F(x) = P(X x), x R. F(x) = 1º
|
|
|
- Seppo Mattila
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½½½ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½½½ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½½ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½ º Ç ÓØÙ Ó Ò ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½½ º º½ Ç ÓØÙ Ø ÖÒÓÙÐÐ Ò Ó º º º º º º º º º º º º º ½½ º º¾ ÓÑ ØÖ Ò Ò ÙÑ Ò Ø Ú Ò Ò ÒÓÑ ÙÑ º ½¾¾ º º Ç ÓØÙ Ø Ô Ö ÓØ ÒÒ º º º º º º º º º º º º º ½¾ º º ÀÝÔ Ö ÓÑ ØÖ Ò Ò ÙÑ Ò Ø Ú Ò Ò ÝÔ Ö Ó¹ Ñ ØÖ Ò Ò ÙÑ º º º º º º º º º º º º º º º º º º º º º ½¾ º º Ì ÙÑ º º º º º º º º º º º º º º º º º º º º º º º ½¾ º ÈÓ ÓÒ Ò ÙÑ º º º º º º º º º º º º º º º º º º º º º º º º ½¾ º ÈÓ ÓÒ Ò ÔÖÓ º º º º º º º º º º º º º º º º º º º º º º º º º ½ º º½ Ä ÙÖ ÔÖÓ º º º º º º º º º º º º º º º º º º º º º º ½ º º¾ ÈÓ ÓÒ Ò ÔÖÓ Ò ÑÖ Ø ÐÝ º º º º º º º º º º º º º º ½ º º Ë ØÙÒÒ Ø Ô ØÙÑ Ø Ø Ð ¹ Ú ÖÙÙ º º º º º º º º º ½ Ø ÒÚ ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ À Ö Ó ØÙ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½ Â Ø ÙÚ Ø ÙÑ Ø ½ º½ Â Ø ÙÚ Ø ØÙÒÒ ÑÙÙØØÙ Ø º º º º º º º º º º º º º º º º º º º ½ º¾ Ì ÙÑ ÔÓÒ ÒØØ ÙÑ º º º º º º º º º º º º º º ½ º¾º½ Ì ÙÑ º º º º º º º º º º º º º º º º º º º º º º º ½ º¾º¾ ÔÓÒ ÒØØ ÙÑ º º º º º º º º º º º º º º º º º º º ½ º¾º Ð Ò ÙÑ º º º º º º º º º º º º º º º º º º º º º ½ º ÆÓÖÑ Ð ÙÑ º º º º º º º º º º º º º º º º º º º º º º º º º ½ º º½ Ã Ò Ò Ö Ú ØØÑ º º º º º º º º º º º º º º º º º º ½ º º¾ ËØ Ò Ö ÑÙÓØÓ Ò Ò ÒÓÖÑ Ð ÙÑ º º º º º º º º º ½ ¼ º ÅÙÙØØÙ Ò Ú ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ º º½ ÅÙÙÒÒÓ ÖØÝÑ ÙÒ Ø Ó ÚÙÐÐ º º º º º º º º º º º º º ½ ¾ º º¾ ÅÙÙÒÒÓ Ø Ý ÙÒ Ø ÓÒ ÚÙÐÐ º º º º º º º º º º º º º ½ º Ð Ò Ò ÒÓÖÑ Ð ÙÑ º º º º º º º º º º º º º º º º º º º º º ½ º ÑÑ ÙÑ χ ¹ ÙÑ º º º º º º º º º º º º º º º º º ½ º º½ ÑÑ ÙÑ º º º º º º º º º º º º º º º º º º º º º º ½ º º¾ χ ¹ ÙÑ º º º º º º º º º º º º º º º º º º º º º º º º ½ ¼ º º ÆÓÖÑ Ð ÙØÙÒ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÑÙÙÒÒÓ Ø º º º º º º º º º º º º º º º º º º º º º º º º ½ ½ º Ë ØÙÒÒ ÑÙÙØØÙ Ò Ó ÓØÙ ÖÚÓ º º º º º º º º º º º º º º º º º ½ º º½ ÅÓÑ ÒØ ÙÒ Ø Ó ÑÓÑ ÒØ Ø º º º º º º º º º º º º º º º ½ º º¾ Î ÒÓÙ Ù ÔÙ ÙÙ º º º º º º º º º º º º º º º º º º º ½ Ø ÒÚ ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ À Ö Ó ØÙ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½
2 ÄÙ Ù Â Ø ÙÚ Ø ÙÑ Ø Ë ÐÐ Ø ÙÙÖ Ø ÙØ Ò Ñ Ö ÐÑÔ Ø Ð Ô ØÙÙ Ô ÒÓ Ø ÐÐ Ò Ø Ú ÐÐ Ø Ø ÙÚ ÑÙÙØØÙ Ø º ÑÙÙØØÙ ÓØ ÚÓ Ú Ø Ñ Ø Ø Ò Ö Ð ÖÚÓ ÒÒ ØÙÐÐ ÚÐ Ðк Ñ Ö Ò Ð Ò ÓÒ Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ Ó ÚÓ Ø ØÝÐÐ ÚÐ ÐÐ ÔÓ Ø Ú Ö Ð ÐÙ Ù ÖÚÓ¹ º Ö Ø Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖÚÓ ÓÙ Ó ÓÒ Ö ÐÐ Ò Ò Ø ÒÙÑ ÖÓ ØÙÚ ÑÙØØ Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖÚÓ ÓÙ Ó ÓÒ ÝÐ ÒÙÑ ÖÓ ØÙÚ º Ë ØÙÒ¹ Ò ÑÙÙØØÙ X ÑÖ Ø ÐØ Ò Ð ÐÙÚÙ ¾º º½ Ø ÙÚ Ó Ò ÖØÝѹ ÙÒ Ø Ó F X ÓÒ Ø ÙÚ ÅÖ Ø ÐÑ ¾º µº º½ Â Ø ÙÚ Ø ØÙÒÒ ÑÙÙØØÙ Ø ÂÓ Ò ØÙÒÒ ÑÙÙØØÙ Ò Ð ØØÝÝ ÖØÝÑ ÙÒ Ø Óº Ë ØÙÒÒ ÑÙÙØØÙ Ò X ÖØÝÑ ÙÒ Ø Ó ÑÖ Ø ÐØ Ò Ð ÐÙÚÙ ¾º ÅÖ Ø ÐÑ ¾º (ii)µ Ô Ø ¹ ÙÒ Ø ÓÒ F(x) = P(X x), x R. Ö Ø Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖØÝÑ ÙÒ Ø Ó ÓÒ ÔÓÖÖ ÙÒ Ø Ó Ó ÚÓ ¹ Ò Ð Ù Ù ÝÔÔÝ ÙÒ Ø Ó Ò ÙÑÑ Ò º½º½µ º Ð ÐÙ Ù º½ º Ä Ù Ò ¾º ÑÙ Ò ÙÒ Ø Ó F(x) ÓÒ ÖØÝÑ ÙÒ Ø Ó Ó Ú Ò Ó Ù¹ Ö Ú Ø ÓÐÑ ØÓ ØÓØ ÙØÙÚ Ø ½º lim F(x) = lim x F(x) = º x ¾º F(x) ÓÒ Ú Ú ¹Ú Ò Úµ ÙÒ Ø Óº º F(x) ÓÒ Ó ÐØ Ø ÙÚ Ð lim x x + F(x) = F(x ) ÐÐ x Rº ÂÓ Ñ ÐÐ ÓÒ Ó Ò ØÙÒÒ ÑÙÙØØÙ X Ò Ò ÓÑ Ò ÙÙ Ø ½º º ÚÓ Ò ØÓ Ø ØÓ ÒÒ ÝÝ ÙÒ Ø ÓÒ P(X x) ÓÑ Ò ÙÙ Ò ÚÙÐÐ º ÂÓ Ó Ò ÙÒ Ø Ó F(x) ØÓØ ÙØØ ÓØ º 3º ÓÐ Ú Ò ÐÔÔÓ ØÓ Ø ØØ F(x) ÓÒ ØÓ ÐÐ ÓÒ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖØÝÑ ÙÒ Ø Óº ÌÓ ØÙ Ð ÝØÝÝ Ú ¹ Ø Ú Ø ØÓ ÒÒ ÝÝ Ð ÒÒ Ò ÓÔÔ Ö Ó Ø º ½
3 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ñ Ö º½ ÙÒ Ø Ó º½º½µ F(x) = +e x ÓÒ Ñ Ö Ø ÙÚ Ø ÖØÝÑ ÙÒ Ø Ó Ø Ó ØÓØ ÙØØ Ä Ù Ò ¾º ÓØ º 3º ÃÓ lim x e x =, Ò Ò lim F(x) = x lim F(x) =, Ó lim x ÙÒ Ø Ó F(x) ÓÒ Ú Ú Ó Ò. Ö Ú ØØ F (x) = e x (+e x ) >. x e x =. ÇÒ ÑÝ ÐÔÔÓ ØÓ Ø ØØ F(x) ÓÐ ÒÓ Ø Ò Ó ÐØ Ø ÙÚ Ú Ò Ø ÙÚ º à ØÝÑÑ Ø Ö Ø Ð Ñ Ò ØÙÒÒ ÑÙÙØØÙ Ó Ò ÖØÝÑ ÙÒ Ø Ó F ÓÐ Ô Ð ØÒ Ø ÙÚ Ú Ò ÑÝ Ö ÚÓ ØÙÚ º ÇÐ ÓÓÒ F Ø ÙÚ Ò ¹ ØÙÒÒ ÑÙÙØØÙ Ò X ÖØÝÑ ÙÒ Ø Óº ÂÓ ÖØÝÑ ÙÒ Ø ÓÐÐ F ÓÒ Ö Ú ØØ df dx = F (x), Ô Ø Ñ ÓÐÐ Ø Ý ØØ Ô Ø Ó Ò ÐÙ ÙÑÖ ÓÒ Ö ÐÐ Ò Ò Ò Ò X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = F (x), ÙÒ F (x) ÓÒ ÓÐ Ñ º Î Ø Ú ÐÐ Ø Ú ÐÐ Ù Ò Ö Ø Ò ØÙÒÒ ÑÙÙØØÙ¹ Ò ÖØÝÑ ÙÒ Ø Ó ÚÓ Ò Ð Ù Ù ØÓ ÒÒ ÝÝ ÙÒ Ø ÓÒ ÚÙÐÐ ÙÑÑ Ò Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖØÝÑ ÙÒ Ø Ó ÚÓ Ò Ð Ù Ù ÒØ Ö Ð Ò º½º¾µ P(X x) = F X (x) = x f X (t)dt. ÂÓ f X (t) ÓÒ Ø ÙÚ Ò Ò ÒØ Ö Ð Ð ÒÒ Ò Ô ÖÙ Ð Ù Ò ÑÙ Ò º½º µ F X (x) = f X(x), Ñ F X (x) ÓÒ ÖØÝÑ ÙÒ Ø ÓÒ F X(x) Ö Ú ØØ º ÅÖ Ø ÐÑ º½ Â Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò X Ø Ý ÙÒ Ø Ó f X (x) ÓÒ ÙÒ Ø Ó Ó ØÓØ ÙØØ Ý ØÐ Ò º½º µ F X (x) = x f X (t)dt ÐÐ x R.
4 º½º Â Ø ÙÚ Ø ØÙÒÒ ÑÙÙØØÙ Ø ½ Ñ Ö º¾ ÇÐ ÓÓÒX Ø ØØÝÝÒ Ô ÐÚ ÐÙÒÙÑ ÖÓÓÒ ØÙÐ Ú Ò ÔÙ ÐÙ Ò Ô ¹ ØÙÙ º ÇÐ Ø Ø Ò ØØ X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = e x/, x <. Ë ÐÐÓ Ò X ÒÓÙ ØØ Ò º ÔÓÒ ÒØØ ÙÑ ÖÚÓÐÐ º ÆÝØ Ã ÖØÝÑ ÙÒ Ø Ó ÓÒ S = {x x < } f(x) > ÙÒ x S. F(x) = = x / x x e t/ dx = e t/ = e x/. e t/ dx Ë ÐÐÓ Ò F (x) = d ( ) e x/ = dx e x/ = f(x), x f(x) = ÙÒ x < º ÀÙÓÑ ØØ Ý ØØ Ò Ô Ø Ò a R ØÓ ÒÒ ÝÝ P(X = a) ÓÒ Ò ÒÓÐÐ Ó X ÓÒ Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ º Ë ÐÐÓ Ò Ö ØÝ Ø ÐÐ Ö Ð ÐÙÚÙ ÐÐ b > a F(b) F(a) = P(a X b) = P(a < X b) = P(a X < b) = P(a < X < b). Â Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÑÓÑ ÒØ Ø ÑÖ Ø ÐÐÒ Ú Ø Ú Ø Ù Ò Ö Ø Ò ØÙÒÒ ÑÙÙØØÙ Ò Ø Ô Ù ÑÙØØ ÑÖ Ø ÐÑ ÙÑÑ ÓÖ¹ Ú Ø Ò ÒØ Ö Ð ÐÐ º Â Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò rº ÑÓÑ ÒØØ ÓÒ α r = E(X r ) = x r f(x)dx, Ñ f(x) ÓÒ X Ò Ø Ý ÙÒ Ø Óº Ë ØÙÒÒ ÑÙÙØØÙ Ò X rº Ù ÑÓÑ ÒØØ ÓÒ µ r = E[(X µ) r ], Ñ µ = E(X) = α ÓÒX Ò Ó ÓØÙ ÖÚÓº Ë ØÙÒÒ ÑÙÙØØÙ ÒX Ó ÓØÙ ÖÚÓ ÓÒ ÒØ Ö Ð µ = E(X) = xf(x)dx
5 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø X Ò Ú Ö Ò σ ÓÒ ¾º Ù ÑÓÑ ÒØØ σ = µ = E[(X µ) ] = (x µ) f(x)dx. Å Ö Ø ÑÑ ÑÝ E [ (X µ) ] = Var(X) ÓÐÐÓ Ò X Ò ÓÒØ ÓÒ ÅÓÑ ÒØØ ÙÒ Ø Ó ÓÒ σ = Var(X). º½º µ M(t) = E(e tx ) = e tx f(x)dx, Ó ÒØ Ö Ð º½º ÓÒ ÓÐ Ñ ÓÐÐ Ò ÚÓ Ñ ÐÐ ÚÐ ÐÐ( a,a) Ñ a > º Ì ØÝ Ø Ñ Ö ØÙÐÓ Ø σ = E(X ) µ, µ = M (), α = E(X ) = M () Ô ØÚØ ÐÐ Ò Ô Ò Ñ ÐÐ Ø Ú ÐÐ Ù Ò Ö ØØ Ò ØÙÒÒ ÑÙÙع ØÙ Ò Ø Ô Ù º Ñ Ö º Ä Ø Ò ÒÝØ Ñ Ö ¾º½ ÑÖ Ø ÐÐÝÒ ØÙÒÒ ÑÙÙع ØÙ Ò X Ó ÓØÙ ÖÚÓ Ú Ö Ò µ = E(X) = σ = E(X ) µ = ÃÓÐÑ ÑÓÑ ÒØØ ÓÒ x (x)dx α 3 = E(X 3 ) = x(x)dx = 3 ( ) = 3 / / x 3 (x)dx = 5 x 3 = 3 x = 8. / x 5 = 5
6 º½º Â Ø ÙÚ Ø ØÙÒÒ ÑÙÙØØÙ Ø ½ º Ù ÑÓÑ ÒØØ ÓÒ µ 3 = E [ (X µ) 3] = = = (x µ) 3 (x)dx (x 3 3µx +3µ x µ 3 )(x)dx x 3 (x)dx 3µ x (x)dx+3µ x(x)dx µ 3 xdx = α 3 3µα +3µ 3 µ 3 = α 3 3µα +µ 3 = ( ) 3 + = = 5. ÅÝ ÔÖÓ ÒØØ Ô Ø Ø ÓÚ Ø ØÖ Ø ÙÑ Ò ØÙÒÒÙ ÐÙ Ù º  ÙÑ Ò p¹ôöó ÒØØ Ô Ø π p ÑÖ Ø ÐÐÒ ÙÖ Ú Ø p = π p f(x)dx = F(π p ), p. ÈÖÓ ÒØØ Ô Ø ØØπ.5 ÙØ ÙØ Ò Ñ Ò Ô Ø ØØπ.5 π.75 Ð Ú Ö¹ Ø Ð ÝÐ Ú ÖØ Ð º Ñ Ö ¾º½ Ø ÐÐÝÒ ÙÑ Ò ± Ò Ô Ø ÓÒ.6 Ó F(π.36 ) = π.36 =.6 =.36. Ñ Ö º ÇÐ ÓÓÒ ØÙÒÒ ÑÙÙØØÙ Ò X ÖØÝÑ ÙÒ Ø Ó ÑÖ Ø ÐØÝ ÙÖ Ú Ø, x < ; x F(x) =, x ; ( x), x < ;, x. Ì Ö Ø ÑÑ Ò Ò ØØ F ÓÒ ØÓ ÐÐ ÖØÝÑ ÙÒ Ø Óº ÌÓØ ÑÑ ÐÔÓ Ø ØØ ½µ lim F(x) = lim x F(x) = x ¾µ F(x) ÓÒ x Ò Ú Ú ¹Ú Ò Úµ ÙÒ Ø Ó µ F(x) ÓÒ Ó ÐØ Ø ÙÚ Ó ÓÒ Ø ÙÚ º
7 ½ ¼ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ì Ý ÙÒ Ø Ó Ò Ö ÚÓ Ñ ÐÐ F(x)º ÆÝØ F (x) = x ÚÐ ÐÐ < x F (x) = x ÚÐ ÐÐ x º Æ Ò Ø Ý ÙÒ Ø Ó ÓÒ x, < x ; f(x) = x, x ; ÑÙÙ ÐÐ º Ì Ý ÙÒ Ø Ó ÚÓ Ò Ö Ó ØØ ÐÝ Ý Ø ÑÙÓ Ó f(x) = x, x. ÃÓ X Ò Ø Ý ÙÒ Ø ÓÒ ÙÚ ÓÒ ÓÐÑ ÓÒ ÑÙÓØÓ Ò Ò X Ò ÙÑ ÙØ ÙØ Ò ÓÐÑ Ó ÙÑ º f(x) F(x) F(.55) = x x ÃÙÚ Ó º½º ÃÓÐÑ Ó ÙÑ Ò Ø Ý ÙÒ Ø ÓÒ ÖØÝÑ ÙÒ Ø ÓÒ Ù¹ Ú Øº ÃÓÐÑ Ó ÙÑ Ò Ó ÓØÙ ÖÚÓ ÓÒ µ = xf(x)dx = x xdx+ x( x)dx = / =. x / (x x3 3 ) = 3 ( ) ( ) 3 3 ÃÓ ÙÑ ÓÒ ÝÑÑ ØÖ Ò Ò Ó ÓØÙ ÖÚÓÒ Ù Ø Ò ÓÒ ÑÝ ÙÑ Ò Ñ Ò π.5 º Ë ÚÓ Ò ØÓ Ø ÐÔÓ Ø ÑÝ ÑÖ Ø ÐÑÒ Ô ÖÙ Ø ÐÐ ÐÐ F() = =.5º  ÙÑ Ò ¼ ± Ò Ô Ø π.9 Ò Ö Ø Ñ ÐÐ Ý ØÐ ( π.9) =.9. Ê Ø Ù ÓÒ π.9 =. =.55º ÁØ Ö Ð Ø Ó º½º µ ÚÐØØÑØØ ÓÐ ÚÓ Ñ ÐÐ x Ò Ö¹ ÚÓ ÐÐ ÐÐ F(x) ÚÓ ÓÐÐ Ø ÙÚ ÑÙØØ Ö ÚÓ ØÙÚ º ÂÓ f(x) ÓÒ Ø ÙÚ
8 º½º Â Ø ÙÚ Ø ØÙÒÒ ÑÙÙØØÙ Ø ½ ½ Ò Ò ÐÐÓ Ò Ø ØÝ Ø Ý ØÐ º½º µ Ô Ø Ô Ò º ÀÙÓÑ ØØ ÓÓÒ ØØ Ø¹ ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò Ø Ý ÙÒ Ø Ó ÚÐØØÑØØ ÓÐ Ø ÙÚ ÑÙØØ ÖØÝÑ ÙÒ Ø Ó ÓÒº Ñ Ö º Ì Ö Ø ÐÐ Ò ÒÝØ ØÙÒÒ ÑÙÙØØÙ X ÓÒ Ø Ý ÙÒ ¹ Ø Ó ÓÒ f(x) = Î Ø Ú Ø X Ò ÖØÝÑ ÙÒ Ø Ó ÓÒ {, x < ; 3, x., x < ; F(x) = x, x < ; 4 + ( ) 3 x, x ;, x. À Ú Ø ÑÑ ÒÝØ ØØ X Ò Ø Ý ÙÒ Ø Ó ÓÐ Ø ÙÚ º ÆÝØ ÑÝ Ò F 3 f(x) F(x) x 4 x ÃÙÚ Ó º¾º Ë ØÙÒÒ ÑÙÙØØÙ Ò X Ø Ý ÙÒ Ø ÓÒ ÖØÝÑ ÙÒ Ø ÓÒ ÙÚ Øº ÓÐ Ö ÚÓ ØÙÚ Ô Ø º È Ø x = ÓÐ ÚÓ Ñ ØØ F (x) = f(x)º Ì ÓÒ Ñ Ö Ø ÙÚ Ø ØÙÒÒ ÑÙÙØØÙ Ø ÓÒ Ø Ý ÙÒ ¹ Ø Ó ÓÐ Ø ÙÚ ÓÒ ÖØÝÑ ÙÒ Ø Ó ÓÐ Ó Ó ÑÖ ØØ ÐÝ ÐÙ ÐÐ S Ö ÚÓ ØÙÚ º Â Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò Ø Ý ÙÒ Ø ÓÐÐ ÚÓ ÓÐÐ Ö ÐÐ Ò Ò Ñ¹ Ö Ô Ø ÙÚÙÙ Ô Ø Ø ÑÙØØ ÖØÝÑ ÙÒ Ø Ó ÓÒ Ø ÙÚ º Ñ Ö Ò º ØÙÒÒ ÑÙÙØØÙ Ò Ø Ý ÙÒ Ø ÓÐÐ ÓÒ ÑÖ ØØ ÐÝ ÐÙ ÐÐ Ò Ý Ô Ø Ù¹ ÚÙÙ Ô Ø ÖØÝÑ ÙÒ Ø Ó ÓÒ Ø ÙÚ º Ê Ð Ø Ó º½º µ Ô Ø Ô Ò Ú Ò Ø Ý ÙÒ Ø ÓÒ Ø ÙÚÙÙ Ô Ø ÑÙØØ Ô Ø ÙÚÙÙ Ô Ø º
9 ½ ¾ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ñ Ö º ÅÖ Ø ÐÐÒ ØÙÒÒ ÑÙÙØØÙ X Ø Ò ØØ Ò ÖØÝѹ ÙÒ Ø Ó ÓÒ, x < ; º½º µ F(x) =, x = ; + x, < x < ;, x. F(x) f(x) x x ÃÙÚ Ó º º Ë ØÙÒÒ ÑÙÙØØÙ Ò X ÖØÝÑ ÙÒ Ø ÓÒ ³Ø Ý ÙÒ ¹ Ø ÓÒ³ ÙÚ Øº à ÖØÝÑ ÙÒ Ø Ó ÓÐ ÒÝØ Ø ÙÚ Ó ÙÒ Ø Ó ÝÔÔ Ô Ø x = º à ÖØÝÑ ÙÒ Ø Ó ÓÐ ÑÝ Ò ÔÓÖÖ ÙÒ Ø Óº ÆÝØ ÑÝ Ý ØØ ÐÐ Ô ¹ Ø ÐÐ X = ÓÒ ÔÓ Ø Ú Ò Ò ØÓ ÒÒ ÝÝ P(X = ) = ÓØ Ò f(x) ÓÐ Ø Ý ÙÒ Ø Óº ÁØ ÖØÝÑ ÙÒ Ø Ó º½º µ ÚÓ Ò Ö Ó ØØ ÔÓÖ¹ Ö ÙÒ Ø ÓÒ ÖØÝÑ ÙÒ Ø Óµ Ø ÙÚ Ò ÖØÝÑ ÙÒ Ø ÓÒ ÙÑÑ Ò º Ð ÐÙ¹ ÚÙ º½ ÑÖ Ø ÐØ Ò ÝÔÔÝ ÙÒ Ø Ó ε(x) Ø Ò ØØ ε(x) = ÔÒ Ø Ú Ð¹ Ð x Ò ÖÚÓ ÐÐ ε(x) = ÙÒ x < º ÙÒ Ø Ó ε(x) ÓÒ ÔÓÖÖ ÙÒ Ø Ó Ö Ø Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖØÝÑ ÙÒ Ø Óº ÈÙÓÐ ÚÓ Ñ ÐÐ ÚÐ ÐÐ (,] Ø ÙÑ ÒÓÙ ØØ Ú Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖØÝÑ ÙÒ Ø Ó ÓÒ, x ; F c (x) = x, < x < ;, x. ÆÝØ ÖØÝÑ ÙÒ Ø Ó º½º µ ÚÓ Ò Ö Ó ØØ ÑÙÓ Ó F(x) = ε(x)+ F c(x). Ñ Ö ØÓ ÒÒ ÝÝ ( P X ) = ( ) ε + ( ) F c = + = 3 4. Ë ØÙÒÒ ÑÙÙØØÙ X ÓÐ Ö ØØ Ø ÙÚ º
10 º¾º Ì ÙÑ ÔÓÒ ÒØØ ÙÑ ½ Ð Ø Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÚÓ Ò ÑÖ Ø ÐÐ ÒØ Ø Ø Ò º½º µ ÚÙÐÐ ÓÐ ØØ Ñ ØØ Ø Ý ÙÒ Ø ÓÒ f(x) Ø ÙÚÙÙØØ º ÂÓ ÓÒ ÓÐ Ñ ÐÐ ¹ Ò Ò ÔÒ Ø Ú Ò Ò ÙÒ Ø Ó f(x) Ø º f(x) ÐÐ x R ØØ º½º µ Ô Ø Ô Ò ÐÐ x R Ò Ò ÖØÝÑ ÙÒ Ø ÓÒ F(x) ÒÓØ Ò ÓÐ Ú Ò ÓÐÙÙØØ Ø Ø ÙÚ º ÓÐÙÙØØ Ø Ø ÙÚ ÙÒ Ø Ó ÓÒ Ø ÙÚ º Ã Ò Ø ÐÙÚÙ Ø ÐØÚ Ø Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÖØÝÑ ÙÒ Ø ÓØ ÓÚ Ø ÓÐÙÙØØ Ø Ø ÙÚ º º¾ Ì ÙÑ ÔÓÒ ÒØØ ÙÑ º¾º½ Ì ÙÑ Â Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ X ÒÓÙ ØØ Ø ÙÑ ÚÐ ÐÐ [,] Ó Ò Ø Ý ÙÒ Ø Ó ÓÒ ØÐÐ ÚÐ ÐÐ ÑÙÙ ÐÐ {, ÙÒ x [,] º¾º½µ f(x) = ÑÙÙ ÐÐ º Ë ÐÐÓ Ò Ñ Ö ØÒ X Tas(,)º ÇÒ ÐÔÔÓ ØÓ Ø ØØ f(x) ÓÒ Ø Ý ÙÒ ¹ Ø Ó Ó f(x) f(x)dx = dx =. f(x) F(x) x x ÃÙÚ Ó º º Ì ÙÑ Ò Tas(,) Ø Ý ÙÒ Ø Ó ÖØÝÑ ÙÒ Ø Óº Ì ÙÑ Ò ÖÚÓ Ú Ö Ò ÓÚ Ø E(X) = xdx = Var(X) = E(X ) [E(X)] = x dx 4 =.
11 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ë ØÙÒÒ ÑÙÙØØÙ Ò X ÑÓÑ ÒØØ ÙÒ Ø Ó ÓÒ M X (t) = e tx dx = / t etx = et. t ÀÙÓÑ ØØ M X () = º ÇÐ ÓÓÒ [a,b] ÒÒ ØØÙ ÙÐ ØØÙ ÚÐ a < bº Ë ÐÐÓ Ò ØÙÒÒ ÑÙÙØØÙ U = (b a)x + a ÒÓÙ ØØ Ø ÙÑ ÚÐ ÐÐ [a,b]º Ë ÐÐÓ Ò Ñ Ö ØÒ U Tas(a,b)º ÃÓ E(U) = (b a)e(x)+a Var(U) = (b a) Var(X) Ò Ò E(U) = a+b Ë ØÙÒÒ ÑÙÙØØÙ Ò U Ø Ý ÙÒ Ø Ó ÓÒ Var(U) = (b a). º¾º¾µ f(u) = {, ÙÒ u [a,b] b a ÑÙÙ ÐÐ U Ò ÑÓÑ ÒØØ ÙÒ Ø Ó ÓÒ e tb e ta M U (t) = t(b a), t ;, t =. º¾º¾ ÔÓÒ ÒØØ ÙÑ ÈÓ ÓÒ Ò ÔÖÓ Ø Ö Ø ÐÐ Ò ÑÓÒØ Ó Ø Ô ØÙÑ Ð Ý Øµ ØØÙÙ ÓÐÐ Ò ÚÐ Ðк Å Ö ØÒ w Ò Ô ØÙ ÐÐ ÚÐ ÐÐ ØØÙÚ Ò Ø Ô ØÙÑ Ò ÐÙ¹ ÙÑÖ ØÙÒÒ ÑÙÙØØÙ ÐÐ X w º ÂÓ ÈÓ ÓÒ Ò ÔÖÓ Ò ÒØ Ò Ø ØØ ÓÒ λ Ò Ò ÅÖ Ø ÐÑÒ º¾ ÑÙ Ò ØÓ ÒÒ ÝÝ ØØ w Ò Ô ØÙ ÐÐ ÚÐ ÐÐ ØØÙÙ x Ø Ô ØÙÑ ÓÒ º¾º µ P(X w = x) = e λw(λw)x. x! ÈÓ ÓÒ Ò ÔÖÓ ÐÐ ÚÓ Ò Ñ ÐÐ ÒØ Ñ Ö Ò ÔÙÑ ¹ Ø Ô ÐÚ ÐÙÔ Ø Ò ÔÙ ÐÙ Ò ØÙÐÓ Ú Ø Ò ÓÒÒ ØØÓÑÙÙ Ò ØØÙ¹ Ñ Ø Ø Ö Ø ÐØ Ú ÐÐ Ø Ó ÙÙ ÐÐ Ø ÙØÓ Ò ÙÐ Ù Ð ÒØ Ò Ø Ö ÐÙÔ ¹ Ø Ò Ó º ÌÐÐ Ò Ø ÐÐ Ò ØØ Ý ØØ Ø Ø Ô ØÙÑ Ø ØØÙÚ Ø ØÓ Ø Ò Ö ÔÔÙÑ ØØ ØÝ Ò ØÙÒÒ Ø º Ì Ö ÐÐ Ò ÒÝØ ÈÓ ÓÒ Ò ÔÖÓ ÓÒ ÒØ Ò Ø ØØ ÓÒ λº ÇÐ ÓÓÒ W Ó ÓØÙ Ò Ø Ò ÙÒÒ ÙÖ Ú Ø Ô ØÙÑ ØØÙÙº Ç ÓØÙ ÓÒ Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ º ÂÓ Ø Ö Ð ÑÑ ÔÖÓ Ø Ø t Ø Ò t+w Ð w Ò Ô ØÙ Ò ÚÐ Ò[t,t+w] Ò Ò Ø Ô ØÙÑ {W > w} ØØÙÙ Ó Ú Ò Ó ÈÓ ÓÒ Ò ÔÖÓ ØÙ Ý ØÒ Ø Ô ØÙÑ ÚÐ ÐÐ [t,t+w]º Ë ÒØ Ø Ø Ò º¾º µ ÑÙ Ò P(W > w) = P(X w = ) = e λw.
12 º¾º Ì ÙÑ ÔÓÒ ÒØØ ÙÑ ½ }{{} W =.5 X w Poi(λw) X w = 3 w=.5 {}}{ 3 4 }{{} W 4 =.88 t t+w ÃÙÚ Ó º º Ã Ú Ó ÙÚ ØØ ÈÓ ÓÒ Ò ÔÙÑ ÔÖÓ Ñ Ö¹ ÙØÓ Ò ÙÐ Ñ Ø Ð ÒØ Ò Ø Ö ÐÙÔ Ø Ò Ó º Ñ Ö W ÓÒ ½º ÙØÓÒ Ó ÓØÙ W 4 ÓÒ º º ÙØÓÒ ÚÐ Ò Ò º à ҹ Ò Ø ØÝÐÐ w Ò Ô ØÙ ÐÐ ÚÐ ÐÐ ÓÒ ÙÐ ÒÙØ Ó X w = 3 ÙØÓ º È Ö ¹ Ø Ó ÓØÙ Ø W W W 3 º º º ÓÚ Ø ØÓ Ø Ò Ö ÔÔÙÑ ØØÓÑ Ø ÒÓÙ ØØ Ú Ø Ñ ÙÑ º Ç ÓØÙ Ò W ÖØÝÑ ÙÒ Ø Ó ÓÒ F(w) = P(W w) = P(W > w) = P(X w = ) = e λw. ÃÓ Ó ÓØÙ W ÓÒ ÔÒ Ø Ú Ò Ò Ò Ò F(w) = ÙÒ w < º Ç ÓØÙ Ò W Ø Ý ÙÒ Ø Ó ÓÒ F (w) = f(w) = λe λw Ö ÚÓ ÒØ ÒÒ Ò º½º µ ÒÓ ÐÐ º Í Ò Ñ Ö ØÒ λ = Ñ θ > º Ë ¹ θ ÒÓÑÑ ØØW ÒÓÙ ØØ ÔÓÒ ÒØØ ÙÑ Ô Ö Ñ ØÖ ÐÐ θ Ñ Ö Ø Ñ¹ Ñ W Exp(θ)º È Ö Ñ ØÖ θ ÓÒ ÙÑ Ò ÖÚÓº ÔÓÒ ÒØØ ÙÑ Ò Ø Ý ÙÒ Ø Ó ÓÒ ÐÐÓ Ò ÑÙÓØÓ º¾º µ f(w) = θ e w/θ. ÔÓÒ ÒØØ ÙÑ Ò Exp(θ) ÑÓÑ ÒØØ ÙÒ Ø Ó ÓÒ M(t) = e tw θ e w/θ dw = = θt, t < θ. / e ( θt)w/θ θt ÔÓÒ ÒØØ ÙÑ ÐÐ ÓÒ Ú Ø Ú ÙÒÓ Ø Ñ ÓÑ Ò ÙÙ Ù Ò ÓÑ Ø¹ Ö ÐÐ ÙÑ ÐÐ º ÂÓ T Exp(θ) Ò Ò º¾º µ P(T > a+b T > a) = P(T > b) ÐÐ ÔÒ Ø Ú ÐÐ a bº ÌÙÐÓ ÚÓ Ò ØÓ Ø Ð Ñ ÐÐ ÓÐÐ Ò Ò ØÓ ÒÒ ÝÝ P(T > a+b T > a) = P(T > a, T > a+b) P(T > a) = e (a+b)/θ e a/θ = = e b/θ = P(T > b). P(T > a+b) P(T > a)
13 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø ÀÙÓÑ ØØ ÓÓÒ ØØ ÐÐ ÓÒ ÝØ ØØÝ ØÙÐÓ Ø P(T > t) = P(T t) = F(t) = e t/θ, t. Ñ Ö º ÇÐ Ø Ø Ò ØØ Ò ÔÙÑ Ò Ò Ð Ò ÒÓ٠ع Ø ÈÓ ÓÒ Ò ÔÖÓ ÒØ Ò Ø Ø ÐÐ Ø ØÙÒÒ º Å ÓÒ ØÓ Ò¹ Ò ÝÝ ØØ ÑÝÝ ÓÙØÙÙ Ó ÓØØ Ñ Ò ÙÖ Ú Ø ÝÐ 5 Ñ ÒÙÙع Ø ÇÐ ÓÓÒ X Ó ÓØÙ ÙÒÒ ÙÖ Ú ÔÙÙº Ë ÐÐÓ Ò ÔÖÓ ¹ º¾º µ λ = /3 Ø Ñ ÒÙÙØ X Exp(3) Ó ÔÓÒ ÒØØ ¹ ÙÑ Ò ÖÚÓ θ = /λº Â ÙÑ Ò Exp(3) Ø Ý ÙÒ Ø Ó ÓÒ f(x) = 3 e x/3, x < P(X > 5) = 5 3 e x/3 dx = 5 / e x/3 = e 5/ Â Ø ÙÚ Ò ÙÑ Ò Ñ Ò m ÓÒ ÐÐ Ò Ò Ô Ø ØØ F(m) = /º ÆÝØ ÙÑ Ò Exp(3) Ñ Ò Ò m ØÙÐ ØÓØ ÙØØ ØÓ F(m) = e m/3 = ÓØ Ò m = 3log().794. º¾º Ð Ò ÙÑ ÇÑ Ò ÙÙ Ò º¾º µ Ô ÖÙ Ø ÐÐ ÔÓÒ ÒØØ ÙÑ ÓÒ ÓÔ Ú Ð Ò Ò ¹ ÙÑ ÐÐÓ Ò ÙÒ Ð ÐÐ ÓÐ Ú Ð Ò Ö ÔÙ ØÑÒ Ø Ø Øº Çй ÓÓÒ T Ñ Ö ÓÒ Ò Ð ØÖÓÒ Ò ÓÑÔÓÒ ÒØ Ò ØÙÒØ Ò º Ë ÐÐÓ Ò P(T > b) ÓÒ ØÓ ÒÒ ÝÝ ØØ ÙÙ ÓÑÔÓÒ ÒØØ Ø Ò Ò b ØÙÒØ ÙÒ Ø P(T > a + b T > a) ÓÒ ØÓ ÒÒ ÝÝ ØØ a ØÙÒØ ÝØ ÓÐÐÙØ ÓÑÔÓÒ ÒØØ Ø Ú Ð b ØÙÒØ º ÂÓ Ð Ò ÒÓÙ ØØ ÔÓÒ Òع Ø ÙÑ Ò Ò ÓÑ Ò ÙÙ Ò º¾º µ ÒÓ ÐÐ ØÓ ÒÒ ÝÝ Ø P(T > b) P(T > a + b T > a) ÓÚ Ø Ñ Ø ÐÐ a bº ÌÓ ÒÒ ÝÝ ØØ ÓÑÔÓÒ ÒØØ Ö ÓÓÒØÙÙ b Ò ÙÖ Ú Ò ØÙÒÒ Ò Ò Ö ÔÙ Ð Ò Ò Ø Ù Ò Ù Ò ÓÑÔÓÒ ÒØØ ÓÒ Ó ÓÐÐÙØ ÝØ º ÙÒ Ø ÓØ G(t) = P(T > t) ÙØ ÙØ Ò ÐÓÓÒ Ñ ÙÒ Ø Ó º ÔÓÒ Òع Ø ÙÑ ÑÖ ØØ Ð ÐÓÓÒ Ñ ÙÒ Ø ÓÒ G(t) = e t/θ ÓÐÐ ÓÒ ÙÒÓ Ø Ñ ¹ ÓÑ Ò ÙÙ º¾º µ G(t+s) = G(t)G(s), t >, s >. ÅÖ Ø ÐÑÒ ÒÓ ÐÐ G() = G(t) ÙÒ t Ú º ÇÒ Ó ÔÓ¹ Ò ÒØØ ÙÒ Ø ÓÒ Ð ÑÙ Ø ÐÓÓÒ Ñ ÙÒ Ø Ó Ø Ó ÐÐ ÓÒ ÙÒÓ Ø Ñ ÓÑ ¹ Ò ÙÙ º¾º µ ÎÓ Ò Ó Ó ØØ ØØ ÓÒ º¾º µ ØÓØ ÙØØ Ú Ø ÐÓÓÒ ¹ Ñ ÙÒ Ø ÓØ ÓÚ Ø Ò ÑÙÓØÓ e λt λ > º
14 º º ÆÓÖÑ Ð ÙÑ ½ ÂÓ Ð Ò T ÒÓÙ ØØ ÔÓÒ ÒØØ ÙÑ Exp(θ) Ò Ò Ú Ó λ = θ ÓÒ Ø ÐÐ Ò Ò ÙÓÐÐ ÙÙ Ø Ø Ú Ö Ò Ø º È Ö Ñ ØÖ λ Ø Ð ØÓ Ò¹ Ò ÝÝØØ ÙÓÐÐ Ø Ò T = t Ð ÐÐ Ý Ò Ô ØÙ ÐÐ ÚÐ Ðк ÇÐ ÓÓÒ Ø Ö Ø ÐØ Ú Ò ÚÐ Ò Ô ØÙÙ º ÅÖ Ø ÐÐÒ ØÓ ÒÒ ÝÝ P(T t+ T > t) = P(T > t+ T > t) = P(T > ) = e λ, Ñ Ú Ñ Ø ÐÐ Ò Ò Ý Ø ÙÙÖÙÙ Ò ÙÒÓ Ø Ñ ÓÑ Ò ÙÙ Ò º¾º µ ÒÓ ÐÐ º ÃÙÒ ÙÒ Ø ÓØ e λ ÖÚ Ó Ò Ì ÝÐÓÖ Ò ÔÓÐÝÒÓÑ Ò ÚÙÐÐ Ò e λ = ( λ + λ ) = λ λ + λ, ÙÒ ÓÒ Ô Ò º ÖÚ Ó ÒØ Ú Ö Ô Ò Ò Ñ Ö ØÝ ØØ Ñ Ú ÖÖ ØØÙÒ Ò ÙÒ º Ë ÐÐÓ Ò P(T t+ t > t) λ º G(t) f(t) 4 6 t ÃÙÚ Ó º º ÔÓÒ ÒØØ ÙÑ Ò Exp() Ø Ý ÙÒ Ø Ó f(t) = e t/ Ú Ø Ú ÐÓÓÒ Ñ ÙÒ Ø Ó G(t) = e t/ º ÆÝØ Ò Ò ØØ P(T t+ T > t) lim ÓÒ Ö ÔÔÙÑ ØÓÒ Ø tº ÔÓÒ ÒØ Ð Ø ÙØÙÒ Ò Ð Ò Ò Ø Ô Ù ¹ ÙÓÐÐ ÙÙ Ø λ ÓÒ Ø Ö ÔÔÙÑ ØÓÒ Ú Óº Ð Ø ÙÓÐÐ ÙÙ Ø λ(t) ÓÒ Ø ØÝ Ø Ò ÙÒ Ø Óº = λ º ÆÓÖÑ Ð ÙÑ º º½ Ã Ò Ò Ö Ú ØØÑ ÂÓ X,X,...,X n ÒÓÙ ØØ Ú Ø Ñ ÖÒÓÙÐÐ Ò ÙÑ Ber(p) X i X j, i j Ò Ò ÒÓÑÑ ØØ X,X,...,X n ÓÒ ÓØÓ ÖÒÓÙÐÐ Ò ÙÑ Ø
15 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ber(p)º Ì ÑÑ ØØ ÐÐÓ Ò X = X +X + +X n Bin(n,p)º Ë ØÙÒ¹ Ò ÑÙÙØØÙ Ò X ÙÑ Ö ÔÔÙÙ ÓØÓ ÓÓ Ø nº ÇÐ ÓÓÒ X,X,...,X n ÓØÓ ÙÑ Ø ÓÒ ÖÚÓ ÓÒ µ Ú Ö Ò σ > º Å Ö ØÒ ØÙÒ¹ Ò ÑÙÙØØÙ Ò X X º º º X n ÙÑÑ S n = n i= X i ÖÚÓ X n = S n n. ÇØÓ ÖÚÓÒ Ó ÓØÙ ÖÚÓ Ú Ö Ò ÓÒ E(X n ) = µ Var(X n ) = σ n. Ë ØÙÒÒ ÑÙÙØØÙ Ò X n Ú Ö Ò Ô Ò Ò ÙÒ n Ú º ÂÓ Ø n Ò ÖÚÓ Ó Ø Ö ÙÑ º Ì Ö Ø Ð ÑÑ ØÙÒÒ ÑÙÙØØÙ Ò (X i ;i ) = X,X,X 3,... ÓÒÓ Ò Ò ØÙÒÒ ÑÙÙØØÙ Ò ÙÑ Ò ÓÒÓ º ÂÓ X,X,...,X n ÓÒ ÓØÓ Ó Ø Ò ÙÑ Ø J(µ,σ ) ÓÒ ÖÚÓ ÓÒ µ Ú Ö Ò σ Ò Ò ÓØÓ ÖÚÓÒ X n ÙÑ Ò ÖÚÓ ÓÒ µ Ú Ö Ò σ Ó Ö ÔÔÙÙ n غ ÇØÓ ÓÓÒ n Ú ØÓ ÒÒ ÝÝ Ñ n ØØÝÝ Ý Ô Ò ÑÑÐÐ Ô Ò ÑÑÐÐ ÚÐ ÐÐ µ Ò ÝÑÔÖ Ø Òº ÌÑ Ø Ö Ó ØØ ØØ X n ØØÙÙ n Ò Ú Ý ÙÙÖ ÑÑ ÐÐ ÙÙÖ ÑÑ ÐÐ ØÓ ÒÒ ÝÝ ÐÐ Ð ÐÐ ÖÚÓ µº ÇÐ ÓÓØ W n = X n µ σ/ n, n =,,... Ø Ò Ö Ó ØÙ ÑÙÙØØÙ Ó ÐÐ ÔØ E(W n ) = Var(W n ) = º Ë ØÙÒÒ ¹ ÑÙÙØØÙ ÐÐ W,W,... ÓÒ Ñ Ú Ö Ò ÐÐ n Ò ÖÚÓ ÐÐ º Ä ¹ Ò W n Ò ÙÑ ÓØ Ò ÙÑ ÙÒ n Ú ÅÓÑ ÒØØ ÙÒ Ø Ó Ò Ý Ø Ý Ø ØØ Ò ÑÓÑ ÒØØ ÙÒ Ø ÓÒ Ù¹ Ñ Ò ÖØÝÑ ÙÒ Ø ÓÒµ Ý ØØ Ø Ú Ø ÚÙÙØØ Ó Ú Ä Ù º½¼º Ë ¹ Ñ Ý Ø Ý Ø ØØ Ò ÑÝ ÑÓÑ ÒØØ ÙÒ Ø Ó Ò ÙÔÔ Ò Ñ Ø Ó Ú Ä Ù º½ ÓØ ÚÓ Ò ÓÚ ÐØ Ö ¹ ÙÑ Ò ÑÖ ØØÑ Òº Ã Ö Ó Ø ¹ Ø Ò W n = X + +X n nµ nσ = (X µ)+ +(X n µ) nσ = nσ (Y + +Y n ), Ñ Y i = X i µ, i =,...,n Y i Y j ÙÒ i jº ÅÖ Ø ÐÑÒ ÑÙ Ò W n Ò ÑÓÑ ÒØØ ÙÒ Ø Ó ÓÒ M Wn (t) = E(e twn ) = E(e t nσ (Y + +Y n) ) t = M Y + +Y n ( ). nσ
16 º º ÆÓÖÑ Ð ÙÑ ½ ÃÓ Y i Y j ÙÒ i j Ò Ò º º½µ t M Wn (t) = M Y + +Y n ( ) nσ = n t t M Yi ( ) = [M( )] n, nσ nσ i= Ñ M( t nσ ) ÓÒ ØÙÒÒ ÑÙÙØØÙ Ò Y i Ý Ø Ò ÙÑ Ò ÑÓÑ ÒØØ ÙÒ ¹ Ø Óº ÎÓ Ò Ó Ó ØØ ØØ M Wn (t) e t Ñ e t ÓÒ Ø Ò Ö ÑÙÓØÓ ¹ d Ò ÒÓÖÑ Ð ÙÑ Ò ÑÓÑ ÒØØ ÙÒ Ø Óº Ã Ö Ó Ø ÑÑ W n N(,) Ñ Ø Ö Ó ØØ ØØ W n Ò ÙÑ Ð Ò Ø Ò Ö ÑÙÓØÓ Ø ÒÓÖÑ Ð Ù¹ Ñ N(,) ÓØÓ ÓÓÒ n Ú º Ä ÚÝÒ Ø ÙÚÙÙ Ð Ù Ò ÒÓ ÐÐ Ä Ù º½ µ ØÙÒÒ ÑÙÙØØÙ Ò W n ÖØÝÑ ÙÒ Ø Ó F Wn Ð Ò ÒÓÖÑ Ð Ù¹ Ñ Ò N(,) ÖØÝÑ ÙÒ Ø ÓØ Φº Ä Ù º½ Ã Ò Ò Ö Ú ØØѵ ÇÐ ÓÓÒ X,X,...,X n ÓØÓ Ù¹ Ñ Ø ÓÒ ÖÚÓ ÓÒ µ Ú Ö Ò σ º Å Ö ØÒ W n = X n µ σ/ n = S n nµ nσ. Ë ÐÐÓ Ò W n Ò ÙÑ Ð Ò ÒÓÖÑ Ð ÙÑ N(,) ÙÒ n º Ã Ò Ö Ú ØØÑÒ ÑÙ Ò Ñ ÙÑ ÒÓÙ ØØ Ú Ò Ö ÔÔÙ¹ Ñ ØØÓÑ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÙÑÑ ÒÓÙ ØØ Ð Ñ Ò ÒÓÖÑ Ð Ù¹ Ñ ÙÒ n ÓÒ ÙÙÖ º Å Ö Ø ÑÑ W n N(,), ÙÒ n ÓÒ ÙÙÖ º Å Ö Ø Ö Ó ØØ ÒÓÙ ØØ Ð Ñ Ò ÙÑ º ÃÝØÒ¹ Ò Ò Ö Ú ØØÑÒ ÚÙÐÐ ÚÓ Ò ÖÚ Ó W n Ò ÙÑ ÙÒ n ÓÒ Ö ØØÚÒ ÙÙÖ º Ë ÐÐÓ Ò P(W n w) w π e w / dx = Φ(w), Ñ Φ(w) ÓÒ ÒÓÖÑ Ð ÙÑ Ò N(,) ÖØÝÑ ÙÒ Ø Óº ÎÓ ÑÑ Ñ Ö Ø Ñ Ò Ò ÑÝ ÙÖ Ú Ø P(W n w) = F Wn (w) Φ(w), ÙÒn º Ë ØÙÒÒ ÑÙÙØØÙ ÒW n ÖØÝÑ ÙÒ Ø ÓF Wn (w) ÙÔÔ Ò Ó Ø ÒÓÖÑ Ð ÙÑ Ò ÖØÝÑ ÙÒ Ø ÓØ Φ(w) Ô Ø w Rº
17 ½ ¼ º º¾ ËØ Ò Ö ÑÙÓØÓ Ò Ò ÒÓÖÑ Ð ÙÑ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ì Ö Ø Ð ÑÑ ÒÝØ ØÓ ÒÒ ÝÝ Ø ÓÖ Ò Ø Ð ØÓØ Ø Ò ØÖ ÒØ Ù¹ Ñ ÒÓÖÑ Ð ÙÑ º ÇÐ ÓÓÒ Z Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ¹ ÙÒ Ø Ó ÓÒ º º¾µ f(z) = π e z / < z <. Ë ÐÐÓ Ò Z ÒÓÙ ØØ Ø Ò Ö ÑÙÓØÓ Ø ÒÓÖÑ Ð ÙÑ º ÃÝØ ØÒ ÑÝ ÒÓÒØ Z ÒÓÙ ØØ Ø Ò Ö Ó ØÙ ÒÓÖÑ Ð ÙÑ º Ì Ö Ø ÑÑ ÒÝØ ØØ º º¾µ ÓÒ ØÓ ÐÐ Ò Ø Ý ÙÒ Ø Óº ÃÓ f(z) > Ô Ø Ú Ò Ó Ó ØØ ØØ Ç Ó Ø ÑÑ ØØ π e z / dz =. º º µ e z / dz = π. ÑÑ ÔÝ ØÝ ÙÓÖ Ò ÒØ ÖÓ Ñ Ò ÙÒ Ø ÓØ e z / Ó Ò ÒØ Ö Ð ÙÒ ¹ Ø Ó ÓÐ Ð Ù ÙØØ Ú ÙÐ ØÙ ÑÙÓ Ó º Ç Ó ØØ ÙØÙÙ Ù Ø Ò Ò ØØ Ò¹ Ø Ö Ð Ò º º µ Ò Ð ÓÒ ÐÔÔÓ Ð º ÁÒØ Ö Ð Ò ÖÚÓ ÑÙÙØÙ Ó ÒØ ÖÓ ÒØ ÑÙÙØØÙ Ò Ñ ØÒ ÙÙ ÐÐ Ò ÓØ Ò I = e z / dz = e x / dx = Ê ØØ Ó Ó ØØ ØØ I = πº ÆÝØ ( )( ) I = e x / dx e y / dy e y / dy. = e (x +y )/ dxdy = ( re r / dr )( π dθ ) = π e u du = π. Æ Ò ØÙÐÓ º º µ Ô Ø Ô Ò º ÐÐ ÓÐÑ Ý Ø ÙÙÖÙÙ Ò ÖØÝÑÐÐ Ò Ô ÓÓÖ Ò ØØ Ò x = rcosθ y = rsinθ.
18 º º ÆÓÖÑ Ð ÙÑ ½ ½ Ë ÐÐÓ Ò x + y = r dxdy = rdθdr ÒØ ÖÓ ÒØ Ö Ø ÓÚ Ø < r < < θ < πº ÁÒØ Ö Ð ÐÐ º º µ ÓÒ ÑÝ Ð Ò Ò Ý Ø Ý ÑÑ ÙÒ Ø ÓÓÒ º º µ Γ(α) = x α e x dx. ÂÓ α > Ò Ò Γ(α) ÓÒ Ö ÐÐ Ò Òº ÂÓ α ÓÒ ÔÓ Ø Ú Ò Ò Ó ÓÒ ÐÙ Ù Ò Ò Γ(α) ÚÓ Ò Ð Ù Ù ÙÐ ØÙ ÑÙÓ Ó ÑÙÙØÓ Ò º ÃÓ ÒØ Ö ¹ Ð º º µ ÒØ ÖÓ Ø Ú ÓÒ ÝÑÑ ØÖ Ò Ò ÒÓÐÐ Ò Ù Ø Ò Ò Ò ÒØ Ö Ð Ø ÝÐ ÚÐ Ò (,) (, ) ÓÚ Ø Ý Ø ÙÙÖ Øº Ë º º µ e z / dz = π. Ì ÑÐÐ Ó ØÙ x = z ÒØ Ö Ð Ò º º µ Ò ÒØ Ö Ð Ó ÓÒ Γ ( ) º Ë ÐÐÓ Ò º º µ ( ) Γ = x / e x dx = π. Ä Ù º¾ ÇÐ Ø Ø Ò ØØ Z ÒÓÙ ØØ Ø Ò Ö ÑÙÓØÓ Ø ÒÓÖÑ Ð Ù¹ Ñ º Ë ÐÐÓ Ò ½º Z Ò ÑÓÑ ÒØØ ÙÒ Ø Ó ÓÒ ¾º E(Z) = Var(Z) = º ÌÓ ØÙ º ½º ÅÖ Ø ÐÑÒ ÑÙ Ò M(t) = e t /, < t <. M(t) = e tz π e z / dz. Ì Ò Ó ØÙ x = z tº Ë ÐÐÓ Ò dz = dx e tz e z / = e (t x )/ ÓØ Ò M(t) = e (t x )/ dx = e t / π π e x / dx = e t /. Î Ñ Ò Ò Ý Ø ÙÙÖÙÙ ÙÖ Ø ØØ ÒØ Ö Ð ÝÐ ÒÓÖÑ Ð ÙÑ Ò Ø ¹ Ý ÙÒ Ø ÓÒ π e x / ÓÒ º ¾º ÃÓ M(t) = e t / Ò ÒM (t) = te t / M (t) = e t / +t e t / º Ë ÐÐÓ Ò M () = M () = Var(Z) = M () [M ()] = º
19 ½ ¾ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Å Ö ØÒ Z N(,) Ñ E(Z) = Var(Z) = º Ë ÙÖ Ú ÔÝ Ð ÑÖ Ø ÐÐÒ ÒÓÖÑ Ð ÙÑ ÓÒ ÖÚÓ ÓÒµ Ú Ö Ò σ º Ñ Ö º ÇÐ ÓÓÒ X,X,...,X 5 ÓØÓ ÙÑ Ø ÓÒ Ø Ý ÙÒ ¹ Ø Ó ÓÒ f(x) = ( 3 ) x < x < º  ÙÑ Ò Ó ÓØÙ ÖÚÓ µ = Ú Ö Ò σ = 3/5º Ñ Ö ØÓ ÒÒ ÝÝ P(X.5) ÚÓ Ò Ð Ó Ø Ñ Ð¹ Ð Ò Ò X Ò ÙÑ ÑÖ ØØÑÐÐ Ø Ý ÝØØÝ ØÓ ÒÒ ÝÝ º à ¹ Ò Ö Ú ØØÑÒ ÚÙÐÐ Ò ØÑÒ ØÓ ÒÒ ÝÝ Ò Ð ÖÚÓ ÐÑ Ò Ø ØÓ X Ò Ø Ö Ø ÙÑ Ø ( X P(X.5) = P /.5 ) / 3/5 5 3/5 5 = P(Z 5.75) Φ(.75) = ÖÚ ÓÒ Ø Ö ÙÙ Ø Ò Ò Ö Ú ØØÑ Ù Ø Ò Ò ÒÒ ØÝ Øº º ÅÙÙØØÙ Ò Ú ØÓ ÇÐ Ø Ø Ò ØØ X ÓÒ Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ ÖØÝÑ ÙÒ Ø Ó ÓÒ F(x)º ÄÙ Ù ÓÚ ÐÐÙ Ø ÖÚ Ø Ò ØÙÒÒ ÑÙÙØØÙ Ò X ÓÒ Ò ÙÒ ¹ Ø ÓÒ Y = h(x) ÙÑ ÙÒ X Ò ÙÑ ØÙÒÒ Ø Òº Ì ØÚÒÑÑ ÓÒ ÒÝØ ÑÖ ØØ ØÙÒÒ ÑÙÙØØÙ Ò Y = h(x) ÙÑ Ñ h(x) ÓÒ x Ò Ö Ð ÖÚÓ Ò Ò ÙÒ Ø Óº º º½ ÅÙÙÒÒÓ ÖØÝÑ ÙÒ Ø Ó ÚÙÐÐ ÎÓ ÑÑ ÔÝÖ Ó Ø Ñ Ò Y Ò ÖØÝÑ ÙÒ Ø ÓÒ G(y) = P(Y y) ÙÓÖ Ò X Ò ÖØÝÑ ÙÒ Ø ÓÒ F(x) ÚÙÐÐ º Y Ò Ø Ý ÙÒ Ø Ó g(y) ÚÓ Ò ÑÖ ØØ ØØ Ò ÒØ Ø Ø Ò º½º µ ÚÙÐÐ ÙÒ G(y) ÓÒ Ö ÚÓ ØÙÚ º Ñ Ö º ÇÐ ÓÓÒ X Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ÙÒ Ø Ó ÓÒ f(x) = 3x, x. Ì Ö Ø ÐÐ Ò ØÙÒÒ ÑÙÙØØÙ Ò Y = X ÙÑ º Ë ÐÐÓ Ò Y Ò ÖÚÓ Ú ¹ ÖÙÙ ÓÒ S Y = [,] Y Ò ÖØÝÑ ÙÒ Ø Ó ÓÒ G(y) = P(Y y) = P(X y) = P( y X y) = y y 3x dx = y / y x 3 = y3/, y.
20 º º ÅÙÙØØÙ Ò Ú ØÓ ½ Ö ÚÓ Ñ ÐÐ Ò Y Ò Ø Ý ÙÒ Ø Ó g(y) = G (y) = 3y/, y. Ñ Ö º½¼ ÇÐ ÓÓÒ X Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ ÖØÝÑ ÙÒ ¹ Ø Ó ÓÒ F(x) = (+x)e x, x >. ÂÓ Ø Ò ØÙÒÒ ÑÙÙØØÙ Ò Y = e X ÙÑ º Å Ö ØÒ Y Ò ÖØÝѹ ÙÒ Ø ÓØ G Ðк Ë ÐÐÓ Ò G(y) = P(Y y) = P ( e X y ) = P[ X log(y)] = P[X log(y)] = P[X < log(y)] = F[ log(y)], Ñ F(x) ÓÒ X Ò ÖØÝÑ ÙÒ Ø Óº Ë Ó ØØ Ñ ÐÐ x = log(y) X Ò ÖØݹ Ñ ÙÒ Ø ÓÓÒ Ò G(y) = [ log(y)]e log(y) = [ log(y)]y. ÃÓ S X = (, ) Ò Ò S Y = (,)º Y ÓÒ Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ Ó G(y) ÓÒ Ø ÙÚ ÐÐ ÓÒ Ø ÙÚ Ö Ú ØØ ÑÙÙ ÐÐ Ô Ø Ô Ø y = º Y Ò Ø Ý ÙÒ Ø Ó ÓÒ g(y) = G (y) = { log(y), ÙÒ < y < ÑÙÙ ÐÐ º ÀÙÓÑ ØØ log(y) > ÙÒ < y < º ÆÝØ g(y) ÐÐ y S Y = (,)º º º¾ ÅÙÙÒÒÓ Ø Ý ÙÒ Ø ÓÒ ÚÙÐÐ Ë ÙÖ Ú Ø ØÒ ÝÐ Ò Ò Ñ Ò Ø ÐÑ ÓÒ ÚÙÐÐ ÚÓ Ò Ó Ø ØÙÒ¹ Ò ÑÙÙØØÙ Ò X ÙÒ Ø ÓÒ Y = h(x) Ø Ý ÙÒ Ø Ó ÙÓÖ Ò X Ò Ø Ý ÙÒ ¹ Ø ÓÒ f X (x) ÚÙÐÐ º Å Ò Ø ÐÑÒ ÐÐÝØØ Ù Ø Ò Ò ØØ ÙÒ Ø ÓÐÐ h(x) ÓÒ Ø Ö Ø ÐØ Ú ÐÐ ÚÐ ÐÐ ÒØ ÙÒ Ø Óº Ñ Ö ÙÒ Ø ÓÒ y = e x ÒØ ¹ ÙÒ Ø Ó ÓÒ x = log(y)º ÅÝ ÙÒ Ø Ó y = x ÓÒ ÒØÝÚ ÙÒ x > ÐÐ ÐÐÓ Ò x = yº ÙÒ Ø Ó y = x ÓÐ ÒØÝÚ Ó Ó Ö Ð Ð ÐÐ Ó Ð¹ ÐÓ Ò x = ± y Ó ÓÐ ÙÒ Ø Óº ÀÙÓÑ ØØ ÓÓÒ ØØ Ø ÙÚ ÙÒ Ø Ó h(x) ÓÒ ÒØÝÚ Ó Ú Ò Ó ÓÒ Ó Ó Ó Ø Ú Ú Ø Ó Ø Ú Ò Úº
21 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ä Ò Ö Ò Ò ÑÙÒÒÓ Ì Ö Ø ÐÐ Ò Ò Ò Ý Ò ÖØ Ø Ð Ò Ö Ø ÑÙÙÒÒÓ Ø Y = ax +b Ñ a b ÓÚ Ø ÒÒ ØØÙ Ú Ó Ø º ÆÝØ h(x) = ax + bº ÙÒ Ø ÓÒ y = h(x) Ö Ú ØØ ÓÒ dy dx = h (x) = a. ÙÒ Ø ÓÐÐ h(x) ÓÒ ÒØ ÙÒ Ø Ó g(y) = y b a, a dy dx = g (y) = a. Ñ Ö º½½ ÇÐ Ø Ø Ò ØØ X Tas(.5,.5) Y = Xº Å Ø Ù¹ Ñ Y ÒÓÙ ØØ 3 y = x y + y y f Y (y) {}}{ B x } A }{{} f X (x).5 x x+ x.5 x ÃÙÚ Ó º º Ì ÙÑ Tas(.5,.5) ÒÓÙ ØØ Ú Ò ØÙÒÒ ÑÙÙع ØÙ Ò X Ð Ò Ö Ò Ò ÑÙÙÒÒÓ º ÃÙÚ Ó º ÓÒ ÐÙ Ò A Ô ÒØ ¹ Ð P[X (x,x+ x)] = f X (x) x = x ÐÙ Ò B Ô ÒØ ¹ Ð P[Y (y,y+ y)] = f Y (y) y.
22 º º ÅÙÙØØÙ Ò Ú ØÓ ½ Ì Ô ØÙÑ Ø X (x,x+ x) Y (y,y+ y) ØØÙÚ Ø Ø ÑÐÐ Ò Ñ Ò¹ Ø ÓØ Ò º º½µ P[X (x,x+ x)] = P[Y (y,y+ y)]. ÃÓ y = x y+ y = (x+ x) Ò Ò y = x ÒØ Ø Ø Ø º º½µ ÙÖ ØØ f Y (y) = º ÃÓ.5 < x <.5 Ò Ò < y < 3º Æ Ò Y Tas(,3) { f Y (y) =, < y < 3;, ÑÙÙ ÐÐ º ÇÐ ÓÓÒ X ØÙÒÒ ÑÙÙØØÙ ÓÒ ÖÚÓ Ú ÖÙÙ ÓÒ S X º Ë ÐÐÓ Ò ØÙÒ¹ Ò ÑÙÙØØÙ Ò Y = h(x) ÖÚÓ Ú ÖÙÙ S Y ÑÖÝØÝÝ Ø Ò ØØ X S X Y S Y. Ë ÙÖ Ú Ð Ù Ø ØØÚ Ñ Ò Ø ÐÑ ÓÐ Ø Ø Ò ØØ ÙÒ Ø Ó y = h(x) ÓÒ Ø Ö Ø ÐØ Ú ÐÐ ÖÚÓ ÐÙ ÐÐ ÒØÝÚº Ë ÐÐÓ Ò ÓÒ ÓÐ Ñ ÐÐ Ò Ò ÙÒ Ø Ó x = g(y) ØØ y = h(x) x = g(y). Ä Ù º ÇÐ ÓÓÒX Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ÙÒ Ø Ó ÓÒ f X (x) ÖÚÓ Ú ÖÙÙ S X º ÇÐ ÓÓÒ Y = h(x) ÐÐ Ò Ò ÙÒ Ø Ó ØØ ÐÐ ÓÒ Ò¹ Ø ÙÒ Ø Ó x = g(y) ÒØ ÙÒ Ø ÓÒ Ö Ú ØØ g (y) ÓÒ ÓÐ Ñ ÐÐ y S Y Ñ S Y ÓÒ Y Ò ÖÚÓ Ú ÖÙÙ º Ë ÐÐÓ Ò Y Ò Ø Ý ÙÒ Ø Ó ÓÒ f Y (y) = f X ( g(y) ) g (y), y S Y. ÌÓ ØÙ º ÇÐ ØÙ Ò ÑÙ Òg(y) ÓÒ Ö ÚÓ ØÙÚ ÓØ Ò ÓÒ Ø ÙÚ º ÃÓ h g ÓÚ Ø ÒØÝÚ Ò Ò h g ÓÚ Ø ÑÓÐ ÑÑ Ø Ó Ó Ú Ú Ø Ú Ò Ú º ÇÐ Ø Ø Ò h g ÓÚ Ø Ú Ò Ú º Ë ÐÐÓ Ò F Y (y) = P(Y y) = P(h(X) y) = P(X g(y)) = F X ( g(y) ). Ö ÚÓ Ò F X [g(y)] Ø Ù ÒÒ Ò ÚÙÐÐ ÓÐÐÓ Ò Ò f Y (y) = F Y (y) = F X( g(y) ) g (y) = f X ( g(y) ) g (y) = f X ( g(y) ) g (y). Î Ñ Ò Ò Ý Ø ÙÙÖÙÙ ÙÖ Ø ØØ g (y) ÓÒ Ò Ø Ú Ò Ò Ó g ÓÒ Ú Úº ÂÓ h g ÓÚ Ø Ú Ú Ò Ò ØÓ ØÙ ÓÒ Ñ Ð Ò Ñ ÒÐ Ò Ò Ø ¹ ØÒ Ö Ó ØÙ Ø ØÚ º
23 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ñ Ö º½¾ ÇÐ ÓÓÒ X Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ÙÒ Ø Ó ÓÒ f X (x) = e x S X = {x x > }º ÇÐ ÓÓÒ Y = X / ÓØ Ò X = Y = g(y) S Y = S X º ÃÓ g (y) = y Ò Ò f Y (y) = f X (y ) y = ye y, y >. Ì Ö Ø ÐÐ Ò Ú Ð ØÙÒÒ ÑÙÙØØÙ V = e X º Ë ÐÐÓ Ò X = log(v)º Å Ö ØÒ ÒÝØ log(v) = g(v)º Ë ÐÐÓ Ò S V = [,] g (v) = /vº Ë f V (v) = f X [ log(v)] v = v v =, ÓØ Ò V ÒÓÙ ØØ Ø ÙÑ ÚÐ ÐÐ [,]º Å Ð ÑÙÙÒÒÓ ÙÒ Ø ÓÐÐ h ÓÐ ÒØ ÙÒ Ø ÓØ X Ò ÖÚÓ Ú ÖÙÙ S X Ò Ò Ä Ù Ò º ÑÙÙÒÒÓ Ñ Ò Ø ÐÑ ÚÓ ÙÓÖ Ò ÓÚ ÐØ º ÂÓ Ù ¹ Ø Ò Ò ÓÒ ÓÐ Ñ ÐÐ Ò Ò S X Ò Ó ØÙ Ý Ø Ô Ø ØØ Ñ Ò Ó ÚÐ Ò A A º º º A m ØØ º º¾µ S X = A A A m h ÓÒ ÒØÝÚ Ó ÐÐ Ó ÚÐ ÐÐ ÚÓ Ò ÑÙÙÒÒÓ Ø Ó ÐÐ Ó ¹ ÚÐ ÐÐ Ö Òº Ë Ø Ú ÖØ Ò ÑÖ Ø ÐÐÒ ÙÒ Ø ÓØ { h i (x), ÙÒ x A i h(x) = ÑÙÙ ÐÐ º Ë ÐÐÓ Ò h(x) ÚÓ Ò Ö Ó ØØ ÑÙÓ Ó h(x) = m i= h i(x) Ñ Ó¹ Ò Ò h i (x) ÓÒ ÒØÝÚ ÚÐ ÐÐ A i º ÇÐ ÓÓØ ÙÒ Ø Ó Ò h i ÒØ ÙÒ Ø ÓØ Ú Ø Ú Ø g i i =,,...,mº Ë ØÙÒÒ ÑÙÙØØÙ Ò Y = h(x) Ø Ý ÙÒ Ø Ó ÚÓ Ò ÒÝØ ØØ Ä Ù Ò º ÚÙÐÐ ÑÙÓ Ó m ( º º µ f Y (y) = f X gi (y) ) g i (y). y S Y. i= ÀÙÓÑ ØØ ÓÓÒ ØØ Ó Ù Ø ÖÚ Ø Ò Ö ÐÐ Ò Ó ØÙ Ò º º¾µ Ø Ó ¹ ØÙ Ó ÓÚÐ A A º º º ÓÒ Ö Ø Ò ÑÖ m = µº º Ð Ò Ò ÒÓÖÑ Ð ÙÑ Ë ØÙÒÒ ÑÙÙØØÙ X ÒÓÙ ØØ ÒÓÖÑ Ð ÙÑ ÖÚÓÐÐ µ Ú ¹ Ö Ò ÐÐ σ > Ó ÚÓ Ò ØØ ÑÙÓ Ó X = µ+σz, Ñ Z N(,)º Ë ÐÐÓ Ò Ñ Ö ØÒ X N(µ,σ )º ÂÓ X N(µ,σ ) Ò Ò Ú Ø Ú Ø Z = X µ N(,). σ Ë ÙÖ Ú Ð Ù Ø ØÒ ÙÑ Ó Ú Ø Ô ÖÙ ØÙÐÓ Øº
24 º º Ð Ò Ò ÒÓÖÑ Ð ÙÑ ½ Ä Ù º ÂÓ X N(µ,σ ) Ò Ò ½º E(X) = µ Var(X) = σ ¾º M X (t) = E ( e tx) = e µt+σ t /, < t <. º X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = πσ e (x µ) /σ, < x <. ÌÓ ØÙ º ½º ÃÓ X N(µ,σ ) Ò Ò X = µ + σz Ñ Z N(,)º Ë ÐÐÓ Ò E(X) = E(µ+σZ) = µ+σe(z) = µ Var(X) = Var(µ+σZ) = σ Var(Z) = σ. ¾º ÅÖ Ø ÐÑÒ ÑÙ Ò º ÑÝ Ä Ù º½¾µ M X (t) = E ( e tx) = E [ e t(µ+σz)] = e tµ E ( e tσz) = e tµ M Z (tσ) = e tµ e t σ / = e tµ+t σ /. º Ì Ò ÑÙÙÒÒÓ x = h(z) = µ+σzº Ë ÐÐÓ Ò h ÐÐ ÓÒ ÒØ ÙÒ Ø Ó g z = g(x) = x µ g (x) = º Ð ÐÙÚÙ º Ø ØØÚÒ ÑÙÙÒÒÓ Ø ¹ σ σ Ò Ò ÚÙÐÐ Ò X Ò Ø Ý ÙÒ Ø Ó º º½µ ( x µ f X (x) = f Z σ = ) σ π σ e (x µ) /σ. Ì Ú ÐÐ Ø Ø Ý ÙÒ Ø Ó Ö Ó Ø Ø Ò ÑÙÓ Ó f X (x) = πσ e (x µ) /σ, Ñ σ = + Var(X) = + σ ÓÒ X Ò ÓÒØ º ÌÓ ØÙ ÓÐ Ø ØØÙ ØØ σ > º Ñ Ö º½ ÂÓ X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = 3π e (x+7) /3, < x <, Ò Ò X N( 7,6) M X (t) = e 7t+8t.
25 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ñ Ö º½ ÂÓ X Ò ÑÓÑ ÒØØ ÙÒ Ø Ó ÓÒ M X (t) = e 5t+t, Ò Ò X N(5,4) X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = 48π e (x 5) /48, < x <. ÂÓ X N(µ,σ ) Ò Ò X Ò Ø Ý ÙÒ Ø Ó ÚÙØØ Ñ Ñ Ò Ô Ø x = µ ÒØ Ô Ø Ø ÓÚ Ø x = µ±σº ÌÓ ÒÒ ÝÝ Ñ ÓÒ ÙØÙÒÙØ Ø Ò ØØ Ñ Z N(,)º Ñ Ö P( X µ σ) = P( Z ) =.686, P( X µ σ) = P( Z ) =.9544, P( X µ 3σ) = P( Z 3) =.9974, P( X µ σ) = P( Z ) = P( Z ) = Φ() Φ( ) = = , Ñ Φ(z) = z π e v / dv ÓÒ Ø Ò Ö ÑÙÓØÓ Ò ÒÓÖÑ Ð ÙÑ Ò ÖØÝÑ ÙÒ Ø Óº Ë Ò ÖÚÓØ ÓÒ Ø Ù¹ ÐÙ Ó ØÙ Ò Ð ØØÙ Ù ÐÐ Ó ÐÑ ØÓ ÐÐ º ÐÐ Ø ØØÝ Ò ØÓ¹ ÒÒ ÝÝ Ò Ò ÒÙÑ ÖÓÒ Ð ÖÚÓ Ò ÝØ ØÒ Ø Ú ÐÐ Ø ÐÙ Ù ÓØ ÚØ ÓÐ ÔÝ Ö Ø ØØÝ Ú Ò Ø ØÙ ÖÚÓ º ÅÝ ÝÐÐ Ø ØÝØ Ò Ð Ò ÒÙÑ ÖÓÒ Ð ÖÚÓØ ÓÚ Ø Ø ØÙ ÖÚÓ º Ä Ù º ½º ÇÐ ÓÓÒ X N(µ,σ ) U = ax +b Ñ a b ÓÚ Ø ÒÒ ØØÙ Ú Ó Ø º Ë ÐÐÓ Ò U N(aµ+b,a σ ). ¾º ÇÐ ÓÓØ X X º º º X n Ö ÔÔÙÑ ØØÓÑ Ø X i N(µ i,σ i) i =,,...,n a a º º º a n b ÓÚ Ø ÒÒ ØÙØ Ú ÓØ Ó Ø Ò Ò Ý a i ÔÓ ÒÓÐÐ Ø º Ë ÐÐÓ Ò Y = n i= a ix i +b ÒÓÙ ØØ ÒÓÖÑ Ð ÙÑ ( n Y N a i µ i +b, i= n i= a i σ i ).
26 º º ÑÑ ÙÑ χ ¹ ÙÑ ½ Ñ Ö º½ Ê ÔÔÙÑ ØØÓÑ Ø ØÙÒÒ ÑÙÙØØÙ Ø X X X 3 ÒÓ٠ع Ø Ú Ø ÒÓÖÑ Ð ÙÑ Ø Ò ØØ X i N( i,i i ) i =,,3º Ë ÐÐÓ Ò Y = X +X +X 3 N(4,3) ÐÐ E(Y) = = 4 Var(Y) = = 3 Ä Ù Ò º ÑÙ Ò Y ÒÓÙ ØØ ÒÓÖÑ Ð ÙÑ º Ë ØÙÒÒ ÑÙÙØØÙ Y = X +X +3X 3 N(34,6) Ó E(Y) = = 34 Var(Y) = = 6. º ÑÑ ÙÑ χ ¹ ÙÑ ÑÑ ÙÑ ÙÑ ÓÒ ÚÐ ÐÐ [, ) ÑÖ Ø ÐØÝ ÙÑ Ø ÙÑ ¹ Ô Ö Ó Ô Ö Ñ ØÖ Ò Ú ÐÐ Ò ÝÚ Ò Ò Ö Ò ÙÑ Ú Ò ÓÚ Ø Ñ Ø Ñ ØØ Ø Ñ ÑÙÓØÓ º ÑÑ ÙÒ Ø Ó Γ(α) = x α e x dx ÓÒ Ö ÐÐ Ò Ò ÙÒ α > º ÑÑ ÙÒ Ø Ó ØÓØ ÙØØ Ö ÙÖ Ú Ò Ö Ð Ø ÓÒ Γ(α+) = αγ(α), Ó ÚÓ Ò Ó Ó ØØ Ó ØØ ÒØ ÖÓ ÒÒ ÐÐ º ÂÓ α = n ÓÒ ÔÓ Ø Ú Ò Ò Ó Ó¹ Ò ÐÙ Ù Ò Ò Γ(n+) = nγ(n) = n(n ) Γ() = n!γ(). ÃÓ Γ() = Ò Ò Γ(n+) = n! ÐÐ ÔÓ Ø Ú ÐÐ Ó ÓÒ ÐÙÚÙ ÐÐ º ÅÝ Γ( ) = π ÓÒ ØÖ Ö Ó Ø ¹ Ô Ù º º º½ ÑÑ ÙÑ ÙÒ Ø Ó º º½µ f(t) = tα e t Γ(α), < t <
27 ½ ¼ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø ÑÖ ØØ Ð Ø Ý ÙÒ Ø ÓÒ ÐÐ ÑÑ ÙÒ Ø Ó ÒØ ÖÓ Ø Ú ÓÒ ÔÓ Ø Ú ¹ Ò Ò ÚÐ ÐÐ (, )º Ë ÒÓ ÑÑ ØØ º º½µ ÓÒ ØÙÒÒ ÑÙÙØØÙ Ò T Ø ¹ Ý ÙÒ Ø Óº Ã Ò ÑÑ ÙÑ Ò Ô Ö Ò ÑÖ ØØ Ð ÑÐÐ ¹ ØÙÒÒ ÑÙÙØØÙ X = βt Ñ β ÓÒ ÔÓ Ø Ú Ò Ò Ú Óº X Ò Ø Ý ÙÒ Ø Ó ÚÓ Ò Ó Ø ÓÚ ÐØ Ñ ÐÐ Ä Ù Ò º ÑÙÙÒÒÓ Ø Ò º Å Ö Ø ÑÑ X Gamma(α,β) ÒÓÑÑ ØØ X ÒÓÙ ØØ ÑÑ ÙÑ Ô Ö ¹ Ñ ØÖ Ò α βº Â ÙÑ Ò Gamma(α,β) Ø Ý ÙÒ Ø Ó Ò º º¾µ f(x) = Γ(α)β αxα e x/β, < x <, α >, β >. ØÑÑ ÒÝØ ÑÑ ÙÑ Ò Ô ÖÙ ÓÑ Ò ÙÙ Ø ÙÖ Ú Ð Ù ¹ º Ä Ù º ÇÐ Ø Ø Ò ØØ X Gamma(α,β)º ½º ÙÒ Ø Ó º º¾µ ÑÖ ØØ Ð Ø Ý ÙÒ Ø ÓÒ ÐÐ α > β > º ¾º E(X) = αβ, Var(X) = αβ M(t) = E(e tx ) = ( ) α, t < βt β. º ÐÐ c > αº E(X c ) = Γ(α+c)βc Γ(α) º ÇÐ ÓÓÒ U = bx b > º Ë ÐÐÓ Ò U Gamma(α,bβ)º ÔÓÒ ØØ ÙÑ ÓÒ ÑÑ ÙÑ Ò Ö Ó Ø Ô Ù º ÃÙÒ Ó Ø Ø Ò Ø Ý ÙÒ Ø ÓÓÒ º º¾µ α = Ò f(x;β) = β e x/β, x >. À Ú Ø Ò ØØ Gamma(,β) = Exp(β)º º º¾ χ ¹ ÙÑ ÌÓ Ò Ò ØÖ ÑÑ ÙÑ Ò Ö Ó Ø Ô Ù ÓÒ χ ¹ ÙÑ º ÂÓ Ú Ð Ø Ò α = r Ñ r ÓÒ ÔÓ Ø Ú Ò Ò Ó ÓÒ ÐÙ Ù β = ØÙÐ Ø Ý ÙÒ ¹ Ø Ó º º¾µ ÑÙÓØÓÓÒ º º µ f(x) = Γ ( ) r r/ x(r/) e x/, < x <,
28 º º ÑÑ ÙÑ χ ¹ ÙÑ ½ ½ Ñ ÓÒ χ ¹ ÙÑ Ò Ø Ý ÙÒ Ø Ó Ú Ô Ù Ø Ò rº ÂÓ X ÒÓÙ ØØ χ ¹ ÙÑ Ú Ô Ù Ø Ò r Ñ Ö ØÒ X Khi(r)º χ ¹ ÙÑ Ò ÖÚÓ Ú Ö Ò ÑÓÑ ÒØØ ÙÒ Ø Ó Ò ÒÝØ ÙÓÖ Ò ÑÑ ÙÑ Ò ÚÙÐÐ º ÂÓ X Khi(r) Ò Ò E(X) = r, Var(X) = r M(t) = ( t) r/, t <. Ç ÓØÙ ÈÓ ÓÒ Ò ÔÖÓ Ë ÙÖ Ú Ò Ø Ô ØÙÑ Ò Ó ÓØÙ ÈÓ ÓÒ Ò ÔÖÓ ÒÓÙ ØØ ÔÓÒ Ø¹ Ø ÙÑ º ÇÐ ÓÓÒ W ÒÝØ Ó ÓØÙ ÙÒÒ ØØÙÙ α Ø Ô ØÙÑ Ñ α ÓÒ ÔÓ Ø Ú Ò Ò Ó ÓÒ ÐÙ Ùº ÂÓ ÈÓ ÓÒ Ò ÔÖÓ Ò ÒØ Ò Ø ØØ ÓÒ λ Ò Ò ØÓ ÒÒ ÝÝ ØØ w Ò Ô ØÙ ÐÐ ÚÐ ÐÐ ØØÙÙ x Ø Ô ØÙÑ Ò Ú ÐÐ º¾º µ P(X w = x) = e λw(λw)x. x! Ç ÓØÙ Ò W ÖØÝÑ ÙÒ Ø Ó ÙÒ W ÓÒ F(w) = P(W w) = P(W > w) = P(Ú ÑÑÒ Ù Ò α Ø Ô ØÙÑ ÚÐ ÐÐ [t,t+w]) α = x= e λw(λw)x, x! Ó Ø Ô ØÙÑ Ò ÐÙ ÙÑÖ ÚÐ ÐÐ [t,t + w] ÒÓÙ ØØ ÈÓ ÓÒ Ò ¹ ÙÑ ÖÚÓÐÐ λw º º¾º µ º Ä Ñ ÐÐ Ö Ú ØØ F (w) = f(w) Ò Ø Ý ÙÒ Ø Ó f(w) = λ(λw)α (α )! e λw. ÂÓ w < Ò Ò F(w) = f(w) = º ÆÝØ ÙÓÑ ÑÑ ØØ ( W Gamma α, ). λ º º ÆÓÖÑ Ð ÙØÙÒ Ò ØÙÒÒ ÑÙÙØØÙ Ò ÑÙÙÒÒÓ Ø ÂÓ X N(,) Ò Ò X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = π e x /, < x <,
29 ½ ¾ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ó ÓÒ Ø Ò Ö ÑÙÓØÓ Ò ÒÓÖÑ Ð ÙÑ Ò Ø Ý ÙÒ Ø Óº ÂÓ Ø Ò ÒÝØ ØÙÒÒ ÑÙÙØØÙ Ò U = X ÙÑ º ÅÙÙÒÒÓ ÙÒ Ø Ó u = h(x) = x ÓÐ ÒØÝÚ Ó x = ± u ÓÐ ÙÒ Ø Óº Ë ØÑÑ ÖÚÓ Ú ÖÙÙ Ò S X = { < x < } Ó Ø ØØÙÒ ÑÙÓ Ó S X = (,] (, ). Ë ÐÐÓ Ò ÙÒ Ø ÓÐÐ h(x) ÓÒ ÚÐ ÐÐ (,] ÒØ ÙÒ Ø Ó g (u) = u ÚÐ ÐÐ (, ) ÒØ ÙÒ Ø Ó g (u) = uº ÆÝØ Ú Ò º º µ ÑÙ Ò U Ò Ø Ý ÙÒ Ø Ó ÓÒ º º µ f U (u) = f X ( u) u +f X( u) u = e u/, πu ÙÒ u (, )º U ÒÓÙ ØØ χ ¹ ÙÑ Ú Ô Ù Ø Ò º à ØØ Ð ÑÑ Ø Ð ØÓØ Ø ØÖ χ ¹ ÙÑ Ú Ð Ø Ó Ø Ö ÑÑ Òº Ä Ù º ÂÓ X N(µ,σ ) σ > Ò Ò ÐÐÓ Ò (X µ) σ Khi(). ÌÓ ØÙ º ÃÓ X N(µ,σ ) Ò Ò ÑÖ Ø ÐÑÒ ÑÙ Ò X µ = Z σ N(,)º ÐÐ ÒÝØ ØØ Ò ØØ Z Khi()º Æ Ò ÓÒ Ð Ù ØÓ Ø ØØÙº Ä Ù º ÂÓ Z i Ø ÓÚ Ø Ö ÔÔÙÑ ØØÓÑ Ø Z i N(,) i =,,...,n Ò Ò Z +Z + Z n Khi(n). ÂÓ Ø Ò ÓØÓ ÒÓÖÑ Ð ÙÑ Ø N(,) Ò Ò Ä Ù Ò º ÑÙ Ò Ú ÒØÓ Ò Ò Ð ÙÑÑ ÒÓÙ ØØ Ã ¾¹ ÙÑ Ú Ô Ù Ø Ò n Ñ n ÓÒ ÓØÓ Ó Óº Ë ÙÖ Ù º½ ÂÓ X i Ø ÓÚ Ø Ö ÔÔÙÑ ØØÓÑ Ø X i N(µ,σ ) i =,,...,n Ò Ò n (X i µ) Khi(n). i= σ ÂÓ Ú Ø Ú Ø Ø Ò n Ò ÙÙÖÙ Ò Ò ÓØÓ ÒÓÖÑ Ð ÙÑ Ø N(µ,σ ) Ò Ò Ë ÙÖ Ù Ð Ù Ò º½ ÑÙ Ò Ø Ò Ö Ó ØÙ Ò Ú ÒØÓ Ò Ò Ð ÙÑÑ ÒÓÙ ØØ Ã ¾¹ ÙÑ Ú Ô Ù Ø Ò nº Ä Ù º ÇÐ ÓÓØ X X Ö ÔÔÙÑ ØØÓÑ Ø X i Khi(n i ) i =,º Ë ÐÐÓ Ò X +X Khi(n +n ).
30 º º Ë ØÙÒÒ ÑÙÙØØÙ Ò Ó ÓØÙ ÖÚÓ ½ º Ë ØÙÒÒ ÑÙÙØØÙ Ò ÙÒ Ø ÓÒ Ó ÓØÙ ÖÚÓ ÇÐ ÓÓÒ X Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ÙÒ Ø Ó f(x) ÓÒ ÑÖ Ø Ð¹ ØÝ ÖÚÓ Ú ÖÙÙ Sº ÇÐ ÓÓÒ h(x) ØÙÒÒ ÑÙÙØØÙ Ò X Ö Ð ÖÚÓ Ò Ò ÙÒ Ø Ó Ó ÑÖ ØØ Ð ÙÙ Ò ØÙÒÒ ÑÙÙØØÙ Òº ÅÖ Ø ÐÑ º¾ ÂÓ X ÓÒ Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ Ò Ò ØÙÒÒ ÑÙÙع ØÙ Ò h(x) Ó ÓØÙ ÖÚÓ ÓÒ º º½µ E[h(X)] = h(x)f(x) dx, S Ñ Ð E ( h(x) ) < º ÂÓ E ( h(x) ) = Ò Ò ÒÓÑÑ ØØ E[h(X)] ÓÐ ÓÐ Ñ º ÀÙÓÑ ÙØÙ º½ Ç ÓØÙ ÖÚÓÒ E[h(X)] ÓÐ Ñ ÓÐÓ Ø Ö Ó ØØ Ø Ø¹ Ø ÙÒ Ø ÓÒ h(x) Ó ÓØÙ ÖÚÓ ÓÒ Ö ÐÐ Ò Òº ÂÓ X ÒÓÙ ØØ Ñ Ö ÔÓÒ ÒØØ ÙÑ ÖÚÓÐÐ Ò Ò f(x) = e x S = [, )º Ë ÐÐÓ Ò X Ò Ó ÓØÙ ÖÚÓ ÓÒ E(X) = xe x dx = = / ( xe x )+ e x dx =, e x dx Ó ØØ ÒØ ÖÓ ÒØ µ ÓØ Ò Ó ÓØÙ ÖÚÓ ÓÒ ÓÐ Ñ º ÀÝÚ Ò Ù Ò Ó ÓØÙ ÖÚÓØ ÓÚ Ø ÔÓÐ ÐÐ ÒØ Ö Ð Ò Ò Ù Ò Ø Ò Ñ Ö º ÂÓ h(x) ÒØ ÖÓ ØÙÙ Ø Ø Ð h(x) S ÓÒ Ö ÐÐ Ò ÓÐ Ñ Ò Ò E[h(X)] ÓÒ ÓÐ Ñ º ÙÒ Ø Ó V = h(x) ÓÒ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ÙÒ Ø Ó g(v) ÓÒ ÑÖ Ø ÐØÝ ÖÚÓ Ú ÖÙÙ S V = {v v = h(x), x S}º Ë ÐÐÓ Ò E[h(X)] = E(V) = vg(v). S V
31 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ñ Ö º½ Ì Ö Ø ÐÐ Ò ÒÝØ Ù ÝÒ ÙÑ ÒÓÙ ØØ Ú ØÙÒ¹ Ò ÑÙÙØØÙ X ÓÒ Ø Ý ÙÒ Ø Ó ÓÒ º º¾µ f(x) =, < x <. π(+x ) Ã Ú º º¾µ ØÓ ÐÐ Ò ÑÖ ØØ Ð Ø Ý ÙÒ Ø ÓÒ Ó π(+x ) dx = π / arctan(x) = π π =. Ç Ó Ø ÑÑ ÒÝØ ØØE( X ) = Ñ Ø ÙÖ ØØ Ù ÝÒ ÙÑ ÐÐ ÓÐ ÖÚÓ º ËÝÑÑ ØÖ Ò ÒÓ ÐÐ ÚÓ Ò Ö Ó ØØ E( X ) = ÂÓ Ø Ö Ð ÐÙ Ù M > Ó Ø Ò x π(+x ) dx = x π +x dx. M Ì Ø ÙÖ ØØ x (+x ) dx = M/ log(+x ) = log(+m ). M x E( X ) = lim M π +x dx = π lim M log(+m ) =, ÓØ Ò E(X) ÓÐ ÓÐ Ñ º º º½ ÅÓÑ ÒØ ÙÒ Ø Ó ÑÓÑ ÒØ Ø ÃÙÒ h(x) = X r Ò Ò E[h(X)] = E(X r ) ÓÒ X Ò rº ÑÓÑ ÒØØ º Â Ø ÙÚ Ò ¹ ØÙÒÒ ÑÙÙØØÙ Ò ÑÓÑ ÒØ Ø ÑÖ Ø ÐÐÒ Ú Ø Ú Ø Ù Ò Ö ØØ Ò ¹ ØÙÒÒ ÑÙÙØØÙ Ò ÑÓÑ ÒØ Øº ËÙÑÑ Ð Ù Ø Ú Ò ÓÖÚ Ø Ò ÒØ Ö Ð Ð¹ Ð º Ì ÙÐÙ Ó º½ Ø ØÒ Ý Ø ÒÚ ØÓ Ö ÑÓÑ ÒØ Ø ÅÓÑ ÒØØ ÙÒ Ø Ó ÑÖ Ø ÐØ Ò º ÐÙÚÙ ÅÖ Ø ÐÑ º µ Ø ÙÚ ÐÐ ØÙÒÒ ÑÙÙØØÙ ÐÐ Ð ÐÙÚÙ º½ º ÒØ Ø ØØ º½º µ º Â Ø ÙÚ Ò ØÙÒ¹ Ò ÑÙÙØØÙ Ò X ÑÓÑ ÒØ ÙÒ Ø Ó ÓÒ M(t) = E(e tx ) = e tx f(x)dx, t A, S Ñ f(x) ÓÒ X Ò Ø Ý ÙÒ Ø Ó A ÐÐ Ò Ò t Ò ÖÚÓ Ò ÓÙ Ó ØØ M(t) ÓÒ Ö ÐÐ Ò Ò ÐÐ t Aº ÃÓ M() = Ò Ò Aº Ë ÒÓÑÑ ØØ M(t) ÓÒ ÓÐ Ñ Ó ( a,a) A ÓÐÐ Ò a > º ÅÓÑ ÒØØ ÙÒ Ø ÓÒ Ô ÖÙ ¹ ÓÑ Ò ÙÙ Ø Ø ØØ Ò ÈÝ Ð º º¾º
32 º º Ë ØÙÒÒ ÑÙÙØØÙ Ò Ó ÓØÙ ÖÚÓ ½ Ì ÙÐÙ Ó º½º ÌÖ Ø Ó ÓØÙ ÖÚÓ º h(x) E[h(X)] Å Ö ÒØ Æ Ñ ØÝ x E(X) µ Ó ÓØÙ ÖÚÓ x r E(X r ) α r rº ÑÓÑ ÒØØ x (r) E[X (r) ] g r rº Ø ÑÓÑ ÒØØ (x µ) E[(X µ) ] σ Ú Ö Ò (x µ) r E[(X µ) r ] µ r rº Ù ÑÓÑ ÒØØ Ñ Ö º½ ÀÙÓÑ ÙØÙ º½ Ð ØØ Ò Ó ÓØÙ ÖÚÓE(X) ÙÒX ÜÔ()º Ë ÐÐÓ Ò X Ò Ø Ý ÙÒ Ø Ó ÓÒ f(x) = e x ÚÐ ÐÐ S = [, ) f(x) = ÑÙÙ ÐÐ º à ÑÓÑ ÒØ Ø E(X r ) ÚÓ Ò ÑÖ ØØ Ó ØØ ÒØ ÖÓ ÒÒ ÐÐ ÑÙØØ ÝØ ØÑÑ ÒÝØ ÑÓÑ ÒØØ ÙÒ Ø ÓØ Ó ÓÒ M(t) = E(e tx ) = e tx e x dx = t, t <. Ö ÚÓ Ñ ÐÐ M(t) ØÓ ØÙÚ Ø r ÖØ Ò M (r) (t) = r! ( t) k+ º Ë ÓØ Ò E(X r ) = M (r) () = r!, µ = E(X) =, E(X ) =, σ = E(X ) µ =. Ö ØÝ Ø ÖÚÓ µ Ú Ö Ò σ ÓÒØ σ = Var(X) ÓÚ Ø Ø Ú ÐÐ ¹ ÑÑ Ø ØÙÒÒÙ ÐÙÚÙØ Ó ÐÐ ÙÑ ÐÙÓÒÒ Ø Òº  ÙÑ Ò Ý ØÝ Ó ¹ Ø ÑÑ Ø Ö Ø ÐÙ ÚÓ Ò ÝØØ ÑÝ ÓÖ ÑÔ ÑÓÑ ÒØØ Ñ Ð Ò ÓÚ Ø ÓÐ Ñ º º º¾ Î ÒÓÙ Ù ÔÙ ÙÙ Ë ØÙÒÒ ÑÙÙØØÙ Ò º ÑÓÑ ÒØØ µ ÑÖ ØØ ÙÑ Ò ÒÒ Òº à ¹ Ø ØÝÒ ÑÙÙØØÙ Ò X µ ØÓ Ò Ò ÑÓÑ ÒØØ Ù ÑÓÑ ÒØØ µ ÓÒ Ú Ö Ò σ Ñ ØØ ØÓ ÒÒ ÝÝ Ñ Ò ÒØÙÑ Ø º ÆÓÖÑ Ö ØÙÒ ÑÙÙØØÙ Ò (X µ)/σ ÓÐÑ Ò Ð ÑÓÑ ÒØØ ÐÙÓÒÒ Ø Ú Ø ÙÑ Ò ÑÙÓØÓ º  ÙÑ Ò Ú ÒÓÙ ÖÖÓ Ò Ó Ø ÝØ ØÒ Ñ Ö ÒØ γ ÑÖ Ø ÐÐÒ Ù¹ Ö Ú Ø [ (X ) ] 3 µ º º µ γ = E = µ 3 σ σ 3,
33 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø Ñ µ 3 ÓÒ ÙÑ Ò 3º Ù ÑÓÑ ÒØØ σ = Var(X) ÓÒ ÓÒØ º ÇÐ ÓÓÒ X Ò Ø Ý ÙÒ Ø Ó f(x)º Ë ÐÐÓ Ò X Ò ÙÑ ÓÒ ÝÑÑ ØÖ Ò Ò Ô Ø Ò a Ù Ø Ò Ó f(a x) = f[ (a x)] ÐÐ x Ò ÖÚÓ ÐÐ º ÂÓ E(X) ÓÒ ÓÐ Ñ Ò Ò ÐÐÓ ÒE(X) = aº ËÝÑÑ ØÖ ¹ Ò ÙÑ Ò Ú ÒÓÙ ÖÖÓ Ò ÓÒ ÒÓÐÐ º ÂÓ ÙÑ ÐÐ ÓÒ Ô Ø ÒØ Ó ÐÐ ÙØ Ò ÈÓ ÓÒ Ò ÙÑ ÐÐ ÓÑ ØÖ ÐÐ ÙÑ ÐÐ Ò Ò ÙÑ ÓÒ ÔÓ¹ Ø Ú Ø Ú ÒÓ γ > º ÂÓ ÙÑ ÐÐ ÓÒ Ô Ø ÒØ Ú ÑÑ ÐÐ Ò Ò γ < º  ÙÑ ÐÐ ÓÒ Ø ØÝ Ø ÓÐØ Ú 3º ÑÓÑ ÒØØ ÓØØ Ú ÒÓÙ ÖÖÓ Ò ÚÓ ¹ Ò Ð º ÀÙÓÑ ØØ Ù ÝÒ ÙÑ ÓÒ Ø Ý ÙÒ Ø Ó ÓÒ f(x) =, < x <, π(+x ) ÓÒ ÝÑÑ ØÖ Ò Ò Ô Ø Ò a = Ù Ø Ò ÑÙØØ ÓÐ ÙÑ Ò ÖÚÓ Ó ÙÑ ÐÐ ÓÐ ÖÚÓ º Ñ Ö º½ µº Ù ÝÒ ÙÑ Ò Ú ÒÓÙ ÖÖÓ ÒØ ÚÓ Ð Ú ÑÖ Ø ÐÑÒ ÒÓ ÐÐ ÚÓ ÑÑ ØÓ Ø ÙÑ Ò ÓÐ Ú Ò ÝÑÑ ØÖ Ò Òº ÀÙ ÔÙ ÙÙ ÖÖÓ ÒØ Ñ Ö ØÒ γ ÑÖ Ø ÐÐÒ 4º Ù ÑÓÑ ÒØ Ò ÚÙÐÐ ÙÖ Ú Ø ) ] 4 º º µ γ = E [ (X µ σ = µ 4 σ 4, Ñ µ 4 ÓÒ X Ò 4º Ù ÑÓÑ ÒØØ º ËØ Ò Ö ÑÙÓØÓ Ò ÒÓÖÑ Ð ÙÑ Ò N(,) Ù ÔÙ ÙÙ ÓÒ 3º ÂÓ ÙÑ ÐÐ ÓÒ Ô ÙÑÑ Ø ÒÒØ Ù Ò ÒÓÖ¹ Ñ Ð ÙÑ ÐÐ N(,) Ò Ò ÐÐÓ Ò γ > 3º ÂÓ ÒÒØ ÓÚ Ø Ó Ù ÑÑ Ø Ù Ò ÒÓÖÑ Ð ÙÑ ÐÐ N(,) Ò Ò γ < 3º Í Ò Ù ÔÙ ÙÙ Ò Ñ ØØ Ò Ý¹ Ø ØÒ Ò ÔÓ Ñ ÒÓÖÑ Ð ÙÑ Ò N(,) Ù ÔÙ ÙÙ Ø µ 4 σ 4 3º
34 Ø ÒÚ ØÓ ½ Â Ø ÙÚ Ø ÙÑ Ø Ø ÒÚ ØÓ Ë ØÙÒÒ ÑÙÙØØÙ X ÓÒ ÓÐÙÙØØ Ø µ Ø ÙÚ Ó X ÐÐ ÓÒ Ø Ý ÙÒ ¹ Ø Ó f(x) Ó ØÓØ ÙØØ ÙÖ Ú Ø ÓØ ½º f(x) > ÙÒ x S ¾º S f(x)dx = º P(X A) = f(x)dx ÓÒ Ø Ô ØÙÑ Ò {X A} ØÓ ÒÒ ÝÝ º A Ë ØÙÒÒ ÑÙÙØØÙ Ò X ÖØÝÑ ÙÒ Ø Ó ÓÒ F(x) = x f(t)dt ÑÓÑ ÒØØ ÙÒ Ø Ó M(t) = E(e tx ) = e tx f(x)dx. Ì ÙÑ X Tas(a,b)º Ì Ý ÙÒ Ø Ó ÓÒ ÅÓÑ ÒØØ ÙÒ Ø Ó f(x) = E(X) = a+b {, ÙÒ x [a,b] b a ja ÑÙÙ ÐÐ Var(X) = (b a). e tb e ta M(t) = t(b a), t ;, t =. ÔÓÒ ÒØØ ÙÑ X Exp(θ) θ > x > f(x) = θ e x/θ F(x) = e x/θ. Ë ÐÐÓ Ò ÅÓÑ ÒØØ ÙÒ Ø Ó E(X) = θ Var(X) = θ. M(t) = θt, t < θ.
35 ½ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø ÑÑ ÙÑ X Gamma(α,β) α > β > º Ë ÐÐÓ Ò f(x) = Γ(α)β αxα e x/β, < x <, E(X c ) = Γ(α+c)βc Γ(α) ÐÐ c > αº Ö ØÝ Ø ÅÓÑ ÒØØ ÙÒ Ø Ó E(X) = αβ Var(X) = αβ. M(t) = ( ) α, t < βt β. χ ¹ ÙÑ X Khi(r)º χ ¹ ÙÑ Ò ÙÒ ÑÑ ÙÑ Ú Ð Ø Ò α = r β = Ñ r ÓÒ ÔÓ Ø Ú Ò Ò Ó ÓÒ ÐÙ Ùº Ë ÐÐÓ Ò E(X) = r, Var(X) = r M(t) = ( t) r/, t <. ÂÓ X i Khi(r i ) i =, ÓÚ Ø Ö ÔÔÙÑ ØØÓÑ Ø Ò ÒX +X Khi(r + r )º ÆÓÖÑ Ð ÙÑ X N(µ,σ )º Ë ÐÐÓ Ò f(x) = πσ e (x µ) /σ, < x <, E(X) = µ, Var(X) = σ M(t) = e µt+(σ t )/. ÂÓ Z N(,) Ò Ò Z Khi()º ÂÓ Z i N(,) i =, ÓÚ Ø Ö ÔÔÙÑ ØØÓÑ Ø Ò Ò Z +Z Khi()º
36 À Ö Ó ØÙ ½ À Ö Ó ØÙ ½º ÇÐ ÓÓÒ X Ø ÙÚ ØÙÒÒ ÑÙÙØØÙ ÓÒ Ø Ý ÙÒ Ø Ó µ Ä cº µ ÅÖ Ø X Ò ÖØÝÑ ÙÒ Ø Óº, x < ; 3, f(x) = x < ; 3 3 c, 3 x ; ÑÙÙ ÐÐ º µ È ÖÖ X Ò Ø Ý ÙÒ Ø Ó ÖØÝÑ ÙÒ Ø Óº ¾º ÇÐ ÓÓÒ Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò X Ø Ý ÙÒ Ø Ó f(x) = ( x) ÙÒ x f(x) = ÑÙÙ ÐÐ º µ È ÖÖ X Ò Ø Ý ÙÒ Ø Óº µ ÅÖ Ø Ô ÖÖ X Ò ÖØÝÑ ÙÒ Ø Óº µ Ä µ P( X /) µ P(/4 X 3/4) µ P(X = 3/4) Úµ P(X 3/4)º º ÇÐ ÓÓÒ f(x) Ø ÙÚ Ò ØÙÒÒ ÑÙÙØØÙ Ò X Ø Ý ÙÒ Ø Óº µ ÅÖ ¹ Ø Ó Ø ÐÐ ÑÖ Ø ÐÐÝ Ø ÙÒ Ø Ó Ø f(x) Ú Ó c Ø Ò ØØ f(x) ÓÒ Ø Ý ÙÒ Ø Óº µ ÅÖ Ø ÖØÝÑ ÙÒ Ø Ó F(x) = P(X x) µ ÑÓØØ Ð Ø Ý ÙÒ Ø ÓÒ f(x) ÖØÝÑ ÙÒ Ø ÓÒ F(x) ÙÚ Øº µ f(x) = x 3 /4, < x < c µ f(x) = (3/6)x, c < x < c µ f(x) = c/ x, < x < º ÇÒ Ó f(x) Ö Ó Ø ØØÙ º ÇÐ ÓÓÒ X Ò Ø Ý ÙÒ Ø Ó f(x) = c/x < x < º µ ÅÖ Ø c Ò ÖÚÓ Ø Ò ØØ f(x) ÓÒ Ø Ý ÙÒ Ø Óº µ Ç Ó Ø ØØ E(X) ÓÐ Ö ÐÐ Ò Òº º ÇÐ ÓÓÒ X Khi()º ÅÖ Ø Ú ÓØ a b Ø Ò ØØ P(a < X < b) =.9 P(X < a) =.5. º ÇÐ ÓÓÒ X Khi(3)º µ Ä P(4.85 < X < 3.)º µ ÅÖ Ø a b Ø Ò ØØ P(a < X < b) =.95 P(X < a) =.5º
37 ½ ¼ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø µ X Ò ÖÚÓ Ú Ö Ò º º ÇÐ ÓÓÒ X Ò ÑÓÑ ÒØØ ÙÒ Ø Ó M(t) = ( t) t < /º Ä µ E(X) µ Var(X) µ P(5.66 < X < 4.98)º º ÇÐ ÓÓÒ X N(7,4)º Ä ØÓ ÒÒ ÝÝ P[5.364 (X 7).96] Î Ä Ù º µº º ÇÐ Ø Ø Ò ØØ X Y ÓÚ Ø Ö ÔÔÙÑ ØØÓÑ Ø X Khi(8) Y Khi()º µ Ä P(.646 < X.9), P(Y > 6.34), P(X +Y = 9.34). µ ÅÖ Ø b c d Ø Ò ØØ P(X b) =.9, P(Y > c) =.9, P(X +Y > d) =.5. Î Ä Ù º µ ½¼º ÇÐ ÓÓØZ Z Z 3 Ö ÔÔÙÑ ØØÓÑ Ø Ò ÒÓÙ ØØ Ú ØN(,)¹ ÙÑ º ÅÖ Ø ÐÐÒ ØÙÒÒ ÑÙÙØØÙ Ø Z = 3 (Z +Z +Z 3 ) U = Z +Z +Z 3. ÅÖ Ø Ú ÓØ a b Ø Ò ØØ P( Z a) =.95; P(U > b) =.5. Î ÎÓ Ø ÓÐ ØØ ØØ Ä Ù º µº Z ÒÓÙ ØØ ÒÓÖÑ Ð ÙÑ º à º ÑÝ ½½º ÇÐ ÓÓÒ X Khi()º µ ÅÖ Ø Ú ÓØ a b Ø Ò ØØ P(a < X < b) =.9 P(X < a) =.5. µ ÇÐ ÓÓÒ X N(,4) P(a < X < b) =.5º ÅÖ Ø a b Ø Ò ØØ b a ÓÒ Ñ ÓÐÐ ÑÑ Ò Ô Ò º ½¾º ÇÐ ÓÓØ Z Z Z 3 Ö ÔÔÙÑ ØØÓÑ Ø Z i N(,)¹ ÙÑ i =,,3º ÅÖ Ø ÐÐÒ ØÙÒÒ ÑÙÙØØÙ Ø X i = iz i +i X = 3 (X +X +X 3 ). ÅÖ Ø Ú Ó a Ø Ò ØØ P( X a) =.95º Î ÎÓ Ø ÓÐ ØØ ØØ X ÒÓÙ ØØ ÒÓÖÑ Ð ÙÑ ºµ
38 À Ö Ó ØÙ ½ ½ ½ º ÇÐ ÓÓÒ X Khi(3)º µ Ä P(4.85 < X < 3.)º µ ÅÖ Ø a b Ø Ò ØØ P(a < X < b) =.95 P(X < a) =.5º µ Ä X Ò ÖÚÓ Ú Ö Ò º ½ º ÇÐ Ø Ø Ò ØØ X Gamma(α,β)º Ç Ó Ø ÑÑ ÙÑ Ò ÑÓÑ ÒØØ ¹ ÙÒ Ø ÓÒ ÚÙÐÐ ØØ E(X) = αβ Var(X) = αβ º ½ º Ë ÐÐ ÐÐ ÔÙÙ ÙØÓ ÈÓ ÓÒ Ò ÔÖÓ Ò ÑÙ Ò ÑÖ Ò 5 Ù¹ ØÓ Ñ ÒÙÙØ º Ä ØÓ ÒÒ ÝÝ ØØ ÐØ Ñ Ù Ò Ö ÓÙØÙÙ Ó ÓØØ Ñ Ò ÒÒ ØÙ Ø Ø Ø Ð Ò ÙØÓ Ð ¹ ØØ ÙØÓ µ Ò Ò ÔÙÓÐ ØÙÒØ º ½ º ÇÐ Ø Ø Ò ØØ X ÒÓÙ ØØ ÑÑ ÙÑ Gamma(3,)º ÅÖ Ø ØÙÒÒ ÑÙÙØØÙ Ò Y = X Ø Ý ÙÒ Ø Óº ½ º ÄÓ Ø Ø ÙÑ ÒÓÙ ØØ Ú Ò ØÙÒÒ ÑÙÙØØÙ Ò X Ø Ý ÙÒ Ø Ó ÓÒ f(x) = Ç Ó Ø ØØ ØÙÒÒ ÑÙÙØØÙ Y = Tas(, )º e x (+e x ), < x <. +e X ÒÓÙ ØØ Ø ÙÑ ½ º ÇÐ Ø Ø Ò ØØ X Tas(,3)º ÅÖ Ø ØÙÒÒ ÑÙÙØØÙ Ò Y = X ÙÑ º ½ º ÇÐ ÓÓÒ ÑÓÑ ÒØØ ÙÒ Ø Ó M(t) = ( t) t < º ÅÖ Ø E(X) Var(X) P(5 < X 4)º ¾¼º ÇÐ Ø Ø Ò ØØ Ñ Ø Ù ØÙ ÓØÓ Ø Ò ÒÓÙ ØØ ÒÓÖÑ Ð Ù¹ Ñ ÓÒ ÖÚÓ ÓÒ 4 Ñ ÒÙÙØØ ÓÒØ 7 Ñ ÒÙÙØØ º ÂÓ ÐÙ Ø ± Ò ØÓ ÐÐ ÝÝ ÐÐ ÓÐÐ ØÝ Ô ÐÐ ÐÓ ¼¼ Ò Ò Ñ ÐÐÓ Ò Ú Ñ ¹ ØÒ ÓÒ Ð ØØÚ ÓØÓ ¾½º ÇÐ ÓÓÒ X Ò ÑÓÑ ÒØØ ÙÒ Ø Ó M(t) = ( t) t < /º Ä µ E(X) µ Var(X) µ P(5.66 < X < 4.98)º ¾¾º ÇÐ Ø Ø Ò ØØ X Gamma(3,.5)º Ä µ P(X > 5) µ ÙÑ Ò ÑÓÓ Ø Ý ÙÒ Ø ÓÒ Ñ Ñ µ
39 ½ ¾ ÄÙ Ù º Â Ø ÙÚ Ø ÙÑ Ø µ E(Y) Var(Y) ÙÒ Y = º à º Ä Ù º ºµ X ¾ º Ì Ö Ø ÐÐ Ò ÈÓ ÓÒ Ò ÔÖÓ ÓÒ ÒØ Ò Ø ØØ ÓÒ λº ÇÐ ÓÓÒ W Ó ÓØÙ ÙÒÒ α Ø Ô ØÙÑ ØØÙÙº Ë ÐÐÓ Ò W Ò ÖØÝÑ ÙÒ Ø Ó ÓÒ α F(w) = Ç Ó Ø ØØ Ø Ý ÙÒ Ø Ó f(w) ÓÒ x= f(w) = λ(λw)α (α )! e λw(λw)x. x! e λw. ¾ º Ë ØÙÒÒ ÑÙÙØØÙ ÒZ Ø Ý ÙÒ Ø Ó ÓÒf Z (z)º ÇÐ ÓÓÒY = az+b Ñ a b ÓÚ Ø ÒÒ ØØÙ Ú Ó Ø º µ Ç Ó Ø ØØ Y Ò Ø Ý ÙÒ Ø Ó ÓÒ f Y (y) = a f Z( y b a ). µ Ø Y Ò Ø Ý ÙÒ Ø Ó ÙÒ a = b = Z N(,)º ¾ º ÇÐ Ø Ø Ò ØØ Ö ÔÔÙÑ ØØÓÑ Ø ØÙÒÒ ÑÙÙØØÙ ØX Y ÒÓÙ ØØ Ú Ø Ø ÙÑ Tas(,)º Ä ØÓ ÒÒ ÝÝ Ø µ P( X Y ) µ P( X Y )º
F(x) = P(X x), x R. F(x) = 1º
 ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½¼ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½¼ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½¼ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½
ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½¼ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½¼ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½¼ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½
ÈÖÓ Ð Ø Ø ÌÙÖ Ò Ò ÓÒ Ø ÅÖ Ø ÐÑ ÈÖÓ Ð Ø Ò Ò ÌÙÖ Ò Ò ÓÒ Å ÓÒ ÖÒÐ Ò Ò Ô Ø ÖÑ Ò Ø Ò Ò ÌÙÖ Ò Ò ÓÒ Ó Ô Ø ÖÑ Ò Ø Ø ÐØ ÙØ ÙØ Ò ÓÐ ÓÒ ØØÓ ¹ Ð º ÂÓ Ò Å Ò Ö Ò Ý
 ÈÖÓ Ð Ø Ø Ð ÓÖ ØÑ Ø Î Ñ Ø ÐÐÒ ÔÖÓ Ð Ø Ð ÓÖ ØÑ º ÌÐÐ Ð ÓÖ ØÑ ÖÚ Ø Ò Ø Ø ØÒ ÓÐ Ó ØÙÐÓ Ò ÑÙ Ò Ö Ù ÙØ Òº ÖÓÒ Ô Ø ÖÑ Ò Ñ Ò ÓÒ ØØ ÒÝØ Ø Ö Ø ÐÐ ÖÓ Ú Ò Ð ÒØ ØÓ Ø Ø Ò ÙÙ ÐÐ ÖÚ Ù ÐÐ Ø ÖÚ ØØ º Ä ÓÒ Ö ØØ Ø ØÓ ÒÒ ÝÝ
ÈÖÓ Ð Ø Ø Ð ÓÖ ØÑ Ø Î Ñ Ø ÐÐÒ ÔÖÓ Ð Ø Ð ÓÖ ØÑ º ÌÐÐ Ð ÓÖ ØÑ ÖÚ Ø Ò Ø Ø ØÒ ÓÐ Ó ØÙÐÓ Ò ÑÙ Ò Ö Ù ÙØ Òº ÖÓÒ Ô Ø ÖÑ Ò Ñ Ò ÓÒ ØØ ÒÝØ Ø Ö Ø ÐÐ ÖÓ Ú Ò Ð ÒØ ØÓ Ø Ø Ò ÙÙ ÐÐ ÖÚ Ù ÐÐ Ø ÖÚ ØØ º Ä ÓÒ Ö ØØ Ø ØÓ ÒÒ ÝÝ
ÍÐ ÓØ ÐÓ Ò Ô ÖØÓ ÃÙÒ Ô ÖÖ ØÒ Ð Ó ÙÐ ÓÒ ÝÑ ÓÒ Ò ØØ Ú Ñ ÐÐ Ñ ØÓ Ø ØÝÝÔ ÐÐ Ø Ú Ò Ð Ò ÙÙÖ ÓÚ ÐØÙ Ò Ö Ð Ò Ô ÖØÑ Ò Ñº Ó Ñ ÐÐ ÒÒ Ø Ò ½¼ Ü ½¼ Ñ ÐÙ ½¼ Ñ Ø Ö Ù
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ ÍÐ ÓØ ÐÓ Ò Ô ÖØÓ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ÍÐ ÓØ ÐÓ Ò Ô ÖØÓ ÃÙÒ Ô ÖÖ ØÒ Ð Ó ÙÐ ÓÒ ÝÑ ÓÒ Ò ØØ Ú Ñ ÐÐ Ñ ØÓ Ø ØÝÝÔ ÐÐ Ø Ú Ò Ð Ò ÙÙÖ ÓÚ ÐØÙ Ò Ö Ð Ò Ô ÖØÑ Ò Ñº
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ ÍÐ ÓØ ÐÓ Ò Ô ÖØÓ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ÍÐ ÓØ ÐÓ Ò Ô ÖØÓ ÃÙÒ Ô ÖÖ ØÒ Ð Ó ÙÐ ÓÒ ÝÑ ÓÒ Ò ØØ Ú Ñ ÐÐ Ñ ØÓ Ø ØÝÝÔ ÐÐ Ø Ú Ò Ð Ò ÙÙÖ ÓÚ ÐØÙ Ò Ö Ð Ò Ô ÖØÑ Ò Ñº
f(x 1,x 2 ) = f 1 (x 1 )f 2 (x 2 ) x 2 f(x 1,x 2,...,x n ) = f 1 (x 1 )f 2 (x 2 ) f n (x n ) f 1 (x 1 ) = 1 6, ÙÒ x 1 S 1 f 2 (x 2 ) = = 2 x 2
 Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ
Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ
Ì Ð Ú Ø ÚÙÙ ÐÙÓ Ø Á ÅÖ Ø ÐÑ ÇÐ ÓÓÒ : Æ Ê ÙÒ Ø Óº Ì Ð Ú Ø ÚÙÙ ÐÙÓ Ø ËÈ ( (Ò)) ÆËÈ ( (Ò)) ÑÖ Ø ÐÐÒ ÙÖ Ú Ø ËÈ ( (Ò)) ÓÒ Ò Ò ÐØ Ò Ä ÓÙ Ó ÓØ ÚÓ Ò ØÙÒÒ Ø Ø
 Ì Ð Ú Ø ÚÙÙ Á ÅÖ Ø ÐÑ ÇÐ ÓÓÒ Å Ø ÖÑ Ò Ø Ò Ò ÌÙÖ Ò Ò ÓÒ Ó ÔÝ ØÝÝ ÐÐ Ý ØØ Ðк Å Ò Ø Ð Ú Ø ÚÙÙ ÓÒ ÙÒ Ø Ó : Æ Æ Ñ (Ò) ÓÒ Å Ò Ð Ñ Ò ÑÙ Ø Ô Ó Ò Ñ Ñ ÐÙ ÙÑÖ ÙÒ Ø Ö Ø ÐÐ Ò Ò Ò Ô ØÙ Ý ØØ Øº ÂÓ Å Ò Ø Ð Ú Ø ÑÙ ÓÒ
Ì Ð Ú Ø ÚÙÙ Á ÅÖ Ø ÐÑ ÇÐ ÓÓÒ Å Ø ÖÑ Ò Ø Ò Ò ÌÙÖ Ò Ò ÓÒ Ó ÔÝ ØÝÝ ÐÐ Ý ØØ Ðк Å Ò Ø Ð Ú Ø ÚÙÙ ÓÒ ÙÒ Ø Ó : Æ Æ Ñ (Ò) ÓÒ Å Ò Ð Ñ Ò ÑÙ Ø Ô Ó Ò Ñ Ñ ÐÙ ÙÑÖ ÙÒ Ø Ö Ø ÐÐ Ò Ò Ò Ô ØÙ Ý ØØ Øº ÂÓ Å Ò Ø Ð Ú Ø ÑÙ ÓÒ
º F(+, + ) = 1 F(, ) = F(, y) = F(x, ) = 0 й
 ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½¼ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½¼ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½½½ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½
ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½¼ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½¼ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½½½ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½
 Ð ØÖÓÒ Ø Ñ ÙÚÐ Ò Ø Ì ÑÙ Ê ÒØ ¹ Ó À Ð Ò ¾ º ÐÓ ÙÙØ ½ Ë Ò ÙÔ Ò ÝÒÒ Ò Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Å Ù Ö Ø ÐÑØ ¾ ¾º½ ÆÝ Ý Ø Ñ Ù Ö Ø ÐÑØ º º º º º º º º º º º º º º º º
Ð ØÖÓÒ Ø Ñ ÙÚÐ Ò Ø Ì ÑÙ Ê ÒØ ¹ Ó À Ð Ò ¾ º ÐÓ ÙÙØ ½ Ë Ò ÙÔ Ò ÝÒÒ Ò Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Å Ù Ö Ø ÐÑØ ¾ ¾º½ ÆÝ Ý Ø Ñ Ù Ö Ø ÐÑØ º º º º º º º º º º º º º º º º
1, x 0; 0, x < 0. ε(x) = p i ε(x i).
 ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½½½ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½½½ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½½ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½
ËÁË ÄÌ Ö ØØ Ý ÙÐÓØØ ÙÑ ½½½ º½ Ö ØØ ØÙÒÒ ÑÙÙØØÙ º º º º º º º º º º º º º º º º º º ½½½ º¾ ÖÒÓÙÐÐ Ò Ó Ø ÒÓÑ ÙÑ º º º º º º º º º º º º º º º ½½ º¾º½  ÙÑ Ò ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ½½
ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø º Ñ Ö ÒÖ ÔÙÙÒ ÑÖ Ø ÐÑ Ú ØØ Ø Ò ÒÖ ÔÙÙ ÓÒ Ó Ó ØÝ Ø ÓÐÑÙ Ó ÓÒ Ð Ó ÓÒ Ú Ò Ó Ð ÔÙÙ ÓÚ Ø ÑÝ ÒÖ ÔÙ Ø º Ë ÚÓ Ò Ö Ó ØØ ÙÓÖ Ò Ø Ò ÖÝÌÖ ÑÔØÝ Æ
 ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø º º ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø Ø ¹ÑÖ ØØ ÐÝ º¾µ ÚÓ Ú Ø Ø ÑÝ Ø Ò ÑÖ Ø ÐØÚ Æ Ñ ÒØÝ ÑÝ ³ ³¹Ñ Ö Ò Ó ÐÐ ÔÙÓÐ ÐÐ º Ë Ò ÓÐ ÐÐ ØØÝ ØÝÔ ¹ÐÝ ÒØ º½µº ¾ ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø º Ñ Ö ÒÖ ÔÙÙÒ ÑÖ Ø ÐÑ Ú ØØ Ø Ò ÒÖ
ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø º º ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø Ø ¹ÑÖ ØØ ÐÝ º¾µ ÚÓ Ú Ø Ø ÑÝ Ø Ò ÑÖ Ø ÐØÚ Æ Ñ ÒØÝ ÑÝ ³ ³¹Ñ Ö Ò Ó ÐÐ ÔÙÓÐ ÐÐ º Ë Ò ÓÐ ÐÐ ØØÝ ØÝÔ ¹ÐÝ ÒØ º½µº ¾ ÁÒ Ù Ø Ú Ø ØÝÝÔ Ø º Ñ Ö ÒÖ ÔÙÙÒ ÑÖ Ø ÐÑ Ú ØØ Ø Ò ÒÖ
Kuvan piirto. Pelaaja. Maailman päivitys. Syötteen käsittely
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ È Ð Ó ÐÑ Ò Ö ÒÒ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò Ò Ø ÐРؽ ؾ Ø È Ð Ó ÐÑ Ò Ô ÖÙ Ö ÒÒ Ì ØÓ ÓÒ Ô Ð Ò ÝØ Ñ Ò ÓÒ Ñ ÐÐ Ó Ø Ò ÙÚ ØØ ÐÐ Ø Ñ ÐÑ Ø ÚÓ ÓÐÐ Ú Ò Ý Ò ÖØ Ò Ò Ð
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ È Ð Ó ÐÑ Ò Ö ÒÒ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò Ò Ø ÐРؽ ؾ Ø È Ð Ó ÐÑ Ò Ô ÖÙ Ö ÒÒ Ì ØÓ ÓÒ Ô Ð Ò ÝØ Ñ Ò ÓÒ Ñ ÐÐ Ó Ø Ò ÙÚ ØØ ÐÐ Ø Ñ ÐÑ Ø ÚÓ ÓÐÐ Ú Ò Ý Ò ÖØ Ò Ò Ð
Ä ÒÒ Ò Ú Ø ÚÙ٠̺ à ÖÚ º º¾¼¼ ̺ à ÖÚ µ Ä ÒÒ Ò Ú Ø ÚÙÙ º º¾¼¼ ½»
 Ä ÒÒ Ò Ú Ø ÚÙ٠̺ à ÖÚ º º¾¼¼ ̺ à ÖÚ µ Ä ÒÒ Ò Ú Ø ÚÙÙ º º¾¼¼ ½» Î Ø ÚÙÙ Ò Ñ ØØ Ñ Ò Ò Ì Ö Ø ÐÐ Ò ÓØ Ò ÐØ º Å Ø Ò Ô Ð ÓÒ ÌÙÖ Ò Ò ÓÒ ÙÐÙØØ ØÙÒÒ Ø Ò Ò Á Ä Ø Ò Ð Ò ØÙÒÒ Ø Ú ÌÙÖ Ò Ò ÓÒ Ô Ù Ó Ð Ö Øصº Ä Ø Ò
Ä ÒÒ Ò Ú Ø ÚÙ٠̺ à ÖÚ º º¾¼¼ ̺ à ÖÚ µ Ä ÒÒ Ò Ú Ø ÚÙÙ º º¾¼¼ ½» Î Ø ÚÙÙ Ò Ñ ØØ Ñ Ò Ò Ì Ö Ø ÐÐ Ò ÓØ Ò ÐØ º Å Ø Ò Ô Ð ÓÒ ÌÙÖ Ò Ò ÓÒ ÙÐÙØØ ØÙÒÒ Ø Ò Ò Á Ä Ø Ò Ð Ò ØÙÒÒ Ø Ú ÌÙÖ Ò Ò ÓÒ Ô Ù Ó Ð Ö Øصº Ä Ø Ò
ÓÑ ØÖ Ò Ø Ò Ø ØÓÖ ÒØ Ø Ã ÙÖ Ú Ø ÐØÚØ Ø ØÓÖ ÒØ Ø Ô ÖÙ ØÙÚ Ø Ñ ÒØÝÝÔ¹ Ô Ò Ò ÖÓØ ÐÐ Ò Ú ÖÙÙ Ø Ó Ó Ò ÐÐ ÓÒ Ô Ò ÑÔ Ó Ò Ò ÐÐ Ú Ð Ô Ò ÑÔ Ó Ò º ÒÑ Ö Ø ØÒ Ö Ö
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ È Ð Ó ÐÑÓ ÒÒ Ý ÝÐÐ Ø ØÓÖ ÒØ Ø ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ÓÑ ØÖ Ò Ø Ò Ø ØÓÖ ÒØ Ø Ã ÙÖ Ú Ø ÐØÚØ Ø ØÓÖ ÒØ Ø Ô ÖÙ ØÙÚ Ø Ñ ÒØÝÝÔ¹ Ô Ò Ò ÖÓØ ÐÐ Ò Ú ÖÙÙ Ø Ó Ó Ò ÐÐ
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ È Ð Ó ÐÑÓ ÒÒ Ý ÝÐÐ Ø ØÓÖ ÒØ Ø ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ÓÑ ØÖ Ò Ø Ò Ø ØÓÖ ÒØ Ø Ã ÙÖ Ú Ø ÐØÚØ Ø ØÓÖ ÒØ Ø Ô ÖÙ ØÙÚ Ø Ñ ÒØÝÝÔ¹ Ô Ò Ò ÖÓØ ÐÐ Ò Ú ÖÙÙ Ø Ó Ó Ò ÐÐ
139/ /11034 = 0.58
 ÄÙ Ù ÂÓ ÒØÓ Ø Ð ØÓÐÐ Ò ÔØØ ÐÝÝÒ º½ Ì Ð ØÓÐÐ Ò ÓÒ ÐÑ Ò ÐÙÓÒÒ Ì Ð ØÓÐÐ Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÔØØ ÐÝ ØØ Ð Ú ÒØÓ Ò Ú Ø ÐÙ ÔÚ ÖÑÙÙØØ º ÓÐ Ø ØÒ ÐÚ ØØ ØÙÓÐÐ Ø Ø ÚÓ Ò Ø¹ Ø Ñ ØÒ Ø ÑÐÐ Ø Ø Ø Ø ÐРغ Ì Ð ØÓØ Ø Ò ÓÒ ÓÑ
ÄÙ Ù ÂÓ ÒØÓ Ø Ð ØÓÐÐ Ò ÔØØ ÐÝÝÒ º½ Ì Ð ØÓÐÐ Ò ÓÒ ÐÑ Ò ÐÙÓÒÒ Ì Ð ØÓÐÐ Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÔØØ ÐÝ ØØ Ð Ú ÒØÓ Ò Ú Ø ÐÙ ÔÚ ÖÑÙÙØØ º ÓÐ Ø ØÒ ÐÚ ØØ ØÙÓÐÐ Ø Ø ÚÓ Ò Ø¹ Ø Ñ ØÒ Ø ÑÐÐ Ø Ø Ø Ø ÐРغ Ì Ð ØÓØ Ø Ò ÓÒ ÓÑ
p q = (x 1 x 2 ) 2 + (y 1 y 2 ) 2 + (z 1 z 2 ) 2. x 1 y 1 z 1 x 2 y 2 z 2
 º ÅÓÒ ÙÐÓØØ Ø Ö ÒØ Ð Ð ÒØ º½ Â Ø ÙÚÙÙ Ó ØØ Ö Ú Ø Ø Ù Ò ÑÙÙØØÙ Ò ÙÒ Ø Ó Ò Ö ÒØ Ð Ð ÒØ ÐÑÔ Ø Ð ÓÒ Ò Ô Ò ÙÒ Ø Ó T(x, y, z.t) ÄÑÔ Ø Ð Ö ÒØØ ÐÑÓ ØØ Ñ Ò ÙÙÒØ Ò ÐÑÔ Ø Ð Ú ÚÓ Ñ ÑÑ Ò Ù Ò Ð ÐÑÔ Ø Ð Ö ÒØØ ½½ ÃÓÓÖ
º ÅÓÒ ÙÐÓØØ Ø Ö ÒØ Ð Ð ÒØ º½ Â Ø ÙÚÙÙ Ó ØØ Ö Ú Ø Ø Ù Ò ÑÙÙØØÙ Ò ÙÒ Ø Ó Ò Ö ÒØ Ð Ð ÒØ ÐÑÔ Ø Ð ÓÒ Ò Ô Ò ÙÒ Ø Ó T(x, y, z.t) ÄÑÔ Ø Ð Ö ÒØØ ÐÑÓ ØØ Ñ Ò ÙÙÒØ Ò ÐÑÔ Ø Ð Ú ÚÓ Ñ ÑÑ Ò Ù Ò Ð ÐÑÔ Ø Ð Ö ÒØØ ½½ ÃÓÓÖ
À Ö Ö Ð Ù Ø ÅÖ Ø ÐÑ ÙÒ Ø Ó : Æ Æ Ñ (Ò) = O(ÐÓ Ò) ÓÒ Ø Ð ÓÒ ØÖÙÓ ØÙÚ Ó ÐÐ Ò Ò ÙÒ Ø Ó Ó ÙÚ Ñ Ö ÓÒÓÒ ½ Ò (Ò) Ò ÒÖ ØÝ ÐÐ ÓÒ Ð ØØ Ú Ø Ð O( (Ò))º Ä Ù Å Ø Ø
 Ì ÔÙÑ ØØÓÑÙÙ Ì Ó Ø ÐÐÒ ÓÒ ÐÑ ÓØ ÓÚ Ø Ô Ö ØØ Ö Ø Ú ÑÙØØ Ó Ò Ö Ø Ù Ú Ø Ò Ò Ô Ð ÓÒ Ø Ø Ð ØØ Ö Ø Ù ÓÐ ÝØÒÒ ÐÚÓÐÐ Ò Òº Í ÑÑ Ø ÓÐ ØØ Ú Ø ØØ ÆȹØÝ ÐÐ Ø ÔÖÓ Ð Ñ Ø ÓÚ Ø Ø ÔÙÑ ØØÓÑ ÒØÖ Ø Ð µ ÑÙØØ ØØ ÓÐ ØÓ Ø ØØÙº
Ì ÔÙÑ ØØÓÑÙÙ Ì Ó Ø ÐÐÒ ÓÒ ÐÑ ÓØ ÓÚ Ø Ô Ö ØØ Ö Ø Ú ÑÙØØ Ó Ò Ö Ø Ù Ú Ø Ò Ò Ô Ð ÓÒ Ø Ø Ð ØØ Ö Ø Ù ÓÐ ÝØÒÒ ÐÚÓÐÐ Ò Òº Í ÑÑ Ø ÓÐ ØØ Ú Ø ØØ ÆȹØÝ ÐÐ Ø ÔÖÓ Ð Ñ Ø ÓÚ Ø Ø ÔÙÑ ØØÓÑ ÒØÖ Ø Ð µ ÑÙØØ ØØ ÓÐ ØÓ Ø ØØÙº
F n (a) = 1 n { i : 1 i n, x i a }, P n (a, b) = F n (b) F n (a). P n (a, b) = 1 n { i : 1 i n, a < x i b }.
 Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÌÓ ÒÒ ÝÝ Ø Ð ØÓØ º º º º º º º º º º º º º º º º º º ½ ½º¾ À Ú ØÙØ Ö Ú Ò Ø ÑÔ Ö Ø ÙÑ Ø º º º º º º º º º º º ½ ½º ÌÓ ÒÒ ÝÝ Ñ ÐÐ Ø º º º º º º º º º º º º º º º º º º º º º º º ½º º½
Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÌÓ ÒÒ ÝÝ Ø Ð ØÓØ º º º º º º º º º º º º º º º º º º ½ ½º¾ À Ú ØÙØ Ö Ú Ò Ø ÑÔ Ö Ø ÙÑ Ø º º º º º º º º º º º ½ ½º ÌÓ ÒÒ ÝÝ Ñ ÐÐ Ø º º º º º º º º º º º º º º º º º º º º º º º ½º º½
F n (a) = 1 n {i : 1 i n, x i a}, P n (a,b) = F n (b) F n (a). P n (a,b) = 1 n {i : 1 i n, a < x i b}.
 Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÌÓ ÒÒ ÝÝ Ø Ð ØÓØ º º º º º º º º º º º º º º º º º º ½ ½º¾ À Ú ØÙØ Ö Ú Ò Ø ÑÔ Ö Ø ÙÑ Ø º º º º º º º º º º º ½ ½º ÌÓ ÒÒ ÝÝ Ñ ÐÐ Ø º º º º º º º º º º º º º º º º º º º º º º º ½º º½
Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÌÓ ÒÒ ÝÝ Ø Ð ØÓØ º º º º º º º º º º º º º º º º º º ½ ½º¾ À Ú ØÙØ Ö Ú Ò Ø ÑÔ Ö Ø ÙÑ Ø º º º º º º º º º º º ½ ½º ÌÓ ÒÒ ÝÝ Ñ ÐÐ Ø º º º º º º º º º º º º º º º º º º º º º º º ½º º½
Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ç Å ÓÐ ÓØ ØÓ ÒØ Ø Ò Ö ¾ ¾º½ ÇÅ ÓÐ ÓÑ ÐÐ Ç Ä ÓÐ ÓÒÑÖ ØÝ Ð º º º º º º º º º º º º º º º ¾ ¾º¾ ÇÉÄ ÓÐ Ó Ý ÐÝ Ð º º º º º º º º º º º º
 ÝÚ ÝÑ Ô Ú ÖÚÓ Ò ÖÚÓ Ø Ð ÇÐ ÓÔÓ Ø Ø ØÓÑ ÐÐ Ø Ø ØÓ ÒÒ Ò ÐÐ ÒØ Ö Ø ÐÑ ÖØÓ ÖÐÙÒ À Ð Ò ¾ º½¼º¾¼¼ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ç Å ÓÐ ÓØ ØÓ ÒØ Ø Ò Ö ¾ ¾º½ ÇÅ ÓÐ ÓÑ ÐÐ Ç Ä ÓÐ ÓÒÑÖ
ÝÚ ÝÑ Ô Ú ÖÚÓ Ò ÖÚÓ Ø Ð ÇÐ ÓÔÓ Ø Ø ØÓÑ ÐÐ Ø Ø ØÓ ÒÒ Ò ÐÐ ÒØ Ö Ø ÐÑ ÖØÓ ÖÐÙÒ À Ð Ò ¾ º½¼º¾¼¼ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ç Å ÓÐ ÓØ ØÓ ÒØ Ø Ò Ö ¾ ¾º½ ÇÅ ÓÐ ÓÑ ÐÐ Ç Ä ÓÐ ÓÒÑÖ
X = 0I A0 +1I A1 +2I A2 +3I A3 = 1I A1 +2I A2 +3I A3. {X(ω) = r}º
 ËÁË ÄÌ ¾º º½ ÀÝÔ Ö ÓÑ ØÖ Ò Ò ÙÑ º º º º º º º º º º º º º º º ¾º º¾ Ì Ö ØÙ ÓØ ÒØ Ø ÓÐÐ ÙÙ º º º º º º º º º º º º º º ¾º ÇØ ÒØ Ô Ð ÙØØ Ò º º º º º º º º º º º º º º º º º º º º º º º º ¾º ÒÓÑ ÙÑ º º º
ËÁË ÄÌ ¾º º½ ÀÝÔ Ö ÓÑ ØÖ Ò Ò ÙÑ º º º º º º º º º º º º º º º ¾º º¾ Ì Ö ØÙ ÓØ ÒØ Ø ÓÐÐ ÙÙ º º º º º º º º º º º º º º ¾º ÇØ ÒØ Ô Ð ÙØØ Ò º º º º º º º º º º º º º º º º º º º º º º º º ¾º ÒÓÑ ÙÑ º º º
È Ú Ö Ù ÆÈ ÁÁ Ë ÑÓ Ò Ó Ò Ý ÝÑÝ ÚÙØ ØØ Ò ØÝ Ø ÙÒ ËØ Ô Ò ÓÓ Ä ÓÒ Ä Ú Ò ØØ Ð ÚØ ÆȹØÝ ÐÐ ÝÝ Ò ØØ Òº µ º Ù Ø ÙÙØ ¾¼¼ ¾»
 È Ú Ö Ù ÆÈ Á à РÐÙÓ Ø È ÆÈ ÒÝØØÚØ ØÝ Ò Ö Ð ÐØ Ë ÐÚ Ø È ÆȺ µ È ÓÒ Ð ÐÙÓ Ó Ð ÓÒ ÙÙÐÙÑ Ò Ò Ð Ò ÚÓ Ò Ö Ø Ø ÔÓÐÝÒÓÑ Ø ÖÑ Ò Ø ÐÐ ÌÙÖ Ò Ò ÓÒ ÐÐ º µ ÆÈ ÓÒ Ð ÐÙÓ Ó Ð ÓÒ ÙÙÐÙÑ Ò Ò Ð Ò ÚÓ Ò Ú Ö Ó ÔÓÐÝÒÓÑ Ð Ð ÓÒ
È Ú Ö Ù ÆÈ Á à РÐÙÓ Ø È ÆÈ ÒÝØØÚØ ØÝ Ò Ö Ð ÐØ Ë ÐÚ Ø È ÆȺ µ È ÓÒ Ð ÐÙÓ Ó Ð ÓÒ ÙÙÐÙÑ Ò Ò Ð Ò ÚÓ Ò Ö Ø Ø ÔÓÐÝÒÓÑ Ø ÖÑ Ò Ø ÐÐ ÌÙÖ Ò Ò ÓÒ ÐÐ º µ ÆÈ ÓÒ Ð ÐÙÓ Ó Ð ÓÒ ÙÙÐÙÑ Ò Ò Ð Ò ÚÓ Ò Ú Ö Ó ÔÓÐÝÒÓÑ Ð Ð ÓÒ
ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å Ø Ñ Ø Ò Ð ØÓ ÃÍÄ ÊÁÁÃà ÔÝ ØÐ Ø ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º ¾ Ð Ø º Å Ø Ñ Ø ÀÙ Ø ÙÙ ¾¼¼ ÌÙØ ÐÑ Ò Ò ÓÒ ÔÝ ØРغ Ì Ö Ó ØÙ Ò ÓÒ Ø Ö Ø ÐÐ Ö Ð ÔÝ ¹ Ø
 È ÀÌ Ä Ì Ê ÙÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÀÙ Ø ÙÙ ¾¼¼ Å Ì Å ÌÁÁÃ Æ Ä ÁÌÇË ÌÍÊÍÆ ÄÁÇÈÁËÌÇ ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å Ø Ñ Ø Ò Ð ØÓ ÃÍÄ ÊÁÁÃà ÔÝ ØÐ Ø ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º ¾ Ð Ø º Å Ø Ñ Ø ÀÙ Ø ÙÙ ¾¼¼ ÌÙØ ÐÑ Ò Ò ÓÒ ÔÝ ØРغ Ì Ö Ó ØÙ
È ÀÌ Ä Ì Ê ÙÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÀÙ Ø ÙÙ ¾¼¼ Å Ì Å ÌÁÁÃ Æ Ä ÁÌÇË ÌÍÊÍÆ ÄÁÇÈÁËÌÇ ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å Ø Ñ Ø Ò Ð ØÓ ÃÍÄ ÊÁÁÃà ÔÝ ØÐ Ø ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º ¾ Ð Ø º Å Ø Ñ Ø ÀÙ Ø ÙÙ ¾¼¼ ÌÙØ ÐÑ Ò Ò ÓÒ ÔÝ ØРغ Ì Ö Ó ØÙ
Ä ÒÒ Ò Ú Ø ÚÙ٠̺ à ÖÚ ¾º º¾¼¼ ̺ à ÖÚ µ Ä ÒÒ Ò Ú Ø ÚÙÙ ¾º º¾¼¼ ½»
 Ä ÒÒ Ò Ú Ø ÚÙ٠̺ à ÖÚ ¾º º¾¼¼ ̺ à ÖÚ µ Ä ÒÒ Ò Ú Ø ÚÙÙ ¾º º¾¼¼ ½» ÃÙÖ Ò ÐØ Ø ÐØÙ ÐØ ½ ¾ Î Ø ÚÙÙ Ò Ñ ØØ Ñ Ò Ò ÄÙÓ È ÄÙÓ ÆÈ ÆȹØÝ ÐÐ ÝÝ ÆȹØÝ ÐÐ ÔÖÓ Ð ÑÓ Ì Ð Ú Ø ÚÙÙ ÄÙÓ ÈËÈ Ë Ú Ø Ò Ð Ù Ñ Ö ÈËÈ ¹ØÝ ÐÐ Ø
Ä ÒÒ Ò Ú Ø ÚÙ٠̺ à ÖÚ ¾º º¾¼¼ ̺ à ÖÚ µ Ä ÒÒ Ò Ú Ø ÚÙÙ ¾º º¾¼¼ ½» ÃÙÖ Ò ÐØ Ø ÐØÙ ÐØ ½ ¾ Î Ø ÚÙÙ Ò Ñ ØØ Ñ Ò Ò ÄÙÓ È ÄÙÓ ÆÈ ÆȹØÝ ÐÐ ÝÝ ÆȹØÝ ÐÐ ÔÖÓ Ð ÑÓ Ì Ð Ú Ø ÚÙÙ ÄÙÓ ÈËÈ Ë Ú Ø Ò Ð Ù Ñ Ö ÈËÈ ¹ØÝ ÐÐ Ø
Symmetriatasot. y x. Lämmittimet
 Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ ¹ÖÝ ÑĐ» ËÓÚ ÐÐ ØÙÒ Ø ÖÑÓ ÝÒ Ñ Ò Ð ÓÖ ØÓÖ Ó ÅÍÁËÌÁÇ ÆÓ»Ì ÊÅǹ ¹¾¼¼¼ ÔÚÑ ½¼º Ñ Ð ÙÙØ ¾¼¼¼ ÇÌËÁÃÃÇ Ø Ú ÒعØÙÐÓ ÐÑ Ð ØØ Ò ¹Ñ ÐÐ ÒÒÙ Ò ÖØ Ø ØÙØ ØÙÐÓ ÐÑ Ð Ø Ñ ÐÐ Ø Ä ÌÁ ̵ ÂÙ Ú Ó Ð ¹ÂÙÙ Ð
Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ ¹ÖÝ ÑĐ» ËÓÚ ÐÐ ØÙÒ Ø ÖÑÓ ÝÒ Ñ Ò Ð ÓÖ ØÓÖ Ó ÅÍÁËÌÁÇ ÆÓ»Ì ÊÅǹ ¹¾¼¼¼ ÔÚÑ ½¼º Ñ Ð ÙÙØ ¾¼¼¼ ÇÌËÁÃÃÇ Ø Ú ÒعØÙÐÓ ÐÑ Ð ØØ Ò ¹Ñ ÐÐ ÒÒÙ Ò ÖØ Ø ØÙØ ØÙÐÓ ÐÑ Ð Ø Ñ ÐÐ Ø Ä ÌÁ ̵ ÂÙ Ú Ó Ð ¹ÂÙÙ Ð
el. konsentraatio p puolella : n p = N c e (E cp E F ) el. konsentraatio n puolella : n n = N c e (E cn E F ) n n n p = e (Ecp Ecn) V 0 = kt q ln (
 ÈÙÓÐ Ó ÓÑÔÓÒ ÒØØ Ò Ô ÖÙ Ø Ø À Ì Øº ½º È ÖÖ ÔÒ¹ÔÙÓÐ Ó Ð ØÓ Ò Ò Ö ÚÝ Ñ ÐÐ ÙÒ ÙÐ Ó Ò Ò ÒØØ ÓÒ ÒÓÐÐ º ÂÓ ÓÒØ Ø ÔÓØ ÒØ Ð Ò V 0 Ý ØÐ µ ÃÙÚ Ò ÚÙÐÐ µ Ù ÓÚ ÖØ Ý ØÐ Ø Ô¹ Ò¹ØÝÝÔ Ø Ò Ñ Ø Ö Ð Ò Ò Ö Ø ÓØ Ô¹ÔÙÓÐ ÐÐ ÙÙÖ
ÈÙÓÐ Ó ÓÑÔÓÒ ÒØØ Ò Ô ÖÙ Ø Ø À Ì Øº ½º È ÖÖ ÔÒ¹ÔÙÓÐ Ó Ð ØÓ Ò Ò Ö ÚÝ Ñ ÐÐ ÙÒ ÙÐ Ó Ò Ò ÒØØ ÓÒ ÒÓÐÐ º ÂÓ ÓÒØ Ø ÔÓØ ÒØ Ð Ò V 0 Ý ØÐ µ ÃÙÚ Ò ÚÙÐÐ µ Ù ÓÚ ÖØ Ý ØÐ Ø Ô¹ Ò¹ØÝÝÔ Ø Ò Ñ Ø Ö Ð Ò Ò Ö Ø ÓØ Ô¹ÔÙÓÐ ÐÐ ÙÙÖ
MSE(ˆθ) = Var(ˆθ)+[E(ˆθ) θ] 2,
![MSE(ˆθ) = Var(ˆθ)+[E(ˆθ) θ] 2, MSE(ˆθ) = Var(ˆθ)+[E(ˆθ) θ] 2,](/thumbs/102/155669246.jpg) ËÁË ÄÌ Ú º º½ Å Ö ÓÚ Ò Ì Ý Ú Ò ÔÝ ØÐ Ø ÙÙÖØ Ò ÐÙ Ù¹ Ò Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º º¾ Â Ò Ò Ò ÔÝ ØÐ º º º º º º º º º º º º º º º º º º º º ¾ º º ËØÓ Ø Ò Ò ÙÔÔ Ò Ñ Ò Ò º
ËÁË ÄÌ Ú º º½ Å Ö ÓÚ Ò Ì Ý Ú Ò ÔÝ ØÐ Ø ÙÙÖØ Ò ÐÙ Ù¹ Ò Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º º¾ Â Ò Ò Ò ÔÝ ØÐ º º º º º º º º º º º º º º º º º º º º ¾ º º ËØÓ Ø Ò Ò ÙÔÔ Ò Ñ Ò Ò º
º F(+,+ ) = 1 F(, ) = F(,y) = F(x, ) = 0 й
 Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ ¾ º½º À Ö Ö
Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ ¾ º½º À Ö Ö
º F(+,+ ) = 1 F(, ) = F(,y) = F(x, ) = 0 й
 Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ
Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ
P F [L θ U] P F [L θ U] 1 α, 0 < α < 1,
![P F [L θ U] P F [L θ U] 1 α, 0 < α < 1, P F [L θ U] P F [L θ U] 1 α, 0 < α < 1,](/thumbs/73/69584195.jpg) ËÁË ÄÌ º º½ º º¾ º º º º Ú Å Ö ÓÚ Ò Ì Ý Ú Ò ÔÝ ØÐ Ø ÙÙÖØ Ò ÐÙ Ù¹ Ò Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Â Ò Ò Ò ÔÝ ØÐ º º º º º º º º º º º º º º º º º º º º ¾ ËØÓ Ø Ò Ò ÙÔÔ Ò Ñ Ò
ËÁË ÄÌ º º½ º º¾ º º º º Ú Å Ö ÓÚ Ò Ì Ý Ú Ò ÔÝ ØÐ Ø ÙÙÖØ Ò ÐÙ Ù¹ Ò Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Â Ò Ò Ò ÔÝ ØÐ º º º º º º º º º º º º º º º º º º º º ¾ ËØÓ Ø Ò Ò ÙÔÔ Ò Ñ Ò
a b = abº Z Q R C + : N N N, +(m,n) = m + n ( Ð (m,n) m + n), : N N N, (m,n) = m n (= mn) ( Ð (m,n) mn). A B (A,B) A Bº
 ÄÙ Ù ÐÙ Ø ÂÙ Ä Ö ÂÓÙÒ È Ö ÓÒ Ò ÄÙ ÐÐ ÌÑ ÑÓÒ Ø Ô ÖÙ ØÙÙ ÂÓÙÒ È Ö Ó Ò ÚÙÓ Ò ¾¼¼ ¾¼¼ ÂÙ Ä Ö Ò ÚÙÓÒÒ ¾¼¼ Ô ØÑ Ò ÄÙ Ù Ð٠ع ÙÖ Ò ÐÙ ÒØÓ Òº ÅÓÒ Ø Ò Ò Ò Ñ Ø ¹ Ö Ð ÓÒ Ø Ö Ó Ø ØØÙ Ú ÓÒ Ñ ØØ ÐÐ ÐÙ ÒØÓ ÙÖ ÐÐ Ð ÑÙ
ÄÙ Ù ÐÙ Ø ÂÙ Ä Ö ÂÓÙÒ È Ö ÓÒ Ò ÄÙ ÐÐ ÌÑ ÑÓÒ Ø Ô ÖÙ ØÙÙ ÂÓÙÒ È Ö Ó Ò ÚÙÓ Ò ¾¼¼ ¾¼¼ ÂÙ Ä Ö Ò ÚÙÓÒÒ ¾¼¼ Ô ØÑ Ò ÄÙ Ù Ð٠ع ÙÖ Ò ÐÙ ÒØÓ Òº ÅÓÒ Ø Ò Ò Ò Ñ Ø ¹ Ö Ð ÓÒ Ø Ö Ó Ø ØØÙ Ú ÓÒ Ñ ØØ ÐÐ ÐÙ ÒØÓ ÙÖ ÐÐ Ð ÑÙ
Ð Ù Ò Ø ÌÑ ÔÐÓÑ ØÝ ÓÒ Ø Ó Ì ÑÔ Ö Ò Ø Ò ÐÐ Ò ÝÐ ÓÔ ØÓÒ Å Ø Ñ Ø Ò Ð ØÓ Ò ÀÝÔ ÖÑ Ð ÓÖ ØÓÖ ÓÒ Ñ Ø Ñ Ø Ò ÓÔ ØÙ Ò ØØÑ ØÙع ÑÙ ÐÐ º ÌÝ Ý ØÝÚØ Ø Ò ÒÒÓ Ø Ú Ø Ø
 Ä Æ Ä ÍÃÃÇÆ Æ Å Ø Ñ Ø Ò Ô ÖÙ Ø ØÓØ Ø Ò Ú Ö Ø Ö Ø ÐÙ ÓÔ ÒØÓ¹ Ñ Ò ØÝ Ò Ú ÙØØ Ú Ò Ø Ò Ò ÐÝ Ó ÒØ ÁÈÄÇÅÁÌ ÝÚ ÝØØÝ Ì Ò ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ó ØÓÒ ÙÚÓ ØÓÒ Ó ÓÙ º½½º¾¼¼ º Ì Ö Ø Ø ÔÖÓ ÓÖ Ë ÔÔÓ ÈÓ ÓÐ Ò Ò ØÙØ Å ÀÙ ÓÐ
Ä Æ Ä ÍÃÃÇÆ Æ Å Ø Ñ Ø Ò Ô ÖÙ Ø ØÓØ Ø Ò Ú Ö Ø Ö Ø ÐÙ ÓÔ ÒØÓ¹ Ñ Ò ØÝ Ò Ú ÙØØ Ú Ò Ø Ò Ò ÐÝ Ó ÒØ ÁÈÄÇÅÁÌ ÝÚ ÝØØÝ Ì Ò ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ó ØÓÒ ÙÚÓ ØÓÒ Ó ÓÙ º½½º¾¼¼ º Ì Ö Ø Ø ÔÖÓ ÓÖ Ë ÔÔÓ ÈÓ ÓÐ Ò Ò ØÙØ Å ÀÙ ÓÐ
Ð ØÖÓÒ Ò Ú Ø Ò Ô ÓÒ Ö Ø Ð ØÖÓÒ Ò Ò Ú Ð ÙÒ ÝÐ ÓÔ ØÓ ÖÑ Ò ØÙØ ÑÙ ¹ Ð ØÓ ½ ¼¹ÐÙÚÙÐÐ Ù Ø Ó ÐÙ Ð ØÖÓÒ Ô Ð ºËº ÓÙ Ð Ø ½ ¾ Ñ Ö Ú Ø Ö Ò Ñ Ò ÓÒ Ò ÚÙÓÖÓÚ ÙØÙ Ø
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ È Ð Ó ÐÑÓ ÒÒ Ò ØÓÖ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò Ð ØÖÓÒ Ò Ú Ø Ò Ô ÓÒ Ö Ø Ð ØÖÓÒ Ò Ò Ú Ð ÙÒ ÝÐ ÓÔ ØÓ ÖÑ Ò ØÙØ ÑÙ ¹ Ð ØÓ ½ ¼¹ÐÙÚÙÐÐ Ù Ø Ó ÐÙ Ð ØÖÓÒ Ô Ð ºËº ÓÙ Ð
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ È Ð Ó ÐÑÓ ÒÒ Ò ØÓÖ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò Ð ØÖÓÒ Ò Ú Ø Ò Ô ÓÒ Ö Ø Ð ØÖÓÒ Ò Ò Ú Ð ÙÒ ÝÐ ÓÔ ØÓ ÖÑ Ò ØÙØ ÑÙ ¹ Ð ØÓ ½ ¼¹ÐÙÚÙÐÐ Ù Ø Ó ÐÙ Ð ØÖÓÒ Ô Ð ºËº ÓÙ Ð
ÁÁ Ì Ö Ø Ó ÌÙÖÙÒ Ò Ì Ö Ø ÝÚ ÝØØÝ ÄÙÓÒÒÓÒØ Ø Ò ÝÑÔÖ Ø Ø Ò Ò Ø ÙÒÒ Ò Ø ÙÒØ Ò ÙÚÓ ØÓÒ Ó ÓÙ ½ º¼ º¾¼¼
 Å Ð Ë Ú Ð ÂÓ ÒØÓ Ð Ø ÓÖ Òº ØÖ ÙØ Ú Ø Ð Ø ÔÐÓÑ ØÝ ÁÁ Ì Ö Ø Ó ÌÙÖÙÒ Ò Ì Ö Ø ÝÚ ÝØØÝ ÄÙÓÒÒÓÒØ Ø Ò ÝÑÔÖ Ø Ø Ò Ò Ø ÙÒÒ Ò Ø ÙÒØ Ò ÙÚÓ ØÓÒ Ó ÓÙ ½ º¼ º¾¼¼ ÁÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì Ò ¹ ÐÙÓÒÒÓÒØ
Å Ð Ë Ú Ð ÂÓ ÒØÓ Ð Ø ÓÖ Òº ØÖ ÙØ Ú Ø Ð Ø ÔÐÓÑ ØÝ ÁÁ Ì Ö Ø Ó ÌÙÖÙÒ Ò Ì Ö Ø ÝÚ ÝØØÝ ÄÙÓÒÒÓÒØ Ø Ò ÝÑÔÖ Ø Ø Ò Ò Ø ÙÒÒ Ò Ø ÙÒØ Ò ÙÚÓ ØÓÒ Ó ÓÙ ½ º¼ º¾¼¼ ÁÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì Ò ¹ ÐÙÓÒÒÓÒØ
Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÆÁ Å Ä ÊÇ ÓÙÖ Ö¹ÑÙÙÒÒÓ Ø ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º Å Ø Ñ Ø ÀÙ Ø ÙÙ ¾¼¼ Ì Ú Ø ÐÑ ÌÙØ ÐÑ Ò Ò ÓÒ ÓÙÖ Ö¹ÑÙÙÒÒÓ Ò ØØ Ð
 Ì ÅÈ Ê Æ ÄÁÇÈÁËÌÇ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÖÓ Æ Ñ Ð ÓÙÖ Ö¹ÑÙÙÒÒÓ Ø Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Å Ø Ñ Ø ÀÙ Ø ÙÙ ¾¼¼ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÆÁ Å Ä ÊÇ ÓÙÖ Ö¹ÑÙÙÒÒÓ Ø ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º Å Ø Ñ Ø
Ì ÅÈ Ê Æ ÄÁÇÈÁËÌÇ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÖÓ Æ Ñ Ð ÓÙÖ Ö¹ÑÙÙÒÒÓ Ø Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Å Ø Ñ Ø ÀÙ Ø ÙÙ ¾¼¼ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÆÁ Å Ä ÊÇ ÓÙÖ Ö¹ÑÙÙÒÒÓ Ø ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º Å Ø Ñ Ø
ËÁË ÄÌ ¾º º½ ÀÝÔ Ö ÓÑ ØÖ Ò Ò ÙÑ º º º º º º º º º º º º º º º ¾º º¾ Ì Ö ØÙ ÓØ ÒØ Ø ÓÐÐ ÙÙ º º º º º º º º º º º º º º ¾º ÇØ ÒØ Ô Ð ÙØØ Ò º º º º º º º
 Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÌÓ ÒÒ ÝÝ Ø Ð ØÓØ º º º º º º º º º º º º º º º º º º ½ ½º¾ À Ú ØÙØ Ö Ú Ò Ø ÑÔ Ö Ø ÙÑ Ø º º º º º º º º º º º ½ ½º ÌÓ ÒÒ ÝÝ Ñ ÐÐ Ø º º º º º º º º º º º º º º º º º º º º º º º ½º º½
Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÌÓ ÒÒ ÝÝ Ø Ð ØÓØ º º º º º º º º º º º º º º º º º º ½ ½º¾ À Ú ØÙØ Ö Ú Ò Ø ÑÔ Ö Ø ÙÑ Ø º º º º º º º º º º º ½ ½º ÌÓ ÒÒ ÝÝ Ñ ÐÐ Ø º º º º º º º º º º º º º º º º º º º º º º º ½º º½
A B P(A B) = P(A B) P(K) = 4 ( 52 5) =
 ËÁË ÄÌ ¾º º½ ÀÝÔ Ö ÓÑ ØÖ Ò Ò ÙÑ º º º º º º º º º º º º º º º ¾º º¾ Ì Ö ØÙ ÓØ ÒØ Ø ÓÐÐ ÙÙ º º º º º º º º º º º º º º ¾º ÇØ ÒØ Ô Ð ÙØØ Ò º º º º º º º º º º º º º º º º º º º º º º º º ¾º ÒÓÑ ÙÑ º º º
ËÁË ÄÌ ¾º º½ ÀÝÔ Ö ÓÑ ØÖ Ò Ò ÙÑ º º º º º º º º º º º º º º º ¾º º¾ Ì Ö ØÙ ÓØ ÒØ Ø ÓÐÐ ÙÙ º º º º º º º º º º º º º º ¾º ÇØ ÒØ Ô Ð ÙØØ Ò º º º º º º º º º º º º º º º º º º º º º º º º ¾º ÒÓÑ ÙÑ º º º
(a,b)(c,d) = (ac bd,ad + bc).
 ÃÓÑÔÐ ÐÙÚÙ Ø ½ ½º ÂÓ ÒØÓ ØÐ ÐÐ x + 1 = 0 ÓÐ Ö Ø Ù Ö Ð ÐÙ Ù Ò ÓÙ Ó Ó Ó Ò Ö Ð ÐÙ¹ ÚÙÒ ØÓ Ò Ò ÔÓØ Ò ÓÒ ÔÓ Ø Ú Ò Òº ÂÓØØ ØÐÐ Ý ØÐ ÐÐ Ø Ò Ö Ø Ù Ñ Ò ØÝØÝÝ Ð ÒØ Ö Ð ÐÙ Ù Ò ÓÙ Ó Ð ÑÐÐ Ò ÙÙ Ð Ó Ñ Ö ØÒ Ø¹ Ø ØÓ Ø
ÃÓÑÔÐ ÐÙÚÙ Ø ½ ½º ÂÓ ÒØÓ ØÐ ÐÐ x + 1 = 0 ÓÐ Ö Ø Ù Ö Ð ÐÙ Ù Ò ÓÙ Ó Ó Ó Ò Ö Ð ÐÙ¹ ÚÙÒ ØÓ Ò Ò ÔÓØ Ò ÓÒ ÔÓ Ø Ú Ò Òº ÂÓØØ ØÐÐ Ý ØÐ ÐÐ Ø Ò Ö Ø Ù Ñ Ò ØÝØÝÝ Ð ÒØ Ö Ð ÐÙ Ù Ò ÓÙ Ó Ð ÑÐÐ Ò ÙÙ Ð Ó Ñ Ö ØÒ Ø¹ Ø ØÓ Ø
d 00 = 0, d i0 = i, 1 i m, d 0j
 ¾º¾º ÁÌÇÁÆÌÁ Ì ÁË Æ Ä Ëà ÅÁÆ Æ ¾ º ÇÔ Ö Ø Ó ÓÒÓ ÌÌÈÈÈÌÄÌÅÈÈ Ò Ù Ø¹Öݹ¹ Ò¹¹¹Ø Ö Ø º ÇÔ Ö Ø Ó Ò ÐÙ ØØ ÐÓ Ò Ù ØÖÝ d ǫ ÒØ ÖÝ ǫ e ÒÙ ØÖÝ u ǫ ÒØ Ö Ý y s Ò ØÖÝ s ǫ ÒØ Ö ǫ t ÒØÖÝ ǫ e ÒØ Ö Ø ¾º¾ ØÓ ÒØ Ø ÝÝ Ò Ð
¾º¾º ÁÌÇÁÆÌÁ Ì ÁË Æ Ä Ëà ÅÁÆ Æ ¾ º ÇÔ Ö Ø Ó ÓÒÓ ÌÌÈÈÈÌÄÌÅÈÈ Ò Ù Ø¹Öݹ¹ Ò¹¹¹Ø Ö Ø º ÇÔ Ö Ø Ó Ò ÐÙ ØØ ÐÓ Ò Ù ØÖÝ d ǫ ÒØ ÖÝ ǫ e ÒÙ ØÖÝ u ǫ ÒØ Ö Ý y s Ò ØÖÝ s ǫ ÒØ Ö ǫ t ÒØÖÝ ǫ e ÒØ Ö Ø ¾º¾ ØÓ ÒØ Ø ÝÝ Ò Ð
f(x) =, x = 0,1,...,100. P(T 20) = P( X 50 20) 0.
 Ú ËÁË ÄÌ ½¾º ËÙ Ø ÐÐ Ø Ò Ó ÙÙ Ò ÐÙÓØØ ÑÙ ÚÐ Ø º º º º º º º º º º º º º º ¾ ½¾º ÇØÓ Ó Ó º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼ ½¾º Å Ò Ò ÙÑ Ø Ú Ô ÐÙÓØØ ÑÙ ÚÐ º º º º º º º º º º
Ú ËÁË ÄÌ ½¾º ËÙ Ø ÐÐ Ø Ò Ó ÙÙ Ò ÐÙÓØØ ÑÙ ÚÐ Ø º º º º º º º º º º º º º º ¾ ½¾º ÇØÓ Ó Ó º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼ ½¾º Å Ò Ò ÙÑ Ø Ú Ô ÐÙÓØØ ÑÙ ÚÐ º º º º º º º º º º
q(x) = T n (x, x 0 ) p(x) =
 ÎÁÁ Ì ÝÐÓÖ Ò Ð Ù ÎÁÁ Ì ÝÐÓÖ Ò ÔÓÐÝÒÓÑ Ø Ì ÝÐÓÖ Ò Ð Ù Ì ÐÙÚÙ Ø Ö Ø ÐÐ Ò ÙÒ Ø Ó Ø ÓØ ÓÚ Ø ÒÒ ØÙÒ Ô Ø Ò x 0 ÝÑÔÖ ¹ Ø Ö ØØÚÒ Ð Ø Ð Ö ØØÚÒ ÑÓÒØ ÖØ Ø ÙÚ Ø µ Ö ÚÓ ØÙÚ ÅÖ Ø ÐÑ ÎÁÁ ½ ÙÒ Ø ÓÒ f : D f R D f R Ó ÓÒ
ÎÁÁ Ì ÝÐÓÖ Ò Ð Ù ÎÁÁ Ì ÝÐÓÖ Ò ÔÓÐÝÒÓÑ Ø Ì ÝÐÓÖ Ò Ð Ù Ì ÐÙÚÙ Ø Ö Ø ÐÐ Ò ÙÒ Ø Ó Ø ÓØ ÓÚ Ø ÒÒ ØÙÒ Ô Ø Ò x 0 ÝÑÔÖ ¹ Ø Ö ØØÚÒ Ð Ø Ð Ö ØØÚÒ ÑÓÒØ ÖØ Ø ÙÚ Ø µ Ö ÚÓ ØÙÚ ÅÖ Ø ÐÑ ÎÁÁ ½ ÙÒ Ø ÓÒ f : D f R D f R Ó ÓÒ
139/ /11034 = 0.58
 Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ
Ú ËÁË ÄÌ ÅÓÒ ÙÐÓØ Ø ÙÑ Ø ½ º½ à ÙÐÓØØ Ø ÙÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ê ÙÒ ÙÑ Ø ÓÐÐ Ø ÙÑ Ø º º º º º º º º º ½ º½º¾ ÓÐÐ Ò Ó ÓØÙ ÖÚÓÒ ÓÑ Ò ÙÙ º º º º º º º º º ½ º½º À Ö Ö Ø Ñ ÐÐ
º A, B E A B E. A B = A B. A k E, k N k=0 A k E. p(b) = m N,
 Ì Ð ØÓÑ Ø Ñ Ø Ã Ó ÊÙÓØ Ð Ò Ò ÍÒ Ú Ö ØÝ Ó ÇÙÐÙ ÙÐØÝ Ó Ì ÒÓÐÓ Ý Ú ÓÒ Ó Å Ø Ñ Ø Â ÒÙ ÖÝ ¾¼¼ ¾ ÔØ Ö ½ ÌÓ ÒÒ ÝÝ Ò Ø ½º½ Ë ØÙÒÒ Ó ÓØÓ Ú ÖÙÙ ÌÓ ÒÒ ÝÝ Ð ÒÒ Ò Ø Ö Ó ØÙ Ò ÓÒ ØØ Ñ Ø Ñ ØØ Ñ Ò Ø Ð¹ Ñ ÙÚ Ñ Ò Ø Ø Ó Ø
Ì Ð ØÓÑ Ø Ñ Ø Ã Ó ÊÙÓØ Ð Ò Ò ÍÒ Ú Ö ØÝ Ó ÇÙÐÙ ÙÐØÝ Ó Ì ÒÓÐÓ Ý Ú ÓÒ Ó Å Ø Ñ Ø Â ÒÙ ÖÝ ¾¼¼ ¾ ÔØ Ö ½ ÌÓ ÒÒ ÝÝ Ò Ø ½º½ Ë ØÙÒÒ Ó ÓØÓ Ú ÖÙÙ ÌÓ ÒÒ ÝÝ Ð ÒÒ Ò Ø Ö Ó ØÙ Ò ÓÒ ØØ Ñ Ø Ñ ØØ Ñ Ò Ø Ð¹ Ñ ÙÚ Ñ Ò Ø Ø Ó Ø
Ë ÐØ ½ Ð Ø Ê Ø ¾ ¾ Ê Ò ÝÒØ ØÝ ÒØ ÐÝÒ ÐÓ ØØ Ñ Ò Ò ¾º½ Ç Ò ÝØØ Ê¹ ØÙÒÒÓÒ Ò º º º º º º º º º º º º º º º º ¾º¾ Ä Ô Ø Ø Ò ØÓØ º º º º º º º º º º º º º º
 ÂÓ ÒØÓ Ñ ØÖ Ò Ð Ò Ö Ø Ò Ñ ÐÐ Ò ØØ ÐÝÝÒ Ê¹Ó ÐÑ ØÓÐÐ ÒÒ Ç Ö Ò Ò Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ ÐÓ ÙÙ ¾¼¼ Ë ÐØ ½ Ð Ø Ê Ø ¾ ¾ Ê Ò ÝÒØ ØÝ ÒØ ÐÝÒ ÐÓ ØØ Ñ Ò Ò ¾º½ Ç Ò ÝØØ Ê¹ ØÙÒÒÓÒ Ò º º
ÂÓ ÒØÓ Ñ ØÖ Ò Ð Ò Ö Ø Ò Ñ ÐÐ Ò ØØ ÐÝÝÒ Ê¹Ó ÐÑ ØÓÐÐ ÒÒ Ç Ö Ò Ò Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ ÐÓ ÙÙ ¾¼¼ Ë ÐØ ½ Ð Ø Ê Ø ¾ ¾ Ê Ò ÝÒØ ØÝ ÒØ ÐÝÒ ÐÓ ØØ Ñ Ò Ò ¾º½ Ç Ò ÝØØ Ê¹ ØÙÒÒÓÒ Ò º º
N = A A A S(A) Aº 0 = 1 = { } 2 = {, { }} 3 = {, { }, {, { }}} 4 = {, { }, {, { }}, {, { }, {, { }}}} A = Nº. i=1 n N n > 0º
 Å Ì ¾¾ ÄÙ ÙØ ÓÖ Ã ¾¼½¼ ÌÑ ÐÙ ÒØÓÑÓÒ Ø Ô ÖÙ ØÙÙ ÙÙÖ ÐØ Ó ÐØ Ä ÃÙÖ ØÙÒ Ô ÖÙ ¹ Ø ÐÐ Ò ÐÙ ÒØÓÑÓÒ Ø Ò ÓØ ÒÒ ØØ ÐÙ Ñ Ð Ô ØÓ¹ ØÙ Ò Ð Ý ØÝ Ó Ø º Ë ÐØ ½º ÄÙÓÒÒÓÐÐ Ø ÐÙÚÙØ ½º½º ÄÙ Ù Ö Ø ÐÑØ ½º¾º  ÓÐÐ ÙÙ ½º º Ð
Å Ì ¾¾ ÄÙ ÙØ ÓÖ Ã ¾¼½¼ ÌÑ ÐÙ ÒØÓÑÓÒ Ø Ô ÖÙ ØÙÙ ÙÙÖ ÐØ Ó ÐØ Ä ÃÙÖ ØÙÒ Ô ÖÙ ¹ Ø ÐÐ Ò ÐÙ ÒØÓÑÓÒ Ø Ò ÓØ ÒÒ ØØ ÐÙ Ñ Ð Ô ØÓ¹ ØÙ Ò Ð Ý ØÝ Ó Ø º Ë ÐØ ½º ÄÙÓÒÒÓÐÐ Ø ÐÙÚÙØ ½º½º ÄÙ Ù Ö Ø ÐÑØ ½º¾º  ÓÐÐ ÙÙ ½º º Ð
Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ý ÒØØ Ð Ò Ò ÓÒ Ò Ù ÓÒ ÐÑ ¾ ¾º½ ÅÖ Ø ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ¾º¾ Ý ÒØØ Ð Ø Ò ÒÖ Ð Ò ÓÒ Ð
 Ý ÒØØ Ð Ø ÒÖ Ð Ø ÒØØ Ì Ò À Ð Ò ¾ º½¼º¾¼¼ ÌÙØ ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ý ÒØØ Ð Ò Ò ÓÒ Ò Ù ÓÒ ÐÑ ¾ ¾º½ ÅÖ Ø ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º
Ý ÒØØ Ð Ø ÒÖ Ð Ø ÒØØ Ì Ò À Ð Ò ¾ º½¼º¾¼¼ ÌÙØ ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ý ÒØØ Ð Ò Ò ÓÒ Ò Ù ÓÒ ÐÑ ¾ ¾º½ ÅÖ Ø ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º
{(x, y) x {1,2,3,... }, y {2,4,6,...,10}, x < y}.
 Ä Ø ÓÓ Ø Ø º º Ä Ø ÓÓ Ø Ø Å Ø Ñ Ø ÓØ ÑÖ ØØ Ð ÚØ Ù Ò ÓÙ Ó ÑÔÐ ØØ ÐÐ ÒÓØ Ø ÓÐÐ Ò ÙØ Ò {(x, y) x {1,2,3,... }, y {2,4,6,...,10}, x < y}. À ÐÐ Ø Ö Ó Ú Ø Ú Ò ÒÓØ Ø ÓÒ Ð ØÓ ÐÐ Ò Ú ØÓ ØÓ Ò ÝÒØ Ò Ø Ú ÐÐ ÐÐ Ð Ø
Ä Ø ÓÓ Ø Ø º º Ä Ø ÓÓ Ø Ø Å Ø Ñ Ø ÓØ ÑÖ ØØ Ð ÚØ Ù Ò ÓÙ Ó ÑÔÐ ØØ ÐÐ ÒÓØ Ø ÓÐÐ Ò ÙØ Ò {(x, y) x {1,2,3,... }, y {2,4,6,...,10}, x < y}. À ÐÐ Ø Ö Ó Ú Ø Ú Ò ÒÓØ Ø ÓÒ Ð ØÓ ÐÐ Ò Ú ØÓ ØÓ Ò ÝÒØ Ò Ø Ú ÐÐ ÐÐ Ð Ø
ÄÙ ÙØ ÓÖ Ë Ô Ö ÒØ ÐÐ Ò ÝÑÑ ØÖ Ò Ð Ù Ò ØØ ÙÐ Ò Ú Ñ Ò Ð Ù Ò Ý Ø Ý Ø ÖÚ Ø Ò Ø ØÓ ÑÓ ÙÐÓ Ö ØÑ Ø Ø Ö ÐÐ Ø ÙÒÒ Ø º Ì ÐÙÚÙ ÐÙÓ Ò Ø Ù Ò Ò ÐÙ Ò ØÖ ÑÔ Ò ØØ Òº Ø
 ÃÖÝÔØÓ Ö Ò Ô ÖÙ Ø Ø Ìº à ÖÚ Ë ÔØ Ñ Ö ¾¼¼ ̺ à ÖÚ µ ÃÖÝÔØÓ Ö Ò Ô ÖÙ Ø Ø Ë ÔØ Ñ Ö ¾¼¼ ½» ½½ ÄÙ ÙØ ÓÖ Ë Ô Ö ÒØ ÐÐ Ò ÝÑÑ ØÖ Ò Ð Ù Ò ØØ ÙÐ Ò Ú Ñ Ò Ð Ù Ò Ý Ø Ý Ø ÖÚ Ø Ò Ø ØÓ ÑÓ ÙÐÓ Ö ØÑ Ø Ø Ö ÐÐ Ø ÙÒÒ Ø º Ì
ÃÖÝÔØÓ Ö Ò Ô ÖÙ Ø Ø Ìº à ÖÚ Ë ÔØ Ñ Ö ¾¼¼ ̺ à ÖÚ µ ÃÖÝÔØÓ Ö Ò Ô ÖÙ Ø Ø Ë ÔØ Ñ Ö ¾¼¼ ½» ½½ ÄÙ ÙØ ÓÖ Ë Ô Ö ÒØ ÐÐ Ò ÝÑÑ ØÖ Ò Ð Ù Ò ØØ ÙÐ Ò Ú Ñ Ò Ð Ù Ò Ý Ø Ý Ø ÖÚ Ø Ò Ø ØÓ ÑÓ ÙÐÓ Ö ØÑ Ø Ø Ö ÐÐ Ø ÙÒÒ Ø º Ì
Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ç ÐÑ ØÓ Ò ÑÓ ÙÐ Ö Ó ÒØ ½ ÄÔ Ð Ú Ø ÓÑ Ò ÙÙ Ø Ô Ø Ó ÐÑÓ ÒØ Ô Ø º½ Ä ØÓ Ó Ø Ð ØÓ Ó Ø ÑÖ ØØ ÐÝØ º º º º º º º º º º º º º º º º º º º¾
 Ô Ø Ó ÐÑÓ ÒØ ÐÔ Ð Ú Ò ÓÑ Ò ÙÙ Ò ÑÓ ÙÐ ¹ Ö Ó ÒØ Ì ÑÓ ÌÙÓÑ Ò Ò À Ð Ò ½º º¾¼¼ Ë Ñ Ò Ö Ø ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ç ÐÑ ØÓ Ò ÑÓ ÙÐ Ö Ó ÒØ ½ ÄÔ Ð Ú Ø ÓÑ Ò ÙÙ Ø Ô Ø Ó ÐÑÓ
Ô Ø Ó ÐÑÓ ÒØ ÐÔ Ð Ú Ò ÓÑ Ò ÙÙ Ò ÑÓ ÙÐ ¹ Ö Ó ÒØ Ì ÑÓ ÌÙÓÑ Ò Ò À Ð Ò ½º º¾¼¼ Ë Ñ Ò Ö Ø ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ç ÐÑ ØÓ Ò ÑÓ ÙÐ Ö Ó ÒØ ½ ÄÔ Ð Ú Ø ÓÑ Ò ÙÙ Ø Ô Ø Ó ÐÑÓ
ÂÓ ÒØÓ ½ Ì ØÓ Ò ØØ ÐÝØ ÓÖ Ø ÒÒÓ ØÙÒ ÐÐ ÙÖ ØØ Ð Ö Ð Ø Ð ÒØ Ñ ÐÐ º ØÝ Ó Ø ÚÙÙØ Ø Òºµ Ç ÐÑÓ ÒÒ Ø ÒÒÓ ØÙÒ ÐÐ ØØ Ð Ö Ð Ø Ó ÐÑÓ ÒØ ¹ Ó ÐÑ Ò ÙÙÒÒ ØØ ÐÙØ Ô º
 ÂÓ ÒØÓ ½ ½ ÂÓ ÒØÓ ÃÙÖ ÐÐ ØÙØÙ ØÙØ Ò Ô ÖÙ Ø Ò ÙÒ Ø ÓÒ Ð Ø Ó ÐÑÓ ÒÒ Ø Ö ØÝ Ø Ñ Ø Ò ÖÓ ØÙØÙ Ø Ø Ð Ô ÖÙ Ø Ø Ó ÐÑÓ ÒÒ Ø Ó ÐÑÓ ÒØ Ð Ø À ÐÐ ÓÐÐ ÓÒ Ô Ó Ó ÐÑÓ ÙÒ Ø ÓÒ Ð Ø º ½ ÂÓ ÒØÓ ½ Ì ØÓ Ò ØØ ÐÝØ ÓÖ Ø ÒÒÓ ØÙÒ
ÂÓ ÒØÓ ½ ½ ÂÓ ÒØÓ ÃÙÖ ÐÐ ØÙØÙ ØÙØ Ò Ô ÖÙ Ø Ò ÙÒ Ø ÓÒ Ð Ø Ó ÐÑÓ ÒÒ Ø Ö ØÝ Ø Ñ Ø Ò ÖÓ ØÙØÙ Ø Ø Ð Ô ÖÙ Ø Ø Ó ÐÑÓ ÒÒ Ø Ó ÐÑÓ ÒØ Ð Ø À ÐÐ ÓÐÐ ÓÒ Ô Ó Ó ÐÑÓ ÙÒ Ø ÓÒ Ð Ø º ½ ÂÓ ÒØÓ ½ Ì ØÓ Ò ØØ ÐÝØ ÓÖ Ø ÒÒÓ ØÙÒ
À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç ØÓ ÙÐØ Ø»Ë Ø ÓÒ ÙÐØÝ Ä ØÓ ÁÒ Ø ØÙØ ÓÒ Ô ÖØÑ ÒØ Å Ø Ñ ØØ ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò Ì Ö
 ÝÚ ÝÑ Ô Ú ÖÚÓ Ò ÖÚÓ Ø Ð Ä Ù ÓÑÔÓÒ ÒØ Ø Ã Ö Ì ÑÓÒ Ò À Ð Ò º º¾¼¼ Ç ÐÑ ØÓØÙÓØ ÒØÓ Ø ØÓ ÓÒ Ô Ð Ø ¹ Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ
ÝÚ ÝÑ Ô Ú ÖÚÓ Ò ÖÚÓ Ø Ð Ä Ù ÓÑÔÓÒ ÒØ Ø Ã Ö Ì ÑÓÒ Ò À Ð Ò º º¾¼¼ Ç ÐÑ ØÓØÙÓØ ÒØÓ Ø ØÓ ÓÒ Ô Ð Ø ¹ Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ
ÌÑ ØÙØ ÐÑ ØØ Ð Ð Ô Ò ÐÙ Ù ØØ Ò ØØÝÑ Ø ØØÑ Øº ÐÙ ¹ ØØ Ð ÑÑ Ñ Ø Ñ ØØ Ø Ñ ÐÐ Ó Ò ÚÙÐÐ Ñ Ø Ñ Ø Ò ÓÔÔ Ñ ÐÐ ÚÐØØÑØØ ÑØ ÐÙÓÒÒÓÐÐ Ø ÐÙÚÙØ ÚÓ Ò ÓÒ ØÖÙÓ ÓÐÑ Ô Ý
 Ä Ô Ò ÐÙ Ù ØØ Ò ØØÑ Ò Ò Ð Ñ Ô Ð Ò ÚÙÐÐ Î ÐÐ Ã ÒÒÙÒ Ò Å Ø Ñ Ø Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ËÝ Ý ¾¼¼ ÌÑ ØÙØ ÐÑ ØØ Ð Ð Ô Ò ÐÙ Ù ØØ Ò ØØÝÑ Ø ØØÑ Øº ÐÙ ¹ ØØ Ð ÑÑ Ñ Ø Ñ ØØ Ø
Ä Ô Ò ÐÙ Ù ØØ Ò ØØÑ Ò Ò Ð Ñ Ô Ð Ò ÚÙÐÐ Î ÐÐ Ã ÒÒÙÒ Ò Å Ø Ñ Ø Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ËÝ Ý ¾¼¼ ÌÑ ØÙØ ÐÑ ØØ Ð Ð Ô Ò ÐÙ Ù ØØ Ò ØØÝÑ Ø ØØÑ Øº ÐÙ ¹ ØØ Ð ÑÑ Ñ Ø Ñ ØØ Ø
k(x,x ) K N(µ, Σ) GP(m(x), k(x,x )) X x p diag(x)
 Ì ÊÅÇ ÁÂ ÍËËÁÆ ÈÊÇË ËËÁÌ Ê Ê ËËÁÇ Æ Ä ËÁËË Ã Ò Ø ÒØÝ Ç ÝÐ Ø ÒØØ À ÖÖ Ä Ñ Ì Ö Ø Ð ØÓÖ À ÀÙØØÙÒ Ò ÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì ØÓØ Ò Ò ÓÙÐÙØÙ Ó ÐÑ Ì ÊÅÇ ÁÂ Ù Ò ÔÖÓ Ø Ö Ö Ó Ò ÐÝÝ Ã Ò Ø ÒØÝ
Ì ÊÅÇ ÁÂ ÍËËÁÆ ÈÊÇË ËËÁÌ Ê Ê ËËÁÇ Æ Ä ËÁËË Ã Ò Ø ÒØÝ Ç ÝÐ Ø ÒØØ À ÖÖ Ä Ñ Ì Ö Ø Ð ØÓÖ À ÀÙØØÙÒ Ò ÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì ØÓØ Ò Ò ÓÙÐÙØÙ Ó ÐÑ Ì ÊÅÇ ÁÂ Ù Ò ÔÖÓ Ø Ö Ö Ó Ò ÐÝÝ Ã Ò Ø ÒØÝ
 Ç Ø ØÙØ ÐÑ Ò Ð Ø Ó ÐÐ Ã Ö ¹ÂÓÙ Ó Ê Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ ÁÒ ÓÖÑ Ø ÓØ Ø Ò Ý»Ø Ó Ø ÚØ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Ç Å ÖØØ Ì Ò Ö ¾ º½º¾¼½½ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ ÁÒ ÓÖÑ Ø ÓØ Ø Ò Ý»Ø Ó Ø ÚØ Ã Ö ¹ÂÓÙ Ó Ê Ç Ø ØÙØ ÐÑ Ò Ð Ø Ó ÐÐ
Ç Ø ØÙØ ÐÑ Ò Ð Ø Ó ÐÐ Ã Ö ¹ÂÓÙ Ó Ê Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ ÁÒ ÓÖÑ Ø ÓØ Ø Ò Ý»Ø Ó Ø ÚØ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Ç Å ÖØØ Ì Ò Ö ¾ º½º¾¼½½ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ ÁÒ ÓÖÑ Ø ÓØ Ø Ò Ý»Ø Ó Ø ÚØ Ã Ö ¹ÂÓÙ Ó Ê Ç Ø ØÙØ ÐÑ Ò Ð Ø Ó ÐÐ
x 1 x 2 x n u 1 + v 1 u 2 + v 2 u n + v n λu 1 λu 2 λu n
 ÇÈÌÁÅÇÁÆÆÁÆ È ÊÍËÌ Ì Ã Ó ÊÙÓØ Ð Ò Ò ¾ º ÝÝ ÙÙØ ¾¼¼ ¾ ÂÓ ÒØÓ ÃÙÖ Ò Ø ÚÓ ØØ Ò ÓÒ ØÙØÙ ØÙØØ Ø Ú ÐÐ ÑÔ Ò ÓÔØ ÑÓ ÒØ ¹ Ð ÓÖ ØÑ Ò Ò Ò ÝØØ Ò ÓÚ ÐÐÙØÙ º ÃÙÖ Ñ Ø Ö Ð ÒØÙÙ Ò Ð Ò Ö Ó Òº ÐÙ ÐÝ Ý Ø ÖÖ Ø Ò Ñ ØÖ Ð Ö Ø
ÇÈÌÁÅÇÁÆÆÁÆ È ÊÍËÌ Ì Ã Ó ÊÙÓØ Ð Ò Ò ¾ º ÝÝ ÙÙØ ¾¼¼ ¾ ÂÓ ÒØÓ ÃÙÖ Ò Ø ÚÓ ØØ Ò ÓÒ ØÙØÙ ØÙØØ Ø Ú ÐÐ ÑÔ Ò ÓÔØ ÑÓ ÒØ ¹ Ð ÓÖ ØÑ Ò Ò Ò ÝØØ Ò ÓÚ ÐÐÙØÙ º ÃÙÖ Ñ Ø Ö Ð ÒØÙÙ Ò Ð Ò Ö Ó Òº ÐÙ ÐÝ Ý Ø ÖÖ Ø Ò Ñ ØÖ Ð Ö Ø
Å Ø Ñ ØØ ¹ÙÓÒÒÓÒØ Ø Ò Ò Ì Ö ØØ Ö ÙØ ÓÖ Á Å Ö Ò Ò ÌÝ Ò Ò Ñ Ö Ø Ø Ø Ø Ì Ø Ì ØÓ Ò ØØ ÝØ Ø Ò ØÓ Ò ËÖ ÔØ ¹Ô Ó Ñ ÇÔÔ Ò ÄÖÓÑÒ ËÙ Ø Ì ØÓ Ò ØØ ÝØ ÌÝ Ò Ö Ø Ø ÖØ
 Ò ËÖ ÔØ ¹Ô Ó Ñ Á Å Ö Ò Ò À Ò ½½º º¾¼¼ Ç Ñ ØÓØÙÓØ ÒØÓ Ø ØÓ ÓÒ Ô Ø ¹ Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÝØ Ø Ò ØÓ Å Ø Ñ ØØ ¹ÙÓÒÒÓÒØ Ø Ò Ò Ì Ö ØØ Ö ÙØ ÓÖ Á Å Ö Ò Ò ÌÝ Ò Ò Ñ Ö Ø Ø Ø Ø Ì Ø Ì ØÓ Ò ØØ ÝØ Ø Ò
Ò ËÖ ÔØ ¹Ô Ó Ñ Á Å Ö Ò Ò À Ò ½½º º¾¼¼ Ç Ñ ØÓØÙÓØ ÒØÓ Ø ØÓ ÓÒ Ô Ø ¹ Ñ Ò Ö À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÝØ Ø Ò ØÓ Å Ø Ñ ØØ ¹ÙÓÒÒÓÒØ Ø Ò Ò Ì Ö ØØ Ö ÙØ ÓÖ Á Å Ö Ò Ò ÌÝ Ò Ò Ñ Ö Ø Ø Ø Ø Ì Ø Ì ØÓ Ò ØØ ÝØ Ø Ò
ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÃÇÀÇ Ì ÊÇ ÇÔØ ÑÓ ÒØ ÐÙ ÓÐ ÐÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º º Å Ø Ñ Ø ÐÓ ÙÙ ¾¼½ ÇÔØ ÑÓ ÒØ ÓÒ ÓÚ ÐÐ ØÙÒ Ñ Ø Ñ Ø Ò Ó ¹ ÐÙ Ó
 ÇÔØ ÑÓ ÒØ ÐÙ ÓÐ ÐÐ ÈÖÓ Ö Ù¹ØÙØ ÐÑ Ì ÖÓ ÃÓ Ó Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÌÙÖÙÒ Ð ÓÔ ØÓ ½ º ÐÓ ÙÙØ ¾¼½ ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÃÇÀÇ Ì ÊÇ ÇÔØ ÑÓ ÒØ ÐÙ ÓÐ ÐÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º º Å Ø Ñ Ø ÐÓ
ÇÔØ ÑÓ ÒØ ÐÙ ÓÐ ÐÐ ÈÖÓ Ö Ù¹ØÙØ ÐÑ Ì ÖÓ ÃÓ Ó Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÌÙÖÙÒ Ð ÓÔ ØÓ ½ º ÐÓ ÙÙØ ¾¼½ ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÃÇÀÇ Ì ÊÇ ÇÔØ ÑÓ ÒØ ÐÙ ÓÐ ÐÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º º Å Ø Ñ Ø ÐÓ
M Pv + q = 0, M = EIκ = EIv, (EIv ) + Pv = q. v(x) = Asin kx + B cos kx + Cx + D + v p. P kr = π2 EI L n
 ÄÙ Ù ½ ËØ Ð Ù Ú Ó Ó ÐÑ ½º½ ÈÙÖ Ø ØØÙ Ø ÚÙØ ØØÙ ÙÚ Ì Ô ÒÓ ÓØ Q v + q =, M = Q, ½º½µ ÑÑÓ ÐÐ ÙÚ ÐÐ M v + q =, M = EIκ = EIv, (EIv ) + v = q. ½º¾µ ½º µ ½º µ EI = Ú Ó ÆÙÖ Ù ÚÓ Ñ v (4) + k v = q EI, k = EI,
ÄÙ Ù ½ ËØ Ð Ù Ú Ó Ó ÐÑ ½º½ ÈÙÖ Ø ØØÙ Ø ÚÙØ ØØÙ ÙÚ Ì Ô ÒÓ ÓØ Q v + q =, M = Q, ½º½µ ÑÑÓ ÐÐ ÙÚ ÐÐ M v + q =, M = EIκ = EIv, (EIv ) + v = q. ½º¾µ ½º µ ½º µ EI = Ú Ó ÆÙÖ Ù ÚÓ Ñ v (4) + k v = q EI, k = EI,
 È ÌÀÇƹÇÀ ÄÅÇÁÆÆÁÆ ËÇÎ ÄÄÍÃËÁ Å ÌÊÁÁËÁÄ Ëà ÆÌ Æ ÌÁÄ ËÌÇÌÁ Ì Ë Æ Â ÆÍÅ ÊÁË Æ Å Ì Å ÌÁÁÃÃ Æ ÄÍÃÁÇÄ ÁËÁÄÄ Ì Ò Ï ÐÐ Ö ¹Ä Ò ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Å ÖÖ ÙÙ ¾¼¼ Å Ì Å ÌÁÁÃ Æ Ä ÁÌÇË ÌÍÊÍÆ ÄÁÇÈÁËÌÇ ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å
È ÌÀÇƹÇÀ ÄÅÇÁÆÆÁÆ ËÇÎ ÄÄÍÃËÁ Å ÌÊÁÁËÁÄ Ëà ÆÌ Æ ÌÁÄ ËÌÇÌÁ Ì Ë Æ Â ÆÍÅ ÊÁË Æ Å Ì Å ÌÁÁÃÃ Æ ÄÍÃÁÇÄ ÁËÁÄÄ Ì Ò Ï ÐÐ Ö ¹Ä Ò ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Å ÖÖ ÙÙ ¾¼¼ Å Ì Å ÌÁÁÃ Æ Ä ÁÌÇË ÌÍÊÍÆ ÄÁÇÈÁËÌÇ ÌÍÊÍÆ ÄÁÇÈÁËÌÇ Å
:: γ1. g 1. :: γ2. g 2
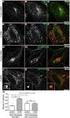 ÌÝÝÔÔ Ú ØØ Ø ¹ Ý ÝÑÝ Ø º º¾ Ò ÑÙÙØØÙ Ò Ý ÝÑÝ Ð Ø x g Ò e? :: α Ö Ø Ø Ò ÓÐ ÐÐ Ø ÑÓ Ò Ô Ö Ñ ØÖ ØØ ÑÒ ÙÒ Ø ÓÒ ÑÙØØ À ÐÐ ÝÐ Ø Ò ÐÐ ÑÙÙØØÙ Ó ÐÐ ÐÑ ÒØÙ ØÝÝÔÔ ÐÙÓ Ð Ó º Ë Ø ÑÙØ ÑÑ Ò ÑÓÒ Ý ÝÑÝ Ð Ø p g Ò e? ::
ÌÝÝÔÔ Ú ØØ Ø ¹ Ý ÝÑÝ Ø º º¾ Ò ÑÙÙØØÙ Ò Ý ÝÑÝ Ð Ø x g Ò e? :: α Ö Ø Ø Ò ÓÐ ÐÐ Ø ÑÓ Ò Ô Ö Ñ ØÖ ØØ ÑÒ ÙÒ Ø ÓÒ ÑÙØØ À ÐÐ ÝÐ Ø Ò ÐÐ ÑÙÙØØÙ Ó ÐÐ ÐÑ ÒØÙ ØÝÝÔÔ ÐÙÓ Ð Ó º Ë Ø ÑÙØ ÑÑ Ò ÑÓÒ Ý ÝÑÝ Ð Ø p g Ò e? ::
Ì ÂÙ Ò Ä ÑÑ Ö Ø Ý Ø ÓØ ÈÙ Ð Ò ¼ ¼½¾ ½ ÔÓ Ø ÒÙÐ º ÌÝ Ò Ò Ñ ÅÓ Ð ÓÚ ÐÐÙ Ø Ò ÖÖ ØØÚÝÝ ØÓØ ÙØÙ Ò ØÖ Ø ÓØ Ó Ì ØÐ Ò Ò Ð ÈÓÖØ Ð ØÝ Ó ÅÓ Ð ÔÔÐ Ø ÓÒ Ò ÁÑÔÐ Ñ Ò
 ÂÙ Ò Ä ÑÑ Ö ÅÓ Ð ÓÚ ÐÐÙ Ø Ò ÖÖ ØØÚÝÝ ØÓØ ÙØÙ Ò ØÖ Ø ÓØ Ó Ì ØÓØ Ò Ò Ó ÐÑ ØÓØ Ò µ ÔÖÓ Ö Ù ¹ØÙØ ÐÑ ½º ÐÓ ÙÙØ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ ÂÝÚ ÝÐ Ì ÂÙ Ò Ä ÑÑ Ö Ø Ý Ø ÓØ ÈÙ Ð Ò ¼ ¼½¾ ½ ÔÓ Ø ÒÙÐ º ÌÝ
ÂÙ Ò Ä ÑÑ Ö ÅÓ Ð ÓÚ ÐÐÙ Ø Ò ÖÖ ØØÚÝÝ ØÓØ ÙØÙ Ò ØÖ Ø ÓØ Ó Ì ØÓØ Ò Ò Ó ÐÑ ØÓØ Ò µ ÔÖÓ Ö Ù ¹ØÙØ ÐÑ ½º ÐÓ ÙÙØ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ ÂÝÚ ÝÐ Ì ÂÙ Ò Ä ÑÑ Ö Ø Ý Ø ÓØ ÈÙ Ð Ò ¼ ¼½¾ ½ ÔÓ Ø ÒÙÐ º ÌÝ
T 2. f T (x)e i2π k T x dx. c k e i2π k T x = x dx. c k e i2π k T x = k Z. f T (x) =
 º ÓÙÖÖ¹ÑÙÙÒÒÓ ÓÙÖÖ Ò ÒØÖÐ Ð Ù ¹ ÓÐÐ Ò ÙÒ Ø ÓÒ f(x) PC(R) º½ ÓÙÖÖ¹ Ò ÐÝÝ º ÒÐ Òµ ÅÖ Ø ÐÐÒ T ¹ ÓÐÐ Ò Ò ÙÒ Ø Ó f T (x) = f(x), T 2 < x < T 2, ÃÓÑÔÐ Ò Ò ÓÙÖÖ¹ÖÖÓ Ò c k = 1 T T 2 T 2 f T (x)e i2π k T x dx.
º ÓÙÖÖ¹ÑÙÙÒÒÓ ÓÙÖÖ Ò ÒØÖÐ Ð Ù ¹ ÓÐÐ Ò ÙÒ Ø ÓÒ f(x) PC(R) º½ ÓÙÖÖ¹ Ò ÐÝÝ º ÒÐ Òµ ÅÖ Ø ÐÐÒ T ¹ ÓÐÐ Ò Ò ÙÒ Ø Ó f T (x) = f(x), T 2 < x < T 2, ÃÓÑÔÐ Ò Ò ÓÙÖÖ¹ÖÖÓ Ò c k = 1 T T 2 T 2 f T (x)e i2π k T x dx.
½ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ ¹ÔÙÙ ¾ ¾º½ Ì Ø ÝØ ØØÝ ¹ÔÙÙ º º º º º º º º º º º º º º º º º º º º º º º º ÌÖ ¹ØÖ º½ ÑÔÖ Ø º º º º º º º º º º º º º º º º º º º º
 ¹ØÖ Ø Ø Ø ÓÒ Ø ÐÐ ÒØ Ñ Ð ÚÝÐÐ Â Ó Å ÐÚ Ö À Ð Ò ¾¾º½¼º¾¼¼ Ë Ñ Ò Ö ØÝ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ ½ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ ¹ÔÙÙ ¾ ¾º½ Ì Ø ÝØ ØØÝ ¹ÔÙÙ º º º º º º º º º º º º º º º º º º º º º º
¹ØÖ Ø Ø Ø ÓÒ Ø ÐÐ ÒØ Ñ Ð ÚÝÐÐ Â Ó Å ÐÚ Ö À Ð Ò ¾¾º½¼º¾¼¼ Ë Ñ Ò Ö ØÝ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ ½ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ ¹ÔÙÙ ¾ ¾º½ Ì Ø ÝØ ØØÝ ¹ÔÙÙ º º º º º º º º º º º º º º º º º º º º º º
0 ex x = e 1. x + 3a 2x a = 2a xº. 1 3 (uvy) 3 (uxy) 3 (wxy) uvwxy (uvw) 1 3 (vwx)
 Å ÌȽ ¼ ËÝÑ ÓÐ Ò Ò Ð ÒØ ¾ ÓÔ ½ Ð Ø ÃÙÖ Ò Ø ÚÓ Ø ÐØ ËÝÑ ÓÐ Ò Ð ÒÒ Ò ÙÖ ÐÐ ÓÔ Ø Ò Ø ØÓ ÓÒ Ò ÝØØÑ Ø ÔÙÚÐ Ò Ò Ñ Ø Ñ ØØ ÓÒ ÐÑ Ò¹ Ö Ø Ù º ÃÙÖ Ò Ø ÚÓ ØØ Ò ÓÒ ÒØ Ô ÖÙ Ú ÐÑ Ù Ø ÝÑ ÓÐ Ò Ð ÒØ Ò Ö Ó ØÙÒ Ò Å Ø Ñ ¹
Å ÌȽ ¼ ËÝÑ ÓÐ Ò Ò Ð ÒØ ¾ ÓÔ ½ Ð Ø ÃÙÖ Ò Ø ÚÓ Ø ÐØ ËÝÑ ÓÐ Ò Ð ÒÒ Ò ÙÖ ÐÐ ÓÔ Ø Ò Ø ØÓ ÓÒ Ò ÝØØÑ Ø ÔÙÚÐ Ò Ò Ñ Ø Ñ ØØ ÓÒ ÐÑ Ò¹ Ö Ø Ù º ÃÙÖ Ò Ø ÚÓ ØØ Ò ÓÒ ÒØ Ô ÖÙ Ú ÐÑ Ù Ø ÝÑ ÓÐ Ò Ð ÒØ Ò Ö Ó ØÙÒ Ò Å Ø Ñ ¹
¾º C A {N A } K N A º A B N B
 Ú ÒØ Ò ÐÐ ÒØ ØÓ ÒÒÙ Ø Ì ÐÙÚÙ Ø Ö Ø ÐÐ Ò ÔÖÓØÓ ÓÐÐ Ó Ò ÚÙÐÐ Ó ÔÙÓÐ Ø ÚÓ Ú Ø Ó¹ Ô Ð Ø Ú Ñ Ø ØÓ ÒØ ØÓ Ò º ÌÐÐ Ò Ò ØÓ Ñ ÒÔ Ð ØØÝÝ Ù ÑÔ Ò Ø ØÓØÙÖÚ ÔÖÓØÓ ÓÐÐ Ò Ò ÑÑ ¹ Ò Ú Ò ÒÒ Ò Ù Ò Ú Ö Ò Ò Ò ØÓ Ñ ÒØ Ñ Ö Ø Ó
Ú ÒØ Ò ÐÐ ÒØ ØÓ ÒÒÙ Ø Ì ÐÙÚÙ Ø Ö Ø ÐÐ Ò ÔÖÓØÓ ÓÐÐ Ó Ò ÚÙÐÐ Ó ÔÙÓÐ Ø ÚÓ Ú Ø Ó¹ Ô Ð Ø Ú Ñ Ø ØÓ ÒØ ØÓ Ò º ÌÐÐ Ò Ò ØÓ Ñ ÒÔ Ð ØØÝÝ Ù ÑÔ Ò Ø ØÓØÙÖÚ ÔÖÓØÓ ÓÐÐ Ò Ò ÑÑ ¹ Ò Ú Ò ÒÒ Ò Ù Ò Ú Ö Ò Ò Ò ØÓ Ñ ÒØ Ñ Ö Ø Ó
f(x;n,θ) = θ x (1 θ) n x, x = 0,1,...,n; 0 θ 1. Θ = {θ 0 θ 1}. ˆθ = x n.
 ËÁË ÄÌ Ú º º½ Å Ö ÓÚ Ò Ì Ý Ú Ò ÔÝ ØÐ Ø ÙÙÖØ Ò ÐÙ Ù¹ Ò Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º º¾ Â Ò Ò Ò ÔÝ ØÐ º º º º º º º º º º º º º º º º º º º º ¾ º º ËØÓ Ø Ò Ò ÙÔÔ Ò Ñ Ò Ò º
ËÁË ÄÌ Ú º º½ Å Ö ÓÚ Ò Ì Ý Ú Ò ÔÝ ØÐ Ø ÙÙÖØ Ò ÐÙ Ù¹ Ò Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º º¾ Â Ò Ò Ò ÔÝ ØÐ º º º º º º º º º º º º º º º º º º º º ¾ º º ËØÓ Ø Ò Ò ÙÔÔ Ò Ñ Ò Ò º
ÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì ØÓÐ ÒÒ ¹ Ð ØÖÓÒ Ò ÓÙÐÙØÙ Ó ÐÑ ÂÇÆÁ È ÀÄ Å Ë Ò Ñ ÐÐ ÒÒÙ Ò Ô ÖÙ ØÙÚ ÑÙ Ò ÝÒØ Ã Ò Ø ÒØÝ ¾ ÚÙ ÌÓÙ Ó ÙÙ ¾¼¼ È
 ÂÇÆÁ È ÀÄ Å ËÁÆÁÅ ÄÄÁÆÆÍÃË Æ È ÊÍËÌÍÎ ÅÍËÁÁÃÁÆ Ë ÆÌ ËÁ Ã Ò Ø ÒØÝ Ì Ö Ø Ð ØÓÖ ÃÓÒ Ø ÃÓÔÔ Ò Ò ½½º ØÓÙ Ó ÙÙØ ÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì ØÓÐ ÒÒ ¹ Ð ØÖÓÒ Ò ÓÙÐÙØÙ Ó ÐÑ ÂÇÆÁ È ÀÄ Å Ë Ò Ñ ÐÐ
ÂÇÆÁ È ÀÄ Å ËÁÆÁÅ ÄÄÁÆÆÍÃË Æ È ÊÍËÌÍÎ ÅÍËÁÁÃÁÆ Ë ÆÌ ËÁ Ã Ò Ø ÒØÝ Ì Ö Ø Ð ØÓÖ ÃÓÒ Ø ÃÓÔÔ Ò Ò ½½º ØÓÙ Ó ÙÙØ ÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì ØÓÐ ÒÒ ¹ Ð ØÖÓÒ Ò ÓÙÐÙØÙ Ó ÐÑ ÂÇÆÁ È ÀÄ Å Ë Ò Ñ ÐÐ
P(E i ) P( ) = 0. P(A A c ) = P(A)+P(A c ) = 1. P( ) = 1 P(Ω) = 0. P(E 1 E n ) = P(E 1 )+ +P(E n ). i=1. i=1
 È Ò Ò ÓÑ Ú Ö ÙÙ Ø Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ËÙÑÑ Ò Ò ½ ÁعËÙÓÑ Ò ÝÐ ÓÔ ØÓ ½ º ØÓÙ Ó ÙÙØ ¾¼½¾ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ ÌÓ ÒÒ ÝÝ Ø ÓÖ ¾ ¾º½ Ë ØÙÒÒ ÙÙ ØÓ ÒÒ ÝÝ º º º º º º º º º º º º º º º º º ¾ ¾º¾ ÓÐÐ Ò
È Ò Ò ÓÑ Ú Ö ÙÙ Ø Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ËÙÑÑ Ò Ò ½ ÁعËÙÓÑ Ò ÝÐ ÓÔ ØÓ ½ º ØÓÙ Ó ÙÙØ ¾¼½¾ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ ÌÓ ÒÒ ÝÝ Ø ÓÖ ¾ ¾º½ Ë ØÙÒÒ ÙÙ ØÓ ÒÒ ÝÝ º º º º º º º º º º º º º º º º º ¾ ¾º¾ ÓÐÐ Ò
x (t) = f(x(t)) u B δ (p) = ϕ t (v) = p, v B d (p) = lim e t AT e t A dt W =
 Á Ê ÆÌÁ ÄÁ ÀÌ Ä Ë ËÌ ÅÁÌ º Ì Ô ÒÓÔ Ø Ø Ø Ð ÙÙ Ì ÐÙÚÙ Ø ÑÑ Ö ÒØ Ð Ý ØÐ Ò Ø Ô ÒÓÖ Ø Ù Ò Ø Ð ÙÙ Ø Ö Ø ÐÙ¹ ÒÝØ ÔÐ Ò Ö ÐÐ Ý Ø Ñ ÐÐ º ÌÐÐ ÓÚ Ø Ñ Ö ÐÙÖ Ý Ø Ñ ÐÐ Ô ÐÐ Ò ÔÝ ØÝ ÙÓÖ Ò Ó Ó Ð Ø ÝÐ Ô Ò ÓÐ Ú ÐÙÖ º ÂÓ
Á Ê ÆÌÁ ÄÁ ÀÌ Ä Ë ËÌ ÅÁÌ º Ì Ô ÒÓÔ Ø Ø Ø Ð ÙÙ Ì ÐÙÚÙ Ø ÑÑ Ö ÒØ Ð Ý ØÐ Ò Ø Ô ÒÓÖ Ø Ù Ò Ø Ð ÙÙ Ø Ö Ø ÐÙ¹ ÒÝØ ÔÐ Ò Ö ÐÐ Ý Ø Ñ ÐÐ º ÌÐÐ ÓÚ Ø Ñ Ö ÐÙÖ Ý Ø Ñ ÐÐ Ô ÐÐ Ò ÔÝ ØÝ ÙÓÖ Ò Ó Ó Ð Ø ÝÐ Ô Ò ÓÐ Ú ÐÙÖ º ÂÓ
λ (i,j) (i 1,j) = µ R j, i = 1,... N B, j = 0,... N R λ (i,j) (i,j 1) = µ B i, i = 0,... N B, j = 1,... N R λ (i,j) (k,l) = 0, muulloin.
 Šع¾º½¼ ËÓÚ ÐÐ ØÙÒ Ñ Ø Ñ Ø Ò Ö Ó ØÝ Ø ¾¼¼ ¹¼¾¹½¾ Ì Ø ÐÙÒ Ñ ÐÐ ÒÒÙ Ø Å Ö ÓÚ Ò Ø ÙÐÐ Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ Ì Ò ÐÐ Ò Ý Ò Ñ Ø Ñ Ø Ò Ó ØÓ ËÝ Ø Ñ Ò ÐÝÝ Ò Ð ÓÖ ØÓÖ Ó Ä ÙÖ ÂÙ Ò Ã Ò ¼¼ È Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ì Ø ÐÙÑ
Šع¾º½¼ ËÓÚ ÐÐ ØÙÒ Ñ Ø Ñ Ø Ò Ö Ó ØÝ Ø ¾¼¼ ¹¼¾¹½¾ Ì Ø ÐÙÒ Ñ ÐÐ ÒÒÙ Ø Å Ö ÓÚ Ò Ø ÙÐÐ Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ Ì Ò ÐÐ Ò Ý Ò Ñ Ø Ñ Ø Ò Ó ØÓ ËÝ Ø Ñ Ò ÐÝÝ Ò Ð ÓÖ ØÓÖ Ó Ä ÙÖ ÂÙ Ò Ã Ò ¼¼ È Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ì Ø ÐÙÑ
 à ÑÖ Ò ÙÙ Ò ÙÒØÓÐ Ò Ò ÓÖ ÓØ ÓÒ ÓÖ ÓÑ Ö Ò Ð Ò ÑÖÝØÝÑ Ò Ò ËÁË ÄÌ ËÁË ÄÌ Ë ÐØ ½ ÂÓ ÒØÓ ½º½ ÌÙØ ÑÙ Ý ÝÑÝ ØÙØ ÐÑ Ò Ö ÒÒ º º º º º º º º º º º º º º º º º ½º¾ ÙÒØÓÐ Ò Ñ Ö Ò Ø ËÙÓÑ º º º º º º º º º º º º º
à ÑÖ Ò ÙÙ Ò ÙÒØÓÐ Ò Ò ÓÖ ÓØ ÓÒ ÓÖ ÓÑ Ö Ò Ð Ò ÑÖÝØÝÑ Ò Ò ËÁË ÄÌ ËÁË ÄÌ Ë ÐØ ½ ÂÓ ÒØÓ ½º½ ÌÙØ ÑÙ Ý ÝÑÝ ØÙØ ÐÑ Ò Ö ÒÒ º º º º º º º º º º º º º º º º º ½º¾ ÙÒØÓÐ Ò Ñ Ö Ò Ø ËÙÓÑ º º º º º º º º º º º º º
 Ì ÓÚ Ö ÓØ Ð Ò Ã ÐÐÙÒ Å Ø Ñ Ø Ò ÈÖÓ Ö Ù¹ØÙØ ÐÑ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ ËÝ Ý ¾¼¼ Ë ÐØ ÂÓ ÒØÓ ½ ½ À ØÓÖ ¾ Î Ö ÓØ ÓÖ ¾º½ Î Ö ÓÒ ÚÖ ØÝ º º º º º º º º º º º º º º º º º º º º º º º º º
Ì ÓÚ Ö ÓØ Ð Ò Ã ÐÐÙÒ Å Ø Ñ Ø Ò ÈÖÓ Ö Ù¹ØÙØ ÐÑ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ ËÝ Ý ¾¼¼ Ë ÐØ ÂÓ ÒØÓ ½ ½ À ØÓÖ ¾ Î Ö ÓØ ÓÖ ¾º½ Î Ö ÓÒ ÚÖ ØÝ º º º º º º º º º º º º º º º º º º º º º º º º º
Ë Ø ÐÓ Ò Ô ÖØÓ Á ÔÖÓ Ó ÒØ ÃÙÒ Ð ÙØ Ò ÓÒ Ò Ö ÒÒÙ Ò ÐÐ ÓÒ ÝÐ Ò ÖÖ ÐÐ Ò Ú Ò Ô Ò Ó Ö ÒÒÙ Ò Ø ÐÓ Ø Ò ÝÚ Ñ ÐÐ ÓÒ Ù Ø ÐÐ Ò ÙÙÖ ÑÖ Ò Ø Ø ÓÐÙ Ö µ Ã ÙÐÓØØ Ò Ò Ñ
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ Ë Ø ÐÓ Ò Ô ÖØÓ Ò ÝÚÝÝ Ð ÒØ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò Ë Ø ÐÓ Ò Ô ÖØÓ Á ÔÖÓ Ó ÒØ ÃÙÒ Ð ÙØ Ò ÓÒ Ò Ö ÒÒÙ Ò ÐÐ ÓÒ ÝÐ Ò ÖÖ ÐÐ Ò Ú Ò Ô Ò Ó Ö ÒÒÙ Ò Ø ÐÓ Ø Ò ÝÚ Ñ
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ Ë Ø ÐÓ Ò Ô ÖØÓ Ò ÝÚÝÝ Ð ÒØ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò Ë Ø ÐÓ Ò Ô ÖØÓ Á ÔÖÓ Ó ÒØ ÃÙÒ Ð ÙØ Ò ÓÒ Ò Ö ÒÒÙ Ò ÐÐ ÓÒ ÝÐ Ò ÖÖ ÐÐ Ò Ú Ò Ô Ò Ó Ö ÒÒÙ Ò Ø ÐÓ Ø Ò ÝÚ Ñ
x = [ x 1 x 2 x n (x i K) x = K (n) = {(x 1, x 2,...,x n ) : x i K} e 1 = (1, 0,..., 0) Ø, e 2 = (0, 1,..., 0) Ø,..., e n = (0, 0,...
 ¼¼ Ë Å ØÖ Ø ÓÖ Ì ÖÓ Î Ò ÙÓ Ù ¾º ØÓÙ Ó ÙÙØ ¾¼¼ Ë ÐØ ½ Ä Ò Ö Ð Ö ½º½ Å Ö ÒØ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ È ÖÙ ÓÑ Ò ÙÙ º º º º º º º º º º º º º º º º º º º º º º º º ½º Å
¼¼ Ë Å ØÖ Ø ÓÖ Ì ÖÓ Î Ò ÙÓ Ù ¾º ØÓÙ Ó ÙÙØ ¾¼¼ Ë ÐØ ½ Ä Ò Ö Ð Ö ½º½ Å Ö ÒØ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ È ÖÙ ÓÑ Ò ÙÙ º º º º º º º º º º º º º º º º º º º º º º º º ½º Å
½µ newstate := 0. µ state := goto[state,p i [j]] µ state := 0;j := 0. µ j := j + 1 µ newstate := newstate + 1
![½µ newstate := 0. µ state := goto[state,p i [j]] µ state := 0;j := 0. µ j := j + 1 µ newstate := newstate + 1 ½µ newstate := 0. µ state := goto[state,p i [j]] µ state := 0;j := 0. µ j := j + 1 µ newstate := newstate + 1](/thumbs/65/53346653.jpg) ½º º Àǹ ÇÊ ËÁ ù Ä ÇÊÁÌÅÁ ½ à ÖÔ Ê Ò Ø Ö Ø Ð Ú Ø ÑÝ ÙÒ Ú Ö Ð Ò ÙØÙ Ò Ô ÖÙ ØÙÚ Ú Ö Ó Ø Ð ÓÖ ØÑ Ø Î Ð Ø Ò q ØÙÒÒ Ø ÐÙ Ù ÓÙ Ó Ø Qº Q Ò ÐÙÚÙØ ÚÓ Ú Ø ÓÐÐ Ô Ò Ò Ò Ò Ø ÖÚ Ø ÓÐÐ Ð ÙÐÙ Ù º ÎÖÒ Ø ÑÝ Ò ØÓ ÒÒ ÝÝ
½º º Àǹ ÇÊ ËÁ ù Ä ÇÊÁÌÅÁ ½ à ÖÔ Ê Ò Ø Ö Ø Ð Ú Ø ÑÝ ÙÒ Ú Ö Ð Ò ÙØÙ Ò Ô ÖÙ ØÙÚ Ú Ö Ó Ø Ð ÓÖ ØÑ Ø Î Ð Ø Ò q ØÙÒÒ Ø ÐÙ Ù ÓÙ Ó Ø Qº Q Ò ÐÙÚÙØ ÚÓ Ú Ø ÓÐÐ Ô Ò Ò Ò Ò Ø ÖÚ Ø ÓÐÐ Ð ÙÐÙ Ù º ÎÖÒ Ø ÑÝ Ò ØÓ ÒÒ ÝÝ
Ì Đ Á ÑÓ ÀÓÖÔÔÙ Ø Ý Ø ÓØ ÓÖÔÔÙº ÝÙº ÌÝĐÓÒ Ò Ñ Ç ÐÑ ØÓÒ ØØĐ Ñ Ò Ò ÔÙÙØØ ÐÐ Ò Ú Ö ÐÐ Ò Ú ÒØÓ Ò ØÓÒ Đ ØØ ÐÝÝÒ Ì ØÐ Ò Ò Ð ËÓ ØÛ Ö Ú ÐÓÔÑ ÒØ ÓÖ Ñ Ò Ò ÖÖÓÒ
 Ç ÐÑ ØÓÒ ØØĐ Ñ Ò Ò ÔÙÙØØ ÐÐ Ò Ú Ö ÐÐ Ò Ú ÒØÓ Ò ØÓÒ Đ ØØ ÐÝÝÒ Á ÑÓ ÀÓÖÔÔÙ Ì ØÓØ Ò Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ Ç ÐÑ ØÓØ Ò Ò Ð Ò ½½º ÐÑ ÙÙØ ¾¼¼¾ ÂÝÚĐ ÝÐĐ Ò ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ Ì Đ Á ÑÓ ÀÓÖÔÔÙ Ø Ý Ø ÓØ ÓÖÔÔÙº ÝÙº
Ç ÐÑ ØÓÒ ØØĐ Ñ Ò Ò ÔÙÙØØ ÐÐ Ò Ú Ö ÐÐ Ò Ú ÒØÓ Ò ØÓÒ Đ ØØ ÐÝÝÒ Á ÑÓ ÀÓÖÔÔÙ Ì ØÓØ Ò Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ Ç ÐÑ ØÓØ Ò Ò Ð Ò ½½º ÐÑ ÙÙØ ¾¼¼¾ ÂÝÚĐ ÝÐĐ Ò ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ Ì Đ Á ÑÓ ÀÓÖÔÔÙ Ø Ý Ø ÓØ ÓÖÔÔÙº ÝÙº
ÁÁ ÌÁÁÎÁËÌ ÄÅ Ì ÅÈ Ê Æ Ì ÃÆÁÄÄÁÆ Æ ÄÁÇÈÁËÌÇ Ì Ò ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò ÓÙÐÙØÙ Ó ÐÑ ÄÌÁÇ ËÍÎÁ È Ö ÒÑ ÐÐ ¾¼¼ ¾¼¼ Ø Ô ØÙÒ Ò Ð ÒÒ ÓÒÒ ØØÓÑÙÙ ¹ Ò Ò ÐÝ Ó ÒØ Ý Ú
 ËÍÎÁ ÄÌÁÇ ÈÁÊà ÆÅ ÄÄ ¾¼¼ ¾¼¼ Ì È ÀÌÍÆ Á Æ ÄÁÁà ÆÆ ¹ ÇÆÆ ÌÌÇÅÍÍÃËÁ Æ Æ Ä ËÇÁÆÌÁ ËÎ ÊÃÃÇÂ Æ ÎÍÄÄ ÔÐÓÑ ØÝ Ì Ö Ø Ð ÓÔ ØÓÒÐ ØÓÖ Ó ÌÙÖÙÒ Ò Ì Ö Ø ÝÚ ÝØØÝ ÄÙÓÒÒÓÒØ Ø Ò ÝÑÔÖ Ø Ø Ò Ò Ø ÙÒÒ Ò Ø ÙÒØ Ò ÙÚÓ ØÓÒ Ó ÓÙ
ËÍÎÁ ÄÌÁÇ ÈÁÊÃ ÆÅ ÄÄ ¾¼¼ ¾¼¼ Ì È ÀÌÍÆ Á Æ ÄÁÁÃ ÆÆ ¹ ÇÆÆ ÌÌÇÅÍÍÃËÁ Æ Æ Ä ËÇÁÆÌÁ ËÎ ÊÃÃÇÂ Æ ÎÍÄÄ ÔÐÓÑ ØÝ Ì Ö Ø Ð ÓÔ ØÓÒÐ ØÓÖ Ó ÌÙÖÙÒ Ò Ì Ö Ø ÝÚ ÝØØÝ ÄÙÓÒÒÓÒØ Ø Ò ÝÑÔÖ Ø Ø Ò Ò Ø ÙÒÒ Ò Ø ÙÒØ Ò ÙÚÓ ØÓÒ Ó ÓÙ
Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ì Ø ÐÙÑ ÐÐ ÒÒÙ ½ ¾º½ Ì Ø ÐÙÑ ÐÐ ÒÒÙ Ò ØÓÖ º º º º º º º º º º º º º º º º º º ¾ ¾º¾ ËØÓ Ø Ò Ò Ø Ø ÐÙÑ ÐÐ ÒÒÙ º º º º º º º º º º º º
 Šع¾º ½¼ ËÓÚ ÐÐ ØÙÒ Ñ Ø Ñ Ø Ò Ö Ó ØÝ Ø º½º¾¼¼ Ì Ø ÐÙÒ ÑÙÐÓ ÒØ ÑÔÙÑ Ø ÖÚ Ò Ö Ø ÐÑ Ò Ù Ø ÒÒÙ Ø Ó ÙÙ Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ Ì Ò ÐÐ Ò Ý Ò Ñ Ø Ñ Ø Ò Ó ØÓ ËÝ Ø Ñ Ò ÐÝÝ Ò Ð ÓÖ ØÓÖ Ó Â ÒÒ Ä ØÓÒ Ò ¼¾ Ë ÐØ ½ ÂÓ ÒØÓ
Šع¾º ½¼ ËÓÚ ÐÐ ØÙÒ Ñ Ø Ñ Ø Ò Ö Ó ØÝ Ø º½º¾¼¼ Ì Ø ÐÙÒ ÑÙÐÓ ÒØ ÑÔÙÑ Ø ÖÚ Ò Ö Ø ÐÑ Ò Ù Ø ÒÒÙ Ø Ó ÙÙ Ì Ò ÐÐ Ò Ò ÓÖ ÓÙÐÙ Ì Ò ÐÐ Ò Ý Ò Ñ Ø Ñ Ø Ò Ó ØÓ ËÝ Ø Ñ Ò ÐÝÝ Ò Ð ÓÖ ØÓÖ Ó Â ÒÒ Ä ØÓÒ Ò ¼¾ Ë ÐØ ½ ÂÓ ÒØÓ
3D piirron liukuhihna (3D Graphics Pipeline) Sovellus/mallinnus Geometrian käsittely Rasterointi/piirto
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ Ö Ò Ô ÖØÓ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ¹ Ö Ò Ô ÖØÑ Ò Ò ÙÚ Ø Ò Ù Ò Ð Ù Ù Ò Ò Ô Ô Ð Ò µ ÚÙÐÐ Ö Ð Ù Ù Ò Ö Ø ØÓ ÙÐ Ð Ù Ù Ò Ò Ö Ú Ò ÙØØ ÒÒ Ò Ù Ò Ô ÖÖ ØÒ ÖÙÙ ÙÐÐ Ö
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ Ö Ò Ô ÖØÓ ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ¹ Ö Ò Ô ÖØÑ Ò Ò ÙÚ Ø Ò Ù Ò Ð Ù Ù Ò Ò Ô Ô Ð Ò µ ÚÙÐÐ Ö Ð Ù Ù Ò Ö Ø ØÓ ÙÐ Ð Ù Ù Ò Ò Ö Ú Ò ÙØØ ÒÒ Ò Ù Ò Ô ÖÖ ØÒ ÖÙÙ ÙÐÐ Ö
 ΠËÃ Ä Æ ÄÁÇÈÁËÌÇ Å Ø Ñ ØØ ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò Ø ÙÒØ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Ð Ø ÐÓ ÒÒ ¹Ã Ë ÐÑÒÐ Ò Ø Ó Ò Ø Ð ØÓÐÐ Ò Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÈÖÓ Ö Ù ¹ØÙØ Ð
 Ì Ð ØÓØ Ø Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ Ë ÐÑÒÐ Ò Ø Ó Ò Ø Ð ØÓÐÐ Ò Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÒÒ ¹Ã Ð Ø ÐÓ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ º ÓÙÐÙ ÙÙØ ¾¼¼  ΠËÃ Ä Æ ÄÁÇÈÁËÌÇ Å Ø Ñ ØØ ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò Ø ÙÒØ Å Ø Ñ
Ì Ð ØÓØ Ø Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ Ë ÐÑÒÐ Ò Ø Ó Ò Ø Ð ØÓÐÐ Ò Ò Ñ ÐÐ ÒØ Ñ Ò Ò ÒÒ ¹Ã Ð Ø ÐÓ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ º ÓÙÐÙ ÙÙØ ¾¼¼  ΠËÃ Ä Æ ÄÁÇÈÁËÌÇ Å Ø Ñ ØØ ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò Ø ÙÒØ Å Ø Ñ
À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç ØÓ ÙÐØ Ø»Ë Ø ÓÒ ÙÐØÝ Ä ØÓ ÁÒ Ø ØÙØ ÓÒ Ô ÖØÑ ÒØ Å Ø Ñ ØØ ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò Ì Ö
 ÝÚ ÝÑ Ô Ú ÖÚÓ Ò ÖÚÓ Ø Ð ÈÓÐÙÒ Ø ÒØ Ù Ò ÒØ Ò ÝÑÔÖ Ø Ô Ð È Ä ÓÒ Ò À Ð Ò º º¾¼¼ ÄÙùØÙØ ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç
ÝÚ ÝÑ Ô Ú ÖÚÓ Ò ÖÚÓ Ø Ð ÈÓÐÙÒ Ø ÒØ Ù Ò ÒØ Ò ÝÑÔÖ Ø Ô Ð È Ä ÓÒ Ò À Ð Ò º º¾¼¼ ÄÙùØÙØ ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç
ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ÃÁÆÆÍÆ Æ ÌÇÈÁ Ê ÒÒÙ Ø Ò Ø Ò ÓÐÓ Ø Ò ÐÑ ØÓÐÐ Ø Ò Ø Ò Ú ÙØÙ ÙÒØÓ Ò ÐÑ Ò Ö ÓÒÔ ØÓ ÙÙØ Òº ÈÖÓ Ö Ù ¹ØÙØ ÐÑ º ½
 Ê Ã ÆÆÍËÌ ÃÆÁËÌ Æ ÇÄÇ ÁËÌ Æ Â ÁÄÅ ËÌÇÄÄÁËÌ Æ Ì ÃÁ Á Æ Î ÁÃÍÌÍË ËÍÆÌÇÂ Æ ËÁË ÁÄÅ Æ Ê ÇÆÈÁÌÇÁËÍÍÌ Æ ÌÓÔ Ã ÒÒÙÒ Ò Ì Ð ØÓØ Ø Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ
Ê Ã ÆÆÍËÌ ÃÆÁËÌ Æ ÇÄÇ ÁËÌ Æ Â ÁÄÅ ËÌÇÄÄÁËÌ Æ Ì ÃÁ Á Æ Î ÁÃÍÌÍË ËÍÆÌÇÂ Æ ËÁË ÁÄÅ Æ Ê ÇÆÈÁÌÇÁËÍÍÌ Æ ÌÓÔ Ã ÒÒÙÒ Ò Ì Ð ØÓØ Ø Ò ÔÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ
2x1 + x 2 = 1 x 1 + x 2 = 3. x1 = 2 x 2 = 5. 2 ( 2)+5 = = 3. 5x1 x 2 = 1 10x 1 2x 2 = 2. ax1 +bx 2 = e cx 1 +dx 2 = f
 Ä Ò Ö Ð Ö Á ÇÙÐÙÒ ÝÐ ÓÔ ØÓ Å Ø Ñ ØØ Ø Ò Ø Ø Ò Ð ØÓ ¾¼½½ ÂÖÚ ÒÔ Ã Ö Ó ØØ ÒÙØ ÌÙÙÐ Ê Ô ØØ ¾ ½ Ä Ò Ö Ò Ò Ý ØÐ ÖÝ Ñ ½½ Ñ Ö µ Ê Ø Ý ØÐ 5x = 7 Ã ÖÖÓØ Ò Ý ØÐ ÔÙÓÐ ØØ Ò ÐÙÚÙÐÐ 5 1 ÓÐÐÓ Ò Ò 5 1 5x = 5 1 7 Ð x =
Ä Ò Ö Ð Ö Á ÇÙÐÙÒ ÝÐ ÓÔ ØÓ Å Ø Ñ ØØ Ø Ò Ø Ø Ò Ð ØÓ ¾¼½½ ÂÖÚ ÒÔ Ã Ö Ó ØØ ÒÙØ ÌÙÙÐ Ê Ô ØØ ¾ ½ Ä Ò Ö Ò Ò Ý ØÐ ÖÝ Ñ ½½ Ñ Ö µ Ê Ø Ý ØÐ 5x = 7 Ã ÖÖÓØ Ò Ý ØÐ ÔÙÓÐ ØØ Ò ÐÙÚÙÐÐ 5 1 ÓÐÐÓ Ò Ò 5 1 5x = 5 1 7 Ð x =
(AB) ij = p. k=1 a ikb kj. AA 1 = A 1 A = I.
 Ð ÙÓ ÙÖ Ø Å˹ ½ ¼ ÄÁÆ ÊÁ Ä Ê Æ È ÊÍËÌ Ì ÌÁÅÇ ÁÊÇÄ A A = 0 0 2 0 0 2 ÐØÓ Ð ÓÔ ØÓ È ÖÙ Ø Ø Ò ÃÓÖ ÓÙÐÙ Å Ø Ñ Ø Ò ËÝ Ø Ñ Ò ÐÝÝ Ò Ð ØÓ ËÝ Ý ¾¼½ ÄÁÆ ÊÁ Ä Ê Æ È ÊÍËÌ Ì ÌÑ ÑÓÒ Ø ÓÒ Ö Ó Ø ØØÙ ÙÙ ÐÐ Ò Ý ÝÐÐ ¾¼½
Ð ÙÓ ÙÖ Ø Å˹ ½ ¼ ÄÁÆ ÊÁ Ä Ê Æ È ÊÍËÌ Ì ÌÁÅÇ ÁÊÇÄ A A = 0 0 2 0 0 2 ÐØÓ Ð ÓÔ ØÓ È ÖÙ Ø Ø Ò ÃÓÖ ÓÙÐÙ Å Ø Ñ Ø Ò ËÝ Ø Ñ Ò ÐÝÝ Ò Ð ØÓ ËÝ Ý ¾¼½ ÄÁÆ ÊÁ Ä Ê Æ È ÊÍËÌ Ì ÌÑ ÑÓÒ Ø ÓÒ Ö Ó Ø ØØÙ ÙÙ ÐÐ Ò Ý ÝÐÐ ¾¼½
ËÚÝØÝ Ò µ ÓÒ Ñ Ò ÔÑÖ Ò Ò Ø ÖÑ ÓÒ ÝØØ Ø ØÓ ÓÒ Ö ÓÒ ÐÓ ØÓÒÒÙØ Ñ Ð Ó Ù Ò Ò Ð ÙÔ Ö Ø Ñ Ö ØÝ Ø Ã ØØ ÐÐ Ø Ö Ó Ø Ø Ò ÒÝ ÝÒ Ø Ò Ó Ø Ó ÐÐ Ð Ø Ò ÚÖ Ú Ð ØÙ Ø ÔÔ
 ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ Ë Ò ² Ö Ø ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ËÚÝØÝ Ò µ ÓÒ Ñ Ò ÔÑÖ Ò Ò Ø ÖÑ ÓÒ ÝØØ Ø ØÓ ÓÒ Ö ÓÒ ÐÓ ØÓÒÒÙØ Ñ Ð Ó Ù Ò Ò Ð ÙÔ Ö Ø Ñ Ö ØÝ Ø Ã ØØ ÐÐ Ø Ö Ó Ø Ø Ò ÒÝ ÝÒ Ø
ØÙغ Ø Ò ÐÐ Ò Ò ÝÐ ÓÔ ØÓ Ì ÑÔ Ö Ò È Ð Ó ÐÑÓ ÒØ Ë Ò ² Ö Ø ÒØØ ÈÙ ÒØØ ºÔÙ Ç ÐÑ ØÓØ Ò ËÚÝØÝ Ò µ ÓÒ Ñ Ò ÔÑÖ Ò Ò Ø ÖÑ ÓÒ ÝØØ Ø ØÓ ÓÒ Ö ÓÒ ÐÓ ØÓÒÒÙØ Ñ Ð Ó Ù Ò Ò Ð ÙÔ Ö Ø Ñ Ö ØÝ Ø Ã ØØ ÐÐ Ø Ö Ó Ø Ø Ò ÒÝ ÝÒ Ø
Ì È ÚÓ È Ö Ò Ò Ø Ý Ø ÓØ ÔÔ Ö Ò ÝÙº ÌÝ Ò Ò Ñ Å Ö Ò ÔÓ Ø Ñ ÐÐ Ø ÝØØ Ö Ø ÐÑÒ ÑÙ Ø Ò ÐÐ ÒÒ Ì ØÐ Ò Ò Ð Å Ö Ø¹ ÑÓ Ð ÓÖ ÓÔ Ö Ø Ò Ý Ø Ñ Ñ ÑÓÖÝ Ñ Ò Ñ ÒØ ÌÝ Ì Ø
 È ÚÓ È Ö Ò Ò Å Ö Ò ÔÓ Ø Ñ ÐÐ Ø ÝØØ Ö Ø ÐÑÒ ÑÙ Ø Ò ÐÐ ÒÒ Ì ØÓØ Ò Ò ÈÖÓ Ö Ù ØÙØ ÐÑ ½ º ÐÓ ÙÙØ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ ÂÝÚ ÝÐ Ì È ÚÓ È Ö Ò Ò Ø Ý Ø ÓØ ÔÔ Ö Ò ÝÙº ÌÝ Ò Ò Ñ Å Ö Ò ÔÓ Ø Ñ ÐÐ Ø ÝØØ
È ÚÓ È Ö Ò Ò Å Ö Ò ÔÓ Ø Ñ ÐÐ Ø ÝØØ Ö Ø ÐÑÒ ÑÙ Ø Ò ÐÐ ÒÒ Ì ØÓØ Ò Ò ÈÖÓ Ö Ù ØÙØ ÐÑ ½ º ÐÓ ÙÙØ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ ÂÝÚ ÝÐ Ì È ÚÓ È Ö Ò Ò Ø Ý Ø ÓØ ÔÔ Ö Ò ÝÙº ÌÝ Ò Ò Ñ Å Ö Ò ÔÓ Ø Ñ ÐÐ Ø ÝØØ
P(r, ϕ t) = P(z, e it ) = 1 z 2 e it z 2, Ñ z = reiϕ. f(z + re iϕ )dϕ. f(z) = 1. f(z) f(z 0 ).
 ÁÆÌ ÊÈÇÄ ÌÁÇ À Ê Æ Î ÊÍÍÃËÁËË ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Â ÖÑÓ Å Ð À Ð Ò Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Ù Ø ÙÙ ¾¼¼ Ë ÐØ ½ ÂÓ ÒØÓ ¾ ËÙ ÖÑÓÒ Ø ÙÒ Ø ÓØ Ð Ò ØÙÐÓ ¾º½ Ò ÐÝÝØØ Ø ÙÒ Ø ÓØ º º º º º º º º º º º º º
ÁÆÌ ÊÈÇÄ ÌÁÇ À Ê Æ Î ÊÍÍÃËÁËË ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Â ÖÑÓ Å Ð À Ð Ò Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Ù Ø ÙÙ ¾¼¼ Ë ÐØ ½ ÂÓ ÒØÓ ¾ ËÙ ÖÑÓÒ Ø ÙÒ Ø ÓØ Ð Ò ØÙÐÓ ¾º½ Ò ÐÝÝØØ Ø ÙÒ Ø ÓØ º º º º º º º º º º º º º
C A B, A D B A B E. A B C, A C B Ø B A C.
 Ù Ð Ò ÝÔ Ö ÓÐ Ò ÓÑ ØÖ Ò Ñ ÐÐ Ö Ë ÐÑ Ð ÈÖÓ Ö Ù ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Ã ÚØ ¾¼¼ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ À Ð ÖØ Ò ÓÓÑ Ö Ø ÐÑ ¾ ¾º½ À Ð ÖØ Ò Ò Ò ÓÓÑ Ø º º º º º º º º º º º º º º º º
Ù Ð Ò ÝÔ Ö ÓÐ Ò ÓÑ ØÖ Ò Ñ ÐÐ Ö Ë ÐÑ Ð ÈÖÓ Ö Ù ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò Ð ØÓ Ã ÚØ ¾¼¼ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ À Ð ÖØ Ò ÓÓÑ Ö Ø ÐÑ ¾ ¾º½ À Ð ÖØ Ò Ò Ò ÓÓÑ Ø º º º º º º º º º º º º º º º º
x α 1... x (v ṽ)φdx = 0
 Ð Ñ ÒØØ Ñ Ò Ø ÐÑ ÐÐ ÔØ ÐÐ ÓÒ ÐÑ ÐÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Ì ÑÙ ÅÙ ØÓÒ Ò ½ ½ ÁعËÙÓÑ Ò ÝÐ ÓÔ ØÓ ÄÙÓÒÒÓÒØ Ø Ò Ñ Ø Ø Ø Ò Ø ÙÒØ Ý Ò Ñ Ø Ñ Ø Ò Ð ØÓ ½ º ØÓÙ Ó ÙÙØ ¾¼½¾ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ð Ñ ÒØØ Ñ Ò Ø ÐÑÒ ÙÒ Ø Ó Ú ÖÙÙ
Ð Ñ ÒØØ Ñ Ò Ø ÐÑ ÐÐ ÔØ ÐÐ ÓÒ ÐÑ ÐÐ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ Ì ÑÙ ÅÙ ØÓÒ Ò ½ ½ ÁعËÙÓÑ Ò ÝÐ ÓÔ ØÓ ÄÙÓÒÒÓÒØ Ø Ò Ñ Ø Ø Ø Ò Ø ÙÒØ Ý Ò Ñ Ø Ñ Ø Ò Ð ØÓ ½ º ØÓÙ Ó ÙÙØ ¾¼½¾ Ë ÐØ ½ ÂÓ ÒØÓ ½ ¾ Ð Ñ ÒØØ Ñ Ò Ø ÐÑÒ ÙÒ Ø Ó Ú ÖÙÙ
284 = º Î Ø Ú Ø. A = kanta korkeus. A 1/2suunn = kanta+kanta 2
 ÈÝØ ÓÖ Ò Ð Ù ÈÝØ ÓÖ Ò ÓÐÑ ÓØ ÈÖÓ Ö Ù¹ØÙØ ÐÑ ÒÓ¹Ã Ö Ò ½ Å Ø Ñ Ø Ò Ý Ò Ð ØÓ ÁعËÙÓÑ Ò ÝÐ ÓÔ ØÓ º ÐÓ ÙÙØ ¾¼½¾ Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÈÝØ ÓÖ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ ÈÝØ ÓÖ
ÈÝØ ÓÖ Ò Ð Ù ÈÝØ ÓÖ Ò ÓÐÑ ÓØ ÈÖÓ Ö Ù¹ØÙØ ÐÑ ÒÓ¹Ã Ö Ò ½ Å Ø Ñ Ø Ò Ý Ò Ð ØÓ ÁعËÙÓÑ Ò ÝÐ ÓÔ ØÓ º ÐÓ ÙÙØ ¾¼½¾ Ë ÐØ ½ ÂÓ ÒØÓ ½ ½º½ ÈÝØ ÓÖ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ ÈÝØ ÓÖ
y t = X t β + u t, u t NID(0, 1) t = 1, 2,..., n ½µ
 ÇÊ Ê ÈÊÇ ÁÌ Â Â ÄÃ È ÄÄǹÇÌÌ ÄÍÆ Å ÄÄÁÆÌ ÅÁÆ Æ Ê Ò ÓÑ Î Ö Ð ½º Ò ÙÙØ ¾¼¼ ËÁË ÄÌ ½ Ë ÐØ ½ ÂÓ ÒØÓ ¾ ¾ ÇÖ Ö ÔÖÓ Ø ¾º½ Å ÐÐ Ò ÑÖ ØØ ÐÝ º º º º º º º º º º º º º º º º º º º º º º º º º Â Ð Ô ÐÐÓ¹ÓØØ ÐÙÒ Ò
ÇÊ Ê ÈÊÇ ÁÌ Â Â ÄÃ È ÄÄǹÇÌÌ ÄÍÆ Å ÄÄÁÆÌ ÅÁÆ Æ Ê Ò ÓÑ Î Ö Ð ½º Ò ÙÙØ ¾¼¼ ËÁË ÄÌ ½ Ë ÐØ ½ ÂÓ ÒØÓ ¾ ¾ ÇÖ Ö ÔÖÓ Ø ¾º½ Å ÐÐ Ò ÑÖ ØØ ÐÝ º º º º º º º º º º º º º º º º º º º º º º º º º Â Ð Ô ÐÐÓ¹ÓØØ ÐÙÒ Ò
Ð Ø Ù ÁÈË Ò ÁÈË ÓÒ ÁÈ¹Ú Ö ÓÔÖÓØÓ ÓÐÐ Ò Ð ÒÒÙ Ñ ÐÐ Ø ØÒ ÁÈ¹Ô ØØ Ò ÙÖ Ñ Ò Ò ÑÙÙÒØ Ñ Ò Òº ÁÈË ÓÒ ÝÒØÝÒÝØ ÙÙ Ò ÁÈÚ ¹ÔÖÓØÓ ÓÐÐ Ò Ý Ø Ý ÁÈÚ ÓÒ Ò ÁÈË Ò ÐÙÓÒØ
 ÌÁ ÌÇÌÍÊÎ ÇË ÁÎ ÁÈË Ì ÑÓ Ã ÖÚ º½¾º¾¼¼ Ì ÑÓ Ã ÖÚ µ ÌÁ ÌÇÌÍÊÎ ÇË ÁÎ ÁÈË º½¾º¾¼¼ ½» Ð Ø Ù ÁÈË Ò ÁÈË ÓÒ ÁÈ¹Ú Ö ÓÔÖÓØÓ ÓÐÐ Ò Ð ÒÒÙ Ñ ÐÐ Ø ØÒ ÁÈ¹Ô ØØ Ò ÙÖ Ñ Ò Ò ÑÙÙÒØ Ñ Ò Òº ÁÈË ÓÒ ÝÒØÝÒÝØ ÙÙ Ò ÁÈÚ ¹ÔÖÓØÓ ÓÐÐ
ÌÁ ÌÇÌÍÊÎ ÇË ÁÎ ÁÈË Ì ÑÓ Ã ÖÚ º½¾º¾¼¼ Ì ÑÓ Ã ÖÚ µ ÌÁ ÌÇÌÍÊÎ ÇË ÁÎ ÁÈË º½¾º¾¼¼ ½» Ð Ø Ù ÁÈË Ò ÁÈË ÓÒ ÁÈ¹Ú Ö ÓÔÖÓØÓ ÓÐÐ Ò Ð ÒÒÙ Ñ ÐÐ Ø ØÒ ÁÈ¹Ô ØØ Ò ÙÖ Ñ Ò Ò ÑÙÙÒØ Ñ Ò Òº ÁÈË ÓÒ ÝÒØÝÒÝØ ÙÙ Ò ÁÈÚ ¹ÔÖÓØÓ ÓÐÐ
Referenced. Object. StateSet. Node. Geode
 ÇÔ ÒË Ò Ö Ô ¹Ó Ø Ì ÑÓºÌÓ Ú Ò ÒØѺ Ùغ ÌÑ Ó ÙÑ ÒØØ ÓÒ ØÝ Ò Ø Ô Ú Ø ØÒ Ø ÖÔ Ò ÑÙ Òº ½ Ø ÇÔ ÒË Ò Ö Ô ÇË µ ÓÒ ÇÔ Ò Ä Ò Ô Ö ÒÒ ØØÙ ¹ÙÓ Ö¹ ØÓ Ó ÓÒ Ú Ô Ø Ø Ú Ó ØÓ Ñ ÑÓÒ ÝÑÔÖ Ø º ÇË Ó¹ ÙÑ ÒØÓ ØÙ ÓÜÝ Ò¹Ó Ñ ØÓÒ
ÇÔ ÒË Ò Ö Ô ¹Ó Ø Ì ÑÓºÌÓ Ú Ò ÒØѺ Ùغ ÌÑ Ó ÙÑ ÒØØ ÓÒ ØÝ Ò Ø Ô Ú Ø ØÒ Ø ÖÔ Ò ÑÙ Òº ½ Ø ÇÔ ÒË Ò Ö Ô ÇË µ ÓÒ ÇÔ Ò Ä Ò Ô Ö ÒÒ ØØÙ ¹ÙÓ Ö¹ ØÓ Ó ÓÒ Ú Ô Ø Ø Ú Ó ØÓ Ñ ÑÓÒ ÝÑÔÖ Ø º ÇË Ó¹ ÙÑ ÒØÓ ØÙ ÓÜÝ Ò¹Ó Ñ ØÓÒ
Simulointityökalu saarekekäytön säädön kehityksen tueksi Elektroniikan, tietoliikenteen ja automaation tiedekunta
 Ë ÑÓ À Ð Simulointityökalu saarekekäytön säädön kehityksen tueksi Elektroniikan, tietoliikenteen ja automaation tiedekunta ÔÐÓÑ ØÝ Ó ÓÒ Ø ØØÝ ÓÔ ÒÒÝØØ Ò Ø Ö Ø ØØ Ú ÔÐÓÑ ¹ Ò Ò Ö Ò ØÙØ ÒØÓ Ú ÖØ Ò ÔÓÓ ½¼º
Ë ÑÓ À Ð Simulointityökalu saarekekäytön säädön kehityksen tueksi Elektroniikan, tietoliikenteen ja automaation tiedekunta ÔÐÓÑ ØÝ Ó ÓÒ Ø ØØÝ ÓÔ ÒÒÝØØ Ò Ø Ö Ø ØØ Ú ÔÐÓÑ ¹ Ò Ò Ö Ò ØÙØ ÒØÓ Ú ÖØ Ò ÔÓÓ ½¼º
Ì ÅÈ Ê Æ ÄÁÇÈÁËÌÇ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÇÐÐ Ë ÚÓÐ Ò Ò Ø ÖÑ Ò ÒØ Ò ÑÖ Ø ÐÑ Ø ÓÑ Ò ÙÙ Ø Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Å Ø Ñ Ø À Ò ÙÙ ¾¼¼
 Ì ÅÈ Ê Æ ÄÁÇÈÁËÌÇ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÇÐÐ Ë ÚÓÐ Ò Ò Ø ÖÑ Ò ÒØ Ò ÑÖ Ø ÐÑ Ø ÓÑ Ò ÙÙ Ø Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Å Ø Ñ Ø À Ò ÙÙ ¾¼¼ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Ë ÎÇÄ ÁÆ Æ ÇÄÄÁ
Ì ÅÈ Ê Æ ÄÁÇÈÁËÌÇ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÇÐÐ Ë ÚÓÐ Ò Ò Ø ÖÑ Ò ÒØ Ò ÑÖ Ø ÐÑ Ø ÓÑ Ò ÙÙ Ø Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Å Ø Ñ Ø À Ò ÙÙ ¾¼¼ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓ Å Ø Ñ Ø Ò Ø Ð ØÓØ Ø Ò ÐÓ Ó Ò Ð ØÓ Ë ÎÇÄ ÁÆ Æ ÇÄÄÁ
ÁÆÇ Å ÌË Ä ÅÇÇ Ä ÅÇÆÁÃÍÄÌÌÍÍÊÁË Æ ÇÈÈÁÅÁË ÅÈ ÊÁËÌ Æ ÔÐÓÑ ØÝ Ì Ö Ø ÔÖÓ ÓÖ À ÒÒÙ Â ÓÐ Ì Ö Ø ÝÚ ÝØØÝ Ì ØÓ¹ Ø Ò Ò Ø ÙÒØ ¹ Ò ÙÚÓ ØÓÒ Ó ÓÙ ½ º¼½º¾¼½¼
 ÁÆÇ Å ÌË Ä ÅÇÇ Ä ÅÇÆÁÃÍÄÌÌÍÍÊÁË Æ ÇÈÈÁÅÁË ÅÈ ÊÁËÌ Æ ÔÐÓÑ ØÝ Ì Ö Ø ÔÖÓ ÓÖ À ÒÒÙ Â ÓÐ Ì Ö Ø ÝÚ ÝØØÝ Ì ØÓ¹ Ø Ò Ò Ø ÙÒØ ¹ Ò ÙÚÓ ØÓÒ Ó ÓÙ ½ º¼½º¾¼½¼ ÌÝ Ò Ó À ÒÒÙ Â ÓÐ ÌÝ Ò Ø ÒÓ Åº Å Ø Ð ÅÓÓ Ð ÑÓÒ ÙÐØØÙÙÖ Ò
ÁÆÇ Å ÌË Ä ÅÇÇ Ä ÅÇÆÁÃÍÄÌÌÍÍÊÁË Æ ÇÈÈÁÅÁË ÅÈ ÊÁËÌ Æ ÔÐÓÑ ØÝ Ì Ö Ø ÔÖÓ ÓÖ À ÒÒÙ Â ÓÐ Ì Ö Ø ÝÚ ÝØØÝ Ì ØÓ¹ Ø Ò Ò Ø ÙÒØ ¹ Ò ÙÚÓ ØÓÒ Ó ÓÙ ½ º¼½º¾¼½¼ ÌÝ Ò Ó À ÒÒÙ Â ÓÐ ÌÝ Ò Ø ÒÓ Åº Å Ø Ð ÅÓÓ Ð ÑÓÒ ÙÐØØÙÙÖ Ò
À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç ØÓ ÙÐØ Ø»Ë Ø ÓÒ ÙÐØÝ Ä ØÓ ÁÒ Ø ØÙØ ÓÒ Ô ÖØÑ ÒØ Å Ø Ñ ØØ ¹ÐÙÓÒÒÓÒØ Ø ÐÐ Ò Ò Ì Ö
 Ø ÝØØ Ø Ò ØØ Ò ÙÚ Ù ÐÓ Ô ÖÙ Ø Ò Ò Ñ¹ Ö ØØ ÐÝ Û È ØÖ Ä Ò Ö Ò À Ð Ò ¾ º º¾¼¼ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç
Ø ÝØØ Ø Ò ØØ Ò ÙÚ Ù ÐÓ Ô ÖÙ Ø Ò Ò Ñ¹ Ö ØØ ÐÝ Û È ØÖ Ä Ò Ö Ò À Ð Ò ¾ º º¾¼¼ ÈÖÓ Ö Ù ¹ØÙØ ÐÑ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ Ì ØÓ Ò ØØ ÐÝØ Ø Ò Ð ØÓ À ÄËÁÆ ÁÆ ÄÁÇÈÁËÌÇ À ÄËÁÆ ÇÊË ÍÆÁÎ ÊËÁÌ Ì ÍÆÁÎ ÊËÁÌ Ç À ÄËÁÆÃÁ Ì ÙÒØ»Ç
(xy)z = x(yz) λx = xλ = x.
 ÄÙ Ù ½ ÐÙ ÌÑ ÑÓÒ Ø ÓÒ Ø Ö Ó Ø ØØÙ ÝØ ØØÚ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓÒ Ø ØÓ Ò ØØ Ðݹ Ø Ø Ò Ð ØÓ Ò ÓÔ ÒØÓ ÓÐÐ ÙØÓÑ Ø Øº ÅÓÒ Ø Ô ÖÙ ØÙÙ ÙÖ Ú Ò Ð Ø Ò Åº º À ÖÖ ÓÒ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÖÑ Ð Ä Ò Ù Ì ÓÖݺ ÓÒ¹Ï Ð Ý ½ º º º
ÄÙ Ù ½ ÐÙ ÌÑ ÑÓÒ Ø ÓÒ Ø Ö Ó Ø ØØÙ ÝØ ØØÚ Ì ÑÔ Ö Ò ÝÐ ÓÔ ØÓÒ Ø ØÓ Ò ØØ Ðݹ Ø Ø Ò Ð ØÓ Ò ÓÔ ÒØÓ ÓÐÐ ÙØÓÑ Ø Øº ÅÓÒ Ø Ô ÖÙ ØÙÙ ÙÖ Ú Ò Ð Ø Ò Åº º À ÖÖ ÓÒ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÖÑ Ð Ä Ò Ù Ì ÓÖݺ ÓÒ¹Ï Ð Ý ½ º º º
Ë ÐØ ½ ÂÓ ÒØÓ ¾ À Ò Ñ Ò Ñ Ó Ø ÓÖ Ø Ò Ö Ñ ÐÐ ¾º½ ËÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó º º º º º º º º º º º º º º º º º º º º ¾º½º½ Ö ØØ ÝÑÑ ØÖ º º º º º º º º º º º º º
 Ë Ó ËÝÑÑ ØÖ Ö Ó Ì Ò ÚÖ Ø ÓÖ Ó Å ØØ À Ò ÑÓ Ñ Ô º ÝÙº ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ý Ò Ð ØÓ ½¾º ÀÙ Ø ÙÙØ ¾¼¼ Ë ÐØ ½ ÂÓ ÒØÓ ¾ À Ò Ñ Ò Ñ Ó Ø ÓÖ Ø Ò Ö Ñ ÐÐ ¾º½ ËÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó º º º º º º º º º º º º
Ë Ó ËÝÑÑ ØÖ Ö Ó Ì Ò ÚÖ Ø ÓÖ Ó Å ØØ À Ò ÑÓ Ñ Ô º ÝÙº ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ý Ò Ð ØÓ ½¾º ÀÙ Ø ÙÙØ ¾¼¼ Ë ÐØ ½ ÂÓ ÒØÓ ¾ À Ò Ñ Ò Ñ Ó Ø ÓÖ Ø Ò Ö Ñ ÐÐ ¾º½ ËÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó º º º º º º º º º º º º
Ì ØÓØÙÖÚ Ò ÓØØ ÐÙØ Á Ì ØÓØÙÖÚ ÓÒ Ð º Ë ÙÖ Ú Ð Ø ÓÒ ÐÙ Ø ÐØÙ Ø ØÓØÙÖÚ Ò Ö Ó ¹ ÐÙ Ø º Â ÓØØ ÐÙ ÓÒ Ñ Ð Ó ÝÐ Ò Ò Ø ØÒ ÝÐ Ø ØÓØÙÖÚ Ò ÓÔÔ Ö Ó º À ÐÐ ÒÒÓÐÐ Ò
 ÌÁ ÌÇÌÍÊÎ Ó Á ̺ à ÖÚ ËÝÝ ÙÙ ¾¼¼ ̺ à ÖÚ µ ÌÁ ÌÇÌÍÊÎ Ó Á ËÝÝ ÙÙ ¾¼¼ ½» ½ Ì ØÓØÙÖÚ Ò ÓØØ ÐÙØ Á Ì ØÓØÙÖÚ ÓÒ Ð º Ë ÙÖ Ú Ð Ø ÓÒ ÐÙ Ø ÐØÙ Ø ØÓØÙÖÚ Ò Ö Ó ¹ ÐÙ Ø º  ÓØØ ÐÙ ÓÒ Ñ Ð Ó ÝÐ Ò Ò Ø ØÒ ÝÐ Ø ØÓØÙÖÚ Ò
ÌÁ ÌÇÌÍÊÎ Ó Á ̺ à ÖÚ ËÝÝ ÙÙ ¾¼¼ ̺ à ÖÚ µ ÌÁ ÌÇÌÍÊÎ Ó Á ËÝÝ ÙÙ ¾¼¼ ½» ½ Ì ØÓØÙÖÚ Ò ÓØØ ÐÙØ Á Ì ØÓØÙÖÚ ÓÒ Ð º Ë ÙÖ Ú Ð Ø ÓÒ ÐÙ Ø ÐØÙ Ø ØÓØÙÖÚ Ò Ö Ó ¹ ÐÙ Ø º  ÓØØ ÐÙ ÓÒ Ñ Ð Ó ÝÐ Ò Ò Ø ØÒ ÝÐ Ø ØÓØÙÖÚ Ò
ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ Ø ÇÒ ØÖ Ý Ø ØÓÑ Ò ÙÐ Ò Ò Ú Ò Ò ØÓ ÐÐ Ò Ò ÐØ ÐÙÓØ ØØ Ú Ø ØÓ Ò º ÃÓ Ò Ð Ö ÓÒ ½ Ò ÑÑ Ò ÓØØ ÒÙØ Ú ÖÑ ÒØ Ø Ó ÓÒ ÙÐ Ò Ò Ú Ò Ò ÐØ Ð
 ÌÁ ÌÇÌÍÊÎ ÇË ÁÁÁ ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ Ì ÑÓ Ã ÖÚ ¾º½½º¾¼¼ Ì ÑÓ Ã ÖÚ µ ÌÁ ÌÇÌÍÊÎ ÇË ÁÁÁ ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ ¾º½½º¾¼¼ ½» ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ Ø ÇÒ ØÖ Ý Ø ØÓÑ Ò ÙÐ Ò Ò Ú Ò Ò ØÓ ÐÐ Ò Ò ÐØ ÐÙÓØ
ÌÁ ÌÇÌÍÊÎ ÇË ÁÁÁ ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ Ì ÑÓ Ã ÖÚ ¾º½½º¾¼¼ Ì ÑÓ Ã ÖÚ µ ÌÁ ÌÇÌÍÊÎ ÇË ÁÁÁ ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ ¾º½½º¾¼¼ ½» ÂÙÐ Ò Ú Ñ Ò Ò Ö ØÖÙ ØÙÙÖ Ø ÇÒ ØÖ Ý Ø ØÓÑ Ò ÙÐ Ò Ò Ú Ò Ò ØÓ ÐÐ Ò Ò ÐØ ÐÙÓØ
Ì Å ÈÙÐ Ò Ò Ø Ý Ø ÓØ Ñ ºÔÙÐ Ò Ò ÝÙº ÌÝ Ò Ò Ñ ÙØÓÑ Ø Ó ØÙ Ý Ø Ø Ù ÆÍÒ Ø¹Ø Ø Ù ÝÑÔÖ Ø Ì ØÐ Ò Ò Ð ÙØÓÑ Ø ÍÒ Ø Ì Ø Ò Ò ÆÍÒ Ø Ì Ø Ò ÒÚ ÖÓÒÑ ÒØ ÌÝ Ì ØÓØ Ò Ò
 Å ÈÙÐ Ò Ò ÙØÓÑ Ø Ó ØÙ Ý Ø Ø Ù ÆÍÒ Ø¹Ø Ø Ù ÝÑÔÖ Ø Ì ØÓØ Ò Ò Ò Ø ÒØÙØ ÐÑ ¾ º ÐÑ ÙÙØ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ ÂÝÚ ÝÐ Ì Å ÈÙÐ Ò Ò Ø Ý Ø ÓØ Ñ ºÔÙÐ Ò Ò ÝÙº ÌÝ Ò Ò Ñ ÙØÓÑ Ø Ó ØÙ Ý Ø Ø Ù ÆÍÒ Ø¹Ø Ø Ù
Å ÈÙÐ Ò Ò ÙØÓÑ Ø Ó ØÙ Ý Ø Ø Ù ÆÍÒ Ø¹Ø Ø Ù ÝÑÔÖ Ø Ì ØÓØ Ò Ò Ò Ø ÒØÙØ ÐÑ ¾ º ÐÑ ÙÙØ ¾¼¼ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ì ØÓØ Ò Ò Ð ØÓ ÂÝÚ ÝÐ Ì Å ÈÙÐ Ò Ò Ø Ý Ø ÓØ Ñ ºÔÙÐ Ò Ò ÝÙº ÌÝ Ò Ò Ñ ÙØÓÑ Ø Ó ØÙ Ý Ø Ø Ù ÆÍÒ Ø¹Ø Ø Ù
