Ë ÐØ ½ ÂÓ ÒØÓ ¾ À Ò Ñ Ò Ñ Ó Ø ÓÖ Ø Ò Ö Ñ ÐÐ ¾º½ ËÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó º º º º º º º º º º º º º º º º º º º º ¾º½º½ Ö ØØ ÝÑÑ ØÖ º º º º º º º º º º º º º

Transkriptio

1 Ë Ó ËÝÑÑ ØÖ Ö Ó Ì Ò ÚÖ Ø ÓÖ Ó Å ØØ À Ò ÑÓ Ñ Ô º ÝÙº ÈÖÓ Ö Ù ¹ØÙØ ÐÑ ÂÝÚ ÝÐÒ ÝÐ ÓÔ ØÓ Ý Ò Ð ØÓ ½¾º ÀÙ Ø ÙÙØ ¾¼¼

2 Ë ÐØ ½ ÂÓ ÒØÓ ¾ À Ò Ñ Ò Ñ Ó Ø ÓÖ Ø Ò Ö Ñ ÐÐ ¾º½ ËÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó º º º º º º º º º º º º º º º º º º º º ¾º½º½ Ö ØØ ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º ¾º½º¾ Â Ø ÙÚ ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º º ¾º½º ÓÐ ØÓÒ Ò Ó ÓÒ Ø º º º º º º º º º º º º º º º º º º º º ½¼ ¾º¾ À Ò Ñ Ò Ñ º º º º º º º º º º º º º º º º º º º º º º º º ½½ ¾º ÏË¹Ì ÓÖ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½¾ ¾º º½ Å ØØ Ó ÓÒ Ò Ñ Ø º º º º º º º º º º º º º º º º º º ½¾ ¾º º¾ ÃÝØ ÒØ ÖÑ ÓÒ Ò º º º º º º º º º º º º º º º º º º ½ ¾º º ÖÑ ÓÒ Ò Ñ Ø º º º º º º º º º º º º º º º º º º º º ½ ¾º º À Ò Ó ÓÒ º º º º º º º º º º º º º º º º º º º º º º º ½ ÄÙÓÒÒÓÐÐ ÙÙ ÓÒ ÐÑ Ø Ò Ö Ñ ÐÐ ¾¼ º½ Å Ò Ö ÒÓÖÑ Ð Ø Ó Ù Û ¹Ø ÓÖ º º º º º º º º º º º º ¾½ º½º½ Ú Ö Ó Ú Ø Ö Ø º º º º º º º º º º º º º º º º º º º º ¾½ º½º¾ Ê ÒÓÖÑ Ð Ø Ó º º º º º º º º º º º º º º º º º º º º º º ¾ º½º ÃÓÖ Ù Ø ÖÑ Ø º º º º º º º º º º º º º º º º º º º º º º º ¾ Ì Ò ÚÖ ¾ º½ Å Ò Ñ Ð Ò Ò Ø Ò ÚÖ Ø ÓÖ º º º º º º º º º º º º º º º º º º º ¾ º¾ Ä ÒÒ ØØÙ Ø Ò ÚÖ º º º º º º º º º º º º º º º º º º º º º º º º¾º½ ÖÑ ÓÒ Ò Ø Ò Ô ÓÒ Ò Ñ Ø º º º º º º º º º º º º º¾º¾ Å Ù ÑÙÙØØ Ú Ò ÙØÖ Ð Ú ÖØ º º º º º º º º º º º º º º ÃÚ Ð Ú Ø Ò ÚÖ º º º º º º º º º º º º º º º º º º º º º º º º º º½ Ö ÑÑ º º º º º º º º º º º º º º º º º º º º º º ¼ º Ë ÓØ Ø Ö ÙÙ Ñ ØØ Ù Ø º º º º º º º º º º º º º º º º º º ÒÓÑ Ð Ó Ò ÙÑÓÙØÙÑ Ò Ò º º º º º º º º º º º º º º º º º º º º½ Ï ØØ Ò Ò ÒÓÑ Ð º º º º º º º º º º º º º º º º º º º º º º¾ Å ØØ ¹ ÒÓÑ Ð Ø º º º º º º º º º º º º º º º º º º º º º º Å Ò Ñ Ð Ò Ò Ú Ð Ú Ø Ò ÚÖ Ñ ÐÐ º½ SU(N) Ò ÓÖ ÑÑ Ø ØÝ Ø º º º º º º º º º º º º º º º º º º¾ Ø Ú Ò Ò Ø ÓÖ º º º º º º º º º º º º º º º º º º º º º º º º º¾º½ Ã Ö Ð ÝÑÑ ØÖ º º º º º º º º º º º º º º º º º º º º º º¾º¾ Ì Ò Ô ÓÒ Ø º º º º º º º º º º º º º º º º º º º º º º º º º¾º ÃÝØ ÒØ ÓÓÒ ØÓÖ Ò º º º º º º º º º º º º ½ º¾º ÃÝØ ÒØ Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ Ò º º º º º º º º º ¾ ½

3 º ÒÓÑ ÒÓÐÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º½ Ð ÔØÓÒ Ô Ö Ò ØÙÓØØÓ º º º º º º º º º º º º º º º º º º º º º º¾ Ä ÔØÓÒ Ò Ó Ñ Ò Ò º º º º º º º º º º º º º º º º º º º º º À Ò Ù Ò Ó Ñ Ò Ò º º º º º º º º º º º º º º º º ζ Ò ÒØ Ò ÙØÖ ÒÓÒ ØÙÓØØÓ º º º º º º º º º º º º º º º ½ Ø ÒÚ ØÓ ¾ ¾

4 ½ ÂÓ ÒØÓ À Ù Ý Ò Ø Ò Ö Ñ ÐÐ ÐÙÓÒÒÓÒ ÚÙÓÖÓÚ ÙØÙ Ø Ö Ú Ø ¹ Ø ÓØ ÐÙ ÙÙÒÓØØ Ñ ØØ Ð Ø ØÒ Ú ÒØØ ÒØØØ ÓÖ ÐÐ º ËØ Ò Ö Ñ ÐÐ ¹ ÙØÙÙ ÓÓÒ Ú Ú Ò ØÓÖ Òº Î Ú ØÓÖ Ð É ÕÙ Ò¹ ØÙÑ ÖÓÑÓ ÝÒ Ñ Ú ÒØØ ÚÖ ÝÒ Ñ µ ½ ÙÚ Ú Ö Ò ÚÐ Ú ÚÓ ÚÙÓÖÓÚ ÙØÙ Ò Ø ÚÙÓÖÓÚ ÙØÙ ÚÐ ØØÚ Ñ ØØ Ó¹ ÓÒ ÐÙÓÒ º Ë Ó ØÓÖ ÔÙÓÐ Ø Ò ÐØ Ñ Ò ØØ ¹ Ò ÓÒ ÚÙÓÖÓÚ ÙØÙ Òº ËØ Ò Ö Ñ ÐÐ Ó ØÓÖ Ù¹ Ú Ø Ò Ð ÓÛ¹Ï Ò Ö ¹Ë Ð Ñ¹Ø ÓÖ ÐÐ ÏË¹Ø ÓÖ µ ¾ º Ì Ø ÓÖ ÓÒ ÓÐ ÐÐ Ø ÔÓÒØ Ò Ó ÝÑÑ ØÖ Ö Ó ÓÒ ØÙØ Ñ Ò Ø ØÝ ØÝØÒº ËØ Ò Ö Ñ ÐÐ Ó ÚÙÓÖÓÚ ÙØÙ ÙÚ Ø Ò Ö ÓÙØÙÑ Ø¹ ØÓÑ SU() U(1)¹ ÝÑÑ ØÖ ÐÐ Ø ÓÖ ÐÐ º Ì Ø ÓÖ Ù Ø Ò Ò ÚÓ ÒØÝ Ñ Ø ÖÑ Ñ ØØ Ó ÓÒ ÐÐ Ø ÖÑ ÓÒ ÐÐ ÐÐ Ò Ö ÓÚ Ø Ñ ØØ ÒÚ Ö Ò º Ë Ñ ÐÐ Ò ÐÐÝØ ØÒ ÑÝ Ð Ö Ò Ò À Ò ÒØغ ÌÑ ÒØØ ÙØØ ÔÓÒØ Ò Ò ÝÑÑ ØÖ Ö ÓÒ ÓÒ ÙÖ Ù Ò ÓØ Ñ ØØ ÒØØ W ± Z Ú Ø ÒÓÐÐ Ø ÔÓ Ú Ò Ñ ¹ Ò ÑÙØØ Ñ Ò ØØ Ø ÚÙÓÖÓÚ ÙØÙ Ø ÚÐ ØØÚ ÓØÓÒ ÐÝÝ Ñ ¹ ØØÓÑ Ò º ÌÐÐ Ò Ó ÝÑÑ ØÖ ÓÒ Ö ÓÙØÙÒÙØ Ö ÐÐ ¹ Ñ Ò ØØ Ó ÚÙÓÖÓÚ ÙØÙ º ÌØ Ñ Ò Ñ ÙØ ÙØ Ò À Ò Ñ Ò Ñ º ËØ Ò Ö Ñ ÐÐ ÓÒ ÓÐÐÙØ Ö ÑÑ Ò Ø Ó Ø Ò Ø Ó ¹ ÚÙØ ØÙÒ Ò Ö Ð Ò Ø Ú Ò Ø ÓÖ Ò º Ë Ò ÒÒÙ Ø Ø ÓÒ ÔÝ ØÝØØÝ Ø ¹ Ø Ñ Ò ÐÙ Ù ÝØØ Ñ ÑѺ Ä È Ä Ö Ð ØÖÓÒ¹ÈÓ ØÖÓÒ ÓÐÐ ¹ Ö ÊÆ Ò ØÓ Ñ ÒÒ µ ËÄ ËØ Ò ÓÖ Ä Ò Ö ÓÐÐ Ö ÍË µ Ì Ú ØÖÓÒ ÖÑ Ð ÍË µ ÓÒ Ú ØØÙ ØØ Ø Ò Ö Ñ ÐÐ Ò ÑÙ Ø Ýع ÒÒØ Ò Ò Ó Ù Ò Ú Ú ØÓÖ ÓÚ Ø ÙÙÖ ÐÐ Ø Ö ÙÙ ÐÐ Ó Ò º Ì ÙÐÙ Ó ½ ÓÒ Ø ØØÝ Ö Ò Ø Ò Ö Ñ ÐÐ Ò ÒÒÙ Ø Ñ ÙÙÖ Ø Ò Ò Ó ÐÐ Ø Ñ Ø ØØÙ ÖÚÓ º À Ò Ù Ø Ù Ø Ò Ò ÓÐ Ð Ý ØØÝ º À Ò Ù Ò ÓÐ ¹ Ñ ÓÐÓÒ Ó ÐÐ Ò Ò Ú Ú Ø Ñ Ò Ò Ò ÓÑ Ò ÙÙ Ò Ø Ö ÑÔ ØÙØ ¹ Ñ Ò Ò ÓÒ Ò Ý ØÖ ÑÑ Ø Ø ØÚ Ø ÙÙ ÄÀ ¹ ÝØØ Ñ Ä Ö¹ À ÖÓÒ ÓÐÐ Ö ÊÆ ØÓ Ñ ÒØ Ð ÚÙÓ Ò ¾¼¼ ÙÐÙ µº ÄÀ Ò Ð ÙÙÒÒ ØØ ÐÐ ÓÒ ÙÙ Ð ØÖÓÒ ¹ÔÓ ØÖÓÒ ¹ ÝØ Ò ÁÄ ÁÒØ ÖÒ Ø ÓÒ Ð Ä Ò Ö ÓÐÐ Öµ ÓÐÐ Ô Ø Ò ¼¼ Î Ò ÑÝ ÑÑ Ò ÓÔ ½ Ì Î Ò Ñ Ô Ø ¹ Ò Ö Ò e e + ¹Ø ÖÑÝ º

5 Ì ÙÐÙ Ó ½º ËØ Ò Ö Ñ ÐÐ Ò ÒÒÙ Ø Ñ ÙÙÖ Ø Ò Ò Ó ÐÐ ¹ Ø ÑÖ Ø ØÝ ÖÚÓ º È Ð Ó ÐÐ ÙÚ Ñ Ø ØÙÒ ÖÚÓÒ ÔÓ ¹ Ñ Ø Ò Ö ÔÓ Ñ µ Ø Ò Ö Ñ ÐÐ Ò ÒÒÙ Ø Ø º ÀÙÓÐ Ñ ØØ Ø Ò Ö Ñ ÐÐ Ò ÙÙÖ Ø Ñ Ò ØÝ Ø Ñ ØØ Ù ØÙÐÓ Ø Ò ¹ Ð ØØÑ Ò Ð ØØÝÝ ÓÒ ÐÑ ÏË¹Ø ÓÖ Ò ÐØÑ À Ò Ù ¹ Ò Ò ÓÒ Ð Ö Ò Ò Ð Ù Ò Ò ØÐÐ Ò Ù Ò ÓÐ Ñ ÓÐÓ

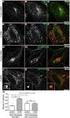
6 ÐØ Ø ÓÖ Ò Ö ÒØ Ò Ð ØØÝÚ ÓÒ ÐÑ º Æ Ø ÓÚ Ø Ò Ò ÙØ ÙØÙØ ÐÙÓÒÒÓÐÐ ÙÙ ¹ Ö Ö ¹ ØÖ Ú Ð ÙÙ ÓÒ ÐÑ Øº ÐÐ Ñ Ò ØÙØ ÓÒ ÐÑ Ø ÓÚ Ø ÐÙÓÒØ ÐØ Ò Ø ÓÖ Ò Ñ Ø Ñ ØØ Ò ÓÒ¹ Ø Ò Ò Ð ØØÝÚ ÚØ ÙÓÖ Ò Ð ØÝ Ø ÓÖ Ò ÒØ Ñ Ò ÒÒÙ Ø Òº À ¹ Ú ÒØÓ ÓØ ÙÓÖ Ò Ú ØØ Ú Ø Ø Ò Ö Ñ ÐÐ Ò ÙÐ ÓÔÙÓÐ Ò Ý Ò ÓÒ ÝÚ Ò Ú Òº ØÐÐ Ò Ò Ú ÒØÓ ÓÒ Ò ÙØÖ ÒÓ Ò Ñ Øº ËØ Ò Ö Ñ Ð¹ Ð Ò ÑÙ Ò Ò ÙØÖ ÒÓØ ÓÚ Ø Ñ ØØÓÑ ÑÙØØ Ú ÒØÓ Ò ÑÙ Ò Ò Ùع Ö ÒÓ ÐÐ Ù Ø Ò Ò ÓÒ Ô Ò Ñ º Î Ø Ò ÓØ Ò Ø Ò Ö Ñ ÐÐ Ò ÙÐ ÓÔÙÓÐ Ø Ý Ð ØØÑÒ Ú ÒÒÓØ Ò ÙØÖ ÒÓ Ò Ñ Ó Ø º ËØ Ò Ö Ñ ÐÐ ÑÝ Ò ÔÝ ØÝ Ð ØØÑÒ Ô Ñ Ò Ò Ò ÓÒ ÐÑ Ñ ÐÑ Ò Ù ÓÒ ÖÙÒ Ø Ò Ò ÙØ ÙØØÙ Ô Ñ Ò ØØ Ð ¹ Ø Ò ÙØÖ Ð ³Ò ÝÑØ Òس Ñ Ø Ö Ó Ø Ð Ñ Ò ØØ Ø Ø Ðݺ º ÌÑ Ò Ò ÑÙÙÒ ÑÙ Ø Ö Ð Ñ ÐÐ Ð Ò Ö ÙÒÓ ÐÐ ÓÐ Ú Ò Ø Ø Ò ÖØÓÒÓÔ ÙØØ Ð Ò Ô Ø Ò ÝÑÔÖ º ÌÑ Ú Ø Ö Ú Ø Ø ÓØ ÓÖ Ò ÒÒÙ Ø ØØ Ñ Ð Ð Ò Ñ ÓÓ ØÙÙ Ú Ò Ò ÝÚ Ø Ò Ø º Ë Ð ØÝØÝÝ Ò ÓÐÐ Ò ÝÚÒ Ò Ò Ð Ô Ñ Ò Ø¹ Ø Ó ÑÙÙØØ Ö Ú Ø Ø ÓÔÓØ ÒØ Ð º ÃÙÚ ½º À Ú ØØÙ ÖØÓÒÓÔ Ù Ð Ò Ô Ø Ò ÝÑÔÖ Ø ¹ ÝÝ Ò Ô Ø Ø ÙÒ Ø ÓÒ º È Ø Ú Ú ÓÒ Ò ÝÚÒ Ò Ò Ø ÓÚ Ú Ô Ñ Ò Ò Ò ÓÒØÖ ÙÙØ Óº ÃÙÚ Ð Ø Ø ½¼

7 ÃÙÚ Ò ½ ØØÑ ÖØÓÒÓÔ Ù ÚÓ Ø Ò Ð ØØ ÑÝ ÐÐ ØØ Ô ÒÓÚÓ ¹ Ñ ØÓ Ñ Ö Ø Ú ÐÐ ÙÙÖ ÐÐ Ø ÝÝ Ðк ÌÑ Ò Ñ ÐÐ Ù Ø Ò Ò Ó Ó ØØ Ù¹ ØÙÙ ÚÖ ÙÒ Ø Ö Ø ÐÐ Ò Ò Ð ÐÙ Ø Ö Ò Ø ÖÑÝ Øº Æ ÝÚ Ò ÐÙ Ø Ö ÓÒ ÔÓ Ò Ú ØÝÔÐ Ñ Ó ÚÙÓÖÓÚ ÙØØ Ø ÖÑÝ ØÓ Ò ÐÙ Ø Ö Ò ÔÐ Ñ Ò Ò Ð Ò Ó Ø ÚÙÓÖÓÚ ÙØØ ¹ Ú Ø Ô Ñ Ø Ò Ø º Ë Ö Ú Ø Ø ÓÔÓØ ÒØ Ð ÓÒ ØØÝÒÝØ ØÙÓÐÐ ¹ Ò Ø ÖÑÝ Ò Ð Ò Ö Ó Ø Ò Ù Ò Ò ÝÚ Ò º ÌÑ Ø Ð ÒÒ Ò ÝÝ ÐÚ Ø ÙÚ ¾º ½¼ ÃÙÚ ¾º Ö Ú Ø Ø Ó¹Ø ÔÓØ ÒØ Ð ÝÖØ ÐÙ Ø Ö Ø ½ ¼ ¹ º ƹ ÝÚ Ò ÓÒ Ú ØÝÔÐ Ñ Ó ÓÒ ÐÚ Ø ØØÝÒÝØ Ö Ó Ø Ò Ù Ò Ö Ú Ø Ø ÓÔÓØ ÒØ Ð Ò Ù Ø ÓØ Ò ÝÚØ Ú Ö ÐÐ Ñ Ö ØØÝ Ò Ø ÔÓØ ÒØ Ð ÝÖ Ò Ô Ø Òº ÃÙÚ Ð Ø Ø ½¼ º ÆÑ Ú ÒÒÓØ ØÙ Ú Ø Ø ÓÖ ÓÒ ÑÙ Ò Ð Ò Ô Ñ ¹ Ò ÓÓ ØÙÙ Ó Ø ÚÙÓÖÓÚ ÙØØ Ú Ø Ñ Ú Ø Ù Ø º ÇÒ Ø ØØÝ ÑÝ ØØ Ô Ñ Ò ÚÓ ÓÓ ØÙ Ñ Ú Ø ÓÑÔ Ø Ø Ó Ø Ø ÑÙØØ ÓÒ Ú ÓÒ ØÖÙÓ Ñ ÐÐ Ó ØÐÐ Ó Ø ÝÒØÝ Ö Ø¹ ØÚ Ø º ËØ Ò Ö Ñ ÐÐ Ù Ø Ò Ò ÐÐ ÐÐ Ø Ù Ø Ó Ø Ó Ø ÚÙÓÖÓÚ ÙØØ Ú Ô Ñ Ò ÚÓ ÐÙÓÒØ Ú Ø ÓÓ ØÙ º Ì Ø Ó ØÙ Ò Ø Ò Ö Ñ ÐÐ ÔÝÖ ØÒ Ð ÒØ Ñ Ò Ø Ò ØØ ÒÑ ÓÒ ÐÑ Ø ÔÓ ØÙ Ú Ø ÑÙØØ Ñ ÐÐ Ò ÙÙÖ Ø Ö ÙÙ Ñ ØØ Ù ØÙÐÓ Ø Ò ÒÒÙ ¹ Ø Ñ ÐÝ º Ø Ô Ð ÒØ Ø Ò Ö Ñ ÐÐ ÓÚ Ø Ò Ò ÙØ ÙØÙØ

8 Ø Ò ÚÖ Ø ÓÖ Ø ½½ ½¾ ½ ½ ½ ½ ½ ½ º Æ Ø ÓÖ Ó À Ò ØÓÖ ÓÖÚ Ø Ò ÙÙ ÐÐ Ú Ú Ø ÚÙÓÖÓÚ ÙØØ Ú ÐÐ ØÓÖ ÐÐ Ó ÐØ ÙÙ ÖÑ ÓÒ Ø Ò Ú Ö Ò Ò Ó Ñ Ò ÙÙ Ò Ú Ú Ò ÚÙÓÖÓ¹ Ú ÙØÙ Òº ÌÐÐ Ò Ò Ø ÓÖ ÔÝ ØÝÝ Ú Ø Ñ Ò ÓÒ ÝÑÑ ØÖ Ò Ö ÓÙØÙÑ Ø ÐÑ Ò Ø ÖÚ ØØ ÓÒ ÐÑ ÐÐ ÐÐ Ð Ö Ù ÐÐ º Ì Ò Ú¹ Ö Ø ÓÖ ÚÓ ÑÝ Ú Ø Ø Ô Ñ Ò Ò Ò ÓÒ ÐÑ Òº ÂÓ Ø ÓÖ Ò Ô Ö Ñ ØÖ Ø Ú Ð Ø Ò Ø ØÝÐÐ Ø Ú ÐÐ ÚÓ Ø ÓÖ ÐØ Ù Ò Ó ÓÐ ÐÙÓÒÒÓÐÐ Ò Ò Ò ØØ Ó Ø ÚÙÓÖÓÚ ÙØØ Ú Ô Ñ Ò ½ ¾¼ º Ì ØÝ ØÙØ Ø Ò Ó ÝÑÑ ØÖ Ö Ó Ø Ò ÚÖ Ø ÓÖ Ó º

9 ¾ À Ò Ñ Ò Ñ Ó Ø ÓÖ Ø Ò¹ Ö Ñ ÐÐ Ì Ö Ø ÐÐ Ò ÐÙ Ø Ò Ö Ñ ÐÐ Ò Ó ØÓÖ À Ò Ñ ¹ Ò Ñ º Ì ÓÒ ÓÐ ÐÐ Ø ÔÓÒØ Ò Ò ÝÑÑ ØÖ Ö ÓÒ ÐÑ Ò Ð ØØÝÚØ ÓÐ ØÓÒ Ò Ó ÓÒ Øº ÌÙØ Ø Ò ÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó À Ò Ñ Ò Ñ Ò Ò ÝÐ Ø ØØ Ò Ø Ò Ö Ñ ÐÐ Ò ÏË¹Ø ÓÖ º ¾º½ ¾º½º½ ËÔÓÒØ Ò ÝÑÑ ØÖ Ö Ó Ö ØØ ÝÑÑ ØÖ ÌÙØ Ø Ò φ 4 ¹Ø ÓÖ ÓÒ Ä Ö Ò Ò Ø Ý ÓÒ L = 1 ( µφ) + 1 µ φ λ 4! φ4 ½µ Ñ ÒÝØ µ > 0 Ð Ñ Ø ÖÑ ÓÒ ÚÖÒ Ñ Ö Ò Òº ÃÓÖÚ Ø Ò ÒÝØ φ φ = φ ÓÐÐÓ Ò L(φ ) = 1 ( µ( φ)) + 1 µ ( φ) λ 4! ( φ)4 = 1 ( µφ) + 1 µ φ λ 4! φ4 = L(φ) Ð L ÓÒ ÒÚ Ö ÒØØ ÑÙÙÒÒÓ φ φº L Ò À Ñ ÐØÓÒ Ò ÙÒ Ø Ó ÓÒ ( ) H = d 3 x(π(x) φ(x) L) = d 3 x φ(x) ( 0 φ) (1 µφ µ φ) L ( = d 3 x( φ (x) L) = d 3 x φ (x) 1 ( µφ) 1 µ φ + λ ) 4! φ4 ( 1 = d 3 x π + 1 ( φ) 1 µ φ + λ ) 4! φ4 ¾µ µ ÂÓ Ø ÔÓØ ÒØ Ð V (φ) = 1 µ φ + λ 4! φ4 º ÈÓØ ÒØ Ð Ò Ö Ú ØØ ÓÒ Ø Ò ¼ ÙÒ V (φ) = µ φ + λ 3! φ3 = 0 6 φ = 0 Ø φ = ± µ =: ±v, λ µ

10 Ñ φ = 0 ÓÒ ÐÓ Ð Ñ Ñ φ = ±v ÓÚ Ø Ñ Ò Ñ º à ÒØÒ ÖÚÓ Ó ÔÓØ ÒØ Ð ÐÐ Î ÓÒ Ñ Ò Ñ ÙØ ÙØ Ò ÒØÒ Ú ÙÙÑ Ó ÓØÙ ÖÚÓ º Ë ÖÖ ØÒ ÒÝØ ÒØØ Ö Ó Ø Ø Ò Ä Ö Ò Ò Ø Ý ÔÓØ ÒØ Ð Ò Ñ ¹ Ò Ñ Ò ÝÑÔÖ Ø Ð Ø Ò ÑÙÙØØÙ ÒÚ ØÓ φ(x) = v + σ(x)º ÌÐÐ Ò L = 1 ( µ(v + σ)) + 1 µ (v + σ) λ (v + σ)4 4! = 1 ( µσ) + 1 µ (v + vσ + σ ) λ 4! (v4 + 4v 3 σ + 6v σ + 4vσ 3 + σ 4 ) = 1 ( µσ) µ σ λ 6 µσ3 λ 4! σ4. µ ÌÑ ÓÒ µ¹ñ Ò Ð Ö ÒØÒ Ä Ö Ò Ò Ø Ý Ó ÓÒ σ 3 σ 4 ÚÙÓÖÓÚ ÙØÙ Ø Ó ÓÐ ÒÚ Ö ÒØØ ÑÙÙÒÒÓ σ σº ÌÑ ÝÑÑ ØÖ ÓÒ Ö ÓÙØÙÒÙØ ÙÒ ÒØØ ÓÒ Ø ØØÝ ÔÓØ ÒØ Ð Ò Ñ Ò Ñ Ò Ð Ý Ð Ò Ú ÙÙÑ Ò Ù Ø Òº ¾º½º¾ Â Ø ÙÚ ÝÑÑ ØÖ ÌÙØ Ø Ò Ä Ö Ò Ò Ø ÝØØ L = 1 ( µφ i ) + 1 µ (φ i ) λ 4 (φi ) 4, µ Ñ ÙÑÑ Ø Ò Æ Ò ÒØÒ {φ i } N i=1 ÝÐ Ø ÖÑ (φ i ) º ÂÐÐ Ò µ > 0 Ð Ñ Ø ÖÑ ÓÒ ÚÖÒ Ñ Ö Ò Òº ÃÓ L Ö ÔÔÙÙ Ú Ò (φ i ) Ø Ð φ Ò ÒÓÖÑ Ò Ò Ð Ø ÓÒ Ö ÔÔÙÑ ØÓÒ φ Ò ÙÙÒÒ Ø Ø º L ÓÒ ÒÚ Ö ÒØØ ÖÓØ ¹ Ø Ó º ÃÙØ Ò ÐÐ Ò ÔÓØ ÒØ Ð V (φ i ) = 1 µ (φ i ) + λ 4 (φi ) 4, µ ÓÒ Ö Ú ØØ ÓÒ ¼ ÙÒ V (φ i ) = µ φ i + λ(φ i ) 3 = 0, µ Ð φ i = 0 Ø (φ i ) = µ º Æ Ø ÓÖ Ó ÓÒ ÐÓ Ð Ñ Ñ ÔÓØ ÒØ Ð ÐÐ ÓÒ λ Ñ Ò Ñ ÙÒ φ Ò ÒÓÖÑ ÓÒ φ = µ =: v. µ λ

11 Ë Ö ØÒ ÒÝØ ÒØØ Ñ Ò Ñ Ò Ó ÐÐ ÙÙÒØ Ò (0, 0,..., 0,v) ½ Ð Ø Ò ÑÙÙØØÙ ÒÚ ØÓ ÌÐÐ Ò φ(x) (π 1 (x),π (x),...,π N 1 (x),v + σ(x)) = ( π(x),v + σ(x)). L = 1 ( µπ i ) + 1 ( µ(v + σ)) + 1 µ ((π i ) + (v + σ) ) ½¼µ λ 4 ((πi ) + (v + σ) ) = 1 ( µπ i ) + 1 ( µσ) µ σ λµ(π i ) σ λ (πi ) σ ½½µ λµσ 3 λ 4 σ4 λ 4 (πi ) 4, Ñ ÙÑÑ Ø Ò Æ¹½ Ò ÒØÒ {π i } N 1 i=1 ÝÐ Ø ÖÑ (π i ) º Ë Ø Ò σ ÓÒ Ñ Ú Ò Ò ÒØØ π i Ø Ñ ØØÓÑ º Ä Ö Ò Ò Ø Ý ÓÒ ÐÐ Ò Ýѹ Ñ ØÖ Ò Ò π i ¹ ÒØØ Ò ÖÓØ Ø Ó Ò Ù Ø Ò ÑÙØØ ÓÐ ÝÑÑ ØÖ Ò Ò Ò¹ ØÒ σ ÖÓØ Ø Ó Ò Ù Ø Òº ËÝÑÑ ØÖ Ò Ö ÓÙØÙÑ Ò Ò ÐÓ Ý Ò Ñ ¹ Ú Ò Æ¹½ Ñ ØÓÒØ ÒØغ Æ Ø Ñ ØØÓÑ Ó ÓÒ ÒØØ Ùع ÙØ Ò ÓÐ ØÓÒ Ò Ó ÓÒ º ÀÙÓÑ ØØ Ú Ù Ø Ò Ò ÓÒ ØØ Ø Ä Ö Ò Ò Ø Ý ÓÒ ÐÐ Ò ÒÚ Ö ÒØØ Ð ÙÔ Ö Ò ÑÙÙÒÒÓ Ò Ù Ø Òº Ë ÖØÝÑ Ò Ò ÒØÒ Ñ Ò Ñ Ò Ð Ý Ð Ò Ú ÙÙÑ Ò ÓÒ Ú Ò ÑÙÙØØÙ Ò¹ Ú ØÓ Ø Ò Ö Ó Ð ÙÔ Ö Ø ÝÑÑ ØÖ º ÃÓ Ù Ø Ò Ò Ý Ð Ø ÒØØ Ö Ó Ø Ø Ò Ý Ð Ò Ú ÙÙÑ Ò Ù Ø Ò ÚØ Ò ØÓØ ÙØ Ð ÙÔ ¹ Ö Ø ÝÑÑ ØÖ º ¾º½º ÓÐ ØÓÒ Ò Ó ÓÒ Ø ÓÐ ØÓÒ Ò Ø ÓÖ Ñ Ò ÑÙ Ò Ø ÙÚ Ò ÝÑÑ ØÖ Ò Ö ÓÙØÙ ÝÒØÝÝ ¹ Ò Ñ ØØÓÑ Ó ÓÒ ÒØØ Ò º ÓÐ ØÓÒ Ò Ó ÓÒ ¾½ ¾¾ º ÌÓ Ø ¹ Ø Ò ØÑ ØÙØ Ñ ÐÐ ÒØØ L = f(φ i, µ φ i ) V (φ i ) Ñ f й Ø Ú Ò Ø ÖÑ ÓØ Ö ÔÔÙÚ Ø φ Ò Ö Ú ØÓ Ø º ÇÐ ÓÓÒ ÔÓØ ÒØ Ð ÒÝØ ÐÐ Ò Ò ØØ ÐÐ ÓÒ Ñ Ò Ñ ÓÐÐ Ò ÒÓÐÐ Ø ÔÓ Ú ÐÐ ÒØÐÐ φ a 0 Ð V φ a φ a (x)=φ a = 0º Ã Ö Ó Ø Ø Ò Î Ö φa 0 0 Ò ÝÑÔÖ Ø ØÓ ÖØ ¹ ÐÙÚÙ V (φ) = V (φ 0 ) + 1 ( ) (φ φ 0) a (φ φ 0 ) b φ a φ bv, ½¾µ φ 0 ( ) Ó Ø V =: m φ a φ b ab ÓÒ Ñ Ñ ØÖ ÓÒ ÓÑ Ò ÖÚÓØ ÓÚ Ø Ý ¹ φ 0 Ð Ò Ú ÙÙÑ Ò Ù Ø Ò Ø ØØÝ Ò ÒØØ Ò Ñ Øº ½ ÎÓ Ø Ò Ú Ð Ø Ñ Ø Ò ÑÙÙ Ò Ô Ø Ó ØÓØ ÙØØ Ý ØÐ Ò µ ½¼

12 Ì Ö Ø ÐÐ Ò ØØ Ò ÝÑÑ ØÖ ÑÙÙÒÒÓ Ø φ a φ a + α a (φ) Ñ α ÓÒ Ò Ò Ø Ñ Ð Ò Ò a (φ) ÓÒ ÒØØ Ò {φ i } ÙÒ Ø Óº Ì Ö Ø ÐÐ Ò Ú Ó¹ ÒØØ ÓÐÐÓ Ò f(φ, µ φ) = 0 Ø Ò Î Ò ÓÒ ÓÐØ Ú ÒÚ Ö ÒØØ ÑÙÙÒÒÓ Ð V (φ a ) = V (φ a + α a (φ)), ½ µ Ó Ø Ö Ó ØØ Ñ ÐÐ Ý ØÐ Ò Ó ÐÐ ÔÙÓÐ ÐÐ Î Ö φ a Ò Ù Ø Ò Ò Ø Ò ÓÒ ÓÐØ Ú V (φ a ) V (φ a ) + α a (φ) φav (φ), ½ µ a (φ) φav (φ) = 0. ½ µ Ö ÚÓ Ñ ÐÐ ØØ φ b Ò Ù Ø Ò Ò Ô Ø φ = φ 0 ( ) ( ) ( ) a (φ) V (φ) + a (φ φ b φ 0 φ a 0 ) φ 0 φ a φ bv = 0 φ 0 ( V Ì = 0 ÓØ Ò ÓÒ ÓÐØ Ú φ )φ=φ a 0 ( ) a (φ 0 ) φ a φ bv = 0. φ 0 ½ µ ½ µ ÂÓ a (φ 0 ) = 0 Ò Ò ÝÑÑ ØÖ ÓÐ Ö ÓÙØÙÒÙØ ÒØÒ φ a Ó ÐØ Ð L ÓÒ Ý Ð Ò Ú ÙÙÑ Ò Ù Ø Ò Ø ØØÝÒ ÐÐ Ò ÝÑÑ ØÖ Ò Ò ÑÙÙØÓ Ò φ a φ a + α a ((φ) Ù Ø Òº ) ÂÓ Ø a (φ 0 ) 0 Ð ÝÑÑ ØÖ ÓÒ Ö ÓÙØÙ¹ ÒÙØ ÓÒ ÓÐØ Ú V = 0 Ø º φ a φ b φ 0 m ab = 0, ½ µ Ð ÓÒ ÝÒØÝÒÝØ Ñ ØÓÒ Ó ÓÒ ÒØغ Ë Ø Ò ÓÐ ØÓÒ Ò Ø ÓÖ Ñ ÓÒ ØÓ ¹ Ø ØØÙº ÓÐ ØÓÒ Ò Ø ÓÖ Ñ Ô ÙÓÖ Ò Ø ÑÙÓ Ó Ó Ø ÓÖ ÓÐ ÄÓÖ ÒØÞ¹ ÒÚ Ö ÒØØ º Ë Ø Ð ÒØ Ó Ñ ÐÐ Ò Ò ÔÓØ ÒØ Ð µ 0 Ø ÒØØ ÓÚ Ø ÔÖ Ð Ø Ú Ø ÚÓ ÝÒØÝÒ Ò ÓÐ ØÓÒ Ò Ó ÓÒ Ò ÑÖ ÓÐÐ Ö Ù Ò Ö ÓÙØÙÒ Ò Ò Ö ØØÓÖ Ò ÑÖº ¾º¾ À Ò Ñ Ò Ñ À Ò Ñ Ò Ñ Ñ ØØ Ó ÓÒ Ø Ú Ø Ñ Ò ÔÓÒØ Ò Ò ÝÑÑ ØÖ Ö ¹ ÓÒ Ú ÙØÙ Ø º ÌÙØ Ø Ò ÒØØ L Ó ÓÒ Ð Ö ÒØØ Ò {φ i } ÙÒ Ø Ó ½½

13 ÒÚ Ö ÒØØ ÓÒ Ò ÝÑÑ ØÖ ÖÝ ÑÒ Ù Ø Ò Ñ Ø ØØ ÑÙÙÒ¹ ÒÓ φ i (1 + iα a t a ) ij φ j Ñ α ÓÒ Ò Ò Ø Ñ Ð Ò Òº ÇÐ Ø Ø Ò ØØ φ i Ø ÓÚ Ø Ö Ð ÓÐÐÓ Ò t a Ò ÓÒ ÓÐØ Ú Ñ Ò Ö Ø Ò ÖÑ ØØ ÝÝ Ò ÒÓ ÐÐ ÒØ ÝÑÑ ØÖ º Å Ö ØÒ t a ij = itij a Ñ T a ÓÒ Ö Ð Ò Ò Ò¹ Ø ÝÑÑ ØÖ Ò Òº ÂÓ ÓÒ ÐÓ Ð Ñ ØØ ÝÑÑ ØÖ ÓÒ ÓÚ Ö ÒØØ Ö Ú ØØ ØÐÐ Ò D µ φ = ( µ iga a µt a )φ = ( µ + ga a µt a )φ, ½ µ Ñ A a Ø ÓÚ Ø Ñ ØØ ÒØغ Ë Ø Ò Ò ØØ Ò Ò Ø ÖÑ L ÓÒ 1 (D µφ i ) = 1 ( µφ i ) + ga a µ( µ φ i T a ijφ j ) + 1 g A a µa bµ (T a φ) i (T b φ) i. ¾¼µ ÇÐ ÓÓÒ ÒÝØ φ ÐÐ ÒÓÐÐ Ø ÔÓ Ú Ú ÙÙÑ Ó ÓØÙ ÖÚÓ φ i = (φ 0 ) i º ÌÐÐ Ò Ø Ô Ø Ø ÖÑ 1 g A a µa bµ (T a φ) i (T b φ) i = 1 m ab Aa µa bµ ÓÒ Ñ ØØ ÒØØ Ò A a Ñ Ø ÖÑ Ñ Ñ Ñ ØÖ ÓÒ m ab = g (T a φ 0 ) i (T b φ 0 ) i º Å Ø ÓÚ Ø Ó Ò Ñ Ö Ð ÔÓ Ø Ú ÐÐ ÓÒ Ð Ð ÓØ m aa = g (T a φ 0 ) 0 a. ¾½µ ÃÙ Ø Ò Ò Ó Ó Ò Ò Ò Ö ØØÓÖ Ø T a ØØ Ú ÙÙÑ Ò ÒÚ Ö ÒØ ÓÒ ØÐÐ Ò T a φ 0 = 0 Ø Ò Ý Ò Ò Ñ ØØ Ó ÓÒ Ñ ØØÓÑ º ¾º ¾º º½ ÏË¹Ì ÓÖ Å ØØ Ó ÓÒ Ò Ñ Ø Ð ÓÛ¹Ï Ò Ö ¹Ë Ð Ñ ¹Ø ÓÖ ÙÚ Ñ Ò ØØ Ó ÚÙÓ¹ ÖÓÚ ÙØÙ º ÌÙØ Ø Ò SU() U(1)¹ ÝÑÑ ØÖ Ø Ù Ð ØØ ÒØØ Ó ÓÒ ÒÚ Ö ÒØØ Ñ ØØ ÑÙÙÒÒÓ φ e iαa τ a e i β φ, ¾¾µ Ñ τ a = 1 σa È ÙÐ Ò σ¹ñ ØÖ µº Ë Ð Ö ÒØØ φ ÚÓ Ò Ö Ó ØØ ÑÙÓ¹ ØÓÓÒ φ(x) = U(x) 1 ( ) 0, ¾ µ v + h(x) Ñ h(x) ÓÒ Ö Ð ÖÚÓ Ò Ò ÒØØ ÓÐÐ h(x) = 0 U(x) ÓÒ Ó Ò ËÍ ¾µ¹ ÑÙÙÒÒÓ º ÃÓ φ ÓÒ ËÍ ¾µ¹Ñ ØØ ÒÚ Ö ÒØØ ÚÓ Ò U(x) ÔÓ Ø Ñ ØØ ÑÙÙÒ¹ ÒÓ ÐÐ º ÌÑ Ñ ØØ ÑÙÙÒÒÓ Ú Ø Ò Ò ÙØÙ ÙÒ ÙÒ Ø Ö Ñ Ø Ò Ú Ð ÒØ º ÇÐ Ø Ø Ò ÒÝØ φ ÐÐ φ 4 ¹Ä Ö Ò Ò Ø Ý L = D µ φ + µ φ φ λ(φ φ), ¾ µ ½¾

14 Ó Ø Ò ÔÓØ ÒØ Ð V (φ) = µ φ φ λ(φ φ) = 1 µ (v + h(x)) 1 4 λ(v + h(x))4. ¾ µ Ë Ø Ò ÔÓØ ÒØ Ð Ò Ö Ú ØØ ÓÒ ¼ ÙÒ V (φ) = µ (v + h(x)) λ(v + h(x)) 3 = 0, ¾ µ Ð v + h(x) = 0 Ñ Ñ µ Ø v + h(x) = µ λ Ñ Ò Ñ µº ÃÓ h(x) = 0 Ò Ú ÙÙÑ Ó ÓØÙ ÖÚÓ v = µ λ º Ë Ó ØØ Ñ ÐÐ ØÑ ÔÓØ ÒØ Ð Ò Ò V (φ) = 1 ( ) µ λ µ + h 1 ( ) 4 µ 4 λ λ + h = µ h λµh λh4 = 1 λ m hh m hh λh4, ¾ µ Ñ m h = µ = λv ÓÒ À Ò Ó ÓÒ Ò Ñ º Ì Ö Ø ÐÐ Ò ÒÝØ Ò Ò Ø Ñ Ð Ø Ñ ØØ ÑÙÙÒÒÓ Ø Ó α 1 = α = 0 α 3 = βº ÌÐÐ Ò e iαa τ a e i β φ = e i β (1+σ3) φ (1 + iβ (1 + σ3 )) φ = φ + iβ ( ( )) ( ) = φ 0 1 v ¾ µ Ð φ ÐÝÝ ÒÚ Ö ÒØØ Ò Ø ÑÙÙÒÒÓ Ø Ò Ú Ø Ú Ñ ØØ Ó ÓÒ Ñ ØØÓÑ º ÅÙÙØ ÓÐÑ Ñ ØØ Ó ÓÒ Ú Ø ÒÓÐÐ Ø ÖÓ Ú Ò Ñ Ò À Ò Ñ Ò Ñ Ò ÙØØ º ÆÝØ ÓÚ Ö ÒØØ Ö Ú ØØ ÓÒ D µ φ = ( µ iga a µτ a i g B µ)φ, ¾ µ Ó A a µ Ø ÓÚ Ø SU()¹Ñ ØØ ÒØØ B µ ÓÒ U(1)¹Ñ ØØ ÒØØ g g Ò Ò ÝØ ÒÚ Óغ Å ØØ Ó ÓÒ Ò Ñ Ø ÖÑ Ø Ò D µ φ Ò Ò Ð Ø ÙÒ Ø Ø Ò φ = φ º ÌÐÐ Ò (D µ φ) (D µ φ) = φ T (iga a µτ a + i g B µ)( iga bµ τ b i g Bµ ) φ + Ø ÖÑ µ φ = 1 ) ( ) 0 v (ga a 0 8 µ σ a + g B µ )(ga bµ σ b + g B )( µ +... v = v 8 (g (A 1 µ) + g (A µ) + ( ga 3 µ + g B µ ) ) +... ¼µ ½

15 Å Ö ØÒ ÒÝØ W ± µ = 1 (A 1 µ ia µ), ÓÐÐÓ Ò Z 0 µ = A µ = 1 g + g (ga3 µ g B µ ), 1 g + g (g A 3 µ + gb µ ), v 8 (g (A 1 µ) + g (A µ) + ( ga 3 µ + g B µ ) ) = v (g 4 W µ + + g 4 W µ (g + g ) Zµ 0 ) Ì Ø ÚÓ Ò ÐÙ Ñ ØØ Ó ÓÒ Ò Ñ Ø m W = gv, m Z = g + g v, m A = 0. ÌÙØ Ø Ò ÖÑ ÓÒ ÓÐÐ ÓÒ Í ½µ¹Ú Ö Ù Y º ÌÐÐ Ò ½µ ¾µ µ D µ = µ iga a µt a ig Y B µ = µ ig ( 1 (A 1 µ ia µ)(t 1 + it ) + 1 ) (A 1 µ + ia µ)(t 1 it ) i g + g 1 g + g (ga3 µ g B µ )(g T 3 g Y ) gg 1 i A 3 g + g g + g (g µ + gb µ )(T 3 + Y ) = µ i g (W µ + T + + Wµ T 1 ) i g + g Z µ(g T 3 g Y ) gg i g + g A µ(t 3 + Y ) µ Ñ T ± = (T 1 ± it ) = 1 (σ1 ± iσ )º ÃÙÒ ØÙÐ Ø Ò Ñ ØÓÒ Ó ÓÒ A µ ÓØÓÒ ÚÓ Ò ÒØ Ó Ð Ø¹ ÖÓÒ Ò Ú Ö Ù gg e = µ g + g ½

16 Ñ Ò ØØ Ò Ò Ú Ö Ù Q = T 3 +Y º ÅÖ Ø ÐÐÒ θ w Ø Ò ØØ cos θ w = g g sin θ +g w = g ÓÐÐÓ Ò g = e g +g sin θ w m W = m Z cos θ w º Æ Ò ÚÙÐÐ D µ Ò ÑÙÓØÓÓÒ D µ = µ i g (W µ + T + +Wµ T g ) i Z µ (T 3 sin θ w Q) iea µ Q, µ cos θ w Ó ÓÒ Ú Ò Ú Ô Ø Ô Ö Ñ ØÖ g Ø eµ θ w º ¾º º¾ ÃÝØ ÒØ ÖÑ ÓÒ Ò ÃÓ Ó Ò Ñ ØØ Ó ÓÒ Ò ÓÒ Ú ØØÙ ÝØ ÚÒ ÒÓ Ø Ò Ú Ò ¹ Ø Ò ÖÑ ÓÒ Ò Ø Ò ÖÑ ÓÒ ÒØÒ Ò ØØ Ò Ò Ø ÖÑ Ö ÐÐ Ò Ó Ò Ú Ò¹ Ó Ø ÐÐ ÒØ ÐÐ ψi/ ψ = ψ L i/ ψ L + ψ R i/ ψ R µ ÃÙÒ ÖÑ ÓÒ ÒØØ ÝØ ØÒ SU()¹Ñ ØØ ÒØØÒ Ð ÓÖÚ Ø Ò µ D µ Ø Ø Ò Ú Ò Ø Ø ÖÑ ÓÒ Ø ËÍ ¾µ¹ Ù Ð Ø Ó Ø Ø Ò Ð Ø ¹ º Ë Ø Ò Ó Ø ÐÐ ÒØ ÐÐ T i = 0 ÐÐ i ÐÐ Ò Q = T 3 ( + Y ) = Y ÓØ Ò Y er = 1 Y ur = Ò º Î Ò Ø ÐÐ ÒØ ÐÐ E νe 3 L = e ( ) ( ) L u 1 0 Q L = ÓÒ T d 3 = 1 σ3 = 1 Ø Ò Y 0 1 EL = 1 Y Q L = 1º 6 L ÃÓ Ú Ò¹ Ó Ø Ø ÖÑ ÓÒ ÒØØ ÓÚ Ø SU() Ò Ö ØÝ ØÝÝÔ ÐÐ Ò Ò Ñ Ø ÖÑ ÑÙÓØÓ m e (ē L e R + ē R e L ) ÓÐ Ñ ØØ ÒÚ Ö ÒØØ º ÁÐÑ Ò Ñ Ø ÖÑ ÚÓ Ò ÝØ ÒØ Ö Ó ØØ L = ĒL(i /D)E L + ē R (i /D)e R + Q L (i /D)Q L + ū R (i /D)u R + d R (i /D)d R. µ ÃÙÒ Ø Ò Ó Ø Ø Ò Ý ØÐ µ Ó ØØÙ ÑÙÓØÓ D µ ÐÐ Ò L =ĒL(i/ )E L + ē R (i/ )e R + Q L (i/ )Q L + ū R (i/ )u R + d R (i/ )d R + g (ĒLγ µ (W + µ T + + W µ T )E L + Q L γ µ (W + µ T + + W µ T )Q L + g cos θ w (ĒL γ µ Z µ (T 3 sin θ w Q)E L + ē R γ µ Z µ ( sin θ w Q)e R + Q L γ µ Z µ (T 3 sin θ w Q)Q L + ū R γ µ Z µ ( sin θ w Q)u R + d R γ µ Z µ ( sin θ w Q)d R ) µ + e(ēl γ µ A µ QE L + ē R γ µ A µ Qe R + Q L γ µ A µ QQ L + ū R γ µ A µ Qu R + d R γ µ A µ Qd R ). ½

17 ÆÝØ Ē L γ µ (W + µ T + + W µ T )E L = ( ν e ē ) L γµ (W + µ Ú Ø Ú Ø ÐÐ Ò ( ) Wµ 0 0 = W + µ ν L γ µ e L + W µ ē L γ µ ν L, Q L γ µ (W + µ T + + W µ T )Q L = W + µ ū L γ µ d L + W µ d L γ µ u L. ( ))( 0 0 νe 1 0 e Ē L γ µ Z µ (T 3 sin θ w Q)E L = Z µ ( 1 ν Lγ µ ν L + ē L γ µ ( 1 + sin θ w )e L ), Q L γ µ Z µ (T 3 sin θ w Q)Q L = Z µ ( ū L γ µ ( 1 3 sin θ w )u L + d L γ µ ( sin θ w )d L ). Å Ö ØÒ ÒÝØ Ñ Ò Ò ØØ Ø Ú ÖØ Ú Ö ØØÙ Ò ÙØÖ Ð Ó Ú ÖØ ( J µ Z = 1 ν L γ µ1 cos θ w ν L + ē L γ µ ( 1 + sin θ w )e L + ē R γ µ sin θ w e R + ū L γ µ ( 1 3 sin θ w )u L + ū R γ µ ( 3 sin θ w )u R ) L + d L γ µ ( sin θ w )d L + d R γ µ ( 1 3 sin θ w )d R ), ¼µ J µ EM = ēγµ ( 1)e + ūγ µ 3 u + dγ µ ( 1 3 d), J µ+ W = 1 ( ν L γ µ e L + ū L γ µ d L ), J µ W = 1 (ē L γ µ ν L + d L γ µ u L ). Æ Ò Ò ÐÓÔÙÐØ L =ĒL(i/ )E L + ē R (i/ )e R + Q L (i/ )Q L + ū R (i/ )u R + d R (i/ )d R + g(w µ + J µ+ W + W µ J µ W + Z µj µ Z ) + ea µj µ EM ½µ ½

18 ¾º º ÖÑ ÓÒ Ò Ñ Ø ÐÐ Ó ØÙ Ø Ä Ö Ò Ò Ø Ý Ø ÔÙÙØØÙÙ Ú Ð ÖÑ ÓÒ Ò Ñ Ø Ö¹ Ñ Øº Æ Ò Ð Ñ Ø ÓÖ Ò ÙÓÑ Ø Ò ØØ ÑÝ ÙÖ Ú ÒÐ Ò Ò Ø Ö¹ Ñ ÓÒ Ñ ØØ ÒÚ Ö ÒØØ L e = λ e Ē L φe R + h.c. ¾µ ÃÙÒ ØÑ Ø ØÒ φ Ò Ú ÙÙÑ Ó ÓØÙ ÖÚÓ Ò Ð ØÖÓÒ ÐÐ Ñ ¹ Ø ÖÑ ( ) ) 1 0 L e = λ e ( νl ē L e v R + h.c = λ e vē L e R + h.c., µ Ñ Ø ÚÓ Ò ÐÙ Ð ØÖÓÒ Ò Ñ m e = 1 λ e vº ÅÝ Ú Ö ÐÐ Ò Ñ Ø ÙÒ Ö Ó Ø Ø Ò L q = λ d QL φd R λ u ǫ ab QLa φ b u R + h.c., Ñ Ú ÙÙÑ Ó ÓØÙ ÖÚÓ ÒØ L q = λ d (ūl dl ) 1 ( 0 v ) = λ d v d L d R λ u vū L u R + h.c. d R λ u ū L 1 vu R + h.c µ µ Ì Ø ÚÓ Ò ÐÙ Ú Ö Ò Ñ Ø m u = 1 λ u v m d = 1 λ d vº ÃÙÒ Ø ÓÖ Ò Ð ØÒ ÙÙ ÖÑ ÓÒ Ù ÙÔÓÐÚ Ò Ò ÐÐ Ñ Ø Ú Ø Ú Ø º Ë Ñ ÐÐ ÝÒØÝÝ ÑÝ Ø ÖÑ ÓØ ÝØ ÚØ Ù ÙÔÓÐÚ Ø ØÓ Ò¹ Ñ Ö ØÒ Ù¹ ¹ØÝÝÔ Ò Ú Ö u i L = (u L,c L,t L ) d i L = (d L,s L,b L )º Ã Ö Ó Ø Ø Ò ÒÑ ÒÝØ Ñ Ò ÓÑ Ò ÒÒ º Ì Ò Ô ØÒ ÙÒ Ø Ö ¹ ÑÙÙÒÒÓ ÐÐ u i L = Uij u u j L di L = Uij d d j L º ÌÐÐ Ò Ú Ö ØØÙ Ú ÖØ ØÙÐ Ú Ö ¹ Ò Ó ÐØ ÑÙÓØÓÓÒ J µ+ W = 1 ū i Lγ µ d i L = 1 ū i Lγ µ (U uu d ) ij d j L. µ Ì (U uu d ) ij =: V ij ÓÒ ÙÒ Ø Ö Ò Ò Ó¹ÃÓ Ý ¹Å Û ¹Ñ ØÖ º V ij Ò ¹ ÓÒ Ð Ø ÖÑ Ø Ñ ÓÐÐ Ø Ú Ø Ú Ö Ù ÙÔÓÐÚ Ò Ó ØØÙÑ Ò ÓÒ Ú Ö ØÙÒ Ú ÖÖ Ò ÚÐ ØÝ Ðк ½

19 ¾º º À Ò Ó ÓÒ Ì Ö Ø ÐÐ Ò Ú Ð À Ò Ù Ò ÚÙÓÖÓÚ ÙØÙ º ÃÓÚ Ö ÒØ Ò Ö Ú ¹ Ø Ò µ ÚÙÐÐ Ò À Ò Ó ÓÒ Ò Ò ØØ Ò Ò Ø ÖÑ D µ φ = 1 ( µ(v + h)) (( ( ) ( ))( )) + g W µ+ + W µ v + h ( ( ) ( ))( ) W µ+ + W µ g cos θ w 1 8 (( Z µ ( v + h )) ( )) ( 0 v + h Z µ ( = 1 ( µh) + g 4 W µ + W µ (v + h) + 1 Z 8 cos µ Z µ (v + h) θ w = 1 ( µh) + (m WW + µ W µ + 1 m ZZ µ Z µ )(1 + h v ). g )) ( ) 0 v + h µ Ì Ø ÔÓØ ÒØ Ð Ø ¾ µ ÚÓ Ò ÐÙ ÝÒÑ Ò Ò ÒÒ Ø Ú ÖØ ÐÐ ÓØ ÐØÚØ À Ò Ó ÓÒ Ò Ñ ØØ Ó ÓÒ º Ë Ò Ú ÖØ Ø {W + W h} = i m W v gµν, {Z 0 Z 0 h} = i m Z v gµν, λ {hhh} = 6i m h = 3i m h v {hhhh} = iλ. µ Ä Ö Ó ØØ Ñ ÐÐ Ù ÖÑ ÓÒ Ò Ñ Ø ÖÑ Ø Ò L e = λ e Ē L φe R = 1 ) ( ) 0 λ e ( νl ē L e v + h R + h.c. = m e ē L e R (1 + h µ v ) + h.c. L q = λ d QL φd R λ u ǫ ab QLa φ b u R + h.c. = m d dl d R (1 + h v ) m uū L u R (1 + h v ) + h.c. ¼µ ½

20 Ë Ø Ò Ò Ú Ð ÝÒÑ Ò Ò ÒØ À Ò Ó ÓÒ Ò ÖÑ ÓÒ ¹ ÒØ ÖÑ ÓÒ ¹ Ô Ö Ò Ú ÖØ ÐÐ {f fh} = i m f v. ½µ ØÐ Ò ¾ µ Ð Ò Ø ØÝ ÙÒ Ø Ö Ñ Ø Ò Ú Ð ÒØ ÔÓ Ø Ø ÓÖ Ø ÓÐ ØÓ¹ Ò Ò Ó ÓÒ Øº ÂÓ Ú Ð Ø Ò Ó Ò ØÓ Ò Ò Ñ ØØ Ø ÓÖ ÒØÝÝ À Ò Ù ¹ Ò Ð ÒØØ φ + φ φ 0 ÓØ ÙÒ Ø Ö Ñ Ø ÓÚ Ø Ó Ò Ñ Ø¹ Ø Ó ÓÒ Ò ÐÓÒ ØÙ Ò Ð Ø ÓÑÔÓÒ ÒØ Øº Ä Ñ Ø Ò Ú Ð ÒÒ Ø Ö ÔÔÙ Ò Ø ÓÖ ÒØÝÝ Ò Ò ÙØ ÙØØÙ Ú¹ÈÓÔÓÚ¹ Ú Ø º ÆÑ ÓÚ Ø Ô Ý¹ Ð Ù ÓØ ÚÓ Ú Ø Ù Ø Ò Ò ÒØÝ ÝÒÑ ÒÒ Ò Ö ÑÑ Ò ÚÐ Ø Ð Ù Ò º ½

21 ÄÙÓÒÒÓÐÐ ÙÙ ÓÒ ÐÑ Ø Ò Ö Ñ ÐÐ ÂÓ Ø ÓÖ ÒØÝÝ Ó Ò ÝÚ Ò Ô Ò Ø Ö Ò ³ ØØݳ Ô Ö Ñ ØÖ ÖØØ Ý ÝÑÝ Ò Ø Ñ ØÐÐ Ô Ö Ñ ØÖ ÐÐ ÓÒ ÙÙÖ Ý Ò Ò ÒÓ¹ ØØÝ ÖÚÓº ÌØ ÓÒ ÐÑ ÙØ ÙØ Ò ÐÙÓÒÒÓÐÐ ÙÙ ÓÒ ÐÑ º ÌÐÐ Ò ÒÓ ØÝÒ Ô Ö Ñ ØÖ Ò ÒÓØ Ò ÓÐ Ú Ò Ø Ò Ø ÐÙÓÒÒÓй Ð Ò Ò Ñ Ð Ø ÐÝ ÓÖ Ù Ø Ò ÖÚÓÓÒ ÓÚ Ø ÑÙÐØ ÔÐ Ø Ú ÐÐ Øй Ð Ò ÙÙÖ Ò ÖÚÓ ÔÝ ÝÝ Ô Ò Ò Ø ÐÝ ÓÖ Ù º ÌÐÐ Ò Ò Ø Ð ÒÒ ÝÒ¹ ØÝÝ Ñ Ð Ý Ò Ô Ö Ñ ØÖ Ò ÖÚÓÒ ØÑ Ò Ò ÒÓÐÐ Ò ÝÒÒÝØØ Ø ÓÖ Ò ÝÑÑ ØÖ Ò Ó Ø ÒÓÐÐ Ø ÔÓ Ú Ø Ø ÐÝ ÓÖ Ù Ø Ô Ö Ñ ØÖ Ò Ö¹ ÚÓÓÒ ÖØ ÐÙÚÙ º ÐÐ Ò Ð ØØÑØØ Ñ ÖÚÓ ÓÒ ÙÙÖ Ý Ò Ò ÑÙØØ ÙÒ ÓÒ ÖÖ Ò ØØÝ ÔÝ ÝÝ Ñ ÙÙÖÙÙ ÐÙÓ ¹ Ø ÐÝ ÓÖ Ù Ø ÙÓÐ Ñ ØØ º ÌÝÝÔ ÐÐ Ø ÖÑ ÓÒ ÒØØ Ò ØØ Ñ Ò Ò Ñ ØØÓÑ ÐÙÓ Ö Ð Ò ÝÑÑ ØÖ Ò ÓÒ ÚÙÓ Ø ÐÝ ÓÖ Ù Ø Ö¹ Ñ ÓÒ Ò Ñ Ò ÓÚ Ø ØÙÓÐÐÓ Ò ÑÝ ÒÓÐÐ º Ë Ø Ò ÖÑ ÓÒ Ò Ñ Ø ÓÚ Ø Ø Ò Ø ÐÙÓÒÒÓÐÐ º Ë Ð Ö Ù Ò Ø Ô Ù ØÐÐ Ø ÝÑÑ ØÖ ÝÒÒݺ Ë Ø ¹ ÐÝ ÓÖ Ù Ø Ð Ö Ò Ð Ù Ò Ñ Ò ÓÚ Ø Ø Ú Ø Ò ÝÒÒÝØØÚØ Ð Ö Ù ÐÐ ÒÓÐÐ Ø ÔÓ Ú Ò Ñ Ò Ú ÔÙÙ¹ Ø ÓÐÐ ØØ Ò ÒÓÐÐ º Ë Ð Ö Ù Ò Ñ ÓÙ ÙØ Ò ¹ ØÑÒ ÙÙ Ø Ò ÖØ ÐÙÚÙ ÓØØ ÔÝ Ý ÒÒ ØÙ ÙÙ¹ ÖÙÙ ÐÙÓ º Æ Ò ÓÐÐ Ò Ð Ö Ù Ò Ø Ö Ò ØØÝ Ñ ÓÒ Ý¹ Ú Ò ÔÐÙÓÒÒÓÐÐ Ò Ò Ú Ø ÓÒ ÒÐ Ò Ð ØÝ Òº ÈÓ Ù Ò Ø Ò ÓÚ Ø ÓÐ ØÓÒ Ò Ó ÓÒ Ø ÓØ ÚÓ Ú Ø ÓÑ Ø Ø Ò Ø ÐÙÓÒÒÓÐÐ Ò Ô Ò Ò Ñ Ò ÔÓÒØ Ò Ø Ö ÓÙØÙÒ Ò ÝÑÑ ØÖ Ò ÚÙÓ º ÌÓ Ò Ò ÔÓ Ù ÓÒ ÐÐ Ò Ò Ð Ö Ù Ò Ò Ó ÓÐ Ð Ù Ò Ò Ú Ò ÓÓ ØÙÙ ¹ Ð Ö Ø Ð Ù Ø º ÌÑÒ Ñ Ò Ñ ØØ Ò ÑÖÝØÝÝ ÓÒ Ø ØÙ ÒØØ Ù Ø Ò ÝÒ Ñ Ò Ô ÖÙ Ø ÐÐ Ø Ò Ø ÐÝ ÓÖ Ù ÙÓÖ Ò Ú Ò ÚРй Ð Ø ÓÒ Ø ØÙ ÒØØ Ù Ø Ò ÝÒ Ñ Ò Ú ÙØØ Ú Ò Ø ÐÝ ÓÖ Ù Ø Ò ÙØØ º ËØ Ò Ö Ñ ÐÐ À Ò Ó ÓÒ ÙÙÐÙ ÙÑÔ Ò Ò Ò Ø ÐÙÓ Ø Ø Ò Ò Ñ Ò Ð ØØÝÝ ÐÙÓÒÒÓÐ ÙÙ ÓÒ ÐÑ º Ì Ö Ø ÐÐ Ò Ñ Ö Ò Ù Û ¹Ø ÓÖ Ò Ö ÒÓÖÑ Ð Ó ÒØ Ý ÐÑÙ ¹ Ø ÓÐÐ Ó ÔÐ ØØ Ø Ò Ò Ð Ö Ò ÖÑ ÓÒ Ò Ñ ÓÖ Ù Ø Ò ÖÓº Ë Ñ Ò ØÝÝÔ Ø ÓÖ Ù Ø Ò ÑÝ Ø Ò Ö Ñ ÐÐ Ò Ó Ø ÓÖ º ¾¼

22 º½ Å Ò Ö ÒÓÖÑ Ð Ø Ó Ù Û ¹Ø ÓÖ º½º½ Ú Ö Ó Ú Ø Ö Ø Ì Ö Ø ÐÐ Ò Ù Û ¹Ø ÓÖ ÓÒ Ä Ö Ò Ò Ø Ý ÓÒ L = 1 ( µφ 0 ) 1 m 0φφ 0 + ψ 0 (i/ m 0ψ )ψ 0 ig 0 ψ0 γ 5 ψ 0 φ 0, ¾µ Ñ φ ÓÒ Ö Ð Ò Ò Ð Ö ÒØØ ψ ÓÒ ÖÑ ÓÒ ÒØغ Ð Ò ¹ ¼ Ú ØØ Ò ØØ Ý ÓÚ Ø Ö ÒÓÖÑ Ð Ó Ñ ØØÓÑ Ø ÒØØ Ñ Ø ÝØ ÒÚ Óغ Ì Ø ÚÓ Ò ÙÓÖ Ò ÐÙ Ö ÒÓÖÑ Ð Ó Ñ ØØÓÑ Ò Ø ÓÖ Ò ÝÒÑ Ò Ò ÒÒ Ø = i(/k+m 0ψ) k m 0ψ = i k m 0φ = g 0 γ 5 Ì ÓÖ Ò Ú Ö Ó Ú Ø n¹ô Ø ÙÒ Ø ÓØ Ò ÐÚ ÐÐ Ø Ö Ø Ð Ñ ÐÐ Ö ¹ Ò Ú Ö Ò Ò Ò ÒÒ Ø Ø ØØ Dº ÃÙ Ò ÐÑÙ ØÙÓØØ ÒØ ÖÓ ÒÒ Ò ¹ÙÐÓØØ Ò Ú ÖÙÙ Ò ÝÐ º ÃÙ Ò Ð Ö ÔÖÓÖ ØØÓÖ ØÙÓØØ ÒØ Ö Ð Ò Ò Ñ ØØ Ò Ø ÖÑ Ò k Ù Ò ÖÑ ÓÒ ÔÖÓÔ ØØÓÖ ØÙÓØØ Ò Ñ ØØ Ò Ø ÖÑ Ò kº Ë Ø Ò ÒÒ ØÙÒ Ö Ò Ú Ö Ò Ò Ò ÒÒ Ò Ò Ø ÓÒ D = 4L p φ p ψ, µ Ñ L ÓÒ ÐÑÙ Ó Ò ÑÖ p φ ÓÒ Ø Ò Ð Ö ÔÖÓÔ ØØÓÖ Ò ÑÖ p ψ ÓÒ Ø Ò ÖÑ ÓÒ ÔÖÓÔ ØØÓÖ Ò ÑÖº ÆÝØ Ö Ú Ö Ó Ó D 0º ÐÐ Ò Ù Ò ÔÖÓÔ ØØÓÖ ØÙÓØØ ÒØ Ö Ð Ò Ð ¹ ÑÖÒ ÝÐ Ù Ò Ú ÖØ ØÓÓ Ý Ò Ð ÑÖÒ Ò Ð Ð ÑÖÒ Ðݹ Ñ Ò ÚÙÓ ÑÙØØ Ý Ú ÖØ Ø ØÓÓ ÒÓ Ø Ò Ò Ð Ð ÑÖÒ ¹ ÐÝÑ Ò Ó Ó Ö Ø Ò Ú ÙØ ÒØ ÖÓ ÒØ Ò ÑÖÒº Ã Ò ÐÑÙ ÒØ Ö Ð Ò ÑÖ ÓÒ Ø Ò L = p φ + p ψ v + 1, µ Ñ v ÓÒ Ú ÖØ Ò ÑÖº ÆÝØ Ò Ð Ö ÔÖÓÔ ØØÓÖ Ò ÝØ ÝØÝÝ Ò Ú ÖØ ÙÐ Ó Ò Ð Ö Ð Ò Ý Ú ÖØ º Ä Ý Ø Ò Ú ÖØ Ò ÝØ ÝØÝÝ Ò Ý Ð Ö ÙÐ Ó Ò Ò Ð Ø Ò Ò ÔÖÓÔ Ø¹ ØÓÖ µº Ë Ø Ò ÔØ v = p φ + n φ, µ ¾½

23 Ñ n φ ÓÒ ÙÐ Ó Ø Ò Ð Ö Ð Ó Ò ÑÖº Ë Ñ ÒÐ Ò Ö ÙÑ ÒØ Ò ÒÓ ÐÐ ÖÑ ÓÒ ÐÐ ÔØ v = p ψ + n ψ, µ Ñ n ψ ÓÒ ÙÐ Ó Ø Ò ÖÑ ÓÒ Ð Ó Ò ÑÖº Æ Ø Ý ØÐ Ø Ò Ò¹ Ò ØÙÒ Ö Ò Ú Ö Ò Ò Ò ÒÒ Ø D = 4L p φ p ψ = p φ + 3p ψ = v n φ + 3v 3 n ψ 4v + 4 = 4 3 n ψ nφ. µ ÌÑÒ Ô ÖÙ Ø ÐÐ Ú Ö Ó Ú n¹ô Ø ÙÒ Ø Ó Ø ÓÒ ÃÙ Ø Ò Ò ÙÓÑ Ø Ò ØØ Ð Ö Ò Ò ½¹Ô Ø ÙÒ Ø Ó ÓÒ Ý ÐÑÙ Ø ÓÐÐ d 4 k Tr(iγ 5 (/k + m 0ψ )) = g 0 (π) 4 (k m 0ψ )(k m 0φ ) = 0, ÐÐ Tr(γ 5 (/k + m 0ψ )) = 0º Ë Ø Ò Ð Ö Ò Ò ½¹Ô Ø ÙÒ Ø Ó Ú º ÐÐ Ò Ð Ö Ò Ò ¹Ô Ø ÙÒ Ø Ó Ý ÐÑÙ Ø ÓÐÐ ÓÒ ÆÝØ (1) = (ig 0 ) 3 d 4 k (π) 4 Tr(γ 5 (/k + m 0ψ )γ 5 (/k/p + m 0ψ )γ 5 (/k/q + m 0ψ )) (k m 0ψ )((k + p ) m 0ψ )((k + q) m 0ψ ) µ Ì Tr(γ 5 (/k + m 0ψ )γ 5 (/k/p + m 0ψ )γ 5 (/k/q + m 0ψ )) = m 0ψ k α (k + p ) β Tr(γ 5 γ α γ β ) + m 0ψ k α (k + q) β Tr(γ 5 γ α γ β ) = 0 + m 0ψ (k + p ) α (k + q) β Tr(γ α γ 5 γ β ) ¾¾ µ

24 Ë ÐÐ Tr(γ 5 γ α γ β ) = 0º Ë Ø Ò (1) = 0º Î Ø Ú Ø () = 0 ÓØ Ò ÑÝ Ð ¹ Ö Ò Ò ÓÐÑ Ô Ø ÙÒ Ø Ó Ú º Ã Ò Ú Ö Ó Ú n¹ô Ø ÙÒ Ø Ó Ø ÓÒ = iσ s = iσ f = iγ = im º½º¾ Ê ÒÓÖÑ Ð Ø Ó ÃÓ Ð Ö Ò Ò Ò Ð Ô Ø ÙÒ Ø Ó ÓÒ Ú Ö Ó Ú ØÙÐ Ø ÓÖ ÒØÝÑÒ ØÑÒ Ú Ø Ø ÖÑ Ò Ø Ú Ø Ð Ö Ò Ò Ò Ð Ô Ø Ú ÖØ º ÌÑÒ ÚÙÓ Ð ØÒ Ø ÓÖ Ò ÑÝ Ö ÒÓÖÑ Ð Ó Ñ ØÓÒ Ò Ð Ú ÖØ = iλ 0, Ó Ò Ò Ð ÑÐÐ Ä Ö Ò Ò Ø ÝØ Ò Ø ÖÑ L = λ 0 4! φ4 0. ¼µ Ë Ð Ø Ò ÒÝØ ÒØØ φ 0 ψ 0 Ø Ò ØØ φ 0 = Z s φ ψ 0 = Z f ψº ÌÐÐ Ò L = 1 Z s( µ φ) 1 m 0φZ s φ +Z f ψ(i / m 0ψ )ψ ig 0 Z f Zs ψγ 5 ψφ Z s λ 0 4! φ4. ½µ ¾

25 ÅÖ Ø ÐÐÒ ØØ Ò Ú Ø Ø ÖÑ Ø δ s = Z s 1, δ f = Z f 1, δ mφ = m 0φZ s m φ, δ mψ = m 0ψ Z f m ψ, δ g = Z f Zs g 0 g, δ λ = Zsλ 0 λ, ¾µ ÓÐÐÓ Ò L = 1 ( µφ) 1 m φφ + ψ(i/ m ψ )ψ ig ψγ 5 ψφ λ 4! φ4 + 1 δ s( m uφ) 1 δ m φ φ + ψ(iδ f / δ mψ )ψ iδ g ψγ 5 ψφ δ λ 4! φ4, µ Å ÒÝØ ÐÑ Ò Ð Ò ¼ ÒØÝÚØ Ô Ö Ñ ØÖ Ø ÓÚ Ø Ý Ð Ø ÒØØ Ñ Ø ÝØ ÒÚ Óغ Ì Ø ÚÓ Ò ÐÙ Ö ÒÓÖÑ Ð Ó ÙÒ Ø ÓÖ Ò ÝÒ¹ Ñ Ò Ò ÒÒ Ø = i(/k + m ψ) k m ψ = i k m φ = gγ 5 = iλ = i(δ s k δ mφ ) ¾

26 = i(δ f k δ mψ ) = δ g γ 5 = iδ λ à ÒÒ Ø ØÒ ÙÖ Ú Ö ÒÓÖÑ Ð Ø ÓÔ Ø º ÃÓ ÓÐ ÑÑ ÒÝØ ÒÓ ¹ ØÙÒ Ø Ú Ò Ñ Ò Ö ÒÓÖÑ Ð Ó ÒÒ Ø Ø ØÒ Ö ÒÓÖÑ Ð Ø Ó ÓØ Ýع ÒÚ Ó ÐÐ λ g Ö Ó ØØ Ñ ØØ º Î Ø Ò ØØ ÔÖÓÔ ØØÓÖ Ò Ò Ú Ø ÓÚ Ø Ù Ø Ò Ñ Ò Ó ÐÐ Ù Ø Ò ÓÐÐ Ñ ÙÓÖ ÐÐ Ò ØØ Ò Ò Ò ÔÓ Ò Ö Ý ÓÒ ½º Ì Ø Ò Ö ÒÓÖÑ Ð Ø Ó ÓØ Σ f (/k = m ψ ) = 0 dσ f = 0 d/k /k=mψ Σ s (k = m φ) = 0 µ º½º ÃÓÖ Ù Ø ÖÑ Ø dσ s k = 0 dk =m φ ÖÑ ÓÒ Ò Ñ ÓÖ Ù ÖÑ ÓÒ Ò Ñ ÓÖ Ù Ò ÑÖ ØØÑ Ð Ø Ò ÔÐ ØØ Ø Σ f Ý ÐÑÙ Ø ÓÐÐ º ÆÝØ iσ f (/q) = Ì Ð ÑÑ Ò Ò Ó ÓÒ i(δ f/p δ mψ ) Ò ÑÑ Ò Ò ÓÒ (ig) d 4 k γ 5 (/k + m ψ )γ 5 (π) 4 (k m ψ )((q µ k) m φ ). ¾

27 ÃÝØØÑÐÐ ÝÒÑ Ò Ò Ô Ö Ñ ØÖ Ò Ò Ñ ØØ ÑÙÓØÓÓÒ 1 1 (k m ψ )((q k) m φ ) = = = dx (x((q k) m φ ) (1 x)(k m ψ )) dx (k xq k + xq xm φ (1 x)m ψ ) dx (l ), µ Ñ l = k xq = xm φ + (1 x)m ψ x(1 x)q º ÅÙÙØØÙ ÒÚ ÓÐÐ l = k xq Ó Ó ØØ ØÙÐ ÑÙÓØÓÓÒ γ 5 (/k + m ψ )γ 5 = /k + m ψ = /l x/q + m ψ. µ ÃÓ /l ÓÒ l Ò Ô Ö ØÓÒ ÙÒ Ø Ó Ú ÒØ ÖÓ ÒÒ Ó Ó Ð ÑÖ Ú ¹ ÖÙÙ Ò ÝÐ Ø Ò Ó Ó ØØ ØÙÐ x/q + m ψ. µ Ã Ò Ò 1 g 0 dx d 4 l x/q m 1 ψ (π) 4 (l ) = ig 0 d 4 l E dx x/q m ψ µ (π) 4 (le + ), Ñ ÓÒ ÙÓÖ Ø ØØÙ Ï Ò ÖÓØ Ø Ó l 0 ile 0 º Ì Ð Ò E Ú ØØ Ò ØØ ÒØ Ö Ð ÓÒ ÒÝØ ¹ÙÐÓØØ Ò Ù Ð Ò Ú ÖÙÙ Ò ÝÐ º ËÙÓÖ ¹ Ø Ø Ò ÒØ Ö Ð Ñ Ò ÓÒ Ð Ø Ö ÙÐ Ö Ó ÒØ ÝØØ Ò Ð ÖÖÝØÒ d¹ Ñ Ò Ó Ò Ù Ð Ò Ú ÖÙÙØ Òº ÌÐÐ Ò Ò 1 ig µ 4 d 0 = g µ 4 d 1 = ig (4π) d d l E x/q m ψ dx (π) d (le + ) dx dx x /q m ψ (4π) d ( ǫ γ E + log Γ( d) d Γ() ( ) 4πµ + log m ψ ( m ) ) ψ (x/q m ψ ), ¼µ ¾

28 Ñ ǫ = 4 d γ E ÓÒ ÙРֹŠÖÓÒ ¹Ú Ó µ ÓÒ Ñ Ð Ú ÐØ Ò Ò Ñ Ò Ñ Ò Ó Ò Ò Ô Ö Ñ ØÖ º ÌÑ ÙØÙÙ Ö ÐÐ Ò Ú Ö Ó Ú Ò Ó Ò Ó Ø Ú Ö Ó Ú Ó ÓÒ ig (4π) Ö ÐÐ Ò Ò Ó ÓÒ ( ǫ γ E + log ig 1 dx(x/q m (4π) ψ ) log 0 ( ÃÝØ ØÒ ÒÝØ Ö ÒÓÖÑ Ð Ø Ó ØÓ ÓÐÐÓ Ò Ò dσ f d/k /k=mψ = δ f + + = 0, 1 0 g (4π) ( )) 4πµ ( 1 m ψ / q m ψ ), ½µ m ψ xm φ + (1 x)m ψ x(1 x)q dσ f d/q ). ¾µ /q=m ψ = 0, µ ( 1 ǫ γ E + 1 ( 4πµ ) log m ψ ( ( m ) ψ dx x log xm φ + (1 + x) m ψ Ó Ø ( δ f = g 1 (4π) ǫ γ E + 1 ( 4πµ ) log m ψ + 1 ÐÐ Ò Ó Ø Ò 0 ( ( m ) ψ dx x log xm φ + (1 + x) m ψ Σ f (/q = m ψ ) = iδ f m ψ δ mψ + m ψ 1 0 Σ f (/q = m ψ ) = 0 (1 x)m ψ xm φ + (1 x) m ψ (1 x)m ψ xm φ + (1 x) m ψ ) ). ( ig 1 (4π) ǫ γ E + 1 ( 4πµ ) log m m ψ ψ ( m ) ) ψ dx(1 x) log xm φ + (1. x) m ψ ¾ ) ) µ µ µ µ

29 ÃÙÒ Ø Ò Ó Ø Ø Ò ÐÐ ÓÐ Ú Ð Ù δ f ÐÐ Ò ( δ mψ = ig m ψ ( 4πµ ) (4π) ǫ γ E + log m ψ ( (1 x)m ψ dx xm φ + (1 x) m ψ ( m )) ) ψ + log xm φ + (1. x) m ψ µ Ì Ø Ò Ò ÔÐ ØØ Ø ØØ ÖÑ ÓÒ Ò Ñ ÓÖ Ù δ mψ ÓÒ Ú ÖÖ Ò¹ ÒÓÐÐ Ò Ò ÖÑ ÓÒ Ò Ñ Ò m ψ º Ë Ø Ò ÖÑ ÓÒ Ò Ñ ÓÒ ÙÓ Ø Ðݹ ÓÖ Ù ÐØ Ò Ñ Ð ØØ Ø ÐÝ ÓÖ Ù Ø ÓÚ Ø Ú Ò ÖØÓ Ñ ÔÙÙØ ¹ ÓÒ Ñ Òº Ë Ð Ö Ò Ñ ÓÖ Ù Ä Ø Ò ØØ Ò Σ s Ý ÐÑÙ Ø ÓÐÐ º ÆÝØ iσ s (q ) = Ò ÑÑ Ò Ò Ö ÓÒ ( ig) ( d 4 k Tr γ 5 (/k + m ψ )γ 5 (/k + /q + m ψ ) ) (π) 4 (k m ψ )((k + q) m ψ ). µ ÂÐ ÚÓ Ò ÐÔÓ Ø Ð Tr ( γ 5 (/k + m ψ )γ 5 (/k + /q + m ψ ) ) = Tr ( ( /k + m ψ )(/k + /q + m ψ ) ) = 4m ψ k α (k + q) β Tr(γ α γ β ) = 4(m ψ k k q). ÝÒÑ Ò Ò Ô Ö Ñ ØÖ ÐÐ Ð ÖÖ Ø Ò ¼µ 1 1 (k m ψ )((k + q) m ψ ) = = ((1 x)(k m ψ ) + x((k + q) m ψ )) 1 (l ), ½µ Ñ l = k + xq = m ψ x(1 x)q º ÌÐÐ ÑÙÙØØÙ ÒÚ ÓÐÐ ÝÐ ÖØ ØÙÐ ÑÙÓØÓÓÒ 4(m ψ k k q = 4( l + x(1 x)q + m ψ), ¾µ ¾

30 Ñ l Ò Ô Ö ØØÓÑ Ø Ø ÖÑ Ø ÓÒ Ø ØØÝ ÔÓ ÐÐ Ò Ú ÚØ ÒØ ÖÓ ÒÒ Ó Ó Ð ÑÖ Ú ÖÙÙ Ò ÝÐ º ËÙÓÖ Ø Ø Ò ÒÝØ Ï Ò ÖÓØ Ø Ó l 0 il 0 E ÖÖÝØÒ Ñ Ò ÓÓÒ d ÓÐÐÓ Ò ÒØ Ö Ð ÓÒ Ó ÓÒ ÙÙ Ò 1 4ig µ ǫ = = 4ig (4π) = 4ig (4π) d d l E le dx + x(1 x)q + m ψ (π) d (le + ) dx µǫ 4ig (4π) d ( d Γ(1 d ) Γ() d 1 + Γ( d) ) d (x(1 x)q + m Γ() ψ) ( dx (1 ǫ ) + x(1 x)q + m ψ dx ( ( ǫ γ E)α + α log ( ) Γ( ǫ ) ( 4πµ ) ǫ ) 4πµ α log ( 1 x(1 x) q ) ), m ψ m ψ µ Ñ α = 3x(1 x)q m ψ º ÌÓ Ò Ò Ö ÓÒ i 1 d 4 λ k i. µ (π) 4 k m φ Ì Ò ÐÐ Ò Ï Ò ÖÓØ Ø Ó ÖÖÝØÒ Ñ Ò ÓÓÒ d ÓÐÐÓ Ò Ò i 1 λµǫ d d k E (π) d 1 k E + m φ = iλµǫ (4π) d = iλm φ (4π) Γ(1 d) (m Γ(1) φ) d 1 ( ǫ γ E + + log ( )) 4πµ. m φ µ ÆÝØ Ö ÒÓÖÑ Ð Ø Ó ØÓ dσ s (q ) q = 0 µ dq =m φ ÒØ ( ) δ s = 4g 1 (4π) ( ǫ γ E) + 1 log( 4πµ ) + A, µ m ψ ¾

31 Ñ A = 1 0 dx ( 3x(1 x) log(1 x(1 x) m φ ) x(1 x)(3x(1 x)m φ m ψ ) m ψ x(1 x)m φ ), m ψ µ ÐÐ Ò Ó Ø Ò Σ s (q = m φ) = 0 µ δ mφ = 1 (4π) ( λm φ 4g m ψ ) ( ǫ γ E + log ( 4πµ ) ) + 4g A + B, ¼µ m φ (4π) Ñ 1 B = λm φ (4π) + 0 dx ( 3x(1 x)m φ m ψ ) ( m φ ) log 1 x(1 x). ½µ m ψ ÇÐ ÐÐ Ø ÓÒ ÒÝØ ÙÓÑ Ø ØØ δ mφ Ò ÐÐ Ø Ú Ó ÓÒ Ú ÖÖ ÒÒÓÐÐ Ò Ò Ø ¹ Ò λm φ 4g m ψ º Ì Ø Ó ØÙ Ò φ Ò Ñ ÓÖ Ù ÓÐ ÒÓ Ø Ò ÖÖÓ Ò ÔÙÙØ ÓÒ Ñ Ò m φ Ú Ò ÐØ ÑÝ Ø ÖÑ Ò Ó Ð ØÒ ÔÙÙØ ÓÒ Ñ Òº Æ Ò ÓÐÐ Ò Ð Ö Ù Ò Ñ ÓÐ ÙÓ Ø ¹ ÐÝ ÓÖ Ù ÐØ Ú Ò ÔÝÖ Ú Ñ Ò Ó ÖØ ÐÙÚÙ º ÌÑ ÐÑ ÓÐ ÓÑ Ò Ò Ò ÒÓ Ø Ò Ø Ø ÐÐÝÐÐ Ù Û ¹Ø ÓÖ ÐÐ Ú Ò Ò¹ ØÝÝ Ò ÙÒ Ø ÓÖ ÐØ ÙÒ Ñ ÒØ Ð Ò Ð Ö Ô ÖØ Ð Òº ÌÓ Ò Ò Ø ¹ Ô Ò ØÑ ÐÑ ÓÒ ØÙÐ Ø Ø ÓÖ Ø Ú Ø ÓÖ Ó ÔØ ÓÒ ÙÒ Ò Ö Ð Ò Λ Ð ÔÙÓÐ ÐÐ º ÌÐÐ Ò Ð Ö Ù Ò Ñ ÓÖ Ù δ mφ ÓÒ ÙØ¹Ó ¹Ö ÙÐ Ö Ø Ó Ú ÖÖ ÒÒÓÐÐ Ò Ò Ø Ò Λ º ËØ Ò Ö Ñ ÐÐ Ò Ø Ô Ù ØÑ Ø Ö Ó ØØ Ø ØØ Ó ØÙÐ Ø Ò Ø Ò Ö Ñ ÐÐ Ø Ú ¹ Ø ÓÖ ÓÒ ÔØ ÚÝÝ ÐÙ ÔØØÝÝ Ð Ò Λ 1 Ì Î ÓÒ À Ò Ù Ò Ñ ÓÖ Ù δ mh Λ º ÌÐÐ Ò Ú Ø ÙÙÖØ ÒÓ Ø ÓØØ À Ò Ù Ò Ñ Ò ÔÝ ÝÑÒ ØÓ Ò Î Ò ÙÙÖÙÙ ÐÙÓ ¹ º Ë Ð Ö Ò À Ò Ù Ò Ð ØØÝÝ ÑÝ ÑÙ Ø ÐÙÓÒØ ÐØ Ò Ñ Ò ØÝÝÔÔ ÓÒ ÐÑ ¾ º Æ Ø ÓÚ Ø Ò Ò ÙØ ÙØØÙ Ö Ö ÓÒ ÐÑ ØÖ Ú ¹ Ð ÙÙ ÓÒ ÐÑ º À Ö Ö ÓÒ ÐÑ ÝÒØÝÝ Ø ØØ Ñ Ò Ð Ø ¹ ÓÒ ÝÑÑ ØÖ Ö ÓÒ Ò Ö Ð Ò ÓÐ Ø ØÙÒ Í̹ Ð Ò Ú ÐØ Ú Ù ¹ Ø ÐÐ Ø ÖÓ º ÌÖ Ú Ð ÙÙ ÓÒ ÐÑ ÝÒØÝÝ ÙÒ Ø Ö Ø ÐÐ Ò À Ò Ù ¹ Ò Ø ÝØ ÒÒÒ ÝØ ÒÚ ÓÒ Ð ÚÓÐÙÙØ ÓØ º ÃÝØ ÒÚ ÓÒ ÚÓ Ò ¼

32 ÒÒ ØÙÐÐ Ð ÐÐ µ ÖÚ Ó ÓÐ Ú Ò ½ λ(µ) λ(λ). ¾µ λ(λ) log Λ 16π µ ØÑ Ú ÐÐ µ ÙÒ Λ º Ë ÓÒ ÔÐÙÓÒÒÓÐÐ Ø ØØ À Ò Ø ÝØ ÒØ ÓÒ Ö Ù Ò ÒÓÐÐ º À Ò Ù Ò Ð ØØÝÚ ÓÒ ÐÑ ÚÓ Ò ÔÝÖ Ö Ø Ñ Ò Ù Ð¹ Ð Ö Ø Ú ÐÐ º ËÙÔ Ö ÝÑÑ ØÖ Ø Ñ ÐÐ Ø ¾ ÐØÚØ ÙÙÖ Ò ÑÖÒ Ø Ò Ö¹ Ñ ÐÐ Ò ÙÐ ÓÔÙÓÐ Ù ÓØ ÓÒ Ö Ø ÐØÝ Ø Ò ØØ ÓÒ ÐÑ ÐÐ Ø ÓÒØÖ ÙÙØ ÓØ ÙØ Ò ÐÐ Ø ØØÝ Ð Ö Ù Ò Ñ Ò Ø ÐÝ ÓÖ Ù ÙÑÓÙØÙÚ Øº Ì Ò ÚÖ Ø ÓÖ Ó À Ò Ù Ò Ò ÓÐ Ð Ù Ò Ò Ú Ò Ø Ò¹ Ö Ñ ÐÐ Ò ÙÐ ÓÔÙÓÐ Ø Ò Ù Ø Ò Ø Ò Ú Ö Ò ÓØØÙ Ø Ð º ÌÐÐ Ò Ø ÓÖ ÐÐ Ð Ò Ò Ð Ö Ø Ð Ù Ø Ø Ò ÑÝ Ò ¹ Ò Ð ØØÝÚ ÓÒ ÐÑ º Ì Ö Ø ÐÐ Ò ÒÝØ Ð ÑÑ Ò Ø Ò ÚÖ Ø ÓÖ º ½

33 Ì Ò ÚÖ Ì Ò ÚÖ Ø ÓÖ Ó ÓØ Ø Ò Ð Ø Ó Ø Ò Ö Ñ ÐÐ ÐÑ Ò À Ò ¹ ØÓÖ º Ë Ò Ó ØÓÖ ÓÓ ØÙÙ SU() U(1)¹Ñ ØØ ÒØ Ø ÓØ ÓÚ Ø Ð Ø Ó Ø Ø Ñ ØØÓÑ º Ì ÓÖ Ò Ð ØÒ ÙÙ ÖÑ ÓÒ Ó Ø Ò Ñ Ø ØÒ Ø Ò Ú Ö º ÆÑ Ó Ú Ø ÙÙ Ò Ú Ú Ò ÚÙÓÖÓÚ ÙØÙ Ò ÓØ ÙÚ Ø Ò ÚÖ ÖÝ Ñ SU(N TC )º ÌÑ Ú Ú ÚÙÓÖÓÚ ÙØÙ ÓÒ ÐÙÓÒ¹ Ø ÐØ Ò Ô Ø ÐØ É Ò Ú Ú Ò ÚÙÓÖÓÚ ÙØÙ Ò ÐØ Ò Òº Ë ØÓÓ Ø Ò ¹ Ú Ö Ø ÓÒ Ò Ø ÓÒ ÑÙÓ Ó ØÙÑ Ò Ò Ö ÓÓ Ø Ò Ú Ö Ò Ö ¹ Ð ÝÑÑ ØÖ Òº ÌÑÒ ÝÑÑ ØÖ Ö ÓÒ Ý Ø Ý ÝÒØÝÝ ÓÐ ØÓÒ Ò Ó Ó¹ Ò ÓØ ÓÖ Ó ØÙÚ Ø Ó Ò Ñ ØØ Ó ÓÒ Ò Ñ Ó Ø Ò Ö ÓÚ Ø ÓÒ ÝÑÑ ØÖ Òº ÌÐÐ Ò Ó ÝÑÑ ØÖ Ö ¹ Ó Ø Ô ØÙÙ ÝÒ Ñ Ø Ó ÔÓ Ø ÏË¹Ø ÓÖ ÒØÝÚØ Ö Ö ¹ ØÖ Ú Ð ÙÙ ¹ ÐÙÓÒÒÓÐÐ ÙÙ ÓÒ ÐÑ Øº º½ Å Ò Ñ Ð Ò Ò Ø Ò ÚÖ Ø ÓÖ Ì Ö Ø ÐÐ Ò Ø ÓÖ Ó ÓÒ Ø Ò Ö Ñ ÐÐ Ò ÙÐ ÓÔÙÓÐ Ø Ñ ØÓÒ¹ Ø ÖÑ ÓÒ T Bº Ë Ó Ø Ø Ò ÒÑ Ú Ò Ø Ò Ù Ð ØØ Ò Ø Ò Ó Ø Ò Ò Ð ØØ Ò ÙØ Ò Ø Ò Ö Ñ ÐÐ Ò Ò ÖÑ ÓÒ Ø Q TC L = ( T B ) L Q TC R = (T R,B R ), µ ÒÒ Ø Ò Ò ÐÐ ÝÔ ÖÚ Ö Ù Ø Y L = 0 Y R = ( 1, 1 )º ÆÑ Ó Ú Ø Ú ¹ Ú Ò ÚÙÓÖÓÚ ÙØÙ Ò ÓÒ Ò ÖÓ ÖÝ Ñ G TC = SU(N TC ) Ñ N TC ÓÒ Ø Ò ÚÖ Ò ÑÖº ÃÓ Ø Ò Ú Ö Ø ÓÚ Ø Ñ ØØÓÑ Ø ÓÖ Ò Ä Ö Ò¹ Ò Ø Ý ÒÒÝ Ñ Ø ÖÑ Ø m ( T L T R + T R T L ) m ( B L B R + B R B L ). Ë Ø Ò Ø ÓÖ ÓÒ ÒÚ Ö ÒØØ Ó ¹ Ú Ò Ø ÖÓØ Ø Ó Ð ÐÐ ÓÒ SU() L SU() R ¹ Ö Ð ÝÑÑ ØÖ º Ê ÓØ Ò ÒÝØ Ö Ð ÝÑÑ ØÖ ÒØ Ñ ÐÐ ÒØØÓÔ Ö ØØÓÖ ÐÐ TT + BB ÒÓÐÐ Ø ÔÓ Ú Ú ÙÙÑ Ó ÓØÙ ÖÚÓ TT + BB 0. µ ¾

34 ÌÐÐ Ò Ý Ð Ò Ò Ú ÙÙÑ ÓÒ Ò ÒÚ Ö ÒØØ ÖÓØ Ø Ó Ó Ú Ò¹ Ó Ø Ø ÖÓØ Ø ÓØ ÓÚ Ø Ú Ú Ð ÒØ Øº ÌÑ Ö ÓÓ SU() L SU() R ¹ Ö Ð ÝÑÑ ØÖ Ò SU() Isospin ¹ ÝÑÑ ØÖ º Ë Ø Ò ÝÒØÝÝ ÓÐÑ Ñ ØÓÒ¹ Ø ÓÐ ØÓÒ Ò Ó ÓÒ º ÃÙØ ÙØ Ò Ò Ø Ø Ò Ô ÓÒ Ñ Ö ØÒ Ò Ø π TC a, a = 1,, 3º Ì Ò Ô ÓÒ Ò Ó Ñ Ú Ó f TC ÑÖ Ø ÐÐÒ Ø Ò ØØ 0 J µ 5 a π TC b = f TC q µ δ ab, µ Ñ J µ 5 a = Qγ µ γ 5 τa Q a = 1,, 3 ÓÚ Ø Ó Ô Ò¹ Ð Ú ÖÖ Øº ÃÝØ ØÒ ÓÒ SU() L U(1)¹Ø ÓÖ Ò Ñ ØØ ÒØØ Ø Ò Ú Ö ¹ Òº ÆÝØ À Ò ÒØØ ÓÐ Ø Ò Ñ ØØ Ó ÓÒ Ø W ±,W 0 B ÓÚ Ø Ñ ØØÓÑ º Ì Ö Ø ÐÐ Ò W ± ¹ Ó ÓÒ Ò ÔÖÓÔ ØØÓÖ º Ë Ú ÙÙÑ ÔÓ¹ Ð Ö Ø Ó ÓÖ Ù Ò D W ±(q) = igµν q igµν q (1 Π(q )), µ Ñ Π(q ) ÓÒ Ú ÙÙÑ ÔÓÐ Ö Ø Óº Î ÙÙÑ ÔÓÐ Ö Ø ÓÒ ÑÖ ØØÑ Ø Ö Ø ÐÐ Ò Ø ÖÑ L = g W ± µ J µ, µ Ñ g ÓÒ SU() L ¹ ÝØ ÒÚ Ó J µ ÓÒ Ó Ô Ò¹Ú ÖØ Ó ÝØ W Ò Ø Ò ¹ Ú Ö Òº J µ ÙØÙÙ Ú ØÓÖ ¹ Ð Ó Ò Ø Ò ØØ J µ = J µ V Jµ 5 aº Æ Ø Ú Ò Ð Ú ÖØ J µ 5 a ØÙÓØØ ÓÒØÖ ÙÙØ ÓÒ W ¹ÔÖÓÔ ØØÓÖ Ò Ò ¹ Ô Òº Ë ÚÓ Ò Ö Ó ØØÙ ØÙØ Ñ Ò Ø ÖÑ L a = g W ± µ J µ 5 a. µ Ã Ö Ó Ø Ø Ò ÒÝØ Ý ØÐ µ ÓÔ Ö ØØÓÖ ÑÙÓ Ó ÌÑÒ ÚÙÐÐ Ø ÖÑ µ ØÙÐ ÑÙÓØÓÓÒ 1 Q TC γ µ γ 5 τ a Q TC = f TC µ π TC b δ ab. µ L a = g f TCW ± µ µ π TC a, ½¼¼µ Ó Ø ÔØ ÐÐÒ ØØ ÝÒÑ Ò Ò ÒØ W ± Ò Ø Ò Ô ÓÒ Ò ÝØ ÚÐÐ Ú Ö¹ Ø ÐÐ ÓÒ g f TCq µ º ÌÑÒ ÚÙÐÐ ÚÓ Ò Ú ÙÙÑ ÔÓÐ Ö Ø Ó ÐÙ ¹ Ö ÑÑ Ø

35 W ± π TC W ± 1 g f TC q g f TC º Ì Ø Ò Ú ÙÙÑ ÔÓÐ Ö Ø Ó Π(q ) q 0 g f TC 4q. ½¼½µ Ë Ø Ò W ± ¹ÔÖÓÔ ØØÓÖ ÓÒ D W ±(q) = igµν q g f TC 4. ½¼¾µ ÌÐÐ ÓÒ Ò Ô Ô Ø q = g f TC 4 Ø Ò ÚÓ Ò ÐÙ W ± Ò Ñ m W = g f TC. ½¼ µ ÐÐ Ò Ò ÙØÖ Ð ÐÐ Ñ ØØ Ó ÓÒ ÐÐ W 0 B ÚÓ Ò ÐÙ Ñ Ñ Ø¹ Ö Ò Ð ÓØ Ú ÙÙÑ ÔÓÐ Ö Ø Ó Ö ÑÑ Ø W 0 W 0 W 0 B B B g g 1 g 1 g g g 1 Ñ g 1 ÓÒ U(1)¹ ÝØ ÒÚ Óº Ì Ø Ò ( ) g m = g 1 g f TC q 1 g g1 4. ½¼ µ ÌÑÒ ÓÑ Ò ÖÚÓØ ÓÚ Ø 0 (g1 + g) f TC 4 º ÌÙÐ Ø Ò ØÑÒ Ñ ØÖ Ò ÓÑ ¹ Ò Ø Ð Ø Ý Ð ÒØ Z 0 A ÓÐÐÓ Ò Ò Z 0 Ò ÓØÓÒ Ò γ Ñ Ø m Z = g1 + g f TC ½¼ µ m γ = 0.

36 ÂÓ ÒÝØ ÑÖ Ø ÐÐÒ ÙØ Ò Ø Ò Ö Ñ ÐÐ g g 1 + g = cos θ w, ½¼ µ Ò Z 0 Ò W ± Ò Ñ Ó ÐÐ Ù m W = m Z cos θ w, ½¼ µ ÙØ Ò Ø Ò Ö Ñ Ð Ò ÒÒÙ Ø º ÌÑ Ñ ÐÐ Ò ÖÓ Ñ ØØ Ó ÓÒ ÐÐ Ó Ø Ñ Ø ÙÒ Ò Ú Ò Ø Ò Ô ÓÒ Ò Ó Ñ Ú Ó f TC ØÒ Ó Ò ÙÙÖÙ º ÌÐÐ Ý Ò ÖØ ÐÐ Ø Ò ÚÖ Ñ ÐÐ ÐÐ ÚÓ Ø Ò ØÙÓØØ Ó Ñ ¹ Ô ØÖ Ø Ò Ö Ñ ÐÐ Ò Ñ ØØ Ó ÓÒ ÐÐ ÐÑ Ò ÙÒ Ñ ÒØ Ð Ø Ð Ö Ô Ö¹ Ø Ð º Î Ø Ú Ø Ñ ØØ Ó ÓÒ Ò Ñ Ô ØÖ ÚÓ Ò ØÙÓØØ ÑÓÒ ÔÙÓ¹ Ð ÑÑ ÐÐ Ò Ø Ò ÚÖ Ñ ÐÐ ÐÐ Ó ÓÒ Ù ÑÔ Ø Ò ÖÑ ÓÒ Ù ÙÔÓÐÚ º ÌÐÐ Ò Ù Ø Ò Ò Ö ÓÙØÙÚ Ö Ð ÝÑÑ ØÖ ÖÝ Ñ ÓÒ ÙÙÖ ÑÔ Ø Ò ÓÐ ØÓÒ Ò Ó ÓÒ Ð Ø Ò Ô ÓÒ ÝÒØÝÝ Ò ÑÑÒº ÐÐ Ò ÓÐÑ Ò ¹ Ø Ú Ø ÓÖ Ø Ñ ØØ Ó ÓÒ Ò Ñ Ó ÑÙØØ ÐÓÔÙØ ÒØÝÚØ Ø ÓÖ Ý Ð Ò Ù Ò ¾ ¾ ¾ º ÌÐÐ Ò Ø ÓÖ Ò ØÝØÝÝ ÓØ Ò Ò Ð ØØ Ñ Ò Ø Ù ÓÐ Ú ØØÙ Ø Ò Ø Ó º ÌÑ ÚÓ Ò Ð ÑÐÐ Ø ÓÖ Ò Ñ Ò Ñ Ó Ò ÖÓ Ò ÐÐ Ù ÐÐ Ö ØØÚÒ ÙÙÖ Ø Ñ Øº º¾ º¾º½ Ä ÒÒ ØØÙ Ø Ò ÚÖ ÖÑ ÓÒ Ò Ø Ò Ô ÓÒ Ò Ñ Ø ËØ Ò Ö Ñ ÐÐ À Ò ÒØØ ÐÙÓ Ñ Ø Ñ ØØ Ó ÓÒ ÐÐ ØØ Ö¹ Ñ ÓÒ ÐÐ º ÐÐ ÙÚ ØÙÒ ÐØ Ò Ò Ø Ò ÚÖ Ø ÓÖ ÔÝ ØÝ Ò ÖÓ Ñ Ò Ñ Ø¹ Ø Ó ÓÒ Ò Ñ Ø ÑÙØØ ÐÐ Ñ Ò Ñ ÖÑ ÓÒ Ò Ñ Ó Ò ÐÙÓ¹ Ñ º ÖÑ ÓÒ Ò Ñ Ø ÖÑ Ø Ò Ö Ó ØØ Ñ ÐÐ Ø ÓÖ Ò Ò Ð ÖÑ ÓÒ ÚÙÓÖÓÚ ÙØÙ F L F QTC R L Q TC R, ½¼ µ Ó ÝØ Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ Ø Ø Ò ÖÑ ÓÒ Ø ØÓ Ò º Ì F L F R ÙÚ Ú Ø Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ ÒØØ Q TC L Q TC R Ø Ò Ú Ö ¹ ÒØØ º ÃÙÒ Ø Ò Ú Ö Ò Ö Ð ÝÑÑ ØÖ ÓÒ Ö ÓØØÙ Ò ÑÙÓ Ó Ø Ú Ø TC ÓÒ Ò Ø Ò Q ÓÐÐÓ Ò Ø ÖÑ ½¼ µ ØÙÐ ÑÙÓØÓÓÒ L QTC R Q TC L Q TC R F L F R. ½¼ µ

37 ÌÑ ÓÒ Ø Ú ÐÐ Ò Ò Ö Ò Ñ Ø ÖÑ Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ ÐÐ F º Ìй Ð Ò Ò Ø ÖÑ ÓÒ Ù Ø Ò Ò ¹Ö ÒÓÖÑ Ð Ó ØÙÚ º Ë Ò ÓÒ ÓÐØ Ú ÙÖ Ù Ø Ó Ø Ò ÓÖ ÑÑ Ò Ò Ö Ð Ò ÔÖÓ Ø º Æ Ð ÖÑ ÓÒ ÚÙÓÖÓÚ ÙØÙ Ñ Ø Ð ÐÐ Ò Ö Ð ÐÐ Ò Ø Ú ¹ Ø ÙÒ Ø Ø Ò Ø Ò ÚÖ ÖÝ Ñ G TC Ð ÒÒ ØÙÒ Ø Ò ÚÖ ¹ ÖÝ ÑÒ G ETC Ð ÖÝ Ñ º Ì Ñ ÐÐ ETC¹Ñ ØØ ÝÑÑ ØÖ Ö ÓÙØÙÙ ÓÐÐ Ò ÓÖ ÐÐ Ò Ö Ð ÐÐ Λ ETC Ø Ò ÚÖ Ò Ñ ØØ ÝÑÑ ØÖ º Ä ¹ ÒÒ ØØÙ Ø Ò ÚÖ ÐØ ÙÙ Ò Ñ ØØ Ó ÓÒ Ò Ó ÝØ Ø Ò Ú Ö Ø Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ Ø ØÓ Ò Ö ÑÑ Ò Q TC L Λ ETC F L F R Q TC L ÚÐ ØÝ Ðк ÃÓ ØÑ Ñ ØØ Ó ÓÒ ÓÒ ÝÚ Ò Ñ Ú Ò Ò ÚÓ Ò ØÝÝÔ ÐÐ ¹ ÐÐ Ò Ö ÐÓ ÐÐ q << Λ ETC ØØ ÚÙÓÖÓÚ ÙØÙ Ø ÝÚ Ò ÔÖÓ ÑÓ ÖÑ Ò Ò Ð Ô Ø ÚÙÓÖÓÚ ÙØÙ ÐÐ Q TC L F L F R Q TC R º Æ Ò ÓÐÐ Ò Ø ÓÖ ÒØÝÝ Ø Ú Ò Ò Ò Ð ÖÑ ÓÒ ÚÙÓÖÓÚ ÙØÙ Ø Ò ¹ Ú Ö Ò Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ Ò ÚÐ ÐÐ Ó ÐÙÓ ÖÑ ÓÒ ÐÐ Ñ Òº Æ Ò ÝÒØÝÒ Ò Ñ Ø ÖÑ Ò Ð ÚÓ Ò ÑÖ ØØ Ö Ø F L Q TC L Q TC R F R º

38 Ì ÖÑ Ô ÐÐÓ ÙÚ Ø Ò ÖÑ ÓÒ Ò ÝÒ Ñ Ø Ñ º ÅÝ Ø Ò ¹ Ô ÓÒ ÐÐ Ò Ñ ETC¹ÚÙÓÖÓÚ ÙØÙ Ò ÙØØ º Ë Ò Ò ÖÓ Ö Q TC R Q TC R π TC πtc Q TC Q TC L L º ÐÐ ÓÐ Ú Ø Ö Ø ÚÓ Ò ÐÙ Ø Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ Ò Ñ ¹ Ð m f g ETC TC Q Λ L Q TC R ETC, ½½¼µ ETC TC Ñ Q L QTC R ETC ÓÒ Ø Ò Ú Ö ÓÒ Ò Ø Ò ÖÚÓ ETC¹ Ð g ETC ÓÒ ETC¹ ÝØ ÒÚ Óº Î Ø Ú Ø Ø Ò Ô ÓÒ Ò Ñ Ð ÓÒ m π TC g ETC f TC Λ ETC ( Q TC L Q TC R ) ETC. ½½½µ Ì Ò Ú Ö ÓÒ Ò Ø Ò ÖÚÓ ETC¹ Ð Ò Ò ÖÚÓ Ø TC¹ ÝÑÑ ØÖ Ö ÓÒ Ð Ý ØÐ Ø ¾ TC Q L Q TC TC R ETC = Q L Q TC R TC exp Λ ETC Λ TC dµ γ m (µ), µ ½½¾µ Ñ γ m ÓÒ ÓÔ Ö ØØÓÖ Ò QQ ÒÓÑ Ð Ò Ò Ñ Ò Óº ÂÓ γ m << 1 ÓÒ ØÐÐ Ò TC Q L Q TC TC R ETC Q L Q TC R TC. ½½ µ É Ò Ð Ù Ø ÚÓ Ò ÖÚ Ó ØØ Q TC L Q TC R TC 4πf 3 TC, ½½ µ ÓØ Ò Ý ØÐ Ø ½½½µ Ò Ø Ò Ô ÓÒ Ò Ñ ÐÐ ÖÚ Ó m π TC (4π) getc f4 TC. ½½ µ Λ ETC

39 º¾º¾ Å Ù ÑÙÙØØ Ú Ò ÙØÖ Ð Ú ÖØ ÖÑ ÓÒ Ò Ñ Ó Ò ØÙÓØØ Ñ Ð ØÝÒ ETC¹ÚÙÓÖÓÚ ÙØÙ Ò ÚÐØع ÑØ Ò ÙÖ Ù ÓÒ Ñ Ù ÑÙÙØØ Ú Ò Ò ÙØÖ Ð Ò Ú ÖÖ Ò ÔÖÓ Øº ÆÑ ÝÒ¹ ØÝÚØ Ö ÑÑ Ø q Q TC q q QTC q Ñ q q ÓÚ Ø Ö Ù ÙÔÓÐÚ Ò Ú Ö º ÌØ Ö ÑÑ ÚÓ Ò Ð¹ Ð Ò ÔÖÓ ÑÓ Ò Ð ÖÑ ÓÒ ÚÙÓÖÓÚ ÙØÙ ÐÐ ÓÐÐÓ Ò Ò Ø Ú Ò Ò Ö ÑÑ q Q TC q q Q TC q ÌÑ ÐÙÓ Ø ÓÖ Ò ÚÙÓÖÓÚ ÙØÙ Ò L qq = g ETC V qq qγ µ q qγ Λ µq + h.c., ETC ½½ µ Ñ V qq ÓÒ Ú Ö Ù ÙÔÓÐÚ Ò q q Ó ØÙ Ø ÓÒ ÓÐ Ø Ø Ò ÓÐ Ú Ò Ú Ø Ú Ò Ó¹ ÙÐÑ Ò ÐÙÓ º Γ µ Γ µ ÓÚ Ø ETC¹Ú ÖØ Ò Ð ØØÝÚØ Ö Ð ÙÙ Ñ ØÖ Ø Γ µ γ µ (1 γ 5 )º Ì Ø ÚÓ Ò ÙÓÖ Ò Ð ÖÚ Ó Ò ÙØÖ Ð Ò ÓÒ Ò Ñ ÖÓÓÒ M K ÙÒ Ø Ø Ò q = d q = sº ÌÐÐ Ò Ò M K = g ETC V ds K 0 M K Λ dγ µ s dγ µs K 0 + c.c. ETC g ETC Re(V ds ) fkm K, Λ ETC ½½ µ

40 Ñ ÓÒ ÖÚ Ó ØÙ Ω dγ µ γ 5 s K 0 (p) = i f K p µ º ¾ Ì Ω ÓÒ Ý Ð Ò Ò Ú ÙÙÑ f K ÓÒ Ã¹Ñ ÓÒ Ò Ó Ñ Ú Ó f K 110 Šκ ÃÓ ÐÐ Ø ¼ Ø ØÒ ØØ M K 3, Ì Î Ó Ø ÙÖ ØØ Λ ETC g ETC Re(V ds ) 1300 TeV. ½½ µ ÃÙÒ ØÑ Ó Ø Ø Ò Ý ØÐ Ò ½½ µ Ò Ø Ò Ô ÓÒ Ò Ñ ÐÐ ÝÐÖ m πtc 4πf TC Re(V ds ) 1300TeV, ½½ µ Ó Ö Ð Ø ÐÐ V ds Ò f TC Ò ÖÚÓ ÐÐ V ds 0.1 f TC 50 Î ÒØ ÝÐÖ m πtc < 10 GeV. ½¾¼µ ÌÑ ÓÒ ÐÚ Ø Ð Ò Ô Ò Ñ ÓØØ ØÐÐ Ø Ù Ø ÓÐ Ó ¹ Ú ØØÙ Ø Ò Ø Ó º ÂÓØØ Ø Ò Ô ÓÒ Ø ÚÓ Ú Ø ÓÐÐ Ñ Ú ÑÔ ØÙÐ ETC¹ Ð Ò Λ ETC ÓÐÐ ÐÚ Ø Ô Ò ÑÔ º Î Ø ÑÙ Ñ Ù ÑÙÙØØ ¹ Ú Ò Ò ÙØÖ Ð Ò Ú ÖÖ Ò ÓÙ Ø ØÓ ÐØ Ø Ò Ô ÓÒ Ò Ñ Ú ÙÙ Ø ÒØ Ú Ø Ö Ø Ö Ø Ú Ø ÑÙ Ð Ò Λ ETC ÙÙÖÙÙ ÐÐ º º ÃÚ Ð Ú Ø Ò ÚÖ ÐÐ Ø Ò Ô ÓÒ Ò Ñ ÖÚ Ó Ø ÓÐ Ø ØØ Ò Ý ØÐ ½½¾µ ØØ γ m 1º ÌÑ Ó Ø ÓÒ ÐÑ Ò Ý Ñ Ù ÑÙÙØØ Ú Ò Ò ÙØÖ Ð Ò Ú ÖÖ Ò Ò º ÇÒ ÐÑ ÚÓ Ò Ö Ø Ø ÒØ Ñ ÐÐ Ì ¹ ÝØ ÒÚ ÓÒ α TC ÔÝ Ý Ð Ú ¹ ÓÒ Ò Ö ÐÓ Ò Λ TC Λ ETC ÚÐ ÐÐ ÐÙ ÐÐ º Ì Ò ÚÖ Ø ÓÖ Ó ÝØ ÒÚ ÓÒ Ð ÚÓÐÙÙØ Ó ÓÒ Ø ÙØ ÙØ Ò Ú Ð Ú Ø Ò ÚÖ º ÌÐÐ Ò Ø ÓÖ Ò β¹ ÙÒ Ø Ó β(µ) 1 ÙÒ Λ TC µ Λ ETC γ m 1 ½ º Ë Ø Ò Ý ØÐ Ø ½½¾µ Ò Λ ETC TC Q L Q TC TC R ETC Q L Q TC R TC exp 1 dµ µ Λ TC ½¾½µ ÌÐÐ Ò Ý ØÐ ½½ µ ØÙÐ ÑÙÓØÓÓÒ = Λ ETC TC Q L Q TC R TC. Λ TC m π TC (4π) g ETC f4 TC Λ ETC ¾ Æ Ò ÒÓØØÙ Ú ÙÙÑ ØÙÖ Ø Ó ÔÔÖÓ Ñ Ø Ó ¾ Λ ETC, ½¾¾µ Λ TC

41 Ø Ò Ñ Ù ÑÙÙØØ Ú Ò Ò ÙØÖ Ð Ò Ú ÖÖ Ò ÙÙÖÙÙ ÐÙÓ Ø ØÙ ÖÚ Ó ½½ µ ÒØ ÑÓ Ò Ö ÙÑ ÒØ Ò Ù Ò ÐÐ Ø Ò Ô ÓÒ Ò Ñ Ò ÝÐÖ m πtc 4πfTC Λ ETC. Re(V ds ) 1300TeV Λ TC ÂÓ ÝØ ÒÚ Ó α TC Ú Ð Ñº Ò ÖØ ÐÙÓ Ò ÝÐ Ð Ó ½¾ µ Λ ETC Λ TC 10, ½¾ µ ÓÒ Ý ØÐ Ò ½¾ µ ÝÐÖ ÒÝØ ÑÓ Ò ÓÐ ØÙ Ò V ds Ò f TC Ò ÖÚÓ ÐÐ Ù Ò ÐÐ m πtc < 1 TeV. ½¾ µ ÌÑ Ñ ÓÒ Ó Ö ØØÚÒ ÙÙÖ ÓØØ ØÐÐ Ø Ù Ø ÓÐ Ú ØØÙ Ø Ò Ø Ó º ÃÚ Ð Ú Ø Ò ÚÖ Ñ ÐÐ ÚÓ Ò ÓÚ ØØ Ý Ø Ò ØÓ ÐØ Ñ Ù ÑÙÙØØ Ú Ò Ò ÙØÖ Ð Ò Ú ÖÖ Ò ÓÙ ØÓ ÐØ Ø Ò Ô ÓÒ Ò Ö ØØÚÒ ÙÙÖ Ñ º º º½ Ö ÑÑ ÈÝÖ ØÒ ØØ Ò ÓÒ ØÖÙÓ Ñ Ò ØÐÐ Ò Ò Ú Ð Ú Ø Ò ÚÖ Ñ ÐÐ º ÂÓØØ ÒÒ Ø¹ ØÙ Ø Ò ÚÖ Ø ÓÖ ÓÐ Ú Ð Ú ØÝØÝÝ Ò ØÓØ ÙØØ ÑÙÙØ Ñ ØÓ º Ò¹ ÒÒ Ò Ø ÓÖ Ò β¹ ÙÒ Ø ÓÐÐ Ô Ø ÓÐÐ ¹ØÖ Ú Ð ÒÓÐÐ Ó Ø ÝØ ÒÚ ÓÒ ÖÚÓÐÐ α 0º ÂÓØØ Ø ÓÖ ÓÐ ÝÑÔØÓÓØØ Ø Ú Ô ÓÒ β¹ ÙÒ Ø ÓÒ Ò¹ ÑÑ ÖØ ÐÙÚÙ ÓÐØ Ú Ò Ø Ú Ò Ò Ø º β 0 < 0º ÂÓ Ù Ø Ò Ò ØÓ Ò ÖØ ÐÙÚÙÒ ÖÖÓ Ò ÓÒ ÔÓ Ø Ú Ò Ò Ð β 1 > 0 ÚÓ β¹ ÙÒ Ø ÓÐÐ ÓÐÐ ØÐÐ Ò Ò ¹ØÖ Ú Ð ÒÓÐÐ Ó Ø º ÃÙÚ ÓÒ Ñ ØØ Ø Ø ØØÝÒ Ö ØÝÝÔÔ β¹ ÙÒ Ø Ó Ø º ÌÓ Ò Ò ÙÓÑ Ó Ø Ú ÓÒ ÓÒ Ò Ø Ò QQ ÑÙÓ Ó ØÙÑ Ò Ò Ø Ò Ö Ð ÝÑÑ ØÖ Ò Ö ÓÙØÙÑ Ò Òº ÌÑ Ø Ô ØÙÙ ÓÐÐ Ò ÙÓ Ú Ò ÝØ Ò¹ Ú ÓÒ ÖÚÓÐÐ α c º ÇÐ ÐÐ Ø ÓÒ ÒÝØ Ò Ò ÖÚÓ Ò Ö ØÝ Ò Ö Ð ÐÐ º Æ Ò Ù Ò ÙÒ β¹ ÙÒ Ø Ó ÔÝ ÝÝ Ò Ø Ú Ò Ú ÝØ ÒÚ Ó α ÖÖÝع Ø Ò Ö ¹ Ð ÐÐ Ó Ø Ñ Ø Ð ÑÔ Ò Ö º ÂÓ α c ÚÙØ Ø Ò Ò Ò Ø Ò ÖÑ ÓÒ Ø ÓÒ Ò Ó ØÙÚ Ø ÓÐÐÓ Ò Ø ÓÖ Ò β¹ ÙÒ Ø Ó ÑÙÙØØÙÙ Ö Ð Ò ÝÑÑ ØÖ Ò Ö ÓÙØÙÑ Ò ÚÙÓ º ÌÐÐ Ò ÓÐ Ø Ø Ò ØØ β 1 Ò ÖÚÓ ÑÙÙع ØÙÙ Ò Ø Ú Ø Ò ÒØÓÔ Ø ØØ Ó β 0 ÚÙØ Ø º ÌÐÐ Ò Ø ÓÖ ÓÐ Ú Ð Úº ÂÓ Ø α ÚÙØ Ø Ò Ò Ò β¹ ÙÒ Ø Ó ÚÙع Ø ÖÚÓÒ ¼ ÓÐÐÓ Ò ÝØ ÒÚ ÓÒ ÚÓÐÙÙØ Ó ÔÝ ØÝݺ Æ Ò ÓÐÐ Ò ÝØ ÒÚ Ó Ó Ò ÚÙØ ÖÚÓ α c Ö Ð Ò Ò ÝÑÑ ØÖ Ö ÓÙ Ùº ÌÐÐ Ò ÑÝ Ò ÝÒÒÝ ÓÐ ØÓÒ Ò Ó ÓÒ ÓØ Ñ ØØ Ó ÓÒ Ø ÚØ Ñ Ø¹ ØÓÑ º ÃÚ Ð ÚÒ Ø Ò ÚÖ Ø ÓÖ Ò ØÝØÝÝ ÓÐÐ ÐÐ Ò Ò Ó α α c º ¼

42 ÃÖ ØØ Ò ÝØ ÒÚ ÓÒ α c ÖÚÓÐÐ ÚÓ Ò Ó Ø ÖÚ Ó ¾ α c = πn 3C (R), ½¾ µ Ñ C (R) ÓÒ Ø Ò ÚÖ ÖÝ ÑÒ SU(N) ØÝ Ò Ê Ò Ð ÐÐ Ò Ò Ñ Ö¹ ÓÔ Ö ØØÓÖ º ÃÙÚ º Î ÑÑ ÒÔÙÓÐ ÙÚ β 0 ØØ β 1 ÓÚ Ø ÔÓ¹ Ø Ú º Ë Ø Ò β¹ ÙÒ Ø Ó ÓÒ ÔÓ Ø Ú Ò Ò ÐÐ ÝØ ÒÚ ÓÒ Ö¹ ÚÓ ÐÐ º ÌÐÐ Ò Ø ÓÖ ÓÐ ÝÑÔØÓÓØØ Ø Ú Ô ÐÐ ÓÐ ¹ØÖ Ú Ð ÒØÓÔ Ø Øغ à ÑÑ ÙÚ β 0 ØØ β 1 ÓÚ Ø Ò Ø Ú º Ë Ø Ò β¹ ÙÒ Ø Ó ÓÒ Ò Ø Ú Ò Ò ÐÐ Ýع ÒÚ ÓÒ ÖÚÓ ÐÐ º ÌÐÐ Ò Ø ÓÖ ÓÒ ÝÑÔØÓÓØØ Ø Ú Ô ÑÙØØ ÐÐ ÓÐ ¹ØÖ Ú Ð ÒØÓÔ Ø Øغ Ç Ò ÔÙÓÐ ÙÚ β 0 ÓÒ Ò Ø Ú Ò Ò β 1 ÔÓ Ø Ú Ò Òº Ë Ø Ò β¹ ÙÒ Ø Ó ÓÒ Ò Ø Ú ¹ Ò Ò Ô Ò ÐÐ ÝØ ÒÚ ÓÒ ÖÚÓ ÐÐ ÔÓ Ø Ú Ò Ò ÙÙÖ ÐÐ º ÌÐÐ Ò Ø ÓÖ ÓÒ ÝÑÔØÓÓØØ Ø Ú Ô ÐÐ ÓÒ ¹ØÖ Ú Ð ÒØÓÔ Ø α º ÌÙØ Ø Ò ÒÝØ Ø Ò ÚÖ Ø ÓÖ Ó ÓÒ N f Ø Ò Ú Ö N Ø Ò ÚÖ Ð Ø Ò ÚÖ ÖÝ Ñ ÓÒ SU(N)º ÌÐÐ Ò Ø ÓÖ Ò β¹ ÙÒ Ø Ó ÓÒ ÐÑÙ ¹ Ø ÓÐÐ g 3 β(g) = β 0 (4π) + β g 5 1 (4π) 4, ½¾ µ Ñ Nβ 0 = 11 3 C (G) + 4 T(R) ½¾ µ 3 (N) β 1 = 34 3 C (G) C (G)T(R) + 4C (R)T(R). ½¾ µ Ì C (R) ÓÒ ØÝ Ò Ê Ò Ð ÐÐ Ò Ò Ñ Ö¹ÓÔ Ö ØØÓÖ ÓÐÐ ÔØ T a RT a R = C (R), ½ ¼µ ½

43 Ñ T a R ÓÚ Ø ÖÝ ÑÒ Ò Ö ØØÓÖ Ø ØÝ Êº Î Ø Ú Ø C (G) ÓÒ Ð Ø¹ ØÓ ØÝ Ò Ò Ð ÐÐ Ò Ò Ñ Ö¹ÓÔ Ö ØØÓÖ T(R) ÓÒ ØÝ Ò Ê Ò ÓÐÐ ÔØ N f C (R)d(R) = T(R)d(G), ½ ½µ Ñ d(r) ÓÒ ØÝ Ò Ê d(g) Ð ØØÓ ØÝ Ò Ñ Ò Óº ÃÙØ Ò ÐÐ ÓÒ ÙÚ ØØÙ Ø ÓÖ ÚÓ ÓÐÐ ÝÑÔØÓÓØØ Ø Ú Ô Ó β 0 ÓÒ Ò Ø Ú Ò Òº ØØ Ñ ÐÐ β 0 = 0 Ò Ý ØÐ Ø ½¾ µ ½ ½µ ÝÐÖ Ø Ò Ú Ö Ò ÑÖÐÐ f = 11 d(g)c (G) 4 d(r)c (R). N af ½ ¾µ ÌØ ÙÙÖ ÑÑ ÐÐ ÑÖÐÐ Ø Ò Ú Ö Ñ Ù Ø ÓÖ ÓÐ ÝÑÔØÓÓØØ ¹ Ø Ú Ô º ÂÓØØ β¹ ÙÒ Ø ÓÐÐ ÓÐ ¹ØÖ Ú Ð ÒÓÐÐ Ó Ø Ð Ò Ö ÔÙÒ ÒØÓÔ Ø ØÝØÝÝ β 1 Ò ÓÐÐ ÔÓ Ø Ú Ò Òº Ë Ø Ò ØØ Ñ ÐÐ β 1 = 0 Ò Ý ØÐ ¹ Ø ½¾ µ ½ ½µ Ð Ö Ø Ò Ú Ö Ò ÑÖÐÐ f = d(g)c (G) 17C (G) d(r)c (R) 10C (G) + 6C (R). N ir ½ µ ÌØ Ô Ò ÑÑÐÐ ÑÖÐÐ Ø Ò Ú Ö Ø ÓÖ ÐÐ Ò Ö ÔÙÒ ÒØÓ¹ Ô Ø Øغ ØÐ Ø ½¾ µ ÚÓ Ò Ö Ø Ø Ø ÓÖ Ò Ò Ö ÔÙÒ ÒØÓÔ Ø ÙÒ ¹ Ø Ò β(g) = 0º ÌÐÐ Ò Ò α = g 4π = 4πβ 0 β 1. ½ µ Ë Ø Ò ØØ Ñ ÐÐ α = α c Ò Ý ØÐ Ø ½¾ µ ½ µ Ø Ò Ú Ö Ò ÑÖÐÐ Ö ØØ Ò Ò ÖÚÓ ÓÒ ÝÐÔÙÓÐ ÐÐ Ø ÓÖ ÓÒ ÓÒ ÓÖÑ Ð Ò Ò Nf c = d(g)c (G) 17C (G) + 66C (R) d(r)c (R) 10C (G) + 30C (R). ½ µ SU(N) Ò Ô ÖÙ ØÝ ÓÐ ÐÐ Ø ÖÝ ÑØ ÓÖ ØØ Ø ÙÙÖ Ø ÓÚ Ø d(f) = N, C (F) = N 1, ½ µ Ð ØØÓ ØÝ ÐÐ d(g) = N 1, C (G) = N. ½ µ ¾

44 Ë Ø Ò Ý ØÐ Ø ½ ¾µ ½ µ ½ µ Ò N af f = 11 N, N ir f = 34N3 13N 3, N c f = 5 N 50N 33 5N 3. ÃÙÚ ÓÒ Ø ØØÝ ÒÑ ÖÚÓØ Ø Ò ÚÖ Ò ÑÖÒ N ÙÒ Ø ÓÒ º ½ µ ÃÙÚ SU(N) Ò Ô ÖÙ ØÝ Ò Ö ÑÑ º Ð ÑÑ ÐÙ¹ β 0 > 0 Ø ÓÖ ÓÐ ÝÑÔØÓÓØØ Ø Ú Ô º Ð ÑÑ ÐÙ β 1 < 0 Ø ÓÖ ÓÐ Ò Ö ÔÙÒ ÒØÓÔ Ø Øغ À Ö¹ Ñ ÐÐ Ñ Ö ØØÝ ÐÙ ÓÒ Ò º ÓÒ ÓÖÑ ¹ ÙÒ Ó Nf c N f N af f º ÌÑÒ ÐÙ Ò Ð Ö ÐÐ Ø ÓÖ Ò Ó ÓØ Ø Ò ÓÐ Ú Ò Ú Ð Úº È ÖÙ ØÝ Ø ÖÚ ØØ Ú Ò Ø Ò Ú Ö Ò ÑÖ ÓÒ Ú Ö Ò ÙÙÖ º Ñ Ö SU() Ò Ø Ô Ù Ø ÖÚ Ø Ò N f 8 SU(3) Ò Ø Ô Ù Ó N f 1º º Ë ÓØ Ø Ö ÙÙ Ñ ØØ Ù Ø ËØ Ò Ö Ñ ÐÐ Ò ÒÒÙ Ø Ø ÚÓ Ò Ó ÐÐ Ø Ø Ø Ø ÝÚ Ò Ø Ö Ø Ò Ò ÙØ ÙØØÙ Ò Ó Ò Ø Ö ÙÙ Ñ ØØ Ù Ø Ò ÚÙÐÐ º ËØ Ò Ö Ñ ÐÐ Ò Ùй ÓÔÙÓÐ Ø Ò Ù Ø Ò Ú ÙØÙ Ø Ò ÐÐ Ñ ØØ Ù ÐÐ Ø Ú Ò ÒÒÙ Ø Ò

45 ÚÓ Ò ÙÚ Ø ÓÐÑ ÐÐ Ô Ö Ñ ØÖ ÐÐ S T Uº ÆÑ ÑÖ Ø ÐÐÒ Ø Ò ØØ Ø Ò Ö Ñ ÐÐ S = T = U = 0 Ò Ò ÔÓ Ñ ÒÓÐÐ Ø ÙÚ ÙÙ Ò Ý Ò Ó ÙÙØØ Ó Ò Ø Ö ÙÙ Ñ ØØ Ù Ø Ò ØÙÐÓ Òº È Ö ¹ Ñ ØÖ Ø S T U ÚÓ Ò ÑÖ Ø ÐÐ ÓÒ Ø ÓÖ Ò Ñ ØØ Ó ÓÒ Ò Ú ¹ ÙÙÑ ÔÓÐ Ö Ø Ó Ò ÚÙÐÐ º Å Ö ØÒ ÒÝØ Ú ÙÙÑ ÔÓÐ Ö Ø ÓØ I J µ ν = Π µν IJ Ñ I J ÓÚ Ø γ Z 0 W + Ø W º Â Ø Ò ØÑ ØØ Ò Ø Ò ÓÖ Ö ÒØ Ò ÑÙ Ò Π µν IJ (q) = Π IJ(q )g µν + (q )q µ q ν. ½ µ (q ) ÓÐ Ó Ò Ø Ö ÙÙ Ñ ØØ Ù Ø Ò ÒÒ ÐØ ÓÐ ÐÐ Ò Òº Ä Ù¹ Ò ÐÔÓØØ Ñ ÑÖ Ø ÐÐÒ ÒÝØ Π IJ Ø Ú Ø Ú Ø Ú ÙÙÑ ÔÓÐ Ö Ø ÓØ Ö ÓÙØÙÑ ØØÓÑ Ò ÓÒ Ò ÓÑ Ò ÒÒ Ð Ú ÒØØ ÐÙ Ù Ò T 1 T 3 Q ÚÙÐÐ º ÆÑ Ð ØØÝÚØ Ñ ØØ Ó ÓÒ Ò Ñ Ò ÓÑ Ò ÒÒ ÑÖ Ø ÐØÝ Ò Ú ÙÙÑ ÔÓÐ Ö Ø Ó Ò ÙÖ Ú ÐÐ Ø Ú ÐÐ Π γγ = e Π QQ, e ( ) Π γz = Π3Q s s W c WΠ QQ, W Π ZZ = e ( ) Π33 s WΠ 3Q + s 4 WΠ QQ, s W c W Π WW = e Π s 11. W ½ ¼µ Ì s W = sinθ W c W = cos θ W º Ë Ú Ö Ù Ò Q Ñ Ø ÚÓ Ò ÝØØ Ú ÒØØ ÐÙ ÙÒ ÑÝ Ó ÝÔ ÖÚ Ö Ù Ø Y º ÌÐÐ Ò Π 3Y = (Π 3Q Π 33 ) ½ ½µ Æ Ò ÚÙÐÐ Ô Ö Ñ ØÖ Ø S T U ÚÓ Ò ÑÖ Ø ÐÐ ÙÖ Ú Ø S = 16π Π 3Y (m Z ) Π 3Y (0), m Z T = 4π Π 11(0) Π 33 (0), s W c W m Z ( Π11 (m Z ) Π 11(0) ) ( Π 33 (m Z ) Π 33(0) ) U = 16π m Z. ½ ¾µ

46 S¹Ô Ö Ñ ØÖ ÙÚ ÙÙ Ò Ý Ò ÙØØ Ñ Ú ÙÙÑ ÔÓÐ Ö Ø ÓÒ ¹ Ð ÚÓÐÙÙØ ÓØ ÙÒ Ø T ¹Ô Ö Ñ ØÖ ÙÚ SU()¹ Ó Ô Ò ÝÑÑ ØÖ Ò Ö ÓÙ¹ ØÙÑ Ø º U ÓÒ Ú ÖÖ ÒÒÓÐÐ Ò Ò T Ò Ö Ú ØØ Ò Ø Ò ÝÐ Ò T Ò ÓÐÐ Ô Ò ÓÒ ÑÝ U Ô Ò º ÌÝÝÔ ÐÐ Ø Ø Ò ÚÖ Ø ÓÖ Ó T U ÓÚ Ø ÝÚ Ò Ð ÐÐ ÒÓÐÐ S Ò ÑÙÓ Ó ØÙ ÓÒ ÐÑ ÐÐ º ÅÖ Ø ÐÐÒ ÐÐ Ò ÝÐ ¹ Ø Ú ÙÙÑ ÔÓÐ Ö Ø ÓØ Ò ÓÖ Ø Π µν LL Ò Ø Ø Ú ÖØ Π µν LR Πµν LR Ø Ò ØØ Πµν LL ÝØ Ú ¹ Ú Ò¹ Ó Ø Ò Ú ÖÖ Ò Ø Ò ÒÑ Ò Ú Ø Ú ÐÐ Ø Ú ÐÐ Ø Ò ÓÖ Ö ÒØ Ò ÑÙ Ò Ù Ò Ðк Æ Ò ÚÙÐÐ ÚÓ Ò Ð ÙÙ Ò ÖÑ ÓÒ Ù Ð Ø Ò Ú ÙØÙ Ô Ö Ñ Ø¹ Ö Ò S Ô ÖÙ ØÝ º Ì Ö Ø ÐÐ Ò Ø ÙÙØØ ÖÑ ÓÒ u dº Ò¹ Ò Ø Ò ÒÝØ Ó Ø ÐÐ ÖÑ ÓÒ ÐÐ d R ÝÔ ÖÚ Ö Ù Yd R Ø Ø Ò ØÓ Ò Ó Ø Ò ÖÑ ÓÒ Ò u R ÝÔ ÖÚ Ö Ù ÒÓÐÐ º ÇÐ ÓÓÒ Ú Ò Ø Ø Ò ÖÑ Ó¹ Ò Ò ÝÔ ÖÚ Ö Ù Ø Y L u = Y L d =: Y L º ÌÐÐ Ò Π 3Y = 1 Y L (Π d LL Π u LL) 1 Y R d Π u LR. ½ µ ÅÖ Ø ØÒ ØØ Ò Π LL º L L = iπ µν LL Ó iπ µν LL = Ì Ð ÓÒ d 4 k Tr(iγ µ 1 (1 γ5 )i(/k + m)iγ ν 1(1 γ5 )i(/k + /q + m)). (π) 4 (k m )((k + q) m ) ½ µ Tr(iγ µ1 (1 γ5 )i(/k + m)iγ ν 1 (1 γ5 )i(/k + /q + m)) = 8(k µ (k + q) ν + k ν (k + q) µ k (k + q)g µν k α (k + q) β ǫ βµαν ), ÝÒÑ Ò Ò Ô Ö Ñ ØÖ Ò ÚÙÐÐ Ò Ñ ØØ ØÙÐ ÑÙÓØÓÓÒ 1 1 (k m )((k + q) m ) = 0 1 dx (l ), Ñ l = k+xq = x(1 x)q +m º ÌÐÐ ÑÙÙØØÙ ÒÚ ÓÐÐ Ó Ó ØØ ÓÒ k µ (k + q) ν + k ν (k + q) µ k (k + q)g µν k α (k + q) β ǫ βµαν = ( d 1)l g µν + x(1 x)q g µν,

47 Ñ ÓÒ Ø ØØÝ ÔÓ Ø ÖÑ Ø ÓØ ÚØ ÓÐ Ú ÖÖ ÒÒÓÐÐ Ñ ØÖ Ò Ø Ò ÓÖ Ò g µν º Ë Ø Ò 1 iπ LL = 0 = i (4π) dx 1 0 d d l ( d 1)l + x(1 x)q (π) d (l ) ( dx(x(1 x)q m ) ǫ γ E + log ( 4πµ )). ½ µ Î Ø Ú Ø iπ µν LR = Ó Ø Ò Ë Ø Ò d 4 k Tr(iγ µ 1 (1 γ5 )i(/k + m)iγ ν 1(1 + γ5 )i(/k + /q + m)), (π) 4 (k m )((k + q) m ) ½ µ iπ LR = i (4π) 1 Π LL (m Z) Π LL (0) = 4 (4π) 0 ( ( )) 4πµ dx m ǫ γ E + log. ½ µ ( m Z 6 Ñ ÓÒ ÖÚ Ó ØÙ m >> m Z º ÐÐ Ò ( ǫ γ E + log ( )) 4πµ m ) m Z, 1 ½ µ Π LR (m Z) Π LR (0) = 1 (4π) m Z 3. ½ µ Ë Ø Ò Ý ØÐ Ø ½ µ ½ µ ½ µ Ò Π 3Y (m Z) Π 3Y (0) = 1 m Z (4π) 6 Ø Ò Ý ØÐ Ò ½ ¾µ ÑÙ Ø S = 1 6π ( Y L log ( Y L log ( ) m d m u ( ) m d m u 1 ) Y d R, ½ ¼µ 1 ) Y d R. ½ ½µ ÂÓ ÒÝØ Ø Ø Ò ÙØ Ò Ñ Ø Ò Ö Ñ ÐÐ Ò Ð ÔØÓÒ ÐÐ Y L = 1 Yd R = ÓÐ Ø Ø Ò ØØ ÙÙ Ø ÖÑ ÓÒ Ø ÓÚ Ø Ñ Ò Ñ Ð m u = m d Ò S Ò ÖÚÓ S = 1 º Ì Ò ÚÖ Ø ÓÖ ÙÙ ÖÑ ÓÒ Ù Ð ØØ 6π

48 ÓÒ N f d(r) ÔÔ Ð ØØ Ó Ø Ù Ò ÙØØ S Ò ÐÐ ÙÚ ØÙÒ ÓÒØÖ ¹ ÙÙØ ÓÒº Ë Ø Ò Ø Ò ÚÖ Ø ÓÖ S = 1 N f d(r). ½ ¾µ 6π ÐÐ Ò Ø Ò ØØ Ú Ð ÚÒ Ø ÓÖ Ò Ö ÒØ Ñ Ø ÖÚ Ø Ò SU() Ò Ø ¹ Ô Ù Ú ÒØÒ SU(3) Ò Ø Ô Ù Ú ÒØÒ ½¾ Ú Ö ÙÒ ÓÐÐ Ò SU(N) Ò Ô ÖÙ ØÝ º ÌÐÐ Ò d(r) = N ÓØ Ò SU()¹Ø ÓÖ S = SU(3)¹Ø ÓÖ S = º ÃÓ ÐÐ Ø ¼ S 0. 3π π ÓØ Ò ÒÑ ÖÚÓØ ÓÚ Ø Ð Ò ÙÙÖ º ÃÚ Ð Ú Ø Ò ÚÖ Ø ÓÖ ÚÓ ÓÐÐ SU(N) Ó ÖÑ ÓÒ Ø ÓÚ Ø Ô ÖÙ ØÝ º ÂÓ Ø Ò Ú Ö Ø ÓÚ Ø SU(N) Ò Ó Ò ÓÖ ÑÑ ØÝ Ò Ø Ø Ø Ò Ù Ø Ò Ò Ø ÖÚ Ø Ú Ñ¹ ÑÒº Ì Ø ÝÝ Ø ÚÓ ÓÐÐ Ö Ú ØÙØ ØÐÐ Ø Ø Ò ÚÖ Ø ÓÖ º Ì Ö ¹ Ø ÐÐ Ò Ù Ø Ò Ò Ò Ò Ó Ø Ò ÒÓÑ Ð Ó Ø ÓØ Ö Ó ØØ Ú Ø Ñ ÓÐÐ Ø Ò Ø ÓÖ Ó Ò Ú Ð Ó Ñ º º º º½ ÒÓÑ Ð Ó Ò ÙÑÓÙØÙÑ Ò Ò Ï ØØ Ò Ò ÒÓÑ Ð Æ Ò ÙØ ÙØØÙ Ï ØØ Ò Ò ÒÓÑ Ð ÒØÝÝ Ø ÓÖ Ó Ó ÓÒ ÚÙÓÖÓÚ ¹ ÙØÙ Ò SU()¹ ÒØØÒ ÝØ ØÒ Ô Ö ØÓÒ ÑÖ ÖÑ ÓÒ Ù Ð ØØ º ÂÓ ØÙ Ò SU() Ò ØÓÔÓÐÓ Ø ÙÒ Ø ÓÒ Ð ¹ ÒØ Ö Ð ÝÐ Ô Ö ØØÓÑ Ò Ñ¹ ÖÒ ÖÑ ÓÒ ÒØØ ÚÓ Ö Ú Ø ÑÖ Ø Ðк ËØ Ò Ö Ñ ÐÐ ÐØ Ô ¹ Ö ÐÐ Ò ÑÖÒ Ú Ò Ø ÖÑ ÓÒ Ù Ð ØØ ÓØ Ò Ò ÒÒÝ Ï ØØ ¹ Ò Ò ÒÓÑ Ð º Ì Ø ÝÝ Ø Ñ Ò Ø Ò Ð ÒÒÙ Ò Ø Ò Ö Ñ ÐÐ Ò ØÙÐ ÓÐÐ ÐÐ Ò Ò ØØ Ø Ò ÐÐ Ï ØØ Ò Ò ÒÓÑ Ð º Ë Ó Ø Ò Ö Ñ ÐÐ Ò ÐÙØ Ò Ð Ø ÖÑ ÓÒ ÓØ ÝØ ØÒ ÓÓÒ ÚÙÓÖÓ¹ Ú ÙØÙ Ò Ú Ò Ø Ò Ù Ð ØØ Ò ØÙÐ Ò Ø Ù Ð ØØ ÓÐÐ Ô Ö ÐÐ Ò Ò ÑÖº Ì Ò ÚÖ Ø ÓÖ Ò ÒÒ ÐØ ØÑ Ø Ö Ó ØØ Ø ØØ Ó Ó Ø Ò Ú Ö ¹ Ù Ð ØØ ÓÒ ÓÐØ Ú Ô Ö ÐÐ Ò Ò ÑÖ Ð ÓÐØ Ú 1 N fd(r) = Ô Ö ÐÐ Ò Ò Ø ØØ Ò Ø ÓÖ Ò ÓÒ Ð ØØÚ Ø Ò Ú Ö Ò Ð ÑÙ Ø Ò ÖÑ ÓÒ Ø Ò ØØ ÙÙ Ò ÖÑ ÓÒ Ù Ð ØØ Ò ÑÖ Ý Ø Ò ÓÒ Ô Ö ÐÐ Ò Òº ÂÐ ÑÑ ¹ Ø Ô Ù Ö ÐÙÓÒÒÓÐÐ Ò Ò Ò ØØ ÙÙ ÖÑ ÓÒ Ù Ð Ø ÓÐ ÙÙ Ð ÔØÓÒ Ù ÙÔÓÐÚ º º º¾ Å ØØ ¹ ÒÓÑ Ð Ø ÃÐ Ø Ø ÓÖ Ò ÒÚ Ö Ò Ø ÓÒ Ò ÑÙÙÒÒÓ Ò Ù Ø Ò ÙÖ ÆÓ Ø ¹ Ö Ò Ø ÓÖ Ñ Ò ÑÙ Ø ÐÝÚ Ú ÖØ º ÃÙ Ø Ò Ò Ð ØØ Ø ÓÖ ÓÖ¹ ÑÔ Ò ÖØ ÐÙ ÙÙÒ ØØ Ú Ø Ø ÐÝ ÓÖ Ù Ø ØÙÓØØ Ú ÖÖ Ò ÐÝÑ ¹

49 Ø Ö ÓÚ Ø ÖÑ º ÌÐÐ ÐÑ Ø ÙØ ÙØ Ò Ñ ØØ ¹ ÒÓÑ Ð Ó º ÀÝÚ Ò ÑÖ Ø ÐÐÝ Ø ÓÖ Ñ ØØ ¹ ÒÓÑ Ð Ó Ò ØÙÐ ÙÑÓÙØÙ Ø Ò ØØ Ñ ØØ ¹ ÝÑÑ ØÖ Ò Ô ÖÙ Ø ÐÐ Ó ÓØ ØØÙ Ú ÖÖ Ò ÐÝÑ Ò Ò ÔØ Ø ÐÝ ÓÖ Ù Ø ÙÓÐ Ñ ØØ º ËØ Ò Ö Ñ ÐÐ Ò ÒÒ ÐØ ÓÐ ÐÐ Ò ÒÓÑ Ð ÓÒ Ò Ò ÙØ ÙØØÙ Ð Ú ÖØ ¹ ÒÓÑ Ð º ÌÙØ Ø Ò ÒÝØ ÝÐ Ø Ø ÓÖ Ó ÝØ ØÒ Ñ ØØÓÑ ÖÑ ÓÒ Ó ÓÒ Ò ¹ Ð Ò Ñ ØØ ÒØØÒº ËØ Ò Ö Ñ ÐÐ Ò ÖÑ ÓÒ Ø ÓÚ Ø Ù Ñ¹ Ñ Ø Ð ÒØ ÝÚÒ ÔÔÖÓ Ñ Ø ÓÒ Ñ ØØÓÑ ÓØ Ò ØÑÒ ÒÓ¹ Ñ Ð Ò ÙÑÓÙØÙÑ Ò Ò Ø Ò Ö Ñ ÐÐ Ò Ñ ÓÐÐ Ð ÒÒÙ ÓÒ ÓÐ ÐÐ Ø º ÃÓ ÖÑ ÓÒ Ø ÓÚ Ø Ñ ØØÓÑ Ø ÓÖ ÐÐ Ø ÖÑ Óع Ó ØØ Ú Ø Ú Ò¹ Ó Ø ÖÑ ÓÒ ÒÒº Ë Ø Ò Ú Ò¹ Ó ¹ Ø Ø Ò Ú ÖØÓ Ò ÓÐ Ø Ø Ò ÐÝÚÒ Ö Òº ÆÑ Ú ÖÖ Ø ÚÓ Ò ÑÝ ÐÑÓ ØØ Ú ØÓÖ ¹ Ð Ú ÖØÓ Ò Ð Ò Ö ÓÑ Ò Ø ÓÒ º Ì Ø ÙÖ ØØ ÑÝ Ú ØÓÖ ¹ Ð Ú ÖØÓ Ò ØÙÐ ÐÝ Ö Òº ÌÙÐ ÓÐÐ µ j µa = 0 µ j µ5a = 0, ½ µ Ñ j µa = ψγ µ t a ψ ÓÒ Ú ØÓÖ Ú ÖØ j µ5a = ψγ µ γ 5 t a ψ ÓÒ Ð Ú ÖØ º Î ØÓÖ Ú ÖÖ Ò Ú Ö Ò ÓÒ ÒÓÐÐ ÑÙØØ Ð Ú ÖØ Ò Ð ØØÝÝ ÒÓÑ Ð Ò Ò ÒÓÐÐ Ø ÔÓ Ú Ú Ö Ò º ÌÙØ Ø Ò ÒÝØ Ö ÑÑ p µ a k ν b = im λ c q Ñ Ú ÖØ ÓÐÑ ÓÒ Ö ÙÚ Ð Ú ÖØ j µ5a ÙÐ Ó Ø ÒØØ ÓÚ Ø Ø ÓÖ Ò Ñ ØØ ÒØØ Ú Ø Ú Ö ÑÑ im Ó ÖÑ ÓÒ ¹ Ú ÖØ ÖØ ØÓ Ò ÙÙÒØ Òº Ì t a ÓÒ Ø ÓÖ Ò ¹ Ð Ò Ñ ØØ ÒØÒ Ò Ö ØØÓÖ º ÆÝØ ( d im = (ig) 4 k (π) 4Tr γ µ γ 5 t i(/k /p) a t b i/k t ci(/k + ) /q) (k p) γν k γλ (k + q) = ig Tr(t a t b t c ) d 4 k (π) 4Tr ( γ µ γ 5 /k /p (k p) γν /k k γλ /k + /q (k + q) ). ½ µ

50 ÂÓ ÝØ ÒØ Ñ ØØ ÒØØ Ò ÐØ Ø ÖÑ Ò γ 5 ØÐÐ ÓÐ Ñ Ö ØÝ Ø ÐÐ γ 5 Ø ÚÓ Ò Ö Ø Ú Ö Ò (γ 5 ) 3 = γ 5 º im ÓÒ Ñ Ð Ù Ó ÓÒ Ú ØØÙ (p,ν,b) (q,λ,c)º ÆÝØ Ý ØÐ Ò ½ µ Ô ÖÙ Ø ÐÐ Ó ÓØ ØØ Ò ØØ p,ν,b;q,λ,c µ j µ5a 0 = 0. ½ µ Ú Ö Ò µ j µ5a Ú Ø Ð ÑÖ ØÝ ØÙÐÓ (p + q) µ j µ5a º Šع Ö Ð Ñ ÒØ Ò ½ µ ÑÖ ØØÑ ÓØ Ø Ò ÒÝØ Ö ÑÑ im ØÑ ØÙÐÓ ÓÐÐÓ Ò ÓÖÚ Ø Ò γ µ γ 5 (p + q) µ γ µ γ 5 = (/k + /q)γ 5 + γ 5 (/k /p)º ÌÐÐ Ò M ØÙÐ ÑÙÓØÓÓÒ im = ig Tr(t a t b t c ) ( d 4 k /k /p (π) 4Tr γ 5 /k γ 5 /k /k + /q (k p) γν k γλ k γλ (k + q) γν ½ µ ËÙÓÖ Ø Ø Ò ÒÝØ Ò ÑÑ Ø ÖÑ ÑÙÙØØÙ Ò Ú ØÓ k k + p ÓÐÐÓ Ò Ò im = ig Tr(t a t b t c ) ( d 4 k (π) 4Tr γ 5 /k /k + /p γ 5 /k /k + /q k γν (k + p) γλ k γλ (k + q) γν ½ µ Ä ÑÖ ÒØ Ö Ð ÓÒ ÒÝØ ÐÚ Ø ÒØ ÝÑÑ ØÖ Ò Ò Ú ÓÒ (p,ν,b) (q,λ,c) Ù Ø Ò ÓØ Ò Ò ÒÒ Ø M + M = 0 ÒÓÑ Ð Ø ÒÓÐÐ Ø ÔÓ Ú Ò Ð Ú Ö Ò ÒÒݺ ÃÙ Ø Ò Ò ÒØ Ö Ð Ó ÑÙÙØØÙ Ò¹ Ú ØÓ k k + p ÙÓÖ Ø ØØ Ò ÓÒ Ú Ö Ó Ú º Ë Ø Ø ÑÙÙØØÙ ÒÚ Ó Ø ØØ Ð ÐÐ ÒÓÐÐ Ø ÔÓ Ú Ø ÖÑ º Ì Ö Ø ÐÐ Ò Ø Ð ÒÒ ØØ ¹ Ñ Ò ÓÒ Ð Ö ÙÐ Ö Ø Ó º ÅÖ Ø ÐÐÒ γ 5 Ñ Ò Ó d Ø Ò Ø¹ Ø ÒØ ÓÑÑÙØÓ γ µ Ò Ò ÙÒ µ = 0, 1,, 3 ÑÙØØ ÓÑÑÙØÓ γ µ Ò Ò ÑÙ ÐÐ µ Ò ÖÚÓ ÐÐ º Â Ø Ò ØØ Ò ÒØ ÖÓ ÒØ ÑÙÙØØÙ k Ø Ò ØØ k = k + k Ñ k ÐØ k Ò ÓÑÔÓÒ ÒØ Ø Ò Ð ÙÐÓØØÙÚÙÙ k ÐÓÔÙØ ÓÑÔÓÒ ÒØ Ø d 4 ÙÐÓØØÙÚÙÙ º ÌÐÐ Ò ØÙÐÓ (p + q) µ j µ5a ÒØ γ µ γ 5 (p + q) µ γ µ γ 5 = (/k + /q)γ 5 + γ 5 (/k /p) γ 5 /k º ÌÐÐ Ò Ð ¹ ØØ ÙÑÑ M + M Ò ÑÑ Ø Ø ÖÑ ÙÑÓÙØÙÚ Ø ÙØ Ò ÐÐ ÓÒ ÒÝØ ØØÝ ÑÙØØ Ú Ñ Ø Ø ÖÑ Ø ÓÒØÖ ÙÙØ Ó im = ig Tr(t a t b t c ) ). ). ( d d k /k /p (π) dtr γ 5 /k /k /k + ) /q. (k p) γν k γλ (k + q) ½ µ ÝÒÑ Ò Ò Ô Ö Ñ ØÖ Ò ÚÙÐÐ ØÑ Ò ÑÙÓØÓÓÒ 1 im = 8g Tr(t a t b t c ) 0 dxdy d d l l (π) d (l ) 3p αq β ǫ ανβλ, ½ µ

51 Ñ ÓÒ ÙÓÖ Ø ØØÙ ÑÙÙØØÙ ÒÚ ØÓ l = k + yq xp = x(1 x)p y(1 y)q + xyp q ÓØ ØØÙ Ð Ö Ò Ñ ØÖ Ò ÝÐ º ËÝÑÑ ØÖ ÒØ Ö Ð ÚÓ Ò ÓÖÚ Ø l d 4 d l º Ì Ò ØØ Ò Ï Ò ÖÓØ Ø Ó ÙÓÖ Ø Ø Ò ÒØ Ö Ð Ø ÓÐÐÓ Ò Ò im = ig (4π) p αq β ǫ ανβλ Tr(t a t b t c ). ½ ¼µ ÌÑ ÓÒ ÝÑÑ ØÖ Ò Ò Ú ÓÒ (p,ν) (q,λ) Ù Ø Ò ÓØ Ò Ó ÓÒ ÙÙ ¹ Ò Ò M + M = g 8π p αq β ǫ ανβλ Tr(t a {t b,t c }). ½ ½µ Æ Ò ÓÐÐ Ò Ñ ØÖ Ð Ñ ÒØØ ½ µ ÓÒ p,ν,b;q,λ,c µ j µ5a 0 = g 8π p αq β ǫ ανβλ A abc, ½ ¾µ Ñ A abc = Tr(t a {t b,t c })º Ð Ú ÖØ ÐÝ ÐÐ A abc ÓÐ ÒÓÐÐ Ø Ó Ø ÓÖ ÐØ Ù Ø Ñ ØØ ÒØØ ÖÑ ÓÒ ØÙÐ ÙÑÑ Ò Ò Ò Ò Ð ØØÝÚ Ø Ø Ø A abc ÓÐÐ ÒÓÐÐ º ÃÓ Ø ÓÖ Ò Ö ÒØ Ò ÒÒ ÐØ ÓÒ ÓÐ ÐÐ Ø ØØ Ð Ú ÖØ ÓÒ ÐÝÚ Ú ÖØ ÓÒ Ú ØØ Ú ØØ ¹ Ö Ð Ø ÓÖ Ó Ø Ò A abc ÙÑÑ Ú º ÅÙÙ Ø Ô Ù Ø ÓÖ ÚÓ Ö Ú Ø ÑÖ Ø Ðк Ì Ö Ø ÐÐ Ò ØØ Ò Ð Ú ÖØ ¹ ÒÓÑ Ð Ò ÙÑÓÙØÙÑ Ø Ø Ò Ö Ñ Ð¹ Ð Ó ÐØ Ý Ò Ô Ö Ò Ñ ØØÓÑ Ú Ö Ý Ò Ô Ö Ò Ñ ØØÓÑ Ð ÔØÓÒ º Å ÓÐÐ Ò Ð Ú ÖØ ¹ ÒÓÑ Ð Ò ÓÒØÖ ÙØÓ ¹ Ú Ø Ö ÑÑ Ø ÓÚ Ø ÓÐÑ Ò Ñ ØØ Ó ÓÒ Ò ÚÐ Ø ÓÐÑ Ó Ö ÑÑ Ø I J K Ì I J K ÓÚ Ø Ø Ò Ö Ñ ÐÐ Ò Ñ ØØ ÒØØ Ð U(1) SU() Ø SU(3)º ÀÙÓÑ Ó Ò ÑÝ Ñ ÓÐÐ Ò Ò Ö Ú Ø Ø ÓÒ Ú ÒØØ Ø ÓÖ ÓÐÐÓ Ò Ø Ò Ö Ñ ÐÐ Ò ÐÐÝØ ØÒ ÙÙ Ñ ØØ Ó ÓÒ Ö Ú ØÓÒ º Ö Ó ¼

52 ÓÐÑ Ñ ØØ ÒØØ ÓÚ Ø Ú Ò¹Ó ¹ ÝÑÑ ØÖ Ø ÖÚ Ø ÓØØ ÙÓÑ ÓÓÒ ÐÐ ÒÑ ÚØ ÓÒØÖ ÙØÓ Ð Ú ÖØ ¹ ÒÓÑ Ð Òº Ø Óع ÐØÚØ Ý Ò SU()¹ Ø SU(3)¹ Ó ÓÒ Ò ÓÚ Ø Ú ÖÖ ÒÒÓÐÐ Ð Ò Tr(τ a ) = 0 Ø Tr(t a ) = 0 ÓÚ Ø Ø Ò ÒÓÐÐ º ÐÐ Ò ÓÐÑ Ò SU()¹ Ó ÓÒ Ò Ú ÖØ ÒØ ÒÓÐÐ Ò ÐÐ {τ a,τ b } = 1 4 δab Ø Ò Ð A abc = 0º Ë Ø Ò Ð ÐÐ ÚØ Ö ÑÑ Ø ÓÚ Ø ÓÐÑ Ò U(1)¹ ÒØÒ Ý Ò U(1)¹ ÒØÒ Ò SU()¹ ÒØÒ Ý Ò U(1)¹ ÒØÒ Ò SU(3)¹ ÒØÒ Ý Ò U(1)¹ ÒØÒ Ò Ö Ú Ø Ø Ó ÒØÒ ÚÐ Ø Ú ÖØ Øº Æ Ô Ø ÙÑÑ Ø Ò Ö Ð Ú ÒØØ Ò ÖÑ ÓÒ Ò ÝÐ º Ò U(1)¹ Ó ÓÒ Ò Ò SU(3)¹ Ó ÓÒ Ò ÚÐ Ò Ò Ú ÖØ ÒØ A abc = Tr(t a t b Y ) = δ ab q Y q, ½ µ Ñ ÙÑÑ ÓÒ Ó ¹ Ú Ò Ø Ø Ò Ú Ö Ò ÝÔ ÖÚ Ö Ù Ø Ò ÝÐ º ËØ Ò¹ Ö Ñ ÐÐ Ò ÑÙ ÐÐ ÝÔ ÖÚ Ö Ù ÐÐ Ò Y q = = 0 ½ µ g Ø Ò ØÑ Ö ØÙÓØ ÓÒØÖ ÙÙØ ÓØ Ð Ú ÖØ ¹ ÒÓÑ Ð Òº Î ¹ Ø Ú Ø U(1)¹ Ó ÓÒ Ò Ò SU()¹ Ó ÓÒ Ò ÚÐ Ò Ò Ú ÖØ ÒØ A abc = Tr(τ a τ b Y ) = δ ab f L Y fl, ½ µ Ñ ÙÑÑ ÓÒ Ò Ú Ò Ø Ø Ò ÖÑ ÓÒ Ò ÝÔ ÖÚ Ö Ù Ø Ò ÝÐ º Âй Ð Ò Ø Ò Ö Ñ ÐÐ Ò ÑÙ ÐÐ ÝÔ ÖÚ Ö Ù ÐÐ Ò Y fl = ( 1 ) 3 1 = 0, ½ µ 6 f L Ñ Ø ÓÐÑ ØÙÐ Ø ØØ Ú Ö Ò ÓÐÑ Ö ÚÖ ØÙÐ Ð Ö Ò ÑÙ Òº ÌÑ Ò Ö ØÙÓØ ÓÒØÖ ÙÙØ ÓØ Ð Ú ÖØ ¹ ÒÓÑ Ð Òº ÐÐ Ò ÓÐÑ Ò U(1)¹ Ó ÓÒ Ò Ö ØÙÓØØ A abc = Tr(Y 3 ) = f Y 3 f ( = ( 1 )3 + ( 1) 3 3 ( ( 1 6 )3 ( 3 )3 ( 1 3 )3)) = 0, ½ µ Ñ ÙÑÑ ÓÒ ÝÐ Ò ÖÑ ÓÒ Ò Ú Ñ Ò U(1)¹ Ó ÓÒ Ò Ò Ö Ú ØÓÒ Ò Ö ØÙÓØØ A abc = Tr(Y ) = Y f f ( = ( 1 ) + ( 1) 3( ( 1 6 ) ( 3 ) ( 1 3 ))) = 0. ½ µ ½