È(a < θ < b X = x) = ( ) θ x n. ba n. x (1 θ) n x dθ

Transkriptio

1 Ê Ö ÈÖ Ù Ì ÓÑ Ý Ò Öع Ò Ë¹ÌÁÄ ËÌÇÌÁ º ¾¼¼ ÒØØ È ÒØØ Ò Ò ÂÝÚ ÝÒ Ý ÓÔ ØÓ Å Ø Ñ ØÒ Ø ØÓØØÒ ØÓ Ý Ìº ½ µº Ò Ý ØÓÛ Ö ÓÚ Ò ÔÖÓ Ñ Ò Ø ÓØÖ Ò Ó Ò º ÈÓ ÓÔ ÌÖ Ò Ø ÓÒ Ó Ø ÊÓÝ ËÓØÝ ¼½ º Ê ÔÖ ÒØ Û Ø Ó¹ Ö Ô ÒÓØ Ý º º ÖÒ Ö Ò ÓÑ ØÖ ¾ ½ ½ ºµ Ó Ø ØÓÒÒ ÝÝ Ø Ý Ò ÙÓ¹ Ñ Ò Òº ÌÙØÑÙ ØØ ÙÖÚ ÔÖÓ Ñ ÂÓ X Ò(n, θ) ÒÒ Ñ ÓÒ È(a < θ < b X = x)? Ý Ò Ö Ø Ù Ó ( ) ba n θ x x (1 θ) n x dθ È(a < θ < b X = x) = ( ). 10 n θ x x (1 θ) n x dθ ½ ½º ÂÓ ÒØÓ Å Ø Ý ¹Ø ØÓØ ÓÒ ÒÙØ ÙÒ ÃÙ Ó ÖÖ Ý Ì ÓÑ Ý ½ ¼¾ ½½µ Ì ÓÑ Ý ÓÒ ÒØ ÒÙØ Ò Ñ Ò Ý ¹ Ò Ú Ý ¹Ø ØÓØØ º Ý ¹ Ø ØÓØ ØÙÒÒ ØØÒ ½ ¼¼¹ÙÚÙ ÒØ ¹ Ø Ò ØÓÒÒ ÝÝ Ò Ñ Ò Ø ÑÒº ÂÓ Ø Ò ÙÓÑ Ó Ø Ý ÝÝØÒ ØØÝÝ ÚÚ Ó Ó Ò Ò ¹ Ø Ù º Ë ÓÒ Ó ½ ¼¼¹ÙÚÙÒ ÓÔÙ Ø Ò ÓÙØ Ý Ú ØÓØÓ Ò Ò ØÝÑ Ø Ô Ø¹ Ø Ò ÔØØ ÝÝÒ ÑÝ Ø Øݺ Ò¹ Ò Ø ØÓØØÒ ÙÙ ÚÓÒ ÚØ Ó Ý ¹Ø ØÓØØÒ ÒÒ ØØÒ Ú ØÙ ØÒº ÎÒ ÑØÙÙ ÔÖÑØØ Ø Ý Ø ÓØ ÓÚ Ø Ú Ø Ý ¹Ø ÓÖ ÑѺ ÓÒÑ ¹ Ö Ø ÙÒ ÓÖÑÙÓ ÒØ Ø Ô Ò º Ì ÓÑ Ý Ó Ò ÒØ Ò Ò ÒØÓÒ ÓÖ¹ Ñ Ø ÔÖ ÝØÖ Ö Ú ÓÖ ÖÖ Ø Ñ ¹ Ø ÑØ Óº ¾ Ö ØÝ Ø ½¼¹ÙÚÙÒ Ù Ø Ò Ý ¹ Ø ØÓØ ÓÒ ØØÒÝØ ØÓØ Ò¹ Ò ØÝ Ù Ó Ò ÚÙ ÚÓÒ ¹ ØÝ ÝÚ ÒÒ ÓÑÔ ÔÖÓ ÑÓ Ø ØÝÑ Ø Ú Ø ÓÒ ØÙÙØ ÙÓ ØØÙ

2 ÂÓ Ø Ò ÚÒ ÒÓ ËÙØÚ Ø ØÓÒÒ ÝÝØ ÔÖ ÓÖ ØØÓ ÔÓ Ø Ö ÓÖ ØØÓ ÔÖØÚ Ò Ò ÙÑ Ö Ö Ø Ñ Ø Å Ö ÓÚ Ò Ø Ù ÅÓÒØ ÖÓº Ý ¹ ÒØ Ã Ò Ò ØÝ Ù ÓÒ Å Ö ÓÚ Ò Ø Ù ÅÓÒØ ÖÓ ¹Ñ Ò Ø Ñ Å Å µº Ë Ò Ñ ÖØÝ ÓÒ Ò ÖØ Ó Ú ØØÙ Ý ¹Ø ØÓØØ ÖØ Ò º º Ò ËÑ Ø º ºÅº ½¼µº Ë ÑÔ Ò ¹ ÔÔÖÓ ØÓ Ù Ø Ò Ñ ÖÒ Ò Ø º ÂÓÙÖÒ Ó Ø Ñ ÖÒ ËØ Ø Ø ÓØ ÓÒ ¾ ¾ º ËÓÚ Ù Ø Ò ÒÒ Ø ØÖ Ó Ñ ØÓØÝ ¹ Ù ÓÒ Í Ë Ý Ò Í Ó Ë ÑÔ Ò µº Ë Ø ØÙÒ ÝØØÑÒ ØÒ ÙÖ ÅÖ Ø Ò ØÓÒÒ ÝÝ ÓÑ È½ Ⱦ È(E H) 0 E H È(H H) = 1 H È È(E F H) = È(E H)+È(F H) ÙÒ E F ÓÚ Ø ØÓ Ò ÔÓ ÙÚ È È(E F, H) È(F H) = È(E F H) E F H Å Ø ÑØØ Ø ÑÙÚÙÙ Ý Ø Ó Ø ØÒ È È ÓÒ ÚÓ Ñ ÒÙÑ ÖÓ ØÙÚ ÓÒÓ E 1, E 2,... Ô ÖØØÒ ØÓ Ò ÔÓ ÙÚ Ø ÔØÙÑ È˺ ÅÙ ØÙØ ØÒ ÑÒ ØÙØÙØ ØÓÒÒ ÝÝÒ ¹ ÓÑ Ø Ò º ÃÓÑÓ ÓÖÓÚ Ò ÓÑ Øµ È(E) 0 È(Ω) = 1 Ω ÓÒ Ó Ó Ú ÖÙÙ È( ne n) = n È(En) En Ò Ô ÖØØÒ Ô Ø ÚÖØ ÒÙÑ ÖÓ ØÙÚ ¾º ÌÓÒÒ ÝÝ ÔÚ ÖÑÙÙÒ Ñ ØØ Ò E Ø ÔØÙÑ H Ø Ù Ø ØØÓ Ó Ù ÝÔÓØ µ È(E H) E Ò ØÓÒÒ ÝÝ Ó Hº Å ØØ ÔÚ ÖÑÙÙØØ Ø ÓÒ H Ú Ó ÃÓÑÑ ÒØØ ½º Ⱦ È(E H) = 1 Ó E Ò ØÝ ÔÚ ÖÑÙÙØØ ¾º È È(E H) = È(E H)+È( H) ØÝ ÓÙÓµº ÂÓ E Ñ ÓØÓÒ ÒÒ È(E H) = 0º º È(E F, H) = È(E F H)/È(F H) È(E H) = 1 Ó Ó Ø Ú ÖÑ ØØ E Ø ÔØÙÙ È(E H) = 0 Ó Ó Ø Ú ÖÑ ØØ E Ø Ô Ù È(E H) = p, 0 < p < 1 E Ò ØØÝÝ ÔÚ ÖÑÙÙØØ ÑÙØØ ÚØØÑØØ ØÙÒÒ ÙÙØØ µ ÂÓ E Ò ÔÚ ÖÑÙÙ ÓÒ ÔÒ ÑÔ Ù Ò F Ò ÒÒ È(E H) > È(F H) º º È(E H) È(F H) Ó E F º ÅÙØØ Ø Ø ÙÖ Ñ ÓÒÑ Ã Ø Ö Ø ÚÓ Ó Ö ØÝ ÔÚ Ö¹ ÑÙÙ Ø Ö H µº ÌÓÒÒ ÝÝ ÑÙÙØØÙÙ ÙÒ Ò ÓÖÑØ Ó ÑÙÙع ØÙÙº Ë ÙÖ Ù Ý ¹Ø ÓÖ Ô ÖÙ ØÙÙ ÙØÚ Ò ØÓÒÒ ÝÝ Òº

3 Å Ø Ò È(E H) Ã Ñ Ö º ÎÓÒÝ ÒØ Î ØÓ E Ø ÚÓÒÝ ÒØ Ù Ø Ø Ó µ ω : 1 Ô ÒÓ Ø µ M Ø Ö Ó ØØ Ó E ØÓØ Ù Ù Ñ Ò ØØ M Ó E ØÓØ ÙØÙÙ ÚÓ Ø Ø ω Mº ÂÓ Ù ÓØ ÚÚ Ø E Ò ÝÚ ÝØ ÚÓÒ Ô¹ Ò ω(h) ω ÖÔÔÙÙ H Ø µº Ç ÓÓÒ ω(h) ÖÙÒ Ô Ò ÚÓÒÝ ÒØ Ù º ÊÙ Ô ¹ È(E H) ω(h)m + È(Ē H) ( M) = 0, Ñ Ē ÓÒ E Ò ÓÑÔ Ñ ÒØØ º E Ò ÔÚ Ö¹ ÑÙÙ Ò ØÓÒÒ ÝÝ 1 È(E H) = 1 + ω(h). Ì Ø Ú ÚÓÒÝ ÒØ ÚÓÒ ÝØØ Ù ¹ ØÚ Ò ØÓÒÒ ÝÝÒ ÓÒ ØÖÙ Ø ÓÓÒº À ÚÒØÓ ÑÙÙØØ ØÓÒÒ ÝÝØØ ÅÖ ØØ Ø E Ò ØØÝÚÒ ÔÚ ÖÑÙÙÒ ¹ Ó Ò µ ØÓÒÒ ÝÝØ Ò È(E H)º À ÒØ ÙÙØØ ØØÓ F ÓÔ Ø Øº ÆÝØ E Ò ØØÝÚ ÔÚ ÖÑÙÙ ÚØØÑØØ Ò Ó È(E H) ÚÒ È(E F, H)º Ñ ¾º½ ÀØ ØÒ Ô Ò ÓÒ ØÓ Ò Ò ÔÙÓ Ù¹ Ú ÔÙÓ µ ÓÒ ÙÔ Ö º Ç ÓÓÒ ØÙÓ 0 Ó ÙÚ ÔÙÓ ÓÒ Ý Ô Ò 1 Ó ÓÒ Ô Òº Å Ö º E Ø ÔØÙ¹ Ñ 1 º ÒÒ Ó ØÝ ÔÚ ÖÑÙÙ Ø Ó ÓÓÒ È(E H) = 1 2 Ø ÓØÒ ÑÙÙØ µº Ç ÓÓÒ F Ó Ö Ó ÓÒ 10 ØØÓ ¼ ¼ ¼ ¼ ¼ ½ ½ ¼ ¼ ½ ÌÑÒ Ò ÔÚ ÖÑÙÙ ÓÒ È(E F, H) < 1 2 º Ì ØÓØ ÓÒ ØØÓ Å Ø Ò ÚÓÒ ÓÔ¹ Ô ÚÒÒÓ ØØ º Ñ Ø Ò ÚÓÒ ÔÒ Ò¹ Ø Ó ÓÒÒ Ò ØØÝÚ ÔÚ ÖÑÙÙØØ º Ý ¹Ø ØÓØ ÓÔ ÖÓ ØÓÒÒ ÝÝ Ò ÚÙ º ½½ ÀÙÓÑ ÚÓÒÝ ÒØ Ù ÓÒ Ø ØØÝ Ù Ô ¹ Ò Ò º ÌÓÒÒ ÝÝ ÒÒ Ø ØÓع Ø ÚÓÒÝ ÒØ Ù E Ò ÔÙÓ Ø ÓÒ ØÓÒÒ ¹ ÝÝ Ò Ù È(E H)/È(Ē H) E Ø Ú ØÒ ÓÒ È(Ē H)/È(E H) º º ÃÝØ ØÒ Ø ÒÖ ØÓÒÒ ÝÝ ¹ Ò Óµ ÄØÓ ÓÒ r ÔÙÒ Ø s Ò Ø Ô Ó º ÔÓ Ñ ØÒ E = Ô Ó ÔÙÒÒ Òº ÅÖ ¹ Ø Ò ÝÑÑ ØÖ Ò Ô ÖÙ ØÙ Ò È(E H) = r r + s. ÎÓÒÝ ÒØ Ù Ó µ ÎÓÒÝ ÒØ Ù E Ò ÔÙÓ Ø F Ú Ø Ó H ÓÒ È(E H) È(F H) 1 Ø Ú ØÒ ØÓÒÒ ÝÝ È(E H) ØÓÒÒ ÝÝØØ È(F H) Ø Ú ØÒº ÌÑ ÓÒ Ù Ò ÙÓÒÒÓ ÑÔ Ø Ù Ò ØÓ¹ ÒÒ ÝÝ ÔÓÑÔ ÑÖ Ø µ ÚÖغ Ñ ¾º½º ÅÝ ÔØ ÒØÓØ ÓÖ Ö ¹ Ò ÝÝ Ý Ø ÝØØÚØ ÚÓÒÝ ÒØ Ù ¹ ØØ º ½¼ ½¾

4 ÊÔÔÙÑ ØØÓÑÙÙ ÒÔ ÒÒ µ ÅÖº E F ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó H Ó È(E F H) = È(E H) È(F H). Å ÖÒÒ ÝÒØÑ ÔÙ ÓØ ØÒ Ú Ø ¹ ØÓ H ÔÓ ÌÓÒÒ ÝÝØ ÓÚ Ø Ò Ó Ý ¹Ø ÓÖ ØÓÒÒ ÝÝØ ÓÚ Ø Ó ¹ º Ë Ö Ó Ø ØÒ E F ÓÚ Ø ÖÔÔÙÑ ØØÓÑ ¹ Ó Ó È(E F) = È(E) È(F) º ÌÑ ÓÒ Ý ØÔ ØÚ Ò Ò ØØ È(E F) = È(E) = È(E F) Ø È(F E) = È(F) º À ÙÖ Ø Ø E F ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó ØÓ Ò E Ø F µ ØÙÒØ Ñ Ò Ò ÑÙÙØ ¹ ØÝ Ø ØÓ Ò ÔÚ ÖÑÙÙ Ø º F Ø ÓÔ Ø ÙÒ ÔÓ ØÒ E Ò ÔÚ ÖÑÙÙØØ º ½ Ý Ò Ú ½º ÃÓ ÓÒ ØÓÒÒ ÝÝ Ç ÓÓÒ H 1, H 2,... ÓÙ ÓÒ Ω Ó ØÙ Ø º H i H j = i j nh n = Ωº Ë Ó Ò ØÓ Ø µ È(E) = n È(E H n) È(H n). ¾º ÃÒØ Ø ØÓÒÒ ÝÝØ È(H n E) ÃÓ È(H n E)È(E) = È(E H n ) = È(H n )È(E H n ), ÒÒ È(H n E) = È(Hn)È(E Hn) È(E) = È(Hn)È(E Hn) k È(H k)è(e H k ) È(H n)è(e H n). ÌØ ÙØ ÙØÒ Ý Ò Ú º ÀÙÓѺ È(H j E) È(H k E) = È(H j) È(H k ) È(E H j) È(E H k ). ÈÓ Ø Ö ÓÖ ÚÓÒÝ ÒØ Ù ÔÖ ÓÖ ÚÓÒÝ ÒØ Ù E Ò ÔÚ ÖÑÙÙ Ò Ù ¹ º ½ ÊÔÔÙÑ ØØÓÑÙÙ Ó ÑÙØØÓÒ Ñº ¾º¾ ÄØÓ ÓÒ r ÔÙÒ Ø k Ú Ó Ø Ô ¹ Ó º Ì Ò ÓØ ÒØ Ø Ò Ó ØØÒº E ÔÙÒ ½º ÚÓ F ÔÙÒ ¾º ÚÓ Ì Ô Ù ½ ÈÙÒ Ø Ò Ù p = r/(r + k) ØÙÒÒ ØÒº ÌÒ È(F E) = p = È(F) ÓØ Ò E F ÓÚ Ø ÖÔ¹ ÔÙÑ ØØÓѺ Æ Ò Ø Ò ØÓÒÒ ¹ ÝÝ ÒÒ º Ì Ô Ù ¾ ÈÙÒ Ø Ò Ó ÙÙØØ ØÙÒÒ Ø º ÌÒ E F ÚØ Ó ÖÔÔÙÑ ØØÓÑ Ú ÓØ ÒÒ Ø ÓÚ Øº ËÝÝ ÓÒ ØØ E Ø Ò Ò ÓÖÑØ ÓØ ÔÙÒ ¹ Ø Ò Ó ÙÙ Ø Ú ÙØØ F Ò Ó Ò ØÓÒ¹ Ò ÝÝØÒº ÅÙØØ Ú p Ó ØÙÒÒ ØØÙ ÒÒ ÚÓ ÑÑ Ö Ó ØØ Ó Ø ØÓÒÒ ÝÝØ Ø¹ Ø Ñ ØØ p ÓÒ ØÙÒÒ ÑÙÙØØ٠ع Ø ÚÓÒ ÙØ Ù Ñ ÒØ Ñ µ È(E p) = È(E F, p) = p. E F ÓÚ Ø Ó Ø ÖÔÔÙÑ ØØÓÑ ¹ Ó pº Ì ØØ Ù ÓÒ ØÖ Ñ ÖØÝ Ø ØÓ ¹ Ñ ÒØ Ñ º ½ Ѻ ¾º Ç Ø ØÒ ØØ ØÝØ Ò ÝÒØÝÑÒ ØÓÒ¹ Ò ÝÝ ÓÒ 1 º Ì Ö Ø Ò ØÓÒÒ ÝÝØØ ØØ 2 Ó Ø ÓÚ Ø ØÝØغ ÇÒ Ó ØÑ ØÓÒÒ ÝÝ 1 4 Î Ø Ù ÓÒ ØØ Ó Ã Ó Ø ÚÓ Ú Ø Ó ÒØØ Ø ÑÓÒÓØ Ý ÓÓØØ Øµ Ñ Ö º M Ø ¹ ÒØØ Ø Ø Ý ÓÓØØ Øµ Ñ Ö º Dº ÁÒØØ ¹ Ø Ó Ø ÓÚ Ø Ò Ñ Ù ÙÔÙÓØ P ÔÓ T ØÝØØ µº È(TT M) = È(PP M) = 1 ; È(TP M) = 0; 2 È(TT D) = È(PP D) = 1 4 ; È(TP D) = 1 2. È(TT) = È(TT M)È(M) + È(TT D)È(D) = 1 2 È(M) + 1 [1 È(M)] 4 = 1 [È(M) + 1] 4 Ì Ø ÙÖ ØØ È(TT) > 1 4 Ó È(M) > 0º Ë ÚÙØÙÓØØÒ Ò È(M) = 4È(TT) 1. ÌÑÒ ÒØ ØØ Ò ÚÙ ÚÓÒ Ø ÑÓ ÒØØ ¹ Ø Ò Ó Ø Ò Ó ÙÙ ÔÓÔÙØ Ó Ó È(TT) ÚÓ ¹ Ò Ø ÑÓ Ú Ø Ö Ø Ö Øº ½

5 º Å Ø Ñ Ö Ñ Ø Ê Ò ØØÓ ØØ ÓÒ Ó Ö ÝÑÑ ØÖ Ò Òº Ø Ò ÓÒ ØØÓ Ô Ø Ø Ó Ö Ø ÖÙÙ¹ ÒÒ Ù Ø Ò Ò ÖÚ Ò ÓÒ θº Ç ÓÓÒ E Ø ÔØÙÑ ØÙÓ ÓÒ ÖÙÙÒº Ë Ó Ò ÚÓÒ Ñ ÖØ ØØ Ñ µ È(E θ) = θ. Ê Ò ØÓØ ØÙ Ú Ø ÒÝØ Ó Ø ÖÔÔÙ¹ Ñ ØØÓÑ º Ì ÓÒ Ý ¹Ø ØÓØØÒ ÖÓ Ò ØÓÒ¹ Ò ÝÝ ÒØÒ Ò Ø ØÓØØ Ò Ã Ò Ò Ê Ò ØÓØ ÓÚ Ø ÖÔÔÙÑ ØØÓÑ ÖÙÙÒ Ò ØÓÒÒ ÝÝÒ Ó θº Ý ÂÓ θ ÓÒ ØÙÒÒ ØØÙ Ó Ò Ö Ò ØÓØ ÓÚ Ø ¹ Ó Ø ÖÔÔÙÑ ØØÓÑ Ó θ Ù Ò ¹ ØÓ ÖÙÙÒ Ò ÒØÝÑ ØÓÒÒ ÝÝ ÓÒ θº Ë ¹ ÒÓÑÑ ØØ ÚÒÒÓØ ÓÚ Ø Ú ÒÒ º ÖÓ Ý ¹ ØÝÑ Ø Ú Ñ ÓÒ ØÙÒØ Ñ ØÓÒ ÙÙÖ θ ÑÙØØ ØÙÒØ Ñ ØØÓÑ ØÓÒÒ ÝÝ ¹ µº ÃÓ θ ÓÒ ØÙÒØ Ñ ØÓÒ ÓÒ ØÙÒÒ ¹ ÑÙÙØØÙ ÓÒ ÙÑ Ô ÖÙ ØÙÙ Ø Ù Ø ØØÓÓÒº ½ ÆÓÖÑ Ñ Ñº º½ Ú Ò ³Ò Ø Ó Ò ÒØ ¹ Ò Ò ÝÝ Ó À ÒÖÝ Ú Ò ½ ½ ½ ½¼µ ÔÝÖ ÑÖ ØØÑÒ ÑÔ ÓÒ Ø ÝÒº º º¾ º º º º º ¾ º¾ º º º º½ º¾ º º ¾ º º º º º º º º Ñ Ò Ñ Ü ÖÚÓ ÓÒØ º½ º º ¼º½ ¾ frekvenssi Cavendish data y ½ Ì Ö Ø Ý ØÝ Ó Ø ÑÑ Ò Ñ Ø Ò ÔÚ ÖÑÙÙ ØØÝÝ ØØÓ Ö º Ç ÓÓÒ E Ò ÑÑ Ò Ò ØØÓ ÓÒ ÖÙÙÒº Å ÓÒ Ë Ó Ò È(E) = È(E θ) = θ. g(θ)è(e θ)dθ = (θ) Ñ g(θ) ÓÒ θ Ò ØÓÒÒ ÝÝ ÙÑ º Ç ÓÓÒ F ØÓ Ò Ò ØØÓ ÓÒ ÖÙÙÒº Ë Ó Ò È(F E, θ) = θ, È(F E) = (θ E), È(E F) = (θ 2 ). ÂÑÑ Ò Ò ÙÖ Ø ØØ È(E, F θ) = È(E F θ) = È(E θ)è(f θ) = θ 2 º È(F E) Ò Ó ØÓ È(E F) È(F E) = È(E) = (θ2 ) (θ) Î Ö(θ) + (θ)2 = (θ) = Î Ö(θ) (θ) + (θ) = Î Ö(θ) (θ) + È(F) È(F). Ø ÙÙÖÙÙ ÓÒ ÚÓ Ñ Ó ÚÒ Ó Î Ö(θ) = 0º ½ Å ÝØ Ô Ö Ñ ØÖ Ø ÚÒÒÓÒ Ò ÓÖ¹ ÑØ ÓÒ ØÓ Ò º ÒÖØÒ Ò Ñ ÓÒ Ù¹ ÖÚ Ó ØØÒ Ñ ØØ Ù Ø ÖÙÙÒ ØÙÒÒ ØÙ ¹ µ ÚÒÒÓØ y 1,..., y n ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó θ y i θ Æ(θ,0.04) ÀÙÓÑ ØØ Ó Ú ÓÒ ÙØÚ Ø º Í ÓØ ¹ ÚÒØÓÒ Ó Ò ÖÔÔÙÑ ØØÓÑÙÙØÒ ÒÓÖÑ ¹ ÙÙØÒ Ø ØØÝÝÒ Ú ÖÒ Òº ÌÑ ÚÓÒ Ý Ø º º Ù ÓØÒ ÒÓ ¹ ØÒ Ó Ò ÖÔÔÙÑ ØØÓÑÙÙØÒ Ó¹ Ñ Ò Ô Ö Ñ ØÖ Øµ ÚÒØÓÒ ÒÓÖѹ ÙÙØÒ ÓÓ Ò y i θ, σ 2 Æ(θ, σ 2 ) ÚÒÒÓØ ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó (θ, σ 2 )º Ì ØÓØØÒ Ô ÖÙ ÙÖ Ó Ø ØØÒ ÚÒØÓÒ ÖÔ¹ ÔÙÑ ØØÓÑÙÙ x i Æ(θ, σ 2 ) Ñ ÓÒ Ö º ¾¼

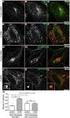
6 Å Ø Ò ÔÓ Ø Ö ÓÖ ÙÑ ÝØ ØÒ ÒÖ Ò ¹ Ò Ú ÒÒ Ñ Ö ÚÒØÓÒ y 1,..., y n Ý Ø Ù¹ Ñ Ó θ ÓÒ ( )n 1 2 p(y 1,..., y n θ) = e 1 ni= (y i θ) 2. 2π 0.04 Ë ÒÓÑÑ ØØ ÚÒÒÓØ y 1,..., y n ÓÚ Ø Ú ¹ ÒÒ ÜÒ µ Ó ÒÒ Ý Ø ¹ ÙÑ p(y 1,..., y n θ) Ó θ ÔÝ ÝÝ Ñ ¹ Ò Ú ÚÒØÓÒ Ö ØÝ Ø Ô ÖÑÙØÓ ¹ Òº Ñ Ö Ó Ò Ò ÖÔÔÙÑ ØØÓÑÙÙ ÚÒØÓ¹ Ò Ñ ÙÑ ØÚ Ø Ú ÒÒ ÙÙÒº Ë Ò ¹ Ò ÚÒÒÓØ y 1,..., y n ÚØ Ó Ñ ÖÒ Ø ÖÔ¹ ÔÙÑ ØØÓѺ ÀÙÓÑ p(y 1,..., y n θ) Ø ØÙÒ θ Ò ÙÒ Ø ÓÒ ÓÒ ÓØÓ Ò y 1,..., y n Ù ÓØØ ÚÙÙ ÙÒ Ø Óº º ÃÙÚº ÎÓÒ ÔÖØ ÔÓ Ø Ö ÓÖ Ù¹ Ñ Ò ÙÚ ÙÒ Ñ(θ) 2º ÂÓ θ = (θ 1,..., θ k ) ÒÒ Ù Ò ÝØ ØÒ Ñ ÖÒ ÔÓ Ø Ö ÓÖ Ù¹ ÑÒ p(θ i y) = p(θ y)dθ 1 dθ i 1 dθ i+1 dθ k ÙÚ i = 1,..., kº ÆÑ ØØÚØ Ó Ø¹ Ø Ø Ò ÓÖÑØ ÓØ ÔÓ Ø Ö ÓÖ Ø ÑÙØØ ¹ ÚØ Ñ Ô Ö Ñ ØÖÒ Ú Ø ÔÓ Ø Ö ÓÖ ¹ Ø µ ÖÔÔÙÚÙÙØØ º ÎÓÒ ÑÝ ÙÚ Ø ¹ Ò Ô Ö Ñ ØÖ Ò θ i θ j ÙÓØØ Ø Ñ Ö¹ Ò ÔÓ Ø Ö ÓÖº º Ö Ò ØÝ Ò Ø ÔÓ Ø Ö ÓÖ Ù¹ Ñ ÚÓÒ ÙÚ Ø ØÙÒÒÙ Ù ÙÒ ÚÙ º Í Ò ÝØ ØÒ Ý ÙÓØØ θ ÙÚ Ù Ø ÖÚÓ ÓÒØ ½¼±¹Ö ¼±¹Ö ¾½ Ñ a%¹ö ÓÒ ÖÚÓ θ a Ó È(θ < θ a y) = a 100 º Ó Ø µº ¾ º ÈÖ ÓÖ ÔÓ Ø Ö ÓÖ ÔÖØÚ Ø ÙÑ Ø Ý ¹Ø ØÓØØ Ó ØÓÔØ Ø Ô ÖÙ Ø ØÒ ÔÓ ¹ Ø Ö ÓÖ ÙÑÒ p(θ data). Ì Ö Ø Ò Ò Ò Ñ Ø Ò ÔÓ Ø Ö ÓÖ ÙÑ ÝØ ¹ ØÒ Ó ØÓÔØ Ø Ò Ø Ó º Ë Ò Ò ØÙØØÒ Ñ ¹ Ø Ò ÔÓ Ø Ö ÓÖ ÙÑ ÓÒ ØÖÙÓÒº º½ ÈÓ Ø Ö ÓÖ ÒÖ Ò Ò Ú ÒÒ Ç Ø ØÒ ØØ y ÓÒ ÚØØÙ Ò ØÓ Ó Ø Ø Ú Ø ÖÓ ØØ Ú Ó ØÙ º Ç ÓÓÒ θ ØÙÒØ Ñ ØÓÒ ÙÙÖ º Ë ÓÒ Ù Ò Ô ¹ Ö Ñ ØÖ ÚØÓÖ µ ÑÙØØ ÚÓ ÑÝ Ó ÔÙÙع ØÙÚ ÚÒØÓ ÚØÓÖ µ Ø Ú Ô Ø ÒØØ ÑÙÙØØÙº Ý ¹Ø ØÓØØ Ò Ò Ö ØÝÝÔÔ Ø Ò ÑÙÙØØÙ Ò Ú Ø ÖÓ Æ ÓÚ Ø ØÙÒØ Ñ ØØÓѺ Ç Ø ØÒ ØØ ÝØ ÓÒ θ Ò ÔÓ Ø ¹ Ö ÓÖ ÙÑ p(θ y)º Ë ÓÒ ØÙÒØ Ñ ØØÓÑ Ò ÙÙÖÒ θ Ó Ò Ò ØÓÒÒ ÝÝ ÙÑ Ó ÚÒØÓ yº ¾¾ º Î Ø ÑÓ ÒØ ÙÒ Ñ(θ) = 1µº ÅÖ¹ ØÒ a b Ø Ò ØØ P(a θ b y) = 1 ǫ. ÌØ ÙØ ÙØÒ ØÒ¹Ú Ý ¹ÙÓØØÓÚ Ö ÒØ ÖÚ µº Ê Ø Ù Ó Ý ØØÒ Òº Ì Ú ÑÑ Ø ÓÒ ØÖÙ ¹ Ø ÓÔ Ö ØØØ ÓÚ Ø ÝÒ Ú ÝÑÑ ØÖ Ò Ò Ú º º P(θ a y) = ǫ 2 P(θ b y) = ǫ 2 º ÙÙÖ ÑÑ Ò Ø ÝÒ Ú À Á Ø Ò ØÝ ÒØ ÖÚ µ ÑÓÒ ÙÓØØ Ø Ô Ù À Ê Ö ¹ ÓÒµ ÙÑ Ò Ø Ý ÙÒ Ø Ó ÓÒ Ú Ò ÙÙ¹ Ö ÑÔ Ù Ò Ñ Ò Ú Ò Ù ÓÔÙÓ Ô Ø º ÌÑ ÓÒ ØÝÝÔ Ò Ò Ý Ò Ò Ú ØÓØÓ ¾

7 p( θ y) À Á ÝÑÑ ØÖ Ò Ò Ý ¹Ú Suurimman tiheyden väli p( θ y) Symmetrinen Bayes väli º ÈÓ Ø Ö ÓÖ Ø ÚÓÒ Ñ ÒÒÓ ¹ Ø Ø º ØÓÒÒ ÝÝ È(θ A y) Ñ A ÓÒ ØÙØÒ ÑÖÑ Ø ÔØÙÑ Ù Ò ÝÔÓØ º a 1 ε b θ º ÀÝÔÓØ ÒØ Ø Ù º ÇÒ ÒÒ ØØÙ ÝÔÓØ ÙØ Ò À : θ > 0º Ä ØÒ È(À y) = È(θ > 0 y) = p(θ y)dθ 0 = ØÒ ØØ ÝÔÓØ ÓÒ ØÓ Ó Ò ØÓ yº ÀÙÓÑ ØØ ØÑ ÓÒ ØÓ Ò ÝÔÓØ Ò ÝÚ ¹ ÝÑ Ò ØÓÒÒ ÝÝ º Ë Ò Ò Ò Ò Ô¹ ÖÚÓ Ó ÝÔÓØ Ò Ý Ñ Ò ØÓÒÒ ÝÝ _ ε 2 _ ε 2 θ ÀÙÓÑ ½ Ý ¹Ñ Ò Ø Ñ ÓÒ ØÝÝÔ Ø ØÓÒÒ ÝÝ ÙØ Ò Ý ¹ÙÓØØÓ¹ Úº Ò Ò ÒØ ÓÒ ØØ ÔÓ Ø Ö ÓÖ ¹ ÙÑ ÚÓÒ Ø Ø Ñ ØÒ¹ÙÑ ÓÒ ØØÙ º ÀÙÓÑ ¾ ÈÓ Ø Ö ÓÖ ÙÑÒ Ô ÖÙ ØÙÚ Ò¹ Ö Ò ÖÓ Ø ÒÖ Ò Ø ÙÓ¹ Ñ ØØ Ú Ø Ô¹ ÖÚÓ ÙÓØØ ÑÙ Ú Ø ØÓ Ø Ñ ÖØ ÚÝÝØØ ÖØØÓÑÙÙع Ø ººº ¾ ¾ º È Ø ¹ Ø ÑÓ ÒØ º À ÙØÒ ØÚ Ø ÔÓ Ø ¹ Ö ÓÖ ÙÑ Ò Ò ÓÖÑØ Ó Ý ØÒ ÖÚÓÓÒ θ Ò Ý ¹ Ø ÑØØÒº Î ØÓØÓ θ = Ö Ñ Üp(θ x) ÔÓ Ø Ö ÓÖ ÑÓÓ ˆθ ÔÓ Ø Ö ÓÖ Ñ Ò ÙÑ Ò p(θ y) Ñ ¹ Ò θ = (θ y) ÔÓ Ø Ö ÓÖ ÖÚÓ Æ Ø Ò ÑÑ Ò Ò ÓÒ Ò ÓÒ Ò ÙÙÖ Ñ¹ Ñ Ò Ù ÓØØ ÚÙÙÒ Ø ÑØØÓÖ Ò Ò º Ë ¹ Ø ÒÓØÒ Å È Å Ü ÑÙÑ ÈÓ Ø Ö ÓÖ ¹ Ø Ñ ØÓÖµ ¹ Ø ÑØØÓÖ º ÇÒ ÙÓÑ ØØ Ú ØØ Ý ¹Ø ØÓØ ÚØØ Ô ¹ Ò Ô Ø ¹ Ø ÑØ Ò ÝØØ Ó ØØÓ θ Ò ÔÚ ÖÑÙÙ Ø ØØÓÒ ÓÒ ÔÓ Ø Ö ÓÖ Ù¹ Ñ µº Í Ò ÒÒ ØÒ θ Ò ÔÓ Ø Ö ÓÖ Ù¹ Ñ Ò ÓÒØ s.d. Æ Ø Ù Ø Ò Ò Ô ØÙØ Ô Ø ¹ Ø ÑØØÒ ÚÒ Ô ÑÑ ÒÒ ÔÓ Ø Ö ÓÖ Ù¹ Ñ Ò ÙÚ Ù Ò ÒÒ Ò ÓÒÒ Ò Ñ ØØÓ Ò µº ¾ º¾ ÈÖ ÓÖ ÙÑ Å Ø Ò ÔÓ Ø Ö ÓÖ ÙÑ ÑÙÓ Ó Ø ØÒ Ì ÖÚ ØÒ Ñ ÚÒÒÓ p(y θ) ÔÖ ÓÖ ÙÑ ØÙÒØ Ñ ØØÓÑ θ Æ Ø Ò Ò ÓÒ Ù ÓØØ ÚÙÙ ÙÒ Ø Ó L(θ; y) = p(y θ)º Ë ÙÚ ÚÒÒÓÒ ØÙÒØ Ñ ØØÓÑ Ò ÙÙÖÒ Ú Ø Ý Ø ÝØغ ÌÑ ÓÒ Ø ÑÒ Ñ Ù Ò Ò Ø ØÓØØÒ Ù ÓØØ ÚÙÙ ÙÒ Ø Óº ÂÑÑ Ò Ò ÓÒ ÙØÚ Ò Òµ ÒÒ Ó ØÝ ØÙÒ¹ Ø Ñ ØØÓÑ Ø θ Ø ÒÒ Ó ØÝ Ø ØÒ Ù¹ Ñ Ò ÚÙ º ÆÑ Ý Ø ØÒ Ý Ò ¹ Ú Ò ÚÙ p(θ y) = p(θ)p(y θ) p(y) = p(θ)p(y θ) p(θ )p(y θ )dθ. Ë ÔÓ Ø Ö ÓÖÔÖ ÓÖ Ù ÓØØ ÚÙÙ ÒÓÖÑÖ ØÒ ÙÑ º ¾

8 Ã Ò Ò Ø ØÓØ Ô ÖÙ ØÙÙ Ô ÓØ Ù ¹ ÓØØ ÚÙÙØÒ L(θ; y) = p(y θ) ÙÒ Ø Ý ¹ Ø ØÓØ ÔÓ Ø Ö ÓÖ ÙÑÒ p(θ y)º ¹ ÑÑ Ò Ò ÓÒ ØÓÒÒ ÝÝ ÙÑ Ñ Ø Ù ÓØØ ÚÙÙ Ø Ó º ÀÙÓÑ ½ ÈÓ Ø Ö ÓÖ ÓÒ ÒÓÖÑÖ Ù Ø Ú ÔÖ ÓÖ Ù ÓØØ ÚÙÙ p(θ y) p(θ) p(y θ). Å ÖÒØ Ø Ö Ó ØØ ³ ÙÓÖÒ Ú ÖÖ ÒÒÓ ¹ Ò Ò³ºµ ÂÓ ÔÖ ÓÖ Ù ÓØØ ÚÙÙ ÙÒ Ø Ó ØÙÒÒ ØÒ ÒÒ ÔÓ ¹ Ø Ö ÓÖ ØÙÒÒ ØÒ ÒÓÖÑÖ Ù Ø Ú º Ä ÒÒ Ø ÓÒÑ Ø ØØÝÚØ ÔÓ Ø Ö ÓÖ Ò ÒÓÖÑÖ Ù Ò Ø º Ò¹ ØÖ Ò p(θ) p(y θ)dθ Ñ Òº ÌÓ Ø ÔÓ Ø Ö ÓÖ Ù ÓÒ p(θ y) p(θ y) = p(θ) p(θ ) p(y θ) p(y θ ). Ë ÝØ Óº ÒØÖ Ò Ñ Ø º Ѻ º½ ÆÓÖÑ Ñ Ç ÓÓÒ ÚÒÒÓØ y = (y 1,..., y n ) y i θ Æ(θ, v) Ú ÖÒ v ØÙÒÒ ØØÙ ÓØÓ ÖÔÔÙÑ ØÓÒ Ó¹ θº Ç Ø ØÒ Ú ØØ ÔÖ ÓÖ p(θ) ÓÒ ÒÓÖÑ Ø º θ Æ(m, w), Ñ m w ÓÚ Ø ØÙÒÒ ØØÙº À ÚÒØÓ Ò Ô ÖÙ ØÙÚ Ù ÓØØ ÚÙÙ ÙÒ Ø Ó ÓÒ n p(y θ) = p(y 1,..., y n θ) = p(y i θ) i=1 ÜÔ 1 n (y i θ) 2 2v i=1 Ó Ò ÖÔÔÙÑ ØØÓÑÙÙÒ Ô ÖÙ Ø º Ò ÔÖ ÓÖ ÓÒ p(θ) = 1 2πw e 1 2w (θ m)2 e 1 2w (θ m)2. ¾ ½ ÀÙÓÑ ¾ Ý ¹ Ò ÝÝ Ô ÖÙ ØÙÙ ØÒ Ò ÓÖÑØ Ó Ø Ò Ó Ò ØÙÒØ Ñ ØÓÒØ ÙÙÖ ØØ θº ÆÑ ÓÚ Ø Ò ØÓ p(y θ) Ò ÙØØ ÒÒ Ó ØÝ p(θ) Ò ÙØØ º ÈÓ Ø Ö ÓÖ ÚÓÒ Ö Ó ØØ ÑÙÓ Ó p(θ y) e 1 2w (θ m)2 e 1 2v ni=1 (y i θ) 2 = e 1 2 Q, Ñ ( 1 Q = w + n v ) (θ m 1 ) 2 + Ú Ó, ( m m 1 = w + nȳ ) ( 1 / v w + n ). v Ä Ñ Ò Ò Ô ÖÙ ØÙÙ Ò Ò ØÝÒØÑ Òº ÈÓ Ø Ö ÓÖ ÓÒ θ y Æ(m 1, v 1 ) Ø º ÒÓÖÑ ¹ ÙÑ { p(θ y) ÜÔ 1 ( 1 m 1 = v 1 = w + n v ( 1 w + n v } (θ m 1 ) 2, 2v 1 ) 1 ( m w + nȳ ), v ) 1 ÂÓ ÔÖ ÓÖ ÔÓ Ø Ö ÓÖ ÙÙÙÚ Ø ÑÒ ÙÑ Ô Ö¹ Ò ÒÒ ÔÙ ÙØÒ ÓÒ Ù ØØ Ô Ö Øº ÆÓÖ¹ Ñ ÔÖ ÓÖ ÖÚÓÔ Ö Ñ ØÖ ÙÒ Ú ÖÒ ÓÒ ØÙÒ¹ Ò ØØÙµ ÓÒ ÒÓÖÑ Ñ Ò º ÓÒ Ù ØØ ÔÖ ÓÖ º ¼ ¾

9 Ѻ º¾ Ú Ò ³ Ø Ø ºµ ÔÖ ÓÖ Ú ÖÑ Ø θ > 1 Ú Ò Ø Ý ½µ ÒÒ Ó ¹ Ø ÑØØ θ = 5º Ç ÓÓÒ θ Æ(5,0.5)º Ù ÓØØ ÚÙÙ ÆÓÖÑ Ú ÖÒ Ó ØÙ 0.04 Ú Ó Ñ ØØ Ù Ø ÖÙÙ µº ÔÓ Ø Ö ÓÖ θ y Æ(m 1, v 1 ) Ñ m 1 = ( ) ( / ) 23 = v 1 = ( ) 1 = ÃÙÚ ÈÖ ÓÖ ØØ Ø ÓÚÚ µ ÔÓ Ø Ö ÓÖ Ý Ø Ò ¹ Ò Ò ÚÚ µº ÈÖ ÓÖ ÙÚ θ Ò ØØÝÚ ÔÚ ÖÑÙÙØØ ÒÒ Ò Øº Ò ØÓ Ø ÓÔ ØÒ ÔÓ Ø Ö ÓÖ ÙÚ ØØ ÔÚ ÖÑÙÙØØ ÚÒØÓÒ Òº Ø Ö Ø ØÙ ÔÓ Ø Ö ÓÖ Ò Ó ØÓ ÒÓÙØÙÙ ÚÚ Ø ÓÒ Ù ØØ ÙÙØÒº ÃÙÒ Ø ÙÓÚÙ¹ ØÒ Ø ÑÙØ ØÙÚ Øº ÅÓÖÒ Ø Ô ÔÓ Ø Ö ÓÖ Ý Ø ÓÒ ÝØØ Å Å ¹ Ñ Ò Ø Ñ ÑÙÓ Òصº Å ÒÒÒ ÒÝØ Ñ Ò Ó Ò ØÒ Ñº º¾º ÔÓ Ø Ö ÓÖ ÙÑ Í Ë ¹Ó Ñ Ú ÖØÙÒ ÚÙÓ ¹ º ØÝ Ó Ø ÑÔ Ø Ö Ø Ù Ø Ò ÙÖ Ò ØÓ ¹ Ó ºµ Á Ò ÓÒ ÑÖ Ø Å Ö ÓÚ Ò Ø Ù ÓÒ Ø Ô¹ ÒÓÙÑ Ò ÓÒ ÑÙÓ Ø Ú ÔÓ Ø Ö ÓÖ º ÌØ Ø Ù ÑÙÓÒ Ù Ø ÖÚÓ Ø ØÒ ÔÓ Ø Ö ÓÖ»Ø Ò ØØÝÚ ÙÚ Ù º Ë ÙÖÚ ÚÙ Ó Ú Í Ë¹Ó Ñ ÓÖ Ò ½ Ƶ ßÝ ÒÓÖÑ ØØ ¾ µ ÑÖ ØØ Ù ÓØØ ÚÙÙÒ ÚÒÒÓÒ Ñ Òµ tiheysfunktio ØØ ÒÓÖÑ ¾µ ÑÖ ØØ ÔÖ ÓÖ Òº ÀÙÓÑ Î ÖÒ Ò Í Ë ÝØ ÒÓÖÑ Ù¹ Ñ Ò ÓÒØ Ô Ö Ñ ØÖ Ò ÒØ Ø Ú ÖÒ Ò¹ ØÒ Ò Ú ÖÒ Ø ÖÙÙ µ τ = 1/σ 2 25 = 1/ = 1/0.5º theta ÈÓ Ø Ö ÓÖ ÙÑ ÓÒ ÙÖÚ Ñº º¾ Ø ºµ ÈÓ Ø Ö ÓÖ Ò ÑÙÓ ÒØ Í Ë ÑÓ ß ÓÖ Ò ½ Ƶ ß Ý ÒÓÖÑ ØØ ¾ µ ØØ ÒÓÖÑ ¾µ tiheysfunktio theta Ø Ø Ý º º¾ º º º º º ¾ º¾ º º º º½ º¾ º º ¾ º º º º º º º ºµ Æ ¾ µ Ò Ø Ø ØØ µ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÑÒ Å ÖÖÓÖ Ú Ô ÑÒ Ú Ô Ø ÖØ ÑÔ ØØ º ¼º¼ ½¾½ º ¹ º ½ º º½ ½ ¾¼¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ Ì Ø ÚÓÒ 90% Ò ØÓÒÒ ÝÝ ¹ Ú ÑÔ ÓÒ Ø Ý ÓÒ (5.415,5.552) º ÑÙÓ ØÙ Å Ö ÓÚ Ò Ø ÙÒ Ö Ø Ó Ó Ø ÔÓ ¹ Ø Ö ÓÖ ØÒ Ã ÖÖ ØÒ Ú Ø ÝØ Ó ØÙ Ø ÓØ ÓÚ Ø Ó Ø ÒØ Ø Ò ØÙÓ Ò ½µ À ÚÒÒÓØ ÒÓÖÑ Ø Ú ÖÒ ØÙÒÒ ØØÙ Ú Óº ¾µ À ÚÒÒÓØ Ó Ø ÖÔÔÙÑ ØØÓÑ Ø Ó θ Ú ÒÒ µ µ ÈÖ ÓÖ ÓÒ ÒÓÖÑ Ñ Ó Ô Ò ÓÖÑ ØÚ Ò Òº theta indeksi

10 ÈÓ Ø Ö ÓÖ ÙÑ Ò ØÓ Ö ÑÑ ØØÙ¹ Ò Ø Ý ÙÒ Ø Ó µº Ø Ò Ò Ò ÚÚ ÓÒ Ø Ó¹ ÖØØ Ø ØØÙ ÒÓÖÑ Ò Ò ÔÓ Ø Ö ÓÖ º À ¹ ØÓ Ö ÑÑ ÓÒ ØØÙ Å Ö ÓÚ Ò Ø ÙÒ ÑÙ¹ Ó ÒÒ Ø º º Ý Ò Ú Ò Ô Ö ÝØØ Ç Ø ØÒ ØØ ÔÖ ÓÖ ÓÒ p(θ) Ù ÓØØ ÚÙÙ p(y θ)º Ç ÓÓÒ ÚÒØÓ y 1 Ò Ô ÖÙ ØÙ¹ Ú ÔÓ Ø Ö ÓÖ p(θ y 1 )º posteriori theta ÀÙÓÑ ØØ ØÓ Ö ÑÑ ÓÒ ØØÙ Ñ Ò ÒØÖÓ Ò¹ غ ÁØ Ò Ñ Ò ÓÒ Ø ÖÚ ØØÙ ÔÓ Ø Ö ÓÖ ¹ ÙÑ Ò Ø Ý ÙÒ Ø ÓØ Ø Ò ØØ ÒÓÖÑÖ Ù Ø ¹ Ø ÖÚ Ø ØÙÒØ ØÖ ÔÖÖ ÓÑÔ Ñ ¹ µº Ì Ò ÙÙ ÚÒØÓ y 2 Ó ÓÒ ÖÔÔÙÑ ¹ ØÓÒ y 1 Ø Ó θº ÅÓ ÑÔÒ ÚÒØÓ Ò Ô ÖÙ ØÙÚ ÔÓ Ø Ö ÓÖ ÓÒ p(θ y 1, y 2 ) p(θ) p(y 1, y 2 θ) = p(θ) p(y 1 θ) p(y 2 θ) p(θ y 1 ) p(y 2 θ) ÎÓÒ Ø ØØ ÔÓ Ø Ö ÓÖ p(θ y 1, y 2 ) Ò Ú ½º À ÚÒØÓ y 1 ÓÔ ØØ ÔÖ ÓÖ p(θµ ØÙÓ ¹ Ò ÓÒ ÔÓ Ø Ö ÓÖ p(θ y 1 )º ¾º y 2 ÓÔ ØØ ÔÖ ÓÖ p(θ y 1 µ ØÙÓ Ò ÔÓ ¹ Ø Ö ÓÖ p(θ y 1, y 2 ) º Ò Ò ØÓ Ñ ÑÝ ÒØ Ö ØÝ º º p(θ y 2 ) ÓÔ Ø Ø ØÒ ÚÒÒÓ y 1 ÖÔÔÙÑ ØØ Ø Ñ Ö ØÝ ÚÒÒÓØ ÓÒ ØØݵº Ñ ÖÒ º¾ Ñ ÚÓÒ ØØ ÙÙÒÒ Ø¹ ØÙÒ Ö Ò ¹ Ö Ø Ý Ö Ô µº ÑÔ Ò Ò µ ÓÒ ÚÒØÓ y i º À ÚÒØÓ ÑÖ ØØ Ñ Ò Ó ÓÒ Ý ØÙÒØ Ñ ØÓÒ ÙÙÖ ÖÚÓµ θ ØÙÒÒ ØØÙ Ú ÖÒ v ÑÑ ¹ Ò Ò Ø Óµº ÌÙÒØ Ñ ØÓÒ ÙÙÖ ÑÖ ØØ ÔÖ ÓÖ Ò Ó ÓÒ ØØÝÝ ¹ Ô Ö Ñ ØÖ m w ÑÓ ÑÑ Ø Ø ØØÙ ØÙÒÒ ØÙ Ý Ò Ø Óµº º À ÚÒÒÓÒ Ñ ÖÒ ÙÑ ÈÖ ÓÖ ¹ ÔÓ Ø Ö ÓÖ ÙÑ Ø ÓÚ Ø ØÒ¹ÙÑ Ô Ö ¹ Ñ ØÖÚ ÖÙÙ Θ ÙÒ Ø Ñ ÓÒ ØÓÒÒ ¹ ÝÝ ÙÑ ÓØÓ Ú ÖÙÙ Ñ ÖØÒ Ø Y µº ÇÒ Ø ÖÔÒ Ô Ø ÔÓ Ø Ö ÓÖ Ø Ø ÔÖ ÓÖ Ø µ ع Ò ÓØÓ Ú ÖÙÙØÒº ÌÑÒ ÚÙÓ ÑÖ Ø Ò ÙÙØØ ÙÑ Ò Ò ÚÒÒÓÒ Ñ ÖÒ ÙÑ ØØ Ò ÔÖØÚ Ò Ò ÙÑ ÙÚÙ º µº Ì ÙØ Ò y ÓÒ ÚÒØÓº Ë ÚÓ Ó Ö ÚØÓÖ ººº º m=5 w=0.5 Ç Ø ØÒ Ò ØØ ÔÖ ÓÖ ÓÒ p(θ) Ù ¹ ÓØØ ÚÙÙ p(y θ)º ÅÖØÒ ÚÒÒÓÒ y ¹ ÙÑ Óº ÚÒÒÓÒ Ñ ÖÒ ÙÑ p(y)º Ë Ø ÚÓÒ ÑÝ ÙØ Ù ÚÒÒÓÒ ÔÖ¹ ØÚ ÙÑ ºµ θ v=0.04 p(y) = p(y, θ)dθ = p(y θ)p(θ)dθ. y i ÌÑ ÓÒ Ö Ù Ò ÚÒÒÓÒ ÙÑ Ø ØÓØØ Ó ÚÒÒÓÒ ÙÑ Ø Ö Ó Ø ØÒ Ó Ø ÙÑ p(y θ)º ¼

11 À ÚÒÒÓÒ Ñ ÖÒ ÙÑ ÝØ Ò ¹ ØÓ Ò Ò Ë Ø Ú Ø ÙÒ Ó ØÙ ÔÖ ÓÖ Ø Ó Ø º Ë ÓÒ ÒÒÙ Ø ØÙ Ú ¹ ÚÒÒÓ ÙÒ Ù ÓØØ ÚÙÙ ÔÖ ÓÖ ÓÒ Ú ØØÙ ÑÙØØ ÚÒØÓ Ó ØØݵº  ÙÑ p(y) ÚÓÒ ÝØØ ÑѺ ØÙØع Ø ÔÖ ÓÖ ÙÑ Ò ÖÚÝÝØغ ÈÖ ÓÖ Ø¹ ØÓ Ù ÓØØ ÚÙÙ Ó Ø Ú Ø ÚÒÒÓÒ Ù¹ ÑÒº Ó Ú ÚÓÒ ÑÝ Ý Ø ÚÓ ¹ Ñ Ó Ú Ó Ø Ñ ØÒ ¹ µ (y) = θ (y θ) Î Ö(y) = θ Î Ö(y θ) + Î Ö θ (y θ) ÆÑ Ú Ø ÒÒ ØØ ÔÒ ÑÒ Ú ¹ Ø ÙÙÒ Ú Ö Ø ½ Ѻ º Ú Ò ³ Ø Ø ºµ Ç ÓÓÒ θ Æ(5,0.5) ỹ θ Æ(θ,0.04) Ý ÚÒØÓ Ñ Ø µº ÅÖØØÚ ỹ Ò ÙÑ p(ỹ)º ÇÓØ Ó ÚØ ØÒ ÒØÖÓ ÒØ Ã Ö Ó Ø ØÒ ỹ = (ỹ θ) + θ. ÆÝØ ỹ θ θ Æ(0,0.04) θ Æ(5,0.5)º Ò ỹ θ θ ÓÚ Ø ÖÔÔÙÑ ØØÓѺ ÌÒ ỹ ÓÒ Ò ÒÓÖÑ ÙØÙÒÒ ØÙÒÒ ¹ ÑÙÙØØÙÒ ÙÑÑ Ò ÒÓÖÑ ÙØÙÒÙØ (ỹ) = (ỹ θ) + (θ) = = 5 Î Ö(ỹ) = Î Ö(ỹ θ) + Î Ö(θ) = = 0.54 Ì Ø ÙÖ ØØ ỹ Æ(5,0.54)º º ÈÖØÚ Ò Ò ÙÑ Ç Ø ØÒ ØØ Ò ØÓÓÒ y Ô ÖÙ ØÙÚ ÔÓ ¹ Ø Ö ÓÖ ÓÒ p(θ y)º Ë ÙÑÑ θ Ó Ú Ò ÔÚ ÖÑÙÙÒ ÚÒÒÓÒ y Ø Ñ Ò Òº Ì Ò ÙÙ ÚÒØÓ ỹ Ó ÓÒ ÖÔÔÙÑ ¹ ØÓÒ y Ø Ó θº ÌÒ ÒÒÙ Ø ÙÑ ÔÖØÚ Ò Ò ÙÑ ÔÖØÚ Ò Ò ÔÓ Ø ¹ Ö ÓÖ ÙÑ µ ỹ ÓÒ ỹ Ò Ó Ò Ò ÙÑ Ó y Ñ Ö º p(ỹ y)º ÂÓ ØÒ p(ỹ y) = = p(ỹ θ, y)p(θ y)dθ p(ỹ θ)p(θ y)dθ marginaalijakauma Ë ÓÒ Ó ØÙ ÙÑ ÙÑ Ø p(ỹ θ) Ñ ¹ θ Ò ÔÒÓ Ò ÓÒ ÔÓ Ø Ö ÓÖ ÙÑ Ò p(θ y) ÖÚÓغ y ¾

12 Ø ºµ Ѻ º Ú Ò ³ Ø Ø ºµ Ç ÓÓÒ Ò θ Æ(5,0.5) y θ Æ(θ,0.04)º Ź ÖØØÚ ÙÑ p(ỹ y)º ÃÝØ ØÒ Ñ ØÖ Ù Ò Ñ Ö ỹ = (ỹ θ) + θ. ÆÝØ ỹ θ θ Æ(0,0.04) θ y Æ(5.483,0.0017)º Ò ỹ θ θ ÓÚ Ø ÖÔÔÙÑ ØØÓѺ Ì ÓÒ ÑÙÓ ØÙ Å Ö ÓÚ Ò Ø Ù Ó Ø ¹ Ú ÖÙÙ ÓÒ Θ Yº ÌÙÓ Ò Ò Ø Ù º Æ Ø Ý ÑÔ ÝØ ØÒ ÖÚÓÔ Ö Ñ ØÖ Ò ÔÓ Ø Ö ÓÖ ¹ ÙÑ Ò Ñ Ò ÑÔ ÙÙÒ Ú ÒÒÓÒ ÔÖ ¹ ØÚ Ò ÙÑ Ò Ñ Òº Ì Ø ÙÖ ØØ ỹ y Æ(5.483,0.0417)º prediktiivinen jakauma theta indeksi y ypred ÃÙÚ ÓÓÒ ÓÒ ÑÝ ÔÖÖ ØØÝ x ¹ ÚØØÙ Ò ¹ ØÓº indeksi Ѻ º Ú Ò Ø ºµ Å Ø Ò ÔÖØÚ Ò Ò ÙÑ ØÒ ÑÙÓ Ñ Ò ÑÖ Ø Ò Ù ÓØØ ÚÙÙ ÔÖ ÓÖ ÙØ Ò ¹ ÑÑ Òµ ÑÙØØ ÓØ ØÒ ÙÙ ÑÙÙØØÙ ÝÔÖ ÙÚÑÒ ÙÙØØ ÚÒØÓ º ÂÓ ÖÚÓÔ Ö ¹ Ñ ØÖ Ò ØØ Ø ÖØ Ó ÑÙÓÒ ÝÔÖ Ò ÖÚÓ ¹ ÚÒÒÓÒ ÙÑ Ø Æ(ØØ,0.04) Ó ØØ º ÑÓ ß ÓÖ Ò ½ Ƶ ß Ý ÒÓÖÑ ØØ ¾ µ ØØ ÒÓÖÑ ¾µ ÝÔÖ ÒÓÖÑ ØØ ¾ µ Ø Ø Ý º º¾ º º º º º ¾ º¾ º º º º½ º¾ º º ¾ º º º º º º º ºµ Æ ¾ µ Ò Ø Ø ØØ ÝÔÖµ ÈÖØÚ Ò Ò ÙÑ ØØÙ ØÓ Ö ÑÑ µ Ó¹ ÓÒ ØØÙ ÑÙÓ ÒÒ Ø º Ø Ò Ò Ò ÚÚ ÙÚ Ø ÓÖØØ Ø ÔÖ ØÚ Ø ÙѺ posteriori ypred ÑÒ Å ÖÖÓÖ Ú ¾º Ô Ú º Ô Ø ÖØ ÑÔ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ØØ º ¼º¼ ½¾½ º ¹ º ¼¾ º ½ ¾¼¼¼ ÝÔÖ º ¼º¾¼ ½ ¼º¼¼ º¼ º ½ ¾¼¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÈÖØÚ Ò ÙÑ Ò ÖÚÓ ÓÒ Ø Ö Ö¹ ÚÓ ÓÒ 5.483µ Ú ÖÒ = µº Ì ÖÙÙØØ ÚÓ Ø Ú ØØ Ñ ÑÙÓ ÒØÒ Ñ¹ Ö ÒÝØ ÓÒ 2000µº

13 º Ô Ö Ñ ØÖ Ñ º½ ÆÓÖÑ ÓØÓ ÖÚÓ ØÙÒØ Ñ ØÓÒ ÚÖغ ÄÙ Ù À ÚÒÒÓØ y 1,..., y n merk. y y i θ Æ(θ, v) ÖÔÔÙÑ ØØÓÑ Ó θ Ú ÖÒ v ØÙÒÒ ØØÙ θ Æ(m, w) ÔÖ ÓÖ µ Ë Ó Ò ÔÓ Ø Ö ÓÖ ÓÒ θ y m 1 = v 1 = Æ(m 1, v 1 ), Ñ m w + nȳ v 1 w + n, ȳ = 1 n v ( 1 w + n ) 1 v n y i, i=1 ÃÓÒ Ù ØØ Ô Öº ÈÖ ÓÖ Æ ÔÓ Ø Ö ÓÖ Æº ÆÓÖ¹ Ñ ÓØÓ ÒÓÖÑ ÔÖ ÓÖ ÒÓØÒ ÓÒ Ù ØØ ¹ ÙÑ º ËÖÖÝØØ ÔÖ ÓÖ Ø ÔÓ Ø Ö ÓÖÒ ÚÒ¹ ØÓ Ô Ú ØØ ÒÓÖÑ ÙÑ Ò ÖÚÓÔ Ö Ñ ØÖ Ú ÖÒ º ÃÓ Ø Ö ØØ ÑÝÝØØ Å Ø Ø ÔØÙÙ ÔÓ Ø Ö ÓÖ ÖÚÓ ÙÒ n m 1 ȳ, ÙÒ n. Ì Ø Ô Ù ÔÖ ÓÖ ØØÓ ÓÒ ÔÓ¹ Ò Òº ÃÙÒ ÔÖ ÓÖ ØØÓ ÓÒ Ó ÚÒÒÓÒ Ò¹ ÓÖÑØ Ó ÙÙÖ ÓØÓ Ó Ó n ÙÙÖ µ ÒÒ Ô¹ ÔÖÓ Ñ ØÚ Ø θ y 1,..., y n Æ(ȳ, v n ). Ì Ø ÙÖ Ñ Ö ØØ 95% Ò À Á ÓÒ ÑÖ Ò v ȳ ± 1.96 n. ÆÙÑÖ Ø 95% Ò À Á ÓÒ Ø Ø Ô Ù ¹ Ñ Ù Ò Ò Ò 95% Ò ÙÓØØ ÑÙ Ú¹ ÑÙØØ ÚÒ ÒÙÑÖ Ø µ ØÙÒØ ÓÒ Ö º ½ ÀÓ ÔÖ ÓÖ Å Ø Ò ÔÖ ÓÖ ÓØÓ Ò ÝÚØ ÔÓ Ø Ö ÓÖ ÖÚÓ ¹ Ì Ö Ø Ò ÔÓ Ø Ö ÓÖ ÖÚÓ m 1 º Ë ÚÓ ¹ Ò Ö Ó ØØ ÑÙÓ Ó m 1 = v 1 w m + v 1 v/n ȳ. m 1 ÓÒ ÔÖ ÓÖ ÖÚÓÒ m ÓØÓ ÖÚÓÒ ȳ ÔÒÓØ ØØÙ ÙÑÑ º ÈÒÓØ ÙÚÚ Ø ÔÖ ÓÖ Ø¹ ÓÒ ÚÒÒÓÒ Ù Ø Ø ÚÓ Ñ ÙÙØØ º ÌÑ Ò ÝÝ Ø ØØ ÔÒÓÒ Ù ÓÒ v 1 v/n v 1w = w v/n. Ë ÓÒ ÔÖ ÓÖ Ú ÖÒ Ò w ÓØÓ ÖÚÓÒ Ú ¹ ÖÒ Ò v/n Ù º ÈÓ Ø Ö ÓÖ ÖÚÓ ÓÒ ÓØÓ ÖÚÓÒ ÙØ ¹ ØÙ Ö Òµ Ó Ø ÔÖ ÓÖ ÖÚÓ º ¼ Ý ¹Ø ØÓØØ Ù Ò ÝØ ØÒ ¹ Ó ÔÖ ÓÖ Ñ ÑÒ ØØÑØØ ÑÝÝØØ Ù¹ Ø Ò p(θ) κ (vakio) θ Æ(0, σ 2 ), σ 2 ÙÙÖ. Æ ÔÔÖÓ ÑÓÒ Ó ÔÖ ÓÖº Ó Ú Ø ÔÖ ÓÖ Ø Ò ÑÑ Ò Ò ÓÒ Ò º ÔØÓ ÔÖ ÓÖ ÒØÖÓÙµº ÃÙ Ø ÒÒ ÔÓ ¹ Ø Ö ÓÖ ÚÓ Ó ØÓ ÙØ Ò Ø Ø Ô Ù ¹ µ κp(y θ) p(θ y) = κp(y θ )dθ ÜÔ 1 n (y i θ) 2 2v. i=1 ÌÑ ÓÒ ØÓ ÔÖ ÓÖ Ó ÒØÖ ÙÔÔ Òº ÜÔ 1 2v n (y i θ ) 2 dθ i=1 ¾

14 ÊÓ Ù Ø ÔÖ ÓÖ ÎÓÒ ÑÝ Ú Ö ÙØÙ Ò ØØ ÔÖ ÓÖ Ó Ò ÖÓ ØØ Úº Ñ Ö ÚÓÒ Ø ÙÖÚ ÒÒ ÓØØÓ À ÚÒÒÓØ ÓÚ Ø ØØÝÒØ ÓÒÒ ÒÒ Ø ØÝÒ Ô Ö Ñ Ø¹ ÖÖÚÓÒ θ 0 ÝÑÔÖ ÑÙØØ ÙÙÖ ØÒ ÔÓ¹ Ñ Ø Ø Ø ÖÚÓ Ø ÚÓ Ú Ø ØÙ Ý ÝÑÝ ¹ Òº ÌÒ ÝØ ØÒ ÚÒØ Ø ÔÖ ÓÖ Ù¹ Ø Ò Ø¹ÙÑÒ Ø º θ θ 0 Ø(ν) Ó Ò Ú Ô Ù ØÒ ÑÖ νº t jakauma on leveähäntäinen ÈÖ ÓÖ Ò ÓÒ ØÖÙÓ ÒØ ÌÙÒØ Ñ ØÓÒ ÙÙÖ θ ÑÖ Ø ÑÒ ÑÙ¹ Ò ÖÚÓ Ú Ø [0,1]º Ë Ó Ò ÔÖ ÓÖ ÓÒ Ñ¹ Ö Ø ØÚ Ø Ú º ÂÓÙ Ø Ú ÔÖ ÓÖ ÙÑ θ ÓÒ ØØ Ù¹ Ñ Ø (α, β) α > 0, β > 0 p(θ α, β) = Γ(α + β) Γ(α)Γ(β) θα 1 (1 θ) β 1, 0 θ 1 θ α 1 (1 θ) β 1, tiheysfunktio theta Ñ Γ(ν) = 0 tν 1 e t dt ÓÒ Ò º ÑÑÙÒ Ø Óº ÙÖ Ó ÑÑÙÒ Ø ÓÒ ÓÑ Ò ÙÙ Ò Γ(ν) = (ν 1)Γ(ν 1) ÖÙÖ Ó Ú µ Γ(n) = (n 1)!, n = 1,2,..., Γ(1) = 0 Γ(0) = Γ(ν) 2π e ν ν ν 1 2 ËØ Ö ÒÒ Ú µ º¾º ÒÓÑ ÓØÓ ÓØÓÑ Ò Ò ÚÒØÓ y i Ò º ÖÒÓÙ ³Ò Ó º y ÖÚÓØ 0 1º ÖÚÓÒ 1 ØØÙ ÔÙ¹ ÙÑÑ ÓÒÒ ØÙÑ Ø ÖÙÙÒ ÚÓ ØØÓ ÙÓ¹ Ñ µº Ò ÖÒÓÙ ³Ò Ó Ò Ñ Ñ θ = È(y i = 1 θ) Ù ÓØØ ÚÙÙ p(y i θ) = θ y i (1 θ) 1 y i, y i = 0,1 n Ò ØÓ ØÓÒ Ó y = (y 1,..., y n ) Ó Ø ÖÔÔÙÑ ØØÓÑ Ó θ p(y θ) = n i=1 { θ y i (1 θ) 1 y i} = θ s (1 θ) n s s = n i=1 y i ÀÙÓÑ s θ Ò(n, θ) (s θ) = nθ Î Ö(s θ) = nθ(1 θ) º ÈÓ Ø Ö ÓÖ y i θ Ò(1, θ), ÖÔÔÙÑ ØØÓÑ Ó θ θ Ø (α, β) ÈÓ Ø Ö ÓÖ ÓÒ s = n i=1 y i µ p(θ y) θ α 1 (1 θ) β 1 θ s (1 θ) n s θ α+s 1 (1 θ) β+n s 1, Ó ÓÒ Ø (α + s, β + n s) ¹ÙÑ º ÀÙÓÑ ØØ ØÝÝÔÔ p(θ) θ a (1 θ) b, θ [0,1] Ó ¹ Ú ÙÑ ÓÒ Ò ØØ ÙÑ ÓÒ Ô Ö Ñ ØÖ Ø ÓÚ Ø α = a + 1 β = b + 1ºµ ØØ ÔÖ ÓÖ ÓÒ ÓÒ Ù ØØ ÔÖ ÓÖ ÒÓÑ ÓØÓ ¹ Ó ÑÝ ÔÓ Ø Ö ÓÖ ÓÒ ØØ Ù¹ Ñ º ÇØÓ Ô Ú ØØ ÙÑ Ò Ô Ö Ñ ØÖ Ø ÔÖ ÓÖ α β ÔÓ Ø Ö ÓÖ α + s β + n s

15 ËÙÙÖØ Ò ÓØÓ Ø Ò Ø Ô Ù ØØ ÙÑ Ò ÓÑ Ò ÙÙ Ä Ñ ÚÓÒ Ó Ó ØØ Ø ÖÚ Ø Ò¹ ØÖÓµ ØØ (θ α, β) = α α + β α β Î Ö(θ α, β) = (α + β) 2 (α + β + 1) ÑÓÓ = α 1 α + β 2. Ó Ú Ø ÔØ ÚØ ÙÑ Ø (α, β)º Ì Ø Ò ÙÓÖ Ó ØÙ α α+s β β+n s ÔÓ Ø Ö ÓÖ ÙÑ Ò ØÙÒÒÙ Ø Ñ Ö α + s (θ y) = α + β + n α + s 1 ÑÓÓ = α + β + n 2. ÃÙÒ n ÒÒ (θ y) = α n + n s α n + β n + 1 s (= ȳ); n È ÝØÒ Ò ÙÙÖ ÑÑ Ò Ù ÓØØ ¹ ÚÙÙÒ Ø ÑØØÓÖÒº ÅÝ ÄÌ Ò Ò Ö ¹ ÖÚÓ Ù Ôص θ (θ y) y Æ(0,1). Î Ö(θ y) Ì Ò Ô ÖÙ ØÙ٠Ѻ 95% Ò À Á Ò ÔÔÖÓ ¹ ÑØ Ó (θ y) ± 1.96 Î Ö(θ y). Å Ø Ò ÖÚÓ ØØÒ Ë ÙÖÚ ØÖ ÓÒ ÝÝ Ò Ò Ú Ø Ò (θ α, β) 1 Γ(α + β) = θ 0 Γ(α)Γ(β) θα 1 (1 θ) β 1 dθ Γ(α + 1)Γ(α + β) 1 Γ(α + β + 1) = Γ(α)Γ(α + β + 1) 0 Γ(α + 1)Γ(β) θ(α+1) 1 (1 θ) β 1 dθ = αγ(α) Γ(α) Γ(α + β) (α + β)γ(α + β) α = α + β, Ó º Ö Ú Ò ÒØÖ ÓÒ ØØ ÙÑ Ò Ø Ý ÙÒ Ø ÓÒ ÒØÖ Ý Ô Ö Ñ ØÖÚ ÖÙÙ¹ Ò ÓÒ 1º Î ØÚ Ø ÚÓÒ Ú ÖÒ Ñ ¹ Ò Ò (θ 2 y) Ø Î Ö(θ y) = (θ 2 y) (θ y) 2. ÈÖ ÓÖ Ò ÓÒ ØÖÙÓ ÒØ ÚÓÒÝ ÒØ Ù ØÒ ÚÙ ÂÓ ÙÒ ÓÒ ÔÓÑÔ Ø ÚÓÒÝ ÒØ Ù ¹ ØÒ ÙØØ ÎÓÒÝ ÒØ Ù ÓÒÒ ØÙÑ Ú º ÔÓÒÒ ØÙÑ ÓÒ ÌÒ θ = φ = ÙÑ Ø ÓÖ ÂÓ θ Ø (α, β) ÒÒ β α φ = θ 1 θ, θ [0,1]. 1, φ [0, ]. 1 + φ 1 βθ α(1 θ) 2α,2β ËÒ ÓÖ Ò ¹ÙÑ µ 1 2 log φ log ( β α (log φ) log ( α 1 ) Þ 2α,2β Ö Ò Þ¹ÙÑ µ 2 β 1 2 ) Î Ö(log φ) 1 α + 1 β ¼

16 Ѻ º½ Ç ÓÓÒ ØÙÒØ Ñ ØÓÒ ÙÙÖ θ ÓÖÒ ¹ Ø Ò Ó ÙÙ ÓØ ÒÒ ØØ Ú Ø ÙÓ Ñ ÒÖ Ò ØÙ Ø º Ç Ø ØÒ ØØ ÔÖ ÓÖ ÓÒ θ Ø Ó (θ) = 0.6 = 0.3º Í Ò ÔÖ ÓÖ ÒÒ ØÒ ÙÙÖ Ø ÑÙÓ Ó ÓÒ Ö Ø Ø Ú α βµº º ØØ ÙÑ Ò Ô Ö Ñ ØÖ Ø Ò Ý Ø Ø α α + β = 0.6 αβ = 0.3 2, (α + β)(α + β + 1) Ó Ø Ö Ø ÙÒ ÓÒ α = 1 β = 2 º ÈÖ ÓÖ ÓÒ 3 p(θ) (1 θ) 1 3, 0 θ 1. º Ì Ò Ó Ó n = 1000 Ó Ú ÓØÓ yº ÇØÓ ¹ Ò ØÙ Ø s = 650 ÒÒ ØØ ÙÓ Ñ ÒÖ Ò ØÙ ¹ Ø º ÈÓ Ø Ö ÓÖ ÓÒ Ø (651, ) Ø º p(θ y) θ 650 (1 θ) Ò (θ y) = = ( )( ) 3 Î Ö(θ y) = ( )2 (1 + 2 = ) 3 (θ y) = À Á ¼ºµ = (0.620,0.679) À Á Ò Ñ ÓÒ ÝØ ØØÝ ÝÑÔØÓÓØØ Ø ÔÔ¹ ÖÓ ÑØ ÓØ ± º ½ Ñ º½ Ø ÙÙ Í Ë¹ ÓÚ Ù ËÙÓÖ Ø ØÒ ÙØ Í Ë¹Ó Ñ º ÃÓ Ø ÓÒ ÒÒ ØØÙ ÓÒÒ ØÙÑ Ø Ò ÑÖÒ s ØÝ ÒØÚ ØÙÒÒÙ ¹ Ù Ùµ ØÓ ØÓÒ ÑÖÒ n ÒÒ ÝØ ØÒ ØØÓ ØØ s θ Ò(θ, n) ÓØÓ Ó Ó ÓÒ Ý º ÑÓ ß Ý Ò ØØ Òµ ØØ Ø ½ ¼º µ Ø Ø Ý ¼ Ò ½¼¼¼µ Ò Ø Ø Øؼº µ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÑÒ Å ÖÖÓÖ Ú ¾º Ô Ú º Ô Ø ÖØ ÑÔ ØØ ¼º ¼º¼½ º ¾¹ ¼º ½ ¼º ¾ ½ ¾¼¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ theta Index tiheysfunktio tiheysfunktio priori ( ) ja posteriori (yhten.) theta posteriorijakauma theta ¾ ÈÖØÚ Ò Ò ÙÑ y i θ θ θ y Ò(1, θ), ÖÔÔÙÑ ØØÓÑ Ó θ Ø (α, β) ÔÖ ÓÖ Ø (α + s, β + n s) ÔÓ Ø Ö ÓÖ Ç ÓÓÒ ÙÙ ÚÒØÓ ỹ ÖÔÔÙÑ ØÓÒ y Ø ¹ Ó θº Ä ØØ Ú ÔÖØÚ Ò Ò ÙÑ p(ỹ y)º 1 È(ỹ = 1 y) = È(ỹ = 1 θ) p(θ y)dθ 0 1 = θ p(θ y) dθ 0 α + s n = α + β + n, s = y i. i=1 ÈÖØÚ Ò Ò ÙÑ ÓÒ ( ) α + s ỹ y Ò 1, α + β + n ÀÙÓÑ ÂÓ α = β = 1 ÔÖ ÓÖ ÓÒ Ø ÙÑ ÒÒ È(ỹ = 1 y) = s + 1 n + 2 ; Ì Ø ÒÒ ØØ ÙÙÒ ÚÒÒÓÒ ÙÑ Ò Ó ÚÒÒÓÒ ÙÑ Ò(1, θ) ÚÒ ÓØÒ Ú Ò ÑÙÙ¹ Ø º ÌÑÒ ÙÑ Ò ÑÝ Ì ÓÑ Ý º

17 Ѻ º½ Ø ÙÙ Ñ Ö ÑÑ ÙÙÒ ÚÒÒÓÒ Ý Ò Ò¹ Ò Ñ Ô µ ỹ Ó Ø ÒÓÙØØ ¹ ÒÓÑ ÙÑ Ó È(ỹ y) = = Í Ë ØØÙÒ ÑÓ ß Ý Ò ØØ Òµ ØØ Ø ½ ¼º µ ÝÔÖ ÖÒ ØØ µ Ø Ø Ý ¼ Ò ½¼¼¼µ Ò Ø Ø Øؼº ÝÔÖ ½µ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÑÒ Å ÖÖÓÖ Ú ¾º Ô Ú º Ô Ø ÖØ ÑÔ ØØ ¼º ¼º¼½ º ¹ ¼º ½ ¼º¼¾ ½ ¾¼¼¼ ÝÔÖ ¼º ¼º ¼º¼½¼ ¼º¼ ½º¼ ½ ¾¼¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ È Ö Ñ ØÖ Ò θ ÖÓÓ ÂÓ y θ ÈÓ ÓÒ(θ) ÒÒ (y θ) = θ Î Ö(y θ) = θ ÃÓÒ Ù ØØ ÔÖ ÓÖ ÈÓ ÓÒ¹ÓØÓ θ ÑÑ (α, β) Ñ α ÓÒ ÑÙÓØÓÔ Ö Ñ ØÖ β ÓÒ ÒØÒ Òµ Ô Ö Ñ ØÖ ÀÙÓÑ ØØ Ó Ù ÝØ ØÒ Ô Ö ¹ Ñ ØÖ 1/βºµ Ë Ò Ø Ý ÙÒ Ø Ó ÓÒ p(θ) = βα Γ(α) θα 1 e βθ, θ > 0, Ñ Γ(α) = 0 uα 1 e u du ÓÒ ÑÑÙÒ Ø Óº º ÈÓ ÓÒ¹ÓØÓ Ñ Ö Ñ Ø Ó ÓÒ ÈÓ ÓÒ¹ÓØÓ Ø¹ ØÝÝ Ì Ö Ø Ò Ø ÔØÙÚ ÑØ Ó Ø Ö Ø Ö Ò Ø ÔØÙÑ ¹ غ Å Ö¹ ØÒ N(I) Ø Ô Ù Ø Ò Ù ÙÑÖ Ú I È(N( t) = 1 θ) = θ t + o( t ) È(N( t) 2 θ) = o( t ) Ì ÔØÙÑ Ø Ö Ú ÓÚ Ø ÖÔÔÙ¹ Ñ ØØÓÑ Ó θµº Ì o(h) : o(h)/h 0 ÙÒ h 0ºµ ÂÓ I ÓÒ Ú Ò i Ô ØÙÙ ÒÒ ØÒ È(N(I) = k θ) = (θ I )k e θ I, k = 0,1,2,..., k! Ó ÓÒ ÔÓ ÓÒÙÑ º Ó Ú ÑØ ÒÓØ ÔÓ ÓÒÔÖÓ Ó ÓÒ Ý Ø ÝØ ØØÝ Ñ ÑѺ ÓÒÓØ ÓÖ º Ó ÚÒ ÔÓ ØÙØØÒ ÒÓ ÔÓ ÓÒÔÖÓ ÓÒ Ñ ÖÚ Ò Ø ÔØÙÑ º ÑÑ ÙÑ Ò ÖÚÓ Ú ÖÒ ÑÓÓ Ã ÖÚÓÒ Ó ØÓ (θ α, β) = = (θ α, β) = α β Î Ö(θ α, β) = α β 2 ÑÓÓ = α 1 β θ βα 0 Γ(α + 1) βγ(α) = αγ(α) βγ(α) 1 = α β. Γ(α) θα 1 e βθ dθ 0 β α+1 Γ(α + 1) θ(α+1) 1 e βθ dθ È Ö Ñ ØÖÒ α β ØÙÒØ Ç Ø ØÒ ØØ θ ÑÑ (α,1) ÂÓ θ = 1 β θ ÒÒ ÚÓÒ ÔÓ Ø Ó Ó ØØ ØØ θ ÑÑ (α, β). Ë Ø Ò 1 ÓÒ Ô Ö Ñ ØÖ º β

18 ÈÓ Ø Ö ÓÖ Ò Ó Ø Ñ Ò Ò Ç ÓÓÒ y = (y 1,..., y n ) ÈÓ ÓÒ¹ÓØÓ y i θ ÈÓ ÓÒ(θ) y i Ø ÖÔÔÙÑ ØØÓÑ Ó θ ÓÓ Ò Ù ÓØØ ÚÙÙ ÓÒ [ ] n θ y i p(y θ) = i=1 y i! e θ θ s e nθ, Ñ s = n i=1 y i º Ç ÓÓÒ θ ÑÑ (α, β)º ÌÒ p(θ y) p(θ) p(y θ) θ α 1 e βθ θ s e nθ θ α+s 1 e (β+n)θ, Ó ÓÒ ÑÑ (α + s, β + n) º ÈÓ Ø Ö ÓÖ ÖÚÓ (θ y) = α+s β+n Ë Ò ØÚ Ò Ò ÒÓÑ ÙÑ Ò ¹ Ó ØÙ Ò ÔÓ ÓÒÙÑ Ø ÆÒ(y α, β) = ÈÓ ÓÒ(y θ) ÑÑ (θ α, β)dθ.  ÙÑ ÝØ ØÒ Ø ØÓØØ ¹ ÝÓÒØ Ø ÒØ Óº Ø ÖÓ Ò Ø Ò Ò ØÓÒ Ñ ÒØ Ñ º ÀÙÓѺ ÂÓ Ù ÝØ ØÒ Ô Ö Ñ ØÖ Ó ÒØ (α, p) Ñ ¹ p = β ) ÙØ Ò ½ ØÝ Ê µº β+1 ÈÖØÚ Ò Ò ÙÑ Î ØÚ Ø ÚÓÒ Ó Ø ÔÖØÚ Ò Ò ÔÓ ¹ Ø Ö ÓÖ µùñ ØÙ Ú ÚÒÒÓ ỹ ÙÒ ÓÒ Ó ÚØØÙ y 1,..., y n º  ÙÑ p(ỹ y) ÓÒ ÆÒ(α + s, β + n). ÈÓ Ø Ö ÓÖ Ú ÖÒ Î Ö(θ y) = α+s (β+n) 2 ÀÙÓÑ ËÙÙÖ ÓØÓ (θ y) s n = ȳ Ù¹ Ø ÑØØÓÖ µ ÖÔÔÙÑ ØØ Ô Ö Ñ ØÖ Ø α β ½ Å ÖÒ ÙÑ Ý ÚÒÒÓ µ Ç Ø ØÒ ØØ Ö ÚÒØÓ y θ ÈÓ ÓÒ(θ) θ ÑÑ (α, β)º ÇÒ ØØ Ú Ñ Ö¹ Ò ÙÑ p(y) = θ y β α = 0 y! e θ Γ(α) θα 1 e βθ dθ Γ(α + y)β α (β + 1) α+y = y!(β + 1) α+y Γ(α) 0 Γ(α + y) θα+y 1 e (β+1)θ dθ Γ(α + y)β α = y!(β + 1) α+y Γ(α) ( ) α ( ) y (α + y 1)(α + y 2) αγ(α) β 1 = Γ(α)y! β + 1 β + 1 ( ) ( ) α ( ) y α + y 1 β 1 = y β + 1 β + 1 ( ) ( ) α ( ) y α + y 1 β 1 = y = 0,1,2,... α 1 β + 1 β + 1 ËØÙ ÙÑ ÓÒ Ò ØÚ Ò Ò ÒÓÑ Ù¹ Ñ ÆÒ(α, β) Ó (y α, β) = α β Î Ö(y α, β) = α β2(β + 1) ¼ Ѻ º¾º ËÓÚ Ù Ô Ñ ÓÓÒ Ç Ø ØÒ ØØ ÑÙÙØØÙ y i ÙÚ Ö ØÙ¹ ÒÒ Ù ÙÑÖ Ù iº Ä Ø¹ ØÒ Ó ÓØ ØØ Ú Ó Ú Ö ØÙÒÒ Ñ¹ Ö x i Ù iº ÌÑ ÙÙÖ Ò Ö ¹ Ø Ö Ø ÓØØ ÙÓÑ ÓÓÒ ÚÙÚÙÒ ¹ Ù ÙÔÙÓ ÙÑ Ò Ó ÓÓÒÓÑ Ò Ø ØÙ Òº Ô Ñ ÓÓ ØÒ Ò º Ø ÒÖ Ó ØÙ Ö Ø ÚÙÙ Ù Ù ËÁʵ Ó ÓÒ y i /x i º Ç Ø ØÒ ØØ y i θ, x i ÈÓ ÓÒ(θx i ) y 1,..., y K ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó θ, xº θ ÑÑ (α, β) Ì θ ÓÒ ØÙØØ Ú Ö Ø ÚÙÙ Ö º ÇÒ ÔÔÓ ÚØ ØØ Ñ ÓÒ Ó Ò Ö Ò Ò Ñ log (y i θ, x i ) = log θ + log x i, Ñ log x i ÓÒ ÒÒ Ø ØØÝ Ò º Ó Øµ ÑÙÙØØÙº ¾

19 Ѻ º¾ Ø ÙÙµ ÈÓ Ø Ö ÓÖ ÓÒ ÒÝØ p(θ y) K i=1 ÓØ Ò ÔÓ Ø Ö ÓÖ ÓÒ { (θxi ) y i e θx } i θ α 1 e βθ θ α+ K i=1 y i 1 e (β+ K i=1 x i )θ ÑÑ (α + i y i, β + i x i ). Ѻ º Ø ÙÙµ Ý ¹ Ò ÝÝ Ç Ø ØÒ ØØ y i θ ÈÓ ÓÒ(θ) ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó θº Î ØÒ ÔÖ ÓÖ θ ÑÑ (4,0.5) ÓÒ ÖÚÓ ÓÒ 8 ÓÒØ 4µº ÈÓ Ø Ö ÓÖ ÓÒ θ y ÑÑ (110,15.5)º ÌÙÒÒÙ Ù Ù ÖÚÓ Ú ÖÒ ÓÒØ ± Ò À Á , ÃÒÒ Ø ØÒ ÙÓÑ ÓØ ÙÖÚÒ Ò ÈÓ Ø Ö ÓÖ Ò ÖÚÓ ÓÒ (θ y, x) = α + y i β +. x i ÃÙÒ ØØ Ú ÖÖ ØÒ Ù¹ Ø ÑØØÓÖÒ ˆθ = i y i, ÒÒ ÚØÒ ØØ Ý ¹ Ø ÑØØÓÖ ÙØ Ø Ó ¹ Ø ÔÖ ÓÖº ËØ ÒÖ Ó ØÙ Ö ØÙÑ Ù Ù ÓÒ Ù¹ Ø ÑØØ i x i θ ÈÓ ÓÒ¹Ñ ÙÒ θ Ú Ø ÙØØÒºµ posteriori Theta:n posteriori theta Ѻ º ÌÙØÑÙ Ù ÓÓ ØÙÙ 15 Ø 100 Ñ 2 Ò ÖÙÙ¹ Ù Ø Ó Ø ÓÒ ØØÙ ÒØÓ ÓÒ Ø Ò ÖÚÒ Ù ÙÑÖØ ØØÝ Øº À ÚÒ¹ ØÓÒ ØÓ ÓÒ 5,7,7,12,2,14,7,8,5,6,18,6,4,1,4. Ò ØÓ Ø ØØÙ ÖÚÓ ÓÒ 7.07 Ú ÖÒ ¹ ÓÒØ 4.51º frekvenssi havaitut frekvenssit Ñ º Ø ÙÙµ ÈÖØÚ Ò Ò ÔÓ Ø Ö ÓÖ ÙÑ ÙÙ ÚÒÒÓ¹ µ ÓÒ ÆÒ 110,15.5µ Ó pistetodennäköisyys ÖÚÓ Ú ÖÒ ÓÒØ predidtiivinen jakauma ÀÙÓÑ Ê ½ ØÝ ÝØØ Ò ØÚ Ò ÒÓÑ ¹ ÙÑ Ò Ô Ö Ñ ØÖ Ó ÒØ (α, p = β µ Ø º ÙÑ ÓÒ β+1 Ó Ò ( ) α + y 1 p(y) = p y α (1 p) y, y = 0,1,2,... y

20 Ѻ º Ñ Ò Ò Í Ë ÑÓ ß ÓÖ Ò ½ Ƶ ßÝ ÔÓ ØØ µ ØØ ÑÑ ¼º µ ÝÔÖ ÔÓ ØØ µ Ø Ø Ý ½¾ ¾ ½ ½ ½ µ Æ ½ µ Ò Ø Ø Øؽ¼ ÝÔÖ ½¾µ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÑÒ Å ÖÖÓÖ Ú ¾º Ô Ú º Ô Ø ÖØ ÑÔ ØØ º½¼ ¼º¼ ¼º¼½ ¾ º º¾ ½ ¾¼¼¼ ÝÔÖ º¼ ¾º ¼º¼ ¾º¼ ½ º¼ ½ ¾¼¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ theta Index ypred Index Í h(y θ) ÑÖ Ø Ò ÙÒ Ø ÓÒ h(y θ) = p(y θ) S(y θ), y > 0. À ÙÖ Ø Ø h(y θ) y ÓÒ ÑÒ Ý Ø Ù Ò È( ÙÓ Ñ Úº (y, y + y) Ó Ø y, θ) ÔÓÒ ÒØØ ÙÑ h(y θ) = θ Ú Óµº ÅÝ ÒØÒ Ò ÓÒ ÚÓ Ñ Ó Ù ÓÒ Ú Ó ÒÒ Ù¹ Ñ ÓÒ ÔÓÒ ÒØØ Ò Òº Í ÑÖ ØØ Ý Øع Ø ÙÑ Òºµ ÂÓ Ø ÔØÙÑ Ø ÒÓÙØØ Ú Ø ÔÓ ÓÒÔÖÓ ¹ ÚÖغ Ù Ù º µ ÒÒ Ó Ò Ø ÔØÙÑÒ Ú Ø Ø ÒÓÙØØ Ú Ø ÔÓÒ ØØ Ø Ù¹ Ѻ ÌÑ ÓÒ Ö ÔÓÒ ÒØØ Ò ÙÑ Ò ÖØ Ö Ó ÒØ Histogram of theta Histogram of ypred Frequency Frequency theta ypred º ÇØÓ ÔÓÒ ÒØØ Ø Ñ Ø ÁÑ Â Ø ÙÚ ÑÙÙØØÙ y Ó ÔÓ Ø¹ Ú Ö ÖÚÓ Ñ ØØ Ò º ÒÖ¹ ØÒ Ò Ñ ÓÒ ÔÓÒ ØØ Ò Ò ÙÑ p(y θ) = θ e θy, y > 0, θ > 0, Ó ÓÒ ÖÓ Ø Ô Ù ÑÑ ÙÑ Ø ÑÑ (1, θ)º Ë ÔØ ÚØØÙÒ Ø Ó ÓÒ (y θ) = 1 θ, Î Ö(y θ) = 1 θ 2 S(t θ) = È(y > t θ) = e θt, t > 0. ÔÓÒ ÒØØ ÙÑ ÓÒ ÙÒÓ Ø ÚÙÙ ¹ ÓÑ Ò ÙÙ ÂÓ t, h > 0 È(y > t + h y > t, θ) = È(y > t + h θ) È(y > t θ) = e θ(t+h) e θt = e θh, Ó ÖÔÙ t غ ÌÑ Ø Ö Ó ØØ Ø ØØ Ø Ú ÒÒº Ç ÓÓÒ ÒÝØ ÓØÓ y i θ ÜÔ(θ) y = (y 1,..., y n ) Ó Ø ÖÔÔÙÑ ØØÓÑ Ó θº ÌÒ Ù ÓØØ ÚÙÙ ÓÒ n { } p(y θ) = θe θy i i=1 = θ n e θs, Ñ s = n i=1 y i º ÀÙÓÑ ØØ s θ ÑÑ (n, θ). ÃÓÒ Ù ØØ ÔÖ ÓÖ ÓÒ θ ÑÑ (α, β)º ÈÓ Ø Ö ÓÖ ÓÒ p(θ y) θ n e θs θ α 1 e βθ θ α+n 1 e (β+s)θ, Ø º ÑÑ (α + n, β + s) Ó (θ y) = α+n α+n β+s ; Î Ö(θ y) = (β+s) 2 ¼

21 Ѻ º Ë Ò ÙÖÓ ÒØ ÒÑ ÇØ Ò ÙÖÓ ØÙ ÓØÓ ÇØÓ Ó Ó n À ÚÒÒÓØ y 1,..., y k, k n ÄÓÔÙ Ø (n k) Ø ÚÒÒÓ Ø ØØÒ ØØ Ò y j > y 0 Ñ y 0 ÓÒ ØÙÒÒ ØØÙ Ò¹ ÙÖÓ ÒØÓ Øº Ç ÓÓÒ y i θ ÜÔ(θ) ÚÒÒÓØ Ó Ø ÖÔÔÙÑ ØØÓÑ Ó θº Ñº º Ç Ø ØÒ ØØ ÓÒ ØØÝ ÙÖÚ Ø Ò¹ ÚÒÒÓØ 1.54, 0.70, 1.23, 0.82, 0.99, 1.33, 0.38, 0.99, 1.97, 1.10, 0.40 Ò ØÓÒ ØØÒ Ó Ú Ò ÓØ Ò ÙÖÓÙÒ Ö¹ ÚÓÓÒ y o = 2.0 Ò ÙÖÓ ØÙÒ ÚÒØÓÒ ÑÖ ÓÒ 4º ÇØÓ Ò Ó Ó ÓÒ 15º Ç Ø ØÒ ØØ y i θ ÜÔ(θ) ØØ ÚÒÒÓØ ÓÚ Ø Ó Ø ÖÔÔÙÑ ØØÓѺ Ç ÓÓÒ ÔÖ ÓÖ θ ÑÑ (2,1) ÓÓ Ò ÔÖ ÓÖ ÖÚÓ ÓÒ 2 ÔÖ ÓÖ Ú ÖÒ 2 ÓÒØ 1.42µº Ñ ÖÒ º Ô ÖÙ ØÙ Ò ÔÓ Ø Ö ÓÖ ÓÒ ÑÑ (13.00,20.45), Ò ÖÚÓ ÓÒ ÓÒØ % Ò ÝÑѺ Ý ¹Ú (0.338,1.025)º ÓÒ ÔÖ ÓÖ Ò Ø ÓÚÚ µ ÔÓ Ø Ö ÓÖ Ò Ý ØÒ Ò Ò ÚÚ µ ÙÚغ Î ØÒ ÓÒ Ù ØØ ÔÖ ÓÖ θ ÑÑ (α, β)º À ÚÒÒÓ Ø y i, i = k + 1,..., n ØØÒ ÚÒ ØØ y i > y 0 Ñ Ò ÓÒ Ò ÓÖÑØ ÓØ ØÙ ÝÝÒ¹ صº ÌÑÒ Ø Ô Ù Ò ØÓÒÒ ÝÝ ÓÒ È(y i > y 0 θ) = e θy0 = S(y 0 θ). tiheysfunktio theta ½ Ѻ º Ø ÙÙµ Ë Ò ÙÖÓÙÒ ÓØÓ Ò Ù ÓØØ ÚÙÙ ÙÒ Ø Ó ÓÒ k { } p(y θ) = θe θy i [S(y0 θ)] (n k) i=1 = θ k e θs k e (n k)θy 0 = θ k e θ[s k+(n k)y 0 ], Ñ s k = k i=1 y i º ÈÓ Ø Ö ÓÖ ÓÒ ÒÝØ p(θ y) θ k e θ[s k+(n k)y 0 ] θ α 1 e βθ = θ α+k 1 e [β+s k+(n k)y 0 ]θ, Ó ÓÒ ÑÑ (α + k, β + s k + (n k)y 0 ) º Ë Ò ÔÓ Ø Ö ÓÖ ÖÚÓ ¹Ú ÖÒ ÓÚ Ø (θ y) = Î Ö(θ y) = α + k, β + s k + (n k)y 0 α + k (β + s k + (n k)y 0 ) 2. Ë Ò ÙÖÓ ÒÒ Ò Ø Ñ Ò Ò ÓÒ Ö ØØ Ò ØÖ Ò¹ ØÙØÑÙ Ù Ò Ò ØÓ ÓÒ Ò ÙÖÓ ØÙº ¾ Ѻ º Ø ºµ Å Ø Ò ØÑ Ø Ò Í Ë ÇÒ ÙÓÑ ØØ Ú ØØ y i θ ÜÔ(θ), ÙÒ i = 1,..., k y i θ Ò(1, e y0θ ), ÙÒ i = k + 1,..., n. Ò ÚÒØÓ ÖÚÓØ y k+1, y k+2,..., y n ÓÚ Ø Ý Ó Ò ÓÚ Ø Ö Ò Ý ØØÚ Ò ÙÖÓ ØÙ ÚÒØÓ ÑÓ ß ØØ ÑÑ ¾ ½µ Ôݼ ¹ ÜÔ ¹ØØ Ý¼µ ÓÖ Ò ½µ ßÝ ÜÔ ØØ µ ÓÖ Ò ½µ Òµ ßÝ ÖÒ Ôݼµ Ø Ø Ý ½º ¼º ¼ ½º¾ ¼º ¾ ¼º ½º ¼º ¼º ½º ½º½¼ ¼º ¼ ½ ½ ½ ½µ ½½ Ò ½ ݼ ¾µ Ò Ø Ø Øؼº µ

22 Ë ÑÙÓ ÒØ ØÙÓ ÑÙÓ ÒØÒ ÑÖ ¾ ¼¼ ÑÑ ØÝ ¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÑÒ Å ÖÖÓÖ Ú ¾º Ô Ú º Ô ÑÔ ØØ ¼º ¼º½ ¼º¼¼ ¼º ¾ ½º¼ ¾ ¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÙÖ Ó ÁÑÑ ¹ÙÑÒ ÅÖ Ø Ñ V ÁÑÑ (α, β) Ó U = 1 V Ì Ý ÙÒ Ø ÓÒ Ó ØÓ U ÑÑ (α, β) ÓÓ Ò ÑÑ (α, β)º theta Index ÂÓ ÙØÒ ÔÖØÚ Ò Ò ÙÑ ÒÒ Ó ¹ ÑÓÓÒ ÓÔÔÙÙÒ ÓÒ ØØÚ p U (u) = βα Γ(α) uα 1 e βu, u > 0. Ç ÓÓÒ V = U 1 º ÌÒ p V (v) = p U (u(v)) du dv ( ) α 1 = βα 1 e β/v 1 Γ(α) v v 2 = βα Γ(α) v (α+1) e β/v, v > 0. ÝÔÖ ÜÔ ØØ µ Ô Ö Ñ ØÖÒ Ù ØÙ Ò Ù ÖÚÓ Ñº Ø Øؼº ÝÔÖ ¼º¾µ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ ÑÒ Å ÖÖÓÖ Ú ¾º Ô Ú º Ô ÑÔ ÝÔÖ ½º ½º ¼º¼¾ ¾ ¼º¼ º ¾ ¾ ¼¼ ¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹ º ÆÓÖÑ ÓØÓ Ú ÖÒ ØÙÒØ Ñ ØÓÒ ÖÚÓ ØÙÒÒ ØØÙ Ç Ø ØÒ ØØ y i θ, φ Æ(θ, φ) θ ØÙÒÒ ØØÙ φ ØÙÒØ Ñ ØÓÒ ÒÒÓ ØÙ Ò Ó µº y = (y 1,..., y n ) ÖÔÔÙÑ ØÓÒ Ó φº Í ÓØØ ÚÙÙ p(y θ) φ n 2 e 2φ 1 ni=1 (y i θ) 2 φ n 2 e n 2φ s2 0, Ñ s 2 0 = 1 n ni=1 (y i θ) 2 º ÃÓÒ Ù ØØ ÔÖ ÓÖ ÓÒ ÒØÒ Ò ÑÑ Ù¹ Ñ ÁÑÑ (α, β) ÓÒ Ø Ù ÙÒ Ø Ó ÓÒ p(φ) φ (α+1) e β φ, φ > 0.  ÙÑ Ò ÖÚÓ Ú ÖÒ ÓÚ Ø ÈÓ Ø Ö ÓÖ p(φ y) φ (α+1) e β φ φ n 2e n 2φ s2 0 φ (α+n 2 +1) e (β+n 2 s2 0 )/φ, Ó ÓÒ ÁÑÑ (α + n 2, β + n 2 s2 0 ) º ÈÓ Ø Ö ÓÖ ÖÚÓ ¹Ú ÖÒ ÓÚ Ø (φ y) = β+n 2 s2 0 α+ n 2 1 (β+ Î Ö(φ y) = n 2 s2 0 )2 (α+ n 2 1)2 (α+ n 2 2) ËÙÙÖ ÓØÓ (φ y) s 2 0 = 1 n ni=1 (y i θ) 2 Ó ÓÒ Ù¹ Ø ÑØØÓÖ (φ) = β α 1, α > 1, β > 0, β Î Ö(φ) = 2 (α 1) 2 (α 2), α > 2, β > 0.

23 º Ô Ö Ñ ØÖ Ò ÔÓÒ ÒØØ Ò Ô Ö¹ Ò ÓÒ Ù ØØ Ô Ö Ç Ø ØÒ ØØ Ý Òµ ÚÒÒÓÒ ÙÑ Ò Ø Ý ÙÒ Ø Ó ÓÒ p(y i θ) = f(y i )g(θ)e φ(θ)u(y i). Ë ÒÓÑÑ ØØ y i Ò ÙÑ ÙÙÙÙ ÔÓ¹ Ò ØØ Ò Ô Ö Òº Ѻ º y i θ Ò(1, θ)º ÎÓÒ Ö Ó ØØ p(y i θ) = θ yi (1 θ) ( 1 yi θ = (1 θ) 1 θ ) yi = (1 θ) e log( 1 θ)yi θ. ( Ë Ó Ò f(y i ) = 1 g(θ) = (1 θ) φ(θ) = log u(y i ) = y i º θ 1 θ) Ë Ø Ò ÒÓÑ ÙÑ ÙÙÙÙ Ý Ô Ö Ñ ØÖ Ò ÔÓ¹ Ò ÒØØ Ò Ô Ö Òº ÂÓ ÔÖ ÓÖ ÓÒ ÒÓÖÑÖ Ù Ø Ú µ ÑÙÓØÓ p(θ) g(θ) η e φ(θ)ν Ó Ò Ô Ö Ñ ØÖ η ν ÒÒ Ó Ò ÔÓ ¹ Ø Ö ÓÖ ÓÒ p(θ y) g(θ) η+n e φ(θ)(ν+t(y)), Ñ ÓÒ Ñ ÑÙÓØÓ Ù Ò ÔÖ ÓÖ ÙÑ º Ö ØÝ Ø ÔÖ ÓÖ Ò Ô Ö Ñ ØÖ Ø Ô Ú ØÝÚØ ÔÓ ¹ Ø Ö ÓÖ ÙÖÚ Ø Ñº º Ø µº ÒÓÑ ÙÑ η ν η + n ν + t(y) p(θ) (1 θ) η e log(θ/(1 θ))ν = θ ν (1 θ) η ν, Ó ÓÒ Ø (ν +1, η ν +1)º ÑÑ Ò ÝØ ØØÒ Ô ¹ Ö Ñ ØÖ α = ν + 1 β = η ν + 1º ÈÓ Ø Ö ÓÖ ÓÒ Ø ((ν+t(y))+1,(η+n) (ν+t(y))+1) Ø (α + t(y), β + n t(y)). ½ Ç Ø ØÒ ÒÝØ ØØ y 1,..., y n ÓÚ Ø ÖÔÔÙÑ Ø¹ ØÓÑ Ó θ Ý Ô Ö Ñ ØÖ Ø ÔÓÒ Òع Ø Ø Ô Ö Øº Ë Ó Ò Ù ÓØØ ÚÙÙ ÓÒ p(y θ) = = n f(y i ) g(θ) n e φ(θ) n i=1 u(y i ) i=1 n f(y i ) g(θ) n e φ(θ) t(y), i=1 Ñ t(y) = n i=1 u(y i ) ÓÒ ØÝ ÒØÚ ØÙÒ¹ ÒÙ Ù Ù φ(θ) ÓÒ Ò º ÙÓÒÒÓ Ò Ò Ô Ö Ñ ØÖ º Ñ º Ø µº Ò(1, θ) ØÝ ÒØÚ ØÙÒÒÙ Ù Ù ÓÒ n t(y) = i=1 ÙÓÒÒÓ Ò Ò Ô Ö Ñ ØÖ ( ) θ φ(θ) = log = logit(θ). 1 θ ÇÒÑ Å ÓÒ ÓÒ Ù ØØ ÔÖ ÓÖ y i º ÂÖ Ý ³ Ò Ô Ò ÓÖÑ ØÚ Ò Ò ÔÖ ÓÖ ÂÖ Ý Ë Ö À ÖÓ ÂÖ Ý ½½ ½ µ Ó Ö ØØ ¹ Ò Ò Ñ Ø ÑØ Ó Ø ØÓØØ Ó ÝÝ Ó ØÖÓÒÓÑ º È ØÒ ÓÒÑÒ Ó ÒÒ ÓØØÓ Ó º Ë ÙÖÚ Ö Ø Ù ÓÒ Ø Ö Ó Ñ Ö¹ µ y θ Æ(θ, v), v ØÙÒÒ ØØÙ θ Æ(0, w), w ÙÙÖ y θ Æ(θ, v), v ØÙÒÒ ØØÙ p(θ) κ y φ Æ(θ, φ), θ ØÙÒÒ ØØÙ p(φ) 1/φ y θ Ò(1, θ) θ Ø (1,1) Ø ÙÑ µ ¼ ¾

24 ÂÖ Ý ³ Ò Ñ Ò Ø Ñ Ç Ø ØÒ ØØ y θ p(y θ) ÓØ ÒØ Ñ p(θ) ÔÖ ÓÖ Ç ÓÓÒ ψ = h(θ) ÙÙ ÒØ Ò Ý Øع Ò Ò Ô Ö Ñ ØÖ Ó ÒØ º Ì Ö Ø Ò ÓÒÑ ÙÖÚ Ò Ñ ÖÒ ÚÙ y θ Ò(1, θ) Ñ Ó ÒÒ Ó Ò ÓÖÑØ ÓØ θ Ø º ÇÒ ³ÙÓÒÒÓ Ø ³ Ú Ø ÔÖ ÓÖ p(θ) 1 Ò º Ý ¹Ä Ô³Ò ÔÖ ÓÖ µº ÅÙØØ Ó Ò Ñ ÑÝ ¹ Ò Ó Ò ÓÖÑØ ÓØ Ô Ö Ñ ØÖ Ø ψ = θ 2 º Ò Ò Ú ÒØ Ó Ø ÑÙÙÒÒÓ Ú Ò Ô ÖÙ Ø ÔÖ ÓÖÒ p(ψ) 1 ψ, Ó Ó Ø ÙÑ º ÂÓ ØÓÔØ Ò ÓÒ ØØ Ø ¹ ÙÑ Ò Ú ÒÒ Ø ÙÖ Ô ÖÓ º ÌÑ ÓÒ Ó¹ ÙØ Ý Ý Ò Ó ØÙÒÙØ Ý Ñ ÌÓ º [ d J(ψ) = 2 ] log p(y ψ) dψ 2 ψ [ d = 2 log p(y θ = h 1 (ψ)) dθ 2 = J(θ) dθ dψ 2. Ë J(ψ) 1 2 = J(θ) 1 2 dθ dψ º ÌÒ p(ψ y) J(ψ) 1 2 p(y ψ) = J(θ) 1 2 dθ dψ p(y ψ) = J(θ) 1 2 p(y θ) p(θ y). dθ ] dψ 2 θ ÂÖ Ý ³ Ò ÔÖ ÓÖ Ó Ø ÑÒ ÔÓ Ø Ö ÓÖÒ ½¹½ ¹Ô Ö Ñ ØÖ Ó ÒÒ º ÂÖ Ý ³ Ò Ô Ö Ø Ô Ò ÓÖÑ ØÚ Ò ÔÖ Ó¹ Ö Ò ØÙ Ó Ø ÑÒ ÔÓ Ø Ö ÓÖ ÙÑÒ Ó ½¹½ ¹ØÖ Ò ÓÖÑÓÙ Ô Ö Ñ ØÖ ψº ÌÑÒ Ô Ö ØØÒ ØÓØ ÙØØ ÂÖ Ý ³ Ò ÔÖ Ó¹ Ö p(θ) [J(θ)] 1 2 Ñ ( ) 2 [ J(θ) = dlog p(y θ) θ d = 2 ] log p(y θ) dθ dθ 2 θ ÓÒ ÚÒÒÓÒ Ö¹ Ò ÓÖÑØ Óº Ѻ º ÂÖ Ý ³ Ò ÔÖ ÓÖ ÒÓÑ ÙÑ y θ Ò(n, θ) p(y θ) = ( ) n θ y y (1 θ) n y log p(y θ) = y log θ+(n y) log(1 θ)+log d dθ log p(y θ) = y θ n y 1 θ d 2 y dθ2 log p(y θ) = θ 2 n y (1 θ) 2 ( ) n y ( d2 dθ2 log p(y θ) θ) = nθ θ 2 + n nθ (1 θ) 2 = n θ(1 θ) ÂÖ Ý ³ Ò ÔÖ ÓÖ ÓÒ p(θ) θ 1 2(1 θ) 1 2 Ó ÓÒ Ø ( 1 2, 1 2 ) ¹ÙÑ º ÀÙÓÑ Ý ¹Ä Ô³Ò Ô Ò ÓÖÑ ØÚ Ò Ò ÔÖ ÓÖ ÓÒ Ø (1,1) Ø ÙÑ µº ÀÙÓÑ ÂÖ Ý ³ Ò ÔÖ ÓÖ Ò Ó ÝÚ ØÙÓ Òº ÅÓÒ ÙÓØØ Ô Ö Ñ ØÖ Ò ÝØØ ÓÒ Ò º

25 º ÂÓ ØÒ Ý Ô Ö ØØØ º½ ÔÓ ÙÙ ØÝ ÒØÚÝÝ ÔÓ ÙÙ Ò º Ò Ö ØÝ ØÝ ÒØÚÝÝ Ò º Ù ÒÝ Ç Ø ØÒ ØØ ØÙÒØ Ñ ØÓÒ ÙÙÖ ÓÒ θ Ø Ò ÙÑÑ ÑÑ Ò Ô Ó Ñ ØØ µ ÔÖ ÓÖ θ p(θ) Ù ÓØØ ÚÙÙ p(y θ)º ÔÓ ÙÙ º Å Ø Ø ÔØÙÙ Ó Ò ØÓÒ y ÙÑ ¹ Ó θ Ù ÓØØ ÚÙÙ µ p(y θ) ÖÔÙ θ Ø ÌÒ p(θ y) p(θ), Ø º ÔÓ Ø Ö ÓÖ =ÔÖ ÓÖ º ÌÑ Ñ ÖØ Ø Ø¹ Ø ÚÒÒÓ Ø y ÓÔ Ø Ø ØÓ Ò ÒÓ Ò y ÓÒ Ô Ò ÓÖÑ ØÚ Ò Ò θ º Ì Ö Ø Ò Ó ØØÙ ÔÓ Ø Ö ÓÖ p(θ y) p(θ) p(z x, θ). Ë ÖÔÔÙ z Ò Ó Ø ÙÑ Ø Ó x θµº ÈÓ Ø Ö ÓÖ Ø ÔÓ ¹ Ò ØÓÒ Ó x Ó Ø ØÙÒ ÙÑ Òº ÌÝ ÒØÚÝÝ ÂÓ p(z x, θ) 1 ÒÒ ÒÓÑÑ ØØ x ÓÒ ØÝ ÒØÚ θ º Ë Ó Ò p(θ x, z) = p(θ x) p(θ) p(x θ). ÈÓ Ø Ö ÓÖ Ø Ò Ó ØÓÔØ Øµ ÖÔÙ Ò Ò z Ø º º Å Ø Ø ÔØÙÙ Ó Ò ØÓ y ÓÒ Ó ØØÒ Ô Ò ÓÖÑ ØÚ Ò Ò θ Ç Ø ØÒ ØØ y = (x, z)º ÎÓÒ Ø ¹ Ø Ò ØØ Ò ØÓ y ÚÒØÒ Ó Ò Ò x ØØ Ò zº À ÚØÒ Ò Ò x ÓÓ Ò ÓÔ ØÙ ÓÒ p(θ x) p(θ) p(x θ). À ÚØÒ ØÑÒ Ò z ÓÓ Ò ÓÔ ØÙ ÓÒ p(θ y) = p(θ x, z) p(θ x) p(z x, θ) p(θ) p(x θ) p(z x, θ) ÂÓ p(x θ) 1 ÒÒ x ÓÒ ÔÓ Ò Ò θ º ÌÒ p(θ x) = p(θ) Ø Ò p(θ y) = p(θ x, z) p(θ) p(z x, θ). ÀÙÓÑ Ò Ó Ò Ø ØÓØØ Òº Ã Ø ØÓØØ ½º Ø ØÒ Ù ØÙÒÒÙ Ù Ù ÔÓ Ò Òµ Ó¹ Ø ØÒ ¾º Ø ØÒ ØÝ ÒØÚ ØÙÒÒÙ Ù Ù ÝØ ØÒ ÒØ Ø ÑØØÓÖØ Ø Ø ÙÙÖØ ÓØ ÓÚ Ø ØÝ Ò¹ ØÚÒ ØÙÒÒÙ ÙÚÙÒ ÙÒ Ø ÓØ º Ý ¹Ø ØÓØØ ½º Ø Ñ ØÒ Ò ÝÚ º Ã Ó ØÙ٠ع ØÒ ÔÓ Ø Ö ÓÖ ØØ Ñº º½ Ç Ø ØÒ ØØ x i θ Ò(1, θ) ÖÔÔÙÑ ØØÓÑ Ó θ x = (x 1,..., x n )º Å ÖØÒ s = n i=1 x i ÓÒÒ ØÙÑ Ø Ò Ñ¹ Öµº ÌÒ Ù ÓØØ ÚÙÙ ÓÒ n p(x θ) = θ x i(1 θ) 1 x i i=1 = θ s (1 θ) n s ½¼¼

26 Ë Ó Ò p(x s, θ) 1 Ó ÖÔÙ θ Ø º Ë s ÓÒ ØÝ ÒØÚ θ º ÌÙÒØ ÃÙÒ s = n i=1 x i ØÙÒÒ ØÒ ÒÒ ÚÒØÓÒ x 1,..., x n ØÙÒØ Ñ Ò Ò ÓÔ Ø ¹ θ Ø º ÎÓÒ ØÓ Ñ ÔÓ Ø Ö ÓÖ p(θ x) Ø p(θ s)º Ѻ º¾ Ç Ø ØÒ ØØ y i θ N(θ,1) i = 1,2º Ç Ø ØÒ ØØ ÚÒÒÓØ ÓÓ ØÙÚ Ø Ñ ØØ Ù ¹ Ø x = y 1 y 2 z = y 1 + y 2 ÚÒØÓ Ó ÑÙÙØØÙ Ø y 1 y 2 µº ÎÓÒ ÔÓ Ø Ó Ó ØØ ØØ p(x, z θ) = p(x) p(z θ). ÁØ x θ Æ(0,2) z θ Æ(2θ,2) Ä x z ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ó θµº ÌÒ ÔÓ Ø Ö ÓÖ ÓÒ p(θ x, z) p(θ) p(θ z). Ì Ø ÙÖ ØØ z ÓÒ ØÝ ÒØÚ θ x ÓÒ Ô¹ Ó Ò Òº Ì Ú p(z x, θ) = p(z θ)º ½¼½ º ÀÝÔÓØ ÒØ Ø Ù Ç Ø ØÒ ØØ Ô Ö Ñ ØÖÚ ÖÙÙ ÓÒ Θº ÀÝÔÓØ H Ø Ö Ó Ø ØÒ Ô Ö Ñ ØÖÚ ÖÙÙ¹ Ò Ó ÓÙÓ Θ H Θ ÙØ Ò Ø ØÓØØ µº Ç ÓÓÒ Ø Ø ØØ Ú ÝÔÓØ H 0 : θ Θ 0 Ú ØÝÔÓØ H 1 : θ Θ 1 Ñ Θ 0 Θ 1 = Θ Θ 0 Θ 1 = º Ì Ø Ù Ø ÒØ ÓÒ Ú ØØ Ú H 0 Ò H 1 Ò Ú Øº Ç ÓÓÒ Ò ØÓ yº Ã Ø Ø Ø ÓÖ Ø Ø ÓÒ ÓØÓ Ú ÖÙÙÒ Ó R = {y y Ó Ø H 0 Ò Ý Ñ Ò }. R ÒÓØÒ ÑÝ Ý Ñ Ù º Ë ÑÖØÒ ØØ Ñ ÖÚÓ ÙÙÖ È(y R θ), θ Θ 0 1 È(y R θ), θ Θ 1. Æ Ò ØÓÒÒ ÝÝ Ò Ý Ø Ý ÔÙ ÙØÒ Á ¹ Ò ÁÁ Ò Ú Ö Øºµ ½¼ º¾ Ô Ò ÓÖÑ ØÚ Ò Ò ÔÝ ÝØØÑ Ò Ò Â ØØÒ Ñ Ö º½º Ç Ø ØÒ ØØ n Ó ÒÒ Ø ØØݺ  ØØÒ ØÓ ØÓ ÙÒÒ Ò r ÓÒÒ ØÙÑ Ø º ÆÝØ n ÓÒ ØÙÒÒÒ Òº Í ÓØØ ÚÙÙ ÓÒ p(n θ) = = ( ) n 1 θ r 1 (1 θ) (n 1) (r 1) θ r 1 ( ) n 1 θ r (1 θ) n r r 1 θ r (1 θ) n r, n = r, r + 1,.... ÃÙÒ n ÓÒ ÒÒ Ø ØØÝ r ØÙÒÒÒ Òµ ÒÒ ( ) n p(r θ, n) = θ r (1 θ) n r r θ r (1 θ) n r. ÃÓ ÙÑÑ Ò Ø Ô Ù Ù ÓØØ ÚÙÙ ÓÒ Ñ ÒÒ ÑÝ ÔÓ Ø Ö ÓÖ ÓÒ Ñ ÑÓ Ò Ý ¹Ø ØÓØØ Ó ØÙØ Ó ØÓÔØ Øº Ã Ø ØÓØØ Ù¹ Ø ÑØØÓÖ ÓÒ ÙÑÑ Ò Ø Ô Ù ˆθ = r/n ÑÙØØ ¹ ÙÑ Ø ÓÖ ÓÒ Ö Ñ µº ½¼¾ Ý ¹Ø ØÓØØ Ø ÒÒ ÓÒ ÚÒ Ý ¹ ÒÖØ ÑÔ º ÅÖ Ø Ò ÔÖ ÓÖ ØÓÒÒ ¹ ÝÝØ π 0 = È(θ Θ 0 ) π 1 = È(θ Θ 1 ) ÔÓ Ø Ö ÓÖ ØÓÒÒ ÝÝØ p 0 = È(θ Θ 0 y) p 1 = È(θ Θ 1 y). ÈÖ ÓÖ ÚÓÒÝ ÒØ Ù ÓÒ π 0 /π 1 ÔÓ Ø Ö Ó¹ Ö ÚÓÒÝ ÒØ Ù p 0 /p 1 º Ò Ò Ò Ø Ù¹ Ú Ù Ò Ô ÓÒ Ù ÓÑÑ ÝÔÓØ Ò H 0 Ù Ø ÝÔÓØ Ò H 1 ÔÖ ÓÖ ÑÑ ¹ Ò Ò ÚÒÒÓÒ y Òº Ý ¹Ø ÒÓØÒ Ù ØØ B = p 0/p 1 π 0 /π 1. B ÓÒ ÚÓÒÝ ÒØ Ù H 0 Ò ÔÙÓ Ø H 1 Ø Ú ØÒ Ó Ó ØÙÙ Ø Ø yº ½¼

27 ÌÓÒÒ ÝÝ p 0 = È(θ Θ 0 y) ÚÓÒ ØØ B Ò ÚÙ ÙÖÚ Ø 1 p 0 = [1 + π 1 π B 1 ]. 0 Ë Ø Ò B Ñ ØØ Ù Ò Ø ÑÙÙØØ ÔÖ ÓÖ ¹ ØÝ Øº Ý ¹Ø ÓÚ ØÙÙ ÝÚ Ò Ô ØÝÔÓØ Ò Ø Ö¹ Ø ÙÙÒ Ç Ø ØÒ ÒÝØ ØØ Θ 0 = {θ 0 } Θ 1 = {θ 1 }º ÌÒ Ò ÓØ Ò p 0 = È(θ = θ 0 y) π 0 p(y θ 0 ) p 1 = È(θ = θ 1 y) π 1 p(y θ 1 ). p 0 p 1 = π 0 π 1 p(y θ 0) p(y θ 1 ), B = p(y θ 0) p(y θ 1 ) = Ù ÓØØ ÚÙÙ Ó ÑÖ. ½¼ Ѻ º¾ À ÑÓ Ò Ô Ö ÝØÝÑ Ò Òº ÅÒ Ô Ö Ñ Æ Ò Ô Ö Ñ Å Ö º Ó ÖÓÑÓ ÓÑ Ø Ö ÙÒ Ùع Ø Òº Å ÓÒ Ø ÖÚ Ó Ö Ó ÆÒ Ò ÓÒ Ø ÖÚ Ó Ø ÙÒÒØ Ó Ö Ó ÇÒÑ ÌØÒ ØØ ÒÒ Ò Ó ¹ Ö ÚÒ Ø ÖÚ Ø ÒØ µº Ä Ø¹ ØÒ ØØ Ò Ò Ø Ó Ö Ú ÓÒ ¹ Ö º ØØ Ò Ò ÔÓ ÓÚ Ø Ø ÖÚ¹ غ ÇÒ ÔØ ØÚ ÓÒ Ó ÒÒ Ò Ø ÙÒÒØ Ú Ø ÖÚ µº ÃÚ Ó Ô Ö ÑÑ Ò Ñ Ø ÓÒ ÙÖÚ ¹ ÚÙ º ½¼ ÂÓ Ò Ò Θ 0 Θ 1 ÓÚ Ø ÓÙÓ ÝÔÓØ ÒÒ ØÙÒØ ÓÒ Ò ÑÔ p(y θ)p(θ)/π 0 dθ B = Θ0 p(y θ)p(θ)/π 1 dθ, Θ1 Ñ π i = p(θ)dθ i = 0,1º ÌÑ Ñ ØØ ÙÓ¹ Θi ÖÒ Ô ÓÒ Ó Ø Ú ÙØØ Ù Ø Ò π 0 /π 1 ÚÒ ÓÒ ÔÒÓØ ØØÙÒ Ù ÓØØ ÚÙÙ Ò Ù B = Θ0 p(y θ)p(θ)dθ/ Θ1 p(y θ)p(θ)dθ π 0 /π 1. Ѻ º¾ Ø ºµ ÃÚ Ó Ô Ö Ñ Ø Ñº º½ Ú Ò ³ Ò Ø µ y i Æ(θ,0.1) y i Ø ÖÔÔÙÑ ØØÓÑ Ó θº Ì Ø ØÒ ÝÔÓØ H 0 : θ = 5.4 Ú º θ = 5.5º Ç ÓÓÒ π 0 = 0.8 π 1 = 0.2 ÚÚ ÒÒ Ò¹ ÓØØÓ H 0 Ò ÔÙÓ Ø µº ÌÒ π 0 /π 1 = 4.0 p 0 = 0.8 p e [ i (y i 5.4) 2 (y i 5.5) 2 ] = B = º ÈÓ Ø Ö ÓÖ ÚÓÒÝ ÒØ Ù ÓÒ ÒÓ Ò 1 : 2 ÚÒØÓ ÑÙÙØØ ØÝ ØÑÑ H 1 Ò ÙÙÒØÒº ½¼ ½¼

28 Ѻ º¾ Ø ºµ ÌØÒ Ú ØØ Ñ Ø º Ú Óµ ØØ Ò Ò Ø ÓÒ ÒØ º Å ÖØÒ θ = 1 Ó ÒÒ Ò ÓÒ ÒØ θ = 0 Ó Ø ÖÚ ¹ÒØ µº Ç ÓÓÒ ÔÖ ÓÖ È(θ = 1) = 1 2 º Ò ØÓ Å ÖØÒ y i = 1 Ó ÔÓ i ÓÒ Ö y i = 0 Ó Ø ÖÚ i = 1,2º À ÚØÒ y = (0,0)º Í ÓØØ ÚÙÙ È(y 1 = 0, y 2 = 0 θ = 1) = = 1 4 È(y 1 = 0, y 2 = 0 θ = 0) = 1 ÈÓ Ø Ö ÓÖ Ò Ñ È(θ = 1 y = (0,0)) È(y = (0,0) θ = 1)È(θ = 1) = È(y = (0,0) θ = 1)È(θ = 1) + È(y = (0,0) θ = 0)È(θ = 0). 1/4 1/2 = 1/4 1/ /2 = 1 5 = ÆÒ ØØ Ø ÖÚÒ ÔÓÒ ÑÖ ÔÓ Ø ¹ Ö ÓÖ ØÓÒÒ ÝÝØغ ½¼ º ÂÓ ØÙ ÑÓÒ Ô Ö Ñ ØÖ Ò Ñ Ò º½ Ã Ù Ô Ö Ñ ØÖÒ Ñ ÒÓ ÒØ Ç ÓÓÒ ØÙÒØ Ñ ØÓÒ ÙÙÖ Ù Ò Ô Ö Ñ ØÖ µ θ Ñ(θ) = p > 1º Ã Ô Ö Ñ ØÖ Ø ÚØ ÚØØÑØØ ÒÒÓ ¹ Ø ÑÙØØ ÒØ Ø ÖÚ ØÒ ÓØØ Ñ Ò Ö ÒÒ Ó ÖÚº Ì Ý ÑÖ Ô Ö Ñ Ø¹ Ö ÒÓØ Ù Ô Ö Ñ ØÖ ÒÙ Ò µ ÚÖغ Ù Ù º½º Å ÖØÒ θ = (θ 1, θ 2 ) Ñ θ 1 ÓÓ ØÙÙ ÒÒÓ Ø Ú Ø Ô Ö Ñ ØÖ Ø θ 2 ÓÓ ØÙÙ Ù Ô Ö Ñ ØÖ Ø º Ѻ y µ, σ 2 Æ(µ, σ 2 ) ÒÒÓ ØÙ Ó ØÙÙ ÒØ Ô Ö Ñ ØÖÒ µ ÓÒØ Ô Ö Ñ ØÖ Ò σ 2 Ó¹ Ù Ô Ö Ñ ØÖ º ÌÒ θ = (θ 1, θ 2 ) Ñ ¹ θ 1 = µ θ 2 = σ 2 º ½½½ Ѻ º¾ Ø ºµ ÓÖÑÙÓÒ Ñ ÖÒ Ý ÝÑÝ Ý ¹ Ò ÝÔÓØ ÒØ Ø Ù Ò Ñ H 0 : θ = 0 H 1 : θ = 1º ÌÒ ÚÓÒÝ ÒØ Ù ØØ ÓÚ Ø π 0 = È(H 0) π 1 È(H 1 ) = 1 p 0 = È(H 0 y) p 1 È(H 1 y) = = 4.0 Ý ¹Ø ÓÒ B = p 0/p 1 π 0 /π 1 = 4.0. ÇÒ ÚÚ ÒÝØØ Ø ØØ ÒÒ Ò Ó ÒØ º ÀÙÓѺ ½ ÎÓÒ ÝÔÓØ Ò ÔÓ Ø Ö ÓÖ ØÓÒ¹ Ò ÝÝØ p 0 = È(H 0 y) = 0.80 p 1 = È(H 1 y) = 0.20º ÆÑ ÓÚ Ø ØÓ Ò ØÓÒÒ ÝÝ º ÇÒ ÑÙ ¹ Ø ØØ Ú ØØ Ò Ò È¹ ÖÚÓ ÓÒ Ò ÓØÒ ÑÙÙØ º ÀÙÓѺ ¾ Ì Ø ÒØ ÝÔÓØ ÒØ Ø Ù ÓÒ Ö¹ Ú Ó ÓÒ ÚÒ Ñ Ó Ø Ú ÖÖ ØÒº ƹ Ò Ú Ó ÑÙ Ø Ñ º ½½¼ Ç Ø ØÒ ØØ Ò ØÓ ÓÒ yº ÂÓ θ = (θ 1, θ 2 ) θ 2 ÓÒ Ù Ô Ö Ñ ØÖ ÒÒ ÑØ ÒÒ Ò ÒÒÓ Ø Ý Ø ÔÓ Ø Ö ÓÖ p(θ 1, θ 2 y) ÚÒ Ñ Ö¹ Ò ÔÓ Ø Ö ÓÖ p(θ 1 y)º Å ÖÒ ÔÓ Ø Ö ÓÖ ÚÓÒ Ó Ø Ø ¹ Ú ½º Ø ÔÓ Ø Ö ÓÖ Ø Ó ÓÒ p(θ 1, θ 2 y) p(y θ 1, θ 2 ) p(θ 1, θ 2 ). ÌÒ Ñ ÖÒ ÔÓ Ø Ö ÓÖ Ò ÒØÖÓ ¹ Ñ Ù Ô Ö Ñ ØÖ ÙÓ Ø º p(θ 1 y) = p(θ 1, θ 2 y)dθ 2. ¾º Ø ÔÓ Ø Ö ÓÖ ÚÓÒ ØÒ Ù¹ ÖÚ Ø p(θ 1, θ 2 y) = p(θ 1 θ 2, y) p(θ 2 y), ÓÓ Ò p(θ 1 y) = p(θ 1 θ 2, y) p(θ 2 y)dθ 2. ÂÑÑ Ø ÝØ ØÒ Ý Ø ÔÓ Ø ¹ Ö ÓÖ Ò ÑÙÓ ÒÒ º ½½¾

29 º¾ ÆÓÖÑ ÓØÓ Ò ØØÝÚ Ø Ö Ø Ù¹ ÆÓÖÑ ÓØÓ ¹ Ô Ò ÓÖÑ ØÚ Ò Ò ÔÖ ÓÖ Ç Ø ØÒ ØØ ÓØ ÒØ ÙÑ ÓÒ y i µ, σ 2 Æ(µ, σ 2 ) Ñ ÒÝØ µ σ 2 ÓÚ Ø ØÙÒØ Ñ ØØÓ¹ Ѻ Ç Ø ØÒ ØØ ÚÒÒÓØ y 1,..., y n ÓÚ Ø ¹ Ó Ø ÖÔÔÙÑ ØØÓÑ Ó µ, σ 2 º Ì Ò ÔÖ ÓÖ Ø ÙÖÚ Ø Ó ØÙ Ø µ σ 2 ÓÚ Ö ÖÔÔÙÑ ØØÓÑ ÔÖ ÓÖ º (µ,log σ) Ø (R 2 ) º Ì Ø ÙÖ ØØ p(µ, σ 2 ) 1 σ 2 º Å ÖØÒ ȳ = 1 n y i ÓØÓ ÖÚÓµ n i=1 s 2 = 1 n (y i ȳ) 2 ÓØÓ Ú ÖÒ µ n 1 i=1 ½½ Å ÖÒ ÔÓ Ø Ö ÓÖ p(σ 2 y) ÓÒ Ó p(σ 2 y) (σ 2 ) (n ) e n 1 ( n 1 ÁÑÑ 2, n 1 ) 2 s2, (σ 2 y) = n 1 n 3 s2 Î Ö(σ 2 y) = 2 s2 /σ 2 2(n 1) 2 (n 3) 2 (n 5) s4. ÈÖØÚ Ò Ò ÙÑ p(ỹ y) ÓÒ p(ỹ y) = p(ỹ µ, σ 2 )p(µ, σ 2 y)dµdσ 2 ( Ø n 1 ȳ,(1 + 1 ) n )s2. ÅÝ ÑÑ Ò ØÙÒ ÙÓÑÑÒ ØØ Ò ¹ ÙÑ Ø ÓÖØØ ØÙÓ ÓÒ Ý ¹ Ò ØÓ Ò ÝÝ ÚÒ ØÓÖ Ø ÖÚÓ º Ø Ù ÙÚ Ø ÔÓÑÑ Ò ÑÙÓ ÒØ ¹ ØÒ Ó º ½½ Ø ÔÓ Ø Ö ÓÖ ÓÒ ÒÝØ p(µ, σ 2 y) (σ 2 ) (n 2 +1) e 1 2σ 2 ni=1 (y i µ) 2 (σ 2 ) (n 2 +1) e 1 2σ 2 [(n 1)s2 +n(ȳ µ) 2 ] Å ÖÒ ÔÓ Ø Ö ÓÖ p(µ y) Ò [ ] n p(µ y) 1 + n(µ ȳ)2 2 (n 1)s 2 Øn 1 (ȳ, s2 n ) Ó (µ y) = ȳ Î Ö(µ y) = n 1 n 3 s2 n º Î ØÓØÓ Ò Ò ØÝ ÓÒ µ ȳ s/ n y Ø n 1(0,1) Ø Ú Ò Ò t¹ùñ ÖÔÙ Ù Ô Ö ¹ Ñ ØÖ Ø σ 2 µº ÀÙÓÑ Ã Ø ØÓØØ ȳ µ s/ n µ Ø n 1(0,1). ÆÓÖÑ ÓØÓ ¹ ÓÒ Ù ØØ ÔÖ ÓÖ ÃÒØÒ Ò χ 2 ¹ÙÑ ÂÓ ÑÙÙØØÙ x ÑÑ ( ν 0 2, 2 1 ) ÒÒ Ó Ò x χ 2 (ν 0 ) χ 2 ¹ÙÑ Ú Ô Ù ØÒ ν 0 µº ÂÓ ÒÝØ y = σ2 0 ν 0 x ÒÒ ÒÓØÒ ØØ y ÒÓÙ¹ ØØ ÒØ Ø χ 2 ¹ÙÑ Ñ Ö º y ÁÒÚχ 2 (ν 0, σ0 2)º ÃÓÒ Ù ØØ ÔÖ ÓÖ ÒÓÖÑ ÓØÓ ÓÒ p(µ, σ 2 ) = p(σ 2 ) p(µ σ 2 ), Ñ σ 2 ÁÒÚχ 2 (ν 0, σ0 2) µ σ 2 Æ(µ 0, σ2 κ ) 0 º  ÙÑ ÒÓØÒ Æ¹ÁÒÚχ 2 ¹ÙÑ º ̹ Ò Ý Ø ÔÓ Ø Ö ÓÖ ÓÒ ÑÝ Æ¹ÁÒÚχ 2 ¹ÙÑ º Ò µ y Ø σ 2 y ÁÒÚχ 2 º ½½ ½½

30 ÆÓÖÑ ÓØÓ ¹ ÑÓÒ Ù ØØ ÔÖ ÓÖ ÂÓ Ó Ú Ý Ø ÔÖ ÓÖ p(µ, σ 2 ) = p(σ 2 ) p(µ σ 2 ) Ó Ø ØÒ ØØ σ 2 ÁÒÚχ 2 (ν 0, σ 2 0 ) µ Æ(µ 0, τ 2 0 ) Ó ÖÔÙ σ2 Ø µ ÒÒ µ σ 2 ÓÚ Ø ÖÔÔÙÑ ØØÓÑ ÔÖ ÓÖ º ÌÑ Ó Ø ÓÑÔ Ò ÔÓ Ø Ö ÓÖÒ ÑÙع Ø ÓÒ ÝÝ Ò Ò ÝØ ØØ ÑÙÓ ÒØ ÔÓ ¹ Ø Ö ÓÖ ØØ º ÈÖ ÓÖ Ò ÓÒ ØÖÙÓ ÒØ Ú ÖÒ σ 2 Ç Ø ØÒ ØØ ÔÖ ÓÖ σ 2 ÁÑÑ (α.β) º º (σ 2 ) = 0.04 (σ 2 ) = 0.02º ÌÒ α = 6.0 β = 0.2º ÃÒØ Ú ÖÒ τ = 1/σ 2 ÔØ Ó Òº τ ÑÑ (6.0,0.2) (τ) = 30 (τ) = 12.25º Ë ÑÙÓ ÒÒ ØÙØ Ñ ÖÒ ÔÓ Ø Ö ÓÖ Ø ØÙÒ¹ Ø Ñ ØØÓÑ ÙÙÖ ÙÙÒ ÚÒÒÓÒ ÔÖØÚ Ò Ò ÙÑ ÓÚ Ø ÒÓ ÑÒ ¾º ± ÑÒ º ± ÑÙ º ¼º¼ ¼ º ¼¾ º¾ º½ Ñ ¾ ¼º¼ ¼º¼¼ ¼º¼¾ ¼º¼ ¼º¼ ¾ Ø Ù ¾ º¾ º ½ º½ ¾ º º½ ÝÔÖ º ¼º¾¼¾ º¼ º º ½½ ½½ Ѻ º½ ÆÓÖÑ ÓØÓ Ó ÖÚÓ ØØ Ú ÖÒ ÓÚ Ø ØÙÒØ Ñ ØØÓÑÒ Ý Ó ÒØ ÝØÒÒ º ËÓÚ ØÒ ÑÙÓ ÒØ Ú Ø ¹ ØÒ ÑÝ ÑÑ Òµ ÝØØ Ò Í Ë¹Ó ÑÓ Ò¹ Ø Í Ë Ý Ò ÒÖ Ò Í Ò Ë ÑÔ Ò µº Ç Ø ØÒ ØØ y i µ, σ 2 Æ(µ, σ 2 ) y 1,..., y n Ó Ø ÖÔÔÙÑ ØØÓÑ Ó µ, σ 2 º Ò ØÓÒ ÓÒ Ú Ò ³ Ò Ø ÚÖغ Ù Ù µ º º¾ º º º º º ¾ º¾ º º º º½ º¾ º º ¾ º º º º º º º º Ç Ø ØÒ ØØ µ σ 2 ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ø ÔÖ ÓÖ ÒÒ Ø Ó Ò Ò ÖÓ ØÙ µ µ Æ(5,0.5) ÙØ Ò ÑÑ Òº Ѻ º½ Ø ºµ Í Ë ¹ ÓÓ Ó Ò Ò Ñ ØØÒ ÑÓ ß ÓÖ Ò ½ Ƶ ß Ý ÒÓÖÑ ÑÙ Ø Ùµ ÑÙ ÒÓÖÑ ¾µ Ø Ù ÑÑ ¼º¾µ Ñ ¾ ¹ ½»Ø Ù ÝÔÖ ÒÓÖÑ ÑÙ Ø Ùµ Ø Ø Ý º º¾ º º º º º ¾ º¾ º º º º½ º¾ º º ¾ º º º º º º º ºµ Æ ¾ µ Ò Ø Ø ÑÙ Ø Ù¼ ÝÔÖµ ÈÓ Ø Ö ÓÖ Ø ÔÖØÚ Ò Ò ÙÑ ÓÒ ØØÙ Ù¹ ÖÚ Ø ÑÙÓ ÒÒ Ø 2000 ÑÙÓ Òص ½½ ½¾¼

31 ½ È Ö Ú ÖØÙ mu ÌÒ m = n (x i, y i ) ÑÙÓ Ó Ø Ú Ø Ú Ö¹ Ö ÒÒÓ Ø Ô Ö Ø Ó Ò Ù Ò Ñ ØØ Ù ¹ ÑÓ Ø Ý Øº Ì ÒÒ Ô ÙØÙÙ Ý Ò ÓØÓ Ò Ø Ô Ù Ò Ó sigma z i = x i y i δ, ω Æ(δ, ω), ω = φ + ψ Ó ÚÒÒÓØ x i y i ÓÚ Ø Ó Ø ÖÔÔÙÑ ØØÓѵº ¾ ÊÔÔÙÑ ØØÓÑ Ø ÓØÓ Ø Ú ÖÒ Ø ØÙÒÒ ¹ ØÙØ tau ÒÖØ Ò Ø ÒÒ ÓÒ Ó λ µ ÓÚ Ø ÖÔÔÙÑ ØØÓÑ ÔÖ ÓÖ p(λ) 1 p(µ) 1º ÌÒ λ x Æ( x, φ m ) ypred µ y Æ(ȳ, ψ n ) δ x, y Æ( x ȳ, φ m + ψ n ) ½¾½ ½¾ ÃÒ ÒÓÖÑ ÔÓÔÙØ ÓÒ ÖÚÓÒ Ú ÖØÙ Ç Ø ØÒ ØØ x i λ, φ Æ(λ, φ) x 1,..., x m ÓÒ ÖÔÔÙÑ ØÓÒ ÓØÓ Ó λ, φº Î ØÚ Ø y i µ, ψ Æ(µ, ψ) y 1,..., y n ÓÒ ØÓ Ò Ò ÖÔÔÙÑ ØÓÒ ÓØÓ Ó µ, ψº ÅÓ ÑÑ Ø ÓØÓ Ø Ó Ø ØÒ ØÓ ØÒ ÖÔ¹ ÔÙÑ ØØÓÑ º ÃÒÒÓ ØÙ Ò Ó ØÒ ÓÒ ÖÚÓÒ λ µ Ú ÖØÙ Ø º ÒÖ Ò Ø Ò ÖÓØÙ Ø δ = λ µº Ì ÒÒ ÚÓÒ Ò Ò Ø Ô Ù Ò Ù¹ Ø Ò Ø ØÓØØ ÒÝØ ØÙ Ô ÖÙ ÙÖ µ ½º Ô Ö Ú ÖØÙ Ô ÖÙ ÙÖ Ò ÖÔÔÙÚ Ø ÓØÓ Ø Ú ÖÖ ÒÒÓ Ø Ô Ö Ø µ ¾º ÖÔÔÙÑ ØØÓÑ Ø ÓØÓ Ø Ú ÖÒ Ø ØÙÒÒ ØÙØ º Ú ÖÒ Ø Ý Ø ÙÙÖ Ø ÑÙØØ ØÙÒØ Ñ ØØÓÑ Ø º Ú ÖÒ Ø ØÙÒØ Ñ ØØÓÑ Ø Æ Ø Ó Ø ÓÒ ÙÑ Ø ÓÖØØ Ø Ú¹ ÑÙØØ ÚÓÒ Ø ÑÝ ÑÑ Ò ¹ Ø ØÚ ÑÙÓ ÒØ Ñ Ò Ø Ñ ÔÓ Ø º ½¾¾ Î ÖÒ Ò Ý Ø ÙÙÖ Ø ÑÙØØ ØÙÒØ Ñ ØØÓ¹ Ñ Ø Ç Ø ØÒ ØØ ψ = φ ØØ ÔÖ ÓÖ ÓÒ Ô Ò¹ ÓÖÑ ØÚ Ò Ò ÌÒ ÔÓ Ø Ö ÓÖ ÓÒ p(λ, µ, φ) 1 φ. p(λ, µ, φ x, y) = p(λ, µ, φ) p(x λ, φ) p(y µ, φ). ËÙÓÖÒ ÙÒ Ø Ø Ò Ó p(δ, φ x, y) = p(φ s 2 ) p(δ x ȳ, φ), p(δ x ȳ, φ) Æ( x ȳ, φ( 1 m + 1 n )) º ÈÓ Ø Ö ÓÖ ÓÒ Ñ δ ( x ȳ) s 1m + 1 n x, y Ø n+m 2 (0,1), s 2 = (m 1)s2 x + (n 1)s 2 y m + n 2. ½¾

32 Ѻ º¾ Ë ÑÙÓ ÒØ Ý ÒÖØ Ø ØÑÒ¹ Ò Ø ÒØÒ ÝØÒÒ Ò Ø ¹ Ò ÝÝ º ¹ Ñ Ö Ò ØÓÒ ÓÒ Ò ÒØÙ Ò Ö Ù¹ Ø Ò Ò ÖÙÓ ÓÖØØÙÒ Òµ Ô Ø ÔÓ Ñ ØØÙÒ ÒÑÙÒÒ Ô Ñ Ø Ø ÑÑ Ö ÙØ Ò Ò ¾¾º¼ ¾ º ¾¼º ¾ º ¾ º¼ ¾ º¼ ¾½º ¾ º ¾¾º ¾ º½ ÖÙÓ ÓÖØØÙÒ Ò ¾ º¾ ¾¾º¼ ¾¾º¾ ¾½º¾ ¾½º ¾½º ¾¾º¼ ¾¾º ¾¾º Ò ØÓÒ ØÙÒÒÙ ÙÙ ØØÙÒ Ê¹ÝÑÔÖ Ø µ ÙÑÑ ÖÝ ¹ Ø ÑÙ½ ÑÒ Üµ Ú Ö½ Ú Ö Üµ ½ ܵ ÑÙ¾ ÑÒ Ýµ Ú Ö¾ Ú Ö Ýµ ¾ ݵµ Ø º Ö Ñ ÙÑÑ Öݵ ÑÙ½ Ú Ö½ ½ ÑÙ¾ Ú Ö¾ ¾ ½ ¾ º½ ½º½½½½ ½º¾ ¼ ¾¾º¾ ¼º ¾¾ ¼º ÁÑ Ø Ø Ø Ô Ù Ó Ô ÖÙ Ø ØÙ Ó ØØ ØØ ÔÓÔÙØ Ó Ò Ú ÖÒ Ø Ó ¹ Ú Ø Ý Ø ÙÙÖ Øº Ì Ò ÙÖÚ Ø Ó ØÙ Ø x i Æ(µ 1, σ 2 1 ) ÖÔÔÙÑ ØØÓÑ Ó µ 1, σ 2 1 º y j Æ(µ 2, σ 2 2 ) ÖÔÔÙÑ ØØÓÑ Ó µ 2, σ 2 2 º ÇØÓ Ø ÖÔÔÙÑ ØØÓѺ ÇÒ Ú ÖÖ ØØ Ú ÖÚÓ ÑÝ Ú ÖÒ ¹ º ½¾ Ñ º¾ Ø º Ä Ñ ÝØ ØØÝ Í Ë ¹ ÓÓ ÑÓ ß ÓÖ Ò ½ Æµß Ü ÒÓÖÑ ÑÙ½ Ø Ù½µ ÓÖ Ò ½ Åµß Ý ÒÓÖÑ ÑÙ¾ Ø Ù¾µ ÑÙ½ÒÓÖÑ ¾¾º¼ ¼º¾ µ ÑÙ¾ÒÓÖÑ ¾¾º¼ ¼º¾ µ Ø Ù½ÑÑ ¼º½ ¼º½µ Ø Ù¾ÑÑ ¼º½ ¼º½µ Ñ ½ ¹½»Ø Ù½ Ñ ¾ ¹½»Ø Ù¾ عÑÙ½¹ÑÙ¾ Ö ¹Ø Ù¾»Ø Ù½ Ø Ø Ü ¾¾º¼ ¾ º ¾¼º ¾ º ¾ º¼ ¾ º¼ ¾½º ¾ º ¾¾º ¾ º½µ Ý ¾ º¾ ¾¾º¼ ¾¾º¾ ¾½º¾ ¾½º ¾½º ¾¾º¼ ¾¾º ¾¾º µ Æ ½¼ ŵ Ò Ø Ø ÑÙ½ ¾¼º¼ ÑÙ¾ ¾¼º¼ Ø Ù½ ½ Ø Ù¾ ½µ ½¾ Ñ º¾ Ø º Ì Ò ÙÖÚ Ø ÔÖ ÓÖ Ú ÒÒ Ø µ 1 Æ(22.0,4) µ 2 Æ(22.0,4) 1/σ 2 1 ÑÑ (0.1,0.1) 1/σ 2 2 ÑÑ (0.1,0.1) Ô Ö Ñ ØÖ Ø ÔÖ ÓÖ ÖÔÔÙÑ ØØÓÑ Ø ØÒÚ ØÓ Ñ ÖÒ ÔÓ Ø Ö ÓÖ ÙÑ Ø ÖÚÓ ÓÒØ ÑÙÓ ÒØ Ú Ö ¼± Ò ØÒ¹Ú µº Ì Ñ ½ ÓÒ σ 2 1 Ñ ¾ ÓÒ σ2 2 Ø ÓÒ µ 1 µ 2 Ö ÓÒ σ 2 1 /σ2 2 º ÒÓ ÑÒ Å ÖÖÓÖ º¼± º¼± ÑÙ½ ¾ º¼ ¼º ¼º¼¼ ¾ ¾¾º ½ ¾ º ÑÙ¾ ¾¾º¼ ¼º¾¾ ¼º¼¼ ¾½º ¾¾º Ñ ½ ½º ½º ½ ¼º¼¾ ¼º ¾¼ º½¾ Ñ ¾ ¼º ¼º ¼ ¼º¼¼ ¼½ ¼º¾½ ½ ½º½ ½ Ø ¼º ¼º ¼ ¼º¼½½½ ¼º½ ¾½ ½º ¼ Ö º º ½ ¼º¼ ½º½ ½ ½½º ÅÓÒ ÙÓØØÒ Ò ÒÓÖÑ ÓØÓ Ý Ý Ø À ÚÒØÓ y i ÓÒ d 1 ÚØÓÖ ÓÒ ÖÚÓÚØÓÖ ÓÒ µ d 1 ÚØÓÖ µ ÓÚ ÖÒ Ñ ØÖ Σ d d Ñ ØÖ µº À ÚÒÒÓÒ ÓØ ÒØ ÙÑ ÓÒ { p(y µ,σ) Σ 2 ÜÔ 1 1 } 2 (y µ)t Σ 1 (y µ). Ç ÓÓÒ y 1,..., y n Ó µ,σ ÖÔÔÙÑ ØØÓÑ Ø ÚÒ¹ ÒÓØ ÓÓ Ò Ù ÓØØ ÚÙÙ ÙÒ Ø Ó ÓÒ { p(y 1,..., y n µ,σ) Σ n 2 ÜÔ 1 } 2 ØÖ(Σ 1 S 0 ), Ñ S 0 = n i=1 (y i µ)(y i µ) T º ½ Σ ØÙÒÒ ØØÙ ÃÓÒ Ù ØØ ÔÖ ÓÖ µ Æ(µ 0,Λ 0 ) ÓÓ Ò ÔÓ Ø Ö ÓÖ Ò µ y Æ(µ n,λ n ) º º µ n = (Λ nσ 1 ) 1 (Λ 1 Λ 1 n = Λ nσ 1. 0 µ 0 + nσ 1 ȳ) Ô Ò ÓÖÑ ØÚ Ò Ò ÔÖ ÓÖ µ ÓÒ p(µ) 1 º ¾ Σ ØÙÒØ Ñ ØÓÒ ÃÓÒ Ù ØØ ÔÖ ÓÖ (µ,σ) ÓÒ Æ¹ ÒØÒ Ò Ï ÖØ ¹ ÙÑ ØÙÓ ÒÓÖÑ ÙÑ Ø ÒØ Ø Ï ¹ ÖØ Ò ÙÑ Ø µº Ï ÖØ Ò ÙÑ ÝØÝÝ Ù¹ Ñ Ø ÙÙ Ó Ø º Σ ÁÒÚ¹Ï ÖØ ν0 (Λ 1 0 ) µ Σ Æ(µ 0,Σ/κ 0 ) ½¾ ½¾

33 ÀÝÔ ÖÔ Ö Ñ ØÖ Ø ÓÚ Ø (λ 0, κ 0 ; ν 0,Λ 0 ). ÌÒ ÑÝ ÔÓ Ø Ö ÓÖ ÓÒ Æ¹ÁÒÚ¹Ï Öغ Ô Ò ÓÖÑ ØÚ Ò Ò ÔÖ ÓÖ ÓÒ p(µ,σ) Σ d+1 2, ÓÓ Ò Ñ ÖÒ ÔÓ Ø Ö ÓÖ Ò Σ y ÁÒÚ¹Ï ÖØ n 1 (S) µ Σ, y Æ(ȳ, 1 n Σ). Ì S ÓÒ ÓØÓ ÓÚ ÖÒ Ñ ØÖ º ÇØ ÒØ ÙÑ ( ) n p(y θ) = θ y1 y 1 y 1 θyk k, k θ i 0 k i=1 θ i = 1 k i=1 y i = n ÒÓØÒ ÑÙØ ÒÓ¹ Ñ ÙÑ º ÃÙÒ k = 2 ÒÒ Ø ÒÒ Ô ÙØÙÙ ÒÓÑ ÙÑ º Ì ( ) n = y 1 y k n! y 1!y 2! y k!. ÃÓÒ Ù ØØ ÔÖ ÓÖ ÑÙØ ÒÓÑ ÓØÓ ÓÒ ¹ Ö Ø³Ò ÙÑ θ Ö(α 1,..., α k ) Ó ÑÖ Ø Ò ÙØ Ò k p(θ) θ α i 1 i, θ i > 0, i=1 Ñ α i > 0º k θ i = 1, i=1 Ö Ø³Ò ÙÑ ÓÒ ÙÖÚ ØÙÒØ ÂÓ Ø Ý ÙÒ Ø ÓØ Ø Ö Ø Ò ÝÔ ÖÔ Ö ¹ Ñ ØÖÒ α i ÙÒ Ø ÓÒ ÒÒ α i Ú Ø ÙÓÒ i ÖÚ Ò ÙÒ ÚÒØÓÒ ÓÒ k i=1 α i º Ò Ö Ø³Ò ÙÑ Ô ÙØÙ٠ع Ø ÙÑÒ Ø (α 1, α 2 ) ÙÒ k = 2º ½¾ ½ ½ º ÅÙØ ÒÓÑ ÓØÓ ÒÓÑ ÓØÓ ØØÝÝ Ø ÒØ Ò Ó Ú ØÓ¹ ØÓ ÓÒ ÙÒ Ø ÑÙØ ÒÓÑ ÓØÓ ØØÝÝ Ù Ò ÙÓØØ ÙÚ ØÓ ÓÒ Ø Ô Ù Òº Ç ÓÓÒ k ÙÓ ÒÙÑ ÖÓ ØÙ ÙØ Ò 1,2,..., k ÙÓØ ÚØ Ó Ö Ø ØØݵº ÄÙÓØØ ÙÑ ÓÒ ÙÖÚ Ω ÓÒ ÙÓØ Ø Ú Ý µ È(Ω j {i} θ i ) = θ i Ó i = 1,..., k, Ñ k i=1 θ i = 1 º Å ÖØÒ θ = (θ 1,..., θ k )º ËÙÑÑ Ù ØÓ Ø Ö Ó ØØ Ø ØØ Ý ÙÓ¹ Ø Ò Ú ÖÑ Ø Ó ÓÒÒ k Ø ÙÓ Ø º ÇØ ÒØ Ñ ÄÙÓØ Ò n Ý ØÓ ØÒ ÖÔÔÙÑ ØØ º Å ÖØÒ y i ÙÓÒ i ÙÓ¹ Ø ØÙÒ ÑÖ i = 1,..., kº ÃÓ Ó ÙÓ¹ ØØ ÙÔ ÝØÖ ÓÒ y = (y 1,..., y k )º ÃÓ ÙÓØØ ÙØ ÓÚ Ø ÖÔÔÙÑ ØØÓÑ Ø ÒÒ k p(y θ) θ y i i. i=1 ½ ¼ ÃÓÒ Ù ØØ ÔÖ ÓÖ Ò Ø Ô Ù ÔÓ Ø Ö ÓÖ ÓÒ p(θ y) p(y θ) p(θ) k θ y k i i θ α i 1 i i=1 i=1 k θ α i+y i 1 i, i=1 Ó ÓÒ Ö(α 1 + y 1,..., α k + y k ) º Ѻ º Ê ÓÙÙØ Ø Ò ÝÝ ÙÙ ¾¼¼½ Ø Ñ Ø ØØ ÙØÙØÑÙ Ý ÝØØÒ ÔÙÓÙÒ ÒÒ ¹ ØÙ Ø º À Ø Ø Ø Ú Ò Ó ½¾ Ò º ÌÙÓ ¹ ØØÙÒ ÒÒ ØÙ Ø ÒÒ ØÙ ÔÖÓ ÒØ Ø µ Ó Ë È Ã ÃÓ ÎÖ Î ÑÙÙ Ý Ø ½ ¾ ½ ¾¾¾ ½¾ ¾ º¼ ¾ º½ ¾¼º¾ ½¾º º¼ ½½º¾ ½¼¼± Î ØÒ ÔÖ ÓÖ Ö(1,1,1,1,1,1)º Å ÖÒ ÔÓ Ø ¹ Ö ÓÖÒ ÙÚ Ù ÒÓ ÑÒ ¾º ± ÑÒ º ± Øؽ ¼º¾ ¼º¼¼ ¾ ¼º¾¾¼ ¼º¾ ¼º¾ Øؾ ¼º¾ ¼ ¼º¼¼ ¼º¾½¾ ¼º¾ ¼ ¼º¾½ ØØ ¼º¾¼½ ¼º¼¼ ¾ ¼º½ ¼º¾¼½ ¼º¾¾¼ ØØ ¼º½¾ ¼º¼¼ ¼º½¼ ¼º½¾ ¼º½ ØØ ¼º¼ ¼ ¼º¼¼ ¼º¼ ¼º¼ ¼¾ ¼º½¼ ¾ ØØ ¼º½½ ¼º¼¼ ¾¾ ¼º¼ ¼º½½ ½ ¼º½¾ ½ ¾

34 Ó Ú ÔÓ Ø Ö ÓÖ ÓÒ ØØÙ Å Å ¹ ÑÙÓ ÒÒ ÝØØ Ò Í Ë ¹Ó Ѻ Ç ¹ ÑÓÓ ÓÒ ÙÖÚ ÑÓ ß Ý ½ à ÑÙØ Øؽ à Ƶ Øؽ Ã Ö Ô ½ à µ Æ ¹ ÙÑ Ý µ Ø Ø Ã Ô ½ ½ ½ ½ ½ ½µ Ý ½ ¾ ½ ¾¾¾µµ Ò Ø Ø ØØ ¼º¾ ¼º¾ ¼º¾ ¼º½ ¼º½ ¼º½µ Ѻ º Ø ºµ Å ÓÒ ÔÓ Ø Ö ÓÖ ØÓÒÒ ÝÝ ØØ Ë È Ò ÒÒ ØÙ ÓÒ ÙÙÖ ÑÔ Ù Ò µ Ã Ù Ø Ò µ ÃÓ ÓÓÑÙ Ò ÃÝØ ØÒ Ò Ñ Ö¹ Ø³Ò ÔÖ ÓÖ Ó α i = 1 iº ÒÓ ÑÒ ¾º ± ÑÒ º ± Ø ½ ¼º¼¼¼¾ ¼º¼½ ¹¼º¼¾½ ¼º¼¼¼ ¼º¼ Ø ¾ ¼º¼ ½ ¼º¼½ ½ ¼º¼¼ ¼º¼ ¼º¼ Ô½ ¼º ½ ¾ ¼º½ ¼º¼ ½º¼ ½º¼ Ô¾ ¼º ¼º¼ ¼ ½º¼ ½º¼ ½º¼ ½ º ÂÓ ØÙ ÔÓ Ø Ö ÓÖ ÙÑ Ò ÑÙÓ Ò¹ ØÒ Ì Ö Ø Ò Ø Ý Ø Ý Ñ ÖÒ ÔÓ ¹ Ø Ö ÓÖ Ò Ñ Ø ÑÙÓ ÒÒ º Ç Ø ØÒ ØØ ØÙÒØ Ñ ØÓÒ ÙÙÖ ÓÒ θ = (θ 1,, θ p ) ÑØ ÒÒÓ Ø Ö ØÝ Ø p(θ 1 y)º ÅÙÙØ Ô Ö Ñ ØÖ Ø Ø ÖÚ ØÒ Ñ Ò Ô Ó ¹ Ñ ºµ È ÙØ ØÒ ÑÒ ØØ p(θ 1 y) = p(θ y)dθ 2 dθ p. Å ÖÒ ÔÓ Ø Ö ÓÖ Ò Ñ Ø ÖÚ Ø p 1 ¹ÙÓØØÒ Ò ÒØÖ Ø Ò ÚÓÒ ÒÓ Ø¹ Ø ÒÙÑÖ Ø Ñ Ò Ø ÑØ ÓÚ Ø ØÓØ ÑÓÒ ÙÓع Ø Ò ÙÒ Ø ÓÒ ÓÔØ ÑÓ ÒÒ ÑÙØØ ÑÓÒ ÙÓØØÒ Ò ÒÙÑÖ Ò Ò ÒØÖÓ ÒØ ÚÙØÙÙ Ñ Ò ÓÒ Ú ¹ Ò º ÓÙÖ Ó Ñ Ò ÓÒµº Ë ÑÙÓ ÒØ ÓÒ ØÓ Ú ØÓØÓ ÑÓÒ ÙÓØØ Ø Ò ÒØÖÒ Ñ º Ç Ø ØÒ ØØ θ (1), θ (2),..., θ (N) ÓÒ ÑÙ¹ Ó ÒØÙ ÓØÓ Ý Ø ÔÖ ÓÖ Ø p(θ y) Ó Ó Ý ¹ ØÑ ÓÒ ÑÙÓ ØÙº ÅÝ ÑÑ Ò ÖÖÓØÒ Ñ Ø Ò Ø Òºµ ½ ÌÑ ØÒ Ñ ÙÖÚ Ó ÑÓÓ Ò ¹ ØÓÒ Ù ÖÚÓÒ Ó ÙØ Ò µ ÑÓ ß Ý ½ à ÑÙØ Øؽ à Ƶ Øؽ Ã Ö Ô ½ à µ Æ ¹ ÙÑ Ý µ Ø ½ ¹Øؽ ¹Øؾ Ø ¾ ¹Øؽ ¹ØØ Ô½ ¹ Ø Ô Ø ½µ Ô¾ ¹ Ø Ô Ø ¾µ θ 1 Ò ÑÔÖ Ò Ò Ñ ÖÒ ÔÓ Ø Ö ÓÖ Ò ÙÓ¹ ÖÒ Ñ ÖÒ ÓØÓ Ø θ (1) 1,..., θ(n) 1 ÙÒÓ ¹ Ø Ñ ÑÙÙØ ÓÑÔÓÒ ÒØ Øµ θ (1) 1 θ (1) 2 θ (1) 3 θ p (1) θ (2) 1 θ (2) 2 θ (2) 3 θ p (2) θ (3) 1 θ (3) 2 θ (3) 3 θ p (3) º º º º θ (N) 1 θ (N) 2 θ (N) 3 θ p (N) ½º ÑÙÓ ÒØ ¾º ÑÙÓ ÒØ º ÑÙÓ ÒØ º Æ ÑÙÓ ÒØ Ò ÑÑ Ò Ò Ö ÓÒ ÓØÓ ÙÑ Ø p(θ 1 y)º ÂÓ ÓÒ ØØ Ú Ó ÓØÙ ÖÚÓ (h(θ 1 ) y) = h(θ 1 ) p(θ y)dθ = h(θ 1 ) p(θ 1 y)dθ 1 Óº ÓØÓ Ò ÚÙ ÓÒ ÚØØÑØØ Ø Ö¹ Ú Ø Ó ÖÔÔÙÑ ØÓÒ ÓØÓ µ ÒÒ ½ (h(θ 1 ) y) 1 N h(θ (k) N 1 ). k=1 ÔÔÖÓ ÑØ ÓØ ØØ ÚØÓÖ Ò θ Óѹ ÔÓÒ ÒØ Ø ÑÙÓÒ ÑÙØØ ÚÒ Ò ÑÑ Ò Óѹ ÔÓÒ ÒØ Ò θ 1 ÑÙÓ ØÙ ÖÚÓ ÝØ ØÒ (h(θ 1 ) y) Ò Ñ º ½