800346A Differentiaaliyhtälöt II. Martti Kumpulainen
|
|
|
- Seppo Väänänen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 8346A Differentiaaliyhtälöt II Martti Kumpulainen 6. maaliskuuta 214
2 DIFFERENTIAALIYHTÄLÖT II Kesto: 3 op. Luentoja 3 h, harjoituksia 16 h. Opintojaksossa tarkastellaan erikoisfunktioita, ortogonaalikehitelmiä ja integraalimuunnoksia, sekä sovelletaan niitä mallintamisessa käytettävien lineaaristen differentiaaliyhtälöiden ja osittaisdifferentiaaliyhtälöiden ratkaisemiseen. Sisältö: Erikoisfunktioista, esimerkkeinä Gammafunktio ja Besselin funktiot. Funktioavaruuksista, funktioiden sisätulo, ortogonaalisuus, ortogonaalipolynomit ja ortogonaalikehitelmät. Sovelluksina funktioiden esittäminen Fourier- sarjoina ja Sturm-Liouvillen reunaarvoprobleemat. Integraalimuunnoksista, mm. Laplace- ja Fourier-muunnokset. Lineaaristen differentiaaliyhtälöiden ja osittaisdifferentiaaliyhtälöiden, esim. lämpö- ja aaltoyhtälöiden sekä Laplacen yhtälön ratkaiseminen ortogonaalikehitelmien ja integraalimuunnosten avulla. Tarvittavat esitiedot: Lineaarialgebra I & II, Analyysi I & II sekä Differentiaaliyhtälöt I. i
3 Sisältö 1 Frobeniuksen menetelmä Frobeniuksen menetelmä Ratkaisut säännöllisen erikoispisteen tapauksessa Indeksiyhtälön ratkaisut reaaliset ja erisuuret Indeksiyhtälön ratkaisut reaaliset ja yhtäsuuret Indeksiyhtälön ratkaisut kompleksisia Erikoisfunktioista Gammafunktio Betafunktio Besselin funktioista Besselin differentiaaliyhtälön ratkaisu Besselin funktioiden rekursiokaavat Besselin funktioiden generoiva funktio Besselin differentiaaliyhtälön toinen lineaarisesti riippumaton ratkaisu 14 3 Ortogonaalikehitelmät funktioavaruudessa Funktioavaruus Funktioiden sisätulo ja normi Ortogonaalisuus, suppeneminen Ortogonaalikehitelmät ii
4 3.5 Ortogonaalipolynomeista Legendren polynomit Legendren polynomien generoiva funktio Hermiten polynomit Lisätieto: ensimmäisen lajin Chebyshevin polynomit Fourier n sarjat Määritelmiä Fourier n kosini- ja sinisarjat Kompleksiarvoisen funktion Fourier n sarja Sturm-Liouvillen ominaisarvo-ongelma Sturm-Liouvillen differentiaaliyhtälö Singulaarisia Sturm-Liouvillen ominaisarvo-ongelmia Besselin yhtälön reuna-arvo-ongelma Laplace-muunnos Esimerkkejä ja olemassaololauseita Laplace-muunnoksen ominaisuuksia Käänteismuunnos ja konvoluutio Sovellutus lineaarisiin differentiaaliyhtälöihin Fourier-muunnos Määritelmä ja ominaisuuksia Konvoluutio ja käänteismuunnos Toisen kertaluvun lineaarisista osittaisdifferentiaaliyhtälöistä Johdanto Lämpöyhtälö iii
5 8.2.1 Lämpöyhtälön johto Yksiulotteinen lämpöyhtälön ratkaiseminen muuttujien erottamismenetelmällä Kaksiulotteinen lämpöyhtä1ö Laplacen yhtälö ulottoinen tapaus alueena suorakulmio Aaltoyhtälö Aaltoyhtälön johtaminen Värähtelevän kielen liikeyhtälön ratkaisu muuttujanerottamismenetelmällä Aaltoyhtälön toinen ratkaisumenetelmä d Alembertin ratkaisu aaltoyhtälölle Laplace- ja Fourier-muunnoksien käytöstä osittaisdifferentiaaliyhtälöiden ratkaisemisessa Osittaisdifferentiaaliyhtälöiden ratkaisemisesta Laplace-muunnoksen avulla Osittaisdifferentiaaliyhtälöiden ratkaisemisesta Fourier-muunnoksen avulla Liite 73 iv
6 Luku 1 Frobeniuksen menetelmä Määritelmä 1.1. Funktio f on analyyttinen pisteessä a, jos sillä on muotoa f(x = a n (x a n = a o +a 1 (x a+a 2 (x a 2 +. n= oleva potenssisarjaesitys eräällä välillä (a r, a + r, r >. Määritelmä Piste a on yhtälön (1.1 y +p(xy +q(xy = säännöllinen piste, jos kerroinfunktiot p, q ovat analyyttisiä pisteessä a. 2. Piste on yhtälön (1.1 säännöllinen (heikko erikoispiste, jos funktiot P(x = (x ap(x, Q(x = (x a 2 q(x ovat analyyttisiä pisteessä a ts. jos yhtälö (1.1 voidaan esittää muodossa missä P ja Q ovat analyyttisiä pisteessä a. (x a 2 y +(x ap(xy +Q(xy =, 3. Ellei a ole yhtälön (1.1 säännöllinen piste, eikä säännöllinen erikoispiste, sanotaan sitä vahvaksi erikoispisteeksi. Esimerkki 1.3. Piste on Eulerin yhtälön säännöllinen erikoispiste. Esimerkki 1.4. Piste on yhtälön vahva erikoispiste. x 2 y +axy +by = x 2 y y by = Suorittamalla muuttujan vaihto x a = t eli x = a + t, saadaan a:n sijasta säännölliseksi erikoispisteeksi. Jatkossa voidaan siis olettaa, että a =. 1
7 1.1 Frobeniuksen menetelmä Oletetaan, että on yhtälön (1.2 x 2 y +xp(xy +Q(xy =, säännöllinen erikoispiste. Tällöin on olemassa sellainen R >, että (1.3 P(x = p n x n, Q(x = q n x n, x I = ( R,R. n= n= Frobeniuksen menetelmä yhtälön 1.2 ratkaisemiseksi Frobeniuksen menetelmä on seuraava 1. Valitaan yritefunktioksi y yleistetty potenssisarja (1.4 y = x r c n x n = c n x n+r, c, n= n= 2. sijoitetaan yritefunktio y ja yhtälön (1.3 sarjat yhtälöön (1.2, 3. määrätään eksponentti r ja kertoimet c n niin, että yhtälö (1.2 toteutuu. Koska funktioilla y ja y on potenssisarjaesitykset y = (r+nc n x n+r 1 = x r 1 (r+nc n x n, y = n= (r+n(r+n 1c n x n+r 2 = x r 2 (r+n(r+n 1c n x n, n= n= n= niin x 2 y = x r (r +n(r +n 1c n x n, n= ( n xp(xy = x r (r +nc n x n p n x n = x r (r+kc k p n k x n, n= n= n= k= ( n Q(xy = x r c n x n q n x n = x r c k q n k x n. n= n= n= k= Sijoittamalla nämä esitykset yhtälöön (1.2 saadaan [ ] n ( x r (r+n(r +n 1c n + (r+kpn k +q n k ck x n =. n= k= 2
8 Tämä yhtälö pätee kaikilla x (,R jos ja vain jos n ( (1.5 (r +n(r +n 1c n + (r +kpn k +q n k ck =, n =,1,... Kun n = ja yhtälö (1.5 jaetaan kertoimella c, saadaan (1.6 = r(r 1+p r +q = r 2 +(p 1r+q. k= Yhtälöä (1.6 kutsutaan yhtälön (1.2 indeksiyhtälöksi ja se määrää ne luvun r arvot, joilla yritefunktio (1.4 saattaa olla yhtälön (1.2 ratkaisu. Määritellään f kaavalla f(z = z(z 1+p z +q. Tällöin indeksiyhtälö (1.6 on yhtäpitävä yhtälön f(r = kanssa. Merkitsemällä lisäksi c n = c n (r, n =,1,..., saadaan yhtälö (1.5 muotoon eli (r+n(r+n 1c n (r+ ( n 1 ( (r+np +q cn (r+ (r+kpn k +q n k ck (r =, n 1 ( (1.7 f(r+nc n (r = (r+kpn k +q n k ck (r. k= Antamalla kertoimelle c (r määrätty arvo, saadaan muut kertoimet kaavasta (1.7, mikäli f(r + n kaikilla n = 1,2,... Voidaan osoittaa, että näin saatu sarja suppenee, kun < x < R. k= 1.2 Ratkaisut säännöllisen erikoispisteen tapauksessa Olkoon a yhtälön (1.8 (x a 2 y +(x ap(xy +Q(xy =, säännöllinen erikoispiste, ts. on olemassa sellainen R >, että P(x = p n (x a n, Q(x = q n (x a n, x I = (a R,a+R. n= n= Kappaleen 1.1 tuloksista seuraa: jos funktio y(x,r = (x a r c n (r(x a n c (r c, n= on differentiaaliyhtälön (1.8 ratkaisu, on r indeksiyhtälön (1.9 f(r = r(r 1+p r +q = ratkaisu, ja kertoimet c n (r, n = 1,2,... saadaan ns. palautuskaavasta n 1 [ ] n [ ] (1.1 f(r+nc n (r = (r+kpn k +q n k ck (r = (r+n kpk +q k cn k (r. k= k=1 3
9 1.2.1 Indeksiyhtälön ratkaisut reaaliset ja erisuuret Olkoot r 1 ja r 2 indeksiyhtälön (1.9 ratkaisut. Tällöin 1. funktio y 1 (x = y(x,r 1 on yhtälön (1.8 ratkaisu välillä (a,a+r ja yhtälön toinen ratkaisu y 2 voidaan määrittää seuravien ohjeiden perusteella 2. funktio y 2 (x = y(x,r 2 on y 1 :stä lineaarisesti vapaa (ei y 1 :n vakiokerrannainen differentiaaliyhtälön (1.8 ratkaisu välillä(a, a+r, jos toinen seuraavista ehdoista toteutuu (a r 1 r 2 ei ole kokonaisluku, (b r 1 r 2 = N on kokonaisluku ja palautuskaavan (1.1 oikea puoli on, kun r = r 2 ja n = N. 3. funktio y 2 (x = r (r r 2y(x,r r=r2 on yhtälön (1.8 ratkaisustay 1 lineaarisesti vapaa ratkaisu välillä(a,a+r, josr 1 r 2 = N on kokonaisluku ja palautuskaavan (1.1 oikea puoli ei ole, kun r = r 2 ja n = N. Edellä mainituissa tapauksissa y 1 ja y 2 muodostavat differentiaaliyhtälön (1.8 ratkaisujen perusjärjestelmän välillä (a, a + R Indeksiyhtälön ratkaisut reaaliset ja yhtäsuuret Olkoon r 1 indeksiyhtälön r(r 1+p r +q = kaksinkertainen juuri. Tällöin funktiot (1.11 y 1 (x = y(x,r 1 = (x a r 1 ja c n (r 1 (x a n, n= y 2 (x = r y(x,r r=r 1 = y 1 (xln(x a+(x a r 1 c n(r 1 (x a n muodostavat differentialiyhtälön (1.8 ratkaisujen perusjärjestelmän välillä (a,a+r. n= Indeksiyhtälön ratkaisut kompleksisia Olkoon r 1 = α+iβ ja c n (r 1 = α n +iβ n, n N. Sijoittamalla nämä y(x,r 1 :n lausekkeeseen (1.11 saadaan y = y 1 +iy 2, missä [ y 1 (x = (x a α cos ( βln(x a α n (x a n sin ( βln(x a ] β n (x a n n= 4 n=
10 ja [ y 2 (x = (x a α cos ( βln(x a β n (x a n +sin ( βln(x a α n (x a ]. n n= n= Funktioty 1 jay 2 muodostavat differentiaaliyhtälön (1.8 ratkaisujen perusjärjestelmän välillä (a,a+r. 5
11 Luku 2 Erikoisfunktioista Matematiikan sovelluksissa esiintyviä (transkendenttifunktioita, jotka määritellään joko alkeisfunktioiden integraaleina tai 2. kertaluvun lineaaristen differentiaaliyhtälöiden ratkaisuina sanotaan erikoisfunktioiksi. 2.1 Gammafunktio Määritelmä 2.1. Gammafunktio Γ määritellään ns. 2. lajin Eulerin integraalin avulla seuraavasti: (2.1 Γ(z = t z 1 e t dt, z C, Rez >. Kuva 1. Gammafunktion kuvaaja. Huomautus 2.2. Kaavassa (2.1 on positiivinen reaaliluku t korotettuna kompleksiseen potenssiin z 1, ja tällaisille lausekkeille pätevät tutut potenssin laskusäännöt (paitsi potenssin 6
12 potenssi. Yleensä kompleksisille potensseille eivät päde tutut potenssin laskusäännöt, sillä kompleksiluvun kompleksinen potenssi on moniarvoinen. Lause 2.3. Gammafunktiolle on voimassa 1. Γ(z +1 = zγ(z, Rez >, 2. Γ(z +n = (z +n 1(z +n 2 zγ(z, Rez >, n = 1,2,..., 3. Γ(n+1 = n!, n =,1,..., 4. Γ( 1 2 = π. Esimerkki 2.4. Laske Γ(n+ 1 2 Esimerkki 2.5. Esitä ( x n Gamma-funktion avulla. Lauseen kohdasta seuraa, että (2.2 Γ(z = Γ(z +1. z Yhtälön (2.2 oikea puoli on määritelty myös, kun 1 < Rez <. Valitaan (2.2 Gammafunktion määritelmäksi edellä mainitussa yhdensuuntaisvyössä, sitten yhdensuuntaisvyössä 2 < Re z < 1 jne. (ks. Kuva 1, jossa x on reaalimuuttuja. Gammafunktiolle on voimassa Stirlingin kaava: (2.3 Γ(x+1 = ( 1 2πxx x e (1+ǫ x x, missä ǫ( 1 kun x. Lisäksi voidaan osoittaa, että x (2.4 Γ(zΓ(1 z = π sinπz, kun yhtälön molemmat puolet ovat määritellyt. 2.2 Betafunktio Määritelmä 2.6. Betafunktio määritellään kaavalla B(z,w = 1 Lause 2.7. Kun Rez > ja Rew >, niin t z 1 (1 t w 1 dt B(z,w = Γ(zΓ(w Γ(z +w. Todistus. Harjoitustehtävä. 7
13 2.3 Besselin funktioista Kaksi-ulotteinen aaltoyhtälö napakoordinaatteissa on (2.5 u tt = c 2 (u rr +r 1 u r +r 2 u θθ. Sijoittamalla u = R(rΘ(θT(t aaltoyhtälö (2.5 tulee muotoon T c 2 T = R R + R rr + Θ r 2 Θ. Koska edellisen yhtälön vasen puoli on muuttujan t funktio ja oikea puoli muuttujien r ja θ funktio, niin molempien puolien täytyy olla sama vakio, jota merkitään termillä µ 2. Tällöin sen oikea puoli voidaan kirjoittaa muotoon r 2 R R + rr R +µ2 r 2 = Θ Θ, joten edellisen yhtälön molempien puolien täytyy olla sama vakioν 2. Näin päädytään kahteen tavalliseen differentiaaliyhtälöön T +c 2 µ 2 T = ja Θ +ν 2 Θ =, jotka ovat tuttuja DYI-kurssilta, sekä yhtälöön (2.6 r 2 R (r+rr (r+(µ 2 r 2 ν 2 R(r =. Yhtälöä (2.6 voidaan yksinkertaistaa muuttujan vaihdolla sijoittamalla x = µ r. Tällöin sijoitetaan R(r = y(µr, R (r = µy (µr, R (r = µ 2 y (µr ja r = x µ yhtälöön (2.6 ja saadaan ( x 2µ 2 y (x+ x µ µ µy (x+(x 2 ν 2 y(x =, josta sieventämällä tulee yhtälö (2.7 x 2 y (x+xy (x+(x 2 ν 2 y(x =. Yhtälö (2.7 on ν:n kertaluvun Besselin differentiaaliyhtälö. Tämä yhtälö ja sen variantit esiintyvät monissa fysiikan ja insinööritieteiden ongelmissa, joihin liittyy ympyräsymmetria tasossa (annetun kiinteän pisteen suhteen symmetria tasossa. Tästä syystä sen ratkaisuja kutsutaan sylinterifunktioiksi, mutta niistä käytetään nimitystä Besselin funktiot Besselin differentiaaliyhtälön ratkaisu Tarkastelemalla Besselin yhtälöä (2.8 x 2 y +xy +(x 2 ν 2 y = 8
14 huomataan, että piste x = on sen säännöllinen erikoispiste (P(x = 1 = p ja Q(x = ν 2 +x 2 = q +q 2 x 2. Yhtälö ratkaistaan Frobeniuksen menetelmällä valitsemalla yritteeksi sarjan y = x r a k x k = a k x r+k, a. k= Sijoittamalla tämä yrite yhtälöön (2.8 ja sieventämällä saadaan k= (2.9 [(r +k 2 ν 2 ]a k x r+k + a k 2 x r+k =. k= k=2 Jotta sijoitettu yrite on ratkaisu, täytyy kerrointen toteuttaa seuraavat yhtälöt (2.1 (2.11 (2.12 (r 2 ν 2 a o = (k =, [(r+1 2 ν 2 ]a 1 = (k = 1, [(r+k 2 ν 2 ]a k +a k 2 =, kun k = 2,3,... Koska oletuksen mukaan a o, niin r = ±ν. Valitaan juuri r = ν. Tällöin yhtälö (2.11 tulee muotoon (2ν+1a 1 =, joten a 1 =, paitsi kun ν = 1/2. Vaikka ν = 1/2, voidaan valita a 1 = ja tämä ei aiheuta ongelmia jatkossa. Yhtälöstä (2.12 saadaan palautuskaava a k 2 (2.13 a k = (ν +k 2 ν = a k 2 2 k(k +2ν, k = 2,3,... Koska a 1 =, kaikki parittomat kertoimet ovat nollia eli a 2k+1 =, k =,1,2,... Parilliset kertoimet saadaan a :n avulla seuraavasti: a o a 2 = 2(2+2ν, a 2 a 4 = 4(4+2ν = a 2 4(2+2ν (4+2ν, ja yleisesti parillinen kerroin saadaan laskettua muotoon a 2k = ( 1 k a 2 4 (2k(2+2ν(4+2ν (2k +2ν (2.14 = ( 1 k a 2 2k k!(1+ν(2+ν (k +ν. Edellä esitetyssä ratkaisumentelmässä joudutaan hankaluuksiin vain tapauksessa ν on negatiivinen kokonaisluku tai puolikas negatiivisesta kokonaisluvusta. Jos ν = n, niin kertoimia a 2k ei voida laskea kaavasta (2.14, kun k n (nolla nimittäjässä, ja emme saa ratkaisua. Jos ν = n/2 ja n on pariton, niin kaavan (2.13 nimittäjässä termi k + 2ν on nolla, kun k = n. Tällöin kertoimia a 2k+1 ei voida laskea siitä, kun k (n 1/2. Jos yhtälöön (2.12 sijoitetaan ν = n/2, niin kertoimille a 2k+1 tulee arvo nolla, kun k =,1,...,(n 2/2 (a 1 =, ja lisäksi yhtälö a n = a n 2 pätee. Koska a n 2 =, niin voidaan valita a n = (jos valitaan a n, niin saadaan toinen ratkaisu. Tällöin y(x = a k= ( 1 k x 2k+ν 2 2k k!(1+ν(2+ν (k +ν 9
15 on Besselin differentiaaliyhtälön (2.8 ratkaisu, kun ν ei ole negatiivinen kokonaisluku. Valitaan vielä kerroin a. Gammafunktion ominaisuudesta Γ(z + 1 = zγ(z seuraa, että Γ(k +ν +1 = (k +ν (1+νΓ(ν +1. Valitsemalla ratkaisu y(x tulee muotoon a = 1 2 ν Γ(ν +1 (2.15 J ν (x = k= ( 1 k x 2k+ν. k!γ(ν +k +1( 2 Suhdetestin avulla voidaan osoittaa, että tämä sarja suppenee kaikilla x (ja myös, kun x = tapauksissa ν. Funktio J ν (x on 1. lajin Besselin funktio kertalukua ν. Kun ν = n N, niin k! = Γ(k +1 ja J n (x = k= ( 1 k!(n+k!( k x 2k+n. 2 MääritelläänJ n (x sijoittamallaν:n paikalle n kaavassa (2.15 (huom!1/(k+n! = 1/Γ(k+ n+1 =, k +n <, koska lim z m Γ(z = ±, m Z {}: J n (x = k= ( 1 k!( n+k!( k x 2k n ( 1 k+n x 2k+n. = 2 (k +n!k!( 2 k= Seuraus: J n (x = ( 1 n J n (x. Kuva 2. Besselin ensimmäisen lajin funktioiden J n (x kuvaajia, kun n =,1,...,5. Edellä tarkastellun perusteella seuraava lause pätee. 1
16 Lause 2.8. Besselin funktio y = J ν (x, ν, on Besselin yhtälön ratkaisu. x 2 y +xy +(x 2 ν 2 y = Edellinen lause voidaan todistaa myös suoraan Besselin funktion määritelmän (2.14 avulla Besselin funktioiden rekursiokaavat Lause 2.9. Besselin funktiot (2.16 J ν (x = toteuttavat seuraavat rekursiot (2.17 (2.18 (2.19 (2.2 (2.21 (2.22 aina, kun x ja ν R. k= ( 1 k x 2k+ν k!γ(ν +k +1( 2 d dx [x ν J ν (x] = x ν J ν+1 (x d dx [xν J ν (x] = x ν J ν 1 (x xj ν(x νj ν (x = xj ν+1 (x xj ν(x+νj ν (x = xj ν 1 (x xj ν 1 (x+xj ν+1 (x = 2νJ ν (x J ν 1 (x J ν+1 (x = 2J ν(x Todistus. Kaava (2.17. Koska k= d dx [x ν J ν (x] = d dx = k=1 k= ( 1 k x 2k 2 2k+ν k!γ(ν +k +1 = ( 1 k (2kx 2k 1 2 2k+ν k!γ(ν +k +1 k=1 ( 1 k x 2k 1 2 2k+ν 1 (k 1!Γ(ν +k +1, niin vaihtamalla summausindeksi k viimeisessä sarjassa k +1:ksi saadaan ( 1 k+1 x 2k+1 2 2k+ν+1 k!γ(ν +k +2 = ( 1 k x 2k+ν+1 x ν 2 2k+ν+1 k!γ(ν +k +2 = x ν J ν+1 (x. Kaavan (2.18 todistus on samanlainen: d dx [xν J ν (x] = d dx = k= k= k= ( 1 k x 2k+2ν 2 2k+ν k!γ(ν +k +1 = k= ( 1 k x 2k+2ν 1 2 2k+ν 1 k!γ(ν +k = xν J ν 1 (x, 11 ( 1 k (2k +2νx 2k+2ν 1 2 2k+ν k!γ(ν +k +1
17 koska Γ(ν +k +1 = (ν +kγ(ν +k. Poistamalla sulut kaavoista (2.17 ja (2.18 (suorittamalla derivointi kaavojen (2.17 ja (2.18 vasemmalla puolella saadaan νx ν 1 J ν (x+x ν J ν(x = x ν J ν+1 (x, νx ν 1 J ν (x+x ν J ν(x = x ν J ν 1 (x. Kertomalla ensimmäinen näistä yhtälöistä puolittain termillä x ν+1 ja toinen yhtälö puolittain termillä x ν+1 saadaan kaavat (2.19 ja (2.2. Vähentämällä kaavat (2.19 ja (2.2 puolittain saadaan kaava (2.21. Lopuksi laskemalla kaavat (2.19 ja (2.2 yhteen puolittain seuraa kaava (2.22. Harjoitustehtävän 2 nojalla (ν 2 = 1/4 J1(x = 2 2 πx sinx ja J 1 (x = 2 2 πx cosx. Kuva 3. Besselin funktioiden J n+ 1(x kuvaajia, kun n =,1,...,5. 2 Näiden ja lauseen 2.9 yhtälön (2.21-kohdan avulla voidaan määrätä J n+ 1(x, kun n Z. 2 Esimerkki 2.1. Määrää J5(x alkeisfunktioiden avulla Besselin funktioiden generoiva funktio Lukujonon (a n n= jäsenten a n generoiva funktio on potenssisarja a n z n. Esimerkiksi jonon (a n n=, a n = 1 aina, kun n N, generoiva funktio on ääretön geometrinen sarja f(z = z n = 1, z < 1. 1 z n= 12
18 Jos b n = 1/n!, kun n N, niin f(z = n= z n n! = ez on lukujonon (b n n= generoiva funktio, ja sitä esittävä potenssisarja suppenee kaikilla z:n arvoilla. Vastaavasti kahden muuttujan funktiota G : C R C sanotaan funktiojonon (g n n= generoivaksi funktioksi, jos on olemassa sellainen reaaliluku r > ja väli I R, joille (2.23 G(z, x = n= g n (xz n ja ko. sarja suppenee, kun < z < r, missä r on positiivinen vakio, aina, kun x on välin I piste. Toisin sanoen G(z, x voidaan kehittää Laurentin sarjaksi muuttujan z suhteen ja z n :n kerroin on funktiojonon (g n n= alkio g n (x aina, kun n = ±1,±2,. Jos (g n n= on polynomijono, niin G(z,x on Taylorin sarja muuttujana z. Lause Besselin funktioiden jonolle (J n (x n= pätee (2.24 G(z, x = n= [ x J n (xz n = exp z 2( 1 ] z kaikilla x ja z. Todistus. Soveltamalla eksponenttifunktion sarjakehitelmää saadaan exp ( xz = 2 j= z j!( j x j ja exp 2 ( x = 2z k= ( 1 k ( x k. z k k! 2 Koska nämä sarjat suppenevat itseisesti (eksponenttifunktion suppenemissäde R =, niin ne voidaan kertoa keskenään ja tuloksena saatavassa tuplasarjassa summaus voidaan suorittaa järjestyksestä välittämättä, joten [ x exp z 2( 1 ] = exp z ( xz exp 2 ( x = 2z j,k= ( 1 k z j k ( x j!k! 2 j+k. Summataan nämä sarjat summaamalla ensi kaikki ne termit, joissa onz n eli asetetaanj k = n (j = k +n. Tällöin saadaan [ x exp z 2( 1 ] = z n= [ k= ( 1 k x ] 2k+n z k!(k +n!( n = 2 n= J n (xz n, koska 1/(k + n! = 1/Γ(k + n + 1 =, kun k + n < (huom! lim z m Γ(z = ±, kun m Z {}. Esimerkki Osoita generoivan funktion avulla, että Besselin funktioille J n (x pätee seuraavaa. J n (x on parillinen, kun n on parillinen, ja pariton, kun n on pariton ts. J n ( x = ( 1 n J n (x, n =,1,2,... 13
19 Ratkaisu Koska ja G(z, x = exp [ x ( z 1 ] = 2 z n= J n ( xz n [ x ( G(z, x = exp z 1 ] [ x = exp ( z 2 z 2( 1 ] = G(x, z ( z = J n (x( z n = ( 1 n J n (xz n, n= n= niin J n ( x = ( 1 n J n (x, n =,1,2,... Kaavassa (2.24 z voi olla mikä tahansa kompleksiluku. Erityisesti, jos valitaan z = e iθ, jolloin 1 2 (z z 1 = isinθ, niin (2.25 e ixsinθ = n= J n (xe inθ. Koska edellisen yhtälön molempien puolien reaaliosat ovat yhtäsuuret ja imaginaariosat ovat yhtäsuuret, niin cos(xsinθ = n= J n (xcos(nθ ja sin(xsinθ = n= Näitä hyväksi käyttäen voidaan johtaa ns. Besselin integraalikaava (2.26 J n (x = 1 π π cos(xsinθ nθdθ. J n (xsin(nθ. Tämän kaavan avulla voidaan osoittaa, että J n (x 1 aina, kun x R. Sama epäyhtälö pätee myös funktion J n (x kaikille derivaatoille ts. J (k n (x 1, kun k = 1,2, Besselin differentiaaliyhtälön toinen lineaarisesti riippumaton ratkaisu Frobeniuksen menetelmällä saatu indeksiyhtälön juurta r = ν vastaava ratkaisu (2.27 J ν (x = m= ( 1 m x 2m ν m!γ(m ν +1( 2 on lineaarisesti riippumaton ratkaisusta J ν (x, kun ν / Z. Näin ollen {J ν (x,j ν (x} on Besselin yhtälön ratkaisujen perusjoukko, kun ν / Z. 14
20 Lemma Besselin funktioiden J ν (x ja J ν (x Wronskin determinantti on (2.28 W[J ν,j ν ](x = 2 πx sin(νπ. Jos ν Z, niin funktiot J ν ja J ν ovat lineaarisesti riippuvat, ja Besselin yhtälön toinen ratkaisu joudutaan määrittelemään toisin. Oletetaan, että ν ei ole kokonaisluku. Besselin toisen lajin funktio määritellään kaavalla (2.29 Y ν (x = cos(νπj ν(x J ν (x. sin(νπ Kun ν on kokonaisluku n, niin toisen lajin Besselin funktio määritellään raja-arvona cos(νπj ν (x J ν (x (2.3 Y n (x = lim Y(ν,x = lim Y ν (x = lim. ν n ν n ν n sin(νπ Kuva 4. Besselin toisen lajin funktioiden Y n (x kuvaajia, kun n =,1,...,5. Lause Yhtälöllä (2.3 määritelty funktio on Besselin differentiaaliyhtälön x 2 y +xy +(x 2 n 2 y = ratkaisu ja joukko {J n (x,y n (x} on lineaarisesti riippumaton. 15
21 Luku 3 Ortogonaalikehitelmät funktioavaruudessa Lineaarialgebrassa tutkittiin milloin annettu vektori voidaan esittää lineaariyhdistelynä jonkin saman vektoriavaruuden vektorijoukon avulla. Ongelma on aina ratkeava, jos vektorijoukko on kyseisen avaruuden kanta. Vastaavaa ongelmaa voidaan tutkia myös funktioiden tapauksessa. Jos meillä on välillä J määritelty reaaliarvoinen funktio f ja samalla välillä määriteltyjen reaaliarvoisten funktioiden joukko {ϕ 1,ϕ 2,...ϕ n }, niin voidaanko funktio f esittää muodossa n f = a k ϕ k, k=1 missä a k, k = 1,2,...n, on reaaliluku? Yleisessä tapauksessa, jossa funktioiden ϕ k joukko on ääretön funktiojono (ϕ k k=1 edellä oleva summa korvataa äärettömällä summalla f = k=1 a k ϕ k = lim n (a 1 ϕ 1 + +a n ϕ n. Tämä tehtävä on mielekäs sellaisessa funktioavaruudessa, jossa on määritelty funktioiden lineaariset yhdistelyt ja suppeneminen. 3.1 Funktioavaruus Tarkastellaan vain reaalimuuttujan reaaliarvoisten funktioiden muodostamaa funktiojoukkoa. Määritelmä 3.1. Funktioavaruus on sellainen funktiojoukko F, jolla on seuraavat ominaisuudet 1. joukon F funktioilla on sama määritysjoukko W, 2. af +bg F aina, kun f, g F ja a, b R, 16
22 missä (af +bg(x = af(x+bg(x x W. Esimerkiksi joukossa W määritellyt jatkuvat reaaliarvoiset funktiot muodostavat funktioavaruudenf. Tätä avaruutta merkitään symbolillac(w (C(W = {f : W R f on jatkuva}. Funktioavaruus on siten vektoriavaruus, jonka alkioina ovat funktiot. Seuraavassa J on reaalilukuväli (se voi olla avoin väli (a,b R tai suljettu väli [a,b] R. Määritelmä 3.2. Funktio f : J R on paloittain jatkuva, jos (i sillä on vain äärellinen määrä epäjatkuvuuspisteitä x 1,x 2,...,x n ja (ii jokaisessa välin pisteessä x k,k = 1,2,...,n, sekä oikean- että vasemmanpuoleiset rajaarvot f(x k = lim h +f(x k h ja f(x k + = lim h +f(x k +h ovat olemassa äärellisinä. Jos päätepiste a (vast. b on epäjatkuvuuspiste, edellytetään vain oikeanpuoleisen (vast. vasemmanpuoleisen raja-arvon olemassaolo. Tällöin merkitään f PC(J = {f : J R f on paloittain jatkuva}. Määritelmä 3.3. Funktio f : J R on paloittain säännöllinen, jos (i se on paloittain jatkuva ja (ii derivaattaf on olemassa ja jatkuva paitsi äärellisessä pistejoukossax 1,x 2,...,x N, jossa ovat myös funktion f epäjatkuvuuspisteet, ja toispuoleiset raja-arvot f (a+, f (b, f (x k ja f (x k + (k = 1,...,N ovat olemassa äärellisinä. Tällöin merkitään f PS(J = {f : J R f on paloittain säännöllinen}. Kuvan avulla tulkittuna: f on paloittain säännöllinen, jos sen kuvaaja on sileä käyrä paitsi pisteissä, joissa se voi hypätä (epäjatkuvuuskohta tai sillä on taitos (derivaatan epäjatkuvuuskohta. Esimerkki 3.4. Tutki ovatko seuraavat funktiot paloittain säännöllisiä:, kun 2 x < 1, a f(x = 3 x, 2 x 2, b g(x = x, kun 1 x < 1 1 x, kun 1 x 2 x+4, kun 2 x < 1 c h(x = x 3 x, kun 1 x < 1 sin(4πx, kun 1 x 2. 17
23 Funktioiden kuvaajat alla. Kohta a Kohta b Kohta c Esimerkki 3.5. JoukotPC(J japs(j ovat funktioavaruuksia japs(j PC(J. Näiden ja jatkuvien funktioiden avaruuden C(J lisäksi joukot ovat funktioavaruuksia. C n (J = {f : J R f (n on jatkuva}, L 1 (J = { f : J R f on integroituva ja L 2 (J = { f : J R f 2 on integroituva ja b a b a f(x dx < } ja f(x 2 dx < } 18
24 3.2 Funktioiden sisätulo ja normi AvaruudestaR n voidaan valita luonnollinen kanta, jonka avulla jokainen vektori voidaan esittää yksikäsitteisenä summana kantavektoreista kerrotuna reaalilukuvakioilla. Kantavektorien valinta voidaan tehdä avaruuden R n sisätulon avulla (siis kohtisuoruuskäsitteen avulla ja tulokseksi saatu vektorijoukko on pienin mahdollinen. Herää kysymys: voidaanko funktioavaruudessa F määritellä vastaava operaatio (jota kutsutaan myös sisätuloksi, jonka avulla voidaan valita sellainen funktiojoukko avaruudesta F, että sen avulla mahdollisimman moni avaruuden F funktio voidaan esittää mielivaltaisen tarkasti summana näistä funktioista reaaliluvuilla kerrottuna? Käsitteeseen mielivaltaisen tarkasti palataan seuraavassa kappaleessa. Tätä varten yleistetään sisätulon käsite funktioavaruudelle. Määritelmä 3.6. Funktioavaruuden F sisätulo on kuvaus, joka liittää jokaiseen avaruuden F funktiopariin (f, g reaaliluvun (f g, ja sillä on seuraavat ominaisuudet. Kaikilla f, g, h F ja a, b R 1. (f f ja (f f = jos ja vain jos f = θ (θ on nollafunktio, 2. (f g = (g f, 3. (af +bg h = a(f h+b(g h. Sisätulon ominaisuuksista 2 ja 3 seuraa, että 4. (h af +bg = a(h f+b(h g. Esimerkki 3.7. Yhtälö (3.1 (f g = J f(xg(xdx määrittelee sisätulon funktioavuuksissa C(J ja C n (J. Jos ne funktiot samaistetaan, jotka saavat eri arvoja vain äärellisellä määrällä muuttujan arvoja, niin edellinen yhtälö määrittelee sisätulon myös avaruuksissa PC(J, PS(J ja L 2 (J. Seuraavassa oletetaan, että F on funktioavaruus, jossa on määritelty sisätulo. Määritelmä 3.8. Normi funktioavaruudessa F määritellään yhtälöllä (3.2 f = (f f, f F. Esimerkiksi sisätuloa (3.1 vastaava normi on ( f 2 = f(x 2 dx J
25 Lause 3.9 (Schwarz in epäyhtälö. Kaikilla f, g F on (f g f g. Lause 3.1. Yhtälöllä (3.2 määritelty normi toteuttaa kaikilla f, g F ja c R ehdot 1. f ja = jos ja vain jos f = θ(= -funktio 2. cf = c f 3. f +g f + g (kolmioepäyhtälö. Huomautus Lauseen 3.1 ehdot 1 2 toteuttaava normi : F R voidaan määritellä myös ilman sisätuloa. Esimerkiksi yhtälö f = sup{ f(x x J} määrittelee normin jokaisessa esimerkin 3.5 funktioavaruudessa, sekä myös avaruudessa B(J = {f: J R f on rajoitettu}. Lause Normi f = (f f toteuttaa suunnikassäännön: (3.3 f +g 2 + f g 2 = 2 f 2 +2 g 2. Kääntäen, jos normi toteuttaa yhtälön (3.3, niin yhtälö määrittelee sisätulon. Huomautus Lauseke (f g = 1 4 ( f +g 2 + f g 2 f 1 = J f(x dx määrittelee normin avaruudessa L 1 (J, mutta normi ei toteuta suunnikassääntöä. Näin ollen L 1 (J varustettuna normilla f 1 ei ole sisätuloavaruus. (Valitse J = [,1], f(t = t ja g(t = 1 t. 3.3 Ortogonaalisuus, suppeneminen Olkoon F funktioavaruus, jossa on määritelty sisätulo. Määritelmä Sanotaan, että funktioavaruuden F funktiot f ja g ovat ortogonaaliset, merkitään f g, jos (f g =. Funktioavaruuden F funktiojonoa (f n n=1 sanotaan ortogonaaliseksi, jos (f j f k =, kun j k. Lause 3.15 (Pythagoraan teoreema. Jos f g, niin (3.4 f +g 2 = f 2 + g 2. 2
26 Huomautus Induktiolla (3.4 yleistyy muotoon f 1 + +f n 2 = f f n 2, jos f j f k, kun j k. Lause Jos jono (g k k=1 on ortogonaalinen ja f = n k= a kg k, niin a k = (f g k (g k g k = (f g k g k 2, k =,1,...,n. Olkoon F funktioavaruus, jossa on määritelty normi. Jos tarkastellaan kahta avaruuden R k vektoria a ja b, niin a b on pisteiden a ja b euklidinen etäisyys. Tämän perusteella on luonnollista määritellä, että vektorijono (a n suppenee kohti vektoria a jos ja vain jos a n a, eli a n a. Tästä johtuen funktiojonojen suppeneminen määritellään seuraavasti. Määritelmä Funktioavaruuden F funktiojono (f n n=1 suppenee kohti F:n funktiota f, jos lim n f n f =. Tällöin merkitään lim n f n = f. Avaruudessa L 2 (J tämä tarkoittaa, että f n n f normin suhteen joss f f n 2 2 = J f(x f n (x 2 dx n, eli erotus f n f menee nollaan sopivan keskiarvon suhteen välillä J. Tästä ei seuraa pisteittäinen suppeneminen, eikä pisteittäisestä suppenemisesta seuraa suppeneminen normin suhteen (ks. Analyysi I:n luennot. Esimerkiksi olkoon J = [,1]. Jos määritellään { 1, kun x 1 n f n (x =,, muutoin, n = 1,2,..., niin f n 2 2 = 1 f n (x 2 dx = 1/n dx = 1 n, joten f n normin suhteen. Toisaalta f n ( = 1 kaikilla n, joten f n ei suppene pisteittäin kohti nollafunktiota. Jos määritellään g n (x = { n, kun < x < 1 n,, muutoin, n = 1,2,..., niin g n pisteittäin (g n ( = kaikilla n, ja jos x >, niin g n (x = aina, kun n > x 1. Toisaalta g n 2 2 = joten g n normin suhteen. 1 g n (x 2 dx = 1/n 21 n 2 dx = n,
27 Lause Jos f n f tasaisesti välillä J, niin f n f normin suhteen. Todistus. Tasainen suppeneminen tarkoittaa, että on olemassa sellainen positiivisten reaalilukujen jono (M n, että f n (x f(x M n kaikilla x J ja M n, kun n. Tällöin f n f 2 2 = f n (x f(x 2 dx Mndx 2 = l(jmn, 2 J missä l(j on välin J pituus, joten f n f 2 menee nollaan, koska M n menee nollaan, kun n. Esimerkki 3.2. Olkoon F = B(J, f = sup f(x. Silloin x J f n n f joss sup f n (x f(x n joss x J j f n n f tasaisesti välillä J. 3.4 Ortogonaalikehitelmät Seuraavassa oletetaan, että F on funktioavaruus, jossa on sisätulon indusoima normi f = (f f. Määritelmä Funktioavaruuden F ortogonaalinen kanta on sellainen F:n ortogonaalinen funktiojono (g k k=, että jokainen avaruuden F funktio voidaan esittää muodossa n f = a k g k = lim a k g k. n k= Lause Jos (g k k= on F:n ortogonaalinen kanta ja f F, niin (3.5 f = a k g k, missä a k = (f g k (g k g k = (f g k g k, k =,1,... 2 k= Lisäksi on voimassa Parsevalin yhtälö f 2 = a 2 k(g k g k = k= k= a 2 k g k 2. k= Huomautus Esitys (3.5 tarkoittaa sitä, että n lim a k g k f =. n k= Tästä ei seuraa, että sarjan k= a kg k (x summa olisi f(x jokaisella x J, mutta "melkein"jokaisessa pisteessä (Tätä selvitetään Analyysi III:n kurssilla tarkemmin. Sen vuoksi merkitään kaavan (3.5 sijasta myös (3.6 f(x a k g k (x, x J. Yhtäsuuruuden voimassaolo kaavassa (3.6, on tarkasteltava erikseen. k= 22
28 3.5 Ortogonaalipolynomeista Aloitetaan ortogonaalipolynomien tarkastelu hyödyllisellä aputuloksella. Lemma Olkoon (p n n= on sellainen polynomien jono, että polynomin p n aste (merkitään deg(p n on tarkalleen n, n =,1,2,... Tällöin jokainen k-asteinen polynomi, k =,1,2,..., on polynomien p,p 1,...,p k lineaariyhdelmä. Todistus. Jos f on k-asteinen polymomi, valitaan sellainen vakio c k, että polynomien f ja c k p k on potenssin x k kerroin on molemmissa sama. Tällöin polynomin f c k p k aste on k 1, ja voidaan valita sellainen kerroin c k 1, että polynomien f c k p k ja c k 1 p k 1 potenssin x k 1 kerroin on sama. Tällöin polynomin f c k p k c k 1 p k 1 aste on k 2. Jatkamalla samalla tavalla valitaan kertoimet c k 2,...,c, ja päädytään yhtälöön f k n= c np n =. Määritelmä Painofunktio on välillä (a,b ( a < b määritelty jatkuva positiiviarvoinen funktio w, jolle b a w(xx n dx <, n =,1,2,... Määritelmä Funktioavaruus PC 2 w(a,b on kaikkien välillä (a,b määriteltyjen ja sen jokaisella suljetulla osavälillä paloittain jatkuvien reaalifunktioiden f joukko, joille b a w(xf 2 (xdx <. Määritelmä Painofunktion w suhteen ortogonaalinen polynomijono (ϕ n n= on sellainen joukko funktioita ϕ n, että ϕ n on n:nnen asteen polynomi ja (ϕ n ϕ m = b a w(xϕ n (xϕ m (xdx =, joss n m. Lause Polynomijono (ϕ n n=, joka on ortogonaalinen painofunktion w suhteen äärellisellä välillä (a,b, on funktioavaruuden PC 2 w(a,b ortogonaalinen kanta. Lauseen 3.28 mukaan on jokaisella funktioavaruuden PCw(a,b 2 funktiolla f sarjakehitelmä f(x c n ϕ n (x, c n = (f ϕ b n (ϕ n= n ϕ n = w(xf(xϕ a n(xdx b w(xϕ a n(x 2 dx. Seuraavissa kolmessa kappaleessa on esimerkkejä ortogonaalisista polynomijonoista ja sarjoista Legendren polynomit Määritelmä Legendren polynomit määritellään Rodriguesin kaavalla seuraavasti: (3.7 P n (x = 1 d n 1 n. 2 n n! dx n(x2 P n on n:s Legendren polynomi. 23
29 Funktio (x 2 1 n on 2n-asteinen polynomi, jonka johtotermi (korkeimman potenssin termi on x 2n. Täten P n on polynomi, jonka aste on n. Neljä ensimmäistä Legendren polynomia ovat P o (x = 1, P 1 (x = x, P 2 (x = 1 2 (3x2 1, P 3 (x = 1 2 (5x3 3x, ja P 4 (x = 1 8 (35x4 3x Kuva 1. Legendren polynomien kuvaajia. Polynomin P n kertoimet voidaan laskea soveltamalla binomikaavaa lausekkeeseen (x 2 1 n ja sitten derivoimalla n kertaa. Lause 3.3. Kun n 2 on luvun n kokonaisosa, on 2 (3.8 P n (x = n 2 k= 2 n ( 1 k (2n 2k! k!(n k!(n 2k! xn 2k. Seuraus P n (x on n:nnen asteen polynomi ja (3.9 P n ( x = ( 1 n P n (x. Seuraaviin tarkasteluihin tarvitaan vain johtotermin kerrointa (x:n korkeimman potenssin kerroin (3.1 P n (x = 1 d n + = 1 2 n n! dx n(x2n 2 n n! [(2n(2n 1 (n+1xn + ] = (2n! +, 2 n (n! 2xn missä pisteet ovat alemman asteen termit. Tutkitaan Legendren polynomien ortoganaaliominaisuuksia avaruudessa L 2 ( 1,1 painofunktion w(x 1 suhteen. 24
30 Lause Legendren polynomit {P n } n= ovat ortogonaalisia avaruudessa L 2 ( 1,1, ja (3.11 P n 2 = 2 2n+1. Todistus. Todistuksen avain on huomata, että jos f on C (n -luokan funktio, niin ( n n!(f P n = = f(x dn 1 n dx = ( 1 n dx n(x2 f (n (x(1 x 2 n dx. 1 f (n (x(x 2 1 n dx Tulos on saatu osittaisintegroimalla n kertaa ja huomioimalla, että sijoitustermi on nolla jokaisessa vaiheessa, koska termin (x 2 1 n = (x 1 n (x+1 n derivaatat häviävät sijoituksissa x = 1 ja x = 1 kertalukuun n 1 asti. Jos f on polynomi, jonka aste on pienempi kuin n, niin f (n, joten (f P n =. Erityisesti, tämä pätee polynomeille P,P 1,...P n 1, joten (P m P n =, kun m < n. Jos m > n, niin samasta syystä (vaihtamalla n ja m keskenään pätee (P m P n =, kun m > n. Täten Legendren polynomit P n ovat ortogonaalisia avaruudessa L 2 ( 1,1. Jos valitaan f = P n, niin kaavan (3.1 nojalla joten f (n (x = (2n!n! 2 n (n! 2 = (2n 1, P n 2 = (2n 1 2 n n! 1 1 (1 x 2 n dx. Sijoittamalla x = y Beta-funktion kaavan (Harjoitusehtävä 5 b avulla edellinen integraali voidaan laskea ja 1 1 (1 x 2 n dx = 2 1 (1 x 2 n dx = 1 (1 y n y 1/2 dy = Γ(n+1Γ(1 2 Γ(n+ 3 2 = n! π Γ(n+ 3 2 = n! ( 1 2 (3 2 (n+ 1 2 = 2 n+1 n! (2n+1, joten P n 2 = (2n 1 2 n n! 2 n+1 n! (2n+1 = 2 2n+1. Legendren differentiaaliyhtälö (1 x 2 y 2xy +n(n+1y = voidaan kirjoittaa yhtäpitävään muotoon [(1 x 2 y ] +n(n+1y =. 25
31 Lause Jokaisella n N (3.13 [(1 x 2 P n(x] +n(n+1p n (x =. Todistus. Olkoon g(x = [(1 x 2 P n(x]. Koska polynomin P n aste on n 1, niin polynomin x 2 P n asteluku on n+1, joten polynomin g asteluku on n. Yhtälön (3.1 nojalla polynomin g johtotermi on (2n! d [ ] ( x 2 (nx n 1 = n(n+1 (2n! 2 n (n! 2 dx 2 n (n! 2 xn. Näin ollen polynomin g+n(n+1p n aste on n 1, joten lemman 3.24 nojalla se on lineaariyhdelmä polynomeista P,...,P n 1 : n 1 g(x+n(n+1p n (x = [(1 x 2 P n(x] +n(n+1p n (x = c k P k (x. Kertoimet c k voidaan laskea sisätulon avulla käyttäen hyväksi polynomien P k ortogonaalisuutta, ja c k = (g +n(n+1p n P k = (g P k+n(n+1(p n P k P k 2 P k 2 Tällöin (P n P k =, kun k < n, ja (g P k = 1 1 [(1 x 2 P n(x] P k (xdx, joka saadaan kaksi kertaa osittaisintegroimalla muotoon (g P k = 1 1 P n (x[(1 x 2 P k(x] dx, koska reunatermit häviävät (x 2 1 =, kun x = ±1. Integraalin sisällä oleva lauseke [(1 x 2 P k (x] on k-asteinen polynomi ja siten lineaariyhdelmä polynomeista P,...,P k. Jokainen näistä polynomeista on ortogonaalinen polynomin P n kanssa, joten kaikki kertoimet c k ovat nollia, kun k =,1,...,n 1. Näin ollen väite pätee. k= Legendren polynomien generoiva funktio Samalla tavalla kuin Besselin funktioilla (J n myös Legendren polynomeilla (P n n= on generoiva funktio. Lause Funktio (1 2xt + t on Legendren polynomien P n (x, n R, generoiva funktio, ts. aina, kun 1 x 1 ja t < 1, niin P n (xt n = (1 2xt+t = F(x,t. n= 26
32 Todistus. Määrätään ensin funktion Taylorin sarja origossa. Derivoimalla saadaan Täten missä Siten f(y = (1+y 1 2 = 1 1+y f (k (y = ( 1 2 ( ( 1 2 k +1(1+y 1 2 k, k =,1,2,... f(y = k= f (k ( y k = k! c k y k, c k = ( 1 2 ( ( 1 k +1 2 = ( 1k 1 3 (2k 1 k! 2 k k! = ( 1k (2k 2 k k!2 4 (2k = ( 1k (2k!. 2 2k (k! 2 (3.14 f(y = (1+y 1 2 = k= k= ( 1 k (2k! 2 2k (k! 2 y k. Tämä sarja suppenee, kun y < 1. Oletetaan, että x 1 ja t < 2 1. Tällöin 2xt t 2 2 x t + t 2 < 1. Sijoitetaan y = 2xt+t 2 = t(t 2x yhtälöön (3.14: F(x,t = (1 2xt+t = k= Soveltamalla binomikaavaa termiin (t 2x k saadaan (1 2xt+t = = = k= k i= [ n= 2i n [ n/2 n= i= ( 1 k (2k! 2 2k (k! 2 t k (t 2x k. ( 1 k (2k! 2 2k (k! 2 k! i!(k i! tk+i ( 2x k i n = k +i ] ( 1 n i (2n 2i!(n i!( 1 n 2i 2 n 2i x n 2i t n 2 2n 2i ((n i! 2 i!(n 2i! ( 1 i 2 n (2n 2i! i!(n i!(n 2i! xn 2i ] t n = P n (xt n. n= Esimerkki Osoita, että P n (1 = 1, P n ( 1 = ( 1 n, n N. Lause Legendren polynomeille on voimassa palautuskaavat 27
33 1. (n+1p n+1 (x = (2n+1xP n (x np n 1 (x, n 1, 2. xp n(x P n 1(x = np n (x, n 1, 3. P n+1(x P n 1(x = (2n+1P n (x, n 1. Lause Jos f C[ 1,1], on funktiolle f voimassa kehitelmä f(x = n= a n P n (x, a n = 2n P n (xf(xdx, n N. Huomautus Jos f on paloittain säännöllinen, pätee lauseen 3.37 tulos muualla paitsi epäjatkuvuuspisteissä. Legendren polynomit ovat ortogonaaliset painofunktion w(x 1 suhteen välillä ( 1, 1. Lisäksi (P n P n = 2 2n+1, joten jokaisella f PC2 w( 1,1 on Legendren sarjakehitelmä (3.15 f(x n= c n P n (x, c n = 2n f(xp n (xdx. Lause Jos f P S[ 1, 1], pätee kaavassa (3.15 yhtäsuuruus funktion f jatkuvuuspisteissä. Epäjatkuvuuspisteissä f(x on korvattava lausekkeella f(x++f(x Hermiten polynomit Hermiten polynomit määritellään kaavalla Ensimmäiset viisi Hermiten polynomia ovat H n (x = ( 1 n dn x2 e. dx ne x2 H (x = 1, H 1 (x = 2x, H 2 (x = 4x 2 2, H 3 (x = 8x 3 12x, H 4 (x = 16x 4 48x Niiden kuvaajat ovat seuraavalla sivulla. Yleisesti pätee joten e x2 H n (x = ( 1 n dn = d dx ne x2 dx [e x2 H n 1 (x] = e x2 [2xH n 1 (x H n 1(x], (3.16 H n (x = 2xH n 1 (x H n 1(x. 28
34 Kuva 2. Hermiten polynomien kuvaajia. Lause 3.4. Hermiten polynomit {H n } n= ovat ortogonaalisia painofunktio w(x = e x2 suhteen reaalilukujoukossa R, ja (3.17 H n 2 w = 2 n n! π. Todistus. Jos f on mikä tahansa polynomi, niin (f H n w = = f(xh n (xe x2 dx = ( 1 n f (n (xe x2 dx. f(x dn dx dx ne x2 Viimeinen edellistä yhtälöistä saadaan osittaisintegroimalla n kertaa ja ottamalla huomioon, että reunatermit häviävät, koska P(xe x2, kun x ± aina, kun P on polynomi. Jos f on polynomi, jonka aste on pienempi kuin n, ja erityisesti kun f = H m, m < n, niin f (n, joten (f H n =. Toisaalta, jos f = H n, niin f(x = (2x n + alemman asteen termit, joten f (n = 2 n n!, ja H n 2 w = 2 n n! e x2 dx = 2 n n! π. Voidaan osoittaa, että (H n n= on avaruuden L 2 w(r ortogonaalikanta (Ks. Folland s.185, ja se on myös avaruuden PCw(R 2 kanta (huom! PCw(R 2 L 2 w(r. Lisäksi jokaisella f PCw(R 2 on Hermiten sarjakehitelmä 1 (3.18 f(x c n H n (x, c n = 2 n n! e x2 f(xh n (xdx, π n= kun edellinen integraali on äärellinen, ja seuraava lause pätee. 29
35 Lause Jos f PS(R ja integraali e x2 f(x 2 dx on äärellinen, niin yhtäsuuruus pätee kaavassa (3.18 jos f on jatkuva pisteessä x. Epäjatkuvuuspisteissä sarjan arvo on f(x++f(x. 2 Hermiten polynomeilla on generoivafunktio. Lause Kaikilla x R ja z C pätee (3.19 n= H n (x zn n! = e2xz z2. Todistus. Lauseen todistus on Harjoitustehtävä Lisätieto: ensimmäisen lajin Chebyshevin polynomit Ensimmäisen lajin Chebyshevin polynomit saadaan lausekkeesta T n (x = cos(n arccosx = n 2 n= n!x n 2k (x 2 1 k, x ( 1,1 (2k!(n 2k! ja ne ovat ortogonaaliset painofunktion w(x = (1 x suhteen välillä ( 1,1. Lisäksi { 1 T 2 (T n T n = n(x dx = π, n =, 1 1 x 2 π, n = 1,2,..., 2 joten jokaisella f PC 2 w( 1,1 on Chebyshevin sarjakehitelmä (3.2 f(x c 2 T (x+ c n T n (x, c n = 2 π n=1 1 1 f(xt n (x 1 x 2 dx. Lause Jos f P S[ 1, 1], pätee kaavassa (3.2 yhtäsuuruus funktion f jatkuvuuspisteissä. Epäjatkuvuuspisteissä f(x on korvattava lausekkeella f(x++f(x. 2 Esimerkki Määrää Chebyshevin sarjakehitelmä funktiolle f(x = x, x < 1. 3
36 Luku 4 Fourier n sarjat Fourier-sarjoja käytetään jaksollisten funktioiden tutkimiseen. Niiden avulla voidaan ratkaista tietyn tyyppisiä osittaisdifferentiaaliyhtälöitä, jotka mallintavat erilaisia luonnonilmiöitä. Näitä esiintyy muunmuassa sähkötekniikassa, optiikassa, signaalin- ja kuvankäsittelyssä sekä datan pakkaamisessa. Fourier-sarjan vahvuus on, että useimmille käytännön sovelluksissa tarvittaville funktioille voidaan kehittää Fourier-sarja, joka approksimoi tarkasti alkuperäistä funktiota myös epäjatkuvassa tapauksessa. 4.1 Määritelmiä Määritelmä 4.1. Funktion f P C[ π, π] Fourier n sarjaesitys määritellään kaavalla (4.1 f(x 1 2 a + (a n cosnx+b n sinnx, missä a n = 1 π (4.2 b n = 1 π π π π π n=1 f(xcosnxdx, n =,1,... f(xsinnxdx, n = 1,2,... Voidaan osoittaa, että funktiot { 1 2, cosnx, sinnx n = 1,2,... } muodostavat funktioavaruuden PC[ π,π] ortogonaalisen kannan sisätulon suhteen ja että (f g = π π f(xg(xdx ( = π, (cosnx cosnx = (sinnx sinnx = π,
37 joten sarjakehitelmä (4.1,(4.2 seuraa luvun 3 tuloksista. Tarkemmin: Jos f P C[ π, π], niin π π [ f(x 1 2 a N ] 2 (a n cosnx+b n sinnx dx N. n=1 Parsevalin yhtälöstä seuraa: Jos f PC[ π,π], niin 1 π f 2 (xdx = 1 π π 2 a2 + (a 2 n +b 2 n. n=1 Pisteittäiselle suppenemiselle pätee seuraava tulos: Lause 4.2. Jos f: R R on paloittain säännöllinen välillä [ π,π ja jos sen jakso on 2π, niin funktion f Fourier n sarjan (4.1 summa on 1. f(x, jos f on jatkuva pisteessä x; 2. f(x +f(x+, jos f on epäjatkuva pisteessä x. 2 Esimerkki 4.3. Määrää funktion Fourier n sarja. f(x = {, π x <, x, x < π Ratkaisu. Lasketaan ensin kertoimet a n ; ja joten a n = 1 π π a = 1 π π πf(xdx = 1 π πf(xcosnxdx = 1 π π π xdx = xcosnxdx = π 1 π x2 2 = π 2, = 1 1 πn2(cosnπ 1 = 1, kun n = 1,2,..., πn 2(( 1n π 1 [ xsinnx cosnx ] π n n 2 2 a 2n = ja a 2n+1 =, kun n =,1,2,... π(2n+1 Samalla tavalla osittaisintegroimalla saadaan b n = 1 π = π πf(xsinnxdx 1 π xsinnxdx = π 1 [ xcosnx + sinnx ] π π n n 2 = 1 [ πcosnπ ] = ( 1n+1, kun n = 1,2,..., π n n 32
38 Funktion f Fourier-sarja on (4.3 f(x π 4 2 π n=1 cos(2n 1x (2n n=1 ( 1 n+1sinnx n. Kuva 1. Funktion f ja sen Fourier-sarjan alun (n = 8 kuvaajat. Koska f(x ajatellaan jatketuksi koko reaalilukujoukkoon 2π-jaksolliseksi funktioksi, niin lauseen 4.2 nojalla sarja (4.3 suppenee pisteessä x = π kohti arvoa 1 2 [f(π +f(π+] = π 2. Kun sarjaan (4.3 sijoitetaan x = π saadaan parittomien positiivisten kokonaislukujen käänteislukujen nelöiden summa n=1 1 (2n 1 = π2 + = Sama summa voidaan laske sijoittamalla x = sarjaan (4.3. Lukijalle jätetään tehtäväksi 1 laskea sarjan (4.3 avulla summa (Vastaus π2 n 2 6. n=1 4.2 Fourier n kosini- ja sinisarjat Seuraavaksi tutkitaan miten funktion f yksinkertaiset symmetriaominaisuudet vaikuttavat sen Fourier-sarjaan. Määritelmä 4.4. Funktio f: R R on 33
39 1. parillinen, jos f( x = f(x kaikilla x R. 2. pariton, jos f( x = f(x kaikilla x R. Lemma 4.5. Oletetaan, että f : ( a, a R, a >, on integroituva. 1. Jos f parillinen, niin a f(xdx = 2 a a 2. Jos f on pariton, niin a f(xdx =. a Todistus. Harjoitustehtävä. Lause 4.6. Olkoon f paloittain jatkuva ja 2π-jaksoinen. f(xdx. 1. Jos f on parillinen, on funktion f Fourier n sarja muotoa f(x 1 2 a + a n cosnx, a n = 2 π n= π 2. Jos f on pariton, on funktion f Fourier n sarja muotoa f(x b n sinnx, b n = 2 π n=1 π f(xcosnxdx. f(xsinnxdx. Jos f :], π] R on paloittain jatkuva, niin se voidaan jatkaa aina joko parilliseksi tai parittomaksi funktioksi välille [ π, π] (suorita funktion jatko parilliseksi ja parittomaksi välille [ π,π]. Tällöin sen kosinisarja on ja sinisarja f(x 1 2 a + f(x a n cosnx, a n = 2 π n=1 b n sinnx, b n = 2 π n=1 π π f(xcosnxdx, f(xsinnxdx. Esimerkki 4.7. Määrää funktion f(x = x, π x π, Fourier n sarja. Ratkaisu. Koska f(x on parillinen funktio, kertoimet b n ovat nollia ja sen Fourier-sarja on kosinisarja. Lauseen 4.5 kohdan 1. nojalla a n = 2 π π x cosnxdx = 2 π π xcosnxdx. Kertoimen a arvo on helppo laskea ja a = π. Osittaisintegroimalla saadaan a n = 2 2 πn2(cosnπ 1 = 1, kun n = 1,2,..., πn 2(( 1n 34
40 joten 4 a 2n = ja a 2n 1 = π(2n 1 2, kun n = 1,2,... Koska funktion f(x 2π-jaksollinen jatke on jatkuva koko reaalilukujoukossa R, niin f(x = π 2 4 cos(2n 1x = π π (2n ( cosx+ cos3x + cos5x +. π n=1 Kuva 2. Funktion f ja sen Fourier-kosinisarjan alun (n = 8 kuvaajat. Tarkastellaan miten funktion Fourier-sarja saadaan määrättyä, kun se on määritelty välillä [ L, L] ja L π. Jos g P C[ L, L], niin merkitsemällä (4.4 x = πt ( Lx L, f(x = g = g(t, π x π, π saadaan funktio f P C[ π, π]. Suorittamalla funktion f Fourier n sarjaan (4.1 ja sen kertoimien lausekkeisiin (4.2 muunnokset (4.4, saadaan (4.5 g(t 1 [ ( nπt ( nπt ] 2 a + a n cos +b n sin, L L missä a n = 1 L b n = 1 L L L L L n=1 ( nπt g(t cos L ( nπt g(t sin L dt, n =,1,... dt, n = 1,2,... Koska yhtälön (4.5 oikea puoli on määritelty ja 2L-jaksoinen koko R:ssä, voidaan g korvata koko R:ssä määritellyllä 2L-jaksoisella jatkeella. Jos g on parillinen (vast. pariton, on sitä myös yhtälöllä (4.4 määritelty f, joten sarja (4.5 supistuu kosinisarjaksi (vast. sinisarjaksi. 35
41 4.3 Kompleksiarvoisen funktion Fourier n sarja Jos f: [ π,π] C on paloittain jatkuva, ovat funktion f Fourier n sarjan (4.6 f(x 1 2 a + (a n cosnx+b n sinnx kertoimet a n = 1 π b n = 1 π π π π π n=1 f(xcosnxdx, n =,1,... f(xsinnxdx, n = 1,2,... kompleksilukuja, sillä funktio f on muotoa f = u + iv ja π π f(xdx = π π u(xdx+i π π v(x dx. Eulerin kaavoista seuraa, että e ±iϕ = cosϕ±i sinϕ cosnx = 1 2 einx e inx, sinnx = 1 2i einx 1 2i e inx. Sijoittamalla nämä kaavaan (4.6 saadaan (4.7 f(x c n e inx, n= missä c = a 2, c n = 1 2 (a n ib n, c n = 1 2 (a n +ib n, n = 1,2,... Kertoimet kehitelmässä (4.7 saadaan myös osoittamalla, että funktiot g n (x = e inx, n =,±1,±2,... muodostavat ortogonaalisen jonon sisätulon (f g = π π f(xg(xdx suhteen. Siten c n = (f g n (g n g n = 1 π f(xe inx dx, n =,±1,±2,... 2π π 36
42 Luku 5 Sturm-Liouvillen ominaisarvo-ongelma 5.1 Sturm-Liouvillen differentiaaliyhtälö Ominaisarvotehtävä on lukijalle tuttu lineaarialgebran kurssilta. OlkoonA : V V,V = R n tai C n, on lineaarinen kuvaus. Luku λ (reaali- tai kompleksiluku on operaattorin A ominaisarvo ja vektori v sen ominaisvektori, jos Av = λv. Kaikkien sellaisten vektorien joukko, joilleav = λv,λon kiinteä luku, on avaruudenv aliavaruus ns. invariantti aliavaruus. Ominaisarvot saadaan ratkaisemalla yhtälö det(a λi =. Invariantin aliavaruuden dimensio on aina pienempi tai yhtäsuuri kuin juuren λ kertaluku. Ominaisarvo, jonka kertaluku on yksi on yksinkertainen (degeneroitumaton. Seuraavassa tutkitaan ominaisarvoprobleemaa, joka liittyy differentiaalioperaattoriin L : C 2 (a,b C 2 (a,b. Avaruus C 2 (a,b on välillä (a,b kaksi kertaa jatkuvasti derivoituvien reaaliarvoisten funktioiden avaruus. Lisäksi oletetaan, että nämä funktiot toteuttavat tietyt reunaehdot. Osittaisdifferentiaaliyhtälöiden ratkaiseminen muuttujien erottamismismenetelmällä johtaa ominaisarvotehtävään, joka voidaan ratkaista tässä luvussa tarkasteltujen menetelmien avulla. Tarkastellaan differentiaaliyhtälöä (5.1 a (xy +a 1 (xy +a 2 (xy =. Kun yhtälö (5.1 kerrotaan puolittain lausekkeella saadaan yhtälö 1 a (x ep(x, missä P(x = (5.2 Ly = (py +qy =, missä p = e P ja q = a 2 a e P. a1 (x a (x dx, Yhtälöä (5.2 kutsutaan yhtälön (5.1 itseadjungoiduksi muodoksi. 37
43 Esimerkki 5.1. Besselin yhtälön x 2 y +xy +(x 2 α 2 y = itseadjungoitu muoto on Määritelmä 5.2. (xy + (x α2 y =. x 1. Differentiaaliyhtälöä (5.3 Ly +λry = (py +qy +λry =. kutsutaan Sturm-Liouvillen differentiaaliyhtälöksi. 2. Yhtälö (5.3 yhdessä reunaehtojen { B 1 (y = αy(a+βy (a =, α + β >, (5.4 B 2 (y = γy(b+δy (b =, γ + δ > kanssa on Sturm-Liouvillen reuna-arvoprobleema. 3. Jos Sturm-Liouvillen probleemalla (5.5 Ly = λry, B 1 (y =, B 2 (y =. on annettua lukua λ R kohti ei-triviaali ratkaisu y, sanomme, että λ on Sturm- Liouvillen reuna-arvo-ongelman (5.5 ominaisarvo ja y ominaisarvoa λ vastaava ominaisfunktio. 4. Sturm-Liouvillen reuna-arvo-ongelman (5.5 ratkaiseminen tarkoittaa sen kaikkien ominaisarvojen ja ominaisfunktioiden määräämistä. Määritelmä 5.3. Ongelmaa (5.3,(5.4 sanotaan säännölliseksi, jos funktiot p, q ja r ovat jatkuvia välillä [a,b] sekä p(x > ja r(x > kaikilla x [a,b]. Esimerkki 5.4. Ratkaise ominaisarvoprobleema { y +λy =, λ R, y( = y(c = c >. Lause 5.5. Säännöllisen Sturm-Liouvillen probleeman eri ominaisarvoja vastaavat ominaisfunktiot ovat ortogonaaliset sisätulon suhteen. (u v = b a r(xu(xv(xdx, u, v F 38
44 Lause 5.6. Säännöllisen Sturm-Liouvillen reuna-arvoprobleeman (5.3,(5.4 ominaisarvot muodostavat kasvavan jonon, joka kasvaa rajatta, ts. λ 1 < λ 2 < < λ n <, ja lim λ n =. n Vastaavat ominaisfunktiot y n, n = 1,2,... ovat vakiota vaille yksikäsitteisesti määrätyt. Huomautus 5.7. Jos reunaehdot (5.4 korvataan jaksollisuusehdoilla, pätevät lauseiden 5.5 ja 5.6 tulokset muutoin, paitsi että samaa ominaisarvoa voi vastata useampi lineaarisesti vapaa ominaisfunktio. Sturm-Liouvillen reuna-arvoprobleeman ominaisfunktiot (y n n=1 muodostavat ortogonaalijonon painofunktion r(x suhteen avaruudessa C 2 (a,b. Jokainen funktio f C 2 (a,b voidaan kehittää sarjaksi tämän ortogonaalijonon avulla f c n y n. n=1 5.2 Singulaarisia Sturm-Liouvillen ominaisarvo-ongelmia Jos Sturm-Liouvillen ominaisarvo-ongelmassa 1. väli (a,b on ääretön tai 2. väli (a,b on äärellinen ja p(x tai r(x saa arvon tai ei ole määritelty päätepisteessä a tai b, niin ongelman (5.3 ratkaisu ei välttämättä ole määritelty pisteessä a tai b. Silloin vastaava reunaehto (5.4 joudutaan korvaamaan ehdolla, että ratkaisulla y ja sen derivaatalla y on äärellinen raja-arvo ko. päätepisteessä. Tällöin joudutaan ns. singulaariseen Sturm-Liouvillen probleemaan. Lauseiden 5.5 ja 5.6 tulokset pätevät myös eräille singulaarisille probleemoille. Seuraavassa esimerkkejä. Legendren ominaisarvo-ongelma { ((1 x 2 y +λy =, 1 < x < 1, ratkaisulla y ja sen derivaatalla y on äärelliset raja-arvot pisteissä ±1. Ominaisarvot ja vastaavat ominaisfunktiot: λ n = n(n+1, y n = P n (x n =,1,... 39
800346A Differentiaaliyhtälöt II. Seppo Heikkilä, Martti Kumpulainen, Janne Oinas
 8346A Differentiaaliyhtälöt II Seppo Heikkilä, Martti Kumpulainen, Janne Oinas 6. toukokuuta 9 DIFFERENTIAALIYHTÄLÖT II Kesto: 3 op. Luentoja 3 h, harjoituksia 16 h. Opintojaksossa tarkastellaan erikoisfunktioita,
8346A Differentiaaliyhtälöt II Seppo Heikkilä, Martti Kumpulainen, Janne Oinas 6. toukokuuta 9 DIFFERENTIAALIYHTÄLÖT II Kesto: 3 op. Luentoja 3 h, harjoituksia 16 h. Opintojaksossa tarkastellaan erikoisfunktioita,
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
Differentiaaliyhtälöiden jatkokurssi A, 5 op Syksy 2015
 Differentiaaliyhtälöiden jatkokurssi 82334A, 5 op Syksy 215 1 Frobeniuksen menetelmä 1 2 Gamma ja betafunktiot 4 3 Besselin funktiot 7 4 Ortogonaalipolynomit 13 4.1 Legendren polynomit..........................
Differentiaaliyhtälöiden jatkokurssi 82334A, 5 op Syksy 215 1 Frobeniuksen menetelmä 1 2 Gamma ja betafunktiot 4 3 Besselin funktiot 7 4 Ortogonaalipolynomit 13 4.1 Legendren polynomit..........................
Differentiaaliyhtälöiden jatkokurssi A, 5 op Syksy 2017
 Differentiaaliyhtälöiden jatkokurssi 82334A, 5 op Syksy 217 1 Frobeniuksen menetelmä 3 2 Gamma ja betafunktiot 6 3 Besselin funktiot 9 4 Ortogonaalipolynomit 15 4.1 Legendren polynomit..........................
Differentiaaliyhtälöiden jatkokurssi 82334A, 5 op Syksy 217 1 Frobeniuksen menetelmä 3 2 Gamma ja betafunktiot 6 3 Besselin funktiot 9 4 Ortogonaalipolynomit 15 4.1 Legendren polynomit..........................
Kompleksianalyysi, viikko 6
 Kompleksianalyysi, viikko 6 Jukka Kemppainen Mathematics Division Funktion erikoispisteet Määr. 1 Jos f on analyyttinen pisteen z 0 aidossa ympäristössä 0 < z z 0 < r jollakin r > 0, niin sanotaan, että
Kompleksianalyysi, viikko 6 Jukka Kemppainen Mathematics Division Funktion erikoispisteet Määr. 1 Jos f on analyyttinen pisteen z 0 aidossa ympäristössä 0 < z z 0 < r jollakin r > 0, niin sanotaan, että
8 Potenssisarjoista. 8.1 Määritelmä. Olkoot a 0, a 1, a 2,... reaalisia vakioita ja c R. Määritelmä 8.1. Muotoa
 8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
Kompleksianalyysi, viikko 5
 Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
2. Fourier-sarjoista. Aaltoliikkeen ja lämmöjohtumisen matemaattinen tarkastelu
 2. Fourier-sarjoista Fourier-analyysi: Aaltoliikkeen ja lämmöjohtumisen matemaattinen tarkastelu Matemaattisen analyysin täkein työväline "Jokainen funktio" voidaan esittää harmonisten värähtelyjen, so.
2. Fourier-sarjoista Fourier-analyysi: Aaltoliikkeen ja lämmöjohtumisen matemaattinen tarkastelu Matemaattisen analyysin täkein työväline "Jokainen funktio" voidaan esittää harmonisten värähtelyjen, so.
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012
 KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
1 Lineaariavaruus eli Vektoriavaruus
 1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
u(0, t) = 0 kaikille t > 0: lämpötila pidetään vakiona pisteessä x = 0;
 3. Lämmönjohtumisyhtälö I Yksiulotteisessa lämmönjohtumisyhtälössä u t = u γ x tuntematon funktio u = u(x, t) kuvaa lämpötilaa yksiulotteisen kappaleen (ohut sauva; x-akseli) kohdassa x hetkellä t. Kun
3. Lämmönjohtumisyhtälö I Yksiulotteisessa lämmönjohtumisyhtälössä u t = u γ x tuntematon funktio u = u(x, t) kuvaa lämpötilaa yksiulotteisen kappaleen (ohut sauva; x-akseli) kohdassa x hetkellä t. Kun
Osoita, että täsmälleen yksi vektoriavaruuden ehto ei ole voimassa.
 LINEAARIALGEBRA Harjoituksia 2016 1. Olkoon V = R 2 varustettuna tavallisella yhteenlaskulla. Määritellään reaaliluvulla kertominen seuraavasti: λ (x 1, x 2 ) = (λx 1, 0) (x 1, x 2 ) R 2 ja λ R. Osoita,
LINEAARIALGEBRA Harjoituksia 2016 1. Olkoon V = R 2 varustettuna tavallisella yhteenlaskulla. Määritellään reaaliluvulla kertominen seuraavasti: λ (x 1, x 2 ) = (λx 1, 0) (x 1, x 2 ) R 2 ja λ R. Osoita,
Fourier-sarjat ja -muunnos
 24. marraskuuta 2016 Jaksolliset funktiot, trigonometriset sarjat, parilliset ja p Jaksolliset funktiot Funktio f : R R on jaksollinen, jos on olemassa p > 0 siten, että f (x + p) = f (x) kaikilla x R
24. marraskuuta 2016 Jaksolliset funktiot, trigonometriset sarjat, parilliset ja p Jaksolliset funktiot Funktio f : R R on jaksollinen, jos on olemassa p > 0 siten, että f (x + p) = f (x) kaikilla x R
802320A LINEAARIALGEBRA OSA I
 802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
1 Sisätulo- ja normiavaruudet
 1 Sisätulo- ja normiavaruudet 1.1 Sisätuloavaruus Määritelmä 1. Olkoon V reaalinen vektoriavaruus. Kuvaus : V V R on reaalinen sisätulo eli pistetulo, jos (a) v w = w v (symmetrisyys); (b) v + u w = v
1 Sisätulo- ja normiavaruudet 1.1 Sisätuloavaruus Määritelmä 1. Olkoon V reaalinen vektoriavaruus. Kuvaus : V V R on reaalinen sisätulo eli pistetulo, jos (a) v w = w v (symmetrisyys); (b) v + u w = v
802320A LINEAARIALGEBRA OSA II
 802320A LINEAARIALGEBRA OSA II Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 64 Sisätuloavaruus Määritelmä 1 Olkoon V reaalinen vektoriavaruus. Kuvaus on reaalinen
802320A LINEAARIALGEBRA OSA II Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 64 Sisätuloavaruus Määritelmä 1 Olkoon V reaalinen vektoriavaruus. Kuvaus on reaalinen
Ortogonaaliprojektio äärellisulotteiselle aliavaruudelle
 Ortogonaaliprojektio äärellisulotteiselle aliavaruudelle Olkoon X sisätuloavaruus ja Y X äärellisulotteinen aliavaruus. Tällöin on olemassa lineaarisesti riippumattomat vektorit y 1, y 2,..., yn, jotka
Ortogonaaliprojektio äärellisulotteiselle aliavaruudelle Olkoon X sisätuloavaruus ja Y X äärellisulotteinen aliavaruus. Tällöin on olemassa lineaarisesti riippumattomat vektorit y 1, y 2,..., yn, jotka
5 Ominaisarvot ja ominaisvektorit
 5 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin A
5 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin A
y x1 σ t 1 = c y x 1 σ t 1 = y x 2 σ t 2 y x 2 x 1 y = σ(t 2 t 1 ) x 2 x 1 y t 2 t 1
 1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
1. Tarkastellaan funktiota missä σ C ja y (y 1,..., y n ) R n. u : R n R C, u(x, t) e i(y x σt), (a) Miksi funktiota u(x, t) voidaan kutsua tasoaalloksi, jonka aaltorintama on kohtisuorassa vektorin y
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
Funktion raja-arvo ja jatkuvuus Reaali- ja kompleksifunktiot
 3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
Analyysi III. Jari Taskinen. 28. syyskuuta Luku 1
 Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
1. Viikko. K. Tuominen MApu II 1/17 17
 1. Viikko Keskeiset asiat ja tavoitteet: 1. Kompleksiluvut, kompleksitaso, polaariesitys, 2. Kompleksilukujen peruslaskutoimitukset, 3. Eulerin ja De Moivren kaavat, 4. Potenssi ja juuret, kompleksinen
1. Viikko Keskeiset asiat ja tavoitteet: 1. Kompleksiluvut, kompleksitaso, polaariesitys, 2. Kompleksilukujen peruslaskutoimitukset, 3. Eulerin ja De Moivren kaavat, 4. Potenssi ja juuret, kompleksinen
1 Ominaisarvot ja ominaisvektorit
 1 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) 1 missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin
1 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) 1 missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin
MATEMATIIKAN JA TILASTOTIETEEN LAITOS
 f ( n) JYVÄSKYLÄN YLIOPISTO MATEMATIIKAN JA TILASTOTIETEEN LAITOS n Funktionaalianalyysi Ei harjoituksia 1.4.2015 Funktionaalista viihdettä pääsiäistauolle: viikolla 14 (ma 30.3., ti 31.3. ja ke 1.4.)
f ( n) JYVÄSKYLÄN YLIOPISTO MATEMATIIKAN JA TILASTOTIETEEN LAITOS n Funktionaalianalyysi Ei harjoituksia 1.4.2015 Funktionaalista viihdettä pääsiäistauolle: viikolla 14 (ma 30.3., ti 31.3. ja ke 1.4.)
4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt
 4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt 4.1 Homogeeniset lineaariset differentiaaliyhtälöt Homogeeninen yhtälö on muotoa F(x, y,, y (n) ) = 0. (1) Yhtälö on lineaarinen, jos se voidaan
4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt 4.1 Homogeeniset lineaariset differentiaaliyhtälöt Homogeeninen yhtälö on muotoa F(x, y,, y (n) ) = 0. (1) Yhtälö on lineaarinen, jos se voidaan
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus
 Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
Matematiikka B3 - Avoin yliopisto
 2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
4 Korkeamman kertaluvun differentiaaliyhtälöt
 Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Täydellisyysaksiooman kertaus
 Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
u = 2 u (9.1) x + 2 u
 9. Poissonin integraali 9.. Poissonin integraali. Ratkaistaan Diriclet n reuna-arvotehtävä origokeskisessä, R-säteisessä ympyrässä D = {(x, y) R x +y < R }, t.s. kun f : D R on annettu jatkuva funktio,
9. Poissonin integraali 9.. Poissonin integraali. Ratkaistaan Diriclet n reuna-arvotehtävä origokeskisessä, R-säteisessä ympyrässä D = {(x, y) R x +y < R }, t.s. kun f : D R on annettu jatkuva funktio,
Toispuoleiset raja-arvot
 Toispuoleiset raja-arvot Määritelmä Funktiolla f on oikeanpuoleinen raja-arvo a R pisteessä x 0 mikäli kaikilla ɛ > 0 löytyy sellainen δ > 0 että f (x) a < ɛ aina kun x 0 < x < x 0 + δ; ja vasemmanpuoleinen
Toispuoleiset raja-arvot Määritelmä Funktiolla f on oikeanpuoleinen raja-arvo a R pisteessä x 0 mikäli kaikilla ɛ > 0 löytyy sellainen δ > 0 että f (x) a < ɛ aina kun x 0 < x < x 0 + δ; ja vasemmanpuoleinen
5 Differentiaaliyhtälöryhmät
 5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
Rollen lause polynomeille
 Rollen lause polynomeille LuK-tutkielma Anna-Helena Hietamäki 7193766 Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 015 Sisältö 1 Johdanto 1.1 Rollen lause analyysissä.......................
Rollen lause polynomeille LuK-tutkielma Anna-Helena Hietamäki 7193766 Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 015 Sisältö 1 Johdanto 1.1 Rollen lause analyysissä.......................
Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: b) 0 e x + 1
 Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
1 sup- ja inf-esimerkkejä
 Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Luku 4. Derivoituvien funktioiden ominaisuuksia.
 1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
3.3 Funktion raja-arvo
 3.3 Funktion raja-arvo Olkoot A ja B kompleksitason joukkoja ja f : A B kuvaus. Kuvauksella f on pisteessä z 0 A raja-arvo c, jos jokaista ε > 0 vastaa δ > 0 siten, että 0 < z z 0 < δ ja z A f(z) c < ε.
3.3 Funktion raja-arvo Olkoot A ja B kompleksitason joukkoja ja f : A B kuvaus. Kuvauksella f on pisteessä z 0 A raja-arvo c, jos jokaista ε > 0 vastaa δ > 0 siten, että 0 < z z 0 < δ ja z A f(z) c < ε.
9. Lineaaristen differentiaaliyhtälöiden ratkaisuavaruuksista
 29 9 Lineaaristen differentiaaliyhtälöiden ratkaisuavaruuksista Tarkastelemme kertalukua n olevia lineaarisia differentiaaliyhtälöitä y ( x) + a ( x) y ( x) + + a ( x) y( x) + a ( x) y= b( x) ( n) ( n
29 9 Lineaaristen differentiaaliyhtälöiden ratkaisuavaruuksista Tarkastelemme kertalukua n olevia lineaarisia differentiaaliyhtälöitä y ( x) + a ( x) y ( x) + + a ( x) y( x) + a ( x) y= b( x) ( n) ( n
Mat / Mat Matematiikan peruskurssi C3-I / KP3-I Harjoitus 5 / vko 42, loppuviikko, syksy 2008
 Mat-.3 / Mat-.33 Matematiikan peruskurssi C3-I / KP3-I Harjoitus 5 / vko 4, loppuviikko, syksy 8 Ennen malliratkaisuja, muistin virkistämiseksi kaikkien rakastama osittaisintegroinnin kaava: b a u(tv (t
Mat-.3 / Mat-.33 Matematiikan peruskurssi C3-I / KP3-I Harjoitus 5 / vko 4, loppuviikko, syksy 8 Ennen malliratkaisuja, muistin virkistämiseksi kaikkien rakastama osittaisintegroinnin kaava: b a u(tv (t
e int) dt = 1 ( 2π 1 ) (0 ein0 ein2π
 Matematiikan ja tilastotieteen laitos Funktionaalianalyysin peruskurssi Kevät 9) Harjoitus 7 Ratkaisuja Jussi Martin). E Hilbert avaruus L [, π]) ja gt) := t, t [, π]. Määrää funktion g Fourier kertoimet
Matematiikan ja tilastotieteen laitos Funktionaalianalyysin peruskurssi Kevät 9) Harjoitus 7 Ratkaisuja Jussi Martin). E Hilbert avaruus L [, π]) ja gt) := t, t [, π]. Määrää funktion g Fourier kertoimet
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
Avaruuden R n aliavaruus
 Avaruuden R n aliavaruus 1 / 41 Aliavaruus Esimerkki 1 Kuva: Suora on suljettu yhteenlaskun ja skalaarilla kertomisen suhteen. 2 / 41 Esimerkki 2 Kuva: Suora ei ole suljettu yhteenlaskun ja skalaarilla
Avaruuden R n aliavaruus 1 / 41 Aliavaruus Esimerkki 1 Kuva: Suora on suljettu yhteenlaskun ja skalaarilla kertomisen suhteen. 2 / 41 Esimerkki 2 Kuva: Suora ei ole suljettu yhteenlaskun ja skalaarilla
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
KOMPLEKSIANALYYSI I KURSSI SYKSY exp z., k = 1, 2,... Eksponenttifunktion z exp(z) Laurent-sarjan avulla
 KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 11. Integrointi erillisen erikoispisteen ympäri Olkoot f analyyttinen punkteeratussa kiekossa D(z 0.r\{z 0 }. Funktiolla f on erikoispiste z 0.
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 11. Integrointi erillisen erikoispisteen ympäri Olkoot f analyyttinen punkteeratussa kiekossa D(z 0.r\{z 0 }. Funktiolla f on erikoispiste z 0.
MS-C1340 Lineaarialgebra ja
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi kevät 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Idea Lineaarisen systeemin ratkaiseminen Olkoon
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi kevät 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Idea Lineaarisen systeemin ratkaiseminen Olkoon
Matriisilaskenta, LH4, 2004, ratkaisut 1. Hae seuraavien R 4 :n aliavaruuksien dimensiot, jotka sisältävät vain
 Matriisilaskenta LH4 24 ratkaisut 1 Hae seuraavien R 4 :n aliavaruuksien dimensiot jotka sisältävät vain a) Kaikki muotoa (a b c d) olevat vektorit joilla d a + b b) Kaikki muotoa (a b c d) olevat vektorit
Matriisilaskenta LH4 24 ratkaisut 1 Hae seuraavien R 4 :n aliavaruuksien dimensiot jotka sisältävät vain a) Kaikki muotoa (a b c d) olevat vektorit joilla d a + b b) Kaikki muotoa (a b c d) olevat vektorit
Lineaarialgebra ja matriisilaskenta II. LM2, Kesä /141
 Lineaarialgebra ja matriisilaskenta II LM2, Kesä 2012 1/141 Kertausta: avaruuden R n vektorit Määritelmä Oletetaan, että n {1, 2, 3,...}. Avaruuden R n alkiot ovat jonoja, joissa on n kappaletta reaalilukuja.
Lineaarialgebra ja matriisilaskenta II LM2, Kesä 2012 1/141 Kertausta: avaruuden R n vektorit Määritelmä Oletetaan, että n {1, 2, 3,...}. Avaruuden R n alkiot ovat jonoja, joissa on n kappaletta reaalilukuja.
x = y x i = y i i = 1, 2; x + y = (x 1 + y 1, x 2 + y 2 ); x y = (x 1 y 1, x 2 + y 2 );
 LINEAARIALGEBRA Ratkaisuluonnoksia, Syksy 2016 1. Olkoon n Z +. Osoita, että (R n, +, ) on lineaariavaruus, kun vektoreiden x = (x 1,..., x n ), y = (y 1,..., y n ) identtisyys, yhteenlasku ja reaaliluvulla
LINEAARIALGEBRA Ratkaisuluonnoksia, Syksy 2016 1. Olkoon n Z +. Osoita, että (R n, +, ) on lineaariavaruus, kun vektoreiden x = (x 1,..., x n ), y = (y 1,..., y n ) identtisyys, yhteenlasku ja reaaliluvulla
7. Tasaisen rajoituksen periaate
 18 FUNKTIONAALIANALYYSIN PERUSKURSSI 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
18 FUNKTIONAALIANALYYSIN PERUSKURSSI 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Kompleksiluvut Riikka Korte (muokannut Riikka Kangaslammen materiaalin pohjalta) Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.11.2015 1 /
MS-A0102 Differentiaali- ja integraalilaskenta 1 Kompleksiluvut Riikka Korte (muokannut Riikka Kangaslammen materiaalin pohjalta) Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.11.2015 1 /
1.1 Vektorit. MS-A0004/A0006 Matriisilaskenta. 1.1 Vektorit. 1.1 Vektorit. Reaalinen n-ulotteinen avaruus on joukko. x 1. R n.
 ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
Numeeriset menetelmät
 Numeeriset menetelmät Luento 13 Ti 18.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 13 Ti 18.10.2011 p. 1/43 p. 1/43 Nopeat Fourier-muunnokset Fourier-sarja: Jaksollisen funktion esitys
Numeeriset menetelmät Luento 13 Ti 18.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 13 Ti 18.10.2011 p. 1/43 p. 1/43 Nopeat Fourier-muunnokset Fourier-sarja: Jaksollisen funktion esitys
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
1 Kompleksiluvut 1. y z = (x, y) Kuva 1: Euklidinen taso R 2
 Sisältö 1 Kompleksiluvut 1 1.1 Määritelmä............................ 1 1. Kertolasku suorakulmaisissa koordinaateissa.......... 4 1.3 Käänteisluku ja jakolasku..................... 9 1.4 Esimerkkejä.............................
Sisältö 1 Kompleksiluvut 1 1.1 Määritelmä............................ 1 1. Kertolasku suorakulmaisissa koordinaateissa.......... 4 1.3 Käänteisluku ja jakolasku..................... 9 1.4 Esimerkkejä.............................
MATP153 Approbatur 1B Ohjaus 2 Keskiviikko torstai
 MATP15 Approbatur 1B Ohjaus Keskiviikko 4.11. torstai 5.11.015 1. (Opiskeluteht. 6 s. 0.) Määritä sellainen vakio a, että polynomilla x + (a 1)x 4x a on juurena luku x = 1. Mitkä ovat tällöin muut juuret?.
MATP15 Approbatur 1B Ohjaus Keskiviikko 4.11. torstai 5.11.015 1. (Opiskeluteht. 6 s. 0.) Määritä sellainen vakio a, että polynomilla x + (a 1)x 4x a on juurena luku x = 1. Mitkä ovat tällöin muut juuret?.
Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus Malliratkaisut (Sauli Lindberg)
 Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus 4 9.4.-23.4.200 Malliratkaisut (Sauli Lindberg). Näytä, että Lusinin lauseessa voidaan luopua oletuksesta m(a)
Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus 4 9.4.-23.4.200 Malliratkaisut (Sauli Lindberg). Näytä, että Lusinin lauseessa voidaan luopua oletuksesta m(a)
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
3 Toisen kertaluvun lineaariset differentiaaliyhtälöt
 3 Toisen kertaluvun lineaariset differentiaaliyhtälöt 3.1 Homogeeniset lineaariset differentiaaliyhtälöt Toisen kertaluvun differentiaaliyhtälö on lineaarinen, jos se voidaan kirjoittaa muotoon Jos r(x)
3 Toisen kertaluvun lineaariset differentiaaliyhtälöt 3.1 Homogeeniset lineaariset differentiaaliyhtälöt Toisen kertaluvun differentiaaliyhtälö on lineaarinen, jos se voidaan kirjoittaa muotoon Jos r(x)
Kertausta: avaruuden R n vektoreiden pistetulo
 Kertausta: avaruuden R n vektoreiden pistetulo Määritelmä Vektoreiden v R n ja w R n pistetulo on v w = v 1 w 1 + v 2 w 2 + + v n w n. Huom. Pistetulo v w on reaaliluku! LM2, Kesä 2012 227/310 Kertausta:
Kertausta: avaruuden R n vektoreiden pistetulo Määritelmä Vektoreiden v R n ja w R n pistetulo on v w = v 1 w 1 + v 2 w 2 + + v n w n. Huom. Pistetulo v w on reaaliluku! LM2, Kesä 2012 227/310 Kertausta:
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Sinin jatkuvuus. Lemma. Seuraus. Seuraus. Kaikilla x, y R, sin x sin y x y. Sini on jatkuva funktio.
 Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
k=0 saanto jokaisen kolmannen asteen polynomin. Tukipisteet on talloin valittu
 LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
LIS AYKSI A kirjaan Reaalimuuttujan analyysi 1.6. Numeerinen integrointi: Gaussin kaavat Edella kasitellyt numeerisen integroinnin kaavat eli kvadratuurikaavat Riemannin summa, puolisuunnikassaanto ja
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
Seuraava topologisluonteinen lause on nk. Bairen lause tai Bairen kategorialause, n=1
 FUNKTIONAALIANALYYSIN PERUSKURSSI 115 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
FUNKTIONAALIANALYYSIN PERUSKURSSI 115 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
3 TOISEN KERTALUVUN LINEAARISET DY:T
 3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 17 R. Kangaslampi Vektoriavaruudet Vektoriavaruus
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Vektoriavaruudet Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 17 R. Kangaslampi Vektoriavaruudet Vektoriavaruus
Harjoitus Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia:
 Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Kertausta: avaruuden R n vektoreiden pistetulo
 Kertausta: avaruuden R n vektoreiden pistetulo Määritelmä Vektoreiden v R n ja w R n pistetulo on v w = v 1 w 1 + v 2 w 2 + + v n w n. Huom. Pistetulo v w on reaaliluku! LM2, Kesä 2014 164/246 Kertausta:
Kertausta: avaruuden R n vektoreiden pistetulo Määritelmä Vektoreiden v R n ja w R n pistetulo on v w = v 1 w 1 + v 2 w 2 + + v n w n. Huom. Pistetulo v w on reaaliluku! LM2, Kesä 2014 164/246 Kertausta:
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
1 Kompleksiluvut. Kompleksiluvut 10. syyskuuta 2005 sivu 1 / 7
 Kompleksiluvut 10. syyskuuta 2005 sivu 1 / 7 1 Kompleksiluvut Lukualueiden laajennuksia voi lähestyä polynomiyhtälöiden ratkaisemisen kautta. Yhtälön x+1 = 0 ratkaisemiseksi tarvitaan negatiivisia lukuja.
Kompleksiluvut 10. syyskuuta 2005 sivu 1 / 7 1 Kompleksiluvut Lukualueiden laajennuksia voi lähestyä polynomiyhtälöiden ratkaisemisen kautta. Yhtälön x+1 = 0 ratkaisemiseksi tarvitaan negatiivisia lukuja.
FyMM IIa Kertausta loppukoetta varten
 Tiistai 27.2.2018 1/11 FyMM IIa Kertausta loppukoetta varten 2018 Tiistai 27.2.2018 2/11 1 Kokeesta yleisesti 2 3 4 5 6 Koealue jakaantuu neljään pääalueeseen: 1 Ensimmäisen kertaluvun ODY:t 2 Toisen kertaluvun
Tiistai 27.2.2018 1/11 FyMM IIa Kertausta loppukoetta varten 2018 Tiistai 27.2.2018 2/11 1 Kokeesta yleisesti 2 3 4 5 6 Koealue jakaantuu neljään pääalueeseen: 1 Ensimmäisen kertaluvun ODY:t 2 Toisen kertaluvun
Reaalilukuvälit, leikkaus ja unioni (1/2)
 Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
8. Avoimen kuvauksen lause
 116 FUNKTIONAALIANALYYSIN PERUSKURSSI 8. Avoimen kuvauksen lause Palautamme aluksi mieleen Topologian kursseilta ehkä tutut perusasiat yleisestä avoimen kuvauksen käsitteestä. Määrittelemme ensin avoimen
116 FUNKTIONAALIANALYYSIN PERUSKURSSI 8. Avoimen kuvauksen lause Palautamme aluksi mieleen Topologian kursseilta ehkä tutut perusasiat yleisestä avoimen kuvauksen käsitteestä. Määrittelemme ensin avoimen
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori = (,..., ). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori = (,..., ). Reaalisten m n-matriisien joukkoa merkitään
Oletetaan ensin, että tangenttitaso on olemassa. Nyt pinnalla S on koordinaattiesitys ψ, jolle pätee että kaikilla x V U
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 018 Harjoitus 4 Ratkaisuehdotukset Tehtävä 1. Olkoon U R avoin joukko ja ϕ = (ϕ 1, ϕ, ϕ 3 ) : U R 3 kaksiulotteisen C 1 -alkeispinnan
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 018 Harjoitus 4 Ratkaisuehdotukset Tehtävä 1. Olkoon U R avoin joukko ja ϕ = (ϕ 1, ϕ, ϕ 3 ) : U R 3 kaksiulotteisen C 1 -alkeispinnan
Funktiojonot ja funktiotermiset sarjat Funktiojono ja funktioterminen sarja Pisteittäinen ja tasainen suppeneminen
 4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
H7 Malliratkaisut - Tehtävä 1
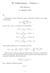 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
Vektorianalyysi I MAT Luennoitsija: Ritva Hurri-Syrjänen Luentoajat: ti: 14:15-16:00, to: 12:15-14:00 Helsingin yliopisto 21.
 Vektorianalyysi I MAT21003 Luennoitsija: Ritva Hurri-Syrjänen Luentoajat: ti: 14:15-16:00, to: 12:15-14:00 Helsingin yliopisto 21. syyskuuta 2017 1 Sisältö 1 Euklidinen avaruus 3 1.1 Euklidinen avaruus
Vektorianalyysi I MAT21003 Luennoitsija: Ritva Hurri-Syrjänen Luentoajat: ti: 14:15-16:00, to: 12:15-14:00 Helsingin yliopisto 21. syyskuuta 2017 1 Sisältö 1 Euklidinen avaruus 3 1.1 Euklidinen avaruus
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
Kanta ja dimensio 1 / 23
 1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
