8 Potenssisarjoista. 8.1 Määritelmä. Olkoot a 0, a 1, a 2,... reaalisia vakioita ja c R. Määritelmä 8.1. Muotoa
|
|
|
- Antero Saaristo
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen potenssisarja suppenee (vakioiden a 0, a, a 2,... arvoista riippumatta) pisteessä x c. On myös mahdollista, että piste x c on ainoa piste, jossa potenssisarja suppenee (ks. esimerkki 8.). Toisaalta potenssisarja voi supeta koko reaalilukujoukossa (ks. esimerkki 8.2) tai sitten jollakin äärellisellä välillä (ks. muut esimerkit ja luku 8.2). Esimerkki 8.. Osamäärätarkastimen nojalla potenssisarja (x c) k suppenee vain, kun x c. Jos nimittäin x c, niin (k + )! (x c) k+ (x c) k (k + ) x c, kun k. Esimerkki 8.2. Potenssisarja xk x k suppenee kaikilla x R (esimerkki 7.2, s. 55). Esimerkki 8.3. Esimerkin 7.3 (s. 56) perusteella potenssisarja (x c) n n n suppenee täsmälleen silloin, kun x [c, c + [. 75
2 Esimerkki 8.4. Olkoon A 0. Geometrisen sarjan (esimerkki 7., s. 55) suppenemisesta seuraa, että potenssisarja A(x c) k A (x c) k suppenee täsmälleen silloin, kun x c < eli kun x ]c, c + [. Jos erityisesti A ja c 0, on kyseessä potenssisarja x k eli tavallinen geometrinen sarja. Tämä suppenee, kun x ], [. Esimerkki 8.5. Käyttämällä osamäärätarkastinta ja Leibnizin lausetta voidaan osoittaa, että potenssisarja ( ) k 2k + x2k+ suppenee täsmälleen silloin, kun x [, ] (harjoitustehtävä). Lause 8.. Jos potenssisarja suppenee pisteessä x c ja r x c, niin sarja suppenee (vieläpä itseisesti) myös välillä { x R x c < r } ]c r, c + r[. Todistus. Oletetaan, että sarja a k (x c) k suppenee ja x c. Koska suppenevan sarjan termit ovat rajoitettuja, on olemassa sellainen M > 0, että a k r k a k (x c) k M k N eli Siis a k M r k k N. M r k x c k M ( ) k x c x R k N. r Täten sarja ak (x c) k M k N suppenee itseisesti majoranttiperiaatteen nojalla, kun x c < r (majoranttina suppeneva geometrinen sarja). 76
3 Seuraus 8.2. Jos sarja a k (x c) k hajaantuu ja x c > x c ( r), myös sarja hajaantuu. 77
4 8.2 Potenssisarjan suppenemissäde ja -väli Luvun 8. esimerkeistä ja tuloksista havaitaan, että yleisesti potenssisarja näyttäisi suppenevan jollakin välillä (tai vain pisteessä x c). Tarkastellaan nyt asiaa täsmällisemmin. Määritelmä 8.2. Jos joukko S { x c suppenee } on ylhäältä rajoitettu, niin potenssisarjan suppenemissäde R sup S. Jos joukko S ei ole ylhäältä rajoitettu, niin R. Lauseen 8. nojalla saadaan välittömästi seuraavat tulokset (harjoitustehtävä). Lause 8.3. Potenssisarjan suppenemissäteellä R on seuraavat ominaisuudet. (i) Jos R 0, niin sarja suppenee vain, kun x c. (ii) Jos R, niin sarja suppenee kaikilla x R. (iii) Jos 0 < R <, niin sarja suppenee, kun x c < R, ja sarja hajaantuu, kun x c > R. Huomautus 8.4. Jos 0 < R <, niin lauseen 8.3 kohdan (iii) perusteella potenssisarja suppenee välillä ]c R, c + R[. Kyseistä väliä kutsutaan potenssisarjan suppenemisväliksi. Jos R 0, niin potenssisarjan suppenemisväli surkastuu pisteeksi c, ja jos R, niin suppenemisväli on koko reaalilukujoukko. Huomautus 8.5. Suppenemisvälin päätepisteissä c R ja c + R potenssisarja voi supeta tai hajaantua (ks. esimerkki 8.7, s. 79). Huomautus 8.6. Potenssisarjan suppeneminen ja itseinen suppeneminen ovat yhtäpitäviä muualla paitsi mahdollisesti pisteissä c R ja c + R. Joskus potenssisarjan suppenemisvälillä tarkoitetaan väliä, joka sisältää nyt määritellyn suppenemisvälin (eli avoimen välin) lisäksi myös välin päätepisteet tai päätepisteen, jos potenssisarja suppenee kyseisissä pisteissä. 78
5 Esimerkki 8.6. Esimerkin 8. (s. 75) potenssisarjan suppenemissäde on 0 ja esimerkin 8.2 (s. 75) potenssisarjan suppenemissäde on. Esimerkki 8.7. Esimerkkien 8.3 (s. 75), 8.4 (s. 76) ja 8.5 (s. 76) jokaisen potenssisarjan suppenemissäde on. Suppenemisvälin päätepisteissä esimerkkien sarjat kuitenkin käyttäytyvät eri tavalla. Esimerkin 8.4 potenssisarja hajaantuu suppenemisvälin molemmissa päätepisteissä, esimerkin 8.5 sarja suppenee suppenemisvälin molemmissa päätepisteissä ja esimerkin 8.3 sarja suppenee toisessa päätepisteessä ja hajaantuu toisessa päätepisteessä. Jos potenssisarjan kertoimet ovat itseisarvoltaan pienempiä tai yhtäsuuria kuin jonkin toisen potenssisarjan kertoimet, niin potenssisarjojen suppenemissäteet ovat käänteisessä järjestyksessä. Tämä nähdään seuraavasta lauseesta. Lause 8.7. Olkoot R ja R 2 (järjestyksessä) potenssisarjojen ja b k (x c) k suppenemissäteet. Jos on olemassa sellainen k 0 N, että (8.) a k b k k > k 0, niin R R 2. Todistus. Olkoon x jokin välin ]c R 2, c + R 2 [ piste. Tällöin sarja b k (x c) k suppenee itseisesti. Ehdosta (8.) seuraa täten majoranttiperiaatteen nojalla, että myös sarja a k (x c) k suppenee itseisesti. Siis sarja n0 n0 suppenee kaikissa välin ]c R 2, c + R 2 [ pisteissä. Täten R R 2. 79
6 Esimerkki 8.8. Olkoon M > 0 ja m > 0. Tutkitaan potenssisarjan suppenemissädettä R. Esimerkin 8.4 (s. 76) perusteella potenssisarjat m(x c) k ja M(x c) k molemmat suppenevat täsmälleen silloin, kun x c <, joten kummankin sarjan suppenemissäde on yksi. Olkoon k 0 N. Lauseen 8.7 perusteella saadaan nyt seuraavat tulokset. (i) Jos a k M kaikilla k > k 0, niin R. (ii) Jos a k m kaikilla k > k 0, niin R. (iii) Jos m a k M kaikilla k > k 0, niin R. Seuraava lause antaa käyttökelpoisen ja usein helpon tavan määrittää potenssisarjan suppenemissäde. Lause 8.8. Jos a k lim k a k+ A (0 A < tai A ), niin potenssisarjan suppenemissäde R A. Todistus. Jos x c, niin tarkasteltava potenssisarja suppenee. Jos taas x c, niin a k+ (x c) k+ a (8.2) lim k lim k+ k a x c x c, k A joten sarjan suppenemista voidaan tutkia osamäärätarkastinta käyttäen. : Jos A 0 ja x c, niin raja-arvo (8.2) on ääretön. Täten sarja hajaantuu, kun x c. Siis R A ( 0). 2 : Jos A, niin raja-arvo (8.2) on nolla. Täten sarja suppenee kaikilla x R. Siis R A ( ). 80
7 3 : Jos 0 < A <, niin sarja suppenee, kun ja hajaantuu, kun Siis R A. x c < eli x c < A, A x c > eli x c > A. A Esimerkki 8.9. Määritetään potenssisarjan suppenemissäde R. Koska k + lim k (k + ) + (k + ) x k lim k k + k + 2, niin lauseen 8.8 nojalla R. Suppenemisvälin päätepisteissä x ± sarja hajaantuu hajaantumistarkastimen nojalla, joten sarja suppenee täsmälleen silloin, kun x <. Esimerkki 8.0. Määritetään potenssisarjan n suppenemissäde R. Kun n, niin n n / n! (n + ) n+ / (n + )! n n n! xn nn n! (n + )! (n + ) n+ nn (n + ) (n + ) n+ e. ( n ) n n + ( + n Täten R lauseen 8.8 nojalla. Sarja siis suppenee, kun x <, ja hajaantuu, e e kun x >. Suppenemissäde ei kuitenkaan kerro mitään sarjan suppenemisesta e pisteissä x ±, joten näissä pisteissä suppeneminen on tutkittava erikseen. e 8 ) n
8 Esimerkki 8.. Oletetaan, että n 2 a n n 4 kaikilla n Z +. Määritetään potenssisarjan a n x n suppenemissäde R. n Olkoot R 2 ja R 4 (järjestyksessä) potenssisarjojen n 2 x n n ja n 4 x n n suppenemissäteet. Koska n 2 a n n 4 kaikilla n Z +, niin lauseen 8.7 nojalla R 2 R R 4. Toisaalta lim n n 2 ja lim (n + ) 2 n n 4 (n + ) 4, joten lauseen 8.8 nojalla R 2 R 4. Siis R. 82
9 8.3 Potenssisarjan määrittelemä funktio Tutkitaan seuraavaksi potenssisarjan summafunktiota. Potenssisarjan suppenemisominaisuuksista seuraa, että potenssisarjan summafunktio on määritelty jollakin välillä (tai mahdollisesti vain yhdessä pisteessä). Luvussa 7 osoitettiin, että jos funktiosarja suppenee tasaisesti jollakin välillä, sarjan termien jatkuvuus ja integroituvuus periytyvät sarjan summafunktiolle. Siksi aloitetaan osoittamalla, että potenssisarja suppenee aina tasaisesti jokaisella suppenemisvälin suljetulla osavälillä. Seurauksena saadaan sitten välittömästi summafunktion jatkuvuutta ja integroituvuutta koskevat tulokset. Lause 8.9. Olkoon n0 potenssisarja, jonka suppenemissäde R > 0. Tällöin sarja suppenee tasaisesti jokaisella välillä I r [c r, c + r], missä 0 < r < R. Todistus. Koska ja sarja ak x c k a k r k x I r ja k N a k r k a k ((c + r) c) k suppenee (huomautus 8.6, s. 78), niin Weierstrassin M-testin (lause 7.4, s. 64) nojalla sarja suppenee tasaisesti välillä I r. Lause 8.0. Olkoon f(x) potenssisarja, jonka suppenemissäde R > 0. Tällöin sarja määrittelee koko suppenemisvälillä ]c R, c + R[ jatkuvan funktion f. Todistus. Sarjan termit ovat jatkuvia kaikilla x R ja kaikilla k N, joten lauseen 7.2 (s. 62) nojalla myös sarjan summafunktio f on jatkuva jokaisella lauseen 8.9 välillä I r. Koska r voi olla mielivaltaisen lähellä lukua R, summafunktio on jatkuva koko välillä ]c R, c + R[. 83
10 Lause 8.. Potenssisarja f(x) voidaan integroida termeittäin jokaisella sarjan suppenemisvälin ]c R, c + R[ (R > 0) suljetulla osavälillä [a, b] eli b a f(x) dx b dx. n0 a Todistus. Lauseen 8.9 nojalla sarja suppenee tasaisesti välillä [a, b]. Koska sarjan termit ovat lisäksi jatkuvia välillä [a, b], väite seuraa lauseesta 7.6 (s. 67). Koska potenssisarjan termit voidaan helposti integroida, lauseen 8. tulos saadaan muotoon b a f(x) dx n0 b a dx a k k + / b a (x c) k+ a ( k (b c) k+ (a c) k+). k + Valitsemalla yllä a c ja b x saadaan termeittäin integrointia koskevalle tulokselle seuraava muoto. Seuraus 8.2. Olkoon f(x) potenssisarja, jonka suppenemissäde R > 0. Jos x ]c R, c + R[, niin x c f(t) dt a k k + (x c)k+. 84
11 Esimerkki 8.2. Osoitetaan, että arc tan x Otetaan lähtökohdaksi potenssisarja ( ) k t 2k ( ) k 2k + x2k+ x [, ]. ( t 2 ) k + t 2, jonka suppenemisväli on geometrisena sarjana ], [. Täten lauseen 8. perusteella x 0 + t 2 dt x ( 0 ) ( ) k t 2k dt x 0 ( ) k 0 ( ) k t 2k dt / x t 2k+ 2k + kaikilla x ], [. Toisaalta ( ) k 2k + x2k+ kaikilla x R, joten x 0 arc tan x + t 2 dt / x 0 arc tan t arc tan x ( ) k 2k + x2k+ x ], [. Tutkimalla tasaista suppenemista (Leibnizin lause) hyödyntäen sarjan summafunktion jatkuvuutta voidaan osoittaa, että saatu tulos on voimassa myös pisteissä x ± (harjoitustehtävä). Täten arc tan x ( ) k 2k + x2k+ x [, ]. Tarkastellaan sitten potenssisarjojen derivointia termeittäin. Aluksi osoitetaan, että jos muodostetaan uusi sarja derivoimalla jonkin potenssisarjan termit, tuloksena on potenssisarja, jolla on sama suppenemissäde kuin alkuperäisellä potenssisarjalla. 85
12 Lause 8.3. Potenssisarjoilla on sama suppenemissäde. ja k k Todistus. Olkoot R ja R 2 (järjestyksessä) sarjojen suppenemissäteet. Koska ja k k a k ka k k Z +, niin lauseen 8.7 (s. 79) nojalla R R 2. Osoitetaan sitten, että R R 2. Olkoon 0 < r < R. Tällöin sarja suppenee pisteessä x c + r. Koska suppenevan sarjan termit ovat rajoitettuja, on olemassa sellainen M > 0, että a k r k ak ((c + r) c) k M k Z+ eli a k M r k k Z +. Siis k M k x c k rk kaikilla x R ja kaikilla k Z +. Edelleen sarja M k r x c r M k x c k M x c k k k r r r k r suppenee (esimerkki 8.9, s. 8) aina, kun x c < eli x c < r. r Täten sarja k k k suppenee majoranttiperiaatteen nojalla aina, kun x c < r. Siis sarja suppenee kaikilla x ]c r, c + r[, joten R 2 r. Koska r voidaan valita mielivaltaisen läheltä lukua R, niin R 2 R ja edelleen R R 2. 86
13 Seuraus 8.4. Jos sarja integroidaan termeittäin (yli välin [c, x]), niin saadulla sarjalla on sama suppenemissäde kuin alkuperäisellä sarjalla. Huomautus. Termeittäin derivoimalla tai integroimalla saadun sarjan suppenemisesta suppenemisvälin päätepisteissä c R ja c + R edellä olevat tulokset eivät kerro mitään. Lause 8.5. Potenssisarja voidaan derivoida termeittäin jokaisessa suppenemisvälinsä ]c R, c + R[ (R > 0) pisteessä eli (8.3) d dx k x ]c R, c + R[. k Todistus. Jokaisella välillä I r [c r, c + r], missä 0 < r < R, on voimassa : 2 : suppenee (sillä r < R), k suppenee tasaisesti (lause 8.3 ja lause 8.9), k 3 : termit (k N) ja k (k Z + ) ovat jatkuvia. Täten sarja voidaan lauseen 7.8 (s. 7) nojalla derivoida termeittäin ja yhtälö (8.3) on voimassa jokaisella välillä I r. Koska r voidaan valita mielivaltaisen läheltä lukua R, niin voidaan derivoida termeittäin koko välillä ]c R, c + R[ ja d dx k k kaikilla x ]c R, c + R[. 87
14 Esimerkki 8.3. Määritetään sarjan f(x) k x k k summa välillä ], [. Esimerkin 8.3 (s. 75) nojalla sarjan suppenemissäde R. Täten f (x) d dx k x k k k k x k k x k k x k x kaikilla x ], [. Koska myös D( log( x)) x, niin integraalilaskennan peruslauseen nojalla on olemassa sellainen C R, että f(x) log( x) + C kaikilla x ], [. Koska f(0) 0, niin C 0 ja kaikilla x ], [. f(x) log( x) Seuraus 8.6. Potenssisarjan summafunktiolla S(x) on sarjan suppenemisvälillä ]c R, c + R[ (R > 0) kaikkien kertalukujen derivaatat ja (8.4) S (n) (x) k (k ) (k (n )) a k (x c) k n kn kaikilla x ]c R, c + R[. Huomautus 8.7. Potenssisarjan S(x) summafunktion derivaatat S (n) (x) ovat sarjan suppenemisvälillä tietenkin myös jatkuvia. 88
15 Jos yhtälössä (8.4) erityisesti x c, niin summalausekkeen muut termit kuin k n ovat nollia. Täten S (n) (c) n (n ) (n (n )) a n n! a n eli a n n! S(n) (c) kaikilla n N. Siis S(x) S (k) (c) (x c) k x ]c R, c + R[. Näin on tullut todistetuksi seuraus 8.8. Seuraus 8.8. Jos funktio f voidaan esittää välillä ]c h, c + h[ (h > 0) potenssisarjana f(x), niin tämä esitys on yksikäsitteinen ja kaikilla k N. a k f (k) (c) Lause 8.9 (Yksikäsitteisyyslause). Jos jollakin välillä ]c h, c + h[ (h > 0) on voimassa b k (x c) k, niin a k b k kaikilla k N. Todistus. Jos potenssisarjojen yhteinen summafunktio välillä ]c h, c + h[ on S(x), niin seurauksen 8.8 nojalla kaikilla k N. a k S(k) (c) b k 89
16 8.4 Taylorin sarja Tähän asti funktiosarjoja tutkittaessa pääasiallisena tavoitteena on ollut määrittää sarjojen summafunktioita. Seuraavaksi tarkastellaan käänteistä tehtävää eli etsitään potenssisarjaa, jonka summafunktio on jokin haluttu funktio Taylorin polynomi Ennen varsinaista tarkastelua esitetään yksi käyttökelpoinen aputulos, jonka avulla pystytään mahdollisesti arvioimaan löydetyn potenssisarjan virhetermiä. Lause 8.20 (Taylorin lause). Jos funktio f ja sen derivaatat f, f,..., f (n) ovat jatkuvia välillä [a, b] ja derivaatta f (n+) on olemassa välillä ]a, b[, niin on olemassa sellainen ξ ]a, b[, että f(b) n f (k) (a) (b a) k + f (n+) (ξ) (n + )! (b a)n+. Todistus. Merkitään ja jolloin F (x) F (x) d ( f(x) + dx f (x) + n f (k) (x) g(x) (b x) n+, n k f (k) (x) ( n f (k+) (x) k (b x) k (b x) k ) (b x) k f (k) ) (x) (b x)k (k )! ja f (n+) (x) n! (b x) n g (x) (n + )(b x) n. Lauseen oletusten nojalla funktiot g(x) ja F (x) ovat jatkuvia välillä [a, b] ja derivoituvia välillä ]a, b[. Täten (differentiaalilaskennan) yleistetyn väliarvolauseen nojalla on olemassa sellainen ξ ]a, b[, että (8.5) F (ξ)[g(b) g(a)] g (ξ)[f (b) F (a)] 90
17 eli Siis f (n+) (ξ) n! sekä edelleen ja Koska F (b) f(b), ja niin (b ξ) n [g(b) g(a)] (n + )(b ξ) n [F (b) F (a)]. f (n+) (ξ) n! f (n+) (ξ) (n + )! [g(b) g(a)] (n + ) [F (b) F (a)] [g(b) g(a)] [F (b) F (a)] F (b) F (a) + f (n+) (ξ) (n + )! F (a) n f (k) (a) [g(a) g(b)]. (b a) k g(a) g(b) (b a) n+ 0 (b a) n+, f(b) n f (k) (a) (b a) k + f (n+) (ξ) (n + )! (b a)n+. Jos b < a ja Taylorin lauseen oletukset ovat voimassa väleillä [b, a] ja ]b, a[, niin Taylorin lauseen todistuksessa ξ ]b, a[ ja yhtälö (8.5) korvautuu yhtälöllä F (ξ)[g(a) g(b)] g (ξ)[f (a) F (b)], joka on yhtäpitävä yhtälön (8.5) kanssa. Täten voidaan esittää seuraava huomautus. Huomautus 8.2. Taylorin lause on voimassa myös, kun b < a. Tällöin tietysti ξ ]b, a[ ja lauseen oletuksia on tarkasteltava väleillä [b, a] ja ]b, a[. Taylorin lauseen oletuksia tarkasteltaessa havaitaan, että jos derivaatta f (n) (n Z + ) on jatkuva välillä [a, b], myös derivaatat f, f,..., f (n ) ovat jatkuvia välillä [a, b]. Muutenhan derivaattaa f (n) ei voitaisi muodostaa. Täten olisi riittänyt olettaa pelkästään derivaatan f (n) jatkuvuus. Jos vastaavasti derivaatta f (n+) on olemassa jollakin välillä I, niin derivaattojen f, f,..., f (n) on oltava jatkuvia välillä I. Näin ollen voidaan esittää seuraava Taylorin lauseen seuraus. 9
18 Seuraus Jos funktio f on n+ kertaa derivoituva pisteen c jossakin ympäristössä I ja x I (x c), niin on olemassa sellainen ξ ]c, x[ (tai ξ ]x, c[, jos x < c), että (8.6) f(x) n f (k) (c) (x c) k + f (n+) (ξ) (n + )! (x c)n+. Todistus. Sovelletaan Taylorin lausetta välillä [c, x] (tai [x, c]). Huomautus Jos x c, niin yhtälö (8.6) on voimassa kaikilla luvun ξ arvoilla, sillä n f (k) (c) (c c) k + f (n+) (ξ) (n + )! (c c)n+ f (0) (c) 0! + 0 f(c). Määritelmä 8.3. Yhtälössä (8.6) esiintyvää summaa T n (x) n f (k) (c) (x c) k kutsutaan funktion f(x) Taylorin polynomiksi pisteessä c. Jos erityisesti c 0, niin polynomia kutsutaan funktion f(x) Maclaurinin polynomiksi. Taylorin polynomia käyttäen seuraukselle 8.22 saadaan jonkin verran selkeämpi esitysmuoto. Huomautus Jos funktio f on n+ kertaa derivoituva pisteen c jossakin ympäristössä I ja x I (x c), niin on olemassa sellainen ξ ]c, x[ (tai ξ ]x, c[, jos x < c), että f(x) T n (x) + R n (x), missä R n (x) f (n+) (ξ) (n + )! (x c)n+. Taylorin lauseessa arvio jäännöstermille saatiin differentiaalilaskennan yleistettyä väliarvolausetta käyttäen. Käyttämällä osittaisintegrointia voidaan helposti todistaa (induktiolla, harjoitustehtävä) Taylorin lauseen jäännöstermille täsmällinen esitys ( huomautus 8.25). Tällöin on oletettava myös derivaatan f (n+) jatkuvuus. 92
19 Huomautus Jos funktio f ja sen derivaatat f, f,...,f (n+) ovat jatkuvia pisteen c jossakin ympäristössä I ja x I, niin f(x) T n (x) + R n (x), missä R n (x) n! x c f (n+) (t) (x t) n dt. Esimerkki 8.4. Muodostetaan funktion f(x) log( + x) Taylorin polynomi pisteessä c 0 (eli funktion Maclaurinin polynomi). Funktiolla f(x) log( + x) on selvästi kaikkien kertalukujen (jatkuvat) derivaatat, kun x >. Olkoon siis x >. Derivoimalla funktio muutamia kertoja havaitaan, että f (x) + x ( + x), f (x) ( ) ( + x) 2, f (x) ( )( 2) ( + x) 3, f (4) (x) ( )( 2)( 3) ( + x) 4, Induktiolla voidaan nyt helposti todistaa, että joten. f (k) (x) ( ) k (k )! ( + x) k ( )k (k )! ( + x) k k, f (k) (0) ( ) k (k )! k. Koska f(0) 0, niin funktion f Maclaurinin polynomi on T n (x) n f (k) (0) x k n k ( ) k (k )! x k n ( ) k x k k k kaikilla n N. Jos n 0, niin yllä T 0 (x) 0. Lisäksi huomautuksien 8.25 ja 8.24 nojalla (x >, n N) log( + x) T n (x) + R n (x), 93
20 missä R n (x) n! n! x 0 x 0 f (n+) (t) (x t) n dt ( ) n n! ( + t) n+ (x t)n dt x ( ) n (x t) n dt ( + t) n+ 0 tai (jos x 0) R n (x) f (n+) (ξ) (n + )! xn+ ( ) n (n + ) ( + ξ) n+ xn+, missä ξ ]0, x[ (tai ξ ]x, 0[, jos x < 0) Taylorin sarja Tarkastellaan sitten varsinaista tehtävää eli etsitään potenssisarjaa, jonka summafunktio on haluttu funktio f. Lähtökohdan tarjoaa seuraus 8.8 (s. 89), sillä jos funktiolla f(x) on välillä ]c h, c + h[ (h > 0) potenssisarjakehitelmä niin seurauksen 8.8 nojalla Siis etsitty potenssisarja on f(x) a k, f (k) (c). (8.7) f (k) (c) (x c) k. Määritelmä 8.4. Sarjaa (8.7) kutsutaan funktion f(x) Taylorin sarjaksi (tai sarjakehitelmäksi) pisteessä c. Jos Taylorin sarjassa c 0, niin sarjaa kutsutaan funktion f(x) Maclaurinin sarjaksi. 94
21 Funktion f(x) Taylorin sarja voidaan muodostaa pisteessä c silloin, kun f (k) (c) on olemassa kaikilla k N eli funktiolla f on pisteessä c kaikkien kertalukujen derivaatat. Tällöin derivaatat f (k) (x) ovat olemassa (ja ne ovat jatkuvia) myös jollakin välillä ]c h, c + h[ (h > 0), sillä f (k+) (c) voidaan muodostaa vain, jos derivaatta f (k) (c) on määritelty pisteen c jossakin ympäristössä. Funktion f(x) pisteessä c muodostetun Taylorin sarjan summa ei välttämättä ole f(x) kaikilla x R. Ensinnäkin sarja voi hajaantua muuttujan x joillakin arvoilla. Toisaalta on mahdollista, että vaikka sarja suppenee jollakin välillä I, niin sarjan summa ei ole f(x) välillä I (ks. esimerkki 8.23, s. 20). Pisteessä x c sarjan summa on aina f(c), sillä f (k) (c) (c c) k f (0) (c) 0! f(c), mutta yleisesti Taylorin sarjan summa on f(x) vain, kun sarjan osasumma eli vastaava Taylorin polynomi T n (x) lähestyy arvoa f(x), kun n. Toisin sanoen jos funktion f Taylorin sarja voidaan muodostaa pisteessä c, niin f(x) f (k) (c) (x c) k täsmälleen silloin, kun lim T n(x) f(x) eli lim R n (x) 0, n n missä R n (x) on huomautuksissa 8.24 ja 8.25 esiintyvä Taylorin polynomia T n (x) vastaava jäännöstermi. Esitetään asia vielä täsmällisesti lauseen muodossa. Lause Oletetaan, että funktiolla f on kaikkien kertalukujen derivaatat pisteessä c. Tällöin f (k) (c) f(x) (x c) k täsmälleen silloin, kun lim R n(x) 0, n missä R n (x) on huomautuksissa 8.24 ja 8.25 esiintyvä Taylorin polynomia T n (x) vastaava jäännöstermi. Jos funktion f Taylorin sarjan summa pisteessä x on f(x), sanotaan, että sarja esittää funktiota f pisteessä x. Taylorin sarjan voimassaoloalue on niiden pisteiden joukko, joissa sarja esittää funktiota f. 95
22 Esimerkki 8.5. Muodostetaan funktion f(x) sin x Maclaurinin sarja, ja osoitetaan, että sarja esittää funktiota sin x kaikilla x R (eli sarjan voimassaoloalue on koko reaalilukujen joukko). Induktiolla voidaan helposti todistaa, että f (2k) (x) ( ) k sin x ja f (2k+) (x) ( ) k cos x kaikilla k N ja kaikilla x R. Täten kaikilla k N. Siis f (2k) (0) 0 ja f (2k+) (0) ( ) k f (k) (0) x k ( ) k (2k + )! x2k+ on funktion f(x) sin x Maclaurinin sarja. Osoitetaan vielä, että tämän sarjan summa on sin x kaikilla x R. Jos x 0, niin sekä sarjan summa että sinin arvo ovat nollia, joten sarja esittää funktiota sin x. Olkoon sitten x 0. Taylorin lauseen (huomautus 8.24) nojalla sin x T n (x) + R n (x), missä T n (x) on funktion sin x Maclaurinin polynomi (n N) ja R n (x) f (n+) (ξ) (n + )! xn+ (ξ ]0, x[ tai ξ ]x, 0[ ). Nyt kaikilla n N ja joten Siis lauseen 8.26 nojalla R n (x) f (n+) (ξ) (n + )! xn+ lim n x n+ (n + )! 0, lim R n(x) 0. n x n+ (n + )! eli sin x ( ) k (2k + )! x2k+ x R sin x x x3 3! + x5 x R. 5! 96
23 Taylorin lauseen vaatima funktion derivaattojen laskeminen ja jäännöstermitarkastelu on usein työlästä. Seuraava jo aluksi esitetty huomio tarjoaa mahdollisuuden käyttää Taylorin lauseen sijasta jo aiemmin muodostettuja potenssisarjoja. Huomautus Jos funktiolla f(x) on välillä ]c h, c + h[ (h > 0) potenssisarjakehitelmä (8.8) f(x), niin seurauksen 8.8 (s. 89) nojalla tämä sarja on funktion f(x) Taylorin sarja pisteessä c. Huomautuksen 8.27 Taylorin sarjan voimassaoloalue on vähintään huomautuksen väli ]c h, c + h[, mutta voimassaoloalue voi olla laajempikin. Voimassaoloalue sisältää esimerkiksi kaikki ne väliin ]c h, c + h[ kuulumattomat pisteet x, joille on jo osoitettu, että ehto (8.8) on voimassa. Tällöinhän muodostettu Taylorin sarja esittää funktiota f(x) myös pisteessä x. Tällainen tilanne voi esiintyä esimerkiksi, jos ]c h, c + h[ on tarkasteltavan Taylorin sarjan suppenemisväli ja väliin kuulumaton piste on suppenemisvälin päätepiste. Aiemmin muodostettuja potenssisarjoja voidaan nyt yrittää hyödyntää joko suoraan tai muokkaamalla niitä sopivasti. Jos on aiemmin osoitettu, että jonkin oikeaa muotoa olevan potenssisarjan summa on jossakin pisteen c ympäristössä funktio, jonka Taylorin sarjaa etsitään, niin tehtävä on sarjan muodostamisen osalta jo suoritettu. Jäljellä on mahdollisesti vielä sarjan voimassaoloalueen määrittäminen, jos voimassaoloalue ei selviä aiemman tarkastelun perusteella. Jos toisaalta edellä mainittua potenssisarjaa ei ole tiedossa, voidaan yrittää muokata tunnettuja potenssisarjoja siten, että uuden sarjan summa on haluttu funktio. Mahdollisia tapoja ovat esimerkiksi sarjojen derivointi ja integrointi, sarjojen kertominen keskenään, funktioiden sijoittaminen sarjoihin muuttujan x tilalle tai sopivien (esimerkiksi trigonometristen) kaavojen käyttö. Lähtökohdan tarjoaa esimerkiksi geometrinen sarja joka potenssisarjana on funktion Maclaurinin sarja välillä ], [. x k x, f(x) x 97
24 Esimerkki 8.6. Muodostetaan funktion f(x) log( + x) Maclaurinin sarja, ja osoitetaan, että sarja esittää funktiota log( + x) kaikilla x ], ]. Esimerkissä 7.3 (s. 69) osoitettiin geometrista sarjaa integroimalla, että (8.9) log( + x) ( ) k x k x ], [. k k Täten funktiolla f(x) log( + x) on Maclaurinin sarja ainakin välillä ], [. Osoitetaan vielä, että yhtälö (8.9) pätee myös, kun x. Esimerkin 8.4 perusteella kaikilla n N on olemassa sellainen ξ ]0, [, että f() T n () + R n (), missä T n () on funktion log( + x) Maclaurinin polynomi ja Täten kaikilla n N. Koska niin myös Siis lauseen 8.26 nojalla R n () f (n+) (ξ) (n + )! n+ R n () ( ) n (n + ) ( + ξ) n+. (n + )( + ξ) n+ n + lim n n + 0, lim R n() 0. n log( + x) ( ) k x k x ], ]. k k Jos x > tai x, niin sarja ( ) k x k k k hajaantuu (harjoitustehtävä). Täten sarjan summa ei voi olla log(+x) (ja log(+x) ei edes ole määritelty, kun x ). Siis funktio log(+x) voidaan esittää Maclaurin sarjana ainoastaan välillä ], ], jolloin log( + x) k ( ) k k x k x x2 2 + x3 3 x
25 Esimerkki 8.7. Määritetään kosinin Maclaurinin sarja ja sarjan voimassaoloalue. Kosinin Maclaurinin sarja voidaan tietysti määrittää vastaavasti kuin sinin Maclaurinin sarja esimerkissä 8.5. Menetellään nyt kuitenkin toisin ja hyödynnetään esimerkissä 8.5 muodostettua sarjaa sin x ( ) k (2k + )! x2k+ x R. Koska tämä sarja voidaan potenssisarjana derivoida termeittäin, niin cos x D(sin x) D ( ( ) k ) (2k + )! x2k+ ( ) k (2k + )! D(x2k+ ) ( ) k (2k + ) x2k (2k + )! ( ) k (2k)! x2k kaikilla x R. Siis funktion cos x Maclaurinin sarja on cos x ( ) k (2k)! x2k x2 2! + x4 4! x6 + x R. 6! Esimerkki 8.8. Esimerkissä 8.2 (s. 85) osoitettiin geometrista sarjaa integroimalla, että arc tan x ( ) k 2k + x2k+ x x3 3 + x5 x [, ]. 5 Huomautuksen 8.27 nojalla kyseinen sarja on funktion arc tan x Maclaurinin sarja välillä [, ]. Jos x >, niin sarja hajaantuu (esimerkki 8.5, s. 76), joten sarjan summa ei tietenkään ole arc tan x (eli sarja ei esitä funktiota arc tan x). Esimerkki 8.9. Esimerkissä 7.5 (s. 73) osoitettiin, että e x x k xk x R. Huomautuksen 8.27 nojalla kyseinen sarja on funktion e x Maclaurinin sarja (kaikilla x R). 99
26 Esimerkki Määritetään funktion a x (a > 0) Maclaurinin sarja ja sarjan voimassaoloalue. Esimerkin 8.9 perusteella a x e x log a (x log a) k (log a) k x k x R, joten huomautuksen 8.27 nojalla a x (log a) k x k x R. Esimerkki 8.2. Määritetään funktion f(x) e 3x+ Maclaurinin sarja ja sarjan voimassaoloalue. Esimerkin 8.9 perusteella e 3x+ e e 3x (3x) k e e3 k x k x R. Esimerkki Määritetään funktion e x, kun x 0, f(x) x, kun x 0, Maclaurinin sarja ja sarjan voimassaoloalue. Esimerkin 8.9 perusteella e x x k k x k x R, joten Lisäksi e x x x k 0 k (k + )! x k k x k x k (k + )! + 0 2! + 0 3! + f(0), x 0. joten sarja esittää funktiota f(x) myös pisteessä x 0. Täten huomautuksen 8.27 nojalla f(x) (k + )! xk x R. 200
27 Esimerkki Olkoon e x f(x) 2, kun x 0, 0, kun x 0. Voidaan suhteellisen helposti osoittaa, että f (n) (0) 0 kaikilla n N (harjoitustehtävä). Täten funktion f(x) Maclaurinin sarja on n0 f (n) (0) n! x n n0 0 n! xn 0 0 x R. n0 Sarja tietenkin suppenee kaikilla x R mutta antaa funktion f(x) arvon vain pisteessä x Sovelluksia Taylorin sarjaa voidaan käyttää esimerkiksi funktion raja-arvon ja ääriarvon määrittämiseen (korvaamalla funktio Taylorin sarjallaan), derivaattojen määrittämiseen pisteessä c sekä yleensäkin erilaisiin likiarvotehtäviin. Esimerkki Määritetään derivaatta f (n) (0), kun e x, kun x 0, f(x) x, kun x 0. Esimerkin 8.22 nojalla f(x) n0 (n + )! xn x R. Täten seurauksen 8.8 (s. 89) nojalla f (n) (0) n! (n + )! n N ja edelleen Siis esimerkiksi f (n) (0) n + f (204) (0) 205. n N. 20
28 Esimerkki Määritetään raja-arvo lim x 0 e x x x2 x x 3 arc tan x Tehtävä voidaan ratkaista käyttämällä neljä kertaa l Hospitalin sääntöä, mutta tällöin joudutaan kohtuullisen mutkikkaisiin derivointeihin. Määritetään raja-arvo nyt l Hospitalin säännnön sijasta käyttämällä funktioiden potenssisarjaesityksiä. Esimerkin 8.9 nojalla joten e x + x + x2 2! + x3 3! + x4 4! + x5 5! + x6 + x R, 6! e x x x2 2 x3 6 x4 4! + x5 5! + x6 6! + ( x 4 4! + x ) 5! + x2 6! + kaikilla x R. Esimerkin 8.8 nojalla taas joten arc tan x x x3 3 + x5 x [, ], 5 ( ) x 3 arc tan x x 3 x x3 3 + x5 5 ( ) x 4 x2 3 + x4 5 kaikilla x [, ]. Jos siis 0 < x, niin e x x x2 x3 2 6 x 3 arc tan x ( x4 + x + x2 + ) 4! 5! 6! ( x 4 x 2 + x4 ) x + x2 + 4! 5! 6! x2 + x4, 3 5 josta nähdään suoraan, että lim x 0 e x x x2 x3 2 6 x 3 arc tan x 4!
29 Esimerkki Määritetään integraalille 0 e x2 dx sellainen likiarvo, että virhe on korkeintaan 0 2. Esimerkin 8.9 perusteella ( x 2 ) k e x2 ( ) k x 2k x R. Potenssisarjana sarja voidaan integroida termeittäin, joten 0 e x2 dx ( 0 ( ) k ) x 2k dx ( ) k x 2k dx 0 / 0 ( ) k (2k + ) x2k+ ( ) k (2k + ). Tulokseksi saatu sarja toteuttaa selvästi Leibnizin lauseen ehdot, joten sarja suppenee ja jäännöstermille saadaan arvio R n (2(n + ) + )(n + )! (2n + 3)(n + )! kaikilla n N. Virheelle asettu vaatimus toteutuu nyt, jos eli (2n + 3)(n + )! 0 2 (2n + 3)(n + )! 00. Pienin epäyhtälön toteuttava kokonaisluku on 3, joten esimerkiksi 0 e x2 dx 3 tuottaa halutun tarkkkuuden. ( ) k (2k + )
30 Esimerkki Arvioidaan funktiota f(x) sin x välillä [0, π 4 ] tarkkuudella 0 4. Esimerkissä 8.5 osoitettiin, että sin x T n (x) + R n (x), missä T n (x) on funktion sin x Maclaurinin polynomi (n N) ja R n (x) x n+ (n + )! kaikilla x R ja kaikilla n N. Välillä [0, π ] tarvittavaksi ehdoksi tulee täten 4 joka toteutuu, kun n 6. ( ) π n+ < 0 4, (n + )! 4 Siis riittävän tarkka tulos saadaan, kun valitaan arvioksi esimerkiksi T 6 (x). Täten kaikilla x [0, π ] on voimassa arvio 4 missä δ < 0 4. sin x T 6 (x) + R 6 (x) x x3 3! + x5 5! δ, 204
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
Funktiojonot ja funktiotermiset sarjat Funktiojono ja funktioterminen sarja Pisteittäinen ja tasainen suppeneminen
 4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
V. POTENSSISARJAT. V.1. Abelin lause ja potenssisarjan suppenemisväli. a k (x x 0 ) k M
 V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Luku 4. Derivoituvien funktioiden ominaisuuksia.
 1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
Kompleksianalyysi, viikko 5
 Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
MS-A0104 Differentiaali- ja integraalilaskenta 1 (ELEC2) MS-A0106 Differentiaali- ja integraalilaskenta 1 (ENG2)
 MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Tenttiin valmentavia harjoituksia
 Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
funktiojono. Funktiosarja f k a k (x x 0 ) k
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
VI. TAYLORIN KAAVA JA SARJAT. VI.1. Taylorin polynomi ja Taylorin kaava
 VI. TAYLORIN KAAVA JA SARJAT VI.. Taylorin polynomi ja Taylorin kaava Olkoon n N ja x, c, c, c 2,..., c n R. Tehtävä: Etsittävä sellainen R-kertoiminen polynomi P, että sen aste deg P n ja P (x ) = c,
VI. TAYLORIN KAAVA JA SARJAT VI.. Taylorin polynomi ja Taylorin kaava Olkoon n N ja x, c, c, c 2,..., c n R. Tehtävä: Etsittävä sellainen R-kertoiminen polynomi P, että sen aste deg P n ja P (x ) = c,
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
Sarja. Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,...,
 Sarja Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): Määritelmä 1 s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,..., n s n = a k. Jos osasummien jonolla (s n ) on raja-arvo s R,
Sarja Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): Määritelmä 1 s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,..., n s n = a k. Jos osasummien jonolla (s n ) on raja-arvo s R,
Taylorin sarja ja Taylorin polynomi
 Taylorin sarja ja 1 Potenssisarja c k (x a) k = f (x) määrittelee x:n funktion. Seuraavaksi toteamme mikä yhteys potenssisarjalla on sen määrittelemän funktion derivaattoihin f (a),f (a),f (a),f (3) (a),...
Taylorin sarja ja 1 Potenssisarja c k (x a) k = f (x) määrittelee x:n funktion. Seuraavaksi toteamme mikä yhteys potenssisarjalla on sen määrittelemän funktion derivaattoihin f (a),f (a),f (a),f (3) (a),...
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
Analyysi III. Jari Taskinen. 28. syyskuuta Luku 1
 Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
Analyysi 1. Harjoituksia lukuihin 4 7 / Syksy Tutki funktion f(x) = x 2 + x 2 jatkuvuutta pisteissä x = 0 ja x = 1.
 Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 2 Funktion derivaatta 2.1 Määritelmiä ja perusominaisuuksia 1. Määritä suoraan derivaatan määritelmää käyttäen f (0), kun (a) + 1, (b) (2 + ) sin(3). 2. Olkoon
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 2 Funktion derivaatta 2.1 Määritelmiä ja perusominaisuuksia 1. Määritä suoraan derivaatan määritelmää käyttäen f (0), kun (a) + 1, (b) (2 + ) sin(3). 2. Olkoon
(b) = x cos x 1 ( cos x)dx. = x cos x + cos xdx. = sin x x cos x + C, C R.
 Calculus Kurssikoe..7. Laske (a) x sin x, (b) x x + x. (a) Merkitään u(x) = x ja v (x) = sin x, jolloin u (x) =, v(x) = cos x ja osittaisintegroimalla saadaan x sin x = u(x)v (x) = u(x)v(x) u (x)v(x) =
Calculus Kurssikoe..7. Laske (a) x sin x, (b) x x + x. (a) Merkitään u(x) = x ja v (x) = sin x, jolloin u (x) =, v(x) = cos x ja osittaisintegroimalla saadaan x sin x = u(x)v (x) = u(x)v(x) u (x)v(x) =
Derivaattaluvut ja Dini derivaatat
 Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012
 KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
Positiivitermisten sarjojen suppeneminen
 Positiivitermisten sarjojen suppeneminen Jono (b n ) n= on kasvava, jos b n+ b n kaikilla n =, 2,... Lemma Jokainen ylhäältä rajoitettu kasvava jono (b n ) n= raja-arvo on lim n b n = sup n Z+ b n. suppenee
Positiivitermisten sarjojen suppeneminen Jono (b n ) n= on kasvava, jos b n+ b n kaikilla n =, 2,... Lemma Jokainen ylhäältä rajoitettu kasvava jono (b n ) n= raja-arvo on lim n b n = sup n Z+ b n. suppenee
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 14.9.2016 Pekka Alestalo, Jarmo Malinen
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 14.9.2016 Pekka Alestalo, Jarmo Malinen
2 Taylor-polynomit ja -sarjat
 2 Taylor-polynomit ja -sarjat 2. Taylor-polynomi Taylor-polynomi P n (x; x 0 ) funtion paras n-asteinen polynomiapprosimaatio (derivoinnin annalta) pisteen x 0 lähellä. Maclaurin-polynomi: tapaus x 0 0.
2 Taylor-polynomit ja -sarjat 2. Taylor-polynomi Taylor-polynomi P n (x; x 0 ) funtion paras n-asteinen polynomiapprosimaatio (derivoinnin annalta) pisteen x 0 lähellä. Maclaurin-polynomi: tapaus x 0 0.
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos September 13, 2017 Pekka Alestalo,
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos September 13, 2017 Pekka Alestalo,
MS-A010{2,3,4,5} (SCI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat
 M-A010{2,3,4,5} (CI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: arjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos eptember 12, 2018 Pekka
M-A010{2,3,4,5} (CI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: arjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos eptember 12, 2018 Pekka
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausta 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat: 1. Potenssisarjojen suppenemissäe, suppenemisväli ja suppenemisjoukko. 2. Derivaatan laskeminen
Matematiikan tukikurssi Kertausta 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat: 1. Potenssisarjojen suppenemissäe, suppenemisväli ja suppenemisjoukko. 2. Derivaatan laskeminen
Vastausehdotukset analyysin sivuainekurssin syksyn välikokeeseen
 Vastausehdotukset analyysin sivuainekurssin syksyn 015 1. välikokeeseen Heikki Korpela November 1, 015 1. Tehtävä: funktio f : R R toteuttaa ehdot ax, kun x 1 f(x) x + 1, kun x < 1 Tutki, millä vakion
Vastausehdotukset analyysin sivuainekurssin syksyn 015 1. välikokeeseen Heikki Korpela November 1, 015 1. Tehtävä: funktio f : R R toteuttaa ehdot ax, kun x 1 f(x) x + 1, kun x < 1 Tutki, millä vakion
5 Funktion jatkuvuus ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT Määritelmä ja perustuloksia
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 5 Funktion jatkuvuus 5.1 Määritelmä ja perustuloksia 1. Tarkastellaan väitettä a > 0: b > 0: c > 0: d U c (a): f(d) / U b (f(a)), missä a, b, c, d R. Mitä funktion
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 5 Funktion jatkuvuus 5.1 Määritelmä ja perustuloksia 1. Tarkastellaan väitettä a > 0: b > 0: c > 0: d U c (a): f(d) / U b (f(a)), missä a, b, c, d R. Mitä funktion
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Potenssisarja, suppenemissäde. Potenssisarja ja derivointi. Potenssisarja ja analyyttiset funktiot. Potenssisarja ja integrointi.
 Matematiikan peruskurssi KP3 I OSA 4: Taylorin sarja, residymenetelmä A.Rasila J.v.Pfaler 26. syyskuuta 2007 Kompleksista sarjoista Jono, suppeneminen, summasarja Potenssisarja, suppenemissäde ja analyyttiset
Matematiikan peruskurssi KP3 I OSA 4: Taylorin sarja, residymenetelmä A.Rasila J.v.Pfaler 26. syyskuuta 2007 Kompleksista sarjoista Jono, suppeneminen, summasarja Potenssisarja, suppenemissäde ja analyyttiset
5 Funktion jatkuvuus ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT Määritelmä ja perustuloksia. 1. Tarkastellaan väitettä
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 5 Funktion jatkuvuus 5.1 Määritelmä ja perustuloksia 1. Tarkastellaan väitettä a > 0: b > 0: c > 0: d U c (a): f(d) / U b (f(a)), missä a, b, c, d R. Mitä funktion
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 5 Funktion jatkuvuus 5.1 Määritelmä ja perustuloksia 1. Tarkastellaan väitettä a > 0: b > 0: c > 0: d U c (a): f(d) / U b (f(a)), missä a, b, c, d R. Mitä funktion
Sisältö. Sarjat 10. syyskuuta 2005 sivu 1 / 17
 Sarjat 10. syyskuuta 2005 sivu 1 / 17 Sisältö 1 Peruskäsitteistöä 2 1.1 Määritelmiä 2 1.2 Perustuloksia 4 2 Suppenemistestejä positiivitermisille sarjoille 5 3 Itseinen ja ehdollinen suppeneminen 8 4 Alternoivat
Sarjat 10. syyskuuta 2005 sivu 1 / 17 Sisältö 1 Peruskäsitteistöä 2 1.1 Määritelmiä 2 1.2 Perustuloksia 4 2 Suppenemistestejä positiivitermisille sarjoille 5 3 Itseinen ja ehdollinen suppeneminen 8 4 Alternoivat
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
Perusidea: Jaetaan väli [a, b] osaväleihin ja muodostetaan osavälejä vastaavat suorakulmiot/palkit, joiden korkeus funktion arvot kyseisellä välillä.
![Perusidea: Jaetaan väli [a, b] osaväleihin ja muodostetaan osavälejä vastaavat suorakulmiot/palkit, joiden korkeus funktion arvot kyseisellä välillä. Perusidea: Jaetaan väli [a, b] osaväleihin ja muodostetaan osavälejä vastaavat suorakulmiot/palkit, joiden korkeus funktion arvot kyseisellä välillä.](/thumbs/96/129910971.jpg) Lähtötilanne Lähtötilanne Tavoite: Määritellään funktion f : [a, b] R integraali siten, että integraalin arvo yhtyy funktion f kuvaajan ja x-akselin väliin jäävän alueen pinta-alaan. Perusidea: Jaetaan
Lähtötilanne Lähtötilanne Tavoite: Määritellään funktion f : [a, b] R integraali siten, että integraalin arvo yhtyy funktion f kuvaajan ja x-akselin väliin jäävän alueen pinta-alaan. Perusidea: Jaetaan
Johdantoa INTEGRAALILASKENTA, MAA9
 Lyhyehkö johdanto integraalilaskentaan. Johdantoa INTEGRAALILASKENTA, MAA9 Integraalilaskennan lähtökohta 1: Laskutoimitukset + ja ovat keskenään käänteisiä, samoin ja ovat käänteisiä, kunhan ei jaeta
Lyhyehkö johdanto integraalilaskentaan. Johdantoa INTEGRAALILASKENTA, MAA9 Integraalilaskennan lähtökohta 1: Laskutoimitukset + ja ovat keskenään käänteisiä, samoin ja ovat käänteisiä, kunhan ei jaeta
Matematiikan tukikurssi: kurssikerta 12
 Matematiikan tukikurssi: kurssikerta 2 Tenttiin valmentavia harjoituksia Huomio. Tähän tulee lisää ratkaisuja sitä mukaan kun ehin niitä kirjoittaa. Kurssilla käyään läpi tehtävistä niin monta kuin mahollista.
Matematiikan tukikurssi: kurssikerta 2 Tenttiin valmentavia harjoituksia Huomio. Tähän tulee lisää ratkaisuja sitä mukaan kun ehin niitä kirjoittaa. Kurssilla käyään läpi tehtävistä niin monta kuin mahollista.
ANALYYSI 3. Tero Kilpeläinen
 ANALYYSI 3 Tero Kilpeläinen Luentomuistiinpanoja syksyltä 2005 14. helmikuuta 2014 Sisältö 1. Esitietoja 2 1.1. Riemann-integraali............................ 2 1.2. Derivaatta.................................
ANALYYSI 3 Tero Kilpeläinen Luentomuistiinpanoja syksyltä 2005 14. helmikuuta 2014 Sisältö 1. Esitietoja 2 1.1. Riemann-integraali............................ 2 1.2. Derivaatta.................................
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
nyky-ymmärryksemme mukaan hajaantuvaan sarjaan luvun 1 2 kun n > N Huom! Määritelmä on aivan sama C:ssä ja R:ssä. (Kuva vain on erilainen.
 Sarjaoppia Käsitellään kompleksi- ja reaalisarjat yhdessä. Reaalilukujen ominaisuuksista (kuten järjestys) riippuvat asiat tulevat lisämausteena mukaan. Kirjallisuutta: 1. [KRE] Kreyszig: Advanced Engineering
Sarjaoppia Käsitellään kompleksi- ja reaalisarjat yhdessä. Reaalilukujen ominaisuuksista (kuten järjestys) riippuvat asiat tulevat lisämausteena mukaan. Kirjallisuutta: 1. [KRE] Kreyszig: Advanced Engineering
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
Matematiikan tukikurssi, kurssikerta 5
 Matematiikan tukikurssi, kurssikerta 5 1 Jonoista Matematiikassa jono (x n ) on yksinkertaisesti järjestetty, päättymätön sarja numeroita Esimerkiksi (1,, 3, 4, 5 ) on jono Jonon i:ttä jäsentä merkitään
Matematiikan tukikurssi, kurssikerta 5 1 Jonoista Matematiikassa jono (x n ) on yksinkertaisesti järjestetty, päättymätön sarja numeroita Esimerkiksi (1,, 3, 4, 5 ) on jono Jonon i:ttä jäsentä merkitään
Sarjojen suppenemisesta
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Terhi Mattila Sarjojen suppenemisesta Matematiikan ja tilastotieteen laitos Matematiikka Huhtikuu 008 Tampereen yliopisto Matematiikan ja tilastotieteen laitos
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Terhi Mattila Sarjojen suppenemisesta Matematiikan ja tilastotieteen laitos Matematiikka Huhtikuu 008 Tampereen yliopisto Matematiikan ja tilastotieteen laitos
1 Reaaliset lukujonot
 Jonot 10. syyskuuta 2005 sivu 1 / 5 1 Reaaliset lukujonot Reaaliset lukujonot ovat funktioita f : Z + R. Lukujonosta käytetään merkintää (a k ) k=1 tai lyhyemmin vain (a k). missä a k = f(k). Täten lukujonot
Jonot 10. syyskuuta 2005 sivu 1 / 5 1 Reaaliset lukujonot Reaaliset lukujonot ovat funktioita f : Z + R. Lukujonosta käytetään merkintää (a k ) k=1 tai lyhyemmin vain (a k). missä a k = f(k). Täten lukujonot
H7 Malliratkaisut - Tehtävä 1
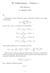 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä
 Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä. L Hospitalin sääntö on tuttu Analyysi :n kurssilta. Se on näppärä keino laskea tiettyjä raja-arvoja, mutta sen käytössä on oltava kuitenkin varovainen.
Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä. L Hospitalin sääntö on tuttu Analyysi :n kurssilta. Se on näppärä keino laskea tiettyjä raja-arvoja, mutta sen käytössä on oltava kuitenkin varovainen.
3.1 Väliarvolause. Funktion kasvaminen ja väheneminen
 Väliarvolause Funktion kasvaminen ja väheneminen LAUSE VÄLIARVOLAUSE Oletus: Funktio f on jatkuva suljetulla välillä I: a < x < b f on derivoituva välillä a < x < b Väite: On olemassa ainakin yksi välille
Väliarvolause Funktion kasvaminen ja väheneminen LAUSE VÄLIARVOLAUSE Oletus: Funktio f on jatkuva suljetulla välillä I: a < x < b f on derivoituva välillä a < x < b Väite: On olemassa ainakin yksi välille
Yleisiä integroimissääntöjä
 INTEGRAALILASKENTA, MAA9 Yleisiä integroimissääntöjä Integroiminen eli annetun funktion f integraalifunktion F määrittäminen (löytäminen) on yleisesti haastavaa. Joskus joutuu jopa arvata tai kokeilla.
INTEGRAALILASKENTA, MAA9 Yleisiä integroimissääntöjä Integroiminen eli annetun funktion f integraalifunktion F määrittäminen (löytäminen) on yleisesti haastavaa. Joskus joutuu jopa arvata tai kokeilla.
Matematiikan tukikurssi
 Matematiian tuiurssi Kurssierta 5 Sarjojen suppeneminen Kiinnostusen ohteena on edelleen sarja a n = a + a 2 + a 3 + a 4 + n= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan että sarja
Matematiian tuiurssi Kurssierta 5 Sarjojen suppeneminen Kiinnostusen ohteena on edelleen sarja a n = a + a 2 + a 3 + a 4 + n= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan että sarja
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
3 Derivoituvan funktion ominaisuuksia
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 3 Derivoituvan funktion ominaisuuksia 31 l Hospitalin sääntö 1 Määritä 2 5 4 2 + 2 7 12 + 11, e 1 2, (c) tan sin 2 Määritä 2012 3 704 + 2 6 30 13 10 + 7, 3 2017
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 3 Derivoituvan funktion ominaisuuksia 31 l Hospitalin sääntö 1 Määritä 2 5 4 2 + 2 7 12 + 11, e 1 2, (c) tan sin 2 Määritä 2012 3 704 + 2 6 30 13 10 + 7, 3 2017
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Derivaatta 1.1 Derivaatta Erilaisia lähestymistapoja: I geometrinen
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Derivaatta 1.1 Derivaatta Erilaisia lähestymistapoja: I geometrinen
Sarjat ja integraalit
 Sarjat ja integraalit Peter Hästö 1. huhtikuuta 2015 Matemaattisten tieteiden laitos Eteneminen pvm luku v 11 2.1, 2.2 v 12 2.3, 2.4 v 13 3.0, 3.1 v 14 3.2 v 15 4 v 16 5.1 v 17 5.2 v 18 6.1 v 19 6.2 Peter
Sarjat ja integraalit Peter Hästö 1. huhtikuuta 2015 Matemaattisten tieteiden laitos Eteneminen pvm luku v 11 2.1, 2.2 v 12 2.3, 2.4 v 13 3.0, 3.1 v 14 3.2 v 15 4 v 16 5.1 v 17 5.2 v 18 6.1 v 19 6.2 Peter
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 . Lasketaan valmiiksi derivaattoja ja niiden arvoja pisteessä x = 2: f(x) = x + 3x 3 + x 2 + 2x + 8, f(2) = 56, f (x) = x 3 + 9x 2 + 2x + 2, f (2) = 7, f (x) = 2x 2 + 8x + 2, f (2) = 86, f (3) (x) = 2x
. Lasketaan valmiiksi derivaattoja ja niiden arvoja pisteessä x = 2: f(x) = x + 3x 3 + x 2 + 2x + 8, f(2) = 56, f (x) = x 3 + 9x 2 + 2x + 2, f (2) = 7, f (x) = 2x 2 + 8x + 2, f (2) = 86, f (3) (x) = 2x
1 sup- ja inf-esimerkkejä
 Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Ratkaisuehdotus 2. kurssikoe
 Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Matemaattisen analyysin tukikurssi
 Matemaattisen analyysin tukikurssi 5. Kurssikerta Petrus Mikkola 10.10.2016 Tämän kerran asiat Raja-arvo ja toispuolinen raja-arvo Funktion suurin ja pienin arvo Lukujono Lukujonon suppeneminen Kasvava
Matemaattisen analyysin tukikurssi 5. Kurssikerta Petrus Mikkola 10.10.2016 Tämän kerran asiat Raja-arvo ja toispuolinen raja-arvo Funktion suurin ja pienin arvo Lukujono Lukujonon suppeneminen Kasvava
Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on
![Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on](/thumbs/47/23658224.jpg) Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 19 Derivaatan määritelmä Määritelmä
Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 19 Derivaatan määritelmä Määritelmä
Ratkaisuehdotus 2. kurssikokeeseen
 Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Sinin jatkuvuus. Lemma. Seuraus. Seuraus. Kaikilla x, y R, sin x sin y x y. Sini on jatkuva funktio.
 Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
MATEMATIIKAN PERUSKURSSI II kevät 2018 Ratkaisut 1. välikokeen preppaustehtäviin. 1. a) Muodostetaan osasummien jono. S n =
 MATEMATIIKAN PERUSKURSSI II kevät 208 Ratkaisut. välikokeen preppaustehtäviin. a) Muodostetaan osasummien jono S n = n ( k k) k= josta saadaan = ( 0 ) + ( 2) + ( 2 3) + ( n 2 n ) + ( n n) = n, n =, 2,...,
MATEMATIIKAN PERUSKURSSI II kevät 208 Ratkaisut. välikokeen preppaustehtäviin. a) Muodostetaan osasummien jono S n = n ( k k) k= josta saadaan = ( 0 ) + ( 2) + ( 2 3) + ( n 2 n ) + ( n n) = n, n =, 2,...,
Poistumislause Kandidaatintutkielma
 Poistumislause Kandidaatintutkielma Mikko Nikkilä 013618832 26. helmikuuta 2011 Sisältö 1 Johdanto................................... 2 2 Olemassaolon ja yksikäsitteisyyden historiaa............ 3 3 Esitietoja..................................
Poistumislause Kandidaatintutkielma Mikko Nikkilä 013618832 26. helmikuuta 2011 Sisältö 1 Johdanto................................... 2 2 Olemassaolon ja yksikäsitteisyyden historiaa............ 3 3 Esitietoja..................................
Funktiojonon tasainen suppeneminen
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Taina Saari Funktiojonon tasainen suppeneminen Matematiikan ja tilastotieteen laitos Matematiikka Elokuu 2009 Tampereen yliopisto Matematiikan ja tilastotieteen
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Taina Saari Funktiojonon tasainen suppeneminen Matematiikan ja tilastotieteen laitos Matematiikka Elokuu 2009 Tampereen yliopisto Matematiikan ja tilastotieteen
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Rollen lause polynomeille
 Rollen lause polynomeille LuK-tutkielma Anna-Helena Hietamäki 7193766 Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 015 Sisältö 1 Johdanto 1.1 Rollen lause analyysissä.......................
Rollen lause polynomeille LuK-tutkielma Anna-Helena Hietamäki 7193766 Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 015 Sisältö 1 Johdanto 1.1 Rollen lause analyysissä.......................
ANALYYSI 3 HELI TUOMINEN
 ANALYYSI 3 HELI TUOMINEN Alkusanat Tässä on muistiinpanot syksyllä 202 luennoimastani kurssista Analyysi 3. Kurssin pohana on Tero Kilpeläisen luentomoniste samannimiselle kurssille. Tässä monisteessa
ANALYYSI 3 HELI TUOMINEN Alkusanat Tässä on muistiinpanot syksyllä 202 luennoimastani kurssista Analyysi 3. Kurssin pohana on Tero Kilpeläisen luentomoniste samannimiselle kurssille. Tässä monisteessa
Outoja funktioita. 0 < x x 0 < δ ε f(x) a < ε.
 Outoja funktioita Differentiaalilaskentaa harjoitettiin miltei 200 vuotta ennen kuin sen perustana olevat reaaliluvut sekä funktio ja sen raja-arvo määriteltiin täsmällisesti turvautumatta geometriseen
Outoja funktioita Differentiaalilaskentaa harjoitettiin miltei 200 vuotta ennen kuin sen perustana olevat reaaliluvut sekä funktio ja sen raja-arvo määriteltiin täsmällisesti turvautumatta geometriseen
saadaan kvanttorien järjestystä vaihtamalla ehto Tarkoittaako tämä ehto mitään järkevää ja jos, niin mitä?
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
Differentiaali- ja integraalilaskenta 1 Ratkaisut 2. viikolle /
 MS-A008 Differentiaali- ja integraalilaskenta, V/207 Differentiaali- ja integraalilaskenta Ratkaisut 2. viikolle / 8. 2.4. Jatkuvuus ja raja-arvo Tehtävä : Määritä raja-arvot a) 3 + x, x Vihje: c)-kohdassa
MS-A008 Differentiaali- ja integraalilaskenta, V/207 Differentiaali- ja integraalilaskenta Ratkaisut 2. viikolle / 8. 2.4. Jatkuvuus ja raja-arvo Tehtävä : Määritä raja-arvot a) 3 + x, x Vihje: c)-kohdassa
MATP153 Approbatur 1B Harjoitus 6 Maanantai
 . (Teht. s. 93.) Määrää raja-arvo MATP53 Approbatur B Harjoitus 6 Maanantai 7..5 cos x x. Ratkaisu. Suora sijoitus antaa epämääräisen muodon (ei auta). Laventamalla päädytään muotoon ja päästään käyttämään
. (Teht. s. 93.) Määrää raja-arvo MATP53 Approbatur B Harjoitus 6 Maanantai 7..5 cos x x. Ratkaisu. Suora sijoitus antaa epämääräisen muodon (ei auta). Laventamalla päädytään muotoon ja päästään käyttämään
Täydellisyysaksiooman kertaus
 Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
Vastaus: 10. Kertausharjoituksia. 1. Lukujonot lim = lim n + = = n n. Vastaus: suppenee raja-arvona Vastaus:
 . Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
. Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
saadaan kvanttorien järjestystä vaihtamalla ehto Tarkoittaako tämä ehto mitään järkevää ja jos, niin mitä?
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 4 Funktion raja-arvo 4. Määritelmä. Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: f) A < ε aina, kun 0 < a < δ, saadaan kvanttorien järjestystä vaihtamalla
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 4 Funktion raja-arvo 4. Määritelmä. Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: f) A < ε aina, kun 0 < a < δ, saadaan kvanttorien järjestystä vaihtamalla
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M)
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
1 Supremum ja infimum
 Pekka Alestalo, 2018 Tämä moniste täydentää reaalilukuja ja jatkuvia reaalifunktioita koskevaa kalvosarjaa lähinnä perustelujen ja todistusten osalta. Suurin osa määritelmistä jms. on esitetty jo kalvoissa,
Pekka Alestalo, 2018 Tämä moniste täydentää reaalilukuja ja jatkuvia reaalifunktioita koskevaa kalvosarjaa lähinnä perustelujen ja todistusten osalta. Suurin osa määritelmistä jms. on esitetty jo kalvoissa,
MS-A010X Differentiaali- ja integraalilaskenta 1
 MS-A010X Differentiaali- ja integraalilaskenta 1 Pekka Alestalo Aalto-yliopisto 1.9.2016 Pekka Alestalo (Aalto-yliopisto) MS-A010X Differentiaali- ja integraalilaskenta 1 1.9.2016 1 / 200 Sisältö Nämä
MS-A010X Differentiaali- ja integraalilaskenta 1 Pekka Alestalo Aalto-yliopisto 1.9.2016 Pekka Alestalo (Aalto-yliopisto) MS-A010X Differentiaali- ja integraalilaskenta 1 1.9.2016 1 / 200 Sisältö Nämä
u(0, t) = 0 kaikille t > 0: lämpötila pidetään vakiona pisteessä x = 0;
 3. Lämmönjohtumisyhtälö I Yksiulotteisessa lämmönjohtumisyhtälössä u t = u γ x tuntematon funktio u = u(x, t) kuvaa lämpötilaa yksiulotteisen kappaleen (ohut sauva; x-akseli) kohdassa x hetkellä t. Kun
3. Lämmönjohtumisyhtälö I Yksiulotteisessa lämmönjohtumisyhtälössä u t = u γ x tuntematon funktio u = u(x, t) kuvaa lämpötilaa yksiulotteisen kappaleen (ohut sauva; x-akseli) kohdassa x hetkellä t. Kun
Numeerinen integrointi ja derivointi
 Numeerinen integrointi ja derivointi Keijo Ruotsalainen Division of Mathematics Interpolaatiokaavat Approksimoitava integraali I = b a f(x)dx. Tasavälinen hila: x i = a+ (b a)i n, i = 0,...,n Funktion
Numeerinen integrointi ja derivointi Keijo Ruotsalainen Division of Mathematics Interpolaatiokaavat Approksimoitava integraali I = b a f(x)dx. Tasavälinen hila: x i = a+ (b a)i n, i = 0,...,n Funktion
Sarjoja ja analyyttisiä funktioita
 3B Sarjoja ja analyyttisiä funktioita 3B a Etsi funktiolle z z 5 potenssisarjaesitys kiekossa B0, 5. b Etsi funktiolle z z potenssisarjaesitys kiekossa, jonka keskipiste on z 0 4. Mikä on tämän potenssisarjan
3B Sarjoja ja analyyttisiä funktioita 3B a Etsi funktiolle z z 5 potenssisarjaesitys kiekossa B0, 5. b Etsi funktiolle z z potenssisarjaesitys kiekossa, jonka keskipiste on z 0 4. Mikä on tämän potenssisarjan
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 2015 / ORMS1010 Matemaattinen Analyysi 7. harjoitus, viikko 17 R1 ma 16 18 D115 (20.4.) R2 ke 12 14 B209 (22.4.) 1. Määritä funktiolle f (x) 1 + 0,1x Taylorin sarja kehityskeskuksena
Vaasan yliopisto, kevät 2015 / ORMS1010 Matemaattinen Analyysi 7. harjoitus, viikko 17 R1 ma 16 18 D115 (20.4.) R2 ke 12 14 B209 (22.4.) 1. Määritä funktiolle f (x) 1 + 0,1x Taylorin sarja kehityskeskuksena
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1. Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS
 DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
Sarjat ja differentiaaliyhtälöt
 Sarjat ja differentiaaliyhtälöt Johdanto Tämä luentomoniste on tarkoitettu korvaamaan luentomuistiinpanoja Sarjat ja differentiaaliyhtälöt-kurssilla. Tämä ei kuitenkaan ole oppikirja, mikä tarkoittaa sitä,
Sarjat ja differentiaaliyhtälöt Johdanto Tämä luentomoniste on tarkoitettu korvaamaan luentomuistiinpanoja Sarjat ja differentiaaliyhtälöt-kurssilla. Tämä ei kuitenkaan ole oppikirja, mikä tarkoittaa sitä,
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Analyysi 1. Harjoituksia lukuihin 1 3 / Syksy Osoita täsmällisesti perustellen, että joukko A = x 4 ei ole ylhäältä rajoitettu.
 Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
ANALYYSI 2. Camilla Hollanti. Tampereen yliopisto 2010. x 3. a x 1. x 4 x 11. x 2
 ANALYYSI 2 Camilla Hollanti _ M M a x x 2 x 3 x 4 x b Tampereen yliopisto 200 Sisältö. Preliminäärejä 3 2. Riemann-integraali 5 2.. Pinta-alat ja porrasfunktiot....................... 5 2... Pinta-ala
ANALYYSI 2 Camilla Hollanti _ M M a x x 2 x 3 x 4 x b Tampereen yliopisto 200 Sisältö. Preliminäärejä 3 2. Riemann-integraali 5 2.. Pinta-alat ja porrasfunktiot....................... 5 2... Pinta-ala
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
3 Lukujonon raja-arvo
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 3 Lukujonon raja-arvo 3 Määritelmä Osoita, että 6n + 2n + 3 3 < 4 n ja määritä jokin sellainen n 0 Z +, että 6n + 2n + 3 3 < 0 87 aina, kun n > n 0 2 Olkoon x n
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 3 Lukujonon raja-arvo 3 Määritelmä Osoita, että 6n + 2n + 3 3 < 4 n ja määritä jokin sellainen n 0 Z +, että 6n + 2n + 3 3 < 0 87 aina, kun n > n 0 2 Olkoon x n
MATP153 Approbatur 1B Harjoitus 5 Maanantai
 MATP153 Approbatur 1B Harjoitus 5 Maanantai 30.11.015 1. (Opiskelutet. 0 s. 81.) Selvitä, miten lauseke sin(4x 3 + cos x ) muodostuu perusfunktioista (polynomeista, trigonometrisistä funktioista jne).
MATP153 Approbatur 1B Harjoitus 5 Maanantai 30.11.015 1. (Opiskelutet. 0 s. 81.) Selvitä, miten lauseke sin(4x 3 + cos x ) muodostuu perusfunktioista (polynomeista, trigonometrisistä funktioista jne).
Kompleksiset sarjat ja potenssisarjat
 MS-C1300 Kompleksianalyysi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto K Kytölä & A Gutiérrez Syksy 2018 Ratkaisut 3A 3A Kompleksiset sarjat ja potenssisarjat 3A1 Laske seuraavien sarjojen
MS-C1300 Kompleksianalyysi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto K Kytölä & A Gutiérrez Syksy 2018 Ratkaisut 3A 3A Kompleksiset sarjat ja potenssisarjat 3A1 Laske seuraavien sarjojen
