Newton-Cotesin ja Gaussin integrointimenetelmistä
|
|
|
- Teemu Melasniemi
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 TAMPEREEN YLIOPISTO Pro grdu -tutkielm Anniin Julku Newton-Cotesin j Gussin integrointimenetelmistä Informtiotieteiden yksikkö Mtemtiikk Toukokuu 215
2 Tmpereen yliopisto Informtiotieteiden yksikkö JULKU, ANNIINA: Newton-Cotesin j Gussin integrointimenetelmistä Pro grdu -tutkielm, 37 s. Mtemtiikk Toukokuu 215 Tiivistelmä Tämä tutkielm käsittelee numeerisen integroinnin kht integrointimenetelmää, Newton-Cotesin j Gussin integrointimenetelmiä. Grfisesti integrointi trkoitt tietyn käyrän j x-kselin väliin jäävän pint-ln määrittämistä integrointivälin päätepisteiden välissä, kun käyrää vstv funktio on positiivinen. Newton-Cotesin integrointimenetelmä on yleisin numeerisist integrointimenetelmistä. Menetelmä perustuu siihen, että hnklsti integroitv funktio korvtn pproksimoidull funktioll, jok on helppo integroid. Kun trkstelln integrointivälin tsvälistä jko j käytetään Lgrngen interpoltiokv, pproksimoidulle polynomille sdn johdettu summluseke pinoineen j pisteineen. Eri pinot vstvt Newton-Cotesin kvoj. Yleensä Newton-Cotesin kvoj ei sovellet koko integrointivälille, vn yksitellen osväleillä, joihin integrointiväli on jettu. Kun integrli rvioidn osvälien pproksimtioiden summll, sdn yhdistettyjä sääntöjä. Gussin integrointimenetelmässä integrli on esitetty pinofunktion j funktion tulon. Integrointiväliä ei kuitenkn jet tsisiin väleihin, sillä päästään prempiin tuloksiin, jos pisteet vlitn trkn integroitumisen knnlt optimlisell tvll. Ennen Gussin integrointisääntöjen muotoilu käydään läpi keskeisiä tuloksi pinofunktioist, ortogonlisist polynomeist j tridigonlimtriiseist. Pinofunktio j sklritulo määritellään, j käydään läpi ortogonlisiin polynomeihin liittyviä luseit, jotk krkterisoivt pinoj j pisteitä. Lopuksi trkstelln Gussin integrointikvoj etukäteen kiinnitetyillä luvuill j pinoill. Näin sdn säännöt Rdun j Lobtton integroinnille. Tärkeimmät viitekirjt työssä ovt J. Stoerin j R. Bulirschin Introduction to Numericl Anlysis j P. J. Dvisin j P. Rbinowitzin Methods of Numericl Integrtion. 2
3 Sisältö 1 Johdnto 4 2 Esitietoj 6 3 Newton-Cotesin integrointimenetelmistä Newton-Cotesin kvoist Yhdistetyistä säännöistä Gussin integrointimenetelmistä Pinofunktioist Perustuloksi ortogonlisist polynomeist Tridigonlimtriiseist Gussin integrointikvoist etukäteen määrätyillä luvuill.. 31 Viitteet 37 3
4 1 Johdnto Olkoon f(x) jokin nnettu relinen funktio. Kyseisen funktion määrätyn integrlin f(x) dx rvon lskeminen on klssinen ongelm. Voimme esittää joidenkin yksinkertisten integrndien f(x) integrlin x f(x) dx = F (x), missä F (x) = f(x), suljetuss muodoss, muuttujn x lgebrllisen esityksenä j tunnettuin lkeisfunktioin. Tällöin smme integrlille trkn rvon lskemll (1.1) f(x) dx = F (b) F (), missä F (x) on funktion f(x) määräämätön integrli (ntiderivtt). Jos määräämätön integrli on helposti stviss j riittävän yksinkertinen, kvll (1.1) voimme sd erittäin nopeit lskutoimituksi. Usein integrointi joht kuitenkin uusiin lkeisfunktioihin. Esimerkiksi integroimll lusekkeen funktion 1 x dx smme logritmin, mikä ei ole lgebrllinen funktio, vikk se onkin lkeisfunktio. Toislt integroimll funktion e x2 dx, smme funktion, jot emme voi esittää lkeisfunktioiden vull. Vikk määräämätön integrli olisi lkeisfunktio j sisimme sen ilmn kohtuutont työmäärää, sen luseke voi oll niin pitkä j monimutkinen, että keskeytämme lskemisen ennen kvn (1.1) soveltmist. Näiden syiden tki rvioimme usein integrlej. (Vrt. [2, s. 2]). Yleensä lskemme määrättyjä integrlej rvioimll integrli äärellisillä summill siten, että summt vstvt integrointivälin [, b] jko. Simpsonin sääntö on tyypillinen esimerkki edellä minitust menetelmästä, j se on yhä prhiten tunnetttu j eniten käytetty integrointimenetelmä Newton- Cotesin kvoist. (Vrt. [6, s. 117]). Tässä pro grdu -tutkielmss trkstelemme Newton-Cotesin j Gussin integrointimenetelmiä. Luvuss 2 esitämme interpoltion perusiden sekä Lgrngen j Hermiten interpoltiokvt lusein. Luvuss 3 esitämme 4
5 muutmi Newton-Cotesin integrointisääntöjä koko integrointivälille j sen osväleille. Luvuss 4 määrittelemme pinofunktion, sklritulon, ortogonlisuuden j todistmme keskeisiä tuloksi ortogonlisist polynomeist. Lopuksi esitämme Gussin integrointisääntöjen erikoistpuksi sekä Lobtton j Rdun integroinnin. Edellytämme lukijlt joidenkin nlyysin, diskreetin mtemtiikn j linerilgebrn perussioiden tuntemist. Edellytämme muun muss, että lukij tuntee yhden muuttujn differentili- j integrlilskennn perusteet. Pääsillisin lähdeteoksin käytämme J. Stoerin j R. Bulirschin Introduction to Numericl Anlysis -kirj j P. J. Dvisin j P. Rbinowitzin Methods of Numericl Integrtion -kirj. 5
6 2 Esitietoj Käymme tässä luvuss läpi pro grdu -tutkielmss käytettäviä merkintöjä sekä Lgrngen j Hermiten interpoltiokvt. (Vrt. [6, s , s. 49, s , s. 56]). Esitämme luksi muutmn merkinnän huomtuksin. Huomutus 2.1. Merkitsemme symbolill Π n kikkien polynomien P, P (x) = + 1 x + + n x n, joukko, joiden ste on korkeintn n. Huomutus 2.2. Käytämme merkintää Π n := {P P (x) = + 1 x + + n 1 x n 1 + x n } stett n olevien normeerttujen polynomien joukolle. Normeermme polynomit P siten, että polynomin korkeimmn steen termin kerroin on 1. Huomutus 2.3. Merkinnällä := trkoitmme on määritelmän mukn. Merkinnällä trkoitmme, että ovt yhtäpitäviä (ekvivlenttej). Olkoot p j q luseit. Nyt luse p := q trkoitt, että p on määritelmän mukn q. Luse p q trkoitt, että p on yhtäpitävä luseen q knss. Huomutus 2.4. Merkinnällä V = C n [, b] trkoitmme funktioiden, joill on jtkuv n:s derivtt välillä [, b], muodostm joukko. Merkinnällä C[, b] trkoitmme jtkuvien funktioiden joukko. Huomutus 2.5. Merkinnällä I[x,..., x n, x] trkoitmme pienintä väliä, jok sisältää luvut x,..., x n j x. Määrittelemme seurvksi, mitä trkoitmme integrointimenetelmän kertluvull. Voimme trkstell kertluku polynomien integrointitrkkuuden ti virhervion vull. Esitämme seurvksi määritelmän kertluvust, jok perustuu virhervioon j jot käytämme jtkoss trkstellessmme Newton- Cotesin yhdistettyjä sääntöjä (ks. luku 3.2). Määritelmä 2.1. Jos osvälien jkmiseen perustuvn yhdistetyn säännön virhe on suuruusluokk O(h r ), mutt ei suuruusluokk O(h r+1 ), snomme, että kyseenomisen menetelmän kertluku on r. (Vrt. [3, s. 1 12]). Yleisesti, jos r = m + 1, numeerinen sääntö integroi osväleillä trksti polynomin, jonk ste on m, mutt ei polynomi stett m + 1. Tällöin menetelmän kertluku on m, j kertluku perustuu integrointitrkkuuteen. Käytämme tätä määritelmää kertluvulle luvuss
7 Ennen käytimme polynomien interpoltiot, kun interpoloimme tulukoist kerättyjen funktioiden rvoj. Menetelmällä rvioimme nnettu funktiot nnetull välillä. Nykyisten tietokoneiden ikkudell meillä ei ole enää trvett käyttää tulukoituj funktioiden rvoj. Kuitenkin polynomien interpoltio on tärkeä teoreettinen pohj useille numeerisen integroinnin kvoille, joten käymme seurvksi läpi interpoltion perusiden j muutmi interpoltiokvoj. Trkoitmme polynomien interpoltioll polynomin sovitust dtn. Olkoot nnettu dtpisteet x, x 1,..., x n 1, y, y 1,..., y n 1. Kun hlumme sovitt polynomin dtn, meidän on vlittv korkeintn (n 1):ttä stett olev polynomi, jolle (2.1) p(x k ) y k, missä k =,..., n 1. Jos vdimme, että yllä olev ehto toteutuu täsmällisesti, kyseessä on interpoltiotehtävä. Jos pisteet x k ovt erillisiä, smme yksikäsitteisen rtkisun. Esitämme seurvksi luseen, jonk mukn voimme rtkist interpoltio-ongelmn in polynomien vull. Luse 2.1 (Lgrngen interpoltiokv). Olkoot n + 1 kpplett pisteprej (x i, f i ), missä i =,..., n, x i x k jokisell i k. Näitä pisteprej kohti on olemss yksikäsitteinen polynomi P Π n, jolle P (x i ) = f i, missä i =,..., n. Todistus. Todistmme ensin yksikäsitteisyyden. Olkoot P 1, P 2 Π n kksi mielivltist polynomi, joille on voimss P 1 (x i ) = P 2 (x i ) = f i, missä i =,..., n. Polynomin P := P 1 P 2 Π n ste on korkeintn n, j sillä on vähintään n + 1 eri nollkoht, nimittäin x i, missä i =,..., n. Jos polynomi ei ole identtisesti noll, lgebrn perusluseest seur, että polynomin juurien määrä on korkeintn polynomin steen verrn. Polynomin P ste on korkeintn n, mutt sillä on nollkohti n + 1 kpplett, missä on ristiriit. Täten polynomin P täytyy oll identtisesti noll, jolloin P 1 = P 2. Todistmme seurvksi olemssolon. Konstruoimme interpoloivn polynomin P eksplisiittisesti polynomien L i Π n, missä i =,..., n, vull, joille on voimss 1, jos i = k, (2.2) L i (x k ) = δ ik =, jos i k. 7
8 Seurvt Lgrngen polynomit (2.3) L i (x) : (x x ) (x x i 1 )(x x i+1 ) (x x n ) (x i x ) (x i x i 1 )(x i x i+1 ) (x i x n ) ω(x) (x x i )ω (x i ), missä n ω(x) : (x x i ), täyttävät ehdon (2.2). Huomutmme, että tähän stinen todistus osoitt inostn sen, että ehto (2.2) määrää yksikäsitteisesti Lgrngen polynomit. Voimme nyt ilmist interpoltio-ongelmn rtkisun P suorn polynomien L i termien vull, jolloin P (x) f i L i (x) f i n k= k i x x k x i x k. Määritelmä 2.2. Snomme luseess 2.1 esiintyvä kv (2.4) P (x) f i L i (x) f i Lgrngen interpoltiokvksi. n k= k i x x k x i x k. Lgrngen interpoltiokv osoitt, että polynomin P kertoimet riippuvt lineerisesti luvuist f i. Vikk Lgrngen kv on teoreettisesti tärkeä, emme voi yleensä käyttää sitä vrsiniseen lskemiseen, vrsinkin jos dtpisteitä on pljon. Jok kert kun vihdmme dtpistettä x i, joudumme lskemn uudelleen kikki Lgrngen polynomit. Lgrngen kv on kuitenkin hyödyllinen tilnteess, joss rtkisemme interpoltio-ongelmn smoill dtpisteillä x i, mutt eri luvuill f i (i =,..., n). Esitämme seurvksi esimerkin Lgrngen interpoltiokvn käytöstä. Esimerkki 2.1. Olkoon n = 3. Olkoot (x i, f i ) prej siten, että x i f i 1 3 4, 8
9 kun i =, 1, 2, 3. Etsimme polynomin P (z) Π 3 rvo muuttujn z rvoll 5, kun P (x i ) = f i kikill i =, 1, 2, 3. Smme Lgrngen polynomeiksi Smme L (x) = (x x 1)(x x 2 )(x x 3 ) (x x 1 )(x x 2 )(x x 3 ) L 1 (x) = (x x )(x x 2 )(x x 3 ) (x 1 x )(x 1 x 2 )(x 1 x 3 ) L 2 (x) = (x x )(x x 1 )(x x 3 ) (x 2 x )(x 2 x 1 )(x 2 x 3 ) L 3 (x) = (x x )(x x 1 )(x x 2 ) (x 3 x )(x 3 x 1 )(x 3 x 2 ) = (x 1)(x 2)(x 3) ( 1)( 2)( 3), = (x )(x 2)(x 3) (1 )(1 2)(1 3), = (x )(x 1)(x 3) (2 )(2 1)(2 3), = (x )(x 1)(x 2) (3 )(3 1)(3 2). P (5) = 1 L (5) + L 1 (5) + 3 L 2 (5) + 4 L 3 (5) = = 1 ( 4) ( 2) = 24. Esitämme seurvksi Hermiten interpoltiokvn, jonk vull voimme myös rtkist interpoltio-ongelmi. Luse 2.2 (Hermiten interpoltiokv). Mielivltisi relilukuj ξ < ξ 1 < < ξ m j y (k) i, missä k =, 1,..., n i 1 j i =, 1,..., m, kohti on olemss täsmälleen yksi polynomi jok toteutt ehdon m P Π n, missä n := n i 1, (2.5) P (k) (ξ i ) = y (k) i, missä k =, 1,..., n i 1 j i =, 1,..., m. Todistus. Osoitmme ensin yksikäsitteisyyden. Trkstelemme polynomej P 1, P 2 Π n, joille Q(x) := P 1 (x) P 2 (x). Vlitsemme polynomit siten, että ehto (2.5) on voimss polynomeille P 1 j P 2. Kosk Q (k) (ξ i ) =, missä k =, 1,..., n i 1 j i =, 1,..., m, 9
10 niin ξ i on polynomin Q inkin n i -kertinen juuri. Polynomill Q on yhteensä inkin m n i = n + 1 juurt, joist jokinen on lskettu esiintymiskertojens mukn. Täten Q:n on oltv noll, sillä sen ste on pienempi kuin n + 1. Olemssolo seur yksikäsitteisyydestä. Kvn (2.5) yhtälöt muodostvt yhtälöryhmän, joss on n + 1 linerist yhtälöä j n + 1 kpplett polynomin P (x) = c + c 1 x + + c n x n tuntemttomi kertoimi c j. Tätä yhtälöryhmää vstv mtriisi on kääntyvä, kosk sillä on yksikäsitteiset rtkisut. Täten tällöin linerisell yhtälöryhmällä (2.5) on yksikäsitteiset rtkisut mielivltisille oiken puolen rvoille y (k) i. Esitämme lopuksi luseen, jot trvitsemme myöhemmin luvuss 4. Luse 2.3. Olkoon relifunktio f n + 1 kert differentioituv välillä [, b]. Trkstelemme pisteitä ξ i [, b], joille ξ < ξ 1 < < ξ m j joit on m + 1 kpplett. Jos polynomi P on korkeintn stett n, toisin snoen m n i = n + 1, j P toteutt interpoltion ehdot P (k) (ξ i ) = f (k) (ξ i ), missä k =, 1,..., n i 1 j i =, 1,..., m, niin tällöin jokist luku x [, b] kohti on olemss ξ I[ξ,..., ξ m, x] siten, että f( x) P ( x) = ω( x)f (n+1) ( ξ), (n + 1)! missä ω(x) := (x ξ ) n (x ξ 1 ) n1 (x ξ m ) nm. Todistus (vrt. [3, s. 311]). Sivuutmme todistuksen. 1
11 3 Newton-Cotesin integrointimenetelmistä Tässä luvuss trkstelemme Newton-Cotesin integrointimenetelmiä. Ensiksi esitämme Newton-Cotesin kvt koko integrointivälille, j sitten sovellmme kvoj integrointivälin osväleille, jolloin smme yhdistettyjä sääntöjä. (Ks. [6, s ]). 3.1 Newton-Cotesin kvoist Smme Newton-Cotesin integrointikvt, kun korvmme integrndin sopivll polynomill P (x). Tällöin integrli on pproksimoitu rvo integrlille P (x) dx f(x) dx. Trkstelemme suljetun välin [, b] tsvälistä jko, jonk jkopisteet voimme kirjoitt muodoss missä jkovälin pituus h on x i = + ih, missä i =,..., n, h := (b ), missä n Z +. n Olkoon P n (x) interpoltiopolynomi, jolle deg (P n ) n j jolle pätee P n (x i ) = f i := f(x i ), missä i =, 1,..., n. Lgrngen interpoltiokvn nojll smme, että P n (x) f i L i (x), missä L i (x) = n k= k i x x k x i x k. Kun esittelemme uuden muuttujn t siten, että x = +ht, voimme kirjoitt jälkimmäisen lusekkeen uudelleen muodoss L i (x) = ϕ i (t) := 11 n k= k i t k i k.
12 Integroimll smme P n (x) dx = f i L i (x) dx n =h f i ϕ i (t) dt =h f i α i, missä α i := n ϕ i (t) dt. Kertoimet ti pinot α i riippuvt inostn n:stä. Erityisesti huommme, että pinot eivät riipu integroitvst funktiost f ti integrointivälin päätepisteistä j b. Seurvksi esitämme kksi esimerkkiä, jotk hvinnollistvt pproksimointi. Esimerkki 3.1. Olkoon n = 2. Tällöin α = α 1 = α 2 = t 1 1 t 2 2 dt = 1 2 (t 2 3t + 2t) dt = 1 ( ) = 1 3, t 1 t dt = t 2 t dt = 1 2 (t 2 t) dt = Smme seurvn pproksimtion integrlille ( ) 8 (t 2 2t) dt = 3 4 = 4 3, P 2 (x) dx = h 3 (f + 4f 1 + f 2 ) f(x) dx. ( = 2) 1 3. Approksimtioss f j f 2 ovt funktion f rvot integrointivälin päätepisteissä j f 1 on funktion rvo välin keskipisteessä. Tämä on Simpsonin sääntö. Simpsonin säännössä interpoloimme funktiot 2. steen polynomill tsvälisellä jkovälillä eli sovitmme dtpisteisiin prbelin. 12
13 Esimerkki 3.2. Olkoon n = 3. Tällöin smme pinoiksi 3 t 1 α = 1 t 2 2 t 3 3 dt = 1 ( t 3 + 6t 2 11t + 6) dt 6 = 1 ( 81 ) = 3 8, 3 t α 1 = 1 t t dt = 1 2 = 1 ( ) = 9 8, 3 t α 2 = 2 t t dt = 1 2 = 1 ( ) = 9 2 8, 3 t α 3 = 3 t t dt = 1 6 = 1 ( ) = 3 8. Smme seurvn pproksimtion integrlille (t 3 5t 2 + 6t) dt ( t 3 + 4t 2 3t) dt (t 3 3t 2 + 2t) dt P 3 (x) dx = 3h 8 (f + 3f 1 + 3f 2 + f 3 ) f(x) dx. Tämä on 3/8-sääntö. Approksimtioss f j f 3 ovt funktion f rvot integrointivälin päätepisteissä sekä f 1 j f 2 ovt funktion rvoj päätepisteiden välissä. Voimme joht muit Newton-Cotesin kvoj vstvll tvll kuin esimerkeissä 3.1 j 3.2. Newton-Cotesin kvoill (3.1) P n (x) dx = h f i α i, missä f i = f( + ih) j h = b, missä n Z n +, smme pproksimtion integrlille f(x) dx. 13
14 Pinoj α i, missä i =, 1,..., n, on tulukoitu. Ne ovt rtionlilukuj, joill on ominisuus (3.2) α i = n. Smme johdettu tämän ominisuuden seurvll tvll. Asetmme, että f(x) : 1. Tällöin soveltmll funktion rvo kvn (3.1) smme, että polynomi P n (x) : 1, sillä Newton-Cotesin kv on integrlin f(x) trkk pproksimtio. Tällöin smme ominisuuden (3.2). Jos s on pinojen α i yhteinen jkj, niin tällöin luvut σ i =: sα i, missä i =, 1,..., n, ovt kokonislukuj. Smme kvn (3.1) muotoon (3.3) P n (x) dx = h f i α i = b ns σ i f i. Approksimoinneiss syntyy in virheitä, kosk rvioimme lkuperäistä integrli. Voimme osoitt, että smme pproksimointivirheen seurvn muotoon (ks. [5, s. 167]) (3.4) P n (x) dx f(x) dx = h p+1 K f (p) (ξ), missä ξ (, b), missä h = b on jkovälin pituus, K on relilukuvkio, p on derivtn n kertluku j f (p) on funktion f p:s derivtt. Edellä (, b) trkoitt voint väliä :st b:hen. Lukujen p j K rvot riippuvt vin luvust n, mutt eivät integrndist f. Esimerkiksi puolisuunnikssäännön (ks. tulukko 1) pproksimointivirhe on h f (2) (ξ), kun p = 2 j K = 1 kvss (3.4). Myös virheitä on tulukoitu. 12 Seurvn tulukkoon olemme koonneet Newton-Cotesin kvoj, kun n = 1, 2,..., 6. Suuremmill n:n rvoill joistkin luvun σ i rvoist tulee negtiivisi. Näitä rvoj vstvt kvt ovt sopimttomi numeerisiin trkoituksiin, sillä termejä kumoutuu lskiessmme summ (3.3) j tällöin lskuihin syntyy virheitä. 14
15 Tulukko 1: Newton-Cotesin sääntöjä. n σ i ns Virhe Nimi h 3 1 (ξ) 12 Puolisuunnikssääntö h 5 1 (ξ) 9 Simpsonin sääntö h 5 3 (ξ) 8 3/8-sääntö h 7 8 (ξ) 945 Milnen sääntö h (ξ) h 9 9 (ξ) 14 Weddlen sääntö Esitämme seurvksi esimerkin 3/8-säännöstä. Esimerkki 3.3. Etsimme funktion f(x) = 5x 5 4x 4 + 3x 3 2x 2 + 1x +, 25 integrlin pproksimtiot 3/8-säännöllä integrointivälillä nollst khteen. Tiedämme, että f() =, 25 j f(2) = 11 4, 25 j integrlin trkk rvo on 364, 5. Kuv 1: Funktion f(x) määrätty integrli välillä [, 2]. Nyt h = b = 2 = Luvun h vull smme tsvälisen jon j sitä vstvt funktion rvot, jolloin f() =, 25; f( ) = 3 972, f( ) =, f(2) = 11 4,
16 Pisteet x, x 1, x 2 j x 3 ovt tsvälisen jon pisteet, joiden rvot olemme lskeneet edellä. Nyt 2 f(x) 3h 8 [f(x ) + 3f(x 1 ) + 3f(x 2 ) + f(x 3 )] = [, = 3889, , 25] Integrlin trkk rvo j pproksimtio erovt toisistn 3889, , 5 364, 5 1 % = 6, 8 %. Virheen ylärjss luku ξ on tuntemton, mutt voimme rvioid, että luseke f (4) (ξ) on suurimmilln silloin, kun funktion f(x) neljäs derivtt f (4) (x) = 6 x 96 s suurimmn rvons välillä [, 2]. Tällöin smme lusekkeen f (4) (x) rvoksi Nyt smme virheeen ylärjksi kun h = 2 3 h f (4) (ξ) = = 11 4 = 545, 1851; on jkovälin pituus. Smme lisää integrointikvoj integrndin f Hermiten interpoltioll (ks. luku 2 luse 2.2) käyttämällä polynomi P Π n, jonk ste on pienempi ti yhtä suuri kuin n. Yksinkertisimmss tpuksess korvmme integrndin f polynomill P Π 3, jolle P () = f(), P () = f (), P (b) = f(b), P (b) = f (b). Kun käytämme yleistettyä Lgrngen kv (ks. [6, s. 53]) tpuksess = j b = 1, polynomille P pätee P (t) =f()[(t 1) 2 + 2t(t 1) 2 ] + f(1)[t 2 2t 2 (t 1)] + f ()t(t 1) 2 + f (1)t 2 (t 1). Kun integroimme tämän polynomin, smme 1 P (t) dt = 1 2 (f() + f(1)) (f () f (1)). Smme yllä olevst kvst integrointisäännön yksinkertisell muuttujn vihdoksell yleisessä tpuksess, kun < b (h := b ), jolloin (3.5) f(x) dx M(h) := h h2 (f() + f(b)) (f () f (b)). 16
17 Jos f C 4 [, b], voimme kirjoitt säännön (3.5) pproksimointivirheen seurvss muodoss (ks. [6, s. 12]) (3.6) M(h) f(x) dx = h5 72 f (4) (ξ), missä ξ (, b) j h = (b ). Jos luvut x i, missä i =, 1,..., n, x = j x n = b, eivät ole jkutuneet tsisesti välille h, smme integrndin f(x) interpoloinnill eri integrointisääntöjä. Tällä tvll smme myös Gussin integrointisääntöjä, joit käsittelemme myöhemmin luvuss Yhdistetyistä säännöistä Emme yleensä sovell Newton-Cotesin kvoj ti muit vstvi kvoj koko integrointivälille [, b], vn käytämme niitä yksitellen osväleillä, joihin kyseinen integrointiväli on jettu. Arvioimme koko integrli osvälien pproksimtioiden summll. Snomme, että pikllisesti käytetty integrointisääntö on ljennettu, mistä smme yhdistetyn säännön. Jtkmme trkstelemll joitkin tällisi yhdistettyjä sääntöjä tässä liluvuss. Kun n = 1, smme puolisuunnikssäännöstä (ks. tulukko 1) pproksimoidun rvon I i := h 2 [f(x i) + f(x i+1 )] osvälillä [x i, x i+1 ] j osituksell x i = + ih, missä i =, 1,..., N j missä h := (b )/N. Smme koko integrointivälille pproksimtion T (h) := N 1 I i = h[ f() 2 + f( + h) + f( + 2h) + + f(b h) + f(b) 2 ], mikä on puolisuunnikssumm jkovälin pituudelle h. Jokisell osvälillä [x i, x i+1 ] smme virheeksi I i x i+1 x i f(x) dx = h3 12 f (2) (ξ i ), missä ξ i (x i, x i+1 ), kun oletmme, että f C 2 [, b]. Kun lskemme kikkien osvälien virheet yhteen, smme T (h) f(x) dx = h3 N 1 f (2) (ξ i ) = h (b ) 1 N 1 f (2) (ξ i ). N Kosk minf (2) (ξ i ) 1 N 1 f (2) (ξ i ) mxf (2) (ξ i ) i N i 17
18 j funktio f (2) (x) on jtkuv, niin on olemss ξ [min i ξ i, mx i ξ i ] (, b) j f (2) (ξ) = 1 N N 1 f (2) (ξ i ), kun [min i ξ i, mx i ξ i ] on väli ξ i :n pienimmästä rvost suurimpn rvoon. Nyt smme virheeksi T (h) f(x) dx = b 12 h2 f (2) (ξ), missä ξ (, b). Kun pienennämme jkovälin pituutt h (j ksvtmme smll luku N), pproksimtiovirhe lähestyy noll nopeudell h 2, joten menetelmä on toist kertluku. Jos N on prillinen, voimme sovelt Simpsonin sääntöä yksitellen jokisell osvälillä [x 2i, x 2i+1, x 2i+2 ], missä i =, 1,..., N/2 1, jolloin smme pproksimtion h 3 (f(x 2i) + 4f(x 2i+1 ) + f(x 2i+2 )). Kun lskemme yhteen N/2 pproksimtiot, smme Simpsonin säännön yhdistetyn säännön S(h) = h [f() + 4f( + h) + 2f( + 2h) + 4f( + 3h) f(b 2h) + 4f(b h) + f(b)] koko integrointivälille. Smme yhdistetyn säännön S(h) virheen, kun lskemme kikki yksittäiset N/2 virhettä yhteen, jolloin S(h) f(x) dx = h5 (N/2) 1 9 f (4) (ξ i ) = h4 9 b 2 2 N (N/2) 1 f (4) (ξ i ). Voimme sd vstvill perusteluill kuin puolisuunnikssummll virheeksi S(h) f(x) dx = b 18 h4 f (4) (ξ), missä ξ (, b), kun f C 4 [, b]. Tällöin menetelmä on neljättä kertluku, sillä pproksimtiovirhe lähestyy noll nopeudell h 4. Kun ljennmme yhtälön (3.5) integrointisääntöä M(h), huommme merkittävän vikutuksen. Kun lskemme yhteen jokisen osintegrlin rvot x i+1 x i f(x) dx, missä i =, 1,..., N 1, 18
19 kikki sisäpuoliset derivtt f (x i ), missä < i < N, kumoutuvt. Smme nyt seurvn pproksimtion koko integrlille. Tällöin U(h) :=h [ f() 2 + f( + h) + + f(b h) + f(b) ] + h [f () f (b)] = T (h) + h2 12 [f () f (b)]. Voimme jtell tätä kv puolisuunnikssummn T (h) korjuksen. Voimme ljent integrointisäännön M(h) virheen (3.6) yhdistetyn säännön U(h) virhekvksi vstvll tvll kuin iemmin. Täten (3.7) U(h) f(x) dx = b 72 h4 f (4) (ξ), missä ξ (, b), kun f C 4 [, b]. Kun vertmme tätä virhettä puolisuunnikssummn virheeseen, huommme, että menetelmän kertluku on prntunut khdell. Simme prnnuksen ikn hyvin pienellä lisätyöllä - derivttojen f () j f (b) lskemisell. Jos nämä kksi rjderivtt ovt smoj (esimerkiksi jksoittisill funktioill), puolisuunnikssumm itsessään trjo menetelmän, jonk kertluku on vähintään 4. 19
20 4 Gussin integrointimenetelmistä Tässä luvuss trkstelemme integrlej, jotk ovt muoto I(f) := ω(x)f(x) dx. Tässä integrndiss funktio ω(x) on nnettu ei-negtiivinen pinofunktio välillä [, b]. Pinofunktioiden määrittelyn jälkeen käymme läpi keskeisiä tuloksi ortogonlisist polynomeist. Näiden tulosten vull voimme myöhemmin muotoill Gussin integrointisääntöjä. (Ks. [6, s ] j [2, s , s. 29]). 4.1 Pinofunktioist Määrittelemmme ensin pinofunktion ω(x) välillä [, b]. Määritelmä 4.1. Olkoon ω(x) nnettu ei-negtiivinen funktio välillä [, b]. Snomme funktion ω(x) olevn pinofunktio, jos se toteutt seurvn ehdon. Jos funktio ω(x) kikill x [, b] j ω(x) dx >, niin tällöin pinofunktio ω(x) on määritelty välillä [, b]. Esitämme seurvksi esimerkin pinofunktiost. Esimerkki 4.1. Jos funktio ω(x) on positiivinen j jtkuv äärellisellä suljetull välillä [, b], niin määritelmän 4.1 ehdo toteutuu. Tällöin funktio ω(x) on pinofunktio. Oletmme jtkoss, että integrndi ω(x)f(x) on Riemnn-integroituv j pinofunktio ω(x) on jtkuv. Huomutus 4.1. Olkoot s(x) ei-negtiivisi polynomej välillä [, b]. Jos integrli ω(x)s(x) dx =, niin tällöin kikille polynomeille s(x) pätee s(x). Tämä on ekvivlentti sen knss, että ω(x) dx >. (Ks. [6, s. 156]). 2
21 Siirrymme seurvksi tutkimn integrlin pproksimtioit j summlusekkeit, jotk ovt muoto (4.1) Ĩ(f) := ω i f(x i ), i=1 missä Ĩ trkoitt integrlin I likirvo. Newton-Cotesin kvt (ks. luku 3) ovt myös tätä muoto, mutt tällöin vdimme lukujen x i muodostvn tsvälisen jon välillä [, b]. Tässä luvuss lievennämme kyseistä rjoitust. Yritämme vlit luvut x i j pinot ω i siten, että smme mhdollisimmn suuren kertluvun integrointimenetelmälle. Tässä kertluku perustuu integrointitrkkuuteen. Yritämme siis sd mhdollisimmn suuren steen, johon sti polynomit integroituvt trksti kvn 4.1 vull. Huommme, että tämä on mhdollist j että se joht luokkn hyvinmääriteltyjä Gussin integrointisääntöjä ti Gussin kvdrtuuristen kvojen luokkn. Trvitsemme ensin joitkin perustuloksi ortogonlisist polynomeist ennen, kuin voimme määrittää Gussin integrointisääntöjen pisteet j pinot. 4.2 Perustuloksi ortogonlisist polynomeist Määrittelemme luksi, mitä trkoitmme funktioiden ortogonlisuudell. Määritelmä 4.2. Olkoon V = C[, b]. Olkoon pinofunktio ω(x) Riemnn-integroituv välillä [, b] siten, että ω(x) dx >. Snomme, että funktioiden f, g V sklritulo on (f, g) := ω(x)f(x)g(x) dx. Snomme, että funktiot f j g ovt ortogonlisi, mikäli niiden sklritulolle pätee (f, g) =. Olkoon edelleen V = C[, b]. Jos f, f 1,... on V :n äärellinen ti ääretön osjoukko siten, että (f i, f j ) =, missä i j, niin osjoukko on ortogonlinen. Jos lisäksi niin osjoukko on ortonormli. (f i, f i ) = 1, missä i =, 1,..., 21
22 Huomutus 4.2. Merkintä xp i trkoitt polynomi, jok s rvon xp i (x) kikill x. Seurv luse osoitt preittin ortogonlisten polynomien, jotk liittyvät pinofunktioon ω(x), jonon olemssolon. Luse 4.1. On olemss polynomit p j Π j, missä j =, 1, 2,..., siten, että (p i, p k ) = kikill i k. Ne voidn määritellä yksikäsitteisesti rekursioll (4.2) p (x) 1, (4.3) p i+1 (x) (x δ i+1 )p i (x) γ 2 i+1p i 1 (x), jos i, j missä p 1 (x), (4.4) δ i+1 := (xp i, p i ), jos i, (p i, p i ) (4.5) γ 2 i+1 := { (p i,p i ) (p i 1,p i 1 ), kun i =,, kun i 1. Todistus. Todistmme luseen 4.1 induktioll. Voimme konstruoid polynomej rekursiivisesti Grm-Schmidt ortogonlistio -tekniikll. Näemme selvästi, että polynomi p (x) 1, sillä Π = {p p(x) = x = 1}. Oletmme sitten induktio-oletuksen, että kikki ortogonliset polynomit, joill on luseess 4.1 minitut ominisuudet, on konstruoitu jokiselle j i. Oletmme lisäksi, että nämä polynomit on osoitettu yksikäsitteisiksi. Osoitmme seurvksi, että on olemss yksikäsitteinen polynomi p i+1 Π i+1, jonk sklritulo (4.6) (p i+1, p j ) = kikill j i j jok toteut luseen 4.1 ehdon (4.3). Jokinen polynomi p i+1 Π i+1 voidn kirjoitt yksikäsitteisesti muodoss p i+1 (x) (x δ i+1 )p i (x) + c i 1 p i 1 (x) + c i 2 p i 2 (x) c p (x), kosk suurimmn termin j polynomien p j, missä j i, suurimpien termien kertoimien rvot ovt 1. Kosk (p j, p k ) = kikill j, joille k i j j k, kv (4.6) on voimss, jos j vin jos (4.7) (p i+1, p i ) = (xp i, p i ) δ i+1 (p i, p i ) =, 22
23 (4.8) (p i+1, p j 1 ) = (xp j 1, p i ) + c j 1 (p j 1, p j 1 ) = kikill j i. Huomutuksen 4.1 ehto, missä on vstvsti käytetty polynomej p 2 i j p 2 j 1 ei-negtiivisen polynomin s, estää sen, että sklrituloille pätisi (p i, p i ) =, (p j 1, p j 1 ) =, kun 1 j i. Täten voimme rtkist yhtälöt (4.7) j (4.8) yksikäsitteisesti. Yhtälöstä (4.7) smme yhtälön (4.4). Induktio-oletuksest seur, että p j (x) (x δ j )p j 1 (x) γ 2 j p j 2 (x) kikill j i. Kun rtkisemme tästä polynomin xp j 1 (x), rtkisun vull voimme osoitt, että (xp j 1, p i ) = (p j, p i ) jokisell j i. Täten smme rtkisemll yhtälön (4.8), että c j 1 = (p { j, p i ) γ (p j 1, p j 1 ) = 2 i+1, kun j = i,, kun j < i. Täten luseen koht (4.3) pätee rvoll i + 1. Huomutus 4.3. Jtkoss polynomi p n trkoitt luseess 4.1 esiintyvää polynomi. Voimme esittää jokisen polynomin p Π k ortogonlisten polynomien p i, kun i k, linerikombintion. Smme seurvn seuruksen. Seurus 4.1. Sklritulo (p, p n ) = kikill polynomeill p Π n 1. Luse 4.2. Polynomin p n juuret x i, missä i = 1,..., n, ovt relisi j yksinkertisi. Kikki polynomin p n juuret x i kuuluvt voimelle välille (, b). Todistus. Trkstelemme polynomin p n juuri, jotk kuuluvt voimelle välille (, b) j jotk ovt pritont kertluku. Toisin snoen juuret ovt kohdiss, joiss polynomi p n viht merkkiä eli Polynomi < x 1 < < x l < b. l q(x) := (x x j ) Π l j=1 on sellinen, että polynomi p n (x)q(x) ei muut merkkiänsä suljetull välillä [, b], joten huomutuksen 4.1 nojll (p n, q) = ω(x)p n (x)q(x)dx. Täten polynomin q steelle on voimss, että deg(q) = l = n, sillä muuten pätisi (p n, q) = seuruksen 4.1 nojll. 23
24 Luse 4.3. Jos A on n n mtriisi, missä p (t 1 )... p (t n ) A :=.., p n 1 (t 1 )... p n 1 (t n ) niin mtriisi A on kääntyvä kikill keskenään erillisillä rgumenteill t i, missä i = 1,..., n. Todistus. Teemme vstoletuksen, ettei mtriisi A ole kääntyvä. Tällöin on olemss sellinen rivivektori c, että c T = (c,..., c n 1 ), j rivivektorin j mtriisin tulolle on voimss c T A =. Siis polynomill q(x) : n 1 c i p i (x), jolle deg (p) < n, on n erillistä juurt t 1,..., t n j polynomin täytyy oll identtisesti noll. Olkoon l suurin indeksi, joll c l. Tällöin pätee p l (x) = 1 l 1 c i p i (x). c l Tämä on ristiriit, sillä oikenpuoleisen polynomin ste on pienempi kuin polynomin p l Π l ste. Edellinen luse osoitt, että interpoltio-ongelm, jok koskee muoto (4.9) p(x) n 1 c i p i (x), missä p(t i ) = f i (i = 1,..., n), olevn funktion löytämistä, on in yksikäsitteisesti rtkistviss. Luseen ehdon mukn millä thns muoto (4.9) olevll polynomill on korkeintn n 1 nollkoht. Seurvksi totemme j todistmme tämän luvun päätuloksen. Luse 4.4. () Olkoot x 1, x 2,..., x n n:nnen steen ortogonlisen polynomin p n (x) juuret. Olkoon w 1, w 2,..., w n kääntyvää mtriisi vstvn yhtälöryhmän { (p, p (4.1) p k (x i )w i = ), jos k =,, jos k = 1, 2,..., n 1, i=1 rtkisu. Tällöin w i > kikill i = 1, 2,..., n, j kikill polynomeill p Π 2n 1 pätee, että (4.11) ω(x)p(x)dx = w i p(x i ). i=1 Snomme, että positiiviset luvut w i ovt "pinoj". 24
25 (b) Kääntäen, jos luvut x i j w i, missä i = 1,..., n, ovt sellisi, että ehto (4.11) pitää pikkns kikill p Π 2n 1, niin luvut x i ovt polynomin p n juuret j pinot w i toteuttvt ehdon (4.1). (c) Ei ole mhdollist löytää sellisi pisteitä x i j w i, missä i = 1,..., n, että ehto (4.11) pitäisi pikkns kikill polynomeill p Π 2n. Todistus. Luseen 4.2 mukn polynomin p n juuret x i, missä i = 1,..., n, ovt relisi j preittin erillisiä lukuj välillä (, b). Tällöin n n-mtriisi p (x 1 )... p (x n ) (4.12) A =.. p n 1 (x 1 )... p n 1 (x n ) on kääntyvä luseen (4.3) nojll, sillä kikki rgumentit ovt erillisiä. Täten yhtälöryhmällä (4.1) on yksikäsitteinen rtkisu. Trkstelemme stunnist polynomi p Π 2n 1. Voimme kirjoitt sen muodoss (4.13) p(x) p n (x)q(x) + r(x), missä q j r ovt polynomej joukost Π n 1. Voimme ilmist polynomit q j r ortogonlisten polynomien linerisin kombintioin j q(x) r(x) n 1 k= n 1 k= α k p k (x) β k p k (x). Kosk p (x) 1, ehdost (4.13) j seuruksest 4.1 seur, että ω(x)p(x)dx = (p n, q) + (r, p ) = β (p, p ). Toislt ehdost (4.13) (sillä p n (x i ) = ) j yhtälöstä (4.1) seur, että ( n 1 n ) w i p(x i ) = w i r(x i ) = β k w i p k (x i ) = β (p, p ). i=1 i=1 k= Siis ω(x)p(x) dx = β (p, p ) = w i p(x i ). i=1 Täten ehto (4.11) on täytetty. Todistmme seurvksi puväitteen ennen, kuin stmme todistuksen loppuun. 25
26 Apuväite 4.1. Jos luvut x i j w i, missä i = 1,..., n, ovt sellisi, että yhtälö (4.11) pitää pikkns kikill polynomeill p Π 2n 1, niin w i > kikill i = 1,..., n. Voimme todent tämän tuloksen soveltmll yhtälöä (4.11) polynomeihin n p j (x) : (x x h ) 2 Π 2n 2, h=1 h j missä j = 1,..., n. Huommme, että n < ω(x) p j (x) dx = w i p j (x i ) = w j i=1 h=1 h j (x j x h ) 2 huomutuksen 4.1 nojll. Tämä täydentää luseen 4.4 kohdn () todistuksen. Stmme nyt loppuun luseen todistuksen. Oletmme, että luvut x i j w i, missä i = 1,..., n, ovt sellisi, että ehto (4.11) pätee kikill polynomeill p Π 2n. Tällöin n p(x) : (x x j ) 2 Π 2n, j=1 mikä iheutt ristiriidn oletuksemme knss, sillä huomutuksen 4.1 nojll < ω(x) p(x) dx = w i p(x i ) =. Tämä todist luseen 4.4 kohdn (c). Todistksemme luseen 4.4 kohdn (b) oletmme seurvksi, että luvut x i j w i, missä i = 1,..., n, ovt sellisi, että yhtälö (4.11) pitää pikkns kikill p Π 2n 1. Pisteiden x i pitää oll erilliset, sillä muuten voisimme muodost smn integrointisäännön käyttäen vin n 1 kpplett lukuj x i, mikä on ristiriidss luseen 4.4 kohdn (c) knss. Soveltmll yhtälöä (4.11) ortogonlisiin polynomeihin p = p k, missä k =,..., n 1, smme { (p, p w i p k (x i ) = ω(x)p k (x) dx = (p k, p ) = ), jos k =,, jos k = 1,..., n 1. i=1 Toisin snoen pinojen w i täytyy toteutt yhtälö (4.1). Kun sovellmme yhtälöä (4.11) polynomeihin i=1 p(x) : p k (x)p n (x), missä k =,..., n 1, 26
27 smme seuruksen 4.1 nojll = (p k, p n ) = w i p n (x i )p k (x i ), missä k =,..., n 1. i=1 Toisin snoen vektori c := (w 1 p n (x 1 ),..., w n p n (x n )) T rtkisee homogeenisen yhtälöryhmän Ac =, missä mtriisi A on muoto (4.12). Kosk pisteet x i, missä i = 1,..., n, ovt erilliset, mtriisi A on kääntyvä luseen (4.3) nojll. Täten c = j w i p n (x i ) = kikill i = 1,..., n. Kosk pinoille pätee w i > puväitteen 4.1 nojll, smme p n (x i ) =, missä i = 1,..., n. Tämä stt loppuun luseen 4.4 kohdn (b) todistuksen. Guss on ensimmäisenä todistnut luseen 4.4 yleisimmällä pinofunktioll ω(x) 1 j suljetull välillä [ 1, 1]. Vstvt ortogonliset polynomit ovt (4.14) p k (x) : k! d k (2k)! dx k (x2 1) k, missä k =, 1,.... Näille polynomeille on voimss, että p k Π k, j osittisintegrointi osoitt, että sklritulolle pätee (p i, p k ) =, kun i k. Snomme, että polynomit (4.14) ovt Legendren polynomej kerroint lukuun ottmtt. Legendren polynomit ovt Legendren differentiliyhtälön (ks. [2, s ]) (1 x 2 )y 2xy + n(n + 1)y =, missä y = P n (x), rtkisut, kun n on luonnollinen luku. Legendren polynomit voidn määritellä myös rekursiivisesti siten, että (n + 1)P n+1 (x) = (2n + 1)xP n (x) np n 1 (x), missä P (x) = 1 j P 1 (x) = 1. Voimme esittää Legendren polynomit myös Rodriguesin kvn vull muodoss d n P n (x) = 1 2 n n! dx n [(x2 1) n ]. Seurvss tulukoss nnmme joitkin rvoj luvuille x i j pinoille w i tässä tärkeässä erityistpuksess. Enemmän rvoj löytyy kirjst Ntionl Bureu of Stndrd s Hndbook of Mthemticl Functions (ks. [1, s. 916]). 27
28 Tulukko 2: Pinoj w i j lukuj x i. n w i x i 1 w 1 = 2 x 1 = 2 w 1 = w 2 = 1 x 2 = x 1 =, w 1 = w 3 = 5 9 x 3 = x 1 =, w 2 = 8 9 x 2 = 4 w 1 = w 4 =, x 4 = x 1 =, w 2 = w 3 =, x 3 = x 2 =, w 1 = w 5 =, x 5 = x 1 =, w 2 = w 4 =, x 4 = x 2 =, w 3 = x 3 = Muit tärkeitä tpuksi, jotk johtvt Gussin integrointisääntöihin, on myös tulukoitu (ks. [6, s. 148]). 4.3 Tridigonlimtriiseist Olemme krkterisoineet luvut x i j pinot w i, jotk voimme sijoitt Gussin integrointisäännöille nnetuille pinofunktioille. Emme ole vielä esitelleet menetelmiä, joill vrsinisesti lskemme Gussin integrointisääntöjen sijoituksi. Sijoitmme Gussin integrointisääntöihin pisteitä, jotk ovt ortogonlisen polynomin nollkohti. Voimme ilmist Gussin integrointisäännöt muodoss ω(x)f(x) dx = w i f(x i ), b missä ω(x) on nnettu pinofunktio j missä n on nnettu luonnollinen luku (ks. [4, s. 121]). Trkstelemme edellä minittu ongelm sellisen oletuksen pohjlt, että rekursion (4.2) j (4.3) kertoimet δ i j γ i on nnettu (ks. luse 4.1). Ortogonlisten polynomien teori liittyy relisten tridigonlimtriisien δ 1 γ 2 γ 2 (4.15) J n = i=1 γ n γ n δ n 28
29 j niiden päälimtriisien δ 1 γ 2 γ 2 J j = γ j γ j δ j teorin. Hvitsemme, että päälimtriisin J j krkteristiset polynomit p j toteuttvt rekursion (4.2) j (4.3) luseess 4.1, kun mtriisin lkiot δ i j γ i ovt kertoimin (ks. [6, s. 149]). Täten p n on tridigonlimtriisin J n krkteristinen polynomi. Smme seuruksen seurvn luseen. Luse 4.5. Ortogonlisen polynomin p n juuret x i, missä i = 1,..., n, ovt tridigonlimtriisin J n ominisrvot. Esitämme seurvksi luseen, jok liittää pinot w i tridigonlimtriiseihin J n. Luse 4.6. Olkoon J n tridigonlimtriisi (4.14) j v (i) := (v (i) 1,..., v (i) n ) T sen ominivektori ominisrvoll x i siten, että J n v (i) = x i v (i). Olkoon lisäksi v (i) sklttu siten, että Tällöin pinoille pätee v (i)t v (i) = (p, p ) = ω(x) dx. w i = (v (i) 1 ) 2, missä i = 1,..., n. Todistus (ks. [6, s ]). Todistus sivuutetn. Lopuksi rvioimme Gussin integrointimenetelmän virhettä. Luse 4.7. Jos f C 2n [, b], niin jollekin ξ (, b). ω(x)f(x) dx i=1 w i f(x i ) = f (2n) (ξ) (p n, p n ) (2n)! Todistus. Trkstelemme Hermiten interpoltio-ongelmn (ks. luku 2 luse 2.2) h(x i ) = f(x i ), h (x i ) = f (x i ), missä i = 1,..., n, rtkisu h Π 2n 1. 29
30 Kosk deg(h) < 2n, niin luseen 4.4 nojll ω(x)h(x) dx = w i h(x i ) = w i f(x i ). i=1 i=1 Täten smme virhetermille integrliesityksen ω(x)f(x) dx w i f(x i ) = ω(x)f(x) dx ω(x)h(x) dx i=1 = ω(x)(f(x) h(x)) dx. Polynomin p n (x) Π n juuret ovt x i. Nyt smme luseen 2.3 nojll f(x) h(x) = f (2n) (ζ) (2n)! (x x 1 ) 2 (x x n ) 2 = f (2n) (ζ) p 2 (2n)! n(x) jollekin ζ = ζ(x) välillä I(x 1,..., x n, x). Tässä väli I(x 1,..., x n, x) trkoitt pienintä voint väliä, jok sisältää luvut x 1,..., x n j x. Lisäksi f (2n) (ζ(x)) (2n)! = f(x) h(x) p 2 n(x) on jtkuv välillä [, b], joten voimme käyttää integrlilskennn yleistettyä välirvolusett. Tällöin ω(x)(f(x) h(x)) dx = jollekin luvulle ξ (, b). ω(x)f (2n) (ζ(x)) (2n)! p 2 n(x) dx = f (2n) (ξ) (p n, p n ) (2n)! Kun vertmme Newton-Cotesin j Gussin integrointimenetelmiä, huommme, että Gussin menetelmä on numeerisesti stbiili. Gussin integrointikvojen pinot ovt in positiivisi riippumtt pisteiden lukumäärästä n. Gussin integrointimenetelmä nt myös trkimmt tulokset, jos lskennllinen työskentely on smnveroist molemmiss menetelmissä. Jos tietäisimme etukäteen, kuink n pitäisi vlit siten, että svuttisimme ennlt määrätyn trkkuuden mille thns integrlille, Gussin integrointimenetelmä olisi ylivoiminen verrttun muihin numeerisiin integrointimenelmiin. Vlitettvsti meillä ei kuitenkn usein ole mhdollisuutt käyttää lusett 4.7 tätä trkoitust vrten, kosk derivtn korken kertluvun vuoksi trvittvien pisteiden määrän ennlt rvioiminen voi oll viket. Edellä minittujen syiden tki sovellmme yleensä Gussin integrointimenetelmää ksvvill n:n rvoill, kunnes peräkkäiset pproksimtiot täsmäävät tietylle trkkuudelle. Kosk emme yleensä voi käyttää luvulle n lskettuj funktion rvoj myös luvulle n + 1 (inkn klssisess tpuksess ω(x) 1), menetämme nopesti Gussin integrtiomenetelmän ilmeiset edut. 3
31 4.4 Gussin integrointikvoist etukäteen määrätyillä luvuill Tässä liluvuss trkstelemme Gussin integrointikvoj, kun meillä on tietty määrä etukäteen määrättyjä lukuj (ks. [2, s ]). Trkoitmme tällä kv, jok on muoto (4.16) m ω(x)f(x) dx k f(y k ) + ω k f(x k ), k=1 k=1 missä olemme kiinnittäneet j määränneet luvut y k etukäteen j määritämme m + 2n vkiot k, ω k j x k siten, että sääntö on trkk mhdollisimmn korke-steiselle polynomille (eli polynomille, jonk ste on m + 2n 1). Olkoot r(x) j s(x) sellisi polynomej, että r(x) = (x y 1 )(x y 2 ) (x y m ) j s(x) = (x x 1 )(x x 2 ) (x x n ). Luse 4.8. Sääntö (4.16) on trkk kikille polynomeille, joiden ste on pienempi ti yhtä suuri kuin m + 2n 1, jos j vin jos () se on trkk kikille polynomeille, joiden ste on m + n 1, (b) jos jokisen polynomin p(x) steluku on korkeitn n 1, niin tällöin ω(x)r(x)s(x)p(x) dx =. Todistus. Luseen 4.8 kohdn () välttämättömyys on trivili. Olkoon polynomi p(x) stett deg(p(x)) n 1. Tällöin polynomi t(x) = r(x)s(x)p(x) on polynomi, jonk ste on korkeintn m + 2n 1. Täten, jos kv (4.16) on trkk polynomille t(x), niin m ω(x)t(x) dx = k t(y k ) + ω k t(x k ). b k=1 k=1 Mutt nyt on voimss t(y k ) =, missä k = 1, 2,..., m, j t(x k ) =, missä k = 1, 2,..., n. Täten kohdn (b) välttämättömyys seur. Oletetn kääntäen, että kohdt () j (b) pitävät pikkns. Olkoon t(x) polynomi, jonk ste on korkeintn m + 2n 1. Tällöin kyseinen polynomi voidn kirjoitt muodosss t(x) = r(x)s(x)q(x) + v(x), missä q(x) on polynomi korkeintn stett n 1 j v(x) on polynomi, jonk ste on korkeintn 31
32 m + n 1. Nyt on voimss, että t(y k ) = v(y k ), missä k = 1, 2,..., m, j t(x k ) = v(x k ), missä k = 1, 2,..., n. Tällöin smme ω(x)t(x) dx = = ω(x)[r(x)s(x)q(x) + v(x)] dx ω(x)v(x) dx, sillä kohdn (b) nojll ω(x)r(x)s(x)q(x) dx =. Mutt kohdst () smme, että Tämä todist riittävyyden. m ω(x)v(x) dx = k v(y k ) + ω k v(x k ) k=1 k=1 m = k t(y k ) + ω k t(x k ). k=1 k=1 Jott voisimme edetä numeerisesti, meidän täytyy määritellä polynomit s(x) = (x x 1 ) (x x n ) ortogonlisin polynomein välillä [, b] pinon ω(x)r(x) suhteen. Tällöin smme Gussin integrointimenetelmän pohjksi kyseiset polynomit siten, että niiden ortogonlisuusreltioiss esiintyvät pinofunktiot ovt integrndin tekijöinä. Luse 4.9. Olkoot p n (x), missä n =, 1,..., ortonormlisi polynomej välillä [, b] pinon ω(x) suhteen. Olkoon r(x) = (x y 1 )(x y 2 ) (x y m ) välillä [, b]. Oletetn, että luvut y i ovt erillisiä. Oletetn lisäksi, että polynomit q n (x), missä n =, 1,..., ovt ortogonlisi polynomej välillä [, b] pinon ω(x)r(x) suhteen. Tällöin p n (x) p n+1 (x) p n+m (x) p n (y 1 ) p n+1 (y 1 ) p n+m (y 1 ) (4.17) r(x)q n (x) =.... p n (y m ) p n+1 (y m ) p n+m (y m ) Todistus. On selvää, että kvn (4.17) oike puoli kuuluu joukkoon Π n+m. Lisäksi oike puoli kto, kun x = y 1, x = y 2,..., x = y m eli determinntin vkrivit ovt yhtä suuret. Täten se voidn kirjoitt muodoss r(x)q n (x), missä q n (x) Π n. 32
33 Osoitmme seurvksi, että polynomi q n (x) on ortogonlinen eli kohtisuorss kikki joukon Π n 1 lkioit vstn pinon ω(x)r(x) suhteen. Olkoon q(x) Π n 1. Kosk r(x)q n (x) on selvästi tietty linerikombintio polynomeist p n (x),..., p n+m (x), niin smme Smme, että ω(x)r(x)q n (x)q(x) dx = r(x)q n (x) = c 1 p n (x) + + c m+1 p n+m (x). ω(x)[c 1 p n (x) + + c m+1 p n+m (x)]q(x) dx =, sillä jokinen ortonormli polynomi on ortogonlinen lemmn steen polynomien suhteen. Lopuksi osoitmme, että polynomin q n (x) ste on täsmälleen n. Smme osoitettu tämän näyttämällä, ettei polynomin p n+m (x) kerroin c m+1 ole noll. Tämä kerroin on p n (y 1 ) p n+1 (y 1 ) p n+m 1 (y 1 ) (4.18) c m+1 =.... p n (y m ) p n+1 (y m ) p n+m 1 (y m ) Jos olisi c m+1 =, löytäisimme vkiot d 1, d 2,..., d m, joist kikki eivät ole nolli, siten, että polynomi (4.19) s(x) = d 1 p n (x) + d 2 p n+1 (x) + + d m p n+m 1 (x) ktoisi, kun x = y 1, x = y 2,..., x = y m. Nyt polynomi s(x) olisi muoto s(x) = r(x)t(x), missä t(x) Π n 1. Lisäksi s(x) olisi tietenkin ortogonlinen kikkien joukon Π n 1 lkioiden suhteen. Tästä seurisi, että = ω(x)s(x)t(x) dx = ω(x)r(x)t 2 (x) dx. Tällöin t(x) huomutuksen 4.1 nojll. Tämä on ristiriidss sen knss, että kikki luvut d i eivät ole nolli. Jos otmme integrointivälin päätepisteet mukn khteen yleisimpään Gussin integrointisääntöön j vlitsemme pinoiksi ω(x) = 1 j loput pisteet x k siten, että smme mhdollisimmn korken kertluvun menetelmälle, päädymme Rdun j Lobtton integrointiin. (Ks. [2, s ]). Esitämme nämä lusein 4.1 j
34 Luse 4.1 (Rdun integrointi). Olkoon funktio f(x) C 2n 1 [ 1, 1]. Tällöin (4.2) 1 1 f(x) dx = 2 n 1 n f( 1) + 2 j=1 ω j f(x j ) + E, missä x j on j:s noll lusekkeess (4.21) missä P n 1 (x) + P n (x), P (x) = Legendren polynomi (ks. luku 4.2), x 1 (4.22) ω j = 1 n 2 1 x j [P n 1 (x j )] 2 = 1 1 x j 1 [P n 1(x j )] 2, j missä (4.23) E = E(f) = 22n 1 n [(2n 1)!] 3 [(n 1)!]4 f (2n 1) (ξ), missä 1 < ξ < 1. Seurvss luseess esitämme Lobtton integroinnin. Luse 4.11 (Lobtton integrointi). Olkoon f(x) C 2n 2 [ 1, 1]. Tällöin (4.24) 1 1 f(x) dx = n 1 2 n(n 1) [f(1) + f( 1)] + ω j f(x j ) + E, j=2 missä x j on polynomin P n 1(x) (j 1):s nollkoht, kun P (x) on Legendren polynomi. Tässä kvss (4.24) luvuille ω j j E pätee, että (4.25) ω j = j (4.26) 2 n(n 1)[P n 1 (x j )] 2, missä x j 1, x j 1, E = E(f) = n(n 1)3 2 2n 1 [(n 2)!] 4 (2n 1)[(2n 2)!] 3 f (2n 2) (ξ), missä 1 < ξ < 1. Rdun j Lobtton integrointisäännöt ovt usein hyödyllisiä pproksimoinniss seurviss tilnteiss (vrt. [2, s ]). (1) Funktio s pisteessä 1 ti 1 yksinkertisen rvon, esimerkiksi nolln. 34
35 (2) Rdun kv on hyödyllinen, kun rtkisemme tvllisen yhden muuttujn differentiliyhtälön (4.27) y = f(x, y) seurvsti (4.28) y(1) = y( 1) f(x, y) dx y( 1) + 2 n 1 n f( 1, y( 1)) + 2 i=1 w i f(x i, y(x i )). Tässä luvut x i ovt Rdun integrointisäännön lukuj j ω i vstvi pinoj. Jos lskemme rvot f(x i, y(x i )) jollkin stndrdimenetelmällä, niin ylläolev pproksimtio prnt termin y(1) rvo. Lopuksi nnmme esimerkin Rdun j Lobtton integrointisäännöistä eri integrndeill. Esimerkki 4.2. Olkoot L 4 Lobtton neljän pisteen sääntö, L 1 Lobtton kymmenen pisteen sääntö, R 6 Rdun kuuden pisteen vsemmn puoleinen sääntö j R 6 kuuden pisteen oiken puoleinen sääntö. Näissä säännöissä esimerkiksi neljän pisteen säännössä n = 4 j kymmenen pisteen säännössä n = 1. Rdun vsemmn puoleisell säännöllä trkoitmme, että olemme vlinneet pisteet integrointivälin osvälien vsemmlt puolelt. Vstvsti Rdun oiken puoleisell säännöllä trkoitmme, että olemme vlinneet pisteet integrointivälin osvälien oikelt puolelt. All oleviin tulukkoihin olemme koonneet sääntöjä vstvi tuloksi eri integrndeill. Tulukko 3: Sääntöjä vstvi tuloksi. Sääntö 1 x 1 2 dx 1 x 3 2 dx 1 1 dx x dx 1+x 4 L 4, , , , L 1, , 4 199, , R 6, , 4 232, , R 6, , , , Trkk rvo, , 4, ,
36 Tulukko 4: Sääntöjä vstvi tuloksi. 1 Sääntö L 4, , L 1, , R 6, , R 6, , Trkk rvo, , dx 1+e x 1 2 dx 2+sin 1πx Kun trkstelemme n:n pisteen Gussin säännön G n j n 1:n pisteen Lobtton säännön virhetermejä (ks. luseet 4.7 j 4.11), huommme, että termien f (2n) (ξ) kertoimet näissä khdess säännösssä ovt melkein smt j vstkkismerkkiset. Tällöin jos f (2n) ei muut merkkiänsä integrointivälillä, niin integrlin I(f) rvo on näiden khden rvon välillä. Pinotetull keskirvoll n + 1 2n + 1 G n + n 2n + 1 L n+1 smme yleensä premmn pproksimtion integrlin I(f) rvolle kuin kummllkn säännöllä G n ti L n+1. Kun luvun n rvo on suuri j funktio on hyvin käyttäytyvä, tämä pitää yleisesti pikkns. 36
37 Viitteet [1] Abrmowitz, M., nd Stegun, I. A., Hndbook of Mthemticl Functions. Ntionl Bureu of Stndrds, Applied Mthemtics series 55. 6th ed. Wshington DC.: U.S. Government Printing Office, [2] Dvis, P.J., nd Rbinowitz P., Methods of numericl integrtion, 2nd ed. The United Sttes of Americ: Acdemic Press, Inc., [3] Kincid, D., nd Cheney, W., Numericl Anlysis, Interntionl Student Edition. The United Sttes of Americ: Wdsworth, Inc., [4] Press, W. H., Flnnery, B. P., Teukolsky, S. A., Vetterling, W. T., Numericl Recipes. The Art of Scientific Computing. The United Sttes of Americ: The Cmbridge University Press, [5] Steffensen, J. F., Interpoltion, 2nd ed. New York: Chelse Publishing Co., 195. [6] Stoer, J., nd Bulirsch, R., Introduction to numericl nlysis, The United Sttes of Americ: Springer-Verlg New York Inc,
Numeeriset menetelmät TIEA381. Luento 9. Kirsi Valjus. Jyväskylän yliopisto. Luento 9 () Numeeriset menetelmät / 29
 Numeeriset menetelmät TIEA381 Luento 9 Kirsi Vljus Jyväskylän yliopisto Luento 9 () Numeeriset menetelmät 17.4.2013 1 / 29 Luennon 9 sisältö Numeerisest integroinnist Newtonin j Cotesin kvt Luento 9 ()
Numeeriset menetelmät TIEA381 Luento 9 Kirsi Vljus Jyväskylän yliopisto Luento 9 () Numeeriset menetelmät 17.4.2013 1 / 29 Luennon 9 sisältö Numeerisest integroinnist Newtonin j Cotesin kvt Luento 9 ()
x k 1 Riemannin summien käyttö integraalin approksimointiin ei ole erityisen tehokasta; jatkuvasti derivoituvalle funktiolle f virhe b
 5 Integrlien lskemisest 51 Riemnnin summt [A2], [4, 61] Rjoitetun funktion f : [, b] R Riemnn-integroituvuudelle ytäpitäväksi on kurssill Anlyysi 2 osoitettu, että Riemnnin summill S P := f(ξ k ) ( ),
5 Integrlien lskemisest 51 Riemnnin summt [A2], [4, 61] Rjoitetun funktion f : [, b] R Riemnn-integroituvuudelle ytäpitäväksi on kurssill Anlyysi 2 osoitettu, että Riemnnin summill S P := f(ξ k ) ( ),
5 Epäoleellinen integraali
 5 Epäoleellinen integrli 5. Integrlin suppeneminen Olkoon f sellinen välillä [, b[ (ei siis välttämättä pisteessä b) määritelty funktio, että f on Riemnn-integroituv välillä [, ] kikill ], b[ eli on olemss
5 Epäoleellinen integrli 5. Integrlin suppeneminen Olkoon f sellinen välillä [, b[ (ei siis välttämättä pisteessä b) määritelty funktio, että f on Riemnn-integroituv välillä [, ] kikill ], b[ eli on olemss
5 Riemann-integraali ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT Ala- ja yläintegraali
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 9 5 Riemnn-integrli 5. Al- j yläintegrli Voit olett tunnetuksi ll esitetyt supremumin j infimumin ominisuudet (joukot A j B ovt rjoitettuj sekä epätyhjiä j λ R). Jos
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 9 5 Riemnn-integrli 5. Al- j yläintegrli Voit olett tunnetuksi ll esitetyt supremumin j infimumin ominisuudet (joukot A j B ovt rjoitettuj sekä epätyhjiä j λ R). Jos
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
 II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
3 Integraali ja derivaatta
 3 Integrli j erivtt 3.1 Integrli ylärjns funktion Olkoon funktio f Riemnn-integroituv välin I jokisell suljetull osvälillä j välin I jokin kiinteä luku. Tällöin integrli määrittelee funktion G(): I R,
3 Integrli j erivtt 3.1 Integrli ylärjns funktion Olkoon funktio f Riemnn-integroituv välin I jokisell suljetull osvälillä j välin I jokin kiinteä luku. Tällöin integrli määrittelee funktion G(): I R,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 9: Integroimismenetelmät
 MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 10.10.2016 Pekk Alestlo, Jrmo Mlinen (Alto-yliopisto,
MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 10.10.2016 Pekk Alestlo, Jrmo Mlinen (Alto-yliopisto,
1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [
![1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [ 1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [](/thumbs/58/42571602.jpg) 1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
Analyysi 2. Harjoituksia lukuihin 1 3 / Kevät Anna sellainen välillä ] 2, 2[ jatkuva ja rajoitettu funktio f, että
![Analyysi 2. Harjoituksia lukuihin 1 3 / Kevät Anna sellainen välillä ] 2, 2[ jatkuva ja rajoitettu funktio f, että Analyysi 2. Harjoituksia lukuihin 1 3 / Kevät Anna sellainen välillä ] 2, 2[ jatkuva ja rajoitettu funktio f, että](/thumbs/58/42210707.jpg) Anlyysi Hrjoituksi lukuihin 3 / Kevät 5. Ann sellinen välillä ], [ jtkuv j rjoitettu funktio f, että () sup A m A j inf A min A, (b) sup A m A j inf A = min A, (c) sup A = m A j inf A min A, (d) sup A
Anlyysi Hrjoituksi lukuihin 3 / Kevät 5. Ann sellinen välillä ], [ jtkuv j rjoitettu funktio f, että () sup A m A j inf A min A, (b) sup A m A j inf A = min A, (c) sup A = m A j inf A min A, (d) sup A
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 7: Integraali ja analyysin peruslause
 MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 3.10.2016 Pekk Alestlo, Jrmo Mlinen
MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 3.10.2016 Pekk Alestlo, Jrmo Mlinen
Riemannin integraalista
 Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 9: Integroimismenetelmät
 MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 27, 2017 Pekk Alestlo,
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 9: Integroimismenetelmät Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 27, 2017 Pekk Alestlo,
Käydään läpi: ääriarvo tarkastelua, L Hospital, integraalia ja sarjoja.
 DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
DI mtemtiikn opettjksi: Täydennyskurssi, kevät Luentorunko j hrjoituksi viikolle : ti 9.. klo :-5:, to.. klo 9:5-: j klo 4:5-6: Käydään läpi: äärirvo trkstelu, L Hospitl, integrli j srjoj.. Kerrtn äärirvojen
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 7: Integraali ja analyysin peruslause
 MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 20, 2017
MS-A010{2,3,4,5} (SCI,ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November 20, 2017
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
SARJAT JA DIFFERENTIAALIYHTÄLÖT Funktiojonot 1
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 JOUNI PARKKONEN Sisältö 0. Tästä tekstistä. Funktiojonot 0. Tästä tekstistä Tämä moniste on trkoitettu käytettäväksi kurssin Srjt j differentiliyhtälöt luentomterilin.
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 JOUNI PARKKONEN Sisältö 0. Tästä tekstistä. Funktiojonot 0. Tästä tekstistä Tämä moniste on trkoitettu käytettäväksi kurssin Srjt j differentiliyhtälöt luentomterilin.
6 Integraalilaskentaa
 6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
7 Funktiosarjoista. 7.1 Funktiosarjojen suppeneminen
 7 Funktiosrjoist 7. Funktiosrjojen suppeneminen Seurvksi trkstelln srjoj, joiden termit ovt (lukujen sijst) jollkin välillä I määriteltyjä funktioit. Täsmällisemmin funktiosrjll (ti lyhyemmin srjll) trkoitetn
7 Funktiosrjoist 7. Funktiosrjojen suppeneminen Seurvksi trkstelln srjoj, joiden termit ovt (lukujen sijst) jollkin välillä I määriteltyjä funktioit. Täsmällisemmin funktiosrjll (ti lyhyemmin srjll) trkoitetn
a = x 0 < x 1 < x 2 < < x n = b f(x) dx = I. lim f(x k ) x k=1
 5 Integrli 5.1 Määritelmä j ominisuudet Olkoon f : [, b] R jtkuv. Muodostetn välin [, b] jko = x 0 < x 1 < x 2 < < x n = b j siihen liittyvä yläsumm S = n M k (x k x k 1 ), M k = mx{f(x) x k 1 x x k },
5 Integrli 5.1 Määritelmä j ominisuudet Olkoon f : [, b] R jtkuv. Muodostetn välin [, b] jko = x 0 < x 1 < x 2 < < x n = b j siihen liittyvä yläsumm S = n M k (x k x k 1 ), M k = mx{f(x) x k 1 x x k },
2 Riemann-integraali. 2.1 Porrasfunktion integraali. Aloitetaan integraalin täsmällinen määrittely tutkimalla porrasfunktion integraalia.
 2 Riemnn-integrli 2.1 Porrsfunktion integrli Aloitetn integrlin täsmällinen määrittely tutkimll porrsfunktion integrli. Määritelmä 2.1 (Porrsfunktion integrli). Olkoon f : [, b] R porrsfunktio j P = {x
2 Riemnn-integrli 2.1 Porrsfunktion integrli Aloitetn integrlin täsmällinen määrittely tutkimll porrsfunktion integrli. Määritelmä 2.1 (Porrsfunktion integrli). Olkoon f : [, b] R porrsfunktio j P = {x
Riemannin integraali
 LUKU 5 iemnnin integrli Tässä luvuss funktion f iemnnin integrli merkitään - b f = - b f() d. Vstvsti funktion f Lebesgue in integrli merkitään f = f() dm(). [,b] [,b] Luse 5.1. Olkoon f : [, b] rjoitettu
LUKU 5 iemnnin integrli Tässä luvuss funktion f iemnnin integrli merkitään - b f = - b f() d. Vstvsti funktion f Lebesgue in integrli merkitään f = f() dm(). [,b] [,b] Luse 5.1. Olkoon f : [, b] rjoitettu
Numeerinen integrointi
 Pitkärnt: Lj mtemtiikk IX9 Numeerinen integrointi IX9 Numeerinen integrointi Numeerisell integroinnill trkoitetn määrätyn integrlin, eli reliluvun I(f,,b) = f(x)dx lskemist numeerisin keinoin (likimäärin)
Pitkärnt: Lj mtemtiikk IX9 Numeerinen integrointi IX9 Numeerinen integrointi Numeerisell integroinnill trkoitetn määrätyn integrlin, eli reliluvun I(f,,b) = f(x)dx lskemist numeerisin keinoin (likimäärin)
2.4 Pienimmän neliösumman menetelmä
 2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
sin θ θ θ r 2 sin 2 θ φ 2 = 0.
 Mtemtiikn j tilstotieteen litos Osittisdifferentiliyhtälöt Kevät 21 Hrjoitus 9 Rtkisuj Jussi Mrtin 1. Osoit, että Lplce-yhtälö pllokoordinteiss on 2 u 1 r 2 2 u r r 1 r 2 sin θ u 1 2 u sin θ θ θ r 2 sin
Mtemtiikn j tilstotieteen litos Osittisdifferentiliyhtälöt Kevät 21 Hrjoitus 9 Rtkisuj Jussi Mrtin 1. Osoit, että Lplce-yhtälö pllokoordinteiss on 2 u 1 r 2 2 u r r 1 r 2 sin θ u 1 2 u sin θ θ θ r 2 sin
Kertymäfunktio. Kertymäfunktio. Kertymäfunktio: Mitä opimme? 2/2. Kertymäfunktio: Mitä opimme? 1/2. Kertymäfunktio: Esitiedot
 TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
 MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
Reaalinen lukualue. Millainen on luku, jossa on päättymätön ja jaksoton desimaalikehitelmä?
 Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Esimerkki 8.1 Määritellään operaattori A = x + d/dx. Laske Af, kun f = asin(bx). Tässä a ja b ovat vakioita.
 8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
Numeerinen integrointi.
 Numeerinen integrointi. Differentili- j integrlilskent 1, syksy 2015 Hrri Vrpnen Mtemtiikn j systeeminlyysin litos Alto-yliopisto Tiisti 6.10.2015 Sisältö Tylor-menetelmä. Käyttökelpoinen silloin, kun
Numeerinen integrointi. Differentili- j integrlilskent 1, syksy 2015 Hrri Vrpnen Mtemtiikn j systeeminlyysin litos Alto-yliopisto Tiisti 6.10.2015 Sisältö Tylor-menetelmä. Käyttökelpoinen silloin, kun
Sisältö. Integraali 10. syyskuuta 2005 sivu 1 / 20
 Integrli 10. syyskuut 2005 sivu 1 / 20 Sisältö 1 Määrätty integrli j integrlifunktio 2 1.1 Integroituvist funktioit 3 1.2 Määrätyn integrlin ominisuuksi 4 1.3 Integrlifunktio 5 1.4 Integrlilskennn tärkeimmät
Integrli 10. syyskuut 2005 sivu 1 / 20 Sisältö 1 Määrätty integrli j integrlifunktio 2 1.1 Integroituvist funktioit 3 1.2 Määrätyn integrlin ominisuuksi 4 1.3 Integrlifunktio 5 1.4 Integrlilskennn tärkeimmät
MS-A010{2,3,4,5} (SCI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
 MS-A1{2,3,4,5} (SC, ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 8: ntegrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November
MS-A1{2,3,4,5} (SC, ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 8: ntegrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November
Kuvausta f sanotaan tällöin isomorfismiksi.
 Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Differentiaali- ja integraalilaskenta 1 (CHEM) Laskuharjoitus 4 / vko 47, mallivastaukset
 Differentili- j integrlilskent (CHEM) Lskuhrjoitus / vko 7, mllivstukset Johdntotehtävä x dx = ln.693, joten rvo ln voidn pproksimoid integroimll numeerisesti funktiot x välillä [,]. Jetn väli [,] khteen
Differentili- j integrlilskent (CHEM) Lskuhrjoitus / vko 7, mllivstukset Johdntotehtävä x dx = ln.693, joten rvo ln voidn pproksimoid integroimll numeerisesti funktiot x välillä [,]. Jetn väli [,] khteen
Johdatus reaalifunktioihin P, 5op
 Johdtus relifunktioihin 802161P, 5op Os 3 Pekk Slmi 19. lokkuut 2015 Pekk Slmi FUNK 19. lokkuut 2015 1 / 48 Integrlit 1 Määrätty integrli = oike integrli: esim. 1 0 x 2 dx = reliluku 2 Määräämätön integrli
Johdtus relifunktioihin 802161P, 5op Os 3 Pekk Slmi 19. lokkuut 2015 Pekk Slmi FUNK 19. lokkuut 2015 1 / 48 Integrlit 1 Määrätty integrli = oike integrli: esim. 1 0 x 2 dx = reliluku 2 Määräämätön integrli
Kertausta ja täydennystä
 LUKU 1 Kertust j täydennystä 1.1. Merkintöjä N = {k Z k 0} = {0, 1, 2,... }, luonnollisten lukujen joukko. Z + = {k Z k > 0} = {1, 2,... }, positiivisten kokonislukujen joukko. (, b) on relikselin voin
LUKU 1 Kertust j täydennystä 1.1. Merkintöjä N = {k Z k 0} = {0, 1, 2,... }, luonnollisten lukujen joukko. Z + = {k Z k > 0} = {1, 2,... }, positiivisten kokonislukujen joukko. (, b) on relikselin voin
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa II
 MS-A7 ifferentili- j integrlilskent (Chem Yhteenveto, os II G. Gripenberg Alto-yliopisto 9. helmikuut 16 G. Gripenberg (Alto-yliopisto MS-A7 ifferentili- j integrlilskent (Chem Yhteenveto, 9. helmikuut
MS-A7 ifferentili- j integrlilskent (Chem Yhteenveto, os II G. Gripenberg Alto-yliopisto 9. helmikuut 16 G. Gripenberg (Alto-yliopisto MS-A7 ifferentili- j integrlilskent (Chem Yhteenveto, 9. helmikuut
Newtonin, Riemannin ja Henstock-Kurzweilin integraalit
 TAMPEREEN YLIOPISTO Pro grdu -tutkielm Annik Heinonen Newtonin, Riemnnin j Henstock-Kurzweilin integrlit Informtiotieteiden yksikkö Mtemtiikk Helmikuu 2013 Sisältö 1 Johdnto 1 2 Newtonin integrli 2 2.1
TAMPEREEN YLIOPISTO Pro grdu -tutkielm Annik Heinonen Newtonin, Riemnnin j Henstock-Kurzweilin integrlit Informtiotieteiden yksikkö Mtemtiikk Helmikuu 2013 Sisältö 1 Johdnto 1 2 Newtonin integrli 2 2.1
2 Epäoleellinen integraali
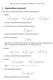 ANALYYSI C, HARJOITUSTEHTÄVIÄ, SYKSY 8 Epäoleellinen integrli Integrointivihje: Hyödynnä yhdistetyn funktion integrointisääntöä.. Määritä 9 9 (c) ( ). Tutki, millä vkion p rvoill epäoleellinen integrli
ANALYYSI C, HARJOITUSTEHTÄVIÄ, SYKSY 8 Epäoleellinen integrli Integrointivihje: Hyödynnä yhdistetyn funktion integrointisääntöä.. Määritä 9 9 (c) ( ). Tutki, millä vkion p rvoill epäoleellinen integrli
Ville Turunen: Mat Matematiikan peruskurssi P1 3. välikokeen alueen teoriatiivistelmä 2007
 Ville Turunen: Mt-.4 Mtemtiikn peruskurssi P 3. välikokeen lueen teoritiivistelmä 27 Mterili: kirjt [Adms] R. A. Adms: Clculus, complete course (6th edition), [Ly] D. C. Ly: Liner lgebr nd its pplictions
Ville Turunen: Mt-.4 Mtemtiikn peruskurssi P 3. välikokeen lueen teoritiivistelmä 27 Mterili: kirjt [Adms] R. A. Adms: Clculus, complete course (6th edition), [Ly] D. C. Ly: Liner lgebr nd its pplictions
4 Taso- ja avaruuskäyrät
 P2-luentoj kevät 2008, Pekk Alestlo 4 Tso- j vruuskäyrät Tässä luvuss tutustutn tso- j vruuskäyriin, niiden krenpituuteen j krevuuteen. Konkreettisin sovelluksin trkstelln nnettu rt pitkin liikkuvn hiukksen
P2-luentoj kevät 2008, Pekk Alestlo 4 Tso- j vruuskäyrät Tässä luvuss tutustutn tso- j vruuskäyriin, niiden krenpituuteen j krevuuteen. Konkreettisin sovelluksin trkstelln nnettu rt pitkin liikkuvn hiukksen
Määritelmä Olkoon C R m yksinkertainen kaari ja γ : [a, b] R m sen yksinkertainen parametriesitys, joka on paloittain C 1 -polku.
![Määritelmä Olkoon C R m yksinkertainen kaari ja γ : [a, b] R m sen yksinkertainen parametriesitys, joka on paloittain C 1 -polku. Määritelmä Olkoon C R m yksinkertainen kaari ja γ : [a, b] R m sen yksinkertainen parametriesitys, joka on paloittain C 1 -polku.](/thumbs/69/59950302.jpg) Muodostetn vektorikentän kri-integrli yksinkertisen kren tpuksess. Plutetn mieleen, että joukko C R m on yksinkertinen kri, jos löytyy sellinen jtkuv bijektio γ : [, b] C, jok on ploittin C 1 -funktio
Muodostetn vektorikentän kri-integrli yksinkertisen kren tpuksess. Plutetn mieleen, että joukko C R m on yksinkertinen kri, jos löytyy sellinen jtkuv bijektio γ : [, b] C, jok on ploittin C 1 -funktio
Integraalilaskenta. Määrätty integraali
 9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 3 Määrätyn integrlin lskeminen Aiemmin määrittelimme määrätyn integrlin f (x)dx funktion f (x) l- j yläsummien rj-rvon. Määrätyllä integrlill on kksi intuitiivist tulkint:.
Mtemtiikn tukikurssi Kurssikert 3 Määrätyn integrlin lskeminen Aiemmin määrittelimme määrätyn integrlin f (x)dx funktion f (x) l- j yläsummien rj-rvon. Määrätyllä integrlill on kksi intuitiivist tulkint:.
TEHTÄVÄ 1. Olkoon (f n ) jono jatkuvia funktioita f n : [a, b] R, joka suppenee välillä [a, b] tasaisesti kohti funktiota f : [a, b] R.
![TEHTÄVÄ 1. Olkoon (f n ) jono jatkuvia funktioita f n : [a, b] R, joka suppenee välillä [a, b] tasaisesti kohti funktiota f : [a, b] R. TEHTÄVÄ 1. Olkoon (f n ) jono jatkuvia funktioita f n : [a, b] R, joka suppenee välillä [a, b] tasaisesti kohti funktiota f : [a, b] R.](/thumbs/61/45986920.jpg) Topologi I Hrjoitus 10, rtkisuj AP TEHTÄVÄ 1. Olkoon (f n ) jono jtkuvi funktioit f n : [, b] R, jok suppenee välillä [, b] tsisesti kohti funktiot f : [, b] R. Osoit, että tällöin f n (x) dx f(x) dx.
Topologi I Hrjoitus 10, rtkisuj AP TEHTÄVÄ 1. Olkoon (f n ) jono jtkuvi funktioit f n : [, b] R, jok suppenee välillä [, b] tsisesti kohti funktiot f : [, b] R. Osoit, että tällöin f n (x) dx f(x) dx.
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA
 OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
Lebesguen integraali - Rieszin määritelmä
 Lebesguen integrli - Rieszin määritelmä Tru Lehtonen Mtemtiikn pro grdu-tutkielm Jyväskylän yliopisto Mtemtiikn j tilstotieteen litos Kevät 216 Tiivistelmä Jyväskylän Yliopisto Lehtonen, Tru Puliin: Lebesguen
Lebesguen integrli - Rieszin määritelmä Tru Lehtonen Mtemtiikn pro grdu-tutkielm Jyväskylän yliopisto Mtemtiikn j tilstotieteen litos Kevät 216 Tiivistelmä Jyväskylän Yliopisto Lehtonen, Tru Puliin: Lebesguen
Integraalilaskentaa. 1. Mihin integraalilaskentaa tarvitaan? MÄNTÄN LUKIO
 Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
2.1 Vaillinaiset yhtälöt
 .1 Villiniset yhtälöt Yhtälö, jok sievenee muotoon x + bx + c = 0 (*) on yleistä normlimuoto olev toisen steen yhtälö. Tämän rtkiseminen ei olekn enää yhtä meknist kuin normlimuotoisen ensisteen yhtälön
.1 Villiniset yhtälöt Yhtälö, jok sievenee muotoon x + bx + c = 0 (*) on yleistä normlimuoto olev toisen steen yhtälö. Tämän rtkiseminen ei olekn enää yhtä meknist kuin normlimuotoisen ensisteen yhtälön
Matematiikan perusteet taloustieteilijöille 2 800118P
 Mtemtiikn perusteet tloustieteilijöille 2 800118P Luentomoniste Kri Myllylä Niin Korteslhti Oulun yliopisto Mtemttisten tieteiden litos Kevät 2014 Sisältö 1 Mtriisilgebr j optimointi 4 11 Määritelmä 4
Mtemtiikn perusteet tloustieteilijöille 2 800118P Luentomoniste Kri Myllylä Niin Korteslhti Oulun yliopisto Mtemttisten tieteiden litos Kevät 2014 Sisältö 1 Mtriisilgebr j optimointi 4 11 Määritelmä 4
Pinta-alan laskeminen
 Pint-ln lskeminen Esimerkki Välillä, jtkuvn, einegtiivisen funktion f määrätt integrli nt suorn pint-ln, eli f = A. INTEGRAALILASKENTA, MAA9 A = f Toislt, jos f on välillä,, eipositiivinen, eli f R, niin
Pint-ln lskeminen Esimerkki Välillä, jtkuvn, einegtiivisen funktion f määrätt integrli nt suorn pint-ln, eli f = A. INTEGRAALILASKENTA, MAA9 A = f Toislt, jos f on välillä,, eipositiivinen, eli f R, niin
3.3 KIELIOPPIEN JÄSENNYSONGELMA Ratkaistava tehtävä: Annettu yhteydetön kielioppi G ja merkkijono x. Onko
 3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
Riemannin integraalista
 TAMPEREEN YLIOPISTO Pro grdu -tutkielm Aij Stenberg Riemnnin integrlist Mtemtiikn j tilstotieteen litos Mtemtiikk Syyskuu 2010 2 Tmpereen yliopisto Mtemtiikn j tilstotieteen litos STENBERG, AIJA: Riemnnin
TAMPEREEN YLIOPISTO Pro grdu -tutkielm Aij Stenberg Riemnnin integrlist Mtemtiikn j tilstotieteen litos Mtemtiikk Syyskuu 2010 2 Tmpereen yliopisto Mtemtiikn j tilstotieteen litos STENBERG, AIJA: Riemnnin
ANALYYSI I, kevät 2009
 ANALYYSI I, kevät 009 Sisältö Relilukujen peruskäsitteitä Lukujonoist 4. Lukujonon rj-rvo....................... 4. Monotoniset jonot..........................3 Osjonot.............................. 7.4
ANALYYSI I, kevät 009 Sisältö Relilukujen peruskäsitteitä Lukujonoist 4. Lukujonon rj-rvo....................... 4. Monotoniset jonot..........................3 Osjonot.............................. 7.4
ANALYYSI I, kevät 2009
 5 Riemnnin integrli 7 ANALYYSI I, kevät 9 5. Integrlin perusominisuuksi................. 76 5. Anlyysin perusluse....................... 8 Sisältö Relilukujen peruskäsitteitä Lukujonoist 3. Lukujonon rj-rvo.......................
5 Riemnnin integrli 7 ANALYYSI I, kevät 9 5. Integrlin perusominisuuksi................. 76 5. Anlyysin perusluse....................... 8 Sisältö Relilukujen peruskäsitteitä Lukujonoist 3. Lukujonon rj-rvo.......................
Matematiikan tukikurssi. Hannu Kivimäki
 Mtemtiikn tukikurssi Hnnu Kivimäki Sisältö I Ensimmäinen välikoe Integrointi 2 Osittisintegrointi 5 3 Osmurtohjotelm 4 Lisää osmurtoj 4 5 Sijoituskeino 9 6 Määrätty integrli 2 7 Ylä- j lsumm 22 8 Määrätyn
Mtemtiikn tukikurssi Hnnu Kivimäki Sisältö I Ensimmäinen välikoe Integrointi 2 Osittisintegrointi 5 3 Osmurtohjotelm 4 Lisää osmurtoj 4 5 Sijoituskeino 9 6 Määrätty integrli 2 7 Ylä- j lsumm 22 8 Määrätyn
i 2 n 3 ( (n 1)a (i + 1) 3 = 1 +
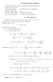 I. INTEGRAALILASKENTA Arkhimedes (287 22 e.kr.) prbelin segmentin pint-l Newton (642 727) j Leibniz (646 76) keksivät diff.- j int.-lskennn Cuhy (789 857) ε, δ Riemnn (826 866) Riemnnin integrli Lebesgue
I. INTEGRAALILASKENTA Arkhimedes (287 22 e.kr.) prbelin segmentin pint-l Newton (642 727) j Leibniz (646 76) keksivät diff.- j int.-lskennn Cuhy (789 857) ε, δ Riemnn (826 866) Riemnnin integrli Lebesgue
ANALYYSI I, kevät 2009
 ANALYYSI I, kevät 2009 Sisältö Relilukujen peruskäsitteitä 2 Lukujonoist 3 2. Lukujonon rj-rvo....................... 3 2.2 Monotoniset jonot......................... 7 2.3 Osjonot..............................
ANALYYSI I, kevät 2009 Sisältö Relilukujen peruskäsitteitä 2 Lukujonoist 3 2. Lukujonon rj-rvo....................... 3 2.2 Monotoniset jonot......................... 7 2.3 Osjonot..............................
10. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA
 MAA0 0. Määrätyn integrlin käyttö eräiden pint-lojen lskemisess 0. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA Edellä on todettu, että f (x)dx nt x-kselin j suorien x =, x = sekä funktion
MAA0 0. Määrätyn integrlin käyttö eräiden pint-lojen lskemisess 0. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA Edellä on todettu, että f (x)dx nt x-kselin j suorien x =, x = sekä funktion
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.2014 Ratkaisut ja arvostelu
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Harri Lehtinen. Kongruenssista
 TAMPEREEN YLIOPISTO Pro grdu -tutkielm Hrri Lehtinen Kongruenssist Mtemtiikn, tilstotieteen j filosofin litos Mtemtiikk Helmikuu 006 Tmpereen yliopisto Mtemtiikn, tilstotieteen j filosofin litos LEHTINEN,
TAMPEREEN YLIOPISTO Pro grdu -tutkielm Hrri Lehtinen Kongruenssist Mtemtiikn, tilstotieteen j filosofin litos Mtemtiikk Helmikuu 006 Tmpereen yliopisto Mtemtiikn, tilstotieteen j filosofin litos LEHTINEN,
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS
 11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS Tilvuus on sen verrn rkielämässä viljelty käsite, että useimmiten sen syvemmin edes miettimättä ymmärretään, mitä juomlsin ti pikkuvuvn kylpymmeen tilvuudell trkoitetn.
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS Tilvuus on sen verrn rkielämässä viljelty käsite, että useimmiten sen syvemmin edes miettimättä ymmärretään, mitä juomlsin ti pikkuvuvn kylpymmeen tilvuudell trkoitetn.
4. Reaalifunktioiden määrätty integraali
 6 4. Relifunktioiden määrätt integrli Vrsinisesti termi "integrli" tulee seurvss esitettävästä määrätstä integrlist, jok on läheistä suku summmiselle. Yhtes derivttn on sitten perustv ltu olev tulos, jot
6 4. Relifunktioiden määrätt integrli Vrsinisesti termi "integrli" tulee seurvss esitettävästä määrätstä integrlist, jok on läheistä suku summmiselle. Yhtes derivttn on sitten perustv ltu olev tulos, jot
HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI
 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunt/Ossto Fkultet/Sektion Fculty Litos Institution Deprtment Mtemttis-luonnontieteellinen Tekijä Förfttre Author Antti Khri Työn
HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunt/Ossto Fkultet/Sektion Fculty Litos Institution Deprtment Mtemttis-luonnontieteellinen Tekijä Förfttre Author Antti Khri Työn
Painopiste. josta edelleen. x i m i. (1) m L A TEX 1 ( ) x 1... x k µ x k+1... x n. m 1 g... m n g. Kuva 1. i=1. i=k+1. i=1
 Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
A-Osio. Valitse seuraavista kolmesta tehtävästä kaksi, joihin vastaat. A-osiossa ei saa käyttää laskinta.
 MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
4 DETERMINANTTI JA KÄÄNTEISMATRIISI
 4 DETERMINANTTI JA KÄÄNTEISMATRIISI Neliömtriisin determinntti Neliömtriisin A determinntti on luku, jot merkitään det(a) ti A. Lskeminen: -mtriisin A determinntti: det(a) -mtriisin A determinntti esim.
4 DETERMINANTTI JA KÄÄNTEISMATRIISI Neliömtriisin determinntti Neliömtriisin A determinntti on luku, jot merkitään det(a) ti A. Lskeminen: -mtriisin A determinntti: det(a) -mtriisin A determinntti esim.
Luku 15. Integraali. Esimerkki Suoraan edellisen luvun derivointikaavojen perusteella on voimassa
 Luku 5. Integrli Merkitsemme seurvss [, b]:llä lukusuorn suljettu väliä { R : b}. Olkoon f välillä [, b] määritelty funktio. Snomme, että välillä [, b] määritelty funktio g on funktion f integrlifunktio
Luku 5. Integrli Merkitsemme seurvss [, b]:llä lukusuorn suljettu väliä { R : b}. Olkoon f välillä [, b] määritelty funktio. Snomme, että välillä [, b] määritelty funktio g on funktion f integrlifunktio
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ PISTEYTYSKOKOUS
 0 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 30 PISTEYTYSKOKOUS 0 ) Sijoitetn x 0 Rtkistn = 0/04,0000 b) Jos neliön sivu on s, niin lävistäjä on s Ehto: s 6 s + s = 6, s 6 3 4s 6,70, joten piiri ) Suorn yhtälö
0 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 30 PISTEYTYSKOKOUS 0 ) Sijoitetn x 0 Rtkistn = 0/04,0000 b) Jos neliön sivu on s, niin lävistäjä on s Ehto: s 6 s + s = 6, s 6 3 4s 6,70, joten piiri ) Suorn yhtälö
Tampereen teknillinen yliopisto hum Konstruktiotekniikan laitos. MEC-2430 Elementtimenetelmän perusteet. Luento vk 1 Syksy 2012.
 mpereen teknillinen yliopisto hum 3.8. Konstruktiotekniikn litos MEC-430 Elementtimenetelmän perusteet. Luento vk Syksy 0. Mtemtiikn j mtriisilskennn kertust Yleistä Kirjoittelen tänne joitin kurssin keskeisiä
mpereen teknillinen yliopisto hum 3.8. Konstruktiotekniikn litos MEC-430 Elementtimenetelmän perusteet. Luento vk Syksy 0. Mtemtiikn j mtriisilskennn kertust Yleistä Kirjoittelen tänne joitin kurssin keskeisiä
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 5 1 Jtkuvuus Trkstelln funktiot fx) josskin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jtkuv ti epäjtkuv. Jtkuvuuden ymmärtää prhiten trkstelemll epäjtkuv
Mtemtiikn tukikurssi Kurssikert 5 1 Jtkuvuus Trkstelln funktiot fx) josskin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jtkuv ti epäjtkuv. Jtkuvuuden ymmärtää prhiten trkstelemll epäjtkuv
Analyysin perusteet kauppatieteilijöille 800118P
 Anlyysin perusteet kupptieteilijöille 800118P Luentomoniste Kri Myllylä Niin Korteslhti Topi Törmä Oulun yliopisto Mtemttisten tieteiden litos Kevät 2015 Sisältö 1 Derivtt 3 1.1 Määritelmä..............................
Anlyysin perusteet kupptieteilijöille 800118P Luentomoniste Kri Myllylä Niin Korteslhti Topi Törmä Oulun yliopisto Mtemttisten tieteiden litos Kevät 2015 Sisältö 1 Derivtt 3 1.1 Määritelmä..............................
Ristitulo ja skalaarikolmitulo
 Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
521. 522. 523. 524. 525. 526. 527. 12. Lisää määrätystä integraalista. 12.1. Integraalin arvioimisesta. Osoita: VASTAUS: Osoita: Osoita:
 12. Lisää määrätystä integrlist 12.1. Integrlin rvioimisest 521. Osoit: 1 + x 2 22 1 < < 1 + x21 21. 522. Osoit: x 3 < 5 x 6 + 8x + 9 < 15 1 5. 523. Osoit: 2 2 < e x2 x < 2e 2. e 524. Olkoon k >. Osoit:
12. Lisää määrätystä integrlist 12.1. Integrlin rvioimisest 521. Osoit: 1 + x 2 22 1 < < 1 + x21 21. 522. Osoit: x 3 < 5 x 6 + 8x + 9 < 15 1 5. 523. Osoit: 2 2 < e x2 x < 2e 2. e 524. Olkoon k >. Osoit:
Pertti Koivisto. Analyysi C
 Pertti Koivisto Anlyysi C TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 68/28 TAMPERE 28 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 68/28 JOULUKUU 28 Pertti Koivisto Anlyysi
Pertti Koivisto Anlyysi C TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 68/28 TAMPERE 28 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 68/28 JOULUKUU 28 Pertti Koivisto Anlyysi
Analyyttiset funktiot ja integrointiteorian alkeita
 Anlyyttiset funktiot j integrointiteorin lkeit 6. helmikuut 2006 isältö 1 Kertust 1 2 Anlyyttiset funktiot 2 2.1 Anlyyttiset funktiot tsoll................... 2 2.2 Monogeeniset funktiot vruudess R n.............
Anlyyttiset funktiot j integrointiteorin lkeit 6. helmikuut 2006 isältö 1 Kertust 1 2 Anlyyttiset funktiot 2 2.1 Anlyyttiset funktiot tsoll................... 2 2.2 Monogeeniset funktiot vruudess R n.............
R4 Harjoitustehtävien ratkaisut
 . Mitkä seurvist lusekkeist eivät ole polynomej? Miksi eivät? Polynomin termine eksponentti on luonnollinen luku, ne lusekkeet, joiss eksponentti ei ole luonnollinen luku ei ole myöskään polynomi.. x x
. Mitkä seurvist lusekkeist eivät ole polynomej? Miksi eivät? Polynomin termine eksponentti on luonnollinen luku, ne lusekkeet, joiss eksponentti ei ole luonnollinen luku ei ole myöskään polynomi.. x x
4 Pinta-alasovelluksia
 Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Pertti Koivisto. Analyysi B
 Pertti Koivisto Anlyysi B TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 67/8 TAMPERE 8 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 67/8 JOULUKUU 8 Pertti Koivisto Anlyysi
Pertti Koivisto Anlyysi B TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 67/8 TAMPERE 8 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 67/8 JOULUKUU 8 Pertti Koivisto Anlyysi
Analyysi B. Derivaatta ja integraali. Pertti Koivisto
 Anlyysi B Derivtt j integrli Pertti Koivisto Kevät 7 Alkusnt Tämä moniste on trkoitettu oheislukemistoksi Tmpereen yliopistoss pidettävälle kurssille Anlyysi B. Monisteen tvoitteen on tuke luentojen seurmist,
Anlyysi B Derivtt j integrli Pertti Koivisto Kevät 7 Alkusnt Tämä moniste on trkoitettu oheislukemistoksi Tmpereen yliopistoss pidettävälle kurssille Anlyysi B. Monisteen tvoitteen on tuke luentojen seurmist,
Sisältö. Funktiojonot ja -sarjat 10. syyskuuta 2005 sivu 1 / 15
 Funktiojonot j -srjt 10. syyskuut 2005 sivu 1 / 15 Sisältö 1 Funktiojonoist 2 2 Funktiosrjoist 5 3 Funktiojonojen j -srjojen derivointi j integrointi 7 4 Potenssisrjt 9 5 Tylorin polynomit j srjt 12 5.1
Funktiojonot j -srjt 10. syyskuut 2005 sivu 1 / 15 Sisältö 1 Funktiojonoist 2 2 Funktiosrjoist 5 3 Funktiojonojen j -srjojen derivointi j integrointi 7 4 Potenssisrjt 9 5 Tylorin polynomit j srjt 12 5.1
MITEN MÄÄRITÄN ASYMPTOOTIT?
 MITEN MÄÄRITÄN ASYMPTOOTIT? Asmptootti Asmptootti on suor ti muu kärä, jot funktion kuvj f() rjtt lähest, kun muuttujn rvot lähestvät tiettä luku ti ääretöntä. Rjoitutn luksi niihin tpuksiin, joiss smptootti
MITEN MÄÄRITÄN ASYMPTOOTIT? Asmptootti Asmptootti on suor ti muu kärä, jot funktion kuvj f() rjtt lähest, kun muuttujn rvot lähestvät tiettä luku ti ääretöntä. Rjoitutn luksi niihin tpuksiin, joiss smptootti
Olkoon. äärellinen automaatti. Laajennetaan M:n siirtymäfunktio yksittäisistä syötemerkeistä merkkijonoihin: jos q Q, x Σ, merkitään
 T 79.00/002 Tietojenkäsittelyteorin perusteet 2. Äärellisten utomttien minimointi Voidn osoitt, että jokisell äärellisellä utomtill on yksikäsitteinen ekvivlentti (so. smn kielen tunnistv) tilmäärältään
T 79.00/002 Tietojenkäsittelyteorin perusteet 2. Äärellisten utomttien minimointi Voidn osoitt, että jokisell äärellisellä utomtill on yksikäsitteinen ekvivlentti (so. smn kielen tunnistv) tilmäärältään
7 Numeerinen derivointi ja integrointi
 7 Numeerinen derivointi j integrointi 7.1 Derivttojen estimointi Numeerisell derivoinnill trkoitetn likirvon lskemist funktion f : R R derivtlle f ilmn derivtn nlyyttistä lusekett. Jos funktion f rvo tunnetn
7 Numeerinen derivointi j integrointi 7.1 Derivttojen estimointi Numeerisell derivoinnill trkoitetn likirvon lskemist funktion f : R R derivtlle f ilmn derivtn nlyyttistä lusekett. Jos funktion f rvo tunnetn
Preliminäärikoe Pitkä Matematiikka 5.2.2013
 Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
Matematiikan johdantokurssi, syksy 2017 Harjoitus 6, ratkaisuista. 1. Onko jokin demojen 5 tehtävän 3 relaatioista
 Mtemtiikn johntokurssi, syksy 07 Hrjoitus 6, rtkisuist. Onko jokin emojen 5 tehtävän reltioist ) R := {(, ), (, ), (, ), (, ), (, ), (, ), (, ), (, )}, ) S := {(, ), (, ), (, ), (, ), (, ), (, ), (, ),
Mtemtiikn johntokurssi, syksy 07 Hrjoitus 6, rtkisuist. Onko jokin emojen 5 tehtävän reltioist ) R := {(, ), (, ), (, ), (, ), (, ), (, ), (, ), (, )}, ) S := {(, ), (, ), (, ), (, ), (, ), (, ), (, ),
Olkoon. M = (Q, Σ, δ, q 0, F)
 T 79.148 Tietojenkäsittelyteorin perusteet 2.4 Äärellisten utomttien minimointi Voidn osoitt, että jokisell äärellisellä utomtill on yksikäsitteinen ekvivlentti (so. smn kielen tunnistv) tilmäärältään
T 79.148 Tietojenkäsittelyteorin perusteet 2.4 Äärellisten utomttien minimointi Voidn osoitt, että jokisell äärellisellä utomtill on yksikäsitteinen ekvivlentti (so. smn kielen tunnistv) tilmäärältään
.) (b) Vertaa p :tä vastaavaa kineettistä energiaa perustilan kokonaisenergiaan. ( ) ( ) = = Ek
 S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
Sinilause ja kosinilause
 Siniluse j kosiniluse GEOMETRI M3 Mikäli kolmion korkeus j knt tiedetään, voidn pint-l lske. Esimerkki: Lske kolmion l, kun 38 kulmn viereiset sivut ovt 8, j 6,8. Nyt knt tiedetään, korkeutt ei! 38 8,
Siniluse j kosiniluse GEOMETRI M3 Mikäli kolmion korkeus j knt tiedetään, voidn pint-l lske. Esimerkki: Lske kolmion l, kun 38 kulmn viereiset sivut ovt 8, j 6,8. Nyt knt tiedetään, korkeutt ei! 38 8,
Sarjat ja integraalit
 Srjt j integrlit c Mtemttisten tieteiden litos, Oulun yliopisto Versio: 9.3.0 Viimeksi muoknnut: Peter Hästö Sisältö Funktion rj-rvo j jtkuvuus. Peruskäsitteitä........................................
Srjt j integrlit c Mtemttisten tieteiden litos, Oulun yliopisto Versio: 9.3.0 Viimeksi muoknnut: Peter Hästö Sisältö Funktion rj-rvo j jtkuvuus. Peruskäsitteitä........................................
Suorat, käyrät ja kaarevuus
 Suort, käyrät j krevuus Jukk Tuomel Professori Mtemtiikn litos, Joensuun yliopisto Suor? Tämä kirjoitus on eräänlinen jtko Timo Tossvisen suorn määritelmää koskevn kirjoitukseen Solmun numeross 2/2002.
Suort, käyrät j krevuus Jukk Tuomel Professori Mtemtiikn litos, Joensuun yliopisto Suor? Tämä kirjoitus on eräänlinen jtko Timo Tossvisen suorn määritelmää koskevn kirjoitukseen Solmun numeross 2/2002.
Paraabelikin on sellainen pistejoukko, joka määritellään urakäsitteen avulla. Paraabelin jokainen piste toteuttaa erään etäisyysehdon.
 5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
VEKTOREILLA LASKEMINEN
 ..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
Vakioiden variointi kolmannen kertaluvun yhtälölle
 Vkioiden vriointi kolmnnen kertluvun yhtälölle Olkoon trksteltvn kolmnnen kertluvun linerinen epähomogeeninen differentiliyhtälö > diffyht:= (-1)*diff(y(), $3)-*diff(y(), $2)+diff(y(), )=ep(^2); diffyht
Vkioiden vriointi kolmnnen kertluvun yhtälölle Olkoon trksteltvn kolmnnen kertluvun linerinen epähomogeeninen differentiliyhtälö > diffyht:= (-1)*diff(y(), $3)-*diff(y(), $2)+diff(y(), )=ep(^2); diffyht
Viikon aiheet. Pinta-ala
 info Viikon iheet Mpu I:sen voit suoritt: Kurssin loppukokeess 23.10. Arvosn: koe + lskrit Mikäli yo. ik ei sovi, voit suoritt loppukokeen yleistenttitilisuudess 24.11. Arvosn: koe + lskrit. Ilmoittudu
info Viikon iheet Mpu I:sen voit suoritt: Kurssin loppukokeess 23.10. Arvosn: koe + lskrit Mikäli yo. ik ei sovi, voit suoritt loppukokeen yleistenttitilisuudess 24.11. Arvosn: koe + lskrit. Ilmoittudu
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentili- j integrlilskent 1 Riikk Korte (Pekk Alestlon klvojen pohjlt) Alto-yliopisto 22.11.2016 Sisältö Pint-l Integrli 1.1 Pint-l: Suorkulmio Seurvss trkstelln umpinisten tsokäyrien rjmi
MS-A0102 Differentili- j integrlilskent 1 Riikk Korte (Pekk Alestlon klvojen pohjlt) Alto-yliopisto 22.11.2016 Sisältö Pint-l Integrli 1.1 Pint-l: Suorkulmio Seurvss trkstelln umpinisten tsokäyrien rjmi
Neliömatriisin A determinantti on luku, jota merkitään det(a) tai A. Se lasketaan seuraavasti: determinantti on
 4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Integrointi Integrointi on derivoinnin käänteistoimitus: jos funktion F(x) derivtt on f (x), niin funktion f (x) integrli on F(x). Täten, kosk esimerkiksi funktion x + e x derivtt
Mtemtiikn tukikurssi Integrointi Integrointi on derivoinnin käänteistoimitus: jos funktion F(x) derivtt on f (x), niin funktion f (x) integrli on F(x). Täten, kosk esimerkiksi funktion x + e x derivtt
Integroimistehtävät, 10. syyskuuta 2005, sivu 1 / 29. Perustehtäviä. Tehtävä 1. Osoita, että vakiofunktio f(x) c on Riemann-integroituva välillä
 Integroimistehtävät,. syyskuut 5, sivu / 9 Perustehtäviä Tehtävä. Osoit, että vkiofunktio f(x) c on Riemnn-integroituv välillä [, b] j lske suorn määritelmän perusteell b f(x). Tehtävä. Osoit, että funktio,
Integroimistehtävät,. syyskuut 5, sivu / 9 Perustehtäviä Tehtävä. Osoit, että vkiofunktio f(x) c on Riemnn-integroituv välillä [, b] j lske suorn määritelmän perusteell b f(x). Tehtävä. Osoit, että funktio,
Sarjaratkaisun etsiminen Maplella
 Srjrtkisun etsiminen Mplell Olkoon trksteltvn ensimmäisen kertluvun differentiliyhtälö: > diffyht:= diff(y(x, x=1y(x^; d diffyht := = dx y( x 1 y( x Tälle pyritään etsimään srjrtkisu origokeskisenä potenssisrjn.
Srjrtkisun etsiminen Mplell Olkoon trksteltvn ensimmäisen kertluvun differentiliyhtälö: > diffyht:= diff(y(x, x=1y(x^; d diffyht := = dx y( x 1 y( x Tälle pyritään etsimään srjrtkisu origokeskisenä potenssisrjn.
Pythagoraan lause. Pythagoras Samoslainen. Pythagoraan lause
 Pythgorn luse Pythgors Smoslinen Pythgors on legendrinen kreikklinen mtemtiikko j filosofi. Tiedot hänen elämästään ovt epävrmoj j ristiriitisi. Tärkein Pythgorst j pythgorlisi koskev lähde on Lmlihosin
Pythgorn luse Pythgors Smoslinen Pythgors on legendrinen kreikklinen mtemtiikko j filosofi. Tiedot hänen elämästään ovt epävrmoj j ristiriitisi. Tärkein Pythgorst j pythgorlisi koskev lähde on Lmlihosin
