Luku Lineaarinen harmoninen oskillaattori
|
|
|
- Arto Siitonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Luku 4 Värähdysliikkeet Kun fysikaalista systeemiä häiritään, se alkaa usein oskilloida. Toisaalta erilaiset jaksolliset tapahtumat voidaan kuvailla oskillaatioina tai niiden superpositioina. Niinpä värähdysliikkeen osaaminen onkin yksi tärkeimpiä fysiikan perusasioita. Varsin yleisesti värähdysliikkeen yhtälö on muotoa q + f(q, q, t) =, (4.) missä q on liikettä kuvaava koordinaatti. Jos f ei riipu eksplisiittisesti ajasta, liikettä kutsutaan autonomiseksi ja jos se ei sisällä myöskään nopeutta q, niin systeemi on konservatiivinen. Jos f on tämän lisäksi q:n lineaarinen funktio, on kyseessä harmonisen oskillaattorin kaltainen tilanne. Esimerkki ei-autonomisesta ja ei-konservatiivisesta värähtelijästä on muotoa q + f(q, q) = F (t), (4.2) missä nopeusriippuvuus kuvaa oskillaation vaimenemista ja F (t) ajasta riippuvaa pakkovoimaa. Tarkastelemme tällä kurssilla pääasiassa lineaarisia värähtelijöitä. Luonnon makroskooppiset oskillaatiot ovat usein epälineaarisia, mutta mikäli oskillaation amplitudi voidaan olettaa pieneksi, yhtälöt voidaan linearisoida. Meillä on jo ollut esimerkki myös epälineaarisesta oskillaattorista, nimittäin luvun matemaattinen heiluri. Kuten olemme nähneet heilahduskulman ollessa pieni (sin θ θ) heiluria voi approksimoida lineaarisena harmonisena oskillaatorina. Tämä usein myös halutaan tehdä, koska kuten tulemme jatkossa näkemään epälineaaristen oskillaatoreiden käsittely on yleensä hyvin hankalaa. 4. Lineaarinen harmoninen oskillaattori Tarkastellaan aluksi vakiomassaista (m) hiukkasta, joka liikkuu potentiaalissa U(q). Systeemi on staattisessa tasapainossa, kun yleistetty voima on nolla eli Q = du/dq =. Tällöin siis potentiaalilla on ääriarvo. Riippuen siitä, onko kyseessä potentiaalin minimi vaiko maksimi, tasapaino on joko stabiili tai epästabiili (Kuva 4.). Värähtelyliike voi syntyä vain stabiilin tasapainotilanteen ympärille. Usein tasapaino 59
2 LUKU 4. VÄRÄHDYSLIIKKEET 6 on stabiili vain lokaalisti eli jos systeemiä häiritään liian voimakkaasti (häiriöamplitudi on liian suuri), systeemi ajautuu epästabiiliksi. U = E U Merkitään koordinaatin tasapainokohtaa q :lla ja poikkeamaa x = q q. q x x 2 Kuva 4.. Stabiili (vasen) ja epästabiili (oikea) tasapainoasema. x q U(q) = U(q ) + du dq Kehitetään potentiaali U Taylorin sarjaksi q :n ympäristössä (HT: kertaa Taylorin sarjat MAPU:sta tai mistä sitten oletkin ne oppinut!) x + q 2! d 2 U dq 2 q x (4.3) Valitaan potentiaalin nollataso siten, että ensimmäinen termi on nolla. Toinen termi on tasapainossa määritelmän mukaan nolla (tasapaino on ääriarvo), joten toista kertalukua myöten U(q) = d 2 U q 2 dq 2 x 2. (4.4) Kun vielä valitaan fiksusti koordinaatiston origoksi q, niin U(x) = 2 kx2, (4.5) missä k = d 2 U/dq 2 q. Näin olemme päässeet luvusta 2 tutun Hooken lain muotoiseen potentiaaliin. Systeemin kineettinen energia on T = 2 m q2 = [ ] d 2 2 m dt (x + q ) = 2 mẋ2, (4.6) ja niinpä meillä on systeemin Lagrangen funktio L = 2 mẋ2 2 kx2. (4.7) Liikeyhtälö löytyy jälleen laskemalla L:n derivaatat Lagrangen yhtälöiden mukaisesti. Tulos on tietenkin tuttu lineaarinen harmoninen oskillaattori mẍ + kx =. (4.8) Otetaan käyttöön merkintä k/m = ω 2, jolloin ẍ + ω 2 x =. (4.9) ω :n fysikaalinen dimensio on selvästi taajuus (SI-yksikkö s ). Vaikka tulos onkin ennestään tuttu, ei saavutus ole vähäpätöinen. Onhan tulos saatu pelkästään tarkastelemalla massapisteen liikettä stabiilin tasapainoaseman lähellä ja käyttämällä Lagrangen yhtälöitä. Yhtälö (4.9) on tavallinen lineaarinen differentiaaliyhtälö, jonka ratkaisuille pätee superpositioperiaate, eli löydettyjen ratkaisujen lineaarikombinaatiot ovat myös yhtälön ratkaisuja. Ratkaisu löytyy tunnetusti
3 LUKU 4. VÄRÄHDYSLIIKKEET 6 yritteellä x = e rt. Sijoittamalla tämä yhtälöön (4.9) saadaan karakteristinen yhtälö r 2 = ω 2 eli r:llä on kaksi kompleksista ratkaisua r = ±iω. Näiden ratkaisujen superpositio on yhtälön yleinen ratkaisu x(t) = 2 A e iωt + 2 A 2e iωt. (4.) Koska x on järkevää olettaa reaaliseksi, on integroimisvakioiden A ja A 2 oltava toistensa kompleksikonjugaatteja. Kirjoitetaan A = a ib ja A 2 = a + ib (a ja b ovat reaalilukuja), jolloin ratkaisu saadaa Eulerin kaavan e iωt = cos ωt + i sin ωt avulla muotoon x(t) = a cos ω t + b sin ω t. (4.) Otetaan alkuarvoiksi t =, x = x ja ẋ = v. Tällöin a = x ja b = v /ω. Ratkaisu voidaan kirjoittaa myös muodossa x(t) = A sin(ω t + δ), (4.2) missä A antaa oskillaation amplitudin ja δ vaiheen. HT: Määritä A ja δ ylläoleville alkuarvoille. Tässä yhteydessä on hyvä paikka kerrata MAPU:lta tavallisten differentiaaliyhtälöiden ratkaisumenetelmät sekä laskeminen kompleksiluvuilla. 4.2 Vaimennettu värähtelijä Jos värähtelijään vaikuttaa nopeuteen verrannollinen vastusvoima, Lagrangen yhtälön suoraviivainen käyttäminen on hankalampaa, koska systeemin kokonaisenergia ei säily (HT: Minne energia menee?). Ongelman tarkastelu on yksinkertaisinta lähtemällä suoraan harmonisen oskillaattorin newtonilaisesta liikeyhtälöstä (4.9) ja lisäämällä siihen vastustermi 2βẋ, missä β oletetaan yksinkertaisuuden vuoksi positiiviseksi vakioksi. Liikeyhtälöksi tulee ẍ + 2βẋ + ω 2 x =. (4.3) Käyttämällä yritettä e rt, saadaan yhtälön (4.3) karakteristisen yhtälön juuriksi r = β + β 2 ω 2 r 2 = β β 2 ω 2 ja yleinen ratkaisu on jälleen superpositio x(t) = e βt (A e β 2 ω 2 t + A 2 e β 2 ω 2 t ). (4.4)
4 LUKU 4. VÄRÄHDYSLIIKKEET 62 Tapaus ω 2 > β2 Merkitään ω 2 = ω2 β2, jolloin ω 2 > ja juurilausekkeet β 2 ω 2 ovat imaginaarisia. Tällöin ratkaisu saa muodon x(t) = e βt (A e iω t + A 2 e iω t ). (4.5) Tämä voidaan kirjoittaa (HT) myös muodossa x(t) = Ae βt cos(ω t δ). (4.6) x Kuva 4.2. Alivaimennettu värähtelijä. t Nyt amplitudi on muotoa Ae βt ja siten se pienenee ajan myötä eli oskillaatio vaimenee. Suure ω muistuttaa taajuutta siinä mielessä, että sen käänteisluku kuvaa verhokäyrän x = Ae βt ja oskillaatiota kuvaavan käyrän peräkkäisten sivuamiskohtien ajallista etäisyyttä, vaikka nämä pisteet eivät olekaan täsmällisesti periodisia (Kuva 4.2). Tätä tapausta kutsutaan alivaimennetuksi värähtelyksi. Samaa yhtälöä voi käyttää kuvaamaan tilannetta, missä β <. Tällöin jokin prosessi syöttää energiaa oskillaattorille ja oskillaatio kasvaa. Tällainen värähtelijä on epästabiili ja oskillaatio ajan mittaan joko kasvaa epälineaariseksi tai systeemin jokin muu ominaisuus alkaa rajoittaa amplitudin kasvua. Huom. Karakteristisen yhtälön ratkaisun imaginaariosa vastaa oskillaation taajuutta ja reaaliosa vaimennusta. Käytännössä oskilloiva suure (esim. sähkökenttä) kirjoitetaan usein muodossa x(t) = A e iωt = A e i(ω +iβ)t = Ae βt e iω t, jolloin siis kompleksisen taajuuden ω = ω + iβ reaaliosa (ω ) antaa oskillaatiotaajuuden ja imaginaariosa (β) vaimennuskertoimen. Tällaisten lausekkeiden merkkien kanssa on tärkeää olla huolellinen. Aikariippuvuus kirjoitetaan usein e iωt. Tällöin taajuus eli ω:n reaaliosan itseisarvo säilyy samana, mutta β:n merkki muuttuu eli negatiivinen β vaimentaa ja positiivinen kasvattaa oskillaatiota. Tapaus ω 2 < β2 Tässä tapauksessa karakteristisen yhtälön ratkaisut ovat reaaliset ja differentiaaliyhtälön yleinen ratkaisu on x(t) = e βt (A e ω 2t + A 2 e ω 2t ), (4.7) missä ω 2 = β 2 ω 2. Tämä ratkaisu ei siten oskilloi. Koska β > ω 2, systeemi hakeutuu aina lopulta (t ) lepoon eli poikkeama tasapainotilasta x. Tapausta kutsutaan ylivaimennetuksi värähtelyksi.
5 LUKU 4. VÄRÄHDYSLIIKKEET 63 Tapaus ω 2 = β2 Nyt karakteristisen yhtälön juuret ovat yhtäsuuret (r = β), jolloin ei suoraan saada kahta lineaarisesti riippumatonta ratkaisua. Nyt ratkaisua kannattaa yrittää muodossa x = A(t)e βt (ns. vakion varioimismenetelmä). Näin saadaan ẋ = ( A βa)e βt ẍ = (Ä 2β A + β 2 A)e βt = ẍ + 2βẋ + β 2 x = Äe βt eli Ä = A = A + A 2 t. Näin siis saadaan kahden riippumattoman ratkaisun superpositio muodossa x(t) = (A + A 2 t)e βt. (4.8) Tämäkään ratkaisu ei osikilloi vaan on sellainen, joka saavuttaa lepotilan mahdollisimman nopeasti. Tällaista vaimennusta kutsutaan kriittiseksi vaimennukseksi. 4.3 Ajasta riippuva ulkoinen voima Oskillaattoria ajaa usein joku ulkoinen pakkovoima. Tämä on varsin yleinen tapaus sähköisissä värähtelypiireissä, joihin ajetaan vaihtovirtoja joko jonkin värähtelylähteen tai vaikka esimerkiksi vastaanottoantennin kautta. Tarkastellaan ensiksi tilannetta, jossa ei ole mukana vaimennusta ẍ + ωx 2 = F (t). (4.9) m Yhtälön ratkaisemiseksi otetaan käyttöön kompleksinen muuttuja z = ẋ iω x. Tämän tempun juju on siinä, että ż = ẍ iω ẋ = ẍ iω (z + iω x) = ẍ + ω 2 x iω z (4.2) ż + iω z = F (t) (4.2) m eli meillä on ensin ratkaistavana ensimmäisen kertaluvun epähomogeeninen differentiaaliyhtälö. Semmoinenhan ratkaistaan ratkaisemalla ensin homogeeninen yhtälö ż h + iω z h = yleisesti ja etsimällä sen jälkeen epähomogeenisen yhtälön erikoisratkaisu. Homogeenisen yhtälön ratkaisu on yksinkertaisesti z h = Ae iω t. (4.22) Erikoisratkaisulle tehdään taas yrite Nyt z e = A(t)e iω t. ż e = A(t)e iω t iω A(t)e iω t (4.23) A(t)e iωt = ż e + iω z e = F (t). (4.24) m
6 LUKU 4. VÄRÄHDYSLIIKKEET 64 Tästä saadaa A(t) integroimalla Näin on ratkaistu z A(t) A() = m z(t) = e iω t t ( A() + m dt e iω t F (t ). (4.25) t joka antaa määritelmänsä mukaan sekä x:n että ẋ:n ) dt e iω t F (t ), (4.26) ẋ = Re z ; x = ω Im z. (4.27) Sivuhuomautus: Lneaarisen. kertaluvun differentiaaliyhtälön ẏ + P (t)y = Q(t) voi ratkaista yleisesti seuraavasti: kerro yhtälön molemmat puolet lausekkeella e t P (t ) dt ja huomaa, että yhtälön vasemalla puolella on nyt lausekkeen ye t P (t ) dt aikaderivaatta. Näin voit siis integroida yhtälön ja saat (HT) t t ye P (t ) dt t y() = e P (t ) dt Q(t ) dt. Yllä annettu ratkaisu (4.26) seuraa tästä suoraan (HT). Edellä esitetyn vakion varioimismenetelmän etuna on kuitenkin se, että kikka toimii usein myös ratkaistaessa korkeampaa kertalukua olevia lineaarisia differentiaaliyhtälöjä. Siirtyminen kompleksitasoon on olennaisesti muuttanut toisen kertaluvun differentiaaliyhtälön kahdeksi ensimmäisen kertaluvun differentiaaliyhtälöksi paikalle ja nopeudelle. Radan määräämiseen meillä on kaksi alkuehtoa, värähtelijän nopeus ja paikka hetkellä t =, jotka määrävät (kompleksisen) alkuarvon A() = z() = x() iω ẋ(). Tarkastellaan esimerkkinä heiluria, joka on aluksi levossa origossa ja johon alkaa hetkellä t = vaikuttaa vakiovoima F. Hiukkasen paikka hetkellä τ saadaan suoraan integraalista z(τ) = e iω τ m = F e iω τ m τ τ F e iω t dt e iω t dt = F e iω τ imω (e iω τ ). (4.28) Eulerin kaavan avulla löydetään jälleen ratkaisun reaali- ja imaginaariosat, jonka jälkeen oskillaattorin paikka saadaan kaavan (4.27) avulla x(τ) = Im z = 2F ω mω 2 sin 2 ( ω τ 2 ). (4.29)
7 LUKU 4. VÄRÄHDYSLIIKKEET Vaimennettu ulkoisen voiman ajama värähtelijä Jos ulkoisen voiman ajama oskillaattori on lisäksi vaimeneva niin kuin kaikki todelliset makroskooppiset oskillaattorit varmaankin ovat, on meillä ratkaistavana yhtälö, joka on muotoa ẍ + 2βẋ + ω 2 x = f(t). (4.3) Jos β on vakio, ei tämän yhtälön ratkaiseminen ole periaatteessa yhtään sen hankalampaa kuin edellä esitetyn tapauksen β =. Tällöin nimittäin yhtälön vasen puoli voidaan kirjoittaa muodossa (D r )(D r 2 )x (D r )z = ż r z, missä r ja r 2 ovat edellä ratkaistut karakteristisen yhtälön juuret ja D = d/dt. Tämä kikka muuntaa siis taas yhtälön kahdeksi ensimmäistä kertalukua olevaksi DY:ksi ż r z = f(t) ẋ r 2 x = z(t), joihin puree edellä johdettu yleinen menetelmä, jossa nyt alivaimennetulle tapaukselle x = Im z Im r 2, mutta kriittisesti vaimennetulle ja ylivaimennetulle tapaukselle (Im r,2 = ) joudutaan toinenkin yhtälö ratkaisemaan ensimmäisen tapaan. Tarkastellaan seuraavaksi kuitenkin sinimuotoista voimaa, jolle ratkaisun voi löytää paljon näppärämmin sopivasti valitulla yritteellä. Useimmat fysikaalisissa ongelmissa esiintulevat pakkovoimat ovat funktionaaliselta muodoltaan sen verran siistejä, että ne voidaan esittää Fourier-sarjoina (FYMM I) esimerkiksi muodossa f(t) = n f n cos(nωt). (4.3) Tarkastellaan tässä esimerkkinä vain yhtä fourier-komponenttia eli kulmataajudella ω oskilloivaa pakkovoimaa ja tehdään epähomogeeniselle yhtälölle yrite f = f cos(ωt) (4.32) x e = A cos(ωt δ). Sijoitetaan tämä täydelliseen liikeyhtälöön (4.3). Yhtälöstä tulee algebrallinen yhtälö (HT) {f A[(ω 2 ω 2 ) cos δ + 2ωβ sin δ]} cos ωt + {A[(ω 2 ω 2 ) sin δ 2ωβ cos δ]} sin ωt =. (4.33)
8 LUKU 4. VÄRÄHDYSLIIKKEET 66 Koska sin ωt ja cos ωt ovat lineaarisesti riippumattomia funktioita, toteutuu yhtälö kaikilla t vain jos kummankin funktion kertoimet ovat erikseen nollia. Jos A, saadaan sin ωt:n kertoimesta lasketuksi tan δ = ω 2 2ωβ, (4.34) ω2 josta voidaan laskea sin δ ja cos δ. Toisaalta cos ωt:n kertoimesta saadaan yritteen amplitudiksi A = f (ω 2 ω2 ) cos δ + 2ωβ sin δ (4.35) Sijoittamalla tähän sin δ ja cos δ saadaan amplitudiksi A = f (ω 2 ω 2 ) 2 + 4ω 2 β 2. (4.36) ja täydellisen yhtälön (4.3) erikoisratkaisu on siten x e (t) = f cos(ωt δ). (4.37) (ω 2 ω 2 ) 2 + 4ω 2 β2 Merkitsemällä jaksossa 4.2 löydettyjä homogeenisen yhtälön yleisiä ratkaisuja x h (t) on yhtälön (4.3) täydellinen ratkaisu muotoa x(t) = x h (t) + x e (t). (4.38) Vaimennetulle oskillaattorille x h (t) on tärkeä vain ratkaisun alussa, sillä sehän vaimenee ajan myötä pieneksi ja pakkovoima määrää oskillaattorin värähtelytaajuuden. Oskillaattorin ominaisvärähtelytaajuus ja vaimennuskerroin vaikuttavat värähtelyn amplitudiin ja vaiheeseen. Kun pakkovoiman taajuus kasvaa, siirtyy vaihekulma δ: π (HT: piirrä kuva!). Erikoistapaus: Resonanssi Jos pakotetun oskillaattorin vaimennus menee nollaksi, on selvää, että yllä löydetty erikoisratkaisu divergoi kun ω ω eli kun pakkovoima on resonanssissa oskillaattorin ominaistaajuuden kanssa. Vaimennetulle oskillaattorille tämä amplitudiresonanssi löydetään etsimällä A(ω):n maksimi da dω =, (4.39) ωres joka on kohdassa ω res = ω 2 2β2. (4.4) Tultaessa liian lähelle resonanssikohtaa heikosti vaimennettu mekaaninen systeemi joko murtuu tai systeemin epälineaariset ominaisuudet alkavat kasvattaa vaimennusta.
9 LUKU 4. VÄRÄHDYSLIIKKEET 67 *Esimerkki: Parametrinen resonanssi Edellä käsitelty amplitudiresonanssi toteutuu ulkoisen pakkovoiman vuoksi, vaikka systeemi olisi alunperin levossa. Käsitellään tässä esimerkkiä systeemistä, joka pysyy levossa, jos se on alunperin levossa, mutta joka ajautuu itsestään epästabiiliksi, jos sen tila poikkeaa vähänkin tasapainosta. Ajatellaan, että systeemin ulkopuolinen vaikutus rajoittuu vain jonkun systeemiä kuvaavan parametrin ajalliseen kehitykseen. Esimerkiksi käy vaikka harmoninen heiluri, jonka ripustuspiste liikkuu ylös-alas. Tällaista tilannetta voi kuvailla yhtälöllä ẍ + ω 2 (t)x =. (4.4) Nyt ajasta riippuva ominaistaajuus oletetaan periodiseksi siten, että ω(t+t ) = ω(t). Jos siis x(t) on liikeyhtälön ratkaisu, niin myös x(t+t ) on ratkaisu. Oletetaan, että x ja x 2 ovat liikeyhtälön kaksi riippumatonta ratkaisua, joten niiden täytyy muuntua itsensä lineaarikombinaatioiksi, kun t t + T. Nyt on mahdollista valita x ja x 2 siten, että x (t+t ) = c x (t) ja x 2 (t+t ) = c 2 x 2 (t). Yleisimmät tällaiset ratkaisut ovat muotoa x i (t) = c t/t i Π i (t) ; i =, 2, (4.42) missä Π i :t ovat periodisia funktioita periodinaan T. Kertoimille c i löytyy sidosehto. Kerrotaan yhtälö ẍ + ω 2 (t)x = x 2 :llä ja yhtälö ẍ 2 + ω 2 (t)x 2 = x :llä ja vähennetään ne toisistaan. Lyhyt lasku antaa tuloksen ẋ x 2 x ẋ 2 = vakio. (4.43) Koska x i :t ovat muotoa (4.42), niin t:n korvaaminen t + T :llä kertoo yhtälön (4.43) vasemman puolen tekijällä c c 2, joten yhtälön voimassaolo edellyttää, että c c 2 =. (4.44) Koska alkuperäisen differentiaaliyhtälön kertoimet ovat reaalisia, täytyy ratkaisun kompleksikonjugaatin olla myös yhtälön ratkaisu. Tästä seuraa, että joko c ja c 2 ovat toistensa kompleksikonjugaatteja, jolloin molempien itseisarvot ovat ykkösen suuruisia, tai molemmat ovat reaalisia, jolloin toinen on toisen käänteisluku. Jälkimmäisessä tapauksessa siis riippumattomat ratkaisut ovat x (t) = c +t/t Π (t) (4.45) x 2 (t) = c t/t Π 2 (t). (4.46) Nyt toinen ratkaisuista (negatiivinen eksponentti) vaimenee ajan myötä, mutta toinen (positiivinen eksponentti) kasvaa nopeasti olipa alkuperäinen häiriö kuinka pieni tahansa. Tätä tilannetta kutsutaan parametriseksi resonanssiksi. Olemme vasta osoittaneet, että periodisen ominaistaajuden tapauksessa systeemillä voi olla ratkaisu, joka kasvaa eksponentiaalisesti. Jotta voisimme sanoa, milloin tämä ratkaisu todella kuvaa systeemiä, pitää ω(t) kiinnittää. Landaun ja Lifshitzin kirjassa tarkastellaan tapausta ω 2 (t) = ω 2 ( + h cos γt), missä h (systeemin ominaistaajudessa on siis pieni sinimuotoinen osa suuren vakion rinnalla). Osoittautuu,
10 LUKU 4. VÄRÄHDYSLIIKKEET 68 että parametrinen resonanssi on vahvimmillaan, jos ominaistaajuuden vaihtelufrekvenssi on γ 2ω, eli noin tuplasti systeemin (häiriötön) ominaistaajuus. Tämän tietää itseasiassa jokainen pikkulapsi, joka osaa keinua riippukeinussa! Liikuttamalla itseään ylös-alas kaksi kertaa keinun ominaistaajuudella lapsi saa keinun nopeasti epälineaarisen suurelle heilahduskulmalle, kunhan keinu aluksi liikahtaa vain vähänkin. 4.5 Kytketyt harmoniset värähtelijät Edellä olleessa tarkastelussa ei Lagrangen formalismia käytetty hyväksi kovinkaan tehokkaasti, sillä liikeyhtälöt olivat löydettävissä varsin helposti suoraan Newtonin mekaniikasta. Siirryttäessä tarkastelemaan useampaa toisiinsa kytkeytynyttä oskillaattoria formalismin edut tulevat kuitenkin näkyviin, sillä suoraviivainen koordinaattitarkastelu käy äkkiä liian raskaaksi. Esimerkki: Kaksoisheiluri tasossa ϕ ϕ 2 l m l 2 m2 Tarkastellaan tasossa liikkuuvaa heiluria (m, l ), jonka vapaasta päästä riippuu toinen samassa tasossa liikkuva heiluri (m 2, l 2 ) (Kuva 4.4). Merkitään heilureiden heilahduskulmia pystysuunnasta ϕ, ϕ 2. Koska molemmilla heilureilla on luonnollinen sidosehto eli heilurin vakiopituus alunperin neljä koordinaattia (x, y, x 2, y 2 ) voidaan ilmaista näiden kahden kulman avulla x = l cos ϕ Kuva 4.4. Kaksoisheiluri. y = l sin ϕ x 2 = l cos ϕ + l 2 cos ϕ 2 y 2 = l sin ϕ + l 2 sin ϕ 2. Seuraavaksi sijoitetaan nämä kineettisen energian lausekkeeseen T = T + T 2 = 2 Potentiaalienergiat ovat puolestaan 2 m i (ẋ 2 i + ẏi 2 ). i= U = m gl cos ϕ U 2 = m 2 g(l cos ϕ + l 2 cos ϕ 2. Kaksoisheilurin Lagrangen funktioksi tulee siten L = 2 (m + m 2 )l 2 ϕ m 2l 2 ϕ m 2 l l ϕ ϕ 2 cos(ϕ ϕ 2 ) +(m + m 2 )gl cos ϕ + m 2 gl 2 cos ϕ 2. Tämä on voimassa kaikille heilahduskulmille. Jos molemmat kulmat voidaan olettaa pieniksi, tämä yksinkertaistuu muotoon L = 2 (m + m 2 )l 2 ϕ m 2l 2 ϕ m 2 l l 2 ϕ ϕ 2 2 (m + m 2 )gl ϕ 2 2 m 2gl 2 ϕ 2 2,
11 LUKU 4. VÄRÄHDYSLIIKKEET 69 josta on sitten suoraviivaista johtaa liikeyhtälöt kummallekin kulmalle käyttäen Lagrangen yhtälöitä. Nämä yhtälöt voidaan sitten ratkaista tässä luvussa käsiteltävin menetelmin. Opiskelijalle jää omatoimiseksi harjoitustehtäväksi vaakuuttautua, että ongelma on aika hankala käsiteltäväksi suoraan ilman Lagrangen formalismia. Tämä vielä kohtuullisen yksinkertainen esimerkki kertoo jotain niistä vaikeuksista, joita liittyy kytkettyjen värähtelijöiden maailmaan. Monenlaisia fysikaalisia systeemejä voi kuvailla toisiinsa kytkettyjen oskillaatoreiden avulla. Esimerkkeinä käyvät moniatomiset molekyylit, akustiset tai mekaaniset värähtelyt taikka sähköiset värähtelypiirit. Samoin jatkuvasti jakautunut kimmoisa aine usein värähtelee tietyillä ominaistaajuksillaan. Jos värähtelyt pysyvät pieninä, systeemin voidaan ajatella koostuvan useasta harmonisesta oskillaattorista. Usean oskillaattorin kytkeminen toisiinsa lisää kuitenkin oskillaattorien välisten resonanssien mahdollisuutta, jolloin mahdollisuus liukastua epälineaariselle alueelle kasvaa nopeasti. Yksinkertainen esimerkki tilanteesta oli jo edellä käsitelty parametrinen resonanssi, jossa oskillaatiota moduloinut pumppuaalto kytkeytyi oskillaattorin ominaistaajuuteen. Koska nyt tarkasteltavissa tapauksissa on useita oskillaatoreita, niissä on useita riippumattomia vapausasteita. Merkitään kaikkia systeemin riippumattomia koordinaatteja q i, i =,..., n. Annetaan systeemin potentiaalienergia näiden funktiona U = U(q,..., q n ). Oletetaan, että systeemillä on tasapainoasema eli potentiaalin minimikohta koordinaattien arvoilla {q, q 2,..., q n}. Merkitään koordinaattien poikkeamia tasapainosta jälleen muuttujilla x i ja kirjoitetaan Taylorin kehitelmä U(q,..., q n ) = U(q )+ i U q x i + 2 U q x i x j +..., (4.47) q i 2! q i,j i q j missä on otettu käyttöön lyhennysmerkintä q {q, q 2,..., q n}. Kaksi ensimmäistä termiä voidaan asettaa nolliksi samoilla oletuksilla kuin yhden oskillaattorin tapauksessa. Rajaamalla tarkastelu lineaarisiin oskillaattoreihin, jäljelle jää vain toisen derivaatan termi, joten potentiaali voidaan kirjoittaa muodossa U = k ij x i x j, (4.48) 2 i,j missä jousivakiot k ij muodostavat nyt kaksiulotteisen matriisin K. Matriisinotaatiossa potentiaali on siis U = 2 xt K x, (4.49) missä x on pystyvektori ja x T on sen transpoosi (siis vaakavektori). (HT: Kertaa matriisijutut MAPU:sta!!)
12 LUKU 4. VÄRÄHDYSLIIKKEET 7 Selvitetään seuraavaksi, mitä kineettinen energia tarkoittaa tällaisessa tapauksessa. Merkitään karteesisia koordinaatteja tällä kertaa {y k } ja kuhunkin koordinaattiin liittyvää massaa m k. Oletetaan yksinkertaisuuden vuoksi, että sidosehdot ovat skeloronomisia (ajasta riippumattomia), joten muunnosyhtälöt yleistettyihin koordinaatteihin ovat muotoa Nopeuskomponentit muuntuvat kuten y k = y k (q, q 2,..., q n ). (4.5) ẏ k = j y k q j q j (4.5) ja näiden neliöiksi tulee ẏ 2 k = i,j y k q i y k q j q i q j. (4.52) Koska q i = qi + x i, on q i = ẋ i ja kineettiselle energialle saadaan lauseke ( ) T = m k ẏk 2 2 = y k y k m k q i q j. (4.53) 2 q i q j Otetaan käyttöön merkintä k k i,g jolloin Lagrangen funktioksi tulee k m k y k q i y k q j m ij, L = m ij ẋ i ẋ j k ij x i x j. (4.54) 2 2 i,j Tämä on hyödyllistä esittää matriisimuodossa kirjoittamalla M = (m ij ) ja K = (k ij ) i,j L = 2ẋT M ẋ 2 xt K x. (4.55) Lagrangen yhtälöt ovat tietenkin muodollisesti samanlaiset kuin aiemminkin ( ) d L L = dt q j q j kaikilla j =,..., n. Massamatriisi (m ij ) ja jousivakiomatriisi (k ij ) ovat määritelmiensä perusteella reaalisia ja symmetrisiä, joten ei ole väliä, kummanko indeksin yli summaus tehdään. Sijottamalla L Lagrangen liikeyhtälöihin saadaan newtonilaisiksi liikeyhtälöiksi poikkeamille {x j } (m ij ẍ j + k ij x j ) = (4.56) j kaikilla i =,..., n. Kyseessä on siis n:n liikeyhtälön yhtälöryhmä. Valitaan yritteeksi jo vahvalla rutiinilla x j = Ca j e iωt,
13 LUKU 4. VÄRÄHDYSLIIKKEET 7 missä C on kompleksiluku ja kertoimet a j ovat reaalisia. Sijoittamalla tämä liikeyhtälöön saadaan (Ca j e iωt k ij Cω 2 a j e iωt m ij ) = (4.57) j (k ij a j ω 2 m ij a j ) =. (4.58) j Tämä on matriisimuodossa ominaisarvoyhtälö missä (K ω 2 M) a =, (4.59) a = a a 2. a n Ei-triviaaleilta ratkaisuilta edellytetään. det(k ω 2 M) =. (4.6) Kirjoittamalla determinantti auki saadaan sekundaariyhtälöksi kutsuttu n:n kertaluvun polynomiyhtälö ω 2 :lle. Sijoittamalla tästä ratkaistut ω:t yksi kerrallaan ominaisarvoyhtälöön, voidaan ratkaista niitä vastaavat ominaisvektorit a, joita on yhtä monta kuin ratkaisuja ω. Numeroidaan nämä alaindekseillä i =,..., n. Nyt voidaan osoittaa, että ωi 2 :t ovat reaalisia (HT) ja (ω 2 i ω 2 j )(a T j M a i ) = a T j ω 2 i M a i (ω 2 j M a j ) T a i = (4.6) a T j K a i (K a j ) T a i =. Jos i j ja ω 2 i ω 2 j, niin at j M a i = eli vektorit a j ja a i ovat ortogonaalisia matriisin M yli. Näinollen voidaan valita normitus a T i M a j = δ ij, (4.62) missä δ ij on Kroneckerin delta eli ykkönen, kun i = j ja muulloin nolla. Määritellään matriisi A = (a, a 2,..., a n ). Tämän matriisin sarakkeina ovat siis pystyvektorit a i. Koska a i :t ovat reaalisia, niin myös A on reaalinen. Nyt (A T M A) ij = a T i M a j = δ ij. (4.63) Siis A T M A = I eli yksikkömatriisi. Nyt ominaisarvoyhtälöstä (4.59) seuraa, että A diagonalisoi myös K:n: (A T K A) ij = ω 2 j δ ij (4.64) A T K A = Ω 2, (4.65)
14 LUKU 4. VÄRÄHDYSLIIKKEET 72 missä Ω 2 = ω 2. ω ω 2 n Nyt systeemin todelliset värähtelyt (x i :t) ovat superpositioita löydetyistä ominaisarvoista. Koska ratkaisu kuitenkin diagonalisoituu, voidaan tehdä koordinaatiston muunnos normaalikoordinaatteihin, joista jokainen värähtelee vain yhdellä ominaistaajuudella. Merkitään näitä koordinaatteja {η i } ja määritellään muunnos x = A η η = A x. Nyt selvästikin A = A T M. Kirjoitetaan Lagrangen funktio uusissa koordinaateissa (HT) L = 2 ηt A T M A η 2 ηt A T K A η ja liikeyhtälöryhmäksi tulee = 2 ηt η 2 ηt Ω 2 η = ( η i 2 ωi 2 ηi 2 ) (4.66) 2 i η i + ω 2 i η i = (4.67) kaikilla i =,..., n. Ongelma on saatu siten palautetuksi yksittäisten oskillaattoreiden liikeyhtälön ratkaisemiseen. Yhtälöiden (4.67) ratkaisut ovat tietenkin η i = C i cos(ω i t + δ i ) (4.68) kaikilla i. Koordinaateissa x i = j a ijη j ratkaisut ovat pulestaan x i = n C j a ij cos(ω j t + δ j ), (4.69) j= missä δ j, C j :t ovat alkuarvoista määräytyviä vakioita. Esimerkki: Lineaarinen kolmiatominen molekyyli Tarkastellaan sellaista yksiulotteisen molekyylin mallia, jossa on keskellä massa M ja sen molemmilla puolilla massat m. Oletetaan, että massat m on sidottu keskusatomiin jousilla, joiden jousivakiot ovat k ja tasapainoasemassa kummankin etäisyys keskusatomista on b. Merkitään massojen paikkoja q, q 2, q 3, joista q 2 on massan M koordinaatti. Nyt molekyylin kineettinen ja potentiaalienergia ovat T = m 2 ( q2 + q 2 3) + M 2 q2 2 U = k 2 (q 2 q b) 2 + k 2 (q 3 q 2 b) 2.
15 LUKU 4. VÄRÄHDYSLIIKKEET 73 Merkitään tasapainoasemia q i ja x i = q i q i. Nyt b = q 2 q = q 3 q 2. Tästä seuraa T = m 2 (ẋ2 + ẋ 2 3) + M 2 ẋ2 2 U = k 2 (x2 + 2x x 2 3 2x x 2 2x 2 x 3 ). Poimitaan näistä sitten massa- ja jousivakiomatriisien komponentit m ij ja k ij, joten matriisit ovat M = m M m ; K = k 2 Ominaisarvoyhtälöksi (K ω 2 M) a = on matriisimuodossa k ω 2 m k k 2k ω 2 M k k k ω 2 m a a 2 a 3 = Tämän karakteristinen yhtälö eli determinantin nollakohdat antava yhtälö on ω 2 (k ω 2 m)[mmω 2 k(2m + M)] =, jonka juuret eli ominaistaajuudet ovat ω 2 = ω 2 2 = k m ω 2 3 = k m ( + 2m ) M. Sijoittamalla ensimmäinen ominaistaajuus ω 2 = ominaisarvoyhtälöön saadaan ominaisvektori, jonka kaikki elementit ovat yhtä suuria a = a 2 = a 3 a. Normitetaan tämä vektorin M yli (a T M a = ), josta a 2 (2m + M) = a = / 2m + M eli ensimmäinen ominaisvektori on a =. 2m + M Toinen ominaistaajuus ω2 2 = k/m tuottaa ominaisarvot a 2 =, a 3 = a a ja normitusehdosta tulee a = / 2m. Toinen ominaisvektori on siten a 2 = 2m. Samalla reseptillä saadaan kolmanneksi ominaisvektoriksi M a 3 = (2mM + 4m 2 2m/M. )
16 LUKU 4. VÄRÄHDYSLIIKKEET 74 Jos nyt halutaan siirtyä normaalikoordinaatteihin {η i }, meidän on laskettava muunnosmatriisi A, joksi saadaan A = M 2m+M 2m (2mM+4m 2 ) 2m+M 2m M M (2mM+4m 2 ) 2m+M M 2m (2mM+4m 2 ) Tämä antaa koordinaatistojen väliset muunnosyhtälöt x = η + η 2 + 2m + M 2m x 2 = x 3 = η + 2m 2m + M M η η 2 + 2m + M 2m. M (2mM + 4m 2 ) η 3 M (2mM + 4m 2 ) η 3 M (2mM + 4m 2 ) η 3. Jos on tarpeen, {η i }:t voi ratkaista tästä yhtälöryhmästä tai laskemalla η = A T M x. Normaalikoordinaattien fysikaalinen merkitys on tässä tapauksessa seuraavanlainen. Oletetaan, että vain η koordinaatti on virittynyt soimaan, jolloin η 2 = η 3 =. Tällöin systeemi värähtelee taajuudella ω, joka tällä kertaa on nolla. Tällöin x = x 3 = x 3 ja tarkasteltava molekyyli liikkuu jäykkänä kappaleena. Jos taas η 2 soi ominaistaajuudellaan ω 2 = k/m, mutta η 2 = η 3 =, on x 2 = ja x 3 = x. Tässä tilanteessa M pysyy paikallaan ja ulommat atomit oskilloivat siten, että niiden välillä on π:n vaihesiirto (miinusmerkki). Kolmas perustapaus (vain η 3 soi) on puolestaan sellainen, jossa x 2 = (2m/M)x ja x 3 = x. Tässä tapauksessa myös keskimmäinen massa värähtelee ulompien suhteen siten, että massakeskipiste pysyy paikallaan. Näitä kolmea normaalikoordinaateissa tapahtuvaa perusvärähtelyä kutsutaan systeemin normaalimoodeiksi. Koska yhden normaalikoordinaatin suhteen taajuus on nolla, molekyyli liikkuu jäykkänä kappaleena. Koska systeemiin ei vaikuta muita voimia, voitaisiin tarkastelu alusta alkaen siirtää molekyylin massakeskipistekoordinaatistoon, jolloin vapausasteita olisi vain kaksi, matriisit olisivat 2 2-matriiseja ja vektoreilla olisi vain kaksi komponenttia. Toisaalta tätä ei tiedetty laskun aluksi. Edellä käsiteltiin vain vaimentamattomia, vapaita, kytkettyjä lineaarisia oskillaattoreita. Jos systeemiin liitetään mukaan vaimennus ja pakkovoima, sen käsittely on olennaisesti vaikeampaa (Goldsteinin oppikirjassa on esitetty lyhyesti teorian perusteet). Näillä ominaisuuksilla on kuitenkin olennaista merkitystä esimerkiksi tarkasteltaessa toisiinsa kytkettyjä sähköisiä värähtelypiirejä. Siellä potentiaalienergiaa kuvaavan K- matriisin elementtien käänteisluvut vastaavat kapasitansseja, kineettistä energiaa kuvaavan M-matriisin elementit induktansseja ja vaimennusta kuvaamaan tuodaan uusi matriisi, jonka elementit vastaavat resistansseja. Pakkovoimia sovelletaan tilanteen mukaan yhteen tai useampaan oskillaattoreista.
17 LUKU 4. VÄRÄHDYSLIIKKEET *Jännitetyn kielen värähtelyt Kuten jo aiemmin on tullut mainituksi Lagrangen mekaniikkaa sovelletaan usein kenttäteorioihin, jotka ovat olennaisesti jatkuvia systeemejä, joissa on ääretön määrä vapausasteita. Esitellään tässä esimerkkinä jatkuvasti jakautuneen aineen alueelta jännitetty kieli, jonka pituus on l, massa pituusyksikköä kohti µ ja kieltä jännittävä voima F. Kielen molemmat päät oletetaan liikkumattomiksi. Arvatenkaan ongelmaa ei kannata lähteä ratkomaan äärettömän monen yleistetyn koordinaatin avulla. Tarkastellaan kielen poikittaista siirtymää jatkuvana funktiona y = y(x, t), joka mitataan kielen tasapainoasemasta. Pienen pituuselementin dx kineettinen energia on (/2)(µdx)ẏ 2. Huom. tässä pisteellä merkitään osittaisaikaderivaattaa ẏ = y/ t aiemmasta käytännöstä poiketen. Koko väräjävän kielen kineettinen energia on siten T = l 2 µẏ2 dx. (4.7) Kun kieli siirtyy tasapainostaan, sen täytyy venyä, joten l + l = l ( + y 2 ) /2 dx, (4.7) missä pilkku puolestaan tarkoittaa y:n osittaisderivaattaa paikan suhteen y = y/ x. Jännitysvoimaa F vastaan tehty työ on F l, mikä siis on häirittyyn kieleen varastoitunutta potentiaalienergiaa. Oletetaan siirtymä pieneksi, jolloin ( + y 2 ) /2 + 2 y 2 ja voiman potentiaalifunktioksi saadaan Lagrangen funktio on nyt L = U = l l 2 F y 2 dx. (4.72) ( 2 µẏ2 ) 2 F y 2 dx. (4.73) Kielen voidaan siis ajatella muodostuvan äärettömän monesta kytketystä oskillaattorista, jolloin Lagrangen funktiossa summaus oskillaattoreiden yli korvautuu integraalilla. Tämä on erikoistapaus muotoa L = l L(y, ẏ, y ) dx (4.74) Periaatteessahan voima F ei ole vakio vaan kasvaa kieltä venytettäessä. Jos kieli on kuitenkin valmiiksi kiristetty, jännitysvoiman muutos on pieni ja F voidaan olettaa vakioksi pienessä venytyksessä.
18 LUKU 4. VÄRÄHDYSLIIKKEET 76 olevasta Lagrangen funktiosta. Tässä L on Lagrangen tiheys. Liikeyhtälöt saadaan jälleen lähtien Hamiltonin periaatteesta määrittelemällä vaikutusintegraali I = t2 l t L(y, ẏ, y ) dx dt. (4.75) Tarkastellaan siis variaatiota δy(x, t), joka häviää, kun t = t ja t = t 2. Oletetaan myös, että päätepisteet ovat kiinteät eli δy =, kun x = ja x = l. Vaikutusintegraalin variaatio on δi = t2 l t [ L y δy + L ẏ t (δy) + L y ] x (δy) dx dt. (4.76) Osittaisintegroidaan toinen termi t:n suhteen ja kolmas termi x:n suhteen. Sijoitustermit häviävät, koska δy = kaikilla neljällä rajalla. Näin on saatu δi = t2 l t [ L y t ( ) L ẏ x ( )] L y δy(x, t) dx dt. (4.77) Jotta tämä katoaisi kaikilla oletetun kaltaisilla y:n variaatioilla, täytyy integrandin olla aina nolla. Niinpä on saatu Lagrangen liikeyhtälö L y ( ) L ( ) L t ẏ x y =. (4.78) Sijoitetaan tähän jännitetyn kielen Lagrangen tiheyden derivaatat L y =, L ẏ = µẏ, L y = F y. Ottamalla vielä keskimmäisen lausekkeen aikaderivaatta saadaan lopulta liikeyhtälö µÿ = F y 2 y t 2 = C2 2 y x 2 (4.79) eli aaltoyhtälö, jossa aallon etenemisnopeus on C = F/µ. Ja sitten vain soitinta virittämään, eli säätämään voimaa F! 4.7 Epälineaarisista värähtelijöistä On tärkeää muistaa, että edellisissä tarkasteluissa muuttuja x on tarkoittanut värähtelijän koordinaatin q poikkeamaa tasapainokohdasta q eli x = q q. Tähän asti on oletettu, että poikkeama on pieni ja potentiaalin Taylorin sarjasta riittää tarkastella vain toista derivaattaa, jolloin oskillaattorin liikeyhtälöt ovat olleet lineaarisia differentiaaliyhtälöitä. Edellä käsitelty resonanssi-ilmiö johtaa kasvaessaan kuitenkin ilmeisesti niin suureen poikkeamaan x, ettei potentiaalin Taylorin sarjaa enää voida katkaista toisen derivaatan kohdalta ja tilannetta kuvailevasta differentiaaliyhtälöstä tulee muuttujan x suhteen epälineaarinen. Luvussa käsitelty matemaattinen heiluri on myös epälineaarisen värähtelijän malliesimerkki, sillä yhtälö θ + g sin θ = (4.8) l
19 LUKU 4. VÄRÄHDYSLIIKKEET 77 on tietenkin kulmamuuttujan θ epälineaarinen yhtälö (sinifunktio). Tämä linearisoituu oletuksella, että kulma on pieni, jolloin sin θ θ. Epälineaarisia differentiaaliyhtälöitä on paljon ja erilaisia eikä edes yksinkertaisimmille niistä ole yleisiä ratkaisuja. Hyvinkin yksinkertaisella epälineaarisella yhtälöllä voi olla useita erilaisia ratkaisuperheitä riippuen yhtälön kertoimien välisistä suhteista. Tarkastellaan tässä esimerkkinä yksiulotteisia epälineaarisia systeemejä, joissa potentiaali on konservatiivinen U(x). Ajatellaan, että systeemin muodostaa hiukkanen, joka liikkuu tässä potentiaalissa. Tällöin systeemin kokonaisenergia on E = T + U = 2 mẋ2 + U(x). (4.8) Koska hiukkasen nopeus on ẋ = ± 2(E U)/m, hiukkanen voi liikkua ainoastaan alueessa, missä kokonaisenergia ylittää potentiaalienergian. Jos potentiaali on nyt sellaista muotoa, että sillä on kaksi huippua, jotka ylittävät kokonaisenergian, niin hiukkanen oskilloi näiden huippujen välissä (Kuva 4.). Olkoot pisteet x ja x 2 kohdat, joissa E = U. Tällöin edestakaisen liikkeen periodi (värähdysaika) on m x2 (E) dx τ(e) = 2, (4.82) 2 x (E) E U(x) missä käännepisteiden ja värähdysajan riippuvuus energiasta on kirjoitettu näkyviin Faasi-integraali ja faasikäyrä Tarkastellaan sitten oskillaattorin liikettä tasossa (x, ẋ). Tällaista tasoa kutsutaan faasitasoksi tai faasiavaruudeksi (tai vaiheavaruudeksi). Edestakainen liike muodostaa tässä tasossa suljetun lenkin, jonka yli otettua integraalia J = p dx (4.83) kutsutaan faasi-integraaliksi (tai vaiheintergraaliksi). Nyt edellä määritelty oskillaattorin periodi voidaan kirjoittaa (HT) muodossa τ = dj/de. (4.84) Epälineaaristen ongelmien käsittelyssä nk. faasikäyrämenetelmä on usein hyödyllinen. Tarkastellaan aluksi vaimentamatonta lineaarista oskillaattoria, jonka rata on muotoa x(t) = A sin(ω t + δ) ja nopeus ẋ(t) = ω A cos(ω t+δ). Korotetaan nämä neliöön ja lasketaan puolittain yhteen, jolloin saadaan yhtälö x 2 A 2 + ω 2 ẋ2 A2 =, (4.85) joka on ellipsin yhtälö faasiavaruudessa eli tässä tapauksessa tasossa (x, ẋ). Koska A 2 = 2E/k ja ω 2 = k/m, ovat ellipsin iso- ja pikkuakselit
20 LUKU 4. VÄRÄHDYSLIIKKEET 78 energian E funktioita. Suurempaa energiaa vastaava ellipsi on aina pienempää energiaa vastaavan ulkopuolella. Faasikäyrän differentiaaliyhtälö dẋ dx = x ω2 (4.86) ẋ saadaan alkuperäisestä differentiaaliyhtälöstä ẍ+ω 2 x = (HT). Saadun differentiaaliyhtälön ratkaisu on siis faasikäyrän yhtälö. ẋ = ẋ(x) (4.87) Tarkastellaan sitten epälineaarista oskillaattoria ja kehitetään potentiaali Taylorin sarjaksi tasapainoaseman ympärillä (ensimmäinen ja toinen termi ovat nollia samoin perustein kuin luvun alussa käsitellyissä lineaarisissa oskillaattoreissa) U(q) = d 2 U q 2! dq 2 x 2 + d 3 U q 3! dq 3 x 3 + d 4 U q 4! dq 4 x (4.88) Ottamalla käyttöön vakiot k, λ ja ε määritelmillä d 2 U q 2! dq 2 2 k d 3 U q 3! dq 3 3 mλ d 4 U q 4! dq 4 4 mε saadaan potentiaalin sarjakehitelmä muotoon U(x) = 2 kx2 3 mλx3 4 mεx (4.89) Oletetaan ensin, että poikkeama harmonisen oskillaattorin paraabelin muotoisesta potentiaalista on muotoa 4 mεx4. Potentiaali on edelleen symmetrinen tasapainoaseman suhteen. Jos ε >, potentiaali on laakeampi kuin harmoninen potentiaali ja oskillaattoria palauttava voima kasvaa hitaammin siirryttäessä kauemmaksi tasapainosta. Tapausta kutsutaan pehmeneväksi. Jos ε <, potentiaali on jyrkempi ja tapausta kutsutaan joskus myötölujenevaksi. Siis palauttava voima vahvistuu, kun siirrytään kauemmaksi tasapainosta. Muotoa 3 mλx3 oleva epäharmonisuus tekee potentiaalista puolestaan on epäsymmetrisen tasapainoaseman suhteen. Riippuen λ:n merkistä palauttava voima on pehmenevä toiseen ja myötölujeneva toiseen suuntaan. (HT: Hahmottele faasikäyrä tällaiselle potentiaalille parilla eri energialla.) van der Polin oskillaattori ja attraktorit Tärkeä ryhmä värähtelijöitä ovat nk. kvasiharmoniset oskillaattorit, joille ẍ + ω 2 x = f(x, ẋ). (4.9)
21 LUKU 4. VÄRÄHDYSLIIKKEET 79 Tällainen on mm. van der Polin oskillaattori, jonka liikeyhtälö on ẍ κ(x 2 x 2 )ẋ + ω 2 x =, (4.9) missä κ ja x ovat vakioita. Epälineaarisuus on siis muotoa x 2 ẋ, mikä on selvästi ei-konservatiivinen termi. Skaalataan muuttujat dimensiottomiksi x/x x ja ω t t ẍ ɛ( x 2 )ẋ + x =, (4.92) missä ɛ = κx 2 /ω. Faasikäyrän differentiaaliyhtälöksi tulee dẋ dx + ẋ x = ɛ( x2 ), (4.93) josta saadaan d dt (x2 + ẋ 2 ) = 2ɛ( x 2 )ẋ 2. (4.94) Jos ɛ =, on x 2 + ẋ 2 = R 2, missä R on vakio, eli faasikäyrä on ympyrä. Tutkitaan sitten tapausta, jossa ɛ on pieni positiivinen luku eli < ɛ. Tällöin liike on kvasiperiodista. Integroidaan yhtälö (??) yhden jakson yli t = T 2π R 2 = T 2ɛ 2ɛ( x 2 )ẋ 2 dt 2π = 2πɛR 2 ( R2 4 ), ( R 2 cos 2 ϕ)r 2 sin 2 ϕ dϕ (4.95) missä on käytetty hyväksi relaatioita x = R cos ϕ ja ẋ = R sin ϕ, approksimoitu R vakioksi ja integrointimuuttujaksi on vaihdettu vaihekulma ajan sijasta dϕ dt. (??):n perusteella R 2 =, kun R = 2. Jos R < 2, niin R 2 >, ja jos R > 2, niin R 2 < eli olipa oskillaattorin radan säde faasitasossa suurempi tai pienempi kuin R = 2, se lähestyy ympyrää R = 2. Palaamalla takaisin dimensiollisiin muuttujiin tämä rajaympyrä vastaa ellipsiä x 2 4x 2 + ẋ2 4x 2 ω2 Tällaista rajakäyrää kutsutaan attraktoriksi. =. (4.96) Jos ɛ ei ole pieni, tilanne pysyy kvalitatiivisesti samanlaisena, mutta systeemi hakeutuu edelleenkin attraktorille. Nyt attraktorin muoto kuitenkin deformoituu. (HT: van der Polin oskillaattoreista löytyy hyviä esimerkkejä webistä. Etsi sopiva sivu ja tutustu kuviin, jotka esittävät oskillaatorin vaimenemista eri ɛ:in arvoilla.) Jos van der Polin oskillaattoriin lisätään sopivan muotoinen ulkoinen ajasta riippuva voima (esim. muotoa cos ω D t, missä ω D on lähellä oskillaattorin ominaistaajuutta ω ), attraktori muuttuu nk. oudoksi attraktoriksi. Saapuessaan attraktorille ratkaisu saattaa hypätä eri paikkaan vaiheavaruutta ja liikkeen ennustaminen käy mahdottomaksi. Tämä on esimerkki kaoottisesta liikkeestä, johon tutustutaan lähemmin luentojen viimeisessä luvussa.
22 LUKU 4. VÄRÄHDYSLIIKKEET Approksimatiivisia ratkaisuja Epälineaaristen yhtälöiden ratkaisemiseksi ei ole olemassa yleisiä menetelmiä, mutta sitä vastoin monenlaisia kikkoja etsiä ainakin approksimatiivisia ratkaisuja. Tutustuaan tässä pariin käyttökelpoiseen esimerkkiin. Duffingin menetelmä Duffingin menetelmä perustuu peräkkäisiin approksimaatioihin. Tarkastellaan esimerkkinä potentiaalissa U(x) = 2 kx2 4 mεx4 (ε < ) (4.97) liikkuvaa m-massaista hiukkasta, johon vaikuttaa lisäksi ulkoinen pakkovoima mf cos ωt. Liikeyhtälö on siten Arvataan ensimmäinen yrite ẍ = εx 3 ω 2 x + f cos ωt. (4.98) x = A cos ωt. Sijoitetaan tämä liikeyhtälön oikealle puolelle ẍ = εa 3 cos 3 ωt ω 2 A cos ωt + f cos ωt. (4.99) Trigonometrian kaavakokoelmista löytyy tulos cos 3 ωt = 4 cos 3ωt + 3 cos ωt 4 ( ) 3 ẍ = 4 εa3 ωa 2 + f cos ωt + 4 εa3 cos 3ωt. (4.) Tämä vihjaa siihen, että yrite x 2 = A cos ωt + B cos 3ωt olisi jo paljon parempi arvaus. Sijoittamalla tämä alkuperäisen yhtälön oikealle puolelle saataisiin sinne muotoa cos 5ωt oleva termi ja niin edelleen. Tuloksena olisi siis taajuusspektri ω:n parittomille monikerroille. Tyydytään tässä kuitenkin oletukseen, että epälineaarisuus on sen verran heikkoa, että x 2 on jo itsessään riittävän hyvä approksimaatio. Sijoitetaan se alkuperäisen yhtälön molemmille puolille, jolloin saadaan yhtälö ω 2 A cos ωt 9ω 2 B cos 3ωt = ε(a cos ωt + B cos 3ωt) 3 ω 2 (A cos ωt + B cos 3ωt) + f cos ωt. (4.) Jotta tällainen kehitelmä yleensä johtaisi johonkin, täytyy korkeampien ylä-äänien (siis ω:n monikertojen) amplitudien olla alempia pienempiä. Jos ylläolevassa näin on, voidaan oikean puolen ensimmäisen termin ylä-ääni jättää pienenä pois, varsinkin kun se on vielä kerrottu pieneksi
23 LUKU 4. VÄRÄHDYSLIIKKEET 8 oletetulla ε:lla. Kehitetään sitten cos 3 ωt jälleen samalla kaavalla kuin edellä ja kootaan perus- ja ylä-äänien lausekkeet yhteen ( ) 3 4 εa3 + ω 2 A ωa 2 + f cos ωt+ (9ω 2 B ω 2B + 4 ) εa3 cos 3ωt =. (4.2) Funktiot cos ωt ja cos 3 ωt ovat riippumattomia toisistaan, joten molempien kertoimien täytyy olla erikseen nollia. Tästä saadaan yhtälöpari 3 4 εa3 + (ω 2 ω 2)A + f = (4.3) εa 3 B = 4(ω 2 9ω2 ), (4.4) joista jälkimmäistä käyttäen toisen kertaluvun approksimaatio on x 2 (t) = A cos ωt + εa 3 4(ω 2 cos 3ωt. (4.5) 9ω2 ) Ylä-äänessä esiintyvä resonanssi ei ole yleensä ole oikea vaan seurausta käytetystä approksimaatiosta ja katoaa mentäessä seuraavaan kertalukuun. Nyt on vielä ratkaistava perusäänen amplitudin kolmannen asteen yhtälö. Selvästikin ratkaisun amplitudi riippuu sekä pakkovoiman voimakkuudesta että taajuudesta. Kolmannen asteen yhtälö voidaan tietenkin ratkaista analyyttisesti, mutta ratkaisun tarkastelu on näppärintä tehdä graafisesti. Tätä varten piirretään saman koordinaatiston (y, A)- tasoon suora y = (ω 2 ω 2 )A f ja kuutioparaabeli y = 3 4 εa3, jolloin ratkaisut löytyvät näiden leikkauspisteestä. Kuvassa 4.3 on hahmoteltu ko. käyrien lisäksi näin saatu amplitudi taajuuden funktiona. (Pisteet, 2 ja 3 on saatu peilaamalla pisteet ω-akselin suhteen, eli määrittelemällä amplitudi aina positiiviseksi.) Häiriökehitelmä Hyvin yleinen tapa ratkoa hankalia ongelmia fysiikassa on tehdä häiriökehitelmiä. Tarkastellaan tässä esimerkkinä epäsymmetristä potentiaalia joka antaa liikeyhtälöksi U(x) = 2 kx2 3 mλx3, (4.6) ẍ + ω 2 x λx 2 =. (4.7) Tässä tapauksessa ei siis ole mukana ulkoista pakkovoimaa. Oletetaan, että vakio λ on pieni eli epälineaarisuus on pienillä amplitudeilla vähäinen korjaus lineaariseen värähtelijään. Kirjoitetaan ratkaisuyrite λ:n potenssisarjana x(t) = x (t) + λx (t) + λ 2 x 2 (t) +...,
24 LUKU 4. VÄRÄHDYSLIIKKEET 82 y A ω= A ω=ω ω 6 ω>ω 7 8 Kuva 4.3. Yhtälön (??) graafinen ratkaiseminen. missä x (t) on häiriöttömän oskillaatorin ratkaisu. Sijoitetaan tämä yrite liikeyhtälöön ja jätetään λ:n toista ja korkeampia kertalukuja olevat termit pois. Tällöin (ẍ + ω 2 x ) + λ(ẍ + ω 2 x x 2 ) =. (4.8) Ensimmäinen sulkulauseke on nolla, koska x on häiritsemättömän värähtelijän ratkaisu. λ:n kerroin on puolestaan nolla sillä edellytyksellä, että korkeamman kertaluvun termit voidaan jättää huomiotta. Näin meillä on yhtälöpari ẍ + ω 2 x = (4.9) ẍ + ω 2 x x 2 =. (4.) Ensimmäinen osataan ratkaista jo kyllästymiseen asti: x = A cos ω t. Käyttäen hyväksi trigonometrista tulosta cos 2 ω t = (/2)( + cos 2ω t) toinen yhtälöistä saa muodon ẍ + ωx 2 = A2 2 + A2 2 cos 2ω t. (4.) Homogeenisen yhtälön ratkaisu on jo mukana x :ssa. Lisätään tähän epähomogeenisen yhtälön erikoisratkaisu, joka on muotoa x (t) = B cos 2ω t + C. (4.2)
25 LUKU 4. VÄRÄHDYSLIIKKEET 83 Sijoittamalla tämä x :n yhtälöön saadaan 3ω 2 B cos 2ω t + ω 2 C = A2 2 + A2 2 cos 2ω t, (4.3) josta saadaan lasketuksi B ja C B = A2 6ω 2 ; C = A2 2ω 2. (4.4) Siis λ:n ensimmäistä kertalukua myöten alkuperäisen liikeyhtälön ratkaisu on x(t) = A cos ω t λ A2 6ω 2 (cos 2ω t 3). (4.5) Tällä kertaa ensimmäinen ylä-ääni on 2ω. Menemällä korkeampiin kertalukuihin spektriin tulee ylä-ääniä 3ω, 4ω,.... Mitattaessa jotakin luonnossa havaittavaa tai vaikka elektronisessa värähtelypiirissä ilmenevää oskillaatiota, sen spektrissä nähdään usein ylä-ääniä, vaikka itse oskillaatiolla ei sellaisia pitäisikään olla. Tällöin ylä-äänispektriä analysoimalla saadaan tietoa oskillaation epälineaarisuusominaisuuksista. Edellä oli kaksi esimerkkiä, joista jälkimmäinen tuotti ylä-ääniä kaikilla perusäänen monikerroilla ja ensimmäinen puolestaan vain perusäänen parittomilla monikerroilla. Vaikkakaan analysointi ei välttämättä ole helppoa, voidaan esim. amplitudin pienenemisestä yrittää arvioida epälineaarisuuden voimakkuutta.
Värähdysliikkeet. q + f (q, q, t) = 0. q + f (q, q) = F (t) missä nopeusriippuvuus kuvaa vaimenemista ja F (t) on ulkoinen pakkovoima.
 Torstai 18.9.2014 1/17 Värähdysliikkeet Värähdysliikkeet ovat tyypillisiä fysiikassa: Häiriö oskillaatio Jaksollinen liike oskillaatio Yleisesti värähdysliikettä voidaan kuvata yhtälöllä q + f (q, q, t)
Torstai 18.9.2014 1/17 Värähdysliikkeet Värähdysliikkeet ovat tyypillisiä fysiikassa: Häiriö oskillaatio Jaksollinen liike oskillaatio Yleisesti värähdysliikettä voidaan kuvata yhtälöllä q + f (q, q, t)
Useita oskillaattoreita yleinen tarkastelu
 Useita oskillaattoreita yleinen tarkastelu Useita riippumattomia vapausasteita q i, i =,..., n ja potentiaali vastaavasti U(q, q 2,..., q n). Tasapainoasema {q 0, q0 2,..., q0 n} q 0 Käytetään merkintää
Useita oskillaattoreita yleinen tarkastelu Useita riippumattomia vapausasteita q i, i =,..., n ja potentiaali vastaavasti U(q, q 2,..., q n). Tasapainoasema {q 0, q0 2,..., q0 n} q 0 Käytetään merkintää
Esimerkki 1 Ratkaise differentiaaliyhtälö
 Esimerkki 1 Ratkaise differentiaaliyhtälö x 2 y xy =1/x. 1 / K. Tuominen kimmo.i.tuominen@helsinki.fi MApu II 1/20 20 Esimerkki 2 Ratkaise differentiaaliyhtälö x(ln y)y y ln x =0. 2 / K. Tuominen kimmo.i.tuominen@helsinki.fi
Esimerkki 1 Ratkaise differentiaaliyhtälö x 2 y xy =1/x. 1 / K. Tuominen kimmo.i.tuominen@helsinki.fi MApu II 1/20 20 Esimerkki 2 Ratkaise differentiaaliyhtälö x(ln y)y y ln x =0. 2 / K. Tuominen kimmo.i.tuominen@helsinki.fi
Luento 13: Periodinen liike. Johdanto Harmoninen värähtely Esimerkkejä F t F r
 Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi
 Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
BM30A0240, Fysiikka L osa 4
 BM30A0240, Fysiikka L osa 4 Luennot: Heikki Pitkänen 1 Oppikirja: Young & Freedman: University Physics Luku 14 - Periodic motion Luku 15 - Mechanical waves Luku 16 - Sound and hearing Muuta - Diffraktio,
BM30A0240, Fysiikka L osa 4 Luennot: Heikki Pitkänen 1 Oppikirja: Young & Freedman: University Physics Luku 14 - Periodic motion Luku 15 - Mechanical waves Luku 16 - Sound and hearing Muuta - Diffraktio,
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Epähomogeenisen yhtälön ratkaisu
 Epähomogeenisen yhtälön ratkaisu Lause Olkoot a = a(x), b = b(x) ja f = f(x) jatkuvia funktioita välillä I R ja olkoot y 1 = y 1 (x) ja y 2 = y 2 (x) eräs homogeeniyhtälön y + a(x)y + b(x)y = 0 ratkaisujen
Epähomogeenisen yhtälön ratkaisu Lause Olkoot a = a(x), b = b(x) ja f = f(x) jatkuvia funktioita välillä I R ja olkoot y 1 = y 1 (x) ja y 2 = y 2 (x) eräs homogeeniyhtälön y + a(x)y + b(x)y = 0 ratkaisujen
Ei-inertiaaliset koordinaatistot
 orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
Luento 14: Periodinen liike, osa 2. Vaimennettu värähtely Pakkovärähtely Resonanssi F t F r
 Luento 14: Periodinen liike, osa 2 Vaimennettu värähtely Pakkovärähtely Resonanssi θ F µ F t F r m g 1 / 20 Luennon sisältö Vaimennettu värähtely Pakkovärähtely Resonanssi 2 / 20 Vaimennettu värähtely
Luento 14: Periodinen liike, osa 2 Vaimennettu värähtely Pakkovärähtely Resonanssi θ F µ F t F r m g 1 / 20 Luennon sisältö Vaimennettu värähtely Pakkovärähtely Resonanssi 2 / 20 Vaimennettu värähtely
Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle /
 Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle / 16. 18.5. Lineaariset differentiaaliyhtälöt, homogeeniset differentiaaliyhtälöt Tehtävä 1: a) Määritä differentiaaliyhtälön y 3y = 14e 4x
Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle / 16. 18.5. Lineaariset differentiaaliyhtälöt, homogeeniset differentiaaliyhtälöt Tehtävä 1: a) Määritä differentiaaliyhtälön y 3y = 14e 4x
a 1 y 1 (x) + a 2 y 2 (x) = 0 vain jos a 1 = a 2 = 0
 6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
Numeeriset menetelmät TIEA381. Luento 5. Kirsi Valjus. Jyväskylän yliopisto. Luento 5 () Numeeriset menetelmät / 28
 Numeeriset menetelmät TIEA381 Luento 5 Kirsi Valjus Jyväskylän yliopisto Luento 5 () Numeeriset menetelmät 3.4.2013 1 / 28 Luennon 5 sisältö Luku 4: Ominaisarvotehtävistä Potenssiinkorotusmenetelmä QR-menetelmä
Numeeriset menetelmät TIEA381 Luento 5 Kirsi Valjus Jyväskylän yliopisto Luento 5 () Numeeriset menetelmät 3.4.2013 1 / 28 Luennon 5 sisältö Luku 4: Ominaisarvotehtävistä Potenssiinkorotusmenetelmä QR-menetelmä
Luento 11: Periodinen liike
 Luento 11: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä θ F t m g F r Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä Johdanto Tarkastellaan
Luento 11: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä θ F t m g F r Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä Johdanto Tarkastellaan
Tehtävä 4.7 Tarkastellaan hiukkasta, joka on pakotettu liikkumaan toruksen pinnalla.
 Tehtävä.7 Tarkastellaan hiukkasta, joka on pakotettu liikkumaan toruksen pinnalla. x = (a + b cos(θ)) cos(ψ) y = (a + b cos(θ)) sin(ψ) = b sin(θ), a > b, θ π, ψ π Figure. Toruksen hajoituskuva Oletetaan,
Tehtävä.7 Tarkastellaan hiukkasta, joka on pakotettu liikkumaan toruksen pinnalla. x = (a + b cos(θ)) cos(ψ) y = (a + b cos(θ)) sin(ψ) = b sin(θ), a > b, θ π, ψ π Figure. Toruksen hajoituskuva Oletetaan,
2. kl:n DY:t. Lause. Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.
 2. kl:n DY:t Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.) Lause Olkoon f(x 2, x 1, t) funktio, ja oletetaan, että f, f/ x 1 ja f/ x
2. kl:n DY:t Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.) Lause Olkoon f(x 2, x 1, t) funktio, ja oletetaan, että f, f/ x 1 ja f/ x
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
Numeeriset menetelmät TIEA381. Luento 12. Kirsi Valjus. Jyväskylän yliopisto. Luento 12 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
3 Toisen kertaluvun lineaariset differentiaaliyhtälöt
 3 Toisen kertaluvun lineaariset differentiaaliyhtälöt 3.1 Homogeeniset lineaariset differentiaaliyhtälöt Toisen kertaluvun differentiaaliyhtälö on lineaarinen, jos se voidaan kirjoittaa muotoon Jos r(x)
3 Toisen kertaluvun lineaariset differentiaaliyhtälöt 3.1 Homogeeniset lineaariset differentiaaliyhtälöt Toisen kertaluvun differentiaaliyhtälö on lineaarinen, jos se voidaan kirjoittaa muotoon Jos r(x)
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
1 Di erentiaaliyhtälöt
 Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
4 Korkeamman kertaluvun differentiaaliyhtälöt
 Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina
 Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 MAT-1345 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 9 Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa
1 MAT-1345 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 9 Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa
4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
Normaaliryhmä. Toisen kertaluvun normaaliryhmä on yleistä muotoa
 Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
5 Differentiaaliyhtälöryhmät
 5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
17. Differentiaaliyhtälösysteemien laadullista teoriaa.
 99 17. Differentiaaliyhtälösysteemien laadullista teoriaa. Differentiaaliyhtälön x'(t) = f(x(t),t), x(t) n määrittelemän systeemin sanotaan olevan autonominen, jos oikea puoli ei eksplisiittisesti riipu
99 17. Differentiaaliyhtälösysteemien laadullista teoriaa. Differentiaaliyhtälön x'(t) = f(x(t),t), x(t) n määrittelemän systeemin sanotaan olevan autonominen, jos oikea puoli ei eksplisiittisesti riipu
H7 Malliratkaisut - Tehtävä 1
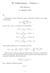 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
Luento 13: Periodinen liike
 Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä ~F t m~g ~F r ELEC-A3110 Mekaniikka (5 op) Sami Kujala Syksy 2016 Mikro- ja nanotekniikan laitos Ajankohtaista
Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä ~F t m~g ~F r ELEC-A3110 Mekaniikka (5 op) Sami Kujala Syksy 2016 Mikro- ja nanotekniikan laitos Ajankohtaista
1 Peruskäsitteet. Dierentiaaliyhtälöt
 Teknillinen korkeakoulu Matematiikka Dierentiaaliyhtälöt Alestalo Tässä monisteessa käydään läpi tavallisiin dierentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Esimerkkejä luennoilla
Teknillinen korkeakoulu Matematiikka Dierentiaaliyhtälöt Alestalo Tässä monisteessa käydään läpi tavallisiin dierentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Esimerkkejä luennoilla
Kertausta: Vapausasteet
 Maanantai 8.9.2014 1/19 Kertausta: Vapausasteet Liikkeen kuvailu: massapisteen koordinaatit (x, y, z) ja nopeudet (v x, v y, v z ). Vapaasti liikkuvalla massapisteellä on kolme vapausastetta. N:llä vapaasti
Maanantai 8.9.2014 1/19 Kertausta: Vapausasteet Liikkeen kuvailu: massapisteen koordinaatit (x, y, z) ja nopeudet (v x, v y, v z ). Vapaasti liikkuvalla massapisteellä on kolme vapausastetta. N:llä vapaasti
Luento 11: Periodinen liike
 Luento 11: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä ~F t m~g ~F r Konseptitesti 1 Tehtävänanto Kuvassa on jouseen kytketyn massan sijainti ajan funktiona. Kuvaile
Luento 11: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä ~F t m~g ~F r Konseptitesti 1 Tehtävänanto Kuvassa on jouseen kytketyn massan sijainti ajan funktiona. Kuvaile
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
- suurempi voima aiheuttaa nopeampaa liikettä kuin pieni voima - samanlainen voima aiheuttaa samalle kappaleelle aina samanlaisen vaikutuksen
 3 Dynamiikka 3.1 Voima (force) - Jos työnnät jotain kevyttä kappaletta, se alkaa liikkua - jos työnnät sitä kovemmin, se liikkuu nopeammin Kyseinen suure on voima - suurempi voima aiheuttaa nopeampaa liikettä
3 Dynamiikka 3.1 Voima (force) - Jos työnnät jotain kevyttä kappaletta, se alkaa liikkua - jos työnnät sitä kovemmin, se liikkuu nopeammin Kyseinen suure on voima - suurempi voima aiheuttaa nopeampaa liikettä
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Voima ja potentiaalienergia II Energian kvantittuminen
 Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt
 4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt 4.1 Homogeeniset lineaariset differentiaaliyhtälöt Homogeeninen yhtälö on muotoa F(x, y,, y (n) ) = 0. (1) Yhtälö on lineaarinen, jos se voidaan
4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt 4.1 Homogeeniset lineaariset differentiaaliyhtälöt Homogeeninen yhtälö on muotoa F(x, y,, y (n) ) = 0. (1) Yhtälö on lineaarinen, jos se voidaan
Mat Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ
 Mat-48 Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ L ẋ = x ẋ = g L sin x rx Epälineaarisen systeemin tasapainotiloja voidaan
Mat-48 Dynaaminen optimointi, mallivastaukset, kierros Vaimennetun heilurin tilanyhtälöt on esitetty luennolla: θ = g sin θ r θ L ẋ = x ẋ = g L sin x rx Epälineaarisen systeemin tasapainotiloja voidaan
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen)
 Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
2. Viikko. CDH: luvut (s ). Matematiikka on fysiikan kieli ja differentiaaliyhtälöt sen yleisin murre.
 2. Viikko Keskeiset asiat ja tavoitteet: 1. Peruskäsitteet: kertaluku, lineaarisuus, homogeenisuus. 2. Separoituvan diff. yhtälön ratkaisu, 3. Lineaarisen 1. kl yhtälön ratkaisu, CDH: luvut 19.1.-19.4.
2. Viikko Keskeiset asiat ja tavoitteet: 1. Peruskäsitteet: kertaluku, lineaarisuus, homogeenisuus. 2. Separoituvan diff. yhtälön ratkaisu, 3. Lineaarisen 1. kl yhtälön ratkaisu, CDH: luvut 19.1.-19.4.
läheisyydessä. Piirrä funktio f ja nämä approksimaatiot samaan kuvaan. Näyttääkö järkeenkäyvältä?
 BM20A5840 - Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2017 1. Tunnemme vektorit a = [ 1 2 3 ] ja b = [ 2 1 2 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
BM20A5840 - Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2017 1. Tunnemme vektorit a = [ 1 2 3 ] ja b = [ 2 1 2 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori = (,..., ). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori = (,..., ). Reaalisten m n-matriisien joukkoa merkitään
6. Differentiaaliyhtälösysteemien laadullista teoriaa.
 1 MAT-13450 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 2010 6. Differentiaaliyhtälösysteemien laadullista teoriaa. Olemme keskittyneet tässä kurssissa ensimmäisen kertaluvun
1 MAT-13450 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 2010 6. Differentiaaliyhtälösysteemien laadullista teoriaa. Olemme keskittyneet tässä kurssissa ensimmäisen kertaluvun
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Matematiikka B3 - Avoin yliopisto
 2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
5 OMINAISARVOT JA OMINAISVEKTORIT
 5 OMINAISARVOT JA OMINAISVEKTORIT Ominaisarvo-ongelma Käsitellään neliömatriiseja: olkoon A n n-matriisi. Luku on matriisin A ominaisarvo (eigenvalue), jos on olemassa vektori x siten, että Ax = x () Yhtälön
5 OMINAISARVOT JA OMINAISVEKTORIT Ominaisarvo-ongelma Käsitellään neliömatriiseja: olkoon A n n-matriisi. Luku on matriisin A ominaisarvo (eigenvalue), jos on olemassa vektori x siten, että Ax = x () Yhtälön
12. Hessen matriisi. Ääriarvoteoriaa
 179 12. Hessen matriisi. Ääriarvoteoriaa Tarkastelemme tässä luvussa useamman muuttujan (eli vektorimuuttujan) n reaaliarvoisia unktioita : R R. Edellisessä luvussa todettiin, että riittävän säännöllisellä
179 12. Hessen matriisi. Ääriarvoteoriaa Tarkastelemme tässä luvussa useamman muuttujan (eli vektorimuuttujan) n reaaliarvoisia unktioita : R R. Edellisessä luvussa todettiin, että riittävän säännöllisellä
= vaimenevan värähdysliikkeen taajuus)
 Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 7: MEKAANINEN VÄRÄHTELIJÄ Teoriaa Vaimeneva värähdysliike y ŷ ŷ ŷ t T Kuva. Vaimeneva värähdysliike ajan funktiona.
Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 7: MEKAANINEN VÄRÄHTELIJÄ Teoriaa Vaimeneva värähdysliike y ŷ ŷ ŷ t T Kuva. Vaimeneva värähdysliike ajan funktiona.
5 Ominaisarvot ja ominaisvektorit
 5 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin A
5 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin A
10. Toisen kertaluvun lineaariset differentiaaliyhtälöt
 37. Toisen kertaluvun lineaariset differentiaalihtälöt Tarkastelemme muotoa () ( x) + a( x) ( x) + a( x) ( x) = b( x) olevia htälöitä, missä kerroinfunktiot ja oikea puoli ovat välillä I jatkuvia. Edellisen
37. Toisen kertaluvun lineaariset differentiaalihtälöt Tarkastelemme muotoa () ( x) + a( x) ( x) + a( x) ( x) = b( x) olevia htälöitä, missä kerroinfunktiot ja oikea puoli ovat välillä I jatkuvia. Edellisen
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
1 Matriisit ja lineaariset yhtälöryhmät
 1 Matriisit ja lineaariset yhtälöryhmät 11 Yhtälöryhmä matriisimuodossa m n-matriisi sisältää mn kpl reaali- tai kompleksilukuja, jotka on asetetettu suorakaiteen muotoiseksi kaavioksi: a 11 a 12 a 1n
1 Matriisit ja lineaariset yhtälöryhmät 11 Yhtälöryhmä matriisimuodossa m n-matriisi sisältää mn kpl reaali- tai kompleksilukuja, jotka on asetetettu suorakaiteen muotoiseksi kaavioksi: a 11 a 12 a 1n
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt. osa 2 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 1 R. Kangaslampi Matriisihajotelmista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt. osa 2 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 1 R. Kangaslampi Matriisihajotelmista
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
 S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva).
 6 DIFFERENTIAALIYHTÄLÖISTÄ Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva). Newtonin II:n lain (ma missä Yhtälö dh dt m dh dt F) mukaan mg, on kiihtyvyys ja
6 DIFFERENTIAALIYHTÄLÖISTÄ Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva). Newtonin II:n lain (ma missä Yhtälö dh dt m dh dt F) mukaan mg, on kiihtyvyys ja
Luento 15: Mekaaniset aallot. Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot
 Luento 15: Mekaaniset aallot Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot 1 / 40 Luennon sisältö Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa
Luento 15: Mekaaniset aallot Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot 1 / 40 Luennon sisältö Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa
Liike pyörivällä maapallolla
 Liike pyörivällä maapallolla Voidaan olettaa: Maan pyöriminen tasaista Maan rataliikkeen näennäisvoimat tasapainossa Auringon vetovoiman kanssa Riittää tarkastella Maan tasaisesta pyörimisestä akselinsa
Liike pyörivällä maapallolla Voidaan olettaa: Maan pyöriminen tasaista Maan rataliikkeen näennäisvoimat tasapainossa Auringon vetovoiman kanssa Riittää tarkastella Maan tasaisesta pyörimisestä akselinsa
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät y' P. α φ
 76336A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät 217 1. Koordinaatiston muunnosmatriisi (a) y' P r α φ ' Tarkastellaan, mitä annettu muunnos = cos φ + y sin φ, y = sin φ + y cos φ, (1a) (1b) tekee
76336A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät 217 1. Koordinaatiston muunnosmatriisi (a) y' P r α φ ' Tarkastellaan, mitä annettu muunnos = cos φ + y sin φ, y = sin φ + y cos φ, (1a) (1b) tekee
1 Ominaisarvot ja lineaariset di erenssiyhtälöt
 Taloustieteen mat.menetelmät syksy 27 materiaali II-4 Ominaisarvot ja lineaariset di erenssiyhtälöt. Idea a b Ajatellaan di erenssiyhtälöä z k+ Az k, A : Jos A olisi diagonaalimatriisi, eli b c, niin muuttujat
Taloustieteen mat.menetelmät syksy 27 materiaali II-4 Ominaisarvot ja lineaariset di erenssiyhtälöt. Idea a b Ajatellaan di erenssiyhtälöä z k+ Az k, A : Jos A olisi diagonaalimatriisi, eli b c, niin muuttujat
5 DIFFERENTIAALIYHTÄLÖRYHMÄT
 5 DIFFERENTIAALIYHTÄLÖRYHMÄT 5. Ensimmäisen kl:n DY-ryhmät Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Useimmat voidaan mallintaa ensimmäisen kertaluvun DY-ryhmien avulla. Ensimmäisen kl:n
5 DIFFERENTIAALIYHTÄLÖRYHMÄT 5. Ensimmäisen kl:n DY-ryhmät Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Useimmat voidaan mallintaa ensimmäisen kertaluvun DY-ryhmien avulla. Ensimmäisen kl:n
MS-A0004/A0006 Matriisilaskenta
 4. MS-A4/A6 Matriisilaskenta 4. Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto..25 Tarkastellaan neliömatriiseja. Kun matriisilla kerrotaan vektoria, vektorin
4. MS-A4/A6 Matriisilaskenta 4. Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto..25 Tarkastellaan neliömatriiseja. Kun matriisilla kerrotaan vektoria, vektorin
Kompleksiluvut., 15. kesäkuuta /57
 Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
Dynaamisten systeemien teoriaa. Systeemianalyysilaboratorio II
 Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
, on säännöllinen 2-ulotteinen pinta. Määrää T x0 pisteessä x 0 = (0, 1, 1).
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 017 Harjoitus 4 Ratkaisuehdotukset 4.1. Osoita, että tasa-arvojoukko S F (0), F : R 3 R, F (x) = 3x 1 x 3 + e x + x e x 3, on säännöllinen
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 017 Harjoitus 4 Ratkaisuehdotukset 4.1. Osoita, että tasa-arvojoukko S F (0), F : R 3 R, F (x) = 3x 1 x 3 + e x + x e x 3, on säännöllinen
Numeeriset menetelmät
 Numeeriset menetelmät Luento 6 To 22.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 6 To 22.9.2011 p. 1/38 p. 1/38 Ominaisarvotehtävät Monet sovellukset johtavat ominaisarvotehtäviin Yksi
Numeeriset menetelmät Luento 6 To 22.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 6 To 22.9.2011 p. 1/38 p. 1/38 Ominaisarvotehtävät Monet sovellukset johtavat ominaisarvotehtäviin Yksi
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Kompleksiluvun logaritmi: Jos nyt z = re iθ = re iθ e in2π, missä n Z, niin saadaan. ja siihen vaikuttava
 Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
MS-A Differentiaali- ja integraalilaskenta 1 (CHEM) Harjoitus 6 loppuviikko
 MS-A0107 - Differentiaali- integraalilaskenta 1 (CHEM) Harjoitus 6 loppuviikko 1 Tehtävä Etsi seuraavien yhtälöiden yleiset ratkaisut: Ratkaisu: a) y y 2y = 4x, b) y + 4y = sin 3x, c) y + 2y + 5y = e x
MS-A0107 - Differentiaali- integraalilaskenta 1 (CHEM) Harjoitus 6 loppuviikko 1 Tehtävä Etsi seuraavien yhtälöiden yleiset ratkaisut: Ratkaisu: a) y y 2y = 4x, b) y + 4y = sin 3x, c) y + 2y + 5y = e x
Kanta ja Kannan-vaihto
 ja Kannan-vaihto 1 Olkoon L vektoriavaruus. Äärellinen joukko L:n vektoreita V = { v 1, v 2,..., v n } on kanta, jos (1) Jokainen L:n vektori voidaan lausua v-vektoreiden lineaarikombinaationa. (Ts. Span(V
ja Kannan-vaihto 1 Olkoon L vektoriavaruus. Äärellinen joukko L:n vektoreita V = { v 1, v 2,..., v n } on kanta, jos (1) Jokainen L:n vektori voidaan lausua v-vektoreiden lineaarikombinaationa. (Ts. Span(V
1 Ominaisarvot ja ominaisvektorit
 1 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) 1 missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin
1 Ominaisarvot ja ominaisvektorit Olkoon A = [a jk ] n n matriisi. Tarkastellaan vektoriyhtälöä Ax = λx, (1) 1 missä λ on luku. Sellaista λ:n arvoa, jolla yhtälöllä on ratkaisu x 0, kutsutaan matriisin
1.1 Vektorit. MS-A0004/A0006 Matriisilaskenta. 1.1 Vektorit. 1.1 Vektorit. Reaalinen n-ulotteinen avaruus on joukko. x 1. R n.
 ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
ja kompleksiluvut ja kompleksiluvut 1.1 MS-A0004/A0006 Matriisilaskenta 1. ja kompleksiluvut Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 8.9.015 Reaalinen
E p1 = 1 e 2. e 2. E p2 = 1. Vuorovaikutusenergian kolme ensimmäistä termiä on siis
 763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys102 Kevät 2010 Jukka Maalampi LUENTO 6 Yksinkertainen harmoninen liike yhteys ympyräliikkeeseen energia dynamiikka Värähdysliike Knight Ch 14 Heilahtelut pystysuunnassa ja gravitaation
Mekaniikan jatkokurssi Fys102 Kevät 2010 Jukka Maalampi LUENTO 6 Yksinkertainen harmoninen liike yhteys ympyräliikkeeseen energia dynamiikka Värähdysliike Knight Ch 14 Heilahtelut pystysuunnassa ja gravitaation
Matriisi-vektori-kertolasku, lineaariset yhtälöryhmät
 Matematiikan peruskurssi K3/P3, syksy 25 Kenrick Bingham 825 Toisen välikokeen alueen ydinasioita Alla on lueteltu joitakin koealueen ydinkäsitteitä, joiden on hyvä olla ensiksi selvillä kokeeseen valmistauduttaessa
Matematiikan peruskurssi K3/P3, syksy 25 Kenrick Bingham 825 Toisen välikokeen alueen ydinasioita Alla on lueteltu joitakin koealueen ydinkäsitteitä, joiden on hyvä olla ensiksi selvillä kokeeseen valmistauduttaessa
1 Rajoittamaton optimointi
 Taloustieteen matemaattiset menetelmät 7 materiaali 5 Rajoittamaton optimointi Yhden muuttujan tapaus f R! R Muistutetaan mieleen maksimin määritelmä. Funktiolla f on maksimi pisteessä x jos kaikille y
Taloustieteen matemaattiset menetelmät 7 materiaali 5 Rajoittamaton optimointi Yhden muuttujan tapaus f R! R Muistutetaan mieleen maksimin määritelmä. Funktiolla f on maksimi pisteessä x jos kaikille y
Numeeriset menetelmät
 Numeeriset menetelmät Luento 12 To 13.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 12 To 13.10.2011 p. 1/38 p. 1/38 Tavalliset differentiaaliyhtälöt Yhtälöissä tuntematon funktio Tavalliset
Numeeriset menetelmät Luento 12 To 13.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 12 To 13.10.2011 p. 1/38 p. 1/38 Tavalliset differentiaaliyhtälöt Yhtälöissä tuntematon funktio Tavalliset
[xk r k ] T Q[x k r k ] + u T k Ru k. }.
![[xk r k ] T Q[x k r k ] + u T k Ru k. }. [xk r k ] T Q[x k r k ] + u T k Ru k. }.](/thumbs/61/45563797.jpg) Mat-2.48 Dynaaminen optimointi Mitri Kitti/Ilkka Leppänen Mallivastaukset, kierros 3. Johdetaan lineaarisen aikainvariantin seurantatehtävän yleinen ratkaisu neliöllisellä kustannuksella. Systeemi: x k+
Mat-2.48 Dynaaminen optimointi Mitri Kitti/Ilkka Leppänen Mallivastaukset, kierros 3. Johdetaan lineaarisen aikainvariantin seurantatehtävän yleinen ratkaisu neliöllisellä kustannuksella. Systeemi: x k+
SEISOVA AALTOLIIKE 1. TEORIAA
 1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
1 Kompleksiluvut. Kompleksiluvut 10. syyskuuta 2005 sivu 1 / 7
 Kompleksiluvut 10. syyskuuta 2005 sivu 1 / 7 1 Kompleksiluvut Lukualueiden laajennuksia voi lähestyä polynomiyhtälöiden ratkaisemisen kautta. Yhtälön x+1 = 0 ratkaisemiseksi tarvitaan negatiivisia lukuja.
Kompleksiluvut 10. syyskuuta 2005 sivu 1 / 7 1 Kompleksiluvut Lukualueiden laajennuksia voi lähestyä polynomiyhtälöiden ratkaisemisen kautta. Yhtälön x+1 = 0 ratkaisemiseksi tarvitaan negatiivisia lukuja.
Mapu 1. Laskuharjoitus 3, Tehtävä 1
 Mapu. Laskuharjoitus 3, Tehtävä Lineaarisessa approksimaatiossa funktion arvoa lähtöpisteen x 0 ympäristössä arvioidaan liikkumalla lähtöpisteeseen sovitetun tangentin kulmakertoimen mukaisesti: f(x 0
Mapu. Laskuharjoitus 3, Tehtävä Lineaarisessa approksimaatiossa funktion arvoa lähtöpisteen x 0 ympäristössä arvioidaan liikkumalla lähtöpisteeseen sovitetun tangentin kulmakertoimen mukaisesti: f(x 0
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 3 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 28 R. Kangaslampi Matriisihajotelmista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 3 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 28 R. Kangaslampi Matriisihajotelmista
W el = W = 1 2 kx2 1
 7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
3 TOISEN KERTALUVUN LINEAARISET DY:T
 3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
Differentiaaliyhtälöt II, kevät 2017 Harjoitus 5
 Differentiaaliyhtälöt II, kevät 27 Harjoitus 5 Heikki Korpela 26. huhtikuuta 27 Tehtävä 2. Määrää seuraavan autonomisen systeemin kriittiset pisteet, ratakäyrät ja luonnostele systeemin aikakehitys: (t)
Differentiaaliyhtälöt II, kevät 27 Harjoitus 5 Heikki Korpela 26. huhtikuuta 27 Tehtävä 2. Määrää seuraavan autonomisen systeemin kriittiset pisteet, ratakäyrät ja luonnostele systeemin aikakehitys: (t)
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 17. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 17. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
y + 4y = 0 (1) λ = 0
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 6 mallit Kevät 2019 Tehtävä 1. Ratkaise yhtälöt a) y + 4y = x 2, b) y + 4y = 3e x. Ratkaisu: a) Differentiaaliyhtälön yleinen
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 6 mallit Kevät 2019 Tehtävä 1. Ratkaise yhtälöt a) y + 4y = x 2, b) y + 4y = 3e x. Ratkaisu: a) Differentiaaliyhtälön yleinen
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
