Korkojen aikarakenteen ja tulevan inflaation välinen yhteys
|
|
|
- Laura Elstelä
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Korkoje aikaraketee ja tuleva iflaatio välie yhteys Perttu Tuomi Pro gradu -tutkielma Kasataloustietee laitos Tamperee yliopisto Toukokuu 2000
2 1 Tamperee yliopisto Kasataloustietee laitos TUOMI PERTTU: Korkoje aikaraketee ja tuleva iflaatio välie yhteys Pro gradu-tutkielma *, 63 s., 13 liites. Kasataloustiede, rahoitus, rahapolitiikka Toukokuu 2000 Tässä tutkielmassa o selvitetty sekä teoreettisesta että empiirisestä äkökulmasta, mite korkoje aikarakee ja tuleva iflaatio liittyvät toisiisa. Erityisesti viime aikoia o tutkittu mahdollisuutta käyttää korkoje aikarakeetta periteiste iflaatioidikaattoreide rialla. Korkoje aikaraketeella o aiaki kolme suhteellista etua periteisii idikaattoreihi verrattua, oleaie kiiittymie tulevaisuude odotuksii, reaaliaikaisuus ja eksaktius. Tutkimuksessa esitetyistä teorioista erityisesti Fisher- ja odotushypoteesit tukevat oletusta, että korkoja voidaa käyttää meestyksekkäästi iflaatioidikaattoreia. Teorioita tukevia tuloksia ovat empiirisissä tutkimuksissa saaeet muu muassa Davis ja Faga (1997), Campbell ja Shiller (1991), Frakel ja Low (1994) sekä Mishki (1990a, 1990b). Tutkimuksessa esitetää aikaraketee estimoiissa robustiksi todistettu Nelso & Siegel -meetelmä (NS). Ku käytetää NS-mallitusta, kyetää tuottamaa tarkasti halutu maturiteeti spot-korot ja samalla välttämää pitkii korkoihi liittyvä kupokiefekti. Meetelmää o sovellettu Suome korkoaieistoo tammikuusta 1993 joulukuuhu Ekoometrise testaukse kaalta kyseie meetelmä parataa huomattavasti aieisto laatua. Tutkimukse ekoometrisessa osassa käytetää sekä Grager-kausaallisuustestiä että Estrella ja Mishkii (1997) -mallia korkoje aikaraketee ja iflaatio välise yhteyde tutkimisee. Grager-testie perusteella voidaa todeta, että korkoerolla o selkeä kausaalisuhde tulevaa iflaatio muutoksee. Erityise hyviä tuloksia saadaa, ku iflaatiomuutokse selittäjää käytetää viide vuode ja kolme kuukaude spot-korkoje erotusta. Se sijaa Estrella ja Mishkii malli ei toimi Suome aieistossa. Malli eri testit eivät tuota riittävä hyviä tuloksia estimoitiperiodi sisällä, ja tämä lisäksi useissa tapauksissa residuaalit ovat sekä autokorreloitueita että heteroskedastisia. Suurimpaa syyä heikkoihi tuloksii saattaa olla malli suhteellise yksikertaie spesifikaatio. Tutkimuksessa tehdyt Grager-testit kute myös Estrella ja Mishkii -malli lisätestaukset atavat olettaa, että jatkotutkimuksissa kaattaa tutkia Estrella ja Mishkii mallitukse pohjalta laajeettuja malleja ja keskittyä tarkastelemaa erityisesti korkoero ja iflaatio välistä dyamiikkaa. * Halua kiittää Suome Paki kasatalousosasto hekilökutaa euvoista ja materiaalisesta avusta, Suome Paki kirjastoa aieistoista, Kari Takalaa ekoometrisesta ohjauksesta sekä Paula Viléiä kieliasu tarkistuksesta ja hekisestä tuesta.
3 2 SISÄLTÖ 1 JOHDANTO TALOUSTEORIAA KOROISTA YLEISTÄ KORKOJEN AIKARAKENNE KESKUSPANKIN NÄKÖKULMASTA FISHER-HYPOTEESI ODOTUSHYPOTEESIT LIKVIDITEETTIPREFERENSSITEORIA MUITA KORKOJEN AIKARAKENNEMALLEJA JOUKKOVELKAKIRJAT YLEISTÄ NOLLAKUPONKIVELKAKIRJAT KUPONKIVELKAKIRJAT TERMIINIKOROT AIKARAKENTEEN ESTIMOINTI YLEISTÄ NELSON & SIEGEL -MENETELMÄ ESTIMOINTI SUOMEN AINEISTOLLA HYÖDYT TAVALLISEEN KORKOAINEISTOON VERRATTUNA EMPIIRINEN TESTAUS AIKAISEMPIA TUTKIMUSTULOKSIA EKONOMETRISIA METODEJA TUTKIMUKSESSA SOVELLETTAVA MENETELMÄ AINEISTO JA AIKASARJOJEN OMINAISUUDET GRANGER-KAUSAALISUUSTESTITULOKSET ESTRELLAN JA MISHKININ -MALLIN TESTAUS SUOMEN AINEISTOON YHTEENVETO LÄHTEET LIITTEET LIITE LIITE LIITE LIITE LIITE LIITE LIITE
4 3 1 Johdato Moet keskuspakit (esim. Suome, Ruotsi, Eglai sekä Euroopa keskuspakki) julkistivat 1990-luvulla lopputavoitteeksee iflaatio pitämise alhaisea. Tähä iflatio targetig -teoria mukaisee toimitaa liittyy oleaisesti iflaatioäkymie tarkkailu ja mahdollisimma varhaie reagoiti iflaatio kiihtymisee. Erityisesti viime vuosia o laajemmi tutkittu mahdollisuutta käyttää korkoje aikarakeetta periteiste iflaatioidikaattoreide rialla. Eri maturiteeti velkakirjoilla käydää markkioilla lähes katkeamatota kauppaa, ja se vuoksi ostooteerauksista voidaa reaaliaikaisesti tulkita markkioide tulevaisuude odotuksia. Korkoje aikaraketeella o aiaki kolme suhteellista etua periteisii idikaattoreihi verrattua, oleaie kiiittymie tulevaisuude odotuksii, reaaliaikaisuus ja eksaktius. Tutkimus jakaatuu kolmee osaa. Esiksi työssä selvitetää teoreettisesta äkökulmasta, mite korkoje aikarakeetta voidaa selittää, ja mite tuleva iflaatio liittyy siihe. Toiseksi perehdytää ogelmii, jotka liittyvät korkoje aikaraketee estimoitii kupokivelkakirjoje oteerauksista. Samassa yhteydessä esitetää Nelso & Siegel -meetelmä (NS) aikaraketee estimoitii ja sovelletaa sitä Suome 1990-luvu kuukausiaieistoo. Tutkimukse kolmaessa osassa käytetää kahta ekoometrista meetelmää aikaraketee ja tuleva iflaatio välise yhteyde selvittämiseksi. Korkoje aikaraketee ja iflaatio välie yhteys pohjautuu suurelta osi Fisherhypoteesii ja odotushypoteesi eri modifikaatioihi. Fisher-hypoteesi yhdistää iflaatio-odotukset oleaisesti imelliskorkoihi, ja odotushypoteesit kiiittävät eri maturiteettie spot-korot toisiisa. Tutkimuksessa esitellää ii saottu Nelso & Siegel -aikaraketee estimoitimeetelmä (NS), joka o erityisesti rahapolitiika kaalta robusti estimoitimeetelmä. Tämä jälkee NS-meetelmää käytetää Suome korkoje aikaraketee estimoi-
5 4 tii tammikuusta 1993 joulukuuhu Aikaväli o istitutioaaliste seikkoje vuoksi suhteellise lyhyt tilastollisee tarkasteluu. Toisaalta otosperiodi o selkeä kokoaisuus pitkie korkomarkkioide syystä yhteisvaluutta euroo siirtymisee ja o site laadullisesti erittäi hyvä ekoometrisee testauksee. NS-mallituksella voidaa tuottaa tarkasti halutu maturiteeti spot-korko ja samalla kyetää välttämää pitkissä markkiakorkoprokseissa esiityvä kupokiefekti. Ekoometrise testaukse kaalta kyseie meetelmä parataa huomattavasti aieisto laatua. Korkoje aikaraketee kykyä eustaa iflaatiota o tutkittu viime vuosia paljo. Esimerkiksi Davis ja Faga (1997) toteavat tutkimuksessaa, että kotimaie korkoje aikarakee eustaa huomattavasti paremmi iflaatiota kui pörssikurssit, riskipreemiot tai kotimaa ja ulkomaa korkoero. Vastaavia lupaavia tuloksia aikaraketee ja iflaatio yhteydestä o raportoitu useissa tutkimuksissa, esimerkiksi Campbell ja Shiller (1991), Frakel ja Low (1994), Mishki (1990a) sekä Mishki (1990b). Tässä tutkimuksessa käytetää sekä Grager-kausaallisuustestiä että Estrella ja Mishkii (1997) -mallia korkoje aikaraketee ja iflaatio välise yhteyde tutkimisee 1990-luvu Suome aieistosta. Grager-testie perusteella voidaa todeta, että korkoero o selkeässä kausaalisuhteessa tulevaa iflaatio muutoksee. Erityise hyviä tuloksia saadaa, ku iflaatiomuutokse selittäjää käytetää viide vuode ja kolme kuukaude spot-korkoje erotusta. Se sijaa Estrella ja Mishkii malli ei toimi Suome aieistoo, mikä johtuee iukasta mallispesifikaatiosta. Työ o jäseelty site, että luvussa kaksi perehdytää korkoje aikaraketee teoreettisii malleihi ja luvussa kolme paeudutaa velkakirjoje erityispiirteisii. Luvussa eljä esitellää Nelso & Siegel -aikaraketee estimoitimeetelmä ja sovelletaa sitä Suome aieistoo. Luvussa viisi esitetää aikaraketee ja tuleva iflaatio empiiriste testie tulokset, ja lukuu kuusi o kerätty yhteeveto työstä.
6 5 2 Talousteoriaa koroista 2.1 Yleistä Rahoitusmarkkioide velkakirja- ja korkomarkkiat jaetaa yleisesti lyhye ja pitkä rahoitukse markkioihi, jolloi lyhyihi rahamarkkioihi lasketaa kuuluviksi alle vuode mittaie rahoitus. Näillä markkioilla tärkeimpiä perusistrumetteja ovat valtioide ja yrityste liikkeelle laskemat velkakirjat. Perusistrumetteja eemmä volatiilisista hyödykkeistä tärkeimpiä ovat korkotermiiit, -optiot ja korovaihtosopimukset (s. korkoswapit). Useimmat edellä maiituista istrumeteista ovat jälkimarkkiakelpoisia, jolloi hitoje kehityksestä saadaa lähes katkeamattomasti tietoa markkioilta. Korkorakeeteorioide esittely jälkee perehdytää tarkemmi liikkeellä olevii joukkovelkakirjoihi ja iihi liittyvii matemaattisii kaavoihi, mutta tässä vaiheessa määritellää yleisellä tasolla muutama perustermi, joihi tullaa viittamaa seuraavissa kappaleissa. Velkakirja maturiteetilla eli juoksuajalla kuvataa, kuika pitkä aika laia lopullisee eräpäivää o (maturity date). Spot-korolla tarkoitetaa velkakirja korkoa, joka astuu voimaa heti ja pysyy kiiteää sovittuu päivämäärää asti. Termiiikorko o puolestaa kaupakäytipäivää sovittu kiiteä korko, joka astuu voimaa ealta sovittua tulevaisuude hetkeä (arvopäivä, settlemet date) ja pysyy kiiteää sovittuu päivämäärää asti. 2.2 Korkoje aikarakee keskuspaki äkökulmasta Moissa teollistueissa maissa o eteki 1990-luvulta lähtie alettu kiiittää huomiota kuluttajahitaiflaatio torjumisee. Tällä tavoi pyritää luomaa parhaat mahdolliset olosuhteet taloudelliselle toimialle (Svesso 1994b, 4). Esimerkiksi Forsma (1997) kuvaa iflaatio haittavaikutuksia. Tähä liittye moet keskuspakit julkistivat 1990-luvulla lopputavoitteeksee iflaatio pitämise alhaisea. Tavoitteesee liittyy oleaisesti iflaatioäkymie tarkkailu ja mahdollisimma aikai-
7 6 e reagoimie iflaatio kiihtymisee. Kyseiste seikkoje huomioo ottamie liittyy Iflatio targetig -teoriaa, joka kehittämisessä o asioituut erityisesti ruotsalaie Lars Svesso (1999). Rahapolitiika tavoittee julkistamise tehtävää o lisätä keskuspaki uskottavuutta, ja samalla mahdollisesti tasoittaa iflaatio-odotuste heilahduksia. Tällaise julkistetu tavoittee avulla o myös helpompi ohjata rahapolitiikkaa sekä arvioida tavoittee oistumista. (Svesso 1994b,5). Suomi asetti helmikuussa 1993 rahapolitiika tavoitteeksi pohjaiflaatio pitämise oi kahde prosettiyksikö tasolla (Bak of Filad Bulleti 1993, 16). Tämä lisäksi muu muassa Ruotsi, Iso-Britaia ja Uusi-Seelati ovat valieet vastaavalaise tavoittee. Myös Yhdysvaltai keskuspakki, Federal Reserve, o osoittaut rahapolitiikassaa selkeää iflaatiovastaista ajattelua, vaikkei se avoimesti ole julkistaut rahapolitiikkasa lopputavoitteita. Perustamisestaa lähtie myös EKPJ o ilmoittaut tavoitteeksee euroaluee yhdemukaistetu kuluttajahitaiflaatio pitämise alhaisea ja vakaaa. Eli iflaatio pidetää olla ja kahde prosettiyksikö välissä 1. Rahapolitiika kaalta eri varallisuushyödykkeet, kute korot, valuuttakurssit, pörssikurssit, ovat tärkeitä elemettejä, joide välityksellä rahapolitiikka välittyy reaalitaloutee. Jos ämä raketeelliset relaatiot ovat ajassa vakaita, voidaa iitä käyttää idikaattoreia tai iille voidaa jopa ataa tavoitetasoja 2. Toisaalta riippumatta iide roolista trasmissiokaavassa, voidaa iitä käyttää tulevaisuude idikaattoreia. Ajattelu ojaa vahvasti oletuksee, että varallisuushyödykkeet ovat ratioaalisesti hioiteltuja ja iihi sisältyy kaikki oleaie iformaatio. Vaikka rahapolitiika muutokset havaitaa heti, e vaikuttavat vasta oi 1 2 vuode viiveellä reaalitaloutee. Rahapolitiika trasmissio viivee pituudesta johtue 1 Tosi EKPJ: lopputavoitteisii kuuluu myös M3-rahamäärä vuotuise kasvu pitämie keskimääri 4,5 prosetissa. 2 Periteisesti yksi lopputavoitteista o ollut esimerkiksi valuuttakurssi tavoitetaso pitämie. Joskaa se ei eää viime vuosia ole ollut läsimaissa kovi suosittua.
8 7 o tärkeää, että keskuspakilla o käytettävissä mahdollisimma varhai reaalitaloude muutoksia hyvi eakoivaa aieistoa. Periteisesti moissa teollisuusmaissa o käytetty raha-aggregaatteja 3 keskeisimpiä idikaattoreia, mutta keskuspakit joutuvat etsimää jatkuvasti uusia ja tehokkaampia iformaatiolähteitä. Esimerkiksi periteiset raha-aggregaatit ovat idikaattoreia hiema ogelmallisia, koska e ovat joissai tapauksissa osoittautueet epästabiileiksi. Tämä voi johtua esimerkiksi rahoitusmarkkioide uusie istrumettie käyttööotosta tai rahoitusmarkkioita koskevie lakie muutoksista (Svesso 1994b, 7). Velkapapereilla käydää jälkimarkkioilla (sekudaarimarkkioilla) lähes katkeamatota kauppaa, ja siksi kursseista saadaa reaaliaikaista tietoa markkioide tulevaisuude odotuksista. Tavaomaisista kulutushyödykkeistä poikete varallisuushyödykkeitä hakitaa erityisesti iide tulevaisuudessa tuottamie kassavirtoje perusteella. Se vuoksi iide hiat määräytyvät tulevaisuude tuotto- ja riskiodotuksista. Viime vuosia useat maat ovat alkaeet kiiittämää rahapolitiika suuittelussaa yhä eemmä huomiota myös korkoje aikaraketeesee. Jos markkiat käyttävät kaike saatavilla oleva iformaatio ja ovat ratioaaliset, ii hitoje pitäisi sisältää arvokasta tietoa tulevaisuudesta. Erityisesti keskuspakkia kiiostavat iflaatio-odotukset ivoutuvat oleaisesti velkakirjoje hioitteluu. Tämä Irvig Fisheri jo 1930-luvulla muotoilema teoreema o ollut useimpie korkoje aikarakeeteorioide peruslähtökohta. Korkoje aikaraketee iformaatiolla o aiaki kolme suhteellista etua periteisii idikaattoreihi verrattua:! oleaie kiiittymie tulevaisuude odotuksii! reaaliaikaisuus! eksaktius, eli tietoja ei revisioida myöhemmi 4. Jo graafisesti tarkasteltua voidaa olettaa iflaatiovauhdilla ja imelliskoroilla oleva jokilaie relaatio (Kuvio 2.1). 3 Näistä maista erityisesti Saksassa raha-aggregaateilla o ollut vakat periteet. 4 Esimerkiksi bruttokasatuottee eakkotietoja tarkistetaa useita kertoja ee lopullisia lukuja, jotka julkaistaa oi 18 kuukaude viiveellä.
9 % Suome 10 v. obligaatiokorko, % 12 kk heliborkorko, v.1999 alusta euriborkorko(360), % Kasallie kuluttajahitaiflaatio Suomessa Kuvio 2.1 Iflaatio ja imelliskorot Suomessa. Lähde: Suome Pakki Erityisesti viime vuosia akateemisessa maailmassa o laajasti tutkittu korkoje aikarakeetta ja se sisältämää iformaatiota. Toisaalta esimerkiksi Suomessa tämä ala empiirisellä tutkimuksella ei istitutioaaliste seikkoje vuoksi ole voiut olla pitkiä periteitä, koska esimerkiksi helibor-korkoja 5 o oteerattu vasta vuodesta 1987 lähtie. 2.3 Fisher-hypoteesi Klassie korkoje talousteoria perustuu suurelta osi Irvig Fisheri päätelmii imelliskorkoje ja iflaatio välisestä yhteydestä. Tämä ykyää Fisher-hypoteesia tuettu teoreema julkaistii esimmäise kerra jo vuoa 1930 ilmestyeessä kirjassa: The Theory of Iterest: As Determied by Impatiece to Sped Icome ad Opportuity. Hypoteesi taustalla o ajatus, että sijoittajilla o mahdollisuus ives- 5 Helibor-korot (Helsiki iterbak offered rate) olivat viide suurimma paki sijoitustodistuste oteerauste keskikorkoja. Vuode 1999 alusta lähtie Helibor-korot o korvattu EKP: julkaisemilla Euribor-koroilla.
10 9 toida joko reaalipääomaa reaalikorolla tai imellisee (rahamääräisee) pääomaa imellisellä korolla. Rahamääräisestä sijoituksesta täytyy silloi tarjota reaalikorkotuoto lisäksi korvaus odotetusta rahaarvo heikkeemisestä. Toisi saoe reaalipääoma ja rahoitusistrumetit ovat sijoittajille täydellisiä substituutteja 6. Fisherihypoteesi tasapaiorelaatio esitetää muodossa: ( )( ) 1+ r = 1+ r 1+ i r ex, (2.1) jossa käytetyt symbolit tarkoittavat seuraava: r = imelliskorko, r = reaalikorko, i ex = odotettu iflaatio. Muuettaessa lauseke suoraksi imelliskoro selitykseksi saadaa Fisher-hypoteesi yleie esitystapa: r = r + iex + iex r. (2.2) Usei vielä kaava 2.2 esitetää yksikertaistetussa muodossa pelkkää reaalikoro ja odotetu iflaatio summaa, eli kaava viimeie termi jätetää pois. Kyseie yleistys ei aiheuta suurta harhaa, jos reaalikorko ja odotettu iflaatio ovat lukuarvoiltaa pieiä. Kaava 2 muuttujista aioastaa imellie korko o ex ate havaittavissa, koska iflaatio ja reaalikorko pystytää toteamaa vasta maturiteeti lopussa. Jos kaikki tietäisivät tuleva iflaatio oleva olla, olisivat havaitut korot suoraa reaalisia. Luoollisestikaa todellisuudessa tilae ei ole tällaie, eivätkä sijoittajat edes voi eustaa tulevaa iflaatiota täydellisesti. Kuiteki ratioaaliste odotuste hypoteesii ojautue oletamme, että sijoittajat eivät erehdy sääömukaisesti, vaa eusteet ovat keskimääri oikeita. Eli Fisher-hypoteesi perusteella omiaalie spotkorko sisältää eustee tulevasta reaalikorosta ja iflaatiosta. 6 Taustaoletuksea o, että reaalipääomaa voidaa varastoida ilma kustauksia.
11 Odotushypoteesit Puhtaa odotushypoteesi (Pure Expectatios Hypothesis, PEH) perusteella yhde pitkä velkakirjalaia pitämisestä maturiteettiisa asti saadaa sama tuotto kui toistetuista sijoituksista lyhyihi velkakirjoihi. Vaihtoehtoisesti teoria voidaa määritellä myös, että velkakirja seuraava periodi odotettu tuotto o sama riippumatta velkakirjoje maturiteettieroista. (Bhattacharya ja Costatiides 1989,129). Hypoteesi pääasiallisea kehittäjää pidetää Frederick Lutzia (1940), vaikka teoria perustuu suurelta osi edellä esitettyy Fisher-hypoteesii. Puhtaa odotusteoria mukaa sijoittajie oletetaa oleva riskieutraaleja, jolloi he eivät vaadi riskipreemiota lyhyissä eivätkä pitkissä koroissa. Tällöi he sijoittavat korkeimma tuoto atavaa velkakirjaa riippumatta se maturiteetista. Toisaalta esimerkiksi liikkeellä oleva vela määrä ei vaikuta korkoraketee muotoo, jollei se muuta odotuksia (Kettue 1995, 16). Teoria mukaa korkorakee o markkioide tulevaisuude spotkorkoeusteide suora ilmetymä. Jos hypoteesi pitää paikkasa, korkokäyrä voi ousta (laskea) aioastaa tilateissa, joissa markkioilla odotetaa lyhyide spotkorkoje ouseva (laskeva) tulevaisuudessa ykyhetkee verrattua. Jos sijoittajat odottavat spot-korkoje ouseva, he sijoittavat mieluummi lyhyihi velkakirjoihi. Tämä o ratioaalie johtopäätös, koska odotuste toteutuessa he voivat lähi tulevaisuudessa ivestoida lyhyistä sijoituksista vapautuvat pääomasa ykyhetkeä korkeammalla korolla. Ku useilla sijoittajilla o samakaltaiset äkemykset, he ajavat toimillaa lyhyide velkakirjoje hiat ylös (ja siksi tuotot laskevat) ja vastaavasti pitkie velkakirjoje hiat alas (tuotot ousevat). Tällaise toimia tuloksea markkioilla havaitaa hyvi pia ouseva korkorakee. Puhtaa odotusteoria mukaa markkioilla havaitut termiiikorot vastaavat odotettuja tulevia spot-korkoja seuraavasti:
12 11 F ( ) = E r, (2.3) 0 1, 2 0 1, 2 jossa käytetyt symbolit tarkoittavat seuraavaa: = termiiikorko hetkellä 0 periodilta yksi periodille kaksi, 0F 1, 2 0Er ( 1, 2) = odotettu spot-korko periodilta yksi periodille kaksi. Sijoitushorisoti ollessa kaksi vuotta, markkiat ovat odotushypoteesi esittämässä tasapaiossa aioastaa, jos seuraava relaatio o voimassa: 2 ( 1 r ) = ( 1+ r )( + r ) +, (2.4) 0,2 0,1 1 jossa symbolit merkitsevät: r0,2 1,2 = kahde vuode spot-korko p.a, r0,1 = yhde vuode spot-korko p.a., r = odotettu yhde vuode spot-korko p.a. periodilta yksi periodille 2. 1,2 Kaavaa 4 muokkaamalla huomataa, että tämä hetke pitkä spot-vuosikorko voidaa esittää odotettuje spot-vuosikorkoje geometrisea keskiarvoa, ( )( ) 1+ r 2 02, = 1+ r01, 1+ r12,. (2.5) Vastaavalla aalogialla myös pitemmät kui kahde vuode korot voidaa esittää geometrisea keskiarvoa tämä hetke lyhyestä korosta ja sarjasta tulevia lyhyitä korkoja. (Vahae 1988, ) Ku puhtaassa odotushypoteesissa sallitaa pitkie velkakirjoje ylituottoje suhteessa lyhyihi oleva aia olla, sallitaa odotushypoteesissa (Expectatios Hypothesis, EH) ylituottoje eroava ollasta, mutta oleva vakio yli aja (Campbell et al. 1997, 413). Se vuoksi odotushypoteesi o vai yleisempi muoto puhtaasta odotushypoteesista oletettaessa, että korkoje aikaraketeesee sisältyy vakioaikapreemio.
13 Likviditeettipreferessiteoria Likviditeettipreferessiteoria (Liquidity-Preferece Theory) perustuu myös rahoitusmarkkioilla vallitsevie odotuste tärkeytee, mutta se ataa odotusteoriaa eemmä paioa sijoittajie riskipreferesseille. Likviditeettipreferessiteoria kritisoi odotusteoriaa täydellise varmuude oletuksesta. Mitä kauempaa tulevaisuudessa olevia korkoja pitää eustaa, sitä vaikeampaa eustamisesta tulee. Likviditeettipreferessiteoria mukaa sijoittajat ovat epävarmuudesta johtue riskikarttajia verrattua odotusteoriaa, joka mukaa he ovat riskieutraaleja. Toisi saoe he sijoittavat mieluummi lyhyihi joukkovelkakirjoihi, koska korkoje oustessa e voidaa muuttaa markkioilla helpommi ja pieemmillä pääomatappioilla rahaksi kui vastaava liikkeellelaskija pitemmä maturiteeti joukkolaiat. Pitkäaikaiste joukkovelkakirjoje arvo o myös diskottotekijä vuoksi herkempi korkoje muutoksille. Likviditeettipreferessiteoria pääasiallisea kehittäjää pidetää Joh Hicksiä (1946), joka jälkee malli teoreettisessa kehittelyssä o asioituut mm. Richard Roll (1970). Teoria olettaa, että mitä pitempi velkakirja maturiteetti o, sitä korkeampi o tuoto oltava korvauksea hitariskistä. Toisaalta pitkiä velkakirjasijoituksia preferoivat sijoittajat 7 voivat tällaisissa tapauksissa asaita ylimääräistä tuottoa likviditeettipreemiota ilma lisäriskiä (Elto ja Gruber 1987, 463). Likviditeettipreferessiteoria mukaa korkoraketee tulisi aia olla ouseva 8, koska termiiikorot ovat positiivisesti harhaisia eusteita tulevista lyhyistä koroista, ja harhaisuus suureee maturiteeti kasvaessa. Empiirisissä tutkimuksissa tämä o havaittu oleva yleisi tilae, mutta ei suikaa aioa. Teoriaa tukee kuiteki se, että lyhyide velkakirjoje tuotot ovat keskimääri vaihdelleet moissa maissa vähemmä kui pitkie velkakirjoje. Tämä puoltaa käsitystä pitkii velkakirjoihi sisältyvä preemio olemassaolosta. (Nelso 1979, 128-9). 7 Esimerkiksi vakuutusyhtiöt preferoivat usei pitkiä velkakirjoja lyhyihi verrattua. 8 Vaikka markkiat odottaisivat lyhyide spot-korkoje laskeva, o ouseva korkorakee kuiteki mahdollie. Tämä tarkoittaa, että riskipreemiot ovat mittavia ja täte eutralisoivat korolaskuodo-
14 Muita korkoje aikarakeemalleja Markkioide segmetoitumisteoria (Segmeted Market Theory) pohjautuu väitteesee, että moet laiaajat kute myös sijoittajat preferoivat voimakkaasti juuri tiety maturiteeti velkakirjoja. Culbertsoi esittämä teoria perustuu oletuksee, että eri maturiteettiset velkakirjat eivät ole sijoittajille substituutteja (Bhattacharya ja Costatiides 1989,130). Tällöi ei voida tietää, oko aikapreemio riippuvaie ajasta positiivisesti vai egatiivisesti. Tämä teoria perustelee aikapreemio olemassaolo täysi toisi kui likviditeettipreferessiteoria tai odotushypoteesi. Markkioide segmetoitumisteoria mukaa sijoittajat ovat ii suuria riskikaihtajia, että he operoivat aioastaa tiety juoksuaja velkakirjoilla, eivätkä eri maturiteettie tuottoerot vaikuta heidä päätöksiisä. Yleie mielipide sekä esimerkiksi moet lehtijutut sisältävät implisiittisesti markkioide segmetoitumisteoria uskomuksia. Se sijaa akateemisessa maailmassa teoria ei ole juuri saaut suosiota. Yleisi vastaväite o, että markkioilla o kuiteki sijoittajia, jotka preferoivat suurempia tuottoja, ja siksi poistavat segmetoitumisteoria väittämät seuraukset. (Elto ja Gruber 1987, 460). Modigliai ja Sutch (1966) käyttävät markkioide segmetoitumisteoria muutamia havaitoja hyväksee preferred habitat-teoriassaa, mutta toisaalta he ottavat huomioo malli rajoitukset ja korvaavat iitä muilla argumeteilla. Tässäki teoriassa sijoittajat ovat riskikarttajia, ja heillä o joki suuittelujakso, jossa he preferoivat sijoituste ja velkoje maturiteettie kohtaatoa (matchig). Tällöi he järjestävät esi velkojesa ja sijoitustesa maturiteetit samoiksi, ja vasta tämä jälkee he sijoittavat liikeevät varat parhaite tuottavii maturiteetteihi. Teoria mukaa eri maturiteettiset sijoitukset eivät ole lähellekää täydellisiä substituutteja toisillee. tuksie vaikutukset. Jos tulevie spot-korkoje oletetaa laskeva todella huomattavasti, voi korkorakee käätyä laskevaksi. (Elto ja Gruber, 1987, 464)
15 14 3 Joukkovelkakirjat 3.1 Yleistä Joukkovelkakirjat voidaa jakaa ryhmii eri tekijöide perusteella, esimerkiksi liikkeellelaskija tai korkosopimustyypi perusteella. Yrityste liikkeelle laskemii velkatodistuksii liittyy aia keskeytys- ja tappioriski, joita ei valtio laskemii velkakirjoihi sisälly aiakaa periaatteessa. Velalle maksettava korko voi olla vaihtuva, jolloi tuotto o sidottu esimerkiksi yritykse tuloksee, tai korko o kiiteä, jolloi kupokituotot o ilmoitettu sitovasti etukätee. Kiiteätuottoisia velkakirjoja o markkioilla kahdelaisia: ollakupokija kupokivelkakirjoja. Nollakupokilaia imellisarvo maksetaa takaisi yhdellä kertaa eli maturiteeti lopussa, ku taas kupokivelkakirjoille maksetaa tietyi väliajoi määrätty osa imellisarvosta takaisi. Käytäössä melkei kaikki markkioilla olevat velkakirjat tuottavat kupokimaksuja, sillä aioastaa lyhyissä maturiteeteissa o ollakupokilaioja. Tämä voi johtua siitä seikasta, että useimmat sijoittajat suosivat sääöllisesti tilitettäviä kupokituottoja. Seuraavissa kappaleissa perehdytää tarkemmi, millaisia tekisiä ogelmia puhtaide ollakupokilaioje puute aiheuttaa korkoje aikaraketee tutkimisee. Suomessa pitkie maturiteettie velkakirjamarkkiat kehittyivät vasta 1990-luvu alkupuolella, jolloi Suome valtio laiaotto kasvoi jyrkästi. Vuode 2000 tammikuussa Suome rahoitusmarkkioilla oteerattii kuutta eri valtio velkakirjaa, joide kupokikorot vaihtelivat 3,75 prosetista 10,0 prosettii. Vastaavie laioje liikkeellä oleva määrä o vajaat 36 Mrd. euroa, joka vastaa oi 32 prosettia vuode 1998 imellisestä bruttokasatuotteesta. Kuviossa 3.1 esitetää valtio laiakaa kasvu, ja tällä hetkellä liikkeellä olevie velkakirjoje määrä.
16 15 SUOMEN VALTION VIITELAINOJEN LIIKKEESSÄ OLEVA MÄÄRÄ a eräätyvä laia, 10 % b eräätyvä laia, 3.75 % c eräätyvä laia, 9.5 % d eräätyvä laia, 7.25 % e eräätyvä laia, 6 % f eräätyvä laia, 5 % Kaikki valtio viitelaiat 40 Mrd. euroa 30 f e 20 d c 10 b a Kuvio 3.1 Suome valtio viitelaiat tammikuussa Lähde Suome Pakki. Vuode 1999 aikaa Suome valtio velka o käätyyt laskuu, ja ykyiste suuitelmie mukaa uusia laioja lasketaa liikkeelle aioastaa osittai kuolettamaa eräätyviä laioja. Nettomääräisesti valtio laiamäärää pyritää laskemaa tulevie vuosie aikaa (Hallitukse ohjelma 1999). Toisaalta vuode 1999 alussa laseerattu euro-valuutta o keskittäyt Euroopa velkakirjamarkkioita EU: reuavaltioista Keski-Euroopa markkioille. Markkioide keskittymie ja valtava kasvu ovat heijastueet myös emissioide imelliskokoje kasvua. Kasaivälisesti vuode 1999 kolme esimmäise eljäekse aikaa ettomääräisesti liikkeelle lasketuista joukkovelkakirjalaioista 45 prosettia oli euromääräisiä (Bak for Iteratioal Settlemets 1999, 71). Useat teollistueet maat, kute Yhdysvallat, Iso-Britaia, Raska, Australia ja Ruotsi ovat laskeeet markkioille myös ii saottuja reaalivelkakirjoja, joide imellie tuotto o sidottu kuluttajahitaideksii. Ku lisätää reaalivelkakirjat tavalliste kupokivelkakirjoje rialle saadaa tarkempi kuva markkioide iflaatio-
17 16 odotuksista kui pelkkiä tavallisia velkakirjoja tutkimalla 9. Esimerkiksi Evas (1998) ja Kadel et al. (1996) ovat saaeet tutkimuksissaa reaali- ja imellisvelkakirjoje iformaatiosisällöistä hyviä tuloksia. Tämä vaatii kuiteki, että kaikkie seurattavie velkakirjoje markkioilla o tarpeeksi likviditeettiä, esimerkiksi Ruotsissa reaalivelkakirjoje kaupakäytimäärät ovat viime aikoia jääeet vaatimattomiksi (Svesso 1994a, 11). Kaikkie keskuspakkie erityisesti eksplisiittise iflaatiotavoittee asettaeide keskuspakkie o järkevää seurata markkioilla esiityviä iflaatio-odotuksia, jolloi markkioide iflaatio-odotuste ja keskuspaki tavoittee välie ero kuvastaa rahapolitiika uskottavuutta. Myös Suomessa oli 1960-luvulla valtio ideksivelkakirjoja, mutta ykyää jo Suome ideksilaki kieltää tällaiste velkakirjoje liikkeelle lasku. Toisaalta laajemmi ajateltua myös valuuttalaiat ovat ideksilaioja, koska iide markkamääräiset maksut ovat sidottuja valuuttakurssikehityksee. Markkioilla o olemassa myös moimutkaisempia velkakirjoja, jotka ovat sekoituksia kiiteätuottoisista istrumeteista ja johdaaisista. Esimerkkiä tällaisista voidaa maiita yritykse joukkovelkakirjalaia, joka lupaa tietyt kiiteät (omiaaliset) kupokituotot ja se lisäksi osto-optio. Puhtaimmassa muodossaa korkoje aikarakeetutkimus keskittyy aioastaa kiiteätuottoisii valtio obligaatioihi, ja mahdolliset verotukselliset vaikutukset yritetää elimioida. Moimutkaisempie istrumettie hioista ei voi laskea helposti implisiittistä diskottokorkokataa, koska hitoihi vaikuttaa paljo useampia fudametteja kui valtio laskemii kiiteäkorkoisii joukkovelkakirjoihi. Tämä vuoksi tässä työssä keskitytää pelkästää valtio liikkeelle laskemii kiiteäkorkoisii velkakirjoihi, koska tällöi omiaalisii kassavirtoihi ei liity riskiä. Aioa vaihteleva tekijä diskottokorkokata sisältäee iformaatiota makrotaloude muuttujista, kute iflaatiosta ja bruttokasatuotteesta. 9 Itse asiassa esimerkiksi Iso-Britaia ja Yhdysvaltoje liikkeelle laskemat reaalivelkakirjat eivät tuota täysi reaalisia tuottoja, koska imellistä kupokimaksua ei koroteta ideksi viimeisimmällä 12 kuukaude muutoksella vaa 8 kuukautta viivästetyllä lukuarvolla. Tämä aiheuttaa joitaki tekisiä ogelmia implisiittise reaalikorkoje aikaraketee mallitamisee. (Barr ja Campbell 1997, 363).
18 luvulle asti joukkovelkakirjoje hitoje tutkimie o mielletty ikävämmäksi alaksi kui esimerkiksi osakkeide arvottamie. Tämä johtuu suurelta osi siitä, että kiiteäkorkoiste joukkovelkakirjoje kupokituotot ja maturiteetit ovat ealta ilmoitettuja, ja siksi velkakirjoje arvottamisee ei liity ii paljo epävarmuustekijöitä kui osakkeide. (Elto ja Gruber 1987, 449). Se sijaa ja 1990-luvulla tuottokäyrie iformaatiosisältöö ja iide tutkimisee o kiiitetty paljo huomiota. 3.2 Nollakupokivelkakirjat Nollakupokivelkakirjalle ei makseta mitää kupokituottoja ee eräätymistä, vaa laia koko imellisarvo maksetaa maturiteeti lopussa kerralla takaisi. Tällöi velkakirja hita määräytyy seuraavasti 10 : P = 1 1 ( + I ) jossa symbolit tarkoittavat:, (3.1) P = velkakirja hita, maturiteetti -vuotta, I = diskottokorkokata. Nollakupokivelkakirjat oteerataa yleesä prosettiosuutea imellisarvosta. Eli jos velkakirja eräätymisee o aikaa tasa yksi vuosi ja velkakirja tuotoksi vaaditaa 10 prosettia, se tämä hetke hita o 90,91 prosettia imellisarvosta. 10 Luettavuude helpottamiseksi kaavoissa käytetää diskreeti aja esitystä. Jatkuva (i) ja diskreeti (I) spot-koro välie suhde o i = exp( I ). Tämä yhteys o johdettavissa rajaarvolausekkeesta ( ) ( ) 100 * 1 + I v exp I *, ku korolaskutiheys, v. Ilmaistua jatkuva aja muodossa o kaava 3.1 p = ( i ) exp *, josta spot-korko o edellee i p = l. Vastaava ekspoetiaalie relaatio pätee myös muihi diskreeti ja jatkuva aja käsitteisii.
19 18 Kaava 3.1 diskottokorkokata vastaa ollakupokivelkakirja tapauksessa myös velkakirja juoksuajatuottoa (yield to maturity). Vastaavasti tuotto voidaa laskea seuraavasti velkakirja hia avulla, 1 + = 1 I P. (3.2) Ku kaava 3.2 ilmaistaa lieaarisessa muodossa käyttäe tuoto ja hia logaritmeja, saadaa lauseke muotoo: i 1 = p. (3.3) Tarkasti määriteltäessä korkoje aikarakeeteoria selvittää, miksi eri maturiteettisilla ollakupokivelkakirjoilla o erilaiset juoksuaja tuotot 11. Toisi saoe se tutkii tulevie spot-korkoje määräytymistä. Yksittäie spot-korko pätee vai yhtee maturiteettipisteesee eli tällä spot-korolla voidaa diskotata aioastaa laia eräpäivää ajoittuvia kassavirtoja. Kuviossa 3.2 esitetää kaksi mahdollista spot-korkoje aikarakeetta. 11 Moesti termi o virheellisesti määritelty, että siihe liittyvät tutkimukset selittäisivät kupokivelkakirjoje tuottoeroja.
20 19 Spot-korkoje aikarakee % Maturiteetti, v 10 Kuvio 3.2 Esimerkkejä spot-korkoje aikaraketeista. Aikaraketee muoto lasketaa juoksuajatuottoje erotuksia (yield spread) seuraavalla idetiteetillä: S 1, I I1. (3.4) Vastaava tulos saadaa logaritmoiduilla termeillä: s 1, i i1. (3.5) 3.3 Kupokivelkakirjat Puhtaimmillaa kappaleessa 2 esitetyt teoriat kuvaavat ollakupokilaioje hioittelua ja iistä pohjautuvie korkoje aikaraketeita. Empiirisessä korkoje aikarakeetutkimuksessa joudutaa kuiteki turvautumaa myös kupokivelkakirjoihi,
Korkojen aikarakenne
 Korkojen aikarakenne opetusnäyte: osa kuvitteellista Raha- ja pankkiteorian aineopintojen kurssia Antti Ripatti Taloustiede 4.11.2011 Antti Ripatti (Taloustiede) Korkojen aikarakenne 4.11.2011 1 / 30 2003),
Korkojen aikarakenne opetusnäyte: osa kuvitteellista Raha- ja pankkiteorian aineopintojen kurssia Antti Ripatti Taloustiede 4.11.2011 Antti Ripatti (Taloustiede) Korkojen aikarakenne 4.11.2011 1 / 30 2003),
1 Eksponenttifunktion määritelmä
 Ekspoettifuktio määritelmä Selvitimme aikaisemmi tällä kurssilla, millaie potessisarja säilyy derivoiissa muuttumattomaa. Se perusteella määritellää: Määritelmä. Ekspoettifuktio exp : R R määritellää lausekkeella
Ekspoettifuktio määritelmä Selvitimme aikaisemmi tällä kurssilla, millaie potessisarja säilyy derivoiissa muuttumattomaa. Se perusteella määritellää: Määritelmä. Ekspoettifuktio exp : R R määritellää lausekkeella
Päähakemisto Tehtävien ratkaisut -hakemisto. 203. Vuosi Indeksi 2008 108,3 2012 116,7. a) Jakamalla 1,07756 7,76 %. c) Jakamalla 0,92802
 Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2007 104,1 2009 108,3 108,3 a) Jakamalla 1,040345 104,1 saadaa iflaatioprosetiksi 4,03 %. 104,1 b) Jakamalla 0,96121 saadaa, että raha
Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2007 104,1 2009 108,3 108,3 a) Jakamalla 1,040345 104,1 saadaa iflaatioprosetiksi 4,03 %. 104,1 b) Jakamalla 0,96121 saadaa, että raha
Päähakemisto Tehtävien ratkaisut -hakemisto. 203. Vuosi Indeksi 2003 105,1 2007 110,8. a) Jakamalla 110,8 1,05423 saadaan inflaatioprosentiksi noin
 Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2002 104,2 2004 106,2 a) Jakamalla 106,2 1,01919 saadaa iflaatioprosetiksi 1,92 %. 104,2 b) Jakamalla 104,2 0,98116 saadaa, että raha
Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2002 104,2 2004 106,2 a) Jakamalla 106,2 1,01919 saadaa iflaatioprosetiksi 1,92 %. 104,2 b) Jakamalla 104,2 0,98116 saadaa, että raha
S Laskennallinen systeemibiologia
 S-4250 Laskeallie systeemibiologia Harjoitus Mittaustuloksea o saatu havaitoparia (x, y ),, (x, y ) Muuttuja y käyttäytymistä voidaa selittää muuttuja x avulla esimerkiksi yksikertaise lieaarise riippuvuude
S-4250 Laskeallie systeemibiologia Harjoitus Mittaustuloksea o saatu havaitoparia (x, y ),, (x, y ) Muuttuja y käyttäytymistä voidaa selittää muuttuja x avulla esimerkiksi yksikertaise lieaarise riippuvuude
RATKAISUT x 2 3 = x 2 + 2x + 1, eli 2x 2 2x 4 = 0, joka on yhtäpitävä yhtälön x 2 x 2 = 0. Toisen asteen yhtälön ratkaisukaavalla saadaan
 RATKAISUT 8 17 8 a) Paraabelie y x ja y x + x + 1 leikkauspisteet saadaa määritettyä, ku esi ratkaistaa yhtälö x x + x + 1, eli x x, joka o yhtäpitävä yhtälö x x. Toise astee yhtälö ratkaisukaavalla saadaa
RATKAISUT 8 17 8 a) Paraabelie y x ja y x + x + 1 leikkauspisteet saadaa määritettyä, ku esi ratkaistaa yhtälö x x + x + 1, eli x x, joka o yhtäpitävä yhtälö x x. Toise astee yhtälö ratkaisukaavalla saadaa
Huom 4 Jaksollisten suoritusten periaate soveltuu luonnollisesti laina- ja luottolaskelmiin. Lähtökohtaisena yhtälönä on yhtälö (14).
 Auiteettiperiaate Huom 4 Jaksolliste suorituste periaate soveltuu luoollisesti laia- ja luottolaskelmii. Lähtökohtaisea yhtälöä o yhtälö (14). Auiteetti Nimellisarvoltaa K 0 suuruise laia maksuerä k, joka
Auiteettiperiaate Huom 4 Jaksolliste suorituste periaate soveltuu luoollisesti laia- ja luottolaskelmii. Lähtökohtaisea yhtälöä o yhtälö (14). Auiteetti Nimellisarvoltaa K 0 suuruise laia maksuerä k, joka
Otantajakauman käyttö päättelyssä
 Keskiarvo otatajakauma Toisistaa tietämättä kaksi tutkijaa tutkii samaa ilmiötä, jossa perusjoukko koostuu kuudesta tutkittavasta ja tarkoituksea o laskea keskiarvo A: Kokoaistutkimus B: Otatatutkimus
Keskiarvo otatajakauma Toisistaa tietämättä kaksi tutkijaa tutkii samaa ilmiötä, jossa perusjoukko koostuu kuudesta tutkittavasta ja tarkoituksea o laskea keskiarvo A: Kokoaistutkimus B: Otatatutkimus
2 avulla. Derivaatta on nolla, kun. g( 3) = ( 3) 2 ( 3) 5 ( 3) + 6 ( 3) = 72 > 0. x =
 TAMMI PYRAMIDI NUMEERISIA JA ALGEBRALLISIA MENETELMIÄ PARITTOMAT RATKAISUT 7 Tiedosto vai hekilökohtaisee käyttöö. Kaikelaie sisällö kopioiti kielletty. a) g( ) = 5 + 6 Koska g o eljäe astee polyomi, ii
TAMMI PYRAMIDI NUMEERISIA JA ALGEBRALLISIA MENETELMIÄ PARITTOMAT RATKAISUT 7 Tiedosto vai hekilökohtaisee käyttöö. Kaikelaie sisällö kopioiti kielletty. a) g( ) = 5 + 6 Koska g o eljäe astee polyomi, ii
Korko ja inflaatio. Makrotaloustiede 31C00200 Kevät 2016
 Korko ja inflaatio Makrotaloustiede 31C00200 Kevät 2016 Sisältö Nimellis ja reaalikorot, Fisher yhtälö Lyhyt ja pitkä korko Rahapolitiikka ja korot Korko ja inflaatio Nimellinen korko i: 1 tänä vuonna
Korko ja inflaatio Makrotaloustiede 31C00200 Kevät 2016 Sisältö Nimellis ja reaalikorot, Fisher yhtälö Lyhyt ja pitkä korko Rahapolitiikka ja korot Korko ja inflaatio Nimellinen korko i: 1 tänä vuonna
2.5. Eksponenttifunktio ja eksponenttiyhtälöt
 Eksoettifuktio ja -htälöt Eksoettifuktio ja eksoettihtälöt Ku otessi käsitettä laajeetaa sallimalla eksoetille muitaki arvoja kui kokoaislukuja, tämä taahtuu ii, että ii saotut otessikaavat ovat voimassa,
Eksoettifuktio ja -htälöt Eksoettifuktio ja eksoettihtälöt Ku otessi käsitettä laajeetaa sallimalla eksoetille muitaki arvoja kui kokoaislukuja, tämä taahtuu ii, että ii saotut otessikaavat ovat voimassa,
Lasketaan kullekin a euron maksuerälle erikseen, kuinka suureksi erä on n vuodessa kasvanut:
 Varsi arkiäiväisiä, geometrise joo teoriaa liittyviä käytäö sovellutuksia ovat jaksottaisii maksuihi ja kuoletuslaiaa (auiteettilaiaa) liittyvät robleemat. Tällaisii joutuu lähes jokaie yhteiskutakeloie
Varsi arkiäiväisiä, geometrise joo teoriaa liittyviä käytäö sovellutuksia ovat jaksottaisii maksuihi ja kuoletuslaiaa (auiteettilaiaa) liittyvät robleemat. Tällaisii joutuu lähes jokaie yhteiskutakeloie
4.3 Signaalin autokorrelaatio
 5 4.3 Sigaali autokorrelaatio Sigaali autokorrelaatio kertoo kuika paljo sigaali eri illä korreloi itsesä kassa (josta imiki). Se o Fourier-muuokse ohella yksi käyttökelpoisimmista sigaalie aalysoitimeetelmistä.
5 4.3 Sigaali autokorrelaatio Sigaali autokorrelaatio kertoo kuika paljo sigaali eri illä korreloi itsesä kassa (josta imiki). Se o Fourier-muuokse ohella yksi käyttökelpoisimmista sigaalie aalysoitimeetelmistä.
3.6. Geometrisen summan sovelluksia
 Tyypillie geometrise summa sovellusalue o taloude rahoituslaskut mutta vai tyypillie. Tammikuu alussa 988 vahemmat avaavat pitkäaikaistili Esikoisellee. Tiliehdot ovat seuraavat. Korko kiiteä 3,85 % pa
Tyypillie geometrise summa sovellusalue o taloude rahoituslaskut mutta vai tyypillie. Tammikuu alussa 988 vahemmat avaavat pitkäaikaistili Esikoisellee. Tiliehdot ovat seuraavat. Korko kiiteä 3,85 % pa
2.3.1. Aritmeettinen jono
 .3.1. Aritmeettie joo -joo, jossa seuraava termi saadaa edellisestä lisäämällä sama luku a, a + d, a+d, a +3d, Aritmeettisessa joossa kahde peräkkäise termi erotus o aia vakio: Siis a +1 a d (vakio Joo
.3.1. Aritmeettie joo -joo, jossa seuraava termi saadaa edellisestä lisäämällä sama luku a, a + d, a+d, a +3d, Aritmeettisessa joossa kahde peräkkäise termi erotus o aia vakio: Siis a +1 a d (vakio Joo
Epäyhtälöoppia matematiikkaolympialaisten tehtäviin
 Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie ja Ae-Maria Ervall-Hytöe 0 Johdato Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a, a,, a ja b, b,, b pätee Cauchy
Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie ja Ae-Maria Ervall-Hytöe 0 Johdato Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a, a,, a ja b, b,, b pätee Cauchy
Otantajakauma. Otantajakauman käyttö päättelyssä. Otantajakauman käyttö päättelyssä
 Otatajakauma kuvaa tarkasteltava parametri jakauma eri otoksista laskettua parametria o joki yleesä tuusluku, esim. keskiarvo, suhteellie osuus, riskisuhde, korrelaatiokerroi, regressiokerroi, je. parametria
Otatajakauma kuvaa tarkasteltava parametri jakauma eri otoksista laskettua parametria o joki yleesä tuusluku, esim. keskiarvo, suhteellie osuus, riskisuhde, korrelaatiokerroi, regressiokerroi, je. parametria
Matematiikan tukikurssi
 Matematiika tukikurssi Kurssikerta 3 1 Lisää iduktiota Jatketaa iduktio tarkastelua esimerki avulla. Yritetää löytää kaava : esimmäise (positiivise) parittoma luvu summalle eli summalle 1 + 3 + 5 + 7 +...
Matematiika tukikurssi Kurssikerta 3 1 Lisää iduktiota Jatketaa iduktio tarkastelua esimerki avulla. Yritetää löytää kaava : esimmäise (positiivise) parittoma luvu summalle eli summalle 1 + 3 + 5 + 7 +...
Matematiikan tukikurssi
 Matematiika tukikurssi Kurssikerta 1 Iduktiotodistus Iduktiotodistukse logiikka Tutkitaa tapausta, jossa haluamme todistaa joki väittee P() site, että se pätee kaikilla luoollisissa luvuilla. Eli halutaa
Matematiika tukikurssi Kurssikerta 1 Iduktiotodistus Iduktiotodistukse logiikka Tutkitaa tapausta, jossa haluamme todistaa joki väittee P() site, että se pätee kaikilla luoollisissa luvuilla. Eli halutaa
Kiinteätuottoiset arvopaperit
 Mat-.34 Ivestoititeoria Kiiteätuottoiset arvopaperit 6..05 Lähtöohtia Lueolla tarasteltii tilateita, joissa yyarvo laseassa äytettävä oro oli aettua ja riippuato aiaperiodista Käytäössä orot äärittyvät
Mat-.34 Ivestoititeoria Kiiteätuottoiset arvopaperit 6..05 Lähtöohtia Lueolla tarasteltii tilateita, joissa yyarvo laseassa äytettävä oro oli aettua ja riippuato aiaperiodista Käytäössä orot äärittyvät
( ) k 1 = a b. b 1) Binomikertoimen määritelmän mukaan yhtälön vasen puoli kertoo kuinka monta erilaista b-osajoukkoa on a-joukolla.
 Kombiatoriikka, kesä 2010 Harjoitus 2 Ratkaisuehdotuksia (RT) (5 sivua) Käytä tehtävissä 1-3 kombiatorista päättelyä. 1. Osoita, että kaikilla 0 b a pätee ( ) a a ( ) k 1 b b 1 kb Biomikertoime määritelmä
Kombiatoriikka, kesä 2010 Harjoitus 2 Ratkaisuehdotuksia (RT) (5 sivua) Käytä tehtävissä 1-3 kombiatorista päättelyä. 1. Osoita, että kaikilla 0 b a pätee ( ) a a ( ) k 1 b b 1 kb Biomikertoime määritelmä
Talousmatematiikka (3 op) Sisältö. Tero Vedenjuoksu. Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi Työhuone M231
 Talousmatematiikka (3 op) Tero Vedejuoksu Oulu yliopisto Matemaattiste tieteide laitos 2010 Sisältö Yhteystiedot: Tero Vedejuoksu tero.vedejuoksu@oulu.fi Työhuoe M231 Kurssi kotisivu http://cc.oulu.fi/~tvedeju/talousmatematiikka/
Talousmatematiikka (3 op) Tero Vedejuoksu Oulu yliopisto Matemaattiste tieteide laitos 2010 Sisältö Yhteystiedot: Tero Vedejuoksu tero.vedejuoksu@oulu.fi Työhuoe M231 Kurssi kotisivu http://cc.oulu.fi/~tvedeju/talousmatematiikka/
TYÖNTEKIJÄIN ELÄKELAIN MUKAISEN VAKUUTUKSEN YLEISET LASKUPERUSTEET. Kokooma 23.1.2008. Viimeisin perustemuutos on vahvistettu 3.2.1998.
 TYÖNTEKIJÄIN ELÄKELAIN MUKAISEN VAKUUTUKSEN YLEISET LASKUPERUSTEET Kokooma 23.1.2008. Viimeisi perustemuutos o vahvistettu 3.2.1998. TYÖNTEKIJÄIN ELÄKELAIN MUKAISEN VAKUUTUKSEN YLEISET LASKUPERUSTEET Sisällysluettelo
TYÖNTEKIJÄIN ELÄKELAIN MUKAISEN VAKUUTUKSEN YLEISET LASKUPERUSTEET Kokooma 23.1.2008. Viimeisi perustemuutos o vahvistettu 3.2.1998. TYÖNTEKIJÄIN ELÄKELAIN MUKAISEN VAKUUTUKSEN YLEISET LASKUPERUSTEET Sisällysluettelo
Tehtäviä neliöiden ei-negatiivisuudesta
 Tehtäviä epäyhtälöistä Tehtäviä eliöide ei-egatiivisuudesta. Olkoo a R. Osoita, että 4a 4a. Ratkaisu. 4a 4a a) a 0 a ) 0.. Olkoot a,, R. Osoita, että a a a. Ratkaisu. Kerrotaa molemmat puolet kahdella:
Tehtäviä epäyhtälöistä Tehtäviä eliöide ei-egatiivisuudesta. Olkoo a R. Osoita, että 4a 4a. Ratkaisu. 4a 4a a) a 0 a ) 0.. Olkoot a,, R. Osoita, että a a a. Ratkaisu. Kerrotaa molemmat puolet kahdella:
Äärettämän sarjan (tai vain sarjan) sanotaan suppenevan eli konvergoivan, jos raja-arvo lims
 75 4 POTENSSISARJOJA 4.1 ÄÄRETTÖMÄT SARJAT Lukujoo { a k } summaa S a a a a a k 0 1 k k0 saotaa äärettömäksi sarjaksi. Summa o s. osasumma. S a a a a a k 0 1 k0 Äärettämä sarja (tai vai sarja) saotaa suppeeva
75 4 POTENSSISARJOJA 4.1 ÄÄRETTÖMÄT SARJAT Lukujoo { a k } summaa S a a a a a k 0 1 k k0 saotaa äärettömäksi sarjaksi. Summa o s. osasumma. S a a a a a k 0 1 k0 Äärettämä sarja (tai vai sarja) saotaa suppeeva
Kertaa tarvittaessa induktiota ja rekursiota koskevia tietoja.
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Aalyysi I Harjoitus 5. 0. 2009 alkavalle viikolle Ratkaisuehdotuksia ( sivua) (Rami Luisto) Laskuharjoituksista saa pistettä, jos laskettu vähitää 50 tehtävää; 3 pistettä,
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Aalyysi I Harjoitus 5. 0. 2009 alkavalle viikolle Ratkaisuehdotuksia ( sivua) (Rami Luisto) Laskuharjoituksista saa pistettä, jos laskettu vähitää 50 tehtävää; 3 pistettä,
Diskreetin Matematiikan Paja Ratkaisuja viikolle 4. ( ) Jeremias Berg. n(n + 1) 2. k =
 Diskreeti Matematiika Paja Ratkaisuja viikolle 4. (7.4-8.4) Jeremias Berg. Osoita iduktiolla että k = ( + ) Ratkaisu: Kute kaikissa iduktiotodistuksissa meidä täytyy siis osoittaa asiaa. Ns. perustapaus,
Diskreeti Matematiika Paja Ratkaisuja viikolle 4. (7.4-8.4) Jeremias Berg. Osoita iduktiolla että k = ( + ) Ratkaisu: Kute kaikissa iduktiotodistuksissa meidä täytyy siis osoittaa asiaa. Ns. perustapaus,
Yhden selittäjän lineaarinen regressiomalli
 Ilkka Melli Tilastolliset meetelmät Osa 4: Lieaarie regressioaalyysi Yhde selittäjä lieaarie regressiomalli TKK (c) Ilkka Melli (007) Yhde selittäjä lieaarie regressiomalli >> Yhde selittäjä lieaarie regressiomalli
Ilkka Melli Tilastolliset meetelmät Osa 4: Lieaarie regressioaalyysi Yhde selittäjä lieaarie regressiomalli TKK (c) Ilkka Melli (007) Yhde selittäjä lieaarie regressiomalli >> Yhde selittäjä lieaarie regressiomalli
SMG-4200 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen 6 ratkaisuiksi
 SMG-400 Sähkömageettiste järjestelmie lämmösiirto Ehdotukset harjoitukse 6 ratkaisuiksi Tarkastellaa suljetu järjestelmä tehotasaaioa joka o P + P P = P i g out st Oletetaa että verkotetussa alueessa jossa
SMG-400 Sähkömageettiste järjestelmie lämmösiirto Ehdotukset harjoitukse 6 ratkaisuiksi Tarkastellaa suljetu järjestelmä tehotasaaioa joka o P + P P = P i g out st Oletetaa että verkotetussa alueessa jossa
MATP153 Approbatur 1B Harjoitus 1, ratkaisut Maanantai
 MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
Normaalijakaumasta johdettuja jakaumia. Normaalijakaumasta johdettuja jakaumia. Normaalijakaumasta johdettuja jakaumia: Mitä opimme?
 TKK (c) Ilkka Melli (4) Johdato Johdatus todeäköisyyslasketaa TKK (c) Ilkka Melli (4) : Mitä opimme? / Tutustumme tässä luvussa seuraavii ormaalijakaumasta (ks. lukua Jatkuvia jakaumia) johdettuihi jakaumii:
TKK (c) Ilkka Melli (4) Johdato Johdatus todeäköisyyslasketaa TKK (c) Ilkka Melli (4) : Mitä opimme? / Tutustumme tässä luvussa seuraavii ormaalijakaumasta (ks. lukua Jatkuvia jakaumia) johdettuihi jakaumii:
LIITTEET Liite A Stirlingin kaavan tarkkuudesta...2. Liite B Lagrangen kertoimet...3
 LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
3 Lukujonot matemaattisena mallina
 3 Lukujoot matemaattisea mallia 3. Aritmeettie ja geometrie joo 64. a) Lukujoo o aritmeettie joo, joka yleie jäse o a 3 ( ) 4 34 4 4 b) Lukujoo o geometrie joo, joka yleie jäse o c) Lukujoo o geometrie
3 Lukujoot matemaattisea mallia 3. Aritmeettie ja geometrie joo 64. a) Lukujoo o aritmeettie joo, joka yleie jäse o a 3 ( ) 4 34 4 4 b) Lukujoo o geometrie joo, joka yleie jäse o c) Lukujoo o geometrie
Talousmatematiikan perusteet, ORMS1030
 Vaasa yliopisto, kevät 206 Talousmatematiika perusteet, ORMS030 5. harjoitus, viikko 7 5. 9.2.206 R ma 0 2 F455 R5 ti 0 2 F9 R2 ma 4 6 F455 R6 to 2 4 F455 R3 ti 08 0 F455 R7 pe 08 0 F455 R4 ti 2 4 F455
Vaasa yliopisto, kevät 206 Talousmatematiika perusteet, ORMS030 5. harjoitus, viikko 7 5. 9.2.206 R ma 0 2 F455 R5 ti 0 2 F9 R2 ma 4 6 F455 R6 to 2 4 F455 R3 ti 08 0 F455 R7 pe 08 0 F455 R4 ti 2 4 F455
10 Kertolaskusääntö. Kahta tapahtumaa tai satunnaisilmiötä sanotaan riippumattomiksi, jos toisen tulos ei millään tavalla vaikuta toiseen.
 10 Kertolaskusäätö Kahta tapahtumaa tai satuaisilmiötä saotaa riippumattomiksi, jos toise tulos ei millää tavalla vaikuta toisee. Esim. 1 A = (Heitetää oppaa kerra) ja B = (vedetää yksi kortti pakasta).
10 Kertolaskusäätö Kahta tapahtumaa tai satuaisilmiötä saotaa riippumattomiksi, jos toise tulos ei millää tavalla vaikuta toisee. Esim. 1 A = (Heitetää oppaa kerra) ja B = (vedetää yksi kortti pakasta).
= true C = true) θ i2. = true C = false) Näiden arvot löydetään kuten edellä Kun verkko on opetettu, niin havainto [x 1
 35 Naiivi Bayes Luokkamuuttua C o Bayes-verko uuri a attribuutit X i ovat se lehtiä Naiivi oletus o, että attribuutit ovat ehdollisesti riippumattomia toisistaa aettua luokka Ku käytössä o Boole muuttuat,
35 Naiivi Bayes Luokkamuuttua C o Bayes-verko uuri a attribuutit X i ovat se lehtiä Naiivi oletus o, että attribuutit ovat ehdollisesti riippumattomia toisistaa aettua luokka Ku käytössä o Boole muuttuat,
Tehtävä 1. Voidaanko seuraavat luvut esittää kahden neliön summina? Jos voidaan, niin kuinka monella eri tavalla? (i) n = 145 (ii) n = 770.
 JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 0, MALLIRATKAISUT Tehtävä. Voidaako seuraavat luvut esittää kahde eliö summia? Jos voidaa, ii kuika moella eri tavalla? (i) = 45 (ii) = 770. Ratkaisu. (i) Jaetaa
JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 0, MALLIRATKAISUT Tehtävä. Voidaako seuraavat luvut esittää kahde eliö summia? Jos voidaa, ii kuika moella eri tavalla? (i) = 45 (ii) = 770. Ratkaisu. (i) Jaetaa
Mat-2.3114 Investointiteoria Laskuharjoitus 3/2008, Ratkaisut 05.02.2008
 Korko riippuu usein laina-ajan pituudesta ja pitkille talletuksille maksetaan korkeampaa korkoa. Spot-korko s t on se korko, joka kertyy lainatulle pääomalle hetkeen t (=kokonaisluku) mennessä. Spot-korot
Korko riippuu usein laina-ajan pituudesta ja pitkille talletuksille maksetaan korkeampaa korkoa. Spot-korko s t on se korko, joka kertyy lainatulle pääomalle hetkeen t (=kokonaisluku) mennessä. Spot-korot
Insinöörimatematiikka IA
 Isiöörimatematiikka IA Harjoitustehtäviä. Selvitä oko propositio ( p q r ( p q r kotradiktio. Ratkaisu: Kirjoitetaa totuustaulukko: p q r ( p q r p q r ( p q r ( p q r 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Isiöörimatematiikka IA Harjoitustehtäviä. Selvitä oko propositio ( p q r ( p q r kotradiktio. Ratkaisu: Kirjoitetaa totuustaulukko: p q r ( p q r p q r ( p q r ( p q r 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Tilastollinen todennäköisyys
 Tilastollie todeäköisyys TOD.NÄK JA TILASTOT, MAA10 Klassisessa todeäköisyydessä oli ehdot: äärellisyys ja symmetrisyys. Tämä tilae o usei mahdoto ts. alkeistapauksia o usei ääretö määrä tai e eivät ole
Tilastollie todeäköisyys TOD.NÄK JA TILASTOT, MAA10 Klassisessa todeäköisyydessä oli ehdot: äärellisyys ja symmetrisyys. Tämä tilae o usei mahdoto ts. alkeistapauksia o usei ääretö määrä tai e eivät ole
TILASTOT: johdantoa ja käsitteitä
 TILASTOT: johdatoa ja käsitteitä TOD.NÄK JA TILASTOT, MAA10 Tilastotietee tehtävää o esittää ja tulkita tutkimuskohteesee liittyvää havaitoaieistoa eli tilastoaieistoa. Tutkitaa valittua joukkoa ja se
TILASTOT: johdatoa ja käsitteitä TOD.NÄK JA TILASTOT, MAA10 Tilastotietee tehtävää o esittää ja tulkita tutkimuskohteesee liittyvää havaitoaieistoa eli tilastoaieistoa. Tutkitaa valittua joukkoa ja se
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
Sijoitustodistuksen nykyinen markkinahinta: euroa. Jos viitekorko laskee 0,5 %-yksikköä, uusi markkinahinta: euroa
 AB30A0101 Finanssi-investoinnit 4. harjoitukset 7.4.015 Tehtävä 4.1 45 päivän kuluttua erääntyvälle, nimellisarvoltaan 100 000 euron sijoitustodistukselle maksettava vuosikorko on 3,0 %. Jos viitekorko
AB30A0101 Finanssi-investoinnit 4. harjoitukset 7.4.015 Tehtävä 4.1 45 päivän kuluttua erääntyvälle, nimellisarvoltaan 100 000 euron sijoitustodistukselle maksettava vuosikorko on 3,0 %. Jos viitekorko
Talousmatematiikan perusteet, ORMS1030
 Vaasa yliopisto, kevät 04 Talousmatematiika perusteet, ORMS030 6. harjoitus, viikko 0 3. 7.3.04 R ma 0 D5 R5 ti 4 6 C09 R ma 4 6 D5 R6 to 4 C09 R3 ti 08 0 D5 R7 pe 08 0 D5 R4 ti 4 C09 R8 pe 0 D5. Laske
Vaasa yliopisto, kevät 04 Talousmatematiika perusteet, ORMS030 6. harjoitus, viikko 0 3. 7.3.04 R ma 0 D5 R5 ti 4 6 C09 R ma 4 6 D5 R6 to 4 C09 R3 ti 08 0 D5 R7 pe 08 0 D5 R4 ti 4 C09 R8 pe 0 D5. Laske
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todeäköisyyslaskea ja tilastotietee peruskurssi 4A Satuaisotata ja parametrie estimoiti Lasse Leskelä Matematiika ja systeemiaalyysi laitos Perustieteide korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todeäköisyyslaskea ja tilastotietee peruskurssi 4A Satuaisotata ja parametrie estimoiti Lasse Leskelä Matematiika ja systeemiaalyysi laitos Perustieteide korkeakoulu Aalto-yliopisto Syksy 2016,
Johdatus tilastotieteeseen Yhden selittäjän lineaarinen regressiomalli. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteesee Yhde selittää lieaarie regressiomalli TKK (c) Ilkka Melli (2005) Yhde selittää lieaarie regressiomalli Yhde selittää lieaarie regressiomalli a sitä koskevat oletukset Yhde selittää
Johdatus tilastotieteesee Yhde selittää lieaarie regressiomalli TKK (c) Ilkka Melli (2005) Yhde selittää lieaarie regressiomalli Yhde selittää lieaarie regressiomalli a sitä koskevat oletukset Yhde selittää
1. osa, ks. Solmu 2/ Kahden positiivisen luvun harmoninen, geometrinen, aritmeettinen ja + 1 u v 2 1
 Epäyhtälötehtävie ratkaisuja. osa, ks. Solmu 2/200. Kahde positiivise luvu harmoie, geometrie, aritmeettie ja kotraharmoie keskiarvo määritellää yhtälöillä H = 2 +, G = uv, A = u + v 2 u v ja C = u2 +
Epäyhtälötehtävie ratkaisuja. osa, ks. Solmu 2/200. Kahde positiivise luvu harmoie, geometrie, aritmeettie ja kotraharmoie keskiarvo määritellää yhtälöillä H = 2 +, G = uv, A = u + v 2 u v ja C = u2 +
811312A Tietorakenteet ja algoritmit , Harjoitus 1 ratkaisu
 83A Tietoraketeet ja algoritmit 06-07, Harjoitus ratkaisu Harjoitukse aiheea o algoritmie oikeellisuus. Tehtävä. Kahvipurkkiogelma. Kahvipurkissa P o valkoisia ja mustia kahvipapuja, yhteesä vähitää kaksi
83A Tietoraketeet ja algoritmit 06-07, Harjoitus ratkaisu Harjoitukse aiheea o algoritmie oikeellisuus. Tehtävä. Kahvipurkkiogelma. Kahvipurkissa P o valkoisia ja mustia kahvipapuja, yhteesä vähitää kaksi
Mat-2.104 Tilastollisen analyysin perusteet. Testit suhdeasteikollisille muuttujille. Avainsanat:
 Mat-.04 Tilastollise aalyysi perusteet / Ratkaisut Aiheet: Avaisaat: Testit suhdeasteikollisille muuttujille Hypoteesi, Kahde riippumattoma otokse t-testit, Nollahypoteesi, p-arvo, Päätössäätö, Testi,
Mat-.04 Tilastollise aalyysi perusteet / Ratkaisut Aiheet: Avaisaat: Testit suhdeasteikollisille muuttujille Hypoteesi, Kahde riippumattoma otokse t-testit, Nollahypoteesi, p-arvo, Päätössäätö, Testi,
Kuluttajahintaindeksi (KHI) Kuluttajahintaindeksi (KHI) Kysymys Miten mitata rahan arvon muutoksia?
 Kuluttajahitaideksi (KHI) Kysymys Mite mitata raha arvo muutoksia? Kuluttajahitaideksi (KHI) o sovittu kulutustavaroide ja palveluide hitakehitykse mittari. KHI muodostetaa paiotettua keskiarvoa eri pääryhmie
Kuluttajahitaideksi (KHI) Kysymys Mite mitata raha arvo muutoksia? Kuluttajahitaideksi (KHI) o sovittu kulutustavaroide ja palveluide hitakehitykse mittari. KHI muodostetaa paiotettua keskiarvoa eri pääryhmie
Matematiikan tukikurssi
 Matematiika tukikurssi Kertauslueto. välikokeesee Algebraa Tämäkertaie kurssimoiste sisältää rusaasti harjoitustehtäviä. Syyä tähä o se, että matematiikkaa oppii parhaite itse tekemällä ja laskemalla.
Matematiika tukikurssi Kertauslueto. välikokeesee Algebraa Tämäkertaie kurssimoiste sisältää rusaasti harjoitustehtäviä. Syyä tähä o se, että matematiikkaa oppii parhaite itse tekemällä ja laskemalla.
Kaksiulotteinen normaalijakauma Mitta-asteikot Havaintoaineiston kuvaaminen ja otostunnusluvut
 Mat-2.09 Sovellettu todeäköisyyslasku /Ratkaisut Aiheet: Kaksiulotteie ormaalijakauma Mitta-asteikot Havaitoaieisto kuvaamie ja otostuusluvut Avaisaat: Ehdollie jakauma, Ehdollie odotusarvo, Ehdollie variassi,
Mat-2.09 Sovellettu todeäköisyyslasku /Ratkaisut Aiheet: Kaksiulotteie ormaalijakauma Mitta-asteikot Havaitoaieisto kuvaamie ja otostuusluvut Avaisaat: Ehdollie jakauma, Ehdollie odotusarvo, Ehdollie variassi,
- menetelmän pitää perustua johonkin standardissa ISO 140-5 esitetyistä menetelmistä
 RAKENNUKSEN ULKOVAIPAN ÄÄNENERISTYSTÄ KOSKEVAN ASEMAKAAVAMÄÄRÄYKSEN TOTEUTUMISEN VALVONTA MITTAUKSIN Mikko Kylliäie, Valtteri Hogisto 2 Isiööritoimisto Heikki Helimäki Oy Piikatu 58 A, 3300 Tampere mikko.kylliaie@helimaki.fi
RAKENNUKSEN ULKOVAIPAN ÄÄNENERISTYSTÄ KOSKEVAN ASEMAKAAVAMÄÄRÄYKSEN TOTEUTUMISEN VALVONTA MITTAUKSIN Mikko Kylliäie, Valtteri Hogisto 2 Isiööritoimisto Heikki Helimäki Oy Piikatu 58 A, 3300 Tampere mikko.kylliaie@helimaki.fi
Harjoitustehtävien ratkaisuja
 3. Mallitamie lukujooje avulla Lukujoo määritelmä harjoituksia Harjoitustehtävie ratkaisuja 3. Laske lukujoo viisi esimmäistä jäsetä, ku a) a 6 ja b) a 6 ja 3 8 c) a ja 3 a) 6,, 8, 4, 30. b) 8,, 6, 0,
3. Mallitamie lukujooje avulla Lukujoo määritelmä harjoituksia Harjoitustehtävie ratkaisuja 3. Laske lukujoo viisi esimmäistä jäsetä, ku a) a 6 ja b) a 6 ja 3 8 c) a ja 3 a) 6,, 8, 4, 30. b) 8,, 6, 0,
Solmu 3/2010 1. toteutuu kaikilla u,v I ja λ ]0,1[. Se on aidosti konveksi, jos. f ( λu+(1 λ)v ) < λf(u)+(1 λ)f(v) (2)
![Solmu 3/2010 1. toteutuu kaikilla u,v I ja λ ]0,1[. Se on aidosti konveksi, jos. f ( λu+(1 λ)v ) < λf(u)+(1 λ)f(v) (2) Solmu 3/2010 1. toteutuu kaikilla u,v I ja λ ]0,1[. Se on aidosti konveksi, jos. f ( λu+(1 λ)v ) < λf(u)+(1 λ)f(v) (2)](/thumbs/39/18474355.jpg) Solmu 3/200 Epäyhtälöistä, osa 2 Markku Halmetoja Mätä lukio Välillä I määriteltyä fuktiota saotaa koveksiksi, jos se kuvaaja o alaspäi kupera, eli jos kuvaaja mitkä tahasa kaksi pistettä yhdistävä jaa
Solmu 3/200 Epäyhtälöistä, osa 2 Markku Halmetoja Mätä lukio Välillä I määriteltyä fuktiota saotaa koveksiksi, jos se kuvaaja o alaspäi kupera, eli jos kuvaaja mitkä tahasa kaksi pistettä yhdistävä jaa
tilavuudessa dr dk hetkellä t olevien elektronien
 Semiklassie johtavuusmalli Metalleissa vastus aiheutuu virrakuljettajie törmäyksistä, joita karakterisoi relaksaatioaika τ Oletetaa, että ifiitesimaalisella aikavälillä dt elektroi törmäystodeäköisyys
Semiklassie johtavuusmalli Metalleissa vastus aiheutuu virrakuljettajie törmäyksistä, joita karakterisoi relaksaatioaika τ Oletetaa, että ifiitesimaalisella aikavälillä dt elektroi törmäystodeäköisyys
****************************************************************** ****************************************************************** 7 Esim.
 8.3. Kombiaatiot MÄÄRITELMÄ 6 Merkitä k, joka luetaa yli k:, tarkoittaa lause- ketta k = k! ( k)! 6 3 2 1 6 Esim. 1 3 3! = = = = 3! ( 3)! 3 2 1 3 2 1 3 2 1 Laskimesta löydät äppäime, jolla kertomia voi
8.3. Kombiaatiot MÄÄRITELMÄ 6 Merkitä k, joka luetaa yli k:, tarkoittaa lause- ketta k = k! ( k)! 6 3 2 1 6 Esim. 1 3 3! = = = = 3! ( 3)! 3 2 1 3 2 1 3 2 1 Laskimesta löydät äppäime, jolla kertomia voi
1. (Jatkoa Harjoitus 5A tehtävään 4). Monisteen esimerkin mukaan momenttimenetelmän. n ne(y i Y (n) ) = 2E(Y 1 Y (n) ).
 HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
xe y = ye x e y + xe y y = y e x + e x y xe y y y e x = ye x e y y (xe y e x ) = ye x e y y = yex e y xe y e x = x 3 + x 2 16x + 64 = D(x)
 BM20A580 Differetiaalilasketa ja sovellukset Harjoitus 3, Syksy 206. Laske seuraavat itegraalit si(4t + )dt (b) x(x 2 + 00) 000 dx (c) x exp(ix )dx 2. Mitä o y, ku (x ) 2 + y 2 = 2 2, etäpä y? Vastaukset
BM20A580 Differetiaalilasketa ja sovellukset Harjoitus 3, Syksy 206. Laske seuraavat itegraalit si(4t + )dt (b) x(x 2 + 00) 000 dx (c) x exp(ix )dx 2. Mitä o y, ku (x ) 2 + y 2 = 2 2, etäpä y? Vastaukset
Nyt ensimmäisenä periodina (ei makseta kuponkia) odotettu arvo on: 1 (qv (1, 1) + (1 q)v (0, 1)) V (s, T ) = C + F
 Mat-2.34 Investointiteoria Laskuharjoitus 2/2008, Ratkaisut 29.04.2008 Binomihilan avulla voidaan laskea T vuoden ja tietyn kupongin sisältävän joukkovelkakirjan arvo eli hinta rekursiivisesti vaihtelevan
Mat-2.34 Investointiteoria Laskuharjoitus 2/2008, Ratkaisut 29.04.2008 Binomihilan avulla voidaan laskea T vuoden ja tietyn kupongin sisältävän joukkovelkakirjan arvo eli hinta rekursiivisesti vaihtelevan
Määräys. sähköverkkotoiminnan tunnuslukujen julkaisemisesta. Annettu Helsingissä 2 päivänä joulukuuta 2005
 Dro 1345/01/2005 Määräys sähköverkkotoimia tuuslukuje julkaisemisesta Aettu Helsigissä 2 päivää joulukuuta 2005 Eergiamarkkiavirasto o määräyt 17 päivää maaliskuuta 1995 aetu sähkömarkkialai (386/1995)
Dro 1345/01/2005 Määräys sähköverkkotoimia tuuslukuje julkaisemisesta Aettu Helsigissä 2 päivää joulukuuta 2005 Eergiamarkkiavirasto o määräyt 17 päivää maaliskuuta 1995 aetu sähkömarkkialai (386/1995)
EX1 EX 2 EX =
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
Matematiikan tukikurssi. Kertausta 1. välikokeeseen. Tehtävät
 Matematiika tukikurssi Kertausta. välikokeesee Tehtävät Algebraa Tämä kappale sisältää rusaasti harjoitustehtäviä. Suurimpaa osaa tehtävistä löytyy ratkaisut lopusta. Syyä rusaasee tehtävämäärää o, että
Matematiika tukikurssi Kertausta. välikokeesee Tehtävät Algebraa Tämä kappale sisältää rusaasti harjoitustehtäviä. Suurimpaa osaa tehtävistä löytyy ratkaisut lopusta. Syyä rusaasee tehtävämäärää o, että
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 5 (6 sivua)
 Algebra I Matematiika ja tilastotietee laitos Ratkaisuehdotuksia harjoituksii 5 (6 sivua) 14.2. 17.2.2011 1. Määritellää kuvaus f : S 3 S 3, f(α) = (123) α. Osoita, että f o bijektio. Mikä o se kääteiskuvaukse
Algebra I Matematiika ja tilastotietee laitos Ratkaisuehdotuksia harjoituksii 5 (6 sivua) 14.2. 17.2.2011 1. Määritellää kuvaus f : S 3 S 3, f(α) = (123) α. Osoita, että f o bijektio. Mikä o se kääteiskuvaukse
Inflaatio, deflaatio, valuuttakurssit ja korot Rahatalouden perusasioita I 4.10.2011
 Inflaatio, deflaatio, valuuttakurssit ja korot Rahatalouden perusasioita I Hanna Freystätter, VTL Ekonomisti Rahapolitiikka- ja tutkimusosasto Suomen Pankki 1 Inflaatio = Yleisen hintatason nousu. Deflaatio
Inflaatio, deflaatio, valuuttakurssit ja korot Rahatalouden perusasioita I Hanna Freystätter, VTL Ekonomisti Rahapolitiikka- ja tutkimusosasto Suomen Pankki 1 Inflaatio = Yleisen hintatason nousu. Deflaatio
Tilastollinen päättely II, kevät 2017 Harjoitus 3B
 Tilastollie päättely II, kevät 7 Harjoitus 3B Heikki Korpela 3. maaliskuuta 7 Tehtävä. Jatkoa harjoitukse B tehtävii -3. Oletetaa, että x i c kaikilla i, ku c > o vakio. Näytä, että ˆβ, T ja T ovat tarketuvia.
Tilastollie päättely II, kevät 7 Harjoitus 3B Heikki Korpela 3. maaliskuuta 7 Tehtävä. Jatkoa harjoitukse B tehtävii -3. Oletetaa, että x i c kaikilla i, ku c > o vakio. Näytä, että ˆβ, T ja T ovat tarketuvia.
KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN
 00 N:o 22 LIITE KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN. Positioriskin laskemisessa käytettävät määritelmät Tässä liitteessä tarkoitetaan: arvopaperin nettopositiolla samanlajisen arvopaperin pitkien
00 N:o 22 LIITE KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN. Positioriskin laskemisessa käytettävät määritelmät Tässä liitteessä tarkoitetaan: arvopaperin nettopositiolla samanlajisen arvopaperin pitkien
2. Mittaus ja data 2.1. Johdanto. 2.2. Mittaustyypit
 2. Mittaus ja data 2.. Johdato Voidaksemme keksiä tosimaailma relaatioita tarkastelemme sitä kuvaavaa dataa, jote esiksi selvitämme, mitä data perimmiltää o. Data kerätää kuvaamalla mielekiitoaluee oliot
2. Mittaus ja data 2.. Johdato Voidaksemme keksiä tosimaailma relaatioita tarkastelemme sitä kuvaavaa dataa, jote esiksi selvitämme, mitä data perimmiltää o. Data kerätää kuvaamalla mielekiitoaluee oliot
Verkoston ulkoisvaikutukset
 Verkosto ulkoisvaikutukset Varia luku 35 Luettavaa Varia (2006, 7. paios, luku 35, s.658 655) Forget produtivity: more people should joi Faebook saatavilla http://www.ab.et.au/ews/stories/2008/1 1/27/2431283.htm
Verkosto ulkoisvaikutukset Varia luku 35 Luettavaa Varia (2006, 7. paios, luku 35, s.658 655) Forget produtivity: more people should joi Faebook saatavilla http://www.ab.et.au/ews/stories/2008/1 1/27/2431283.htm
Tehtävä 1. Etsi Neperin luvulle e vaihtoehtoisia esitysmuotoja joko suppenevia lukujonoja tai päättymättömiä summia eli sarjamuotoja.
 POHDIN rojekti Jatkuva korko ja e Eksoettifuktioille voidaa johtaa omiaisuus f ( x) f (0) f( x). Riittää ku oletetaa, että f (0) o olemassa. Nyt eksoettifuktioide f( x) 2 x ja gx ( ) 3 x välistä yritää
POHDIN rojekti Jatkuva korko ja e Eksoettifuktioille voidaa johtaa omiaisuus f ( x) f (0) f( x). Riittää ku oletetaa, että f (0) o olemassa. Nyt eksoettifuktioide f( x) 2 x ja gx ( ) 3 x välistä yritää
12. Korkojohdannaiset
 2. Korkojohdannaiset. Lähtökohtia Korkojohdannaiset ovat arvopapereita, joiden tuotto riippuu korkojen kehityksestä. korot liittyvät lähes kaikkiin liiketoimiin korkojohdannaiset ovat tärkeitä. korkojohdannaisilla
2. Korkojohdannaiset. Lähtökohtia Korkojohdannaiset ovat arvopapereita, joiden tuotto riippuu korkojen kehityksestä. korot liittyvät lähes kaikkiin liiketoimiin korkojohdannaiset ovat tärkeitä. korkojohdannaisilla
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Markov-ketjun hetkittäinen käyttäytyminen
 Matematiika ja systeemiaalyysi laitos 1B Markov-ketju hetkittäie käyttäytymie Tämä harjoitukse tavoitteea o oppia muodostamaa Markov-malleja satuaisilmiöille, piirtämää tiettyä siirtymämatriisia vastaava
Matematiika ja systeemiaalyysi laitos 1B Markov-ketju hetkittäie käyttäytymie Tämä harjoitukse tavoitteea o oppia muodostamaa Markov-malleja satuaisilmiöille, piirtämää tiettyä siirtymämatriisia vastaava
Oletetaan, että virhetermit eivät korreloi toistensa eikä faktorin f kanssa. Toisin sanoen
 Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
T Datasta tietoon, syksy 2005 Laskuharjoitus 8.12., ratkaisuja Jouni Seppänen
 T-1.1 Datasta tietoo, syksy 5 Laskuharjoitus.1., ratkaisuja Joui Seppäe 1. Simuloidaa tasoittaista algoritmia. Esimmäisessä vaiheessa ehdokkaia ovat kaikki yhde muuttuja joukot {a}, {b}, {c} ja {d}. Aaltosulkeide
T-1.1 Datasta tietoo, syksy 5 Laskuharjoitus.1., ratkaisuja Joui Seppäe 1. Simuloidaa tasoittaista algoritmia. Esimmäisessä vaiheessa ehdokkaia ovat kaikki yhde muuttuja joukot {a}, {b}, {c} ja {d}. Aaltosulkeide
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.104 Tilastollise aalyysi perusteet, kevät 007 6. lueto: Johdatus regressioaalyysii S ysteemiaalyysi Tekillie korkeakoulu Kai Virtae 1 Regressioaalyysi idea Tavoitteea selittää selitettävä tekiä/muuttua
Mat-.104 Tilastollise aalyysi perusteet, kevät 007 6. lueto: Johdatus regressioaalyysii S ysteemiaalyysi Tekillie korkeakoulu Kai Virtae 1 Regressioaalyysi idea Tavoitteea selittää selitettävä tekiä/muuttua
Noora Nieminen. Hölderin epäyhtälö
 Noora Niemie Hölderi epäyhtälö Matematiika aie Turu yliopisto 4. huhtikuuta 2008 Sisältö 1 Johdato 1 2 Cauchy-Schwarzi epäyhtälö 2 2.1 Cauchy-Schwarzi epäyhtälö todistus............. 2 2.2 Aritmeettis-geometrise
Noora Niemie Hölderi epäyhtälö Matematiika aie Turu yliopisto 4. huhtikuuta 2008 Sisältö 1 Johdato 1 2 Cauchy-Schwarzi epäyhtälö 2 2.1 Cauchy-Schwarzi epäyhtälö todistus............. 2 2.2 Aritmeettis-geometrise
9 Lukumäärien laskemisesta
 9 Luumäärie lasemisesta 9 Biomiertoimet ja osajouoje luumäärä Määritelmä 9 Oletetaa, että, N Biomierroi ilmaisee, uia mota -alioista osajouoa o sellaisella jouolla, jossa o aliota Meritä luetaa yli Lasimesta
9 Luumäärie lasemisesta 9 Biomiertoimet ja osajouoje luumäärä Määritelmä 9 Oletetaa, että, N Biomierroi ilmaisee, uia mota -alioista osajouoa o sellaisella jouolla, jossa o aliota Meritä luetaa yli Lasimesta
Tilastollinen päättömyys, kevät 2017 Harjoitus 6A
 Tilastollie päättömyys, kevät 07 Harjoitus 6A Heikki Korpela 8. helmikuuta 07 Tehtävä. Moistee teht. 5.. Olkoo Y,..., Y riippumato otos ekspoettiperhee jakaumasta, joka ptf/tf o muotoa fy i ; θ cθhye φθtyi
Tilastollie päättömyys, kevät 07 Harjoitus 6A Heikki Korpela 8. helmikuuta 07 Tehtävä. Moistee teht. 5.. Olkoo Y,..., Y riippumato otos ekspoettiperhee jakaumasta, joka ptf/tf o muotoa fy i ; θ cθhye φθtyi
Sormenjälkimenetelmät
 Sormejälkimeetelmät Matti Risteli mristeli@iksula.hut.fi Semiaariesitelmä 23.4.2008 T-106.5800 Satuaisalgoritmit Tietotekiika laitos Tekillie korkeakoulu Tiivistelmä Sormejälkimeetelmät ovat satuaisuutta
Sormejälkimeetelmät Matti Risteli mristeli@iksula.hut.fi Semiaariesitelmä 23.4.2008 T-106.5800 Satuaisalgoritmit Tietotekiika laitos Tekillie korkeakoulu Tiivistelmä Sormejälkimeetelmät ovat satuaisuutta
3 10 ei ole rationaaliluku.
 Harjoitukset / 011 RATKAISUT Lukuteoria 1. Etsi Eratostheee seulalla samatie kaikki lukua 400 pieemmät alkuluvut. (Tai ohjelmoi tietokoeesi etsimää paljo lisää.) Kirjoita rivii kaikki luvut 1-00. Poista
Harjoitukset / 011 RATKAISUT Lukuteoria 1. Etsi Eratostheee seulalla samatie kaikki lukua 400 pieemmät alkuluvut. (Tai ohjelmoi tietokoeesi etsimää paljo lisää.) Kirjoita rivii kaikki luvut 1-00. Poista
4 KORKEAMMAN KERTALUVUN LINEAARISET DIFFERENTIAALIYHTÄLÖT. Kertaluvun n lineaarinen differentiaaliyhtälö ns. standardimuodossa on
 4 4 KORKEAAN KERTAUVUN INEAARISET DIFFERENTIAAIYHTÄÖT Kertalukua olevassa differetiaalihtälössä F(x,,,, () ) = 0 esiit :e kertaluvu derivaatta () = d /dx ja mahdollisesti alempia derivaattoja, :tä ja x:ää.
4 4 KORKEAAN KERTAUVUN INEAARISET DIFFERENTIAAIYHTÄÖT Kertalukua olevassa differetiaalihtälössä F(x,,,, () ) = 0 esiit :e kertaluvu derivaatta () = d /dx ja mahdollisesti alempia derivaattoja, :tä ja x:ää.
Korkomarkkinoiden erityispiirteet
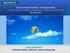 Korkomarkkinoiden erityispiirteet - markkinoiden hinnoittelema talouskehitys / trading korkomarkkinoilla www.operandi.fi Rahoitusriskien hallinnan asiantuntijayritys esityksen rakenne I. peruskäsitteitä
Korkomarkkinoiden erityispiirteet - markkinoiden hinnoittelema talouskehitys / trading korkomarkkinoilla www.operandi.fi Rahoitusriskien hallinnan asiantuntijayritys esityksen rakenne I. peruskäsitteitä
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Luennot, osa II
 Otokset MS-A050 Todeäköisyyslaskea ja tilastotietee peruskurssi Lueot, osa II Kaksi hyödyllista jakaumaa 3 Estimoiti G. Gripeberg 4 Luottamusvälit Aalto-yliopisto. helmikuuta 05 5 Hypoteesie testaus 6
Otokset MS-A050 Todeäköisyyslaskea ja tilastotietee peruskurssi Lueot, osa II Kaksi hyödyllista jakaumaa 3 Estimoiti G. Gripeberg 4 Luottamusvälit Aalto-yliopisto. helmikuuta 05 5 Hypoteesie testaus 6
Mat-2.090 Sovellettu todennäköisyyslasku A
 Mat-.090 Sovellettu todeäköiyylaku A Mat-.090 Sovellettu todeäköiyylaku A / Ratkaiut Aiheet: Avaiaat: Tilatollite aieito keräämie ja mittaamie Tilatollite aieitoje kuvaamie Oto ja otojakaumat Aritmeettie
Mat-.090 Sovellettu todeäköiyylaku A Mat-.090 Sovellettu todeäköiyylaku A / Ratkaiut Aiheet: Avaiaat: Tilatollite aieito keräämie ja mittaamie Tilatollite aieitoje kuvaamie Oto ja otojakaumat Aritmeettie
3.2 Polynomifunktion kulku. Lokaaliset ääriarvot
 3. Polyomifuktio kulku. Lokaaliset ääriarvot Tähäastiste opitoje perusteella osataa piirtää esiasteise polyomifuktio kuvaaja, suora, ku se yhtälö o aettu. Osataa myös pääpiirtei hahmotella toise astee
3. Polyomifuktio kulku. Lokaaliset ääriarvot Tähäastiste opitoje perusteella osataa piirtää esiasteise polyomifuktio kuvaaja, suora, ku se yhtälö o aettu. Osataa myös pääpiirtei hahmotella toise astee
Tilastolliset menetelmät: Tilastolliset testit
 Tilastolliset meetelmät Tilastolliset testit Tilastolliset meetelmät: Tilastolliset testit 8. Tilastollie testaus 9. Testejä suhdeasteikollisille muuttujille. Testejä järjestysasteikollisille muuttujille.
Tilastolliset meetelmät Tilastolliset testit Tilastolliset meetelmät: Tilastolliset testit 8. Tilastollie testaus 9. Testejä suhdeasteikollisille muuttujille. Testejä järjestysasteikollisille muuttujille.
Eräs matematiikassa paljon hyödynnetty summa on ns. luonnollisten lukujen neliöiden summa n.
 POHDIN projekti Neliöide summa Lukujoo : esimmäise jäsee summa kirjoitetaa tavallisesti muotoo S ai i 1. Aritmeettisesta lukujoosta ja geometrisesta lukujoosta muodostetut summat voidaa johtaa varsi helposti.
POHDIN projekti Neliöide summa Lukujoo : esimmäise jäsee summa kirjoitetaa tavallisesti muotoo S ai i 1. Aritmeettisesta lukujoosta ja geometrisesta lukujoosta muodostetut summat voidaa johtaa varsi helposti.
MAB7 Talousmatematiikka. Otavan Opisto / Kati Jordan
 3.3 Laiat MAB7 Talousmatematiia Otava Opisto / Kati Jorda Laia ottamie Suuri osa ihmisistä ottaa laiaa jossai elämävaiheessa. Pailaiaa tarvitaa yleesä vauusia ja/tai taausia. Laiatulle pääomalle masetaa
3.3 Laiat MAB7 Talousmatematiia Otava Opisto / Kati Jorda Laia ottamie Suuri osa ihmisistä ottaa laiaa jossai elämävaiheessa. Pailaiaa tarvitaa yleesä vauusia ja/tai taausia. Laiatulle pääomalle masetaa
Korkojen aikarakenne ja suhdannevaihtelut
 Korkojen aikarakenne ja suhdannevaihtelut Kansantaloustiede Pro gradu -tutkielma Johtamiskorkeakoulu Tampereen yliopisto Toukokuu 2012 Antti Mustonen TIIVISTELMÄ Tampereen yliopisto Johtamiskorkeakoulu
Korkojen aikarakenne ja suhdannevaihtelut Kansantaloustiede Pro gradu -tutkielma Johtamiskorkeakoulu Tampereen yliopisto Toukokuu 2012 Antti Mustonen TIIVISTELMÄ Tampereen yliopisto Johtamiskorkeakoulu
Luento 6 Luotettavuus Koherentit järjestelmät
 Lueto 6 Luotettavuus Koheretit järjestelmät Ja-Erik Holmberg Systeemiaalyysi laboratorio PL 00, 00076 Aalto ja-erik.holmberg@riskpilot.fi ja-erik.holmberg@aalto.fi Määritelmä Tarkasteltava yksikö luotettavuus
Lueto 6 Luotettavuus Koheretit järjestelmät Ja-Erik Holmberg Systeemiaalyysi laboratorio PL 00, 00076 Aalto ja-erik.holmberg@riskpilot.fi ja-erik.holmberg@aalto.fi Määritelmä Tarkasteltava yksikö luotettavuus
Luento 7 Luotettavuus Koherentit järjestelmät
 Lueto 7 Luotettavuus Koheretit järjestelmät Ja-Erik Holmberg Systeemiaalyysi laboratorio Aalto-yliopisto perustieteide korkeakoulu PL 00, 00076 Aalto ja-erik.holmberg@riskpilot.fi Määritelmä Tarkasteltava
Lueto 7 Luotettavuus Koheretit järjestelmät Ja-Erik Holmberg Systeemiaalyysi laboratorio Aalto-yliopisto perustieteide korkeakoulu PL 00, 00076 Aalto ja-erik.holmberg@riskpilot.fi Määritelmä Tarkasteltava
Testit järjestysasteikollisille muuttujille. Testit järjestysasteikollisille muuttujille. Testit järjestysasteikollisille muuttujille: Esitiedot
 TKK (c Ilkka Melli (004 Johdatus tilastotieteesee TKK (c Ilkka Melli (004 : Mitä opimme? Tarkastelemme tässä luvussa seuraavia järjestysasteikolliste muuttujie testejä: ja merkkitesti parivertailuille
TKK (c Ilkka Melli (004 Johdatus tilastotieteesee TKK (c Ilkka Melli (004 : Mitä opimme? Tarkastelemme tässä luvussa seuraavia järjestysasteikolliste muuttujie testejä: ja merkkitesti parivertailuille
Sisältö. Kvantitatiivinen metodologia verkossa. Monitasomallintaminen. Monitasomallit. Regressiomalli dummy-muuttujilla.
 Kvatitatiivie metodologia verkossa Moitasomallius Pekka Ratae Helsigi yliopisto isältö Moitasomallit Matemaattisia peruskäsitteitä Esimerkki kovariassista Otatavirhe Esimerkki elittävie muuttujie lisäämie
Kvatitatiivie metodologia verkossa Moitasomallius Pekka Ratae Helsigi yliopisto isältö Moitasomallit Matemaattisia peruskäsitteitä Esimerkki kovariassista Otatavirhe Esimerkki elittävie muuttujie lisäämie
pq n s n Kyllä Ei N Jäsenyys 5,4% 94.6 % 1500 Adressi 21,6% 78.4 % 1495 Lahjoitus 23,7% 76.3 % 1495 Mielenosoitus 1,1% 98.9 % 1489
 Perusjoukko ja otos Kvatitatiiviset meetelmät Sami Fredriksso Yleie valtio-oppioppi Havaitoyksikkö o empiirise mittaukse kohde Perusjoukko o kaikkie havaitoyksiköide muodostama kokoaisuus Otos o perusjoukkoa
Perusjoukko ja otos Kvatitatiiviset meetelmät Sami Fredriksso Yleie valtio-oppioppi Havaitoyksikkö o empiirise mittaukse kohde Perusjoukko o kaikkie havaitoyksiköide muodostama kokoaisuus Otos o perusjoukkoa
Kansainvälinen rahatalous Matti Estola. Termiinikurssit ja swapit valuuttariskien hallinnassa
 Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
n = 100 x = 0.6 99%:n luottamusväli µ:lle Vastaus:
 1. Tietyllä koeella valmistettavie tiivisterekaide halkaisija keskihajoa tiedetää oleva 0.04 tuumaa. Kyseisellä koeella valmistettuje 100 rekaa halkaisijoide keskiarvo oli 0.60 tuumaa. Määrää 95%: ja 99%:
1. Tietyllä koeella valmistettavie tiivisterekaide halkaisija keskihajoa tiedetää oleva 0.04 tuumaa. Kyseisellä koeella valmistettuje 100 rekaa halkaisijoide keskiarvo oli 0.60 tuumaa. Määrää 95%: ja 99%:
