2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
|
|
|
- Annika Haavisto
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1
2 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja näin ollen päädymme tarkastelemaan systeemejä joissa fluidin lämpö muuttuu mekaaniseksi työksi, ja toisinpäin. Sisäenergia (internal energy), käsite jonka olemassaoloon viitattiin aiemmin mutta joka jätettiin siltä erää käsittelemättä, tulee muodostumaan tässä tarkastelussa keskeiseksi käsitteeksi.
3 Jotta voidaan käsitellä termodynaamisia prosesseja, täytyy ensin määritellä tarkastelun alla oleva termodynaaminen systeemi (thermodynamic system). Määritellään mitkä objektit ovat osa systeemiä ja mitkä eivät (Esimerkkinä veden keittäminen kattilassa. Onko kattila osa tarkasteltavaa systeemiä, vai pelkkä vesi? Onko liesi?). 3 Kaikkea sitä mikä ei kuulu käsiteltävään systeemiin, kutsutaan ympäristöksi (surroundings). Systeemiä ja ympäristöä erottaa raja (boundary), joka usein on pikemminkin määritelmällinen kuin fyysinen. Systeemillä voi olla mahdollisuus vuorovaikuttaa ympäristön kanssa vaihtamalla sen kanssa lämpöä, työtä tai materiaa. Toisaalta voidaan määritellä että kyseisiä vuorovaikutuksia ei tapahdu. Näitä määritelmiä kutsutaan reunaehdoiksi (boundary conditions).
4 4 Systeemillä on aina jokin tarkasti määriteltävissä oleva tila (state). Tämä tila voidaan määritellä kun tunnetaan tilamuuttujat (state variables). Prosessia jossa systeemi muuttaa tilaansa, kutsutaan termodynaamiseksi prosessiksi (thermodynamic process).
5 2.1 Fluidin tekemä työ kun tilavuus muuttuu Määritellään ensin lämmön ja työn etumerkit. Kun pitäytyy laskuissa systemaattisesti tietyssä valinnassa, pienenee huomattavasti todennäköisyys tehdä merkkivirheitä. 5 Määritellään seuraavat ilmiöt kantamaan positiivista etumerkkiä: Systeemiin tuodaan lämpöä. Systeemi tekee työtä (esimerkiksi kaasun paine työntää mäntää ulospäin). Määritellään seuraavat ilmiöt kantamaan negatiivista etumerkkiä: Systeemistä poistuu lämpöä. Systeemiin tehdään työtä (esimerkiksi ulkoinen voima puristaa kaasua kokoon).
6 6 Tiedetään että paine jonka kaasu kohdistaa säiliön reunoihin koostuu suuresta määrästä yksittäisiä kaasumolekyylien törmäyksiä. Ajatellaan kuvan mukaista tilannetta. Säiliössä on kaasua, ja kaasua voidaan männän avulla joko laajentaa tai puristaa kokoon. Vasemman kuvan tapauksessa kaasumolekyyli törmää mäntään joka liikkuu oikealle (kaasu laajenee). Molekyyli kimpoaa takaisn pienemmällä nopeudella kuin mikä sillä alussa oli; toisin sanoen, molekyyli luovuttaa osan kineettisestä energiastaan mäntään.
7 Kun suuri määrä kaasumolekyylejä tekee saman, kaasu työntää mäntää poispäin. Kaasu tekee siis työtä (work). 7 Oikean puoleisessa kuvassa mäntä liikkuu oikealle (kaasu puristuu kokoon). Kaasumolekyyli joka kimpoaa männästä, kimpoaa takaisin suuremmalla kineettisellä energialla kuin mikä sillä alussa oli; toisin sanoen, mäntä luovuttaa energiaansa kaasumolekyylille. Kaasu saa männältä lisää energiaa; mäntä tekee siis työtä kaasuun (voidaan ilmaista myös niin että kaasumolekyylit tekevät negatiivista työtä mäntään).
8 Oletetaan nyt että männän pinta-ala (joka on kontaktissa kaasun kanssa) on A, ja kaasun mäntään kohdistama paine on p (toki männän kaasuun kohdistama paine on sama). Kaasu siis kohdistaa mäntään voiman F = pa. 8 Kun mäntä liikkuu oikealle matkan dx, tekee kaasu työtä määrän dw = F dx = padx verran. Toisaalta koska Adx = dv, voidaan kirjoittaa dw = pdv. Kun kaasun tilavuus muuttuu arvosta V 1 arvoon V 2, se tekee siis työn W = V2 V 1 pdv. Äsken käsitellyt pv -diagrammit muodostuvat tämän kaasun tekemän työn tarkastelussa erittäin käteviksi.
9 9 Oletetaan että systeemi on aluksi tilassa 1 ja käy läpi termodynaamisen prosessin päätyen tilaan 2. Fluidin tekemä työ W on nyt helposti visualisoitavissa; se on kuvassa näkyvän käyrän alle jäävä pinta-ala. Huomataan toinenkin erittäin merkittävä havainto: jotta työ voidaan määritellä, täytyy tuntea reitti (path) jota pitkin systeemi päätyy toiseen tilaan! Tieto alku- ja lopputilasta ei siis vielä riitä. Kuvassa sis Work A Work B.
10 Tämän havainnon valossa onkin parempi ilmaista fluidin tekemä työ muodossa W = pdv. path 0 Olettaen että paine p pysyy vakiona, saadaan W = p(v 2 V 1 ). Huomaa että tulos on positiivinen kun kaasu laajenee, ja negatiivinen kun kaasu puristuu (äsken määriteltyjen etumerkkisopimusten mukaan).
11 1 Tarkastellaan fluidin tekemää työtä kun pisteestä 1 päädytään pisteeseen 2 eri reittejä. Kun pv -diagrammissa siirrytään pisteestä 1 pisteeseen 3, se tarkoitta että paine pidetään vakiona p 1 :ssä, ja kaasu laajenee tilavuudesta V 1 tilavuuteen V 2.
12 Kaasu tekee siis työn p 1 (V 2 V 1 ), jota edustaa se pinta-ala joka jää vaaka-akselin ja janan 1 3 alle. Siirtymä 3 2 ei tee työtä, koska tilavuus pysyy silloin vakiona. 2 Vastaavasti jos pisteestä 1 siirrytään pisteeseen 2 alareittiä, ei siirtymä 1 4 tee työtä, ja siirtymässä 4 2 tehdään työ p 1 (V 2 V 1 ), jota edustaa se pinta-ala joka jää vaaka-akselin ja janan 4 2 alle. Huomataan siis jälleen että tehty työ riippuu siitä, mitä reittiä pv -diagrammilla kuljettin. Samalla huomataan että kuvassa näkyvä neliö edustaa syklistä prosessia (cyclic process). Riippuen siitä kuljetaanko reitti 1 1 myötäpäivään vai vastapäivään, fluidi päätyy tekemään joko positiivisen tai negatiivisen määrän työtä. Tätä tehtyä työtä edustaa se ala-joka jää neliön sisään.
13 3 Tarkastellaan kuvan systeemiä. Aluksi säiliössä on kaasua tietyssä lämpötilassa ja tietyssä paineessa. Syötetään kaasuun hitaasti lämpöä alla näkyvästä lämmittimestä. Samalla kaasu painaa mäntää oikealle. Tehdään prosessi hitaasi niin, että kaasun lämpötila pysyy koko ajan vakiona (pieni laajeneminen pudottaisi lämpötilaa, ja juuri tämän verran tuodaan lämmittimestä lisää).
14 4 Yllä oleva kuva esittää tilanetta ennen laajentamisen/lämmittämisen aloittamista, ja sen jälkeen. Kaasu on laajentunut alkutilavuudesta V 1 lopputilavuuteen V 2. Tässä termodynaamisessa prosessissa kaasuun on syötetty energiaa määrän Q verran, ja se on tehnyt työtä määrän W verran. Energian säilymislain nojalla näiden täytyy olla yhtäsuuret, siis Q = W.
15 5 Tarkastellaan prosessia jossa päädytään samasta alkutilasta samaan lopputilaan (sama määrä kaasua n, sama lämpötila T, sama alku- ja lopputilavuus, V 1, V 2 ). Prosessi on kuitenkin täysin erilainen; kaasuun ei tuoda ulkopuolelta lämpöä, eikä kaasu laajetessaan tee työtä. Männän työntämisen sijaan kaasu laajenee vapaasti (free expansion). Sekä systeemiin tuotu lämpö että kaasun tekemä työ ovat nollia, siis Q = W = 0.
16 Huomataan siis että näissä kahdessa prosessissa alkutilat olivat samat, ja lopputilat olivat samat. Kuitenkaan systeemiin tuotu lämpö, tai systeemin tekemä työ eivät olleet samoja. 6 Mainitsemisen arvoista on, että riippumatta kumman prosessin kaasu käy läpi, sisäenergia ennen laajenemista, U 1, on sama molemmissa tapauksissa. Myös sisäenergia laajenemisen jälkeen, U 2, on sama molemimssa tapauksissa. Kun pidetään mielessä että kaasun tilan määrittelevät tilamuuttujat, p, V, T, niin toki sisäenergioiden täytyykin olla samat.
17 2.2 Sisäenergia (Internal energy) Nyt viimein pääsemme määrittelemään sisäenergian, käsitteen joka on yksi termodynamiikan yksi keskeisimpiä käsitteitä. 7 Kuten jo tiedämme, systeemin sisäenergia voi termodynaamisessa prosessissa muuttua arvosta U 1 arvoon U 2. Merkitään tätä sisäenergian muutosta symbolilla U. Prosessissa jossa systeemiin tuodaan ulkopuolelta lämpöä, mutta jossa systeemi ei tee työtä, sisäenergian muutos on U = Q. Toistaalta prosessissa jossa systeemi tekee työtä, mutta se ei luovuta eikä vastaanota lämpöä ympäristöstään, on sen sisäenergian muutos U = W.
18 Prosessissa, jossa systeemi tekä vastaanottaa lämpöä että tekee työtä, on sisäenergian muutos U = Q W. Tämä havainto, joka on itse asiassa energian säilymislain yleistys, on nimeltään termodynamiikan ensimmäinen pääsääntö. 8 Nykyisin tiedetään että energiaa ei koskaan katoa eikä sitä myöskään koskaan ilmesty tyhjästä; energia vain muuttaa muotoaan. Laajimmillaan tämä määritelmä pitää sisällään myös sen, että massakin on pohjimmiltaan energiaa. On tässä vaiheessa mainitsemisen arvoista että äsken käydyssä esimerkkiparissa ensimmäisessä tapauksessa U = Q W = 0, vaikkakin Q 0 ja W 0. Toisessa tapauksessa U = Q W = 0, ja myös Q = 0 ja W = 0.
19 Systeemin sisäenergiaa voidaan ajatella systeemin atomien/molekyylien kineettisten energioiden ja potentiaalienergioiden summana. Tämä on käytännöllinen ajatus summittaisena määritelmänä, mutta on pidettävä mielessä että näin määriteltyä sisäenergiaa on erittäin hankala, ehkä jopa mahdoton, määritellä tarkasti. 9 Emme siis tule koskaan tarkstelemaan systeemin sisäenergian määrää, ainoastaan sen muutosta. Tämä tilanne on samankaltainen kuin mekaniikassa potentiaalienergian kanssa. Emme koskaan määrittele mikä on systeemin kokonaispotentiaalienergia, vaan keskitymme ainoastaan sen muutokseen. Kuten potentiaalienergiallekin, sisäenergialle voidaan tarpeen vaatiessa sopia nollataso, johon verraten muutoksia mitataan.
20 Korostettakoon vielä tämän tarkestelun tuloksena saatua tärkeintä havaintoa: 0 Vaikka Q ja W riippuvat reitistä, U = Q W ei riipu. Systeemin sisäenergian muutos termodynaamisessa prosessissa riippuu vain sen alkutilasta ja lopputilasta. Systeemin tilan määrittelevät tilamuuttujat p, V, T.
21 Sisäenergian muutoksen yhtälö, U = Q W, voidaan ilmaista myös differentiaalisessa muodossa: 1 du = dq dw. Systeemeissä joista tulemme tässä käsittelyssä puhumaan on työ fluidin tilavuuden muutosta, joten yhtälö voidaan ilmaista myös muodossa du = dq pdv.
22 On huomattava, että ideaalikaasun sisäenergia riippuu vain lämpötilasta (!). Reaalisten kaasujen sisäenergiaan vaikuttavat myös p ja V. 2 Kuten aiemmin käytiin läpi, ideaalikaasu on yksinkertaistettu malli missä kaasumolekyylit lentävät kukin omia lentoratojaan ja kimpoavat astian seinistä täydellisen elastisilla törmäyksillä, mutta eivät vaikuta toisiinsa. Ajattele äsken käsiteltyä esimerkkiä, jossa kaasua on tietyssä alkutilavuudessa, luukku välistä avataan ja kaasu pääsee vapaasi laajenemaan suurempaan tilavuuteen. Kun kerran on niin, että ideaalikaasun molekyylit eivät vaikuta toisiinsa, koostuu näin ollen ideaalikaasun sisäenergia vain molekyylien kineettisestä energiasta.
23 3 Tämä selittää sen, että ideaalikaasun sisäenergia ei muutu tässä prosessissa: yhdenkään kaasumolekyylin kineettinen energia ei muutu, vaikka kaasumolekyylit pääsevätkin liikkumaan suuremmassa tilavudessa. Se, että reaalisissa kaasuissa kaasumolekyylit vaikuttavat toisiinsa (potentiaalienergia), selittää sen että reaalisten kaasujen tapauksessa vastaava prosessi muuttaa kaasun sisäenergiaa.
24 Sellaista prosessia jossa sisäenergia alussa on sama kuin sisäenergia lopussa, U 1 = U 2, kutsutaan sykliseksi prosessiksi (cyclic process). Syklisessä prosessissa systeemin tila käy läpi erinäisiä muutoksia, mutta systeemi päätyy lopulta samaan tilaan mistä se lähti. 4 Vaikka U 1 = U 2 eli U = 0, tämä ei kuitenkaan tarkoita että Q tai W olisivat nollia. Yhtälö U = Q W pitää paikkansa vaikka Q ja W poikkeavat nollasta, kunhan Q = W. Sellaista prosessia joka ei vuorovaikuta ollenkaan ympäristönsä kanssa sanotaan eristetyksi prosessiksi (isolated process). Tälläisessä prosessissa Q = W = 0, ja näin ollen U 1 = U 2 = U = 0.
25 2.3 Erityisiä termodynaamisia prosesseja Kuten aiemmin mainittiin, voidaan fluidin tekemä työ yleisessä tapauksessa laskea kaavalla W = path pdv. 5 Käsitellään seuraavaksi neljä erityitapausta, joissa jokin tilamuuttuja tai muu suure pysyy vakiona, ja tilanteen käsittely on näin ollen helpompaa (vältytään integroinnilta). Kyseiset tapaukset edustavat myös suurta otosta prosesseja, joten moni monimutkaisempikin prosessi voidaan käsitellä näiden yhdistelmänä.
26 2.3.1 Adiabaattinen prosessi (Adiabatic process) Adiabaattisen prosessin määritelmä on se, että prosessissa systeemi ei vaihda lämpöä ympäristön kanssa (ei vastaanota eikä luovuta). Toisin sanoen, Q = 0. 6 Tämä tarkoittaa että sisäenergian muutoksen yhtälö menee muotoon U = W. Hyvä esimerkki adiabaattisesta prosessista on kaasu sylinterissä, joka laajenee ja painaa mäntää ulospäin tai jota mäntä puristaa kasaan. Kaasu tekee näin positiivisen tai negatiivisen työn, mutta ei ota eikä luovuta lämpöä ympäristöstä.
27 2.3.2 Isokoorinen prosessi (Isochoric process) Isokoorisen prosessin määritelmä on se, että se tapahtuu vakiotilavuudessa, siis V = 0. 7 Koska fluidin tekemän työn määrittelee juuri tilavuuden muutos, on siis W = 0. Näin ollen sisäenergian muutos voidaan ilmaista U = Q. Hyvä esimerkki isokoorisesta prosessista on kaasun lämmittäminen/viilentäminen kiinteässä säiliössä. Kaasun tilavuus ei muutu, mutta se voi vastaanottaa tai luovuttaa lämpöä.
28 2.3.3 Isobaarinen prosessi (Isobaric process) Isobaarisen prosessin määritelmä on se, että se tapahtuu vakiopaineessa. Mikään suureista U, Q, W ei välttämättä ole nollia, mutta silti työn laskeminen on helppoa (ei tarvitse integroida). 8 Kuten aiemmin jo mainittiinkin, saadaan työ paineen ollessa vakio laskettua yhtälöllä W = p(v 2 V 1 ). Hyvä esimerkki isobaarisesta prosessista on veden keittäminen kattilassa ilman kantta; vaikka vesi kiehuessaan laajenee, ei huoneen ilmanpaine tässä prosessissa kuitenkaan mainittavasti kasva.
29 2.3.4 Isoterminen prosessi (Isothermal process) Isotermisen prosessin määritelmä on se, että se tapahtuu vakiolämpötilassa. 9 Tämä tarkoittaa sitä, että prosessi tapahtuu sen verran hitaasti, että aina kun systeemiin tuodaan pieni määrä lämpöä, tekee systeemi saman verran työtä; tai vastaavasti jos syteemiin tehdään työtä, se luovuttaa välittömästi saamansa lämmön systeemistä ulos. Ideaalikaasujen tapauksessa isotermiset prosessit ovat merkittävässä asemassa, koska ideaalikaasun sisäenergia riippuu vain yksinomaan sen lämpötilasta. Näin ollen ideaalikaasuille isotermisessä prosesissa U = 0 ja näin ollen Q = W.
30 0 Ylläolevaan kuvaan on koottu kaikkien neljän edellä käsitellyn prosessin kuvaajat pv -koordinaatistoon.
31 2.4 Ideaalikaasun lämpökapasiteetit 1 Edellisessä kappaleessa määriteltiin aineen ominaislämpökapasiteetti. Käsittely oli riittävä kalorimetrian tarpeisiin, mutta kaasujen tapauksessa kannattaa pitää mielessä että lämpökapasiteetti riippuu olosuhteista joissa se määritellään.
32 Määritellään ideaalikaasulle moolinen lämpökapasiteetti vakiotilavuudessa, C V, ja moolinen lämpökapasiteetti vakiopaineessa, C p. 2 Kaasu ei vakiotilavuudessa laajene eikä näin ollen tee työtä. Sen sijaan pysyäkseen vakiopaineessa kaasun on lämmetessään laajettava. Laajetessaan kaasu tekee työtä, ja näin ollen osa kaasun saamasta energiasta menee työhön, ei kaasun lämpötilan nostamiseen. Voidaan siis jo nyt päätellä että C p on suurempi kuin C V. (Jos halutaan lämmittää yksi mooli kaasua yhden Kelvinin, pitää vakiopaineolosuhteissa syöttää enemmän lämpöä; osa lämmittämiseen, osa kaasun laajentamiseen.)
33 Jotta voidaan nostaa kaasun lämpötilaa vakiotilavuudessa määrällä T, täytyy lämpöä tuoda määrä Q = nc V T. 3 Vakiotilavuudessa systeemi ei tee työtä, joten W = 0 ja näin ollen U = Q. Jotta voidaan nostaa kaasun lämpötilaa vakiopaineessa, täytyy lisäksi tuoda systeemiin lämpöä kaasun tekemän työn verran, eli W = p(v 2 V 1 ) = nr(t 2 T 1 ) = nr T Vakiopaineessa siis W 0, ja U = Q + W. Saadaan siis nc p T = nc V T + nr T...ja tästä huomataan yhteys C p = C V + R.
34 Lämpökapasiteettien C V ja C p suhdetta kutsutaan lämpökapasiteettisuhteeksi (ratio of heat capacities), ja sitä merkitään symbolilla γ (gamma). 4 Määritellään siis γ = C p C V. Huomataan että koska C p on aina suurempi kuin C V, on γ aina ykköstä suurempi. C V, C p ja γ muodostuvat tärkeiksi käsitteiksi käsiteltäessä ideaalikaasun adiabaattisia prosesseja.
35 Ideaalikaasun adiabaattisille prosesseille pätee: T V (γ 1) = vakio 5 pv γ = vakio Koska Q = 0 ja täten U = W, pätevät myös W = nc V (T 1 T 2 ) = C V R (p 1V 1 p 2 V 2 ) = 1 1 γ (p 1V 1 p 2 V 2 ).
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt
 14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Termodynamiikan toinen pääsääntö (Second Law of Thermodynamics)
 e1 3 Termodynamiikan toinen pääsääntö (Second Law of Thermodynamics) Tärkeä käsite termodynamiikassa on termodynaamisen prosessin suunta. Kaikki prosessit ovat oikeasti irreversiibelejä (irreversible),
e1 3 Termodynamiikan toinen pääsääntö (Second Law of Thermodynamics) Tärkeä käsite termodynamiikassa on termodynaamisen prosessin suunta. Kaikki prosessit ovat oikeasti irreversiibelejä (irreversible),
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
3Työ. 3.1 Yleinen määritelmä
 3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Thermodynamics is Two Laws and a Li2le Calculus
 Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
VII LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ
 II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
W el = W = 1 2 kx2 1
 7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori!
 6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / TERVETULOA! Termodynamiikan 1. pääsääntö 9/25/2017
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 25.9.2017 TERVETULOA! v. 03 / T. Paloposki Tämän päivän ohjelma: Termodynamiikan 1. pääsääntö 1 Termodynamiikan 1. pääsääntö (energian säilymisen laki,
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 25.9.2017 TERVETULOA! v. 03 / T. Paloposki Tämän päivän ohjelma: Termodynamiikan 1. pääsääntö 1 Termodynamiikan 1. pääsääntö (energian säilymisen laki,
dl = F k dl. dw = F dl = F cos. Kun voima vaikuttaa kaarevalla polulla P 1 P 2, polku voidaan jakaa infinitesimaalisen pieniin siirtymiin dl
 Kun voima vaikuttaa kaarevalla polulla P 2, polku voidaan jakaa infinitesimaalisen pieniin siirtymiin dl Kukin siirtymä dl voidaan approksimoida suoraviivaiseksi, jolloin vastaava työn elementti voidaan
Kun voima vaikuttaa kaarevalla polulla P 2, polku voidaan jakaa infinitesimaalisen pieniin siirtymiin dl Kukin siirtymä dl voidaan approksimoida suoraviivaiseksi, jolloin vastaava työn elementti voidaan
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
TEHTÄVIEN RATKAISUT. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 712 p m 105 kg
 TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
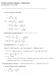 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Luku6 Tilanyhtälö. Ideaalikaasun N V. Yleinen aineen. paine vakio. tilavuus vakio
 Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Luento 11: Potentiaalienergia. Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia
 Luento 11: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia 1 / 22 Luennon sisältö Potentiaalienergia Konservatiiviset voimat
Luento 11: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia 1 / 22 Luennon sisältö Potentiaalienergia Konservatiiviset voimat
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
Ensimmäinen pääsääntö
 4 Ensimmäinen ääsääntö Luvuissa 2 ja 3 käsiteltiin eri taoja siirtää energiaa termodynaamisten systeemien välillä joko lämmön tai työn kautta. 1840-luvulla erityisesti Robert Julius von Mayern ja James
4 Ensimmäinen ääsääntö Luvuissa 2 ja 3 käsiteltiin eri taoja siirtää energiaa termodynaamisten systeemien välillä joko lämmön tai työn kautta. 1840-luvulla erityisesti Robert Julius von Mayern ja James
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 28.9.2015 / T. Paloposki / v. 01 Tämän päivän ohjelma: Tilanyhtälöt (kertaus) Termodynamiikan 1. pääsääntö (energian häviämättömyyden laki)
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 28.9.2015 / T. Paloposki / v. 01 Tämän päivän ohjelma: Tilanyhtälöt (kertaus) Termodynamiikan 1. pääsääntö (energian häviämättömyyden laki)
DEE-11110 Sähkötekniikan perusteet
 DEE-11110 Sähkötekniikan perusteet Antti Stenvall Peruskäsitteet Luennon keskeinen termistö ja tavoitteet sähkövaraus teho ja energia potentiaali ja jännite sähkövirta Tarkoitus on määritellä sähkötekniikan
DEE-11110 Sähkötekniikan perusteet Antti Stenvall Peruskäsitteet Luennon keskeinen termistö ja tavoitteet sähkövaraus teho ja energia potentiaali ja jännite sähkövirta Tarkoitus on määritellä sähkötekniikan
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
3.4 Liike-energiasta ja potentiaalienergiasta
 Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
Työperiaatteeksi (the work-energy theorem) kutsutaan sitä että suljetun systeemin liike-energian muutos Δ on voiman systeemille tekemä työ W Tämä on yksi konservatiivisen voiman erityistapaus Työperiaate
Käytetään lopuksi ideaalikaasun tilanyhtälöä muutoksille 1-2 ja 3-1. Muutos 1-2 on isokorinen, joten tilanyhtälöstä saadaan ( p2 / p1) = ( T2 / T1)
 LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Luento 9: Potentiaalienergia
 Luento 9: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Laskettuja esimerkkejä Luennon sisältö Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta
Luento 9: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Laskettuja esimerkkejä Luennon sisältö Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
Tarvittavat välineet: Kalorimetri, lämpömittari, jännitelähde, kaksi yleismittaria, sekuntikello
 1 LÄMPÖOPPI 1. Johdanto Työssä on neljä eri osiota, joiden avulla tutustutaan lämpöopin lakeihin ja ilmiöihin. Työn suoritettuaan opiskelijan on tarkoitus ymmärtää lämpöopin keskeiset käsitteet, kuten
1 LÄMPÖOPPI 1. Johdanto Työssä on neljä eri osiota, joiden avulla tutustutaan lämpöopin lakeihin ja ilmiöihin. Työn suoritettuaan opiskelijan on tarkoitus ymmärtää lämpöopin keskeiset käsitteet, kuten
Energia, energian säilyminen ja energiaperiaate
 E = γmc 2 Energia, energian säilyminen ja energiaperiaate Luennon tavoitteet Lepoenergian, liike-energian, potentiaalienergian käsitteet haltuun Työ ja työn merkki* Systeemivalintojen miettimistä Jousivoiman
E = γmc 2 Energia, energian säilyminen ja energiaperiaate Luennon tavoitteet Lepoenergian, liike-energian, potentiaalienergian käsitteet haltuun Työ ja työn merkki* Systeemivalintojen miettimistä Jousivoiman
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Luvun 8 laskuesimerkit
 Luvun 8 laskuesimerkit Esimerkki 8.1 Heität pallon, jonka massa on 0.40 kg seinään. Pallo osuu seinään horisontaalisella nopeudella 30 m/s ja kimpoaa takaisin niin ikään horisontaalisesti nopeudella 20
Luvun 8 laskuesimerkit Esimerkki 8.1 Heität pallon, jonka massa on 0.40 kg seinään. Pallo osuu seinään horisontaalisella nopeudella 30 m/s ja kimpoaa takaisin niin ikään horisontaalisesti nopeudella 20
3 Raja-arvo ja jatkuvuus
 3 Raja-arvo ja jatkuvuus 3. Raja-arvon käsite Raja-arvo kuvaa funktion kättätmistä jonkin lähtöarvon läheisdessä. Raja-arvoa tarvitaan toisinaan siksi, että funktion arvoa ei voida laskea kseisellä lähtöarvolla
3 Raja-arvo ja jatkuvuus 3. Raja-arvon käsite Raja-arvo kuvaa funktion kättätmistä jonkin lähtöarvon läheisdessä. Raja-arvoa tarvitaan toisinaan siksi, että funktion arvoa ei voida laskea kseisellä lähtöarvolla
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 17.3.2016 Susanna Hurme Päivän aihe: Energian, työn ja tehon käsitteet sekä energiaperiaate (Kirjan luku 14) Osaamistavoitteet: Osata tarkastella partikkelin kinetiikkaa
KJR-C1001 Statiikka ja dynamiikka Luento 17.3.2016 Susanna Hurme Päivän aihe: Energian, työn ja tehon käsitteet sekä energiaperiaate (Kirjan luku 14) Osaamistavoitteet: Osata tarkastella partikkelin kinetiikkaa
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2012 Insinöörivalinnan fysiikan koe 30.5.2012, malliratkaisut
 A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit
 19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: b) 0 e x + 1
 Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 24.3.2016 Susanna Hurme Rotaatioliikkeen liike-energia, teho ja energiaperiaate (Kirjan luku 18) Osaamistavoitteet Ymmärtää, miten liike-energia määritetään kiinteän
KJR-C1001 Statiikka ja dynamiikka Luento 24.3.2016 Susanna Hurme Rotaatioliikkeen liike-energia, teho ja energiaperiaate (Kirjan luku 18) Osaamistavoitteet Ymmärtää, miten liike-energia määritetään kiinteän
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 9/26/2016
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 26.9.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 1 Kotilasku 2 Kotilasku 2 2 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 26.9.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 1 Kotilasku 2 Kotilasku 2 2 Termodynamiikan
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
