REAKTIOT JA ENERGIA, KE3. Kaasut
|
|
|
- Siiri Leppänen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen malli, joka kuvaa reaalikaasua. Kerrataan lyhyesti muutama fysiikan käsite ja kaasulait (4.- ja 2.-kurssit). Määritelmiä: Kimmoisa törmäys: Liikemäärä p = mv ja liike-energia E kin = 1 2 mv2 säilyvät. Kimmoton törmäys: Liikemäärä p säilyy, mutta liike-energia E kin ei säily. Täysin kimmoton törmäys: Kappaleet takertuvat toisiinsa. Liikemäärä p säilyy, mutta liike-energia E kin ei säily. Kaasulait: Boylen laki: Vakiolämpötilassa kaasun paine ja tilavuus ovat kääntäen verrannolliset, eli pv=vakio. Puhutaan isotermisestä tilanmuutoksesta. Charlesin laki: Vakiotilavuudessa kaasun paine on suoraan verrannollinen sen absoluuttiseen lämpötilaan (Kelvin-asteet), eli p =vakio. Puhutaan isokoorisesta T tilanmuutoksesta. Gay-Lussacin laki: Vakiopaineessa kaasusysteemin tilavuus on suoraan verrannollinen sen absoluuttiseen lämpötilaan (Kelvin-asteet), eli V T =vakio. Puhutaan isobaarisesta tilanmuutoksesta. 1
2 Aineen olomuodoista juuri kaasu on helpommin tutkittavissa fysikaalisin ja kemiallisin keinoin. Palautetaan mieleen tärkeät suureet, paine, tilavuus ja lämpötila. 1. Kaasun paine, p Aiheutuu molekyylien törmäyksistä astian seinämiin. Paine on voima jaettuna pinta-alalla, siis p = F. Yksikköjä ovat A Pascal Pa, bar ja atm. Normaali ilmanpaine on 101,325 kpa. 2. Kaasun tilavuus, V Kaasu täyttää aina koko astian, eli käytettävän tilan ja kaasun tilavuus on sama kuin astian tilavuus. 3. Kaasun lämpötila, T Kaikissa kaasulaskuissa käytetään absoluuttista lämpötila-asteikkoa, eli yksikkönä on Kelvin, K. Kaasulaskuissa käteviä yksikkömuunnoksia: 1 atm = 101,325 kpa = 1,01325 bar T K = t + 273,15 T = t K 273,15 Tarkastellaan näiden suureiden vaikutuksia kaasuun lyhyesti kuvien avulla. Tarkempi tarkastelu ja kuvaajien piirto p, V-koordinaatistoon fysiikan kursseilla! Sama ainemäärä n, T=vakio. Kun V pienenee, niin paine eli törmäykset seinämiin kasvaa. Havaitaan Boyle V 1 p V, T=vakio. Jos toisessa on suurempi p, on oltava suurempi ainemäärä n. (enemmän törmäyksiä). Siis havaitaan p n 2
3 Sama paine ja lämpötila eli p, T=vakio. Jos toisen astian V suurempi, on siellä oltava myös suurempi n. Siis havaitaan verrannollisuus V n V, n=vakio. Jos toisessa on suurempi T, sen rakenneosilla enemmän energiaa eli liikkuvat nopeammin enemmän törmäyksiä aikayksikköä kohden suurempi p. Siis havaitaan Charles p T Italialainen fyysikko Amadeo Avogadro tutki, miten eri kaasut käyttäytyvät, kun niillä on sama paine ja lämpötila. Hän esitti vuonna 1811 koetulostensa perusteella hypoteesinsa, tunnetaan nykyisin Avogadron lakina. Avogadron laki: Kaikki samoissa lämpötiloissa ja paineissa olevat kaasut sisältävät yhtä suurissa tilavuuksissa yhtä monta molekyyliä (=yhtä suuren ainemäärän). Siis V 1 = n 1, kun p ja T pysyvät vakiona. V 2 n 2 Heliumia Happea Metaania 3
4 Yhdistämällä eri kaasulait saadaan ns. kaasujen yleinen tilanyhtälö (erittäin käyttökelpoinen pitää osata!) pv = nrt, missä R on verrannollisuuskerroin, kutsutaan mooliseksi kaasuvakioksi. Huomaa, että R riippuu mitä paineen yksikköä käyttää. Nämä löytyvät MAOL:sta. J bar l R = 8,3145 = 0, mol K mol K Muista 1 J = 1 N m = 1 Pa m 2 m = 1 Pa m 3. Kaasulaskuissa ja tarkasteluissa käytetään hyvin usein NTP-olosuhteita eli normaalitilaa (Normal pressure and temperature), jolloin normaalilämpötila on T 0 = 273,15 K ja normaalipaine p 0 = 1 atm = 101,325 kpa, lyhenne atm tulee sanasta atmosphere=ilmakehä, joka on yhtä suuri kuin keskimääräinen ilmanpaine merenpinnan tasolla Pariisin leveysasteella, sopimus v Näissä olosuhteissa yhden kaasumoolin tilavuus eli kaasun moolitilavuus V m on vakio V m = V n = 22,41 l mol, V = V m n Laske tämä itsenäisesti kotona! 4
5 Esimerkki 1: Lämpötilan vaikutus veden olomuotoon ja tilavuuteen. Kuvassa on 1 mooli vettä kiinteänä, nesteenä ja kaasuna. Voit kokeilla miten paine vaikuttaa veden kiehumiseen Ota ruisku ja laita hieman vettä. Vedä mäntä ulospäin ja saat alipaineen. Miksi vesi alkaa kuplia eli kiehua? Esimerkki 2: 3,45 kuutiometrin kokoiseen typpisäiliöön imettiin vakuumipumpulla tyhjiö. Säiliön loppupaineeksi mitattiin 6, Pa ja lämpötilaksi 22. Laske säiliöön jääneen typpikaasun ainemäärä. Ratkaisu: Kaasujen yleisestä tilanyhtälöstä pv = nrt ratkaistaan ainemäärä n. Saadaan n = pv RT = 6, Pa 3,45 m 3 = 9,3770 J mol 8,3145 mol K 273, K Esimerkki 3 (kaasun moolimassa): 62,6 mg erästä kaasumaista hiilivetyä on suljettu 34,9 cm 3 :n suuruiseen astiaan. Hiilivedyn paine on 102,9 kpa ja lämpötila on 100. a) Laske hiilivedyn moolimassa b) Polttoanalyysin perusteella hiilivedyssä on 88,82 m-% hiiltä ja 11,18 m-% vetyä. Mikä on yhdisteen molekyylikaava? c) Yhdisteen reaktio bromin Br 2 kanssa osoitti, että siinä on kaksi kaksoissidosta. Piirrä hiilivedyn viivakaava. 5
6 Ratkaisu: a) Kaasujen yleinen tilanyhtälö pv = nrt ja ainemäärän määritelmän n = m avulla voidaan laskea kaasun moolimassa M: M pv = nrt pv = m mrt RT M = M pv J 0,0626 g 8, , K M = mol K 102,9 kpa 0, m 3 = 54,06 g mol b) Yhdisteen empiirinen kaava C 2 H 3 x : hiilen massa, m C = 0, ,6 mg = 55,60132 mg ja vastaavasti vedyn massa, m H = 0, ,6 mg = 6,99868 mg. Näin ollen ainemääriksi saadaan, n C = 0, g = 4, mol ja n H = 0, g = 6,9 12,01 g/mol 1,008 g/mol 10 3 mol. Siis, hiilen ja vedyn suhteiksi saadaan = 4, = 0, n H 6, Koska yhden C 2 H 3 yksikön moolimassa on 2 12, ,008 = 27,044, niin kerroin x:ksi tulee 54,06 27,044 = 1, Molekyylikaavaksi tulee C 2 H 3 2 = C 4 H 6. c) Kyseinen hiilivety on 1,3-butadieeni. n C Esimerkki 4: Pekka ajoi Ferrarillaan koulusta kotiin. Matkalla kului 7,5 litraa bensiiniä (tiheys 0,71 kg/l). Oletetaan, että bensiini on oktaanin ja iso-oktaanin seosta, molekyylikaava C 8 H 18, ja se palaa täydellisesti. Laske matkan aikana muodostuneen hiilidioksidin ja vesihöyryn yhteistilavuus, kun palamiskaasujen lämpötila on 450 ja paine on 202 kpa. Ratkaisu: Suureet ja arvot: p = 202 kpa = 2,02 bar, R = 0, bar dm3, mol K T = ,15 K = 723,15 K, V C 8 H 18 = 7,5 l, ρ C 8 H 18 = 0,71 kg/l ja M C 8 H 18 = 114,224 g/mol. Bensiinin täydellistä palamista kuvaava tasapainotettu reaktioyhtälö on 2 C 8 H 18 g + 25 O 2 g 16 CO 2 g + 18 H 2 O g. Kuluneen bensiinin massa saadaan tiheyden ja tilavuuden kautta ρ = m V, eli m C 8 H 18 = ρ C 8 H 18 V C 8 H 18 = 0,71 kg/l 7,5 l = 5325 g, joten ainemääräksi tulee n C 8 H 18 = m C 8H g = = 46,62 mol. M C 8 H ,224 g/mol 6
7 Tasapainotetun reaktioyhtälön mukaan n CO 2 = 16 n C 8 H 18 2, n H 2 O = 18 n C 8 H 18 2, josta saadaan n CO 2 = 8 n C 8 H 18, n H 2 O = 9 n C 8 H 18, Eli n kaasut = n CO 2 + n H 2 O = 8 n C 8 H n C 8 H 18 = 17 n C 8 H 18 = 17 46,62 mol = 792,5 mol. Kaasujen yleistä tilanyhtälöä hyödyntäen saadaan kaasujen tilavuudeksi V kaasut = nrt bar dm 792,5 mol R = 0, = mol K 723,15 K p 2,02 bar = dm 3 = 24 m 3. Kaasuseoksen kokonaispaine on osapaineiden summa, Daltonin laki. 7
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Bensiiniä voidaan pitää hiilivetynä C8H18, jonka tiheys (NTP) on 0,703 g/ml ja palamislämpö H = kj/mol
 Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella:
 ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Lukion kemia 3, Reaktiot ja energia. Leena Piiroinen Luento 2 2015
 Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
luku 1.notebook Luku 1 Mooli, ainemäärä ja konsentraatio
 Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Tehtävä 2. Selvitä, ovatko seuraavat kovalenttiset sidokset poolisia vai poolittomia. Jos sidos on poolinen, merkitse osittaisvaraukset näkyviin.
 KERTAUSKOE, KE1, SYKSY 2013, VIE Tehtävä 1. Kirjoita kemiallisia kaavoja ja olomuodon symboleja käyttäen seuraavat olomuodon muutokset a) etanolin CH 3 CH 2 OH höyrystyminen b) salmiakin NH 4 Cl sublimoituminen
KERTAUSKOE, KE1, SYKSY 2013, VIE Tehtävä 1. Kirjoita kemiallisia kaavoja ja olomuodon symboleja käyttäen seuraavat olomuodon muutokset a) etanolin CH 3 CH 2 OH höyrystyminen b) salmiakin NH 4 Cl sublimoituminen
Luku 13 KAASUSEOKSET
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Luento 9 Kemiallinen tasapaino CHEM-A1250
 Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
PULLEAT JA VALTAVAT VAAHTOKARKIT
 sivu 1/6 PULLEAT JA VALTAVAT VAAHTOKARKIT LUOKKA-ASTE/KURSSI Soveltuu ala-asteelle, mutta myös yläkouluun syvemmällä teoriataustalla. ARVIOTU AIKA n. 1 tunti TAUSTA Ilma on kaasua. Se on yksi kolmesta
sivu 1/6 PULLEAT JA VALTAVAT VAAHTOKARKIT LUOKKA-ASTE/KURSSI Soveltuu ala-asteelle, mutta myös yläkouluun syvemmällä teoriataustalla. ARVIOTU AIKA n. 1 tunti TAUSTA Ilma on kaasua. Se on yksi kolmesta
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
TKK, TTY, LTY, OY, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 31.5.2006
 TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
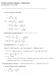 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
Lämpötila, lämpö energiana
 Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila, lämpö energiana Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila, lämpö energiana Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
PULLEAT VAAHTOKARKIT
 PULLEAT VAAHTOKARKIT KOHDERYHMÄ: Työ soveltuu alakouluun kurssille aineet ympärillämme ja yläkouluun kurssille ilma ja vesi. KESTO: Työ kestää n.30-60min MOTIVAATIO: Työssä on tarkoitus saada positiivista
PULLEAT VAAHTOKARKIT KOHDERYHMÄ: Työ soveltuu alakouluun kurssille aineet ympärillämme ja yläkouluun kurssille ilma ja vesi. KESTO: Työ kestää n.30-60min MOTIVAATIO: Työssä on tarkoitus saada positiivista
Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa.
 Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Pituuden lämpötilalaajeneminen ja -kutistuminen
 8 Lämpölaajeneminen Lämpölaajeneminen tarkoittaa, että kun kappaleen lämpötila kasvaa, kasvaa myös sen koko. Vastaavasti lämpötilan laskeminen pienentää kappaleen kokoa. Kiinteiden kappaleiden pituuden
8 Lämpölaajeneminen Lämpölaajeneminen tarkoittaa, että kun kappaleen lämpötila kasvaa, kasvaa myös sen koko. Vastaavasti lämpötilan laskeminen pienentää kappaleen kokoa. Kiinteiden kappaleiden pituuden
Leena Ylivuori ja Tarja Ihalin/ DFCL3/ LAB/ raportti/ webbiversio/ 8. kokonaisuus. 8. Lämpöoppi 1. : Tilanyhtälö
 Leena Ylivuori ja Tarja Ihalin/ DFCL3/ LAB/ raportti/ webbiversio/ 8. kokonaisuus 8. Lämpöoppi 1. : Tilanyhtälö 1. Johdanto Tässä työkokonaisuudessa on tutkittu lämmittämisen, jäähdyttämisen ja puristuksen
Leena Ylivuori ja Tarja Ihalin/ DFCL3/ LAB/ raportti/ webbiversio/ 8. kokonaisuus 8. Lämpöoppi 1. : Tilanyhtälö 1. Johdanto Tässä työkokonaisuudessa on tutkittu lämmittämisen, jäähdyttämisen ja puristuksen
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Lämpötila ja lämpöenergia
 Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila ja lämpöenergia Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila ja lämpöenergia Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Sukunimi: Etunimi: Henkilötunnus:
 K1. Onko väittämä oikein vai väärin. Oikeasta väittämästä saa 0,5 pistettä. Vastaamatta jättämisestä tai väärästä vastauksesta ei vähennetä pisteitä. (yhteensä 10 p) Oikein Väärin 1. Kaikki metallit johtavat
K1. Onko väittämä oikein vai väärin. Oikeasta väittämästä saa 0,5 pistettä. Vastaamatta jättämisestä tai väärästä vastauksesta ei vähennetä pisteitä. (yhteensä 10 p) Oikein Väärin 1. Kaikki metallit johtavat
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Luku 2. Kemiallisen reaktion tasapaino
 Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Ainemäärien suhteista laskujen kautta aineiden määriin
 REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Törmäysteoria. Törmäysteorian mukaan kemiallinen reaktio tapahtuu, jos reagoivat hiukkaset törmäävät toisiinsa
 Törmäysteoria Törmäysteorian mukaan kemiallinen reaktio tapahtuu, jos reagoivat hiukkaset törmäävät toisiinsa tarpeeksi suurella voimalla ja oikeasta suunnasta. 1 Eksotermisen reaktion energiakaavio E
Törmäysteoria Törmäysteorian mukaan kemiallinen reaktio tapahtuu, jos reagoivat hiukkaset törmäävät toisiinsa tarpeeksi suurella voimalla ja oikeasta suunnasta. 1 Eksotermisen reaktion energiakaavio E
Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin.
 1.2 Elektronin energia Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin. -elektronit voivat olla vain tietyillä energioilla (pääkvanttiluku n = 1, 2, 3,...) -mitä kauempana
1.2 Elektronin energia Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin. -elektronit voivat olla vain tietyillä energioilla (pääkvanttiluku n = 1, 2, 3,...) -mitä kauempana
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Kemian koe, Ke3 Reaktiot ja energia RATKAISUT Perjantai VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN
 Kemian koe, Ke3 Reaktiot ja energia RATKAISUT Kannaksen lukio Perjantai 26.9.2014 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN 1. A. Selitä käsitteet ja määritelmät (lyhyesti), lisää tarvittaessa kemiallinen merkintätapa:
Kemian koe, Ke3 Reaktiot ja energia RATKAISUT Kannaksen lukio Perjantai 26.9.2014 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN 1. A. Selitä käsitteet ja määritelmät (lyhyesti), lisää tarvittaessa kemiallinen merkintätapa:
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Syksy 009 Jukka Maalampi LUENTO 8 Paine nesteissä Nesteen omalla painolla on merkitystä Nestealkio korkeudella y pohjasta: dv Ady dm dv dw gdm gady paino Painon lisäksi alkioon
Mekaniikan jatkokurssi Fys10 Syksy 009 Jukka Maalampi LUENTO 8 Paine nesteissä Nesteen omalla painolla on merkitystä Nestealkio korkeudella y pohjasta: dv Ady dm dv dw gdm gady paino Painon lisäksi alkioon
Joensuun yliopisto Kemian valintakoe/3.6.2009
 Joesuu yliopisto Kemia valitakoe/.6.009 Mallivastaukset 1. Selitä lyhyesti (korkeitaa kolme riviä), a) elektroegatiivisuus b) elektroiaffiiteetti c) amfolyytti d) diffuusio e) Le Chatelieri periaate. a)
Joesuu yliopisto Kemia valitakoe/.6.009 Mallivastaukset 1. Selitä lyhyesti (korkeitaa kolme riviä), a) elektroegatiivisuus b) elektroiaffiiteetti c) amfolyytti d) diffuusio e) Le Chatelieri periaate. a)
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
0, mol 8,3145 (273,15 37)K mol K. Heliumkaasun paine saadaan kaasujen tilanyhtälöstä pv = nrt. K mol kpa
 4. Kaasut 9. Palauta ieleen Reaktio 1 s. 19 olouodoista ja niiden eroista. a) Kaasussa rakenneosat ovat kaukana toisistaan, joten kaasu on aljon harveaa kuin neste. Ts. kaasun tiheys on ienei kuin nesteen
4. Kaasut 9. Palauta ieleen Reaktio 1 s. 19 olouodoista ja niiden eroista. a) Kaasussa rakenneosat ovat kaukana toisistaan, joten kaasu on aljon harveaa kuin neste. Ts. kaasun tiheys on ienei kuin nesteen
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Luku 13. Kertausta Hydrostaattinen paine Noste
 Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
kertausta Boltzmannin jakauma infoa Ideaalikaasu kertausta Maxwellin ja Boltzmannin vauhtijakauma
 infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
Ideaalikaasut. 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista?
 Ideaalikaasut 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista? 2. Auton renkaan paineeksi mitattiin huoltoasemalla 2,2 bar, kun lämpötila oli + 10 ⁰C. Pitkän ajon jälkeen rekkaan
Ideaalikaasut 1. Miksi normaalitila (NTP) on tärkeä puhuttaessa kaasujen tilavuuksista? 2. Auton renkaan paineeksi mitattiin huoltoasemalla 2,2 bar, kun lämpötila oli + 10 ⁰C. Pitkän ajon jälkeen rekkaan
S , Fysiikka III (S) I välikoe Malliratkaisut
 S-4.35, Fysiikka III (S) I välikoe 9.0.000 Malliratkaisut Tehtävä Kuution uotoisessa säiliössä, jonka särän pituus on 0,0, on 3,0 0 olekyyliä happea (O) 300 K läpötilassa. a) Kuinka onta kertaa kukin olekyyli
S-4.35, Fysiikka III (S) I välikoe 9.0.000 Malliratkaisut Tehtävä Kuution uotoisessa säiliössä, jonka särän pituus on 0,0, on 3,0 0 olekyyliä happea (O) 300 K läpötilassa. a) Kuinka onta kertaa kukin olekyyli
TUNTEMATON KAASU. TARINA 1 Lue etukäteen argonin käyttötarkoituksista Jenni Västinsalon kandidaattitutkielmasta sivut 12-15. Saa lukea myös kokonaan!
 TUNTEMATON KAASU KOHDERYHMÄ: Työ soveltuu lukiolaisille, erityisesti kurssille KE3 ja FY2. KESTO: Noin 60 min. MOTIVAATIO: Oppilaat saavat itse suunnitella koejärjestelyn. TAVOITE: Työn tavoitteena on
TUNTEMATON KAASU KOHDERYHMÄ: Työ soveltuu lukiolaisille, erityisesti kurssille KE3 ja FY2. KESTO: Noin 60 min. MOTIVAATIO: Oppilaat saavat itse suunnitella koejärjestelyn. TAVOITE: Työn tavoitteena on
Yhdisteiden nimeäminen
 Yhdisteiden nimeäminen Binääriyhdisteiden nimeäminen 1. Ioniyhdisteet 2. Epämetallien väliset yhdisteet Kompleksiyhdisteiden nimeäminen Kemiallinen reaktio 1. Reaktioyhtälö 2. Määrälliset laskut 3. Reaktionopeuteen
Yhdisteiden nimeäminen Binääriyhdisteiden nimeäminen 1. Ioniyhdisteet 2. Epämetallien väliset yhdisteet Kompleksiyhdisteiden nimeäminen Kemiallinen reaktio 1. Reaktioyhtälö 2. Määrälliset laskut 3. Reaktionopeuteen
Fysiikan kurssit. MAOL OPS-koulutus Naantali 21.11.2015 Jukka Hatakka
 Fysiikan kurssit MAOL OPS-koulutus Naantali 21.11.2015 Jukka Hatakka Valtakunnalliset kurssit 1. Fysiikka luonnontieteenä 2. Lämpö 3. Sähkö 4. Voima ja liike 5. Jaksollinen liike ja aallot 6. Sähkömagnetismi
Fysiikan kurssit MAOL OPS-koulutus Naantali 21.11.2015 Jukka Hatakka Valtakunnalliset kurssit 1. Fysiikka luonnontieteenä 2. Lämpö 3. Sähkö 4. Voima ja liike 5. Jaksollinen liike ja aallot 6. Sähkömagnetismi
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
c) Tasapainota seuraava happamassa liuoksessa tapahtuva hapetus-pelkistysreaktio:
 HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
Alkuaineita luokitellaan atomimassojen perusteella
 IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
KOTITEKOINEN PALOSAMMUTIN (OSA 1)
 KOTITEKOINEN PALOSAMMUTIN (OSA 1) Johdanto Monet palosammuttimet, kuten kuvassa esitetty käsisammutin, käyttävät hiilidioksidia. Jotta hiilidioksidisammutin olisi tehokas, sen täytyy vapauttaa hiilidioksidia
KOTITEKOINEN PALOSAMMUTIN (OSA 1) Johdanto Monet palosammuttimet, kuten kuvassa esitetty käsisammutin, käyttävät hiilidioksidia. Jotta hiilidioksidisammutin olisi tehokas, sen täytyy vapauttaa hiilidioksidia
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
KE4, KPL. 3 muistiinpanot. Keuruun yläkoulu, Joonas Soininen
 KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
Seoksen pitoisuuslaskuja
 Seoksen pitoisuuslaskuja KEMIAA KAIKKIALLA, KE1 Analyyttinen kemia tutkii aineiden määriä ja pitoisuuksia näytteissä. Pitoisuudet voidaan ilmoittaa: - massa- tai tilavuusprosentteina - promilleina tai
Seoksen pitoisuuslaskuja KEMIAA KAIKKIALLA, KE1 Analyyttinen kemia tutkii aineiden määriä ja pitoisuuksia näytteissä. Pitoisuudet voidaan ilmoittaa: - massa- tai tilavuusprosentteina - promilleina tai
PAINOPISTE JA MASSAKESKIPISTE
 PAINOPISTE JA MASSAKESKIPISTE Kappaleen painopiste on piste, jonka kautta kappaleeseen kohdistuvan painovoiman vaikutussuora aina kulkee, olipa kappale missä asennossa tahansa. Jos ajatellaan kappaleen
PAINOPISTE JA MASSAKESKIPISTE Kappaleen painopiste on piste, jonka kautta kappaleeseen kohdistuvan painovoiman vaikutussuora aina kulkee, olipa kappale missä asennossa tahansa. Jos ajatellaan kappaleen
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Näiden aihekokonaisuuksien opetussuunnitelmat ovat luvussa 8.
 9. 11. b Oppiaineen opetussuunnitelmaan on merkitty oppiaineen opiskelun yhteydessä toteutuva aihekokonaisuuksien ( = AK) käsittely seuraavin lyhentein: AK 1 = Ihmisenä kasvaminen AK 2 = Kulttuuri-identiteetti
9. 11. b Oppiaineen opetussuunnitelmaan on merkitty oppiaineen opiskelun yhteydessä toteutuva aihekokonaisuuksien ( = AK) käsittely seuraavin lyhentein: AK 1 = Ihmisenä kasvaminen AK 2 = Kulttuuri-identiteetti
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Ongelmanratkaisu ja Tekstikoe HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Ongelmanratkaisu ja Tekstikoe HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
Laskun vaiheet ja matemaattiset mallit
 Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 26. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 26. syyskuuta 2016 1 / 14 Hieman kertausta
Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 26. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 26. syyskuuta 2016 1 / 14 Hieman kertausta
a) Oletetaan, että happi on ideaalikaasu. Säiliön seinämiin osuvien hiukkasten lukumäärä saadaan molekyylivuon lausekkeesta = kaava (1p) dta n =
 S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
( ) ( ) on nimeltään molekyylisironnan mikroskooppinen vaikutusala). Sijoittamalla numeroarvot saadaan vapaaksi matkaksi
 S-4.35, FYSIIKKA III, Syksy 00, LH, Loppuiikko 38 LH-* Laske happimolekyylin keskimääräinen apaa matka 300 K lämpötilassa ja,0 baarin paineessa. Voit olettaa, että molekyyli on pallon muotoinen ja pallon
S-4.35, FYSIIKKA III, Syksy 00, LH, Loppuiikko 38 LH-* Laske happimolekyylin keskimääräinen apaa matka 300 K lämpötilassa ja,0 baarin paineessa. Voit olettaa, että molekyyli on pallon muotoinen ja pallon
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Syksy 010 Jukka Maalampi LUENTO 9 Paine nesteissä Nesteen omalla painolla on merkitystä Nestealkio korkeudella y pohjasta: dv Ady dm dv dw gdm gady paino Painon lisäksi alkioon
Mekaniikan jatkokurssi Fys10 Syksy 010 Jukka Maalampi LUENTO 9 Paine nesteissä Nesteen omalla painolla on merkitystä Nestealkio korkeudella y pohjasta: dv Ady dm dv dw gdm gady paino Painon lisäksi alkioon
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Käyttämällä annettua kokoonpuristuvuuden määritelmää V V. = κv P P = P 0 = P. (b) Lämpölaajenemisesta johtuva säiliön tilavuuden muutos on
 766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma
 KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
