VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
|
|
|
- Leo Majanlahti
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET Kiertoprosessin ja termodynaamisen koneen määritelmä Termodynaamisten koneiden hyötysuhde Lämpövoimakone Lämpöpumpun tehokerroin Jäähdytyskoneen tehokerroin Ideaalikaasun Carnotin prosessi Carnotin prosessin hyötysuhde Käänteinen Carnotin prosessi Carnotin prosessin ja muiden kiertoprosessien vertailua
2 196 VIII Kiertoprosessit ja termodynaamiset koneet VIII Kiertoprosessit ja termodynaamiset koneet 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä Kiertoprosessilla tarkoitetaan kahden tai useamman tilanmuutoksen sarjaa, jossa systeemi palaa lopuksi alkuperäiseen termodynaamiseen tilaansa. Termodynaaminen kone on vastaavasti laite joka (1) toteuttaa toistuvasti kiertoprosessia, (2) ottaa ja luovuttaa lämpöä kiertoprosessin eri vaiheissa ja (3) tekee konfiguraatiotyötä ympäristöön nähden. Jos koneen tekemä työ on positiivinen, kyseessä on lämpövoimakone. Jos taas ympäristön tekemä työ on positiivinen, kyseessä on jäähdytyskone tai lämpöpumppu. Jälkimmäisten väliseen eroon palaamme myöhemmin. Seuraavissa tarkasteluissa oletamme, että koneet ovat ideaalisia eivätkä Kuva 8-1 Termodynaamisten koneiden energiavirrat. kitkan kaltaiset häviöt vaikuta koneiden hyötysuhteeseen. Kuvassa 8.1 W on systeemin tekemä työ, Q A systeemin alemmasta lämpövarastosta ottama lämpö ja Q Y systeemin ylemmästä lämpövarastosta ottama lämpö. Työn ja lämpömäärien etumerkit riippuvat termodynaamisen koneen tyypistä taulukon 8.1 mukaisesti. Termodynaamisen koneen yhden kierroksen aikana tekemän työn ja koneen saamien lämpömäärien summa on nolla. Lämpöopin ensimmäinen pääsääntö voidaan esittää termodynaamisille koneille muodossa W Q Q = Y + A. (8.1)
3 8.2 Termodynaamisten koneiden hyötysuhde Termodynaamisten koneiden hyötysuhde Lämpövoimakone Kiertoprosessin hyötysuhde määritellään prosessista ympäristöön saatavan "hyötyenergian" suhteena prosessiin "sijoitettuun" energiaan. Lämpövoimakoneen tavoitteena on tehdä mahdollisimman paljon työtä jokaista ylemmästä lämpövarastosta otettua energiayksikköä kohden. Hyötysuhde määritellään yhtälöllä W QY QA QA η = = = 1, (8.2) QY QY QY ts. hyötysuhde on systeemin tekemän työn suhde sen ylemmästä lämpövarastosta ottamaan lämpöön. Jos hyötysuhde ilmoitetaan ylemmästä varastosta otetun lämmön ja alempaan lämpövarastoon luovutetun lämmön avulla, on muistettava, että alempaan lämpövarastoon luovutettu lämpö on Q A. Taulukko 8.1 Energiavirtojen suunta termodynaamisissa koneissa Lämpövoimakone Lämpöpumppu ja jäähdytyskone W > 0 kone tekee työtä Q Y > 0 kone ottaa lämpöä ylemmästä lämpövarastosta Q A < 0 kone luovuttaa lämpöä alempaan lämpövarastoon W < 0 ympäristö tekee työtä Q Y < 0 kone luovuttaa lämpöä ylempään lämpövarastoon A Q > 0 kone ottaa lämpöä alemmasta lämpövarastosta Lämpöpumpun tehokerroin Lämpöpumpun tavoitteena on luovuttaa ylempään lämpövarastoon mahdollisimman paljon energiaa jokaista ympäristön tekemän työn energiayksikköä kohden. Hyötysuhteen sijaan puhutaan kuitenkin tehokertoimesta, joka määritellään
4 198 VIII Kiertoprosessit ja termodynaamiset koneet QY 1 ε L = W = η. (8.3) Tehokerroin on systeemin ylempään lämpövarastoon luovuttaman lämmön suhde ympäristön tekemään työhön. Lämpöpumpulle W < 0, Q Y < 0 ja Q A > 0. Lämpöpumpun tehokerroin on vastaavaa (reversiibeliä) kiertoprosessia suorittavan lämpövoimakoneen hyötysuhteen käänteisluku. Palaamme tähän Carnotin koneen yhteydessä Jäähdytyskoneen tehokerroin Jäähdytyskoneen tavoitteena on poistaa mahdollisimman paljon lämpöä alemmasta varastosta jokaista ympäristön tekemän työn energiayksikköä kohden, joten sen tehokerroin määritellään ε J QA W QY = = = εl 1. (8.4) W W Tehokerroin on siis alemmasta varastosta poistettu energia jaettuna ympäristön tekemällä työllä. Yhtälössä 8.4 jäähdytyskoneen tehokerroin on esitetty myös vastaavan lämpöpumpun tehokertoimen avulla käyttäen hyväksi ensimmäisestä pääsäännöstä seuraavaa yhtälöä 8.1. Kiertoprosessissa tehdyn työn ja hyötysuhteen laskemi- Esimerkki 8.1. nen. Tarkastellaan kuvan 8-2 prosessia. Sylinterissä on 58 g ilmaa, joka suorittaa seuraavan kiertoprosessin: 1 2 isobaarinen laajeneminen, 2 3 isokoorinen jäähdytys ja 3 1 adiabaattinen puristus. Lasketaan ilman tekemä työ ja prosessin hyötysuhde, kun tunnetaan tilaavuudet 3 3 V 1 = 20,0 dm ja V2 = V3 = 50,0 dm sekä paineet p1 = p2 = 5 bar ja p 3 = 1,39 bar. Kuva 8-2 Kiertoprosessin hyötysuhteen laskeminen. Lasketaan aluksi moolimäärä. Ilman keskimääräinen molekyylipaino on 29,0 g/mol, joten ν = 2. Happi ja typpi ovat
5 8.2 Termodynaamisten koneiden hyötysuhde 199 kaksiatomisia molekyylejä. Oletamme, että niillä on 5 aktiivista vapausastetta ( f = 5 ). Ominaislämmöt ovat cv = 5/2R ja cp = 7/2R ja adiabaattivakio γ = cp/ cv = 1,40. Lasketaan kaasun saama lämpömäärä eri osaprosesseissa. 1 2 Isobaarinen laajeneminen: QY = Q12 = νcp ( T2 T1 ) = ν( 7/2 ) R ( T2 T1 ) = ( 7/2 )( pv 2 2 pv 1 1) = 52,2 kj. 2 3 Isokoorinen jäähdytys: QA = Q23 = νcv ( T3 T2 ) = ν( 5/2 ) R ( T2 T3 ) = ( 5/2 )( pv 2 2 pv 3 3) = 45,2 kj 3 1 adiabaattisessa prosessissa Q 31 = 0. Systeemin tekemä työ = ylemmästä varastosta saadun lämmön ja alempaan varastoon luovutetun lämmön erotus W = QY QA = 7,3 kj, joten hyötysuhteeksi saadaan määritelmän mukaan η = W / Q Y = 14 %. Esimerkki 8.2. Ideaalinen Ottoprosessi on autoissa yleisesti käytetty kiertoprosessi. Oheinen kuva esittää Otto-prosessin tilanmuutokset: 0 1 Kaasu imetään sylinteriin. Imu oletetaan häviöttömäksi. Kaasuuntuneen polttoaineen ja ilman seos on ulkoilman paineessa. 1 2 Adiabaattinen puristus minimitilavuuteen. Oletetaan, että puristus on nopea, joten lämpöä ei ehdi siirtyä seinämiin, mutta samalla riittävän hidas, jotta prosessi on kvasistaattinen (kaasu homogeenista). Kuva 8-3 Ideaalisen Otto-prosessin tilanmuutokset. 2 3 Isokoorinen muutos polttoaineen palaessa räjähdyksenomaisesti ja luovuttaessa lämpömäärän Q Y > 0 systeemiin. 3 4 Kaasu laajenee adiabaattisesti ja tekee työtä. 4 5 Isokoorinen jäähtyminen paineen laskiessa normaali-ilmanpaineeseen. Tämä on karkea approksimaatio, sillä tyhjennyksen alkaessa palokaa-
6 200 VIII Kiertoprosessit ja termodynaamiset koneet sujen lämpötila on huomattavan korkea. Kaasu luovuttaa lämpöä ympäristöön, joten Q A < Jäähtyneen ja yhden ilmankehän paineeseen laajentuneen kaasun kitkaton työntäminen pois sylinteristä. Hyötysuhteen laskeminen Ylemmästä lämpövarastosta otetaan energiaa isokoorisessa muutoksessa 2 3. Saatu lämpömäärä on QY = νcv( T3 T2) > 0. Alempaan lämpövarastoon luovutetaan energiaa isokoorisessa muutoksessa 4 1, jolloin kaasun saama lämpömäärä on (<0) QA = νcv( T1 T4) < 0. Lämpövoimakoneen hyötysuhteen määritelmän mukaan η W QY QA QA T T = = = = 1 QY QY QY T3 T2. (8.5) Sievennetään 8.5 käyttämällä ideaalikaasun adiabaattiselle prosessille päteviä yhtälöitä pv γ = vakio ja p = ν RT / V. Sijoittamalla jälkimmäisestä saatu paine edelliseen saamme uudeksi adiabaattista prosessia kuvaavaksi yhtälöksi TV γ 1 = vakio. (8.6) Yhtälön (8.6) avulla saadaan TV 3 3 γ TV 4 4 γ ; TV 2 2 γ TV 1 1 γ = =. Kuvan 8-3 mukaan V1 = V4 ja V2 = V3, joten Ratkaistaan tästä suhde T1/ T 2: TV 3 3 γ TV 4 1 γ ; TV 2 3 γ TV 1 1 γ = =. T3 T4 T3 T2 T4 T1 T1 T4 T1 = = = T2 T1 T2 T1 T2 T3 T2 Sijoittamalla tämä yhtälöön 8.5 saadaan hyötysuhteeksi. η =. (8.7) 1 T1/ T2 1/( γ -1) Hyötysuhde 8.7 voidaan esittää puristussuhteen ε = ( V / V ) = ( T / T ) (adiabaattinen prosessi) avulla muodossa ( γ 1) η = 1 ε. (8.8)
7 8.2 Termodynaamisten koneiden hyötysuhde 201 Yhtälöstä 8.8 nähdään, että hyötysuhde kasvaa puristussuhteen ε kasvaessa. Korkea puristussuhde johtaa kaasuseoksen lämpenemiseen puristuksen aikana. Polttoaineen itsesytytys pyritään estämään polttoaineseoksen sopivalla koostumuksella (lisäaineilla). Esimerkki 8.3. Ideaalinen Dieselprosessi on toinen autojen voimanlähteiden yleinen kiertoprosessi. Kuva 8-4 esittää ideaalisen Diesel-prosessin tilanmuutoksia. 0 1 Ilma imetään sylinteriin. 1 2 Ilman adiabaattinen puristus yläkuolokohtaan. 2 3 Palovaihe, jolloin polttoaine ruiskutetaan sylinteriin. Polttoaine Kuva 8-4 Diesel-prosessin tilanmuutokset palaa isobaarisesti, jolloin kaasu laajenee ja tekee työtä. Tässä vaiheessa systeemiin (kaasuseokseen) tuodaan lämpö Q Y kemiallisena energiana. 3 4 Palamistuotteet laajenevat adiabaattisesti ja tekevät lisää työtä männän siirtyessä alakuolokohtaan Isokoorinen paineenlasku, jäädytys ja palamistuotteiden poisto kuten ottomoottorissakin (karkea yksinkertaistus). Hyötysuhteen laskeminen Isobaarisessa prosessissa 2 3 saadaan lämpöä systeemiin, joten QY = νcp ( T3 T2 ) > 0. Vastaavasti lämpöä luovutetaan alempaan lämpövarastoon isokoorisessa prosessissa 4 1: QA = νcv( T1 T4) < 0. Lämpövoimakoneen hyötysuhteen määritelmän perusteella onη = 1 QA / QY. Sijoittamalla saadaan Diesel-prosessin hyötysuhteeksi η ( 4 1) ( ) cv T T = 1 cp T3 T2. (8.9) Sijoittamalla adiabaattivakio γ = cp/ cv yhtälöön 8.9 saadaan hyötysuhde muotoon
8 202 VIII Kiertoprosessit ja termodynaamiset koneet η 1 1 T4 T1 1 T4 T T2 = = γ T3 T2 γ T1 T1 T1 (8.10) Diesel-prosessia kuvattaessa tarvitaan kaksi parametria. Puristussuhde määritellään kuten Otto-prosessissakin: ε ( γ ) 1/ 1 V1 T2 = = V2 T1 (8.11) Toinen parametri on polttosuhde eli täyspainesuhde φ, jonka määrää pääasiassa polttoaineen ruiskutuksen kesto, V3 T3 V2 T2 φ = =. (8.12) Esitämme seuraavaksi hyötysuhteen 8.10 näiden parametrien avulla. Prosessi 2 3 on isobaarinen joten p2 = νrt2/ V2 = p3 = νrt3/ V3. Osaprosessi 3 4 on adiabaattinen, joten käyttämällä yhtälöä 1 TV γ = vakio ja määritelmiä 8.11 ja (8.12) γ 1 γ 1 γ 1 T4 V3 V3 φ = = = T3 V4 V1 ε ja γ 1 T4 T4 T3 T2 φ γ 1 γ = = φ ε = φ. T1 T3 T2 T1 ε Sijoittamalla näistä yhtälöistä lämpötilasuhteet yhtälöön 8.10 saadaan η γ 1 φ 1 = 1 γ 1 ε γ φ ( 1). (8.13) γ Polttosuhteen sisältävä tekijä ( φ 1) γ( φ 1) on aina suurempi kuin yksi. Samalla puristussuhteen arvolla Diesel-prosessin hyötysuhde on siis pienempi kuin ottoprosessin, ja hyötysuhde lähestyy Otto-prosessin arvoa, kun polttosuhde pienenee kohti ykköstä. Diesel-moottorissa käytettävä polttoaine, dieselöljy, mahdollistaa kuitenkin korkeamman puristussuhteen, mikä suurentaa moottorin hyötysuhdetta.
9 8.3 Ideaalikaasun Carnotin prosessi Ideaalikaasun Carnotin prosessi Carnotin (N.L. Carnot ) kiertoprosessi on termodynamiikassa erityisasemassa, koska se on tehokkain tapa muuttaa lämpöä työksi kahden lämpövaraston välissä toimivassa termodynaamisessa koneessa. Carnotin prosessin työaineena voi olla mikä tahansa termodynaaminen systeemi: kaasu, neste, kiinteä aine tai paramagneettinen väliaine. Carnotin kone toimii kahden lämpövaraston välissä, ja pvt-systeemin Carnotin kiertoprosessi koostuu seuraavista neljästä prosessista: Kuva 8-5 Carnotin prosessia toistavan koneen toimintaperiaate. Sylinterin seinät, mäntä ja eriste E ovat ideaalisia eristeitä, kun taas sylinterin kansi on täydellinen johde. Isoterminen lämmönotto ylemmästä lämpövarastosta T Y. Lämpö Q Y > 0 siirtyy kaasuun samalla kun kaasu laajenee ja tekee työtä. Prosessi 1 2 kuvissa 8-5,6. Adiabaattinen siirtyminen alempaan lämpötilaan T A. Sylinterikansi on kosketuksessa eristeeseen B ja kaasu laajenee edelleen adiabaattisesti ja tekee lisää työtä. Samalla kaasu jäähtyy alemman lämpövaraston lämpötilaan T A. Prosessi 2 3 kuvissa 8-5,6. Kuva 8-6 Carnotin kiertoprosessin osat p- V tasossa.
10 204 VIII Kiertoprosessit ja termodynaamiset koneet Isoterminen lämmön luovutus alempaan lämpövarastoon. Isoterminen puristus, jossa kansi on kontaktissa alempaan lämpövarastoon Q A < 0. Prosessi 3 4 kuvissa 8-5,6. Adiabaattinen paluu lämpötilaan T Y. Kaasua puristetaan lisää adiabaattisesti, jolloin kaasu lämpenee ylemmän lämpövaraston lämpötilaan T Y. Prosessi 4 1 kuvissa 8-5,6. Taulukko 8.2 Carnotin kiertoprosessin tilamuutoksien työt ja lämpömäärät Prosessi Työ Lämpömäärä Perustelu 1 2 W12 = ν RTY ln V2 V1 V2 QY = ν RTY ln V1 Isoterminen prosessi, W = Q Y 2 3 W23 = νc ( T T ) Q = 0 Adiabaattinen prosessi V Y A 3 4 W 34 4 A ln V = ν RT V3 Q V RT 4 = V3 A ν A ln Isoterminen prosessi, W = Q A 4 1 W41 = νc ( T T ) Q = 0 Adiabaattinen prosessi V A Y Carnotin prosessin hyötysuhde Käyttämällä isotermisten ja adiabaattisten prosessien ominaisuuksia saadaan osaprosesseihin liittyvät työt ja lämmöt. Ideaalikaasulle systeemin tekemä työ isotermisessä prosessissa on W = ν RTln ( V2 / V1) ja adiabaattisessa prosessissa vastaavasti W fνr( T T ) νc ( T T ) = (1/ 2) 1 2 = V 1 2. Käyttämällä lisäksi ensimmäistä pääsääntöä saamme taulukon 8.2. Systeemin kiertoprosessin aikana tekemä kokonaistyö on ( ) ν ( ) W Q Q RT V V RT V V = Y A = ν Y ln 2 / 1 + Aln 4 / 3. (8.14) = vakio saa- Käyttämällä adiabaattiselle prosessille pätevää yhtälöä daan 1 TV γ
11 8.3 Ideaalikaasun Carnotin prosessi 205 TV TV V. TV = γ 1 γ 1 Y 2 = A 3 V2 3 (jakamalla puolittain) γ 1 γ 1 = V Y 1 TV A 4 1 V4 Sijoittamalla tämä työn lausekkeeseen saadaan ( ) W R T T V V = ν ( Y A)ln 2 / 1. (8.15) Tästä saadaan Carnotin prosessia toteuttavan lämpövoimakoneen hyötysuhteelle: W TY TA TA ηc = = = 1. (8.16) Q T T Y Y Y Käänteinen Carnotin prosessi Käänteisellä Carnotin prosessilla tarkoitetaan kuvan 8.6 kiertoprosessia ( ). Kaikki kaasun saamat lämpömäärät ja työt vaihtavat etumerkkinsä kiertosuunnan vaihtuessa. Kaasun kiertoprosessin aikana tekemä työ on siis W ν R( TA TY)ln ( V2 / V1) vutettu lämpömäärä Q ν RT ln ( V / V ) = ja ylempään lämpövarastoon luo- Y Y 2 1. Käänteistä Carnotin prosessia hyödyntävän lämpöpumpun tehokerroin on siis määritelmän mukaan QY TY 1 ε L = 1 W = TY T = A η >. (8.17) c Käänteistä Carnotin prosessia hyödyntävän jäähdytyskoneen tehokerroin on vastaavasti ( ) ε = ε 1 = T / T T. (8.18) J L A Y A Carnotin prosessin ja muiden kiertoprosessien vertailua Osoitamme seuraavaksi, että Carnotin prosessin hyötysuhde on suurin mahdollinen termodynaamiselle koneelle, joka toimii lämpövarastojen T Y ja T A välillä. Kuva 8.7 esittää kahta kytkettyä termodynaamista konetta. Kone A on tuntematonta kiertoprosessia toteuttava lämpövoimakone, jonka hyötysuhteen η * oletamme korkeammaksi kuin käänteistä Carnotin prosessia toteuttavan lämpöpumpun B hyötysuhteen η c. Lämpövoimakoneen A
12 206 VIII Kiertoprosessit ja termodynaamiset koneet tuottama mekaaninen työ käytetään lämpöpumpussa B lämmön siirtämiseen alemmasta lämpövarastosta ylempään lämpövarastoon. Oletamme, että kone A tuottaa työtä * määrän W = QY η *, joka käytetään kokonaisuudessaan koneessa B lämmön siirtämiseen käänteisellä Carnotin prosessilla alemmasta lämpövarastosta ylempään lämpövarastoon. Käänteisessä Carnotin prosessissa B ylempään varastoon siirretylle lämmölle saadaan taulukon 8.2 perusteella, vaihtamalla työn ja lämpömäärän etumerkki, Kuva 8-7 Carnotin koneen B ja muun lämpövoimakoneen A yhdistelmä. ( ) * * * Y / ηc Y η ηc Y Q = W = Q > Q. (8.19) Lämpöä olisi tällöin siirretty alemmasta lämpövarastosta ylempään ilman ulkoista työtä! Tämä on havaittu kokeellisesti mahdottomaksi ja kyseistä empiiristä havaintoa kutsutaan lämpöopin toiseksi pääsäännöksi. Käsittelemme toista pääsääntöä lähemmin seuraavassa luvussa. Toisesta pääsäännöstä seuraa, että ylempään * lämpövarastoon luovutettavalle lämpömäärälle pätee QY QY, josta edelleen yhtälön 8.19 perusteella η* ηc. Koneen A hyötysuhde voi siis olla enintään Carnotin prosessin hyötysuhde η c.
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
Käytetään lopuksi ideaalikaasun tilanyhtälöä muutoksille 1-2 ja 3-1. Muutos 1-2 on isokorinen, joten tilanyhtälöstä saadaan ( p2 / p1) = ( T2 / T1)
 LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 14.11. ja tiistai 15.11. Kurssin aiheet 1. Lämpötila ja lämpö
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 14.11. ja tiistai 15.11. Kurssin aiheet 1. Lämpötila ja lämpö
Luku6 Tilanyhtälö. Ideaalikaasun N V. Yleinen aineen. paine vakio. tilavuus vakio
 Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
6-1 Hyötysuhde ja tehokerroin
 67 6 Lämpövoimakoneet ja jäähdyttimet 6-1 Hyötysuhde ja tehokerroin Lämpövoimakone (engl. heat engine) on laite, joka muuttaa lämpöenergiaa työksi. Tavallisesti laitteessa tapahtuu kiertoprosessi, jonka
67 6 Lämpövoimakoneet ja jäähdyttimet 6-1 Hyötysuhde ja tehokerroin Lämpövoimakone (engl. heat engine) on laite, joka muuttaa lämpöenergiaa työksi. Tavallisesti laitteessa tapahtuu kiertoprosessi, jonka
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 9 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 9 / 14.11.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Vielä vähän entropiasta... Termodynamiikan 2. pääsääntö Entropian rooli 2. pääsäännön yhteydessä
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 9 / 14.11.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Vielä vähän entropiasta... Termodynamiikan 2. pääsääntö Entropian rooli 2. pääsäännön yhteydessä
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
Lämpöopin pääsäännöt. 0. pääsääntö. I pääsääntö. II pääsääntö
 Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
VII LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ
 II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-445, Fysiikka III (Sf) tentti/välikoeuusinta 43 välikokeen alue ristetyssä astiassa, jonka lämötila idetään, kelvinissä, on nestemäistä heliumia tasaainossa helium kaasun kanssa Se on erotettu toisesta
S-445, Fysiikka III (Sf) tentti/välikoeuusinta 43 välikokeen alue ristetyssä astiassa, jonka lämötila idetään, kelvinissä, on nestemäistä heliumia tasaainossa helium kaasun kanssa Se on erotettu toisesta
Termodynaamiset syklit Todelliset tehosyklit
 ermodynaamiset syklit odelliset tehosyklit Luennointi: k Kati Miettunen Esitysmateriaali: k Mikko Mikkola HYS-A00 ermodynamiikka (FM) 09..05 Syklien tyypit Sisältö Kaasusyklit s. höyrysyklit Suljetut syklit
ermodynaamiset syklit odelliset tehosyklit Luennointi: k Kati Miettunen Esitysmateriaali: k Mikko Mikkola HYS-A00 ermodynamiikka (FM) 09..05 Syklien tyypit Sisältö Kaasusyklit s. höyrysyklit Suljetut syklit
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Luku 6 TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 6 TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Pentti Saarenrinne Copyright TUT and The McGraw-Hill Companies,
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 6 TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Pentti Saarenrinne Copyright TUT and The McGraw-Hill Companies,
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
Valitse seuraavista joko tehtävä 1 tai 2
 PHYS-A0120 Termodynamiikka, syksy 2016 Kotitentti Vastaa tehtäviin 1/2, 3, 4/5, 6/7, 8 ja 9 (yhteensä kuusi vastausta). Tehtävissä 1 ja 2 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2016 Kotitentti Vastaa tehtäviin 1/2, 3, 4/5, 6/7, 8 ja 9 (yhteensä kuusi vastausta). Tehtävissä 1 ja 2 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, Luku 7 ENTROPIA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt
 14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit
 19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
Termodynamiikan toinen pääsääntö (Second Law of Thermodynamics)
 e1 3 Termodynamiikan toinen pääsääntö (Second Law of Thermodynamics) Tärkeä käsite termodynamiikassa on termodynaamisen prosessin suunta. Kaikki prosessit ovat oikeasti irreversiibelejä (irreversible),
e1 3 Termodynamiikan toinen pääsääntö (Second Law of Thermodynamics) Tärkeä käsite termodynamiikassa on termodynaamisen prosessin suunta. Kaikki prosessit ovat oikeasti irreversiibelejä (irreversible),
Oikeasta vastauksesta (1p): Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
Luku Pääsääntö (The Second Law)
 Luku 3 2. Pääsääntö (he Second Law) Some things happen naturally, some things don t Spontaneous must be interpreted as a natural tendency that may or may not be realized in prac=ce. hermodynamics is silent
Luku 3 2. Pääsääntö (he Second Law) Some things happen naturally, some things don t Spontaneous must be interpreted as a natural tendency that may or may not be realized in prac=ce. hermodynamics is silent
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
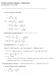 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
n = = RT S Tentti
 S-5 Tetti 500 a) Kuika suuri o molekyylie traslaatioliikkee kieettie eergia kuutiometrissä ilmaa jos ilma lämpötila o 00 K ja paie 0 bar? b) Mikä o kieettise eergia kokoaismäärä ku myös muut liikelajit
S-5 Tetti 500 a) Kuika suuri o molekyylie traslaatioliikkee kieettie eergia kuutiometrissä ilmaa jos ilma lämpötila o 00 K ja paie 0 bar? b) Mikä o kieettise eergia kokoaismäärä ku myös muut liikelajit
Tekijä: Markku Savolainen. STIRLING-moottori
 Tekijä: Markku Savolainen STIRLING-moottori Perustietoa Perustietoa Palaminen tapahtuu sylinterin ulkopuolella Moottorin toiminta perustuu työkaasun kuumentamiseen ja jäähdyttämiseen Työkaasun laajeneminen
Tekijä: Markku Savolainen STIRLING-moottori Perustietoa Perustietoa Palaminen tapahtuu sylinterin ulkopuolella Moottorin toiminta perustuu työkaasun kuumentamiseen ja jäähdyttämiseen Työkaasun laajeneminen
S , Fysiikka III (ES) Tentti Tentti / välikoeuusinta. Laaditaan taulukko monisteen esimerkin 3.1. tapaan ( nj njk Pk
 S-.35, Fysiia III (ES) entti 8..3 entti / välioeuusinta I älioeen alue. Neljän tunnistettavissa olevan hiuasen miroanonisen jouon mahdolliset energiatasot ovat, ε, ε, 3ε, ε,, jota aii ovat degeneroitumattomia.
S-.35, Fysiia III (ES) entti 8..3 entti / välioeuusinta I älioeen alue. Neljän tunnistettavissa olevan hiuasen miroanonisen jouon mahdolliset energiatasot ovat, ε, ε, 3ε, ε,, jota aii ovat degeneroitumattomia.
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
