vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
|
|
|
- Anton Hakala
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen
2 ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin tehty työ on systeemin sisäenergian muutos, ts. U = Q + W DEE-5400 Risto Mikkonen
3 ilavuuden muutostyö W 1 =? 3 DEE-5400 Risto Mikkonen
4 ilavuuden muutostyö W 1 =? W p dv DEE-5400 Risto Mikkonen
5 Esimerkki olttomoottorin sylinterin kaasun ominaissisäenergia on 800 kj/kg ja ominaistilavuus 0.06 m 3 paisunnan alkaessa. aisunta tapahtuu paineesta 55 bar paineeseen 1.4 bar, jolloin paineen riippuvuus ominaistilavuudesta on pv 1.5 vakio aisunnan jälkeen ominaissisäenergia on 30 kj/kg. Määritä sylinteristä jäähdytysveteen siirtynyt lämpö sylinterissä olevaa kaasun massayksikköä kohti. 5 DEE-5400 Risto Mikkonen
6 Esimerkki (Cont.) Alussa: u 1 = 800 kj/kg, v 1 = 0.06 m 3 /kg p 1 = 55 bar u p v Lopussa: u = 30 kj/kg, p = 1.4 bar 6 DEE-5400 Risto Mikkonen
7 Entropia Lämmön tasaantumisilmiöitä kuvaava suure Suljetun systeemin entropia ei koskaan pienene termodynaamisessa prosessissa. ämä tarkoittaa systeemin kehittymistä kohti todennäköisempiä ja vähemmän järjestäytyneitä tiloja. Jos entropia pysyy vakiona, prosessi on reversiibeli (käänteinen), ja voi siis tapahtua kumpaan suuntaan tahansa. Jos entropia kasvaa, prosessi ei ole reversiibeli, ja sen kehitys voi edetä vain yhteen suuntaa. 7 DEE-5400 Risto Mikkonen
8 Entropia (Cont.) S dq Mikäli kappaleen lämpötila muutuu 1 :stä :een olomuodon pysyessä muuttumattomana S 1 mcd mc ln 1 S tot S t y 0 8 DEE-5400 Risto Mikkonen
9 Carnot -prosessi 9 DEE-5400 Risto Mikkonen
10 Carnot n hyötysuhde c 1 out in 10 DEE-5400 Risto Mikkonen
11 Esimerkki Kumpi on tehokkaampi tapa kahden lämpösäiliön välillä toimivan Carnot n voimakoneen hyötysuhteen nostamiseksi: korkeamman lämpötilan 1 nostaminen alemman lämpötilan pysyessä vakiona vai :n laskeminen 1 :n pysyessä vakiona. 11 DEE-5400 Risto Mikkonen
12 Esimerkki Määritä vaadittava minimityö jäähdytettäessä kg vettä lämpötilaan 5 0 C allulämpötilasta 5 0 C vakiopaineessa. Veden ominaislämpö C p = kj/kgk. Ympäristön lämpötila on 5 0 C. 1 DEE-5400 Risto Mikkonen
13 Entalpia ja Gibbsin vapaa energia G ; aineeseen sitoutunut kokonaisenergia sisäenergian ja paisuntatyön summa = U + pv G; maksimi sähköenergia prosessista saatu maksimityö G = U + pv - S 13 DEE-5400 Risto Mikkonen
14 ilasuureet Sisäenergia Entalpia Gibbsin vapaa energia U = Q + W = U + pv G = S elmholtzin vapaa energia F = U - S 14 DEE-5400 Risto Mikkonen
15 ilasuureet - differentiaalimuodot du = ds dv d = ds + V d dg = - S d + V d da = - S d dv 15 DEE-5400 Risto Mikkonen
16 ilasuureiden väliset differentiaalikaavat avoitteena on 1. Johtaa eri tilasuureiden (p, V,, S, U,, F ja G) väliset differentiaaliyhtälöt. Valita riippumattomiksi suureiksi helposti mitattavat suureet, kuten p, V, Maxwellin yhtälöt 16 DEE-5400 Risto Mikkonen
17 Maxwellin yhtälöt v s p s v p s v s p p v s v v p s p 17 DEE-5400 Risto Mikkonen
18 Esimerkki soita, että ideaalikaasulle (vety, vesihöyry) Entalpia Sisäenergia h (, p) = h() u (, v) = u() 18 DEE-5400 Risto Mikkonen
19 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. Ideaalitapauksessa koko Gibbsin energia muuttuu sähköksi. Kennon reversiibeli tyhjäkäyntijännite 1 19 DEE-5400 Risto Mikkonen
20 Molaarinen lämpökapasiteetti dh = ds + v dp = dq + v dp Kun paine on vakio dh = dq dq d p dh d p c p C p on siis mitta sille, kuinka paljon lämpöä tasetila tarvitsee tietyn lämpötilaeron aikaansaamiseksi vakiopaineessa d s 1 dh 0 DEE-5400 Risto Mikkonen
21 Molaarinen lämpökapasiteetti C p DEE-5400 Risto Mikkonen : : : C C C p p p
22 Avogadron luku Yksi mooli mitä tahansa ainetta sisältää aina saman määrän molekyylejä 6.0 x 10 3 ( = N ) Yksi mooli elektroneja käsittää siis N kpl elektroneja Kokonaisvaraus siis N x e (e = 1.60 x C) Faraday n vakio F = N x e C DEE-5400 Risto Mikkonen
23 Reversiibeli tyhjäkäyntijännite Fosforihappokenno: Kaksi elektronia kulkeutuu ulkoisen ( op = 00 0 C) piirin kautta yhtä tuotettua vesimolekyyliä ja yhtä vetymolekyyliä kohti. Kokonaisvaraus: - x N x e = - x F Siis: ehty työ = varaus x jännite = - x F x e = g g 0000 J E F C V 3 DEE-5400 Risto Mikkonen
24 Reversiibeli tyhjäkäyntijännite (Cont.) Yleisesti E z g F z: siirrettyjen elektronien lukumäärä jokaista polttoainemolekyyliä kohti arjoitus: Määritä suoran metanolipolttokennon reversiibeli tyhjäkäyntijännite. 4 DEE-5400 Risto Mikkonen
25 olttokennon hyötysuhde tuotettusähköenergia Gibbsin vapaanenergian muutos polttoainemolekyylintuottamasähköenergia h max g h 100 % ermodynaaminen hyötysuhde 5 DEE-5400 Risto Mikkonen
26 olttokennon hyötysuhde (Cont.) Mikäli vedyn koko energia (entalpian muutos) voidaan muuttaa sähköksi: E h F 1.48 V ( V ) V : vedyn ylempi lämpöarvo (reaktiossa syntynyt vesi nesteenä) LV : vedyn alempi lämpöarvo (reaktiossa syntynyt vesi kaasuna) V c % V c todellinen kennojännite f Vc % f reagoineen ja sisäänsyötetyn polttoainemäärän suhde 6 DEE-5400 Risto Mikkonen
27 G = G (,, c) j J + k K m M Ideaalikaasulle aktiivisuus 0 0 = 0.1 Ma g g 0 R ln a j J a a m M k K R yleinen kaasuvakio = J / mol K 7 DEE-5400 Risto Mikkonen
28 erusreaktioyhtälö DEE-5400 Risto Mikkonen 8 1 a a a R g g 1 0 ln E a a a F R F g E ln Nernstin yhtälö
29 Nernstin yhtälö DEE-5400 Risto Mikkonen ; ; a a a ln F R E E
30 Nernstin yhtälö (Cont.) Kun prosessin paineet yksikössä bar 0 = 1 E E 0 R F ln 1 30 DEE-5400 Risto Mikkonen
31 Nernstin yhtälö (Cont.) olttokennon reaktioissa olevat kaasut ovat usein jonkinlaisia seoksia (katodille ilmaa, anodilla vedyn seassa hiilidioksidia) ; ; on prosessipaine E E 0 R F ln DEE-5400 Risto Mikkonen
32 Nernstin yhtälö (Cont.) E E 0 R ln 1 R ln ( ) F 4 F 3 DEE-5400 Risto Mikkonen
33 arjoitus arkastele a) systeemin paineen b) vedyn osapaineen c) hapen osapaineen vaikutusta kennon tyhjäkäyntijännitteeseen 33 DEE-5400 Risto Mikkonen
34 Esimerkki arkastellaan polttokennon anodilla ja katodilla tapahtuvia seuraavia reaktioita C 5 C 3 C e 1 e Mistä sovellutuksesta on kysymys? 34 DEE-5400 Risto Mikkonen
35 35 DEE-5400 Risto Mikkonen
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE Kryogeniikka
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold tip tirling aim com mod.jpg Introduced about
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold tip tirling aim com mod.jpg Introduced about
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
Luku Pääsääntö (The Second Law)
 Luku 3 2. Pääsääntö (he Second Law) Some things happen naturally, some things don t Spontaneous must be interpreted as a natural tendency that may or may not be realized in prac=ce. hermodynamics is silent
Luku 3 2. Pääsääntö (he Second Law) Some things happen naturally, some things don t Spontaneous must be interpreted as a natural tendency that may or may not be realized in prac=ce. hermodynamics is silent
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Termodynaamiset syklit Todelliset tehosyklit
 ermodynaamiset syklit odelliset tehosyklit Luennointi: k Kati Miettunen Esitysmateriaali: k Mikko Mikkola HYS-A00 ermodynamiikka (FM) 09..05 Syklien tyypit Sisältö Kaasusyklit s. höyrysyklit Suljetut syklit
ermodynaamiset syklit odelliset tehosyklit Luennointi: k Kati Miettunen Esitysmateriaali: k Mikko Mikkola HYS-A00 ermodynamiikka (FM) 09..05 Syklien tyypit Sisältö Kaasusyklit s. höyrysyklit Suljetut syklit
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
4. Termodynaamiset potentiaalit
 Statistinen fysiikka, osa A (FYSA241) uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty
Statistinen fysiikka, osa A (FYSA241) uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Lämpöopin pääsäännöt. 0. pääsääntö. I pääsääntö. II pääsääntö
 Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Kemiallinen reaktio
 Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
7 Termodynaamiset potentiaalit
 82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / TERVETULOA! Termodynamiikan 1. pääsääntö 9/25/2017
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 25.9.2017 TERVETULOA! v. 03 / T. Paloposki Tämän päivän ohjelma: Termodynamiikan 1. pääsääntö 1 Termodynamiikan 1. pääsääntö (energian säilymisen laki,
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 25.9.2017 TERVETULOA! v. 03 / T. Paloposki Tämän päivän ohjelma: Termodynamiikan 1. pääsääntö 1 Termodynamiikan 1. pääsääntö (energian säilymisen laki,
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics is Two Laws and a Li2le Calculus
 Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Luento 2: Lämpökemiaa, osa 1 Torstai klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
vetyteknologia Muut kennotyypit 1 Polttokennot ja vetyteknologia Risto Mikkonen
 DEE-5400 Polttokennot ja vetyteknologia Muut kennotyypit 1 Polttokennot ja vetyteknologia Risto Mikkonen Alkaalipolttokennot Anodi: Katodi: H 4OH 4 H O 4e O e H O 4OH 4 Avaruussovellutukset, ajoneuvokäytöt
DEE-5400 Polttokennot ja vetyteknologia Muut kennotyypit 1 Polttokennot ja vetyteknologia Risto Mikkonen Alkaalipolttokennot Anodi: Katodi: H 4OH 4 H O 4e O e H O 4OH 4 Avaruussovellutukset, ajoneuvokäytöt
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
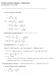 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
4. Termodynaamiset potentiaalit
 FYSA241, kevät 2012 uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2012 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty järjestelmä
FYSA241, kevät 2012 uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2012 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty järjestelmä
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 9/26/2016
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 26.9.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 1 Kotilasku 2 Kotilasku 2 2 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 26.9.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 1 Kotilasku 2 Kotilasku 2 2 Termodynamiikan
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen
 KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
4. Termodynaamiset potentiaalit
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2015 4. ermodynaamiset potentiaalit 1 ermodynaaminen tasapaino kanonisessa joukossa Mikrokanoninen
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2015 4. ermodynaamiset potentiaalit 1 ermodynaaminen tasapaino kanonisessa joukossa Mikrokanoninen
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
DEE Polttokennot ja vetyteknologia
 DEE-54020 Polttokennot ja vetyteknologa Polttokennon hävöt 1 Polttokennot ja vetyteknologa Rsto Mkkonen Polttokennon tyhjäkäyntjännte Teoreettnen tyhjäkäyntjännte E z g F Todellnen kennojännte rppuu er
DEE-54020 Polttokennot ja vetyteknologa Polttokennon hävöt 1 Polttokennot ja vetyteknologa Rsto Mkkonen Polttokennon tyhjäkäyntjännte Teoreettnen tyhjäkäyntjännte E z g F Todellnen kennojännte rppuu er
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
Biofysiikka Luento Entropia, lämpötila ja vapaa energia. Shannonin entropia. Boltzmannin entropia. Lämpötila. Vapaa energia.
 Biofysiikka Luento 7 1 6. Entropia, lämpötila ja vapaa energia Shannonin entropia Boltzmannin entropia M I NK P ln P S k B j1 ln j j Lämpötila Vapaa energia 2 Esimerkkiprobleemoita: Miten DNA-sekvenssistä
Biofysiikka Luento 7 1 6. Entropia, lämpötila ja vapaa energia Shannonin entropia Boltzmannin entropia M I NK P ln P S k B j1 ln j j Lämpötila Vapaa energia 2 Esimerkkiprobleemoita: Miten DNA-sekvenssistä
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
6. Entropia, lämpötila ja vapaa energia
 6. Entropia, lämpötila a vapaa energia 1 Luento 6 24.2.2017: Shannonin entropia M I NK P ln P 1 Boltzmannin entropia S k B ln Lämpötila Vapaa energia 2 Probleemoita: Miten DNA-sekvenssistä määräytyvän
6. Entropia, lämpötila a vapaa energia 1 Luento 6 24.2.2017: Shannonin entropia M I NK P ln P 1 Boltzmannin entropia S k B ln Lämpötila Vapaa energia 2 Probleemoita: Miten DNA-sekvenssistä määräytyvän
Konventionaalisessa lämpövoimaprosessissa muunnetaan polttoaineeseen sitoutunut kemiallinen energia lämpö/sähköenergiaksi höyryprosessin avulla
 Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 28.9.2015 / T. Paloposki / v. 01 Tämän päivän ohjelma: Tilanyhtälöt (kertaus) Termodynamiikan 1. pääsääntö (energian häviämättömyyden laki)
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 28.9.2015 / T. Paloposki / v. 01 Tämän päivän ohjelma: Tilanyhtälöt (kertaus) Termodynamiikan 1. pääsääntö (energian häviämättömyyden laki)
Ideaalikaasulaki johdettuna mikroskooppisen tarkastelun perusteella! Lämpötila vaikuttaa / johtuu molekyylien kineettisestä energiasta
 HYS-A00 Termodynamiikka (TFM), Luentomuistiinpanot Luennot 7-8, kertaus, mitkä olivat oppimistavoitteet? Kineettinen kaasuteoria Oletukset: - kaasun tiheys on riittävän suuri - molekyylin koko on paljon
HYS-A00 Termodynamiikka (TFM), Luentomuistiinpanot Luennot 7-8, kertaus, mitkä olivat oppimistavoitteet? Kineettinen kaasuteoria Oletukset: - kaasun tiheys on riittävän suuri - molekyylin koko on paljon
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
Oikeasta vastauksesta (1p): Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
Entrooppiset voimat. Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit
 Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-445, Fysiikka III (Sf) tentti/välikoeuusinta 43 välikokeen alue ristetyssä astiassa, jonka lämötila idetään, kelvinissä, on nestemäistä heliumia tasaainossa helium kaasun kanssa Se on erotettu toisesta
S-445, Fysiikka III (Sf) tentti/välikoeuusinta 43 välikokeen alue ristetyssä astiassa, jonka lämötila idetään, kelvinissä, on nestemäistä heliumia tasaainossa helium kaasun kanssa Se on erotettu toisesta
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
