Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
|
|
|
- Sofia Laine
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole vuorovaikutuksessa ympäristönsä kanssa Eristettyyn systeemiin muodostuu itsestään termodynaaminen tasapaino Suljettu systeemi Vaihtaa ympäristönsä kanssa energiaa, mutta ei ainetta Avoin systeemi Vaihtaa ympäristönsä kanssa sekä ainetta, että energiaa Eristetty systeemi Suljettu systeemi Avoin systeemi ympäristö energiaa ainetta energiaa
2 Energian säilymislaki Myös systeemin sisäenergia huomioitava rakenneosasten lämpöliikkeen ja rakenneosasten välisten vuorovaikutusten potentiaalienergioiden summa Vain sisäenergian muutos voidaan mitata Lämpötila Tilastollinen suure, joka määritellään aineen rakennehiukkasten keskimääräisen liike-energian avulla. Absoluuttinen nollapiste -273,15 C = 0 K. Lämpö Ei voida koskaan saavuttaa Makrotaso: Lämpötilaerosta johtuvaa energian siirtymistä korkeammasta lämpötilasta matalampaan Mikrotaso: Termisen energian eli aineen rakenneosasten lämpöliikkeeseen liittyvän energian siirtymistä (systeemistä ympäristöön tai päinvastoin)
3 Lämmön siirtyminen Kuljettuminen (konvektio) Termistä energiaa siirtyy liikkuvan aineen mukana Merivirrat, tuulet, keskuslämmitysjärjestelmä Johtuminen Tarvitaan väliaine, joka on osa termodynaamista systeemiä Metallit ovat hyviä lämmönjohteita Säteily Termistä alkuperää oleva energia siirtyy kappaleesta ympäristöön sähkömagneettisena säteilynä Ei tarvitse väliainetta Infrapunasäteily Lämpölaajeneminen Verrannollinen alkuperäiseen pituuteen/pinta-alaan/tilavuuteen Verrannollinen lämpötilan muutokseen ΔT Riippuu aineesta (pituuden lämpötilakerroin = )
4 Ideaalikaasu Matemaattinen malli (yksinkertaistus) reaalikaasuista kaasumolekyylit pistemäisiä (tilavuus oletetaan nollaksi) rakenneosaset jatkuvassa, satunnaisessa ja suoraviivaisessa liikkeessä törmäysten vuoksi liikerata on murtoviiva rakenneosat törmäilevät toisiinsa ja säiliön seiniin täysin kimmoisasti ei muuta vuorovaikutusta toisiinsa ideaalikaasun tilanyhtälö Avogadron laki pv T vakio Samassa lämpötilassa ja paineessa yhtä suuret tilavuudet eri kaasuja sisältävät yhtä monta molekyyliä NTP-tilassa yksi mooli ideaalikaasua vaatii tilavuuden 22,4 l nr
5 Aineen olomuodot (eli faasit) kiinteä neste kaasu (plasma, kondensaatit) Olomuodon muutoksissa sitoutuu tai vapautuu energiaa Faasikaaviolla kuvataan aineen olomuotoja (T,p)-koordinaatistossa kolmoispisteen paineessa ja lämpötilassa kaikki kolme olomuotoa ovat tasapainossa neste-kaasu-tasapainokäyrä päättyy kriittiseen pisteeseen, jota suuremmissa lämpötiloissa ja paineissa nestemäisen ja kaasumaisen olomuodon raja häviää kriittisen lämpötilan alapuolella höyry voidaan aina tiivistää nesteeksi kriittisen lämpötilan alapuolella puhutaan (vesi)höyrystä ja yläpuolella kaasusta Haihtuminen nesteen höyrystymistä nesteen vapaasta pinnasta tapahtuu kaikissa lämpötiloissa Kiehuminen tapahtuu kaikkialla nesteessä tapahtuu lämpötilassa, jossa nesteen sisäinen höyrynpaine ulkoinen paine härmistyminen
6 Lämpökapasiteetti C = Q/ΔT ilmaisee kuinka paljon kappale voi ottaa vastaan tai luovuttaa energiaa lämpönä yhtä lämpötilayksikköä kohti ominaislämpökapasiteetti c ilmaisee aineen lämpönä luovuttaman tai vastaanottaman energian massa- ja lämpötilayksikköä kohti Q = cmδt ominaishöyrystymislämpö r = Q/m se energia Q massayksikköä m kohti, joka on vietävä lämpönä kiehumispisteessä olevaan nesteeseen, jotta se höyrystyisi ominaissulamislämpö s = Q/m se energia Q massayksikköä m kohti, joka on vietävä lämpönä sulamispisteessä olevaan kiinteään aineeseen, jotta se sulaisi nesteeksi Laskutehtävissä piirrä kaavio, josta näkee mihin prosesseihin (lämmitys, olomuodon muutokset) lämpömäärä kuluu
7 Yo-tehtävä, K2000/5 Termospullossa on 0,60 kg vettä, jonka lämpötila on 25 C. Pulloon kaadetaan 0,41 kg jääpaloja, joiden lämpötila on -8,0 C, ja sekoitetaan. Kuinka paljon jäätä jää sulamatta? Kuinka pitkän ajan kuluttua jää on kokonaan sulanut, kun ympäristöstä siirtyy pulloon lämpövirta 11 kj/h? Termospullon lämpökapasiteetti on 0,15 kj/ C. Ratkaisu: Mitä tapahtuu? Mitä säilymislakia voidaan soveltaa? Termospullon ja termospullon veden lämpö lämmittää jään sulamispisteeseen ja sulattaa osan jäästä. Q t termospullo C = 0,15 kj/ C T T jään lämmitys j m j = 0,41 kg Q j T 1 = 25 C => 0 C c j = 2,09 kj/kg C T 2 = -8 C => 0 C lämmin vesi m v = 0,60 kg vesi ja termospullo jäähtyy Q v c v = 4,19 kj/kg C jään sulatus m s =? s = 333 kj/kg Q s
8 Tasapainotila saavutetaan käytännössä niin nopeasti, ettei sekoitusaikana pulloon siirtyvää lämpömäärää tarvitse huomioida. Kaavion perusteella saadaan siis yhtälö Q t + Q v = Q j + Q s C T + c v m v T = c j m j T j + sm s m s = C T + c vm v T c j m j T j s 0,15 kj kj 25 K + 4,19 K m s = m s 0,1794 kg kj 0,60 kg 25 K 2,09 kg K 333 kj kg Sulamatta jäi 0,41 kg 0,1794 kg = 0,2306 kg 0,23 kg Sulamiseen vaaditaan energiamäärä Q = sm = 333 kj 0,2306 kg 76,79 kj kg Lämpöä virtaa systeemiin teholla P = 11 kj/h. Sulamiseen kuluu aika: t = Q P = 76,79 kj 11 kj/h 7,0 h V: Sulamiseen kuluu aikaa 7 tuntia 0,41 kg 8 K kg K
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Kaasu Neste Kiinteä aine Plasma
 Olomuodot Kaasu: atomeilla/molekyyleillä suuri nopeus, vuorovaikuttavat vain törmätessään toisiinsa Neste: atomit/molekyylit/ionit liukuvat toistensa lomitse, mutta pysyvät yhtenä nestetilavuutena (molekyylien
Olomuodot Kaasu: atomeilla/molekyyleillä suuri nopeus, vuorovaikuttavat vain törmätessään toisiinsa Neste: atomit/molekyylit/ionit liukuvat toistensa lomitse, mutta pysyvät yhtenä nestetilavuutena (molekyylien
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
Lämpöistä oppia Fysiikan ja kemian perusteet ja pedagogiikka
 Lämpöistä oppia Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2012 Alkudemonstraatio Käsi lämpömittarina Laittakaa kolmeen eri altaaseen kylmää, haaleaa ja lämmintä vettä. 1) Pitäkää
Lämpöistä oppia Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2012 Alkudemonstraatio Käsi lämpömittarina Laittakaa kolmeen eri altaaseen kylmää, haaleaa ja lämmintä vettä. 1) Pitäkää
Aineen olomuodot. Fysiikka 2 tiivistelmä. Lämpö. Nimityksiä: systeemit. Paine. Lämpötila F A
 http://www.foxitsoftware.com For evaluation only. 7..0 Aineen olomuodot Fysiikka tiivistelmä Juhani Kaukoranta Raahen lukio 0 Kiinteä Pitää oman muotonsa astiassa Neste Saa astian muodon Kaasu Jos kansi,
http://www.foxitsoftware.com For evaluation only. 7..0 Aineen olomuodot Fysiikka tiivistelmä Juhani Kaukoranta Raahen lukio 0 Kiinteä Pitää oman muotonsa astiassa Neste Saa astian muodon Kaasu Jos kansi,
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
Lämpöistä oppia ja energiaa Fysiikan ja kemian perusteet ja pedagogiikka
 Lämpöistä oppia ja energiaa Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2014 Alkudemonstraatio: Käsi lämpömittarina Laitetaan kolmeen eri altaaseen kylmää, haaleaa ja lämmintä vettä.
Lämpöistä oppia ja energiaa Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2014 Alkudemonstraatio: Käsi lämpömittarina Laitetaan kolmeen eri altaaseen kylmää, haaleaa ja lämmintä vettä.
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
Kemiallinen reaktio
 Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
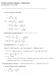 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Peruslaskutehtävät fy2 lämpöoppi kurssille
 Peruslaskutehtävät fy2 lämpöoppi kurssille Muista että kurssissa on paljon käsitteitä ja ilmiöitä, jotka on myös syytä hallita. Selvitä itsellesi kirjaa apuna käyttäen mitä tarkoittavat seuraavat fysiikan
Peruslaskutehtävät fy2 lämpöoppi kurssille Muista että kurssissa on paljon käsitteitä ja ilmiöitä, jotka on myös syytä hallita. Selvitä itsellesi kirjaa apuna käyttäen mitä tarkoittavat seuraavat fysiikan
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa.
 Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella:
 ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Lämpötila ja lämpöenergia
 Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila ja lämpöenergia Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila ja lämpöenergia Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
13 KALORIMETRI. 13.1 Johdanto. 13.2 Kalorimetrin lämmönvaihto
 13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
Lämpötila, lämpö energiana
 Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila, lämpö energiana Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
Matematiikan, fysiikan ja kemian opettajan kandiohjelma Didaktisen fysiikan kokeellisuus I Lämpötila, lämpö energiana Tilanmuuttujien perushahmotus Lämpötila, paine, tasapaino Lämpötilalla tarkoitetaan
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 1: Lämpötila ja lämpö Maanantai 30.10. ja tiistai 31.10. A theory is the more impressive the greater the simplicity of its
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 1: Lämpötila ja lämpö Maanantai 30.10. ja tiistai 31.10. A theory is the more impressive the greater the simplicity of its
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Työ 3: Veden höyrystymislämmön määritys
 Työ 3: Veden höyrystymislämmön määritys Työryhmä: Tehty (pvm): Hyväksytty (pvm): Hyväksyjä: 1. Tavoitteet Työssä vettä höyrystetään uppokuumentimella ja mitataan jäljellä olevan veden painoa sekä höyrystymiseen
Työ 3: Veden höyrystymislämmön määritys Työryhmä: Tehty (pvm): Hyväksytty (pvm): Hyväksyjä: 1. Tavoitteet Työssä vettä höyrystetään uppokuumentimella ja mitataan jäljellä olevan veden painoa sekä höyrystymiseen
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
Lämpöopin pääsäännöt. 0. pääsääntö. I pääsääntö. II pääsääntö
 Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
Konventionaalisessa lämpövoimaprosessissa muunnetaan polttoaineeseen sitoutunut kemiallinen energia lämpö/sähköenergiaksi höyryprosessin avulla
 Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
Kuivauksen fysiikkaa. Hannu Sarkkinen
 Kuivauksen fysiikkaa Hannu Sarkkinen 28.11.2013 Kuivatusmenetelmiä Auringon säteily Mikroaaltouuni Ilmakuivatus Ilman kosteus Ilman suhteellinen kosteus RH = ρ v /ρ vs missä ρ v = vesihöyryn tiheys (g/m
Kuivauksen fysiikkaa Hannu Sarkkinen 28.11.2013 Kuivatusmenetelmiä Auringon säteily Mikroaaltouuni Ilmakuivatus Ilman kosteus Ilman suhteellinen kosteus RH = ρ v /ρ vs missä ρ v = vesihöyryn tiheys (g/m
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
kertausta Boltzmannin jakauma infoa Ideaalikaasu kertausta Maxwellin ja Boltzmannin vauhtijakauma
 infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
KOSTEUS. Visamäentie 35 B 13100 HML
 3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
Lämpötila ja lämpö. 2.1 Terminen tasapaino
 2 Lämpötila ja lämpö Lämpötila ja lämpö ovat meille arkipäivästä tuttuja käsitteitä jo oman aistimaailmamme kautta. Me tunnemme "lämmön"ja "kylmän"ja lämpömittareiden lukemat säätelevät päivittäistä toimintaamme:
2 Lämpötila ja lämpö Lämpötila ja lämpö ovat meille arkipäivästä tuttuja käsitteitä jo oman aistimaailmamme kautta. Me tunnemme "lämmön"ja "kylmän"ja lämpömittareiden lukemat säätelevät päivittäistä toimintaamme:
Kiiännö!! b) Fysiikan tunnilla tutkittiin lääkeruiskussa olevan ilman paineen riippuvuutta lämpötilasta vakiotilavuudessa ruiskuun kiinnitetyn
 FYSKKA (FY02l: 2. KURSS: Lämpö vasraa KUUTEEN (6) TEHnÄVÄÄN il KOE 21.02.2013 1. a) Suuren matkustajalentokoneen lentokorkeus maahan nähden on 10,5 km, vauhti980 km/h ja massa 310 000 kg. Laske lentokoneen
FYSKKA (FY02l: 2. KURSS: Lämpö vasraa KUUTEEN (6) TEHnÄVÄÄN il KOE 21.02.2013 1. a) Suuren matkustajalentokoneen lentokorkeus maahan nähden on 10,5 km, vauhti980 km/h ja massa 310 000 kg. Laske lentokoneen
Energia-alan keskeisiä termejä. 1. Energiatase (energy balance)
 Energia-alan keskeisiä termejä 1. Energiatase (energy balance) Energiataseet perustuvat energian häviämättömyyden lakiin. Systeemi rajataan ja siihen meneviä ja sieltä tulevia energiavirtoja tarkastellaan.
Energia-alan keskeisiä termejä 1. Energiatase (energy balance) Energiataseet perustuvat energian häviämättömyyden lakiin. Systeemi rajataan ja siihen meneviä ja sieltä tulevia energiavirtoja tarkastellaan.
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Aineen rakenne the structure of matter
 1 Termodynaaminen systeemi Aineen rakenne the structure of matter Kaikki aine rakentuu atomeista. Kaikki atomit rakentuvat protoneista, neutroneista ja elektroneista. All matter is atoms, and all atoms
1 Termodynaaminen systeemi Aineen rakenne the structure of matter Kaikki aine rakentuu atomeista. Kaikki atomit rakentuvat protoneista, neutroneista ja elektroneista. All matter is atoms, and all atoms
KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT
 KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT Lämpölaajeneminen Pituuden lämpölaajeneminen: l = αl o t lo l l = l o + l = l o + αl o t l l = l o (1 + α t) α = pituuden lämpötilakerroin esim. teräs: α = 12 10
KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT Lämpölaajeneminen Pituuden lämpölaajeneminen: l = αl o t lo l l = l o + l = l o + αl o t l l = l o (1 + α t) α = pituuden lämpötilakerroin esim. teräs: α = 12 10
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
VASTAUKSIA YO-KYSYMYKSIIN KURSSISTA FY2: Lämpö
 VASTAUKSIA YO-KYSYMYKSIIN KURSSISTA FY2: Lämpö 1. Selitä fysikaalisesti, miksi: a) sateessa kastuneet vaatteet tuntuvat kylmältä, b) pyykit kuivuvat myös pakkasessa, c) uunista pudonneen hehkuvan hiilenpalan
VASTAUKSIA YO-KYSYMYKSIIN KURSSISTA FY2: Lämpö 1. Selitä fysikaalisesti, miksi: a) sateessa kastuneet vaatteet tuntuvat kylmältä, b) pyykit kuivuvat myös pakkasessa, c) uunista pudonneen hehkuvan hiilenpalan
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Luvun 12 laskuesimerkit
 Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
Luku 3 Puhtaiden aineiden ominaisuudet
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 3 Puhtaiden aineiden ominaisuudet Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 3 Puhtaiden aineiden ominaisuudet Copyright The McGraw-Hill Companies, Inc. Permission required
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
KEMIAN MIKROMAAILMA, KE2 VESI
 VESI KEMIAN MIKROMAAILMA, KE2 Johdantoa: Vesi on elämälle välttämätöntä. Se on hyvä liuotin, energian ja aineiden siirtäjä, lämmönsäätelijä ja se muodostaa vetysidoksia, jotka tekevät siitä poikkeuksellisen
VESI KEMIAN MIKROMAAILMA, KE2 Johdantoa: Vesi on elämälle välttämätöntä. Se on hyvä liuotin, energian ja aineiden siirtäjä, lämmönsäätelijä ja se muodostaa vetysidoksia, jotka tekevät siitä poikkeuksellisen
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
4 Aineen olomuodot. 4.2 Höyrystyminen POHDI JA ETSI
 4 Aineen olomuodot 4.2 Höyrystyminen POHDI JA ETSI 4-1. a) Vesi asettuu astiassa vaakatasoon Maan vetovoiman ja veden herkkäliikkeisyyden takia. Painovoima tekee työtä, kunnes veden potentiaalienergia
4 Aineen olomuodot 4.2 Höyrystyminen POHDI JA ETSI 4-1. a) Vesi asettuu astiassa vaakatasoon Maan vetovoiman ja veden herkkäliikkeisyyden takia. Painovoima tekee työtä, kunnes veden potentiaalienergia
Lämpöoppia. Haarto & Karhunen. www.turkuamk.fi
 Läpöoppia Haarto & Karhunen Läpötila Läpötila suuren atoi- tai olekyylijoukon oinaisuus Liittyy kiinteillä aineilla aineen atoeiden läpöliikkeeseen (värähtelyyn) ja nesteillä ja kaasuilla liikkeisiin Atoien
Läpöoppia Haarto & Karhunen Läpötila Läpötila suuren atoi- tai olekyylijoukon oinaisuus Liittyy kiinteillä aineilla aineen atoeiden läpöliikkeeseen (värähtelyyn) ja nesteillä ja kaasuilla liikkeisiin Atoien
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
