Luku6 Tilanyhtälö. Ideaalikaasun N V. Yleinen aineen. paine vakio. tilavuus vakio
|
|
|
- Juha Saarnio
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, )
2 Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla tasoilla. Vakiopainekäyrät saadaan painepinnan ja VT suuntaisten tasojen leikkauspisteistö.
3 Kriittinen piste Kaksi eri polkua kaasun nesteyttämiseksi. Vain punaista polkua pitkin havaitaan faasimuutos.
4 Molekyylien välinen vuorovaikutus Yksinkertainen malli molekyylien väliselle vuorovaikutukselle. r 0 on molekyylin säde ja r 12 molekyylien välinen etäisyys. korjaus partitiofunktioon Pienillä etäisyyksillä molekyylit hylkivät toisiaan kuten biljardipallot, suurilla etäisyyksillä niitä vetää puoleensa heikko van der Waalsin voima, joka aiheutuu elektronien naapurimolekyyliin indusoitumasta dipolimomentista
5 Korkeissa lämpötiloissa tiheyden kasvaessa kaasun paine on korkeampi kuin ideaalikaasun tilanyhtälön arvo efektiivinen tilavuus on koko tilavuutta pienempi Matalissa lämpötiloissa reaalikaasun paine on alempi kuin ideaalikaasun paineen muutos on suoraan verrannollinen paritörmäyksiin, jotka taas ovat verrannollisia tiheyteen
6
7 nestefaasi ei puristu kokoon! Van der Waalsin isotermit van der Waals! lähestyvät toisiaan kaikissa lämpötiloissa =yhteinen efektiivinen tilavuus T>> T C : reaalikaasu ja ideaalikaasu lähes identtisiä ideaalikaasu ja reaalikaasu eroavat kuitenkin hard coren takia
8 Työ ja lämpö lämmönvaihto korkeammasta kylmempään lämpötilaan! U kasvaa konfiguraatiotyö U pienenee Kun systeemiin tuodaan energiaa (ulkoisen) työn kautta, jokin systeemiä rajoittava pinta liikkuu tai muuttaa muotoaan. Q>0, kun lämpöä ulkoa systeemiin ja W>0, kun systeemin työ on positiivista Lämpöenergia tuodaan systeemiin satunnaisissa mikroskooppisissa erissä
9 sisäenergian muutos Lämpöeristetylle systeemille systeemin tekemä makroskooppinen työ ympäristön tekemä työ
10 Työn laskeminen Differentiaalinen työ dw = Fdx= padx= pdv Geometrinen tulkinta: Kuvan (a) viivoitettu alue 2 Makroskooppinen työ W = pdv V1 Geometrinen tulkinta: Kuvan (a) harmaa alue. Makroskooppinen työ riippuu tilanmuutospolusta (kuva b). V
11 Kiertoprosessi, lämpövoimakoneet Kiertoprosesseissa systeemi palaa alkupisteeseen kahden tai useamman tilanmuutoksen jälkeen. Kaasun laajetessa reittiä (1) kaasun tekemä työ on positiivinen ja yhtä suuri kuin kuvaajan (1) ja V-akselin väliin jäävän alueen pinta-ala. Kaasun puristuessa (2) sen tekemä työ on negatiivinen eli kuvaajan (2) ja V-akselin välinen pinta-ala negatiivisena. Kokonaistyö V V 2 1 W = pdv + pdv = reitti (1) V reitti(2) 1 2 Kuvan punainen alue V
12 Työ kvasistaattisessa prosessissa Isobaarinen laajeneminen Isoterminen laajeneminen Työ isobaarisessa laajenmisessa V 2 W = pdv = p( V V ) V Ideaalikaasun isoterminen työ V 2 2 dv W = pdv = knt = knt V V V V 1 1 V ln V 2 1
13 Lämpöopin I pääsääntö = energian säilyminen termodynamiikassa U = Q - W U = Q + Wext kaasun sisäenergian muutos = kaasun lämpömäärä kaasun tekemä työ
14 Q W W ext U Positiivinen systeemi saa lämpöä systeemi tekee työtä ympäristö tekee työtä sisäenergia kasvaa Negatiivinen systeemi luovuttaa lämpöä ympäristö tekee työtä systeemi tekee työtä sisäenergia pienenee
15 Lämpöopin ensimmäinen pääsääntö Adiabaattinen prosessi: lämpöeristetty tilanmuutoksen aikana Isokoorinen prosessi: pdv=0 Ideaalikaasun isoterminen prosessi Näitä tuloksia tarvitaan paljon!!! Ideaalikaasun lämpömäärä isotermisessä prosessi = kaasun tekemä työ
16 Kiertoprosessi Systeemi palaa alkuperäiseen tilaansa Ideaalikaasu: kiertonopeus esim. 100 kertaa minuutissa, laske kaasun tekemän työn teho
17 Ominaislämpö, pvt:n funktiona Triviaali kokeellinen havainto: kaasun tai nesteen lämpötila kasvaa, kun siihen virtaa lämpöenergiaa. Kaasulla on lämpötilan lisäksi aina toinen riippumaton tilanmuuttuja, lämpötila ei siis yksin riitä kuvaamaan termodynaamista tilaa. Systeemin lämpökapasiteetti moolia kohti on Lämpömäärä riippuu prosessista, yleiselle vakiotilamuuttujalle käytetään alaindeksiä x=p,v,... tilavuus vakio paine vakio
18 Systeemin kokonaislämpökapasiteetti Jos ominaislämpö on vakio
19 Lämmön siirtymismekanismit Johtuminen Säteily Kuljettuminen
20 Termodynaamiset koneet syklisiä koneen tekemä työ ympäristön tekemä työ on positiivinen
21 Lämpövoimakone W > 0 kone tekee työtä Q Y > 0 kone ottaa lämpöä ylemmästä lämpövarastosta Q A < 0 kone luovuttaa lämpöä alempaan lämpövarastoon Lämpöpumppu ja jäähdytyskone W< 0 ympäristö tekee työtä Q Y < 0 kone luovuttaa lämpöä ylempään lämpövarastoon Q A > 0 kone oottaa lämpöä alemmasta lämpövarastosta
22 Jääkaapin toimintaperiaate
23 Lämpövoimakone
24 Höyryturbiini/Generaattori
25 Jäähdytyskoneen tehokerroin ε J QA W QY = = = εl 1 W W isobaarinen laajeneminen Esim. 58 g ilmaa V 1 =20 dm 3, V 2 =V 3 =50 dm 3 p 1 =p 2 = 5 bar p 3 = 1,39 bar adiabaattinen puristus isokoorinen jäähdytys
26 Auton ottomoottori 2-3 isokoorinen muutos (räjähdys) Q Y >0 koneeseen 3-4 adiabaattinen kaasun laajeneminen, kaasu tekee työtä 1-2 adiabaattinen puristus, kvasistaattinen systeemi, nopeahko prosessi, dq=0 4-5 isokoorinen jäähtyminen (ideaalitapaus) 0 1 kaasu sylinteriin, paine ei muutu 5-6 jäähtyneen ja alhaisen paineen laajentuneen kaasun työntäminen pois sylinteristä
27 Diesel-moottori polttoaine sylinteriin, isobaarinen palaminen, kaasu laajenee ja tekee työtä, lämpö on kemiallista energiaa! 1-2 adiabaattinen puristus, mäntä liikkuu 0-1 ilmaa sylinteriin 3-4 adiabaattinen laajeneminen, kaasu tekee lisää työtä mäntä siirtyy alakuolokohtaan isokoorinen paineen lasku, jäähdytys ja ja kaasujen poisto
28 lämpö kaasuun Carnotin kiertoprosessi adiabaattinen puristus ja lämpeäminen ylempään lämpötilaan kaasu laajenee ja tekee työtä kaasu laajenee edelleen, mutta jäähtyy ja tekee lisää työtä lämmön luovutus alempaan lämpövarastoon, isoterminen puristus 1 June Aug 1832 isotermiset prosessit sylinterin kansi täydellinen johde, muut osat eristeitä adiabaattiset prosessit dq=0
29 Prosessi Työ Lämpömäärä Perustelu 1 2 Isoterminen prosessi 2 3 Q=0 Adiabaattinen prosessi 3 4 Isoterminen 4 1 Q=0 Adiabaattinen prosessi
30 Kiteen elektronien potentiaalienergia Kiteessä elektronien potentiaalienergia on periodinen funktio, jossa on minimi kunkin atomin ytimen kohdalla. Lähellä ydintä elektronien potentiaalienergia on varsin samanlainen kuin vapaassa yksittäisessä atomissa.
31 Energiavöiden muodostuminen Kiteessä vapaiden atomien diskreeteistä energiatiloista tulee energiavöitä. Lähellä ydintä olevien elektronien energiatilat säilyvät lähes ennallaan. Uloimpien elektronien energiavyöt ovat leveitä ja peittävät usein toisiaan. Puolijohdekomponettien toiminnan kannalta vain kaksi ulointa osin tai kokonaan miehittynyttä energiavyötä ovat tärkeitä.
32 Energiavyöt itseispuolijohteessa Itseispuolijohteessa on nolla lämpötilassa valenssivyö täysi ja johtovyö tyhjä. Äärellisessä lämpötilassa elektroneja virittyy termisesti johtovyöhön. Jos energia-aukko on suuri terminen virittyminen on hyvin vähäistä ja materiaali on eriste tai puoli-eriste. Jokaista johtovyön elektronia kohden jää valenssivyöhön yksi aukko.
33 Donori ja akseptoritasot puolijohteessa n-tyypin puolijohde p-tyypin puolijohde Seostetussa puolijohteessa donoriatomit (a) luovuttavat yhden elektronin johtovyöhön, tai akseptoriatomit (b) sitovat valenssivyöstä yhden elektronin jättäen jälkeensä aukon.
34 Tilatiheys puolijohteissa Puolijohteissa johtovyön tilatiheys on samanmuotoinen kuin metallin johtoelektronien tilatiheys. Elektronin lepomassa korvautuu efektiivisellä massalla joka on noin % lepomassasta. 3/2 * V 2m e 1/2 ge( E) = ( E E ) 2 2 C 2π h Huomaa, että energia lasketaan johtovyön alareunasta (niin kuin metallin johtoelektroneillekin)
35 Puolijohteen Fermienergia Valenssivyössä elektronin efektiivinen massa on negatiivinen ja tilatiheys on peilikuva johtovyön tilatiheydestä. 3/2 * V 2m h gh( E) = E 2 2 V E 2π h ( ) Energia lasketaan valenssivyön reunasta ja efektiivisen massan arvona käytetään tyhjän elektronitilan massaa, joka on tähän tilaan liittyvän elektronimassan vastaluku ja siis positiivinen. Koska jokaista johtoelektronia kohden jää valenssivyöhön yksi aukko, aukkojen ja elektronien lukumäärät (tiheydet) ovat yhtä suuret. 1/2 n e Ne = = nh = V N V h
36 Fermienergian määrääminen n = 3/2 1/2 ( E E ) * 1 2m e C 2 de = 2 ( E E )/ 2 F kt π h e + 1 e EC * 3/2 EV 1 2mh 1/2 1 h = ( ) V ( E EF )/ kt π h e n E E de Huomaa,että aukon esiintymistodennäköisyys = 1- elektronin esiintymistodennäköisyys: f 1 1 = 1 f = 1 = ( F) / ( F )/ e + 1 e + 1 h e E E kt E E kt
37 Boltzmann approksimaatio Jos fermienergia on kaukana valenssivyön ja johtovyön reunasta ( E EF) / kt ( E EF) / kt e + 1 e (useimmille puolijohteille ( E EF) > 0,5 ev, jolloin ( E EF) / kt > 20 huonelämpötilassa) Elektronitiheys voidaan nyt integroida analyyttisesti * 3/2 1/2 1 2m e h = = 2 2 / c F C 2π F h E e h V V F * 3/2 * mkt e mkt h C = 2 ; N 2 2 V = 2 ( E EC ) ( ) ( E E ) kt n de N exp E E / kt Vastaavasti aukoille n = N exp ( E E )/ kt N C 2π h 2πh 3/2
38 Fermienergia ( ) ( ) NCexp EF EC / kt = NV exp EV EF / kt NC = exp ( V EC 2 F )/ N E + E kt V EV + EC 3 ( * * E ln / ) F = + kt m i h me 2 4 Itseispuolijohteen fermienergia on nollalämpötilassa kielletyn energiaalueen eli energiaaukon puolivälissä, huonelämpötilassa Fermienergia on siirtynyt muutama kymmentä mev lähemmäs johtovyötä.
39 Kvasifermitasapaino Puolijohdelasereissa johtovyöhön johdetaan elektroneja ja valenssivyöhön aukkoja (valenssivyöstä johdetaan pois elektroneita) Johtovyössä olevien elektronien lukumäärä on paljon suurempi kuin termisen virittymisen tapauksessa = populaatioinversio Koska vöiden välinen tasapaino muodostuu hyvin hitaasti,vyöt ovat sisäisessä tasapainossa, vaikka vyöt eivät ole kskinäisessä tasapainossa.
40 Kokonaisdifferentiaalit
41 Carnotin prosessi ja muut prosessit
42 Kaasun irreversiibeli purkautuminen
43 Termodynaamiset koneet Lämpövoimakone Lämpöpumppu
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Isotermit ja isobaarit. Luku6 Tilanyhtälö. Kriittinen piste. Molekyylien välinen vuorovaikutus. Ideaalikaasun N V. Yleinen aineen
 Luku6 Tilanyhtälö Isotermit ja isobaarit paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta Yleinen aineen p= f T pinta (, ) akiolämpötilakäyrät saadaan leikkaamalla painepinta p suuntaisilla tasoilla.
Luku6 Tilanyhtälö Isotermit ja isobaarit paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta Yleinen aineen p= f T pinta (, ) akiolämpötilakäyrät saadaan leikkaamalla painepinta p suuntaisilla tasoilla.
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
Puolijohteet. luku 7(-7.3)
 Puolijohteet luku 7(-7.3) Metallit vs. eristeet/puolijohteet Energia-aukko ja johtavuus gap size (ev) InSb 0.18 InAs 0.36 Ge 0.67 Si 1.11 GaAs 1.43 SiC 2.3 diamond 5.5 MgF2 11 Valenssivyö Johtavuusvyö
Puolijohteet luku 7(-7.3) Metallit vs. eristeet/puolijohteet Energia-aukko ja johtavuus gap size (ev) InSb 0.18 InAs 0.36 Ge 0.67 Si 1.11 GaAs 1.43 SiC 2.3 diamond 5.5 MgF2 11 Valenssivyö Johtavuusvyö
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
VII LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ
 II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-445, Fysiikka III (Sf) tentti/välikoeuusinta 43 välikokeen alue ristetyssä astiassa, jonka lämötila idetään, kelvinissä, on nestemäistä heliumia tasaainossa helium kaasun kanssa Se on erotettu toisesta
S-445, Fysiikka III (Sf) tentti/välikoeuusinta 43 välikokeen alue ristetyssä astiassa, jonka lämötila idetään, kelvinissä, on nestemäistä heliumia tasaainossa helium kaasun kanssa Se on erotettu toisesta
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 10: Reaalikaasut Pe 1.4.2016 1 AIHEET 1. Malleja, joissa pyritään huomioimaan
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 10: Reaalikaasut Pe 1.4.2016 1 AIHEET 1. Malleja, joissa pyritään huomioimaan
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
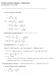 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt
 14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
3Työ. 3.1 Yleinen määritelmä
 3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
LIITTEET...2. Liite A Stirlingin kaavan tarkkuudesta Liite B Lagrangen kertoimet... 3
 LIITTEET... Liite A Stirlingin kaavan tarkkuudesta... Liite B Lagrangen kertoimet... 3 Liite C Kokonaisdifferentiaaleista... 7 C.1 Ristiderivaattojen riippumattomuus derivointijärjestyksestä... 7 C. Osittaisderivaattoja
LIITTEET... Liite A Stirlingin kaavan tarkkuudesta... Liite B Lagrangen kertoimet... 3 Liite C Kokonaisdifferentiaaleista... 7 C.1 Ristiderivaattojen riippumattomuus derivointijärjestyksestä... 7 C. Osittaisderivaattoja
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
VI TILANYHTÄLÖ
 VI TILANYHTÄLÖ... 150 6.1 Ideaalikaasun tilanyhtälö...150 6. Van der Waalsin tilanyhtälö...151 6..1 Semiempiirinen lähestymistapa...151 6.. Van der Waalsin kaasun ominaisuuksia:...154 6..3 Van der Waalsin
VI TILANYHTÄLÖ... 150 6.1 Ideaalikaasun tilanyhtälö...150 6. Van der Waalsin tilanyhtälö...151 6..1 Semiempiirinen lähestymistapa...151 6.. Van der Waalsin kaasun ominaisuuksia:...154 6..3 Van der Waalsin
Käytetään lopuksi ideaalikaasun tilanyhtälöä muutoksille 1-2 ja 3-1. Muutos 1-2 on isokorinen, joten tilanyhtälöstä saadaan ( p2 / p1) = ( T2 / T1)
 LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 9 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 9 / 14.11.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Vielä vähän entropiasta... Termodynamiikan 2. pääsääntö Entropian rooli 2. pääsäännön yhteydessä
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 9 / 14.11.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Vielä vähän entropiasta... Termodynamiikan 2. pääsääntö Entropian rooli 2. pääsäännön yhteydessä
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Lämpöopin pääsäännöt. 0. pääsääntö. I pääsääntö. II pääsääntö
 Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 14.11. ja tiistai 15.11. Kurssin aiheet 1. Lämpötila ja lämpö
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 14.11. ja tiistai 15.11. Kurssin aiheet 1. Lämpötila ja lämpö
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
PUOLIJOHTEISTA. Yleistä
 39 PUOLIJOHTEISTA Yleistä Pyrittäessä löytämään syy kiinteiden aineiden erilaiseen sähkön johtavuuteen joudutaan perehtymään aineen kidehilassa olevien atomien elektronisiin energiatiloihin. Seuraavassa
39 PUOLIJOHTEISTA Yleistä Pyrittäessä löytämään syy kiinteiden aineiden erilaiseen sähkön johtavuuteen joudutaan perehtymään aineen kidehilassa olevien atomien elektronisiin energiatiloihin. Seuraavassa
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
kertausta Boltzmannin jakauma infoa Ideaalikaasu kertausta Maxwellin ja Boltzmannin vauhtijakauma
 infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
S Fysiikka III (Est), 2 VK Malliratkaisut (Arvosteluperusteita täydennetään vielä)
 S-.7 Fysiikka III (st), VK 8.5.008 Malliratkaisut (Arvosteluperusteita täydennetään vielä). Näytä, että sekä symmetrinen aaltofunktio ψn( x ) ψn ( x) + ψn( x) ψn, että antisymmetrinen aaltofunktioψn( x)
S-.7 Fysiikka III (st), VK 8.5.008 Malliratkaisut (Arvosteluperusteita täydennetään vielä). Näytä, että sekä symmetrinen aaltofunktio ψn( x ) ψn ( x) + ψn( x) ψn, että antisymmetrinen aaltofunktioψn( x)
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ... 2 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 2. Termodynamiikan perusteet 1 Termodynamiikka ja Statistinen Mekaniikka Statistisesta
Kemiallinen reaktio
 Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
1 Johdanto. energiavyö, saavutetaan (1) missä E on
 35 PUOLIJOHTEEN ENERGIA-AUKKO 1 Johdanto Kiinteissä aineissa aineen elektronitt ovat järjestyneet niin kutsutuille energiavöille. Hyvissä sähkönjohteissa ylin elektroneita sisältävä energiavyö on vain
35 PUOLIJOHTEEN ENERGIA-AUKKO 1 Johdanto Kiinteissä aineissa aineen elektronitt ovat järjestyneet niin kutsutuille energiavöille. Hyvissä sähkönjohteissa ylin elektroneita sisältävä energiavyö on vain
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
Thermodynamics is Two Laws and a Li2le Calculus
 Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
DEE-11110 Sähkötekniikan perusteet
 DEE-11110 Sähkötekniikan perusteet Antti Stenvall Peruskäsitteet Luennon keskeinen termistö ja tavoitteet sähkövaraus teho ja energia potentiaali ja jännite sähkövirta Tarkoitus on määritellä sähkötekniikan
DEE-11110 Sähkötekniikan perusteet Antti Stenvall Peruskäsitteet Luennon keskeinen termistö ja tavoitteet sähkövaraus teho ja energia potentiaali ja jännite sähkövirta Tarkoitus on määritellä sähkötekniikan
Luento 8. Lämpökapasiteettimallit Dulong-Petit -laki Einsteinin hilalämpömalli Debyen ääniaaltomalli. Sähkönjohtavuus Druden malli
 Luento 8 Lämpökapasiteettimallit Dulong-Petit -laki Einsteinin hilalämpömalli Debyen ääniaaltomalli Sähkönjohtavuus Druden malli Klassiset C V -mallit Termodynamiikka kun Ei ennustetta arvosta! Klassinen
Luento 8 Lämpökapasiteettimallit Dulong-Petit -laki Einsteinin hilalämpömalli Debyen ääniaaltomalli Sähkönjohtavuus Druden malli Klassiset C V -mallit Termodynamiikka kun Ei ennustetta arvosta! Klassinen
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 9: Fotonit ja relativistiset kaasut Ke 30.3.2016 1 AIHEET 1. Fotonikaasun termodynamiikkaa.
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 9: Fotonit ja relativistiset kaasut Ke 30.3.2016 1 AIHEET 1. Fotonikaasun termodynamiikkaa.
3.1 Varhaiset atomimallit (1/3)
 + 3 ATOMIN MALLI 3.1 Varhaiset atomimallit (1/3) Thomsonin rusinakakkumallissa positiivisesti varautuneen hyytelömäisen aineen sisällä on negatiivisia elektroneja kuin rusinat kakussa. Rutherford pommitti
+ 3 ATOMIN MALLI 3.1 Varhaiset atomimallit (1/3) Thomsonin rusinakakkumallissa positiivisesti varautuneen hyytelömäisen aineen sisällä on negatiivisia elektroneja kuin rusinat kakussa. Rutherford pommitti
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Entrooppiset voimat. Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit
 Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
13 KALORIMETRI. 13.1 Johdanto. 13.2 Kalorimetrin lämmönvaihto
 13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
6-1 Hyötysuhde ja tehokerroin
 67 6 Lämpövoimakoneet ja jäähdyttimet 6-1 Hyötysuhde ja tehokerroin Lämpövoimakone (engl. heat engine) on laite, joka muuttaa lämpöenergiaa työksi. Tavallisesti laitteessa tapahtuu kiertoprosessi, jonka
67 6 Lämpövoimakoneet ja jäähdyttimet 6-1 Hyötysuhde ja tehokerroin Lämpövoimakone (engl. heat engine) on laite, joka muuttaa lämpöenergiaa työksi. Tavallisesti laitteessa tapahtuu kiertoprosessi, jonka
