Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
|
|
|
- Hilja Karjalainen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla tai vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä): C6H6 + C3H6 C6H5CH(CH3) Laske bentseenin tasapainokonversio 400 C lämpötilassa, kun syöttö on stoikiometrinen ja paine on 1 bar. Pohdi, miten tasapainokonversio muuttuu, jos a) syöttö on stoikiometrinen ja 10 bar paine b) kolminkertainen propeeniylimäärä ja 1 bar paine c) lähtöaineiden moolisuhde stoikiometrinen, kolmasosa syötöstä inerttiä ja 1 bar paine Kirjallisuudesta: YHDISTE C6H6 C3H6 C6H5CH(CH3) ΧfG o (T) [J/mol] (T/K) (T/K) (T/K) Vinkit Laske Gibbsin energia reaktiolle annetuista komponenttien Gibbsin energioista, ΧrG = (tuotteet) (lähtöaineet). Muista myös stoikiometriset kertoimet! Gibbsin energian ja tasapainovakion välinen yhteys on ΧrG = -RT ln(ka). Tee stoikiometriataulukko tasapainotilanteesta, jonka avulla määrität yhtälön Ka:lle Ratkaisu Gibbsin energia komponenttien muodostumiselle on annettu. Näistä saadaan Gibbsin energia reaktiolle (ΧrG) tyylillä tuotteet miinus lähtöaineet stoikiometria huomioiden. Δ () = / Δ () = = (673)
2 Δ (673 ) = 1815 / Nyt tasapainovakion ja Gibbsin energian välillä on riippuvuus: Δ = ( ) = Δ = 1815 = 1, Tehdään stoikiometriataulukko systeemille, jossa esitetään alkutila sekä tasapainotila. Taulukossa kunkin komponentin määrät ilmoitetaan mooleina, jolloin ei tarvitse ottaa huomioon tilavuuden muutosta reaktion aikana. Ptot = 1 bar C6H6 + C3H6 C6H5CH(CH3) Ρn alussa tp-tila 1-x 1-x x -x Huomaa, että nyt kulunut lähtöaineen määrä on x moolia, jolloin tällä merkinnällä tasapainokonversion suuruus on x. Yhtälö tasapainovakiolle, joka esitetään ainemäärien funktiona, on: = () Σ Stoikiometriasta: Ρµ = = -1 K φ = fugasiteettikerrointasapainovakio ideaalikaasuille 1 =1 1 (1 ) x,38 4,76 1,38 = 0 = 0,35 a) Ptot = 10 bar = () = ( ) = 1,38 (1 ) = 1,38 josta saadaan = 0,74
3 b) Syöttösuhde 1:3 Ptot = 1 bar C6H6 + C3H6 C6H5CH(CH3) Ρn alussa tp-tila 1-x 3-x x 4-x = = 0,50 (1 )(3 ) 1 4 x = 1,38 c) Ptot = 1 bar C6H6 + C3H6 C6H5CH(CH3) inertti Ρn alussa tp-tila 1-x 1-x x 1 3-x = = 0,7 1 (1 ) 3 x = 1,38 Tehtävä. Tasapainovakio van t Hoffin yhtälöllä, reaktorin mitoitus tasapainoreaktiolle A ja B reagoivat kaasufaasireaktiossa ideaalisesti toimivassa sekoitussäiliöreaktorissa paineessa 1 bar. Syöttövirrassa on A:ta ja B:tä stoikiometrisessa suhteessa ja kokonaissyöttö reaktoriin on 00 mol/h. Lämpötilassa 00 C tapahtuu oheinen alkeisreaktio + + A:n kulumisen reaktionopeusvakio reaktiolämpötilassa 00 C:ssa on k1 = 0,05 h -1 ja reaktion tasapainovakion arvo lämpötilassa 5 C on,0. Kuinka suuri reaktori tarvitaan, jotta saavutetaan 30 % konversio, jos reaktioentalpia ΧrH on a) -10 kj/mol b) 10 kj/mol Mitä huomaat kyseisten tasapainovakioiden lämpötilariippuvuuksista?
4 Vinkit Laske tasapainovakiot kummallekin tapaukselle lämpötilassa 00 C van t Hoffin yhtälön avulla = 1 1 Kun sijoitat CSTR:n mitoitusyhtälöön reaktionopeuden lauseketta, muista myös käänteisreaktio! Tasapainovakio Ka = k1/k-1 Ratkaisu: Ratkaistaan van t Hoffin yhtälöstä tasapainovakiot 00 C:ssa = 1 1 ( ) = ( ) 1 1 Kun reaktioentalpia ΧrH=-10 kj/mol (eksoterminen reaktio) 10 ( ) = () 1 (5 + 73) 1 ( ) = 0,80 = 0,45 Kun reaktioentalpia ΧrH=10 kj/mol (endoterminen reaktio) 10 ( ) = () 1 (5 + 73) 1 ( ) =,18 = 8,90 Huomataan, että eksotermisen reaktion tasapainovakio pienenee lämpötilan kasvaessa, ja endotermisen reaktion tasapainovakio kasvaa lämpötilan kasvaessa, aivan kuten termodynamiikan mukaan kuuluukin tapahtua. Reaktionopeuslausekkeessa otetaan huomioon nyt myös käänteisreaktio, jossa A:ta syntyy. Tasapainovakio Ka on reaktionopeusvakioiden k1 ja k-1 suhde eli ra on muotoa = = Kyseessä on kaasufaasireaktio, jossa syötössä ca0 = cb0 jossa moolimäärä ei muutu (δ=0), joten konsentraatiot ovat = = 1 1+ = (1 )
5 = = + 1+ = jossa θc on C:n moolinen syöttosuhde verrattuna A:han (nyt nolla, syötössä ei C:tä) ja a ja c stoikiometriset kertoimet reaktioyhtälöstä (molemmat ykkösiä). Sijoitetaan sekoitussäiliöreaktorin mitoitusyhtälöön = ( ) = ( 0) = (1 ) Lasketaan A:n konsentraatio syötössä ideaalikaasulain avulla. Koska syöttö on stoikiometrinen, sekä A:n että B:n mooliosuus syötössä on 0,5 = =0, = 1,7 ( ) Sijoitetaan arvot mitoitusyhtälöön. Huomaa, että kokonaissyötöstä puolet on A:ta eli A:n moolivirta reaktoriin on 100 mol/h. Eksotermiselle reaktiolle saadaan = 100 /h 0,3 0,05 h 1,7 1,7 (1 0,3) 0,3 0,45 = 1,8 Ja endotermiselle reaktiolle = 100 /h 0,3 0,05 h 1,7 1,7 (1 0,3) 0,3 8,90 = 7,7 Huomaa, että 5 C:ssa molempien reaktioiden vaatima reaktoritilavuus olisi sama, sillä tuossa lämpötilassa molempien tasapainovakion arvo on yhtä suuri ja reaktionopeusyhtälö siis samanlainen.
6 Tehtävä 3. Tasapainokonversion laskenta Alkeisreaktiota A (g) B (g) ajetaan sekoitussäiliöreaktorissa. Reaktiolämpötila on 00 C. Reaktoriin syötetään A:ta 00 mol/h ja A:n konsentraatio syötössä on 0 mol/m 3. Tutkituissa reaktioolosuhteissa reaktionopeusvakion arvo on 0 h -1. Kuinka suuri reaktori tarvitaan, jos tavoitteena on 80% tasapainokonversiosta? Tasapainovakio noudattaa kokeellista korrelaatiota (HUOM: lämpötila Kelvineinä) log = ,510 log + 1,871 Vinkit: Laske ensin tasapainovakio annetusta korrelaatiosta ja laske sen avulla tasapainokonversio määrittämällä yhtälö tasapainovakiolle konversion funktiona. CSTR:n mitoitusyhtälöön sijoitetaan reaktionopeusyhtälö tasapainoreaktiolle, muista myös käänteisreaktio ja tasapainovakion sisällyttäminen reaktionopeusyhtälöön! Tasapainovakio Ka = k1/k-1 Ratkaisu: Lasketaan annetusta korrelaatiosta tasapainovakion arvo reaktiolämpötilassa 473 K log = 790 K + 1,510 log = 0,0115 K=1,03 Lausutaan tasapainovakio pitoisuuksien avulla K + 1,871 = 790 K 473 K 473 K + 1,510 log K + 1,871 A B ni syöttö 1 0 tasapaino 1-x x 1 = = 1 1 = 1 Ratkaistaan edellisestä yhtälöstä tasapainokonversio xe = +1 = 1,03 1, = 0,507 Nyt halutaan operoida konversiotasolla, joka on 80 % tasapainokonversiosta, eli haluttu konversio on 0,405. Reaktorin mitoitusta varten tarvitaan reaktionopeusyhtälö -ra. Reaktionopeuslausekkeessa otetaan huomioon nyt myös käänteisreaktio, jossa A:ta syntyy. Tasapainovakio Ka on reaktionopeusvakioiden k1 ja k-1 suhde eli ra on muotoa
7 = = = (1 ) Sijoitetaan reaktorin mitoitusyhtälöön = ( ) = = 1,0 (1 ) = 00 h 0,405 0 h 0 0,405 (1 0,405) 1,03 Tehtävä 4: Onko seos termodynaamisessa tasapainossa Isoamyleenien tasapainoa tutkitaan isomeroimalla -metyyli-1-buteenia (M1B) -metyyli-- buteeniksi (MB). Seoksen koostumus 100 C:ssa on 0 mol-% M1B:tä, 30 mol-% MB:tä ja loput on inerttiä hiilivetyä. Laske reaktioseoksen tasapainovakion arvo ja päättele onko reaktioseos saavuttanut termodynaamisen tasapainotilan. Komponentti ΔGf (kj/mol) -metyyli-1-buteeni 65,6 -metyyli--buteeni 59,7 Vinkit: Laske tasapainovakiolle arvo kahdella tavalla: 1. annetusta koostumuksesta. annetuista termodynaamisista arvoista, ΧrG = -RT ln(ka). Vertaa saamiasi tuloksia toisiinsa Ratkaisu: Tasapainovakio termodynaamisista arvoista: Lasketaan ensin Gibbsin energia reaktiolle annetuista komponenttien Gibbsin energioista stoikiometria huomioiden, ΧrG = ΧGf 0 (MB) - ΧGf 0 (M1B) = 59,7 kj/mol 65,6 kj/mol = -5,9 kj/mol Gibbsin energian ja tasapainovakion välinen yhteys on ΧrG = -RT ln(ka) eli ln = = 5900 = 1,90 ( ) 373 Ka = 6,70
8 Sijoitetaan reaktioseoksen koostumus tasapainovakion lausekkeeseen, jolloin saadaan arvo, jota voidaan verrata termodynaamisista arvoista laskettuun termodynaamisen tasapainovakion Ka arvoon. Reaktiossa ei tapahdu moolimäärän muutosta, joten tasapainovakion lauseke supistuu komponenttien suhteeksi = = 1 = = 0,3 0, = 1,5 Huomataan, että termodynaaminen tasapainovakio (6,70) on melko kaukana kokeellisesta koostumuksesta laskettua (1,5). Termodynaamisessa tasapainotilassa olisi siis suurempi osuus MB:tä, joten reaktio ei ole vielä saavuttanut termodynaamista tasapainotilaa. Tehtävä 5. Mekanismi tasapainoreaktiolle Fosgeenin muodostumisreaktiolle on ehdotettu seuraavaa mekanismia: Cl Cl (1) Cl + Cl Cl3 () Cl3 + CO COCl + Cl (3) Johda ehdotetun mekanismin pohjalta nopeusyhtälö fosgeenin muodostumiselle. Reaktiot (1) ja () voidaan olettaa molempiin suuntiin erittäin nopeiksi suhteessa reaktioon (3). Vinkit Muodosta reaktionopeuslauseke fosgeenin (COCl) muodostumiselle. Reaktiot 1 ja ovat erittäin nopeita eli niiden voi olettaa olevan likimäärin tasapainossa. Radikaalien konsentraatiot voidaan lausua reaktioiden 1 ja tasapainovakioiden avulla. Ratkaisu Aiemmin tämän kurssin aikana tasapainoreaktiot on kirjotettu kahdeksi erilliseksi reaktioksi, jotka etenevät vastakkaisiin suuntiin. Tämän tehtävän pystyy ratkaisemaan myös aiemmin esitetyllä tavalla. Nyt käsitellään kutakin reaktiota reversiibelinä, ja otetaan lisäksi käyttöön tasapainovakiot reaktiolle. Tehtävänannon mukaan reversiibelit reaktiot (1) ja () ovat nopeita, joten oletetaan niiden olevan likimäärin tasapainossa. Tällöin radikaalikonsentraatioiden lausekkeet saadaan ratkaistua tasapainovakion lausekkeiden avulla: K K 1 k < k k < k 1, 1 < < Ζ Ζ Cl Cl ΖCl3 ΖCl ΖCl,. () (1)
9 Yhtälöiden (1) ja () perusteella: ΖCl < Ζ K 1 Cl ja Cl 3 < K Cl Cl < K K1 Cl Ζ Ζ Ζ Ζ 3 / (3) (4) Muodostetaan lauseke fosgeenin muodostumiselle: ΖCl Ζ CO, k ΖCOCl Ζ rcocl < k 3 3, 3 Cl (5) johon sijoitetaan yhtälöt (3) ja (4): ΖCl 3/ ΖCO, k K ΖCOCl ΖCl rcocl < k3k K 1, 3 eli vakiotermit yhdistämällä nopeusyhtälö saadaan muotoon COCl ΖCl 3/ ΖCO k' ΖCOCl ΖCl r < k, 1 (6) (7)
CHEM-A1110 Virtaukset ja reaktorit. Laskuharjoitus 9/2016. Energiataseet
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
Luento 9 Kemiallinen tasapaino CHEM-A1250
 Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luku 2. Kemiallisen reaktion tasapaino
 Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
KEMA221 2009 KEMIALLINEN TASAPAINO ATKINS LUKU 7
 KEMIALLINEN TASAPAINO Määritelmiä Kemiallinen reaktio A B pyrkii kohti tasapainoa. Yleisessä tapauksessa saavutetaan tasapainoa vastaava reaktioseos, jossa on läsnä sekä lähtöaineita että tuotteita: A
KEMIALLINEN TASAPAINO Määritelmiä Kemiallinen reaktio A B pyrkii kohti tasapainoa. Yleisessä tapauksessa saavutetaan tasapainoa vastaava reaktioseos, jossa on läsnä sekä lähtöaineita että tuotteita: A
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut
 Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
HSC-ohje laskuharjoituksen 1 tehtävälle 2
 HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
Esimerkiksi ammoniakin valmistus typestä ja vedystä on tyypillinen teollinen tasapainoreaktio.
 REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
Luku 8. Reaktiokinetiikka
 Luku 8 Reaktiokinetiikka 234 8.1 Reaktion nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista
Luku 8 Reaktiokinetiikka 234 8.1 Reaktion nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
KE Prosessien perusteet
 KE-40.2500 Prosessien perusteet Tentiss2i saa kiiyttia1 materiaalina vain fysikaalisen kemian taulukoita kirjaa sek?i kemian laitetekniikan taulukoita ja piinoksia kirjaa' TENTT 10.3.20088-13. 1. Selit8
KE-40.2500 Prosessien perusteet Tentiss2i saa kiiyttia1 materiaalina vain fysikaalisen kemian taulukoita kirjaa sek?i kemian laitetekniikan taulukoita ja piinoksia kirjaa' TENTT 10.3.20088-13. 1. Selit8
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Luku 21. Kemiallisten reaktioiden nopeus
 Luku 21. Kemiallisten reaktioiden nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista tasapainoreaktiota:
Luku 21. Kemiallisten reaktioiden nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista tasapainoreaktiota:
Lukion kemia 3, Reaktiot ja energia. Leena Piiroinen Luento 2 2015
 Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Teddy 2. välikoe kevät 2008
 Teddy 2. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 2. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin?
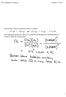 Esimerkki: Mihin suuntaan etenee reaktio CO (g) + H 2 O (g) CO 2 (g) + H 2 (g), K = 0,64, kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin? 1 Le Châtelier'n
Esimerkki: Mihin suuntaan etenee reaktio CO (g) + H 2 O (g) CO 2 (g) + H 2 (g), K = 0,64, kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin? 1 Le Châtelier'n
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiotekniikka. Prosessi- ja ympäristötekniikan perusta Teema 4 Kaisa Lamminpää
 Reaktiotekniikka Prosessi- ja ympäristötekniikan perusta Teema 4 Kaisa Lamminpää Luennon sisältö Johdanto ja termejä Reaktiotekniikka Kemiallinen prosessitekniikka Kemialliset reaktiot Reaktioiden jaottelu
Reaktiotekniikka Prosessi- ja ympäristötekniikan perusta Teema 4 Kaisa Lamminpää Luennon sisältö Johdanto ja termejä Reaktiotekniikka Kemiallinen prosessitekniikka Kemialliset reaktiot Reaktioiden jaottelu
b) Laske prosentteina, paljonko sydämen keskimääräinen teho muuttuu suhteessa tilanteeseen ennen saunomista. Käytä laskussa SI-yksiköitä.
 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
7 Termodynaamiset potentiaalit
 82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
Teddy 10. harjoituksen malliratkaisu syksy 2011
 Teddy. harjoituksen malliratkaisu syksy 2. Tarkastellaan reaktioketjua k O 3 O2 +O () O 2 +O k O 3 (2) O 3 +O k 2 O 2 +O 2 (3) Vakiotilaolettamuksen mukaan välituotteen konsentraatio pysyy vakiona lyhyen
Teddy. harjoituksen malliratkaisu syksy 2. Tarkastellaan reaktioketjua k O 3 O2 +O () O 2 +O k O 3 (2) O 3 +O k 2 O 2 +O 2 (3) Vakiotilaolettamuksen mukaan välituotteen konsentraatio pysyy vakiona lyhyen
1.1 Homogeeninen kemiallinen tasapaino
 1.1 Homogeeninen kemiallinen tasapaino 1. a) Mitä tarkoittaa käsite kemiallinen tasapaino? b) Miten kemiallinen tasapaino ilmaistaan reaktioyhtälössä? c) Mistä tekijöistä tasapainossa olevan reaktioseoksen
1.1 Homogeeninen kemiallinen tasapaino 1. a) Mitä tarkoittaa käsite kemiallinen tasapaino? b) Miten kemiallinen tasapaino ilmaistaan reaktioyhtälössä? c) Mistä tekijöistä tasapainossa olevan reaktioseoksen
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
Ratkaisu. Tarkastellaan aluksi Fe 3+ - ja Fe 2+ -ionien välistä tasapainoa: Nernstin yhtälö tälle reaktiolle on:
 Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
LUKU 16 KEMIALLINEN JA FAASITASAPAINO
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 LUKU 16 KEMIALLINEN JA FAASITASAPAINO Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 LUKU 16 KEMIALLINEN JA FAASITASAPAINO Copyright The McGraw-Hill Companies, Inc. Permission required
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä.
 FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
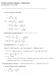 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe
 Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
Korkealämpötilakemia
 Korkealämpötilakemia Ellingham-diagrammit To 9.11.2017 klo 8-10 SÄ114 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Sisältö Mikä on Ellinghamin diagrammi?
Korkealämpötilakemia Ellingham-diagrammit To 9.11.2017 klo 8-10 SÄ114 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Sisältö Mikä on Ellinghamin diagrammi?
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
Yhdisteiden nimeäminen
 Yhdisteiden nimeäminen Binääriyhdisteiden nimeäminen 1. Ioniyhdisteet 2. Epämetallien väliset yhdisteet Kompleksiyhdisteiden nimeäminen Kemiallinen reaktio 1. Reaktioyhtälö 2. Määrälliset laskut 3. Reaktionopeuteen
Yhdisteiden nimeäminen Binääriyhdisteiden nimeäminen 1. Ioniyhdisteet 2. Epämetallien väliset yhdisteet Kompleksiyhdisteiden nimeäminen Kemiallinen reaktio 1. Reaktioyhtälö 2. Määrälliset laskut 3. Reaktionopeuteen
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
Ainemäärien suhteista laskujen kautta aineiden määriin
 REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
Lämpö- eli termokemiaa
 Lämpö- eli termokemiaa Endoterminen reaktio sitoo ympäristöstä lämpöenergiaa. Eksoterminen reaktio vapauttaa lämpöenergiaa ympäristöön. Entalpia H kuvaa systeemin sisäenergiaa vakiopaineessa. Entalpiamuutos
Lämpö- eli termokemiaa Endoterminen reaktio sitoo ympäristöstä lämpöenergiaa. Eksoterminen reaktio vapauttaa lämpöenergiaa ympäristöön. Entalpia H kuvaa systeemin sisäenergiaa vakiopaineessa. Entalpiamuutos
2CHEM-A1210 Kemiallinen reaktio Kevät 2017 Laskuharjoitus 7.
 HEM-A0 Kemiallinen reaktio Kevät 07 Laskuharjoitus 7.. Metalli-ioni M + muodostaa ligandin L - kanssa : kompleksin ML +, jonka pysyvyysvakio on K ML + =,00. 0 3. Mitkä ovat kompleksitasapainon vapaan metalli-ionin
HEM-A0 Kemiallinen reaktio Kevät 07 Laskuharjoitus 7.. Metalli-ioni M + muodostaa ligandin L - kanssa : kompleksin ML +, jonka pysyvyysvakio on K ML + =,00. 0 3. Mitkä ovat kompleksitasapainon vapaan metalli-ionin
Bensiiniä voidaan pitää hiilivetynä C8H18, jonka tiheys (NTP) on 0,703 g/ml ja palamislämpö H = kj/mol
 Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta.
 Helsingin yliopiston kemian valintakoe 10.5.2019 Vastaukset ja selitykset Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta. Reaktio
Helsingin yliopiston kemian valintakoe 10.5.2019 Vastaukset ja selitykset Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta. Reaktio
ja piirrä sitä vastaavat kaksi käyrää ja tarkista ratkaisusi kuvastasi.
 Harjoituksia yhtälöryhmistä ja matriiseista 1. Ratkaise yhtälöpari (F 1 ja F 2 ovat tuntemattomia) cos( ) F 1 + cos( ) F 2 = 0 sin( ) F 1 + sin( ) F 2 = -1730, kun = -50 ja = -145. 2. Ratkaise yhtälöpari
Harjoituksia yhtälöryhmistä ja matriiseista 1. Ratkaise yhtälöpari (F 1 ja F 2 ovat tuntemattomia) cos( ) F 1 + cos( ) F 2 = 0 sin( ) F 1 + sin( ) F 2 = -1730, kun = -50 ja = -145. 2. Ratkaise yhtälöpari
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Luku 13 KAASUSEOKSET
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Luento 10:Kertausta: Kemiallinen tasapaino + Kiinteän olomuodon kemia CHEM-A1250
 Luento 10:Kertausta: Kemiallinen tasapaino + Kiinteän olomuodon kemia 9.2.2017 CHEM-A1250 Tasapaino ja tasapainovakio Kaksisuuntainen reaktio a A+ b B p P + r R Eteenpäin menevän reaktion nopeus: rr 1
Luento 10:Kertausta: Kemiallinen tasapaino + Kiinteän olomuodon kemia 9.2.2017 CHEM-A1250 Tasapaino ja tasapainovakio Kaksisuuntainen reaktio a A+ b B p P + r R Eteenpäin menevän reaktion nopeus: rr 1
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen
 KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
Chem-C2400 Luento 3: Faasidiagrammit Ville Jokinen
 Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Kemian koe, Ke3 Reaktiot ja energia RATKAISUT Perjantai VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN
 Kemian koe, Ke3 Reaktiot ja energia RATKAISUT Kannaksen lukio Perjantai 26.9.2014 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN 1. A. Selitä käsitteet ja määritelmät (lyhyesti), lisää tarvittaessa kemiallinen merkintätapa:
Kemian koe, Ke3 Reaktiot ja energia RATKAISUT Kannaksen lukio Perjantai 26.9.2014 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN 1. A. Selitä käsitteet ja määritelmät (lyhyesti), lisää tarvittaessa kemiallinen merkintätapa:
c) Tasapainota seuraava happamassa liuoksessa tapahtuva hapetus-pelkistysreaktio:
 HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Törmäysteoria. Törmäysteorian mukaan kemiallinen reaktio tapahtuu, jos reagoivat hiukkaset törmäävät toisiinsa
 Törmäysteoria Törmäysteorian mukaan kemiallinen reaktio tapahtuu, jos reagoivat hiukkaset törmäävät toisiinsa tarpeeksi suurella voimalla ja oikeasta suunnasta. 1 Eksotermisen reaktion energiakaavio E
Törmäysteoria Törmäysteorian mukaan kemiallinen reaktio tapahtuu, jos reagoivat hiukkaset törmäävät toisiinsa tarpeeksi suurella voimalla ja oikeasta suunnasta. 1 Eksotermisen reaktion energiakaavio E
KOTITEKOINEN PALOSAMMUTIN (OSA 1)
 KOTITEKOINEN PALOSAMMUTIN (OSA 1) Johdanto Monet palosammuttimet, kuten kuvassa esitetty käsisammutin, käyttävät hiilidioksidia. Jotta hiilidioksidisammutin olisi tehokas, sen täytyy vapauttaa hiilidioksidia
KOTITEKOINEN PALOSAMMUTIN (OSA 1) Johdanto Monet palosammuttimet, kuten kuvassa esitetty käsisammutin, käyttävät hiilidioksidia. Jotta hiilidioksidisammutin olisi tehokas, sen täytyy vapauttaa hiilidioksidia
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
PROSESSISUUNNITTELUN SEMINAARI. Luento 5.3.2012 3. vaihe
 PROSESSISUUNNITTELUN SEMINAARI Luento 5.3.2012 3. vaihe 1 3. Vaihe Sanallinen prosessikuvaus Taselaskenta Lopullinen virtauskaavio 2 Sanallinen prosessikuvaus Prosessikuvaus on kirjallinen kuvaus prosessin
PROSESSISUUNNITTELUN SEMINAARI Luento 5.3.2012 3. vaihe 1 3. Vaihe Sanallinen prosessikuvaus Taselaskenta Lopullinen virtauskaavio 2 Sanallinen prosessikuvaus Prosessikuvaus on kirjallinen kuvaus prosessin
Reaktiolämpö KINEETTINEN ENERGIA POTENTIAALI- ENERGIA
 POTENTIAALI- ENERGIA KINEETTINEN ENERGIA Reaktiolämpö REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa
POTENTIAALI- ENERGIA KINEETTINEN ENERGIA Reaktiolämpö REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella:
 ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Ellinghamin diagrammit
 Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
Luento 2: Lämpökemiaa, osa 1 Torstai klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
(a) Potentiaali ja virtafunktiot saadaan suoraan summaamalla lähteen ja pyörteen funktiot. Potentiaalifunktioksi
 Tehtävä 1 Tornadon virtauskenttää voidaan approksimoida kaksiulotteisen nielun ja pyörteen summana Oleta, että nielun voimakkuus on m < ja pyörteen voimakkuus on > (a Määritä tornadon potentiaali- ja virtafunktiot
Tehtävä 1 Tornadon virtauskenttää voidaan approksimoida kaksiulotteisen nielun ja pyörteen summana Oleta, että nielun voimakkuus on m < ja pyörteen voimakkuus on > (a Määritä tornadon potentiaali- ja virtafunktiot
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
KE03. Kurssikalvot. Tuomas Hentunen. Kevät Tuomas Hentunen KE03 Kevät / 26
 KE03 Kurssikalvot Tuomas Hentunen Kevät 2016 Tuomas Hentunen KE03 Kevät 2016 1 / 26 Reaktioyhtälöt ja niiden tasapainottaminen Kemiallista reaktiota kuvataan reaktioyhtälöllä reaktioyhtälöstä selviää:
KE03 Kurssikalvot Tuomas Hentunen Kevät 2016 Tuomas Hentunen KE03 Kevät 2016 1 / 26 Reaktioyhtälöt ja niiden tasapainottaminen Kemiallista reaktiota kuvataan reaktioyhtälöllä reaktioyhtälöstä selviää:
Helsingin yliopisto/tampereen yliopisto Henkilötunnus - Molekyylibiotieteet/Bioteknologia Etunimet valintakoe Tehtävä 3 Pisteet / 30
 Helsingin yliopisto/tampereen yliopisto Henkilötunnus - hakukohde Sukunimi Molekyylibiotieteet/Bioteknologia Etunimet valintakoe 20.5.2013 Tehtävä 3 Pisteet / 30 3. Osa I: Stereokemia a) Piirrä kaikki
Helsingin yliopisto/tampereen yliopisto Henkilötunnus - hakukohde Sukunimi Molekyylibiotieteet/Bioteknologia Etunimet valintakoe 20.5.2013 Tehtävä 3 Pisteet / 30 3. Osa I: Stereokemia a) Piirrä kaikki
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
