Oikeasta vastauksesta (1p): Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
|
|
|
- Urho Sariola
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C Laske teräksen lämpötila koko systeemin saavutettua uuden termisen tasapainon Astian lämpenemistä ei tarvitse huomioida m j m v m t t (g) (g) (g) ( C) A B C D Jään sulattamiseen vaadittava lämpö: Q s = L j m j = 333 kj 0,118 kg = 39,3 kj kg eräs voi enimmillään luovuttaa sulavalle jäälle lämmön: Q t,max = c t m t t,max = 0,460 kj kg C 0,312 kg (0 808 C) = 116 kj Oikeasta vastauksesta : l trk+1 l trk+1 (K) (K) ( C) ( C) A: ,4 36,3 36,29 B: ,1 19,9 19,92 C: ,3 28,2 28,18 D: ,5 15,4 15,37 ehtävän tarkkuus on kolme numeroa Jään sulamisen tarkistus puuttuu, max 5p Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö: Q s Q t,max (kj) (kj) A 39,3 116 B 54,6 103 C 47,3 110 D 61,3 101 Koska Q s < Q t,max niin kaikki jää sulaa ja vesi lämpenee eräksen luovuttama lämpö menee jään sulattamiseen ja veden lämmittämiseen tai Q luovutettu = Q vastaanotettu tai eristetty systeemi, eikä tapahdu lämpöhäviöitä eli c t m t ( t l ) = L {{ j m j + c v (m j + m v )( l v ), {{{{ (++) (++) missä v on vesi-jää seoksen alkulämpötila, 0 C tai 273,15 K (++), ja l on teräs-vesi-systeemin loppulämpötila kun terminen tasapaino on saavutettu eräs-vesi seoksen loppulämpötilaksi saadaan: l = c tm t t + c v (m j + m v ) v L j m j = 309 K c v (m j + m v ) + c t m t {{ (++)
2 A2 Oheisessa kytkentäkaaviossa virtamittarin ja jännitemittarin sisäiset resistanssit ovat R A = 1,70 Ω ja R V = 1,00 kω Jännitelähteellä E ei ole sisäistä resistanssia a) Kytkennässä virtamittarin lukema on 0,260 A ja jännitemittarin lukema on 12,0 V Kuinka suuri on vastuksen R resistanssi? (2p) b) Piirrä kytkentä kun kytkentää muutetaan siten, että jännitemittari mittaa vastuksessa R tapahtuvaa jännitehäviötä ja virtamittari mittaa jännitelähteen E läpi kulkevaa sähkövirtaa ällöin virtamittarin lukema on 0,271 A Kuinka suuri jännitemittarin lukema on? (4p) R A R V I a U a I b (Ω) (kω) (A) (V) (A) A 1,70 1,00 0,260 12,0 0,271 B 2,26 1,00 0,310 12,0 0,321 C 3,00 1,00 0,450 12,0 0,459 D 2,60 1,00 0,350 12,0 0,360 R E V A ehtävän 2a kytkentäkaavio a) (max 2p) apa 1: Virtamittari ja vastus R on kytketty sarjaan eli niiden kokonaisresistanssi on R kok,a = R + R A (++) Vastuksen resistanssi R voidaan ratkaista Ohmin laista (++) kun tunnetaan sarjaan kytkettyjen vastusten läpi kulkeva virta I a ja vastusten yli vaikuttava jännite U a : U a = R kok,a I a = (R + R A )I a = R = U a I a R A = 44,5 Ω apa 2: Kirchhoffin silmukkasäännön tai Kirchhoff II tai Ohmin lain (++) mukaan E I a R I a R A = 0 (++) b) (max 4p) apa 1: R on kytketty rinnan jännitemittarin kanssa Kokonaisresistanssi vastukselle ja jännitemittarille on 1 R RV,b = 1 R + 1 R V = R RV,b = RR V R + R V R E V A ehtävän 2b kytkentäkaavio Virtamittarin mittaama virta I b on sama kuin R RV,b :n läpi kulkeva virta Ohmin laista saadaan U b = R RV,b I b = RR V I R + R b = U b = 11,5 V V apa 2: Kirchhoffin silmukkasäännöllä E U V I a R A = 0 Lähdejännite saadaan a-kohdasta, joten Oikeasta vastauksesta : U V = E I a R A = U b = 11,5 V U b trk+1 (V) (V) A: 11,5 11,53 B: 11,3 11,29 C: 10,6 10,61 D: 11,1 11,06 ehtävän tarkkuus on kolme numeroa b-kohdasta 0p, jos kuvaa ei ole tai kuva on väärin Jännitemittari mittaa suoraan lähdejännitettä E, joten U a = (R + R A )I a Oikeasta vastauksesta (++): R trk+1 (Ω) (Ω) A: 44,5 44,45 B: 36,4 36,45 C: 23,7 23,67 D: 31,7 31,69
3 A3 Oheisessa kuvassa on vauhtipyörä A, joka pyörii kitkatta kiinteän akselin S ympäri kulmanopeudella 12,3 rad/s Vauhtipyörään A liitetään nopeasti vauhtipyörä B, joka ei aluksi pyöri Liittämisen jälkeen vauhtipyörät pyörivät kitkatta yhteisellä kulmanopeudella Vauhtipyörän A hitausmomentti on 1,07 kgm 2 ja vauhtipyörän B hitausmomentti 0,503 kgm 2 akselin S suhteen ilmoitettuna a) Kuinka suuri on vauhtipyörien yhteinen kulmanopeus liittämisen jälkeen? b) Kuinka suuri on systeemin mekaanisen energian muutos? ω A J A J B (rad/s) (kgm 2 ) (kgm 2 ) A 12,3 1,07 0,503 B 13,0 1,47 0,466 C 12,9 1,23 0,472 D 11,6 1,03 0,568 S A B ehtävän 3 kuva a) (max 3p) Vauhtipyörien yhteenliittämisessä pyörimismäärä säilyy (++), eli pyörimismäärä ennen yhteenliittämistä on yhtä suuri kuin yhteenliitettyjen vauhtipyörien pyörimismäärä: J A ω A = J AB ω AB (++) Yhteenliitettyjen vauhtipyörien muodostaman systeemin hitausmomentti on yhtä suuri kuin vauhtipyörien A ja B yhteenlaskettu hitausmomentti, eli J AB = J A + J B (++) b) (max 3p) Alussa vain vauhtipyörä A:lla on pyörimisenergia, E A = 1 2 J Aω 2 A Systeemin pyörimisenergia yhteenliittämisen jälkeen on E AB = 1 2 (J A + J B )ωab 2 = 1 ( ) 2 (J JA ω 2 A + J B ) A = 1 JA 2 ω2 A J A + J B 2 J A + J B Systeemin mekaanisen energian muutos on siis E = E AB E A = 1 2 Oikeasta vastauksesta : JA 2 ω2 A 1 J A + J B 2 J AωA 2 = 1 ( ) 2 J AωA 2 JA 1 = 25,9 J J A + J B E trk+1 E A E AB (J) (J) (J) (J) A: -25,9-25,88 80,94 55,06 B: -29,9-29,90 124,2 94,32 C: -28,4-28,38 102,3 73,96 D: -24,6-24,63 69,30 44,67 ehtävän tarkkuus on kolme numeroa b)-kohdan vastauksen merkkiä ei arvostella a)-kohta laskettu energian säilymisellä, tehtävästä 0p Nyt voidaan ratkaista systeemin kulmanopeus yhteenliittämisen jälkeen: Oikeasta vastauksesta : ω AB = J Aω A J AB = J Aω A J A + J B = 8,37 rad/s ω AB trk+1 (rad/s) (rad/s) A: 8,37 8,367 B: 9,87 9,871 C: 9,32 9,323 D: 7,48 7,477
4 A4 214 Pb-näytteen radioaktiivisuutta on mitattu 10 minuutin välein oheiseen taulukkoon Näytteen aktiivisuus A on suoraan verrannollinen radioaktiivisten ydinten lukumäärään, A = λn, missä radioaktiivisten ytimien lukumäärä N noudattaa hajoamislakia N = N 0 e λt Aika t (min) 0,0 10,0 20,0 30,0 40,0 50,0 Aktiivisuus A (Bq) a) Määritä graafisesti 214 Pb-isotoopin puoliintumisaika b) Kuinka monta lyijy-ydintä koko 50 minuutin mittauksen aikana on hajonnut? a) (max 3p) ln(a/a 0 ) ln(a/a 0 ) t 30 Aika (min) 40 Kuvaaja, apa 1 apa 1: Näytteen aktiivisuudelle pätee 50 Aktiivisuus (Bq) A = A 0 e λt, Aika (min) Kuvaaja, apa 2 missä A 0 = N 0 /λ on näytteen aktiivisuus ajanhetkellä t = 0 min ja λ on 214 P-ytimen hajoamisvakio Jakamalla yllä oleva yhtälö A 0 :lla ja ottamalla luonnollinen logaritmi puolittain saadaan ln(a/a 0 ) = λt Yllä oleva yhtälö vastaa suoraa jonka kulmakerroin on λ Piirretään ln(a/a 0 ):n kuvaaja ajan funktiona ja määritetään suoran kulmakerroin graafisesti : 50 apa 2: Piirretään kuvaaja A(t) ja merkitään kuvaajaan kohta jossa aktiivisuus on puolittunut (A=605 Bq) Kohtaa vastaava aika on näytteen puoliintumisaika 1/2 = 27 min b) (max 3p) Aktiivisten ydinten ja aktiivisuuden välinen yhteys on A = λn Hajoamisvakio λ saadaan ratkaistua puoliintumisajasta: Hajonneiden ydinten lukumäärä on λ = ln 2 = 0, s 1 1/2 {{ A(0) A(50) N = N(0) N(50) = = [A(0) A(50)] 1/2 {{ λ ln 2 trk+1: 2, kpl, = 2, kpl ehtävän tarkkuus on kaksi numeroa Kuvaajaan vaaditaan: yksiköt akseleilla, symbolit akseleilla, akselien jaotus, kaikki pisteet, graafinen tasoitus Kukin puute: (-1/3p) a)-kohta apa 1: Jos on piirretty ln A t:n funktiona, kuvaajasta 0p a)-kohta apa 2: Jos sovitettu A(t)-kuvaajaan suora, kuvaajasta 0p λ = ln(a/a 0) t Puoliintumisaika ratkaistaan hajoamisvakiosta: = 0, s 1 1/2 = ln 2 λ = 27 min trk+1: 26,8 min,
5 A5 Kesälomalla oleva teekkari si ee kylmää juomaa laiturinnokassa aurinkoisena päivänä Hän on vähän huolimaton lisätessään jäitä juomaansa ja pudottaa jääpalan järveen Kauhuissaan hän muistaa entropia-luennon kevään ermodynamiikka-kurssilta ja luulee, että hän on nyt järkyttänyt universumin tasapainoa ja kokonaisentropia termodynamiikan toisen pääsäännön vastaisesti universumissa pienenee Auta hätääntynyttä teekkaria Määritä jääpalan entropian muutos kun jää a) lämpenee, b) sulaa vedeksi, c) sulamisvesi lämpenee d) Laske järviveden entropian muutos ja osoita, että universumin entropian muutos on positiivinen (3p) Jääpalan massa ja alkulämpötila ovat 12,0 g ja -10,8 C Järviveden lämpötila on 17,0 C ja sen lämpötila ei muutu m j i f (g) ( C) ( C) A 12,0 10,8 17,0 B 21,0 10,0 17,0 C 18,0 10,0 17,0 D 15,0 10,0 16,6 a) (max 1p) Jääpalan lämmetessä sen lämpötila muuttuu lämpötilasta i = 10,0 C = 263,2 K lämpötilaan a = 0 C = 273,2 K Jääpalan entropian muutos on kaavan (6) mukaan S a = c j m j ln a = 1,02 J/K (++) {{ i b) (max 1p) Jääpalan sulaessa sen entropian muutos on kaavan (3) mukaan S b = Q b = L jm j = 14,6 J/K (++) {{ a a c) (max 1p) Sulamisveden lämmetessä veden entropian muutos on kaavan (6) mukaan S c = c v m j ln f = 3,04 J/K, (++) {{ a missä f = 17,0 C = 290,2 K d) (max 3p) Järvivesi luovuttaa jääpalalle lämmön ( ) Q d = c j m j ( a i ) + L j m j + c v m j ( f a ) Entropian muutos järvivedelle saadaan kaavan (3) avulla: (++) S d = Q d = c jm j ( a i ) + L j m j + c v m j ( f a ) = 17,7 J/K (++) f f {{ Jääpala-järvivesi -systeemin entropian muutos on siis S kok = S a + S b + S c + S {{ d = 1,03 J/K (++) (++) ämä on samalla universumin entropian muutos, sillä muita lämpöjä ei prosesseissa vaihdu Oikeat vastaukset: S a trk+1 S b trk+1 S c trk+1 S d trk+1 S kok trk+1 (J/K) (J/K) (J/K) (J/K) (J/K) (J/K) (J/K) (J/K) (J/K) (J/K) A: 1,02 1,017 14,6 14,63 3,04 3,036-17,7-17,66 1,03 1,026 B: 1,64 1,645 25,6 25,60 5,31 5,313-30,8-30,78 1,78 1,782 C: 1,41 1,410 21,9 21,94 4,55 4,554-26,4-26,38 1,53 1,527 D: 1,17 1,175 18,3 18,29 3,71 3,708-21,9-21,93 1,24 1,243 ehtävän tarkkuus on kolme numeroa Laskuissa käytetty C kelvineiden sijaan, koko tehtävästä max 2p
6 A6 Oheisessa pv-tason kuvaajassa on esitetty syklinen prosessi ideaalikaasulle Prosessi koostuu kolmesta osaprosessista Prosessi a b on isokoorinen, prosessi b c isoterminen ja prosessi c a isobaarinen Ideaalikaasun muodostama systeemi on suljettu a) Määritä entropian muutoksen merkki (+/-) jokaiselle osaprosessille Perustele b) Hahmottele kaasun prosessin pv-tason kuvaajaa vastaava kuvaaja entropialämpötilatasossa, eli S-tasossa ehtävän 6 kuvaaja a) (max 3p) Prosessi a b: Kaavan (7) mukaan entropian muutos on isokoorisessa prosessissa S a b = C V ln b a Kyseessä on ideaalikaasu, joten tilanyhtälön mukaan pv = nr b) (max 3p) Kuvaajan pisteytys: a b: S kasvaa, kasvaa (++), b c: S kasvaa, vakio (++), c a: S pienenee, pienenee (++) Syklinen prosessi (++), suunta a)-kohdan perustelupisteitä ei anneta, jos vastaus väärin b)-kohta: hyväksytään sekä S- että S-kuvaaja S S-kuvaajan hahmotelma, akselit eivät ole lineaarisia ilavuuden pysyessä muuttumattomana ja paineen kasvaessa lämpötila nousee, eli b > a (++) Näin ollen S a b > 0 Vastaus: + Prosessi b c: Isotermisessä prosessissa ideaalikaasulle, kaasun sisäenergia ei muutu ermodynamiikan ensimmäisestä pääsäännöstä seuraa silloin että Q b c = W b c Koska kaasu laajenee kaasun ympäristöön tekemä työ on positiivinen ja kaasu näin ollen myös vastaanottaa lämpöä ympäristöstä (Q b c > 0) (++) Kaavasta (3) seuraa silloin että S b c > 0 Vastaus: + Prosessi c a: Kaavan (6) mukaan entropian muutos on S c a = C p ln a c Paineen pysyessä muuttumattomana ja tilavuuden pienentyessä ideaalikaasun tilanyhtälöstä seuraa että lämpötila laskee, eli a < c (++) Näin ollen S c a < 0 Vastaus: -
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 1.6.2005, malliratkaisut.
 1 Kuvaan 1 on piiretty kahden suoraviivaisesti samaan suuntaan liikkuvan auton ja B nopeudet ajan funktiona. utot ovat rinnakkain ajanhetkellä t = 0 s. a) Kuvaile auton liikettä ajan funktiona. Kumpi autoista
1 Kuvaan 1 on piiretty kahden suoraviivaisesti samaan suuntaan liikkuvan auton ja B nopeudet ajan funktiona. utot ovat rinnakkain ajanhetkellä t = 0 s. a) Kuvaile auton liikettä ajan funktiona. Kumpi autoista
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
2. Vastuksen läpi kulkee 50A:n virta, kun siihen vaikuttaa 170V:n jännite. Kuinka suuri resistanssi vastuksessa on?
 SÄHKÖTEKNIIKKA LASKUHARJOITUKSIA; OHMIN LAKI, KIRCHHOFFIN LAIT, TEHO 1. 25Ω:n vastuksen päiden välille asetetaan 80V:n jännite. Kuinka suuri virta alkaa kulkemaan vastuksen läpi? 2. Vastuksen läpi kulkee
SÄHKÖTEKNIIKKA LASKUHARJOITUKSIA; OHMIN LAKI, KIRCHHOFFIN LAIT, TEHO 1. 25Ω:n vastuksen päiden välille asetetaan 80V:n jännite. Kuinka suuri virta alkaa kulkemaan vastuksen läpi? 2. Vastuksen läpi kulkee
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
RATKAISUT: 22. Vaihtovirtapiiri ja resonanssi
 Physica 9. painos (0) RATKAST. Vaihtovirtapiiri ja resonanssi RATKAST:. Vaihtovirtapiiri ja resonanssi. a) Vaihtovirran tehollinen arvo on yhtä suuri kuin sellaisen tasavirran arvo, joka tuottaa vastuksessa
Physica 9. painos (0) RATKAST. Vaihtovirtapiiri ja resonanssi RATKAST:. Vaihtovirtapiiri ja resonanssi. a) Vaihtovirran tehollinen arvo on yhtä suuri kuin sellaisen tasavirran arvo, joka tuottaa vastuksessa
Kuva 1. Ohmin lain kytkentäkaavio. DC; 0 6 V.
 TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
1. Tasavirta. Virtapiirin komponenttien piirrosmerkit. Virtapiiriä havainnollistetaan kytkentäkaaviolla
 Fy3: Sähkö 1. Tasavirta Virtapiirin komponenttien piirrosmerkit Virtapiiriä havainnollistetaan kytkentäkaaviolla Sähkövirta I Sähkövirran suunta on valittu jännitelähteen plusnavasta miinusnapaan (elektronit
Fy3: Sähkö 1. Tasavirta Virtapiirin komponenttien piirrosmerkit Virtapiiriä havainnollistetaan kytkentäkaaviolla Sähkövirta I Sähkövirran suunta on valittu jännitelähteen plusnavasta miinusnapaan (elektronit
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Ionisoiva säteily. Tapio Hansson. 20. lokakuuta 2016
 Tapio Hansson 20. lokakuuta 2016 Milloin säteily on ionisoivaa? Milloin säteily on ionisoivaa? Kun säteilyllä on tarpeeksi energiaa irrottaakseen aineesta elektroneja tai rikkoakseen molekyylejä. Milloin
Tapio Hansson 20. lokakuuta 2016 Milloin säteily on ionisoivaa? Milloin säteily on ionisoivaa? Kun säteilyllä on tarpeeksi energiaa irrottaakseen aineesta elektroneja tai rikkoakseen molekyylejä. Milloin
7. Resistanssi ja Ohmin laki
 Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Omnia AMMATTIOPISTO Pynnönen
 MMTTOSTO SÄHKÖTEKNKK LSKHJOTKS; OHMN LK, KCHHOFFN LT, TEHO, iirrä tehtävistä N piirikaavio, johon merkitset kaikki virtapiirin komponenttien tunnisteet ja suuruudet, jännitteet ja virrat. 1. 22:n vastuksen
MMTTOSTO SÄHKÖTEKNKK LSKHJOTKS; OHMN LK, KCHHOFFN LT, TEHO, iirrä tehtävistä N piirikaavio, johon merkitset kaikki virtapiirin komponenttien tunnisteet ja suuruudet, jännitteet ja virrat. 1. 22:n vastuksen
Sähkövirran määrittelylausekkeesta
 VRTAPRLASKUT kysyttyjä suureita ovat mm. virrat, potentiaalit, jännitteet, resistanssit, energian- ja tehonkulutus virtapiirin teho lasketaan Joulen laista: P = R 2 sovelletaan Kirchhoffin sääntöjä tuntemattomien
VRTAPRLASKUT kysyttyjä suureita ovat mm. virrat, potentiaalit, jännitteet, resistanssit, energian- ja tehonkulutus virtapiirin teho lasketaan Joulen laista: P = R 2 sovelletaan Kirchhoffin sääntöjä tuntemattomien
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Insinöörivalinnan fysiikan koe 1.6.2011, malliratkaisut
 A1 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Täydennä kuhunkin kohtaan yhtälöstä puuttuva suure tai vakio alla olevasta taulukosta. Anna vastauksena kuhunkin kohtaan ainoastaan
A1 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2011 Täydennä kuhunkin kohtaan yhtälöstä puuttuva suure tai vakio alla olevasta taulukosta. Anna vastauksena kuhunkin kohtaan ainoastaan
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
Fy06 Koe 20.5.2015 Kuopion Lyseon lukio (KK) 1/7
 Fy06 Koe 0.5.015 Kuopion Lyseon lukio (KK) 1/7 alitse kolme tehtävää. 6p/tehtävä. 1. Mitä mieltä olet seuraavista väitteistä. Perustele lyhyesti ovatko väitteet totta vai tarua. a. irtapiirin hehkulamput
Fy06 Koe 0.5.015 Kuopion Lyseon lukio (KK) 1/7 alitse kolme tehtävää. 6p/tehtävä. 1. Mitä mieltä olet seuraavista väitteistä. Perustele lyhyesti ovatko väitteet totta vai tarua. a. irtapiirin hehkulamput
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Radioaktiivinen hajoaminen
 radahaj2.nb 1 Radioaktiivinen hajoaminen Radioaktiivinen hajoaminen on ilmiö, jossa aktivoitunut, epästabiili atomiydin vapauttaa energiaansa a-, b- tai g-säteilyn kautta. Hiukkassäteilyn eli a- ja b-säteilyn
radahaj2.nb 1 Radioaktiivinen hajoaminen Radioaktiivinen hajoaminen on ilmiö, jossa aktivoitunut, epästabiili atomiydin vapauttaa energiaansa a-, b- tai g-säteilyn kautta. Hiukkassäteilyn eli a- ja b-säteilyn
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
SMG-2100: SÄHKÖTEKNIIKKA
 SMG-2100: SÄHKÖTEKNIIKKA Vastusten kytkennät Energialähteiden muunnokset sarjaankytkentä rinnankytkentä kolmio-tähti-muunnos jännitteenjako virranjako Käydään läpi vastusten keskinäisten kytkentöjen erilaiset
SMG-2100: SÄHKÖTEKNIIKKA Vastusten kytkennät Energialähteiden muunnokset sarjaankytkentä rinnankytkentä kolmio-tähti-muunnos jännitteenjako virranjako Käydään läpi vastusten keskinäisten kytkentöjen erilaiset
Aineopintojen laboratoriotyöt 1. Veden ominaislämpökapasiteetti
 Aineopintojen laboratoriotyöt 1 Veden ominaislämpökapasiteetti Aki Kutvonen Op.nmr 013185860 assistentti: Marko Peura työ tehty 19.9.008 palautettu 6.10.008 Sisällysluettelo Tiivistelmä...3 Johdanto...3
Aineopintojen laboratoriotyöt 1 Veden ominaislämpökapasiteetti Aki Kutvonen Op.nmr 013185860 assistentti: Marko Peura työ tehty 19.9.008 palautettu 6.10.008 Sisällysluettelo Tiivistelmä...3 Johdanto...3
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
kipinäpurkauksena, josta salama on esimerkki.
 Sähkö 25 Esineet saavat sähkövarauksen hankauksessa kipinäpurkauksena, josta salama on esimerkki. Hankauksessa esineet voivat varautua sähköisesti. Varaukset syntyvät, koska hankauksessa kappaleesta siirtyy
Sähkö 25 Esineet saavat sähkövarauksen hankauksessa kipinäpurkauksena, josta salama on esimerkki. Hankauksessa esineet voivat varautua sähköisesti. Varaukset syntyvät, koska hankauksessa kappaleesta siirtyy
Katso Opetus.tv:n video: Kirchhoffin 1. laki http://opetus.tv/fysiikka/fy6/kirchhoffin-lait/
 4.1 Kirchhoffin lait Katso Opetus.tv:n video: Kirchhoffin 1. laki http://opetus.tv/fysiikka/fy6/kirchhoffin-lait/ Katso Kimmo Koivunoron video: Kirchhoffin 2. laki http://www.youtube.com/watch?v=2ik5os2enos
4.1 Kirchhoffin lait Katso Opetus.tv:n video: Kirchhoffin 1. laki http://opetus.tv/fysiikka/fy6/kirchhoffin-lait/ Katso Kimmo Koivunoron video: Kirchhoffin 2. laki http://www.youtube.com/watch?v=2ik5os2enos
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
Coulombin laki. Sähkökentän E voimakkuus E = F q
 Coulombin laki Kahden pistemäisen varatun hiukkasen välinen sähköinen voima F on suoraan verrannollinen varausten Q 1 ja Q 2 tuloon ja kääntäen verrannollinen etäisyyden r neliöön F = k Q 1Q 2 r 2, k =
Coulombin laki Kahden pistemäisen varatun hiukkasen välinen sähköinen voima F on suoraan verrannollinen varausten Q 1 ja Q 2 tuloon ja kääntäen verrannollinen etäisyyden r neliöön F = k Q 1Q 2 r 2, k =
SMG-1100: PIIRIANALYYSI I
 SMG-1100: PIIIANALYYSI I Vastusten kytkennät Energialähteiden muunnokset sarjaankytkentä rinnankytkentä kolmio-tähti-muunnos jännitteenjako virranjako Kirja: luku 3 Luentomoniste: luvut 4.2, 4.3 ja 4.4
SMG-1100: PIIIANALYYSI I Vastusten kytkennät Energialähteiden muunnokset sarjaankytkentä rinnankytkentä kolmio-tähti-muunnos jännitteenjako virranjako Kirja: luku 3 Luentomoniste: luvut 4.2, 4.3 ja 4.4
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Kaksi yleismittaria, tehomittari, mittausalusta 5, muistiinpanot ja oppikirjat. P = U x I
 Pynnönen 1/3 SÄHKÖTEKNIIKKA Kurssi: Harjoitustyö : Tehon mittaaminen Pvm : Opiskelija: Tark. Arvio: Tavoite: Välineet: Harjoitustyön tehtyäsi osaat mitata ja arvioida vastukseen jäävän tehohäviön sähköisessä
Pynnönen 1/3 SÄHKÖTEKNIIKKA Kurssi: Harjoitustyö : Tehon mittaaminen Pvm : Opiskelija: Tark. Arvio: Tavoite: Välineet: Harjoitustyön tehtyäsi osaat mitata ja arvioida vastukseen jäävän tehohäviön sähköisessä
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
c) Missä ajassa kappale selvittää reitin b-kohdan tapauksessa? [3p]
![c) Missä ajassa kappale selvittää reitin b-kohdan tapauksessa? [3p] c) Missä ajassa kappale selvittää reitin b-kohdan tapauksessa? [3p]](/thumbs/50/26318972.jpg) Fysiikan valintakoe 11.5.2016 klo 9-12 1. Kappale lähtee levosta liikkeelle pisteessä A (0,3) ja liukuu kitkattomasti, ensin kaltevaa tasoa pitkin pisteeseen B (x,0) ja siitä edelleen vaakaatasoa pitkin
Fysiikan valintakoe 11.5.2016 klo 9-12 1. Kappale lähtee levosta liikkeelle pisteessä A (0,3) ja liukuu kitkattomasti, ensin kaltevaa tasoa pitkin pisteeseen B (x,0) ja siitä edelleen vaakaatasoa pitkin
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
Radioaktiivisen säteilyn läpitunkevuus. Gammasäteilty.
 Fysiikan laboratorio Työohje 1 / 5 Radioaktiivisen säteilyn läpitunkevuus. Gammasäteilty. 1. Työn tavoite Työn tavoitteena on tutustua ionisoivaan sähkömagneettiseen säteilyyn ja tutkia sen absorboitumista
Fysiikan laboratorio Työohje 1 / 5 Radioaktiivisen säteilyn läpitunkevuus. Gammasäteilty. 1. Työn tavoite Työn tavoitteena on tutustua ionisoivaan sähkömagneettiseen säteilyyn ja tutkia sen absorboitumista
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
AVOIMEN SARJAN VASTAUKSET JA PISTEITYS
 AVOIME SARJA VASTAUKSET JA PISTEITYS 1. Käytössäsi on viivoitin, 10 g:n punnus, 2 :n kolikko sekä pyöreä kynä. Määritä kolikon ja viivoittimen massa. Selosta vastauksessa käyttämäsi menetelmät sekä esitä
AVOIME SARJA VASTAUKSET JA PISTEITYS 1. Käytössäsi on viivoitin, 10 g:n punnus, 2 :n kolikko sekä pyöreä kynä. Määritä kolikon ja viivoittimen massa. Selosta vastauksessa käyttämäsi menetelmät sekä esitä
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
RATKAISUT: 17. Tasavirtapiirit
 Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Fysiikan valintakoe 10.6.2014, vastaukset tehtäviin 1-2
 Fysiikan valintakoe 10.6.2014, vastaukset tehtäviin 1-2 1. (a) W on laatikon paino, F laatikkoon kohdistuva vetävä voima, F N on pinnan tukivoima ja F s lepokitka. Kuva 1: Laatikkoon kohdistuvat voimat,
Fysiikan valintakoe 10.6.2014, vastaukset tehtäviin 1-2 1. (a) W on laatikon paino, F laatikkoon kohdistuva vetävä voima, F N on pinnan tukivoima ja F s lepokitka. Kuva 1: Laatikkoon kohdistuvat voimat,
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 31.5.2006, malliratkaisut ja arvostelu.
 1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
Atomin ydin. Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N
 Atomin ydin ytimen rakenneosia, protoneja (p + ) ja neutroneja (n) kutsutaan nukleoneiksi Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N saman
Atomin ydin ytimen rakenneosia, protoneja (p + ) ja neutroneja (n) kutsutaan nukleoneiksi Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N saman
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
Tehtävä 1. a) sähkövirta = varausta per sekunti, I = dq dt = 1, A = 1, C s protonin varaus on 1, C
 Tehtävä a) sähkövirta = varausta per sekunti, I = dq dt =, 5 0 3 =, 5 0 3 C s protonin varaus on, 6 0 9 C Jaetaan koko virta yksittäisille varauksille:, 5 0 3 C s kpl = 9 05, 6 0 9 s b) di = Jd = J2πrdr,
Tehtävä a) sähkövirta = varausta per sekunti, I = dq dt =, 5 0 3 =, 5 0 3 C s protonin varaus on, 6 0 9 C Jaetaan koko virta yksittäisille varauksille:, 5 0 3 C s kpl = 9 05, 6 0 9 s b) di = Jd = J2πrdr,
VASTUSMITTAUKSIA. 1 Työn tavoitteet
 Oulun yliopisto Fysiikan opetuslaboratorio Sähkö ja magnetismiopin laboratoriotyöt VASTUSMTTAUKSA Työn tavoitteet Tässä työssä tutustut Ohmin lakiin ja joihinkin menetelmiin, joiden avulla vastusten resistansseja
Oulun yliopisto Fysiikan opetuslaboratorio Sähkö ja magnetismiopin laboratoriotyöt VASTUSMTTAUKSA Työn tavoitteet Tässä työssä tutustut Ohmin lakiin ja joihinkin menetelmiin, joiden avulla vastusten resistansseja
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
TEHTÄVÄT KYTKENTÄKAAVIO
 TEHTÄÄT KYTKENTÄKIO 1. a) Mitkä kytkentäkaavion hehkulampuista hehkuvat? b) Kuinka monta eri kulkureittiä sähkövirralla on pariston plusnavalta miinusnavalle? 2. Piirrä sähkölaitteen tai komponentin piirrosmerkki.
TEHTÄÄT KYTKENTÄKIO 1. a) Mitkä kytkentäkaavion hehkulampuista hehkuvat? b) Kuinka monta eri kulkureittiä sähkövirralla on pariston plusnavalta miinusnavalle? 2. Piirrä sähkölaitteen tai komponentin piirrosmerkki.
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2009, insinöörivalinnan fysiikan koe 27.5.2009, malliratkaisut
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2009, insinöörivalinnan fysiikan koe 27.5.2009, malliratkaisut 1 Huvipuiston vuoristoradalla vaunu (massa m v = 1100 kg) lähtee levosta liikkeelle
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2009, insinöörivalinnan fysiikan koe 27.5.2009, malliratkaisut 1 Huvipuiston vuoristoradalla vaunu (massa m v = 1100 kg) lähtee levosta liikkeelle
KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT
 KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT Lämpölaajeneminen Pituuden lämpölaajeneminen: l = αl o t lo l l = l o + l = l o + αl o t l l = l o (1 + α t) α = pituuden lämpötilakerroin esim. teräs: α = 12 10
KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT Lämpölaajeneminen Pituuden lämpölaajeneminen: l = αl o t lo l l = l o + l = l o + αl o t l l = l o (1 + α t) α = pituuden lämpötilakerroin esim. teräs: α = 12 10
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
SÄHKÖENERGIATEKNIIIKKA. Harjoitus - luento 6. Tehtävä 1.
 SÄHKÖENERGIATEKNIIIKKA Harjoitus - luento 6 Tehtävä 1. Aurinkokennon virta I s 1,1 A ja sen mallissa olevan diodin estosuuntainen kyllästysvirta I o 1 na. Laske aurinkokennon maksimiteho suhteessa termiseen
SÄHKÖENERGIATEKNIIIKKA Harjoitus - luento 6 Tehtävä 1. Aurinkokennon virta I s 1,1 A ja sen mallissa olevan diodin estosuuntainen kyllästysvirta I o 1 na. Laske aurinkokennon maksimiteho suhteessa termiseen
Fysiikan laboratoriotyöt 3 Sähkömotorinen voima
 Fysiikan laboratoriotyöt 3 Sähkömotorinen voima Työn suorittaja: Antti Pekkala (1988723) Mittaukset suoritettu 8.10.2014 Selostus palautettu 16.10.2014 Valvonut assistentti Martti Kiviharju 1 Annettu tehtävä
Fysiikan laboratoriotyöt 3 Sähkömotorinen voima Työn suorittaja: Antti Pekkala (1988723) Mittaukset suoritettu 8.10.2014 Selostus palautettu 16.10.2014 Valvonut assistentti Martti Kiviharju 1 Annettu tehtävä
13 KALORIMETRI. 13.1 Johdanto. 13.2 Kalorimetrin lämmönvaihto
 13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Tarvittavat välineet: Kalorimetri, lämpömittari, jännitelähde, kaksi yleismittaria, sekuntikello
 1 LÄMPÖOPPI 1. Johdanto Työssä on neljä eri osiota, joiden avulla tutustutaan lämpöopin lakeihin ja ilmiöihin. Työn suoritettuaan opiskelijan on tarkoitus ymmärtää lämpöopin keskeiset käsitteet, kuten
1 LÄMPÖOPPI 1. Johdanto Työssä on neljä eri osiota, joiden avulla tutustutaan lämpöopin lakeihin ja ilmiöihin. Työn suoritettuaan opiskelijan on tarkoitus ymmärtää lämpöopin keskeiset käsitteet, kuten
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
Lineaarialgebra MATH.1040 / Piirianalyysiä
 Lineaarialgebra MATH.1040 / Piirianalyysiä 1 Kirchoffin ensimmäinen laki: Missä tahansa virtapiirin liitoskohdassa pisteeseen saapuvien sähkövirtojen summa on yhtä suuri kuin siitä poistuvien sähkövirtojen
Lineaarialgebra MATH.1040 / Piirianalyysiä 1 Kirchoffin ensimmäinen laki: Missä tahansa virtapiirin liitoskohdassa pisteeseen saapuvien sähkövirtojen summa on yhtä suuri kuin siitä poistuvien sähkövirtojen
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
Käytetään lopuksi ideaalikaasun tilanyhtälöä muutoksille 1-2 ja 3-1. Muutos 1-2 on isokorinen, joten tilanyhtälöstä saadaan ( p2 / p1) = ( T2 / T1)
 LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa.
 Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
Ohjeita fysiikan ylioppilaskirjoituksiin
 Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
S SÄHKÖTEKNIIKKA Kimmo Silvonen
 S55.103 SÄHKÖTKNKK 21.12.2000 Kimmo Silvonen Tentti: tehtävät 1,3,4,8,9 1. välikoe: tehtävät 1,2,3,4,5 2. välikoe: tehtävät,7,8,9,10 Oletko jo ehtinyt vastata palautekyselyyn Voit täyttää lomakkeen nyt.
S55.103 SÄHKÖTKNKK 21.12.2000 Kimmo Silvonen Tentti: tehtävät 1,3,4,8,9 1. välikoe: tehtävät 1,2,3,4,5 2. välikoe: tehtävät,7,8,9,10 Oletko jo ehtinyt vastata palautekyselyyn Voit täyttää lomakkeen nyt.
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
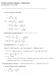 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä
 Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Erään piirikomponentin napajännite on nolla, eikä sen läpi kulje virtaa ajanhetkellä 0 jännitteen ja virran arvot ovat. 500t.
 DEE- Piirianalyysi Harjoitus / viikko 4 Erään piirikomponentin napajännite on nolla, eikä sen läpi kulje virtaa ajanhetkellä jännitteen ja virran arvot ovat t Kun t, v te t 5t 8 V, i te t 5t 5 A, a) Määritä
DEE- Piirianalyysi Harjoitus / viikko 4 Erään piirikomponentin napajännite on nolla, eikä sen läpi kulje virtaa ajanhetkellä jännitteen ja virran arvot ovat t Kun t, v te t 5t 8 V, i te t 5t 5 A, a) Määritä
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2013 Insinöörivalinnan fysiikan koe 29.5.2013, malliratkaisut
 A1 Ampumahiihtäjä ampuu luodin vaakasuoraan kohti maalitaulun keskipistettä. Luodin lähtönopeus on v 0 = 445 m/s ja etäisyys maalitauluun s = 50,0 m. a) Kuinka pitkä on luodin lentoaika? b) Kuinka kauaksi
A1 Ampumahiihtäjä ampuu luodin vaakasuoraan kohti maalitaulun keskipistettä. Luodin lähtönopeus on v 0 = 445 m/s ja etäisyys maalitauluun s = 50,0 m. a) Kuinka pitkä on luodin lentoaika? b) Kuinka kauaksi
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Perusopintojen Laboratoriotöiden Työselostus 1
 Perusopintojen Laboratoriotöiden Työselostus 1 Kalle Hyvönen Työ tehty 1. joulukuuta 008, Palautettu 30. tammikuuta 009 1 Assistentti: Mika Torkkeli Tiivistelmä Laboratoriossa tehdyssä ensimmäisessä kokeessa
Perusopintojen Laboratoriotöiden Työselostus 1 Kalle Hyvönen Työ tehty 1. joulukuuta 008, Palautettu 30. tammikuuta 009 1 Assistentti: Mika Torkkeli Tiivistelmä Laboratoriossa tehdyssä ensimmäisessä kokeessa
Harjoitustehtäviä kokeeseen: Sähköoppi ja magnetismi
 Harjoitustehtäviä kokeeseen: Sähköoppi ja magnetismi 3. Selitä: a. Suljettu virtapiiri Suljettu virtapiiri on sähkövirran reitti, jonka muodostavat johdot, paristot ja komponentit. Suljetussa virtapiirissä
Harjoitustehtäviä kokeeseen: Sähköoppi ja magnetismi 3. Selitä: a. Suljettu virtapiiri Suljettu virtapiiri on sähkövirran reitti, jonka muodostavat johdot, paristot ja komponentit. Suljetussa virtapiirissä
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
