7 Termodynaamiset potentiaalit
|
|
|
- Markus Kahma
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan. Monet käytännön kannalta tärkeät prosessit tapahtuvat kuitenkin systeemeissä, jotka eivät ole eristettyjä. ällaiset systeemit voivat vaihtaa lämpöä ja mekaanista energiaa ympäristönsä kanssa, joten E ja eivät ole välttämättä vakioita. ässä kappaleessa johdetaan entropiaperiaatteen yleistys, jonka avulla voidaan saada selville, mihin suuntaan prosessit etenevät tällaisissa ympäristönsä kanssa vuorovaikuttavissa systeemeissä (joiden oletetaan kuitenkin edelleen olevan suljettuja, joten N on vakio). Entropiaperiaatteen mukaan eristetyn systeemin tilan muuttuessa tilasta 1 tilaksi 2 systeemin entropia joko kasvaa (irreversiibeleissä prosesseissa) tai ääritapauksissa pysyy vakiona (reversiibeleissä prosesseissa): S S 2 S 1 0. (7.1) arkastellaan kuvan 1 mukaista systeemiä, joka on kytketty sekä termisesti että mekaanisesti lämpökylpyyn. ämä merkitsee sitä, että systeemin ja lämpökylvyn välinen rajapinta voi olla liikkuva ja lämpöä johtava. Lämpökylvyn koko on niin suuri, että rajapinnan läpi siirtyvä lämpömäärä ja rajapinnan liike eivät muuta kylvyn lämpötilaa 0 Kuva 1.
2 tai painetta 0. Näin ollen voidaan sanoa, että lämpökylpy toimii myös painekylpynä. Systeemi ja lämpökylpy eivät välttämättä ole tarkasteltavalla hetkellä keskinäisessä tasapainossa, ts. niiden lämpötilat ja paineet eivät välttämättä ole samat. Systeemin ei tarvitse olla myöskään sisäisessä tasapainossa esimerkiksi sen lämpötila ja paine voivat olla eri kohdissa erilaisia. Lämpökylvyn oletetaan kuitenkin olevan koko ajan sisäisessä tasapainossa. Systeemi ja lämpökylpy muodostavat yhdessä eristetyn kokonaissysteemin, jonka entropia on systeemin ja lämpökylvyn entropioiden S ja S 0 summa: 83 S tot = S + S 0. (7.2) Entropiaperiaatteen (7.1) mukaan kokonaissysteemin kaikissa muutoksissa S tot kasvaa tai pysyy vakiona: S tot = S + S 0 0. (7.3) arkastellaan prosessia, jossa systeemiin siirtyy lämpökylvystä lämpömäärä Q ja systeemin tilavuus muuttuu :n verran. Koska lämpökylpy on koko ajan sisäisessä tasapainossa lämpötilassa 0 ja paineessa 0, prosessi on lämpökylvyn kannalta reversiibeli ja isoterminen. Näin ollen lämpökylvyn entropian muutos on yhtälön (5.35) mukaan S 0 = Q 0. (7.4) Sijoittamalla tämä yhtälö epäyhtälöön (7.3) ja kertomalla puolittain 0 :lla saadaan tulos 0 S Q 0. (7.5) Ensimmäisen pääsäännön (2.7) mukaan Q = E W, missä E on tarkasteltavan systeemin sisäisen energian muutos ja W on siihen tehty työ. Näin ollen epäyhtälö (7.5) voidaan esittää muodossa 0 S E + W 0. (7.6) ilavuuden muutoksen takia lämpökylpy tekee systeemiin yhtälön (2.15) mukaan työn W = 0. (7.7) Jos systeemiin ei tehdä mitään muuta työtä, W = W ja epäyhtälöstä (7.6) saadaan (siirtämällä termit -merkin oikealle puolelle) Clausiuksen epäyhtälö E S 0, (7.8) missä =- ja <-merkit pätevät reversiibeleille ja irreversiibeleille prosesseille. Epäyhtälö (7.8) on Clausiuksen entropiaperiaatteen (7.1) yleistys, joka määrää termisesti ja mekaanisesti lämpökylpyyn kytketyssä suljetussa systeemissä tapahtuvien luonnollisten prosessien suunnan. rosessia pidetään luonnollisena tai spontaanina, jos systeemiin tehty työ on pelkästään normaalia (ja väistämätöntä) ympäristön paineen aiheuttamaa tilavuudenmuutostyötä ( -työtä). ällöin W = W = 0, eikä systeemiin vaikuteta ulkopuolelta tekemällä siihen jotakin muuta työtä. Alkuperäinen Clausiuksen entropiaperiaate (7.1) on voimassa ilman tällaista lisäehtoa, koska eristettyyn systeemiin ei tehdä ulkoapäin mitään työtä, ei edes tilavuudenmuutostyötä. Eristetyn systeemin kaikki prosessit ovat siis tämän määritelmän mukaan luonnollisia.
3 Yleisessä tapauksessa Clausiuksen epäyhtälö (7.8) sisältää systeemin tilamuuttujien (E, ja S) lisäksi myös sen ympäristön tilamuuttujia ( 0 ja 0 ). On kuitenkin olemassa erikoistapauksia, joissa epäyhtälö riippuu vain itse systeemin ominaisuuksista. Esimerkiksi ympäristön lämpötilassa tapahtuvissa isotermisissä prosesseissa, joissa systeemin tilavuus ei muutu, epäyhtälö (7.8) redusoituu sijoituksilla 0 = ja = 0 muotoon joka sisältää vain systeemin tilamuuttujia. 84 E S 0, (7.9) Jos määritellään systeemin ja sen ympäristön tilamuuttujien funktio A (engl. availability) yhtälöllä A E S, (7.10) Clausiuksen epäyhtälö (7.8) saa kompaktin muodon A 0. (7.11) ästä nähdään, että funktio A pyrkii pienenemään tarkastellun systeemin kaikissa luonnollisissa prosesseissa. Se määrää myös systeemin tasapainotilan se on tila, jossa A saavuttaa miniminsä. Clausiuksen epäyhtälö (7.11) voidaan helposti yleistää tapauksiin, joissa systeemiin tehdään lämpökylvyn paineen 0 aiheuttaman tilavuudenmuutostyön W = 0 lisäksi muutakin työtä. Jos tätä muuta työtä merkitään W X :llä, systeemiin tehty kokonaistyö on W = W + W X = 0 + W X. (7.12) Kun tämä W :n lauseke sijoitetaan epäyhtälöön (7.6), saadaan 0 S E 0 + W X 0, (7.13) joka voidaan funktion A määritelmää (7.10) A = E S käyttäen kirjoittaa muotoon A W X. (7.14) ämä on Clausiuksen epäyhtälön (7.11) yleistys. Se redusoituu alkuperäiseksi epäyhtälöksi, jos ylimääräinen työ W X on nolla (tällöin prosessia voidaan pitää luonnollisena ). Jos prosessia muutetaan tekemällä systeemiin W X :n verran muuta kuin -työtä, funktion A ei tarvitse välttämättä pienentyä, vaan se voi kasvaa enintään W X :n verran. Epäyhtälö (7.14) voidaan kirjoittaa myös muotoon W X A, (7.15) missä W X on systeemin tekemä käyttökelpoinen työ (engl. useful work). ällä tarkoitetaan työtä, jota voidaan käyttää hyväksi jossakin toisessa systeemissä. Systeemin tekemää tilavuudenmuutostyötä W = 0 ei voida käyttää tässä mielessä hyväksi. Se menee ko. toisen systeemin kannalta hukkaan, koska se kuluu ympäristön paineen voittamiseen systeemin tilavuuden kasvaessa (ja muuttuu ympäristön lämpöenergiaksi). Epäyhtälö (7.15) osoittaa, että systeemi voi tehdä käyttökelpoista työtä korkeintaan A:n verran. Systeemistä voidaan siis vapauttaa käyttökelpoista energiaa enintään A:n pienenemisen A = A 1 A 2 verran. ästä syystä funktiota A voitaisiin kutsua systeemin vapaaksi
4 energiaksi. Suomen kielessä A:lle ei kuitenkaan ole olemassa mitään vakiintunutta nimitystä ermodynaamiset potentiaalit Edellisessä kappaleessa osoitettiin, että yhtälöllä (7.10) määritelty funktio A määrää termisesti ja mekaanisesti lämpökylpyyn kytketyssä suljetussa systeemissä tapahtuvien luonnollisten prosessien suunnan ja tällaisen systeemin tasapainotilan. Jos systeemissä tapahtuvia prosesseja rajoitetaan joillakin side-ehdoilla, saadaan A:n tilalle muita funktioita, jotka määräävät prosessien suunnan. Eristetyllä systeemillä E = = 0, joten funktion A = E S muutos on A = 0 S. (7.16) ällöin Clausiuksen epäyhtälö A 0 redusoituu alkuperäiseksi Clausiuksen entropiaperiaatteeksi (7.1): S 0. (7.17) Systeemin entropia S määrää siis eristetyn systeemin tasapainotilan (se on tila, jossa S on maksimissaan). Helmholtzin vapaa energia arkastellaan systeemiä, jonka lämpötila on alku- ja lopputilassa (tiloissa 1 ja 2) sama kuin lämpökylvyn lämpötila 0 ( 1 = 2 = = 0 ) ja jonka tilavuus on alkutilassa sama kuin lopputilassa ( 1 = 2, joten = 2 1 = 0). ällaisen systeemin tapauksessa funktion A muutos on A = E S = (E S) F 0, (7.18) sillä ( S) = 2 S 2 1 S 1 = S 2 S 1 = (S 2 S 1 ) = S. ässä epäyhtälössä esiintyvä funktio F = E S on yhtälön (5.10) mukaan Helmholtzin vapaa energia (tai Helmholtzin funktio), joka riippuu vain systeemin (ei ympäristön) ominaisuuksista. ällaisessa systeemissä F määrää luonnollisten prosessien suunnan: se pyrkii pienenemään ja saavuttaa tasapainotilassa miniminsä. ässä suhteessa se käyttäytyy samalla tavalla kuin mekaanisen systeemin potentiaalienergia, joka määrää systeemin tasapainotilan. ästä syystä Helmholtzin vapaata energiaa sanotaan termodynaamiseksi potentiaaliksi. Epäyhtälö (7.18) on voimassa siinäkin tapauksessa, että systeemin lämpötila muuttuu prosessin aikana, edellyttäen että alku- ja loppulämpötilat ovat samat. Käytännössä näin tapahtuu varsin usein. yypillisessä tapauksessa systeemi on aluksi termisessä tasapainossa lämpötilassa olevan lämpökylvyn kanssa. Systeemissä tapahtuu esimerkiksi eksoterminen kemiallinen reaktio A + B AB, josta vapautuva energia nostaa systeemin lämpötilaa. Reaktion jälkeen ylimääräinen energia siirtyy kuitenkin lämpökylpyyn ja systeemi jäähtyy lopulta takaisin alkulämpötilaansa. Epäyhtälö (7.18) on tällöin voimassa, jos alku- ja lopputilavuudet ovat samat. Samalla tavalla systeemin tilavuus voi prosessin aikana muuttua, edellyttäen että lopputilavuus on sama kuin alkutilavuus. Clausiuksen epäyhtälön yleistyksen (7.15) mukaan tarkasteltava systeemi voi tehdä käyttökelpoista työtä korkeintaan F :n verran: W X F. (7.19)
5 Jos siis Helmholtzin vapaa energia pienenee prosessin aikana esimerkiksi 100 J, systeemistä vapautuu käyttökelpoista energiaa reversiibelissä prosessissa 100 J ja irreversiibelissä prosessissa vähemmän. Hyvin usein joudutaan tarkastelemaan vakiopaineessa (esimerkiksi systeemiä ympäröivän ilmakehän paineessa) tapahtuvia prosesseja. Yleensä systeemi on tällöin termisessä kontaktissa lämpökylvyn kanssa, mutta se voi olla myös lämpöeristetty. Näissä tapauksissa saadaan kaksi erilaista systeemin tasapainotilan määräävää ehtoa. Näitä ehtoja varten määritellään kaksi uutta tilamuuttujaa, joita myös sanotaan termodynaamisiksi potentiaaleiksi. Gibbsin vapaa energia Jos systeemi on sekä termisessä että mekaanisessa kontaktissa lämpökylvyn kanssa siten, että systeemin lämpötila ( ) ja paine ( ) ovat alku- ja lopputilassa samat kuin lämpökylvyllä ( 1 = 2 = = 0, 1 = 2 = = 0 ), Clausiuksen epäyhtälö (7.11) saa muodon A = E + S = (E + S) G 0, (7.20) sillä ( ) = = 2 1 = ( 2 1 ) =. ässä epäyhtälössä on määritelty Gibbsin vapaa energia (Gibbsin funktio tai vapaa entalpia) G: G E + S. (7.21) Näin ollen G (joka on vain systeemin ominaisuuksien funktio) pienenee kaikissa tällaisen systeemin spontaaneissa prosesseissa ja saavuttaa tasapainossa miniminsä. Epäyhtälön (7.15) mukaan tällainen systeemi voi tehdä käyttökelpoista työtä korkeintaan Gibbsin vapaan energian pienenemisen ( G) verran: 86 W X G. (7.22) Entalpia Jos systeemi on mekaanisessa tasapainossa vakiopaineisen ympäristön kanssa, sen paine on koko prosessin ajan kaikkialla sama kuin ympäristön paine 0. ällöin siihen tehty tilavuudenmuutostyö on yhtälön (2.15) mukaan W = W = 0 =. Jos systeemiin ei tehdä mitään muuta työtä, siihen siirtynyt lämpömäärä on termodynamiikan ensimmäisen pääsäännön (2.7) mukaan Q = E W = E + = (E + ) H, (7.23) missä on määritelty systeemin entalpia (engl. enthalpy): H E +. (7.24) akiopaineessa olevaan systeemiin sen luonnollisissa prosesseissa siirtyvä lämpömäärä Q on sama kuin systeemin entalpian muutos H. Entalpia H on tilamuuttuja, joka riippuu vain tarkasteltavan systeemin ominaisuuksista. Sitä sanotaan joskus systeemin lämpösisällöksi (engl. heat content), sillä yhtälön (7.23)
6 87 Kuva 2. mukaan hypoteettinen systeemin luominen tyhjästä (alkutilasta E = = H = 0) vaatisi vakiopaineessa = 0 kokonaislämpömäärän Q = H = E +. ällaiseen systeemiin tuotu lämpöenergia kuluisi osaksi sisäisen energian kasvattamiseen (0 E) ja osaksi tilavuudenmuutostyöhön ( ). Entalpia ottaa siis automaattisesti huomioon myös sen työn, joka systeemin on tehtävä luodakseen tarvitsemansa tilan ympäristössä, jonka paine on. Jos systeemi häviäisi täydellisesti, vapautuva energia olisi H, johon E:n lisäksi kuuluu myös ympäristön tekemä tilavuudenmuutostyö. Jos vakiopaineessa oleva systeemi on lämpöeristetty, Q on nolla ja entalpia on vakio: Q = H = 0. (7.25) Clausiuksen epäyhtälön esimuoto (7.5) redusoituu tapauksessa Q = 0 muotoon S 0. (7.26) Näin ollen entropia S kasvaa kaikissa lämpöeristetyn systeemin prosesseissa ja saavuttaa tasapainotilassa maksiminsa. Jos systeemin paine on lisäksi koko prosessin ajan vakio, myös sen entalpia on yhtälön (7.25) mukaan vakio. ällaisen kuvan 2 mukaisen systeemin tasapainotila löydetään siis maksimoimalla entropia pitäen entalpia vakiona. Systeemin mekaanisesta tasapainosta ympäristön kanssa seuraa, että systeemin tilavuuden muutos tapahtuu reversiibelisti. Systeemin ei kuitenkaan tarvitse olla muuten tasapainotilassa, joten prosessi voi olla kokonaisuutena irreversiibeli ja systeemin entropia voi siis kasvaa. Analogisesti eristetyssä systeemissä entropia maksimoidaan pitäen energia vakiona. Esimerkki: Kemiallisen reaktion SO O 2 SO 3 vaatima lämpömäärä, reaktiolämpö, on Q = Q = 97, 03 kj/mol, kun reaktio tapahtuu vakiotilavuudessa alku- ja loppulämpötilan ollessa 25 C (reaktio tuottaa lämpömäärän Q = 97, 03 kj/mol). Kuinka suuri on vakiopaineessa mitattu reaktiolämpö?
7 Jos systeemin tilavuus ei muutu, siihen ei tehdä lainkaan työtä (edellyttäen, että käytetyssä koejärjestelyssä mikään muu kuin ympäristön paineen tekemä -työ ei ole mahdollinen), joten ensimmäisen pääsäännön (2.7) mukaan reaktiolämpö Q = Q on sama kuin sisäisen energian muutos: 88 Q = E. (7.27) Jos systeemi on mekaanisessa tasapainossa vakiopaineisen ympäristön kanssa, reaktiolämpö Q = Q on yhtälön (7.23) mukaan sama kuin entalpian muutos, joka voidaan yhtälöiden (7.24) ja (7.27) avulla kirjoittaa muodossa Q = H = E + ( ) = Q + ( ). (7.28) Jos SO 2 :n, O 2 :n ja SO 3 :n tilanyhtälöitä approksimoidaan 25 C:n lämpötilassa ideaalikaasun tilanyhtälöllä = nr, saadaan :n muutokseksi ( ) = = n 2 R n 1 R = n R, (7.29) missä n = n 2 n 1 ja n 1 ja n 2 ovat reaktioon osallistuvien aineiden moolien lukumäärät alku- ja lopputilassa. ällöin entalpian muutos on H = E + n R. (7.30) ässä tapauksessa n 1 on reagoivien aineiden (SO 2 :n ja O 2 :n) moolien lukumäärien summa = 3 2 ja n 2 on reaktion lopputuloksen (SO 3 :n) moolien lukumäärä 1. Näin ollen n = n 2 n 1 = = 1 2 ja yhtälön (7.30) mukaan H = E 1 2 R, josta saadaan lämpötilassa 25 C = 298 K tulos H = 98, 27 kj/mol. Reaktio tuottaa siis vakiopaineessa enemmän lämpöä kuin vakiotilavuudessa ( Q = 98, 27 kj/mol ja Q = 97, 03 kj/mol). ämä johtuu siitä, että systeemin tilavuus pienenee moolien lukumäärän pienentyessä, jolloin kaasuun tehdään positiivista työtä (W = = n R ), joka muuttuu lämmöksi. On huomattava, että tämä työ ei riipu lainkaan systeemin paineesta. Useimmat kemialliset reaktiot tapahtuvat vakiopaineessa, jossa reaktiolämpö on sama kuin entalpian muutos. Yhdisteen muodostumisentalpia normaalitilassa, H f, on entalpian muutos reaktiossa, jossa tämä yhdiste muodostuu alkuaineistaan kaikkien reaktioon osallistuvien aineiden ollessa alussa ja lopussa annetussa normaalitilassa. Aineen normaalitila osoitetaan yläindeksillä (tai ) ja se tarkoittaa tilaa, jossa aine on stabiili annetussa lämpötilassa 1 atm:n paineessa (ko. absoluuttinen lämpötila merkitään näkyviin alaindeksinä tai suluissa). Esim. SO 2 :n H f :n arvo on sama kuin reaktion S + O 2 SO 2 H :n arvo ( H298 = 296, 9 kj/mol). Muodostumisentalpioista on julkaistu laajoja taulukoita, ja niiden avulla voidaan helposti laskea minkä tahansa reaktion H :n arvo.
8 89 Esimerkki: Kuinka suuren lämpömäärän metaani (CH 4 ) tuottaa palaessaan 1 atm:n paineessa lämpötilan ollessa alussa ja lopussa 25 C? Metaanin palamisreaktio on CH O 2 CO H 2 O, missä CH 4, O 2 ja CO 2 ovat normaalitilassaan 1 atm:n paineessa ja 25 C:n lämpötilassa kaasuja ja H 2 O on neste. Näiden yhdisteiden muodostumisentalpioiden H f (298) taulukkoarvot ovat 74, 75 kj/mol (CH 4 ), 393, 513 kj/mol (CO 2 ) ja 285, 830 kj/mol (nestemäinen H 2 O). O 2 :n H f on määritelmän perusteella nolla, koska O 2 on alkuaine. Reaktioyhtälön vasemmalla ja oikealla puolella olevien aineiden (1 mol CH mol O 2 ja 1 mol CO mol H 2 O) muodostumisentalpiat ovat 74, = 74, 75 kj ja 393, , 830 = 965, 173 kj. Reaktiossa tapahtuva entalpian muutos on siis H298 = 965, , 75 = 890, 42 kj/mol. akiopaineessa tapahtuvan reaktion H on sama kuin reaktiolämpö Q, joten palaminen tuottaa lämpömäärän Q = 890, 42 kj/mol. Analogisesti H f :n määritelmän kanssa yhdisteen Gibbsin vapaa muodostumisenergia normaalitilassa, G f, määritellään Gibbsin vapaan energian muutokseksi reaktiossa, jossa tämä yhdiste muodostuu alkuaineistaan kaikkien reaktioon osallistuvien aineiden ollessa alussa ja lopussa normaalitilassa. Myös sen arvoista on julkaistu laajoja taulukoita, joiden avulla voidaan laskea minkä tahansa reaktion G :n arvo. Esimerkki: oiko sykloheksaania C 6 H 12 muodostua spontaanisti grafiitista ja vedystä reaktiolla 6 C + 6 H 2 C 6 H 12 1 atm:n paineessa alku- ja loppulämpötilan ollessa 25 C? Yhtälön (7.20) mukaan Gibbsin vapaa energia G pienenee kaikissa spontaaneissa prosesseissa, jotka tapahtuvat vakiopaineessa ja -lämpötilassa. ästä syystä tällaisessa prosessissa tapahtuvan G:n muutoksen G vastalukua G kutsutaan usein prosessin käyttövoimaksi. Kemiallisen reaktion G saadaan laskemalla tulosaineiden G:n summa ja vähentämällä siitä lähtöaineiden G:n summa. Sama tulos saadaan, jos G:n sijasta käytetään Gibbsin vapaata muodostumisenergiaa G f : G = G(tulosaineet) G(lähtöaineet) = G f (tulosaineet) G f (lähtöaineet). ässä tapauksessa lähtöaineet ovat alkuaineita (C ja H 2 ), joten reaktion G on sama kuin tulosaineen (C 6 H 12 ) G f. Sykloheksaanin G f :n arvo on normaalitilassa 1 atm:n paineessa ja 25 C:n lämpötilassa G f (298) = 31, 8 kj/mol. Reaktion G on siis positiivinen, eikä se näin ollen voi edetä spontaanisti, ts. ilman ulkopuolelta tehtyä ylimääräistä työtä (so. muuta kuin ympäristön paineen aiheuttamaa -työtä). arkastellussa sykloheksaanin muodostumisreaktiossa entalpia pienenee: H = H f (298) = 123, 2 kj/mol. Jos reaktio etenisi spontaanisti, se tuottaisi yhtälön (7.23) mukaan positiivisen lämpömäärän Q = H = 123, 2 kj/mol ja systeemin sisäinen energia E pienenisi (osa lämmöstä tulisi yhtälön (7.30) mukaisesti -työstä). Gibbsin vapaa energia voidaan kirjoittaa G:n ja H:n määritelmien (7.21) ja (7.24) avulla muodossa G = H S, (7.31)
9 josta nähdään, että entalpian pieneneminen johtaa G:n pienenemiseen. Näin ollen G:n entalpiatermi H suosii tarkasteltua reaktiota, joten sen estymisen täytyy johtua G:n entropiatermistä S. Reaktioon osallistuvien aineiden entropioiden taulukkoarvot 1 atm:n paineessa ja 25 C:n lämpötilassa, S (298), ovat 5, 744 J/(K mol) (C, grafiitti), 130, 66 J/(K mol) (H 2 ) ja 298, 4 J/(K mol) (C 6 H 12 ). Jos alkutilassa on 6 moolia hiiltä ja 6 moolia vetyä, kokonaisentropia on S 1 = 6 (5, , 66) J/K = 818, 42 J/K. Lopputilassa on tällöin 1 mooli sykloheksaania, jonka entropia on S 2 = 298, 4 J/K. Näin ollen entropian muutos on S = S (298) = S 2 S 1 = 520, 0 J/(K mol). Entropia pienenee reaktiossa voimakkaasti, koska atomit muodostavat paremmin järjestyneitä ryhmiä. Entropiatermin S muutos on siis S = 298, 15 K ( 520, 0) J/mol = 155, 0 kj/mol. ästä seuraa, että G saa positiivisen arvon G = H S = 123, 2 kj/mol + 155, 0 kj/mol = 31, 8 kj/mol. aikka reaktio siis johtaa alempaan energiaan, se samalla lisää systeemin järjestystä ja pienentää entropiaa niin paljon, että prosessi ei voi edetä spontaanisti. 90 ässä kappaleessa on tarkasteltu Clausiuksen epäyhtälöä (7.11) neljän erilaisen (käytännössä tärkeän) side-ehdon vaikuttaessa. Näissä erikoistapauksissa epäyhtälö redusoituu seuraaviin muotoihin: S 0 (E ja vakioita), (7.32 a) F 0 ( ja vakioita), (7.32 b) G 0 ( ja vakioita), (7.32 c) S 0 (H ja vakioita). (7.32 d) Muunkinlaiset side-ehdot ovat mahdollisia. Esimerkiksi systeemin tilavuus ja entropia S voivat olla lopputilassa samoja kuin alkutilassa ( = S = 0). ällöin funktion A = E S muutos on A = E 0. (7.33) ässä tapauksessa systeemin sisäinen energia E pyrkii luonnollisissa prosesseissa pienenemään ja saavuttaa tasapainotilassa miniminsä: E 0 (S ja vakioita). (7.34) Yleensä systeemin termodynaamisiksi potentiaaleiksi sanotaan sen sisäistä energiaa E, entalpiaa H = E +, Helmholtzin vapaata energiaa F = E S ja Gibbsin vapaata energiaa G = E + S. Niillä kaikilla on energian yksikkö. 7-3 Maxwellin relaatiot Maxwellin relaatiot ovat tilamuuttujien,, ja S osittaisderivaattojen välisiä yhtälöitä. Ne on johdettu termodynamiikan perusrelaation (5.25) avulla suoraan termodynaamisten potentiaalien E, F, G ja H määritelmistä, joten ne ovat yleisesti voimassa kaikille tasapainotiloissa oleville -systeemeille (so., systeemeille, joiden tila voidaan spesifioida täydellisesti :n, :n ja :n avulla). Ne ovat hyödyllisiä erityisesti siksi, että niiden avulla on mahdollista esittää entropian muutoksen lauseke :n, :n ja :n funktiona.
10 Koska systeemin sisäinen energia E on tilamuuttuja, joka voidaan esittää esimerkiksi tilamuuttujien S ja funktiona, E:n infinitesimaalinen muutos voidaan esittää kokonaisdifferentiaalina ( ) ( ) E E de = ds + d. (7.35) ertaamalla tätä termodynamiikan perusrelaatioon nähdään, että ja voidaan esittää osittaisderivaattoina = S de = ds d (5.25) ( ) E ja = 91 ( ) E. (7.36) S oidaan osoittaa, että tilamuuttujan toinen osittaisderivaatta kahden eri muuttujan suhteen on riippumaton derivoimisjärjestyksestä: 2 f/ x y = 2 f/ y x. Yhtälöistä (7.36) saadaan tätä ominaisuutta hyväksi käyttäen :n ja :n derivaattojen relaatio ( ) ( = S ( ) ) ( E = S ämä tulos on ensimmäinen Maxwellin relaatio. Kun Helmholtzin vapaan energian ( ) ) E S ( ) =. (7.37) F (E,, S) = E S (5.10) kokonaisdifferentiaalin lausekkeessa esiintyvän de:n paikalle sijoitetaan termodynamiikan perusrelaation (5.25) mukainen lauseke de = ds d, saadaan df = de ds S d = ( ds d ) ds S d = S d d. (7.38) ämän täytyy olla funktion F (, ) kokonaisdifferentiaali, josta voidaan tunnistaa osittaisderivaatat ( ) ( ) F F S = ja =. (7.39) Näiden avulla saadaan toinen Maxwellin relaatio ( ) ( ( ) ) ( F = = ( ) ) F = ( ). (7.40) Sijoittamalla termodynamiikan perusrelaatio vastaavalla tavalla Gibbsin vapaan energian G(E,,,, S) (7.21) kokonaisdifferentiaaliin saadaan tulos dg = de + d + d ds S d = ( ds d ) + d + d ds S d = d S d. (7.41) ämä on funktion G(, ) kokonaisdifferentiaali, josta saadaan osittaisderivaatat S = ( ) G ja = ( ) G. (7.42)
11 Näitä yhtälöitä käyttämällä saadaan kolmas Maxwellin relaatio ( ) ( ( ) ) ( ( ) ) ( ) G G = = =. (7.43) Lopuksi saadaan entalpian H(E,, ) (7.24) kokonaisdifferentiaaliksi termodynamiikan perusrelaatiota käyttämällä dh = de + d + d = ( ds d ) + d + d = ds + d, (7.44) mistä saadaan :lle ja :lle lausekkeet ( ) H = ja = Näistä seuraa edelleen neljäs Maxwellin relaatio ( ) ( ( ) ) H = = S S ( 92 ( ) H. (7.45) S ( ) ) H S = ( ). (7.46) Yhtälöistä (7.36), (7.39), (7.42) ja (7.45) nähdään, että tilamuuttujat,, ja S voidaan esittää termodynaamisten potentiaalien E, F, G ja H osittaisderivaattoina. ässä suhteessa E, F, G ja H käyttäytyvät analogisesti sähköstaattisen potentiaalin φ kanssa, josta saadaan sähkökentän komponentit E x, E y ja E z muodostamalla φ:n (negatiiviset) osittaisderivaatat koordinaattien x, y ja z suhteen: E x = φ/ x, E y = φ/ y ja E z = φ/ z. 7-4 ermodynamiikan kolmas pääsääntö Yhtälön (4.27) mukaan todennäköisyys sille, että termisessä tasapainossa lämpötilassa olevan systeemin energia on E r, on p(e r ) = 1 Z g(e r)e E r/k, (4.27) missä g(e r ) on energiatilan E r degeneraatio (niiden mikrotilojen lukumäärä, joilla on energia E r ). Energian E s ja alimman mahdollisen energian E 1 (E 1 < E s ) esiintymistodennäköisyyksien suhde on siis p(e s ) p(e 1 ) = g(e s) g(e 1 ) e (E s E 1 )/k. (7.47) ämän yhtälön oikea puoli lähestyy nollaa, kun lämpötila lähestyy nollaa. ämä merkitsee sitä, että kaikkien E 1 :n yläpuolella olevien energioiden E s esiintymistodennäköisyydet p(e s ) lähestyvät tällöin nollaa. ästä voidaan päätellä, että absoluuttista nollapistettä lähestyessään systeemi asettuu alimpaan mahdolliseen energiatilaan, perustilaan: p(e 1 ) = 1 ja p(e s ) = 0, kun s > 1. Koska perustilaan kuuluvien mikrotilojen lukumäärä on Ω(E 1 ) = g(e 1 ), Boltzmannin entropian määritelmän (4.3) mukaan systeemin entropian raja-arvo lämpötilan lähestyessä nollaa on lim S = k ln Ω(E 1) = k ln g(e 1 ). (7.48) 0
12 Sama tulos saadaan myös entropian yleisestä lausekkeesta (5.5) sijoittamalla siihen mikrokanonisen joukon todennäköisyysjakauma (p r = 1/g(E 1 ), kun r = 1, 2,..., g(e 1 ), ja p r = 0, kun r > g(e 1 )). Jos oletetaan, että perustilan degeneraatio g(e 1 ) ei riipu systeemin tilamuuttujista (esimerkiksi tilavuudesta tai paineesta), myös entropian raja-arvo (7.48) on näistä muuttujista riippumaton vakio. Näin saadaan Walther Nernstin muotoilema termodynamiikan kolmas pääsääntö: sisäisessä tasapainossa olevan systeemin entropia on absoluuttisessa nollapisteessä systeemin tilamuuttujista riippumaton vakio. Monissa ideaalisissa systeemeissä g(e 1 ) = 1, ts., perustilaan kuuluu vain yksi mikrotila. Esimerkiksi kappaleessa 4-2 tarkastellussa esimerkissä havaittiin, että ulkoiseen magneettikenttään B sijoitetun paramagneettisen kiinteän aineen alimpaan mahdolliseen energiaan E 1 = Nµ B kuuluu vain se mikrotila, missä kaikki magneettiset dipolit ovat kentän suuntaisia. Myös puhtaan aineen virheettömän kiteen perustilassa atomien, ionien tai molekyylien geometrinen järjestys on yksikäsitteinen. ällaisissa tapauksissa entropian raja-arvo on yhtälön (7.48) mukaan nolla: 93 lim S = k ln 1 = 0. (7.49) 0 ämä tulos johtaa seuraavaan Max lanckin esittämään termodynamiikan kolmannen pääsäännön muotoiluun: sisäisessä tasapainossa olevan puhtaan aineen entropia on absoluuttisessa nollapisteessä nolla. Kolmannen pääsäännön avulla voidaan helposti johtaa eräitä kaikille aineille yhteisiä ominaisuuksia, jotka ilmenevät matalissa lämpötiloissa. Jos systeemin lämpötila muuttuu reversiibelisti 1 :stä 2 :een tilavuuden pysyessä vakiona, entropian muutos S = S( 2, ) S( 1, ) voidaan laskea yhtälöiden (5.34) ja (5.36) avulla. Näin ollen entropian arvo lämpötilassa 2 voidaan esittää muodossa S( 2, ) = S( 1, ) + 2 C ( ) 1 d. (7.50) Kolmannen pääsäännön (7.48) mukaan S( 1, ) lähestyy lämpötilan 1 laskiessa vakioarvoa k ln g(e 1 ) (joka voi olla nolla), joten S( 2, ) = k ln g(e 1 ) C ( ) d. (7.51) Koska entropian S( 2, ) täytyy olla äärellisessä lämpötilassa 2 äärellinen, yhtälön (7.51) oikealla puolella oleva integraali ei saa divergoida. ästä seuraa, että vakiotilavuudessa määritetyn lämpökapasiteetin C ( ) raja-arvon C (0) täytyy olla nolla. Samalla tavalla voidaan osoittaa, että myös vakiopaineessa määritetyn lämpökapasiteetin, C ( ), täytyy lähestyä nollaa, kun lähestyy nollaa: lim C ( ) = lim C ( ) = 0. (7.52) 0 0 Kuva 3 esittää kuparin C :n ja C :n mitattuja arvoja lämpötilan funktiona. Nämä koetulokset, jotka ovat tyypillisiä kaikille kiinteille aineille, osoittavat teoreettiset ennusteet (7.52) oikeiksi.
13 94 Kuva 3. Kolmannen Maxwellin relaation (7.43) mukaan ( ) ( ) =. (7.43) Kolmannen pääsäännön mukaan entropia S(, ) lähestyy lämpötilan laskiessa paineesta riippumatonta vakiota. Näin ollen S(, ):n osittaisderivaatan (/ ) täytyy lähestyä nollaa, kun lähestyy nollaa. ästä syystä myös yhtälön (7.43) oikean puolen täytyy lähestyä nollaa: ( ) lim = 0. (7.53) 0 ämä merkitsee sitä, että matalissa lämpötiloissa tilavuus ei riipu lämpötilasta, ts. tilavuuden lämpölaajenemiskertoimen β( ) (1/ )( / ) (3.13) raja-arvo on nolla: ( ) 1 lim β( ) = lim = 0. (7.54) 0 0 Kuvan 4 esittämät koetulokset kuparille osoittavat myös tämän ennusteen oikeaksi. (Kuvassa on esitetty myös kuparin kokoonpuristuvuus κ( ) (1/ )( / ), jonka rajaarvo ei ole nolla.) Samalla tavalla saadaan Maxwellin toisesta relaatiosta (7.40) tulos ( ) ( ) lim = lim = 0, (7.55) 0 0
14 95 Kuva 4. joka osoittaa, että matalissa lämpötiloissa paine ei riipu lämpötilasta.
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
4. Termodynaamiset potentiaalit
 Statistinen fysiikka, osa A (FYSA241) uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty
Statistinen fysiikka, osa A (FYSA241) uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt
 14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi
4. Termodynaamiset potentiaalit
 FYSA241, kevät 2012 uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2012 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty järjestelmä
FYSA241, kevät 2012 uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2012 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty järjestelmä
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
Luku Pääsääntö (The Second Law)
 Luku 3 2. Pääsääntö (he Second Law) Some things happen naturally, some things don t Spontaneous must be interpreted as a natural tendency that may or may not be realized in prac=ce. hermodynamics is silent
Luku 3 2. Pääsääntö (he Second Law) Some things happen naturally, some things don t Spontaneous must be interpreted as a natural tendency that may or may not be realized in prac=ce. hermodynamics is silent
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut
 Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 8 / 7.11.2016 v. 02 / T. Paloposki Tämän päivän ohjelma: Sisäenergia (kertaus) termodynamiikan 1. pääsääntö Entropia termodynamiikan 2. pääsääntö 1 Termodynamiikan
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
S , Fysiikka III (Sf) tentti/välikoeuusinta
 S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
S-114.45, Fysiikka III (Sf) tentti/välikoeuusinta.11.4 1. välikokeen alue 1. Osoita, että hyvin alhaisissa lämpötiloissa elektronin FD systeemin energia on U = (3/ 5) ε F. Opastus: oleta, että kaikki tilat
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
4. Termodynaamiset potentiaalit
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2015 4. ermodynaamiset potentiaalit 1 ermodynaaminen tasapaino kanonisessa joukossa Mikrokanoninen
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2015 4. ermodynaamiset potentiaalit 1 ermodynaaminen tasapaino kanonisessa joukossa Mikrokanoninen
Luento 2: Lämpökemiaa, osa 1 Torstai klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
 766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
Kemiallinen reaktio
 Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
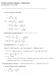 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
infoa tavoitteet E = p2 2m kr2 Klassisesti värähtelyn amplitudi määrää kokonaisenergian Klassisesti E = 1 2 mω2 A 2 E = 1 2 ka2 = 1 2 mω2 A 2
 infoa tavoitteet Huomenna keskiviikkona 29.11. ei ole luentoa. Oppikirjan lukujen 12-13.3. lisäksi kotisivulla laajennettu luentomateriaali itse opiskeltavaksi Laskarit pidetään normaalisti. Ymmärrät mitä
infoa tavoitteet Huomenna keskiviikkona 29.11. ei ole luentoa. Oppikirjan lukujen 12-13.3. lisäksi kotisivulla laajennettu luentomateriaali itse opiskeltavaksi Laskarit pidetään normaalisti. Ymmärrät mitä
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 1: Lämpötila ja Boltzmannin jakauma Ke 24.2.2016 1 YLEISTÄ KURSSISTA Esitietovaatimuksena
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 1: Lämpötila ja Boltzmannin jakauma Ke 24.2.2016 1 YLEISTÄ KURSSISTA Esitietovaatimuksena
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Biofysiikka Luento Entropia, lämpötila ja vapaa energia. Shannonin entropia. Boltzmannin entropia. Lämpötila. Vapaa energia.
 Biofysiikka Luento 7 1 6. Entropia, lämpötila ja vapaa energia Shannonin entropia Boltzmannin entropia M I NK P ln P S k B j1 ln j j Lämpötila Vapaa energia 2 Esimerkkiprobleemoita: Miten DNA-sekvenssistä
Biofysiikka Luento 7 1 6. Entropia, lämpötila ja vapaa energia Shannonin entropia Boltzmannin entropia M I NK P ln P S k B j1 ln j j Lämpötila Vapaa energia 2 Esimerkkiprobleemoita: Miten DNA-sekvenssistä
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
3. Statistista mekaniikkaa
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 3. Statistista mekaniikkaa 1 Mikrotilojen laskenta Kvanttimekaniikka: diskreetit
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 3. Statistista mekaniikkaa 1 Mikrotilojen laskenta Kvanttimekaniikka: diskreetit
Ideaalikaasulaki johdettuna mikroskooppisen tarkastelun perusteella! Lämpötila vaikuttaa / johtuu molekyylien kineettisestä energiasta
 HYS-A00 Termodynamiikka (TFM), Luentomuistiinpanot Luennot 7-8, kertaus, mitkä olivat oppimistavoitteet? Kineettinen kaasuteoria Oletukset: - kaasun tiheys on riittävän suuri - molekyylin koko on paljon
HYS-A00 Termodynamiikka (TFM), Luentomuistiinpanot Luennot 7-8, kertaus, mitkä olivat oppimistavoitteet? Kineettinen kaasuteoria Oletukset: - kaasun tiheys on riittävän suuri - molekyylin koko on paljon
766328A Termofysiikka Harjoitus no. 10, ratkaisut (syyslukukausi 2014)
 7668A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 4). Johdetaan yksiatomisen klassisen ideaalikaasun kemiallisen potentiaalin µ(t,, N) lauseke. (a) Luentojen yhtälön mukaan kemiallinen potentiaali
7668A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 4). Johdetaan yksiatomisen klassisen ideaalikaasun kemiallisen potentiaalin µ(t,, N) lauseke. (a) Luentojen yhtälön mukaan kemiallinen potentiaali
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Fysiikan maailmankuva 2015 Luento 8. Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa?
 Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Oikeasta vastauksesta (1p): Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa eräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808 C
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, Luku 7 ENTROPIA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Luku 2. Kemiallisen reaktion tasapaino
 Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Entrooppiset voimat. Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit
 Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Reaktiolämpö KINEETTINEN ENERGIA POTENTIAALI- ENERGIA
 POTENTIAALI- ENERGIA KINEETTINEN ENERGIA Reaktiolämpö REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa
POTENTIAALI- ENERGIA KINEETTINEN ENERGIA Reaktiolämpö REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa
Luento 8 6.3.2015. Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit
 Luento 8 6.3.2015 1 Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) 2 Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Luento 8 6.3.2015 1 Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) 2 Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Termodynaamiset syklit Todelliset tehosyklit
 ermodynaamiset syklit odelliset tehosyklit Luennointi: k Kati Miettunen Esitysmateriaali: k Mikko Mikkola HYS-A00 ermodynamiikka (FM) 09..05 Syklien tyypit Sisältö Kaasusyklit s. höyrysyklit Suljetut syklit
ermodynaamiset syklit odelliset tehosyklit Luennointi: k Kati Miettunen Esitysmateriaali: k Mikko Mikkola HYS-A00 ermodynamiikka (FM) 09..05 Syklien tyypit Sisältö Kaasusyklit s. höyrysyklit Suljetut syklit
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
DEE Kryogeniikka
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold tip tirling aim com mod.jpg Introduced about
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold tip tirling aim com mod.jpg Introduced about
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
KLASSISET TASAPAINOJOUKOT (AH 4.3, , 7.2) Yleisesti joukoista
 KLASSISET TASAPAINOJOUKOT (AH 4.3, 6.1-6.7, 7.2) 1 Yleisesti joukoista Seuraavaksi tarkastelemme konkreettisella tasolla erilaisia termodynaamisia ensemblejä eli joukkoja, millä tarkoitamme tiettyä makrotilaa
KLASSISET TASAPAINOJOUKOT (AH 4.3, 6.1-6.7, 7.2) 1 Yleisesti joukoista Seuraavaksi tarkastelemme konkreettisella tasolla erilaisia termodynaamisia ensemblejä eli joukkoja, millä tarkoitamme tiettyä makrotilaa
