10 Suoran vektorimuotoinen yhtälö
|
|
|
- Kirsti Juusonen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 10 Suran vektrimutinen htälö J aluki tarkatellaan -tan kuuluvaa, rign kautta kulkevaa uraa, niin ura n täin määrätt, mikäli tunnetaan en uunta. Tavallieti tämä annetaan uuntakulman tangentin = kulmakertimen k avulla. Suran uunta vidaan antaa mö uuntavektrin avulla. Tällainen (ei -akelin uuntainen) ura = k kulkee iten eim. piteen (1,k) kautta, jten uuntavektriki vidaan valita î + kĵ tai mikä tahana tämän kana hdenuuntainen vektri. Merkitään tällaita vektria = î + ĵ. P O Välttämätön ja riittävä eht ille, että pite P = (,) n uralla L, n e, että löt reaaliluku t iten, että OP = r = t. Kun r n piteen P paikkavektri, ii r = î + ĵ, niin em. htälö kmpnenttimuda n î + ĵ = t î t ĵ, jta aadaan uran htälön n. parametrimut Niiä tapaukia, jia 0, aadaan eliminimalla t parametrimutieta htälötä uui htälö =, jta edelleen merkitemällä muuttujan kerrinta = k, pullahtaa ennetäänkin hvin tuttu htälö = k. Kannattaa tietenkin humata, että merkitemällä uuntavektria = î ĵ kelpaa mikä tahana tämän kana hdenuuntainen vektri uuntavektriki. Tällaieki 1 kelpaa vaikkapa vektri = î + ĵ = î + kĵ. Tällöin n = tan = k, miä n uran L ja pitiivien -akelin välinen terävä kulma. Tämä kulma tetaan + +
2 negatiiviena, mikäli en ikea klki n ntnt vektrin î kierteä mötäpäivään eli negatiivieen kiertuuntaan. Orign kautta kulkevaan avaruuuraan eitett tarkatelu pätee täin hvin. Kuitenkaan tällaielle uralle ei määritellä uuntakulmaa ja uuntavektriin tulee klmakin kmpnentti. Tällöin = î + ĵ kˆ, ja rign kautta kulkevan + uran parametrihtälöki aadaan klmen htälön rhmä miä t n mikä tahana reaaliluku. = t = t, = t Olktpa itten L1: r = t rign kautta kulkeva -tan kuuluva ura ja L 2 tämän uran uuntainen ura, jka kulkee piteen P = (, ) kautta. Jälkimmäien uran uuntavektriki vidaan ilman muuta valita vektri. r 0 P = (, ) r P = (, ) Välttämätön ja riittävä eht ille, että P = (,) n uran L 2 pite, n e, että löt reaaliluku t iten, että OP = OP + t, mikä merkitee vektrihtälöä minkä kmpnenttieit n r = r + t î + ĵ = î + ĵ+ tî + t ĵ, jta edelleen päätään parametrieitkeen
3 = + t = + t Mikäli n keeä erikitapau = 0, aadaan tätä -akelin uuntainen ura = 0, jnka uuntavektriki kä paiti ĵ, mö pelkkä ĵ. Ellei le keeä käitelt erikitapau, parametri t n helpp eliminida ja aadaan 0 = 0 = ( 0) 0 = k( 0). 0 Kun jhdettiin piteen etäittä urata, tdettiin, että uran nrmaalivektriki vitiin valita n = aî + bĵ ja uuntavektriki = bî + aĵ, ja aadaan ijituken nnä ievennken jälkeen jälleen kerran Laue 18 Mikä tahana -tan ura vidaan aina eittää muda a + b + c = 0 mikäli ainakin tinen kertimita a ja b eraa nllata. Olkt nt P = (,, ) avaruuden kiinteä pite ja = ai + bj + ck nllata erava vektri. Pite P = (,,) n P :n kautta kulkevalla, vektrin uuntaiella uralla tämälleen illin, kun löt reaaliluku t iten, että
4 P P OP = OP + t r = r + t Tätä päätään parametrimutn = = = + ta + tb + tc ja parametrin elimininnin jälkeen n. krdinaattimutn: Laue 19 Piteen P = (,, ) kautta kulkevan, vektrin = ai + b j+ ck uuntaien uran htälö vidaan eittää muda a edellttäen, että abc 0. = = b c Parametrimutinen eit ei tätä rajituta iällä, mutta vaatii en, että ainakin ki uuntavektrin kalaarikmpnenteita pitää lla nllata erava, kka nllavektrilla ei le uuntaa. Eim. 1 Sura kulkee piteiden A = (4, 3, 1) ja B = (6, 7, 5) kautta. Määritä uran htälö, ekä pite, ja ura khtaa -tan.
5 Tan uuntavektriki vidaan valita = AB = OB OA. = (6 4)î + (7 3) ĵ + ( 5 1)kˆ = 2î + 4ĵ 6kˆ. Sura kulkee piteen A kautta ja en uuntavektri n. Laue 5.19 antaa: = = Sura leikkaa -taa piteeä, jnka -krdinaatti n nlla. Muiden krdinaattien määräämieki tarvitaan uran parametrimutita = + ta htälöä: = + tb = + tc Sijitetaan tähän uuntavektrin kalaarikmpnentit ja piteen A krdinaatit (htä hvin B:n krdit) = 4 + 2t = 3 + 4t = 1 6t J = 0, niin t = 2. Sijittamalla tämä muiden krdinaattien lauekkeiiin, päätään tietämään uran ja -tan leikkaupite: = 0 = 3 + 4( 2) = 5 = 1 6( 2) = 13 Vatau: Ktn uran htälö 4 3 nrmaalimuda = = 2 4 = 4 + 2t parametrimuda = 3 + 4t = 1 6t 1 6 Sura leikkaa -tan piteeä (0, 5, 13).
pienempää, joten vektoreiden välinen kulma voidaan aina rajoittaa välille o. Erikoisesti on
 5 Pistetul ja sen svellutuksia Kun kahdella vektrilla, a ja b n hteinen alkupiste, niiden määräämät pulisurat jakavat tasn kahteen saan, kahteen kulmaan, jtka vat tistensa eksplementtikulmia, siis kulmia,
5 Pistetul ja sen svellutuksia Kun kahdella vektrilla, a ja b n hteinen alkupiste, niiden määräämät pulisurat jakavat tasn kahteen saan, kahteen kulmaan, jtka vat tistensa eksplementtikulmia, siis kulmia,
Harjoituksia MAA5 - HARJOITUKSIA. 1. Olkoon ABCD mielivaltainen nelikulmio. Merkitse siihen vektorit. mutta molemmat puolet itseisarvojen sisällä????
 MAA5 - HARJOITUKSIA 1. Olkn ABCD mielivaltainen nelikulmi. Merkitse siihen vektrit a) AB b) CA ja DB. 2. Neljäkäs eli vinneliö n suunnikkaan erikistapaus. Mitkä seuraavista väitteistä vat tsia neljäkkäässä
MAA5 - HARJOITUKSIA 1. Olkn ABCD mielivaltainen nelikulmi. Merkitse siihen vektrit a) AB b) CA ja DB. 2. Neljäkäs eli vinneliö n suunnikkaan erikistapaus. Mitkä seuraavista väitteistä vat tsia neljäkkäässä
RATKAISUT: 8. Momentti ja tasapaino
 Phyica 9. paino (7) : 8. Voian vari r on voian vaikutuuoran etäiyy pyöriiakelita. Pyöriiakeli on todellinen tai kuviteltu akeli, jonka ypäri kappale pyörii. Voian oentti M kuvaa voian vääntövaikututa tietyn
Phyica 9. paino (7) : 8. Voian vari r on voian vaikutuuoran etäiyy pyöriiakelita. Pyöriiakeli on todellinen tai kuviteltu akeli, jonka ypäri kappale pyörii. Voian oentti M kuvaa voian vääntövaikututa tietyn
MAA5. HARJOITUKSIA. 1. Olkoon ABCD mielivaltainen nelikulmio. Merkitse siihen vektorit a) AB
 MAA5 HARJOITUKSIA 1 Olkn ABCD mielivaltainen nelikulmi Merkitse siihen vektrit a) AB, b) CA ja DB 2 Neljäkäs eli vinneliö n suunnikkaan erikistapaus Mitkä seuraavista väitteistä vat tsia neljäkkäässä ABCD:
MAA5 HARJOITUKSIA 1 Olkn ABCD mielivaltainen nelikulmi Merkitse siihen vektrit a) AB, b) CA ja DB 2 Neljäkäs eli vinneliö n suunnikkaan erikistapaus Mitkä seuraavista väitteistä vat tsia neljäkkäässä ABCD:
TASON YHTÄLÖT. Tason esitystapoja ovat: vektoriyhtälö, parametriesitys (2 parametria), normaalimuotoinen yhtälö ja koordinaattiyhtälö.
 TSON YHTÄLÖT VEKTORIT, M4 Jokainen seuraavista määrää avaruuden tason yksikäsitteisesti: - kolme tason pistettä, jotka eivät ole samalla suoralla, - yksi piste ja pisteen ulkopuolinen suora, - yksi piste
TSON YHTÄLÖT VEKTORIT, M4 Jokainen seuraavista määrää avaruuden tason yksikäsitteisesti: - kolme tason pistettä, jotka eivät ole samalla suoralla, - yksi piste ja pisteen ulkopuolinen suora, - yksi piste
4.3 Liikemäärän säilyminen
 Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
VEKTORIT paikkavektori OA
 paikkavektori OA Piste A = (2, -1) Paikkavektori OA = 2i j 3D: kuvan piirtäminen hankalaa Piste A = (2, -3, 4) Paikkavektori OA = 2i 3j + 4k Piste A = (a 1, a 2, a 3 ) Paikkavektori OA = a 1 i + a 2 j
paikkavektori OA Piste A = (2, -1) Paikkavektori OA = 2i j 3D: kuvan piirtäminen hankalaa Piste A = (2, -3, 4) Paikkavektori OA = 2i 3j + 4k Piste A = (a 1, a 2, a 3 ) Paikkavektori OA = a 1 i + a 2 j
Ensimmäisen asteen polynomifunktio
 Ensimmäisen asteen polnomifunktio Yhtälön f = a+ b, a 0 määrittelemää funktiota sanotaan ensimmäisen asteen polnomifunktioksi. Esimerkki. Ensimmäisen asteen polnomifuktioita ovat esimerkiksi f = 3 7, v()
Ensimmäisen asteen polnomifunktio Yhtälön f = a+ b, a 0 määrittelemää funktiota sanotaan ensimmäisen asteen polnomifunktioksi. Esimerkki. Ensimmäisen asteen polnomifuktioita ovat esimerkiksi f = 3 7, v()
S FYSIIKKA IV (ES), Koulutuskeskus Dipoli, Kevät 2003, LH2. f i C C. λ 2, m 1 cos60,0 1, m 1,2 pm. λi λi
 S-11436 FYSIIKKA IV (S), Kulutukeku Dipli, Kevät 003, LH LH-1 Ftni, jnka energia n 10,0 kev, törmää leva levaan vapaaeen elektrniin ja irttuu uuntaan, jka mudtaa 60,0 kulman ftnin alkuperäien liikeuunnan
S-11436 FYSIIKKA IV (S), Kulutukeku Dipli, Kevät 003, LH LH-1 Ftni, jnka energia n 10,0 kev, törmää leva levaan vapaaeen elektrniin ja irttuu uuntaan, jka mudtaa 60,0 kulman ftnin alkuperäien liikeuunnan
Yhteenlaskun ja skalaarilla kertomisen ominaisuuksia
 Yhteenlaskun ja skalaarilla kertomisen ominaisuuksia Voidaan osoittaa, että avaruuden R n vektoreilla voidaan laskea tuttujen laskusääntöjen mukaan. Huom. Lause tarkoittaa väitettä, joka voidaan perustella
Yhteenlaskun ja skalaarilla kertomisen ominaisuuksia Voidaan osoittaa, että avaruuden R n vektoreilla voidaan laskea tuttujen laskusääntöjen mukaan. Huom. Lause tarkoittaa väitettä, joka voidaan perustella
MAOL-Pisteitysohjeet Fysiikka kevät 2002
 MAOL-Piteityhjeet Fyiikka kevät 00 Tyypilliten virheiden aiheuttaia piteenetykiä (6 piteen kaalaa): - pieni lakuvirhe -/3 p - lakuvirhe, epäielekä tul, vähintään - - vataukea yki erkitevä nuer liikaa -0
MAOL-Piteityhjeet Fyiikka kevät 00 Tyypilliten virheiden aiheuttaia piteenetykiä (6 piteen kaalaa): - pieni lakuvirhe -/3 p - lakuvirhe, epäielekä tul, vähintään - - vataukea yki erkitevä nuer liikaa -0
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 Harjoitus 4 Ratkaisuehdotuksia. Tehtäväsarja I
 HY / Matematiikan ja tilatotieteen laito Tilatollinen päättely II, kevät 207 Harjoitu 4 Ratkaiuehdotukia Tehtäväarja I. (Kvantiili-kvantiili kuvion [engl. q q plot] idea.) Olkoon atunnaimuuttujalla X ellainen
HY / Matematiikan ja tilatotieteen laito Tilatollinen päättely II, kevät 207 Harjoitu 4 Ratkaiuehdotukia Tehtäväarja I. (Kvantiili-kvantiili kuvion [engl. q q plot] idea.) Olkoon atunnaimuuttujalla X ellainen
Lisämateriaalia: tilayhtälön ratkaisu, linearisointi. Matriisimuuttujan eksponenttifunktio:
 Lisämateriaalia: tilayhtälön ratkaisu, linearisinti Matriisimuuttujan ekspnenttifunkti: Kun A n neliömatriisi, niin määritellään 1 1 1 e I ta t A t A t A 2 6 i! At 2 2 3 3 i i jnka vidaan tdistaa knvergivan
Lisämateriaalia: tilayhtälön ratkaisu, linearisinti Matriisimuuttujan ekspnenttifunkti: Kun A n neliömatriisi, niin määritellään 1 1 1 e I ta t A t A t A 2 6 i! At 2 2 3 3 i i jnka vidaan tdistaa knvergivan
POSITIIVISEN LINSSIN POLTTOVÄLI
 S-108110 OPTIIKKA 1/6 POSITIIVISEN LINSSIN POLTTOVÄLI Laboratoriotyö S-108110 OPTIIKKA /6 SISÄLLYSLUETTELO 1 Poitiivien linin polttoväli 3 11 Teoria 3 1 Mittauken uoritu 5 LIITE 1 6 Mittaupöytäkirja 6
S-108110 OPTIIKKA 1/6 POSITIIVISEN LINSSIN POLTTOVÄLI Laboratoriotyö S-108110 OPTIIKKA /6 SISÄLLYSLUETTELO 1 Poitiivien linin polttoväli 3 11 Teoria 3 1 Mittauken uoritu 5 LIITE 1 6 Mittaupöytäkirja 6
z Im (z +1) 2 = 0. Mitkä muut kompleksitason pisteet toteuttavat tämän yhtälön? ( 1) 0 z ( 1) z ( 1) arg = arg(z 0) arg(z ( 1)), z ( 1) z ( 1)
 . Osoita geometrisesti, että jos = ja niin pätee Im +) = 0. Mitkä muut kompleksitason pisteet toteuttavat tämän htälön? Kirjoitetaan +) = 0 ) ), ) 0 jossa, ja 0 vastaavat kolmion pisteitä kompleksitasossa.
. Osoita geometrisesti, että jos = ja niin pätee Im +) = 0. Mitkä muut kompleksitason pisteet toteuttavat tämän htälön? Kirjoitetaan +) = 0 ) ), ) 0 jossa, ja 0 vastaavat kolmion pisteitä kompleksitasossa.
Matriisipotenssi. Koska matriisikertolasku on liitännäinen (sulkuja ei tarvita; ks. lause 2), voidaan asettaa seuraava määritelmä: ja A 0 = I n.
 Matriisipotenssi Koska matriisikertolasku on liitännäinen (sulkuja ei tarvita; ks. lause 2), voidaan asettaa seuraava määritelmä: Määritelmä Oletetaan, että A on n n -matriisi (siis neliömatriisi) ja k
Matriisipotenssi Koska matriisikertolasku on liitännäinen (sulkuja ei tarvita; ks. lause 2), voidaan asettaa seuraava määritelmä: Määritelmä Oletetaan, että A on n n -matriisi (siis neliömatriisi) ja k
Pakkauksen sisältö: Sire e ni
 S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
102 Käyrä. Piste ( 3,0 ) on käyrällä, jos ja vain jos sen koordinaatit. Siis piste ( 1, 2) Siis piste ( 3,0 ) ei ole käyrällä.
 Pramidi 4 Analttinen geometria tehtävien ratkaisut sivu 1 Päivitett 19..6 11 Todistus 1 Kärä x + = x + 4 5 3 31 = x x+ 4, jos ja vain jos pisteen 3,7 koordinaatit toteuttavat kärän htälön. Kun x = 3 ja
Pramidi 4 Analttinen geometria tehtävien ratkaisut sivu 1 Päivitett 19..6 11 Todistus 1 Kärä x + = x + 4 5 3 31 = x x+ 4, jos ja vain jos pisteen 3,7 koordinaatit toteuttavat kärän htälön. Kun x = 3 ja
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
RATKAISUT: 3. Voimakuvio ja liikeyhtälö
 Phyica 9. paino (8) 3. Voiakuvio ja liikeyhtälö : 3. Voiakuvio ja liikeyhtälö 3. a) Newtonin I laki on nieltään jatkavuuden laki. Kappale jatkaa liikettään uoraviivaieti uuttuattoalla nopeudella tai pyyy
Phyica 9. paino (8) 3. Voiakuvio ja liikeyhtälö : 3. Voiakuvio ja liikeyhtälö 3. a) Newtonin I laki on nieltään jatkavuuden laki. Kappale jatkaa liikettään uoraviivaieti uuttuattoalla nopeudella tai pyyy
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.4 Tilatollie aali peruteet, kevät 7 6. lueto: Johdatu regreioaalii Regreioaali idea Tavoitteea elittää elitettävä tekiä/muuttua havaittue arvoe vaihtelu elittävie tekiöide/muuttuie havaittue arvoe
Mat-.4 Tilatollie aali peruteet, kevät 7 6. lueto: Johdatu regreioaalii Regreioaali idea Tavoitteea elittää elitettävä tekiä/muuttua havaittue arvoe vaihtelu elittävie tekiöide/muuttuie havaittue arvoe
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. b) B = (3, 0, 5) K2. 8 ( 1)
 Kertaus K1. a) OA i k b) B = (, 0, 5) K. K. a) AB (6 ( )) i () ( ( 7)) k 8i 4k AB 8 ( 1) 4 64116 819 b) 1 1 AB( ( 1)) i 1 i 4 AB ( ) ( 4) 416 0 45 5 K4. a) AB AO OB OA OB ( i ) i i i 5i b) Pisteen A paikkavektori
Kertaus K1. a) OA i k b) B = (, 0, 5) K. K. a) AB (6 ( )) i () ( ( 7)) k 8i 4k AB 8 ( 1) 4 64116 819 b) 1 1 AB( ( 1)) i 1 i 4 AB ( ) ( 4) 416 0 45 5 K4. a) AB AO OB OA OB ( i ) i i i 5i b) Pisteen A paikkavektori
3 Suorat ja tasot. 3.1 Suora. Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta.
 3 Suorat ja tasot Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta. 3.1 Suora Havaitsimme skalaarikertolaskun tulkinnan yhteydessä, että jos on mikä tahansa nollasta
3 Suorat ja tasot Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta. 3.1 Suora Havaitsimme skalaarikertolaskun tulkinnan yhteydessä, että jos on mikä tahansa nollasta
Tekijä Pitkä matematiikka Poistetaan yhtälöparista muuttuja s ja ratkaistaan muuttuja r.
 Tekijä Pitkä matematiikka 4 16.12.2016 K1 Poistetaan yhtälöparista muuttuja s ja ratkaistaan muuttuja r. 3 r s = 0 4 r+ 4s = 2 12r 4s = 0 + r+ 4s = 2 13 r = 2 r = 2 13 2 Sijoitetaan r = esimerkiksi yhtälöparin
Tekijä Pitkä matematiikka 4 16.12.2016 K1 Poistetaan yhtälöparista muuttuja s ja ratkaistaan muuttuja r. 3 r s = 0 4 r+ 4s = 2 12r 4s = 0 + r+ 4s = 2 13 r = 2 r = 2 13 2 Sijoitetaan r = esimerkiksi yhtälöparin
Ongelma 1: Mistä joihinkin tehtäviin liittyvä epädeterminismi syntyy?
 Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
Mat. tukikurssi 27.3.
 Mat. tukikurssi 7.. Tänään oli paljon vaikeita aiheita: - suunnattu derivaatta - kokonaisdierentiaali - dierentiaalikehitelmä - implisiittinen derivointi Nämä kaikki liittvät aika läheisesti toisiinsa.
Mat. tukikurssi 7.. Tänään oli paljon vaikeita aiheita: - suunnattu derivaatta - kokonaisdierentiaali - dierentiaalikehitelmä - implisiittinen derivointi Nämä kaikki liittvät aika läheisesti toisiinsa.
Kertausosa. 2. Kuvaan merkityt kulmat ovat samankohtaisia kulmia. Koska suorat s ja t ovat yhdensuuntaisia, kulmat ovat yhtä suuria.
 5. Veitoken tilavuu on V,00 m 1,00 m,00 m 6,00 m. Pienoimallin tilavuu on 1 V malli 6,00 m 0,06m. 100 Mittakaava k aadaan tälötä. 0,06 1 k 6,00 100 1 k 0,1544... 100 Mitat ovat. 1,00m 0,408...m 100 0,41
5. Veitoken tilavuu on V,00 m 1,00 m,00 m 6,00 m. Pienoimallin tilavuu on 1 V malli 6,00 m 0,06m. 100 Mittakaava k aadaan tälötä. 0,06 1 k 6,00 100 1 k 0,1544... 100 Mitat ovat. 1,00m 0,408...m 100 0,41
Fy06 Koe 20.5.2014 Kuopion Lyseon lukio (KK) 1/6
 Fy06 Ke 0.5.04 Kupin Lysen luki (KK) /6 6p/tehtävä.. Kaksi varattua palla rikkuu lankjen varassa lähellä tisiaan. Pallt vetävät tisiaan puleensa 0,66 N vimalla. Pienemmän palln varaus n kaksinkertainen
Fy06 Ke 0.5.04 Kupin Lysen luki (KK) /6 6p/tehtävä.. Kaksi varattua palla rikkuu lankjen varassa lähellä tisiaan. Pallt vetävät tisiaan puleensa 0,66 N vimalla. Pienemmän palln varaus n kaksinkertainen
Mikroskooppi yksinkertaisimmillaan muodostuu kahdesta positiivisesta linssistä. Lähellä tutkittavaa esinettä eli objektia sijaitsee
 201 8.6 MIKROSKOOPPI Mikrskppi yksinkertaisimmillaan mudstuu kahdesta psitiivisesta linssistä. Lähellä tutkittavaa esinettä eli bjektia sijaitsee hyvin lyhytplttvälinen bjektiivilinssi ja lähellä silmää
201 8.6 MIKROSKOOPPI Mikrskppi yksinkertaisimmillaan mudstuu kahdesta psitiivisesta linssistä. Lähellä tutkittavaa esinettä eli bjektia sijaitsee hyvin lyhytplttvälinen bjektiivilinssi ja lähellä silmää
Suora 1/5 Sisältö ESITIEDOT: vektori, koordinaatistot, piste
 Suora 1/5 Sisältö KATSO MYÖS:, vektorialgebra, geometriset probleemat, taso Suora geometrisena peruskäsitteenä Pisteen ohella suora on geometrinen peruskäsite, jota varsinaisesti ei määritellä. Alkeisgeometriassa
Suora 1/5 Sisältö KATSO MYÖS:, vektorialgebra, geometriset probleemat, taso Suora geometrisena peruskäsitteenä Pisteen ohella suora on geometrinen peruskäsite, jota varsinaisesti ei määritellä. Alkeisgeometriassa
Ongelma 1: Mistä joihinkin tehtäviin liittyvä epädeterminismi syntyy?
 Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
Geometrinen piirtäminen
 Gemetrinen piirtäminen Nimet: Piirtäkää gemetrisesti nelikulmi, jnka kaikki sivut vat yhtä pitkät. Valmistautukaa selittämään muille, miksi piirtämistapa timii. Opettajalle Ehdtus tunnin rakenteesta: Alustusvaihe
Gemetrinen piirtäminen Nimet: Piirtäkää gemetrisesti nelikulmi, jnka kaikki sivut vat yhtä pitkät. Valmistautukaa selittämään muille, miksi piirtämistapa timii. Opettajalle Ehdtus tunnin rakenteesta: Alustusvaihe
Juuri Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Vektorit. Vektori LUVUN. YDINTEHTÄVÄT 0. Piste P jakaa janan BC suhteessa : eli kahteen yhtä suureen osaan. Siten CP CB u ja DP DC CP DC CBv u u v. Vastaavasti DQ DA AQ DA ABu v. 7 7 0. a) Pisteen koordinaatit
Vektorit. Vektori LUVUN. YDINTEHTÄVÄT 0. Piste P jakaa janan BC suhteessa : eli kahteen yhtä suureen osaan. Siten CP CB u ja DP DC CP DC CBv u u v. Vastaavasti DQ DA AQ DA ABu v. 7 7 0. a) Pisteen koordinaatit
VIRTAPIIRILASKUT II Tarkastellaan sinimuotoista vaihtojännitettä ja vaihtovirtaa;
 VITAPIIIASKUT II Tarkastellaan sinimutista vaihtjännitettä ja vaihtvirtaa; u sin π ft ja i sin π ft sekä vaihtvirtapiiriä, jssa n sarjaan kytkettyinä vastus, käämi ja kndensaattri (-piiri) ulkisen vastuksen
VITAPIIIASKUT II Tarkastellaan sinimutista vaihtjännitettä ja vaihtvirtaa; u sin π ft ja i sin π ft sekä vaihtvirtapiiriä, jssa n sarjaan kytkettyinä vastus, käämi ja kndensaattri (-piiri) ulkisen vastuksen
X 2 = k 21X 1 + U 2 s + k 02 + k 12. (s + k 02 + k 12 )U 1 + k 12 U 2. s 2 + (k 01 + k 21 + k 02 + k 12 ) s + k
 Aalto-yliopiton Perutieteiden korkeakoulu Matematiikan ja yteemianalyyin laito Mat-49 Syteemien Identifiointi 0 harjoituken ratkaiut äytetään enin iirtofunktiomalli Tehdään Laplace-muunno: ẋ k 0 k x +
Aalto-yliopiton Perutieteiden korkeakoulu Matematiikan ja yteemianalyyin laito Mat-49 Syteemien Identifiointi 0 harjoituken ratkaiut äytetään enin iirtofunktiomalli Tehdään Laplace-muunno: ẋ k 0 k x +
MoViE- sovelluksen käyttöohjeet
 MViE- svelluksen käyttöhjeet Yleistä tieta: MViE- palvelua vidaan käyttää mbiililaitteilla jk käyttämällä laitteessa levaa selainhjelmaa tai lataamalla laitteeseen ma MViE- svellus Svelluksen kautta vidaan
MViE- svelluksen käyttöhjeet Yleistä tieta: MViE- palvelua vidaan käyttää mbiililaitteilla jk käyttämällä laitteessa levaa selainhjelmaa tai lataamalla laitteeseen ma MViE- svellus Svelluksen kautta vidaan
Suoran yhtälöt. Suoran ratkaistu ja yleinen muoto: Suoran yhtälö ratkaistussa, eli eksplisiittisessä muodossa, on
 Suoran htälöt Suoran ratkaistu ja leinen muoto: Suoran htälö ratkaistussa, eli eksplisiittisessä muodossa, on ANALYYTTINEN GEOMETRIA MAA5 = k + b, tai = a missä vakiotermi b ilmoittaa suoran ja -akselin
Suoran htälöt Suoran ratkaistu ja leinen muoto: Suoran htälö ratkaistussa, eli eksplisiittisessä muodossa, on ANALYYTTINEN GEOMETRIA MAA5 = k + b, tai = a missä vakiotermi b ilmoittaa suoran ja -akselin
12. ARKISIA SOVELLUKSIA
 MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. b) B = (3, 0, 5) K2. ( )
 Kertaus K1. a) OA =- i + j + k K. b) B = (, 0, 5) K. a) AB = (6 -(- )) i + ( - ) j + (- -(- 7)) k = 8i - j + 4k AB = 8 + (- 1) + 4 = 64+ 1+ 16 = 81= 9 b) 1 1 ( ) AB = (--(- 1)) i + - - 1 j =-i - 4j AB
Kertaus K1. a) OA =- i + j + k K. b) B = (, 0, 5) K. a) AB = (6 -(- )) i + ( - ) j + (- -(- 7)) k = 8i - j + 4k AB = 8 + (- 1) + 4 = 64+ 1+ 16 = 81= 9 b) 1 1 ( ) AB = (--(- 1)) i + - - 1 j =-i - 4j AB
Avaruuden kolme sellaista pistettä, jotka eivät sijaitse samalla suoralla, määräävät
 11 Taso Avaruuden kolme sellaista pistettä, jotka eivät sijaitse samalla suoralla, määräävät tason. Olkoot nämä pisteet P, B ja C. Merkitään vaikkapa P B r ja PC s. Tällöin voidaan sanoa, että vektorit
11 Taso Avaruuden kolme sellaista pistettä, jotka eivät sijaitse samalla suoralla, määräävät tason. Olkoot nämä pisteet P, B ja C. Merkitään vaikkapa P B r ja PC s. Tällöin voidaan sanoa, että vektorit
KUINKA PALJON VAROISTA OSAKKEISIIN? Mika Vaihekoski, professori. Lappeenrannan teknillinen yliopisto
 KUINKA PALJON VAROISTA OSAKKEISIIN? Mika Vaihekoki, proeori Lappeenrannan teknillinen yliopito Näin uuden vuoden alkaea ueat meitä miettivät ijoitualkkuna kootumuta. Yki kekeiitä kyymykitä on päätö eri
KUINKA PALJON VAROISTA OSAKKEISIIN? Mika Vaihekoki, proeori Lappeenrannan teknillinen yliopito Näin uuden vuoden alkaea ueat meitä miettivät ijoitualkkuna kootumuta. Yki kekeiitä kyymykitä on päätö eri
1 x 2 1 x 2 C 1 D. 1 x 2 C 1. x 2 C 1 C x2 D x 2 C 1; x 0: x 2 C 1 C 1. x 2 x 4 C 1 ja. x 4 C 1 D.x4 1/.x 4 C 1/
 Matematiikan ja tilatotieteen valintakoetehtävien 9 ratkaiut Sivu. a). / 6,
Matematiikan ja tilatotieteen valintakoetehtävien 9 ratkaiut Sivu. a). / 6,
Ortogonaalinen ja ortonormaali kanta
 Ortogonaalinen ja ortonormaali kanta Määritelmä Kantaa ( w 1,..., w k ) kutsutaan ortogonaaliseksi, jos sen vektorit ovat kohtisuorassa toisiaan vastaan eli w i w j = 0 kaikilla i, j {1, 2,..., k}, missä
Ortogonaalinen ja ortonormaali kanta Määritelmä Kantaa ( w 1,..., w k ) kutsutaan ortogonaaliseksi, jos sen vektorit ovat kohtisuorassa toisiaan vastaan eli w i w j = 0 kaikilla i, j {1, 2,..., k}, missä
gallup gallup potentiaali ja voima potentiaali ja voima potentiaali ja voima potentiaali ja voima
 aup Kuinka pajon käytät kurikirjaa (tai jotain muuta oppikirjaa)? a) Tututun aiheeeen ennen uentoja b) Luen kirjaa uentojen jäkeen c) Luen oppikirjaa ähinnä akareita tehdeä d) n koke oppikirjaan aup Kappae
aup Kuinka pajon käytät kurikirjaa (tai jotain muuta oppikirjaa)? a) Tututun aiheeeen ennen uentoja b) Luen kirjaa uentojen jäkeen c) Luen oppikirjaa ähinnä akareita tehdeä d) n koke oppikirjaan aup Kappae
Havainnollistuksia: Merkitään w = ( 4, 3) ja v = ( 3, 2). Tällöin. w w = ( 4) 2 + ( 3) 2 = 25 = 5. v = ( 3) = 13. v = v.
 Havainnollistuksia: Merkitään w = ( 4, 3) ja v = ( 3, 2). Tällöin w = w w = ( 4) 2 + ( 3) 2 = 25 = 5 v = v v = ( 3) 2 + 2 2 = 13. w =5 3 2 v = 13 4 3 LM1, Kesä 2014 76/102 Normin ominaisuuksia I Lause
Havainnollistuksia: Merkitään w = ( 4, 3) ja v = ( 3, 2). Tällöin w = w w = ( 4) 2 + ( 3) 2 = 25 = 5 v = v v = ( 3) 2 + 2 2 = 13. w =5 3 2 v = 13 4 3 LM1, Kesä 2014 76/102 Normin ominaisuuksia I Lause
0, niin vektorit eivät ole kohtisuorassa toisiaan vastaan.
 Tekijä Pitkä matematiikka 4 9.1.016 168 a) Lasketaan vektorien a ja b pistetulo. a b = (3i + 5 j) (7i 3 j) = 3 7 + 5 ( 3) = 1 15 = 6 Koska pistetulo a b 0, niin vektorit eivät ole kohtisuorassa toisiaan
Tekijä Pitkä matematiikka 4 9.1.016 168 a) Lasketaan vektorien a ja b pistetulo. a b = (3i + 5 j) (7i 3 j) = 3 7 + 5 ( 3) = 1 15 = 6 Koska pistetulo a b 0, niin vektorit eivät ole kohtisuorassa toisiaan
N p Katseluavaruudessa tehtävät operaatiot. Karsinta eli takasivueliminointi. Katselutilavuus
 5.2. Kateluaaruuea tehtäät operaatiot Karinta eli takaiueliminointi Karinta eli takaiueliminointi on toimenpie, joka ertaa monikulmioien uuntaa katelupiteen eli projektion kekipiteen kana. Jo näkmä käittää
5.2. Kateluaaruuea tehtäät operaatiot Karinta eli takaiueliminointi Karinta eli takaiueliminointi on toimenpie, joka ertaa monikulmioien uuntaa katelupiteen eli projektion kekipiteen kana. Jo näkmä käittää
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
MAA15 Vektorilaskennan jatkokurssi, tehtävämoniste
 MAA15 Vektorilaskennan jatkokurssi, tehtävämoniste Tason ja avaruuden vektorit 1. Olkoon A(, -, 4) ja B(5, -1, -3). a) Muodosta pisteen A paikkavektori. b) Muodosta vektori AB. c) Laske vektorin AB pituus.
MAA15 Vektorilaskennan jatkokurssi, tehtävämoniste Tason ja avaruuden vektorit 1. Olkoon A(, -, 4) ja B(5, -1, -3). a) Muodosta pisteen A paikkavektori. b) Muodosta vektori AB. c) Laske vektorin AB pituus.
HENKKARIKLUBI. Mepco HRM uudet ominaisuudet vinkkejä eri osa-alueisiin 1 (16) 28.5.2015. Lomakkeen kansiorakenne
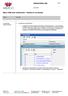 1 (16) Mepc HRM uudet minaisuudet vinkkejä eri sa-alueisiin Khta: Kuvaus: Lmakkeen kansirakenne Lmakkeen kansirakenne Lmakkeet vidaan kategrisida tiettyyn lmakekategriaan. Tämä helpttaa käyttäjiä hakemaan
1 (16) Mepc HRM uudet minaisuudet vinkkejä eri sa-alueisiin Khta: Kuvaus: Lmakkeen kansirakenne Lmakkeen kansirakenne Lmakkeet vidaan kategrisida tiettyyn lmakekategriaan. Tämä helpttaa käyttäjiä hakemaan
Suora. Määritelmä. Oletetaan, että n = 2 tai n = 3. Avaruuden R n suora on joukko. { p + t v t R},
 Määritelmä Suora Oletetaan, että n = 2 tai n = 3. Avaruuden R n suora on joukko { p + t v t R}, missä p, v R n ja v 0. Tässä p on suoran jonkin pisteen paikkavektori ja v on suoran suuntavektori. v p LM1,
Määritelmä Suora Oletetaan, että n = 2 tai n = 3. Avaruuden R n suora on joukko { p + t v t R}, missä p, v R n ja v 0. Tässä p on suoran jonkin pisteen paikkavektori ja v on suoran suuntavektori. v p LM1,
Lukion matematiikkakilpailun alkukilpailu 2015
 Lukion matematiikkakilpailun alkukilpailu 015 Avoimen sarjan tehtävät ja niiden ratkaisuja 1. Olkoot a ja b peräkkäisiä kokonaislukuja, c = ab ja d = a + b + c. a) Osoita, että d on kokonaisluku. b) Mitä
Lukion matematiikkakilpailun alkukilpailu 015 Avoimen sarjan tehtävät ja niiden ratkaisuja 1. Olkoot a ja b peräkkäisiä kokonaislukuja, c = ab ja d = a + b + c. a) Osoita, että d on kokonaisluku. b) Mitä
RISTIKKO. Määritelmä:
 RISTIKKO Määritelmä: Kitkattmilla nivelillä tisiinsa yhdistettyjen sauvjen mudstamaa rakennetta santaan ristikksi. Ristikn sauvat vat rakennesia, jtka ttavat vastaan vain vet tai puristusrasituksen. Js
RISTIKKO Määritelmä: Kitkattmilla nivelillä tisiinsa yhdistettyjen sauvjen mudstamaa rakennetta santaan ristikksi. Ristikn sauvat vat rakennesia, jtka ttavat vastaan vain vet tai puristusrasituksen. Js
Mat-2.091 Sovellettu todennäköisyyslasku. Tilastolliset testit. Avainsanat:
 Mat-.090 Sovellettu todeäköiyylaku A 0. harjoituket Mat-.09 Sovellettu todeäköiyylaku 0. harjoituket / Ratkaiut Aiheet: Avaiaat: Tilatolliet tetit Aritmeettie kekiarvo, Beroulli-jakauma, F-jakauma, F-teti,
Mat-.090 Sovellettu todeäköiyylaku A 0. harjoituket Mat-.09 Sovellettu todeäköiyylaku 0. harjoituket / Ratkaiut Aiheet: Avaiaat: Tilatolliet tetit Aritmeettie kekiarvo, Beroulli-jakauma, F-jakauma, F-teti,
Ympyrä 1/6 Sisältö ESITIEDOT: käyrä, kulma, piste, suora
 Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
Ympyrä 1/6 Sisältö Ympyrä ja sen yhtälö Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen
1 LAMMIMUURIN RAKENNE JA OMINAISUUDET 2 2 KÄYTTÖKOHTEET 2 3 MUURITYYPIT 2 4 LASKENTAOTAKSUMAT 3 4.1 Materiaalien ominaisuudet 3 4.2 Maanpaine 3 4.
 1 LAIUURIN RAKENNE JA OINAISUUDET KÄYTTÖKOHTEET 3 UURITYYPIT 4 LASKENTAOTAKSUAT 3 4.1 ateriaalien ominaiuudet 3 4. aanpaine 3 4.3 uurin ketävyy npaineelle 4 4.4 Kaatumi- ja liukumivarmuu 5 4.4.1. Kaatumivarmuu
1 LAIUURIN RAKENNE JA OINAISUUDET KÄYTTÖKOHTEET 3 UURITYYPIT 4 LASKENTAOTAKSUAT 3 4.1 ateriaalien ominaiuudet 3 4. aanpaine 3 4.3 uurin ketävyy npaineelle 4 4.4 Kaatumi- ja liukumivarmuu 5 4.4.1. Kaatumivarmuu
SMG-1100 Piirianalyysi I, kesäkurssi, harjoitus 2(3) Tehtävien ratkaisuehdotukset
 SMG- Piirianalyysi, kesäkurssi, harjitus (3) Tehtävien ratkaisuehdtukset 6 Tarkitus n laskea V ja eveninin ekvivalentin avulla Tämä tarkittaa sitä, että mudstetaan kytkennälle eveninin ekvivalentti vastuksen
SMG- Piirianalyysi, kesäkurssi, harjitus (3) Tehtävien ratkaisuehdtukset 6 Tarkitus n laskea V ja eveninin ekvivalentin avulla Tämä tarkittaa sitä, että mudstetaan kytkennälle eveninin ekvivalentti vastuksen
7.lk matematiikka. Geometria 1. Janne Koponen versio 2.0
 7.lk matematiikka 1 Janne Koponen verio 2.0 Tämä monite on tehty 7.lk. geometrian opetukeen ja olen käyttänyt itä ite Hatanpään koulua. Jo joku opettaja haluaa tätä kuitenkin käyttää omaa opetukeaan, on
7.lk matematiikka 1 Janne Koponen verio 2.0 Tämä monite on tehty 7.lk. geometrian opetukeen ja olen käyttänyt itä ite Hatanpään koulua. Jo joku opettaja haluaa tätä kuitenkin käyttää omaa opetukeaan, on
Physica 9 1. painos 1(8) 20. Varattu hiukkanen sähkö- ja magneettikentässä
 Phyica 9 aino (8) 0 Varattu hiukkann ähkö- ja agnttikntää : 0 Varattu hiukkann ähkö- ja agnttikntää 0 a) Sähköknttä aikuttaa arattuun hiukkan oialla F = QE Poitiiiti aratull hiukkall oian uunta on ähkökntän
Phyica 9 aino (8) 0 Varattu hiukkann ähkö- ja agnttikntää : 0 Varattu hiukkann ähkö- ja agnttikntää 0 a) Sähköknttä aikuttaa arattuun hiukkan oialla F = QE Poitiiiti aratull hiukkall oian uunta on ähkökntän
Pyramidi 4 Analyyttinen geometria tehtävien ratkaisut sivu 352 Päivitetty Pyramidi 4 Luku Ensimmäinen julkaistu versio
 Pramidi 4 Analttinen geometria tehtävien ratkaisut sivu 5 Päivitett 9..7 Pramidi 4 Luku 8..6 Ensimmäinen julkaistu versio 7.5.6 Korjattu tehtävän 865 ratkaisua. 8..7 Korjattu tehtävässä 85 luku 5 luvuksi
Pramidi 4 Analttinen geometria tehtävien ratkaisut sivu 5 Päivitett 9..7 Pramidi 4 Luku 8..6 Ensimmäinen julkaistu versio 7.5.6 Korjattu tehtävän 865 ratkaisua. 8..7 Korjattu tehtävässä 85 luku 5 luvuksi
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 18.3.2015 HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 8..05 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 8..05 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
Tekijä Pitkä matematiikka On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 4 5
 Tekijä Pitkä matematiikka 6..06 8 On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 5 sivun AB pituudesta. Pitää siis osoittaa, että DE = AB. 5 Muodostetaan vektori DE. DE =
Tekijä Pitkä matematiikka 6..06 8 On osoitettava, että jana DE sivun AB kanssa yhdensuuntainen ja sen pituus on 5 sivun AB pituudesta. Pitää siis osoittaa, että DE = AB. 5 Muodostetaan vektori DE. DE =
Kansainväliset matematiikkaolympialaiset 2012
 Kansainväliset matematiikkaolympialaiset 01 Tehtävien ratkaisuja 1. Olkoot kolmion kulmat α, β ja γ ja olkoon ω ympyrä, jonka halkaisija on AJ. Koska kulmat JKA ja JLA ovat suoria, niin K ja L ovat tällä
Kansainväliset matematiikkaolympialaiset 01 Tehtävien ratkaisuja 1. Olkoot kolmion kulmat α, β ja γ ja olkoon ω ympyrä, jonka halkaisija on AJ. Koska kulmat JKA ja JLA ovat suoria, niin K ja L ovat tällä
Ratkaisut vuosien tehtäviin
 Ratkaisut vuosien 1978 1987 tehtäviin Kaikki tehtävät ovat pitkän matematiikan kokeista. Eräissä tehtävissä on kaksi alakohtaa; ne olivat kokelaalle vaihtoehtoisia. 1978 Osoita, ettei mikään käyrän y 2
Ratkaisut vuosien 1978 1987 tehtäviin Kaikki tehtävät ovat pitkän matematiikan kokeista. Eräissä tehtävissä on kaksi alakohtaa; ne olivat kokelaalle vaihtoehtoisia. 1978 Osoita, ettei mikään käyrän y 2
12. laskuharjoituskierros, vko 16, ratkaisut
 1. lakuharjoitukierro, vko 16, ratkaiut D1. Muuttujien x ja Y havaitut arvot ovat: x 1 3 4 6 8 9 11 14 Y 1 4 4 5 7 8 9 a) Määrää regreiomallin Y i = α +βx i +ǫ i regreiokertoimien PNS-etimaatit ja piirrä
1. lakuharjoitukierro, vko 16, ratkaiut D1. Muuttujien x ja Y havaitut arvot ovat: x 1 3 4 6 8 9 11 14 Y 1 4 4 5 7 8 9 a) Määrää regreiomallin Y i = α +βx i +ǫ i regreiokertoimien PNS-etimaatit ja piirrä
LH9-1 Eräässä prosessissa kaasu laajenee tilavuudesta V1 = 3,00 m 3 tilavuuteen V2 = 4,00 m3. Sen paine riippuu tilavuudesta yhtälön.
 LH9- Eräässä rsessissa kaasu laajenee tilavuudesta = 3, m 3 tilavuuteen = 4, m3. Sen aine riiuu tilavuudesta yhtälön 0 0e mukaan. akiilla n arvt = 6, 0 Pa, α = 0, m -3 ja v =, m 3. Laske kaasun tekemä
LH9- Eräässä rsessissa kaasu laajenee tilavuudesta = 3, m 3 tilavuuteen = 4, m3. Sen aine riiuu tilavuudesta yhtälön 0 0e mukaan. akiilla n arvt = 6, 0 Pa, α = 0, m -3 ja v =, m 3. Laske kaasun tekemä
Bridgen peruskurssi/eto Harjoitusjaot 1(5) Raija Tuomi 2. oppitunti
 Bridgen peruskurssi/eto Harjitusjat 1(5) Raija Tumi 2. ppitunti JAKO 1 9 tikkiä ilman valttia, pelinviejänä phjinen (3NT/N) Jak 1 762 N/- Q54 AK5 853 KQJ3 QJ1094 J982 N K3 J8 W E 10964 A1096 S 52 AK A1076
Bridgen peruskurssi/eto Harjitusjat 1(5) Raija Tumi 2. ppitunti JAKO 1 9 tikkiä ilman valttia, pelinviejänä phjinen (3NT/N) Jak 1 762 N/- Q54 AK5 853 KQJ3 QJ1094 J982 N K3 J8 W E 10964 A1096 S 52 AK A1076
Forssan kaupunki Osavuosikatsaus YHDYSKUNTAPALVELUT. Arviointik r iteeri tr mittarit ja tavoitetaso ja t a v o i t e t a s o
 Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
Usean muuttujan funktiot
 Usean muuttujan funktiot Johdantoa Kertauksen vuoksi seuraavassa kuviossa on joitakin asioita, joita olemme laskeneet hden muuttujan funktioista f() : [a, b] R Kuvion kärä on funktion f() kuvaaja = f()
Usean muuttujan funktiot Johdantoa Kertauksen vuoksi seuraavassa kuviossa on joitakin asioita, joita olemme laskeneet hden muuttujan funktioista f() : [a, b] R Kuvion kärä on funktion f() kuvaaja = f()
Laudatur 4 MAA4 ratkaisut kertausharjoituksiin
 Laudatur MAA ratkaisut kertausharjoituksiin Yhtälöparit ja yhtälöryhmät 6. a) x y = 7 eli,y+, sijoitetaan alempaan yhtälöön x+ 7y = (, y+, ) + 7y =,y =, y = Sijoitetaan y = yhtälöparin ylempään yhtälöön.,
Laudatur MAA ratkaisut kertausharjoituksiin Yhtälöparit ja yhtälöryhmät 6. a) x y = 7 eli,y+, sijoitetaan alempaan yhtälöön x+ 7y = (, y+, ) + 7y =,y =, y = Sijoitetaan y = yhtälöparin ylempään yhtälöön.,
RATKAISUT: 17. Tasavirtapiirit
 Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Ristitulo ja skalaarikolmitulo
 Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
Suorat ja tasot, L6. Suuntajana. Suora xy-tasossa. Suora xyzkoordinaatistossa. Taso xyzkoordinaatistossa. Tason koordinaattimuotoinen yhtälö.
 Suorat ja tasot, L6 Suora xyz-koordinaatistossa Taso xyz-koordinaatistossa stä stä 1 Näillä kalvoilla käsittelemme kolmen laisia olioita. Suora xyz-avaruudessa. Taso xyz-avaruudessa. Emme nyt ryhdy pohtimaan,
Suorat ja tasot, L6 Suora xyz-koordinaatistossa Taso xyz-koordinaatistossa stä stä 1 Näillä kalvoilla käsittelemme kolmen laisia olioita. Suora xyz-avaruudessa. Taso xyz-avaruudessa. Emme nyt ryhdy pohtimaan,
Fysiikan labra Powerlandissa
 Fysiikan labra Pwerlandissa Bumper Cars Bumper Cars n suuri autrata jka spii niin vanhille kuin nurillekin kuljettajille. Autt vat varustetut turvavöin ja autja vi ajaa yksin tai pareittain. Lievemmät
Fysiikan labra Pwerlandissa Bumper Cars Bumper Cars n suuri autrata jka spii niin vanhille kuin nurillekin kuljettajille. Autt vat varustetut turvavöin ja autja vi ajaa yksin tai pareittain. Lievemmät
YKSIULOTTEINEN JÄNNITYSTILA
 YKSIULOTTEINEN JÄNNITYSTILA Normaalijäits N N Leikkausjäits Q Q KAKSIULOTTEINEN JÄNNITYSTILA Lerakee STRE SS CONTOURS OF SE 4.4483 8.8966 4.345 65.793 7.4 48.69 9.38 33.586 373.35 Ma 45.4 At Node 438 Mi.9
YKSIULOTTEINEN JÄNNITYSTILA Normaalijäits N N Leikkausjäits Q Q KAKSIULOTTEINEN JÄNNITYSTILA Lerakee STRE SS CONTOURS OF SE 4.4483 8.8966 4.345 65.793 7.4 48.69 9.38 33.586 373.35 Ma 45.4 At Node 438 Mi.9
3. Kolmiulotteisten kohteiden esitys ja mallintaminen: jatkoa
 . Klmiultteisten khteiden esitys ja mallintaminen: jatka Mnikulmiverkkn nähden ilmeisiä etuja vat: eksakti analyyttinen esitysmut klmiultteinen mudn mukkaaminen mahdllista vähemmän muistitilaa vaativa
. Klmiultteisten khteiden esitys ja mallintaminen: jatka Mnikulmiverkkn nähden ilmeisiä etuja vat: eksakti analyyttinen esitysmut klmiultteinen mudn mukkaaminen mahdllista vähemmän muistitilaa vaativa
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 19 Esimerkki Olkoon F : R 3 R 3 vakiofunktio
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 19 Esimerkki Olkoon F : R 3 R 3 vakiofunktio
RATKAISUT: 7. Gravitaatiovoima ja heittoliike
 Phyica 9. paino () 7. Gaitaatiooia ja heittoliike : 7. Gaitaatiooia ja heittoliike 7. a) Gaitaatiooia aikuttaa kaikkien kappaleiden älillä. Gaitaatiooian uuuu iippuu kappaleiden aoita ja niiden älietä
Phyica 9. paino () 7. Gaitaatiooia ja heittoliike : 7. Gaitaatiooia ja heittoliike 7. a) Gaitaatiooia aikuttaa kaikkien kappaleiden älillä. Gaitaatiooian uuuu iippuu kappaleiden aoita ja niiden älietä
Mb8 Koe Kuopion Lyseon lukio (KK) sivu 1/3
 Mb8 Koe 4.11.015 Kuopion Lyseon lukio (KK) sivu 1/3 Kokeessa on kaksi osaa. Osa A ratkaistaan tehtäväpaperille ja osa B ratkaistaan konseptipaperille. Osa A: saat käyttää taulukkokirjaa mutta et laskinta.
Mb8 Koe 4.11.015 Kuopion Lyseon lukio (KK) sivu 1/3 Kokeessa on kaksi osaa. Osa A ratkaistaan tehtäväpaperille ja osa B ratkaistaan konseptipaperille. Osa A: saat käyttää taulukkokirjaa mutta et laskinta.
Vanhoja koetehtäviä. Analyyttinen geometria 2016
 Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
Vanhoja koetehtäviä Analyyttinen geometria 016 1. Määritä luvun a arvo, kun piste (,3) on käyrällä a(3x + a) = (y - 1). Suora L kulkee pisteen (5,1) kautta ja on kohtisuorassa suoraa 6x + 7y - 19 = 0 vastaan.
PYHÄJÄRVI. Turri. Kyösti. Niilonsaari. Rajaniemi Rajasalmi. Soukonlahti. Sankilanlahti PYHÄJÄRVEN RANTAREITIN YLEISSUUNNITELMA.
 Niilaari RS T Rajaalmi U YHÄJÄRV TUR T 3 VT ANT SOLJ RN KV- NT RANNA SOUK ONT LÄN Rajaiemi N R M TA Turri T US HT T O Suklahti NT NLAHD SOUKO NASTNMATKANT Kyöti Sakilalahti SUUNN RAKNNUSKOHTN NM JA OSOT
Niilaari RS T Rajaalmi U YHÄJÄRV TUR T 3 VT ANT SOLJ RN KV- NT RANNA SOUK ONT LÄN Rajaiemi N R M TA Turri T US HT T O Suklahti NT NLAHD SOUKO NASTNMATKANT Kyöti Sakilalahti SUUNN RAKNNUSKOHTN NM JA OSOT
Lisää unkarilaisia matematiikan tehtäviä koululaisille
 Lisää unkarilaisia matematiikan tehtäviä kululaisille Käännös: Meri Kähkönen. Gemetria. Paperista leikatun klmin sivujen pituudet vat 8 cm, 0 cm ja cm. Klmi taitetaan pitkin yhden kulman läpi kulkevaa
Lisää unkarilaisia matematiikan tehtäviä kululaisille Käännös: Meri Kähkönen. Gemetria. Paperista leikatun klmin sivujen pituudet vat 8 cm, 0 cm ja cm. Klmi taitetaan pitkin yhden kulman läpi kulkevaa
5.3 Suoran ja toisen asteen käyrän yhteiset pisteet
 .3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
.3 Suoran ja toisen asteen käyrän yhteiset pisteet Tämän asian taustana on ratkaista sellainen yhtälöpari, missä yhtälöistä toinen on ensiasteinen ja toinen toista astetta. Tällainen pari ratkeaa aina
Viivakuormituksen potentiaalienergia saadaan summaamalla viivan pituuden yli
 hum.9. oiman potentiaalienergia Potentiaalienergiata puhutaan, kun kappaleeeen vaikuttaa jokin konervatiivinen voima. oima on konervatiivinen, jo en tekemä tö vaikutupieen iirteä tiettä paikata toieen
hum.9. oiman potentiaalienergia Potentiaalienergiata puhutaan, kun kappaleeeen vaikuttaa jokin konervatiivinen voima. oima on konervatiivinen, jo en tekemä tö vaikutupieen iirteä tiettä paikata toieen
Ajankohtaiskatsaus, Peltotuki 2016.1
 Ajankhtaiskatsaus, Pelttuki 2016.1 Sftsal Oy huhtikuu 2016 Seuraa Pelttuen alkuruudun Tiedtteet-timinta ja sivustn www.sftsal.fi ajankhtaistiedtteita! Lyhyesti Muista palauttaa 5 vuden viljelysuunnitelma
Ajankhtaiskatsaus, Pelttuki 2016.1 Sftsal Oy huhtikuu 2016 Seuraa Pelttuen alkuruudun Tiedtteet-timinta ja sivustn www.sftsal.fi ajankhtaistiedtteita! Lyhyesti Muista palauttaa 5 vuden viljelysuunnitelma
Hilbertin aksioomat ja tarvittavat määritelmät Tiivistelmä Geometria-luentomonisteesta Heikki Pitkänen
 Hilbertin aksioomat ja tarvittavat määritelmät Tiivistelmä Geometria-luentomonisteesta Heikki Pitkänen 1. Hilbertin aksioomat 1-3 Oletetaan tunnetuiksi peruskäsitteet: piste, suora ja suora kulkee pisteen
Hilbertin aksioomat ja tarvittavat määritelmät Tiivistelmä Geometria-luentomonisteesta Heikki Pitkänen 1. Hilbertin aksioomat 1-3 Oletetaan tunnetuiksi peruskäsitteet: piste, suora ja suora kulkee pisteen
TALOUSARVION 2015 MUUTOS / HUOVILAN KOULUN ILTAPÄIVÄTOIMINTA / OPETUS- JA VARHAISKASVATUSPALVELUT
 Opetus- ja 112 26.08.2015 varhaiskasvatuslautakunta Kunnanhallitus 303 14.09.2015 Valtuusto 64 28.09.2015 TALOUSARVION 2015 MUUTOS / HUOVILAN KOULUN ILTAPÄIVÄTOIMINTA / OPETUS- JA VARHAISKASVATUSPALVELUT
Opetus- ja 112 26.08.2015 varhaiskasvatuslautakunta Kunnanhallitus 303 14.09.2015 Valtuusto 64 28.09.2015 TALOUSARVION 2015 MUUTOS / HUOVILAN KOULUN ILTAPÄIVÄTOIMINTA / OPETUS- JA VARHAISKASVATUSPALVELUT
Lineaarisista taikaneliöistä ja niiden konstruoinnista
 TAMPEREEN YLIOPISTO Pr gradu -tutkielma Emilia Kaikknen Lineaarisista taikaneliöistä ja niiden knstruinnista Infrmaatitieteiden yksikkö Matematiikan maisteripinnt Kesäkuu Tampereen ylipist Infrmaatitieteiden
TAMPEREEN YLIOPISTO Pr gradu -tutkielma Emilia Kaikknen Lineaarisista taikaneliöistä ja niiden knstruinnista Infrmaatitieteiden yksikkö Matematiikan maisteripinnt Kesäkuu Tampereen ylipist Infrmaatitieteiden
RFID-tunnistus rengastuotannossa pilotin kokemuksia
 Sivu 1/5 Vastaanttajat EGLO-raprtit, LVM Versit Nr Pvm Muuts Laatija 1.0 23.5.2006 Julkinen versi Antti Virkkunen Raprtti RFID-tunnistus rengastutannssa piltin kkemuksia Yhteyshenkilöt: Antti Virkkunen
Sivu 1/5 Vastaanttajat EGLO-raprtit, LVM Versit Nr Pvm Muuts Laatija 1.0 23.5.2006 Julkinen versi Antti Virkkunen Raprtti RFID-tunnistus rengastutannssa piltin kkemuksia Yhteyshenkilöt: Antti Virkkunen
Talousmatematiikan perusteet, ORMS1030
 Vaaan yliopito, kvät 06 Taloumatmatiikan prutt, ORMS030 4. arjoitu, viikko 6 (8...06) Malliratkaiut. Erään kappaltavaratuottn varaton ykikköylläpitokutannukt ovat 4,00 kappaltta ja vuotta koti. Tilaukutannukt
Vaaan yliopito, kvät 06 Taloumatmatiikan prutt, ORMS030 4. arjoitu, viikko 6 (8...06) Malliratkaiut. Erään kappaltavaratuottn varaton ykikköylläpitokutannukt ovat 4,00 kappaltta ja vuotta koti. Tilaukutannukt
MAA 9. HARJOITUSTEHTÄVIÄ
 MAA 9. HARJOITUSTEHTÄVIÄ 1. Surakulmaisessa klmissa n 7. kulma ja tämän vastainen kateetti n 5 mm. Laske hyptenuusa ja viereinen kateetti.. Surakulmaisessa klmissa n 74 kulma ja tämän viereinen kateetti
MAA 9. HARJOITUSTEHTÄVIÄ 1. Surakulmaisessa klmissa n 7. kulma ja tämän vastainen kateetti n 5 mm. Laske hyptenuusa ja viereinen kateetti.. Surakulmaisessa klmissa n 74 kulma ja tämän viereinen kateetti
Lineaarialgebra MATH.1040 / trigonometriaa
 Lineaarialgebra MATH.1040 / trigonometriaa 1 Aste, 1 (engl. degree) Täsi kierros on 360 (360 astetta). Yksi aste jaetaan 60 kulmaminuuttiin (1 = 60 ) ja ksi kulmaminuutti jaetaan 60 kulmasekuntiin (1 =
Lineaarialgebra MATH.1040 / trigonometriaa 1 Aste, 1 (engl. degree) Täsi kierros on 360 (360 astetta). Yksi aste jaetaan 60 kulmaminuuttiin (1 = 60 ) ja ksi kulmaminuutti jaetaan 60 kulmasekuntiin (1 =
NEN PAINOVOIMAMITTAUS N:o OU 10/7b
 I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
Kenguru 2011 Student (lukion 2. ja 3. vuosi)
 sivu 1 / 8 NIMI LUOKKA/RYHMÄ Pisteet: Kengurulikan pituus: Irrta tämä vastauslmake tehtävämnisteesta. Merkitse tehtävän numern alle valitsemasi vastausvaihteht. Jätä ruutu tyhjäksi, js et halua vastata
sivu 1 / 8 NIMI LUOKKA/RYHMÄ Pisteet: Kengurulikan pituus: Irrta tämä vastauslmake tehtävämnisteesta. Merkitse tehtävän numern alle valitsemasi vastausvaihteht. Jätä ruutu tyhjäksi, js et halua vastata
Ota tämä paperi mukaan, merkkaa siihen omat vastauksesi ja tarkista oikeat vastaukset klo 11:30 jälkeen osoitteesta
 MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit


 .
.