Länsitunneli Rakennettavuusselvitys
|
|
|
- Albert Salonen
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Länsitunneli Rkennettvuusselvitys GEO 6.. KAUPUNKSUUNNTTELUVRASTO, LKENNESUUNNTTELUOSASTO KNTESTÖVRASTO, GEOTEKNNEN OSASTO
2 RAKENNETTAVUUSSELVTYS Jyrki Alstlo / ksv Pekk Holopinen / kv GEO / 6.. (4) LÄNSTUNNEL. Tehtävä Tään rkennettvuusselvityksen trkoituksen on selvittää tekniset edellytykset j krke kustnnustso utoliikennetunnelille, jok lähtee Länsistst j yhtyy Keskusttunnelin länsiosn. Ajtuksen on, että tunneli voisi vrsinisen stn utoliikenteen lisäksi käyttää yös uu Jätkäsren liikenne. Tehtävää ohjsi työryhä, johon kuului: Ktriin Brn, ksv, pj AnnMij Fro, Hels Pekk Holopinen, kv/geo Jri Huhtniei, ksv Seij Nrvi, ksv Ann Nervol, ksv Outi Säntti, Tske lkk Vähäho, kv/geo. Rportin ltivt Jyrki Alstlo / ksv, los j Pekk Holopinen / kv, geo.. Liikenteelliset näkökohdt Länsitunnelin on jteltu plvelevn sekä Länsist että Jätkäsren uut luett. Tunnelin rkentinen vin stn liikennettä vrten ei liene relistist. Länsistn livliikenteen iheutt liikenneäärä on noin 4 4 jon/vrk (henkilöutot, kuorutot, bussit j rekt). Jos oletetn, että siitä liikenneäärästä suuntutuu Länsiväylälle noin /3, niin tunneli käyttäisi stn liikenteestä noin 3 jon/vrk. Jätkäsren suinlueelt on yös yhteys Länsitunneliin. Liikennesuunnitteluosstoll ei ole vielä rvioitu Jätkäsren suntolueen tuotti liikenneääriä Länsitunneliss. Keskusttunnelin läntinen suuukko on kistinen j sijoittuu Slisrenkdun jtkeeksi Länsiväylän itäpuolell. Tunnelin käyttäinen osn Länsitunneli edellyttää, että suuukko levennetään 3kistiseksi j että Keskusttunneli rkennetn vliiksi noin 4 etrin tkll hutusn ll. Keskusttunnelin suunnitel uutetn siten, että länteen päin on kole kist suunnitelss olevn khden kistn sijn. Kols kist uodostuu Sttunnelist tulevst kistst, jok johdetn suorn Länsiväylälle. tään riittää kksi kist siten, että erkneinen Sttunneliin tphtuu betonitunneliosuudelle rkennettvn erkneiskistn vull. Sttunneli toteutetn kistisen klliotunnelin siten, että josuunnt ovt oiss tunneleissn. PL 99 HELSNGN KAUPUNK Geotekninen ossto Mlin setie 3 A (9) 3 3 Fx (9)
3 RAKENNETTAVUUSSELVTYS Jyrki Alstlo / ksv Pekk Holopinen / kv GEO / 6.. (4) LÄNSTUNNEL 3. Reunehdot tunnelille Jätkäsren päässä ino relistinen hdollisuus järjestää sisäänjo klliotunneliin on Bunkkeri rkennuksen eteläreun. Bunkkeri on perustettu ielle klliosrelle. Rkennuksen eteläpuoleinen lue on kvoitettu pelikentiksi. Täten betonitunnelin rkentinen sille, täyttö tkisin nykyiseen korkeustsoon j pelikenttien rkentinen tään jälkeen on hdollist. Tunnelin suuripn pituuskltevuuten on käytetty 6 % lspäin j % ylöspäin. Se on suuri rskille joneuvoille, utt voitneen pitää hdollisen. Tunnelin linjukselle osuvt oless olevt etrotunnelit j Kppi Slisri yhteiskäyttötunneli. Tulevisuudess kvillut tunnelilinjt sen sijn ovt sovitettviss yhteen Länsitunnelin knss. Turvllisuussioiss on oletettu, että kupikin josuunt on erotettv oksi osstokseen. Käytännössä tää trkoitt kht erillistä klliotunneli. Lisäksi poistuisyhteyksiä npinnlle on oletettu trvittvn 3 välein. Kllioperässä ei tiedoss itään sellisi heikkousvyöhykkeitä, jotk vikuttisivt oleellisesti kyseisen suuntisen tunnelin linjukseen tässä suunnitteluviheess. 4. Tunnelin linjus j rkenne Kksoistunnelin pituus on noin, k. Tästä noin, k on yhteistä rkennett Keskusttunnelin knss. Tunnelin linjus, pituusleikkukset j poikkileikkukset on esitetty liitepiirustuksiss. Länsistn päässä voluiskn pituus on. Se on sijoitettu tulevlle ktulueelle. Trvittess voluisk voidn linjt yös stlueelle. Lisäsi sen yläpäätä voi kääntää vpsti krresäteiden slliiss rjoiss. Länsitunneli j sen lkupään sijoittinen on oleellinen eleentti lkneelle stlueen hnkesuunnittelulle. Länsistn pään betonitunneli on rkenteellisesti vtiv. Osuuden pituus on 9. Se joudutn upottn perään, joss ylipänä on pilntunutt t j sen lpuolell sve. Rtkisun on jteltu käytettävän vesitiiviitä porpluseiniä, joiden väliin on rkennettu erillinen, väliseinäinen betonitunneli. Klliotunnelin osuus hrutuu Keskusttunneli lähestyttäessä khdeksi toisistn loittonevksi rppitunneliksi. Länteen johtvn rppitunnelin kllioktto stt osoittutu liin pieneksi hutusn kohdll. Ongel on kuitenkin rtkistviss sijoittll ideäksi rppitunnelin liittäinen Keskusttunneliin. Mnpinnlle ulottuvien tuuletus j hätäpoistuiskuilujen sijintej ei ole tässä viheess trksteltu. PL 99 HELSNGN KAUPUNK Geotekninen ossto Mlin setie 3 A (9) 3 3 Fx (9)
4 RAKENNETTAVUUSSELVTYS Jyrki Alstlo / ksv Pekk Holopinen / kv GEO / (4) LÄNSTUNNEL Länsiväylän puoleisess päässä pääos Keskusttunnelin rkenteist tulee toteutt, vikk Länsitunneli otettisiin käyttöön jo ennen sen rkentist. Avoluisk j betonitunneliosuus vtii länteen päin suuntutuvlle liikenteelle yhden lisäkistn. Yliääräisenä tehtävänä trksteltiin, olisiko Hernesren liikenne helposti yhdistettävissä Länsitunneliin. Jätkäsren j Hernesren välisellä erilueell klliopint on syvyydellä noin. Tää edellyttää tunnelin pohjtsoksi noin. Tunneliss olisi 6%:n jtkuv nousu kiloetrin tkll. Kokonispituutt kertyy n.,4 k, joten odotettviss olevill liikenneäärillä tunneli ei void pitää perusteltun.. Kustnnukset. Kustnnusrvion perusteet Kikki kustnnukset on esitetty tikuun kustnnustsoss j lv %. Lähtökohtn on pidetty Keskustn huoltotunneli, jok on toteutettu tiiviisti rkennetuss kupunkiypäristössä. Sen kokoniskustnnukset olivt 33 e / tunneli vuoden 7 kustnnustsoss. Mrkennuksen kustnnusindeksi on noussut kesäkuust 7 tikuuhun yhteensä,9 %. Täten Keskustn huoltotunnelin kustnnus uutettun tikuun kustnnustsoon on,9 x 33 e eli 4 e / tunneli. Keskustn huoltotunneli uodostuu yhdestä klliotunnelist (B = 4, H = 8 ). Pääos Länsitunnelist puolestn koostuu khdest erillisestä klliotunnelist (B = 8, H = 6 ). Länsitunnelin tunneliprin yksikkökustnnukset rvioidn neljänneksen suureiksi kuin vstvn Keskustn huoltotunnelin yksiputkisen tunnelin kustnnukset. Täten Länsitunnelin kksoistunnelin kllioosuuden kustnnuksiksi uodostuu, x 4 e eli e / tunnelipri. Os Länsitunnelist koostuu khdest selvästi toisistn erillään olevst klliotunnelist. Tässä tpuksess yksittäisen klliotunnelin (B = 8, H = 6 ) kustnnukseksi on jteltu s kuin Keskustn huoltotunnelill, kuitenkin vähennettynä pieneän poikkileikkuksen louhinnn kustnnuksell ( e/3). Täten yksittäisen klliotunnelin hinnksi uodostuu 4 7 = 33 e / tunneli. Trondheiiss on vuonn toteutettu liikennetunnelin os svikoll. Työnikinen tuent on toteutettu porpluill j tunneliosuus betoniltikkon. 3 pitkän rkenteen kokonishinnksi uodostui 7 Me. (keskustelu 6.. Teräplupäivillä). Tällä perusteell stpään betonitunneliosuuden yksikköhinnksi on rvioitu e / kksoistunneli. Tään lisäksi tulevt pilntuneist ist syntyvät kustnnukset. PL 99 HELSNGN KAUPUNK Geotekninen ossto Mlin setie 3 A (9) 3 3 Fx (9)
5 RAKENNETTAVUUSSELVTYS Jyrki Alstlo / ksv Pekk Holopinen / kv GEO / (4) LÄNSTUNNEL. Kustnnusrvio.. Avoluisk stpäässä, e yht. 4 Me.. Betonitunneli stpäässä 9, e 73 Me..3 Pilntuneet t stpäässä 3, e 4 Me kolsos kivettvist ssoist..4 Klliotunneli kksoistunnelin, e 6 Me.. Yksittäinen klliotunneli 94, 33 e 3 Me..6 Betonitunneli Länsiväylän päässä 8, e 4 Me..7 Avoluisk Länsiväylän päässä, e Me Kustnnukset yhteensä iln rkennuttjn kustnnuksi Kustnnukset yhteensä l. rkennuttjn kustnnukset (%) 6 Me Me Betonitunnelit ovt klliit verrttun klliotunneleihin. Niiden kustnnukset ovt puolet koko hnkkeest, vikk ne edustvt vin noin % koko pituudest. Myös trvittvien pystykuilujen sijoittinen vliiseen kupunkirkenteeseen on erkittävä kustnnustekijä. Me kokoniskustnnuksist Keskusttunnelin osuudeksi voidn lske Me j Länsitunnelin Me. LTEPRUSTUKSET. Krtt, pv.8.., A3. Pituus j poikkileikkukset, pv.8.., A3 N:\projekti\holoppe\\rs.docx PL 99 HELSNGN KAUPUNK Geotekninen ossto Mlin setie 3 A (9) 3 3 Fx (9)
6 VSS6 M LTE L r k 4 VSS66T Z YK33T YK MAR34 YK9K3 L4 44 VSS66A tr k vj Z34T M MAR3 L VSS M VSS MAR6 YK33T6 L M 3 YK Sirl k Z34TK L4S Z Z34TK4 MAR VSS tr k Z34TK 4 Z34TK3 M VSS MAR36 VSS66PT 4 YK H349T4 V8S VSS66K YK9T7 H349S H H349T VSS66K3 H349T H388T V H H388K 4 H3S V8S 6 H349TA 3 MAR H3S H349T M 9 YK H H388K H349S V 6 7S H H388S H384S VS YK366S VS 8 M6S s V YK366A YK366K 7 M YK YK9S3 K Y H 7 H H4S H H4T H 6 VSS VSS44TS VSS44TS H H4K VSS44T H4S K Y M H M 8 H4K3 V YK366T4 M M 7 H M 9 M 4 L L4 J6K J r k J J6T Z L4S H 3 L s r k 3 J J4T J 4 VSS39 VSS VSS 9 6 H 9 MK4 J 8 HS HS HS6T HS J L sij. ep{v. J 7 J k JK L HS JK6 L sij. ep{v. HS6A L HS6S Tunnelilinjus, voluisk 3 Tunnelilinjus, klliotunneli 3 Tunnelilinjus, betoni Bunkkeri Liikuntpuisto Oless olevt nliset tilt 3 Arvioitu klliopinnn tsokyrst Entisen sren rntviiv (sispuolell entiset korkeuskyrt) Entinen klliosri 4 3 Keskusttunneli 3 9 Piir. n:o TUNNELYHTEYS 3 L NSV YL L NSSATAMA Suhde Korv Korvttu Piirt. Lt. MLe JAl Trk. Pv. Ehd. 3 6 J 8.. Hyv. HELSNGN KAUPUNGN KNTESTVRASTO GEOTEKNNEN OSASTO HELSNGN KAUPUNKSUUNNTTELUVRASTO LKENNESUUNNTTELUOSASTO K.os
7 TUNNELYHTEYS L NSV YL L NSSATAMA LTE L nsiv yl L nsist Pituusleikkukset 3. Mrin sirln huoltotunneli S=4 S=4. Avoluisk Metro Betonitunneli 3 4 S= S=.6 S=4 S=4.4 Klliotunneli Arvioitu klliopint L nsistl nsiv yl 3 Keskusttunneli. 3 4 S=4 S=4.4 S=4 Metro S=4. S=3 S=3 Keskusttunneli. Yhteisk ytt tunneli S=4 S=4. Yhteisk ytt tunneli Kliotunnelin poikkileikkus vp korkeus 4.8 vp korkeus HELSNGN KAUPUNGN KNTEST VRASTO GEOTEKNNEN OSASTO HELSNGN KAUPUNKSUUNNTTELUVRASTO LKENNESUUNNTTELUOSASTO / JAl, MLe 8..
4 Pinta-alasovelluksia
Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Helsingin kaupunki / Liikennesuunnitteluosasto 26.2.2014 16:21 Anitta Vähäkuopus 1 (3) Koje vaihdetaan ja muutetaan minikojeeksi (ITC-2bM).
Helsinin kupunki / Liikennesuunnitteluossto 26.2.204 6:2 Anitt Vähäkuopus (3) TYÖSELTE Telkkktu/Pursimiehenktu Risteys 256 Kojeuusint Yleistä Koje vihdetn j muutetn minikojeeksi (TC-2M). Klusteet j työ
LINSSI- JA PEILITYÖ TEORIAA. I Geometrisen optiikan perusaksioomat
(0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
3.3 KIELIOPPIEN JÄSENNYSONGELMA Ratkaistava tehtävä: Annettu yhteydetön kielioppi G ja merkkijono x. Onko
3.3 KILIOPPIN JÄSNNYSONGLMA Rtkistv tehtävä: Annettu yhteydetön kielioppi G j merkkijono x. Onko x L(G)? Rtkisumenetelmä = jäsennyslgoritmi. Useit vihtoehtoisi menetelmiä, erityisesti kun G on jotin rjoitettu
Riemannin integraalista
Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
6 Integraalilaskentaa
6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
ICS-C2000 Tietojenkäsittelyteoria Kevät 2016
ICS-C2 Tietojenkäsittelyteori Kevät 2 Kierros,. 5. helmikuut Demonstrtiotehtävien rtkisut D: Sievennä seurvi säännöllisiä lusekkeit (so. konstruoi yksinkertisemmt lusekkeet smojen kielten kuvmiseen): ()
10. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA
MAA0 0. Määrätyn integrlin käyttö eräiden pint-lojen lskemisess 0. MÄÄRÄTYN INTEGRAALIN KÄYTTÖ ERÄIDEN PINTA-ALOJEN LASKEMISESSA Edellä on todettu, että f (x)dx nt x-kselin j suorien x =, x = sekä funktion
Tee B-osion konseptiin etusivulle pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Välivaiheet perustelevat vastauksesi!
MAA8 Koe 4.4.016 Jussi Tyni Tee B-osion konseptiin etusivulle pisteytysruudukko! Muist kirjt nimesi j ryhmäsi. Väliviheet perustelevt vstuksesi! A-osio. Ilmn lskint. MAOLi s käyttää. Mksimissn 1h ik. Lske
Painopiste. josta edelleen. x i m i. (1) m L A TEX 1 ( ) x 1... x k µ x k+1... x n. m 1 g... m n g. Kuva 1. i=1. i=k+1. i=1
Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
S Laskennallinen systeemibiologia
S-4.50 Lsknnllinn systmiiologi 4. Hrjoitus. Viill tutkittvll ljill (,, c, j ) on määrätty täisyyt c 0 8 8 8 0 8 8 8 c 0 4 4 0 0 Määritä puurknn käyttän UPGMA-mntlmää. Näytä kunkin vihn osrkntt vstvin täisyyksinn.
Integraalilaskentaa. 1. Mihin integraalilaskentaa tarvitaan? MÄNTÄN LUKIO
Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
Laskennan mallit (syksy 2010) 1. kurssikoe, ratkaisuja
582206 Lskennn mllit (syksy 2010) 1. kurssikoe, rtkisuj 1. [2+2+2 pistettä] Säännöllisissä lusekkeiss on käytetty tuttu lyhennysmerkintää Σ = ( ). () merkkijonot, joiden kksi ensimmäistä merkkiä ovt joko
NASTOLAN YRITYSPUISTO RAKENNUSTAPAOHJEET NASTOLAN YRITSPUISTON ALUEEN KORTTELEITA 500, 501, 504-511 KOSKEVAT RAKENNUSTAPAOHJEET
NASTOLAN YRISPUISTO RAKENNUSTAPAOHJEET NASTOLAN YRITSPUISTON ALUEEN KORTTELEITA 00, 0, 0 - KOSKEVAT RAKENNUSTAPAOHJEET NASTOLAN YRITSPUISTON ALUEEN KORTTELEITA 00, 0, 0 - KOSKEVAT RAKENNUSTAPAOHJEET YLEISTÄ
Teoriaa tähän jaksoon on talvikurssin luentomonisteessa luvussa 10. Siihen on linkki sivulta
Jkso 10. Sähkömgneettinen induktio Näytä ti plut tämän jkson tehtävät viimeistään tiistin 13.6.2017. Ekstr-tehtävät vstvt kolme tvllist tehtävää, kun lsketn lskuhrjoituspisteitä. Teori tähän jksoon on
θ 1 θ 2 γ γ = β ( n 2 α + n 2 β = l R α l s γ l s 22 LINSSIT JA LINSSIJÄRJESTELMÄT 22.1 Linssien kuvausyhtälö
22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
Kuvausta f sanotaan tällöin isomorfismiksi.
Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA
OSA 1: POLYNOMILASKENNAN KERTAUSTA, BINOMIN LASKUSÄÄNTÖJÄ JA YHTÄLÖNRATKAISUA Tekijät: Ari Heimonen, Hellevi Kupil, Ktj Leinonen, Tuomo Tll, Hnn Tuhknen, Pekk Vrniemi Alkupl Tiedekeskus Tietomn torninvrtij
Näytä tai jätä tarkistettavaksi tämän jakson tehtävät viimeistään tiistaina 18.6. ylimääräisessä tapaamisessa.
Jkso 12. Sähkömgneettinen induktio Tässä jksoss käsitellään sähkömgneettist induktiot, jok on tärkeimpiä sioit sähkömgnetismiss. Tätä tphtuu koko jn rkisess ympäristössämme, vikk emme sitä välttämättä
T Syksy 2002 Tietojenkäsittelyteorian perusteet Harjoitus 5 Demonstraatiotehtävien ratkaisut. ja kaikki a Σ ovat säännöllisiä lausekkeita.
T-79.8 Syksy 22 Tietojenkäsittelyteorin perusteet Hrjoitus 5 Demonstrtiotehtävien rtkisut Säännölliset lusekkeet määritellään induktiivisesti: j kikki Σ ovt säännöllisiä lusekkeit. Mikäli α j β ovt säännöllisiä
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.2014 Ratkaisut ja arvostelu
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
Vuoden 2014 tuloveroprosentti. Vuoden 2014 kiinteistöveroprosentit
Kunnnvltuusto KOKOUSKUTSU Kokousik Perjnti 15.11.2013 klo 14.00-15.00 Kokouspikk Käsiteltävät sit Asino Liite no Svukosken kunnnvirsto 1 60 Järjestäytymissit 2 61 1-2 Vuoden 2014 tuloveroprosentti 3 62
Suorakaidekanavat. lindab suorakaidekanavat
Suorkideknvt lind suorkideknvt lind suorkideknvt Sisällysluettelo Suorkideknvt Knv LKR... Liitosost Liitoslist LS... Liitoslist LS-... Kulmyhde LBR... Liitoslist LS... S-mutk LBXR... LBSR... Liitoslist
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS
11. MÄÄRÄTTY INTEGRAALI JA TILAVUUS Tilvuus on sen verrn rkielämässä viljelty käsite, että useimmiten sen syvemmin edes miettimättä ymmärretään, mitä juomlsin ti pikkuvuvn kylpymmeen tilvuudell trkoitetn.
766328A Termofysiikka Harjoitus no. 12, ratkaisut (syyslukukausi 2014)
7668A Termofysiikk Hrjoitus no 1, rtkisut (syyslukukusi 14) 1 Lämpötilss T K elektronien energit eivät ylitä Fermin energi (ɛ i ɛ F ), lämpötilprmetri β j kemillinen potentili vst Fermin energi (µ() ɛ
V Päästön havaittavuus ja valvonta VI Päästön todennäköisyys
I suunt II Mperä j pint Riskinro, 0410901 I tieliikenn e j tienpito vlttiet 3 j 10, tie 130 Vlttiet 3 j 10 kuuluvt korkeimpn kunnosspitoluo kkn Is (normlisti in pljn). Molemmt tiet ovt merkittäviä vrllisten
Syksyn 2015 Pitkän matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
Paraabelikin on sellainen pistejoukko, joka määritellään urakäsitteen avulla. Paraabelin jokainen piste toteuttaa erään etäisyysehdon.
5. Prbeli Prbelikin on sellinen pistejoukko, jok määritellään urkäsitteen vull. Prbelin jokinen piste toteutt erään etäissehdon. ********************************************** MÄÄRITELMÄ : Prbeli on tson
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
Ristitulo ja skalaarikolmitulo
Ristitulo j sklrikolmitulo Opetussuunnitelmn 00 mukinen kurssi Vektorit (MAA) sisältää vektoreiden lskutoimituksist keskeisenä ineksen yhteenlskun, vähennyslskun, vektorin kertomisen luvull j vektoreiden
MS-A010{2,3,4,5} (SCI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
MS-A1{2,3,4,5} (SC, ELEC*, ENG*) Differentili- j integrlilskent 1 Luento 8: ntegrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos November
YLÄPUOLINEN VESIKOURU JA LUMIESTE 1/5 VESIKOURU LYIJYLEVYÄ 1 mm YLÄPÄÄ TAIVUTETAAN KATTOTIILIRIVIN ALLE ALAPÄÄ TUETAAN LUMIESTEESEEN
Tolerance.: pproved 4 5 6-9,2 9 Tolerance.: 05..2009 Section top alu-tre 5 H-ikkuna TES pproved 4 5 1713-26 PRELIMINRY 1-0 +0,5 5,2 9 PYSTYLEIKKUS 1/5 YLÄPUOLINEN VESIKOURU J LUMIESTE 1/5 VESIKOURU LYIJYLEVYÄ
Numeerinen integrointi
Pitkärnt: Lj mtemtiikk IX9 Numeerinen integrointi IX9 Numeerinen integrointi Numeerisell integroinnill trkoitetn määrätyn integrlin, eli reliluvun I(f,,b) = f(x)dx lskemist numeerisin keinoin (likimäärin)
Matematiikan tukikurssi
Mtemtiikn tukikurssi Kurssikert 5 1 Jtkuvuus Trkstelln funktiot fx) josskin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jtkuv ti epäjtkuv. Jtkuvuuden ymmärtää prhiten trkstelemll epäjtkuv
1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [
![1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [](/thumbs/58/42571602.jpg "1. Derivaatan Testi. Jos funktio f on jatkuva avoimella välillä ]a, b[ ja x 0 ]a, b[ on kriit. tai singul. piste niin. { f (x) > 0, x ]a, x 0 [")
1. Derivtn Testi Jos funktio f on jtkuv voimell välillä ], b[ j x 0 ], b[ on kriit. ti singul. piste niin { f (x) < 0, x ], x 0 [ f x (x) > 0, x ]x 0, b[ 0 on lokli minimipiste (1) { f (x) > 0, x ], x
Vastaa tehtäviin 1-4 ja valitse toinen tehtävistä 5 ja 6. Vastaat siis enintään viiteen tehtävään.
S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
Sähkömagneettinen induktio
ähkömgneettinen inuktio Kun johinsilmukn läpi menevä mgneettikentän vuo muuttuu, silmukkn inusoituu jännite j silmukss lk kulke sähkövit. Mgneettikentässä liikkuvn johtimeen syntyy myös jännite. Näitä
x k 1 Riemannin summien käyttö integraalin approksimointiin ei ole erityisen tehokasta; jatkuvasti derivoituvalle funktiolle f virhe b
5 Integrlien lskemisest 51 Riemnnin summt [A2], [4, 61] Rjoitetun funktion f : [, b] R Riemnn-integroituvuudelle ytäpitäväksi on kurssill Anlyysi 2 osoitettu, että Riemnnin summill S P := f(ξ k ) ( ),
Sarjaratkaisun etsiminen Maplella
Srjrtkisun etsiminen Mplell Olkoon trksteltvn ensimmäisen kertluvun differentiliyhtälö: > diffyht:= diff(y(x, x=1y(x^; d diffyht := = dx y( x 1 y( x Tälle pyritään etsimään srjrtkisu origokeskisenä potenssisrjn.
Kohteen turvaluokitus on
LVI 03-10517 SIT 13-610091 KH X4-00513 INFRA 053-710109 ST 41.01 HANKETIETOKORTTI HT12 Hnketietokortiss esitetään rkennuskohteen lähtötiedot j tiljn edellyttämä ltutso suunnittelun työmäärän rviointi vrten.
Tehtävä 1. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi
Tehtävä. Jtk loogisesti oheisi jonoj khdell seurvksi tulevll termillä. Perustele vstuksesi lyhyesti. ), c, e, g, b),,, 7,, Rtkisut: ) i j k - oike perustelu j oiket kirjimet, nnetn p - oike perustelu,
Valmennuksen ja arvioinnin tukijärjestemä (VAT)
Vlmennuksen j rvioinnin tukijärjestemä (VAT) Työhön kuntoutuksen trkoitus on utt sikst kuntoutumn siten, että siirtyminen koulutukseen ti työelämään on mhdollist. VAT -järjestelmä on kehitetty kuntoutumisen
Viittomakielten fonologisista prosesseista
Viittomkielten fonologisist prosesseist Tommi Jntunen Helsingin yliopisto Yleisen kielitieteen litos tjjntun@ling.helsinki.fi Seurvss esitellään joitkin tyypillisimpiä fonologisi prosessej viitotuiss kielissä.
HIOMAKONEEN AUTOMATIIKKAVENTTIILIT. Asennus-, käyttöja huolto-ohjeet 5 GA 71 fi Painos 5/02
HIOMAKONEEN AUTOMATIIKKAVENTTIILIT Asennus-, käyttöj huolto-ohjeet 5 GA 71 fi Pinos 5/02 2 Sisällysluettelo 1 TOIMINTASELOSTUS................. 3 1.1 Yleistä.......................... 3 1.2 Pääkomponentit..................
Y56 Mikron jatkokurssi kl 2008: HARJOITUSTEHTÄVÄT 2 Mallivastaukset
Y6 Mikron jtkokurssi kl 008: HARJOITUSTEHTÄVÄT Mllivstukset Kuluttjn vlint (Muokttu Burketist 006, 07) Olkoon Mrkon udjettirjoite = 40 Mrkoll on hvin kättätvät referenssit j Mrkon rjusustituutiosuhde on
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
RTS 16:2. Tässä ohjeessa esitetään ajoneuvojen ja yleisimpien autotyyppien mittoja, massoja sekä liikenteeseen hyväksymistä koskevia rajoituksia.
RTS 16:2 RT XX-XXXXX KH XX-XXXXX Infr x-x AJONEUVOJEN MITTOJA OHJEET xxxkuu 2016 1 (8) korv RT 98-10914 Tässä ohjeess esitetään joneuvojen j yleisimpien utotyyppien mittoj, mssoj sekä liikenteeseen hyväksymistä
Aluevarausmerkinnät: T/kem Maakuntakaava
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Kustaankartanon vanhustenkeskus Vanhainkoti Päivätoiminta Palvelukeskus
Kustnkrtnon vnhustenkeskus Vnhinkoti Päivätoimint Plvelukeskus 1 Kustnkrtnoss tärkeinä pidettyjä sioit: sukkn hyvä olo hyvä elämä hyvä yhteistyö omisten knss gerontologisen hoidon osminen työntekijöiden
2.1 Vaillinaiset yhtälöt
.1 Villiniset yhtälöt Yhtälö, jok sievenee muotoon x + bx + c = 0 (*) on yleistä normlimuoto olev toisen steen yhtälö. Tämän rtkiseminen ei olekn enää yhtä meknist kuin normlimuotoisen ensisteen yhtälön
Korkotuettuja osaomistusasuntoja
Korkotuettuj osomistussuntoj Hvinnekuv suunnitelmst. Titeilijn näkemys Asunto Oy Espoon Stulmkri Stulmkrintie 1, 02780 ESOO Asunto Oy Espoon Stulmkri Kerv Kuklhti Iso Mntie 2 Espoo Vihdintie Keh III Hämeenlinnnväylä
Myynti:
Juplcon ovli kivonknsistot liikennelueiden kpelinkivoihin j pumppmoihin : o k k u li p v o v m m 0 6 5 x 1170 Lt Juplcon vlurutiset kivonknsistot pääkuvsto osoitteest Knsistortkisu kikille suurt vpt ukko
YRITYSTEN HENKILÖSTÖKOULUTUS
AIKUISKOULUTUSTILASTOT M Itell Posti Oy YRITYSTEN HENKILÖSTÖKOULUTUS VUONNA 2010 'CONTINUING VOCATIONAL TRAINING SURVEY - CVTS4' TIEDUSTELU PERUSTUU TILASTOLAKIIN (LAKI 280/04) KYSELYLOMAKE SÄHKÖINEN LOMAKE:
Esimerkki 8.1 Määritellään operaattori A = x + d/dx. Laske Af, kun f = asin(bx). Tässä a ja b ovat vakioita.
8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
Matematiikan tukikurssi
Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Matematiikan johdantokurssi, syksy 2017 Harjoitus 6, ratkaisuista. 1. Onko jokin demojen 5 tehtävän 3 relaatioista
Mtemtiikn johntokurssi, syksy 07 Hrjoitus 6, rtkisuist. Onko jokin emojen 5 tehtävän reltioist ) R := {(, ), (, ), (, ), (, ), (, ), (, ), (, ), (, )}, ) S := {(, ), (, ), (, ), (, ), (, ), (, ), (, ),
VEKTOREILLA LASKEMINEN
..07 VEKTOREILL LSKEMINEN YHTEENLSKU VEKTORIT, M4 Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on vektorin
Preliminäärikoe Pitkä Matematiikka 5.2.2013
Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
Diskreetin matematiikan perusteet Laskuharjoitus 6 / vko 13
MS-A040 Diskreetin mtemtiikn perusteet, IV/07 Kngslmpi / Jkosson Diskreetin mtemtiikn perusteet Lskuhrjoitus / vko Tuntitehtävät 4-4 lsketn lkuviikon hrjoituksiss j tuntitehtävät 45-4 loppuviikon hrjoituksiss.
b) (max 3p) Värähtelijän jaksonajan ja taajuuden välinen yhteys on T = 1/ f, eli missä k on jousen jousivakio. Neliöimällä yllä oleva yhtälö saadaan
A1 Lbortoriokokeess keveen kierrejouseen ripustettiin eri mssisi punnuksi. Punnust vedettiin lspäin j sntneen hrmonisen värähteln jksonik mitttiin. Värähtelijän tjus f = 2π 1 k mp. Oheisess tulukoss on
sin θ θ θ r 2 sin 2 θ φ 2 = 0.
Mtemtiikn j tilstotieteen litos Osittisdifferentiliyhtälöt Kevät 21 Hrjoitus 9 Rtkisuj Jussi Mrtin 1. Osoit, että Lplce-yhtälö pllokoordinteiss on 2 u 1 r 2 2 u r r 1 r 2 sin θ u 1 2 u sin θ θ θ r 2 sin
ICS-C2000 Tietojenkäsittelyteoria Kevät 2015
ICS-C2 Tietojenkäsittelyteori Kevät 25 Kierros 3, 26. 3. tmmikuut Demonstrtiotehtävien rtkisut D: Ldi epädeterministinen äärellinen utomtti, jok test onko nnetun inäärijonon kolmnneksi viimeinen merkki,
Mat Dynaaminen optimointi, mallivastaukset, kierros 8
Mt-.148 Dynminen optimointi, mllivstukset, kierros 8 1. Idelisess tsvirtmoottoriss vääntömomentti on suorn verrnnollinen virtn. Moottori pyörittää ikiliikkuj (ei kitk- ti sähkömgneettisi vstusvoimi). Moottorin
763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 1 Kevät 2014
763333A KIINTEÄN AINEEN FYSIIKKA Rtkisut 1 Kevät 014 1. Tehtävä: Lske, kuink mont hilpistettä on yksikkökopiss ) yksinkertisess kuutiollisess, b) tkk:ss j c) pkk:ss. (Ot huomioon, että esimerkiksi yksikkökopin
Numeeriset menetelmät TIEA381. Luento 9. Kirsi Valjus. Jyväskylän yliopisto. Luento 9 () Numeeriset menetelmät / 29
Numeeriset menetelmät TIEA381 Luento 9 Kirsi Vljus Jyväskylän yliopisto Luento 9 () Numeeriset menetelmät 17.4.2013 1 / 29 Luennon 9 sisältö Numeerisest integroinnist Newtonin j Cotesin kvt Luento 9 ()
Poirot. POIROT 1/7. Koko alueen kerrosala edot:
Poirot. Suunnitelmn lähtökohtn on uistomiseksi kehite ävä länteen vutuv jokimisem, johon kor eleiden iht sekä lähes kikki sunnot vutuvt. Pistetlotyologi on kehite y siten, e ä muodou selkeäs hhmote vi
6 Kertausosa. 6 Kertausosa
Kertusos Kertusos. ) b). ) b). ) ( ( ) : ) ( : ) b) { : [ ( ) ]} { :[ - ]} { : } -{ - } -{} c) ( ) : - ( ) ( ) ( ) ( 9) 9 9 Kertusos. ) ( ) b) ( ). ) ) ) b) / / c) : 7 7. ) ) ) b) Kertusos c) : 7 ( 9)
Kasvihuonekaasupäästöjen kehitys pääkaupunkiseudulla
YTV MUISTIO 1 Asi 7 / Liite 1 PÄÄKAUPUNKISEUDUN ILMASTOSTRATEGIA 2030 YTV:n hllitus on kokouksessn 14.12.2006 hyväksynyt Pääkupunkiseudun ilmstostrtegiluonnoksen 2030 lusuntojen j knnnottojen pyytämistä
-kortiston näyte RT 09-10692 ESTEETÖN LIIKKUMIS- JA TOIMIMISYMPÄRISTÖ SISÄLLYSLUETTELO YLEISTÄ
RT 09-09 ohjetiedosto mliskuu 999 () ESTEETÖN LIIKKUMIS- JA TOIMIMISYMPÄRISTÖ liikkumisesteiset, toimimisesteiset, esteettömyys hndikppde, funktionshindrde, tillgänglighet disled persons, ccessiility Tämä
TYÖ 30. JÄÄN TIHEYDEN MÄÄRITYS. Tehtävänä on määrittää jään tiheys.
TYÖ 30 JÄÄN TIHEYDEN MÄÄRITYS Tehtävä älineet Tusttietoj Tehtävänä on äärittää jään tiheys Byretti (51010) ti esi 100 l ittlsi (50016) j siihen sopivi jääploj, lkoholi (sopii jäähdytinneste lsol), nlyysivk
7 Funktiosarjoista. 7.1 Funktiosarjojen suppeneminen
7 Funktiosrjoist 7. Funktiosrjojen suppeneminen Seurvksi trkstelln srjoj, joiden termit ovt (lukujen sijst) jollkin välillä I määriteltyjä funktioit. Täsmällisemmin funktiosrjll (ti lyhyemmin srjll) trkoitetn
T Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (Predikaattilogiikka )
T-79.3001 Kevät 2009 Logiikk tietotekniikss: perusteet Lskuhrjoitus 7 (Predikttilogiikk 9.1 10.2) 19.3. 23.3. 2009 Rtkisuj demotehtäviin Tehtävä 9.1 Rtkisuss on käytetty usen otteeseen rjoitettuj universli-
2 7: :281 LOUHINTA SIPOON KUNNAN OMISTAMALLA KIINTEISTÖLLÄ 2:57 ERILLISELLÄ LUVALLA KIRJOVERKKOPERHOSELLE PERUSTETTU KOMPENSAATIOALUE
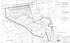2 ERKINNÄT EV-1 KULJETUKSET OTTISLUEEN / TOIINT-LUEEN RJ (osa-alue C 6,2 ha + osa-alue B 2,9 ha = 66,1 ha) Kaikki ottotoimintaan liittyvät toiminnot sijoittuvat rajauksen sisälle (mm. pintamaiden ja kiviaineksen
VESIPATTERIN ASENNUS TBLA Thermo Guard-jäätymissuojalla GOLD koko 11-32, versio B
VESIPATTERIN ASENNUS TBLA -jäätymissuojll GOLD koko 11-32, versio B ASENNUS 1. Knvliitäntä on tehtävä seurvsti: ) TBLA 000-031 j 000-040 Vesiptteri voidn sent suorn kierresumttuun knvn. Ptteri on vrustettu
MITEN MÄÄRITÄN ASYMPTOOTIT?
MITEN MÄÄRITÄN ASYMPTOOTIT? Asmptootti Asmptootti on suor ti muu kärä, jot funktion kuvj f() rjtt lähest, kun muuttujn rvot lähestvät tiettä luku ti ääretöntä. Rjoitutn luksi niihin tpuksiin, joiss smptootti
POHJOIS-SAVON SAIRAANHOITOPIIRIN KUNTAYHTYMÄ
1 2012 POHJOIS-SAVON SAIRAANHOITOPIIRIN KUNTAYHTYMÄ CyberKnife KYSiin, s. 4 KYSin rkenteet kevenevät, s. 14 Nope kotiutus vähentää kustnnuksi, s. 24 Henkreikä 1 / 2012 Pääkirjoitus... 3 Trkkuussädehoitolite
VAIHTOEHTO 4, PÄÄVESIJOHTO JA PÄÄJÄTEVESIVIEMÄRI YHTEISKÄYTTÖTUNNELISSA JÄTEVESIVIEMÄRISSÄ YKSI VÄLIPUMPPAUS
1 LIITE 2 VAIHTOEHTO 4, PÄÄVESIJOHTO JA PÄÄJÄTEVESIVIEMÄRI YHTEISKÄYTTÖTUNNELISSA JÄTEVESIVIEMÄRISSÄ YKSI VÄLIPUMPPAUS Mitoitus Vaihtoehdossa on selvitetty mahdollisuutta johtaa jätevedet yhteiskäyttötunneliin
Kirjallinen teoriakoe
11 Kirjllinen teorikoe Päivämäärä: Osllistujn nimi: Kirjllinen teorikoe Arviointi koostuu khdest osst: "yleiset kysymykset "j lskutehtävät" Kokeen hyväksytty rj on 51% molemmist osioist erikseen. St 1
Kognitiivinen mallintaminen I, kevät Harjoitus 1. Joukko-oppia. MMIL, luvut 1-3 Ratkaisuehdotuksia, MP
Kognitiivinen mllintminen I, kevät 007 Hrjoitus. Joukko-oppi. MMIL, luvut -3 Rtkisuehdotuksi, MP. Määritellään joukot: A = {,,, 3, 4, 5} E = {, {}, } B = {, 4} F = C = {, } G = {{, }, {,, 4}} D = {, }
Tasogeometriassa käsiteltiin kuvioita vain yhdessä tasossa. Avaruusgeometriassa tasoon tulee kolmas ulottuvuus, jolloin saadaan kappaleen tilavuus.
KOLMIULOTTEISI KPPLEIT Tsogeometriss käsiteltiin kuvioit vin ydessä tsoss. vruusgeometriss tsoon tulee kolms ulottuvuus, jolloin sdn kppleen tilvuus. SUORKULMINEN SÄRMIÖ Suorkulmisess särmiössä kikki kulmt
Säännöt 2 7. Regler 8 13. Regler. Regler. Rules 26 31
Säännöt 8 9 Rules B tyhjä suositusruutu krtt rhmittri vesiruutu viinitrhruutu utio viinitrhruutu Sisällys C pelilut Viiniyhdistyksen suositus -ltt hintmerkkiä Ltikoit: punviiniltikko vlkoviiniltikko smppnjltikko
3 Mallipohjainen testaus ja samoilutestaus
Tietojenkäsittelytiede 24 Joulukuu 2005 sivut 8 21 Toimittj: Jorm Trhio c kirjoittj(t) Historiljennus mllipohjisess testuksess Timo Kellomäki Tmpereen teknillinen yliopisto Ohjelmistotekniikn litos 1 Johdnto
5.4 Ellipsi ja hyperbeli (ei kuulu kurssivaatimuksiin, lisätietoa)
5.4 Ellipsi j hypereli (ei kuulu kurssivtimuksiin, lisätieto) Aurinkokuntmme plneett kiertävät Aurinko ellipsin (=litistyneen ympyrän) muotoist rt, jonk toisess polttopisteessä Aurinko on. Smoin Mt kiertävät
****************************************************************** MÄÄRITELMÄ 4:
. Murtopotessi MÄÄRITELMÄ : O Olkoo prillie, positiivie kokoisluku. Ei egtiivise luvu :s juuri trkoitt sellist ei-egtiivist luku b, jok :s potessi o. Merkitää b. Kute eliöjuureki tpuksess, luku b täyttää
SAVUKOSKEN KUNTA Sosiaalilautakunta 21.03.2012
Sosililutkunt 21.03.2012 11 Sosililutkunt Aik: Keskiviikko 21.03.2012 klo 16.00 17.35 Pikk: Vnhinkoti Asit 9 Sosililutkunnlle tiedoksi 10 Plvelussuhteen päättyminen 11 Rvitsemistyöntekijän tehtävien hoito
ICS-C2000 Tietojenkäsittelyteoria Kevät 2016
ICS-C2000 Tietojenkäsittelyteori Kevät 2016 Kierros 5, 8. 12. helmikuut Demonstrtiotehtävien rtkisut D1: Hhmolusekkeet ovt esimerkiksi UN*X-järjestelmien tekstityökluiss käytetty säännöllisten lusekkeiden
VEKTOREILLA LASKEMINEN
3..07 VEKTOREILLA LASKEMINEN YHTEENLASKU VEKTORIT, MAA Vektoreiden j summ on vektori +. Tämän summvektorin + lkupiste on vektorin lkupiste j loppupiste vektorin loppupiste, kun vektorin lkupisteenä on
4 Taso- ja avaruuskäyrät
P2-luentoj kevät 2008, Pekk Alestlo 4 Tso- j vruuskäyrät Tässä luvuss tutustutn tso- j vruuskäyriin, niiden krenpituuteen j krevuuteen. Konkreettisin sovelluksin trkstelln nnettu rt pitkin liikkuvn hiukksen
Pythagoraan lause. Pythagoras Samoslainen. Pythagoraan lause
Pythgorn luse Pythgors Smoslinen Pythgors on legendrinen kreikklinen mtemtiikko j filosofi. Tiedot hänen elämästään ovt epävrmoj j ristiriitisi. Tärkein Pythgorst j pythgorlisi koskev lähde on Lmlihosin
KANDIDAATINTYÖ: TEOLLISUUSKIINTEISTÖN ILMANVAIHTOKONEEN LTO- LAITTEISTON HYÖTYSUHTEEN PARANTAMINEN
LAPPEENRANNAN TEKNILLINEN YLIOPISTO Teknillinen tiedekunt Energitekniikn koulutusohjelm KANDIDAATINTYÖ: TEOLLISUUSKIINTEISTÖN ILMANVAIHTOKONEEN LTO- LAITTEISTON HYÖTYSUHTEEN PARANTAMINEN Lppeenrnnss 1.2.2010
Asennusopas. Daikin Altherma - Matalan lämpötilan Monoblocin varalämmitin EKMBUHCA3V3 EKMBUHCA9W1. Asennusopas. Suomi
Dikin Altherm - Mtln lämpötiln Monolocin vrlämmitin EKMBUHCAV EKMBUHCA9W Suomi Sisällysluettelo Sisällysluettelo Tietoj sikirjst. Tieto tästä sikirjst... Tietoj pkkuksest. Vrlämmitin..... Vrusteiden poistminen
7.lk matematiikka. Geometria 1
7.lk mtemtiikk 1 Htnpään koulu 7B j 7C Kevät 2017 2 Sisällys 1. Koordintisto... 4 2. Kulmien nimeäminen j luokittelu... 8 3. Kulmien mittminen j piirtäminen... 10 4. Ristikulmt j vieruskulmt... 14 5. Suort,
1 250 opiskelijapaikan lisääminen ammatillisen peruskoulutuksen järjestämislupiin 1.1.2010 lukien
KTPO/Ammtillisen koulutuksen yksikkö PM 4.12.29 1 25 opiskelijpikn lisääminen mmtillisen peruskoulutuksen järjestämislupiin 1.1.21 lukien Tust Aikisemmt opiskelijmäärälisäykset Hllitusohjelmn j vltiontlouden
JÄMSÄN KAUPUNKI. MAANKÄYTTÖ- JA RAKENNUSLAIN 63 :n MUKAINEN OSALLISTUMIS- JA ARVIOINTISUUNNITELMA
JÄMSÄN KAUPUNKI MAANKÄYTTÖ- JA RAKENNUSLAIN 63 :n MUKAINEN OSALLISTUMIS- JA ASEMAKAAVAN MUUTOS KOSKEE Jämsän kupungiss, 1. kupunginosss os korttelist 15 sekä puisto-, ktu-, stm- j vesilueit. uj nk pä Se
Tässä on vanhoja Sähkömagnetismin kesäkurssin tenttejä. Tentaattorina on ollut näissä tenteissä sama henkilö kuin tänä vuonna eli Hanna Pulkkinen.
Tässä on vnhoj Sähkömgnetismin kesäkurssin tenttejä. Tentttorin on ollut näissä tenteissä sm henkilö kuin tänä vuonn eli Hnn Pulkkinen. 766319A Sähkömgnetismi, kesäkurssi 2012 Päätekoe 11.6.2012 1. Esitä
A-Osio. Valitse seuraavista kolmesta tehtävästä kaksi, joihin vastaat. A-osiossa ei saa käyttää laskinta.
MAA Loppukoe 5.. Jussi Tyni Tee pisteytysruudukko konseptin yläreunn! Vstuksiin väliviheet, jotk perustelevt vstuksesi! Lue ohjeet huolellisesti! A-Osio. Vlitse seurvist kolmest tehtävästä kksi, joihin
Kajaanin kaupunki ASEMAKAAVAN MUUTOS KAJAANI KAJAANI KAUPUNGINOSA 14 KUURNA KORTTELIN 22 TONTTI 2 VIREILLETULO SELOSTUS 15.5.
ASEMAKAAVAN MUUTOS KAJAANI KAUPUNGINOSA KUURNA KORTTELIN TONTTI Muodostuu: Kjnin kupunki Ympäristötekninen toimil PL 870 Kjni VIREILLETULO 6..07 SELOSTUS..07 YMTK KAJAANI KAUPUNGINOSA KUURNA KORTTELIN
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 7: Integraali ja analyysin peruslause
MS-A010{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 7: Integrli j nlyysin perusluse Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 3.10.2016 Pekk Alestlo, Jrmo Mlinen
( ) Pyramidi 4 Analyyttinen geometria tehtävien ratkaisut sivu 321 Päivitetty 19.2.2006. Saadaan yhtälö. 801 Paraabeli on niiden pisteiden ( x,
Pyrmidi Anlyyttinen geometri tehtävien rtkisut sivu Päivitetty 9..6 8 Prbeli on niiden pisteiden (, y) joukko, jotk ovt yhtä kukn johtosuorst j polttopisteestä. Pisteen (, y ) etäisyys suorst y = on d
Runkovesijohtoputket
Runkovesijohtoputket PUTKET JA PUTKEN OSAT SSAB:n vlmistmi pinnoitettuj putki j putken osi käytetään lähinnä runkovesijohtolinjoihin, joiden hlkisij on DN 400-1200. Ost vlmistetn teräksisistä pineputkist