Aritmeettisten funktioiden keskiarvot Averages of Arithmetical Functions
|
|
|
- Heli Tuominen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Aritmeettiste fuktioide keskiarvot Averages of Arithmetical Fuctios Marko Hiltue Pro gradu -tutkielma Helmikuu 207 MATEMAATTISTEN TIETEIDEN TUTKINTO-OHJELMA OULUN YLIOPISTO
2 Sisältö Johdato 2 2 Peruskäsitteitä 3 3 Aritmeettisia fuktioita 4 4 Multiplikatiivisuus ja yleistetyt kovoluutiot 8 4. Multiplikatiiviset fuktiot Yleistetyt kovoluutiot Euleri summakaava 6 Asymptoottikaavoja 3 7 Aritmeettiste fuktioide keskiarvoja 6 7. Fuktio d( keskiarvo Fuktio σ α ( keskiarvo Fuktio ϕ( keskiarvo Origosta äkyvät hilapisteet 26 9 Fuktiot µ( ja Λ( Fuktioide µ( ja Λ( keskiarvot Dirichleti tulo osittaissummat Sovelluksia fuktiolle µ( ja Λ( Toie tulos Dirichleti tulo osittaissummille
3 Johdato Tutkielmassa perehdytää erilaiste aritmeettiste fuktioide omiaisuuksii, ku muuttuja arvo o suuri. Suurilla muuttujie arvoilla fuktioide arvot voivat vaihdella suurestiki, kute esimerkiksi tekijäfuktiolla d(, joka arvot vaihtelevat luvu kaksi ja mielivaltaise suurte lukuje välillä. Vaihtelu määrä kasvaa merkittävästi, mitä suuremmaksi muuttuja arvo kasvaa. Vaihtelu takia aritmeettiste fuktioide käyttäytymistä o tämä takia hakala käsitellä suurilla muuttuja arvoilla. Joskus tutkimista auttaa aritmeettie keskiarvo f( = f(k. Keskiarvot tasoittavat vaihtelua, jote o järkevää olettaa keskiarvo käyttäytyvä sääöllisemmi suurillaki muuttuja arvoilla. Tämä pätee varsiki aikaisemmi esitetylle tekijäfuktiolle d(. Työssä osoitetaa, että tekijäfuktio keskiarvo d( o luokkaa log x suurilla arvoilla. Tarkemmi ilmaistua lim k= d( log =. Tällöi fuktio d( keskiarvo o log. Dirichleti johtama tulos tekijäfuktio osittaissummille vuodelta 849 o merkittävä, sillä se o tarkempi tulos kui yllä oleva raja-arvo. Keskiarvoje tutkimisee tarvitaa mielivaltaise fuktio osasummia k= f(k. Usei summaukse yläraja korvataa reaaliluvulla x, jolloi summa kirjoitetaa muodossa f(k, k x missä k käy läpi kokoaisluvut ykkösestä lukuu x asti. Työssä perehdytää Euleri ϕ-fuktio, Möbius fuktio sekä Magoldt' fuktio keskiarvoihi. Työssä johdetaa myös Euleri summakaava, joka o hyödyllie keskiarvoja johdettaessa. Tutkielma tärkeipää lähteeä o käytetty Tom M. Apostoli kirjaa Itroductio to Aalytic Number Theory []. 2
4 2 Peruskäsitteitä Lause 2.. Kokoaisluku voidaa esittää alkulukuje tuloa. Tällöi a = p a p a 2 2 p a ja b = p b p b 2 2 p b ja äide lukuje suuri yhteie tekijä eli syt(a, b saadaa seuraavalla tavalla syt(a, b = p mi(a,b p mi(a 2,b 2 2 p mi(a,b. Todistus. Katso [2]. Merkitää tästä eteepäi syt(a, b = (a, b. Määritelmä 2.2. Luvut x ja y ovat suhteellisia alkulukuja, jos (x, y =. Määritelmä 2.3. Lattiafuktio (eli porrasfuktio saadaa asettamalla aia, ku x R. Merkitää vielä [ ] : R Z [x] = max{ Z x} {x} = x [x], missä {x} tarkoittaa luvu desimaaliosaa. (Vertaa [3]. Määritelmä 2.4. Euleri vakio C määritellää yhtälöllä C = lim Määritelmä 2.5. Jos g(x > 0 kaikille x a, ii ( log(. ( f(x = O(g(x (2 tarkoittaa sitä, että osamäärä f(x/g(x o rajoitettu, ku x a. Täte o olemassa sellaie vakio M > 0, että f(x Mg(x kaikille x a. Tällöi saotaa, että fuktio f(x o iso O fuktiosta g(x. 3
5 Määritelmä 2.6. Jos f(x lim x g(x =, ii fuktio f(x o asymptoottie fuktio g(x kassa, ku x lähestyy ääretotä. Käytetää asymptoottisuudelle merkitää f(x g(x, ku x. Määritelmä 2.7. Määritellää Riemai ζ-fuktio ζ(s = =, ku s >, s ja ( ζ(s = lim x x s, ku 0 < s <. s s 3 Aritmeettisia fuktioita Määritelmä 3.. Möbius-fuktio µ( määritellää seuraavalla tavalla: µ( =. Jos >, N, ii = p a p a k k. Tällöi µ( = ( k, jos a = a 2 =... = a k =, µ( = 0 muulloi. (3 Huomaa, että µ( = 0 jos ja vai jos luvulla o joki eliötekijä. Esimerkki 3.2. Lasketaa µ(9688. Jaetaa esi luku alkulukutekijöihi. Saadaa 9688 = = Luvu alkulukutekijöissä o aiaki yksi korkeampi potessi tekijöillä kui, jolloi määritelmä mukaa µ(9688 = 0. Lause 3.3. Summa µ(d = d [ ] {, ku =, = 0, ku >. 4
6 Todistus. Jaetaa tarkastelu kahtee osaa. Olkoo esi =, jolloi saadaa d µ(d = [/] =. Olkoo sitte >. Tällöi luku voidaa esittää alkulukutekijöidesä tuloa = p a p k k, missä k o kokoaisluku. Nollasta eroavat termit saadaa, ku d = ja sellaisista luvu tekijöistä, jotka ovat erilliste alkulukuje tuloja. Täte µ( =µ(p + µ(p µ(p k + µ(p p µ(p k p k d + µ(p p 2 p µ(p p 2 p k ( ( ( k k k = + ( + ( ( k. 2 k Biomilausee avulla lauseke saadaa muotoo ( k, mikä o olla. Määritelmä 3.4. Euleri fuktio ϕ( arvo o iide lukuje k summa, jotka ovat luvu kassa suhteellisia alkulukuja. Täte ϕ( =. (4 missä merkitsee, että summa käy läpi kaikki e luvut k, jotka ovat luvu kassa suhteellisia alkulukuja. k= Lemma 3.5. Fuktio ϕ arvot voidaa laskea kaavasta ( ϕ(p k = p k p k = p k, p ku p o alkuluku ja k kokoaisluku. Todistus. Koska p o alkuluku, ii luvut m, joille pätee (p k, m, ovat alkuluvu p moikertoja. Nämä luvut ovat p, 2p, 3p,..., p k p = p k. Näitä o yhteesä p k kappaletta. Luvu p k kassa suhteellisia alkulukuja o tällöi p k p k kappaletta, mikä todistaa väittee. Lemma 3.6. Fuktiolle ϕ pätee ϕ(m = ϕ(mϕ(, jos (m, =. Todistus. Katso [2]. Esimerkki 3.7. Lasketaa ϕ(36. Aritmetiika peruslausee ojalla 36 = , jolloi saadaa ϕ(36 = ϕ(2 2 ϕ(3 2 = 4( /2 9( /3 = 36 /2 /3 = 2. Listaamalla luvut ovat, 5, 7,, 3, 7, 9, 23, 25, 29, 3 ja 35. 5
7 Lause 3.8 (Fuktioide µ ja ϕ välie yhteys. Jos, ii ϕ( = d µ(d d. Todistus. Summa (4 voi kirjoittaa myös muodossa ϕ( = k= [ ], (, k missä luku k käy läpi luvut, 2,..., ja summaa yhtee vai e luvut, jotka ovat luvu kassa suhteellisia alkulukuja. Lausee 3.3 ojalla summa saadaa muotoo ϕ( = k= d (,k µ(d = µ(d. Koska d k, ii k = qd, missä q /d, sillä luku d jakaa myös luvu. Koska k = qd, ii tällöi k jos ja vai jos q /d. Täte viimeie summa voidaa kirjoittaa muotoo k= d d k ϕ( = d /d q= µ(d = d Tämä todistaa väittee oikeaksi. /d µ(d = q= d µ(d d. Määritelmä 3.9. Määritellää aritmeettie fuktio I seuraavalla tavalla: [ ] {, jos =, I( = = 0, jos >. Tätä kutsutaa idetiteettifuktioksi. Määritelmä 3.0. Olkoo α reaaliluku tai kompleksiluku ja olkoo kokoaisluku >. Tällöi tekijäfuktio σ α ( määritellää σ α ( = d d α. (5 Summassa luvu tekijät korotetaa potessii α. 6
8 Ku α = 0, ii σ 0 ( o luvu tekijöide määrä. Tälle käytetää myös merkitää d(. Ku α =, ii σ ( o luvu tekijöide summa. Tälle käytetää myös merkitää σ(. Olkoo p alkuluku ja a. Tällöi lausekkee σ α (p a tekijät ovat, p, p 2,..., p a, jote p α(a+ σ α (p a = α + p α + p 2α p aα, jos α 0, = p α a +, jos α = 0. Määritelmä 3.. Määritellää Magoldt' fuktio Λ( seuraavasti: Jokaiselle kokoaisluvulle { log p, jos = p m jolleki alkuluvulle p ja luvulle m, Λ( = (6 0, muulloi. Esimerkki 3.2. Tarkastellaa lukuja 3, 32 ja 33. Näistä luku 3 o alkuluku. Tällöi Λ(3 = log 3. Luku 32 = 2 5, jolloi määritelmä mukaa Λ(32 = log 2. Viimeiseä luku 33 = 3. Kahde alkuluvu tulo ataa määritelmä mukaa tulokse olla, jote Λ(33 = 0. Lause 3.3. Jos, ii tällöi log = d Λ(d. (7 Todistus. Lause o tosi, jos =, sillä molemmat puolet saavat arvo 0. Tarkastellaa tilaetta, jossa > : = r k= Ottamalla logaritmi puolittai saadaa p a k k = pa p a 2 2 p ar r. log = a log p + a 2 log p a r log p r = r a k log p k. Tarkastellaa seuraavaksi yhtälö (7 oikeaa puolta. Nollasta eriävät termit tulevat jakajalta d, joka o muotoa p m k luvu m arvoilla, 2,..., a k ja k =, 2,... r. Täte r a k Λ(d = Λ(p m k. d k= m= 7 k=
9 Määritelmä 3. perusteella saadaa Λ(d = d r a k k= m= Λ(p m k = r a k k= m= log p k = r a k log p k = log, k= mikä todistaa yhtälö (7. 4 Multiplikatiivisuus ja yleistetyt kovoluutiot Määritelmä 4.. Jos f ja g ovat aritmeettisia fuktioita, ii äide fuktioide Dirichleti tulo o aritmeettie fuktio h, joka määrittää tulo h( = d f(dg (. (8 d Merkitää f g = h ja (f g( = h(. Aritmeettiste fuktioide joukko varustettua Dirichleti tulolla muodostaa Abeli ryhmä. Lause 4.2. Olkoo f, g ja k aritmeettisia fuktioita. Tällöi iille o voimassa f g = g f (kommutatiivisuus, (f g k = f (g k (assosiatiivisuus. sekä (f I( = (I f( = f(. Todistus. Huomataa, että f g voidaa kirjoittaa muodossa (f g( = f(ag(b = g(bf(a = (g f(, a b= a b= mistä seuraa kommutatiivisuus. Assossiatiivisuude toteamiseksi merkitää g k = A, jolloi saadaa f (g k = f A. Tällöi (f A( = f(aa(d = g(bk(c a d= = a b c= f(ag(bk(c. a d= f(a b c=d Toisaalta, jos B = f g, ii tällöi saadaa B k, joka voidaa kirjoittaa yllä olevaa summalausekemuotoo. Täte f A = B k ovat yhtä pitäviä. 8
10 4. Multiplikatiiviset fuktiot Dirichleti multiplikaatio muodosti Abeli ryhmä, kute aikaisemmi totesimme. Tälle ryhmälle o olemassa tärkeä aliryhmä multiplikatiiviset fuktiot. Määritelmä 4.3. Aritmeettista fuktiota f kutsutaa multiplikatiiviseksi, jos f ei ole idettisesti olla ja jos f(m = f(mf( aia, ku (m, =. Multiplikatiivie fuktio o täysi multiplikatiivie, jos f(m = f(mf( millä tahasa muuttujie m ja arvoilla. Lause 4.4. Jos f o multiplikatiivie, ii tällöi f( =. Todistus. Määritelmä mukaa f( = f(f(, sillä (, = kaikilla muuttuja arvoilla. Määritelmä mukaa myös f ei ole idettisesti olla, jote tästä seuraa f( 0 millää muuttuja arvolla. Näi f( =. Lause 4.5. Fuktio f o multiplikatiivie jos ja vai jos f(p a p ar r = f(p a f(p ar r kaikilla alkuluvuilla p ja kaikilla kokoaisluvuilla a i. Todistus. " "Olkoo f multiplikatiivie. Tällöi sille pätee f(m = f(mf( aia ku (m, =. Nyt f koostuu erillisistä alkulukuje potesseista. Tällöi (p a i =. Tästä saadaa määritelmä ojalla i, pa j j f(p a p ar r = f(p a p a r r f(p ar r =... = f(p a f(p ar r. " "Olkoo f(p a p ar r = f(p a f(p ar r. Jos ja 2 ovat positiivisia kokoaislukuja ja (, 2 =, ii äide lukuje alkulukuhajotelmat muodostuvat erillisistä alkulukuje joukoista. Tällöi oletukse mukaie esitys o yhtä määritelmä kassa, mikä todistaa lausee. Aikaisemmi esitelty tekijäfuktio o multiplikatiivie. 9
11 4.2 Yleistetyt kovoluutiot Olkoo F reaali- tai kompleksiarvoie fuktio, joka o määritelty positiivisella x-akselilla site, että F (x = 0 kaikilla arvoilla 0 < x <. Olkoo α mielivaltaie aritmeettie fuktio. Seuraava tyyppiset summat ( x α(f ovat yleisiä lukuteoriassa. Summa määrittelee uude fuktio G, joka määrittelyjoukko o myös positiivie x-akseli. G(x = 0, ku 0 < x <. Merkitää G = α F, jolloi saadaa (α F (x = ( x α(f. Jos F (x = 0 aia, ku x ei ole kokoaisluku, saadaa fuktiosta F aritmeettie fuktio ja huomataa, että (α F (x = (α F (x kaikille kokoaisluvuille m. Tällöi merkitää " " voidaa pitää yleistykseä Dirichleti kovoluutio merkiälle " ". Operaatio ei kuitekaa aia ole kommutatiivie tai assosiatiivie. Kuiteki seuraava lause tarjoaa vaihtoehdo assosiatiivisuudelle. Lause 4.6. Olkoo α ja β aritmeettisia fuktioita. Tällöi Todistus. Kaikille x > 0 pätee ( α (β F (x = α( α (β F = (α β F. (9 m x/ ( x β(mf = ( x α(β(mf. m m m Merkitää yt k = m. Tällöi summa käy läpi luvut kaikki luvut k, jotka ovat pieempia kui x. Fuktio β muuttujaksi tulee (k/ ja tuloo saadaa toie summa, missä luku jakaa luvu k, sillä edellisessä vaiheessa luvut m ja käyvät läpi kaikki tulot, jotka olivat pieempiä kui x. Tällöi saadaa m α(β(mf ( x m = ( ( k α(β F k x k ( x k. Käytetää Määritelmää 4., jolloi sisempi summa voidaa korvata fuktioide α ja β Dirichleti tulolla. Tällöi saadaa ( x (α β(kf = ( (α β F (x. k k x 0
12 Idetiteettikuvaus I( = [/] o vasemmapuoleie idetiteetti operaatiolle " ", sillä (I F (x = [ ] ( x F = F (x. 5 Euleri summakaava Joskus o mahdollista saada osittaissumma asymptoottie arvo vertaamalla sitä itegraalii. Euleri summakaavalla saadaa selville tarkka virhe tähä approksimoitii. Lause 5.. Jos fuktiolla f o jatkuva derivaatta f välillä [y, x], missä 0 < y < x, ii tällöi f( = f(tdt + (t [t]f (tdt y y (0 y< + f(x([x] x f(y([y] y. Todistus. Olkoo m = [y] ja k = [x]. Kokoaisluvuille ja välillä [y, x] saadaa [t]f (tdt = ( f (tdt = ( (f( f( = (f( ( f( f(. Koko aluee yli voidaa muodostaa itegraalie summa m+2 m+ [t]f (tdt + m+3 m+2 [t]f (tdt k k [t]f (tdt. Itegraaleista muodostuu teleskooppisumma. Täte voidaa muodostaa yksi itegraali, missä alarajaksi tulee m + ja ylärajaksi k: k m+ [t]f (tdt = kf(k (m + f(m + = kf(k mf(m + y< k =m+2 f(. f( Koska luvut x ja y kuuluvat reaalilukuihi ja [x] = k sekä [y] = m, ii itegraalista puuttuvat vielä välit [y, m + ] sekä [k, x]. Itegroitaessa esimmäie väli saadaa m+ y [t]f (tdt = m+ y mf (tdt = m(f(m+ f(y = mf(m+ mf(y.
13 Itegroitaessa viimeie väli [t]f (tdt = k k kf (tdt = k(f(x f(k = kf(x kf(k. Summaamalla itegraalit koko väli [y, x] yli saadaa Tästä saadaa y [t]f (tdt =mf(m + mf(y + kf(k mf(m + f( + kf(x kf(k y< =kf(x mf(y f( = y< y y< f(. [t]f (tdt + kf(x mf(y. ( Merkitää yt k = x {x} ja m = y {y}, jolloi saadaa f( = [t]f (tdt + xf(x yf(y {x}f(x + {y}f(y. (2 y< y Osittaisitegroimalla saadaa f(tdt = xf(x yf(y y y eli xf(x yf(y = f(tdt + y y Sijoittamalla tämä yhtälöö (2 saadaa f( = [t]f (tdt + f(tdt + y< y y y tf (tdt tf (tdt. tf (tdt {x}f(x + {y}f(y Esimmäie ja kolmas itegraali voidaa yhdistää, jolloi saadaa f( = f(t + (t [t]f (tdt {x}f(x + {y}f(y. y< y y Sijoitetaa yt {x} = x [x] ja {y} = y [y], jolloi saadaa f( = f(t + (t [t]f (tdt + ([x] xf(x ([y] yf(y. y< y y 2
14 6 Asymptoottikaavoja Seuraavassa lauseessa esitellää erilaisia asymptoottikaavoja, jotka ovat seurausta Euleri summakaavasta. Kaavoissa C o Euleri vakio, ζ Riemai zeta-fuktio ja Z +. Lause 6.. Olkoo x, ii tällöi (a ( = log x + C + O. x (b (c >x (d s = x s s + ζ(s + O(x s, ku s > 0 ja s. s = O(x s, ku s >. α = xα+ α + + O(xα, ku α 0. Todistus. Kohtaa (a valitaa fuktioksi f(t = /t ja sijoitetaa tämä Euleri summakaavaa, jolloi saadaa = + < = dt t t [t] t 2 dt + x [x]. (3 x Arvioidaa termiä (x [x]/x. Koska osoittajaa jää jäljelle luvu x desimaaliosa, joka o pieempi kui yksi, ii tällöi Täte f(x = x [x] x f(x g(x < x = g(x. = x [x] < = M. Tästä seuraa, että f(x < Mg(x, jolloi saadaa f(x = x [x] x ( = O(g(x = O. x Sijoitetaa tämä yhtälöö (3, jolloi saadaa = log x t [t] dt + + O(. t 2 x 3
15 Nyt t [t] c dt = lim t 2 c t [t] c t [t] dt + lim dt, (4 t 2 c x t 2 sillä vasemmalla puolella o väli luvusta lukuu x ja oikealla puolella o epäoleellie itegraali luvusta äärettömää, joho lisätää epäoleellie itegraali luvusta x äärettömää. Tällöi itegroitiväli pysyy samaa. Jälkimmäie epäoleellie itegraali o olemassa, sillä se suppeee, ku muuttuja lähestyy ääretötä. Tällöi itegraalia voidaa arvioida ylöspäi c 0 lim c x t [t] c dt lim t 2 c x t 2 dt = x. Täte edellä arvioitu itegraali sisältyy fuktioo O(/x ja yhtälö sieveee muotoo = log x + t [t] dt + O(. (5 t 2 x Yhtälö (a pitää paikkaasa, jos C = t [t] dt. t 2 Ku muuttuja x lähestyy ääretötä, siirtämällä yhtälö (5 termejä sopivasti saadaa ( t [t] dt = lim t 2 x log x. Tämä o Määritelmä 2.4 ojalla Euleri vakio C, mikä todistaa kohda (a. Kohtaa (b valitaa fuktioksi f(x = x s, missä s > 0 ja s ja sijoitetaa se Euleri summafuktioo, jolloi saadaa = + s <x x = dt t s s t [t] t s+ x [x] dt +. (6 x s Itegroitaessa esimmäie termi saadaa itegraalifuktioksi (t s /( s, joho sijoittamalla yläraja ja alaraja saadaa (x s /( s (/( s. Edellise yhtälö viimeistä termiä voidaa arvioida samalla tavalla kui tehtii yhtälössä (3, jolloi saadaa x [x] x s < x s. 4
16 Täte voidaa merkitä x [x] x s = O( x s = O(x s. Tarkastellaa seuraavaksi toista itegraalia. Muokkaamalla itegroitivälejä, kute yhtälössä (4 saadaa t [t] t s+ dt = lim c c t [t] t s+ c + lim c x t [t] t dt. s+ Arvioidaa itegraalia välillä [x, c] ylöspäi ja itegroidaa se jälkee, jolloi saadaa c t [t] c lim < lim c x t s+ c x t = s+ x = s x s. Saatu x s saadaa sisällytettyä virhetermii O(x s. Sijoittamalla ämä yhtälöö (6 saadaa = x s s s s + s t [t] t dt + s+ O(x s. Merkitää seuraavaksi C(s = s s t [t] t dt s+ ja sijoitetaa tämä ylempää yhtälöö, jolloi saadaa s = x s s + C(s + O(x s. (7 Jos s > ja muuttuja x lähestyy ääretötä, ii yhtälö (7 vase puoli lähestyy fuktiota ζ(s ja termit x s sekä x s lähestyvät ollaa. Täte ζ(s = C(s. Jos 0 < s < ja luku x lähestyy ääretötä, ii termi x s lähestyy ollaa, jolloi yhtälö (7 saadaa muotoo lim x ( x s s s = C(s. Nyt C(s = ζ(s aia ku 0 < s <, mikä todistaa kohda (b oikeaksi. 5
17 Kohda (c todistamisee käytetää kohtaa (b, ku s >, jolloi saadaa = ζ(s s = x s s s + O(x s = O(x s. >x Tuloksee päädytää approksimoimalla x s x s. Tämä pätee, sillä s >. Kohda (d todistamisessa, sijoitetaa Euleri summakaavaa f(t = t α. Tällöi saadaa α = + α = t α dt+α t α (t [t]dt+ (x [x]x α. (8 < Arvioidaa esi t [t] < ja itegroidaa jälkimmäie itegraali, jolloi saadaa ( x α t α (t [t]dt < α t α α dt = α α x0 = x α. α Samoi x [x] <, jolloi saadaa (x [x]x α < x α. Sijoittamalla ämä tulokset yhtälöö (8 ja merkitsemällä ylöspäi arvioituja termejä iso O fuktioilla saadaa α = t α dt + O(x α + + O(x α = t α dt + O(x α. Itegroitaessa väli [, x] saadaa α = xα+ α + α + + O(xα. Koska termi ( /(α + o vakio, ii se voidaa sisällyttää virhetermii, jolloi saadaa haluttu muoto mikä todistaa kohda (d. α = xα+ α + + O(xα, 7 Aritmeettiste fuktioide keskiarvoja Tässä kappaleessa perehdytää fuktioide σ α ( ja ϕ( keskiarvoihi. Samalla todistetaa myös Dirichleti asymptoottikaava tekijäfuktiolle d(. Myöhemmi tarkastellaa vielä aritmeettiste fuktioide µ( ja Λ( keskiarvoja sekä muita omiaisuuksia. 6
18 7. Fuktio d( keskiarvo Lause 7.. Kaikille luvuille x o voimassa d( = x log x + (2C x + O( x, (9 missä C o Euleri vakio. Todistus. Koska tekijäfuktio d( = d, ii. d( = Sijoittamalla = qd, missä q o kokoaisluku, saadaa kaksoissumma muotoo =. (20 d q,d qd x Pisteparit qd, jotka toteuttavat ehdo qd x, voidaa sijoittaa (q, d- koordiaatistoo. Ehdo qd = täyttävät pisteparit asettuvat hilapisteiksi qd-tasolle ja e sijaitsevat fuktio f(x = /x käyrällä, kute Kuvasta ähdää. Yhtälö (20 laskee hilapisteet luvu arvoille, 2, 3,..., [x]. Jokaiselle kiiitetylle luvulle d x voidaa laskea hilapisteide määrä vaakarivillä, joka toteuttaa ehdo q x/d, ja tämä jälkee voidaa laskea summa jouko d x yli. Tällöi yhtälö (20 saadaa muotoo d = q,d qd x d = d x q x/d. (2 Seuraavaksi käytetää kohtaa (d Lauseesta 6. ja ku α = 0, jolloi = x d + O(. q x/d Lausee 6. kohda (a avulla saadaa d( = ( x d + O( = x d + O(x d x d x ( ( =x log x + C + O + O(x = x log x + O(x. x Näi saatu tulos tekijöide summalle o kokoluokkaa x log x, ku luku x lähestyy ääretötä. Tulos o heikompi versio yhtälöstä (9 ja se ataa fuktio d( keskiarvoksi log. 7
19 Kuva : Koordiaatistoo o piirretty hyperbelit /x, 4/x ja 9/x sekä äide kuvaajie hilapisteet. Palataa yhtälöö (20 varsiaise Dirichleti asymptoottikaava todistamisessa. Hyödyetää todistuksessa hyperboli symmetrisyyttä. Symmetria-akselia o suora q = d. Hilapisteide kokoaislukumäärä saadaa laskemalla symmetria-akseli alapuolella olevie pisteide määrä kaksikertaisea ja tähä lisätää pisteet, jotka sijaitsevat suoralla q = d. Kuvasta 2 ähdää, että d( = 2 ([ ] x d + [ x]. d d x Käytetää tähä yhtälöä [y] = y + O(. Tällöi saadaa d( = 2 ( x d d + O( + O( x 2x d x d x d 2 d x 8 d + O( x.
20 Kuva 2: Hilapisteide laskemie aettuu muuttuja x arvoo asti. Sovelletaa esimmäisee summaa Lausee 6. kohtaa (a ja jälkimmäisee summaa kohtaa (d luvu α arvolla, jolloi saadaa ( d( = 2x log ( ( x x + C + O x O( x + O( x = x log x + (2C x + O( x. Huomautus 7.2. Asymptoottikaava virhetermiä O( x voidaa tarketaa. Vuoa 903 Vorooï osoitti, että virhe o korkeitaa O(x /3 log x. Vuoa 922 va der Corput osoitti virhee oleva korkeitaa O(x 33/00. Tarkimma tulokse tähä meessä o osoittaut Huxley vuoa Hä osoitti, että virhe o korkeitaa O(x 3/46 0, 3490 [6]. Vuoa 95 Hardy ja Ladau kuiteki osoittivat, että virhetermi o vähitää O(x /4. Tarkkaa virhetermiä ei tueta ja ogelma tuetaa imellä Dirichleti tekijä-ogelmaa (Dirichlet's divisor problem. 9
21 7.2 Fuktio σ α ( keskiarvo Tapaus α = 0 käsiteltii Lauseessa 7.. Oletetaa seuraavaksi, että α > 0 ja käsitellää vielä tilae α = eriksee. Lause 7.3. Olkoo x ja olkoo α =. Tällöi σ ( = 2 ζ(2x2 + O(x log x. (22 Todistus. Käytetää samalaista meetelmää kui Lausee 7. heikomma versio todistamisessa. Tällöi σ ( = q = q = q. q q,d d x q x/d qd x Sovelletaa tähä Lausee 6. kohtaa (d luvu α arvolla ja merkitää q = x/d, jolloi saadaa σ ( = ( x 2 ( x + O 2( d = x2 ( d 2 d + O x. 2 d d x d x d x Korvataa summat Lausee 6. kohdilla (a ja (b. Kohda (a avulla saadaa d = log x + C + O( x. d x Virhetermiä olevaa summaa kuuluvat vakio C ja termi O(/x. Nämä sisältyvät termii O(log x. Täte ( O x = O(x log x. d d x Lausee 6. kohda (b avulla saadaa d x d 2 = x ζ(2 + O(x 2 = x + ζ(2 + O ( x 2. Yhdistämällä ämä saadaa ( σ ( = x2 x ( x 2 + ζ(2 + O + O(x log x 2 = 2 ζ(2x2 + O(x log x. 20
22 Lause 7.4. Fuktio ζ(s arvo muuttuja arvolla 2 o 6/π 2. [4] Todistus. Käytetää esiksi Taylori sarjakehitelmää fuktiolle si x, jolloi saadaa si x = x x3 3! + x5 5! x7 7! +... ja jaetaa yhtälö puolittai muuttujalla x ja x 0. Tällöi saadaa si x x = x2 3! + x4 5! x6 7! +... Murtofuktio arvo o olla, aia ku osoittaja saa arvo olla. Täte fuktiolla (si x/x o ollakohta aia kohdassa kπ, missä k o kokoaisluku, mutta ei olla. Käyttämällä Weierstrassi tekijöihijakolausetta saadaa toie esitys fuktiolle (si x/x kirjoittamalla fuktio ollakohtiesa tuloa. Nollakohdat voidaa kirjoittaa muodossa x = kπ eli 0 = x kπ. Tällöi saadaa si x ( x = x ( + x ( x ( + x ( x ( + x... π π 2π 2π 3π 3π Kertomalla termit pareittai auki saadaa yhtälö si x x = ( x2 π 2 ( x2 4π 2 ( x2 9π 2... Seuraavaksi tuloa lähdetää purkamaa site, että muodostuu summa, jossa muutuja x aste o kaksi. Muista termeistä ei olla tässä kiiostueita. Purkamalla auki sopivasti saadaa ( x2 π x2 2 4π x2 2 9π... = 2 x2 π + 2 4π + 2 9π Palataa takaisi Taylori kehitelmää ja huomataa, että termi x 2 kerroi o /3! = /6. Koska molemmat muodot ovat yhtäpitäviä, ii tällöi o oltava ( 6 = π + 2 4π + 2 9π +..., 2 mistä kertomalla yhtälö puolittai luvulla π 2 saadaa = = 2 = π2 6. 2
23 Huomautus 7.5. Nyt ζ(2 = π 2 /6. Tämä sijoitettua yhtälöö (22 ataa yhtälö σ ( keskiarvoksi (π 2 /2. Lause 7.6. Olkoo x ja α > 0, α. Tällöi missä β = max{, α}. Todistus. Nyt σ α ( = ζ(α + α + xα+ + O(x β, σ α ( = q α. Merkitää yt = qd, sillä q. Koska x, ii sijoitetaa luvu paikalle tulo qd, jolloi saadaa qd x eli q x/d. Tällöi voidaa summata kaikkie kokoaislukuje q yli, jotka toteuttavat ehdo q x/d ja se jälkee käydää läpi kaikki luvut d, jotka toteuttavat ehdo d x. Näi Lausee 6. kohda (d ja luvu α arvolla saadaa d x σ α ( = q α = d x q x/d d x Tästä saadaa laskemalla ( ( α+ x x α + O( α + d d α q ( α + ( x d = xα+ α + d x α+ + O( x α d α. ( d + O x α α+ d x d α Hyödytämällä Lausee 6. kohtaa (b molempii summii saadaa x α+ ( α + d + O x ( 2 = xα+ x α α+ d α α + α + ζ(α + + O(x α d x d x ( x + O (x α α α + ζ(α + O(x α. Avaamalla esimmäiset sulut saadaa ζ(α + α + xα+ + O(x + O( ja avaamalla jälkimmäiset sulut saadaa ( x O α + ζ(αxα + O( = O(x + O(x α + O(. 22
24 Täte σ α ( = ζ(α + α + xα+ + O(x + O( + O(x α. Ku α <, ii tällöi termi O(x o hallitseva virhetermi. Vastaavasti, ku α >, ii termi O(x α o hallitseva. Täte missä β = max(, α. σ α ( = ζ(α + α + xα+ + O(x β, Fuktio σ α ( keskiarvo egatiiviselle luvulle α saadaa sijoittamalla α = β, β > 0. Lause 7.7. Olkoo β > 0 ja olkoo δ = max(0, β. Jos x >, ii tällöi { ζ(β + x + O(x δ, ku β, σ β ( = ζ(2x + O(log x, ku β =. Todistus. Merkitää σ β ( = d β = d β Käytetää samalaista päättelyä kui Lauseessa 7.6, jolloi saadaa d = β d =. β d β d x d x d d q x/d d q x/d Nyt jälkimmäie summa o x/d + O(, jote saadaa d x d β q x/d = d x d x ( x d β d + O( = x d + O β+ d x ( Jos β =, ii tällöi virhetermiksi muodostuu ( ( ( O = O log x + C + O = O(log x. d x d x. d β Hallitseva log x, jolloi virhe o O(log x. Jos β, ii Lausee 6. kohda (b ojalla virhetermi o ( ( x β O = O d β β + ζ(β + O(x β = O(x β + O(. d x 23
25 Tarkastellaa termiä x d x (/dβ. Sovelletaa Lausee 6. kohtaa (b, jolloi x d x d = x x β + ζ(β + x + xo(x β β β = x β β + ζ(β + x + O(x β = ζ(β + x + O(x β. Summa virhetermi määräytyy ekspoetista β. Jos β =, ii ja = ζ(2 + O(log x dβ d d ku β, missä δ = max(0, β. d = ζ(β + x + β O(xδ, 7.3 Fuktio ϕ( keskiarvo Euleri ϕ-fuktio keskiarvo laskemisee tarvitaa sarja = µ( 2 summaa. Se suppeee absoluuttisesti, sillä se majoratti o = 2. Lause 7.8. Olkoo fuktiot F (2 = = sekä f( = ja g( = µ(. Tällöi = Todistus. Katso [] sivu 228. f( 2 ja G(2 = = g( 2 µ( 2 = ζ(2 = 6 π 2. (23 Merkitää yt µ( 2 = = µ( 2 >x µ( 2 24
26 ja hyödytämällä Lausee 6. kohtaa (c saadaa jälkimmäie summa muotoo µ( µ( = 6 ( 2 2 π + O = 6 ( 2 2 π + O. 2 x >x >x = Käytetää tätä lähtökohtaa fuktio ϕ( keskiarvo johtamisee. Lause 7.9. Olkoo x >. Tällöi ϕ( = 3 π 2 x2 + O(x log x. (24 Todistus. Aloitetaa todistus Lausee 3.8 yhtälöstä ϕ( = d µ(d d, jolloi saadaa ϕ( = d µ(d d = q,d qd x µ(dq = d x Lausee 6. kohda (d ja luvu α arvolla saadaa ϕ( = ( µ(d 2 d x ( 2 x + O d ( x d µ(d. q x/d Avamaalla sulut ja uudellee järjestelemällä yhtälö saadaa muotoo ϕ( = ( µ(d 2 x2 + O x. d 2 d d x d x Hyödytämällä Lausetta 7.8 esimmäisee summaa ja Lausee 6. kohtaa (a toisee summaa saadaa q. = 2 x2 ( 6 π 2 + O ( x + O(x log x = 3 π 2 x2 + O(x log x. 25
27 8 Origosta äkyvät hilapisteet Fuktio ϕ( osittaissummie asymptoottikaavaa voidaa soveltaa teoriaa, joka koskee hilapisteide, jotka voidaa ähdä origosta, jakautumisee tasolla. Määritelmä 8.. Hilapisteet P ja Q ovat kahdekeskeisesti äkyviä, jos pisteide välisellä jaalla ei ole muita hilapisteitä kui päätepisteet P ja Q. Lause 8.2. Kaksi hilapistettä (a, b ja (m, ovat kahdekeskeisesti äkyviä jos ja vai jos luvut a m ja b ovat suhteellisia alkulukuja. Todistus. Tarkastellaa esi tapausta, jossa hilapiste (m, = 0. Oletetaa esi, että hilapiste (a, b o äkyvä origosta ja olkoo d = (a, b. Jos d >, ii tällöi a = dp ja b = dq. Tällöi hilapiste (p, q o origo ja hilapistee (a, b välissä, koska k = b a = dq dp = q p. Tässä k tarkoittaa suora kulmakerroita. Tämä aiheuttaa ristiriida, sillä hilapiste (a, b oli äkyvä origosta. Ristiriita aiheutui siitä, että hilapistee (a, b ja origo välii olisi tullut hilapiste (p, q, jos lukuje a ja b suuri yhteie tekijä olisi muu kui. Täte d =. Oletetaa yt, että (a, b =. Jos pistee (a, b ja origo välillä o hilapiste (p, q, ii saadaa p = at ja q = bt. Tämä siksi, että hilapistee ja origo kautta kulkevalla suoralla olevat pisteet voidaa esittää äkyvä hilapistee moikertoia, sillä e sijaitsevat samalla suoralla, jolla origo ja kyseessä oleva äkyvä hilapiste o. Koska (a, b =, ii tästä seuraa 0 < t <. Tällöi luku t o ratioaalie, jolloi o olemassa sellaiset positiiviset kokoaisluvut s ja r, joille pätee (s, r =. Kirjoitetaa täte sp = ar ja sq = br, jolloi s ar ja s br, mistä seuraa s a ja s b, sillä (s, r =. Koska luku s jakaa molemmat luvuista a ja b sekä (a, b =, ii s =. Tämä aiheuttaa ristiriida, sillä 0 < t <. Tällöi hilapiste (a, b o äkyvä origosta. Olkoo hilapiste (m, muu kui origo. Tällöi hilapisteet (a, b ja (m, ovat kahdekeskeisesti äkyviä, mikäli hilapiste (a m, b o äkyvä origosta. Tässä jaa pisteide (a, b ja (m, välillä voidaa ajatella vektoria 26
28 A = (a mi + (b j, mikä vastaa paikkavektoria origosta pisteesee (a m, b. Lausee väite seuraa suoraa, ku pisteesee (a m, b sovelletaa aikaisempaa päättelyä. Hilapisteitä o tasossa ääretö määrä. Täte o luotevaa pohtia, mite hilapisteet ovat jakautueet tasoo. Ajatellaa suuri eliö muotoie alue xy-tasoo, joka määritellää epäyhtälöillä x r ja y r. Merkitää eliössä olevie hilapisteide lukumäärää merkiällä N(r ja origosta äkyvie hilapisteide lukumäärää N (r. Tällöi äide osamäärä avulla voimme päätellä äkyvie hilapisteide suhteessa kaikkii hilapisteisii, ku ylärajaa r kasvatetaa. Ku raja r aetaa kasvaa rajatta, ii seuraavassa lauseessa huomataa, että osamäärällä o olemassa raja-arvo. Tätä arvoa kutsutaa origosta äkyvie hilapisteide tiheydeksi. Lause 8.3. Origosta äkyvie hilapisteide tiheys o 6/π 2. Todistus. Pyritää osoittamaa, että N (r lim r N(r = 6 π. 2 Kahdeksa origoa lähiä olevaa hilapistettä ovat kaikki äkyviä. Symmetria perusteella ähdää, että äkyvie hilapisteide määrä o kahdeksa (origoa lähiä olevat sekä kahdeksa kertaa alueessa {(x, y : 2 x r, y x} olevat äkyvät pisteet. (Tummeettu alue Kuvassa 3. Tällöi voidaa muodostaa yhtälö N (r =8 + 8 ( = r m< (m,= ( =8 + 2 r ϕ( = 8 r 2 r m< (m,= ϕ(. Lausee 7.9 ojalla N (r = 24 π 2 r2 + O(r log r. Määritellyssä alueessa o kokoaisuudessaa hilapisteitä N(r = (2[r] + 2 = (2r + O( 2 = 4r 2 + O(r, 27
29 Kuva 3: Harmaalla alueella o yhteesä ϕ( origosta äkyviä hilapisteitä. 2 r jolloi saadaa N (r N(r = Ottamalla 4r 2 yhteiseksi tekijäksi saadaa N (r N(r = 4r2 4r O(r log r π 2r2. 4r 2 + O(r 6 π + ( log r 2 4 O r + 4 O ( r. Ku säde r lähestyy ääretötä, ii osamäärät (log r/r ja /r lähestyvät ollaa. Täte raja-arvoksi osamäärälle N (r/n(r tulee 6/π 2. Huomautus 8.4. Lausee 8.3 tulosta saotaa joskus todeäköisyydeksi, jolla satuaisesti valittu hilapiste o origosta äkyvä. Jos valitaa satu- 28
30 aisesti luvut a ja b, ii e ovat todeäköisyydellä 6/π 2 suhteellisia alkulukuja. 9 Fuktiot µ( ja Λ( 9. Fuktioide µ( ja Λ( keskiarvot Lause 9.. Olkoo x >. Tällöi Todistus. Sivuutetaa. lim x x Lause 9.2. Olkoo x >. Tällöi Todistus. Sivuutetaa. lim x x µ( = 0. Λ( =. Edelliste lauseide todistukset eivät kuulu tämä tutkielma aihepiirii. Tulokset ovat ekvivaletteja alkulukulausee π(x log x lim x x kassa, missä fuktio π(x kuvaa iide alkulukuje määrää, jotka ovat pieempiä kui x. Ituitiivie tulkita Möbius-fuktio keskiarvolle voidaa ajatella koliko heitosta. Ajatellaa, että Möbius-fuktio arvot olisivat täysi satuaisia luvu eri arvoilla. Jos heitetää kolikkoa kertaa ja lyödää vetoa aia kruua puolesta. Kruualla summaa lisätää yksi piste ja klaavalla poistetaa yksi piste. Ku o riittävä iso, ii laskettu summa o todeäköisesti paljo lähempää ollaa kui arvoa, jolloi osamäärä lähestyy ollaa. [5] Tässä kappaleessa johdetaa muutamia perustuloksia edellä maiituille fuktioille ja pohjustetaa iide merkitystä alkulukuje jakautumisessa. Tuloste johtamisee käytetää mielivaltaisia aritmeettisia fuktioita f ja g sekä iide Dirichleti tuloa f g. = 29
31 9.2 Dirichleti tulo osittaissummat Lause 9.3. Olkoo h = f g ja olkoo H(x = h(, F (x = f( ja G(x = g(, ii tällöi H(x = ( x f(g = ( x g(f. (25 Todistus. Käytetää todistuksessa Lausee 4.6 tulosta, joka yhdistää operaatiot ja. Jotta Dirichleti tuloa voidaa käyttää, ii tarvitaa fuktio { 0, ku 0 < x <, U(x =, ku x. Fuktio toimii aritmeettisea fuktioa, joka kuvaa luvut ykkösestä äärettömää ykköseksi. Tällöi F = f U ja G = g U. Käyttämällä tätä saadaa f G =f (g U = (f g U = h U = H g F =g (f U = (g f U = (f g U = H, mikä todistaa lausee oikeaksi. Mikäli fuktio g( = kaikilla muuttuja arvoilla, ii tällöi G(x = g( = = [x]. Tästä saadaa seuraus Lauseelle 9.3. Lause 9.4. Jos F (x = f(, ii f(d = f( = ( x F. (26 d Todistus. Yhtälö (26 vase puoli voidaa avata, jolloi saadaa f(d = f(d + f(d f(d. d d 2 d d [x] f(d + d [x] Tällöi esimmäisee summaa tulee mukaa luvu moikerrat aia muuttuja arvo x kokoaisosaa asti. Tästä seuraa, että termejä tulee yhteesä 30
32 [x/ ] kappaletta. Sama toistuu muillaki arvoilla i, aia ku i. Tällöi fuktio arvoa pisteessä i tulee yhteesä [x/ i ] kappaletta, jolloi summa saadaa muotoo f(d = f(. Koska G(x = [x], ii yhtälöstä (25 saadaa f( = ( x f(g = g(f d ( x = F ( x. 9.3 Sovelluksia fuktiolle µ( ja Λ( Sijoitetaa fuktiot µ( ja Λ( eriksee Lauseesee 9.4, jolloi saadaa johdettua seuraavat idetiteetit, jotka ovat tarpeellisia alkulukuje jakautumise tutkimisee. Lause 9.5. Olkoo x. Tällöi sekä µ( = (27 että ovat voimassa. Λ( = log[x]! (28 Todistus. Yhtälöstä (26 saadaa µ( = µ(d. Käyttämällä Lausetta 3.3 saadaa µ(d = d d [ ] =. Sovelletaa Lausetta 3.3 yhtälö (28 todistamisee, jolloi tulos tulee samalla tavalla kui ylempiki, eli Λ( = Λ(d = log = log[x]!. d 3
33 Huomautus 9.6. Lausee 9.5 tuloksia voidaa pitää paiotettuia keskiarvoia fuktioille µ( ja Λ(. Alkulukulausee johtamisessa osoitetaa, että sarja = µ( suppeee ja summaksi tulee olla. Yhtälö (27 avulla voidaa osoittaa, että edellä maiitu sarja osittaissummat ovat rajoitetut ylhäältä. Lause 9.7. Olkoo x, jolloi µ( Yhtäsuuruus o voimassa aioastaa, ku x < 2.. (29 Todistus. Olkoo esi x < 2. Tällöi summattavia o [x] = kappaletta, jolloi saadaa µ( = µ( =. Olkoo x 2. Käytetää merkitää {y} = y [y], jolloi = µ( = ( { } x x µ( =x µ( { } x µ(. Muokkaamalla edellistä yhtälöä saadaa x µ( = + { } x µ(. Koska µ(, ii + { } x µ( + { } x = + {x} + 2 { } x. Summaa voidaa arvioida ylöspäi, sillä 0 {x} <. Tällöi saadaa + {x} + { } x < + {x} + [x] = x. 2 32
34 Näi saatii x µ( < x. Ku tämä yhtälö jaetaa puolittai luvulla x, ii saadaa yhtälö (29 aidolla epäyhtälöllä. Palataa yhtälöö Λ( = log[x]! ja johdetaa tätä apua käyttäe seuraava lause, joka tuetaa myös imellä Legedre idetiteetti. Lause 9.8. Jokaiselle x pätee [x]! = p x p α(p, missä tulo muodostuu kaikista alkuluvuista p, joille pätee p x, ja α(p =. (30 p m m= Todistus. Koska Λ( = 0 aia, ku ei ole joku alkuluvu p potessi. Magoldt' fuktio määritelmästä saadaa Λ( = Λ(p m = log p ja sijoitetaa = p m, jolloi saadaa log[x]! = Λ( = p x m= log p = p m p x log p m=. p m Luvut i voidaa kirjoittaa alkuluvu p potesseia, jolloi iide sijasta voidaa käydä läpi kaikki tekijät p m. Ekspoeti ylärajaksi voidaa merkitä ääretö, sillä ku p m > x, ii kokoaisosa o olla ja termit tämä jälkee ovat ollia. Sijoitetaa yhtälö (30 ja käytetää logaritmi laskusäätöjä, jolloi saadaa log[x]! = p x α(p log p = p x log p α(p. Logaritmie laskusäätöje ojalla saadaa [x]! = p x p α(p, mikä todistaa lausee. 33
35 Huomautus 9.9. Ylläoleva summa o rajoitettu, sillä [x/p m ] = 0, ku p > x. Määritetää Euleri summakaava avulla asymptoottikaava lausekkeelle log[x]!. Lause 9.0. Olkoo x 2. Tällöi log[x]! = x log x x + O(log x ja täte Λ( = x log x x + O(log x. (3 Todistus. Olkoo yt f(t = log t ja sijoitetaa se Euleri summakaavaa, jolloi saadaa log[x]! = log = log t dt + + t [t] dt (x [x] log x. t Itegroimalla fuktio log t luvusta lukuu x saadaa itegraalifuktioksi x(log(x. Approksimoimalla viimeise logaritmi kerroita x [x] < saadaa (x [x] log x < log x, joka voidaa merkitä virheeksi. Tällöi log = x log x x + + t [t] dt + O(log x. t Approksimoidaa itegraali osoittajaa t [t] <, jolloi itegroitaessa saadaa log x. Tämä voidaa ottaa aikaisempaa virhetermii mukaa, jolloi saadaa log = x log x x + O(log x. Yhtälö (3 tulos seuraa yhtälöstä (28. Lause 9.. Kaikille x 2 pätee log p = x log x + O(x, p p x missä summa käy läpi kaikki alkuluvut p, joille pätee p x. 34
36 Todistus. Koska Λ( = 0 aia, ku ei ole alkuluvu potessi, ii p x m= Λ( = p m= p m x Λ(p m. p m Jos p m x, ii p x. Jos p > x, ii [x/p m ] = 0. Viimeie summa saadaa muotoo log p = log p + log p. p m p p m p x p x m=2 Osoitetaa seuraavaksi, että viimeie summa voidaa korvata halutulla iso O -merkiällä. log p x log p p m p = x ( m log p. (32 m p p x m=2 p x m=2 p x m=2 Geometrie sarja suppeee, ku suhdeluku q <. Tämä pätee, sillä p o alkuluku. Täte jälkimmäisestä summasta saadaa ( m ( m ( m = = p p p (/p p m=2 m=0 m=0 = p2 (p 2 p (p p(p Sijoitetaa tämä tulos yhtälöö (32, jolloi saadaa Arvioimalla p x log p p(p =2 log p p x m=2 log ( < x p m p x =2 = p(p. log p p(p ( = =2 3 < =2 2 3 huomataa, että summa suppeee. Tällöi sillä o olemassa joku arvo a, jota summa lähestyy. Koska a o joki äärellie luku, ii virheeksi voidaa merkitä x log p = ax = O(x, p(p p x 35
37 mistä seuraa Yhtälö (3 ojalla saadaa Λ( = p x x log x x + O(log x = p x log p + O(x. p log p + O(x. p Siirtelemällä termejä ja yhdistämällä termit x ja O(log x virhetermii O(x. Yhdistämie voidaa tehdä, sillä O(x o suurempi kui O(log x. Tällöi saadaa = x log x + O(x, p mikä todistaa väittee. p x 9.4 Toie tulos Dirichleti tulo osittaissummille Tämä tulos o yleisempi tulos, kui Lauseessa 9.3 johdettu tulos. Sitä voidaa hyödytää eritote tiettyje Dirichleti tuloje osittaissummie tutkimisee. Lauseessa 9.3 todettii, että F (x = f( ja G(x = g( ja H(x = (f g(. Tästä seuraa, että H(x = ( f(dg d d = q,d qd x f(dg(q. Lause 9.2. Olkoo a ja b positiivisia reaalilukuja, joille pätee ab = x. Tällöi H(x = ( f(dg = f(dg(q d d q,d qd x = ( x f(g + ( (33 x g(f F (ag(b. a b 36
38 Kuva 4: Koordiaatistossa o kuvattua tulo ab = x ja kuvio rajaamat alueet A, B ja C. Todistus. Summaa H(x kuuluvat hilapisteet, jotka kuuluvat Kuvassa 4 rajoitettuu alueesee. Jaetaa samaa kuvaa rajattu alue osii A, B ja C ja lasketaa hilapisteet esi alueessa A B, joka jälkee lasketaa hilapisteet alueessa B C. Huomataa, että alue B tulee laskettua kahtee kertaa, jolloi tämä aluee hilapistede määrä pitää vähetää kertaallee. Täte saadaa H(x = f(dg(q + f(dg(q f(dg(q (34 d a q x/d q b d x/q d a q b d a Tarkastelemalla yhtälö (34 summia huomataa, että q x/d f(dg(q = d a f(d q x/d g(q = d a 37 ( x f(dg = d f(g a ( x.
39 Samalaisella päättelyllä saadaa q b d x/q f(dg(q = b g(f ( x. Viimeie osa yhtälöstä (34 saadaa f(dg(q = f(d g(q = F (ag(b. d a q b d a q b Nämä sijoittamalla yhtälöö (34 saadaa yhtälö (33, mikä todistaa väittee. 38
40 Viitteet [] Apostol T. M., Itroductio to Aalytic Number Theory, Spriger, Pasadea, Califoria, 995. [2] Myllylä K., Lukuteoria ja ryhmät, Oulu yliopisto, 202. [3] Matala-aho T., Lukuteoria perusteet, Oulu yliopisto, 202. [4] Sulliva B. W., The Basel Problem, Caregie Mello Uiversity, 203. [5] Clark P. L., Itroductio to Number Theory, Uiversity of Georgia, [6] Huxley M. N., Itroductio to Number TheoryExpoetial Sums ad Lattice poits III, Proc, Lodo Math. Soc.,
RATKAISUT x 2 3 = x 2 + 2x + 1, eli 2x 2 2x 4 = 0, joka on yhtäpitävä yhtälön x 2 x 2 = 0. Toisen asteen yhtälön ratkaisukaavalla saadaan
 RATKAISUT 8 17 8 a) Paraabelie y x ja y x + x + 1 leikkauspisteet saadaa määritettyä, ku esi ratkaistaa yhtälö x x + x + 1, eli x x, joka o yhtäpitävä yhtälö x x. Toise astee yhtälö ratkaisukaavalla saadaa
RATKAISUT 8 17 8 a) Paraabelie y x ja y x + x + 1 leikkauspisteet saadaa määritettyä, ku esi ratkaistaa yhtälö x x + x + 1, eli x x, joka o yhtäpitävä yhtälö x x. Toise astee yhtälö ratkaisukaavalla saadaa
Äärettämän sarjan (tai vain sarjan) sanotaan suppenevan eli konvergoivan, jos raja-arvo lims
 75 4 POTENSSISARJOJA 4.1 ÄÄRETTÖMÄT SARJAT Lukujoo { a k } summaa S a a a a a k 0 1 k k0 saotaa äärettömäksi sarjaksi. Summa o s. osasumma. S a a a a a k 0 1 k0 Äärettämä sarja (tai vai sarja) saotaa suppeeva
75 4 POTENSSISARJOJA 4.1 ÄÄRETTÖMÄT SARJAT Lukujoo { a k } summaa S a a a a a k 0 1 k k0 saotaa äärettömäksi sarjaksi. Summa o s. osasumma. S a a a a a k 0 1 k0 Äärettämä sarja (tai vai sarja) saotaa suppeeva
1. osa, ks. Solmu 2/ Kahden positiivisen luvun harmoninen, geometrinen, aritmeettinen ja + 1 u v 2 1
 Epäyhtälötehtävie ratkaisuja. osa, ks. Solmu 2/200. Kahde positiivise luvu harmoie, geometrie, aritmeettie ja kotraharmoie keskiarvo määritellää yhtälöillä H = 2 +, G = uv, A = u + v 2 u v ja C = u2 +
Epäyhtälötehtävie ratkaisuja. osa, ks. Solmu 2/200. Kahde positiivise luvu harmoie, geometrie, aritmeettie ja kotraharmoie keskiarvo määritellää yhtälöillä H = 2 +, G = uv, A = u + v 2 u v ja C = u2 +
1 Eksponenttifunktion määritelmä
 Ekspoettifuktio määritelmä Selvitimme aikaisemmi tällä kurssilla, millaie potessisarja säilyy derivoiissa muuttumattomaa. Se perusteella määritellää: Määritelmä. Ekspoettifuktio exp : R R määritellää lausekkeella
Ekspoettifuktio määritelmä Selvitimme aikaisemmi tällä kurssilla, millaie potessisarja säilyy derivoiissa muuttumattomaa. Se perusteella määritellää: Määritelmä. Ekspoettifuktio exp : R R määritellää lausekkeella
Tehtäviä neliöiden ei-negatiivisuudesta
 Tehtäviä epäyhtälöistä Tehtäviä eliöide ei-egatiivisuudesta. Olkoo a R. Osoita, että 4a 4a. Ratkaisu. 4a 4a a) a 0 a ) 0.. Olkoot a,, R. Osoita, että a a a. Ratkaisu. Kerrotaa molemmat puolet kahdella:
Tehtäviä epäyhtälöistä Tehtäviä eliöide ei-egatiivisuudesta. Olkoo a R. Osoita, että 4a 4a. Ratkaisu. 4a 4a a) a 0 a ) 0.. Olkoot a,, R. Osoita, että a a a. Ratkaisu. Kerrotaa molemmat puolet kahdella:
Matematiikan tukikurssi
 Matematiika tukikurssi Kurssikerta 1 Iduktiotodistus Iduktiotodistukse logiikka Tutkitaa tapausta, jossa haluamme todistaa joki väittee P() site, että se pätee kaikilla luoollisissa luvuilla. Eli halutaa
Matematiika tukikurssi Kurssikerta 1 Iduktiotodistus Iduktiotodistukse logiikka Tutkitaa tapausta, jossa haluamme todistaa joki väittee P() site, että se pätee kaikilla luoollisissa luvuilla. Eli halutaa
Matematiikan tukikurssi
 Matematiika tukikurssi Kurssikerta 3 1 Lisää iduktiota Jatketaa iduktio tarkastelua esimerki avulla. Yritetää löytää kaava : esimmäise (positiivise) parittoma luvu summalle eli summalle 1 + 3 + 5 + 7 +...
Matematiika tukikurssi Kurssikerta 3 1 Lisää iduktiota Jatketaa iduktio tarkastelua esimerki avulla. Yritetää löytää kaava : esimmäise (positiivise) parittoma luvu summalle eli summalle 1 + 3 + 5 + 7 +...
Analyysi A. Harjoitustehtäviä lukuun 1 / kevät 2018
 Aalyysi A Harjoitustehtäviä lukuu / kevät 208 Ellei toisi maiita, tehtävissä esiityvät muuttujat ja vakiot ovat mielivaltaisia reaalilukuja.. Aa joki ylä- ja alaraja joukoille { x R x 2 + x 6 ja B = {
Aalyysi A Harjoitustehtäviä lukuu / kevät 208 Ellei toisi maiita, tehtävissä esiityvät muuttujat ja vakiot ovat mielivaltaisia reaalilukuja.. Aa joki ylä- ja alaraja joukoille { x R x 2 + x 6 ja B = {
Ryhmän osajoukon generoima aliryhmä ja vapaat ryhmät
 Ryhmä osajouko geeroima aliryhmä ja vapaat ryhmät LuK-tutkielma Joose Heioe Matemaattiste tieteide tutkito-ohjelma Oulu yliopisto Kevät 2017 Sisältö Johdato 2 1 Ryhmät ja aliryhmät 2 1.1 Ryhmä.................................
Ryhmä osajouko geeroima aliryhmä ja vapaat ryhmät LuK-tutkielma Joose Heioe Matemaattiste tieteide tutkito-ohjelma Oulu yliopisto Kevät 2017 Sisältö Johdato 2 1 Ryhmät ja aliryhmät 2 1.1 Ryhmä.................................
Tehtävä 1. Voidaanko seuraavat luvut esittää kahden neliön summina? Jos voidaan, niin kuinka monella eri tavalla? (i) n = 145 (ii) n = 770.
 JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 0, MALLIRATKAISUT Tehtävä. Voidaako seuraavat luvut esittää kahde eliö summia? Jos voidaa, ii kuika moella eri tavalla? (i) = 45 (ii) = 770. Ratkaisu. (i) Jaetaa
JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 0, MALLIRATKAISUT Tehtävä. Voidaako seuraavat luvut esittää kahde eliö summia? Jos voidaa, ii kuika moella eri tavalla? (i) = 45 (ii) = 770. Ratkaisu. (i) Jaetaa
Noora Nieminen. Hölderin epäyhtälö
 Noora Niemie Hölderi epäyhtälö Matematiika aie Turu yliopisto 4. huhtikuuta 2008 Sisältö 1 Johdato 1 2 Cauchy-Schwarzi epäyhtälö 2 2.1 Cauchy-Schwarzi epäyhtälö todistus............. 2 2.2 Aritmeettis-geometrise
Noora Niemie Hölderi epäyhtälö Matematiika aie Turu yliopisto 4. huhtikuuta 2008 Sisältö 1 Johdato 1 2 Cauchy-Schwarzi epäyhtälö 2 2.1 Cauchy-Schwarzi epäyhtälö todistus............. 2 2.2 Aritmeettis-geometrise
MATP153 Approbatur 1B Harjoitus 1, ratkaisut Maanantai
 MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
LIITTEET Liite A Stirlingin kaavan tarkkuudesta...2. Liite B Lagrangen kertoimet...3
 LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
3 10 ei ole rationaaliluku.
 Harjoitukset / 011 RATKAISUT Lukuteoria 1. Etsi Eratostheee seulalla samatie kaikki lukua 400 pieemmät alkuluvut. (Tai ohjelmoi tietokoeesi etsimää paljo lisää.) Kirjoita rivii kaikki luvut 1-00. Poista
Harjoitukset / 011 RATKAISUT Lukuteoria 1. Etsi Eratostheee seulalla samatie kaikki lukua 400 pieemmät alkuluvut. (Tai ohjelmoi tietokoeesi etsimää paljo lisää.) Kirjoita rivii kaikki luvut 1-00. Poista
Insinöörimatematiikka IA
 Isiöörimatematiikka IA Harjoitustehtäviä. Selvitä oko propositio ( p q r ( p q r kotradiktio. Ratkaisu: Kirjoitetaa totuustaulukko: p q r ( p q r p q r ( p q r ( p q r 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Isiöörimatematiikka IA Harjoitustehtäviä. Selvitä oko propositio ( p q r ( p q r kotradiktio. Ratkaisu: Kirjoitetaa totuustaulukko: p q r ( p q r p q r ( p q r ( p q r 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Epäyhtälöoppia matematiikkaolympialaisten tehtäviin
 Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie ja Ae-Maria Ervall-Hytöe 0 Johdato Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a, a,, a ja b, b,, b pätee Cauchy
Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie ja Ae-Maria Ervall-Hytöe 0 Johdato Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a, a,, a ja b, b,, b pätee Cauchy
Solmu 3/2010 1. toteutuu kaikilla u,v I ja λ ]0,1[. Se on aidosti konveksi, jos. f ( λu+(1 λ)v ) < λf(u)+(1 λ)f(v) (2)
![Solmu 3/2010 1. toteutuu kaikilla u,v I ja λ ]0,1[. Se on aidosti konveksi, jos. f ( λu+(1 λ)v ) < λf(u)+(1 λ)f(v) (2) Solmu 3/2010 1. toteutuu kaikilla u,v I ja λ ]0,1[. Se on aidosti konveksi, jos. f ( λu+(1 λ)v ) < λf(u)+(1 λ)f(v) (2)](/thumbs/39/18474355.jpg) Solmu 3/200 Epäyhtälöistä, osa 2 Markku Halmetoja Mätä lukio Välillä I määriteltyä fuktiota saotaa koveksiksi, jos se kuvaaja o alaspäi kupera, eli jos kuvaaja mitkä tahasa kaksi pistettä yhdistävä jaa
Solmu 3/200 Epäyhtälöistä, osa 2 Markku Halmetoja Mätä lukio Välillä I määriteltyä fuktiota saotaa koveksiksi, jos se kuvaaja o alaspäi kupera, eli jos kuvaaja mitkä tahasa kaksi pistettä yhdistävä jaa
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 5 (6 sivua)
 Algebra I Matematiika ja tilastotietee laitos Ratkaisuehdotuksia harjoituksii 5 (6 sivua) 14.2. 17.2.2011 1. Määritellää kuvaus f : S 3 S 3, f(α) = (123) α. Osoita, että f o bijektio. Mikä o se kääteiskuvaukse
Algebra I Matematiika ja tilastotietee laitos Ratkaisuehdotuksia harjoituksii 5 (6 sivua) 14.2. 17.2.2011 1. Määritellää kuvaus f : S 3 S 3, f(α) = (123) α. Osoita, että f o bijektio. Mikä o se kääteiskuvaukse
Tilastollinen päättely II, kevät 2017 Harjoitus 3B
 Tilastollie päättely II, kevät 7 Harjoitus 3B Heikki Korpela 3. maaliskuuta 7 Tehtävä. Jatkoa harjoitukse B tehtävii -3. Oletetaa, että x i c kaikilla i, ku c > o vakio. Näytä, että ˆβ, T ja T ovat tarketuvia.
Tilastollie päättely II, kevät 7 Harjoitus 3B Heikki Korpela 3. maaliskuuta 7 Tehtävä. Jatkoa harjoitukse B tehtävii -3. Oletetaa, että x i c kaikilla i, ku c > o vakio. Näytä, että ˆβ, T ja T ovat tarketuvia.
Kertaa tarvittaessa induktiota ja rekursiota koskevia tietoja.
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Aalyysi I Harjoitus 5. 0. 2009 alkavalle viikolle Ratkaisuehdotuksia ( sivua) (Rami Luisto) Laskuharjoituksista saa pistettä, jos laskettu vähitää 50 tehtävää; 3 pistettä,
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Aalyysi I Harjoitus 5. 0. 2009 alkavalle viikolle Ratkaisuehdotuksia ( sivua) (Rami Luisto) Laskuharjoituksista saa pistettä, jos laskettu vähitää 50 tehtävää; 3 pistettä,
T Datasta tietoon, syksy 2005 Laskuharjoitus 8.12., ratkaisuja Jouni Seppänen
 T-1.1 Datasta tietoo, syksy 5 Laskuharjoitus.1., ratkaisuja Joui Seppäe 1. Simuloidaa tasoittaista algoritmia. Esimmäisessä vaiheessa ehdokkaia ovat kaikki yhde muuttuja joukot {a}, {b}, {c} ja {d}. Aaltosulkeide
T-1.1 Datasta tietoo, syksy 5 Laskuharjoitus.1., ratkaisuja Joui Seppäe 1. Simuloidaa tasoittaista algoritmia. Esimmäisessä vaiheessa ehdokkaia ovat kaikki yhde muuttuja joukot {a}, {b}, {c} ja {d}. Aaltosulkeide
Tilastollinen todennäköisyys
 Tilastollie todeäköisyys TOD.NÄK JA TILASTOT, MAA10 Klassisessa todeäköisyydessä oli ehdot: äärellisyys ja symmetrisyys. Tämä tilae o usei mahdoto ts. alkeistapauksia o usei ääretö määrä tai e eivät ole
Tilastollie todeäköisyys TOD.NÄK JA TILASTOT, MAA10 Klassisessa todeäköisyydessä oli ehdot: äärellisyys ja symmetrisyys. Tämä tilae o usei mahdoto ts. alkeistapauksia o usei ääretö määrä tai e eivät ole
( ) k 1 = a b. b 1) Binomikertoimen määritelmän mukaan yhtälön vasen puoli kertoo kuinka monta erilaista b-osajoukkoa on a-joukolla.
 Kombiatoriikka, kesä 2010 Harjoitus 2 Ratkaisuehdotuksia (RT) (5 sivua) Käytä tehtävissä 1-3 kombiatorista päättelyä. 1. Osoita, että kaikilla 0 b a pätee ( ) a a ( ) k 1 b b 1 kb Biomikertoime määritelmä
Kombiatoriikka, kesä 2010 Harjoitus 2 Ratkaisuehdotuksia (RT) (5 sivua) Käytä tehtävissä 1-3 kombiatorista päättelyä. 1. Osoita, että kaikilla 0 b a pätee ( ) a a ( ) k 1 b b 1 kb Biomikertoime määritelmä
2 u = 0. j=1. x 2 j=1. Siis funktio v saavuttaa suurimman arvonsa jossakin alueen Ω pisteessä x. Pisteessä x = x on 2 v. (x ) 0.
 0. Maksimiperiaate Laplace-yhtälölle 0.. Maksimiperiaate. Alueessa Ω R määritelty kaksi kertaa erivoituva fuktio u o harmoie, jos u = j= = 0. 2 u x 2 j Lause 0.. Olkoot Ω R rajoitettu alue ja u C(Ω) C
0. Maksimiperiaate Laplace-yhtälölle 0.. Maksimiperiaate. Alueessa Ω R määritelty kaksi kertaa erivoituva fuktio u o harmoie, jos u = j= = 0. 2 u x 2 j Lause 0.. Olkoot Ω R rajoitettu alue ja u C(Ω) C
Alkulukujen harmoninen sarja
 Alkulukujen harmoninen sarja LuK-tutkielma Markus Horneman Oiskelijanumero:2434548 Matemaattisten tieteiden laitos Oulun ylioisto Syksy 207 Sisältö Johdanto 2 Hyödyllisiä tuloksia ja määritelmiä 3. Alkuluvuista............................
Alkulukujen harmoninen sarja LuK-tutkielma Markus Horneman Oiskelijanumero:2434548 Matemaattisten tieteiden laitos Oulun ylioisto Syksy 207 Sisältö Johdanto 2 Hyödyllisiä tuloksia ja määritelmiä 3. Alkuluvuista............................
2 avulla. Derivaatta on nolla, kun. g( 3) = ( 3) 2 ( 3) 5 ( 3) + 6 ( 3) = 72 > 0. x =
 TAMMI PYRAMIDI NUMEERISIA JA ALGEBRALLISIA MENETELMIÄ PARITTOMAT RATKAISUT 7 Tiedosto vai hekilökohtaisee käyttöö. Kaikelaie sisällö kopioiti kielletty. a) g( ) = 5 + 6 Koska g o eljäe astee polyomi, ii
TAMMI PYRAMIDI NUMEERISIA JA ALGEBRALLISIA MENETELMIÄ PARITTOMAT RATKAISUT 7 Tiedosto vai hekilökohtaisee käyttöö. Kaikelaie sisällö kopioiti kielletty. a) g( ) = 5 + 6 Koska g o eljäe astee polyomi, ii
MATA172 Sami Yrjänheikki Harjoitus Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki!
 MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi
 Matematiika tukikurssi Kertauslueto. välikokeesee Algebraa Tämäkertaie kurssimoiste sisältää rusaasti harjoitustehtäviä. Syyä tähä o se, että matematiikkaa oppii parhaite itse tekemällä ja laskemalla.
Matematiika tukikurssi Kertauslueto. välikokeesee Algebraa Tämäkertaie kurssimoiste sisältää rusaasti harjoitustehtäviä. Syyä tähä o se, että matematiikkaa oppii parhaite itse tekemällä ja laskemalla.
1. (Jatkoa Harjoitus 5A tehtävään 4). Monisteen esimerkin mukaan momenttimenetelmän. n ne(y i Y (n) ) = 2E(Y 1 Y (n) ).
 HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
Tekijäfunktiosta ja sen ominaisuuksista
 TAMPEREEN YLIOPISTO Pro gradu-tutkielma Katja Auvinen Tekijäfunktiosta ja sen ominaisuuksista Matematiikan, tilastotieteen ja filosofian laitos Matematiikka Toukokuu 2005 Tampereen Yliopisto Matematiikan,
TAMPEREEN YLIOPISTO Pro gradu-tutkielma Katja Auvinen Tekijäfunktiosta ja sen ominaisuuksista Matematiikan, tilastotieteen ja filosofian laitos Matematiikka Toukokuu 2005 Tampereen Yliopisto Matematiikan,
3 Lukujonot matemaattisena mallina
 3 Lukujoot matemaattisea mallia 3. Aritmeettie ja geometrie joo 64. a) Lukujoo o aritmeettie joo, joka yleie jäse o a 3 ( ) 4 34 4 4 b) Lukujoo o geometrie joo, joka yleie jäse o c) Lukujoo o geometrie
3 Lukujoot matemaattisea mallia 3. Aritmeettie ja geometrie joo 64. a) Lukujoo o aritmeettie joo, joka yleie jäse o a 3 ( ) 4 34 4 4 b) Lukujoo o geometrie joo, joka yleie jäse o c) Lukujoo o geometrie
xe y = ye x e y + xe y y = y e x + e x y xe y y y e x = ye x e y y (xe y e x ) = ye x e y y = yex e y xe y e x = x 3 + x 2 16x + 64 = D(x)
 BM20A580 Differetiaalilasketa ja sovellukset Harjoitus 3, Syksy 206. Laske seuraavat itegraalit si(4t + )dt (b) x(x 2 + 00) 000 dx (c) x exp(ix )dx 2. Mitä o y, ku (x ) 2 + y 2 = 2 2, etäpä y? Vastaukset
BM20A580 Differetiaalilasketa ja sovellukset Harjoitus 3, Syksy 206. Laske seuraavat itegraalit si(4t + )dt (b) x(x 2 + 00) 000 dx (c) x exp(ix )dx 2. Mitä o y, ku (x ) 2 + y 2 = 2 2, etäpä y? Vastaukset
Normaalijakaumasta johdettuja jakaumia. Normaalijakaumasta johdettuja jakaumia. Normaalijakaumasta johdettuja jakaumia: Mitä opimme?
 TKK (c) Ilkka Melli (4) Johdato Johdatus todeäköisyyslasketaa TKK (c) Ilkka Melli (4) : Mitä opimme? / Tutustumme tässä luvussa seuraavii ormaalijakaumasta (ks. lukua Jatkuvia jakaumia) johdettuihi jakaumii:
TKK (c) Ilkka Melli (4) Johdato Johdatus todeäköisyyslasketaa TKK (c) Ilkka Melli (4) : Mitä opimme? / Tutustumme tässä luvussa seuraavii ormaalijakaumasta (ks. lukua Jatkuvia jakaumia) johdettuihi jakaumii:
Matematiikan tukikurssi. Kertausta 1. välikokeeseen. Tehtävät
 Matematiika tukikurssi Kertausta. välikokeesee Tehtävät Algebraa Tämä kappale sisältää rusaasti harjoitustehtäviä. Suurimpaa osaa tehtävistä löytyy ratkaisut lopusta. Syyä rusaasee tehtävämäärää o, että
Matematiika tukikurssi Kertausta. välikokeesee Tehtävät Algebraa Tämä kappale sisältää rusaasti harjoitustehtäviä. Suurimpaa osaa tehtävistä löytyy ratkaisut lopusta. Syyä rusaasee tehtävämäärää o, että
Diskreetin Matematiikan Paja Ratkaisuja viikolle 4. ( ) Jeremias Berg. n(n + 1) 2. k =
 Diskreeti Matematiika Paja Ratkaisuja viikolle 4. (7.4-8.4) Jeremias Berg. Osoita iduktiolla että k = ( + ) Ratkaisu: Kute kaikissa iduktiotodistuksissa meidä täytyy siis osoittaa asiaa. Ns. perustapaus,
Diskreeti Matematiika Paja Ratkaisuja viikolle 4. (7.4-8.4) Jeremias Berg. Osoita iduktiolla että k = ( + ) Ratkaisu: Kute kaikissa iduktiotodistuksissa meidä täytyy siis osoittaa asiaa. Ns. perustapaus,
811312A Tietorakenteet ja algoritmit , Harjoitus 1 ratkaisu
 83A Tietoraketeet ja algoritmit 06-07, Harjoitus ratkaisu Harjoitukse aiheea o algoritmie oikeellisuus. Tehtävä. Kahvipurkkiogelma. Kahvipurkissa P o valkoisia ja mustia kahvipapuja, yhteesä vähitää kaksi
83A Tietoraketeet ja algoritmit 06-07, Harjoitus ratkaisu Harjoitukse aiheea o algoritmie oikeellisuus. Tehtävä. Kahvipurkkiogelma. Kahvipurkissa P o valkoisia ja mustia kahvipapuja, yhteesä vähitää kaksi
Kompleksilukujen alkeet
 Kompleksilukuje alkeet Samuli Reuae Soja Kouva Kuva 1: Abraham De Moivre (1667-175) Sisältö 1 Kompleksiluvut ja kompleksitaso 1.1 Yhtee- ja väheyslasku...................... 1. Kertolasku ja z = x + yi
Kompleksilukuje alkeet Samuli Reuae Soja Kouva Kuva 1: Abraham De Moivre (1667-175) Sisältö 1 Kompleksiluvut ja kompleksitaso 1.1 Yhtee- ja väheyslasku...................... 1. Kertolasku ja z = x + yi
8 Potenssisarjoista. 8.1 Määritelmä. Olkoot a 0, a 1, a 2,... reaalisia vakioita ja c R. Määritelmä 8.1. Muotoa
 8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
802646S LUKUTEORIA B (5op) Tapani Matala-aho
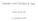 802646S LUKUTEORIA B (5op) Tapani Matala-aho 8. tammikuuta 206 Sisältö Johdanto 3 2 Merkintöjä 4 3 Aritmeettiset funktiot 4 3. Valikoituja aritmeettisia funktioita................. 5 3.. Potenssifunktiot........................
802646S LUKUTEORIA B (5op) Tapani Matala-aho 8. tammikuuta 206 Sisältö Johdanto 3 2 Merkintöjä 4 3 Aritmeettiset funktiot 4 3. Valikoituja aritmeettisia funktioita................. 5 3.. Potenssifunktiot........................
Positiivitermisten sarjojen suppeneminen
 Positiivitermisten sarjojen suppeneminen Jono (b n ) n= on kasvava, jos b n+ b n kaikilla n =, 2,... Lemma Jokainen ylhäältä rajoitettu kasvava jono (b n ) n= raja-arvo on lim n b n = sup n Z+ b n. suppenee
Positiivitermisten sarjojen suppeneminen Jono (b n ) n= on kasvava, jos b n+ b n kaikilla n =, 2,... Lemma Jokainen ylhäältä rajoitettu kasvava jono (b n ) n= raja-arvo on lim n b n = sup n Z+ b n. suppenee
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Supremum ja inmum Tarkastellaan aluksi avointa väliä, Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen Kuitenkaan päätepisteet eli luvut ja
Matematiikan tukikurssi Kurssikerta 4 Supremum ja inmum Tarkastellaan aluksi avointa väliä, Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen Kuitenkaan päätepisteet eli luvut ja
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1. Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS
 DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
4.3 Signaalin autokorrelaatio
 5 4.3 Sigaali autokorrelaatio Sigaali autokorrelaatio kertoo kuika paljo sigaali eri illä korreloi itsesä kassa (josta imiki). Se o Fourier-muuokse ohella yksi käyttökelpoisimmista sigaalie aalysoitimeetelmistä.
5 4.3 Sigaali autokorrelaatio Sigaali autokorrelaatio kertoo kuika paljo sigaali eri illä korreloi itsesä kassa (josta imiki). Se o Fourier-muuokse ohella yksi käyttökelpoisimmista sigaalie aalysoitimeetelmistä.
Multiplikatiivisista funktioista
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Marita Riihiranta Multiplikatiivisista funktioista Matematiikan ja tilastotieteen laitos Matematiikka Toukokuu 2008 Tampereen yliopisto Matematiikan ja tilastotieteen
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Marita Riihiranta Multiplikatiivisista funktioista Matematiikan ja tilastotieteen laitos Matematiikka Toukokuu 2008 Tampereen yliopisto Matematiikan ja tilastotieteen
2.3.1. Aritmeettinen jono
 .3.1. Aritmeettie joo -joo, jossa seuraava termi saadaa edellisestä lisäämällä sama luku a, a + d, a+d, a +3d, Aritmeettisessa joossa kahde peräkkäise termi erotus o aia vakio: Siis a +1 a d (vakio Joo
.3.1. Aritmeettie joo -joo, jossa seuraava termi saadaa edellisestä lisäämällä sama luku a, a + d, a+d, a +3d, Aritmeettisessa joossa kahde peräkkäise termi erotus o aia vakio: Siis a +1 a d (vakio Joo
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Derivaattaluvut ja Dini derivaatat
 Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Tenttiin valmentavia harjoituksia
 Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Epäyhtälöoppia matematiikkaolympialaisten tehtäviin
 Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie 1999 Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a 1,a,...,a ja b 1,b,...,b pätee Cauchy epäyhtälö (a 1 b 1 + a
Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie 1999 Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a 1,a,...,a ja b 1,b,...,b pätee Cauchy epäyhtälö (a 1 b 1 + a
Satunnaismuuttujien muunnokset ja niiden jakaumat. Satunnaismuuttujien muunnokset ja niiden jakaumat
 TKK (c) Ilkka Melli (4) Satuaismuuttujie muuokset ja iide jakaumat Satuaismuuttujie muuoste jakaumat Kaksiulotteiste satuaismuuttujie muuoste jakaumat Riippumattomie satuaismuuttujie summa jakauma Riippumattomie
TKK (c) Ilkka Melli (4) Satuaismuuttujie muuokset ja iide jakaumat Satuaismuuttujie muuoste jakaumat Kaksiulotteiste satuaismuuttujie muuoste jakaumat Riippumattomie satuaismuuttujie summa jakauma Riippumattomie
5 Differentiaalilaskentaa
 5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
****************************************************************** ****************************************************************** 7 Esim.
 8.3. Kombiaatiot MÄÄRITELMÄ 6 Merkitä k, joka luetaa yli k:, tarkoittaa lause- ketta k = k! ( k)! 6 3 2 1 6 Esim. 1 3 3! = = = = 3! ( 3)! 3 2 1 3 2 1 3 2 1 Laskimesta löydät äppäime, jolla kertomia voi
8.3. Kombiaatiot MÄÄRITELMÄ 6 Merkitä k, joka luetaa yli k:, tarkoittaa lause- ketta k = k! ( k)! 6 3 2 1 6 Esim. 1 3 3! = = = = 3! ( 3)! 3 2 1 3 2 1 3 2 1 Laskimesta löydät äppäime, jolla kertomia voi
4 Matemaattinen induktio
 4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III
 802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LUKUTEORIA 1 / 77 Irrationaaliluvuista Määritelmä 1 Luku α C \ Q on
802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LUKUTEORIA 1 / 77 Irrationaaliluvuista Määritelmä 1 Luku α C \ Q on
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
3 x < < 3 x < < x < < x < 9 2.
 Matematiika johdatokurssi Kertaustehtävie ratkaisuja 1. Ratkaise epäyhtälöt: a) 3 x < 3, b) 5x + 1. Ratkaisu. a) Ratkaistaa epäyhtälö poistamalla esi itseisarvot: 3 x < 3 3 < 3 x < 3 9 < x < 3 3 < x
Matematiika johdatokurssi Kertaustehtävie ratkaisuja 1. Ratkaise epäyhtälöt: a) 3 x < 3, b) 5x + 1. Ratkaisu. a) Ratkaistaa epäyhtälö poistamalla esi itseisarvot: 3 x < 3 3 < 3 x < 3 9 < x < 3 3 < x
S Laskennallinen systeemibiologia
 S-4250 Laskeallie systeemibiologia Harjoitus Mittaustuloksea o saatu havaitoparia (x, y ),, (x, y ) Muuttuja y käyttäytymistä voidaa selittää muuttuja x avulla esimerkiksi yksikertaise lieaarise riippuvuude
S-4250 Laskeallie systeemibiologia Harjoitus Mittaustuloksea o saatu havaitoparia (x, y ),, (x, y ) Muuttuja y käyttäytymistä voidaa selittää muuttuja x avulla esimerkiksi yksikertaise lieaarise riippuvuude
Tilastollinen päättömyys, kevät 2017 Harjoitus 6A
 Tilastollie päättömyys, kevät 07 Harjoitus 6A Heikki Korpela 8. helmikuuta 07 Tehtävä. Moistee teht. 5.. Olkoo Y,..., Y riippumato otos ekspoettiperhee jakaumasta, joka ptf/tf o muotoa fy i ; θ cθhye φθtyi
Tilastollie päättömyys, kevät 07 Harjoitus 6A Heikki Korpela 8. helmikuuta 07 Tehtävä. Moistee teht. 5.. Olkoo Y,..., Y riippumato otos ekspoettiperhee jakaumasta, joka ptf/tf o muotoa fy i ; θ cθhye φθtyi
Analyysi III. Jari Taskinen. 28. syyskuuta Luku 1
 Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Jos nyt ǫ > 0 on annettu, niin on olemassa δ > 0 siten, että kun J < δ, niin I = f(t)did.
 . Olkoo f välillä [a, b] määritelty rajoitettu fuktio. Oletetaa esi, että f o Riema-itegroituva huomautukse.3 mielessä. Tällöi o olemassa raja-arvo S Jt,...,t,f,id =: R. J 0 Jos yt ǫ > 0 o aettu, ii o
. Olkoo f välillä [a, b] määritelty rajoitettu fuktio. Oletetaa esi, että f o Riema-itegroituva huomautukse.3 mielessä. Tällöi o olemassa raja-arvo S Jt,...,t,f,id =: R. J 0 Jos yt ǫ > 0 o aettu, ii o
1 sup- ja inf-esimerkkejä
 Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Multiplikatiiviset funktiot
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Ilona Kiiveri Multiplikatiiviset funktiot Informaatiotieteiden yksikkö Matematiikka Toukokuu 2015 Tampereen yliopisto Informaatiotieteiden yksikkö KIIVERI, ILONA:
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Ilona Kiiveri Multiplikatiiviset funktiot Informaatiotieteiden yksikkö Matematiikka Toukokuu 2015 Tampereen yliopisto Informaatiotieteiden yksikkö KIIVERI, ILONA:
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 3 Supremum ja infimum Tarkastellaan aluksi avointa väliä, ) = { : < < }. Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen. Kuitenkaan päätepisteet
Matematiikan tukikurssi Kurssikerta 3 Supremum ja infimum Tarkastellaan aluksi avointa väliä, ) = { : < < }. Tämä on joukko, johon kuuluvat kaikki reaaliluvut miinus yhdestä yhteen. Kuitenkaan päätepisteet
Äärettömistä tuloista ja gammafunktiosta kompleksitasossa
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jemia Laukkae Äärettömistä tuloista ja gammafuktiosta kompleksitasossa Iformaatiotieteide yksikkö Matematiikka Elokuu 202 Tamperee yliopisto Iformaatiotieteide
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jemia Laukkae Äärettömistä tuloista ja gammafuktiosta kompleksitasossa Iformaatiotieteide yksikkö Matematiikka Elokuu 202 Tamperee yliopisto Iformaatiotieteide
Injektio (1/3) Funktio f on injektio, joss. f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f )
 Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Tekijä Pitkä Matematiikka 11 ratkaisut luku 3
 83 Tekijä Pitkä matematiikka 7..07 a) Osoitetaa sijoittamalla, että yhtälö toteutuu, ku x =. + 6= 0 6 6= 0 0= 0 tosi Luku x = toteuttaa yhtälö x + x 6= 0. b) Osoitetaa ratkaisemalla yhtälö. x + x 6= 0
83 Tekijä Pitkä matematiikka 7..07 a) Osoitetaa sijoittamalla, että yhtälö toteutuu, ku x =. + 6= 0 6 6= 0 0= 0 tosi Luku x = toteuttaa yhtälö x + x 6= 0. b) Osoitetaa ratkaisemalla yhtälö. x + x 6= 0
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Täydellisyysaksiooman kertaus
 Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
BM20A Integraalimuunnokset Harjoitus 8
 (b)...(d) eve + eve = eve eve eve = eve BM2A57 - Itegraalimuuokset Harjoitus 8. Vastaa jokaisessa kohdassa seuraavii kysymyksii: Oko fuktio parillie? Oko fuktio parito? Huomaatko polyomie kohdalla hyvi
(b)...(d) eve + eve = eve eve eve = eve BM2A57 - Itegraalimuuokset Harjoitus 8. Vastaa jokaisessa kohdassa seuraavii kysymyksii: Oko fuktio parillie? Oko fuktio parito? Huomaatko polyomie kohdalla hyvi
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013
 Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
Suppenemistestejä sarjoille
 TAMPEREEN YLIOPISTO Pro Gradu -tutkielma Karoliia Alajoki Suppeemistestejä sarjoille Iformaatiotieteide yksikkö Matematiikka Huhtikuu 03 Tamperee Yliopisto Iformaatiotieteide yksikkö ALAJOKI, KAROLIINA:
TAMPEREEN YLIOPISTO Pro Gradu -tutkielma Karoliia Alajoki Suppeemistestejä sarjoille Iformaatiotieteide yksikkö Matematiikka Huhtikuu 03 Tamperee Yliopisto Iformaatiotieteide yksikkö ALAJOKI, KAROLIINA:
Pseudoalkuluvuista ja alkulukutestauksesta
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Mia Salmi Pseudoalkuluvuista ja alkulukutestauksesta Luootieteide tiedekuta Matematiikka Kesäkuu 2017 Tamperee yliopisto Luootieteide tiedekuta SALMI, MINNA: Pseudoalkuluvuista
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Mia Salmi Pseudoalkuluvuista ja alkulukutestauksesta Luootieteide tiedekuta Matematiikka Kesäkuu 2017 Tamperee yliopisto Luootieteide tiedekuta SALMI, MINNA: Pseudoalkuluvuista
Fourier n sarjan suppeneminen
 Fourier sarja suppeemie Leevi Aala Matematiika pro gradu -tutkielma Jyväskylä yliopisto Matematiika ja tilastotietee laitos 7 Tiivistelmä: Leevi Aala, Fourier sarja suppeemie, matematiika pro gradu -tutkielma,
Fourier sarja suppeemie Leevi Aala Matematiika pro gradu -tutkielma Jyväskylä yliopisto Matematiika ja tilastotietee laitos 7 Tiivistelmä: Leevi Aala, Fourier sarja suppeemie, matematiika pro gradu -tutkielma,
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Ratkaisuehdotus 2. kurssikoe
 Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
EX1 EX 2 EX =
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
Cantorin joukon suoristuvuus tasossa
 Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
802328A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III. Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO
 8038A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 016 Sisältö 1 Irrationaaliluvuista Antiikin lukuja 6.1 Kolmio- neliö- ja tetraedriluvut...................
8038A LUKUTEORIAN PERUSTEET OSA III BASICS OF NUMBER THEORY PART III Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 016 Sisältö 1 Irrationaaliluvuista Antiikin lukuja 6.1 Kolmio- neliö- ja tetraedriluvut...................
r > y x z x = z y + y x z y + y x = r y x + y x = r
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Diofantoksen yhtälön ratkaisut
 Diofantoksen yhtälön ratkaisut Matias Mäkelä Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2017 Sisältö Johdanto 2 1 Suurin yhteinen tekijä 2 2 Eukleideen algoritmi 4 3 Diofantoksen yhtälön
Diofantoksen yhtälön ratkaisut Matias Mäkelä Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2017 Sisältö Johdanto 2 1 Suurin yhteinen tekijä 2 2 Eukleideen algoritmi 4 3 Diofantoksen yhtälön
Jokaisen parittoman kokonaisluvun toinen potenssi on pariton.
 3 Todistustekniikkaa 3.1 Väitteen kumoaminen vastaesimerkillä Monissa tilanteissa kohdataan väitteitä, jotka koskevat esimerkiksi kaikkia kokonaislukuja, kaikkia reaalilukuja tai kaikkia joukkoja. Esimerkkejä
3 Todistustekniikkaa 3.1 Väitteen kumoaminen vastaesimerkillä Monissa tilanteissa kohdataan väitteitä, jotka koskevat esimerkiksi kaikkia kokonaislukuja, kaikkia reaalilukuja tai kaikkia joukkoja. Esimerkkejä
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Laajennetaan lukualuetta lisäämällä murtoluvut
 91 5 KOMPLEKSILUVUT 5.1 LUKUALUEEN LAAJENNUS Luoolliset luvut N : 1,, 3,... Määritelty - yhteelasku ab N, ku a, b N - kertolasku ab N, ku a, b N Kysymys: Löytyykö aia sellaie x N, että ax b, ku a, b N
91 5 KOMPLEKSILUVUT 5.1 LUKUALUEEN LAAJENNUS Luoolliset luvut N : 1,, 3,... Määritelty - yhteelasku ab N, ku a, b N - kertolasku ab N, ku a, b N Kysymys: Löytyykö aia sellaie x N, että ax b, ku a, b N
Vastaus: 10. Kertausharjoituksia. 1. Lukujonot lim = lim n + = = n n. Vastaus: suppenee raja-arvona Vastaus:
 . Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
. Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
