VI. TAYLORIN KAAVA JA SARJAT. VI.1. Taylorin polynomi ja Taylorin kaava
|
|
|
- Niko Härkönen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 VI. TAYLORIN KAAVA JA SARJAT VI.. Taylorin polynomi ja Taylorin kaava Olkoon n N ja x, c, c, c 2,..., c n R. Tehtävä: Etsittävä sellainen R-kertoiminen polynomi P, että sen aste deg P n ja P (x ) = c, P (x ) = c,..., P (n ) (x ) = c n. Ratkaisu: Jos P on olemassa, niin P (x) = b +b x+...+b n x n. Sijoitetaan x = x +(x x ), jolloin P tulee muotoon P (x) = a + a (x x ) a n (x x ) n. Tutkitaan, voidaanko kertoimet a, a,..., a n R valita niin, että vaaditut ehdot ovat voimassa. Lauseen V.2.5 mukaan P (k) (x ) = a k, k =,, 2,..., n (ja P (k) (x ) = kaikilla k n). Siispä P toteuttaa vaaditut ehdot a = c, a = c, 2! a 2 = c 2,..., (n )! a n = c n n c k P (x) = c + (x x ) k kaikilla x R. Löydettiin siis -käsitteinen ratkaisu (itse asiassa tämä seuraa potenssisarjan yksikäsitteisyyslauseesta 2.6, koska polynomi on potenssisarja, jonka lopputermit ovat nollia). Huom. Jos ei vaadita, että deg P n, ehdot P (x ) = c, P (x ) = c,..., P (n ) (x ) = c n toteuttavia polynomeja P on ääretön määrä (P (x) = a + a (x x ) a m (x x ) m, m n = a n, a n+,..., a m saavat olla mitä tahansa). Toisaalta voi olla deg P < n (jos c n = ). Merkitään B(x, h) = ]x h, x + h[, kun h >. Oletetaan, että f: B(x, h) R on funktio, jolle - on olemassa derivaatat f (x), f (2) (x),..., f (n 2) (x) kaikilla x B(x, h), - on olemassa f (n ) (x ). Valitsemalla edellä c = f(x ) ja c k = f (k) (x ), kun k =, 2,..., n, saadaan f:n pisteeseen x kuuluva Taylorin polynomi n T n (x; x ) = f(x ) + f (k) (x ) (x x ) k ; P (x) = T n (x; x ) on se -käsitteinen polynomi, jolla deg P n ja P (x ) = f(x ), P (x ) = f (x ),..., P (n ) (x ) = f (n ) (x ). Erikoistapauksessa x = puhutaan myös Maclaurinin polynomista. (Taylor ja Maclaurin ) Uusi tehtävä: Tutkittava erotusta f(x) T n (x; x ). Vahvennetaan hieman f:ää koskevia oletuksia.
2 .. Taylorin kaava. Olkoon x R, n N. Jos f C n (B(x, h)) eräällä h >, niin kaikilla x B(x, h) on f(x) = T n (x; x ) + R n (x; x ), missä jäännöstermi R n (x; x ) saadaan kaavasta R n (x; x ) = x f (n) (t)(x t) n dt. (n )! x Tod. (d Alembert , Lagrange ) Induktio n:n suhteen. n = : Jos f C (B(x, h)) eli f on jatkuva, niin kaikilla x B(x, h) on f(x) = f(x ) + (f(x) f(x )) = f(x ) + = R (x; x ) = f(x) T (x; x ) = / x x f(t) = T (x; x ) + x x f (t) dt. x x f (t) dt n > : Jos f C n (B(x, h)), niin myös f C n (B(x, h)). Induktio-oletuksen perusteella kaikilla x B(x, h) on x f(x) T n 2 (x; x ) = f (n ) (t)(x t) n 2 dt. (n 2)! x Väite seuraa osittaisintegroinnilla: x x f (n ) (t)(x t) n 2 dt = / x x f (n ) (t) (x t)n n = f (n ) (x ) (x x ) n + n n = f(x) T n 2 (x; x ) f (n ) (x ) (x x ) n = (n )! }{{} = T n (x; x ) x f (n) (x t)n (t) x n x x f (n) (t)(x t) n dt dt x f (n) (t)(x t) n dt. (n )! x Huom. ) Taylorin kaavan jäännöstermi R n (x; x ) ei ole yleensä minkään (suppenevan) sarjan jäännöstermi eikä edes määritelty kaikilla n N. 2) Seuraavassa lauseessa R n (x; x ) esitetään käytännöllisemmässä muodossa..2. Lagrangen jäännöstermimuoto. Edellisen lauseen tilanteessa R n (x; x ) = f (n) (ξ) (x x ) n x B(x, h), missä ξ = ξ x on jokin x :n ja x:n välissä oleva luku. Tod. R n (x; x ):n lausekkeessa funktio t (x t) n säilyttää merkkinsä integroimisvälillä [x, x] (tai [x, x ]) ja f (n) on jatkuva. Integraalilaskennan yleistetyn väliarvolauseen I.4.2.a) mukaan 2
3 R n (x; x ) = x (n )! = f (n) (ξ) (n )! / x jollakin ξ, joka on x :n ja x:n välissä. x x f (n) (t)(x t) n dt = (x t)n n = f (n) (ξ) (x x ) n x (n )! f (n) (ξ) (x t) n dt x Huom. ) Erikoistapauksessa n = on R (x; x ) = f (ξ)(x x ) ja T (x; x ) = f(x ). Tällöin siis f(x) = f(x ) + f (ξ)(x x ) eli saadaan diff.-laskennan väliarvolause, joten Lagrangen jäännöstermi on sen yleistys. 2) Muista: Taylorin kaava ja Lagrangen jäännöstermi pätevät kaikille f C n (B(x, h)); f:llä ei tarvitse olla potenssisarjaesitystä eikä edes (n + ):ttä derivaattaa..3. Esimerkkejä. ) Funktiolle f(x) = e x on f (k) (x) = e x ja siis f (k) () = kaikilla k. Kun n N ja x R, on siis missä ξ x on :n ja x:n välissä. T n (x; ) = + x + x2 2! xn (n )! ja R n (x; ) = eξ x xn, 2) Jos f(x) = sin x, niin f (x) = cos x, f (x) = sin x, f (3) (x) = cos x, f (4) (x) = sin x,..., joten (f (k) ()) k= = (,,,,,,...). Kun n N, x R, on siis T 2n (x; ) = T 2n (x; ) = x x3 3! + x5 5!... + ( )n x 2n (2n )!, R 2n (x; ) = R 2n+ (x; ) = f (2n+) (ξ x ) (2n + )! missä ξ x on :n ja x:n välissä. x 2n+ = ( ) n cos ξ x (2n + )! x2n+, 3) Jos f(x) = cos x, niin f (x) = sin x, f (x) = cos x, f (3) (x) = sin x, f (4) (x) = cos x,..., joten (f (k) ()) k= = (,,,,,,...). Kun n N, x R, on siis T 2n 2 (x; ) = T 2n (x; ) = x2 2! + x4 4!... + ( )n x 2n 2 (2n 2)!, R 2n (x; ) = R 2n (x; ) = f (2n) (ξ x ) (2n)! missä ξ x on :n ja x:n välissä. 4) Olkoon f(x) = x 3 ja keskus x =. Tällöin 3x 2, kun x >, f (x) = 3x 2, kun x <,, kun x =, x 2n = ( ) n cos ξ x (2n)! x2n, 6x, kun x >, ja f (x) = 6x, kun x <,, kun x =. Koska f () = ja f () =, niin T 2 (x; ) =. Nyt kuitenkaan f (3) () ei ole olemassa, joten myöskään T 3 (x; ) ei ole olemassa. 3
4 Jos f (n) (x) M < kaikilla x B(x, h), niin L.2 mukaan f(x) T n (x; x ) = R n (x; x ) M hn kaikilla x B(x, h). Tästä on hyötyä, jos halutaan approksimoida f:ää polynomilla T n (x; x )..4. Esimerkkejä. ) Laskettava Taylorin kaavan avulla /e niin tarkasti, että virhe < 4. Ratk. Edell. esim..3.) mukaan e x = + x + x2 2! xn (n )! + R n(x; ) ja R n (x; ) = eξ xn, missä ξ on :n ja x:n välissä. Valitaan x =, jolloin < ξ < ja R n ( ; ) = eξ e ξ ( )n = <. Koska 7! = 54 ja 8! = 432, niin R 8 ( ; ) < /8! <, Kun valitaan n = 8, saadaan siis e T 7( ; ) = + 2! 3! + 4! 5! + 6! 7! = = 3 (, 36786), 28 missä virhe <, Jos tulos ilmoitetaan desimaalilukuna 3/28, 3679, niin pyöristysvirhe <, 5 4. Koska tällöin vielä (, 25 +, 5) 4 < 4, niin /e, 3679 on riittävän tarkka likiarvo. 2) Approksimoitava funktiota f(x) = cos x välillä ] π/4, π/4[ sopivalla Taylorin polynomilla niin, että virhe < 4. Ratk. Esimerkin.3.3) mukaan f(x) = T 2n 2 (x; ) + R 2n (x; ), missä R 2n (x; ) = cos ξ x x 2n x2n (2n)! (2n)! < (π/4)2n (2n)! < ] (2n)!, kun x π 4, π [ 4 (ξ x on :n ja x:n välissä). Koska (2 3)! = 72 ja (2 4)! = 432, niin riittävän tarkka approksimaatio saadaan, kun valitaan n = 4. Vaaditulla tarkkuudella siis cos x T 6 (x; ) = x2 2 + x4 24 x6 72, x < π 4. VI.2. Kehitelmän yksikäsitteisyys Palautetaan mieleen Diff.I.:stä: Jos on olemassa f (x ) ja merkitään ε(x) = f(x) f(x ) x x f (x ), x x, niin lim ε(x) = ja ε(x)(x x ) = f(x) f(x ) f (x )(x x ). x x f(x ) + f (x )(x x ) = T (x; x ), joten Saadussa lausekkeessa on f(x) = T (x; x ) + (x x )ε(x), missä lim ε(x) =. x x 4
5 Jos f C n (B(x, h)), niin Taylorin kaavan ja Lagrangen jäännöstermin mukaan on f(x) T n (x; x ) = R n (x; x ) = f (n) (ξ x ) (x x ) n, missä ξ x on x :n ja x:n välissä. Jos merkitään ε(x) = f (n) (ξ x ) (x x ), niin f(x) T n (x; x ) = (x x ) n ε(x), missä ε(x) = f (n) (ξ x ) (x x ), kun x x. Itse asiassa voidaan helposti saada vähän vahvempikin muoto: 2.. Lause. Jos f C n (B(x, h)), niin f:llä on Taylorin kehitelmä f(x) = T n (x; x ) + (x x ) n ε(x), missä lim ε(x) =. x x Tod. Kuten edellä f(x) T n (x; x ) = f (n) (ξ x ) (x x ) n, missä ξ x on x :n ja x:n välissä. Koska f (n) on jatkuva pisteessä x, niin lim x x f (n) (x) = f (n) (x ). Kun x x, niin ξ x x, joten f (n) (ξ x ) = f (n) (x ) + ε (x), missä ε (x), kun x x. Siis f(x) = T n (x; x ) + f (n) (x ) (x x ) n + ε (x) (x x ) n = T n (x; x ) + (x x ) n ε(x), missä ε(x) = ε (x). x x 2.2. Yksikäsitteisyyslause. Olkoon f määritelty ympäristössä B(x, h) ja olkoon f(x) = a + a (x x ) a n (x x ) n + (x x ) n ε (x) = b + b (x x ) b n (x x ) n + (x x ) n ε 2 (x), missä lim x x ε j (x) =, j =, 2. Tällöin a k = b k kaikilla k ja siis ε (x) = ε 2 (x) kaikilla x B(x, h), ts. kehitelmät ovat identtiset. Tod. Vastaoletus: a k b k jollakin k {,, 2,..., n}. Olkoon k pienin tällainen indeksi. Tällöin kaikilla x B(x, h) on = f(x) f(x) = (a k b k )(x x ) k (a n b n )(x x ) n + (x x ) n [ε (x) ε 2 (x)] Oletetaan, että x x ja jaetaan (x x ) k :lla, jolloin kaikilla x B(x, h), x x, on = (a k b k ) (a n b n )(x x ) n k + (x x ) n k [ε (x) ε 2 (x)]. Kun annetaan x x, niin a k b k = eli a k = b k, RISTIRIITA. Täytyy siis olla a k = b k kaikilla k, ja siten myös ε (x) = ε 2 (x), kun x x. 5
6 2.3. Seuraus. Jos f C n (B(x, h)) ja f:llä on edelläoleva kehitelmä f(x) = a + a (x x ) a n (x x ) n + (x x ) n ε(x) kaikilla x B(x, h), missä lim x x ε(x) =, niin kyseessä on f:n Taylorin kehitelmä, ts. kaikilla x B(x, h) on { Tn (x; x ) = a + a (x x ) a n (x x ) n R n+ (x; x ) = (x x ) n ε(x). Tod. Lauseen 2. mukaan f:llä on Taylorin kehitelmä ja L 2.2 nojalla Taylorin kehitelmä on identtinen annetun kehitelmän kanssa. Huom. ) Seurauksessa 2.3 on (x x ) n ε(x) = R n+ (x; x ) = f(x) T n (x; x ), joten ε(x) = f(x) T n(x; x ) (x x ) n kaikilla x B(x, h), x x. Siten mm. on olemassa jatkuvat derivaatat ε (x),..., ε (n) (x), kun < x x < h. 2) Seurauksen 2.3 merkitys on siinä, että sen avulla Taylorin polynomit on usein helpompi muodostaa kuin laskemalla derivaatat Lause. Olkoon potenssisarjan a k (x x ) k suppenemissäde R >. Jos f(x) = k= a k (x x ) k kaikilla x B(x, h) (missä siis h R), niin f:n pisteeseen x liittyvät Taylorin k= polynomit ovat sarjan osasummat T n (x; x ) = ja jäännöstermillä on lauseke R n+ (x; x ) = n a k (x x ) k k= k=n+ a k (x x ) k, kun x B(x, h). Tod. L V.2.5 = f C (B(x, h)) ja f (k) (x ) = a k. Siis f(x) = T n (x; x ) + a k (x x ) k = T n (x; x ) + (x x ) n ε(x), missä ε(x) = väitteen. k=n+ k=n+ a k (x x ) k n. Lauseen V.2.2 nojalla 2.5. Esimerkkejä. ) Muodosta T n (x; ) funktiolle f, f(x) = x 2. Ratk. Geometrisen sarjan summakaavan mukaan kaikilla x ], [ on Koska f C (B(, )), niin f(x) = x 2 = + x2 + x x 2k +... = lim ε(x) =, joten Seuraus 2.3 antaa x x (x 2 ) k = k= x 2k. k= T n (x; ) = + x 2 + x x 2k, kun n = 2k tai n = 2k +. 6
7 2) Muodosta T 4 (x; ) funktiolle f: R R, f(x) = e x2. Ratk. Taylorin kaavan nojalla on Sijoittamalla y = x 2 saadaan e y = + y + y2 2 + y2 ε(y), missä lim y ε(y) =. ( ) e x2 = + x 2 + x4 2 + x4 ε(x), ε(x) = ε(x 2 ). Koska lim ε(x) = lim ε(x 2 ) = ja f C 4 (R) (jopa f C (R)), niin edellä ( ):ssä on saatu f:n x x Taylorin kehitelmä, joten erityisesti on T 4 (x; ) = + x x4 funktiolle f. 3) Esim. IV.3.7 mukaan f(x) = ln( + x) = ( ) k xk k = x x2 2 + x3 3 x4 +..., kun x <. 4 Lisäksi ketjusäännön mukaan f C (B(, )), joten L 2.4 ja S 2.3 perusteella f:llä on Taylorin kehitelmä ln( + x) = x x2 2 + x3 3 x4 xn ( )n 4 n + xn ε(x), lim ε(x) =. x 4) Muodosta T 4 (x; ) funktiolle f: R R, f(x) = ln(+2x 2 ), lähtemällä funktion x ln(+x) kehitelmästä. Ratk. Kun y <, niin ln( + y) = y 2 y2 + y 2 ε(y), missä lim ε(y) =. Sijoitetaan y y = 2x 2 : 2x 2 < x < / 2. Jos siis x < / 2, niin ( ) f(x) = ln( + 2x 2 ) = 2x 2 2 4x4 + 4x 4 ε(2x 2 ) = 2x 2 2x 4 + x 4 ε(x), missä ε(x) = 4ε(2x 2 ), kun x. Koska lisäksi f C 4 (R), niin ( ) on f:n Taylorin kehitelmä ja siis T 4 (x; ) = 2x 2 2x 4. Erityisesti f () =, f () = 2! 2 = 4, f (3) () = ja f (4) () = 4! ( 2) = Lause. Oletetaan, että f, g C n (B(x, h)) ja α R on vakio. Olkoot f:n ja g:n Taylorin kehitelmät missä f(x) = T f n (x; x ) + R f n+ (x; x ) ja g(x) = T g n(x; x ) + R g n+ (x; x ), { T f n (x; x ) = a + a (x x ) a n (x x ) n = T f (x) T g n(x; x ) = b + b (x x ) b n (x x ) n = T g (x) ja jäännöstermit ovat muotoa R f n+ (x; x ) = (x x ) n ε f (x), R g n+ (x; x ) = (x x ) n ε g (x), 7 lim ε f (x) =, x x lim ε g (x) =. x x
8 Tällöin a) summafunktiolla f + g on Taylorin kehitelmä f(x) + g(x) = [T f n (x; x ) + T g n(x; x )] + [R f n+ (x; x ) + R g n+ (x; x )], b) funktiolla αf on Taylorin kehitelmä ja c) tulofunktiolla f g on Taylorin kehitelmä (αf)(x) = αt f n (x; x ) + αr f n+ (x; x ) f(x)g(x) = T fg n (x; x ) + (x x ) n ε(x), missä Tn fg (x; x ) = a b + (a b + a b )(x x ) (a b n + a b n a n b )(x x ) n ja ε(x), kun x x. Tod. a) Koska (f + g) (k) (x) = f (k) (x) + g (k) (x) ja deg(tn f (x; x ) + Tn(x; g x ) n, niin Tn f (x; x )+Tn(x; g x ) on (f +g):n n:s Taylorin polynomi. Koska lisäksi R f n+ (x; x )+R g n+ (x; x ) = (x x ) n ε(x), missä ε(x) = ε f (x) + ε g (x), kun x x, ja f + g C n (B(x, h)), niin kohta a) on todistettu. b) Vastaavasti. c) Todetaan aluksi, että f, g C n (B(x, h)) = fg C n (B(x, h)). Perustelu: D(fg) = Df g + f Dg = D (2) (fg) = D (2) f g + Df Dg + Df Dg + f D (2) g = D (2) f g + 2Df Dg + f D (2) g ja yleisesti D (k) (fg) = binomikerroin. Nyt i+j=k ( i j ) D (i) f D (j) g, missä f(x)g(x) = Tn fg (x; x ) + (x x ) n+ Q(x) + T f (x)(x x ) n ε g (x) + T g (x)(x x ) n e f (x) + (x x ) n+n ε f (x)ε g (x) = Tn fg (x; x ) + (x x ) n ε(x) missä Q(x) on korkeintaan astetta n oleva polynomi ja ε(x) = (x x )Q(x) + T f (x)ε g (x) + T g (x)e f (x) + (x x ) n ε f (x)ε g (x). ( i j ) on Koska tässä ε(x), kun x x, niin saatu kehitelmä on fg:n Taylorin kehitelmä. Esim. Muodostettava T 4 (x; ) funktiolle f(x) = sin x ln( + x). Ratk. Käytetään suoraan yksikäsitteisyyslauseen seurausta 2.3 (eikä vedota edelliseen lauseeseen). Esim..3.2) ja 2.5.3) mukaan sin x = x 6 x3 + x 4 ε (x) (x R), ln( + x) = x 2 x2 + 3 x3 + x 3 ε 2 (x) ( x < ), missä lim x ε i (x) =, i =, 2. Siis kaikilla x ], [ on sin x ln( + x) = x x x 2 x2 + x 3 x3 + x x 3 ε 2 (x) 6 x3 x + 6 x3 2 x2 6 x3 3 x3 6 x3 x 3 ε 2 (x) + x 4 ε (x) x x 4 ε (x) 2 x2 + x 4 ε (x) 3 x3 + x 4 ε (x) x 3 ε 2 (x) 8
9 = x 2 2 x3 + 6 x4 + x 4 ε(x), missä ε(x) = ε 2 (x) + x [ 2 + ε (x)] + x 2 [ 8 2 ε (x) 6 ε 2(x)] + x 3 [ 3 ε (x) + ε (x)ε 2 (x)]. Koska ε(x), kun x, ja f C 4 (], [), niin on saatu Taylorin kehitelmä, ja erityisesti T 4 (x; ) = x 2 2 x3 + 6 x4. Siten f() = f () =, f () = 2! = 2, f (3) () = 3! ( 2 ) = 3 ja f (4) () = 4!/6 = 4. Huom. Koska sin x:n ja ln( + x):n kehitelmissä vakiotermi =, niin T 4 (x; ):n saamiseksi funktiolle f(x) = sin x ln( + x) riitti ottaa T 3 (x; ):t sin x:lle ja ln( + x):lle. VI.3. Taylorin kaavan sovelluksia 3.. Raja-arvojen laskeminen. Jos on olemassa kehitelmä f(x) = T n (x; x ) + R n+ (x; x ) pisteen x ympäristössä, niin f:n käyttäytyminen x :n lähellä hallitaan hyvin (sitä paremmin mitä suurempi n on). Tästä voi olla hyötyä laskettaessa raja-arvoja, joissa x x. sin x x Esim.. Määritä lim x x( cos x). Ratk. Aikaisempien esimerkkien perusteella kaikilla x R on sin x = x 6 x3 + x 4 ε (x) ja cos x = 2 x2 + x 3 ε 2 (x), missä lim x ε i (x) = (i =, 2). Kun < x < π, on siis sin x x x( cos x) = 6 x3 + x 4 ε (x) 2 x3 x 4 ε 2 (x) = 6 + xε (x) 2 xε 2(x) /6 x /2 = 3. ( Esim. 2. Määritä lim cos ( x ) ) n 2, kun x R. n n Ratk. cos ( x ) x >, kun n n < π 2 n > 2 ( π x. Merkitään y n = cos ( x ) ) n 2 ja tarkastellaan jonoa (ln y n ). n Koska niin cos y = 2 y2 + y 3 ε (y), lim ε (y) =, y ln( + z) = z + zε 2 (z) = z( + ε 2 (z)), z <, ( ln y n = n 2 ln cos ( x = ln y n = n 2 z( + ε 2 (z)) = (kun n, niin z ). Siis lim ε 2 (z) =, z n) ) = n 2 ln( + z), missä z = x 2 ( x + 2( n) n ( 2 x2 + x3 n ε ( x n lim y n = lim n n eln y n = e 2 x2. 9 ) 3ε ( x ) n ) ) ( + ε 2 (z)) n 2 x2
10 Esim. 3. Määritä lim x sin(sin x) sin x x 3. sin y = y 6 y3 + y 4 ε(y), lim ε(y) =. y Sijoittamalla y = sin x saadaan sin(sin x) = sin x 6 (sin x)3 + (sin 4 x)ε(sin x) = sin(sin x) sin x x 3 = 6 ( sin x x ) 3 ( sin x ) 3(sin + x)ε(sin x) x x 6 + = Integraalien likiarvot. Esim.. Lasketaan e x2 dx, :n tarkkuudella. e y = + y + y2 2! yn (n )! + eξ yn, missä ξ on :n ja y:n välissä ja y. Sijoittamalla y = x 2 saadaan e x2 = + x 2 + x4 2! x2(n ) (n )! + eξ x2n, < ξ < x 2. Nyt < x = < ξ < x 2 = R 2n (x) = eξ x2n e x2n, joten integroitaessa virhetermille saadaan arvio R 2n (x) dx e x 2n dx = e / x 2n+ (2n + ) = e <,, (2n + ) kun n 5 (tällöin itse asiassa on virhe <, 3). Haettu likiarvo on (pyöristys desimaaliluvuksi mahtuu vielä virheeseen mukaan) ) ( + x 2 + x4 2 + x6 6 + x8 dx = = 5, Esim. 2. Laske likiarvo integraalille ln( + x) dx, :n tarkkuudella korvaamalla in- x tegroitava sopivalla Taylorin polynomilla.,2 Ratk. Esimerkin IV.3.7 mukaan ln( + x) = ( ) k xk, kun x <, joten k ln( + x) x = ( ) k xk k kun x, x <.
11 ln( + x) Koska nyt lim x x nimittäin määritellään =, niin integraalin epäoleellisuus alarajalla on vain näennäistä. Jos niin g on jatkuva ja { ln( + x) g: ], [ R, g(x) =, kun x ], [, x x, kun x =,,2 ln( + x) dx = x,2 g(x) dx. Tällöin g(x) = ( ) k xk k = T n (x; ) + R n (x; ), x <. Sarja toteuttaa Leibnizin lauseen oletukset, kun < x <, joten ja R n (x; ) < xn n +, kun < x <, ja R n(; ) = (n =, 2,...),2,2,2 x n /,2 R n (x; ) dx R n (x; ) dx < n + dx = x n+ (, 2)n+ = (n + ) 2 (n + ) 2. Jos n =, niin (, 2)2 2 2 =,. Siis riittää korvata g(x) T (x; ) =, jolloin,2 ln( + x) dx = x,2 g(x) dx,2 dx =, Ääriarvot. Kertausta: Jos f:llä on (lokaali) ääriarvokohta pisteessä x ja jos on olemassa f (x ), niin f (x ) = (ei kääntäen). Jos lisäksi on olemassa f (x ), niin x on minimikohta, kun f (x ) >, ja x on maksimikohta, kun f (x ) <. Jos kuitenkin f (x ) =, ei tiedetä vielä mitään Lause. Olkoon f C n (B(x, h)) ja oletetaan, että f (x ) = f (x ) =... = f (n ) (x ) = ja f (n) (x ). Tällöin a) n parillinen, f (n) (x ) < = x on (oleellinen lokaali) maksimikohta, b) n parillinen, f (n) (x ) > = x on (oleellinen lokaali) minimikohta, c) n pariton = ei ääriarvoa x :ssa. Tod. Koska f (x ) = f (x ) =... = f (n ) (x ) =, niin T n (x; x ) = f(x ). Jos siis < x x < h, niin Taylorin kaavan mukaan on ( ) f(x) f(x ) = f (n) { (ξ x ) (x x ) n ]x, x[, jos x > x, ξ x, ]x, x [, jos x < x. Oletuksen mukaan f (n) on jatkuva pisteessä x, joten on olemassa sellainen r >, r h, että f (n) (x) on samanmerkkinen kuin f (n) (x ) aina, kun x x < r. Siis myös f (n) (ξ x ) on samanmerkkinen kuin f (n) (x ) aina, kun < x x < r ( ξ x x < x x ). Kun < x x < r, voidaan tapauksissa a) c) päätellä:
12 a) Koska f (n) (ξ x ) < ja (x x ) n >, niin ( ) = f(x) f(x ) <, joten x on maksimikohta (ja oleellinen). b) Nyt f (n) (ξ x ) >, (x x ) n >, joten ( ) = f(x) f(x ) > ja siis x on minimikohta (myös oleellinen). { >, kun x > c) Koska (x x ) n x, ja f (n) (ξ <, kun x < x x ) säilyttää merkkinsä, niin ( ):n mukaan f(x) f(x ) vaihtaa merkkinsä, kun x ohitetaan, joten x ei ole ääriarvokohta. Esim. Onko funktiolla f, f(x) = cos x + cosh x, ääriarvoa kohdassa x =? f (x) = sin x + sinh x = f () = f (x) = cos x + cosh x = f () = + = f (x) = sin x + sinh x = f () = f (4) (x) = cos x + cosh x = f (4) () = + = 2 >, 4 parillinen Siis f:llä on :ssa lokaali minimi. VI.4. Taylorin sarja Olkoon x R, h > ja B(x, h) = ]x h, x + h[. Kun f C (B(x, h)), potenssisarja (TS) f(x ) + f (k) (x ) (x x ) k k= on f:n Taylorin sarja riippumatta siitä, suppeneeko sarja vai ei (sopimalla f () (x ) = f(x ) voidaan tämäkin termi siirtää summaan mukaan). 4.. Esim. Olkoon potenssisarjan a k (x x ) k suppenemissäde h ja f ko. sarjan summafunktio. Lauseen V.2.5 mukaan f C (B(x, h)) ja f (k) (x ) = ()a k kaikilla k, ts. on summafunktionsa f Taylorin sarja. a k (x x ) k Olkoon f C (B(x, h)) ja n N. Funktion f Taylorin sarjan (TS) n:s osasumma on f:n Taylorin polynomi T n (x; x ). Koska f C n (B(x, h)), niin Taylorin kaavan mukaan ja Lagrangen jäännöstermin mukaan on missä ξ x,n on x :n ja x:n välissä. f(x) T n (x; x ) = R n (x; x ) = f (n) (ξ x,n ) (x x ) n, 4.2. Lause. Funktio f C (B(x, h)) on välillä ]x r, x +r[ ( < r h) jonkin suppenevan potenssisarjan a k (x x ) k summa k= R n (x; x ) n kaikilla x ]x r, x + r[. 2 k=
13 Tällöin a k (x x ) k on f:n Taylorin sarja (TS), ja siis k= ( ) f(x) = f(x ) + f (k) (x ) (x x ) k x ]x r, x + r[. Tod. = : Esim. 4. = ( ) pätee. Taylorin kaavan jäännöstermi on nyt tämän suppenevan sarjan jäännöstermi. =: Kun x B(x, h), niin R n (x; x ) n T n (x; x ) n f(x) (TS) suppenee ja sen summa = f(x). Funktio f C (B(x, h)) ei välttämättä ole suppenevan potenssisarjan summa millään välillä ]x r, x + r[. Tällaisessa tapauksessa joko (TS) suppenee vain pisteessä x (ts. suppenemissäde = ) tai (TS):n suppenemissäde >, mutta ( ) ei päde millään r >. Esimerkin V.2. funktio f C (R) ja f (k) () = kaikilla k. Tästä seuraa, että f:n Taylorin sarja (TS) (jossa x = ) on =, joten (TS):n summa = < f(x) kaikilla x >. Siten ( ) ei päde millään r > Muutamien funktioiden Taylorin sarjoja:. Eksponenttifunktio. Jo esimerkissä IV.3.9.2) todettiin, että e x = k= x k = + x + x2 2! + x3 3! +... x R. Tämän tuloksen voi johtaa myös e x :n Taylorin kehitelmien avulla: Esim..3.) mukaan kaikilla n N ja x R on e x = + x + x2 2! xn (n )! + R n(x; ), missä R n (x; ) = eξx,n missä ξ x,n on :n ja x:n välissä. Kiinteällä x R on siis x k koska sarja suppenee. k= Jos x R, on siis myös R n (x; ) max(, e x ) x n e x = e x +(x x ) = e x e x x = e x + ex ts. e x saatiin kehitettyä (x x ):n potenssien mukaan. Jos kantalukuna on a >, saadaan a x = e x ln a = + ln a!, n x n,! (x x ) + ex 2! (x x ) x R, (ln a)2 x + x x R. 2! 3
14 2. Trigonometriset funktiot. Esimerkin.3.2) mukaan kaikilla n N ja x R on sin x = x x3 3! + x5 5!... + ( )n x 2n (2n )! + R 2n+(x; ), R 2n+ (x; ) = ( ) n cos ξ x,n (2n + )! x2n+ (ξ x,n on :n ja x:n välissä). Koska jokaisella kiinteällä x R on R 2n+ (x; ) x 2n+ (2n + )! sin x = x x3 3! + x5 5!... x R., niin n Vastaavasti cos x = x2 2! + x4 4!... x R. Samoin 3. Logaritmifunktio. Esimerkissä IV.3.7 todettiin, että ln( + x) = x x2 2 + x3 3 x4 +..., kun < x. 4 ln( x) = x x2 2 x3 3 x4 +..., kun x <. 4 Koska ln + x = ln( + x) ln( x), niin eo. kehitelmistä vähentämällä saadaan x ln + x x = 2 ( x + x3 3 + x ), kun < x <. Tästä sarjasta voi laskea luvun ln y likiarvoja millä tahansa y >, sillä jokaista y > kohti on olemassa yksikäsitteinen x ], [ s.e. y = ( + x)/( x): + x y = y + x = y xy x = x y +. Esim. Koska 2 = + x x x = ( 3, niin ln 2 = ( ) 3 3 ( ) 5 ) Tämä 3 suppenee huomattavasti nopeammin kuin sarja ln 2 = Jos merkitään 4 R 2n+ = ln 2 2( 3 + ( ) 3 3 ( ) 2n ) n, 3 niin ( < R 2n+ = 2 = 2 2n + ( 3 ( ) 2n+ 2n + ( ) 2n+3 ) + 3 2n ) 2n+ ( + 2n + ) 2 2n + ) 4 ) n + 3( 3 2n + 5( 3 4
15 2 < 2n + ( 3 2 = 2n + ( 3 Jos valitaan n = 3, niin < R 7 < 4 7( 3 ) 2n+ ( ( ) 2 ( 4 ) ) ) 2n+ (/9) = ln 2 2( 3 + ( ) 3 3 ( ) 5 ) missä virhe <, 2 (laskin ln 2 =, ). ( 4(2n + ) 3 ) 5 = 684 < 2 4, joten 4. Arkustangenttifunktio. Esimerkin V.2.8.2) mukaan ) 2n. = 842 =, , 25 arc tan x = x x3 3 + x5 5 x x [, ]. 7 Luvun π likiarvojen laskemiseen saadaan tehokkaampi sarja seuraavasti. Todistetaan ensin ns. Machin in kaava: (M) π 4 = 4 arc tan arc tan Merkitään β = arc tan(/5), γ = arc tan(/239) ja α = 4β γ. Koska kaikilla x > on < arc tan x < x, niin < 4β < (4/5), < γ < (/239) ja (/239) < α < (4/5), joten erityisesti 2 π < α < 2π. Siten riittää osoittaa, että tan α = = tan(π/4). Tangentin yhteenlaskukaavan nojalla saadaan tan 2β = ja tan α = 2 tan β tan 2 β = 2/5 /25 = 5 2 tan 2β, tan 4β = 2 tan 2 2β = /2 25/44 = 2 9 tan 4β tan γ + tan 4β tan γ joten (M) on osoitettu oikeaksi. Koska arc tan x = ( ) k x2k+, x [, ], niin 2k + k= 2/9 / = = + 2/(9 239) =, ( ) k π = 6 (2k + ) 5 2k+ 4 ( ) k (2k + ) 239 2k+ k= k= ( = ) ( ) Molemmat sarjat toteuttavat Leibnizin lauseen ehdot, joten esimerkiksi ( π ) < 4 ( = π ) ±, 3, 46 ±, Vielä pari esimerkkiä Taylorin sarjoista: 5
16 4.4. Esimerkkejä. ) Muodosta (x+3):n potenssien mukaan etenevä Taylorin sarja funktiolle x x 2 4. Ratk. Merkitään x + 3 = t. Ol. x ±2. x 2 4 = [ 4 x 2 ] = [ x t 5 ] t = [ 4 t ] [ 5 = (t/5) 4 t k 5 k= ( = ) ( 4 5 k+ t k = ( 4 5 k= k= k= ( ) ] k t 5 ) k+ ) (x + 3) k, kun x+3 = t < eli 4 < x < 2, jolloin molemmat edelläolevat geometriset sarjat suppenevat. 2) Muodosta x:n potenssien mukaan etenevä Taylorin sarja funktiolle x 2 π π/2 dt x cos 2 t. Ratk. Jos x <, niin myös x cos 2 t <, joten integroitava voidaan kehittää geometriseksi sarjaksi x cos 2 t = + x cos2 t + x 2 cos 4 t + x 3 cos 6 t x k cos 2k t Olkoon x ], [ kiinteä. Koska tällöin x k cos 2k t x k kaikilla t R ja k x k suppenee, niin Weierstrassin lauseen mukaan eo. sarja suppenee tasaisesti arvoilla t R, erityisesti arvoilla t [, 2π]. Voidaan siis integroida termeittäin: 2 π π/2 dt x cos 2 t = 2 π ( π/2 π 2 + x cos 2 t dt + x 2 = + 2 x x π/2 cos 4 t dt x k 3... (2k ) (2k) kaikilla < x < (integroinnista katso esim. I.8.B.2, s. 27). π/2 x k +... ) cos 2k t dt Trigonometristen funktioiden olemassaolo. Seuraavassa esitetään tapa, millä sinija kosinifunktiot voidaan määritellä käyttämättä kulman käsitettä. Unohdetaan kaikki, mitä olemme kuvitelleet tietävämme sini- ja kosinifunktioista. Tarkastellaan potenssisarjoja (s) x x3 3! + x5 5!... ja (c) x2 2! + x4 4!.... 6
17 o. Sarjat (s) ja (c) suppenevat itseisesti kaikilla x R. Tod. Merkitään f k (x) = ( ) k x 2k+. Jos x, niin (2k + )! f k+ (x) f k (x) = x 2k+3 (2k + )! (2k + 3)! x 2k+ = x 2 (2k + 2)(2k + 3) k ts. (s) suppenee suhdetestin mukaan itseisesti arvolla x; sarja (c) vastaavasti. Määritellään nyt sin x = x x3 3! + x5 5!... x R, cos x = x2 2! + x4 4!... x R ja todetaan seuraavat ominaisuudet. 2 o. sin = ja cos = selvästi. 3 o. Sarjoista termeittäin derivoimalla saadaan D sin x = cos x ja D cos x = sin x. Olkoon x R, jota pidetään kiinteänä. Merkitään A(y) = sin(x + y) sin x cos y cos x sin y, A() = sin x sin x =, B(y) = cos(x + y) cos x cos y + sin x sin y, B() = cos x cos x =, { A (y) = cos(x + y) + sin x sin y cos x cos y = B(y) = B (y) = sin(x + y) + cos x sin y + sin x cos y = A(y). Määritellään F (y) = A(y) 2 + B(y) 2 kaikilla y R. Tällöin F (y) = 2A(y)A (y) + 2B(y)B (y) = 2A(y)B(y) 2B(y)A(y) = kaikilla y R, joten F (y) = C (vakio) kaikilla y R. Koska F () =, niin C =, joten kaikilla y R on F (y) = = A(y) 2 + B(y) 2 A(y) = = B(y). Siis kaikilla x, y R on voimassa sin(x + y) = sin x cos y + cos x sin y cos(x + y) = cos x cos y sin x sin y. 4 o. Sarjojen määritelmien mukaan sin( x) = sin x ja cos( x) = cos x, joten = cos = cos(x x) = cos x cos( x) sin x sin( x) = cos 2 x + sin 2 x kaikilla x R. 5 o. Kun x, niin sin x x = x2 3! +... = sin x x. x Yhteyden trigonometriasta tunnettuihin määritelmiin antaa seuraava tulos: Huom. Olkoon s yksikköympyrän pisteiden (, ) ja (x, y ) välisen kaaren pituus. Silloin on x = cos s ja y = sin s. Tod. Kaarella on parametriesitys α(t) = (x(t), y(t)) = (cos t, sin t), t t, jossa x = x(t ) = cos t ja y = y(t ) = sin t. Kaaren pituus on s = t x (t) 2 + y (t) 2 dt = t 7 sin 2 t + cos 2 t dt = t.
18 4.6. Binomisarja. Olkoon µ R vakio. Tarkastellaan funktiota f(x) = ( + x) µ, kun x > (eräillä µ R on ( + x) µ määritelty myös muilla x:n arvoilla). Selvästi f C (], [) ja f (k) (x) = µ(µ )... (µ k + )( + x) µ k x >. Erityisesti f (k) () = µ(µ )... (µ k + ) kaikilla k N, joten funktion f origossa muodostettu Taylorin sarja on µ(µ )... (µ k + ) (BS) + x k = + a k x k. }{{} =a k Jos µ = n N {}, on a k = (Binomikerroin binomikaava Huom. Yleisesti n(n )... (n k + ) ( ) n k = ( n k ), kun k > n, =, kun k n. (n k)! on Pascalin kolmion n:nnen rivin k:s alkio, k =,,..., n.) ( + x) n = + ( ) ( ) n n = ja k n k (a + b) n = a n( + b a n a k x k = ( ) n =. ) n = a n n k= n k= ( ) n ( b k a ( ) n x k x R. k ) k = n k= ( ) n a n k b k. k Saadaan siis Osoitamme, että myös tapauksessa µ N {} sarjan (BS) summa = ( + x) µ, kun x < Lause. Kaikilla x ], [ on ( + x) µ = + a k x k, a k = µ(µ )... (µ k + ) Tod. Tapaus µ N {} on selvä (polynomi, päättyvä sarja). Olkoon µ N {}. Tällöin a k kaikilla k ja a k = µ(µ )... (µ k + ) (k + )! µ(µ )... (µ k) = k + µ k = + (/k) (µ/k) a k+., k joten (BS):n suppenemisväli on ], [. Olkoon S(x) = (BS):n summa, kun x ], [. Tällöin S on derivoituva välillä ], [ ja (termeittäin derivoimalla) S (x) = µ(µ )... (µ k + ) x k = (k )! }{{} =b k 8 b k x k,
19 missä b k = ka k. Nyt ja tässä b k+ + b k = b k µ k k ( + x)s (x) = b k x k + b k x k = µ + b k x k + b k x k ( ) ( + x)s (x) = µ + k=2 = µ + b k+ x k + b k x k = µ + (b k+ + b k )x k + b k = b k ( µ k k ( µa k x k = µ + ) + = b k µ k = µa k, jolloin a k x k) = µs(x) x ], [. Olkoon g(x) = S(x)( + x) µ, kun x <. Tällöin kaikilla x ], [ on g (x) = S (x)( + x) µ + S(x)( µ)( + x) µ = ( + x) µ [( + x)s (x) µs(x)] = ( ), joten g(x) = C = vakio. Koska C = g() = S() =, niin S(x) = ( + x) µ, kun x < Esimerkkejä. ) Tuttu geometrinen sarja on myös binomisarja: kun x <, niin + x = ( + x) = x + ( )( 2) x 2 + ( )( 2)( 3) x ! 3! = x + x 2 x ) Kun x <, niin + x = ( + x) /2 = + = 2 x x x ( 2 )( 2 )... ( 2 k + ) x k 3) Funktiolle x arc sin x saadaan sarjakehitelmä, koska sen derivaatta voidaan kehittää binomisarjaksi. t 2 = ( t2 ) /2 = + ( 2 )( 2 )... ( 2 k + ) ( t 2 ) k = + 2 t t t6 +..., t < x dt = arc sin x = = t 2 = x + 2 x x x , x <. 9
20 4.9. Juurien likiarvot. Olkoon a > ja n N. Muodostettava sarjakehitelmä luvulle n a ja etsittävä sen avulla likiarvo juurelle n a. Olkoon q luvun n a likiarvo ja merkitään r = a q n ja α = r. Kun lähtökohdaksi valitaan qn niin tarkka likiarvo, että α <, niin binomisarjasta saadaan n a = a /n = (r + q n ) /n = q( + α) /n = q [ + n α + n ( n ) α 2 + 2! ja tästä voidaan laskea likiarvoja juurelle n a. n ( n )( n 2) 3! ] α Esim. Etsittävä sarjakehitelmä luvulle 3 ja laskettava sen avulla 3:n likiarvo 4 :n tarkkuudella. Ratk. Valitaan q = 7/4 =, 75, jolloin α = / = 6 = 7 49 = = 7 4 = 7 [ 2 + ( 2 )... ( 2 k + ) 4 = 7 4 = 7 4 missä < x k = 7 8 < [ 2 [ k=2 49 k=2 ( ) k +k ( ) /2 49 ( ) k ] 49 2 ( 2 )... (k 2 ) ( k ] 49) 3... (2k 3) ( k ] 2 k = 49) (2k 3) ( ) k ( ) k, < kun k 2. Koska (2k) k=n+ x k < k=n+ ( 49 kun n 2, niin riittävällä tarkkuudella on (laskimella 3 =, ). ) k = ( 49 ) n+ 7 x k, k=2 (/49) = 49 n 48 < 4, = 9 =,
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
8 Potenssisarjoista. 8.1 Määritelmä. Olkoot a 0, a 1, a 2,... reaalisia vakioita ja c R. Määritelmä 8.1. Muotoa
 8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
V. POTENSSISARJAT. V.1. Abelin lause ja potenssisarjan suppenemisväli. a k (x x 0 ) k M
 V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
Luku 4. Derivoituvien funktioiden ominaisuuksia.
 1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
H7 Malliratkaisut - Tehtävä 1
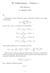 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
MS-A0104 Differentiaali- ja integraalilaskenta 1 (ELEC2) MS-A0106 Differentiaali- ja integraalilaskenta 1 (ENG2)
 MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
Differentiaali- ja integraalilaskenta 1 Ratkaisut 3. viikolle /
 MS-A008 Differentiaali- ja integraalilaskenta, V/07 Differentiaali- ja integraalilaskenta Ratkaisut 3. viikolle / 5. 7.4. Taylorin Polynomit, Taylorin sarjat, potenssisarjat, Newtonin menetelmä Tehtävä
MS-A008 Differentiaali- ja integraalilaskenta, V/07 Differentiaali- ja integraalilaskenta Ratkaisut 3. viikolle / 5. 7.4. Taylorin Polynomit, Taylorin sarjat, potenssisarjat, Newtonin menetelmä Tehtävä
Kompleksianalyysi, viikko 5
 Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 . Lasketaan valmiiksi derivaattoja ja niiden arvoja pisteessä x = 2: f(x) = x + 3x 3 + x 2 + 2x + 8, f(2) = 56, f (x) = x 3 + 9x 2 + 2x + 2, f (2) = 7, f (x) = 2x 2 + 8x + 2, f (2) = 86, f (3) (x) = 2x
. Lasketaan valmiiksi derivaattoja ja niiden arvoja pisteessä x = 2: f(x) = x + 3x 3 + x 2 + 2x + 8, f(2) = 56, f (x) = x 3 + 9x 2 + 2x + 2, f (2) = 7, f (x) = 2x 2 + 8x + 2, f (2) = 86, f (3) (x) = 2x
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
MATEMATIIKAN PERUSKURSSI II kevät 2018 Ratkaisut 1. välikokeen preppaustehtäviin. 1. a) Muodostetaan osasummien jono. S n =
 MATEMATIIKAN PERUSKURSSI II kevät 208 Ratkaisut. välikokeen preppaustehtäviin. a) Muodostetaan osasummien jono S n = n ( k k) k= josta saadaan = ( 0 ) + ( 2) + ( 2 3) + ( n 2 n ) + ( n n) = n, n =, 2,...,
MATEMATIIKAN PERUSKURSSI II kevät 208 Ratkaisut. välikokeen preppaustehtäviin. a) Muodostetaan osasummien jono S n = n ( k k) k= josta saadaan = ( 0 ) + ( 2) + ( 2 3) + ( n 2 n ) + ( n n) = n, n =, 2,...,
Funktiojonot ja funktiotermiset sarjat Funktiojono ja funktioterminen sarja Pisteittäinen ja tasainen suppeneminen
 4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Derivaatta 1.1 Derivaatta Erilaisia lähestymistapoja: I geometrinen
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Derivaatta 1.1 Derivaatta Erilaisia lähestymistapoja: I geometrinen
Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua.
 6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausta 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat: 1. Potenssisarjojen suppenemissäe, suppenemisväli ja suppenemisjoukko. 2. Derivaatan laskeminen
Matematiikan tukikurssi Kertausta 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat: 1. Potenssisarjojen suppenemissäe, suppenemisväli ja suppenemisjoukko. 2. Derivaatan laskeminen
Taylorin sarja ja Taylorin polynomi
 Taylorin sarja ja 1 Potenssisarja c k (x a) k = f (x) määrittelee x:n funktion. Seuraavaksi toteamme mikä yhteys potenssisarjalla on sen määrittelemän funktion derivaattoihin f (a),f (a),f (a),f (3) (a),...
Taylorin sarja ja 1 Potenssisarja c k (x a) k = f (x) määrittelee x:n funktion. Seuraavaksi toteamme mikä yhteys potenssisarjalla on sen määrittelemän funktion derivaattoihin f (a),f (a),f (a),f (3) (a),...
Analyysi III. Jari Taskinen. 28. syyskuuta Luku 1
 Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 6: Alkeisfunktioista
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 6: Alkeisfunktioista Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 28.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 6: Alkeisfunktioista Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 28.9.2016 Pekka Alestalo,
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
funktiojono. Funktiosarja f k a k (x x 0 ) k
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
Integroimistekniikkaa Integraalifunktio
 . Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
. Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
Matematiikan tukikurssi: kurssikerta 12
 Matematiikan tukikurssi: kurssikerta 2 Tenttiin valmentavia harjoituksia Huomio. Tähän tulee lisää ratkaisuja sitä mukaan kun ehin niitä kirjoittaa. Kurssilla käyään läpi tehtävistä niin monta kuin mahollista.
Matematiikan tukikurssi: kurssikerta 2 Tenttiin valmentavia harjoituksia Huomio. Tähän tulee lisää ratkaisuja sitä mukaan kun ehin niitä kirjoittaa. Kurssilla käyään läpi tehtävistä niin monta kuin mahollista.
2 Taylor-polynomit ja -sarjat
 2 Taylor-polynomit ja -sarjat 2. Taylor-polynomi Taylor-polynomi P n (x; x 0 ) funtion paras n-asteinen polynomiapprosimaatio (derivoinnin annalta) pisteen x 0 lähellä. Maclaurin-polynomi: tapaus x 0 0.
2 Taylor-polynomit ja -sarjat 2. Taylor-polynomi Taylor-polynomi P n (x; x 0 ) funtion paras n-asteinen polynomiapprosimaatio (derivoinnin annalta) pisteen x 0 lähellä. Maclaurin-polynomi: tapaus x 0 0.
l 1 2l + 1, c) 100 l=0 AB 3AC ja AB AC sekä vektoreiden AB ja
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
Derivaatan sovellukset (ääriarvotehtävät ym.)
 Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 15.11.2016 Sisältö Alkeisfunktiot 1.1 Funktio I Funktio f : A! B on sääntö, joka liittää
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 15.11.2016 Sisältö Alkeisfunktiot 1.1 Funktio I Funktio f : A! B on sääntö, joka liittää
Ratkaisuehdotus 2. kurssikokeeseen
 Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
Ratkaisuehdotus 2. kurssikoe
 Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
MATP153 Approbatur 1B Harjoitus 5 Maanantai
 MATP153 Approbatur 1B Harjoitus 5 Maanantai 30.11.015 1. (Opiskelutet. 0 s. 81.) Selvitä, miten lauseke sin(4x 3 + cos x ) muodostuu perusfunktioista (polynomeista, trigonometrisistä funktioista jne).
MATP153 Approbatur 1B Harjoitus 5 Maanantai 30.11.015 1. (Opiskelutet. 0 s. 81.) Selvitä, miten lauseke sin(4x 3 + cos x ) muodostuu perusfunktioista (polynomeista, trigonometrisistä funktioista jne).
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Analyysi 1. Harjoituksia lukuihin 4 7 / Syksy Tutki funktion f(x) = x 2 + x 2 jatkuvuutta pisteissä x = 0 ja x = 1.
 Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
H5 Malliratkaisut - Tehtävä 1
 H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa
H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
Mat / Mat Matematiikan peruskurssi C3-I / KP3-I Harjoitus 5 / vko 42, loppuviikko, syksy 2008
 Mat-.3 / Mat-.33 Matematiikan peruskurssi C3-I / KP3-I Harjoitus 5 / vko 4, loppuviikko, syksy 8 Ennen malliratkaisuja, muistin virkistämiseksi kaikkien rakastama osittaisintegroinnin kaava: b a u(tv (t
Mat-.3 / Mat-.33 Matematiikan peruskurssi C3-I / KP3-I Harjoitus 5 / vko 4, loppuviikko, syksy 8 Ennen malliratkaisuja, muistin virkistämiseksi kaikkien rakastama osittaisintegroinnin kaava: b a u(tv (t
MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 25.9.2017 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on
![Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on](/thumbs/47/23658224.jpg) Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 19 Derivaatan määritelmä Määritelmä
Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 19 Derivaatan määritelmä Määritelmä
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio
 MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä
 Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä. L Hospitalin sääntö on tuttu Analyysi :n kurssilta. Se on näppärä keino laskea tiettyjä raja-arvoja, mutta sen käytössä on oltava kuitenkin varovainen.
Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä. L Hospitalin sääntö on tuttu Analyysi :n kurssilta. Se on näppärä keino laskea tiettyjä raja-arvoja, mutta sen käytössä on oltava kuitenkin varovainen.
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 2 Funktion derivaatta 2.1 Määritelmiä ja perusominaisuuksia 1. Määritä suoraan derivaatan määritelmää käyttäen f (0), kun (a) + 1, (b) (2 + ) sin(3). 2. Olkoon
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 2 Funktion derivaatta 2.1 Määritelmiä ja perusominaisuuksia 1. Määritä suoraan derivaatan määritelmää käyttäen f (0), kun (a) + 1, (b) (2 + ) sin(3). 2. Olkoon
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M)
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
Numeerinen integrointi ja derivointi
 Numeerinen integrointi ja derivointi Keijo Ruotsalainen Division of Mathematics Interpolaatiokaavat Approksimoitava integraali I = b a f(x)dx. Tasavälinen hila: x i = a+ (b a)i n, i = 0,...,n Funktion
Numeerinen integrointi ja derivointi Keijo Ruotsalainen Division of Mathematics Interpolaatiokaavat Approksimoitava integraali I = b a f(x)dx. Tasavälinen hila: x i = a+ (b a)i n, i = 0,...,n Funktion
Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: b) 0 e x + 1
 Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tehtävä : Tehtävänanto oli ratkaista seuraavat määrätyt integraalit: a) a) x b) e x + Integraali voisi ratketa muuttujanvaihdolla. Integroitava on muotoa (a x ) n joten sopiva muuttujanvaihto voisi olla
Tenttiin valmentavia harjoituksia
 Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Funktion määrittely (1/2)
 Funktion määrittely (1/2) Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon a täsmälleen yhden B:n alkion b. Merkitään b = f (a). Tässä A = M f on f :n määrittelyjoukko, B on f :n maalijoukko.
Funktion määrittely (1/2) Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon a täsmälleen yhden B:n alkion b. Merkitään b = f (a). Tässä A = M f on f :n määrittelyjoukko, B on f :n maalijoukko.
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Muuttujan vaihto. Viikon aiheet. Muuttujan vaihto. Muuttujan vaihto. ) pitää muistaa lausua t:n avulla. Integroimisen työkalut: Kun integraali
 Viikon aiheet Integroimisen työkalut: Rationaalifunktioiden jako osamurtoihin Rekursio integraaleissa CDH: Luku 4, Prujut206: Luvut 4-4.2.5, Prujut2008: s. 89-6 Kun integraali h(x) ei näytä alkeisfunktioiden
Viikon aiheet Integroimisen työkalut: Rationaalifunktioiden jako osamurtoihin Rekursio integraaleissa CDH: Luku 4, Prujut206: Luvut 4-4.2.5, Prujut2008: s. 89-6 Kun integraali h(x) ei näytä alkeisfunktioiden
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
2.2.1 Ratkaiseminen arvausta sovittamalla
 2.2.1 Ratkaiseminen arvausta sovittamalla Esimerkki: lomitusjärjestäminen (edellä) Yleistys: Ratkaistava T (1) c T (n) g(t (1),..., T (n 1), n) missä g on n ensimmäisen parametrin suhteen kasvava. (Ratkaisu
2.2.1 Ratkaiseminen arvausta sovittamalla Esimerkki: lomitusjärjestäminen (edellä) Yleistys: Ratkaistava T (1) c T (n) g(t (1),..., T (n 1), n) missä g on n ensimmäisen parametrin suhteen kasvava. (Ratkaisu
Sarja. Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,...,
 Sarja Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): Määritelmä 1 s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,..., n s n = a k. Jos osasummien jonolla (s n ) on raja-arvo s R,
Sarja Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): Määritelmä 1 s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,..., n s n = a k. Jos osasummien jonolla (s n ) on raja-arvo s R,
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012
 KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
RATKAISUT a + b 2c = a + b 2 ab = ( a ) 2 2 ab + ( b ) 2 = ( a b ) 2 > 0, koska a b oletuksen perusteella. Väite on todistettu.
 RATKAISUT 198 197 198. Olkoon suorakulmion erisuuntaisten sivujen pituudet a ja b sekä neliön sivun pituus c. Tehtävä on mielekäs vain, jos suorakulmio ei ole neliö, joten oletetaan, että a b. Suorakulmion
RATKAISUT 198 197 198. Olkoon suorakulmion erisuuntaisten sivujen pituudet a ja b sekä neliön sivun pituus c. Tehtävä on mielekäs vain, jos suorakulmio ei ole neliö, joten oletetaan, että a b. Suorakulmion
Funktion raja-arvo ja jatkuvuus Reaali- ja kompleksifunktiot
 3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
2. Fourier-sarjoista. Aaltoliikkeen ja lämmöjohtumisen matemaattinen tarkastelu
 2. Fourier-sarjoista Fourier-analyysi: Aaltoliikkeen ja lämmöjohtumisen matemaattinen tarkastelu Matemaattisen analyysin täkein työväline "Jokainen funktio" voidaan esittää harmonisten värähtelyjen, so.
2. Fourier-sarjoista Fourier-analyysi: Aaltoliikkeen ja lämmöjohtumisen matemaattinen tarkastelu Matemaattisen analyysin täkein työväline "Jokainen funktio" voidaan esittää harmonisten värähtelyjen, so.
Seuraava topologisluonteinen lause on nk. Bairen lause tai Bairen kategorialause, n=1
 FUNKTIONAALIANALYYSIN PERUSKURSSI 115 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
FUNKTIONAALIANALYYSIN PERUSKURSSI 115 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Funktioiden approksimointi ja interpolointi
 Funktioiden approksimointi ja interpolointi Keijo Ruotsalainen Division of Mathematics interpolaatio-ongelma 8 Eksponenttifunktion exp(x) interpolointi 3.5 Funktion e^{0.25x} \sin(x) interpolointi 7 3
Funktioiden approksimointi ja interpolointi Keijo Ruotsalainen Division of Mathematics interpolaatio-ongelma 8 Eksponenttifunktion exp(x) interpolointi 3.5 Funktion e^{0.25x} \sin(x) interpolointi 7 3
Pisteessä (1,2,0) osittaisderivaatoilla on arvot 4,1 ja 1. Täten f(1, 2, 0) = 4i + j + k. b) Mihin suuntaan pallo lähtee vierimään kohdasta
 Laskukarnevaali Matematiikka B. fx, y, z) = x sin z + x y, etsi f,, ) Osittaisderivaatat ovat f f x = sin z + xy, y = x, f z = x cos z Pisteessä,,) osittaisderivaatoilla on arvot 4, ja. Täten f,, ) = 4i
Laskukarnevaali Matematiikka B. fx, y, z) = x sin z + x y, etsi f,, ) Osittaisderivaatat ovat f f x = sin z + xy, y = x, f z = x cos z Pisteessä,,) osittaisderivaatoilla on arvot 4, ja. Täten f,, ) = 4i
Analyysi 1. Harjoituksia lukuihin 1 3 / Syksy Osoita täsmällisesti perustellen, että joukko A = x 4 ei ole ylhäältä rajoitettu.
 Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Demonstraatiot III, 4.5..06. Mikä on funktion f suurin mahdollinen määrittelyjoukko, kun f(x) x? Mikä on silloin f:n arvojoukko? Etsi f:n käänteisfunktio f ja tarkista, että löytämäsi
Matematiikan peruskurssi Demonstraatiot III, 4.5..06. Mikä on funktion f suurin mahdollinen määrittelyjoukko, kun f(x) x? Mikä on silloin f:n arvojoukko? Etsi f:n käänteisfunktio f ja tarkista, että löytämäsi
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 12 1 Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan
Matematiikan tukikurssi Kurssikerta 12 1 Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1. Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS
 DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
Maksimit ja minimit 1/5 Sisältö ESITIEDOT: reaalifunktiot, derivaatta
 Maksimit ja minimit 1/5 Sisältö Funktion kasvavuus ja vähenevyys; paikalliset ääriarvot Jos derivoituvan reaalifunktion f derivaatta tietyssä pisteessä on positiivinen, f (x 0 ) > 0, niin funktion tangentti
Maksimit ja minimit 1/5 Sisältö Funktion kasvavuus ja vähenevyys; paikalliset ääriarvot Jos derivoituvan reaalifunktion f derivaatta tietyssä pisteessä on positiivinen, f (x 0 ) > 0, niin funktion tangentti
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
sin(x2 + y 2 ) x 2 + y 2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 2017 Harjoitus 2 Ratkaisuedotukset 2.1. Tutki funktion g : R 2 R, g(0, 0) = 0, jatkuvuutta. g(x, y) = sin(x2 + y 2 ) x 2 + y 2, kun (x,
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 2017 Harjoitus 2 Ratkaisuedotukset 2.1. Tutki funktion g : R 2 R, g(0, 0) = 0, jatkuvuutta. g(x, y) = sin(x2 + y 2 ) x 2 + y 2, kun (x,
3 x 1 < 2. 2 b) b) x 3 < x 2x. f (x) 0 c) f (x) x + 4 x 4. 8. Etsi käänteisfunktio (määrittely- ja arvojoukkoineen) kun.
 Matematiikka KoTiA1 Demotehtäviä 1. Ratkaise epäyhtälöt x + 1 x 2 b) 3 x 1 < 2 x + 1 c) x 2 x 2 2. Ratkaise epäyhtälöt 2 x < 1 2 2 b) x 3 < x 2x 3. Olkoon f (x) kolmannen asteen polynomi jonka korkeimman
Matematiikka KoTiA1 Demotehtäviä 1. Ratkaise epäyhtälöt x + 1 x 2 b) 3 x 1 < 2 x + 1 c) x 2 x 2 2. Ratkaise epäyhtälöt 2 x < 1 2 2 b) x 3 < x 2x 3. Olkoon f (x) kolmannen asteen polynomi jonka korkeimman
1 sup- ja inf-esimerkkejä
 Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Ratkaisu: Tutkitaan derivoituvuutta Cauchy-Riemannin yhtälöillä: f(x, y) = u(x, y) + iv(x, y) = 2x + ixy 2. 2 = 2xy xy = 1
 1. Selvitä missä tason pisteissä annetut funktiot ovat derivoituvia/analyyttisiä. Määrää funktion derivaatta niissä pisteissä, joissa se on olemassa. (a) (x, y) 2x + ixy 2 (b) (x, y) cos x cosh y i sin
1. Selvitä missä tason pisteissä annetut funktiot ovat derivoituvia/analyyttisiä. Määrää funktion derivaatta niissä pisteissä, joissa se on olemassa. (a) (x, y) 2x + ixy 2 (b) (x, y) cos x cosh y i sin
0. Kertausta. Luvut, lukujoukot (tavalliset) Osajoukot: Yhtälöt ja niiden ratkaisu: N, luonnolliset luvut (1,2,3,... ) Z, kokonaisluvut
 0. Kertausta Luvut, lukujoukot (tavalliset) N, luonnolliset luvut (1,2,3,... ) Z, kokonaisluvut Rationaaliluvut n/m, missä n,m Z Reaaliluvut R muodostavat jatkumon fysiikan lukujoukko Kompleksiluvut C:z
0. Kertausta Luvut, lukujoukot (tavalliset) N, luonnolliset luvut (1,2,3,... ) Z, kokonaisluvut Rationaaliluvut n/m, missä n,m Z Reaaliluvut R muodostavat jatkumon fysiikan lukujoukko Kompleksiluvut C:z
Diskreetti derivaatta
 Diskreetti derivaatta LuK-tutkielma Saara Sadinmaa 43571 Matemaattisten tieteiden koulutusohjelma Oulun yliopisto Syksy 017 Sisältö Johdanto 1 Peruskäsitteitä 3 Ominaisuuksia 4 3 Esimerkkejä 8 4 Potenssifunktioita
Diskreetti derivaatta LuK-tutkielma Saara Sadinmaa 43571 Matemaattisten tieteiden koulutusohjelma Oulun yliopisto Syksy 017 Sisältö Johdanto 1 Peruskäsitteitä 3 Ominaisuuksia 4 3 Esimerkkejä 8 4 Potenssifunktioita
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Fysiikan matematiikka P
 Fysiikan matematiikka 763101P Luennoija: Kari Rummukainen, Fysikaalisten tieteiden laitos Tavoite: tarjota opiskelijalle nopeasti fysikaalisten tieteiden tarvitsemia matematiikan perustietoja ja taitoja.
Fysiikan matematiikka 763101P Luennoija: Kari Rummukainen, Fysikaalisten tieteiden laitos Tavoite: tarjota opiskelijalle nopeasti fysikaalisten tieteiden tarvitsemia matematiikan perustietoja ja taitoja.
Numeeriset menetelmät
 Numeeriset menetelmät Luento 7 Ti 27.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 7 Ti 27.9.2011 p. 1/39 p. 1/39 Interpolointi Ei tunneta funktion f : R R lauseketta, mutta tiedetään funktion
Numeeriset menetelmät Luento 7 Ti 27.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 7 Ti 27.9.2011 p. 1/39 p. 1/39 Interpolointi Ei tunneta funktion f : R R lauseketta, mutta tiedetään funktion
saadaan kvanttorien järjestystä vaihtamalla ehto Tarkoittaako tämä ehto mitään järkevää ja jos, niin mitä?
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Differentiaali- ja integraalilaskenta 1 Ratkaisut 2. viikolle /
 MS-A008 Differentiaali- ja integraalilaskenta, V/207 Differentiaali- ja integraalilaskenta Ratkaisut 2. viikolle / 8. 2.4. Jatkuvuus ja raja-arvo Tehtävä : Määritä raja-arvot a) 3 + x, x Vihje: c)-kohdassa
MS-A008 Differentiaali- ja integraalilaskenta, V/207 Differentiaali- ja integraalilaskenta Ratkaisut 2. viikolle / 8. 2.4. Jatkuvuus ja raja-arvo Tehtävä : Määritä raja-arvot a) 3 + x, x Vihje: c)-kohdassa
ANALYYSI 3. Tero Kilpeläinen
 ANALYYSI 3 Tero Kilpeläinen Luentomuistiinpanoja syksyltä 2005 14. helmikuuta 2014 Sisältö 1. Esitietoja 2 1.1. Riemann-integraali............................ 2 1.2. Derivaatta.................................
ANALYYSI 3 Tero Kilpeläinen Luentomuistiinpanoja syksyltä 2005 14. helmikuuta 2014 Sisältö 1. Esitietoja 2 1.1. Riemann-integraali............................ 2 1.2. Derivaatta.................................
Olkoon funktion f määrittelyjoukkona reaalilukuväli (erityistapauksena R). Jos kaikilla määrittelyjoukon luvuilla x 1 ja x 2 on voimassa ehto:
 4 Reaalifunktiot 4. Funktion monotonisuus Olkoon funktion f määrittelyjoukkona reaalilukuväli (erityistapauksena R). Jos kaikilla määrittelyjoukon luvuilla x ja x on voimassa ehto: "jos x < x, niin f (x
4 Reaalifunktiot 4. Funktion monotonisuus Olkoon funktion f määrittelyjoukkona reaalilukuväli (erityistapauksena R). Jos kaikilla määrittelyjoukon luvuilla x ja x on voimassa ehto: "jos x < x, niin f (x
MATEMATIIKAN JA TILASTOTIETEEN LAITOS
 f ( n) JYVÄSKYLÄN YLIOPISTO MATEMATIIKAN JA TILASTOTIETEEN LAITOS n Funktionaalianalyysi Ei harjoituksia 1.4.2015 Funktionaalista viihdettä pääsiäistauolle: viikolla 14 (ma 30.3., ti 31.3. ja ke 1.4.)
f ( n) JYVÄSKYLÄN YLIOPISTO MATEMATIIKAN JA TILASTOTIETEEN LAITOS n Funktionaalianalyysi Ei harjoituksia 1.4.2015 Funktionaalista viihdettä pääsiäistauolle: viikolla 14 (ma 30.3., ti 31.3. ja ke 1.4.)
Viikon aiheet. Funktion lineaarinen approksimointi
 Viikon aiheet Funktion ääriarvot Funktion lineaarinen approksimointi Vektorit, merkintätavat, pituus, yksikkövektori, skalaarilla kertominen, kanta ja kannan vaihto Funktion ääriarvot 6 Väliarvolause Implisiittinen
Viikon aiheet Funktion ääriarvot Funktion lineaarinen approksimointi Vektorit, merkintätavat, pituus, yksikkövektori, skalaarilla kertominen, kanta ja kannan vaihto Funktion ääriarvot 6 Väliarvolause Implisiittinen
Sarjoja ja analyyttisiä funktioita
 3B Sarjoja ja analyyttisiä funktioita 3B a Etsi funktiolle z z 5 potenssisarjaesitys kiekossa B0, 5. b Etsi funktiolle z z potenssisarjaesitys kiekossa, jonka keskipiste on z 0 4. Mikä on tämän potenssisarjan
3B Sarjoja ja analyyttisiä funktioita 3B a Etsi funktiolle z z 5 potenssisarjaesitys kiekossa B0, 5. b Etsi funktiolle z z potenssisarjaesitys kiekossa, jonka keskipiste on z 0 4. Mikä on tämän potenssisarjan
LUKU 3. Ulkoinen derivaatta. dx i 1. dx i 2. ω i1,i 2,...,i k
 LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
Miten osoitetaan joukot samoiksi?
 Miten osoitetaan joukot samoiksi? Määritelmä 1 Joukot A ja B ovat samat, jos A B ja B A. Tällöin merkitään A = B. Kun todistetaan, että A = B, on päättelyssä kaksi vaihetta: (i) osoitetaan, että A B, ts.
Miten osoitetaan joukot samoiksi? Määritelmä 1 Joukot A ja B ovat samat, jos A B ja B A. Tällöin merkitään A = B. Kun todistetaan, että A = B, on päättelyssä kaksi vaihetta: (i) osoitetaan, että A B, ts.
