ANALYYSI 3. Tero Kilpeläinen
|
|
|
- Auvo Karvonen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 ANALYYSI 3 Tero Kilpeläinen Luentomuistiinpanoja syksyltä helmikuuta 2014
2 Sisältö 1. Esitietoja Riemann-integraali Derivaatta Analyysin peruslause Taylor-polynomit Taylorin lause Jäännöstermin lauseke ja arvioita Funktiojonot Lukusarjat Sarjan suppeneminen ja itseinen suppeneminen Suppenemistestejä Sarjan ehdollinen suppeneminen Potenssisarjat Funktiosarjat ja niiden suppeneminen Potenssisarjat
3 Analyysi 3 1 Teksti sisältää muistiinpanoja syksyllä Tämän paketin tarkoitus on tukea omien muistiinpanojen tekoa, ei korvata niitä. Matematiikkaa oppii parhaiten itse kirjoittaen ja ongelmia ratkoen.
4 Analyysi Esitietoja Muistellaan Analyysi 1 ja 2 -kurssien tärkeitä määritelmiä ja tuloksia: Funktio f : I R, I R, on jatkuva pisteessä x 0 I, jos jokaisella ε > 0 on olemassa δ > 0 siten, että f(x) f(x 0 ) < ε, kun x x 0 < δ (x,x 0 I). Edelleen f : I R on jatkuva välillä I, jos f on jatkuva jokaisessa pisteessä x 0 I. Jatkuvuus voidaaan karakterisoida myös raja-arvojen avulla: muista, että luku a R on funktion f raja-arvo pisteessä x 0, merkitään lim f(x) = a, x x 0 jos jokaisella ε > 0 on olemassa δ > 0 siten, että f(x) a < ε aina, kun 0 < x x 0 < δ. Nyt pätee lause: Tällöin f on jatkuva pisteessä x 0, jos ja vain, jos f:llä on raja-arvo f(x 0 ) pisteessä x 0, ts. lim x x 0 f(x) = f(x 0 ) Riemann-integraali Integrointi ja differentiointi (derivointi) ovat kaksi analyysin keskeisintä rajaprosessia. Analyysin peruslause ilmaisee, että derivointi ja integrointi ovat toistensa käänteisprosesseja. Olkoon I rajoitettu väli, jonka päätepisteet ovat a,b R, a < b. Välin I jaon muodostavat luvut (äärellisen monta) a = x 0 < x 1 < x 2 < < x n = b. Funktio g : I R on porrasfunktio, jos on olemassa välin I jako P = (x 0,x 1,x 2,...,x n )
5 Analyysi 3 3 ja luvut a j R, j = 1,2,...,n, joille g(x) = a j kaikilla x ]x j 1,x j [. Porrasfunktion g : [a,b] R integraali (yli välin [a,b]) on b a g := n a j (x j x j 1 ), missä P = (x 0,x 1,x 2,...,x n ) on välin [a,b] jako siten, että g(x) = a j kaikilla x I j =]x j 1,x j [. Rajoitettu funktio f : [a, b] R on (Riemann-)integroituva, jos b ala b f = ylä f. a a Tällöin f:n (Riemann-)integraali yli välin [a, b] on b f := b b f(x)dx := ala b f = ylä f. a a a a Tässä b ala b f := sup{ g : g porrasfunktio ja g f välillä [a,b]} a a ja f:n yläintegraali yli välin [a,b] b ylä b f := inf{ h : g porrasfunktio ja h f välillä [a,b]}. a a Jatkuvat funktiot ovat integroituvia. Riemannin ehto antaa erään keinon tarkastella integroituvuutta: (Analyysi 2, Lause 1.1)
6 Analyysi Lause. (Riemannin ehto) Rajoitettu funktio f : [a,b] R on Riemannintegroituva, välillä [a, b], jos ja vain jos jokaisella ε > 0 on olemassa porrasfunktiot g ja h siten, että g f h välillä [a,b] ja b hdx b gdx < ε. a a Jatkuva funktio saa keskiarvonsa välillä [a, b] (Analyysi 2, Lause 1.14): 1.2. Lause. (Integraalilaskennan väliarvolause (IVAL)) Olkoon f jatkuva välillä [a,b]. Tällöin on olemassa ξ [a,b], jolle b a f(x)dx = f(ξ)(b a). Tarvitsemme tästä myös yleistetyn version (Analyysi 2, Lause 1.16): 1.3. Lause. (Yleistetty integraalilaskennan väliarvolause) Olkoon f jatkuva ja p ei-negatiivinen, Riemann-integroituva välillä [a, b]. Tällöin on olemassa ξ [a, b], jolle b b fpdx = f(ξ) pdx. a a 1.2. Derivaatta Olkoon f ]a,b[ R ja x ]a,b[. Sanotaan, että f on derivoituva ja f (x) f:n derivaatta pisteeessä x, jos raja-arvo on olemassa (ja reaaliluku!). f(x+h) f(x) lim h 0 h = f (x) Edelleen, jos f on derivoituva välillä ]a,b[, niin sen derivaatta f määrittelee myös funktion f ]a,b[ R: mikäli derivaattafunktio f on derivoituva, niin f on kahdesti derivoituva ja f:n toinen derivaatta on f (x) = (f ) (x).
7 Analyysi 3 5 Jatkamalla näin, f:n kolmas derivaatta f = f (3) on f:n toisen derivaatan f derivaatta, mikäli sellainen on olemassa jne. Seuraava väliarvolause (Analyysi 2, lause 2.7) on alkeisdifferentiaalilaskennan ehkä tärkein ja hyödyllisin lause Lause. (Väliarvolause, VAL) Olkoon f [a, b] R jatkuva suljetulla välillä [a,b] ja derivoituva avoimella välillä ]a,b[. Tällöin on olemassa ξ ]a,b[ siten, että f (ξ) = f(b) f(a) b a Tarvitsemme jatkossa myös sen yleistettyä muotoa (Analyysi 2, lause 2.13): Lause. (Yleistetty väliarvolause) Olkoon f ja g jatkuvia suljetulla välillä [a, b] ja derivoituvia avoimella välillä ]a, b[. Jos niin on olemassa ξ ]a,b[ siten, että g (x) 0 kaikilla x ]a,b[, f(b) f(a) g(b) g(a) = f (ξ) g (ξ) Analyysin peruslause Analyysin peruslause sitoo integroinnin ja derivoinnin toisiinsa (ks Analyysi 2, luku 3): 1.6. Lause. (Analyysin peruslause) Olkoon f :]a, b[ R jatkuvasti derivoituva ja x 0 ]a,b[. Tällöin f(x) = f(x 0 )+ x x 0 f (t)dt kaikilla x ]a,b[. Kääntäen, jos g on jatkuva funktio välillä [a,b] ja x 0 [a,b], niin integraalifunktio G(x) = x x 0 g(t)dt, on jatkuvasti derivoituva välillä ]a,b[ ja G (x) = g(x) kaikilla x ]a,b[.
8 Analyysi Taylor-polynomit 2.1. Taylorin lause Analyysi 1 -kurssilla opittiin, että jos funktio f on jatkuva pisteesä x 0, niin sen käyttäytymistä voidaan (lähellä pistettä x 0 ) approksimoida vakiofunktiolla (y = f(x 0 )), sillä f(x) f(x 0 ) = o(1) = o( x x 0 0 ) kun x x 0, toisin sanoen 1 f(x) = f(x 0 )+ǫ(x), missä lim x x 0 ǫ(x) x x 0 0 = lim x x 0 ǫ(x) = 0. Vakiopolynomi p 0 (x) = f(x 0 ) on siis jatkuvan funktion f paras approksimointi 0. asteen polynomilla pisteen x 0 lähistöllä. Jos f on hieman sileämpi, approksimointikin sujuu paremmin: olkoon f derivoituva pisteessä x 0. Tällöin (yhtäpitävästi) f(x) (f(x 0 )+f (x 0 )(x x 0 )) = o( x x 0 ) kun x x 0, toisin sanoen derivoituvaa funktiota voidaan approksimoida pisteen x 0 ympäristössä affiinilla funktiolla eli ensimmäisen asteen polynomilla niin, että virhetermi on pienempi kuin lineaarinen. Siten tämä polynomi p 1 (x) = f(x 0 )+f (x 0 )(x x 0 ) 1 Muista: pikku-o ja iso-o merkinnät (Analyysi 2): mikä tarkoittaa, että ja f(x) = o(g(x)), kun x x 0, f(x) lim x x 0 g(x) = 0, f(x) = O(g(x)), kun x x 0, mikä tarkoittaa, että on olemassa vakio C > 0 siten, että kunhan x on tarpeeksi lähellä pistettä x 0. f(x) C g(x),
9 Analyysi 3 7 antaa ensimmäiseen asteen polynomeista parhaan approksimoinnin f:lle pisteen x 0 lähellä. Nyt voisi arvata, että kahdesti derivoituvaa funktioita voisi approksimoida toisen asteen polynomilla niin, että virhetermi olisi muotoa o((x x 0 ) 2 ). Lasketaan tämä ensin 2. asteen polynomille: p 2 (x) = a 2 x 2 +a 1 x+a 0, jolloin p 2 (x) p 2 (x 0 ) = a 2 (x 2 x 2 0 )+a 1(x x 0 ) = a 2 (x x 0 ) 2 +2a 2 x 0 (x x 0 )+a 1 (x x 0 ) = 1 2 p 2(x 0 )(x x 0 ) 2 +p 2(x 0 )(x x 0 ). Tämän opastamana arvaamme, että kahdesti derivoituvaa funktiota f voidaan parhaiten approksimoida polynomilla Näin onkin asian laita: q 2 (x) = f(x 0 )+f (x 0 )(x x 0 )+ 1 2 f (x 0 )(x x 0 ) Lause. Olkoon funktiolla f jatkuva toinen derivaatta f välillä ]a,b[. Jos x 0 ]a,b[ ja q 2 (x) = f(x 0 )+f (x 0 )(x x 0 )+ 1 2 f (x 0 )(x x 0 ) 2, niin f(x) q 2 (x) = o( x x 0 2 ), kun x x 0, ts. kaikilla ε > 0 on δ > 0, jolle f(x) q 2 (x) ε x x 0 2, kun x x 0 < δ. Todistus: Olkoon F = f q 2. Tällöin F:llä on jatkuva toinen derivaatta ja F(x 0 ) = F (x 0 ) = F (x 0 ) = 0. Väite todistetaan soveltamalla väliarvolausetta 1.4 kahdesti: Ensiksi, löydetään sellainen piste x 1 pisteiden x 0 ja x välistä, jolle F(x) = F(x) F(x 0 ) = F (x 1 )(x x 0 )
10 Analyysi 3 8 ja edelleen piste x 2 pisteiden x 0 ja x 1 välistä, jolle F (x 1 ) = F (x 1 ) F (x 0 ) = F (x 2 )(x 1 x 0 ). Siten yhdistämällä nämä F(x) = F (x 2 )(x 1 x 0 )(x x 0 ) F (x 2 ) (x x 0 ) 2. Koska F on jatkuva ja F (x 0 ) = 0, on jokaista ε > 0 kohden sellainen δ > 0, jolle F (x) < ε kaikilla x, joille x x 0 < δ. Koska piste x 2 pisteiden x 0 ja x välissä, saadaan tästä f(x) g 2 (x) = F(x) F (x 2 ) (x x 0 ) 2 ε(x x 0 ) 2 kaikilla x, joille x x 0 < δ. Seuraavaksi havaitsemme, että n. asteen polynomille pätee p(x) = a n x n +a n 1 x n 1 + +a 1 x+a 0, (2.1) p(x) = p(x 0 )+p (x 0 )(x x 0 )+ 1 2 p (x 0 )(x x 0 ) p(n) (x 0 ) (x x 0 ) n. n! Tämän toteamiseksi kirjoitetaan (x = x 0 +h ja) p(x 0 +h) = n a j (x 0 +h) j = j=0 n b j h j, j=0 jolloin b 0 = p(x 0 ). Muut kertoimet b j saadaan laskemalla eo. lausekkeen derivaatat h:n suhteen pisteessä h = 0: ensiksi p (x 0 +h) = n jb j h j 1, mistä p (x 0 ) = b 1. Laskemalla samoin kaikki n derivaattaa samoin päädytään kaavaan (2.1). Jos f on n kertaa derivoituva, niin kaavan (2.1) oikean puolen polynomi voidaan muodostaa (kun p korvataan f:llä). Sitä kutsutaan f:n Taylorin polynomiksi:
11 Analyysi Määritelmä. Olkoon f n kertaa derivoituva välillä ]a, b[. Funktion f n. Taylorin polynomi pisteessä x 0 ]a,b[ on T n,x0 f(x) = f(x 0 )+f (x 0 )(x x 0 )+ 1 2 f (x 0 )(x x 0 ) f(n) (x 0 ) (x x 0 ) n. n! Kaavan (2.1) mukaan korkeintaan n. asteen polynomille p pätee: T n,x0 p(x) = p(x) kaikilla x R. Yleiselle funktiolle f sen Taylorin polynomi on tietysti eri kuin funktio itse. Funktiota R n,x0 f, joka ilmaisee kuinka paljon n. Taylorin polynomi eroaa f:stä sanotaan f:n n. jäännöstermiksi. Siis R n,x0 f(x) = f(x) T n,x0 f(x). Seuraava Taylorin lause kertoo, että jäännöstermi on varsin pieni sileälle funktiolle: 2.3. Lause. (Taylorin lause/kaava) Olkoon funktio f n kertaa jatkuvasti derivoituva välillä ]a,b[ ja x 0 ]a,b[. Tällöin f(x) = T n,x0 f(x)+r n,x0 f(x) kaikilla x ]a,b[, missä R n,x0 f(x) = o( x x 0 n ), kun x x 0. Todistus: (vrt Lauseen 2.1 todistus.) Osoitetaan väliarvolauseen avulla, että Ensiksi havaitaan, että R n,x0 (x) = R n,x0 f(x) = o( x x 0 n ), kun x x 0. R n,x0 (x 0 ) = R n,x 0 (x 0 ) = R n,x 0 (x 0 ) = = R (n) n,x 0 (x 0 ) = 0, jolloin soveltamalla väliarvolausetta jäännöstermiin ja sen derivaattoihin löydetään pisteet x 1,x 2,...,x n pisteiden x ja x 0 välistä, joille R n,x0 (x) = R n,x 0 (x 1 )(x x 0 ) R n,x 0 (x 1 ) = R n,x 0 (x 2 )(x 1 x 0 )... R (n 1) n,x 0 (x n 1 ) = R (n) n,x 0 (x n )(x n 1 x 0 ).
12 Analyysi 3 10 Yhdistämällä nämä saadaan josta R n,x0 (x) = R (n) n,x 0 (x n )(x x 0 )(x 1 x 0 )(x 2 x 0 ) (x n 1 x 0 ), R n,x0 (x) R (n) n,x 0 (x n ) x x 0 n, joten väite seuraa, koska jatkuvuuden nojalla lim R n,x (n) x x 0 (x n ) = lim R n,x (n) 0 (y) = R n,x (n) 0 (x 0 ) = 0. 0 y x0 Esimerkki. Eksponenttifunktion Taylor-approksimointi origossa on e x = 1+x+ x2 2! + x3 xn + + 3! n! +xn ǫ(x), missä ǫ(x) 0. Samalla tavalla saadaan suoraan derivoimalla, että missä ǫ 2k+1 (x) 0 ja sinx = x x3 3! + x5 5! + +( 1)k x 2k+1 (2k +1)! +x2k+1 ǫ 2k+1 (x), missä ǫ 2k (x) 0. cosx = 1 x2 2! + x4 x2k + +( 1)k 4! (2k)! +x2k ǫ 2k (x), Näiden avulla voidaan laskea esimerkiksi lim x 0 sinx x x(cosx 1) = lim x 0 = lim x x3 3! +x 3 ǫ 3 (x) x x(1 x2 2! +x 2 ǫ 2 (x) 1) x3 x 0 x3 3! +x 3 ǫ 3 (x) 2! +x 3 ǫ 2 (x) = lim x 0 1 3! +ǫ 3(x) 1 2! +ǫ 2(x) = 1 3.
13 Analyysi 3 11 Huomaa, että Taylorin lause kertoo, että n. Taylorin polynomi approksimoi funktiota hyvin pisteen x 0 lähellä, muttei mitään siitä, mitä tapahtuu kauempana. Huomaa myös, että Taylorin polynomit voivat muuttua paljonkin, kun pistettä x 0 muutetaan. Myöhemmin tutkimme lähemmin, miten funktiota voidaan approksimoida pisteittäin tai globaalimmin. Taylorin polynomi voidaan aina laskea derivoimalla f riittävän monta kertaa. Tämä on kuitenkin usein kohtuuttoman työlästä. Siksi on hyvä havaita seuraava yksikäsitteisyystulos: 2.4. Lause. Olkoon f n kertaa jatkuvasti derivoituva välillä ]a,b[ ja x 0 ]a,b[. Jos p on n. asteen polynomi, jolle f(x) p(x) = o( x x 0 n ), kun x x 0, niin p(x) = T n,x0 f(x) kaikilla x. Todistus: Koska Taylorin lauseen 2.3 mukaan f(x) p(x) = o( x x 0 n ) ja f(x) T n,x0 f(x) = o( x x 0 n ) niin p(x) T n,x0 f(x) x x 0 n 0, kun x x 0. Siten kirjoittamalla p(x) T n,x0 f(x) = n a j (x x 0 ) j j=0 ja antamalla x x 0 nähdään, että a 0 = 0 ja edelleeen a 1 = 0, a 2 = 0... ja a n = 0. Edelläolevan yksikäsitteisyyslauseen (eräs) hyöty on se, että riittää löytää millä tahansa keinolla tai konstilla n. asteen polynomi p, jolle f(x) p(x) = o( x x 0 n ), sillä tämän polynomin täytyy olla f:n n. Taylorin polynomi. Esimerkiksi kahden funktion f ja g Taylorin polynomien tulosta saadaan tulofunktiolle f g Taylorin polynomi, kun tulopolynomista otetaan mukaan vain termit joiden aste on korkeintaan n(silläkorkeammille potensseillek > npätee x x 0 k = o( x x 0 n )).Hetkenpäästä muitakin esimerkkejä.
14 Analyysi 3 12 Esimerkki. (Geometrinen sarja) Olkoon n 1 S n = 1+q +q 2 + +q n 1 = n termin geometrinen summa. Induktiolla todetaan, että kunhan q 1 (jos q = 1 on S n = n). S n = 1 qn 1 q, Tarkastellaan nyt funktiota g :],1[ R, g(t) = 1 1 t. Nyt ylläolevasta geometrisestä sarjasta saamme (kaikilla n N) josta integroimalla (x < 1) log(1 x) = k=0 q k g(t) = 1+t+t 2 + +t n 1 + tn 1 t, = x 0 x 0 dt 1 t = x+ x2 2 n = (1+t+t 2 + +t n 1 )dt+ + + xn n R n(x) x j j R n(x), x 0 t n 1 t dt missä Nyt x R n (x) = 0 t n 1 t dt. x t n dt x n+1 =, kun x 0, 0 n+1 R n (x) 1 x t n dt x n+1 =, kun x [0,1[, 1 x (1 x)(n+1) 0
15 Analyysi 3 13 Siten kaikilla x [ 1,1[ f(x) = log(1 x) = missä R n (x) 0, kun n. Koska lisäksi n x j j +R n(x), R n (x) = o( x x 0 n ), kun x 0, on Taylorin polynomin yksikäsitteisyystuloksen 2.4 nojalla funktion n. Taylorin polynomi nollassa f(x) = log(1 x) T n,x0 f(x) = Huomaa, että yo. laskun avulla saamme n x j j. log2 = , minkä tarkka merkitys selviää myöhemmin sarjoja käsittelevässä luvussa Jäännöstermin lauseke ja arvioita Taylorin kaavan sovellutuksissa on usein tarpeen tietää enemmän jäännöstermistä kuin, mitä lauseesta 2.3 käy ilmi. Ensin todistamme sille tarkan integraalimuodon: 2.5. Lause. (Taylorin kaava, integroitu muoto) Olkoon funktio f n + 1 kertaa jatkuvasti derivoituva välillä ]a,b[ ja x 0 ]a,b[. Tällöin missä jäännöstermi on f(x) = T n,x0 f(x)+r n,x0 f(x) kaikilla x ]a,b[, x R n,x0 f(x) = 1 (x t) n f (n+1) (t)dt. n! x 0
16 Analyysi 3 14 Todistus: Tämä voidaan todistaa myös suoraan osittaisintegroimalla ja induktiolla, mikä tehtäneen harjoituksissa. Seuraavassa todistuksessa käytetään Lauseen 2.3 kaavaa: kaikilla x,y ]a,b[ R n,y f(x) = f(x) T n,y f(x) = f(x) f(y) f (y)(x y) 1 2 f (y)(x y) 2 f(n) (y) (x y) n, n! mistä laskemalla derivaatta y:n suhteen saadaan tulon derivoimissäännön avulla d dy R n,yf(x) =0 f (y) (f (y)(x y) f (y)) ( 1 2 f (y)(x y) 2 f (y)(x y))... ( f(n+1) (y) (x y) n f(n) (y) n! (n 1)! (x y)n 1 ) = f(n+1) (y) (x y) n, n! koska summassa joka toinen termi kumoaa toisensa. Koska R n,x f(x) = 0, saadaan analyysin peruslauseen nojalla ja väite on todistettu. R n,x0 f(x) = R n,x0 f(x) R n,x f(x) = = x 0 x x x 0 d dy R n,yf(x)dy = x x 0 f (n+1) (y) (x y) n dy, n! d dy R n,yf(x)dy Integraalilaskennan väliarvolauseesta 1.2 saadaan seuraava arvio jäännöstermille: 2.6. Lause. (Cauchyn muoto jäännöstermille) Olkoon funktio f n + 1 kertaa jatkuvasti derivoituva välillä ]a,b[ ja x 0 ]a,b[. Taylorin polynomin n. jäännöstermille pätee: kaikilla x ]a,b[ on olemassa ξ pisteiden x ja x 0 välissä, jolle R n,x0 f(x) = f(n+1) (ξ) (x ξ) n (x x 0 ). n!
17 Analyysi 3 15 Todistus: Seuraa suoraan jäännöstermin integraalimuodosta ja integraalilaskennan väliarvolauseesta 1.2 sillä x R n,x0 f(x) = 1 (x t) n f (n+1) (t)dt n! x 0 missä ξ on eräs piste pisteiden x ja x 0 välissä. = 1 n! f(n+1) (ξ)(x ξ) n (x x 0 ), Yleistetystä integraalilaskennan väliarvolauseesta 1.3 saadaan seuraava arvio jäännöstermille: 2.7. Lause. (Lagrangen muoto jäännöstermille) Olkoon funktio f n + 1 kertaa jatkuvasti derivoituva välillä ]a,b[ ja x 0 ]a,b[. Taylorin polynomin n. jäännöstermille pätee: kaikilla x ]a,b[ on olemassa ξ pisteiden x ja x 0 välissä, jolle R n,x0 f(x) = f(n+1) (ξ) (n+1)! (x x 0) n+1. Todistus: Seuraa suoraan jäännöstermin integraalimuodosta ja yleistetystä integraalilaskennan väliarvolauseesta 1.3 sillä x R n,x0 f(x) = 1 (x t) n f (n+1) (t)dt n! x 0 missä ξ on eräs piste pisteiden x ja x 0 välissä. x = 1 n! f(n+1) (ξ) (x t) n dt x 0 = 1 1 n! f(n+1) (ξ) n+1 (x x 0) n+1, Seuraavassa eräs esimerkki Taylorin kaavan sovellutuksesta: 2.8. Lause. Olkoon funktio f n kertaa jatkuvasti derivoituva välillä ]a,b[ ja x 0 ]a,b[. Jos f (x 0 ) = f (x 0 ) = f (3) (x 0 ) = = f (n 1) (x 0 ) = 0 ja f (n) (x 0 ) > 0, niin f:llä on lokaali minimi pisteessä x 0, jos n 2 on parillinen. Piste x 0 ei ole f:n ääriarvokohta jos n on pariton.
18 Analyysi 3 16 Todistus: Seuraa Taylorin kaavasta. Yksityiskohdat: HT.
19 Analyysi Funktiojonot Muistetaan Analyysi 1 -kurssilta suppenevan pistejonon määritelmä: 3.1. Määritelmä. Olkoon x 1,x 2,... jono reaalilukuja. Sanotaan, että jono (x n ) suppenee kohti reaalilukua a, jos jokaisella ε > 0 on olemassa luku N = N(ε,jono) N siten, että x n a < ε kaikilla n N. Tällöin a on jonon (x n ) raja-arvo ja sitä merkitään lim x n = a tai x n a kun n. n Esimerkki. Olkoon x [0,1]. Tällöin jono (x n ) suppenee ja lim n xn = { 0, jos 0 x < 1, 1, jos x = 1, Jos x = 0 tai x = 1, on asia selvä. Jos 0 < x < 1, tämä nähdään esimerkiksi Bernoullin epäyhtälön 2 avulla ( ) n x n 1 = 1+( 1 1) x Koska Bernoullin epäyhtälöstä seuraa, että 1 1+n( 1 x 1) x n = (1 (1 x)) n 1 n(1 x) 1 2 x n(1 x) 0., kun 1 1 2n x 1, huomataan, että jonon suppenemisvauhti riippuu pisteestä x, ts. se kohta (indeksi n), mistä jonon loppuosa on annettua lukua ε lähempänä raja-arvoa, riippuu x:n arvosta. Jono voidaan myös kirjoittaa funktioiden avulla: f n : [0,1] R, f n (x) = x n, n N. Tällöin jonoa (f n ) kutsutaan funktiojonoksi. 2 Bernoullin epäyhtälö: jos y > 1, niin (1+y) n 1+ny kaikilla n N.
20 Analyysi 3 18 Jos A R ja f n : A R, n N, ovat funktioita, niin (f n ) n = (f n ) n N = (f n ) = f 1,f 2,f 3,..., on funktiojono. Funktiojono (f n ) tuottaa jokaisella x A lukujonon (f n (x)). Sanotaan, että funktiojono (f n ) suppenee (pisteittäin) joukossa A, jos lukujonot (f n (x)) suppenevat jokaisella x A, ts. jokaisella x A on olemassa reaaliluku f(x), jolle lim f n(x) = f(x). n Nämä raja-arvot f(x) määrittelevät uuden funktion f : A R ja sanotaan, että funktiojono (f n ) suppenee (pisteittäin) kohti funktiota f, tätä merkitään f n f tai lim f n = f. n Huomaa, että suppenemisvauhti f n (x) f(x) riippuu yleensä pisteestä x, vrt. esimerkki edellä. Edelläolevan määritelmän mukaan siis funktiojono f n suppenee pisteittäin (joukossa A) kohti funktiota f, jos jokaisella x ja jokaisella ε > 0 on olemassa luku N = N(x,ε,jono) N siten, että f n (x) f(x) < ε kaikilla n N. Lukujono suppenee, jos se täyttää Cauchyn kriteerion; funktiojonolle tämä kertoo seuraavaa: funktiojono (f n ) suppenee pisteittäin joukossa A (kohti jotain funktiota f : A R), jos jokaisella x ja jokaisella ε > 0 on olemassa luku N = N(x,ε,jono) N siten, että f n (x) f m (x) < ε kaikilla n,m N. Pisteittäisessä suppenemisessa jokaista lukua ε > 0 kohti on luku N, jota suuremmille indekseillä jonon funktioiden arvot pisteessä x poikkeavat rajafunktion arvosta pisteessä x vähemmän kuin ε. Se kuinka suuri luvun N tulee olla, riipuu yleensä pisteestä x. Esimerkki. Olkoon f n : R R, n N, f n (x) = { sin(πx), jos x [n,2n] 0, muutoin.
21 Analyysi 3 19 Tällöin f n on jono jatkuvia funktioita f n : R R ja f n 0, koska kiinteällä x f n (x) = 0 kunhan n > x. Siten valitsemalla N > x (N N) saamme (kaikilla ε > 0) f n (x) 0 < ε, kunhan n N. Kuitenkaan lukua N ei voida valita pisteestä x riippumattomaksi (mikäli ε < 1) koska kaikilla n pätee f n (x) 0 = f n (n+ 1 ) = 1 > ε. 2 Seuraavassa määritellään pisteittäistä konvergenssia vahvempi konvergenssin käsite funktiojonoille: 3.2. Määritelmä. Sanotaan, että jono funktioita f n : A R suppenee tasaisesti joukossa A kohti funktiota f : A R, jos kaikilla ε > 0 on olemassa luku N = N(ε,jono) N siten, että f n (x) f(x) < ε kaikilla x A, kunhan n N. Tätä merkitään joskus f n f tasaisesti A:ssa. Tasaisesti suppeneva funktiojono suppenee tietysti pisteittäin, mutta käänteinen väite ei ole tosi, kuten yllä olevissa esimerkeissä näimme. Huomaa, että tasaisessa suppenemisessa lukua ε vastaava luku N pitää voida valita pisteestä x riippumattomalla tavalla. Tämä tarkoittaa sitä, että funktiot f n ovat jostain indeksistä alkaen lähellä funktiota f, ns. ε-putkessa.
22 Analyysi 3 20 f +ε 6 f f ε ε-putki Tasaista suppenemista voi hahmottaa niin, että siinä mitataan funktioiden välisiä etäisyyksiä; tässä tietysti pitää käyttää soveltuvaa mittaa ( metriikkaa ): jos f ja g ovat joukossa A määriteltyjä funktioita, niin d(f,g) = sup f(x) g(x) x A on niiden välinen etäisyys. Tämän etäisyyden avulla funktiojonon tasainen suppeneminen vastaa reaalilukujonon suppenemista, kun vain objektien välisiä etäisyyksiä mitataan oikealla tavalla: 3.3. Lause. Olkoot f n,f : A R funktioita. Tällöin f n f tasaisesti A:ssa, jos ja vain, jos lim d(f n,f) = 0, n ts. kaikilla ε > 0 on olemassa luku N N siten, että sup f n (x) f(x) < ε, kaikilla n N. x A
23 Analyysi 3 21 Todistus: Olkoon ε > 0. Jos f n f tasaisesti A:ssa, niin on N N, jolle (kun n N) joten Kääntäen, jos kun n N, niin joten f n f tasaisesti A:ssa. f n (x) f(x) < ε 2 kaikilla x A, sup f n (x) f(x) ε x A 2 < ε. sup f n (x) f(x) < ε, x A f n (x) f(x) < ε kaikilla x A, Seuraava Cauchyn ehto kertoo, milloin funktiojono suppenee tasaisesti kohti jotain funktiota, mistä ei tarvitse olla mitään tietoa Lause. (Tasainen Cauchyn kriteerio) Olkoot f n : A R funktioita. Tällöin funktiojono (f n ) suppenee tasaisesti joukossa A (kohti jotain funktiota f : A R), jos ja vain, jos jokaisella ε > 0 on olemassa luku N N siten, että f n (x) f m (x) < ε kaikilla n,m N ja kaikilla x A. Todistus: Se, että tasaisesta suppenemisesta seuraa tasainen Cauchyn ehto menee aivan samoin kuin lukujonon Cauchyn ehdon todistuksessa (ks Analyysi 1, Lause 4.9) yksityiskohdat harjoituksissa. Jos taas jono toteuttaa tasaisen Cauchyn ehdon, niin jokaisella x lukujono f n (x) on Cauchy-jono ja siten suppenee kohti reaalilukua f(x). Näin saadaan rajafunktioehdokas f : A R. Se on jonon f n tasainen raja: Olkoon ε > 0 ja valitaan tasaisen Cauchyn ehdon antama N, jolle f n (x) f m (x) < ε 2 kaikilla n,m N ja kaikilla x A. Kun x A, f n (x) f(x), joten voimme valita luvun m x N, jolle m x > N ja f(x) f mx (x) < ε 2. Näin ollen f n (x) f(x) f n (x) f mx (x) + f mx (x) f(x) < ε 2 + ε 2 = ε; erityisesti, f n (x) f(x) < ε kaikilla x, kunhan n N, ts. jono f n suppenee tasaisesti A:ssa (kohti funktiota f).
24 Analyysi 3 22 Pisteittäinen konvergenssi on lokaali ominaisuus: se ottaa huomioon jonon funktioiden arvot vain tarkasteltavassa pisteessä. Tasaisen konvergenssi on luonteeltaan globaalimpi: tasaisesti suppenevan jonon funktiot tulevat kauttaaltaan lähelle rajafunktiota. Täten jonon funktioiden ominaisuudet heijastuvat myös rajafunktioon paremmin, mm. jatkuvuus säilyy tasaisessa konvergenssissa: 3.5. Lause. Olkoot f n : A R funktioita, jotka ovat jatkuvia pisteessä x 0 A. Jos f n f tasaisesti A:ssa, on rajafunktio f myös jatkuva pisteessä x 0. Todistus: Olkoon ε > 0. Valitaan n N, jolle sup f n (x) f(x) < ε x A 3. Koska f n on jatkuva pisteessä x 0, on δ > 0, jolle f n (x) f n (x 0 ) < ε 3 kaikilla x A, joilla x x 0 < δ. Siten sellaisella x f(x) f(x 0 ) f(x) f n (x) + f n (x) f n (x 0 ) + f n (x 0 ) f(x 0 ) < ε 3 + ε 3 + ε 3 = ε. Löysästi puhuen edellinen lause on osa periaatetta jos suppeneminen on tasaista, kahden peräkkäisen rajankäynnin järjestys voidaan vaihtaa. Seuraava lause antaa tästä integraaliversion: 3.6. Lause. Olkoot f n : [a,b] R Riemann-integroituvia funktioita. Jos f n f tasaisesti välillä [a, b], on rajafunktio f myös Riemann-integroituva ja b b lim f n dx = f dx. n a a Todistus: Käytetään Riemannin ehtoa 1.1. Olkoon ε > 0. Valitaan sellainen n N, jolle ε sup f n (x) f(x) < x A 3(b a).
25 Analyysi 3 23 Sitten valitaan Riemannin ehdon mukaiset porrasfunktiot g n ja h n, joille g n f n h n ja jolloin myös Asettamalla g = g n saadaan porrasfunktiot, joille ε g = g n 3(b a) f n ja b a hdx b a b a b a h n dx h n dx ε 3(b a) b a b a g n dx < ε 3 f n dx < ε 3. ja h = h n + ε 3(b a) f f n + gdx = joten f on Riemann-integroituva ja b a fdx b a b a h n dx f n dx b a b a hdx ε 3(b a) ε 3(b a) h n + g n dx+2 ε 3 < ε, b a gdx < ε 3. ε 3(b a) = h Derivoituvuus ei yleensä säily tasaisessa konvergenssissa, mikä näkyy allaolevasta kuvasta. Derivoituvuus ei säily tasaisessa konvergenssissa.
26 Analyysi 3 24 Kuitenkin, jos funktioiden jatkuvat derivaatat myös suppenevat tasaisesti, niin rajafunktiokin on derivoituva: 3.7. Lause. Olkoot f n :]a,b[ R jatkuvasti derivoituvia funktioita. Jos f n f tasaisesti välillä ]a,b[ ja jos derivaattojen f n jono suppenee myös tasaisesti välillä ]a,b[ kohti funktiota g, niin f on (jatkuvasti) derivoituva ja f = g. Todistus: Riittää osoittaa, että f on derivoituva ja f = g; derivaatan jatkuvuus seuraaa Lauseesta 3.5. Tapa 1.Käytetäänanalyysinperuslausetta1.6:Kiinnitetäänx 0 ]a,b[.analyysin peruslauseen nojalla f n (x) = f n (x 0 )+ x x 0 f n (t)dt. Antamalla n yhtälön vasen puoli suppenee kohti lukua f(x), oikean puolen integraalin hoitaa edeltävä integraalien konvergenssilause 3.6: f(x) = lim f n (x) = lim f n (x 0 )+ lim f n (t)dt n n n x 0 = f(x 0 )+ x x 0 g(t)dt, joten väite seuraa analyysin peruslauseen nojalla. Tapa 2. Käytetään väliarvolausetta 1.4: Kiinnitetään x 0 ]a,b[. Olkoon h R sellainen, että x 0 ± h ]a,b[. Väliarvolauseen nojalla jokaisella n N on piste ξ n, jolle x 0 h ξ n x 0 + h ja x f n (x 0 +h) f n (x 0 ) h = f n(ξ n ). Bolzano-Weierstrassin lauseen (Analyysi 1) nojalla on piste z h [x 0 h,x 0 + h ], jota kohti eräs ξ n :n osajono (jota merkitään edelleen ξ n :llä) suppenee. Nyt derivaattojen tasaisesta konvergenssista ja jatkuvuudesta seuraa (HT), että lim n f n (ξ n) = g(z h ),
27 Analyysi 3 25 joten f(x 0 +h) f(x 0 ) h = lim n f n (x 0 +h) f n (x 0 ) h = lim n f n(ξ n ) = g(z h ). Koska z h [x 0 h,x 0 + h ] ja koska g on jatkuva (Lause 3.5), erotusosamäärällä on raja-arvo: f(x 0 +h) f(x 0 ) lim = limg(z h ) = g(x 0 ). h 0 h h 0 Taylorin polynomeja käsiteltäessä opimme, että sileätä funktiota voidaan lokaalisti approksimoida hyvin polynomilla. Seuraava lause (jota emme todista tällä kurssilla) kertoo, että jatkuvaa funktiota voidaan aina approksimoida polynomeilla tasaisesti suljetulla välillä Lause. (Weierstrassin approksimointilause) Olkoon f jatkuva välillä [a, b]. Tällöin on olemassa jono polynomeja p j, joka suppenee kohti f:ää tasaisesti välillä [a,b]. Seuraava Dinin konvergenssilause on hyödyllistä tietää; huomaa, että oletus suljetusta ja rajoitetusta välistä on siinä oleellinen (HT) Lause. (Dini) Olkoon f n vähenevä jono jatkuvia funktioita suljetulla välillä [a,b]. Jos f n f pisteittäin ja jos f on myös jatkuva, niin f n f tasaisesti välillä [a,b]. Todistus: Tarkastelemalla funktioita f n = f n f voidaan olettaa, että f 0. Ellei konvergenssi ole tasaista, löydämme luvut ε > 0 ja x n [a,b], joille f n (x n ) ε. Osajonoon siirtymällä voimme Bolzano-Weierstrassin lauseen (Analyysi 1) nojalla olettaa, että on olemassa x 0 [a,b], jolle lim x n = x 0. n Koska jono f n on vähenevä pätee kaikilla j n: f j (x n ) f n (x n )) ε,
28 Analyysi 3 26 joten jatkuvuudesta seuraa, että f j (x 0 ) = lim n f j (x n ) ε kaikilla j, joten f j (x 0 ) 0, kun j, mikä on vastoin pisteittäisen konvergenssin oletusta.
29 Analyysi Lukusarjat Olkoot a j reaalilukuja, j N. Äärellisen monen reaaliluvun a 1,a 2,...,a n yhteenlasku on tuttua puuhaa ja niiden summa on n a j = a 1 +a 2 + +a n. Tässä luvussa tarkastellaan, mitä äärettömällä summalla eli sarjalla a j tarkoitetaan (vai tarkoitetaanko mitään). Karkeana ideana on laskea jonon (a j ) alusta yhä useampia ja useampia termejä yhteen ja toivoa, että näin saadut summat tulevat lähestymään jotain lukua. Toisin sanoen muodostetaan summat a 1, a 1 +a 2, a 1 +a 2 +a 3, a 1 +a 2 +a 3 +a 4,..., n a j,... ; nämä summat muodostavat uuden reaalilukujonon, joka joko suppenee (jolloin niiden raja-arvoa sanotaan sarjaksi a j tai sarjan summaksi) tai hajaantuu (jolloin sanotaan, että sarja a j hajaantuu) Sarjan suppeneminen ja itseinen suppeneminen 4.1. Määritelmä. Olkoot a j reaalilukuja, j N. Muodollista summaa a j = a 1 +a sanotaan (luku)sarjaksi. Sen j. termi on luku x j ja (äärellinen) summa S n = n a j = a 1 +a 2 + +a n, n N,
30 Analyysi 3 28 on sarjan a j n. osasumma. Jos näiden osasummien (S n ) n N muodostama jono suppenee kohti reaalilukua S, sanotaan että sarja a j suppenee (eli konvergoi) ja raja-arvo on sen summa; merkitään S = lim n S n a j = S = lim n n a j. Ellei sarja suppene, niin sanotaan että se hajaantuu (eli divergoi) Huomautus. (a) Sarja siis hajaantuu, jos sen osasummien jonolla ei ole raja-arvoa (tai jos mahdollinen raja-arvo on ± ). (b) Usein sarjassa summataan indeksejä 0:stä tai jostain muusta luvusta äärettömään. Ilmeinen pieni muokkaus määritelmään kertoo, mitä silloin tarkoitetaan. (c) Jos sarjat a j ja b j, suppenevat, niin termien summien ja vakiolla kerrottujen termien muodostamat sarjat suppenevat myös ja (a j +b j ) = a j + b j sekä (ca j ) = c a j, kun c R. (d) Huomaa, että termien summausjärjestys vaikuttaa sarjan suppenemiseen; tästä esimerkkejä myöhemmin (ks 4.18 ja 4.19).
31 Analyysi 3 29 Esimerkki. Sarja j=0 x j j! suppenee kaikilla x R kohti lukua e x, koska osasummien jono on eksponenttifunktion n. Taylorin polynomi, jonka jäännöstermille pätee e ξ R n,0 exp(x) = (n+1)! xn+1 (n+1)! xn+1 0, kun n. e x 4.3. Lause. Jos sarja a j suppenee, niin lim a j = 0. j Todistus: Termit saadaan helposti osasummista, joten a n = S n S n 1 = n n 1 a j a j a j a j = 0. Termien suppeneminen nollaan on välttämätön, vaan ei riittävä ehto sarjan suppenemiselle, kuten esimerkiksi harmonisesta sarjasta (Esim. 4.5) opimme Huomautus. Lukujono suppenee, jos se täyttää Cauchyn kriteerion; sarjoihin sovellettuna se kertoo, että sarja suppenee, jos ja vain, jos sen osasummien jono on Cauchy-jono, minkä kanssa on edelleen yhtäpitävää, että kaikilla ε > 0 on N N, jolle n m n S n S m = a j a j = a j < ε kunhan n > m N. j=m+1
32 Analyysi Esimerkki. (harmoninen sarja) Sarjaa sanotaan harmoniseksi sarjaksi. Se hajaantuu (tosin hyvin hitaasti), vaikka termit suppenevat nollaan, 1 0. Hajaantuminen nähdään helposti: jos n N, niin n S n S 2n = 2n j=n+1 1 j 1 j = 1 n n n 1 n+n + 1 n+n n+n = n 1 2n = 1 2, joten osasummien jono ei ole Cauchy eikä näin ollen suppene. Suoremmin hajaantuminen nähdään seuraavasti: n S 2 n = 1+ (S 2 j S 2 j 1) 1+n 1 2, kun n, joten harmoninen sarja ei suppene.. Induktiolla on (melko) helppo nähdä (ks 4.15), että log(n+1) joten hajaantuminen on hidasta (HT). n 1 j 1+logn, Esimerkki. Vuorotteleva harmoninen sarja ( 1) j+11 j suppenee, koska osasummien jono on Cauchy-jono: havaitaan, että kaikilla k S 2k 1 S 2k 1 1 2k + 1 2k +1 = S 2k+1 S 2k+1 1 2k +2 = S 2k+2 = S 2k + 1 2k k +2 S 2k,
33 Analyysi 3 31 joten kaikilla n,m 2k S n S m S 2k 1 S 2k = 1 2k. Siis (S n ) on Cauchy-jono ja siten suppenee. Huom. Logaritmin Taylor polynomi on log(1 x) = n x j j +R n(x), kun x < 1, missä R n (x) 0, kun n. Tämän avulla saamme toisen tavan todeta vuorottelevan harmonisen sarjan suppeneminen. Lisäksi ( 1) j+11 j = log(2). Esimerkki. (aritmeettinen sarja) Sarja a j on aritmeettinen, jos kahden peräkkäisen termin erotus on vakio, ts. kaikilla j ts. aritmeettinen sarja on muotoa a j+1 a j = d, (a 1 +(j 1)d). Aritmeettinen sarja hajaantuu (ellei sen kaikki termit ole = 0), koska n a j = n ellei a 1 = 0 = d. a 1 +(j 1)d = na 1 + n(n 1)d 2 = n a 1 +(a 1 +(n 1)d), 2 Esimerkki. (geometrinen sarja) Sarja a j on geometrinen, jos jokaisen kahden peräkkäisen termin suhde on vakio, ts. on sellainen luku q, jolle kaikilla j a j+1 = qa j.
34 Analyysi 3 32 Ts. geometrinen sarja on muotoa aq j 1. Vaihdetaan summausindeksiä, jolloin summa on helpompi muistaa: aq j 1 = aq k. k=0 Induktiolla toteamme, että n. osasumma on n aq k = a k=0 n q k a 1 qn+1, jos q 1 = 1 q a(n+1), jos q = 1. k=0 Tästä näemme, että geometrinen sarja suppenee, jos ja vain, jos sen suhdeluvulle q pätee q < 1. Tällöin sarjan summa on aq k = a k=0 k=0 q k = a, jos q 1. 1 q 4.6. Määritelmä. Olkoota j R,j = 1,2,...Sanotaan,ettäsarja a j suppenee itseisesti (tai absoluuttisesti), jos termien itseisarvojen muodostama sarja suppenee. a j Suppeneva sarja ei välttämättä suppene itseisesti, sillä esimerkiksi vuorotteleva harmoninen sarja ( 1) j1 j suppenee, mutta ei itseisesti. Käänteinen kuitenkin pätee:
35 Analyysi Lause. Itseisesti suppeneva sarja suppenee ja a j a j. Todistus: Kolmioepäyhtälön nojalla kaikille b j R ja n N (4.1) n n b j b j, joten osasummien jonolle pätee (kun n > m) S n = n a j S n S m = n j=m+1 a j n j=m+1 a j = n a j m a j < ε, kun n ja m tarpeeksi suuria, koska itseisarvojen osasummien jono on suppenevana jonona Cauchy-jono. Siis (S n ) on myös Cauchy-jono, siis suppeneva. Väitteen epäyhtälö seuraa kolmioepäyhtälöstä (4.1), koska kaikilla n N n n a j a j a j. Seuraavasta lauseesta saadaan riiittävä ja välttämätön ehto itseiselle suppenemiselle Lause. Jos b j 0 kaikilla j, niin sarja b j suppenee, jos ja vain, jos sen osasummien jono muodostaa rajoitetun jonon, ts. on olemassa M R, jolle n b j M kaikilla n. Todistus: Osasummien jono on nouseva; nouseva jono suppenee täsmälleen silloin kun se on rajoitettu.
36 Analyysi Suppenemistestejä Seuraavassa esitetään kokoelma testejä sarjojen (itseisen) supenemisen toteamiseksi Lause. (Vertailutesti) Olkoot a j R, j N. (a) Jos on olemassa luvut b j 0, joille a j b j kaikilla j N ja sarja b j suppenee, niin sarja a j suppenee (itseisesti). (b) Jos on olemassa luvut c j 0, joille a j c j 0 kaikilla j N ja sarja c j hajaantuu, niin sarja a j hajaantuu. Todistus: Tämä seuraa lähes välittömästi lauseesta 4.8 (HT). Vertailutestiä on joskus kätevä käyttää seuraavassa rajamuodossa: Lause. (Vertailutesti 2) Olkoot a j 0 ja b j 0, j N. (a) Jos (b) Jos a j lim = a ]0, [, j b j niin sarja a j suppenee, jos ja vain, jos sarja b j suppenee. a j lim = 0 j b j ja jos sarja b j suppenee, niin myös sarja a j suppenee.
37 Analyysi 3 35 (c) Jos a j lim = j b j ja jos sarja b j hajaantuu, niin myös sarja a j hajaantuu. Todistus: Seuraa Lauseesta 4.9, koska äärellisen monen termin muuttaminen ei vaikuta sarjan suppenemiseen (HT). Esimerkki. Sarja hajaantuu, koska ja harmoninen sarja hajaantuu. lim j j j 2 +j +1 j j 2 +j+1 1 j 1 j = Lause. (Suhdetesti) Olkoot a j R, a j 0 kaikilla j N. (a) Jos on olemassa luvut ρ < 1 ja N N, joille a j+1 a j ρ kaikilla j N,, niin sarja a j suppenee (itseisesti). (b) Jos on olemassa luvut η > 1 ja N N, joille a j+1 a j η kaikilla j N, niin sarja a j hajaantuu.
38 Analyysi 3 36 Todistus: a) Koska a j ρ a j 1 ρ 2 a j 2 ρ j N a N, sarjaa majoroi suppeneva geometrinen sarja a j j=n a N ρ j N, j=n joten väite a) seuraa vertailutestistä 4.9. b) Nyt a j η a j 1 η 2 a j 2 η j N a N, kun j, joten sarja a j hajaantuu (Lause 4.3) Huomautus. Lauseesta 4.11 saadaan helposti raja-arvoversio (a j 0): (a) Jos niin sarja a j suppenee (itseisesti). a j+1 lim < 1, j a j (b) Jos niin sarja a j hajaantuu. a j+1 lim > 1, j a j Huomaa, että jos suhdetestissä ρ = 1 tai η = 1 tai jos suhteen raja-arvo on itseisarvoltaan 1, niin suppenemisesta ei voida päätellä mitään, esimerkiksi harmoninen sarja hajaantuu ja vuorotteleva harmoninen sarja suppenee, vaikka molemmille a j+1 a j = j < 1 kaikilla j. j +1
39 Analyysi 3 37 Esimerkki. Sarja suppenee koska 1 (n+1)! 1 n! 1 n! = 1 n < 1. Seuraavaa juuritestiä on usein hieman vaikeampi käyttää kuin edellisiä testejä, mutta se on kuitenkin tärkeä suppenemistesti Lause. (Juuritesti) Olkoot a n R, n N. (a) Jos on olemassa luvut ρ < 1 ja N N, joille n an ρ kaikilla n N, niin sarja a n suppenee (itseisesti). (b) Jos on olemassa luvut η > 1 ja N N, joille n an η kaikilla n N, niin sarja a n hajaantuu. Erityisesti, jos on olemassa raja-arvo lim n n an = L, niin sarja a n suppenee (itseisesti), jos L < 1 ja hajaantuu, jos L > 1. Todistus: (a) Koska a n ρ n, niin sarjalla sarja n=n n=n ρ n, joten väite seuraa vertailutestistä 4.9. a n on majoranttina suppeneva (b) Tällöin a n η n 1 äärettömän monella n, joten termit a n eivät suppene nollaan eikä sarja siten voi supeta (Lause 4.3).
40 Analyysi 3 38 Esimerkki. Sarja 1 n2 n suppenee, koska lim n n 1 n2 = 1 n 2 lim n 1 n n = = 1 2 < 1. Seuraavasta 2 m -testistä on joskus hyötyä: Lause. (2 m -testi) Olkoot a n R laskeva jono ei-negatiivisia lukuja (ts. a 1 a 2 0), joille lim a n = 0. n Tällöin sarja a n suppenee, jos ja vain, jos sarja 2 m a 2 m suppenee. m=0 Todistus: Jos : Olkoon N N ja valitaan se kokonaisluku M, jolle 2 M 1 N < 2 M. Tällöin N a n 2 M 1 a n = a 1 +(a 2 +a 3 )+(a 4 +a 5 +a 6 +a 7 )+ +(a 2 M 1 + +a 2 M 1) 2 0 a a a M 1 a 2 M 1 = M 1 m=0 2 m a 2 m 2 m a 2 m <, m=0 joten osasummien jono on rajoitettu ja sarja a n siten suppenee.
41 Analyysi 3 39 Vain jos : Samaan tapaan, sillä 1 2 M 2 m a 2 m = m=1 Yksityiskohdat HT. M 2 m 1 a 2 m m=1 (a 1 +a 2 )+(a 3 +a 4 )+(a 5 +a 6 +a 7 +a 8 )+... +(a 2 M a 2 M a 2 M) a n <. Esimerkki. (Yli- ja aliharmoniset sarjat) Tarkastellaan sarjaa Käytetään 2 m -testiä 4.14, missä a n = n p : 2 m a 2 m = m=0 1, missä p > 0. np m=0 2 m (2 m ) = p m=0 ( 1 2 p 1 ) m, mikä on geometrinen sarja, joka suppenee jos ja vain, jos 1/2 p 1 < 1 eli p > 1. Siis yliharmoninen sarja 1, p > 1, suppenee np ja aliharmoninen (ja harmoninen) sarja 1, 0 < p 1, hajaantuu. np Lause. (Integraalitesti) Olkoon f : [1, ) [0, ) jatkuva ja vähenevä funktio ja a n = f(n).
42 Analyysi 3 40 Tällöin sarja a n suppenee jos ja vain, jos epäoleellinen integraali f(x)dx suppenee. 1 a 1 a 2 a 3 a 4 y = f(x) Todistus: 1 5 Väite seuraa, koska kaikilla N (ks. kuva) N a n = n=2 = N f(n) = n=2 N 1 f(x)dx N 1 = a n. N n n=2 n 1 N 1 Yksityiskohdat jätetään harjoitustehtäväksi. f(n)dx n+1 n f(n)dx N n n=2 n 1 f(x)dx Esimerkki. Sarja 1 (n+2)log(n+2)
43 Analyysi 3 41 hajaantuu, koska määrittelemällä f(x) = 1 (x+2)log(x+2), x 1, voidaan soveltaa integraalitestiä ja laskemme: a 1 kun a. f(x)dx = = a 1 / a 1, 1 (x+2) log(x+2) dx log(log(x+2)) = log(log(a+2)) log(log(3)) Huomautus. Yksi suppenemistesti ei sovellu joka sarjaan, vaan usein pitää kokeilla useampia testejä ennen kuin onnistuu. Huomaa myös, että esimerkiksi vertailutestin käytössä riittää löytää karkea epäyhtälö (ja vain häntäpään termeille), esimerkiksi ehto a n n 2, kun n > on ihan riittävä takaamaan sarjan a n itseisen suppenemisen. Muista myös erottaa oleelliset osat epäoleellisista, esimerkiksi luvussa 2 n n 7 osa 2 n on määräävä isoilla n Sarjan ehdollinen suppeneminen Kun sarjan termit eivät kaikki ole samanmerkkisiä, niin suppeneva sarja ei välttämättä suppene itseisesti. Tällaisista esimerkkinä on vuorotteleva harmoninen sarja ( 1) n1 n, joka suppenee, mutta ei itseisesti. Joskus halutaan korostaa, ei-itseistä (eiabsoluuttista) konvergenssiä ja sanotaan, että sarja suppenee ehdollisesti. Tässä jaksossa tarkastellaan tähän liittyviä ilmiöitä.
44 Analyysi Lause. (Leibnitzin testi vuorotteleville sarjoille) Olkoon a n vähenevä jono ei-negatiivisia reaalilukuja, ts. a 1 a 2 a n 0. Jos niin vuorotteleva sarja ( 1) n 1 a n jonolle pätee S 2n lim a n = 0, n suppenee. Edelleen, sarjan osasummien S n ( 1) j 1 a j S 2n 1 kaikilla n. Todistus: Kun S n = n ( 1) j 1 a j, niin 2n 1 S 2n 1 = ( 1) j 1 a j = S 2n+1 +(a 2n a 2n+1 ) S 2n+1, koska jono a j on vähenevä. Siten jono (S 2n 1 ) n on vähenevä. Samoin nähdään, että jono (S 2n ) n on kasvava: S 2n = 2n ( 1) j 1 a j = S 2n+2 (a 2n+1 a 2n+2 ) S 2n+2. Koska lisäksi S 1 S 2n 1 = S 2n +a 2n S 2n S 2, ovat molemmat jonot (S 2n 1 ) n ja (S 2n ) n rajoitettuja, joten niillä on reaaliset rajaarvot: lim n S 2n 1 = S ja lim S 2n = S. n Koska 0 S 2n 1 S 2n = a 2n 0, on S = S ja väite seuraa.
45 Analyysi 3 43 Esimerkki. Kuten tiedämme vuorotteleva harmoninen sarja ( 1) n 11 n, suppenee, mutta ei itseisesti. Vaihdetaan seuraavassa sen termien a n = ( 1) n 11 n summausjärjestystä: olkoon b 1 = a n ja valitaan summataan parittomien indeksien termejä kunnes termien summa on 2. Sitten otetaan seuraavaksi b-termiksi ensimmäinen negatiivinen termi a 2 = 1 ja sitten taas summataan parittomia indeksejä, 2 posiitivisia termejä, kunnes kokonaissumma ylittää arvon 3. Nyt lisätään a 4 = 1 ja 4 jatketaan positiivitermien summaamista. Näin jatkamalla saadaan termit helposti järjestetyksi niin, että uudessa järjestyksessä summattu sarja hajaantuu (ks. yksityiskohdat tarkemmin alla 4.19). Ei-itseisesti suppenevan sarjan suppenemista sanotaan joskus ehdolliseksi juuri sen tähden, että summausjärjestystä vaihtamalla suppeneminen voidaaan kadottaa. Itseisesti suppenevalle sarjalle on ihan sama, missä järjestyksessä termit lasketaan yhteen: Sanotaan, että sarja b n on saatu sarjasta a n summausjärjestystä vaihtamalla, jos on olemassa bijektio j : N N, jolle b j(n) = a n kaikilla n Lause. Olkoon sarja b n saatu sarjasta a n summausjärjestystä vaihta- malla. Jos sarja a n suppenee itseisesti, niin sarja b n suppenee myös itseisesti ja a n = b n. Todistus: Olkoon S j sarjan a n osasummien jono ja S sen raja-arvo. Olkoon T j uudelleen järjestetyn sarjan b n osasummien jono. Jos ε > 0, niin voidaan valita sellainen M, jolle a n < ε 2, n=m+1
46 Analyysi 3 44 jolloin myös S j S < ε 2 kaikilla j M. Valitaan N niin suureksi, että kaikki M ensimmäistä a n -termiä ovat N ensimmäisen b n -termin joukossa, ts. Tällöin kaikilla n N joten {a 1,a 2,...,a M } {b 1,b 2,...,b N }. S M T n n=m+1 a n < ε 2, T n S S S M + S M T n < ε 2 + ε 2 = ε. Ei-itseisesti suppenevan sarjan voi uudelleen järjestäminen sekoittaa pahoin: Lause. (Riemannin uudelleenjärjestyslause) Olkoon sarja a n suppeneva, mutta ei itseisesti suppeneva. Jokaisella s R voidaan sarjasta a n summausjär- jestystä vaihtamalla muodostaa sarja b n, joka suppenee kohti lukua s. Todistus: Olkoot p 1,p 2,... sarjan a n ei-negatiiviset termit alkuperäisessä järjestyksessään lueteltuina. Samoin q 1,q 2,... onnegatiivisten termien jono. Nyt sarjat p n ja q n hajaantuvat, koska jos ne molemmat suppenesivat, niin sarja a n suppenesi itseisesti. Jos taas toinen em. sarjoista suppenisi ja toinen hajaantuisi, niin sarjan osasummien jono lähestyisi joko postiivista tai negatiivista äärettömyyttä. Koska alkuperäinen sarja suppenee, sen termit suppenevat nollaan; siten lim n p n = 0 ja lim n q n = 0. a n
47 Analyysi 3 45 Näiden alkuvalmistelujen jälkeen voimme järjestää sarjan termit uudelleen: Valitaan ensin positiivitermit p 1,p 2,...,p k1, missä k 1 on ensimmäinen indeksi, jolle k 1 p n > s. Tällainen k 1 on mahdollista valita koska positiivitermien sarja hajaantuu. Sitten summataan negatiivisia termejä q 1,q 2,...,q l1 missä l 1 on ensimmäinen indeksi, jolle k 1 p n + l 1 q n < s. Jatketaan summaamalla positiivitermejä, kunnes päästään kokonaissummassa taas yli luvun s; sitten negatiivisia, kunnes taas s:n alapuolelle jne. Positiivisia termejä summattaessa ((n + 1). kertaa) osasummien arvo on lukujen s + q ln ja s + p kn+1 välissä. Negatiivisia termejä summattaessa (n. kertaa) osasummien arvo on lukujen s+q ln ja s+p kn välissä. Koska lim p n = 0 ja lim q n = 0, n n osasummat väkisin suppenevat kohti haluttua lukua s. Olkoot seuraavassa a n ja b n kaksi itseisesti suppenevaa sarjaa. Pyritään muodostamaan termeistä tuloja, joiden muodostama sarja suppenisi kohti lukua ( )( ) a n b n. Lasketaan muodollisesti: (a 1 +a 2 +a 3 +a )(b 1 +b 2 +b 3 +b ) = a 1 b 1 +(a 2 b 1 +a 1 b 2 )+(a 3 b 1 +a 2 b 2 +a 1 b 3 )+(a 4 b 1 + +a 1 b 4 )+... = c 1 +c 2 +c , missä n c n = a j b n j+1. Sarjaa c n sanotaan sarjojen a n ja b n Cauchyn tuloksi.
48 Analyysi Lause. Olkoot a n ja b n kaksi itseisesti suppenevaa sarjaa. Tällöin niiden Cauchyn tulo suppenee itseisesti ja ( )( ) a n b n = c n, missä siis c n = n a j b n j+1. Todistus: Tarkastellaan sarjaa (4.2) a 1 b 1 +a 2 b 1 +a 2 b 2 +a 1 b 2 +a 3 b 1 +a 3 b 2 +a 3 b 3 +a 2 b 3 +a 1 b a n b 1 +a n b 2 +a n b 3 + +a n b n +a n 1 b n + +a 1 b n Tämän k 2. osasumma on tulo ( k )( k ) a n b n. Koska alkuperäiset sarjat suppenevat itseisesti, niin sarjan (4.2) termien itseisarvojen osasummilla on ylärajana tulo ( a n )( b n ) <, joten sarja (4.2) suppenee itseisesti. Näin ollen sen termien summausjärjestystä voidaan vaihtaa eikä suppeneminen eikä sarjan summa tästä muutu(lause 4.18). Koska Cauchyn tulo saadaan selvästi sarjasta (4.2) summausjärjestystä vaihtamalla, väite seuraa koska, jos S k on sarjan (4.2) k. osasumma, niin lim S ( k )( k ) ( )( ) k = lim S k 2 = lim a n b n = a n b n. k k k
49 Analyysi 3 47 Esimerkki. Geometrisestä sarjasta tiedämme, että kaikilla x ] 1, 1[ 1 1 x = x n = n=0 k=1 x k 1 ja sarja suppenee itseisesti, kun x ] 1,1[. Siten sen Cauchyn tulo itsensä kanssa antaa 1 (1 x) = 2 k=1 k x j 1 x k j+1 1 = k x k 1 = k=1 kx k 1 = (n+1)x n, k=1 n=0 mikä Lauseen 4.20 nojalla suppenee itseisesti kaikilla x ] 1, 1[.
50 Analyysi Potenssisarjat Tässä luvussa tarkastellaan funktioiden f j : A R muodostamia sarjoja f j ; lähinnä muotoa olevia potenssisarjoja. a j (x x 0 ) j j= Funktiosarjat ja niiden suppeneminen Aluksi yleistetään sarjan käsite funktioiden summille aivan samoin kuin luvussa 3 yleistimme lukujonon suppenemisen funktioiden jonoille: 5.1. Määritelmä. (Funktiosarjat)Olkoonf n : A R,n = 1,2,...Muodollista summaa f n = f 1 +f sanotaan funktiosarjaksi. Sanotaan, että funktiosarja f n suppenee (pisteittäin) joukossa A, jos sarjat f n (x) suppenevat jokaisella x A. Funktiosarja f n suppenee itseisesti, jos itseisarvofunktioiden sarja f n suppenee. Edelleen sanotaan, että funktiosarja f n suppenee tasaisesti joukossa A, jos osasummien S k, S k (x) = k f n (x),
51 Analyysi 3 49 jono suppenee tasaisesti joukossa A. Toisin sanoen on olemassa funktio f : A R, jolle kaikilla ε > 0 on N N, jolle S k (x) f(x) < ε kaikilla x A, kun k N Huomautus. a) Suppeneva funktiosarja f n määrää siis funktion f : A R, jonka arvo pisteessä x on lukusarjan f n (x) summa, Tällöin siis osasummafunktiot S k, f(x) = S k (x) = f n (x). k f n (x), suppenevat kohti funktiota f joko pisteittäin tai tasaisesti rippuen siitä kummalla lailla sarja suppenee. Luvun 3 funktiojonojen suppenemista ja luvun 4 sarjojen suppenemista koskevat tulokset ovat nyt käytettävissä. b) Tasaisen suppenemisen Cauchyn kriteerio 3.4 tulkittuna funktiosarjoille kertoo, että funktiosarja f n suppenee tasaisesti (kohti jotain funktiota f : A R) jos ja vain jos kaikilla ε > 0 on N = N(ε) N, jolle sup x A k n=m+1 f n (x) = sup S k (z) S m (z) < ε, kun k > m N. x A c) Jos sarja f n suppenee tasaisesti joukossa A, niin funktiojono f n suppenee tasaisesti kohti nollafunktiota, koska f n = n n 1 f k f k, k=1 k=1 (vrt. Lause 4.3).
52 Analyysi 3 50 Funktiojonoja koskevista tuloksista saamme heti seuraavan Lause. Olkoot f n : I R funktioita, joille funktiosarja f n suppenee tasaisesti välillä I. (a) Jos funktiot f n ovat jatkuvia, niin summafunktio f n on jatkuva. (b) Jos funktiot f n ovat Riemann-integroituvia välillä [a,b] I, niin summafunktio f n on Riemann-integroituva ja b a f n (x)dx = b a f n (x)dx. (c) Jos funktiot f n ovat jatkuvasti derivoituvia ja jos myös derivaattafunktioiden sarja f n suppenee tasaisesti (avoimella) välillä I, niin summafunktio on jatkuvasti derivoituva ja d dx f n (x) = f n (x) kaikilla x I. Todistus: a) on Lause 3.5, b) Lause 3.6 ja c) Lause 3.7. f n Seuraava Weierstrassin M-testi on erittäin tärkeä apukeino funktiosarjoja käsitellessä: funktiosarja suppenee tasaisesti, jos funktioiden itseisarvojen supremumien muodostama lukusarja suppenee Lause (Weierstrassin M-testi). Olkoon f n : A R jono funktioita, joille kaikilla n N on sellainen M n <, että f n (x) M n kaikilla x A. Jos sarja M n suppenee, niin funktiosarja f n suppenee itseisesti ja tasaisesti joukossa A.
53 Analyysi 3 51 Todistus: Itseinen suppeneminen seuraa vertailutestistä 4.9. Olkoon S m (z) = Nyt kun k > m, niin kaikilla x A S m (x) S k (x) = ( k kun k > m N ε, sillä ) M n k = m f n (x). k n=m+1 k n=m+1 k M n f n (x) f n (x) k n=m+1 m M n < ε, M n on Cauchy-jono, koska se suppenee. Siten f n toteuttaa tasaisen suppenemisen Cauchyn kriteerion ja suppenee siten tasaisesti A:ssa Potenssisarjat Olkoon a j R ja x 0 R Muotoa a j (x x 0 ) j j=0 olevaa funktiosarjaa (muuttujana on luku x) sanotaan potenssisarjaksi tai Taylorsarjaksi. Luvut a j ovat potenssisarjan a j (x x 0 ) j kertoimetjapiste x 0 sen keskus. j=0 Vertaamalla potenssisarjaa geometriseen sarjaan saadaan seuraava tulos: 5.5. Lause. Jospotenssisarja a j (x x 0 ) j suppenee, kunx = x 1,niinsesuppenee j=0 itseisesti kaikilla x, joille x x 0 < x 1 x 0. Jos potenssisarja a j (x x 0 ) j hajaantuu, kun x = x 2, niin se hajaantuu kaikilla j=0 x, joille x x 0 > x 2 x 0.
54 Analyysi 3 52 Todistus: Olkoon x x 0 < x 1 x 0 (voidaan olettaa, että x x 0 ). Koska sarja a j (x 1 x 0 ) j suppenee, sen termit suppenevat nollaan (Lause 4.3) ja siis on luvut j=0 M R ja N N, joille Näin ollen a j (x 1 x 0 ) j M kaikilla j N. a j (x x 0 ) j = a j (x 1 x 0 ) j x x ( ) 0 j j x 1 x 0 M x x0 kaikilla j N, j x 1 x 0 joten koska x x 0 x 1 x 0 < 1, sarjaa a j (x x 0 ) j majoroi suppeneva geometrinen sarja j=0 M j=0 ja siten se suppenee itseisesti (Lause 4.9). ( ) j x x0, x 1 x 0 Sarjan a j (x x 0 ) j hajaantuminen, kun x x 0 > x 2 x 0, nähdään samaan j=0 tapaan vertaamalla sitä geometriseen sarjaan (HT). Esimerkki. Tarkastellaan potenssisarjaa Kun x = 1, kyseessä on harmoninen sarja, joka hajaantuu. Siten lauseen 5.5 mukaan ko. potenssisarja hajaantuu aina, kun x > 1. Kun taas x = 1, kyseesä on vuorotteleva harmoninen sarja, joka suppenee. Lauseen 5.5 nojalla potenssisarja suppenee itseisesti, kun x < 1. Näin ollen esimerkin potenssisarja suppenee täsmälleen välillä [ 1,1[, itseisesti avoimella välillä ] 1,1[. x j j.
55 Analyysi Määritelmä. Potenssisarjan a j (x x 0 ) j suppenemissäde on luku j=0 R = sup{ x x 0 : sarja a j (x x 0 ) j suppenee }. j=0 Tällöin 0 R ja avoin väli ]x 0 R,x 0 +R[ on potenssisarjan a j (x x 0 ) j suppenemisväli. j=0 Huomaa, että jos R = 0, on suppenemisväli tyhjä ja potenssisarja suppenee tällöin vain keskuksessaan x = x 0. Jos taas R =, potenssisarja suppenee koko R:ssä Lause. Olkoon R potenssisarjan a j (x x 0 ) j suppenemissäde ja 0 < r < j=0 R. Tällöin potenssisarja a j (x x 0 ) j suppenenee itseisesti suppenemisvälillään j=0 ]x 0 R,x 0 +R[ ja tasaisesti välillä [x 0 r,x 0 +r]. Edelleen potenssisarja a j (x x 0 ) j hajaantuu jokaisella x / [x 0 R,x 0 +R]. j=0 Todistus: Itseistä suppenemista ja hajaantumista koskevat väitteet seuraavat lauseesta 5.5. Tasainen konvergenssi seuraa Weierstrassin M-testistä 5.4, sillä kun x [x 0 r,x 0 +r], niin a j (x x 0 ) j a j r j ja sarja a j r j suppenee sillä sen termit ovat potenssisarjan a j (x x 0 ) j termien j=0 itseisarvoja pisteessä x = x 0 +r, joka kuuluu suppenemisvälille. j=0 Esimerkki. Millä x:n arvoilla sarja ( 1) n (x 1) n 2 n n 2
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
8 Potenssisarjoista. 8.1 Määritelmä. Olkoot a 0, a 1, a 2,... reaalisia vakioita ja c R. Määritelmä 8.1. Muotoa
 8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
8 Potenssisarjoista 8. Määritelmä Olkoot a 0, a, a 2,... reaalisia vakioita ja c R. Määritelmä 8.. Muotoa a 0 + a (x c) + a 2 (x c) 2 + olevaa sarjaa sanotaan c-keskiseksi potenssisarjaksi. Selvästi jokainen
Konvergenssilauseita
 LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
LUKU 4 Konvergenssilauseita Lause 4.1 (Monotonisen konvergenssin lause). Olkoon (f n ) kasvava jono Lebesgueintegroituvia funktioita. Asetetaan f(x) := f n (x). Jos f n
Sisältö. Sarjat 10. syyskuuta 2005 sivu 1 / 17
 Sarjat 10. syyskuuta 2005 sivu 1 / 17 Sisältö 1 Peruskäsitteistöä 2 1.1 Määritelmiä 2 1.2 Perustuloksia 4 2 Suppenemistestejä positiivitermisille sarjoille 5 3 Itseinen ja ehdollinen suppeneminen 8 4 Alternoivat
Sarjat 10. syyskuuta 2005 sivu 1 / 17 Sisältö 1 Peruskäsitteistöä 2 1.1 Määritelmiä 2 1.2 Perustuloksia 4 2 Suppenemistestejä positiivitermisille sarjoille 5 3 Itseinen ja ehdollinen suppeneminen 8 4 Alternoivat
Funktiojonon tasainen suppeneminen
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Taina Saari Funktiojonon tasainen suppeneminen Matematiikan ja tilastotieteen laitos Matematiikka Elokuu 2009 Tampereen yliopisto Matematiikan ja tilastotieteen
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Taina Saari Funktiojonon tasainen suppeneminen Matematiikan ja tilastotieteen laitos Matematiikka Elokuu 2009 Tampereen yliopisto Matematiikan ja tilastotieteen
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 14.9.2016 Pekka Alestalo, Jarmo Malinen
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 14.9.2016 Pekka Alestalo, Jarmo Malinen
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos September 13, 2017 Pekka Alestalo,
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos September 13, 2017 Pekka Alestalo,
Sarja. Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,...,
 Sarja Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): Määritelmä 1 s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,..., n s n = a k. Jos osasummien jonolla (s n ) on raja-arvo s R,
Sarja Lukujonosta (a k ) k N voi muodostaa sen osasummien jonon (s n ): Määritelmä 1 s 1 = a 1, s 2 = a 1 + a 2, s 3 = a 1 + a 2 + a 3,..., n s n = a k. Jos osasummien jonolla (s n ) on raja-arvo s R,
V. POTENSSISARJAT. V.1. Abelin lause ja potenssisarjan suppenemisväli. a k (x x 0 ) k M
 V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
MS-A010{2,3,4,5} (SCI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: Sarjat
 M-A010{2,3,4,5} (CI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: arjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos eptember 12, 2018 Pekka
M-A010{2,3,4,5} (CI, ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 2: arjat Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos eptember 12, 2018 Pekka
funktiojono. Funktiosarja f k a k (x x 0 ) k
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
ANALYYSI 3 HELI TUOMINEN
 ANALYYSI 3 HELI TUOMINEN Alkusanat Tässä on muistiinpanot syksyllä 202 luennoimastani kurssista Analyysi 3. Kurssin pohana on Tero Kilpeläisen luentomoniste samannimiselle kurssille. Tässä monisteessa
ANALYYSI 3 HELI TUOMINEN Alkusanat Tässä on muistiinpanot syksyllä 202 luennoimastani kurssista Analyysi 3. Kurssin pohana on Tero Kilpeläisen luentomoniste samannimiselle kurssille. Tässä monisteessa
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Funktiojonot ja funktiotermiset sarjat Funktiojono ja funktioterminen sarja Pisteittäinen ja tasainen suppeneminen
 4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
Analyysi III. Jari Taskinen. 28. syyskuuta Luku 1
 Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Analyysi III Jari Taskinen 28. syyskuuta 2002 Luku Sisältö Sarjat 2. Lukujonoista........................... 2.2 Rekursiivisesti määritellyt lukujonot.............. 8.3 Sarja ja sen suppenminen....................
Kompleksianalyysi, viikko 5
 Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
Kompleksianalyysi, viikko 5 Jukka Kemppainen Mathematics Division Kompleksiset jonot Aloitetaan jonon suppenemisesta. Määr. 1 Kompleksiluvuista z 1,z 2,...,z n,... koostuva jono suppenee kohti raja-arvoa
Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä
 Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä. L Hospitalin sääntö on tuttu Analyysi :n kurssilta. Se on näppärä keino laskea tiettyjä raja-arvoja, mutta sen käytössä on oltava kuitenkin varovainen.
Sarjat ja differentiaaliyhtälöt, harjoitustehtäviä. L Hospitalin sääntö on tuttu Analyysi :n kurssilta. Se on näppärä keino laskea tiettyjä raja-arvoja, mutta sen käytössä on oltava kuitenkin varovainen.
Sarjat ja differentiaaliyhtälöt
 Sarjat ja differentiaaliyhtälöt Johdanto Tämä luentomoniste on tarkoitettu korvaamaan luentomuistiinpanoja Sarjat ja differentiaaliyhtälöt-kurssilla. Tämä ei kuitenkaan ole oppikirja, mikä tarkoittaa sitä,
Sarjat ja differentiaaliyhtälöt Johdanto Tämä luentomoniste on tarkoitettu korvaamaan luentomuistiinpanoja Sarjat ja differentiaaliyhtälöt-kurssilla. Tämä ei kuitenkaan ole oppikirja, mikä tarkoittaa sitä,
1 sup- ja inf-esimerkkejä
 Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Nollakohdan olemassaolo. Kaikki tuntevat
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1. Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS
 DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
DIFFERENTIAALI- JA INTEGRAALILASKENTA I.1 Ritva Hurri-Syrjänen/Syksy 1999/Luennot 6. FUNKTION JATKUVUUS Huomautus. Analyysin yksi keskeisimmistä käsitteistä on jatkuvuus! Olkoon A R mielivaltainen joukko
Sarjojen suppenemisesta
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Terhi Mattila Sarjojen suppenemisesta Matematiikan ja tilastotieteen laitos Matematiikka Huhtikuu 008 Tampereen yliopisto Matematiikan ja tilastotieteen laitos
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Terhi Mattila Sarjojen suppenemisesta Matematiikan ja tilastotieteen laitos Matematiikka Huhtikuu 008 Tampereen yliopisto Matematiikan ja tilastotieteen laitos
Matematiikan tukikurssi, kurssikerta 5
 Matematiikan tukikurssi, kurssikerta 5 1 Jonoista Matematiikassa jono (x n ) on yksinkertaisesti järjestetty, päättymätön sarja numeroita Esimerkiksi (1,, 3, 4, 5 ) on jono Jonon i:ttä jäsentä merkitään
Matematiikan tukikurssi, kurssikerta 5 1 Jonoista Matematiikassa jono (x n ) on yksinkertaisesti järjestetty, päättymätön sarja numeroita Esimerkiksi (1,, 3, 4, 5 ) on jono Jonon i:ttä jäsentä merkitään
III. SARJATEORIAN ALKEITA. III.1. Sarjan suppeneminen. x k = x 1 + x 2 + x ,
 III. SARJATEORIAN ALKEITA Sarja on formaali summa III.. Sarjan suppeneminen = x + x 2 + x 3 +..., missä R aiilla N (merintä ei välttämättä taroita mitään reaaliluua). Luvut x, x 2,... ovat sarjan yhteenlasettavat
III. SARJATEORIAN ALKEITA Sarja on formaali summa III.. Sarjan suppeneminen = x + x 2 + x 3 +..., missä R aiilla N (merintä ei välttämättä taroita mitään reaaliluua). Luvut x, x 2,... ovat sarjan yhteenlasettavat
Luku 4. Derivoituvien funktioiden ominaisuuksia.
 1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
nyky-ymmärryksemme mukaan hajaantuvaan sarjaan luvun 1 2 kun n > N Huom! Määritelmä on aivan sama C:ssä ja R:ssä. (Kuva vain on erilainen.
 Sarjaoppia Käsitellään kompleksi- ja reaalisarjat yhdessä. Reaalilukujen ominaisuuksista (kuten järjestys) riippuvat asiat tulevat lisämausteena mukaan. Kirjallisuutta: 1. [KRE] Kreyszig: Advanced Engineering
Sarjaoppia Käsitellään kompleksi- ja reaalisarjat yhdessä. Reaalilukujen ominaisuuksista (kuten järjestys) riippuvat asiat tulevat lisämausteena mukaan. Kirjallisuutta: 1. [KRE] Kreyszig: Advanced Engineering
VI. TAYLORIN KAAVA JA SARJAT. VI.1. Taylorin polynomi ja Taylorin kaava
 VI. TAYLORIN KAAVA JA SARJAT VI.. Taylorin polynomi ja Taylorin kaava Olkoon n N ja x, c, c, c 2,..., c n R. Tehtävä: Etsittävä sellainen R-kertoiminen polynomi P, että sen aste deg P n ja P (x ) = c,
VI. TAYLORIN KAAVA JA SARJAT VI.. Taylorin polynomi ja Taylorin kaava Olkoon n N ja x, c, c, c 2,..., c n R. Tehtävä: Etsittävä sellainen R-kertoiminen polynomi P, että sen aste deg P n ja P (x ) = c,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
Tenttiin valmentavia harjoituksia
 Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
Tenttiin valmentavia harjoituksia Alla olevissa harjoituksissa suluissa oleva sivunumero viittaa Juha Partasen kurssimonisteen siihen sivuun, jolta löytyy apua tehtävän ratkaisuun. Funktiot Harjoitus.
3 Lukujonon raja-arvo
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 3 Lukujonon raja-arvo 3 Määritelmä Osoita, että 6n + 2n + 3 3 < 4 n ja määritä jokin sellainen n 0 Z +, että 6n + 2n + 3 3 < 0 87 aina, kun n > n 0 2 Olkoon x n
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 209 3 Lukujonon raja-arvo 3 Määritelmä Osoita, että 6n + 2n + 3 3 < 4 n ja määritä jokin sellainen n 0 Z +, että 6n + 2n + 3 3 < 0 87 aina, kun n > n 0 2 Olkoon x n
Perusidea: Jaetaan väli [a, b] osaväleihin ja muodostetaan osavälejä vastaavat suorakulmiot/palkit, joiden korkeus funktion arvot kyseisellä välillä.
![Perusidea: Jaetaan väli [a, b] osaväleihin ja muodostetaan osavälejä vastaavat suorakulmiot/palkit, joiden korkeus funktion arvot kyseisellä välillä. Perusidea: Jaetaan väli [a, b] osaväleihin ja muodostetaan osavälejä vastaavat suorakulmiot/palkit, joiden korkeus funktion arvot kyseisellä välillä.](/thumbs/96/129910971.jpg) Lähtötilanne Lähtötilanne Tavoite: Määritellään funktion f : [a, b] R integraali siten, että integraalin arvo yhtyy funktion f kuvaajan ja x-akselin väliin jäävän alueen pinta-alaan. Perusidea: Jaetaan
Lähtötilanne Lähtötilanne Tavoite: Määritellään funktion f : [a, b] R integraali siten, että integraalin arvo yhtyy funktion f kuvaajan ja x-akselin väliin jäävän alueen pinta-alaan. Perusidea: Jaetaan
1 sup- ja inf-esimerkkejä
 Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Kaarenpituus. Olkoon r: [a, b] R
Alla olevat kohdat (erityisesti todistukset) ovat lähinnä oheislukemista reaaliluvuista, mutta joihinkin niistä palataan myöhemmin kurssilla. 1 sup- ja inf-esimerkkejä Kaarenpituus. Olkoon r: [a, b] R
Analyysi 1. Harjoituksia lukuihin 1 3 / Syksy Osoita täsmällisesti perustellen, että joukko A = x 4 ei ole ylhäältä rajoitettu.
 Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
Analyysi Harjoituksia lukuihin 3 / Syksy 204. Osoita täsmällisesti perustellen, että joukko { 2x A = x ]4, [. x 4 ei ole ylhäältä rajoitettu. 2. Anna jokin ylä- ja alaraja joukoille { x( x) A = x ], [,
Vastausehdotukset analyysin sivuainekurssin syksyn välikokeeseen
 Vastausehdotukset analyysin sivuainekurssin syksyn 015 1. välikokeeseen Heikki Korpela November 1, 015 1. Tehtävä: funktio f : R R toteuttaa ehdot ax, kun x 1 f(x) x + 1, kun x < 1 Tutki, millä vakion
Vastausehdotukset analyysin sivuainekurssin syksyn 015 1. välikokeeseen Heikki Korpela November 1, 015 1. Tehtävä: funktio f : R R toteuttaa ehdot ax, kun x 1 f(x) x + 1, kun x < 1 Tutki, millä vakion
Reaaliluvut. tapauksessa metrisen avaruuden täydellisyyden kohdalla. 1 fi.wikipedia.org/wiki/reaaliluku 1 / 13
 Reaaliluvut Reaalilukujen joukko R. Täsmällinen konstruointi palautuu rationaalilukuihin, jossa eri mahdollisuuksia: - Dedekindin leikkaukset - rationaaliset Cauchy-jonot - desimaaliapproksimaatiot. Reaalilukujen
Reaaliluvut Reaalilukujen joukko R. Täsmällinen konstruointi palautuu rationaalilukuihin, jossa eri mahdollisuuksia: - Dedekindin leikkaukset - rationaaliset Cauchy-jonot - desimaaliapproksimaatiot. Reaalilukujen
infoa Viikon aiheet Potenssisarja a n = c n (x x 0 ) n < 1
 infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
infoa Viikon aiheet Tentti ensi viikolla ma 23.0. klo 9.00-3.00 Huomaa, alkaa tasalta! D0 (Sukunimet A-) E204 (Sukunimet S-Ö) Mukaan kynä ja kumi. Ei muuta materiaalia. Tentissä kaavakokoelma valmiina.
1 Supremum ja infimum
 Pekka Alestalo, 2018 Tämä moniste täydentää reaalilukuja ja jatkuvia reaalifunktioita koskevaa kalvosarjaa lähinnä perustelujen ja todistusten osalta. Suurin osa määritelmistä jms. on esitetty jo kalvoissa,
Pekka Alestalo, 2018 Tämä moniste täydentää reaalilukuja ja jatkuvia reaalifunktioita koskevaa kalvosarjaa lähinnä perustelujen ja todistusten osalta. Suurin osa määritelmistä jms. on esitetty jo kalvoissa,
Matemaattisen analyysin tukikurssi
 Matemaattisen analyysin tukikurssi 5. Kurssikerta Petrus Mikkola 10.10.2016 Tämän kerran asiat Raja-arvo ja toispuolinen raja-arvo Funktion suurin ja pienin arvo Lukujono Lukujonon suppeneminen Kasvava
Matemaattisen analyysin tukikurssi 5. Kurssikerta Petrus Mikkola 10.10.2016 Tämän kerran asiat Raja-arvo ja toispuolinen raja-arvo Funktion suurin ja pienin arvo Lukujono Lukujonon suppeneminen Kasvava
(b) = x cos x 1 ( cos x)dx. = x cos x + cos xdx. = sin x x cos x + C, C R.
 Calculus Kurssikoe..7. Laske (a) x sin x, (b) x x + x. (a) Merkitään u(x) = x ja v (x) = sin x, jolloin u (x) =, v(x) = cos x ja osittaisintegroimalla saadaan x sin x = u(x)v (x) = u(x)v(x) u (x)v(x) =
Calculus Kurssikoe..7. Laske (a) x sin x, (b) x x + x. (a) Merkitään u(x) = x ja v (x) = sin x, jolloin u (x) =, v(x) = cos x ja osittaisintegroimalla saadaan x sin x = u(x)v (x) = u(x)v(x) u (x)v(x) =
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012
 KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
KOMPLEKSIANALYYSI I KURSSI SYKSY 2012 RITVA HURRI-SYRJÄNEN 8. Integraalilauseiden sovelluksia 1. Analyyttisen funktion sarjaesitys. (eli jokainen analyyttinen funktio on lokaalisti suppenevan potenssisarjan
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Johdantoa INTEGRAALILASKENTA, MAA9
 Lyhyehkö johdanto integraalilaskentaan. Johdantoa INTEGRAALILASKENTA, MAA9 Integraalilaskennan lähtökohta 1: Laskutoimitukset + ja ovat keskenään käänteisiä, samoin ja ovat käänteisiä, kunhan ei jaeta
Lyhyehkö johdanto integraalilaskentaan. Johdantoa INTEGRAALILASKENTA, MAA9 Integraalilaskennan lähtökohta 1: Laskutoimitukset + ja ovat keskenään käänteisiä, samoin ja ovat käänteisiä, kunhan ei jaeta
reaalifunktioiden ominaisuutta, joiden perusteleminen on muita perustuloksia hankalampaa. Kalvoja täydentää erillinen moniste,
 Reaaliluvuista Pekka Alestalo Matematiikan ja systeemianalyysin laitos Aalto-yliopiston perustieteiden korkeakoulu Nämä kalvot sisältävät tiivistelmän reaaliluvuista ja niihin liittyvistä käsitteistä.
Reaaliluvuista Pekka Alestalo Matematiikan ja systeemianalyysin laitos Aalto-yliopiston perustieteiden korkeakoulu Nämä kalvot sisältävät tiivistelmän reaaliluvuista ja niihin liittyvistä käsitteistä.
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
x > y : y < x x y : x < y tai x = y x y : x > y tai x = y.
 ANALYYSIN TEORIA A Kaikki lauseet eivät ole muotoiltu samalla tavalla kuin luennolla. Ilmoita virheistä yms osoitteeseen mikko.kangasmaki@uta. (jos et ole varma, onko kyseessä virhe, niin ilmoita mieluummin).
ANALYYSIN TEORIA A Kaikki lauseet eivät ole muotoiltu samalla tavalla kuin luennolla. Ilmoita virheistä yms osoitteeseen mikko.kangasmaki@uta. (jos et ole varma, onko kyseessä virhe, niin ilmoita mieluummin).
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Ratkaisuehdotus 2. kurssikoe
 Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikokeeseen
 Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
2 Funktion derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 2018 2 Funktion derivaatta 1. Määritä derivaatan määritelmää käyttäen f (), kun (a), (b) 1 ( > 0). 2. Tutki, onko funktio sin(2) sin 1, kun 0, 2 0, kun = 0, derivoituva
Täydellisyysaksiooman kertaus
 Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
Täydellisyysaksiooman kertaus Luku M R on joukon A R yläraja, jos a M kaikille a A. Luku M R on joukon A R alaraja, jos a M kaikille a A. A on ylhäältä (vast. alhaalta) rajoitettu, jos sillä on jokin yläraja
ANALYYSI 2. Camilla Hollanti. Tampereen yliopisto 2010. x 3. a x 1. x 4 x 11. x 2
 ANALYYSI 2 Camilla Hollanti _ M M a x x 2 x 3 x 4 x b Tampereen yliopisto 200 Sisältö. Preliminäärejä 3 2. Riemann-integraali 5 2.. Pinta-alat ja porrasfunktiot....................... 5 2... Pinta-ala
ANALYYSI 2 Camilla Hollanti _ M M a x x 2 x 3 x 4 x b Tampereen yliopisto 200 Sisältö. Preliminäärejä 3 2. Riemann-integraali 5 2.. Pinta-alat ja porrasfunktiot....................... 5 2... Pinta-ala
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
3 Lukujonon raja-arvo
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 3 Lukujonon raja-arvo 3 Määritelmä Osoita, että 6n + 2n + 3 3 < 4 n ja määritä jokin sellainen n 0 Z +, että 6n + 2n + 3 3 < 0 87 aina, kun n > n 0 2 Olkoon x n
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 3 Lukujonon raja-arvo 3 Määritelmä Osoita, että 6n + 2n + 3 3 < 4 n ja määritä jokin sellainen n 0 Z +, että 6n + 2n + 3 3 < 0 87 aina, kun n > n 0 2 Olkoon x n
Taylorin sarja ja Taylorin polynomi
 Taylorin sarja ja 1 Potenssisarja c k (x a) k = f (x) määrittelee x:n funktion. Seuraavaksi toteamme mikä yhteys potenssisarjalla on sen määrittelemän funktion derivaattoihin f (a),f (a),f (a),f (3) (a),...
Taylorin sarja ja 1 Potenssisarja c k (x a) k = f (x) määrittelee x:n funktion. Seuraavaksi toteamme mikä yhteys potenssisarjalla on sen määrittelemän funktion derivaattoihin f (a),f (a),f (a),f (3) (a),...
H7 Malliratkaisut - Tehtävä 1
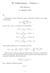 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
Matematiikan tukikurssi: kurssikerta 12
 Matematiikan tukikurssi: kurssikerta 2 Tenttiin valmentavia harjoituksia Huomio. Tähän tulee lisää ratkaisuja sitä mukaan kun ehin niitä kirjoittaa. Kurssilla käyään läpi tehtävistä niin monta kuin mahollista.
Matematiikan tukikurssi: kurssikerta 2 Tenttiin valmentavia harjoituksia Huomio. Tähän tulee lisää ratkaisuja sitä mukaan kun ehin niitä kirjoittaa. Kurssilla käyään läpi tehtävistä niin monta kuin mahollista.
Tasainen suppeneminen ja sen sovellukset
 Tasainen suppeneminen ja sen sovellukset Tuomas Hentunen Matematiikan pro gradu tutkielma Kesäkuu 2014 Tiivistelmä: Tuomas Hentunen, Tasainen suppeneminen ja sen sovellukset (engl. Uniform convergence
Tasainen suppeneminen ja sen sovellukset Tuomas Hentunen Matematiikan pro gradu tutkielma Kesäkuu 2014 Tiivistelmä: Tuomas Hentunen, Tasainen suppeneminen ja sen sovellukset (engl. Uniform convergence
MATEMATIIKAN PERUSKURSSI II kevät 2018 Ratkaisut 1. välikokeen preppaustehtäviin. 1. a) Muodostetaan osasummien jono. S n =
 MATEMATIIKAN PERUSKURSSI II kevät 208 Ratkaisut. välikokeen preppaustehtäviin. a) Muodostetaan osasummien jono S n = n ( k k) k= josta saadaan = ( 0 ) + ( 2) + ( 2 3) + ( n 2 n ) + ( n n) = n, n =, 2,...,
MATEMATIIKAN PERUSKURSSI II kevät 208 Ratkaisut. välikokeen preppaustehtäviin. a) Muodostetaan osasummien jono S n = n ( k k) k= josta saadaan = ( 0 ) + ( 2) + ( 2 3) + ( n 2 n ) + ( n n) = n, n =, 2,...,
1 Reaaliset lukujonot
 Jonot 10. syyskuuta 2005 sivu 1 / 5 1 Reaaliset lukujonot Reaaliset lukujonot ovat funktioita f : Z + R. Lukujonosta käytetään merkintää (a k ) k=1 tai lyhyemmin vain (a k). missä a k = f(k). Täten lukujonot
Jonot 10. syyskuuta 2005 sivu 1 / 5 1 Reaaliset lukujonot Reaaliset lukujonot ovat funktioita f : Z + R. Lukujonosta käytetään merkintää (a k ) k=1 tai lyhyemmin vain (a k). missä a k = f(k). Täten lukujonot
Derivaattaluvut ja Dini derivaatat
 Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Derivaattaluvut Dini derivaatat LuK-tutkielma Helmi Glumo 2434483 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Taustaa 2 2 Määritelmät 4 3 Esimerkkejä lauseita 7 Lähdeluettelo
Funktion raja-arvo ja jatkuvuus Reaali- ja kompleksifunktiot
 3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
3. Funktion raja-arvo ja jatkuvuus 3.1. Reaali- ja kompleksifunktiot 43. Olkoon f monotoninen ja rajoitettu välillä ]a,b[. Todista, että raja-arvot lim + f (x) ja lim x b f (x) ovat olemassa. Todista myös,
Positiivitermisten sarjojen suppeneminen
 Positiivitermisten sarjojen suppeneminen Jono (b n ) n= on kasvava, jos b n+ b n kaikilla n =, 2,... Lemma Jokainen ylhäältä rajoitettu kasvava jono (b n ) n= raja-arvo on lim n b n = sup n Z+ b n. suppenee
Positiivitermisten sarjojen suppeneminen Jono (b n ) n= on kasvava, jos b n+ b n kaikilla n =, 2,... Lemma Jokainen ylhäältä rajoitettu kasvava jono (b n ) n= raja-arvo on lim n b n = sup n Z+ b n. suppenee
4.3 Moniulotteinen Riemannin integraali
 4.3 Moniulotteinen Riemannin integraali Tässä luvussa opitaan miten integroidaan usean muuttujan reaaliarvoista tai vektoriarvoista funktiota, millaisten joukkojen yli jatkuvaa funktiota voi integroida,
4.3 Moniulotteinen Riemannin integraali Tässä luvussa opitaan miten integroidaan usean muuttujan reaaliarvoista tai vektoriarvoista funktiota, millaisten joukkojen yli jatkuvaa funktiota voi integroida,
Funktion approksimointi
 Funktion approksimointi Päivikki Vesterinen Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2015 Tiivistelmä: Päivikki Vesterinen, Funktion approksimointi (engl.
Funktion approksimointi Päivikki Vesterinen Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2015 Tiivistelmä: Päivikki Vesterinen, Funktion approksimointi (engl.
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Outoja funktioita. 0 < x x 0 < δ ε f(x) a < ε.
 Outoja funktioita Differentiaalilaskentaa harjoitettiin miltei 200 vuotta ennen kuin sen perustana olevat reaaliluvut sekä funktio ja sen raja-arvo määriteltiin täsmällisesti turvautumatta geometriseen
Outoja funktioita Differentiaalilaskentaa harjoitettiin miltei 200 vuotta ennen kuin sen perustana olevat reaaliluvut sekä funktio ja sen raja-arvo määriteltiin täsmällisesti turvautumatta geometriseen
Analyysi 1. Harjoituksia lukuihin 4 7 / Syksy Tutki funktion f(x) = x 2 + x 2 jatkuvuutta pisteissä x = 0 ja x = 1.
 Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
Analyysi 1 Harjoituksia lukuihin 4 7 / Syksy 014 1. Tutki funktion x + x jatkuvuutta pisteissä x = 0 ja x = 1.. Määritä vakiot a ja b siten, että funktio a x cos x + b x + b sin x, kun x 0, x 4, kun x
LUKU 3. Ulkoinen derivaatta. dx i 1. dx i 2. ω i1,i 2,...,i k
 LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
LUKU 3 Ulkoinen derivaatta Olkoot A R n alue k n ja ω jatkuvasti derivoituva k-muoto alueessa A Muoto ω voidaan esittää summana ω = ω i1 i 2 i k dx i 1 dx i 2 1 i 1
Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus Malliratkaisut (Sauli Lindberg)
 Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus 4 9.4.-23.4.200 Malliratkaisut (Sauli Lindberg). Näytä, että Lusinin lauseessa voidaan luopua oletuksesta m(a)
Matematiikan ja tilastotieteen laitos Reaalianalyysi I Harjoitus 4 9.4.-23.4.200 Malliratkaisut (Sauli Lindberg). Näytä, että Lusinin lauseessa voidaan luopua oletuksesta m(a)
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Käytännön asiat Jonot Sarjat 1.1 Opettajat luennoitsija Riikka Korte
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Käytännön asiat Jonot Sarjat 1.1 Opettajat luennoitsija Riikka Korte
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
termit on luontevaa kirjoittaa summamuodossa. Tällöin päädymme lukusarjojen teoriaan: a k = s.
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 7 3. Luusarjat Josus luujonon (b ) termit on luontevairjoittaa summamuodossa. Tällöin päädymme luusarjojen teoriaan: Määritelmä 3.. Oloon ( ), R luujono. Symboli (3.)
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 7 3. Luusarjat Josus luujonon (b ) termit on luontevairjoittaa summamuodossa. Tällöin päädymme luusarjojen teoriaan: Määritelmä 3.. Oloon ( ), R luujono. Symboli (3.)
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
5 Funktion jatkuvuus ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT Määritelmä ja perustuloksia. 1. Tarkastellaan väitettä
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 5 Funktion jatkuvuus 5.1 Määritelmä ja perustuloksia 1. Tarkastellaan väitettä a > 0: b > 0: c > 0: d U c (a): f(d) / U b (f(a)), missä a, b, c, d R. Mitä funktion
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 2019 5 Funktion jatkuvuus 5.1 Määritelmä ja perustuloksia 1. Tarkastellaan väitettä a > 0: b > 0: c > 0: d U c (a): f(d) / U b (f(a)), missä a, b, c, d R. Mitä funktion
Analyysin peruslause
 LUKU 10 Analyysin peruslause 10.1. Peruslause I Aiemmin Cantorin funktion ψ kohdalla todettiin, että analyysin peruslause II ei päde: [0,1] ψ (x) dm(x) < ψ(1) ψ(0). Kasvavalle funktiolle analyysin peruslauseesta
LUKU 10 Analyysin peruslause 10.1. Peruslause I Aiemmin Cantorin funktion ψ kohdalla todettiin, että analyysin peruslause II ei päde: [0,1] ψ (x) dm(x) < ψ(1) ψ(0). Kasvavalle funktiolle analyysin peruslauseesta
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
=p(x) + p(y), joten ehto (N1) on voimassa. Jos lisäksi λ on skalaari, niin
 FUNKTIONAALIANALYYSI, RATKAISUT 1 KEVÄT 211, (AP) 1. Ovatko seuraavat reaaliarvoiset funktiot p : R 3 R normeja? Ovatko ne seminormeja? ( x = (x 1, x 2, x 3 ) R 3 ) a) p(x) := x 2 1 + x 2 2 + x 2 3, b)
FUNKTIONAALIANALYYSI, RATKAISUT 1 KEVÄT 211, (AP) 1. Ovatko seuraavat reaaliarvoiset funktiot p : R 3 R normeja? Ovatko ne seminormeja? ( x = (x 1, x 2, x 3 ) R 3 ) a) p(x) := x 2 1 + x 2 2 + x 2 3, b)
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausta 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat: 1. Potenssisarjojen suppenemissäe, suppenemisväli ja suppenemisjoukko. 2. Derivaatan laskeminen
Matematiikan tukikurssi Kertausta 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat: 1. Potenssisarjojen suppenemissäe, suppenemisväli ja suppenemisjoukko. 2. Derivaatan laskeminen
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kuinka määritellään 2 3?
 Kuinka määritellään 2 3? y Nyt 3 = 1,7320508.... Luvut 3 2 x x 3 2 x 2 1 = 2, 2 1,7 3,2490, 2 1,73 3,3173, 2 1,732 3,3219,... ovat hyvin määriteltyjä koska näihin tarvitaan vain rationaalilukupotenssin
Kuinka määritellään 2 3? y Nyt 3 = 1,7320508.... Luvut 3 2 x x 3 2 x 2 1 = 2, 2 1,7 3,2490, 2 1,73 3,3173, 2 1,732 3,3219,... ovat hyvin määriteltyjä koska näihin tarvitaan vain rationaalilukupotenssin
Todista raja-arvon määritelmään perustuen seuraava lause: Jos lukujonolle a n pätee lima n = a ja lima n = b, niin a = b.
 2 Lukujonot 21 Lukujonon määritelmä 16 Fibonacci n luvut määritellään ehdoilla Osoita: 17 a 1 = a 2 = 1; a n+2 = a n+1 + a n, n N a n = 1 [( 1 + ) n ( 2 1 ) n ] 2 Olkoon a 1 = 3, a 2 = 6, a n+1 = 1 n (na
2 Lukujonot 21 Lukujonon määritelmä 16 Fibonacci n luvut määritellään ehdoilla Osoita: 17 a 1 = a 2 = 1; a n+2 = a n+1 + a n, n N a n = 1 [( 1 + ) n ( 2 1 ) n ] 2 Olkoon a 1 = 3, a 2 = 6, a n+1 = 1 n (na
Epälineaaristen yhtälöiden ratkaisumenetelmät
 Epälineaaristen yhtälöiden ratkaisumenetelmät Keijo Ruotsalainen Division of Mathematics Perusoletus Lause 3.1 Olkoon f : [a, b] R jatkuva funktio siten, että f(a)f(b) < 0. Tällöin funktiolla on ainakin
Epälineaaristen yhtälöiden ratkaisumenetelmät Keijo Ruotsalainen Division of Mathematics Perusoletus Lause 3.1 Olkoon f : [a, b] R jatkuva funktio siten, että f(a)f(b) < 0. Tällöin funktiolla on ainakin
(2n 1) = n 2
 3.5 Induktiotodistus Induktiota käyttäen voidaan todistaa luonnollisia lukuja koskevia väitteitä, jotka ovat muotoa väite P (n) on totta kaikille n =0, 1, 2,... Tässä väite P (n) riippuu n:n arvosta. Todistuksessa
3.5 Induktiotodistus Induktiota käyttäen voidaan todistaa luonnollisia lukuja koskevia väitteitä, jotka ovat muotoa väite P (n) on totta kaikille n =0, 1, 2,... Tässä väite P (n) riippuu n:n arvosta. Todistuksessa
Riemannin sarjateoreema
 Riemannin sarjateoreema LuK-tutielma Sami Määttä 2368326 Matemaattisten tieteiden laitos Oulun yliopisto Sysy 206 Sisältö Johdanto 2 Luujonot 3 2 Sarjat 4 2. Vuorottelevat sarjat........................
Riemannin sarjateoreema LuK-tutielma Sami Määttä 2368326 Matemaattisten tieteiden laitos Oulun yliopisto Sysy 206 Sisältö Johdanto 2 Luujonot 3 2 Sarjat 4 2. Vuorottelevat sarjat........................
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Osa 5. lukujonot ja sarjat.
 Osa 5. lukujonot ja sarjat. Summamerkintä Kurssilla on jo tullut vastaan ns. summamerkintä (kreikkalainen iso sigma): n k=1 Indeksin loppuarvo Indeksi jonka suhteen summataan a k =a 1 +a +a 3 +...+a n
Osa 5. lukujonot ja sarjat. Summamerkintä Kurssilla on jo tullut vastaan ns. summamerkintä (kreikkalainen iso sigma): n k=1 Indeksin loppuarvo Indeksi jonka suhteen summataan a k =a 1 +a +a 3 +...+a n
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
f(x) sin k x dx, c k = 1
 f ( n) n 3. Fourier n sarjoista I [1, 8.16, luku 11], [, luku 15], [3, luku IX, 8 9]. [5, luku I], [6, luku XII, 3], [7, luku 8], [8, luku 4], [9, luku 8] Trigonometrinen polynomi on muotoa a + ( ak cos
f ( n) n 3. Fourier n sarjoista I [1, 8.16, luku 11], [, luku 15], [3, luku IX, 8 9]. [5, luku I], [6, luku XII, 3], [7, luku 8], [8, luku 4], [9, luku 8] Trigonometrinen polynomi on muotoa a + ( ak cos
7. Tasaisen rajoituksen periaate
 18 FUNKTIONAALIANALYYSIN PERUSKURSSI 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
18 FUNKTIONAALIANALYYSIN PERUSKURSSI 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
Alkulukujen harmoninen sarja
 Alkulukujen harmoninen sarja LuK-tutkielma Markus Horneman Oiskelijanumero:2434548 Matemaattisten tieteiden laitos Oulun ylioisto Syksy 207 Sisältö Johdanto 2 Hyödyllisiä tuloksia ja määritelmiä 3. Alkuluvuista............................
Alkulukujen harmoninen sarja LuK-tutkielma Markus Horneman Oiskelijanumero:2434548 Matemaattisten tieteiden laitos Oulun ylioisto Syksy 207 Sisältö Johdanto 2 Hyödyllisiä tuloksia ja määritelmiä 3. Alkuluvuista............................
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
Seuraava topologisluonteinen lause on nk. Bairen lause tai Bairen kategorialause, n=1
 FUNKTIONAALIANALYYSIN PERUSKURSSI 115 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
FUNKTIONAALIANALYYSIN PERUSKURSSI 115 7. Tasaisen rajoituksen periaate Täydellisyydestä puristetaan maksimaalinen hyöty seuraavan Bairen lauseen avulla. Bairen lause on keskeinen todistettaessa kahta funktionaalianalyysin
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
