Pisteet ja viivat. Multigraafi
|
|
|
- Akseli Jääskeläinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Pisteet ja viivat Josuv on viiva, niin pisteetujav ovat viivanuv päätepisteet (endpoints) ja u jav ovat vierekkäisiä eli vieruspisteitä (neighbours, adjacent points). Piste on irtopiste (isolated point) jos sillä ei ole vieruspisteitä. Viivate 1 jae 2 ovat vierekkäiset, jos niillä on yhteinen päätepiste. 1 / 30 Multigraafi Multigraafi: Kahden pisteen välillä sallitaan yhtä useampi viiva ja viivan päätepisteet voivat olla samat Multigraafissa muotoa uu olevia viivoja Useita viivoja kahden eri pisteen välillä. Jokainen graafi on myös multigraafi. 2 / 30 1
2 Graafin 2. määrittely Toinen määrittely: Graafi Yksinkertainen graafi (=Simple graph) Multigraafi Graafi 3 / 30 Suunnattu graafi Suunnattu graafi (Directed graph, Digraph)D = (V,E) on järjestetty pari, missäv on äärellinen joukko ja E V V.Lisäksi aina kun(u,v) E, onu v. Suunnatussa graafissa on viivauv vu, kunujav ovat eri pisteet. 4 / 30 2
3 Esimerkki suunnatusta graafista a c b d 5 / 30 Väritys ja etäisyys Funktioα : V G K on pisteiden väritys (vertex colouring)joukonk väreillä. Funktioα : E G K on viivojen väritys (edge colouring) joukonk väreillä. YleensäK = {1,2,...,k}. JosK R, niinα:aa kutsutaan myös paino- tai etäisyysfunktioksi. 6 / 30 3
4 Graafien isomorfia Kaksi graafiagjah ovat isomorfiset, merkitääng = H, jos on olemassa bijektioα : V G V H, jolleuv E G jos ja vain josα(u)α(v) E H aina kunu,v V G. SiisGjaH ovat pisteiden nimeämistä vaille yksinkäsitteisiä. 7 / 30 Esimerkki 8 / 30 4
5 Lukumääriä Graafien ja ei-isomorfisten graafien lukumääriä: Pisteitä Graafeja Ei-isomorfisia / 30 Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. GraafinG = (V,E),V = {v 1,v 2,...,v n } vieruspistematriisi (adjacency matrix)onn nmatriisi M = (M ij ), missänong:n pisteiden lukumäärä ja { 0 v i v j / E, M ij = 1 v i v j E. Vieruspistematriisi on aina symmetrinen. Lause 9.1. Kaksi graafia ovat isomorfisia täsmälleen silloin kun niillä on yhteinen vieruspistematriisi. Kahdella isomorfisella graafilla on täsmälleen samat vieruspistematriisit. 10 / 30 5
6 Graafin aste GraafinG = (V,E) pisteenv naapurusto (neighbourhood) on joukko N G (v) = {u V vu E} Pisteenv aste (degree) graafissagdeg G (v) (lyhyemmindeg(v)) onv:n naapuruston pisteiden lukumäärä. deg G (v) = N G (v). Irtopiste:deg G (v) = 0 lehti, loppupiste (leaf, endpoint):deg G (v) = 1 11 / 30 Handshaking lemma Lause 9.2.(Euler 1736, Handshaking lemma): Jokaiselle graafille G = (V, E) on deg G (v) = 2 E v G elig:n pisteiden asteiden summa on kaksi kertaag:n viivojen lukumäärä. Lisäksi parittoman asteen omaavien pisteiden lukumäärä on aina parillinen Tod / 30 6
7 Graafityyppejä Graafi on nollagraafi, jos se ei sisällä yhtään pistettä. Graafi on triviaali (trivial), jos se sisältää korkeintaan yhden pisteen. GraafiG = K V on täydellinen graafi pistejoukossav,jos se sisältää kaikki mahdolliset viivat eli jokainen piste on kaikkien muiden pisteiden vieruspiste. Kaikki täydellisetnpistettä sisältävät graafit ovat isomorfisia. Niitä merkitäänk n :llä. Selvästi E Kn = n(n 1) 2 E G n(n 1) 2 aina kungonn:n pisteen graafi,n / 30 Graafin komplementti GraafinGkomplementti (complement)on graafig, missä V G = V G jae G = {e E(V) e / E G }. Täydellisten graafien komplementteja K n kutsutaan erillisiksi graafeiksi (discrete graphs). 14 / 30 7
8 Säännöllinen graafi Graafi on säännöllinen (regular), jos jokaisella graafin pisteellä on sama aste. Jos tämä aste onr, niin graafia kutsutaan r-säännölliseksi (r-regular). Erillinen graafi on0-säännöllinen. K n onn 1-säännöllinen. 15 / 30 Petersenin graafi Petersenin graafi on3-säännöllinen. 16 / 30 8
9 Kaksijakoinen graafi Kaksijakoinen(bipartite) graafi G = (V, E): pistejoukollav on sellainen ositusx,y,että jokaisen viivanuv E toinen päätepiste on joukonx ja toinen päätepiste joukony piste. Silloin(X, Y) on graafin G kaksijako (bipartition of G) ja G on(x, Y)-kaksijakoinen ((X, Y)-bipartite). 17 / 30 Kaksijakoiset graafit 2 Kaksijakoinen graafi G = (V, E) on täydellinen(m, k)-kaksijakoinen graafi (complete(m, k)-bipartite graph), jos X = m, Y = k jauv E aina kunu X jav Y. Kaikki täydelliset(m,k)-kaksijakoiset graafit ovat isomorfisia keskenään. Merkitään niitä K m,k :lla Graafi on täydellinen kaksijakoinen graafi, jos se on täydellinen(m,k)-kaksijakoinen graafi jollain luvuillam,k. GraafiK 1,n on tähti (star). 18 / 30 9
10 Aligraafit 19 / 30 Määritelmiä Määritelmä. GraafiH = (V H,E H ) on graafing = (V G,E G ) aligraafi (subgraph), josv H V G jae H E G. Silloin merkitäänh G. JosH G jav H = V G, niinh ong:n virittävä aligraafi (spanning subgraph). Viivojen osajoukkof E G muodostaa yksikäsitteisen graafingvirittävän aligraafin G[F] = (V G,F). 20 / 30 Indusoitu aligraafi JosH G jae H = E G E(V H ) (elih sisältää kaikkig:n viivat, joiden molemmat päätepisteet ovatv H :n pisteitä), niinh on pistejoukonv H indusoimag:n aligraafi (induced subgraph). PistejoukollaA V G on olemassa yksikäsitteineng:stä indusoitu aligraafi G[A] = (A,E G E(A)). 21 / 30 10
11 9.2. Polut ja piirit. Graafin yhtenäisyys 22 / 30 Polut Sovelluksissa usein oleellista: Pisteiden läpikäyminen (esimerkiksi etsintäalgoritmit) Pisteiden välinen etäisyys (esimerkiksi sähköpostin kulkemien solmukoneiden lukumäärä) 23 / 30 Kulku Olkoote i = u i u i+1 E G graafingviivoja aina kuni = 1,2,...,k. Viivate i jae i+1 ovat vierekkäisiä, sillä niillä on yhteinen päätepisteu i+1. JonoW = e 1 e 2 e k onk:n pituinen kulku (walk) pisteestäu 1 pisteeseenu k+1 Kulusta käytetään myös merkintöjä W : u 1 u 2 u k u k+1, k jaw : u 1 u 2 u k+1 sekäw : u 1 uk+1. u 1 uk+1 : On olemassa kulku pisteestäu 1 pisteeseenu k+1. W : u 1 uk+1 tarkoittaa aina tiettyä kulkuaw = e 1 e 2 e k. Kulun W pituutta merkitään W :llä. 24 / 30 11
12 Polku ja piiri KulkuW = e 1 e 2 e k (e i = u i u i+1 ) on a)suljettu (closed), josu 1 = u k+1, b)polku (path), josu i u j aina kuni j, c) reitti (trail),jose i e j aina kuni j, d) piiri (cycle), josu 1 = u k+1 ja muulloinu i u j aina kuni j, e)triviaali polku (trivial path), jos W = / 30 Esimerkki kuluista Kulku, joka ei ole reitti: g e d c b e d Kulku, joka ei ole polku: g e d c b e c 26 / 30 12
13 Esimerkki jatkoa: Polkujab d: b e d,b e c d b c d,b c e d b a f c d jab a f c e d. Piiri: b a f c b b a f c e d c b ei ole piiri 27 / 30 Käsitteitä KulunW : u = u 1 u 2 u k+1 = v käänteiskulku (inverse of W) on kulku W 1 : v = u k+1 u k u 1 = u. Pisteuon kulunp päätepiste (end ofp ), josp alkaa tai päättyy pisteeseenu. PolutP jaqovat erilliset (disjoint), jos niillä ei ole yhteisiä pisteitä (eikä siis myöskään yhteisiä viivoja) ja riippumattomat (independent), jos vain niiden päätepisteet ovat samat. 28 / 30 13
14 Käsitteitä 2 PolunP käänteispolkup 1 on polku. Kahden polun yhdiste ei välttämättä ole polku. Graafi (tai aligraafi)p k on graafi joka muodostuuk 1:sen pituisesta polusta (k 1viivaa,k pistettä). Graafi (tai aligraafi)c k onk:n pituinen piiri. Josk on parillinen, niin polkuap k (piiriäc k ) kutsutaan parilliseksi poluksi (parilliseksi piiriksi). Josk on pariton, niinp k (vastaavastic k ) on pariton polku (piiri). 29 / 30 Lause 9.3. Lause 9.3. Aina kunw : u v on kulku jau v, niin on olemassa polkup : u v, joka on saatuw :stä poistamalla siitä pisteitä ja viivoja. Tod / 30 14
0 v i v j / E, M ij = 1 v i v j E.
 Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
6.4. Järjestyssuhteet
 6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
Graafin virittävä puu 1 / 20
 Graafin virittävä puu 1 / 20 Graafin virittävä puu PuuT on graafingvirittävä puu (spanning tree), jos se sisältää kaikkig:n pisteet. Virittäviä puita: 2 / 20 Yhdistämisongelma Yhdistämisongelma:(Connector
Graafin virittävä puu 1 / 20 Graafin virittävä puu PuuT on graafingvirittävä puu (spanning tree), jos se sisältää kaikkig:n pisteet. Virittäviä puita: 2 / 20 Yhdistämisongelma Yhdistämisongelma:(Connector
7.4. Eulerin graafit 1 / 22
 7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Todistus (2.2) Todistus (2.2) jatkoa. (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio.
 Todistus (2.2) (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio. Selvästi bittijono f sisältää ainakin yhden1:sen. Voidaan olettaa, että f 1
Todistus (2.2) (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio. Selvästi bittijono f sisältää ainakin yhden1:sen. Voidaan olettaa, että f 1
8.5. Järjestyssuhteet 1 / 19
 8.5. Järjestyssuhteet 1 / 19 Määritelmä Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä).
8.5. Järjestyssuhteet 1 / 19 Määritelmä Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä).
Kysymys: Voidaanko graafi piirtää tasoon niin, että sen viivat eivät risteä muualla kuin pisteiden kohdalla?
 7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
Luentorunko Kevät Matti Peltola.
 GRAAFITEORIA 031029S Luentorunko Kevät 2009 Matti Peltola http://www.ee.oulu./mpa/graate.htm Hyödyllistä tietoa Matematiikan jaoksen tuottamasta opetuksesta löytyy osoitteesta http://s-mat-pcs.oulu./opetus
GRAAFITEORIA 031029S Luentorunko Kevät 2009 Matti Peltola http://www.ee.oulu./mpa/graate.htm Hyödyllistä tietoa Matematiikan jaoksen tuottamasta opetuksesta löytyy osoitteesta http://s-mat-pcs.oulu./opetus
GRAAFITEORIA. Keijo Ruohonen
 GRAAFITEORIA Keijo Ruohonen 2013 Sisältö 1 I MÄÄRITELMIÄ JA PERUSTULOKSIA 1 1.1 Määritelmiä 5 1.2 Kulku. Reitti. Polku. Piiri. Yhtenäisyys. Komponentti 10 1.3 Graafien operaatioita 14 1.4 Irrotus 17 1.5
GRAAFITEORIA Keijo Ruohonen 2013 Sisältö 1 I MÄÄRITELMIÄ JA PERUSTULOKSIA 1 1.1 Määritelmiä 5 1.2 Kulku. Reitti. Polku. Piiri. Yhtenäisyys. Komponentti 10 1.3 Graafien operaatioita 14 1.4 Irrotus 17 1.5
GRAAFITEORIAA. Pertti Koivisto Riitta Niemistö
 GRAAFITEORIAA Pertti Koivisto Riitta Niemistö Esipuhe Tämän monisteen tarkoituksena on tutustuttaa lukija graafiteorian peruskäsitteisiin ja -tuloksiin. Vaikka algoritminen graafiteoria on tietokoneiden
GRAAFITEORIAA Pertti Koivisto Riitta Niemistö Esipuhe Tämän monisteen tarkoituksena on tutustuttaa lukija graafiteorian peruskäsitteisiin ja -tuloksiin. Vaikka algoritminen graafiteoria on tietokoneiden
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Pertti Koivisto ja Riitta Niemistö. Graafiteoriaa
 Pertti Koivisto ja Riitta Niemistö Graafiteoriaa TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMPERE 2018 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMMIKUU
Pertti Koivisto ja Riitta Niemistö Graafiteoriaa TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMPERE 2018 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMMIKUU
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Graafiteoria matematiikkaako?
 Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
PARITUS KAKSIJAKOISESSA
 PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
Diskreetit rakenteet
 Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005
 Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Graphs in Social Network Analysis And Modeling. Graafit sosiaalisten verkostojen mallintamisessa
 Hypermedian jatko-opintoseminaari 2008 2009 1 Graphs in Social Network Analysis And Modeling Graafit sosiaalisten verkostojen mallintamisessa 28.11.2008 Thumas Miilumäki thumas.miilumaki@tut.fi Sisältö
Hypermedian jatko-opintoseminaari 2008 2009 1 Graphs in Social Network Analysis And Modeling Graafit sosiaalisten verkostojen mallintamisessa 28.11.2008 Thumas Miilumäki thumas.miilumaki@tut.fi Sisältö
keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 1 b 3 a 5
 Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Puiden karakterisointi
 Puiden karakterisointi LuK-tutkielma Airta Ella 2502661 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2018 Sisältö Johdanto 2 1 Johdatus verkkoteoriaan 3 1.1 Verkko käsitteenä.........................
Puiden karakterisointi LuK-tutkielma Airta Ella 2502661 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2018 Sisältö Johdanto 2 1 Johdatus verkkoteoriaan 3 1.1 Verkko käsitteenä.........................
Berge-perfektit graafit ja Shannonin kapasiteetti
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Joel Syvänen Berge-perfektit graafit ja Shannonin kapasiteetti Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Joel Syvänen Berge-perfektit graafit ja Shannonin kapasiteetti Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
Hamiltonin sykleistä graateoriassa
 Hamiltonin sykleistä graateoriassa Pro gradu -tutkielma Ohto Nordberg 1335868 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2013 Sisältö Johdanto 2 1 Historiaa 3 1.1 Euler................................
Hamiltonin sykleistä graateoriassa Pro gradu -tutkielma Ohto Nordberg 1335868 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2013 Sisältö Johdanto 2 1 Historiaa 3 1.1 Euler................................
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
Verkkojen elementaarinen ekvivalenssi
 Verkkojen elementaarinen ekvivalenssi Mikko Männikkö pro gradu -tutkielma Matematiikan ja tilastotieteen laitos Helsingin yliopisto Lokakuu 2004 Sisältö 1. Johdanto 3 2. Perusteet 4 2.1 Verkot 4 2.2 Ensimmäisen
Verkkojen elementaarinen ekvivalenssi Mikko Männikkö pro gradu -tutkielma Matematiikan ja tilastotieteen laitos Helsingin yliopisto Lokakuu 2004 Sisältö 1. Johdanto 3 2. Perusteet 4 2.1 Verkot 4 2.2 Ensimmäisen
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT GRAAFITEHTÄVIÄ JA -ALGORITMEJA Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) GRAAFIN LÄPIKÄYMINEN Perusta useimmille
A274101 TIETORAKENTEET JA ALGORITMIT GRAAFITEHTÄVIÄ JA -ALGORITMEJA Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) GRAAFIN LÄPIKÄYMINEN Perusta useimmille
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Rakenteellinen tasapaino ja transitiivisyys
 1 Hypermedian jatko-opintoseminaari 2008-2009 Rakenteellinen tasapaino ja transitiivisyys 20.2.2009 Seppo Pohjolainen 2 Rakenteellinen tasapaino Käsitteitä: Arvotettu graafi (signed graph) (+ tai - ) Suuntaamaton
1 Hypermedian jatko-opintoseminaari 2008-2009 Rakenteellinen tasapaino ja transitiivisyys 20.2.2009 Seppo Pohjolainen 2 Rakenteellinen tasapaino Käsitteitä: Arvotettu graafi (signed graph) (+ tai - ) Suuntaamaton
Rinnakkaistietokoneet luento S
 Rinnakkaistietokoneet luento 4 521475S Rinnakkaiset ei-numeeriset algoritmit: transitiivisulkeuma (transitive closure) Oletetaan suunnattu graafi G = (V,E) ja halutaan tietää onko olemassa kahta pistettä
Rinnakkaistietokoneet luento 4 521475S Rinnakkaiset ei-numeeriset algoritmit: transitiivisulkeuma (transitive closure) Oletetaan suunnattu graafi G = (V,E) ja halutaan tietää onko olemassa kahta pistettä
b) Olkoon G vähintään kaksi solmua sisältävä puu. Sallitaan verkon G olevan
 Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 5 ratkaisut (Hannu Niemistö) Tehtävä 1 OlkootGjaG neljän solmun verkkoja Määritä, milloing = 2 G eli verkot ovat osittaisesti isomorfisia kahden muuttujan suhteen
Äärellisten mallien teoria Harjoituksen 5 ratkaisut (Hannu Niemistö) Tehtävä 1 OlkootGjaG neljän solmun verkkoja Määritä, milloing = 2 G eli verkot ovat osittaisesti isomorfisia kahden muuttujan suhteen
Johdatus verkkoteoriaan 4. luento
 Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Tehtävä 5 : 1. Tehtävä 5 : 2
 Tehtävä 5 : 1 Merkitään kirjaimella H kuvan punaisten solmujen virittämää verkon G yhtenäistä aliverkkoa, jossa on yhteensä kolme särmää. Aliverkosta H voidaan kahdella tavalla valita kahden solmun joukko
Tehtävä 5 : 1 Merkitään kirjaimella H kuvan punaisten solmujen virittämää verkon G yhtenäistä aliverkkoa, jossa on yhteensä kolme särmää. Aliverkosta H voidaan kahdella tavalla valita kahden solmun joukko
VERKKOTEORIAN ALKEITA. Martti E. Pesonen 28.2.2013
 VERKKOTEORIAN ALKEITA Martti E. Pesonen 28.2.2013 1 Sisältö 1 VERKOISTA 1 1.1 Mitä matemaattiset verkot ovat?................ 1 1.1.1 Verkkoteorian synty.................... 1 1.2 Suuntaamaton verkko.......................
VERKKOTEORIAN ALKEITA Martti E. Pesonen 28.2.2013 1 Sisältö 1 VERKOISTA 1 1.1 Mitä matemaattiset verkot ovat?................ 1 1.1.1 Verkkoteorian synty.................... 1 1.2 Suuntaamaton verkko.......................
Tehtävä 8 : 1. Tehtävä 8 : 2
 Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
Kurssikoe on maanantaina 29.6. Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
Ratkaisu. Tulkitaan de Bruijnin jonon etsimiseksi aakkostossa S := {0, 1} sanapituudelle n = 4. Neljän pituisia sanoja on N = 2 n = 16 kpl.
 iskreetti matematiikka, syksy 00 arjoitus, ratkaisuista. seta 8 nollaa ja 8 ykköstä renkaaksi niin, että jokainen yhdistelmä 0000, 000,..., esiintyy täsmälleen kerran. Vihje: Tulkitse de ruijnin jonon
iskreetti matematiikka, syksy 00 arjoitus, ratkaisuista. seta 8 nollaa ja 8 ykköstä renkaaksi niin, että jokainen yhdistelmä 0000, 000,..., esiintyy täsmälleen kerran. Vihje: Tulkitse de ruijnin jonon
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
Suunnatut, etumerkilliset ja arvotetut graafit Sosiaalisten verkostojen analysoinnin näkökulmalla
 Suunnatut, etumerkilliset ja arvotetut graafit Sosiaalisten verkostojen analysoinnin näkökulmalla Hypermedian jatko-opintoseminaari 2008-2009 12.12.2008 Jaakko Salonen jaakko.salonen@tut.fi TTY / Hypermedialaboratorio
Suunnatut, etumerkilliset ja arvotetut graafit Sosiaalisten verkostojen analysoinnin näkökulmalla Hypermedian jatko-opintoseminaari 2008-2009 12.12.2008 Jaakko Salonen jaakko.salonen@tut.fi TTY / Hypermedialaboratorio
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
Tietojenkäsittelytieteen ja tilastotieteen matematiikkaa 1/137
 Tietojenkäsittelytieteen ja tilastotieteen matematiikkaa 1/137 Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi...
Tietojenkäsittelytieteen ja tilastotieteen matematiikkaa 1/137 Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi...
VERKOT. SUHTEIKOT JA VERKOT 1. Johdanto... 1 2. Pisteiden asteet...7 3. Yhtenäisyys... 11 4. Kulku suhteikossa... 18 5. Hamiltonin kulut...
 Heikki Junnila VERKOT. LUKU I SUHTEIKOT JA VERKOT 1. Johdanto..... 1 2. Pisteiden asteet...7 3. Yhtenäisyys.... 11 4. Kulku suhteikossa.... 18 5. Hamiltonin kulut....... 26 Harjoitustehtäviä......35 LUKU
Heikki Junnila VERKOT. LUKU I SUHTEIKOT JA VERKOT 1. Johdanto..... 1 2. Pisteiden asteet...7 3. Yhtenäisyys.... 11 4. Kulku suhteikossa.... 18 5. Hamiltonin kulut....... 26 Harjoitustehtäviä......35 LUKU
Tasograafit ja väritykset
 Solmu /06 Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta
Solmu /06 Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta
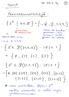 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) OT
 Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) 31.1.-4.2.2011 OT 1. Määritellään kokonaisluvuille laskutoimitus n m = n + m + 5. Osoita, että (Z, ) on ryhmä.
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) 31.1.-4.2.2011 OT 1. Määritellään kokonaisluvuille laskutoimitus n m = n + m + 5. Osoita, että (Z, ) on ryhmä.
Sisätuloavaruudet. 4. lokakuuta 2006
 Sisätuloavaruudet 4. lokakuuta 2006 Tässä esityksessä vektoriavaruudet V ja W ovat kompleksisia ja äärellisulotteisia. Käydään ensin lyhyesti läpi määritelmiä ja perustuloksia. Merkitään L(V, W ) :llä
Sisätuloavaruudet 4. lokakuuta 2006 Tässä esityksessä vektoriavaruudet V ja W ovat kompleksisia ja äärellisulotteisia. Käydään ensin lyhyesti läpi määritelmiä ja perustuloksia. Merkitään L(V, W ) :llä
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
v 8 v 9 v 5 C v 3 v 4
 Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Luku 7. Verkkoalgoritmit. 7.1 Määritelmiä
 Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Jaollisuus kymmenjärjestelmässä
 Jaollisuus kymmenjärjestelmässä Lauseen 4.5 mukaan jokaiselle n N on yksikäsitteiset kokonaisluvut s 0 ja a 0, a 1,..., a s, joille n = a s 10 s + a s 1 10 s 1 + + a 1 10 + a 0 = a s a a 1... a 0, (1)
Jaollisuus kymmenjärjestelmässä Lauseen 4.5 mukaan jokaiselle n N on yksikäsitteiset kokonaisluvut s 0 ja a 0, a 1,..., a s, joille n = a s 10 s + a s 1 10 s 1 + + a 1 10 + a 0 = a s a a 1... a 0, (1)
Tasograafit ja väritykset
 Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-Yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta kärkiä; sekä
Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-Yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta kärkiä; sekä
9. Graafit. 9.1. Graafin abstrakti tietotyyppi
 9. Graafit Graafeilla eli verkoilla esitetään yhteystietoja. Esimerkkejä niistä ovat kaupunkikartan kadut ja tietoverkon tietokoneet. Tämä luku tarkastelee verkkojen perusasioita. 9.1. Graafin abstrakti
9. Graafit Graafeilla eli verkoilla esitetään yhteystietoja. Esimerkkejä niistä ovat kaupunkikartan kadut ja tietoverkon tietokoneet. Tämä luku tarkastelee verkkojen perusasioita. 9.1. Graafin abstrakti
Kokonaislukukapasiteetti. Max-Flow Min-Cut
 Kokonaislukukapasiteetti Seuraus 10.2.2. JosN on siirtoverkko, jonka kapasiteettifunktion α arvot ovat kokonaislukuja, niin silloinn:llä on olemassa sellainen maksimivirtausf, ettäf(e) on kokonaisluku
Kokonaislukukapasiteetti Seuraus 10.2.2. JosN on siirtoverkko, jonka kapasiteettifunktion α arvot ovat kokonaislukuja, niin silloinn:llä on olemassa sellainen maksimivirtausf, ettäf(e) on kokonaisluku
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen
 V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
Eulerin verkkojen karakterisointi
 Eulerin verkkojen karakterisointi Pro Gradu -tutkielma Jenni Heikkilä 373175 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 018 Sisältö Johdanto 1 Verkkojen peruskäsitteet 3 1.1 Verkon määrittely.........................
Eulerin verkkojen karakterisointi Pro Gradu -tutkielma Jenni Heikkilä 373175 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 018 Sisältö Johdanto 1 Verkkojen peruskäsitteet 3 1.1 Verkon määrittely.........................
TIETOTEKNIIKAN MATEMATIIKKA
 TIETOTEKNIIKAN MATEMATIIKKA Harjoitus 4 syksy 2016 Ratkaisut 1. Mitä ehtoja joukkojen M ja N tulee täyttää (kussakin kohdassa erikseen), jotta seuraavat väittämät olisivat tosia a) M = b) N \ M = c) M
TIETOTEKNIIKAN MATEMATIIKKA Harjoitus 4 syksy 2016 Ratkaisut 1. Mitä ehtoja joukkojen M ja N tulee täyttää (kussakin kohdassa erikseen), jotta seuraavat väittämät olisivat tosia a) M = b) N \ M = c) M
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten. Ratkaisuehdotelma
 Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
A = a b B = c d. d e f. g h i determinantti on det(c) = a(ei fh) b(di fg) + c(dh eg). Matriisin determinanttia voi merkitä myös pystyviivojen avulla:
 11 Determinantti Neliömatriisille voidaan laskea luku, joka kertoo muun muassa, onko matriisi kääntyvä vai ei Tätä lukua kutsutaan matriisin determinantiksi Determinantilla on muitakin sovelluksia, mutta
11 Determinantti Neliömatriisille voidaan laskea luku, joka kertoo muun muassa, onko matriisi kääntyvä vai ei Tätä lukua kutsutaan matriisin determinantiksi Determinantilla on muitakin sovelluksia, mutta
Näytetään nyt relaatioon liittyvien ekvivalenssiluokkien olevan verkon G lohkojen särmäjoukkoja. Olkoon siis f verkon G jokin särmä.
 Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Kiinalaisen postimiehen ongelma
 Kiinalaisen postimiehen ongelma Kimmo Kontio 1.12.2015 Ohjaaja/Valvoja: Harri Ehtamo [5] Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki oikeudet pidätetään.
Kiinalaisen postimiehen ongelma Kimmo Kontio 1.12.2015 Ohjaaja/Valvoja: Harri Ehtamo [5] Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki oikeudet pidätetään.
Tehtävä 10 : 1. Tehtävä 10 : 2
 Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
1 Lukujen jaollisuudesta
 Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Johdatus graafiteoriaan
 Johdatus graafitoriaan Syksy 2017 Lauri Hlla Tamprn yliopisto Luonnontitidn tidkunta 2 Luku 1 Pruskäsittitä 1.1 Määritlmiä 1.2 Esimrkkjä 1.3 Trminologiaa 1.4 Joitakin rikoisia yksinkrtaisia graafja 1.5
Johdatus graafitoriaan Syksy 2017 Lauri Hlla Tamprn yliopisto Luonnontitidn tidkunta 2 Luku 1 Pruskäsittitä 1.1 Määritlmiä 1.2 Esimrkkjä 1.3 Trminologiaa 1.4 Joitakin rikoisia yksinkrtaisia graafja 1.5
Algoritmi on periaatteellisella tasolla seuraava:
 Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Ortogonaaliprojektio äärellisulotteiselle aliavaruudelle
 Ortogonaaliprojektio äärellisulotteiselle aliavaruudelle Olkoon X sisätuloavaruus ja Y X äärellisulotteinen aliavaruus. Tällöin on olemassa lineaarisesti riippumattomat vektorit y 1, y 2,..., yn, jotka
Ortogonaaliprojektio äärellisulotteiselle aliavaruudelle Olkoon X sisätuloavaruus ja Y X äärellisulotteinen aliavaruus. Tällöin on olemassa lineaarisesti riippumattomat vektorit y 1, y 2,..., yn, jotka
811312A Tietorakenteet ja algoritmit, , Harjoitus 6, Ratkaisu
 811312A Tietorakenteet ja algoritmit, 2016-2017, Harjoitus 6, Ratkaisu Harjoituksen aiheet ovat verkkojen leveys- ja syvyyshakualgoritmit Tehtävä 6.1 Hae leveyshakualgoritmia käyttäen lyhin polku seuraavan
811312A Tietorakenteet ja algoritmit, 2016-2017, Harjoitus 6, Ratkaisu Harjoituksen aiheet ovat verkkojen leveys- ja syvyyshakualgoritmit Tehtävä 6.1 Hae leveyshakualgoritmia käyttäen lyhin polku seuraavan
Luku 5. Löwenheimin ja Skolemin lause. kompaktisuuslause. Tässä luvussa tutustumme tärkeimpiin täydellisyyslauseen (ja sen todistuksen) seurauksiin.
 Luku 5 Löwenheimin ja Skolemin lause, kompaktisuuslause Tässä luvussa tutustumme tärkeimpiin täydellisyyslauseen (ja sen todistuksen) seurauksiin. Löwenheimin ja Skolemin lause Sanomme, että kaavajoukko
Luku 5 Löwenheimin ja Skolemin lause, kompaktisuuslause Tässä luvussa tutustumme tärkeimpiin täydellisyyslauseen (ja sen todistuksen) seurauksiin. Löwenheimin ja Skolemin lause Sanomme, että kaavajoukko
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
Yhtäpitävyys. Aikaisemmin osoitettiin, että n on parillinen (oletus) n 2 on parillinen (väite).
 Yhtäpitävyys Aikaisemmin osoitettiin, että n on parillinen (oletus) n 2 on parillinen (väite). Toisaalta ollaan osoitettu, että n 2 on parillinen (oletus) n on parillinen (väite). Nämä kaksi väitelausetta
Yhtäpitävyys Aikaisemmin osoitettiin, että n on parillinen (oletus) n 2 on parillinen (väite). Toisaalta ollaan osoitettu, että n 2 on parillinen (oletus) n on parillinen (väite). Nämä kaksi väitelausetta
(1) refleksiivinen, (2) symmetrinen ja (3) transitiivinen.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
Sosiaalisten verkostojen datan notaatio. Notation for Social Network Data
 Sosiaalisten verkostojen datan notaatio Notation for Social Network Data Jari Jussila 14.11.2008 2 Notaatio Notaatiota tarvitaan / auttaa kuvaamaan: toimijat tai toimijoiden muodostamat joukot, toimijoiden
Sosiaalisten verkostojen datan notaatio Notation for Social Network Data Jari Jussila 14.11.2008 2 Notaatio Notaatiota tarvitaan / auttaa kuvaamaan: toimijat tai toimijoiden muodostamat joukot, toimijoiden
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 2 ratkaisut Tehtävä 1 Olkoon X = {a, b, c} kolmen alkion joukko. a) Mikä on joukon X eri laskutoimitusten lukumäärä? b) Kuinka moni näistä laskutoimituksista on
Äärellisten mallien teoria Harjoituksen 2 ratkaisut Tehtävä 1 Olkoon X = {a, b, c} kolmen alkion joukko. a) Mikä on joukon X eri laskutoimitusten lukumäärä? b) Kuinka moni näistä laskutoimituksista on
Matikkapaja keskiviikkoisin klo Lineaarialgebra (muut ko) p. 1/210
 Matikkapaja keskiviikkoisin klo 14-16 Lineaarialgebra (muut ko) p. 1/210 Lineaarialgebra (muut ko) p. 2/210 Operaatiot Vektoreille u = (u 1,u 2 ) ja v = (v 1,v 2 ) Yhteenlasku: u+v = (u 1 +v 1,u 2 +v 2
Matikkapaja keskiviikkoisin klo 14-16 Lineaarialgebra (muut ko) p. 1/210 Lineaarialgebra (muut ko) p. 2/210 Operaatiot Vektoreille u = (u 1,u 2 ) ja v = (v 1,v 2 ) Yhteenlasku: u+v = (u 1 +v 1,u 2 +v 2
Kenguru 2017 Cadet (8. ja 9. luokka)
 sivu 1 / 16 3 pistettä 1. Kello on 17.00. Kuinka paljon kello on 17 tunnin kuluttua? (A) 8.00 (B) 10.00 (C) 11.00 (D) 12.00 (E) 13.00 17 tuntia on 7 tuntia vaille täysi vuorokausi. 17 7 = 10, joten 17
sivu 1 / 16 3 pistettä 1. Kello on 17.00. Kuinka paljon kello on 17 tunnin kuluttua? (A) 8.00 (B) 10.00 (C) 11.00 (D) 12.00 (E) 13.00 17 tuntia on 7 tuntia vaille täysi vuorokausi. 17 7 = 10, joten 17
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
T : Max-flow / min-cut -ongelmat
 T-61.152: -ongelmat 4.3.2008 Sisältö 1 Määritelmät Esimerkki 2 Max-flow Graafin leikkaus Min-cut Max-flow:n ja min-cut:n yhteys 3 Perusajatus Pseudokoodi Tarkastelu 4 T-61.152: -ongelmat Virtausverkko
T-61.152: -ongelmat 4.3.2008 Sisältö 1 Määritelmät Esimerkki 2 Max-flow Graafin leikkaus Min-cut Max-flow:n ja min-cut:n yhteys 3 Perusajatus Pseudokoodi Tarkastelu 4 T-61.152: -ongelmat Virtausverkko
Algoritmit 1. Luento 9 Ti Timo Männikkö
 Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Tehtävä 4 : 2. b a+1 (mod 3)
 Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Kuva 1: Funktion f tasa-arvokäyriä. Ratkaisu. Suurin kasvunopeus on gradientin suuntaan. 6x 0,2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
Liite: Verkot. TKK (c) Ilkka Mellin (2004) 1
 Liite: Verkot TKK (c) Ilkka Mellin (2004) 1 : Mitä opimme? Verkkoteoria on hyödyllinen sovelletun matematiikan osa-alue, jolla on sovelluksia esimerkiksi logiikassa, operaatiotutkimuksessa, peli-ja päätösteoriassa
Liite: Verkot TKK (c) Ilkka Mellin (2004) 1 : Mitä opimme? Verkkoteoria on hyödyllinen sovelletun matematiikan osa-alue, jolla on sovelluksia esimerkiksi logiikassa, operaatiotutkimuksessa, peli-ja päätösteoriassa
d ) m d (I n ) = 2 d n d. Koska tämä pätee kaikilla
 MAT21007 Mitta ja integraali Harjoitus 2 viikko 25.3-29.3 2019) Palauta mieleen: monisteen luku 0; Topologia I) avaruuden d euklidinen etäisyys, avoimet kuulat ja joukot. Ohjausta laskuharjoitusten tekoon:
MAT21007 Mitta ja integraali Harjoitus 2 viikko 25.3-29.3 2019) Palauta mieleen: monisteen luku 0; Topologia I) avaruuden d euklidinen etäisyys, avoimet kuulat ja joukot. Ohjausta laskuharjoitusten tekoon:
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 3.5 Reedin-Mullerin koodit Olkoon tässä kappaleessa F = F2 = Z2 ja n = 2 m. Määritellään avaruuteen F n kertolasku koordinaateittain:
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 3.5 Reedin-Mullerin koodit Olkoon tässä kappaleessa F = F2 = Z2 ja n = 2 m. Määritellään avaruuteen F n kertolasku koordinaateittain:
Kanta ja dimensio 1 / 23
 1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
3x + y + 2z = 5 e) 2x + 3y 2z = 3 x 2y + 4z = 1. x + y 2z + u + 3v = 1 b) 2x y + 2z + 2u + 6v = 2 3x + 2y 4z 3u 9v = 3. { 2x y = k 4x + 2y = h
 HARJOITUSTEHTÄVIÄ 1. Anna seuraavien yhtälöryhmien kerroinmatriisit ja täydennetyt kerroinmatriisit sekä ratkaise yhtälöryhmät Gaussin eliminointimenetelmällä. { 2x + y = 11 2x y = 5 2x y + z = 2 a) b)
HARJOITUSTEHTÄVIÄ 1. Anna seuraavien yhtälöryhmien kerroinmatriisit ja täydennetyt kerroinmatriisit sekä ratkaise yhtälöryhmät Gaussin eliminointimenetelmällä. { 2x + y = 11 2x y = 5 2x y + z = 2 a) b)
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa I
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetyhteenveto, 3. osahuhtikuuta
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetyhteenveto, 3. osahuhtikuuta
6 Vektoriavaruus R n. 6.1 Lineaarikombinaatio
 6 Vektoriavaruus R n 6.1 Lineaarikombinaatio Määritelmä 19. Vektori x œ R n on vektorien v 1,...,v k œ R n lineaarikombinaatio, jos on olemassa sellaiset 1,..., k œ R, että x = i v i. i=1 Esimerkki 30.
6 Vektoriavaruus R n 6.1 Lineaarikombinaatio Määritelmä 19. Vektori x œ R n on vektorien v 1,...,v k œ R n lineaarikombinaatio, jos on olemassa sellaiset 1,..., k œ R, että x = i v i. i=1 Esimerkki 30.
Määritelmä Olkoon T i L (V i, W i ), 1 i m. Yksikäsitteisen lineaarikuvauksen h L (V 1 V 2 V m, W 1 W 2 W m )
 Määritelmä 519 Olkoon T i L V i, W i, 1 i m Yksikäsitteisen lineaarikuvauksen h L V 1 V 2 V m, W 1 W 2 W m h v 1 v 2 v m T 1 v 1 T 2 v 2 T m v m 514 sanotaan olevan kuvausten T 1,, T m indusoima ja sitä
Määritelmä 519 Olkoon T i L V i, W i, 1 i m Yksikäsitteisen lineaarikuvauksen h L V 1 V 2 V m, W 1 W 2 W m h v 1 v 2 v m T 1 v 1 T 2 v 2 T m v m 514 sanotaan olevan kuvausten T 1,, T m indusoima ja sitä
6. Tekijäryhmät ja aliryhmät
 6. Tekijäryhmät ja aliryhmät Tämän luvun tavoitteena on esitellä konstruktio, jota kutsutaan tekijäryhmän muodostamiseksi. Konstruktiossa lähdetään liikkeelle jostakin isosta ryhmästä, samastetaan alkioita,
6. Tekijäryhmät ja aliryhmät Tämän luvun tavoitteena on esitellä konstruktio, jota kutsutaan tekijäryhmän muodostamiseksi. Konstruktiossa lähdetään liikkeelle jostakin isosta ryhmästä, samastetaan alkioita,
Avaruuden R n aliavaruus
 Avaruuden R n aliavaruus 1 / 41 Aliavaruus Esimerkki 1 Kuva: Suora on suljettu yhteenlaskun ja skalaarilla kertomisen suhteen. 2 / 41 Esimerkki 2 Kuva: Suora ei ole suljettu yhteenlaskun ja skalaarilla
Avaruuden R n aliavaruus 1 / 41 Aliavaruus Esimerkki 1 Kuva: Suora on suljettu yhteenlaskun ja skalaarilla kertomisen suhteen. 2 / 41 Esimerkki 2 Kuva: Suora ei ole suljettu yhteenlaskun ja skalaarilla
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 10.4.18 Netspace Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon duaali, verkon upottaminen, verkon genus, verkon komplementti,
Johdatus verkkoteoriaan luento 10.4.18 Netspace Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon duaali, verkon upottaminen, verkon genus, verkon komplementti,
Graafit ja verkot. Joukko solmuja ja joukko järjestämättömiä solmupareja. eli haaroja. Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria
 Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Paikkatiedon käsittely 4. Diskreettiä geometriaa
 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Paikkatiedon käsittely 4. Diskreettiä geometriaa Antti Leino antti.leino@cs.helsinki.fi 25.1.2007 Tietojenkäsittelytieteen laitos Laskentatarkkuuden
HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Paikkatiedon käsittely 4. Diskreettiä geometriaa Antti Leino antti.leino@cs.helsinki.fi 25.1.2007 Tietojenkäsittelytieteen laitos Laskentatarkkuuden
Symmetrisistä ryhmistä symmetriaryhmiin
 Symmetrisistä ryhmistä symmetriaryhmiin 16. marraskuuta 2006 1 Symmetrisistä ryhmistä... Bijektiivistä kuvausta {1,..., n} {1,..., n} kutsutaan n-permutaatioksi. Merkitään n-permutaatioden joukkoa S n.
Symmetrisistä ryhmistä symmetriaryhmiin 16. marraskuuta 2006 1 Symmetrisistä ryhmistä... Bijektiivistä kuvausta {1,..., n} {1,..., n} kutsutaan n-permutaatioksi. Merkitään n-permutaatioden joukkoa S n.
Transversaalit ja hajoamisaliryhmät
 Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
8. Kieliopit ja kielet
 8. Kieliopit ja kielet Suomen kielen sanoja voidaan yhdistellä monella eri tavalla. Kielioppi määrää sen, milloin sanojen yhdistely antaa oikein muodostetun lauseen. "Mies räpyttää siipiään" on kieliopillisesti
8. Kieliopit ja kielet Suomen kielen sanoja voidaan yhdistellä monella eri tavalla. Kielioppi määrää sen, milloin sanojen yhdistely antaa oikein muodostetun lauseen. "Mies räpyttää siipiään" on kieliopillisesti
