Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005
|
|
|
- Hannes Mäki
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla graafin 3-värittyvyyttä voidaan tutkia sekä esitetään algoritmi, jonka avulla voidaan löytää graafin 3-väritys tai todeta, että graafi ei ole 3-värittyvä. Teoreettisella tarkastelulla ja algoritmilla saadaan 3-väritys ratkaistua vain osasta graafeista. 1 Johdanto Graafin G = (V, E) solmuväritys on kuvaus c : V S niin että c(v) c(w) kun v ja w ovat vierekkäiset. Joukon S alkioita sanotaan käytettävissä oleviksi väreiksi. Meitä kiinnostaa S:n koko: tyypillisesti kysytään mikä on pienin kokonaisluku k niin että G:llä on k-väritys, solmuväritys C : V {1,..., k}. Tämä k on G:n kromaattinen luku; sitä merkitään χ(g):llä. Jos χ(g) k, sanotaan graafia G k-värittyväksi [Diestel]. 2 Kirjallisuuskatsaus 2.1 Graafin kaksijakoisuus 2-värittyvyys on sama asia kuin kaksijakoisuus [West]. Lause Graafi G on kaksijakoinen jos ja vain jos G ei sisällä yhtään parittoman pituista sykliä [Jungnickel]. Modifioitua leveyshaku (Breadth-first search) -algoritmia voidaan käyttää graafin kaksijakoisuuden tutkintaan. Tällainen algoritmi tarkistaa onko annettu yhtenäinen graafi kaksijakoinen vai ei, ja jos se on, löytää sen solmujoukon kaksijaon [Jungnickel]. 1
2 2.2 Graafin kriittisyys Jos χ(h) < χ(g) = k kaikille aidoille G:n aligraafeille H, niin G on k-kriittinen [West]. Graafi G on 4-kriittinen, jos se on 4-värittyvä ja poistamalla mikä tahansa sen kaarista tai solmuista saadaan 3-värittyvä graafi [Pyatkin]. Parittomat syklit ovat 3-kriittisiä graafeja [West]. 2.3 Ahne väritys Ahne väritys suhteessa V (G):n solmujen järjestykseen v 1,..., v n saadaan värittämallä solmut järjestyksessä v 1,..., v n antamalla v i :lle pienin väri-indeksi jota ei ole vielä käytetty sen pienempi-indeksoiduissa naapureissa [West]. Lause χ(g) (G) + 1 [West]. (G)+1 on huonoin yläraja mitä ahne väritys voi tuottaa. Valitsemalla solmujen järjestys huolellisesti saadaan parannuksia [West]. Propositio Jos graafilla G on astejärjestys d 1... d n, niin χ(g) 1+max i min {d i, i 1} [West]. χ(g) = 1 + (G) täydellisillä graafeilla sekä parittomilla sykleillä [West]. Lause Jos G on yhtenäinen graafi, joka ei ole täydellinen graafi tai pariton sykli, niin χ(g) (G) [West]. 2.4 Muuta teoriaa Lause Jokainen tasograafi, jossa ei ole kolmiota on 3-värittyvä. [Diestel] Seuraavassa lauseita, joiden avulla voidaan havaita, ettei annettu graafi ole 3- värittyvä: Lause Graafi, jossa on silmukka, ei ole 3-värittyvä. Todistus. Tulos on ilmeinen. Lause Graafi, jonka aligraafina on K 4 tai suurempi klikki, ei ole 3-värittyvä. Todistus. Vastaoletus: K 4 on 3-värittyvä. K 4 :ssä solmun naapureista vähintään kahdella täytyy olla sama väri, koska käytettäviä värejä on vain kolme kappaletta. Näiden kahden solmun välillä on kuitenkin kaari, joten tästä seuraa ristiriita. Suurempien klikkien kuin K 4 aligraafina on K 4, joten ne eivät ole 3-värittyviä. Maksimiklikin löytämistä graafista käsitellään artikkelissa [Babel]. 2
3 3 Laskennallisesta vaativuudesta Hyvää karakterisointia 4-kriittisille graafeille tai testiä 3-värittyvyydelle ei tunneta. Hyvä karakterisointi tarkoittaa karakterisointia ehdolla, joka voidaan tarkastaa polynomisessa ajassa. [West]. P-ongelmia NP-täydellisiä ongelmia 2-VÄRITTYVYYS k-värittyvyys (k 3) TASOMAISUUS Taulukko 1. Eräiden ongelmien vaativuusluokkia [West]. 4 Algoritmi Tehtävänä oli kehittää algoritmi, joka etsii graafille 3-väritystä ja pysähtyy kun 3-väritys on löytynyt tai kun on selvää ettei graafi ole 3-värittyvä. Kehitetty algoritmi käy läpi kaikki värivaihtoehdot ja tutkii onko graafi 3- värittyvä. Alussa kaikille solmuille annetaan väri 0: solmujen värejä voidaan kuvata tällöin 3-järjestelmän luvulla Jos graafi ei ole värittyvä näillä väreillä, kasvatetaan lukua yhdellä. Luku on nyt Seuraavaksi tutkitaan väritystä luvuilla ja jne. kunnes väritys löytyy tai kaikki värivaihtoehdot on käyty läpi. Eri värivaihtoehtoja on 3 n(g) kappaletta. Ensimmäisen solmun väri voidaan kuitenkin kiinnittää 0:ksi ilman että menetetään 3-värityksen löytymismahdollisuuksia. Eri värivaihtoehtoja on siten 3 n(g) 1 = 1 3 3n(G) kappaletta. Tutkittavassa matriisissa on alkioita n(g) n(g) kappaletta. Algoritmin suorituskykyä tutkittiin eri astetta olevilla graafeilla, joiden viimeisessä solmussa on silmukka ja joissa ei ole muita kaaria. Näin algoritmi huomaa mahdollisimman myöhäisessä vaiheessa, että graafi ei ole 3-värittyvä (tutkiminen etenee naapuruusmatriisin vasemmasta yläkulmasta alkaen rivi riviltä vasemmalta oikealle). 3
4 18 solmun kokoisen tutkittavan graafin naapuruusmatriisi on G = Tarvittava (lähes pahimman tapauksen) laskenta-aika näkyy kuvasta 1 (Prosessori Intel Celeron 2.4 GHz). Kuva 1. Lähes pahimman tapauksen laskenta-ajat eri kokoisille tutkittaville graafeille. 4
5 Kuvasta nähdään, että algoritmi soveltuu käytännössä vain graafeille, joiden solmumäärä on alle Yhteenveto Projektityöohjeen mukaan algoritmia pitäisi testata graafeilla, jotka löytyvät Pyatkinin artikkelista [Pyatkin]. Näistä toinen, asteeltaan pienempi, on 157- solmuinen eräs ns. circulant. Sitä merkitään merkinnällä G = (157; 8, 14). Todetaan tässä, että graafi G on 6-säännöllinen 4-kriittinen graafi. Graafi on asteeltaan aivan liian suuri tutkittavaksi tässä artikkelissa esitetyllä algoritmilla. Samoin tässä artikkelissa esitetyn teorian perusteella ei voida löytää G:n 4-kriittisyyttä eli mm. sitä, että kun siitä poistetaan mikä tahansa kaari, niin syntynyt graafi on 3-värittyvä. Kuvassa 2 kuvataan niiden graafien joukot, joiden 3-väritys voidaan tutkia tässä artikkelissa esitellyllä algoritmilla tai toisaalta tässä artikkelissa esitellyllä teorialla. Nämä joukot menevät osittain päällekkäin. Kuvasta nähdään, että on joukko graafeja, joiden 3-värittyvyyttä ei voida tutkia kummallakaan tavalla. Tähän joukkoon kuuluu myös graafi G. Ei 3 värittyvät 3 värittyvät A B C D algoritmilla lauseilla algoritmilla lauseilla G = (157;8,14) Kuva 2. A,C : Graafit, joiden 3-väritys voidaan käytännössä tutkia tässä artikkelissa esitellyllä algoritmilla. B,D : Graafit, joiden 3-väritys voidaan tutkia tässä artikkelissa esitellyllä teorialla. 5
6 6 Viitteet [Babel] Luitpold Babel, Finding Maximum Cliques in Arbitrary and in Special Graphs, Computing,46: ,1991 [Diestel] R.Diestel, Graph Theory, 2nd ed., Springer, New York NY, 2000 [Jungnickel] Dieter Jungnickel, Graphs, Networks and Algorithms, Springer- Verlag, 2002 [Pyatkin] A.V. Pyatkin, 6-regular 4-critical Graph, J Graph Theory 41: , 2002 [West] Douglas B. West, Introduction to graph theory, Second Edition, Prentice- Hall,
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Verkon värittämistä hajautetuilla algoritmeilla
 Verkon värittämistä hajautetuilla algoritmeilla 5 12 30 19 72 34 Jukka Suomela 15 77 18 4 9. tammikuuta 2012 19 2 68 Verkko 2 Verkko solmu 3 Verkko solmu kaari 4 Hajautettu järjestelmä solmu (tietokone)
Verkon värittämistä hajautetuilla algoritmeilla 5 12 30 19 72 34 Jukka Suomela 15 77 18 4 9. tammikuuta 2012 19 2 68 Verkko 2 Verkko solmu 3 Verkko solmu kaari 4 Hajautettu järjestelmä solmu (tietokone)
Johdatus verkkoteoriaan 4. luento
 Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Algoritmit 1. Luento 9 Ti Timo Männikkö
 Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
0 v i v j / E, M ij = 1 v i v j E.
 Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Algoritmi on periaatteellisella tasolla seuraava:
 Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Kysymys: Voidaanko graafi piirtää tasoon niin, että sen viivat eivät risteä muualla kuin pisteiden kohdalla?
 7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Rekursiolause. Laskennan teorian opintopiiri. Sebastian Björkqvist. 23. helmikuuta Tiivistelmä
 Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Tehtävä 10 : 1. Tehtävä 10 : 2
 Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen
 V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m.
 Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
Verkon värittäminen ja riippumattomat joukot: johdantoa ja sovelluksia
 hyväksymispäivä arvosana arvostelija Verkon värittäminen ja riippumattomat joukot: johdantoa ja sovelluksia Janne Korhonen Helsinki 8.12.2009 Seminaariraportti HELSINGIN YLIOPISTO Tietojenkäsittelytieteen
hyväksymispäivä arvosana arvostelija Verkon värittäminen ja riippumattomat joukot: johdantoa ja sovelluksia Janne Korhonen Helsinki 8.12.2009 Seminaariraportti HELSINGIN YLIOPISTO Tietojenkäsittelytieteen
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
Graafiteoria matematiikkaako?
 Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
6.4. Järjestyssuhteet
 6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
Algoritmit 2. Luento 11 Ti Timo Männikkö
 Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Luku 7. Verkkoalgoritmit. 7.1 Määritelmiä
 Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Tarkennamme geneeristä painamiskorotusalgoritmia
 Korotus-eteen-algoritmi (relabel-to-front) Tarkennamme geneeristä painamiskorotusalgoritmia kiinnittämällä tarkasti, missä järjestyksessä Push- ja Raise-operaatioita suoritetaan. Algoritmin peruskomponentiksi
Korotus-eteen-algoritmi (relabel-to-front) Tarkennamme geneeristä painamiskorotusalgoritmia kiinnittämällä tarkasti, missä järjestyksessä Push- ja Raise-operaatioita suoritetaan. Algoritmin peruskomponentiksi
Kurssikoe on maanantaina 29.6. Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
811312A Tietorakenteet ja algoritmit, , Harjoitus 6, Ratkaisu
 811312A Tietorakenteet ja algoritmit, 2018-2019, Harjoitus 6, Ratkaisu Harjoituksen aiheet ovat verkkojen leveys- ja syvyyshakualgoritmit Tehtävä 6.1 Hae leveyshakualgoritmia käyttäen lyhin polku seuraavan
811312A Tietorakenteet ja algoritmit, 2018-2019, Harjoitus 6, Ratkaisu Harjoituksen aiheet ovat verkkojen leveys- ja syvyyshakualgoritmit Tehtävä 6.1 Hae leveyshakualgoritmia käyttäen lyhin polku seuraavan
Algoritmit 2. Luento 10 To Timo Männikkö
 Algoritmit 2 Luento 10 To 19.4.2018 Timo Männikkö Luento 10 Peruutusmenetelmä Osajoukon summa Verkon 3-väritys Pelipuut Pelipuun läpikäynti Algoritmit 2 Kevät 2018 Luento 10 To 19.4.2018 2/34 Algoritmien
Algoritmit 2 Luento 10 To 19.4.2018 Timo Männikkö Luento 10 Peruutusmenetelmä Osajoukon summa Verkon 3-väritys Pelipuut Pelipuun läpikäynti Algoritmit 2 Kevät 2018 Luento 10 To 19.4.2018 2/34 Algoritmien
- painottamattoman graafin solmujen järjestäminen. - painotetun graafin solmujen järjestäminen
 1. DEMO TUOTTEEN OMINAISUUKSISTA Tuotteesta demotaan seuraavat asiat: - käyttöliittymä - painottamattoman graafin solmujen järjestäminen - painotetun graafin solmujen järjestäminen - yhden maksimiklikin
1. DEMO TUOTTEEN OMINAISUUKSISTA Tuotteesta demotaan seuraavat asiat: - käyttöliittymä - painottamattoman graafin solmujen järjestäminen - painotetun graafin solmujen järjestäminen - yhden maksimiklikin
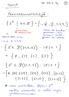 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet )
 T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
7.4. Eulerin graafit 1 / 22
 7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan koulutusohjelma. Kaariväritysongelma. Kandidaatintyö. 29. huhtikuuta 2012. Sami J.
 Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan koulutusohjelma Kaariväritysongelma Kandidaatintyö 29. huhtikuuta 2012 Sami J. Lehtinen Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan
Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan koulutusohjelma Kaariväritysongelma Kandidaatintyö 29. huhtikuuta 2012 Sami J. Lehtinen Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan
Kokonaislukuoptimointi
 Kokonaislukuoptimointi Algebrallisen geometrian sovelluksia Sisältö Taustaa algebrallisesta geometriasta Gröbnerin kanta Buchbergerin algoritmi Kokonaislukuoptimointi Käypyysongelma Algoritmi ratkaisun
Kokonaislukuoptimointi Algebrallisen geometrian sovelluksia Sisältö Taustaa algebrallisesta geometriasta Gröbnerin kanta Buchbergerin algoritmi Kokonaislukuoptimointi Käypyysongelma Algoritmi ratkaisun
811312A Tietorakenteet ja algoritmit , Harjoitus 2 ratkaisu
 811312A Tietorakenteet ja algoritmit 2017-2018, Harjoitus 2 ratkaisu Harjoituksen aiheena on algoritmien oikeellisuus. Tehtävä 2.1 Kahvipurkkiongelma. Kahvipurkissa P on valkoisia ja mustia kahvipapuja,
811312A Tietorakenteet ja algoritmit 2017-2018, Harjoitus 2 ratkaisu Harjoituksen aiheena on algoritmien oikeellisuus. Tehtävä 2.1 Kahvipurkkiongelma. Kahvipurkissa P on valkoisia ja mustia kahvipapuja,
Valitaan alkio x 1 A B ja merkitään A 1 = A { x 1 }. Perinnöllisyyden nojalla A 1 I.
 Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
VAATIMUSMÄÄRITTELY. PROJEKTITYÖ Tik Wclique
 VAATIMUSMÄÄRITTELY PROJEKTITYÖ Tik-76.115 SISÄLLYSLUETTELO Sisällysluettelo... 2 Versiohistoria... 3 1. JOHDANTO... 4 1.1 Algoritmi... 4 1.2 Graafi... 4 1.3 Nauty... 5 1.4 Mermaid... 5 2. YLEISKUVAUS...
VAATIMUSMÄÄRITTELY PROJEKTITYÖ Tik-76.115 SISÄLLYSLUETTELO Sisällysluettelo... 2 Versiohistoria... 3 1. JOHDANTO... 4 1.1 Algoritmi... 4 1.2 Graafi... 4 1.3 Nauty... 5 1.4 Mermaid... 5 2. YLEISKUVAUS...
8.5. Järjestyssuhteet 1 / 19
 8.5. Järjestyssuhteet 1 / 19 Määritelmä Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä).
8.5. Järjestyssuhteet 1 / 19 Määritelmä Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä).
Berge-perfektit graafit ja Shannonin kapasiteetti
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Joel Syvänen Berge-perfektit graafit ja Shannonin kapasiteetti Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Joel Syvänen Berge-perfektit graafit ja Shannonin kapasiteetti Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä.
 Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
C C. x 2. x 3 x 3. Lause 3SAT p m VC Todistus. Olk. φ = C 1 C 2 C m 3-cnf-kaava, jossa esiintyvät muuttujat. φ toteutuva:
 Lause 3SAT p m VC Todistus. Olk. φ = C 1 C C m 3-cnf-kaava, jossa esiintyvät muuttujat x 1,..., x n. Vastaava solmupeiteongelman tapaus G, k muodostetaan seuraavasti. G:ssä on solmu kutakin literaalia
Lause 3SAT p m VC Todistus. Olk. φ = C 1 C C m 3-cnf-kaava, jossa esiintyvät muuttujat x 1,..., x n. Vastaava solmupeiteongelman tapaus G, k muodostetaan seuraavasti. G:ssä on solmu kutakin literaalia
Graafit ja verkot. Joukko solmuja ja joukko järjestämättömiä solmupareja. eli haaroja. Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria
 Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
PARITUS KAKSIJAKOISESSA
 PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Jaollisuus kymmenjärjestelmässä
 Jaollisuus kymmenjärjestelmässä Lauseen 4.5 mukaan jokaiselle n N on yksikäsitteiset kokonaisluvut s 0 ja a 0, a 1,..., a s, joille n = a s 10 s + a s 1 10 s 1 + + a 1 10 + a 0 = a s a a 1... a 0, (1)
Jaollisuus kymmenjärjestelmässä Lauseen 4.5 mukaan jokaiselle n N on yksikäsitteiset kokonaisluvut s 0 ja a 0, a 1,..., a s, joille n = a s 10 s + a s 1 10 s 1 + + a 1 10 + a 0 = a s a a 1... a 0, (1)
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä4. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä4. ym.,
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä14.
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä14.
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Permutaatiot
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Permutaatiot
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Ryhmät Permutaatiot
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Ryhmät Permutaatiot
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko
 DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
Markov-ketjut pitkällä aikavälillä
 2A Markov-ketjut pitkällä aikavälillä Tämän harjoituksen tavoitteena on oppia lukemaan siirtymämatriisista tai siirtymäkaaviosta, milloin Markov-ketju on yhtenäinen ja jaksoton; oppia tunnistamaan, milloin
2A Markov-ketjut pitkällä aikavälillä Tämän harjoituksen tavoitteena on oppia lukemaan siirtymämatriisista tai siirtymäkaaviosta, milloin Markov-ketju on yhtenäinen ja jaksoton; oppia tunnistamaan, milloin
Laskennan vaativuus ja NP-täydelliset ongelmat
 Laskennan vaativuus ja NP-täydelliset ongelmat TRAK-vierailuluento 13.4.2010 Petteri Kaski Tietojenkäsittelytieteen laitos Tietojenkäsittelytiede Tietojenkäsittelytiede tutkii 1. mitä tehtäviä voidaan
Laskennan vaativuus ja NP-täydelliset ongelmat TRAK-vierailuluento 13.4.2010 Petteri Kaski Tietojenkäsittelytieteen laitos Tietojenkäsittelytiede Tietojenkäsittelytiede tutkii 1. mitä tehtäviä voidaan
A = a b B = c d. d e f. g h i determinantti on det(c) = a(ei fh) b(di fg) + c(dh eg). Matriisin determinanttia voi merkitä myös pystyviivojen avulla:
 11 Determinantti Neliömatriisille voidaan laskea luku, joka kertoo muun muassa, onko matriisi kääntyvä vai ei Tätä lukua kutsutaan matriisin determinantiksi Determinantilla on muitakin sovelluksia, mutta
11 Determinantti Neliömatriisille voidaan laskea luku, joka kertoo muun muassa, onko matriisi kääntyvä vai ei Tätä lukua kutsutaan matriisin determinantiksi Determinantilla on muitakin sovelluksia, mutta
1 Lukujen jaollisuudesta
 Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Näytetään nyt relaatioon liittyvien ekvivalenssiluokkien olevan verkon G lohkojen särmäjoukkoja. Olkoon siis f verkon G jokin särmä.
 Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
TOIMINNALLINEN MÄÄRITTELY. PROJEKTITYÖ Tik Wclique
 TOIMINNALLINEN MÄÄRITTELY PROJEKTITYÖ Tik-7.115 SISÄLLYSLUETTELO Sisällysluettelo... Versiohistoria... 1. JOHDANTO... 4 1.1 Tarkoitus ja kattavuus... 4 1. Tuote... 4 1. Määritelmät, termit ja lyhenteet...
TOIMINNALLINEN MÄÄRITTELY PROJEKTITYÖ Tik-7.115 SISÄLLYSLUETTELO Sisällysluettelo... Versiohistoria... 1. JOHDANTO... 4 1.1 Tarkoitus ja kattavuus... 4 1. Tuote... 4 1. Määritelmät, termit ja lyhenteet...
Sosiaalisten verkostojen datan notaatio. Notation for Social Network Data
 Sosiaalisten verkostojen datan notaatio Notation for Social Network Data Jari Jussila 14.11.2008 2 Notaatio Notaatiota tarvitaan / auttaa kuvaamaan: toimijat tai toimijoiden muodostamat joukot, toimijoiden
Sosiaalisten verkostojen datan notaatio Notation for Social Network Data Jari Jussila 14.11.2008 2 Notaatio Notaatiota tarvitaan / auttaa kuvaamaan: toimijat tai toimijoiden muodostamat joukot, toimijoiden
Algoritmit 1. Luento 2 Ke Timo Männikkö
 Algoritmit 1 Luento 2 Ke 11.1.2017 Timo Männikkö Luento 2 Algoritmin esitys Algoritmien analysointi Suoritusaika Asymptoottinen kertaluokka Peruskertaluokkia NP-täydelliset ongelmat Algoritmit 1 Kevät
Algoritmit 1 Luento 2 Ke 11.1.2017 Timo Männikkö Luento 2 Algoritmin esitys Algoritmien analysointi Suoritusaika Asymptoottinen kertaluokka Peruskertaluokkia NP-täydelliset ongelmat Algoritmit 1 Kevät
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Jenna Laine. Ramseyn teoria
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jenna Laine Ramseyn teoria Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta LAINE, JENNA: Ramseyn teoria Pro
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jenna Laine Ramseyn teoria Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta LAINE, JENNA: Ramseyn teoria Pro
Tehtävä 4 : 2. b a+1 (mod 3)
 Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
9. Graafit. 9.1. Graafin abstrakti tietotyyppi
 9. Graafit Graafeilla eli verkoilla esitetään yhteystietoja. Esimerkkejä niistä ovat kaupunkikartan kadut ja tietoverkon tietokoneet. Tämä luku tarkastelee verkkojen perusasioita. 9.1. Graafin abstrakti
9. Graafit Graafeilla eli verkoilla esitetään yhteystietoja. Esimerkkejä niistä ovat kaupunkikartan kadut ja tietoverkon tietokoneet. Tämä luku tarkastelee verkkojen perusasioita. 9.1. Graafin abstrakti
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 8.5.2018 Timo Männikkö Luento 13 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys Kertaus ja tenttivinkit Algoritmit 2 Kevät
Algoritmit 2 Luento 13 Ti 8.5.2018 Timo Männikkö Luento 13 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys Kertaus ja tenttivinkit Algoritmit 2 Kevät
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
TOIMINNALLINEN MÄÄRITTELY. PROJEKTITYÖ Tik Wclique
 TOIMINNALLINEN MÄÄRITTELY PROJEKTITYÖ Tik-.115 SISÄLLYSLUETTELO Sisällysluettelo... Versiohistoria... 1. JOHDANTO... 4 1.1 Tarkoitus ja kattavuus... 4 1. Tuote... 4 1. Määritelmät, termit ja lyhenteet...
TOIMINNALLINEN MÄÄRITTELY PROJEKTITYÖ Tik-.115 SISÄLLYSLUETTELO Sisällysluettelo... Versiohistoria... 1. JOHDANTO... 4 1.1 Tarkoitus ja kattavuus... 4 1. Tuote... 4 1. Määritelmät, termit ja lyhenteet...
Taulun avoimista haaroista saadaan kelvolliset lausejoukot
 T-79.5101 kevät 2006 Laskennallisen logiikan jatkokurssi Laskuharjoitus 11 Ratkaisut 1. M : a, Q b c d Lauseen X( UQ) sulkeuma: CL ( X( UQ) ) = { X( UQ), X( UQ), UQ, X ( UQ), ( UQ),, Q, X ( UQ),, } Muodostetaan
T-79.5101 kevät 2006 Laskennallisen logiikan jatkokurssi Laskuharjoitus 11 Ratkaisut 1. M : a, Q b c d Lauseen X( UQ) sulkeuma: CL ( X( UQ) ) = { X( UQ), X( UQ), UQ, X ( UQ), ( UQ),, Q, X ( UQ),, } Muodostetaan
 0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
Sudokun matematiikkaa
 Sudokun matematiikkaa Pro Gradu -tutkielma Marjo Silventoinen 175843 Itä-Suomen yliopisto 30. elokuuta 2012 Sisältö 1 Johdanto 1 2 Tausta 3 2.1 Latinalainen neliö......................... 3 2.2 Graateoriaa...........................
Sudokun matematiikkaa Pro Gradu -tutkielma Marjo Silventoinen 175843 Itä-Suomen yliopisto 30. elokuuta 2012 Sisältö 1 Johdanto 1 2 Tausta 3 2.1 Latinalainen neliö......................... 3 2.2 Graateoriaa...........................
Ennakkotehtävän ratkaisu
 Ennakkotehtävän ratkaisu Ratkaisu [ ] [ ] 1 3 4 3 A = ja B =. 1 4 1 1 [ ] [ ] 4 3 12 12 1 0 a) BA = =. 1 + 1 3 + 4 0 1 [ ] [ ] [ ] 1 0 x1 x1 b) (BA)x = =. 0 1 x 2 x [ ] [ ] [ 2 ] [ ] 4 3 1 4 9 5 c) Bb
Ennakkotehtävän ratkaisu Ratkaisu [ ] [ ] 1 3 4 3 A = ja B =. 1 4 1 1 [ ] [ ] 4 3 12 12 1 0 a) BA = =. 1 + 1 3 + 4 0 1 [ ] [ ] [ ] 1 0 x1 x1 b) (BA)x = =. 0 1 x 2 x [ ] [ ] [ 2 ] [ ] 4 3 1 4 9 5 c) Bb
Totaalisesti unimodulaariset matriisit voidaan osoittaa olevan rakennettavissa oleellisesti verkkomalleihin liittyvistä matriiseista
 8. Verkkomallit Totaalisesti unimodulaariset matriisit voidaan osoittaa olevan rakennettavissa oleellisesti verkkomalleihin liittyvistä matriiseista (P. D. Seymour, Journal of Combinatorial Theory (B),
8. Verkkomallit Totaalisesti unimodulaariset matriisit voidaan osoittaa olevan rakennettavissa oleellisesti verkkomalleihin liittyvistä matriiseista (P. D. Seymour, Journal of Combinatorial Theory (B),
Oikeasta tosi-epätosi -väittämästä saa pisteen, ja hyvästä perustelusta toisen.
 Tietorakenteet, kevät 2012 Kurssikoe 2, mallivastaukset 2. (a) Järjestämistä ei voi missään tilanteessa suorittaa nopeammin kuin ajassa Θ(n log n), missä n on järjestettävän taulukon pituus. Epätosi: Yleisessä
Tietorakenteet, kevät 2012 Kurssikoe 2, mallivastaukset 2. (a) Järjestämistä ei voi missään tilanteessa suorittaa nopeammin kuin ajassa Θ(n log n), missä n on järjestettävän taulukon pituus. Epätosi: Yleisessä
Algoritmit 1. Luento 8 Ke Timo Männikkö
 Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Hakupuut. tässä luvussa tarkastelemme puita tiedon tallennusrakenteina
 Hakupuut tässä luvussa tarkastelemme puita tiedon tallennusrakenteina hakupuun avulla voidaan toteuttaa kaikki joukko-tietotyypin operaatiot (myös succ ja pred) pahimman tapauksen aikavaativuus on tavallisella
Hakupuut tässä luvussa tarkastelemme puita tiedon tallennusrakenteina hakupuun avulla voidaan toteuttaa kaikki joukko-tietotyypin operaatiot (myös succ ja pred) pahimman tapauksen aikavaativuus on tavallisella
VAATIMUSMÄÄRITTELY. PROJEKTITYÖ Tik Wclique
 VAATIMUSMÄÄRITTELY PROJEKTITYÖ Tik-76.115 SISÄLLYSLUETTELO Sisällysluettelo... 2 Versiohistoria... 3 1. JOHDANTO... 4 1.1 Algoritmi... 4 1.2 Graafi... 4 1.3 Nauty... 5 1.4 Mermaid... 5 2. YLEISKUVAUS...
VAATIMUSMÄÄRITTELY PROJEKTITYÖ Tik-76.115 SISÄLLYSLUETTELO Sisällysluettelo... 2 Versiohistoria... 3 1. JOHDANTO... 4 1.1 Algoritmi... 4 1.2 Graafi... 4 1.3 Nauty... 5 1.4 Mermaid... 5 2. YLEISKUVAUS...
811312A Tietorakenteet ja algoritmit, , Harjoitus 6, Ratkaisu
 811312A Tietorakenteet ja algoritmit, 2016-2017, Harjoitus 6, Ratkaisu Harjoituksen aiheet ovat verkkojen leveys- ja syvyyshakualgoritmit Tehtävä 6.1 Hae leveyshakualgoritmia käyttäen lyhin polku seuraavan
811312A Tietorakenteet ja algoritmit, 2016-2017, Harjoitus 6, Ratkaisu Harjoituksen aiheet ovat verkkojen leveys- ja syvyyshakualgoritmit Tehtävä 6.1 Hae leveyshakualgoritmia käyttäen lyhin polku seuraavan
3. Kongruenssit. 3.1 Jakojäännös ja kongruenssi
 3. Kongruenssit 3.1 Jakojäännös ja kongruenssi Tässä kappaleessa esitellään kokonaislukujen modulaarinen aritmetiikka (ns. kellotauluaritmetiikka), jossa luvut tyypillisesti korvataan niillä jakojäännöksillä,
3. Kongruenssit 3.1 Jakojäännös ja kongruenssi Tässä kappaleessa esitellään kokonaislukujen modulaarinen aritmetiikka (ns. kellotauluaritmetiikka), jossa luvut tyypillisesti korvataan niillä jakojäännöksillä,
Algoritmit 2. Luento 14 To Timo Männikkö
 Algoritmit 2 Luento 14 To 2.5.2019 Timo Männikkö Luento 14 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydelliset ongelmat Kertaus ja tenttivinkit Algoritmit
Algoritmit 2 Luento 14 To 2.5.2019 Timo Männikkö Luento 14 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydelliset ongelmat Kertaus ja tenttivinkit Algoritmit
2017 = = = = = = 26 1
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 2, MALLIRATKAISUT Tehtävä 1. Sovella Eukleiden algoritmia ja (i) etsi s.y.t(2017, 753) (ii) etsi kaikki kokonaislukuratkaisut yhtälölle 405x + 141y = 12. Ratkaisu
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 2, MALLIRATKAISUT Tehtävä 1. Sovella Eukleiden algoritmia ja (i) etsi s.y.t(2017, 753) (ii) etsi kaikki kokonaislukuratkaisut yhtälölle 405x + 141y = 12. Ratkaisu
Algoritmit 2. Luento 12 Ke Timo Männikkö
 Algoritmit 2 Luento 12 Ke 26.4.2017 Timo Männikkö Luento 12 Rajoitehaku Kauppamatkustajan ongelma Lyhin virittävä puu Paikallinen etsintä Vaihtoalgoritmit Geneettiset algoritmit Simuloitu jäähdytys Algoritmit
Algoritmit 2 Luento 12 Ke 26.4.2017 Timo Männikkö Luento 12 Rajoitehaku Kauppamatkustajan ongelma Lyhin virittävä puu Paikallinen etsintä Vaihtoalgoritmit Geneettiset algoritmit Simuloitu jäähdytys Algoritmit
= k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko
 238 7.2 Luokka NP Luokka NP on: NP = { NTIME(t) t on polynomi } = k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko P NP Luokan NP ongelmista
238 7.2 Luokka NP Luokka NP on: NP = { NTIME(t) t on polynomi } = k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko P NP Luokan NP ongelmista
1. (a) Seuraava algoritmi tutkii, onko jokin luku taulukossa monta kertaa:
 Tietorakenteet, laskuharjoitus 10, ratkaisuja 1. (a) Seuraava algoritmi tutkii, onko jokin luku taulukossa monta kertaa: SamaLuku(T ) 2 for i = 1 to T.length 1 3 if T [i] == T [i + 1] 4 return True 5 return
Tietorakenteet, laskuharjoitus 10, ratkaisuja 1. (a) Seuraava algoritmi tutkii, onko jokin luku taulukossa monta kertaa: SamaLuku(T ) 2 for i = 1 to T.length 1 3 if T [i] == T [i + 1] 4 return True 5 return
Puiden karakterisointi
 Puiden karakterisointi LuK-tutkielma Airta Ella 2502661 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2018 Sisältö Johdanto 2 1 Johdatus verkkoteoriaan 3 1.1 Verkko käsitteenä.........................
Puiden karakterisointi LuK-tutkielma Airta Ella 2502661 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2018 Sisältö Johdanto 2 1 Johdatus verkkoteoriaan 3 1.1 Verkko käsitteenä.........................
MS-A0003/A0005 Matriisilaskenta Malliratkaisut 5 / vko 48
 MS-A3/A5 Matriisilaskenta Malliratkaisut 5 / vko 48 Tehtävä (L): a) Onko 4 3 sitä vastaava ominaisarvo? b) Onko λ = 3 matriisin matriisin 2 2 3 2 3 7 9 4 5 2 4 4 ominaisvektori? Jos on, mikä on ominaisarvo?
MS-A3/A5 Matriisilaskenta Malliratkaisut 5 / vko 48 Tehtävä (L): a) Onko 4 3 sitä vastaava ominaisarvo? b) Onko λ = 3 matriisin matriisin 2 2 3 2 3 7 9 4 5 2 4 4 ominaisvektori? Jos on, mikä on ominaisarvo?
Algebra I, harjoitus 5,
 Algebra I, harjoitus 5, 7.-8.10.2014. 1. 2 Osoita väitteet oikeiksi tai vääriksi. a) (R, ) on ryhmä, kun asetetaan a b = 2(a + b) aina, kun a, b R. (Tässä + on reaalilukujen tavallinen yhteenlasku.) b)
Algebra I, harjoitus 5, 7.-8.10.2014. 1. 2 Osoita väitteet oikeiksi tai vääriksi. a) (R, ) on ryhmä, kun asetetaan a b = 2(a + b) aina, kun a, b R. (Tässä + on reaalilukujen tavallinen yhteenlasku.) b)
Lineaarikuvauksen R n R m matriisi
 Lineaarikuvauksen R n R m matriisi Lauseessa 21 osoitettiin, että jokaista m n -matriisia A vastaa lineaarikuvaus L A : R n R m, jolla L A ( v) = A v kaikilla v R n. Osoitetaan seuraavaksi käänteinen tulos:
Lineaarikuvauksen R n R m matriisi Lauseessa 21 osoitettiin, että jokaista m n -matriisia A vastaa lineaarikuvaus L A : R n R m, jolla L A ( v) = A v kaikilla v R n. Osoitetaan seuraavaksi käänteinen tulos:
ICS-C2000 Tietojenkäsittelyteoria Kevät 2016
 ICS-C2000 Tietojenkäsittelyteoria Kevät 206 Kierros 0, 2. 24. maaliskuuta Huom! Perjantaina 25. maaliskuuta ei ole laskareita (pitkäperjantai), käykää vapaasti valitsemassanne ryhmässä aiemmin viikolla.
ICS-C2000 Tietojenkäsittelyteoria Kevät 206 Kierros 0, 2. 24. maaliskuuta Huom! Perjantaina 25. maaliskuuta ei ole laskareita (pitkäperjantai), käykää vapaasti valitsemassanne ryhmässä aiemmin viikolla.
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten. Ratkaisuehdotelma
 Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
Verkkojen värittäminen
 Verkkojen värittäminen Pro gradu -tutkielma Tiina Aaltonen 165231 Itä-Suomen yliopisto Fysiikan ja matematiikan laitos 10. tammikuuta 2012 Sisältö 1 Johdanto 1 2 Verkkojen peruskäsitteitä 4 2.1 Solmu,
Verkkojen värittäminen Pro gradu -tutkielma Tiina Aaltonen 165231 Itä-Suomen yliopisto Fysiikan ja matematiikan laitos 10. tammikuuta 2012 Sisältö 1 Johdanto 1 2 Verkkojen peruskäsitteitä 4 2.1 Solmu,
Todistusmenetelmiä Miksi pitää todistaa?
 Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti!
 MAA11 Koe.4.014 Jussi Tyni Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti! A-Osio: Ei saa käyttää laskinta. MAOL saa olla alusta asti käytössä. Maksimissaan
MAA11 Koe.4.014 Jussi Tyni Tee konseptiin pisteytysruudukko! Muista kirjata nimesi ja ryhmäsi. Lue ohjeet huolellisesti! A-Osio: Ei saa käyttää laskinta. MAOL saa olla alusta asti käytössä. Maksimissaan
Silmukkaoptimoinnista
 sta TIE448 Kääntäjätekniikka, syksy 2009 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. joulukuuta 2009 Sisällys Sisällys Seuraava deadline Vaihe F maanantai 14.12. klo 12 rekisteriallokaatio Arvostelukappale
sta TIE448 Kääntäjätekniikka, syksy 2009 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. joulukuuta 2009 Sisällys Sisällys Seuraava deadline Vaihe F maanantai 14.12. klo 12 rekisteriallokaatio Arvostelukappale
Lisää pysähtymisaiheisia ongelmia
 Lisää pysähtymisaiheisia ongelmia Lause: Pysähtymättömyysongelma H missä H = { w111x w validi koodi, M w ei pysähdy syötteellä x } ei ole rekursiivisesti lueteltava. Todistus: Pysähtymisongelman komplementti
Lisää pysähtymisaiheisia ongelmia Lause: Pysähtymättömyysongelma H missä H = { w111x w validi koodi, M w ei pysähdy syötteellä x } ei ole rekursiivisesti lueteltava. Todistus: Pysähtymisongelman komplementti
Käänteismatriisin. Aiheet. Käänteismatriisin ominaisuuksia. Rivioperaatiot matriisitulona. Matriisin kääntäminen rivioperaatioiden avulla
 Käänteismatriisi, L5 1 Tässä kalvosarjassa käsittelemme neliömatriiseja. Ilman asian jatkuvaa toistamista oletamme seuraavassa, että kaikki käsittelemämme matriisit ovat neliömatriiseja. Määritelmä. Olkoon
Käänteismatriisi, L5 1 Tässä kalvosarjassa käsittelemme neliömatriiseja. Ilman asian jatkuvaa toistamista oletamme seuraavassa, että kaikki käsittelemämme matriisit ovat neliömatriiseja. Määritelmä. Olkoon
GRAAFITEORIAA. Pertti Koivisto Riitta Niemistö
 GRAAFITEORIAA Pertti Koivisto Riitta Niemistö Esipuhe Tämän monisteen tarkoituksena on tutustuttaa lukija graafiteorian peruskäsitteisiin ja -tuloksiin. Vaikka algoritminen graafiteoria on tietokoneiden
GRAAFITEORIAA Pertti Koivisto Riitta Niemistö Esipuhe Tämän monisteen tarkoituksena on tutustuttaa lukija graafiteorian peruskäsitteisiin ja -tuloksiin. Vaikka algoritminen graafiteoria on tietokoneiden
keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 1 b 3 a 5
 Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Harjoitus 3 (3.4.2014)
 Harjoitus 3 (3..) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i, j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Harjoitus 3 (3..) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i, j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
