Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella:
|
|
|
- Ritva Pakarinen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti. Vesihöyryä voi olla ilmassa vain tietty enimmäismäärä, jonka suuruus riippuu ilman lämpötilasta. Vesihöyryn sanotaan tällöin olevan kylläistä. Kylläinen höyry on dynaamisessa tasapainotilassa, jossa höyrystyminen ja tiivistyminen ovat yhtä runsasta. Tällaisessa tilassa olevaa höyryä sanotaan siis kylläiseksi höyryksi ja vallitsevaa höyryn painetta kylläisen höyryn paineeksi. Kylläisen vesihöyryn paine eri lämpötiloissa on esitetty taulukossa (ks. MAOL s. 80 (80)). Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella: missä h % hö ä hö.äö. Ilman suhteellinen kosteus voidaan laskea myös toisella tavalla; ilman absoluuttisen kosteuden X ja kyseistä lämpötilaa vastaavan maksimikosteuden Xmax osamääränä, joka ilmoitetaan usein prosentteina; % Ilman absoluuttinen kosteus X tarkoittaa ilman todellista vesihöyryn tiheyttä. Se siis ilmoittaa ilmassa olevan vesihöyryn massan tilavuusyksikköä kohti. Tiettyä lämpötilaa vastaava maksimikosteus Xmax kertoo vesihöyryn suurimman mahdollisen massan tilavuusyksikköä kohden. Maksimikosteus Xmax on siis vesihöyryn suurin mahdollinen tiheys ilmassa. Maksimikosteus Xmax riippuu lämpötilasta. Jos ilman kosteus on 100 %, niin ilma on vesihöyryn kyllästämä. Ilma sisältää maksimimäärän vettä ja esimerkiksi avoimesta astiasta ei haihdu vettä ilmaan. Saunassa ilmankosteus voi olla 100 %. Löylyä heitettäessä vettä tiivistyy iholle ja ikkunoihin. Asunnoissa suhteellisen kosteuden tulisi olla noin 40 % - 55 %. (Lehto-Luoma: Fysiikka 3: Lämpö ja energia, Tammi, 5-9. uudistettu painos 2002, s , 71).
2 Jos ilman lämpötila laskee, ilman suurin mahdollinen kosteus pienenee. Jos ilman lämpötila laskee niin paljon, että tätä lämpötilaa vastaava kylläisen vesihöyryn paine (ks. MAOL s. 80(80)) on yhtä suuri kuin ilmassa olevan vesihöyryn osapaine, vesihöyry alkaa tiivistyä vedeksi. Tätä lämpötilaa kutsutaan kastepisteeksi. Kun lämpötila laskee kastepisteen alapuolelle, (näkymättömän) vesihöyryn tiivistyminen vedeksi jatkuu. Silloin maan pinnalla näkyy usein sumua, ja kastepisaroita tiivistyy ruohoon. Jos huoneen lämpötila laskee kastepisteen alapuolelle, kosteus tiivistyy ikkunoihin ja tekstiileihin, ja huonekalut tuntuvat kosteilta. Mikäli kastepiste on sulamispistettä alempi, esimerkiksi ruohoon muodostuu jäähileitä. Auton ikkunoihin voi muodostua silloin jäätä. Ilmiötä, jossa vesihöyry muuttuu kiinteäksi (jääksi), kutsutaan härmistymiseksi. Kosteustaulukko. Suhteellinen kosteus (%) -liian kostea puu mätänee 90 - vilun tunne 80 - maalit lohkeilevat 70 - soittimet epävireessä -sopiva kosteus liian kuiva kurkku aamuisin kipeä huonekalut rapistuvat 0 Astmaattisten ja allergisten ihmisten ja varsinkin pienten lasten terveydelle ilman suhteellisella kosteudella on suuri merkitys. Huoneilman suhteellinen kosteus vaikuttaa myös kotieläinten terveyteen ja kasvien sekä soittimien kuntoon.
3 TEHTÄVIÄ: Teht. 1. Asuinhuoneessa on kosteusmittarin mukaan suhteellinen kosteus 52 %. Huoneen lämpötila on 21 o C ja tilavuus 48 m 3. Laske a) huoneilman vesihöyryn osapaine b) vesihöyryn osatiheys ilmassa. c) Kuinka paljon (g) huoneilmassa on vettä? Teht. 2. Tehtävän 1 asuinhuoneessa on kosteusmittarin mukaan suhteellinen kosteus 52 %, huoneen lämpötila on 21 o C ja tilavuus 48 m 3. Kastepiste on lämpötila, jossa vesihöyry alkaa tiivistyä vedeksi. Määritä asuinhuoneen kastepiste. Teht. 3. Työpöytäsi vieressä oleva kosteusmittari osoittaa suhteellisen kosteuden arvoa 39 %. Huoneen lämpötila on 21 o C. a) Laske huoneilman vesihöyryn osapaine. b) Määritä kastepisteen arvo. Teht. 4. Huoneilman lämpötila on 19 o C ja suhteellinen kosteus 49 %. Laske a) huoneilman vesihöyryn osapaine b) veden osatiheys ilmassa. c) Kuinka paljon (g) huoneilmassa on vettä? Huoneen tilavuus on 52 m 3. d) Kuinka suuri on huoneilman kastepiste? Teht. 5. Huoneen ilman suhteellinen kosteus on 60 % ja lämpötila 21 o C. a) Kuinka suuri on absoluuttinen kosteus? b) Kuinka paljon ilmassa on vettä, jos huoneen tilavuus on 36 m 3? Teht. 6. Määritä kastepisteen suuruus tehtävän 5 tapauksessa. Teht. 7. Ilman lämpötila on 20 o C ja suhteellinen kosteus 59 %. a) Kuinka suuri on absoluuttinen kosteus? b) Mikä on kastepiste? Teht. 8. Luokkahuoneen tilavuus on 180 m 3 ja sen sisältämän ilman lämpötila 24 o C sekä suhteellinen kosteus 48 %. Mikä on luokkahuoneen sisältämän vesihöyryn massa?
4 RATKAISUT TEHTÄVIIN 1-8. Teht. 1. Asuinhuoneessa on kosteusmittarin mukaan suhteellinen kosteus 52 %. Huoneen lämpötila on 21 o C ja tilavuus 48 m 3. Laske a) huoneilman vesihöyryn osapaine b) vesihöyryn osatiheys ilmassa. c) Kuinka paljon (g) huoneilmassa on vettä? Teht. 1. Ratkaisu: 0,52 T ( ,15)K 294,15 K V 48 m 3 Taulukosta (MAOL s. 80(80)) nähdään, että kylläisen vesihöyryn paine lämpötilassa 21 o C on 24,86. Ilman suhteellinen kosteus on, josta saadaan huoneilman vesihöyryn osapaine 0,52 24,86 12, V: Huoneilman vesihöyryn osapaine on 13 mbar. b) Vesihöyryn osatiheys ilmassa on Ilmassa olevan vesihöyryn massa m (g) on, (MAOL s ( )) missä äää. h. Veden H2O moolimassa on Mv (2 1, ,00) g/mol 18,0 g/mol. Vedyn H suhteellinen atomimassa on 1,008 ja hapen O suhteellinen atomimassa 16,00. (ks. hapen ja vedyn suhteelliset atomimassat; MAOL s. 169, 171 (161, 163)). Oletetaan, että kaasujen yleinen tilanyhtälö on voimassa. Kaasujen yleisestä tilanyhtälöstä saadaan vesihöyryn ainemäärä, missä on a)-kohdassa laskettu huoneilman vesihöyryn osapaine. Vesihöyryn massa. Vesihöyryn osatiheys on,,,, 0, , , ,15 9, Vesihöyryn osatiheys ilmassa on 9,5 10 9,5 10.
5 c) Huoneilmassa olevan veden massa on 9, g. Yksikkötarkastelu: Vesihöyryn osatiheys on. Oikein. Teht. 2. Tehtävän 1 asuinhuoneessa on kosteusmittarin mukaan suhteellinen kosteus 52 %, huoneen lämpötila on 21 o C ja tilavuus 48 m 3. Kastepiste on lämpötila, jossa vesihöyry alkaa tiivistyä vedeksi. Määritä asuinhuoneen kastepiste. Teht. 2. Ratkaisu: Tehtävässä 1 laskettiin asuinhuoneen vesihöyryn osapaineeksi 12, Huoneen lämpötilan on laskettava niin alas, että tätä lämpötilaa vastaava kylläisen vesihöyryn paine on 12,9 mbar 13 mbar. Kastepiste on tätä kylläisen höyryn painetta vastaava lämpötila, joka taulukon (MAOL s. 80(80)) mukaan on noin 11 o C. V: kastepiste on 11 o C. Teht. 3. Työpöytäsi vieressä oleva kosteusmittari osoittaa suhteellisen kosteuden arvoa 39 %. Huoneen lämpötila on 21 o C. a) Laske huoneilman vesihöyryn osapaine. b) Määritä kastepisteen arvo. Teht. 3. Ratkaisu: a) Ilman suhteellinen kosteus 0,39 ja lämpötila t 21 o C. Kylläisen vesihöyryn paine taulukkokirjan (MAOL s. 80(80)) mukaan tässä lämpötilassa on 24,86. Ilman suhteellinen kosteus on josta saadaan huoneilman vesihöyryn osapaine 0,39 24,86 9,6954 9,7. V: Huoneilman vesihöyryn osapaine on 9,7 mbar., b) Jos ilman lämpötila laskee niin paljon, että tätä lämpötilaa vastaava kylläisen vesihöyryn paine (taulukosta) on yhtä suuri kuin ilmassa olevan vesihöyryn osapaine eli a)-kohdan perusteella pv 9,7 mbar, niin vesihöyry alkaa tiivistyä vedeksi. Lämpötilaa, jossa tämä tapahtuu, sanotaan kastepisteeksi. Vesihöyryn osapainetta pv 9,7 mbar 10 mbar vastaa taulukon mukaan (MAOL s. 80(80)) lämpötila 7 o C. V: kastepiste on 7 o C.
6 Teht. 4. Huoneilman lämpötila on 19 o C ja suhteellinen kosteus 49 %. Laske a) huoneilman vesihöyryn osapaine b) veden osatiheys ilmassa. c) Kuinka paljon (g) huoneilmassa on vettä? Huoneen tilavuus on 52 m 3. d) Kuinka suuri on huoneilman kastepiste? Teht. 4. Ratkaisu: 0,49 T ( ,15)K 292,15 K V 52 m 3 Taulukosta (MAOL s. 80(80)) nähdään, että kylläisen vesihöyryn paine lämpötilassa 19 o C on 21,96. Ilman suhteellinen kosteus on, josta saadaan huoneilman vesihöyryn osapaine 0,49 21,96 10, V: Huoneilman vesihöyryn osapaine on 11 mbar. b) Vesihöyryn osatiheys ilmassa on Ilmassa olevan vesihöyryn massa m (g) on, (MAOL s ( )) missä äää. h. Veden H2O moolimassa on Mv (2 1, ,00) g/mol 18,0 g/mol. (ks. hapen ja vedyn suhteelliset atomimassat; MAOL s. 169, 171 (161, 163)). Oletetaan, että kaasujen yleinen tilanyhtälö on voimassa. Kaasujen yleisestä tilanyhtälöstä saadaan vesihöyryn ainemäärä, missä on a)-kohdassa laskettu huoneilman vesihöyryn osapaine. Vesihöyryn massa. Vesihöyryn osatiheys on,,,, 0, , , ,15 7, Vesihöyryn osatiheys ilmassa on 8,0 10 8,0 10.
7 c) Huoneilmassa olevan veden massa on 7, ,6 415g. d) Kastepisteessä kylläisen vesihöyryn paine on yhtä suuri kuin vesihöyryn osapaine 10,76. Taulukosta (MAOL s. 80(80)) nähdään, että tätä vesihöyryn osapainetta 10,76 vastaava lämpötila on 8 o C. V: kastepiste on 8 o C. Teht. 5. Huoneen ilman suhteellinen kosteus on 60 % ja lämpötila 21 o C. a) Kuinka suuri on absoluuttinen kosteus? b) Kuinka paljon ilmassa on vettä, jos huoneen tilavuus on 36 m 3? Teht. 5. Ratkaisu: a) Ilman suhteellinen kosteus on absoluuttisen kosteuden X ja maksimikosteuden Xmax osamäärä;. Absoluuttinen kosteus ratkaistaan tästä suhteellisen kosteuden yhtälöstä, jolloin saadaan. Taulukon mukaan (MAOL s. 80(80)) 21 o C:n lämpötilassa maksimikosteus ( kylläisen vesihöyryn tiheys) on Xmax 18,33 g/m 3. Sijoittamalla lukuarvot saadaan absoluuttiseksi kosteudeksi 0,60 18,33 10,998. V: 11 b) Huoneilmassa olevan veden massa m saadaan tiheyden ja tilavuuden tulona (m ρv) eli tehtävän merkinnöillä m X V 10,998 g/m 3 36 m g m 400 g. Teht. 6. Määritä kastepisteen suuruus tehtävän 5 tapauksessa. Teht. 6. Ratkaisu: Edellisessä tehtävässä saatiin huoneen ilman absoluuttiseksi kosteudeksi 11 g/m 3. Katsotaan taulukosta (MAOL s. 80(80)), missä lämpötilassa se on maksimikosteus. Taulukon mukaan lämpötilassa 12 o C kylläisen vesihöyryn tiheys on 10,66 g/m 3. V: Kastepiste on siis noin 12 o C.
8 Teht. 7. Ilman lämpötila on 20 o C ja suhteellinen kosteus 59 %. a) Kuinka suuri on absoluuttinen kosteus? b) Mikä on kastepiste? Teht. 7. Ratkaisu: a) Suhteellinen kosteus on, missä X absoluuttinen kosteus ja Xmax maksimikosteus. Absoluuttinen kosteus on siten Taulukon mukaan lämpötilaa 20 o C vastaa kylläisen vesihöyryn tiheys, joka on maksimikosteus Xmax 17,29 g/m 3. Absoluuttiseksi kosteudeksi saadaan näin ollen 0,59 17,29 10,201. V: Absoluuttinen kosteus on X 10 g/m 3. b) Absoluuttisen kosteuden arvoa eli kylläisen vesihöyryn tiheyttä 10,2 g/m 3 vastaa taulukon mukaan (MAOL s. 80(80)) lämpötila, joka on noin 11 o C. V: Kastepiste on noin 11 o C. Teht. 8. Luokkahuoneen tilavuus on 180 m 3 ja sen sisältämän ilman lämpötila 24 o C sekä suhteellinen kosteus 48 %. Mikä on luokkahuoneen sisältämän vesihöyryn massa? Teht. 8. Ratkaisu: Sovelletaan vesihöyryyn kaasujen yleistä tilanyhtälöä pv nrt. Kylläisen vesihöyryn paine lämpötilassa 24 o C on 29,82 mbar (MAOL s. 80(80)). Ilman suhteellinen kosteus on, josta saadaan huoneilman vesihöyryn osapaine 0,48 29,82 14, , , , , Lämpötila on kaasujen yleisessä tilanyhtälössä eli ideaalikaasujen tilanyhtälössä ilmoitettava aina kelvineinä (K): T ( ,15)K 297,15 K. Kaasujen yleisen tilanyhtälön mukaan RT (*) jossa vesihöyryn ainemäärä on veden massa m (g) jaettuna veden moolimassalla (ks. MAOL s ( )). äää. Veden H2O moolimassa on Mv (2 1, ,00) g/mol 18,0 g/mol. Vedyn H suhteellinen atomimassa on 1,008 ja hapen O suhteellinen atomimassa 16,00. (ks. hapen ja vedyn suhteelliset atomimassat; MAOL s. 169, 171 (161, 163)).
9 Sijoitetaan ainemäärän lauseke kaasujen yleiseen tilanyhtälöön (*), jolloin saadaan, josta ratkaistaan vesihöyryn massa m; 18,0 1, m 8, ,15 18,0 1, m 8, , : Luokkahuoneen sisältämän vesihöyryn massa on 1,9 kg. Yksikkötarkastelu. [ ]. Oikein.
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
, voidaan myös käyttää likimäärälauseketta
 ILMAN KOSTEUS Ilma sisältää aina jonkin verran vesihöyryä. Ilman vesihöyrypitoisuudella eli kosteudella on huomattava merkitys ihmisten viihtyvyydelle ja terveydelle, erilaisten materiaalien ja esineiden
ILMAN KOSTEUS Ilma sisältää aina jonkin verran vesihöyryä. Ilman vesihöyrypitoisuudella eli kosteudella on huomattava merkitys ihmisten viihtyvyydelle ja terveydelle, erilaisten materiaalien ja esineiden
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
KOSTEUS. Visamäentie 35 B 13100 HML
 3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
4 Aineen olomuodot. 4.2 Höyrystyminen POHDI JA ETSI
 4 Aineen olomuodot 4.2 Höyrystyminen POHDI JA ETSI 4-1. a) Vesi asettuu astiassa vaakatasoon Maan vetovoiman ja veden herkkäliikkeisyyden takia. Painovoima tekee työtä, kunnes veden potentiaalienergia
4 Aineen olomuodot 4.2 Höyrystyminen POHDI JA ETSI 4-1. a) Vesi asettuu astiassa vaakatasoon Maan vetovoiman ja veden herkkäliikkeisyyden takia. Painovoima tekee työtä, kunnes veden potentiaalienergia
10B16A. LÄMPÖLAAJENEMINEN JA ILMAN SUHTEELLINEN KOSTEUS
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 1B16A. LÄMPÖLAAJENEMINEN JA ILMAN SUHTEELLINEN KOSTEUS A. LÄMPÖLAAJENEMINEN Pituuden lämpötilakertoimen määrittäminen vesihauteen avulla 1. Työn tavoite Tutkitaan aineen
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 1B16A. LÄMPÖLAAJENEMINEN JA ILMAN SUHTEELLINEN KOSTEUS A. LÄMPÖLAAJENEMINEN Pituuden lämpötilakertoimen määrittäminen vesihauteen avulla 1. Työn tavoite Tutkitaan aineen
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
KE4, KPL. 3 muistiinpanot. Keuruun yläkoulu, Joonas Soininen
 KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa.
 Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Valintakoe 2016/FYSIIKKA Vastaa kaikkiin kysymyksiin. Oheisista kaavoista ja lukuarvoista saattaa olla apua laskutehtäviin vastatessa. Boltzmannin vakio 1.3805 x 10-23 J/K Yleinen kaasuvakio 8.315 JK/mol
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
KARTOITUSRAPORTTI. Rälssitie 13 01510 VANTAA 567/2609 25.9.2013
 KARTOITUSRAPORTTI Rälssitie 13 01510 VANTAA 567/2609 25.9.2013 KARTOITUSRAPORTTI 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 JOHTOPÄÄTÖKSET JA SUOSITUKSET...
KARTOITUSRAPORTTI Rälssitie 13 01510 VANTAA 567/2609 25.9.2013 KARTOITUSRAPORTTI 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 JOHTOPÄÄTÖKSET JA SUOSITUKSET...
Puu luovuttaa (desorptio) ilmaan kosteutta ja sitoo (adsorptio) ilmasta kosteutta.
 Puun kosteus Hygroskooppisuus Puu luovuttaa (desorptio) ilmaan kosteutta ja sitoo (adsorptio) ilmasta kosteutta. Tasapainokosteus Ilman lämpötilaa ja suhteellista kosteutta vastaa puuaineen tasapainokosteus.
Puun kosteus Hygroskooppisuus Puu luovuttaa (desorptio) ilmaan kosteutta ja sitoo (adsorptio) ilmasta kosteutta. Tasapainokosteus Ilman lämpötilaa ja suhteellista kosteutta vastaa puuaineen tasapainokosteus.
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
KARTOITUSRAPORTTI. Asematie Vantaa 1710/
 Asematie 7 01300 Vantaa 1710/6416 26.3.2018 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 KÄYTETTY MITTAKALUSTO... 4 MITTAUSPÖYTÄKIRJA... 5 YHTEENVETO... 7 3 KOHDETIEDOT
Asematie 7 01300 Vantaa 1710/6416 26.3.2018 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 KÄYTETTY MITTAKALUSTO... 4 MITTAUSPÖYTÄKIRJA... 5 YHTEENVETO... 7 3 KOHDETIEDOT
ENSIRAPORTTI/MITTAUSRAPORTTI
 Martinkyläntie 5 01620 VANTAA Raportointi pvm: 22.2.2012 ENSIRAPORTTI/MITTAUSRAPORTTI Työ A12162 KOHDE: ASUNNOT: Martinkyläntie 5 01620 VANTAA/Myllymäen koulu Liikuntasali ja pukuhuonetilat TILAAJA: Reino
Martinkyläntie 5 01620 VANTAA Raportointi pvm: 22.2.2012 ENSIRAPORTTI/MITTAUSRAPORTTI Työ A12162 KOHDE: ASUNNOT: Martinkyläntie 5 01620 VANTAA/Myllymäen koulu Liikuntasali ja pukuhuonetilat TILAAJA: Reino
ENSIRAPORTTI. Työ A11849. Läntinen Valoisenlähteentie 50 A Raportointi pvm: 01.12.2011. A - Kunnostus- ja kuivauspalvelut Oy Y-tunnus: 1911067-2
 ENSIRAPORTTI Läntinen Valoisenlähteentie 50 A Raportointi pvm: 01.12.2011 Työ TILAT: ISÄNNÖINTI: TILAAJA: LASKUTUSOSOITE: VASTAANOTTAJA (T): Läntinen valkoisenlähteentie 50 A Lummenpolun päiväkoti Päiväkodin
ENSIRAPORTTI Läntinen Valoisenlähteentie 50 A Raportointi pvm: 01.12.2011 Työ TILAT: ISÄNNÖINTI: TILAAJA: LASKUTUSOSOITE: VASTAANOTTAJA (T): Läntinen valkoisenlähteentie 50 A Lummenpolun päiväkoti Päiväkodin
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka. Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU
 MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
luku 1.notebook Luku 1 Mooli, ainemäärä ja konsentraatio
 Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
Viikkoharjoitus 2: Hydrologinen kierto
 Viikkoharjoitus 2: Hydrologinen kierto 30.9.2015 Viikkoharjoituksen palautuksen DEADLINE keskiviikkona 14.10.2015 klo 12.00 Palautus paperilla, joka lasku erillisenä: palautus joko laskuharjoituksiin tai
Viikkoharjoitus 2: Hydrologinen kierto 30.9.2015 Viikkoharjoituksen palautuksen DEADLINE keskiviikkona 14.10.2015 klo 12.00 Palautus paperilla, joka lasku erillisenä: palautus joko laskuharjoituksiin tai
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
TUNTEMATON KAASU. TARINA 1 Lue etukäteen argonin käyttötarkoituksista Jenni Västinsalon kandidaattitutkielmasta sivut 12-15. Saa lukea myös kokonaan!
 TUNTEMATON KAASU KOHDERYHMÄ: Työ soveltuu lukiolaisille, erityisesti kurssille KE3 ja FY2. KESTO: Noin 60 min. MOTIVAATIO: Oppilaat saavat itse suunnitella koejärjestelyn. TAVOITE: Työn tavoitteena on
TUNTEMATON KAASU KOHDERYHMÄ: Työ soveltuu lukiolaisille, erityisesti kurssille KE3 ja FY2. KESTO: Noin 60 min. MOTIVAATIO: Oppilaat saavat itse suunnitella koejärjestelyn. TAVOITE: Työn tavoitteena on
PL 6007 00021, Laskutus 153021000 / Anne Krokfors. A - Kunnostus- ja kuivauspalvelut Oy Y-tunnus: 1911067-2
 ENSIRAPORTTI raportointipäivä : 4.8.2011 Työ : TILAAJA: Vantaan kaupunki ISÄNNÖINTI: Vantaan kaupunki / HUOLTO: Kouluisäntä: 0400 765 713 LASKUTUSOSOITE: Vantaan Kaupunki PL 6007 00021, Laskutus 153021000
ENSIRAPORTTI raportointipäivä : 4.8.2011 Työ : TILAAJA: Vantaan kaupunki ISÄNNÖINTI: Vantaan kaupunki / HUOLTO: Kouluisäntä: 0400 765 713 LASKUTUSOSOITE: Vantaan Kaupunki PL 6007 00021, Laskutus 153021000
Kosteusmittausten haasteet
 Kosteusmittausten haasteet Luotettavuutta päästökauppaan liittyviin mittauksiin, MIKES 21.9.2006 Martti Heinonen Tavoite Kosteusmittaukset ovat haastavia; niiden luotettavuuden arviointi ja parantaminen
Kosteusmittausten haasteet Luotettavuutta päästökauppaan liittyviin mittauksiin, MIKES 21.9.2006 Martti Heinonen Tavoite Kosteusmittaukset ovat haastavia; niiden luotettavuuden arviointi ja parantaminen
ARK-A.3000 Rakennetekniikka (4op) Lämpö- ja kosteustekniset laskelmat. Hannu Hirsi.
 ARK-A.3000 Rakennetekniikka (4op) Lämpö- ja kosteustekniset laskelmat Hannu Hirsi. SRakMK ja rakennusten energiatehokkuus : Lämmöneristävyys laskelmat, lämmöneristyksen termit, kertausta : Lämmönjohtavuus
ARK-A.3000 Rakennetekniikka (4op) Lämpö- ja kosteustekniset laskelmat Hannu Hirsi. SRakMK ja rakennusten energiatehokkuus : Lämmöneristävyys laskelmat, lämmöneristyksen termit, kertausta : Lämmönjohtavuus
Kartoitusraportti. Kisatie 21 Ruusuvuoren koulu Vantaa 297/
 Kartoitusraportti Kisatie 21 Ruusuvuoren koulu Vantaa 297/3920 5.5.2015 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 JOHTOPÄÄTÖKSET JA SUOSITUKSET... 4 MITTAUSPÖYTÄKIRJA...
Kartoitusraportti Kisatie 21 Ruusuvuoren koulu Vantaa 297/3920 5.5.2015 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 JOHTOPÄÄTÖKSET JA SUOSITUKSET... 4 MITTAUSPÖYTÄKIRJA...
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
MOOLIMASSA. Vedyllä on yksi atomi, joten Vedyn moolimassa M(H) = 1* g/mol = g/mol. ATOMIMASSAT TAULUKKO
 MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT
 KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT Lämpölaajeneminen Pituuden lämpölaajeneminen: l = αl o t lo l l = l o + l = l o + αl o t l l = l o (1 + α t) α = pituuden lämpötilakerroin esim. teräs: α = 12 10
KIINTEÄN AINEEN JA NESTEEN TILANYHTÄLÖT Lämpölaajeneminen Pituuden lämpölaajeneminen: l = αl o t lo l l = l o + l = l o + αl o t l l = l o (1 + α t) α = pituuden lämpötilakerroin esim. teräs: α = 12 10
b) Laske prosentteina, paljonko sydämen keskimääräinen teho muuttuu suhteessa tilanteeseen ennen saunomista. Käytä laskussa SI-yksiköitä.
 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
Kuivauksen fysiikkaa. Hannu Sarkkinen
 Kuivauksen fysiikkaa Hannu Sarkkinen 28.11.2013 Kuivatusmenetelmiä Auringon säteily Mikroaaltouuni Ilmakuivatus Ilman kosteus Ilman suhteellinen kosteus RH = ρ v /ρ vs missä ρ v = vesihöyryn tiheys (g/m
Kuivauksen fysiikkaa Hannu Sarkkinen 28.11.2013 Kuivatusmenetelmiä Auringon säteily Mikroaaltouuni Ilmakuivatus Ilman kosteus Ilman suhteellinen kosteus RH = ρ v /ρ vs missä ρ v = vesihöyryn tiheys (g/m
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
MITTAUSRAPORTTI. Työ : 514/3248. Kohde: Hämeenkylän koulu. Raportointipäivä : 24.6.2014. A - Kunnostus- ja kuivauspalvelut Oy Y-tunnus: 1911067-2
 MITTAUSRAPORTTI Kohde: Hämeenkylän koulu Raportointipäivä : 2462014 Työ : 514/3248 etunimisukunimi@akumppanitfi 01740 Vantaa wwwkuivauspalvelutfi KOHDE: Hämeenkylän koulu TILAN VUOKRALAINEN: TILAAJA: Vantaan
MITTAUSRAPORTTI Kohde: Hämeenkylän koulu Raportointipäivä : 2462014 Työ : 514/3248 etunimisukunimi@akumppanitfi 01740 Vantaa wwwkuivauspalvelutfi KOHDE: Hämeenkylän koulu TILAN VUOKRALAINEN: TILAAJA: Vantaan
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
Luvun 12 laskuesimerkit
 Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luento 9 Kemiallinen tasapaino CHEM-A1250
 Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
TEHTÄVÄ 1 *palautettava tehtävä (DL: 3.5. klo. 10:00 mennessä!) TEHTÄVÄ 2
 Aalto-yliopisto/Insinööritieteiden korkeakoulu/energiatalous ja voimalaitostekniikka 1(5) TEHTÄVÄ 1 *palautettava tehtävä (DL: 3.5. klo. 10:00 mennessä!) Ilmaa komprimoidaan 1 bar (abs.) paineesta 7 bar
Aalto-yliopisto/Insinööritieteiden korkeakoulu/energiatalous ja voimalaitostekniikka 1(5) TEHTÄVÄ 1 *palautettava tehtävä (DL: 3.5. klo. 10:00 mennessä!) Ilmaa komprimoidaan 1 bar (abs.) paineesta 7 bar
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Hydrologia. Säteilyn jako aallonpituuden avulla
 Hydrologia L3 Hydrometeorologia Säteilyn jako aallonpituuden avulla Ultravioletti 0.004 0.39 m Näkyvä 0.30 0.70 m Infrapuna 0.70 m. 1000 m Auringon lyhytaaltoinen säteily = ultavioletti+näkyvä+infrapuna
Hydrologia L3 Hydrometeorologia Säteilyn jako aallonpituuden avulla Ultravioletti 0.004 0.39 m Näkyvä 0.30 0.70 m Infrapuna 0.70 m. 1000 m Auringon lyhytaaltoinen säteily = ultavioletti+näkyvä+infrapuna
Kasvihuoneen kasvutekijät. ILMANKOSTEUS Tuula Tiirikainen Keuda Mäntsälä Saari
 Kasvihuoneen kasvutekijät ILMANKOSTEUS Tuula Tiirikainen Keuda Mäntsälä Saari Kasvien kasvuun vaikuttavat: - Lämpö - Valo - Vesi - Ilmankosteus - Hiilidioksidi - Ravinteet - Kasvin perinnölliset eli geneettiset
Kasvihuoneen kasvutekijät ILMANKOSTEUS Tuula Tiirikainen Keuda Mäntsälä Saari Kasvien kasvuun vaikuttavat: - Lämpö - Valo - Vesi - Ilmankosteus - Hiilidioksidi - Ravinteet - Kasvin perinnölliset eli geneettiset
Alkuaineita luokitellaan atomimassojen perusteella
 IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
Luku 13. Kertausta Hydrostaattinen paine Noste
 Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
ENSIRAPORTTI. Työ A Jokiniemen koulu Valkoisenlähteentie 51, Vantaa. raportointipäivä:
 ENSIRAPORTTI raportointipäivä: 22.3.2011 Työ TILAAJA: Vantaan kaupunki / Anne Krokfors LASKUTUSOSOITE: Vantaan kaupunki PL 6007 00021 Laskutus Viite: 153021000/Anne Krokfors VASTAANOTTAJA (T): Anne Krokfors
ENSIRAPORTTI raportointipäivä: 22.3.2011 Työ TILAAJA: Vantaan kaupunki / Anne Krokfors LASKUTUSOSOITE: Vantaan kaupunki PL 6007 00021 Laskutus Viite: 153021000/Anne Krokfors VASTAANOTTAJA (T): Anne Krokfors
Bensiiniä voidaan pitää hiilivetynä C8H18, jonka tiheys (NTP) on 0,703 g/ml ja palamislämpö H = kj/mol
 Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Luku 13. Kertausta Hydrostaattinen paine Noste
 Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Luku 13 Kertausta Hydrostaattinen paine Noste Uutta Jatkuvuusyhtälö Bernoullin laki Virtauksen mallintaminen Esitiedot Voiman ja energian käsitteet Liike-energia ja potentiaalienergia Itseopiskeluun jää
Kaasu Neste Kiinteä aine Plasma
 Olomuodot Kaasu: atomeilla/molekyyleillä suuri nopeus, vuorovaikuttavat vain törmätessään toisiinsa Neste: atomit/molekyylit/ionit liukuvat toistensa lomitse, mutta pysyvät yhtenä nestetilavuutena (molekyylien
Olomuodot Kaasu: atomeilla/molekyyleillä suuri nopeus, vuorovaikuttavat vain törmätessään toisiinsa Neste: atomit/molekyylit/ionit liukuvat toistensa lomitse, mutta pysyvät yhtenä nestetilavuutena (molekyylien
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
S , Fysiikka III (S) I välikoe Malliratkaisut
 S-4.35, Fysiikka III (S) I välikoe 9.0.000 Malliratkaisut Tehtävä Kuution uotoisessa säiliössä, jonka särän pituus on 0,0, on 3,0 0 olekyyliä happea (O) 300 K läpötilassa. a) Kuinka onta kertaa kukin olekyyli
S-4.35, Fysiikka III (S) I välikoe 9.0.000 Malliratkaisut Tehtävä Kuution uotoisessa säiliössä, jonka särän pituus on 0,0, on 3,0 0 olekyyliä happea (O) 300 K läpötilassa. a) Kuinka onta kertaa kukin olekyyli
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Liike ja voima. Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä
 Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Ainemäärien suhteista laskujen kautta aineiden määriin
 REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
Ekvipartitioperiaatteen mukaisesti jokaiseen efektiiviseen vapausasteeseen liittyy (1 / 2)kT energiaa molekyyliä kohden.
 . Hiilidioksidiolekyyli CO tiedetään lineaariseksi a) Mitkä ovat eteneisliikkeen, pyöriisliikkeen ja värähtelyn suuriat ekvipartitioperiaatteen ukaiset läpöenergiat olekyyliä kohden, kun kaikki vapausasteet
. Hiilidioksidiolekyyli CO tiedetään lineaariseksi a) Mitkä ovat eteneisliikkeen, pyöriisliikkeen ja värähtelyn suuriat ekvipartitioperiaatteen ukaiset läpöenergiat olekyyliä kohden, kun kaikki vapausasteet
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
TEHTÄVIEN RATKAISUT N = 1,40 N -- 0,84 N = 0,56 N. F 1 = p 1 A = ρgh 1 A. F 2 = p 2 A = ρgh 2 A
 TEHTÄVIEN RATKAISUT 8-1. Jousivaa an lukema suolavedessä on pienempi kuin puhtaassa vedessä, koska suolaveden tiheys on suurempi kuin puhtaan veden ja siksi noste suolavedessä on suurempi kuin puhtaassa
TEHTÄVIEN RATKAISUT 8-1. Jousivaa an lukema suolavedessä on pienempi kuin puhtaassa vedessä, koska suolaveden tiheys on suurempi kuin puhtaan veden ja siksi noste suolavedessä on suurempi kuin puhtaassa
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
Oppikirjan tehtävien ratkaisut
 Oppikirjan tehtävien ratkaisut Liukoisuustulon käyttö 10. a) Selitä, mitä eroa on käsitteillä liukoisuus ja liukoisuustulo. b) Lyijy(II)bromidin PbBr liukoisuus on 1,0 10 mol/dm. Laske lyijy(ii)bromidin
Oppikirjan tehtävien ratkaisut Liukoisuustulon käyttö 10. a) Selitä, mitä eroa on käsitteillä liukoisuus ja liukoisuustulo. b) Lyijy(II)bromidin PbBr liukoisuus on 1,0 10 mol/dm. Laske lyijy(ii)bromidin
Sääilmiöt tapahtuvat ilmakehän alimmassa kerroksessa, troposfäärissä (0- noin 15 km).
 Sää ja ilmasto Sää (engl. weather) =ilmakehän alaosan, fysikaalinen tila määrätyllä hetkellä määrätyllä paikalla. Ilmasto (engl. climate) = pitkäaikaisten (> 30 vuotta) säävaihteluiden keskiarvo. Sääilmiöt
Sää ja ilmasto Sää (engl. weather) =ilmakehän alaosan, fysikaalinen tila määrätyllä hetkellä määrätyllä paikalla. Ilmasto (engl. climate) = pitkäaikaisten (> 30 vuotta) säävaihteluiden keskiarvo. Sääilmiöt
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
KARTOITUSRAPORTTI. Seurantaraportti Valkoisenlähteentie Vantaa 86/
 Seurantaraportti Valkoisenlähteentie 51 01370 Vantaa 86/3342 28.8.2014 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 JOHTOPÄÄTÖKSET JA SUOSITUKSET... 5 KÄYTETTY
Seurantaraportti Valkoisenlähteentie 51 01370 Vantaa 86/3342 28.8.2014 2 KOHDETIEDOT... 3 LÄHTÖTIEDOT... 4 RAKENTEET... 4 SUORITETUT TYÖT SEKÄ HAVAINNOT... 4 JOHTOPÄÄTÖKSET JA SUOSITUKSET... 5 KÄYTETTY
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
VASTAUKSIA YO-KYSYMYKSIIN KURSSISTA FY2: Lämpö
 VASTAUKSIA YO-KYSYMYKSIIN KURSSISTA FY2: Lämpö 1. Selitä fysikaalisesti, miksi: a) sateessa kastuneet vaatteet tuntuvat kylmältä, b) pyykit kuivuvat myös pakkasessa, c) uunista pudonneen hehkuvan hiilenpalan
VASTAUKSIA YO-KYSYMYKSIIN KURSSISTA FY2: Lämpö 1. Selitä fysikaalisesti, miksi: a) sateessa kastuneet vaatteet tuntuvat kylmältä, b) pyykit kuivuvat myös pakkasessa, c) uunista pudonneen hehkuvan hiilenpalan
PAINOPISTE JA MASSAKESKIPISTE
 PAINOPISTE JA MASSAKESKIPISTE Kappaleen painopiste on piste, jonka kautta kappaleeseen kohdistuvan painovoiman vaikutussuora aina kulkee, olipa kappale missä asennossa tahansa. Jos ajatellaan kappaleen
PAINOPISTE JA MASSAKESKIPISTE Kappaleen painopiste on piste, jonka kautta kappaleeseen kohdistuvan painovoiman vaikutussuora aina kulkee, olipa kappale missä asennossa tahansa. Jos ajatellaan kappaleen
Kosteusmittausyksiköt
 Kosteusmittausyksiköt Materiaalit Paino-% kosteus = kuinka monta prosenttia vettä materiaalissa on suhteessa kuivapainoon. kg/m3 kosteus = kuinka monta kg vettä materiaalissa on suhteessa yhteen kuutioon.
Kosteusmittausyksiköt Materiaalit Paino-% kosteus = kuinka monta prosenttia vettä materiaalissa on suhteessa kuivapainoon. kg/m3 kosteus = kuinka monta kg vettä materiaalissa on suhteessa yhteen kuutioon.
Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Tehtävä 2. Selvitä, ovatko seuraavat kovalenttiset sidokset poolisia vai poolittomia. Jos sidos on poolinen, merkitse osittaisvaraukset näkyviin.
 KERTAUSKOE, KE1, SYKSY 2013, VIE Tehtävä 1. Kirjoita kemiallisia kaavoja ja olomuodon symboleja käyttäen seuraavat olomuodon muutokset a) etanolin CH 3 CH 2 OH höyrystyminen b) salmiakin NH 4 Cl sublimoituminen
KERTAUSKOE, KE1, SYKSY 2013, VIE Tehtävä 1. Kirjoita kemiallisia kaavoja ja olomuodon symboleja käyttäen seuraavat olomuodon muutokset a) etanolin CH 3 CH 2 OH höyrystyminen b) salmiakin NH 4 Cl sublimoituminen
Termiikin ennustaminen radioluotauksista. Heikki Pohjola ja Kristian Roine
 Termiikin ennustaminen radioluotauksista Heikki Pohjola ja Kristian Roine Maanpintahavainnot havaintokojusta: lämpötila, kostea lämpötila (kosteus), vrk minimi ja maksimi. Lisäksi tuulen nopeus ja suunta,
Termiikin ennustaminen radioluotauksista Heikki Pohjola ja Kristian Roine Maanpintahavainnot havaintokojusta: lämpötila, kostea lämpötila (kosteus), vrk minimi ja maksimi. Lisäksi tuulen nopeus ja suunta,
Algebran ja Geometrian laskukokoelma
 Algebran ja Geometrian laskukokoelma A. Potenssien laskusäännöt Sievennä 1. (r 3 ) 4 2. (2a 3 ) 3 3. x 3 x 5 4. k11 k 5 5. 2a2 a 7 5a 3 6. (-3x 2 y 3 ) 3 7. ( 1 4 ) 3 8. (2 a2 Lisätehtäviä b 3)3 9. (a
Algebran ja Geometrian laskukokoelma A. Potenssien laskusäännöt Sievennä 1. (r 3 ) 4 2. (2a 3 ) 3 3. x 3 x 5 4. k11 k 5 5. 2a2 a 7 5a 3 6. (-3x 2 y 3 ) 3 7. ( 1 4 ) 3 8. (2 a2 Lisätehtäviä b 3)3 9. (a
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
a) Oletetaan, että happi on ideaalikaasu. Säiliön seinämiin osuvien hiukkasten lukumäärä saadaan molekyylivuon lausekkeesta = kaava (1p) dta n =
 S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
KOSTEUSKARTOITUS. Ruusuvuoren koulu Kisatie Vantaa 1/5. Työnumero: Scan-Clean Oy Y-tunnus:
 1/5 KOSTEUSKARTOITUS Ruusuvuoren koulu Kisatie 21 01450 Vantaa Työnumero: 09089 Scan-Clean Oy Y-tunnus: 0690693-8 www.asb.fi 24 h päivytys puh: +358 40 717 9330 Konalankuja 4, 00390 Helsinki puh: 0207
1/5 KOSTEUSKARTOITUS Ruusuvuoren koulu Kisatie 21 01450 Vantaa Työnumero: 09089 Scan-Clean Oy Y-tunnus: 0690693-8 www.asb.fi 24 h päivytys puh: +358 40 717 9330 Konalankuja 4, 00390 Helsinki puh: 0207
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin.
 1.2 Elektronin energia Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin. -elektronit voivat olla vain tietyillä energioilla (pääkvanttiluku n = 1, 2, 3,...) -mitä kauempana
1.2 Elektronin energia Käytetään nykyaikaista kvanttimekaanista atomimallia, Bohrin vetyatomi toimii samoin. -elektronit voivat olla vain tietyillä energioilla (pääkvanttiluku n = 1, 2, 3,...) -mitä kauempana
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Ennakoiva Laadunohjaus 2016 Kosteudenhallinta. Vaasa Tapani Hahtokari
 Ennakoiva Laadunohjaus 2016 Kosteudenhallinta Rakennuksen kosteuslähteet Rakennusfysikaalinen toimivuus Materiaalien säilytys työmaalla Rakennekosteus ja materiaalien kuivuminen Rakennedetaljit Rakennuksen
Ennakoiva Laadunohjaus 2016 Kosteudenhallinta Rakennuksen kosteuslähteet Rakennusfysikaalinen toimivuus Materiaalien säilytys työmaalla Rakennekosteus ja materiaalien kuivuminen Rakennedetaljit Rakennuksen
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2012 Insinöörivalinnan fysiikan koe 30.5.2012, malliratkaisut
 A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
Laskun vaiheet ja matemaattiset mallit
 Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 26. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 26. syyskuuta 2016 1 / 14 Hieman kertausta
Laskun vaiheet ja matemaattiset mallit Jukka Sorjonen sorjonen.jukka@gmail.com 26. syyskuuta 2016 Jukka Sorjonen (Jyväskylän Normaalikoulu) Mallit ja laskun vaiheet 26. syyskuuta 2016 1 / 14 Hieman kertausta
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
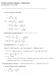 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
Keski-Suomen fysiikkakilpailu
 Keski-Suomen fysiikkakilpailu 28.1.2016 Kilpailussa on kolme kirjallista tehtävää ja yksi kokeellinen tehtävä. Kokeellisen tehtävän ohjeistus on laatikossa mittausvälineiden kanssa. Jokainen tehtävä tulee
Keski-Suomen fysiikkakilpailu 28.1.2016 Kilpailussa on kolme kirjallista tehtävää ja yksi kokeellinen tehtävä. Kokeellisen tehtävän ohjeistus on laatikossa mittausvälineiden kanssa. Jokainen tehtävä tulee
