b) Laske prosentteina, paljonko sydämen keskimääräinen teho muuttuu suhteessa tilanteeseen ennen saunomista. Käytä laskussa SI-yksiköitä.
|
|
|
- Hanna-Mari Korpela
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus ennen saunomista on 5, l/min ja saunomisen aikana 9,6 l/min. Käytä tehtävässä näitä arvoja. Lisäksi voidaan olettaa aortan poikkileikkauksen pinta-alaksi,0 cm² sekä keskimääräiseksi aorttapaineeksi ennen saunomista ja saunomisen aikana 0 mmhg. a) Laske sydämen iskutilavuus ennen saunomista (syke 75 lyöntiä minuutissa) ja saunomisen aikana (syke 0 lyöntiä minuutissa). (4 p) inuuttitilavuus = syke iskutilavuus (sv) 5, l/min 9,6 l/min Ennen: sv 0,0708 l 7 ml, aikana: sv 0,076 l 76 ml 75/ min 0 / min b) Laske prosentteina, paljonko sydämen keskimääräinen teho muuttuu suhteessa tilanteeseen ennen saunomista. Käytä laskussa SI-yksiköitä. (6 p) Sydämen keskimääräinen teho,5 7 P q p q A 6 kg m Paine pascaleina: p Hg gh 600 9,8 0,0 m 475 Pa m s Ennen:,5 050 kg/m 5,0 m 7 kg 5,0 m P 475,49 W,4 W (0,000 m ) 60 s 6 m s 60 s Aikana:, 5050 kg/m 9,6 0 m 7 kg 9,6 0 m P 475,545 W,5 W (0,000 m ) 60 s 6 m s 60 s,545,49 uutos-%: 00 % 79,5 % 79 %,49 8 e D i m e n s i o 00
2 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä c) Laske kuvassa olevan mallin avulla, paljonko ihonalaiskudoksen virtausvastus muuttuu PRU-yksiköissä (perifeerinen vastusyksikkö) tilanteissa ennen saunomista ja saunomisen aikana. Saunomisen aikana perifeerinen kokonaisvirtausvastus laskee 4 % ja ennen saunomista verenvirtauksesta 6,0 % kulkee ihonalaiskudoksen kautta. Saunomisen aikana muun kehon perifeerinen vastus =, PRU. olemmissa tapauksissa keskimääräinen aortta- ja laskimopaineen ero p = 98 mmhg. Huomioi miten PRU-yksikkö on määritelty. (8 p) p sydän muu keho ihonalaiskudos Ihonalaiskudoksen virtaus, ennen: 50 ml ml 0,06 5, eli: 60 s s 98 mmhg PRUiho 8,456 PRU 5, ml/s 98 mmhg uun kudoksen virtaus, aikana: Q muu 89, 0909 ml/s 545 ml/min, PRU Ihon kautta: Q 960 ml/min 545 ml/min 85 ml/min eli: PRU iho iho 98 mmhg 60 s,54 PRU 85 ml PRU iho pienenee 8,456 PRU,54 PRU = 6,9 PRU 7 PRU (Tai muu loogisesti etenevä ja oikeaan tulokseen johtava ratkaisutapa) [Galenos: 406, 40, 40-4, ] e D i m e n s i o 00 9
3 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 8 pistettä Normaalisti valtimoveren hiilidioksidiosapaine (pco ) on 5, kpa, ph 7,40 ja vetykarbonaatti-ionin konsentraatio 6,6 mmol/l. Saunomisen aikana hiilidioksidin osapaine voi kohota kapillaariveren plasmassa arvoon 7,5 kpa ja veren ph laskea arvoon 7,6. itkä ovat tällöin kapillaariveren plasmaan liuenneen hiilidioksidin ja vetykarbonaatti-ionin konsentraatiot (mmol/l)? uita mahdollisia veren ph-arvoon vaikuttavia tekijöitä ei oteta huomioon. pk a -arvo hiilidioksidi-vetykarbonaattipuskurijärjestelmälle voidaan ratkaista sijoittamalla normaalitilanteen arvot yhtälöön: ph pk pk a a A log HA A ph log pco H 6,6 7,40 log 6,0 (5, 0,5) Saunomisen aikana liuenneen CO :n konsentraatio kapillaariveressä: c CO = p CO H (Henryn vakio) c CO = 7,5 kpa 0,50 mmol/(l kpa) c CO =,79 mmol/l HCO : HCO 7,6 6,0 log,79 log HCO, 6,79 HCO 4, 45,79 [HCO ] = 5,9 mmol/l [Galenos: 59, 9, 90, 9] 0 e D i m e n s i o 00
4 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 0 4 pistettä RIA on eräs klassinen tapa määrittää esim. veren hormonipitoisuus. RIA:aan tarvitaan hormonia spesifisesti sitova vasta-aine (A), radioaktiivisesti merkitty hormoni ( ) sekä näyte, jonka sisältämän hormonin () pitoisuus mitataan. Näytteen sisältämä hormoni kilpailee radioaktiivisen hormonin kanssa sitoutumisesta vasta-aineeseen. + A A () + A A () Voimassa ovat siis tasapainot A K ja K A A A Yksinkertaistuksen vuoksi oletamme, että jokainen vasta-ainemolekyyli sitoo vain yhden hormonimolekyylin. Kun reaktiot ovat saavuttaneet tasapainon, A eristetään ja sen pitoisuus ([ A]) määritetään radioaktiivisuuden mittauksen avulla. [ A] on em. reaktioiden pohjalta kääntäen verrannollinen näytteen sisältämän hormonin pitoisuuteen (mitä pienempi radioaktiivisuus, sitä suurempi näytteen hormonipitoisuus; ks. kuva 4). monipitoisuus näytteessä voidaan laskea, koska A:n ja :n pitoisuudet ja reaktioiden tasapainovakiot tunnetaan. Eräs koetilanne, jossa näytteen hormonikonsentraatio määritettiin: Reaktioseokset (kokonaistilavuus = V =,000 ml) verrokkiseos (ei näytettä): 0,800 ml puskuriliuosta, 0,00 ml vasta-ainetta sisältävää liuosta (A-liuos) ja 0,00 ml radioaktiivista hormonia sisältävää liuosta ( -liuos) näytteen sisältävä seos: 0,600 ml puskuriliuosta, 0,00 ml näytettä, 0,00 ml A-liuosta ja 0,00 ml -liuosta vasta-aineen kokonaiskonsentraatio (kummassakin seoksessa) = C A = [A] + [ A] + [A] =, mol/l Kuva 4. radioaktiivisen hormonin kokonaiskonsentraatio (kummassakin seoksessa) = C =, mol/l K = K =, l/mol e D i m e n s i o 00
5 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Verrokkiseoksessa (ei näytettä; C = 0) [ A] = 4, mol/l (tasapainotila). Näytettä sisältävässä seoksessa [ A] =, mol/l (tasapainotila). Laske tehtävämonisteessa mainitussa koetilanteessa olevien vakioiden ja mittaustulosten perusteella alkuperäisen näytteen hormonikonsentraatio. Oleta, että vapaiden hormonien ( ja ) konsentraatio reaktioseoksessa ei muutu merkittävästi niiden sitoutuessa A:han (ylimäärä :a ja :a suhteessa A:han) eli C [ ] ja C []. Vihje: ratkaisu saadaan C A :n lausekkeesta. K A A A A A A K A K A K Yllä olevan perusteella saadaan A K A Sijoitetaan yhtälöön C A K A K A A A A CA K CA A K 6,00 0 mol l,00 0 7,74 0 mol l 0,69 0 mol l 0 A A A mol l,00 0 9,00 0 l mol Näyte laimeni, kun sitä lisättiin reaktioseokseen: alkuperäisen näytteen hormonikonsentraatio =,000 ml/0,00 ml [] =,000/0,00, mol/l = 8, mol/l 0 mol l [Galenos: 5-54, 75, 4, ] e D i m e n s i o 00
6 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 8 pistettä Kun erästä saunaa, jonka tilavuus on 7,8 m³, lämmitetään koivuhaloilla, kestää saunan lämpötilan nousu huoneenlämmöstä ( ºC) saunomislämpötilaan (85 ºC) 65 min ja energiaa saunan lämmittämiseen kuluu J. a) Kiuas korvataan sähkökiukaalla, jossa kolme identtistä vastusta on kukin erikseen kytketty 0 V teholliseen jännitteeseen. Kuinka suuri pitää kunkin vastuksen resistanssin olla, jotta lämmitysaika pysyisi samana? (5 p) P = UI, U = RI I = U/R, P = U² /R, E/ = Pt = U² t/r R = U² t/e E = J = 0 6 J, U = 0 V. t = 65 min = s R = (0V) 6065 s 6 0 J = 8, 8 b) Jos saunan on täysin kuivaa ja npaine saunassa on 05 kpa kun saunomislämpötila saavutetaan, niin kuinka suuri osuus lämmitykseen käytetystä energiasta on kulunut sillä hetkellä saunassa olevan n lämmittämiseen? Tässä oletetaan, että n lämpötila on kaikkialla saunassa sama. c p, =,0 kj/(kg K), (85 ºC) =,0 kg/m (5 p) W = E, W = c T c m T c V T p, p, = 85 C C = 6 K, E = J = c p, =,0 kj/ (kg K) =,0 0 J/ K) (kg, 6 0 J, V = 7,8 m (85 C ) =,0 kg/ m E V p,,0 0 J/(kg K),0 kg/m 7,8 m 6 K = 0,06 0,0, % 6 0 J T e D i m e n s i o 00
7 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä c) ikäli kiukaalle heitetään,5 dl vettä ( ºC), joka höyrystyy kokonaan, ja oletetaan, ettei (hetkellisesti) pääse poistumaan saunasta sekä odotetaan, kunnes lämpötila ja nkosteus saunan sisällä ovat tasaantuneet, niin kuinka paljon npaine saunassa on noussut löylynheittoa edeltävään hetkeen verrattuna? Voit käsitellä sekä a että höyryä ideaalikaasuina ja voit olettaa niiden olevan kaikkialla saunassa 85 ºC lämpötilassa. (8 p) Dalton n höyry = p m tot p p p = höyry höyry m höyry V p höyry, phöyry V höyry = n höyry RT T = 85 C = (85+7,5) K = 58,5 K, R = 8,4 J/( mol K ), V höyry = 7,8 m V =,5 dl = 0,5 0 m, ( C ) =,0 0 kg/ m = H + O =, 0 g/mol + 6, 0 g/mol = 8,0 0 kg/mol V R T p p höyry = = V höyry,0 0 kg/m 0,50 8,0 0 m 8,4 J/(mol K) 58,5 K kg/mol7,8 m = 5, J/ m 5,7 kpa [Galenos: 7, 6, 75, 76, 79, 5, 5] 4 e D i m e n s i o 00
LÄÄKETIETEEN ALAN VALINTAKOE 28.5.2009 VASTAUSANALYYSIT TEHTÄVÄKOHTAISET PISTEET: yhteensä
 LÄÄKETIETEEN ALAN VALINTAKOE 8.5.009 VASTAUSANALYYSIT TEHTÄVÄKOHTAISET PISTEET: 1 5 9 0 10 14 6 10 9 1 14 7 11 17 16 18 4 8 yhteensä 18 11 159 Vastausanalyysissä määritellään yleisesti kunkin tehtävän
LÄÄKETIETEEN ALAN VALINTAKOE 8.5.009 VASTAUSANALYYSIT TEHTÄVÄKOHTAISET PISTEET: 1 5 9 0 10 14 6 10 9 1 14 7 11 17 16 18 4 8 yhteensä 18 11 159 Vastausanalyysissä määritellään yleisesti kunkin tehtävän
KandiakatemiA Kandiklinikka
 Kandiklinikka Pääsykoe 2009 Opiskelijan koe LÄÄKETIETEEN PÄÄSYKOE 2009, OPISKELIJAN KOE Lääketieteen pääsykoe on kuluneina vuosina sisältänyt tehtäviä biologiasta, kemiasta sekä fysiikasta. Pääsykokeen
Kandiklinikka Pääsykoe 2009 Opiskelijan koe LÄÄKETIETEEN PÄÄSYKOE 2009, OPISKELIJAN KOE Lääketieteen pääsykoe on kuluneina vuosina sisältänyt tehtäviä biologiasta, kemiasta sekä fysiikasta. Pääsykokeen
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
TUTKIMUS IKI-KIUKAAN ENERGIASÄÄSTÖISTÄ YHTEISKÄYTTÖSAUNOISSA
 TUTKIMUS IKI-KIUKAAN ENERGIASÄÄSTÖISTÄ YHTEISKÄYTTÖSAUNOISSA IKI-Kiuas Oy teetti tämän tutkimuksen saatuaan taloyhtiöiltä positiivista palautetta kiukaistaan. Asiakkaat havaitsivat sähkölaskujensa pienentyneen,
TUTKIMUS IKI-KIUKAAN ENERGIASÄÄSTÖISTÄ YHTEISKÄYTTÖSAUNOISSA IKI-Kiuas Oy teetti tämän tutkimuksen saatuaan taloyhtiöiltä positiivista palautetta kiukaistaan. Asiakkaat havaitsivat sähkölaskujensa pienentyneen,
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella:
 ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
Helsingin yliopisto/tampereen yliopisto Henkilötunnus - Biokemian/bioteknologian valintakoe Etunimet Tehtävä 5 Pisteet / 20
 Helsingin yliopisto/tampereen yliopisto Henkilötunnus - Biokemian/bioteknologian valintakoe Sukunimi 24.5.2006 Etunimet Tehtävä 5 Pisteet / 20 Glukoosidehydrogenaasientsyymi katalysoi glukoosin oksidaatiota
Helsingin yliopisto/tampereen yliopisto Henkilötunnus - Biokemian/bioteknologian valintakoe Sukunimi 24.5.2006 Etunimet Tehtävä 5 Pisteet / 20 Glukoosidehydrogenaasientsyymi katalysoi glukoosin oksidaatiota
Luku 2. Kemiallisen reaktion tasapaino
 Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT JA PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
2CHEM-A1210 Kemiallinen reaktio Kevät 2017 Laskuharjoitus 7.
 HEM-A0 Kemiallinen reaktio Kevät 07 Laskuharjoitus 7.. Metalli-ioni M + muodostaa ligandin L - kanssa : kompleksin ML +, jonka pysyvyysvakio on K ML + =,00. 0 3. Mitkä ovat kompleksitasapainon vapaan metalli-ionin
HEM-A0 Kemiallinen reaktio Kevät 07 Laskuharjoitus 7.. Metalli-ioni M + muodostaa ligandin L - kanssa : kompleksin ML +, jonka pysyvyysvakio on K ML + =,00. 0 3. Mitkä ovat kompleksitasapainon vapaan metalli-ionin
KEMIA HYVÄN VASTAUKSEN PIIRTEET
 BILÄÄKETIETEEN enkilötunnus: - KULUTUSJELMA Sukunimi: 20.5.2015 Etunimet: Nimikirjoitus: KEMIA Kuulustelu klo 9.00-13.00 YVÄN VASTAUKSEN PIIRTEET Tehtävämonisteen tehtäviin vastataan erilliselle vastausmonisteelle.
BILÄÄKETIETEEN enkilötunnus: - KULUTUSJELMA Sukunimi: 20.5.2015 Etunimet: Nimikirjoitus: KEMIA Kuulustelu klo 9.00-13.00 YVÄN VASTAUKSEN PIIRTEET Tehtävämonisteen tehtäviin vastataan erilliselle vastausmonisteelle.
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 31.5.2006, malliratkaisut ja arvostelu.
 1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin?
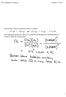 Esimerkki: Mihin suuntaan etenee reaktio CO (g) + H 2 O (g) CO 2 (g) + H 2 (g), K = 0,64, kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin? 1 Le Châtelier'n
Esimerkki: Mihin suuntaan etenee reaktio CO (g) + H 2 O (g) CO 2 (g) + H 2 (g), K = 0,64, kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin? 1 Le Châtelier'n
Luvun 12 laskuesimerkit
 Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
1. Muunna seuraavat yksiköt. Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu. Oppilaitos:.. Koulutusala:...
 MATEMATIIKAN KOE Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu Nimi: Oppilaitos:.. Koulutusala:... Luokka:.. Sarjat: LAITA MERKKI OMAAN SARJAASI. Tekniikka ja liikenne:..
MATEMATIIKAN KOE Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu Nimi: Oppilaitos:.. Koulutusala:... Luokka:.. Sarjat: LAITA MERKKI OMAAN SARJAASI. Tekniikka ja liikenne:..
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Luento 9 Kemiallinen tasapaino CHEM-A1250
 Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
TKK, TTY, LTY, OY, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 31.5.2006
 TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
a) Oletetaan, että happi on ideaalikaasu. Säiliön seinämiin osuvien hiukkasten lukumäärä saadaan molekyylivuon lausekkeesta = kaava (1p) dta n =
 S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
MATEMATIIKAN KOE. AMMATIKKA top 17.11.2005. 2. asteen ammatillisen koulutuksen kaikkien alojen yhteinen matematiikka kilpailu. Oppilaitos:.
 AMMATIKKA top 17.11.005 MATEMATIIKAN KOE. asteen ammatillisen koulutuksen kaikkien alojen yhteinen matematiikka kilpailu Nimi: Oppilaitos:. Koulutusala:... Luokka:.. Sarjat: MERKITSE OMA SARJA 1. Tekniikka
AMMATIKKA top 17.11.005 MATEMATIIKAN KOE. asteen ammatillisen koulutuksen kaikkien alojen yhteinen matematiikka kilpailu Nimi: Oppilaitos:. Koulutusala:... Luokka:.. Sarjat: MERKITSE OMA SARJA 1. Tekniikka
Veden ionitulo ja autoprotolyysi TASAPAINO, KE5
 REAKTIOT JA Veden ionitulo ja autoprotolyysi TASAPAINO, KE5 Kun hapot ja emäkset protolysoituvat, vesiliuokseen muodostuu joko oksoniumioneja tai hydroksidi-ioneja. Määritelmä: Oksoniumionit H 3 O + aiheuttavat
REAKTIOT JA Veden ionitulo ja autoprotolyysi TASAPAINO, KE5 Kun hapot ja emäkset protolysoituvat, vesiliuokseen muodostuu joko oksoniumioneja tai hydroksidi-ioneja. Määritelmä: Oksoniumionit H 3 O + aiheuttavat
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
Esimerkiksi ammoniakin valmistus typestä ja vedystä on tyypillinen teollinen tasapainoreaktio.
 REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
Demo 5, maanantaina 5.10.2009 RATKAISUT
 Demo 5, maanantaina 5.0.2009 RATKAISUT. Lääketieteellisen tiedekunnan pääsykokeissa on usein kaikenlaisia laitteita. Seuraavassa yksi hyvä kandidaatti eli Venturi-mittari, jolla voi määrittää virtauksen
Demo 5, maanantaina 5.0.2009 RATKAISUT. Lääketieteellisen tiedekunnan pääsykokeissa on usein kaikenlaisia laitteita. Seuraavassa yksi hyvä kandidaatti eli Venturi-mittari, jolla voi määrittää virtauksen
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Bensiiniä voidaan pitää hiilivetynä C8H18, jonka tiheys (NTP) on 0,703 g/ml ja palamislämpö H = kj/mol
 Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe
 Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
Vinkkejä opettajille ja odotetut tulokset SIVU 1
 Vinkkejä opettajille ja odotetut tulokset SIVU 1 Konteksti palautetaan oppilaiden mieliin käymällä Osan 1 johdanto uudelleen läpi. Kysymysten 1 ja 2 tarkoituksena on arvioida ovatko oppilaat ymmärtäneet
Vinkkejä opettajille ja odotetut tulokset SIVU 1 Konteksti palautetaan oppilaiden mieliin käymällä Osan 1 johdanto uudelleen läpi. Kysymysten 1 ja 2 tarkoituksena on arvioida ovatko oppilaat ymmärtäneet
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka. Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU
 MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen
 KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
Käyttämällä annettua kokoonpuristuvuuden määritelmää V V. = κv P P = P 0 = P. (b) Lämpölaajenemisesta johtuva säiliön tilavuuden muutos on
 766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta.
 Helsingin yliopiston kemian valintakoe 10.5.2019 Vastaukset ja selitykset Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta. Reaktio
Helsingin yliopiston kemian valintakoe 10.5.2019 Vastaukset ja selitykset Tehtävä 1. Avaruussukkulan kiihdytysvaiheen kiinteänä polttoaineena käytetään ammonium- perkloraatin ja alumiinin seosta. Reaktio
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma
 KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
RATKAISUT: 22. Vaihtovirtapiiri ja resonanssi
 Physica 9. painos (0) RATKAST. Vaihtovirtapiiri ja resonanssi RATKAST:. Vaihtovirtapiiri ja resonanssi. a) Vaihtovirran tehollinen arvo on yhtä suuri kuin sellaisen tasavirran arvo, joka tuottaa vastuksessa
Physica 9. painos (0) RATKAST. Vaihtovirtapiiri ja resonanssi RATKAST:. Vaihtovirtapiiri ja resonanssi. a) Vaihtovirran tehollinen arvo on yhtä suuri kuin sellaisen tasavirran arvo, joka tuottaa vastuksessa
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
TEHTÄVÄ 1 *palautettava tehtävä (DL: 3.5. klo. 10:00 mennessä!) TEHTÄVÄ 2
 Aalto-yliopisto/Insinööritieteiden korkeakoulu/energiatalous ja voimalaitostekniikka 1(5) TEHTÄVÄ 1 *palautettava tehtävä (DL: 3.5. klo. 10:00 mennessä!) Ilmaa komprimoidaan 1 bar (abs.) paineesta 7 bar
Aalto-yliopisto/Insinööritieteiden korkeakoulu/energiatalous ja voimalaitostekniikka 1(5) TEHTÄVÄ 1 *palautettava tehtävä (DL: 3.5. klo. 10:00 mennessä!) Ilmaa komprimoidaan 1 bar (abs.) paineesta 7 bar
Oppikirjan tehtävien ratkaisut
 Oppikirjan tehtävien ratkaisut Liukoisuustulon käyttö 10. a) Selitä, mitä eroa on käsitteillä liukoisuus ja liukoisuustulo. b) Lyijy(II)bromidin PbBr liukoisuus on 1,0 10 mol/dm. Laske lyijy(ii)bromidin
Oppikirjan tehtävien ratkaisut Liukoisuustulon käyttö 10. a) Selitä, mitä eroa on käsitteillä liukoisuus ja liukoisuustulo. b) Lyijy(II)bromidin PbBr liukoisuus on 1,0 10 mol/dm. Laske lyijy(ii)bromidin
Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan
 Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan 1. Kolmiossa yksi kulma on 60 ja tämän viereisten sivujen suhde 1 : 3. Laske
Tekniikan valintakokeen laskutehtävät (osio 3): Vastaa kukin tehtävä erilliselle vastauspaperille vastaukselle varattuun kohtaan 1. Kolmiossa yksi kulma on 60 ja tämän viereisten sivujen suhde 1 : 3. Laske
Integroidut tunnit II Tuntitehtävät
 Integroidut tunnit II Tuntitehtävät Ledeillä (LED = light emitting diode) toteutettu valaistus on huomattavasti hehkulanka- tai loisteputkivalaisimia parempi hyötysuhteeltaan. Valaisin perustuu puolijohdetekniikkaan,
Integroidut tunnit II Tuntitehtävät Ledeillä (LED = light emitting diode) toteutettu valaistus on huomattavasti hehkulanka- tai loisteputkivalaisimia parempi hyötysuhteeltaan. Valaisin perustuu puolijohdetekniikkaan,
Kiiännö!! b) Fysiikan tunnilla tutkittiin lääkeruiskussa olevan ilman paineen riippuvuutta lämpötilasta vakiotilavuudessa ruiskuun kiinnitetyn
 FYSKKA (FY02l: 2. KURSS: Lämpö vasraa KUUTEEN (6) TEHnÄVÄÄN il KOE 21.02.2013 1. a) Suuren matkustajalentokoneen lentokorkeus maahan nähden on 10,5 km, vauhti980 km/h ja massa 310 000 kg. Laske lentokoneen
FYSKKA (FY02l: 2. KURSS: Lämpö vasraa KUUTEEN (6) TEHnÄVÄÄN il KOE 21.02.2013 1. a) Suuren matkustajalentokoneen lentokorkeus maahan nähden on 10,5 km, vauhti980 km/h ja massa 310 000 kg. Laske lentokoneen
5 LIUOKSEN PITOISUUS Lisätehtävät
 LIUOKSEN PITOISUUS Lisätehtävät Esimerkki 1. a) 100 ml:ssa suolaista merivettä on keskimäärin 2,7 g NaCl:a. Mikä on meriveden NaCl-pitoisuus ilmoitettuna molaarisuutena? b) Suolaisen meriveden MgCl 2 -pitoisuus
LIUOKSEN PITOISUUS Lisätehtävät Esimerkki 1. a) 100 ml:ssa suolaista merivettä on keskimäärin 2,7 g NaCl:a. Mikä on meriveden NaCl-pitoisuus ilmoitettuna molaarisuutena? b) Suolaisen meriveden MgCl 2 -pitoisuus
Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2 1/2 p = 2 p.
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 014 Insinöörivalinnan kemian koe 8.5.014 MALLIRATKAISUT ja PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 014 Insinöörivalinnan kemian koe 8.5.014 MALLIRATKAISUT ja PISTEET Lasku- ja huolimattomuusvirheet ½ p. Loppupisteiden puolia pisteitä ei korotettu
Teddy 2. välikoe kevät 2008
 Teddy 2. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 2. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
B sivu 1(6) AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE
 B sivu 1(6) TEHTÄVÄOSA 7.6.2004 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän
B sivu 1(6) TEHTÄVÄOSA 7.6.2004 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän
KE5 Kurssikoe Kastellin lukio 2012 Valitse kuusi (6) tehtävää. Piirrä pisteytystaulukko.
 KE5 Kurssikoe Kastellin lukio 01 Valitse kuusi (6) tehtävää. Piirrä pisteytystaulukko. 1. a) Selvitä, mitä tarkoitetaan seuraavilla käsitteillä lyhyesti sanallisesti ja esimerkein: 1) heikko happo polyproottinen
KE5 Kurssikoe Kastellin lukio 01 Valitse kuusi (6) tehtävää. Piirrä pisteytystaulukko. 1. a) Selvitä, mitä tarkoitetaan seuraavilla käsitteillä lyhyesti sanallisesti ja esimerkein: 1) heikko happo polyproottinen
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
KOSTEUS. Visamäentie 35 B 13100 HML
 3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
Sähkövirran määrittelylausekkeesta
 VRTAPRLASKUT kysyttyjä suureita ovat mm. virrat, potentiaalit, jännitteet, resistanssit, energian- ja tehonkulutus virtapiirin teho lasketaan Joulen laista: P = R 2 sovelletaan Kirchhoffin sääntöjä tuntemattomien
VRTAPRLASKUT kysyttyjä suureita ovat mm. virrat, potentiaalit, jännitteet, resistanssit, energian- ja tehonkulutus virtapiirin teho lasketaan Joulen laista: P = R 2 sovelletaan Kirchhoffin sääntöjä tuntemattomien
Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu
 MATEMATIIKAN KOE Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu Nimi: Oppilaitos:.. Koulutusala:... Luokka:.. AIKAA KOKEEN TEKEMISEEN 90 MINUUTTIA MUKANA KYNÄ, KUMI,
MATEMATIIKAN KOE Ammatillisen koulutuksen kaikkien alojen yhteinen matematiikan valmiuksien kilpailu Nimi: Oppilaitos:.. Koulutusala:... Luokka:.. AIKAA KOKEEN TEKEMISEEN 90 MINUUTTIA MUKANA KYNÄ, KUMI,
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
Jos olet käynyt kurssin aikaisemmin, merkitse vuosi jolloin kävit kurssin nimen alle.
 1(4) Lappeenrannan teknillinen yliopisto School of Energy Systems LUT Energia Nimi, op.nro: BH20A0450 LÄMMÖNSIIRTO Tentti 13.9.2016 Osa 1 (4 tehtävää, maksimi 40 pistettä) Vastaa seuraaviin kysymyksiin
1(4) Lappeenrannan teknillinen yliopisto School of Energy Systems LUT Energia Nimi, op.nro: BH20A0450 LÄMMÖNSIIRTO Tentti 13.9.2016 Osa 1 (4 tehtävää, maksimi 40 pistettä) Vastaa seuraaviin kysymyksiin
Verikaasuanalyysi. Esitys (anestesia)hoitajille. Vesa Lappeteläinen 3.10.2013
 Verikaasuanalyysi Esitys (anestesia)hoitajille Vesa Lappeteläinen 3.10.2013 Yleistä Yleensä valtimoverestä otettava verinäyte, joka analysoidaan vieritestianalysaattorilla Nopein tapa saada keskeistä tietoa
Verikaasuanalyysi Esitys (anestesia)hoitajille Vesa Lappeteläinen 3.10.2013 Yleistä Yleensä valtimoverestä otettava verinäyte, joka analysoidaan vieritestianalysaattorilla Nopein tapa saada keskeistä tietoa
TEHTÄVIEN RATKAISUT. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 712 p m 105 kg
 TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
BI4 IHMISEN BIOLOGIA
 BI4 IHMISEN BIOLOGIA Verenkierto toimii elimistön kuljetusjärjestelmänä 6 Avainsanat fibriini fibrinogeeni hiussuoni hyytymistekijät imusuonisto iso verenkierto keuhkoverenkierto laskimo lepovaihe eli
BI4 IHMISEN BIOLOGIA Verenkierto toimii elimistön kuljetusjärjestelmänä 6 Avainsanat fibriini fibrinogeeni hiussuoni hyytymistekijät imusuonisto iso verenkierto keuhkoverenkierto laskimo lepovaihe eli
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
Sukunimi: Etunimi: Henkilötunnus:
 K1. Onko väittämä oikein vai väärin. Oikeasta väittämästä saa 0,5 pistettä. Vastaamatta jättämisestä tai väärästä vastauksesta ei vähennetä pisteitä. (yhteensä 10 p) Oikein Väärin 1. Kaikki metallit johtavat
K1. Onko väittämä oikein vai väärin. Oikeasta väittämästä saa 0,5 pistettä. Vastaamatta jättämisestä tai väärästä vastauksesta ei vähennetä pisteitä. (yhteensä 10 p) Oikein Väärin 1. Kaikki metallit johtavat
Kemian opetuksen keskus Helsingin yliopisto Veden kovuus Oppilaan ohje. Veden kovuus
 Huomaat, että vedenkeittimessäsi on valkoinen saostuma. Päättelet, että saostuma on peräisin vedestä. Haluat varmistaa, että vettä on turvallista juoda ja viet sitä tutkittavaksi laboratorioon. Laboratoriossa
Huomaat, että vedenkeittimessäsi on valkoinen saostuma. Päättelet, että saostuma on peräisin vedestä. Haluat varmistaa, että vettä on turvallista juoda ja viet sitä tutkittavaksi laboratorioon. Laboratoriossa
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Ongelmanratkaisu ja Tekstikoe HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Ongelmanratkaisu ja Tekstikoe HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim. 2½ p. = 2 p.
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 DI-kemian valintakoe 31.5. Malliratkaisut Lasku- ja huolimattomuusvirheet - ½ p. Loppupisteiden puolia pisteitä ei korotettu ylöspäin, esim.
Luku 3. Protolyysireaktiot ja vesiliuoksen ph
 Luku 3 Protolyysireaktiot ja vesiliuoksen ph 1 MIKÄ ALKUAINE? Se ei ole metalli, kuten alkalimetallit, se ei ole jalokaasu, vaikka onkin kaasu. Kevein, väritön, mauton, hajuton, maailmankaikkeuden yleisin
Luku 3 Protolyysireaktiot ja vesiliuoksen ph 1 MIKÄ ALKUAINE? Se ei ole metalli, kuten alkalimetallit, se ei ole jalokaasu, vaikka onkin kaasu. Kevein, väritön, mauton, hajuton, maailmankaikkeuden yleisin
c) Tasapainota seuraava happamassa liuoksessa tapahtuva hapetus-pelkistysreaktio:
 HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
Kuva 1. Ohmin lain kytkentäkaavio. DC; 0 6 V.
 TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
HENGITYSKAASUJEN VAIHTO
 HENGITYSKAASUJEN VAIHTO Tarja Stenberg KAASUJENVAIHDON VAIHEET Happi keuhkoista vereen -diffuusio alveolista kapillaariin -ventilaatio-perfuusio suhde Happi veressä kudokseen -sitoutuminen hemoglobiiniin
HENGITYSKAASUJEN VAIHTO Tarja Stenberg KAASUJENVAIHDON VAIHEET Happi keuhkoista vereen -diffuusio alveolista kapillaariin -ventilaatio-perfuusio suhde Happi veressä kudokseen -sitoutuminen hemoglobiiniin
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
Opiskeluintoa ja menestystä tuleviin valintakokeisiin!
 RATKAISUT TESTIKYSYMYKSIIN Tästä löydät astaukset lääketieteen alintakoetyyppisiin testikysymyksiin. Jos osa kysymyksistä tuotti sinulle paljon päänaiaa, älä masennu, keään alintakokeeseen on ielä pitkä
RATKAISUT TESTIKYSYMYKSIIN Tästä löydät astaukset lääketieteen alintakoetyyppisiin testikysymyksiin. Jos osa kysymyksistä tuotti sinulle paljon päänaiaa, älä masennu, keään alintakokeeseen on ielä pitkä
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Spektrofotometria ja spektroskopia
 11 KÄYTÄNNÖN ESIMERKKEJÄ INSTRUMENTTIANALYTIIKASTA Lisätehtävät Spektrofotometria ja spektroskopia Esimerkki 1. Mikä on transmittanssi T ja transmittanssiprosentti %T, kun absorbanssi A on 0, 1 ja 2. josta
11 KÄYTÄNNÖN ESIMERKKEJÄ INSTRUMENTTIANALYTIIKASTA Lisätehtävät Spektrofotometria ja spektroskopia Esimerkki 1. Mikä on transmittanssi T ja transmittanssiprosentti %T, kun absorbanssi A on 0, 1 ja 2. josta
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
1. Tasavirta. Virtapiirin komponenttien piirrosmerkit. Virtapiiriä havainnollistetaan kytkentäkaaviolla
 Fy3: Sähkö 1. Tasavirta Virtapiirin komponenttien piirrosmerkit Virtapiiriä havainnollistetaan kytkentäkaaviolla Sähkövirta I Sähkövirran suunta on valittu jännitelähteen plusnavasta miinusnapaan (elektronit
Fy3: Sähkö 1. Tasavirta Virtapiirin komponenttien piirrosmerkit Virtapiiriä havainnollistetaan kytkentäkaaviolla Sähkövirta I Sähkövirran suunta on valittu jännitelähteen plusnavasta miinusnapaan (elektronit
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
Rasvattoman maidon laktoosipitoisuuden määritys entsymaattisesti
 Rasvattoman maidon laktoosipitoisuuden määritys entsymaattisesti 1. Työn periaate Esikäsitellyn näyteliuoksen sisältämä laktoosi hajotetaan (hydrolysoidaan) entsymaattisesti D-glukoosiksi ja D-galaktoosiksi
Rasvattoman maidon laktoosipitoisuuden määritys entsymaattisesti 1. Työn periaate Esikäsitellyn näyteliuoksen sisältämä laktoosi hajotetaan (hydrolysoidaan) entsymaattisesti D-glukoosiksi ja D-galaktoosiksi
MATEMATIIKKA. Matematiikkaa pintakäsittelijöille. Ongelmanratkaisu. Isto Jokinen 2017
 MATEMATIIKKA Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017 SISÄLTÖ 1. Matemaattisten ongelmien ratkaisu laskukaavoilla 2. Tekijäyhtälöt 3. Laskukaavojen yhdistäminen 4. Yhtälöiden
MATEMATIIKKA Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017 SISÄLTÖ 1. Matemaattisten ongelmien ratkaisu laskukaavoilla 2. Tekijäyhtälöt 3. Laskukaavojen yhdistäminen 4. Yhtälöiden
Coulombin laki. Sähkökentän E voimakkuus E = F q
 Coulombin laki Kahden pistemäisen varatun hiukkasen välinen sähköinen voima F on suoraan verrannollinen varausten Q 1 ja Q 2 tuloon ja kääntäen verrannollinen etäisyyden r neliöön F = k Q 1Q 2 r 2, k =
Coulombin laki Kahden pistemäisen varatun hiukkasen välinen sähköinen voima F on suoraan verrannollinen varausten Q 1 ja Q 2 tuloon ja kääntäen verrannollinen etäisyyden r neliöön F = k Q 1Q 2 r 2, k =
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE /5 TEHTÄVÄOSA/ Ongelmanratkaisu..08 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA:
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE /5 TEHTÄVÄOSA/ Ongelmanratkaisu..08 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA:
Valitkoituja esimerkkejä & vastaustekniikkaa
 Valitkoituja esimerkkejä & vastaustekniikkaa Liukoisuus Lääketieteellisen tiedekunnan valintakoe vuonna 2000 t.5 Virtsakiviä muodostuu, kun niukkaliukoisia suoloja muodostavien ioninen pitoisuus virtsassa
Valitkoituja esimerkkejä & vastaustekniikkaa Liukoisuus Lääketieteellisen tiedekunnan valintakoe vuonna 2000 t.5 Virtsakiviä muodostuu, kun niukkaliukoisia suoloja muodostavien ioninen pitoisuus virtsassa
2.2 Gaussin eliminaatio. 2.2 Gaussin eliminaatio. 2.2 Gaussin eliminaatio. 2.2 Gaussin eliminaatio
 x = x 2 = 5/2 x 3 = 2 eli Ratkaisu on siis x = (x x 2 x 3 ) = ( 5/2 2) (Tarkista sijoittamalla!) 5/2 2 Tämä piste on alkuperäisten tasojen ainoa leikkauspiste Se on myös piste/vektori jonka matriisi A
x = x 2 = 5/2 x 3 = 2 eli Ratkaisu on siis x = (x x 2 x 3 ) = ( 5/2 2) (Tarkista sijoittamalla!) 5/2 2 Tämä piste on alkuperäisten tasojen ainoa leikkauspiste Se on myös piste/vektori jonka matriisi A
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Harjoitus 3: Hydrauliikka + veden laatu
 Harjoitus 3: Hydrauliikka + veden laatu 14.10.015 Harjoitusten aikataulu Aika Paikka Teema Ke 16.9. klo 1-14 R00/R1 1) Globaalit vesikysymykset Ke 3.9 klo 1-14 R00/R1 1. harjoitus: laskutupa Ke 30.9 klo
Harjoitus 3: Hydrauliikka + veden laatu 14.10.015 Harjoitusten aikataulu Aika Paikka Teema Ke 16.9. klo 1-14 R00/R1 1) Globaalit vesikysymykset Ke 3.9 klo 1-14 R00/R1 1. harjoitus: laskutupa Ke 30.9 klo
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2012 Insinöörivalinnan fysiikan koe 30.5.2012, malliratkaisut
 A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
TITRAUKSET, KALIBROINNIT, SÄHKÖNJOHTAVUUS, HAPPOJEN JA EMÄSTEN TARKASTELU
 Oulun Seudun Ammattiopisto Raportti Page 1 of 6 Turkka Sunnari & Janika Pietilä 23.1.2016 TITRAUKSET, KALIBROINNIT, SÄHKÖNJOHTAVUUS, HAPPOJEN JA EMÄSTEN TARKASTELU PERIAATE/MENETELMÄ Työssä valmistetaan
Oulun Seudun Ammattiopisto Raportti Page 1 of 6 Turkka Sunnari & Janika Pietilä 23.1.2016 TITRAUKSET, KALIBROINNIT, SÄHKÖNJOHTAVUUS, HAPPOJEN JA EMÄSTEN TARKASTELU PERIAATE/MENETELMÄ Työssä valmistetaan
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
SAIPPUALIUOKSEN SÄHKÖKEMIA 09-2009 JOHDANTO
 SAIPPUALIUOKSEN SÄHKÖKEMIA 09-009 JOHDANTO 1 lainaus ja kuvat lähteestä: Työssä tutkitaan johtokyky- ja ph-mittauksilla tavallisen palasaippuan kemiallista koostumusta ja misellien ja aggregaattien muodostumista
SAIPPUALIUOKSEN SÄHKÖKEMIA 09-009 JOHDANTO 1 lainaus ja kuvat lähteestä: Työssä tutkitaan johtokyky- ja ph-mittauksilla tavallisen palasaippuan kemiallista koostumusta ja misellien ja aggregaattien muodostumista
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
c) Missä ajassa kappale selvittää reitin b-kohdan tapauksessa? [3p]
![c) Missä ajassa kappale selvittää reitin b-kohdan tapauksessa? [3p] c) Missä ajassa kappale selvittää reitin b-kohdan tapauksessa? [3p]](/thumbs/50/26318972.jpg) Fysiikan valintakoe 11.5.2016 klo 9-12 1. Kappale lähtee levosta liikkeelle pisteessä A (0,3) ja liukuu kitkattomasti, ensin kaltevaa tasoa pitkin pisteeseen B (x,0) ja siitä edelleen vaakaatasoa pitkin
Fysiikan valintakoe 11.5.2016 klo 9-12 1. Kappale lähtee levosta liikkeelle pisteessä A (0,3) ja liukuu kitkattomasti, ensin kaltevaa tasoa pitkin pisteeseen B (x,0) ja siitä edelleen vaakaatasoa pitkin
Luku 5: Diffuusio kiinteissä aineissa
 Luku 5: Diffuusio kiinteissä aineissa Käsiteltävät aiheet... Mitä on diffuusio? Miksi sillä on tärkeä merkitys erilaisissa käsittelyissä? Miten diffuusionopeutta voidaan ennustaa? Miten diffuusio riippuu
Luku 5: Diffuusio kiinteissä aineissa Käsiteltävät aiheet... Mitä on diffuusio? Miksi sillä on tärkeä merkitys erilaisissa käsittelyissä? Miten diffuusionopeutta voidaan ennustaa? Miten diffuusio riippuu
Ylioppilastutkintolautakunta S tudentexamensnämnden
 Ylioppilastutkintolautakunta S tudentexamensnämnden MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ.9.013 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden ja sisältöjen luonnehdinta ei sido ylioppilastutkintolautakunnan
Ylioppilastutkintolautakunta S tudentexamensnämnden MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ.9.013 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden ja sisältöjen luonnehdinta ei sido ylioppilastutkintolautakunnan
