Yhden bitin tiedot. Digitaalitekniikan matematiikka Luku 1 Täsmätehtävä Tehtävä 1. Luettele esimerkkejä yhden bitin tiedoista.
|
|
|
- Aleksi Haapasalo
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista. Ovi auki - ovi kiinni Virta kulkee - virta ei kulje Lamppu palaa - lamppu ei pala Lompakossa on rahaa - lompakossa ei ole rahaa Ruoka on hyvää - ruoka ei ole hyvää Datayhteys toimii - datayhteys on poikki
2 Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä 2 Koodin bittimäärä ja vaihtoehdot Montako erilaista vaihtoehtoa saadaan kahdella bitillä? Vaihtoehdot,, ja eli neljä erilaista Entä kolmella bitillä? Vaihtoehdot,,,,, ja eli kahdeksan erilaista Minkä säännön mukaan vaihtoehtojen määrä riippuu bittimäärästä? Vaihtoehtojen määrä = 2 bittimäärä ASCII-koodilla voidaan esittää 28 erilaista merkkiä. Montako bittiä siinä on? 28 = 2 7. Bittejä on siis seitsemän
3 Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä 3 Binaariluvun arvon laskeminen Laske binaarilukujen ja arvo kymmenjärjestelmän lukuna Esimerkki: = = = 3 = = = 6 = = = 7
4 Digitaalitekniikan matematiikka Luku 2 Täsmätehtävä Tehtävä Eri tyyppisten piirien käyttö laitteissa Yhdistä kukin laite niihin piirityyppeihin, joita siinä on järkevää käyttää. Vakiopiirit Huippukännykkä Laiteharrastajan hilavitkutin Liikennevalojen ohjausjärjestelmä PC:n emolevy Puhuva nukke TV-studion ääni- ja kuvaohjauspöytä 3G-verkon tukiasema Asiakaspiirit Ohjelmoitavat logiikkaverkot
5 Digitaalitekniikan matematiikka Luku 2 Täsmätehtävä Tehtävä 2 Tuotekehitysprosessi Yhdistä kukin tuotekehitysprosessissa syntyvä tuotos oikeaan vaiheeseen. Määrittely Suunnittelu Toteutus Asiakaskysely Laitteen prototyyppi Piirikaavio Ohjelmalistaus Testiraportti Tuotantotestausohje Kannattavuuslaskelma Kotelon piirustus Testaussuunnitelma Komponenttien asettelurobotin ohjelma Testaus Tuotantoon vienti
6 Digitaalitekniikan matematiikka Luku 2 Täsmätehtävä Tehtävä 3 Puheen kulku digitaalisessa puhelinverkossa Mitä reittiä puhe kulkee, kun kännykästä soitetaan analogiseen pöytäpuhelimeen? Millä reitin osilla puhe on digitaalisessa muodossa? Digitaalinen Analoginen
7 Digitaalitekniikan matematiikka Luku 3 Täsmätehtävä Tehtävä Kombinaatio- ja sekvenssipiirit Mitkä seuraavista toiminnoista voidaan tehdä kombinaatiopiirillä, mitkä vaativat sekvenssipiirin? Kahden binaariluvun yhteenlasku K Ohi ajaneiden autojen lukumäärän laskenta S Kunkinhetkisen lämpötilan numeronäyttö K Vuorokauden maksimilämpötilan näyttö Mikroaaltouunin käynnistyksen ajastin S S Mikroaaltouunin lämmitystehon säätöpiiri K
8 Digitaalitekniikan matematiikka Luku 3 Täsmätehtävä Tehtävä 2 Totuustaulu Funktiot F ja G riippuvat muuttujista A ja B seuraavasti: F saa arvon, kun muuttujilla A ja B on sama arvo, ja arvon muulloin G saa arvon, kun molemmat muuttujat A ja B saavat arvon, ja arvon muulloin. Laadi funktioiden F ja G totuustaulu. Esimerkki totuustaulusta A B F G A B F
9 Digitaalitekniikan matematiikka Luku 3 Täsmätehtävä Tehtävä 3 JA- ja TAI-funktiot Millä funktiolla voidaan toteuttaa kukin seuraavista toiminnoista? Kirjoita myös lauseke. Raitiovaunun oven avaus A painikkeilla P, P2, P3 ja P4 riittää, että yhtä painiketta painetaan: siis TAI-funktio: A = P + P2 + P3 + P4 TAI Levyleikkurin terän T iskun ohjaus kahdella painikkeella P ja P2 turvallisuussyistä molempia painikkeita on painettava yhtä aikaa: siis JA-funktio: T = P P2 JA Windowsin kirjautumisnäkymän kutsu K näppäimillä Ctrl, Alt ja Delete kaikkia näppäimiä on painettava yhtä aikaa: siis JA-funktio: K = Ctrl Alt Delete JA Porraskäytävän lampun L sytytys kerroksissa olevilla painikkeilla P - P6 riittää, että yhtä painiketta painetaan: siis TAI-funktio: L = P + P2 + P3 + P4 + P5 + P6 TAI
10 Digitaalitekniikan matematiikka Luku 3 Täsmätehtävä Tehtävä 4 EI-funktio Mitkä seuraavista ovat tosia lauseita eli missä niistä esitetty funktio on EIfunktio? Pullo on täysi = Pullo on tyhjä lause ei ole tosi: pullo voi olla myös esimerkiksi puolillaan Valo palaa = Valo ei pala lause on tosi, funktio on EI-funktio EI Opintotuki ei riitä = Opintotuki on liian pieni lause ei ole tosi: viiva on liikaa, ilman viivaakin on kyseenalaista, onko lause tosi Tilillä on rahaa = Tili on tyhjä tai miinuksella lause on tosi, funktio on EI-funktio EI
11 Digitaalitekniikan matematiikka Luku 3 Täsmätehtävä Tehtävä 5 Lausekkeena esitetyn funktion arvo Laske alla olevien lausekkeena esitettyjen funktioiden F ja G arvo, kun A = ja B = C =. F = A C+B = + = + = + = G= (A + B) (B + C) = ( + ) ( + ) = ( + ) ( + ) = =
12 Digitaalitekniikan matematiikka Luku 3 Täsmätehtävä Tehtävä 6 Piirikaavio Piirrä lauseketta F = AB+ C vastaava piirikaavio. JA-portti & A B C & F TAI-portti EI-piiri
13 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä De Morganin kaavojen käyttö Sovella De Morganin kaavoja seuraaviin lausekkeisiin. Pyri siihen, että lopuksi lausekkeessa ei ole yhtään pitkää viivaa. Viimeisessä tehtävässä kaavaa pitää käyttää useita kertoja. Muista, että A = A + A + B = A B = A B A B C = A + B + C = A + B + C (A + B) (A + B) = (A + B) + (A + B) = A B + A B = A B + A B
14 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä 2 SOP- ja POS-muodot Mitkä seuraavista lausekkeista ovat tulojen summamuotoisia (SOP), mitkä summien tulomuotoisia (POS) ja mitkä eivät kumpaakaan muotoa? (A + B + C) (A + B + C) (A + B + C) (A + B + C) POS A + B C + C D + B C D E SOP (A + B) (B + C) SOP POS A + B C SOP (A + B) C POS A + B + C + D SOP POS
15 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä 3 Minimi- ja maksimitermit Mitkä tulotermit seuraavissa lausekkeissa ovat minimitermejä ja mitkä summatermit maksimitermejä? F(A, B, C) = A B + B C A + C A B + B min G(X, Y) = (X + Y) (X + Y) MAX H(A, B, C, D) = (A + B + C) (A + B + C + D) (A + B + C) (A + B + C) MAX K(A, B, C) = A B C min
16 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä 4 Funktion totuustaulua vastaava kanoninen SOP Laadi alla olevaa totuustaulua vastaava kanoninen tulojen summamuotoinen (SOP) lauseke ja esitä se kaikilla kolmella eri esitystavalla. A B F F(A, B) = A B+ A B F(A, B) = m + m2 F(A, B) = m (, 2)
17 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä 5 Funktion totuustaulua vastaava kanoninen POS Laadi alla olevaa totuustaulua vastaava kanoninen summien tulomuotoinen (POS) lauseke ja esitä se kaikilla kolmella eri esitystavalla. A B F F(A, B) = (A + B) (A + B) F(A, B) = M M3 F(A, B) = M (, 3)
18 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä 6 Funktion SOP-lauseketta vastaava totuustaulu Laadi alla esitetyn funktion F tulojen summamuotoista (SOP) lauseketta vastaava totuustaulu. AB F F(A, B) = A B + B
19 Digitaalitekniikan matematiikka Luku 4 Täsmätehtävä Tehtävä 7 Funktion POS-lauseketta vastaava totuustaulu Laadi alla esitetyn funktion F summien tulomuotoista (POS) lauseketta vastaava totuustaulu. AB F F(A, B) = (A + B) (A + B)
20 Digitaalitekniikan matematiikka Luku 5 Täsmätehtävä Tehtävä Karnaugh'n kartan ryhmät ja vastaavat tulotermit Esitä oheisissa Karnaugh'n kartoissa olevia ryhmiä vastaavat tulotermit. A A C B D C A B A B D C B D B C A B C D A B D
21 Digitaalitekniikan matematiikka Luku 5 Täsmätehtävä Tehtävä 2 Perustermit ja olennaiset perustermit Mitkä oheisessa Karnaugh'n kartassa olevia ryhmiä vastaavat tulotermit ovat perustermejä ja mitkä olennaisia perustermejä? F A A C D P P OP A C D A B C C B D A C B C D A B OP P OP
22 Digitaalitekniikan matematiikka Luku 5 Täsmätehtävä Tehtävä 3 Kolmen muuttujan SOP-lauseke Piirrä totuustaulun funktion F Karnaugh'n kartta ja esitä funktion yksinkertaisin SOP-lauseke. A B C F F C B A F = A B + A C + A B C
23 Digitaalitekniikan matematiikka Luku 5 Täsmätehtävä Tehtävä 4 Neljän muuttujan POS-lauseke A B C D F Piirrä totuustaulun funktion F Karnaugh'n kartta ja esitä funktion yksinkertaisin POS-lauseke. F C B A F =(A+B) (C+D) (B+C+D) D
24 Digitaalitekniikan matematiikka Luku 5 Täsmätehtävä Tehtävä 6 Hälläväliä-arvoja sisältävän funktion SOP-lauseke Piirrä totuustaulun epätäydellisesti määrittelemän funktion F Karnaugh'n kartta ja esitä funktion yksinkertaisin SOP-lauseke. A B C F X X X F C X X A X B F = B + A C
25 Digitaalitekniikan matematiikka Luku 6 Täsmätehtävä Tehtävä JA-EI ja TAI-EI-funktiot ja -piirit Mikä on lähtösignaalin arvo seuraavissa piireissä? & & & & & &
26 Digitaalitekniikan matematiikka Luku 6 Täsmätehtävä Tehtävä 2 Kytkentäfunktion toteutus JA-EI-porteilla Muokkaa alla oleva funktion F SOP-muotoinen lauseke De Morganin kaavaa käyttäen kaksituloisilla JA-EI-porteilla toteutettavaksi ja esitä toteutus. F = A B + A C = A B + A C = A B A C A B & C & & & F
27 Digitaalitekniikan matematiikka Luku 6 Täsmätehtävä Tehtävä 3 Kytkentäfunktion toteutus TAI-EI-porteilla Muokkaa alla oleva funktion F POS-muotoinen lauseke De Morganin kaavaa käyttäen kaksituloisilla TAI-EI-porteilla toteutettavaksi ja esitä toteutus. F = (A + B) (A + C) = (A + B) (A + C) = (A + B) + (A + C) A B C F
28 Digitaalitekniikan matematiikka Luku 6 Täsmätehtävä Tehtävä 4 Kytkentäfunktion I-SOP-toteutus Alla on esitetty funktion F Karnaugh'n kartta. Esitä funktion F SOP-lauseke. Laadi funktion F komplementin F Karnaugh'n kartta. Esitä funktion F I-SOP-lauseke. F A C Totuustaulun -alueista saadaan SOP-lauseke F = A B + B C. B F:n Karnaugh'n kartta saadaan F:n kartasta vaihtamalla :t ja :t. F C A Totuustaulun -alueista saadaan F:n SOP-lauseke F = B + A C ja siitä B F:n I-SOP-lauseke F = B + A C.
29 Digitaalitekniikan matematiikka Luku 6 Täsmätehtävä Tehtävä 5 Porttipiirin analyysi Analysoi oheinen porttipiiri. Muodosta ensin kytkentäfunktio ja laadi sitten totuustaulu. K L MN A & B F C & F = M + B + N = A C + B + K L = A C + B + AC A B C F
30 Digitaalitekniikan matematiikka Luku 7 Täsmätehtävä Tehtävä Logiikkasopimus Yhdistä L ja H nollaan ja ykköseen oikein alla olevassa kuvassa. Negatiivinen logiikkasopimus Positiivinen logiikkasopimus H H L L
31 Digitaalitekniikan matematiikka Luku 7 Täsmätehtävä Tehtävä 2 Negaatiomerkintä ja napaisuusmerkintä Piirrä kaksituloisen JA-EI-portin piirrosmerkki käyttäen negaatiomerkintää ja napaisuusmerkintää. Negaatiomerkintä Napaisuusmerkintä & &
32 Digitaalitekniikan matematiikka Luku 7 Täsmätehtävä Tehtävä 3 Etenemisviive ja muutosajat Arvioi oheisen aikakaavion perusteella JA-EI-portin etenemisviiveet t PHL ja t PLH sekä laskuaika t f ja nousuaika t r. A B & A B A B t PHL = 4 ns t f =,8 2 ns =,6 ns t PLH = 6 ns t r =,8 4 ns = 3,2 ns A B t / ns
33 Digitaalitekniikan matematiikka Luku 7 Täsmätehtävä Tehtävä 4 Piirrosmerkkien käsitteet Kirjoita kunkin käsitteen perään sitä vastaavat kirjaimet. Huomaa, että jokin käsite saattaa liittyä useaan kohtaan ja samaan kohtaan saattaa liittyä useita käsitteitä. A B JA-toiminta Kolmitilalähtö Looginen komplementointi Looginen napaisuus Loogisella tasolla L aktiivinen tulo Sallintatulo Samanlaiset lohkot TAI-toiminta Tarkennusmerkki Yleinen tarkennusmerkki Yhteinen lähtösignaali Yhteinen ohjauslohko C D B F F E, F K A A, B, C, D, E, F, G A, C, G H J C E F J K & EN X/Y D G H
34 Digitaalitekniikan matematiikka Luku 8 Täsmätehtävä Tehtävä EHDOTON TAI -portti Johda oheisesta EHDOTON TAI -funktion totuustaulusta sen summien tulomuotoinen (POS-) lauseke. A B A B A B = (A + B) (A + B)
35 Digitaalitekniikan matematiikka Luku 8 Täsmätehtävä Tehtävä 2 Dekooderin toiminta Mitkä ovat kuvien dekooderien lähtösignaalien arvot? 2 EN X/Y EN X/Y 2 3
36 Digitaalitekniikan matematiikka Luku 8 Täsmätehtävä Tehtävä 3 Tulovalitsin Esitä kuvien tulovalitsimien lähtösignaalien arvot. MUX EN MUX EN G 3 G
37 Digitaalitekniikan matematiikka Luku 8 Täsmätehtävä Tehtävä 4 Kytkentäfunktion toteuttaminen tulovalitsimella Esitä kytkennät, joilla alla oleva tulovalitsin saadaan toteuttamaan totuustaulun mukainen funktio. MUX A B Y B A 2 3 G 3 Y
38 Digitaalitekniikan matematiikka Luku 8 Täsmätehtävä Tehtävä 5 Kytkentäfunktion toteuttaminen tulovalitsimella Esitä kytkennät, joilla alla oleva tulovalitsin saadaan toteuttamaan totuustaulun mukainen funktio. B A C C F = F = C F = C F = A B C F F MUX 2 3 G 3
39 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä Kantaluvun esittäminen Täytä alla esitetty taulukko. Järjestelmä Luku Alaindeksi Kirjain Ohjelmointikieli Binaari 2 B - Oktaali Q 765 Desimaali Heksadesimaali 3928 FAFFA D 3928 FAFFA 6 FAFFAH xfaffa
40 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä 2 Etumerkittömien lukujen esittäminen ja tulkinta Tulkitse seuraavat luvut eli laske niiden arvo kymmenjärjestelmän lukuina. 2 Q x = = 2 + = 3 = = 8 + = 9 = = 6 + = 7
41 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä 3 Etumerkittömät binaarikokonaisluvut Esitä seuraavat etumerkittömät binaariluvut 8-bittisinä. = = =
42 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä 4 Etumerkittömät kiinteän pilkun binaariluvut Esitä seuraavat etumerkittömät kiinteän pilkun binaariluvut 6-bittisinä. Kokonaisosassa on 2 bittiä.,, =, =, =,
43 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä 5 Kahden komplementin muodostaminen Muodosta seuraavien kahdeksanbittisten lukujen kahden komplementit. kaksi nollaa ja ykkönen säilyvät, muut kääntyvät kaikki bitit säilyvät vain ykkönen säilyy, muut kääntyvät
44 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä 6 Muunnokset etumerkki-itseisarvoesityksen ja kahden komplementtiesityksen välillä Muunna seuraavat kahdeksanbittiset etumerkki-itseisarvomuotoiset binaariluvut kahden komplementtimuotoon. negatiivinen suuruusosa komplementoidaan negatiivinen suuruusosa komplementoidaan positiivinen ei muutosta
45 Digitaalitekniikan matematiikka Luku 9 Täsmätehtävä Tehtävä 7 Kahden komplementtimuotoisen luvun sananpituuden muuttaminen Lyhennä seuraavat 6-bittiset kahden komplementtimuotoiset luvut kahdeksanbittisiksi, mikäli se on mahdollista. alussa 9 merkkibittiä voidaan lyhentää alussa 9 merkkibittiä voidaan lyhentää alussa vain 8 merkkibittiä ei voida lyhentää
Yhden bitin tiedot. Binaariluvun arvon laskeminen. Koodin bittimäärä ja vaihtoehdot ? 1
 Luku Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Opetuskerta Sivu Luku Opetuskerta Sivu Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista.
Luku Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Opetuskerta Sivu Luku Opetuskerta Sivu Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista.
Digitaalitekniikan matematiikka Harjoitustehtäviä
 arjoitustehtäviä Sivu 6 6.3.2 e arjoitustehtäviä uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä jossa käytävän kummassakin päässä on kytkin ja käytävän keskellä lamppu. amppu
arjoitustehtäviä Sivu 6 6.3.2 e arjoitustehtäviä uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä jossa käytävän kummassakin päässä on kytkin ja käytävän keskellä lamppu. amppu
Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) Kytkentäalgebra A + 1 = 1 A = A A + B C = (A + B) (A + C) A 0 = 0. Maksimitermi.
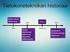 Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) A + 1 = 1 A + B C = (A + B) (A + C) F(A, B, C) = Σ m (2, 3, 5, 7) Maksimitermi A = A m0 A 0 = 0 M7 A + B = A B Minimitermi Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) A + 1 = 1 A + B C = (A + B) (A + C) F(A, B, C) = Σ m (2, 3, 5, 7) Maksimitermi A = A m0 A 0 = 0 M7 A + B = A B Minimitermi Digitaalitekniikan matematiikka
Lukujärjestelmät. Digitaalitekniikan matematiikka Luku 9 Sivu 3 (26) Lukujärjestelmät ja lukujen esittäminen Fe
 Digitaalitekniikan matematiikka Luku 9 Sivu 3 (26) Lukujärjestelmät ja lukujen esittäminen.9.2 Fe Lukujärjestelmät Kymmen- eli desimaalijärjestelmä: kantaluku perinteisesti käytetty ja tuttu numerot,,
Digitaalitekniikan matematiikka Luku 9 Sivu 3 (26) Lukujärjestelmät ja lukujen esittäminen.9.2 Fe Lukujärjestelmät Kymmen- eli desimaalijärjestelmä: kantaluku perinteisesti käytetty ja tuttu numerot,,
C = P Q S = P Q + P Q = P Q. Laskutoimitukset binaariluvuilla P -- Q = P + (-Q) (-Q) P Q C in. C out
 Digitaalitekniikan matematiikka Luku ivu (2).9.2 Fe C = Aseta Aseta i i = n i > i i i Ei i < i i i Ei i i = Ei i i = i i -- On On On C in > < = CI CO C out -- = + (-) (-) = + = C + Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku ivu (2).9.2 Fe C = Aseta Aseta i i = n i > i i i Ei i < i i i Ei i i = Ei i i = i i -- On On On C in > < = CI CO C out -- = + (-) (-) = + = C + Digitaalitekniikan matematiikka
ANSI/IEEE Std
 Digitaalitekniikan matematiikka Luku 9 Sivu 1 (26) Lukujärjestelmät ja lukujen esittäminen ANSI/IEEE Std 754-2008 0 1 0 1 1 0 0 0 B = Σ B i 2 i Digitaalitekniikan matematiikka Luku 9 Sivu 2 (26) Johdanto
Digitaalitekniikan matematiikka Luku 9 Sivu 1 (26) Lukujärjestelmät ja lukujen esittäminen ANSI/IEEE Std 754-2008 0 1 0 1 1 0 0 0 B = Σ B i 2 i Digitaalitekniikan matematiikka Luku 9 Sivu 2 (26) Johdanto
Digitaalitekniikan matematiikka Luku 6 Sivu 1 (20) Kombinaatiopiirit & & A B A + B
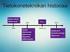 igitaalitekniikan matematiikka Luku 6 Sivu (20).9.20 e 0 0 0 0 0 + 0 0 0 0 0 0 0 igitaalitekniikan matematiikka Luku 6 Sivu 2 (20).9.20 e Johdanto Tässä luvussa esitellään porttipiirityypit J-EI ja TI-EI
igitaalitekniikan matematiikka Luku 6 Sivu (20).9.20 e 0 0 0 0 0 + 0 0 0 0 0 0 0 igitaalitekniikan matematiikka Luku 6 Sivu 2 (20).9.20 e Johdanto Tässä luvussa esitellään porttipiirityypit J-EI ja TI-EI
Digitaalitekniikan matematiikka Luku 8 Sivu 1 (23) Kombinaatiopiirielimet MUX X/Y 2 EN
 Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe DX G = G EN X/Y Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe Johdanto Tässä luvussa esitetään keskeisiä kombinaatiopiirielimiä ne ovat perusporttipiirejä
Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe DX G = G EN X/Y Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe Johdanto Tässä luvussa esitetään keskeisiä kombinaatiopiirielimiä ne ovat perusporttipiirejä
Digitaalilaitteen signaalit
 Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä
Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä
Digitaalitekniikan matematiikka Luku 3 Sivu 1 (19) Kytkentäfunktiot ja perusporttipiirit
 Digitaalitekniikan matematiikka Luku 3 Sivu (9) && Digitaalitekniikan matematiikka Luku 3 Sivu 2 (9) Johdanto Tässä luvussa esitetään digitaalilaitteen signaalit ja digitaalipiirien perustyypit esitellään
Digitaalitekniikan matematiikka Luku 3 Sivu (9) && Digitaalitekniikan matematiikka Luku 3 Sivu 2 (9) Johdanto Tässä luvussa esitetään digitaalilaitteen signaalit ja digitaalipiirien perustyypit esitellään
Digitaalitekniikan matematiikka Luku 10 Sivu 1 (14) Lukujärjestelmämuunnokset. 2 s s
 Digitaalitekniikan matematiikka Luku 10 Sivu 1 (14) k 10 2 10 2 s 10 10 8 10 16 10 2 10 2 s 2 8 8 2 2 16 16 2 Digitaalitekniikan matematiikka Luku 10 Sivu 2 (14) Johdanto Tässä luvussa perustellaan, miksi
Digitaalitekniikan matematiikka Luku 10 Sivu 1 (14) k 10 2 10 2 s 10 10 8 10 16 10 2 10 2 s 2 8 8 2 2 16 16 2 Digitaalitekniikan matematiikka Luku 10 Sivu 2 (14) Johdanto Tässä luvussa perustellaan, miksi
Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: JA-EI-portti A B. TAI-EI-portti A B = 1
 Digitaalitekniikan matematiikka Luku 6 Sivu () Kombinaatiopiirit.9. Fe J-EI- (NND) ja TI-EI- (NOR) -portit Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: NND? B B & B B = & B + B + B
Digitaalitekniikan matematiikka Luku 6 Sivu () Kombinaatiopiirit.9. Fe J-EI- (NND) ja TI-EI- (NOR) -portit Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: NND? B B & B B = & B + B + B
Digitaalitekniikan matematiikka Luku 5 Sivu 1 (22) Lausekkeiden sieventäminen F C F = B + A C. Espresso F = A (A + B) = A A + A B = A B
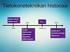 igitaalitekniikan matematiikka Luku 5 Sivu (22).9.2 e = + = ( + ) = + = Espresso igitaalitekniikan matematiikka Luku 5 Sivu 2 (22).9.2 e Johdanto Tässä luvussa esitetään perusteet lausekemuodossa esitettyjen
igitaalitekniikan matematiikka Luku 5 Sivu (22).9.2 e = + = ( + ) = + = Espresso igitaalitekniikan matematiikka Luku 5 Sivu 2 (22).9.2 e Johdanto Tässä luvussa esitetään perusteet lausekemuodossa esitettyjen
ELEC-C3240 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä
 ELE-324 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä Materiaalia otettu myös: https://www.allaboutcircuits.com/textbook/digital/chpt-8/introduction-to-karnaughmapping/
ELE-324 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä Materiaalia otettu myös: https://www.allaboutcircuits.com/textbook/digital/chpt-8/introduction-to-karnaughmapping/
Käytännön logiikkapiirit ja piirrosmerkit
 Digitaalitekniikan matematiikka Luku 7 Sivu (27) EN 2 EN X/Y X/Y 0 2 3 2 EN X/Y X/Y 0 2 3 Digitaalitekniikan matematiikka Luku 7 Sivu 2 (27) Johdanto Tässä luvussa esitellään käsitteet logiikkaperhe ja
Digitaalitekniikan matematiikka Luku 7 Sivu (27) EN 2 EN X/Y X/Y 0 2 3 2 EN X/Y X/Y 0 2 3 Digitaalitekniikan matematiikka Luku 7 Sivu 2 (27) Johdanto Tässä luvussa esitellään käsitteet logiikkaperhe ja
Harjoitustehtävien ratkaisuja
 igitaalitekniikan matematiikka arjoitustehtävien ratkaisuja Sivu (22) 6.3.2 e arjoitustehtävien ratkaisuja uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä, jossa käytävän kummassakin
igitaalitekniikan matematiikka arjoitustehtävien ratkaisuja Sivu (22) 6.3.2 e arjoitustehtävien ratkaisuja uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä, jossa käytävän kummassakin
ELEC-C3240 Elektroniikka 2
 ELEC-C324 Elektroniikka 2 Marko Kosunen Marko.kosunen@aalto.fi Digitaalielektroniikka Tilakoneet Materiaali perustuu kurssiins-88. Digitaalitekniikan perusteet, laatinut Antti Ojapelto Luennon oppimistavoite
ELEC-C324 Elektroniikka 2 Marko Kosunen Marko.kosunen@aalto.fi Digitaalielektroniikka Tilakoneet Materiaali perustuu kurssiins-88. Digitaalitekniikan perusteet, laatinut Antti Ojapelto Luennon oppimistavoite
Sekvenssipiirin tilat
 igitaalitekniikka (piirit) Luku Täsmätehtävä Tehtävä Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan seuraavissa sekvenssipiireissä: Painikkeella ohjattava lampun sytytys ja sammutus. Näyttöä ohjaava
igitaalitekniikka (piirit) Luku Täsmätehtävä Tehtävä Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan seuraavissa sekvenssipiireissä: Painikkeella ohjattava lampun sytytys ja sammutus. Näyttöä ohjaava
Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset
 Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset Metropolia/AK. Mealyn koneessa on kolme tulosignaalia, joista yksi vaikuttaa pelkästään lähtösignaaleihin, yksi pelkästään koneen tilaan ja yksi
Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset Metropolia/AK. Mealyn koneessa on kolme tulosignaalia, joista yksi vaikuttaa pelkästään lähtösignaaleihin, yksi pelkästään koneen tilaan ja yksi
SISÄLLYS - DIGITAALITEKNIIKKA
 SISÄLLYS - DIGITAALITEKNIIKKA Digitaalitekniikan perusteita...2 Bitti (bit)...2 Tavu (bytes)...2 Sana (word)...2 Yksiköt...2 Binääri järjestelmän laskutapa...2 Esimerkki: Digikuvan siirron kestoaika...2
SISÄLLYS - DIGITAALITEKNIIKKA Digitaalitekniikan perusteita...2 Bitti (bit)...2 Tavu (bytes)...2 Sana (word)...2 Yksiköt...2 Binääri järjestelmän laskutapa...2 Esimerkki: Digikuvan siirron kestoaika...2
Digitaalitekniikan matematiikka Luku 1 Sivu 1 (19) Johdatus digitaalitekniikkaan
 Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdatus digitaalitekniikkaan Digitaalitekniikan matematiikka Luku Sivu 2 (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdanto
Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdatus digitaalitekniikkaan Digitaalitekniikan matematiikka Luku Sivu 2 (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdanto
Harjoitustehtävien ratkaisuja
 Sivu (52) 27.2.2 Fe Johdatus digitaalitekniikkaan - Luettele erilaisia tekstitiedon ja liikkumattoman kuvan ilmenemismuotoja (esimerkiksi oppikirjan teksti ja valokuva). Miten niitä voidaan tallettaa,
Sivu (52) 27.2.2 Fe Johdatus digitaalitekniikkaan - Luettele erilaisia tekstitiedon ja liikkumattoman kuvan ilmenemismuotoja (esimerkiksi oppikirjan teksti ja valokuva). Miten niitä voidaan tallettaa,
Harjoitustehtävien ratkaisut
 Sivu (22) 29.8.2 Fe/Ko Luku Sekvenssipiirit. Tutki luentokalvo- ja opetusmonisteessa esitettyä esimerkkiä synkronisesta sekvenssipiiristä. a) Montako tilaa piirissä on? Koska piirissä on kaksi tilasignaalia,
Sivu (22) 29.8.2 Fe/Ko Luku Sekvenssipiirit. Tutki luentokalvo- ja opetusmonisteessa esitettyä esimerkkiä synkronisesta sekvenssipiiristä. a) Montako tilaa piirissä on? Koska piirissä on kaksi tilasignaalia,
F = AB AC AB C C Tarkistus:
 Digitaalitekniikka I, tenttitehtäviä ratkaisuineen I 3..995 2. c) esitä seuraava funktio kanonisten summien tulona f(,,) = + Sovelletaan DeMorganin teoreemaa (työläs). Teoriaminimointia ei ole käytetty!
Digitaalitekniikka I, tenttitehtäviä ratkaisuineen I 3..995 2. c) esitä seuraava funktio kanonisten summien tulona f(,,) = + Sovelletaan DeMorganin teoreemaa (työläs). Teoriaminimointia ei ole käytetty!
DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU
 OPINNÄYTETYÖ - AMMATTIKORKEAKOULUTUTKINTO TEKNIIKAN JA LIIKENTEEN ALA DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU T E K I J Ä : Toni Halonen SAVONIA-AMMATTIKORKEAKOULU OPINNÄYTETYÖ
OPINNÄYTETYÖ - AMMATTIKORKEAKOULUTUTKINTO TEKNIIKAN JA LIIKENTEEN ALA DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU T E K I J Ä : Toni Halonen SAVONIA-AMMATTIKORKEAKOULU OPINNÄYTETYÖ
Digitaalitekniikka (piirit) Luku 14 Sivu 1 (16) Sekvenssipiirit. Kombinaatiopiiri. Tilarekisteri
 Digitaalitekniikka (piirit) Luku 4 Sivu (6).8.24 Fe/AKo Tilarekisteri Kombinaatiopiiri Digitaalitekniikka (piirit) Luku 4 Sivu 2 (6).8.24 Fe/AKo Johdanto Tässä luvussa todetaan esimerkin avulla kombinaatiopiirien
Digitaalitekniikka (piirit) Luku 4 Sivu (6).8.24 Fe/AKo Tilarekisteri Kombinaatiopiiri Digitaalitekniikka (piirit) Luku 4 Sivu 2 (6).8.24 Fe/AKo Johdanto Tässä luvussa todetaan esimerkin avulla kombinaatiopiirien
OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012
 OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012 Luento 6: Tiedon esittäminen tietokoneessa, osa 1 Tekijät: Antti Virtanen, Timo Lehtonen, Matti Kujala, Kirsti Ala-Mutka, Petri M. Gerdt et al. Luennon
OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012 Luento 6: Tiedon esittäminen tietokoneessa, osa 1 Tekijät: Antti Virtanen, Timo Lehtonen, Matti Kujala, Kirsti Ala-Mutka, Petri M. Gerdt et al. Luennon
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 2. Lukujen esittäminen ja aritmetiikka 2.1 Kantajärjestelmät ja lukujen esittäminen Käytettävät lukujoukot: Luonnolliset luvut IN = {0,1,2,3,... } Positiiviset kokonaisluvut
811120P Diskreetit rakenteet 2016-2017 2. Lukujen esittäminen ja aritmetiikka 2.1 Kantajärjestelmät ja lukujen esittäminen Käytettävät lukujoukot: Luonnolliset luvut IN = {0,1,2,3,... } Positiiviset kokonaisluvut
Kappale 20: Kantaluvut
 Kappale 20: Kantaluvut 20 Johdanto: Kantaluvut... 328 Kantalukujen syöttäminen ja muuntaminen... 329 Matemaattiset toiminnot Hex- ja Bin-luvuilla... 330 Bittien vertaileminen ja manipulointi... 331 Huom!
Kappale 20: Kantaluvut 20 Johdanto: Kantaluvut... 328 Kantalukujen syöttäminen ja muuntaminen... 329 Matemaattiset toiminnot Hex- ja Bin-luvuilla... 330 Bittien vertaileminen ja manipulointi... 331 Huom!
Johdatus digitaalitekniikkaan
 Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Johdatus digitaalitekniikkaan Johdanto
Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Johdatus digitaalitekniikkaan Johdanto
Esimerkkitentin ratkaisut ja arvostelu
 Sivu (5) 2.2.2 Fe Seuraavassa on esitetty tenttitehtävien malliratkaisut ja tehtäväkohtainen arvostelu. Osassa tehtävistä on muitakin hyväksyttäviä ratkaisuja kuin malliratkaisu. 2 Tehtävät on esitetty
Sivu (5) 2.2.2 Fe Seuraavassa on esitetty tenttitehtävien malliratkaisut ja tehtäväkohtainen arvostelu. Osassa tehtävistä on muitakin hyväksyttäviä ratkaisuja kuin malliratkaisu. 2 Tehtävät on esitetty
Luku- ja merkkikoodit. Digitaalitekniikan matematiikka Luku 12 Sivu 1 (15)
 Digitaalitekniikan matematiikka Luku 12 Sivu 1 (15) A = a = i i w i Digitaalitekniikan matematiikka Luku 12 Sivu 2 (15) Johdanto Tässä luvussa esitetään kymmenjärjestelmän lukujen eli BCD-lukujen esitystapoja
Digitaalitekniikan matematiikka Luku 12 Sivu 1 (15) A = a = i i w i Digitaalitekniikan matematiikka Luku 12 Sivu 2 (15) Johdanto Tässä luvussa esitetään kymmenjärjestelmän lukujen eli BCD-lukujen esitystapoja
Elektroniikan laboratorio Lisätehtävät 17.9.2003. Mallivastauksia
 OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät 7.9. Mallivastauksia. Mitkä loogiset operaatiot oheiset kytkennät toteuttavat? Vihje: kytkin johtaa, kun ohjaava signaali =. Käytä
OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät 7.9. Mallivastauksia. Mitkä loogiset operaatiot oheiset kytkennät toteuttavat? Vihje: kytkin johtaa, kun ohjaava signaali =. Käytä
LABORAATIOSELOSTUSTEN OHJE H. Honkanen
 LABORAATIOSELOSTUSTEN OHJE H. Honkanen Tämä ohje täydentää ja täsmentää osaltaan selostuskäytäntöä laboraatioiden osalta. Yleinen ohje työselostuksista löytyy intranetista, ohjeen on laatinut Eero Soininen
LABORAATIOSELOSTUSTEN OHJE H. Honkanen Tämä ohje täydentää ja täsmentää osaltaan selostuskäytäntöä laboraatioiden osalta. Yleinen ohje työselostuksista löytyy intranetista, ohjeen on laatinut Eero Soininen
Ohjelmoitavat logiikkaverkot
 Digitaalitekniikka (piirit) Luku 9 Sivu (3) Ohjelmoitavat logiikkaverkot.8.24 Fe/AKo Ohjelmoitavat logiikkaverkot Ohjelmoitavat logiikkaverkot Programmable logic logic PLD-piirit Programmable logic logic
Digitaalitekniikka (piirit) Luku 9 Sivu (3) Ohjelmoitavat logiikkaverkot.8.24 Fe/AKo Ohjelmoitavat logiikkaverkot Ohjelmoitavat logiikkaverkot Programmable logic logic PLD-piirit Programmable logic logic
Kombinatorisen logiikan laitteet
 Kombinatorisen logiikan laitteet Kombinatorinen logiikka tarkoittaa logiikkaa, jossa signaali kulkee suoraan sisääntuloista ulostuloon Sekventiaalisessa logiikassa myös aiemmat syötteet vaikuttavat ulostuloon
Kombinatorisen logiikan laitteet Kombinatorinen logiikka tarkoittaa logiikkaa, jossa signaali kulkee suoraan sisääntuloista ulostuloon Sekventiaalisessa logiikassa myös aiemmat syötteet vaikuttavat ulostuloon
Synkronisten sekvenssipiirien suunnittelu
 Digitaalitekniikka (piirit) Luku 6 Sivu (5) Synkronisten sekvenssipiirien suunnittelu.8.24 Fe/AKo Synkronisten sekvenssipiirien suunnittelu Digitaalitekniikka (piirit) Luku 6 Sivu 2 (5) Synkronisten sekvenssipiirien
Digitaalitekniikka (piirit) Luku 6 Sivu (5) Synkronisten sekvenssipiirien suunnittelu.8.24 Fe/AKo Synkronisten sekvenssipiirien suunnittelu Digitaalitekniikka (piirit) Luku 6 Sivu 2 (5) Synkronisten sekvenssipiirien
Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena
 Mikrotietokone Moderni tietokone Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena Sen käyttötarkoitus on yleensä työnteko, kissavideoiden katselu internetistä tai pelien pelaaminen. Tietokoneen
Mikrotietokone Moderni tietokone Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena Sen käyttötarkoitus on yleensä työnteko, kissavideoiden katselu internetistä tai pelien pelaaminen. Tietokoneen
Tervetuloa opiskelemaan DIGITAALI- TEKNIIKKAA!
 igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e Yleistä opintojaksosta Laajuus op = 8 h, kokonaan syyslukukauden
igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e Yleistä opintojaksosta Laajuus op = 8 h, kokonaan syyslukukauden
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen
 Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2012-2013 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2012-2013 Lasse Lensu 2 Transistori yhdessä
Oppikirjan harjoitustehtävien ratkaisuja
 Sivu (27) 26.2.2 e 7 Muistipiirit 7- Tietokoneen muistin koko on 256 K 6 b. Montako sanaa muistissa on? Mikä on sen sananpituus? Montako muistialkiota muistissa on? Muistissa on 256 kibisanaa eli 262 44
Sivu (27) 26.2.2 e 7 Muistipiirit 7- Tietokoneen muistin koko on 256 K 6 b. Montako sanaa muistissa on? Mikä on sen sananpituus? Montako muistialkiota muistissa on? Muistissa on 256 kibisanaa eli 262 44
Digitaalitekniikka (piirit) Luku 18 Sivu 1 (32) Rekisterit ja laskurit R C1 SRG4 R C1/ CTRDIV16 1R G2 2CT=15 G3 C1/2,3 + CT 3
 Digitaalitekniikka (piirit) Luku 8 Sivu (32) R C D SRG4 R C/ D CTRDIV6 R G2 2CT=5 G3 C/2,3 + CT 3 Digitaalitekniikka (piirit) Luku 8 Sivu 2 (32) Johdanto Tässä luvussa esitellään keskeiset salpoja ja kiikkuja
Digitaalitekniikka (piirit) Luku 8 Sivu (32) R C D SRG4 R C/ D CTRDIV6 R G2 2CT=5 G3 C/2,3 + CT 3 Digitaalitekniikka (piirit) Luku 8 Sivu 2 (32) Johdanto Tässä luvussa esitellään keskeiset salpoja ja kiikkuja
c) loogiset funktiot tulojen summana B 1 = d) AND- ja EXOR-porteille sopivat yhtälöt
 IGITLITEKNIIKK I 5 Tentti:.. ELEKTRONIIKN LORTORIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) b) minimoituna summien
IGITLITEKNIIKK I 5 Tentti:.. ELEKTRONIIKN LORTORIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) b) minimoituna summien
Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008
 Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008 Kilpailijan nimi: 1) Oheisen kytkennän kokonaisresistanssi on n. 33 Ohm 150 Ohm a) 70 Ohmia b) 100 Ohmia c) 120 Ohmia 120 Ohm 2) Oheisen kytkennän
Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008 Kilpailijan nimi: 1) Oheisen kytkennän kokonaisresistanssi on n. 33 Ohm 150 Ohm a) 70 Ohmia b) 100 Ohmia c) 120 Ohmia 120 Ohm 2) Oheisen kytkennän
 LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
Ohjelmoijan binaarialgebra ja heksaluvut
 Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoinaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoinaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Inputs: b; x= b 010. x=0. Elektroniikkajärjestelmät ETT_2068
 Elektroniikkajärjestelmät ETT_2068 tentti 1) Oheisessa sekvenssilogiikassa tiloille on jo annettu bittivaste 000, 001 jne. Tehtävänäsi on nyt konstruoda sekvenssilogiikka vaihe vaiheelta standarditavalla.
Elektroniikkajärjestelmät ETT_2068 tentti 1) Oheisessa sekvenssilogiikassa tiloille on jo annettu bittivaste 000, 001 jne. Tehtävänäsi on nyt konstruoda sekvenssilogiikka vaihe vaiheelta standarditavalla.
Sekvenssipiirin tilat. Synkroninen sekvenssipiiri ? 1 ? 2
 Luku igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AKo igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AK Opetuskerta Sivu 4 Luku Opetuskerta Sivu Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan
Luku igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AKo igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AK Opetuskerta Sivu 4 Luku Opetuskerta Sivu Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan
Palautteita. Tutoriaalit olivat vaikeat! Totta, tentti on onneksi helpompi
 Palautteita Tutoriaalit olivat vaikeat! Totta, tentti on onneksi helpompi 504 Mitä range() tekee? range on funktio, joka palauttaa listan esim. a = range(5,10) Palauttaa listan [5,6,7,8,9] Siis nämä kolme
Palautteita Tutoriaalit olivat vaikeat! Totta, tentti on onneksi helpompi 504 Mitä range() tekee? range on funktio, joka palauttaa listan esim. a = range(5,10) Palauttaa listan [5,6,7,8,9] Siis nämä kolme
c) loogiset funktiot tulojen summana B 1 = C 2 C 1 +C 1 C 0 +C 2 C 1 C 0 e) logiikkakaavio
 IGITLITEKNIIKK I 5 Tentti:.. ntti Mäntyniemi ELEKTONIIKN LOTOIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) ykkösten
IGITLITEKNIIKK I 5 Tentti:.. ntti Mäntyniemi ELEKTONIIKN LOTOIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) ykkösten
Digitaalitekniikan matematiikka Luku 1 Sivu 1 (19) Johdatus digitaalitekniikkaan
 Digitaalitekniikan matematiikka Luku 1 Sivu 1 (19) Digitaalitekniikan matematiikka Luku 1 Sivu 2 (19) Johdanto Tässä luvussa esitellään tiedon lajeja ja tiedolle tehtävää käsittelyä käsitellään tiedon
Digitaalitekniikan matematiikka Luku 1 Sivu 1 (19) Digitaalitekniikan matematiikka Luku 1 Sivu 2 (19) Johdanto Tässä luvussa esitellään tiedon lajeja ja tiedolle tehtävää käsittelyä käsitellään tiedon
Ongelma(t): Miten tietokoneen komponentteja voi ohjata siten, että ne tekevät yhdessä jotakin järkevää? Voiko tietokonetta ohjata (ohjelmoida) siten,
 Ongelma(t): Miten tietokoneen komponentteja voi ohjata siten, että ne tekevät yhdessä jotakin järkevää? Voiko tietokonetta ohjata (ohjelmoida) siten, että se pystyy suorittamaan kaikki mahdolliset algoritmit?
Ongelma(t): Miten tietokoneen komponentteja voi ohjata siten, että ne tekevät yhdessä jotakin järkevää? Voiko tietokonetta ohjata (ohjelmoida) siten, että se pystyy suorittamaan kaikki mahdolliset algoritmit?
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen
 Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2013-2014 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2013-2014 Lasse Lensu 2 Transistori yhdessä
Digitaalitekniikka (piirit) Luku 15 Sivu 1 (17) Salvat ja kiikut 1D C1 C1 1T 1J C1 1K S R
 igitaalitekniikka (piirit) Luku 5 ivu (7).8.24 Fe/AKo C J C K C T C C J C K igitaalitekniikka (piirit) Luku 5 ivu 2 (7).8.24 Fe/AKo Johdanto Tässä luvussa esitetään salpapiirit, jotka ovat yksinkertaisimpia
igitaalitekniikka (piirit) Luku 5 ivu (7).8.24 Fe/AKo C J C K C T C C J C K igitaalitekniikka (piirit) Luku 5 ivu 2 (7).8.24 Fe/AKo Johdanto Tässä luvussa esitetään salpapiirit, jotka ovat yksinkertaisimpia
Paavo Räisänen. Ohjelmoijan binaarialgebra ja heksaluvut. www.ohjelmoimaan.net
 Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoimaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoimaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Matematiikan didaktiikka, osa II Algebra
 Matematiikan didaktiikka, osa II Algebra Sarenius Kasvatustieteiden tiedekunta, Oulun yksikkö Mitä on algebra? Algebra on aritmetiikan yleistys. Algebrassa siirrytään operoimaan lukujen sijaan niiden ominaisuuksilla.
Matematiikan didaktiikka, osa II Algebra Sarenius Kasvatustieteiden tiedekunta, Oulun yksikkö Mitä on algebra? Algebra on aritmetiikan yleistys. Algebrassa siirrytään operoimaan lukujen sijaan niiden ominaisuuksilla.
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset
 Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
ASM-kaavio: reset. b c d e f g. 00 abcdef. naytto1. clk. 01 bc. reset. 10 a2. abdeg. 11 a3. abcdg
 Digitaalitekniikka (piirit) Metropolia / AKo Pikku nnitteluharjoitus: Suunnitellaan sekvenssipiiri, jolla saadaan numerot juoksemaan seitsensegmenttinäytöllä: VHDL-koodin generointi ASM-kaavioista Tässä
Digitaalitekniikka (piirit) Metropolia / AKo Pikku nnitteluharjoitus: Suunnitellaan sekvenssipiiri, jolla saadaan numerot juoksemaan seitsensegmenttinäytöllä: VHDL-koodin generointi ASM-kaavioista Tässä
Ratkaisu. Ensimmäinen kuten P Q, toinen kuten P Q. Kolmas kuten P (Q R):
 Diskreetti matematiikka, sks 2010 Harjoitus 2, ratkaisuista 1. Seuraavassa on kuvattu kolme virtapiiriä, joissa on paristo, sopiva lamppu L ja katkaisimia P, Q, R, joiden läpi virta kulkee (1) tai ei kulje
Diskreetti matematiikka, sks 2010 Harjoitus 2, ratkaisuista 1. Seuraavassa on kuvattu kolme virtapiiriä, joissa on paristo, sopiva lamppu L ja katkaisimia P, Q, R, joiden läpi virta kulkee (1) tai ei kulje
Harjoitustyön 2 aiheiden kuvaukset
 Sivu 1 (5) 1 Raitiovaunun oven avaamis- ja sulkemispiiri Raitiovaunun oven vieressä on matkustajan avauspainike. Kun vaunu on paikallaan, matkustajan avauspainikkeen painaminen antaa signaalin, joka avaa
Sivu 1 (5) 1 Raitiovaunun oven avaamis- ja sulkemispiiri Raitiovaunun oven vieressä on matkustajan avauspainike. Kun vaunu on paikallaan, matkustajan avauspainikkeen painaminen antaa signaalin, joka avaa
5. Laskutoimitukset eri lukujärjestelmissä
 5. Laskutoimitukset eri lukujärjestelmissä Lukujen esitykset eri lukujärjestelmissä Muunnokset lukujärjestelmien välillä Laskutoimitukset eri lukujärjestelmissä. 5.1. Muunnokset lukujärjestelmien välillä
5. Laskutoimitukset eri lukujärjestelmissä Lukujen esitykset eri lukujärjestelmissä Muunnokset lukujärjestelmien välillä Laskutoimitukset eri lukujärjestelmissä. 5.1. Muunnokset lukujärjestelmien välillä
PERUSLASKUJA. Kirjoita muuten sama, mutta ota välilyönti 4:n jälkeen 3/4 +5^2
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä /+^2 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen / +^2 Kopioi molemmat matematiikka-alueet ja liiku alueen sisällä
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä /+^2 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen / +^2 Kopioi molemmat matematiikka-alueet ja liiku alueen sisällä
Sähkötekniikan perusteet
 Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Taitaja2005/Elektroniikka. 1) Resistanssien sarjakytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden rinnankytkentä
 1) Resistanssien sarjakytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden rinnankytkentä 2) Kahdesta rinnankytketystä sähkölähteestä a) kuormittuu enemmän se, kummalla on
1) Resistanssien sarjakytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden rinnankytkentä 2) Kahdesta rinnankytketystä sähkölähteestä a) kuormittuu enemmän se, kummalla on
PERUSLASKUJA. Kirjoita muuten sama, mutta ota välilyönti 4:n jälkeen 3/4 +5^2 3
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/+^ 3 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen 3/ +^ 3 Liiku matematiikka alueella nuolinäppäimin. Kokeile
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/+^ 3 Kirjoita muuten sama, mutta ota välilyönti :n jälkeen 3/ +^ 3 Liiku matematiikka alueella nuolinäppäimin. Kokeile
Kenguru 2012 Cadet (8. ja 9. luokka)
 sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
1. Logiikan ja joukko-opin alkeet
 1. Logiikan ja joukko-opin alkeet 1.1. Logiikkaa 1. Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa muotoon p q, ts. että propositio (p q) ( p q) on identtisesti tosi. 2. Todista
1. Logiikan ja joukko-opin alkeet 1.1. Logiikkaa 1. Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa muotoon p q, ts. että propositio (p q) ( p q) on identtisesti tosi. 2. Todista
S SÄHKÖTEKNIIKKA Kimmo Silvonen
 S55.3 SÄHKÖTKNIIKK..999 Kimmo Silvonen Tentti: tehtävät,3,4,8,. välikoe: tehtävät,,3,4,5. välikoe: tehtävät,7,8,9, Oletko muistanut vastata palautekyselyyn Voit täyttää lomakkeen nyt.. aske virta I. =Ω,
S55.3 SÄHKÖTKNIIKK..999 Kimmo Silvonen Tentti: tehtävät,3,4,8,. välikoe: tehtävät,,3,4,5. välikoe: tehtävät,7,8,9, Oletko muistanut vastata palautekyselyyn Voit täyttää lomakkeen nyt.. aske virta I. =Ω,
815338A Ohjelmointikielten periaatteet Harjoitus 2 vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
Ehto- ja toistolauseet
 Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
1. Osoita, että joukon X osajoukoille A ja B on voimassa toinen ns. de Morganin laki (A B) = A B.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
Negatiiviset luvut ja laskutoimitukset
 7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
Laskentaa kirjaimilla
 MAB1 Polynomit Laskentaa kirjaimilla Tähän asti olemme laskeneet luvuilla, jotka on esitetty numeroiden avulla. Matematiikan säännöt, laskentamenetelmät, kaavat samoin kuin fysiikan ja itse asiassa kaikkien
MAB1 Polynomit Laskentaa kirjaimilla Tähän asti olemme laskeneet luvuilla, jotka on esitetty numeroiden avulla. Matematiikan säännöt, laskentamenetelmät, kaavat samoin kuin fysiikan ja itse asiassa kaikkien
Insinöörimatematiikka A
 Insinöörimatematiikka A Demonstraatio 3, 3.9.04 Tehtävissä 4 tulee käyttää Gentzenin järjestelmää kaavojen johtamiseen. Johda kaava φ (φ ) tyhjästä oletusjoukosta. ) φ ) φ φ 3) φ 4) φ (E ) (E ) (I, ) (I,
Insinöörimatematiikka A Demonstraatio 3, 3.9.04 Tehtävissä 4 tulee käyttää Gentzenin järjestelmää kaavojen johtamiseen. Johda kaava φ (φ ) tyhjästä oletusjoukosta. ) φ ) φ φ 3) φ 4) φ (E ) (E ) (I, ) (I,
kipinäpurkauksena, josta salama on esimerkki.
 Sähkö 25 Esineet saavat sähkövarauksen hankauksessa kipinäpurkauksena, josta salama on esimerkki. Hankauksessa esineet voivat varautua sähköisesti. Varaukset syntyvät, koska hankauksessa kappaleesta siirtyy
Sähkö 25 Esineet saavat sähkövarauksen hankauksessa kipinäpurkauksena, josta salama on esimerkki. Hankauksessa esineet voivat varautua sähköisesti. Varaukset syntyvät, koska hankauksessa kappaleesta siirtyy
(a) Kyllä. Jokainen lähtöjoukon alkio kuvautuu täsmälleen yhteen maalijoukon alkioon.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 015 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I Seuraavat tehtävät liittyvät kuvauksiin. 1. Merkitään X = {1,,, 4}. Ovatko seuraavat säännöt
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 015 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I Seuraavat tehtävät liittyvät kuvauksiin. 1. Merkitään X = {1,,, 4}. Ovatko seuraavat säännöt
Digitaalitekniikan matematiikka Luku 13 Sivu 1 (10) Virheen havaitseminen ja korjaus
 Digitaalitekniikan matematiikka Luku 13 Sivu 1 (10) Digitaalitekniikan matematiikka Luku 13 Sivu 2 (10) Johdanto Tässä luvussa esitetään virheen havaitsevien ja korjaavien koodaustapojen perusteet ja käyttösovelluksia
Digitaalitekniikan matematiikka Luku 13 Sivu 1 (10) Digitaalitekniikan matematiikka Luku 13 Sivu 2 (10) Johdanto Tässä luvussa esitetään virheen havaitsevien ja korjaavien koodaustapojen perusteet ja käyttösovelluksia
Testaa taitosi 1: Lauseen totuusarvo
 Testaa taitosi 1: Lauseen totuusarvo 1. a) Laadi lauseen A (B A) totuustaulu. b) Millä lauseiden A ja B totuusarvoilla a-kohdan lause on tosi? c) Suomenna a-kohdan lause, kun lause A on olen vihainen ja
Testaa taitosi 1: Lauseen totuusarvo 1. a) Laadi lauseen A (B A) totuustaulu. b) Millä lauseiden A ja B totuusarvoilla a-kohdan lause on tosi? c) Suomenna a-kohdan lause, kun lause A on olen vihainen ja
T Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 (lauselogiikka )
 T-79.3001 Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 (lauselogiikka 2.1 3.4) 5.2. 9.2. 2009 Ratkaisuja demotehtäviin Tehtävä 2.1 Merkitään lausetta φ:llä, ja valitaan atomilauseiden
T-79.3001 Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 (lauselogiikka 2.1 3.4) 5.2. 9.2. 2009 Ratkaisuja demotehtäviin Tehtävä 2.1 Merkitään lausetta φ:llä, ja valitaan atomilauseiden
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 1 1 Matemaattisesta päättelystä Matemaattisen analyysin kurssin (kuten minkä tahansa matematiikan kurssin) seuraamista helpottaa huomattavasti, jos opiskelija ymmärtää
Matematiikan tukikurssi Kurssikerta 1 1 Matemaattisesta päättelystä Matemaattisen analyysin kurssin (kuten minkä tahansa matematiikan kurssin) seuraamista helpottaa huomattavasti, jos opiskelija ymmärtää
Tietorakenteet (syksy 2013)
 Tietorakenteet (syksy 2013) Harjoitus 1 (6.9.2013) Huom. Sinun on osallistuttava perjantain laskuharjoitustilaisuuteen ja tehtävä vähintään kaksi tehtävää, jotta voit jatkaa kurssilla. Näiden laskuharjoitusten
Tietorakenteet (syksy 2013) Harjoitus 1 (6.9.2013) Huom. Sinun on osallistuttava perjantain laskuharjoitustilaisuuteen ja tehtävä vähintään kaksi tehtävää, jotta voit jatkaa kurssilla. Näiden laskuharjoitusten
1. Mittausjohdon valmistaminen 10 p
 1 1. Mittausjohdon valmistaminen 10 p Valmista kuvan mukainen BNC-hauenleuka x2 -liitosjohto. Johtimien on oltava yhtä pitkät sekä mittojen mukaiset. 60 100 mm 1 000 mm Puukko ja BNC-puristustyökalu ovat
1 1. Mittausjohdon valmistaminen 10 p Valmista kuvan mukainen BNC-hauenleuka x2 -liitosjohto. Johtimien on oltava yhtä pitkät sekä mittojen mukaiset. 60 100 mm 1 000 mm Puukko ja BNC-puristustyökalu ovat
1. a) Laske lukujen 1, 1 ja keskiarvo. arvo. b) Laske lausekkeen. c) Laske integraalin ( x xdx ) arvo. MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 13..015 MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 13..015 MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
LAUSEKKEET JA NIIDEN MUUNTAMINEN
 LAUSEKKEET JA NIIDEN MUUNTAMINEN 1 LUKULAUSEKKEITA Ratkaise seuraava tehtävä: Retkeilijät ajoivat kahden tunnin ajan polkupyörällä maantietä pitkin 16 km/h nopeudella, ja sitten vielä kävelivät metsäpolkua
LAUSEKKEET JA NIIDEN MUUNTAMINEN 1 LUKULAUSEKKEITA Ratkaise seuraava tehtävä: Retkeilijät ajoivat kahden tunnin ajan polkupyörällä maantietä pitkin 16 km/h nopeudella, ja sitten vielä kävelivät metsäpolkua
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
Talousmatematiikan perusteet, L3 Prosentti, yhtälöt Aiheet
 Talousmatematiikan perusteet, L3 Prosentti, t Toisen Prosentti 1 Jos b on p% luvusta a, eli niin b = p 100 a a = perusarvo (Mihin verrataan?) (Minkä sadasosista on kysymys.) p = prosenttiluku (Miten monta
Talousmatematiikan perusteet, L3 Prosentti, t Toisen Prosentti 1 Jos b on p% luvusta a, eli niin b = p 100 a a = perusarvo (Mihin verrataan?) (Minkä sadasosista on kysymys.) p = prosenttiluku (Miten monta
1. Yleistä asiaa tietoliikenneyhteyden toiminnasta.
 TTSE Tietoliikenteen perusteet Metropolia/A. Koivumäki Aiheita viikolla 5. Yleistä asiaa tietoliikenneyhteyden toiminnasta.. Samaa asiaa englanniksi.. Binäärimatematiikan kertausta.. Kirjan lukuun.. Traffi
TTSE Tietoliikenteen perusteet Metropolia/A. Koivumäki Aiheita viikolla 5. Yleistä asiaa tietoliikenneyhteyden toiminnasta.. Samaa asiaa englanniksi.. Binäärimatematiikan kertausta.. Kirjan lukuun.. Traffi
VIII. Osa. Liitteet. Liitteet Suoritusjärjestys Varatut sanat Binääri- ja heksamuoto
 Osa VIII Liitteet Liitteet A B C Suoritusjärjestys Varatut sanat Binääri- ja heksamuoto Osa VIII A. Liite Operaattoreiden suoritusjärjestys On tärkeää ymmärtää, että operaattoreilla on prioriteettinsa,
Osa VIII Liitteet Liitteet A B C Suoritusjärjestys Varatut sanat Binääri- ja heksamuoto Osa VIII A. Liite Operaattoreiden suoritusjärjestys On tärkeää ymmärtää, että operaattoreilla on prioriteettinsa,
Kojemeteorologia. Sami Haapanala syksy 2013. Fysiikan laitos, Ilmakehätieteiden osasto
 Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Datan käsittely ja tallentaminen Käytännössä kaikkien mittalaitteiden ensisijainen signaali on analoginen Jotta tämä
Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Datan käsittely ja tallentaminen Käytännössä kaikkien mittalaitteiden ensisijainen signaali on analoginen Jotta tämä
Yhtälön oikealla puolella on säteen neliö, joten r. = 5 eli r = ± 5. Koska säde on positiivinen, niin r = 5.
 Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
Luvuilla laskeminen. 1. Laske. a) 2 5 b) 6 11 c) 4 + ( 4) d) 1 ( 7) Ratkaisu. a) 2 5 = 7 b) 6 11 = 5 c) 4 + ( 4) = 4 4 = 0 d) 1 ( 7) = = 6
 Luvuilla laskeminen. Laske. 6 4 + ( 4) d) ( 7) = 7 6 = 4 + ( 4) = 4 4 = 0 d) ( 7) = + 7 = 6. Laske. ( 9) 7 ( 8) 8 : ( ) d) 4 : 6 ( 9) = 7 7 ( 8) = 6 8 : ( ) = 9 d) 4 : 6 = 7. Muunna 8 sekaluvuksi 6 sekaluvuksi
Luvuilla laskeminen. Laske. 6 4 + ( 4) d) ( 7) = 7 6 = 4 + ( 4) = 4 4 = 0 d) ( 7) = + 7 = 6. Laske. ( 9) 7 ( 8) 8 : ( ) d) 4 : 6 ( 9) = 7 7 ( 8) = 6 8 : ( ) = 9 d) 4 : 6 = 7. Muunna 8 sekaluvuksi 6 sekaluvuksi
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
MAA2.3 Koontitehtävät 2/2, ratkaisut
 MAA.3 Koontitehtävät /, ratkaisut. (a) 3x 5x 4 = 0 x = ( 5) ± ( 5) 4 3 ( 4) 6 (b) (x 4) = (x 4)(x + 4) (x 4)(x 4) = (x 4)(x + 4) x 8x + 6 = x 6 x 6 8x = 3 : 8 x = 4 = 5 ± 73 6 (c) 4 x + x + = 0 4 x + 4x
MAA.3 Koontitehtävät /, ratkaisut. (a) 3x 5x 4 = 0 x = ( 5) ± ( 5) 4 3 ( 4) 6 (b) (x 4) = (x 4)(x + 4) (x 4)(x 4) = (x 4)(x + 4) x 8x + 6 = x 6 x 6 8x = 3 : 8 x = 4 = 5 ± 73 6 (c) 4 x + x + = 0 4 x + 4x
Preliminäärikoe Pitkä Matematiikka 3.2.2009
 Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
Taulukkolaskentaa selkokielellä EXCEL
 Taso 1 1 MICROSOFT Taulukkolaskentaa selkokielellä EXCEL Tuomas Seitsemän veljeksen Tuomas on vakaa ja vahva kuin tammi. Hänellä ei ole juuri mielikuvitusta, hän ei keksi mitään itse, vaan ideat tulevat
Taso 1 1 MICROSOFT Taulukkolaskentaa selkokielellä EXCEL Tuomas Seitsemän veljeksen Tuomas on vakaa ja vahva kuin tammi. Hänellä ei ole juuri mielikuvitusta, hän ei keksi mitään itse, vaan ideat tulevat
Algoritmit 2. Luento 8 To Timo Männikkö
 Algoritmit 2 Luento 8 To 4.4.2019 Timo Männikkö Luento 8 Algoritmien analysointi Algoritmien suunnittelu Rekursio Osittaminen Rekursioyhtälöt Rekursioyhtälön ratkaiseminen Master-lause Algoritmit 2 Kevät
Algoritmit 2 Luento 8 To 4.4.2019 Timo Männikkö Luento 8 Algoritmien analysointi Algoritmien suunnittelu Rekursio Osittaminen Rekursioyhtälöt Rekursioyhtälön ratkaiseminen Master-lause Algoritmit 2 Kevät
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio
 MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
1 Logiikkaa. 1.1 Logiikan symbolit
 1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
