Elektroniikan laboratorio Lisätehtävät Mallivastauksia
|
|
|
- Albert Elstelä
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät 7.9. Mallivastauksia. Mitkä loogiset operaatiot oheiset kytkennät toteuttavat? Vihje: kytkin johtaa, kun ohjaava signaali =. Käytä apuna totuustauluja. V = Päätellään totuustaulu... + GN = V = GN = Vastaus: + eli NOR Päätellään totuustaulu... Vastaus: eli NN. Toteuta looginen funktio = neljällä -tuloisella NN-portilla. Käytössäsi on muuttujista vain suorat versiot,,,. Ratkaisu vaatii yhtälön kasittelyä oolen algebralla (mm. emorganin teoreeman käyttöä). (Kts. myös laskuharjoitusmonisteen esim c) (+)(+)).. Toteuta looginen funktio = + neljällä -tuloisella NOR-portilla. Käytössäsi on muuttujista vain suorat versiot,,,.ratkaisu vaatii yhtälön kasittelyä oolen algebralla (mm. emorganin teoreeman käyttöä). = + = + + = ( + ) = ( + ) ( + ) = ( + ) + ( + ) = Onko mahdollista toteuttaa mikä tahansa looginen funktio käyttäen pelkästään -tuloisia NNportteja. Miksi? Perustele. Kytkentäfunktio voidaan aina saattaa tulojen summa -muotoon. Näin kaikki funktiot voidaan toteuttaa -tuloisilla NN-porteilla. Invertointikin onnistuu NNillä. Kts. myös luentomonisteen s Suunnittele kombinaatiologiikka, johon tulee 4 tulosignaalia,, ja. Logiikalla on kaksi lähtöä ja Y. Lähtö = vain silloin, kun tulot ja ovat molemmat ykkösiä, mutta samalla ja eivät ole molemmat yhtäaikaa ykkösiä. Vastaavasti lähtö Y = vain silloin, kun ja ovat molemmat ykkösiä, mutta samalla ja eivät ole molemmat yhtäaikaa ykkösiä. Saat käyttää - tuloisia NN- ja NOR-portteja. Käytössäsi on muuttujista vain suorat versiot,,,. Kuusi kpl -tuloisia logiikkaportteja riittää (4 NNiä ja NORia), mikäli huomaa hyödyntää yhteisiä termejä :n ja Y:n lausekkeissa. Samoin tarvitset vain suorat versiot muuttujista. Ratkaisu vaatii yhtälön käsittelyä oolen algebralla (mm. emorganin teoreeman käyttöä). pua on myös tämän monisteen tehtävistä ja. = ( + ) + ( + ) = + = opyright ntti Mäntyniemi opyright ntti Mäntyniemi
2 Laaditaan Karnaug h kartat lähdöille: : = + = ( + ) = = + Y:? Y Y = + Y = ( + ) Y = Y = + OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Tuntitehtävät Toteuta oheista kombinaatiologiikkaa vastaava looginen funktio joko pelkillä NN-porteilla tai pelkillä NOR-porteilla. Käytössäsi on joko yhteensä 5 kpl -, - ja 4-tuloisia NN-portteja tai 4 kpl -tuloisia NOR-portteja. Perustele vastauksesi K-kartalla ja esitä minimoitu lauseke! ( + ) = (++) =+ Vastaus / nswer +++ =++ = + Eli 5xNN ( + ) = (++)( + ) =(+)(+) = =(++)(++)(++) = Eli 4xNOR Α Β Y. Toteuta kuvan esittämä logiikka käyttäen -tuloisia TI-EI-portteja (NOR). Toteutuksen tulee olla mahdollisimman yksinkertainen. Esitä piirikaavio ja perustele vastaus. M N M N = ++ eli, NN-portti, jonka tulot invertoidaan, vastaa OR-porttia Z taas NN-portista OR-portti, parittomalle tasolle tuleva ulkoinen muuttuja joutuu kulkemaan invertterin läpi, tosin tässä OR-lauseke muuttujan itsensä kanssa ei tee mitään. TI-taso. J-taso toisensa kumoavat invertterit, eli NN-portista tulee N-portti. TI-taso Z = MN + MN + MN = M(N+N) + N(M+M) = M + N MN nollien mukaan M Z = (M+N) = + M+N N Z opyright ntti Mäntyniemi opyright ntti Mäntyniemi
3 OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät a) nalysoi ja minimoi oheinen multiplekserikytkentä. Signaaleista on tarjolla sekä suorat (,, ) että käännetyt versiot (,, ). Toteuta minimoitu looginen yhtälö käyttäen mahdollisimman vähän b) -tuloisia NN-portteja ykkösillä minimoidusta emorgan... = /Y MU G G G G = + + ykkösillä nollilla + tai ( + ) ( + ) minimoitu yhtälö =. a) nalysoi ja minimoi oheinen demultiplekserikytkentä. Signaaleista on tarjolla sekä suorat (,, ) että käännetyt versiot (,, ). Toteuta minimoitu looginen yhtälö käyttäen mahdollisimman vähän MU G MU G Toteuta minimoitu looginen yhtälö käyttäen mahdollisimman vähän b) -tuloisia NN-portteja ykkösillä minimoidusta emorgan... = 5 7 = minimoitu yhtälö = + tai ( + ) ( + ) c) -tuloisia NOR-portteja nollilla minimoidusta emorgan... = ( + ) + ( + ) c) -tuloisia NOR-portteja nollilla minimoidusta emorgan... = ( + ) + ( + ) opyright ntti Mäntyniemi opyright ntti Mäntyniemi
4 . Mitkä seuraavista kombinaatiologiikan esimerkeistä vastaavat toisiaan loogiselta toiminnaltaan? Perustele! = (+)(+)(+) = ΠM(,7) 4 = = m(,,,6) Vastaus (lisää oikeat alaindeksit): Perustelut! 6 =(+)(+)(+)(++) Graafinen emorgan G 7 = 6 = 7 = 4 = OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät viikko 4. Suunnittele digitaalinen komparaattori, joka vertailee kahta -bittistä binäärilukua P ja (bitit P P J ). Komparaattorissa on kolme lähtöä: P =, P < ja P >. a) esitä totuustaulut ja/tai K-kartat. b) minimoi lähtöjen loogiset funktiot. c) piirrä lähtöjen logiikkakaaviot haluamillasi logiikkaporteilla (N, OR, INV, NN, NOR, EOR, ENOR, MU, MU=EOER...). P P : P = P P : P < = P P +P P +P P +P P P P : P > = P (P + P ) + P (P + P ) = (P + P ) (P + P ) = P P = P + P P + P = P + P + P P 4. Mitkä seuraavista kombinaatiologiikan esimerkeistä vastaavat toisiaan loogiselta toiminnaltaan? Perustele! G MU = ++ + MU G Graafinen emorgan = = (++)(+) 6 = = = + + Vastaus (lisää oikeat alaindeksit): = 4 = 6 = 7 = Perustelut! huomaa invertteri = (+) (+) = (+)(+)(+) 6 7. Suunnittele binäärisummainlogiikka, joka summaa kaksi -bittistä binäärilukua P ja (bitit PPP J ). Käytössäsi on koko- ja puolisummaimia. (ull dder =, Half dder = H). Kts. luentomoniste s. 8. Yksinkertaisin ja hitain rakenne on oheisen kuvan mukainen ripple-carrysummain (ripple = käydä läpi, levitä (vähitellen)). P H o P i o o o P i o muistinumerot H = Half dder = puolisummain = ull dder = kokosummain o o P P++o P++o P+ = = = =. Suunnittele binäärikertojalogiikka, joka kertoo kaksi -bittistä binäärilukua (PPP J ). Käytössäsi on koko- ja puolisummaimia ja N-portteja. a) Esitä tarvittavat binääriset kertolaskut ja summaukset (kynä ja paperi -menetelmällä, katso luentomoniste s. ). b) Montako N-porttia tarvitaan? c) Montako summainta tarvitaan (koko- ja puolisummaimia yhteensä)? Huomaa, että esim. kokosummaimessa on vain kolme tuloa = summattavat bitit ja muistinumerobitti edellisestä asteesta. Et voine suoraan summata neljää bittiä, vaan homma on jaettava ainakin kahteen vaiheeseen? d) Montako bittiä kertolaskun tuloksessa on? e) Piirrä kertojan logiikkakaavio. o P o P opyright ntti Mäntyniemi opyright ntti Mäntyniemi
5 a) Tarkastellaan tarvittavia laskutoimituksia kyna ja paperi -menetelmällä. Merkitään tulotermejä lyhennettynä, esim. P = b) tarvitaan 9 N-porttia. c) esim. kertolaskun tuloksen bitti P vaatii neljän bitin summaamista, kun taas kokosummain summaa kolme bittiä. Laskenta täytyy siis jakaa vaiheisiin. Esimerkkeinä ripple-carry summain (yksinkertaisin ja hitain) ja carry-save-summain (nopeampi kuin ripple-carry). Tarvitaan puolisummainta (H) ja kokosummainta (). P P P Π5 Π4 Π Π Π Π arry-save-summain, pisin viivepolku 4 summainta P P P o o 4 o 4 o 5 o 5 o 6 6 Π5 Π4 Π Π Π Π Ripple-carry-summain, pisin viivepolku 5 summainta o 4 o 4 P P o P P P P H o o Π Π P P P P P P o 5 o 6 6 Π5 Π4 H o i o o 5 Π o o P H 4 o o 4 P P Π Π Π H o i o o i 5 o o 5 6 o 6 Π Π Π Π Π4 Π5 P P H o o P P P i o P o i 4 o o 4 H o i o 5 o 5 6 o 6 Π Π Π4 Π5 opyright ntti Mäntyniemi opyright ntti Mäntyniemi
6 OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävä viikko 4 Suunnittele laskuri, joka käy edestakaisin läpi sekvenssiä,,,,,,,,,... Ensi silmäyksellä laskurissa näyttäisi olevan 4 tilaa. Mutta miten laskuri saadaan kulkemissuunnasta riippuen menemään tilasta tilaan tai ja tilasta tilaan tai kolme? Ei mitenkään ilman ylimääräistä (piilotettua) tilamuuttujaa, joka vaihtaa tilaansa aina laskurin sopivassa tilassa ja muistaa tilansa sopivan ajan. Tilamuuttujien kaksi alinta bittiä sisältävät toivotun laskuritoiminnan ja eniten merkitsevä bitti kertoo laskemissuunnan. Laskurin todellinen sekvenssi on,,,,6,5,,,... Koodataan ylimääräisten tilojen 4 ja 7 seuraaviksi tiloiksi don t care (d), niin saadaan minimitoteutus silläkin uhalla, että esim. tilan 7 seuraavaksi tilaksi koodataan 7, jos don t care tilaksi tulkitaan minimoinnissa tila eli 7. Laaditaan laskurille tilansiirtotaulukko ja tilakaavio käyttäen kolmea tilamuuttujaa. Nykytila tila Seuraava d d d d d d Minimoidaan K-kartoilla: d d d d = + = + = LK d d don t caret valittiin minimoinnissa näin, eli tilasta 4 tilaan 5 ja tilasta 7 tilan 4 kautta tilaan 5, eli ei jäädä jumiin! OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävä viikko 4 Ratkaistaan edellinen tehtävä myös käyttämällä kahta keskenään kommunikoivaa tilakonetta. Laskurina toimii yleiskäyttöinen -bittinen ylös/alas-laskuri, jossa suunnan määrää ohjaustulo (own). Kun =, laskuri laskee alaspäin, muuten ylöspäin. Laskentasuuntaa kontrolloi -bittinen tilakone, joka vaihtaa tilaansa sopivasti laskurin tilojen perusteella. Laskurissa on lähtösignaaleja, joihin koodataan sopivien tilojen tunnistus, tässä tapauksessa tilat ja, kuten ajoituskaaviosta voidaan päätellä. Jotta laskuri osaisi vaihtaa suuntaa tilan kolme kohdalla, täytyy ohjaustilakoneen saada siitä tieto tilan kohdalla, jotta seuraavan kellon reunan jälkeen ohjaustilakoneen generoima = olisi valmiina laskurille. Vastaavasti laskenta vaihtaa suuntaa tilan kohdalla, kunhan tilan aikana ohjaustilakone saa tiedon tilassa olemisesta ja osaa vaihtaa tilansa nollaksi. y = = LK [..] TIL TIL -bittisen ylös/alas-laskurin tilansiirtotaulukko: = Nykytila Seuraava tila Lähdöt = ( + )+ ( + ) TIL TIL = ( )+ ( ) = ( )+ ( ) = TIL = TIL = = Suunnanvaihtotilakoneen tilansiirtotaulukko: Tilakoneella on kaksi ohjaustuloa: y (ykköseksi), jolla tilakone saadaan vaihtamaan tilansa -> ja n (nollaksi), jolla tilakone saadaan vaihtamaan tilansa ->. Näihin ohjaustuloihin kytketään ylös/alaslaskurin TIL-lähdöt siten, että TIL = nollaksi ja TIL = ykköseksi. Sovitaan vielä, että ykköseksi ja nollaksi eivät voi yhtäaikaa olla ykkösiä -> don t care tilaan jos olisivat. Tulkitaan don t caret ykkösiksi minimoinnissa. Nykytila Seuraava tila yn d d yn d d yn y = y + n y+y n = y + n = yn opyright ntti Mäntyniemi opyright ntti Mäntyniemi
7 Piirretään molempien tilakoneiden logiikkakaaviot ja ylemmän abstraktiotason kuva, jossa käytetään tilakoneista muodostettuja komponentteja. Lisätään kiikkuihin myös asynkroninen nollaustulo. OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Tuntitehtävät viikko 4 = LK RESETN = = = R R TIL TIL toimintatilan valinta M=mode -bittinen laskuri TR M[OWN] +/- T= T= T= [] [] lähdöt ykkösiä laskurin sopivassa tilassa T= asynkroninen nollaus eli laskurin tila menee nollaksi T= kellosignaalista riippumatta toimintatilassa laskurin tilaa kasvaa yhdellä toimintatilassa laskurin tilaa pienenee yhdellä. nalysoi oheisen kuvan tilakone. Esitä vastauksena tilakaavio ja riittävät välivaiheet perusteluksi. Tilakaavio: KELLO K-karttana: Tilansiirtotaulukkona: = + NT ST, -. nalysoi myös oheisen kuvan tilakone. Esitä vastauksena tilakaavio ja riittävät välivaiheet perusteluksi. n y LK RESETN = y + n R KELLO a) = = RESETN LK TR M[OWN] +/- T= T= T= [] [] y n R Erilaisia tapoja merkitä väylä [..] (:) [:] <:> b) Nykytila Seuraava tila Kahden bitin GRY-koodilaskuri c) opyright ntti Mäntyniemi opyright ntti Mäntyniemi
8 Laskuharjoitusmoniste 5. nalysoi oheisen kuvan tilakone. nna vastaus tilakaaviona (tilakarttana). 4.J.TI.J.TI LK nalysoidaan takaisinkytkennän kombinaatiologiikka. = ( + ) ( + ) + ( + ) = + + = + Nykytila Tulo Seuraava tila : TI : Nykytila Tulo Seuraava tila Kotitehtävät 6... Palautus viimeistään maanantaina nalysoi oheisen logiikkakaavion esittämän tilakoneen toiminta. lkutila on ja tulo on synkronoitu kelloon LK. voi olla ykkönen useiden kellojaksojen ajan. Esitä vastauksenasi toiminnan esittävä tilakaavio ja riittävät välivaiheet (esim. kiikkujen herätetulojen yhtälöt, tilansiirtotaulukko...). Selitä myös yhdellä lauseella mitä logiikka tekee. LK LK Z Z = + = = + = + Nykytila Seuraava tila Lähtö Z Tilakaavio Selitys: Logiikka tunnistaa ykköstä tulossa, jolloin lähtö Z=..nalysoi oheinen synkroninen tilakone. nna vastauksena: a) minimoidut kiikkujen herätetulojen loogiset funktiot, b) tilansiirtotaulukko ja c) tilakaavio. KELLO MU G MU G Z= Z= Z= Z= a) = + = + + = (+) + (+) = + b) Nykytila Seuraava tila c) opyright ntti Mäntyniemi opyright ntti Mäntyniemi
9 Lisätehtävät... Esitä puolisummaimen vaatima logiikka seuraavilla eri tavoilla: a) totuustauluna b) K-kartoilla Summataan siis kaksi -bittistä binäärilukua, jolloin saadaan neljä erilaista vaihtoehtoa. + desim.- binääri- lukuna lukuna o o + Tarvitaan lähtöön kaksi bittiä, summabitti ja muistinumero o c) tulojen summana: ykkösten mukaan o =, = + d) summien tulona: nollien mukaan o =, = ( + ) ( + ) e) hajalogiikalla (N-, OR-, NOT-porteilla) = + o = f) -tuloisilla NN-porteilla g) -tuloisilla NOR-porteilla edellisten kohtien lausekkeisiin tai logiikkakaavioihin sovelletaan emorganin teoreemaa. = + o = = ( + ) ( + ) o = = ( + ) ( + ) o = h) minimimäärällä mitä tahansa logiikkaportteja ykkösten mukaan o =, = + = i) 4-tuloisilla multipleksereillä Nelituloisella multiplekserillä voidaan suoraan toteuttaa kahden muuttujan loogiset funktiot kytkemällä multiplekserin tuloihin ykköset ja nollat totuustaulun mukaisesti. j) -tuloisilla multipleksereillä -tuloisen muxin sisäinen rakenne on seuraavanlainen: G G Y MU G G + GY = o o MU G Kuten kohdan a) totuustaulussa myös tässä muuttuja ajatellaan enemmän merkitseväksi, jolloin se tulee kytkeä muxin enemmän merkitsevään valintatuloon. Kun vaikkapa yhtälö = + sovitetaan -tuloiselle muxille saadaan seuraavat vaihtoehdot: MU G MU G Vastaavasti o = saa seuraavat muodot: MU G MU G = = o = + o o o = opyright ntti Mäntyniemi opyright ntti Mäntyniemi
10 k) -to-4 IN/LIN-dekoodereilla ja hajalogiikalla Myös -to-4 IN/LIN-dekoodereilla ja OR-portilla voidaan suoraan toteuttaa kahden muuttujan loogiset funktiot kytkemällä dekooderin sopivat lähdöt OR-portin tuloihin -to-4 IN/LIN-dekooderin sisäinen rakenne on seuraavanlainen: G G G G G G G G = G G = G G = G G = G G Kun yhtälöt = + ja o = sovitetaan -to-4 IN/LIN-dekooderille saadaan seuraavaa: IN/LIN Β Α G Α Β Α Β Α Β Α Β o. Esitä kokosummaimen vaatima logiikka seuraavilla eri tavoilla: a) totuustauluna b) K-kartoilla Summataan siis kaksi -bittistä binäärilukua ( ja ) ja muistinumero (i), jolloin saadaan kahdeksan erilaista vaihtoehtoa. ++i desim.- lukuna binääri- lukuna o i i o Tarvitaan lähtöön kaksi bittiä, summabitti ja muistinumero o l) -to- IN/LIN-dekooderilla ja hajalogiikalla -to- IN/LIN-dekooderin sisäinen rakenne voisi olla seuraavanlainen: IN/LIN G = G G = G Eli -to- IN/LIN-dekooderin lähdöissä on yhden tulomuuttujan IN/LIN kannalta komplementti ja muuttuja itse. G o c) tulojen summana: ykkösten mukaan o = + i + i = i + i + i + i d) summien tulona: nollien mukaan o = (+)(+i)(+i) S = (++i)(++i)(++i)(++i) e) hajalogiikalla (N-, OR-, NOT-porteilla) i i i i i i i i -to- IN/LIN-dekooderi sallintatulolla (= MU demultiplekseri) voisi olla seuraavanlainen: G = G = G IN/LIN G Α Β Α Β IN/LIN G i i o i i o Α Β Α Β o opyright ntti Mäntyniemi opyright ntti Mäntyniemi
11 f) -tuloisilla NN-porteilla g) -tuloisilla NOR-porteilla edellisten kohtien lausekkeisiin tai logiikkakaavioihin sovelletaan oolen algebraa, jolla lausekkeet ryhmitellään uudelleen muotoon, jossa esiintyy vain -tuloisia operaatioita. Sitten käytetään emorganin teoreemaa = i + i + i + i = (i+i)+( i+i) = (i+i) ( i+i) = i i i i h) minimimäärällä mitä tahansa logiikkaportteja tai digitaalilohkoja Kirjoitetaan lausekkeet uudelleen hieman eri muodossa: o = + i + i = + i(+) = + i( ) (OR-funktio kahden peräkkäisen puolisummaimen muistinumerolähtöjen välillä) = i + i + i + i = (i + i) + ( i + i) = ( i) + ( i) = i (kaksi puolisummaimen summalähtöä peräkkäin) H o H o = i i( ) i i i i Yhteiseksi tekijäksi esim. o o = + i + i = ( + i) + i = ( + i) i = i i i i i i i i i i o i i) 8-tuloisilla multipleksereillä 8-tuloisella multiplekserillä voidaan suoraan toteuttaa kolmen muuttujan loogiset funktiot kytkemällä multiplekserin tuloihin ykköset ja nollat totuustaulun mukaisesti. MU G 7 4 o j) 4-tuloisilla multipleksereillä Samoin kuin toteutettaessa puolisummain -tuloisilla muxeilla, myös tässä pitää yksi muuttujista tuoda muxin datatuloihin ja kahdella muuttujalla hoitaa muxin valintatulojen ohjaus. Tätä voi havainnollistaa K-kartalla, jonka ruutuihin tuodaan ykkösten ja nollien lisäksi muuttujia (VEMkartta, Variable Entered Map). Tässä tapauksessa on kolme mahdollisuutta. Itse asiassa VEM-kartan ruutujen arvo (, tai muuttuja) on suoraan se mitä kytketään muxin datatuloihin, kun valintatuloja ohjataan VEM-kartan indeksointiin käytetyillä muuttujilla. o = + i + i i = i + i + i + i i i MU G 7 i +i = i i o = + i( ) i i Kuten kohdan a) totuustaulussa myös tässä muuttuja ajatellaan enemmän merkitseväksi, jolloin se tulee kytkeä muxin enemmän merkitsevään valintatuloon. + = i i + = opyright ntti Mäntyniemi opyright ntti Mäntyniemi
12 Tässä esimerkkinä vaihtoehto, jossa muuttujat ja muxien valintatuloissa ja sopivasti datatuloissa. m) puolisummaimilla ja hajalogiikalla Tämä taisi tulla tehdyksi jo kohdassa h). i i MU G o i i i i MU G. Toteuta invertteri eli looginen EI-operaatio, NOT, käyttäen vuorollaan yhtä oheisen kuvan mukaisista logiikkaporteista: a) NN-portilla b) NOR-portilla c) E-OR-portilla d) E-NOR-portilla e) -tuloisella multiplekserillä, MU f) -lähtöisellä (-to-) demultiplekserillä, MU k) -to-8 IN/LIN-dekoodereilla ja hajalogiikalla Myös -to-8 IN/LIN-dekoodereilla ja OR-portilla voidaan suoraan toteuttaa kolmen muuttujan loogiset funktiot kytkemällä dekooderin sopivat lähdöt OR-portin tuloihin IN/LIN i Β Α 4 G 7 Α Β i Α Β i Α Β i Α Β i Α Β i 4 Α Β i 5 Α Β i 6 Α Β i 7 l) -to-4 IN/LIN-dekoodereilla ja hajalogiikalla Lähdetään siitä olettamuksesta, että -to-4 IN/LIN-dekooderissa on sallintatulo. IN/LIN i Β Α i Β Α G Α Β i Α Β i Α Β i Α Β i IN/LIN G Α Β i Α Β i Α Β i Α Β i o Ylemmän dekooderin sallintatulossa on, jolloin lähdöissä on tarjolla min-termit m, m, m ja m. lemmän dekooderin sallintatulossa on, jolloin lähdöissä on tarjolla min-termit m4, m5, m6 ja m7. o = = MU G MU G a) b) c) d) e) f) Lähestytään asiaa totuustaulun avulla kohdissa a) - d). a) Jos toinen tulo on ykkönen lähtö on toisen tulon komplementti tai jos molemmissa tuloissa sama arvo, lähtö on tämän arvon komplementti d) = Jos toinen tulo on nolla lähtö on toisen tulon komplementti ERI-EI = = b) + Jos toinen tulo on nolla lähtö on toisen tulon komplementti tai jos molemmissa tuloissa sama arvo, lähtö on tämän arvon komplementti e) c) = MU G Mux toteuttaa suoraan totuustaulun Jos toinen tulo on ykkönen lähtö on toisen tulon komplementti f) MU G ERI MU toimii, kun nolla-aktiivinen sallintatulo nollassa, lähtö on kun = eli = opyright ntti Mäntyniemi opyright ntti Mäntyniemi
13 4. Toteuta a) kolmen muuttujan N-operaatio -tuloisilla NN-porteilla = () = h) kolmen muuttujan NOR-operaatio -tuloisilla NN-porteilla = (+)+ = + = b) kolmen muuttujan N-operaatio -tuloisilla NOR-porteilla = () = + = loitteleva digitaalisuunnittelija yritti tehdä loogisen funktion = + komplementin väärin = + oppimansa säännön mukaisesti: vaihdetaan kaikki J-operaatiot TI-operaatioiksi ja kaikki TI-operaatiot J-operaatioiksi sekä komplementoidaan kaikki muuttujat.(lustavissa testeissä logiikasta nousi savu.) Missä meni pieleen? Esitä :n oikean komplementin oikein looginen funktio summien tulona ja esitä myös totuustaulujen ja K-karttojen avulla loogisten funktioiden, väärin ja oikein toiminta. c) kolmen muuttujan NN-operaatio -tuloisilla NN-porteilla = () = d) kolmen muuttujan NN-operaatio -tuloisilla NOR-porteilla = () = + = + + e) kolmen muuttujan OR-operaatio -tuloisilla NOR-porteilla = (+)+ = + + f) kolmen muuttujan OR-operaatio -tuloisilla NN-porteilla = (+)+ = + = g) kolmen muuttujan NOR-operaatio -tuloisilla NOR-porteilla = (+)+ = + + väärin oikein väärin oikein = +, sovelletaan emorganin sääntöä = + tai luetaan K-kartasta nollien mukaan = oikein = ( + ) eli sulut unohtuivat! = ( + ), tai suoraan alkuperäisellä säännöllä, mutta muistetaan sulut! 6. Suunnittele vanhentuneiden logiikkaporttien kolmioviseen varastoon valaistusjärjestelmän ohjauslogiikka. Järjestelmä sisältää kolme kytkintä, ja, yhden kunkin oven pielessä. Varaston valot voi sytyttää tai sammuttaa millä tahansa kytkimellä muiden kytkinten asennosta riippumatta. Merkitään kytkimien tiloja esim. seuraavasti: (eli =) ja (eli =), ja vastaavasti. Merkitään logiikan lähtöä :llä. Mikäli valon halutaan olevan päällä =. a) Esitä logiikan totuustaulu. b) Esitä logiikan minimoitu funktio. c) Piirrä ohjauslogiikan logiikkakaavio. Käytössäsi on korkeintaan 5 logiikkaporttia! tai a) tai in tai Gray b) tai : tai : ei minimoidu! = = = ( + ) + ( + ) = ( ) + ( ) = = ( + ) + ( + ) = ( ) + ( ) = ( ) c) tai = = = = opyright ntti Mäntyniemi opyright ntti Mäntyniemi
14 7. Suunnittele TRIV-laskuri, dekadilaskuri, joka laskee tilat,,...9 ja pyörähtää sitten ympäri tilaan ja sekvenssi alkaa uudelleen, eli laskurissa on kymmenen tilaa. Laskurissa on sallintatulo, jonka ollessa laskenta on sallittu, muuten laskuri säilyttää tilansa. Laskurissa on myös T-lähtö (Terminal ount, viimeinen tila), joka kertoo laskurin olevan tilassa 9. Kuvataan laskurin toiminta tilakaaviona ja tilansiirtotaulukkona, (Mooren tilakone). 8 T= 7 T= 9 T= T= T= 6 T= 5 T= opyright ntti Mäntyniemi 4 T= T= T= Nykytila Seuraava tila, Lähtö T d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d Määritellään sekvenssiin kuulumattomille tiloille seuraavaksi tilaksi don t care (d). Minimoidaan K-kartoilla. d d d d d d : d d : d d d d d d d d d d d d d d d d = d d : d d d d = d d d d d d = d d : d d d d = = = = = = + + tai = ( + ) = tai = = + + tai = = + tai = T = Miten don t care t tulkittiin minimoinnissa? Voiko laskuri jäädä jumiin? d d d d d d Kymmenlaskurin logiikkasymboli voisi olla seuraavanlainen. kun sallintatulo G on laskurin tilaa kasvaa yhdellä kymmenlaskuri sallintatulo kellotulo 8. Suunnittele TRIV6-laskuri, joka laskee tilat,,...5 ja pyörähtää sitten ympäri tilaan ja sekvenssi alkaa uudelleen, eli laskurissa on kuusi tilaa. Laskurissa on sallintatulo, jonka ollessa laskenta on sallittu, muuten laskuri säilyttää tilansa. Laskurissa on myös T-lähtö (Terminal ount, viimeinen tila), joka kertoo laskurin olevan tilassa 5. opyright ntti Mäntyniemi TR IV G + T=9 T= [] [] [4] [8] asynkroninen nollaus eli laskurin tila menee nollaksi, T=, kellosignaalista riippumatta lähtö ykkönen, kun tila 9 Kuvataan laskurin toiminta tilakaaviona ja tilansiirtotaulukkona, (Mooren tilakone). Nykytila Seuraava tila, Lähtö T= T 5 T= T= 4 T= T= T= d d d d d d Määritellään sekvenssiin kuulumattomille tiloille seuraavaksi tilaksi don t care (d). Minimoidaan K-kartoilla. d : d d d d : d d d d d d d d d d : d d d = + + = + + = + T =
15 TRIV6-laskurin logiikkasymboli voisi olla seuraavanlainen. kun sallintatulo G on laskurin tilaa kasvaa yhdellä laskurilla 6 tilaa sallintatulo kellotulo TR IV 6 G + T=5 T= [] [] [4] lähtö ykkönen, kun tila 9 Jos kellosignaalin taajuus on Hz, voidaan kymmenlaskurin sallintatulo kytkeä kiinteästi loogiseen ykköseen. TRIV6:n sallintasignaali on suoraan kymmenlaskurin T-lähtö. LK RESETN TR IV G + T=9 T= [] [] [4] [8] T asynkroninen nollaus eli laskurin tila menee nollaksi, T=, kellosignaalista riippumatta 9. Edellisen tehtävän laskureita käyttämällä suunnittele laskurijärjestelmä, joka osaa laskea minuutin sekunnit. Tulosignaaleina ovat MHz:n kellosignaali LK sekä sallintasignaali, joka on µs:n mittainen ylhäällä aktiivinen pulssi sekunnin välein. Laskurissa on T-lähtö, joka on ykkönen µs:n ajan laskurin ollessa tilassa 59. (Laskuria tullaan käyttämään osana suurempaa synkronista logiikkaa, jota kellotetaan MHz:n kellolla.) Miten tilanne muuttuu, jos laskuri saa kellokseen Hz:n kellosignaalin? TR IV 6 G + T=5 T= [] [] [4] LK RESETN TR IV G + T=9 T= T [] [] [4] [8] TR IV 6 G + T=5 T= [] [] [4] opyright ntti Mäntyniemi opyright ntti Mäntyniemi
16 Viikon 4 lisätehtävä. Suunnittele /7-segmentti-dekooderi. ( = inary oded ecimal). Eli tuloina 4-bittinen -sana (..9) ja lähtönä 7 segmenttiohjaussignaalia (a,b,c,d,e,f,g), joiden kombinaatiot edustavat numerosymboleja 7-segmenttinäytössä. -koodiin kuulumattomien tulokombinaatioiden lähtönä voi olla don't care, niin saadaan minimitoteutus. a b c d e f g d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d a: d d d d d d c: d d d d d d b: d d d d d d d: d d d d d d e: d d d d d d f: d d d d d d g: d d d d d a = b = + + c = + + d = e = + f = g = opyright ntti Mäntyniemi
F = AB AC AB C C Tarkistus:
 Digitaalitekniikka I, tenttitehtäviä ratkaisuineen I 3..995 2. c) esitä seuraava funktio kanonisten summien tulona f(,,) = + Sovelletaan DeMorganin teoreemaa (työläs). Teoriaminimointia ei ole käytetty!
Digitaalitekniikka I, tenttitehtäviä ratkaisuineen I 3..995 2. c) esitä seuraava funktio kanonisten summien tulona f(,,) = + Sovelletaan DeMorganin teoreemaa (työläs). Teoriaminimointia ei ole käytetty!
c) loogiset funktiot tulojen summana B 1 = d) AND- ja EXOR-porteille sopivat yhtälöt
 IGITLITEKNIIKK I 5 Tentti:.. ELEKTRONIIKN LORTORIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) b) minimoituna summien
IGITLITEKNIIKK I 5 Tentti:.. ELEKTRONIIKN LORTORIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) b) minimoituna summien
c) loogiset funktiot tulojen summana B 1 = C 2 C 1 +C 1 C 0 +C 2 C 1 C 0 e) logiikkakaavio
 IGITLITEKNIIKK I 5 Tentti:.. ntti Mäntyniemi ELEKTONIIKN LOTOIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) ykkösten
IGITLITEKNIIKK I 5 Tentti:.. ntti Mäntyniemi ELEKTONIIKN LOTOIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) ykkösten
ELEC-C3240 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä
 ELE-324 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä Materiaalia otettu myös: https://www.allaboutcircuits.com/textbook/digital/chpt-8/introduction-to-karnaughmapping/
ELE-324 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä Materiaalia otettu myös: https://www.allaboutcircuits.com/textbook/digital/chpt-8/introduction-to-karnaughmapping/
Digitaalitekniikan matematiikka Harjoitustehtäviä
 arjoitustehtäviä Sivu 6 6.3.2 e arjoitustehtäviä uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä jossa käytävän kummassakin päässä on kytkin ja käytävän keskellä lamppu. amppu
arjoitustehtäviä Sivu 6 6.3.2 e arjoitustehtäviä uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä jossa käytävän kummassakin päässä on kytkin ja käytävän keskellä lamppu. amppu
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen
 Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2012-2013 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2012-2013 Lasse Lensu 2 Transistori yhdessä
Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: JA-EI-portti A B. TAI-EI-portti A B = 1
 Digitaalitekniikan matematiikka Luku 6 Sivu () Kombinaatiopiirit.9. Fe J-EI- (NND) ja TI-EI- (NOR) -portit Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: NND? B B & B B = & B + B + B
Digitaalitekniikan matematiikka Luku 6 Sivu () Kombinaatiopiirit.9. Fe J-EI- (NND) ja TI-EI- (NOR) -portit Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: NND? B B & B B = & B + B + B
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen
 Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2013-2014 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2013-2014 Lasse Lensu 2 Transistori yhdessä
Sekvenssipiirin tilat
 igitaalitekniikka (piirit) Luku Täsmätehtävä Tehtävä Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan seuraavissa sekvenssipiireissä: Painikkeella ohjattava lampun sytytys ja sammutus. Näyttöä ohjaava
igitaalitekniikka (piirit) Luku Täsmätehtävä Tehtävä Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan seuraavissa sekvenssipiireissä: Painikkeella ohjattava lampun sytytys ja sammutus. Näyttöä ohjaava
Esimerkkitentin ratkaisut ja arvostelu
 Sivu (5) 2.2.2 Fe Seuraavassa on esitetty tenttitehtävien malliratkaisut ja tehtäväkohtainen arvostelu. Osassa tehtävistä on muitakin hyväksyttäviä ratkaisuja kuin malliratkaisu. 2 Tehtävät on esitetty
Sivu (5) 2.2.2 Fe Seuraavassa on esitetty tenttitehtävien malliratkaisut ja tehtäväkohtainen arvostelu. Osassa tehtävistä on muitakin hyväksyttäviä ratkaisuja kuin malliratkaisu. 2 Tehtävät on esitetty
Digitaalitekniikan matematiikka Luku 8 Sivu 1 (23) Kombinaatiopiirielimet MUX X/Y 2 EN
 Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe DX G = G EN X/Y Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe Johdanto Tässä luvussa esitetään keskeisiä kombinaatiopiirielimiä ne ovat perusporttipiirejä
Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe DX G = G EN X/Y Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe Johdanto Tässä luvussa esitetään keskeisiä kombinaatiopiirielimiä ne ovat perusporttipiirejä
kwc Nirni: Nimen selvennys : ELEKTRONIIKAN PERUSTEET 1 Tentti La / Matti Ilmonen / Vastaukset kysymyspapereille. 0pisk.
 Tentti La 20.01.2001 / Matti Ilmonen / Vastaukset kysymyspapereille. Nirni: Nimen selvennys : 1 2 3 4 5 z -.. 0pisk.no: ARVOSANA 1. Selvita lyhyesti seuraavat kiitteet ( kohdat a... j ) a) Kokosummain?
Tentti La 20.01.2001 / Matti Ilmonen / Vastaukset kysymyspapereille. Nirni: Nimen selvennys : 1 2 3 4 5 z -.. 0pisk.no: ARVOSANA 1. Selvita lyhyesti seuraavat kiitteet ( kohdat a... j ) a) Kokosummain?
Oppikirjan harjoitustehtävien ratkaisuja
 Sivu (27) 26.2.2 e 7 Muistipiirit 7- Tietokoneen muistin koko on 256 K 6 b. Montako sanaa muistissa on? Mikä on sen sananpituus? Montako muistialkiota muistissa on? Muistissa on 256 kibisanaa eli 262 44
Sivu (27) 26.2.2 e 7 Muistipiirit 7- Tietokoneen muistin koko on 256 K 6 b. Montako sanaa muistissa on? Mikä on sen sananpituus? Montako muistialkiota muistissa on? Muistissa on 256 kibisanaa eli 262 44
Digitaalilaitteen signaalit
 Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä
Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä
Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset
 Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset Metropolia/AK. Mealyn koneessa on kolme tulosignaalia, joista yksi vaikuttaa pelkästään lähtösignaaleihin, yksi pelkästään koneen tilaan ja yksi
Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset Metropolia/AK. Mealyn koneessa on kolme tulosignaalia, joista yksi vaikuttaa pelkästään lähtösignaaleihin, yksi pelkästään koneen tilaan ja yksi
Digitaalitekniikan matematiikka Luku 6 Sivu 1 (20) Kombinaatiopiirit & & A B A + B
 igitaalitekniikan matematiikka Luku 6 Sivu (20).9.20 e 0 0 0 0 0 + 0 0 0 0 0 0 0 igitaalitekniikan matematiikka Luku 6 Sivu 2 (20).9.20 e Johdanto Tässä luvussa esitellään porttipiirityypit J-EI ja TI-EI
igitaalitekniikan matematiikka Luku 6 Sivu (20).9.20 e 0 0 0 0 0 + 0 0 0 0 0 0 0 igitaalitekniikan matematiikka Luku 6 Sivu 2 (20).9.20 e Johdanto Tässä luvussa esitellään porttipiirityypit J-EI ja TI-EI
Yhden bitin tiedot. Digitaalitekniikan matematiikka Luku 1 Täsmätehtävä Tehtävä 1. Luettele esimerkkejä yhden bitin tiedoista.
 Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista. Ovi auki - ovi kiinni Virta kulkee - virta ei kulje Lamppu palaa - lamppu ei pala
Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista. Ovi auki - ovi kiinni Virta kulkee - virta ei kulje Lamppu palaa - lamppu ei pala
Digitaalitekniikan matematiikka Luku 3 Sivu 1 (19) Kytkentäfunktiot ja perusporttipiirit
 Digitaalitekniikan matematiikka Luku 3 Sivu (9) && Digitaalitekniikan matematiikka Luku 3 Sivu 2 (9) Johdanto Tässä luvussa esitetään digitaalilaitteen signaalit ja digitaalipiirien perustyypit esitellään
Digitaalitekniikan matematiikka Luku 3 Sivu (9) && Digitaalitekniikan matematiikka Luku 3 Sivu 2 (9) Johdanto Tässä luvussa esitetään digitaalilaitteen signaalit ja digitaalipiirien perustyypit esitellään
ELEC-C3240 Elektroniikka 2
 ELEC-C324 Elektroniikka 2 Marko Kosunen Marko.kosunen@aalto.fi Digitaalielektroniikka Tilakoneet Materiaali perustuu kurssiins-88. Digitaalitekniikan perusteet, laatinut Antti Ojapelto Luennon oppimistavoite
ELEC-C324 Elektroniikka 2 Marko Kosunen Marko.kosunen@aalto.fi Digitaalielektroniikka Tilakoneet Materiaali perustuu kurssiins-88. Digitaalitekniikan perusteet, laatinut Antti Ojapelto Luennon oppimistavoite
Harjoitustehtävien ratkaisut
 Sivu (22) 29.8.2 Fe/Ko Luku Sekvenssipiirit. Tutki luentokalvo- ja opetusmonisteessa esitettyä esimerkkiä synkronisesta sekvenssipiiristä. a) Montako tilaa piirissä on? Koska piirissä on kaksi tilasignaalia,
Sivu (22) 29.8.2 Fe/Ko Luku Sekvenssipiirit. Tutki luentokalvo- ja opetusmonisteessa esitettyä esimerkkiä synkronisesta sekvenssipiiristä. a) Montako tilaa piirissä on? Koska piirissä on kaksi tilasignaalia,
Kombinatorisen logiikan laitteet
 Kombinatorisen logiikan laitteet Kombinatorinen logiikka tarkoittaa logiikkaa, jossa signaali kulkee suoraan sisääntuloista ulostuloon Sekventiaalisessa logiikassa myös aiemmat syötteet vaikuttavat ulostuloon
Kombinatorisen logiikan laitteet Kombinatorinen logiikka tarkoittaa logiikkaa, jossa signaali kulkee suoraan sisääntuloista ulostuloon Sekventiaalisessa logiikassa myös aiemmat syötteet vaikuttavat ulostuloon
Synkronisten sekvenssipiirien suunnittelu
 Digitaalitekniikka (piirit) Luku 6 Sivu (5) Synkronisten sekvenssipiirien suunnittelu.8.24 Fe/AKo Synkronisten sekvenssipiirien suunnittelu Digitaalitekniikka (piirit) Luku 6 Sivu 2 (5) Synkronisten sekvenssipiirien
Digitaalitekniikka (piirit) Luku 6 Sivu (5) Synkronisten sekvenssipiirien suunnittelu.8.24 Fe/AKo Synkronisten sekvenssipiirien suunnittelu Digitaalitekniikka (piirit) Luku 6 Sivu 2 (5) Synkronisten sekvenssipiirien
BL40A1711 Johdanto digitaaleketroniikkaan: Sekvenssilogiikka, pitopiirit ja kiikut
 BL40A1711 Johdanto digitaaleketroniikkaan: Sekvenssilogiikka, pitopiirit ja kiikut Sekvenssilogiikka Kombinatooristen logiikkapiirien lähtömuuttujien nykyiset tilat y i (n) ovat pelkästään riippuvaisia
BL40A1711 Johdanto digitaaleketroniikkaan: Sekvenssilogiikka, pitopiirit ja kiikut Sekvenssilogiikka Kombinatooristen logiikkapiirien lähtömuuttujien nykyiset tilat y i (n) ovat pelkästään riippuvaisia
Digitaalitekniikan matematiikka Luku 5 Sivu 1 (22) Lausekkeiden sieventäminen F C F = B + A C. Espresso F = A (A + B) = A A + A B = A B
 igitaalitekniikan matematiikka Luku 5 Sivu (22).9.2 e = + = ( + ) = + = Espresso igitaalitekniikan matematiikka Luku 5 Sivu 2 (22).9.2 e Johdanto Tässä luvussa esitetään perusteet lausekemuodossa esitettyjen
igitaalitekniikan matematiikka Luku 5 Sivu (22).9.2 e = + = ( + ) = + = Espresso igitaalitekniikan matematiikka Luku 5 Sivu 2 (22).9.2 e Johdanto Tässä luvussa esitetään perusteet lausekemuodossa esitettyjen
AUTO3030 Digitaalitekniikan jatkokurssi, harjoitus 2, ratkaisuja
 AUTO3030 Digitaalitekniikan jatkokurssi, harjoitus 2, ratkaisuja s2009 1. D-kiikku Toteuta DE2:lla synkroninen laskukone, jossa lasketaan kaksi nelibittistä lukua yhteen. Tulos esitetään ledeillä vasta,
AUTO3030 Digitaalitekniikan jatkokurssi, harjoitus 2, ratkaisuja s2009 1. D-kiikku Toteuta DE2:lla synkroninen laskukone, jossa lasketaan kaksi nelibittistä lukua yhteen. Tulos esitetään ledeillä vasta,
Yhden bitin tiedot. Binaariluvun arvon laskeminen. Koodin bittimäärä ja vaihtoehdot ? 1
 Luku Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Opetuskerta Sivu Luku Opetuskerta Sivu Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista.
Luku Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Opetuskerta Sivu Luku Opetuskerta Sivu Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista.
Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena
 Mikrotietokone Moderni tietokone Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena Sen käyttötarkoitus on yleensä työnteko, kissavideoiden katselu internetistä tai pelien pelaaminen. Tietokoneen
Mikrotietokone Moderni tietokone Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena Sen käyttötarkoitus on yleensä työnteko, kissavideoiden katselu internetistä tai pelien pelaaminen. Tietokoneen
C = P Q S = P Q + P Q = P Q. Laskutoimitukset binaariluvuilla P -- Q = P + (-Q) (-Q) P Q C in. C out
 Digitaalitekniikan matematiikka Luku ivu (2).9.2 Fe C = Aseta Aseta i i = n i > i i i Ei i < i i i Ei i i = Ei i i = i i -- On On On C in > < = CI CO C out -- = + (-) (-) = + = C + Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku ivu (2).9.2 Fe C = Aseta Aseta i i = n i > i i i Ei i < i i i Ei i i = Ei i i = i i -- On On On C in > < = CI CO C out -- = + (-) (-) = + = C + Digitaalitekniikan matematiikka
T clk > t DFF + t critical + t setup -> T clk > 3 ns + (2+2) ns + 2 ns > 9 ns -> F clk < MHz. t DFF t critical t setup CLK NA1 CLK2,CLK3 Q2,D3
 . a) Kriittisen polun mukaan (DFF - DFF): (DFF = D Flip-Flop = D-kiikku) T clk > t DFF t critical t setup -> T clk > ns () ns ns > 9 ns -> F clk
. a) Kriittisen polun mukaan (DFF - DFF): (DFF = D Flip-Flop = D-kiikku) T clk > t DFF t critical t setup -> T clk > ns () ns ns > 9 ns -> F clk
Inputs: b; x= b 010. x=0. Elektroniikkajärjestelmät ETT_2068
 Elektroniikkajärjestelmät ETT_2068 tentti 1) Oheisessa sekvenssilogiikassa tiloille on jo annettu bittivaste 000, 001 jne. Tehtävänäsi on nyt konstruoda sekvenssilogiikka vaihe vaiheelta standarditavalla.
Elektroniikkajärjestelmät ETT_2068 tentti 1) Oheisessa sekvenssilogiikassa tiloille on jo annettu bittivaste 000, 001 jne. Tehtävänäsi on nyt konstruoda sekvenssilogiikka vaihe vaiheelta standarditavalla.
Digitaalitekniikan perusteet
 HAMK Riihimäki Versio 1.0 Väinö Suhonen Digitaalitekniikan perusteet Loogiset funktiot ja portit Kombinaatiologiikan elimiä Rekisterilogiikan perusteet Rekisteri- ja sekvenssilogiikan elimiä ena up/ down
HAMK Riihimäki Versio 1.0 Väinö Suhonen Digitaalitekniikan perusteet Loogiset funktiot ja portit Kombinaatiologiikan elimiä Rekisterilogiikan perusteet Rekisteri- ja sekvenssilogiikan elimiä ena up/ down
OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012
 OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012 Luento 6: Tiedon esittäminen tietokoneessa, osa 1 Tekijät: Antti Virtanen, Timo Lehtonen, Matti Kujala, Kirsti Ala-Mutka, Petri M. Gerdt et al. Luennon
OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012 Luento 6: Tiedon esittäminen tietokoneessa, osa 1 Tekijät: Antti Virtanen, Timo Lehtonen, Matti Kujala, Kirsti Ala-Mutka, Petri M. Gerdt et al. Luennon
Digitaalitekniikka (piirit) Luku 14 Sivu 1 (16) Sekvenssipiirit. Kombinaatiopiiri. Tilarekisteri
 Digitaalitekniikka (piirit) Luku 4 Sivu (6).8.24 Fe/AKo Tilarekisteri Kombinaatiopiiri Digitaalitekniikka (piirit) Luku 4 Sivu 2 (6).8.24 Fe/AKo Johdanto Tässä luvussa todetaan esimerkin avulla kombinaatiopiirien
Digitaalitekniikka (piirit) Luku 4 Sivu (6).8.24 Fe/AKo Tilarekisteri Kombinaatiopiiri Digitaalitekniikka (piirit) Luku 4 Sivu 2 (6).8.24 Fe/AKo Johdanto Tässä luvussa todetaan esimerkin avulla kombinaatiopiirien
Kerta 2. Kerta 2 Kerta 3 Kerta 4 Kerta 5. 1. Toteuta Pythonilla seuraava ohjelma:
 Kerta 2 Kerta 3 Kerta 4 Kerta 5 Kerta 2 1. Toteuta Pythonilla seuraava ohjelma: 2. Tulosta Pythonilla seuraavat luvut allekkain a. 0 10 (eli, näyttää tältä: 0 1 2 3 4 5 6 7 8 9 10 b. 0 100 c. 50 100 3.
Kerta 2 Kerta 3 Kerta 4 Kerta 5 Kerta 2 1. Toteuta Pythonilla seuraava ohjelma: 2. Tulosta Pythonilla seuraavat luvut allekkain a. 0 10 (eli, näyttää tältä: 0 1 2 3 4 5 6 7 8 9 10 b. 0 100 c. 50 100 3.
Ongelma(t): Miten tietokoneen komponentteja voi ohjata siten, että ne tekevät yhdessä jotakin järkevää? Voiko tietokonetta ohjata (ohjelmoida) siten,
 Ongelma(t): Miten tietokoneen komponentteja voi ohjata siten, että ne tekevät yhdessä jotakin järkevää? Voiko tietokonetta ohjata (ohjelmoida) siten, että se pystyy suorittamaan kaikki mahdolliset algoritmit?
Ongelma(t): Miten tietokoneen komponentteja voi ohjata siten, että ne tekevät yhdessä jotakin järkevää? Voiko tietokonetta ohjata (ohjelmoida) siten, että se pystyy suorittamaan kaikki mahdolliset algoritmit?
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 2. Lukujen esittäminen ja aritmetiikka 2.1 Kantajärjestelmät ja lukujen esittäminen Käytettävät lukujoukot: Luonnolliset luvut IN = {0,1,2,3,... } Positiiviset kokonaisluvut
811120P Diskreetit rakenteet 2016-2017 2. Lukujen esittäminen ja aritmetiikka 2.1 Kantajärjestelmät ja lukujen esittäminen Käytettävät lukujoukot: Luonnolliset luvut IN = {0,1,2,3,... } Positiiviset kokonaisluvut
SISÄLLYS - DIGITAALITEKNIIKKA
 SISÄLLYS - DIGITAALITEKNIIKKA Digitaalitekniikan perusteita...2 Bitti (bit)...2 Tavu (bytes)...2 Sana (word)...2 Yksiköt...2 Binääri järjestelmän laskutapa...2 Esimerkki: Digikuvan siirron kestoaika...2
SISÄLLYS - DIGITAALITEKNIIKKA Digitaalitekniikan perusteita...2 Bitti (bit)...2 Tavu (bytes)...2 Sana (word)...2 Yksiköt...2 Binääri järjestelmän laskutapa...2 Esimerkki: Digikuvan siirron kestoaika...2
Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) Kytkentäalgebra A + 1 = 1 A = A A + B C = (A + B) (A + C) A 0 = 0. Maksimitermi.
 Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) A + 1 = 1 A + B C = (A + B) (A + C) F(A, B, C) = Σ m (2, 3, 5, 7) Maksimitermi A = A m0 A 0 = 0 M7 A + B = A B Minimitermi Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) A + 1 = 1 A + B C = (A + B) (A + C) F(A, B, C) = Σ m (2, 3, 5, 7) Maksimitermi A = A m0 A 0 = 0 M7 A + B = A B Minimitermi Digitaalitekniikan matematiikka
Diskreetin matematiikan perusteet Malliratkaisut 2 / vko 38
 Diskreetin matematiikan perusteet Malliratkaisut 2 / vko 38 Tuntitehtävät 11-12 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 15-16 loppuviikon harjoituksissa. Kotitehtävät 13-14 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Malliratkaisut 2 / vko 38 Tuntitehtävät 11-12 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 15-16 loppuviikon harjoituksissa. Kotitehtävät 13-14 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Harjoitustehtäväkierros 1
 T-06.50 kurssihenkilökunta deadline Tiistai 20.0.2009 2:5 Johdanto Tämä tehtäväkierros käsittelee pääasiassa toisen luennon sisältöä. Harjoituksia saa tehdä yksin tai yhdessä. Yhdessä tekeminen on suositeltavaa,
T-06.50 kurssihenkilökunta deadline Tiistai 20.0.2009 2:5 Johdanto Tämä tehtäväkierros käsittelee pääasiassa toisen luennon sisältöä. Harjoituksia saa tehdä yksin tai yhdessä. Yhdessä tekeminen on suositeltavaa,
1. Mikä on lukujen 10, 9, 8,..., 9, 10 summa? 2. Mikä on lukujen 10, 9, 8,..., 9, 10 tulo? =?
 Tehtävät 1 1. Mikä on lukujen 10, 9, 8,..., 9, 10 summa? 2. Mikä on lukujen 10, 9, 8,..., 9, 10 tulo? 3. 16 125 250 =? 4. Kirjoita lausekkeeseen sulut siten, että tulos on nolla. 2 + 2 2 2 : 2 + 2 2 2
Tehtävät 1 1. Mikä on lukujen 10, 9, 8,..., 9, 10 summa? 2. Mikä on lukujen 10, 9, 8,..., 9, 10 tulo? 3. 16 125 250 =? 4. Kirjoita lausekkeeseen sulut siten, että tulos on nolla. 2 + 2 2 2 : 2 + 2 2 2
Kappale 20: Kantaluvut
 Kappale 20: Kantaluvut 20 Johdanto: Kantaluvut... 328 Kantalukujen syöttäminen ja muuntaminen... 329 Matemaattiset toiminnot Hex- ja Bin-luvuilla... 330 Bittien vertaileminen ja manipulointi... 331 Huom!
Kappale 20: Kantaluvut 20 Johdanto: Kantaluvut... 328 Kantalukujen syöttäminen ja muuntaminen... 329 Matemaattiset toiminnot Hex- ja Bin-luvuilla... 330 Bittien vertaileminen ja manipulointi... 331 Huom!
ASM-kaavio: reset. b c d e f g. 00 abcdef. naytto1. clk. 01 bc. reset. 10 a2. abdeg. 11 a3. abcdg
 Digitaalitekniikka (piirit) Metropolia / AKo Pikku nnitteluharjoitus: Suunnitellaan sekvenssipiiri, jolla saadaan numerot juoksemaan seitsensegmenttinäytöllä: VHDL-koodin generointi ASM-kaavioista Tässä
Digitaalitekniikka (piirit) Metropolia / AKo Pikku nnitteluharjoitus: Suunnitellaan sekvenssipiiri, jolla saadaan numerot juoksemaan seitsensegmenttinäytöllä: VHDL-koodin generointi ASM-kaavioista Tässä
(0 1) 010(0 1) Koska kieli on yksinkertainen, muodostetaan sen tunnistava epädeterministinen q 0 q 1 q 2 q3
 T-79.48 Tietojenkäsittelyteorian perusteet Tentti 25..23 mallivastaukset. Tehtävä: Kuvaa seuraavat kielet sekä säännölisten lausekkeiden että determinististen äärellisten automaattien avulla: (a) L = {w
T-79.48 Tietojenkäsittelyteorian perusteet Tentti 25..23 mallivastaukset. Tehtävä: Kuvaa seuraavat kielet sekä säännölisten lausekkeiden että determinististen äärellisten automaattien avulla: (a) L = {w
SGN-1200 Signaalinkäsittelyn menetelmät Välikoe
 SGN-00 Signaalinkäsittelyn menetelmät Välikoe 9.3.009 Sivuilla - on. Älä vastaa siihen, jos et ollut ensimmäisessä välikokeessa. Tentin kysymykset ovat sivuilla 3-4. Vastaa vain jompaan kumpaan kokeeseen,
SGN-00 Signaalinkäsittelyn menetelmät Välikoe 9.3.009 Sivuilla - on. Älä vastaa siihen, jos et ollut ensimmäisessä välikokeessa. Tentin kysymykset ovat sivuilla 3-4. Vastaa vain jompaan kumpaan kokeeseen,
DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU
 OPINNÄYTETYÖ - AMMATTIKORKEAKOULUTUTKINTO TEKNIIKAN JA LIIKENTEEN ALA DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU T E K I J Ä : Toni Halonen SAVONIA-AMMATTIKORKEAKOULU OPINNÄYTETYÖ
OPINNÄYTETYÖ - AMMATTIKORKEAKOULUTUTKINTO TEKNIIKAN JA LIIKENTEEN ALA DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU T E K I J Ä : Toni Halonen SAVONIA-AMMATTIKORKEAKOULU OPINNÄYTETYÖ
MAB Jussi Tyni. Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista kirjoittaa nimesi. Kysymyspaperin saa pitää.
 MAB6. 014 Jussi Tyni Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista kirjoittaa nimesi. Kysymyspaperin saa pitää. A-OSIO: Ei saa käyttää laskinta. MAOL saa olla esillä. Maksimissaan
MAB6. 014 Jussi Tyni Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista kirjoittaa nimesi. Kysymyspaperin saa pitää. A-OSIO: Ei saa käyttää laskinta. MAOL saa olla esillä. Maksimissaan
Lue tehtävänannot huolella. Tee pisteytysruudukko 1. konseptin yläreunaan. ILMAN LASKINTA -OSIO! LASKE KAIKKI SEURAAVAT TEHTÄVÄT:
 MAA Koe 8.1.014 Arto Hekkanen ja Jussi Tyni Lue tehtävänannot huolella. Tee pisteytysruudukko 1. konseptin yläreunaan. ILMAN LASKINTA -OSIO! LASKE KAIKKI SEURAAVAT TEHTÄVÄT: 1. a) Laske polynomien x x
MAA Koe 8.1.014 Arto Hekkanen ja Jussi Tyni Lue tehtävänannot huolella. Tee pisteytysruudukko 1. konseptin yläreunaan. ILMAN LASKINTA -OSIO! LASKE KAIKKI SEURAAVAT TEHTÄVÄT: 1. a) Laske polynomien x x
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008
 Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008 Kilpailijan nimi: 1) Oheisen kytkennän kokonaisresistanssi on n. 33 Ohm 150 Ohm a) 70 Ohmia b) 100 Ohmia c) 120 Ohmia 120 Ohm 2) Oheisen kytkennän
Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008 Kilpailijan nimi: 1) Oheisen kytkennän kokonaisresistanssi on n. 33 Ohm 150 Ohm a) 70 Ohmia b) 100 Ohmia c) 120 Ohmia 120 Ohm 2) Oheisen kytkennän
Se mistä tilasta aloitetaan, merkitään tyhjästä tulevalla nuolella. Yllä olevassa esimerkissä aloitustila on A.
 Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
1. Osoita, että joukon X osajoukoille A ja B on voimassa toinen ns. de Morganin laki (A B) = A B.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset
 Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
Digitaalitekniikka (piirit) Luku 18 Sivu 1 (32) Rekisterit ja laskurit R C1 SRG4 R C1/ CTRDIV16 1R G2 2CT=15 G3 C1/2,3 + CT 3
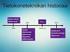 Digitaalitekniikka (piirit) Luku 8 Sivu (32) R C D SRG4 R C/ D CTRDIV6 R G2 2CT=5 G3 C/2,3 + CT 3 Digitaalitekniikka (piirit) Luku 8 Sivu 2 (32) Johdanto Tässä luvussa esitellään keskeiset salpoja ja kiikkuja
Digitaalitekniikka (piirit) Luku 8 Sivu (32) R C D SRG4 R C/ D CTRDIV6 R G2 2CT=5 G3 C/2,3 + CT 3 Digitaalitekniikka (piirit) Luku 8 Sivu 2 (32) Johdanto Tässä luvussa esitellään keskeiset salpoja ja kiikkuja
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Taitaja2005/Elektroniikka. 1) Resistanssien sarjakytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden rinnankytkentä
 1) Resistanssien sarjakytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden rinnankytkentä 2) Kahdesta rinnankytketystä sähkölähteestä a) kuormittuu enemmän se, kummalla on
1) Resistanssien sarjakytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden rinnankytkentä 2) Kahdesta rinnankytketystä sähkölähteestä a) kuormittuu enemmän se, kummalla on
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon
 Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä
 Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Käy vastaamassa kyselyyn kurssin pedanet-sivulla (TÄRKEÄ ensi vuotta ajatellen) Kurssin suorittaminen ja arviointi: vähintään 50 tehtävää tehtynä (vihkon palautus kokeeseen tullessa) Koe Mahdolliset testit
Sekvenssipiirin tilat. Synkroninen sekvenssipiiri ? 1 ? 2
 Luku igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AKo igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AK Opetuskerta Sivu 4 Luku Opetuskerta Sivu Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan
Luku igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AKo igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AK Opetuskerta Sivu 4 Luku Opetuskerta Sivu Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan
A/D-muuntimia. Flash ADC
 A/D-muuntimia A/D-muuntimen valintakriteerit: - bittien lukumäärä instrumentointi 6 16 audio/video/kommunikointi/ym. 16 18 erikoissovellukset 20 22 - Tarvittava nopeus hidas > 100 μs (
A/D-muuntimia A/D-muuntimen valintakriteerit: - bittien lukumäärä instrumentointi 6 16 audio/video/kommunikointi/ym. 16 18 erikoissovellukset 20 22 - Tarvittava nopeus hidas > 100 μs (
815338A Ohjelmointikielten periaatteet Harjoitus 2 vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
Paavo Räisänen. Ohjelmoijan binaarialgebra ja heksaluvut. www.ohjelmoimaan.net
 Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoimaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoimaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 18.3.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 18.3.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
OPERAATIOVAHVISTIN. Oulun seudun ammattikorkeakoulu Tekniikan yksikkö. Elektroniikan laboratoriotyö. Työryhmä Selostuksen kirjoitti 11.11.
 Oulun seudun ammattikorkeakoulu Tekniikan yksikkö Elektroniikan laboratoriotyö OPERAATIOVAHVISTIN Työryhmä Selostuksen kirjoitti 11.11.008 Kivelä Ari Tauriainen Tommi Tauriainen Tommi 1 TEHTÄVÄ Tutustuimme
Oulun seudun ammattikorkeakoulu Tekniikan yksikkö Elektroniikan laboratoriotyö OPERAATIOVAHVISTIN Työryhmä Selostuksen kirjoitti 11.11.008 Kivelä Ari Tauriainen Tommi Tauriainen Tommi 1 TEHTÄVÄ Tutustuimme
Käytännön logiikkapiirit ja piirrosmerkit
 Digitaalitekniikan matematiikka Luku 7 Sivu (27) EN 2 EN X/Y X/Y 0 2 3 2 EN X/Y X/Y 0 2 3 Digitaalitekniikan matematiikka Luku 7 Sivu 2 (27) Johdanto Tässä luvussa esitellään käsitteet logiikkaperhe ja
Digitaalitekniikan matematiikka Luku 7 Sivu (27) EN 2 EN X/Y X/Y 0 2 3 2 EN X/Y X/Y 0 2 3 Digitaalitekniikan matematiikka Luku 7 Sivu 2 (27) Johdanto Tässä luvussa esitellään käsitteet logiikkaperhe ja
Ehto- ja toistolauseet
 Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
Sähkötekniikan perusteet
 Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Verilogvs. VHDL. Janne Koljonen University of Vaasa
 Verilogvs. VHDL Janne Koljonen University of Vaasa Sälää Huom! Verilogistauseita versioita: 1995, 2001 ja 2005. Kommentit Javasta tutut // ja /* */ ovat kommenttimerkkejä. Case sensitivity Isot ja pienet
Verilogvs. VHDL Janne Koljonen University of Vaasa Sälää Huom! Verilogistauseita versioita: 1995, 2001 ja 2005. Kommentit Javasta tutut // ja /* */ ovat kommenttimerkkejä. Case sensitivity Isot ja pienet
MATEMATIIKKA. Matematiikkaa pintakäsittelijöille. Ongelmanratkaisu. Isto Jokinen 2017
 MATEMATIIKKA Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017 SISÄLTÖ 1. Matemaattisten ongelmien ratkaisu laskukaavoilla 2. Tekijäyhtälöt 3. Laskukaavojen yhdistäminen 4. Yhtälöiden
MATEMATIIKKA Matematiikkaa pintakäsittelijöille Ongelmanratkaisu Isto Jokinen 2017 SISÄLTÖ 1. Matemaattisten ongelmien ratkaisu laskukaavoilla 2. Tekijäyhtälöt 3. Laskukaavojen yhdistäminen 4. Yhtälöiden
2.3 Juurien laatu. Juurien ja kertoimien väliset yhtälöt. Jako tekijöihin. b b 4ac = 2
 .3 Juurien laatu. Juurien ja kertoimien väliset yhtälöt. Jako tekijöihin. Toisen asteen yhtälön a + b + c 0 ratkaisukaavassa neliöjuuren alla olevaa lauseketta b b 4ac + a b b 4ac a D b 4 ac sanotaan yhtälön
.3 Juurien laatu. Juurien ja kertoimien väliset yhtälöt. Jako tekijöihin. Toisen asteen yhtälön a + b + c 0 ratkaisukaavassa neliöjuuren alla olevaa lauseketta b b 4ac + a b b 4ac a D b 4 ac sanotaan yhtälön
Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, sekä voi olla apua.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
Vektoreiden virittämä aliavaruus
 Vektoreiden virittämä aliavaruus Määritelmä Oletetaan, että v 1, v 2,... v k R n. Näiden vektoreiden virittämä aliavaruus span( v 1, v 2,... v k ) tarkoittaa kyseisten vektoreiden kaikkien lineaarikombinaatioiden
Vektoreiden virittämä aliavaruus Määritelmä Oletetaan, että v 1, v 2,... v k R n. Näiden vektoreiden virittämä aliavaruus span( v 1, v 2,... v k ) tarkoittaa kyseisten vektoreiden kaikkien lineaarikombinaatioiden
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 5.5.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 5.5.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
MAA9.2 2014 Jussi Tyni Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista kirjoittaa nimesi. Kysymyspaperin saa pitää.
 MAA9. 014 Jussi Tyni Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista kirjoittaa nimesi. Kysymyspaperin saa pitää. A-OSIO: Ei saa käyttää laskinta. MAOL saa olla esillä. Maksimissaan
MAA9. 014 Jussi Tyni Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista kirjoittaa nimesi. Kysymyspaperin saa pitää. A-OSIO: Ei saa käyttää laskinta. MAOL saa olla esillä. Maksimissaan
-Matematiikka on aksiomaattinen järjestelmä. -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi
 -Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
-Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
c) 22a 21b x + a 2 3a x 1 = a,
 Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. 1. Lukion A ja lukion B oppilasmäärien suhde oli a/b vuoden 2017 lopussa. Vuoden 2017 aikana
Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. 1. Lukion A ja lukion B oppilasmäärien suhde oli a/b vuoden 2017 lopussa. Vuoden 2017 aikana
Digitaalitekniikka (piirit) Luku 15 Sivu 1 (17) Salvat ja kiikut 1D C1 C1 1T 1J C1 1K S R
 igitaalitekniikka (piirit) Luku 5 ivu (7).8.24 Fe/AKo C J C K C T C C J C K igitaalitekniikka (piirit) Luku 5 ivu 2 (7).8.24 Fe/AKo Johdanto Tässä luvussa esitetään salpapiirit, jotka ovat yksinkertaisimpia
igitaalitekniikka (piirit) Luku 5 ivu (7).8.24 Fe/AKo C J C K C T C C J C K igitaalitekniikka (piirit) Luku 5 ivu 2 (7).8.24 Fe/AKo Johdanto Tässä luvussa esitetään salpapiirit, jotka ovat yksinkertaisimpia
Flash AD-muunnin. Ominaisuudet. +nopea -> voidaan käyttää korkeataajuuksisen signaalin muuntamiseen (GHz) +yksinkertainen
 Flash AD-muunnin Koostuu vastusverkosta ja komparaattoreista. Komparaattorit vertailevat vastuksien jännitteitä referenssiin. Tilanteesta riippuen kompraattori antaa ykkösen tai nollan ja näistä kootaan
Flash AD-muunnin Koostuu vastusverkosta ja komparaattoreista. Komparaattorit vertailevat vastuksien jännitteitä referenssiin. Tilanteesta riippuen kompraattori antaa ykkösen tai nollan ja näistä kootaan
Python-ohjelmointi Harjoitus 5
 Python-ohjelmointi Harjoitus 5 TAVOITTEET Kerrataan silmukkarakenteen käyttäminen. Kerrataan jos-ehtorakenteen käyttäminen. Opitaan if else- ja if elif else-ehtorakenteet. Matematiikan sisällöt Tehtävät
Python-ohjelmointi Harjoitus 5 TAVOITTEET Kerrataan silmukkarakenteen käyttäminen. Kerrataan jos-ehtorakenteen käyttäminen. Opitaan if else- ja if elif else-ehtorakenteet. Matematiikan sisällöt Tehtävät
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset
 815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
Signaalien datamuunnokset. Näytteenotto ja pito -piirit
 Signaalien datamuunnokset Muunnoskomponentit Näytteenotto ja pitopiirit Multiplekserit A/D-muuntimet Jännitereferenssit D/A-muuntimet Petri Kärhä 26/02/2008 Signaalien datamuunnokset 1 Näytteenotto ja
Signaalien datamuunnokset Muunnoskomponentit Näytteenotto ja pitopiirit Multiplekserit A/D-muuntimet Jännitereferenssit D/A-muuntimet Petri Kärhä 26/02/2008 Signaalien datamuunnokset 1 Näytteenotto ja
Ohjelmoijan binaarialgebra ja heksaluvut
 Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoinaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoinaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Alkuarvot ja tyyppimuunnokset (1/5) Alkuarvot ja tyyppimuunnokset (2/5) Alkuarvot ja tyyppimuunnokset (3/5)
 Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Harjoitustyön 2 aiheiden kuvaukset
 Sivu 1 (5) 1 Raitiovaunun oven avaamis- ja sulkemispiiri Raitiovaunun oven vieressä on matkustajan avauspainike. Kun vaunu on paikallaan, matkustajan avauspainikkeen painaminen antaa signaalin, joka avaa
Sivu 1 (5) 1 Raitiovaunun oven avaamis- ja sulkemispiiri Raitiovaunun oven vieressä on matkustajan avauspainike. Kun vaunu on paikallaan, matkustajan avauspainikkeen painaminen antaa signaalin, joka avaa
ELEC-C5070 Elektroniikkapaja (5 op)
 (5 op) Luento 5 A/D- ja D/A-muunnokset ja niiden vaikutus signaaleihin Signaalin A/D-muunnos Analogia-digitaalimuunnin (A/D-muunnin) muuttaa analogisen signaalin digitaaliseen muotoon, joka voidaan lukea
(5 op) Luento 5 A/D- ja D/A-muunnokset ja niiden vaikutus signaaleihin Signaalin A/D-muunnos Analogia-digitaalimuunnin (A/D-muunnin) muuttaa analogisen signaalin digitaaliseen muotoon, joka voidaan lukea
Digitaalitekniikka (piirit) Metropolia / AKo Joitakin vinkkejä harjoitustyö 2:n aihesiin Aihe Tuloja Lähtöjä Sitten vinkkejä
 Digitaalitekniikka (piirit) Joitakin vinkkejä harjoitustyö 2:n aihesiin Metropolia / AKo Sille ei voi mitään, että jotkut harjoitustyöaiheet ovat vaikeammin lähestyttäviä kuin jotkut muut. Siltä varalta,
Digitaalitekniikka (piirit) Joitakin vinkkejä harjoitustyö 2:n aihesiin Metropolia / AKo Sille ei voi mitään, että jotkut harjoitustyöaiheet ovat vaikeammin lähestyttäviä kuin jotkut muut. Siltä varalta,
6. Analogisen signaalin liittäminen mikroprosessoriin 2 6.1 Näytteenotto analogisesta signaalista 2 6.2. DA-muuntimet 4
 Datamuuntimet 1 Pekka antala 19.11.2012 Datamuuntimet 6. Analogisen signaalin liittäminen mikroprosessoriin 2 6.1 Näytteenotto analogisesta signaalista 2 6.2. DA-muuntimet 4 7. AD-muuntimet 5 7.1 Analoginen
Datamuuntimet 1 Pekka antala 19.11.2012 Datamuuntimet 6. Analogisen signaalin liittäminen mikroprosessoriin 2 6.1 Näytteenotto analogisesta signaalista 2 6.2. DA-muuntimet 4 7. AD-muuntimet 5 7.1 Analoginen
Fourier-analyysi, I/19-20, Mallivastaukset, Laskuharjoitus 7
 MS-C14, Fourier-analyysi, I/19- Fourier-analyysi, I/19-, Mallivastaukset, Laskuharjoitus 7 Harjoitustehtävä 7.1. Hetkellä t R olkoon s(t) 1 + cos(4πt) + sin(6πt). Laske tämän 1-periodisen signaalin s Fourier-kertoimet
MS-C14, Fourier-analyysi, I/19- Fourier-analyysi, I/19-, Mallivastaukset, Laskuharjoitus 7 Harjoitustehtävä 7.1. Hetkellä t R olkoon s(t) 1 + cos(4πt) + sin(6πt). Laske tämän 1-periodisen signaalin s Fourier-kertoimet
(a) Kyllä. Jokainen lähtöjoukon alkio kuvautuu täsmälleen yhteen maalijoukon alkioon.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 015 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I Seuraavat tehtävät liittyvät kuvauksiin. 1. Merkitään X = {1,,, 4}. Ovatko seuraavat säännöt
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 015 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I Seuraavat tehtävät liittyvät kuvauksiin. 1. Merkitään X = {1,,, 4}. Ovatko seuraavat säännöt
815338A Ohjelmointikielten periaatteet Harjoitus 6 Vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
SGN Signaalinkäsittelyn perusteet Välikoe Heikki Huttunen
 SGN- Signaalinkäsittelyn perusteet Välikoe.5.4 Heikki Huttunen Tentissä ja välikokeessa saa käyttää vain tiedekunnan laskinta. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla -3 on. Sivuilla 4-5 on. Sivulla
SGN- Signaalinkäsittelyn perusteet Välikoe.5.4 Heikki Huttunen Tentissä ja välikokeessa saa käyttää vain tiedekunnan laskinta. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla -3 on. Sivuilla 4-5 on. Sivulla
Varauspumppu-PLL. Taulukko 1: ulostulot sisääntulojen funktiona
 Varauspumppu-PLL Vaihevertailija vertaa kelloreunoja aikatasossa. Jos sisääntulo A:n taajuus on korkeampi tai vaihe edellä verrattuna sisääntulo B:hen, ulostulo A on ylhäällä ja ulostulo B alhaalla ja
Varauspumppu-PLL Vaihevertailija vertaa kelloreunoja aikatasossa. Jos sisääntulo A:n taajuus on korkeampi tai vaihe edellä verrattuna sisääntulo B:hen, ulostulo A on ylhäällä ja ulostulo B alhaalla ja
Python-ohjelmointi Harjoitus 2
 Python-ohjelmointi Harjoitus 2 TAVOITTEET Kerrataan tulostuskomento ja lukumuotoisen muuttujan muuttaminen merkkijonoksi. Opitaan jakojäännös eli modulus, vertailuoperaattorit, ehtorakenne jos, input-komento
Python-ohjelmointi Harjoitus 2 TAVOITTEET Kerrataan tulostuskomento ja lukumuotoisen muuttujan muuttaminen merkkijonoksi. Opitaan jakojäännös eli modulus, vertailuoperaattorit, ehtorakenne jos, input-komento
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
TIEP114 Tietokoneen rakenne ja arkkitehtuuri, 3 op. FT Ari Viinikainen
 TIEP114 Tietokoneen rakenne ja arkkitehtuuri, 3 op FT Ari Viinikainen Tietokoneen rakenne Keskusyksikkö, CPU Keskusmuisti Aritmeettislooginen yksikkö I/O-laitteet Kontrolliyksikkö Tyypillinen Von Neumann
TIEP114 Tietokoneen rakenne ja arkkitehtuuri, 3 op FT Ari Viinikainen Tietokoneen rakenne Keskusyksikkö, CPU Keskusmuisti Aritmeettislooginen yksikkö I/O-laitteet Kontrolliyksikkö Tyypillinen Von Neumann
Piirikytkentäiset kytkentäkentät. Kapeakaistakenttä kytkee PCM-aikavälejä
 Piirikytkentäiset kytkentäkentät Mitä ja miksi Aikakytkentä Tilakytkentä Analogiat Tila-tila Aika-tila AA AT TA TT Rka/ML -k000 Tiedonvälitystekniikka I 4 - Kapeakaistakenttä kytkee PCM-aikavälejä PCM30
Piirikytkentäiset kytkentäkentät Mitä ja miksi Aikakytkentä Tilakytkentä Analogiat Tila-tila Aika-tila AA AT TA TT Rka/ML -k000 Tiedonvälitystekniikka I 4 - Kapeakaistakenttä kytkee PCM-aikavälejä PCM30
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-1200 Signaalinkäsittelyn menetelmät, Tentti 21.3.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SG-1200 Signaalinkäsittelyn menetelmät, Tentti 21.3.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
Näppäimistö CT 1000. Käyttäjäopas. Global Safety & Security Solutions Oy E-mail: info@globalsafety.fi. CT1000v.5
 Näppäimistö CT 1000 Käyttäjäopas CT1000v.5 Global Safety & Security Solutions Oy E-mail: info@globalsafety.fi Sivu 2 CT 1000 Rajoitukset Kaikki oikeudet tähän ohjekirjaan ovat Global Safety & Security
Näppäimistö CT 1000 Käyttäjäopas CT1000v.5 Global Safety & Security Solutions Oy E-mail: info@globalsafety.fi Sivu 2 CT 1000 Rajoitukset Kaikki oikeudet tähän ohjekirjaan ovat Global Safety & Security
Toinen muotoilu. {A 1,A 2,...,A n,b } 0, Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun 1 / 13
 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun {A 1,A 2,...,A n,b } 0, jatkoa jatkoa 1 / 13 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin
2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun {A 1,A 2,...,A n,b } 0, jatkoa jatkoa 1 / 13 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin
