3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE
|
|
|
- Hilja Lehtilä
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 3. MATERIALISTISTEN HIUKKASTEN AALTOLUONNE 3.1. DE BROGLIE AALLOT 1905: Aaltojen hiukkasominaisuudet 1924: Hiukkasten aalto-ominaisuudet: de Broglien hypoteesi Liikkuvat hiukkaset käyttäytyvät aaltojen tavoin. Fotonin liikemäärä: p hf c h, josta aallonpituus: h p De Broglien hypoteesin mukaan λ=h/p pätee sekä hiukkasille että aalloille. Myös hiukkasten liikkeeseen liittyy siis aaltoliike, jonka aallonpituus h h m0 m on hiukkasen relativistinen massa m 2 2 p mv 1 v / c De Broglie päätyi aineaaltoihin Bohrin atomimallista (käsitellään myöhemmin), jossa vain kvantittuneet energiatilat ovat mahdollisia. Aineaallot havaittiin elektronien diffraktiossa kiteestä (käsitellään myöhemmin). 1
2 ESIMERKKI 3.1 Laske de Broglie aallonpituudet a) 46 g painavalle golf pallolle, jonka nopeus on 30 m/s. b) elektronille, jonka nopeus on 10 7 m/s (elektronin massa 9, kg). 2
3 3.2. TODENNÄKÖISYYSKÄSITE de Broglie aallon amplitudi heijastaa todennäköisyyttä löytää siihen liittyvä hiukkanen tietystä paikasta tietyllä hetkellä. Liikkuvaan hiukkaseen liittyy aaltofunktio ψ, jolla ei ole fysikaalista vastinetta vaan aaltofunktio on abstrakti käsite. (tätä tullaan käsittelemään paljon myöhemmin) Aaltofunktio liittyy todennäköisyyteen löytää liikkuva hiukkanen x,y,z-avaruuden tietystä pisteestä hetkellä t. Kuitenkin aaltofunktion amplitudi voi saada sekä positiivisia että negatiivisia arvoja, joten sellaisenaan se ei toimi todennäköisyytenä vaan todennäköisyys löytää hiukkanen, jota kuvaa aaltofunktio ψ, paikasta (x, y, z) ajanhetkellä t on verrannollinen aaltofunktion neliöön ψ 2 Jos ψ 2 on suuri todennäköisyys hiukkasen olemassaololle on suuri Jos ψ 2 on pieni todennäköisyys hiukkasen olemassaololle on pieni Jos ψ 2 0 on todennäköisyys hiukkasen löytymiselle Jos ψ 2 = 0 hiukkanen ei voi olla pisteessä (x,y,z) ajanhetkellä t 3
4 Vaikka sanotaan, että aaltofunktio kuvaa hiukkasen levinneisyyttä avaruudessa, se ei tarkoita, että hiukkanen itsessään olisi hajonnut avaruuteen. Mitatessa elektroneja, saadaan aina mitattua kokonainen elektroni tietyssä paikassa tietyllä hetkellä (esim. 20% todennäköisyys havaita koko elektroni, ei havaita 20% elektronista) Jos suurella hiukkasjoukolla on sama aaltofunktio ψ, hiukkastiheys on verrannollinen aaltofunktion neliöön ψ 2. 4
5 3.3. AALLON KUVAAMINEN Miten nopeasti hiukkaseen liittyvät aallot liikkuvat? Onko liikkuvaa hiukkasta kuvaavan de Broglie aallon nopeus sama kuin hiukkasen nopeus? Määritetään de Broglie aallon nopeus: λ = h mv ja E = hf = mc 2 f = mc2 h De Broglie aallon nopeus voidaan määrittää. v p = fλ = mc2 h h mv = c2 v Koska aina hiukkasen nopeus v < c, de Broglie aallon vaihenopeus > c de Broglie aallot kulkevat valoa nopeammin? Voidaanko siis havaita valoa nopeampia aaltoja? 5
6 Hieman aaltoliikeoppia tähän väliin: Tarkastellaan yksinkertaista aaltoa, jonka maksimi arvo y-akselilla on +A (= aallon amplitudi) ja se saavuttaa sen paikassa x = 0 ajanhetkellä t = 0. Ajan kuluessa seuraavat y-akselin arvot saadaan yhtälöstä: y Acos 2 f t A t=0 t Yhtälö kertoo aallon yksittäisen pisteen paikan ajan funktiona y-akselin suunnassa. Tahdomme kuitenkin yhtälön, joka kertoo y:n arvon jokaisessa pisteessä x eri ajanhetkinä. 6 6
7 Ravistetaan köyttä: Aalto lähtee etenemään köydessä +x-suuntaan nopeudella v p. Nopeus riippuu köyden ominaisuuksista. Aalto liikkuu ajan t kuluessa matkan x = v p t ts. aikavälin x/v p jälkeen aalto on kohdassa x. y:n arvo pisteessä x ajanhetkellä t = y:n poikkeama pisteessä x=0 ajanhetkellä t = - x/v p. Sijoitetaan y:n yhtälöön t:n paikalle (t - x/v p ) y A cos 2 f t x v p 7 7
8 8 x t f Acos 2 y Aaltoyhtälö saadaan muotoon: joka antaa y:n arvon eri x ja t arvoilla. Määritetään: Kulmataajuus ω = 2πf Aaltoluku k = 2π λ = ω v p ja saadaan aaltoyhtälö muotoon p p p p f k f f v v 2 v v t kx Acos y 8 x t f f f x t f f x t f x t f p p A cos 2 A cos 2 v A cos 2 v A cos 2 y Muokataan vähän yhtälöä: Sij. v p =fλ
9 3.4. AALLON VAIHE- JA RYHMÄNOPEUS de Broglie aallon amplitudi heijastaa todennäköisyyttä löytää hiukkanen tietystä paikasta tietyllä hetkellä. Kuitenkin yleinen aaltoyhtälö y Acos t kx kuvaa päättymätöntä sarjaa aaltoja, joilla on sama amplitudi. Sillä ei voi kuvata hiukkasen de Broglie aaltoa. Sen sijaan ajatellaan, että liikkuvaa hiukkasta vastaa aaltopaketti tai aaltoryhmä: Matemaattisesti aaltoryhmä on yksittäisten interferoivien aaltojen summa. Ryhmänopeus = aaltoryhmien nopeus 9 9
10 Aallon ryhmänopeus v g voidaan johtaa tarkastelemalla kahden aallon y 1 = A cos(ωt kx) y 2 = A cos ω + Δω t k + Δk x summa-aaltoa. Aalloilla on sama amplitudi A ja niiden kulmataajuuksien ero on Δω ja aaltolukujen ero on Δk. Summa-aalto saadaan sievennyksien jälkeen muotoon: y = 2A cos ωt kx cos 1 2 Δωt Δkx Summa-aallon ensimmäinen osa on saman muotoinen kuin alkuperäiset aallot ja jälkimmäinen osa on moduloiva osa, joka aiheuttaa ryhmät Vaihenopeus v p = ω k Ryhmänopeus v g = Δω Δk Kun ω ja k ovat jatkuvia, ryhmänopeus: g d dk Riippuen vaihenopeuden ja aaltoluvun erosta, ryhmänopeus voi olla pienempi tai suurempi kuin osa-aaltojen vaihenopeus. Jos vaihenopeus on sama kaikille aallonpituuksille (kuten valolla tyhjiössä), ryhmä- ja vaihenopeus ovat samat. v 10 10
11 ESIMERKKI 3.2 Määritä ryhmä- ja vaihenopeus de Broglie aalloille
12 Yhteenveto: Hiukkasen liikettä kuvaa aaltoryhmän liike. Ryhmä muodostuu äärettömästä määrästä yksittäisiä aaltoja. Yksittäisen aallon nopeus voi olla suurempi kuin valonnopeus. Yksittäisen aallon nopeutta ei voida havaita. Voidaan havaita paikallisen häiriön, aaltoryhmän nopeus, joka on v g < c 12
13 ESIMERKKI 3.3 Elektronin de Broglie aallonpituus on 2.00 pm. Mikä on sen kineettinen energia? Laske myös de Broglie aallon vaihe- ja ryhmänopeudet? 13 13
14 3.5. HIUKKASTEN DIFFRAKTIO De Broglie aaltojen olemassa olo eli materialististen hiukkasten aaltoluonne todistettiin Davisson-Germerin kokeella Elektronisuihku kiihdytetään ja sillä pommitetaan kidettä. Elektronit siroavat kiteestä detektorille, jolla havaitaan sironneet elektronit eri kulmilla. Klassisen fysiikan mukaan elektronit voivat sirota kaikkiin suuntiin. Davisson ja Germer havaitsivat (vahingossa) kuitenkin kuumennetulta puhtaalta nikkelipinnalta voimakkaan sironnan tiettyyn kulmaan, joka riippui elektronien energiasta. Kuumennus aiheutti nikkelin rakenteen muuttumisen useampiin yksittäiskiteisiin, joista elektronit siroavat (kuten rtg-säteet kiteestä). Braggin laista voidaan laskea elektronin aallonpituus, joka vastaa hyvin de Broglien aallonpituutta: Davisson-Germerin koe todistaa de Broglien hypoteesin liikkuvien hiukkasten aaltoluonteesta!
15 ESIMERKKI 3.4 a) Amerikkalaiset Davisson ja Germer pommittivat kuuluisassa kokeessaan vuonna 1927 nikkelikidettä elektroneilla, joiden liike-energia oli 54 ev. Ensimmäisen kertaluvun heijastuksen kulmaksi mitattiin 65 astetta. Kuinka suuri on tätä vastaava nikkelin kiteiden atomitasojen välimatka? 15
16 Sovellus: Elektronioptiikka Mikroskoopin erotuskyky on aallonpituuden suuruusluokkaa ~1 nm Elektronimikroskoopilla päästään parempaan erotuskykyyn, koska hiukkasten aallonpituutta voidaan helposti muuttaa kiihdytysjännitettä muuttamalla erotuskyky paranee aallonpituuden pienentyessä. Elektronien varaus mahdollistaa magneettiset linssien rakentamisen. Sovellukset: solubiologia, lääketiede, metallurgia Oulun yliopistossa toimii Mikroskopian ja nanoteknologian keskus Tarjoaa puhdastila-, tutkimus- ja analyysipalveluja yliopiston laitoksille ja elinkeinoelämälle. Keskuksella on käytössään useita pyyhkäisyelektronimikroskooppeja (SEM) ja läpäisyelektronimikroskooppi 16 16
17 Elektronimikroskooppikuvia Kuvaaja: Raija Peura, alkuperäiset kuvat mustavalkoisia, väritys Raija Peura) Sääsken silmä Vaaksiaisen ihoa 17
18 3.6. HIUKKANEN LAATIKOSSA Rajoitetaan liikkuvan hiukkanen laatikkoon, jonka leveys on L. Liikkuvan hiukkasen aaltoluonne vaikuttaa hiukkasen liikkeeseen. Tarkastellaan hiukkasen liikettä: Oletetaan, että hiukkanen ei menetä energiaa törmätessään seiniin. Oletetaan, että hiukkasen nopeus on niin pieni, ettei relativistisuutta tarvitse huomioida. Käsitellään tapausta tarkemmin myöhemmin, tehdään nyt vain karkea analyysi: Aaltoluonteen näkökulmasta hiukkanen on kuin seisova aalto, jonka solmukohdat ovat laatikon seinillä. Seinillä aaltofunktio ψ =0, koska aalto pysähtyy niissä. Hiukkasen mahdolliset (de Broglie) aallonpituudet riippuvat laatikon leveydestä L
19 Pisin aallonpituus λ=2l, seuraavat λ=l, λ=2l/3 Sallitut aallonpituudet: 2L n n 1, 2, 3,... n Tässä mallissa hiukkasella ei ole potentiaalienergiaa, joten hiukkasen kokonaisenergia saadaan liike-energiasta: ( mv) 2m E EKin 2 mv h m Koska mv = h/λ Sijoitetaan tähän sallitut aallonpituudet ja saadaan hiukkasen energiaksi: 2 2 n h E n n 1, 2, 3, mL Hiukkasen energia voi siis saada vain tiettyjä arvoja eli energia on kvantittunut E n = energiataso n=kvanttiluku 19 19
20 Yhtälöstä voidaan tehdä kolme johtopäätöstä, jotka pätevät kaikille tiettyyn tilaan rajatuille hiukkasille (myös atomin elektroneille): 1) Hiukkasen energia ei voi saada mitä tahansa arvoja. Mahdolliset energiat riippuvat hiukkasen massasta ja rajatun avaruuden koosta. 2) Hiukkasen energia ei voi olla nolla. 3) Energian kvantittuminen on merkittävää vain kun m ja L ovat pieniä
21 ESIMERKKI 3.5 a) Laske sallitut energiat 10g marmorikuulalle, joka on 10 cm laatikossa. b) Laske sallitut energiat elektronille, joka on 0.10 nm laatikossa (atomin suuruusluokkaa)
22 3.7. VIELÄ TODENNÄKÖISYYSKÄSITTEESTÄ Hiukkanen (jota kuvaa aaltoryhmä), voi sijaita missä tahansa aaltoryhmän sisällä. de Broglie aallon amplitudi heijastaa todennäköisyyttä löytää siihen liittyvä hiukkanen tietystä paikasta tietyllä ajanhetkellä. Todennäköisyys löytää hiukkanen, jota kuvaa aaltofunktio ψ, paikasta (x, y, z) ajanhetkellä t on verrannollinen aaltofunktion neliöön ψ 2. ψ 2 on suurimmillaan keskellä ryhmää hiukanen on todennäköisimmin siinä. Se voi kuitenkin sijata missä tahansa kohdassa, missä ψ
23 ESIMERKKI 3.6 Elektroni on yksiulotteisessa potentiaalilaatikossa, joka rajoittaa sen liikkeen x-akselin välille [0,a]. Mikä on todennäköisyys sille, että alimmalla energiatilalla oleva elektroni on x-akselin välillä [0, a/3]? Perustilaa kuvaava aaltofunktio on muotoa φ x = 2 a 1/2 sin πx a 23
24 3.8. HEISENBERGIN EPÄTARKKUUSPERIAATE Aaltoryhmän kuvaaman hiukkasen paikan ja liikemäärän mittaus ei ole tarkkaa. Hiukkanen (jota aaltoryhmä kuvaa), voi sijaita missä tahansa ryhmän sisällä. Mitä kapeampi aaltoryhmä, sen tarkempi hiukkasen paikka. Silloin kuitenkin aallonpituus tulee epätarkaksi, koska ei ole tarpeeksi aaltoja tarkkaan mittaukseen. Koska aallonpituutta ei saada mitattua tarkasti, myöskään liikemäärän määritys ei ole tarkka. Mitä laajempi aaltoryhmä, sen tarkemmin saadaan määritettyä hiukkasen aallonpituus ja liikemäärä, mutta paikan määritys muuttuu epätarkaksi
25 Heisenbergin epätarkkuusperiaate: On mahdotonta tietää tarkasti samaan aikaan hiukkasen paikkaa ja liikemäärää. (Werner Heisenberg 1927) Optimitilanteessa, jossa aaltoryhmä on Gaussin funktion muotoinen, voidaan johtaa (kts. kirjan kappale 3.7) aaltoryhmän paikan x ja aaltoluvun k epätarkkuuksille ΔxΔk 1 2 Koska de Broglie aallonpituus hiukkaselle on λ = h p ja aaltoluku k = 2π λ saadaan k = 2πp h p = hk 2π Δp = hδk 2π Sijoittamalla edelliseen Δk 1 2Δx, saadaan ΔxΔp h 4π = ħ 2 ħ = h 2π Koska h on hyvin pieni, epätarkkuusperiaate koskee vain mikromaailmaa. Epätarkkuusperiaate ei ole vain negatiivista, vaan sen avulla voidaan ymmärtää monta atomitason ilmiötä
26 ESIMERKKI 3.7 Protonin paikka voidaan mitata tarkkuudella ± m. Mikä on protonin paikan epätarkkuus 1.00 s jälkeen. Oletetaan, että protonin nopeus on paljon pienempi kuin valonnopeus
27 ESIMERKKI 3.8 Tyypillinen atomin ytimen säde on n m. Käytä epätarkkuusperiaatetta määrittämään alaraja energialle, joka täytyy elektronilla olla, jos se on osa atomiydintä. 27
28 ESIMERKKI 3.9 Vetyatomin säde on m. Käytä epätarkkuusperiaatetta ja arvioi mikä on pienin energia, jonka elektroni voi saada tässä atomissa
29 ESIMERKKI 3.10 Epätarkkuusperiaate koskee myös energiaa ja aikaa. Jos atomaarisessa prosessissa vapautuu sähkömagneettista säteilyä (energiaa) ajan Δt kuluessa, taajuuden määrityksen epätarkkuus 1 f t E hf jolloin energian epätarkkuus on h E tai Et h t Tarkempi käsittely antaa epätarkkuusperiaatteeksi energialle ja ajalle: Et 2 Viritetty atomi voi emittoida säteilyä tietyllä taajuudella (käsitellään myöhemmin). Keskimääräinen aika virityksen ja viritystilan purkautumisen välillä on s. Mikä on emittoituvan fotonin taajuuden epätarkkuus? 29 29
Osallistumislomakkeen viimeinen palautuspäivä on maanantai
 Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
Aineen aaltoluonne. Yliopistonlehtori, TkT Sami Kujala. Kevät Harris luku 4. Mikro- ja nanotekniikan laitos
 Aineen aaltoluonne Harris luku 4 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Aineaallot Heisenbergin epätarkkuusperiaate Fourier-muunnos ja epätarkkuusperiaate Aineaaltojen
Aineen aaltoluonne Harris luku 4 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Aineaallot Heisenbergin epätarkkuusperiaate Fourier-muunnos ja epätarkkuusperiaate Aineaaltojen
Kvantittuminen. E = hf f on säteilyn taajuus h on Planckin vakio h = 6, Js = 4, evs. Planckin kvanttihypoteesi
 Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen)
 Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Fysiikka 8. Aine ja säteily
 Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
Fysiikka 8 Aine ja säteily Sähkömagneettinen säteily James Clerk Maxwell esitti v. 1864 sähkövarauksen ja sähkövirran sekä sähkö- ja magneettikentän välisiä riippuvuuksia kuvaavan teorian. Maxwellin teorian
1240eV nm. 410nm. Kun kappaleet saatetaan kontaktiin jännite-ero on yhtä suuri kuin työfunktioiden erotus ΔV =
 S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
1. JOHDANTOA. Makroskooppinen aine koostuu atomeista ja molekyyleistä. Atomit koostuvat ytimestä ja elektroneista.
 1. JOHDANTOA Makroskooppinen aine koostuu atomeista ja molekyyleistä. Atomit koostuvat ytimestä ja elektroneista. 1 Atomifysiikka käsittelee atomin elektroniverhon fysiikka Ydinfysiikka käsittelee ytimen
1. JOHDANTOA Makroskooppinen aine koostuu atomeista ja molekyyleistä. Atomit koostuvat ytimestä ja elektroneista. 1 Atomifysiikka käsittelee atomin elektroniverhon fysiikka Ydinfysiikka käsittelee ytimen
Todennäköisyys ja epämääräisyysperiaate
 Todennäköisyys ja epämääräisyysperiaate Luento 7 Hiukkas-aaltodualismi vaatii uudenlaisen kielenkäytön omaksumista kuvaamaan iukkasten liikettä ja paikkaa. Newtonin mekaniikassa iukkanen on aina jossain
Todennäköisyys ja epämääräisyysperiaate Luento 7 Hiukkas-aaltodualismi vaatii uudenlaisen kielenkäytön omaksumista kuvaamaan iukkasten liikettä ja paikkaa. Newtonin mekaniikassa iukkanen on aina jossain
Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus
 Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus värähtelytiheyden. 1 Funktiot ja aallot Aiemmin käsiteltiin funktioita ja miten niiden avulla voidaan kuvata fysiikan
Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus värähtelytiheyden. 1 Funktiot ja aallot Aiemmin käsiteltiin funktioita ja miten niiden avulla voidaan kuvata fysiikan
Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa
 Potentiaalikuoppa Luento 9 Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa U( x ) = U U( x ) = 0 0 kun x < 0 tai x > L, kun 0 x L. Kuopan kohdalla hiukkanen on vapaa,
Potentiaalikuoppa Luento 9 Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa U( x ) = U U( x ) = 0 0 kun x < 0 tai x > L, kun 0 x L. Kuopan kohdalla hiukkanen on vapaa,
Aatofunktiot ja epätarkkuus
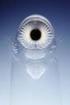 Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
Aatofunktiot ja epätarkkuus Aaltofunktio sisältää tiedon siitä, millä todennäköisyydellä hiukkanen on missäkin avaruuden pisteessä. Tämä tunnelointimikroskoopilla grafiitista otettu kuva näyttää elektronin
S Fysiikka III (EST) (6 op) 1. välikoe
 S-114.1327 Fysiikka III (EST) (6 op) 1. välikoe 1.3.21 Ilkka Tittonen 1. Vastaa seuraaviin kysymyksiin perustellusti, mutta ytimekkäästi (esim. 5-1 lausetta) (2p per kohta). a) Mikä on sidottu tila? Anna
S-114.1327 Fysiikka III (EST) (6 op) 1. välikoe 1.3.21 Ilkka Tittonen 1. Vastaa seuraaviin kysymyksiin perustellusti, mutta ytimekkäästi (esim. 5-1 lausetta) (2p per kohta). a) Mikä on sidottu tila? Anna
Aikariippuva Schrödingerin yhtälö
 Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
Aineaaltodynamiikka Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit Aikariippuva Schrödingerin
5.10. HIUKKANEN POTENTIAALIKUOPASSA
 5.10. HIUKKANEN POTENTIAALIKUOPASSA eli miten reunaehdot ja normitus vaikuttavat aaltofunktioihin Yleensä Schrödingerin yhtälön ratkaiseminen matemaattisesti on hyvin työlästä ja edellyttää vahvaa matemaattista
5.10. HIUKKANEN POTENTIAALIKUOPASSA eli miten reunaehdot ja normitus vaikuttavat aaltofunktioihin Yleensä Schrödingerin yhtälön ratkaiseminen matemaattisesti on hyvin työlästä ja edellyttää vahvaa matemaattista
Aineaaltodynamiikkaa
 Aineaaltodynamiikkaa Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit = kuinka hiukkasen fysikaaliset
Aineaaltodynamiikkaa Aineaaltokenttien riippuvuus ajasta aikariippuva Schrödingerin yhtälö Stationääriset ja ei-stationääriset tilat Aaltopaketit Kvanttimekaniikan postulaatit = kuinka hiukkasen fysikaaliset
766326A Atomifysiikka 1 - Syksy 2013
 766326A Atomifysiikka 1 - Syksy 2013 Luennot n. 46 tuntia Torstaisin 8-10 sali IT116 Perjantaisin 8-10 sali L6 Poikkeuksia: to 19.9. luento vain 8-9 to 17.10. luento vain 8-9 to 14.11. luento vain 8-9
766326A Atomifysiikka 1 - Syksy 2013 Luennot n. 46 tuntia Torstaisin 8-10 sali IT116 Perjantaisin 8-10 sali L6 Poikkeuksia: to 19.9. luento vain 8-9 to 17.10. luento vain 8-9 to 14.11. luento vain 8-9
S Fysiikka III (EST) Tentti ja välikoeuusinta
 S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
 S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
Voima ja potentiaalienergia II Energian kvantittuminen
 Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
780392A/782631S Fysikaalinen kemia II, 5 op / 4 op
 78392A/782631S Fysikaalinen kemia II, 5 op / 4 op Luennot: 5.9.-15.11.216 Ma klo 8-1 PR12 Ti klo 12-14 PR12 Risto Laitinen (22.2.-14.3.) Epäorgaanisen kemian tutkimusyksikkö (KE 313) PL 3 914 Oulun yliopisto
78392A/782631S Fysikaalinen kemia II, 5 op / 4 op Luennot: 5.9.-15.11.216 Ma klo 8-1 PR12 Ti klo 12-14 PR12 Risto Laitinen (22.2.-14.3.) Epäorgaanisen kemian tutkimusyksikkö (KE 313) PL 3 914 Oulun yliopisto
Tfy Fysiikka IIB Mallivastaukset
 Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
Shrödingerin yhtälön johto
 Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Lisävaatimuksia aaltofunktiolle
 Lisävaatimuksia aaltofunktiolle (1) Koska Ψ*Ψ on äärellinen => Ψ on äärellinen. () Koska P = Ψ*Ψdτ => Ψ on yksiselitteinen. (3) Ψ on jatkuva. (4) dψ/dτ on jatkuva. Esimerkki Epäkelpoja aaltofunktioita
Lisävaatimuksia aaltofunktiolle (1) Koska Ψ*Ψ on äärellinen => Ψ on äärellinen. () Koska P = Ψ*Ψdτ => Ψ on yksiselitteinen. (3) Ψ on jatkuva. (4) dψ/dτ on jatkuva. Esimerkki Epäkelpoja aaltofunktioita
ψ(x) = A cos(kx) + B sin(kx). (2) k = nπ a. (3) E = n 2 π2 2 2ma 2 n2 E 0. (4)
 76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
9 VALOAALTOJEN SUPERPOSITIO
 09 9 VALOAALTOJEN SUPERPOSITIO Edellisissä kappaleissa olemme tutkineet valon heijastumista peileissä ja taittumista linsseissä geometrisen optiikan approksimaation avulla Approksimaatiossa valon aaltoluonnetta
09 9 VALOAALTOJEN SUPERPOSITIO Edellisissä kappaleissa olemme tutkineet valon heijastumista peileissä ja taittumista linsseissä geometrisen optiikan approksimaation avulla Approksimaatiossa valon aaltoluonnetta
Luento 6. Mustan kappaleen säteily
 Mustan kappaleen säteily Luento 6 Pintaa, joka absorboi kaiken siihen osuvan sähkömagneettisen säteilyn, kutsutaan mustaksi kappaleeksi. Tällainen pinta myös säteilee kaikilla aallonpituuksilla. Sen sanotaan
Mustan kappaleen säteily Luento 6 Pintaa, joka absorboi kaiken siihen osuvan sähkömagneettisen säteilyn, kutsutaan mustaksi kappaleeksi. Tällainen pinta myös säteilee kaikilla aallonpituuksilla. Sen sanotaan
Kvanttisointi Aiheet:
 Kvanttisointi Luento 5 4 Aiheet: Valosähköilmiö Einsteinin selitys Fotonit Aineaallot ja energian kvantittuminen Bohrin kvanttimalli atomille Bohrin malli vetyatomille Vedyn spektri Mitä olet oppinut?
Kvanttisointi Luento 5 4 Aiheet: Valosähköilmiö Einsteinin selitys Fotonit Aineaallot ja energian kvantittuminen Bohrin kvanttimalli atomille Bohrin malli vetyatomille Vedyn spektri Mitä olet oppinut?
KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
Luento 15: Mekaaniset aallot. Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot
 Luento 15: Mekaaniset aallot Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot 1 / 40 Luennon sisältö Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa
Luento 15: Mekaaniset aallot Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa Energia Aallon heijastuminen Seisovat aallot 1 / 40 Luennon sisältö Mekaaniset aallot Eteneminen Aallon nopeus väliaineessa
Nyt n = 1. Tästä ratkaistaan kuopan leveys L ja saadaan sijoittamalla elektronin massa ja vakiot
 S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
ja KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
Atomi- ja ydinfysiikka -verkkokurssin toteuttaminen
 Atomi- ja ydinfysiikka -verkkokurssin toteuttaminen Janne Klemola Oulun yliopisto Fysiikan tutkinto-ohjelma Pro gradu -tutkielma Toukokuu 2017 Sisältö Johdanto 1 1 Kurssin asiasisältö 2 1.1 Sähkömagneettisten
Atomi- ja ydinfysiikka -verkkokurssin toteuttaminen Janne Klemola Oulun yliopisto Fysiikan tutkinto-ohjelma Pro gradu -tutkielma Toukokuu 2017 Sisältö Johdanto 1 1 Kurssin asiasisältö 2 1.1 Sähkömagneettisten
ja siis myös n= nk ( ). Tällöin dk l l
 Tästä havaitaan, että jos nopeus ei riipu aallonpituudesta, ts. ei ole dispersiota, vg = v p. Tilanne on tällainen esimerkiksi tyhjiössä, missä vg = v p = c. Dispersiivisessä väliaineessa v p = c/ n, missä
Tästä havaitaan, että jos nopeus ei riipu aallonpituudesta, ts. ei ole dispersiota, vg = v p. Tilanne on tällainen esimerkiksi tyhjiössä, missä vg = v p = c. Dispersiivisessä väliaineessa v p = c/ n, missä
Ch7 Kvanttimekaniikan alkeita. Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset.
 Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
Ch7 Kvanttimekaniikan alkeita Tässä luvussa esitellään NMR:n kannalta keskeiset kvanttimekaniikan tulokset. Spinnittömät hiukkaset Hiukkasta kuvaa aineaaltokenttä eli aaltofunktio. Aaltofunktio riippuu
Atomien rakenteesta. Tapio Hansson
 Atomien rakenteesta Tapio Hansson Ykköskurssista jo muistamme... Atomin käsite on peräisin antiikin Kreikasta. Demokritos päätteli alunperin, että jatkuva aine ei voi koostua äärettömän pienistä alkeisosasista
Atomien rakenteesta Tapio Hansson Ykköskurssista jo muistamme... Atomin käsite on peräisin antiikin Kreikasta. Demokritos päätteli alunperin, että jatkuva aine ei voi koostua äärettömän pienistä alkeisosasista
Vapaat tilat. Yliopistonlehtori, TkT Sami Kujala. Kevät Harris luku 6. Mikro- ja nanotekniikan laitos
 Vapaat tilat Harris luku 6 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Potentiaaliaskel Potentiaalivalli ja tunneloituminen Aaltopaketti ja aineaallon eteneminen Potentiaaliaskel
Vapaat tilat Harris luku 6 Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Potentiaaliaskel Potentiaalivalli ja tunneloituminen Aaltopaketti ja aineaallon eteneminen Potentiaaliaskel
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys12 Kevät 21 Jukka Maalampi LUENTO 11 Mekaaninen aaltoliike alto = avaruudessa etenevä järjestäytynyt häiriö. alto altoja on kahdenlaisia: Poikittainen aalto - poikkeamat kohtisuorassa
Mekaniikan jatkokurssi Fys12 Kevät 21 Jukka Maalampi LUENTO 11 Mekaaninen aaltoliike alto = avaruudessa etenevä järjestäytynyt häiriö. alto altoja on kahdenlaisia: Poikittainen aalto - poikkeamat kohtisuorassa
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
 766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
Kvanttimekaniikka: Luento 2. Mar$kainen Jani- Petri
 Kvanttimekaniikka: Luento 2 Mar$kainen Jani- Petri Assarointimainos Fyssa tarvitsee assareita Noin 30 euroa tun$+ lisiä tyypillises$ n. 4h/viikko, muba voi olla enemmän/vähemmän Opintosuoritukset+ lyhyt
Kvanttimekaniikka: Luento 2 Mar$kainen Jani- Petri Assarointimainos Fyssa tarvitsee assareita Noin 30 euroa tun$+ lisiä tyypillises$ n. 4h/viikko, muba voi olla enemmän/vähemmän Opintosuoritukset+ lyhyt
Infrapunaspektroskopia
 ultravioletti näkyvä valo Infrapunaspektroskopia IHMISEN JA ELINYMPÄ- RISTÖN KEMIAA, KE2 Kertausta sähkömagneettisesta säteilystä Sekä IR-spektroskopia että NMR-spektroskopia käyttävät sähkömagneettista
ultravioletti näkyvä valo Infrapunaspektroskopia IHMISEN JA ELINYMPÄ- RISTÖN KEMIAA, KE2 Kertausta sähkömagneettisesta säteilystä Sekä IR-spektroskopia että NMR-spektroskopia käyttävät sähkömagneettista
LIITE 11A: VALOSÄHKÖINEN ILMIÖ
 LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
3.1 Varhaiset atomimallit (1/3)
 + 3 ATOMIN MALLI 3.1 Varhaiset atomimallit (1/3) Thomsonin rusinakakkumallissa positiivisesti varautuneen hyytelömäisen aineen sisällä on negatiivisia elektroneja kuin rusinat kakussa. Rutherford pommitti
+ 3 ATOMIN MALLI 3.1 Varhaiset atomimallit (1/3) Thomsonin rusinakakkumallissa positiivisesti varautuneen hyytelömäisen aineen sisällä on negatiivisia elektroneja kuin rusinat kakussa. Rutherford pommitti
766334A Ydin- ja hiukkasfysiikka
 1 766334A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 4 Juhani Lounila Oulun yliopisto, Fysiikan laitos, 01 6 Radioaktiivisuus Kuva 1 esittää radioaktiivisen aineen ydinten lukumäärää
1 766334A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 4 Juhani Lounila Oulun yliopisto, Fysiikan laitos, 01 6 Radioaktiivisuus Kuva 1 esittää radioaktiivisen aineen ydinten lukumäärää
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina
 Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Luento 13: Periodinen liike. Johdanto Harmoninen värähtely Esimerkkejä F t F r
 Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
(1) (2) Normalisointiehdoksi saadaan nytkin yhtälö (2). Ratkaisemalla (2)+(3) saamme
 S-446 Fysiikka IV (Sf) Tentti 3934 Oletetaan, että φ ja φ ovat ajasta riippumattoman Scrödingerin yhtälön samaan ominaisarvoon E liittyviä ominaisfunktioita Nämä funktiot ovat normitettuja, mutta eivät
S-446 Fysiikka IV (Sf) Tentti 3934 Oletetaan, että φ ja φ ovat ajasta riippumattoman Scrödingerin yhtälön samaan ominaisarvoon E liittyviä ominaisfunktioita Nämä funktiot ovat normitettuja, mutta eivät
YLEINEN AALTOLIIKEOPPI
 YLEINEN AALTOLIIKEOPPI KEVÄT 2017 1 Saana-Maija Huttula (saana.huttula@oulu.fi) Maanantai Tiistai Keskiviikko Torstai Perjantai Vk 8 Luento 1 Mekaaniset aallot 1 Luento 2 Mekaaniset aallot 2 Ääni ja kuuleminen
YLEINEN AALTOLIIKEOPPI KEVÄT 2017 1 Saana-Maija Huttula (saana.huttula@oulu.fi) Maanantai Tiistai Keskiviikko Torstai Perjantai Vk 8 Luento 1 Mekaaniset aallot 1 Luento 2 Mekaaniset aallot 2 Ääni ja kuuleminen
Fysiikan valintakoe klo 9-12
 Fysiikan valintakoe 2.5.208 klo 9-2. Koripalloilija heittää vapaaheiton. Hän lähettää pallon liikkeelle korkeudelta,83 m alkuvauhdilla 7,53 m/s kulmassa 43,2 vaakatason yläpuolella. Pallon lähtöpisteen
Fysiikan valintakoe 2.5.208 klo 9-2. Koripalloilija heittää vapaaheiton. Hän lähettää pallon liikkeelle korkeudelta,83 m alkuvauhdilla 7,53 m/s kulmassa 43,2 vaakatason yläpuolella. Pallon lähtöpisteen
Tilat ja observaabelit
 Tilat ja observaabelit Maksimaalinen informaatio systeemistä tietyllä ajanhetkellä sisältyy tilaan ψ (ket). Tila = vektori Hilbertin avaruudessa sisätulo ψ ψ C ψ c 1 ψ 1 + c 2 ψ 2 = c 1 ψ ψ 1 + c 2 ψ ψ
Tilat ja observaabelit Maksimaalinen informaatio systeemistä tietyllä ajanhetkellä sisältyy tilaan ψ (ket). Tila = vektori Hilbertin avaruudessa sisätulo ψ ψ C ψ c 1 ψ 1 + c 2 ψ 2 = c 1 ψ ψ 1 + c 2 ψ ψ
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 2 Kevät 207. Nelinopeus ympyräliikkeessä On siis annettu kappaleen paikkaa kuvaava nelivektori X x µ : Nelinopeus U u µ on määritelty kaavalla x µ (ct,
Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa. Tapio Hansson
 Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa Tapio Hansson Laskentoa SI-järjestelmä soveltuu hieman huonosti kvantti- ja hiukaksfysiikkaan. Sen perusyksiköiden mittakaava
Suhteellisuusteoriasta, laskuista ja yksiköistä kvantti- ja hiukkasfysiikassa Tapio Hansson Laskentoa SI-järjestelmä soveltuu hieman huonosti kvantti- ja hiukaksfysiikkaan. Sen perusyksiköiden mittakaava
1. (a) (2p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori
 FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
FYSA5 Kvanttimekaniikka I, Osa B 7.. tentti: 4 tehtävää, 4 tuntia. a) p.) Systeemin infinitesimaalista siirtoa matkan ɛ verran esittää operaattori T ɛ) = iɛ h P. Osoita tämän avulla, että äärellistä siirtoa
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi
 Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Luku 9: Kvanttimekaniikan soveltaminen eri liiketyyppeihin:
 Luku 9: Kvanttimekaniikan soveltaminen eri liiketyyppeihin: Translaatioliike (hiukkanen laatikossa) Rotaatio eli pyörimisliike Vibraatio eli värähdysliike 1 Vapaan hiukkasen (V =0) Schrödingerin yhtälön
Luku 9: Kvanttimekaniikan soveltaminen eri liiketyyppeihin: Translaatioliike (hiukkanen laatikossa) Rotaatio eli pyörimisliike Vibraatio eli värähdysliike 1 Vapaan hiukkasen (V =0) Schrödingerin yhtälön
Braggin ehdon mukaan hilatasojen etäisyys (111)-tasoille on
 763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
Luento 15: Ääniaallot, osa 2
 Luento 15: Ääniaallot, osa 2 Aaltojen interferenssi Doppler Laskettuja esimerkkejä Luennon sisältö Aaltojen interferenssi Doppler Laskettuja esimerkkejä Aaltojen interferenssi Samassa pisteessä vaikuttaa
Luento 15: Ääniaallot, osa 2 Aaltojen interferenssi Doppler Laskettuja esimerkkejä Luennon sisältö Aaltojen interferenssi Doppler Laskettuja esimerkkejä Aaltojen interferenssi Samassa pisteessä vaikuttaa
Kvanttimekaniikan perusteet
 Kvanttimekaniikan perusteet Schrödingerin yhtälö Sironta potentiaaliaskeleesta Elektronitilat potentiaalikuopassa Harmoninen oskillaattori Tilatiheys lisää sirontailmiöistä Aineaaltokenttä ja todennäköisyystiheys
Kvanttimekaniikan perusteet Schrödingerin yhtälö Sironta potentiaaliaskeleesta Elektronitilat potentiaalikuopassa Harmoninen oskillaattori Tilatiheys lisää sirontailmiöistä Aineaaltokenttä ja todennäköisyystiheys
BM30A0240, Fysiikka L osa 4
 BM30A0240, Fysiikka L osa 4 Luennot: Heikki Pitkänen 1 Oppikirja: Young & Freedman: University Physics Luku 14 - Periodic motion Luku 15 - Mechanical waves Luku 16 - Sound and hearing Muuta - Diffraktio,
BM30A0240, Fysiikka L osa 4 Luennot: Heikki Pitkänen 1 Oppikirja: Young & Freedman: University Physics Luku 14 - Periodic motion Luku 15 - Mechanical waves Luku 16 - Sound and hearing Muuta - Diffraktio,
2. Fotonit, elektronit ja atomit
 Luento 4 2. Fotonit, elektronit ja atomit Valon kvanttiteoria; fotoni Valosähköinen ilmiö ja sen kvanttiselitys Valon emissio ja absorptio Säteilyn spektri; atomin energiatasot Atomin rakenne Niels Bohrin
Luento 4 2. Fotonit, elektronit ja atomit Valon kvanttiteoria; fotoni Valosähköinen ilmiö ja sen kvanttiselitys Valon emissio ja absorptio Säteilyn spektri; atomin energiatasot Atomin rakenne Niels Bohrin
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 3 Kevät E 1 + c 2 m 2 = E (1) p 1 = P (2) E 2 1
 763306A JOHDATUS SUHTLLISUUSTORIAAN Ratkaisut 3 Kevät 07. Fuusioreaktio. Lähdetään suoraan annetuista yhtälöistä nergia on suoraan yhtälön ) mukaan + m ) p P ) m + p 3) M + P 4) + m 5) Ratkaistaan seuraavaksi
763306A JOHDATUS SUHTLLISUUSTORIAAN Ratkaisut 3 Kevät 07. Fuusioreaktio. Lähdetään suoraan annetuista yhtälöistä nergia on suoraan yhtälön ) mukaan + m ) p P ) m + p 3) M + P 4) + m 5) Ratkaistaan seuraavaksi
Liikemäärän säilyminen Vuorovesivoimat Jousivoima
 Liikemäärän säilyminen Vuorovesivoimat Jousivoima Tämän luennon tavoitteet Liikemäärän säilyminen Vuorovesivoimat ja binomiapproksimaatio gravitaatio jatkuu viime viikolta Jousivoima: mikä se on ja miten
Liikemäärän säilyminen Vuorovesivoimat Jousivoima Tämän luennon tavoitteet Liikemäärän säilyminen Vuorovesivoimat ja binomiapproksimaatio gravitaatio jatkuu viime viikolta Jousivoima: mikä se on ja miten
Fononit. Värähtelyt lineaarisessa atomiketjussa Dispersiorelaatio Kaksi erilaista atomia ketjussa Fononit kolmessa dimensiossa
 Fononit Värähtelyt lineaarisessa atomiketjussa Dispersiorelaatio Kaksi erilaista atomia ketjussa Fononit kolmessa dimensiossa Atomien lämpövärähtely Mikä on atomien värähtelyn taajuus ja amplitudi? Tarkastellaan
Fononit Värähtelyt lineaarisessa atomiketjussa Dispersiorelaatio Kaksi erilaista atomia ketjussa Fononit kolmessa dimensiossa Atomien lämpövärähtely Mikä on atomien värähtelyn taajuus ja amplitudi? Tarkastellaan
KEMIAN MIKROMAAILMA, KE2 Kvanttimekaaninen atomimalli
 KEMIAN MIKROMAAILMA, KE2 Kvanttimekaaninen atomimalli Aineen rakenteen teoria alkoi hahmottua, kun 1800-luvun alkupuolella John Dalton kehitteli teoriaa atomeista jakamattomina aineen perusosasina. Toki
KEMIAN MIKROMAAILMA, KE2 Kvanttimekaaninen atomimalli Aineen rakenteen teoria alkoi hahmottua, kun 1800-luvun alkupuolella John Dalton kehitteli teoriaa atomeista jakamattomina aineen perusosasina. Toki
n=5 n=4 M-sarja n=3 L-sarja n=2 Lisäys: K-sarjan hienorakenne K-sarja n=1
 10.1 RÖNTGENSPEKTRI Kun kiihdytetyt elektronit törmäävät anodiin, syntyy jatkuvaa säteilyä sekä anodimateriaalille ominaista säteilyä (spektrin terävät piikit). Atomin uloimpien elektronien poistamiseen
10.1 RÖNTGENSPEKTRI Kun kiihdytetyt elektronit törmäävät anodiin, syntyy jatkuvaa säteilyä sekä anodimateriaalille ominaista säteilyä (spektrin terävät piikit). Atomin uloimpien elektronien poistamiseen
Teoreetikon kuva. maailmankaikkeudesta
 Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
Teoreetikon kuva Teoreetikon kuva hiukkasten hiukkasten maailmasta maailmasta ja ja maailmankaikkeudesta maailmankaikkeudesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Lapua 5. 5. 2012 Miten
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Työssä mitataan välillisesti elektronien taipumiskulmat ja lasketaan niiden sekä elektronin energian avulla grafiitin hilavakioita.
 FYSA230/1 ELEKTRONIEN DIFFRAKTIO 1 Johdanto Elektronien diffraktio on interferenssi-ilmiö, joka osoittaa hiukkasilla olevan aaltoluonteen. Hiukkasten aaltoluonne on hyvin fundamentaalisesti fysiikan maailmankuvaan
FYSA230/1 ELEKTRONIEN DIFFRAKTIO 1 Johdanto Elektronien diffraktio on interferenssi-ilmiö, joka osoittaa hiukkasilla olevan aaltoluonteen. Hiukkasten aaltoluonne on hyvin fundamentaalisesti fysiikan maailmankuvaan
Ydin- ja hiukkasfysiikka 2014: Harjoitus 5 Ratkaisut 1
 Ydin- ja hiukkasfysiikka 04: Harjoitus 5 Ratkaisut Tehtävä a) Vapautunut energia saadaan laskemalla massan muutos reaktiossa: E = mc = [4(M( H) m e ) (M( 4 He) m e ) m e ]c = [4M( H) M( 4 He) 4m e ]c =
Ydin- ja hiukkasfysiikka 04: Harjoitus 5 Ratkaisut Tehtävä a) Vapautunut energia saadaan laskemalla massan muutos reaktiossa: E = mc = [4(M( H) m e ) (M( 4 He) m e ) m e ]c = [4M( H) M( 4 He) 4m e ]c =
FYSIIKAN LABORATORIOTYÖT 2 HILA JA PRISMA
 FYSIIKAN LABORATORIOTYÖT HILA JA PRISMA MIKKO LAINE 9. toukokuuta 05. Johdanto Tässä työssä muodostamme lasiprisman dispersiokäyrän ja määritämme työn tekijän silmän herkkyysrajan punaiselle valolle. Lisäksi
FYSIIKAN LABORATORIOTYÖT HILA JA PRISMA MIKKO LAINE 9. toukokuuta 05. Johdanto Tässä työssä muodostamme lasiprisman dispersiokäyrän ja määritämme työn tekijän silmän herkkyysrajan punaiselle valolle. Lisäksi
Bohr Einstein -väittelyt. Petteri Mäntymäki Timo Kärkkäinen
 Bohr Einstein -väittelyt Petteri Mäntymäki Timo Kärkkäinen Esityksen sisältö Kvanttivallankumous Epätarkkuusperiaate Väittelyt Yhteenveto 24.4.2013 2 Kvanttivallankumous Alkoi 1900-luvulla (Einstein, Planck,
Bohr Einstein -väittelyt Petteri Mäntymäki Timo Kärkkäinen Esityksen sisältö Kvanttivallankumous Epätarkkuusperiaate Väittelyt Yhteenveto 24.4.2013 2 Kvanttivallankumous Alkoi 1900-luvulla (Einstein, Planck,
Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori!
 6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
L a = L l. rv a = Rv l v l = r R v a = v a 1, 5
 Tehtävä a) Energia ja rataliikemäärämomentti säilyy. Maa on r = AU päässä auringosta. Mars on auringosta keskimäärin R =, 5AU päässä. Merkitään luotaimen massaa m(vaikka kuten tullaan huomaamaan sitä ei
Tehtävä a) Energia ja rataliikemäärämomentti säilyy. Maa on r = AU päässä auringosta. Mars on auringosta keskimäärin R =, 5AU päässä. Merkitään luotaimen massaa m(vaikka kuten tullaan huomaamaan sitä ei
Theory Finnish (Finland) Suuri hadronitörmäytin (Large Hadron Collider, LHC) (10 pistettä)
 Q3-1 Suuri hadronitörmäytin (Large Hadron Collider, LHC) (10 pistettä) Lue erillisessä kuoressa olevat yleisohjeet ennen tämän tehtävän aloittamista. Tässä tehtävässä tarkastellaan maailman suurimman hiukkasfysiikan
Q3-1 Suuri hadronitörmäytin (Large Hadron Collider, LHC) (10 pistettä) Lue erillisessä kuoressa olevat yleisohjeet ennen tämän tehtävän aloittamista. Tässä tehtävässä tarkastellaan maailman suurimman hiukkasfysiikan
1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria
 Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Opettajaopiskelijoiden käsityksiä kvanttimekaniikasta
 Opettajaopiskelijoiden käsityksiä kvanttimekaniikasta Eetu Laukka Pro gradu -tutkielma Joulukuu 2015 Fysiikan ja matematiikan laitos Itä-Suomen yliopisto i Eetu Laukka Työn ohjaajat Opettajaopiskelijoiden
Opettajaopiskelijoiden käsityksiä kvanttimekaniikasta Eetu Laukka Pro gradu -tutkielma Joulukuu 2015 Fysiikan ja matematiikan laitos Itä-Suomen yliopisto i Eetu Laukka Työn ohjaajat Opettajaopiskelijoiden
J 2 = J 2 x + J 2 y + J 2 z.
 FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
FYSA5 Kvanttimekaniikka I, Osa B.. tentti: 4 tehtävää, 4 tuntia. Tarkastellaan pyörimismääräoperaattoria J, jonka komponentit toteuttavat kommutaatiorelaatiot [J x, J y ] = i hj z, [J y, J z ] = i hj x,
4. ATOMI. Kuva atomista?
 4. ATOMI Kuva atomista? 4. ATOMIN RAKENNE YDIN 8-luvun lopulla useimmat tutkijat jo uskoivat, että materiaalit koostuvat atomeista pienistä jakamattomista osista 898 J.J. Thomson löysi elektronit ja esitti
4. ATOMI Kuva atomista? 4. ATOMIN RAKENNE YDIN 8-luvun lopulla useimmat tutkijat jo uskoivat, että materiaalit koostuvat atomeista pienistä jakamattomista osista 898 J.J. Thomson löysi elektronit ja esitti
Atomin ydin. Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N
 Atomin ydin ytimen rakenneosia, protoneja (p + ) ja neutroneja (n) kutsutaan nukleoneiksi Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N saman
Atomin ydin ytimen rakenneosia, protoneja (p + ) ja neutroneja (n) kutsutaan nukleoneiksi Z = varausluku (järjestysluku) = protonien määrä N = neutroniluku A = massaluku (nukleoniluku) A = Z + N saman
Esitehtävä (ks. sivu 5) tulee olla tehtynä mittausvuorolle tultaessa!
 FYSA2031 / K1 ELEKTRONIEN DIFFRAKTIO 1 Johdanto Elektronien diffraktio on interferenssi-ilmiö, joka osoittaa hiukkasilla olevan aaltoluonteen. Hiukkasten aaltoluonne on hyvin fundamentaalisesti fysiikan
FYSA2031 / K1 ELEKTRONIEN DIFFRAKTIO 1 Johdanto Elektronien diffraktio on interferenssi-ilmiö, joka osoittaa hiukkasilla olevan aaltoluonteen. Hiukkasten aaltoluonne on hyvin fundamentaalisesti fysiikan
Energian säilymislain perusteella elektronin rekyylienergia on fotnien energioiden erotus: (1)
 S-11446 Fysiikka IV (Sf), I Väliko 544 1 Osoita, ttä Comptonin sironnassa lktronin suurin mahdollinn rkyylinrgia voidaan sittää muodossa E Kin hf 1 + mc /hf Enrgian säilymislain prustlla lktronin rkyylinrgia
S-11446 Fysiikka IV (Sf), I Väliko 544 1 Osoita, ttä Comptonin sironnassa lktronin suurin mahdollinn rkyylinrgia voidaan sittää muodossa E Kin hf 1 + mc /hf Enrgian säilymislain prustlla lktronin rkyylinrgia
kertausta Boltzmannin jakauma infoa Ideaalikaasu kertausta Maxwellin ja Boltzmannin vauhtijakauma
 infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
infoa kertausta Boltzmannin jakauma Huomenna itsenäisyyspäivänä laitos on kiinni, ei luentoa, ei laskareita. Torstaina laboratoriossa assistentit neuvovat myös laskareissa. Ensi viikolla tiistaina vielä
Aineen olemuksesta. Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto
 Aineen olemuksesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Miten käsitys aineen perimmäisestä rakenteesta on kehittynyt aikojen kuluessa? Mitä ajattelemme siitä nyt? Atomistit Loogisen päättelyn
Aineen olemuksesta Jukka Maalampi Fysiikan laitos Jyväskylän yliopisto Miten käsitys aineen perimmäisestä rakenteesta on kehittynyt aikojen kuluessa? Mitä ajattelemme siitä nyt? Atomistit Loogisen päättelyn
.) (b) Vertaa p :tä vastaavaa kineettistä energiaa perustilan kokonaisenergiaan. ( ) ( ) = = Ek
 S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
S-446, FYSIIKKA IV (Sf) Kevät 5, HSf Rtkisut HSf- Kvnttimekninen hrmoninen värähtelijä on perustillln (mss m) Värähtelyn mplitudi on A () ske p (Värähtelijä sijitsee välillä A ) (b) Vert p :tä vstv kineettistä
S Fysiikka IV (SE, 3,0 ov) S Fysiikka IV (Sf, 4,0 ov )
 S-114.326 Fysiikka IV (SE, 3,0 ov) S-114.426 Fysiikka IV (Sf, 4,0 ov ) KVANTTIFYSIIKAN TUTKIMUSALA: Aineen atomirakenne Elektronitilat Aineen sähköiset ja optiset ominaisuudet Sähkömagneettisen kentän
S-114.326 Fysiikka IV (SE, 3,0 ov) S-114.426 Fysiikka IV (Sf, 4,0 ov ) KVANTTIFYSIIKAN TUTKIMUSALA: Aineen atomirakenne Elektronitilat Aineen sähköiset ja optiset ominaisuudet Sähkömagneettisen kentän
2 Mekaaninen aalto. Mekaaniset aallot kulkevat jossain materiaalissa, jota kutsutaan tässä yhteydessä väliaineeksi (medium).
 2 Mekaaninen aalto Mekaaniset aallot kulkevat jossain materiaalissa, jota kutsutaan tässä yhteydessä väliaineeksi (medium). 1 Mekaanisten aaltojen vastakohtana ovat sähkömagneettiset allot, jotka kulkevat
2 Mekaaninen aalto Mekaaniset aallot kulkevat jossain materiaalissa, jota kutsutaan tässä yhteydessä väliaineeksi (medium). 1 Mekaanisten aaltojen vastakohtana ovat sähkömagneettiset allot, jotka kulkevat
Kvanttimekaniikkaa yhdessä ulottuvuudessa
 Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
Kvanttimekaniikkaa yhdessä ulottuvuudessa Kvanttiefektit ovat tärkeitä nanoskaalassa. Tässä on ksenon-atomeilla tehtyjä kirjaimia metallipinnalla. Luennon tavoite: Ymmärtää kvanttimekaniikan perusperiaatteet
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Synkrotronisäteily ja elektronispektroskopia. Tutkimus Oulun yliopistossa
 Synkrotronisäteily ja elektronispektroskopia Tutkimus Oulun yliopistossa Ryhmätyö Keskustelkaa n. 4 hengen ryhmissä, mitä on synkrotronisäteily ja miten sitä tuotetaan. Kirjoittakaa ylös ajatuksianne.
Synkrotronisäteily ja elektronispektroskopia Tutkimus Oulun yliopistossa Ryhmätyö Keskustelkaa n. 4 hengen ryhmissä, mitä on synkrotronisäteily ja miten sitä tuotetaan. Kirjoittakaa ylös ajatuksianne.
π yd cos 2 b) Osoita, että lauseke intensiteetille sirontakulman funktiona on I
 PHYS-A140 Aineen rakenne C34 1. Monokromaattinen valo kulkee kaden vierekkäisen raon läpi. Rakojen takana olevalla varjostimella avaitaan valoisia ja mustia juovia. Rakojen välimatka d on samaa suuruusluokkaa
PHYS-A140 Aineen rakenne C34 1. Monokromaattinen valo kulkee kaden vierekkäisen raon läpi. Rakojen takana olevalla varjostimella avaitaan valoisia ja mustia juovia. Rakojen välimatka d on samaa suuruusluokkaa
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 4 Kevät 2017
 763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 4 Keät 207. Rekyyli Luentomonisteessa on käsitelty tilanne, jossa hiukkanen (massa M) hajoaa kahdeksi hiukkaseksi (massat m ja m 2 ). Tässä käytetään
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 4 Keät 207. Rekyyli Luentomonisteessa on käsitelty tilanne, jossa hiukkanen (massa M) hajoaa kahdeksi hiukkaseksi (massat m ja m 2 ). Tässä käytetään
SEISOVA AALTOLIIKE 1. TEORIAA
 1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
Fysiikka 1. Coulombin laki ja sähkökenttä. Antti Haarto
 ysiikka 1 Coulombin laki ja sähkökenttä Antti Haarto 7.1.1 Sähkövaraus Aine koostuu Varauksettomista neutroneista Positiivisista protoneista Negatiivisista elektroneista Elektronien siirtyessä voi syntyä
ysiikka 1 Coulombin laki ja sähkökenttä Antti Haarto 7.1.1 Sähkövaraus Aine koostuu Varauksettomista neutroneista Positiivisista protoneista Negatiivisista elektroneista Elektronien siirtyessä voi syntyä
KVANTTIMEKANIIKAN PERUSTEET...57
 KVANTTIMEKANIIKAN PERUSTEET...57.1 Johdanto... 57. Aaltofunktio ja todennäköisyystiheys... 58.3 Schrödingerin yhtälö... 61.3.1 Vapaan hiukkasen aaltofunktio... 6.4 Hiukkasen sironta potentiaaliaskeleesta...
KVANTTIMEKANIIKAN PERUSTEET...57.1 Johdanto... 57. Aaltofunktio ja todennäköisyystiheys... 58.3 Schrödingerin yhtälö... 61.3.1 Vapaan hiukkasen aaltofunktio... 6.4 Hiukkasen sironta potentiaaliaskeleesta...
Linssin kuvausyhtälö (ns. ohuen linssin approksimaatio):
 Fysiikan laboratorio Työohje 1 / 5 Optiikan perusteet 1. Työn tavoite Työssä tutkitaan valon kulkua linssisysteemeissä ja perehdytään interferenssi-ilmiöön. Tavoitteena on saada perustietämys optiikasta
Fysiikan laboratorio Työohje 1 / 5 Optiikan perusteet 1. Työn tavoite Työssä tutkitaan valon kulkua linssisysteemeissä ja perehdytään interferenssi-ilmiöön. Tavoitteena on saada perustietämys optiikasta
Luento 10: Työ, energia ja teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho Ajankohtaista Konseptitesti 1 Kysymys Ajat pyörällä ylös jyrkkää mäkeä. Huipulle vie kaksi polkua, toinen kaksi kertaa pidempi kuin
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho Ajankohtaista Konseptitesti 1 Kysymys Ajat pyörällä ylös jyrkkää mäkeä. Huipulle vie kaksi polkua, toinen kaksi kertaa pidempi kuin
