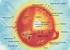
n=5 n=4 M-sarja n=3 L-sarja n=2 Lisäys: K-sarjan hienorakenne K-sarja n=1

Transkriptio

1 10.1 RÖNTGENSPEKTRI Kun kiihdytetyt elektronit törmäävät anodiin, syntyy jatkuvaa säteilyä sekä anodimateriaalille ominaista säteilyä (spektrin terävät piikit). Atomin uloimpien elektronien poistamiseen atomista tarvitaan näkyvän alueen fotoneja, kun taas sisäkuorten elektronit ovat tiukasti sidottuna atomiin. Esim. natrium 3s 5.13 ev p 31 ev s 63 ev 1s 1041 ev Röntgenputkessa kiihdytetty elektroni poistaa anodimateriaalin atomista sisäkuoren elektronin. Syntynyt aukko täyttyy ylemmän kuoren elektronilla ja vapautuu röntgenkvantti. 1

2 n=5 n=4 n=3 M-sarja L-sarja n= Lisäys: K-sarjan hienorakenne K-sarja n=1

3 Röntgensiirtymien taajuuksia voidaan approksimoida esimerkiksi seuraavasti: K α siirtymä L-kuorelta (n=) K-kuorelle (n=1) L kuoren elektroni kokee ytimen varauksen Ze vähennettynä varjostuksella, jonka yksi K kuoren elektroni aiheuttaa. Elektroni kokee siis ytimen varauksen (Z-1)e Korvataan vetyatomin energiayhtälössä E n e 8π r 0 n e 8π 0 πme n h 0 4 me 8n h 0 n 1,, 3,... varaus e 4 varauksella (Z-1) e 4 ja lasketaan alkutilan n i = ja lopputilan n f =1 välinen energiaero taajuuden avulla: f f m( Z 1) e 3 8h 0 3cR( Z 1) n f 1 n i cr( Z 1 1 1) 1 4 me R h c 0 7 m 1 3

4 Elektronivolteissa K α siirtymän energia on likimain: E(K α ) = 10. (Z-1) ev Tätä voidaan käyttää näyteatomin järjestysluvun Z määrittämiseen brittifyysikko H.G.J. Moseley mittaili ensimmäisenä kokeellisesti atomien järjestyslukuja. Näiden perusteella jaksollinen järjestelmä voitiin järjestää atomiluvun mukaiseen järjestykseen. Sitä ennen jaksollinen järjestelmä oli määritetty massaluvun mukaan. Tutkimuksissaan Moseley huomasi myös, että mittaukissa oli hyppäys Z=43, 61, 7 ja 75 kohdilla eli niitä alkuaineita ei vielä tähän aikaan tunnettu. Alkuaineet löydettiin kyllä myöhemmin (kahdella ensimmäisellä ei ole stabiilia isotooppeja ja kaksi viimeistä pystyttiin eristämään 190 luvulla). 4

5 ESIMERKKI 10.1 Minkä alkuaineen K α siirtymän aallonpituus on nm? 5

6 Atomien optisen alueen spektreistä - Vety 6

7 Natrium 7

8 Helium 8

9 Elohopea 9

10 10.. AUGER-ILMIÖ Atomin sisäkuorella oleva aukko voi täyttyä myös ns. Auger siirtymällä, jossa ylemmän kuoren elektroni täyttää aukon ja samalla toinen yläkuoren elektroni emittoituu. Irronneen ns. Auger-elektronin energia: E Auger =E sidos (K)-E sidos (L 1 )-E sidos (L,3 ) Auger siirtymä on todennäköisempi kuin röntgen-emissio pienillä alkuaineilla ja ulommilla kuorilla. Röntgen-emissio on hallitseva, kun aukko ison atomin sisäkuorella. 10

11 ESIMERKKI 10.. Kadmiumin K- ja L- absorptiorajat ovat nm sekä nm, nm ja nm. Laske termien energia kev:nä ja piirrä energiatasokaavio. Laske K α1 ja K α viivojen aallonpituudet. Laske kadmiumin Auger elektronien (K-LL) energiat. Oletetaan, että elektronin poistamiseen tarvittava energia on riippumaton siitä, että yksi elektroni on jo poistettu. 11

12 MITEN TUTKIMUSTA TEHDÄÄN? ESIMERKKI 8.9 Neonin Auger-spektri Kokeelliset mittaukset: Meet ELO Varastorenkaassa kiertää yksi tai useampia hiukkas kimppuja vakionopeudella, joka on lähellä valonnopeutta Säteilyn syntyminen varastorenkaassa: 1) Elektronitykki - elektronisuihkun synnyttäminen ) LINAC = lineaarinen kiihdytin (+Kiihdytinrengas (booster ring) - elektronien kiihdytys) Esim. MAX-III ringissä lineaarikiihdyttimen jälkeen elektronien energia on 99,9999% valonnopeudesta ja massa lähes 800 x elektronin lepomassa (400 MeV). 1

13 3) Varastorengas suorat osat ja elektronien rataa kaareuttavat magneettiset laitteet a) Taivutusmagneetti - Yksi magneettinen napapari, jatkuva säteilyspektri b) Wiggleri Magneettijonolähde, voimakkaat magneettikentät, jatkuva säteilyspektri c) Undulaattori Magneettijonolähde, vähemmän oskillaatiota, interferenssi -> terävät piikit 13

14 4) Säteilylinjat lähtevät magneettisista laitteista ja ohjaavat säteilyn mittauslaitteelle. Säteilyn monokromatisointi (erilaiset peilit ja hilat) Esim. tasohilamonokromaattori Tyhjiön ylläpitämiseen liittyviä laitteita (erilaiset tyhjiöpumput, venttiilit) MAX-II laboratorio, BL I

15 Kohdistetaan säteily näyteaineeseen ja mitataan emittoituneet elektronit esim. puolipalloanalysaattorin avulla 15

16 Mitäs meidän pitäisi spektrissä nähdä? 16