Jouni Sampo. 5. helmikuuta 2014
|
|
|
- Urho Heikkilä
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 B1 Jouni Sampo 5. helmikuuta 2014
2 Sisältö 1 Usean muuttujan funktioista Raja arvot ja jatkuvuus Osittaisderivaatat Normaalivektori, normaalisuora ja tangenttitaso Korkeamman kertaluvun derivaatat Ketjusääntö Differentioituvien funktioiden arvojen muutoksen tutkiminen ja approksimointi Lineaariset approksimaatiot Differentioituvuus ja differentiaalit Gradientti Suunnattu derivaatta Taylorin polynomi Implisiittifunktiot Funktion ääriarvot Kriittisten pisteiden luokittelu Funktioiden ääriarvojen etsintä rajoitteiden läsnä ollessa Lagrangen kertoimet Lineaarinen optimointi Pienimmän neliösumman menetelmä Kaksiulotteinen integraali 26 5 Parametrisia tehtäviä Derivoinnin ja integroinnin järjestyksen vaitaminen Verhokäyrät Implisiittisesti määriteltyjen funktioiden arviointi
3 1 Usean muuttujan funktioista Usean reaalimuuttujan funktio f on kuvaus, jossa jokaista funktion määrittelyjoukkoon D(f) kuuluvaa pistettä (x 1, x 2, x 3,..., x n ) R n vastaa yksikäsitteinen reaaliluku f(x 1, x 2,..., x n ). Määrittelyalueeksi (domain)d(f) on usein valittavissa jopa koko R n, mutta käytännön tilanteissa sitä voi olla järkevää rajoittaa. Kuten yhdenkin muuttujan funktioilla, usean muuttujan funktion f arvojoukko (range) R(f) koostuu kaikista funktion saamista arvoista, eli R(f) = {f(x 1, x 2,..., x n ) (x 1, x 2,..., x n ) D(f)}. Käytännössä arvojoukko voi olla erittäin haastavaa määrittää. Esimerkki 1.1. Painoindeksi w lasketaan kaavalla w = y/x 2 missä y on paino (kilogrammoina) ja x on pituus (metreinä). Painoindeksia voidaan siis ajatella kahden muuttujan funktiona w = f(x, y). a) Määritä R(f) jos D(f) = {(x, y) R x 2, 40 y 160}. b) Edellinen määrittelyjoukko ei mahdollista kaikille pituuksille samoja painoindeksejä. Mikä olisi määrittelyjoukon oltava jotta kaikille pituuksille 1.5 x 2 olisi mahdollista saada painoindeksiksi mikä tahansa luku väliltä [15, 40]? Kun muuttujia on korkeintaan kaksi, on funktioita vielä suhteellisen yksinkertaista kuvata graafisesti. Tällöin funktion f(x, y) kuvaaja, on joukko pisteitä R 3 :ssa, joiden koordinaatit ovat (x, y, f(x, y)). Kahden muuttujan funktio voidaan esittää graafisesti myös tasokäyrinä f(x, y) = C xy tasossa (topografinen kartta). Tasokäyrä on siis kuvaajan z = f(x, y) ja tason z = C leikkauskäyrän projektio, xy tasoon. Koska funktio saa tasokäyrän pisteissä aina vain samoja arvoja, kutsutaan tätä käyrää myös nimellä tasa-arvokäyrä. Esimerkki 1.2. Hahmottele funktion f(x 1, x 2 ) = x x 2 2 kuvaaja piirtämällä ensin muutamia tasokäyriä. Esimerkki 1.3. Olkoon f(x, y) = cos(x 2 y). Hahmottele tasokäyrät f(x, y) = 1 ja f(x, y) = 1. Esitä myös määrittely- ja arvojoukko f:lle ja yritä hahmotella f:n kuvaaja. 1.1 Raja arvot ja jatkuvuus Esitämme tässä raja-arvon määritelmän kahden muuttujan funktiolle: Raja arvo lim (x,y) (a,b) f(x, y) = L jos ja vain jos jokaista positiivista kokonaislukua ɛ vastaa positiivinen luku δ = δ(ɛ) siten, että f(x, y) L < ɛ, kun 0 < (x a) 2 + (y b) 2 < δ. (1) Yllä olevasta raja-arvosta on hyvä huomata kuinka samankaltainen se on A1 kurssilla esitettyyn yhden muuttujan raja-arvoon. Raja-arvon määritelmä yleistyisi n:n muuttujan funktioille 2
4 aivan samalla tavalla. Edellisestä määritelmästä seuraa että jos raja arvo on olemassa, se on yksikäsitteinen. Siis jotta raja arvo olisi olemassa, on f(x, y):n lähestyttävä lukua L, kun (x, y) lähestyy (a, b):tä mitä tahansa reittiä pitkin xy tasossa. Tämä tekee usein suhteellisen helpoksi tutkia sellainen tapaus jossa raja-arvoa ei ole olemassa. Esimerkki 1.4. Onko funktiolla f(x, y) = Ratkaisu: Reittiä y = 0 pitkin raja-arvoksi tulee lim (x,y) (0,0) Toisaalta reittiä y = x pitkin lim (x,y) (0,0) 2xy x 2 + y 2 = 2xy x 2 + y 2 = 2xy x 2 +y 2 raja arvoa, kun (x, y) (0, 0) lim (x,y) (0,0) 0 x 2 = lim 2x 2 (x,y) (0,0) 2x = 2 lim 0 = 0. (x,y) (0,0) lim 1 = 1. (x,y) (0,0) Koska eri reittejä pitkin saadut arvot eroavat toisistaan, ei funktiolla ole pisteessä (0, 0) rajaarvoa. Huom! Kun yhden muuttujan funktion tapauksessa raja-arvon olemassa oloa tutkittiin, voitiin tutkia erikseen raja-arvoa pistettä vasemmalta- ja oikealtapuolelta lähestyttäessä. Jos nämä raja-arvot täsmäsivät, oli raja-arvo olemassa. Koska useamman muuttujan funktiolla on mahdollisia lähestymissuuntia äärettömän monta eikä kaikkia voida millään käydä lävitse, rajaarvon olemassa olon todistamiseksi ainut matemaattisesti "vedenpitävä"menetelmä on suora raja-arvon määritelmän soveltaminen. Useamman muuttujan funktioiden raja arvot noudattavat samoja sääntöjä kuin yhden muuttujan funktioiden raja arvot, esim. jos lim (x,y) (a,b) f(x, y) = L ja lim (x,y) (a,b) g(x, y) = M lim (f(x, y) ± g(x, y)) = L ± M (x,y) (a,b) lim f(x, y)g(x, y) = LM (x,y) (a,b) f(x, y) lim (x,y) (a,b) g(x, y) = L M (2) Lisäksi jos F (t) on jatkuva, kun t = L, lim F (f(x, y)) = F (L). (3) (x,y) (a,b) Funktio f(x, y) on jatkuva pisteessä (a, b) jos ja vain jos lim f(x, y) = f(a, b). (4) (x,y) (a,b) 3
5 Esimerkki 1.5. Olkoon g(x, y) = e 1/(x2 +y 2) /(x 2 + y 2 ) kun (x, y) (0, 0). Kuinka g(0, 0) täytyisi määritellä jostta g olisi jatkuva koko R 2 :ssa? Ratkaisu: Merkitsemällä x 2 + y 2 = t funktio g(x, y) = e t 1 /t = F (t). Selvästi t on jatkuva funktio ja kun (x, y) (0, 0) niin t 0 +. Täten L Hospitalin säännön avulla saadaan lim (x,y) (0,0) g(x, y) = lim F (t) = lim t 0 + t 0 + t 1 e t 1 = lim t 0 + t 2 t 2 e t 1 1 = lim = 0. t 0 + e t 1 Täytyisi siis määritellä g(0, 0) = Osittaisderivaatat Kuten yhden muuttujan funktioiden tapauksessakin, useamman muuttujan funktioiden kasvua kuvataan derivaattojen avulla. Nyt kasvunopeus vain voi olla erilainen, riippuen siitä mihin suuntaan kasvua tarkastellaan. Mietitään ensin kahden muuttujan funktion kasvuominaisuuksia kun kuljetaan x tai y akselin suuntaan. Funktion f(x, y) ensimmäiset osittaisderivaatat muuttujien x ja y suhteen ovat funktiot f 1 (x, y) ja f 2 (x, y), jotka määritellään seuraavasti: f(x + h, y) f(x, y) f 1 (x, y) = lim h 0 h (5) f(x, y + k) f(x, y) f 2 (x, y) = lim, k 0 k (6) mikäli kyseiset raja arvot ovat olemassa. Huom! Kun kaavassa (5) määriteltiin lauseketta f 1 (x, y), laskettiin itseasiassa normaali derivaatta g funktiolle g(x) = f 1 (x, y), eli y muuttuja pidettiin vakiona. Samoin kun kaavassa (6) määriteltiin lauseketta f 2 (x, y), laskettiin itseasiassa normaali derivaatta h funktiolle h(y) = f 2 (x, y), eli x muuttuja pidettiin vakiona. Osittaisderivaattoja laskettaessa pätevätkin siis täysin samat laskusäännöt kuin yhden muuttujan funktioiden derivaattoja laskiessa! Esimerkki 1.6. Derivoi funktio g(x) = sin(ax) + 5ax 2. Laske osittaisderivaatat f 1 (x, y) ja f 2 (x, y) funktiolle f(x, y) = sin(yx) + 5yx 2. Ratkaisu: dg dx = a cos(ax) + 10ax, f 1(x, y) = y cos(yx) + 10yx ja f 2 (x, y) = x cos(yx) + 10x 2. Esimerkki 1.7. Laske osittaisderivaatat funktiolle f(x, y) = 1/2 + xy 3 + cos(xy) + ye y. Graafisesti osittaisderivaatat kuvaavat kasvunopeutta tiettyyn suuntaan: f 1 (a, b) on kuvaajan z = f(x, y) ja tason y = b leikkauskäyrän kulmakerroin pisteessä x = a. Esimerkki 1.8. Laske osittaisderivaatan f 2 (x, y) arvo pisteessä (x, y) = (0, 1/ 2) funktiolle f(x, y) = 1 x 2 y 2. Hahmottele tilanne myös graafisesti. 4
6 Esimerkki 1.9. Henkilö kävelee pitkin erästä pintaa joka on funktion f(x, y) kuvaaja. Aina ottaessaan h pituisen askeleen x akselin suuntaan, henkilö nousee 4h:n verran ylöspäin. Aina ottaessaan h pituisen askeleen y akselin suuntaan, henkilö laskeutuu 3h:n verran alaspäin. Määritä lausekkeet funktioille f 1 (x, y), f 2 (x, y) ja f(x, y). Kuten yhden muuttujan funktion derivaatoilla, on myös osittaisderivaatoilla useita vaihtoehtoisia merkintätapoja, esimerkiksi kahden muuttujan funktiolle z = f(x, y) Osittaisderivaatat pisteessä (a, b): ( z x (a,b) = x z y (a,b) = z x = x f(x, y) = f 1(x, y) = D 1 f(x, y) z y = y f(x, y) = f 2(x, y) = D 2 f(x, y) (7) ) f(x, y) ) ( f(x, y) y (a,b) = f 1 (a, b) = D 1 f(a, b) (a,b) = f 2 (a, b) = D 2 f(a, b) (8) Joskus käytetään myös merkintöjä f x ja f y. Edelliset merkintätavat yleistyvät myös useamman kuin kahden muuttujan funktioille. Esimerkki Tiedetään että eräästä prosessista mitattava suure y noudattaa mallia y = ce at missä c ja a ovat (mahdollisesti säädettäviä) prosessin parametreja ja t on aika. Laske prosessin säätöä/suunnittelua varten y, f ja f c t 3 kun y = f(t, c, a). Määritä myös f 3 (2, 3, ɛ) kun ɛ on jokin positiivinen vakio. Ratkaisu: y c = eat, f t = aceat, f 3 = tce at ja f 3 (2, 3, ɛ) = 2 3e ɛ 2. Esimerkki Laske osittaisderivaatat f Määritä myös arvo f 3 (1, 2, 0, 3). x, f u ja f 4 kun f(x, u, v, w) = x+xu+xuv +xuvw. Esimerkki Oletetaan että funktio f(x, y, z) kuvaa pisteen (x, y, z) etäisyyttä origosta. Laske f, f f ja. Laske myös f x y z 2(0, 1, 2). Esimerkki Olkoon g(x 1,..., x n ) = n i=1 xi i. Laske g x j sievennä myös n k=1 (g k(1, 1,..., 1)) 2. kaikille j = 1,..., n. Laske ja 1.3 Normaalivektori, normaalisuora ja tangenttitaso Seuraavat käsitteet yleistyisivät myös useamman kuin kahden muuttujan funktioille, tarkastelemme tässä kuitenkin vain kahden muuttujan tapausta. 5
7 Pinnan z = f(x, y) normaalivektori pisteessä (a, b, f(a, b)) on n = f 1 (a, b)i + f 2 (a, b)j k (9) Jos normaalivektori on siis esim. z-akselin suuntainen, on funktion kuvaaja (mikäli on sileä) pisteen (a, b) läheisyydessä xy-tason suuntainen (ja pisteessä (a, b) on mahdollisesti funktion minimi tai maksimikohta). Taso joka on kohtisuorassa normaalivektoria kohti ja kulkee pisteen (a, b) kautta on pinnan z = f(x, y) tangenttitaso pisteessä (a, b, f(a, b)). Tangenttitason yhtälö: Pinnan z = f(x, y) normaalisuoran yhtälö: z = f(a, b) + f 1 (a, b)(x a) + f 2 (a, b)(y b). (10) x a f 1 (a, b) = y b f 2 (a, b) = z f(a, b) 1 (11) On hyvä huomata että yhtälöissä (10) ja (11) on kyse aivan tavallisista (A2 kurssilta tutuista) tason ja suoran yhtälöistä. Esimerkki Etsi kuvaajan z = sin(xy) normaalivektori ja tangenttitason ja normaalisuoran yhtälöt pisteessä x = π/3, y = 1. Etsi myös ne pisteet jotka ovat normaalisuoralla ja joiden etäisyys on 5 yksikköä pisteestä (x, y, z) = ( π 3, 1, sin( π 3 )). Ratkaisu: Suoraan kaavoihin sijoittamalla, tangenttitaso ja normaalisuora z = sin( π 3 ( 1)) + ( 1) cos(π 3 ( 1))(x π 3 ) + π 3 cos(π ( 1))(y ( 1)) 3 x π 3 ( 1) cos( π 3 ( 1)) = Ilmoitetaan kysytyt pisteet paikkavektorin muodossa: y ( 1) π cos( π( 1)) = z sin( π ( 1)) r = π 3 i j + sin( π 3 )k + t n n, missä t = ±5 ja n = cos( π( 1))i + π cos( π ( 1))j k Esimerkki Muodosta tangenttitaso ja normaalisuora funktiolle f(x 1, x 2 ) = sin(x 2 x 1 ) + 5x 2 x 2 1 pisteessä (x 1, x 2 ) = (π/4, 1). 1.4 Korkeamman kertaluvun derivaatat Kahden muuttujan funktiolle z = f(x, y), voidaan laskea toisen kertaluvun derivaatat: Puhtaat toiset osittaisderivaatat x:n tai y:n suhteen 2 z x = z 2 x x = f 11(x, y) = f xx (x, y) 2 z y = z 2 y y = f 22(x, y) = f yy (x, y) (12) 6
8 Toiset sekaderivaatat x:n ja y:n suhteen: 2 z x y = x z y = f 21(x, y) = f yx (x, y) 2 z y x = z y x = f 12(x, y) = f xy (x, y) (13) Korkeamman kertaluvun derivaatoille ja useamman muuttujan funktiolle on aivan vastaavat merkinnät, esim. w = f(x, y, z) 5 w y x y 2 z = y x y w y z = f 32212(x, y, z) = f zyyxy (x, y, z) (14) Oletetaan, että funktion f kaksi n:nnen kertaluvun sekaderivaattaa sisältää samat derivoinnit mutta eri järjestyksessä. Jos f ja kaikki n:ää alemman kertaluvun osittaisderivaatat ovat jatkuvia pisteen P ympäristössä niin silloin edellä mainitut sekaderivaatat ovat samoja pisteessä P (tai yksinkertaisesti sanottuna: derivoimisjärjestys ei vaikuta lopputulokseen). Esimerkki Laske 2 f x 2, 3 f x 2 y kun f(x, y) = sin(xy). Ratkaisu: Ensinäkin 2 f x = 2 x ( f x ) = x (y cos(xy)) = y2 sin(xy). Koska vaikka kuinka derivoisi, lausekkeeseen ei selvästi ilmesty mistään jakajia, logaritmeja yms. tilanteita mistä epäjatkuvuutta voisi syntyä, voidaan varmasti derivoimisjärjestystä vaihtaa, jolloin saadaan käytettyä edellä laskettua hyväksi: 3 f x 2 y = 2 f y x = 2 y ( y2 sin(xy)) = 2y sin(xy) y 2 x cos(xy) Esimerkki Osoita suoraan laskemalla että f 223 (x, y, z) = f 232 (x, y, z) = f 322 (x, y, z) kun f(x, y, z) = e x 2y+3z. Korkeamman kertaluvun osittaisderivaattoja esiintyy muunmuassa osittaisdifferentiaaliyhtälöissä jotka ovat monen insinööritieteen kulmakiviä: tapa muotoilla ongelma matemaattiseen muotoon ratkaisua varten. Differentiaaliyhtälöiden ratkaiseminen voi olla haastavaa (ja tehdään usein numeerisesti) mutta annetun (analyyttisen) ratkaisun kelpoisuuden toteaminen on suoraviivainen sijoitustehtävä. Esimerkki Osoita että z = e kx cos(ky) sekä z = e kx sin(ky) kelpaavat kummatkin ratkaisuksi Laplacen yhtälölle 2 z x + 2 z 2 y = 0 (15) 2 Esimerkki Yksiulotteinen Aaltoyhtälö on muotoa 2 w t = 2 w 2 c2 (16) x 2 Osoita että ratkaisuiksi kelpaavat ainakin funktiot jotka ovat muotoa w(x, t) = f(x ct) + g(x + ct), olettaen että f ja g ovat kahdesti derivoituvia. 7
9 1.5 Ketjusääntö Matematiikka A1 kurssista tuttu yhdistetyn funktion derivoimiskaava on D(f(g(x))) = f (g(x))g (x). Merkintöjä y = f(u) ja u = g(x) käyttäen tämä voidaan kirjoittaa myös muodossa dy dx = df du du dx. (17) Käytettiin kumpaa tahansa muodoista, voidaan puhua ketjusäännöstä, joskin se on yleisempää jälkimmäisen kohdalla. Useamman muuttujan funktioiden kohdalla ketjusääntö muuttaa hieman muotoaan: Jos z on x:n ja y:n jatkuva funktio, jolla on jatkuvat ensimmäiset osittaisderivaatat ja jos x ja y ovat t:n derivoituvia funktioita, on voimassa dz dt = z dx x dt + z dy y dt (18) Yleisemmin: Olkoon f(x 1, x 2,..., x n ) jatkuva funktio, jolla on jatkuvat ensimmäiset osittaisderivaatat. Olkoon lisäksi x i, i = 1,..., n muuttujan t jatkuvia funktioita. Tällöin df dt = f dx 1 x 1 dt + f dx 2 x 2 dt + + f dx n x n dt. (19) Edellä on hyvä huomata että on aivan luonnollista tutkia derivaattaa df dt f on t:n funktio. koska pohjimmiltaan Esimerkki Laske ketjusäännön avulla dz dt kun z(x, y) = xy + y2, x = cos(t) ja y = t 2. Ratkaisu: dz dt = z dx x dt + z dy y dt = y dx + (x + 2y)dy dt dt = y sin(t) + (x + 2y)2t = t 2 sin(t) + ( cos(t) + 2t 2 )2t Esimerkki Olkoon f(x, y) = e x +x 2 +y 3, y = cos(t) ja x = e t. Laske df dt b) sijoittamalla ensin x:n ja y:n lausekkeet ja sitten derivoimalla. a) ketjusäännöllä Esimerkki Laske ketjusäännön avulla h f kun h(f, x) = ef x 2, f = ln(t) ja x = t. Esimerkki Laske ketjusäännöllä df dt kun f(x 1,..., x n ) = n i=1 xi i ja x j = t j, j = 1,..., n. 8
10 Koska osittaisderivaatat lasketaan aivan normaalien derivaattojen tapaan, ketjusääntö ei oleellisesti monimutkaistu vaikka "sisäfunktioilla"olisi useampiakin muuttujia. Oleellisin ero on että "d"merkit muuttuvat " "merkeiksi muistuttamaan siitä että funktion arvon taustalla on mahdollisesti useampia muuttujia. Esimerkiksi jos kolmen muuttujan funkton f(x, y, z) muuttujat x, y ja z riippuvat vielä muuttujista t ja s, niin voi olla mielenkiintoista tutkia funkton muutosta näiden muuttujien suhteen, eli laskea osittasiderivaatat f s = f x x s + f y y s + f z z s ja f t = f x x t + f y y t + f z z t (20) Esimerkki Eräässä piirissä virta I riippuu jännitteistä U 1, U 2 ja resistansseista R 1 ja R 2 kaavan I = U 1 /R 1 + U 2 /R 2 mukaisesti. Ajanhetkellä t = 0 on U 1 = U 2 = 0, ja R 1 = 1, R 2 = 10. Jos virran I muutosnopeudeksi hetkellä t = 0 tahdotaan 3 (ampeeria sekunnissa), mikä on oltava jännitteen U 1 muutosnopeus kun U 2 :n muutosnopeus on 4 (volttia sekunnissa), R 2 on vakio ja R 1 :n muutosnopeus on 3? Esimerkki Funktio z(x, y) = 2xy 3 + x 2, x = t 3 + cos(s) ja y = s 2. Laske z t ketjusäännön z s = z x x s + z y y s z t = z x x t + z y y t ja z s (21) avulla. Ketjusäännön kaavat ovat usein pitkiä erityisesti korkeamman kertaluvun derivaatoille ja niitä löytyy myös kaavakirjoista. Korkeamman kertaluvunkin derivaattoja voidaan kuitenkin laskea suoraviivaisesti derivoimalla "yksi derivaatta kerrallaan". Esimerkki Laske 3 f kun f(x, y) = t 2 s ex + y 2 missä x = s 4 ja y = s cos(t). Tee tämä ensin ketjusääntöä soveltamalla ja sitten sijoittamalla ennen derivointia x:n ja y:n lausekkeet. Ratkaisu: Koska 3 f = f f, lasketaan ensin t 2 s t t s tulon derivoimissääntöä kahdesti käyttäen saadaan f t s = ( e x 4s 3 + 2y cos(t) ) t = f s x = 4s 3 t ex + 2y cos(t) t = 4s 3 e x x t + 2 cos(t) t y + 2y t cos(t) = 4s 3 e x cos(t)( s sin(t)) + 2y( sin(t)) = 2 sin(t)(s cos(t) + y) x + f y = s y s ex 4s 3 + 2y cos(t). Täten 9
11 ja lopulta f t t s = ( 2 sin(t)(s cos(t) + y)) t = 2(s cos(t) + y) t sin(t) 2 sin(t) (s cos(t) + y) t = 2(s cos(t) + y) cos(t) 2 sin(t)( s sin(t) s sin(t)) = 4s(cos 2 (t) sin 2 (t)) Sijoittamalla: f(x, y) = e s4 +s 2 cos 2 (t). Täten f = s es4 4s 4 +2s cos 2 (t) ja t 4s sin(2t), eli = 8s cos(2t). t t f s f s = 0+2s( 2 sin(t) cos(t)) = Edellisessä esimerkissä ensimmäinen tapa oli paljon pidempi siitä syystä että tällä kertaa lausekkeessa x ja y esiintyivät hyvin harvoissa kohdissa, jolloin suora sijoitus tuli melko yksinkertaiseksi. Jos f:n x:n ja y:n lausekkeet olisivat pitkiä niin ketjusäännön käyttäminen toisi selvää etua myös laskun pituuteen sillä sisäfunktioiden derivaatat tulevat esiintymään aina vain kertaalleen. Esimerkki Laske ketjusääntöä soveltamalla sekä ilman ketjusääntöä (suoraan sijoittamalla) dl2 f funktiolle f(x, y) = ye 2x +y 4 kun x = sin(t) ja y = t. Laske myös kyseisen derivaatan dt 2 arvo kun t = 0. Ketjusäännön "ketju"voi olla pidempikin. Kolmelle sisäkkäiselle yhden muuttujan funktiolle saadaan derivoimiskaava soveltamalla kaksi kertaa ketjusääntöä: D(f(g(h(x)))) = f (g(h(x)))d(g(h(x))) = f (g(h(x)))g (h(x))h (x). Samoin voidaan toimia useamman muuttujan funktioiden kanssa. Esimerkki Määritä ketjusäännön avulla f z 1 kun f(x 1, x 2 ) = 2x 1 x 4 2, x 1 = 6y 1, x 2 = y 1 + cos(y 2 ), y 1 = 2z 2 2, y 2 = 7z 1 + 8z 2. Ratkaisu: Ketjusäännön mukaan f z 1 = f x 1 x 1 z 1 + f x 2 x 2 z 1 ( x2 y 1 + x ) 2 y 2 y 1 z 1 y 2 z 1 = f x 1 y 1 + f x 1 y 1 z 1 x 2 = 2x x 1 x 3 2 (1 0 sin(y 2 ) 7) = 56x 1 x 3 2 sin(y 2 ) = 56(6 2z 2 2(2z cos(7z 1 + 8z 2 ))) 3 Esimerkki Määritä ketjusäännön avulla f s kun f(x, y, z) = ex +y 2 +cos(x)z, x = h 2 +g, y = sin(hg), z = g 3, h = 2s + 3t + 4u, ja g = cos(s + u). Huomaa että f on pohjimmiltaan siis s:n, t:n ja u:n funktio. 10
12 Ketjusääntöä voidaan käyttää esimerkiksi kun: Ilmiö mallinnetaan osa kerrallaan ja ilmiön muutosnopeus eri muuttujien suhteen kiinnostaa. Tunnettuja tuloksia (kaavoja) muunnetaan hieman muuttuneeseen tilanteeseen tai tarkoituksenmukaisempaan muotoon, esimerkiksi kun siirrytään erilaiseen koordinaatistoon. Teoreettisten tulosten johtamisessa Esimerkki Olkoon g(z, y, z) = x 2 + y 2 + z 2. a) Määritä ketjusäännön avulla kuinka nopeasti g on muuttumassa ajan t suhteen ajanhetkellä t = 0 kun x(t) = sin(t), y(t) = cos(t) ja z(t) = t 2. b) Jos pisteen (x, y, z) muutosnopeus ajan suhteen z suunnassa pystytään mittaamaan, i) pystytäänkö pisteen muutosnopeus päättelemään myös x ja y suunnassa? ii) pystytäänkö funktion g muutosnopeus t:n suhteen päättelemään? Esimerkki Osoita että Laplacen yhtälö napakoordinaateissa on 2 z r + 1 z 2 r r z r 2 θ = 0 (22) 2 2 Differentioituvien funktioiden arvojen muutoksen tutkiminen ja approksimointi 2.1 Lineaariset approksimaatiot Käyrän y = f(x) tangenttisuoraa pisteessä x = a voidaan käyttää approksimaationa f(x):n arvoille, kun x on lähellä a:ta: f(x) L(x) = f(a) + f (a)(x a) (23) Funktiota L(x) kutsutaan f:n linearisaatioksi tai lineaariseksi approksimaatioksi pisteessä a. Vastaavasti funktion f(x, y) lineaarinen approksimaatio pisteessä (a, b) on f(x, y) L(x, y) = f(a, b) + f 1 (a, b)(x a) + f 2 (a, b)(y b) (24) Funktion f(x 1,..., x n ) linearisaatio pisteessä a = (a 1,..., a n ) määritellään samoin: L(x 1,..., x n ) = f(a 1,..., a n ) + n i=1 f x i a (x i a i ) (25) Linearisaatio L(x) on ekvivalentti Pisteeseen a asetetun tangenttitason kanssa Taylorin 1. asteen polynomin kanssa (tähän palataan myöhemmin) 11
13 Esimerkki 2.1. a) Muodosta funktiolle f(x, y) = x 2 + x sin(y) linearisaatio eli lineaarinen approksimaatio piteessä (2, 0). b) Olkoon f(x 1, x 2, x 3 ) = x x 2 + x 2 3. Muodosta f:lle lineaarinen approksimaatio pisteessä (1, 10, 0) ja arvioi tämän avulla mitä on f(1.02, 10 + a, 0.01), missä a on jokin vakio. Ratkaisu: a) Osittaisderivaatat ovat f 1 (x, y) = 2x + sin(y) ja f 2 (x, y) = x cos(y), joten f 1 (2, 0) = 4 ja f 2 (2, 0) = 2. Lisäksi f(2, 0) = 4, joten suoraan kaavaan (24) sijoittamalla saadaan L(x, y) = 4 + 4(x 2) + 2(y 0) b) Osittaisderivaatat ovat f 1 (x 1, x 2, x 3 ) = 2x 1 f 2 (x 1, x 2, x 3 ) = 1 ja f 3 (x 1, x 2, x 3 ) = 2x 3, joten f 1 (1, 10, 0) = 2 f 2 (1, 10, 0) = 1 f 3 (1, 10, 0) = 0 ja f(1, 10, 0) = 11. Täten suoraan kaavaan (25) sijoittamalla L(x 1, x 2, x 3 ) = (x 1 1) + 1 (x 2 10) + 0 (x 3 0) ja L(1.02, 10 + a, 0.01) = a. Esimerkki 2.2. a) Muodosta funktiolle f(x, y) = xy + x linearisaatio eli lineaarinen approksimaatio piteessä (1, 1). b) Olkoon f(u, v, w) = u 2 + v 2 + w 2. Muodosta f:lle lineaarinen approksimaatio pisteessä (0, 1, 2) ja arvioi tämän avulla mitä on f(0.01, 0.95, 2.02). Yhden muuttujan funktioille linearisaatiota ei voida laske jos derivaatta ei ole määritelty. Useamman muuttujan funktioilla tilanne on se että osittaisderivaatat voivat olla määritellyt (eli linearisaatio pystytään teknisesti ottaen muodostamanaan), vaikka funktio olisi sellainen että linearisaatio olisi surkea approksimaatio funktiolle f jopa lähellä pistettä a. Tälläiset funktiot eivät ole differentioituva pisteen a ympäristössä. Funktion differentioituvuus voidaankin määritellä asettamalla laatuvaatimus linearisaatiolle: 2.2 Differentioituvuus ja differentiaalit Funktio f(x, y) on differentioituva pisteessä (a, b), jos f(a + h, b + k) f(a, b) hf 1 (a, b) kf 2 (a, b) lim = 0. (26) (h,k) (0,0) h2 + k 2 Tämä tarkoittaa että pistettä (a, b) lähestyessä funktion f(x, y) ja sen pisteeseen (a, b) muodostetun tangenttitason arvot lähenevät toisiaan oleellisesti nopeammin kuin mitä (x, y) piste lähestyy pistettä (a, b). Esimerkki 2.3. Hahmottele funktio (sen kuvaaja) jolle linearisaatio voidaan teknisesti ottaen muodostaa pisteessä (0, 0), mutta joka ei ole differentioituva kyseisessä pisteessä. Koska differentioituvuus on usein algoritmeille tärkeä ominaisuus, on käytännöllistä että varsin yksinkertaiset ehdot varmistavat tämän. Seuraava tulos on varsin hyödyllinen tieto: Jos f 1 ja f 2 ovat jatkuvia pisteen (a, b) ympäristössä niin tällöin f on differentioituva pisteessä (a, b). 12
14 Esimerkki 2.4. Osoita että f(x 1, x 2 ) = e x 1x 2 + cos(x 2 ) on kaikkialla differentioituva. Väliarvolause (mean value theorem): Jos f 1 (x, y) ja f 2 (x, y) ovat jatkuvia pisteen (a, b) ympäristössä ja jos h:n ja k:n itseisarvot ovat riittävän pieniä, on olemassa luvut θ 1 ja θ 2, molemmat 0:n ja 1:n välillä, siten, että f(a + h, b + k) f(a, b) = hf 1 (a + θ 1 h, b + k) + kf 2 (a, b + θ 2 k) (27) Väliarvolauseella on merkitystä usein matemaattisten menetelmien ja algoritmien tutkimisessa ja kehittämisessä mutta insinööri joutuu sitä harvemmin arkipäivän laskennassa käyttämään (luvut θ 1 ja θ 2 ovat useinmiten varsin hankalia määrittää). Sellaisessa pisteessä jossa funktiolla z = f(x 1,..., x n ) on jatkuvat ensimmäiset osittaisderivaatat, voidaan funktion arvon muutosta kuvaava (kokonais) differentiaali määritellä kaavalla dz = df = z x 1 dx z x n dx n = f 1 (x 1,..., x n )dx f n (x 1,..., x n )dx n. (28) Differentiaali sisältää saman informaation kuin ketjusääntö: jos (28) jaetaan puolittain dt:llä ja x i :t ajatellaan t:stä riippuvaisiksi niin saadaan näkyviin täsmälleen ketjusäännön mukainen kaava. Differentiaalia on kuitenkin usein ketjusääntöä suoraviivaisempaa käyttää käytännön laskuissa: Koska differentiaalit dx i ajatellaan mielivaltaisen pieniksi, korvaamalla ne pienillä luvuilla x i, differentiaalilla df voidaan arvioida f:n arvojen muutosta ilman että tarvitsee miettiä muuttujia x i sitovaa taustamuuttujaa t kuten ketjusäännön kaavassa täytyisi: f = f(x 1 + x 1,..., x n + x n ) f(x 1,..., x n ) f 1 (x 1,..., x n ) x f n (x 1,..., x n ) x n (29) Tälläisien approksimaatioiden käyttö on varsin yleistä insinööritieteissä. On opettavaista huomata ettei tässäkään approksimaatiossa ole itseasiassa kyse mistään muusta kuin linearisaation käyttämisestä funktion arvon muutoksen arviointiin. Esimerkki 2.5. Oletetaan että g(x, y) on differentioituva funktio. Jos g(0, 0) = 1, g 1 (0, 0) = 2 ja g 2 (0, 0) = 0.2, arvioi differentiaalin avulla funktion g arvoa pisteessä (0.1, 0.25). Esimerkki 2.6. Arvioi differentiaalin avulla prosentuaalista muutosta heilurin heilahdusajassa L T = 2π g, (30) jos pituus L kasvaa 2% ja gravitaatiokiihtyvyys g pienenee 0.6%? 2.3 Gradientti Jos pinnan normaalivektorista jätetään viimeinen komponentti pois, saadaan gradienttivektori f(x, y) = gradf(x, y) = f 1 (x, y)i + f 2 (x, y)j, (31) 13
15 missä (nabla) on vektoridifferentiaalioperaattori = i x + j y Useamman muuttujan funktiolle määritelmä menee samoin: ( f f(x 1,..., x n ) =,..., f ) x 1 x n (32) (33) Huomaa että edellisessä vektoria merkitään avaruuden R n pisteenä sen sijaan että koordinaattiakselien suuntaiset yksikkövektorit kirjoitettaisiin näkyviin. Kyseessä on vain (lyhyempi) merkintätapa. Esimerkki 2.7. a) Laske gradienttivektori pisteessä (x, y) = (1, 2) funktiolle f(x, y) = x 2 y + ln(x). b) Laske funktion f(x, y, z) = x 2 + y 2 + z 2 gradienttivektorin ja vektorin v = (1, 2, 0) pistetulo. Ratkaisu: a) Gradienttivektori pisteessä (x, y) on f(x, y) = f 1 (x, y)i + f 2 (x, y)j = (2xy + 1/x)i + x 2 j, joten piseessä (1,2) f(1, 2) = 5i + j. b) Gradienttivektori f(x, y, z) = (2x, 2y, 2z), joten pistetulo f(x, y, z) v = (2x, 2y, 2z) (1, 2, 0) = 2x 1 + 2y 2 + 2z 0 = 2x + 4y. Esimerkki 2.8. Määritä gradienttivektorit funktioille f(x, y) = e x y, g(x, y, z) = sin(xy) + cos(yz) ja h(x 1, x 2, x 3, x 4 ) = 3x 1 + 2x 3 + e x 4. Esimerkki 2.9. Laske gradienttivektori seuraaville funktioille a) f(x, y) = cos(x) sin(y). b) x(y, z), kun x + ye x = z 2 c) g(x 1,..., x n ) = n i=1 a ix i, missä luvut a i ovat vakioita. Gradienttivektorin ominaisuuksia: Jos f(x, y) on derivoituva pisteessä (a, b) ja f(a, b) 0, niin f(a, b) on pisteen (a, b) kautta kulkevan f:n tasokäyrän normaalivektori. Funktion f(x, y) muutosnopeus pisteessä (a, b) on nolla pisteen (a, b) kautta kulkevan funktion f tasokäyrän suunnassa, eli kohtisuorassa vektoria f(a, b) vastaan. Pisteessä (a, b) funktio f(x, y) kasvaa nopeimmin gradienttivektorin f(a, b) suuntaan. Kasvun maksiminopeus on f(a, b). Pisteessä (a, b) funktio f(x, y) vähenee nopeimmin vektorin f(a, b) suuntaan. Vähenemisen maksiminopeus on f(a, b). 14
16 Aivan vastaavat ominaisuudet pätevät myös useamman muuttujan funktoille, tietystikin tällöin ei voida puhua tasokäyristä vaan esim. kolmen muuttujan funktion tapauksessa tasa-arvo pinnoista. Esimerkki Olkoon f(x, y) = e (x2 +y 2). a) Mihin suuntaan f kasvaa nopeimmin pisteessä (1, 1) b) Määritä se xy-tason käyrä joka kulkee pisteen (1, 1) kautta ja jota pitkin kulkiessa f:n arvo ei muutu. c) Määritä ne (x, y) pisteet joissa f(x, y) = 1 Esimerkki Olkoon f(x, y) = 20(3 + x 2 + 2y 2 ) 1. Mitä pisteen (3, 2) kautta kulkevaa xy-tason käyrää pitkin f(x, y) vähenee nopeimmin? 2.4 Suunnattu derivaatta Gradientti ja osittaisderivaatat kertovat funktion kasvunopeudesta tietyissä suunnissa, mutta entäpä jos kasvunopeutta pitäisi kuvata mielivaltaisesti valitussa suunnassa? Suunnattu derivaatta auttaa tässä. Olkoon u = ui + vj yksikkövektori, ts. u 2 + v 2 = 1. Funktion f(x, y) suunnattu derivaatta pisteessä (a, b) vektorin u suuntaan on f(x, y):n muutosnopeus suhteessa pisteestä (a, b) mitattuun etäisyyteen pitkin u:n suuntaista sädettä xy tasossa. Suunnattu derivaatta voidaan määritellä esim. tai f(a + hu, b + hv) f(a, b) D u f(a, b) = lim h 0+ h (34) D u f(a, b) = d dt f(a + tu 1, b + tu 2 ) t=0, (35) jos tämä derivaatta on olemassa. Ensimmäisessä muodossa joudutaan laskemaan raja-arvo. Jälkimmäinen muoto on varsin näppärä laskea ketjusäännön avulla, mikäli ketjusäänön oletukset ovat voimassa (jatkuva funktio, jatkuvat osittaisderivaatat). Tämä ketjusäännön käyttäminen voidaan kuitenkin kirjoittaa lyhyesti Gradientin avulla. Gradientti on siis usein kätevä työkalu suunntatun derivaatan laskemiseksi: Jos f on derivoituva pisteessä (a, b) ja u = ui + vj yksikkövektori, niin f:n suunnattu derivaatta pisteessä (a, b) vektorin u suuntaan on D u f(a, b) = u f(a, b). (36) Vektorin v suuntainen yksikkövektori saadaan jakamalla vektori sen pituudella. Näin ollen suunnattu derivaatta vektorin v suuntaan on D v/ v f(a, b) = v f(a, b). (37) v Mille tahansa yksikkövektorille u on voimassa missä θ on vektorien u ja f(a, b) välinen kulma. D u f(a, b) = u f(a, b) = f(a, b) cos θ, (38) 15
17 Esimerkki a) Laske funktion h(x, y) = sin(x) + cos(y) suunnattu derivaatta vektorin u = 2i j suuntaan pisteessä P = (0, π/2). b) Määritä vektori v siten että pisteessä P funktion h(x, y) suunnattu derivaatta vektorin v suuntaan on Ratkaisu: a) Lasketaan ensin kaavassa (37) tarvittavan gradientin arvo. Ensinä h(x, y) = cos(x)i sin(y)j joten h(0, π/2) = i j. Sijoitetaan nyt kaikki edellä mainittuun kaavan D u/ u h(0, π/2) = u h(0, π/2) = 2i u j ( 1) ( 1) (i j) = = Edelliset määritelmät ja ominaisuudet yleistyvät myös useamman muuttujan funktioille. Erityisesti: Jos f(x 1,..., x n ) on differentioituva pisteessä (a 1,..., a n ), niin f:n suunnattu derivaatta pisteessä (a 1,..., a n ) vektorin u suuntaan on D u f(a 1,..., a n ) = u f(a 1,..., a n ). (39) Esimerkki Laske suunnattu derivaatta funktiolle g(x, y) = x + 2yx pisteessä (1, 0) vektorin 2i + 3j suuntaan. Esimerkki Laske suunnattu derivaatta funktiolle g(x, y, z, t) = (x+2yx+3z+4t)pisteessä (1, 0, 3, 2) vektorin (2, 3, 0, 5) suuntaan. f(a, b), eli suun- HUOM! Usein suunnattu derivaatta määritellään kaavalla D v f(a, b) = v tavektorin normalisaatio on sisällytetty määritelmään. v 2.5 Taylorin polynomi Taylorin polynomin käsite on usean muuttujan funktioille samanlainen kuin yhden muuttujan funktiollekin: Funktio f(x, y), jolla on vähintään n:n kertaluvun jatkuvat osittaisderivaatat, voidaan lausua Taylorin polynomin ja jäännöstermin avulla: missä f(x, y) = f(a + h, b + k) = P n (x, y) + R n, (40) P n (x, y) = n 1 j=0 ( 1 h j! x + k ) j f(a, b) (41) y ja R n = 1 ( h n! x + k ) n f(a + θh, b + θk), 0 < θ < 1 (42) y Jäännöstermissä R n esiintyvä luku θ riippuu x:n ja y : n arvoista ja on yleensä hyvin hankala, jollei peräti mahdoton määrittää. Polynomia käytetäänkin yleensä approksimaationa alkuperäiselle funktiolle, eli f(x, y) P n (x, y) (43) ja jotta approksimaatio olisi hyvä, on piste (a, b) syytä valita sellaiseksi että se on kiinnostavien (x, y) pisteiden lähistöllä (eli h ja k ovat aina pieniä). 16
18 Esimerkki Muodosta toisen asteen Taylorin polynomi funktiolle (kolmannen asteen polynomille) f(x, y) = x 3 + xy + y 3 a) pisteessä (0, 0) kehitettynä ja laske P 2 (1, 1). b) pisteessä (1, 2) kehitettynä ja laske P 2 (1, 1). 1. Laske molemmissa tapauksissa approksimaatiovirheen f(1, 1) P 2 (1, 1) suuruus. Joskus polynomiapproksimaatio usean muuttujan funktiolle on kätevä rakentaa käyttämällä yhden muuttujan Taylorin polynomeja. Esimerkki Muodosta sellainen polynomi jolla voidaan approksimoidan funktion f(x, y, z) arvoja pisteen (1, 1, π) läheisyydessä kun f(x, y, z) = cos(xyz) + sin(x 2 ) cos(z). Käytä apuna ensimmäisen asteen (yhden muuttujan) Taylorin polynomeja funktioille cos(t) ja sin(t). Virhearviotarkastelu voi tietysti olla vielä monimutkaisempaa tälläisessä tapauksessa sillä kyseessä ei välttämättä ole enää (usean muuttujan) Taylorin polynomi eikä voida tarkastella yksittäistä virhetermiä. 2.6 Implisiittifunktiot Jo kurssilla Matematiikka A1 laskettiin funktion y = f(x) derivaatalle lausekkeita tapauksessa jossa y on määritelty implisiittisesti lausekkeen F (x, y) = 1 avulla. Virkistetään hieman muistia Esimerkki Olkoon y + e y = (x + x 3 )/2. a) Määritä lauseke dy dx. b) Laske y (x) siinä pisteessä x jolle y = 1. c) Kun x = 1 niin y = 0. Jos mahdollista, laske y (1) ja x (0). Jälkimmäisessä x:ää siis ajatellaan y:n funktiona. d) Edellisten perusteella, mieti kuinka 1. asteen Taylorin polynomia voisi käyttää arvioimaan käyrän kulkua pisteen (1, 0) läheisyydessä. Muotoillaan nyt edellisessä esimerkissä käytettyjä laskutoimenpiteitä hieman yleisempään muotoon: Oletetaan, että piste (a, b) toteuttaa yhtälön F (x, y) = 0 ja että funktiolla F on jatkuvat ensimmäiset osittaisderivaatat kaikissa pisteissä (a, b):n lähellä. Jos tästä yhtälöstä voidaan y ratkaista x:n funktiona, niin y:n derivaatta x:n suhteen pisteessä x = a voidaan ratkaista derivoimalla yhtälö F (x, y) = 0 puolittain (ketjusääntöä soveltamalla) x:n suhteen ja laskemalla tulos pisteessä (a, b): F 1 (x, y) + F 2 (x, y) dy = 0, (44) dx josta saadaan (ehdolla F 2 (a, b) 0) dy dx x=a = F 1(a, b) F 2 (a, b) (45) 17
19 Ongelmia aiheuttavat lähinnä pisteet joissa jakaja menee nollaksi: Tälläisissä pisteissä voi olla ettei käyrä edes määrittele pisteen (a, b) läheisyydessä y:tä x:n funktiona, varmaa on että numeerisia ongelmia tulee jos jokin algoritmi käyttää derivaatan arvoja. Vastaavasti jos ajateltaisiin x:ää muuttujan y funktiona, saataisiin F 1 (x, y) dx dy + F 2(x, y) = 0, (46) josta dx dy y=b = F 2(a, b) F 1 (a, b). (47) Esimerkki a) Olkoon F (x, y) = x 2 + y 2 1. Päättele ilman laskemista minkä pisteiden läheisyydessä yhtälö F (x, y) = 0 ei määrittele y:tä x : n funktiona. Laske näissä pisteissä F 1 (x, y). Päättele ilman laskemista ne pisteet joissa F 2 (x, y) = 0. b) Muodosta funktio F (x, y) siten että yhtälö F (x, y) = 0 määrittelee pisteen (0, 1) läheisyydessä x:n muuttujan y funktiona mutta F 1 (x, y) = 0. Ajatus toimii myös useamman muuttujan tapauksessa: esim. jos ajatellaan että yhtälö F (x, y, z) = 0 määrittelee z:n muuttujien x ja y funktiona, saadaan z x (x 0,y 0 ) = F 1(x 0, y 0, z 0 ) F 3 (x 0, y 0, z 0 ) ja z y (x 0,y 0 ) = F 2(x 0, y 0, z 0 ) F 3 (x 0, y 0, z 0 ) (48) Esimerkki a) Olkoon F (x, y, z) = x 3 y 2 + z 2. Ajatellaan y:tä x:n ja z:n funktiona. Määritä lausekkeet y, y x z ja z x b) Olkoon F (x, y, z) = x 2 + y 2 + z 2 1. Määritä ilman laskemista ne pisteet joissa i) F 1 (x, y, z) = 0, ii) F 2 (x, y, z) = 0, iii) F 1 (x, y, z) = 0. Mikäli edellä esiintyneissä osittaisderivaattojen lausekkeissa jakajat eivät mene nollaan, voidaan implisiittisestikin määritellylle funktiolle etsiä approksimaatioita. Esimerkki Jos mahdollista, muodosta pisteeseen (x, y) = (0, 1) asetettu tangenttitaso (eli Taylorin 1. asteen polynomi) funktiolle z(x, y) jonka määrittelee yhtälö z 5 + xz + y = sin(y)x 2 + x. Edellä olemme käsitelleet tapauksia joissa funktion määrittelee yksi yhtälö ja funktiolla voi olla yksi tai useampia muuttujia. Entäpä jos yhtälöitä olisi useampia? Esim. tarkastellaan yhtälöryhmää { F (x, y, z, w) = 0 (49) G(x, y, z, w) = 0 18
20 Koska muuttujia on neljä ja yhtälöitä kaksi niin mahdolliseti kaksi muuttujaa voidaan eliminoida: Ratkaistaan ylemmästä yhtälöstä x (riippuu y:stä, z:sta ja w:stä) ja sijoitetaan se alempaan yhtälöön jonka jälkeen tästä yhtälöstä ratkaistaan y (joka tulee siis riippumaan z:sta ja w:stä) nyt saatu y:n lauseke sijoitetaan edellä laskettuun x:n lausekkeeseen, jolloin myös x riippuu enää z:sta jaw:stä. Tällä tavoin ratkaisten ollaan siis saatu x = x(z, w) ja y = y(z, w). Se mitkä muuttujat tahdotaan ratkaista (sidotut muuttujat) toisten muuttujien (vapaat muuttujat) funktioina riippuu sovelluksesta. Edelläkin olisi yhtä hyvin voitu yrittää ratkaista y ja w, jolloin muuttujiksi olisi jäänyt x ja z. Käytännössä, valittiin muuttujiksi mitkä tahansa, on tälläisten yhtälöryhmien ratkaisu hyvin haastavaa, usein mahdotonta, käsin laskien. Numeeriset ratkaisumenetelmät taasen tarvitsevat usein osittaisderivaattojen lausekkeita. Näitä osittaisderivaattoja määrittäessä täytyykin olla selvänä se mitä alkuperäisitä muuttujista ajatellaan vakioina (eli vapaina muuttujina) ja mitkä muuttujat riippuvat näistä vapaista muuttujista (eli ovat sidottuja muuttujia). Voidaan käyttää esimerkiksi seuraavia merkintöjä: ( ) x z w ( ) x z y vastaa tulkintaa vastaa tulkintaa { x = x(z, w) y = y(z, w) { x = x(y, z) w = w(y, z) Edellä mainitut osittaisderivaatat voidaan yrittää laskea esim. differentioimalla lausekkeita puolittain ja ratkaisemalla näin saadusta yhtälöryhästä haluttu derivaatta. (50) (51) Esimerkki Olkoon x + y + xzw = 0 ja yx + zw + w = 0. Määritä implisiittistä differentiointia ja ketjusääntöä soveltamalla ( ) y z x Muuttujien ja yhtälöiden määrän kasvaessa lisääntyy myös erilaisten tulkintojen määrä. Kun vapaat muuttujat on päätetty, voidaan hyvin yksinkertaisesti tarkistaa että sidottuja muuttujia voidaan ajatella vapaiden muuttujien funktoina. Tämä tapahtuu tarkastelemalla n.k. Jacobin determinanttia: Funktioiden F (x 1, x 2, x 3,..., x n ) ja G(x 1, x 2, x 3,..., x n ) Jacobin determinantti muuttujien x 1 ja x 2 suhteen on (F, G) (x 1, x 2 ) = F F x 1 x 2 G G = F 1 F 2 G 1 G 2 (52) x 1 Jos (F,G) 0, niin muuttujat x (x 1,x 2 ) 1 ja x 1 voidaan ajatella muuttujien x 3,..., x n funktioina jotka määritellään yhtälöillä F (x 1, x 2, x 3,..., x n ) = 0 ja G(x 1, x 2, x 3,..., x n ) = 0. Erityisesti tällöin myös osittaisderivaatat x 1 x j ja x 2 x j voidaan ratkaista esimerkiksi implisiittisesti differentioimalla (ja ketjusääntöä soveltamalla) kaikille j = 3,..., n. Huomaa että mikäli Jacobin determinantti on 0 jossain pisteessä niin saattaa olla että x 1 ja x 2 voidaan silti ratkaista muiden muuttujien funktoina. Kuitenkin tällöin on odotettavissa että osittaisderivaattoja (tai Jacobin matriisia) käyttävät algoritmit ovat todennäköisesti vaikeuksissa. x 2 Esimerkki Laske Jacobin determinantti muuttujien x ja y suhteen kun F (x, y, z, w) = x 2 + y 2 + z 2 w ja (x 1) 2 + y 2 + z 2 w 2 ) 19
21 3 Funktion ääriarvot Matematiika A1 kurssilta (ja lukiosta) tuttua: yhden muuttujan funktiolla f(x) on lokaali maksimiarvo (lokaali minimiarvo) pisteessä a, jos f(x) < f(a) (f(x) > f(a)) kaikilla x:n arvoilla riittävän lähellä a:ta. Jos epäyhtälö pätee kaikilla x:n arvoilla, f:llä on absoluuttinen maksimi (minimi) pisteessä a. Ääriarvoja voi esiintyä 1. kriittisissä pisteissä, joissa f (x) = 0 2. singulaaripisteissä, joissa f (x) ei ole olemassa 3. f:n määrittelyalueen päätepisteissä. Vastaavasti kahden muuttujan funktiolla on lokaali maksimi tai suhteellinen maksimi määrittelyalueensa pisteessä (a, b), jos f(x, y) < f(a, b) kaikille (x, y) pisteille, jotka ovat riittävän lähellä pistettä (a, b). Jos epäyhtälö pätee kaikille (x, y) (jotka kuuluvat f:n määrittelyalueeseen), f:llä on globaali maksimi (absoluuttinen maksimi) pisteessä (a, b). Vastaavasti määritellään lokaali ja globaali minimi. Välttämättömät ehdot ääriarvojen olemassaololle: Funktiolla f(x, y) voi olla lokaali tai globaali ääriarvo pisteessä (a, b) vain, jos (a, b) on 1. f:n kriittinen piste, ts. piste, jossa f(a, b) = 0 tai 2. f:n singulaarinen piste, ts. piste, jossa f(a, b) ei ole olemassa tai 3. f:n määrittelyalueen reunapiste. Vain tämäntyyppisistä pisteistä voi siis löytyä ääriarvoja. Miellyttävää on että nämä ehdot on hyvin helppo tarkistaa annetulle (a, b) pisteelle ja ne pätevät myös useammankin muuttujan funktioille. Ongelmallista on että pisteen (a, b) löytäminen, joka täyttää jonkin ehdoista (erityisesti 1. ehdon) voi olla hyvinkin haastavaa. Ja reunapisteiden tutkiminen kokonaan oma ongelmansa. Eikä yksikään näistä ehdoista vielä takaa sitä että pisteessä (a, b) todella olisi ääriarvo! Esimerkki 3.1. a) Osoita että funktiolla f(x, y) = e xy +x 2 y ei voi olla maksimia tai minimiä pisteessä (1, 2). b) Etsi funktion f(x, y) = x 2 y + x 1/2 mahdolliset kriittiset pisteet ja singulaaripisteet. Edellä käsitellyt ehdot ovat siis välttämättömiä, mutta eivät vielä riittäviä, varmistamaan että ääriarvo esiintyisi pisteessä (a,b). Mikä tahansa ehdoista saattaa siis olla voimassa ilman että maksimia tai minimiä esiintyy. Esimerkki 3.2. Osoita että (0, 0) on funktion f(x, y) = x 3 y 2 kriittinen piste mutta ei ole lokaali ääriarvopiste. Hahmottele myös sellaisen funktion kuvaaja joka on singulaarinen pisteessä (0, 0), mutta kyseinen piste ei ole funktion lokaali ääriarvopiste. Lopuksi hieman lisää terminolgiaa ja teoriaa: 20
22 Joukko R n on rajoitettu, jos se sisältyy kokonaisuudessaan palloon x 2 1 +x x 2 n R 2, missä säde R on äärellinen. Riittävät ehdot ääriarvojen olemassaololle: Jos f on jatkuva n:n muuttujan funktio, jonka määrittelyalue on suljettu ja rajoitettu joukko R n :ssä, niin f:n arvojoukko on rajoitettu joukko reaalilukuja ja sen määrittelyalueessa on pisteitä, joissa f saa absoluuttisia maksimi ja minimiarvoja. Jos (a, b) on funktion f määrittelyjoukon sisäpiste (ei rajalla oleva piste) ja myös f:n kriittinen piste niin sitä kutsutaan satulapisteeksi mikäli f:llä ei ole ko. pisteessä maksimi eikä minimiarvoa. Edellä esitetty riittävä ehto ääriarvon olemassa ololle on siinä mielessä tärkeä että sen avulla voidaan (tietyissä tilanteissa) sanoa että ongelmalla on ratkaisu. Se kuinka ratkaisu löydetään onkin sitten täysin toinen tarina. Satulapisteet ovat yksinkertaisesti pisteitä joista yhteen suuntaan edetessä funktio lähtee kasvuun johonkin toiseen suuntaan edetessä funktio lähtee vähenemään. 3.1 Kriittisten pisteiden luokittelu Maksimi-, minimi-, ja satulapisteiden toisistaan erottaminen suoraan f:n lausekkeesta voi olla välillä varsin vaikeaa. Yhden muuttujan funktioille voidaan ongelma ratkaista muodostamalla derivaatan merkkitaulukko. Usemamman muuttujan funktioilla tämä ratkaisu ei tietenkään onnistu. Yhden muuttujan funktoiden kriittiset pisteet voidaan yrittää määritellä myös käyttäen 2. derivaatan testiä. Tämä testi laajenee myös käytettäväksi useamman muuttujan funktioille: Toisen derivaatan testi: Olkoon (a, b) funktion f(x, y) kriittinen piste f:n määrittelyalueen sisällä. Oletetaan, että f:n toiset osittaisderivaatat ovat jatkuvia(a, b):n läheisyydessä ja niillä on arvot A = f 11 (a, b), B = f 12 (a, b) = f 21 (a, b), C = f 22 (a, b) (53) 1. Jos B 2 < AC ja A > 0, niin f:llä on lokaali minimi pisteessä (a, b) 2. Jos B 2 < AC ja A < 0, niin f:llä on lokaali maksimi pisteessä (a, b) 3. Jos B 2 > AC, niin f:llä on satulapiste pisteessä (a, b) 4. Jos B 2 = AC, ei testi anna informaatiota. Esimerkki 3.3. Etsi ja luokittele kriittiset pisteet funktiolle a) f(x, y) = 2x 3 6xy + 3y 2, b) f(x, y) = xye (x2 +y 2 )/2 kriittiset pisteet. Molemmissa tapauksissa tutki myös onko f:llä absoluuttista maksimia tai minimiä? Useamman kuin kahden muuttujan funktioille on olemassa samanlaiset, varsin suoraviivaiset, luokittelusäännöt mutta niitä ei käsitellä tällä kurssilla. Säännöt löytyvät esim. Betataulukkokirjasta mutta käsitteiden ymmärtäminen saattaa vaatia hieman kokemusta B2 kurssin aihealueelta. 21
23 3.2 Funktioiden ääriarvojen etsintä rajoitteiden läsnä ollessa Tilanteet joissa funktion f(x, y) muutujan arvoja ei ole rajoitettu millään tavalla ovat melko harvinaisia. Usein on asetettava esimerkiksi positiivisuusehtoja eli x 0 ja/tai y 0 jos muuttujat edustavat tiettyjen suureiden arvoja esim. pituutta tai painoa. Samoin geometriset rajoitteet voivat asettaa rajoitteita jotka ovat esim. muotoa x 2 +y 2 5. Ensimmäiset rajoitteet jättäisivät määrittelyalueen osittain avoimeksi kun taasen jälkimmäisessä tapauksessa määrittelyalue olisi suljettu. Ääriarvojen tutkimisesta rajoitteiden kanssa voidaan todeta aivan samat perusasiat kuin A1 kurssilla yhden muuttujan funktioiden tapauksessa: Jos jatkuvan funktion määrittelyalue on suljettu ja rajoitettu, sillä on absoluuttisia ääriarvoja. Suljetulla välillä määritellyn jatkuvan funktion ääriarvot löytyvät joko kriittisistä pisteistä, singulaaripisteistä tai sitten määrittelyjoukon rajoilta. Jos määrittelyalue on jostakin päin avoin, täytyy rajat silti tutkia. Tällöin saatetaan joutua laskemaan raja-arvoja. Maksimi- ja/tai minimiarvoja saattaa löytyä tai olla löytymättä, riippuen kriittisten pisteiden laadusta ja funktion (raja-)arvoista avoimilla rajoilla. Käytännössä ääriarvojen tutkiminen aloitetaan yleensä kuten edellisessäkin kappaleessa: Lasketaan kriittiset pisteet ja luokitellaan ne, sekä tutkitaan singulaaripisteet. Tämän jälkeen siirrytään tutkimaan rajoja. Tällä kurssilla käymme läpi kaksi eri menetelmää: 1. Muuttujien redusointi sijoituksen avulla (tässä kappaleessa) 2. Lagrangen kertoimien menetelmä (katso seuraava kappale) Esimerkki 3.4. Etsi funktion f(x, y) = 2xy minimi ja maksimiarvot suljetussa puolikiekossa x 2 + y 2 4, y 0. Esimerkki 3.5. Etsi funktion g(x, y, z) = x 2 +y 2 +y+z 2 minimi- ja maksimipisteet rajoitteella x 2 + (y/2) 2 + (z/4) 2 1 Kun sijoitus on tehty, voi lauseke olla vielä sen verran hankala että sen minimin tai maksimin löytäminen analyyttisesti on hankalaa tai jopa mahdotonta. Tällöin voidaan käyttää numeerisia algoritmeja mm. kriittisten pisteiden etsintään. Mutta mitä tehdä jos rajoitetta ei pystytä muokkaamaan sellaiseen muotoon että sijoituksen voisi tehdä? 3.3 Lagrangen kertoimet Olivat rajoitteet sitten yhtälöitä tai epäyhtälöitä, Lagrangen kertoimien menetelmää voidaan käyttää. Jälkimmäisessä tapauksessa täytyy vain alueen sisäpisteet tutkia erikseen (edellisten kappaleiden tyyliin). Reunapisteiden tutkiminen on sitten ekvivalentti yhtälörajoitteiden tutkimisen kanssa. Tästä syystä keskitymme tässä kappaleessa yhtälörajoitteisiin. Voidaan puhua myös sidotusta ääriarvotehtävästä. Sidotussa (constrained) ääriarvotehtävässä optimoitavan funktion muuttujat voivat riippua toisistaan rajoiteyhtälöiden tai epäyhtälöiden kautta. Esimerkkejä: 22
24 Maksimoi funktio f(x, y) ehdolla g(x, y) = C Minimoi funktio f(x, y, z, w) ehdoilla g(x, y, z, w) = C 1 ja h(x, y, z, w) = C 2 Maksimoi funktio f(x, y, z) ehdolla g(x, y, z) C Rajoitteet voivat siis olla yhtälömuotoisia (kaksi ensimmäistä tapausta) tai epäyhtälöitä (viimeinen tapaus). Rajoiteyhtälöiden ratkaisu on usein vaikeaa tai mahdotonta. Tällöin voidaan käyttää Lagrangen menetelmää. Teoreettinen viitekehys kahden muuttujan ja yhden rajoitteen tapauksessa on seuraava: Olkoon f(x, y) funktio jonka minimi ja maksimiarvot tahdotaan löytää käyrällä joka on osa yhtälön g(x, y) = 0 määräämää tasokäyrää. Oletetaan että 1. Funktiolla f ja g on jatkuvat ensimmäiset derivaatat lähellä pistettä P 0 = (x 0, y 0 ) käyrällä C, jonka yhtälö on g(x, y) = 0 2. Kun rajoitutaan käyrällä C oleviin pisteisiin, funktiolla f(x, y) on lokaali maksimi tai minimiarvo P 0 :ssa 3. P 0 ei ole C:n päätepiste 4. f(p 0 ) 0 Tällöin on olemassa luku λ 0 siten, että (x 0, y 0, λ 0 ) on Lagrangen funktion L(x, y, λ) = f(x, y) + λg(x, y) (54) kriittinen piste. Lukuja λ kutsutaan Lagrangen kertoimiksi. Jos teoreettinen Lagrangen kertoiminen viitekehys voi näyttääkin hieman monimutkaiselta ja antaa vain tiettyjen oletusten voimassa ollessa välttämättömän ehdon sille että piste olisi minimi tai maksimipiste, niin käytännön algoritmi on suoraviivainen: 1. Etsitään funktion L ja funktion g kriittiset pisteet (ja funktion f kriittiset pisteet, ellei niitä ole aiemmin laskettu). Arvoa λ:lle ei ole välttämätöntä määrittää. 2. Etsitään ne pisteet joissa gradientti f:lle tai g:lle ei ole olemassa 3. Valitaan jatkotarkasteluun ne edellisissä kohdissa lasketut pisteet jotka toteuttavat rajoitteen. 4. Lasketaan funktion f arvot edellisissä kohdassa valituissa pisteissä sekä rajoiteyhtälön (käyrän) mahdollisissa päätepisteissä. Edellistä algoritmia käyttääkseen täytyy osata i) derivoida (onnistuu aina) ii) ratkaista yhtälöryhmiä (tämä voi olla vaikeaa, mutta numeerisia menetelmiä on olemassa) Esimerkki 3.6. Etsi Lagrangen kertoimien menetelmää käyttäen funktion f(x, y) = 2xy minimi ja maksimiarvot suljetussa puolikiekossa x 2 + y 2 4, y 0. Kuinka tilanne muuttuisi jos kiekko puolikiekko olisi avoin, eli x 2 + y 2 < 4, y < 0 23
25 Lagrangen kertoimien menetelmä yleistyy myös useamman muuttujan funktioille ja useammalle rajoitteelle (kunhan rajoitteita ei ole yhtä paljoa kuin tutkittavalla funktiolla muuttujia). Esimerkiksi kolmiulotteinen ongelma, jossa on etsittävä funktion f(x, y, z) ääriarvot ehdoilla g(x, y, z) = 0 ja h(x, y, z) = 0, voidaan ratkaista käyttäen Lagrangen funktiota L(x, y, z, λ, µ) = f(x, y, z) + λg(x, y, z) + µh(x, y, z). (55) Tässä lukuja λ ja µ kutsutaan Lagrangen kertoimiksi. Esimerkki 3.7. a) Ratkaise Lagrangen kertoimien menetelmällä pisteen (0, 0, 1) lyhin etäisyys pinnan z = x 2 + 2y 2 ja tason x = z leikkauskäyrältä. b) Ratkaise sama tehtävä käyttäen muuttujien redusointia. Vastaavasti menetelmä pätee myös n:n muuttujan funktioille (katso esim. Beta-kaavakirja). 3.4 Lineaarinen optimointi Lineaarisen funktion minimien ja maksimien etsimistä lineaaristen rajoitteiden läsnäollessa kutsutaan lineaariseksi ohjelmoinniksi. Tästä on oma kurssinsakin, "Lineaarinen optimointi". Tällä kurssilla rajoitumme vain kahden muuttujan tapaukseen ja suoritamme maksimien (tai minimien) etsintään graafisesti. Oletetaan siis että f(x, y) = ax+by missä c ja d ovat vakioita. Lisäksi on n rajoitetta jotka ovat nyt joko muotoa y a i x + b i tai muotoa y a i x + b i, i = 1,..., n. Jos merkitään f(x, y) = c, etsitään siis (minimin etsinnässä) mahdollisimman pientä lukua c jolle x ja y toteuttavat edellä kuvatut ehdot. Algoritmillisesti voidaan toimia vaikka seuraavasti: 1. Määritetään ensin ehtojen rajaama alue (suhteellisen helppo piirtää). Olkoon tämä alue A. 2. Hahmoitellaan suora c = ax + by (eli y = ax + c ) jollakin luvun c arvolla. b b 3. Jos hahmoteltua suoraa nyt nostetaan (tai lasketaan) muuttamatta kulmakerrointa a/b, vaihdetaan oleellisesti c:n arvoa. Nostetaan tai (laseketaan) siis hahmoteltua suoraa niin ylös (tai alas) kuin mahdollista (eli edes yksi suoran piste kuuluu alueeseen A). Se liikutetaanko ylos vai alas päin riippuu b:n merkistä ja siitä ollaanko minimoimassa vai maksimoimassa. 4. Edellisessä kohdassa löydetty piste on minimi (tai maksimi) piste. Esimerkki 3.8. a) Etsi funktion f(x, y) = x + 2y maksimi- jaminimi arvot kun x 0, y x 4, y x + 6 ja y 3. b) Olkoon rajoitteet samat kuin edellä. Mikä olisi oltava luvun a jotta f(x, y) = x + ay saisi maksimiarvonsa useissa eri pisteissä? Tämäntyyppistä geometrista optimointia voidaan myös harjoittaa silloin kun vain minimoitava (tai maksimoitava) funktio on lineaarinen mutta rajoitteet eivät. Esimerkki 3.9. Määritä funktion f(x, y) = x y maksimi- ja minimiarvot kun x 2 + y 2 = 9. 24
2 Osittaisderivaattojen sovelluksia
 2 Osittaisderivaattojen sovelluksia 2.1 Ääriarvot Yhden muuttujan funktiolla f(x) on lokaali maksimiarvo (lokaali minimiarvo) pisteessä a, jos f(x) f(a) (f(x) f(a)) kaikilla x:n arvoilla riittävän lähellä
2 Osittaisderivaattojen sovelluksia 2.1 Ääriarvot Yhden muuttujan funktiolla f(x) on lokaali maksimiarvo (lokaali minimiarvo) pisteessä a, jos f(x) f(a) (f(x) f(a)) kaikilla x:n arvoilla riittävän lähellä
BM20A0300, Matematiikka KoTiB1
 BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
Matematiikka B1 - avoin yliopisto
 28. elokuuta 2012 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Nettitehtävät Kurssin sisältö 1/2 Osittaisderivointi Usean muuttujan funktiot Raja-arvot Osittaisderivaatta Pinnan
28. elokuuta 2012 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Nettitehtävät Kurssin sisältö 1/2 Osittaisderivointi Usean muuttujan funktiot Raja-arvot Osittaisderivaatta Pinnan
1.7 Gradientti ja suunnatut derivaatat
 1.7 Gradientti ja suunnatut derivaatat Funktion ensimmäiset osittaisderivaatat voidaan yhdistää yhdeksi vektorifunktioksi seuraavasti: Missä tahansa pisteessä (x, y), jossa funktiolla f(x, y) on ensimmäiset
1.7 Gradientti ja suunnatut derivaatat Funktion ensimmäiset osittaisderivaatat voidaan yhdistää yhdeksi vektorifunktioksi seuraavasti: Missä tahansa pisteessä (x, y), jossa funktiolla f(x, y) on ensimmäiset
Matematiikka B1 - TUDI
 Osittaisderivointi Osittaisderivaatan sovellukset Matematiikka B1 - TUDI Miika Tolonen 3. syyskuuta 2012 Miika Tolonen Matematiikka B2 - TUDI 1 Osittaisderivointi Osittaisderivaatan sovellukset Kurssin
Osittaisderivointi Osittaisderivaatan sovellukset Matematiikka B1 - TUDI Miika Tolonen 3. syyskuuta 2012 Miika Tolonen Matematiikka B2 - TUDI 1 Osittaisderivointi Osittaisderivaatan sovellukset Kurssin
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018 1. (a) Tunnemme vektorit a = [ 5 1 1 ] ja b = [ 2 0 1 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2018 1. (a) Tunnemme vektorit a = [ 5 1 1 ] ja b = [ 2 0 1 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio.
 MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
läheisyydessä. Piirrä funktio f ja nämä approksimaatiot samaan kuvaan. Näyttääkö järkeenkäyvältä?
 BM20A5840 - Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2017 1. Tunnemme vektorit a = [ 1 2 3 ] ja b = [ 2 1 2 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
BM20A5840 - Usean muuttujan funktiot ja sarjat Harjoitus 1, Kevät 2017 1. Tunnemme vektorit a = [ 1 2 3 ] ja b = [ 2 1 2 ]. Laske (i) kummankin vektorin pituus (eli itseisarvo, eli normi); (ii) vektorien
Antti Rasila. Kevät Matematiikan ja systeemianalyysin laitos Aalto-yliopisto. Antti Rasila (Aalto-yliopisto) MS-A0204 Kevät / 16
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Antti Rasila Matematiikan ja systeemianalyysin laitos
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Antti Rasila Matematiikan ja systeemianalyysin laitos
Kuva 1: Funktion f tasa-arvokäyriä. Ratkaisu. Suurin kasvunopeus on gradientin suuntaan. 6x 0,2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
3 = Lisäksi z(4, 9) = = 21, joten kysytty lineaarinen approksimaatio on. L(x,y) =
 BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 6, Syksy 2016 1. (a) Olkoon z = z(x,y) = yx 1/2 + y 1/2. Muodosta z:lle lineaarinen approksimaatio L(x,y) siten että approksimaation ja z:n arvot
BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 6, Syksy 2016 1. (a) Olkoon z = z(x,y) = yx 1/2 + y 1/2. Muodosta z:lle lineaarinen approksimaatio L(x,y) siten että approksimaation ja z:n arvot
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Suunnattu derivaatta Aluksi tarkastelemme vektoreita, koska ymmärrys vektoreista helpottaa alla olevien asioiden omaksumista. Kun liikutaan tasossa eli avaruudessa
Matematiikan tukikurssi Kurssikerta 8 1 Suunnattu derivaatta Aluksi tarkastelemme vektoreita, koska ymmärrys vektoreista helpottaa alla olevien asioiden omaksumista. Kun liikutaan tasossa eli avaruudessa
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
Johdatus tekoälyn taustalla olevaan matematiikkaan
 Johdatus tekoälyn taustalla olevaan matematiikkaan Informaatioteknologian tiedekunta Jyväskylän yliopisto 3. luento 17.11.2017 Neuroverkon opettaminen (ohjattu oppiminen) Neuroverkkoa opetetaan syöte-tavoite-pareilla
Johdatus tekoälyn taustalla olevaan matematiikkaan Informaatioteknologian tiedekunta Jyväskylän yliopisto 3. luento 17.11.2017 Neuroverkon opettaminen (ohjattu oppiminen) Neuroverkkoa opetetaan syöte-tavoite-pareilla
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 3: Osittaisderivaatta
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 3: Osittaisderivaatta Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu Antti Rasilan luentomonisteeseen
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 3: Osittaisderivaatta Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu Antti Rasilan luentomonisteeseen
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 4: Ketjusäännöt ja lineaarinen approksimointi
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 4: Ketjusäännöt ja lineaarinen approksimointi Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 4: Ketjusäännöt ja lineaarinen approksimointi Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1
12. Hessen matriisi. Ääriarvoteoriaa
 179 12. Hessen matriisi. Ääriarvoteoriaa Tarkastelemme tässä luvussa useamman muuttujan (eli vektorimuuttujan) n reaaliarvoisia unktioita : R R. Edellisessä luvussa todettiin, että riittävän säännöllisellä
179 12. Hessen matriisi. Ääriarvoteoriaa Tarkastelemme tässä luvussa useamman muuttujan (eli vektorimuuttujan) n reaaliarvoisia unktioita : R R. Edellisessä luvussa todettiin, että riittävän säännöllisellä
a) on lokaali käänteisfunktio, b) ei ole. Piirrä näiden pisteiden ympäristöön asetetun neliöruudukon kuva. VASTAUS:
 6. Käänteiskuvaukset ja implisiittifunktiot 6.1. Käänteisfunktion olemassaolo 165. Määritä jokin piste, jonka ympäristössä funktiolla f : R 2 R 2, f (x,y) = (ysinx, x + y + 1) a) on lokaali käänteisfunktio,
6. Käänteiskuvaukset ja implisiittifunktiot 6.1. Käänteisfunktion olemassaolo 165. Määritä jokin piste, jonka ympäristössä funktiolla f : R 2 R 2, f (x,y) = (ysinx, x + y + 1) a) on lokaali käänteisfunktio,
Derivaatta: funktion approksimaatio lineaarikuvauksella.
 Viikko 5 Tällä viikolla yleistetään R 2 :n ja R 3 :n vektorialgebran peruskäsitteet n-ulotteiseen avaruuteen R n, ja määritellään lineaarikuvaus. Tarkastellaan funktioita, joiden määrittelyjoukko on n-ulotteisen
Viikko 5 Tällä viikolla yleistetään R 2 :n ja R 3 :n vektorialgebran peruskäsitteet n-ulotteiseen avaruuteen R n, ja määritellään lineaarikuvaus. Tarkastellaan funktioita, joiden määrittelyjoukko on n-ulotteisen
Injektio (1/3) Funktio f on injektio, joss. f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f )
 Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
Injektio (1/3) Määritelmä Funktio f on injektio, joss f (x 1 ) = f (x 2 ) x 1 = x 2 x 1, x 2 D(f ) Seurauksia: Jatkuva injektio on siis aina joko aidosti kasvava tai aidosti vähenevä Injektiolla on enintään
, on säännöllinen 2-ulotteinen pinta. Määrää T x0 pisteessä x 0 = (0, 1, 1).
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 017 Harjoitus 4 Ratkaisuehdotukset 4.1. Osoita, että tasa-arvojoukko S F (0), F : R 3 R, F (x) = 3x 1 x 3 + e x + x e x 3, on säännöllinen
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 017 Harjoitus 4 Ratkaisuehdotukset 4.1. Osoita, että tasa-arvojoukko S F (0), F : R 3 R, F (x) = 3x 1 x 3 + e x + x e x 3, on säännöllinen
f(x, y) = x 2 y 2 f(0, t) = t 2 < 0 < t 2 = f(t, 0) kaikilla t 0.
 Ääriarvon laatu Jatkuvasti derivoituvan funktion f lokaali ääriarvokohta (x 0, y 0 ) on aina kriittinen piste (ts. f x (x, y) = f y (x, y) = 0, kun x = x 0 ja y = y 0 ), mutta kriittinen piste ei ole aina
Ääriarvon laatu Jatkuvasti derivoituvan funktion f lokaali ääriarvokohta (x 0, y 0 ) on aina kriittinen piste (ts. f x (x, y) = f y (x, y) = 0, kun x = x 0 ja y = y 0 ), mutta kriittinen piste ei ole aina
Pisteessä (1,2,0) osittaisderivaatoilla on arvot 4,1 ja 1. Täten f(1, 2, 0) = 4i + j + k. b) Mihin suuntaan pallo lähtee vierimään kohdasta
 Laskukarnevaali Matematiikka B. fx, y, z) = x sin z + x y, etsi f,, ) Osittaisderivaatat ovat f f x = sin z + xy, y = x, f z = x cos z Pisteessä,,) osittaisderivaatoilla on arvot 4, ja. Täten f,, ) = 4i
Laskukarnevaali Matematiikka B. fx, y, z) = x sin z + x y, etsi f,, ) Osittaisderivaatat ovat f f x = sin z + xy, y = x, f z = x cos z Pisteessä,,) osittaisderivaatoilla on arvot 4, ja. Täten f,, ) = 4i
Viikon aiheet. Funktion lineaarinen approksimointi
 Viikon aiheet Funktion ääriarvot Funktion lineaarinen approksimointi Vektorit, merkintätavat, pituus, yksikkövektori, skalaarilla kertominen, kanta ja kannan vaihto Funktion ääriarvot 6 Väliarvolause Implisiittinen
Viikon aiheet Funktion ääriarvot Funktion lineaarinen approksimointi Vektorit, merkintätavat, pituus, yksikkövektori, skalaarilla kertominen, kanta ja kannan vaihto Funktion ääriarvot 6 Väliarvolause Implisiittinen
Tutki, onko seuraavilla kahden reaalimuuttujan reaaliarvoisilla funktioilla raja-arvoa origossa: x 2 + y 2, d) y 2. x + y, c) x 3
 2. Reaaliarvoiset funktiot 2.1. Jatkuvuus 23. Tutki funktion f (x,y) = xy x 2 + y 2 raja-arvoa, kun piste (x,y) lähestyy origoa pitkin seuraavia xy-tason käyriä: a) y = ax, b) y = ax 2, c) y 2 = ax. Onko
2. Reaaliarvoiset funktiot 2.1. Jatkuvuus 23. Tutki funktion f (x,y) = xy x 2 + y 2 raja-arvoa, kun piste (x,y) lähestyy origoa pitkin seuraavia xy-tason käyriä: a) y = ax, b) y = ax 2, c) y 2 = ax. Onko
(d) f (x,y,z) = x2 y. (d)
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 2, Kevät 2017 Tässä harjoituksessa ja tulevissakin merkitään punaisella tähdellä sellaisia tehtäviä joiden tyyppisten osaamattomuus tentissä/välikokeessa
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 2, Kevät 2017 Tässä harjoituksessa ja tulevissakin merkitään punaisella tähdellä sellaisia tehtäviä joiden tyyppisten osaamattomuus tentissä/välikokeessa
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan peruskurssi (MATY020) Harjoitus 10 to
 Matematiikan peruskurssi (MATY00) Harjoitus 10 to 6.3.009 1. Määrää funktion f(x, y) = x 3 y (x + 1) kaikki ensimmäisen ja toisen kertaluvun osittaisderivaatat. Ratkaisu. Koska f(x, y) = x 3 y x x 1, niin
Matematiikan peruskurssi (MATY00) Harjoitus 10 to 6.3.009 1. Määrää funktion f(x, y) = x 3 y (x + 1) kaikki ensimmäisen ja toisen kertaluvun osittaisderivaatat. Ratkaisu. Koska f(x, y) = x 3 y x x 1, niin
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on
![Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on](/thumbs/47/23658224.jpg) Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 19 Derivaatan määritelmä Määritelmä
Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 19 Derivaatan määritelmä Määritelmä
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Matematiikan tukikurssi Kurssikerta 8 Väliarvolause Oletetaan, että funktio f on jatkuva jollain reaalilukuvälillä [a, b] ja derivoituva avoimella välillä (a, b). Funktion muutos tällä välillä on luonnollisesti
Reaalilukuvälit, leikkaus ja unioni (1/2)
 Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 1 Implisiittinen derivointi Tarkastellaan nyt yhtälöä F(x, y) = c, jossa x ja y ovat muuttujia ja c on vakio Esimerkki tällaisesta yhtälöstä on x 2 y 5 + 5xy = 14
Matematiikan tukikurssi Kurssikerta 9 1 Implisiittinen derivointi Tarkastellaan nyt yhtälöä F(x, y) = c, jossa x ja y ovat muuttujia ja c on vakio Esimerkki tällaisesta yhtälöstä on x 2 y 5 + 5xy = 14
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Luku 4. Derivoituvien funktioiden ominaisuuksia.
 1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
1 MAT-1343 Laaja matematiikka 3 TTY 1 Risto Silvennoinen Luku 4 Derivoituvien funktioiden ominaisuuksia Derivaatan olemassaolosta seuraa funktioille eräitä säännöllisyyksiä Näistä on jo edellisessä luvussa
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi Kurssikerta 10 1 Funktion monotonisuus Derivoituva funktio f on aidosti kasvava, jos sen derivaatta on positiivinen eli jos f (x) > 0. Funktio on aidosti vähenevä jos sen derivaatta
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Derivaatta 1.1 Derivaatta Erilaisia lähestymistapoja: I geometrinen
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 24.10.2016 Sisältö Derivaatta 1.1 Derivaatta Erilaisia lähestymistapoja: I geometrinen
f(x 1, x 2 ) = x x 1 k 1 k 2 k 1, k 2 x 2 1, 0 1 f(1, 1)h 1 = h = h 2 1, 1 12 f(1, 1)h 1 h 2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 7 Harjoitus 6 Ratkaisuehdotukset 6.. Olkoon f : G R, G = {(x, x ) R x > }, f(x, x ) = x x. Etsi differentiaalit d k f(, ), k =,,. Ratkaisu:
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 7 Harjoitus 6 Ratkaisuehdotukset 6.. Olkoon f : G R, G = {(x, x ) R x > }, f(x, x ) = x x. Etsi differentiaalit d k f(, ), k =,,. Ratkaisu:
Mapu 1. Laskuharjoitus 3, Tehtävä 1
 Mapu. Laskuharjoitus 3, Tehtävä Lineaarisessa approksimaatiossa funktion arvoa lähtöpisteen x 0 ympäristössä arvioidaan liikkumalla lähtöpisteeseen sovitetun tangentin kulmakertoimen mukaisesti: f(x 0
Mapu. Laskuharjoitus 3, Tehtävä Lineaarisessa approksimaatiossa funktion arvoa lähtöpisteen x 0 ympäristössä arvioidaan liikkumalla lähtöpisteeseen sovitetun tangentin kulmakertoimen mukaisesti: f(x 0
Vektorianalyysi II (MAT21020), syksy 2018
 Vektorianalyysi II (MAT21020), syksy 2018 Ylimääräisiä harjoitustehtäviä 1. Osoita, että normin neliö f : R n R, f(x) = x 2 on differentioituva pisteessä a R n ja, että sen derivaatalle on voimassa 2.
Vektorianalyysi II (MAT21020), syksy 2018 Ylimääräisiä harjoitustehtäviä 1. Osoita, että normin neliö f : R n R, f(x) = x 2 on differentioituva pisteessä a R n ja, että sen derivaatalle on voimassa 2.
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos
 Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Vesanen MS-A0205/6 Differentiaali- ja integraalilaskenta 2, kevät 2017 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Vesanen MS-A0205/6 Differentiaali- ja integraalilaskenta 2, kevät 2017 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Luento 9: Yhtälörajoitukset optimoinnissa
 Luento 9: Yhtälörajoitukset optimoinnissa Lagrangen kerroin Oletetaan aluksi, että f, g : R R. Merkitään (x 1, x ) := (x, y) ja johdetaan Lagrangen kerroin λ tehtävälle min f(x, y) s.t. g(x, y) = 0 Olkoon
Luento 9: Yhtälörajoitukset optimoinnissa Lagrangen kerroin Oletetaan aluksi, että f, g : R R. Merkitään (x 1, x ) := (x, y) ja johdetaan Lagrangen kerroin λ tehtävälle min f(x, y) s.t. g(x, y) = 0 Olkoon
3 x 1 < 2. 2 b) b) x 3 < x 2x. f (x) 0 c) f (x) x + 4 x 4. 8. Etsi käänteisfunktio (määrittely- ja arvojoukkoineen) kun.
 Matematiikka KoTiA1 Demotehtäviä 1. Ratkaise epäyhtälöt x + 1 x 2 b) 3 x 1 < 2 x + 1 c) x 2 x 2 2. Ratkaise epäyhtälöt 2 x < 1 2 2 b) x 3 < x 2x 3. Olkoon f (x) kolmannen asteen polynomi jonka korkeimman
Matematiikka KoTiA1 Demotehtäviä 1. Ratkaise epäyhtälöt x + 1 x 2 b) 3 x 1 < 2 x + 1 c) x 2 x 2 2. Ratkaise epäyhtälöt 2 x < 1 2 2 b) x 3 < x 2x 3. Olkoon f (x) kolmannen asteen polynomi jonka korkeimman
1 Rajoittamaton optimointi
 Taloustieteen matemaattiset menetelmät 7 materiaali 5 Rajoittamaton optimointi Yhden muuttujan tapaus f R! R Muistutetaan mieleen maksimin määritelmä. Funktiolla f on maksimi pisteessä x jos kaikille y
Taloustieteen matemaattiset menetelmät 7 materiaali 5 Rajoittamaton optimointi Yhden muuttujan tapaus f R! R Muistutetaan mieleen maksimin määritelmä. Funktiolla f on maksimi pisteessä x jos kaikille y
Oletetaan ensin, että tangenttitaso on olemassa. Nyt pinnalla S on koordinaattiesitys ψ, jolle pätee että kaikilla x V U
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 018 Harjoitus 4 Ratkaisuehdotukset Tehtävä 1. Olkoon U R avoin joukko ja ϕ = (ϕ 1, ϕ, ϕ 3 ) : U R 3 kaksiulotteisen C 1 -alkeispinnan
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 018 Harjoitus 4 Ratkaisuehdotukset Tehtävä 1. Olkoon U R avoin joukko ja ϕ = (ϕ 1, ϕ, ϕ 3 ) : U R 3 kaksiulotteisen C 1 -alkeispinnan
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 4: Derivaatta Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 21.9.2016 Pekka Alestalo, Jarmo
y (0) = 0 y h (x) = C 1 e 2x +C 2 e x e10x e 3 e8x dx + e x 1 3 e9x dx = e 2x 1 3 e8x 1 8 = 1 24 e10x 1 27 e10x = e 10x e10x
 BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
VEKTORIANALYYSIN HARJOITUKSET: VIIKKO 4
 VEKTORIANALYYSIN HARJOITUKSET: VIIKKO 4 Jokaisen tehtävän jälkeen on pieni kommentti tehtävään liittyen Nämä eivät sisällä mitään kovin kriittistä tietoa tehtävään liittyen, joten niistä ei tarvitse välittää
VEKTORIANALYYSIN HARJOITUKSET: VIIKKO 4 Jokaisen tehtävän jälkeen on pieni kommentti tehtävään liittyen Nämä eivät sisällä mitään kovin kriittistä tietoa tehtävään liittyen, joten niistä ei tarvitse välittää
MATP153 Approbatur 1B Harjoitus 5 Maanantai
 MATP153 Approbatur 1B Harjoitus 5 Maanantai 30.11.015 1. (Opiskelutet. 0 s. 81.) Selvitä, miten lauseke sin(4x 3 + cos x ) muodostuu perusfunktioista (polynomeista, trigonometrisistä funktioista jne).
MATP153 Approbatur 1B Harjoitus 5 Maanantai 30.11.015 1. (Opiskelutet. 0 s. 81.) Selvitä, miten lauseke sin(4x 3 + cos x ) muodostuu perusfunktioista (polynomeista, trigonometrisistä funktioista jne).
Differentiaalilaskenta 1.
 Differentiaalilaskenta. a) Mikä on tangentti? Mikä on sekantti? b) Määrittele funktion monotonisuuteen liittyvät käsitteet: kasvava, aidosti kasvava, vähenevä ja aidosti vähenevä. Anna esimerkit. c) Selitä,
Differentiaalilaskenta. a) Mikä on tangentti? Mikä on sekantti? b) Määrittele funktion monotonisuuteen liittyvät käsitteet: kasvava, aidosti kasvava, vähenevä ja aidosti vähenevä. Anna esimerkit. c) Selitä,
Tilavuus puolestaan voidaan esittää funktiona V : (0, ) (0, ) R,
 Vektorianalyysi Harjoitus 9, Ratkaisuehdotuksia Anssi Mirka Tehtävä 1. ([Martio, 3.4:1]) Millä suoralla sylinterillä, jonka tilavuus on V > on pienin vaipan ja pohjan yhteenlaskettu pinta-ala? Ratkaisu
Vektorianalyysi Harjoitus 9, Ratkaisuehdotuksia Anssi Mirka Tehtävä 1. ([Martio, 3.4:1]) Millä suoralla sylinterillä, jonka tilavuus on V > on pienin vaipan ja pohjan yhteenlaskettu pinta-ala? Ratkaisu
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
4 (x 1)(y 3) (y 3) (x 1)(y 3)3 5 3
 . Taylorin polynomi; funktion ääriarvot.1. Taylorin polynomi 94. Kehitä funktio f (x,y) = x 2 y Taylorin polynomiksi kehityskeskuksena piste ( 1,2) a) laskemalla osittaisderivaatat, b) kirjoittamalla muuttujat
. Taylorin polynomi; funktion ääriarvot.1. Taylorin polynomi 94. Kehitä funktio f (x,y) = x 2 y Taylorin polynomiksi kehityskeskuksena piste ( 1,2) a) laskemalla osittaisderivaatat, b) kirjoittamalla muuttujat
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos
 Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Ojalammi MS-A0203 Differentiaali- ja integraalilaskenta 2, kevät 2016 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Ojalammi MS-A0203 Differentiaali- ja integraalilaskenta 2, kevät 2016 Laskuharjoitus 4A (Vastaukset) alkuviikolla
H7 Malliratkaisut - Tehtävä 1
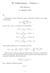 H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
H7 Malliratkaisut - Tehtävä Eelis Mielonen 7. lokakuuta 07 a) Palautellaan muistiin Maclaurin sarjan määritelmä (Taylorin sarja origon ympäristössä): f n (0) f(x) = (x) n Nyt jos f(x) = ln( + x) saadaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
Matematiikan perusteet taloustieteilij oille I
 Matematiikan perusteet taloustieteilijöille I Harjoitukset syksy 2006 1. Laskeskele ja sieventele a) 3 27 b) 27 2 3 c) 27 1 3 d) x 2 4 (x 8 3 ) 3 y 8 e) (x 3) 2 f) (x 3)(x +3) g) 3 3 (2x i + 1) kun, x
Matematiikan perusteet taloustieteilijöille I Harjoitukset syksy 2006 1. Laskeskele ja sieventele a) 3 27 b) 27 2 3 c) 27 1 3 d) x 2 4 (x 8 3 ) 3 y 8 e) (x 3) 2 f) (x 3)(x +3) g) 3 3 (2x i + 1) kun, x
Derivaatan sovellukset (ääriarvotehtävät ym.)
 Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
f(x) f(y) x y f f(x) f(y) (x) = lim
 Y1 (Matematiikka I) Haastavampia lisätehtäviä Syksy 1 1. Funktio h määritellään seuraavasti. Kuvan astiaan lasketaan vettä tasaisella nopeudella 1 l/min. Astia on muodoltaan katkaistu suora ympyräkartio,
Y1 (Matematiikka I) Haastavampia lisätehtäviä Syksy 1 1. Funktio h määritellään seuraavasti. Kuvan astiaan lasketaan vettä tasaisella nopeudella 1 l/min. Astia on muodoltaan katkaistu suora ympyräkartio,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
Matematiikan tukikurssi Kurssikerta 9 Korkeamman asteen derivaatat Tutkitaan nyt funktiota f, jonka kaikki derivaatat on olemassa. Kuten tunnettua, funktion toista derivaattaa pisteessä x merkitään f (x).
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
Funktion derivoituvuus pisteessä
 Esimerkki A Esimerkki A Esimerkki B Esimerkki B Esimerkki C Esimerkki C Esimerkki 4.0 Ratkaisu (/) Ratkaisu (/) Mielikuva: Funktio f on derivoituva x = a, jos sen kuvaaja (xy-tasossa) pisteen (a, f(a))
Esimerkki A Esimerkki A Esimerkki B Esimerkki B Esimerkki C Esimerkki C Esimerkki 4.0 Ratkaisu (/) Ratkaisu (/) Mielikuva: Funktio f on derivoituva x = a, jos sen kuvaaja (xy-tasossa) pisteen (a, f(a))
VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN
 Matematiikan kurssikoe, Maa6 Derivaatta RATKAISUT Sievin lukio Torstai 23.9.2017 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN MAOL-taulukkokirja on sallittu. Vaihtoehtoisesti voit käyttää aineistot-osiossa olevaa
Matematiikan kurssikoe, Maa6 Derivaatta RATKAISUT Sievin lukio Torstai 23.9.2017 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN MAOL-taulukkokirja on sallittu. Vaihtoehtoisesti voit käyttää aineistot-osiossa olevaa
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 7: Pienimmän neliösumman menetelmä ja Newtonin menetelmä.
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 7: Pienimmän neliösumman menetelmä ja Newtonin menetelmä. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 7: Pienimmän neliösumman menetelmä ja Newtonin menetelmä. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Funktion kuperuussuunnat Derivoituva funktio f (x) on pisteessä x aidosti konveksi, jos sen toinen derivaatta on positiivinen f (x) > 0. Vastaavasti f (x) on aidosti
Matematiikan tukikurssi Kurssikerta 8 1 Funktion kuperuussuunnat Derivoituva funktio f (x) on pisteessä x aidosti konveksi, jos sen toinen derivaatta on positiivinen f (x) > 0. Vastaavasti f (x) on aidosti
BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 2016
 BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 2016 1. (a) Anna likiarvo lineaarisen approksimaation avulla sille mitä on T (100.5), kun T (100) = 45 ja T (100) = 10. (b) Käyttäen lineaarista
BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 2016 1. (a) Anna likiarvo lineaarisen approksimaation avulla sille mitä on T (100.5), kun T (100) = 45 ja T (100) = 10. (b) Käyttäen lineaarista
l 1 2l + 1, c) 100 l=0 AB 3AC ja AB AC sekä vektoreiden AB ja
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 3: Jatkuvuus Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 19.9.2016 Pekka Alestalo, Jarmo
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 4, Syksy 2016
 BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 4, Syksy 2016 1. Hahmottele karkeasti funktion f : R R 2 piirtämällä sen arvoja muutamilla eri muuttujan arvoilla kaksiulotteiseen koordinaatistoon
BM20A5800 Funktiot, lineaarialgebra ja vektorit Harjoitus 4, Syksy 2016 1. Hahmottele karkeasti funktion f : R R 2 piirtämällä sen arvoja muutamilla eri muuttujan arvoilla kaksiulotteiseen koordinaatistoon
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 4: Ketjusäännöt ja lineaarinen approksimointi
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 4: Ketjusäännöt ja lineaarinen approksimointi Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 4: Ketjusäännöt ja lineaarinen approksimointi Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
Vektoreiden A = (A1, A 2, A 3 ) ja B = (B1, B 2, B 3 ) pistetulo on. Edellisestä seuraa
 Viikon aiheet Pistetulo (skalaaritulo Vektorien tulot Pistetulo Ristitulo Skalaari- ja vektorikolmitulo Integraalifunktio, alkeisfunktioiden integrointi, yhdistetyn funktion derivaatan integrointi Vektoreiden
Viikon aiheet Pistetulo (skalaaritulo Vektorien tulot Pistetulo Ristitulo Skalaari- ja vektorikolmitulo Integraalifunktio, alkeisfunktioiden integrointi, yhdistetyn funktion derivaatan integrointi Vektoreiden
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori = (,..., ). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori = (,..., ). Reaalisten m n-matriisien joukkoa merkitään
Funktiot. funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina.
 Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
Funktiot Tässä luvussa käsitellään reaaliakselin osajoukoissa määriteltyjä funktioita f : A R. Yleensä funktion määrittelyjoukko M f = A on jokin väli, muttei aina. Avoin väli: ]a, b[ tai ]a, [ tai ],
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
BM20A5810 Differentiaalilaskenta ja sovellukset
 BM20A5810 Differentiaalilaskenta ja sovellukset Jouni Sampo 2. joulukuuta 2014 Sisältö 1 Funktioiden käyttäytymistä tutkimassa 2 1.1 Parittomat, parilliset ja jaksolliset funktiot.....................
BM20A5810 Differentiaalilaskenta ja sovellukset Jouni Sampo 2. joulukuuta 2014 Sisältö 1 Funktioiden käyttäytymistä tutkimassa 2 1.1 Parittomat, parilliset ja jaksolliset funktiot.....................
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
Ratkaisuehdotus 2. kurssikokeeseen
 Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Ratkaisuehdotus 2. kurssikokeeseen 4.2.202 (ratkaisuehdotus päivitetty 23.0.207) Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin
Maksimit ja minimit 1/5 Sisältö ESITIEDOT: reaalifunktiot, derivaatta
 Maksimit ja minimit 1/5 Sisältö Funktion kasvavuus ja vähenevyys; paikalliset ääriarvot Jos derivoituvan reaalifunktion f derivaatta tietyssä pisteessä on positiivinen, f (x 0 ) > 0, niin funktion tangentti
Maksimit ja minimit 1/5 Sisältö Funktion kasvavuus ja vähenevyys; paikalliset ääriarvot Jos derivoituvan reaalifunktion f derivaatta tietyssä pisteessä on positiivinen, f (x 0 ) > 0, niin funktion tangentti
Differentiaali- ja integraalilaskenta 2 (CHEM) MS-A0207 Hakula/Vuojamo Kurssitentti, 12.2, 2018, arvosteluperusteet
 ifferentiaali- ja integraalilaskenta 2 (CHEM) MS-A27 Hakula/Vuojamo Kurssitentti, 2.2, 28, arvosteluperusteet T Moniosaisten tehtävien osien painoarvo on sama ellei muuta ole erikseen osoitettu. Kokeessa
ifferentiaali- ja integraalilaskenta 2 (CHEM) MS-A27 Hakula/Vuojamo Kurssitentti, 2.2, 28, arvosteluperusteet T Moniosaisten tehtävien osien painoarvo on sama ellei muuta ole erikseen osoitettu. Kokeessa
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Matematiikan tukikurssi Kurssikerta Eksponenttifuntio Palautetaan mieliin, että Neperin luvulle e pätee: e ) n n n ) n n n n n ) n. Tästä määritelmästä seuraa, että eksponenttifunktio e x voidaan määrittää
Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua.
 6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
r > y x z x = z y + y x z y + y x = r y x + y x = r
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
Numeeriset menetelmät TIEA381. Luento 12. Kirsi Valjus. Jyväskylän yliopisto. Luento 12 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
x + 1 πx + 2y = 6 2y = 6 x 1 2 πx y = x 1 4 πx Ikkunan pinta-ala on suorakulmion ja puoliympyrän pinta-alojen summa, eli
 BM0A5810 - Differentiaalilaskenta ja sovellukset Harjoitus, Syksy 015 1. a) Funktio f ) = 1) vaihtaa merkkinsä pisteissä = 1, = 0 ja = 1. Lisäksi se on pariton funktio joten voimme laskea vain pinta-alan
BM0A5810 - Differentiaalilaskenta ja sovellukset Harjoitus, Syksy 015 1. a) Funktio f ) = 1) vaihtaa merkkinsä pisteissä = 1, = 0 ja = 1. Lisäksi se on pariton funktio joten voimme laskea vain pinta-alan
