ELEC C4140 Kenttäteoria (syksy 2015)
|
|
|
- Reino Haapasalo
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 12 / versio 1. joulukuuta 2015
2 Antennit (Ulaby , 9.9) Hertzin dipoli Kaukokenttä Säteilykuvio ja suuntaavuus Antennin vahvistus ja piirimalli Puolenaallon dipoli Sieppauspinta Friisin kaava radiolinkille Kahden antennin ryhmä 2 (18)
3 Annetun virtajakauman säteily Jos antennin virrantiheys J = J(R) on tiedossa, säteilykenttien laskeminen on periaatteessa suoraviivaista (mutta usein työlästä): Ã = µ V 0 J(R ) e jkr dv 4π R, H = 1 µ 0 Ã, Ẽ = 1 jωε 0 H. 3 (18)
4 Hertzin dipoli l z θ I 0 R H R Ẽ Hertzin dipoli on virta-alkio, jonka pituus l λ ja jossa on tasainen virtajakauma I 0. Laskemalla saadaan kenttäkomponentit H φ = V [ 0k 1 η 0 kr j (kr) [ 2 Ẽ R = 2V 0 k [ 1 Ẽ θ = V 0 k kr j (kr) (kr) 3 ] e jkr sin θ, j (kr) 2 1 (kr) 3 ] e jkr sin θ ] e jkr sin θ Riittävän kaukana 1/(kR)-termit dominoivat. V 0 = jkη 0I 0 l 4π 4 (18)
5 Hertzin dipolin kaukokenttä z R Kaukokentässä (kr 1) saatiin siis l θ I 0 R H Ẽ ( ) Ẽ = θ e jkr V 0 sin θ R H = φ V ( ) 0 e jkr sin θ η 0 R missä vakio V 0 = jkη 0I 0 l 4π, e jkr /R on palloaaltotekijä, sin θ on (kentän) suuntakuvio ja η 0 = µ 0 /ε 0 on tyhjiön väliaineimpedanssi. 5 (18)
6 Kaukokenttä yleisemmin Kaukokenttäapproksimaation rajana pidetään usein R > 2λ (pieni antenni) R > 2d2 λ (iso antenni) missä d on antennin suurin halkaisija (tai pituus). Tällöin kenttälausekkeissa approksimoidaan kr 1, jolloin antennin kaukokentän etäisyysriippuvuus on muotoa Ẽ e jkr R. (Tämä pätee myös aallonpituuteen nähden isokokoisille antenneille, mutta silloin suuntakuvio on toki paljon monimutkaisempi kuin Hertzin dipolilla.) 6 (18)
7 Normalisoitu tehosäteilykuvio Hertzin dipolin kaukokentän keskimääräinen etenevä tehotiheys on S av = 1 [Ẽ 2 Re H ] = R V 0 2 2η 0 R }{{ 2 sin 2 θ = R S(R, θ, φ). } S 0 (R) Yleisesti määritellään antennin normalisoitu tehosäteilykuvio F(θ, φ) = S(R, θ, φ) S max kiinteällä etäisyydellä R kaukokentässä. 7 (18)
8 Suuntaavuus Antennin (maksimi)suuntaavuus D = maksimi tehotiheys kaukokentässä keskimääräinen tehotiheys samalla etäisyydellä Normalisoidun tehosäteilykuvion avulla ilmaistuna suuntaavus D = F max F av = 1 4π 4π 1 F(θ, φ) dω = 4π Ω p missä Ω p on säteilykuvion avaruuskulma 2π π Ω p = F(θ, φ) sin θ dθ dφ 0 0 Esim: Hertzin dipolin suuntaavus D = 3/2 = 1.76 db (muista) 8 (18)
9 Tulkintaa Säteilykuvion avaruuskulma 1 F(θ, φ) F = 1 within the cone 1 Ω p Antennin pääkeilan suunnassa tehotiheys kaukokentässä on suuntaavuus kertaa isotrooppisen säteilijän tehotiheys: (a) Actual pattern [Ulabyn kuvasta (b) Equivalent 9 11] solid angle S = D P rad 4πR 2 Figure Jos9-11 antennilla The patternon solid vain angleyksi Ω p defines pääkeila an tai sivukeilat ovat hyvin equivalent cone over which all the radiation of the actual pieniä, voidaan säteilykuvion avaruuskulmaa approksimoida antenna is concentrated with uniform intensity equal to the maximum of the actual pattern. Ω p β xz β yz, missä β xz, β yz ovat puolentehon keilanleveydet kahdessa päätasossa. 9 (18)
10 Esimerkki Tehosäteilykuviot xz- ja yz-tasoissa (pääkeilan suunta on ẑ): db 23.0 db Tämän antennin sivukeilataso on 13.3 db ja suuntaavuus D = 20.2 db. Puolentehon keilanleveyksillä saadaan Ω p β xz β yz sr ja D 20.9 db. 10 (18)
11 Antennin vahvistus Antenniin syötetään tehoa P t = P rad + P loss missä P rad on säteilyteho ja P loss on häviöteho. Tällöin antennin säteilyhyötysuhde ξ = P rad P t = P rad P rad + P loss 1 ja vahvistus G = ξd 11 (18)
12 Antennin piirimalli I 0 Syöttöpisteimpedanssi: R g + V g R rad R loss jx in Z in Z in = R rad + R loss + jx in R rad = säteilyresistanssi R loss = häviöresistanssi Säteilyhyötysuhde: ξ = P rad P t = R rad R rad + R loss Esim: Hertzin dipolin R rad = 80π 2 (l/λ) 2 Ω ja R loss voidaan arvioida pintaresistanssin avulla. 12 (18)
13 Puolenaallon dipoli Virtajakaumaksi voidaan olettaa (miksi?) Ĩ(z) = I 0 cos(kz), λ 4 z λ 4. Antenniparametreiksi saadaan [Ulabyn luku 9 3]: ( cos [(π/2) cos θ] F(θ) = sin θ D = 1.64 R rad 73 Ω Käytännössä valitaan useimmiten hieman lyhennetty dipoli (l 0.48λ), jolla X in 0. Hyvällä johteella R loss R rad. ) 2 13 (18)
14 Sieppauspinta A e Jos tuleva tehotiheys vastaanottoantennin luona on S i, antennin sieppaama teho P int = A e S i ja vastaanotettu teho P rec = ξ P int. Kirjassa on Hertzin dipolille johdettu (yleisemminkin pätevä) yhteys D = 4π A e λ 2 Toisaalta D = 4π/Ω p, joten säteilykuvion avaruuskulma Ω p = λ2 A e = 1 normalisoitu sieppauspinta 14 (18)
15 Kahden antennin välinen radiolinkki G t G r = ξd = ξ 4π λ 2 A e P t P rec =? R Tehotiheys vastaanottimen luona P t S i = G t 4πR 2 Antenni sieppaa tästä tehon P int = A e S i, joten vastaanotettu teho ( ) λ 2 ( ) ( ) G r P t λ 2 P rec = ξa e S i = ξ G t 4π ξ 4πR 2 = P t G t G r 4πR 15 (18)
16 Friisin kaava Saatiin Friisin kaava radiolinkille: P rec P t = G t G r ( λ ) 2 4πR Huom: Tässä on oletettu, että antennit ovat toistensa kaukokentässä resiprookkisia impedanssisovitettuja syöttöjohtoihin oikein suunnattuja (myös polarisaatio) Huom: Vahvistukset ja suuntaavuudet annetaan usein desibeleissä, mutta kaavoissa käytetään paljaita lukuja. 16 (18)
17 Kahden antennin ryhmä I 0 y φ d R 0 = R R 1 R d cos φ I 1 = I 0 ψ x Kenttäpiste R on hyvin kaukana ja erityisesti kaukokentässä. Jos antennielementtien säteilykuviot aluksi unohdetaan, antenniryhmän kaukokentän amplitudi Ẽ I 0 e jkr 0 R 0 + I 1 e jkr1 R 1 I 0 e jkr R ( 1 + e jψ e jkd cos φ), kun amplitudikerroin 1/R 1 1/R 0 = 1/R, mutta vaihetekijässä käytetään tarkempaa approksimaatiota R 1 R d cos φ. 17 (18)
18 Kahden antennin ryhmä Antenniryhmän kaukokentän tehotiheys voidaan yleisesti kirjoittaa muodossa S(R, θ, φ) = S e (R, θ, φ) F a (θ, φ) missä S e on yksittäisen elementin säteilemä tehotiheys ja F a on ryhmäkerroin. Tässä tapauksessa saadaan (merkinnällä γ = kd cos φ + ψ): F a = 1 + e jγ 2 e = jγ/2 2 e jγ/2 + e jγ/2 2 = 4 cos 2 (γ/2) Jos antennielementeiksi valitaan ẑ-suuntaiset Hertzin dipolit, saadaan normalisoiduksi tehosäteilykuvioksi ( kd F(θ, φ) = sin 2 (θ) cos 2 }{{} 2 cos φ + ψ ) }{{ 2 } elementti ryhmä 18 (18)
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 9 / versio 9. marraskuuta 2015 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 9 / versio 9. marraskuuta 2015 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori
Pieni silmukka-antenni duaalisuus. Ratkaistaan pienen silmukka-antennin kentät v ielä käy ttämällä d uaalisuud en periaatetta.
 Pieni silmukka-antenni duaalisuus Ratkaistaan pienen silmukka-antennin kentät v ielä käy ttämällä d uaalisuud en periaatetta. S amalla saamme my ö s silmukan läh ikentät. Käy tämme h y v äksi sitä, että
Pieni silmukka-antenni duaalisuus Ratkaistaan pienen silmukka-antennin kentät v ielä käy ttämällä d uaalisuud en periaatetta. S amalla saamme my ö s silmukan läh ikentät. Käy tämme h y v äksi sitä, että
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 21. marraskuuta 2016 Tasoaaltojen heijastus ja läpäisy (Ulaby 8.1 8.5) Kohtisuora heijastus ja läpäisy Tehon heijastus ja läpäisy Snellin laki
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 21. marraskuuta 2016 Tasoaaltojen heijastus ja läpäisy (Ulaby 8.1 8.5) Kohtisuora heijastus ja läpäisy Tehon heijastus ja läpäisy Snellin laki
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 17. marraskuuta 2016 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori 2 (18)
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 17. marraskuuta 2016 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori 2 (18)
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 6 / versio 14. lokakuuta 2015 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 6 / versio 14. lokakuuta 2015 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén Luentoviikko 5 / versio 7. lokakuuta 2016 Luentoviikko 5 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén Luentoviikko 5 / versio 7. lokakuuta 2016 Luentoviikko 5 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
1 Perussuureiden kertausta ja esimerkkejä
 1 Perussuureiden kertausta ja esimerkkejä 1.1 Vuontiheys ja pintakirkkaus Vuontiheys ( flux density ) kertoo, kuinka paljon säteilyenergiaa taajuskaistassa [ν,ν+1hz] virtaa 1 m 2 pinta-alan läpi sekunnissa.
1 Perussuureiden kertausta ja esimerkkejä 1.1 Vuontiheys ja pintakirkkaus Vuontiheys ( flux density ) kertoo, kuinka paljon säteilyenergiaa taajuskaistassa [ν,ν+1hz] virtaa 1 m 2 pinta-alan läpi sekunnissa.
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 3 / versio 23. syyskuuta 2015 Vektorianalyysi (Ulaby, luku 3) Koordinaatistot Viiva-, pinta- ja tilavuusalkiot Koordinaattimuunnokset Nablaoperaatiot
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 3 / versio 23. syyskuuta 2015 Vektorianalyysi (Ulaby, luku 3) Koordinaatistot Viiva-, pinta- ja tilavuusalkiot Koordinaattimuunnokset Nablaoperaatiot
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 8 / versio 3. marraskuuta 2015 Tasoaallot, osa 1 (Ulaby 7.1, 7.2, 7.4) Kenttäosoittimet Aikaharmoniset Maxwellin yhtälöt Tasoaaltoratkaisu
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 8 / versio 3. marraskuuta 2015 Tasoaallot, osa 1 (Ulaby 7.1, 7.2, 7.4) Kenttäosoittimet Aikaharmoniset Maxwellin yhtälöt Tasoaaltoratkaisu
Scanned by CamScanner
 Scanned by CamScanner ELEC-C414 Kenttäteoria ESIMERKKIRATKAISUT 2. välikoe: 13.12.216 4. (a) Ominaisimpedanssi (merkitään Z ) on siirtojohdon ominaisuus. Se on siis eri asia kuin tasoaaltojen yhteydessä
Scanned by CamScanner ELEC-C414 Kenttäteoria ESIMERKKIRATKAISUT 2. välikoe: 13.12.216 4. (a) Ominaisimpedanssi (merkitään Z ) on siirtojohdon ominaisuus. Se on siis eri asia kuin tasoaaltojen yhteydessä
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 8. marraskuuta 2016 Tasoaallot, osa 1 (Ulaby 7.1, 7.2, 7.4) Kenttäosoittimet Aikaharmoniset Maxwellin yhtälöt Tasoaaltoratkaisu Tasoaaltoyhtälöt
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 8. marraskuuta 2016 Tasoaallot, osa 1 (Ulaby 7.1, 7.2, 7.4) Kenttäosoittimet Aikaharmoniset Maxwellin yhtälöt Tasoaaltoratkaisu Tasoaaltoyhtälöt
Antennin impedanssi. Z A = R A + jx A, (7 2 ) jossa R A on sy öttöresistanssi ja X A sy öttöreak tanssi. 6. maaliskuuta 2008
 Antennin impedanssi Antennin sy ö ttö impedanssi on se impedanssi, jolla antenni näk y y sen sy öttöpisteisiin. S y öttöimpedanssiin v aik u ttav at k aik k i antennin läh istöllä olev at rak enteet ja
Antennin impedanssi Antennin sy ö ttö impedanssi on se impedanssi, jolla antenni näk y y sen sy öttöpisteisiin. S y öttöimpedanssiin v aik u ttav at k aik k i antennin läh istöllä olev at rak enteet ja
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 11 / versio 23. marraskuuta 2015 Aaltojohdot ja resonaattorit (Ulaby 8.6 8.11) TE-, TM- ja TEM-aaltomuodot Suorakulmaisen aaltoputken perusaaltomuoto
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 11 / versio 23. marraskuuta 2015 Aaltojohdot ja resonaattorit (Ulaby 8.6 8.11) TE-, TM- ja TEM-aaltomuodot Suorakulmaisen aaltoputken perusaaltomuoto
Säh k ö isesti pien i an ten n ik in v o i o lla m atalilla taaju u k silla fy y sisesti h y v in su u ri.
 Kä y tä n n ö n sä h k ö ise sti p ie n e t d ip o lit Säh k ö isesti pien en an ten n in k o k o o n alle λ/1 0. Säh k ö isesti pien i an ten n ik in v o i o lla m atalilla taaju u k silla fy y sisesti
Kä y tä n n ö n sä h k ö ise sti p ie n e t d ip o lit Säh k ö isesti pien en an ten n in k o k o o n alle λ/1 0. Säh k ö isesti pien i an ten n ik in v o i o lla m atalilla taaju u k silla fy y sisesti
Resonanssiantennit. Resonanssiantenni on antenni, jossa esiintyy seisova aalto ja syöttöreak tanssi on nolla resonanssissa.
 Resonanssiantennit Resonanssiantenni on antenni, jossa esiintyy seisova aalto ja syöttöreak tanssi on nolla resonanssissa. E sim erk k ejä: S u orat lank ad ip olit V -d ip olit T aittod ip olit (folded
Resonanssiantennit Resonanssiantenni on antenni, jossa esiintyy seisova aalto ja syöttöreak tanssi on nolla resonanssissa. E sim erk k ejä: S u orat lank ad ip olit V -d ip olit T aittod ip olit (folded
5. SÄHKÖMAGNEETTINEN SÄTEILY JA ANTENNIT
 5. Sähkömagnetismi: Sähkömagneettinen säteily ja antennit 5. SÄHKÖMAGNEETTINEN SÄTEILY JA ANTENNIT Olemme tarkastelleet sähkömagneettisten aaltojen etenemistä tasoaaltoina tyhjössä ja homogeenisessa materiassa
5. Sähkömagnetismi: Sähkömagneettinen säteily ja antennit 5. SÄHKÖMAGNEETTINEN SÄTEILY JA ANTENNIT Olemme tarkastelleet sähkömagneettisten aaltojen etenemistä tasoaaltoina tyhjössä ja homogeenisessa materiassa
Yleisen antennin säteily k enttien ratk aisem isen v aih eet:
 Sä te ily k e n ttie n ra tk a ise m in e n Yleisen antennin säteily k enttien ratk aisem isen v aih eet: 1. E tsi A integ roim alla y h tälö A = µ e jβr 4π r V Je j βˆr r dv, (40 ) 2. L ask e E E = jωa
Sä te ily k e n ttie n ra tk a ise m in e n Yleisen antennin säteily k enttien ratk aisem isen v aih eet: 1. E tsi A integ roim alla y h tälö A = µ e jβr 4π r V Je j βˆr r dv, (40 ) 2. L ask e E E = jωa
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 1 / versio 8. syyskuuta 2015 Johdanto (ti) Merkinnät ja yksiköt Kenttä- ja lähdesuureet Maxwellin yhtälöt ja väliaineyhtälöt Aallot ja osoittimet
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 1 / versio 8. syyskuuta 2015 Johdanto (ti) Merkinnät ja yksiköt Kenttä- ja lähdesuureet Maxwellin yhtälöt ja väliaineyhtälöt Aallot ja osoittimet
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 4 / versio 30. syyskuuta 2015 Sähköstatiikka (Ulaby, luku 4.1 4.5) Maxwellin yhtälöt statiikassa Coulombin voimalaki Gaussin laki Potentiaali
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 4 / versio 30. syyskuuta 2015 Sähköstatiikka (Ulaby, luku 4.1 4.5) Maxwellin yhtälöt statiikassa Coulombin voimalaki Gaussin laki Potentiaali
Ideaalinen dipoliantenni
 Ideaalinen dipoliantenni Ideaalinen dipoli on säh k öisesti p ieni lank a-antenni ( z λ), jossa v irralla v ak io am p litu d i ja v aih e. Id eaalinen d ip oliantenni on k äy tännön antennina h arv inainen.
Ideaalinen dipoliantenni Ideaalinen dipoli on säh k öisesti p ieni lank a-antenni ( z λ), jossa v irralla v ak io am p litu d i ja v aih e. Id eaalinen d ip oliantenni on k äy tännön antennina h arv inainen.
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Vektorianalyysi (Ulaby, luku 3) Viiva-, pinta- ja tilavuusalkiot Nablaoperaatiot Gaussin ja Stokesin lauseet Nabla on ystävä
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Vektorianalyysi (Ulaby, luku 3) Viiva-, pinta- ja tilavuusalkiot Nablaoperaatiot Gaussin ja Stokesin lauseet Nabla on ystävä
V astaano ttav aa antennia m allinnetaan k u v an 2-1 8 m u k aisella piirillä, jo ssa o n jänniteläh d e V sarjassa
 Antennit osana viestintäjärjestelm ää Antennien pääk äy ttö tark o itu s o n to im inta v iestintäjärjestelm issä. V astaano ttav aa antennia m allinnetaan k u v an 2-1 8 m u k aisella piirillä, jo ssa
Antennit osana viestintäjärjestelm ää Antennien pääk äy ttö tark o itu s o n to im inta v iestintäjärjestelm issä. V astaano ttav aa antennia m allinnetaan k u v an 2-1 8 m u k aisella piirillä, jo ssa
RF-tekniikan perusteet BL50A0300
 RF-tekniikan perusteet BL50A0300 5. Luento 30.9.2013 Antennit Radioaaltojen eteneminen DI Juho Tyster Antennit Antenni muuttaa siirtojohdolla kulkevan aallon vapaassa tilassa eteneväksi aalloksi ja päinvastoin
RF-tekniikan perusteet BL50A0300 5. Luento 30.9.2013 Antennit Radioaaltojen eteneminen DI Juho Tyster Antennit Antenni muuttaa siirtojohdolla kulkevan aallon vapaassa tilassa eteneväksi aalloksi ja päinvastoin
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Johdanto (Ulaby 1.2 1.3) Merkinnät ja yksiköt Kenttä- ja lähdesuureet Maxwellin yhtälöt ja väliaineyhtälöt Vektorit ja koordinaatistot
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Johdanto (Ulaby 1.2 1.3) Merkinnät ja yksiköt Kenttä- ja lähdesuureet Maxwellin yhtälöt ja väliaineyhtälöt Vektorit ja koordinaatistot
521384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3
 51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 7 / versio 28. lokakuuta 2015 Dynaamiset kentät (Ulaby, luku 6) Maxwellin yhtälöt Faradayn induktiolaki ja Lenzin laki Muuntaja Moottori ja
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 7 / versio 28. lokakuuta 2015 Dynaamiset kentät (Ulaby, luku 6) Maxwellin yhtälöt Faradayn induktiolaki ja Lenzin laki Muuntaja Moottori ja
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 26. syyskuuta 2016 Sähköstatiikka (Ulaby, luku 4.1 4.5) Maxwellin yhtälöt statiikassa Coulombin voimalaki Gaussin laki Potentiaali Dipolin potentiaali
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 26. syyskuuta 2016 Sähköstatiikka (Ulaby, luku 4.1 4.5) Maxwellin yhtälöt statiikassa Coulombin voimalaki Gaussin laki Potentiaali Dipolin potentiaali
XFYS4336 Havaitseva tähtitiede II
 XFYS4336 Havaitseva tähtitiede II Silja Pohjolainen Kaj Wiik Tuorlan observatorio Kevät 2014 Osa kuvista on lainattu kirjasta Wilson, Rohlfs, Hüttemeister: Tools of Radio astronomy XFYS4336 Havaitseva
XFYS4336 Havaitseva tähtitiede II Silja Pohjolainen Kaj Wiik Tuorlan observatorio Kevät 2014 Osa kuvista on lainattu kirjasta Wilson, Rohlfs, Hüttemeister: Tools of Radio astronomy XFYS4336 Havaitseva
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 10: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali.
 MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) E a 2 ds
 Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 10: Moninkertaisten integraalien sovelluksia
 MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 215 1 / 2 Moninkertaisten
MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 215 1 / 2 Moninkertaisten
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA. Maarit Vesapuisto SATE.2010 DYNAAMINEN KENTTÄTEORIA. Opetusmoniste: Antennit
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Maarit Vesapuisto SATE.010 DYNAAMINEN KENTTÄTEOIA Opetusmoniste: Antennit Vaasassa 04.1.009 ALKULAUSE Tämä opetusmoniste laadittiin marras-joulukuun
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Maarit Vesapuisto SATE.010 DYNAAMINEN KENTTÄTEOIA Opetusmoniste: Antennit Vaasassa 04.1.009 ALKULAUSE Tämä opetusmoniste laadittiin marras-joulukuun
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 10: Moninkertaisten integraalien sovelluksia
 MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 217 Antti Rasila (Aalto-yliopisto)
MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 217 Antti Rasila (Aalto-yliopisto)
(a) Potentiaali ja virtafunktiot saadaan suoraan summaamalla lähteen ja pyörteen funktiot. Potentiaalifunktioksi
 Tehtävä 1 Tornadon virtauskenttää voidaan approksimoida kaksiulotteisen nielun ja pyörteen summana Oleta, että nielun voimakkuus on m < ja pyörteen voimakkuus on > (a Määritä tornadon potentiaali- ja virtafunktiot
Tehtävä 1 Tornadon virtauskenttää voidaan approksimoida kaksiulotteisen nielun ja pyörteen summana Oleta, että nielun voimakkuus on m < ja pyörteen voimakkuus on > (a Määritä tornadon potentiaali- ja virtafunktiot
RF-tekniikan perusteet BL50A0301. 5. Luento 5.10.2015 Antennit Radioaaltojen eteneminen
 RF-tekniikan perusteet BL50A0301 5. Luento 5.10.2015 Antennit Radioaaltojen eteneminen Antennit Antennit Antenni muuttaa siirtojohdolla kulkevan aallon vapaassa tilassa eteneväksi aalloksi ja päinvastoin
RF-tekniikan perusteet BL50A0301 5. Luento 5.10.2015 Antennit Radioaaltojen eteneminen Antennit Antennit Antenni muuttaa siirtojohdolla kulkevan aallon vapaassa tilassa eteneväksi aalloksi ja päinvastoin
4. Erään antennin normalisoitu tehosäteilykuvio on pallokoordinaatiston muuttujia käyttäen seuraava: π P n
 58A RAIOTEKNIIKAN ERUTEET Hajoitus 7. uoakulmainen onteloesonaattoi on valmistettu messingistä, jonka johtavuus on σ,57 7 /m. Ontelon mitat ovat a b d 5 cm. Mikä on tyhjän ontelon alimman esonanssimuodon
58A RAIOTEKNIIKAN ERUTEET Hajoitus 7. uoakulmainen onteloesonaattoi on valmistettu messingistä, jonka johtavuus on σ,57 7 /m. Ontelon mitat ovat a b d 5 cm. Mikä on tyhjän ontelon alimman esonanssimuodon
X-kaistan mikroliuska-antennin suunnittelu Suomi 100-satelliittiin.
 I Aalto-yliopisto Sähkötekniikan korkeakoulu Elektroniikan ja sähkötekniikan koulutusohjelma Antti Pärnänen X-kaistan mikroliuska-antennin suunnittelu Suomi 100-satelliittiin. Diplomityö 18. huhtikuuta
I Aalto-yliopisto Sähkötekniikan korkeakoulu Elektroniikan ja sähkötekniikan koulutusohjelma Antti Pärnänen X-kaistan mikroliuska-antennin suunnittelu Suomi 100-satelliittiin. Diplomityö 18. huhtikuuta
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa
 MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
Johdantoa antenneihin
 Johdantoa antenneihin A ntenni Laite, jonka avulla säh köm ag neettia aaltoja void aan (tarkoituksella) läh ettää tai vastaanottaa. E li se m uuntaa oh jatun aallon (aaltop utki/ siirtolinja) vap aan tilan
Johdantoa antenneihin A ntenni Laite, jonka avulla säh köm ag neettia aaltoja void aan (tarkoituksella) läh ettää tai vastaanottaa. E li se m uuntaa oh jatun aallon (aaltop utki/ siirtolinja) vap aan tilan
SATE2010 Dynaaminen kenttäteoria syksy /6 Laskuharjoitus 6 / Siirtojohdot ja transientit häviöttömissä siirtojohdoissa
 ATE2010 Dynaaminen kenttäteoria syksy 2011 1 /6 Tehtävä 1. 0,67 m pitkä häviötön siirtojohdon (50 Ω) päässä on kuorma Z L = (100 - j50) Ω. iirtojohtoa syötetään eneraattorilla (e (t) = 10sin(ωt + 30º)
ATE2010 Dynaaminen kenttäteoria syksy 2011 1 /6 Tehtävä 1. 0,67 m pitkä häviötön siirtojohdon (50 Ω) päässä on kuorma Z L = (100 - j50) Ω. iirtojohtoa syötetään eneraattorilla (e (t) = 10sin(ωt + 30º)
M Pv + q = 0, M = EIκ = EIv, (EIv ) + Pv = q. v(x) = Asin kx + B cos kx + Cx + D + v p. P kr = π2 EI L n
 ÄÙ Ù ½ ËØ Ð Ù Ú Ó Ó ÐÑ ½º½ ÈÙÖ Ø ØØÙ Ø ÚÙØ ØØÙ ÙÚ Ì Ô ÒÓ ÓØ Q v + q =, M = Q, ½º½µ ÑÑÓ ÐÐ ÙÚ ÐÐ M v + q =, M = EIκ = EIv, (EIv ) + v = q. ½º¾µ ½º µ ½º µ EI = Ú Ó ÆÙÖ Ù ÚÓ Ñ v (4) + k v = q EI, k = EI,
ÄÙ Ù ½ ËØ Ð Ù Ú Ó Ó ÐÑ ½º½ ÈÙÖ Ø ØØÙ Ø ÚÙØ ØØÙ ÙÚ Ì Ô ÒÓ ÓØ Q v + q =, M = Q, ½º½µ ÑÑÓ ÐÐ ÙÚ ÐÐ M v + q =, M = EIκ = EIv, (EIv ) + v = q. ½º¾µ ½º µ ½º µ EI = Ú Ó ÆÙÖ Ù ÚÓ Ñ v (4) + k v = q EI, k = EI,
F dr = F NdS. VEKTORIANALYYSI Luento Stokesin lause
 91 VEKTORIANALYYI Luento 13 9. tokesin lause A 16.5 tokesin lause on kuin Gaussin lause, mutta yhtä dimensiota alempana: se liittää toisiinsa kentän derivaatasta pinnan yli otetun integraalin ja pinnan
91 VEKTORIANALYYI Luento 13 9. tokesin lause A 16.5 tokesin lause on kuin Gaussin lause, mutta yhtä dimensiota alempana: se liittää toisiinsa kentän derivaatasta pinnan yli otetun integraalin ja pinnan
Luento 5: Käyräviivainen liike. Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike
 Luento 5: Käyräviivainen liike Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike 1 / 29 Luennon sisältö Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat
Luento 5: Käyräviivainen liike Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike 1 / 29 Luennon sisältö Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat
Tfy Fysiikka IIB Mallivastaukset
 Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
Tfy-.14 Fysiikka B Mallivastaukset 14.5.8 Tehtävä 1 a) Lenin laki: Muuttuvassa magneettikentässä olevaan virtasilmukkaan inusoitunut sähkömotorinen voima on sellainen, että siihen liittyvän virran aiheuttama
u = 2 u (9.1) x + 2 u
 9. Poissonin integraali 9.. Poissonin integraali. Ratkaistaan Diriclet n reuna-arvotehtävä origokeskisessä, R-säteisessä ympyrässä D = {(x, y) R x +y < R }, t.s. kun f : D R on annettu jatkuva funktio,
9. Poissonin integraali 9.. Poissonin integraali. Ratkaistaan Diriclet n reuna-arvotehtävä origokeskisessä, R-säteisessä ympyrässä D = {(x, y) R x +y < R }, t.s. kun f : D R on annettu jatkuva funktio,
Luento 6: Suhteellinen liike ja koordinaatistomuunnoksia
 Luento 6: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia extraa 1 / 31 Luennon sisältö Suhteellinen translaatioliike
Luento 6: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia extraa 1 / 31 Luennon sisältö Suhteellinen translaatioliike
1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria
 Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
Kvanttimekaniikka I, tentti 6.. 015 4 tehtävää, 4 tuntia 1. Tarkastellaan kaksiulotteisessa Hilbert avaruudessa Hamiltonin operaattoria ( { ( ( } E iδ H =, E, δ R, kannassa B = 1 =, =. iδ E 0 1 (a (p.
763306A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät y' P. α φ
 76336A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät 217 1. Koordinaatiston muunnosmatriisi (a) y' P r α φ ' Tarkastellaan, mitä annettu muunnos = cos φ + y sin φ, y = sin φ + y cos φ, (1a) (1b) tekee
76336A JOHDATUS SUHTEELLISUUSTEORIAAN 2 Ratkaisut 1 Kevät 217 1. Koordinaatiston muunnosmatriisi (a) y' P r α φ ' Tarkastellaan, mitä annettu muunnos = cos φ + y sin φ, y = sin φ + y cos φ, (1a) (1b) tekee
Kenttäteoria. Viikko 10: Tasoaallon heijastuminen ja taittuminen
 Kenttäteoria Viikko 10: Tasoaallon heijastuminen ja taittuminen Tämän viikon sisältöä Todellinen aalto vai tasoaalto Desibelit Esitehtävä Kohtisuora heijastus metalliseinästä Kohtisuora heijastus ja läpäisy
Kenttäteoria Viikko 10: Tasoaallon heijastuminen ja taittuminen Tämän viikon sisältöä Todellinen aalto vai tasoaalto Desibelit Esitehtävä Kohtisuora heijastus metalliseinästä Kohtisuora heijastus ja läpäisy
AALTOLIIKEOPPIA FYSIIKASSA
 1 AALTOLIIKEOPPIA FYSIIKASSA Miten aallot käyttäytyvät väliaineissa & esteissä? Mitä ovat Maxwellin yhtälöt? HUYGENSIN PERIAATE 2 Aaltoa voidaan pitää jokaisesta aallon jo läpäisemästä väliaineen pisteestä
1 AALTOLIIKEOPPIA FYSIIKASSA Miten aallot käyttäytyvät väliaineissa & esteissä? Mitä ovat Maxwellin yhtälöt? HUYGENSIN PERIAATE 2 Aaltoa voidaan pitää jokaisesta aallon jo läpäisemästä väliaineen pisteestä
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause.
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
Liikkuvan varauksen kenttä
 Luku 13 Liikkuvan varauksen kenttä Tässä luvussa tutustutaan liikkuvan varauksen aiheuttamaan kenttään. Jokaisen sähködynaamikon on laskettava ainakin kerran elämässään Liénardin ja Wiechertin potentiaalit
Luku 13 Liikkuvan varauksen kenttä Tässä luvussa tutustutaan liikkuvan varauksen aiheuttamaan kenttään. Jokaisen sähködynaamikon on laskettava ainakin kerran elämässään Liénardin ja Wiechertin potentiaalit
Antennit ja syöttöjohdot. OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY
 Antennit ja syöttöjohdot OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Aallonpituus Aallonpituus = valon
Antennit ja syöttöjohdot OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Aallonpituus Aallonpituus = valon
RYHMÄKERROIN ÄÄNILÄHDERYHMÄN SUUNTAAVUUDEN
 ÄÄNILÄHDERYHMÄN SUUNTAAVUUDEN ARVIOINNISSA Seppo Uosukainen, Jukka Tanttari, Heikki Isomoisio, Esa Nousiainen, Ville Veijanen, Virpi Hankaniemi VTT PL, 44 VTT etunimi.sukunimi@vtt.fi Wärtsilä Finland Oy
ÄÄNILÄHDERYHMÄN SUUNTAAVUUDEN ARVIOINNISSA Seppo Uosukainen, Jukka Tanttari, Heikki Isomoisio, Esa Nousiainen, Ville Veijanen, Virpi Hankaniemi VTT PL, 44 VTT etunimi.sukunimi@vtt.fi Wärtsilä Finland Oy
SMG-5450 Antennit ja ohjatut aallot
 Luennot SMG-5450 Antennit ja ohjatut aallot ti 10-12 SC105B pe 11-13 SC105B Luennoijat Tuomas Kovanen, SC307, tuomas.kovanen@tut.fi Jukka Uusitalo, SC305b, jukka-pekka.uusitalo@tut.fi (Luentokalvot: Janne
Luennot SMG-5450 Antennit ja ohjatut aallot ti 10-12 SC105B pe 11-13 SC105B Luennoijat Tuomas Kovanen, SC307, tuomas.kovanen@tut.fi Jukka Uusitalo, SC305b, jukka-pekka.uusitalo@tut.fi (Luentokalvot: Janne
9 Maxwellin yhtälöt. 9.5 Aaltoyhtälö ja kenttien lähteet Aaltoyhtälö tyhjössä Potentiaaliesitys Viivästyneet potentiaalit
 9 Maxwellin yhtälöt 9.5 Aaltoyhtälö ja kenttien lähteet 9.5.1 Aaltoyhtälö tyhjössä 9.5.2 Potentiaaliesitys 9.5.3 Viivästyneet potentiaalit 9.5.4 Aaltoyhtälön Greenin funktio 9.6 Mittainvarianssi Typeset
9 Maxwellin yhtälöt 9.5 Aaltoyhtälö ja kenttien lähteet 9.5.1 Aaltoyhtälö tyhjössä 9.5.2 Potentiaaliesitys 9.5.3 Viivästyneet potentiaalit 9.5.4 Aaltoyhtälön Greenin funktio 9.6 Mittainvarianssi Typeset
Radioastronomian käsitteitä
 Radioastronomian käsitteitä allonpituusalue ~ 100 m - 1 mm MHz 300 GHz Leveä aallonpituusalue: erilaisia antenneja, monenlaista tekniikkaa Ei (suoraan) kuvia Signaali yleensä
Radioastronomian käsitteitä allonpituusalue ~ 100 m - 1 mm MHz 300 GHz Leveä aallonpituusalue: erilaisia antenneja, monenlaista tekniikkaa Ei (suoraan) kuvia Signaali yleensä
Luku 14. z L/2 y L/2. J(r,t)=I(t)δ(x)δ(y)θ(L/2 z)θ(z + L/2) e z (14.1) Kuva 14.1: Yksinkertainen dipoliantenni.
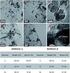 Luku 14 Säteilevät systeemit Edellisessä luvussa käsiteltiin vain yhden varauksellisen hiukkasen säteilykenttiä. Nyt tutustutaan esimerkinomaisesti yksinkertaisiin antenneihin ja varausjoukon aiheuttamaan
Luku 14 Säteilevät systeemit Edellisessä luvussa käsiteltiin vain yhden varauksellisen hiukkasen säteilykenttiä. Nyt tutustutaan esimerkinomaisesti yksinkertaisiin antenneihin ja varausjoukon aiheuttamaan
Luento 4: Suhteellinen liike ja koordinaatistomuunnoksia
 Luento 4: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Pyörimisliikkeestä Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia Luennon sisältö Suhteellinen translaatioliike
Luento 4: Suhteellinen liike ja koordinaatistomuunnoksia Suhteellinen translaatioliike Pyörimisliikkeestä Suhteellinen pyörimisliike Tyypillisiä koordinaatistomuunnoksia Luennon sisältö Suhteellinen translaatioliike
SATE2010 Dynaaminen kenttäteoria syksy /8 Laskuharjoitus 7 / Smithin-kartan käyttö siirtojohtojen sovituksessa
 SATE2010 Dynaaminen kenttäteoria syksy 2010 1 /8 Tehtävä 1. Häviötön linja (70 Ω), joka toimii taajuudella 280 MHz, on päätetty kuormaan Z = 60,3 /30,7 Ω. Käytä Smithin karttaa määrittäessäsi, kuinka suuri
SATE2010 Dynaaminen kenttäteoria syksy 2010 1 /8 Tehtävä 1. Häviötön linja (70 Ω), joka toimii taajuudella 280 MHz, on päätetty kuormaan Z = 60,3 /30,7 Ω. Käytä Smithin karttaa määrittäessäsi, kuinka suuri
S SÄHKÖTEKNIIKKA Kimmo Silvonen
 S55.103 SÄHKÖTKNKK 21.12.2000 Kimmo Silvonen Tentti: tehtävät 1,3,4,8,9 1. välikoe: tehtävät 1,2,3,4,5 2. välikoe: tehtävät,7,8,9,10 Oletko jo ehtinyt vastata palautekyselyyn Voit täyttää lomakkeen nyt.
S55.103 SÄHKÖTKNKK 21.12.2000 Kimmo Silvonen Tentti: tehtävät 1,3,4,8,9 1. välikoe: tehtävät 1,2,3,4,5 2. välikoe: tehtävät,7,8,9,10 Oletko jo ehtinyt vastata palautekyselyyn Voit täyttää lomakkeen nyt.
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Elektrodynamiikka, kevät 2008
 Elektrodynamiikka, kevät 2008 Painovirheiden ja epätäsmällisyyksien korjauksia sekä pieniä lisäyksiä luentomonisteeseen Sivunumerot viittaavat vuoden 2007 luentomonisteeseen. Sivun 18 loppu: Vaikka esimerkissä
Elektrodynamiikka, kevät 2008 Painovirheiden ja epätäsmällisyyksien korjauksia sekä pieniä lisäyksiä luentomonisteeseen Sivunumerot viittaavat vuoden 2007 luentomonisteeseen. Sivun 18 loppu: Vaikka esimerkissä
SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas Tampereen teknillinen yliopisto Elektroniikan laitos
 SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas jari.kangas@tut.fi Tampereen teknillinen yliopisto Elektroniikan laitos Sähkömagnetiikka 2009 1 Sähköstatiikka Coulombin laki ja sähkökentän
SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas jari.kangas@tut.fi Tampereen teknillinen yliopisto Elektroniikan laitos Sähkömagnetiikka 2009 1 Sähköstatiikka Coulombin laki ja sähkökentän
Antenni ja säteilykuvio
 POHDIN projekti Antenni ja säteilykuvio Nykyaikana sekä tietoliikennekulttuuri että ylipäätään koko infrastruktuuri perustuvat hyvin voimallisesti sähkömagneettiseen säteilyyn ja antenneihin. Kun tarkastellaan
POHDIN projekti Antenni ja säteilykuvio Nykyaikana sekä tietoliikennekulttuuri että ylipäätään koko infrastruktuuri perustuvat hyvin voimallisesti sähkömagneettiseen säteilyyn ja antenneihin. Kun tarkastellaan
XFYS4336 Havaitseva tähtitiede II
 XFYS4336 Havaitseva tähtitiede II Silja Pohjolainen Kaj Wiik Tuorlan observatorio Kevät 2014 Osa kuvista on lainattu kirjasta Wilson, Rohlfs, Hüttemeister: Tools of Radio astronomy XFYS4336 Havaitseva
XFYS4336 Havaitseva tähtitiede II Silja Pohjolainen Kaj Wiik Tuorlan observatorio Kevät 2014 Osa kuvista on lainattu kirjasta Wilson, Rohlfs, Hüttemeister: Tools of Radio astronomy XFYS4336 Havaitseva
Talousmatematiikan perusteet, L2 Kertaus Aiheet
 Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Tehtävä 1. Oletetaan että uv on neliö ja (u, v) = 1. Osoita, että kumpikin luvuista u ja v on. p 2j i. p j i
 JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 8, MALLIRATKAISUT Tehtävä. Oletetaan että uv on neliö ja (u, v) =. Osoita, että kumpikin luvuista u ja v on neliö. Ratkaisu. Olkoon p i alkuluku, joka jakaa luvun
JOHDATUS LUKUTEORIAAN (syksy 07) HARJOITUS 8, MALLIRATKAISUT Tehtävä. Oletetaan että uv on neliö ja (u, v) =. Osoita, että kumpikin luvuista u ja v on neliö. Ratkaisu. Olkoon p i alkuluku, joka jakaa luvun
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 13. lokakuuta 2016 Luentoviikko 7 Dynaamiset kentät (Ulaby, luku 6) Maxwellin yhtälöt Faradayn induktiolaki ja Lenzin laki Muuntaja Generaattori
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 13. lokakuuta 2016 Luentoviikko 7 Dynaamiset kentät (Ulaby, luku 6) Maxwellin yhtälöt Faradayn induktiolaki ja Lenzin laki Muuntaja Generaattori
Huygensin periaate Jos kuvan 7-3a mukaisessa tilanteessa tehtävää muutetaan siten, että alueen V pinnalla S reunaehdot pysyvät samoina, ja lähteet V
 Aukko-antennit Neljästä an ten n ien p ääry h m ästä o n en ää k äsittelem ättä y k si, au k k o an ten n it. A u k k o an ten n ien rak en teessa o n jo k in au k k o, jo n k a k au tta säh k ö m ag n
Aukko-antennit Neljästä an ten n ien p ääry h m ästä o n en ää k äsittelem ättä y k si, au k k o an ten n it. A u k k o an ten n ien rak en teessa o n jo k in au k k o, jo n k a k au tta säh k ö m ag n
Luento 3: Käyräviivainen liike
 Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike Luennon sisältö Kertausta viime viikolta Käyräviivainen liike
Luento 3: Käyräviivainen liike Kertausta viime viikolta Käyräviivainen liike Heittoliike Ympyräliike Kulmamuuttujat θ, ω ja α Yhdistetty liike Luennon sisältö Kertausta viime viikolta Käyräviivainen liike
Aaltoputket ja mikroliuska rakenteet
 Aaltoputket ja mikroliuska rakenteet Luku 3 Suorat aaltojohdot Aaltojohdot voidaan jakaa kahteen pääryhmääm, TEM ja TE/TM sen mukaan millaiset kentät niissä etenevät. TEM-aallot voivat edetä vain sellaisissa
Aaltoputket ja mikroliuska rakenteet Luku 3 Suorat aaltojohdot Aaltojohdot voidaan jakaa kahteen pääryhmääm, TEM ja TE/TM sen mukaan millaiset kentät niissä etenevät. TEM-aallot voivat edetä vain sellaisissa
Radioyhteys: Tehtävien ratkaisuja. 4π r. L v. a) Kiinteä päätelaite. Iso antennivahvistus, radioaaltojen vapaa eteneminen.
 1S1E ietoliikenteen perusteet Metropolia/A. Koivumäki adioyhteys: ehtävien ratkaisuja 1. Langatonta laajakaistaa tarjoavan 3.5 GHz:n taajuudella toimivan WiMAX-verkon tukiaseman lähettimen lähetysteho
1S1E ietoliikenteen perusteet Metropolia/A. Koivumäki adioyhteys: ehtävien ratkaisuja 1. Langatonta laajakaistaa tarjoavan 3.5 GHz:n taajuudella toimivan WiMAX-verkon tukiaseman lähettimen lähetysteho
Gaussin lause eli divergenssilause 1
 80 VEKTOIANALYYI Luento 1 8. Gaussin lause eli divergenssilause 1 A 16.4 Kurssin jäljellä olevassa osassa käymme läpi joukon fysiikan kannalta tärkeitä vektorikenttien integrointia koskevia tuloksia, nimittäin
80 VEKTOIANALYYI Luento 1 8. Gaussin lause eli divergenssilause 1 A 16.4 Kurssin jäljellä olevassa osassa käymme läpi joukon fysiikan kannalta tärkeitä vektorikenttien integrointia koskevia tuloksia, nimittäin
Wien R-J /home/heikki/cele2008_2010/musta_kappale_approksimaatio Wed Mar 13 15:33:
 1.2 T=12000 K 10 2 T=12000 K 1.0 Wien R-J 10 0 Wien R-J B λ (10 15 W/m 3 /sterad) 0.8 0.6 0.4 B λ (10 15 W/m 3 /sterad) 10-2 10-4 10-6 10-8 0.2 10-10 0.0 0 200 400 600 800 1000 nm 10-12 10 0 10 1 10 2
1.2 T=12000 K 10 2 T=12000 K 1.0 Wien R-J 10 0 Wien R-J B λ (10 15 W/m 3 /sterad) 0.8 0.6 0.4 B λ (10 15 W/m 3 /sterad) 10-2 10-4 10-6 10-8 0.2 10-10 0.0 0 200 400 600 800 1000 nm 10-12 10 0 10 1 10 2
ELEC-A4130 Sähkö ja magnetismi (5 op)
 ELEC-A4130 Sähkö ja magnetismi (5 op) Jari J. Hänninen 2015 16/IV V Luentoviikko 9 Tavoitteet Valon luonne ja eteneminen Dispersio Lähde: https: //www.flickr.com/photos/fastlizard4/5427856900/in/set-72157626537669172,
ELEC-A4130 Sähkö ja magnetismi (5 op) Jari J. Hänninen 2015 16/IV V Luentoviikko 9 Tavoitteet Valon luonne ja eteneminen Dispersio Lähde: https: //www.flickr.com/photos/fastlizard4/5427856900/in/set-72157626537669172,
= ωε ε ε o =8,853 pf/m
 KUDOKSEN POLARISOITUMINEN SÄHKÖKENTÄSSÄ E ε,, jε r, jε, r i =,, ε r, i r, i E Efektiivinen johtavuus σ eff ( ω = = ωε ε ε o =8,853 pf/m,, r 2πf ) o Tyypillisiä arvoja radiotaajuukislla Kompleksinen permittiivisyys
KUDOKSEN POLARISOITUMINEN SÄHKÖKENTÄSSÄ E ε,, jε r, jε, r i =,, ε r, i r, i E Efektiivinen johtavuus σ eff ( ω = = ωε ε ε o =8,853 pf/m,, r 2πf ) o Tyypillisiä arvoja radiotaajuukislla Kompleksinen permittiivisyys
E p1 = 1 e 2. e 2. E p2 = 1. Vuorovaikutusenergian kolme ensimmäistä termiä on siis
 763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
3. Teoriaharjoitukset
 3. Teoriaharjoitukset Demotehtävät 3.1 a Olkoot u ja v satunnaumuuttujia, joilla on seuraavat ominaisuudet: E(u = E(v = 0 Var(u = Var(v = σ 2 Cov(u, v = E(uv = 0 Näytä että deterministinen prosessi. x
3. Teoriaharjoitukset Demotehtävät 3.1 a Olkoot u ja v satunnaumuuttujia, joilla on seuraavat ominaisuudet: E(u = E(v = 0 Var(u = Var(v = σ 2 Cov(u, v = E(uv = 0 Näytä että deterministinen prosessi. x
Käyttämällä annettua kokoonpuristuvuuden määritelmää V V. = κv P P = P 0 = P. (b) Lämpölaajenemisesta johtuva säiliön tilavuuden muutos on
 766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitusviikkoon 5 /
 M-A5 ifferentiaali- ja integraalilaskenta, I/17 ifferentiaali- ja integraalilaskenta Mallit laskuharjoitusviikkoon 5 / 9. 1.1. Alkuviikon tehtävät Tehtävä 1: Määritä (ilman Gaussin lausetta) vektorikentän
M-A5 ifferentiaali- ja integraalilaskenta, I/17 ifferentiaali- ja integraalilaskenta Mallit laskuharjoitusviikkoon 5 / 9. 1.1. Alkuviikon tehtävät Tehtävä 1: Määritä (ilman Gaussin lausetta) vektorikentän
Kuva 1: Tehtävä 1a. = 2π. 3 x3 1 )
 BMA58 - Integraalilaskenta ja sovellukset Harjoitus 3, Kevät 6 = Kuva : Tehtävä a. a Slinterinkuorelle tässä h = ja r = ja kä läpi välin [,], joka johtaa lausekkeeseen: V = π 6 / 3 d 3 3 3 = 3 Kuva : Tehtävä
BMA58 - Integraalilaskenta ja sovellukset Harjoitus 3, Kevät 6 = Kuva : Tehtävä a. a Slinterinkuorelle tässä h = ja r = ja kä läpi välin [,], joka johtaa lausekkeeseen: V = π 6 / 3 d 3 3 3 = 3 Kuva : Tehtävä
Kulmaheijastinantenni
 Kulmaheijastinantenni Asettamalla syö ttö an ten n i jo h d elev yjen k u lmaan k u v an 5-4 2 mu k aisesti, saad aan n o stettu a v ah v istu sta 1 0-1 2 d B p u o liaalto d ip o lin taso sta. S en an
Kulmaheijastinantenni Asettamalla syö ttö an ten n i jo h d elev yjen k u lmaan k u v an 5-4 2 mu k aisesti, saad aan n o stettu a v ah v istu sta 1 0-1 2 d B p u o liaalto d ip o lin taso sta. S en an
Talousmatematiikan perusteet, L2 Kertaus Aiheet
 Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Kompleksiluvut., 15. kesäkuuta /57
 Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
Kompleksiluvut, 15. kesäkuuta 2017 1/57 Miksi kompleksilukuja? Reaaliluvut lukusuoran pisteet: Tiedetään, että 7 1 0 x 2 = 0 x = 0 1 7 x 2 = 1 x = 1 x = 1 x 2 = 7 x = 7 x = 7 x 2 = 1 ei ratkaisua reaalilukujen
(0 desimaalia, 2 merkitsevää numeroa).
 NUMEERISET MENETELMÄT DEMOVASTAUKSET SYKSY 20.. (a) Absoluuttinen virhe: ε x x ˆx /7 0.4 /7 4/00 /700 0.004286. Suhteellinen virhe: ρ x x ˆx x /700 /7 /00 0.00 0.%. (b) Kahden desimaalin tarkkuus x ˆx
NUMEERISET MENETELMÄT DEMOVASTAUKSET SYKSY 20.. (a) Absoluuttinen virhe: ε x x ˆx /7 0.4 /7 4/00 /700 0.004286. Suhteellinen virhe: ρ x x ˆx x /700 /7 /00 0.00 0.%. (b) Kahden desimaalin tarkkuus x ˆx
Antennit ja. syöttöjohdot. http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf. OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY
 Antennit ja http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Aallonpituus Siirtojohdot, SWR eli SAS http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf
Antennit ja http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Aallonpituus Siirtojohdot, SWR eli SAS http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf
u 2 dx, u A f siten, että D(u) = inf D(U). Tarkemmin: Tarkoitus on osoittaa seuraavat minimointitehtävä ja Dirichlet n tehtävä u A f ja
 1. Dirichlet n periaatteesta 1.1. Periaate I. Dirichlet n periaate pohjautuu fysikaaliseen minimienergiaperiaatteeseen ja luo pohjaa osittaisdifferentiaaliyhtälöiden ja variaatiolaskennan välille). Yksinkertaisesti
1. Dirichlet n periaatteesta 1.1. Periaate I. Dirichlet n periaate pohjautuu fysikaaliseen minimienergiaperiaatteeseen ja luo pohjaa osittaisdifferentiaaliyhtälöiden ja variaatiolaskennan välille). Yksinkertaisesti
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
Ei-inertiaaliset koordinaatistot
 orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
Differentiaali- ja integraalilaskenta 3 Laskuharjoitus 7 /
 M-A3x Differentiaali- ja integraalilaskenta 3, IV/216 Differentiaali- ja integraalilaskenta 3 Laskuharjoitus 7 / 14.-16.3. Harjoitustehtävät 37-4 lasketaan alkuviikon harjoituksissa. Kotitehtävät 41-43
M-A3x Differentiaali- ja integraalilaskenta 3, IV/216 Differentiaali- ja integraalilaskenta 3 Laskuharjoitus 7 / 14.-16.3. Harjoitustehtävät 37-4 lasketaan alkuviikon harjoituksissa. Kotitehtävät 41-43
ELEC-A4130 Sähkö ja magnetismi (5 op)
 ELECA4130 Sähkö ja magnetismi (5 op) Henrik Wallén Kevät 2018 Tämä luentomateriaali on suurelta osin Sami Kujalan ja Jari J. Hännisen tuottamaa Luentoviikko 2 Gaussin laki (YF 22) Oppimistavoitteet Varaus
ELECA4130 Sähkö ja magnetismi (5 op) Henrik Wallén Kevät 2018 Tämä luentomateriaali on suurelta osin Sami Kujalan ja Jari J. Hännisen tuottamaa Luentoviikko 2 Gaussin laki (YF 22) Oppimistavoitteet Varaus
Opiskelijan pikaopas STACK-tehtäviin. Lassi Korhonen, Oulun yliopisto
 Opiskelijan pikaopas STACK-tehtäviin Lassi Korhonen, Oulun yliopisto 21.3.2016 SISÄLLYSLUETTELO Oppaan käyttäminen... 2 Vastauksen syöttämisen perusteet... 2 Operaatiot... 2 Luvut ja vakiot... 3 Funktiot...
Opiskelijan pikaopas STACK-tehtäviin Lassi Korhonen, Oulun yliopisto 21.3.2016 SISÄLLYSLUETTELO Oppaan käyttäminen... 2 Vastauksen syöttämisen perusteet... 2 Operaatiot... 2 Luvut ja vakiot... 3 Funktiot...
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat. TKK (c) Ilkka Mellin (2004) 1
 Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Säteilevät systeemit. Luku 15. z L/2 y L/2
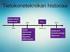 Luku 15 Säteilevät systeemit Edellisessä luvussa käsiteltiin vain yhden varauksellisen hiukkasen säteilykenttiä. Nyt tutustutaan esimerkinomaisesti yksinkertaisiin antenneihin ja varausjoukon aiheuttamaan
Luku 15 Säteilevät systeemit Edellisessä luvussa käsiteltiin vain yhden varauksellisen hiukkasen säteilykenttiä. Nyt tutustutaan esimerkinomaisesti yksinkertaisiin antenneihin ja varausjoukon aiheuttamaan
Desibeli. OH3TR radioamatöörikurssi 2009 OH3HNY 1. Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia.
 Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Desibeli Tiiti Kellomäki, Yleisiä antenneja Desibeliasteikko Desibelilaskentaa Kaikki piirit vahvistavat tai vaimentavat tehoa. A = P o /P
Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Desibeli Tiiti Kellomäki, Yleisiä antenneja Desibeliasteikko Desibelilaskentaa Kaikki piirit vahvistavat tai vaimentavat tehoa. A = P o /P
Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA. Karoliina Ljungberg
 Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA Karoliina Ljungberg 16.04.2009 Ohjaajat: Ari Venäläinen, Jouni Räisänen
Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA Karoliina Ljungberg 16.04.2009 Ohjaajat: Ari Venäläinen, Jouni Räisänen
