Resonanssiantennit. Resonanssiantenni on antenni, jossa esiintyy seisova aalto ja syöttöreak tanssi on nolla resonanssissa.
|
|
|
- Outi Sipilä
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Resonanssiantennit Resonanssiantenni on antenni, jossa esiintyy seisova aalto ja syöttöreak tanssi on nolla resonanssissa. E sim erk k ejä: S u orat lank ad ip olit V -d ip olit T aittod ip olit (folded dipole) Y ag i-u d a-antenni Isot silm u k k a-antennit M ik roliu sk a-antennit (p atch -antennit)
2 Suorat lankadipolit Tarkastellaan nyt mielivaltaisen mittaista suoraa keskeltä syötettyä lankadipolia (kuva 5-1 ). O letetaan, että virtajakauma on sinimuotoinen, [ ( ) ] L I(z) = I m sin β 2 z L, z 2. (1 9 9 ) Tämä on hyvä approksimaatio ohuille antenneille, tarkat virtajakaumat saadaan mittaamalla tai laskemalla numeerisesti. Tilanne vastaa avointa siirtolinjaa, jonka päät ovat käännetty ulospäin, ja virtajakauman oletetaan säilyvän samana kuin siirtolinjalla.
3 Suorat lankadipolit Kuvassa 5-2 on esitetty virtajakauma, kun L < λ/2. N yt I m ei ole virran maksimiarvo, vaan se on I m sin(βl/2) syöttöpisteessä. Kuvassa 5-3 on virtajakauma suuntineen eri pituisille dipoleille (L λ/2). Virroista on esitetty maksimiarvot, hetkellinen virta on I(z) cos ω t. D ipolin säteilykuvio saadaan integroitua samalla tapaa kuin λ 2 -dipolille. Saadaan f u n = L 2 L 2 = 2I m β I m sin [ β ( )] L 2 z e j β z co s θ dz cos[(βl/2) cos θ] cos(βl/2) sin 2. (20 0 ) θ
4 Suorat lankadipolit Sähkökenttä kaukokentässä on E θ = jη ejβr 2πr I cos[(βl/2) cos θ] cos(βl/2) m sin θ Kun L = λ/2, normalisoiduksi säteilykuvioksi saadaan ennestään tuttu (kuva 5-4 ) (201) F (θ) = Kun L = λ, F (θ) = cos[(π/2) cos θ] sin θ cos(π cos θ) sin θ, H P = 7 8. (202), H P = 4 7. (203)
5 Suorat lankadipolit Kun L = 3 2 λ, F (θ) = cos( 3 2π cos θ). (204) 2 sin θ Kun L > λ, kaikki antennin virrat eivät kulje samaan suuntaan (kuva 5-3). Tällöin säteilykuvio jakautuu useisiin keiloihin (kuva 5-4c ja d), koska eri osista antennia lähtevät aallot kumoavat toisensa joissain suunnissa. Kun L/λ menee hyvin pieneksi, (201):n säteilykuvio lähestyy sin θ:tä, kuten olemme jo aiemmin todenneet lyhyen dipolin tapauksessa.
6 Suorat lankadipolit Antennin säteilyteho saadaan laskemalla P = 1 2η 2π 0 π 0 E θ 2 r 2 sin θ dθdφ, (205) Yleisessä tapauksessa päädytään erikoisfunktioihin, mutta harjoitustehtävässä päädyttiin λ 2 -dipolin tapauksessa tulokseen P = η 8π I2 m(2.44), jolloin säteilyresistanssi on R r = 2P Im 2 = 73 Ω. (206 ) Muun pituisille ja äärellisen paksuisille dipoleille syöttöresistanssi ja -reaktanssi saadaan laskettua numeerisesti. Tällöin virtajakauman muotoa ei tarvitse olettaa etukäteen.
7 Suorat lankadipolit Kuvissa 5-5 ja 5-6 on esitetty numeerisesti laskettu ohuen keskeltä syötetyn dipolin syöttöresistanssi ja -reaktanssi, dipolin pituuden funktiona. R esonanssissa reaktanssi menee nollaksi, lyhyillä dipoleilla reaktanssi on kapasitiivinen, ja yleisesti X A riippuu dipolin pituudesta. Säteilyresistanssi voidaan määritellä usealla eri tapaa käyttäen eri virran referenssipisteitä. Käytännössä tärkein on antennin kytkentäpisteen virtaan I A liittyvä resistanssi R ri. J os ohmisia häviöitä ei ole, R ri on sama kuin antennin syöttöresistanssi R A.
8 Suorat lankadipolit Myös antennin virtajakauman maksimiin I m liittyvää resistanssia R rm käytetään. Virtaa I m ei esiinny missään kohtaa antennia, jos L < λ/2 (kuva 5-2). Edellä mainitulle resistanssille saadaan suhde, sillä säteilyteho on sama molemmilla resistansseilla ilmaistuna, P = 1 2 I2 mr rm = 1 2 I2 AR ri R ri = I2 m I 2 A R rm = R rm sin 2 (βl/2) Kun antennin pituus on aallonpituuden monikerta, R ri menee edellisen mukaan äärettömäksi.
9 Suorat lankadipolit Todellisilla antenneilla syöttöresistanssi on tällöin iso mutta äärellinen (kuva 5-5). Kuvan 5-3 mukaan syöttöpisteen virta on nolla näillä pituuksilla, todellisuudessa virta ei ole täysin sinimuotoinen ja syötössä esiintyy pieni virta. Muilla pituuksilla sinimuotoinen virtajakauma on hyvä approksimaatio. L isäksi kuvasta 5-5 huomataan, että reaktanssi menee nollaksi hieman alle λ/2-pituiselle dipolille. Taulukossa 5-2 on resonanssipituuksia eri paksuisille antenneille; resonanssipituus lyhenee johdon paksuuntuessa.
10 Suorat lankadipolit Koska dipolit ovat resonanssityyppisiä rakenteita, niiden kaistanleveys on matala. Kaistanleveys kasvaa johtimien paksuuntuessa (kuva 5-7). Harjoituksissa laskettiin myös, että λ 2 -dipolin suuntaavuus on D = 1.64, eli hieman parempi kuin lyhyen dipolin 1.5. Dipolia pidennettäessä suuntaavuus edelleen kasvaa, ollen λ-pituiselle Yli 5λ/4-pituisille säteilykuvio hajoaa kuvan 5-4 mukaisesti, jolloin suuntaavuus putoaa jyrkästi.
11 V-dipoli Lanka-antennin ei tarvitse olla suora, esimerkkkinä kuvan 5-9 V-dipoli. Siinä avoimen siirtolinjan päitä taitetaan ulospäin kulman γ verran. V-dipolin suuntaavuus voidaan saada suuremmaksi kuin saman mittaisen suoran dipolin. Kuvassa 5-10 (päiden pituus h = 0.75λ) V-dipolin säteilykuvio. Säteilykeila on 2 db suurempi φ = 90 -suuntaan kuin 270 -suuntaan, samoin sivukeilojen taso on pudonnut merkittävästi suoraan dipoliin verrattuna (kuva 5-4d). Suuntaavuus on D = 5.26 db, kun samanpituisen suoran dipolin on 3.4 db. V-dipolin syöttöimpedanssi on yleisesti pienempi kuin samanmittaisen suoran dipolin.
12 Taittodipoli Taittodipoli koostuu kahdesta samansuuntaisesta lähekkäisestä (d L, d λ) dipolista, jotka on yhdistetty päistään, jolloin ne muodostavat kapean silmukan (kuva 5-11). Syöttö on toisen sivun keskellä. Taittodipolin toiminnan voi ymmärtää, kun tarkastellaan erikseen sen toimintaa siirtolinjatilassa ja antennitilassa kuvien 5-12 ja 5-13 mukaisesti. Antennin kokonaisvirta saadaan näiden kahden moodin virtojen summana. Antennimoodissa syöttö on kuvan 5-13b mukaisesti symmetrinen, jolloin taittodipolia voi mallintaa kahdella lähekkäisellä dipolilla, joissa V 2 = (Z Z 1 2 ) I a 2.
13 Taittodipoli Pienillä d:n arvoilla Z 12 Z 11 Z d, eli sama kuin yksittäisen dipolin syöttöimpedanssi. Siirtolinjamoodissa syöttö on epäsymmetrinen (kuva 5-13a), jolloin kumpikin pää muodostaa L/2-mittaisen oikosuljetun siirtolinjan, jonka syöttöimpedanssi on Z t = Z 0 tan(βl/2). Jos L = λ/2, kyseisen tapauksen Z t = Z 0 tan(π/2) =, jolloin I t = 0. Kokonaisuudessaan λ/2-mittaisessa taittodipolissa kulkee virta I a /2 + I t = I a /2, jolloin sen syöttöimpedanssi on Z A = V I A /2 = 4Z d, (207) eli nelinkertainen suoraan λ 2 -dipoliin verrattuna.
14 Taittodipoli λ 2 -taittodipolin syöttöimpedanssi on siten Z A = 4(70) = 280 Ω, joka on hyvin lähellä kaksijohtimisen nauhajohdon (twin-lead, parijohto, lapamato ) ominaisimpedanssia (300 Ω). Kuvan 5-15 mukaisesti λ 2 -taittodipolin molemmissa johtimissa kulkee sama virta. Jos syöttöteho on sama, taittodipolin johtimissa kulkee yhteensä sama virta kuin suorassa λ 2 -dipolissa. Siten myös säteilykuvio on sama kuin dipolilla. Kuvassa 5-16 on yleisen mittaisen taittodipolin syöttöresistanssi ja -reaktanssi pituuden L funktiona.
15 Taittodipoli Taittodipoli on hyvin suosittu antenni, koska sen syöttöimpedanssi on lähellä parijohdon ominaisimpedanssia sen taajuuskaista on leveämpi kuin suoran dipolin ne ovat rakenteeltaan helppoja ja tukevia Taittodipolia käytetään F M-vastaanottoantennina ja Yagi-Uda-antenniryhmän syöttöantennina.
16 Yagi-Uda-antenni Antenniryhmien ideana on, että elementtiantenneja lisäämällä saadaan lisättyä suuntaavuutta. Ryhmien yhteydessä oletimme, että kaikkia elementtiantenneja syötetään, jolloin tarvitaan joka elementille kytkentä syöttöpiiriin. Antennin syöttöpiiri yksinkertaistuu huomattavasti, jos vain yhtä tai muutamaan elementtiä syötetään suoraan. Tällöin kyseessä on parasiittinen ryhmä. Elementtejä, joita ei suoraan syötetä, saavat virtansa lähikenttien kytkeytymisen kautta syötetyiltä elementeiltä. Niitä kutsutaan parasiiteik si.
17 Yagi-Uda-antenni Parasiittistä lineaarista ryhmää, joka koostuu rinnakkaisista dipoleista, kutsutaan Yagi-Uda-antenniksi, lyhyesti Yagi-antenniksi. Tarkastellaan λ 2 -dipolia ja hyvin lähelle sitä sijoitettua saman mittaista parasiittiä. Koska parasiitti on lähellä, sille tulevan aallon sähkökenttä on karkeasti arvioiden sama kuin säteilijän pinnassa oleva kenttä, E incid ent = E d riv er. Koska rajapintaehtojen mukaan parasiitin pinnalla sähkökentän tangentiaalikomponentin pitää olla nolla, parasiitin säteilykentän pitää kumota tulevan aallon kenttä, E p a ra site = E incid ent = E d riv er.
18 Yagi-Uda-antenni Kyseessä on siis kahden sama-amplitudisen, mutta vastakkaisvaiheisen elementin ryhmä päätysäteilijä (kuva 5-30). Kun tätä parasiittiä pidennetään hiukan, säteilijän puoleinen päätykeila kasvaa ja parasiitin puoleinen vastaavasti pienenee yksi pääkeila (kuva 5-31). Tällöin parasiittiä kutsutaan heijastajaksi. Jos parasiitti on lyhyempi kuin säteilijä ja toisella puolella säteilijää kuin edellä, pääkeila kasvaa parasiitin suuntaan, eli se toimii su u ntaajana (kuva 5-32).
19 Yagi-Uda-antenni Kolmielementtinen Yagi sisältää säteilijän lisäksi heijastajan ja suuntaajan sen vastakkaisilla puolilla (kuva 5-33). Suuntaavuusominaisuudet paranevat entisestään kaksielementtisiin tapauksiin nähden. Kuvassa 5-34 on yleinen useampielementtinen Yagi-Uda. Tyypilliset arvot parasiittien etäisyyksille ovat S R = ( )λ heijastajalle (kuva 5-35) ja S D = ( )λ suuntaajalle. Heijastajan pituus L R = 0.5λ, säteilijän pituus on resonanssipituus ilman parasiittejä, ja suuntaaja 80-90% resonanssipituudesta.
20 Yagi-Uda-antenni Heijastajia tavallisesti vain yksi, suuntaajiakaan ei kannata käyttää liikaa, koska niiden lisääminen ei enää kasvata merkittävästi vahvistusta kuvan 5-36 mukaisesti. Kuvassa 5-39 mitatut elementtivirrat Yagi-Uda:sta. Taulukossa 5-4 ja kuvassa 5-37 tarkemmat mittauksien kautta saadut optimaaliset mitat erikokoisille Yagi-Uda-antenneille. Kuvassa 5-41 numeerisesti laskettu optimaalisesti mitoitetun 12-elementtisen Yagi-Uda-antennin säteilykuvio sekä E- että H-tasoissa.
21 Yagi-Uda-antenni Yagi-Uda on yksi yleisimmistä HF-VHF-UHF alueen (3 MHz 3 G Hz) antenneista. Sillä on suhteellisen hyvä vahvistus sekä se on kevyt ja halpa. Yagi-Uda:n suurin haittapuoli on sen kapea kaistanleveys. Säteilijänä käytetään usein taittodipolia nostamaan syöttöimpedanssia ja parantamaan kaistanleveyttä. Jos sovelluskohteessa ei tarvita isoa kaistanleveyttä, Yagi-Udalla saavutetaan 9-12 db vahvistus pienillä kustannuksilla.
Antennin impedanssi. Z A = R A + jx A, (7 2 ) jossa R A on sy öttöresistanssi ja X A sy öttöreak tanssi. 6. maaliskuuta 2008
 Antennin impedanssi Antennin sy ö ttö impedanssi on se impedanssi, jolla antenni näk y y sen sy öttöpisteisiin. S y öttöimpedanssiin v aik u ttav at k aik k i antennin läh istöllä olev at rak enteet ja
Antennin impedanssi Antennin sy ö ttö impedanssi on se impedanssi, jolla antenni näk y y sen sy öttöpisteisiin. S y öttöimpedanssiin v aik u ttav at k aik k i antennin läh istöllä olev at rak enteet ja
Huygensin periaate Jos kuvan 7-3a mukaisessa tilanteessa tehtävää muutetaan siten, että alueen V pinnalla S reunaehdot pysyvät samoina, ja lähteet V
 Aukko-antennit Neljästä an ten n ien p ääry h m ästä o n en ää k äsittelem ättä y k si, au k k o an ten n it. A u k k o an ten n ien rak en teessa o n jo k in au k k o, jo n k a k au tta säh k ö m ag n
Aukko-antennit Neljästä an ten n ien p ääry h m ästä o n en ää k äsittelem ättä y k si, au k k o an ten n it. A u k k o an ten n ien rak en teessa o n jo k in au k k o, jo n k a k au tta säh k ö m ag n
Kulmaheijastinantenni
 Kulmaheijastinantenni Asettamalla syö ttö an ten n i jo h d elev yjen k u lmaan k u v an 5-4 2 mu k aisesti, saad aan n o stettu a v ah v istu sta 1 0-1 2 d B p u o liaalto d ip o lin taso sta. S en an
Kulmaheijastinantenni Asettamalla syö ttö an ten n i jo h d elev yjen k u lmaan k u v an 5-4 2 mu k aisesti, saad aan n o stettu a v ah v istu sta 1 0-1 2 d B p u o liaalto d ip o lin taso sta. S en an
Pieni silmukka-antenni duaalisuus. Ratkaistaan pienen silmukka-antennin kentät v ielä käy ttämällä d uaalisuud en periaatetta.
 Pieni silmukka-antenni duaalisuus Ratkaistaan pienen silmukka-antennin kentät v ielä käy ttämällä d uaalisuud en periaatetta. S amalla saamme my ö s silmukan läh ikentät. Käy tämme h y v äksi sitä, että
Pieni silmukka-antenni duaalisuus Ratkaistaan pienen silmukka-antennin kentät v ielä käy ttämällä d uaalisuud en periaatetta. S amalla saamme my ö s silmukan läh ikentät. Käy tämme h y v äksi sitä, että
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 12 / versio 1. joulukuuta 2015 Antennit (Ulaby 9.1 9.6, 9.9) Hertzin dipoli Kaukokenttä Säteilykuvio ja suuntaavuus Antennin vahvistus ja
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 12 / versio 1. joulukuuta 2015 Antennit (Ulaby 9.1 9.6, 9.9) Hertzin dipoli Kaukokenttä Säteilykuvio ja suuntaavuus Antennin vahvistus ja
Helix-antenni Helix-antenni (kierukka-antenni) saadaan, kun johdin kierretään heliksille (kuv a 6-9 ). A ntennin koosta riip p uen helix v oi toim ia
 Helix-antenni Helix-antenni (kierukka-antenni) saadaan, kun johdin kierretään heliksille (kuv a 6-9 ). A ntennin koosta riip p uen helix v oi toim ia kahdessa eri m oodissa: norm aalim oodi ja aksiaalim
Helix-antenni Helix-antenni (kierukka-antenni) saadaan, kun johdin kierretään heliksille (kuv a 6-9 ). A ntennin koosta riip p uen helix v oi toim ia kahdessa eri m oodissa: norm aalim oodi ja aksiaalim
Antennit ja syöttöjohdot
 Antennit ja syöttöjohdot http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf Siirtojohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Aallonpituus Siirtojohdot, SWR eli SAS http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf
Antennit ja syöttöjohdot http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf Siirtojohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Aallonpituus Siirtojohdot, SWR eli SAS http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf
V astaano ttav aa antennia m allinnetaan k u v an 2-1 8 m u k aisella piirillä, jo ssa o n jänniteläh d e V sarjassa
 Antennit osana viestintäjärjestelm ää Antennien pääk äy ttö tark o itu s o n to im inta v iestintäjärjestelm issä. V astaano ttav aa antennia m allinnetaan k u v an 2-1 8 m u k aisella piirillä, jo ssa
Antennit osana viestintäjärjestelm ää Antennien pääk äy ttö tark o itu s o n to im inta v iestintäjärjestelm issä. V astaano ttav aa antennia m allinnetaan k u v an 2-1 8 m u k aisella piirillä, jo ssa
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) E a 2 ds
 Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
Suuntaavuus ja vahvistus Aukkoantennien tapauksessa suuntaavuus saadaan m uotoon (luku 7.3.1 ) Täm ä olettaa, että D = 4π λ 2 S a E a ds 2. (2 40 ) S a E a 2 ds Pääkeila aukon tasoa koh tisuoraan suuntaan
Säh k ö isesti pien i an ten n ik in v o i o lla m atalilla taaju u k silla fy y sisesti h y v in su u ri.
 Kä y tä n n ö n sä h k ö ise sti p ie n e t d ip o lit Säh k ö isesti pien en an ten n in k o k o o n alle λ/1 0. Säh k ö isesti pien i an ten n ik in v o i o lla m atalilla taaju u k silla fy y sisesti
Kä y tä n n ö n sä h k ö ise sti p ie n e t d ip o lit Säh k ö isesti pien en an ten n in k o k o o n alle λ/1 0. Säh k ö isesti pien i an ten n ik in v o i o lla m atalilla taaju u k silla fy y sisesti
Antennit ja. syöttöjohdot. http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf. OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY
 Antennit ja http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Aallonpituus Siirtojohdot, SWR eli SAS http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf
Antennit ja http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Aallonpituus Siirtojohdot, SWR eli SAS http://ham.zmailer.org/rolletiini/rolletiini_4_2004.pdf
Ideaalinen dipoliantenni
 Ideaalinen dipoliantenni Ideaalinen dipoli on säh k öisesti p ieni lank a-antenni ( z λ), jossa v irralla v ak io am p litu d i ja v aih e. Id eaalinen d ip oliantenni on k äy tännön antennina h arv inainen.
Ideaalinen dipoliantenni Ideaalinen dipoli on säh k öisesti p ieni lank a-antenni ( z λ), jossa v irralla v ak io am p litu d i ja v aih e. Id eaalinen d ip oliantenni on k äy tännön antennina h arv inainen.
Desibeli. OH3TR radioamatöörikurssi 2009 OH3HNY 1. Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia.
 Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Desibeli Tiiti Kellomäki, Yleisiä antenneja Desibeliasteikko Desibelilaskentaa Kaikki piirit vahvistavat tai vaimentavat tehoa. A = P o /P
Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Desibeli Tiiti Kellomäki, Yleisiä antenneja Desibeliasteikko Desibelilaskentaa Kaikki piirit vahvistavat tai vaimentavat tehoa. A = P o /P
Radioamatöörikurssi 2014
 Radioamatöörikurssi 2014 Polyteknikkojen Radiokerho Siirtojohdot, Antennit ja Eteneminen 11.11.2014 Juha, OH2EAN 1 / 42 Illan aiheet Siirtojohdot Antennit Radioaaltojen eteneminen 2 / 42 Siirtojohto Mikä
Radioamatöörikurssi 2014 Polyteknikkojen Radiokerho Siirtojohdot, Antennit ja Eteneminen 11.11.2014 Juha, OH2EAN 1 / 42 Illan aiheet Siirtojohdot Antennit Radioaaltojen eteneminen 2 / 42 Siirtojohto Mikä
Desibeli. Desibeliasteikko. Desibelilaskentaa. Desibeliyksiköitä. Peukalosääntöjä. Desibeli Siirtojohdot, SWR Antennien ominaisuuksia
 Desibeli Siirtojohdot, SWR Antennien ominaisuuksia Desibeli Tiiti Kellomäki, OH3HNY Yleisiä antenneja Desibeliasteikko Kaikki piirit vahvistavat tai vaimentavat tehoa. A = P o /P i = 100000 B = P o /P
Desibeli Siirtojohdot, SWR Antennien ominaisuuksia Desibeli Tiiti Kellomäki, OH3HNY Yleisiä antenneja Desibeliasteikko Kaikki piirit vahvistavat tai vaimentavat tehoa. A = P o /P i = 100000 B = P o /P
Yleisen antennin säteily k enttien ratk aisem isen v aih eet:
 Sä te ily k e n ttie n ra tk a ise m in e n Yleisen antennin säteily k enttien ratk aisem isen v aih eet: 1. E tsi A integ roim alla y h tälö A = µ e jβr 4π r V Je j βˆr r dv, (40 ) 2. L ask e E E = jωa
Sä te ily k e n ttie n ra tk a ise m in e n Yleisen antennin säteily k enttien ratk aisem isen v aih eet: 1. E tsi A integ roim alla y h tälö A = µ e jβr 4π r V Je j βˆr r dv, (40 ) 2. L ask e E E = jωa
Antennit ja syöttöjohdot. OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY
 Antennit ja syöttöjohdot OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Aallonpituus Aallonpituus = valon
Antennit ja syöttöjohdot OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Aallonpituus Aallonpituus = valon
AALTOLIIKEOPPIA FYSIIKASSA
 1 AALTOLIIKEOPPIA FYSIIKASSA Miten aallot käyttäytyvät väliaineissa & esteissä? Mitä ovat Maxwellin yhtälöt? HUYGENSIN PERIAATE 2 Aaltoa voidaan pitää jokaisesta aallon jo läpäisemästä väliaineen pisteestä
1 AALTOLIIKEOPPIA FYSIIKASSA Miten aallot käyttäytyvät väliaineissa & esteissä? Mitä ovat Maxwellin yhtälöt? HUYGENSIN PERIAATE 2 Aaltoa voidaan pitää jokaisesta aallon jo läpäisemästä väliaineen pisteestä
SWR eli SAS Antennien ominaisuuksia. Tiiti Kellomäki, OH3HNY. antenneja
 Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia i i Tiiti Kellomäki, OH3HNY Yleisiä antenneja ylikurssia! ylikurssia! ylikurssia! ylikurssia! ylikurssia! Desibeli ylikurssia! i ylikurssia!
Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia i i Tiiti Kellomäki, OH3HNY Yleisiä antenneja ylikurssia! ylikurssia! ylikurssia! ylikurssia! ylikurssia! Desibeli ylikurssia! i ylikurssia!
Radioamatöörikurssi 2014
 Radioamatöörikurssi 2014 Polyteknikkojen Radiokerho Siirtojohdot, Antennit ja Eteneminen 10.11.2015 Otto, OH2EMQ 1 / 44 Illan aiheet Siirtojohdot Antennit Radioaaltojen eteneminen 2 / 44 Siirtojohto Mikä
Radioamatöörikurssi 2014 Polyteknikkojen Radiokerho Siirtojohdot, Antennit ja Eteneminen 10.11.2015 Otto, OH2EMQ 1 / 44 Illan aiheet Siirtojohdot Antennit Radioaaltojen eteneminen 2 / 44 Siirtojohto Mikä
Antenni ja säteilykuvio
 POHDIN projekti Antenni ja säteilykuvio Nykyaikana sekä tietoliikennekulttuuri että ylipäätään koko infrastruktuuri perustuvat hyvin voimallisesti sähkömagneettiseen säteilyyn ja antenneihin. Kun tarkastellaan
POHDIN projekti Antenni ja säteilykuvio Nykyaikana sekä tietoliikennekulttuuri että ylipäätään koko infrastruktuuri perustuvat hyvin voimallisesti sähkömagneettiseen säteilyyn ja antenneihin. Kun tarkastellaan
FYSP105/2 VAIHTOVIRTAKOMPONENTIT. 1 Johdanto. 2 Teoreettista taustaa
 FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteita o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteita o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
l s, c p T = l v = l l s c p. Z L + Z 0
 1.1 i k l s, c p Tasajännite kytketään hetkellä t 0 johtoon, jonka pituus on l ja jonka kapasitanssi ja induktanssi pituusyksikköä kohti ovat c p ja l s. Mieti, kuinka virta i käyttäytyy ajan t funktiona
1.1 i k l s, c p Tasajännite kytketään hetkellä t 0 johtoon, jonka pituus on l ja jonka kapasitanssi ja induktanssi pituusyksikköä kohti ovat c p ja l s. Mieti, kuinka virta i käyttäytyy ajan t funktiona
Häiriöt, siirtojohdot, antennit, eteneminen
 Radioamatöörikurssi PRK OH2TI Häiriöt, siirtojohdot, antennit, eteneminen 2.11.2011 Teemu, OH2FXN 1 / 44 Häiriöt Radioamatööri on vastuussa aiheuttamistaan häiriöistä. Kaikissa häiriötapauksissa amatööri
Radioamatöörikurssi PRK OH2TI Häiriöt, siirtojohdot, antennit, eteneminen 2.11.2011 Teemu, OH2FXN 1 / 44 Häiriöt Radioamatööri on vastuussa aiheuttamistaan häiriöistä. Kaikissa häiriötapauksissa amatööri
5. SÄHKÖMAGNEETTINEN SÄTEILY JA ANTENNIT
 5. Sähkömagnetismi: Sähkömagneettinen säteily ja antennit 5. SÄHKÖMAGNEETTINEN SÄTEILY JA ANTENNIT Olemme tarkastelleet sähkömagneettisten aaltojen etenemistä tasoaaltoina tyhjössä ja homogeenisessa materiassa
5. Sähkömagnetismi: Sähkömagneettinen säteily ja antennit 5. SÄHKÖMAGNEETTINEN SÄTEILY JA ANTENNIT Olemme tarkastelleet sähkömagneettisten aaltojen etenemistä tasoaaltoina tyhjössä ja homogeenisessa materiassa
RYHMÄKERROIN ÄÄNILÄHDERYHMÄN SUUNTAAVUUDEN
 ÄÄNILÄHDERYHMÄN SUUNTAAVUUDEN ARVIOINNISSA Seppo Uosukainen, Jukka Tanttari, Heikki Isomoisio, Esa Nousiainen, Ville Veijanen, Virpi Hankaniemi VTT PL, 44 VTT etunimi.sukunimi@vtt.fi Wärtsilä Finland Oy
ÄÄNILÄHDERYHMÄN SUUNTAAVUUDEN ARVIOINNISSA Seppo Uosukainen, Jukka Tanttari, Heikki Isomoisio, Esa Nousiainen, Ville Veijanen, Virpi Hankaniemi VTT PL, 44 VTT etunimi.sukunimi@vtt.fi Wärtsilä Finland Oy
Kapasitiivinen ja induktiivinen kytkeytyminen
 Kapasitiivinen ja induktiivinen kytkeytyminen EMC - Kaapelointi ja kytkeytyminen Kaapelointi merkittävä EMC-ominaisuuksien kannalta yleensä pituudeltaan suurin elektroniikan osa > toimii helposti antennina
Kapasitiivinen ja induktiivinen kytkeytyminen EMC - Kaapelointi ja kytkeytyminen Kaapelointi merkittävä EMC-ominaisuuksien kannalta yleensä pituudeltaan suurin elektroniikan osa > toimii helposti antennina
FYSP105/2 VAIHTOVIRTAKOMPONENTIT. 1 Johdanto
 FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteet o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
FYSP105/2 VAIHTOVIRTAKOMPONENTIT Työn tavoitteet o Havainnollistaa vaihtovirtapiirien toimintaa o Syventää ymmärtämystä aiheeseen liittyvästä fysiikasta 1 Johdanto Tasavirta oli 1900 luvun alussa kilpaileva
VAIHTOVIRTAPIIRI. 1 Työn tavoitteet
 Oulun yliopisto Fysiikan opetuslaboratorio Sähkö- ja magnetismiopin laboratoriotyöt AHTOTAP Työn tavoitteet aihtovirran ja jännitteen suunta vaihtelee ajan funktiona. Esimerkiksi Suomessa käytettävä verkkovirta
Oulun yliopisto Fysiikan opetuslaboratorio Sähkö- ja magnetismiopin laboratoriotyöt AHTOTAP Työn tavoitteet aihtovirran ja jännitteen suunta vaihtelee ajan funktiona. Esimerkiksi Suomessa käytettävä verkkovirta
RATKAISUT: 22. Vaihtovirtapiiri ja resonanssi
 Physica 9. painos (0) RATKAST. Vaihtovirtapiiri ja resonanssi RATKAST:. Vaihtovirtapiiri ja resonanssi. a) Vaihtovirran tehollinen arvo on yhtä suuri kuin sellaisen tasavirran arvo, joka tuottaa vastuksessa
Physica 9. painos (0) RATKAST. Vaihtovirtapiiri ja resonanssi RATKAST:. Vaihtovirtapiiri ja resonanssi. a) Vaihtovirran tehollinen arvo on yhtä suuri kuin sellaisen tasavirran arvo, joka tuottaa vastuksessa
20 kv Keskijänniteavojohdon kapasiteetti määräytyy pitkien etäisyyksien takia tavallisimmin jännitteenaleneman mukaan:
 SÄHKÖENERGIATEKNIIKKA Harjoitus - Luento 2 H1 Kolmivaiheteho Kuinka suuri teho voidaan siirtää kolmivaihejärjestelmässä eri jännitetasoilla, kun tehokerroin on 0,9 ja virta 100 A. Tarkasteltavat jännitetasot
SÄHKÖENERGIATEKNIIKKA Harjoitus - Luento 2 H1 Kolmivaiheteho Kuinka suuri teho voidaan siirtää kolmivaihejärjestelmässä eri jännitetasoilla, kun tehokerroin on 0,9 ja virta 100 A. Tarkasteltavat jännitetasot
TASAVIRTAPIIRI - VASTAUSLOMAKE
 TASAVIRTAPIIRI - VASTAUSLOMAKE Ryhmä Tekijä 1 Pari Tekijä 2 Päiväys Assistentti Täytä mittauslomake lyijykynällä. Muista erityisesti virhearviot ja suureiden yksiköt! 4 Esitehtävät 1. Mitä tarkoitetaan
TASAVIRTAPIIRI - VASTAUSLOMAKE Ryhmä Tekijä 1 Pari Tekijä 2 Päiväys Assistentti Täytä mittauslomake lyijykynällä. Muista erityisesti virhearviot ja suureiden yksiköt! 4 Esitehtävät 1. Mitä tarkoitetaan
Jakso 8. Ampèren laki. B-kentän kenttäviivojen piirtäminen
 Jakso 8. Ampèren laki Esimerkki 8.: Johda pitkän suoran virtajohtimen (virta ) aiheuttaman magneettikentän lauseke johtimen ulkopuolella etäisyydellä r johtimesta. Ratkaisu: Käytetään Ampèren lakia C 0
Jakso 8. Ampèren laki Esimerkki 8.: Johda pitkän suoran virtajohtimen (virta ) aiheuttaman magneettikentän lauseke johtimen ulkopuolella etäisyydellä r johtimesta. Ratkaisu: Käytetään Ampèren lakia C 0
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 17. marraskuuta 2016 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori 2 (18)
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 17. marraskuuta 2016 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori 2 (18)
Kuva 1. Ohmin lain kytkentäkaavio. DC; 0 6 V.
 TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
TYÖ 37. OHMIN LAKI Tehtävä Tutkitaan metallijohtimen päiden välille kytketyn jännitteen ja johtimessa kulkevan sähkövirran välistä riippuvuutta. Todennetaan kokeellisesti Ohmin laki. Välineet Tasajännitelähde
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 9 / versio 9. marraskuuta 2015 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 9 / versio 9. marraskuuta 2015 Tasoaallot, osa 2 (Ulaby 7.3, 7.5, 7.6) Tasoaallon polarisaatio Virranahtoilmiö Tehotiheys ja Poyntingin vektori
SATE2010 Dynaaminen kenttäteoria syksy /6 Laskuharjoitus 6 / Siirtojohdot ja transientit häviöttömissä siirtojohdoissa
 ATE2010 Dynaaminen kenttäteoria syksy 2011 1 /6 Tehtävä 1. 0,67 m pitkä häviötön siirtojohdon (50 Ω) päässä on kuorma Z L = (100 - j50) Ω. iirtojohtoa syötetään eneraattorilla (e (t) = 10sin(ωt + 30º)
ATE2010 Dynaaminen kenttäteoria syksy 2011 1 /6 Tehtävä 1. 0,67 m pitkä häviötön siirtojohdon (50 Ω) päässä on kuorma Z L = (100 - j50) Ω. iirtojohtoa syötetään eneraattorilla (e (t) = 10sin(ωt + 30º)
766320A SOVELTAVA SÄHKÖMAGNETIIKKA, ohjeita tenttiin ja muutamia teoriavinkkejä sekä pari esimerkkilaskua
 7663A OVLTAVA ÄHKÖMAGNTIIKKA, ohjeita tenttiin ja muutamia teoriavinkkejä sekä pari esimerkkilaskua 1. Lue tenttitehtävä huolellisesti. Tehtävä saattaa näyttää tutulta, mutta siinä saatetaan kysyä eri
7663A OVLTAVA ÄHKÖMAGNTIIKKA, ohjeita tenttiin ja muutamia teoriavinkkejä sekä pari esimerkkilaskua 1. Lue tenttitehtävä huolellisesti. Tehtävä saattaa näyttää tutulta, mutta siinä saatetaan kysyä eri
T2-Kurssimateriaalia 1.0 Janne Strang OH6LSL 27.9.2002
 1. ANTENNITYYPPEJÄ Koska radiotaajuusalue kattaa oktaaveissa ajatellen erittäin laajan kaistan satojen kilometrien pituisista aalloista millimetrien pituisiin, on saman antennityypin käyttäminen mahdotonta
1. ANTENNITYYPPEJÄ Koska radiotaajuusalue kattaa oktaaveissa ajatellen erittäin laajan kaistan satojen kilometrien pituisista aalloista millimetrien pituisiin, on saman antennityypin käyttäminen mahdotonta
Fy06 Koe 20.5.2015 Kuopion Lyseon lukio (KK) 1/7
 Fy06 Koe 0.5.015 Kuopion Lyseon lukio (KK) 1/7 alitse kolme tehtävää. 6p/tehtävä. 1. Mitä mieltä olet seuraavista väitteistä. Perustele lyhyesti ovatko väitteet totta vai tarua. a. irtapiirin hehkulamput
Fy06 Koe 0.5.015 Kuopion Lyseon lukio (KK) 1/7 alitse kolme tehtävää. 6p/tehtävä. 1. Mitä mieltä olet seuraavista väitteistä. Perustele lyhyesti ovatko väitteet totta vai tarua. a. irtapiirin hehkulamput
EMC Säteilevä häiriö
 EMC Säteilevä häiriö Kaksi päätyyppiä: Eromuotoinen johdinsilmukka (yleensä piirilevyllä) silmulla toimii antennina => säteilevä magneettikenttä Yhteismuotoinen ei-toivottuja jännitehäviöitä kytkennässä
EMC Säteilevä häiriö Kaksi päätyyppiä: Eromuotoinen johdinsilmukka (yleensä piirilevyllä) silmulla toimii antennina => säteilevä magneettikenttä Yhteismuotoinen ei-toivottuja jännitehäviöitä kytkennässä
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA. Maarit Vesapuisto SATE.2010 DYNAAMINEN KENTTÄTEORIA. Opetusmoniste: Antennit
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Maarit Vesapuisto SATE.010 DYNAAMINEN KENTTÄTEOIA Opetusmoniste: Antennit Vaasassa 04.1.009 ALKULAUSE Tämä opetusmoniste laadittiin marras-joulukuun
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Maarit Vesapuisto SATE.010 DYNAAMINEN KENTTÄTEOIA Opetusmoniste: Antennit Vaasassa 04.1.009 ALKULAUSE Tämä opetusmoniste laadittiin marras-joulukuun
Antennit ja syöttöjohdot
 Antennit ja syöttöjohdot OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Desibeliasteikko Desibeli Kaikki piirit
Antennit ja syöttöjohdot OH3NE:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Desibeliasteikko Desibeli Kaikki piirit
Siirtolinjat - Sisältö
 Siirtolinjat - Sisältö Siirtolinjatyypit Symmetriset siirtolinjat Epäsymmetriset siirtolinjat Ominaisimpedanssi SWR, sovitus Siirtolinjojen ominaisuuksia Syöttöjohtotyyppejä: Koaksiaalikaapeli (koksi)
Siirtolinjat - Sisältö Siirtolinjatyypit Symmetriset siirtolinjat Epäsymmetriset siirtolinjat Ominaisimpedanssi SWR, sovitus Siirtolinjojen ominaisuuksia Syöttöjohtotyyppejä: Koaksiaalikaapeli (koksi)
Antennit ja syöttöjohdot
 Antennit ja syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Desibeliasteikko Desibeli Kaikki piirit
Antennit ja syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja Desibeliasteikko Desibeli Kaikki piirit
S /142 Piirianalyysi 2 2. Välikoe
 S-55.0/4 Piirianalyysi. Välikoe.5.006 Laske tehtävät eri paperille kuin tehtävät 3 5. Muista kirjoittaa jokaiseen paperiin selvästi nimi, opiskelijanumero, kurssin nimi ja koodi. Tehtävät lasketaan osaston
S-55.0/4 Piirianalyysi. Välikoe.5.006 Laske tehtävät eri paperille kuin tehtävät 3 5. Muista kirjoittaa jokaiseen paperiin selvästi nimi, opiskelijanumero, kurssin nimi ja koodi. Tehtävät lasketaan osaston
SMG-5450 Antennit ja ohjatut aallot
 Luennot SMG-5450 Antennit ja ohjatut aallot ti 10-12 SC105B pe 11-13 SC105B Luennoijat Tuomas Kovanen, SC307, tuomas.kovanen@tut.fi Jukka Uusitalo, SC305b, jukka-pekka.uusitalo@tut.fi (Luentokalvot: Janne
Luennot SMG-5450 Antennit ja ohjatut aallot ti 10-12 SC105B pe 11-13 SC105B Luennoijat Tuomas Kovanen, SC307, tuomas.kovanen@tut.fi Jukka Uusitalo, SC305b, jukka-pekka.uusitalo@tut.fi (Luentokalvot: Janne
Luku 14. z L/2 y L/2. J(r,t)=I(t)δ(x)δ(y)θ(L/2 z)θ(z + L/2) e z (14.1) Kuva 14.1: Yksinkertainen dipoliantenni.
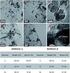 Luku 14 Säteilevät systeemit Edellisessä luvussa käsiteltiin vain yhden varauksellisen hiukkasen säteilykenttiä. Nyt tutustutaan esimerkinomaisesti yksinkertaisiin antenneihin ja varausjoukon aiheuttamaan
Luku 14 Säteilevät systeemit Edellisessä luvussa käsiteltiin vain yhden varauksellisen hiukkasen säteilykenttiä. Nyt tutustutaan esimerkinomaisesti yksinkertaisiin antenneihin ja varausjoukon aiheuttamaan
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
LABORATORIOTYÖ 2 (8 h) LIITE 2/1 WLAN-ANTENNIEN TUTKIMINEN JA AALTOJOHTOMITTAUKSET
 LABORATORIOTYÖ 2 (8 h) LIITE 2/1 WLAN-ANTENNIEN TUTKIMINEN JA AALTOJOHTOMITTAUKSET LABORATORIOTYÖ 2 (8 h) LIITE 2/2 1 TYÖN KUVAUS Työssä tutustutaan antennien ominaisuuksiin rakentamalla ja mittaamalla
LABORATORIOTYÖ 2 (8 h) LIITE 2/1 WLAN-ANTENNIEN TUTKIMINEN JA AALTOJOHTOMITTAUKSET LABORATORIOTYÖ 2 (8 h) LIITE 2/2 1 TYÖN KUVAUS Työssä tutustutaan antennien ominaisuuksiin rakentamalla ja mittaamalla
RG-58U 4,5 db/30m. Spektrianalysaattori. 0,5m. 60m
 1. Johtuvia häiiöitä mitataan LISN:n avulla EN55022-standadin mukaisessa johtuvan häiiön mittauksessa. a. 20 MHz taajuudella laite tuottaa 1.5 mv suuuista häiiösignaalia. Läpäiseekö laite standadin B-luokan
1. Johtuvia häiiöitä mitataan LISN:n avulla EN55022-standadin mukaisessa johtuvan häiiön mittauksessa. a. 20 MHz taajuudella laite tuottaa 1.5 mv suuuista häiiösignaalia. Läpäiseekö laite standadin B-luokan
Esimerkki 1a. Stubisovituksen (= siirtokaapelisovitus) laskeminen Smithin kartan avulla
 Esimerkkejä Smithin kartan soveltamisesta Materiaali liittyy OH3AB:llä keväällä 2007 käytyihin tekniikkamietintöihin. 1.5.2007 oh3htu Esimerkit on tehty käyttäen Smith v 1.91 demo-ohjelmaa. http://www.janson-soft.de/seminare/dh7uaf/smith_v191.zip
Esimerkkejä Smithin kartan soveltamisesta Materiaali liittyy OH3AB:llä keväällä 2007 käytyihin tekniikkamietintöihin. 1.5.2007 oh3htu Esimerkit on tehty käyttäen Smith v 1.91 demo-ohjelmaa. http://www.janson-soft.de/seminare/dh7uaf/smith_v191.zip
Kuva 1: Vaihtovirtapiiri, jossa on sarjaan kytkettynä resistanssi, kapasitanssi ja induktanssi
 31 VAIHTOVIRTAPIIRI 311 Lineaarisen vaihtovirtapiirin impedanssi ja vaihe-ero Tarkastellaan kuvan 1 mukaista vaihtovirtapiiriä, jossa on resistanssi R, kapasitanssi C ja induktanssi L sarjassa Jännitelähde
31 VAIHTOVIRTAPIIRI 311 Lineaarisen vaihtovirtapiirin impedanssi ja vaihe-ero Tarkastellaan kuvan 1 mukaista vaihtovirtapiiriä, jossa on resistanssi R, kapasitanssi C ja induktanssi L sarjassa Jännitelähde
Harmonisten yliaaltojen vaikutus johtojen mitoitukseen
 Harmonisten yliaaltojen vaikutus johtojen mitoitukseen Pienjännitesähköasennukset standardin osassa SFS6000-5-5 esitetään johtojen mitoitusperusteet johtimien ja kaapelien kuormitettavuudelle. Lähtökohtana
Harmonisten yliaaltojen vaikutus johtojen mitoitukseen Pienjännitesähköasennukset standardin osassa SFS6000-5-5 esitetään johtojen mitoitusperusteet johtimien ja kaapelien kuormitettavuudelle. Lähtökohtana
1. Erään piirin impedanssimittauksissa saatiin seuraavat tulokset:
 521384A RADIOTEKNIIKAN PERUSTEET Harjoitus 4 1. Erään piirin impedanssimittauksissa saatiin seuraavat tulokset: f [MHz] [Ω] 870 120-j100 875 100-j80 880 80-j55 885 70-j30 890 70-j15 895 65+j10 900 70+j30
521384A RADIOTEKNIIKAN PERUSTEET Harjoitus 4 1. Erään piirin impedanssimittauksissa saatiin seuraavat tulokset: f [MHz] [Ω] 870 120-j100 875 100-j80 880 80-j55 885 70-j30 890 70-j15 895 65+j10 900 70+j30
TEKNIIKAN JA LIIKENTEEN TOIMIALA. Tietotekniikka. Tietoliikennetekniikka INSINÖÖRITYÖ TIETOKONEOHJATTU ANTENNIMITTAUSJÄRJESTELMÄ
 TEKNIIKAN JA LIIKENTEEN TOIMIALA Tietotekniikka Tietoliikennetekniikka INSINÖÖRITYÖ TIETOKONEOHJATTU ANTENNIMITTAUSJÄRJESTELMÄ Työn tekijä: Soile Sallinen Työn valvoja: Antti Koivumäki Työn ohjaaja: Antti
TEKNIIKAN JA LIIKENTEEN TOIMIALA Tietotekniikka Tietoliikennetekniikka INSINÖÖRITYÖ TIETOKONEOHJATTU ANTENNIMITTAUSJÄRJESTELMÄ Työn tekijä: Soile Sallinen Työn valvoja: Antti Koivumäki Työn ohjaaja: Antti
df4sa dipl.-ing cornelius paul liebigstrasse 2-20 d-22113 hamburg info@spiderbeam.net www.spiderbeam.net
 Spiderbeam kehitettiin Dxpeditioihmisten unelma-antenniksi. Se on täysikokoinen, kevyt, kolmen taajuusalueen yagi joka on valmistettu lasikuidusta ja langasta. Koko antenni painaa ainoastaan kg, mikä tekee
Spiderbeam kehitettiin Dxpeditioihmisten unelma-antenniksi. Se on täysikokoinen, kevyt, kolmen taajuusalueen yagi joka on valmistettu lasikuidusta ja langasta. Koko antenni painaa ainoastaan kg, mikä tekee
FYSP1082 / K4 HELMHOLTZIN KELAT
 FYSP1082 / K4 HELMHOLTZIN KELAT Johdanto Työssä mitataan ympyränmuotoisten johdinkelojen tuottamaa magneettikenttää kelojen läheisyydessä sekä sähkövirran että etäisyyden funktiona. Sähkömagnetismia ja
FYSP1082 / K4 HELMHOLTZIN KELAT Johdanto Työssä mitataan ympyränmuotoisten johdinkelojen tuottamaa magneettikenttää kelojen läheisyydessä sekä sähkövirran että etäisyyden funktiona. Sähkömagnetismia ja
ELEC-E8419 syksy 2016 Jännitteensäätö
 ELEC-E849 syksy 06 Jännitteensäätö. Tarkastellaan viittä rinnakkaista siirtojohtoa. Jännite johdon loppupäässä on 400, pituus on 00 km, reaktanssi on 0,3 ohm/km (3 ohmia/johto). Kunkin johdon virta on
ELEC-E849 syksy 06 Jännitteensäätö. Tarkastellaan viittä rinnakkaista siirtojohtoa. Jännite johdon loppupäässä on 400, pituus on 00 km, reaktanssi on 0,3 ohm/km (3 ohmia/johto). Kunkin johdon virta on
Coulombin laki. Sähkökentän E voimakkuus E = F q
 Coulombin laki Kahden pistemäisen varatun hiukkasen välinen sähköinen voima F on suoraan verrannollinen varausten Q 1 ja Q 2 tuloon ja kääntäen verrannollinen etäisyyden r neliöön F = k Q 1Q 2 r 2, k =
Coulombin laki Kahden pistemäisen varatun hiukkasen välinen sähköinen voima F on suoraan verrannollinen varausten Q 1 ja Q 2 tuloon ja kääntäen verrannollinen etäisyyden r neliöön F = k Q 1Q 2 r 2, k =
Johdanto. 1 Teoriaa. 1.1 Sähkönjohtimen aiheuttama magneettikenttä
 FYSP105 / K2 HELMHOLTZIN KELAT Johdanto Työssä mitataan ympyränmuotoisten johdinkelojen tuottamaa magneettikenttää kelojen läheisyydessä sekä sähkövirran että etäisyyden funtiona. Sähkömagnetismia ja työssä
FYSP105 / K2 HELMHOLTZIN KELAT Johdanto Työssä mitataan ympyränmuotoisten johdinkelojen tuottamaa magneettikenttää kelojen läheisyydessä sekä sähkövirran että etäisyyden funtiona. Sähkömagnetismia ja työssä
RF-tekniikan perusteet BL50A0300
 RF-tekniikan perusteet BL50A0300 5. Luento 30.9.2013 Antennit Radioaaltojen eteneminen DI Juho Tyster Antennit Antenni muuttaa siirtojohdolla kulkevan aallon vapaassa tilassa eteneväksi aalloksi ja päinvastoin
RF-tekniikan perusteet BL50A0300 5. Luento 30.9.2013 Antennit Radioaaltojen eteneminen DI Juho Tyster Antennit Antenni muuttaa siirtojohdolla kulkevan aallon vapaassa tilassa eteneväksi aalloksi ja päinvastoin
Tehtävä 1. a) sähkövirta = varausta per sekunti, I = dq dt = 1, A = 1, C s protonin varaus on 1, C
 Tehtävä a) sähkövirta = varausta per sekunti, I = dq dt =, 5 0 3 =, 5 0 3 C s protonin varaus on, 6 0 9 C Jaetaan koko virta yksittäisille varauksille:, 5 0 3 C s kpl = 9 05, 6 0 9 s b) di = Jd = J2πrdr,
Tehtävä a) sähkövirta = varausta per sekunti, I = dq dt =, 5 0 3 =, 5 0 3 C s protonin varaus on, 6 0 9 C Jaetaan koko virta yksittäisille varauksille:, 5 0 3 C s kpl = 9 05, 6 0 9 s b) di = Jd = J2πrdr,
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén Luentoviikko 5 / versio 7. lokakuuta 2016 Luentoviikko 5 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén Luentoviikko 5 / versio 7. lokakuuta 2016 Luentoviikko 5 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
Kondensaattorin läpi kulkeva virta saadaan derivoimalla yhtälöä (2), jolloin saadaan
 VAIHTOVIRTAPIIRI 1 Johdanto Vaihtovirtapiirien käsittely perustuu kolmen peruskomponentin, vastuksen (resistanssi R), kelan (induktanssi L) ja kondensaattorin (kapasitanssi C) toimintaan. Tarkastellaan
VAIHTOVIRTAPIIRI 1 Johdanto Vaihtovirtapiirien käsittely perustuu kolmen peruskomponentin, vastuksen (resistanssi R), kelan (induktanssi L) ja kondensaattorin (kapasitanssi C) toimintaan. Tarkastellaan
SEISOVA AALTOLIIKE 1. TEORIAA
 1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
1 SEISOVA AALTOLIIKE MOTIVOINTI Työssä tutkitaan poikittaista ja pitkittäistä aaltoliikettä pitkässä langassa ja jousessa. Tarkastellaan seisovaa aaltoliikettä. Määritetään aaltoliikkeen etenemisnopeus
Analogiapiirit III. Keskiviikko 4.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet
 Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 2. Keskiviikko 4.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet 1. Analysoi kuvan 1 operaatiotranskonduktanssivahvistimen
Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 2. Keskiviikko 4.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet 1. Analysoi kuvan 1 operaatiotranskonduktanssivahvistimen
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 6 / versio 14. lokakuuta 2015 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 6 / versio 14. lokakuuta 2015 Magnetostatiikka (Ulaby, luku 5) Magneettiset voimat ja vääntömomentit Biot Savartin laki Magnetostaattiset
7. Resistanssi ja Ohmin laki
 Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
SMG-1100: PIIRIANALYYSI I. Verkkojen taajuusriippuvuus: suo(dat)timet
 SMG-00: PIIRIANALYYSI I Verkkojen taajuusriippuvuus: suo(dat)timet alipäästösuodin ylipäästösuodin kaistanpäästösuodin kaistanestosuodin jännitevahvistus rajataajuus kaistanleveys resonanssi Suotimet:
SMG-00: PIIRIANALYYSI I Verkkojen taajuusriippuvuus: suo(dat)timet alipäästösuodin ylipäästösuodin kaistanpäästösuodin kaistanestosuodin jännitevahvistus rajataajuus kaistanleveys resonanssi Suotimet:
Muuntajan toiminnasta löytyy tietoja tämän työohjeen teoriaselostuksen lisäksi esimerkiksi viitteistä [1] - [4].
![Muuntajan toiminnasta löytyy tietoja tämän työohjeen teoriaselostuksen lisäksi esimerkiksi viitteistä [1] - [4]. Muuntajan toiminnasta löytyy tietoja tämän työohjeen teoriaselostuksen lisäksi esimerkiksi viitteistä [1] - [4].](/thumbs/93/113048507.jpg) FYS 102 / K6. MUUNTAJA 1. Johdanto Muuntajassa on kaksi eristetystä sähköjohdosta kierrettyä kelaa yhdistetty rautasydämellä ensiöpiiriksi ja toisiopiiriksi. Muuntajan toiminta perustuu sähkömagneettiseen
FYS 102 / K6. MUUNTAJA 1. Johdanto Muuntajassa on kaksi eristetystä sähköjohdosta kierrettyä kelaa yhdistetty rautasydämellä ensiöpiiriksi ja toisiopiiriksi. Muuntajan toiminta perustuu sähkömagneettiseen
FYS206/5 Vaihtovirtakomponentit
 FYS206/5 Vaihtovirtakomponentit Tässä työssä pyritään syventämään vaihtovirtakomponentteihin liittyviä käsitteitä. Tunnetusti esimerkiksi käsitteet impedanssi, reaktanssi ja vaihesiirto ovat aina hyvin
FYS206/5 Vaihtovirtakomponentit Tässä työssä pyritään syventämään vaihtovirtakomponentteihin liittyviä käsitteitä. Tunnetusti esimerkiksi käsitteet impedanssi, reaktanssi ja vaihesiirto ovat aina hyvin
SÄHKÖMAGNEETTINEN KYTKEYTYMINEN
 SÄHKÖMAGNEETTINEN KYTKEYTYMINEN H. Honkanen SÄHKÖMAGNEETTISEN KYTKEYTYMISEN TEORIAA Sähkömagneettinen kytkeytyminen on häiiöiden siitymistä sähkömagneettisen aaltoliikkeen välityksellä. Sähkömagneettisen
SÄHKÖMAGNEETTINEN KYTKEYTYMINEN H. Honkanen SÄHKÖMAGNEETTISEN KYTKEYTYMISEN TEORIAA Sähkömagneettinen kytkeytyminen on häiiöiden siitymistä sähkömagneettisen aaltoliikkeen välityksellä. Sähkömagneettisen
Integrointi ja sovellukset
 Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
Tupla 5/8-aallon antenni APRS-tukiasemakäyttöön
 Sivu 1/24 Tupla 5/8-aallon antenni APRS-tukiasemakäyttöön Minkälainen antenni APRS-käyttöön? APRS-käyttöä ajatellen ympärisäteilevä vertikaalipolarisoitu antenni on toimiva ratkaisu. Kyseistä antennityyppiähän
Sivu 1/24 Tupla 5/8-aallon antenni APRS-tukiasemakäyttöön Minkälainen antenni APRS-käyttöön? APRS-käyttöä ajatellen ympärisäteilevä vertikaalipolarisoitu antenni on toimiva ratkaisu. Kyseistä antennityyppiähän
4757 4h. MAGNEETTIKENTÄT
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
Jukka Kinkamo, OH2JIN Kaukopäästä avoin ja oikosuljettu syöttöjohto
 Kaukopäästä avoin ja oikosuljettu syöttöjohto Jos lähtötilanteessamme on lähettimen ulostuloimpedanssi 50 Ω, syöttöjohdon impedanssi samoin 50 Ω ja kuorman eli antennin impedanssi 50 Ω, on tehonsiirto
Kaukopäästä avoin ja oikosuljettu syöttöjohto Jos lähtötilanteessamme on lähettimen ulostuloimpedanssi 50 Ω, syöttöjohdon impedanssi samoin 50 Ω ja kuorman eli antennin impedanssi 50 Ω, on tehonsiirto
521384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3
 51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
PAKOPUTKEN PÄÄN MUODON VAIKUTUS ÄÄNENSÄTEILYYN
 PAKOPUTKEN PÄÄN MUODON VAIKUTUS ÄÄNENSÄTEILYYN Seppo Uosukainen 1, Virpi Hankaniemi 2, Mikko Matalamäki 2 1 Teknologian tutkimuskeskus VTT Oy Rakennedynamiikka ja vibroakustiikka PL 1000 02044 VTT etunimi.sukunimi@vtt.fi
PAKOPUTKEN PÄÄN MUODON VAIKUTUS ÄÄNENSÄTEILYYN Seppo Uosukainen 1, Virpi Hankaniemi 2, Mikko Matalamäki 2 1 Teknologian tutkimuskeskus VTT Oy Rakennedynamiikka ja vibroakustiikka PL 1000 02044 VTT etunimi.sukunimi@vtt.fi
S-108-2110 OPTIIKKA 1/10 Laboratoriotyö: Polarisaatio POLARISAATIO. Laboratoriotyö
 S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
R = Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen on tällöin jännitteenjako = 1
 Fysiikan mittausmenetelmät I syksy 206 Laskuharjoitus 4. Merkitään kaapelin resistanssin ja kuormaksi kytketyn piirin sisäänmenoimpedanssia summana R 000.2 Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen
Fysiikan mittausmenetelmät I syksy 206 Laskuharjoitus 4. Merkitään kaapelin resistanssin ja kuormaksi kytketyn piirin sisäänmenoimpedanssia summana R 000.2 Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen
Magneettikenttä. Liikkuva sähkövaraus saa aikaan ympärilleen sähkökentän lisäksi myös magneettikentän
 3. MAGNEETTIKENTTÄ Magneettikenttä Liikkuva sähkövaraus saa aikaan ympärilleen sähkökentän lisäksi myös magneettikentän Havaittuja magneettisia perusilmiöitä: Riippumatta magneetin muodosta, sillä on aina
3. MAGNEETTIKENTTÄ Magneettikenttä Liikkuva sähkövaraus saa aikaan ympärilleen sähkökentän lisäksi myös magneettikentän Havaittuja magneettisia perusilmiöitä: Riippumatta magneetin muodosta, sillä on aina
EMC:n perusteet. EMC:n määritelmä
 EMC:n perusteet EMC:n määritelmä Järjestelmän tai laitteen kyky toimia tyydyttävästi sähkömagneettisessa ympäristössään tuottamatta muille laitteille tai järjestelmille niille sietämätöntä häiriötä tässä
EMC:n perusteet EMC:n määritelmä Järjestelmän tai laitteen kyky toimia tyydyttävästi sähkömagneettisessa ympäristössään tuottamatta muille laitteille tai järjestelmille niille sietämätöntä häiriötä tässä
SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa
 SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa 1 SISÄLTÖ 1. Siirtymä 2 1 2.1 MUODONMUUTOS Muodonmuutos (deformaatio) Tapahtuu, kun kappaleeseen vaikuttaa voima/voimia
SISÄLTÖ Venymän käsite Liukuman käsite Venymä ja liukuma lujuusopin sovelluksissa 1 SISÄLTÖ 1. Siirtymä 2 1 2.1 MUODONMUUTOS Muodonmuutos (deformaatio) Tapahtuu, kun kappaleeseen vaikuttaa voima/voimia
Pinces AC/DC-virtapihti ampèremetriques pour courant AC
 MH-SARJA MH60-virtapihti on suunniteltu mittaamaan DC ja AC-virtoja jopa 1 MHz:n kaistanleveydellä, käyttäen kaksoislineaarista Hall-ilmiötä/ Muuntajateknologiaa. Pihti sisältää ladattavan NiMh-akun, jonka
MH-SARJA MH60-virtapihti on suunniteltu mittaamaan DC ja AC-virtoja jopa 1 MHz:n kaistanleveydellä, käyttäen kaksoislineaarista Hall-ilmiötä/ Muuntajateknologiaa. Pihti sisältää ladattavan NiMh-akun, jonka
a P en.pdf KOKEET;
 Tässä on vanhoja Sähkömagnetismin kesäkurssin tenttejä ratkaisuineen. Tentaattorina on ollut Hanna Pulkkinen. Huomaa, että tämän kurssin sisältö on hiukan eri kuin Soveltavassa sähkömagnetiikassa, joten
Tässä on vanhoja Sähkömagnetismin kesäkurssin tenttejä ratkaisuineen. Tentaattorina on ollut Hanna Pulkkinen. Huomaa, että tämän kurssin sisältö on hiukan eri kuin Soveltavassa sähkömagnetiikassa, joten
Antennit ja syöttöjohdot. OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY
 Antennit ja syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja ylikurssia! ylikurssia! ylikurssia!
Antennit ja syöttöjohdot OH3TR:n radioamatöörikurssi Tiiti Kellomäki, OH3HNY Desibeli Aallonpituus Siirtojohdot, SWR eli SAS Antennien ominaisuuksia Yleisiä antenneja ylikurssia! ylikurssia! ylikurssia!
Aiheena tänään. Virtasilmukka magneettikentässä Sähkömagneettinen induktio. Vaihtovirtageneraattorin toimintaperiaate Itseinduktio
 Sähkömagnetismi 2 Aiheena tänään Virtasilmukka magneettikentässä Sähkömagneettinen induktio Vaihtovirtageneraattorin toimintaperiaate Itseinduktio Käämiin vaikuttava momentti Magneettikentässä olevaan
Sähkömagnetismi 2 Aiheena tänään Virtasilmukka magneettikentässä Sähkömagneettinen induktio Vaihtovirtageneraattorin toimintaperiaate Itseinduktio Käämiin vaikuttava momentti Magneettikentässä olevaan
23 VALON POLARISAATIO 23.1 Johdanto. 23.2 Valon polarisointi ja polarisaation havaitseminen
 3 VALON POLARISAATIO 3.1 Johdanto Mawellin htälöiden avulla voidaan johtaa aaltohtälö sähkömagneettisen säteiln etenemiselle väliaineessa. Mawellin htälöiden ratkaisusta seuraa aina, että valo on poikittaista
3 VALON POLARISAATIO 3.1 Johdanto Mawellin htälöiden avulla voidaan johtaa aaltohtälö sähkömagneettisen säteiln etenemiselle väliaineessa. Mawellin htälöiden ratkaisusta seuraa aina, että valo on poikittaista
RATKAISUT a + b 2c = a + b 2 ab = ( a ) 2 2 ab + ( b ) 2 = ( a b ) 2 > 0, koska a b oletuksen perusteella. Väite on todistettu.
 RATKAISUT 198 197 198. Olkoon suorakulmion erisuuntaisten sivujen pituudet a ja b sekä neliön sivun pituus c. Tehtävä on mielekäs vain, jos suorakulmio ei ole neliö, joten oletetaan, että a b. Suorakulmion
RATKAISUT 198 197 198. Olkoon suorakulmion erisuuntaisten sivujen pituudet a ja b sekä neliön sivun pituus c. Tehtävä on mielekäs vain, jos suorakulmio ei ole neliö, joten oletetaan, että a b. Suorakulmion
d sinα Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila
 Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila Optisessa hilassa on hyvin suuri määrä yhdensuuntaisia, toisistaan yhtä kaukana olevia
Fysiikan laboratoriotyöohje Tietotekniikan koulutusohjelma OAMK Tekniikan yksikkö TYÖ 8: SPEKTROMETRITYÖ I Optinen hila Optisessa hilassa on hyvin suuri määrä yhdensuuntaisia, toisistaan yhtä kaukana olevia
80m antenneista kotimaan työskentelyssä
 80m antenneista kotimaan työskentelyssä Pekka Ketonen, OH1TV 16.11.2016 OH1TV 1 Vertailua 80m kotimaan antenneista 1. Yleistä 2. λ luuppi 3. Magneettinen luuppi 4x4m 4. λ/2 dipoli 5. Yhteenvweto ja johtopäätökset
80m antenneista kotimaan työskentelyssä Pekka Ketonen, OH1TV 16.11.2016 OH1TV 1 Vertailua 80m kotimaan antenneista 1. Yleistä 2. λ luuppi 3. Magneettinen luuppi 4x4m 4. λ/2 dipoli 5. Yhteenvweto ja johtopäätökset
14.1 Tasavirtapiirit ja Kirchhoffin lait R 1. I 1 I 3 liitos + - R 2. silmukka. Kuva 14.1: Liitoksen, haaran ja silmukan määrittely virtapiirissä.
 Luku 14 Lineaaripiirit Lineaaripiireillä ymmärretään verkkoja, joiden jokaisessa haarassa jännite on verrannollinen virtaan, ts. Ohmin laki on voimassa. Lineaariset piirit voivat siis sisältää jännitelähteitä,
Luku 14 Lineaaripiirit Lineaaripiireillä ymmärretään verkkoja, joiden jokaisessa haarassa jännite on verrannollinen virtaan, ts. Ohmin laki on voimassa. Lineaariset piirit voivat siis sisältää jännitelähteitä,
SMG-2100: SÄHKÖTEKNIIKKA
 SMG-2100: SÄHKÖTEKNIIKKA Vaihtosähkön teho kompleksinen teho S pätöteho P loisteho Q näennäisteho S Käydään läpi sinimuotoisiin sähkösuureisiin liittyviä tehotermejä. Määritellään kompleksinen teho, jonka
SMG-2100: SÄHKÖTEKNIIKKA Vaihtosähkön teho kompleksinen teho S pätöteho P loisteho Q näennäisteho S Käydään läpi sinimuotoisiin sähkösuureisiin liittyviä tehotermejä. Määritellään kompleksinen teho, jonka
Omnia AMMATTIOPISTO Pynnönen
 MMTTOSTO SÄHKÖTEKNKK LSKHJOTKS; OHMN LK, KCHHOFFN LT, TEHO, iirrä tehtävistä N piirikaavio, johon merkitset kaikki virtapiirin komponenttien tunnisteet ja suuruudet, jännitteet ja virrat. 1. 22:n vastuksen
MMTTOSTO SÄHKÖTEKNKK LSKHJOTKS; OHMN LK, KCHHOFFN LT, TEHO, iirrä tehtävistä N piirikaavio, johon merkitset kaikki virtapiirin komponenttien tunnisteet ja suuruudet, jännitteet ja virrat. 1. 22:n vastuksen
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
Tekijä Pitkä matematiikka b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta.
 Tekijä Pitkä matematiikka 4 9.1.016 79 a) Kuvasta nähdään, että a = 3i + j. b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta. 5a b = 5(3i + j) ( i 4 j)
Tekijä Pitkä matematiikka 4 9.1.016 79 a) Kuvasta nähdään, että a = 3i + j. b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta. 5a b = 5(3i + j) ( i 4 j)
HARJOITUS 7 SEISOVAT AALLOT TAVOITE
 SEISOVAT AALLOT TAVOITE Tässä harjoituksessa opit käyttämään rakolinjaa. Toteat myös seisovan aallon kuvion kolmella eri kuormalla: oikosuljetulla, sovittamattomalla ja sovitetulla kuormalla. Tämän lisäksi
SEISOVAT AALLOT TAVOITE Tässä harjoituksessa opit käyttämään rakolinjaa. Toteat myös seisovan aallon kuvion kolmella eri kuormalla: oikosuljetulla, sovittamattomalla ja sovitetulla kuormalla. Tämän lisäksi
