Mat Investointiteoria - Kotitehtävät
|
|
|
- Riikka Kinnunen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Mat Investointiteoria - Kotitehtävät Kotitehtäviä on yhteensä kahdeksan ja ne ratkeavat tavallisilla taulukkolaskentaohjelmistoilla. Jokaisesta kotitehtävistä saa maksimissaan 5 pistettä: 4p/oikea ratkaisu + 1p, jos on valmis esittämään ratkaisunsa annettuna päivämääränä. Esitetyn ratkaisun ei tarvitse olla täysin oikein jotta pisteen saa, mutta ratkaisun on oltava oikeansuuntainen. Kotitehtävät palautetaan palautuslaatikkoon (kyyhkyslakkojen vieressä laskutupaa Y190c vastapäätä, lokero merkitty tekstillä Mat Investointiteoria) tai laskuharjoituksiin siististi kirjoitettuna ja välivaiheet lyhyesti perusteltuina kello mennessä annettuna päivänä. Myöhästyneitä palautuksia ei arvostella. Kotitehtäväpisteet skaalataan kurssin lopullista arvostelua varten. Kurssin kokonaispistemäärä on 40 pistettä ja se muodostetaan seuraavasti: 30p tentistä ja 10p kotitehtävistä. Lisäksi vierailijaluennosta saa yhden läsnäolopisteen. Tehtävä 1 (palautus ja esitys ) Tarkastellaan euron asuntolainaa, jonka laina-ajaksi otetaan 25 vuotta. Lainan viitekoroksi tarjotaan kahta vaihtoehtoa: 12kk euribor + asiakaskohtainen marginaali tai 5v kiinteä korko. Oletetaan tässä, että koko lainapääoma tulee sitoa samaan viitekorkoon. Lainaa lyhennetään annuiteettina kuukausittain. Koroista saatavia verohelpotuksia ei tarvitse huomioida laskuissa. Olkoon asiakkaan marginaali 0,3%, jolloin 12kk euriboriin sidotun lainan koroksi tulee ensimmäiseksi vuodeksi 1,7% + 0,3% = 2,0%. Pankki tarjoaa 5v kiinteäksi (vuotuiseksi) koroksi 3,0%. Oletetaan, että 12kk euribor nousee λ prosenttiyksikköä vuosittain seuraavan 5 vuoden ajan. Tämän viitekorkoon sidotun lainan korontarkistus on kerran vuodessa siten, että ensimmäisen vuoden ajan korko on 2,00%, toisen vuoden ajan (2,00 + λ)%, kolmannen (2,00 + 2λ)% jne. Kiinteäkorkoiseen lainaan 12kk euriborin nousu ei seuraavan 5 vuoden aikana vaikuta. a. Mikä on lainan kuukausittainen annuiteettierä ensimmäisen vuoden ajan 12kk euriboriin sidottuna? Entä kiinteään korkoon sidottuna? (1p) b. Esitä graafisesti λ:n funktiona 12kk euriboriin sidotun lainan kuukausittaisen annuiteettierän suuruus toisena vuonna (eli ensimmäisen korontarkistuksen jälkeen), kun kokonaislaina-aika halutaan säilyttää ennallaan. Käytä λ:n arvoja -0,25%; 0%; 0,25%; 0,50%; 1,00% ja 2,00%. Piirrä samaan kuvaan vertailuksi kiinteäkorkoisen lainan kuukausimaksu. Huomaa laskuissa, että laina on lyhentynyt ensimmäisen vuoden aikana ja ensimmäisenä korontarkistuspäivänä laina-aikaa on jäljellä 24 vuotta. (1p) c. Esitä graafisesti λ:n funktiona kuinka paljon 12kk euriboriin sidotun lainan kokonaislaina-aikaa täytyy muuttaa toisen vuoden alussa, jos kuukausierä halutaan säilyttää ennallaan. Käytä λ:n arvoja -0,25%; 0%; 0,25%; 0,50%; 1,00% ja 2,00%. (1p) d. Tarkastellaan 12kk euriboriin ja 5v kiinteään korkoon sidottujen lainojen annuiteettierien summaa ensimmäisen viiden vuoden aikana. Millä λ:n arvolla (yllä kuvatussa tasaisen vuotuisen kasvun mallissa) 12kk euriboriin sidotun lainan viiden vuoden maksujen summa ylittää kiinteään korkoon sidotun lainan vastaavan ajan maksujen summan? (1p)
2 Tehtävä 2 (palautus ja esitys ) Taulukossa 1 on listattuna viiden eri joukkovelkakirjan tiedot. Kuponkimaksut suoritetaan kerran vuodessa. Taulukko 1 Joukkovelkakirja Hinta ( ) Maturiteetti (v) Nimellisarvo ( ) Kuponkikorko % % % % % a. Määritä joukkovelkakirjojen tietojen avulla korkokäyrä (so. spot-korot) viidelle vuodelle ja esitä käyrä graafisesti. (1p) b. Oletetaan, että odotushypoteesi pätee. Määritä spot-korkojen perusteella lyhyet korot seuraaville viidelle vuodelle. (1p) c. Määritä forward-korot f i,j kaikille pareille (i,j), kun i = 0,1,...,4; j = 1,...,5; j > i. (1p) d. Sijoitat rahaa riskittömän kohteen mukaista tuottoa maksavalle tilille seuraavasti: sijoitat 500 nyt (eli vuoden 1 alussa), 300 vuoden 2 alussa, ja 100 vuoden 3 alussa. Mikä on tilin saldo vuoden 5 lopussa, jos korkokehitys on a-kohdassa määrittämäsi korkokäyrän mukainen? (1p)
3 Tehtävä 3 (palautus ja esitys ) Oletetaan, että spot-korot ovat tehtävässä 2 määrittämäsi korkokäyrän mukaiset. Taulukossa 3 on esitetty kahden joukkovelkakirjan kassavirrat ( ) ja hinnat ( ) sekä pankin tulevat maksusitoumukset ( ) seuraavan neljän vuoden ajalle. Taulukko 3 Vuosi Joukkovelkakirja 1 Joukkovelkakirja 2 Sitoumukset Hinta ( ) a. Muodosta ainoastaan joukkovelkakirjaa 2 käyttäen portfolio, jonka nykyarvo täsmää mahdollisimman hyvin maksusitoumusrakenteen nykyarvon kanssa. (1p) b. Oletetaan, että korkokäyrä siirtyy välittömästi yhden prosenttiyksikön ylöspäin (nk. paralleelisiirtymä). Arvioi duraatioiden avulla, kuinka suureksi sitoumusrakenteen ja a-kohdassa muodostamasi portfolion nykyarvojen erotus muodostuu korkokäyrän paralleelisiirtymän seurauksena. (1p) c. Muodosta nyt molemmista joukkovelkakirjoista maksusitoumusrakenteen immunisoiva portfolio. (1p) d. Arvioi duraatioiden avulla, miten b-kohdan mukainen korkokäyrän paralleelisiirtymä vaikuttaa immunisoidun portfolion ja maksusitoumusrakenteen nykyarvojen erotukseen. Löytyykö immunisointitehtävälle ratkaisua, jossa molempien joukkovelkakirjojen lukumäärät ovat portfoliossa ei-negatiivisia? Perustele vastauksesi duraatioiden avulla. (1p)
4 Tehtävä 4 (palautus ja esitys ) Tarkastellaan sellaisia yksinkertaistettuja markkinoita, joilla on tarjolla kolme osakesarjaa A, B ja C. Taulukossa 2 on listattuna kunkin osakesarjan tiedot. Taulukko 2 Osakesarja Odotettu Tuoton Korrelaatio Korrelaatio Korrelaatio tuotto keskihajonta A:n suhteen B:n suhteen C:n suhteen A 20 % 25 % B 15 % 20 % C 10 % 15 % a. Rakenna A:sta, B:stä ja C:stä koostuva minimivarianssiportfolio siten, että jokaisen osakesarjan suhteellinen osuus tässä portfoliossa on ei-negatiivinen. Mikä on tämän minimivarianssiportfolion tuoton odotusarvo? (1p) b. Rakenna osakesarjojen A, B ja C avulla tehokas portfolio, jonka odotettu tuotto on 18%. Missä suhteessa portfolio sisältää osakesarjoja ja mikä on tämän portfolion tuoton keskihajonta? (1p) c. Oletetaan, että markkinoilla on lisäksi tarjolla riskitön sijoituskohde, jonka tuotto on 5%. Rakenna A:sta, B:stä ja C:stä koostuva portfolio, josta yhdessä riskittömän sijoituskohteen kanssa voidaan muodostaa mikä tahansa tehokas portfolio. Mikä on tämän portfolion tuoton odotusarvo ja keskihajonta? (1p) d. Esitä graafisesti tuotto-keskihajontakaaviossa osakesarjat A, B ja C sekä a-, b- ja c-kohdissa rakentamasi portfoliot. Piirrä samaan kaaviokuvaan lisäksi c-kohdassa muodostamasi portfolion ja riskittömän sijoituskohteen kautta kulkeva suora. (1p)
5 Tehtävä 5 (palautus ja esitys ) Oletetaan, että pörssissä on vain kaksi osakesarjaa A ja B. Taulukossa 1 on listattu osakesarjojen tiedot. Osakesarjojen tuottojen välinen korrelaatio on ρ AB = 1/2. Lisäksi markkinoilla on valtion obligaatioita, joiden tuotto on riskitön. Pörssin oletetaan toimivan CAPM:n mukaisesti ja markkinaportfolion odotetuksi tuotoksi on estimoitu 8.6%. Taulukko 1 Osakesarja Osakkeiden lukumäärä Osakkeen hinta Odotettu tuotto Tuoton keskihajonta A ? 12% B % 6% a. Kuinka suuri on osakesarjan A odotettu tuotto? (1p) b. Laske markkinaportfolion keskihajonta. (1p) c. Määritä molempien osakesarjojen β-kertoimet. (1p) d. Kuinka suuri on valtion obligaatioiden riskitön korko? (1p)
6 Tehtävä 6 (palautus ja esitys ) Maanviljelijä on sitoutunut myymään 5 tonnia kauraa vuoden kuluttua ja on päättänyt suojautua kauran tulevilta hinnanmuutoksilta vehnäfutuurien avulla, koska kaurafutuureita ei ole saatavilla. Kauran ja vehnän tämänhetkiset hinnat sekä vuosittaiset keskihajonnat on esitetty taulukossa 2. Kauran ja vehnän hintojen väliseksi korrelaatioksi on estimoitu 0,50. Taulukko 2 Tuote Hinta Vuotuinen keskihajonta Kaura 150 /tonni 20% Vehnä 180 /tonni 25% a. Muodosta maanviljelijälle minimivarianssisuojaus. (2p) b. Kuinka paljon minimivarianssisuojaus pienentää (prosentuaalisesti) kauraerän myyntiin liittyvää hintariskiä (so. keskihajontaa)? (2p)
7 Tehtävä 7 (palautus ja esitys ) Osakkeen vuotuinen volatiliteetti on 20% ja tämänhetkinen kurssi on 100 euroa. Osakkeeseen kohdistuu myyntioptio (put), jonka toteutushinta on 90 euroa ja päättymispäivä 5 kuukauden kuluttua. Riskitön vuosikorko on 5%. a. Määritä amerikkalaisen myyntioption arvo binomihilalla, jonka perusperiodin pituus on yksi kuukausi. (1p) b. Määritä vastaavan eurooppalaisen myyntioption arvo binomihilalla, jonka perusperiodin pituus on yksi kuukausi. Perustele, ovatko a- ja b-kohdan arvot keskenään johdonmukaiset. (1p) c. Samaan osakkeeseen kohdistuu myös nk. valintaoptio, jonka haltija saa 3 kuukauden kuluttua valita, toteutetaanko optio eurooppalaisena myyntioptiona vai eurooppalaisena osto-optiona. Myös tämän valintaoption toteutushinta on 90 euroa ja päättymispäivä on 5 kuukauden kuluttua. Määritä valintaoption hinta binomihilalla, jonka perusperiodin pituus on yksi kuukausi (jolloin option tyypin valinta tapahtuu periodin 3 päätteeksi). Perustele onko saamasi hinta johdonmukainen b-kohdan kanssa. (2p)
8 Tehtävä 8 (palautus ja esitys ) Harkitset vuokraavasi metsäpalstan, jolla puut kasvavat joka vuosi taulukon 3 mukaisella kertoimella (ensimmäisenä vuonna, hetkien 0 ja 1 välillä puumäärä kasvaa siis kertoimella 1.20 jne.). Puutavaran markkinahinta on stokastinen ja se noudattaa binomihilaa parametrein u = 1.20 ja d = Riskitön vuosikorko on 5.0%. Metsäpalstasta vaadittava vuokra on euroa vuodessa ja se maksetaan kunkin vuoden alussa etukäteen. Metsäpalstalla kasvavien puiden arvo on 2 miljoonaa euroa, jos ne hakattaisiin välittömästi (puun määrä hetkellä 0 kertaa puun hinta hetkellä 0). Puut voidaan kaataa minkä tahansa vuoden lopussa, jonka jälkeen metsäpalsta on annettava pois vuokralta. Puutavara voidaan varastoida ilman kustannuksia. Taulukko 3 Vuosi Kasvu a. Määritä vuokrausmahdollisuuden arvo reaalioptioiden avulla asettamalla perusperiodin pituudeksi yksi vuosi. Vuokrasopimus on korkeintaan 10 vuoden mittainen, eli puut on hakattava viimeistään vuoden 10 lopussa. (2p) b. Mikä on paras hakkuustrategia, kun metsäpalstan vuokra on euroa: missä päätössolmuissa (=minkä vuosien lopussa) puut kannattaa kaataa? Esitä strategia rinnakkaisena päätöshilana, jonka jokaisessa solmussa 0 = maksetaan seuraavan vuoden vuokra ja 1 = kaadetaan ja myydään puut, jolloin vuokraus loppuu. (2p)
Mat-2.11 4 Investointiteoria. Tentti 6.9.2005. Mitd
 .* Mat-2.11 4 Investointiteoria Tentti 6.9.2005 Ki{oita jokaiseen koepapcriin selveisti: o Mat-2.114 Investointiteoria o opintoki{'an numero sekii sukunimi ja viralliset etunimet tekstaten o koulutusohjelma
.* Mat-2.11 4 Investointiteoria Tentti 6.9.2005 Ki{oita jokaiseen koepapcriin selveisti: o Mat-2.114 Investointiteoria o opintoki{'an numero sekii sukunimi ja viralliset etunimet tekstaten o koulutusohjelma
Mat-2.3114 Investointiteoria Laskuharjoitus 3/2008, Ratkaisut 05.02.2008
 Korko riippuu usein laina-ajan pituudesta ja pitkille talletuksille maksetaan korkeampaa korkoa. Spot-korko s t on se korko, joka kertyy lainatulle pääomalle hetkeen t (=kokonaisluku) mennessä. Spot-korot
Korko riippuu usein laina-ajan pituudesta ja pitkille talletuksille maksetaan korkeampaa korkoa. Spot-korko s t on se korko, joka kertyy lainatulle pääomalle hetkeen t (=kokonaisluku) mennessä. Spot-korot
Nyt ensimmäisenä periodina (ei makseta kuponkia) odotettu arvo on: 1 (qv (1, 1) + (1 q)v (0, 1)) V (s, T ) = C + F
 Mat-2.34 Investointiteoria Laskuharjoitus 2/2008, Ratkaisut 29.04.2008 Binomihilan avulla voidaan laskea T vuoden ja tietyn kupongin sisältävän joukkovelkakirjan arvo eli hinta rekursiivisesti vaihtelevan
Mat-2.34 Investointiteoria Laskuharjoitus 2/2008, Ratkaisut 29.04.2008 Binomihilan avulla voidaan laskea T vuoden ja tietyn kupongin sisältävän joukkovelkakirjan arvo eli hinta rekursiivisesti vaihtelevan
Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia
 Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia { z(t k+1 ) = z(t k ) + ɛ(t k ) t t k+1 = t k + t, k = 0,..., N, missä ɛ(t i ), ɛ(t j ), i j ovat toisistaan riippumattomia siten, että
Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia { z(t k+1 ) = z(t k ) + ɛ(t k ) t t k+1 = t k + t, k = 0,..., N, missä ɛ(t i ), ɛ(t j ), i j ovat toisistaan riippumattomia siten, että
Viimeinen erä on korot+koko laina eli 666, 67 + 100000 100667, 67AC.
 Kotitehtäviä 6. Aihepiiri Rahoitusmuodot Ratkaisuehdotuksia 1. Pankki lainaa 100000 bullet-luoton. Laina-aika on 4kk ja luoton (vuotuinen) korkokanta 8% Luoton korot maksetaan kuukausittain ja laskutapa
Kotitehtäviä 6. Aihepiiri Rahoitusmuodot Ratkaisuehdotuksia 1. Pankki lainaa 100000 bullet-luoton. Laina-aika on 4kk ja luoton (vuotuinen) korkokanta 8% Luoton korot maksetaan kuukausittain ja laskutapa
Arvo (engl. value) = varmaan attribuutin tulemaan liittyvä arvo. Päätöksentekijä on riskipakoinen, jos hyötyfunktio on konkaavi. a(x) = U (x) U (x)
 Arvo (engl. value) = varmaan attribuutin tulemaan liittyvä arvo. Hyöty (engl. utility) = arvo, jonka koemme riskitilanteessa eli, kun teemme päätöksiä epävarmuuden (todennäköisyyksien) vallitessa. Vrt.
Arvo (engl. value) = varmaan attribuutin tulemaan liittyvä arvo. Hyöty (engl. utility) = arvo, jonka koemme riskitilanteessa eli, kun teemme päätöksiä epävarmuuden (todennäköisyyksien) vallitessa. Vrt.
, tuottoprosentti r = X 1 X 0
 Ostat osakkeen hintaan ja myyt sen vuoden myöhemmin hintaan X 1. Kokonaistuotto on tällöin R = X 1, tuottoprosentti r = X 1 ja pätee R = 1 + r. Lyhyeksimyymisellä tarkoitetaan, että voit myydä osakkeen
Ostat osakkeen hintaan ja myyt sen vuoden myöhemmin hintaan X 1. Kokonaistuotto on tällöin R = X 1, tuottoprosentti r = X 1 ja pätee R = 1 + r. Lyhyeksimyymisellä tarkoitetaan, että voit myydä osakkeen
Rahoitusriskit ja johdannaiset Matti Estola. luento 8 Optioiden hinnoittelusta
 Rahoitusriskit ja johdannaiset Matti Estola luento 8 Optioiden hinnoittelusta 1. Optioiden erilaiset kohde-etuudet 1.1. Osakeoptiot Yksi optio antaa yleensä oikeuden ostaa/myydä 1 kpl kohdeetuutena olevia
Rahoitusriskit ja johdannaiset Matti Estola luento 8 Optioiden hinnoittelusta 1. Optioiden erilaiset kohde-etuudet 1.1. Osakeoptiot Yksi optio antaa yleensä oikeuden ostaa/myydä 1 kpl kohdeetuutena olevia
Oletetaan, että virhetermit eivät korreloi toistensa eikä faktorin f kanssa. Toisin sanoen
 Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
On olemassa eri lainatyyppiä, jotka eroavat juuri sillä, miten lainaa lyhennetään. Tarkastelemme muutaman yleisesti käytössä olevan tyypin.
 Rahoitusmuodot HUOM. Tässä esitetään vain teoriaa ja joitakin esimerkkejä. Enemmän esimerkkejä ja laskuja löytyy ratkaistuina EXCEL-tiedostosta "Rahoitusmuodot - laskut ja esimerkit", joka on MOODLESSA
Rahoitusmuodot HUOM. Tässä esitetään vain teoriaa ja joitakin esimerkkejä. Enemmän esimerkkejä ja laskuja löytyy ratkaistuina EXCEL-tiedostosta "Rahoitusmuodot - laskut ja esimerkit", joka on MOODLESSA
Verkkokurssin tuotantoprosessi
 Verkkokurssin tuotantoprosessi Tietotekniikan perusteet Excel-osion sisältökäsikirjoitus Heini Puuska Sisältö 1 Aiheen esittely... 3 2 Aiheeseen liittyvien käsitteiden esittely... 3 2.1 Lainapääoma...
Verkkokurssin tuotantoprosessi Tietotekniikan perusteet Excel-osion sisältökäsikirjoitus Heini Puuska Sisältö 1 Aiheen esittely... 3 2 Aiheeseen liittyvien käsitteiden esittely... 3 2.1 Lainapääoma...
ln S(k) = ln S(0) + w(i) E[ln S(k)] = ln S(0) + vk V ar[ln S(k)] = kσ 2
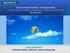
![ln S(k) = ln S(0) + w(i) E[ln S(k)] = ln S(0) + vk V ar[ln S(k)] = kσ 2 ln S(k) = ln S(0) + w(i) E[ln S(k)] = ln S(0) + vk V ar[ln S(k)] = kσ 2](/thumbs/65/53919158.jpg) Moniperiodisten investointitehtäviä tarkasteltaessa sijoituskohteiden hintojen kehitystä mallinnetaan diskeetteinä (binomihilat) tai jatkuvina (Itô-prosessit) prosesseina. Sijoituskohteen hinta hetkellä
Moniperiodisten investointitehtäviä tarkasteltaessa sijoituskohteiden hintojen kehitystä mallinnetaan diskeetteinä (binomihilat) tai jatkuvina (Itô-prosessit) prosesseina. Sijoituskohteen hinta hetkellä
Sijoitustodistuksen nykyinen markkinahinta: euroa. Jos viitekorko laskee 0,5 %-yksikköä, uusi markkinahinta: euroa
 AB30A0101 Finanssi-investoinnit 4. harjoitukset 7.4.015 Tehtävä 4.1 45 päivän kuluttua erääntyvälle, nimellisarvoltaan 100 000 euron sijoitustodistukselle maksettava vuosikorko on 3,0 %. Jos viitekorko
AB30A0101 Finanssi-investoinnit 4. harjoitukset 7.4.015 Tehtävä 4.1 45 päivän kuluttua erääntyvälle, nimellisarvoltaan 100 000 euron sijoitustodistukselle maksettava vuosikorko on 3,0 %. Jos viitekorko
r = r f + r M r f (Todistus kirjassa sivulla 177 tai luennon 6 kalvoissa sivulla 6.) yhtälöön saadaan ns. CAPM:n hinnoittelun peruskaava Q P
 Markkinaportfolio on koostuu kaikista markkinoilla olevista riskipitoisista sijoituskohteista siten, että sijoituskohteiden osuudet (so. painot) markkinaportfoliossa vastaavat kohteiden markkina-arvojen
Markkinaportfolio on koostuu kaikista markkinoilla olevista riskipitoisista sijoituskohteista siten, että sijoituskohteiden osuudet (so. painot) markkinaportfoliossa vastaavat kohteiden markkina-arvojen
OPTIOT Vipua ja suojausta - mutta mitä se maksaa? Remburssi Investment Group 23.5.2000
 OPTIOT Vipua ja suojausta - mutta mitä se maksaa? Remburssi Investment Group 23.5.2000 MARKKINAKATSAUS AGENDA Lyhyt johdanto optioihin Näkemysesimerkki 1: kuinka tehdä voittoa kurssien laskiessa Näkemysesimerkki
OPTIOT Vipua ja suojausta - mutta mitä se maksaa? Remburssi Investment Group 23.5.2000 MARKKINAKATSAUS AGENDA Lyhyt johdanto optioihin Näkemysesimerkki 1: kuinka tehdä voittoa kurssien laskiessa Näkemysesimerkki
12. Korkojohdannaiset
 2. Korkojohdannaiset. Lähtökohtia Korkojohdannaiset ovat arvopapereita, joiden tuotto riippuu korkojen kehityksestä. korot liittyvät lähes kaikkiin liiketoimiin korkojohdannaiset ovat tärkeitä. korkojohdannaisilla
2. Korkojohdannaiset. Lähtökohtia Korkojohdannaiset ovat arvopapereita, joiden tuotto riippuu korkojen kehityksestä. korot liittyvät lähes kaikkiin liiketoimiin korkojohdannaiset ovat tärkeitä. korkojohdannaisilla
r1 2 (1 0,02) 1 0,027556 (1 0, 0125) A250A0100 Finanssi-investoinnit 6. harjoitukset 21.4.2015 Futuuri, termiinit ja swapit
 A50A000 Finanssi-investoinnit 6. harjoitukset.4.05 Futuuri, termiinit ja swapit Tehtävä 6. Mikä on kahden vuoden bonditermiinin käypä markkinahinta, kun kohdeetuutena on viitelaina, jonka nimellisarvo
A50A000 Finanssi-investoinnit 6. harjoitukset.4.05 Futuuri, termiinit ja swapit Tehtävä 6. Mikä on kahden vuoden bonditermiinin käypä markkinahinta, kun kohdeetuutena on viitelaina, jonka nimellisarvo
Optioiden hinnoittelu binomihilassa
 Mat-2.3114 Investointiteoria Optioien hinnoittel binomihilassa 26.3.2015 Yksiperioiset optiot 1/3 Olkoon S kohe-eten arvo perioin alssa siten, että perioin päättyessä sen arvo on S toennäköisyyellä p tai
Mat-2.3114 Investointiteoria Optioien hinnoittel binomihilassa 26.3.2015 Yksiperioiset optiot 1/3 Olkoon S kohe-eten arvo perioin alssa siten, että perioin päättyessä sen arvo on S toennäköisyyellä p tai
Rahoitusriskit ja johdannaiset Matti Estola. luento 7 Swap sopimuksista lisää
 Rahoitusriskit ja johdannaiset Matti Estola luento 7 Swap sopimuksista lisää 1. Pankki swapin välittäjänä Yleensä 2 eri-rahoitusalan yritystä eivät tee swap sopimusta keskenään vaan pankin tai yleensäkin
Rahoitusriskit ja johdannaiset Matti Estola luento 7 Swap sopimuksista lisää 1. Pankki swapin välittäjänä Yleensä 2 eri-rahoitusalan yritystä eivät tee swap sopimusta keskenään vaan pankin tai yleensäkin
Kansainvälinen rahatalous Matti Estola. Termiinikurssit ja swapit valuuttariskien hallinnassa
 Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Helsingin OP Pankki Oyj. Vesa Väätänen
 Helsingin OP Pankki Oyj Vesa Väätänen OP-bonuksia keskittämisestä Palkitsemme asiakkaitamme keskittämisestä markkinoiden parhailla keskittämiseduilla. Viime vuonna asiakkaillemme kertyi OP-bonuksia 195
Helsingin OP Pankki Oyj Vesa Väätänen OP-bonuksia keskittämisestä Palkitsemme asiakkaitamme keskittämisestä markkinoiden parhailla keskittämiseduilla. Viime vuonna asiakkaillemme kertyi OP-bonuksia 195
Mat Investointiteoria Laskuharjoitus 4/2008, Ratkaisut
 Projektien valintapäätöksiä voidaan pyrkiä tekemään esimerkiksi hyöty-kustannus-suhteen (so. tuottojen nykyarvo per kustannusten nykyarvo) tai nettonykyarvon (so. tuottojen nykyarvo - kustannusten nykyarvo)
Projektien valintapäätöksiä voidaan pyrkiä tekemään esimerkiksi hyöty-kustannus-suhteen (so. tuottojen nykyarvo per kustannusten nykyarvo) tai nettonykyarvon (so. tuottojen nykyarvo - kustannusten nykyarvo)
Ratkaisu: a) Aritmeettisen jonon mielivaltainen jäsen a j saadaan kaavalla. n = a 1 n + (n 1)n d = 5 500 + 4 = 501500. 2 500 = 5 + 2001 2
 Kotitehtäviä 5. Ratkaisuehdotuksia. a) Jono a,..., a 500 on aritmeettinen, a = 5 ja erotusvakio d = 4. Laske jäsenet a, a 8 ja a 00 sekä koko jonon summa. b) Jono b,..., b 0 on geometrinen, b = ja suhdeluku
Kotitehtäviä 5. Ratkaisuehdotuksia. a) Jono a,..., a 500 on aritmeettinen, a = 5 ja erotusvakio d = 4. Laske jäsenet a, a 8 ja a 00 sekä koko jonon summa. b) Jono b,..., b 0 on geometrinen, b = ja suhdeluku
Tunnetko asuntolainariskisi?
 Tunnetko asuntolainariskisi? Studia Monetaria 12.10.2010 Peter Palmroos, tutkija Esityksen sisältö Asuntoluottojen riskit lainanottajalle Vakuuksien hinnan kehitys Maksukyvyn säilyminen Pankkien asuntoluottoriskit
Tunnetko asuntolainariskisi? Studia Monetaria 12.10.2010 Peter Palmroos, tutkija Esityksen sisältö Asuntoluottojen riskit lainanottajalle Vakuuksien hinnan kehitys Maksukyvyn säilyminen Pankkien asuntoluottoriskit
Mat Investointiteoria Laskuharjoitus 1/2008, Ratkaisu Yleistä: Laskarit tiistaisin klo luokassa U352.
 Yleistä: Laskarit tiistaisin klo 14-16 luokassa U352. Kysyttävää laskareista yms. jussi.kangaspunta@tkk. tai huone U230. Aluksi hieman teoriaa: Kassavirran x = (x 0, x 1,..., x n ) nykyarvo P x (r), kun
Yleistä: Laskarit tiistaisin klo 14-16 luokassa U352. Kysyttävää laskareista yms. jussi.kangaspunta@tkk. tai huone U230. Aluksi hieman teoriaa: Kassavirran x = (x 0, x 1,..., x n ) nykyarvo P x (r), kun
Talousmatematiikan perusteet: Luento 2. Sarjat Sovelluksia korkolaskentaan
 Talousmatematiikan perusteet: Luento 2 Sarjat Sovelluksia korkolaskentaan Viime luennolla Lukujono on päättyvä tai päättymätön jono reaalilukuja a 1, a 2,, a n, joita sanotaan jonon termeiksi. Erikoistapauksia
Talousmatematiikan perusteet: Luento 2 Sarjat Sovelluksia korkolaskentaan Viime luennolla Lukujono on päättyvä tai päättymätön jono reaalilukuja a 1, a 2,, a n, joita sanotaan jonon termeiksi. Erikoistapauksia
Millainen on Osuuspankin asuntopalvelu?
 Millainen on Osuuspankin asuntopalvelu? 1 Mistä asuntopalvelumme koostuu? Olitpa sitten hankkimassa ensimmäistä omaa kotia tai vaihtamassa nykyistä, saat meiltä juuri sinulle sopivan asuntolainan. Hoidamme
Millainen on Osuuspankin asuntopalvelu? 1 Mistä asuntopalvelumme koostuu? Olitpa sitten hankkimassa ensimmäistä omaa kotia tai vaihtamassa nykyistä, saat meiltä juuri sinulle sopivan asuntolainan. Hoidamme
Tietoja koron-ja valuutanvaihtosopimuksista
 Tietoja koron-ja valuutanvaihtosopimuksista Tämä esite sisältää tietoja Danske ankin kautta tehtävistä koron- ja valuutanvaihtosopimuksista. Koron- ja valuutanvaihtosopimuksilla voidaan käydä Danske ankin
Tietoja koron-ja valuutanvaihtosopimuksista Tämä esite sisältää tietoja Danske ankin kautta tehtävistä koron- ja valuutanvaihtosopimuksista. Koron- ja valuutanvaihtosopimuksilla voidaan käydä Danske ankin
Rahoitusriskit ja johdannaiset Matti Estola. luento 2 Termiini- ja futuurihintojen määräytyminen
 Rahoitusriskit ja johdannaiset Matti Estola luento 2 ermiini- ja futuurihintojen määräytyminen 1. ermiinien hinnoittelusta Esimerkki 1 Olkoon kullan spot -hinta $ 300 unssilta, riskitön korko 5 % vuodessa
Rahoitusriskit ja johdannaiset Matti Estola luento 2 ermiini- ja futuurihintojen määräytyminen 1. ermiinien hinnoittelusta Esimerkki 1 Olkoon kullan spot -hinta $ 300 unssilta, riskitön korko 5 % vuodessa
Rahoitusriskit ja johdannaiset Matti Estola Luento 5. Termiinihinnan määräytyminen
 Rahoitusriskit ja johdannaist Matti Estola Lunto 5 rmiinihinnan määräytyminn 1. rmiinin ylinn hinnoittlukaava Mrkitään trmiinisopimuksn kohd-tuudn spot hintaa sopimuksn tkopäivänä S :lla, kohd-tuudn trmiinihintaa
Rahoitusriskit ja johdannaist Matti Estola Lunto 5 rmiinihinnan määräytyminn 1. rmiinin ylinn hinnoittlukaava Mrkitään trmiinisopimuksn kohd-tuudn spot hintaa sopimuksn tkopäivänä S :lla, kohd-tuudn trmiinihintaa
Tietoja koronvaihtosopimuksista
 Tietoja koronvaihtosopimuksista Tämä esite sisältää tietoja Danske Bankin kautta tehtävistä koronvaihtosopimuksista. Koronvaihtosopimuksilla voidaan käydä kauppaa Danske Bankin kanssa pörssin ulkopuolella
Tietoja koronvaihtosopimuksista Tämä esite sisältää tietoja Danske Bankin kautta tehtävistä koronvaihtosopimuksista. Koronvaihtosopimuksilla voidaan käydä kauppaa Danske Bankin kanssa pörssin ulkopuolella
Korkomarkkinoiden erityispiirteet
 Korkomarkkinoiden erityispiirteet - markkinoiden hinnoittelema talouskehitys / trading korkomarkkinoilla www.operandi.fi Rahoitusriskien hallinnan asiantuntijayritys esityksen rakenne I. peruskäsitteitä
Korkomarkkinoiden erityispiirteet - markkinoiden hinnoittelema talouskehitys / trading korkomarkkinoilla www.operandi.fi Rahoitusriskien hallinnan asiantuntijayritys esityksen rakenne I. peruskäsitteitä
Korkokatto taloyhtiön lainoille Suojaudu korkoriskiltä asettamalla katto korkomenoille
 Korkokatto taloyhtiön lainoille Suojaudu korkoriskiltä asettamalla katto korkomenoille Korkoriski asunto-osakeyhtiössä Yleistyneiden remonttien takia taloyhtiöt ovat joutuneet nostamaan merkittäviä lainapääomia
Korkokatto taloyhtiön lainoille Suojaudu korkoriskiltä asettamalla katto korkomenoille Korkoriski asunto-osakeyhtiössä Yleistyneiden remonttien takia taloyhtiöt ovat joutuneet nostamaan merkittäviä lainapääomia
a) 3500000 (1, 0735) 8 6172831, 68. b) Korkojaksoa vastaava nettokorkokanta on
 Kotitehtävät 4 Ratkaisuehdotukset. 1. Kuinka suureksi 3500000 euroa kasvaa 8 vuodessa, kun lähdevero on 30% ja vuotuinen korkokanta on 10, 5%, kun korko lisätään a) kerran vuodessa b) kuukausittain c)
Kotitehtävät 4 Ratkaisuehdotukset. 1. Kuinka suureksi 3500000 euroa kasvaa 8 vuodessa, kun lähdevero on 30% ja vuotuinen korkokanta on 10, 5%, kun korko lisätään a) kerran vuodessa b) kuukausittain c)
YHTEENVETO LAINATARJOUKSISTA 17.6.2015
 1 YHTEENVETO LAINATARJOUKSISTA 17.6.2015 Danske Bank Oyj Kuntarahoitus Oyj Rantasalmen Osuuspankki Lainan määrä 1.000.000 euroa 1.000.000 euroa 1.000.000 euroa Laina-aika 10 vuotta 15 vuotta 15 vuotta
1 YHTEENVETO LAINATARJOUKSISTA 17.6.2015 Danske Bank Oyj Kuntarahoitus Oyj Rantasalmen Osuuspankki Lainan määrä 1.000.000 euroa 1.000.000 euroa 1.000.000 euroa Laina-aika 10 vuotta 15 vuotta 15 vuotta
Taloyhtiön korjaushankkeen rahoitus
 Taloyhtiön korjaushankkeen rahoitus Taloyhtiölaina / Osakaslaina Saavatko taloyhtiöt lainaa Nordeasta? Millaisia muutoksia on tapahtunut uusien säädösten myötä? Suomen talous edelleen alavireessä, mutta
Taloyhtiön korjaushankkeen rahoitus Taloyhtiölaina / Osakaslaina Saavatko taloyhtiöt lainaa Nordeasta? Millaisia muutoksia on tapahtunut uusien säädösten myötä? Suomen talous edelleen alavireessä, mutta
diskonttaus ja summamerkintä, L6
 diskonttaus ja summamerkintä, L6 1 Edellä aina laskettiin kasvanut pääoma alkupääoman ja koron perusteella. Seuraavaksi pohdimme käänteistä ongelmaa: Miten suuri tulee alkupääoman K 0 olla, jotta n jakson
diskonttaus ja summamerkintä, L6 1 Edellä aina laskettiin kasvanut pääoma alkupääoman ja koron perusteella. Seuraavaksi pohdimme käänteistä ongelmaa: Miten suuri tulee alkupääoman K 0 olla, jotta n jakson
Taloyhtiölaina ja AsuntoJousto
 Taloyhtiölaina ja AsuntoJousto rahoittamisen ratkaisuina Suomen Asunto-osakkeenomistajien ajankohtaiskatsaus 21.11.2011 Mikko Knuutila Johtaja, yritysasiakkaat 1745 Kanta-Helsingin Yrityskonttori Nordea
Taloyhtiölaina ja AsuntoJousto rahoittamisen ratkaisuina Suomen Asunto-osakkeenomistajien ajankohtaiskatsaus 21.11.2011 Mikko Knuutila Johtaja, yritysasiakkaat 1745 Kanta-Helsingin Yrityskonttori Nordea
Rahoitusriskit ja johdannaiset Luentokurssi kevät 2011 Lehtori Matti Estola
 Rahoitusriskit ja johdannaiset Luentokurssi kevät 2011 Lehtori Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Oikeustieteiden laitos, kansantaloustiede Luennot 22 t, harjoitukset
Rahoitusriskit ja johdannaiset Luentokurssi kevät 2011 Lehtori Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Oikeustieteiden laitos, kansantaloustiede Luennot 22 t, harjoitukset
Reaalioptioden käsitteen esittely yksinkertaisen esimerkin avulla
 Reaalioptioden käsitteen esittely yksinkertaisen esimerkin avulla Optimointiopin seminaari - Syksy 2000 / 1 Esitelmän sisältö Investointien peruuttamattomuuden vaikutus investointipäätökseen Investointimahdollisuuksien
Reaalioptioden käsitteen esittely yksinkertaisen esimerkin avulla Optimointiopin seminaari - Syksy 2000 / 1 Esitelmän sisältö Investointien peruuttamattomuuden vaikutus investointipäätökseen Investointimahdollisuuksien
Talousmatematiikan perusteet: Luento 1. Prosenttilaskentaa Korkolaskentaa
 Talousmatematiikan perusteet: Luento 1 Prosenttilaskentaa Korkolaskentaa Luennon sisältö Prosenttilaskennan kertausta Korkolaskentaa Käsitteitä Koron lisäys kerran / m kertaa vuodessa / jatkuvasti Diskonttaus
Talousmatematiikan perusteet: Luento 1 Prosenttilaskentaa Korkolaskentaa Luennon sisältö Prosenttilaskennan kertausta Korkolaskentaa Käsitteitä Koron lisäys kerran / m kertaa vuodessa / jatkuvasti Diskonttaus
8. Vertailuperiaatteita ja johdannaisia
 8. Vertailuperiaatteita ja johdannaisia 1. Hyötyfunktio Nykyarvo ei mittaa riskiasennetta, joka vaikuttaa valintakäyttäytymiseen (minkä investointivaihtoehdon valitset?). Esim. Kumpi seuraavista vaihtoehdoista
8. Vertailuperiaatteita ja johdannaisia 1. Hyötyfunktio Nykyarvo ei mittaa riskiasennetta, joka vaikuttaa valintakäyttäytymiseen (minkä investointivaihtoehdon valitset?). Esim. Kumpi seuraavista vaihtoehdoista
Suojaa ja tuottoa laskevilla markkinoilla. Johannes Ankelo Arvopaperi Aamuseminaari
 Suojaa ja tuottoa laskevilla markkinoilla Commerzbank AG Saksan toiseksi suurin pankki Euroopan johtavia strukturoitujen tuotteiden liikkeellelaskijoita Yli 50 erilaista tuotetyyppiä listattuna Saksan
Suojaa ja tuottoa laskevilla markkinoilla Commerzbank AG Saksan toiseksi suurin pankki Euroopan johtavia strukturoitujen tuotteiden liikkeellelaskijoita Yli 50 erilaista tuotetyyppiä listattuna Saksan
Rahoitusriskit ja johdannaiset Matti Estola Luento 6. Swap -sopimukset
 Rahoitusriskit ja johdannaiset Matti Estola Luento 6 Swap -sopimukset 1. Swapit eli vaihtosopimukset Swap -sopimus on kahden yrityksen välinen sopimus vaihtaa niiden saamat tai maksamat rahavirrat keskenään.
Rahoitusriskit ja johdannaiset Matti Estola Luento 6 Swap -sopimukset 1. Swapit eli vaihtosopimukset Swap -sopimus on kahden yrityksen välinen sopimus vaihtaa niiden saamat tai maksamat rahavirrat keskenään.
Hanken Svenska handelshögskolan / Hanken School of Economics www.hanken.fi
 Sijoittajan sanastoa Pörssisäätiön sijoituskoulu VERO 2014 Prof. Minna Martikainen Hanken School of Economics, Finland Sijoitusmaailman termistö ja logiikka, omat toimet ja näin luen. SIJOITUSMAAILMAN
Sijoittajan sanastoa Pörssisäätiön sijoituskoulu VERO 2014 Prof. Minna Martikainen Hanken School of Economics, Finland Sijoitusmaailman termistö ja logiikka, omat toimet ja näin luen. SIJOITUSMAAILMAN
Solvenssi II:n markkinaehtoinen vastuuvelka
 Solvenssi II:n markkinaehtoinen vastuuvelka Mikä on riskitön korko ja pääoman tuottovaatimus Suomen Aktuaariyhdistys 13.10.2008 Pasi Laaksonen Yleistä Mikäli vastuuvelka on ei-suojattavissa (non-hedgeable)
Solvenssi II:n markkinaehtoinen vastuuvelka Mikä on riskitön korko ja pääoman tuottovaatimus Suomen Aktuaariyhdistys 13.10.2008 Pasi Laaksonen Yleistä Mikäli vastuuvelka on ei-suojattavissa (non-hedgeable)
Talousmatematiikan perusteet: Luento 2. Lukujonot Sarjat Sovelluksia korkolaskentaan
 Talousmatematiikan perusteet: Luento 2 Lukujonot Sarjat Sovelluksia korkolaskentaan Lukujonoista Miten jatkaisit seuraavia lukujonoja? 1, 3, 5, 7, 1, 2, 4, 8, 1, 3, 9, 27, 1, 1, 2, 3, 5, 8, 8.1.2018 2
Talousmatematiikan perusteet: Luento 2 Lukujonot Sarjat Sovelluksia korkolaskentaan Lukujonoista Miten jatkaisit seuraavia lukujonoja? 1, 3, 5, 7, 1, 2, 4, 8, 1, 3, 9, 27, 1, 1, 2, 3, 5, 8, 8.1.2018 2
KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN
 00 N:o 22 LIITE KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN. Positioriskin laskemisessa käytettävät määritelmät Tässä liitteessä tarkoitetaan: arvopaperin nettopositiolla samanlajisen arvopaperin pitkien
00 N:o 22 LIITE KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN. Positioriskin laskemisessa käytettävät määritelmät Tässä liitteessä tarkoitetaan: arvopaperin nettopositiolla samanlajisen arvopaperin pitkien
9 VEROTUS, TALLETUKSET JA LAINAT
 9 VEROTUS, TALLETUKSET JA LAINAT ALOITA PERUSTEISTA 370A. Kunnallisveroprosentti oli 19,5, joten 31 200 tuloista oli maksettava kunnallisveroa 0,195 31 200 = 6084. Vastaus: 6084 euroa 371A. a) Hajuveden
9 VEROTUS, TALLETUKSET JA LAINAT ALOITA PERUSTEISTA 370A. Kunnallisveroprosentti oli 19,5, joten 31 200 tuloista oli maksettava kunnallisveroa 0,195 31 200 = 6084. Vastaus: 6084 euroa 371A. a) Hajuveden
ENSIASUNNON OSTAJAN ABC
 Unelmien koti kiikarissa? ENSIASUNNON OSTAJAN ABC Ensimmäisen oman asunnon ostaminen saattaa tuntua henkisesti ja rahallisesti isolta päätökseltä, johon liittyy paljon uutta ja tuntematonta. Tämä opas
Unelmien koti kiikarissa? ENSIASUNNON OSTAJAN ABC Ensimmäisen oman asunnon ostaminen saattaa tuntua henkisesti ja rahallisesti isolta päätökseltä, johon liittyy paljon uutta ja tuntematonta. Tämä opas
RBS Warrantit NOKIA DAX. SIP Nordic AB Alexander Tiainen Maaliskuu 2011
 RBS Warrantit DAX NOKIA SIP Nordic AB Alexander Tiainen Maaliskuu 2011 RBS Warrantit Ensimmäiset warrantit Suomen markkinoille Kaksi kohde-etuutta kilpailukykyisillä ehdoilla ; DAX ja NOKIA Hyvät spreadit
RBS Warrantit DAX NOKIA SIP Nordic AB Alexander Tiainen Maaliskuu 2011 RBS Warrantit Ensimmäiset warrantit Suomen markkinoille Kaksi kohde-etuutta kilpailukykyisillä ehdoilla ; DAX ja NOKIA Hyvät spreadit
Ensimmäiseen omaan kotiin
 Ensimmäiseen omaan kotiin Tarja Lehtonen 18.11.2014 Ensimmäiseen omaan kotiin Aihealueet Huomioitavaa ennen asunnon ostoa ASP lyhyesti Asuntolaina Korkovaihtoehdot Vakuudet OmaTakaus Vakuutukset Verotus
Ensimmäiseen omaan kotiin Tarja Lehtonen 18.11.2014 Ensimmäiseen omaan kotiin Aihealueet Huomioitavaa ennen asunnon ostoa ASP lyhyesti Asuntolaina Korkovaihtoehdot Vakuudet OmaTakaus Vakuutukset Verotus
Talousmatematiikan perusteet: Luento 1. Prosenttilaskentaa Korkolaskentaa Lukujonot: aritmeettinen ja geometrinen
 Talousmatematiikan perusteet: Luento 1 Prosenttilaskentaa Korkolaskentaa Lukujonot: aritmeettinen ja geometrinen Luennon sisältö Prosenttilaskennan kertausta Korkolaskentaa Käsitteitä Koron lisäys kerran
Talousmatematiikan perusteet: Luento 1 Prosenttilaskentaa Korkolaskentaa Lukujonot: aritmeettinen ja geometrinen Luennon sisältö Prosenttilaskennan kertausta Korkolaskentaa Käsitteitä Koron lisäys kerran
Nykyarvo ja investoinnit, L14
 Nykyarvo ja investoinnit, L14 netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n netto 0 1 2 3 4 5 6...
Nykyarvo ja investoinnit, L14 netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n netto 0 1 2 3 4 5 6...
Millaisia ovat finanssipolitiikan kertoimet
 Millaisia ovat finanssipolitiikan kertoimet Antti Ripatti Helsingin yliopisto, HECER, Suomen Pankki 20.3.2013 Antti Ripatti (HECER) fipon kerroin 20.3.2013 1 / 1 Johdanto Taustaa Finanssipolitiikkaa ei
Millaisia ovat finanssipolitiikan kertoimet Antti Ripatti Helsingin yliopisto, HECER, Suomen Pankki 20.3.2013 Antti Ripatti (HECER) fipon kerroin 20.3.2013 1 / 1 Johdanto Taustaa Finanssipolitiikkaa ei
Työkalut rahoitusriskien hallintaan käytännön ratkaisuja. Jukka Leppänen rahoituspäällikkö, johdannaiset
 1 Työkalut rahoitusriskien hallintaan käytännön ratkaisuja Jukka Leppänen rahoituspäällikkö, johdannaiset KORKORISKI KOKONAISKORKO = Markkinakorko Marginaali Muut kulut Markkinakorko Markkinakorko aiheuttaa
1 Työkalut rahoitusriskien hallintaan käytännön ratkaisuja Jukka Leppänen rahoituspäällikkö, johdannaiset KORKORISKI KOKONAISKORKO = Markkinakorko Marginaali Muut kulut Markkinakorko Markkinakorko aiheuttaa
Talousmatematiikan perusteet: Luento 5. Käänteisfunktio Yhdistetty funktio Raja-arvot ja jatkuvuus
 Talousmatematiikan perusteet: Luento 5 Käänteisfunktio Yhdistetty funktio Raja-arvot ja jatkuvuus Tähän mennessä Funktiolla f: A B, y = f x kuvataan muuttujan y B riippuvuutta muuttujasta x A Jotta funktio
Talousmatematiikan perusteet: Luento 5 Käänteisfunktio Yhdistetty funktio Raja-arvot ja jatkuvuus Tähän mennessä Funktiolla f: A B, y = f x kuvataan muuttujan y B riippuvuutta muuttujasta x A Jotta funktio
MAT INVESTOINTITEORIA. (5 op) Kevät Ville Brummer / Pekka Mild / Ahti Salo
 MAT - 2.114 INVESTOINTITEORIA (5 op) Kevät 2008 Ville Brummer / Pekka Mild / Ahti Salo 1 Opintojakson sisältö Taustaa Kattaa matemaattisen investointiteorian perusteet: Teemoja sivuttu osin muilla Mat-2
MAT - 2.114 INVESTOINTITEORIA (5 op) Kevät 2008 Ville Brummer / Pekka Mild / Ahti Salo 1 Opintojakson sisältö Taustaa Kattaa matemaattisen investointiteorian perusteet: Teemoja sivuttu osin muilla Mat-2
Taloudelliset laskelmat
 Taloudelliset laskelmat Pielisen Tietoverkko Juuka 31.3.214 LUONNOS LASKENTAOLETUKSET 31.3.214 2 Laskentaoletukset Investoinnit Ominaisuus Kuvaus Rakentamisaikataulu Runkoverkon rakentaminen tapahtuu vuonna
Taloudelliset laskelmat Pielisen Tietoverkko Juuka 31.3.214 LUONNOS LASKENTAOLETUKSET 31.3.214 2 Laskentaoletukset Investoinnit Ominaisuus Kuvaus Rakentamisaikataulu Runkoverkon rakentaminen tapahtuu vuonna
Projektin arvon määritys
 Projektin arvon määritys Luku 6, s. 175-186 Optimointiopin seminaari - Syksy 2000 / 1 Tehtävä Johdetaan menetelmä projektiin oikeuttavan option määrittämiseksi kohde-etuuden hinnan P perusteella projektin
Projektin arvon määritys Luku 6, s. 175-186 Optimointiopin seminaari - Syksy 2000 / 1 Tehtävä Johdetaan menetelmä projektiin oikeuttavan option määrittämiseksi kohde-etuuden hinnan P perusteella projektin
Kulutus. Kulutus. Antti Ripatti. Helsingin yliopisto, HECER, Suomen Pankki Antti Ripatti (HECER) Kulutus
 Kulutus Antti Ripatti Helsingin yliopisto, HECER, Suomen Pankki 13.11.2013 Antti Ripatti (HECER) Kulutus 13.11.2013 1 / 11 Indifferenssikäyrät ja kuluttajan teoria Tarkastellaan edustavaa kotitaloutta.
Kulutus Antti Ripatti Helsingin yliopisto, HECER, Suomen Pankki 13.11.2013 Antti Ripatti (HECER) Kulutus 13.11.2013 1 / 11 Indifferenssikäyrät ja kuluttajan teoria Tarkastellaan edustavaa kotitaloutta.
Jaksolliset suoritukset, L13
 , L13 1 Jaksollinen talletus Tarkastellaan tilannetta, jossa asiakas tallettaa pankkitilille toistuvasti yhtäsuuren rahasumman k aina korkojakson lopussa. Asiakas suorittaa talletuksen n kertaa. Lasketaan
, L13 1 Jaksollinen talletus Tarkastellaan tilannetta, jossa asiakas tallettaa pankkitilille toistuvasti yhtäsuuren rahasumman k aina korkojakson lopussa. Asiakas suorittaa talletuksen n kertaa. Lasketaan
Nykyarvo ja investoinnit, L9
 Nykyarvo ja investoinnit, L9 netto netto netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n 0 1 2 3 4 5
Nykyarvo ja investoinnit, L9 netto netto netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n 0 1 2 3 4 5
Valuuttariskit ja johdannaiset
 Valuuttariskit ja johdannaiset Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Sosiaali- ja terveysjohtamisen laitos, kansantaloustiede Lähde: Hull, Options, Futures, & Other
Valuuttariskit ja johdannaiset Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Sosiaali- ja terveysjohtamisen laitos, kansantaloustiede Lähde: Hull, Options, Futures, & Other
Johdannaisanalyysi. Contingent Claims Analysis Juha Leino S ysteemianalyysin. Laboratorio
 Johdannaisanalyysi Contingent Claims Analysis Juha Leino 11.10.2000 Optimointiopin seminaari - Syksy 2000 / 1 Oletukset Yritys tuottaa tuotetta, jonka hinta on x x noudattaa geometrista Brownin liikettä
Johdannaisanalyysi Contingent Claims Analysis Juha Leino 11.10.2000 Optimointiopin seminaari - Syksy 2000 / 1 Oletukset Yritys tuottaa tuotetta, jonka hinta on x x noudattaa geometrista Brownin liikettä
This watermark does not appear in the registered version - http://www.clicktoconvert.com. Hedgehog Oy:n Rapidfire-pääomalaina
 Hedgehog Oy:n Rapidfire-pääomalaina Sisältö Lyhyt lainaesite Hedgehog Oy Rapidfire lainaehdot Rapidfire testaus Miten Rapidfireen voi sijoittaa Yhteystiedot ã 2004 Hedgehog Oy E Koskinen / 2 Rapidfire-pääomalaina
Hedgehog Oy:n Rapidfire-pääomalaina Sisältö Lyhyt lainaesite Hedgehog Oy Rapidfire lainaehdot Rapidfire testaus Miten Rapidfireen voi sijoittaa Yhteystiedot ã 2004 Hedgehog Oy E Koskinen / 2 Rapidfire-pääomalaina
Asumisen palvelumme sinulle
 Asumisen palvelumme sinulle 1 Mistä asumisen palvelumme koostuvat? Olitpa sitten hankkimassa ensimmäistä omaa kotia tai vaihtamassa nykyistä, saat meiltä juuri sinulle sopivan asuntolainan. Hoidamme myös
Asumisen palvelumme sinulle 1 Mistä asumisen palvelumme koostuvat? Olitpa sitten hankkimassa ensimmäistä omaa kotia tai vaihtamassa nykyistä, saat meiltä juuri sinulle sopivan asuntolainan. Hoidamme myös
Todellinen vuosikorko. Efektiivinen/sisäinen korkokanta. Huomioitavaa
 Todellinen vuosikorko Huomioitavaa Edellinen keskimaksuhetkeen perustuva todellinen vuosikorko antaa vain arvion vuosikorosta. Tarkempi arvio todellisesta korosta saadaan ottamalla huomioon mm. koronkorko.
Todellinen vuosikorko Huomioitavaa Edellinen keskimaksuhetkeen perustuva todellinen vuosikorko antaa vain arvion vuosikorosta. Tarkempi arvio todellisesta korosta saadaan ottamalla huomioon mm. koronkorko.
YHTEENVETO LAINATARJOUKSISTA 2.3.2015
 1 YHTEENVETO LAINATARJOUKSISTA 2.3.2015 Danske Bank Oyj Kuntarahoitus Oyj Nordea Pankki Suomi Oyj Laina-aika 1+ 9 vuotta 10 tai 15 vuotta 10 vuotta Lyhennykset Tasalyhennyksin puolivuosittain. Tasalyhennyksin
1 YHTEENVETO LAINATARJOUKSISTA 2.3.2015 Danske Bank Oyj Kuntarahoitus Oyj Nordea Pankki Suomi Oyj Laina-aika 1+ 9 vuotta 10 tai 15 vuotta 10 vuotta Lyhennykset Tasalyhennyksin puolivuosittain. Tasalyhennyksin
Määräykset ja ohjeet 4/2011
 Määräykset ja ohjeet 4/2011 Asuntoluoton ennenaikaisesta takaisinmaksusta perittävän enimmäiskorvauksen laskentaan käytettävät Dnro FIVA 9/01.00/2011 Antopäivä 15.12.2011 Voimaantulopäivä 31.3.2012 FIASSIVALVOTA
Määräykset ja ohjeet 4/2011 Asuntoluoton ennenaikaisesta takaisinmaksusta perittävän enimmäiskorvauksen laskentaan käytettävät Dnro FIVA 9/01.00/2011 Antopäivä 15.12.2011 Voimaantulopäivä 31.3.2012 FIASSIVALVOTA
Korko ja inflaatio. Makrotaloustiede 31C00200 Kevät 2016
 Korko ja inflaatio Makrotaloustiede 31C00200 Kevät 2016 Sisältö Nimellis ja reaalikorot, Fisher yhtälö Lyhyt ja pitkä korko Rahapolitiikka ja korot Korko ja inflaatio Nimellinen korko i: 1 tänä vuonna
Korko ja inflaatio Makrotaloustiede 31C00200 Kevät 2016 Sisältö Nimellis ja reaalikorot, Fisher yhtälö Lyhyt ja pitkä korko Rahapolitiikka ja korot Korko ja inflaatio Nimellinen korko i: 1 tänä vuonna
Kirjanpito ja laskentatoimi A-osa
 1. Arvon määritys a) Mitkä tekijät vaikuttavat osto- ja myyntioptioiden arvoon ja miten? b) Yrityksen osingon oletetaan olevan ensi vuonna 3 euroa per osake ja osinkojen uskotaan kasvavan 6 % vuosivauhtia.
1. Arvon määritys a) Mitkä tekijät vaikuttavat osto- ja myyntioptioiden arvoon ja miten? b) Yrityksen osingon oletetaan olevan ensi vuonna 3 euroa per osake ja osinkojen uskotaan kasvavan 6 % vuosivauhtia.
Talousmatematiikka (3 op)
 Talousmatematiikka (3 op) Tero Vedenjuoksu Oulun yliopisto Matemaattisten tieteiden laitos 2011 Talousmatematiikka 2011 Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi Työhuone M231 Kurssin kotisivu
Talousmatematiikka (3 op) Tero Vedenjuoksu Oulun yliopisto Matemaattisten tieteiden laitos 2011 Talousmatematiikka 2011 Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi Työhuone M231 Kurssin kotisivu
(1) Katetuottolaskelma
 (1) Katetuottolaskelma Katetuottolaskelmalla tarkastellaan yrityksen kannattavuutta myyntituotto - muuttuvat kustannukset (mukut) = katetuotto katetuotto - kiinteät kustannukset (kikut) = tulos (voitto
(1) Katetuottolaskelma Katetuottolaskelmalla tarkastellaan yrityksen kannattavuutta myyntituotto - muuttuvat kustannukset (mukut) = katetuotto katetuotto - kiinteät kustannukset (kikut) = tulos (voitto
Optiot 2. Tervetuloa webinaariin!
 Optiot 2 Tervetuloa webinaariin! Optiot 2 on jatkokurssi optioista kiinnostuneelle sijoittajalle. Webinaarissa jatketaan optioiden käsittelyä ja syvennymme johdannaisten maailmaan. Webinaarissa käydään
Optiot 2 Tervetuloa webinaariin! Optiot 2 on jatkokurssi optioista kiinnostuneelle sijoittajalle. Webinaarissa jatketaan optioiden käsittelyä ja syvennymme johdannaisten maailmaan. Webinaarissa käydään
Talousmatematiikka (3 op)
 Talousmatematiikka (3 op) Tero Vedenjuoksu Oulun yliopisto Matemaattisten tieteiden laitos 2011 Talousmatematiikka 2011 Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi Työhuone M231 Kurssin kotisivu
Talousmatematiikka (3 op) Tero Vedenjuoksu Oulun yliopisto Matemaattisten tieteiden laitos 2011 Talousmatematiikka 2011 Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi Työhuone M231 Kurssin kotisivu
Johdatus f90/95 ohjelmointiin. H, R & R luvut 1-3
 Johdatus f90/95 ohjelmointiin H, R & R luvut 1-3 Fortran-kieli ( 3.1-3) IBM 1954, FORmula TRANslator ISO/ANSI standardit f90, f95, f2003 tieteellinen & teknillinen laskenta rinnakkaislaskenta (HPF, openmp)
Johdatus f90/95 ohjelmointiin H, R & R luvut 1-3 Fortran-kieli ( 3.1-3) IBM 1954, FORmula TRANslator ISO/ANSI standardit f90, f95, f2003 tieteellinen & teknillinen laskenta rinnakkaislaskenta (HPF, openmp)
Projektin arvon aleneminen
 Projektin arvon aleneminen sivut 99-07 Optimointiopin seminaari - Syksy 000 / Arvon aleneminen Jatketaan projektin arvon tutkimista. Nyt huomioidaan arvon aleneminen. Syitä esimerkiksi: kaluston vanheneminen
Projektin arvon aleneminen sivut 99-07 Optimointiopin seminaari - Syksy 000 / Arvon aleneminen Jatketaan projektin arvon tutkimista. Nyt huomioidaan arvon aleneminen. Syitä esimerkiksi: kaluston vanheneminen
Tietoja osakeoptioista
 Tietoja osakeoptioista Tämä esite sisältää yleisiä tietoja osakeoptioista, joilla voidaan käydä kauppaa Danske Bankin välityksellä. AN OTC TRANSACTION WITH DANSKE BANK AS COUNTERPARTY. ESITTELY Osakeoptioilla
Tietoja osakeoptioista Tämä esite sisältää yleisiä tietoja osakeoptioista, joilla voidaan käydä kauppaa Danske Bankin välityksellä. AN OTC TRANSACTION WITH DANSKE BANK AS COUNTERPARTY. ESITTELY Osakeoptioilla
Asunto Oy Vantaan Kaneli Tikkurilantie 35,01370 Vantaa Asunto Oy Vantaan Kaneli sijaitsee omalla tontilla.
 Asunto Oy Vantaan Kaneli Tikkurilantie 35,01370 Vantaa Asunto Oy Vantaan Kaneli sijaitsee omalla tontilla. MYYNTIHINTALUETTELO pvm 26.1.2015 Hinnat voimassa toistaiseksi Päivitetty 4.1.2016 Huoneisto tyyppi
Asunto Oy Vantaan Kaneli Tikkurilantie 35,01370 Vantaa Asunto Oy Vantaan Kaneli sijaitsee omalla tontilla. MYYNTIHINTALUETTELO pvm 26.1.2015 Hinnat voimassa toistaiseksi Päivitetty 4.1.2016 Huoneisto tyyppi
Talousmatematiikan perusteet
 kevät 2019 / orms.1030 Talousmatematiikan perusteet 5. harjoitus, viikko 7 11.02. 15.02.2019 R01 Ma 12 14 F453 R08 Ke 10 12 F453 R02 Ma 16 18 F453 L To 08 10 A202 R03 Ti 08 10 F425 R06 To 12 14 F140 R04
kevät 2019 / orms.1030 Talousmatematiikan perusteet 5. harjoitus, viikko 7 11.02. 15.02.2019 R01 Ma 12 14 F453 R08 Ke 10 12 F453 R02 Ma 16 18 F453 L To 08 10 A202 R03 Ti 08 10 F425 R06 To 12 14 F140 R04
SIJOITUSANALYYSI 2h+kk+ph, Kauppurienkatu 5, Oulu KOHDETIEDOT
 KOHDETIEDOT Sivu 1 PERUSTIEDOT VUOKRATIEDOT Sijainti Kauppurienkatu 5, Oulu Vuokra 610,00 /kk Kaupunginosa Keskusta Hoitovastike 110,00 /kk Yhtiö As Oy Kauppurienkatu 5 Rahoitusvastike - Rakennusvuosi
KOHDETIEDOT Sivu 1 PERUSTIEDOT VUOKRATIEDOT Sijainti Kauppurienkatu 5, Oulu Vuokra 610,00 /kk Kaupunginosa Keskusta Hoitovastike 110,00 /kk Yhtiö As Oy Kauppurienkatu 5 Rahoitusvastike - Rakennusvuosi
25.9.2008 klo 9-15. 1. Selvitä vakuutustekniseen vastuuvelkaan liittyvät riskit ja niiltä suojautuminen.
 SHV-tutkinto Vakavaraisuus 25.9.28 klo 9-15 1(5) 1. Selvitä vakuutustekniseen vastuuvelkaan liittyvät riskit ja niiltä suojautuminen. (1p) 2. Henkivakuutusyhtiö Huolekas harjoittaa vapaaehtoista henkivakuutustoimintaa
SHV-tutkinto Vakavaraisuus 25.9.28 klo 9-15 1(5) 1. Selvitä vakuutustekniseen vastuuvelkaan liittyvät riskit ja niiltä suojautuminen. (1p) 2. Henkivakuutusyhtiö Huolekas harjoittaa vapaaehtoista henkivakuutustoimintaa
Talousmatematiikan perusteet
 kevät 219 / orms.1 Talousmatematiikan perusteet 1. Laske integraalit a 6x 2 + 4x + dx, b 5. harjoitus, viikko 6 x + 1x 1dx, c xx 2 1 2 dx a termi kerrallaan kaavalla ax n dx a n+1 xn+1 +C. 6x 2 + 4x +
kevät 219 / orms.1 Talousmatematiikan perusteet 1. Laske integraalit a 6x 2 + 4x + dx, b 5. harjoitus, viikko 6 x + 1x 1dx, c xx 2 1 2 dx a termi kerrallaan kaavalla ax n dx a n+1 xn+1 +C. 6x 2 + 4x +
Esteet, hyppyprosessit ja dynaaminen ohjelmointi
 Esteet, hyppyprosessit ja dynaaminen ohjelmointi Juha Martikainen 4.10.2000 Oppikirjan sivut 83-87 ja 93-98 Optimointiopin seminaari - Syksy 2000 / 1 Esteet (määritelmät) Muistellaan menneitä: Ajelehtiva
Esteet, hyppyprosessit ja dynaaminen ohjelmointi Juha Martikainen 4.10.2000 Oppikirjan sivut 83-87 ja 93-98 Optimointiopin seminaari - Syksy 2000 / 1 Esteet (määritelmät) Muistellaan menneitä: Ajelehtiva
10 Liiketaloudellisia algoritmeja
 218 Liiketaloudellisia algoritmeja 10 Liiketaloudellisia algoritmeja Tämä luku sisältää liiketaloudellisia laskelmia. Aiheita voi hyödyntää vaikkapa liiketalouden opetuksessa. 10.1 Investointien kannattavuuden
218 Liiketaloudellisia algoritmeja 10 Liiketaloudellisia algoritmeja Tämä luku sisältää liiketaloudellisia laskelmia. Aiheita voi hyödyntää vaikkapa liiketalouden opetuksessa. 10.1 Investointien kannattavuuden
Tasaerälaina ja osamaksukauppa
 Tasaerälaina ja osamaksukauppa Merkintöjä Yleensä laskussa lähdetään todellisesta vuosikorosta. Merkitään todellista vuosikorkokantaa kirjaimella i a, jolloin vuosikorkotekijä on (1 + i a ). Vuosi jaetaan
Tasaerälaina ja osamaksukauppa Merkintöjä Yleensä laskussa lähdetään todellisesta vuosikorosta. Merkitään todellista vuosikorkokantaa kirjaimella i a, jolloin vuosikorkotekijä on (1 + i a ). Vuosi jaetaan
A250A0100 Finanssi-investoinnit 5. harjoitukset 14.4.2015 Futuurit ja termiinit
 A250A0100 Finanssi-investoinnit 5. harjoitukset 14.4.2015 Futuurit ja termiinit ehtävä 5.1 Kesäkuun 3. päivä ostaja O ja myyjä M sopivat syyskuussa erääntyvästä 25 kappaleen OMX Helsinki CAP-indeksifutuurin
A250A0100 Finanssi-investoinnit 5. harjoitukset 14.4.2015 Futuurit ja termiinit ehtävä 5.1 Kesäkuun 3. päivä ostaja O ja myyjä M sopivat syyskuussa erääntyvästä 25 kappaleen OMX Helsinki CAP-indeksifutuurin
SAMPO PANKKI KORKO-OBLIGAATIO 1609: KORKOKAULURI XV
 Danske Bank Oyj, www.danskebank.fi SAMPO PANKKI KORKO-OBLIGAATIO 1609: KORKOKAULURI XV Tietoa lainasta: Lainan liikkeeseenlaskija: Danske Bank Oyj Lainan ISIN-koodi: FI4000050000 KORKOKAULURI XV Viiden
Danske Bank Oyj, www.danskebank.fi SAMPO PANKKI KORKO-OBLIGAATIO 1609: KORKOKAULURI XV Tietoa lainasta: Lainan liikkeeseenlaskija: Danske Bank Oyj Lainan ISIN-koodi: FI4000050000 KORKOKAULURI XV Viiden
METSÄLIITTO OSUUSKUNNAN JOUKKOVELKAKIRJALAINA I/2006 LAINAKOHTAISET EHDOT
 METSÄLIITTO OSUUSKUNNAN JOUKKOVELKAKIRJALAINA I/2006 LAINAKOHTAISET EHDOT Nämä lainakohtaiset ehdot muodostavat yhdessä 29.5.2006 päivättyyn ohjelmaesitteeseen sisältyvien Metsäliitto Osuuskunnan joukkovelkakirjojen
METSÄLIITTO OSUUSKUNNAN JOUKKOVELKAKIRJALAINA I/2006 LAINAKOHTAISET EHDOT Nämä lainakohtaiset ehdot muodostavat yhdessä 29.5.2006 päivättyyn ohjelmaesitteeseen sisältyvien Metsäliitto Osuuskunnan joukkovelkakirjojen
Markkinoilla kaupattavia sijoituskohteita (1/2)
 Markkinoilla kaupattavia sijoituskohteita (1/2) Sovelletun matematiikan jatko-opintoseminaari Johdannaissopimushinnoittelun matemaattinen mallinnus ja laskennalliset menetelmät Johdanto TkT Juho Kanniainen
Markkinoilla kaupattavia sijoituskohteita (1/2) Sovelletun matematiikan jatko-opintoseminaari Johdannaissopimushinnoittelun matemaattinen mallinnus ja laskennalliset menetelmät Johdanto TkT Juho Kanniainen
Pankkitalletukset ja rahamarkkinasijoitukset. Henri Huovinen, analyytikko Osakesäästäjien Keskusliitto ry
 Pankkitalletukset ja rahamarkkinasijoitukset Henri Huovinen, analyytikko Osakesäästäjien Keskusliitto ry Korkosijoitukset Korkosijoituksiin luokitellaan mm. pankkitalletukset, rahamarkkinasijoitukset,
Pankkitalletukset ja rahamarkkinasijoitukset Henri Huovinen, analyytikko Osakesäästäjien Keskusliitto ry Korkosijoitukset Korkosijoituksiin luokitellaan mm. pankkitalletukset, rahamarkkinasijoitukset,
Q&A. 1) Kuka voi lainata osakkeita?
 Q&A 1) Kuka voi lainata osakkeita? Kaikki sijoittajat voivat ottaa lainaksi osakkeita, mutta osakkeita voi antaa lainaksi vain sijoittajat, joiden sijoitukset kuuluvat elinkeinoverotuksen piiriin. 2) Mitä
Q&A 1) Kuka voi lainata osakkeita? Kaikki sijoittajat voivat ottaa lainaksi osakkeita, mutta osakkeita voi antaa lainaksi vain sijoittajat, joiden sijoitukset kuuluvat elinkeinoverotuksen piiriin. 2) Mitä
METSÄTILASTOTIEDOTE 52/2014
 Metsäntutkimuslaitos, Metsätilastollinen tietopalvelu METSÄTILASTOTIEDOTE 52/2014 Metsä sijoituskohteena 1983 2013 15.12.2014 Esa Uotila Puuntuotannon sijoitustuotto 4 prosenttia vuonna 2013 Yksityismetsien
Metsäntutkimuslaitos, Metsätilastollinen tietopalvelu METSÄTILASTOTIEDOTE 52/2014 Metsä sijoituskohteena 1983 2013 15.12.2014 Esa Uotila Puuntuotannon sijoitustuotto 4 prosenttia vuonna 2013 Yksityismetsien
Asuntolainan syvin olemus. Toimitusjohtaja Matti Inha
 Asuntolainan syvin olemus Toimitusjohtaja Matti Inha Asuntolainan syvin olemus Miksi yleensä kannattaa ottaa asuntolainaa?? perussyy on mahdollisuus hankkia kallis ja tuloihin nähden aina huomattavan iso
Asuntolainan syvin olemus Toimitusjohtaja Matti Inha Asuntolainan syvin olemus Miksi yleensä kannattaa ottaa asuntolainaa?? perussyy on mahdollisuus hankkia kallis ja tuloihin nähden aina huomattavan iso
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 18.3.2015 HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 8..05 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 8..05 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
200 Opintolaina 20,00 1.nosto
 LAINAT, HENKILÖASIAKKAAT 1.9.2019 Täydellinen palveluhinnasto on nähtävissä pankin konttorissa. Arvo Yks. Huomioitavaa Toimitusmaksu Asuntolainat ennen 1.9.2019 allekirjoitetut kulutusluotto- ja opintolainasopimukset
LAINAT, HENKILÖASIAKKAAT 1.9.2019 Täydellinen palveluhinnasto on nähtävissä pankin konttorissa. Arvo Yks. Huomioitavaa Toimitusmaksu Asuntolainat ennen 1.9.2019 allekirjoitetut kulutusluotto- ja opintolainasopimukset
Ratkaisu: a) Koroton takaisinmaksuaika on 9000 = 7,5 vuotta. 1200 b) Kun vuosituotot pysyvät vakiona, korollinen takaisinmaksuaika määräytyy
 Kotitehtävät 7. Aihepiirinä Investointi Ratkaisuehdotuksia 1. Investoinnin hankintameno on 9000 euroa ja siitä saadaan seuraavina vuosina vuosittain 1200 euron tulot. Määritä a) koroton takaisinmaksuaika
Kotitehtävät 7. Aihepiirinä Investointi Ratkaisuehdotuksia 1. Investoinnin hankintameno on 9000 euroa ja siitä saadaan seuraavina vuosina vuosittain 1200 euron tulot. Määritä a) koroton takaisinmaksuaika
Luentorunko 10: Kv. pääomaliikkeet ja lyhyen aikavälin makrot
 Luentorunko 10: Kv. pääomaliikkeet ja lyhyen aikavälin makrotasapaino Niku, Aalto-yliopisto ja Etla Makrotaloustiede 31C00200, Talvi 2018 Johdanto Kiinteä valuuttakurssi Edelleen lyhyen aikavälin makrotasapaino,
Luentorunko 10: Kv. pääomaliikkeet ja lyhyen aikavälin makrotasapaino Niku, Aalto-yliopisto ja Etla Makrotaloustiede 31C00200, Talvi 2018 Johdanto Kiinteä valuuttakurssi Edelleen lyhyen aikavälin makrotasapaino,
