Kun pilari liittyy muihin ei-jäykkiin kimmoisiin rakenteisiin, kuten kehäpalkkiin tai perustuksiin määritetään nurjahduspituus seuraavilla kaavoilla:
|
|
|
- Ella Tarja Nieminen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Plarn mtotus EC:n mukaan Nurjahdusptuus Yksttäsen plarn nurjahdusptuus ja hokkuus h) Kun plar lttyy muhn e-jäykkn kmmosn rakentesn, kuten kehäpalkkn ta perustuksn määrtetään nurjahdusptuus seuraavlla kaavolla: Svusrtymätön plar ( jäykstetyt sauvat ) (tapaukset a, c, d, f) Plar päden srtymä estetty mulla rakentella; rakennusta jäykstävät muut rakenteet kun tarkasteltava plar, kuten jäykstävät senät L = 0,5 L o k k k + 0,45 + k Svusrtyvä plar ( jäykstämättömät sauvat ) (tapaukset b, e, g ja h) Plarn tosen pään srtymää e ole estetty mulla rakentella kun tarkasteltavalla plarlla; tarkasteltava plar on osa rakennusta jäykstävää rakennekokonasuutta esm. osa rakennusta jäykstävästä jäykkänurkkasesta kehästä (kuten harjotustyössä) ta rakennus on jäykstetty tarkasteltavana olevlla mastoplarella. L 0 k k L + 0 k + k k + k L + + k + k Kaavossa on L 0 on nurjahdusptuus L on plarn todellnen ptuus = vapaa ptuus knntyskohten välltä
2 k ja k ovat plarn päden ja kertymäjoustavuuden (= kertymäjousvakoden kääntesarvojen) suhteellsa arvoja: θ EI k = M L θ on plarn pään knntysmomentta M vastaava kertymstä vastustaven sauvojen esm. palkn ta anturan kertymä θ L plarn lttyvä sauva: = sauvan vastakkasessa päässä nvel M 3 EI θ L = sauvan vastakkanen pää knntetty M 4 EI EI L EI L on plarn tavutusjäykkyys (vodaan laskea halkeamattomana) on plarn ptuus on palkn tavutusjäykkyys (vodaan laskea halkeamattomana) on palkn ptuus täysn jäykkä knntys k=0 vapaast kertyvä pää (nvel ta uloke) k= Ulokeplar: k = L 0 L + 0 k + k L + k kunmk kun k 0,7 < 0,7 Täysn jäykkä knntys e yleensä ole mahdollnen, joten suostellaan vähmmäsarvoa k=0,. Vähmmäsarvoa k =0. ja k =0. vastaava nurjahdusptuus - svusrtymätön plar: plarn molemmssa päät knntettyjä (k =k =0,) L 0 = 0,59 L~0,6L tonen pää knntetty, tosessa päässä nvel (k =0,, k = ) L 0 = 0,77 L~0,8L molemmssa pässä nvel (k = k = ) L 0 = L - svusrtyvä plar plarn molemmat päät knntettyjä (k = k =0,) L 0 =, L~,L uloke; tonen pää vapaa (k = ), tonen pää knntetty (k =0,) L 0 =,8 L~,L Jos samaan nurkkaan lttyy tonenkn plar (esm. ylemp plar), joka myötävakuttaa nurjahduksessa syntyvään kertymään jousvakossa k term EI/L korvataan summalla (EI/L) a +(EI/L) b.
3 Jos plarn lttyy molemmlta puollta palkk, nn term L 4 EI L3 + 4 EI 3 L 4 EI korvataan summalla Huom! Harjotustyössä ylemp elementtplar lttyy kehään nvelellsest, joten sen e oleteta vakuttavan alemman plarn kertymään. Huom! Alapäästä jäykäst knntetty ja yläpäähän lttyy palkk nvellsest (elementt)palkk ja plarn yläpään srtymä vapaa (svusrtyvä) vastaa uloketta, jonka nurjahdusptuus L 0 L Tapaus h) kuvaa svusrtyvän jäykkänurkkasen kehän plara, jossa plar lttyy jäykäst yläpäästään palkkn ja alapäässä on esm. perustus, joka pääsee kertymään. Yläpään ltos e täysn jäykkä, koska plar lttyy kmmosaan palkkn (staattsessa mallssa on palkn kertymäjäykkyyttä vastaava jous, jousvakon kääntesarvo M θ ). Vastaavast alapään ltos e ole täysn jäykkä perustuksen kertymän (staattsessa mallssa jous) vuoks. Plarn yläpää pääsee srtymään (staattsessa mallssa rullat), joten kehä on svusrtyvä; vaakasuuntasen srtymän suhteen anota jäykstävä rakenteta ovat kehän plart. Paalutuksen vakutus nurjahdusptuuteen Tavutusmomentn M rasttaessa paaluanturaa, saa tosen paalurvn paalut purstusta ja tosen vetoa. Paalulle tulevat purstus- ja vetovomat ovat N p M = ± n a mssä n on yhdessä rvssä oleven paalujen lukumäärärä (harj.työssä n=) a on paaluväl Np N p Paalun saamat jänntykset ovat σ p = ja muodonmuutos ε p = mssä Ap Ecmp A p A p on paalun pnta-ala ja E cmp on paalun betonn keskmääränen kmmokerron. Tosen rvn paalut lyhenevät ja tosen rvn ptenevät määrän Lp M Lp on paalun ptuus. Anturan kertymä on θ = = a n E A a θ Lp Plarn alapään kertymäjoustavuus on = M n E A a cmp cmp p p L p = ±ε p L p, mssä L p
4 Esm. Ulokeplar, ptuus L=4 m, pokklekkaus 380*380, beton C5/30 Plarn I=, m 4, E cm =3500 MPa => E cm I/L= 3,68 MNm Paalut + kpl 50*50 paalua,ptuus L p =0 m, paaluväl a=0,8 m, beton C40/50 Paalun pnta-ala A p = 0,065 m, E cmp =3500 MPa n= => θ/m=0,04 /(MNm) Plarn alapään kertymäjoustavuus k = 0,04 3,68 = 0,94 >0, + 0,94 Plarn nurjahdusptuus L 0 = L = L,35 = 9,3m + 0,94 Esm. Edellä olevaan plarn lttyy jäykäst palkk, L = 6 m, pokklekkaus 380*580, beton C5/30. Palkn tosessa päässä on vaakasuuntasen lkkeen sallva nveltuk el rullatuk. Koska palkn tonen pää vo lkkua vaakasuunnassa, nn myös plarn yläpää pääsee lkkumaan vaakasuunnassa, joten plar on svusrtyvä. Palkn I= 6,8 0-3 m 4 θ L = 3 EI M = 0,003 MNm θ EI Yläpään kertymäjoustavuus k = = 0,003 3,68 = 0,4 > 0, M L Plarn nurjahdusptuus k k L + 0 = 4 k + k L0 k + k L + + k + k Plarn nurjahdusptuus on ss L o = 5,39 m 0,94 0,4 + 0 =,35 4 = 5,39 m 0,94 + 0,4 0,94 0,4 = =,3 4 = 5, m ,4 Mussa kun edellä estetyssä tapauksssa (sauvan normaalvoma ta pokklekkaus muuttuva ta rakenne on monmutkasemp) nurjahdusptuus määrtetään esm. numeersella menetelmällä lasketusta (kmmosesta) nurjahduskuormasta seuraavast: L 0 = π EI N B N B on tavutusjäykkyyttä EI vastaava nurjahduskuorma
5 Plarn hokkuus L λ = 0 EI = h on htaussäde ; suorakade = 0,89h ympyrä = 0.5 h EA Tosen kertaluvun vakutukset vodaan jättää ottamatta huomoon, jos nden vakutus on alle 0 % ta hokkuus 0 A B C λ λlm = n A = + 0, ϕ jos vrumalukua e tunneta vodaan käyttää A~0,7 ef B = + ω jos mekaansta raudotusastetta ω e tunneta, vodaan käyttää B~, C=,7-r m jos päätymomentten suhdetta r m e tunneta, vodaan käyttää r m ~0,7 M 0 r m = on. kertaluvun päätymomentten suhde M M 0 M 0 0 Jos M 0 ja M 0 aheuttavat vetoa rakenteen samalle puolelle r m >0 (C,7) Jos M 0 ja M 0 aheuttavat vetoa rakenteen er puollle r m <0 (C>,7) Päätymomentten suhteelle vodaan käyttää arvoa r m =,0 (C=0,7), kun - svusrtyvssä plaressa. kertaluvun momentteja syntyy van ta enssjasest perusepäkesksyyksstä ta pokttaskuormsta (vaakakuormsta) Jos normaalvoma tulee plarlle epäkeskesest, lasketaan r m näden todellsten epäkesksyyksen aheuttamen momentten M 0 ja M 0 perusteella n - svusrtyvssä rakenneosssa yleensä N A f Ed = on suhteellnen normaalvoma A c c cd s yd ω = on mekaannen raudotusaste; kokonasteräsmäärä A f f cd molempen reunojen teräsmäärä yhteensä
6 Tehollnen vrumaluku nurjahdustarkastelussa ϕ ef M = ϕ(, t 0) M 0Eqp 0Ed φ(,t 0 ) M 0Eqp M OEd on vrumaluvun loppuarvo; vodaan olettaa, että t 0 ~8 vrk on. kertaluvun käyttötlan tavutusmomentt ptkäakasessa kuormtusyhdstelmässä on. kertaluvun murtotlan momentt tarkasteltavassa kuormtusyhdstelmässä Vruman vakutusta e tarvtse ottaa huomoon, jos kakk seuraavat kolme ehtoa toteutuvat: ϕ(, t ) 0 λ 75 M0Ed e0d = h NEd h plarpokklekkauksen korkeus A=0,7 B=, C=0,7 => n λ lm λ = lm 0,78 Lsävaakavoma ja perusepäkesksyys n
7 Pokklekkauksen mttapokkeamen vakutus otetaan huomoon materaalen osavarmuusluvussa; ntä e ssällytetä rakenneanalyysn (vomasuureden määrtykseen) Rakenteen ja kuorman sjantn lttyvät mttaepätarkkuudet otetaan huomoon murtorajatlossa, mutta ntä e tarvtse ottaa huomoon käyttörajatlossa. Rakenteen ja kuorman sjantn lttyvät mttaepätarkkuudet estetään rakenteen/rakennuksen vnouden θ ι avulla: Rakenteen vnous θ = θ 0 α h α m Vnouden perusarvo θ 0 = /00 Rakennuksen korkeuteen perustuva vnouden penennyskerron αh = M αh L 3 L on rakenneosan korkeus (m) Pystysuuntasten rakenneosen lukumäärään perustuva vnouden penennyskerron α m = 0,5 ( + ) m m on kokonasvakutuksen aheuttaven (asennettaven) pystysuuntasten rakenneosen lukumäärä (esm. plaren lukumäärä) Vnouden vakutus yksttäsen rakenneosan mtotukseen: L=rakenneosan (plarn) todellnen ptuus m= => α m = Vnouden vakutus jäykstysjärjestelmään: L= rakennuksen korkeus m = pystysuuntasest kuormtettujen pystyrakenneosen lukumäärä (erllsten asennettaven ta valettaven pystyrakenneosen, senen ja plareden lukumäärä) yhdessä lkuntasaumalohkossa Vnouden vakutus levykenttnä tomvn vaakavoma jakavn tasohn: L = kerroskorkeus m=kussakn kerroksessa pystykuormtettujen pystysuuntasten rakenneosen lukumäärä
8 Vnouden vakutus vodaan ottaa huomoon kahdella tavalla: L0 a) normaalvoman N Ed epäkesksyyden e avulla e = θ b) lsävaakavoman H avulla svusrtymättömssä rakenneosssa L 0 :n puolvälssä lsävaakavoma svusrtyvssä rakenneosssa L 0 :n yläpäässä lsävaakavoma H H = N Ed = N Ed θ θ Vnouden vakutus vodaan ottaa huomoon rakenneanalyysssä (vomasuureta laskettaessa) tason kohdalla vakuttavana lsävaakavomana H muden kuormen ohella - vakutus jäykstysjärjestelmään (esm. kehään) H = (NEdb NEda ) θ = NEd θ - vakutus välpohjan levykenttään H = (N Edb + N H - vakutus yläpohjan levykenttään = N Eda θ Eda ) θ N Eda on tason yläpuolsen pystyrakenteen normaalvoma N Edb on tason alapuolsen pystyrakenteen normaalvoma N Ed on tasolta pystyrakenteelle tuleva normaalvoman muutos /θ Rakenteen vnouden θ vakutus erllseen rakenneosaan = 00 L θ L (m)
9 Vnouden penennyskerron pystyrakenteden lukumäärästä α m Pystyrakenteden lukumäärä m (kpl) Rakenteden vnous θ θ L>9 m L=8 m L=7 m L=6 m L=5 m L< 4 m Pystyrakenteden lukumäärä m (kpl)
10 Plarn nurjahdustarkastelu EC:ssa on estetty kaks yksnkertastettua menetelmää a) nmellsjäykkyyteen perustuva menetelmä b) nmellseen kaarevuuteen perustuva menetelmä Nmellseen kaarevuuteen perustuva menetelmä Plarn pokklekkaus ja raudotus muuttumattoma plarn ptuudella L Kaarevuus r K K = r ϕ r 0 n u n Normaalvomasta rppuva korjauskerron K r = kun n>0,4 n n Suhteellnen normaalvoma NEd n = A f c cd K r = u bal kun n 0,4 Lyhyen plarn suhteellnen normaalvomakestävyys = N A f + A f U c cd s yd n = = + ω A f A f u (A s ja ω kokonasteräsmäärä c cd c cd molemmat reunat yhteeensä) Plarpokklekkauksen suurnta tavutuskestävyyttä vastaava suhteellsen normaalvoman arvo n bal =0,4 Alussa teräsmäärää e tunneta, joten oletetaan plarn EC:n mnmraudotus (kokonasteräsmäärä, mol. reunat yhteensä) 0, N Ed As mn = kutenkn vähntään A f smn =0,00 A c yd mekaannen raudotusaste ω=0, n (kokonasteräsmäärä mol. reunat yhteensä) 0,9 n K r = 0,6 + 0, n Maksmraudotus 6 % pokklekkausalasta => ω=,8 (C5/30 -lk) => K r =,64-0,4 n Korjauskerron Kϕ = + β ϕef ottaa huomoon vruman vakutuksen fck λ β = 0,
11 Kaarevuuden korjauskerron K r mnm- ja maksmraudotuksella K r K r =,64-0,4 n ω=, K r ω=0,n 0,9 n = 0,6 + 0, n Suhteellnen normaalvoma n Kaarevuuden perusarvo εyd = r0 0,45 d f yd ε yd = A500HW ε yd =,7 % o (.lk) Es Lsäepäkesksyys e 0 L0 = r c L = r π r L0 0 Jos vakomomentt c=8, paraabel c=9,6 Suorakadepokklekkaukselle : h L0 htaussäde = hokkuus λ = h h ympyräpokklekkaus htaussäde = hokkuus 4 4 Lo λ = h. kertaluvun nmellnen lsämomentt M = N Ed e
12 . kertaluvun momentt Svusrtymättömssä rakentessa: Kun sauvan päden välllä e vakuta vaakavoma, on mtottava. kertaluvun momentt plarjänteen keskellä M 0Ed = 0,6 M0 + 0,4 M 0 > 0,4 M0 M 0 ja M 0 ovat plarn pässä vakuttavat. kertaluvun momentt; M 0 M 0 Svusrtyvssä rakentessa mtottava. kertaluvun momentt on sauvan suurn momentt M 0Ed = M 0 Mtotusmomentt M Ed =M 0Ed + M Ed (θ ) + M mssä M 0Ed on. kertaluvun momentt M Ed (θ ) on vnoudesta (lsävaakavomasta H ta perusepäkesksyydestä) e aheutuva momentt
13 Kuormtusyhdstelmät plarn mtotuksessa Plarssa vakuttaa kaks vomasuuretta: - normaalvoma N Ed - momentt M Ed Osa kuormtustapaukssta aheuttaa sekä normaalvomaa että momentta (esm. epäkeskenen normaalvoma, epäkesksyys e= M/N; myös kehäpalklta tulee plarlle palkn kuormasta pystysuuntanen tukreakto ja tukmomentt). Momentt ja normaalvoma rppuvat tosstaan, rppuvuutta lmasee epäkesksyys e. Osa kuormtustapaukssta aheuttaa van tosta vomasuuretta; esm. vaakasuuntanen tuulkuorma aheuttaa pääsääntösest plarn tavutusmomentta; tavutusmomentt on rppumaton normaalvomasta. Mtotuksessa normaalvomalla oletetaan olevan tetty perusepäkesksyys esm. pystyrakenteden vnouden seurauksena sekä hokalla plarlla lsäepäkesksyys. Normaalvomasta aheutuu ss ana momentta epäkesksyyden ollessa normaalvomasta rppumaton. Hokka plar on geometrsest epälneaarnen, joten nurjahdustarkastelu ja plarn mtotuksessa e vo käyttää superpostoperaatetta, vaan mtotus täytyy tehdä erkseen jokaselle kuormtusyhdstelmälle (N-M-yhdstelmälle rppumattomen muuttuven kuormen yhdstelykertomen ja lkkuven kuormen er vahtoehtojen mukasest). Purstava normaalvoma aheuttaa pokklekkaukseen purstusta ja vähentää tarvttavaa vetoteräsmäärää, tosaalta normaalvoma aheuttaa momentta, joka puolestaan vaat lsää vetoteräsmäärää. Tämän vuoks plarn mtotuksessa on tarkastettava yhdstelmät, jotka aheuttavat sekä penmmän normaalvoman (pysyvän kuorman osavarmuusluku 0,9, e muuttuva kuorma) että suurmman normaalvoman (pysyvän kuorman osavarmuusluku,5, suurmman normaalvoman aheuttama muuttuven kuormen yhdstelmä).
14 Kuormtusohjeden (SFS-EN-990-) mukaan kahden tosstaan rppumattoman er kuormaluokkaan kuuluvan muuttuvan kuorman tapauksessa saadaan seuraavat yhdstelmät:.35 G.5 G +.5 Q.5 G +.5 Q.5 G +.5 Q +.5 ψ 0, Q.5 G +.5 ψ 0, Q +.5 Q 0.9 G 0.9 G +.5 Q 0.9 G +.5 Q 0.9 G +.5 Q +.5 ψ 0, Q 0.9 G +.5 ψ 0, Q +.5 Q Jos rppumattoma muuttuva kuorma on esm. 3, yhdstelmä tulee yhteensä 6 kpl. Kuormtusohjeden (SFS-EN-990-) mukassta kuormtusyhdstelmstä haetaan seuraavat tapaukset, jolle plar mtotetaan:. Suurn normaalvoma N Ed,max ; tavutusmomentt tässä kuormtustapauksessa M Ed. Penn normaalvoma N Ed,mn tavutusmomentt tässä kuormtustapauksessa M Ed 3. Suurn tavutusmomentt M Ed,max normaalvoma tässä kuormtustapauksessa N Ed3 4. Itsesarvoltaan suurn negatvnen tavutusmomentt -M Edmax normaalvoma tässä kuormtustapauksessa N Ed4 5. Kuormtustapaus, joka antaa suurmman reunavetojänntyksen N Ed5 6 M Ed5 σ max = + b h b h 6. Kuormtustapaus, joka antaa suurmman reunavetojänntyksen toseen reunaan N Ed6 6 M Ed6 σmax = + b h b h
15 Pokklekkauksen mtotus Yleensä plart raudotetaan symmetrsest el molemmlla reunolla on sama raudotus. Tällön vodaan käyttää alla olevaa yhtesvakutusdagramma. Suhteellnen momentt µ = M Ed b h fcd Suhteellnen normaalvoma ν = N Ed b h f cd Suhteellnen kokonasteräsmäärä A s,veto + A s,pur f = ω f cd yd b h
16 Rakenteellsa ohjeta - Pääteräksen halkasja vähntään 8 mm; meluummn.6 mm - Haan halkasja vähntään 6 mm; - htsatusta verkosta muodostetussa haassa 5 mm - Hakaväln enmmäsarvo penn seuraavsta: 5* päätankojen halkasja - plarn penn svumtta mm - Pokklekkauksen nurkassa pääteräs sdotaan haalla - Päätanko saa olla (purstetulla puolella) enntään 50 mm:n päässä sdotusta tangosta; - Jos etäsyys suuremp sdotaan ko. tangot välhaolla, joden jako saa olla - kertanen. - Välhaat evät ole tarpeen, kun - plarn svumtta on enntään 380 mm, kun svun keskellä on tanko, - plarn svumtta on enntään 480 mm ja svun keskellä on tankoa - Palkn ta laatan ylä- ja alapuolella sekä lmjatkoksen alueella plarn suurempaa svumttaa vastaavalla matkalla hakojako saa olla enntään 0,6*kertaa em. enmmäsarvo - Lmjatkoksen alueella on oltava kutenkn vähntään 3 hakaa - Pääterästen vähmmäsmäärä A s,mn 0, N Ed f yd 0,00 A c - Suurn suhteellnen teräsmäärä enntään 6 %.
17 Plarn haotus
18 Plarn mtotus- yhteenveto. Lasketaan rakenteen vnous θ. Lasketaan. kertaluvun vomasuureet, normaalvoma N Ed, sauvan pään momentt M 0, M Otetaan vnouden vakutus huomoon. kertaluvun vomasuuressa esm. - antamalla kullekn kuormalle vnoutta vastaava vaakavoma (q h = θ q) ta - mallntamalla rakenne vnoks ta - lsäämällä. kertaluvun momentteja määrällä M Ed (θ I )=N Ed e I 4. Määrtetään plarn päden knntysjoustavuudet k ja k 5. Määrtetään plarn nurjahdusptuus 6. Lasketaan tehollnen vrumaluku φ ef ja kaarevuuden korjauskerron K φ sekä normaalvomasta aheutuva kaarevuuden penennyskerron K r 7. Lasketaan perusepäkesksyys e 8. Lasketaan mtottava. kertaluvun momentt M 0Ed,. kertaluvun lsämomentt sekä lopullnen mtotusmomentt M Ed 9. Lasketaan tarvttava raudotus ja tarkstetaan, että täyttää mnmraudotusvaatmuksen
Puupintaisen sandwichkattoelementin. lujuuslaskelmat. Sisältö:
 Puupntasen sandwchkattoelementn lujuuslaskelmat. Ssältö: Sandwch kattoelementn rakenne ja omnasuudet Laatan laskennan kulku Tulosten vertalua FEM-malln ja analyyttsen malln välllä. Elementn rakenne Puupntasa
Puupntasen sandwchkattoelementn lujuuslaskelmat. Ssältö: Sandwch kattoelementn rakenne ja omnasuudet Laatan laskennan kulku Tulosten vertalua FEM-malln ja analyyttsen malln välllä. Elementn rakenne Puupntasa
levyt toimivat lineaarisen kimmoisesti leikkausrasituksessa runkopuut ovat jäykkiä ja kiinnitetty nivelellisesti toisiinsa
 Kpslevyjäykstysrakenteden suunntteluohje (verso, 4..07) Tämän suunntteluohjeen on laatnut TkL Jarmo Leskelä A-Insnöört Suunnttelu Oy:stä yhtestyössä Sant-Goban Rakennustuotteet Oy:n kanssa. Suunntteluohje
Kpslevyjäykstysrakenteden suunntteluohje (verso, 4..07) Tämän suunntteluohjeen on laatnut TkL Jarmo Leskelä A-Insnöört Suunnttelu Oy:stä yhtestyössä Sant-Goban Rakennustuotteet Oy:n kanssa. Suunntteluohje
JÄNNITETTYJEN ONTELOLAATTOJEN CE-MERKINNÄN MUKAINEN SUUNNITTELU EUROKOODIEN MUKAAN
 05.11.08 1 JÄNNTETTYJEN ONTELOLAATTOJEN CE-ERKNNÄN UKANEN SUUNNTTELU EUROKOODEN UKAAN 5.1. armuuskertomet (1) Betonn osavarmuuslukua vodaan CE-merktyllä tuottella penentää arvoon γ c,red1 1,35. (Kansallnen
05.11.08 1 JÄNNTETTYJEN ONTELOLAATTOJEN CE-ERKNNÄN UKANEN SUUNNTTELU EUROKOODEN UKAAN 5.1. armuuskertomet (1) Betonn osavarmuuslukua vodaan CE-merktyllä tuottella penentää arvoon γ c,red1 1,35. (Kansallnen
Yleistä. Teräsrakenteiden liitokset. Liitos ja kiinnitys
 Ylestä Teäsakenteden ltokset (EC3-1-8, EC3-1-8-NA) Teäsakenteden lttämsessä tosnsa vodaan käyttää seuaava menetelmä: uuv-, ntt- ja nveltappltokset htsausltokset lmaltokset Ltos ja knntys Ltosta asttavan
Ylestä Teäsakenteden ltokset (EC3-1-8, EC3-1-8-NA) Teäsakenteden lttämsessä tosnsa vodaan käyttää seuaava menetelmä: uuv-, ntt- ja nveltappltokset htsausltokset lmaltokset Ltos ja knntys Ltosta asttavan
Betoniteollisuus ry 18.2.2010 1 (43)
 Betonteollsuus r 18.2.2010 1 (43) 2 Jäkstsjärjestelmät... 2 2.1 Rakennuksen jäkstssuunnttelun tehtävät... 4 Alustava jäkstssuunnttelu... 4 Jäkstksen mtotus murtorajatlassa... 6 Jäkstksen mtotus kättörajatlassa...
Betonteollsuus r 18.2.2010 1 (43) 2 Jäkstsjärjestelmät... 2 2.1 Rakennuksen jäkstssuunnttelun tehtävät... 4 Alustava jäkstssuunnttelu... 4 Jäkstksen mtotus murtorajatlassa... 6 Jäkstksen mtotus kättörajatlassa...
RIL lisäohjeet: Stora Enso CLT
 Ar Kevarnmäk RIL 05--07 CLT lsäohjeet 5..07 (5) RIL 05--07 lsäohjeet: Tämä lsäohje koskee Stora Enson valmstamaa ETA-4/049 mukasta rstnlmattua massvpuulevyä CLT Cross Lamnate Tmber. Ohjeessa estetyt :n
Ar Kevarnmäk RIL 05--07 CLT lsäohjeet 5..07 (5) RIL 05--07 lsäohjeet: Tämä lsäohje koskee Stora Enson valmstamaa ETA-4/049 mukasta rstnlmattua massvpuulevyä CLT Cross Lamnate Tmber. Ohjeessa estetyt :n
Galerkin in menetelmä
 hum.9.3 Galerkn n menetelmä Galerknn menetelmän soveltamnen e ole rajottunut van ongelmn, jotka vodaan pukea sellaseen varaatomuotoon, joka on seurauksena funktonaaln mnmomsesta, kuten potentaalenergan
hum.9.3 Galerkn n menetelmä Galerknn menetelmän soveltamnen e ole rajottunut van ongelmn, jotka vodaan pukea sellaseen varaatomuotoon, joka on seurauksena funktonaaln mnmomsesta, kuten potentaalenergan
Sähköstaattinen energia
 ähköstaattnen enega Potentaalenegan a potentaaln suhde on samanlanen kun Coulomn voman a sähkökentän suhde: ähkökenttä vakuttaa vaattuun kappaleeseen nn, että se kokee Coulomn voman, mutta sähkökenttä
ähköstaattnen enega Potentaalenegan a potentaaln suhde on samanlanen kun Coulomn voman a sähkökentän suhde: ähkökenttä vakuttaa vaattuun kappaleeseen nn, että se kokee Coulomn voman, mutta sähkökenttä
COULOMBIN VOIMA JA SÄHKÖKENTTÄ, PISTEVARAUKSET, JATKUVAT VARAUSJAKAUMAT
 COUOMBIN VOIMA JA SÄHKÖKENTTÄ, PISTEVARAUKSET, JATKUVAT VARAUSJAKAUMAT SISÄTÖ: Coulombn voma Sähkökenttä Coulombn voman a sähkökentän laskemnen pstevaaukslle Jatkuvan vaauksen palottelemnen pstevaauksks
COUOMBIN VOIMA JA SÄHKÖKENTTÄ, PISTEVARAUKSET, JATKUVAT VARAUSJAKAUMAT SISÄTÖ: Coulombn voma Sähkökenttä Coulombn voman a sähkökentän laskemnen pstevaaukslle Jatkuvan vaauksen palottelemnen pstevaauksks
r i m i v i = L i = vakio, (2)
 4 TÖRMÄYKSET ILMATYYNYPÖYDÄLLÄ 41 Erstetyn systeemn sälymslat Kun kaks kappaletta törmää tosnsa ne vuorovakuttavat keskenään tetyn ajan Vuorovakutuksella tarkotetaan stä että kappaleet vahtavat keskenään
4 TÖRMÄYKSET ILMATYYNYPÖYDÄLLÄ 41 Erstetyn systeemn sälymslat Kun kaks kappaletta törmää tosnsa ne vuorovakuttavat keskenään tetyn ajan Vuorovakutuksella tarkotetaan stä että kappaleet vahtavat keskenään
1. Luvut 1, 10 on laitettu ympyrän kehälle. Osoita, että löytyy kolme vierekkäistä
 Johdatus dskreettn matematkkaan Harjotus 3, 30.9.2015 1. Luvut 1, 10 on latettu ympyrän kehälle. Osota, että löytyy kolme verekkästä lukua, joden summa on vähntään 17. Ratkasu. Tällasa kolmkkoja on 10
Johdatus dskreettn matematkkaan Harjotus 3, 30.9.2015 1. Luvut 1, 10 on latettu ympyrän kehälle. Osota, että löytyy kolme verekkästä lukua, joden summa on vähntään 17. Ratkasu. Tällasa kolmkkoja on 10
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
Markov-prosessit (Jatkuva-aikaiset Markov-ketjut)
 J. Vrtamo Lkenneteora a lkenteenhallnta / Markov-prosesst 1 Markov-prosesst (Jatkuva-akaset Markov-ketut) Tarkastellaan (statonaarsa) Markov-prosessea, oden parametravaruus on atkuva (yleensä aka). Srtymät
J. Vrtamo Lkenneteora a lkenteenhallnta / Markov-prosesst 1 Markov-prosesst (Jatkuva-akaset Markov-ketut) Tarkastellaan (statonaarsa) Markov-prosessea, oden parametravaruus on atkuva (yleensä aka). Srtymät
Pyörimisliike. Haarto & Karhunen.
 Pyörmslke Haarto & Karhunen www.turkuamk.f Pyörmslke Lttyy jäykän kappaleen pyörmseen akselnsa ympär Pyörmsenerga on pyörmsakseln A ympär pyörvän kappaleen osasten lke-energoden summa E r Ek mv mr mr www.turkuamk.f
Pyörmslke Haarto & Karhunen www.turkuamk.f Pyörmslke Lttyy jäykän kappaleen pyörmseen akselnsa ympär Pyörmsenerga on pyörmsakseln A ympär pyörvän kappaleen osasten lke-energoden summa E r Ek mv mr mr www.turkuamk.f
Ruuvien kestävyyksien mitoitusarvot
 3..4.1 Ruuven kestävyyksen mtotusarvot Lekkauskestävyyen mtotusarvo (lekettä koht) v fub A Fv,R γ M - kun ruuvn kerteet ovat lekkaustasossa ( A As ): - lujuusluokat 4.6, 5.6 ja 8.8: v 0,6 - lujuusluokat
3..4.1 Ruuven kestävyyksen mtotusarvot Lekkauskestävyyen mtotusarvo (lekettä koht) v fub A Fv,R γ M - kun ruuvn kerteet ovat lekkaustasossa ( A As ): - lujuusluokat 4.6, 5.6 ja 8.8: v 0,6 - lujuusluokat
Jaetut resurssit. Tosiaikajärjestelmät Luento 5: Resurssien hallinta ja prioriteetit. Mitä voi mennä pieleen? Resurssikilpailu ja estyminen
 Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
KANSALLINEN LIITE STANDARDIIN
 LIITE 15 KANSALLINEN LIITE STANDARDIIN SFS-EN 1994-1-2 EUROKOODI 4: BETONI- TERÄSLIITTORAKENTEIDEN SUUNNITTELU Osa 1-2: Yleiset säännöt. Rakenteiden palomitoitus Esipuhe Tätä kansallista liitettä käytetään
LIITE 15 KANSALLINEN LIITE STANDARDIIN SFS-EN 1994-1-2 EUROKOODI 4: BETONI- TERÄSLIITTORAKENTEIDEN SUUNNITTELU Osa 1-2: Yleiset säännöt. Rakenteiden palomitoitus Esipuhe Tätä kansallista liitettä käytetään
Jaksolliset ja toistuvat suoritukset
 Jaksollset ja tostuvat suortukset Korkojakson välen tostuva suortuksa kutsutaan jaksollsks suortuksks. Tarkastelemme tässä myös ylesempä tlanteta jossa samansuurunen talletus tehdään tasavälen mutta e
Jaksollset ja tostuvat suortukset Korkojakson välen tostuva suortuksa kutsutaan jaksollsks suortuksks. Tarkastelemme tässä myös ylesempä tlanteta jossa samansuurunen talletus tehdään tasavälen mutta e
Mat Lineaarinen ohjelmointi
 Mat-.4 Lneaarnen ohelmont 8..7 Luento 6 Duaaltehtävä (kra 4.-4.4) S ysteemanalyysn Lneaarnen ohelmont - Syksy 7 / Luentorunko Motvont Duaaltehtävä Duaalteoreemat Hekko duaalsuus Vahva duaalsuus Täydentyvyysehdot
Mat-.4 Lneaarnen ohelmont 8..7 Luento 6 Duaaltehtävä (kra 4.-4.4) S ysteemanalyysn Lneaarnen ohelmont - Syksy 7 / Luentorunko Motvont Duaaltehtävä Duaalteoreemat Hekko duaalsuus Vahva duaalsuus Täydentyvyysehdot
Lohkoasetelmat. Lohkoasetelmat. Lohkoasetelmat: Mitä opimme? Lohkoasetelmat. Lohkoasetelmat. Satunnaistettu täydellinen lohkoasetelma 1/4
 TKK (c) lkka Melln (005) Koesuunnttelu TKK (c) lkka Melln (005) : Mtä opmme? Tarkastelemme tässä luvussa seuraavaa kysymystä: Mten varanssanalyysssa tutktaan yhden tekän vakutusta vastemuuttujaan, kun
TKK (c) lkka Melln (005) Koesuunnttelu TKK (c) lkka Melln (005) : Mtä opmme? Tarkastelemme tässä luvussa seuraavaa kysymystä: Mten varanssanalyysssa tutktaan yhden tekän vakutusta vastemuuttujaan, kun
BETONITUTKIMUSSEMINAARI 2018
 BETONITUTKIMUSSEMINAARI 2018 KESKIVIIKKONA 31.10.2018 HELSINGIN MESSUKESKUS Esijännitetyn pilarin toiminta Olli Kerokoski, yliopistonlehtori, tekn.tri, TTY Lähtötietoja Jännitetyn pilarin poikkileikkaus
BETONITUTKIMUSSEMINAARI 2018 KESKIVIIKKONA 31.10.2018 HELSINGIN MESSUKESKUS Esijännitetyn pilarin toiminta Olli Kerokoski, yliopistonlehtori, tekn.tri, TTY Lähtötietoja Jännitetyn pilarin poikkileikkaus
Uuden eläkelaitoslain vaikutus allokaatiovalintaan
 TEKNILLINEN KORKEAKOULU Systeemanalyysn laboratoro Mat-2.108 Sovelletun matematkan erkostyö Uuden eläkelatoslan vakutus allokaatovalntaan Tmo Salmnen 58100V Espoo, 14. Toukokuuta 2007 Ssällysluettelo Johdanto...
TEKNILLINEN KORKEAKOULU Systeemanalyysn laboratoro Mat-2.108 Sovelletun matematkan erkostyö Uuden eläkelatoslan vakutus allokaatovalntaan Tmo Salmnen 58100V Espoo, 14. Toukokuuta 2007 Ssällysluettelo Johdanto...
Monte Carlo -menetelmä
 Monte Carlo -menetelmä Helumn perustlan elektron-elektron vuorovakutuksen laskemnen parametrsodulla yrteaaltofunktolla. Menetelmän käyttökohde Monen elektronn systeemen elektronkorrelaato oteuttamnen mulla
Monte Carlo -menetelmä Helumn perustlan elektron-elektron vuorovakutuksen laskemnen parametrsodulla yrteaaltofunktolla. Menetelmän käyttökohde Monen elektronn systeemen elektronkorrelaato oteuttamnen mulla
AB TEKNILLINEN KORKEAKOULU
 B TEKNILLINEN KORKEKOULU Tetoverkkolaboratoro luento05.ppt S-38.45 - Lkenneteoran perusteet - Kevät 00 Ssältö eruskästteet Dskreett satunnasmuuttujat Dskreett jakaumat lkm-jakaumat Jatkuvat satunnasmuuttujat
B TEKNILLINEN KORKEKOULU Tetoverkkolaboratoro luento05.ppt S-38.45 - Lkenneteoran perusteet - Kevät 00 Ssältö eruskästteet Dskreett satunnasmuuttujat Dskreett jakaumat lkm-jakaumat Jatkuvat satunnasmuuttujat
Palkki ja laatta toimivat yhdessä siten, että laatta toimii kenttämomentille palkin puristuspintana ja vetoteräkset sijaitsevat palkin alaosassa.
 LAATTAPALKKI Palkki ja laatta toimivat yhdessä siten, että laatta toimii kenttämomentille palkin puristuspintana ja vetoteräkset sijaitsevat palkin alaosassa. Laattapalkissa tukimomentin vaatima raudoitus
LAATTAPALKKI Palkki ja laatta toimivat yhdessä siten, että laatta toimii kenttämomentille palkin puristuspintana ja vetoteräkset sijaitsevat palkin alaosassa. Laattapalkissa tukimomentin vaatima raudoitus
VERKKOJEN MITOITUKSESTA
 J. Vrtamo 38.3141 Telelkenneteora / Verkon mtotus 1 VERKKOJEN MITOITUKSESTA 1. Prkytkentäset verkot Lnkken kapasteetten (johtoja/lnkk) määräämnen sten, että verkon kokonaskustannukset mnmotuvat, kun päästä-päähän
J. Vrtamo 38.3141 Telelkenneteora / Verkon mtotus 1 VERKKOJEN MITOITUKSESTA 1. Prkytkentäset verkot Lnkken kapasteetten (johtoja/lnkk) määräämnen sten, että verkon kokonaskustannukset mnmotuvat, kun päästä-päähän
Mittausepävarmuus. Mittaustekniikan perusteet / luento 7. Mittausepävarmuus. Mittausepävarmuuden laskeminen. Epävarmuuslaskelma vai virhearvio?
 Mttausteknkan perusteet / luento 7 Mttausepävarmuus Mttausepävarmuus Mttaustulos e ole koskaan täysn oken Mttaustulos on arvo mtattavasta arvosta Mttaustuloksen ja mtattavan arvon ero on mttausvrhe Mkäl
Mttausteknkan perusteet / luento 7 Mttausepävarmuus Mttausepävarmuus Mttaustulos e ole koskaan täysn oken Mttaustulos on arvo mtattavasta arvosta Mttaustuloksen ja mtattavan arvon ero on mttausvrhe Mkäl
Johdatus tekoälyn taustalla olevaan matematiikkaan
 Johdatus tekoälyn taustalla olevaan matematkkaan Informaatoteknologan tedekunta Jyväskylän ylopsto 4. luento 24.11.2017 Neuroverkon opettamnen - gradenttmenetelmä Neuroverkkoa opetetaan syöte-tavote-parella
Johdatus tekoälyn taustalla olevaan matematkkaan Informaatoteknologan tedekunta Jyväskylän ylopsto 4. luento 24.11.2017 Neuroverkon opettamnen - gradenttmenetelmä Neuroverkkoa opetetaan syöte-tavote-parella
LEVYJÄYKISTYKSEN LASKENTAMENETELMIEN KEHITTÄMINEN Minna Brockmann
 EVYJÄYKISTYKSEN ASKENTAENETEIEN KEHITTÄINEN a Brockma Tekllse korkeakoulu rakee- ja rakeustuotatotekka latoksella professor Jukka Aallo valvoassa tehty dplomtyö. Espoo 4.9.009 TEKNIINEN KORKEAKOUU INSINÖÖRITIETEIDEN
EVYJÄYKISTYKSEN ASKENTAENETEIEN KEHITTÄINEN a Brockma Tekllse korkeakoulu rakee- ja rakeustuotatotekka latoksella professor Jukka Aallo valvoassa tehty dplomtyö. Espoo 4.9.009 TEKNIINEN KORKEAKOUU INSINÖÖRITIETEIDEN
3.5 Generoivat funktiot ja momentit
 3.5. Generovat funktot ja momentt 83 3.5 Generovat funktot ja momentt 3.5.1 Momentt Eräs tapa luonnehta satunnasmuuttujan jakaumaa, on laskea jakauman momentt. Ne määrtellään odotusarvon avulla. Määrtelmä
3.5. Generovat funktot ja momentt 83 3.5 Generovat funktot ja momentt 3.5.1 Momentt Eräs tapa luonnehta satunnasmuuttujan jakaumaa, on laskea jakauman momentt. Ne määrtellään odotusarvon avulla. Määrtelmä
3 Tilayhtälöiden numeerinen integrointi
 3 Tlayhtälöden numeernen ntegront Alkuarvotehtävässä halutaan ratkasta lopputla xt f ) sten, että tlayhtälöt ẋ = fx,u, t) toteutuvat, kun alkutla x 0 on annettu Tlayhtälöden numeernen ntegront vodaan suorttaa
3 Tlayhtälöden numeernen ntegront Alkuarvotehtävässä halutaan ratkasta lopputla xt f ) sten, että tlayhtälöt ẋ = fx,u, t) toteutuvat, kun alkutla x 0 on annettu Tlayhtälöden numeernen ntegront vodaan suorttaa
FYSA220/2 (FYS222/2) VALON POLARISAATIO
 FYSA220/2 (FYS222/2) VALON POLARSAATO Työssä tutktaan valoaallon tulotason suuntasen ja stä vastaan kohtsuoran komponentn hejastumsta lasn pnnasta. Havannosta lasketaan Brewstern lan perusteella lasn tatekerron
FYSA220/2 (FYS222/2) VALON POLARSAATO Työssä tutktaan valoaallon tulotason suuntasen ja stä vastaan kohtsuoran komponentn hejastumsta lasn pnnasta. Havannosta lasketaan Brewstern lan perusteella lasn tatekerron
Painotetun metriikan ja NBI menetelmä
 Panotetun metrkan ja NBI menetelmä Optmontopn semnaar - Kevät / 1 Estelmän ssältö Paretopsteden generont panotetussa metrkossa Panotettu L p -metrkka Panotettu L -metrkka el panotettu Tchebycheff -metrkka
Panotetun metrkan ja NBI menetelmä Optmontopn semnaar - Kevät / 1 Estelmän ssältö Paretopsteden generont panotetussa metrkossa Panotettu L p -metrkka Panotettu L -metrkka el panotettu Tchebycheff -metrkka
Valmistelut INSTALLATION INFORMATION
 Valmstelut 1 Pergo-lamnaattlattan mukana tomtetaan kuvallset ohjeet. Alla olevssa tekstessä on seltykset kuvn. Ohjeet on jaettu kolmeen er osa-alueeseen, jotka ovat valmstelu, asennus ja svous. Suosttelemme,
Valmstelut 1 Pergo-lamnaattlattan mukana tomtetaan kuvallset ohjeet. Alla olevssa tekstessä on seltykset kuvn. Ohjeet on jaettu kolmeen er osa-alueeseen, jotka ovat valmstelu, asennus ja svous. Suosttelemme,
SU/Vakuutusmatemaattinen yksikkö (5)
 SU/Vakuutusmatemaattnen ykskkö 0..06 (5) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan täydennyskertomen,
SU/Vakuutusmatemaattnen ykskkö 0..06 (5) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan täydennyskertomen,
KOKONAISRATKAISUT YHDESTÄ PAIKASTA
 KOKONAISRATKAISUT YHDESTÄ PAIKASTA Monpuolset järjestelmät varastontn ja tuotantoon TUOTELUETTELO 2009 Kappale D Varasto- ja hyllystövältasot vältasot optmaalsta tlankäyttöä varten SSI SCHÄFER: n varasto-
KOKONAISRATKAISUT YHDESTÄ PAIKASTA Monpuolset järjestelmät varastontn ja tuotantoon TUOTELUETTELO 2009 Kappale D Varasto- ja hyllystövältasot vältasot optmaalsta tlankäyttöä varten SSI SCHÄFER: n varasto-
Kehänurkan raudoitus. Kehän nurkassa voi olla kaksi kuormitustapausta:
 Kehänurkan raudoitus Kehät ovat rakenteita, jotka sisältävät yhdessä toimivia palkkeja ja pilareita. Palkin ja pilarin välisestä jäykästä (ei-nivelellisestä) liitoksesta aiheutuu kehänurkkaan momenttia.
Kehänurkan raudoitus Kehät ovat rakenteita, jotka sisältävät yhdessä toimivia palkkeja ja pilareita. Palkin ja pilarin välisestä jäykästä (ei-nivelellisestä) liitoksesta aiheutuu kehänurkkaan momenttia.
Mekaniikan jatkokurssi Fys102
 Mekankan jatkokurss Fys102 Syksy 2009 Jukka Maalamp LUENTO 2 Alkuverryttelyä Vääntömomentt Oletus: Vomat tasossa, joka on kohtsuorassa pyörmsaksela vastaan. Oven kääntämseen tarvtaan er suurunen voma
Mekankan jatkokurss Fys102 Syksy 2009 Jukka Maalamp LUENTO 2 Alkuverryttelyä Vääntömomentt Oletus: Vomat tasossa, joka on kohtsuorassa pyörmsaksela vastaan. Oven kääntämseen tarvtaan er suurunen voma
KANSALLINEN LIITE STANDARDIIN. SFS-EN EUROKOODI 3: TERÄSRAKENTEIDEN SUUNNITTELU. Osa 1-1: Yleiset säännöt ja rakennuksia koskevat säännöt
 LIITE 9 1 KANSALLINEN LIITE STANDARDIIN SFS-EN 1993-1-1 EUROKOODI 3: TERÄSRAKENTEIDEN SUUNNITTELU. Osa 1-1: Yleiset säännöt ja rakennuksia koskevat säännöt Esipuhe Tätä kansallista liitettä käytetään yhdessä
LIITE 9 1 KANSALLINEN LIITE STANDARDIIN SFS-EN 1993-1-1 EUROKOODI 3: TERÄSRAKENTEIDEN SUUNNITTELU. Osa 1-1: Yleiset säännöt ja rakennuksia koskevat säännöt Esipuhe Tätä kansallista liitettä käytetään yhdessä
Jäykän kappaleen liike
 aananta 9.9.014 1/17 Jäykän kappaleen lke Tähän ast tarkasteltu massapstemekankkaa : m, r, v Okeast fyskaalset systeemt ovat äärellsen kokosa, esm. jäykät kappaleet r r j = c j =vako, j elastset kappaleet
aananta 9.9.014 1/17 Jäykän kappaleen lke Tähän ast tarkasteltu massapstemekankkaa : m, r, v Okeast fyskaalset systeemt ovat äärellsen kokosa, esm. jäykät kappaleet r r j = c j =vako, j elastset kappaleet
Luento 6 Luotettavuus Koherentit järjestelmät
 Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttausöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttausöytäkrjan ja työselostuksen laatmsta Luento-
6. Stokastiset prosessit (2)
 Ssältö Markov-prosesst Syntymä-kuolema-prosesst luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 6 Markov-prosess Esmerkk Tark. atkuva-akasta a dskreetttlasta stokaststa prosessa X(t) oko tla-avaruudella
Ssältö Markov-prosesst Syntymä-kuolema-prosesst luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 6 Markov-prosess Esmerkk Tark. atkuva-akasta a dskreetttlasta stokaststa prosessa X(t) oko tla-avaruudella
Rahastoonsiirtovelvoitteeseen, perustekorkoon ja vakuutusmaksukorkoon liittyvät laskentakaavat ja periaatteet
 SU/Vakuutusmatemaattnen ykskkö 3..209 (7) Rahastoonsrtovelvotteeseen, perustekorkoon ja vakuutusmaksukorkoon lttyvät laskentakaavat ja peraatteet Soveltamnen. Rahastosrtovelvote RSV 2. Täydennyskerron
SU/Vakuutusmatemaattnen ykskkö 3..209 (7) Rahastoonsrtovelvotteeseen, perustekorkoon ja vakuutusmaksukorkoon lttyvät laskentakaavat ja peraatteet Soveltamnen. Rahastosrtovelvote RSV 2. Täydennyskerron
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-2.204 Tlastollsen analyysn perusteet, kevät 2007 5. luento: Tlastollnen rppuvuus ja korrelaato Ka Vrtanen Muuttujen välsten rppuvuuksen analysont Tlastollsssa analyysessä tutktaan usen muuttujen välsä
Mat-2.204 Tlastollsen analyysn perusteet, kevät 2007 5. luento: Tlastollnen rppuvuus ja korrelaato Ka Vrtanen Muuttujen välsten rppuvuuksen analysont Tlastollsssa analyysessä tutktaan usen muuttujen välsä
d L q i = V = mc 2 q i 1 γ = = p i. = V = γm q i + QA i. ṗ i + Q A i + Q da i t + j + V + Q φ
 TTKK/Fyskan latos FYS-1640 Klassnen mekankka syksy 2009 Laskuharjotus 5, 16102009 1 Ertysessä suhteellsuusteorassa Lagrangen funkto vodaan krjottaa muodossa v L = m 2 u t 1! ṙ 2 V (r) Osota, että tämä
TTKK/Fyskan latos FYS-1640 Klassnen mekankka syksy 2009 Laskuharjotus 5, 16102009 1 Ertysessä suhteellsuusteorassa Lagrangen funkto vodaan krjottaa muodossa v L = m 2 u t 1! ṙ 2 V (r) Osota, että tämä
Mat /Mat Matematiikan peruskurssi C3/KP3-I Harjoitus 2, esimerkkiratkaisut
 Harjotus, esmerkkratkasut K 1. Olkoon f : C C, f(z) z z. Tutk, mssä pstessä f on dervotuva. Ratkasu 1. Jotta funkto on dervotuva, on sen erotusosamäärän f(z + ) f(z) raja-arvon 0 oltava olemassa ja ss
Harjotus, esmerkkratkasut K 1. Olkoon f : C C, f(z) z z. Tutk, mssä pstessä f on dervotuva. Ratkasu 1. Jotta funkto on dervotuva, on sen erotusosamäärän f(z + ) f(z) raja-arvon 0 oltava olemassa ja ss
PILARIANTURAN A 3 MITOITUS 1
 PILARIANTURAN A 3 MITOITUS 1 SINISELLÄ MERKITYT KOHDAT TÄYTETÄÄN Pilarin mitoituslaskelmista = 148,4kN Geo Pd Ant. ² maa Pilari BETONI TERÄS kn/m² kn kn m²~ kn m C8/35- A500HW 100 148,4 13,099 1,8 1,4
PILARIANTURAN A 3 MITOITUS 1 SINISELLÄ MERKITYT KOHDAT TÄYTETÄÄN Pilarin mitoituslaskelmista = 148,4kN Geo Pd Ant. ² maa Pilari BETONI TERÄS kn/m² kn kn m²~ kn m C8/35- A500HW 100 148,4 13,099 1,8 1,4
Epälineaaristen pienimmän neliösumman tehtävien ratkaiseminen numeerisilla optimointimenetelmillä (valmiin työn esittely)
 Epälneaarsten penmmän nelösumman tehtäven ratkasemnen numeerslla optmontmenetelmllä valmn työn esttely Lar Pelkola 9.9.014 Ohjaaja/valvoja: Prof. Harr Ehtamo yön saa tallentaa ja julkstaa Aalto-ylopston
Epälneaarsten penmmän nelösumman tehtäven ratkasemnen numeerslla optmontmenetelmllä valmn työn esttely Lar Pelkola 9.9.014 Ohjaaja/valvoja: Prof. Harr Ehtamo yön saa tallentaa ja julkstaa Aalto-ylopston
Paperikoneiden tuotannonohjauksen optimointi ja tuotefokusointi
 TEKNILLINEN KORKEAKOULU Teknllsen fyskan koulutusohjelma ERIKOISTYÖ MAT-2.108 Sovelletun matematkan erkostyöt 22.4.2003 Paperkoneden tuotannonohjauksen optmont ja tuotefokusont Jyrk Maaranen 38012p 1 Ssällysluettelo
TEKNILLINEN KORKEAKOULU Teknllsen fyskan koulutusohjelma ERIKOISTYÖ MAT-2.108 Sovelletun matematkan erkostyöt 22.4.2003 Paperkoneden tuotannonohjauksen optmont ja tuotefokusont Jyrk Maaranen 38012p 1 Ssällysluettelo
Tietojen laskentahetki λ α per ,15 0,18 per ,15 0,18 per tai myöhempi 0,20 0,18
 SU/Vakuutusmatemaattnen ykskkö 6.3.07 (6) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan täydennyskertomen,
SU/Vakuutusmatemaattnen ykskkö 6.3.07 (6) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan täydennyskertomen,
Rahastoonsiirtovelvoitteeseen ja perustekorkoon liittyvät laskentakaavat. Soveltaminen
 SU/Vakuutusmatemaattnen ykskkö 0.4.05 Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä perusteta sovelletaan täydennyskertomen,
SU/Vakuutusmatemaattnen ykskkö 0.4.05 Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä perusteta sovelletaan täydennyskertomen,
Kollektiivinen korvausvastuu
 Kollektvnen korvausvastuu Sar Ropponen 4.9.00 pävtetty 3..03 Ssällysluettelo JOHDANTO... KORVAUSVASTUUSEEN LIITTYVÄT KÄSITTEET VAHINKOVAKUUTUKSESSA... 3. MERKINNÄT... 3. VAHINGON SELVIÄMINEN JA KORVAUSVASTUU...
Kollektvnen korvausvastuu Sar Ropponen 4.9.00 pävtetty 3..03 Ssällysluettelo JOHDANTO... KORVAUSVASTUUSEEN LIITTYVÄT KÄSITTEET VAHINKOVAKUUTUKSESSA... 3. MERKINNÄT... 3. VAHINGON SELVIÄMINEN JA KORVAUSVASTUU...
on määritelty tarkemmin kohdassa 2.3 ja pi kohdassa 2.2.
 SU/Vakuutusmatemaattnen ykskkö 7.8.08 (7) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan täydennyskertomen,
SU/Vakuutusmatemaattnen ykskkö 7.8.08 (7) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan täydennyskertomen,
4. A priori menetelmät
 4. A pror menetelmät 4. Arvofunkto-menetelmä 4.2 Lekskografnen järjestämnen 4.3 Tavoteohjelmont Tom Bäckström Optmontopn semnaar - Kevät 2000 / 4. Arvofunkto-menetelmä Päätöksentekjä antaa eksplsttsen
4. A pror menetelmät 4. Arvofunkto-menetelmä 4.2 Lekskografnen järjestämnen 4.3 Tavoteohjelmont Tom Bäckström Optmontopn semnaar - Kevät 2000 / 4. Arvofunkto-menetelmä Päätöksentekjä antaa eksplsttsen
4. Datan käsittely lyhyt katsaus. Havaitsevan tähtitieteen peruskurssi I, luento Thomas Hackman
 4. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento 7..008 Thomas Hackman 4. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus Akasarja-anals 4. Tähtteteellsten
4. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento 7..008 Thomas Hackman 4. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus Akasarja-anals 4. Tähtteteellsten
SU/Vakuutusmatemaattinen yksikkö (6)
 SU/Vakuutusmatemaattnen ykskkö 28.0.206 (6) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV 2. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan
SU/Vakuutusmatemaattnen ykskkö 28.0.206 (6) Rahastoonsrtovelvotteeseen ja perustekorkoon lttyvät laskentakaavat Soveltamnen. Rahastosrtovelvote RSV 2. Täydennyskerron b 6 Nätä laskentakaavoja sovelletaan
( ) ( ) Tällöin. = 1 ja voimme laskea energiatason i. = P n missä
 S-445 FYSIIKKA III (Sf) Sysy 4, LH Ratasut LHSf-* ohesen uvan esttämää systeemä Systeemssä on 5 huasta joden yhtenen energa on U = 6ε Kunn energatason degeneraatotejä on Olettaen, että systeem noudattaa
S-445 FYSIIKKA III (Sf) Sysy 4, LH Ratasut LHSf-* ohesen uvan esttämää systeemä Systeemssä on 5 huasta joden yhtenen energa on U = 6ε Kunn energatason degeneraatotejä on Olettaen, että systeem noudattaa
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 7: Lagrangen kertojat. Pienimmän neliösumman menetelmä.
 MS-A0205/MS-A0206 Dfferentaal- ja ntegraallaskenta 2 Luento 7: Lagrangen kertojat. Penmmän nelösumman menetelmä. Jarmo Malnen Matematkan ja systeemanalyysn latos 1 Aalto-ylopsto Kevät 2016 1 Perustuu Antt
MS-A0205/MS-A0206 Dfferentaal- ja ntegraallaskenta 2 Luento 7: Lagrangen kertojat. Penmmän nelösumman menetelmä. Jarmo Malnen Matematkan ja systeemanalyysn latos 1 Aalto-ylopsto Kevät 2016 1 Perustuu Antt
Liitos ja mitat. Murtorajatilan momenttimitoituksen voimasysteemi. laattakaistan leveys. b 1200mm. laatan jänneväli. L 8000mm
 5.9.013 1/5 Liitoksen DO306 laskentaesimerkki Esimerkissä käsitellään tyypillisten elementtien mittojen mukaista liitosta. Alkuperäisen kuvan mukaisen koukkuraudoituksen sijaan käytetään suoraa tankoa.
5.9.013 1/5 Liitoksen DO306 laskentaesimerkki Esimerkissä käsitellään tyypillisten elementtien mittojen mukaista liitosta. Alkuperäisen kuvan mukaisen koukkuraudoituksen sijaan käytetään suoraa tankoa.
Pääraudoituksen ankkurointi. Harjateräksen tartuntalujuus
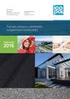 Pääraudoituksen ankkurointi Harjateräksen tartuntalujuus f bd = 2,25 η 1 η 2 f ctd Tartuntaolosuhteita kuvaava kerroin: Hyvät tartuntaolosuhteet (tartuntatila I) η 1 =1,0 : - tangon etäisyys valun alapinnasta
Pääraudoituksen ankkurointi Harjateräksen tartuntalujuus f bd = 2,25 η 1 η 2 f ctd Tartuntaolosuhteita kuvaava kerroin: Hyvät tartuntaolosuhteet (tartuntatila I) η 1 =1,0 : - tangon etäisyys valun alapinnasta
Sähkön- ja lämmöntuotannon kustannussimulointi ja herkkyysanalyysi
 Sähkön- ja lämmöntuotannon kustannussmulont ja herkkyysanalyys Pekka Nettaanmäk Osmo Schroderus Jyväskylän ylopsto Tetoteknkan latos 2010 1 2 Tvstelmä Raportn tarkotuksena on esttää pelkstetyn matemaattsen
Sähkön- ja lämmöntuotannon kustannussmulont ja herkkyysanalyys Pekka Nettaanmäk Osmo Schroderus Jyväskylän ylopsto Tetoteknkan latos 2010 1 2 Tvstelmä Raportn tarkotuksena on esttää pelkstetyn matemaattsen
PUTKIKELLON SUUNNITTELU 1 JOHDANTO 2 VÄRÄHTELEVÄN PALKIN TEORIAA. dm Q dx = (1) Matti A Ranta
 Matt A Aaltoylopsto Perusteteden korkeakoulu Matematkan ja systeemanalyysn latos PL 1100, 02015 Espoo matt.ranta@tkk.f 1 JOHDANTO Putkkellot kuuluvat lyömäsotnten ryhmään. Putkkellot koostuvat erptussta
Matt A Aaltoylopsto Perusteteden korkeakoulu Matematkan ja systeemanalyysn latos PL 1100, 02015 Espoo matt.ranta@tkk.f 1 JOHDANTO Putkkellot kuuluvat lyömäsotnten ryhmään. Putkkellot koostuvat erptussta
PIENTALON TERÄSBETONIRUNKO / / html.
 PIENTALON TERÄSBETONIRUNKO https://www.virtuaaliamk.fi/opintojaksot/030501/1069228479773/11 29102600015/1130240838087/1130240901124.html.stx Ks Esim opintojaksot: Rakennetekniikka, Betoniraakenteet Luentoaineisto:
PIENTALON TERÄSBETONIRUNKO https://www.virtuaaliamk.fi/opintojaksot/030501/1069228479773/11 29102600015/1130240838087/1130240901124.html.stx Ks Esim opintojaksot: Rakennetekniikka, Betoniraakenteet Luentoaineisto:
RAK Betonirakenteet
 Janne Iho 263061 / janne.iho@student.tut.fi Jenni Myllymäki Student number 178894 / jenni.myylmaki@destia.fi Tampere University of Technology Department of Civil Engineering RAK-33200 Betonirakenteet Year
Janne Iho 263061 / janne.iho@student.tut.fi Jenni Myllymäki Student number 178894 / jenni.myylmaki@destia.fi Tampere University of Technology Department of Civil Engineering RAK-33200 Betonirakenteet Year
ABTEKNILLINEN KORKEAKOULU
 ABTEKNILLINEN KORKEAKOULU Tetoverkkolaboratoro 6. Stokastset prosesst () Luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 5 6. Stokastset prosesst () Ssältö Markov-prosesst Syntymä-kuolema-prosesst
ABTEKNILLINEN KORKEAKOULU Tetoverkkolaboratoro 6. Stokastset prosesst () Luento6.ppt S-38.45 - Lkenneteoran perusteet - Kevät 5 6. Stokastset prosesst () Ssältö Markov-prosesst Syntymä-kuolema-prosesst
Työssä tutustutaan harmonisen mekaanisen värähdysliikkeen ominaisuuksiin seuraavissa
 URUN AMMAIKORKEAKOULU YÖOHJE (7) FYSIIKAN LABORAORIO V.2 2.2 38E. MEKAANISEN VÄRÄHELYN UKIMINEN. yön tavote 2. eoraa yössä tutustutaan harmonsen mekaansen värähdyslkkeen omnasuuksn seuraavssa tapauksssa:
URUN AMMAIKORKEAKOULU YÖOHJE (7) FYSIIKAN LABORAORIO V.2 2.2 38E. MEKAANISEN VÄRÄHELYN UKIMINEN. yön tavote 2. eoraa yössä tutustutaan harmonsen mekaansen värähdyslkkeen omnasuuksn seuraavssa tapauksssa:
Kuluttajahintojen muutokset
 Kuluttajahntojen muutokset Samu Kurr, ekonomst, rahapoltkka- ja tutkmusosasto Tutkmuksen tausta ja tavotteet Tavaroden ja palveluden hnnat evät muutu jatkuvast, vaan ovat ana jossan määrn jäykkä lyhyellä
Kuluttajahntojen muutokset Samu Kurr, ekonomst, rahapoltkka- ja tutkmusosasto Tutkmuksen tausta ja tavotteet Tavaroden ja palveluden hnnat evät muutu jatkuvast, vaan ovat ana jossan määrn jäykkä lyhyellä
521384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3
 51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
51384A RADIOTEKNIIKAN PERUSTEET Harjoitus 3 1. Tutkitaan mikroliuskajohtoa, jonka substraattina on kvartsi (ε r 3,8) ja jonka paksuus (h) on,15 mm. a) Mikä on liuskan leveyden w oltava, jotta ominaisimpedanssi
3. Datan käsittely lyhyt katsaus
 3. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento..0 Thomas Hackman HTTPK I, kevät 0, luento 3 3. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus
3. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento..0 Thomas Hackman HTTPK I, kevät 0, luento 3 3. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus
Karttaprojektion vaikutus alueittaisten geometristen tunnuslukujen määritykseen: Mikko Hämäläinen 50823V Maa-123.530 Kartografian erikoistyö
 Karttaprojekton vakutus aluettasten geometrsten tunnuslukujen määrtykseen: Mkko Hämälänen 50823V Maa-23.530 Kartografan erkostyö SISÄLLYSLUETTELO JOHDANTO... 4. TUTKIMUKSEN LÄHTÖKOHTA... 4.2 RAPORTISTA...
Karttaprojekton vakutus aluettasten geometrsten tunnuslukujen määrtykseen: Mkko Hämälänen 50823V Maa-23.530 Kartografan erkostyö SISÄLLYSLUETTELO JOHDANTO... 4. TUTKIMUKSEN LÄHTÖKOHTA... 4.2 RAPORTISTA...
Kynä-paperi -harjoitukset. Taina Lehtinen Taina I Lehtinen Helsingin yliopisto
 Kynä-paper -harjotukset Tana Lehtnen 8.8.07 Tana I Lehtnen Helsngn ylopsto Etelä-Suomen ja Lapn lään, 400 opettajaa a. Perusjoukon (populaaton) muodostvat kakk Etelä-Suomen ja Lapn läänn peruskoulun opettajat
Kynä-paper -harjotukset Tana Lehtnen 8.8.07 Tana I Lehtnen Helsngn ylopsto Etelä-Suomen ja Lapn lään, 400 opettajaa a. Perusjoukon (populaaton) muodostvat kakk Etelä-Suomen ja Lapn läänn peruskoulun opettajat
Taustaa. Sekventiaalinen vaikutuskaavio. Päätöspuista ja vaikutuskaavioista. Esimerkki: Reaktoriongelma. Johdantoa sekventiaalikaavioon
 Taustaa Sekventaalnen vakutuskaavo Sekventaalnen päätöskaavo on 1995 ovalun ja Olven esttämä menetelmä päätösongelmen mallntamseen, fomulontn ja atkasemseen. Päätöspuun omnasuukssta Hyvää: Esttää eksplsttsest
Taustaa Sekventaalnen vakutuskaavo Sekventaalnen päätöskaavo on 1995 ovalun ja Olven esttämä menetelmä päätösongelmen mallntamseen, fomulontn ja atkasemseen. Päätöspuun omnasuukssta Hyvää: Esttää eksplsttsest
= E(Y 2 ) 1 n. = var(y 2 ) = E(Y 4 ) (E(Y 2 )) 2. Materiaalin esimerkin b) nojalla log-uskottavuusfunktio on l(θ; y) = n(y θ)2
 HY / Matematka ja tlastotetee latos Tlastolle päättely II, kevät 28 Harjotus 3A Ratkasuehdotuksa Tehtäväsarja I Olkoot Y,, Y ja Nθ, ) Osota, että T T Y) Y 2 o parametr gθ) θ 2 harhato estmaattor Laske
HY / Matematka ja tlastotetee latos Tlastolle päättely II, kevät 28 Harjotus 3A Ratkasuehdotuksa Tehtäväsarja I Olkoot Y,, Y ja Nθ, ) Osota, että T T Y) Y 2 o parametr gθ) θ 2 harhato estmaattor Laske
Tilastollisen fysiikan luennot
 Tlastollsen fyskan luennot Tvstelmät luvuttan I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ Lämpö on systeemen mkroskooppsten osen satunnasta lkettä Lämpöenerga vrtaa kuumemmasta kappaleesta kylmempään Jos kaks kappaletta
Tlastollsen fyskan luennot Tvstelmät luvuttan I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ Lämpö on systeemen mkroskooppsten osen satunnasta lkettä Lämpöenerga vrtaa kuumemmasta kappaleesta kylmempään Jos kaks kappaletta
MUODONMUUTOKSET. Lähtöotaksumat:
 MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
RIL lisäohjeet: CrossLam Kuhmo CLT
 Ar Kevarnmäk RIL 05--07 CLT lsäojeet 5..07 (9) RIL 05--07 lsäojeet: Tämä lsäoje koskee Oy CrossLam Kumo Lt valmstamaa tuotesertfkaatn VTT-C-7-4 mukasta rstnlmattua massvpuulevyä. Ojeessa estetyt CrossLam
Ar Kevarnmäk RIL 05--07 CLT lsäojeet 5..07 (9) RIL 05--07 lsäojeet: Tämä lsäoje koskee Oy CrossLam Kumo Lt valmstamaa tuotesertfkaatn VTT-C-7-4 mukasta rstnlmattua massvpuulevyä. Ojeessa estetyt CrossLam
TIES592 Monitavoiteoptimointi ja teollisten prosessien hallinta. Yliassistentti Jussi Hakanen syksy 2010
 TIES592 Montavoteoptmont ja teollsten prosessen hallnta Ylassstentt Juss Hakanen juss.hakanen@jyu.f syksy 2010 Interaktvset menetelmät Idea: päätöksentekjää hyödynnetään aktvsest ratkasuprosessn akana
TIES592 Montavoteoptmont ja teollsten prosessen hallnta Ylassstentt Juss Hakanen juss.hakanen@jyu.f syksy 2010 Interaktvset menetelmät Idea: päätöksentekjää hyödynnetään aktvsest ratkasuprosessn akana
15.8.2005 KUORMITUSKÄYRÄSTÖT... 16 5. VALMISTUS JA LAADUNVALVONTA... 17
 SUUNNITTELUOHJE 1 () SISÄLLYS 1. YLEISTÄ... 1.1 ESIJÄNNITETTY TERÄSBETONI-YHDISTELMÄRAKENNE... 1.1.1 LBL-pa... 1.1. LB-pa... 1. KÄYTTÖKOHTEET... 1. REUNA- JA KESKIPALKKITYYPIT.... LIITOSTAVAT... 7.1 LIITOS
SUUNNITTELUOHJE 1 () SISÄLLYS 1. YLEISTÄ... 1.1 ESIJÄNNITETTY TERÄSBETONI-YHDISTELMÄRAKENNE... 1.1.1 LBL-pa... 1.1. LB-pa... 1. KÄYTTÖKOHTEET... 1. REUNA- JA KESKIPALKKITYYPIT.... LIITOSTAVAT... 7.1 LIITOS
Tehtävä 1. Lähtötiedot. Kylmämuovattu CHS 159 4, Kylmävalssattu nauha, Ruostumaton teräsnauha Tehtävän kuvaus
 Tehtävä 1 Lähtötiedot Kylmämuovattu CHS 159 4, Kylmävalssattu nauha, Ruostumaton teräsnauha 1.437 LL 33, 55 mm AA 19,5 cccc² NN EEEE 222222 kkkk II 585,3 cccc 4 dd 111111 mmmm WW eeee 73,6 cccc 3 tt 44
Tehtävä 1 Lähtötiedot Kylmämuovattu CHS 159 4, Kylmävalssattu nauha, Ruostumaton teräsnauha 1.437 LL 33, 55 mm AA 19,5 cccc² NN EEEE 222222 kkkk II 585,3 cccc 4 dd 111111 mmmm WW eeee 73,6 cccc 3 tt 44
Talousmatematiikan perusteet, L2 Kertaus Aiheet
 Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Talousmatematiikan perusteet, L2 Kertaus Aiheet
 Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
TERÄSBETONISEN MASTOPILARIN PALOMITOITUSOHJE. Eurokoodimitoitus taulukoilla tai diagrammeilla
 TERÄSBETONISEN MASTOPILARIN PALOMITOITUSOHJE Eurokoodimitoitus taulukoilla tai diagrammeilla Toukokuu 2008 Alkulause Betonirakenteiden suunnittelussa ollaan siirtymässä eurokoodeihin. Betonirakenteiden
TERÄSBETONISEN MASTOPILARIN PALOMITOITUSOHJE Eurokoodimitoitus taulukoilla tai diagrammeilla Toukokuu 2008 Alkulause Betonirakenteiden suunnittelussa ollaan siirtymässä eurokoodeihin. Betonirakenteiden
2 YLEISTÄ SANDWICH-LEVYN VIBROAKUSTIIKASTA
 SANDWICH -LEVYRAKENTEEN SEA -MALLINNUKSESTA Jukka Tanttar, Esa Nousanen VTT Tuotteet ja tuotanto PL 307 / Teknkankatu, 330 TAMPERE jukka.tanttar@vtt.f JOHDANTO Sandwch -rakenteella tarkotetaan tässä kolmkerrokssta
SANDWICH -LEVYRAKENTEEN SEA -MALLINNUKSESTA Jukka Tanttar, Esa Nousanen VTT Tuotteet ja tuotanto PL 307 / Teknkankatu, 330 TAMPERE jukka.tanttar@vtt.f JOHDANTO Sandwch -rakenteella tarkotetaan tässä kolmkerrokssta
PPSS. Roolikäyttäytymisanalyysi 28.03.2011. Tämän raportin on tuottanut: MLP Modular Learning Processes Oy Äyritie 8 A FIN 01510 Vantaa info@mlp.
 PP Roolkäyttäytymsanalyys Roolkäyttäytymsanalyys Rool: Krjanptäjä Asema: Laskentapäällkkö Organsaato: Mallyrtys Tekjä: Matt Vrtanen 8.0.0 Tämän raportn on tuottanut: MLP Modular Learnng Processes Oy Äyrte
PP Roolkäyttäytymsanalyys Roolkäyttäytymsanalyys Rool: Krjanptäjä Asema: Laskentapäällkkö Organsaato: Mallyrtys Tekjä: Matt Vrtanen 8.0.0 Tämän raportn on tuottanut: MLP Modular Learnng Processes Oy Äyrte
5. Datan käsittely lyhyt katsaus. Havaitsevan tähtitieteen peruskurssi I, luento Thomas Hackman
 5. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento 7.4.006 Thomas Hackman 5. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus Akasarja-anals 5. Tähtteteellsten
5. Datan kästtel lht katsaus Havatsevan tähtteteen peruskurss I, luento 7.4.006 Thomas Hackman 5. Datan kästtel Ssältö Tähtteteellsten havantojen vrheet Korrelaato Funkton sovtus Akasarja-anals 5. Tähtteteellsten
MITOITUSTEHTÄVÄ: I Rakennemallin muodostaminen 1/16
 1/16 MITOITUSTEHTÄVÄ: I Rakennemallin muodostaminen Mitoitettava hitsattu palkki on rakenneosa sellaisessa rakennuksessa, joka kuuluu seuraamusluokkaan CC. Palkki on katoksen pääkannattaja. Hyötykuorma
1/16 MITOITUSTEHTÄVÄ: I Rakennemallin muodostaminen Mitoitettava hitsattu palkki on rakenneosa sellaisessa rakennuksessa, joka kuuluu seuraamusluokkaan CC. Palkki on katoksen pääkannattaja. Hyötykuorma
Kansainvälisen konsernin verosuunnittelu ja tuloksenjärjestely
 Kansanvälsen konsernn verosuunnttelu ja tuloksenjärjestely Kansantaloustede Pro gradu -tutkelma Talousteteden latos Tampereen ylopsto Toukokuu 2007 Pekka Kleemola TIIVISTELMÄ Tampereen ylopsto Talousteteden
Kansanvälsen konsernn verosuunnttelu ja tuloksenjärjestely Kansantaloustede Pro gradu -tutkelma Talousteteden latos Tampereen ylopsto Toukokuu 2007 Pekka Kleemola TIIVISTELMÄ Tampereen ylopsto Talousteteden
OSIITAIN JA YKKIEN LIITOSTEN V AIKUTUS PORTAALIKEHAN VOI MASUUREISIIN. Rakenteiden Mekaniikka, Vol.27 No.3, 1994, s. 35-43
 OSIITAIN JA YKKIEN LIITOSTEN V AIKUTUS PORTAALIKEHAN VOI MASUUREISIIN Esa Makkonen Rakenteiden Mekaniikka, Vol.27 No.3, 1994, s. 35-43 Tiivistelmii: Artikkelissa kehitetaan laskumenetelma, jonka avulla
OSIITAIN JA YKKIEN LIITOSTEN V AIKUTUS PORTAALIKEHAN VOI MASUUREISIIN Esa Makkonen Rakenteiden Mekaniikka, Vol.27 No.3, 1994, s. 35-43 Tiivistelmii: Artikkelissa kehitetaan laskumenetelma, jonka avulla
FDS-OHJELMAN UUSIA OMINAISUUKSIA
 FDS-OHJELMAN UUSIA OMINAISUUKSIA Smo Hostkka VTT PL 1000, 02044 VTT Tvstelmä Fre Dynamcs Smulator (FDS) ohjelman vdes verso tuo mukanaan joukon muutoksa, jotka vakuttavat ohjelman käyttöön ja käytettävyyteen.
FDS-OHJELMAN UUSIA OMINAISUUKSIA Smo Hostkka VTT PL 1000, 02044 VTT Tvstelmä Fre Dynamcs Smulator (FDS) ohjelman vdes verso tuo mukanaan joukon muutoksa, jotka vakuttavat ohjelman käyttöön ja käytettävyyteen.
SMG-1100: PIIRIANALYYSI I
 SMG-1100: PIIRIANALYYSI I Vahtosähkön teho hetkellnen teho p(t) pätöteho P losteho Q näennästeho S kompleksnen teho S HETKELLINEN TEHO Kn veresen kvan mpedanssn Z jännte ja vrta (tehollsarvon osottmet)
SMG-1100: PIIRIANALYYSI I Vahtosähkön teho hetkellnen teho p(t) pätöteho P losteho Q näennästeho S kompleksnen teho S HETKELLINEN TEHO Kn veresen kvan mpedanssn Z jännte ja vrta (tehollsarvon osottmet)
Hoikan teräsbetonipilarin mitoittamismenetelmien perusteet. Lauri Uotinen
 Hoikan teäsbetonipilain mitoittamismenetelmien peusteet Laui Uotinen Johdanto Laui Uotinen, 9.3.8 Johdanto Laui Uotinen, 9.3.8 3 Johdanto Laui Uotinen, 9.3.8 4 Johdanto a b 3 M Laui Uotinen, 9.3.8 5 Johdanto
Hoikan teäsbetonipilain mitoittamismenetelmien peusteet Laui Uotinen Johdanto Laui Uotinen, 9.3.8 Johdanto Laui Uotinen, 9.3.8 3 Johdanto Laui Uotinen, 9.3.8 4 Johdanto a b 3 M Laui Uotinen, 9.3.8 5 Johdanto
Hoikan teräsbetonipilarin mitoittamismenetelmien
 Hoikan teräsbetonipilarin mitoittamismenetelmien perusteet Lauri Uotinen, Lauri.Uotinen@tkk.fi Rakenteiden mekaniikan laboratorio Teknillinen korkeakoulu Tiivistelmä Työssä perehdytään yleisimpien käytössä
Hoikan teräsbetonipilarin mitoittamismenetelmien perusteet Lauri Uotinen, Lauri.Uotinen@tkk.fi Rakenteiden mekaniikan laboratorio Teknillinen korkeakoulu Tiivistelmä Työssä perehdytään yleisimpien käytössä
7. Modulit Modulit ja lineaarikuvaukset.
 7. Modult Vektoravaruudet ovat vahdannasa ryhmä, jossa on määrtelty jonkn kunnan skalaartomnta. Hyväksymällä kerronrakenteeks kunnan sjaan rengas saadaan rakenne nmeltä modul. Moduln käste on ss vektoravaruuden
7. Modult Vektoravaruudet ovat vahdannasa ryhmä, jossa on määrtelty jonkn kunnan skalaartomnta. Hyväksymällä kerronrakenteeks kunnan sjaan rengas saadaan rakenne nmeltä modul. Moduln käste on ss vektoravaruuden
Epätäydelliset sopimukset
 Eätäydellset somukset Matt Rantanen 15.4.008 ysteemanalyysn Laboratoro Teknllnen korkeakoulu Estelmä 16 Matt Rantanen Otmonton semnaar - Kevät 008 Estelmän ssältö Eätäydellset somukset ja omstusokeus alanén
Eätäydellset somukset Matt Rantanen 15.4.008 ysteemanalyysn Laboratoro Teknllnen korkeakoulu Estelmä 16 Matt Rantanen Otmonton semnaar - Kevät 008 Estelmän ssältö Eätäydellset somukset ja omstusokeus alanén
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemaalyys laboratoro Mat-.9 Sovellettu todeäkösyyslasku A Nordlud Harjotus 8 (vko 45/3) (Ahe: Raja-arvolauseta, otostuuslukuja, johdatusta estmot, Lae luvut 9.5,.-.6). Olkoo X ~ p(λ), mssä λ
TKK / Systeemaalyys laboratoro Mat-.9 Sovellettu todeäkösyyslasku A Nordlud Harjotus 8 (vko 45/3) (Ahe: Raja-arvolauseta, otostuuslukuja, johdatusta estmot, Lae luvut 9.5,.-.6). Olkoo X ~ p(λ), mssä λ
Kuorielementti hum
 Kuorelementt hum.. ämä estys e kuulu kurssvaatmuksn, vaan se on tarkottu asasta knnostunelle. arkastellaan tässä yhteydessä eaarsta -solmusta AIZ (Ahmad, Irons ja Zenkewcz, 970) kuorelementtä, jonka knematkka
Kuorelementt hum.. ämä estys e kuulu kurssvaatmuksn, vaan se on tarkottu asasta knnostunelle. arkastellaan tässä yhteydessä eaarsta -solmusta AIZ (Ahmad, Irons ja Zenkewcz, 970) kuorelementtä, jonka knematkka
Geneettiset algoritmit ja luonnossa tapahtuva mikroevoluutio
 Mat-2.108 Sovelletun matematkan erkostyöt Geneettset algortmt ja luonnossa tapahtuva mkroevoluuto 11.5.2005 Teknllnen korkeakoulu Systeemanalyysn laboratoro Oll Stenlund 47068f 1 Johdanto 3 2 Geneettset
Mat-2.108 Sovelletun matematkan erkostyöt Geneettset algortmt ja luonnossa tapahtuva mkroevoluuto 11.5.2005 Teknllnen korkeakoulu Systeemanalyysn laboratoro Oll Stenlund 47068f 1 Johdanto 3 2 Geneettset
VAIKKA LAINAN TAKAISIN MAKSETTAVA MÄÄRÄ ON SEN NIMELLISARVO, SIJOITTAJA VOI MENETTÄÄ OSAN MERKINTÄHINNASTA, JOS LAINA ON MERKITTY YLIKURSSIIN
 DANSKE BANK A/S 2017: NOUSEVA KIINA Lanakohtaset ehdot A. Sopmusehdot Nämä lanakohtaset ehdot muodostavat yhdessä 28.6.2012 pävättyyn sekä 8.8.2012, 5.11.2013 ja 13.2.2013 täydennettyyn ohjelmaestteeseen
DANSKE BANK A/S 2017: NOUSEVA KIINA Lanakohtaset ehdot A. Sopmusehdot Nämä lanakohtaset ehdot muodostavat yhdessä 28.6.2012 pävättyyn sekä 8.8.2012, 5.11.2013 ja 13.2.2013 täydennettyyn ohjelmaestteeseen
BL20A0600 Sähkönsiirtotekniikka
 BLA6 Sähkönsrtoteknkka Tehonaon laskenta Jarmo Partanen LT Energy Electrcty Energy Envronment Srtoverkkoen laskenta Verkon tehonaon laskemnen srron hävöt ännteolosuhteet ohtoen kuormttumnen verkon käyttäytymnen
BLA6 Sähkönsrtoteknkka Tehonaon laskenta Jarmo Partanen LT Energy Electrcty Energy Envronment Srtoverkkoen laskenta Verkon tehonaon laskemnen srron hävöt ännteolosuhteet ohtoen kuormttumnen verkon käyttäytymnen
