Differentiaaliyhtälöt. 1. mpld001.tex (infoverkostot (iv) s. 2001) Ratkaise yhtälö. 2. mpld002.tex (infoverkostot (iv) s. 2001)
|
|
|
- Juho Katajakoski
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e Differentiaaliyhtälöt 1. mpld001.tex (infoverkostot (iv) s. 2001) Ratkaise yhtälö. dy dt = ty a.) Muodosta yleinen ratkaisu. b.) Määritä vakio _C1 alkuehdolle y(0) = 1. c.) Ratkaise alkuarvotehtävä suoraan dsolve:lla. Vihje: Maplen funktio dsolve. b)-kohdassa voit ottaa ratkaisulausekkeen rhs (Righthand side) kiinni. Tarvitset lisäksi komentoja subs ja solve c)?dsolve, [HAM] ss Ratkaisu: > dyht := diff(y(t), t) = t*y(t) a) > ylratk := dsolve(dyht, y(t)) b) > Y := rhs(ylratk) > solve(subs(t = 0, Y) = 1, _C1) Huom! Dokumenttimoodissa alaviiva pudottaa kursorin alaindeksitasolle. "copy/paste" tarvitaan _C1:lle. > eval(%) c) > dsolve({dyht, y(0) = 1}, y(t)) 2. mpld002.tex (infoverkostot (iv) s. 2001) Ratkaise differentiaaliyhtälö sijoittamalla ratkaisuehdotus (REh) annettuun yhtälöön tai esim. integroimalla, arvaamalla tms.: (a) y + y = x 2 2, REh: y = Ce x + x 2 2x (b) y + y = 0, REh: y = a cos x + b sin x (c) y = e x, (d) x + yy = 0, REh: x 2 + y 2 = C (C > 0, vakio). Vihje: (d)-kohta: Derivoi implisiittisesti, ts. oleta, että on olemassa derivoituva funktio x y(x) s.e. x 2 +y(x) = C ja derivoi puolittain. (Tässä tapauksessa olemassaolo tiedetään, onhan y(x) = C x 2 tällainen. Tämän eksplisiittisen lausekkeen käyttö ei silti kannata, se vain mutkistaa asioita, olkaamme siis implisiittisiä.)
2 Ratkaisu: mpld002r.mw ja.pdf ON 3. mpld003.tex [Matlab-versio:...mlD002.tex] (iv3/2001, harj. 1, teht. 2) Millä xy-tason käyrillä on ominaisuus: Käyrän tangentin kulmakerroin jokaisessa pisteessä (x, y) on 4x y? Ratkaise yhtälö muuttujien erottelulla ( separation of variables ). Piirrä suuntakenttä isokliineja apuna käyttäen käsin vaikkapa alueessa [ 2, 2] [ 2, 2]. Ota sitten Maple avuksi. Kokeile ja selitä! Vihje: Kts. [HAM] ss > with(detools) > with(plots) Suuntakenttään:DEplot, grafiikkojen yhdistämiseen: display. Suoraparven saat tyyliin > yparvi:=seq(...,c=[-2,-1,-.5,.5,2,1]) # tms. > isokl:=plot([yparvi],x=...) Yleisemmin isokliinit saadaan piirretyksi implicitplot-funktiolla, mutta tässä saatiin ratkaistussa muodossa suoraan. Avainsanat:MapleDy, diffyhtälöt, suuntakenttä, isokliinit, mpldifferentiaali(yhtälöt) Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, mpld004.tex [Matlab-versio:...mlD004.tex] (iv3/2001, harj. 1, LV teht. 1-2) Laskuvarjohyppääjän yhtälö. Oletetaan, että hyppääjän + varustuksen massa = m ja ilmanvastus on verrannollinen nopeuden neliöön, olkoon verrannollisuskerroin = b. Tällöin Newtonin 2. laki antaa liikeyhtälön: mv = mg bv 2. Olkoon yksinkertaisuuden vuoksi m = 1, b = 1 ja g = 9.81m/s 2. Piirrä suuntakenttä. Oletetaan, että laskuvarjo aukeaa, kun v = 10m/s, valitaan tämä alkuhetkeksi t = 0. Piirrä tämä ratkaisukäyrä suuntakenttäpiirrokseen. Yritä nähdä suuntakentästä, että kaikki ratkaisut näyttävät lähestyvän rajanopeutta v 3.13 ja että ratkaisut ovat joko kasvavia tai pieneneviä (ja millä alkuarvoilla mitäkin, ja mitä tarkoittaa fysikaalisesti) Määritä rajanopeus suoraan yhtälöstä. Käytä Matlab-piirroksiin funktiota dfield8 ja Maplessa DEtools-kirjaston DEplot-funktiota. Vihje: Kts. [HAM] ss tai?deplot
3 > with(detools) > with(plots) Suuntakenttään:DEplot, grafiikkojen yhdistämiseen: display. dfield-ohje: Hae m-tiedosto dfield8 sivulta ja sijoita se Matlab-polkusi varrelle. Kirjoita Matlab-istuntoon : dfield8 Avainsanat: MatlabDy, MapleDy, diffyhtälöt, suuntakenttä, isokliinit, mpldifferentiaali(yhtälöt), mldifferentiaali(yhtälöt) Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, mpld005.tex (iv3/2001, harj. 1, LV teht. 2) Muodosta edellä olevan laskuvarjotehtävän (mpld004) analyyttinen ratkaisu muuttujien erottelulla. Määritä edellä mainittu (v(0) = 10)-ratkaisukäyrä. Tarkista ratkaisu Maplella ja kokeile lopuksi Maplen dsolve- komentoa. (Ohje [HAM]-kirjassa.) Vihje: Ohje analyyttiseen: Muistathan, että osamurtohajoitelma on hyödyllinen rationaalilausekkeen integroinnissa (Maple: convert(lauseke,parfrac,muuttuja); mutta osattava myös käsin). Avainsanat: MapleDy, diffyhtälöt, muuttujien erottelu, mpldifferentiaali(yhtälöt), mldifferentiaali(yhtälöt) Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, mpld006.tex (iv3/2001, harj. 1, LV teht. 3) Vaihdamme tässä LAODE-tyyliseen notaatioon: t on riippumaton muuttuja, x on riippuva muuttuja. Kannattaa totutella eri tyyleihin. Ratkaise alkuarvotehtävä x = x 2 e t, x(0) = 1. Kyseessä on lineaarinen epähomogeeninen (EHY). Tämä lasku ei edellytä mitään uutta muuttujien erottelun lisäksi (ainoastaan uskomista), kaikki on tässä neuvottu. Suorita ratkaisu näin: Ratkaise ensin vastaava (HY) x = x 2 (yleinen ratkaisu). Yritä keksiä jokin (EHY):n erityisratkaisu (siis mikä tahansa (EHY):n toteuttava). Keksiminen on helppoa, kun mietit exp-funktion derivointia. (Määräämätön kerroin ratkaistaan sijoittamalla yrite (EHY):yyn). Lineaaristen teoria sanoo, että (EHY):n yleinen = (HY):n yleinen + (EHY):n erikoinen. Piirrä myös suuntakenttä ja ratkaisukäyriä (Maple: DEtools[DEplot], Matlab: dfield8 tai suuntak1). Miten näet suuntakentästä, että yhtälö ei ole autonominen?
4 Avainsanat: MapleDy, lineaariset diffyhtälöt, mpldifferentiaali(yhtälöt) Viitteet: [LAODE] Golubitzky-Dellnitz: Linear Algebra and Differential Equations using Matlab, Brooks/Cole mpld007.tex (iv3/2001, harj. 2, AV teht. 1) Ratkaise (AA)-tehtävä y 2xy = 1, y(0) = 0.5 Tässä näyttää siltä, että (EHY):n erikoinen olisi helppo löytää, mutta huomaat pian, että luonnolliset yritteet eivät toimi. (Kyseessähän on lineaarinen, mutta ei-vakiokertoiminen yhtälö.) Ratkaise vaan sitten kiltisti integroivan tekijän menettelyllä. Integrointi johtaa erf-funktioon, Maple antaa sen suoraan, voit myös konsultoida KRE-kirjaa hakusanalla erf. Lausu siis ratkaisu erf:n avulla. Piirrä suuntakenttäpiirros Maplen DEtools-pakkauksen DEplot-funktion avulla (kts [HAM] s. 169), voit toki käyttää myös Matlab:n dfield8-funktiota (ohje alla). Valitse alkuarvoja y 0 väliltä ( 1, 0.5) yrittäen löytää kriittistä arvoa y 0, joka jakaa ratrkaisukäyrät plus tai miinus ääretöntä lähestyviin. (Tuo kriittinen ratkaisukäyrä on rajoitettu.) Käytä hyväksesi erf-funktion ominaisuutta lim x erf(x) = 1 laskeaksesi tarkan arvon y 0 :lle. Vihje: dfield-ohje: Hae m-tiedosto dfield8 sivulta ja sijoita se Matlabpolkusi varrelle. Kirjoita Matlab-istuntoon : dfield8 Avainsanat: MapleDy, diffyhtälöt,erf, mpldifferentiaali(yhtälöt) Viitteet: [KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, mpld008.tex (iv3/2001, harj. 2, AV teht. 2) Tarkastellaan (AA)-tehtävää xy = 4y, y(0) = 1. (a) Osoita, että tehtävällä ei ole ratkaisua. Osoita, että tämä ei ole ristiriidassa 1 -lauseen kanssa. (Huom: Lauseen avulla ei voi todistaa epäeksistenssiä, koska lauseen ehdot eivä ole välttämättömät.) (b) Vaihdetaan alkuehdoksi: y(0) = 0. Miten nyt on ratkaisujen laita. (c) Mitä voit sanoa alkuehdon y(x 0 ) = y 0 tapauksessa, jos x 0 0, (A) suoraan ratkaisukaavan avulla, (B) 1 -lauseen avulla. Vihje: Tämä on puhtaasti perinteinen tehtävä, mutta havainnollistus Maple/Matlab-välineillä on hyvinkin paikallaan. Avainsanat: diffyhtälöt, ratkaisun (epä)olemassaolo, eksistenssilause, mpldifferentiaali(yhtälöt) 9. mpld009.tex (iv3/2001, harj. 2, AV teht. 3) Muodosta Picardin iteraatiojonon muutama termi (AA)-tehtäville (a) y = x + y, y(0) = 0 (c) y = y 2, y(0) = 1. (b) y = x + y, y(0) = 1
5 Määritä myös tarkka ratkaisu. Vihje: LV-tehtävässä palataan asiaan Maple-hommana. Tämä on tyypillistä symbolilaskennan vahvuusaluetta. Avainsanat: diffyhtälöt, ratkaisun (epä)olemassaolo, Picard-Lindelöf-menetelmä, Picardin iteraatio, mpldifferentiaali(yhtälöt) 10. Ratkaise yhtälö dy dt = ty. Vihje: Maplen funktio dsolve. 11. mpld010.tex (iv3/2001, harj. 2, LV teht. 1) Muodosta Picardin iteraatiojonoa pitemmälle kuin AV-tehtävässä samoille (AA)-tehtäville (a), (b), (c) ja lisäksi vielä (d): lle. (a) y = x + y, y(0) = 0 (b) y = x + y, y(0) = 1 (c) y = y 2, y(0) = 1. (d) y = 3 y x Laske myös tarkka ratkaisu Maplella ja piirrä se ja iteraatiojonon funktioita. (Jos tuntuu liian pitkältä, niin jätä yksi pois, hyvä olis saada kaikki yhteisesti katetuksi (vaikka parityöskentelyssä sopimalla). Vihje: Malli: Aputiedostossa mpld010apu.zip on L4Picard.mw,L4Picard.pdf,L4exa2.mw, L4exa2.pdf, kts. myös [HAM] ss (dsolve)ja s. 126 Picard Lindelöf Avainsanat: diffyhtälöt, Picard-Lindelöf-menetelmä, Picardin iteraatio, mpldifferentiaali(yhtälöt) Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, mpld011.tex (a) Sovella Picardin iteraatiota (tuttuakin tutumpaan) (AA)-tehtävään y = y, y(0) = 1. Osoita, että iteraatiojono lähestyy ratkaisufunktiota y(x) = e x. (b) (Olkoon vaihteeksi x(t).) Olkoon alkuarvotehtävänä edelleen x = x, x(0) = 1. Osoita, että jos lasketaan likiarvo x n = x h (t n ) EM:llä pisteessä t = t n käyttäen askelpituutta h, niin x h (t n ) = c(h) tn, missä c(h) = (1 + h) 1/h. Osoita tämän nojalla, että kiinteällä t = t n pätee lim h 0 x h (t) = e t. Vihje: Tehtävässä tuskin tarvitaan ohjelmistoja. EM = Eulerin menetelmä 13. mpld012.tex Seuraava toistokäsky soveltaa Eulerin menetelmää alkuarvotehtävän y = sin(xy), y(0) = 1 ratkaisun likiarvon y(1) laskemiseen. Kokeile käskyjä askelpituuksilla h = 0.25, h = 0.1, h = 0.01 ja h = Mikä menee pieleen viimeisessä kohdassa?
6 f:=(x,y)-> sin(x*y); Digits:= 4; n:= 4; h:=1/n; y[0] := 1; for k from 0 to n-1 do # (paina tässä kohti Shift+Enter) y[k+1]:= evalf(y[k]+h*f(k*h,y[k])) # (samoin) end do; Piirrä Eulerin murtoviivat eri väreillä samaan koordinaatistoon. Vihje: Datan piirto sujuu nykyisin Matlab-tyylisesti : > xlista:=[seq(j*h,j=0..n)]; > ylista:=[seq(y[j],j=0..n)] > plot(xlista,ylista) [HAM]-viitteessä ss esitetyt tavat pisteparien listana toimivat myös, mutta s. 96 zip-temppu ei ole enää tarpeen. Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, mpld013.tex Ratkaise alkuarvotehtävä ja piirrä ratkaisun kuvaaja välillä 0 x 10. y + 3y + 3y = 1 e x, y(0) = 2, y (0) = 0, Vihje: Diffyhtälön saat ratkaistua komennolla dsolve. Yhtälössä esiintyvät derivaatat voit ilmoittaa komennolla diff, ja derivaatan pisteessa 0 voit ilmaista derivaattaoperaattorilla D(y)(0). 15. mpld014.tex Maple,Matlab a) Ratkaise alkuarvotehtävä y y = cos x, y(0) = 1 analyyttisesti Maplella ja numeerisesti Matlabilla. Piirrä ratkaisukäyrä. b) Anna alkuarvoksi symboli c ja piirrä ratkaisukäyräparvi sopivalla välillä, kun c = 0.9, 0.8,..., 0. Miltä parvi näyttää suurilla x :n arvoilla. Tässä pitäisi erottua kolmenlaista käytöstä. Vihje: Maple: dsolve, Matlab: ode45 Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
7 Viitteet: Coombes et al: Differential equations with Maple, Wiley Boyce - DiPrima s: Elementary Differential Equations and Boundary Value Problems,Wiley 16. mpld015.tex Maple,Matlab Tarkastellaan (AA)-tehtävää y = 3t 2, y(1) = 0. (3y 2 4) (a) Laske EM:llä ratkaisuapproksimaatiot pisteissä t = 1.2, 1.4, 1.6, 1.8 käyttäen askelta h = 0.1. (b) Tee sama askeleella h = (c) Vertaa tuloksia. (d) Piirrä suuntakenttä ja ratkaisuapproksimaatioita, sekä EM-ratkaisuja. Osaatko selittää, miksi EM toimii kohtuullisesti alussa, mutta kelvottomasti lopussa? Vihje: Eulerin menetelmää voi tässä käyttää ohjelman (MMM) laskintyylillä, kuten edellä tai sitten oikeaksi funktioksi koodatulla versiolla, annetaan tässä nuo koodit. Eulerin menetelmän koodit (sisältyvät myös apupakettiin *apu.zip): Maple: [HAM s. 206] (copy/paste Maple-istuntoon) Euler:=proc(f,a,b,ya,m) local n,h,t,y; h:=evalf((b-a)/m); t[0]:=a;y[0]:=ya; for n from 0 to m do y[n+1]:=y[n]+h*f(t[n],y[n]); t[n+1]:=t[n]+h; end do; seq([t[n],y[n]],n=0..m); end: Esim: y = t y 2 f:=(t,y)->t-y^2; e3:=euler(f,0,5,1,3); plot([e3]); Matlab: (Kts. vastaava Matlab-teht.) Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu. Viitteet: [KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998.
8 17. mpld016.tex (vrt. Matlab: mld007.tex) Tarkastellaan (AA)-tehtävää välillä t [1, 1.8] Ratkaise tehtävä y = 2 y ln t t a) Eulerin menetelmällä askelpituudella h = 0.1, b) Heunin menetelmällä askelpituudella h = 0.2, c) RK4- menetelmällä askelpituudella h = t, y(1) = 0 Määritä tarkka ratkaisu Maple:n dsolve-komennolla ja laske sen avulla virheet, piirrä ja taulukoi kussakin tapauksessa. Huomaa, että näillä askelpituuksien valinnoilla funktion arvojen laskentamäärät ovat samat. Vihje: Eulerin menetelmän koodit (sisältyvät myös apupakettiin mpld016apu.zip): Maple: [HAM s. 206] (copy/paste Maple-istuntoon) Euler:=proc(f,a,b,ya,m) local n,h,t,y; h:=evalf((b-a)/m); t[0]:=a;y[0]:=ya; for n from 0 to m do y[n+1]:=y[n]+h*f(t[n],y[n]); t[n+1]:=t[n]+h; end do; seq([t[n],y[n]],n=0..m); end: Esim: y = t y 2 f:=(t,y)->t-y^2; e3:=euler(f,0,5,1,3); plot([e3]); Laitetaan myös Heun ja RK4 Matlab: (Kts. vastaava Matlab-teht.) Huom: Tästä voi kehitellä monenlaisia tehtävävariaatioita, myös ilman numeeristen menetelmien korostusta. Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu. Viitteet: [KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998.
9 18. mpld017.tex, mld007.tex Huomasimme, että eksponentiaalinen kasvumalli, ns. Malthus n laki y = ky ei toimi USA:n väestödataan pitkällä aikavälillä. Mallia voidaan tarkentaa lisäämällä sopiva kasvua rajoittava termi, tällöin johdutaan ns. logistiseen kasvulakiin: y = ay by 2 USA:n väestödataan liityen Verhulst arvioi v arvot a = 0.03 ja b = , kun t mitataan vuosissa ja väkiluku y(t) miljoonissa. Opettajalle: Tehtävä voidaan käsitellä ehkä luontavamminkin kokonaan erillisenä numeeristen diffyhtälöratkaisujen opetuksesta. Tällöin otetaan vain alla olevat kohdat (c) ja/tai (d). (a) Ratkaise tehtävä (y(0) = 5.3) Eulerin menetelmällä käyttämllä askelpituussa h = 10 (b) rk4:llä käyttäen n. nelinkertaista askelta (voit kokeilla pienempiäkin) (c) Matlabin ode45:llä. (d) Laske analyyttinen ratkaisu Maplella (kyseessähän on Bernoullin yhtälö. Piirrä kuvia ja laske kaikissa tapauksessa ratkaisujen arvot annetuissa taulukkopisteissä. (ode45-tapauksessa onnistuu ainakin sovittamalla dataan splini funktiolla spline, joka on maailman helppokäyttöisin.) kts. (Nykyään (2012) ei tarvita erillistä splinisovitusta, laskentapisteet voidaan antaa suoraan ode45-funktiolle syötteenä.) Vihje: function [T,Y]=eulerS(f,Tspan,ya,n) % Tämä vain kehittely- ja opettelutarkoituksessa. % Funktio eulerv hoitaa niin skalaari- kuin vektoriversion. % ( , modifioitu ) % Esim: y =t+y, y(0)=1 % f=@(t,y)t+y % [T,Y]=eulerS(f,[0 4],1,6), plot(t,y,t,y,.r );shg a=tspan(1);b=tspan(2); h=(b-a)/n; Y=zeros(n+1,1);T=(a:h:b) ; %Pystyvektorit yhdenmukaisesti ode45:n Y(1)=ya; % kanssa for j=1:n Y(j+1)=Y(j)+h*f(T(j),Y(j)); end; Viitteitä: (Listaus yllä) 19. mpld018.tex, mld008.tex Tarkastellaan yhtälöä y = 2α(t 1)y. Ratkaise aluksi analyyttisesti (saat käyttää Mapleakin.) Totea kuvasta ja derivaattaehdosta yhtälön stabiilisuus/epästabiilisuusalueet. Ota kuvassa ja aina tarvittaessa vaikkapa α = 5.
10 Ratkaise yhtälö sekä Eulerilla että BE:llä. Sopivia arvoja voisivat olla vaikkapa h = 0.2, väli: [1, 4.5], y(1) = 1. Vertaa kokeellisesti stabiilisuukäyttäytymistä teorian ennustamaan ja pane merkille, miten epästabiilisuus käytännössä ilmenee. Tämä tehtävä soveltuu erityisen hyvin Maplella tehtäväksi, se on pitkälle ideoitu [HAM] sivulla 124, myös Euler ja BE ovat valmiina. (Koodit saa kurssin maple-hakemistosta.) ** Tulee aputiedostoon ** ** apu puuttuu, editoi viitteet! ** Vihje: Viitteitä: (Listaus yllä) 20. mpld019.tex [mplp017.tex] Opiskelija ottaa lainaa euroa hetkellä k = 0 ja ryhtyy maksamaan sitä takaisin kuukauden päästä hetkellä k = 1. Kuukausikorko on 1% (huh!) ja takaisinmaksu tapahtuu kiintein maksuerin 450 EUR/kk Olkoon y k k:n kuukauden kuluttua jäljellä olevan velan määrä. Kirjoita differenssiyhtälö y k :lle. Muodosta taulukko ja graafinen esitys, jossa on pisteet (k, y k ), ja selvitä sen perusteella, miten kauan velan maksu kestää ja miten paljon rahaa opiskelijaparka käyttää koko projektiin. Luokittelu: Differenssi- ja differentiaaliyhtalot, Maple-perusteet. Vihje: 21. a) Osoita, että funktio arctan y x toteuttaa Laplacen osittaisdifferentiaaliyhtälön 2 u x u y 2 = 0. (Tällaisia funktioita sanotaan harmonisiksi funktioiksi.) b) Oletetaan, että funktioilla u(x, y) ja v(x, y) on jatkuvat toiset osittaisderivaatat ja ne toteuttavat ns. Cauchy-Riemannin yhtälöt: u x = v y, v x = u y Osoita, että u ja v ovat harmonisia.
11 c) Olkoon f(x, y) = x 3 y 2 + x 4 sin y + cos(xy). Laske osittaisderivaatat f xxy, f xyx, f yxx ja totea, että ne ovat samat. 22. Seuraava toistokäsky soveltaa Eulerin menetelmää alkuarvotehtävän y = sin(xy), y(0) = 1 ratkaisun likiarvon y(1) laskemiseen. Kokeile käskyjä askelpituuksilla h = 0.25, h = 0.1, h = 0.01 ja h = Mikä menee pieleen viimeisessä kohdassa? f:=(x,y)-> sin(x*y); Digits:= 4; n:= 4; h:=1/n; y[0] = 1; for k from 0 to n-1 do (paina tässä kohti Shift+Enter) y[k+1]:= y[k]+h*f(k*h,y[k]) (samoin) od; Vihje: 23. Ratkaise alkuarvotehtävä ja piirrä ratkaisun kuvaaja välillä 0 x 10. y + 3y + 3y = 1 e x, y(0) = 2, y (0) = 0, Vihje: Diffyhtälön saat ratkaistua komennolla dsolve. Yhtälössä esiintyvät derivaatat voit ilmoittaa komennolla diff, ja derivaatan pisteessa 0 voit ilmaista derivaattaoperaattorilla D(y)(0). 24. Maple,Matlab (H2T10) a) Ratkaise alkuarvotehtävä y y = cos x, y(0) = 1 analyyttisesti Maplella ja numeerisesti Matlabilla. Piirrä ratkaisukäyrä. b) Anna alkuarvoksi symboli c ja piirrä ratkaisukäyräparvi sopivalla välillä, kun c = 0.9, 0.8,..., 0. Miltä parvi näyttää suurilla x :n arvoilla. Tässä pitäisi erottua kolmenlaista käytöstä. Vihje: Maple: dsolve, Matlab: ode45 Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu. 25. Kirjoita heiluriyhtälö Θ + g sin(θ) = 0 ensimmäisen kertaluvun systeemiksi, tai toisen kertaluvun differentiaaliyhtälöksi. Voit ottaa g/l = L 1.
12 Laske ratkaisu sopivalla aikavälillä (esim. [0, 10]) ja kolmella erilaisella alkuarvolla, joilla saat erityyppiset ratkaisut. Piirrä ratkaisukäyrät aikatasoon ja trajektorit faasitasoon. 26. Ratkaise RA-tehtävä y = y 2 1, y(0) = 0, y(1) = 1. Maplella. Yritä ensin analyyttista. Jos/kun mitään ei palaudu, voit asettaa esim infolevel[dsolve]:=3:. Näet ainakin, mitä Maple yrittää. Siirry sitten tyyppiin numeric, homma sujuu ongelmitta. Muutaman kokeilun jälkeen huomasin, ettei sujukaan. Numeerisen ratkaisun määritteleminen parametrista riippuvaksi funkioksi on aikamoista temppuilua, tällaisella kurssilla ei kannata siihen paneutua, koska Matlab-ratkaisu on hyvin selkeä ja ongelmaton. Muutetaan tehtävä helpommaksi: Suorita Maplella suoraan reuna-arvotehtävän ratkaisu (luultavasti Maple laskee sen differessimenetelmällä). Syntaksi on aivan sama kuin alkuarvotehtävälle, nyt vain annetaan pelkät reunaehdot. Helpin esimerkkien avulla pääset kiinni ratkaisufunktioon. 27. a) Osoita, että funktio arctan y x toteuttaa Laplacen osittaisdifferentiaaliyhtälön 2 u x + 2 u 2 y = 0. 2 (Tällaisia funktioita sanotaan harmonisiksi funktioiksi.) b) Oletetaan, että funktioilla u(x, y) ja v(x, y) on jatkuvat toiset osittaisderivaatat ja ne toteuttavat ns. Cauchy-Riemannin yhtälöt: u x = v y, v x = u y Osoita, että u ja v ovat harmonisia. c) Olkoon f(x, y) = x 3 y 2 + x 4 sin y + cos(xy). Laske osittaisderivaatat f xxy, f xyx, f yxx ja totea, että ne ovat samat.
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos. h=0.5; t=-1:h:1;x=0:h:2 for i=1:5 for j=1:5 K(i,j)=y(i)-x(j) end end
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mldifferentiaali(yhtälöt) 1. mld001.tex (iv3 harj.1 av 2001) Tätä tehtävää harjoitellaan Matlab-teknisesti loppuviikon harjoituksissa. Osattava
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mldifferentiaali(yhtälöt) 1. mld001.tex (iv3 harj.1 av 2001) Tätä tehtävää harjoitellaan Matlab-teknisesti loppuviikon harjoituksissa. Osattava
mplcurve fitting 1. mplcf01.tex [Matlab:../../matlabteht/mlCurveFit/mplCF01.tex] 2. mplcf03.tex, [Matlab:../../matlabteht/mlCurveFit/mlCF15.
![mplcurve fitting 1. mplcf01.tex [Matlab:../../matlabteht/mlCurveFit/mplCF01.tex] 2. mplcf03.tex, [Matlab:../../matlabteht/mlCurveFit/mlCF15. mplcurve fitting 1. mplcf01.tex [Matlab:../../matlabteht/mlCurveFit/mplCF01.tex] 2. mplcf03.tex, [Matlab:../../matlabteht/mlCurveFit/mlCF15.](/thumbs/61/45445326.jpg) Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplcurve fitting 1. mplcf01.tex [Matlab:../../matlabteht/mlCurveFit/mplCF01.tex] Opettajalle: Tehtävän alkuperäinen tarkoitus on demonstroida
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplcurve fitting 1. mplcf01.tex [Matlab:../../matlabteht/mlCurveFit/mplCF01.tex] Opettajalle: Tehtävän alkuperäinen tarkoitus on demonstroida
Käyttäen tätä dataa, arvioi teoksen Sinfonia Concertanten sävellysvuosi, kun tiedetään, että sen Köchel-numero on 364.
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mplaritmetiikka 1. SIIRRETTY (cp) mplperusteet-hakemistoon: mplp005.tex Etsi lukujen 1234 3243 ja 7681 suurin yhteinen tekijä. Vihje: Suurin yhteinen
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mplaritmetiikka 1. SIIRRETTY (cp) mplperusteet-hakemistoon: mplp005.tex Etsi lukujen 1234 3243 ja 7681 suurin yhteinen tekijä. Vihje: Suurin yhteinen
mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011)
![mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011) mplperusteet 1. Tiedosto: mplp001.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x 1 ( mplp002.tex (PA P1 s.2011)](/thumbs/91/107207023.jpg) Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplperusteet. Tiedosto: mplp00.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x ( x )( + x ). Kokeile funktiota simplify. 2. mplp002.tex
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos -e mplperusteet. Tiedosto: mplp00.tex Ohjelmat: Maple, [Mathematica] Sievennä lauseke x ( x )( + x ). Kokeile funktiota simplify. 2. mplp002.tex
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 10: Ensimmäisen kertaluvun differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Numeeriset menetelmät TIEA381. Luento 12. Kirsi Valjus. Jyväskylän yliopisto. Luento 12 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 MAT-1345 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 9 Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa
1 MAT-1345 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 9 Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
2. Viikko. CDH: luvut (s ). Matematiikka on fysiikan kieli ja differentiaaliyhtälöt sen yleisin murre.
 2. Viikko Keskeiset asiat ja tavoitteet: 1. Peruskäsitteet: kertaluku, lineaarisuus, homogeenisuus. 2. Separoituvan diff. yhtälön ratkaisu, 3. Lineaarisen 1. kl yhtälön ratkaisu, CDH: luvut 19.1.-19.4.
2. Viikko Keskeiset asiat ja tavoitteet: 1. Peruskäsitteet: kertaluku, lineaarisuus, homogeenisuus. 2. Separoituvan diff. yhtälön ratkaisu, 3. Lineaarisen 1. kl yhtälön ratkaisu, CDH: luvut 19.1.-19.4.
mplbasic, Mapleperusteet
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mplbasic, Mapleperusteet Luvussa esiintyy Maple-ohjelman perusharjoitteluun sopivia tehtäviä. mplbas000 Teknillinen korkeakoulu Matematiikka Peruskurssien
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mplbasic, Mapleperusteet Luvussa esiintyy Maple-ohjelman perusharjoitteluun sopivia tehtäviä. mplbas000 Teknillinen korkeakoulu Matematiikka Peruskurssien
13. Ratkaisu. Kirjoitetaan tehtävän DY hieman eri muodossa: = 1 + y x + ( y ) 2 (y )
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Differentiaaliyhtälöt, kesä 00 Tehtävät 3-8 / Ratkaisuehdotuksia (RT).6.00 3. Ratkaisu. Kirjoitetaan tehtävän DY hieman eri muodossa: y = + y + y = + y + ( y ) (y
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Differentiaaliyhtälöt, kesä 00 Tehtävät 3-8 / Ratkaisuehdotuksia (RT).6.00 3. Ratkaisu. Kirjoitetaan tehtävän DY hieman eri muodossa: y = + y + y = + y + ( y ) (y
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
Harjoitus Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia:
 Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Kompleksiluvun logaritmi: Jos nyt z = re iθ = re iθ e in2π, missä n Z, niin saadaan. ja siihen vaikuttava
 Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Matemaattiset ohjelmistot MS-E Yleisiä differentiaaliyhtälökäsitteitä. 2 Analyyttinen ratkaiseminen, komento dsolve
 Matemaattiset ohjelmistot MS-E1999 Tavalliset differentiaaliyhtälöt 1 Yleisiä differentiaaliyhtälökäsitteitä Differentiaaliyhtälö tarkoittaa sellaista yhtälöä, jossa esiintyy tuntematon funktio ja sen
Matemaattiset ohjelmistot MS-E1999 Tavalliset differentiaaliyhtälöt 1 Yleisiä differentiaaliyhtälökäsitteitä Differentiaaliyhtälö tarkoittaa sellaista yhtälöä, jossa esiintyy tuntematon funktio ja sen
12. Differentiaaliyhtälöt
 1. Differentiaaliyhtälöt 1.1 Johdanto Differentiaaliyhtälöitä voidaan käyttää monilla alueilla esimerkiksi tarkasteltaessa jonkin kohteen lämpötilan vaihtelua, eksponentiaalista kasvua, sähkölatauksen
1. Differentiaaliyhtälöt 1.1 Johdanto Differentiaaliyhtälöitä voidaan käyttää monilla alueilla esimerkiksi tarkasteltaessa jonkin kohteen lämpötilan vaihtelua, eksponentiaalista kasvua, sähkölatauksen
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
Ratkaisu: Tutkitaan derivoituvuutta Cauchy-Riemannin yhtälöillä: f(x, y) = u(x, y) + iv(x, y) = 2x + ixy 2. 2 = 2xy xy = 1
 1. Selvitä missä tason pisteissä annetut funktiot ovat derivoituvia/analyyttisiä. Määrää funktion derivaatta niissä pisteissä, joissa se on olemassa. (a) (x, y) 2x + ixy 2 (b) (x, y) cos x cosh y i sin
1. Selvitä missä tason pisteissä annetut funktiot ovat derivoituvia/analyyttisiä. Määrää funktion derivaatta niissä pisteissä, joissa se on olemassa. (a) (x, y) 2x + ixy 2 (b) (x, y) cos x cosh y i sin
2v 1 = v 2, 2v 1 + 3v 2 = 4v 2.. Vastaavasti ominaisarvoa λ 2 = 4 vastaavat ominaisvektorit toteuttavat. v 2 =
 TKK, Matematiikan laitos Pikkarainen/Tikanmäki Mat-1.1320 Matematiikan peruskurssi K2 Harjoitus 12, A=alku-, L=loppuviikko, T= taulutehtävä, P= palautettava tehtävä, W= verkkotehtävä 21. 25.4.2008, viikko
TKK, Matematiikan laitos Pikkarainen/Tikanmäki Mat-1.1320 Matematiikan peruskurssi K2 Harjoitus 12, A=alku-, L=loppuviikko, T= taulutehtävä, P= palautettava tehtävä, W= verkkotehtävä 21. 25.4.2008, viikko
y (0) = 0 y h (x) = C 1 e 2x +C 2 e x e10x e 3 e8x dx + e x 1 3 e9x dx = e 2x 1 3 e8x 1 8 = 1 24 e10x 1 27 e10x = e 10x e10x
 BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
Numeeriset menetelmät
 Numeeriset menetelmät Luento 12 To 13.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 12 To 13.10.2011 p. 1/38 p. 1/38 Tavalliset differentiaaliyhtälöt Yhtälöissä tuntematon funktio Tavalliset
Numeeriset menetelmät Luento 12 To 13.10.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 12 To 13.10.2011 p. 1/38 p. 1/38 Tavalliset differentiaaliyhtälöt Yhtälöissä tuntematon funktio Tavalliset
1 Peruskäsitteet. Dierentiaaliyhtälöt
 Teknillinen korkeakoulu Matematiikka Dierentiaaliyhtälöt Alestalo Tässä monisteessa käydään läpi tavallisiin dierentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Esimerkkejä luennoilla
Teknillinen korkeakoulu Matematiikka Dierentiaaliyhtälöt Alestalo Tässä monisteessa käydään läpi tavallisiin dierentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Esimerkkejä luennoilla
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Luento 2: Liikkeen kuvausta
 Luento 2: Liikkeen kuvausta Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Luennon sisältö Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Liikkeen ratkaisu kiihtyvyydestä
Luento 2: Liikkeen kuvausta Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Luennon sisältö Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Liikkeen ratkaisu kiihtyvyydestä
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti. Piirrä integroitavan funktion kuvaaja. Mikä itse asiassa on integraalin arvo?
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos Matlab-tehtäviä, käyrän sovitus -e Differentiaali- ja integraalilaskenta 1. Laske integraali 2π cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti.
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos Matlab-tehtäviä, käyrän sovitus -e Differentiaali- ja integraalilaskenta 1. Laske integraali 2π cos x 13 12 cos 2x dx a) symbolisesti, b) numeerisesti.
sin(x2 + y 2 ) x 2 + y 2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 2017 Harjoitus 2 Ratkaisuedotukset 2.1. Tutki funktion g : R 2 R, g(0, 0) = 0, jatkuvuutta. g(x, y) = sin(x2 + y 2 ) x 2 + y 2, kun (x,
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 2017 Harjoitus 2 Ratkaisuedotukset 2.1. Tutki funktion g : R 2 R, g(0, 0) = 0, jatkuvuutta. g(x, y) = sin(x2 + y 2 ) x 2 + y 2, kun (x,
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 3: Osittaisderivaatta
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 3: Osittaisderivaatta Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu Antti Rasilan luentomonisteeseen
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 3: Osittaisderivaatta Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu Antti Rasilan luentomonisteeseen
4. Differentiaaliyhtälöryhmät 4.1. Ryhmän palauttaminen yhteen yhtälöön
 4 Differentiaaliyhtälöryhmät 41 Ryhmän palauttaminen yhteen yhtälöön 176 Ratkaise differentiaaliyhtälöryhmät a) dt = y +t, b) = y z + sinx x 2 dt = x +t, c) + z = x2 = y + z + cosx + 2y = x a)x = C 1 e
4 Differentiaaliyhtälöryhmät 41 Ryhmän palauttaminen yhteen yhtälöön 176 Ratkaise differentiaaliyhtälöryhmät a) dt = y +t, b) = y z + sinx x 2 dt = x +t, c) + z = x2 = y + z + cosx + 2y = x a)x = C 1 e
Differentiaaliyhtälöryhmä
 Differentiaaliyhtälöryhmä Ensimmäisen kertaluvun differentiaaliyhtälöryhmä vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä voidaan ratkaista numeerisesti täsmälleen samanlaisilla kaavoilla
Differentiaaliyhtälöryhmä Ensimmäisen kertaluvun differentiaaliyhtälöryhmä vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä voidaan ratkaista numeerisesti täsmälleen samanlaisilla kaavoilla
Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva).
 6 DIFFERENTIAALIYHTÄLÖISTÄ Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva). Newtonin II:n lain (ma missä Yhtälö dh dt m dh dt F) mukaan mg, on kiihtyvyys ja
6 DIFFERENTIAALIYHTÄLÖISTÄ Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva). Newtonin II:n lain (ma missä Yhtälö dh dt m dh dt F) mukaan mg, on kiihtyvyys ja
Normaaliryhmä. Toisen kertaluvun normaaliryhmä on yleistä muotoa
 Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
Matematiikan perusteet taloustieteilij oille I
 Matematiikan perusteet taloustieteilijöille I Harjoitukset syksy 2006 1. Laskeskele ja sieventele a) 3 27 b) 27 2 3 c) 27 1 3 d) x 2 4 (x 8 3 ) 3 y 8 e) (x 3) 2 f) (x 3)(x +3) g) 3 3 (2x i + 1) kun, x
Matematiikan perusteet taloustieteilijöille I Harjoitukset syksy 2006 1. Laskeskele ja sieventele a) 3 27 b) 27 2 3 c) 27 1 3 d) x 2 4 (x 8 3 ) 3 y 8 e) (x 3) 2 f) (x 3)(x +3) g) 3 3 (2x i + 1) kun, x
Matematiikka B3 - Avoin yliopisto
 2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
3 = Lisäksi z(4, 9) = = 21, joten kysytty lineaarinen approksimaatio on. L(x,y) =
 BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 6, Syksy 2016 1. (a) Olkoon z = z(x,y) = yx 1/2 + y 1/2. Muodosta z:lle lineaarinen approksimaatio L(x,y) siten että approksimaation ja z:n arvot
BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 6, Syksy 2016 1. (a) Olkoon z = z(x,y) = yx 1/2 + y 1/2. Muodosta z:lle lineaarinen approksimaatio L(x,y) siten että approksimaation ja z:n arvot
Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle /
 Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle / 16. 18.5. Lineaariset differentiaaliyhtälöt, homogeeniset differentiaaliyhtälöt Tehtävä 1: a) Määritä differentiaaliyhtälön y 3y = 14e 4x
Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle / 16. 18.5. Lineaariset differentiaaliyhtälöt, homogeeniset differentiaaliyhtälöt Tehtävä 1: a) Määritä differentiaaliyhtälön y 3y = 14e 4x
5 DIFFERENTIAALIYHTÄLÖRYHMÄT
 5 DIFFERENTIAALIYHTÄLÖRYHMÄT 5. Ensimmäisen kl:n DY-ryhmät Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Useimmat voidaan mallintaa ensimmäisen kertaluvun DY-ryhmien avulla. Ensimmäisen kl:n
5 DIFFERENTIAALIYHTÄLÖRYHMÄT 5. Ensimmäisen kl:n DY-ryhmät Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Useimmat voidaan mallintaa ensimmäisen kertaluvun DY-ryhmien avulla. Ensimmäisen kl:n
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
SARJAT JA DIFFERENTIAALIYHTÄLÖT
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 43 0.5 0.4 0.3 0.2 0.1 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.1 0.2 0.3 0.4 0.5 0.1 0.2 0.3 0.4 0.5 0.6 0.7 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 Kuva 12. Esimerkin 4.26(c kuvauksen
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 43 0.5 0.4 0.3 0.2 0.1 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.1 0.2 0.3 0.4 0.5 0.1 0.2 0.3 0.4 0.5 0.6 0.7 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 Kuva 12. Esimerkin 4.26(c kuvauksen
LDYS06.mw. Alustukset. Seosprobl, HY. Lineaariset differentiaaliyhtälösysteemit L9-> syksyllä 2006
 LDYS06.mw Lineaariset differentiaaliyhtälösysteemit L9- syksyllä 2006 Alustukset with(linearalgebra):with(linalg): with(plots): with(detools): Seosprobl, HY A:=
LDYS06.mw Lineaariset differentiaaliyhtälösysteemit L9- syksyllä 2006 Alustukset with(linearalgebra):with(linalg): with(plots): with(detools): Seosprobl, HY A:=
plot(f(x), x=-5..5, y=-10..10)
 [] Jokaisen suoritettavan rivin loppuun ; [] Desimaalierotin Maplessa on piste. [] Kommentteja koodin sekaan voi laittaa # -merkin avulla. Esim. #kommentti tähän [] Edelliseen tulokseen voi viitata merkillä
[] Jokaisen suoritettavan rivin loppuun ; [] Desimaalierotin Maplessa on piste. [] Kommentteja koodin sekaan voi laittaa # -merkin avulla. Esim. #kommentti tähän [] Edelliseen tulokseen voi viitata merkillä
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Mat-C.1 harj2. Alustuksia f d 1 C sin x 1 C x 2 f := 1 C sin x
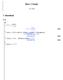 Mat-C.1 harj2 21.3. 2012 Alustuksia 1. a) f d 1 C sin 1 C 2 f := 1 C sin 1 C 2 subs =K2.0, f ; evalf % # Sijoita :n paikalle -2.0 lausekkeessa f. 1 C 0.2000000000 sin K2.0 eval f, =K2.0 plot f, =K5..5
Mat-C.1 harj2 21.3. 2012 Alustuksia 1. a) f d 1 C sin 1 C 2 f := 1 C sin 1 C 2 subs =K2.0, f ; evalf % # Sijoita :n paikalle -2.0 lausekkeessa f. 1 C 0.2000000000 sin K2.0 eval f, =K2.0 plot f, =K5..5
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
Numeeriset menetelmät TIEA381. Luento 11. Kirsi Valjus. Jyväskylän yliopisto. Luento 11 () Numeeriset menetelmät / 37
 Numeeriset menetelmät TIEA381 Luento 11 Kirsi Valjus Jyväskylän yliopisto Luento 11 () Numeeriset menetelmät 24.4.2013 1 / 37 Luennon 11 sisältö Numeerisesta integroinnista ja derivoinnista Adaptiiviset
Numeeriset menetelmät TIEA381 Luento 11 Kirsi Valjus Jyväskylän yliopisto Luento 11 () Numeeriset menetelmät 24.4.2013 1 / 37 Luennon 11 sisältö Numeerisesta integroinnista ja derivoinnista Adaptiiviset
3 TOISEN KERTALUVUN LINEAARISET DY:T
 3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
. Kun p = 1, jono suppenee raja-arvoon 1. Jos p = 2, jono hajaantuu. Jono suppenee siis lineaarisesti. Vastaavasti jonolle r k+1 = r k, suhde on r k+1
 TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio Mat-.39 Optimointioppi Kimmo Berg 8. harjoitus - ratkaisut. a)huomataan ensinnäkin että kummankin jonon raja-arvo r on nolla. Oletetaan lisäksi että
TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio Mat-.39 Optimointioppi Kimmo Berg 8. harjoitus - ratkaisut. a)huomataan ensinnäkin että kummankin jonon raja-arvo r on nolla. Oletetaan lisäksi että
Matemaattinen Analyysi
 Vaasan yliopisto, syksy 2016 / ORMS1010 Matemaattinen Analyysi 8. harjoitus, viikko 49 R1 to 12 14 F453 (8.12.) R2 to 14 16 F345 (8.12.) R3 ke 8 10 F345 (7.11.) 1. Määritä funktion f (x) = 1 Taylorin sarja
Vaasan yliopisto, syksy 2016 / ORMS1010 Matemaattinen Analyysi 8. harjoitus, viikko 49 R1 to 12 14 F453 (8.12.) R2 to 14 16 F345 (8.12.) R3 ke 8 10 F345 (7.11.) 1. Määritä funktion f (x) = 1 Taylorin sarja
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Mat Matematiikan peruskurssi K2
 Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
r > y x z x = z y + y x z y + y x = r y x + y x = r
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
5 Differentiaaliyhtälöryhmät
 5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
1 Johdanto. 1.1 Vakiokertoiminen differentiaaliyhtälö y = ay. Differentiaaliyhtälöt c Pekka Alestalo 2013
 Differentiaaliyhtälöt c Pekka Alestalo 2013 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Differentiaaliyhtälöt c Pekka Alestalo 2013 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Osittaisdifferentiaaliyhtälöt
 Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
Osittaisdifferentiaaliyhtälöt Harjoituskokoelmat 4 ja 5, kevät 2011 Palautus Eemeli Blåstenille to 23.6. klo 16.00 mennessä 1. Ratkaise Dirichlet ongelma u(x, y) = 0, x 2 + y 2 < 1, u(x, y) = y + x 2,
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos
 Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Vesanen MS-A0205/6 Differentiaali- ja integraalilaskenta 2, kevät 2017 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Vesanen MS-A0205/6 Differentiaali- ja integraalilaskenta 2, kevät 2017 Laskuharjoitus 4A (Vastaukset) alkuviikolla
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit
 MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
Differentiaalilaskenta 1.
 Differentiaalilaskenta. a) Mikä on tangentti? Mikä on sekantti? b) Määrittele funktion monotonisuuteen liittyvät käsitteet: kasvava, aidosti kasvava, vähenevä ja aidosti vähenevä. Anna esimerkit. c) Selitä,
Differentiaalilaskenta. a) Mikä on tangentti? Mikä on sekantti? b) Määrittele funktion monotonisuuteen liittyvät käsitteet: kasvava, aidosti kasvava, vähenevä ja aidosti vähenevä. Anna esimerkit. c) Selitä,
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
y + 4y = 0 (1) λ = 0
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 6 mallit Kevät 2019 Tehtävä 1. Ratkaise yhtälöt a) y + 4y = x 2, b) y + 4y = 3e x. Ratkaisu: a) Differentiaaliyhtälön yleinen
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 6 mallit Kevät 2019 Tehtävä 1. Ratkaise yhtälöt a) y + 4y = x 2, b) y + 4y = 3e x. Ratkaisu: a) Differentiaaliyhtälön yleinen
DYNAAMISET SYSTEEMIT 1998
 1. harjoitus, viikko 3 1. Määritä seuraavien differentiaaliyhtälöiden tyyppi (kertaluku, lineaarinen eilineaarinen, jos lineaarinen, niin vakiokertoiminen ei-vakiokertoiminen): a) y + y - x 2 = 0 b) y
1. harjoitus, viikko 3 1. Määritä seuraavien differentiaaliyhtälöiden tyyppi (kertaluku, lineaarinen eilineaarinen, jos lineaarinen, niin vakiokertoiminen ei-vakiokertoiminen): a) y + y - x 2 = 0 b) y
2. kl:n DY:t. Lause. Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.
 2. kl:n DY:t Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.) Lause Olkoon f(x 2, x 1, t) funktio, ja oletetaan, että f, f/ x 1 ja f/ x
2. kl:n DY:t Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.) Lause Olkoon f(x 2, x 1, t) funktio, ja oletetaan, että f, f/ x 1 ja f/ x
Nopeus, kiihtyvyys ja liikemäärä Vektorit
 Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Nopeus, kiihtyvyys ja liikemäärä Vektorit Luento 2 https://geom.mathstat.helsinki.fi/moodle/course/view.php?id=360 Luennon tavoitteet: Vektorit tutuiksi Koordinaatiston valinta Vauhdin ja nopeuden ero
Integroimistekniikkaa Integraalifunktio
 . Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
. Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
Harjoitus 6: Symbolinen laskenta II (Mathematica)
 Harjoitus 6: Symbolinen laskenta II (Mathematica) SCI-C0200 Fysiikan ja matematiikan menetelmien studio SCI-C0200 Fysiikan ja matematiikan menetelmien studio 1 Harjoituksen aiheita Differentiaaliyhtälöiden
Harjoitus 6: Symbolinen laskenta II (Mathematica) SCI-C0200 Fysiikan ja matematiikan menetelmien studio SCI-C0200 Fysiikan ja matematiikan menetelmien studio 1 Harjoituksen aiheita Differentiaaliyhtälöiden
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
Tutki, onko seuraavilla kahden reaalimuuttujan reaaliarvoisilla funktioilla raja-arvoa origossa: x 2 + y 2, d) y 2. x + y, c) x 3
 2. Reaaliarvoiset funktiot 2.1. Jatkuvuus 23. Tutki funktion f (x,y) = xy x 2 + y 2 raja-arvoa, kun piste (x,y) lähestyy origoa pitkin seuraavia xy-tason käyriä: a) y = ax, b) y = ax 2, c) y 2 = ax. Onko
2. Reaaliarvoiset funktiot 2.1. Jatkuvuus 23. Tutki funktion f (x,y) = xy x 2 + y 2 raja-arvoa, kun piste (x,y) lähestyy origoa pitkin seuraavia xy-tason käyriä: a) y = ax, b) y = ax 2, c) y 2 = ax. Onko
MS-A0104 Differentiaali- ja integraalilaskenta 1 (ELEC2) MS-A0106 Differentiaali- ja integraalilaskenta 1 (ENG2)
 MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
JYVÄSKYLÄN YLIOPISTO. Integraalilaskenta 2 Harjoitus Olkoon A := {(x, y) R 2 0 x π, sin x y 2 sin x}. Laske käyräintegraali
 JYVÄSKYLÄN YLIOPISTO MTEMTIIKN J TILSTOTIETEEN LITOS Integraalilaskenta Harjoitus 4 5.4.4. Olkoon := {(x, y) R x π, sin x y sin x}. Laske käyräintegraali + (y dx + x dy) a) suoraan; ja b) Greenin lauseen
JYVÄSKYLÄN YLIOPISTO MTEMTIIKN J TILSTOTIETEEN LITOS Integraalilaskenta Harjoitus 4 5.4.4. Olkoon := {(x, y) R x π, sin x y sin x}. Laske käyräintegraali + (y dx + x dy) a) suoraan; ja b) Greenin lauseen
[4A] DIFFERENTIAALIYHTÄLÖT 1. Alkuarvotehtävät
![[4A] DIFFERENTIAALIYHTÄLÖT 1. Alkuarvotehtävät [4A] DIFFERENTIAALIYHTÄLÖT 1. Alkuarvotehtävät](/thumbs/69/61810803.jpg) [4A] DIFFERENTIAALIYHTÄLÖT 1. Alkuarvotehtävät Numeerisen integroinnin yhteydessä ratkoimme jo tavallisia ensimmäisen kertaluvun alkuarvotehtäviä integroimalla eli t y (t) =f(t, y(t)) y(t) =y(t a )+ f(t,
[4A] DIFFERENTIAALIYHTÄLÖT 1. Alkuarvotehtävät Numeerisen integroinnin yhteydessä ratkoimme jo tavallisia ensimmäisen kertaluvun alkuarvotehtäviä integroimalla eli t y (t) =f(t, y(t)) y(t) =y(t a )+ f(t,
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos
 Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Ojalammi MS-A0203 Differentiaali- ja integraalilaskenta 2, kevät 2016 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Aalto-yliopiston perustieteiden korkeakoulu Matematiikan ja systeemianalyysin laitos Malinen/Ojalammi MS-A0203 Differentiaali- ja integraalilaskenta 2, kevät 2016 Laskuharjoitus 4A (Vastaukset) alkuviikolla
Hermiten interpolaatio: Interpolaatioehdoissa esiintyy myös derivaattoja. Määritä 4. asteen polynomi p, joka toteuttaa ehdot:
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mlcurvefit 1. H2T5.tex/mplCF01.tex Hermiten interpolaatio: Interpolaatioehdoissa esiintyy myös derivaattoja. Määritä 4. asteen polynomi p, joka
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mlcurvefit 1. H2T5.tex/mplCF01.tex Hermiten interpolaatio: Interpolaatioehdoissa esiintyy myös derivaattoja. Määritä 4. asteen polynomi p, joka
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
1 Di erentiaaliyhtälöt
 Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
DI matematiikan opettajaksi: Täydennyskurssi, kevät 2010 Luentorunkoa ja harjoituksia viikolle 13: ti klo 13:00-15:30 ja to 1.4.
 DI matematiikan opettajaksi: Täydennyskurssi, kevät Luentorunkoa ja harjoituksia viikolle 3: ti 33 klo 3:-5:3 ja to 4 klo 9:5-: Käydään läpi differentiaaliyhtälöitä Määritelmä Olkoon A R n n (MatLab:ssa
DI matematiikan opettajaksi: Täydennyskurssi, kevät Luentorunkoa ja harjoituksia viikolle 3: ti 33 klo 3:-5:3 ja to 4 klo 9:5-: Käydään läpi differentiaaliyhtälöitä Määritelmä Olkoon A R n n (MatLab:ssa
Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua.
 6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
6 Alkeisfunktiot Kaikkia alla olevia kohtia ei käsitellä luennoilla kokonaan, koska osa on ennestään lukiosta tuttua. 6. Funktion määrittely Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
l 1 2l + 1, c) 100 l=0 AB 3AC ja AB AC sekä vektoreiden AB ja
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
Harjoitus 6: Symbolinen laskenta II (Mathematica)
 Harjoitus 6: Symbolinen laskenta II (Mathematica) MS-C2107 Sovelletun matematiikan tietokonetyöt MS-C2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Differentiaaliyhtälöiden ja differentiaaliyhtälösysteemien
Harjoitus 6: Symbolinen laskenta II (Mathematica) MS-C2107 Sovelletun matematiikan tietokonetyöt MS-C2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Differentiaaliyhtälöiden ja differentiaaliyhtälösysteemien
a 1 y 1 (x) + a 2 y 2 (x) = 0 vain jos a 1 = a 2 = 0
 6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
BM20A0300, Matematiikka KoTiB1
 BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
BM20A0300, Matematiikka KoTiB1 Luennot: Heikki Pitkänen 1 Oppikirja: Robert A. Adams: Calculus, A Complete Course Luku 12 Luku 13 Luku 14.1 Tarvittava materiaali (luentokalvot, laskuharjoitustehtävät ja
Yleisiä integroimissääntöjä
 INTEGRAALILASKENTA, MAA9 Yleisiä integroimissääntöjä Integroiminen eli annetun funktion f integraalifunktion F määrittäminen (löytäminen) on yleisesti haastavaa. Joskus joutuu jopa arvata tai kokeilla.
INTEGRAALILASKENTA, MAA9 Yleisiä integroimissääntöjä Integroiminen eli annetun funktion f integraalifunktion F määrittäminen (löytäminen) on yleisesti haastavaa. Joskus joutuu jopa arvata tai kokeilla.
13. Taylorin polynomi; funktioiden approksimoinnista. Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
 13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
13. Taylorin polynomi; funktioiden approksimoinnista 13.1. Taylorin polynomi 552. Muodosta funktion f (x) = x 4 + 3x 3 + x 2 + 2x + 8 kaikki Taylorin polynomit T k (x, 2), k = 0,1,2,... (jolloin siis potenssien
Peruskäsitteet 1. Mitkä ovat seuraavien funktiota y = y(x) koskevien differentiaaliyhtälöiden kertaluvut? Ovatko yhtälöt normaalimuotoisia?
 Peruskäsitteet 1. Mitkä ovat seuraavien funktiota y = y(x) koskevien differentiaaliyhtälöiden kertaluvut? Ovatko yhtälöt normaalimuotoisia? a) xy + 2y sinx + y = e x b) y + sin(x + y) = 0 c) y = xy y y
Peruskäsitteet 1. Mitkä ovat seuraavien funktiota y = y(x) koskevien differentiaaliyhtälöiden kertaluvut? Ovatko yhtälöt normaalimuotoisia? a) xy + 2y sinx + y = e x b) y + sin(x + y) = 0 c) y = xy y y
HY / Avoin yliopisto Lineaarialgebra ja matriisilaskenta II, kesä 2015 Harjoitus 1 Ratkaisut palautettava viimeistään maanantaina klo
 HY / Avoin yliopisto Lineaarialgebra ja matriisilaskenta II, kesä 2015 Harjoitus 1 Ratkaisut palautettava viimeistään maanantaina 10.8.2015 klo 16.15. Tehtäväsarja I Tutustu lukuun 15, jossa vektoriavaruuden
HY / Avoin yliopisto Lineaarialgebra ja matriisilaskenta II, kesä 2015 Harjoitus 1 Ratkaisut palautettava viimeistään maanantaina 10.8.2015 klo 16.15. Tehtäväsarja I Tutustu lukuun 15, jossa vektoriavaruuden
Luento 4: Liikkeen kuvausta, differentiaaliyhtälöt
 Luento 4: Liikkeen kuvausta, differentiaaliyhtälöt Digress: vakio- vs. muuttuva kiihtyvyys käytännössä Kinematiikkaa yhdessä dimensiossa taustatietoa Matlab-esittelyä 1 / 20 Luennon sisältö Digress: vakio-
Luento 4: Liikkeen kuvausta, differentiaaliyhtälöt Digress: vakio- vs. muuttuva kiihtyvyys käytännössä Kinematiikkaa yhdessä dimensiossa taustatietoa Matlab-esittelyä 1 / 20 Luennon sisältö Digress: vakio-
4 Korkeamman kertaluvun differentiaaliyhtälöt
 Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Differentiaaliyhtälöt I, kevät 2017 Harjoitus 3
 Differentiaaliyhtälöt I, kevät 07 Harjoitus 3 Heikki Korpela. helmikuuta 07 Tehtävä. Ratkaise alkuarvo-ongelmat a) y + 4y e x = 0, y0) = 4 3 b) Vastaus: xy + y = x 3, y) =.. a) Valitaan integroivaksi tekijäksi
Differentiaaliyhtälöt I, kevät 07 Harjoitus 3 Heikki Korpela. helmikuuta 07 Tehtävä. Ratkaise alkuarvo-ongelmat a) y + 4y e x = 0, y0) = 4 3 b) Vastaus: xy + y = x 3, y) =.. a) Valitaan integroivaksi tekijäksi
mplteht/mpldiffint1, Diff-int 1 Maple
 Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mplteht/mpldiffint1, Diff-int 1 Maple Tässä luvussa on tehtäviä differentiaali- ja integraalilaskentaan Maple- ohjelmalla. (Sopivat yhtä hyvin
Aalto-yliopisto, Matematiikan ja Systeemianalyysin laitos mplteht/mpldiffint1, Diff-int 1 Maple Tässä luvussa on tehtäviä differentiaali- ja integraalilaskentaan Maple- ohjelmalla. (Sopivat yhtä hyvin
Kompleksianalyysi viikko 3
 Kompleksianalyysi viikko 3 Jukka Kemppainen Mathematics Division Derivaatta Oletetaan seuraavassa, että joukko A C on avoin, eli jokaista z 0 A kohti on olemassa sellainen ǫ > 0, että z z 0 < ǫ z A. f
Kompleksianalyysi viikko 3 Jukka Kemppainen Mathematics Division Derivaatta Oletetaan seuraavassa, että joukko A C on avoin, eli jokaista z 0 A kohti on olemassa sellainen ǫ > 0, että z z 0 < ǫ z A. f
2. Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä. y = 2xy, Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä käyristä on kyse?
 2. Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä 2.1. Ensimmäisen kertaluvun yhtälöt 30. Ratkaise alkuarvotehtävä y = 2xy, y(0)=1. Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä
2. Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä 2.1. Ensimmäisen kertaluvun yhtälöt 30. Ratkaise alkuarvotehtävä y = 2xy, y(0)=1. Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä
Suoran yhtälöt. Suoran ratkaistu ja yleinen muoto: Suoran yhtälö ratkaistussa, eli eksplisiittisessä muodossa, on
 Suoran htälöt Suoran ratkaistu ja leinen muoto: Suoran htälö ratkaistussa, eli eksplisiittisessä muodossa, on ANALYYTTINEN GEOMETRIA MAA5 = k + b, tai = a missä vakiotermi b ilmoittaa suoran ja -akselin
Suoran htälöt Suoran ratkaistu ja leinen muoto: Suoran htälö ratkaistussa, eli eksplisiittisessä muodossa, on ANALYYTTINEN GEOMETRIA MAA5 = k + b, tai = a missä vakiotermi b ilmoittaa suoran ja -akselin
MS-A0102 Differentiaali- ja integraalilaskenta 1
 MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 15.11.2016 Sisältö Alkeisfunktiot 1.1 Funktio I Funktio f : A! B on sääntö, joka liittää
MS-A0102 Differentiaali- ja integraalilaskenta 1 Riikka Korte (Pekka Alestalon kalvojen pohjalta) Aalto-yliopisto 15.11.2016 Sisältö Alkeisfunktiot 1.1 Funktio I Funktio f : A! B on sääntö, joka liittää
