Verkon värittäminen ja riippumattomat joukot: johdantoa ja sovelluksia
|
|
|
- Aila Kinnunen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 hyväksymispäivä arvosana arvostelija Verkon värittäminen ja riippumattomat joukot: johdantoa ja sovelluksia Janne Korhonen Helsinki Seminaariraportti HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
2 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta Fakultet Faculty Laitos Institution Department Matemaattis-luonnontieteellinen Tekijä Författare Author Janne Korhonen Työn nimi Arbetets titel Title Tietojenkäsittelytieteen laitos Verkon värittäminen ja riippumattomat joukot: johdantoa ja sovelluksia Oppiaine Läroämne Subject Tietojenkäsittelytiede Työn laji Arbetets art Level Aika Datum Month and year Sivumäärä Sidoantal Number of pages Seminaariraportti sivua Tiivistelmä Referat Abstract Verkon värittäminen ja maksimaalisten riippumattomien joukkojen etsiminen ovat laskentaongelmia, joilla on monia sovelluksia hajautettujen synkronisten algoritmien tutkimuksessa. Tämä raportti toimii lyhyenä johdantona aiheeseen. Määrittelemme kyseiset laskentaongelmat ja osoitamme, että ne palautuvat toisiinsa. Tarkastelemme lisäksi, kuinka muita laskentaongelmia voidaan ratkaista hajautetuilla algoritmeilla käyttämällä verkon värittämisalgoritmeja ja maksimaalisen riippumattoman joukon etsiviä algoritmeja. ACM Computing Classification System (CCS): F.2.2 [Analysis of Algorithms and Problem Complexity]: Nonnumerical Algorithms and Problems, G.2.2 [Discrete Mathematics]: Graph Theory Avainsanat Nyckelord Keywords hajautetut algoritmit, verkot, verkon väritys, maksimaalinen riippumaton joukko Säilytyspaikka Förvaringsställe Where deposited Muita tietoja övriga uppgifter Additional information
3 Sisältö ii 1 Johdanto 1 2 Peruskäsitteitä Verkoista Laskennan malli Laskentaongelmien esittely 3 4 Palautukset ongelmien välillä Maksimaalinen riippumaton joukko värityksestä Väritys maksimaalisesta riippumattomasta joukosta Sovelluksia Maksimaalisen riippumattoman joukon hyödyntäminen Muita värityksiä Algoritmien hajauttaminen värityksen avulla Yhteenveto 14 Lähteet 15
4 1 Johdanto 1 Hajautettujen algoritmien tutkimuksen taustalla ovat käytännön sovellukset erilaisten tietoliikenneverkkojen yhteydessä, mutta siitä huolimatta alalla on päädytty myös tutkimaan puhtaan teoreettisia kysymyksiä. Hajautettujen algoritmien tutkimus onkin tavallaan teoreettisen tietojenkäsittelytieteen mikrokosmos omine algoritmeineen sekä alaraja- ja mahdottomuustuloksineen. Tyypillisesti tutkimuksen tavoitteena on kuitenkin kehittää parempia algoritmeja. Tutustumme tässä raportissa verkon värityksiin ja maksimaalisiin riippumattomiin joukkoihin hajautettujen algoritmien kontekstissa. Tulemme havaitsemaan, että näitä voidaan käyttää hyväksi monien muiden laskentaongelmien hajautetussa ratkaisussa. Keskitymmekin tutkimaan verkon värittämisen ja maksimaalisten riippumattomien joukkojen etsinnän sovelluksia ja suhdetta toisiinsa. Varsinaisia hajautettuja algoritmeja verkon värittämiseen ja maksimaalisten riippumattomien joukkojen etsimiseen emme kuitenkaan esitä tämän raportin puitteissa. Luvussa 3 määrittelemme verkon värittämisongelman ja maksimaalisten riippumattomien joukkojen etsimisongelman sekä käsittelemme näitä laskentaongelmia yleisesti. Luvussa 4 osoitamme, että nämä ongelmat ovat palautettavissa toisiinsa siinä mielessä, että toisen näistä ongelmista ratkaisevaa algoritmia voidaan käyttää kummankin ratkaisuun. Lopulta luvussa 5 näemme, kuinka näitä algoritmeja voidaan hyödyntään monien muiden laskentaongelmien hajautettuun ratkaisuun. 2 Peruskäsitteitä Aloitamme kiinnittämällä merkintöjä ja määritelmiä, joita tulemme tarvitsemaan jatkossa. Käsittelemme ensin lyhyesti verkkoteoriaa ja määrittelemme sitten täsmällisesti käyttämämme hajautetun laskennan mallin. 2.1 Verkoista Käsittelemme tässä raportissa vain suuntaamattomia verkkoja. Esitämme verkon parina G = (V, E), missä V on epätyhjä joukko ja kaaret solmujen u, v V välillä esitetään kahden alkion joukkoina {u, v} E. Merkitsemme lisäksi n = V ja m = E. Solmun v V astetta eli naapurien lukumäärää verkossa G merkitsemme deg G (v).
5 2 Verkon maksimiastetta merkitsemme puolestaan (G), toisin sanoen (G) = max({deg G (v) v V }). Jos sekaannuksen vaaraa ei ole, käytämme lyhennysmerkintöjä deg(v) = deg G (v) ja = (G). Verkon G = (V, E) kaariverkko 1 on verkko G = (V, E ), missä 1. V = E, ja 2. solmujen e, f V välillä on kaari verkossa G, jos kaarilla e ja f on yhteinen päätepiste verkossa G, eli v u. Verkon G kaariverkossa G on korkeintaan V ( V 1)/2 solmua ja sen maksimiaste (G ) on korkeintaan 2( (G) 1). Olkoon edelleen G = (V, E) verkko ja v, u V. Solmujen v ja u etäisyys d(v, u) verkossa G on kaarien lukumäärä lyhimmällä polulla solmusta v solmuun u. Kaikilla k N verkon G potenssiverkko G k on verkko, jonka solmujoukko on V ja solmujen v, u välillä on kaari jos d(v, u) k. 2.2 Laskennan malli Hajautetuille algoritmeille on monia keskenään hyvinkin erilaisia laskennan malleja. Rajoitumme kuitenkin tässä käsittelemään laskentaa synkronisissa hajautetuissa järjestelmissä. Tämä käyttämämme malli on Linialin [Lin92] esittelemä; Peleg [Pel00] kutsuu vastaavaa mallia nimellä LOCAL. Mallissamme verkko G = (V, E) kuvaa laskentalaitteiden sijoittelua ja niiden välisiä yhteyksiä; jokainen solmu v V on yksi laskentalaite, ja kaksi solmua pystyy lähettämään toisilleen viestejä, jos niiden välillä on kaari verkossa G. Jokainen solmu suorittaa samaa algoritmia A. Algoritmi A ei tiedä etukäteen verkon G rakennetta, vaan se saa syötteenä kussakin solmussa tiedon kyseisen solmun naapureista. Laskennan lopuksi jokainen solmu tuottaa paikallisen tulosteen. Varsinainen laskenta tässä mallissa tapahtuu synkronisissa kommunikaatiokierroksissa. Algoritmia A suoritetaan r kierrosta, ja jokaisella kierroksella suoritetaan seuraavat asiat järjestyksessä: 1 englanniksi line graph
6 3 1. Jokainen prosessori suorittaa paikallista laskentaa. Tälle laskennalle ei aseteta mitään rajoituksia, vaan aikaa ja tilaa voidaan käyttää mielivaltaisen paljon. 2. Jokainen prosessori lähettää viestin jokaiselle naapurilleen. Tämän viestin kokoa ei myöskään ole rajoitettu. Emme tarkastele tässä mallissa virheensietoisuutta, vaan oletamme, että kaikki viestit saapuvat aina perille täydellisinä. 3. Jokainen prosessori vastaanottaa viestin jokaiselta naapuriltaan. Oleellista siis on, että kaikki viestit lähetetään ennen yhdenkään vastaanottamista. Kierroksen r jälkeen jokainen prosessori voi vielä tehdä rajoittamattomasti paikallista laskentaa ennen tuloksen tuottamista. Hajautetuissa algoritmeissa on usein kriittistä, kuinka paljon ylimääräistä informaatiota solmuilla on käytettävissään. Oletamme aina, että solmu pystyy erottamaan naapurinsa toisistaan, tai tarkemmin, että jokaisella solmulla v on käytössä jokin kiinnitetty numerointi naapurisolmuilleen luonnollisilla luvuilla 1,..., deg(v). Monet hajautetut algoritmit tarvitsevat kuitenkin myös solmuille uniikit tunnisteet. Solmun v tunniste ID(v) on luonnollinen luku, ja kaikilla verkon solmuilla on eri tunniste. Jos tunnisteita ei ole, sanomme verkon olevan anonyymi. 3 Laskentaongelmien esittely Ryhdymme nyt tarkastelemaan kahta jo mainitsemaamme laskentaongelmaa: verkon värittämistä ja maksimaalisen riippumattoman joukon löytämistä. Tavoitteenamme ei tässä raportissa kuitenkaan ole esittää algoritmeja näiden ongelmien ratkaisuun, vaan tutkia yleisemmin niiden roolia hajautettujen algoritmien tutkimuksessa. Määritelmä 1. Olkoon G = (V, E) verkko. Verkon G (solmujen) väritys on kuvaus c: V S, missä S on jokin joukko ja c(u) c(v) jos {u, v} E. Värityksen maalijoukon S alkioita kutsumme väreiksi. Yleensä joukoksi S valitaan joukko {1,..., k}, jolloin sanomme, että c on k-väritys (ks. kuva 1a). Ongelma 1 (Verkon värittäminen). Etsi annetulle verkolle G jokin väritys c. Hajautettujen algoritmien kontekstissa värittämisongelman syötteenä toimii algoritmia suorittava laskentaverkko G = (V, E) itse. Yksittäisen solmun ei tarvitse tietää lopuksi koko lopputulosta, vaan riittää, että jokainen solmu v G tulostaa oman värinsä c(v).
7 4 Haluamme tyypillisesti löytää mahdollisimman vähän värejä käyttävän värityksen mahdollisimman nopeasti. Jokaisen verkon G värittämiseen riittää aina + 1 väriä, sillä jokaisella solmulla on korkeintaan naapuria ja siten joukosta {1,..., + 1} löytyy aina vapaa väri. Oletetaan, että laskentaverkossa G on käytettävissä solmujen tunnisteet. Tällöin parhaat tunnetut yleisessä tapauksessa toimivat deterministiset ( +1)-värittämisalgoritmit toimivat ajassa O( +log n) [BE09, Kuh09]. Toisaalta Linial on osoittanut, että mikä tahansa deterministinen tai satunnainen ( +1)-värittämisalgoritmi vaatii ainakin 1 2 log n O(1) laskentakierrosta [Lin92]. Puille on olemassa ajassa O(log n) toimiva 3-värittämisalgoritmi [Pel00]. Lisäksi on olemassa odotusarvoisesti ajassa O(log n) toimiva hajautettu satunnaisalgoritmi ( + 1)-värittämiseen (ks. luku 4.2). Tätä algoritmia voidaan käyttää myös anonyymin verkon värittämiseen. Verkon värittäminen optimaalisesti on kuitenkin vaikeampi ongelma. Sanomme, että verkon G kromaattinen luku χ(g) on pienin luonnollinen luku k, jolla on olemassa verkon G solmujen k-väritys. Luvun χ(g) laskeminen on yleisesti NP-kova ongelma. Vastaavasti kaikilla k 3 on NP-täydellinen päätösongelma ratkaista, riittääkö k väriä annetun verkon G värittämiseen [GJ79, s. 191]. Määritelmä 2. Olkoon G = (V, E) verkko. Riippumaton joukko I V on verkon solmujen kokoelma, jossa ei ole kahta vierekkäistä solmua. Riippumaton joukko I on maksimaalinen, jos kaikilla riippumattomilla joukoilla I I pätee I = I, eli joukkoon I ei voi lisätä yhtään solmua rikkomatta sen riippumattomuutta (ks. kuva 1b). Ongelma 2 (Maksimaalisen riippumattoman joukon etsiminen). Etsi annetusta verkosta G jokin maksimaalinen riippumaton joukko I. Hajautettu algoritmi maksimaalisen riippumattoman joukon etsimiseen käyttää jäl- (a) (b) Kuva 1: (a) Verkon väritys kolmella värillä. (b) Eräs maksimaalinen riippumaton joukko (mustat solmut).
8 5 leen syötteenään algoritmia suorittavaa laskentaverkkoa G = (V, E). Laskennan lopuksi jokaisen solmun v V tulee ilmoittaa, kuuluuko se joukkoon I. Hajautetuilla satunnaisalgoritmeilla maksimaalinen riippumaton joukko voidaan rakentaa odotusarvoisesti ajassa O(log n) [Lub86, Pel00]. Maksimaalisen riippumattoman joukon löytäminen ei siis ole erityisen vaativa laskennallinen ongelma. Vastaava optimointiongelma on kuitenkin jälleen vaikeampi. Sanomme, että riippumaton joukko I V on maksimikokoinen, jos ei ole olemassa riippumatonta joukkoa I V, jolla I > I. Maksimikokoisen riippumattoman joukon löytäminen on NP-kova ongelma [GJ79, s. 194]. 4 Palautukset ongelmien välillä Tutkimme nyt esittelemiemme laskentaongelmien suhdetta toisiinsa. Osoitamme tässä luvussa, että ongelmat voidaan palauttaa toisiinsa; toisin sanoen, jos meillä on käytössä joko verkon värittämisalgoritmi tai maksimaalisen riippumattoman joukon etsivä algoritmi, voimme ratkaista molemmat ongelmat. Tulemme näkemään näissä palautuksissa käytettäviä tekniikoita myös muissa sovelluksissa myöhemmin. Perehdymme tarkemmin näiden palautuksien taustalla oleviin ajatuksiin luvussa Maksimaalinen riippumaton joukko värityksestä Maksimaalinen riippumaton joukko voidaan konstruoida helposti hajautetulla laskennalla, jos käytettävissä on väritys. Oletetaan, että G = (V, E) on laskentaverkko ja c on k-väritys verkolle G, niin että jokainen solmu v V tietää oman värinsä. Esitämme nyt algoritmin M, joka rakentaa maksimaalisen riippumattoman joukon I V seuraavasti. Jokainen solmu v V suorittaa laskentaa k synkronista laskentakierrosta seuraavasti: 1. Aluksi solmu v ei kuulu joukkoon I. 2. Kierroksella c(v), jos mikään solmun v naapuri ei ole ilmoittanut liittyneensä joukkoon I, solmu v liittyy joukkoon I ja lähettää tästä ilmoituksen kaikille naapureilleen. Muilla kierroksilla v ei tee mitään muuta viestien vastaanottamisen lisäksi. 3. Laskennan lopuksi v ilmoittaa, liittyikö joukkoon I vai ei.
9 6 (a) (b) (c) i = 1 i = 2 i = 3 Kuva 2: Esimerkki maksimaalisen riippumattoman joukon etsinnästä värityksen pohjalta. (a) 3-väritetty laskentaverkko G. (b) Algoritmin M suoritus kierroksittain; kierroksella i värin i solmut yrittävät liittyä maksimaaliseen riippumattomaan joukkoon. (c) Lopullinen maksimaalinen riippumaton joukko. Esimerkki algoritmin M suorituksesta on esitetty kuvassa 2. Lause 3. Algoritmi M löytää maksimaalisen riippumattoman joukon. Todistus. Olkoon I algoritmin M valitsema joukko verkossa G. Osoitamme ensin, että I on riippumaton. Olkoon u I ja v jokin sen naapuri. Solmu v ei voinut liittyä joukkoon I ennen kierrosta c(u), koska tällöin u ei olisi liittynyt joukkoon I. Koska u ja v ovat naapureita, c(v) c(u), eikä siis v voinut liittyä joukkoon I kierroksella c(u). Kierroksella c(u) lisäksi u ilmoitti solmulle v liittyneensä joukkoon I, joten v ei voinut liittyä joukkoon I kierroksen c(u) jälkeen. Siis v / I. Maksimaalisuuden osoittamiseksi olkoon v V jokin solmu, jonka mikään naapuri ei kuulu valittuun joukkoon I. Tällöin myöskään kierroksella c(v) mikään v:n naapuri ei kuulunut joukkoon I, joten v liittyi joukkoon I. Siis joukon I täytyy olla maksimaalinen riippumaton joukko. Selvästi algoritmi M vaatii täsmälleen k laskentakierrosta. Mikä tahansa hajautettu värittämisalgoritmi voidaan muuttaa maksimaalisen riippumattoman joukon etsiväksi algoritmiksi suorittamalla sen jälkeen algoritmin M. Tästä havainnosta saamme suoraan seuraavan korollaarin. Korollaari 4. Jos käytettävissä verkon värittämisalgoritmi, joka verkolla G vaatii T (G) laskentakierrosta ja tuottaa k(g)-värityksen, voidaan maksimaalinen riippumaton joukko löytää ajassa T (G) + k(g).
10 7 Soveltamalla korollaaria 4 aikaisemmin mainittuihin deterministisiin värittämisalgoritmeihin, saamme deterministisen hajautetun algoritmin, joka löytää tunnisteilla varustetussa verkossa maksimaalisen riippumattoman joukon ajassa O( + log n). 4.2 Väritys maksimaalisesta riippumattomasta joukosta Verkon värittäminen maksimaalisen riippumattoman joukon avulla on jokseenkin monimutkaisempi ongelma. Emme pysty suoraviivaisesti rakentamaan annetun maksimaalisen riippumattoman joukon pohjalta väritystä, mutta maksimaalisen riippumattoman joukon etsivä algoritmi voidaan muuttaa värittämisalgoritmiksi. Käytämme siihen alunperin Lubyn [Lub86] esittämää tekniikkaa. Olkoon G = (V, E) laskentaverkko. Oletamme, että käytössämme on jokin maksimaalisen riippumattoman joukon etsivä algoritmi A. Tällöin voimme värittää verkon G seuraavasti (kuva 3). 1. Konstruoimme verkon G pohjalta uuden verkon G = (V, E ), missä a) jokainen solmu v V korvataan deg(v) + 1:llä kopiolla v 1,..., v deg(v)+1, b) solmut v 1,..., v deg(v)+1 muodostavat klikin, eli ovat kaikki toistensa naapureita, ja c) solmut v i ja u i, missä {v, u} E, ovat naapureita kaikilla 1 i min(deg(v) + 1, deg(u) + 1). 2. Simuloimme maksimaalisen riippumattoman joukon etsivää algoritmia A verkossa G ja saamme tuloksena joukon I V. Jokainen v V siis simuloi solmuja v 1,... v deg(v) Solmu v V valitsee värin i, jos v i V kuuluu löydettyyn maksimaaliseen riippumattomaan joukkoon I. Kutsumme tätä algoritmiksi C. Algoritmin C valitsema väri solmulle v V on hyvin määritelty. Nimittäin vain yksi solmuista v 1,..., v deg(v)+1 voidaan valita maksimaaliseen riippumattomaan joukkoon I, sillä kyseiset solmut muodostavat klikin verkossa G. Toisaalta ainakin yksi näistä solmuista valitaan joukkoon I, koska solmulla v on deg G (v) naapuria, eikä siis kaikilla v i voi olla joukkoon I kuuluvaa naapuria verkossa G. Vastaavasti havaitsemme, että algoritmi C todella tuottaa värityksen. Jos v, u V ovat naapureita ja niille valittaisiin sama väri i, niin tällöin solmujen v i ja u i tulisi
11 8 (a) (b) (c) (d) Kuva 3: Esimerkki verkon värittämisestä maksimaalisen riippumattoman joukon etsivällä algoritmilla. (a) Alkuperäinen laskentaverkko G. (b) Algoritmin C rakentama verkko G. (c) Eräs maksimaalinen riippumaton joukko I = {v 4, u 3, w 2, y 1 } verkossa G. (d) Maksimaalisesta riippumattomasta joukosta I saatu väritys verkolle G. kuulua maksimaaliseen riippumattomaan joukkoon I. Tämä on kuitenkin mahdotonta, koska v i ja u i ovat naapureita. Selvästi esittämämme algoritmi tuottaa ( (G) + 1)-värityksen. Algoritmin C suoritusaika on sama kuin käytetyn maksimaalisen riippumattoman joukon etsimisalgoritmin suoritusaika verkossa G. Huomaamme lisäksi, että V = (deg G (v) + 1) ( (G) + 1) V, v V ja (G ) = 2 (G) + 1. Käyttämällä maksimaalisen riippumattoman joukon etsimiseen aikaisemmin mainitsemaamme odotusarvoisesti ajassa O(log n) toimivaa satunnaisalgoritmia, saamme odotusarvoisesti ajassa O(log n) toimivan väritysalgoritmin, sillä log V log (( (G) + 1) V ) log V 2 = 2 log V. Tällä algoritmilla pystymme siis myös värittämään anonyymeja verkkoja. 5 Sovelluksia Nyt siirrymme käsittelemään värityksien ja maksimaalisten riippumattomien joukkojen soveltamista muiden laskentaongelmien hajautettuun ratkaisuun. Tavoittee-
12 namme on käsitellä, miten väritykset ja maksimaaliset riippumattomat joukot liittyvät muihin verkko-ongelmiin ja niiden hajautettuun ratkaisuun Maksimaalisen riippumattoman joukon hyödyntäminen Näimme luvussa 4.2 kuinka maksimaalisen riippumattoman joukon etsivällä algoritmilla voitiin rakentaa väritys verkossa G siirtymällä ensin uuteen verkkoon G. Vastaavaa lähestymistapaa voidaan soveltaa myös muihin ongelmiin. Määritelmä 5. Olkoon G = (V, E) verkko. Pariutus M E on verkon kaarien kokoelma, jossa e f = kaikilla e, f M. Pariutus M on maksimaalinen, jos kaikilla pariutuksilla M M pätee M = M. Maksimaalinen pariutus voidaan löytää helposti maksimaalisen riippumattoman joukon etsivällä algoritmilla. Olkoon G = (V, E) laskentaverkko, josta haluamme löytää maksimaalisen pariutuksen. Siirrymme alkuperäisen verkon G sijaan tarkastelemaan verkon G kaariverkkoa G = (V, E ), samaan tapaan kuin aikaisemmin algoritmissa C. Jokainen solmu v V simuloi itsestään lähteviä kaaria vastaavia solmuja. Tällöin jokaista solmua e V simuloidaan kahdessa alkuperäisen verkon solmussa, ja nämä kopiot synkronoidaan jokaisella laskentakierroksella. Kun verkosta G etsitään maksimaalinen riippumaton joukko M V, niin joukko M on maksimaalinen pariutus alkuperäisessä verkossa G (kuva 4). Koska verkossa G on korkeintaan V ( V 1)/2 solmua, saamme myös maksimaalisen pariutuksen rakennettua satunnaisalgoritmilla odotusarvoisesti ajassa O(log n). Käyttämällä hyväksi maksimaalista pariutusta saamme edelleen ratkaistua muita verkko-ongelmia. Määritelmä 6. Joukko U V on solmupeite, jos kaikilla {u, v} E joko u U Kuva 4: Maksimaalinen pariutus verkossa G ja vastaava maksimaalinen riippumaton joukko verkon G kaariverkossa G.
13 10 tai v U. Solmupeite U on minimaalinen, jos mikään sen aito osajoukko ei ole solmupeite. Saamme solmupeitteen U V verkossa G = (V, E) maksimaalisesta pariutuksesta M E valitsemalla joukkoon U kaikkien kaarien e M molemmat päätepisteet. Tämä on solmupeite, sillä pariutuksen M maksimaalisuuden nojalla ei ole olemassa kaarta e E, jonka kummastakaan päätepisteestä ei lähtisi joukkoon M kuuluvaa kaarta. Näin saatu solmupeite U ei välttämättä ole minimaalinen solmupeite, mutta se on kuitenkin 2-approksimaatio solmujen lukumäärältä minimikokoisesta solmupeitteestä [Vaz03, s. 3]. Yleisesti yksittäisen riippumattoman joukon tunteminen ei ole kovin hyödyllistä hajautettujen algoritmien kannalta. Maksimaaliset riippumattomat joukot kuitenkin liittyvät läheisesti moneen muuhun verkko-ongelmaan. Esitämme tähän liittyen joukon yksinkertaisia havaintoja. Olkoon jatkossa G = (V, E) mielivaltainen yhtenäinen verkko. Ensinnäkin maksimaalisen riippumattoman joukon I komplementti V \ I on selvästi minimaalinen solmupeite. Määrittelemme lisäksi muita verkko-ongelmia, joilla on yhteys maksimaalisiin riippumattomiin joukkoihin. Määritelmä 7. Joukko U V on dominoiva joukko, jos kaikilla v V \ U on naapuri u U. Dominoiva joukko U on minimaalinen, jos mikään sen aito osajoukko ei ole dominoiva. Maksimaalinen riippumaton joukko I V on myös minimaalinen dominoiva joukko. Jos V > 1, niin myös joukko V \I on dominoiva joukko, mutta ei välttämättä minimaalinen. Yhdessä nämä muodostavat verkon G domaattisen osituksen, eli osituksen erillisiin dominoiviin joukkoihin. Määritelmä 8. Verkon G (solmujen) heikko väritys on kuvaus c: V S, missä S on jokin joukko ja kaikilla solmuilla v V, joilla on naapureita, on ainakin yksi naapuri u V, jolla c(v) c(u). Heikko k-väritys määritellään vastaavasti kuin tavallinen k-väritys. Jos I V on maksimaalinen riippumaton joukko, niin heikko 2-väritys saadaan asettamalla c(u) = 1 kaikille u I ja c(u) = 2 kaikille u V \ I. Heikon värityksen määrittelivät alunperin Naor ja Stockmeyer [NS95], nimenomaan hajautettujen algoritmien yhteydessä. Sitä on myös mahdollista käyttää apuna muiden laskentaongelmien ratkaisussa laskentaverkoissa.
14 Muita värityksiä Olemme jo käsitelleet verkon solmuvärityksiä ja heikkoja solmuvärityksiä. Määrittelemme tässä vielä muita väritystyyppejä, ja tutkimme, miten solmuvärittämisalgoritmeja voidaan soveltaa näiden konstruoimiseen. Määritelmä 9. Olkoon G = (V, E) verkko. Verkon G kaariväritys on kuvaus c: E S, missä S on jokin joukko ja c(e) c(f) jos kaarilla e ja f on yhteinen päätepiste. Vastaavasti kuin solmuvärityksen tapauksessa, joukoksi S valitaan tyypillisesti joukko {1,..., k}, jolloin sanomme, että c on k-kaariväritys. Kaariväritys palautuu helposti solmuväritykseen, sillä voimme jälleen siirtyä alkuperäisestä verkosta G sen kaariverkkoon G. Selvästi kaariverkon solmuväritys on suoraan alkuperäisen verkon kaariväritys. Jos käytämme kaariverkon solmuvärityksen etsimiseen ( + 1)-värittämisalgoritmia, saamme alkuperäiseen verkkoon (2 (G) 1)-kaarivärityksen, koska (G ) 2( (G) 1). Tämä on itse asiassa 2-approksimaatio värien lukumäärältä minimikokoisesta kaarivärityksestä, sillä Vizingin lauseen [Die05, s. 119] nojalla kaariväritykseen vaaditaan aina vähintään väriä ja jokaiselle verkolle on olemassa ( + 1)-kaariväritys. Määritelmä 10. Olkoon G = (V, E) verkko. Verkon G solmujen väritys c: V S on etäisyyden k väritys 2, jos kaikilla v, u V, joilla c(v) = c(u), pätee d(v, u) > k. Havaitsemme, että verkon G etäisyyden k väritykset ovat potenssiverkon G k värityksiä ja päinvastoin. Saamme siis etäisyyden k värityksen rakennettua verkossa G simuloimalla väritysalgoritmin toimintaa verkossa G k. Tämä onnistuu verkossa G suorittamalla jokaisen laskentakierroksen jälkeen k 1 ylimääräistä laskentakierrosta, joiden aikana viestit välitetään verkossa etäisyydellä k oleviin solmuihin. Siis etäisyyden k väritys (G k )+1 värillä voidaan laskea vakiokerrointa k vaille samassa ajassa kuin ( (G) + 1)-solmuväritys. Verkon G etäisyyden 2 väritys voidaan suoraviivaisesti muuntaa kaariväritykseksi. Kaaren {u, v} E väriksi valitaan järjestämätön pari {c(u), c(v)}. Tämä tuottaa kaarivärityksen, sillä jos e = {u, v} ja f = {u, w} ovat eri kaaret, niin etäisyyden 2 värityksen määritelmästä seuraa c(v) c(w) ja kaaret e ja f saavat eri värit. Tämä tekniikka kuitenkin johtaa helposti suureen värimäärään. 2 englanniksi distance-k coloring
15 Algoritmien hajauttaminen värityksen avulla Sovellamme nyt luvussa 4.1 esitetyn algoritmin M ideaa muihin laskentaongelmiin. Algoritmissa M solmujen valitseminen maksimaaliseen riippumattomaan joukkoon I pystyttiin tekemään yhden värin sisällä rinnakkaisesti, sillä nämä päätökset eivät riippuneet toisistaan. Tämä päätösten riippumattomuus puolestaan perustui siihen, että päätös joukkoon I liittymisestä riippui vain solmun naapureista, ja {v V c(v) = i} on riippumaton joukko kaikilla väreillä i. Yleisemmin voimme hajauttaa solmut tai kaaret mielivaltaisessa järjestyksessä käsittelevän keskitetyn sekventiaalisen algoritmin sopivan värityksen avulla, kunhan päätökset ei-vierekkäisten solmujen tai kaarien kohdalla ovat sopivalla tavalla riippumattomia toisistaan. Tällöin voimme suorittaa käsittelyn väri kerrallaan rinnakkaistetusti, kuten algoritmissa M. Käymme nyt läpi esimerkkejä tätä lähestymistapaa hyödyntävistä algoritmeista. Määritelmä 11. Olkoon G = (V, E) verkko. Verkon G leikkaus (S, T ) on joukon V ositus kahteen erilliseen osajoukkoon S ja T, eli S, T V ja T = V \S. Leikkauksen (S, T ) koko on joukon {{s, t} E s S, t T } alkioiden lukumäärä, eli joukkojen S ja T välillä kulkevien kaarien lukumäärä. Leikkaus (S, T ) on maksimikokoinen, jos ei ole olemassa kooltaan suurempaa leikkausta. Maksimikokoisen leikkauksen etsiminen on NP-kova ongelma [GJ79, s. 210]. Saamme kuitenkin 2-approksimaation maksimikokoisesta leikkauksesta seuraavalla keskitetyllä algoritmilla, joka rakentaa leikkauksen (S, T ) verkolle G [SG76]. 1. Aluksi joukot S ja T ovat tyhjiä. 2. Solmut v V käydään läpi mielivaltaisessa järjestyksessä. Jos solmua v käsitellessä {s S {v, s} E} > {t T {v, t} E}, niin solmu v lisätään joukkoon T, ja muussa tapauksessa v lisätään joukkoon S. Olkoon nyt G = (V, E) laskentaverkko ja c jokin k-väritys verkolle G. Voimme tällöin simuloida tätä keskitettyä algoritmia verkossa G käyttämällä k laskentakierrosta. Kierroksella i = 1,..., k, jokainen värin i solmu v suorittaa seuraavat askeleet: 1. Aluksi solmu v laskee aikaisemmilla kierroksilla saamiensa viestien perusteella luvut {s S {v, s} E} ja {t T {v, t} E}.
16 13 2. Mikäli {s S {v, s} E} > {t T {v, t} E}, solmu v liittyy joukkoon T ja muuten se liittyy joukkoon S. 3. Solmu v ilmoittaa naapureilleen liittymisestään joukkoon S tai joukkoon T. Solmujen tekemät päätökset riippuvat vain niiden naapureiden aikaisemmin tekemistä päätöksistä, eivätkä siis rinnakkain tehtävät päätökset voi vaikuttaa toisiinsa. Näin siis saamme simuloitua esittämäämme keskitettyä algoritmia käyttämällä k synkronista laskentakierrosta ja saamme näin 2-approksimaation maksimikokoisesta leikkauksesta. Voimme käyttää tällaisen hajauttamisen pohjana myös muita kuin tavallista solmuväritystä. Tätä lähestymistapaa voidaan soveltaa esimerkiksi maksimaalisen pariutuksen etsimiseen. Olkoon G = (V, E) verkko ja c jokin k-kaariväritys verkolle G. Keskitetysti maksimaalinen pariutus voidaan rakentaa yksinkertaisesti käymällä kaaret mielivaltaisessa järjestyksessä läpi, ja ottamalla kaari mukaan jos mukana ei ole vielä kummastakaan sen päätepisteestä lähtevää kaarta. Tämä algoritmin hajautettu versio puolestaan ottaa mukaan kierroksella i kaikki sopivat kaaret e E, joilla c(e) = i. Näin maksimaalinen pariutus saadaan rakennettua käyttämällä k laskentakierrosta. Algoritmin oikeellisuus perustuu siihen, että koska kahdella samanvärisellä kaarella ei voi olla yhteistä päätepistettä, eivät yhden kierroksen aikana tehtävät päätökset voi vaikuttaa toisiinsa. Tämä algoritmi voidaan tietysti jälleen muuttaa 2-approksimaatioalgoritmiksi solmupeitteelle. Esitämme lopuksi monimutkaisemman sovelluksen väritysten käytöstä keskitettyjen algoritmien hajauttamisessa. Solmujen lukumäärältä minimikokoista dominoivaa joukkoa voidaan approksimoida keskitetyllä ahneella algoritmilla rakentamalla verkossa G = (V, E) joukko U V. 1. Aluksi U on tyhjä. 2. Joka kierroksella joukkoon U lisätään jokin solmu v V, jolla deg(v) deg(u) kaikilla u V. Solmu v ja sen naapurit poistetaan verkosta G. 3. Algoritmi päättyy, kun verkossa G ei ole enää yhtään solmua jäljellä. Tämä algoritmi on oleellisesti sama kuin tunnettu ahne approksimaatioalgoritmi joukkopeitteen etsintään ja se tuottaa O(log )-approksimaation minimikokoisesta dominoivasta joukosta [Joh73]. Olkoon nyt G = (V, E) laskentaverkko ja c verkon G etäisyyden 2 solmuväritys. Oletamme lisäksi, että jokainen solmu tietää verkon G maksimiasteen. Nyt yllä esitetyn keskitetyn algoritmin toimintaa voidaan simuloida verkossa G hajautetulla
17 14 algoritmilla rakentamalla dominoiva joukko U V seuraavasti. Algoritmin suoritus on jaettu vaiheisiin, joissa jokaisessa käsitellään tiettyä astetta δ ja tiettyä väriä i. Joka vaiheessa suoritetaan kaksi laskentakierrosta. 1. Ensimmäisellä kierroksella a) kaikki solmut ensin vähentävät omaa astettaan edellisessä vaiheessa saamiensa poistumisilmoitusten mukaisesti, ja b) solmut v V, joiden aste deg(v) = δ ja väri c(v) = i, liittyvät joukkoon U ja ilmoittavat tästä naapureilleen. 2. Toisella kierroksella solmut, jotka ovat ensimmäisellä kierroksella saaneet naapuriltaan viestin joukkoon U liittymisestä ilmoittavat naapureilleen poistuvansa verkosta ja lopettavat tämän jälkeen laskennan. Käsittely aloitetaan asteesta. Jokaista väriä i = 1,..., k kohti suoritetaan yksi yllä kuvattu algoritmin vaihe. Tämän jälkeen siirrytään asteen 1 solmuihin ja suoritetaan jälleen jokaista väriä kohti yksi algoritmin vaihe. Tätä jatketaan, kunnes kaikki asteet ja värit on käyty läpi; vaiheita siis suoritetaan yhteensä k. Mikäli viimeisen vaiheen jälkeen verkossa on jäljellä asteen 0 solmuja, nämä liittyvät myös joukkoon U. Algoritmi vaatii selvästi 2k laskentakierrosta. Etäisyyden 2 värityksen käyttö takaa, etteivät rinnakkaisesti tehtävät päätökset vaikuta toisiinsa. Käyttämällä kaksi laskentakierrosta joka vaiheessa varmistetaan, että solmut ehtivät saada tiedon verkosta poistetuista naapureistaan ennen kuin itse yrittävät seuraavan kerran liittyä rakennettavaan dominoivaan joukkoon U. Tämä algoritmi tietenkin pääsee samaan approksimaatiosuhteeseen O(log ) kuin pohjana toiminut keskitetty algoritmikin. 6 Yhteenveto Olemme nähneet, kuinka verkon väritykset ja maksimaaliset riippumattomat joukot liittyvät läheisesti toisiinsa. Lisäksi olemme nähneet monia tapoja soveltaa näitä verkkoteoreettisia rakenteita ja niitä etsiviä algoritmeja muiden verkko-ongelmien ratkaisussa laskentaverkoissa. Koska lisäksi sekä värittämiseen että maksimaalisen riippumattoman joukon etsintään tunnetaan tehokkaita hajautettuja algoritmeja, esittelemämme tekniikat tarjoavat selkeästi hyödyllisen peruslähtökohdan hajautettujen algoritmien suunnittelulle. On kuitenkin huomattava, että näin saadut algoritmi eivät välttämättä ole lähelläkään optimaalista, ja suorempi lähestymistapa voisi
18 15 tuottaa parempia ratkaisuja. Käsittelemästämme aiheesta on kuitenkin tehty hyvin vähän systemaattista tutkimusta. Esittämämme lähestymistavat värityksien ja maksimaalisten riippumattomien joukkojen soveltamisesta ovat pitkälti yksittäisiä temppuja. Laajimmin sovellettava menetelmä vaikuttaisi olevan luvussa 5.3 esitetty värityksen etsiminen ja keskitetyn algoritmin hajauttaminen sen avulla. Näiden aiheiden tarkempi tutkiminen voisi siis olla hedelmällistä. Lisäksi on syytä huomata, ettemme käsitelleet ollenkaan miten värityksen olemassaolo vaikuttaa symmetrianrikkomisongelmaan anonyymeissa verkoissa, vaikka tämä kysymys liittyykin luontevasti tämän raportin aihepiiriin. Lähteet BE09 Barenboim, L. ja Elkin, M., Distributed ( + 1)-coloring in linear (in ) time. STOC 09: Proceedings of the 41st Annual ACM Symposium on Theory of Computing. ACM, 2009, sivut Die05 Diestel, R., Graph Theory. Springer-Verlag, GJ79 Joh73 Kuh09 Lin92 Lub86 NS95 Garey, M. R. ja Johnson, D. S., Computers and Intractability, A Guide to the Theory of NP-Completeness. W.H. Freeman and Company, Johnson, D., Approximation algorithms for combinatorial problems. Proceedings of the Fifth Annual ACM Symposium on Theory of Computing. ACM, 1973, sivut Kuhn, F., Weak graph colorings: distributed algorithms and applications. SPAA 09: Proceedings of the Twenty-First Annual Symposium on Parallelism in Algorithms and Architectures. ACM, 2009, sivut Linial, N., Locality in distributed graph algorithms. SIAM Journal on Computing, 21,1(1992), sivut Luby, M., A simple parallel algorithm for the maximal independent set problem. SIAM Journal on Computing, 15,4(1986), sivut Naor, M. ja Stockmeyer, L., What can be computed locally? SIAM Journal on Computing, 24,6(1995), sivut
19 16 Pel00 SG76 Peleg, D., Distributed Computing: a Locality-Sensitive Approach. Society for Industrial and Applied Mathematics, Sahni, S. ja Gonzalez, T., P-complete approximation problems. Journal of the ACM, 23,3(1976), sivut Vaz03 Vazirani, V., Approximation Algorithms. Springer-Verlag, 2003.
Verkon värittämistä hajautetuilla algoritmeilla
 Verkon värittämistä hajautetuilla algoritmeilla 5 12 30 19 72 34 Jukka Suomela 15 77 18 4 9. tammikuuta 2012 19 2 68 Verkko 2 Verkko solmu 3 Verkko solmu kaari 4 Hajautettu järjestelmä solmu (tietokone)
Verkon värittämistä hajautetuilla algoritmeilla 5 12 30 19 72 34 Jukka Suomela 15 77 18 4 9. tammikuuta 2012 19 2 68 Verkko 2 Verkko solmu 3 Verkko solmu kaari 4 Hajautettu järjestelmä solmu (tietokone)
Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005
 Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen
 V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
arvostelija OSDA ja UDDI palveluhakemistoina.
 Hyväksymispäivä Arvosana arvostelija OSDA ja UDDI palveluhakemistoina. HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty/Section Laitos Institution
Hyväksymispäivä Arvosana arvostelija OSDA ja UDDI palveluhakemistoina. HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty/Section Laitos Institution
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Selainpelien pelimoottorit
 Selainpelien pelimoottorit Teemu Salminen Helsinki 28.10.2017 Seminaaritutkielma Helsingin yliopisto Tietojenkäsittelytiede ! 1 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta
Selainpelien pelimoottorit Teemu Salminen Helsinki 28.10.2017 Seminaaritutkielma Helsingin yliopisto Tietojenkäsittelytiede ! 1 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta
Seminaari: Hajautetut algoritmit syksy 2009
 Seminaari: Hajautetut algoritmit syksy 2009 http://www.cs.helsinki.fi/u/josuomel/sem-2009s/ Jukka Suomela 10.9.2009 Seminaari: Hajautetut algoritmit syksy 2009 Seminaarin työmuodot 2 / 38 Aikataulu ja
Seminaari: Hajautetut algoritmit syksy 2009 http://www.cs.helsinki.fi/u/josuomel/sem-2009s/ Jukka Suomela 10.9.2009 Seminaari: Hajautetut algoritmit syksy 2009 Seminaarin työmuodot 2 / 38 Aikataulu ja
6. Approksimointialgoritmit
 6. Approksimointialgoritmit Tässä luvussa käsitellään lyhyesti approksimointiin liittyvät peruskäsitteet ja joitain keskeisiä approksimoituvuustuloksia. Tavoitteena on, että opiskelija näkee approksimointialgoritmien
6. Approksimointialgoritmit Tässä luvussa käsitellään lyhyesti approksimointiin liittyvät peruskäsitteet ja joitain keskeisiä approksimoituvuustuloksia. Tavoitteena on, että opiskelija näkee approksimointialgoritmien
Dominointianalyysi. Teppo Niinimäki. Helsinki Approksimointialgoritmit HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
 Dominointianalyysi Teppo Niinimäki Helsinki 10.5.2010 Approksimointialgoritmit HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta
Dominointianalyysi Teppo Niinimäki Helsinki 10.5.2010 Approksimointialgoritmit HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta
Parinmuodostuksesta tietojenkäsittelytieteen silmin. Petteri Kaski Tietojenkäsittelytieteen laitos Aalto-yliopisto
 Parinmuodostuksesta tietojenkäsittelytieteen silmin Petteri Kaski Tietojenkäsittelytieteen laitos Aalto-yliopisto Suomalainen Tiedeakatemia Nuorten Akatemiaklubi 18.10.2010 Sisältö Mitä tietojenkäsittelytieteessä
Parinmuodostuksesta tietojenkäsittelytieteen silmin Petteri Kaski Tietojenkäsittelytieteen laitos Aalto-yliopisto Suomalainen Tiedeakatemia Nuorten Akatemiaklubi 18.10.2010 Sisältö Mitä tietojenkäsittelytieteessä
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
Valitaan alkio x 1 A B ja merkitään A 1 = A { x 1 }. Perinnöllisyyden nojalla A 1 I.
 Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m.
 Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Laskennan vaativuus ja NP-täydelliset ongelmat
 Laskennan vaativuus ja NP-täydelliset ongelmat TRAK-vierailuluento 13.4.2010 Petteri Kaski Tietojenkäsittelytieteen laitos Tietojenkäsittelytiede Tietojenkäsittelytiede tutkii 1. mitä tehtäviä voidaan
Laskennan vaativuus ja NP-täydelliset ongelmat TRAK-vierailuluento 13.4.2010 Petteri Kaski Tietojenkäsittelytieteen laitos Tietojenkäsittelytiede Tietojenkäsittelytiede tutkii 1. mitä tehtäviä voidaan
Tehtävä 4 : 2. b a+1 (mod 3)
 Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Olkoon seuraavaksi G 2 sellainen tasan n solmua sisältävä suunnattu verkko,
 Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
Yleinen paikallinen vakautuva synkronointialgoritmi
 Yleinen paikallinen vakautuva synkronointialgoritmi Panu Luosto 23. marraskuuta 2007 3 4 putki 1 2 α α+1 α+2 α+3 0 K 1 kehä K 2 K 3 K 4 Lähdeartikkeli Boulinier, C., Petit, F. ja Villain, V., When graph
Yleinen paikallinen vakautuva synkronointialgoritmi Panu Luosto 23. marraskuuta 2007 3 4 putki 1 2 α α+1 α+2 α+3 0 K 1 kehä K 2 K 3 K 4 Lähdeartikkeli Boulinier, C., Petit, F. ja Villain, V., When graph
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Konsensusongelma hajautetuissa järjestelmissä. Niko Välimäki Hajautetut algoritmit -seminaari
 Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki 30.11.2007 Hajautetut algoritmit -seminaari Konsensusongelma Päätöksen muodostaminen hajautetussa järjestelmässä Prosessien välinen viestintä
Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki 30.11.2007 Hajautetut algoritmit -seminaari Konsensusongelma Päätöksen muodostaminen hajautetussa järjestelmässä Prosessien välinen viestintä
Algoritmi on periaatteellisella tasolla seuraava:
 Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
7.4 Sormenjälkitekniikka
 7.4 Sormenjälkitekniikka Tarkastellaan ensimmäisenä esimerkkinä pitkien merkkijonojen vertailua. Ongelma: Ajatellaan, että kaksi n-bittistä (n 1) tiedostoa x ja y sijaitsee eri tietokoneilla. Halutaan
7.4 Sormenjälkitekniikka Tarkastellaan ensimmäisenä esimerkkinä pitkien merkkijonojen vertailua. Ongelma: Ajatellaan, että kaksi n-bittistä (n 1) tiedostoa x ja y sijaitsee eri tietokoneilla. Halutaan
Näytetään nyt relaatioon liittyvien ekvivalenssiluokkien olevan verkon G lohkojen särmäjoukkoja. Olkoon siis f verkon G jokin särmä.
 Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Aika/Datum Month and year Kesäkuu 2012
 Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos/Institution Department Filosofian, historian, kulttuurin ja taiteiden tutkimuksen laitos Humanistinen tiedekunta Tekijä/Författare Author Veera Lahtinen
Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos/Institution Department Filosofian, historian, kulttuurin ja taiteiden tutkimuksen laitos Humanistinen tiedekunta Tekijä/Författare Author Veera Lahtinen
Skedulointi, kuormituksen tasaus, robotin navigaatio
 Skedulointi, kuormituksen tasaus, robotin navigaatio Esitelmä algoritmiikan tutkimusseminaarissa 17.2.2003 Kimmo Palin Tietojenkäsittelytieteen laitos Helsingin Yliopisto Skedulointi, kuormituksen tasaus,
Skedulointi, kuormituksen tasaus, robotin navigaatio Esitelmä algoritmiikan tutkimusseminaarissa 17.2.2003 Kimmo Palin Tietojenkäsittelytieteen laitos Helsingin Yliopisto Skedulointi, kuormituksen tasaus,
A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä.
 Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Stabilointi. Marja Hassinen. p.1/48
 Stabilointi Marja Hassinen marja.hassinen@cs.helsinki.fi p.1/48 Kertausta ja käsitteitä Sisältö Stabilointi Resynkroninen stabilointi Yleinen stabilointi Tarkkailu Alustus Kysymyksiä / kommentteja saa
Stabilointi Marja Hassinen marja.hassinen@cs.helsinki.fi p.1/48 Kertausta ja käsitteitä Sisältö Stabilointi Resynkroninen stabilointi Yleinen stabilointi Tarkkailu Alustus Kysymyksiä / kommentteja saa
Satunnaisalgoritmit. Topi Paavilainen. Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
 Satunnaisalgoritmit Topi Paavilainen Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 1 Johdanto Satunnaisalgoritmit ovat algoritmeja, joiden
Satunnaisalgoritmit Topi Paavilainen Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 1 Johdanto Satunnaisalgoritmit ovat algoritmeja, joiden
Työn laji Arbetets art Level Aika Datum Month and year Sivumäärä Sidoantal Number of pages
 Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Tekijä Författare Author Työn nimi Arbetets titel Title Oppiaine Läroämne Subject Työn laji Arbetets art Level Aika Datum Month
Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Tekijä Författare Author Työn nimi Arbetets titel Title Oppiaine Läroämne Subject Työn laji Arbetets art Level Aika Datum Month
Matematiikan ja tilastotieteen laitos Matematiikka tutuksi Harjoitus 2, malliratkaisut
 Matematiikan ja tilastotieteen laitos Matematiikka tutuksi Harjoitus, malliratkaisut 1.-5.9.009 1. Muodosta joukot A B, A B ja A\B sekä laske niiden alkioiden lukumäärät (mikäli kyseessä on äärellinen
Matematiikan ja tilastotieteen laitos Matematiikka tutuksi Harjoitus, malliratkaisut 1.-5.9.009 1. Muodosta joukot A B, A B ja A\B sekä laske niiden alkioiden lukumäärät (mikäli kyseessä on äärellinen
Department of Mathematics, Hypermedia Laboratory Tampere University of Technology. Roolit Verkostoissa: HITS. Idea.
 Roolit Tommi Perälä Department of Mathematics, Hypermedia Laboratory Tampere University of Technology 25.3.2011 J. Kleinberg kehitti -algoritmin (Hypertext Induced Topic Search) hakukoneen osaksi. n taustalla
Roolit Tommi Perälä Department of Mathematics, Hypermedia Laboratory Tampere University of Technology 25.3.2011 J. Kleinberg kehitti -algoritmin (Hypertext Induced Topic Search) hakukoneen osaksi. n taustalla
Tehtävä 10 : 1. Tehtävä 10 : 2
 Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
Rekursiolause. Laskennan teorian opintopiiri. Sebastian Björkqvist. 23. helmikuuta Tiivistelmä
 Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA. Karoliina Ljungberg
 Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA Karoliina Ljungberg 16.04.2009 Ohjaajat: Ari Venäläinen, Jouni Räisänen
Pro gradu -tutkielma Meteorologia SUOMESSA ESIINTYVIEN LÄMPÖTILAN ÄÄRIARVOJEN MALLINTAMINEN YKSIDIMENSIOISILLA ILMAKEHÄMALLEILLA Karoliina Ljungberg 16.04.2009 Ohjaajat: Ari Venäläinen, Jouni Räisänen
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
j(j 1) = n(n2 1) 3 + (k + 1)k = (k + 1)(k2 k + 3k) 3 = (k + 1)(k2 + 2k + 1 1)
 MS-A0401 Diskreetin matematiikan perusteet Tentti ja välikokeiden uusinta 10.11.015 Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot! Laskimia tai taulukoita ei saa käyttää tässä kokeessa!
MS-A0401 Diskreetin matematiikan perusteet Tentti ja välikokeiden uusinta 10.11.015 Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot! Laskimia tai taulukoita ei saa käyttää tässä kokeessa!
Äärellisten automaattien ja säännöllisten lausekkeiden minimointi
 Äärellisten automaattien ja säännöllisten lausekkeiden minimointi Timi Suominen, Riia Ohtamaa ja Pessi Moilanen Helsinki..01 HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Äärellisten automaattien
Äärellisten automaattien ja säännöllisten lausekkeiden minimointi Timi Suominen, Riia Ohtamaa ja Pessi Moilanen Helsinki..01 HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Äärellisten automaattien
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko
 DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
b) Olkoon G vähintään kaksi solmua sisältävä puu. Sallitaan verkon G olevan
 Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Johnson, A Theoretician's Guide to the Experimental Analysis of Algorithms.
 Kokeellinen algoritmiikka (3 ov) syventäviä opintoja edeltävät opinnot: ainakin Tietorakenteet hyödyllisiä opintoja: ASA, Algoritmiohjelmointi suoritus harjoitustyöllä (ei tenttiä) Kirjallisuutta: Johnson,
Kokeellinen algoritmiikka (3 ov) syventäviä opintoja edeltävät opinnot: ainakin Tietorakenteet hyödyllisiä opintoja: ASA, Algoritmiohjelmointi suoritus harjoitustyöllä (ei tenttiä) Kirjallisuutta: Johnson,
0 v i v j / E, M ij = 1 v i v j E.
 Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Verkkoalgoritmeja. Henry Niveri. hniveri(at)cc.hut.fi
 Verkkoalgoritmeja Henry Niveri hniveri(at)cc.hut.fi Seminaariesitelmä 16.4.008 T-106.5800 Satunnaisalgoritmit Tietotekniikan laitos Teknillinen korkeakoulu Tiivistelmä Tässä esityksessä käsitellään satunnaisalgoritmien
Verkkoalgoritmeja Henry Niveri hniveri(at)cc.hut.fi Seminaariesitelmä 16.4.008 T-106.5800 Satunnaisalgoritmit Tietotekniikan laitos Teknillinen korkeakoulu Tiivistelmä Tässä esityksessä käsitellään satunnaisalgoritmien
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
Joukot. Georg Cantor ( )
 Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
missä on myös käytetty monisteen kaavaa 12. Pistä perustelut kohdilleen!
 Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 8.5.2018 Timo Männikkö Luento 13 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys Kertaus ja tenttivinkit Algoritmit 2 Kevät
Algoritmit 2 Luento 13 Ti 8.5.2018 Timo Männikkö Luento 13 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys Kertaus ja tenttivinkit Algoritmit 2 Kevät
Pysähtymisongelman ratkeavuus [Sipser luku 4.2]
![Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Pysähtymisongelman ratkeavuus [Sipser luku 4.2]](/thumbs/59/42645644.jpg) Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Osoitamme nyt vihdoin, että jotkin Turing-tunnistettavat kielet ovat ratkeamattomia ja jotkin kielet eivät ole edes Turing-tunnistettavia. Lisäksi toteamme,
Pysähtymisongelman ratkeavuus [Sipser luku 4.2] Osoitamme nyt vihdoin, että jotkin Turing-tunnistettavat kielet ovat ratkeamattomia ja jotkin kielet eivät ole edes Turing-tunnistettavia. Lisäksi toteamme,
PARITUS KAKSIJAKOISESSA
 PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Algoritmit 1. Luento 1 Ti Timo Männikkö
 Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Maailman muutosta tallentamassa Marko Vuokolan The Seventh Wave -valokuvasarja avauksena taidevalokuvan aikaan
 Maailman muutosta tallentamassa Marko Vuokolan The Seventh Wave -valokuvasarja avauksena taidevalokuvan aikaan Pro gradu -tutkielma 31.1.2012 Helsingin yliopisto Humanistinen tiedekunta Filosofian, historian,
Maailman muutosta tallentamassa Marko Vuokolan The Seventh Wave -valokuvasarja avauksena taidevalokuvan aikaan Pro gradu -tutkielma 31.1.2012 Helsingin yliopisto Humanistinen tiedekunta Filosofian, historian,
Itsestabilointi: perusmääritelmiä ja klassisia tuloksia
 Itsestabilointi: perusmääritelmiä ja klassisia tuloksia Jukka Suomela Hajautettujen algoritmien seminaari 12.10.2007 Hajautetut järjestelmät Ei enää voida lähteä oletuksesta, että kaikki toimii ja mikään
Itsestabilointi: perusmääritelmiä ja klassisia tuloksia Jukka Suomela Hajautettujen algoritmien seminaari 12.10.2007 Hajautetut järjestelmät Ei enää voida lähteä oletuksesta, että kaikki toimii ja mikään
1 + b t (i, j). Olkoon b t (i, j) todennäköisyys, että B t (i, j) = 1. Siis operaation access(j) odotusarvoinen kustannus ajanhetkellä t olisi.
 Algoritmien DP ja MF vertaileminen tapahtuu suoraviivaisesti kirjoittamalla kummankin leskimääräinen kustannus eksplisiittisesti todennäköisyyksien avulla. Lause T MF ave = 1 + 2 1 i
Algoritmien DP ja MF vertaileminen tapahtuu suoraviivaisesti kirjoittamalla kummankin leskimääräinen kustannus eksplisiittisesti todennäköisyyksien avulla. Lause T MF ave = 1 + 2 1 i
Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukko oppi aksiomaattisesti.
 Joukon määritelmä Joukko on alkioidensa kokoelma. Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukko oppi aksiomaattisesti. Näin ei tässä
Joukon määritelmä Joukko on alkioidensa kokoelma. Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukko oppi aksiomaattisesti. Näin ei tässä
Chomskyn hierarkia ja yhteysherkät kieliopit
 Chomskyn hierarkia ja yhteysherkät kieliopit Laskennan teorian opintopiiri Tuomas Hakoniemi 21. helmikuuta 2014 Käsittelen tässä laskennan teorian opintopiirin harjoitustyössäni muodollisten kielioppien
Chomskyn hierarkia ja yhteysherkät kieliopit Laskennan teorian opintopiiri Tuomas Hakoniemi 21. helmikuuta 2014 Käsittelen tässä laskennan teorian opintopiirin harjoitustyössäni muodollisten kielioppien
Ratkaisu: a) Kahden joukon yhdisteseen poimitaan kaikki alkiot jotka ovat jommassakummassa joukossa (eikä mitään muuta).
 Matematiikan laitos Johdatus Diskreettiin Matematiikaan Harjoitus 1 03.11.2010 Ratkaisuehdotuksia Aleksandr Nuija 1. Tarkastellaan joukkoja A = {1,3,4}, B = {2,3,7,9} ja C = {2, 5, 7}. Määritä joukot (a)
Matematiikan laitos Johdatus Diskreettiin Matematiikaan Harjoitus 1 03.11.2010 Ratkaisuehdotuksia Aleksandr Nuija 1. Tarkastellaan joukkoja A = {1,3,4}, B = {2,3,7,9} ja C = {2, 5, 7}. Määritä joukot (a)
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet )
 T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
AVL-puut. eräs tapa tasapainottaa binäärihakupuu siten, että korkeus on O(log n) kun puussa on n avainta
 AVL-puut eräs tapa tasapainottaa binäärihakupuu siten, että korkeus on O(log n) kun puussa on n avainta pohjana jo esitetyt binäärihakupuiden operaatiot tasapainotus vie pahimmillaan lisäajan lisäys- ja
AVL-puut eräs tapa tasapainottaa binäärihakupuu siten, että korkeus on O(log n) kun puussa on n avainta pohjana jo esitetyt binäärihakupuiden operaatiot tasapainotus vie pahimmillaan lisäajan lisäys- ja
Diofantoksen yhtälön ratkaisut
 Diofantoksen yhtälön ratkaisut Matias Mäkelä Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2017 Sisältö Johdanto 2 1 Suurin yhteinen tekijä 2 2 Eukleideen algoritmi 4 3 Diofantoksen yhtälön
Diofantoksen yhtälön ratkaisut Matias Mäkelä Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2017 Sisältö Johdanto 2 1 Suurin yhteinen tekijä 2 2 Eukleideen algoritmi 4 3 Diofantoksen yhtälön
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Jenna Laine. Ramseyn teoria
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jenna Laine Ramseyn teoria Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta LAINE, JENNA: Ramseyn teoria Pro
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jenna Laine Ramseyn teoria Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta LAINE, JENNA: Ramseyn teoria Pro
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8
 Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
Konsensusongelma hajautetuissa järjestelmissä
 Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki Helsinki 29.10.2007 Seminaarityö HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Sisältö i 1 Johdanto 1 2 Konsensusongelma 2 2.1 Ratkeamattomuustodistus........................
Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki Helsinki 29.10.2007 Seminaarityö HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Sisältö i 1 Johdanto 1 2 Konsensusongelma 2 2.1 Ratkeamattomuustodistus........................
Matemaattisen analyysin tukikurssi
 Matemaattisen analyysin tukikurssi 4. Kurssikerta Petrus Mikkola 4.10.2016 Tämän kerran asiat Funktion raja-arvo Raja-arvon määritelmä Toispuolinen raja-arvo Laskutekniikoita Rationaalifunktion esityksen
Matemaattisen analyysin tukikurssi 4. Kurssikerta Petrus Mikkola 4.10.2016 Tämän kerran asiat Funktion raja-arvo Raja-arvon määritelmä Toispuolinen raja-arvo Laskutekniikoita Rationaalifunktion esityksen
Algoritmit 2. Luento 14 To Timo Männikkö
 Algoritmit 2 Luento 14 To 2.5.2019 Timo Männikkö Luento 14 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydelliset ongelmat Kertaus ja tenttivinkit Algoritmit
Algoritmit 2 Luento 14 To 2.5.2019 Timo Männikkö Luento 14 Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydelliset ongelmat Kertaus ja tenttivinkit Algoritmit
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Injektio. Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim.
 Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
6.4. Järjestyssuhteet
 6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 4 ratkaisut Tehtävä 1. Määritä suurin aste k, johon saakka kuvan verkot G ja G ovat osittaisesti isomorfisia: Ratkaisu 1. Huomataan aluksi, että G =4 G : Ehrenfeucht-Fraïssé
Äärellisten mallien teoria Harjoituksen 4 ratkaisut Tehtävä 1. Määritä suurin aste k, johon saakka kuvan verkot G ja G ovat osittaisesti isomorfisia: Ratkaisu 1. Huomataan aluksi, että G =4 G : Ehrenfeucht-Fraïssé
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Johdatus matemaattiseen päättelyyn
 Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä 2 Todistamisesta 2 3 Joukko-oppia Tässä luvussa tarkastellaan joukko-opin
Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä 2 Todistamisesta 2 3 Joukko-oppia Tässä luvussa tarkastellaan joukko-opin
Yhtenäisyydestä. Johdanto. Lähipisteavaruus. Tuomas Korppi
 Solmu 2/2012 1 Yhtenäisyydestä Tuomas Korppi Johdanto Tarkastellaan kuvassa 1 näkyviä verkkoa 1 ja R 2 :n (eli tason) osajoukkoa. Kuvan 2 verkko voidaan jakaa kolmeen osaan niin, että osien välillä ei
Solmu 2/2012 1 Yhtenäisyydestä Tuomas Korppi Johdanto Tarkastellaan kuvassa 1 näkyviä verkkoa 1 ja R 2 :n (eli tason) osajoukkoa. Kuvan 2 verkko voidaan jakaa kolmeen osaan niin, että osien välillä ei
Kysymys: Voidaanko graafi piirtää tasoon niin, että sen viivat eivät risteä muualla kuin pisteiden kohdalla?
 7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
Hahmon etsiminen syotteesta (johdatteleva esimerkki)
 Hahmon etsiminen syotteesta (johdatteleva esimerkki) Unix-komennolla grep hahmo [ tiedosto ] voidaan etsia hahmon esiintymia tiedostosta (tai syotevirrasta): $ grep Kisaveikot SM-tulokset.txt $ ps aux
Hahmon etsiminen syotteesta (johdatteleva esimerkki) Unix-komennolla grep hahmo [ tiedosto ] voidaan etsia hahmon esiintymia tiedostosta (tai syotevirrasta): $ grep Kisaveikot SM-tulokset.txt $ ps aux
2.1. Tehtävänä on osoittaa induktiolla, että kaikille n N pätee n = 1 n(n + 1). (1)
 Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan koulutusohjelma. Kaariväritysongelma. Kandidaatintyö. 29. huhtikuuta 2012. Sami J.
 Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan koulutusohjelma Kaariväritysongelma Kandidaatintyö 29. huhtikuuta 2012 Sami J. Lehtinen Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan
Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan koulutusohjelma Kaariväritysongelma Kandidaatintyö 29. huhtikuuta 2012 Sami J. Lehtinen Aalto-yliopisto Perustieteiden korkeakoulu Tietotekniikan
 0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
v 8 v 9 v 5 C v 3 v 4
 Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
= k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko
 238 7.2 Luokka NP Luokka NP on: NP = { NTIME(t) t on polynomi } = k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko P NP Luokan NP ongelmista
238 7.2 Luokka NP Luokka NP on: NP = { NTIME(t) t on polynomi } = k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko P NP Luokan NP ongelmista
missä on myös käytetty monisteen kaavaa 12. Pistä perustelut kohdilleen!
 Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Lisää pysähtymisaiheisia ongelmia
 Lisää pysähtymisaiheisia ongelmia Lause: Pysähtymättömyysongelma H missä H = { w111x w validi koodi, M w ei pysähdy syötteellä x } ei ole rekursiivisesti lueteltava. Todistus: Pysähtymisongelman komplementti
Lisää pysähtymisaiheisia ongelmia Lause: Pysähtymättömyysongelma H missä H = { w111x w validi koodi, M w ei pysähdy syötteellä x } ei ole rekursiivisesti lueteltava. Todistus: Pysähtymisongelman komplementti
Koht dialogia? Organisaation toimintaympäristön teemojen hallinta dynaamisessa julkisuudessa tarkastelussa toiminta sosiaalisessa mediassa
 Kohtdialogia? Organisaationtoimintaympäristönteemojenhallinta dynaamisessajulkisuudessatarkastelussatoiminta sosiaalisessamediassa SatuMariaPusa Helsinginyliopisto Valtiotieteellinentiedekunta Sosiaalitieteidenlaitos
Kohtdialogia? Organisaationtoimintaympäristönteemojenhallinta dynaamisessajulkisuudessatarkastelussatoiminta sosiaalisessamediassa SatuMariaPusa Helsinginyliopisto Valtiotieteellinentiedekunta Sosiaalitieteidenlaitos
Luonnontieteiden popularisointi ja sen ideologia
 Luonnontieteiden popularisointi ja sen ideologia Tapauksina Reino Tuokko ja Helsingin Sanomat 1960-luvulla Ahto Apajalahti Helsingin yliopisto Humanistinen tiedekunta Suomen ja Pohjoismaiden historia Pro
Luonnontieteiden popularisointi ja sen ideologia Tapauksina Reino Tuokko ja Helsingin Sanomat 1960-luvulla Ahto Apajalahti Helsingin yliopisto Humanistinen tiedekunta Suomen ja Pohjoismaiden historia Pro
Implementation of Selected Metaheuristics to the Travelling Salesman Problem (valmiin työn esittely)
 Implementation of Selected Metaheuristics to the Travelling Salesman Problem (valmiin työn esittely) Jari Hast xx.12.2013 Ohjaaja: Harri Ehtamo Valvoja: Hari Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston
Implementation of Selected Metaheuristics to the Travelling Salesman Problem (valmiin työn esittely) Jari Hast xx.12.2013 Ohjaaja: Harri Ehtamo Valvoja: Hari Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston
8 Joukoista. 8.1 Määritelmiä
 1 8 Joukoista Joukko on alkoidensa kokoelma. Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukkooppi aksiomaattisesti. Näin ei tässä tehdä
1 8 Joukoista Joukko on alkoidensa kokoelma. Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukkooppi aksiomaattisesti. Näin ei tässä tehdä
Kanta ja dimensio 1 / 23
 1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
Tarkastelemme ensin konkreettista esimerkkiä ja johdamme sitten yleisen säännön, joilla voidaan tietyissä tapauksissa todeta kielen ei-säännöllisyys.
 Ei-säännöllisiä kieliä [Sipser luku 1.4] Osoitamme, että joitain kieliä ei voi tunnistaa äärellisellä automaatilla. Tulos ei sinänsä ole erityisen yllättävä, koska äärellinen automaatti on äärimmäisen
Ei-säännöllisiä kieliä [Sipser luku 1.4] Osoitamme, että joitain kieliä ei voi tunnistaa äärellisellä automaatilla. Tulos ei sinänsä ole erityisen yllättävä, koska äärellinen automaatti on äärimmäisen
Algoritmit 2. Luento 10 To Timo Männikkö
 Algoritmit 2 Luento 10 To 19.4.2018 Timo Männikkö Luento 10 Peruutusmenetelmä Osajoukon summa Verkon 3-väritys Pelipuut Pelipuun läpikäynti Algoritmit 2 Kevät 2018 Luento 10 To 19.4.2018 2/34 Algoritmien
Algoritmit 2 Luento 10 To 19.4.2018 Timo Männikkö Luento 10 Peruutusmenetelmä Osajoukon summa Verkon 3-väritys Pelipuut Pelipuun läpikäynti Algoritmit 2 Kevät 2018 Luento 10 To 19.4.2018 2/34 Algoritmien
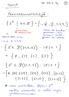 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Matematiikan tukikurssi, kurssikerta 1
 Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus
 Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Avaruuden R n aliavaruus
 Avaruuden R n aliavaruus 1 / 41 Aliavaruus Esimerkki 1 Kuva: Suora on suljettu yhteenlaskun ja skalaarilla kertomisen suhteen. 2 / 41 Esimerkki 2 Kuva: Suora ei ole suljettu yhteenlaskun ja skalaarilla
Avaruuden R n aliavaruus 1 / 41 Aliavaruus Esimerkki 1 Kuva: Suora on suljettu yhteenlaskun ja skalaarilla kertomisen suhteen. 2 / 41 Esimerkki 2 Kuva: Suora ei ole suljettu yhteenlaskun ja skalaarilla
Algoritmit 1. Luento 8 Ke Timo Männikkö
 Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Algoritmit 2. Luento 11 Ti Timo Männikkö
 Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto
 Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
Harjoitustyön testaus. Juha Taina
 Harjoitustyön testaus Juha Taina 1. Johdanto Ohjelman teko on muutakin kuin koodausta. Oleellinen osa on selvittää, että ohjelma toimii oikein. Tätä sanotaan ohjelman validoinniksi. Eräs keino validoida
Harjoitustyön testaus Juha Taina 1. Johdanto Ohjelman teko on muutakin kuin koodausta. Oleellinen osa on selvittää, että ohjelma toimii oikein. Tätä sanotaan ohjelman validoinniksi. Eräs keino validoida
P? = NP Kysymys ratkaisun keksimisestä ja sen tarkistamisesta
 P? = NP Kysymys ratkaisun keksimisestä ja sen tarkistamisesta Juha Nurmonen Matematiikan laitos Helsingin yliopisto Ajatellaanpa esimerkiksi kauppamatkustajan jokapäiväistä ongelmaa: Kauppamatkustajan
P? = NP Kysymys ratkaisun keksimisestä ja sen tarkistamisesta Juha Nurmonen Matematiikan laitos Helsingin yliopisto Ajatellaanpa esimerkiksi kauppamatkustajan jokapäiväistä ongelmaa: Kauppamatkustajan
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
