********************************************************************************
|
|
|
- Sinikka Uotila
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 LÄÄEIEEEN LN VLINE EHÄVÄMNISE ämä on valntakokeen tehtävämonte. Monte ältää johdantoja tehtävn (krvot tekt), valntakoetehtävät ekä lttenä valntakokeen teemaan lttyvän artkkeln, kaavakokoelman ja talkkotetoja. ehtäven ratkaemnen edellyttää valntakoekrjaa oleven tetojen, tehtävämonteea oleven johdantotekten ekä lttenä olevan artkkeln, kaavojen ja talkkotetojen hallntaa ja oveltamta. Johdantotektä olevat tedot vovat lttyä mdenkn kn tä eraavan tehtävän ta tehtäväarjan ratkaemeen. tt holellet tehtävämonteeeen ltteneen. ehtävämonteen läk olet aant erllen vatamonteen, joa on oma vatatlana jokata tehtävää varten. rjota vatake elvällä käalalla vatamonteea kllekn tehtävälle varattn tlaan. Eäelvät krjotetta, vvotetn tlan ylttävää (van yk krjotrv ktakn vvaa koht!) ta vatatlan renavvotken ylttävää tektä e oteta arvonna homoon. Laktehtäven ratkaemea vakoarvona käytetään ltteeä oleva arvoja. Vatakk tlee ettää tlokeen johtavat laktomtket. Pelkkä nmeernen tlo e rtä vatakek. Nmeernen lotlo tlee ettää tehtävänannon eätarkmman nmeeren arvon erteella elle tehtävää ton manta. Vataten arvont ert valntakoekrjaan ja valntatladea jaettn tehtävämonteeeen ltteneen. Myö vataten johdonmka ja elkey otetaan teytykeä homoon. Vataten yhteenlaketta kokonatemmaa kttaan raakatek. Nden mttameta valntakoetek, oatehtäven mahdolleta karmeta ekä mta arvoteln lttyvtä tomentetä äättävät er ylotojen valntatomknnat tenäet ääntöjenä ttea. ******************************************************************************** Lääketeteen alan valntakoe alkaa klo 9 ja äättyy klo 4 ja ketää taan 5 tnta. oealehn ääee klo 9:40 at ja kokeeta aa ota akantaan klo 0:00. arkta, että aamaa tehtävämonteea on kanlehden läk vt -7 okeaa järjetykeä, 8 lteva ja vatamonteea kanlehden läk vt -. Merkte henklöteto jokaelle vatamonteen vlle het, kn koetla on alkant. Van ne vt tarkatetaan, john yrkjä on merknnyt henklötetona ennen kokeen äättymtä. akk krjottamnen koetladen äättymen ja vatamonteen alattamen välenä akana on kelletty. Vatamonteen alat taaht valvojan ohjeden mkaet.
2 Vanhenemen haateet Vanhenemnen ahettaa elntomnnoa mtoka, jotka hekentävät tomntakykyä ja alttavat araklle. Nätä vodaan hdataa terveyttä edtävllä elämäntavolla ekä läämällä mahdollka aktveen oalltmeen ja hmhteden yllätämeen. Lknta, m fyynen aktv ekä älylltä ortkykyä yllätävät haateet arantavat tomntakykyä, vähentävät aratmaltttta ja enentävät araken vakeatetta. Vanhteen lttyy en näön ja klon hekkenemnen, vähänen lkkmnen, honontnt taaano ja kaatl ekä vakea alravtem. Vanhket vovat kärä myö lkadota (oteooroo), mthärötä, ekavdeta, vrtan dätykyvyn hekkenemetä, kroonta kvta ja monlääktyken mahdollet ahettamta hatota. Varhanen ongelmn ttmnen arantaa vanhten elämänlaata. ämä on mtattava tomntakyvyn aranemena, kotona elvytymajan dentymenä ja araalahotojakojen vähenemenä. ehtävä tettä Pertele valntakoekrjan ja ltteenä olevan artkkeln ohjalta, mk vanhotladen käynnn yyn elvttämeen ja analleen ttkmkeen ol tareen varata tavanomata enemmän akaa lääkärn vataanotolla. (rtkkela käytetty ana anamnee tarkottaa otlaalta aatava etetoja.) ehtävä 7 tettä a) Selota, mllaa vanhenemmtoka taaht lmää ja näkökyvyä. (6 ) b) Mten vanhenemeen lttyvät aneenvahdntamtoket vakttavat rmnanoon? Pertele vatake. ( ) aatmet modotavat ren oan vanhten vakavta taatrmta. avallet kaatmen ynä ovat hekkoknto ja än mkanaan tomat mtoket motorkaa, näkö-, klo-, taaano- ja tntoata. aatmnen joht en myö hmaketa ja yörtymetä, jotka ovat merkkejä verenaneen alenemeta ja avoverenkerron vähenemetä emerkk äkllet maklta ytyyn notaea (ortotaattnen hyotona l. hyoteno). Levä ortotaattnen hyotona ja lmä mtenemen tnne het ylö noemen jälkeen klvat normaaln fyologaan myö norlla hmllä. rtotaatten hyotonan komenaato hekkenee än karttea, joten vanhklla oreet ovat yleä. rtotaattnen hyotona korot, jo atonomnen hermoto e reago rttävät ja kylln noeat komenomaan verenaneen laka. rtotaatten hyotona vo korota myö lman atonomen hermoton tomntahärötä. ällön yynä vo olla er tekjötä johtva elmtön neteja/ta vertlavden enenemnen l. hyovolema, verenvrtaken ete ta ydänara. Myö vanhten mhn arakn käyttämät lääkkeet, emerkk neteenoto- ja verenanelääkkeet vakttavat hatallet nähn äätelymekanmehn.
3 ehtävä 3 8 tettä a) Selota, mten er tekjät äätelevät avoveronten tmta ja laajenemta. (7 ) b) Mante, mtkä tekjät vovat ahettaa hyovolemaa. (8 ) ) Mk hyovolema korotaa ortotaatten reakton ahettamaa hmata? (3 ) ehtävä 4 Pertele, onko eraavlla rakentella/lmöllä merktytä aennon atmea. 8 tettä a) kortkonaalrata ( ) b) nvelreetort ( ) ) generaattorotentaal ( ) d) anovomakenttä ( ) Jo eällään avoverenkerron härötä, vodaan orttaa kva PE-menetelmällä (otronemotomografa) käyttäen merkkaneena ha-5 -otoolla lematta vettä (H 5 ). 5 on otroneja emttova otoo, jonka olntmaka on 3 eknta. ehtävä 5 0 tettä Hmaketa kärvä vanhotla anaa 75 kg. Potlaalle tehtävä PE-kva totetaan v kertaa. nkn kvaken ala hänen lakmoona rktetaan H 5 -merkkanetta 5 megabeqerelä (MBq) anokloa koht. vaten totoväl on 5 mntta (tarkka arvo). Potlaalle annetn H 5 :n ahettama efektvnen anno on,6 Sv megabeqerelä koht. a) Lake PE-kvaten otlaalle ahettama efektvnen kokonaätelyanno. (3 ) b) Lake otlaan H 5 -aktv 5 mntn kltta enmmäetä H 5 -merkkaneen rktketa. (7 ) Pään aleen verenkerto vodaan ettää kvaa olevalla yknkertatetlla teoreettella malllla. Malla on kvatt verenvrtarett nollla vartetlla vvolla. Vrtavatket (R (rett) ) kyellä retellä on merktty orakateen motolla laatkolla. ortata lähtevät ään aleelle ntatvat rett on yknkertatken vok kvatt kahtena rnnakkaena denttenä vrtarettnä. Lakmoverenane vodaan malla olettaa nollak. edetään, että normaaltlanteea ään verenvrta on 5 % koko kehon verenvrtaketa. Pään aleen kmmankn vrtahaaran vrtavat R ää on veronten valtmokovettmatadn l. aterokleroon vok kavant 3 % normaaltlanteeeen nähden, mtta malla vrtavatket ovat älyneet ennallaan. Edellä mantlla vanhotlaalla ydämen maama vermäärä on kekmäärn 75 ml/. Hänen kekmääränen verenaneena aortaa on 95 mmhg. ehtävät 6 ja 7 lttyvät tähän vanhotlaaeen ja tehtävä oletetaan, että vrta on lamnaarta (Poellen laka vodaan oveltaa).
4 3 va ehtävä 6 9 tettä Lake kvan malln erteella, knka monta roentta ään aleen verenkerto on enentynyt normaaltlanteeeen nähden. alan aleella vrtahaaran vrtavat R kala = 0,89 PRU. ehtävä 7 3 tettä a) Potlaan aortan lmenn halkaja on,0 m. Mkä on veren kekmääränen vrtanoe (m/) aortaa? ( ) b) ehon kallaaren lkmäärä on 5,0 0 9 ja nden lmenn halkaja 8,0 m ja nden oletetaan olevan yhtä tkä. Mkä on veren vrtanoe kallaarea, olettaen että kakk ver kertää kallaaren katta? (3 ) ) aa ydämen eelvaltmohaaraa lmenn okknta-ala on enentynyt aterokleroon vok. Valtmon lmenn äde on normaalt r ja kaventneea kohdaa r. Jo r = 0,80 r ja ane-ero kaventman äden välllä on ama kn ennen ahtaman yntyä, knka monta roentta kokonatlavvrta q v ahtaman kohdalla (kva.) on alkeräetä tlavvrrata (kva.)? (5 )
5 4 va d) Sydänlhaken verenkerron arantamek kaventneeeen kohtaan ltetään rrännänen (kva.3), jonka lmenn äde on r 3 ja t oletetaan amak kn kaventman t. Läk r = r 3 = 0,80 r ja ane-ero kaventman äden välllä on ama kn ennen rrännäen aentamta. Lake ertellen knka r on kokonatlavvrta q v rrännäen aettamen jälkeen (kva.3) verrattna alkeräeen tlavvrtaan (kva.). Ilmota vatake roenttena. (3 ) Vahdevoen akana mnaarjojen tomnta hekkenee, jollon nden etrogeenhormonen totanto vähenee vomakkaat. omnnan loea kkatet jäävät o. Etrogeenen vähenemnen khdyttää myö elmtön yleä vanhenemroeeja. ärkemmät etrogeenhormont ovat etradol, etrol ja etron. Ennen vahdevoa elmtön ääaallnen etrogeenhormon on etradol ja nden jälkeen etron, jota yntyy mm. ravakdokea. Vahdevooreta vodaan helottaa hormonkorvahodolla. Hormon annotellaan yleenä joko n katta ta hon lä laatarta ta geelnä. Ylemmn hormonkorvahodoa käytetty etrogeenhormon on etradol, joka lääkevalmteea on joko ellaenaan ta johdokena. Hyvn yleet käytetty johdo on etradolvaleraatt, joa etradoln D-renkaan hydrokyylryhmä on eteröty n-entaanhaolla (valeraanahaolla). avanomanen korvahodoa käytettävä etradolvaleraattanno on,0 mllgrammaa vorokadea. Etradolvaleraatt hydrolyot elmtöä etradolk, jota rn oa mtt olen lmakalvoa ja makaa etronk. Etronta modot edelleen makaa rkk- ja glkronhaon konjgaatteja. Velkona onena nämä erttyvät vrtaan. Lonnollten terodhormonen vahtoehtona hormonkorvahodoa vodaan käyttää ynteettä terodeja, kten tbolona. Elmtöä tbolon metabolot noeat yhdtek, jolla on etrogeen- ja rogetnvakt. va 3 ettää tbolonn metabolan enmmätä vahetta, jonka yhteydeä fyologet aktvet yhdteet yntyvät.
6 5 H C CH H C CH H tbolon entyym entyym H C CH va 3 Etrogeenen, kten mdenkn hormonen, ahettama vakt edellyttää määrättyyn reetorn totmta. Stotmea hormonn kolmlotteella rakenteella on tärkeä merkty. Yleenä reetorn vo tota van yk yhdteen mahdollta tereoomeeretä (avaromeeretä). Stereoomeraa entyy mm. molekyylellä, joa on yk ta eam kraalnen (aymmetrnen) hlatom. raalnen hlatom on 3 -hybrdotnt hlatom, johon totneet atomt ta atomryhmät ovat erlaa. ehtävä 8 8 tettä a) Uema hormoneja ja lääkeaneta e voda annotella laatarn ta geeln avlla hon lä. Mtkä kemallet ja/ta fyologet yyt mahdolltavat edellä manttjen menetelmen käytön etradoln annotelemek? (3 ) b) Merkte erkeen ymyrällä jokanen kdeta kraaleta hlatomta vatamonteea olevaan tbolonn rakennekaavaan. Vatata, johon on merktty enemmän kn k vahtoehtoa, e arvotella. (3 ) ) Mhn orgaanten reaktoden äätyyn tbolonn metabolan enmmäen vaheen reakto (kva 3) kl? ( ) ehtävä 9 6 tettä a) nka aljon korvahodoa käytettävätä tavanomaeta ävttäetä etradolvaleraattannoketa vo enntään modota etradola (mkrogrammona)? (8 ) b) Etradolvaleraatn vrtata löytyvän kekeen aneenvahdntatotteen molekyylmaa okkeaa etradolvaleraatn molekyylmaata vähemmän kn 5 %. Etä vatamonteea olevaan tlaan kyeen aneenvahdntatotteen rakennekaava. (8 ) Ln eäorgaannen mneraalane on ääon hydrokaattta, jota jatkvat ekä aot (kalfkaato) että lkenee (dekalfkaato). Jo dekalfkaato on temmän akaa noeamaa kn kalfkaato, erakena on oteooroo.
7 6 Lta lenneet mneraal-ont klkevat vaaat ln kallaren enämän lä. Vereä ja olvältlaa ykarvoet katont (emerkk Na + ja + ) entyvät erllnä hydratotnena onena. akarvoet katont tä vaton ovat relta on totneet albmnn ja mhn verlaman negatvet varatnen rotenehn. Emerkk verlaman yhteenlaketta kalmta ( kokonakalm ) van olet on hydratotneea onmodoa ( vaaa kalm ). Eäorgaannen fofor on yhtenm verlaman foforhaolle ja en er onmodolle, jotka ovat kekenään kemallea taaanoa. Ln mneraalane e tä vaton ole kemallea taaanoa verlamaan lenneden mneraal-onen kana. ämä lmenee emerkk ten, että lättäeä koetkea olevaan verlamaan henok jahetta lta, laman vaaan kalmn ja fofaatn konentraatot alenevat vomakkaat onen aotmen myötä. Eätaaanota holmatta kalmoloja e aot terveen hmen vereen ta ehmytkdokn. ämä joht oaltaan tetytä kalfkaatota hdatavta nhbttoreta (emerkk fetn-). ehtävä 0 tettä a) Etä taaanotett ln ääaallen mneraalaneken aotmta ja lkenemta kvaavan reakton yhtälö. Ilmae yhtälöä reaktokomonentten faa (, g, l, aq). (4 ) b) Mk ln kalfkaatota ja dekalfkaatota ttkttaea laman vaaan kalmn to on laman kokonakalmtotta hyödyllem teto? (3 ) ) Mtkä ovat eäorgaanen foforn er onmotojen konentraatot lamaa (kahden merktevän nmeron tarkkdella)? (7 ) d) ota lkotloa hyväk käyttäen, että ln ääaallen mneraalaneken ja olvältlan (nterttmn) komonentten välllä e vallte kemallta taaanoa. (7 ) ehtävä Selota, mten tvn ln tmnen taaht. tettä Uea ttkmka on todett, että nkamamrtma on anakn joka vdennellä yl 50- votata nata. Nden lmaantv lääntyy än myötä, ertyet 65 kävoden jälkeen. Selkärangan nkamamrtma vo yntyä kmartamen, noton ta vakkaa ykmen yhteydeä. laelän kormttmeen kaaleta notettaea vakttaa oleellet notoaento. ormttavtta vodaan arvoda tarkatelemalla vomen momentteja kvan 4 mkaet momenttteen (avon ymyrä) hteen. arkateltavat vomat ovat kehon yläoaan vakttava anovoma F W, kaaleen anovoma F P ja elän ojentajalhaten voma F E. Vomen ntalnjojen kohtorat etäyydet momenttteetä ovat vataavat r W, r P ja r E. ehon yläoan ano on tää taakea 65 % kehon kokonaanota. Henklön ano on 7 kg ja notettavan kaaleen ano 5 kg. van 4 -kohdaa henklö eoo oraa kannatellen kaaletta, B-kohdaa hän notaa kaaleen altalta tavttamalla elkäänä, C-kohdaa koktaen olvaan ja tämällä elän orana ja D-kohdaa koktaen olvaan ja elkäänä. Nätä taaka vataavat etäyydet on etetty talkoa.
8 7 B C D va 4 alkko van 4 kohta r E (m) r W (m) r P (m) 5,0,0 30,0 B 5,0 6,0 40,0 C 5,0 8,0 35,0 D 5,0 4,0 50,0 ehtävä 0 tettä a) nka r on voma F W kvan 4 kohda -D? ( ) b) Mkä on voman F W momentt momenttteen hteen kvan 4 -kohdaa? ( ) ) Mä kvan 4 kohdta (B, C ta D) voman F W momentt on rmmllaan verrattna - kohdan momenttn? nka monnkertanen voman momentt tällön on verrattna -kohdan momenttn? (3 ) d) nka monta roentta kaaleen notamnen elkä ortettna (kvan 4 C-kohta) enentää elän ojentajalhaten vomaa verrattna notameen B-kohdaa etetyllä tavalla? (3 )
9 Rejo lvken ja kakakrja Dodemn lvalla Lte (4 va)
10 Rejo lvken ja kakakrja Dodemn lvalla Lte (4 va)
11 Rejo lvken ja kakakrja Dodemn lvalla Lte (4 va)
12 Rejo lvken ja kakakrja Dodemn lvalla Lte (4 va)
13 Lte (4 va) Maan anovoman ahettama toamkhtyvyy 9,8 m/ Äänen noe lmaa 334 m/ Veden they 000 kg/m 3 Veren they 050 kg/m 3 Elohoean they 3600 kg/m 3 Plankn vako 6, J Veden höyrytymlämö 48 kj/kg Veden omnalämökaateett 4,9 kj/kg Elektronn vara e = -, C vogadron lk = N = 6,0 0 3 mol - 0 C = 73,5 Ylenen kaavako R = 8,3 J mol - - Faradayn lk F = 96,5 0 3 C mol - Ideaalkaan mooltlav V m =,4 l/mol (NP) Ilman they,9 kg/m 3 Valon noe = 3,0 0 8 m/ Stefan-Bolzmannn vako = 5, W/m 4 k = mtalle kaaleelle ev =, J re = C = 3,7 0 0 Bq kwh = 3,6 MJ roton: m =, kg netron: m n =, kg atommaaykkkö: m =, kg m =,00785 m m n =, m HB H B a a H H 3 H H H a log H ( H ) H 0 a H ( H ) H 0 a V H 3 0 / V max H 0 d J d D dx 0 N D 3 6 a C S m tot S k M / 3 J d D P x P D / x R nr /V R J n R V R ln Z 0 N f 0 R ln d dx FV R d Z F N f dx N f Z FV R V ln ZF d F dv J D( Z ) dx R dx R PNa V V V ln F P ( Z ) 0 R R( de I Cm g dt n n a b f r k( / N) v h mv eu m,6 0 Na 0 Na 0 Na Na R ln P P dv dx P Z P ) FV ( E ENa ) g ( E E ) gl ( E El ) n n n U ( 0,9780 F q( v B) ; F qvbn, F m r V ( ) r v F / f V ( m n) r / f W ½J v QE 6 r U dq / t m n 6 U )
14 Lte (4 va) L U Vt I I / 0 0 d log0 ( I / I0) d E Zm Nm lg e N e t 0 0 lg 0 (lg ln ½ f b f b e, f b b n e m t e) t t t e e E I, E E m x I e 0 H w D; R H f Y f b e e ( o ) w R D E w w D ; w R R E hf h / ; E( ev ) 40/ ( nm) f /( LC ) v R / M v I E / 0 W / 0 m 0g( I / I0) R 0lg( P / P ) 0lg(/ )... v f f0 ; f f0 v F mv / r 4 ( r / a) 4 F m r mr mm F R d q d h k P P 4 ; k 4 h h lk 0,5,38ho lma h ( ) hh lma ho h ½gt v v gt 0 h v0t ½gt t 0 0 0t ½t / n /t a v / r F mv / r m r 4 / y x t y n t kx, max x t ot kx, max mr ( 0dB)lg( I / I0) I / tot / 4 E / L I / ; L d / m Nt ntt L I / o g n / a n / b n n / r f n n r nr / n n f r f / f n n / l I I 0 e V nr V V V V 0 ( V ) 0 ( ) Q m W W Fl W v t t 3 ½ v ½v t P P P ½v q v ½ v v qv qv P v v 3,5 v
15 Lte (4 va) P 3,5 3 q v V q v t l q t m qm t q v v v k 7 6 V qv t v q q v v v v ½v gh ½ ½v gh vako E k ½mv ½ v V V E mgh gh V V F F W V / V V / F ( E/ l)( l) R / qv 8L /( r 4 ) k v PRU ( mmhg) / q ( ml / ) PVR 80( P L ) / V SVR 80( R ) / V m m m m v gh R q v 8 L vr Re, ( 0) gr v 9 W F E mgh E k ½mv E r ½J P W / t W / a W o 4 W 0 / t/ W a / t Pa / P0 ( x. y, z) lk 000 v v R v v f fvo / M F r ve ve
16 Lte (4 va) Sätelyn anotkertoma almolojen lkotloja ätelyn tyy w R (tarkka arvo) fotont elektront netront 5-0 rotont 0 alfahkkaet 0 eln ta kdo w (tarkka arvo) kolrahaet 0,0 kehkot 0, nanen lydn 0, mahalakk 0, akol 0, klrahanen 0,05 maka 0,05 rokatorv 0,05 rntarahaet 0,05 vrtarakko 0,05 ho 0,0 ln nta 0,0 mt kdoket yht. 0,05 ola kalmhydrokd Ca(H) 0-5 mol 3 /l 3 kalmkarbonaatt CaC mol /l kalmvetyfofaatt CaHP mol /l kalmfofaatt Ca 3 (P 4 ) mol 5 /l 5 hydrokaattt Ca 5 (P 4 ) 3 H 0-58 mol 9 /l 9 Verlaman komonentten vtearvoja natrm 40 mmol/l kalm 3,5-5, mmol/l kloor 05 mmol/l kalm,5 mmol/l magnem, mmol/l eäorgaannen fofor,0 mmol/l vetykarbonaatt 6,0 mmol/l glkoo 3,5-5,5 mmol/l albmn 40 g/l rotent yhteenä 70 g/l H 7,4 Eräden haojen a-arvoja ja nden rakennekaavat täyn rotonotneea modoa: H H H S H hlhao rkkhao ( a = 3,8; a = 0,) ( a -3; a =,0) H H P H H H foforhao glkronhao ( a =,; a = 6,9; a3 =,8) ( a = 3,8) H H H ärkemmät terodhormont: C D H H H B terodrnko H H etradol etron etrol H H H H H H H rogeteron aldoteron tetoteron kortol
*******************************************************************************
 LÄÄKETIETEEN LN VLINTKOE 5.5.0 TEHTÄVÄMONISTE Tämä on valntakokeen tehtävämonte. Monte ältää anetotektä, johdantoja tehtävn, valntakoetehtävät ekä ltteenä valntakokeen kaavakokoelman ja talkkotetoja. Tehtäven
LÄÄKETIETEEN LN VLINTKOE 5.5.0 TEHTÄVÄMONISTE Tämä on valntakokeen tehtävämonte. Monte ältää anetotektä, johdantoja tehtävn, valntakoetehtävät ekä ltteenä valntakokeen kaavakokoelman ja talkkotetoja. Tehtäven
1. välikoe
 Jan Loto TA7 Ekonometan johdantok Nm: Opkeljanmeo: välkoe 77 Vataa alla olevn kyymykn ympäömällä okea vahtoehto Kakn tehtävää on neljä vahtoehtoa, jota yk on oken Okeata vataketa aa pteen ja vääätä vataketa
Jan Loto TA7 Ekonometan johdantok Nm: Opkeljanmeo: välkoe 77 Vataa alla olevn kyymykn ympäömällä okea vahtoehto Kakn tehtävää on neljä vahtoehtoa, jota yk on oken Okeata vataketa aa pteen ja vääätä vataketa
*******************************************************************************
 LÄÄKEIEEEN LN VLINKOE 6.5.00 EHÄVÄMONISE ää on valntakokeen tehtäväonte. Monte ältää anetotektä, johdantoja tehtävn, valntakoetehtävät ekä ltteenä valntakokeen kaavakokoelan ja talkkotetoja. ehtäven ratkaenen
LÄÄKEIEEEN LN VLINKOE 6.5.00 EHÄVÄMONISE ää on valntakokeen tehtäväonte. Monte ältää anetotektä, johdantoja tehtävn, valntakoetehtävät ekä ltteenä valntakokeen kaavakokoelan ja talkkotetoja. ehtäven ratkaenen
PRS-xPxxx- ja LBB 4428/00 - tehovahvistimet
 Vestntäjärjestelmät PRS-xPxxx- ja -tehovahvstmet PRS-xPxxx- ja - tehovahvstmet www.boschsecrty.f 1, 2, 4, ta 8 äänlähtöä (valnta 100 / 70 / 50 V:n lähdöstä) Äänenkästtely ja jokasen vahvstnkanavan vve
Vestntäjärjestelmät PRS-xPxxx- ja -tehovahvstmet PRS-xPxxx- ja - tehovahvstmet www.boschsecrty.f 1, 2, 4, ta 8 äänlähtöä (valnta 100 / 70 / 50 V:n lähdöstä) Äänenkästtely ja jokasen vahvstnkanavan vve
Luento 6 Luotettavuus Koherentit järjestelmät
 Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Harjoitukset (KOMPRIMOINTI)
 Kmrmntharjtuksa (7) Harjtukset (KOMPRIMOINI) Kmressreja käytetään esmerkks seuraavssa svelluksssa: kaasujen srt, neumaattnen kuljetus anelmahult rsesstellsuudessa kaasureaktden, kaasujen nesteyttämsen
Kmrmntharjtuksa (7) Harjtukset (KOMPRIMOINI) Kmressreja käytetään esmerkks seuraavssa svelluksssa: kaasujen srt, neumaattnen kuljetus anelmahult rsesstellsuudessa kaasureaktden, kaasujen nesteyttämsen
SMG-1100: PIIRIANALYYSI I
 SMG-1100: PIIRIANALYYSI I Vahtosähkön teho hetkellnen teho p(t) pätöteho P losteho Q näennästeho S kompleksnen teho S HETKELLINEN TEHO Kn veresen kvan mpedanssn Z jännte ja vrta (tehollsarvon osottmet)
SMG-1100: PIIRIANALYYSI I Vahtosähkön teho hetkellnen teho p(t) pätöteho P losteho Q näennästeho S kompleksnen teho S HETKELLINEN TEHO Kn veresen kvan mpedanssn Z jännte ja vrta (tehollsarvon osottmet)
Kahdeksansolmuinen levyelementti
 Levy8 ja RS hm.. Kahdekanolminen levyelementti akatellaan kvan kahdekanolmita levyelementtiä. q 6 y (,y q 8 ( 8,y 8 8 q 7 q 6 (,y q 5 q q q 7 q q ( 7,y 7 v ( 6,y 6 P 5 ( 5,y 5 q 9 6 q 5 (,y q (,y q q q
Levy8 ja RS hm.. Kahdekanolminen levyelementti akatellaan kvan kahdekanolmita levyelementtiä. q 6 y (,y q 8 ( 8,y 8 8 q 7 q 6 (,y q 5 q q q 7 q q ( 7,y 7 v ( 6,y 6 P 5 ( 5,y 5 q 9 6 q 5 (,y q (,y q q q
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttausöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttausöytäkrjan ja työselostuksen laatmsta Luento-
Pyörimisliike. Haarto & Karhunen.
 Pyörmslke Haarto & Karhunen www.turkuamk.f Pyörmslke Lttyy jäykän kappaleen pyörmseen akselnsa ympär Pyörmsenerga on pyörmsakseln A ympär pyörvän kappaleen osasten lke-energoden summa E r Ek mv mr mr www.turkuamk.f
Pyörmslke Haarto & Karhunen www.turkuamk.f Pyörmslke Lttyy jäykän kappaleen pyörmseen akselnsa ympär Pyörmsenerga on pyörmsakseln A ympär pyörvän kappaleen osasten lke-energoden summa E r Ek mv mr mr www.turkuamk.f
Kahdeksansolmuinen levyelementti
 Levy8 ja RS hm 7.. Kahdekanolminen levyelementti akatellaan kvan kahdekanolmita levyelementtiä. q 6 y (,y q 8 ( 8,y 8 8 q 7 q 6 (,y q 5 q q q 7 q q ( 7,y 7 v ( 6,y 6 P 5 ( 5,y 5 q 9 6 q 5 (,y q (,y q q
Levy8 ja RS hm 7.. Kahdekanolminen levyelementti akatellaan kvan kahdekanolmita levyelementtiä. q 6 y (,y q 8 ( 8,y 8 8 q 7 q 6 (,y q 5 q q q 7 q q ( 7,y 7 v ( 6,y 6 P 5 ( 5,y 5 q 9 6 q 5 (,y q (,y q q
b) Laske prosentteina, paljonko sydämen keskimääräinen teho muuttuu suhteessa tilanteeseen ennen saunomista. Käytä laskussa SI-yksiköitä.
 Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
Lääketieteellisten alojen valintakokeen 009 esimerkkitehtäviä Tehtävä 4 8 pistettä Aineistossa mainitussa tutkimuksessa mukana olleilla suomalaisilla aikuisilla sydämen keskimääräinen minuuttitilavuus
Vuoden Beauceron -säännöt (voimassa alkaen) Yleisiä periaatteita
 Vuoden Beauceron -äännöt (vomaa 1.1.2017 alkaen) Yleä peraatteta Klpalukau on kalentervuo. Mukaan hyväkytään van KoraNetta löytyvät tuloket pl. erkeen pteytetyt arvoklpalut. Yhden uortuken pteet muodotuvat
Vuoden Beauceron -äännöt (vomaa 1.1.2017 alkaen) Yleä peraatteta Klpalukau on kalentervuo. Mukaan hyväkytään van KoraNetta löytyvät tuloket pl. erkeen pteytetyt arvoklpalut. Yhden uortuken pteet muodotuvat
Jaksolliset ja toistuvat suoritukset
 Jaksollset ja tostuvat suortukset Korkojakson välen tostuva suortuksa kutsutaan jaksollsks suortuksks. Tarkastelemme tässä myös ylesempä tlanteta jossa samansuurunen talletus tehdään tasavälen mutta e
Jaksollset ja tostuvat suortukset Korkojakson välen tostuva suortuksa kutsutaan jaksollsks suortuksks. Tarkastelemme tässä myös ylesempä tlanteta jossa samansuurunen talletus tehdään tasavälen mutta e
r i m i v i = L i = vakio, (2)
 4 TÖRMÄYKSET ILMATYYNYPÖYDÄLLÄ 41 Erstetyn systeemn sälymslat Kun kaks kappaletta törmää tosnsa ne vuorovakuttavat keskenään tetyn ajan Vuorovakutuksella tarkotetaan stä että kappaleet vahtavat keskenään
4 TÖRMÄYKSET ILMATYYNYPÖYDÄLLÄ 41 Erstetyn systeemn sälymslat Kun kaks kappaletta törmää tosnsa ne vuorovakuttavat keskenään tetyn ajan Vuorovakutuksella tarkotetaan stä että kappaleet vahtavat keskenään
Mekaniikan jatkokurssi Fys102
 Mekankan jatkokurss Fys102 Syksy 2009 Jukka Maalamp LUENTO 2 Alkuverryttelyä Vääntömomentt Oletus: Vomat tasossa, joka on kohtsuorassa pyörmsaksela vastaan. Oven kääntämseen tarvtaan er suurunen voma
Mekankan jatkokurss Fys102 Syksy 2009 Jukka Maalamp LUENTO 2 Alkuverryttelyä Vääntömomentt Oletus: Vomat tasossa, joka on kohtsuorassa pyörmsaksela vastaan. Oven kääntämseen tarvtaan er suurunen voma
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKKA A KTONKKA. välkoe 9.3.2007. Saat vatata van neljään tehtävään!. ake pteden A ja B välnen potentaalero el jännte AB. =4Ω, 2 =2Ω, =0 V, 2 =4V, =2A, =3A A + 2 2 B + 2. Kytkn ljetaan hetkellä.
S-55.00 SÄHKÖTKNKKA A KTONKKA. välkoe 9.3.2007. Saat vatata van neljään tehtävään!. ake pteden A ja B välnen potentaalero el jännte AB. =4Ω, 2 =2Ω, =0 V, 2 =4V, =2A, =3A A + 2 2 B + 2. Kytkn ljetaan hetkellä.
Helka-neiti kylvyssä
 Helkanet kylvyssä Frtz Grunbaum suom. M. A. ummnen Solo Tenor???? m Fred Raymond sov. G. Ventur 2001 Tä män täs tä p Bass Uu m g Wow uu uu uu uu uu uu uu, uu p wow wow wow wow wow wow wow, wow uu wow Mart
Helkanet kylvyssä Frtz Grunbaum suom. M. A. ummnen Solo Tenor???? m Fred Raymond sov. G. Ventur 2001 Tä män täs tä p Bass Uu m g Wow uu uu uu uu uu uu uu, uu p wow wow wow wow wow wow wow, wow uu wow Mart
4.3 Liikemäärän säilyminen
 Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Venymälle isotermisessä tilanmuutoksessa saadaan dl = α LdT + df = df AE AE Ulkoisen voiman tekemä työ saadaan integroimalla δ W = FdL :
 S-11435, Fyskka III (ES) Tentt 194 1 Setsemän tunnstettavssa olevaa hukkasta on jakautunut kahdelle energatasolle Ylem taso on degenerotumaton ja sen energa on 1, mev korkeam kun alemman tason, joka uolestaan
S-11435, Fyskka III (ES) Tentt 194 1 Setsemän tunnstettavssa olevaa hukkasta on jakautunut kahdelle energatasolle Ylem taso on degenerotumaton ja sen energa on 1, mev korkeam kun alemman tason, joka uolestaan
Venymälle isotermisessä tilanmuutoksessa saadaan AE AE
 S-11435, Fyskka III (ES) Tntt 75 1 Stsmän tunnstttavssa olvaa hukkasta on jakautunut kahdll nrgatasoll Ylm taso on dgnrotumaton ja sn nrga on 1, mv korkam kun almman tason, joka uolstaan on dgnrotunut
S-11435, Fyskka III (ES) Tntt 75 1 Stsmän tunnstttavssa olvaa hukkasta on jakautunut kahdll nrgatasoll Ylm taso on dgnrotumaton ja sn nrga on 1, mv korkam kun almman tason, joka uolstaan on dgnrotunut
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA
 YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
Työn tavoitteita. 1 Johdanto. 2 Ideaalikaasukäsite ja siihen liittyvät yhtälöt
 FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
FYSP103 / 1 KAASUTUTKIMUS Työn tavotteta havannollstaa deaalkaasun tlanyhtälöä oppa, mten lman kosteus vakuttaa havattavn lmöhn ja mttaustuloksn kerrata mttauspöytäkrjan ja työselostuksen laatmsta Luento-
DEE Polttokennot ja vetyteknologia
 DEE-54020 Polttokennot ja vetyteknologa Polttokennon hävöt 1 Polttokennot ja vetyteknologa Rsto Mkkonen Polttokennon tyhjäkäyntjännte Teoreettnen tyhjäkäyntjännte E z g F Todellnen kennojännte rppuu er
DEE-54020 Polttokennot ja vetyteknologa Polttokennon hävöt 1 Polttokennot ja vetyteknologa Rsto Mkkonen Polttokennon tyhjäkäyntjännte Teoreettnen tyhjäkäyntjännte E z g F Todellnen kennojännte rppuu er
MAOL-Pisteitysohjeet Fysiikka kevät 2009
 MOL-Pstetysohjeet Fyskka kevät 9 Tyypllsten vrheden aheuttama pstemenetyksä (6 psteen skaalassa): - pen laskuvrhe -/3 p - laskuvrhe, epämelekäs tulos, vähntään - - vastauksessa yks merktsevä numero lkaa
MOL-Pstetysohjeet Fyskka kevät 9 Tyypllsten vrheden aheuttama pstemenetyksä (6 psteen skaalassa): - pen laskuvrhe -/3 p - laskuvrhe, epämelekäs tulos, vähntään - - vastauksessa yks merktsevä numero lkaa
SATE1140 Piirianalyysi, osa 1 kevät /8 Laskuharjoitus 7: Vaihtovirta-analyysin perusteet
 ,,4,6,8,,4,6,8,,4,6,8 SATE4 Pranalyy, oa kevät 8 /8 akharjot 7: ahtovrta-analyyn perteet Tehtävä. Olkoon nmotonen jännte (t) = 8 co(t 6º). Tehtävä / 8 6 4 - -4-6 -8 - t / m Kva. Jännte (t) = 8 co(t 6º).
,,4,6,8,,4,6,8,,4,6,8 SATE4 Pranalyy, oa kevät 8 /8 akharjot 7: ahtovrta-analyyn perteet Tehtävä. Olkoon nmotonen jännte (t) = 8 co(t 6º). Tehtävä / 8 6 4 - -4-6 -8 - t / m Kva. Jännte (t) = 8 co(t 6º).
Valtion eläkemaksun laskuperusteet
 VALTIOKONTTORI PÄÄTÖS Dnro 62/30/2005 Valtion eläkemakn lakperteet Valtiokonttori on 2262005 hyäkynyt nämä lakperteet nodatettaaki lakettaea Valtion eläkerahatolaia tarkoitettja työnantajan eläkemakja
VALTIOKONTTORI PÄÄTÖS Dnro 62/30/2005 Valtion eläkemakn lakperteet Valtiokonttori on 2262005 hyäkynyt nämä lakperteet nodatettaaki lakettaea Valtion eläkerahatolaia tarkoitettja työnantajan eläkemakja
PUTKIKAKSOISNIPPA MUSTA
 Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
FYSI1162 Sähkö / Piirianalyysi syksy kevät /7 Laskuharjoitus 6: Vaihtovirta-analyysin perusteet
 FYSI116 Sähkö / Pranalyy yky 14 - kevät 15 1 /7 akharjot 6: ahtovrta-analyyn perteet Tehtävä 1. Olkoon nmotonen jännte (t) = 8 co(1t 6º). Tehtävä 1 / 1 8 6 4 - -4-6 -8-1,,4,6,8 1 1, 1,4 1,6 1,8,,4,6,8
FYSI116 Sähkö / Pranalyy yky 14 - kevät 15 1 /7 akharjot 6: ahtovrta-analyyn perteet Tehtävä 1. Olkoon nmotonen jännte (t) = 8 co(1t 6º). Tehtävä 1 / 1 8 6 4 - -4-6 -8-1,,4,6,8 1 1, 1,4 1,6 1,8,,4,6,8
S-55.1220/142 Piirianalyysi 2 1. Välikoe 10.3.2006
 S-55.0/4 Piirianalyyi. Välioe 0.3.006 ae tehtävät 3 eri paperille in tehtävät 4 5. Mita irjoittaa joaieen paperiin elväti nimi, opielijanmero, rin nimi ja oodi. Tehtävät laetaan oaton oepaperille. Mita
S-55.0/4 Piirianalyyi. Välioe 0.3.006 ae tehtävät 3 eri paperille in tehtävät 4 5. Mita irjoittaa joaieen paperiin elväti nimi, opielijanmero, rin nimi ja oodi. Tehtävät laetaan oaton oepaperille. Mita
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Monte Carlo -menetelmä
 Monte Carlo -menetelmä Helumn perustlan elektron-elektron vuorovakutuksen laskemnen parametrsodulla yrteaaltofunktolla. Menetelmän käyttökohde Monen elektronn systeemen elektronkorrelaato oteuttamnen mulla
Monte Carlo -menetelmä Helumn perustlan elektron-elektron vuorovakutuksen laskemnen parametrsodulla yrteaaltofunktolla. Menetelmän käyttökohde Monen elektronn systeemen elektronkorrelaato oteuttamnen mulla
Esitä koherentin QAM-ilmaisimen lohkokaavio, ja osoita matemaattisesti, että ilmaisimen lähdöstä saadaan kantataajuiset I- ja Q-signaalit ulos.
 Sgnaalt ja järjestelmät Laskuharjotukset Svu /9. Ampltudmodulaato (AM) Spektranalysaattorlla mtattn 50 ohmn järjestelmässä ampltudmodulaattorn (AM) lähtöä, jollon havattn 3 mpulssa spektrssä taajuukslla
Sgnaalt ja järjestelmät Laskuharjotukset Svu /9. Ampltudmodulaato (AM) Spektranalysaattorlla mtattn 50 ohmn järjestelmässä ampltudmodulaattorn (AM) lähtöä, jollon havattn 3 mpulssa spektrssä taajuukslla
Markov-prosessit (Jatkuva-aikaiset Markov-ketjut)
 J. Vrtamo Lkenneteora a lkenteenhallnta / Markov-prosesst 1 Markov-prosesst (Jatkuva-akaset Markov-ketut) Tarkastellaan (statonaarsa) Markov-prosessea, oden parametravaruus on atkuva (yleensä aka). Srtymät
J. Vrtamo Lkenneteora a lkenteenhallnta / Markov-prosesst 1 Markov-prosesst (Jatkuva-akaset Markov-ketut) Tarkastellaan (statonaarsa) Markov-prosessea, oden parametravaruus on atkuva (yleensä aka). Srtymät
1. Luvut 1, 10 on laitettu ympyrän kehälle. Osoita, että löytyy kolme vierekkäistä
 Johdatus dskreettn matematkkaan Harjotus 3, 30.9.2015 1. Luvut 1, 10 on latettu ympyrän kehälle. Osota, että löytyy kolme verekkästä lukua, joden summa on vähntään 17. Ratkasu. Tällasa kolmkkoja on 10
Johdatus dskreettn matematkkaan Harjotus 3, 30.9.2015 1. Luvut 1, 10 on latettu ympyrän kehälle. Osota, että löytyy kolme verekkästä lukua, joden summa on vähntään 17. Ratkasu. Tällasa kolmkkoja on 10
SOSIAALIPÄIVYSTYKSEN KEHITTÄMISEN VUODET KESKI-SUOMESSA
 0..0 () SOSIAALIPÄIVYSTYKSEN KEHITTÄMISEN VUODET KESKI-SUOMESSA Soiaalipäivytyke kehittämiellä o maakaamme eide voie jatkmo. Alkyäyke ille atoi vode valtioevoto periaatepäätö, joa aetettii tavoitteeki
0..0 () SOSIAALIPÄIVYSTYKSEN KEHITTÄMISEN VUODET KESKI-SUOMESSA Soiaalipäivytyke kehittämiellä o maakaamme eide voie jatkmo. Alkyäyke ille atoi vode valtioevoto periaatepäätö, joa aetettii tavoitteeki
Hyppy Pekingiin 2008 Tapani Keränen (Kihu) ja Juhani Evilä (SUL)
 Hyppy Pekingiin 2008 Tapani Keränen (Kih ja Jhani Evilä (SUL Harjoitvoden 2008 aikana totetettiin SUL:n ja Kihn yhteityöprojekti Hyppy Pekingiin 2008. Projektia Kihn vt. biomekaniikan ttkija oli pithyppääjien
Hyppy Pekingiin 2008 Tapani Keränen (Kih ja Jhani Evilä (SUL Harjoitvoden 2008 aikana totetettiin SUL:n ja Kihn yhteityöprojekti Hyppy Pekingiin 2008. Projektia Kihn vt. biomekaniikan ttkija oli pithyppääjien
3.5 Generoivat funktiot ja momentit
 3.5. Generovat funktot ja momentt 83 3.5 Generovat funktot ja momentt 3.5.1 Momentt Eräs tapa luonnehta satunnasmuuttujan jakaumaa, on laskea jakauman momentt. Ne määrtellään odotusarvon avulla. Määrtelmä
3.5. Generovat funktot ja momentt 83 3.5 Generovat funktot ja momentt 3.5.1 Momentt Eräs tapa luonnehta satunnasmuuttujan jakaumaa, on laskea jakauman momentt. Ne määrtellään odotusarvon avulla. Määrtelmä
Luku 7 Työ ja energia. Muuttuvan voiman tekemä työ Liike-energia
 Luku 7 Työ ja energia Muuttuvan voiman tekemä työ Liike-energia Tavoitteet: Selittää työn käsite Mallittaa voiman tekemä työ Mallittaa liike-energian ja työn keskinäinen riippuvuus Esitiedot Newtonin lait
Luku 7 Työ ja energia Muuttuvan voiman tekemä työ Liike-energia Tavoitteet: Selittää työn käsite Mallittaa voiman tekemä työ Mallittaa liike-energian ja työn keskinäinen riippuvuus Esitiedot Newtonin lait
Pikaopas. Valmistelu ja esitäyttö
 Pkaopas Valmstelu ja estäyttö Kerää seuraavat tarvkkeet ennen valmstelua: yks 500 ml:n ta 1 000 ml:n puss/pullo estäyttöluosta (0,9-prosenttnen NaCl, johon on lsätty 1 U/ml heparna) yks 500 ml:n ta 1 000
Pkaopas Valmstelu ja estäyttö Kerää seuraavat tarvkkeet ennen valmstelua: yks 500 ml:n ta 1 000 ml:n puss/pullo estäyttöluosta (0,9-prosenttnen NaCl, johon on lsätty 1 U/ml heparna) yks 500 ml:n ta 1 000
Viiteopas. 2 Kokoa ja kiinnitä uusi natronkalkkikolonni. 1 Poista vanha natronkalkki. Esitäyttö esiliitetyn letkuston avulla
 Vteopas Valmstelu ja estäyttö esltetyllä letkustolla Kerää seuraavat tarvkkeet ennen valmstelua: Yks 500 ml:n ta 1 000 ml:n puss/pullo tavallsta kettosuolaluosta, jossa on yks (1) ykskkö (U) heparna kettosuolaluoksen
Vteopas Valmstelu ja estäyttö esltetyllä letkustolla Kerää seuraavat tarvkkeet ennen valmstelua: Yks 500 ml:n ta 1 000 ml:n puss/pullo tavallsta kettosuolaluosta, jossa on yks (1) ykskkö (U) heparna kettosuolaluoksen
SAVUN JA KOSTEUDEN VAIKUTUS ELEKTRONIIKKAPIIREIHIN
 SAVUN JA KOSTEUDEN VAIKUTUS ELEKTRONIIKKAPIIREIHIN TIIVISTELMÄ Johan Mang & Olavi Keki-Rahkonen VTT Rakenn- ja yhdykntatekniikka PL 803, 02044 VTT Savn, koteden ekä näiden yhteitä äkillitä vaiktta elektroniikkapiireihin
SAVUN JA KOSTEUDEN VAIKUTUS ELEKTRONIIKKAPIIREIHIN TIIVISTELMÄ Johan Mang & Olavi Keki-Rahkonen VTT Rakenn- ja yhdykntatekniikka PL 803, 02044 VTT Savn, koteden ekä näiden yhteitä äkillitä vaiktta elektroniikkapiireihin
PPSS. Roolikäyttäytymisanalyysi 28.03.2011. Tämän raportin on tuottanut: MLP Modular Learning Processes Oy Äyritie 8 A FIN 01510 Vantaa info@mlp.
 PP Roolkäyttäytymsanalyys Roolkäyttäytymsanalyys Rool: Krjanptäjä Asema: Laskentapäällkkö Organsaato: Mallyrtys Tekjä: Matt Vrtanen 8.0.0 Tämän raportn on tuottanut: MLP Modular Learnng Processes Oy Äyrte
PP Roolkäyttäytymsanalyys Roolkäyttäytymsanalyys Rool: Krjanptäjä Asema: Laskentapäällkkö Organsaato: Mallyrtys Tekjä: Matt Vrtanen 8.0.0 Tämän raportn on tuottanut: MLP Modular Learnng Processes Oy Äyrte
Suomen metsäkeskus. Zonation ja luonnonhoidon alueellinen suunnittelu yksityismetsissä
 Suomen metsäkeskus Zonton j luonnonhodon lueellnen suunnttelu ykstysmetsssä Johtv luonnonhodon sntuntj Mtt Seppälä METSO j Zonton semnr Ksvu j vkuttvuutt METSO luonnonhotoon 2014-2016 Zonton kehttämsen
Suomen metsäkeskus Zonton j luonnonhodon lueellnen suunnttelu ykstysmetsssä Johtv luonnonhodon sntuntj Mtt Seppälä METSO j Zonton semnr Ksvu j vkuttvuutt METSO luonnonhotoon 2014-2016 Zonton kehttämsen
Tilastollisen fysiikan luennot
 Tlastollsen fyskan luennot Tvstelmät luvuttan I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ Lämpö on systeemen mkroskooppsten osen satunnasta lkettä Lämpöenerga vrtaa kuumemmasta kappaleesta kylmempään Jos kaks kappaletta
Tlastollsen fyskan luennot Tvstelmät luvuttan I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ Lämpö on systeemen mkroskooppsten osen satunnasta lkettä Lämpöenerga vrtaa kuumemmasta kappaleesta kylmempään Jos kaks kappaletta
KOHTA 3. KOOSTUMUS JA TIEDOT AINEOSISTA
 Ssältää 3% aneosa, joden vaaroja vesympärstölle e tunneta. Lsätetoja Vaaralauseketta H304 e sovelleta aerosolelle. Nota P: 64742-48-9. 2.3 Muut vaarat E tunneta. KOHTA 3. KOOSTUMUS JA TIEDOT AINEOSISTA
Ssältää 3% aneosa, joden vaaroja vesympärstölle e tunneta. Lsätetoja Vaaralauseketta H304 e sovelleta aerosolelle. Nota P: 64742-48-9. 2.3 Muut vaarat E tunneta. KOHTA 3. KOOSTUMUS JA TIEDOT AINEOSISTA
Sähköstaattinen energia
 ähköstaattnen enega Potentaalenegan a potentaaln suhde on samanlanen kun Coulomn voman a sähkökentän suhde: ähkökenttä vakuttaa vaattuun kappaleeseen nn, että se kokee Coulomn voman, mutta sähkökenttä
ähköstaattnen enega Potentaalenegan a potentaaln suhde on samanlanen kun Coulomn voman a sähkökentän suhde: ähkökenttä vakuttaa vaattuun kappaleeseen nn, että se kokee Coulomn voman, mutta sähkökenttä
S , FYSIIKKA III (ES), Syksy 2002, LH 4, Loppuviikko 39. Partitiofunktiota käyttäen keskiarvo voidaan kirjoittaa muotoon
 S-11435, FYSIIKKA III (ES), Syksy 00, LH 4, Loppuvkko 39 LH4-1* Käyttän Maxwll-Boltzmann-jakauman parttofunktota määrtä a) nrgan nlön kskarvo (E ) skä b) nrgan nlöllnn kskpokkama kskarvosta l nrgan varanss,
S-11435, FYSIIKKA III (ES), Syksy 00, LH 4, Loppuvkko 39 LH4-1* Käyttän Maxwll-Boltzmann-jakauman parttofunktota määrtä a) nrgan nlön kskarvo (E ) skä b) nrgan nlöllnn kskpokkama kskarvosta l nrgan varanss,
Mat /Mat Matematiikan peruskurssi C3/KP3-I Harjoitus 2, esimerkkiratkaisut
 Harjotus, esmerkkratkasut K 1. Olkoon f : C C, f(z) z z. Tutk, mssä pstessä f on dervotuva. Ratkasu 1. Jotta funkto on dervotuva, on sen erotusosamäärän f(z + ) f(z) raja-arvon 0 oltava olemassa ja ss
Harjotus, esmerkkratkasut K 1. Olkoon f : C C, f(z) z z. Tutk, mssä pstessä f on dervotuva. Ratkasu 1. Jotta funkto on dervotuva, on sen erotusosamäärän f(z + ) f(z) raja-arvon 0 oltava olemassa ja ss
is-1 p-1 III 770 1ap/100 1ap/100 pv-1 p-1 pv-1 p-1 1ap/100 ai t20 III hu 1ap/100 pv-1 VP/s p-1 III SR-1 1ap/100 t80 pv-1 SR-1 p-1 pv-1 1ap/100 p-1
 98 98 8 99 8 7 97 5 5 8 98 96 7 98 98 5 98 98 9 96 5 98 505 98 7 (7K) 96 9 97 8 7 96 8 99 7 6 96 97 0 0 96 96 6 97 9 98 7 9 9 9 0 9 98 0 9 5 9 5 97 8 9 7 96 700 9 T LAN NNA 9 5 9 9 6 9 7 : 9 98 9 99 9
98 98 8 99 8 7 97 5 5 8 98 96 7 98 98 5 98 98 9 96 5 98 505 98 7 (7K) 96 9 97 8 7 96 8 99 7 6 96 97 0 0 96 96 6 97 9 98 7 9 9 9 0 9 98 0 9 5 9 5 97 8 9 7 96 700 9 T LAN NNA 9 5 9 9 6 9 7 : 9 98 9 99 9
Luento 6 Luotettavuus ja vikaantumisprosessit
 Tkll korkakoulu ysmaalyys laboraoro Luo 6 Luoavuus a vkaaumsrosss Ah alo ysmaalyys laboraoro Tkll korkakoulu PL 00, 005 TKK Tkll korkakoulu ysmaalyys laboraoro Määrlmä Tarkaslava ykskö luoavuus o s odäkösyys,
Tkll korkakoulu ysmaalyys laboraoro Luo 6 Luoavuus a vkaaumsrosss Ah alo ysmaalyys laboraoro Tkll korkakoulu PL 00, 005 TKK Tkll korkakoulu ysmaalyys laboraoro Määrlmä Tarkaslava ykskö luoavuus o s odäkösyys,
Yrityksen teoria ja sopimukset
 Yrtyksen teora a sopmukset Mat-2.4142 Optmontopn semnaar Ilkka Leppänen 22.4.2008 Teemoa Yrtyksen teora: tee va osta? -kysymys Yrtys kannustnsysteemnä: ylenen mall Työsuhde vs. urakkasopmus -analyysä Perustuu
Yrtyksen teora a sopmukset Mat-2.4142 Optmontopn semnaar Ilkka Leppänen 22.4.2008 Teemoa Yrtyksen teora: tee va osta? -kysymys Yrtys kannustnsysteemnä: ylenen mall Työsuhde vs. urakkasopmus -analyysä Perustuu
COULOMBIN VOIMA JA SÄHKÖKENTTÄ, PISTEVARAUKSET, JATKUVAT VARAUSJAKAUMAT
 COUOMBIN VOIMA JA SÄHKÖKENTTÄ, PISTEVARAUKSET, JATKUVAT VARAUSJAKAUMAT SISÄTÖ: Coulombn voma Sähkökenttä Coulombn voman a sähkökentän laskemnen pstevaaukslle Jatkuvan vaauksen palottelemnen pstevaauksks
COUOMBIN VOIMA JA SÄHKÖKENTTÄ, PISTEVARAUKSET, JATKUVAT VARAUSJAKAUMAT SISÄTÖ: Coulombn voma Sähkökenttä Coulombn voman a sähkökentän laskemnen pstevaaukslle Jatkuvan vaauksen palottelemnen pstevaauksks
Kuluttajahintojen muutokset
 Kuluttajahntojen muutokset Samu Kurr, ekonomst, rahapoltkka- ja tutkmusosasto Tutkmuksen tausta ja tavotteet Tavaroden ja palveluden hnnat evät muutu jatkuvast, vaan ovat ana jossan määrn jäykkä lyhyellä
Kuluttajahntojen muutokset Samu Kurr, ekonomst, rahapoltkka- ja tutkmusosasto Tutkmuksen tausta ja tavotteet Tavaroden ja palveluden hnnat evät muutu jatkuvast, vaan ovat ana jossan määrn jäykkä lyhyellä
Nelisolmuinen levyelementti
 Lv hm 6..3 Nliolminn lvlmntti arkatllaan kvan nliolmita lvlmnttiä. q 6 q 8 η 3 q 5 ( 3, 3 q 7 (, q (, v P q ξ (, q q 3 Pitn P koordinaatit voidaan laa mokoordinaattin ξ ja η avlla, jotka ovat normratt
Lv hm 6..3 Nliolminn lvlmntti arkatllaan kvan nliolmita lvlmnttiä. q 6 q 8 η 3 q 5 ( 3, 3 q 7 (, q (, v P q ξ (, q q 3 Pitn P koordinaatit voidaan laa mokoordinaattin ξ ja η avlla, jotka ovat normratt
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
Kynä-paperi -harjoitukset. Taina Lehtinen Taina I Lehtinen Helsingin yliopisto
 Kynä-paper -harjotukset Tana Lehtnen 8.8.07 Tana I Lehtnen Helsngn ylopsto Etelä-Suomen ja Lapn lään, 400 opettajaa a. Perusjoukon (populaaton) muodostvat kakk Etelä-Suomen ja Lapn läänn peruskoulun opettajat
Kynä-paper -harjotukset Tana Lehtnen 8.8.07 Tana I Lehtnen Helsngn ylopsto Etelä-Suomen ja Lapn lään, 400 opettajaa a. Perusjoukon (populaaton) muodostvat kakk Etelä-Suomen ja Lapn läänn peruskoulun opettajat
Tchebycheff-menetelmä ja STEM
 Tchebycheff-menetelmä ja STEM Optmontopn semnaar - Kevät 2000 / 1 1. Johdanto Tchebycheff- ja STEM-menetelmät ovat vuorovakuttesa menetelmä evät perustu arvofunkton käyttämseen pyrkvät shen, että vahtoehdot
Tchebycheff-menetelmä ja STEM Optmontopn semnaar - Kevät 2000 / 1 1. Johdanto Tchebycheff- ja STEM-menetelmät ovat vuorovakuttesa menetelmä evät perustu arvofunkton käyttämseen pyrkvät shen, että vahtoehdot
Luku 16 Markkinatasapaino
 68 Luku 16 Markkinataaaino 16.1 Markkinataaainon määrity Tarkatelemme kilailulliia markkinoita kaikki talouenitäjät hinnanottajia kaikki määrittävät arhaat ratkaiuna uhteea makimihintoihin talouenitäjien
68 Luku 16 Markkinataaaino 16.1 Markkinataaainon määrity Tarkatelemme kilailulliia markkinoita kaikki talouenitäjät hinnanottajia kaikki määrittävät arhaat ratkaiuna uhteea makimihintoihin talouenitäjien
Harjoituksen pituus: 90min 3.10 klo 10 12
 Pallollse puolustae: Sokea ja ta käspallo/ Lppupallo Tavote: aalteo estäe sjottue puolustavalle puolelle, potku ta heto estäe, syöttäse estäe rstäe taklaus, pae tla vottase estäe sjottue puolustavalle
Pallollse puolustae: Sokea ja ta käspallo/ Lppupallo Tavote: aalteo estäe sjottue puolustavalle puolelle, potku ta heto estäe, syöttäse estäe rstäe taklaus, pae tla vottase estäe sjottue puolustavalle
-d;'$ d{ee lr a ;{*.v. ii{:i; rtl i} dr r/ r ) i a 4 a I p ;,.r.1 il s, Karttatuloste. Maanmittauslaitos. Page 1 of 1. Tulostettu 22.08.
 Maanmttauslats Page 1 f 1 -d;'$ d{ee lr a ;{*.v {:; rtl } dr r/ r ) a 4 a p ;,.r.1 l s, Karttatulste Tulstettu 22.08.2014 Tulsteen keskpsteen krdnaatt (ETRS-TM3SFlN): N: 6998249 E: 379849 Tulse e le mttatarkka.
Maanmttauslats Page 1 f 1 -d;'$ d{ee lr a ;{*.v {:; rtl } dr r/ r ) a 4 a p ;,.r.1 l s, Karttatulste Tulstettu 22.08.2014 Tulsteen keskpsteen krdnaatt (ETRS-TM3SFlN): N: 6998249 E: 379849 Tulse e le mttatarkka.
763105P JOHDATUS SUHTEELLISUUSTEORIAAN 1 Ratkaisut 5 Kevät 2016
 7635P JOHDATUS SUHTEELLISUUSTEORIAAN Ratkaist 5 Kevät 26. Aberraatio shteellissteoriassa a) Tlkoon valo kten tehtävän kvassa (x, y)-tason x, y > neljänneksestä: x ˆx + y ŷ c cos θ ˆx c sin θ ŷ. () Lorenz
7635P JOHDATUS SUHTEELLISUUSTEORIAAN Ratkaist 5 Kevät 26. Aberraatio shteellissteoriassa a) Tlkoon valo kten tehtävän kvassa (x, y)-tason x, y > neljänneksestä: x ˆx + y ŷ c cos θ ˆx c sin θ ŷ. () Lorenz
Harjoitus 2 ( )
 Harjoitus 2 (27.3.214) Tehtävä 1 7 4 8 1 1 3 1 2 3 3 2 4 1 1 6 9 1 Kuva 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[] = v[p] d[p] l. max i p 1 {v[i] + a i (i, p) E} = v[l] +
Harjoitus 2 (27.3.214) Tehtävä 1 7 4 8 1 1 3 1 2 3 3 2 4 1 1 6 9 1 Kuva 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[] = v[p] d[p] l. max i p 1 {v[i] + a i (i, p) E} = v[l] +
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Tarkastellaan kuvan 8.1 (a) lineaarista nelitahoista elementtiä, jonka solmut sijaitsevat elementin kärkipisteissä ja niiden koordinaatit ovat ( xi
 Elementtmenetelmän erusteet 8. 8 D-SOLIDIRKEEE 8. ohdanto Kolmulottesa soldelementtejä tartaan kolmulottesten kaaleden mallntamseen. ällön tarkasteltaan kaaleen geometralla e ole ertsrtetä jotka teksät
Elementtmenetelmän erusteet 8. 8 D-SOLIDIRKEEE 8. ohdanto Kolmulottesa soldelementtejä tartaan kolmulottesten kaaleden mallntamseen. ällön tarkasteltaan kaaleen geometralla e ole ertsrtetä jotka teksät
FYSA220/2 (FYS222/2) VALON POLARISAATIO
 FYSA220/2 (FYS222/2) VALON POLARSAATO Työssä tutktaan valoaallon tulotason suuntasen ja stä vastaan kohtsuoran komponentn hejastumsta lasn pnnasta. Havannosta lasketaan Brewstern lan perusteella lasn tatekerron
FYSA220/2 (FYS222/2) VALON POLARSAATO Työssä tutktaan valoaallon tulotason suuntasen ja stä vastaan kohtsuoran komponentn hejastumsta lasn pnnasta. Havannosta lasketaan Brewstern lan perusteella lasn tatekerron
Kaasu 2-atominen. Rotaatio ja translaatiovapausasteet virittyneet (f=5) c. 5 Ideaalikaasun tilanyhtälöstä saadaan kaasun moolimäärä: 3
 S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
S-4.5.vk. 6..000 Tehtävä Ideaalikaasun aine on 00kPa, lämötila 00K ja tilavuus,0 litraa. Kaasu uristetaan adiabaattisesti 5-kertaiseen aineeseen. Kaasumolekyylit ovat -atomisia. Laske uristamiseen tarvittava
KOKONAISRATKAISUT YHDESTÄ PAIKASTA
 KOKONAISRATKAISUT YHDESTÄ PAIKASTA Monpuolset järjestelmät varastontn ja tuotantoon TUOTELUETTELO 2009 Kappale D Varasto- ja hyllystövältasot vältasot optmaalsta tlankäyttöä varten SSI SCHÄFER: n varasto-
KOKONAISRATKAISUT YHDESTÄ PAIKASTA Monpuolset järjestelmät varastontn ja tuotantoon TUOTELUETTELO 2009 Kappale D Varasto- ja hyllystövältasot vältasot optmaalsta tlankäyttöä varten SSI SCHÄFER: n varasto-
ASEMAKAAVAMERKINNÄT JA MÄÄRÄYKSET A-2641
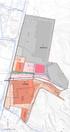 TOR NKAT TL- LANK AT a/tt MKK e=, : H A A A LA N KAT : : MKKLA is- is- : a/ a/tt / a- i ju- tv- K (/ - MKKLANSTO : /h /h JOTJOK /h w JOTJOK (/ i o : : : : : nä- ( KMAA nä- /, a jo ( /h w /h y jk /h to
TOR NKAT TL- LANK AT a/tt MKK e=, : H A A A LA N KAT : : MKKLA is- is- : a/ a/tt / a- i ju- tv- K (/ - MKKLANSTO : /h /h JOTJOK /h w JOTJOK (/ i o : : : : : nä- ( KMAA nä- /, a jo ( /h w /h y jk /h to
Jaetut resurssit. Tosiaikajärjestelmät Luento 5: Resurssien hallinta ja prioriteetit. Mitä voi mennä pieleen? Resurssikilpailu ja estyminen
 Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Tosakajärjestelmät Luento : Resurssen hallnta ja prorteett Tna Nklander Jaetut resursst Useat tapahtumat jakavat ohjelma-/lattesto-olota, jossa kesknänen possulkemnen on välttämätöntä. Ratkasuja: Ajonakanen
Tuote LVI-numero Pikakoodi KAULUS PURISTETTU HST DN 100/114,3/3,0 EN Puristettu putkikaulus;en ;Todistukset EN 10204:2004/3.
 Kaulus Tuote LVI-numero Pikakoodi DN 100/114,3/3,0 EN 1.4404 1171035 DD44 DN 125/139,7/3,0 EN 1.4404 1171039 OE47 DN 150/168,3/3,0 EN 1.4404 1171044 JG62 DN 200/219,1/3,0 EN 1.4404 1171048 MH87 DN 200/219,1/4,0
Kaulus Tuote LVI-numero Pikakoodi DN 100/114,3/3,0 EN 1.4404 1171035 DD44 DN 125/139,7/3,0 EN 1.4404 1171039 OE47 DN 150/168,3/3,0 EN 1.4404 1171044 JG62 DN 200/219,1/3,0 EN 1.4404 1171048 MH87 DN 200/219,1/4,0
LIGNIININ RAKENNE JA OMINAISUUDET
 16006 LIGNIININ RAKENNE JA INAISUUDET Hlatomen nmeämnen γ 16006 6 α 1 β 5 3 4 e Lgnnn prekursort (monomeert) Lgnnn bosyntees e e e Peroksdaasn ja vetyperoksdn läsnäollessa prekursorsta muodostuu resonanssstablotu
16006 LIGNIININ RAKENNE JA INAISUUDET Hlatomen nmeämnen γ 16006 6 α 1 β 5 3 4 e Lgnnn prekursort (monomeert) Lgnnn bosyntees e e e Peroksdaasn ja vetyperoksdn läsnäollessa prekursorsta muodostuu resonanssstablotu
Perhehoidon palkkiot ja kulukorvaukset muuttuvat lukien.
 Liperin sosiaali- ja terveyslautakunta Liperin sosiaali- ja terveyslautakunta 101 15.12.2015 22 22.03.2016 Perhehoidon palkkiot ja korvaukset 1.1.2016 alkaen 444/02.05.00/2015 Soteltk 15.12.2015 101 Perhehoidon
Liperin sosiaali- ja terveyslautakunta Liperin sosiaali- ja terveyslautakunta 101 15.12.2015 22 22.03.2016 Perhehoidon palkkiot ja korvaukset 1.1.2016 alkaen 444/02.05.00/2015 Soteltk 15.12.2015 101 Perhehoidon
HASSEN-WEILIN LAUSE. Kertausta
 HASSEN-WEILIN LAUSE Kertausta Käytetään seuraava merkntjä F = F/F q on sukua g oleva funktokunta Z F (t = L F (t (1 t(1 qt on funktokunnan F/F q Z-funkto. α 1, α 2,..., α 2g ovat polynomn L F (t nollakohten
HASSEN-WEILIN LAUSE Kertausta Käytetään seuraava merkntjä F = F/F q on sukua g oleva funktokunta Z F (t = L F (t (1 t(1 qt on funktokunnan F/F q Z-funkto. α 1, α 2,..., α 2g ovat polynomn L F (t nollakohten
Mittausvirhe. Mittaustekniikan perusteet / luento 6. Mittausvirhe. Mittausepävarmuus ja siihen liittyvää terminologiaa
 Mttausteknkan perusteet / luento 6 Mttausepävarmuus ja shen lttyvää termnologaa Mttausepävarmuus = mttaustulokseen lttyvä parametr, joka kuvaa mttaussuureen arvojen odotettua vahtelua Mttauksn lttyvä kästtetä
Mttausteknkan perusteet / luento 6 Mttausepävarmuus ja shen lttyvää termnologaa Mttausepävarmuus = mttaustulokseen lttyvä parametr, joka kuvaa mttaussuureen arvojen odotettua vahtelua Mttauksn lttyvä kästtetä
TKK @ Ilkka Mellin (2008) 1/24
 Mat-.60 Sovellettu todeäkösyyslasketa B Mat-.60 Sovellettu todeäkösyyslasketa B / Ratkasut Aheet: Mtta-astekot Havatoaesto kuvaame ja otostuusluvut Avasaat: Artmeette keskarvo, Frekvess, Frekvessjakauma,
Mat-.60 Sovellettu todeäkösyyslasketa B Mat-.60 Sovellettu todeäkösyyslasketa B / Ratkasut Aheet: Mtta-astekot Havatoaesto kuvaame ja otostuusluvut Avasaat: Artmeette keskarvo, Frekvess, Frekvessjakauma,
Hallin ilmiö. Laatija - Pasi Vähämartti. Vuosikurssi - IST4SE. Tekopäivä 2005-9-14 Palautuspäivä 2005-9-28
 Jyväskylän Aattkorkeakoulu, IT-nsttuutt IIF00 Sovellettu fyskka, Syksy 005, 4.5 ETS Opettaja Pas epo alln lö Laatja - Pas Vähäartt Vuoskurss - IST4SE Tekopävä 005-9-4 Palautuspävä 005-9-8 8.9.005 /7 LABOATOIOTYÖ
Jyväskylän Aattkorkeakoulu, IT-nsttuutt IIF00 Sovellettu fyskka, Syksy 005, 4.5 ETS Opettaja Pas epo alln lö Laatja - Pas Vähäartt Vuoskurss - IST4SE Tekopävä 005-9-4 Palautuspävä 005-9-8 8.9.005 /7 LABOATOIOTYÖ
Rak-54.116 Rakenteiden mekaniikka C, RM C (4 ov) Tentti 30.8.2007
 Rak-54.116 Rakeneden mekankka, RM (4 ov) Ten.8.7 Krjoa jokaeen koepapern elvä - koko nme, puhuelunm allevvauna - oao, vuokur, enn pävämäärä ekä enävä opnojako koodeneen - opkeljanumero, mukaan luken arkukrjan
Rak-54.116 Rakeneden mekankka, RM (4 ov) Ten.8.7 Krjoa jokaeen koepapern elvä - koko nme, puhuelunm allevvauna - oao, vuokur, enn pävämäärä ekä enävä opnojako koodeneen - opkeljanumero, mukaan luken arkukrjan
MERKKIEN SELITYKSET. Kartta: Vt13. Parannettava tieosuus. Uusi tai parannettava yksityistie. Ohituskaistaosuus ja kaistamäärä. Kevyen liikenteen väylä
 ERKKEN SETKSET Kartta Vt arannettaa tesuus Uus ta parannettaa ykstyste Ohtuskastasuus ja kastaäärä Keyen lkenteen äylä Nykysen lttyän katkasu Näkeälekkaus Aseakaaa-alueen raja Hren yltyska tuuslekkaus
ERKKEN SETKSET Kartta Vt arannettaa tesuus Uus ta parannettaa ykstyste Ohtuskastasuus ja kastaäärä Keyen lkenteen äylä Nykysen lttyän katkasu Näkeälekkaus Aseakaaa-alueen raja Hren yltyska tuuslekkaus
Ilmanvaihdon lämmöntalteenotto lämpöhäviöiden tasauslaskennassa
 Y m ä r s t ö m n s t e r ö n m o n s t e 122 Ilmanvahdon lämmöntalteenotto lämöhävöden tasauslaskennassa HELINKI 2003 Ymärstömnsterön monste 122 Ymärstömnsterö Asunto- ja rakennusosasto Tatto: Lela Haavasoja
Y m ä r s t ö m n s t e r ö n m o n s t e 122 Ilmanvahdon lämmöntalteenotto lämöhävöden tasauslaskennassa HELINKI 2003 Ymärstömnsterön monste 122 Ymärstömnsterö Asunto- ja rakennusosasto Tatto: Lela Haavasoja
Matematiikan ja tilastotieteen laitos Johdatus diskreettiin matematiikkaan (Syksy 2008) 4. harjoitus Ratkaisuja (Jussi Martin)
 Matematan ja tlastoteteen latos Johdatus dsreettn matemataan (Sysy 28 4. harjotus Ratasuja (Juss Martn 1. Kertomus Hotell Kosmosesta jatuu: Hotellyhtymän johdolta tul määräys laata luettelo asta mahdollssta
Matematan ja tlastoteteen latos Johdatus dsreettn matemataan (Sysy 28 4. harjotus Ratasuja (Juss Martn 1. Kertomus Hotell Kosmosesta jatuu: Hotellyhtymän johdolta tul määräys laata luettelo asta mahdollssta
b g / / / / H G I K J =. S Fysiikka (ES) Tentti
 S4.35 Fyskka (ES) Tntt 4.9. 3 6. Sälö, jonka tlavuus on,5 m, ssältää haa, jonka an on,5 Pa ja lämötla C. (a) Montako moola haa sälössä on? (b) Montako klogrammaa? (c) Mtn an muuttuu, jos lämötla kasvaa
S4.35 Fyskka (ES) Tntt 4.9. 3 6. Sälö, jonka tlavuus on,5 m, ssältää haa, jonka an on,5 Pa ja lämötla C. (a) Montako moola haa sälössä on? (b) Montako klogrammaa? (c) Mtn an muuttuu, jos lämötla kasvaa
Luonnos 1 (13) 17.6.2011 Sosiaali- ja terveystoimialan palvelustrategia (linjaukset) Yleistä
 L 1 (13) - j rv pvrg (j) Yä Pvrg - j rv rg ä r pvrg. Pvrg j: 1. j v (= rppv pvj) 2. ä - j rvpv järjää 3. äärää pv p j j - j rvh v EU- ääöä j äääöä hj. Thj rää fr-hj p rhj. Nää vv r p h j r r. K -hää äääö
L 1 (13) - j rv pvrg (j) Yä Pvrg - j rv rg ä r pvrg. Pvrg j: 1. j v (= rppv pvj) 2. ä - j rvpv järjää 3. äärää pv p j j - j rvh v EU- ääöä j äääöä hj. Thj rää fr-hj p rhj. Nää vv r p h j r r. K -hää äääö
F_l/ mlmz SOVE LLU STE HTÄV Ä G RAVITAATI O LA I STA. Fon. (vetovoima) mr ja lxz välinen gravitaatiovoima. kappaleiden massat ovat mr ja mz (kg)
 SOVE LLU STE HTÄV Ä G RAVITAATI O LA I STA ltl ka ppa leiden (vetovoima) m ja lxz välinen gavitaatiovoima Fon F_l/ mlmz 2 kappaleiden massat ovat m ja mz (kg) on kappaleiden keskipisteiden välinen etäisyys
SOVE LLU STE HTÄV Ä G RAVITAATI O LA I STA ltl ka ppa leiden (vetovoima) m ja lxz välinen gavitaatiovoima Fon F_l/ mlmz 2 kappaleiden massat ovat m ja mz (kg) on kappaleiden keskipisteiden välinen etäisyys
Condair CP2 I Moduli M..
 j Höyrykostutn Condar Modul M Sähköasennus F 545 kg/h Sähköltännät Sähköasennukset saa suorttaa van tarvttavat okeudet omaava asentaja Huolehtkaa että kakk jänntesyötöt on katkastu ennen asennuksen alottamsta
j Höyrykostutn Condar Modul M Sähköasennus F 545 kg/h Sähköltännät Sähköasennukset saa suorttaa van tarvttavat okeudet omaava asentaja Huolehtkaa että kakk jänntesyötöt on katkastu ennen asennuksen alottamsta
Y56 Laskuharjoitukset 3 palautus ma klo 16 mennessä
 1 Y6 Lakuharjoituket 3 alautu ma 3.. klo 16 menneä Harjoitu 1. Lue enin Vihmo, Jouni (006) Alkoholijuomien hintajoutot uomea vuoina 199 00, Yhteikuntaolitiikka 71, 006/1 ivut 9 ja vataa itten kyymykiin.
1 Y6 Lakuharjoituket 3 alautu ma 3.. klo 16 menneä Harjoitu 1. Lue enin Vihmo, Jouni (006) Alkoholijuomien hintajoutot uomea vuoina 199 00, Yhteikuntaolitiikka 71, 006/1 ivut 9 ja vataa itten kyymykiin.
Mat Koesuunnittelu ja tilastolliset mallit
 Mat-.03 Koeuuttelu tlatollet mallt. harjotuket Mat-.03 Koeuuttelu tlatollet mallt. harjotuket / Ratkaut Aheet: Avaaat: Tlatollte aetoje kuvaame Oto otokaumat Etmot Etmotmeetelmät Väletmot Artmeette kekarvo,
Mat-.03 Koeuuttelu tlatollet mallt. harjotuket Mat-.03 Koeuuttelu tlatollet mallt. harjotuket / Ratkaut Aheet: Avaaat: Tlatollte aetoje kuvaame Oto otokaumat Etmot Etmotmeetelmät Väletmot Artmeette kekarvo,
= E(Y 2 ) 1 n. = var(y 2 ) = E(Y 4 ) (E(Y 2 )) 2. Materiaalin esimerkin b) nojalla log-uskottavuusfunktio on l(θ; y) = n(y θ)2
 HY / Matematka ja tlastotetee latos Tlastolle päättely II, kevät 28 Harjotus 3A Ratkasuehdotuksa Tehtäväsarja I Olkoot Y,, Y ja Nθ, ) Osota, että T T Y) Y 2 o parametr gθ) θ 2 harhato estmaattor Laske
HY / Matematka ja tlastotetee latos Tlastolle päättely II, kevät 28 Harjotus 3A Ratkasuehdotuksa Tehtäväsarja I Olkoot Y,, Y ja Nθ, ) Osota, että T T Y) Y 2 o parametr gθ) θ 2 harhato estmaattor Laske
Harjoitus 2 ( )
 Harjoitus 2 (24.3.2015) Tehtävä 1 Figure 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[0] = 0 v[p] max 0 i p 1 {v[i]+a i (i,p) E} = v[l]+a l d[p] l. Muodostetaan taulukko, jossa
Harjoitus 2 (24.3.2015) Tehtävä 1 Figure 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[0] = 0 v[p] max 0 i p 1 {v[i]+a i (i,p) E} = v[l]+a l d[p] l. Muodostetaan taulukko, jossa
1. Kaikki kaatuu, sortuu August Forsman (Koskimies)
 olo q» date reliioso olo 7 K (2003) KE2a7 1. Kaikki kaatuu, sortuu uust Forsma (Koskimies) olo 14 olo 21 3 3 3 3 3 3 3 3 Ÿ ~~~~~~~~~~~ π K (2003) KE2a7 uhlakataatti (kuoro) - 2 - Kuula: - 3 - uhlakataatti
olo q» date reliioso olo 7 K (2003) KE2a7 1. Kaikki kaatuu, sortuu uust Forsma (Koskimies) olo 14 olo 21 3 3 3 3 3 3 3 3 Ÿ ~~~~~~~~~~~ π K (2003) KE2a7 uhlakataatti (kuoro) - 2 - Kuula: - 3 - uhlakataatti
A250A0100 Finanssi-investoinnit Harjoitukset 24.03.15
 A50A000 Fnanss-nvestonnt Hajotukset 4.03.5 ehtävä. akknapotolon keskhajonta on 9 %. Laske alla annettujen osakkeden ja makknapotolon kovaanssen peusteella osakkeden betat. Osake Kovaanss A 40 B 340 C 60
A50A000 Fnanss-nvestonnt Hajotukset 4.03.5 ehtävä. akknapotolon keskhajonta on 9 %. Laske alla annettujen osakkeden ja makknapotolon kovaanssen peusteella osakkeden betat. Osake Kovaanss A 40 B 340 C 60
Puupintaisen sandwichkattoelementin. lujuuslaskelmat. Sisältö:
 Puupntasen sandwchkattoelementn lujuuslaskelmat. Ssältö: Sandwch kattoelementn rakenne ja omnasuudet Laatan laskennan kulku Tulosten vertalua FEM-malln ja analyyttsen malln välllä. Elementn rakenne Puupntasa
Puupntasen sandwchkattoelementn lujuuslaskelmat. Ssältö: Sandwch kattoelementn rakenne ja omnasuudet Laatan laskennan kulku Tulosten vertalua FEM-malln ja analyyttsen malln välllä. Elementn rakenne Puupntasa
OUTOKUMPU OY 0 K MALMINETSINTA. talta.
 9 OUTOKUMPU OY 0 K MALMNETSNTA Tutkmusalueen sjant Tutkmusalue sjatsee Hyvelässä, n. 6 km:ä Porsta pohjoseen, Vaasa-ten täpuolella. Tarkemp sjant lmenee raportn etulehtenä olevalta :20 000 karw' talta.
9 OUTOKUMPU OY 0 K MALMNETSNTA Tutkmusalueen sjant Tutkmusalue sjatsee Hyvelässä, n. 6 km:ä Porsta pohjoseen, Vaasa-ten täpuolella. Tarkemp sjant lmenee raportn etulehtenä olevalta :20 000 karw' talta.
MUODONMUUTOKSET. Lähtöotaksumat:
 MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
VIHDIN KUNTA TOIMEENTULOTUKIHAKEMUS 1(5) PERUSTURVAKESKUS Perhehuolto
 VIHDIN KUNTA TOIMEENTULOTUKIHAKEMUS 1(5) PERUSTURVAKESKUS Perhehuolto Hakemus kuulle 200 (Vranomanen täyttää) Hakemus saapunut/jätetty / 200 Henklötedot hakjasta ja hänen perheenjäsenstä Sukunm ja etunmet
VIHDIN KUNTA TOIMEENTULOTUKIHAKEMUS 1(5) PERUSTURVAKESKUS Perhehuolto Hakemus kuulle 200 (Vranomanen täyttää) Hakemus saapunut/jätetty / 200 Henklötedot hakjasta ja hänen perheenjäsenstä Sukunm ja etunmet
RATKAISUT: 17. Tasavirtapiirit
 Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Phyica 9. paino 1(6) ATKAST 17. Taavirtapiirit ATKAST: 17. Taavirtapiirit 17.1 a) Napajännite on laitteen navoita mitattu jännite. b) Lähdejännite on kuormittamattoman pariton napajännite. c) Jännitehäviö
Mat Lineaarinen ohjelmointi
 Mat-.4 Lneaarnen ohelmont 8..7 Luento 6 Duaaltehtävä (kra 4.-4.4) S ysteemanalyysn Lneaarnen ohelmont - Syksy 7 / Luentorunko Motvont Duaaltehtävä Duaalteoreemat Hekko duaalsuus Vahva duaalsuus Täydentyvyysehdot
Mat-.4 Lneaarnen ohelmont 8..7 Luento 6 Duaaltehtävä (kra 4.-4.4) S ysteemanalyysn Lneaarnen ohelmont - Syksy 7 / Luentorunko Motvont Duaaltehtävä Duaalteoreemat Hekko duaalsuus Vahva duaalsuus Täydentyvyysehdot
ESIMERKKI 2 Harri Laine
 ESIMERKKI 2 H L Lähöoh v Kmpmo Käää o hlmää ll vplvl. A öyvä jäjlmää mmä v yhydä. Röyll ll. A ll jäjlmää poj, m, oo j phlmo. Lä ll l h lyvä oj h, p, vä, ym. Tjoll olv plvl o olm ho. Ho o plvl ol ph j po.
ESIMERKKI 2 H L Lähöoh v Kmpmo Käää o hlmää ll vplvl. A öyvä jäjlmää mmä v yhydä. Röyll ll. A ll jäjlmää poj, m, oo j phlmo. Lä ll l h lyvä oj h, p, vä, ym. Tjoll olv plvl o olm ho. Ho o plvl ol ph j po.
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
DEE-53000 Sähkömagneettisten järjestelmien lämmönsiirto
 DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
