815338A Ohjelmointikielten periaatteet: Logiikkaohjelmointi. Logiikkaohjelmointi
|
|
|
- Kaarina Väänänen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Logiikkaohjelmointi Tässä osassa käsitellään toista deklaratiivisen ohjelmoinnin paradigmaa eli logiikkaohjelmointia. Pääasiallisena lähteenä on käytetty Sebestan ([Seb]) lukua 16. Maarit Harsun teoksen [Har] luvussa 14 perehdytään myös logiikkaohjelmointiin. Symboliseen logiikkaan perustuvaa ohjelmointia nimitetään logiikkaohjelmoinniksi ja tällaiseen ohjelmointiin soveltuvia kieliä logiikkaohjelmointikieliksi. Joissakin yhteyksissä nimitys deklaratiivinen kieli rajataan koskemaan pelkästään logiikkaohjelmointikieliä. Logiikkaohjelmointikielen syntaksi ja semantiikka eroaa imperatiivisen ohjelmointikielen vastaavista vielä voimakkaammin kuin funktionaalisten kielten. Logiikkaohjelmoinnissa ohjelmoija ei määrittele ratkaisuun johtavia toimenpiteitä, vaan ratkaisuun johtavia ominaisuuksia eli väittämiä, joiden oikeellisuuden ohjelma pyrkii päättelemään vertailemalla niitä tunnettuihin tosiasioihin. Tulos true merkitsee, että väittämä on oikea, mutta false merkitsee yleensä vain, että väittämää ei pystytty todistamaan oikeaksi. Ihannetapauksessa ohjelmoijan ei tarvitse keskittyä ratkaisuun johtavien toimenpiteiden ohjelmoimiseen vaan ratkaisun löytämisen logiikkaan. 1. Symbolisesta logiikasta Koska logiikkaohjelmointi perustuu vahvasti symbolisen logiikan käyttöön, tarkastellaan hieman sen ominaisuuksia. Diskreettien rakenteiden kurssissa käsitellään myös propositio- ja predikaattilogiikkaa (ks. [Kor], Luku 3). Propositio on looginen väittämä, jolla on totuusarvo. Symbolinen logiikka yksinkertaisimmillaan on propositio- eli lauselogiikkaa. Symbolisen logiikan avulla esitetään propositioiden välisiä suhteita ja johdetaan uusia väittämiä olemassa olevista. Propositiosymboleita (joilla usein on jokin tulkinta, esimerkiksi "On kylmä" tai "Sataa") yhdistellään käyttämällä loogisia konnektiiveja; nämä ovat
2 Nimi Symboli Esimerkki Semantiikka Negaatio a ei a Konjunktio a b a ja b Disjunktio a b a tai b Implikaatio tai a b a b a:sta seuraa b b:stä seuraa a Ekvivalenssi a b a ja b yhtäpitävät Propositiologiikassa negaatiolla on korkein preferenssi, minkä jälkeen tulevat konjunktio, disjunktio ja ekvivalenssi, jotka ovat preferenssiltään korkeammalla kuin implikaatio. Päättely-operaattoreiden = > ja < = > avulla voidaan muodostaa päättelyketjuja, joiden avulla saadaan uusia lauseita esimerkiksi seuraavasti: On kylmä Palelee On kylmä => Palelee Logiikkaohjelmoinnissa tarvittava symbolinen logiikka on predikaattilogiikkaa, jota kuvataan hieman seuraavaksi. Itse asiassa logiikkaohjelmoinnin käyttämä logiikka on jossakin propositio- ja predikaattilogiikan välimaastossa. Propositiologiikka ei sisällä muuttujia, joten se on liian yksinkertaista, predikaattilogiikka taas on ratkeamaton, ts. ei ole tehokasta algoritmia, jonka avulla voitaisiin päätellä onko jokin predikaatti tosi. Predikaattilogiikan avulla voidaan muodostaa ilmauksia, jotka koskevat propositiojoukkoja. Tätä varten loogisten lauseiden esittämisessä sallitaan lisäksi muuttujat, jotka esiintyvät aina kvanttoreiden (universaalikvanttori) ja
3 (eksistenssikvanttori) yhteydessä. Ensin mainittu tarkoittaa, että jokin ominaisuus pätee kaikilla arvoilla ja toinen, että on olemassa jokin arvo, jolle ominaisuus pätee, ts. Y:P Z:Q Kaikilla arvoilla Y P on tosi On olemassa sellainen Z että Q on tosi Presedenssijärjestyksessä kvanttorit ovat samalla tasolla kuin negaatio. Propositio on suljettu lause ja predikaatti on avoin lause, joka saadaan parametrisoimalla propositio. Predikaatista saadaan propositio korvaamalla parametrit eli muuttujat joillakin vakioilla. Predikaattilogiikan perusosat ovat: Vakiot, jotka edustavat tunnettuja alkioita. Vakioita merkitään yleensä pienillä kirjaimilla alkavilla tunnisteilla; lisäksi kokonaisluvut ovat vakioita. Muuttujat, jotka edustavat tuntemattomia alkioita. Niitä merkitään yleensä isoilla kirjaimilla alkavilla tunnisteilla. Funktiosymbolit eli funktorit (nimeävät funktioita). Predikaattisymbolit eli predikaatit, jotka määrittelevät alkioiden väliset relaatiot. Esimerkiksi ">": p(x,y)= X > Y. Termit ovat lausekkeita jotka koostuvat vakioista, muuttujista ja funktoreista. Esimerkiksi f(x) + Y Atomikaava koostuu predikaatista, jonka argumenttina voi olla termi. Esimerkiksi f(z)-x < 0. Kaava saadaan yhdistelemällä atomikaavoja loogisilla konnektiiveilla ja kvanttoreillla. Esimerkiksi Y X: (f(x) < 1) (Y > 0) Loogisella päättelyllä tarkoitetaan johtopäätösten muodostamista premisseistä (tunnetuista lauseista) loogisten päättelysääntöjen nojalla. Formaalisti oikea päättely tapahtuu siten, että kaavojen tai lauseiden semantiikka esitetään formaalisti ja noudatetaan korrektia semantiikkaa kussakin päättelysäännössä. Johtopäätökset vastaavat (yleensä) ihmisen käsitystä loogisista seurauksista. Yksinkertaisimmat lauseet, joita käytetään logiikkaohjelmoinnissa, ovat atomisia propositioita, nämä koostuvat yhdistetyistä termeistä, jotka kirjoitetaan
4 funktiokutsumaisessa muodossa. Yhdistetty termi muodostuu kahdesta osasta; funktorista ja järjestetystä parametrien listasta, esimerkiksi lammas(dolly) syö(dolly,ruoho) ovat yhdistettyjä termejä. Tässä esitetään ainoastaan, että relaatio lammas sisältää alkion {dolly} ja että relaatio syö sisältää järjestetyn kaksikon {dolly,ruoho}. Lauseiden semantiikka on deklaratiivista, ts. se on välittömästi nähtävissä lauseesta itsestään. Mitään tulkintaa lauseisiin ei kuitenkaan sinänsä sisälly. Esimerkiksi jälkimmäinen termi voi tarkoittaa, että dolly syö ruohoa, ruoho syö dollyä tai lause voi tarkoittaa jotakin aivan muuta. Ylläesitetyt lauseet koostuvat vakioista, mutta propositioissa voi myös esiintyä muuttujia. Atomisten propositioiden ja konnektiivien avulla voidaan muodostaa koottuja propositioita, esimerkiksi lammas(dolly) nisäkäs(dolly) syö(dolly,x) liha(x) Jotta logiikkaohjelmointi olisi lainkaan hyödyllistä, siinä täytyy olla jonkinlaisia mekanismeja, joiden avulla johdetaan uusia sääntöjä. Sääntö voidaan johtaa annetuista tosista lauseista soveltamalla niihin äärellistä määrää peräkkäisiä päättelyjä. Logiikkaohjelmoinnissa päättelymekanismit perustuvat modus ponens- sääntöön ja universaalikvanttorin eliminointiin. Modus ponens: Lause A (A B) voidaan korvata termillä B Universaalikvanttorin eliminoimissääntö: Lause X:A(X) voidaan korvata lauseella, jossa kaikki muuttujan X vapaat esiintymät on korvattu jollakin termillä. Koneellisessa loogisessa päättelyssä suureksi ongelmaksi muodostuu keskenään ekvivalenttien lauseiden joukko, joka on kooltaan valtava. Siksi olisi toivottavaa
5 määritellä jokin standardimuoto, jonka avulla propositiot voitaisiin esittää. Eräs tällainen on klausuuli. Klausuulin muoto on B1 B2... BN A1 A2... AM Missä A:t ja B:t ovat termejä. Klausuulin semantiikka: Jos kaikki A:t ovat tosia, ainakin yksi B on tosi. Oikeaa puolta kutsutaan edellytykseksi (antecedent) ja vasenta puolta seuraukseksi (consequent). Vasen puoli toteutuu, kunhan vain oikea puoli voidaan osoittaa todeksi. Voidaan osoittaa, että kaikki predikaattilogiikan propositiot on algoritmisesti mahdollista muuttaa klausuuleiksi. Logiikkaohjelmoinnissa käytetään yleisesti erikoistapausta B A1 A2... AM jota kutsutaan Hornin klausuuliksi. Esimerkiksi syö(dolly,timotei) syö(dolly,ruoho) ruoho(timotei) Mikäli Hornin klausuuli käsittää ainoastaan seurauksen (oikea puoli on tyhjä), sen vasen puoli on varauksetta tosi. Joskus tällaisia klausuuleja sanotaan myös faktoiksi. Alan Robinson kehitti vuonna 1965 ns. resoluutioperiaatteen tutkiessaan mahdollisuuksia automatisoida lauseiden todistusmekanismeja. Resoluutio on päättelymekanismi, jonka avulla annetuista propositioista johdetaan uusia propositioita. Resoluutioaskeleen periaate on hyvin yksinkertainen ja se perustuu modus ponens-eliminointisääntöön. Oletetaan esimerkiksi, että seuraavat säännöt ovat voimassa: P Q (1) R P (2) Tästä saadaan johdettua sääntö R Q (3)
6 Ensimmäisistä klausuuleista voidaan päätellä eräänlainen supistamismekanismi: kirjoitetaan P R Q P Ja "supistetaan" P pois, jolloin jäljelle jää klausuuli (3). Logiikkaohjelmoinnissa resoluutiomekanismissa joudutaan vielä huomioimaan muuttujat ja käyttämään lisäksi universaalikvanttorin eliminointisääntöä. Resoluutio yleistyy myös Hornin klausuuleille, joissa oikealla puolella on useampi termi. Resoluutiomekanismin käyttö logiikkaohjelmassa toimii seuraavasti: Kun halutaan todistaa jokin väite, se esitetään Hornin klausuulin oikeana puolena. Klausuuli yhdistetään tunnettuihin sääntöihin ja mikäli onnistutaan resoluution avulla saavuttamaan tyhjä klausuuli, on väite tosi. Väitettä voidaan myös nimittää kyselyksi (query). Esimerkki. Oletetaan säännöt (1) jalat(x,2) nisäkäs(x) kädet(x,2) (2) jalat(x,4) nisäkäs(x) kädet(x,0) (3) nisäkäs(lammas) (4) kädet(lammas,0) Halutaan todistaa väite jalat(lammas,4) Aluksi kirjoitetaan väite Hornin klausuulin oikeana puolena jalat(lammas,4) Yhdistetään tämä sääntöön (2), jolloin saadaan jalat(x,4) nisäkäs(x) kädet(x,0) jalat(lammas,4)
7 Korvataan x vakiolla lammas: jalat(lammas,4) nisäkäs(lammas) kädet(lammas,0) jalat(lammas,4) Resoluutiolla saadaan supistettua jalat(lammas,4) pois, joten tullaan lausekkeeseen nisäkäs(lammas) kädet(lammas,0) Yhdistetään tämä sääntöön (3): nisäkäs(lammas) nisäkäs(lammas) kädet(lammas,0) Resoluutiolla saadaan supistettua nisäkäs(lammas) pois ja lauseke saadaan muotoon kädet(lammas,0) Yhdistetään lopuksi tämä neljänteen sääntöön ja käytetään taas resoluutiota supistamaan kädet(lammas,0) pois: kädet(lammas,0) kädet(lammas,0) Päästiin siis tyhjään klausuuliin, joten väite on tosi.
8 2. Prolog Tarkastellaan yleisimmän logiikkaohjelmointikielen Prologin ominaisuuksia. Prologin perusrakenteen suunnittelivat Colmerauer, Roussel sekä Kowalski, ja ensimmäinen Prolog-tulkki implementoitiin Marseillessa vuonna Kielestä on syntynyt monia murteita, joilla voi olla hyvinkin erilaiset syntaksit. Edinburghin yliopistossa luotu versio on kuitenkin saavuttanut jonkinlaisen standardin aseman. Kielelle on laadittu vuonna 1995 ISO-standardi, joka pohjautuu Edinburghin versioon. Prolog ei ole puhtaasti logiikkaohjelmointikieli, vaan sisältää piirteitä myös imperatiivisista ohjelmointikielistä. Prologin ominaisuuksia kuvataan tässä lähinnä Loudenin ([Lou], kappale 11) ja Sebestan ([Seb], kappaleet ) mukaisesti. Prologissa käytetään samankaltaista notaatiota Hornin klausuuleille kuin yllä on esitetty, mutta nuolimerkintä on korvattu merkinnällä :- ja and -merkintä pilkulla, ts. Prologissa kirjoitettaisiin esi_isa(x,y) :- vanhempi(x,z), esi_isa(z,y). Prologissa erotetaan muuttujien ja vakioiden sekä predikaattien nimet siten, että muuttujien nimet alkavat isolla kirjaimella. Muuten alkukirjaimena käytetään pientä kirjainta. Prologin jokainen lause päättyy pisteeseen. Prologissa peruslauseista muodostuu oletetun tiedon tietokanta, jota hyväksi käyttäen voidaan johtaa uutta tietoa. Prologissa käytetään kahdentyyppisiä peruslauseita: Lauseet, jotka vastaavat Hornin klausuulien vasenta puolta ja lauseet jotka vastaavat varsinaisia Hornin klausuuleja. Ensin mainitut katsotaan faktoiksi, ts. loogisesti ne tulkitaan tosiksi lauseiksi. Toisen tyypin peruslauseita sanotaan myös säännöiksi. Prologissa väitteitä, joita halutaan todistaa, kutsutaan kyselyiksi (query) tai maalilauseiksi (goal) ja nämä esitetään Prolog -tulkille samassa muodossa kuin faktatkin. Oletetaan, että tietokantaan on syötetty lauseet esi_isa(x,y) :- vanhempi(x,z), esi_isa(z,y). esi_isa(x,x). vanhempi(nooa,haam).
9 Tällöin kysely esi_isa(nooa,haam) tuottaa tuloksen yes (tai true) ja kysely esi_isa(haam,nooa) tuloksen no (tai false). Samoin voidaan tehdä kysely esi_isa(x,haam) jolloin vastauksena saadaan X = nooa ->; (haetaan lisää) X = haam Prolog sisältää määrittelyt aritmeettisille operaatiolle ja niiden evaluoinnille. Prologille on kuitenkin kerrottava, milloin aritmeettista lauseketta tarkastellaan lausekkeena ja milloin se on evaluoitava. Esimerkiksi kirjoittamalla write(5+6). saa vastaukseksi 5+6. Mikäli haluaa Prologin evaluoivan summan, on kirjoitettava esimerkiksi X is 5+6, write(x). jolloin saa vastaukseksi X=11. Tästä aiheutuu mm. se että aritmeettisten lausekkeiden vertailu tuottaa tuloksen "no" mikäli lausekkeet ovat erilaiset siitä huolimatta, että niiden arvot olisivat samat. Siten 3+5 = 5+3 antaa tuloksen no. Jos halutaan vertailla lausekkeita niiden arvon perusteella, voidaan kirjoittaa predikaatti sama_arvo(termi1,termi2) :- X is Termi1, Y is Termi2, X=Y.
10 Tällöin syöttämällä sama_arvo(3+5,5+3) saadaan tulokseksi yes. Instantiointi tarkoittaa tyypin ja arvon liittämistä muuttujaan. Liittämisellä (unification) tarkoitetaan Prologissa prosessia, jolla kaksi muuttujaa instantioidaan sillä tavoin, että muuttujat täsmäävät resoluutiossa. Näin ollen liittäminen tarkoittaa jossakin mielessä kahden termin tekemistä samoiksi. Liittäminen ilmaistaan yhtäsuuruudella, esimerkiksi a = a -> yes (liittäminen onnistui) a = b -> no (eri vakioiden liittäminen ei onnistu) a = X -> X = a (muuttuja, jota ei ole instantioitu, liittyy mihin tahansa ja instantioituu tällä) f(a,z) = f(y,b) -> Z = b -> Y = a (liittäminen onnistuu kun Z=b ja Y = a) f(x) = g(x) -> no (kahden eri funktion liittäminen ei onnistu) Tarkastellaan seuraavaksi resoluution mekanismia Prologissa, ts. minkälaista hakustrategiaa käytetään johdettaessa tulosta. Resoluutiota sovelletaan täysin lineaarisesti siten, että maaleja korvataan vasemmalta oikealle ja tietokannan klausuuleja käydään läpi ylhäältä alaspäin. Alimaalit tarkastellaan välittömästi, kun ne on määrätty. Tällaista strategiaa sanotaan syvyyssuntaiseksi (depth-first). Palataan aiempaan esimerkkiin
11 esi_isa(x,y) :- vanhempi(x,z), esi_isa(z,y). esi_isa(x,x). vanhempi(nooa,haam). Olkoon annettu maali esi_isa(x,haam). Tällöin alimaalit muodostavat seuraavan hakupuun: Prolog palauttaa ensimmäisen vastaantulevan ratkaisun ja mikäli ratkaisuja halutaan lisää, puussa peräydytään (backtrack), kunnes löydetään uusia haaroja joita voidaan kulkea. Tämän kaltainen hakustrategia on tehokas, mutta kärsii samasta ongelmasta kuin rekursiivisesti laskeutuva jäsentäjä: säännöissä ei saa olla vasemmanpuoleista rekursiota. Jos ensimmäinen sääntö olisi kirjoitettu esi_isa(x,y) :- esi_isa(z,y), vanhempi(x,z).
12 Prolog joutuisi ikuiseen silmukkaan maalin johdossa yrittäessään toteuttaa lauseen esi_isa(z,y) soveltamalla toistuvasti ensimmäistä lausetta. Prologin peräytymismekanismia voidaan käyttää silmukoiden ja toistuvien hakujen toteuttamiseen, kunhan vain jotenkin pakotetaan etsinnän jatkaminen, vaikka ratkaisu löytyykin. Tätä varten Prologissa on predikaatti fail. Lisäksi haku voidaan katkaista operaattorilla!, joten ikuiset hakuprosessit voidaan ehkäistä. Tässä ei perehdytä näiden mekanismien yksityiskohtiin. Tarkastellaan vielä Prologin listarakenteita, jotka ovat Prolog-ohjelmoinnissa keskeisessä asemassa. Prologissa listaa merkitään hakasulkeilla, joiden sisällä ovat listan alkiot pilkulla erotettuna (esimerkiksi [a,b,c]), joten syntaksiltaan Prologin listat muistuttavat Haskellin listoja. Merkintä [] tarkoittaa tyhjää listaa. Prologissa ei ole listojen muodostamiseen ja purkamiseen erillisiä funktioita; sen sijaan kielessä käytetään merkintää [H T] tarkoittamaan listaa, jonka pää on H ja häntä T. Prologin listojen muodostamisen perusoperaatioita on append, joka liittää listoja yhteen, esimerkiksi?- Lista = [eka, toka, kolmas]. Lista = [eka, toka, kolmas].?- append($lista,[nelj],klista). Klista = [eka, toka, kolmas, nelj].
13 Prologin append-operaatiota voidaan soveltaa myös päättelemään, minkä listojen yhdistäminen antaa tuloslistan:?- append(x,y,$lista). X = [], Y = [eka, toka, kolmas]; X = [eka], Y = [toka, kolmas]; X = [eka, toka], Y = [kolmas]; X = [eka, toka, kolmas], Y = []; Esitetään vielä, miten listan kääntämisoperaatio voidaan toteuttaa Prologilla: kaanna([],[]). kaanna([h T],K) :- kaanna(t,k1),append(k1,[h],k). Tyhjän listan kääntäminen tuottaa tyhjän listan. Kun operaatiota sovelletaan epätyhjään listaan, käännetään ensin listan häntä, muodostetaan siitä lista K1 ja lisätään alkuun listan pää. Lopuksi käsitellään Prologin puutteita, jotka ainakin jossakin määrin koskevat yleisesti logiikkaohjelmointikieliä. Logiikkaohjelmointikielten piti alun perin muuttaa ohjelmointi spesifioinniksi ja vapauttaa ohjelmoija ratkaisun ohjelmoinnin yksityiskohdista. Tähän on pystytty vain osittain ja logiikkakielten päättelyissään käyttämät algoritmit ovat tuoneet omia ongelmia näillä kielillä ohjelmointiin. Esimerkiksi Prologin liittämisalgoritmi on itse asiassa epäkorrekti, tietyt määrittelyt johtavat sen ikuisiin silmukoihin (ks. [Lou], ). Prologissa on käytetty yksinkertaista ja tehokasta algoritmia, joka ei toimi oikein kaikissa erikoistapauksissa; tehokkaat ja korrektit algoritmit ovat huomattavasti monimutkaisempia. Looginen negaatio muodostuu ongelmalliseksi käsitteeksi logiikkakielissä niiden "suljetun maailman" oletuksen vuoksi. Logiikkakieli pitää väitettä vääränä, ellei sitä voida johtaa annetuista lauseista. Näin ollen väitteen negaatio on tosi, ellei väitettä
14 voida johtaa. Siten negaatio tarkoittaa pikemminkin epäonnistumista kuin loogista epätotuutta ja voi johtaa omalaatuisiin tuloksiin. Tietyssä mielessä myös logiikkaohjelmoinnin perimmäinen idea ratkaisun spesifioinnista sen tarkkojen yksityiskohtien ohjelmoimisen sijaan on ongelmallinen. Esimerkiksi lajitteluohjelman kirjoittaminen luonnollisimmalla tavalla johtaa listan kaikkien mahdollisten permutaatioiden generoimiseen, kunnes tavataan sellainen permutaatio, että lista on järjestyksessä. Tämä on luonnollisesti äärettömän tehoton tapa lajitella eikä sovellu käytännön ohjelmiin. Näin ollen ohjelmoijan on kuitenkin ohjelmoitava jokin konkreettinen lajittelualgoritmi, jolloin logiikkaohjelmointi lähestyy perinteisempiä ohjelmointimenetelmiä. (Prologilla voidaan kyllä esimerkiksi lajittelualgoritmeja kirjoittaa varsin näppärästi). Logiikkakielten pääasialliset sovelluskohteet liittyvät tekoälyyn tavalla tai toisella, kielissä on sovellettu mm. luonnollisen kielen käsittelyyn ja asiantuntijajärjestelmien toteuttamiseen. Tekoälysovellusten ulkopuolella logiikkaohjelmointikieliä on käytetty toistaiseksi varsin vähän, mutta relaatiotietokantojen käsittelyyn niitä on ainakin sovellettu. Lähteet [Har] Harsu, Maarit. Ohjelmointikielet, Periaatteet, käsitteet, valintaperusteet, Talentum [Kor] Kortelainen, Juha. Diskreetit rakenteet P, Luentomoniste. ( [Lou] Louden, Kenneth C. Programming Languages, Principles and Practice, PWS-KENT [Seb] Sebesta, Robert W. Concepts of Programming Languages 10th edition, Pearson 2013.
815338A Ohjelmointikielten periaatteet
 815338A Ohjelmointikielten periaatteet 2015-2016 VII Logiikkaohjelmointi Sisältö 1. Johdanto 2. Predikaattilogiikan käsitteistöä 3. Prolog 815338A Ohjelmointikielten periaatteet, Logiikkaohjelmointi 2
815338A Ohjelmointikielten periaatteet 2015-2016 VII Logiikkaohjelmointi Sisältö 1. Johdanto 2. Predikaattilogiikan käsitteistöä 3. Prolog 815338A Ohjelmointikielten periaatteet, Logiikkaohjelmointi 2
FI3 Tiedon ja todellisuuden filosofia LOGIIKKA. 1.1 Logiikan ymmärtämiseksi on tärkeää osata erottaa muoto ja sisältö toisistaan:
 LOGIIKKA 1 Mitä logiikka on? päättelyn tiede o oppi muodollisesti pätevästä päättelystä 1.1 Logiikan ymmärtämiseksi on tärkeää osata erottaa muoto ja sisältö toisistaan: sisältö, merkitys: onko jokin premissi
LOGIIKKA 1 Mitä logiikka on? päättelyn tiede o oppi muodollisesti pätevästä päättelystä 1.1 Logiikan ymmärtämiseksi on tärkeää osata erottaa muoto ja sisältö toisistaan: sisältö, merkitys: onko jokin premissi
 LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
Logiikan kertausta. TIE303 Formaalit menetelmät, kevät Antti-Juhani Kaijanaho. Jyväskylän yliopisto Tietotekniikan laitos.
 TIE303 Formaalit menetelmät, kevät 2005 Logiikan kertausta Antti-Juhani Kaijanaho antkaij@mit.jyu.fi Jyväskylän yliopisto Tietotekniikan laitos TIE303 Formaalit mentetelmät, 2005-01-27 p. 1/17 Luento2Luentomoniste
TIE303 Formaalit menetelmät, kevät 2005 Logiikan kertausta Antti-Juhani Kaijanaho antkaij@mit.jyu.fi Jyväskylän yliopisto Tietotekniikan laitos TIE303 Formaalit mentetelmät, 2005-01-27 p. 1/17 Luento2Luentomoniste
LOGIIKKA johdantoa
 LOGIIKKA johdantoa LUKUTEORIA JA TO- DISTAMINEN, MAA11 Logiikan tehtävä: Logiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat päättelyt
LOGIIKKA johdantoa LUKUTEORIA JA TO- DISTAMINEN, MAA11 Logiikan tehtävä: Logiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat päättelyt
Nimitys Symboli Merkitys Negaatio ei Konjuktio ja Disjunktio tai Implikaatio jos..., niin... Ekvivalenssi... jos ja vain jos...
 2 Logiikkaa Tässä luvussa tutustutaan joihinkin logiikan käsitteisiin ja merkintöihin. Lisätietoja ja tarkennuksia löytyy esimerkiksi Jouko Väänäsen kirjasta Logiikka I 2.1 Loogiset konnektiivit Väitelauseen
2 Logiikkaa Tässä luvussa tutustutaan joihinkin logiikan käsitteisiin ja merkintöihin. Lisätietoja ja tarkennuksia löytyy esimerkiksi Jouko Väänäsen kirjasta Logiikka I 2.1 Loogiset konnektiivit Väitelauseen
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2017-2018 Yhteenveto Yleistä kurssista Kurssin laajuus 5 op Luentoja 30h Harjoituksia 21h Itsenäistä työskentelyä n. 80h 811120P Diskreetit rakenteet, Yhteenveto 2 Kurssin
811120P Diskreetit rakenteet 2017-2018 Yhteenveto Yleistä kurssista Kurssin laajuus 5 op Luentoja 30h Harjoituksia 21h Itsenäistä työskentelyä n. 80h 811120P Diskreetit rakenteet, Yhteenveto 2 Kurssin
Insinöörimatematiikka A
 Insinöörimatematiikka A Mika Hirvensalo mikhirve@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2018 Mika Hirvensalo mikhirve@utu.fi Luentoruudut 3 1 of 23 Kertausta Määritelmä Predikaattilogiikan
Insinöörimatematiikka A Mika Hirvensalo mikhirve@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2018 Mika Hirvensalo mikhirve@utu.fi Luentoruudut 3 1 of 23 Kertausta Määritelmä Predikaattilogiikan
Prolog kielenä Periaatteet Yhteenveto. Prolog. Toni ja Laura Fadjukoff. 9. joulukuuta 2010
 kielenä 9. joulukuuta 2010 Historia kielenä Historia Sovelluksia kehitettiin vuonna 1972 Kehittäjinä ranskalaiset Pääkehittäjä Alain Colmerauer Philippe Roussel programmation en logique Robert Kowalski
kielenä 9. joulukuuta 2010 Historia kielenä Historia Sovelluksia kehitettiin vuonna 1972 Kehittäjinä ranskalaiset Pääkehittäjä Alain Colmerauer Philippe Roussel programmation en logique Robert Kowalski
-Matematiikka on aksiomaattinen järjestelmä. -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi
 -Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
-Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 3. Logiikka 3.1 Logiikka tietojenkäsittelyssä Pyritään formalisoimaan terveeseen järkeen perustuva päättely Sovelletaan monella alueella tietojenkäsittelyssä, esim.
811120P Diskreetit rakenteet 2016-2017 3. Logiikka 3.1 Logiikka tietojenkäsittelyssä Pyritään formalisoimaan terveeseen järkeen perustuva päättely Sovelletaan monella alueella tietojenkäsittelyssä, esim.
Pikapaketti logiikkaan
 Pikapaketti logiikkaan Tämän oppimateriaalin tarkoituksena on tutustua pikaisesti matemaattiseen logiikkaan. Oppimateriaalin asioita tarvitaan projektin tekemisessä. Kiinnostuneet voivat lukea lisää myös
Pikapaketti logiikkaan Tämän oppimateriaalin tarkoituksena on tutustua pikaisesti matemaattiseen logiikkaan. Oppimateriaalin asioita tarvitaan projektin tekemisessä. Kiinnostuneet voivat lukea lisää myös
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet )
 T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
T-79144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 7 (opetusmoniste, kappaleet 11-22) 26 29102004 1 Ilmaise seuraavat lauseet predikaattilogiikalla: a) Jokin porteista on viallinen
Predikaattilogiikkaa
 Predikaattilogiikkaa UKUTEORIA JA TO- DISTAMINEN, MAA11 Kertausta ogiikan tehtävä: ogiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat
Predikaattilogiikkaa UKUTEORIA JA TO- DISTAMINEN, MAA11 Kertausta ogiikan tehtävä: ogiikka tutkii ajattelun ja päättelyn sääntöjä ja muodollisten päättelyiden oikeellisuutta, ja pyrkii erottamaan oikeat
Approbatur 3, demo 1, ratkaisut A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat.
 Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
815338A Ohjelmointikielten periaatteet Harjoitus 6 Vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
Logiikka 1/5 Sisältö ESITIEDOT:
 Logiikka 1/5 Sisältö Formaali logiikka Luonnollinen logiikka muodostaa perustan arkielämän päättelyille. Sen käyttö on intuitiivista ja usein tiedostamatonta. Mikäli logiikka halutaan täsmällistää esimerkiksi
Logiikka 1/5 Sisältö Formaali logiikka Luonnollinen logiikka muodostaa perustan arkielämän päättelyille. Sen käyttö on intuitiivista ja usein tiedostamatonta. Mikäli logiikka halutaan täsmällistää esimerkiksi
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset
 Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
Diskreetit rakenteet. 3. Logiikka. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1
 811120P 3. 5 op Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 ja laskenta tarkastelemme terveeseen järkeen perustuvaa päättelyä formaalina järjestelmänä logiikkaa sovelletaan
811120P 3. 5 op Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 ja laskenta tarkastelemme terveeseen järkeen perustuvaa päättelyä formaalina järjestelmänä logiikkaa sovelletaan
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet )
 T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet 9.1 9.5) 30.11. 3.12.2004 1. Osoita lauselogiikan avulla oheisten ehtolausekkeiden ekvivalenssi. (a)!(a
T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet 9.1 9.5) 30.11. 3.12.2004 1. Osoita lauselogiikan avulla oheisten ehtolausekkeiden ekvivalenssi. (a)!(a
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 4 Ratkaisuehdotukset
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Etsi lauseen (p 0 (p 1 p 0 )) p 1 kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Etsi lauseen (p 0 (p 1 p 0 )) p 1 kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa
Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi
 Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi LUKUTEORIA JA TODISTAMINEN, MAA11 Esimerkki a) Lauseen Kaikki johtajat ovat miehiä negaatio ei
Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi LUKUTEORIA JA TODISTAMINEN, MAA11 Esimerkki a) Lauseen Kaikki johtajat ovat miehiä negaatio ei
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset
 815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
TIEA241 Automaatit ja kieliopit, syksy Antti-Juhani Kaijanaho. 8. syyskuuta 2016
 TIEA241 Automaatit ja kieliopit, syksy 2016 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. syyskuuta 2016 Sisällys a https://tim.jyu.fi/view/kurssit/tie/ tiea241/2016/videoiden%20hakemisto Matemaattisen
TIEA241 Automaatit ja kieliopit, syksy 2016 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. syyskuuta 2016 Sisällys a https://tim.jyu.fi/view/kurssit/tie/ tiea241/2016/videoiden%20hakemisto Matemaattisen
Luonnollisen päättelyn luotettavuus
 Luonnollisen päättelyn luotettavuus Luotettavuuden todistamiseksi määrittelemme täsmällisesti, milloin merkkijono on deduktio. Tässä ei ole sisällytetty päättelysääntöihin iteraatiosääntöä, koska sitä
Luonnollisen päättelyn luotettavuus Luotettavuuden todistamiseksi määrittelemme täsmällisesti, milloin merkkijono on deduktio. Tässä ei ole sisällytetty päättelysääntöihin iteraatiosääntöä, koska sitä
PROPOSITIOLOGIIKAN RIITTÄMÄTTÖMYYS
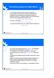 67 PROPOSITIOLOGIIKAN RIITTÄMÄTTÖMYYS Jo äärimmäisen yksinkertaisessa peliesimerkissämme propositiologiikan ilmaisuvoima osoittautuu riittämättömäksi Tietämyskannan alustamiseksi pelin säännöillä meidän
67 PROPOSITIOLOGIIKAN RIITTÄMÄTTÖMYYS Jo äärimmäisen yksinkertaisessa peliesimerkissämme propositiologiikan ilmaisuvoima osoittautuu riittämättömäksi Tietämyskannan alustamiseksi pelin säännöillä meidän
T Syksy 2005 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet )
 T-79.144 Syksy 2005 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3-3.4) 2 5.11.2005 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio R A
T-79.144 Syksy 2005 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3-3.4) 2 5.11.2005 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio R A
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 1: Joukko-oppi ja logiikka Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kiitokset Nämä luentokalvot perustuvat Gustaf
MS-A0402 Diskreetin matematiikan perusteet Osa 1: Joukko-oppi ja logiikka Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kiitokset Nämä luentokalvot perustuvat Gustaf
Loogiset konnektiivit
 Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi... jos ja vain jos... Sulkeita ( ) käytetään selkeyden vuoksi
Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi... jos ja vain jos... Sulkeita ( ) käytetään selkeyden vuoksi
Tehtävä 1. Päättele resoluutiolla seuraavista klausuulijoukoista. a. 1 {p 3 } oletus. 4 {p 1, p 2, p 3 } oletus. 5 { p 1 } (1, 2) 7 (4, 6)
 Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
missä on myös käytetty monisteen kaavaa 12. Pistä perustelut kohdilleen!
 Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Johdatus logiikkaan I Harjoitus 4 Vihjeet
 Johdatus logiikkaan I Harjoitus 4 Vihjeet 1. Etsi lauseen ((p 0 p 1 ) (p 0 p 1 )) kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa normaalimuodossa, (b) konjunktiivisessa normaalimuodossa.
Johdatus logiikkaan I Harjoitus 4 Vihjeet 1. Etsi lauseen ((p 0 p 1 ) (p 0 p 1 )) kanssa loogisesti ekvivalentti lause joka on (a) disjunktiivisessa normaalimuodossa, (b) konjunktiivisessa normaalimuodossa.
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 4. Joukot, relaatiot ja funktiot Osa 3: Funktiot 4.3 Funktiot Olkoot A ja B joukkoja. Funktio joukosta A joukkoon B on sääntö, joka liittää yksikäsitteisesti määrätyn
811120P Diskreetit rakenteet 2016-2017 4. Joukot, relaatiot ja funktiot Osa 3: Funktiot 4.3 Funktiot Olkoot A ja B joukkoja. Funktio joukosta A joukkoon B on sääntö, joka liittää yksikäsitteisesti määrätyn
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 1 Määrittelyjoukoista Tarkastellaan funktiota, jonka määrittelevä yhtälö on f(x) = x. Jos funktion lähtöjoukoksi määrittelee vaikkapa suljetun välin [0, 1], on funktio
Matematiikan tukikurssi Kurssikerta 1 Määrittelyjoukoista Tarkastellaan funktiota, jonka määrittelevä yhtälö on f(x) = x. Jos funktion lähtöjoukoksi määrittelee vaikkapa suljetun välin [0, 1], on funktio
T kevät 2007 Laskennallisen logiikan jatkokurssi Laskuharjoitus 1 Ratkaisut
 T-79.5101 kevät 2007 Laskennallisen logiikan jatkokurssi Laskuharjoitus 1 Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun juureen
T-79.5101 kevät 2007 Laskennallisen logiikan jatkokurssi Laskuharjoitus 1 Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun juureen
Todistusteoriaa. Kun kielen syntaksi on tarkasti määritelty, voidaan myös määritellä täsmällisesti, mitä pätevällä päättelyllä tarkoitetaan.
 Todistusteoriaa Kun kielen syntaksi on tarkasti määritelty, voidaan myös määritellä täsmällisesti, mitä pätevällä päättelyllä tarkoitetaan. Todistusteoriassa annetaan joukko aksioomia ja päättely- sääntöjä,
Todistusteoriaa Kun kielen syntaksi on tarkasti määritelty, voidaan myös määritellä täsmällisesti, mitä pätevällä päättelyllä tarkoitetaan. Todistusteoriassa annetaan joukko aksioomia ja päättely- sääntöjä,
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2018-2019 Kertausta toiseen välikokeeseen Yhteenveto Kurssin sisältö 1. Algoritmin käsite 2. Lukujärjestelmät ja niiden muunnokset; lukujen esittäminen tietokoneessa 3. Logiikka
811120P Diskreetit rakenteet 2018-2019 Kertausta toiseen välikokeeseen Yhteenveto Kurssin sisältö 1. Algoritmin käsite 2. Lukujärjestelmät ja niiden muunnokset; lukujen esittäminen tietokoneessa 3. Logiikka
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
Johdatus matematiikkaan
 Johdatus matematiikkaan Luento 3 Mikko Salo 1.9.2017 Sisältö 1. Logiikasta 2. Suora ja epäsuora todistus 3. Jaollisuus ja alkuluvut Todistus Tähän asti esitetyt todistukset ovat olleet esimerkinomaisia.
Johdatus matematiikkaan Luento 3 Mikko Salo 1.9.2017 Sisältö 1. Logiikasta 2. Suora ja epäsuora todistus 3. Jaollisuus ja alkuluvut Todistus Tähän asti esitetyt todistukset ovat olleet esimerkinomaisia.
T Kevät 2006 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet )
 T-79.3001 Kevät 2006 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3 3.4) 21. 24.3.2006 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio
T-79.3001 Kevät 2006 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (opetusmoniste, kappaleet 2.3 3.4) 21. 24.3.2006 1. Olkoon R kaksipaikkainen predikaattisymboli, jonka tulkintana on relaatio
Lause 5. (s. 50). Olkoot A ja B joukkoja. Tällöin seuraavat ehdot ovat
 jen Kahden joukon A ja B samuutta todistettaessa kannattaa usein osoittaa, että A on B:n osajoukko ja että B on A:n osajoukko. Tällöin sovelletaan implikaation ja ekvivalenssin yhteyttä. Lause 5. (s. 50).
jen Kahden joukon A ja B samuutta todistettaessa kannattaa usein osoittaa, että A on B:n osajoukko ja että B on A:n osajoukko. Tällöin sovelletaan implikaation ja ekvivalenssin yhteyttä. Lause 5. (s. 50).
1 Logiikkaa. 1.1 Logiikan symbolit
 1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
Kirjoita käyttäen propositiosymboleita, konnektiiveja ja sulkeita propositiologiikan lauseiksi:
 1 Logiikan paja, kevät 2011 Ratkaisut viikolle I Thomas Vikberg Merkitään propopositiosymboleilla p i seuraavia atomilauseita: p 0 : vettä sataa p 1 : tänään on perjantai p 2 : olen myöhässä Valitaan konnektiiveiksi,
1 Logiikan paja, kevät 2011 Ratkaisut viikolle I Thomas Vikberg Merkitään propopositiosymboleilla p i seuraavia atomilauseita: p 0 : vettä sataa p 1 : tänään on perjantai p 2 : olen myöhässä Valitaan konnektiiveiksi,
Propositiot: Propositiot ovat väitelauseita. Totuusfunktiot antavat niille totuusarvon T tai E.
 Propositiot: Propositiot ovat väitelauseita. Totuusfunktiot antavat niille totuusarvon T tai E. Perusaksioomat: Laki 1: Kukin totuusfunktio antaa kullekin propositiolle totuusarvoksi joko toden T tai epätoden
Propositiot: Propositiot ovat väitelauseita. Totuusfunktiot antavat niille totuusarvon T tai E. Perusaksioomat: Laki 1: Kukin totuusfunktio antaa kullekin propositiolle totuusarvoksi joko toden T tai epätoden
Ratkaisu: Käytetään induktiota propositiolauseen A rakenteen suhteen. Alkuaskel. A = p i jollain i N. Koska v(p i ) = 1 kaikilla i N, saadaan
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 2 Ratkaisuehdotukset 1. Olkoon totuusjakauma v sellainen että v(p i ) = 1 kaikilla i N ja A propositiolause, jossa
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 2 Ratkaisuehdotukset 1. Olkoon totuusjakauma v sellainen että v(p i ) = 1 kaikilla i N ja A propositiolause, jossa
4 Matemaattinen induktio
 4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 (opetusmoniste, lauselogiikka )
 T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 opetusmoniste, lauselogiikka 2.1-3.5) 21 24.9.2004 1. Määrittele lauselogiikan konnektiivit a) aina epätoden lauseen ja implikaation
T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 opetusmoniste, lauselogiikka 2.1-3.5) 21 24.9.2004 1. Määrittele lauselogiikan konnektiivit a) aina epätoden lauseen ja implikaation
T Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 11 (predikaattilogiikka )
 T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 11 (predikaattilogiikka 14.1 14.5) 23. 25.4.2008 Ratkaisuja demotehtäviin Tehtävä 14.1 Herbrand-universumi U muodostuu termeistä,
T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 11 (predikaattilogiikka 14.1 14.5) 23. 25.4.2008 Ratkaisuja demotehtäviin Tehtävä 14.1 Herbrand-universumi U muodostuu termeistä,
13. Loogiset operaatiot 13.1
 13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
815338A Ohjelmointikielten periaatteet Harjoitus 2 vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 2 vastaukset Harjoituksen aiheena on BNF-merkinnän käyttö ja yhteys rekursiivisesti etenevään jäsentäjään. Tehtävä 1. Mitkä ilmaukset seuraava
1. Logiikan ja joukko-opin alkeet
 1. Logiikan ja joukko-opin alkeet 1.1. Logiikkaa 1. Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa muotoon p q, ts. että propositio (p q) ( p q) on identtisesti tosi. 2. Todista
1. Logiikan ja joukko-opin alkeet 1.1. Logiikkaa 1. Osoita totuusarvotauluja käyttäen, että implikaatio p q voidaan kirjoittaa muotoon p q, ts. että propositio (p q) ( p q) on identtisesti tosi. 2. Todista
Matematiikan tukikurssi, kurssikerta 2
 Matematiikan tukikurssi kurssikerta 1 Relaatioista Oletetaan kaksi alkiota a ja b. Näistä kumpikin kuuluu johonkin tiettyyn joukkoon mahdollisesti ne kuuluvat eri joukkoihin; merkitään a A ja b B. Voidaan
Matematiikan tukikurssi kurssikerta 1 Relaatioista Oletetaan kaksi alkiota a ja b. Näistä kumpikin kuuluu johonkin tiettyyn joukkoon mahdollisesti ne kuuluvat eri joukkoihin; merkitään a A ja b B. Voidaan
Lisää pysähtymisaiheisia ongelmia
 Lisää pysähtymisaiheisia ongelmia Lause: Pysähtymättömyysongelma H missä H = { w111x w validi koodi, M w ei pysähdy syötteellä x } ei ole rekursiivisesti lueteltava. Todistus: Pysähtymisongelman komplementti
Lisää pysähtymisaiheisia ongelmia Lause: Pysähtymättömyysongelma H missä H = { w111x w validi koodi, M w ei pysähdy syötteellä x } ei ole rekursiivisesti lueteltava. Todistus: Pysähtymisongelman komplementti
FORMAALI SYSTEEMI (in Nutshell): aakkosto: alkeismerkkien joukko kieliopin määräämä syntaksi: sallittujen merkkijonojen rakenne, formaali kuvaus
 FORMAALI SYSTEEMI (in Nutshell): Formaali kieli: aakkosto: alkeismerkkien joukko kieliopin määräämä syntaksi: sallittujen merkkijonojen rakenne, formaali kuvaus esim. SSM:n tai EBNF:n avulla Semantiikka:
FORMAALI SYSTEEMI (in Nutshell): Formaali kieli: aakkosto: alkeismerkkien joukko kieliopin määräämä syntaksi: sallittujen merkkijonojen rakenne, formaali kuvaus esim. SSM:n tai EBNF:n avulla Semantiikka:
5.1 Semanttisten puiden muodostaminen
 Luku 5 SEMNTTISET PUUT 51 Semanttisten puiden muodostaminen Esimerkki 80 Tarkastellaan kysymystä, onko kaava = (( p 0 p 1 ) (p 1 p 2 )) toteutuva Tätä voidaan tutkia päättelemällä semanttisesti seuraavaan
Luku 5 SEMNTTISET PUUT 51 Semanttisten puiden muodostaminen Esimerkki 80 Tarkastellaan kysymystä, onko kaava = (( p 0 p 1 ) (p 1 p 2 )) toteutuva Tätä voidaan tutkia päättelemällä semanttisesti seuraavaan
3. Predikaattilogiikka
 3. Predikaattilogiikka Muuttuja mukana lauseessa. Ei yksikäsitteistä totuusarvoa. Muuttujan kiinnittäminen määrän ilmaisulla voi antaa yksikäsitteisen totuusarvon. Esimerkki. Lauseella x 3 8 = 0 ei ole
3. Predikaattilogiikka Muuttuja mukana lauseessa. Ei yksikäsitteistä totuusarvoa. Muuttujan kiinnittäminen määrän ilmaisulla voi antaa yksikäsitteisen totuusarvon. Esimerkki. Lauseella x 3 8 = 0 ei ole
Toinen muotoilu. {A 1,A 2,...,A n,b } 0, Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun 1 / 13
 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun {A 1,A 2,...,A n,b } 0, jatkoa jatkoa 1 / 13 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin
2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin kun {A 1,A 2,...,A n,b } 0, jatkoa jatkoa 1 / 13 2 3 Edellinen sääntö toisin: Lause 2.5.{A 1,A 2,...,A n } B täsmälleen silloin
T Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut
 T-79.146 Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun
T-79.146 Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun
2. Minkä joukon määrittelee kaava P 0 (x 0 ) P 1 (x 0 ) mallissa M = ({0, 1, 2, 3}, P M 0, P M 1 ), kun P M 0 = {0, 1} ja P M 1 = {1, 2}?
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan II, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Mitkä muuttujat esiintyvät vapaina kaavassa x 2 ( x 0 R 0 (x 1, x 2 ) ( x 3 R 0 (x 3, x 0
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan II, syksy 2018 Harjoitus 4 Ratkaisuehdotukset 1. Mitkä muuttujat esiintyvät vapaina kaavassa x 2 ( x 0 R 0 (x 1, x 2 ) ( x 3 R 0 (x 3, x 0
Algebralliset tietotyypit ym. TIEA341 Funktio ohjelmointi 1 Syksy 2005
 Algebralliset tietotyypit ym. TIEA341 Funktio ohjelmointi 1 Syksy 2005 Tällä luennolla Algebralliset tietotyypit Hahmonsovitus (pattern matching) Primitiivirekursio Esimerkkinä binäärinen hakupuu Muistattehan...
Algebralliset tietotyypit ym. TIEA341 Funktio ohjelmointi 1 Syksy 2005 Tällä luennolla Algebralliset tietotyypit Hahmonsovitus (pattern matching) Primitiivirekursio Esimerkkinä binäärinen hakupuu Muistattehan...
T Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (Predikaattilogiikka )
 T-79.3001 Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (Predikaattilogiikka 10.3. 11.4) 26. 30.3. 2009 Ratkaisuja demotehtäviin Tehtävä 10.5 Allaolevat kolme graafia pyrkivät selventämään
T-79.3001 Kevät 2009 Logiikka tietotekniikassa: perusteet Laskuharjoitus 8 (Predikaattilogiikka 10.3. 11.4) 26. 30.3. 2009 Ratkaisuja demotehtäviin Tehtävä 10.5 Allaolevat kolme graafia pyrkivät selventämään
ITKP102 Ohjelmointi 1 (6 op)
 ITKP102 Ohjelmointi 1 (6 op) Tentaattori: Antti-Jussi Lakanen 7. huhtikuuta 2017 Vastaa kaikkiin tehtäviin. Tee jokainen tehtävä erilliselle konseptiarkille. Kirjoittamasi luokat, funktiot ja aliohjelmat
ITKP102 Ohjelmointi 1 (6 op) Tentaattori: Antti-Jussi Lakanen 7. huhtikuuta 2017 Vastaa kaikkiin tehtäviin. Tee jokainen tehtävä erilliselle konseptiarkille. Kirjoittamasi luokat, funktiot ja aliohjelmat
missä on myös käytetty monisteen kaavaa 12. Pistä perustelut kohdilleen!
 Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Matematiikan johdantokurssi Kertausharjoitustehtävien ratkaisuja/vastauksia/vihjeitä. Osoita todeksi logiikan lauseille seuraava: P Q (P Q). Ratkaisuohje. Väite tarkoittaa, että johdetut lauseet P Q ja
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
T Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 5 (lauselogiikka ) A ( B C) A B C.
 T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 5 (lauselogiikka 6.1 7.2) 27. 29.2.2008 Ratkaisuja demotehtäviin Tehtävä 6.1 a) A (B C) Poistetaan lauseesta ensin implikaatiot.
T-79.3001 Logiikka tietotekniikassa: perusteet Kevät 2008 Laskuharjoitus 5 (lauselogiikka 6.1 7.2) 27. 29.2.2008 Ratkaisuja demotehtäviin Tehtävä 6.1 a) A (B C) Poistetaan lauseesta ensin implikaatiot.
Todistamisessa on tärkeää erottaa tapaukset, kun sääntö pätee joillakin tai kun sääntö pätee kaikilla. Esim. On olemassa reaaliluku x, jolle x = 5.
 3.4 Kvanttorit Todistamisessa on tärkeää erottaa tapaukset, kun sääntö pätee joillakin tai kun sääntö pätee kaikilla. Esim. On olemassa reaaliluku x, jolle x = 5. Kaikilla reaaliluvuilla x pätee x+1 >
3.4 Kvanttorit Todistamisessa on tärkeää erottaa tapaukset, kun sääntö pätee joillakin tai kun sääntö pätee kaikilla. Esim. On olemassa reaaliluku x, jolle x = 5. Kaikilla reaaliluvuilla x pätee x+1 >
Karteesinen tulo. Olkoot A = {1, 2, 3, 5} ja B = {a, b, c}. Näiden karteesista tuloa A B voidaan havainnollistaa kuvalla 1 / 21
 säilyy Olkoot A = {1, 2, 3, 5} ja B = {a, b, c}. Näiden karteesista tuloa A B voidaan havainnollistaa kuvalla c b a 1 2 3 5 1 / 21 säilyy Esimerkkirelaatio R = {(1, b), (3, a), (5, a), (5, c)} c b a 1
säilyy Olkoot A = {1, 2, 3, 5} ja B = {a, b, c}. Näiden karteesista tuloa A B voidaan havainnollistaa kuvalla c b a 1 2 3 5 1 / 21 säilyy Esimerkkirelaatio R = {(1, b), (3, a), (5, a), (5, c)} c b a 1
13. Loogiset operaatiot 13.1
 13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, sekä voi olla apua.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
LOGIIKKA, TIETÄMYS JA PÄÄTTELY
 36 LOGIIKKA, TIETÄMYS JA PÄÄTTELY Ryhdymme nyt tarkastelemaan tietämyskannan (knowledge base, KB omaavia agentteja KB:n avulla agentti pyrkii pitämään yllä tietoa vain osittain havainnoimastaan maailmasta
36 LOGIIKKA, TIETÄMYS JA PÄÄTTELY Ryhdymme nyt tarkastelemaan tietämyskannan (knowledge base, KB omaavia agentteja KB:n avulla agentti pyrkii pitämään yllä tietoa vain osittain havainnoimastaan maailmasta
Predikaattilogiikan malli-teoreettinen semantiikka
 Predikaattilogiikan malli-teoreettinen semantiikka February 4, 2013 Muistamme, että predikaattilogiikassa aakkosto L koostuu yksilövakioista c 0, c 1, c 2,... ja predikaattisymboleista P, R,... jne. Ekstensionaalisia
Predikaattilogiikan malli-teoreettinen semantiikka February 4, 2013 Muistamme, että predikaattilogiikassa aakkosto L koostuu yksilövakioista c 0, c 1, c 2,... ja predikaattisymboleista P, R,... jne. Ekstensionaalisia
Ratkaisu: Yksi tapa nähdä, että kaavat A (B C) ja (A B) (A C) ovat loogisesti ekvivalentit, on tehdä totuustaulu lauseelle
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 3 Ratkaisuehdotukset 1. Olkoot A, B ja C propositiolauseita. Näytä, että A (B C) (A B) (A C). Ratkaisu: Yksi tapa
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 3 Ratkaisuehdotukset 1. Olkoot A, B ja C propositiolauseita. Näytä, että A (B C) (A B) (A C). Ratkaisu: Yksi tapa
TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho. 16. maaliskuuta 2011
 TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 16. maaliskuuta 2011 Sisällys Sisällys Väitelauseet lause (tai virke), joka sanoo jonkin asian pitävän paikkaansa
TIEA241 Automaatit ja kieliopit, kevät 2011 (IV) Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 16. maaliskuuta 2011 Sisällys Sisällys Väitelauseet lause (tai virke), joka sanoo jonkin asian pitävän paikkaansa
tään painetussa ja käsin kirjoitetussa materiaalissa usein pienillä kreikkalaisilla
 2.5. YDIN-HASKELL 19 tään painetussa ja käsin kirjoitetussa materiaalissa usein pienillä kreikkalaisilla kirjaimilla. Jos Γ ja ovat tyyppilausekkeita, niin Γ on tyyppilauseke. Nuoli kirjoitetaan koneella
2.5. YDIN-HASKELL 19 tään painetussa ja käsin kirjoitetussa materiaalissa usein pienillä kreikkalaisilla kirjaimilla. Jos Γ ja ovat tyyppilausekkeita, niin Γ on tyyppilauseke. Nuoli kirjoitetaan koneella
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 5 Ratkaisuehdotukset
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 5 Ratkaisuehdotukset 1. Päättele resoluutiolla seuraavista klausuulijoukoista: (a) {{p 0 }, {p 1 }, { p 0, p 2 },
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 5 Ratkaisuehdotukset 1. Päättele resoluutiolla seuraavista klausuulijoukoista: (a) {{p 0 }, {p 1 }, { p 0, p 2 },
Johdatus matemaattiseen päättelyyn
 Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä 2 Todistamisesta 2 3 Joukko-oppia Tässä luvussa tarkastellaan joukko-opin
Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä 2 Todistamisesta 2 3 Joukko-oppia Tässä luvussa tarkastellaan joukko-opin
b) Määritä myös seuraavat joukot ja anna kussakin tapauksessa lyhyt sanallinen perustelu.
 Johdatus yliopistomatematiikkaan Helsingin yliopisto, matematiikan ja tilastotieteen laitos Kurssikoe 23.10.2017 Ohjeita: Vastaa kaikkiin tehtäviin. Ratkaisut voi kirjoittaa samalle konseptiarkille, jos
Johdatus yliopistomatematiikkaan Helsingin yliopisto, matematiikan ja tilastotieteen laitos Kurssikoe 23.10.2017 Ohjeita: Vastaa kaikkiin tehtäviin. Ratkaisut voi kirjoittaa samalle konseptiarkille, jos
Algoritmit. Ohjelman tekemisen hahmottamisessa käytetään
 Ohjelmointi Ohjelmoinnissa koneelle annetaan tarkkoja käskyjä siitä, mitä koneen tulisi tehdä. Ohjelmointikieliä on olemassa useita satoja. Ohjelmoinnissa on oleellista asioiden hyvä suunnittelu etukäteen.
Ohjelmointi Ohjelmoinnissa koneelle annetaan tarkkoja käskyjä siitä, mitä koneen tulisi tehdä. Ohjelmointikieliä on olemassa useita satoja. Ohjelmoinnissa on oleellista asioiden hyvä suunnittelu etukäteen.
Reaalifunktioista 1 / 17. Reaalifunktioista
 säilyy 1 / 17 säilyy Jos A, B R, niin funktiota f : A B sanotaan (yhden muuttujan) reaalifunktioksi. Tällöin karteesinen tulo A B on (aiempia esimerkkejä luonnollisemmalla tavalla) xy-tason osajoukko,
säilyy 1 / 17 säilyy Jos A, B R, niin funktiota f : A B sanotaan (yhden muuttujan) reaalifunktioksi. Tällöin karteesinen tulo A B on (aiempia esimerkkejä luonnollisemmalla tavalla) xy-tason osajoukko,
Todistusmenetelmiä Miksi pitää todistaa?
 Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Heidi Luukkonen. Sahlqvistin kaavat
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Heidi Luukkonen Sahlqvistin kaavat Informaatiotieteiden yksikkö Matematiikka Maaliskuu 2013 Tampereen yliopisto Informaatiotieteiden yksikkö LUUKKONEN, HEIDI: Sahlqvistin
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Heidi Luukkonen Sahlqvistin kaavat Informaatiotieteiden yksikkö Matematiikka Maaliskuu 2013 Tampereen yliopisto Informaatiotieteiden yksikkö LUUKKONEN, HEIDI: Sahlqvistin
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
11.4. Context-free kielet 1 / 17
 11.4. Context-free kielet 1 / 17 Määritelmä Tyypin 2 kielioppi (lauseyhteysvapaa, context free): jos jokainenp :n sääntö on muotoa A w, missäa V \V T jaw V. Context-free kielet ja kieliopit ovat tärkeitä
11.4. Context-free kielet 1 / 17 Määritelmä Tyypin 2 kielioppi (lauseyhteysvapaa, context free): jos jokainenp :n sääntö on muotoa A w, missäa V \V T jaw V. Context-free kielet ja kieliopit ovat tärkeitä
Rakenteiset päättelyketjut ja avoin lähdekoodi
 Rakenteiset päättelyketjut ja avoin lähdekoodi Mia Peltomäki Kupittaan lukio ja Turun yliopiston IT-laitos http://crest.abo.fi /Imped Virtuaalikoulupäivät 24. marraskuuta 2009 1 Taustaa Todistukset muodostavat
Rakenteiset päättelyketjut ja avoin lähdekoodi Mia Peltomäki Kupittaan lukio ja Turun yliopiston IT-laitos http://crest.abo.fi /Imped Virtuaalikoulupäivät 24. marraskuuta 2009 1 Taustaa Todistukset muodostavat
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Roosa Niemi. Riippuvuuslogiikkaa
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Roosa Niemi Riippuvuuslogiikkaa Informaatiotieteiden yksikkö Matematiikka Syyskuu 2011 Tampereen yliopisto Informaatiotieteiden yksikkö ROOSA NIEMI: Riippuvuuslogiikkaa
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Roosa Niemi Riippuvuuslogiikkaa Informaatiotieteiden yksikkö Matematiikka Syyskuu 2011 Tampereen yliopisto Informaatiotieteiden yksikkö ROOSA NIEMI: Riippuvuuslogiikkaa
MS-A0402 Diskreetin matematiikan perusteet
 MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
Ensimmäinen induktioperiaate
 Ensimmäinen induktioperiaate Olkoon P(n) luonnollisilla luvuilla määritelty predikaatti. (P(n) voidaan lukea luvulla n on ominaisuus P.) Todistettava, että P(n) on tosi jokaisella n N. ( Kaikilla luonnollisilla
Ensimmäinen induktioperiaate Olkoon P(n) luonnollisilla luvuilla määritelty predikaatti. (P(n) voidaan lukea luvulla n on ominaisuus P.) Todistettava, että P(n) on tosi jokaisella n N. ( Kaikilla luonnollisilla
Johdatus matemaattiseen päättelyyn
 Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä Luonnollisten lukujen joukko N on joukko N = {1, 2, 3,...} ja kokonaislukujen
Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä Luonnollisten lukujen joukko N on joukko N = {1, 2, 3,...} ja kokonaislukujen
(1) refleksiivinen, (2) symmetrinen ja (3) transitiivinen.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
 1. Algoritmi 1.1 Sisällys Algoritmin määritelmä. Aiheen pariin johdatteleva esimerkki. Muuttujat ja operaatiot (sijoitus, aritmetiikka ja vertailu). Algoritmista ohjelmaksi. 1.2 Algoritmin määritelmä Ohjelmointi
1. Algoritmi 1.1 Sisällys Algoritmin määritelmä. Aiheen pariin johdatteleva esimerkki. Muuttujat ja operaatiot (sijoitus, aritmetiikka ja vertailu). Algoritmista ohjelmaksi. 1.2 Algoritmin määritelmä Ohjelmointi
Vaihtoehtoinen tapa määritellä funktioita f : N R on
 Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: 1 (Alkuarvot) Ilmoitetaan funktion arvot
Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: 1 (Alkuarvot) Ilmoitetaan funktion arvot
Rekursio. Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on
 Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: Rekursio Funktio f : N R määritellään yleensä
Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: Rekursio Funktio f : N R määritellään yleensä
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa I
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 30. syyskuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 30.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 30. syyskuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 30.
Ensimmäinen induktioperiaate
 1 Ensimmäinen induktioperiaate Olkoon P(n) luonnollisilla luvuilla määritelty predikaatti. (P(n) voidaan lukea luvulla n on ominaisuus P.) Todistettava, että P(n) on tosi jokaisella n N. ( Kaikilla luonnollisilla
1 Ensimmäinen induktioperiaate Olkoon P(n) luonnollisilla luvuilla määritelty predikaatti. (P(n) voidaan lukea luvulla n on ominaisuus P.) Todistettava, että P(n) on tosi jokaisella n N. ( Kaikilla luonnollisilla
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
Cantorin joukon suoristuvuus tasossa
 Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
