16. Valikoituja aiheita
|
|
|
- Anni Tuulikki Lahti
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 16. Valikoituja aiheita Materiaalin viimeisessä luvussa käydään läpi väliinjääneitä kuntalaajennoksiin liittyviä tuloksia ja tutustutaan vielä hieman tarkemmin Galois n teoriaan Isomorfismien jatkaminen. On hyödyllistä tietää, millaisessa tilanteessa kuntien välinen isomorfismi voidaan laajentaa algebrallisten laajennosten väliseksi isomorfismiksi. Kuntien välistä homomorfismiaσ:k K vastaa polynomirenkaiden homomorfismik[x] K [X], joka kuvaa polynomin i a ix i polynomille i σ(a i)x i. Myös tätä johdettua homomorfismia merkitään kirjaimella σ, mikäli sekaantumisen vaaraa ei ole. Seuraava lemma kertoo, millä tavalla annettua kuntaisomorfismia voidaan jatkaa yksinkertaiseen algebralliseen laajennokseen. Lause Oletetaan, ettäσ:k K on kuntaisomorfismi. Olkoonf jokin jaoton K-kertoiminen polynomi, olkoon α polynomin f juuri jossain K:n laajennoksessal, ja olkoonα vastaavasti polynominσ(f) juuri jossaink :n laajennoksessal. Tällöin on olemassa isomorfismiτ:k(α) K (α), jolle pätee τ K =σ ja τ(α) =α. L K( ) K L K K( ) Kuva 30. Isomorfismi voidaan jatkaa yksinkertaiseen laajennokseen. Todistus. Merkitääng =σ(f). Koskaf on jaoton jaf(α) = 0, alkionα minimipolynomi on f:n liittoalkio. Täten f virittää alkioon α liittyvän sijoitushomomorfismin ytimen. Vastaava pätee polynomilleg K [X], sillä se on myös jaoton. Algebrojen homomorfialauseesta saadaan K-algebrojen isomorfismit ϕ :K[X]/ f K(α) ja ψ :K [X]/ g K (α). Toisaalta kaava h σ(h) + g määrittelee surjektiivisen rengashomomorfismin χ :K[X] K [X]/ g. Tämän homomorfismin ydin on f, joten algebrojen homomorfialauseesta saadaan isomorfismiχ :K[X]/ f K [X]/ g. Nyt yhdistetty kuvausτ =ψ χ ϕ 1 :K(α) K(α ) on kuntaisomorfismi, jolle pätee τ :α ϕ 1 X + f X χ + g α ψ. Lisäksiτ K =σ, silläϕjaψ kuvaavat vakiopolynomit vastaavasti kuntienk ja K alkioille. 111
2 112 Esimerkki Yllä olevaa lausetta voidaan käyttää myös tilanteessa, jossa K jak ovat sama kunta jaσ=id K. Jos tällöinαjaα ovat saman jaottoman polynomin juuria, niin on olemassa isomorfismik(α) =K(α ), joka kuvaaα α ja joka kiinnittää lähtökunnank. Esimerkiksi polynomix 4 2 on jaoton Q:n suhteen, ja sillä on kompleksijuuret± 4 2 ja±i 4 2. On siis olemassa muun muassa Q-isomorfismiσ: Q( 4 2) Q(i 4 2), jolle päteeσ( 4 2) =i 4 2, sekä automorfismi τ Gal(Q( 4 2)/Q), jolle päteeσ( 4 2) = 4 2. Osoittautuu, että kuntaisomorfismi voidaan aina laajentaa jopa juurikuntien isomorfismiksi. Tämän tuloksen todistus perustuu Zornin lemmaan. Oletetaan, ettäσ :K K on jokink-isomorfismi. OlkoonS ={f i } i I joukkok-kertoimisia polynomeja, ja olkoons ={σ(f i )} vastaava joukkok -kertoimisia polynomeja. Olkoon lisäksilpolynomijoukons jokin juurikuntak:n suhteen, jal vastaavasti S :n jokin juurikunta kunnank suhteen. Lause 16.3 (Isomorfismien jatkaminen). Olkoonα L, ja olkoonpalkionα minimipolynomik:n suhteen. Olkoon lisäksiα L mikä tahansa polynominσ(p) juuri. Tällöin löytyy isomorfismiτ:l L, jolle päteeτ K =σ jaτ(α) =α. Todistus. OlkoonF kaikkien parien (F,ϕ) joukko, missäf on kunnanl alikunta jaϕ:f L on kuntahomomorfismi, jolle päteeϕ K =σ. Tämä joukko sisältää parin (K, σ), joten F. Joukko F voidaan varustaa osittaisjärjestyksellä määrittelemällä (F,ϕ) (F,ϕ ) silloin, kunf F jaϕ F =ϕ. Olkoon {(F i,ϕ i )} i I jokin ketju osittaisjärjestyksessäf. Määrittelemällä F = i IF i ja ϕ(a) =ϕ i (a), kuna F i, saadaan hyvin määritelty pari (F,ϕ) F, joka on ketjun{(f i,ϕ i )} i I yläraja. Zornin lemman perusteella joukossa F on maksimaalinen alkio (M, τ). Osoitetaan, ettäm =Ljaτ(M) =L. JosM L, niin löytyy jokin polynomi f S, jonka kaikki juuret eivät ole kunnassam. Olkoonαjokin tällainen juuri, ja olkoonp = min(k,α). Merkitäänq =σ(p) S. KoskaL on joukons juurikunta, löytyy jokinα L, jolle päteeq(α) = 0. Lauseen 16.1 perusteella on olemassa isomorfismiϕ:m(α) τ(m)(α ), jolle päteeϕ M =τ. Tämä on ristiriidassa parin (M, τ) maksimaalisuuden kanssa, joten M = L. Lisäksi on helppo osoittaa, että juurikunnan kuvaτ(l) on puolestaan polynomijoukons juurikunta kunnan K suhteen, mistä seuraa, ettäτ(l) =L. Isomorfismien jatkamislausetta käytetään usein konstruoimaan annetun laajennoksen automorfismeja eli Galois n ryhmän alkioita. Lisäksi siitä seuraa suoraan juurikuntien ja algebrallisten sulkeumien yksikäsitteisyys. Korollaari Olkoon K kunta, ja olkoon S joukko K-kertoimisia polynomeja. Kaikki S:n juurikunnat kunnan K suhteen ovat isomorfisia K:n laajennoksina. Erityisesti kaikki K:n algebralliset sulkeumat ovat isomorfisia. Todistus. Koska id : K K on kuntaisomorfismi, isomorfismien jatkamislauseesta saadaan K-laajennosten isomorfismi minkä tahansa kahden S:n juurikunnan välille. Toinen väite seuraa tästä suoraan, sillä kunnan K algebrallinen sulkeuma on samalla kaikkien K-kertoimisten polynomien joukon juurikunta.
3 L 16. VALIKOITUJA AIHEITA 113 = M L K K Kuva 31. Isomorfismi voidaan jatkaa juurikuntien isomorfismiksi. Nyt kun on todistettu algebrallisen sulkeuman olemassaolo ja yksikäsitteisyys isomorfiaa vaille, voidaan algebrallisista laajennoksista puhuttaessa aina rajoittua sopivan alkukunnan algebrallisen sulkeuman alikuntiin. Mikä tahansa algebrallinen laajennos nimittäin sisältyy johonkin algebralliseen sulkeumaan, ja kahden sulkeuman välinen isomorfismi kuvaa myös kyseisen laajennoksen tuon ennalta valitun sulkeuman alilaajennokseksi Galois n laajennosten karakterisoinnista. Algebrallinen laajennos L/K on Galois, jos K on suurin L:n alikunta, jonka kaikki K-automorfismit kiinnittävät. Mitä enemmän K-automorfismeja on, sitä suuremman joukon ne kiinnittävät. Voidaan siis päätellä intuitiivisesti, että laajennos on Galois, jos siinä voidaan määritellä mahdollisimman suuri määrä K-automorfismeja. Olkoon L kunnan K algebrallinen laajennos, ja olkoon Ω jokin K:n algebrallinen sulkeuma (jotka ovat siis kaikki keskenään isomorfisia). Isomorfismien jatkamislauseen perusteella jokainen L:n K-automorfismi voidaan jatkaa Ω:n K- automorfismiksi. Mutta mitkä Ω:n automorfismeista rajoittuvat L:n automorfismeiksi? Koska jokaisen K-kertoimisen jaottoman polynomin juuri voidaan isomorfismien jatkamislauseen perusteella kuvata toiselle saman polynomin juurelle, täytyisi L:n sisältää kaikki nämä juuret, jos se sisältää niistä yhdenkin, muuten joukko L ei ole vakaa kyseisessä kuvauksessa. Laajennoksen L täytyisi siis olla jonkin polynomijoukon juurikunta. Tätä ehtoa kutsutaan normaalisuusehdoksi: kunnan L kuvaa jossakin Ω:n K-automorfismissa σ kutsutaan L:n konjugaatiksi, ja normaalisuus takaa, että jokaiselle L:n konjugaatille pätee σ(l) L. (Vertaa tätä aliryhmän normaalisuuden käsitteeseen.) Laajennoksen automorfismien määrä voi rajoittua toisellakin tavalla. Jaottoman polynomin jokaisen juuren voi kuvata mille tahansa toiselle juurelle, mutta joskus käy niin, että erillisten juurien lukumäärä on pienempi kuin polynomin aste. Toisin sanoen jotkin polynomin ensimmäisen asteen tekijöistä ovat samoja. Tämä vähentää myös erilaisten automorfismien määrää. Määritelmä OlkoonK kunta, ja olkoonp K[X] jokin jaoton polynomi. Oletetaan, että L on K:n laajennos ja α L. Jos p on jaollinen polynomilla (X α) n jollainn>1, sanotaan, ettäαon polynominpmoninkertainen juuri. Jos p:llä ei ole lainkaan moninkertaisia juuria juurikunnassaan K:n suhteen, sanotaan, että p on K:n suhteen separoituva.
4 114 L L = K K Kuva 32. Algebrallisen laajennoksen automorfismeja menetetään, jos juuret kuvautuvat laajennoksen ulkopuolelle tai itselleen. Polynomia f kutsutaan separoituvaksi, jos sen jokainen jaoton tekijä on separoituva. Polynomin separoituvuuden selvittämiseksi on olemassa näppärä testi, joka hyödyntää polynomin derivaatan käsitettä. Vaikka polynomialgebrassa ei voidakaan yleensä määritellä metriikkaa eikä raja-arvoja, polynomeja voidaan silti derivoida muodollisesti tutuilla derivointikaavoilla. Lemma OlkoonK kunta, ja olkoonf K[X] polynomi, joka ei ole vakio. Tällöinf on separoituva, jos ja vain jos syt(f,f ) = 1. Todistus. Osoitetaan ensin, että josf,g K[X] jalonk:n laajennos, niinf jagovat keskenään jaottomia renkaassal[x], jos ja vain jos ne ovat keskenään jaottomia renkaassa K[X]. Toinen suunta on selvä, joten oletetaan, että syt(f,g) = 1 renkaassak[x]. Tällöinaf +bg = 1 joillaina,b K[X]. Tämä yhtälö pätee myös renkaassa L[X], joten syt(f, g) = 1 myös renkaassa L[X]. Oletetaan nyt, että syt(f,f ) = 1, ja tarkastellaanf:n jakokuntaal. Josα L on sellainen, ettäf = (X α) 2 g, niin f = 2(X α) g + (X α) 2 g = (X α)(2g + (X α)g ), jotenx α jakaa myös polynominf. Tämä on ristiriita sen kanssa, ettäf jaf ovat keskenään jaottomia renkaassa L[X]. Oletetaan sitten, että polynomi f jakautuu juurikunnassaan L erillisiksi ensimmäisen asteen tekijöiksi, ja merkitäänf = n i=1 (X α i ), missä luvutα i L ovat erillisiä. Tulon derivointisäännön nojalla n f = (X α j ). i=1i j Nyt jokaisellakpäteef (α k ) = k j (X α j) 0, joten polynomeillaf jaf ei ole yhteisiä juuria. Olkoon nytd K[X] jokin polynomienf jaf yhteinen tekijä. KoskaLon polynominf juurikunta jadonf:n tekijä, myösd:n kaikki juuret löytyvät kunnastal. Lisäksi jokainen näistä juurista on polynomienf jaf yhteinen juuri, koska d jakaa molemmat polynomit. Tällaisia juuria ei ole, joten polynomindtäytyy olla vakio. Täten polynomienf jaf suurin yhteinen tekijä on yksikkö.
5 16. VALIKOITUJA AIHEITA 115 Laajennoksen alkiota nimitetään separoituvaksi, jos sen minimipolynomi on separoituva. Koko laajennos on separoituva, jos sen jokainen alkio on separoituva. Seuraava lause, jonka todistuksen perusideaa hahmoteltiin yllä, esittää tärkeimmän tavan karakterisoida Galois n laajennokset. Lause Oletetaan, että L on kunnan K algebrallinen laajennos. Seuraavat ehdot ovat yhtäpitäviä: i) L/K on Galois n laajennos. ii) L/K on normaali ja separoituva. iii) L on jonkin separoituvista polynomeista koostuvan joukon juurikunta kunnan K suhteen. Jos lähtökunnan karakteristika on nolla, derivaattatestin perusteella jokainen laajennos on separoituva. Jos nimittäin f on jaoton polynomi ja polynomeilla f jaf on yhteinen tekijäg, joka ei ole vakio, niing:n täytyy ollaf:n liittoalkio. Silloin deg(f) = deg(g), mutta koska deg(f ) = deg(f) 1, niing ei voi olla polynominf tekijä. Näin saadaan vielä eräs karakterisointi Galois n laajennoksille siinä tapauksessa, että separoituvuutta ei tarvitse erikseen mainita. Lause Oletetaan, että L on kunnan K algebrallinen laajennos ja K:n karakteristika on nolla. TällöinL/K on Galois, jos ja vain jos se on jonkin polynomijoukon juurikunta K:n suhteen Äärelliset kunnat. Luvussa 10 nähtiin, että jokaisen äärellisen kunnan koko onp n, missäpon alkuluku janpositiivinen kokonaisluku. Nyt voidaan lopulta osoittaa, että jokaista tällaista lukuap n kohti on olemassa kyseistä kertalukua oleva kunta. Lisäksi kaikki samaa kertalukua olevat kunnat ovat keskenään isomorfisia. Lause Olkoon p alkuluku ja n positiivinen kokonaisluku. On olemassa kuntak, jonka koko onp n. Lisäksi tämä kunta on isomorfiaa vaille yksikäsitteinen. Todistus. Olkoon Ω kunnan F p algebrallinen sulkeuma. Tarkastellaan polynomiaf =X pn X, ja merkitään sen juurten joukkoal Ω. On helppo nähdä, että joukko L on kunnan Ω alikunta. Tällöin L myös sisältää välttämättä alkukunnan F p. Lisäksif =p n X pn 1 1 = 1, joten derivaattatestin perusteella f on separoituva kunnan F p suhteen. Siispä kaikkif:n juuret ovat erillisiä, joten kunnanlkoko onp n. Olkoon sittenm mikä tahansa kunta, jonka koko onp n. Tämä kunta sisältää alkukuntanaan kunnank, joka on isomorfinen kunnan F p kanssa. Koska M =p n 1, niina pn 1 = 1 kaikillaa M. Täten jokainen kunnanm alkio on polynominf juuri (sillä myös 0 onf:n juuri). Toisaalta polynomillaf on korkeintaanp n juurta, jotenm onf:n juurikunta kunnank suhteen. Isomorfismien jatkamislauseesta seuraa, että kaikki tällaiset juurikunnat ovat keskenään isomorfisia. Äärellisten kuntien multiplikatiivisilla ryhmillä on sellainen merkittävä ominaisuus, että ne ovat kaikki syklisiä. Tämän osoittamiseksi käytetään ryhmän
6 116 eksponentin käsitettä. Ryhmän G eksponentti exp(g) on pienin positiivinen kokonaislukum, jolle päteeg m = 1 kaikillag G. Toisin sanoen eksponentti on ryhmän alkioiden kertalukujen pienin yhteinen jaettava. Lemma Olkoon G vaihdannainen ryhmä. Tällöin löytyy alkio g G, jonka kertaluku on exp(g). Todistus. KoskaK on vaihdannainen, se voidaan kirjoittaap-ryhmien suorana tulonag 1 G n, missä G i =p k i i kaikilla i (todistus harjoitustehtävä). Olkoong i G i se alkio, jonka kertaluku ryhmässäg i on suurin, ja olkoon tämä kertalukum i. RyhmänG i jokaisen alkion kertaluku on jokinp i :n potenssi, mistä seuraa, ettäh m i = 1 kaikillah G i. Olkoon nytg=(g 1,g 2,...,g n ) G, ja olkoong:n kertalukum, jolloin erityisesti exp(g) m. Toisaalta jokaisellaipätee nytg m i = 1, mistä seuraa, että m i m. Jos siish = (h 1,...,h n ) G, niin h m = (h m 1,...,h m n ) = (1,..., 1). Täten myös epäyhtälö exp(g) mpätee, jotengon alkio, jonka kertaluku on exp(g). Lause Jos kuntak on äärellinen, niin (K, ) on syklinen ryhmä. Todistus. Merkitäänm=exp(K ). Jokaisellag K päteeg m = 1, joten jokainen ryhmänk alkio on polynominx m 1 juuri. Tällä polynomilla on kuitenkin korkeintaanmjuurta, joten K m. Toisaalta edellisen lemman mukaanmon jonkin alkiong K kertaluku, joten K =m, jag virittää ryhmän K Polynomien ratkeavuus. Galois pystyi nimeään kantavan teorian avulla lopulta selvittämään täsmälleen, mitkä rationaalikertoimiset polynomit voidaan ratkaista kuntalaskutoimitusten ja juurenoton avulla. Tämä tulos riippuu vahvasti siitä, että tiettyihin kuntalaajennosten ketjuihin liittyy Galois n ryhmän normaali jono, minkä osoittamiseksi puolestaan täytyy tuntea seuraava Galois n teorian peruslauseen jatko-osa. Lause (Galois n teorian peruslause, 2. osa). Oletetaan, että L/K on äärellinen Galois n laajennos, ja merkitään G = Gal(L/K). Jos H = Gal(L/M), missä M on jokin laajennoksen K/L välikunta, niin [L :M] = H ja [M :K] = [G :H]. LisäksiH on normaalig:ssä, jos ja vain josm/k on Galois n laajennos. Tässä tapauksessag/h = Gal(M/K). L M K [L:M] [M:K] {id} H H G/H G
7 16. VALIKOITUJA AIHEITA 117 Todistus. Sivuutetaan. Tutustutaan seuraavaksi polynomin ratkeavuuden määritelmään. Se muistuttaa huomattavasti geometrisen konstruoituvuuden ehtoa. Määritelmä Kunta L on kunnan K juurilaajennos, jos on olemassa jono kuntia K =K 0 K 1 K r =L, missäk i+1 =K i (a i ) jollaina i K i+1, ja lisäksia n i i F i jollainn i N. Josn = max{n i }, missä luvutn i ovat kuten edellisessä määritelmässä, sanotaan, että L/K on kertaluvun n juurilaajennos. Oletetaan, että f K[X]. Jos on olemassa juurilaajennos L/K, jossa f jakautuu ensimmäisen asteen tekijöihin, sanotaan, että f on juurtamalla ratkeava. Käytännössä tämä tarkoittaa sitä, että f:n juuret voidaan kirjoittaa lausekkeina, joissa esiintyy yhteen-, vähennys-, kerto- ja jakolaskun lisäksi mielivaltaisia juurilausekkeita. Seuraava Évariste Galois n todistama lause julkaistiin vasta hänen kuolemansa jälkeen vuonna Lause (Galois). Olkoon K kunta, jonka karakteristika on 0, ja olkoon f K[X]. OlkoonLpolynominf juurikuntak:n suhteen. Tällöinf on juurtamalla ratkeava, jos ja vain jos Gal(L/K) on ratkeava ryhmä. Todistus. (Hahmotelma.) Oletetaan, että f on juurtamalla ratkeava, jolloin on olemassa kertaluvun n juurilaajennos M/K, joka sisältää juurikunnan L. Nyt M/K ei välttämättä ole Galois n laajennos, mutta se on separoituva, koska char(k) = 0. Olkoon M laajennoksen M/K normaali sulkeuma eli pienin normaali laajennos, joka sisältää kunnan M. Tällöin laajennos M/K on Galois. Teknisistä syistä asetetaank 1 =K(ω), missäω one 2πi/n, ykkösenn:s juuri. Voidaan osoittaa, ettäm/k 1 on edelleen kertaluvunnjuurilaajennos, joten on olemassa kuntien jono K =K 0 K 1 K 2 K r =M, missäk i+1 =K i (a i ) jaa n i K i. Tässä kuntajonossa jokainen laajennosk i+1 /K i on Galois, ja jokainen Gal(K i+1 /K i ) on vaihdannainen ryhmä. MerkitäänG=Gal(M/K) jah i = Gal(M/K i ). Galois n teorian peruslauseen perusteella on olemassa aliryhmien jono G =H 0 H 1 H r = 1. Peruslauseen toisen osan mukaanh i+1 on normaali ryhmässäh i kaikillai, sillä K i+1 /K i on Galois n laajennos. Jono ( ) on siis normaali jono. Koska lisäksi tekijä H i /H i+1 = Gal(Ki+1 /K i ) on vaihdannainen ryhmä kaikillai, nähdään, ettäg on ratkeava ryhmä. Ratkeavien ryhmien teorian perusteista seuraa, että myös Gal(L/K) =G/ Gal(M/L) on ratkeava. Toinen suunta etenee samalla periaatteella mutta vaatii vielä enemmän teknisiä aputuloksia. Voidaan kysyä, mitä hyötyä Galois n lauseesta oikeastaan on. Näyttää nimittäin siltä, että sen selvittämiseksi, onko jokin polynomi juurtamalla ratkeava, on ( )
8 118 tunnettava sen juurikunnan Galois n ryhmä. Tämän juurikunnan tunteminen taas tuntuu edellyttävän sitä, että juuret on jo löydetty. Käytännössä kuitenkin voidaan vähäisistä juurten luonnetta koskevista tiedoista päätellä ryhmien teorian avulla yhtä ja toista juurikunnan Galois n ryhmästä, vaikka itse juuria ei tunnettaisi. Seuraavassa tästä eräs esimerkki. Esimerkki Tarkastellaan polynomiaf =X 5 4X +2. Tämä polynomi on Eisensteinin kriteerin perusteella jaoton Q:n suhteen, joten sillä ei ole rationaalijuuria. Toisaalta piirtämällä polynomifunktion x f(x) kuvaaja voidaan päätellä, että f:llä on kolme reaalijuurta, joten se voidaan jakaa tuloksi f = (X α 1 )(X α 2 )(X α 3 ) g, missäα i R kaikillai, jag on toisen asteen reaalikertoiminen polynomi. Kuva 33. Polynomifunktionf(x) =x 5 4x + 2 kuvaaja. Olkoon L C polynomin f juurikunta, jolloin L/K on Galois n laajennos. Polynomilla f on yhteensä viisi kompleksijuurta, ja jokainen juurikunnan Q- automorfismi määräytyy siitä, miten se permutoi näitä juuria. Voidaan siis päätellä, että Gal(L/K) on isomorfinen jonkin ryhmäns 5 aliryhmän kanssa. Polynomi f on jaoton, joten se on itse jokaisen juurensa minimipolynomi. Tästä nähdään, että [L :K] = [L : Q(α 1 )] [Q(α 1 ) : Q] = [L : Q(α 1 )] 5. Galois n peruslauseen toisen osan perusteella Gal(L/K) = [L : K], joten ryhmän Gal(L/K) kertaluku on jaollinen viidellä. Cauchyn lauseesta seuraa, että Gal(L/K) sisältää alkion, jonka kertaluku on 5. RyhmässäS 5 kaikki tällaiset alkiot ovat 5-syklejä. Toisaalta tiedetään, että toisen asteen polynoming juuret ovat toistensa kompleksikonjugaatteja, joten kompleksikonjugoinnin rajoittuma juurikuntaan L on Q-automorfismi, joka vaihtaa keskenään polynomin f ei-reaaliset juuret ja pitää reaaliset paikallaan. RyhmässäS 5 tämä alkio on transpositio. On varsin suoraviivaista osoittaa, että 5-sykli ja transpositio riittävät virittämään koko ryhmäns 5, mistä seuraa, että Gal(L/K) =S 5. KoskaS 5 ei ole ratkeava, myöskään polynomi f ei ole juurtamalla ratkeava.
9 16. VALIKOITUJA AIHEITA 119 Jo ennen Galois ta oli tunnettua, että n:nnen asteen polynomiyhtälöllä ei ole yleistä ratkaisukaavaa, mikäli n 5. Sen olivat nimittäin todistaneet itsenäisesti Ruffini 21 vuonna 1799 ja Abel vuonna Galois n lause tarkentaa tätä tulosta näyttämällä täsmälleen, millä yksittäisillä polynomeilla on ratkaisukaava ja millä ei. Tulos voidaan myös johtaa Galois n lauseesta, kun muistetaan, ettäs n ei ole ratkeava milläänn 5. Lause (Abelin Ruffinin lause). Olkoon K kunta, jonka karakteristika on nolla. Jos n 5, niin n:nnen asteen K-kertoimisella polynomilla ei ole yleistä kaavaa juurten löytämiseksi. Todistus. Yleinen n:nnen asteen polynomi on muotoa f = (X Y 1 )(X Y 2 ) (X Y n ) =X n s 1 X n ( 1) n s n, missä jokaineny i on tuntematon parametri ja jokainens i K[Y 1,...,Y n ] on ns. symmetrinen polynomi. Esimerkiksi s 1 =Y 1 +Y 2 + +Y n s 2 =Y 1 Y 2 +Y 1 Y 3 + +Y 2 Y 3 + +Y n 1 Y n. s n =Y 1 Y 2 Y n. Polynominf kertoimet ovat siis kunnassak 0 =K(s 1,...,s n ) K(Y 1,...,Y n ). Jos on olemassa ratkaisukaava yleiselle n:nnen asteen polynomille, täytyy polynominf olla juurtamalla ratkeava kunnank 0 suhteen. Polynominf juurikunta onl=k(y 1,...,Y n ). Galois n ryhmän Gal(L/K 0 ) alkiot määräytyvät siitä, miten ne permutoivat virittäjiäy i, joten Gal(L/K 0 ) on isomorfinen jonkin symmetrisen ryhmäns n aliryhmän kanssa. Toisaalta mikä tahansa tuntemattomien permutaatio kiinnittää jokaisen symmetrisen polynomin s i, joten Gal(L/K 0 ) =S n. KoskaS n ei ole ratkeava, kunn 5, myöskäänf ei ole juurtamalla ratkeava. Tämä todistaa väitteen. LOPPU 21 Paolo Ruffini ( ), italialainen filosofi ja matemaatikko
15. Laajennosten väliset homomorfismit
 15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit niin sanotut automorfismit auttavat vastaavasti
15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit niin sanotut automorfismit auttavat vastaavasti
15. Laajennosten väliset homomorfismit
 15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit eli niin sanotut automorfismit auttavat vastaavasti
15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit eli niin sanotut automorfismit auttavat vastaavasti
14. Juurikunnat Määritelmä ja olemassaolo.
 14. Juurikunnat Mielivaltaisella polynomilla ei välttämättä ole juuria tarkasteltavassa kunnassa. Tässä luvussa tutkitaan sellaisia algebrallisia laajennoksia, jotka saadaan lisäämällä polynomeille juuria.
14. Juurikunnat Mielivaltaisella polynomilla ei välttämättä ole juuria tarkasteltavassa kunnassa. Tässä luvussa tutkitaan sellaisia algebrallisia laajennoksia, jotka saadaan lisäämällä polynomeille juuria.
13.3. Transkendenttisuudesta. 14. Juurikunnat Määritelmä ja olemassaolo.
 13.3. Transkendenttisuudesta. Luvun todistamiseksi algebralliseksi riittää löytää polynomi, jonka juuri kyseinen luku on. Transkendenttisuuden todistaminen on sen sijaan työläämpää. Jotkut tapaukset ovat
13.3. Transkendenttisuudesta. Luvun todistamiseksi algebralliseksi riittää löytää polynomi, jonka juuri kyseinen luku on. Transkendenttisuuden todistaminen on sen sijaan työläämpää. Jotkut tapaukset ovat
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
[E : F ]=[E : K][K : F ].
![[E : F ]=[E : K][K : F ]. [E : F ]=[E : K][K : F ].](/thumbs/61/46040569.jpg) ALGEBRA II 35 Lause 4.4 (Astelukulause). Olkoot E/K/Fäärellisiä kuntalaajennuksia. Silloin [E : F ]=[E : K][K : F ]. Todistus. Olkoon {α 1,...,α n } kanta laajennukselle E/K ja {β 1,...,β m } kanta laajennukselle
ALGEBRA II 35 Lause 4.4 (Astelukulause). Olkoot E/K/Fäärellisiä kuntalaajennuksia. Silloin [E : F ]=[E : K][K : F ]. Todistus. Olkoon {α 1,...,α n } kanta laajennukselle E/K ja {β 1,...,β m } kanta laajennukselle
koska 2 toteuttaa rationaalikertoimisen yhtälön x 2 2 = 0. Laajennuskunnan
 4. Äärellisten kuntien yleisiä ominaisuuksia 4.1. Laajenuskunnat. Tarkastellaan aluksi yleistä kuntaparia F ja K, missä F on kunnan K alikunta. Tällöin sanotaan, että kunta K on kunnan F laajennuskunta
4. Äärellisten kuntien yleisiä ominaisuuksia 4.1. Laajenuskunnat. Tarkastellaan aluksi yleistä kuntaparia F ja K, missä F on kunnan K alikunta. Tällöin sanotaan, että kunta K on kunnan F laajennuskunta
ei ole muita välikuntia.
 ALGEBRA II 41 Lause 4.15. F q m on polynomin x qm x hajoamiskunta kunnan F q suhteen. Todistus. Olkoon α kunnan F q m primitiivialkio. Nyt F qm =< α > muodostuu täsmälleen polynomin x qm 1 1nollakohdistajatäten
ALGEBRA II 41 Lause 4.15. F q m on polynomin x qm x hajoamiskunta kunnan F q suhteen. Todistus. Olkoon α kunnan F q m primitiivialkio. Nyt F qm =< α > muodostuu täsmälleen polynomin x qm 1 1nollakohdistajatäten
13. Algebralliset laajennokset
 13. Algebralliset laajennokset Vanhoina aikoina algebran tutkimuksen päämääränä oli oppia ratkaisemaan polynomiyhtälöitä. Niinpä erityisen tärkeää osaa klassisessa kuntalaajennosten teoriassa näyttelevät
13. Algebralliset laajennokset Vanhoina aikoina algebran tutkimuksen päämääränä oli oppia ratkaisemaan polynomiyhtälöitä. Niinpä erityisen tärkeää osaa klassisessa kuntalaajennosten teoriassa näyttelevät
1. Hiukan lineaarialgebraa
 ÁÎ ÃÓ Ø ÐÓ ³Ò Ø ÓÖ 1. Hiukan lineaarialgebraa 1.1. Määritelmä. Olkoon K = (K, +, ) kunta (ns. kerroinkunta). Joukko V varustettuna yhteenlaskulla +:V V V ja skalaarikerronnalla :K V V on K- vektoriavaruus,
ÁÎ ÃÓ Ø ÐÓ ³Ò Ø ÓÖ 1. Hiukan lineaarialgebraa 1.1. Määritelmä. Olkoon K = (K, +, ) kunta (ns. kerroinkunta). Joukko V varustettuna yhteenlaskulla +:V V V ja skalaarikerronnalla :K V V on K- vektoriavaruus,
4. Ryhmien sisäinen rakenne
 4. Ryhmien sisäinen rakenne Tässä luvussa tarkastellaan joitakin tapoja päästä käsiksi ryhmien sisäiseen rakenteeseen. Useimmat tuloksista ovat erityisen käyttökelpoisia äärellisten ryhmien tapauksessa.
4. Ryhmien sisäinen rakenne Tässä luvussa tarkastellaan joitakin tapoja päästä käsiksi ryhmien sisäiseen rakenteeseen. Useimmat tuloksista ovat erityisen käyttökelpoisia äärellisten ryhmien tapauksessa.
Äärelliset kunnat ja polynomien jako alkutekijöihin
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Heidi Kananoja Äärelliset kunnat ja polynomien jako alkutekijöihin Matematiikan, tilastotieteen ja filosofian laitos Matematiikka Syyskuu 2007 Tampereen yliopisto
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Heidi Kananoja Äärelliset kunnat ja polynomien jako alkutekijöihin Matematiikan, tilastotieteen ja filosofian laitos Matematiikka Syyskuu 2007 Tampereen yliopisto
ja jäännösluokkien joukkoa
 3. Polynomien jäännösluokkarenkaat Olkoon F kunta, ja olkoon m F[x]. Polynomeille f, g F [x] määritellään kongruenssi(-relaatio) asettamalla g f mod m : m g f g = f + m h jollekin h F [x]. Kongruenssi
3. Polynomien jäännösluokkarenkaat Olkoon F kunta, ja olkoon m F[x]. Polynomeille f, g F [x] määritellään kongruenssi(-relaatio) asettamalla g f mod m : m g f g = f + m h jollekin h F [x]. Kongruenssi
on Abelin ryhmä kertolaskun suhteen. Tämän joukon alkioiden lukumäärää merkitään
 5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
Galois'n teoria polynomien ratkeavuudesta. Wille Lehtomäki
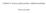 Galois'n teoria polynomien ratkeavuudesta Wille Lehtomäki HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Matemaattis-luonnontieteellinen
Galois'n teoria polynomien ratkeavuudesta Wille Lehtomäki HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Matemaattis-luonnontieteellinen
R 1 = Q 2 R 2 + R 3,. (2.1) R l 2 = Q l 1 R l 1 + R l,
 2. Laajennettu Eukleideen algoritmi Määritelmä 2.1. Olkoot F kunta ja A, B, C, D F [x]. Sanotaan, että C jakaa A:n (tai C on A:n jakaja), jos on olemassa K F [x] siten, että A = K C; tällöin merkitään
2. Laajennettu Eukleideen algoritmi Määritelmä 2.1. Olkoot F kunta ja A, B, C, D F [x]. Sanotaan, että C jakaa A:n (tai C on A:n jakaja), jos on olemassa K F [x] siten, että A = K C; tällöin merkitään
5. Ryhmän kompositiotekijät
 5. Ryhmän kompositiotekijät Jos ryhmästä löydetään normaali aliryhmä, sen suhteen voidaan muodostaa tekijäryhmä, jolla saattaa olla yksinkertaisempi rakenne kuin alkuperäisellä ryhmällä. Ryhmä voidaan
5. Ryhmän kompositiotekijät Jos ryhmästä löydetään normaali aliryhmä, sen suhteen voidaan muodostaa tekijäryhmä, jolla saattaa olla yksinkertaisempi rakenne kuin alkuperäisellä ryhmällä. Ryhmä voidaan
Mitään muita operaatioita symbolille ei ole määritelty! < a kaikilla kokonaisluvuilla a, + a = kaikilla kokonaisluvuilla a.
 Polynomit Tarkastelemme polynomirenkaiden teoriaa ja polynomiyhtälöiden ratkaisemista. Algebrassa on tapana pitää erillään polynomin ja polynomifunktion käsitteet. Polynomit Tarkastelemme polynomirenkaiden
Polynomit Tarkastelemme polynomirenkaiden teoriaa ja polynomiyhtälöiden ratkaisemista. Algebrassa on tapana pitää erillään polynomin ja polynomifunktion käsitteet. Polynomit Tarkastelemme polynomirenkaiden
4. Ryhmien sisäinen rakenne
 3.5. Sisäiset symmetriat. Kuution väritysesimerkissä 3.14 tarkasteltiin yksittäisten alkioiden sijaan niiden konjugaattiluokkia ja todettiin, että konjugaattiluokkia vastaavat luonnollisella tavalla erityyppiset
3.5. Sisäiset symmetriat. Kuution väritysesimerkissä 3.14 tarkasteltiin yksittäisten alkioiden sijaan niiden konjugaattiluokkia ja todettiin, että konjugaattiluokkia vastaavat luonnollisella tavalla erityyppiset
1 Algebralliset perusteet
 1 Algebralliset perusteet 1.1 Renkaat Tämän luvun jälkeen opiskelijoiden odotetaan muistavan, mitä ovat renkaat, vaihdannaiset renkaat, alirenkaat, homomorfismit, ideaalit, tekijärenkaat, maksimaaliset
1 Algebralliset perusteet 1.1 Renkaat Tämän luvun jälkeen opiskelijoiden odotetaan muistavan, mitä ovat renkaat, vaihdannaiset renkaat, alirenkaat, homomorfismit, ideaalit, tekijärenkaat, maksimaaliset
5. Ryhmän kompositiotekijät
 5. Ryhmän kompositiotekijät Ratkeavan ryhmän käsite kuuluu historiallisesti ensimmäisiin varsinaisen ryhmäteorian käsitteisiin. Évariste Galois todisti vuonna 1831, että polynomiyhtälöön liittyy aina tietty
5. Ryhmän kompositiotekijät Ratkeavan ryhmän käsite kuuluu historiallisesti ensimmäisiin varsinaisen ryhmäteorian käsitteisiin. Évariste Galois todisti vuonna 1831, että polynomiyhtälöön liittyy aina tietty
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
rm + sn = d. Siispä Proposition 9.5(4) nojalla e d.
 9. Renkaat Z ja Z/qZ Tarkastelemme tässä luvussa jaollisuutta kokonaislukujen renkaassa Z ja todistamme tuloksia, joita käytetään jäännösluokkarenkaan Z/qZ ominaisuuksien tarkastelussa. Jos a, b, c Z ovat
9. Renkaat Z ja Z/qZ Tarkastelemme tässä luvussa jaollisuutta kokonaislukujen renkaassa Z ja todistamme tuloksia, joita käytetään jäännösluokkarenkaan Z/qZ ominaisuuksien tarkastelussa. Jos a, b, c Z ovat
11. Jaollisuudesta. vuoksi tarkastellaan tässä yhteydessä vain kokonaisalueita.
 11. Jaollisuudesta Kuntalaajennosten yhteydessään käytetään usein apuna jaottomia polynomeja. Tarkastellaan seuraavaksi hieman jaollisuuskäsitettä yleensä ja todistetaan joitain kriteerejä erityisesti
11. Jaollisuudesta Kuntalaajennosten yhteydessään käytetään usein apuna jaottomia polynomeja. Tarkastellaan seuraavaksi hieman jaollisuuskäsitettä yleensä ja todistetaan joitain kriteerejä erityisesti
Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen
 Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen anton.mallasto@aalto.fi. 1. 2. Muista. Ryhmän G aliryhmä H on normaali aliryhmä, jos ah = Ha kaikilla a G. Toisin
Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen anton.mallasto@aalto.fi. 1. 2. Muista. Ryhmän G aliryhmä H on normaali aliryhmä, jos ah = Ha kaikilla a G. Toisin
(x + I) + (y + I) = (x + y)+i. (x + I)(y + I) =xy + I. kaikille x, y R.
 11. Ideaalit ja tekijärenkaat Rengashomomorfismi φ: R R on erityisesti ryhmähomomorfismi φ: (R, +) (R, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin φ
11. Ideaalit ja tekijärenkaat Rengashomomorfismi φ: R R on erityisesti ryhmähomomorfismi φ: (R, +) (R, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin φ
HN = {hn h H, n N} on G:n aliryhmä.
 Matematiikan ja tilastotieteen laitos Algebra I Ratkaisuehdoituksia harjoituksiin 8, 23.27.3.2009 5 sivua Rami Luisto 1. Osoita, että kullakin n N + lukujen n 5 ja n viimeiset numerot kymmenkantaisessa
Matematiikan ja tilastotieteen laitos Algebra I Ratkaisuehdoituksia harjoituksiin 8, 23.27.3.2009 5 sivua Rami Luisto 1. Osoita, että kullakin n N + lukujen n 5 ja n viimeiset numerot kymmenkantaisessa
Viidennen asteen yhtälön ratkaisukaavan olemassaolon mahdottomuus Galois n teorian pohjalta
 Viidennen asteen yhtälön ratkaisukaavan olemassaolon mahdottomuus Galois n teorian pohjalta Teppo Lahti Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2014 Tiivistelmä
Viidennen asteen yhtälön ratkaisukaavan olemassaolon mahdottomuus Galois n teorian pohjalta Teppo Lahti Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2014 Tiivistelmä
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto
 Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
k=1 b kx k K-kertoimisia polynomeja, P (X)+Q(X) = (a k + b k )X k n+m a i b j X k. i+j=k k=0
 1. Polynomit Tässä luvussa tarkastelemme polynomien muodostamia renkaita polynomien ollisuutta käsitteleviä perustuloksia. Teemme luvun alkuun kaksi sopimusta: Tässä luvussa X on muodollinen symboli, jota
1. Polynomit Tässä luvussa tarkastelemme polynomien muodostamia renkaita polynomien ollisuutta käsitteleviä perustuloksia. Teemme luvun alkuun kaksi sopimusta: Tässä luvussa X on muodollinen symboli, jota
Äärellisesti generoitujen Abelin ryhmien peruslause
 Tero Harju (2008/2010) Äärellisesti generoitujen Abelin ryhmien peruslause Merkintä X on joukon koko ( eli #X). Vapaat Abelin ryhmät Tässä kappaleessa käytetään Abelin ryhmille additiivista merkintää.
Tero Harju (2008/2010) Äärellisesti generoitujen Abelin ryhmien peruslause Merkintä X on joukon koko ( eli #X). Vapaat Abelin ryhmät Tässä kappaleessa käytetään Abelin ryhmille additiivista merkintää.
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013
 Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
Tekijäryhmiä varten määritellään aluksi sivuluokat ja normaalit aliryhmät.
 3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
Renkaat ja modulit. Tässä osassa käsiteltävät renkaat ovat vaihdannaisia, ellei toisin mainita. 6. Ideaalit
 Renkaat ja modulit Tässä osassa käsiteltävät renkaat ovat vaihdannaisia, ellei toisin mainita. 6. Ideaalit Tekijärenkaassa nollan ekvivalenssiluokka on alkuperäisen renkaan ideaali. Ideaalin käsitteen
Renkaat ja modulit Tässä osassa käsiteltävät renkaat ovat vaihdannaisia, ellei toisin mainita. 6. Ideaalit Tekijärenkaassa nollan ekvivalenssiluokka on alkuperäisen renkaan ideaali. Ideaalin käsitteen
6 A 5, alternoiva ryhmä ja muita yksinkertaisia ryhmiä
 6 A 5, alternoiva ryhmä ja muita yksinkertaisia ryhmiä Tutustukaamme ensin ryhmään S 5. Jos käytämme syklinotaatiota, toteamme, että se sisältää syklejä, jotka ovat muotoa (12), (123), (1234), (12345),
6 A 5, alternoiva ryhmä ja muita yksinkertaisia ryhmiä Tutustukaamme ensin ryhmään S 5. Jos käytämme syklinotaatiota, toteamme, että se sisältää syklejä, jotka ovat muotoa (12), (123), (1234), (12345),
Resolventtimenetelmästä
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jori Mäntysalo Resolventtimenetelmästä Informaatiotieteiden yksikkö Matematiikka Kesäkuu 2013 Tampereen yliopisto Informaatiotieteiden yksikkö MÄNTYSALO, JORI:
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jori Mäntysalo Resolventtimenetelmästä Informaatiotieteiden yksikkö Matematiikka Kesäkuu 2013 Tampereen yliopisto Informaatiotieteiden yksikkö MÄNTYSALO, JORI:
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdoituksia harjoituksiin 8 (7 sivua)
 Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdoituksia harjoituksiin ( sivua).... Nämä ovat kurssin Algebra I harjoitustehtävien ratkaisuehdoituksia. Ratkaisut koostuvat kahdesta osiosta,
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdoituksia harjoituksiin ( sivua).... Nämä ovat kurssin Algebra I harjoitustehtävien ratkaisuehdoituksia. Ratkaisut koostuvat kahdesta osiosta,
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Tommi Kuusisto
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Tommi Kuusisto Äärellisistä kunnista Matematiikan ja tilastotieteen laitos Matematiikka Huhtikuu 2008 Tampereen yliopisto Matematiikan, tilastotieteen ja filosofian
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Tommi Kuusisto Äärellisistä kunnista Matematiikan ja tilastotieteen laitos Matematiikka Huhtikuu 2008 Tampereen yliopisto Matematiikan, tilastotieteen ja filosofian
Esko Turunen MAT Algebra1(s)
 Määritelmä (4.1) Olkoon G ryhmä. Olkoon H G, H. Jos joukko H varustettuna indusoidulla laskutoimituksella on ryhmä, se on ryhmän G aliryhmä. Jos H G on ryhmän G aliryhmä, merkitään usein H G, ja jos H
Määritelmä (4.1) Olkoon G ryhmä. Olkoon H G, H. Jos joukko H varustettuna indusoidulla laskutoimituksella on ryhmä, se on ryhmän G aliryhmä. Jos H G on ryhmän G aliryhmä, merkitään usein H G, ja jos H
11. Jaollisuudesta. Lemma Oletetaan, että a, b R.
 11. Jaollisuudesta Edellisen luvun esimerkissä tarvittiin tietoa erään polynomin jaottomuudesta. Tämä on hyvin tavallista kuntalaajennosten yhteydessä. Seuraavassa tarkastellaan hieman jaollisuuskäsitettä
11. Jaollisuudesta Edellisen luvun esimerkissä tarvittiin tietoa erään polynomin jaottomuudesta. Tämä on hyvin tavallista kuntalaajennosten yhteydessä. Seuraavassa tarkastellaan hieman jaollisuuskäsitettä
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos Koodausteoria 10 op Kontaktiopetusta 50 h, 26.5. - 26.6. ma 10-14, ti 10-13, to 10-13 Aloitusviikolla poikkeuksellisesti ke 10-13 torstain
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos Koodausteoria 10 op Kontaktiopetusta 50 h, 26.5. - 26.6. ma 10-14, ti 10-13, to 10-13 Aloitusviikolla poikkeuksellisesti ke 10-13 torstain
Proäärelliset ryhmät ja kuntalaajennukset
 Proäärelliset ryhmät ja kuntalaajennukset Matti Åstrand Helsinki 25.5.2009 Pro gradu -tutkielma HELSINGIN YLIOPISTO Matematiikan ja tilastotieteen laitos HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY
Proäärelliset ryhmät ja kuntalaajennukset Matti Åstrand Helsinki 25.5.2009 Pro gradu -tutkielma HELSINGIN YLIOPISTO Matematiikan ja tilastotieteen laitos HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY
Laitos/Institution Department Matematiikan ja tilastotieteen laitos. Aika/Datum Month and year Huhtikuu 2014
 Tiedekunta/Osasto Fakultet/Sektion Faculty Matemaattis-luonnontieteellinen tiedekunta Laitos/Institution Department Matematiikan ja tilastotieteen laitos Tekijä/Författare Author Anna-Mari Pulkkinen Työn
Tiedekunta/Osasto Fakultet/Sektion Faculty Matemaattis-luonnontieteellinen tiedekunta Laitos/Institution Department Matematiikan ja tilastotieteen laitos Tekijä/Författare Author Anna-Mari Pulkkinen Työn
H = : a, b C M. joten jokainen A H {0} on kääntyvä matriisi. Itse asiassa kaikki nollasta poikkeavat alkiot ovat yksiköitä, koska. a b.
 10. Kunnat ja kokonaisalueet Määritelmä 10.1. Olkoon K rengas, jossa on ainakin kaksi alkiota. Jos kaikki renkaan K nollasta poikkeavat alkiot ovat yksiköitä, niin K on jakorengas. Kommutatiivinen jakorengas
10. Kunnat ja kokonaisalueet Määritelmä 10.1. Olkoon K rengas, jossa on ainakin kaksi alkiota. Jos kaikki renkaan K nollasta poikkeavat alkiot ovat yksiköitä, niin K on jakorengas. Kommutatiivinen jakorengas
Rollen lause polynomeille
 Rollen lause polynomeille LuK-tutkielma Anna-Helena Hietamäki 7193766 Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 015 Sisältö 1 Johdanto 1.1 Rollen lause analyysissä.......................
Rollen lause polynomeille LuK-tutkielma Anna-Helena Hietamäki 7193766 Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 015 Sisältö 1 Johdanto 1.1 Rollen lause analyysissä.......................
Esko Turunen Luku 3. Ryhmät
 3. Ryhmät Monoidia rikkaampi algebrallinen struktuuri on ryhmä: Määritelmä (3.1) Olkoon joukon G laskutoimitus. Joukko G varustettuna tällä laskutoimituksella on ryhmä, jos laskutoimitus on assosiatiivinen,
3. Ryhmät Monoidia rikkaampi algebrallinen struktuuri on ryhmä: Määritelmä (3.1) Olkoon joukon G laskutoimitus. Joukko G varustettuna tällä laskutoimituksella on ryhmä, jos laskutoimitus on assosiatiivinen,
TOOLS. Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO TOOLS 1 / 28
 TOOLS Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO 2018 TOOLS 1 / 28 Merkintöjä ja algebrallisia rakenteita Lukujoukkoja N = {0, 1, 2,..., GOOGOL 10,...} = {ei-negatiiviset kokonaisluvut}. TOOLS
TOOLS Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO 2018 TOOLS 1 / 28 Merkintöjä ja algebrallisia rakenteita Lukujoukkoja N = {0, 1, 2,..., GOOGOL 10,...} = {ei-negatiiviset kokonaisluvut}. TOOLS
{I n } < { I n,i n } < GL n (Q) < GL n (R) < GL n (C) kaikilla n 2 ja
 5. Aliryhmät Luvun 4 esimerkeissä esiintyy usein ryhmä (G, ) ja jokin vakaa osajoukko B G siten, että (B, B ) on ryhmä. Määrittelemme seuraavassa käsitteitä, jotka auttavat tällaisten tilanteiden käsittelyssä.
5. Aliryhmät Luvun 4 esimerkeissä esiintyy usein ryhmä (G, ) ja jokin vakaa osajoukko B G siten, että (B, B ) on ryhmä. Määrittelemme seuraavassa käsitteitä, jotka auttavat tällaisten tilanteiden käsittelyssä.
Bijektio. Voidaan päätellä, että kuvaus on bijektio, jos ja vain jos maalin jokaiselle alkiolle kuvautuu tasan yksi lähdön alkio.
 Määritelmä Bijektio Oletetaan, että f : X Y on kuvaus. Sanotaan, että kuvaus f on bijektio, jos se on sekä injektio että surjektio. Huom. Voidaan päätellä, että kuvaus on bijektio, jos ja vain jos maalin
Määritelmä Bijektio Oletetaan, että f : X Y on kuvaus. Sanotaan, että kuvaus f on bijektio, jos se on sekä injektio että surjektio. Huom. Voidaan päätellä, että kuvaus on bijektio, jos ja vain jos maalin
Algebra I, harjoitus 8,
 Algebra I, harjoitus 8, 4.-5.11.2014. 1. Olkoon G ryhmä ja H sen normaali aliryhmä. Todista, että tällöin G/H on ryhmä, kun määritellään laskutoimitus joukossa G/H asettamalla aina, kun x, y G (lauseen
Algebra I, harjoitus 8, 4.-5.11.2014. 1. Olkoon G ryhmä ja H sen normaali aliryhmä. Todista, että tällöin G/H on ryhmä, kun määritellään laskutoimitus joukossa G/H asettamalla aina, kun x, y G (lauseen
1 Lineaariavaruus eli Vektoriavaruus
 1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
kaikille a R. 1 (R, +) on kommutatiivinen ryhmä, 2 a(b + c) = ab + ac ja (b + c)a = ba + ca kaikilla a, b, c R, ja
 Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi binääristä assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme muuten samat ominaisuudet kuin kokonaisluvuilta,
Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi binääristä assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme muuten samat ominaisuudet kuin kokonaisluvuilta,
a 2 ba = a a + ( b) a = (a + ( b))a = (a b)a, joten yhtälö pätee mielivaltaiselle renkaalle.
 Harjoitus 10 (7 sivua) Ratkaisuehdotuksia/Martina Aaltonen Tehtävä 1. Mitkä seuraavista yhtälöistä pätevät mielivaltaisen renkaan alkioille a ja b? a) a 2 ba = (a b)a b) (a + b + 1)(a b) = a 2 b 2 + a
Harjoitus 10 (7 sivua) Ratkaisuehdotuksia/Martina Aaltonen Tehtävä 1. Mitkä seuraavista yhtälöistä pätevät mielivaltaisen renkaan alkioille a ja b? a) a 2 ba = (a b)a b) (a + b + 1)(a b) = a 2 b 2 + a
1. Tarkastellaan esimerkissä 4.9 esiintynyttä neliön symmetriaryhmää
 Ryhmäteoreettinen näkökulma Rubikin kuutioon Matematiikan ja tilastotieteen laitos Syksy 2010 Harjoitus 2 Ratkaisuehdotus 1. Tarkastellaan esimerkissä 4.9 esiintynyttä neliön symmetriaryhmää D 8 = { id,
Ryhmäteoreettinen näkökulma Rubikin kuutioon Matematiikan ja tilastotieteen laitos Syksy 2010 Harjoitus 2 Ratkaisuehdotus 1. Tarkastellaan esimerkissä 4.9 esiintynyttä neliön symmetriaryhmää D 8 = { id,
jonka laskutoimitus on matriisien kertolasku. Vastaavasti saadaan K-kertoiminen erityinen lineaarinen ryhmä
 4. Ryhmät Tässä luvussa tarkastelemme laskutoimituksella varustettuja joukkoja, joiden laskutoimitukselta oletamme muutamia yksinkertaisia ominaisuuksia: Määritelmä 4.1. Laskutoimituksella varustettu joukko
4. Ryhmät Tässä luvussa tarkastelemme laskutoimituksella varustettuja joukkoja, joiden laskutoimitukselta oletamme muutamia yksinkertaisia ominaisuuksia: Määritelmä 4.1. Laskutoimituksella varustettu joukko
Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua)
 Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua) 10.12.2012 Tehtävä 1. Osoita, että tuloryhmän R np R sp indeksi Rubikin paikkaryhmässä R p on täsmälleen kaksi. (Tarkkaan
Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua) 10.12.2012 Tehtävä 1. Osoita, että tuloryhmän R np R sp indeksi Rubikin paikkaryhmässä R p on täsmälleen kaksi. (Tarkkaan
Tekijäryhmän määrittelemistä varten määritellään aluksi sivuluokat ja normaalit aliryhmät. gh = {gh h H}.
 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
a ord 13 (a)
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 4, MALLIRATKAISUT Tehtävä 1. Etsi asteet ord p (a) luvuille a 1, 2,..., p 1 kun p = 13 ja kun p = 17. (ii) Mitkä jäännösluokat ovat primitiivisiä juuria (mod
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 4, MALLIRATKAISUT Tehtävä 1. Etsi asteet ord p (a) luvuille a 1, 2,..., p 1 kun p = 13 ja kun p = 17. (ii) Mitkä jäännösluokat ovat primitiivisiä juuria (mod
Algebran jatkokurssin demo 1,
 Algebran jatkokurssin demo 1, 23.1.2014 0. Tätä nollatehtävää ei käsitellä demoissa, vaan jätetään jokaisen oman harrastuneisuuden varaan käydä läpi nämä kuviot, jotka ovat lähestulkoon identtisiä LAG:n
Algebran jatkokurssin demo 1, 23.1.2014 0. Tätä nollatehtävää ei käsitellä demoissa, vaan jätetään jokaisen oman harrastuneisuuden varaan käydä läpi nämä kuviot, jotka ovat lähestulkoon identtisiä LAG:n
Algebra I, Harjoitus 6, , Ratkaisut
 Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut (MV 6 sivua 1. Olkoot M ja M multiplikatiivisia monoideja. Kuvaus f : M M on monoidihomomorfismi jos 1 f(ab = f(af(b
Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut (MV 6 sivua 1. Olkoot M ja M multiplikatiivisia monoideja. Kuvaus f : M M on monoidihomomorfismi jos 1 f(ab = f(af(b
Avainsanat Nyckelord Keywords Nullstellensatz, Hilbertin nollajoukkolause, algebrallinen geometria
 HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Matemaattis-luonnontieteellinen Tekijä Författare Author Sampo
HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department Matemaattis-luonnontieteellinen Tekijä Författare Author Sampo
8. Avoimen kuvauksen lause
 116 FUNKTIONAALIANALYYSIN PERUSKURSSI 8. Avoimen kuvauksen lause Palautamme aluksi mieleen Topologian kursseilta ehkä tutut perusasiat yleisestä avoimen kuvauksen käsitteestä. Määrittelemme ensin avoimen
116 FUNKTIONAALIANALYYSIN PERUSKURSSI 8. Avoimen kuvauksen lause Palautamme aluksi mieleen Topologian kursseilta ehkä tutut perusasiat yleisestä avoimen kuvauksen käsitteestä. Määrittelemme ensin avoimen
Polynomiyhtälöiden ratkeavuus juurilausekkeilla. Ville Uusivuori
 Polynomiyhtälöiden ratkeavuus juurilausekkeilla Ville Uusivuori HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department
Polynomiyhtälöiden ratkeavuus juurilausekkeilla Ville Uusivuori HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI Tiedekunta/Osasto Fakultet/Sektion Faculty Laitos Institution Department
LUKUTEORIA A. Harjoitustehtäviä, kevät 2013. (c) Osoita, että jos. niin. a c ja b c ja a b, niin. niin. (e) Osoita, että
 LUKUTEORIA A Harjoitustehtäviä, kevät 2013 1. Olkoot a, b, c Z, p P ja k, n Z +. (a) Osoita, että jos niin Osoita, että jos niin (c) Osoita, että jos niin (d) Osoita, että (e) Osoita, että a bc ja a c,
LUKUTEORIA A Harjoitustehtäviä, kevät 2013 1. Olkoot a, b, c Z, p P ja k, n Z +. (a) Osoita, että jos niin Osoita, että jos niin (c) Osoita, että jos niin (d) Osoita, että (e) Osoita, että a bc ja a c,
Eräitä ratkeavuustarkasteluja
 Eräitä ratkeavuustarkasteluja Pro gradu-tutkielma Milla Jantunen 2124227 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2014 Sisältö 1 Ryhmät ja aliryhmät 3 1.1 Ryhmä...............................
Eräitä ratkeavuustarkasteluja Pro gradu-tutkielma Milla Jantunen 2124227 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2014 Sisältö 1 Ryhmät ja aliryhmät 3 1.1 Ryhmä...............................
Tehtävä 8 : 1. Tehtävä 8 : 2
 Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
802355A Algebralliset rakenteet Luentorunko Syksy Markku Niemenmaa Kari Myllylä Topi Törmä Marko Leinonen
 802355A Algebralliset rakenteet Luentorunko Syksy 2016 Markku Niemenmaa Kari Myllylä Topi Törmä Marko Leinonen Sisältö 1 Kertausta kurssilta Algebran perusteet 3 2 Renkaat 8 2.1 Renkaiden teoriaa.........................
802355A Algebralliset rakenteet Luentorunko Syksy 2016 Markku Niemenmaa Kari Myllylä Topi Törmä Marko Leinonen Sisältö 1 Kertausta kurssilta Algebran perusteet 3 2 Renkaat 8 2.1 Renkaiden teoriaa.........................
1 Kertausta algebran kurssilta 1. 4 Kuntalaajennukset Kuntalaajennuksen aste Harppi-viivoitin-konstruktiot Hajoituskunnat 88
 Sisältö 1 Kertausta algebran kurssilta 1 2 Lisää polynomeista 10 3 Kertausta Q:n konstruktiosta; jakokunta 20 4 Kuntalaajennukset 27 5 Kuntalaajennuksen aste 49 6 Harppi-viivoitin-konstruktiot 64 7 Galois
Sisältö 1 Kertausta algebran kurssilta 1 2 Lisää polynomeista 10 3 Kertausta Q:n konstruktiosta; jakokunta 20 4 Kuntalaajennukset 27 5 Kuntalaajennuksen aste 49 6 Harppi-viivoitin-konstruktiot 64 7 Galois
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 4.7 Syklisen koodin jälkiesitys Olkoon F = F q ja K = F q m kunnan F laajennuskunta. Määritelmä 4.7.1. Kuntalaajennuksen K/F jälkifunktioksi
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 4.7 Syklisen koodin jälkiesitys Olkoon F = F q ja K = F q m kunnan F laajennuskunta. Määritelmä 4.7.1. Kuntalaajennuksen K/F jälkifunktioksi
802320A LINEAARIALGEBRA OSA I
 802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
Miten osoitetaan joukot samoiksi?
 Miten osoitetaan joukot samoiksi? Määritelmä 1 Joukot A ja B ovat samat, jos A B ja B A. Tällöin merkitään A = B. Kun todistetaan, että A = B, on päättelyssä kaksi vaihetta: (i) osoitetaan, että A B, ts.
Miten osoitetaan joukot samoiksi? Määritelmä 1 Joukot A ja B ovat samat, jos A B ja B A. Tällöin merkitään A = B. Kun todistetaan, että A = B, on päättelyssä kaksi vaihetta: (i) osoitetaan, että A B, ts.
Algebran ja lukuteorian harjoitustehtäviä. 1. Tutki, ovatko seuraavat relaatiot ekvivalenssirelaatioita joukon N kaikkien osajoukkojen
 Algebran ja lukuteorian harjoitustehtäviä Versio 1.0 (27.1.2006) Turun yliopisto Lukuteoria 1. Tutki, ovatko seuraavat relaatiot ekvivalenssirelaatioita joukon N kaikkien osajoukkojen joukolla: a) C D
Algebran ja lukuteorian harjoitustehtäviä Versio 1.0 (27.1.2006) Turun yliopisto Lukuteoria 1. Tutki, ovatko seuraavat relaatiot ekvivalenssirelaatioita joukon N kaikkien osajoukkojen joukolla: a) C D
Peruskäsitteet. 0. Kertausta
 Peruskäsitteet 0. Kertausta Tässä luvussa käydään läpi sellaiset peruskäsitteet ja merkinnät, joiden oletetaan olevan tuttuja aiemmalta algebran kurssilta. 0.1. Laskutoimitukset. Olkoon X joukko. Joukon
Peruskäsitteet 0. Kertausta Tässä luvussa käydään läpi sellaiset peruskäsitteet ja merkinnät, joiden oletetaan olevan tuttuja aiemmalta algebran kurssilta. 0.1. Laskutoimitukset. Olkoon X joukko. Joukon
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 9 (6 sivua) OT
 Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 9 (6 sivua) 28.3.-1.4.2011 OT 1. a) Osoita, että rengas R = {[0] 10, [2] 10, [4] 10, [6] 10, [8] 10 } on kokonaisalue. Mikä
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 9 (6 sivua) 28.3.-1.4.2011 OT 1. a) Osoita, että rengas R = {[0] 10, [2] 10, [4] 10, [6] 10, [8] 10 } on kokonaisalue. Mikä
x j x k Tällöin L j (x k ) = 0, kun k j, ja L j (x j ) = 1. Alkuperäiselle interpolaatio-ongelmalle saadaan nyt ratkaisu
 2 Interpolointi Olkoon annettuna n+1 eri pistettä x 0, x 1, x n R ja n+1 lukua y 0, y 1,, y n Interpoloinnissa etsitään funktiota P, joka annetuissa pisteissä x 0,, x n saa annetut arvot y 0,, y n, (21)
2 Interpolointi Olkoon annettuna n+1 eri pistettä x 0, x 1, x n R ja n+1 lukua y 0, y 1,, y n Interpoloinnissa etsitään funktiota P, joka annetuissa pisteissä x 0,, x n saa annetut arvot y 0,, y n, (21)
(xa) = (x) (a) = (x)0 = 0
 11. Ideaalit ja tekijärenkaat Rengashomomorfismi : R! R 0 on erityisesti ryhmähomomorfismi :(R, +)! (R 0, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin
11. Ideaalit ja tekijärenkaat Rengashomomorfismi : R! R 0 on erityisesti ryhmähomomorfismi :(R, +)! (R 0, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin
Määritelmä, alkuluku/yhdistetty luku: Esimerkki . c) Huomautus Määritelmä, alkutekijä: Esimerkki
 Alkuluvut LUKUTEORIA JA TODISTAMINEN, MAA11 Jokainen luku 0 on jaollinen ainakin itsellään, vastaluvullaan ja luvuilla ±1. Kun muita eri ole, niin kyseinen luku on alkuluku. Määritelmä, alkuluku/yhdistetty
Alkuluvut LUKUTEORIA JA TODISTAMINEN, MAA11 Jokainen luku 0 on jaollinen ainakin itsellään, vastaluvullaan ja luvuilla ±1. Kun muita eri ole, niin kyseinen luku on alkuluku. Määritelmä, alkuluku/yhdistetty
g : R R, g(a) = g i a i. Alkio g(a) R on polynomin arvo pisteessä a. Jos g(a) = 0, niin a on polynomin g(x) nollakohta.
 ALGEBRA II 27 on homomorfismi. Ensinnäkin G(a + b) a + b G(a)+G(b) (f), G(ab) ab G(a)G(b) G(a) G(b) (f), ja koska kongruenssien vasempien ja oikeiden puolten asteet ovat pienempiä kuin f:n aste, niin homomorfiaehdot
ALGEBRA II 27 on homomorfismi. Ensinnäkin G(a + b) a + b G(a)+G(b) (f), G(ab) ab G(a)G(b) G(a) G(b) (f), ja koska kongruenssien vasempien ja oikeiden puolten asteet ovat pienempiä kuin f:n aste, niin homomorfiaehdot
Tehtävä 1. Arvioi mitkä seuraavista väitteistä pitävät paikkansa. Vihje: voit aloittaa kokeilemalla sopivia lukuarvoja.
 Tehtävä 1 Arvioi mitkä seuraavista väitteistä pitävät paikkansa. Vihje: voit aloittaa kokeilemalla sopivia lukuarvoja. 1 Jos 1 < y < 3, niin kaikilla x pätee x y x 1. 2 Jos x 1 < 2 ja y 1 < 3, niin x y
Tehtävä 1 Arvioi mitkä seuraavista väitteistä pitävät paikkansa. Vihje: voit aloittaa kokeilemalla sopivia lukuarvoja. 1 Jos 1 < y < 3, niin kaikilla x pätee x y x 1. 2 Jos x 1 < 2 ja y 1 < 3, niin x y
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
2.1. Tehtävänä on osoittaa induktiolla, että kaikille n N pätee n = 1 n(n + 1). (1)
 Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
b) Olkoon G vähintään kaksi solmua sisältävä puu. Sallitaan verkon G olevan
 Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
2 1/ /2 ; (a) Todista, että deg P (x)q(x) = deg P (x) + deg Q(x). (b) Osoita, että jos nolla-polynomille pätisi. deg 0(x) Z, Z 10 ; Z 10 [x];
![2 1/ /2 ; (a) Todista, että deg P (x)q(x) = deg P (x) + deg Q(x). (b) Osoita, että jos nolla-polynomille pätisi. deg 0(x) Z, Z 10 ; Z 10 [x]; 2 1/ /2 ; (a) Todista, että deg P (x)q(x) = deg P (x) + deg Q(x). (b) Osoita, että jos nolla-polynomille pätisi. deg 0(x) Z, Z 10 ; Z 10 [x];](/thumbs/97/131422104.jpg) 802656S ALGEBRALLISET LUVUT Harjoituksia 2017 1. Näytä, että (a) (b) (c) (d) (e) 2 1/2, 3 1/2, 2 1/3 ; 2 1/2 + 3 1/2 ; 2 1/3 + 3 1/2 ; e iπ/m, m Z \ {0}; sin(π/m), cos(π/m), tan(π/m), m Z \ {0}; ovat algebrallisia
802656S ALGEBRALLISET LUVUT Harjoituksia 2017 1. Näytä, että (a) (b) (c) (d) (e) 2 1/2, 3 1/2, 2 1/3 ; 2 1/2 + 3 1/2 ; 2 1/3 + 3 1/2 ; e iπ/m, m Z \ {0}; sin(π/m), cos(π/m), tan(π/m), m Z \ {0}; ovat algebrallisia
Lisää ryhmästä A 5 1 / 28. Lisää ryhmästä
 14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 1 / 28 14A.1 14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 Tehtävä: Määrää ryhmän karakteritaulu,
14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 1 / 28 14A.1 14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 Tehtävä: Määrää ryhmän karakteritaulu,
IV. TASAINEN SUPPENEMINEN. f(x) = lim. jokaista ε > 0 ja x A kohti n ε,x N s.e. n n
 IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
IV. TASAINEN SUPPENEMINEN IV.. Funktiojonon tasainen suppeneminen Olkoon A R joukko ja f n : A R funktio, n =, 2, 3,..., jolloin jokaisella x A muodostuu lukujono f x, f 2 x,.... Jos tämä jono suppenee
Sylowin lauseet äärellisten ryhmien luokittelussa
 Sylowin lauseet äärellisten ryhmien luokittelussa Jenna Johansson 21. marraskuuta 2018 Pro gradu -tutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Syksy 2018 Merkintöjä: N Luonnollisten
Sylowin lauseet äärellisten ryhmien luokittelussa Jenna Johansson 21. marraskuuta 2018 Pro gradu -tutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Syksy 2018 Merkintöjä: N Luonnollisten
Kurssikoe on maanantaina Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 05 Harjoitus 6 Ratkaisut palautettava viimeistään tiistaina.6.05 klo 6.5. Huom! Luennot ovat salissa CK maanantaista 5.6. lähtien. Kurssikoe on
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 05 Harjoitus 6 Ratkaisut palautettava viimeistään tiistaina.6.05 klo 6.5. Huom! Luennot ovat salissa CK maanantaista 5.6. lähtien. Kurssikoe on
Ryhmäteoriaa. 2. Ryhmän toiminta
 Ryhmäteoriaa 2. Ryhmän toiminta Permutaatiot kuvaavat jonkin perusjoukon alkioita toisikseen. Eräät permutaatiot jättävät joitain alkioita paikalleen, toiset liikuttavat kaikkia joukon alkioita. Kaikki
Ryhmäteoriaa 2. Ryhmän toiminta Permutaatiot kuvaavat jonkin perusjoukon alkioita toisikseen. Eräät permutaatiot jättävät joitain alkioita paikalleen, toiset liikuttavat kaikkia joukon alkioita. Kaikki
Teema 4. Homomorfismeista Ihanne ja tekijärengas. Teema 4 1 / 32
 1 / 32 Esimerkki 4A.1 Esimerkki 4A.2 Esimerkki 4B.1 Esimerkki 4B.2 Esimerkki 4B.3 Esimerkki 4C.1 Esimerkki 4C.2 Esimerkki 4C.3 2 / 32 Esimerkki 4A.1 Esimerkki 4A.1 Esimerkki 4A.2 Esimerkki 4B.1 Esimerkki
1 / 32 Esimerkki 4A.1 Esimerkki 4A.2 Esimerkki 4B.1 Esimerkki 4B.2 Esimerkki 4B.3 Esimerkki 4C.1 Esimerkki 4C.2 Esimerkki 4C.3 2 / 32 Esimerkki 4A.1 Esimerkki 4A.1 Esimerkki 4A.2 Esimerkki 4B.1 Esimerkki
Transversaalit ja hajoamisaliryhmät
 Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
PERUSASIOITA ALGEBRASTA
 PERUSASIOITA ALGEBRASTA Matti Lehtinen Tässä luetellut lauseet ja käsitteet kattavat suunnilleen sen mitä algebrallisissa kilpatehtävissä edellytetään. Ns. algebrallisia struktuureja jotka ovat nykyaikaisen
PERUSASIOITA ALGEBRASTA Matti Lehtinen Tässä luetellut lauseet ja käsitteet kattavat suunnilleen sen mitä algebrallisissa kilpatehtävissä edellytetään. Ns. algebrallisia struktuureja jotka ovat nykyaikaisen
4 Abelin ryhmät. 4.1 Suorat tulot ja summat
 4 Abelin ryhmät Ensimmäisellä ryhmäteorian kurssilla käytiin läpi lähinnä syklisiä ryhmiä. Tällä kurssilla keskitymme epäkommutatiivisiin esimerkkeihin. On kuitenkin niin, että äärellisesti viritettyjen
4 Abelin ryhmät Ensimmäisellä ryhmäteorian kurssilla käytiin läpi lähinnä syklisiä ryhmiä. Tällä kurssilla keskitymme epäkommutatiivisiin esimerkkeihin. On kuitenkin niin, että äärellisesti viritettyjen
MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen
 MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen Tehtävä 1. Onko joukon X potenssijoukon P(X) laskutoimitus distributiivinen laskutoimituksen suhteen? Onko laskutoimitus distributiivinen laskutoimituksen
MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen Tehtävä 1. Onko joukon X potenssijoukon P(X) laskutoimitus distributiivinen laskutoimituksen suhteen? Onko laskutoimitus distributiivinen laskutoimituksen
4 Yleinen potenssifunktio ja polynomifunktio
 4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
4 Yleinen potenssifunktio ja polynomifunktio ENNAKKOTEHTÄVÄT 1. a) Tutkitaan yhtälöiden ratkaisuja piirtämällä funktioiden f(x) = x, f(x) = x 3, f(x) = x 4 ja f(x) = x 5 kuvaajat. Näin nähdään, monessako
Algebra I, harjoitus 5,
 Algebra I, harjoitus 5, 7.-8.10.2014. 1. 2 Osoita väitteet oikeiksi tai vääriksi. a) (R, ) on ryhmä, kun asetetaan a b = 2(a + b) aina, kun a, b R. (Tässä + on reaalilukujen tavallinen yhteenlasku.) b)
Algebra I, harjoitus 5, 7.-8.10.2014. 1. 2 Osoita väitteet oikeiksi tai vääriksi. a) (R, ) on ryhmä, kun asetetaan a b = 2(a + b) aina, kun a, b R. (Tässä + on reaalilukujen tavallinen yhteenlasku.) b)
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 5 : 1. Tehtävä 5 : 2
 Tehtävä 5 : 1 Merkitään kirjaimella H kuvan punaisten solmujen virittämää verkon G yhtenäistä aliverkkoa, jossa on yhteensä kolme särmää. Aliverkosta H voidaan kahdella tavalla valita kahden solmun joukko
Tehtävä 5 : 1 Merkitään kirjaimella H kuvan punaisten solmujen virittämää verkon G yhtenäistä aliverkkoa, jossa on yhteensä kolme särmää. Aliverkosta H voidaan kahdella tavalla valita kahden solmun joukko
ÄÄRELLISTEN RYHMIEN VAIHDANNAISUUSVERKOT MIIKKA SILFVERBERG
 ÄÄRELLISTEN RYHMIEN VAIHDANNAISUUSVERKOT MIIKKA SILFVERBERG PRO GRADU HELSINGIN YLIOPISTON MATEMATIIKAN LAITOS TOUKOKUU 2008 SISÄLTÖ 1. Merkinnöistä ja määritelmistä 2 2. Johdanto 3 3. Ryhmäteoriaa 5 3.1.
ÄÄRELLISTEN RYHMIEN VAIHDANNAISUUSVERKOT MIIKKA SILFVERBERG PRO GRADU HELSINGIN YLIOPISTON MATEMATIIKAN LAITOS TOUKOKUU 2008 SISÄLTÖ 1. Merkinnöistä ja määritelmistä 2 2. Johdanto 3 3. Ryhmäteoriaa 5 3.1.
Jarkko Peltomäki. Aliryhmän sentralisaattori ja normalisaattori
 Jarkko Peltomäki Aliryhmän sentralisaattori ja normalisaattori Matematiikan aine Turun yliopisto Syyskuu 2009 Sisältö 1 Johdanto 2 2 Määritelmiä ja perusominaisuuksia 3 2.1 Aliryhmän sentralisaattori ja
Jarkko Peltomäki Aliryhmän sentralisaattori ja normalisaattori Matematiikan aine Turun yliopisto Syyskuu 2009 Sisältö 1 Johdanto 2 2 Määritelmiä ja perusominaisuuksia 3 2.1 Aliryhmän sentralisaattori ja
3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2
 3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 Olen valinnut kunkin luvun teemaksi yhden ryhmän. Ensimmäisen luvun teema on pienin epätriviaali ryhmä, eli ryhmä, jossa on kaksi alkiota. Merkitsen
3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 Olen valinnut kunkin luvun teemaksi yhden ryhmän. Ensimmäisen luvun teema on pienin epätriviaali ryhmä, eli ryhmä, jossa on kaksi alkiota. Merkitsen
