Neitola M. T. T. (2006) Delta-sigma A/D-muuntimien mallinnus ja simulointi. Lisensiaatintyö. Oulun Yliopisto, Sähkö- ja tietotekniikan osasto, 98 s.
|
|
|
- Annika Palo
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 2 Neitola M. T. T. (26) Delta-sigma A/D-muuntimien mallinnus ja simulointi. Lisensiaatintyö. Oulun Yliopisto, Sähkö- ja tietotekniikan osasto, 98 s. TIIVISTELMÄ Lisensiaatintyössä on tutkittu delta-sigma A/D-muuntimien suunnittelumenetelmiä. Suunnittelu korkealta abstraktiotasolta valmiiseen piiriin voi olla haastavaa, koska delta-sigma A/D-muuntimen stabiilisuuden varmistaminen vaatii kattavan joukon lineaarisia anayysejä ja epälineaarisia käyttäytymistason simulointeja. Suunnittelijan tulee myös mallintaa tärkeimpiä piiritason epäideaalisuuksia, jotta suorituskyvyn ja stabiilisuuden tunnusluvut täyttyvät varmasti. Tämä siksi, että transistoritasolla mallin simuloinnit ovat stabiilisuusja suorituskykyanalyysiin auttamattoman hitaita. Tunnettujen ilmiöiden ja analyysimenetelmien lisäksi työssä esitellään joukko työssä kehiteltyjä työkaluja muuntimien suunnitteluun, käyttäytymistason simulointiin ja epäideaalisuuksien mallinnukseen. Työssä esitellään myös tunnettuja ja työssä kehitettyjä ja menetelmiä virheenkorjausmenetelmiin nk. monibittisissä delta-sigma A/D-muuntimissa. Avainsanat: delta-sigma, A/D-muunnin, analysointi, mallintaminen, simulointi, virheenkorjaus.
2 3 Neitola M. T. T. (26) Simulation and modeling of delta-sigma A/D-converters. Licentiate thesis. University of Oulu. Department of electrical and information engineering. 98 p. ABSTRACT In this licentiate thesis, design methods for delta-sigma A/D-converters are studied. The design flow from a high level abstraction level to circuit level can be demanding, because ensuring stable behavior of a delta-sigma converter calls for a large variety of linear analyses and nonlinear behavioral simulations. The designer is also required to model the most dominant nonlinearities of the circuit to assure performance and stability. These requirements can not be ensured by slow device level simulations. In addition to known phenomena and analysis methods, this work introduces also an extensive group of known and created methods for converter design, behavioral level simulation and modeling non-ideal behavior. This work also introduces traditional and created methods for the mismatch error correction for so called multi-bit delta-sigma A/D converters. Key words: delta-sigma, A/D-converter, analyzing, modeling, simulation, error correction.
3 4 SISÄLLYSLUETTELO TIIVISTELMÄ ABSTRACT SISÄLLYSLUETTELO ALKULAUSE LYHENTEIDEN JA MERKKIEN SELITYKSET 1. JOHDANTO DELTA-SIGMA A/D-MUUNTIMET Ylinäytteistys ja kohinanmuokkaus Kvantisointikohina Kvantisoijan vahvistus Suunnittelun alkuvaiheet Diskreetti- ja jatkuva-aikainen DS A/D-toteutus SC-integraattori Modulaattorin rakennevaihtoehdot Desimointisuodattimet DELTA-SIGMA MODULAATTORIN ANALYSOINTIMENETELMÄT Lineaarinen malli NTF:n valinta Lineaarinen analyysi Juuren ura Kuvaavan funktion menetelmä Siirtofunktion kompleksiset navat QTF - kvantisoijan mallinnus särön analyysissä Epälineaarinen analyysi TOPOLOGIATASON ESITYS Tärkeimmät topologiat Feed-forward (FF) -topologia Multiple-feedback (MF) -topologia Error feedback -topologia Topologioiden vertailu Topologian piiritoteutukseen liittyvät seikat STF:n muokkaus Topologian kerroinparametrit Parametrien laskenta ja skaalaus Tilamallin ja kertoimien skaalaus Delta-Sigma -muunnintopologian analysointi vuokaaviotasolla Mitoitus vuokaavioanalyysillä Kertoimien typistäminen DISKREETTIAIKAINEN SIMULOINTIMALLI DS-muuntimen simuloinnin periaatteita Käyttäytymistason mallinnus Kvantisoijan efektiivinen vahvistus Kaistan ulkopuolisten häiriösignaalien vaikutus... 57
4 6. ANALOGIAOSIEN EPÄIDEAALISUUDET kt/c-kohina Integraattorin epäideaalisuudet Kellojitteri EPÄIDEAALISUUKSIEN MALLINTAMINEN Analyyttiset mallit ja niiden rajoitukset Mittaukseen perustuva malli Asettumisvirheiden karakterisointi Sovitus ja mallinnuksen tarkkuus Simulointimalli ja suorituskykysimuloinnit Mittaukseen perustuvan polynomimallinnuksen hyöty MONIBITTISET DELTA-SIGMA MUUNTIMET Monibittisen DS A/D-muuntimen lineaarisuusvirheiden korjaaminen Dynamic element matching (DEM) Digitaalinen virheenkorjaus Offline-kalibrointiin perustuva korjaus Background- eli taustakorjaus Adaptiivinen eli online-tyyppinen korjaus POHDINTA YHTEENVETO LÄHDELUETTELO
5 6 ALKULAUSE Tämä lisensiaatintyö koostaa valtaosan viimeisen kuuden vuoden julkaisu- ja tutkimustoiminnan tuloksista. Diplomityön jälkeen olen ollut sähkö- ja tietotekniikan osaston elektroniikan laboratoriossa sekä kokopäiväisenä tutkijana eri projekteissa että assistenttina. Tutkimusprojektit A-CDMA ja ECCON olivat elektroniikan laboratorion projekteja, joka rahoittajia ovat Nokia Mobile Phones, Nokia Telecommunications, National Semiconductor Finland Oy, TEKES ja KTH. A- CDMA-projektin painopiste oli uusien WCDMA-vastaanotin rakenteiden suunnittelussa ja ECCON-projektissa tutkittiin mallinnus- ja suodatustekniikoita sekä digitaalista virheenkorjausta. Työn valvojana ja tarkastajana on toiminut professori Timo Rahkonen jolle kiitokset neuvoista ja opastuksesta. Haluan kiittää myös professori Juha Kostamovaaraa työn tarkastamisesta. Kiitokset myös kotiväelle tuesta ja kannustuksesta. Oulussa Marko Neitola Pinkelikatu 6 B Oulu
6 7 LYHENTEIDEN JA MERKKIEN SELITYKSET A A/D AAF ABCD ABSTOL ADC A DC B C CMOS cov D D/A d 3 DAC DACTF DEM DNL DR DS DWA e E EFB ENOB f f b f s FF FFT FIR fn FS GBW HBF I IIR INL k k FB K L L L1 LMS LSB signaalin amplitudi analogia/digitaali anti-alias -suodatin tilamallin tilamatriisi absoluuttinen toleranssiarvo analogia/digitaali -muunnin dc-vahvistus kvantisoinnissa käytettävien bittien lukumäärä kapasitanssi complementary metal oxide semiconductor kovarianssifunktio desimointikerroin digitaali/analogia kolmannen ja ensimmäisen asteen termin suhde digitaali/analogia -muunnin siirtofunktio DACista lähtöön dynamic element matching differential nonlinearity dynaaminen alue delta-sigma data weighted averaging virhe, Neperin luku virhe taajuustasossa error-feedback (topologia) effective number of bits taajuus signaalikaistan kantataajuuskaistanleveys näytteistystaajuus feed-forward (topologia) nopea Fourier-muunnos finite impulse response -suodatin Nyquist-taajuus full scale, täyden skaalan amplitudi gain bandwidth, yksikkövahvistuskaistanleveys half-band -suodatin virta infinite impulse response -suodatin integral nonlinearity kvantisoijan vahvistus, Bolzmanin vakio vahvistimen takaisinkytkentäkerroin desimointisuodattimen asteluku, kvantisointitasot delta-sigma -muuntimen asteluku silmukkasuodattimen siirtofunktio signaalille silmukkasuodattimen siirtofunktio kohinalle least mean squares -algoritmi least significant bit
7 8 LUT lookup-taulukko M kvantisointitasojen lukumäärä m LMS adaptointiaskel Mag amplitudi desibeleinä MASH useamman delta-sigma -asteen muunnin MEX Matlabissa suoritettava ja käännettävä koodi MF multiple-feedback (topologia) MSB most significant bit MSE mean squared error MTF epäsovitus siirtofunktio N kvantisointitasojen lukumäärä n INL epäsovituksesta johtuva kohina n Q kvantisointikohina n qin kvantisoijan tulosignaalin kohinainen osa NTF kohinan siirtofunktio OSR ylinäytteistyssuhde p integraattorin tk. kerroin Pha vaihe Q hyvyysluku, kvantisointitasojen lkm. q kvantisointiaskel QTF kvantisoijan siirtofunktio R resistanssi RAM random access -muisti RMS root mean square, tehollisarvo s jatkuva-aikainen kompleksinen taajuusmuuttuja SC switched capacitor, kytkinkapasitanssi SFDR Signaalin suhde voimakkaimpaan spurritasoon SNDR signaalin suhde kohinaan ja säröön SNR signaali-kohinasuhde s qin kvantisoijan tulosignaalin signaaliosa SR slew-rate std hajontafunktio STF signaalin siirtofunktio T aikaväli, lämpötila TOL toleranssi u, U DS-muuntimen tulosignaali aika- ja taajuustasossa v, V DS-muuntimen lähtösignaali aika- ja taajuustasossa var varianssifunktio w LMS painokertoimet y, Y kvantisoijan tulosignaali aika- ja taajuustasossa z diskreettiaikainen kompleksinen taajuusmuuttuja vahvistusvirhe siirtofunktion navan virhe jitterilaskennan ajoitusvirhe epälineaarisuusvirhe SC-integraattorin kytkentävaiheet hajonta, varianssi aikavakio kulmataajuus
8 9 1. JOHDANTO Ylinäytteistävän ja kvantisointikohinan spektriä muokkaavan delta-sigma (DS) tyyppisen analogia-digitaali (A/D) -muuntimen suunnittelussa on runsaasti huomioon otettavia seikkoja. Piirisuunnittelijan näkökulmasta tärkeitä asioita ovat piirin sisäisten osien suorituskykyyn ja piirin sisäisten signaalien tilastollisiin tietoihin liittyvät seikat. Ongelmana on yleensä suunnittelun liiallinen empiirisyys: yksittäisellä simuloinnilla saadut tiedot eivät aina kerro koko totuutta. Halutusti toimiva DS-muunnin saattaa joillakin esim. heräteparametreilla olla jopa epästabiili. Tämä on yleensä oire siitä, että on jätetty tekemättä tärkeitä siirtofunktiotason analyysejä, tai jätetty tietyn tyyppisiä käyttäytymistason simulointeja suorittamatta. Delta-sigma -muuntimen suunnittelun haasteellisuudesta kertonee se, että tyhjentävä analyysi on näihin päiviin asti tehty ainoastaan ideaalisille 1. ja 2. asteen muuntimille [1]. Tämän työn tarkoitus on esitellä erilaisia apuvälineitä DS-suunnittelun vaiheisiin. Käyttäytymis- ja siirtofunktiotason analyysiin soveltuvista ohjelmista Matlab on tällä hetkellä suosituin. Matlabin laajennus, graafiseen käyttöliittymään perustuva Simulink on myös oleellisessa asemassa tässä työssä. Internetistä ilmaisena jaettava Richard Schreierin kehittämä Delta-Sigma Toolbox [2] Matlabille on suosittu DS-muuntimien suunnittelun ohjelmistopaketti. DS-toolbox sisältää suuren määrän suunnittelua helpottavia apuvälineitä, joten sitä on lähes mahdoton sivuuttaa. Tässä työssä keskitytään lähinnä diskreettiaikaisena toteutettavan DS A/Dmuuntimen suunnitteluvuohon. Tämä työ ei sinänsä ole tutkielma piiritason suunnittelun vaiheista, vaan lähtökohtana on yleisin DS-sovellus eli diskreettiaikainen, SC-tekniikalla (switched capacitor) toteutettu DS A/D-muunnin. Työssä esitellään laajalti tunnettujen menetelmien ja apuvälineiden lisäksi myös useita omia kontribuutioita, joista mainittakoon: häiriösignaalin vaikutus DS-muuntimen käyttäytymiseen, apuvälineitä siirtofunktioanalyysin vuokaaviotasolla [3,4], muunninkertoimien skaalaamisen ja typistämisen automatisointi, muunninkertoimien adaptointi jälkisuodatuksen ekvalisoinnissa [5], monibittisen DS-muuntimen lineaarisuusvirheiden korjaus offline- ja taustakalibroinnilla sekä adaptiivisen menetelmän avulla [6,7,8] ja mittaukseen perustuva vahvistimen epälineaarisuuden mallinnus. Kappaleessa 2 kerrotaan DS-muuntimien teoriasta, yleisestä suunnitteluvuosta sekä diskreettiaikaisesta A/D-toteutuksesta. Kappale 3 kertoo siirtofunktion valintaan liittyvistä seikoista sekä lineaarisen analyysin keinoista. Lisäksi kerrotaan myös vähemmän tunnetuista epälineaarisista analyysimenetelmistä. Kappaleessa 4 esitellään tärkeimmät DS-topologiat sekä kerrotaan topologiatason muunninkertoimien realisoinnista, skaalauksesta ja typistämisestä. Kappaleessa 5 kerrotaan käyttäytymistason simuloimisesta diskreettiaikaisessa Matlab-ympäristössä korostaen siirtofunktion herkkyyttä kvantisoijan vahvistuksen arvolla eri herätteillä ja kaistan ulkopuolisen häiriön tapauksessa. Kun muuntimen käyttäytyminen ja suorituskyky on varmistettu, seuraava askel on määritellä integraattorin kondensaattoreiden koko suhteessa kt/c-kohinaan sekä
9 1 piirin pinta-alaan. Kappaleessa 6 esiteltävät piirin epäideaalisuudet tuovat oman vaikutuksensa kvantisointikohinaan, johon voidaan vaikuttaa tarkalla suunnittelulla. Myös käyttäytymistason mallin simuloinnit mahdollisimman tarkalla integraattorin mallilla ovat suositeltavia. Piirin epäideaalisuuksien mallintamisesta löytyykin erittäin paljon kirjallisuutta. DS-muuntimet ovat tyypillisesti verrattain suuria mixedsignal-piirejä, jonka simulointi transistoritasolla on erittäin hidasta. Käyttäytymistason simuloinneilla voidaan mallintaa epäideaalisia ilmiöitä, kuten rajallista dcvahvistusta, vahvistimen signaaliriippuvaa asettumisvirhettä sekä piirin komponenttien epäsovitusta. Kappaleessa 7 kerrotaan epäideaalisuuksien mallintamistavoista. Vertailtavana on kaksi menetelmää: analyyttinen sekä mittauksiin perustuvan mallintamismenetelmä. Analyyttinen mallinnus on varsin yleistä, mutta se soveltuu ainoastaan heikosti epälineaarisiin, yksiulotteisesti mallinnettaviin ilmiöihin. Mittauksiin perustuvassa menetelmässä voidaan mallintaa integraattorin virhettä kaksiulotteisesti käyttämällä mittauksia tai realistista tilamallia. Kappaleessa 8 esitellään monibittisen DS:n takaisinkytkentä-d/a-muuntimen (DAC) epälineaarisuusvirheiden korjausmenetelmistä. Kappale käsittelee pintapuolisesti suosittuja dynamic element matching -menetelmiä, mutta pääpaino on digitaalisen virheenkorjauksen menetelmissä. Kuvassa 1 on kooste DS-A/D-muuntimen suunnittelun osa-alueista. Siinä on pyritty kattamaan lisensiaatintyössä esitetyt, muuntimen suunnittelussa huomioitavat asiat ja menetelmät. Keskellä keltaisessa ympyrässä on oleellisia suunnittelun spesifikaatioita, joista ohjelmoitavuus liittyy A/D-muuntimen käytettävyyteen useassa tiedonsiirto-protokollassa (nk. multimode-ominaisuus). -Asteluku, OSR -Siirtofunktiot -Yksi tai monibittinen takaisinkytkentä -Juuren ura -Kuvaava funktio Lineaarinen analyysi -Kvantisoijan vahvistus -Suorituskyky -Kompleksisuus -Tehonkulutus -Ohjelmoitavuus Aikatason simulointi -Silmukkasuodatin/topologia -Epäideaalisuuksien mallinnus (kt/c, integr., jitteri, DAC) -DEM tai digitaal. virheenkorjaus Topologia -FF, MF, vai error feedback, -MASH,Leslie-Singh (rakenteet) -Kertoimet+skaalaus Vuokaavio-analyysi Kuva 1. Suunnittelun osa-alueet lineaarisen analyysin, topologian ja simuloinnin kannalta.
10 11 2. DELTA-SIGMA A/D-MUUNTIMET 2.1 Ylinäytteistys ja kohinanmuokkaus Näytteenottoteoreeman mukaan jatkuva-aikainen kantataajuinen signaali voidaan muodostaa uudelleen diskreettiaikaisten näytearvojensa avulla, mikäli näytteenottotaajuus f s on vähintään kaksi kertaa signaalin kaistanleveys f b. Taajuutta f N kutsutaan Nyquist-taajuudeksi. f s 2 f b = f N (1) Nyquist-taajuudella toimivat muuntimet ovat monibittisiä ja laajakaistaisia A/Dmuuntimia, joten ne tarvitsevat erittäin jyrkän anti-alias -suodatuksen sekä hyvin sovitettuja komponentteja. Jos näytteenottotaajuus on suurempi kuin Nyquist-taajuus, puhutaan ylinäytteistyksestä. Tällöin näytteistetty signaali sisältää enemmän näytteitä, ja spektrin sivukaistojen välinen etäisyys kasvaa. Delta-sigma -muuntimet ovat ylinäytteistäviä sekä kohinaa muokkaavia, ja etenkin korkean resoluution A/D- ja D/A-muuntimien (kuva 2) suunnittelussa DS-muunnintekniikan käyttö on erittäin suosittua. Diskreettiaikaisissa systeemeissä tulosignaali on suoraan näytteistetty, mikä johtaa siihen, että lähellä näytteistystaajuudella olevat signaalikomponentit laskostuvat signaalin kaistalle ilman vaimennusta. Siksi tarvitaan anti-alias (AAF) - suodatin eli laskostumisen estosuodatin ennen tulosignaalin näytteistämistä. Nyquisttaajuudella toimivat muuntimet tarvitsevat jyrkän laskostumisen estosuodattimen, jotta korkeataajuiset harhatoistot saadaan vaimennettua. Analoginen Alipäästösuodatin A/D Digitaalinen Digitaalinen D/A Alipäästösuodatin Analoginen Kuva 2. A/D- ja D/A-muunnos. Ylinäytteistäville A/D-muuntimille ylinäytteistyssuhde tarkoittaa näytteenottotaajuuden suhdetta Nyquist-taajuuteen f N : OSR missä f b on kantataajuuskaistan leveys ja OSR on ylinäytteistyssuhde. f ---- s f N f s = = (2) 2f b Ylinäytteistyssuhde helpottaa AAF-suodattimen jyrkkyysvaatimuksia huomattavasti. Esimerkiksi 2kHz:n signaalin näytteistys Nyquist-taajuudella 4 khz vaatisi ideaaliseen anti-alias -suodattimen (kuva 3a). Jos näytteenottotaajuus olisi 8kHz, anti-alias-suodattimen siirtokaista olisi 4kHz (kuva 3b).
11 12 a) d(t) t d(t) D(f) b) AAF(f) t D(f) AAF(f ) f b f N f s -f b Kuva 3. a) Nyquist-taajuudella näytteistetty signaali ja b) ylinäytteistetty signaali. Kuvassa 4 [9] on esitetty DS-modulointitekniikan käyttöä A/D- ja D/Amuunnoksissa. A/D-muunnoksessa signaali suodatetaan yksinkertaisella laskostumisen estosuodattimella. N-bittiseksi kvantisoidun DS-lähdön korkeataajuinen kvantisointikohina suodatetaan desimointisuodattimella, jonka lähtödata on Nyquist-taajuinen. Vastaavasti DS D/A-muunnoksessa N-bittinen digitaalinen DSlähtö muunnetaan analogiseksi ja korkeataajuinen kvantisointikohina alipäästösuodatetaan. f f a) yksinkert. alipäästö suodatin DS ADC N Digitaalinen desimointisuodatin M (M>>N) b) M Digitaalinen interpolointisuodatin >M N digitaal. yksinkert. DS DAC analoginen alipäästös. Kuva 4. DS-muunninteknologian soveltaminen a) A/D muuntimessa ja b) D/A muuntimessa (N ja M ovat sanaleveyksiä). Ensimmäisen asteen DS-muunnin koostuu integraattorista ja yksibittisestä kvantisoijasta (komparaattorista). Termit delta ja sigma tulevat silmukan matemaattisista operaatioista: negatiivinen takaisinkytkennästä (delta) ja erotussignaalin integroinnista eli akkumulaatiosta (sigma). Kuvan 5a DS-silmukka integroi tulosignaalin ja lähtösignaalin välistä virhettä, jolloin signaali alipäästösuodattuu ja kohina ylipäästösuodattuu: yksibittisen kvantisoinnin kautta kulkeva takaisinkytkentä- ja suodatuspolku muokkaa kvantisointi-kohinan korkeammille taajuuksille, jolloin signaalikaistan kvantisointikohinatehopienenee. Tarkastellaan tilannetta lineaarisella mallilla: kuvassa 5b on 1. asteen DSmuuntimen lineaarinen malli, jossa on diskreettiaikainen integraattori. Kvantisointivirhettä e kuvataan summautuvana kohinalähteenä. Negatiivisen takaisinkytkennän ansiosta komparaattorin lähtösignaalin keskiarvo seuraa tulosignaalin tasoa. Kuvan 5b avulla saadaan ensimmäisen asteen DS-muuntimen lähdölle diskreettiaikaisessa tapauksessa V(z) = z -1 U(z) +( 1-z -1 )E(z) (3)
12 13 a) b) e u + y v u + Integraattori A/D - - z z 1 y v D/A Kuva asteen DS: a) lohkokaavio ja b) lineaarinen malli diskreettiaikaisella integraattorilla. Tällöin siirtofunktiot u:sta ja e:sta lähtöön v ovat: STFz = z 1 NTFz = 1 z 1 (4) missä STF on signaalin siirtofunktio NTF on kohinan siirtofunktio Kuvassa 6 on kohinan siirtofunktion amplitudivaste, joka on ylipäästävä. Kvantisointikohina on siis muokkautunut korkeammille taajuuksille, ja vaimenee suurimmaksi osaksi desimointisuodattimella. Tällä tavalla DS-muunnin saavuttaa korkeamman resoluution verrattuna pelkästään ylinäytteistävään muuntimeen. Tätä ominaisuutta kutsutaan kohinanmuokkaukseksi. 1 NTF (db) f / fs Kuva asteen DS-muuntimen kohinanmuokkausfunktio. Jos muuntimessa on L kappaletta peräkkäisiä integraattoreita, yksibittinen kvantisoija, sekä yksi takaisinkytkentähaara (ns. pure-differentiation topologia), kohinan siirtofunktion voidaan esittää diskreettiaikaisessa muodossa NTFz = 1 z 1 L, (5) missä L on asteluku.
13 14 Integraattoreiden lisääminen em. topologiaan jyrkentää kohinanmuokkausta. Jos muuntimessa on L integraattoria, maksimi signaali-kvantisointikohinasuhteeksi saadaan kaavalla [9]: 3 2B SNR Q db 1log L 1 = OSR + 2L + 1 (6) 2 Kaavasta saadaan yleisesti käytetty estimaatti, jonka mukaan SNR:n parannus ylinäytteistyssuhteen kaksinkertaistuessa on 3(2L+1) db per oktaavi. Tämän mukaan parannus asteen muuntimille ovat 9 db (1.5 bit), 15 db (2.5 bit) ja 21 db (3.5 bit) per oktaavi. Kuva 7 esittää asteen DS-muuntimen spektrien kohinanmuokkausominaisuuksia. Vertailukohteena on myös Nyquist-taajuudella toimivat sekä pelkästään (ei-muokkaavat) ylinäytteistävät muuntimet NTF (db) 2L f N A/D -muuntimet 3. asteen DS 2. asteen DS 1. asteen DS ylinäytteistävät A/D -muuntimet f b f s /2 f Kuva asteen DS-muuntimen kohinanmuokkausominaisuudet. Kuvassa 8 [1] on vertailtu A/D-muunninteknologioita resoluution ja kaistanleveyden kannalta. Delta-sigma -muunnin on oletettu tässä tyypilliseksi diskreettiaikaiseksi. Successive approximation (SAR) -muuntimessa A/D-muunnoksen tulos saadaan vertaamalla tulosignaalia N-bittisen D/A-muuntimen lähtöön N:llä näytteistysjaksolla. Flash-muuntimissa signaalin amplitudia verrataan joukkoon referenssejä (2 N kappaletta), jolloin mittaus tapahtuu yhdessä jaksossa 2 N -1 komparaattorilla. Pipeline-muunninta voidaan pitää SAR- ja Flash-muuntimen välimuotona, jossa hyödynnetään vertailun jäännös-informaatiota (residue).
14 15 Delta-sigma Resoluutio Successive approximation Pipeline Flash Kaistanleveys Kuva 8. Eri A/D-muunnintyyppien vertailu resoluution ja kaistanleveyden suhteen. 2.2 Kvantisointikohina Takaisinkytkentähaarassa oleva kvantisointi on epälineaarinen operaatio: se aiheuttaa dc-tulosignaalin tapauksessa DS:n lähtöön lähes aina havaittavaa rajavärähtelyä (limit cycle oscillation). Rajavärähtely on kvantisointikohinassa oleva periodisesti toistuva virhe-kuvio (pattern), joka aiheuttaa tietyntaajuisia häiriöpiikkejä. Korkeataajuiset häiriöt voivat myös olla haitallisia, koska ne voivat vuotaa signaalin kaistalle keskinäismodulaatiosärön kautta. Vaikka rajavärähtelyn luonne riippuu muuntimen asteluvusta, se on dctulosignaalilla lähes aina dominoiva. Kaavassa (6) laskettu signaalikvantisointikohinasuhde on korreloimattoman kohinan avulla laskettu approksimaatio, mutta todellisuudessa kvantisointikohina korreloi muuntimen tulosignaalin kanssa. Mikäli dc-tulosignaali on referenssijännitteen suhteen rationaaliluku, muuntimen lähtö on 1. asteen DS:lle periodista. Tällöin lähdön spektri on diskreetti ja sillä on useita spektripiikkejä eli spurreja. Tällöin puhutaan ns. kuviokohinasta (pattern noise) [9]. Kohina ei siis todellisuudessa ole luonteeltaan valkoista kohinaa. Kvantisointikohinan spektrin muoto dc-tulosignaalilla riippuu signaalitason lisäksi myös muuntimen asteluvusta. Mitä korkeampi muuntimen asteluku on, sitä satunnaisemman luonteen kvantisointikohina saa. On kuitenkin väärin kuvitella, että asteluvun kasvattaminen poistaisi rajavärähtelyn kokonaan. Kuvassa 9 on 5. asteen yksibittisen DS:n taajuusvaste dc-tulosignaalille, joka on puolet täyden skaalan tulosignaalista. Rajavärähtely osuu taajuudelle fs/4.
15 16 rajavärähtely -5 db taajuus Kuva asteen yksibittisen DS:n amplitudivaste dc-tulosignaalille. Kaavassa (5) esitetyn pure differentiation -topologian astelukua ei voi kasvattaa loputtomiin, koska tässä DS-topologiassa kvantisointikohinan amplitudi on verrannollinen lukuun 2 L. Esimerkiksi yksibittiselle kvantisoijalle L ei voi olla yli kaksi, koska tällöin muunnin on epästabiili. Epästabiilisuudella tarkoitetaan sitä, että modulaattorissa esiintyy amplitudiltaan suurempia signaalin tiloja kuin lineaarinen malli ennustaa. Epästabiililla muuntimella on olemassa jokin matala oskillointitaajuus, joka näkyy lähdössä pitkinä nollien ja ykkösten sekvensseinä. [11] 2.3 Kvantisoijan vahvistus Kvantisoinnissa signaali typistetään lähimpään kvantisointitasoon, jolloin kvantisoijan virhe on maksimissaan puolet kvantisointiaskeleesta. Kuvassa 1 on esitetty 8-tasoisen kvantisoijan vaste ramppimuotoiselle herätteelle, ja tämän kvantisointivirhe. heräte vaste virhe aika aika aika Kuva 1. Ramppimuotoisen herätteen kvantisoitu vaste, sekä kvantisointivirhe. Kun kvantisointitasoja on vähän, kvantisoijan tulon ja lähdön välinen keskiarvoistettu kulmakerroin riippuu ylityksen määrästä. DS-muuntimissa kvantisointikohina korreloi selvästi signaalin kanssa etenkin kun kvantisointitasoja on vähän, jolloin
16 17 lineaarisessa analyysissä kvantisoijaa on syytä mallintaa summattavan kvantisointivirheen lisäksi muuttuvalla vahvistuskertoimella. Tätä kerrointa kutsutaan kvantisoijan vahvistukseksi. 2.4 Suunnittelun alkuvaiheet Seuraavaksi esitellään tyypillinen delta-sigma -muuntimen suunnitteluvuo. Suorituskykyspesifikaatiot ja käytettävä ylinäytteistyssuhde kertovat karkeasti, mikä on muuntimen asteluku. Suunnitteluvuota voidaan kutsua termillä cookbooksuunnittelu [12], joka lähtee liikkeelle kohinan ja signaalin siirtofunktion analysoinnista. Signaalin siirtofunktion tulee olla tasainen ainakin signaalikaistalla. Kohinan siirtofunktion muotoon vaikuttavia asioita ovat kohinan nurkkataajuus ja estokaistan maksimivahvistus, jotka mitoitetaan haluttuihin arvoihin. Analysoinnit sekä lineaarisella siirtofunktiotasolla että aikatason simulointimallilla antavat estimaatin suorituskyvystä. Asteluvun kasvattaminen suorituskyvyn parantamiseksi saattaa tuoda muuntimen stabilisointiin liittyviä ongelmia, jolloin voidaan vaihtoehtoisesti harkita monibittisen muuntimen toteuttamista. Kun tiedetään muuntimen asteluku, OSR ja takaisinkytkentäsignaalin sananleveys, näillä parametriyhdistelmillä suorituskyvylle löytyy aina kattoarvo. Esimerkkinä tästä käy kuva 11 [12], jossa on optimoitu ja simuloitu eri asteluvun yksibittisiä muuntimia ja katsottu SNR-tuloksia OSR:n funktiona. Kun muuntimella on taipumus epästabiilisuuteen (aggressiivinen NTF, kappale 3.1.1) tai on muuten riittämätön suorituskyvyltään, ainoa mahdollisuus on kasvattaa joitain näistä parametreista. L= L=2 L=1 Kuva 11. Signaali-kohinasuhde OSR:n funktiona eri asteluvuilla L. Muuntimet ovat yksibittisiä. Topologian eli DS-muunninrakenteen valintaan vaikuttavat signaalin ja kohinan siirtofunktiot ja muuntimen takaisinkytkentäbittien lukumäärä (yksi- tai monibittinen
17 18 DS). Piirisuunnittelun kannalta myös toteutettavan topologian sisäiset signaalitasot ja piirin kompleksisuus vaikuttavat valintaan. Tyypillisesti kuitenkin valinta kohdistuu johonkin aiemmin toteutettuun, hyväksi todettuun rakenteeseen. Muunnintopologioista kerrotaan kappaleessa 4. Suorituskyvyn arviointiin voidaan käyttää joko describing function -menetelmää, (kappale 3.2.2) tai diskreettiaikaisia simulointeja (kappale 5.1), mieluimmin kumpaakin. Simulointi voidaan tehdä tietylle topologialle, mikä edellyttää topologian kertoimien ratkaisemista. Simulointeja kannattaa tehdä monella herätteellä, ja varsinkin dc-stabiilisuus kannattaa todeta erittäin pitkillä simuloinneilla. Monibittinen takaisinkytkentä parantaa suorityskykyä n. 6dB/bitti ja myös pienentää rajavärähtelyä. Monibittinen takaisinkytkentä vaatii kuitenkin poikkeuksetta linearisointia, josta kerrotaan kappaleessa 8, sillä takaisinkytkennän lineaarisuus saavutetaan automaattisesti vain yksibittisellä takaisinkytkennällä. 2.5 Diskreetti- ja jatkuva-aikainen DS A/D-toteutus Suurin osa tähän asti raportoiduista DS-muuntimista on toteutettu diskreettiaikaisina, CMOS-tekniikalla toteutettuina kytkinkondensaattori- (switched-capacitor, SC) piireillä, jolloin etuna on joustava ja helposti kontrolloitava signaalin- ja kohinansiirtofunktion suunnittelu. SC-suodattimien helppo viritettävyys on tärkeä etu: suodattimen rajataajuus (cut-off -taajuus) on muunneltavissa kellotaajutta muuttamalla [13]. Korkeasta resoluutiostaan huolimatta näillä muuntimilla on saavutettu varsin alhaisia muunnosnopeuksia. Diskreettiaikaiset DS A/D-muuntimet ovat vähemmän alttiita kellojitterille kuin jatkuva-aikaiset DS-muuntimet, mutta niiden ylinäytteistyssuhdetta rajoittaa vahvistimien kaistanleveys. Lisääntyneet vaatimukset nopeille ja tarkoille A/D-muuntimille ovatkin kasvattaneet kiinnostusta jatkuva-aikaisiin DS-muuntimiin [1]. Diskreettiaikaisten muuntimien tehonkulutuksessa valtaosa aiheutuu silmukkasuodattimesta, eli silmukkasuodattimen asettumisvaatimukset asettavat rajan aktiivisten komponenttien kaistanleveyksille. SC-toteutuksessa maksimi näytteenottotaajuutta rajoittaa operaatiovahvistimen yksikkövahvistustaajuus: nyrkkisääntö SC-suodattimen operaatiovahvistimen yksikkövahvistustaajuudeksi on noin viisi kertaa muuntimen näytteenottotaajuus. SC-DS -toteutukset eivät siis voi saavuttaa CMOS-teknologian tarjoamaa suurinta kellotaajuutta. [14] Vaikka jatkuva-aikaiset muuntimet eivät ole helposti integroitavissa, niiden avainetu on se, että näytteistys tehdään muuntimen silmukan sisällä, jolloin silmukkasuodatin ei rajoita näytteenottotaajuutta. Kun asettumisvaatimukset helpottuvat, helpottuvat myös tehonkulutusvaatimukset. Kuten sivulla 11 mainittiin, ylinäytteistys helpottaa laskostumisen estosuotimen vaatimuksia. Jatkuva-aikaisen muuntimen tapauksessa laskostumisen estosuodattimen vaatimukset helpottuvat vielä enemmän näytteistettävään verrattuna, koska nyt näytteistys tapahtuu vasta silmukkasuodattimen jälkeen. Tällöin signaalin kaistalle laskostuneet komponentit vaimenevat. Kirjallisuudessa tätä ilmiötä kutsutaan termillä itseinen (intrinsic) anti-alias-suodatus [15]. Lähteessä [16] kerrotaan jatkuva-aikaisen DS A/D-muuntimen ongelmista, toteutuksesta ja testauksesta.
18 SC-integraattori Valtaosa nykyään toteutetuista delta-sigma A/D-muuntimista on toteutettu SCtekniikalla. Jos kytkimet avataan kuvan 12 vaihekellotuksen mukaan, varaus C S (V1- V2) kulkee kapasitanssin C S läpi. Jos kellojakso on T, virtakeskiarvo on C I S V 1 V 2 V avg V = = , (7) T missä T/C S suhdetta voidaan pitää keskiarvoresistanssina R eq. Kytkinkapasitanssi approksimoituu parhaiten ekvivalentti-resistanssiksi, jos kytkentäintervalli on paljon suurempi kuin aikavakio. Kuvassa 12 on esitetty diskreettiaikaisen kytkinkapasitanssin resistanssi-ekvivalentti. R eq V 1 V 2 C S T =1/f s V1 I avg R eq V2 Kuva 12. Kytkinkapasitanssin ekvivalentti resistanssi. Kuvassa 13 on esitetty SC-integraattoreita eri kytkinkonfiguraatioilla. Valittu integraattoritopologia on suosittu parasiittisille kapasitansseille epäherkkä rakenne. Kytkimen ajoituksella voidaan vaikuttaa integraattorin viiveeseen. Siirtofunktiot kuvan 13 neljälle eri integrointikonfiguraatiolle ovat: Kokonainen viive, ei-invertoiva Puolikas viive, ei-invertoiva Viiveetön, invertoiva Puolikas viive, invertoiva Vout1 Vin Vout2 Vin Vout3 Vin Vout Vin = C S C I C S C I z z 1 z 1 2 = z 1 C S 1 = C I 1 z 1 C S z 1 2 = C I 1 z 1 (8)
19 2 a) C I Vin C S Vout1 Vout2 b) C I Vin C S Vout3 Vout4 Kuva 13. SC-integraattorin 4 konfiguraatiota: a) ei-invertoiva ja b) invertoiva integraattori. Ensimmäisen asteen DS-muuntimen switched-capacitor toteutus on esitetty kuvassa 14. A/D-muunnos tehdään komparaattorilla ja D-kiikulla, ja D/A -muunnin on toteutettu kahdella referenssijännitteellä ja kahdella kytkimellä. Kapasitanssisuhde on 1/2, mikä on todettu optimaaliseksi painokertoimeksi 1. asteen muuntimelle [17]. 2C T u C y D-kiikku 1D q C1 v -Vref Vref Kuva 14. Ensimmäisen asteen DS-muuntimen SC-toteutus.
20 Modulaattorin rakennevaihtoehdot DS-muuntimen topologia tarkoittaa tapaa, jolla silmukkasuodatin toteutetaan, ja tästä kerrotaan tarkemmin kappaleessa 4. Tässä esiteltävät rakenteelliset ratkaisut liittyvät suorituskyvyn ja stabiilisuuden parantamiseen riippumatta topologiasta. Yksibittisille DS-muuntimille asteluvun kasvattamisessa suorituskyvyn parantamiseen tulee yläraja vastaan noin 5. asteen muuntimissa, koska korkean asteluvun muuntimissa on aina suurempi riski epästabiiliin käyttäytymiseen. Korkeamman asteen muuntimille tyypillisiä ongelmia voidaan välttää kolmella tavalla: 1. MASH-DS (kuva 15), joka koostuu monesta (tyypillisesti 2-3) rinnakkaisesta matalan asteluvun muuntimesta, jossa yhtä DS-astetta seuraava aste muuntaa edellisen asteen kvantisointikohinaa ja lopullinen vaste tehdään yhdistämällä (summaamalla) digitaaliset lähdöt sopivalla suodatinvasteella (jälkimmäisten asteiden lähdöt suodatetaan) [9]. Tämä digitaalinen suodatus tuo esille uuden ongelman, koska suodatinfunktio perustuu usean perättäisen DS asteen NTF:sta ja STF:sta: kvantisoijan vahvistuksen muuttumisen aiheuttama epäsovitus aiheuttaa suorituskyvyn alenemista. Tähän on esitetty mm. adaptiiviseen virheenkorjaukseen liittyviä ratkaisuja [18]. Tässä työssä ei juuri käsitellä MASHtyyppisiä muuntimia, koska MASHin yksi aste on kuitenkin perus-ds, jota täytyy myös analysoida sellaisenaan. 2. Monibittinen kvantisointi ja takaisinkytkentä, jonka käyttö helpottaa astelukuvaatimuksia, mutta tuo esille takaisinkytkentähaaran D/A-muuntimen linearisoinnin pakollisuuden (tarkemmin kappaleessa 8). 3. Monibittinen lähtö ja yksibittisen takaisinkytkentä on mahdollista yhdistää ns. Leslie-Singh -rakenteessa [19] (kuva 16), joissa monibittinen lähtö ja suodatettu kvantisointikohina summataan lähtösanaksi. Tällöin vältytään takaisinkytkentä- D/A-muunnoksen epäsovitusongelmilta, mutta digitaalisen suodatuksen epäsovitusongelmat on mahdollisia, kuten MASH-DS:ssa. tulo kvantis. kvantis. kvantis. 1. DS virhe 2. DS virhe virhe M. DS aste Digitaalinen suodatus lähtö Kuva 15. MASH DS, jossa M kappaletta DS-muuntimia.
21 22 tulo DS silmukka suodatin out N + - lähtö 1 MSB out-msb Digitaalinen suodatus Kuva 16. Leslie-Singh -DS (N-bittinen). 2.8 Desimointisuodattimet Desimointisuodattimen tehtävä on muuntaa signaali takaisin Nyquist-taajuudelle siten, että signaalikaistan ulkopuolinen kvantisointikohina ei laskostu signaalin kaistalle. Desimointisuodatus on järkevää tehdä useassa desimointiasteessa, koska se vähentää desimointipiirin kompleksisuutta sananleveysvaatimusten osalta. [2] Tyypillisesti ensimmäinen desimointiaste on sinc-tyyppinen suodatin. Se sisältää K kappaletta DS:n näytteistystaajuudella toimivia integraattoreita, joita seuraa K kappaletta alennetulla näytteistystaajuudella toimivia derivaattoreita. Etuna on yksinkertaisuus: ei tarvita digitaalisia kertojia. Sinc K -suodattimen siirtofunktio on ja taajuusvaste Hz Hj missä D on desimointikerroin, K on asteluku ja on normalisoitu kulmataajuus (...2). Riittävä sinc K -suodattimen asteluku K on tyypillisesti [2] z D = D 1 z 1 (9) K sind 2 = D sin 2, (1) K eli DS:n asteluku plus yksi. K=L+1, (11)
22 23 Kuvassa 17 on esitetty 7. asteen sinc K -suodattimen vaste, jossa on sincamplitudivasteelle ominaiset uurrokset (notch). Sinc K -suodatin vaimentaa tehokkaasti korkeataajuisen kvantisointikohinan, mutta sen siirtokaista on varsin loiva. Siksi viimeinen desimointiaste on tyypillisesti jyrkkä FIR (finite impulse response) - tyyppinen desimointi, jolla on pieni desimointikerroin (usein 2). Suodattimien toteutustapoja on paljon, ja eräs ratkaisu on half-band -suodatin (HBF), jossa päästöja estokaista ovat yhtä leveitä ja niiden rippelit ovat yhtä suuret. Kuvan 17 viimeinen aste ei ole desimoiva, vaan se ekvalisoi loivan sinc-suodattimen aiheuttamaa signaalikaistan reunan muutaman desibelin vaimennusta. Kyseessä on nk. fs lähtö Mag (db) Mag (db) DS lähtö SINC -3 fb Mag (db) fs/2-12 fb HBF Ekvalisointi -8 Mag (db) 1 fb 2*fb Mag (db) Desimoitu. Desimoitu. lähtö Kuva 17. Desimointiasteet: sinc K, jyrkän siirtokaistan suodatin (HBF) ja viimeisenä asteena droop-ekvalisointi. Jos viimeisen desimointiasteen jyrkkyysvaatimukset ovat erittäin suuret (kuten kuvan 17 esimerkin 4-bittisen DS:n lähdön desimoinnissa) voidaan useasta identtisestä halfband suodattimesta koota jyrkkä siirtokaistan suodatin. Tästä esimerkkinä kuva 18, jossa yksittäinen lohko F on 8. asteen half-band -suodatin. Tässä tulosignaali näytteistetään kaksinkertaisella näytteistystaajuudella ns. monivaihe-suodatuksessa (polyphase filtering) [2,21]. fb -12 fb freq F F F F F.5 z -6 z -11 z -11 Kuva 18. Jyrkän siirtokaistan polyphase-desimointiaste, jossa F on yksittäinen halfband -suodatin.
23 24 3. DELTA-SIGMA MODULAATTORIN ANALYSOINTIMENETELMÄT Tässä kappaleessa kerrotaan lähinnä lineaarisen analysoinnin keinoista, joiden perusteella valitaan delta-sigma -muuntimen kohinan siirtofunktio, eli NTF. Siirtofunktiotason analyyseillä voidaan saada hyvä tuntuma muuntimen käyttäytymisestä ja suorituskyvystä jo ennen topologian valintaa ja aikatason simulointeja. 3.1 Lineaarinen malli Kuvassa 19 on yleinen DS-modulaattorin silmukkasuodatinmalli, jossa kvantisoija on linearisoitu ja sen vahvistus k on oletettu ykköseksi. Silmukkasuodattimella on kaksi siirtofunktiota tuloista U ja V lähtöön Y. Tällöin lineaarisen silmukkasuodatinlohkon lähtö Y on: Yz = L zuz + L 1 zvz (12) u v L L1 silmukkasuodatin y k=1 e kvantisoijan kohina v Kuva 19. DS-muuntimen lineaarinen malli, jolla on kaksituloinen silmukkasuodatin. Koska kvantisointivirhe E on V:n ja Y:n erotus, edellinen kaava voidaan muuntaa tulo- ja virhesignaalin U ja E mukaan, jolloin DS-muuntimen lähtö on Vz = STFzUz + NTFzEz, (13) jossa STF on signaalin siirtofunktio ja NTF on kohinan siirtofunktio. Silmukkasuodatin-siirtofunktiot ovat siten
24 25 L z L 1 z = STFz NTFz = NTF z 1 NTFz josta vastaavasti signaalin ja kohinan siirtofunktiot ovat L STFz z = L 1 z NTFz = L 1 z, (14) (15) Signaalin siirtofunktiota voidaan pitää tässä tapauksessa pelkkänä signaalin esisuodattimena, jolloin voidaan keskittyä kohinan siirtofunktioon stabiilisuuden tutkimisessa. Tällainen mallinnustapa valitettavasti kätkee kvantisointikohinan signaaliriippuvuuden. Jos kvantisoijan efektiivinen vahvistus k ei ole kuvan 19 tapaan yksi, kvantisoijan virheeksi tulee Ekz = Vz kyz (16) jolloin uudeksi signaalin ja kohinan siirtofunktioiksi tulee ja NTFk z STFk z missä NTF(z) ja STF(z) ovat kaavasta (15). = = NTFz (17) 1 + k L 1 z k + 1 kntfz k L z = = k STFz, (18) 1 + k L 1 z k + 1 kntfz Nyt siirtofunktiot ovat muuttuneet ja ovat pahimmassa tapauksessa epästabiileja jollakin k:n arvoilla. Kvantisoijan vahvistuksen todellista arvoa voidaan estimoida diskreettiaikaisten simulointitulosten nojalla, jolloin saadaan järkevä arvaus sille, miten vahvistus voi muuttua eri herätteillä tai vaikkapa kaistan ulkopuolisen häiriösignaalin tilanteessa. Vahvistuksen laskennasta kerrotaan tarkemmin kappaleissa (analyyttinen menetelmä) ja 5.3 (simulointiin perustuva menetelmä). Kun kvantisoijan vahvistuksen vaihtelu tiedetään, voidaan varsin tarkasti määritellä, paljonko esim. NTF:n navat voivat liikkua. Tämä on hyvä tietää, koska korkeamman asteen ja pienen ylinäytteistyssuhteen muuntimen tapauksessa siirtofunktion navat voivat siirtyä signaalin kaistalle, mikä voi olla haitallista. Kun jokin parametri signaalissa muuttuu (hyötysignaali tai summautunut häiriösignaali), myös kvantisoijan vahvistus muuttuu. Tämä voi olla suunnittelun kannalta hankalaa. Kuvassa 2 on esitetty testauksen idea, jossa yhden sinimuotoisen häiriösignaalin taajuutta pyyhkäistiin signaalikaistan reunalta aina puoleen näytteistystaajuuteen. Kuvassa 21 on simulointitulosten avulla estimoitu kvantisoijan vahvistusta sinimuotoisen hyötysignaalin amplitudin sekä kaistan ulkopuolisen
25 häiriösignaalin taajuuden funktiona. Tässä häiriösignaalin amplitudi pysyy vakiona (5% täydestä skaalasta). tulosignaali [db] Hyötysignaali signaalikaista tuloon summautunut häiriösignaali f b pyyhkäisysuunta fs/2 Kuva 2. Tuloon summautuvan häiriösignaalin pyyhkäisy kvantisoijan vahvistuksen mittauksessa. Kuvan 21 vaaka-akselissa on näytteistystaajuuteen normalisoitu häiriösignaalin taajuus logaritmisena ja pystyakselilla on hyötysignaalin amplitudi desibeliasteikolla. Kvantisoijan vahvistus muuttuu selvästi välillä [1,2 1,8], joten kohinan siirtofunktiota on syytä tarkastella myös näillä parametreilla käyttäen kaavaa (17). Kvantisoijan vahvistus k ampl (db) log 1 ( f / f s ) Kuva 21. Simuloitu estimaatti kvantisoijan vahvistuksen muuttumisesta hyötysignaalin amplitudin ja häiriösignaalin taajuuden funktiona. Kun kvantisoija ylikuormittuu, sen efektiivinen vahvistus laskee. Tämän seurauksena syntyy yleensä matalataajuinen rajavärähtely, koska takaisinkytketyn signaalin amplitudi on liian pieni verrattuna muihin integraattoreihin tuleviin signaaleihin. Tällöin stabiili tulosignaalitaso on ylitetty. Kaavasta (12) saadaan kvantisoijan tuloksi Ykz = STFk zukz + NTFk z 1Ekz. (19) Nyt termin NTF(z)-1 vahvistus eli yksinkertaisesti NTF:n vahvistus ei saa olla liian suuri. Siirtofunktiolle NTFz = 1 z 1 L ( pure-differentiation -topologia) maksimivahvistus on NTF(-1) = 2 L. Tämä selittää hyvin, miksi asteluvun L kasvaessa voidaan törmätä stabiilisuusongelmiin. Kvantisoijan mallin tulisi siis analyysiä varten olla kehittyneempi. Tällaisesta kerrotaan kappaleessa 4.
26 NTF:n valinta Edellisessä kappaleessa esitetyn kohinan siirtofunktion 1 z 1 L käyttö rajoittuu stabiilisuusongelmiensa takia yleensä teoreettiseen tarkasteluun. Stabiilisuusongelman välttämiseksi siirtofunktiota voidaan muokata lisäämällä siihen napoja, jolloin NTFz 1 z 1 = , (2) Dz missä nimittäjän D(z) tehtävänä on tasoittaa ylipäästävän siirtofunktion korkeataajuista osaa. Oikealla D(z):n valinnalla funktio voi olla esim. Butterworthylipäästöfunktio [12]. D(z):n määrittämiseen vaikuttaa haluttu funktion vahvistuksen maksimi sekä ylinäytteistyssuhde. Butterworth-funktio on yleinen valinta kaupallisissa DS-muunnintoteutuksessa, koska tällöin funktion kompleksisten napaparien hyvyysluku Q saadaan varsin pieneksi. Jos napojen Q on suuri, muunnin on altis ei-toivotulle oskilloinnille, jos tulosignaalissa on samaisella taajuudella häiriösignaalia. Kompleksisten napojen tulisi olla myös kaukana signaalin kaistalta. Toinen yleinen NTF-tyyppi on navoiltaan kaavan (2) mukainen, mutta nollia siirretään pois dc:ltä. Toisin sanoen funktiolla on kompleksisia signaalin taajuuskaistalle olevia nollapareja, jotka vaimentavat päästökaistan vahvistusta, jolloin signaali-kvantisointikohinasuhde saadaan alemmaksi kuin Butterworth-tyypin NTF:llä. Mitä enemmän kompleksisia nollapareja funktiossa on, sitä laajakaistaisemmaksi saadaan kohinan vaimennus signaalilla kaistalla, mutta tällöin piiritoteutus on myös kompleksisempaa. Kuvassa 22 on esitetty tässä mainitut kohinan siirtofunktion muodot. L 1 z 1 L 1 z Dz L Xz Dz kompl. nollat kompl. nollapari Kuva 22. NTF malleja: a) Pure-differentiation, b) Butterworth-navat ja c) Butterworth-navat ja kompleksinen nollapari X(z).
27 28 NTF:n ylipäästösuodatinvaste-tyyppinä Butterworth, kompleksiset nollat (inverse Chebysev), tai maksimaalisen tasainen all-pole vaste ovat raportoiduimpia. Erikoisempaa suodatinta valittaessa täytyy muistaa, että joillakin suodatintyypeillä muuntimen sisäiset kertoimet tai integraattorien lähtösignaalitasot voivat olla toteutuksen kannalta liian suuria. Jotta kohinan siirtofunktio on myös realisoitavissa, sen täytyy olla kausaalinen. Takaisinkytketyn signaalin täytyy siis olla viivästetty vähintään yhdellä näytteistysintervallilla. Jos DS-muunnin todetaan epästabiiliksi, kaistan ulkopuolista maksimivahvistusta pitää pienentää. Monessa julkaisussa päteväksi osoittautuneen nyrkkisäännön mukaan amplitudivasteen vahvistus yksibittisille muuntimille kannattaa skaalata 1,5:ksi (ns. Lee:n nyrkkisääntö [11]). Tämä skaalaus tehdään alentamalla suodattimen nurkkataajuutta. Jos muuntimen signaali-kohinasuhde (SNR) ei ole riittävä, voidaan kokeilla maksimivahvistuksen kasvattamista. Kun tämä maksimivahvistus on lähellä epästabiilisuden rajoja, puhutaan aggressiivisista kohinan siirtofunktioista. Funktion aggressiivisuus näkyy mm. siinä, että tulosignaalin maksimiamplitudia täytyy stabiilisuus-ongelmien takia rajoittaa huomattavasti (esim. 2%:iin täyden skaalan signaalista). Aggressiivinen siirtofunktio voi huomattavasti parantaa suorituskykyä, mutta siinä piilee vaaransa, koska muunnin on stabiilisuuden rajoilla. Tällöin erittäin pienet muutokset piiritason toteutuksessa (piirin kohina sekä kapasitanssisuhteen epäsovitus) voivat aiheuttaa epästabiilin tilanteen, ja kvantisoijan vahvistus elää. Jos ei tiedetä, missä rajoissa kvantisoijan vahvistus käytännössä liikkuu, ovat stabiilisuusongelmat erittäin todennäköisiä. Delta-Sigma Toolbox [2] sisältää kaksi kohinan siirtofunktion synteesifunktiota. Näistä ensimmäinen, synthesizentf on tarkoitettu yksibittisille muuntimille, jossa annetaan argumentit asteluvulle, ylinäytteistyssuhteelle, sekä sille, tuleeko NTF:lle kompleksisia nollapareja. Toinen funktio clans on tarkoitettu monibittisten muunninten NTF:n generoimiseen. Tässä funktiossa optimoidaan iteratiivisesti suljetun silmukan napoja siten, että funktion maksimivahvistus pysyy käyttäjän antamissa rajoissa. Menetelmä perustuu ideaan [22], että kvantisoijan ylikuormituksesta vältytään jos kvantisointi kohina täyttää X kvantisointitasoa, missä X:n maksimiarvo on kvantisointitasojen lukumäärä. Matemaattisesti ehto on muotoa: X ntf 1 1, (21) missä X kertoo montako kvantisointitasoa kvantisointikohina täyttää ja ntf 1 on impulssivasteen ykkösnormi eli impulssivasteen itseisarvojen summa. Alkuperäinen clans-funktio optimoi vain signaalikaistan reunalla olevaa vahvistusta, mikä aiheuttaa ongelmia, jos ylinäytteistyssuhde on pieni. Tällöin NTF voi optimoitua väärin signaalikaistalla. Ongelma ratkaistiin tässä työssä muokkaamalla optimointikriteeriä siten, että asetetaan optimoinnin tunnusluvuksi koko signaalikaistan RMS-kohina. Kuvassa 23 on esitetty alkuperäisen ja parannetun optimoinnin tulos.
28 Max. gain = 4.65 (13.3 db) Max. gain = 3.7 (9.7 db) -1 db clans clans+rms f / f s Kuva 23. Monibittisen, pienen OSR:n (=8) DS:n synteesi: alkuperäinen clansfunktio (vihreä käyrä) ja parannettu versio (musta käyrä). Kun valitaan X eli montako kvantisointitasoa kvantisointikohinan annetaan käyttää, n. 75%:n osuus on konservatiivinen ratkaisu. Lähelle 1% tuottaa aggressiivisen kohinan siirtofunktion. 3.2 Lineaarinen analyysi Yksibittisestä takaisinkytkennän kvantisoinnista johtuen muuntimen epälineaarinen luonne tekee jopa 1. asteen DS:n analyysistä erittäin kompleksista [23]. Koska tyhjentävä matemaattinen analyysi on joko erittäin monimutkaista tai kokonaan vielä ratkaisematta, useimmat suunnittelijat turvautuvat lineaariseen analyysiin sekä simulointeihin. Useimmiten lineaarinen analyysi on kvantisoinnin korvaamista signaalista riippumattomalla kohinalähteellä, jolloin systeemiä voidaan käsitellä siirtofunktiotasolla.
29 Juuren ura Siirtofunktiotasolla voidaan selvittää, millä kvantisoijan vahvistuksen arvolla DSmuunnin pysyy stabiilina. Diskreettiaikaiselle siirtofunktiolle stabiilisuusehtona on funktion napojen pysyminen yksikköympyrän sisällä. Kuvassa 24 on esitettynä toisen ja viidennen asteen muuntimen juuren urat eli napojen liikkuminen, kun kvantisoijan vahvistus k kasvaa.1:stä 3:en. Jälkimmäinen näistä on epästabiili, kun k on pienempi kuin 1. a) b) k=3 k=.1 k=3 k=.1 Kuva 24. NTF:n juuren ura kvantisoijan vahvistuksen kasvaessa a) toisen asteen DS-muuntimelle ja b) viidennen asteen muuntimelle (stabiili, kun k1). Kuvassa 25 on edellisiä juuren uria vastaavat korkeuskäyräkuvat kohinan siirtofunktiosta k:n funktiona. Viidennen asteen muuntimessa huomataan korkeilla taajuuksilla selvää piikitystä, kun k on n. 1 (epästabiili). fs/2 a) 7 fs/2 piikitys b) taajuus (log) taajuus (log) } { signaalikaista k k Kuva 25. NTF:n amplitudivasteen korkeuskäyräkuvaaja (db), a) toisen ja b) viidennen asteen DS:lle. Juuren uraa voidaan käyttää myös rajavärähtelyn synnyn ennustamiseen [24]. Yksibittiselle DS:lle kvantisoijan vahvistuksen lisäksi kvantisoijan aiheuttaman vaiheensiirron vaikutusta voidaan mallintaa lineaarisesti: vaiheensiirto (vaiheepävarmuus, phase uncertainty) johtuu kvantisoijan lähtösignaalin tilan muuttumishetken viiveestä. Juuren ura -menetelmän järkevä käyttö vaatii arvion, millä välillä kvantisoijan vahvistus liikkuu. Seuraavassa kappaleessa kerrotaan eräästä arviointimenetelmästä.
30 Kuvaavan funktion menetelmä Kuvaavan funktion menetelmällä (describing function method) on tarkoitus estimoida kvantisoijan vahvistusta lineaarisella analyysillä. Analyysi tehdään aina tietylle spesifiselle tulosignaalin tyypille (sini tai tasajännite), ja kvantisointi korvataan lineaarisella vahvistuksella, joka minimoi todellisen ja lineaarisen kvantisoijan mallin välisen neliöllisen eron. Kuvaava funktio tarvitsee kvantisoijan vahvistuksesta mallin, joka riippuu signaalin tilastollisista ominaisuuksista. Ardalan ja Paulos [25] kehittivät tällaisen mallin, ja se perustuu yleistettyyn kuvaavan funktion menetelmään. Tässä menetelmässä yksibittinen muunnin jaetaan kahteen lineaariseen systeemiin, toinen signaalille, toinen kohinalle. Tässä esitetyssä mallinnuksessa [12] on käsitelty pelkästään dc-tulosignaaleja ja yksibittistä takaisinkytkentää. Kvantisoijan tulosignaali y voidaan jakaa kahteen osaan (kuva 26): y signaalille, y 1 kohinalle. Tässä y on y:n keskiarvo ja y 1 on satunnainen ja nollakeskiarvoinen komponentti. Jos tulo olisi muuta kuin dc:tä, y olisi komponentti, joka korreloi tulon kanssa ja y 1 olisi edellisen jäännös. Signaali vahvistetaan signaalin kvantisoijan vahvistuksella k ja kohina k1:llä. Kvantisoijan vahvistukset k ja k 1 mallinnetaan siten, että mallinnusvirhe e on mahdollisimman pieni: missä sgn on signum-funktio. e = sgn(y + y1) - k y - k 1 y, (22) u Silmukka- suodatin y y y 1 k k 1 e v Kuva 26. Lineaarinen malli sekä signaalin että kohinan vahvistukselle kvantisoijassa. Mallinnuksessa e minimoidaan pienimmän neliösumman periaatteella. Tässä mallinnustavassa muunnin jaetaan siis kahteen osaan, signaalille ja kohinalle, kuvan 27 mukaisesti.
31 32 a) u L L1 y out b) L L1 y 1 e out Kuva 27. Kvantisoijan vahvistuksen mallinnus a) signaalille ja b) kohinalle. Olettaen, että e on valkoista kohinaa ja STF(z) on yksi, Ardalan ja Paulos päätyivät seuraavanlaisiin tilastollisiin yhteyksiin: Kvantisointikohina e ja lähtö oletetaan korreloimattomiksi, eli virhesignaali e oletetaan valkoiseksi kohinaksi varianssilla e 2 missä erf on virhefunktio y1:n varianssi ja vahvistus k1 ovat : 1 u 2 2 = -- exp 2erf 1 u 2, (23) x erfx = 2 e t2 dt. (24) 1 2 = e 2 2 NTFz 2 (25) k = -- exp 2erf 1 u 2 missä NTF(z) 2 on NTF:n tehovahvistus, eli 2-normi, kun NTF on (26) NTF(z) = L 1 (z) / (1 - k 1 L 1 (z) ) (27) Parametrit y ja k ovat tällöin y = 1 erf 1 u (28) ja y 1 k = ----erf (29) y 2 1
32 33 Delta Sigma toolboxin funktio predictsnr tekee describing function -analyysin halutulle kohinansiirtofunktiolle. Ohjelma laskee eri tulosignaalin tasolle kvantisoijan vahvistuksen dc-tulosignaalin tapauksessa sekä laskee suorituskykyarvion. Suorituskyvyn estimaatti on lähes poikkeuksetta lähellä tarkemmin simuloituja arvoja. Kuvassa 28 on estimoitu 5. asteen muunninta, jossa kvantisoija ylikuormittuu varsin pienellä signaalin tasolla (noin 4% täyden skaalan signaalista). Tämä ohjelma pätee vain yksibittisille muuntimille ja dc-tulosignaaleille. Kappaleessa 5.3 kerrotaan tässä työssä kehitetystä menetelmästä, jossa kvantisoijan vahvistuksia signaali- ja kohina-osalle lasketaan simulointitulosten perusteella minkä tahansa tulosignaalin avulla ja mille tahansa takaisinkytkentäbittien lukumäärälle. 115 SNR (db) amp (db) e 2 k kvantisoijan vahvistus kvantisointikohinateho amp (db) signaalin osuus k kohinan osuus k amp (db) Kuva 28. SNR, virhesignaalin varianssi sekä kvantisoijan vahvistukset signaali ja kohina-osalle.
33 Siirtofunktion kompleksiset navat Pienellä ylinäytteistyssuhteella kompleksiset navat voivat olla ongelmallisia. Koska kompleksiset navat voivat olla haitallisia signaalin kaistalla, kannattaa NTF:n nollanapakarttaa tarkastella jo suunnittelun alkuvaiheessa. Simuloinneilla voidaan myös tarkastaa, voivatko ne esim. liikkua tietyllä hyötysignaalilla tai häiriösignaalilla. Kuvassa 29 on esitetty erään kuudennen asteen muuntimen nollanapakartta, josta huomataan kompleksiset navat signaalikaistalla. Esimerkki on liioiteltu, koska asteluvun kasvattaminen korkeaksi ei juuri hyödytä, kun OSR on 8: kompleksisten napaparien siirtämistä korkeammille taajuuksille rajoittaa sallitun kvantisointikohinan maksimitaso annetulla kvantisoijan tasojen lukumäärällä. /2 kompleksisia napoja... /OSR SIGNAALIKAISTA...signaalikaistalla! /OSR /2 Kuva asteen DS:n NTF:n nollanapa-kartta. OSR on pieni ja kompleksisia napoja ei voida siirtää kaistan ulkopuolelle. Korkeamman asteen NTF:n syntesointi-ohjelmaan (clans) tehtiin lisäyksiä em. ongelman välttämiseksi: asetetaan lisäkriteeriksi napojen sijainti pois signaalin kaistalta ja asetetaan vielä turvamarginaali kvantisoijan vahvistuksen muuttumisen varalle. Kuvassa 3 on esitetty kolmannen asteen muuntimen kvantisoijan vahvistuksen muuttuminen, kun kaistan ulkopuolisen häiriön taajuutta muutetaan (ks. kuva 2, sivulla 26). Vahvistus muuttuukin jonkin verran, ja vasemmalla on NTF:n juuren ura sekä kompleksisen napataajuuden pahimman tapauksen muutos vahvistuksen k muutosalueella. Myös signaalin amplitudia on pyyhkäisty, ja oikealla puolella nähdään kvantisoijan vahvistuksen (kohinalle) ja SNR:n muutokset häiriön taajuuden ja signaalin amplitudin funktiona. Kuvasta 3b havaitaan, että kompleksisten napojen muutosalue näyttäisi pysyvän signaalikaistan ulkopuolella, tosin melko niukasti. Tässä esimerkissä kvantisoijan vahvistusta on estimoitu simuloinneilla kappaleessa 5.3 esitettävällä metodilla.
34 35 a).6.4 Real b) Imag.9 fnapa / fs.8.7 signaalikaistan yläraja Qgain kvantisoijan vahvistus c) amp(db) SNR (db) fblock/fs d) kvantisoijan Knoise vahvistus fblock/fs Kuva asteen yksibittinen feed-forward-ds, jonka OSR on 8. a) Juuren ura kvantisoijan vahvistuksen k vaihtelualueella, b) NTF:n kompleksisen napaparin taajuuden muutos k:n funktiona ja c) SNR ja d) kvantisoijan vahvistus tulosignaalin amplitudin ja häiriösignaalin taajuuden fblock funktiona.
35 QTF - kvantisoijan mallinnus särön analyysissä Tässä kappaleessa esitetään kvantisoijalle keskiarvostettu malli, jolla voidaan ennustaa DS-muuntimen suorituskykyä ja särökäyttäytymistä. Kun DS-muunninta simuloidaan usealla dc-amplitudilla, saadaan kvantisoijan tuloa ja lähtöä keskiarvostamalla kuva kvantisoijan epälineaarisuudesta. Jos tämä kuvaaja sovitetaan kolmannen asteen polynomiin saadaan ns. kvantisoijan siirtofunktio (quantizer transfer function) QTF [12]: v = k 1 y + k 3 y 3, (3) missä termiä k1 voidaan pitää kvantisoijan vahvistuksen estimaattina ja kolmannen asteen termistä voidaan tulkita myös muuntimen aggressiivisuutta. DS-muuntimissa silmukan kohinan tiheysfunktio riippuu dc-tulosignaalista, joten matalalla taajuudella vastetta voidaan mallittaa QTF-funktiolla, joka voidaan ymmärtää keskiarvostettuna epälineaarisuusfunktiona. Kuvan 31 aikatason QTF-funktio sisältää siis tietoa muuntimen siirtofunktiosta kvantisoijan vahvistuksen funktiona (kaava (15)) sekä myös särökäyttäytymisestä. u DC Silmukka- suodatin y QTF v Kuva 31. Matalataajuinen DS-mallinnus kvantisoijan siirtofunktiolla. Kun termi k 1 sijoitetaan NTF:ään ja normalisoidaan kaava (3) k 1 :n suhteen, kvantisoijan siirtofunktiota voidaan käyttää särön analyysiin pientaajuiselle signaalille. Tällöin DS:n lähtöä v approksimoidaan kaavalla. v = y + d 3 u 3, (31) missä u on DS:n tulosignaali y on normalisoitu kvantisoijan tulosignaali särömallissa, y = y/k 1 d 3 on k 3 /k 3 1 Kuvan 32 mukaisesti särökomponentin mallinnuksessa särö voidaan redusoida muuntimen tuloon olettaen, että STF(z) on yksi. Tällöin signaalin suhde kolmannen asteen särö-komponenttiin on [12]: 2log , (32) d 3 A 2 NTFk 1 z missä A on signaalin amplitudi ja NTF(k 1,z) on NTF kvantisoijan vahvistuksella k 1 (kaava (17))
36 37 Kaavaa (32) voidaan tulkita myös säätötekniikan perusteella, eli takaisinkytkentä vaimentaa säröä silmukkavahvistuksen verran [27]. d3 (...) 3 NTF UUSI (z) u = A p-p L = 1/NTF UUSI L1 = 1 - L y Kuva 32. Matalataajuinen särömalli. Kuvassa 33 on julkaisusta [28] poimitulle viidennen asteen muuntimelle laskettu QTF (sama kuin kuvan 28 esimerkki). Kvantisoijan vahvistus pienillä amplitudeilla on sama kuin describing function -menetelmällä saatu. Termi k 1 on siis 2.7 ja särökerroin d3 on noin Lineaarisen termin itseisarvo on suurempi kuin yksi, mikä lupaa melko aggressiivista kohinan siirtofunktiota, joten tässä mallissa maksimi tulosignaalialue on rajoitettu 15%:in täyden skaalan signaalista (-16.5dB). Kohinan siirtofunktion (jossa k 1 on huomioitu) vahvistus signaalikaistan reunalla on n. -8dB ja db:n tulosignaalilla pahimman tapauksen signaali-särösuhde on kaavan (32) mukaan 94 db. Näin siis tasajännitteillä mitattua QTF-käyrää voidaan käyttää ennustamaan muuntimen säröä ja kvantisoijan sallittua signaalialuetta..4 QTF(x) = -13.7x x u y Kuva 33. Viidennen asteen yksibittisen DS:n [28] QTF.
37 Epälineaarinen analyysi Epälineaarisen analyysin menetelmät eivät ole järin suosittuja DS-muuntimen suunnittelijoiden keskuudessa. Epälineaarisen analyysin matemaattisesti erittäin raskaat julkaisut ovat kuitenkin valottaneet joitain tärkeitä aspekteja DS-muuntimen käyttäytymisestä. Spektraalinen analyysi pohjaa ergodiseen teoriaan ja kvantisointikohinan autokorrelaatiofunktioon [29-31]. Sillä on pystytty todistamaan, että (1-z -1 ) L - topologian kvantisointikohina ei ole valkoista vaan tuottaa periodisen lähdön, kun dctulosignaali on rationaaliluku. Lisäksi analyysillä on pystytty todistamaan, että sinc K - suodatin on DS-muuntimelle optimaalinen desimointisuodatin-esiaste [31]. Geometrinen analyysi tutkii integraattorin lähdön liikeratoja, ja pyrkii löytämään ns. lukkiutumisalueen (trapping region), josta integraattorin lähtö ei poikkea [32]. Stabiilisuuden takaaminen tehdään identifioimalla tilamallin tilojen liikeradat toistensa suhteen. Kuvassa 34 [1] on toisen asteen systeemille iteroitu stabiili lukkiutumisalue, jolla voidaan myös todistaa rajavärähtelyä ja stabiilisuutta [1]. Menetelmällä on voitu todistaa yksittäisten asteen muuntimien dc-stabiilisuutta - laskennallinen kompleksisuus tosin kasvaa eksponentiaalisesti muuntimen asteluvun funktiona. (a) (b) Kuva 34. Lukkiutumisalue, jossa x1 ja x2 ovat integraattoreiden lähtösignaaleja: a) Stabiili lukkiutumisalue ja b) dc-tulosignaalitasoa nostetaan stabiilin alueen maksimiin. Kolmas menetelmä, eli epälineaarinen dynamiikka (nonlinear dynamics), keskittyy myös integraattorin käyttäytymiseen, tosin piirin epäideaalisuuden kautta. Tarkoituksena on löytää raja integraattorin dc-vahvistukselle. Kun dc-vahvistus on liian pieni, tietyllä dc-signaalitasojen välillä DS:n lähtö pysyy samana. Tällöin puhutaan dead-zone -alueesta, jolloin muuntimen resoluution huononeminen riippuu alueen koosta. Rajallista dc-vahvistusta mallinnetaan kuvan 35 tapaan integraattorilla, jolla on alle ykkösen takaisinkytkentäkerroin. Analyysin avulla on todettu, että kun dc-tulosignaali on nollatason lähettyvillä, dc-tasot välillä 1 p 1 + p, 1 p1 + p tuottavat saman DS-lähdön. Tämän avulla suunnittelija voi päätellä, millä dc-vahvistuksen arvolla resoluutio pienenee. [33] + + viive Kuva 35. Äärellisen dc-vahvistuksen integraattori (p on pienempi kuin yksi). p
38 39 4. TOPOLOGIATASON ESITYS 4.1 Tärkeimmät topologiat Tietylle siirtofunktiolle voidaan realisoida varsin useita topologioita. Variaatioita on paljon, koska DS:n peruslohkot eli integraattorit ja resonaattoriparit voidaan toteuttaa eri viiveillä. Perusmuotoja DS A/D-muuntimelle on kuitenkin kaksi kappaletta, eli feed-forward ja multiple-feedback -topologiat. Kyseisiä topologioita voidaan käyttää DS D/A-muuntimissakin, mutta yleisin DS D/A-muuntimen topologia on kolmantena esitettävä topologia, eli ns. error-feedback -topologia Feed-forward (FF) -topologia Kuvassa 36 on FF-topologialle ominainen silmukkasuodattimen rakenne. Signaali y kvantisoidaan, ja kvantisoitu DS:n lähtö out toimii silmukkasuodattimen toisena tulona, joten silmukkasuodattimella on kaksi tuloa ja yksi lähtö, kuten sivun 24 lohkokaaviossa. in b1 b2 b3 g1 INT c1 INT a2 y a1 in out b1 b2 b3 b4 g1 INT c1 INT c2 INT a3 a2 a1 out y Kuva 36. FF-topologian 2. ja 3. asteen silmukkasuodatin. Kuvassa 36 on rakenneperiaatteet sekä parillisen että parittoman asteluvun muuntimen rakenteelle. Muunnin koostuu ketjusta integraattoreita, joiden lähdöt summataan painokertoimilla a i ennen kvantisointia. Kertoimet c i ovat
39 4 integraattoriketjun painokertoimia. Kertoimilla g i saadaan aikaan kompleksiset nollat kohinan siirtofunktioon, ja kertoimilla b i voidaan muokata signaalin siirtofunktiota. Perusrakenne ilman g1-kertoimia ja yhdellä tulokertoimella (b 1 ) antaa identtiset silmukkasuodattimet L ja L 1 : L a L z L 1 z 1 a a n = = = z 1 z z 1 n (33) n = 1 ja signaalin ja kohinan siirtofunktion välinen yhteys on: STFz = 1 NTFz. (34) Multiple-feedback (MF) -topologia Kuvassa 37 on vastaava silmukkasuodatinperiaate parillisen ja parittoman asteluvun MF-topologialle. Rakenteellinen ero FF-topologialle on se, että takaisinkytkentähaaroja on aina asteluvun verran, ja vain viimeisen integraattorin lähtö viedään kvantisoijalle. in b1 b2 b3 g1 INT c1 INT c2 y a1 a2 in out b1 b2 b3 b4 g1 INT c1 INT c2 INT c3 y a1 a2 a3 out Kuva 37. MF-topologian 2. ja 3. asteen silmukkasuodatin.
40 41 Perusmuodossaan, eli jälleen ilman resonaattoria ja yhdellä tulokertoimella silmukkasuodattimet ovat: ja L 1 z a 1 L z a 2 = z 1 L z 1 L 1 Kohinan ja signaalin siirtofunktiot ovat: b 1 = z 1 L (35)... L a n = z 1 L n + 1 (36) n = 1 NTFz = z 1 ja STFz Dz L b 1 = NTFzL z = , (37) Dz missä D(z) on siirtofunktion navat (esim. Butterworth-tyypin) Error feedback -topologia Tätä topologiaa käytetään paljon digitaalisissa DS-rakenteissa (DS D/A-muuntimet). Takaisinkytkentäsilmukassa on FIR-suodatin F(z), jolla ei ole napoja. Kuvan 38 error feedback -topologian silmukkasuodattimiksi saadaan: ja L z = (38) 1 Fz Fz L z = , (39) 1 Fz joten kohinan ja signaalin siirtofunktiot ovat NTFz = 1 Fz STFz = 1 (4) + + F(z) + - Kuva 38. Error-feedback topologia.
41 42 Tällöin F(z):n ollessa pelkkä viive saadaan ensimmäisen asteen DS. Toisen asteen NTF (1-z -1 ) 2 saadaan, kun F(z) on 2z -1 - z -2. Napoja sisältävä NTF vaatisi F(z):n IIRsuodatintoteutuksen. Error-feedback topologiaa ei yleensä käytetä DS-ADC:n toteutukseen, koska analoginen FIR vaatisi tarkkoja sample-and-hold piirejä, joita on vaikeampi suunnitella kuin integraattoreita. Mainittakoon vielä, että error feedback -rakennetta käytetään DS D/A-muunnintoteutuksen lisäksi myös monibittisen DS:n DACin epälineaarisuusvirheiden korjauksessa, tarkemmin DAC-elementtien valintalogiikkana (ks. kappale 8.2). 4.2 Topologioiden vertailu MF- ja FF-topologioilla on sama NTF, jos niiden a i -, c i - ja g i -kertoimet ovat kuvien 36 ja 37 merkinnöillä identtiset. Eroavaisuudet ovat silmukkasuodattimen sisäisissä signaalin jakaantumisessa. Jos tulosignaali summautuu ainoastaan ensimmäiseen integraattoriin kummassakin tapauksessa, huomataan että signaalin siirtofunktiot ovat erilaisia. Kuvan 39 kohinan siirtofunktio on sama, mutta MF-topologiassa signaalin siirtofunktio on yhden tulosignaalin tapauksessa poikkeuksetta alipäästöluonteinen. FF-topologialla signaalin siirtofunktio on MF-topologiaan verrattuna tasainen laajalla kaistalla, tosin siinä voi ilmetä lievää korotusta signaalikaistan vieressä. Lisäksi FFtopologiassa on vain yksi takaisinkytkentähaaran D/A-muunnos, mikä on helpotus varsinkin monibittisten muuntimien tapauksessa [34]. Mag (db) NTF STF FF STF MF taajuus / fs Kuva 39. Signaalin siirtofunktiot yksibittiselle 3. asteen muuntimelle. Tulosignaalin kertoimilla b i voidaan helposti säätää tasainen STF. Tällöin NTF pysyy samana, mutta integraattorit prosessoivat pelkkää kvantisointikohinaa. Tämä helpottaa integraattoreiden suorituskykyvaatimuksia [34], koska integraattoreiden
42 43 signaalisvingit ovat tällöin pienemmät. Pienen ylinäytteistyssuhteen muuntimissa on edullista, jos STF on laajalla kaistalla tasainen. Topologian ja STF:n riippuvuutta voidaan tutkia tarkastelemalla integraattoreiden maksimilähtötasoja tasaisella ja ei-tasaisella STF:llä. Kuvassa 4 on 5. asteen yksibittisen DS-muuntimen integraattoreiden lähtöjä dc-tulosignaalin funktiona. Kuvassa 4a on kyseessä MF-topologia yhdellä tulohaaralla, jolloin STF on alipäästöluonteinen. Maksimilähtötasot kasvavat lineaarisesti lähes koko stabiilissa tulosignaalialueessa (-.58 kertaa täyden skaalan signaali). Kuvassa 4b on sama MF-topologia tasaisella STF:llä (usealla tulohaaralla), jolloin maksimilähtötasot eivät ole vahvasti tulosignaalin tasosta riippuvaisia. Kuva 4c kuvaa vastaavia tuloksia FF-topologialla. Maksimilähtötasot pysyvät samana tulosignaalin haarojen määrästä huolimatta, koska STF on tälle topologialle lähes poikkeuksetta laajakaistainen. Tulotasojen amplitudiriippuvuus ei myöskään ole niin selkeää, kuin kuvassa 4a, mutta integraattorin lähtötasot ovat pienemmät kuin kuvassa 4b. Stabiili tulosignaalialue on merkitty kuvissa katkoviivalla ja se on ennustettu kappaleessa mainitulla kuvaavan funktion menetelmällä. 1.4 Integr. 1.2 Ampl /taysi 1 skaala integr. a) 4. integr. b) c) integr. 1. integr. 3. integr Tulosignaalin taso / täysi skaala Kuva 4. Integraattoreiden lähtösvingit eri muunninkonfiguroinnille: a) MF alipäästö-stf:llä, b) MF kun STF=1 ja c) FF (sama tulos, kun STF=1 ja STF=1) Topologian piiritoteutukseen liittyvät seikat Topologian valinta sekä sen sisäisten lohkojen suunnittelu on myös yhteydessä piirisuunnittelussa tehtäviin valintoihin. FF-topologialle karakteristinen tasainen STF (vaikka ilman b i -kertoimia) on myös huomattava etu monibittisen DS:n takaisinkytkennän D/A-muuntimen epäsovitusvirheiden korjauksessa. Tästä kerrotaan kappaleessa 8.1.
43 44 Topologian valinta on valtaosassa toteutuksissa hyvinkin selvää, koska DSmuuntimeksi valitaan yleensä jokin aiemmin toteutettu ja hyväksi todettu topologia. Myös yksinkertaisuus ja pieni pinta-ala ovat tärkeitä kriteerejä: tehdään mahdollisimman pelkistetty muunnin ilman kompleksisia nollapareja ja mahdollisimman pienillä kondensaattoreilla. FF- ja MF-topologialle voidaan saada NTF:n kompleksinen nollapari asettamalla paikallinen takaisinkytkentä, eli nollasta poikkeavat g-kertoimet. Paikallinen takaisinkytkentä muodostaa resonaattorin, joka näkyy kohinan siirtofunktiossa dc:n ulkopuolisina nollina. Jos paikallisessa takaisinkytkennässä toinen integraattori on kuvan 41 tapaan viiveetön, resonaattorilla on ääretön vahvistus resonanssitaajuudella. g z z z -1 Kuva 41. Todellinen resonaattori: viiveellinen ja viiveetön integraattori sekä takaisinkytkentä. Jos kummatkin ovat viiveellisiä, vahvistus ei ole ääretön, eli kahden viiveellisen integraattoriparin muodostama pseudo-resonaattori ei vaimenna täydellisesti resonanssitaajuudella r. Resonaattorien taajuusvasteet ovat kuvassa 42. 8dB 7dB a) b) 6dB r taajuus Kuva 42. Paikallisen resonaattorin amplitudivaste: a) todellinen resonaattori ja b) pseudoresonaattori. Piiritoteutuksen kannalta viiveellisillä integraattoreilla toteutettu piiri on huomattavasti yksinkertaisempi toteuttaa SC-tekniikalla, koska silloin vältytään integraattoriparin asettumisvaatimuksesta yhden asettumisjakson aikana. Todellisen resonaattorin tapauksessa yksittäisen integraattorin asettumisvaatimukset ovat siis tiukemmat. Todellisen resonaattorin siirtofunktio on seuraavanlainen (integraattoriketjun kertoimet on skaalattu ykkösiksi): Rz z = z 2, (41) 2 g z + 1 jolloin resonanssi tapahtuu taajuudella r = arc 1 g (42)
44 45 Integraattorit ovat lopullisen toteutuksen tärkeimmät suunniteltavat lohkot, ja kuten kappaleessa 2 mainittiin, valittavana on viiveetön, puolikkaan viiveen, ja koko viiveen integraattori. Puolikkaat viiveet eivät sinänsä ole vaikeita lohkoja, kunhan muunnin toteuttaa vaaditun kohinan siirtofunktion. Toisaalta niiden mallintaminen diskreettiaikaisessa simulaattorissa saattaa olla hieman ongelmallista. Matlabin siirtofunktio-objekti ei voi sisältää puolikasta viivettä, mutta käyttäytymistason Simulink-mallissa voidaan muunnella näytteistystaajuutta vapaasti STF:n muokkaus STF:n halutaan yleensä toteuttavan mahdollisimman tasaisen vasteen signaalin kaistalla. Myös hieman erikoisempi STF:n säätäminen on mahdollista. Julkaisussa [5] on suunniteltu lähetinpuolen kaistanpäästötyyppinen DS-D/A-muunninta, jossa esitettiin DS-muuntimen signaalinmuokkaus-ominaisuuksien yhdistäminen jälkisuotimen taajuusvasteen korjaamiseen, jolloin erillistä ekvalisaattorisuodinta ei tarvita. Toisin sanoen STF ekvalisoi jälkisuodattimen muotoa, jolloin yhteisvaste on kuvan 43 mukaisesti tasainen. db STF jälkisuodatin & STF jälkisuodatin f-keskitaajuus (MHz) Kuva 43. STF:n käyttö jälkisuodatinvasteen ekvalisointiin. Ekvalisointia suunniteltiin alun perin käyttäen kuvan 43 mukaista analogista FIRsuodatinta (punainen käyrä), jonka ekvalisoinnin vaikutus on helppo nähdä taajuusvasteesta. Kyseisessä julkaisussa käytettiin analogisen FIR-suodattimen asemesta oikean SAW-suodattimen (Surface Acoustic Wave) mallia, joka ekvalisoitiin vastaavasti. Suodattimen mallinnus tehtiin tarkalla IIR-suodatinrekonstruktiolla IF-taajuudelle, koska ylössekoituksen mallintaminen ei ollut tarpeellista. Ennen ekvalisointia kohinan siirtofunktion suunnittelussa osa kompleksisista nollista asetettiin viereisen kanavan taajuudelle, jotta WCDMA-järjestelmän spesifikaatiot viereisien kanavien tehoille minimoituisi. Ekvalisoivan STF:n optimoimisessa DS-muuntimen kertoimia adaptoitiin minimoimalla QAM-herätteen aiheuttamaa virhevektorin suuruutta (EVM, error vector magnitude) siten, että viereisen kanavan teho ei huonone. SAW-suodatinmallin vasteen konstellaatiokuvaajasta laskettiin maksimi virhevektorin arvo rms-suureena
45 46 (EVM rms ), jonka mukaan kertoimet optimoitiin. Optimoinnissa EVM:n merkittävä paraneminen ei välttämättä edes näy spektrissä, vaan se huomataan symbolien keskinäiseen interferenssin (ISI, intersymbol interference) vähenemisenä. Kyseisen tutkimustyön tulos oli Virtexin E-sarjan FPGA-toteutus digitaaliselle DSmuuntimelle. Kuvassa 44 on esitetty simulointitulos, jossa todellisen FPGA:lla toteutetun DS:n lähtödataa suodatetaan SAW-suodatinmallilla. EVM-tulokset lupaavat alle 3%:n rms-arvoja, ja viereisten kanavien tehojen suhteet ovat lähimmästä kauimmaiseen kaistaan ovat ACLR1, ACLR2 ja ACLR3. konstellaatiokuvaaja 981:lle symbolille Q I 3 max = 2.759% % EVM rms.5 16 eri I-Q paria konstellaatiokuvaajasta ACLR3 = db oma kanava ACLR2 = db ACLR1 = db f - keskitaajuus (MHz) Kuva 44. FPGA-toteutuksesta simuloitu virhevektorin RMS-maksimiarvo sekä viereisten kanavien tehojen suhteen oman kanavan tehoon (Adjacent Channel Leakage Power Ratio, ACLR). Tämän tapaisessa muunninkertoimien optimoinnissa ei käytetä lineaarista analyysiä, vaan simulointituloksia, jolloin esim. kvantisoijan vahvistusta kyseiselle herätteelle ja topologialle ei tarvitse arvioida. Optimoinnissa on kuitenkin vaarana epästabiilisuus, koska kertoimien adaptoinnin aikana stabiilisuuden testaaminen kävisi liian hitaaksi; stabiilisuuden testaaminen täytyy tehdä adaptoinnin päättyessä.
46 Topologian kerroinparametrit Kun topologia ja kohinansiirtofunktio on valittu, voidaan kertoimet määrittää. Kertoimien valinnassa on olemassa tiettyjä vapausasteita, toisin sanoen kertoimia voidaan skaalata integraattorin huippuarvojen perusteella. Tämä voi tarkoittaa silmukkasuodattimen tilamallin skaalausta tai esim. integraattoriparista tehdyn resonaattorin siirtofunktion skaalausta Parametrien laskenta ja skaalaus Kohinansiirtofunktion hyväksyminen DS-muunnintoteutukseen voi olla varsin perusteellisen harkinnan tulos. Kun analyysit on tehty ja silmukkasuodatinta on simuloitu tarpeeksi, on vuorossa topologiatason analyysi, jota varten muuntimen kerroinparametrit realisoidaan. Kertoimien generointihan ei periaatteessa ole muuta kuin yhtälöryhmän ratkaisua. Muuntimen realisointiin on delta-sigma toolboxissa on funktio realizentf, joka määrää integraattoriketjun kertoimet ykkösiksi ja laskee muut kertoimet. Delta-sigma toolboxia käyttäen kertoimien realisointi on automaattista, joskin vain muutamalle tarkkaan määritellylle topologialle. Muuntimen kertoimissa mahdollisuus skaalaamiseen on yleensä olemassa, koska kertoimia on yleensä enemmän kuin yhtälöitä. Muunninkertoimien skaalaamisella voidaan vaikuttaa siihen, miten muuntimen sisäiset signaalitasot vaihtelevat. Tyypillinen ongelmatilanne on integraattoreiden lähtösignaalin maksimivaihteluvälin suuruus. Esimerkkinä huonosti skaalatusta muuntimesta on kuvan asteen DS:n integraattorin lähdöt. Kun täyden skaalaan signaali on 3V, viidennen integraattorin maksimi vaihteluväli on seitsenkertainen. Käytännön integraattoritoteutuksessa maksimisvingi voi olla esim. 1,5-2 kertainen täyden skaalan signaaliin, joten tässä signaali leikkautuu (clipping) aiheuttaen oskillointia signaalin kaistalla. x 1 4 int 4 old x 1 4 int 5 old x 1 4 int 6 old Kuva integraattorin lähdön histogrammit 6. asteen 3-bittiselle feedforward DS:lle.
47 48 Integraattorin lähdön svingiä voidaan rajoittaa skaalauksella. Esimerkkinä skaalauksesta on paikallisen resonaattorin sisäisten kertoimien muokkaaminen: kahden integraattorin ja takaisinkytkennän muodostavan systeemin sisäisiä kertoimia muutetaan siten, että resonaattorin siirtofunktio pysyy samana, mutta signaalitasot integraattoreiden lähdössä laskevat. Kuvassa 46 on edellisen esimerkkimuuntimen integraattorin lähdöt onnistuneen skaalauksen jälkeen. x 1 4 int 4 new x 1 4 int 5 new x 1 4 int 6 new Kuva 46. Kuvan 45 DS:n lähtösvingit oikeaoppisesti skaalattuna. Muunninkertoimien skaalausta ei välttämättä tarvitse tehdä kiinnittämällä huomiota tietyn integraattorin svingiin. Varsinkin korkeamman asteen muuntimissa siirtofunktioiden yhteys kertoimiin on paperilla laskien varsin hankala jäljittää. Järkevintä on käyttää säätötekniikan apuneuvoja, kuten silmukkasuodattimen tilamallin balansointia, josta kerrotaan seuraavassa kappaleessa Tilamallin ja kertoimien skaalaus Delta-sigma muuntimen silmukkasuodatin on kaksituloinen ja yksilähtöinen systeemi, jonka tilamallin yhtälöt integraattoreiden tilojen x(n) ja lähdön y(n) laskemiseen ovat: xn + 1 = Axn+ B un vn, (43) yn = Cxn+ D un vn missä A, B, C ja D muodostavat silmukkasuodattimen tilamatriisin: ABCD = AB (44) CD
48 49 Huonosti skaalatun tilamallin balansoiminen on varsin tunnettu säätötekniikan apuväline. Huonosti skaalatun tilamatriisin erottaa helposti matriisin numeroarvojen laajasta skaalasta. Tämä heijastuu suoraan silmukkasuodatin-yhtälöihin L (z) ja L 1 (z). Tilamallin balansointi onnistuu geneerisellä Matlab-komennolla ssbal, mutta Deltasigma toolboxissa skaalaus on pitkälle kustomoitu. Mikäli skaalausta tarvitaan, käyttäjä generoi topologiasta tilamallin stuffabcd -funktiolla. Tämän jälkeen tilamallin voi skaalata scaleabcd -funktiolla, joka pyrkii balansoimaan tilamallin käyttäjän antamien ehtojen mukaan. DS-toolboxin tilamallin balansoinnilla voidaan määrittää jopa integraattoreiden lähtöjen maksimiarvot, mikäli se ylipäätään on mahdollista. Balansointi etenee DS-toolboxilla kuvan 47 komentojen avulla: Tilamalli muutetaan tilamatriisiksi rivillä 1. Tilamalli balansoidaan delta sigma toolboxin scaleabcd -komennolla, rivi 2. Kyseisen funktion argumentti ovat vapaaehtoisia ja niillä voidaan asettaa ylärajat integraattoreiden tiloille (xlim), sekä asettaa yläraja kvantisoijan tulolle (ylim), kun kvantisoijan tasojen lukumäärä on nlev. Rivillä 3 käytetään toolboxin komentoa mapabcd, jolla saadaan tietyn topologian mukaiset, skaalatut muunninkertoimet. 1 [A,B,C,D]=ssdata(SYS);ABCD = [A,B;C,D]; %SYS sisältää STF:n ja NTF:n 2 ABCDs=scaleABCD(ABCD,nlev,xlim,ymax); %balansointi 3 [a,g,b,c]=mapabcd(abcds, CRFF ); %generoidaan topologialle kertoimet Kuva 47. Skaalausproseduuri DS-toolboxin avulla: muodostetaan silmukkasuodattimen tilamatriisi, joka balansoidaan. Tilamallista muunninkertoimiin -muunnos ( mapabcd ) sisältää vain tietyille rakenteille tehdyn muunnos-ohjelman, joita on delta-sigma toolboxissa on vain kourallinen. Pienikin muutos topologiassa vaatisi oman aliohjelmansa, joten skaalaus on jokseenkin rajoittunutta Delta-Sigma -muunnintopologian analysointi vuokaaviotasolla DS-muuntimien analyysi alkaa yleensä siirtofunktiotasolta. Kun siirtofunktio tunnetaan, se realisoidaan tietylle topologialle. Vuokaavioanalyysin kätevyys tulee ilmeiseksi, kun halutaan laskea jollekin topologialle signaalin ja kohinan siirtofunktiot: usean takaisinkytkentähaaran topologiasta on varsin hankalaa laskea siirtofunktioita käsin. Vuokaavioanalyysin etuna on topologian tutkimisen ja topologian muuttamisen nopea analyysi. Käyttäjä voi esimerkiksi muuttaa integraattorit resonaattoriksi, jolloin muunnin muuttuu alipäästävästä kaistanpäästötyyppiseksi. Myös topologian kerroinparametrien ja kvantisoijan vahvistuksen muutoksien tutkiminen onnistuu helposti. Tämä kappale käsittelee tässä työssä kehitettyä automaattista vuokaaviotason analyysityökalua [4], jonka voi ladata ilmaiseksi Mathworksin käyttäjien kontribuutiot -tietokannasta [35]. Työ on jatkokehitystyö perustuen julkaisuun [3], jossa käytettiin vuokaavioanalyysiin sekä Matlab- että Maple-komentoja.
49 5 Vuokaavioanalyysi [26] on matemaattisesti määritellyn järjestelmän kuvausta yhtälöryhmillä. Esimerkiksi kuvan asteen diskreettiaikaiselle DS-muuntimelle yhtälöt kirjoitetaan siten että jokaiselle solmulle (S1-S4) tulevat signaalit summataan: S1=IN+1*S2-a*S4 S2=z -1 *S1 S3=NOI+c*S2 S4=k*S3 1 1 a z 1 c 1 k 1 S1 S2 S3 S4 = IN NOI (45) Matriisiyhtälössä on siis systeemimatriisi, joka kerrottuna solmuvektorilla antaa lähdevektorin. Kahden solmun välisen siirtofunktion ratkaiseminen vaatii systeemimatriisin käänteisfunktion laskemista, joka on helppo ratkaista symbolisesti esimerkiksi Matlabilla tai Maplella. Proseduurin automatisointi perustuu nodelisttyyppisen kuvauksen tulkintaan, jossa kukin signaalivuo on kuvattu tekstitiedostossa omalla rivillään. 1 NOI IN S1 z -1 S2 c S3 k S4 OUT -a Kuva asteen DS:n vuokaaviomalli. Vuokaavioanalyysi etenee kuvan 49 mukaan: Matlab-ohjelma tulkitsee tekstimuotoisen kuvauksen tekstitiedostosta ja muodostaa siitä systeemimatriisin. Tämän jälkeen ratkaistaan ja yksinkertaistetaan haluttujen solmujen välille syntyvä siirtofunktio. Kuvassa on esitetty L:nnen asteen pure differentiation rakenteelle tekstimuotoinen esitys, jolle lasketaan signaalin ja kohinan siirtofunktiot, eli solmujen in ja out välinen siirtofunktion on STF ja solmujen noi ja out välinen on NTF. Vuokaavioanalyysin etuja on myös abstraktiotason vapaa valitseminen. Käyttäjä voi esimerkiksi määritellä integraattorin viiveellä ja summauksella, tai integraattorin siirtofunktiolla. Toinen etu on modulaarisuus:.pre komennolla käyttäjä voi määritellä jonkin sisäisen lohkon siirtofunktion, jota voi käyttää toistuvasti. Käyttäjä voi myös päättää, onko siirtofunktio symbolisen muodon lisäksi siirtofunktioobjektina, jota voidaan käyttää Matlab-ympäristössä numeerisessa säätöteknisessä analyysissä (.post komento). Kuvan esimerkissä tämä optio on poistettu kommentoimalla se (merkki *.post komennon edessä), koska symbolista astelukua L ei voida käyttää numeeriseen säätötekniseen analyysiin.
50 51 L kappaletta integraattoreita H SOLMU in H SOLMU noi H SOLMU out in noi H^L noi out 1 out in -1.pre syms z L.pre H=1/(z-1);.tf in out.tf noi out *.post z=tf('z',1); Kuva 49. pure differentiation topologia ja sen tekstimuotoinen kuvaus. Integraattoreita H on L kappaletta. Kuvassa 5 on esitetty analysointifunktion flow_tf käyttö. Edellisessä kuvassa esitetty tekstimuotoinen kuvaus on tiedostossa MOD_L.flw. Funktio antaa jokaiselle solmulle indeksinumeron ja muodostaa systeemimatriisin Y. Y:n käänteismatriisista saadaan jokaisen solmun välinen siirtofunktio ja funktio antaa lähtöargumenttina ne siirtofunktiot jotka tekstimuotoisessa kuvauksessa on haluttu. >> [NTF]=flow_tf('MOD_L.flw'); SOLMU NUMERO noi 1 out 2 in 3 KOMENTO SOLMULISTA >> pretty(ntf.sym{2}) / 1 \L \z - 1 / = 1 z 1 L SIIRTOFUNKTIO Kuva 5. Automaattinen vuokaavioanalyysi kuvan 49 topologiaesitykselle. Vuokaavioanalyysi-ohjelma flow_tf ei sinänsä ole räätälöity pelkästään DSmuuntimille, vaan ideana oli kehittää yleistyökalu, jolla jatkuva- tai diskreettiaikaisen systeemin siirtofunktiot saadaan generoitua mahdollisimman mutkattomasti ja varmasti. Ohjelma on käyttökelpoinen lukuisiin säätötekniikan sovelluksiin, suodatinsuunnitteluun, s-parametrilaskentaan, vahvistimien suunnitteluun, jne Mitoitus vuokaavioanalyysillä Kuvassa 51 on esitetty eräs vuokaavioanalyysin laajennus. Oletetaan, että käyttäjä on suunnitellut kohinansiirtofunktion NTF(z) ja haluaa tietyn topologian muuntimen kerroinparametrit. Tällöin hän voi generoida vuokaavioanalyysin avulla automaattisesti symbolisen siirtofunktion, jolloin siirtofunktion ratkaisu on pelkän
51 52 yhtälöryhmän ratkaisun takana. Schreierin DS-toolbox tekee kyllä täysin saman, mutta ainoastaan neljälle perustopologialle, joissa kerroinparametrien paikka on ennalta määrätty. Vuokaavioanalyysin käyttö mahdollistaa kustomoinnin, jolloin voidaan tarvittaessa tehdä poikkeavia rakenteita. Ainoa rajoitus on luonnollisesti se, että muuttujia ei saa olla enemmän kuin yhtälöitä, mikä on kuvan 51 esimerkissä vältetty siten, että integraattoriketjun kerroinparametrit on skaalattu ykkösiksi. Parametrien ratkaiseminen find_sdparams ohjelmalla perustuu puhtaasti yhtälöryhmän ratkaisemiseen, joten sillä voidaan ratkaista minkä tahansa symbolisen siirtofunktiojoukon parametrit. Laskenta perustuu siihen, että symbolisen ja numeerisen datan kompleksisen taajuusmuuttujan (s tai z) termit järjestellään yhteneviksi symboliselle ja numeeriselle datalle, esim. z 3 *(3-g1) = z 3 *2.98. Osoittajan ja nimittäjän kaikkien potenssien kertoimet kootaan siis yhtälöryhmään, joka ratkaistaan. out=find_sdparams([ntf 1],[H.sym{2} H.sym{1}]) out = in a1:.6189 a2:.9998 a3: b1:.6189 b2: b3: b4: 1 g1:.231 halutut kohinan ja signaalin siirtofunktiot b1 b2 g1 b3 b4 Vuokaavioanalyysin tulokset symbolisena rakenteena: {2}: NTF {1}: STF e H1 H2 H a1 a2 a3 k=1 out Kuva 51. Kertoimien realisointi vuokaavioanalyysillä. H1 on viiveellinen integraattori ja H2 viiveetön. Kertoimien skaalauksen ja tilamallin balansoimisen voi tehdä myös vuokaavioanalyysin kautta. Jos muuntimella on kertoimet, joihin ei olla tyytyväisiä, silmukkasuodatin-funktiot L (z) ja L 1 (z) voidaan generoida katkaisemalla takaisinkytkentähaara ja asettamalla se silmukkasuodattimen toiseksi tuloksi. Tästä päästään vuokaavio-analyysin kautta silmukkasuodattimen tilamalliin helposti Kertoimien typistäminen Integroivaan SC-vahvistinkytkentään summattavien signaalien kertoimet määräytyvät kapasitanssien suhteilla. Koska tämän suhdeluvun nimittäjän määrää integroiva
52 53 kondensaattori, on piiritoteutuksen kannalta järkevää, jos näillä kertoimilla olisi yhteinen nimittäjä. Tämä nimittäjä ei voi olla joku satunnaisesti valittu sopiva luku, vaan valinnassa tulee minimoida typistämisen vaikutus. Järkevintä on siis etsiä kertoimille kahden kokonaisluvun suhde, jolla on yhteinen nimittäjä ja joiden muutos alkuperäiseen floating-point -tarkkuudella esitettyyn tarkkaan kertoimeen ei vaikuta suorituskykyyn. Typistyksen vaikutusten vertaaminen tehdään siirtofunktiotasolla tarkistamalla pysyykö signaalikaistan kokonaiskohina sekä maksimi kaistan ulkopuolinen vahvistus lähellä alkuperäistä. Toinen vertaus tehdään simulointitasolla: verrataan signaalikohinasuhteita muutamalla tulosignaalin amplitudilla. Jos vertailu tuottaa huonon tuloksen tietyllä toleransseilla, yhteistä nimittäjää kasvatetaan, kunnes tavoitteeseen on päästy. Typistystä varten on tehty ohjelma sd_coeffs_round, joka tekee seuraavat asiat: yksi- ja monibittisen muuntimen NTF:n suunnittelu, dc-stabiilisuuden testaus ja skaalaus. Lopuksi ohjelma hakee tietyllä toleransseilla sopivan yhteisen nimittäjän kertoimille (kuva 52). Kyseinen ohjelma tekee myös vaihtoehtoisesti typistyksen digitaaliselle DS-muuntimelle (DS D/A-muunnin), jolloin kertoimille esitetään minimaalinen CSD-esitys (canonical signed digit, eli 2 N -termien summa). Ohjelman tuloargumenttina voi olla myös valmis topologia kertoimineen, ja myös toleranssit voidaan laittaa argumenteiksi. montako kv. tasoa sallitaan kv. kohinalle asteluku 1: NTF:ssä on kompl. nollat >> result = sd_coeffs_round([6 5 1],3,'CRFF ); takaisinkytkentäbittien lkm. Synthesizing...done Realizing and scaling...done Truncating...done: Smallest common denominator is 99 * NTF is OK. (stable, no complex inband) * Quantizer noise utilizes 5 quantizer levels. * Suites for at least 3-bit modulators. topologia (oikealla resonaatorilla, feed-forward topologialla) a: 49/99 14/99 31/33 18/11 61/99 g: 1/99 1/9 71/99 b: 25/99 1 c: 74/99 5/9 16/33 32/99 4/11 13/99 Kuva 52. Typistysohjelman toiminta: siirtofunktio syntesoidaan spesifikaatioiden mukaan, josta realisoidaan topologialle kertoimet. Tämän jälkeen kertoimet typistetään suorituskyvyn mukaiseksi.
53 54 5. DISKREETTIAIKAINEN SIMULOINTIMALLI 5.1 DS-muuntimen simuloinnin periaatteita Lineaarinen analyysi antaa parhaimmillaan hyvän arvion muuntimen käyttäytymisestä. Todellisen kuvan saa kuitenkin vasta käyttäytymistason simuloinnista, jossa epälineaarisen elementin, eli kvantisoijan vaikutukset todella näkyvät. Simulointimallia tulisi ajaa usealla eri herätetyypillä, jotta saataisiin mahdollisimman varma tieto muuntimen toiminnasta. Aikatason simuloinnit varmistavat, onko muunnin stabiili erityyppisillä signaaleilla (mm. dc- ja sinisignaalilla). Lineaarisella analyysillä voidaan arvioida muuntimen maksimi stabiili tulosignaalin amplitudi, mutta se kannattaa todeta eritaajuisilla sinisignaaleilla sekä dc-tulotasoilla. Myös usean sinisignaalin sekä kaistan ulkopuolisen häiriön simulointeja kannattaa tehdä, varsinkin jos muuntimen siirtofunktio on aggressiivinen (ks. kappale 2.4). Lähtösignaalin spektrin avulla voidaan arvioida muuntimen suorituskykyä sekä mahdollisia oskillointipiikkejä. Valitettavasti spektri ei kerro koko totuutta tai voi olla jopa harhaanjohtava. Esimerkiksi suuresta näytemäärästä otettu ikkunafunktiolla suodatettu diskreetti Fourier-muunnos voi näyttää valkoiselta kohinalta, mutta lyhyeltä aikaväliltä katsottu DS:n lähdön autokorrelaatiofunktio tuo esiin selvän, monen sävelen surinan. Tämä on varsinkin audiototeutuksessa erittäin tärkeä aspekti. Rajavärähtelyn peittäminen voidaan toteuttaa ns. ditherillä, eli summataan sopivan amplitudista valesatunnaista kohinaa kvantisoijan tuloon. Ditheröintitekniikoita on useita, jopa signaalitasosta riippuva dynaaminen ditheröintimenetelmä on raportoitu [12]. 5.2 Käyttäytymistason mallinnus Lineaarisen analyysin tueksi kannattaa siis tehdä useita simulointeja. Simulink on Matlabin oma graafinen käyttäjäliityntä, joka on vuosien varrella kehittynyt käyttöliittymältään erittäin monipuoliseksi ja hyödylliseksi mallinnusympäristöksi. Matlab ja Simulink ovat käyttäjän tarpeen mukaan laajennettavia kokonaisuuksia, ja laajennus-moduuleja kutsutaan toolboxeiksi (Matlab) ja blockseteiksi (Simulink). Delta-sigma toolbox on harvoja ilmaisena jaettavia ohjelmistopaketteja, ja se on laajalti tunnettu DS-muuntimia tutkivien keskuudessa. Cookbook-suunnitteluohjeen (kappale 2.4) mukaan suorituskyvyn analyysit simulointi mukaan lukien voidaan tehdä ennen topologian valintaa. Tämä on järkevää, koska silmukkafunktion mallin simulointi on yleensä nopeampaa abstraktilla tilamallilla. Silmukkasuodattimen tilamalli soveltuu sekä Simulink- että Matlab-ympäristöön. Matlabin DS-toolboxista löytyvä simulointifunktio simulatedsm on C-kielestä käännetty MEX-funktio, jonka simulointi on monta kertaa nopeampi kuin komentorivipohjaisen Matlab-funktion simulointi. Kuva 53 esittää Simulinkin tilamalliin perustuvaa yksibittisen DS:n mallinnusta, jossa on sama periaate kuin em. MEX-funktiolla.
54 55 mux y(n) = Cx(n)+Du(n) x(n) = Ax(n)+B(u(n) tilamalli + alkuarvot relay (komparaattori) Kuva 53. Simulink-malli yksibittiselle DS:lle, jossa silmukkasuodatin on tilamalli. Mainittakoon vielä, että silmukkasuodattimen tilamalli sisältää tiedot sekä signaalin että kvantisointikohinan polusta, eli STF ja NTF voivat olla täysin ennalta määriteltynä. Topologiataso voidaan mallintaa myöhemmin, jolloin voidaan tehdä esim. piirin epäideaalisuuksien mallinnusta (kappale ). Simulointimallinnuksessa kannattaa siis kiinnittää huomiota mallin abstraktiotasoon. Jos esimerkiksi simulointimallissa on desimointisuodatin, kannattaa sinc K - sekä muiden desimointiasteiden suodattimet toteuttaa siirtofunktiotasolla, mikäli ei ole vielä tarkoitus tutkia suodattimen sisäisten sananleveyksien vaikutuksia. Esimerkiksi lähteen [21] half-band suodatin voidaan delta-sigma toolboxissa toteuttaa sekä topologiakerroin- että siirtofunktiotasolla ( designhbf funktio). 5.3 Kvantisoijan efektiivinen vahvistus Kvantisoijan efektiivinen vahvistus kohinalle saadaan kvantisoijan tulo- ja lähtösignaalin korrelaatiokertoimella [12]: k noise N n qin nqoutn = cov y v = n = vary N. (46) n qin n 2 n = missä k noise on kohinan kvantisoijan vahvistus, cov on kovarianssifunktio, var on varianssifunktio, n qin on kvantisoijan tulosignaalin kohinainen osa ja qout on kvantisoijan lähtösignaali Tämä kaava osoittaa kvantisointikohinan signaaliriippuvuuden, joten tarkan lineaarisen mallintamisen edellytys on tieto tulosignaalin tilastollisista ominaisuuksista. Kaavalla (46) saadaan laskettua vahvistus mitatusta datasta, koska sinimuotoisella herätteellä kvantisoijan tulosignaalista voidaan eristää sekä sinimuotoinen signaali että kohinakomponentti. Sinifunktion sovitus tehdään IEEE:n standardin [36] mukaisesti joko pienimmän neliösumman (LSE, least squared error) sovituksella tai
55 56 iteratiivisella pienimmän neliövirheen minimoinnilla. Sovituksen jälkeen kvantisoijan vahvistus voidaan määrittää myös kaavalla (46) kohinalle sekä myös sinisignaalille: k signal N n = N s nqoutn qin (47) n = s qin n 2 missä k signal on signaalin kvantisoijan vahvistus ja s qin on kvantisoijan tulosignaalin hyötysignaaliosa. Kuten aiemmin kuvassa 21 sivulla 26 esitettiin, kvantisoijan vahvistus muuttuu, kun signaalin ominaisuuksia muutetaan. Signaalin kvantisoijan vahvistus on sinisignaalin sovituksessa mahdollista laskea ainoastaan, jos kvantisoijan tulosignaali korreloi tulosignaalin kanssa (sinin sovitus on mahdollista). Pienillä signaalin tasoilla kvantisointivirheen signaalikomponentti hukkuu kohinan alle, jolloin sinisovitusta ei voida tehdä. Kuvassa 54 on esitetty kvantisoijan vahvistuksen mittausten ja describing function -menetelmän tulokset toisen asteen muuntimelle. Muistutettakoon, että kuvaavan funktion menetelmä käyttää dc-tulotasoja, mittaukseen perustuvassa menetelmässä heräte voi olla mikä tahansa, tässä tapauksessa sinisignaali. Kuvassa 54 dc- ja sinisignaalin erot ovat yllättävän suuret. Ero selittyy sillä, että eri herätetyypeillä saadaan eri kvantisoijan vahvistus. Kun DSmuuntimia simuloidaan, dc-stabiili tulosignaalin dynamiikka on lähes poikkeuksetta pienempi kuin mitä sinisignaalilla (tai jollain muulla herätteellä) simuloidut tulokset lupaavat. Siniherätteellä hyviä suorituskykytuloksia lupaava DS-muunnin ei ole välttämättä dc-stabiili. KOHINAN kvant. vahvistus SIGNAALIN kvant. vahvistus simuloitu (sini).5 estimoitu (dc) amp (db) simuloitu (sini).5 estimoitu (dc) amp (db) Kuva 54. Kvantisoijan vahvistukset simuloinnin ja kuvaavan funktion menetelmän perusteella. Kvantisoijan vahvistusta voidaan siis analysoida paitsi perinteisellä kuvaavan funktion menetelmällä, myös LSE-sovituksella.
56 57 Lähteessä [37] puhutaan integraattorin svingin suhteesta signaaliin taajuuteen. Jos yksibittisen DS:n tulosignaalin taajuus on sama kuin kohinan siirtofunktion impulssivasteen värähtelytaajuus, integraattorin svingi kasvaa roimasti ja suorituskyky alenee signaalin leikkautumisen johdosta. Jatkuva-aikaisena tämän ongelmatilanteen voi esittää muodossa: = sig = osc o , (48) 4Q2 NTF missä sig on tulosignaalin taajuus (rad/s), osc on impulssivasteen oskillointitaajuus o on kohinan siirtofunktion kompleksisen navan nurkkataajuus (rad/s) ja Q NTF on jatkuva-aikaisen kohinan siirtofunktion hyvyysluku Ongelmaa pystytään lieventämään skaalaamalla muuntimen kertoimia (kappale 4.3.1). On siis suositeltavaa tehdä suorituskykysimulaatioita eri signaalin taajuudella. Myös seuraavassa kappaleessa esitetty häiriösignaalin vaikutus kannattaa tutkia Kaistan ulkopuolisten häiriösignaalien vaikutus Kvantisoijan vahvistuksen mittauksissa perusajatuksena on katsoa vahvistuksen ja suorituskyvyn muutoksia, kun tulosignaalin ominaisuuksia muutetaan. Testisimulointeja voidaan siis tehdä minkälaisella herätteellä tahansa, joten myös kaistan ulkopuolisten häiriöiden vaikutusten testaus on mahdollista. Kaistan ulkopuolisen sinimuotoisen häiriösignaalin avulla voidaan nähdä, millä taajuudella ja millä dynamiikalla esimerkiksi piirin epäideaalisuuksista aiheutuva särö vaikuttaa suorituskykyyn. Mikäli DS:lla on olemassa napoja lähellä yksikköympyrää (suuri Q- luku), on mahdollista että samalla taajuudella oleva signaali aiheuttaa piirin oskilloimisen. Koska nyrkkisääntöä häiriösignaalin ominaisuuksien ja Q-luvun väliselle suhteelle ei ole, se tulee todeta simuloinneilla. Kuvassa 55 on testattu asiaa 2. ja 5. asteen muuntimella. Sinimuotoisen häiriösignaalin taajuutta on kasvatettu signaalikaistan reunalta puoleen näytteenottotaajuuteen, ja hyötysignaalin amplitudia on kasvatettu -2dB:stä db:in. Häiriösignaali on tässä esimerkissä voimakas: 5% täyden skaalan signaalista. Toisen asteen DS:ssa häiriön vaikutus näkyy SNDR:ssä stabiilin alueen pienenemisessä, mutta ei vaikuta NTF:n kompleksisen navan taajuudella (noin f s /1). Kvantisoijan vahvistukset signaalille ja kohinalle tosin pienenevät häiriön ollessa napataajuudella: selvä vako on havaittavissa kompleksisen navan taajuudella. Viidennen asteen muunnin onkin luonteeltaan aggressiivisempi. Muuntimella on kompleksisia napoja lähellä yksikköympyrää, ja napojen taajuudella (noin f s /4) oleva häiriö aiheuttaa suorituskyvyn romahtamisen ja kvantisoijan vahvistusten putoamisen nollaan. Signaalin siirtofunktio voi olla alipäästävä, jolloin mahdollinen signaaliin summautunut häiriö vaimenee merkityksettömäksi, mikäli se on tarpeeksi kaukana signaalin kaistalta. Kapeakaistainen häiriö voi syntyä myös piirin epälineaarisuuksista, jolloin signaalin suodattaminen ei auta.
57 SNDR (db) 58 SNDR (db) ampl (db) log2(f / fs) ampl (db) -6-4 log2(f / fs) -6-4 log2(f / fs) -6-4 log2(f / fs) -2 3 Ksignal Ksignal ampl (db) log (f / f ) ampl (db) s -2 Knoise Knoise ampl (db) log (f / f ) 2 s ampl (db) -2 Kuva 55. Kaistan ulkopuolisen häiriöpiikin taajuuden ja signaalin amplitudin vaikutus SNR:ään ja kvantisoijan vahvistuksille. Vasemmalla puolella on tulokset 2. asteen ja oikealla 5. asteen DS:lle.
58 59 6. ANALOGIAOSIEN EPÄIDEAALISUUDET Jos piirisuunnittelija ei ota huomioon tarpeeksi piirin sisäisiä epäideaalisuuksia, piirin testausvaiheessa huomataan todennäköisesti harhatoistoja signaalin kaistalla: kvantisointikohinassa ilmenee yllättäviä säröpiikkejä ja suorituskyky romahtaa. Vahvistinketjussa seuraavien vahvistimien särö jaetaan edellisten vahvistimien vahvistuksella. Näin ollen ketjun ensimmäisen vahvistimen särö ei ole redusoitunut, jolloin ensimmäisen vahvistimen suorituskyky vaikuttaa koko DS-muuntimen suorituskykyyn ratkaisevasti. Epälineaarisuudesta johtuva särö voidaan välttää asettamalla ensimmäisen vahvistimen lineaarisuus vähintään muuntimin teoreettisen lineaarisuuden tasolle. 6.1 kt/c-kohina Integroivan vahvistimen lineaarisuuden lisäksi kondensaattoreiden minimikoko määräytyy suorituskyvyn mukaan: kapasitanssien minimikoon määrittää sallitun termisen kohinan taso. Näytteistyskondensaattorin termistä kohinaa voidaan olettaa olevan valkoista kohinaa, jonka tehoa P CS signaalin kaistalla differentiaaliselle toteutukselle voidaan approksimoida kaavalla [38] P 8kT CS = , (49) C S OSR missä k on Bolzmanin vakio (1,38*1-23 J/K), T on lämpötila kelvineissä ja C S on näytteistyskondensaattori 6.2 Integraattorin epäideaalisuudet DC-vahvistus Kuvassa 56b on esitetty, kuinka kuvan 56a integraattorin rajallinen dc-vahvistus (A DC ) vaikuttaa integraattorin taajuusvasteeseen. Vastaava lohkokaavio 1. asteen muuntimelle on kuvassa 56c. Kerroin p aiheuttaa napojen siirtymisen integraattorin siirtofunktiossa. Liian pienen dc-vahvistuksen seuraus on se, että kvantisointikohinan vaimennus signaalin kaistalla pienenee. Vaikutus korostuu jälleen integraattoriketjun ensimmäiseen vahvistimessa. Rajallisen dc-vahvistuksen integraattorin siirtofunktio on: missä Hz C S C I z 1 = z 1 (5)
59 6 1 = C S C I A DC (51) a) C I C S A DC Vout c) b) H(z) (db) Ideaalinen z -1 p A DC taajuus (log) Kuva 56. Rajallinen dc-vahvistus: a) SC-integraattori, b) lohkokaavio ja c) taajuusvaste. Kohinanmuokkaus pienentää dc-vahvistuksen vaatimuksia ensimmäistä integraattoria seuraavissa integraattoreissa. Lähteessä [1] tutkittiin dc-vahvistuksen vaikutusta 2. asteen DS-muuntimen suorituskykyyn ja siinä päädyttiin helppoon nyrkkisääntöön, jonka mukaan suorituskyky ei huonone merkittävästi jos A DC OSR. Mikäli dcvahvistuksen arvo on lähellä ylinäytteistyssuhdetta, on siis syytä tarkastella suorituskykyä simuloinneilla. Kyseinen vaatimus ei ole kovinkaan merkittävä. Kuitenkin, mikäli A DC OSR, esiintyy kappaleessa 3.3 esitetty dead-zone ongelma. Tällöin dc-tulosignaalin ollessa nollatason lähettyvillä dc-tasot välillä 1 p 1 p u DC = (52) 1 + p 1 + p tuottavat saman DS-lähtösignaalin. Termillä p tarkoitetaan ykköstä pienempää integraattorin takaisinkytkentäkerrointa.
60 61 Slew-rate -rajoitus Kun kapasitanssit mitoitetaan termisen kohinan ja spesifikaatioiden perusteella, integroivan vahvistimen asettumisvaatimukset on mitoitettava seuraavaksi. Vahvistimen kaistanleveys (ts. aikavakio ) määrää ns. lineaarisen asettumisajan t exp. Slew-rate (SR) on voimakkaasti epälineaarinen ilmiö, joka määrä lähtöjännitteen maksimaalisen muutosnopeuden. Vahvistimen slew-rate määrää epälineaarista asettumisaikaa t SR. Em. asettumisajat voidaan esittää integraattorin askelvasteella, kuten kuvassa 57. V ideal V todell virhe t SR t exp Kuva 57. Integraattorin lähtöjännitteen askelvaste. t DS-muuntimen (ketjun ensimmäiseen) integraattoriin tuleva signaali koostuu tulosignaalista ja sakaramuotoisesta takaisinkytkennästä. Viiveellisen ja lineaarisen integraattorin lähtöjännite on C s v out t = v out nt T v nt T -- in 2 1 e 1 nt T t nt (53) C I Tämän käyrän maksimikulmakerroin on: Max ----v d dt out t C v in nt T s 2 V S = = K C I C (54) K C C = S C I V S = v in nt T -- 2
61 62 Mikäli vahvistimen slew-rate on suurempi kuin edellisen kaavan maksimiarvo, SRrajoitusta ei ole ja lähtöjännite v out noudattaa kaavaa (53). Jos se on suurempi, jännitteen v out aikavaste noudattaa slew-rate kulmakerrointa. Tällöin lähtöjännite on: [39] v out t v out nt T K C V S SRt SR K C V S e t t SR = + +, (55) missä SRt SR on vout:n arvo ajanhetkellä, jossa SR rajoitus loppuu. Jos mallinnetaan lähtövirran ja tulojännitteen välistä suhdetta kuvan 58 paloittain lineaarisella mallilla [4], vahvistimen lähtövirta saturoituu bias-virran arvoon I MAX. Oletetaan että tulojännite V i liukuu kohti lineaarisen tulojännitteen lineaarista aluetta V lin, jonka jälkeen vahvistin asettuu lineaarisesti. Tällöin liukuminen (slewing) rajoittaa lineaarista asettumisaikaa t SR :n verran missä t SR max V i V lin = (56) SR Tämä aiheuttaa eksponentiaalisen epälineaarisuusvirheen t SR T s t SR = exp = exp T s t SR exp (57) Iout asettumisvirhe [mv] i MAX g m = i MAX V lin V i -V lin V lin V i V lin lineaar. alue Kuva 58. Vahvistimen lähtövirta ja asettumisvirhe tulojännitteen V i funktiona. Epäideaalisuuksia mallinnettaessa slew-rate -rajoitus on hankala ongelma, koska se on luonteeltaan voimakkaasti epälineaarinen ilmiö. Tällaista ilmiötä ei voida esittää suljetussa muodossa, joten sitä on hankala mallintaa analyyttisessa mallissa. Kappaleessa 7.2 kerrotaan mallintamismenetelmästä, jossa asettumisvirheen mallinnus käsittää myös slew-rate -ilmiön.
62 63 Kytkinresistanssi Asettumisvirhe ei ole pelkästään vahvistimen ongelma, koska myös kuvan 56a integraattorin kytkinverkko aiheuttaa asettumisvirheitä. Tällöin integraattorin siirtofunktio on [41] Hz C S z Ts C I 1 z 1 1 2e 4R ON C s = (58) missä Ts on näytteistysintervalli R on on MOS-kytkimen ekvivalentti ON resistanssi ja C S on näytteistyskondensaattori Kerroinkapasitanssien epäsovitus Piirin layout-valmistuksessa näytteistys- ja integrointikondensaattoreiden kapasitanssit voivat poiketa suunnitellusta arvostaan. Mahdollisesta poikkeamasta voi kuitenkin olla jotain tilastollista tietoa, jolloin simulointivaiheessa voidaan katsoa, vaikuttaako pahimman tapauksen poikkeama kerroinparametrissa vahinkoa suorituskyvylle. Ongelmien välttäminen onnistuu parhaiten kohinan siirtofunktion suunnittelussa, eli valitaan vähemmän aggressiivinen kohinan siirtofunktio. Pieni kerroinkapasitanssien epäsovitus voi vaikuttaa kriittisesti suorituskykyyn, kun DS-muuntimessa on kahdesta integraattorista muodostettuja resonaattoreita (kappale 3.1.1). Resonaattorista saadaan kompleksinen nollapari kohinan siirtofunktioon, ja resonaattorin taajuus on herkkä muunninkerrointen pienelle epäsovitukselle Mainittakoon, että kappaleessa mainittu, kerroinparametrien typistys ohjelma on mainio väline juuri em. herkkyyden havainnointiin. Kyseinen ohjelma kertoo, kuinka paljon kertoimia voidaan pyöristää, kun suorituskyvystä ja stabiilisuudesta ei tingitä. Differentiaalinen rakenne Differentiaalinen piiritoteutus on järkevää, koska sillä saadaan karkeasti sama tehonkulutus ja parempi dynamiikka kun yksipäisellä rakenteella. Differentiaalinen rakenne eliminoi epäideaalisuuksia, kuten parillisen asteluvun harmoninen särö sekä käyttöjännitehäiriöiden vaikutukset.
63 Kellojitteri SC-piiri on täysin diskreettiaikainen, ja sen toiminta perustuu varauksen siirtoon kellojaksojen aikana. Niinpä näytteistämisen epäideaalisuus eli jitteri vaikuttaa vain ensimmäisessä näytteenotossa, ja se voidaan mallintaa tulosignaaliin liittyväksi. Näytteistyskellon jitterivirhe kasvattaa DS-lähdön kohinatehoa. Jitterivirhe on suoraan verrannollinen sekä itse jitterin että tulosignaalin tilastollisiin ominaisuuksiin. Kun tulosignaali on sinimuotoinen amplitudilla A ja taajuudella f in, ja näytteistys tapahtuu hetkellä jonka ajoitusvirhe on (aika), tulee virheeksi [43]: (59) Jos jitterivirhe oletetaan Gaussin jakautuneeksi hajonnalla t, jitterin aiheuttama kohina jakautuu tasaisesti koko taajuusalueella ja signaalikaistan kohinateho on tällöin [1] S t 2qf b t 2 = , (6) 8OSR missä t 2 on jitterin varianssi, f b on signaalin kaistanleveys ja q on kvantisointiaskel. Voidaan siis todeta, että diskreettiaikaisten muuntimien jitterivirhettä kasvattaa näytteenoton apertuurivirhe. Ylinäytteistyssuhde pienentää jitterin vaikutusta signaalikaistan kohinatehoon. Jatkuva-aikaisilla DS-muuntimilla jitterivirhe on vakava ongelma, koska se vaikuttaa suoraan jatkuva-aikaisen takaisinkytkentäsignaalin arvoon.
64 65 7. EPÄIDEAALISUUKSIEN MALLINTAMINEN 7.1 Analyyttiset mallit ja niiden rajoitukset Systeemitason mallintamisen tarkoituksena on vähentää suunnitteluvaiheiden määrää. SC-tekniikalla toteutettavan DS-muuntimen käyttäytymistason simulointi on tarkalla transistoritason simulaattorilla (esim. SPICE) tyypillisesti toivottoman hidasta. Piiriin pohjautuvien makromallit ja taulukkoon perustuvat mallit ovat nopeampia, tosin realismin kustannuksella. Diskreettiaikaista simulaattoria, kuten Matlab/Simulink käytetään tavallisesti ideaalisten lohkojen kuvaukseen, ja mahdolliset piirin epäideaalisuudet yleensä mallinnetaan käyttäen tunnettuihin kaavoihin perustuvia epäideaalisuuksien mallintamista. Analyyttinen mallintaminen rajoittuu heikosti epälineaarisiin ilmiöihin, mikä kattaa suurimman osan epäideaalisuuksista. Kuitenkin voimakkaita epälineaarisuuksia kuten slew-ratea ei voida esittää suljetussa lausekemuodossa [27]. SC-vahvistimien asettuminen on kompleksinen epälineaarinen ilmiö. Piirisuunnittelussa asettumisvirhettä voidaan minimoida kasvattamalla biasvirtoja, mikä kasvattaa slew-ratea. Asettumisvirheen mallintamisella voidaan katsoa miten jonkun parametrin muuttaminen (esim. biasvirta) vaikuttaa systeemin suorituskykyyn. Simulointi on diskreettiaikaisella simulaattorilla nopeaa, mutta käyttäytymistason mallin realistisuus riippuu siitä, kuinka tarkasti seuraavat jatkuvaaikaiset ilmiöt on mallinnettu: vahvistimen ominaisuudet kuten kohina, rajallinen dc-vahvistuksen lineaarisuus, äärellinen kaistanleveys, SR-rajoitus ja saturoitumistaso, terminen kohina (kt/c), näytteistyksen kellojitteri, D/A-muunnoksen epälineaarisuus ja kapasitanssien epäsovitus. Kun monibittisen DS:n takaisinkytkentä-dacin epälineaarisuutta ei huomioida, potentiaalisin piirikohinan lähde on integraattoriketjun ensimmäinen integraattori. Kuvan 59 [43] mallinnuksessa on huomioitu em. listan kaksi ensimmäistä kohtaa, ja lopputuloksena on varsin käyttökelpoinen käyttäytymistason malli. tulosignaali lähtösignaali Kuva 59. Kaistanpäästö-tyyppisen DS:n käyttäytymistason malli.
65 66 Lähteessä [42] on vastaava, jopa hieman tarkempi Simulink-mallinnus toisen asteen alipäästö-ds:lle, mutta tämänkin tyyppisessä mallintamisessa on heikkoutensa. Nimittäin mallinnuksissa oletetaan, että SC-integraattorit kellotetaan siten, että tulon varaus siirretään ensin integroivaan kondensaattorin yhden kellojakson aikana ja kuormakapasitanssi on kytkettynä lähtöön seuraavalla jaksolla. Todellisuudessa integraattorin tulosolmussa oleva jännite riippuu myös edellisestä näytteestä. Heikosti epälineaarisia ilmiöitä voidaan toki mallintaa yksiulotteisella funktiolla, mutta tarkka vahvistuksen mallinnus tarvitsee myös tietoa lähtöjännitteestä. Asettumisen mallintaminen on vahvistinkytkennästä riippuen joko pelkästään tulojänniteriippuva (yksiulotteinen mallinnus) tai tämän lisäksi myös edellisen tilan funktio (kaksiulotteinen mallinnus). Kuva 6 esittää yksi- ja kaksiulotteisen mallinnuksen ideaa. Yksiulotteisessa mallinnuksessa varauksensiirtoyhtälössä lähdön tämän hetkinen tila v i riippuu ainoastaan tulojännitteestä V in. Tällöin kaikki tulojännitteestä riippuvat epäideaalisuudet on mallinnettuna yksiulotteisena, analyyttisenä virhefunktiona. Kaksiulotteisessa mallinnuksessa sekä tulon että lähdön tila (v i ja v o ) riippuvat jännitteistä V in ja V out, eli edellinen tila vaikuttaa asettumiseen. (a) V in v i lineaar. kombi- naatio v o skaalaus v i virheen funktio V out (b) V in kaksiulotteinen polynomi tai lookuptaulukko Kuva 6. a) Yksi- ja b) kaksiulotteinen mallinnus, missä v i ja v o ovat tulo- ja lähtöjännitteen alkutiloja. Seuraavassa kappaleessa esitellään varsin seikkaperäisesti mittaukseen perustuva mallinnustapa. Taulukossa 1 on vertailun vuoksi jäsennetty puhtaasti analyyttisen sekä kaksiulotteisen polynomimallinnuksen tärkeimmät eroavaisuudet. V out Taulukko 1: Integraattorin mallinnustapojen vertailu Mallinnettava ilmiö kuvan 59 mukainen analyyttinen malli Mittaukseen perustuva polynomimallinnus Slew-Rate rajoitus ei kyllä Tulojännitteestä riippuvat asettumisvirheet Lähtöjännitteestä riippuvat asettumisvirheet kyllä ei kyllä kyllä Terminen kohina kyllä ei Vahvistimen malli yksinapainen ei rajoituksia
66 Mittaukseen perustuva malli Kaksi- tai useampiulotteisen mallin tarkka toteuttaminen analyyttisillä yhtälöillä ei ole järkevää, koska realistisen yhtälömalliryppään kasvaessa suureksi tulkintakin vaikeutuu. Lisäksi suljetussa muodossa voidaan esittää vain heikosti epälineaarisia ilmiöitä. Kaksiulotteisen polynomimallinnuksen tavoitteena on tehdä diskreettiaikainen simulointimalli, jolla voidaan ennustaa myös integraattorin lähdöstä riippuvat asettumisvirheet. Tällöin sekä nykyisen tulojännitteen että edellisen lähtöjännitteen tiloja käytetään vahvistimen tulon ja lähdön tilan laskemiseen. Kaksiulotteinen malli vahvistinkytkennän asettumisvirheille käyttää mittaus- tai simulointituloksista saatua tietoa. Vahvistinkytkentää ajetaan täydellä skaalalla tulo- ja lähtöjännitteen tilojen v i ja v o valikoitujen kombinaatioiden tuottamat asettumisvirheet. Virhetaulukko, tai pikemminkin virhepinta karakterisoidaan tulon ja lähdön jännitetilojen funktiona kaksiulotteiseksi polynomiksi. Saadun virhepolynomin kertoimilla ei ole mitään fyysistä merkitystä, ja menetelmällä säästytään hankalasti mallinnettavilta 2. kertaluvun ilmiöiltä [44]. Virhetaulukosta voitaisiin tehdä myös taulukkopohjainen (table-based) malli, mutta tämä vaatisi interpolointitekniikoiden käyttöönottoa. Käytännössä karakterisointi on varsin nopeasti tehtävä operaatio, ja virheen polynomimallia käytetään pitempikestoisissa simuloinneissa. Polynomimalli on helppo sisällyttää diskreettiaikaiseen simulointiympäristöön, kuten Simulinkympäristöön. Polynomimallin realistisuus riippuu täysin mittausdatasta. Tämä data voi olla peräisen esim. transistoritason simulaattorista tai tarkasta tilamallista. Puolijohde-tekniikassa tällaista epäanalyyttistä mallinnusta kutsutaan usein device knows best -lähestymistavaksi Asettumisvirheiden karakterisointi Kuvassa 61 on esimerkki tulojännitteen alkuarvon asettumisesta: virhetaulukkoon otetaan talteen kunkin alkutilayhdistelmän aiheuttama asettumisvirhe. Termillä V lin tarkoitetaan lineaarisen tulojännitteen aluetta (ks. sivu 62). Kuvan 62 [44] esimerkissä kaikki kondensaattori voivat olla varattuna tiettyyn jännitteeseen V 1 -V 5. Kun ne ovat kytkettynä, kokonaisvaraus jakaantuu uudelleen ja tulon ja lähdön alkuarvot V i ja V o voidaan laskea. Tästä alkuarvosta vahvistin asettuu ja varauksensiirtoyhtälöstä (61) voidaan esim. laskea onko V i lineaarisella tuloalueella. C 1 + C 2 + C 3 + C p C 3 C 3 C 3 + C L V i V o = (61) C 1 V 1 + C 2 V 2 + C 3 V 3 + C p V 5 + C 1 V 1 + C 2 V 2 + C p V 5 C 3 V 3 + C L V 4 + C L V 4
67 68 v i e t Vlin t SR t exp t t stop Kuva 61. Tulojännitteen tilan muuttuminen yhden näytteistysintervallin aikana. mitattavat alkuarvot - V V V 4 - V 1 V i V o V 4 (a) C 1 C 3 C L C 2 (b) V 2 C 1 C 3 C L C 2 - V V 5 + C p Kuva 62. Alkutilojen V i ja V o laskenta: (a) alkutilat, (b) kondensaattorit kytkettynä jännitteisiin V 1 - V 5. Integraattoriketjun ensimmäisen integraattorin tilamalli muodostetaan kullekin SCintegraattorin vaiheelle puolen kellojakson aikana kuvan esittämällä tavalla. Vaiheessa 1 kondensaattori C S ottaa näytteen, eli C S varataan jännitteeseen Vin. Vaiheessa 2 C S :n varaus Q siirtyy integrointikondensaattoriin C I. V 5 C p a) C I - C L C S + b) Q C I - C L C S + Kuva 63. SC-integraattorin vaiheet: a) vaihe 1 eli näytteistys ja b) vaihe 2 eli varauksen siirto
68 69 Kuvan 63 mallissa näytteistysvaiheessa (vaihe 1) lähtöjännitteen virhe out1 (n) on kaksiulotteinen funktio: out1 n = gu i n u o n 1 (62) missä u i ja u ovat tulo- ja lähtöjännite ja g on potenssisarjana karakterisoitava funktio Varauksen siirtovaiheessa (vaihe 2) virhettä out2 (n) voidaan mallintaa yksiulotteisena: out2 n = gu i n 1 (63) Näytteistysvaiheen (vaihe 1) kaksiulotteisena mallinnettu asettumisvirhe on näistä kahdesta virhemallista dominoiva, joten vastedes puhuttaessa tunnusluvuista käsitellään vain tätä virhemallia. 1. integraattorin malli on kuvan 64 folded-cascode -vahvistin malli, jolle tehtiin tilamalli. Tilamalli mahdollisti nopean konfiguroinnin sekä tarvittavan realistisen käyttäytymisen, kuten siirtofunktio-navan muutoksen vaikutukset. Tiettyjä parametreja pyyhkäisemällä voidaan tarkastella DS-muuntimen suorituskykyä tiettyjen integraattorin tunnuslukujen funktiona. Esimerkiksi kun kuvan 64 piirin ensimmäisen asteen virtalähdettä i1 ja kapasitanssia muutetaan, muuttuvat integroivan vahvistimen slew-rate sekä integraattorin toista napaa (vaihevara). CF i1 max i2 CS Cin gm1 go1 Cp1 gm2 go2 Co Kuva 64. Folded-cascode vahvistimen makromalli. Kuvan 64 vahvistimen tunnusluvut lasketaan kaavakokoelmalla: k = CF FB CS + CF + Cin i1 max Umax = gm1 CF CS C2 = Co + CF CS i1 max SR = C2 C2 = gm1 f gm1 gm2 Adc = go1 g2 missä k FB on takaisinkytkentäkerroin SR on slew-rate Umax on maksimi (lineaarinen) tulojännite H gm1 gm2 = go1 + jcp1 go2 + jc2 Aloop = Adc k FB (64)
69 7 on aikavakio Acd ja Aloop ovat avoimen ja suljetun silmukan dc-vahvistukset H on taajuusvaste on kulmataajuus Kuvassa 65 on vasemmalla esitetty integraattorin tilamallin asettumissimuloinnit (eri tulon ja lähdön alkutilalla), joiden mukaan virhetaulukko saadaan. Asettumisvirheitä on simuloitu n. 1:lla alkutilalla. Virhetaulukko on oikeanpuoleinen virhepinta, jolle tehdään polynomisovitus. Polynomimalli voidaan sijoittaa diskreettiaikaiseen simulointimalliin, ja tällöin ei tarvitse laskea asettumisvirheitä näytevälin sisältä x time x 1-5 V i -1-1 Kuva 65. Asettumiskäyrät ja virhetaulukko. error(t) V o 1 Kuva 66 esittää vahvistimen (tila)mallin asettumisvirhettä i1:n ja Cp1:n funktiona. Asettumisvirhetaulukosta (joka on joukko alkuarvovasteita) on ratkaistu vaste em. integraattorimallia käyttäen parametriparilla virheen tehollisarvon (RMS-virheen) logaritmi. Kuvaan on myös merkittynä slew-rate virran I1 funktiona sekä vaihevaran ja yksikkövahvistus kaistanleveyden (GBW) muutos kapasitanssin Cp1 funktiona. Mainittakoon että kuva 66 vastaa ns. todellisen integraattorin suorituskykyä usealla SR:n ja GBW:n arvoilla, eli tilannetta ennen polynomin karakterisointia. Yksi mittaustulos ja karakterisointi tehdään siis aina tietyllä i1:n ja Cp1:n (SR:n ja GBW:n) arvoilla. Virheen kasvaminen kuvan 66 alalaidassa johtuu slew-rate rajoituksesta, eli epälineaarisen asettumisajan kasvamisesta. Kuvan oikealla puolella virheen kasvu johtuu vaihevaran pienenemisestä, eli oskilloinnista lineaarisella asettumisalueella. Kuvan keskellä on merkittynä ns. lineaarisin alue eli pienin virhe, mitä parametriparilla (i1,cp1) saadaan.
70 71 I1 x SR (V/ns) Lineaarisin alue GBW (MHz) Vaihevara log1(cp1) o 67.3 o 58.6 o 48.8 o 4.8 o 33.4 o 26.6 o 2.8 o Kuva 66. Integraattorimallin todellinen RMS-asettumisvirhe [db] (tilamallista) I1:n ja Cp1:n funktiona. Slew-rate kasvaa I1:n funktiona ja vaihevara pienenee Cp1:n funktiona Sovitus ja mallinnuksen tarkkuus Polynomin sovitus, tarkemmin pienimmän neliösumman ei-rekursiivinen LSEsovitus [45] on sinänsä yksinkertainen matriisioperaatio, jossa kertoimet saadaan virhetaulukon E sekä mallimatriisin F avulla. Näistä jälkimmäinen on lineaarinen alkutiloista muodostettu lineaarinen yhtälöryhmä (havaintomatriisi): v i1 v o1 v2 i1 v2 o1.. v 2 i1 v3 o1 1 v F i2 v o2 v2 i2 v2 o2.. v 2 i2 v3 o2 1 = (65) : : : : : : v in v on v2 in v2 on.. v A in v B on 1 Kertoimet C, jotka sovituksessa saadaan minimoivat yhtälön X pienimmän neliösumman periaatteella, eli X = min{mse(e-fc)} (66) Kun virhevektori E tiedetään, kertoimet saadaan pienimmän neliösumman estimoinnin ratkaisukaavasta: C = F T F 1 FT E (67)
71 72 Sovitusvirhe on todellisen (tilamallin) asettumisvirheen x ja polynomilla sovitetun virhemallin xf erotus. Mallia muodostettaessa vaaditaan, että polynomimalli vastaa tarkasti todellista asettumisvirheen mallia virhetoleranssilla TOL: xf x 1 + TOL xf x x TOL xf x 2 x 2 TOL 2 ja xf x 1 TOL x xf x TOL x xf 2 x 2 TOL 2 joten RMSxf x RMSx TOL, (68) missä x on todellinen asettumisvirhe xf on polynomimallin asettumisvirhe TOL on toleranssi (esim..1 = 1%) RMS(xf-x) on mallinnusvirheen tehollisarvo ja RMS(x) on todellisen virheen tehollisarvo Tilamallin perusteella sovitetun polynomin tarkkuus riippuu myös todellisesta virheestä. Kuvassa 66 tietyillä parametreilla saadaan todella pieni RMS-virhe, joten mallinnusvirheelle täytyy vielä asettaa rajoitus, jonka mukaan pienellä todellisella virheellä mallinnusvirheen sallitaan olevan suurempi, eli RMSxf x RMSx TOL + ABSTOL, (69) missä ABSTOL antaa minimin sallitulle RMS-mallinnusvirheelle. Mallinnusvirheen maksimiarvoa rajoitetaan myös ABSTOL-parametrilla, jotta yksittäisellä tulo- ja lähtöjännitteen tiloilla ei saavuteta liian suurta virhettä, tällöin siis max( xf - x ) < 1*ABSTOL (7) Em. toleranssiehdot määrittävät polynomin asteluvun. Mikäli polynomi ei saavuta tiettyä mallinnustarkkuutta, astelukua kasvatetaan, kunnes onnistutaan. Polynomisovitus ei tunnetusti onnistu mille tahansa virhepinnalle, joten esimerkkisimuloinneissa asteluvun maksimi on 7, TOL on.1 (1%) ja ABSTOL on 1-9/2 V eli noin 3V. Myös tilamallin tarkkuus on huomioitava. Jos virhetaulukko (mittausdata) koostuu liian pienestä määrästä pisteitä, myös polynomimalli on epätarkka. Toleranssirajojen ja näytepisteiden lukumäärää tutkittaessa voidaan käyttää apuna tilastomatematiikan tunnuslukuja. Muuttujien x ja xf välinen Pearsonin korrelaatiokerroin r xy (tulomomenttikerroin) kuvaa kahden muuttujan välistä lineaarista riippuvuutta ja sen määrittelee lauseke [45]:
72 73 r xy N = x xxf xf covx xf = n =, stdx stdxf N N (71) x x xf xf n = n = josta saadaan tilastomatematiikassa käytettävä selityskerroin r xy 2, joka kertoo kuinka suuren osan x:n vaihtelusta xf pystyy selittämään. Kun yhtälössä on vain yksi selittävä muuttuja, r xy 2 on X:n ja Y:n välisen korrelaation neliö. Useamman selittävän muuttujan tapauksessa r xy 2 on selitettävän (x) muuttujan havaitun arvon ja ennustetun arvon korrelaation neliö. Matemaattista selityskerrointa käytettiin varmistamaan tarpeeksi suuri näytepisteiden lukumäärä, minkä jälkeen onnistunut sovitus antoi lähes maksimaalisen selityskertoimen (hieman alle yksi) Simulointimalli ja suorituskykysimuloinnit Polynomimallinnuksessa esimerkkinä käytetty muunnin on esitetty kuvassa 67. Se on 2. asteen yksibittinen DS, jonka ylinäytteistyssuhde on 32. Muuntimen näytteistystaajuus on 1MHz ja integraattorin avoimen silmukan kaistanleveys on noin 65MHz. Topologiaksi on valittu feed-forward tyyppi, jossa molemmat integraattorit ovat viiveellisiä. Tällä on vältetty kahden vahvistimen asettumisvaatimus yhden kellojakson aikana. Mallinnettavalla 1. integraattorilla on kolme tulosignaalia: Vin (tulo), Vref (D/Atakaisinkytkentä) ja Vfb (resonaattoritakaisinkytkentä). Tulosignaaleihin liittyvät kondensaattorit ovat tällöin C 1, C 2 ja C 3. Ideaalisessa tapauksessa lähtö on tällöin V o T C 1 = V in T V ref T V fb T+ V o T 1. (72) C I C 2 C I C 3 C I Varauksen siirto integroivaan kondensaattoriin vaiheessa 2 aiheuttaa toisen asettumistransientin. Esimerkkimuuntimen suorituskyky on melko vaatimaton (SNR n. 6 db), joten.1 pf:n minimikapasitanssin valinta ei vaatinut skaalaamista kt/c-kohinan mukaan.
73 74 u (tulo) IN REF FB out mallinnettava integraattori komparaattori polynomi mallit Vaiheen 1 virhe out1 (n) Vaiheen 2 virhe out2 (n) v (lähtö) Kuva asteen yksibittisen DS:n Simulink-malli polynomimallinnuksella. Integraattorin vaiheet vaativat kummatkin oman virhemallinsa. Kuvassa 68 on sovitusvirhe, jolle tehdään virhetoleranssitarkastus. Kun polynomi täyttää vaaditut toleranssit, tarkastetaan onko polynomissa turhia kertoimia. Turhat kertoimet ovat kertoimia, joita voidaan poistaa rikkomatta virheen toleranssirajoja. 1.5 x 1-5 sovitusvirhe Vin Vop Kuva 68. Mallinnuksen virhe tyypillisillä piirin parametreilla. 1
74 75 Kun polynomimallit (kaksi- ja yksiulotteiset polynomit kummallekin vaiheelle) on karakterisoitu, voidaan aloittaa DS-muuntimen simuloinnit. Sivun 74 kuvassa 67 esitetty malli on Simulink-malli, jossa ensimmäisen integraattorin tulojen (tulosignaali, paikallinen takaisinkytkentä sekä lähdön takaisinkytkentä) sekä integraattorin lähdön perusteella lasketaan polynomimallien mukaiset virheet. Virheenlaskenta on toteutettu Matlab-funktiolla, jonka Simulink-malli lukee. Tuloon summautuva virhe on integrointivaiheen virhe (kaksiulotteinen) ja lähtöön summautuva virhe on varauksen siirtovaiheen virhe (yksiulotteinen). Simulointeja tehdään kuvan 66 mukaisesti eri i1:n ja Cp1:n funktiona, ja simulointituloksista lasketaan muuntimen suorituskyvyn tunnusluvut SNDR ja SFDR. Kuvassa 69 on esimerkki-ds:n SFDR ja SNDR i1:n ja Cp1:n funktiona tulosignaalin amplitudin ollessa 5% täyden skaalan signaalista. Kuvassa korostuu hyvin vaihevaran pienenemisen vaikutus. Katkoviivalla rajatulla alueella sovitettu polynomi ei ole kyennyt saavuttamaan vaadittua virhetoleranssia (asteluvun maksimiraja tuli vastaan). Polynomin asteluku ei kerro kaikkea itse polynomin pituudesta. Polynomilla on ristitermejä (eli vin N * vout M -termejä), joiden minimäärä määritetään sovitusohjelmistolla jokaiselle asteluvulle, kunnes asteluvun yläraja tulee vastaan. Ohjelma myös karsii turhat kertoimet pois, ts. ne kertoimet, jotka eivät vaikuta sovitustulokseen, poistetaan. x i SFDR log 1 (Cp1) 65 i1 SNDR x log 1 (Cp1) Kuva 69. SFDR ja SNDR (db) I1:n ja Cp1:n funktiona.
75 Mittaukseen perustuvan polynomimallinnuksen hyöty Polynomimallinnuksella käyttäytymistason DS-ADC simulointimalliin voidaan sisällyttää SC-DS:n dominoivin epäideaalisuus, eli tuloasteen integraattori. Esimerkkimallina on nyt simuloitu z -1 /(1-z -1 )-tyyppistä täyden viiveen integraattoria, jonka voisi muuttaa myös puolen jakson viiveellä toimivaksi. Jos jälkimmäinen integraattori olisi viiveetön (todellinen resonaattori), mallinnettavana olisi kahden vahvistimen asettuminen saman kellojakson aikana, joten tilamalliinkin pitäisi lisätä toinen vahvistin. SC-integraattorin polynomimallinnuksella voidaan mallintaa lähtöriippuvaa jännitevahvistusta sekä asettumisnopeutta. Näitä ilmiöitä ei voida mallintaa usein käytetyillä yksiulotteisilla analyyttisillä malleilla. Koska malli perustuu mittaustulokseen, voidaan myös simuloida usean siirtofunktio-navan vaikutuksia, jotka näkyvät esim. oskillointina pienen vaihevaran johdosta. Polynomimallin karakterisointi ja liittäminen simulointimalliin on erittäin helppoa. Kuten odottaa saattaa, polynomimallinnus hidastaa Simulink-mallin simulointia verrattuna puhtaasti kaavapohjaiseen malliin. Empiirisen tuntuman mukaan hidastus on noin 7-12-kertainen. Polynomimallinnus optimaalisella simulointinopeudella saadaan Simulinkin versiossa 6. (ja uudemmissa) funktion upottamisella (embedded m-file), jolla vältetään toistuvaa Matlab-tiedoston kutsumista Simulink-mallista. Kuitenkin polynomimallinnuksen voidaan sanoa olevan nopeaa, koska noin tuhannen karakterisoinnin ja simuloinnin parametripyyhkäisy kestää karkeasti puoli vuorokautta (yhdessä simuloinnissa lasketaan noin 65 pistettä). Kun karakterisointi ja sovitus vievät tästä ajasta noin puolet, voidaan sanoa että diskreettiaikaisen simuloinnin nopeusetu transistoritason simulointeihin on voimassa. Myös kappaleessa 7.1 esitetty analyyttinen malli on toteutettu Simulinkympäristössä. Tärkein ero analyyttiseen malliin on siis ainoastaan vahvistimen mallinnustapa, joten itse polynomimallinnuksen simulointeihin voi toki lisätä muitakin virheen käyttäytymismalleja, kuten kellojitterin vaikutuksen.
76 77 8. MONIBITTISET DELTA-SIGMA MUUNTIMET Kun DS-muuntimen lähdön sanaleveyttä kasvatetaan, suorituskyky paranee noin 6 db/bitti. Monibittisyyden ongelmana on kuitenkin takaisinkytkennän D/Amuunnoksen epälineaarisuus. Yksibittisellä D/A-muunnoksella lineaarisuus on taattu: kaksi kvantisointitasoa mahdollistaa täydellisen lineaarisuuden. N-bittisellä muuntimella (kuva 7) on 2 N kvantisointitasoa, joiden sovitusvirheet tuovat signaalikaistalle säröä. Eli kun D/A-yksikköelementit summataan, epäsovitus aiheuttaa INL-virhettä (Integral nonlinearity) digitaaliseen lähtösanaan verrattuna, ja koska takaisinkytkennässä virhe summautuu tulosignaaliin, se ei muokkaudu kuten kvantisointikohina. I MSB D/A muunnin: 2 B yksikköelementtiä (virtalähteitä tai kondensaattoreita) I out Kuva 7. Takaisinkytkentähaaran D/A-muunnin (DAC). Kuvan 7 yksikköelementtien summausta kuvataan termillä lämpömittarikoodaus (thermometer coding), jossa tietty lähtösana kytkee aina samat yksikköelementit. Tällöin epäsovituskohina aiheuttaa aina harmonista säröä signaalitaajuuden lähistölle. Jos DACin lineaarisuus on alle muuntimen ideaalisen suorituskyvyn, epäsovituskohina on dominoiva kohinanlähde. Kuvassa 71 on simuloitu erään 4- bittisen muuntimen SNDR-suorituskyky D/A-muuntimen yksikköelementtien arvon hajonnan () kasvaessa. 1 9 SNDR (db) db / dekadi virheen hajonta Kuva 71. Epäsovituksen vaikutus suorituskykyyn, 4-bittinen muunnin.
77 Monibittisen DS A/D-muuntimen lineaarisuusvirheiden korjaaminen Monibittisen DS-A/D-muuntimen takaisinkytkentähaaran DAC-yksikköelementtien epäsovitusvirheiden linearisointiin on olemassa useita ratkaisuja. Suosituin niistä on DEM (dynamic element matching). Siinä kantavana ajatuksena on satunnaistaa tai jaksottaa yksikköelementtien käyttöä. Tällöin epäsovituskohina joko levittyy laajalle kaistalle, muokkaantuu korkeammille taajuuksille tai moduloituu kapeakaistaiseksi signaalikaistan ulkopuoliseksi signaaliksi. Kuva 72 valottaa hyvin linearisointia: Jos jokaiselle koodille valittujen yksikköelementtien käyttö on yhtä todennäköistä, D/A muunnoksen keskiarvokäyrä on lineaarinen. DAC lähtö DAClähtöjä eri ajanhetkellä keskiarvo digitaalinen lähtö Kuva 72. DAC-yksikköelementtien käytön satunnaistaminen jokaiselle digitaaliselle lähtökoodille: keskiarvo on lineaarinen. Digitaalisessa virheenkorjauksessa ideana on tallettaa DAC-yksikköelementtien INLtai DNL-virheet tarvittavalla tarkkuudella korjaustaulukkoon, jolloin korjaus tapahtuu summaamalla virhe digitaaliseen lähtösanaan. Myös digitaaliselle virheenkorjaukseksi on olemassa useita keinoja. Näistä yksinkertaisin on offlinekorjaus, jossa virheet mitataan tarkasti ennen kun monibittinen muunnin voi aloittaa toimintansa. Kuvan 73 digitaalinen virheenkorjaus tehdään käyttäen summaamalla tallennettuja tarkkoja virhekoodeja DS-muuntimen lähdön kanssa. RAM-lookup-taulukossa (RAM-LUT) olevan virhetiedon resoluutio on verrannollinen DS-muuntimen suorituskykyyn. Virhe-informaation mittaaminen eli kalibrointi voidaan tehdä kolmella tavalla: virheen mittaus ennen itse muuntimen toimintaa, eli ns. offline-korjaus, korjaus rinnakkain monibittisen muuntimen toimiessa, eli background-korjaus ja adaptiivinen virheenkorjaus, jossa elementtien DNL-virheet haetaan DS:n lähtösignaalista. Tämä vaatii oman mittauskaistansa, joka täytyy valitettavasti varata signaalin kaistalta.
78 79 in N N-bit M+N Silmukkasuodatin ADC Desimointi- Suodatin N-bit DAC RAM lookup-taulukko M M>>N Kuva 73. Digitaalinen virheenkorjaus: RAM taulukossa oleva M-bittinen virhe summataan N-bittiseen DS-lähtödataan. 8.2 Dynamic element matching (DEM) Satunnaistamalla yksibittisten yksikkö-dac -elementtien käyttöä (Random Element Swapping) epäsovituskohina muuttuu valkoseksi kohinaksi, joka levittyy tasaisesti koko taajuusalueen yli. Epäsovituskohinan teho on signaalista riippuva, joten se voi peittää kvantisointikohinatason signaalin kaistalla. Jos kvantisointitasoja on monta, esim. 8 kappaletta, satunnaistamislogiikan toteutus on varsin mutkikas, koska se vaatisi kaikkiaan 432 (8!) kombinaation kytkemistä. Tähän ongelmaan onkin esitetty algoritmeja, jotka yksinkertaistavat satunnaistamislogiikkaa [22]. Epäsovituskohinaa voidaan myös moduloida (clocked averaging): Indeksoidaan D/ A-yksikköelementit ja aloitetaan jokainen D/A-muunnos edellisen lähtösanan toisen indeksin elementillä. Harmoninen särö sekoittuu taajuudelle f s /2 B ja sen harmonisille taajuuksille. Rajoittava tekijä on kvantisointitasojen määrä: jos kvantisointitasoja on paljon ja OSR on pieni, moduloitu särö on signaalin kaistalla. Yhteys kvantisointitasojen lukumäärällä ja ylinäytteistyssuhteella on: OSR >,5(1+2 B )2 B (73) Eli jos DAC on 3-bittinen, OSR:n on oltava yli 32, ja 4-bittisellä yli 128. Individual level averaging (ILA) metodi keskittyy kuvan 72 periaatteeseen, eli käytetään jokaista DAC elementtiä yhtä suurella todennäköisyydellä. Menetelmään on kehitetty useampia algoritmeja, ja perusideana on käyttää tietoa edellisten A/Dmuunnoksien DAC-elementtien valinnasta käyttäen kombinaatioita sekventiaalisesti. Suosituin DEM-menetelmä on Data weighted averaging (DWA), jolla saadaan parempia tuloksia kuin edellisillä menetelmillä [46]. 1. asteen DWA-algoritmissa ideana on DAC:n elementtien käyttö syklisesti, eli koodin aloitusindeksi on edellisen koodin viimeistä DAC indeksiä seuraava. Menetelmä käyttää jokaista DAC elementtiä mahdollisimman tasaisesti, jolloin DAC-virheet keskiarvoistuvat mahdollisimman nopeasti ja epäsovituskohina muokkautuu ensimmäisen asteen ylipäästövasteen mukaan. DWA-menetelmästä löytyy paljon variaatioita mm. korkeamman asteen epäsovituskohinan elementinvalintalogiikka sekä toteutuksia kaistanpäästö DS:lle [47]. Kuvassa 74 on DWA-algoritmin Matlab-simulointiskripti kommenteilla.
79 8 Vuorossa olevan lähtösanan arvo sekä edellisen lähtösanan käyttämät yksikköelementit määrittelevät valittavat elementit, joille annetaan aloitus- ja lopetusindeksit n1 ja n2. Jos n2 on pienempi kuin n1, aloitetaan uusi kierros. Koodin syklisyyttä visualisoidaan usein kuvan 74 tapaan pyörivällä osoittimella. Ympyrän sisällä oleva punainen katkottu ympyrä pyrkii hahmottamaan tarvittavaa yksikköelementtien lukumäärää, joka on tässä esimerkissä 4. 3 Koodi: [3, 2, 4, 1,...] Koodin maksimipituus: osoitin NELM=4; % DAC-elementtien lukumäärä E=randn(NELM,1)/1; % virheen oletetaan noudattavan normaalijakaumaa data=round(rand(496,1)*(nelm-1))+1; % kokonaislukujoukko eli DS-lähtö datasum=cumsum(data); % kumuloidaan data indeksointia varten nxtp=[1;mod(datasum,nelm)+1]; % seuraava osoitin-indeksi for ind=1:length(data) if nxtp(ind+1)>nxtp(ind) % jos n1<n2 INL(ind)=sum(E(nxtp(ind):(nxtp(ind+1)-1))); else %jos n1>n2 INL(ind)=sum([E(nxtp(ind):NELM);E(1:nxtp(ind+1)-1)]); end end Kuva 74. DWA-algoritmi: Osoitin valitsee syklisesti kullekin koodille käytettävät DAC-elementit. Alempana on vastaava Matlabilla toteutettu DWA-algoritmi satunnaiselle lähtöarvolle data. NELM on yksikköelementtien lukumäärä ja E on kunkin DAC-elementin DNL-virhe. Epäsovituskohinan muokkausalgoritmeja voidaan esittää geneerisessä muodossa, jossa epäsovituskohinan muokkaukselle saadaan myös korkeamman asteen vaste [51]. Elementinvalintalogiikka tehdään kuvan 75 systeemillä. Vektorikvantisointioperaatiossa VQ(sy,v) v on N-bittinen DS-muuntimen lähtösignaali ja sy on 2 N kappaletta painokertoimia sisältävä vektori. Nämä painokertoimet määräävät, mitkä yksikköelementit valitaan edustamaan lähtösanaa. Esimerkiksi, VQ(sy,v) = VQ([,,2,1] T,3) = [1,,1,1] T, (74)
80 81 missä VQ tarkoittaa vektorikvantisointi-operaatiota. Kyseisessä esimerkissä elementit valittiin vektorin sy kertoman prioriteetin mukaan. N-bittinen lähtöarvo koodataan siis 2N-mittaiseksi nollien ja ykkösien vektoriksi, ja ykkösien osoite kertoo valittavat yksikköelementit. Kuvan 75 elementinvalintalogiikka muodostaa itse asiassa kappaleessa esitetyn digitaalisen error-feedback topologian, jossa F vastaa FIRsuodatinta ja signaali sy on takaisinkytkentäsignaali. Funktiolla min( ) normalisoidaan priorisointivektori sy siten, että nolla on minimiarvo. Jos kuvassa 75 epäsovitussiirtofunktio MTF olisi z -1, olisi vaste sama kuin DWA- menetelmässä. Menetelmän huonoja puolia ovat toteutuksien monimutkaisuus ja korkeamman asteen MTF:n tapauksessa (DS:lle tyypilliset) stabiilisuus-ongelmat. Käytännössä elementinvalinta-algoritmin toteutusta ei tehdä tällä mallilla. F -min( ) - + MTF(z) vektorikvantisointi sy sv yksikkö DAC v [1...2 N ] valintavektori Kuva 75. Korkean asteluvun elementinvalintalogiikka. Vektorikvantisointilohko valitsee vektorin sy painokertoimien perusteella, mitkä elementit valitaan. Korkeamman asteen elementinvalintalogiikalla voidaan tehdä myös kaistanestotyyppinen epäsovituskohinan vaste kaistanpäästötyyppiselle DS:lle. Kuvassa 76b on esitetty 4. asteen epäsovituskohinan muokkauksen elementinvalintataulukko, ja vertailun vuoksi myös vastaava taulukko ilman koodausta (kuva 76a). Schreierin delta-sigma toolboxista löytyy funktio simulateesl DWAmenetelmän sekä korkeamman asteen MTF:n simuloinnille. a) 3 b) 3 Valitut elemtit (vihreällä) Valitut elemtit (vihreällä) 2 4 näyte 2 4 näyte Kuva 76. Elementin valinta a) perinteisellä thermometer-koodauksella b) 4.asteen kaistanpäästötyyppisen muokkauksen mukaan. DEM-menetelmät sopivat sellaisenaan myös DS-D/A-muuntimiin (DS-DAC), jossa digitaalista interpolointia ja DS-modulointia seuraa D/A-muunnin
81 Digitaalinen virheenkorjaus DWA-menetelmässä epäsovituskohinan muokkauksen asteluvun täytyy sopia itse DSmuuntimen astelukuun. Tämän lisäksi pieni ylinäytteistyssuhde asettaa epäsovituskohinan muokkaukselle lisähaasteen, koska signaalin kaista on tällöin suhteellisen leveä. Kuten mainittu, valinta-algoritmin astelukua ei voida kasvattaa mielin määrin, koska tällöin elementin valintalogiikka on monimutkainen ja jopa epästabiili. Riittämättömästä korjauksesta esimerkkinä on kuva 77, jossa on 3- bittisen, 6. asteen DS-muuntimen taajuusvaste ennen ja jälkeen epäsovitusvirheen 2. asteen muokkausta. Muokkauksella saavutetaan noin 17dB:n parannus SFDR:ään, joka ei riitä alkuunkaan. DEM-menetelmistä poiketen digitaalinen virheenkorjaus ei muokkaa epäsovituskohinaa, vaan vaimentaa sen käyttäen epäsovitusvirheen mittausta. Kun jokaisen DAC-yksikköelementin INL-virhe on tallennettu riittävällä tarkkuudella, virheenkorjaus on taulukkopohjaista, ja se on yksinkertaisimmillaan koodiin liittyvän virheen summausta DS-muuntimen lähtösanaan, kuten kuvassa 73 esitettiin. 2 2 a) b) signaali signaali -2-29dB harmoninen 2. harmoninen dB dc fb 2fb -12 dc Kuva asteen 3-bittisen muuntimen (FF-topologia, OSR on 16) taajuusvaste a) ennen ja b) jälkeen 2. asteen epäsovituskohinan muokkausta. fb 2fb DAC-siirtofunktion kompensointi Korjaus on helpoimmillaan yksinkertaista takaisinkytkentä-dacin virheen summausta vastaavan koodiin. Kuitenkin, mikäli siirtofunktio DAC-virhelähteestä DS:n lähtöön ei ole laajakaistainen, optimaalinen korjaus vaatii virheenkorjauksen kompensointia em. siirtofunktiolla [6]. DAC-virheen voidaan ajatella summautuvan integraattoriketjun ensimmäiseen integraattoriin, jolloin DAC-virhesiirtofunktion on
82 83 sama kuin signaalin siirtofunktio ilman tulosignaalin summausta muiden integraattoreiden tuloihin. Kompensoinnilta ei voi välttyä multiple-feedback (MF) topologialla, koska siirtofunktio on tällöin poikkeuksetta alipäästötyyppinen: DACTF(z) = -a1*stf MF (z), (75) missä a1 on ensimmäiseen integraattoriin summautuvan takaisinkytkentähaaran kerroin ja STF MF on MF-topologian signaalin siirtofunktio vain yhdellä tulosignaalihaaralla Sen sijaan feed-forward topologialla on ominaisuutena varsin tasainen STF, joten kompensoinnilta usein vältytään. Kompensointisuodatin on useimmiten DACvirhesiirto-funktion FIR-estimaatti (kuva 78) tai yksinkertaisimmillaan pelkkä viive. Usein asiaan liittyvissä julkaisuissa, kuten [48], ei ole huomioitu kompensointia, koska MF-topologian takaisinkytkentähaaroilla on mallinnuksessa oletettu olevan yhteinen DAC, mikä ei usein ole kovin realistista. Tällöin DAC-virhesiirtofunktio on sama kuin FF-topologian, eli DACTF(z) = -STF FF (z) = 1-NTF(z). (76) missä STF FF on FF-topologian signaalin siirtofunktio vain yhdellä tulosignaalihaaralla ADC B + + M+B desimointi RAM LUT M FIR M>>B Kuva 78. Digitaalisen virheenkorjaus MF-topologialle: FIR-suodatinta tarvitaan DAC-virhesiirtofunktion kompensointiin. MF-topologialla on siis useita takaisinkytkentähaaran D/A-muuntimia. Epäsovituksen virheenkorjaus keskitetään kuitenkin menetelmästä riippumatta aina integraattoriketjun ensimmäiseen integraattoriin summautuvaan epäsovitusvirheeseen, koska muihin integraattoreihin summautuva virhe muokkaantuu ylipäästöfunktiolla (olettaen että kaikki integraattorit ovat viiveellisiä): z 1 n 1 DACTF n z = a n (77) Dz Missä n on integraattorin järjestys (n = 2, 3, 4...), a n on takaisinkytkentäparametri ja D(z) on kohinan ja signaalin siirtofunktion nimittäjä, kuten kaavassa (37). Kaava (75) on siis yleistys kaavasta (77). Korostettakoon vielä, että FF-topologian DS-A/D muuntimilla on aina kaavan (76) mukainen DAC-virhesiirtofunktio johtuen yhdestä takaisinkytkentähaarasta.
83 84 Seuraavissa kappaleissa esitellään kolme kalibrointiin perustuvaa virheenkorjausperiaatetta, eli offline-kalibrointi, taustalla tapahtuva korjaus sekä adaptiivinen virheenkorjaus. Näistä kaksi viimeistä perustuvat kokonaan tässä työssä tehtyihin tutkimuksiin Offline-kalibrointiin perustuva korjaus Offline-tyyppinen virheenkorjaus on varsin laajasti raportoitu virheenkorjausmenetelmä, ensimmäiset julkaisut löytyvät 8-luvun lopulta [49]. Ideana on takaisinkytkentä-dacin virheiden mittaus, minkä jälkeen monibittinen muunnin voi toimia. Virheiden mittaus tehdään ns. kalibrointi-tilassa, jossa käytetään yksibittistä DS-A/D muunninta sekä desimointisuodatinta. Tämä johtuu siitä, että yksibittisessä DS:ssa ei ole lineaarisuusvirheitä. Tämän ns. kalibrointivaiheen yksibittinen muunnin käyttää monibittisen DS:n komponentteja, millä minimoidaan piirin kompleksisuutta. Virheiden korjauksessa mitataan DACin lähtö jokaiselle koodille, eli yksibittisen kalibrointi-ds:n tulona on vakio dc-signaali. Alkuperäinen idea on varsin suoraviivainen eli kumuloituva DAC-elementtien summa jokaiselle koodille tuotiin kalibrointi-ds:n tuloon. Tämä on ongelmallista, koska suuret amplitudivaihtelut voivat johtaa mittaustulosten resoluution muutoksiin, varsinkin jos kalibrointi-ds on yli 2. asteen DS. Tuomalla kalibrointi-ds:aan vuorotellen yhden yksikköelementin arvo, jossa on DNL-virhettä, vältytään suurilta amplitudivaihteluilta. Idea on esitetty kuvassa 79: 1. Laskuri valitsee elementin yksi kerrallaan mittaamiseen tarvitseman ajan määräämällä kalibrointitaajuudella. DS:n näytteistystaajuus on paljon suurempi kuin elementin valintataajuus. 2. Sinc-tyyppinen desimointisuodatin laskee keskiarvon mitattavalle dc-arvolle (plus yksi), josta saadaan estimaatti DNL-virheelle, eli DNL. Desimointisuodattimen lähtösignaalin taajuus on kalibrointitaajuus. 3. Integrointi ennen RAM-taulukkoon tallentamista tarkoittaa, että taulukkoon tallennetaan INL-virheitä INL. Kun kalibroidaan seuraavaa elementtiä, sen DNL-virhe summataan edellisen DNL-virheen kanssa, ja seuraavaan DNLvirheeseen summataan edellinen virheiden summa jne. 4. Kumuloituneet virheet eli INL-virheet tallennetaan RAM-taulukkoon laskurin määräämään osoitteeseen. Kun taulukkoon tallennetaan vain virheet, eikä siihen summautuvaa vakiotasoa, säästetään myös virhetaulukon sanaleveydessä [5]. 5. Kalibrointi on päättynyt, kun kaikkien koodien INL-virheet ovat taulukossa. Tallennettujen virheiden sanaleveys on poikkeuksetta paljon suurempi kuin itse DS:n lähtösanan leveys. Koodin sanaleveys sekä kalibrointi-ds:n ja sitä seuraavan sincdesimointi-asteiden asteluku riippuu halutusta monibittisen DS:n suorituskyvystä. Em. asteluku vaikuttaa myös korjausnopeuteen. Korjausnopeuteen liittyvät seikat pätevät myös seuraavassa kappaleessa esiteltävälle background-tyyppiselle korjaukselle, joten aiheesta kerrotaan tarkemmin siellä.
84 85 1+ DNL yksikköelementit silmukkasuodatin komparaattori N-bittinen laskuri valitun koodin osoite RAM LUT INL z -1 DNL DNL desimointisuodatin Kuva 79. Eräs offline-korjauksen kalibrointiperiaate: lasketaan DNL-virhe ja tallennetaan INL-virhe RAM-taulukkoon integroimalla DNL-virhe. Sininen väri tarkoittaa hitaalla kalibrointitaajuudella näytteistettyä ja punainen nopeammalla näytteistystaajuudella näytteistettyä dataa Background- eli taustakorjaus Kuvassa 8 esitetty taustalla tehtävä virheenkorjaus käyttää pitkälti samoja periaatteita kuin offline-korjaus. Erona on se, että kalibrointi tehdään rinnakkain monibittisen muuntimen ollessa aina toiminnassa. Ideana on mitata DNL-virheet erillisellä kalibrointi-ds:lla siten, että yhtä virhettä mitattaessa muut DAC elementit ovat monibittisen DS:n käytössä. Tällöin tarvitaan yksi ylimääräinen yksikköelementti. [6] in silm. suod. DAC ADC N RAM M, INL + + desimointiin kalibrointi yksibittinen ja sinc K desimointi. Kuva 8. Taustavirheenkorjauksen idea: rinnakkainen kalibrointi ja virheestimaatin tallennus.
85 86 Kun mittaukset on suoritettu, kalibrointi-ds lakkaa toimimasta, ja virheenkorjaus on täsmälleen samanlaista kuin offline-korjauksessa. Background-korjauksessa tallennetut virheet ovat aina DNL-virheitä, koska INL-virhe lasketaan niiden avulla. Koska DAC-elementtejä on vain yksi ylimääräinen, ei myöskään korjausnopeudessa ole paljon eroa offline-korjaukseen. Kalibrointinopeus, eli virheen mittaamiseen tarvittavien näytteiden lukumäärä on kääntäen verrannollinen kalibrointi-ds:n ja sitä seuraavan desimointisuodattimen astelukuun. Kuvassa 81 on korjaustuloksia 3-bittiselle, 6. asteen DS:lle, jonka OSR on 16. Kalibrointi-DS on 3. asteen ja sitä seuraava desimointisuodatin on 4. asteen sinc-aste. Kuvasta huomataan, että yhdessä kalibroinnissa tarvittavien näytteiden lukumäärä on minimissään 256, jotta päästään lähelle ideaalista korjausta. Yhteys korjaustarkkuuden ja suorituskyvyn välillä on ilmeinen: DS-muuntimen resoluutio biteissä (effective number of bits, ENOB) on karkeasti 15 bittiä, kun käytetään kaavaa: ENOB = SNR ,7 (78) 6,23 Kuvasta 81 nähdään että korjaustarkkuudeksi tarvitaan vähintään 15 bittiä. Esimerkkisimuloinnissa suorituskyvyn mittarina on SNDR. Kun SNDRsuorituskykyä katsotaan kalibroinnin keston funktiona eri taajuisilla siniherätteillä, kaavan (78) korjaustarkkuus ei välttämättä riitä: pienet spurritasot korostuvat, varsinkin jos signaalin toinen harmoninen on signaalin kaistalla. Ainakin kahden bitin turvamarginaali on suositeltavaa kalibrointitarkkuudessa, eli kalibrointitarkkuuden on oltava vähintään ENOB+2. 1 a) ideaalinen korjaus SNDR [db] 8 6 tausta- ja offline-korjaus Ei korjausta b) Mittaus resoluutio [Bit] näytettä tarvitaan Näytteiden lukumäärä yhdessä kalibrointisyklissä Näytteiden lukumäärä yhdessä kalibrointisyklissä Kuva 81. Offline- ja background korjaus. a) Suorituskyky ja b) INL-estimaatin tarkkuus yhteen kalibrointisykliin tarvittavien näytteiden lukumäärän funktiona. Kalibrointi-DS on 3. asteen yksibittinen muunnin, jota seuraa 4.asteen sincdesimointisuodatin.
86 87 Em. kalibrointitarkkuus on laskettu kaavalla Tarkkuus 2 y ideal y = log korj Bit, (79) A FS missä y ideal on ideaalinen, nollakeskiarvoinen desimoitu lähtö, y korj on korjattu, nollakeskiarvoinen desimoitu lähtö ja A FS on täyden skaalan taso. Kuvassa 82 on tarkempi kuvaus taustakorjauksesta. Valintalogiikka vastaa kalibroitavien yksikköelementtien valinnasta ja antaa myös RAM-taulukolle korjattua DNL-virhettä vastaavan koodin osoitteen. Tarvittaessa kalibrointi voidaan käynnistää uudestaan, mutta sitä ei voida pitää jatkuvasti toiminnassa. Hidas elementtien rotaatio vastaa sivulla 79 esitettyä clocked averaging -menetelmää, mutta hitauden vuoksi se moduloi matalataajuisen häiriön signaalin kaistalle. Tämä johtuu siitä, että absoluuttista korjaustarkkuutta ei saavuteta, vaan epäsovituskohina pyritään pitämään kvantisointikohinaa pienempänä. Rinnakkaisen korjauksen etuna on erillisen mittausmoodin puuttuminen, mutta valitettavasti siinä tarvitaan erillinen kalibrointilohko (DS ja sinc-desimointi), mikä kasvattaa toteutuksen kompleksisuutta. Tulo signaali silmukka suodatin a) Koodi e) kvantisointi DAC_out DNL_Calib DNL_addr c) Korjattu desimoitu lähtö Decimate OSR: 1 silmukka suodatin (1-bit DS). b) komparaattori DNL_addr_cal valintalogiikka Calib Sinc. Decimator Koodi Osoite Osoite (mittaus) Kalib. lähtö Trig KORJAUS d) out Corrected TRIG kytkin virheenkorjauksen uudelleen aloittamiselle Kuva 82. Background-korjaus: a) monibittinen DS, b)yksibittinen kalibrointi-ds ja desimointi, c) DAC-elementin valintalogiikka, d) RAM-taulukko ja integrointi ja e) monibittisen DS:n desimointiasteet.
87 Adaptiivinen eli online-tyyppinen korjaus Sokeassa eli adaptiivisessa virheenkorjauksessa ei käytetä erillistä testisignaalia, vaan hyödynnetään signaalin jotain tunnettua ominaisuutta kuten amplitudijakaumaa. Amplitudijakaumaa käytetään korjauksessa, jossa D/A-muunnetun datan jakauma eli histogrammin muoto tunnetaan. Monibittisissä DS-muuntimissa amplitudijakauman käyttö ei toimi, koska kvantisointitasoja on niin vähän (tyypillisesti 3-16), että niistä ei voida tehdä luotettavaa jakaumamallia. Tässä työssä D/A-muunnoksen INL-virheiden adaptiivisen etsimisen idea on esitetty julkaisussa [7]. INL-virheiden adaptiivinen etsiminen edellyttää omaa, virheen mittaukseen tarkoitettua taajuuskaistaa. Koska epäsovituskohina dominoi signaalin kaistalla, mittauskaista joudutaan varaamaan sieltä. Erillinen mittauskaista pienentää alkuperäistä signaalin kaistaa, jolloin OSR kasvaa. Kuvassa 83 on esitetty signaali- ja mittauskaista. Mittauskaistan informaatio saadaan desimoidusta ja ylipäästösuodatetusta DS-lähtödatasta. Ampl. (db) signaali Virheen Mittauskaista Kvantisointikohina f f b DAC-epäsovituskohina taajuus (log) Kuva 83. Uusi signaalin kaista ja mittauskaista. Mittauskaista varataan alkuperäisestä signaalin kaistasta. Seuraavassa esimerkissä on tehty adaptiivinen virheenkorjaus 3-bittiselle DS A/Dmuuntimelle, jonka lähdön kvantisointitasot ovat [ ]. Kuvassa 84 on adaptiivisen korjauksen lohkotason esitys. Tarkoituksena on löytää kutakin lähtösanaa vastaava painokerroinvektori INL (haettava INL-virhe), joka minimoi mittauskaistan epäsovituskohinan n INL. N-bittisen DS:n lähtökoodit (eli kvantisointitasot) dekoodataan binääri/lineaari-dekoodauksella vektoriksi A, jossa ykköset painottavat kunkin koodin osoitetta. Vektori, joka minimoisi epäsovituskohinan on K INL, missä K on kvantisointitasot. Eli jos vektori A kerrotaan elementtikohtaisesti K INL :n kanssa, saadun vektorin summa on korjattu koodi. INL-virhevektori INL haetaan korreloimalla mittauskaistalla olevaa virhettä kunkin lähtötilan kanssa. Koska mittauskaista täytyy eristää ennen painokertoimella kertomista, desimointi ja ylipäästösuodatus tulee tehdä ennen sitä. Tämä johtaa siihen, että em. suodatusoperaation tulee tehdä jokaiselle lähtötilalle erikseen, mikä kasvattaa piirin kompleksisuutta huomattavasti. LMS-silmukoita on kolme perustyyppiä: kohinan vaimennus, ekvalisointi ja ennustava [52]. Kuvan 84 LMS-silmukka on ennustava (predictive) LMS-silmukka. Kuvan 84 painokerroinvektorit w ovat adaptoinnin alussa kvantisoijan tasot K, joten koostettu signaali y on adaptoinnin alussa todellinen mittauskaistan sisältö. LMS-algoritmi minimoi virhetermiä e, mikä on y:n ja sen
88 89 viivästetyn signaalin d erotus. Koostettu signaali saavuttaa miniminsä, kun painokertoimet ovat K+' INL, missä ' INL on estimoitu INL-virhe. Desimoitu, mutta ei-ylipäästösuodatettu data (S) kerrotaan painokerroinvektorilla w, ja sadun vektorin summa on korjattu koodi. LMS-silmukka on toteutettu ennustavan adaptoinnin perusteella, ja LMS painokertoimet päivittyvät kaavan (8) mukaan. wn+ 1 missä n on nykyisen näytteen indeksi on adaptointiaskel e on ennustusvirhe u on tulosignaali bin/lin-dekoodaus wn + en un = (8) N signaali+n Q +n INL A demux 2 Desimointi- N Ylipäästö- 2N Suodattimia suodattimia Decim S mux HPF mux u Ennustava LMS silmukka W Z -1 u e d y Z -1 W u S W signaali Kuva 84. Adaptiivinen virheenkorjaus. DS-muuntimen lähtö koodataan osoitteen mukaan 2 N haaran. Jokainen haara desimoidaan ja ylipäästösuodatetaan. Ennustustyypin LMS-adaptoinnin tulos w on INL-estimaatti. Järkevä adaptointiaskeleen arvo löytyy lähteen [52] mukaisesti adaptoituvien kertoimien suuruusluokan (kvantisointitasot) avulla väliltä: K2 LK K = missä K on kvantisointitasot ja L K on kvantisointitasojen lukumäärä. = , (81)
89 9 Adaptiivisen korjauksen nopeus riippuu signaalin luonteesta. Jos mittauskaistalla on selkeitä harmonisia, virhesignaali on suuri ja adaptointi on nopeampaa. Kuvan 85 simulointituloksen spektrogrammi kuvaa hyvin em. ilmiötä: Signaali on sinimuotoinen ja sen taajuus kasvaa ajan funktiona. Kun signaalin toinen harmoninen särökomponentti saavuttaa mittauskaistan, korjaus nopeutuu huomattavasti. Tässä esimerkissä signaalitaajuuden on annettu kasvaa mittauskaistalle, mikä näkyy suorituskyvyn romahtamisena simuloinnin lopussa Alkuperäinen signaalikaista (dc -> fb) Mittauskaista (.5*fb -> fb) (db) taajuus / f s harmoninen särö SIGNAALI Signaalikaista (dc ->.5*fb) aika Kuva 85. Spektrogrammi adaptiivisen korjauksen asettumisnopeudesta signaalin taajuuden kasvaessa. Adaptointialgoritmin tyypillinen suorituskyvyn mitta on neliöllinen virhe (mean square error, MSE). Koska epäsovituskohina saadaan ainoastaan ac-kytkettynä mittauskaistalta, INL-estimaatissa on tyypillisesti hieman kuvan 86 mukaista dc- ja vahvistusvirhettä. Tämä ei juuri näy itse muuntimen suorituskyvyssä, mutta kylläkin MSE-tuloksessa, joten paras mitta adaptoinnin sujumiseen on suorituskykymitta, kuten SNR tai SFDR. Adaptiivisessa menetelmässä myös mittauskaistan leveys on kääntäen verrannollinen korjausnopeuteen. Adaptiivinen korjaus toimii hyvin käyttäytymistason simuloinneissa, mutta toteutus on hyvin raskas, koska desimaattoreita tarvitaan yhtä monta kun on korjattavia koodeja (kvantisointitasoja). Kuvan 87 mukainen LMS-silmukka kohinanvaimennuksella (noise cancellation) on houkuttava idea, koska silloin ylipäästösuodattimia ei tarvittaisi kuin yksi kappale. Valitettavasti tämä ei käy, koska tällöin kohinareferenssi ei saa korreloida signaalin kanssa [52]. On selvää, että
Muuntavat analogisen signaalin digitaaliseksi Vertaa sisääntulevaa signaalia referenssijännitteeseen Sarja- tai rinnakkaismuotoinen Tyypilliset
 Muuntavat analogisen signaalin digitaaliseksi Vertaa sisääntulevaa signaalia referenssijännitteeseen Sarja- tai rinnakkaismuotoinen Tyypilliset valintakriteerit resoluutio ja nopeus Yleisimmät A/D-muunnintyypit:
Muuntavat analogisen signaalin digitaaliseksi Vertaa sisääntulevaa signaalia referenssijännitteeseen Sarja- tai rinnakkaismuotoinen Tyypilliset valintakriteerit resoluutio ja nopeus Yleisimmät A/D-muunnintyypit:
ELEC-C5070 Elektroniikkapaja (5 op)
 (5 op) Luento 5 A/D- ja D/A-muunnokset ja niiden vaikutus signaaleihin Signaalin A/D-muunnos Analogia-digitaalimuunnin (A/D-muunnin) muuttaa analogisen signaalin digitaaliseen muotoon, joka voidaan lukea
(5 op) Luento 5 A/D- ja D/A-muunnokset ja niiden vaikutus signaaleihin Signaalin A/D-muunnos Analogia-digitaalimuunnin (A/D-muunnin) muuttaa analogisen signaalin digitaaliseen muotoon, joka voidaan lukea
Flash AD-muunnin. Ominaisuudet. +nopea -> voidaan käyttää korkeataajuuksisen signaalin muuntamiseen (GHz) +yksinkertainen
 Flash AD-muunnin Koostuu vastusverkosta ja komparaattoreista. Komparaattorit vertailevat vastuksien jännitteitä referenssiin. Tilanteesta riippuen kompraattori antaa ykkösen tai nollan ja näistä kootaan
Flash AD-muunnin Koostuu vastusverkosta ja komparaattoreista. Komparaattorit vertailevat vastuksien jännitteitä referenssiin. Tilanteesta riippuen kompraattori antaa ykkösen tai nollan ja näistä kootaan
Successive approximation AD-muunnin
 AD-muunnin Koostuu neljästä osasta: näytteenotto- ja pitopiiristä, (sample and hold S/H) komparaattorista, digitaali-analogiamuuntimesta (DAC) ja siirtorekisteristä. (successive approximation register
AD-muunnin Koostuu neljästä osasta: näytteenotto- ja pitopiiristä, (sample and hold S/H) komparaattorista, digitaali-analogiamuuntimesta (DAC) ja siirtorekisteristä. (successive approximation register
11. kierros. 1. Lähipäivä
 11. kierros 1. Lähipäivä Viikon aihe AD/DA-muuntimet Signaalin digitalisointi Kvantisointivirhe Kvantisointikohina Kytkinkapasitanssipiirit Mitoitus Kontaktiopetusta: 6 tuntia Kotitehtäviä: 4 tuntia Tavoitteet:
11. kierros 1. Lähipäivä Viikon aihe AD/DA-muuntimet Signaalin digitalisointi Kvantisointivirhe Kvantisointikohina Kytkinkapasitanssipiirit Mitoitus Kontaktiopetusta: 6 tuntia Kotitehtäviä: 4 tuntia Tavoitteet:
A/D-muuntimia. Flash ADC
 A/D-muuntimia A/D-muuntimen valintakriteerit: - bittien lukumäärä instrumentointi 6 16 audio/video/kommunikointi/ym. 16 18 erikoissovellukset 20 22 - Tarvittava nopeus hidas > 100 μs (
A/D-muuntimia A/D-muuntimen valintakriteerit: - bittien lukumäärä instrumentointi 6 16 audio/video/kommunikointi/ym. 16 18 erikoissovellukset 20 22 - Tarvittava nopeus hidas > 100 μs (
Virheen kasautumislaki
 Virheen kasautumislaki Yleensä tutkittava suure f saadaan välillisesti mitattavista parametreistä. Tällöin kokonaisvirhe f määräytyy mitattujen parametrien virheiden perusteella virheen kasautumislain
Virheen kasautumislaki Yleensä tutkittava suure f saadaan välillisesti mitattavista parametreistä. Tällöin kokonaisvirhe f määräytyy mitattujen parametrien virheiden perusteella virheen kasautumislain
Signaalien datamuunnokset
 Signaalien datamuunnokset Datamuunnosten teoriaa Muunnosten taustaa Muunnosten teoriaa Muunnosten rajoituksia ja ongelmia Petri Kärhä 06/02/2004 Luento 4a: Signaalien datamuunnokset 1 Digitaalitekniikan
Signaalien datamuunnokset Datamuunnosten teoriaa Muunnosten taustaa Muunnosten teoriaa Muunnosten rajoituksia ja ongelmia Petri Kärhä 06/02/2004 Luento 4a: Signaalien datamuunnokset 1 Digitaalitekniikan
Signaalien datamuunnokset. Digitaalitekniikan edut
 Signaalien datamuunnokset Datamuunnosten teoriaa Muunnosten taustaa Muunnosten teoriaa Muunnosten rajoituksia ja ongelmia Petri Kärhä 09/02/2009 Signaalien datamuunnokset 1 Digitaalitekniikan edut Tarkoituksena
Signaalien datamuunnokset Datamuunnosten teoriaa Muunnosten taustaa Muunnosten teoriaa Muunnosten rajoituksia ja ongelmia Petri Kärhä 09/02/2009 Signaalien datamuunnokset 1 Digitaalitekniikan edut Tarkoituksena
LABORATORIOTYÖ 2 A/D-MUUNNOS
 LABORATORIOTYÖ 2 A/D-MUUNNOS 2-1 2. A/D-muunnos Työn tarkoitus Tässä työssä demotaan A/D-muunnoksen ominaisuuksia ja ongelmia. Tarkoitus on osoittaa käytännössä, miten bittimäärä ja näytteenottotaajuus
LABORATORIOTYÖ 2 A/D-MUUNNOS 2-1 2. A/D-muunnos Työn tarkoitus Tässä työssä demotaan A/D-muunnoksen ominaisuuksia ja ongelmia. Tarkoitus on osoittaa käytännössä, miten bittimäärä ja näytteenottotaajuus
LABORATORIOTYÖ 2 A/D-MUUNNOS
 LABORATORIOTYÖ 2 A/D-MUUNNOS Päivitetty: 23/01/2009 TP 2-1 2. A/D-muunnos Työn tarkoitus Tässä työssä demotaan A/D-muunnoksen ominaisuuksia ja ongelmia. Tarkoitus on osoittaa käytännössä, miten bittimäärä
LABORATORIOTYÖ 2 A/D-MUUNNOS Päivitetty: 23/01/2009 TP 2-1 2. A/D-muunnos Työn tarkoitus Tässä työssä demotaan A/D-muunnoksen ominaisuuksia ja ongelmia. Tarkoitus on osoittaa käytännössä, miten bittimäärä
6. Analogisen signaalin liittäminen mikroprosessoriin 2 6.1 Näytteenotto analogisesta signaalista 2 6.2. DA-muuntimet 4
 Datamuuntimet 1 Pekka antala 19.11.2012 Datamuuntimet 6. Analogisen signaalin liittäminen mikroprosessoriin 2 6.1 Näytteenotto analogisesta signaalista 2 6.2. DA-muuntimet 4 7. AD-muuntimet 5 7.1 Analoginen
Datamuuntimet 1 Pekka antala 19.11.2012 Datamuuntimet 6. Analogisen signaalin liittäminen mikroprosessoriin 2 6.1 Näytteenotto analogisesta signaalista 2 6.2. DA-muuntimet 4 7. AD-muuntimet 5 7.1 Analoginen
Tuntematon järjestelmä. Adaptiivinen suodatin
 1 1 Vastaa lyhyesti seuraaviin a) Miksi signaaleja ylinäytteistetään AD- ja DA-muunnosten yhteydessä? b) Esittele lohkokaaviona adaptiiviseen suodatukseen perustuva tuntemattoman järjestelmän mallinnus.
1 1 Vastaa lyhyesti seuraaviin a) Miksi signaaleja ylinäytteistetään AD- ja DA-muunnosten yhteydessä? b) Esittele lohkokaaviona adaptiiviseen suodatukseen perustuva tuntemattoman järjestelmän mallinnus.
SGN Signaalinkäsittelyn perusteet Välikoe Heikki Huttunen
 SGN-11 Signaalinkäsittelyn perusteet Välikoe 3.5.16 Heikki Huttunen Laskimen käyttö sallittu. Muiden materiaalien käyttö ei sallittu. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla 1-3 on. Sivuilla 4-5
SGN-11 Signaalinkäsittelyn perusteet Välikoe 3.5.16 Heikki Huttunen Laskimen käyttö sallittu. Muiden materiaalien käyttö ei sallittu. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla 1-3 on. Sivuilla 4-5
2. kierros. 2. Lähipäivä
 2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
2. kierros 2. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Tavoitteet: tietää Yhden navan vasteen ekvivalentti kohinakaistaleveys Vastuksen terminen kohina Termit
Signaalien datamuunnokset. Näytteenotto ja pito -piirit
 Signaalien datamuunnokset Muunnoskomponentit Näytteenotto ja pitopiirit Multiplekserit A/D-muuntimet Jännitereferenssit D/A-muuntimet Petri Kärhä 26/02/2008 Signaalien datamuunnokset 1 Näytteenotto ja
Signaalien datamuunnokset Muunnoskomponentit Näytteenotto ja pitopiirit Multiplekserit A/D-muuntimet Jännitereferenssit D/A-muuntimet Petri Kärhä 26/02/2008 Signaalien datamuunnokset 1 Näytteenotto ja
Flash AD-muunnin. suurin kaistanleveys muista muuntimista (gigahertsejä) pieni resoluutio (max 8) kalliita
 Flash AD-muunnin Flash AD-muunnin koostuu monesta peräkkäisestä komparaattorista, joista jokainen vertaa muunnettavaa signaalia omaan referenssijännitteeseensä. Referenssijännite aikaansaadaan jännitteenjaolla:
Flash AD-muunnin Flash AD-muunnin koostuu monesta peräkkäisestä komparaattorista, joista jokainen vertaa muunnettavaa signaalia omaan referenssijännitteeseensä. Referenssijännite aikaansaadaan jännitteenjaolla:
1 Olkoon suodattimen vaatimusmäärittely seuraava:
 Olkoon suodattimen vaatimusmäärittely seuraava: Päästökaistan maksimipoikkeama δ p =.5. Estokaistan maksimipoikkeama δ s =.. Päästökaistan rajataajuus pb = 5 Hz. Estokaistan rajataajuudet sb = 95 Hz Näytetaajuus
Olkoon suodattimen vaatimusmäärittely seuraava: Päästökaistan maksimipoikkeama δ p =.5. Estokaistan maksimipoikkeama δ s =.. Päästökaistan rajataajuus pb = 5 Hz. Estokaistan rajataajuudet sb = 95 Hz Näytetaajuus
1 Diskreettiaikainen näytteistys. 1.1 Laskostuminen. Laskostuminen
 AD/DA muunnos Lähteet: Pohlman. (1995). Principles of digital audio (3rd ed). Zölzer. (008). Digital audio signal processing (nd ed). Reiss. (008), Understanding sigma-delta modulation: The solved and
AD/DA muunnos Lähteet: Pohlman. (1995). Principles of digital audio (3rd ed). Zölzer. (008). Digital audio signal processing (nd ed). Reiss. (008), Understanding sigma-delta modulation: The solved and
Katsaus suodatukseen
 Katsaus suodatukseen Suodatuksen perustaa, ideaaliset suotimet, käytännön toteutuksia Suodatus Suodatusta käytetään yleensä signaalin muokkaukseen siten, että 2 poistetaan häiritsevä signaali hyötysignaalin
Katsaus suodatukseen Suodatuksen perustaa, ideaaliset suotimet, käytännön toteutuksia Suodatus Suodatusta käytetään yleensä signaalin muokkaukseen siten, että 2 poistetaan häiritsevä signaali hyötysignaalin
ELEC-C5340 - Sovellettu digitaalinen signaalinkäsittely. Äänisignaalien näytteenotto ja kvantisointi Dither Oskillaattorit Digitaalinen suodatus
 L1: Audio Prof. Vesa Välimäki ELEC-C5340 - Sovellettu digitaalinen signaalinkäsittely Luennon sisältö Äänisignaalien näytteenotto ja kvantisointi Dither Oskillaattorit Digitaalinen suodatus Lyhyt FIR-suodin
L1: Audio Prof. Vesa Välimäki ELEC-C5340 - Sovellettu digitaalinen signaalinkäsittely Luennon sisältö Äänisignaalien näytteenotto ja kvantisointi Dither Oskillaattorit Digitaalinen suodatus Lyhyt FIR-suodin
SGN-1200 Signaalinkäsittelyn menetelmät Välikoe
 SGN-00 Signaalinkäsittelyn menetelmät Välikoe 9.3.009 Sivuilla - on. Älä vastaa siihen, jos et ollut ensimmäisessä välikokeessa. Tentin kysymykset ovat sivuilla 3-4. Vastaa vain jompaan kumpaan kokeeseen,
SGN-00 Signaalinkäsittelyn menetelmät Välikoe 9.3.009 Sivuilla - on. Älä vastaa siihen, jos et ollut ensimmäisessä välikokeessa. Tentin kysymykset ovat sivuilla 3-4. Vastaa vain jompaan kumpaan kokeeseen,
IIR-suodattimissa ongelmat korostuvat, koska takaisinkytkennästä seuraa virheiden kertautuminen ja joissakin tapauksissa myös vahvistuminen.
 TL536DSK-algoritmit (J. Laitinen)..5 Välikoe, ratkaisut Millaisia ongelmia kvantisointi aiheuttaa signaalinkäsittelyssä? Miksi ongelmat korostuvat IIR-suodatinten tapauksessa? Tarkastellaan Hz taajuista
TL536DSK-algoritmit (J. Laitinen)..5 Välikoe, ratkaisut Millaisia ongelmia kvantisointi aiheuttaa signaalinkäsittelyssä? Miksi ongelmat korostuvat IIR-suodatinten tapauksessa? Tarkastellaan Hz taajuista
AD/DA muunnos Lähteet: Pohlman. (1995). Principles of digital audio (3rd ed). Zölzer. (1997). Digital audio signal processing
 AD/DA muunnos Lähteet: Pohlman. (1995). Principles of digital audio (3rd ed). Zölzer. (1997). Digital audio signal processing Sisältö: Näytteistys, laskostuminen Kvantisointi, kvantisointivirhe, kvantisointisärö,
AD/DA muunnos Lähteet: Pohlman. (1995). Principles of digital audio (3rd ed). Zölzer. (1997). Digital audio signal processing Sisältö: Näytteistys, laskostuminen Kvantisointi, kvantisointivirhe, kvantisointisärö,
Petri Kärhä 04/02/04. Luento 2: Kohina mittauksissa
 Kohinan ominaisuuksia Kohinamekanismit Terminen kohina Raekohina 1/f kohina (Kvantisointikohina) Kohinan käsittely Kohinakaistanleveys Kohinalähteiden yhteisvaikutus Signaali-kohina suhde Kohinaluku Kohinalämpötila
Kohinan ominaisuuksia Kohinamekanismit Terminen kohina Raekohina 1/f kohina (Kvantisointikohina) Kohinan käsittely Kohinakaistanleveys Kohinalähteiden yhteisvaikutus Signaali-kohina suhde Kohinaluku Kohinalämpötila
Puheenkoodaus. Olivatpa kerran iloiset serkukset. PCM, DPCM ja ADPCM
 Puheenkoodaus Olivatpa kerran iloiset serkukset PCM, DPCM ja ADPCM PCM eli pulssikoodimodulaatio Koodaa jokaisen signaalinäytteen binääriseksi (eli vain ykkösiä ja nollia sisältäväksi) luvuksi kvantisointitasolle,
Puheenkoodaus Olivatpa kerran iloiset serkukset PCM, DPCM ja ADPCM PCM eli pulssikoodimodulaatio Koodaa jokaisen signaalinäytteen binääriseksi (eli vain ykkösiä ja nollia sisältäväksi) luvuksi kvantisointitasolle,
Dynaamisten systeemien identifiointi 1/2
 Dynaamisten systeemien identifiointi 1/2 Mallin rakentaminen mittausten avulla Epäparametriset menetelmät: tuloksena malli, joka ei perustu parametreille impulssi-, askel- tai taajusvaste siirtofunktion
Dynaamisten systeemien identifiointi 1/2 Mallin rakentaminen mittausten avulla Epäparametriset menetelmät: tuloksena malli, joka ei perustu parametreille impulssi-, askel- tai taajusvaste siirtofunktion
z muunnos ja sen soveltaminen LTI järjestelmien analysointiin
 z muunnos ja sen soveltaminen LTI järjestelmien analysointiin muunnoksella (eng. transform) on vastaava asema diskreettiaikaisten signaalien ja LTI järjestelmien analyysissä kuin Laplace muunnoksella jatkuvaaikaisten
z muunnos ja sen soveltaminen LTI järjestelmien analysointiin muunnoksella (eng. transform) on vastaava asema diskreettiaikaisten signaalien ja LTI järjestelmien analyysissä kuin Laplace muunnoksella jatkuvaaikaisten
SIGNAALITEORIAN KERTAUSTA OSA 2
 1 SIGNAALITEORIAN KERTAUSTA OSA 2 Miten spektri lasketaan moduloiduille ja näytteistetyille tietoliikennesignaaleille? KONVOLUUTIO JA KERTOLASKU 2 Kantataajuussignaali (baseband) = sanomasignaali ilman
1 SIGNAALITEORIAN KERTAUSTA OSA 2 Miten spektri lasketaan moduloiduille ja näytteistetyille tietoliikennesignaaleille? KONVOLUUTIO JA KERTOLASKU 2 Kantataajuussignaali (baseband) = sanomasignaali ilman
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 18.3.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 18.3.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-1200 Signaalinkäsittelyn menetelmät, Tentti 24.4.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SG-1200 Signaalinkäsittelyn menetelmät, Tentti 24.4.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
Marko Neitola (1999) Analoginen korrelaattori WCDMA-vastaanottimessa. Diplomityö. Oulun yliopisto, Sähkötekniikan osasto, 60 s.
 2 Marko Neitola (1999) Analoginen korrelaattori WCDMA-vastaanottimessa. Diplomityö. Oulun yliopisto, Sähkötekniikan osasto, 60 s. TIIVISTELMÄ Tässä työssä toteutettiin analoginen korrelaattorirakenne WCDMAvastaanottimeen.
2 Marko Neitola (1999) Analoginen korrelaattori WCDMA-vastaanottimessa. Diplomityö. Oulun yliopisto, Sähkötekniikan osasto, 60 s. TIIVISTELMÄ Tässä työssä toteutettiin analoginen korrelaattorirakenne WCDMAvastaanottimeen.
Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. = K K K M. s 2 3s 2 KK P
 Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Säädön kotitehtävä vk3 t. 1 a) { Y =G K P E H E=R K N N G M Y Yhtälöparista ratkaistiin vuorotellen siirtofunktiot laittamalla muut tulot nollaan. G R s = Y R = GK P s 1 = KK 1 GK P K N G P M s 2 3s 2
Suodattimet. Suodatintyypit: Bessel Chebyshev Elliptinen Butterworth. Suodattimet samalla asteluvulla (amplitudivaste)
 Suodattimet Suodatintyypit: Bessel Chebyshev Elliptinen Butterworth Suodattimet samalla asteluvulla (amplitudivaste) Kuvasta nähdään että elliptinen suodatin on terävin kaikista suodattimista, mutta sisältää
Suodattimet Suodatintyypit: Bessel Chebyshev Elliptinen Butterworth Suodattimet samalla asteluvulla (amplitudivaste) Kuvasta nähdään että elliptinen suodatin on terävin kaikista suodattimista, mutta sisältää
Spektri- ja signaalianalysaattorit
 Spektri- ja signaalianalysaattorit Pyyhkäisevät spektrianalysaattorit Suora pyyhkäisevä Superheterodyne Reaaliaika-analysaattorit Suora analoginen analysaattori FFT-spektrianalysaattori DFT FFT Analysaattoreiden
Spektri- ja signaalianalysaattorit Pyyhkäisevät spektrianalysaattorit Suora pyyhkäisevä Superheterodyne Reaaliaika-analysaattorit Suora analoginen analysaattori FFT-spektrianalysaattori DFT FFT Analysaattoreiden
Luento 8. Suodattimien käyttötarkoitus
 Luento 8 Lineaarinen suodatus Ideaaliset alipäästö, ylipäästö ja kaistanpäästösuodattimet Käytännölliset suodattimet 8..006 Suodattimien käyttötarkoitus Signaalikaistan ulkopuolisen kohinan ja häiriöiden
Luento 8 Lineaarinen suodatus Ideaaliset alipäästö, ylipäästö ja kaistanpäästösuodattimet Käytännölliset suodattimet 8..006 Suodattimien käyttötarkoitus Signaalikaistan ulkopuolisen kohinan ja häiriöiden
SGN-1200 Signaalinkäsittelyn menetelmät Välikoe
 SGN-100 Signaalinkäsittelyn menetelmät Välikoe 6.4.010 Sivuilla 1- on. Älä vastaa siihen, jos et ollut ensimmäisessä välikokeessa. Tentin kysymykset ovat sivuilla 3-4. Vastaa vain jompaan kumpaan kokeeseen,
SGN-100 Signaalinkäsittelyn menetelmät Välikoe 6.4.010 Sivuilla 1- on. Älä vastaa siihen, jos et ollut ensimmäisessä välikokeessa. Tentin kysymykset ovat sivuilla 3-4. Vastaa vain jompaan kumpaan kokeeseen,
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät / systeemitekniikka Jan 019
1 PID-taajuusvastesuunnittelun esimerkki
 Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
Enso Ikonen, Oulun yliopisto, systeemitekniikan laboratorio 2/23 Säätöjärjestelmien suunnittelu 23 PID-taajuusvastesuunnittelun esimerkki Tehtävänä on suunnitella säätö prosessille ( ) = = ( +)( 2 + )
OPERAATIOVAHVISTIN. Oulun seudun ammattikorkeakoulu Tekniikan yksikkö. Elektroniikan laboratoriotyö. Työryhmä Selostuksen kirjoitti 11.11.
 Oulun seudun ammattikorkeakoulu Tekniikan yksikkö Elektroniikan laboratoriotyö OPERAATIOVAHVISTIN Työryhmä Selostuksen kirjoitti 11.11.008 Kivelä Ari Tauriainen Tommi Tauriainen Tommi 1 TEHTÄVÄ Tutustuimme
Oulun seudun ammattikorkeakoulu Tekniikan yksikkö Elektroniikan laboratoriotyö OPERAATIOVAHVISTIN Työryhmä Selostuksen kirjoitti 11.11.008 Kivelä Ari Tauriainen Tommi Tauriainen Tommi 1 TEHTÄVÄ Tutustuimme
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-00 Signaalinkäsittelyn menetelmät, Tentti..005 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle ja sen
SG-00 Signaalinkäsittelyn menetelmät, Tentti..005 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle ja sen
puheen laatu kärsii koodauksesta mahdollisimman vähän. puhe pakkautuu mahdollisimman pieneen määrään bittejä.
 Luku 1 Puheen koodaus Puheen koodauksella tarkoitetaan puhesignaalin esittämiseen tarvittavan bittimäärän pienentämistä sillä tavalla, että puhesignaalin laatu ja ymmärrettävyys kärsivät mahdollisimman
Luku 1 Puheen koodaus Puheen koodauksella tarkoitetaan puhesignaalin esittämiseen tarvittavan bittimäärän pienentämistä sillä tavalla, että puhesignaalin laatu ja ymmärrettävyys kärsivät mahdollisimman
3. kierros. 2. Lähipäivä
 3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
3. kierros. Lähipäivä Viikon aihe (viikko /) Takaisinkytketyt vahvistimet Takaisinkytkentä, suljettu säätöluuppi Nyquistin kriteeri, stabiilisuus Taajuusanalyysi, Boden ja Nyquistin diagrammit Systeemin
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 5.5.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 5.5.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
Digitaalinen Signaalinkäsittely T0125 Luento 4-7.04.2006
 Digitaalinen Signaalinkäsittely T5 Luento 4-7.4.6 Jarkko.Vuori@evtek.fi Z-taso Z-taso on paljon käytetty graafinen esitystapa jonka avulla voidaan tarkastella signaalien taajuussisältöjä sekä järjestelmien
Digitaalinen Signaalinkäsittely T5 Luento 4-7.4.6 Jarkko.Vuori@evtek.fi Z-taso Z-taso on paljon käytetty graafinen esitystapa jonka avulla voidaan tarkastella signaalien taajuussisältöjä sekä järjestelmien
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-1200 Signaalinkäsittelyn menetelmät, Tentti 30.1.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SG-1200 Signaalinkäsittelyn menetelmät, Tentti 30.1.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-1200 Signaalinkäsittelyn menetelmät, Tentti 21.3.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SG-1200 Signaalinkäsittelyn menetelmät, Tentti 21.3.2006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
R = Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen on tällöin jännitteenjako = 1
 Fysiikan mittausmenetelmät I syksy 206 Laskuharjoitus 4. Merkitään kaapelin resistanssin ja kuormaksi kytketyn piirin sisäänmenoimpedanssia summana R 000.2 Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen
Fysiikan mittausmenetelmät I syksy 206 Laskuharjoitus 4. Merkitään kaapelin resistanssin ja kuormaksi kytketyn piirin sisäänmenoimpedanssia summana R 000.2 Ω. Jännite R:n yli suhteessa sisäänmenojännitteeseen
TL5503 DSK, laboraatiot (1.5 op) Suodatus 2 (ver 1.0) Jyrki Laitinen
 TL5503 DSK, laboraatiot (1.5 op) Suodatus 2 (ver 1.0) Jyrki Laitinen TL5503 DSK, laboraatiot (1.5 op), K2005 1 Suorita oheisten ohjeiden mukaiset tehtävät Matlab-ohjelmistoa käyttäen. Kokoa erilliseen
TL5503 DSK, laboraatiot (1.5 op) Suodatus 2 (ver 1.0) Jyrki Laitinen TL5503 DSK, laboraatiot (1.5 op), K2005 1 Suorita oheisten ohjeiden mukaiset tehtävät Matlab-ohjelmistoa käyttäen. Kokoa erilliseen
A / D - MUUNTIMET. 2 Bittimäärä 1. tai. A / D muunnin, A/D converter, ADC, ( Analog to Digital Converter )
 A / D - MUUNTIMET A / D muunnin, A/D converter, ADC, ( Analog to Digital Converter ) H. Honkanen Muuntaa analogisen tiedon ( yleensä jännite ) digitaalimuotoon. Lähtevä data voi olla sarja- tai rinnakkaismuotoista.
A / D - MUUNTIMET A / D muunnin, A/D converter, ADC, ( Analog to Digital Converter ) H. Honkanen Muuntaa analogisen tiedon ( yleensä jännite ) digitaalimuotoon. Lähtevä data voi olla sarja- tai rinnakkaismuotoista.
LOPPURAPORTTI 19.11.2007. Lämpötilahälytin. 0278116 Hans Baumgartner xxxxxxx nimi nimi
 LOPPURAPORTTI 19.11.2007 Lämpötilahälytin 0278116 Hans Baumgartner xxxxxxx nimi nimi KÄYTETYT MERKINNÄT JA LYHENTEET... 3 JOHDANTO... 4 1. ESISELOSTUS... 5 1.1 Diodi anturina... 5 1.2 Lämpötilan ilmaisu...
LOPPURAPORTTI 19.11.2007 Lämpötilahälytin 0278116 Hans Baumgartner xxxxxxx nimi nimi KÄYTETYT MERKINNÄT JA LYHENTEET... 3 JOHDANTO... 4 1. ESISELOSTUS... 5 1.1 Diodi anturina... 5 1.2 Lämpötilan ilmaisu...
SGN-1251 Signaalinkäsittelyn sovellukset Välikoe Heikki Huttunen
 SGN-5 Signaalinkäsittelyn sovellukset Välikoe.. Heikki Huttunen Tentissä ja välikokeessa saa käyttää vain tiedekunnan laskinta. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla - on. Sivuilla 4-6 on. Vastaa
SGN-5 Signaalinkäsittelyn sovellukset Välikoe.. Heikki Huttunen Tentissä ja välikokeessa saa käyttää vain tiedekunnan laskinta. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla - on. Sivuilla 4-6 on. Vastaa
Elektroniikka, kierros 3
 Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
Elektroniikka, kierros 3 1. a) Johda kuvan 1 esittämän takaisinkytketyn systeemin suljetun silmukan vahvistuksen f lauseke. b) Osoita, että kun silmukkavahvistus β 1, niin suljetun silmukan vahvistus f
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SG-00 Signaalinkäsittelyn menetelmät, Tentti 6.3.006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle ja
SG-00 Signaalinkäsittelyn menetelmät, Tentti 6.3.006 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle ja
4. kierros. 1. Lähipäivä
 4. kierros 1. Lähipäivä Viikon aihe Taajuuskompensointi, operaatiovahvistin ja sen kytkennät Taajuuskompensaattorit Mitoitus Kontaktiopetusta: 8 h Kotitehtäviä: 4 h + 0 h Tavoitteet: tietää Operaatiovahvistimen
4. kierros 1. Lähipäivä Viikon aihe Taajuuskompensointi, operaatiovahvistin ja sen kytkennät Taajuuskompensaattorit Mitoitus Kontaktiopetusta: 8 h Kotitehtäviä: 4 h + 0 h Tavoitteet: tietää Operaatiovahvistimen
Boost-hakkuri. Hakkurin tilaesitykset
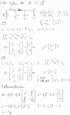 Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
Boost-hakkuri Boost-hakkurilla on toiminnassaan kaksi tilaa. Päällä, jolloin kytkimestä virtapiiri on suljettu ja pois silloin kun virtapiiri on kytkimestä aukaistu. Kummallekin tilalle tulee muodostaa
Missä mennään. systeemi. identifiointi. mallikandidaatti. validointi. malli. (fysikaalinen) mallintaminen. mallin mallin käyttötarkoitus, reunaehdot
 Missä mennään systeemi mallin mallin käyttötarkoitus, reunaehdot käyttö- (fysikaalinen) mallintaminen luonnonlait yms. yms. identifiointi kokeita kokeita + päättely päättely vertailu mallikandidaatti validointi
Missä mennään systeemi mallin mallin käyttötarkoitus, reunaehdot käyttö- (fysikaalinen) mallintaminen luonnonlait yms. yms. identifiointi kokeita kokeita + päättely päättely vertailu mallikandidaatti validointi
Alias-ilmiö eli taajuuden laskostuminen
 Prosessiorientoituneet mallit Todellista hybridijärjestelmää ELEC-C1230 Säätötekniikka Luku 12: Näytteenottoteoreema ja jatkuvien säätimien diskreetit approksimaatiot Prosessiorientoituneet mallit katsotaan
Prosessiorientoituneet mallit Todellista hybridijärjestelmää ELEC-C1230 Säätötekniikka Luku 12: Näytteenottoteoreema ja jatkuvien säätimien diskreetit approksimaatiot Prosessiorientoituneet mallit katsotaan
KOHINA LÄMPÖKOHINA VIRTAKOHINA. N = Noise ( Kohina )
 KOHINA H. Honkanen N = Noise ( Kohina ) LÄMÖKOHINA Johtimessa tai vastuksessa olevien vapaiden elektronien määrä ei ole vakio, vaan se vaihtelee satunnaisesti. Nämä vaihtelut aikaansaavat jännitteen johtimeen
KOHINA H. Honkanen N = Noise ( Kohina ) LÄMÖKOHINA Johtimessa tai vastuksessa olevien vapaiden elektronien määrä ei ole vakio, vaan se vaihtelee satunnaisesti. Nämä vaihtelut aikaansaavat jännitteen johtimeen
Signaalien datamuunnokset
 Signaalien datamuunnokset Muunnoskomponentit Näytteenotto ja pitopiirit Multiplekserit A/D-muuntimet Jännitereferenssit D/A-muuntimet Petri Kärhä 17/02/2005 Luento 4b: Signaalien datamuunnokset 1 Näytteenotto
Signaalien datamuunnokset Muunnoskomponentit Näytteenotto ja pitopiirit Multiplekserit A/D-muuntimet Jännitereferenssit D/A-muuntimet Petri Kärhä 17/02/2005 Luento 4b: Signaalien datamuunnokset 1 Näytteenotto
Kojemeteorologia. Sami Haapanala syksy 2013. Fysiikan laitos, Ilmakehätieteiden osasto
 Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Datan käsittely ja tallentaminen Käytännössä kaikkien mittalaitteiden ensisijainen signaali on analoginen Jotta tämä
Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Datan käsittely ja tallentaminen Käytännössä kaikkien mittalaitteiden ensisijainen signaali on analoginen Jotta tämä
20 Kollektorivirta kun V 1 = 15V 10. 21 Transistorin virtavahvistus 10. 22 Transistorin ominaiskayrasto 10. 23 Toimintasuora ja -piste 10
 Sisältö 1 Johda kytkennälle Theveninin ekvivalentti 2 2 Simuloinnin ja laskennan vertailu 4 3 V CE ja V BE simulointituloksista 4 4 DC Sweep kuva 4 5 R 2 arvon etsintä 5 6 Simuloitu V C arvo 5 7 Toimintapiste
Sisältö 1 Johda kytkennälle Theveninin ekvivalentti 2 2 Simuloinnin ja laskennan vertailu 4 3 V CE ja V BE simulointituloksista 4 4 DC Sweep kuva 4 5 R 2 arvon etsintä 5 6 Simuloitu V C arvo 5 7 Toimintapiste
1 Vastaa seuraaviin. b) Taajuusvasteen
 Vastaa seuraaviin a) Miten määritetään digitaalisen suodattimen taajuusvaste sekä amplitudi- ja vaihespektri? Tässä riittää sanallinen kuvaus. b) Miten viivästys vaikuttaa signaalin amplitudi- ja vaihespektriin?
Vastaa seuraaviin a) Miten määritetään digitaalisen suodattimen taajuusvaste sekä amplitudi- ja vaihespektri? Tässä riittää sanallinen kuvaus. b) Miten viivästys vaikuttaa signaalin amplitudi- ja vaihespektriin?
Digitaalinen signaalinkäsittely Desibeliasteikko, suotimen suunnittelu
 Digitaalinen signaalinkäsittely Desibeliasteikko, suotimen suunnittelu Teemu Saarelainen, teemu.saarelainen@kyamk.fi Lähteet: Ifeachor, Jervis, Digital Signal Processing: A Practical Approach H.Huttunen,
Digitaalinen signaalinkäsittely Desibeliasteikko, suotimen suunnittelu Teemu Saarelainen, teemu.saarelainen@kyamk.fi Lähteet: Ifeachor, Jervis, Digital Signal Processing: A Practical Approach H.Huttunen,
Signaalien generointi
 Signaalinkäsittelyssä joudutaan usein generoimaan erilaisia signaaleja keinotekoisesti. Tyypillisimpiä generoitavia aaltomuotoja ovat eritaajuiset sinimuotoiset signaalit (modulointi) sekä normaalijakautunut
Signaalinkäsittelyssä joudutaan usein generoimaan erilaisia signaaleja keinotekoisesti. Tyypillisimpiä generoitavia aaltomuotoja ovat eritaajuiset sinimuotoiset signaalit (modulointi) sekä normaalijakautunut
Matlab-tietokoneharjoitus
 Matlab-tietokoneharjoitus Tämän harjoituksen tavoitteena on: Opettaa yksinkertaisia piirikaavio- ja yksikkömuunnoslaskuja. Opettaa Matlabin perustyökaluja mittausten analysoimiseen. Havainnollistaa näytteenottotaajuuden,
Matlab-tietokoneharjoitus Tämän harjoituksen tavoitteena on: Opettaa yksinkertaisia piirikaavio- ja yksikkömuunnoslaskuja. Opettaa Matlabin perustyökaluja mittausten analysoimiseen. Havainnollistaa näytteenottotaajuuden,
Kohina. Havaittujen fotonien statistinen virhe on kääntäen verrannollinen havaittujen fotonien lukumäärän N neliö juureen ( T 1/ N)
 Kohina Havaittujen fotonien statistinen virhe on kääntäen verrannollinen havaittujen fotonien lukumäärän N neliö juureen ( T 1/ N) N on suoraan verrannollinen integraatioaikaan t ja havaittuun taajuusväliin
Kohina Havaittujen fotonien statistinen virhe on kääntäen verrannollinen havaittujen fotonien lukumäärän N neliö juureen ( T 1/ N) N on suoraan verrannollinen integraatioaikaan t ja havaittuun taajuusväliin
Laskuharjoitus 4 ( ): Tehtävien vastauksia
 TT12S1E Tietoliikenteen perusteet Metropolia/A. Koivumäki Laskuharjoitus 4 (2.10.2013): Tehtävien vastauksia 1. Tutkitaan signaalista näytteenotolla muodostettua PAM (Pulse Amplitude Modulation) -signaalia.
TT12S1E Tietoliikenteen perusteet Metropolia/A. Koivumäki Laskuharjoitus 4 (2.10.2013): Tehtävien vastauksia 1. Tutkitaan signaalista näytteenotolla muodostettua PAM (Pulse Amplitude Modulation) -signaalia.
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät, Systeemitekniikka Feb 2019
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät, Systeemitekniikka Feb 2019
Mitä on signaalien digitaalinen käsittely
 Mitä on signaalien digitaalinen käsittely Signaalien digitaalinen analyysi: mitä sisältää, esim. mittaustulosten taajuusanalyysi synteesi: signaalien luominen, esim. PC:n äänikortti käsittely: oleellisen
Mitä on signaalien digitaalinen käsittely Signaalien digitaalinen analyysi: mitä sisältää, esim. mittaustulosten taajuusanalyysi synteesi: signaalien luominen, esim. PC:n äänikortti käsittely: oleellisen
SÄÄTÖJÄRJESTELMIEN SUUNNITTELU
 ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
ENSO IKONEN PYOSYS 1 SÄÄTÖJÄRJESTELMIEN SUUNNITTELU Enso Ikonen professori säätö- ja systeemitekniikka http://cc.oulu.fi/~iko Oulun yliopisto Älykkäät koneet ja järjestelmät helmikuu 2019 ENSO IKONEN PYOSYS
SGN Signaalinkäsittelyn perusteet Välikoe Heikki Huttunen
 SGN- Signaalinkäsittelyn perusteet Välikoe.5.4 Heikki Huttunen Tentissä ja välikokeessa saa käyttää vain tiedekunnan laskinta. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla -3 on. Sivuilla 4-5 on. Sivulla
SGN- Signaalinkäsittelyn perusteet Välikoe.5.4 Heikki Huttunen Tentissä ja välikokeessa saa käyttää vain tiedekunnan laskinta. Tenttikysymyksiä ei tarvitse palauttaa. Sivuilla -3 on. Sivuilla 4-5 on. Sivulla
KON-C3004 Kone- ja rakennustekniikan laboratoriotyöt Tiedonkeruu ja analysointi Panu Kiviluoma
 KON-C34 Kone- ja rakennustekniikan laboratoriotyöt Tiedonkeruu ja analysointi Panu Kiviluoma Mitattava suure Tarkka arvo Mittausjärjestelmä Mitattu arvo Ympäristö Mitattava suure Anturi Signaalinkäsittely
KON-C34 Kone- ja rakennustekniikan laboratoriotyöt Tiedonkeruu ja analysointi Panu Kiviluoma Mitattava suure Tarkka arvo Mittausjärjestelmä Mitattu arvo Ympäristö Mitattava suure Anturi Signaalinkäsittely
Signaalimallit: sisältö
 Signaalimallit: sisältö Motivaationa häiriöiden kuvaaminen ja rekonstruointi Signaalien kuvaaminen aikatasossa, determinisitinen vs. stokastinen Signaalien kuvaaminen taajuustasossa Fourier-muunnos Deterministisen
Signaalimallit: sisältö Motivaationa häiriöiden kuvaaminen ja rekonstruointi Signaalien kuvaaminen aikatasossa, determinisitinen vs. stokastinen Signaalien kuvaaminen taajuustasossa Fourier-muunnos Deterministisen
H(s) + + _. Ymit(s) Laplace-tason esitykseksi on saatu (katso jälleen kalvot):
 ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
ELEC-C3 Säätötekniikka 5. laskuharjoitus Vastaukset Quiz: Luennon 4 luentokalvojen (luku 4) lopussa on esimerkki: Sähköpiiri (alkaa kalvon 39 tienoilla). Lue esimerkki huolellisesti ja vastaa seuraavaan:
S Elektroniset mittaukset ja elektroniikan häiriökysymykset. 2 ov
 TKK / Mittaustekniikan laboratorio HUT / Metrology Research Institute S-108.180 Elektroniset mittaukset ja elektroniikan häiriökysymykset 2 ov 7.2.2001 KL kohina.ppt 1 Elektroninen mittaussysteemi MITATTAVA
TKK / Mittaustekniikan laboratorio HUT / Metrology Research Institute S-108.180 Elektroniset mittaukset ja elektroniikan häiriökysymykset 2 ov 7.2.2001 KL kohina.ppt 1 Elektroninen mittaussysteemi MITATTAVA
1 Kohina. 2 Kohinalähteet. 2.1 Raekohina. 2.2 Terminen kohina
 1 Kohina Kohina on yleinen ongelma integroiduissa piireissä. Kohinaa aiheuttavat pienet virta- ja jänniteheilahtelut, jotka ovat komponenteista johtuvia. Myös ulkopuoliset lähteet voivat aiheuttaa kohinaa.
1 Kohina Kohina on yleinen ongelma integroiduissa piireissä. Kohinaa aiheuttavat pienet virta- ja jänniteheilahtelut, jotka ovat komponenteista johtuvia. Myös ulkopuoliset lähteet voivat aiheuttaa kohinaa.
T SKJ - TERMEJÄ
 T-61140 SKJ - termit Sivu 1 / 7 T-61140 SKJ - TERMEJÄ Nimi Opnro Email Signaalinkäsittelyyn liittyviä termejä ja selityksiä Kevät 2005 Täytä lomaketta kevään aikana ja kerää mahdollisesti puuttuvia termejä
T-61140 SKJ - termit Sivu 1 / 7 T-61140 SKJ - TERMEJÄ Nimi Opnro Email Signaalinkäsittelyyn liittyviä termejä ja selityksiä Kevät 2005 Täytä lomaketta kevään aikana ja kerää mahdollisesti puuttuvia termejä
a) I f I d Eri kohinavirtakomponentit vahvistimen otossa (esim. http://www.osioptoelectronics.com/)
 a) C C p e n sn V out p d jn sh C j i n V out Käytetyt symbolit & vakiot: P = valoteho [W], λ = valodiodin ilmaisuvaste eli responsiviteetti [A/W] d = pimeävirta [A] B = kohinakaistanleveys [Hz] T = lämpötila
a) C C p e n sn V out p d jn sh C j i n V out Käytetyt symbolit & vakiot: P = valoteho [W], λ = valodiodin ilmaisuvaste eli responsiviteetti [A/W] d = pimeävirta [A] B = kohinakaistanleveys [Hz] T = lämpötila
Johdanto tieto- viestintäteknologian käyttöön: Äänitystekniikka. Vfo135 ja Vfp124 Martti Vainio
 Johdanto tieto- viestintäteknologian käyttöön: Äänitystekniikka Vfo135 ja Vfp124 Martti Vainio Akustiikka Äänityksen tarkoitus on taltioida paras mahdo!inen signaali! Tärkeimpinä kolme akustista muuttujaa:
Johdanto tieto- viestintäteknologian käyttöön: Äänitystekniikka Vfo135 ja Vfp124 Martti Vainio Akustiikka Äänityksen tarkoitus on taltioida paras mahdo!inen signaali! Tärkeimpinä kolme akustista muuttujaa:
2. kierros. 1. Lähipäivä
 2. kierros. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Mitoitus Kontaktiopetusta: 8 tuntia Kotitehtäviä: 4 + 4 tuntia Tavoitteet: tietää Yhden navan vasteen ekvivalentti
2. kierros. Lähipäivä Viikon aihe Vahvistimet, kohina, lineaarisuus Siirtofunktiot, tilaesitys Mitoitus Kontaktiopetusta: 8 tuntia Kotitehtäviä: 4 + 4 tuntia Tavoitteet: tietää Yhden navan vasteen ekvivalentti
Analogiapiirit III. Tentti 15.1.1999
 Oulun yliopisto Elektroniikan laboratorio nalogiapiirit III Tentti 15.1.1999 1. Piirrä MOS-differentiaalipari ja johda lauseke differentiaaliselle lähtövirralle käyttäen MOS-transistorin virtayhtälöä (huom.
Oulun yliopisto Elektroniikan laboratorio nalogiapiirit III Tentti 15.1.1999 1. Piirrä MOS-differentiaalipari ja johda lauseke differentiaaliselle lähtövirralle käyttäen MOS-transistorin virtayhtälöä (huom.
Dynaamisten systeemien teoriaa. Systeemianalyysilaboratorio II
 Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
Dynaamisten systeemien teoriaa Systeemianalyysilaboratorio II 15.11.2017 Vakiot, sisäänmenot, ulostulot ja häiriöt Mallin vakiot Systeemiparametrit annettuja vakioita, joita ei muuteta; esim. painovoiman
LABORATORIOTYÖ 3 VAIHELUKITTU VAHVISTIN
 LABORATORIOTYÖ 3 VAIHELUKITTU VAHVISTIN Päivitetty: 23/01/2009 TP 3-1 3. VAIHELUKITTU VAHVISTIN Työn tavoitteet Työn tavoitteena on oppia vaihelukitun vahvistimen toimintaperiaate ja käyttömahdollisuudet
LABORATORIOTYÖ 3 VAIHELUKITTU VAHVISTIN Päivitetty: 23/01/2009 TP 3-1 3. VAIHELUKITTU VAHVISTIN Työn tavoitteet Työn tavoitteena on oppia vaihelukitun vahvistimen toimintaperiaate ja käyttömahdollisuudet
Operaatiovahvistimen vahvistus voidaan säätää halutun suuruiseksi käyttämällä takaisinkytkentävastusta.
 TYÖ 11. Operaatiovahvistin Operaatiovahvistin on mikropiiri ( koostuu useista transistoreista, vastuksista ja kondensaattoreista juotettuna pienelle piipalaselle ), jota voidaan käyttää useisiin eri kytkentöihin.
TYÖ 11. Operaatiovahvistin Operaatiovahvistin on mikropiiri ( koostuu useista transistoreista, vastuksista ja kondensaattoreista juotettuna pienelle piipalaselle ), jota voidaan käyttää useisiin eri kytkentöihin.
SIGNAALITEORIAN KERTAUSTA 1
 SIGNAALITEORIAN KERTAUSTA 1 1 (26) Fourier-muunnos ja jatkuva spektri Spektri taajuuden funktiona on kompleksiarvoinen funktio, jonka esittäminen graafisesti edellyttää 3D-kuvaajan piirtämisen. Yleensä
SIGNAALITEORIAN KERTAUSTA 1 1 (26) Fourier-muunnos ja jatkuva spektri Spektri taajuuden funktiona on kompleksiarvoinen funktio, jonka esittäminen graafisesti edellyttää 3D-kuvaajan piirtämisen. Yleensä
T Digitaalinen signaalinkäsittely ja suodatus
 T-63 Digitaalinen signaalinkäsittely ja suodatus 2 välikoe / tentti Ke 4528 klo 6-9 Sali A (A-x) ja B (x-ö)m 2 vk on oikeus tehdä vain kerran joko 75 tai 45 Tee välikokeessa tehtävät, 2 ja 7 (palaute)
T-63 Digitaalinen signaalinkäsittely ja suodatus 2 välikoe / tentti Ke 4528 klo 6-9 Sali A (A-x) ja B (x-ö)m 2 vk on oikeus tehdä vain kerran joko 75 tai 45 Tee välikokeessa tehtävät, 2 ja 7 (palaute)
ELEC-C5070 Elektroniikkapaja. Laboratoriotyö 3 A/D- ja D/A-muuntimet
 ELEC-C5070 Elektroniikkapaja Laboratoriotyö 3 A/D- ja D/A-muuntimet Työohje Syksy 2016 Sisällysluettelo 1 Johdanto... 3 2 Teoriaa... 3 2.1 A/D- ja D/A-muunnos... 3 2.2 Switched capacitor-tekniikka... 4
ELEC-C5070 Elektroniikkapaja Laboratoriotyö 3 A/D- ja D/A-muuntimet Työohje Syksy 2016 Sisällysluettelo 1 Johdanto... 3 2 Teoriaa... 3 2.1 A/D- ja D/A-muunnos... 3 2.2 Switched capacitor-tekniikka... 4
Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu. Vinkit 1 a
 ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
ELEC-C3 Säätötekniikka 9. laskuharjoitus Taajuustason tekniikat: Boden ja Nyquistin diagrammit, kompensaattorien suunnittelu Vinkit a 3. Vaiheenjättökompensaattorin siirtofunktio: ( ) s W LAG s, a. s Vahvistus
S-108.3020 Elektroniikan häiriökysymykset. Laboratoriotyö, kevät 2010
 1/7 S-108.3020 Elektroniikan häiriökysymykset Laboratoriotyö, kevät 2010 Häiriöiden kytkeytyminen yhteisen impedanssin kautta lämpötilasäätimessä Viimeksi päivitetty 25.2.2010 / MO 2/7 Johdanto Sähköisiä
1/7 S-108.3020 Elektroniikan häiriökysymykset Laboratoriotyö, kevät 2010 Häiriöiden kytkeytyminen yhteisen impedanssin kautta lämpötilasäätimessä Viimeksi päivitetty 25.2.2010 / MO 2/7 Johdanto Sähköisiä
Mediaanisuodattimet. Tähän asti käsitellyt suodattimet ovat olleet lineaarisia. Niille on tyypillistä, että. niiden ominaisuudet tunnetaan hyvin
 Mediaanisuodattimet Tähän asti käsitellyt suodattimet ovat olleet lineaarisia. Niille on tyypillistä, että niiden ominaisuudet tunnetaan hyvin niiden analysointiin on olemassa vakiintuneita menetelmiä
Mediaanisuodattimet Tähän asti käsitellyt suodattimet ovat olleet lineaarisia. Niille on tyypillistä, että niiden ominaisuudet tunnetaan hyvin niiden analysointiin on olemassa vakiintuneita menetelmiä
LUKU 6 TÄRKEIMPIEN ASIOIDEN KERTAUS
 LUKU 6 TÄRKEIMPIEN ASIOIDEN KERTAUS 1 (8) Kantatajuisen järjestelmän lähdön (SNR) D = P T /N 0 W käytetään referenssinä verrattaessa eri kantoaaltomodulaatioita keskenään. Analyysissä oletettiin AWGN-kanava,
LUKU 6 TÄRKEIMPIEN ASIOIDEN KERTAUS 1 (8) Kantatajuisen järjestelmän lähdön (SNR) D = P T /N 0 W käytetään referenssinä verrattaessa eri kantoaaltomodulaatioita keskenään. Analyysissä oletettiin AWGN-kanava,
Alipäästösuotimen muuntaminen muiksi perussuotimiksi
 Alipäästösuotimen muuntaminen muiksi perussuotimiksi Usein suodinsuunnittelussa on lähtökohtana alipäästösuodin (LPF), josta voidaan yksinkertaisilla operaatioilla muodostaa ylipäästö- (HPF), kaistanpäästö-
Alipäästösuotimen muuntaminen muiksi perussuotimiksi Usein suodinsuunnittelussa on lähtökohtana alipäästösuodin (LPF), josta voidaan yksinkertaisilla operaatioilla muodostaa ylipäästö- (HPF), kaistanpäästö-
TL5503 DSK, laboraatiot (1.5 op) Suodatus 1 (ver 1.0) Jyrki Laitinen
 TL5503 DSK, laboraatiot (1.5 op) Suodatus 1 (ver 1.0) Jyrki Laitinen TL5503 DSK, laboraatiot (1.5 op), K2005 1 Suorita oheisten ohjeiden mukaiset tehtävät Matlab-ohjelmistoa käyttäen. Kokoa erilliseen
TL5503 DSK, laboraatiot (1.5 op) Suodatus 1 (ver 1.0) Jyrki Laitinen TL5503 DSK, laboraatiot (1.5 op), K2005 1 Suorita oheisten ohjeiden mukaiset tehtävät Matlab-ohjelmistoa käyttäen. Kokoa erilliseen
Uuden sukupolven HF-kommunikaatiotekniikka
 MATINE tutkimusseminaari 16.11.2017 Uuden sukupolven HF-kommunikaatiotekniikka Lauri Anttila 1, Mika Korhonen 1, Juha Yli-Kaakinen 1, Markku Renfors 1, Hannu Tuomivaara 2 1 Elektroniikan ja tietoliikennetekniikan
MATINE tutkimusseminaari 16.11.2017 Uuden sukupolven HF-kommunikaatiotekniikka Lauri Anttila 1, Mika Korhonen 1, Juha Yli-Kaakinen 1, Markku Renfors 1, Hannu Tuomivaara 2 1 Elektroniikan ja tietoliikennetekniikan
Vastekorjaus (ekvalisointi) Lähteet: Zölzer. Digital audio signal processing. Wiley & Sons. Zölzer (ed.) DAFX Digital Audio Effects. Wiley & Sons.
 Vastekorjaus (ekvalisointi) Lähteet: Zölzer. Digital audio signal processing. Wiley & Sons. Zölzer (ed.) DAFX Digital Audio Effects. Wiley & Sons. Sisältö:! Johdanto! IIR vai FIR äänten suodattamiseen?!
Vastekorjaus (ekvalisointi) Lähteet: Zölzer. Digital audio signal processing. Wiley & Sons. Zölzer (ed.) DAFX Digital Audio Effects. Wiley & Sons. Sisältö:! Johdanto! IIR vai FIR äänten suodattamiseen?!
Vahvistimet ja lineaaripiirit. Operaatiovahvistin
 Vahvistimet ja lineaaripiirit Kotitentti 3 (2007) Petri Kärhä 20/01/2008 Vahvistimet ja lineaaripiirit 1 Operaatiovahvistin (Operational Amplifier, OpAmp) Perusvahvistin, toiminta oletetaan suunnittelussa
Vahvistimet ja lineaaripiirit Kotitentti 3 (2007) Petri Kärhä 20/01/2008 Vahvistimet ja lineaaripiirit 1 Operaatiovahvistin (Operational Amplifier, OpAmp) Perusvahvistin, toiminta oletetaan suunnittelussa
MATLAB harjoituksia RST-säädöstä (5h)
 Digitaalinen säätöteoria MATLAB harjoituksia RST-säädöstä (5h) Enso Ikonen Oulun yliopisto, systeemitekniikan laboratorio November 25, 2008 Harjoituskerran sisältö kertausta (15 min) Napojensijoittelu
Digitaalinen säätöteoria MATLAB harjoituksia RST-säädöstä (5h) Enso Ikonen Oulun yliopisto, systeemitekniikan laboratorio November 25, 2008 Harjoituskerran sisältö kertausta (15 min) Napojensijoittelu
Analogiapiirit III. Keskiviikko 4.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet
 Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 2. Keskiviikko 4.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet 1. Analysoi kuvan 1 operaatiotranskonduktanssivahvistimen
Oulun yliopisto Sähkötekniikan osasto Analogiapiirit III Harjoitus 2. Keskiviikko 4.12.2002, klo. 12.15-14.00, TS128. Operaatiovahvistinrakenteet 1. Analysoi kuvan 1 operaatiotranskonduktanssivahvistimen
FYSP105 / K3 RC-SUODATTIMET
 FYSP105 / K3 R-SODATTIMET Työn tavoitteita tutustua R-suodattimien toimintaan oppia mitoittamaan tutkittava kytkentä laiterajoitusten mukaisesti kerrata oskilloskoopin käyttöä vaihtosähkömittauksissa Työssä
FYSP105 / K3 R-SODATTIMET Työn tavoitteita tutustua R-suodattimien toimintaan oppia mitoittamaan tutkittava kytkentä laiterajoitusten mukaisesti kerrata oskilloskoopin käyttöä vaihtosähkömittauksissa Työssä
