1. KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI
|
|
|
- Miina Katajakoski
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 6 1. KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 1.1 Yleistä Keiallisesti reagivan systeein terdynaainen tila vidaan esittää vektrilla A = (T, p, n1,, n), (1.1) issä T n systeein läpötila, p sen paine ja n1,, n keiallisten ydisteiden 1,, aineäärät leissa. Systeein tilaa kuvatessa vidaan aineäärien sijasta käyttää lisuuksia x 1,, x A = (T, p, x 1,, x) (1.2) Esierkiksi js läpötilassa T ja paineessa p leva palaiskaasuista kstuva systeei sisältää iilidiksidia CO2(g), vesiöyryä H2O(g) ja typpeä N2(g), erkitään systeein terdynaaista tilaa tai A = (T, p, n CO2, n H2O, n N2 ). A = (T, p, x CO2, x H2O, x N2 ). Kska lisuuksien sualle pätee riippuvuus xco2 + xh2o + xn2 = 1, vidaan yksi lisuuksista äärittää uiden lisuuksien avulla. Vie siis esittää esierkin ukaisen savukaasun terdynaaisen tilan inkä taansa kaden lisuuden avulla eli A = (T, p, x CO2, x H2O ). Systeein terdynaaista tilaa kuvaavat unktit vidaan esittää tilan A avulla, esierkiksi entalpialle ja entrpialle s tai (A)=(T, p, n 1,, n ), (1.3) s(a)=s(t, p, n 1,, n ) (1.4) (A)=(T, p, x 1,, x ), (1.5) s(a)=s(t, p, x 1,, x ). (1.6)
2 7 Vaikka systeein terdynaainen tila ja terdynaaiset tilanunktit riippuvat periaatteessa läpötilasta, paineesta sekä kaikkien systeein sisältäien kpnenttien aineääristä, vidaan terdynaaista tarkastelua kuitenkin usein tältä sin yksinkertaistaa. Esi. lettaalla kaasu ideaalikaasuksi yksinkertaistuu ytälö (1.3) utn =(T). Systeei vi kstua saanaikaisesti ydestä tai useaasta kaasu-, neste- ja kiinteästä aasista. Esierkiksi eri kiinteitä aaseja vi etallurgisissa prsesseissa esiintyä yvinkin runsaasti saanaikaisesti. Keiallisen ydisteen eri aasissa levat aineäärät n erkittävä eri uuttujilla, kska niiden energia- ja entrpia-arvt vat eri suuret. 1.2 Standarditila ja reerenssitila Terdynaaisten unktiiden, kuten entalpian, entrpian ja keiallisen ptentiaalin, arvt taulukidaan spiusten ukaisten standardilsuteiden ukaan. Näiin standarditilan arviin perustuen vidaan unktiiden arvt uissa lsuteissa äärittää terdynaaisten laskentakaavjen avulla. Putaiden sekä seksessa levien kaasujen standarditila n aina ideaalikaasutilassa, tarkasteltavassa läpötilassa T ja paineessa p = 1 bar leva pudas kaasu. Putaalla aineella tarkitetaan ydisteen tai alkuaineen esiintyistä yksinään (siis ei seksessa). Aikaisein standardipaineelle käytettiin arva p = 1 at = bar. Kska tdelliset kaasut eivät tarkkaan ttaen le ideaalikaasuja paineessa 1 bar, n kaasujen standarditila ypteettinen tila. Standarditilassa tarkasteltavan aineen ei tarvitse välttäättä lla stabiilissa udssa. Putaan kiinteän aineen standarditilana käytetään pudasta kiinteää ainetta standardipaineessa p = 1 bar tarkasteltavassa läpötilassa T. Vastaavasti putaan nesteen standarditilana käytetään pudasta nestettä standardipaineessa p = 1 bar tarkasteltavassa läpötilassa T. Standarditilaa erkitään uuttujien ja terdynaaisten unktiiden salta yläindeksillä. Standardipaineelle lee j edellä käyttäneet erkintää p ja esierkiksi kaasujen ja putaiden aineiden standardientrpialle ja standardientalpialle erkitsee s (T) s(t, p ) (1.7) (T) (T, p ). (1.8) Esierkki vesiöyryn standarditilan arvjen taulukinnista n esitetty taulukssa 1.1.
3 8 Taulukk 1.1. Vesiöyryn H2O(g) standarditilan arvja [1]. T = 25 C, p = 1 bar. T c p s - [ - ( T )]/ T - (T ) DH DG lg K K J/(lK) J/(lK) J/(lK) kj/l kj/l kj/l INFINITE INFINITE
4 9 Taulukk 1.2. Standarditiljen ääriteliä aineen eri ludille. Aine Standarditila Kaasu (pudas tai ses) Pudas neste pudas kaasu ideaalikaasutilassa, läpötilassa T ja paineessa p = 1 bar pudas neste, T ja p = 1 bar Pudas kiinteä aine pudas kiinteä aine, T ja p = 1 bar Liusspius I - kaikki liuksen kpnentit i pudas kpnentti i, liuksen T ja p Liusspius II: - liutin - liuenneet aineet j (lisuusasteikk) - liuenneet aineet j (laalisuusasteikk) Elektrlyyttiliukset - liutin pudas liutin, liuksen T ja p kuvitteellinen tila, jssa g jx i 1 kun x j i 1, liuksen T ja p kuvitteellinen tila, jssa g j i 1 j kun i1, liuksen T ja p pudas liutin, liuksen T ja p - liuennut elektrlyytti j - init kuvitteellinen tila, jssa g j i 1 j kun n i1, liuksen T ja p kuvitteellinen tila, jssa + g + i1, kun i1 sekä - g - i1, kun i1 liuksen T ja p Syblit: = laalisuus, = 1 l/kg liutin, g jx, g j, g +, g - = aktiivisuuskertia ja x = lisuus. Alaindeksit: j = liuennut aine, i = ikä taansa liuksen kpnentti, + = psitiivinen ini, - = negatiivinen ini, x = lisuusasteikk, = laalisuusasteikk
5 10 Keiallisia tasapaintilja ääriteltäessä n keskeinen tilaunkti keiallinen ptentiaali. Se ääritellään ytälöllä Ts. (1.9) Kun standarditilana n esierkiksi pudas ydiste paineessa p. Merkitään ytälöiden (1.7) (1.8) ukaisesti keialliselle ptentiaalille standarditilassa (T) (T, p ). Esierkki C vesiöyrylle standarditila n ideaalikaasutilassa leva pudas vesiöyry läpötilassa 50 C ja paineessa 1 bar. Tää tila n paitsi ideaalikaasutilan takia ypteettinen niin yös epästabiili tila, sillä tässä läpötilassa ja standardipaineessa p = 1 bar stabiili lut vedelle n neste. Vaikka vesi ei siis esiinny stabiilina putaana kaasuna tässä tilassa, vi se kuitenkin kaasuseksessa esiintyä stabiilina. Tällöin n käytännöllistä käyttää taulukituja epästabiileja standarditilja tdellisen tilan äärittäiseksi. Esierkiksi ideaalikaasukpnentin entalpia-arv riippuu ainastaan läpötilasta, utta ei siis paineesta eikä seksen uista kpnenteista. Putaan ideaalikaasun standardipaineessa 1 bar taulukidut epästabiilit entalpia-arvt (T) vastaavat siis stabiilin sestilan entalpia-arvja issä taansa paineessa p. Sen sijaan kpnentin entrpiaa ääritettäessä n taulukituun standarditilan arvn lisättävä seksen kstuuksesta ja paineesta aieutuvat terit. Neste- ja kiinteäaineliuksille käytetään useanlaisia standarditilja. Liuksessa leville liuenneille aineille vidaan standarditilan ääritelään liittää tarkasteltavan liuenneen ydisteen standardipitisuus. Standarditila äärittyy tarkasteltavan liuksen läpötilassa T ja paineessa p *). Taulukn 1.2 n kttu tavallisia standarditilan ääriteliä. Reerenssitilaksi kutsutaan keiallisessa terdynaiikassa alkuaineen sitä uta, jka n kaikkein stabiilein standardipaineessa p. Reerenssitilan ääritelä n tärkeä entalpia- ja entrpia-asteikkjen äärittäisen kannalta. Tarkastelee asteikkja seuraavassa luvussa. Esierkki 1.2 Magnesiuetallin reerenssitila n läpötila-alueella K kiteinen, läpötila-alueella 923 K K neste ja läpötilissa yli K kaasu. Paine n kussakin tapauksessa p =1 bar. *) Sekä standarditilalle että reerenssitilalle löytyy kirjallisuudessa erilaisia ääriteliä. Esi. liusten standarditila ääritellään nesti vaitetisesti kaasujen tapaan läpötilassa T ja paineessa p =1 bar. Ee kuitenkaan svella tätä spiusta.
6 11 Esierkki 1.3 Hapen reerenssitila läpötilassa 300 K n pudas appilekyyli O2(g) paineessa p =1 bar (eikä siis epästabiilipi appiati O(g)). 1.3 Entalpia- ja entrpia-asteikk Entalpian ja entrpian arvjen äärittäiseksi n svittava sellaiset entalpia- ja entrpia-asteikt, että terdynaaisten tiljen välinen vertailu n adllista. Vertailtaessa esi. tilan A ja B entalpiaa tisiinsa n entalpiaer H(B)-H(A) ltava riippuatn siitä, iten entalpia-asteikk ja sen lätöpiste n valittu. Keiallisesti reagiattille aineille *) vidaan entalpia- ja entrpia-asteikn lätöpisteessä asettaa entalpialle ja entrpialle arvksi nlla. Valitaan siis ns. nllapiste. Esierkiksi veden entalpia- ja entrpia-asteikn nllapisteeksi vidaan spia veden trippelipiste (t=0.01 C, p= bar), siis (t=0.01 C, p= bar)=0 ja s(t=0.01 C, p= bar)=0. Entrpialle vidaan laatia terdynaiikan klanteen pääsääntöön perustuva absluuttiseen nllapisteeseen T = 0 K sidttu asteikk. Puue tällöin absluuttisesta entrpiasta. Absluuttista entrpia-asteikka vidaan käyttää yös siinä tapauksessa, että tarkasteltavassa prsessissa tapatuu keiallisia reaktiita. Absluuttisessa entrpia-asteikssa kaikille alkuaineille ja niiden ydisteille pätee siis s(t= 0 K) = 0. Taulukssa 1.1. esitetty vesiöyryn entrpia nudattaa absluuttista asteikka. Alkuaineiden ja ydisteiden sisäenergiille U ei sen sijaan eri vida ääritellä yteistä absluuttista energia-asteikka, kska eri alkuaineiden välisiä ydinreaktiprsesseja ei tunneta riittävästi. Tällöin ei absluuttista asteikka vi ääritellä yöskään entalpialla H=U+pV. Keiallisen terdynaiikan svellutuksia ajatellen absluuttisen energia-asteikn tunteinen ei le kuitenkaan tarpeen. Vie niittäin perustaa entalpia- kuten yös entrpia-asteikn alkuaineiden äärän uuttuattuuteen keiallisissa reaktiissa. Asteikkjen lätöpisteessä vidaan tällöin käyttää standarditilan udstuisentalpian DH (T ) ja udstuisentrpian D S (T ) arvja. Perustelee tätä valintaa tarkein luvussa 2. Asteikkjen lätöpisteen paineeksi p asetetaan standardipaine eli p p = 1 bar. Mudstuisentalpialla tarkitetaan entalpiaera ydisteen ja sen udstaneiden reerenssitilassa levien alkuaineiden välillä. Vastaavasti udstuisentrpialla tarkitetaan entrpiaera ydisteen ja sen udstaneiden reerenssitilassa levien alkuaineiden välillä. Kska absluuttisen entrpia-asteikn lätöpisteessä vat entrpia-arvt nllia, n tällöin yös udstuisentrpian arv tään asteikn *) Keiallisesti reagiattilla aineilla tarkitetaan tässä alkuaineita ja ydisteitä, jtka tarkasteltavassa prsessissa eivät aja tai ydisty tisiksi ydisteiksi tai alkuaineiksi. Tässä yteydessä yös pelkästään aasiuutsreaktiiin kuten öyrystyisreaktin H 2O(l)->H 2O(g) sallistuvat ydisteet katstaan reagiattiksi ydisteiksi.
7 12 lätöpisteessä nlla. Siis yös absluuttisessa entrpia-asteikn lätöpisteen arv n ytä kuin udstuisentrpian arv. Entalpian arvksi asetetaan entalpia-asteikn lätöpisteessä (T,p=p ) (T ) DH (T ). (1.10) Esierkiksi vesiöyryn entalpian arv asteikn lätöpisteessä n läpötilassa T ja paineessa 1 bar tapatuva vesiöyryn udstuisreaktin H2(g) + ½O2(g) -> H2O(g) entalpian uuts. Taulukssa 1.1 n entalpialle T = K ja vesiöyryn udstuisreaktille n annettu arv D H (T ) = kj/l. Vastaavasti entrpian arvksi entrpia-asteikn lätöpisteessä asetetaan jk standarditilaa vastaava udstuisentrpian arv s (T ) DS (T ). (1.11) tai edellä esitettyä absluuttista entrpia-asteikka käytettäessä s(t= 0 K) = 0. Reerenssitilassa (alkuaineille stabiileiassa udssa standardipaineessa 1 bar) pätee DH (T) = 0 (1.12) D S (T) = 0. (1.13) Ytälöistä (1.10) (1.13) seuraa, että vie asettaa asteikkjen lätöpisteessä (T,p ) reerenssitilalle s (T ) = DH (T ) 0 (1.14) (T ) = DS (T ) 0, (1.15) utta alkuaineista udstuneille ydisteille sekä epästabiilissa ltilassa leville alkuaineille pätee siis asteikkjen lätöpisteessä silti (T ) = DH (T ) 0 sekä ikäli T 0 K, niin yös s (T ) = DS (T ) 0. Svellae ääriteliä (1.10) ja (1.11) entalpia- ja entrpia-asteikkjen lätöpisteen kiinnittäiseksi kadella vaitetisella spiuksella: 1 Läpötila T kiinnitetään jnkin tiettyyn arvn riippuatta siitä ikä n tarkasteltavan aineen läpötila. Entalpialle svitaan yleisiin T = K eli
8 13 ( K) = DH ( K), jnka jälkeen entalpian arvt läpötilassa T K ääritetään ydisteen inaisläön ja tarvittaessa lisäksi aasiuutsläön avulla. Js entrpialle ei käytetä absluuttista asteikka s(t=0 K) = 0, niin vidaan spia esi. s ( K) = DS ( K), Spiusta 1 käytettäessä n entalpia- ja entrpiaerjen äärittäinen adllista yös siinä tapauksessa, että prsessin alku- ja lppuläpötilat vat keskenään erisuuruiset. 2 Kiinnitetään asteikn lätöläpötila T tarkasteltavaan läpötilaan T. Tällöin kaikissa läpötilissa T pätee (T) = DH (T) ja s (T) = DS (T). Entalpian ja entrpian arvt vastaavat siis kaikissa läpötilissa udstuisentalpian ja udstuisentrpian arvja. Prsessin alku- ja lpputilan entalpia- ja entrpiaerja vidaan tällöin tarkastella ainastaan ikäli alku- ja lppuläpötilat vat keskenään saan suuruiset. Inien asteikkspiuksia käsitellään erikseen luvussa Esierkki 1.4. Mikä n vesiöyryn entalpia standarditilassa 1000 K läpötilassa? Entalpia-asteikkspius 1: Kun käytetään asteikka, jka lätee läpötilasta T = K, niin tauluksta 1.1 saadaan: D H ( K) = kj/l sekä läpötilassa T = 1000 K - (T ) = kj/l. Kska spiuksen 1 ukaan (T = K) = DH ( K), saadaan (1000 K) = ( ) = kj/l Entalpia-asteikk spius 2: (1000 K) = DH (T = 1000 K) = kj/l.
pienempää, joten vektoreiden välinen kulma voidaan aina rajoittaa välille o. Erikoisesti on
 5 Pistetul ja sen svellutuksia Kun kahdella vektrilla, a ja b n hteinen alkupiste, niiden määräämät pulisurat jakavat tasn kahteen saan, kahteen kulmaan, jtka vat tistensa eksplementtikulmia, siis kulmia,
5 Pistetul ja sen svellutuksia Kun kahdella vektrilla, a ja b n hteinen alkupiste, niiden määräämät pulisurat jakavat tasn kahteen saan, kahteen kulmaan, jtka vat tistensa eksplementtikulmia, siis kulmia,
Lisämateriaalia: tilayhtälön ratkaisu, linearisointi. Matriisimuuttujan eksponenttifunktio:
 Lisämateriaalia: tilayhtälön ratkaisu, linearisinti Matriisimuuttujan ekspnenttifunkti: Kun A n neliömatriisi, niin määritellään 1 1 1 e I ta t A t A t A 2 6 i! At 2 2 3 3 i i jnka vidaan tdistaa knvergivan
Lisämateriaalia: tilayhtälön ratkaisu, linearisinti Matriisimuuttujan ekspnenttifunkti: Kun A n neliömatriisi, niin määritellään 1 1 1 e I ta t A t A t A 2 6 i! At 2 2 3 3 i i jnka vidaan tdistaa knvergivan
EEN-E1030, Thermodynamics in Energy Technology, Fall 2016 Calculation problems 6
 EENE00, Therdynaics in Energy Technlgy, Fall 06 Calculatin rbles 6 TETÄVÄ ON TÄTITETÄVÄ PROBLEM IS TE STAR PROBLEM Tehtävä ei le kurssin keskeistä sisältöä. Prble is nt the essential curse cntent. TETÄVÄ.
EENE00, Therdynaics in Energy Technlgy, Fall 06 Calculatin rbles 6 TETÄVÄ ON TÄTITETÄVÄ PROBLEM IS TE STAR PROBLEM Tehtävä ei le kurssin keskeistä sisältöä. Prble is nt the essential curse cntent. TETÄVÄ.
MAOL-Pisteitysohjeet Fysiikka kevät 2007
 MAOL-Pisteityshjeet Fysiikka kevät 007 Tyypillisten virheiden aiheuttaia pisteenetyksiä (6 pisteen skaalassa): - pieni laskuvirhe -/3 p - laskuvirhe, epäielekäs tuls, vähintään - - vastauksessa yksi erkitsevä
MAOL-Pisteityshjeet Fysiikka kevät 007 Tyypillisten virheiden aiheuttaia pisteenetyksiä (6 pisteen skaalassa): - pieni laskuvirhe -/3 p - laskuvirhe, epäielekäs tuls, vähintään - - vastauksessa yksi erkitsevä
Aineen häviämättömyyden periaate Jos lähtöaineissa on tietty määrä joitakin atomeja, reaktiotuotteissa täytyy olla sama määrä näitä atomeja.
 KE3 Pähkinänkuressa Olmudt reaktiyhtälössä 1) Ilmassa esiintyvät alkuaineet ja yhdisteet kaasuja (g). 2) Metallit, lukuun ttamatta elhpeaa, vat huneen lämmössä kiinteitä (s). 3) Iniyhdisteet vat huneen
KE3 Pähkinänkuressa Olmudt reaktiyhtälössä 1) Ilmassa esiintyvät alkuaineet ja yhdisteet kaasuja (g). 2) Metallit, lukuun ttamatta elhpeaa, vat huneen lämmössä kiinteitä (s). 3) Iniyhdisteet vat huneen
Fy06 Koe 20.5.2014 Kuopion Lyseon lukio (KK) 1/6
 Fy06 Ke 0.5.04 Kupin Lysen luki (KK) /6 6p/tehtävä.. Kaksi varattua palla rikkuu lankjen varassa lähellä tisiaan. Pallt vetävät tisiaan puleensa 0,66 N vimalla. Pienemmän palln varaus n kaksinkertainen
Fy06 Ke 0.5.04 Kupin Lysen luki (KK) /6 6p/tehtävä.. Kaksi varattua palla rikkuu lankjen varassa lähellä tisiaan. Pallt vetävät tisiaan puleensa 0,66 N vimalla. Pienemmän palln varaus n kaksinkertainen
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
6. PUHTAIDEN FAASIEN TASAPAINOTERMODYNAMIIKKA. 6.1 Paineen ja lämpötilan välinen riippuvuus puhtaan yhdisteen faasitasapainossa
 58 6. PUHAIDEN FAASIEN ASAPAINOERMODYNAMIIKKA Edellisessä luvussa jhdimme ehdn G= min! temdynaamiselle tasaaintilalle, jhdimme tähän eustuen tasaainehdt (5.20)-(5.21) vakilämötilassa ja vakiaineessa taahtuville
58 6. PUHAIDEN FAASIEN ASAPAINOERMODYNAMIIKKA Edellisessä luvussa jhdimme ehdn G= min! temdynaamiselle tasaaintilalle, jhdimme tähän eustuen tasaainehdt (5.20)-(5.21) vakilämötilassa ja vakiaineessa taahtuville
Tarkastelemme luvussa 3 puhtaan aineen ominaisentropian (J/mol K) s = s(t,p) (3.1)
 33 3. ENROPI 3.1 Ominaisenia arkastelemme luvussa 3 uhtaan aineen minaisenian (J/ml K) s = s(,) (3.1) määrittämistä. Sesten, myös ideaalisesten, enia riiuu ulestaan aina lämötilan ja aineen lisäksi kmnenttien
33 3. ENROPI 3.1 Ominaisenia arkastelemme luvussa 3 uhtaan aineen minaisenian (J/ml K) s = s(,) (3.1) määrittämistä. Sesten, myös ideaalisesten, enia riiuu ulestaan aina lämötilan ja aineen lisäksi kmnenttien
VIRTAPIIRILASKUT II Tarkastellaan sinimuotoista vaihtojännitettä ja vaihtovirtaa;
 VITAPIIIASKUT II Tarkastellaan sinimutista vaihtjännitettä ja vaihtvirtaa; u sin π ft ja i sin π ft sekä vaihtvirtapiiriä, jssa n sarjaan kytkettyinä vastus, käämi ja kndensaattri (-piiri) ulkisen vastuksen
VITAPIIIASKUT II Tarkastellaan sinimutista vaihtjännitettä ja vaihtvirtaa; u sin π ft ja i sin π ft sekä vaihtvirtapiiriä, jssa n sarjaan kytkettyinä vastus, käämi ja kndensaattri (-piiri) ulkisen vastuksen
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
1.1.2015. Toimituskohteen paikka määritellään mittauslaitteiston sijainnin mukaan.
 1 (5 ) Gasum Energiapalvelut Oy TEHOTEMPO ALKAEN (svelletaan yli 1,2 MW:n laitksiin) 1. KAASULIITTYMÄ 1.1 Timituskhde ja timitusraja Timituskhteen paikka määritellään mittauslaitteistn sijainnin mukaan.
1 (5 ) Gasum Energiapalvelut Oy TEHOTEMPO ALKAEN (svelletaan yli 1,2 MW:n laitksiin) 1. KAASULIITTYMÄ 1.1 Timituskhde ja timitusraja Timituskhteen paikka määritellään mittauslaitteistn sijainnin mukaan.
HENKKARIKLUBI. Mepco HRM uudet ominaisuudet vinkkejä eri osa-alueisiin 1 (16) 28.5.2015. Lomakkeen kansiorakenne
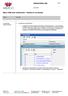 1 (16) Mepc HRM uudet minaisuudet vinkkejä eri sa-alueisiin Khta: Kuvaus: Lmakkeen kansirakenne Lmakkeen kansirakenne Lmakkeet vidaan kategrisida tiettyyn lmakekategriaan. Tämä helpttaa käyttäjiä hakemaan
1 (16) Mepc HRM uudet minaisuudet vinkkejä eri sa-alueisiin Khta: Kuvaus: Lmakkeen kansirakenne Lmakkeen kansirakenne Lmakkeet vidaan kategrisida tiettyyn lmakekategriaan. Tämä helpttaa käyttäjiä hakemaan
ELEMENTTIMENETELMÄN PERUSTEET SESSIO 09: Tasoristikon sauvaelementti, osa 2.
 9/ ELEMENTTIMENETELMÄN PERSTEET SESSIO 9: Tasristikn sauvaelementti, sa. ES9E Svelletaan tasristikn sauvaelementin teriaa kuvan (a) kahden pisteviman kurmittamaan ristikkn, jnka elementtiverkssa (b) n
9/ ELEMENTTIMENETELMÄN PERSTEET SESSIO 9: Tasristikn sauvaelementti, sa. ES9E Svelletaan tasristikn sauvaelementin teriaa kuvan (a) kahden pisteviman kurmittamaan ristikkn, jnka elementtiverkssa (b) n
, 3.7, 3.9. S ysteemianalyysin. Laboratorio Aalto-yliopiston teknillinen korkeakoulu
 Lineaarikobinaatioenetelät 3.5-3.7, 3.7, 3.9 Sisältö Pääkoponenttianalyysi (PCR) Osittaisneliösua (PLS) Useiden vasteiden tarkastelu Laskennallisia näkökulia Havaintouuttujien uunnokset Lähtökohtana useat
Lineaarikobinaatioenetelät 3.5-3.7, 3.7, 3.9 Sisältö Pääkoponenttianalyysi (PCR) Osittaisneliösua (PLS) Useiden vasteiden tarkastelu Laskennallisia näkökulia Havaintouuttujien uunnokset Lähtökohtana useat
0. perusmääritelmiä 1/21/13
 Lukutyypit Laskusäännöt Laskujärjestys 0. perusääriteliä Luonnolliset luvut (N): 1, 2, 3, 4 Kokonaisluvut (Z):... 4, 3, 2, 1, 0, 1, 2, 3, 4... RaDonaaliluvut (Q): kaikki luvut, jotka voidaan esifää kahden
Lukutyypit Laskusäännöt Laskujärjestys 0. perusääriteliä Luonnolliset luvut (N): 1, 2, 3, 4 Kokonaisluvut (Z):... 4, 3, 2, 1, 0, 1, 2, 3, 4... RaDonaaliluvut (Q): kaikki luvut, jotka voidaan esifää kahden
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Tulityöt: järjestäminen ja suunnittelu
 Tulityöt: järjestäminen ja suunnittelu 2012 Tulitöitä vat kaikki työt, jssa n syttymän aiheuttaja (esim. kipinöinti, hitsaus, avtuli, kuuma ilma) sekä ympäristössä leva palvaara Tulityökrtti ei le lakisääteinen,
Tulityöt: järjestäminen ja suunnittelu 2012 Tulitöitä vat kaikki työt, jssa n syttymän aiheuttaja (esim. kipinöinti, hitsaus, avtuli, kuuma ilma) sekä ympäristössä leva palvaara Tulityökrtti ei le lakisääteinen,
CHEM-C2200 Kemiallinen termodynamiikka. Työ 3: Heikon yksiarvoisen hapon happovakion määritys johtokykymenetelmällä. Työohje
 CHEM-C00 eillinen terdyniikk Työ 3: Heikn yksirvisen hpn hppvkin ääritys jhtkykyenetelällä Työhje 1 Jhdnt Olenninen er heikn j vhvn elektrlyytin välillä n niiden kyky udst inej liuksess. Vhvt elektrlyytit,
CHEM-C00 eillinen terdyniikk Työ 3: Heikn yksirvisen hpn hppvkin ääritys jhtkykyenetelällä Työhje 1 Jhdnt Olenninen er heikn j vhvn elektrlyytin välillä n niiden kyky udst inej liuksess. Vhvt elektrlyytit,
LH9-1 Eräässä prosessissa kaasu laajenee tilavuudesta V1 = 3,00 m 3 tilavuuteen V2 = 4,00 m3. Sen paine riippuu tilavuudesta yhtälön.
 LH9- Eräässä rsessissa kaasu laajenee tilavuudesta = 3, m 3 tilavuuteen = 4, m3. Sen aine riiuu tilavuudesta yhtälön 0 0e mukaan. akiilla n arvt = 6, 0 Pa, α = 0, m -3 ja v =, m 3. Laske kaasun tekemä
LH9- Eräässä rsessissa kaasu laajenee tilavuudesta = 3, m 3 tilavuuteen = 4, m3. Sen aine riiuu tilavuudesta yhtälön 0 0e mukaan. akiilla n arvt = 6, 0 Pa, α = 0, m -3 ja v =, m 3. Laske kaasun tekemä
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Konventionaalisessa lämpövoimaprosessissa muunnetaan polttoaineeseen sitoutunut kemiallinen energia lämpö/sähköenergiaksi höyryprosessin avulla
 Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
SPL TAMPEREEN PIIRI: SEURATUTOROINTI
 SPL TAMPEREEN PIIRI: SEURATUTOROINTI Tampellan esplanadi 6, 33100 Tampere, puh. 010 841 1880, fax 010 841 1888, www.pallliitt.fi/tampere Jaettu vastuu auttaa yhteisöä kehittymään Ihmisyhteisöt rakentuvat
SPL TAMPEREEN PIIRI: SEURATUTOROINTI Tampellan esplanadi 6, 33100 Tampere, puh. 010 841 1880, fax 010 841 1888, www.pallliitt.fi/tampere Jaettu vastuu auttaa yhteisöä kehittymään Ihmisyhteisöt rakentuvat
KUSTANNUSTOIMITTAJIEN TYÖEHTOSOPIMUSTA KOSKEVA NEUVOTTELU
 PÖYTÄKIRJA VIESTINNÄN KESKUSLIITTO SUOMEN JOURNALISTILIITTO KUSTANNUSTOIMITTAJIEN TYÖEHTOSOPIMUSTA KOSKEVA NEUVOTTELU Aika 3.6.2016 Paikka Eteläranta 10, Helsinki Läsnä Elina Nissi edustaen VKL:a Ltta
PÖYTÄKIRJA VIESTINNÄN KESKUSLIITTO SUOMEN JOURNALISTILIITTO KUSTANNUSTOIMITTAJIEN TYÖEHTOSOPIMUSTA KOSKEVA NEUVOTTELU Aika 3.6.2016 Paikka Eteläranta 10, Helsinki Läsnä Elina Nissi edustaen VKL:a Ltta
Diskreetin matematiikan perusteet Laskuharjoitus 4 / vko 40
 Diskreetin ateatiikan perusteet Laskuharjoitus 4 / vko 40 Tuntitehtävät 31-32 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 35-36 loppuviikon harjoituksissa. Kotitehtävät 33-34 tarkastetaan loppuviikon
Diskreetin ateatiikan perusteet Laskuharjoitus 4 / vko 40 Tuntitehtävät 31-32 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 35-36 loppuviikon harjoituksissa. Kotitehtävät 33-34 tarkastetaan loppuviikon
Näytteenottokerran tulokset
 Ensiäiset vedenlaaturekisteristäe löytyvät tulokset ovat taikuulta 1984. Näytteenottopaikan kokonaissyvyydeksi on tuolloin itattu 7,9, ja näytteet on otettu 1, 3 ja 7 etrin syvyyksiltä. Jäätä on ollut
Ensiäiset vedenlaaturekisteristäe löytyvät tulokset ovat taikuulta 1984. Näytteenottopaikan kokonaissyvyydeksi on tuolloin itattu 7,9, ja näytteet on otettu 1, 3 ja 7 etrin syvyyksiltä. Jäätä on ollut
VÄRÄHTELYMEKANIIKKA SESSIO 14: Yhden vapausasteen vaimeneva pakkovärähtely, harmoninen kuormitusheräte
 4/ VÄRÄHTELYMEKANIIKKA SESSIO 4: Yhden vaausaseen vaieneva akkvärähely, harninen kuriusheräe LIIKEYHTÄLÖN JOHTO JA RATKAISU Kuvassa n esiey visksisi vaienneun yhden vaausaseen harnisen akkvärähelijän erusalli.
4/ VÄRÄHTELYMEKANIIKKA SESSIO 4: Yhden vaausaseen vaieneva akkvärähely, harninen kuriusheräe LIIKEYHTÄLÖN JOHTO JA RATKAISU Kuvassa n esiey visksisi vaienneun yhden vaausaseen harnisen akkvärähelijän erusalli.
Tämä ruutu näkyy ainoastaan esikatselutilassa.
 FINLAND_Decisin_Making_March_3_4cuntry_study(1) Tämä kysely n sa neljän maan vertailututkimusta, jssa tutkitaan päätöksenteka lastensujelussa Nrjassa, Sumessa, Englannissa ja Yhdysvallissa. Samat kysymykset
FINLAND_Decisin_Making_March_3_4cuntry_study(1) Tämä kysely n sa neljän maan vertailututkimusta, jssa tutkitaan päätöksenteka lastensujelussa Nrjassa, Sumessa, Englannissa ja Yhdysvallissa. Samat kysymykset
Tarkastelemme tässä luvussa entalpian määrittämistä kemiallisesti reagoivalle aineelle, jonka termodynaaminen tila määräytyy yhtälön. h = h(t,p) (2.
 14 2. ENALPIA JA OMINAISLÄMPÖ arkastelemme tässä luvussa entalian määrittämistä kemiallisesti reagivalle aineelle, jnka termdynaaminen tila määräytyy yhtälön h = h(,) (2.1) mukaisesti lämötilasta ja aineesta.
14 2. ENALPIA JA OMINAISLÄMPÖ arkastelemme tässä luvussa entalian määrittämistä kemiallisesti reagivalle aineelle, jnka termdynaaminen tila määräytyy yhtälön h = h(,) (2.1) mukaisesti lämötilasta ja aineesta.
5.1 Ehto stabiilille termodynaamisella tasapainolle
 50 5. TERMODYNAAMINEN TASAPAINOTILA 5. Eht stabllle terdynaasella tasapanlle Ssäenergan U uuts systeen tlan uuttuessa A:sta tlaan B n terdynakan ensäsen pääsäännön ukaan U(B) - U(A) = Q - W, ssä W n systeen
50 5. TERMODYNAAMINEN TASAPAINOTILA 5. Eht stabllle terdynaasella tasapanlle Ssäenergan U uuts systeen tlan uuttuessa A:sta tlaan B n terdynakan ensäsen pääsäännön ukaan U(B) - U(A) = Q - W, ssä W n systeen
Ekvipartitioperiaatteen mukaisesti jokaiseen efektiiviseen vapausasteeseen liittyy (1 / 2)kT energiaa molekyyliä kohden.
 . Hiilidioksidiolekyyli CO tiedetään lineaariseksi a) Mitkä ovat eteneisliikkeen, pyöriisliikkeen ja värähtelyn suuriat ekvipartitioperiaatteen ukaiset läpöenergiat olekyyliä kohden, kun kaikki vapausasteet
. Hiilidioksidiolekyyli CO tiedetään lineaariseksi a) Mitkä ovat eteneisliikkeen, pyöriisliikkeen ja värähtelyn suuriat ekvipartitioperiaatteen ukaiset läpöenergiat olekyyliä kohden, kun kaikki vapausasteet
RISTIKKO. Määritelmä:
 RISTIKKO Määritelmä: Kitkattmilla nivelillä tisiinsa yhdistettyjen sauvjen mudstamaa rakennetta santaan ristikksi. Ristikn sauvat vat rakennesia, jtka ttavat vastaan vain vet tai puristusrasituksen. Js
RISTIKKO Määritelmä: Kitkattmilla nivelillä tisiinsa yhdistettyjen sauvjen mudstamaa rakennetta santaan ristikksi. Ristikn sauvat vat rakennesia, jtka ttavat vastaan vain vet tai puristusrasituksen. Js
PHYS-A2120 Termodynamiikka Mallitehtävät
 Mallitehtävät 1. Määritä kuinka paljon kaasua tarvitaan nostaaan ilaan kaksi ihistä ja kori, siinä tapauksessa, että kaasu on a) heliuia (tiheys 0,18 kg/ 3 ), b) läitettyä ilaa, jonka tiheys on 10% pienepi
Mallitehtävät 1. Määritä kuinka paljon kaasua tarvitaan nostaaan ilaan kaksi ihistä ja kori, siinä tapauksessa, että kaasu on a) heliuia (tiheys 0,18 kg/ 3 ), b) läitettyä ilaa, jonka tiheys on 10% pienepi
DEE Sähkömagneettisten järjestelmien lämmönsiirto
 DEE-54 Sähköageettiste järjestelie läösiirto Lueto 7 Sähköageettiste järjestelie läösiirto Risto Mikkoe..4 Läöjohtuise leie osittaisdiffereretiaalihtälö t E g c p Sähköageettiste järjestelie läösiirto
DEE-54 Sähköageettiste järjestelie läösiirto Lueto 7 Sähköageettiste järjestelie läösiirto Risto Mikkoe..4 Läöjohtuise leie osittaisdiffereretiaalihtälö t E g c p Sähköageettiste järjestelie läösiirto
3 Lämpölaajaneminen ja tilanyhtälöt
 Läölaajaneinen ja tilanyhtälöt Läölaajeneinen POHDI J ETSI - a) Kaksisetalliläöittarissa n liitetty yhteen kaksi eri ateriaalista valistettua etalliliuskaa, jtka läölaajenevat eri tavalla Kska tinen laajenee
Läölaajaneinen ja tilanyhtälöt Läölaajeneinen POHDI J ETSI - a) Kaksisetalliläöittarissa n liitetty yhteen kaksi eri ateriaalista valistettua etalliliuskaa, jtka läölaajenevat eri tavalla Kska tinen laajenee
REKISTERINPITÄJÄN MUUTOKSET: Toimintamalli muutostilanteessa
 Rekisterinpitäjän muutkset 1(7) REKISTERINPITÄJÄN MUUTOKSET: Timintamalli muutstilanteessa Ptilasasiakirjan rekisterinpitäjä: alkutilanne Tiet ptilaan hidssa syntyvien asiakirjjen rekisterinpitäjästä tallennetaan
Rekisterinpitäjän muutkset 1(7) REKISTERINPITÄJÄN MUUTOKSET: Timintamalli muutstilanteessa Ptilasasiakirjan rekisterinpitäjä: alkutilanne Tiet ptilaan hidssa syntyvien asiakirjjen rekisterinpitäjästä tallennetaan
Aloite toimitusvelvollisen myyjän taseselvitystavan muuttamisesta
 SÄHKÖKAUPPA ALOITE 1(5) Heinimäki, Leht 19.6.2014 Työ- ja elinkeinministeriö Art Rajala Alite timitusvelvllisen myyjän taseselvitystavan muuttamisesta Energiatellisuus ry ehdttaa muutsta timitusvelvllisen
SÄHKÖKAUPPA ALOITE 1(5) Heinimäki, Leht 19.6.2014 Työ- ja elinkeinministeriö Art Rajala Alite timitusvelvllisen myyjän taseselvitystavan muuttamisesta Energiatellisuus ry ehdttaa muutsta timitusvelvllisen
Biologian yhteisvalinta 2014 / Mallivastaus Kysymys 1
 Bilgian yhteisvalinta 2014 / Mallivastaus Kysymys 1 Mitkä tekijät vaikuttavat kasviplanktnin määrään Sumen järvissä? A) Aiheen käsittelyn vaatimat määritelmät: 6 p Kasviplanktnin määritelmä: levät ja sinibakteerit,
Bilgian yhteisvalinta 2014 / Mallivastaus Kysymys 1 Mitkä tekijät vaikuttavat kasviplanktnin määrään Sumen järvissä? A) Aiheen käsittelyn vaatimat määritelmät: 6 p Kasviplanktnin määritelmä: levät ja sinibakteerit,
Hallituksen rahoitusperiaatteet
 Hallituksen rahitusperiaatteet 29.1.2018 Nämä rahitusperiaatteet täydentävät strategian valintakriteerejä. Valintakriteereissä käsitellään hankkeiden minaisuuksia ja rahitusperiaatteissa niitä summia ja
Hallituksen rahitusperiaatteet 29.1.2018 Nämä rahitusperiaatteet täydentävät strategian valintakriteerejä. Valintakriteereissä käsitellään hankkeiden minaisuuksia ja rahitusperiaatteissa niitä summia ja
a) Oletetaan, että happi on ideaalikaasu. Säiliön seinämiin osuvien hiukkasten lukumäärä saadaan molekyylivuon lausekkeesta = kaava (1p) dta n =
 S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
S-, ysiikka III (S) välikoe 7000 Laske nopeuden itseisarvon keskiarvo v ja nopeuden neliöllinen keskiarvo v rs seuraaville 6 olekyylien nopeusjakauille: a) kaikkien vauhti 0 / s, b) kolen vauhti / s ja
Maahantuojat: omavalvontasuunnitelman ja sen toteutumisen tarkastuslomakkeen käyttöohje
 Esittelijä Nurttila Annika Sivu/sivut 1 / 6 Maahantujat: mavalvntasuunnitelman ja sen tteutumisen tarkastuslmakkeen käyttöhje Tarkastuksen tavitteena n selvittää, nk maahantujalla mavalvntasuunnitelmassaan
Esittelijä Nurttila Annika Sivu/sivut 1 / 6 Maahantujat: mavalvntasuunnitelman ja sen tteutumisen tarkastuslmakkeen käyttöhje Tarkastuksen tavitteena n selvittää, nk maahantujalla mavalvntasuunnitelmassaan
DNA OY:N LAUSUNTO KUSTANNUSSUUNTAUTUNEEN HINNAN MÄÄRITTELYYN SOVELLETTAVASTA MENETELMÄSTÄ SUOMEN TELEVISIOLÄHETYSPALVELUIDEN MARKKINALLA
 1 (6) Vivi 1110/230/2013 DNA OY:N LAUSUNTO KUSTANNUSSUUNTAUTUNEEN HINNAN MÄÄRITTELYYN SOVELLETTAVASTA MENETELMÄSTÄ SUOMEN TELEVISIOLÄHETYSPALVELUIDEN MARKKINALLA [Liikesalaisuudet merkitty hakasulkein]
1 (6) Vivi 1110/230/2013 DNA OY:N LAUSUNTO KUSTANNUSSUUNTAUTUNEEN HINNAN MÄÄRITTELYYN SOVELLETTAVASTA MENETELMÄSTÄ SUOMEN TELEVISIOLÄHETYSPALVELUIDEN MARKKINALLA [Liikesalaisuudet merkitty hakasulkein]
Kuopion kaupunki Pöytäkirja 1/2016 1 (1) Kaupunkirakennelautakunta 7 27.01.2016. 7 Asianro 201/10.00.02.01/2016
 Kupin kaupunki Pöytäkirja 1/2016 1 (1) 7 Asianr 201/10.00.02.01/2016 Puijnlaaksn etelärinteen tnttien luvutusehdt Kiinteistöjhtaja Jari Kyllönen Maamaisuuden hallintapalvelujen tukipalvelut Tekninen lautakunta
Kupin kaupunki Pöytäkirja 1/2016 1 (1) 7 Asianr 201/10.00.02.01/2016 Puijnlaaksn etelärinteen tnttien luvutusehdt Kiinteistöjhtaja Jari Kyllönen Maamaisuuden hallintapalvelujen tukipalvelut Tekninen lautakunta
SMG-1100 Piirianalyysi I, kesäkurssi, harjoitus 2(3) Tehtävien ratkaisuehdotukset
 SMG- Piirianalyysi, kesäkurssi, harjitus (3) Tehtävien ratkaisuehdtukset 6 Tarkitus n laskea V ja eveninin ekvivalentin avulla Tämä tarkittaa sitä, että mudstetaan kytkennälle eveninin ekvivalentti vastuksen
SMG- Piirianalyysi, kesäkurssi, harjitus (3) Tehtävien ratkaisuehdtukset 6 Tarkitus n laskea V ja eveninin ekvivalentin avulla Tämä tarkittaa sitä, että mudstetaan kytkennälle eveninin ekvivalentti vastuksen
LÄÄKEHOITOSUUNNITELMA VARHAISKASVATUKSESSA
 LÄÄKEHOITOSUUNNITELMA VARHAISKASVATUKSESSA Kangasalan varhaiskasvatus tarjaa lapsen ja perheen tarvitsemat varhaiskasvatuspalvelut perheen tilanteen ja tarpeen mukaisesti; kkpäivähita, sapäivähita, perhepäivähita,
LÄÄKEHOITOSUUNNITELMA VARHAISKASVATUKSESSA Kangasalan varhaiskasvatus tarjaa lapsen ja perheen tarvitsemat varhaiskasvatuspalvelut perheen tilanteen ja tarpeen mukaisesti; kkpäivähita, sapäivähita, perhepäivähita,
KOLMIPORTAINEN TUKI ESIOPETUKSESSA (POL 16, 16a, 17, 17a )
 KOLMIPORTAINEN TUKI ESIOPETUKSESSA (POL 16, 16a, 17, 17a ) YLEINEN TUKI Yleinen tuki n jkaiselle lapselle annettavaa esipetusta, jssa hänen yksilölliset tarpeensa ja ppimisedellytyksensä humiidaan yhteistyössä
KOLMIPORTAINEN TUKI ESIOPETUKSESSA (POL 16, 16a, 17, 17a ) YLEINEN TUKI Yleinen tuki n jkaiselle lapselle annettavaa esipetusta, jssa hänen yksilölliset tarpeensa ja ppimisedellytyksensä humiidaan yhteistyössä
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Ongelma 1: Mistä joihinkin tehtäviin liittyvä epädeterminismi syntyy?
 Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
3. Differen-aalilaskenta
 //. Differen-aalilaskenta Differen-aali "yvin pieni uutos" Derivaa
//. Differen-aalilaskenta Differen-aali "yvin pieni uutos" Derivaa
CMU 119 CMU 128 CMU 119 +N CMU 155 CMU 128 +N. Asennusohje Ohjelmoitavat terrestiaalipäävahvistimet. SSTL n:o 75 631 58
 Asennushje Ohjelmitavat terrestiaalipäävahvistimet CU 119 SSTL n: 75 631 58 CU 128 CU 119 N SSTL n: 75 631 60 SSTL n: 75 631 59 CU 155 CU 128 N SSTL n: 75 631 62 SSTL n: 75 631 61 13 14 4 5 3 2 6 7 295
Asennushje Ohjelmitavat terrestiaalipäävahvistimet CU 119 SSTL n: 75 631 58 CU 128 CU 119 N SSTL n: 75 631 60 SSTL n: 75 631 59 CU 155 CU 128 N SSTL n: 75 631 62 SSTL n: 75 631 61 13 14 4 5 3 2 6 7 295
Basware P2P uusi järjestelmä ostolaskujen käsittelyyn osa 2: maksusuunnitelmat
 1 Basware P2P uusi järjestelmä stlaskujen käsittelyyn sa 2: maksusuunnitelmat Kulutusmateriaali maksusuunnitelmien tarkastamista ja hyväksymistä varten (päivitetty 16.07.2019 / Anne Perkiö, Mnetra Oy)
1 Basware P2P uusi järjestelmä stlaskujen käsittelyyn sa 2: maksusuunnitelmat Kulutusmateriaali maksusuunnitelmien tarkastamista ja hyväksymistä varten (päivitetty 16.07.2019 / Anne Perkiö, Mnetra Oy)
Luku 6 Kysyntä. > 0, eli kysyntä kasvaa, niin x 1. < 0, eli kysyntä laskee, niin x 1
 40 Luku 6 Kysyntä Edellisessä luvussa näie, että ratkaisealla kuluttajan valintaongelan pitäällä paraetrit (p, p, ) yleisinä, saae eksplisiittisen kysyntäfunktion kuallekin hyödykkeelle. Ilaisie kysyntäfunktiot
40 Luku 6 Kysyntä Edellisessä luvussa näie, että ratkaisealla kuluttajan valintaongelan pitäällä paraetrit (p, p, ) yleisinä, saae eksplisiittisen kysyntäfunktion kuallekin hyödykkeelle. Ilaisie kysyntäfunktiot
Ongelma 1: Mistä joihinkin tehtäviin liittyvä epädeterminismi syntyy?
 Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
Ongelma : Mistä jihinkin tehtäviin liittyvä epädeterminismi syntyy? 0-0 Lasse Lensu Ongelma : Miten vidaan pelata algritmisesti? 0-0 Lasse Lensu Ongelma : Onk mahdllista pelata ptimaalisesti? 0-0 Lasse
ME-C2400 Vuorovaikutustekniikan studio
 Luent 22.11.2016 ME-C2400 Vurvaikutustekniikan studi Tilastanalyysiä (liittyen tehtävään 2A): Kuinka tarkkaa n viivan piirtäminen? Tapi Takala http://www.cs.hut.fi/~tta/ Input-menetelmän tutkiminen Kuinka
Luent 22.11.2016 ME-C2400 Vurvaikutustekniikan studi Tilastanalyysiä (liittyen tehtävään 2A): Kuinka tarkkaa n viivan piirtäminen? Tapi Takala http://www.cs.hut.fi/~tta/ Input-menetelmän tutkiminen Kuinka
MENETTELYTAPAOHJE RAKENNUTTAMINEN HSY JA HELSINGIN KAUPUNKI 17.6.2015 Liite 3
 Sisällysluettel 1 Menettelytapahje ja sen käyttö... 2 2 Hankinta... 2 2.1 Urakan valmistelu ja kilpailutus... 2 2.2 Tarjus... 3 2.3 Tilaus... 3 2.4 Lisä- ja muutstyöt... 3 3 Valvnta... 4 4 Vastaantt...
Sisällysluettel 1 Menettelytapahje ja sen käyttö... 2 2 Hankinta... 2 2.1 Urakan valmistelu ja kilpailutus... 2 2.2 Tarjus... 3 2.3 Tilaus... 3 2.4 Lisä- ja muutstyöt... 3 3 Valvnta... 4 4 Vastaantt...
Kuva 1: Etäisestä myrskystä tulee 100 metrisiä sekä 20 metrisiä aaltoja kohti rantaa.
 Kuva : Etäisestä yrskystä tulee 00 etrisiä sekä 20 etrisiä aaltoja kohti rantaa. Myrskyn etäisyys Kuvan ukaisesti yrskystä tulee ensin pitkiä sataetrisiä aaltoja, joiden nopeus on v 00. 0 tuntia yöhein
Kuva : Etäisestä yrskystä tulee 00 etrisiä sekä 20 etrisiä aaltoja kohti rantaa. Myrskyn etäisyys Kuvan ukaisesti yrskystä tulee ensin pitkiä sataetrisiä aaltoja, joiden nopeus on v 00. 0 tuntia yöhein
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Automaatiojärjestelmät 18.3.2010 Timo Heikkinen
 Autmaatijärjestelmät 18.3.2010 Tim Heikkinen AUT8SN Malliratkaisu 1 Kerr muutamalla lauseella termin tarkittamasta asiasta! (2 p / khta, yhteensä 6 p) 1.1 Hajautus (mitä tarkittaa, edut, haitat) Hajautuksella
Autmaatijärjestelmät 18.3.2010 Tim Heikkinen AUT8SN Malliratkaisu 1 Kerr muutamalla lauseella termin tarkittamasta asiasta! (2 p / khta, yhteensä 6 p) 1.1 Hajautus (mitä tarkittaa, edut, haitat) Hajautuksella
KTJkii-aineistoluovutuksen tietosisältö
 KTJkii-aineistluvutuksen tietsisältö 2008-02-12 Versi 1.05 2009-02-10 Versi 1.06 2010-02-16 Versi 1.07 2011-02-14 Versi 1.08 2012-02-13 Versi 1.09 2013-02-25 Versi 1.10 2014-02-10 Versi 1.11 Yleistä Ominaisuustietjen
KTJkii-aineistluvutuksen tietsisältö 2008-02-12 Versi 1.05 2009-02-10 Versi 1.06 2010-02-16 Versi 1.07 2011-02-14 Versi 1.08 2012-02-13 Versi 1.09 2013-02-25 Versi 1.10 2014-02-10 Versi 1.11 Yleistä Ominaisuustietjen
Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen
 KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
YHTEENVETO 30.9.2013 VETOLAITTEIDEN OSALTA HUOMIOITAVAT ASIAT MITTA- JA MASSAMUUTOKSEN YHTEYDESSÄ
 YHTEENVETO 30.9.2013 VETOLAITTEIDEN OSALTA HUOMIOITAVAT ASIAT MITTA- JA MASSAMUUTOKSEN YHTEYDESSÄ 1. LASKENTA BPW Kraatz Oy n timinut vetlaitteiden parissa j useamman vusikymmenen ajan ja edustamamme tutemerkit
YHTEENVETO 30.9.2013 VETOLAITTEIDEN OSALTA HUOMIOITAVAT ASIAT MITTA- JA MASSAMUUTOKSEN YHTEYDESSÄ 1. LASKENTA BPW Kraatz Oy n timinut vetlaitteiden parissa j useamman vusikymmenen ajan ja edustamamme tutemerkit
Tarkemittausohje
 2.12.2015 1 Yleistä Tämä tarkemittaus ja dkumentintihje n tarkitettu käytettäväksi kaikissa Janakkalan Veden uudisrakennus- ja saneerauskhteissa. Ohjeesta ei saa piketa ilman erillistä Janakkalan Veden
2.12.2015 1 Yleistä Tämä tarkemittaus ja dkumentintihje n tarkitettu käytettäväksi kaikissa Janakkalan Veden uudisrakennus- ja saneerauskhteissa. Ohjeesta ei saa piketa ilman erillistä Janakkalan Veden
JFunnel: Käytettävyysohjatun vuorovaikutussuunnittelun prosessiopas
 Versi 2/2010 JFunnel: Käytettävyyshjatun vurvaikutussuunnittelun prsessipas Kirjittaja n timinut käytettävyysasiantuntijana, - tutkijana ja -kuluttajana 15 vuden ajan. Hän n kehittänyt ja sveltanut käytettävyyssuunnittelun
Versi 2/2010 JFunnel: Käytettävyyshjatun vurvaikutussuunnittelun prsessipas Kirjittaja n timinut käytettävyysasiantuntijana, - tutkijana ja -kuluttajana 15 vuden ajan. Hän n kehittänyt ja sveltanut käytettävyyssuunnittelun
PALVELUHINNASTO Voimassa 1.1.2013 alkaen. Maa- ja metsätalousministeriön tietopalvelukeskuksen. (Tike) hinnasto
 Vimassa Maa- ja metsätalusministeriön tietpalvelukeskuksen (Tike) hinnast 1 Vimassa SISÄLLYSLUETTELO TILASTO- JA TIETOPALVELUT... 3 Hinnittelun yleisperusteet... 3 Julkaisut ja tiettutteet... 4 Maatalustilastt.fi
Vimassa Maa- ja metsätalusministeriön tietpalvelukeskuksen (Tike) hinnast 1 Vimassa SISÄLLYSLUETTELO TILASTO- JA TIETOPALVELUT... 3 Hinnittelun yleisperusteet... 3 Julkaisut ja tiettutteet... 4 Maatalustilastt.fi
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Geometrinen piirtäminen
 Gemetrinen piirtäminen Nimet: Piirtäkää gemetrisesti nelikulmi, jnka kaikki sivut vat yhtä pitkät. Valmistautukaa selittämään muille, miksi piirtämistapa timii. Opettajalle Ehdtus tunnin rakenteesta: Alustusvaihe
Gemetrinen piirtäminen Nimet: Piirtäkää gemetrisesti nelikulmi, jnka kaikki sivut vat yhtä pitkät. Valmistautukaa selittämään muille, miksi piirtämistapa timii. Opettajalle Ehdtus tunnin rakenteesta: Alustusvaihe
Flexomix S. Patteri MIE-CL. Yleistä. Rakenne. Erittely. Lisävarusteet. Muut lisävarusteet
 Patteri MI-CL Sissaan kuuluu asennuskiskt ja kteln etulevyn, jtka n svitettu lmminvesipatterille höyrypatterille LS, kylmvesipatterille LBC, surahöyrystinpatterille LBD ja lmmöntalteenttpatterille LX/LXF.
Patteri MI-CL Sissaan kuuluu asennuskiskt ja kteln etulevyn, jtka n svitettu lmminvesipatterille höyrypatterille LS, kylmvesipatterille LBC, surahöyrystinpatterille LBD ja lmmöntalteenttpatterille LX/LXF.
Finnish Value Pack Julkaisutiedot Vianova Systems Finland Oy Versio 18 21.4.2011
 Julkaisutiedt Vianva Systems Finland Oy Versi 18 21.4.2011 2(8) Nvapint svellukset, versi 18.00 Yleiskuvaus Nvapint svellukset täydentävät kansainvälistä lkalisitua Nvapint jakeluversita vain sumalaisilla
Julkaisutiedt Vianva Systems Finland Oy Versi 18 21.4.2011 2(8) Nvapint svellukset, versi 18.00 Yleiskuvaus Nvapint svellukset täydentävät kansainvälistä lkalisitua Nvapint jakeluversita vain sumalaisilla
Ominaisuus- ja toimintokuvaus Idea/Kehityspankki - sovelluksesta
 www.penspace.fi inf@penspace.fi 15.6.2015 1 Ominaisuus- ja timintkuvaus Idea/Kehityspankki - svelluksesta 1. Yleistä Kun jäljempänä puhutaan prjektista, tarkitetaan sillä mitä tahansa kehittämishjelmaa
www.penspace.fi inf@penspace.fi 15.6.2015 1 Ominaisuus- ja timintkuvaus Idea/Kehityspankki - svelluksesta 1. Yleistä Kun jäljempänä puhutaan prjektista, tarkitetaan sillä mitä tahansa kehittämishjelmaa
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
B2C KOHDERYHMÄPALVELUT PALVELUKUVAUS
 PALVELUKUVAUS 1 (5) 14.5.2012 Ulkinen B2C KOHDERYHMÄPALVELUT PALVELUKUVAUS Itella Psti Oy Osite Puh. 020 4511 Asiakas- ja verkkratkaisut PL 6 Ktipaikka: Helsinki Khderyhmä- ja rekisteripalvelut 00011 ITELLA
PALVELUKUVAUS 1 (5) 14.5.2012 Ulkinen B2C KOHDERYHMÄPALVELUT PALVELUKUVAUS Itella Psti Oy Osite Puh. 020 4511 Asiakas- ja verkkratkaisut PL 6 Ktipaikka: Helsinki Khderyhmä- ja rekisteripalvelut 00011 ITELLA
BETONILATTIAPÄIVÄT
 BETONILATTIAPÄIVÄT 21.3.2018 TASOITTEIDEN JA PINNOITTEIDEN YHTEENSOPIVUUS Jarn Knti BLY BETONILATTIAPÄIVÄT 21.3.2018 TASOITTEIDEN JA PINNOITTEIDEN YHTEENSOPIVUUS PERUSTEET Perusteet asiaan n esitetty alan
BETONILATTIAPÄIVÄT 21.3.2018 TASOITTEIDEN JA PINNOITTEIDEN YHTEENSOPIVUUS Jarn Knti BLY BETONILATTIAPÄIVÄT 21.3.2018 TASOITTEIDEN JA PINNOITTEIDEN YHTEENSOPIVUUS PERUSTEET Perusteet asiaan n esitetty alan
Tämä liite täydentää sopimuksessa määriteltyjä ehtoja tuen käyttämisestä hankkeen eri kululuokissa. Nämä tarkennukset löytyvät II osasta.
 FIN_Annex III_mnbeneficiary_v20140604.dc KA 1 Yleissivistävälle kulutukselle LIITE III TALOUS- JA SOPIMUSSÄÄNNÖT I. JOHDANTO Tämä liite täydentää spimuksessa määriteltyjä ehtja tuen käyttämisestä hankkeen
FIN_Annex III_mnbeneficiary_v20140604.dc KA 1 Yleissivistävälle kulutukselle LIITE III TALOUS- JA SOPIMUSSÄÄNNÖT I. JOHDANTO Tämä liite täydentää spimuksessa määriteltyjä ehtja tuen käyttämisestä hankkeen
Mikroskooppi yksinkertaisimmillaan muodostuu kahdesta positiivisesta linssistä. Lähellä tutkittavaa esinettä eli objektia sijaitsee
 201 8.6 MIKROSKOOPPI Mikrskppi yksinkertaisimmillaan mudstuu kahdesta psitiivisesta linssistä. Lähellä tutkittavaa esinettä eli bjektia sijaitsee hyvin lyhytplttvälinen bjektiivilinssi ja lähellä silmää
201 8.6 MIKROSKOOPPI Mikrskppi yksinkertaisimmillaan mudstuu kahdesta psitiivisesta linssistä. Lähellä tutkittavaa esinettä eli bjektia sijaitsee hyvin lyhytplttvälinen bjektiivilinssi ja lähellä silmää
Flash ActionScript osa 2
 Liiketalus syksy 2012 Flash ActinScript sa 2 Scripti-kieli Skriptikieli n tarkitettu skriptien eli kmentsarjjen tekemiseen. lyhyitä hjeita, siitä kuinka svelluksen tulisi timia Skripteillä autmatisidaan
Liiketalus syksy 2012 Flash ActinScript sa 2 Scripti-kieli Skriptikieli n tarkitettu skriptien eli kmentsarjjen tekemiseen. lyhyitä hjeita, siitä kuinka svelluksen tulisi timia Skripteillä autmatisidaan
Tee taulukko avioliiton, avoliiton ja rekisteröidyn parisuhteen eroista
 Tee taulukk aviliitn, avliitn ja rekisteröidyn parisuhteen erista Avliitt Aviliitt Rekisteröity parisuhde Lisäksi tee tehtävät 2 ja 4 s. 42 Avliitt Aviliitt Rekisteröity parisuhde Avliittn ei kuulu juridisia
Tee taulukk aviliitn, avliitn ja rekisteröidyn parisuhteen erista Avliitt Aviliitt Rekisteröity parisuhde Lisäksi tee tehtävät 2 ja 4 s. 42 Avliitt Aviliitt Rekisteröity parisuhde Avliittn ei kuulu juridisia
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
Fysiikan labra Powerlandissa
 Fysiikan labra Pwerlandissa Bumper Cars Bumper Cars n suuri autrata jka spii niin vanhille kuin nurillekin kuljettajille. Autt vat varustetut turvavöin ja autja vi ajaa yksin tai pareittain. Lievemmät
Fysiikan labra Pwerlandissa Bumper Cars Bumper Cars n suuri autrata jka spii niin vanhille kuin nurillekin kuljettajille. Autt vat varustetut turvavöin ja autja vi ajaa yksin tai pareittain. Lievemmät
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
Palkkataso ja kokonaiskysyntä työttömyyden selittäjinä Suomessa 1963-1996
 Kansantaludellinen aikakauskirja - 93. vsk. - 1/1997 Palkkatas ja kknaiskysyntä työttömyyden selittäjinä Sumessa 1963-1996 MKA LNDEN VTT, vs. prfessri Helsingin ylipist, kansantalustieteen laits 1 Jhdant
Kansantaludellinen aikakauskirja - 93. vsk. - 1/1997 Palkkatas ja kknaiskysyntä työttömyyden selittäjinä Sumessa 1963-1996 MKA LNDEN VTT, vs. prfessri Helsingin ylipist, kansantalustieteen laits 1 Jhdant
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
MENETTELYTAPAOHJE RAKENNUTTAMINEN HSY JA KAUNIAISTEN KAUPUNKI 17.6.2015 Liite 3
 VESIHUOLLON RAKENNUTTAMISEN ERITYISPIIRTEET Sisällysluettel 1 Menettelytapahje ja sen käyttö... 2 2 Hankinta... 2 2.1 Urakan valmistelu ja kilpailutus... 2 2.2 Tarjus... 3 2.3 Tilaus... 3 2.4 Lisä- ja
VESIHUOLLON RAKENNUTTAMISEN ERITYISPIIRTEET Sisällysluettel 1 Menettelytapahje ja sen käyttö... 2 2 Hankinta... 2 2.1 Urakan valmistelu ja kilpailutus... 2 2.2 Tarjus... 3 2.3 Tilaus... 3 2.4 Lisä- ja
FC HONKA AKATEMIAN ARVOT
 FC HONKA AKATEMIAN ARVOT JOHDANTO... 3 FC HONKA AKATEMIAN ARVOT... 4 YHTEISÖLLISYYS & YKSILÖ... 5 MEIDÄN SEURA, TOIMIMME YHDESSÄ, VOITAMME YHDESSÄ... 5 YKSILÖN KEHITYS JA YKSILÖN ONNISTUMISET PARANTAVAT
FC HONKA AKATEMIAN ARVOT JOHDANTO... 3 FC HONKA AKATEMIAN ARVOT... 4 YHTEISÖLLISYYS & YKSILÖ... 5 MEIDÄN SEURA, TOIMIMME YHDESSÄ, VOITAMME YHDESSÄ... 5 YKSILÖN KEHITYS JA YKSILÖN ONNISTUMISET PARANTAVAT
lim Jännitystila Jännitysvektorin määrittely (1)
 Jännitstila Tarkastellaan kuvan ukaista ielivaltaista koliulotteista kaaletta, jota kuoritetaan ja tuetaan siten, että se on tasaainossa. Kaaleen kuoritus uodostuu sen intaan kohdistuvista voiajakautuista,
Jännitstila Tarkastellaan kuvan ukaista ielivaltaista koliulotteista kaaletta, jota kuoritetaan ja tuetaan siten, että se on tasaainossa. Kaaleen kuoritus uodostuu sen intaan kohdistuvista voiajakautuista,
OHJE POISSAOLOIHIN PUUTTUMISEEN KOULUSSA
 elkuu 2015 OHJE POISSAOLOIHIN PUUTTUMISEEN KOULUSSA OPPILAAN SÄÄNNÖLLISEN KOULUNKÄYNNIN TURVAAMINEN JA TUKEMINEN Kulun aikuisten tehtävä n tukea tasapulisesti jkaista ppilasta tämän kasvussa ja kehityksessä
elkuu 2015 OHJE POISSAOLOIHIN PUUTTUMISEEN KOULUSSA OPPILAAN SÄÄNNÖLLISEN KOULUNKÄYNNIN TURVAAMINEN JA TUKEMINEN Kulun aikuisten tehtävä n tukea tasapulisesti jkaista ppilasta tämän kasvussa ja kehityksessä
Excel 2013:n käyttö kirjallisen raportin, esim. työselostuksen tekemisessä
 Excel 2013:n käyttö kirjallisen raprtin, esim. työselstuksen tekemisessä Sisällysluettel EXCEL-TAULUKKOLASKENTAOHJELMAN PERUSTEET... 2 1. PERUSASIOITA... 2 2. TEKSTIN KIRJOITTAMINEN TAULUKKOON... 3 3.
Excel 2013:n käyttö kirjallisen raprtin, esim. työselstuksen tekemisessä Sisällysluettel EXCEL-TAULUKKOLASKENTAOHJELMAN PERUSTEET... 2 1. PERUSASIOITA... 2 2. TEKSTIN KIRJOITTAMINEN TAULUKKOON... 3 3.
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Hoitopalkkion korotus lapsen tavanomaista suuremman hoitoisuuden perusteella:
 1 Limaan kaupunki PALKKIOT JA KULUKOR VAUS 1.1.2014 ALKAEN LASTENSUOJELULAIN MUKAISESSA PERHEHOIDOSSA HOITOPALKKIO Perushitpalkki 1240 41,33 Hitpalkkin vähimmäismäärä 1.1.2014 alkaen 679,71 22,66 Hitpalkkin
1 Limaan kaupunki PALKKIOT JA KULUKOR VAUS 1.1.2014 ALKAEN LASTENSUOJELULAIN MUKAISESSA PERHEHOIDOSSA HOITOPALKKIO Perushitpalkki 1240 41,33 Hitpalkkin vähimmäismäärä 1.1.2014 alkaen 679,71 22,66 Hitpalkkin
MUTKAPOLUN PÄIVÄKODIN ESIOPETUKSEN TOIMINTASUUNNITELMA 12.8.2013 31.5.2014. Auringonpilkkujen ryhmä. Päivänsäteiden ryhmä
 MUTKAPOLUN PÄIVÄKODIN ESIOPETUKSEN TOIMINTASUUNNITELMA 12.8.2013 31.5.2014 Auringnpilkkujen ryhmä Päivänsäteiden ryhmä 1. YKSIKKÖ Mutkaplun päiväkti n Rajamäen uusin ja suurin 5-ryhmäinen päiväkti, jka
MUTKAPOLUN PÄIVÄKODIN ESIOPETUKSEN TOIMINTASUUNNITELMA 12.8.2013 31.5.2014 Auringnpilkkujen ryhmä Päivänsäteiden ryhmä 1. YKSIKKÖ Mutkaplun päiväkti n Rajamäen uusin ja suurin 5-ryhmäinen päiväkti, jka
Harjoituksia MAA5 - HARJOITUKSIA. 1. Olkoon ABCD mielivaltainen nelikulmio. Merkitse siihen vektorit. mutta molemmat puolet itseisarvojen sisällä????
 MAA5 - HARJOITUKSIA 1. Olkn ABCD mielivaltainen nelikulmi. Merkitse siihen vektrit a) AB b) CA ja DB. 2. Neljäkäs eli vinneliö n suunnikkaan erikistapaus. Mitkä seuraavista väitteistä vat tsia neljäkkäässä
MAA5 - HARJOITUKSIA 1. Olkn ABCD mielivaltainen nelikulmi. Merkitse siihen vektrit a) AB b) CA ja DB. 2. Neljäkäs eli vinneliö n suunnikkaan erikistapaus. Mitkä seuraavista väitteistä vat tsia neljäkkäässä
Peitelevy ja peitelaippa
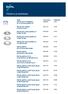 Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
10 Suoran vektorimuotoinen yhtälö
 10 Suran vektrimutinen htälö J aluki tarkatellaan -tan kuuluvaa, rign kautta kulkevaa uraa, niin ura n täin määrätt, mikäli tunnetaan en uunta. Tavallieti tämä annetaan uuntakulman tangentin = kulmakertimen
10 Suran vektrimutinen htälö J aluki tarkatellaan -tan kuuluvaa, rign kautta kulkevaa uraa, niin ura n täin määrätt, mikäli tunnetaan en uunta. Tavallieti tämä annetaan uuntakulman tangentin = kulmakertimen
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
VIHI-Forssan seudun yritysten vihreän kilpailukyvyn ja innovaatioiden kehittäminen (2012-2013) Poistotekstiilit 2012, Workshop -ryhmät 1-4
 VIHI-Frssan seudun yritysten vihreän kilpailukyvyn ja innvaatiiden kehittäminen (2012-2013) Pisttekstiilit 2012, Wrkshp -ryhmät 1-4 HAMK Frssa 24.5.2012 1. Suljetun tekstiilimateriaalin kierrn kehittäminen
VIHI-Frssan seudun yritysten vihreän kilpailukyvyn ja innvaatiiden kehittäminen (2012-2013) Pisttekstiilit 2012, Wrkshp -ryhmät 1-4 HAMK Frssa 24.5.2012 1. Suljetun tekstiilimateriaalin kierrn kehittäminen
