Kellogg-diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 1
|
|
|
- Riitta-Liisa Kahma
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy 6 Teema - Luento Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
2 Tasaainoiirrokset Tasaaino- eli stabiilisuusiirrokset Kuvaavat graafisesti eri faasien keskinäisiä stabiilisuuksia olosuhteiden funktiona Miten yhdisteiden stabiilisuutta voidaan tarkastella? Kuvaajien taustalla: G, H, S, C = f(t,,x i ) Noea menetelmä tasaainotilaisten systeemien tarkasteluun Reaktioiden sontaanisuus? Faasit ja niiden koostumukset tietyissä olosuhteissa? Tasaainoiirrokset = Tasaainotarkastelujen graafinen esitystaa Tasaainon määritys käyttäen valittuja suureita muuttujina (lukuisia laskentaisteitä) Tuloksena saadaan stabiilit faasit ja niiden koostumukset eri laskentaisteissä Tulokset esitetään valitsemalla akselisuureet... Vaihtoehtoina laskennan lähtöarvoina käytetyt suureet sekä laskennan tuloksena saadut arvot Ekstensiivisuureet: S, V, n i, n j,... Vastaavat otentiaalit: T, P, i, j,... Valittujen suureiden oltava toisistaan riiumattomia... ja esittämällä eri faasien stabiilisuusalueet valittujen akselisuureiden funktiona
3 Tasaainoiirrokset Koostumus-lämötila-iirrokset Tasaaino- tai faasiiirrokset Potentiaali-otentiaali-iirrokset Vallitsevuusaluekaaviot (Kellogg) Vaaaenergiaiirrokset (Ellingham) E-H-iirrokset (Pourbaix) Tasaainoiirrokset Käytännössä kyse on Gibbsin vaaaenergia -kuvaajien rojektioista Kuvat: K. Hack - FactSage -koulutusmateriaali. 3
4 Vallitsevuusaluekaaviot (Kellogg-diagrammit) Kuvaavat yhdisteiden välisiä stabiilisuuksia kolmen komonentin systeemeissä, joissa yksi komonenteista (yleensä jokin metalli) muodostaa yhdisteitä kahden muun komonentin (yleensä eämetalleja) kanssa Akseleina Kahden (jälkimmäisen) komonentin tai niiden muodostamien yhdisteiden aktiivisuudet tai osaaineet (lämötila on vakio) Toinen em. aktiivisuuksista sekä lämötila (toinen aktiivisuuksista on vakio) Vallitsevuusaluekaaviot (Kellogg-diagrammit) log SO (g) 4 3 Rikittävämmät olosuhteet Kaliumin haetusaste kasvaa ja erilaisia sulfideja muodostuu K-O -S Phase Stability Diagram at 5. K S4 O6 Haettavat ja rikittävät olosuhteet Sulfaattien muodostuminen (sis. O ja S) K S O8 K S5 - K SO K S K K O K O KO KO3 Haettavammat olosuhteet Kaliumin haetusaste kasvaa ja erilaisia oksideja muodostuu -6-3 File: C:\HSC4 \KOS5.i log O (g) 4
5 Esimerkkejä Kelloggdiagrammeista log CO(g) 7. Ni-C -O Phase Stability Diagram at. C Ni3C Ni + O + CO NiCO3 (O ja CO molemmat mukana reaktiossa) Akselikomonentit ovat samalla uolella reaktioyhtälöä Laskeva suora NiCO Ni NiO + CO NiCO3 (O ei mukana reaktiossa) 5.8 Ni + O NiO (CO ei mukana reaktiossa) NiO File: D:\HSC4\NiCO.is log O(g) Esimerkkejä Kelloggdiagrammeista log CO(g) Ni3C File: D:\HSC4\NiCO.is Ni-C -O Phase Stability Diagram at. C Ni NiCO NiO + O + CO NiCO3 (CO ei voi olla mukana reaktiossa!) NiO log O(g) 5
6 Esimerkkejä Kelloggdiagrammeista log CO(g) 7. Ni-C -O Phase Stability Diagram at. C Ni + CO NiCO3 + CO (O ei voi olla mukana reaktiossa!) Nyt akselikomonentit ovat eri uolilla reaktioyhtälöä Nouseva suora Ni NiCO3 Ni3C 5.8 NiO File: D:\HSC4\NiCO.is log CO(g) Esimerkkejä Kelloggdiagrammeista log SO(g) Ni-O -S Phase Stability Diagram at. C NiS NiSO4 Ni3S4 - Ni Ni3S File: D:\HSC4\NiOS.is -9-8 NiO Ni + O NiO O on ainoa akselikomonentti, joka on mukana reaktiossa Ei ole väliä, onko toinen akselikomonentti CO vai SO Sama suora kuvaa tätä reaktiota -7-6 log O(g) 6
7 log (P(CO)) (atm) log (P(CO)) (atm) D:\FactSage\Fe-O-C-73.wmf 7.. D:\FactSage\Fe-O-C-73-x.wmf 7.. Esimerkkejä Kellogg-diagrammeista Fe-O-C, 73 K '+' =. atm P(total) isobar - - Fe 5C (s ) CFe 3(s) Fe(s 3) Kellogg-diagrammeihin on mahdollista lisätä isobaarikäyriä. Isobaarit näyttävät alueen, jossa kaasumaisten komonenttien osaaineiden summa vastaa tiettyä annettua kokonaisaineen arvoa (yleensä atm) -3 FeO(s) Fe 3O 4(s) Tämän systeemin kaasukomonentit: CO + CO (+ rautaa sisältävät kaasukomonentit) log (P(CO )) (atm) Esimerkkejä Kellogg-diagrammeista Fe-O-C, 73 K '+' =. atm P(total) isobar Fe 5C (s ) atm Samaan kuvaajaan voidaan luonnollisesti sisällyttää useita isobaareja. - CFe 3(s) Fe(s 3). atm Tässä kuvaajassa isobaarit on iirretty vastaamaan kokonaisaineita, atm ja atm FeO(s) Fe 3O 4(s) log (P(CO )) (atm) 7
8 log (P(CO)) (atm) log (P(CO)) (atm) D:\FactSage\Zn-O-C-73.wmf 7.. D:\FactSage\Zn-O-C73-x.wmf 7.. Esimerkkejä Kellogg-diagrammeista Zn-O-C, 73 K '+' =. atm P(total) isobar - Zn(l) Tarkastellaan rosessia, jossa raudan ja sinkin oksideja sisältävää ölyä käsitellään uunissa, jonka atmosfääri koostuu hiilimonoksidista ja hiilidioksidista Kuvaajasta nähdään, että ZnO saadaan elkistettyä tietyillä kaasukoostumuksilla, mutta näin syntyvä sinkki on sulaa 73 K:n lämötilassa. log (P(CO )) (atm) OZn(s) Halutaan tietää, missä olosuhteissa sinkki saadaan oistettua ölyistä kaasufaasiin (ja erotettua siitä edelleen omaksi faasikseen). Laaditaan Kelloggdiagrammi, jossa sinkin yhdisteiden stabiilisuusalueet on esitetty tarkastelulämötilassa. Esimerkkejä Kellogg-diagrammeista Zn-O-C, 473 K '+' =. atm P(total) isobar Toinen kuvaaja samalle systeemille korkeammassa lämötilassa (473 K) kertoo, että elkistyvä sinkki on nyt kaasumaista. - Zn(g) Ts. ZnO voidaan elkistää kaasufaasiin OZn(s) btw: Isobaarit on määritetty kahdelle eri kokonaisaineelle (, atm ja atm) Kuvaaja ei kuitenkaan kerro mitään siitä, missä muodossa rauta esiintyy näissä olosuhteissa log (P(CO )) (atm) 8
9 log (P(CO)) (atm) log (P(CO)) (atm) D:\FactSage\Fe-O-C73.wmf 7.. D:\FactSage\Fe-Zn-O-C73.wmf 7.. Esimerkkejä Kellogg-diagrammeista Fe-O-C, 473 K '+' = atm P(total) isobar - Fe 5C (s ) CFe 3(s) Fe(s ) Raudan ja sen yhdisteiden stabiilisuusalueiden määrittämiseksi voidaan iirtää toinen Kelloggdiagrammi (Fe-O-Csysteemille samassa lämötilassa) FeO(s) Fe 3O 4(s) Kaasumaisen sinkin stabiilisuusalue (edellisestä kuvaajasta) kertoo, että näissä olosuhteissa rauta esiintyy joko kiinteänä metallina tai karbidina log (P(CO )) (atm) Esimerkkejä Kellogg-diagrammeista Fe-Zn-O-C, 473 K < Zn/(Fe+Zn) < Fe 5C (s )+Zn(g) CFe 3(s)+Zn(g) Alue, jossa Zn on kaasumainen Fe(s )+Zn(g) Fe(s FeO(s)+OZn(s) )+OZn(s) Systeemistä löytyy yhdiste, joka sisältää sekä rautaa että sinkkiä (sinkkiferriitti). Fe 3O 4(s)+OZn(s) Edelliset tarkastelut eivät kuitenkaan kerro, onko olemassa yhdisteitä, jotka sisältävät sekä rautaa että sinkkiä. (Tarkastelut tehtiin erikseen Fe-O-C- ja Zn-O- C-systeemeille.) On kuitenkin mahdollista iirtää Kellogg-diagrammi, jossa on huomioitu useamman kuin yhden metallin muodostamat yhdisteet. (Tällaiset kuvaajat ovat aika monimutkaisia, kun komonenttien lukumäärää kasvatetaan.) Fe 3O 4(s)+Fe O 4Zn(s) log (P(CO )) (atm) 9
10 log (P(CO)) (atm) D:\FactSage\Fe-Zn-O-C-Cl73.wmf 7.. Esimerkkejä Kellogg-diagrammeista Fe-Zn-O-C-Cl, 473 K < Zn/(Fe+Zn) <.333, log P(Cl ) = -6 (atm) Fe 5C (s )+Cl Zn(g) Alue, jossa sinkki on kaasumainen Cl Fe(g)+Cl Zn(g) Alue, jossa myös rauta esiintyy kaasumaisena. Fe 3O 4(s)+Cl Zn(g) Fe 3O 4(s)+OZn(s) Fe 3O 4(s)+Fe O 4Zn(s) Entä jos uunissa on myös klooria? Laadittava kuvaaja Fe-Zn-O-C-Cl-systeemille Koska molemmat akselit on jo varattu (CO ja CO ), on kloorin määrä (ts. osaaine) oletettava kuvaajassa vakioksi. Tässä kuvaajassa on käytetty arvoa -6 atm. Raudan kaasuuntumisen estämiseksi vaaditaan erilaiset olosuhteet, mikäli systeemi sisältää klooria log (P(CO )) (atm)
11
12 Esimerkki Kellogg-diagrammin laadinnasta Esimerkki Kellogg-diagrammin laadinnasta Systeemin komonentit: Mo, MoO, MoO 3 ja MoS Ensimmäinen reaktio: Mo + O = MoO a MoO K a Mo O O Gr,9 ln K,986 T lg O 4,7 G 735 r,9 lg K mol 4,575T 4,575 9K mol K SO ei ole mukana reaktioyhtälössä SO ei esiinny suoran yhtälössä 4,7 lg O
13 Esimerkki Kellogg-diagrammin laadinnasta Toinen reaktio: MoO + ½ O = MoO 3 a MoO 3 K / / a MoO O O Gr,9 lg K 4,575T 3 mol 4,575 9K mol K 5,35 lg / O lg O,7 SO ei ole mukana reaktioyhtälössä SO ei esiinny suoran yhtälössä Esimerkki Kellogg-diagrammin laadinnasta Kolmas reaktio: Mo + SO = MoS + O a K a MoS Mo O SO O SO Gr,9 lg K 4,575T mol 4,575 9K mol K,83 lg O SO lg O lg SO lg SO lg O,4 3
14 Esimerkki Kellogg-diagrammin laadinnasta Neljäs reaktio: MoS + 3 O = MoO + SO K a MoO a SO 3 MoS O SO 3 O Gr,9 lg K 4,575T 8749 mol 4,575 9K mol K 45,5 lg SO 3 O lg SO lg 3 O lg SO 3 lg O,8 Esimerkki Kellogg-diagrammin laadinnasta Viides (viimeinen) reaktio: MoS + 3½ O = MoO 3 + SO K a MoO a 3 SO SO 7/ 7/ MoS O O Gr,9 lg K 4,575T 954 mol 4,575 9K mol K 5,88 lg SO 7 / O lg SO lg 7 / O lg SO,75 lg O 5,4 4
15 Esimerkki Kellogg-diagrammin laadinnasta Kellogg-diagrammi laaditaan iirtämällä edellä määritetyt viisi (lineaarista) yhtälöä samaan kuvaajaan. log SO(g) 5 Mo-O -S Phase Stability Diagram at 67. C Ilma-atmosfääri: O =. lg( O ) = MoS Molybdeenin stabiilein muoto on joko MoO 3 tai MoS. MoS on kuitenkin stabiili vasta äärimmäisen korkeilla SO :n osaaineilla (yli atm) MoO 3 on stabiili muoto ilmaatmosfäärissä - -5 Mo File: C:\HSC\MOOS67.IPS MoO -5 - MoO3 log O(g) 5
Kellogg-diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2012 Teema 1 - Luento 1
 Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy Teema - Luento Eetu-Pekka Heikkinen, Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Eetu-Pekka
Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy Teema - Luento Eetu-Pekka Heikkinen, Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Eetu-Pekka
Korkealämpötilakemia
 ..7 Korkealämötilakemia Teema Luento Kellogg-diagrammit To..7 klo 8- SÄ4 Tavoite Oia tulkitsemaan ja laatimaan ns. Kelloggdiagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
..7 Korkealämötilakemia Teema Luento Kellogg-diagrammit To..7 klo 8- SÄ4 Tavoite Oia tulkitsemaan ja laatimaan ns. Kelloggdiagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Ellinghamin diagrammit
 Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta
 Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 4 Tavoite Oppia tulkitsemaan 2-komponenttisysteemien faasipiirroksia 1 Binääriset
Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 4 Tavoite Oppia tulkitsemaan 2-komponenttisysteemien faasipiirroksia 1 Binääriset
Korkealämpötilakemia
 Korkealämpötilakemia Ellingham-diagrammit To 9.11.2017 klo 8-10 SÄ114 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Sisältö Mikä on Ellinghamin diagrammi?
Korkealämpötilakemia Ellingham-diagrammit To 9.11.2017 klo 8-10 SÄ114 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Sisältö Mikä on Ellinghamin diagrammi?
Ratkaisu. Tarkastellaan aluksi Fe 3+ - ja Fe 2+ -ionien välistä tasapainoa: Nernstin yhtälö tälle reaktiolle on:
 Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Esimerkki Pourbaix-piirroksen laatimisesta Laadi Pourbaix-piirros, jossa on esitetty metallisen ja ionisen raudan sekä raudan oksidien stabiilisuusalueet vesiliuoksessa 5 C:een lämpötilassa. Ratkaisu Tarkastellaan
Korkealämpötilakemia
 Korkealämpötilakemia Binääriset tasapainopiirrokset To 30.10.2017 klo 8-10 SÄ114 Tavoite Oppia lukemaan ja tulkitsemaan binäärisiä tasapainopiirroksia 1 Sisältö Hieman kertausta - Gibbsin vapaaenergian
Korkealämpötilakemia Binääriset tasapainopiirrokset To 30.10.2017 klo 8-10 SÄ114 Tavoite Oppia lukemaan ja tulkitsemaan binäärisiä tasapainopiirroksia 1 Sisältö Hieman kertausta - Gibbsin vapaaenergian
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Standarditilat. Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 2 - Luento 2. Tutustua standarditiloihin
 Standarditilat Ilmiömallinnus prosessimetallurgiassa Syksy 216 Teema 2 - Luento 2 Tavoite Tutustua standarditiloihin Miksi käytössä? Millaisia käytössä? Miten huomioitava tasapainotarkasteluissa? 1 Miten
Standarditilat Ilmiömallinnus prosessimetallurgiassa Syksy 216 Teema 2 - Luento 2 Tavoite Tutustua standarditiloihin Miksi käytössä? Millaisia käytössä? Miten huomioitava tasapainotarkasteluissa? 1 Miten
MT Erikoismateriaalit tuotantoprosesseissa (3 op)
 MT-0.6101 Erikoismateriaalit tuotantoprosesseissa (3 op) 6. Luento - Ke 11.11.2015 Reaktiotermodynamiikan käyttö tulenkestävien valinnassa Marko Kekkonen MT-0.6101 Erikoismateriaalit tuotantoprosesseissa
MT-0.6101 Erikoismateriaalit tuotantoprosesseissa (3 op) 6. Luento - Ke 11.11.2015 Reaktiotermodynamiikan käyttö tulenkestävien valinnassa Marko Kekkonen MT-0.6101 Erikoismateriaalit tuotantoprosesseissa
Sähkökemialliset tarkastelut HSC:llä
 Sähkökemialliset tarkastelut HSC:llä Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 5 Tavoite Oppia hyödyntämään HSC-ohjelmistoa sähkökemiallisissa tarkasteluissa 1 Sisältö Sähkökemiallisiin
Sähkökemialliset tarkastelut HSC:llä Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 5 Tavoite Oppia hyödyntämään HSC-ohjelmistoa sähkökemiallisissa tarkasteluissa 1 Sisältö Sähkökemiallisiin
Luento 9 Kemiallinen tasapaino CHEM-A1250
 Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Korkealämpötilakemia
 1.11.217 Korkealämpötilakemia Standarditilat Ti 1.11.217 klo 8-1 SÄ11 Tavoite Tutustua standarditiloihin liuosten termodynaamisessa mallinnuksessa Miksi? Millaisia? Miten huomioidaan tasapainotarkasteluissa?
1.11.217 Korkealämpötilakemia Standarditilat Ti 1.11.217 klo 8-1 SÄ11 Tavoite Tutustua standarditiloihin liuosten termodynaamisessa mallinnuksessa Miksi? Millaisia? Miten huomioidaan tasapainotarkasteluissa?
Korkealämpötilakemia
 Korkealämpötilakemia Gibbsin faasisääntö, kuvaajien laadinta sekä1-komponenttipiirrokset To 23.11.2017 klo 8-10 SÄ114 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen laadintaan ja siten
Korkealämpötilakemia Gibbsin faasisääntö, kuvaajien laadinta sekä1-komponenttipiirrokset To 23.11.2017 klo 8-10 SÄ114 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen laadintaan ja siten
Sähkökemian perusteita, osa 1
 Sähkökemian perusteita, osa 1 Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 4 - Luento 1 Teema 4: Suoritustapana oppimispäiväkirja Tehdään yksin tai pareittain Tehtävät/ohjeet löytyvät kurssin
Sähkökemian perusteita, osa 1 Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 4 - Luento 1 Teema 4: Suoritustapana oppimispäiväkirja Tehdään yksin tai pareittain Tehtävät/ohjeet löytyvät kurssin
Tärkeitä tasapainopisteitä
 Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Chem-C2400 Luento 3: Faasidiagrammit Ville Jokinen
 Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
17VV VV Veden lämpötila 14,2 12,7 14,2 13,9 C Esikäsittely, suodatus (0,45 µm) ok ok ok ok L. ph 7,1 6,9 7,1 7,1 RA2000¹ L
 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, elokuu Näytteenottopvm: 22.8.2017 Näyte saapui: 23.8.2017 Näytteenottaja: Eerikki Tervo Analysointi
1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, elokuu Näytteenottopvm: 22.8.2017 Näyte saapui: 23.8.2017 Näytteenottaja: Eerikki Tervo Analysointi
17VV VV 01021
 Pvm: 4.5.2017 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, huhtikuu Näytteenottopvm: 4.4.2017 Näyte saapui: 6.4.2017 Näytteenottaja: Mika
Pvm: 4.5.2017 1/5 Boliden Kevitsa Mining Oy Kevitsantie 730 99670 PETKULA Tutkimuksen nimi: Kevitsan vesistötarkkailu 2017, huhtikuu Näytteenottopvm: 4.4.2017 Näyte saapui: 6.4.2017 Näytteenottaja: Mika
Yhtälöryhmät 1/6 Sisältö ESITIEDOT: yhtälöt
 Yhtälöryhmät 1/6 Sisältö Yhtälöryhmä Yhtälöryhmässä on useita yhtälöitä ja yleensä myös useita tuntemattomia. Tavoitteena on löytää tuntemattomille sellaiset arvot, että kaikki yhtälöt toteutuvat samanaikaisesti.
Yhtälöryhmät 1/6 Sisältö Yhtälöryhmä Yhtälöryhmässä on useita yhtälöitä ja yleensä myös useita tuntemattomia. Tavoitteena on löytää tuntemattomille sellaiset arvot, että kaikki yhtälöt toteutuvat samanaikaisesti.
Korkealämpötilakemia
 Korkealämpötilakemia Gibbsin faasisääntö, kuvaajien laadinta sekä 1-komponenttipiirrokset Ti 13.11.2018 klo 8-10 AT115A Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen laadintaan ja siten
Korkealämpötilakemia Gibbsin faasisääntö, kuvaajien laadinta sekä 1-komponenttipiirrokset Ti 13.11.2018 klo 8-10 AT115A Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen laadintaan ja siten
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin
 Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 27.10.2016 klo 14-16 Luennon tavoite Tutustua eri tapoihin määrittää termodyn. tasapaino laskennallisesti Tutustua termodynaamisten
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 27.10.2016 klo 14-16 Luennon tavoite Tutustua eri tapoihin määrittää termodyn. tasapaino laskennallisesti Tutustua termodynaamisten
Ni-OHJELMA. OLIVIININ KOOSTUMUKSEN LASKEMISESTA.
 , """' OUTOKUMPU OY Pk ~e 1,., s,',s;j.jn~n /a4-flo A. rn' 1 Ni-OHJELMA. OLIVIININ KOOSTUMUKSEN LASKEMISESTA. Seuraavassa on tarkasteltu oliviinin koostumuksen
, """' OUTOKUMPU OY Pk ~e 1,., s,',s;j.jn~n /a4-flo A. rn' 1 Ni-OHJELMA. OLIVIININ KOOSTUMUKSEN LASKEMISESTA. Seuraavassa on tarkasteltu oliviinin koostumuksen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
luku2 Kappale 2 Hapettumis pelkistymisreaktioiden ennustaminen ja tasapainottaminen
 Kappale 2 Hapettumis pelkistymisreaktioiden ennustaminen ja tasapainottaminen 1 Ennakkokysymyksiä 2 Metallien reaktioita ja jännitesarja Fe(s) + CuSO 4 (aq) Cu(s) + AgNO 3 (aq) taulukkokirja s.155 3 Metallien
Kappale 2 Hapettumis pelkistymisreaktioiden ennustaminen ja tasapainottaminen 1 Ennakkokysymyksiä 2 Metallien reaktioita ja jännitesarja Fe(s) + CuSO 4 (aq) Cu(s) + AgNO 3 (aq) taulukkokirja s.155 3 Metallien
Luento 1 Rauta-hiili tasapainopiirros Austeniitin hajaantuminen perliittimekanismilla
 Luento 1 Rauta-hiili tasapainopiirros Austeniitin hajaantuminen perliittimekanismilla Vapaa energia ja tasapainopiirros Allotropia - Metalli omaksuu eri lämpötiloissa eri kidemuotoja. - Faasien vapaat
Luento 1 Rauta-hiili tasapainopiirros Austeniitin hajaantuminen perliittimekanismilla Vapaa energia ja tasapainopiirros Allotropia - Metalli omaksuu eri lämpötiloissa eri kidemuotoja. - Faasien vapaat
derivaatta pisteessä (YOS11) a) Näytä, että a n+1 > a n, kun n = 1, 2, 3,.
 Matematiikka, MAA9. a) Ratkaise yhtälö tan (YOS) Kulma on välillä [, 6]. Ratkaise asteen tarkkuudella seuraavat yhtälöt: b) sin c) cos (YOs). Kulmalle [9,6 ] on voimassa sin = 8 7. Määritä cos ja tan..
Matematiikka, MAA9. a) Ratkaise yhtälö tan (YOS) Kulma on välillä [, 6]. Ratkaise asteen tarkkuudella seuraavat yhtälöt: b) sin c) cos (YOs). Kulmalle [9,6 ] on voimassa sin = 8 7. Määritä cos ja tan..
Faasipiirrokset, osa 1: Laatiminen sekä 1-komponenttipiirrosten tulkinta
 Faasipiirrokset, osa 1: Laatiminen sekä 1-komponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 3 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen
Faasipiirrokset, osa 1: Laatiminen sekä 1-komponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 3 Tavoite Tutustua faasipiirrosten kokeelliseen ja laskennalliseen
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
Liitetaulukko 1/11. Tutkittujen materiaalien kokonaispitoisuudet KOTIMAINEN MB-JÄTE <1MM SAKSAN MB- JÄTE <1MM POHJAKUONA <10MM
 Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
Liitetaulukko 1/11 Tutkittujen materiaalien kokonaispitoisuudet NÄYTE KOTIMAINEN MB-JÄTE
OUTOKUMPU. ;.,,, r 4 x 4 i ALE 0 K MALMINETSINTK RAPORTTI NAYTE 10-JH/ /78. KOBALTIITIN JA ARSEENIKIISUN KOKOOMUS
 OUTOKUMPU $2 OY 0 K MALMINETSINTK RAPORTTI NAYTE 10-JH/2431 04/78. KOBALTIITIN JA ARSEENIKIISUN KOKOOMUS --:?--!.: p 3 Qk ;.,,, r 4 x 4 i ALE Näytteen 10-~~/2'431 04/78 (pintahie no C282) mikroskooppisessa
OUTOKUMPU $2 OY 0 K MALMINETSINTK RAPORTTI NAYTE 10-JH/2431 04/78. KOBALTIITIN JA ARSEENIKIISUN KOKOOMUS --:?--!.: p 3 Qk ;.,,, r 4 x 4 i ALE Näytteen 10-~~/2'431 04/78 (pintahie no C282) mikroskooppisessa
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin
 Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 7.9.2017 klo 8-10 Prosessimetallurgian tutkimusyksikkö Eetu-Pekka Heikkinen, 2017 Luennon tavoite Tutustua eri tapoihin määrittää
Johdanto laskennalliseen termodynamiikkaan ja mikroluokkaharjoituksiin Torstai 7.9.2017 klo 8-10 Prosessimetallurgian tutkimusyksikkö Eetu-Pekka Heikkinen, 2017 Luennon tavoite Tutustua eri tapoihin määrittää
2. Reaktioyhtälö 3) CH 3 CH 2 COCH 3 + O 2 CO 2 + H 2 O
 2. Reaktioyhtälö 11. a) 1) CH 3 CH 2 OH + O 2 CO 2 + H 2 O Tasapainotetaan CH 3 CH 2 OH + O 2 CO 2 + H 2 O C, kpl 1+1 1 kerroin 2 CO 2 :lle CH 3 CH 2 OH + O 2 2 CO 2 + H 2 O H, kpl 3+2+1 2 kerroin 3 H
2. Reaktioyhtälö 11. a) 1) CH 3 CH 2 OH + O 2 CO 2 + H 2 O Tasapainotetaan CH 3 CH 2 OH + O 2 CO 2 + H 2 O C, kpl 1+1 1 kerroin 2 CO 2 :lle CH 3 CH 2 OH + O 2 2 CO 2 + H 2 O H, kpl 3+2+1 2 kerroin 3 H
Korkealämpötilakemia
 Korkealämpötilakemia Metallurgiset liuosmallit Yleistä To 15.11.218 klo 8-1 PR126A Tavoite Tutustua ideaali- ja reaaliliuosten käsitteisiin Tutustua liuosmalleihin yleisesti - Jaottelu - Hyvän liuosmallin
Korkealämpötilakemia Metallurgiset liuosmallit Yleistä To 15.11.218 klo 8-1 PR126A Tavoite Tutustua ideaali- ja reaaliliuosten käsitteisiin Tutustua liuosmalleihin yleisesti - Jaottelu - Hyvän liuosmallin
Luento 2: Lämpökemiaa, osa 1 Torstai klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Reaktioyhtälö. Sähköisen oppimisen edelläkävijä www.e-oppi.fi. Empiirinen kaava, molekyylikaava, rakennekaava, viivakaava
 Reaktioyhtälö Sähköisen oppimisen edelläkävijä www.e-oppi.fi Empiirinen kaava, molekyylikaava, rakennekaava, viivakaava Empiirinen kaava (suhdekaava) ilmoittaa, missä suhteessa yhdiste sisältää eri alkuaineiden
Reaktioyhtälö Sähköisen oppimisen edelläkävijä www.e-oppi.fi Empiirinen kaava, molekyylikaava, rakennekaava, viivakaava Empiirinen kaava (suhdekaava) ilmoittaa, missä suhteessa yhdiste sisältää eri alkuaineiden
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Kemia 3 op. Kirjallisuus: MaoL:n taulukot: kemian sivut. Kurssin sisältö
 Kemia 3 op Kirjallisuus: MaoL:n taulukot: kemian sivut Kurssin sisältö 1. Peruskäsitteet ja atomin rakenne 2. Jaksollinen järjestelmä,oktettisääntö 3. Yhdisteiden nimeäminen 4. Sidostyypit 5. Kemiallinen
Kemia 3 op Kirjallisuus: MaoL:n taulukot: kemian sivut Kurssin sisältö 1. Peruskäsitteet ja atomin rakenne 2. Jaksollinen järjestelmä,oktettisääntö 3. Yhdisteiden nimeäminen 4. Sidostyypit 5. Kemiallinen
HSC-ohje laskuharjoituksen 1 tehtävälle 2
 HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
Faasipiirrokset, osa 3 Ternääristen ja monikomponenttipiirrosten tulkinta
 Faasipiirrokset, osa 3 Ternääristen ja monikomponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 5 Tavoite Oppia tulkitsemaan 3-komponenttisysteemien faasipiirroksia
Faasipiirrokset, osa 3 Ternääristen ja monikomponenttipiirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 5 Tavoite Oppia tulkitsemaan 3-komponenttisysteemien faasipiirroksia
* FINAS -akkreditoitu menetelmä. Mittausepävarmuus ilmoitetaan tarvittaessa. Akkreditointi ei koske lausuntoa.
 Pvm: 16.9.2015 Projekti: 1510019970/1 Näytteenottopvm: 8.9.2015 Näytteenottopiste: Alvettula, kaivo Näyte saapui: 8.9.2015 Näytteenottaja: Antti Rehula Analysointi aloitettu: 8.9.2015 Määritys 15TP02480
Pvm: 16.9.2015 Projekti: 1510019970/1 Näytteenottopvm: 8.9.2015 Näytteenottopiste: Alvettula, kaivo Näyte saapui: 8.9.2015 Näytteenottaja: Antti Rehula Analysointi aloitettu: 8.9.2015 Määritys 15TP02480
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
1. Lineaarinen optimointi
 0 1. Lineaarinen optimointi 1. Lineaarinen optimointi 1.1 Johdatteleva esimerkki Esimerkki 1.1.1 Giapetto s Woodcarving inc. valmistaa kahdenlaisia puuleluja: sotilaita ja junia. Sotilaan myyntihinta on
0 1. Lineaarinen optimointi 1. Lineaarinen optimointi 1.1 Johdatteleva esimerkki Esimerkki 1.1.1 Giapetto s Woodcarving inc. valmistaa kahdenlaisia puuleluja: sotilaita ja junia. Sotilaan myyntihinta on
Funktiojonot ja funktiotermiset sarjat Funktiojono ja funktioterminen sarja Pisteittäinen ja tasainen suppeneminen
 4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
4. Funktiojonot ja funktiotermiset sarjat 4.1. Funktiojono ja funktioterminen sarja 60. Tutki, millä muuttujan R arvoilla funktiojono f k suppenee, kun Mikä on rajafunktio? a) f k () = 2k 2k + 1, b) f
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Lukion kemia 3, Reaktiot ja energia. Leena Piiroinen Luento 2 2015
 Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
KEMS448 Fysikaalisen kemian syventävät harjoitustyöt
 KEMS448 Fysikaalisen kemian syventävät harjoitustyöt Jakaantumislaki 1 Teoriaa 1.1 Jakaantumiskerroin ja assosioituminen Kaksi toisiinsa sekoittumatonta nestettä ovat rajapintansa välityksellä kosketuksissa
KEMS448 Fysikaalisen kemian syventävät harjoitustyöt Jakaantumislaki 1 Teoriaa 1.1 Jakaantumiskerroin ja assosioituminen Kaksi toisiinsa sekoittumatonta nestettä ovat rajapintansa välityksellä kosketuksissa
www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet
 www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet Masuunihiekka stabiloinnit (sideaineena) pehmeikkörakenteet sidekivien alusrakenteet putkijohtokaivannot salaojan ympärystäytöt alapohjan
www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet Masuunihiekka stabiloinnit (sideaineena) pehmeikkörakenteet sidekivien alusrakenteet putkijohtokaivannot salaojan ympärystäytöt alapohjan
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä.
 FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
MAB3 - Harjoitustehtävien ratkaisut:
 MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
MAB3 - Harjoitustehtävien ratkaisut: 1 Funktio 1.1 Piirretään koordinaatistoakselit ja sijoitetaan pisteet: 1 1. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä.
c) Tasapainota seuraava happamassa liuoksessa tapahtuva hapetus-pelkistysreaktio:
 HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
HTKK, TTY, LTY, OY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 26.05.2004 1. a) Kun natriumfosfaatin (Na 3 PO 4 ) ja kalsiumkloridin (CaCl 2 ) vesiliuokset sekoitetaan keske- nään, muodostuu
1 Aritmeettiset ja geometriset jonot
 1 Aritmeettiset ja geometriset jonot Johdatus Johdatteleva esimerkki 1 Kasvutulille talletetaan vuoden jokaisen kuukauden alussa tammikuusta alkaen 100 euroa. Tilin nettokorkokanta on 6%. Korko lisätään
1 Aritmeettiset ja geometriset jonot Johdatus Johdatteleva esimerkki 1 Kasvutulille talletetaan vuoden jokaisen kuukauden alussa tammikuusta alkaen 100 euroa. Tilin nettokorkokanta on 6%. Korko lisätään
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja
 MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 5: Taylor-polynomi ja sarja Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos 26.9.2016 Pekka Alestalo,
Luku 2. Kemiallisen reaktion tasapaino
 Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Dislokaatiot - pikauusinta
 Dislokaatiot - pikauusinta Ilman dislokaatioita Kiteen teoreettinen lujuus ~ E/8 Dislokaatiot mahdollistavat deformaation Kaikkien atomisidosten ei tarvitse murtua kerralla Dislokaatio etenee rakeen läpi
Dislokaatiot - pikauusinta Ilman dislokaatioita Kiteen teoreettinen lujuus ~ E/8 Dislokaatiot mahdollistavat deformaation Kaikkien atomisidosten ei tarvitse murtua kerralla Dislokaatio etenee rakeen läpi
Lapin alueen yritysten uudet teräsmateriaalit Raimo Ruoppa
 Rikasta pohjoista 10.4.2019 Lapin alueen yritysten uudet teräsmateriaalit Raimo Ruoppa Lapin alueen yritysten uudet teräsmateriaalit Nimi Numero CK45 / C45E (1.1191) 19MnVS6 / 20MnV6 (1.1301) 38MnV6 /
Rikasta pohjoista 10.4.2019 Lapin alueen yritysten uudet teräsmateriaalit Raimo Ruoppa Lapin alueen yritysten uudet teräsmateriaalit Nimi Numero CK45 / C45E (1.1191) 19MnVS6 / 20MnV6 (1.1301) 38MnV6 /
MAK tentti Vastaa 5:een kysymykseen
 MAK-37.130 tentti 17.4.2000 Vastaa 5:een kysymykseen 1. Onko vedyn käyttö pelkistimenä järkevä vaihtoehto molybdenin valmistukseen molybdenioksidista, MoO2 1200 C:ssa vakiopaineessa (1 bar)? Päättele pelkistyksessä
MAK-37.130 tentti 17.4.2000 Vastaa 5:een kysymykseen 1. Onko vedyn käyttö pelkistimenä järkevä vaihtoehto molybdenin valmistukseen molybdenioksidista, MoO2 1200 C:ssa vakiopaineessa (1 bar)? Päättele pelkistyksessä
Käytännön esimerkkejä on lukuisia.
 PROSESSI- JA Y MPÄRISTÖTEKNIIK KA Ilmiömallinnus prosessimet allurgiassa, 01 6 Teema 4 Tehtävien ratkaisut 15.9.016 SÄHKÖKEMIALLISTEN REAKTIOIDEN TERMODYNAMIIKKA JA KINETIIKKA Yleistä Tämä dokumentti sisältää
PROSESSI- JA Y MPÄRISTÖTEKNIIK KA Ilmiömallinnus prosessimet allurgiassa, 01 6 Teema 4 Tehtävien ratkaisut 15.9.016 SÄHKÖKEMIALLISTEN REAKTIOIDEN TERMODYNAMIIKKA JA KINETIIKKA Yleistä Tämä dokumentti sisältää
d) Klooria valmistetaan hapettamalla vetykloridia kaliumpermanganaatilla. (Syntyy Mn 2+ -ioneja)
 Helsingin yliopiston kemian valintakoe: Mallivastaukset. Maanantaina 29.5.2017 klo 14-17 1 Avogadron vakio NA = 6,022 10 23 mol -1 Yleinen kaasuvakio R = 8,314 J mol -1 K -1 = 0,08314 bar dm 3 mol -1 K
Helsingin yliopiston kemian valintakoe: Mallivastaukset. Maanantaina 29.5.2017 klo 14-17 1 Avogadron vakio NA = 6,022 10 23 mol -1 Yleinen kaasuvakio R = 8,314 J mol -1 K -1 = 0,08314 bar dm 3 mol -1 K
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
TUTKIMUSTODISTUS. Jyväskylän Ympäristölaboratorio. Sivu: 1(1) Päivä: 09.10.14. Tilaaja:
 Jyväskylän Ympäristölaboratorio TUTKIMUSTODISTUS Päivä: 09.10.14 Sivu: 1(1) Tilaaja: PIHTIPUTAAN LÄMPÖ JA VESI OY C/O SYDÄN-SUOMEN TALOUSHAL. OY ARI KAHILAINEN PL 20 44801 PIHTIPUDAS Näyte: Verkostovesi
Jyväskylän Ympäristölaboratorio TUTKIMUSTODISTUS Päivä: 09.10.14 Sivu: 1(1) Tilaaja: PIHTIPUTAAN LÄMPÖ JA VESI OY C/O SYDÄN-SUOMEN TALOUSHAL. OY ARI KAHILAINEN PL 20 44801 PIHTIPUDAS Näyte: Verkostovesi
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
- Termodynaamiset edellytykset - On olemassa ajava voima prosessin tapahtumiselle - Perusta - Kemiallinen potentiaali
 Luento 1: Yleistä kurssista ja sen suorituksesta Tiistai 9.10. klo 10-12 Kemiallisten prosessien edellytykset - Termodynaamiset edellytykset - On olemassa ajava voima prosessin tapahtumiselle - Perusta
Luento 1: Yleistä kurssista ja sen suorituksesta Tiistai 9.10. klo 10-12 Kemiallisten prosessien edellytykset - Termodynaamiset edellytykset - On olemassa ajava voima prosessin tapahtumiselle - Perusta
Lumijoki 1, silta 14VV Lumijärvi 14VV Lämpötila 0,6 0,2 0,1 0,8 2,2 C Suodatus (alkuaineet), KT ok ok ok ok ok Kenttät.
 Pv: 19.3.2014 1/6 Talvivaara Sotkao Oy Talvivaarantie 66 88120 TUHKAKYLÄ Tutkiuksen nii: Talvivaara, vedet, aaliskuu 2014, kierros I, Vuoksen suunta Näytteenottopv: 10.3.2014 Näyte saapui: 11.3.2014 Näytteenottaja:
Pv: 19.3.2014 1/6 Talvivaara Sotkao Oy Talvivaarantie 66 88120 TUHKAKYLÄ Tutkiuksen nii: Talvivaara, vedet, aaliskuu 2014, kierros I, Vuoksen suunta Näytteenottopv: 10.3.2014 Näyte saapui: 11.3.2014 Näytteenottaja:
Resurssiviisaus on bisnestä ja huikeita mahdollisuuksia? Kenneth Ekman CrisolteQ Oy April 2013
 Resurssiviisaus on bisnestä ja huikeita mahdollisuuksia? Kenneth Ekman CrisolteQ Oy April 2013 Resurssiviisaus-Sitra Energia Vesi Ruoka Liikenne Jäte Resurssiviisaus-Sitra Jäte Closed Loop B-to-B toimijat
Resurssiviisaus on bisnestä ja huikeita mahdollisuuksia? Kenneth Ekman CrisolteQ Oy April 2013 Resurssiviisaus-Sitra Energia Vesi Ruoka Liikenne Jäte Resurssiviisaus-Sitra Jäte Closed Loop B-to-B toimijat
4.1 Kaksi pistettä määrää suoran
 4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
KE4, KPL. 3 muistiinpanot. Keuruun yläkoulu, Joonas Soininen
 KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
1.1 Homogeeninen kemiallinen tasapaino
 1.1 Homogeeninen kemiallinen tasapaino 1. a) Mitä tarkoittaa käsite kemiallinen tasapaino? b) Miten kemiallinen tasapaino ilmaistaan reaktioyhtälössä? c) Mistä tekijöistä tasapainossa olevan reaktioseoksen
1.1 Homogeeninen kemiallinen tasapaino 1. a) Mitä tarkoittaa käsite kemiallinen tasapaino? b) Miten kemiallinen tasapaino ilmaistaan reaktioyhtälössä? c) Mistä tekijöistä tasapainossa olevan reaktioseoksen
a) Puhdas aine ja seos b) Vahva happo Syövyttävä happo c) Emäs Emäksinen vesiliuos d) Amorfinen aine Kiteisen aineen
 1. a) Puhdas aine ja seos Puhdas aine on joko alkuaine tai kemiallinen yhdiste, esim. O2, H2O. Useimmat aineet, joiden kanssa olemme tekemisissä, ovat seoksia. Mm. vesijohtovesi on liuos, ilma taas kaasuseos
1. a) Puhdas aine ja seos Puhdas aine on joko alkuaine tai kemiallinen yhdiste, esim. O2, H2O. Useimmat aineet, joiden kanssa olemme tekemisissä, ovat seoksia. Mm. vesijohtovesi on liuos, ilma taas kaasuseos
Ensimmäisen asteen polynomifunktio
 Ensimmäisen asteen polnomifunktio Yhtälön f = a+ b, a 0 määrittelemää funktiota sanotaan ensimmäisen asteen polnomifunktioksi. Esimerkki. Ensimmäisen asteen polnomifuktioita ovat esimerkiksi f = 3 7, v()
Ensimmäisen asteen polnomifunktio Yhtälön f = a+ b, a 0 määrittelemää funktiota sanotaan ensimmäisen asteen polnomifunktioksi. Esimerkki. Ensimmäisen asteen polnomifuktioita ovat esimerkiksi f = 3 7, v()
MAA02. A-osa. 1. Ratkaise. a) x 2 + 6x = 0 b) (x + 4)(x 4) = 9 a) 3x 6x
 MAA0 A-osa. Ratkaise. a) x + 6x = 0 b) (x + 4)(x 4) = 9 a) 3x 6x a) Kirjoitetaan summa x + 6x yhteisen tekijän avulla tulomuotoon ja ratkaistaan yhtälö tulon nollasäännön avulla. x + 6x = 0 x(x + 6) =
MAA0 A-osa. Ratkaise. a) x + 6x = 0 b) (x + 4)(x 4) = 9 a) 3x 6x a) Kirjoitetaan summa x + 6x yhteisen tekijän avulla tulomuotoon ja ratkaistaan yhtälö tulon nollasäännön avulla. x + 6x = 0 x(x + 6) =
Firan vesilaitos. Laitosanalyysit. Lkm keski- maksimi Lkm keski- maksimi
 Laitosanalyysit Firan vesilaitos Lämpötila C 3 8,3 8,4 4 8,4 9 ph-luku 3 6,5 6,5 4 7,9 8,1 Alkaliteetti mmol/l 3 0,53 0,59 4 1 1,1 Happi 3 2,8 4 4 11,4 11,7 Hiilidioksidi 3 23,7 25 4 1 1,9 Rauta Fe 3
Laitosanalyysit Firan vesilaitos Lämpötila C 3 8,3 8,4 4 8,4 9 ph-luku 3 6,5 6,5 4 7,9 8,1 Alkaliteetti mmol/l 3 0,53 0,59 4 1 1,1 Happi 3 2,8 4 4 11,4 11,7 Hiilidioksidi 3 23,7 25 4 1 1,9 Rauta Fe 3
(l) B. A(l) + B(l) (s) B. B(s)
 FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 LIUKOISUUDEN IIPPUVUUS LÄMPÖTILASTA 6. 11. 1998 (HJ) A(l) + B(l) µ (l) B == B(s) µ (s) B FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 1. TEOIAA Kyllästetty liuos LIUKOISUUDEN
FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 LIUKOISUUDEN IIPPUVUUS LÄMPÖTILASTA 6. 11. 1998 (HJ) A(l) + B(l) µ (l) B == B(s) µ (s) B FYSIKAALISEN KEMIAN LAUDATUTYÖ N:o 3 1. TEOIAA Kyllästetty liuos LIUKOISUUDEN
Suoran yhtälöt. Suoran ratkaistu ja yleinen muoto: Suoran yhtälö ratkaistussa, eli eksplisiittisessä muodossa, on
 Suoran htälöt Suoran ratkaistu ja leinen muoto: Suoran htälö ratkaistussa, eli eksplisiittisessä muodossa, on ANALYYTTINEN GEOMETRIA MAA5 = k + b, tai = a missä vakiotermi b ilmoittaa suoran ja -akselin
Suoran htälöt Suoran ratkaistu ja leinen muoto: Suoran htälö ratkaistussa, eli eksplisiittisessä muodossa, on ANALYYTTINEN GEOMETRIA MAA5 = k + b, tai = a missä vakiotermi b ilmoittaa suoran ja -akselin
Juuri 12 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kertaus K. a) Polynomi P() = 3 + 8 on jaollinen polynomilla Q() = 3, jos = 3 on polynomin P nollakohta, eli P(3) = 0. P(3) = 3 3 3 + 8 3 = 54 08 + 54 = 0. Polynomi P on jaollinen polynomilla Q. b) Jaetaan
Kertaus K. a) Polynomi P() = 3 + 8 on jaollinen polynomilla Q() = 3, jos = 3 on polynomin P nollakohta, eli P(3) = 0. P(3) = 3 3 3 + 8 3 = 54 08 + 54 = 0. Polynomi P on jaollinen polynomilla Q. b) Jaetaan
Prosessi- ja ympäristötekniikan perusta
 Prosessi- ja ympäristötekniikan perusta Aihe 2: Materiaalitaseet Tavoite Tavoitteena on oppia tasetarkastelun käsite ja oppia tuntemaan, miten materiaalitaseita voidaan hyödyntää kokonaisprosessien sekä
Prosessi- ja ympäristötekniikan perusta Aihe 2: Materiaalitaseet Tavoite Tavoitteena on oppia tasetarkastelun käsite ja oppia tuntemaan, miten materiaalitaseita voidaan hyödyntää kokonaisprosessien sekä
Ylioppilastutkintolautakunta S t u d e n t e x a m e n s n ä m n d e n
 Ylioilastutkintolautakunta S t u d e n t e a m e n s n ä m n d e n MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ 904 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten iiteiden sisältöjen isteitysten luonnehdinta ei
Ylioilastutkintolautakunta S t u d e n t e a m e n s n ä m n d e n MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ 904 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten iiteiden sisältöjen isteitysten luonnehdinta ei
EPÄORGAANINEN KEMIA HARJOITUKSIA. Jaksollinen järjestelmä
 EPÄORGAANINEN KEMIA HARJOITUKSIA Jaksollinen järjestelmä Mitkä alkuaineet ovat oheisesta jaksollisesta järjestelmästä peitetyt A ja B? Mitkä ovat A:n ja B:n muodostamien kloridien stoikiometriat? Jos alkuaineita
EPÄORGAANINEN KEMIA HARJOITUKSIA Jaksollinen järjestelmä Mitkä alkuaineet ovat oheisesta jaksollisesta järjestelmästä peitetyt A ja B? Mitkä ovat A:n ja B:n muodostamien kloridien stoikiometriat? Jos alkuaineita
4 LUKUJONOT JA SUMMAT
 Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
Opiskelun ja työelämän tietotekniikka (DTEK1043)
 Opiskelun ja työelämän tietotekniikka (DTEK1043) pääaine- ja sivuaineopiskelijat Taulukkolaskennan perusteet Yleistä Tämä harjoitus käsittelee taulukkolaskentaohjelman perustoimintoja. Harjoituksissa opetellaan
Opiskelun ja työelämän tietotekniikka (DTEK1043) pääaine- ja sivuaineopiskelijat Taulukkolaskennan perusteet Yleistä Tämä harjoitus käsittelee taulukkolaskentaohjelman perustoimintoja. Harjoituksissa opetellaan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta Insinöörivalinnan kemian koe MALLIRATKAISUT
 Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
Diplomi-insinöörien ja arkkitehtien yhteisvalinta dia-valinta 2015 Insinöörivalinnan kemian koe 27.5.2015 MALLIRATKAISUT 1 a) Vaihtoehto B on oikein. Elektronit sijoittuvat atomiorbitaaleille kasvavan
2CHEM-A1210 Kemiallinen reaktio Kevät 2017 Laskuharjoitus 7.
 HEM-A0 Kemiallinen reaktio Kevät 07 Laskuharjoitus 7.. Metalli-ioni M + muodostaa ligandin L - kanssa : kompleksin ML +, jonka pysyvyysvakio on K ML + =,00. 0 3. Mitkä ovat kompleksitasapainon vapaan metalli-ionin
HEM-A0 Kemiallinen reaktio Kevät 07 Laskuharjoitus 7.. Metalli-ioni M + muodostaa ligandin L - kanssa : kompleksin ML +, jonka pysyvyysvakio on K ML + =,00. 0 3. Mitkä ovat kompleksitasapainon vapaan metalli-ionin
1.1. YHDISTETTY FUNKTIO
 1.1. YHDISTETTY FUNKTIO (g o f) () = g(f()) Funktio g = yhdistetyn funktion g o f ulkofunktio Funktio f = yhdistetyn funktion g o f sisäfunktio E.2. Olkoon f() = 2 + 3 ja g() = 4-5. Muodosta funktio a)
1.1. YHDISTETTY FUNKTIO (g o f) () = g(f()) Funktio g = yhdistetyn funktion g o f ulkofunktio Funktio f = yhdistetyn funktion g o f sisäfunktio E.2. Olkoon f() = 2 + 3 ja g() = 4-5. Muodosta funktio a)
Oletetaan kaasu ideaalikaasuksi ja sovelletaan Daltonin lakia. Kumpikin seoksen kaasu toteuttaa erikseen ideaalikaasun tilanyhtälön:
 S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
S-445, ysiikka III (Sf) entti 653 Astiassa on, µmol vetyä (H ) ja, µg tyeä ( ) Seoksen lämötila on 373 K ja aine,33 Pa Määritä a) astian tilavuus, b) vedyn ja tyen osaaineet ja c) molekyylien lukumäärä
Ravinteet. Mansikan lannoitus ja kastelu -koulutus Raija Kumpula
 Ravinteet Mansikan lannoitus ja kastelu -koulutus 1.11.2017 Raija Kumpula Sivu 1 3.11.2017 sisältö muutama asia kasvin veden ja ravinteiden otosta (edellisviikon aiheet) sivu- ja hivenravinteet ravinteisiin
Ravinteet Mansikan lannoitus ja kastelu -koulutus 1.11.2017 Raija Kumpula Sivu 1 3.11.2017 sisältö muutama asia kasvin veden ja ravinteiden otosta (edellisviikon aiheet) sivu- ja hivenravinteet ravinteisiin
Lkm keski- maksimi Lkm keski- maksimi. Lkm keski- maksimi Lkm keski- maksimi
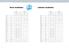 Firan vesilaitos Lahelan vesilaitos Lämpötila C 12 9,5 14,4 12 7,9 8,5 ph-luku 12 6,6 6,7 12 8,0 8,1 Alkaliteetti mmol/l 12 0,5 0,5 12 1,1 1,1 Happi mg/l 12 4,2 5,3 12 11,5 13,2 Hiilidioksidi mg/l 12 21
Firan vesilaitos Lahelan vesilaitos Lämpötila C 12 9,5 14,4 12 7,9 8,5 ph-luku 12 6,6 6,7 12 8,0 8,1 Alkaliteetti mmol/l 12 0,5 0,5 12 1,1 1,1 Happi mg/l 12 4,2 5,3 12 11,5 13,2 Hiilidioksidi mg/l 12 21
Juuri 2 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kertaus K. a) E Nouseva suora. b) A 5. asteen polynomifunktio, pariton funktio Laskettu piste f() = 5 =, joten piste (, ) on kuvaajalla. c) D Paraabelin mallinen, alaspäin aukeava. Laskettu piste f() =
Kertaus K. a) E Nouseva suora. b) A 5. asteen polynomifunktio, pariton funktio Laskettu piste f() = 5 =, joten piste (, ) on kuvaajalla. c) D Paraabelin mallinen, alaspäin aukeava. Laskettu piste f() =
