KIINTEÄN AINEEN FYSIIKKA A. Erkki Thuneberg
|
|
|
- Anne Laaksonen
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 KIINTÄN AINN FYSIIKKA A rkki Thuneberg Fysiikan laitos Oulun yliopisto 2014
2 Järjestelyjä Kurssin verkkosivu on Verkkosivulta löytyy luentomateriaali (tämä moniste), harjoitustehtävät ja myöhemmin myös harjoitustehtävien ratkaisut. Katso sieltä myös mahdolliset muutokset luentoja harjoitusaikoihin. Aikataulut 2014 Luennot: ti ja ke 10-12, , sali L8 (paitsi PR ) Harjoitukset: ti ja ke 12-16, , sali T320 Päätekoe: ti , klo14:00-18:00, L1 Harjoitusassistentit: Susanna Ahola, Tapio Hansson Kurssiin kuuluvat oleellisena osana laskuharjoitukset, joiden tehtävät laitetaan kurssin verkkosivulle pian vastaavan luennon jälkeen. Määräaikaan mennessä näytetyistä tehdyistä harjoituksista saa yhden arvosanapykälän korotuksen loppuarvosanaan. (i pisterajoja, jokainen tehtävä vaikuttaa paitsi että loppuarvosana pyöristetään kokonaisluvuksi.) Korostettakoon että nämä lisäpisteet ovat vain pieni lisä siihen hyötyyn, joka laskuharjoitusten tekemisestä on kurssin asian ymmärtämiselle ja siten tenttimenestykselle. 1. Johdanto Tämän kurssin tarkoituksena on antaa perustiedot kiinteän aineen fysiikasta (solid state physics). Jotkut tutkittavat asiat ovat varsin samanlaisia myös nesteissä. Tämän takia on alettu käyttää termiä condensed matter physics. Tämä sisältää sekä kiinteät aineet että nesteet, joissa molemmissa atomit jatkuvasti vuorovaikuttavat toistensa kanssa. Termistä käytetään suomennoksia tiiviin aineen fysiikka tai kondensoidun materian fysiikka. Tiiviin aineen fysiikka on fysiikan suurin osa-alue. Sillä on tavaton merkitys yhteiskunnallemme, sillä tekniikan edelleen jatkuva nopea kehitys perustuu olennaisesti tiiviin aineen ominaisuuksien ymmärtämiseen. Tämä ei kuitenkaan ole ainoa syy tiiviin aineen fysiikan opiskeluun. Nähdäkseni yhtä tärkeää on se, että tiiviissä aineessa esiintyy monia fysikaalisesti mielenkiintoisia ilmiöitä. Tiiviin aineen ominaisuudet ovat seurausta suuresta määrästä ( ) hiukkasia ja niiden välisistä vuorovaikutuksista. Tällaiseen monen kappaleen ongelmaan ei ole mitään yleistä ratkaisumenetelmää. Sen sijaan on olemassa suuri joukko erilaisia likimääräismenetelmiä ja malleja. On aina helpoin lähteä liikkeelle mahdollisimman yksinkertaisesta mallista. Jos tämä ei auta ymmärtämään tutkittavaa ilmiötä, pyritään vähän korjaamalla saamaan aikaan parempi malli, ja sitten taas parempi, kunnes saavutetaan riittävä tarkkuus. Tätä menetelmää soveltamalla voidaan hyvin monet tiiviin aineen ominaisuudet ymmärtää. Aina kuitenkin jää jäljelle ongelmia, jotka ovat aivan liian vaikeita ratkaistavaksi. Kurssit Atomifysiikka 1, Kiinteän aineen fysiikka ja Ydin- ja hiukkasfysiikka tutustuttavat eri aihepiireihin, jossa kvanttimekaniikalla on olennainen asema. Kvanttimekaniikka on erityisen olennainen monissa tiiviin aineen fysiikan ilmiöissä. Ongelmana on se, että kvanttimekaniikkaa ei ole opittu tässä vaiheessa kunnolla. Siksi monien asioiden kovin syvällinen ymmärtäminen ei juuri ole mahdollista. Lisäksi on vältettävä monimutkaista matematiikkaa. Koska kiinteän aineen fysiikalla on kuitenkin suuri merkitys, on tästä huolimatta tärkeä antaa jonkinlainen perustieto tästä tavattoman laajasta alasta. Tiiviin aineen fysiikasta syvemmin kiinnostuneille suositellaan kvanttimekaniikan opiskelun jälkeen syventävää kurssia Kondensoidun materian fysiikka. sitiedot Kurssilla oletetaan tunnetuksi perustiedot kvanttimekaniikasta siinä laajuudessa, kun on saatu kurssilla Atomifysiikka 1. Myös sähkömagnetismin ja Aaltoliike ja optiikka kurssit ovat hyödyllisiä joissain kohdissa. Lämpöoppi on tärkeää monissa tiiviin aineen ilmiöissä. Jotta nämä kohdat tulisivat ymmärrettyä paremmin suositellaan jatkokurssiksi Termofysiikkaa. Sisällysluettelo johdanto 1
3 kiderakenne hilavärähtelyt elektronirakenne vapaaelektronimalli elektroni jaksollisessa potentiaalissa johteet ja eristeet metallit puolijohteet sähkömagneettisen säteilyn ja kiinteän aineen vuorovaikutus elektroni-elektroni-vuorovaikutus kokeellisia menetelmiä magnetismi suprajohtavuus lopuksi Kirjoja Monisteet. tämä moniste. Suppea, mutta kattaa tässä kurssissa vaaditut asiat. V. Lantto, Materiaalifysiikan perusteet, luentomoniste (1997). Teknillisen tiedekunnan materiaalifysiikan kurssin moniste. Yleiskirjat. Tässä kurssissa käsitellään kiinteää olomuotoa hieman laajemmin kuin näissä. R. isberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles. J. Brehm and J. Mullin, Introduction to the Structure of Matter. M. Alonso and. Finn, Fundamental University Physics III. Kurssi käsittää myös joitain pätkiä osasta II. Kiinteän olomuodon kirjat. Paljon laajempia kuin tarvitaan tässä kurssissa. C. Kittel, Introduction to Solid State Physics. Perinteinen kokeellispainotteinen oppikirja, tämän kurssin olennaisin osa löytyy, mutta paljon muutakin. N. Ashcroft ja D. Mermin, Solid state physics (AM). Selkeä teoreettispainotteinen vanhempi oppikirja, ylittää selvästi tämän kurssin vaatimukset. Kiitokset Kiitän Jani Halista monista korjauksista tähän monisteeseen. Merkintöjä ja vakioita a/bc = a bc laskujärjestyssääntö tässä monisteessa h, Planckin vakio, useammin esiintyy h = h/2π = Js e = C, alkeisvaraus, elektronin varauksen itseisarvo k B = J/K, Boltzmannin vakio N A = /mol, Avogadron vakio u = (0.001 kg/mol)/n A = kg, atomimassayksikkö ɛ 0 = C 2 /Nm 2, sähkövakio (tyhjiön permittiivisyys) µ 0 = 4π 10 7 N/A 2 = 4π 10 7 T 2 m 3 /J, magneettivakio (tyhjiön permeabiliteetti) m e = kg, elektronin massa, useimmiten merkitty vain m:llä 1 ev= J,, sähkökenttä, energia B, magneettikenttä (virallinen nimi magneettivuon tiheys ) H, magnetoiva kenttä (virallinen nimi magneettikentän voimakkuus ) U, 1) elektronin potentiaalienergia U = ev, 2) kiteen muodostumislämpö µ, 1) Fermi-taso (103), 2) magneettisen momentin (109) itseisarvo, µ = µ. exp(x) = e x, cosh x = 1 2 (ex +e x ), sinh x = 1 2 (ex e x ), tanh x = 1/ coth x = sinh x/ cosh x. a, a:n kompleksikonjugaatti H.M. Rosenberg, The Solid State. Teknillisessä tiedekunnassa käytetty kirja, vaikuttaa sopivalla tasolla olevalta. M. Marder, Condensed matter physics. Moderni teoreettispainotteinen, oppikirjana kondensoidun materian fysiikan kurssilla (763628S), ylittää selvästi tämän kurssin vaatimukset. 2
4 2. Kiderakenne Kiinteät aineet muodostuvat atomeista. Atomien välillä on vuorovaikutuksia, joiden seurauksena on tietyissä oloissa kiinteä aine. Kiinteässä aineessa atomit ovat usein järjestyneet säännölliseen järjestykseen. Tällaista ainetta kutsutaan kiteiseksi (crystalline). Kiinteät kappaleet ovat useimmiten monikiteisiä. Tämä tarkoittaa että ne koostuvat useista eri suuntiin olevista yhteenliittyneistä kiteistä. Yksittäisessä kiteessä voi olla esim atomia, kun koko makroskooppisessa kappaleessa on atomia. Tunnelointimikroskoopilla (scanning tunneling microscope, sivu 28) saatu atomiresoluution kuva NbSe 2 - pinnasta. Lähinaapuriatomien välimatka on 0.35 nm. ( Kuvassa näytteitä joissa erikokoisia rikkikiisukiteitä (FeS 2 ). Yleisesti kiinteän aineen rakenne voi olla tavattoman monimutkainen. Vaikka se olisikin muodostunut rakenneyksiköistä, joissa on samat atomit, siinä ei välttämättä ole säännöllisesti toistuvaa rakennetta. simerkki tällaisesta aineesta on lasi, joka muodostuu SiO 2 -yksiköistä. Tällaista ainetta kutsutaan amorfiseksi. Tutkitaan ideaalista tapausta, jossa jätetään kaikki kiteen epätäydellisyydet huomiotta. Tällaisen kiteen kuvaus voidaan jakaa kahteen osaan. 1) joukkoon atomeja (tai mitä tahansa kuvia), joka muodostaa kiteessä toistuvan objektin. Tätä sanotaan kannaksi (basis). 2) avaruuden pistejoukko, joihin kaikkiin paikkoihin kanta on asetettava (vain siirtämällä, ei kääntämällä), jotta saataisiin koko kide muodostettua. Tällainen pistejoukko esitetään muodossa r = n 1 a 1 + n 2 a 2 + n 3 a 3. (1) Kuvassa kaksi kvartsikidettä (SiO 2 ). Useat kiteiset aineet esiintyvät tietyissä muodoissa, joissa tasaiset pinnat kohtaavat toisensa tietyillä vakiokulmilla. Tällaiset muodot voidaan ymmärtää atomien järjestäytymisen pohjalta. Tässä n 1, n 2 ja n 3 ovat kokonaislukuja. Vektoreita a 1, a 2 ja a 3 kutsutaan alkeisvektoreiksi. (Niiden täytyy olla lineaarisesti riippumattomia.) Pistejoukkoa (1) kutsutaan Bravaishilaksi ja sen pisteitä hilapisteiksi. a 3 a 1 a 2 Kuvan mukaista alkeisvektorien määräämää koppia kutsutaan alkeiskopiksi. Kuvassa kaksi kalsiittikidettä (CaCO 3 ), joilla pinnat ovat samoissa kulmissa. + = hila + kanta = kide Kuvassa esimerkki kahdessa ulottuvuudessa. 3
5 a' 2 a a 2 a' 1 a 1 Alkeisvektorien valinta ei ole yksikäsitteistä. Oheisessa kuvassa alkeisvektoreina voidaan käyttää myös a 1 ja a 2. Myös niiden avulla saadaan lausuttua kaikki hilapisteet. Pintakeskeisessä kuutiossa (pkk, engl. face centered cubic, fcc) on yksinkertaiseen kuutiolliseen rakenteeseen lisätty pisteet tahkojen keskelle. yksikkökoppi a 2 a 1 a' 2 alkeiskoppi a' 1 Timanttirakenteessa on lisätty pisteitä pintakeskeiseen kuutiolliseen rakenteeseen siten, että ne ovat neljän lähinaapuripisteen muodostaman tetraedrin keskellä. Tämä rakenne esiintyy mm. piillä (kaikki atomit Si). Lähisukuinen rakenne on sinkkivälkkeellä ZnS, jossa joka toinen atomi on Zn (esim. keltaiset yllä olevassa kuvassa). Tietyissä symmetrisissä hiloissa on alkeisvektorien sijasta käytännöllisempää käyttää suorakulmaisesti valittuja vektoreita (vaikka ne eivät virittäisikään koko hilaa). Niiden määräämää koppia kutsutaan yksikkökopiksi. Yksikkökopin sivujen pituuksia kutsutaan hilavakioiksi. 2.1 simerkkejä kiderakenteista Näissä kuvissa pallot kuvaavat atomiytimien paikkoja. Koko kide saadaan toistamalla kuvattua yksikköä. Natriumkloridirakenne on kuutiollinen, jossa Na- ja Clatomit vuorottelevat. Tämä voidaan nähdä myös pkkhilana, jossa kanta muodostuu yhdestä NaCl-parista. Pintakeskeinen kuutiollinen rakenne muodostaa ns. tiiviin pakkauksen: jos pinotaan kovia kuulia, saavutetaan pkk-hilassa maksimaalinen pakkaustiheys. Alla oleva kuva pyrkii havainnollistamaan kuinka pkk-hila muodostuu tiiviisti pakatuista tasoista. a a a a Yksinkertaisessa kuutiollisessa (simple cubic) rakenteessa kaikki sivut ovat yhtä pitkiä ja kulmat suoria. a Vaihtoehtoinen tiiviin pakkauksen rakenne on heksagonaalinen tiivis pakkaus (htp, engl. hexagonal close packing, hcp). Se muodostuu samanlaisista tasoista kuin yllä, mutta ne on aseteltu eri kohdille. Ideaalisessa (kovien pallojen) tapauksessa c = 8/3 a. Tilakeskeisessä kuutiossa (tkk, engl. body centered cubic, bcc) on lisäksi yksi piste kuution keskellä. 4
6 c a Pkk- ja htp-pakkausten ero voidaan esittää oheisella kuvalla. Kun kuulien päälle laitetaan kolmas kerros, se tulee pkk:ssa kahdessa alemmassa kerroksessa avoimiksi jääneisiin kohtiin c. Htp:ssa kuulat tulevat samoille kohdille a kuin alimmassa kerroksessa. Molemmat tiiviit pakkaukset ovat yleisiä rakenteita erityisesti alkuainemetalleille. Jos atomit käyttäytyisivät kuin kovat pallot, niille olisi yhdentekevää onko niiden järjestys pkk vai htp. Atomit kuitenkin valitsevat jomman kumman, esim. Al, Ni ja Cu ovat pkk ja Mg, Zn ja Co ovat htp. Htp:ssä lisäksi suhde c/a poikkeaa jonkin verran kovien pallojen arvosta. Tiiviiden pakkausten lisäksi myös tilakeskeinen kuutiollinen hila on yleinen alkuaineilla, mm. K, Cr, Mn, Fe. Yksinkertaista kuutiollista rakennetta ei juuri esiinny kiteissä. Natriumkloridirakenne voidaan ymmärtää sillä, että atomien koko on hyvin erilainen: suurien kloori-ionien väliin mahtuu sopivasti pienet natriumionit. Timanttirakenne vastaa varsin harvaa pakkausta. Se esiintyy aineilla, jotka pyrkivät sitoutumaan neljään lähinaapuriin siten että kaikki naapurit ovat samassa kulmassa toisiinsa nähden (109.5 ). Useilla materiaaleilla kiderakenne on monimutkaisempi kuin edellä esitellyt. Oheinen kuva esittää kvartsin kiderakennetta (itse kide on kuvassa edellä). SiO 2 esiintyy usein myös amorfisessa muodossa (lasi). Tarkastelemalla kvartsin monimutkaista kiderakennetta voi ehkä ymmärtää, että jäähdytettäessä nopeasti sulaa SiO 2 :ta, atomit eivät ehdi järjestyä vaan jäävät epäjärjestyneeseen muotoon. Kiteet voidaan luokitella perustuen niiden symmetriaan. Kide on aina symmetrinen siirroissa hilavektorin verran. (Siis kun kidettä siirretään hilavektorin (1) verran, lopputulos on identtinen alkuperäisen kanssa.) Sen lisäksi kiteellä voi olla mm. kierto- ja heijastussymmetrioita. On osoitettu, että eri perusteilla kiteet voidaan jakaa 7 kidejärjestelmään, 14 hilatyyppiin, 32 kideluokkaan ja 230 avaruusryhmään. Monet kiteiden ominaisuudet ovat riippuvaisia kiteen symmetriasta. simerkiksi kuutiollisessa ionikiteessä negatiivisesti ja positiivisesti varattujen ionien painopiste yhtyy, ja siksi materiaalin sähköinen dipolimomentti häviää (esim. NaCl). Jos symmetria on pienempi (esimerkiksi suorakulmaisen särmiön), negatiivisesti ja positiivisesti varattujen ionien painopiste saattaa olla eri. Tällaista materiaalia, jolla on nollasta poikkeava sähköinen dipolimomentti, sanotaan ferroelektriseksi. Toinen tapaus on että dipolimomentti häviää tasapainotilassa. Näin on esim. oheisessa mallikuvassa, jossa negatiiviset varaukset ovat tetraedrin kulmissa ja positiivinen tetraedrin keskellä. Jos tällaista materiaalia puristetaan nuolen suunnassa, eivät varausten painopisteet enää yhdy, ja syntyy sähköinen polarisaatio. Tällaista materiaalia sanotaan pietsoelektriseksi. Ilmiö toimii myös toisin päin: kun pietsoelektrinen kide laitetaan sähkökenttään, muuttaa se muotoaan. Mm. yllä kuvattu kvartsi on pietsoelektrinen, mutta ilmiön tarkempi selittäminen siinä on hankalaa monimutkaisesta kiderakenteesta johtuen. Kiderakenteeseen liittyvä ominaisuus on myös kahtaistaittavuus. Kahtaistaittavissa materiaaleissa valonsäteen kulkunopeus riippuu valon polarisaatiosta (sähkökentän suunnasta). Tämä takia valo jakautuu kahteen eri säteeseen. Malli kvartsin (SiO 2 ) kiderakenteesta. Pallot esittävät happiatomeja, piiatomit (ei näytetty kuvassa) sijaitsevat jokaisen O 4 -tetraedrin keskellä. Bravaishilan kanta muodostuu kolmesta tetraedristä (esim A, B ja C). Kuvassa kahtaistaittavuus kahdessa kalsiittikiteessä (CaCO 3 ). 5
7 2.2 Hilatasot Hilapisteiden kautta kulkevia tasoja kutsutaan hilatasoiksi. Kuvassa on esitetty muutamia eri hilatasoja. Hilatasojen suuntia merkitään usein Millerin indekseillä. Yksinkertaisuuden vuoksi rajoitutaan kuutiolliseen hilaan, missä vektorit a 1, a 2 ja a 3 kiinnitetään yksikkökopin särmien mukaan. Tarkastellaan hilatasoa, joka kulkee pisteiden 3a 1, 1a 2 ja 2a 3 kautta. Muodostetaan kertoimista käänteisluvut: 1 3, 1 ja 1 2. Jotta saataisiin kokonaisluvut kerrotaan nämä 6:lla. Tällöin tason Millerin indeksit ovat (263). Tätä tasoa vastaan kohtisuoraa suuntaa merkitään käyttämällä samoja lukuja kulmasuluissa, [263]. 2a 3 d on samaa suuruusluokkaa kuin atomien etäisyydet kiteessä, syntyy diffraktiokuvio, josta atomien järjestys voidaan päätellä. Aaltoliikkeen yleistä teoriaa käsitellään eri kurssilla. Oletetaan että seuraava Huygensin periaate on tuttu: kun aalto saapuu johonkin pisteeseen, synnyttää se ns. toisioaallon, joka lähtee pisteestä kaikkiin suuntiin. Syntyvä kokonaisaalto saadaan summana toisioaalloista. Tämän mukaan aallot etenevät rintamina, joissa kaikkien aaltojen vaihe on sama. Muissa suunnissa toisioaallot kumoavat toisensa. toisioaalto aaltorintama Huygensin periaatteen mukaan heijastuksessa tasaisesta pinnasta on tulevan aallon ja heijastuneen aallon kulmat samat. AC=BD (263) a 3 yksikkökoppi θ B C θ a 1 a 2 A D 3a 1 Tarkastellaan nyt heijastusta kidetasoista. Jos hilataso ei leikkaa jotain akselia, vastaa se tapausta, missä leikkauspiste menee äärettömän kauas. Tämän käänteisluvuksi tulkitaan 1 = 0. Voidaan osoittaa, että vierekkäisten samansuuntaisten hilatasojen välinen etäisyys d saadaan Millerin indeksistä (hkl) kaavalla a d = h2 + k 2 + l, (2) 2 θ d sin θ θ d missä a on kuutiollisen yksikkökopin sivun pituus. (100) (110) (111) Oheisessa kuvassa on esitetty kolme usein esiintyvää hilatasoa. Huomaa että kuutiollisen hilan symmetrian vuoksi tasot (010) ja (001) ovat samanlaisia tason (100) kanssa. Myös tasot (011), (101) ja (110) ovat keskenään samanlaisia. 2.3 Kiderakenteen kokeellinen määrittäminen Kiderakenne voidaan määrätä kokeellisesti käyttäen säteilyn diffraktiota kiteestä. Jos säteilyn aallonpituus λ Heijastuksissa peräkkäisistä hilatasoista eroaa kuljettu matka 2d sin θ:n verran. Heijastuneet aallot ovat samassa vaiheessa, jos tämä etäisyys on aallonpituuden λ monikerta. Voimakkaalle sironnalle saadaan siis Braggin ehto 2d sin θ = nλ, n = 1, 2, 3,... (3) Kun tämä ehto on voimassa, ovat kaikista hilan pisteistä sironneet aallot samassa vaiheessa ja vahvistavat toisiaan. Kaikkien heijastusten saamiseksi on käytävä kaikki kidetasot läpi. Jotta Braggin piikkejä nähtäisiin, täytyy aallonpituuden λ olla lyhyempi kuin kaksi kertaa hilatasojen etäisyys, 2d. Käytännössä λ 0.02 nm - 1 nm. Voidaan käyttää eri säteilylajeja. sähkömagneettinen säteily. Vaadittu aallonpituus on röntgenalueella, = hν, ν = c λ = ch λ. (4) 6
8 Tässä on energia, h Planckin vakio, ν taajuus, c valon nopeus, λ aallonpituus. simerkiksi röntgenputkessa, jossa kuparinen kohtio, saadaan ns. karakteristista säteilyä vastaten K α -siirtymää energioilla 8027 ja 8047 ev. Näitä vastaavaksi aallonpituudeksi saadaan nm. neutronit. = p2 2m, p = h λ = h2 2mλ 2. (5) Tässä m on neutronin massa ja p liikemäärä. elektronit. Kaavat (5) pätevät myös elektroneille. Matalaenergiset elektronit eivät juuri tunkeudu kiteen sisään, joten niillä saadaan tietoa vain pinnasta. Korkeilla energioilla myös kiteen sisältä. Sirontamittaukset voidaan suorittaa monella eri tavalla. Useimmissa menetelmissä käytetään säteilyä, jossa on vain yksi aallonpituus, esim. karakteristinen röntgensäteily. Jotta sironnat saataisiin mitattua, yksikiteellä on sekä kidettä että havaitsinta kierrettävä sopiviin suuntiin. Vaikka havaitsimena käytettäisiin valokuvauslevyä, saadaan sille heijastuksia vain tietyillä kiteen asennoilla. Röntgen- putki havaitsin kide Toinen vaihtoehto on käyttää pulverinäytettä, jossa on kiteitä satunnaisesti kaikissa eri asennoissa θ 2θ joka on tehty ohutfilmitransistoria varten. Heijastukset on identifioitu koodilla (hkl) joka saadaan kertomalla Millerin indeksissä olevat luvut n:llä, joka esiintyy Braggin kaavassa (3). Lähde: researchweb.watson.ibm.com/journal/rd/451/mitzi.html Heijastuksen sammuminen Tarkastellaan heijastusta tkk-hilan (100)-tasoista. Yksinkertaisesta kuutiollisesta hilasta (hilavakio a) saadaan heijastukset kun 2a sin θ = nλ, n = 1, 2, 3,... (6) Tähän verrattuna tkk:ssa ovat ylimääräiset tasot kunkin tason välissä. Näistä lisätasoista syntyvät heijastukset ovat vastakkaisissa vaiheissa päätasoista syntyvien aaltojen kanssa kun n = 1, tai yleisemmin kun n on pariton. Sanotaan että tkk:ssa nämä heijastukset ovat sammuneet. θ Vastaavaa sammumista ei tapahdu heijastuksissa (110)- tasoista koska nämä tasot ovat samat tkk:ssa ja yksinkertaisessa kuutiollisessa hilassa. ri heijastuksia tutkimalla on pystytty identifioimaan lukuisten materiaalien kiderakenteet. Röntgensironnalla voidaan tutkia myös suuria molekyylejä, mm. DNA. Muodostamalla näistä kiteitä saadaan sironneen säteilyn intensiteetti riittävän suureksi mittauksia varten. 2.4 Kiinteän aineen sidosvoimat Olisi mielenkiintoista teoreettisesti ymmärtää esim. kiinteiden aineiden hilarakenne. Periaatteessa tämä on helppoa. Otetaan Schrödingerin yhtälö elektroneille ja ytimille, määrätään näiden ominaisarvot ja funktiot, jolloin alimman energiatilan ratkaisun pitäisi antaa materiaalin hilarakenne. Pyritään arvioimaan mitä vaatisi selvittää teoreettisesti esim. alumiinin hilarakenne. Oletetaan että elektronin aaltofunktion yhdessä ulottuvuudessa voi diskretoida kymmenellä pisteellä. θ a Ψ(x) x 1 x 10 x Röntgendiffraktio ja scanning electron micrograph (SM) materiaalista (C 6 H 5 C 2 H 4 NH 3 ) 2 SnI 4, Jotta voitaisiin ratkaista ero tkk:n ja htp:n välillä on laskettava minimissään noin 10 atomia. Jokaisessa atomissa on 13 elektronia jotka kukin liikkuvat kolmessa ulottuvuudessa. Ominaisarvo on siis laskettava matriisille jonka 7
9 dimensio on = ja jossa on siis elementtiä. Tämä ylittää monin verroin kaikkien maailman tietokoneiden yhteenlasketun keskusmuistin. Päätellään siis, että monien asioiden laskeminen perusperiaatteista lähtien on käytännössä mahdotonta. Sen sijaan on turvauduttava erilaisiin likimääräismenetelmiin. Näitä on kehitetty valtava määrä eri tarkoituksiin sopivia ja niiden avulla voidaan ymmärtää lukuisia ilmiöitä. Tässä kurssissa tarkastellaan niistä vain yksinkertaisimpia. Pidän hämmästyttävänä, että joidenkin asioiden laskemisen mahdottomuudesta huolimatta kondensoidun aineen fysiikasta tiedetään hyvin paljon. Kiinteiden aineiden sidosvoimien kvantitatiivinen käsittely ei juuri onnistu yksinkertaisin menetelmin. Siksi mainitaan vain lyhyesti päätyypit. Lyhyillä etäisyyksillä kahden atomin välinen voima on aina repulsiivinen. Tämä johtuu suureksi osaksi Paulin kieltosäännöstä, joka estää useampaa kuin yhtä elektronia olemasta samassa tilassa. Myös elektronien välinen Coulombin repulsio on olennainen. Suuremmilla etäisyyksillä voimat ovat usein attraktiivisia. (r) 0 0 Kuvassa on hahmoteltu kahden atomin välinen potentiaalienergia niiden etäisyyden r funktiona. Kovalentti sidos. Attraktiivinen voima johtuu siitä että atomit pareittain jakavat keskenään osan elektroneistaan. Koska elektronit pääsevät liikkumaan laajemmalla alueella, niiden kineettinen energia alenee. (Perustilassa on epämääräisyysperiaatteen mukaan liikemäärä p h/d, missä d on liikkumaväli, ja kineettinen energia kin = p 2 /2m. Toisaalta Paulin kieltosääntö saattaa estää energian alenemisen. Palataan tähän myöhemmin harjoitustehtävänä.) Metallisidos. Suuri joukko atomeja jakaa osan elektroneistaan niin että ne pääsevät liikkumaan koko kiteen läpi. Perustelu muuten samanlainen kuin kovalentillä sidoksella. Ionisidos. Joissain yhdisteissä esim. NaCl, Na luovuttaa lähes kokonaan uloimman elektroninsa klooriatomille. Tässä tapauksessa attraktiivinen voima aiheutuu Coulombin potentiaalista. Kahden ionin (varaukset n 1 e ja n 2 e) välinen potentiaalienergia on r 12 = 1 4πɛ 0 n 1 n 2 e 2 r 1 r 2. (7) NaCl-kiteessä yhdellä Na + -ionilla on kuusi Cl -ionia lähinaapureina. Yhden lähinaapurisidoksen energia on p1 = 1 4πɛ 0 e 2 R, (8) missä R on lähinaapurietäisyys. Seuraavaksi lähimpänä on Na + -ioneja, joita on 12 kpl ja etäisyys d = 2R. tutkitaan tämän naapureita 6 kpl d = R Na + Cl - 8 kpl d = 3 R 12 kpl d = 2 R Yhden Na + ionin vuorovaikutusenergia muiden ionien kanssa saadaan summaamalla vuorovaikutusenergiat kaikilla etäisyyksillä oleviin naapureihin. Täksi energiaksi saadaan ( p = e )... = e2 α 4πɛ 0 R 2 3 4πɛ 0 R. (9) Tässä α on sulkujen sisällä esiintyvä summa, jota kutsutaan Madelungin vakioksi. Sen arvo riippuu hilasta ja on tässä tapauksessa α = Jotta voitaisiin päästä eteenpäin, on keksittävä joku muoto repulsiiviselle voimalle. Yksinkertaisuuden vuoksi oletetaan lauseke p,repulsive = Kokonaispotentiaaliksi saadaan p (R) = e2 4πɛ 0 βe2 4πɛ 0 R n. (10) ( α R β R n ). (11) tsimällä tämän minimi saadaan β = αr n 1 /n ja energia ( p = αe2 1 1 ). (12) 4πɛ 0 R n Koko kiteen sidosenergia U on tämä vastakkaismerkkisenä kerrottuna NaCl-parien määrällä N ( U = Nαe2 1 1 ). (13) 4πɛ 0 R n Tämä on yhtäpitävä mitatun muodostumislämmön kanssa kun valitaan n = 9.4, mikä lienee uskottava arvo. Huomaa että repulsiivisen osuuden vaikutus sidosenergiaan on pieni 10%. Vetysidos. Vedyllä on vain yksi elektroni. Kun vety liittyy esimerkiksi happiatomiin, siirtyy pääosa elektronin aaltofunktiosta hapelle ja vedylle jää positiivinen varaus. Tällä varauksella se voi vetää puoleensa jotain kolmatta atomia, mistä syntyvää sidosta molekyylien välille kutsutaan vetysidokseksi. Tämä sidos on tärkeä mm. jäässä. Van der Waals -vuorovaikutus. Tämä antaa heikon attraktion myös varauksettomien atomien välille. Idea: elektronien kiertoliikkeestä johtuen varauksettomat atomit ovat värähteleviä sähköisiä dipoleja. Hetkellinen dipolimomentti toisessa atomissa synnyttää sähkökentän, joka polarisoi toisen atomin, jolloin niiden välillä vaikuttaa dipolidipoli-voima. Vuorovaikutus riippuu etäisyydestä kuten 1/r 6 ja on olennainen mm. jalokaasuatomien välillä. 8
10 Oheisessa taulukossa on annettu joidenkin kiinteiden aineiden sulamislämpötilat (normaalipaineessa), joista voi päätellä sidosten vahvuutta. Taulukon väliviivat jaottelevat aineet edellä lueteltujen sidostyyppien mukaisesti. aine sulamislämpötila (K) kiderakenne Si 1683 timantti C (4300) timantti GaAs 1511 sinkkivälke SiO Al 2 O Hg Na 371 tkk Al 933 pkk Cu 1356 pkk Fe 1808 tkk W 3683 tkk CsCl 918 NaCl 1075 H 2 O 273 He - Ne 24.5 pkk Ar 83.9 pkk H 2 14 O Hiilellä on timantin lisäksi toinen muoto, grafiitti. Tässä kukin hiiliatomi muodostaa kovalenttisen sidoksen kolmen lähinaapurin kanssa, jolloin muodostuu tasoja. Tasojen väliset voimat ovat van der Waals -tyyppiä ja heikkoja, joten tasot pääsevät helposti liukumaan toistensa suhteen. Grafiitista irrotettua yhtä tasoa kutsutaan grafeeniksi. 3. Hilavärähtelyt Tutkitaan atomien heilahtelua tasapainoasemiensa ympärillä. Yksinkertaisuuden vuoksi tarkastellaan aluksi yksiulotteista atomiketjua. Oletetaan heilahtelun amplitudi pieneksi. Tällöin voidaan olettaa, että atomiin kohdistuvat voimat ovat verrannollisia poikkeamiin lähinaapurietäisyyksissä. Tämä malli on ekvivalentti sen kanssa, että atomit olisi kytketty toisiinsa jousilla. tasapaino a n-1 na n epätasapaino n+1 ξ n-1 ξ n ξ n+1 Tasapainotilassa atomit ovat tasavälein a, eikä niihin kohdistu voimia. Merkitään atomin n paikkaa tasapainossa x n = na. pätasapainotilassa atomi n on paikassa x n = na + ξ n, missä ξ n on siis atomin n poikkeama tasapainoasemastaan. Atomiin n vaikuttaa oikealta puolelta atomista n + 1 voima K(ξ n+1 ξ n ), (14) missä K on jousivakio ja ξ n+1 ξ n on atomien n ja n + 1 välisen jousen venymä. Vasemmalta puolelta atomista n 1 vaikuttava voima on K(ξ n ξ n 1 ). (15) Tässä etumerkki tulee siitä, että voima on negatiiviseen suuntaan, jos ξ n > ξ n 1. Muodostetaan Newtonin liikeyhtälö ja laskemalla voimat yhteen saadaan x M d2 ξ n dt 2 = K(ξ n+1 ξ n ) K(ξ n ξ n 1 ) = K(ξ n+1 2ξ n + ξ n 1 ), (16) Kuvassa grafiitin malli jossa pallot esittävät hiiliatomeja (Wikipedia) Kovalentti sidos muodostuu usein juuri tiettyyn suuntaan. Kovalenttiset kiteet ovat kovia, mutta hauraita, ts. ne murtuvat kovasta iskusta. Metallisidos ei olennaisesti riipu suunnasta. Siksi metalliatomit voivat liukua toistensa ohi mutta sidos silti pitää. Tästä syystä metalleja voidaan muovata esimerkiksi takomalla. missä M on atomin massa. Pyritään ratkaisemaan yhtälö (16) yritteellä Tarkastellaan tätä yritettä hieman. ξ n (t) = Ae i(kna ωt). (17) Yrite (17) on kompleksinen, sillä e iφ = cos φ+i sin φ. Oikea fysikaalinen ratkaisu on tulkittava tämän kompleksisen ratkaisun reaaliosana: ξ fysikaalinen n = Reξ n (18) = (ReA) cos(kna ωt) (ImA) sin(kna ωt). Syy kompleksisen yritteen käyttöön on, että silloin ei tarvitse erikseen kirjoittaa sini- ja kosinifunktioita, vaan molemmat sisältyvät erikoistapauksina kompleksiseen yritteeseen (17). Kaikki laskut voitaisiin yhtä hyvin tehdä käyttäen vain reaalista yritettä (18), mutta silloin ne tulisivat pidemmiksi. Toiseksi huomioidaan, että na x n on atomin n x- koordinaatti (koska oletetaan ξ n a). Yrite (17) on siten 9
11 muotoa Ae i(kx ωt). Tämä kuvaa aaltoa, jonka aaltoluku on k ja kulmataajuus ω. Palautetaan mieliin miten nämä liittyvät aallonpituuteen λ, värähtelytaajuuteen ν ja aallon nopeuteen v: k = 2π λ, ω = 2πν, v = ω k = λν. (19) Aallon nopeuden pystyy parhaiten päättelemään kirjoittamalla yrite (17) muotoon f(x vt). Sijoittamalla yrite (17) liikeyhtälöön (16) ja kumoamalla yhteiset tekijät saadaan Mω 2 = K(e ika 2 + e ika ) = 4K sin 2 ka 2. (20) Tästä voidaan ratkaista kulmataajuus K ω = ±2 M sin ka 2. (21) Tämä ns. dispersiorelaatio on esitetty alla olevassa kuvassa 2 K M 0 ω ω = ck a π Tarkastellaan erikseen eri aaltoluvun k arvoja. (Tapaus ω < 0 ei tuo mitään uutta, joten tutkitaan jatkossa vain tapausta ω 0). 1) 0 < k π/a. Tämä voidaan myös kirjoittaa λ a, eli aallonpituus on paljon suurempi kuin vierekkäisten atomien etäisyys toisistaan. Aalloissa aineen tiheys vaihtelee. Siksi ne voidaan tulkita ääniaalloiksi kiinteässä aineessa. Tällä alueella dispersiorelaatio (21) voidaan approksimoida lineaarisella riippuvuudella k ω = ck, (22) missä c = a K/M tulkitaan äänen nopeudeksi. 2) k π/a. Tässä alueessa aallonpituus on samaa suuruusluokkaa kuin hilavakio a. Kulmataajuus lähenee maksimiarvoa ω max = 2 K/M. Tässä alueessa aallon nopeus v = ω/k (19) poikkeaa arvosta c. Vastaavaa ilmiötä valolle (etenemisnopeuden riippuvuutta aallonpituudesta eli valon väristä) kutsutaan dispersioksi. Tästä johtuu ω:n ja k:n välisen relaation (21) nimi. 3) k < 0. Nämä ratkaisut vastaavat negatiiviseen x- suuntaan kulkevia aaltoja. Ottaen nämä mukaan voidaan piirtää seuraava kuva. - a π 2 K M 0 ω ω = ck 4) k > π/a. Tämä alue ei johda mihinkään uuteen ratkaisuun. Tämä voidaan nähdä kirjoittamalla ratkaisu (17) aaltoluvulle k+(2π/a). Todetaan että ξ n (t) on täysin sama kuin aaltoluvulle k. Alla oleva kuva pyrkii selventämään, että samat ξ n :t voidaan saada useammalla k:lla. Aaltoluvut voidaan siis aina rajata välille k π/a. ξ n a Saadut tulokset osoittavat, että kidevärähtelyt eivät ole mahdollisia tietyn taajuuden yläpuolella. Käytännössä tämä taajuus on kuitenkin hyvin korkea, ν max = ω max /2π Hz. simerkiksi ihmisen kuulemien aaltojen maksimitaajuus on n Hz. Kuuloalueella lineaarinen approksimaatio (22) dispersiorelaatiolle on täysin riittävä. Kaksiatominen kanta Oletetaan että hilassa on kanta, johon kuuluu kaksi erimassaista atomia M 2 M 1 n-1 n n n+1 a epätasapaino x a π η n-1 ξ n η n ξ n+1 k tasapaino Samoin kuin edellä, näille voidaan kirjoittaa liikeyhtälöt Tehdään yritteet M 1 d 2 ξ n dt 2 = K(η n 2ξ n + η n 1 ) M 2 d 2 η n dt 2 = K(ξ n+1 2η n + ξ n ). (23) ξ n (t) = A 1 e i(kna ωt) η n (t) = A 2 e i(kna ωt). (24) Sijoittamalla ja kumoamalla yhteiset tekijät saadaan M 1 ω 2 A 1 = 2KA 1 + K(1 + e ika )A 2 M 2 ω 2 A 2 = K(1 + e ika )A 1 2KA 2. (25) 10
12 Jotta tällä olisi nollasta poikkeava ratkaisu, täytyy kerroindeterminantin hävitä, det ( ) M1 ω 2 2K K(1 + e ika ) K(1 + e ika ) M 2 ω 2 = 0. (26) 2K ω TO 1 TO 2 LA LO TA 1 TA 2 Tästä saadaan M 1 M 2 ω 4 2K(M 1 + M 2 )ω 2 + 4K 2 sin 2 k a 2 = 0, (27) - a π 0 a π k joka voidaan ratkaista ω 2 = K M 1 M 2 [ ] M 1 + M 2 ± M1 2 + M M 1M 2 cos(ka). (28) Kaava (28) antaa kaksi eri ratkaisua. Nämä ratkaisut on hahmoteltu kuvassa. Toinen ratkaisuista, jota kutsutaan akustiseksi haaraksi, on samantyyppinen kuin saatiin edellä identtisten atomien ketjussa (21). Tämän lisäksi saatavaa toista ratkaisua kutsutaan optiseksi haaraksi. - a π 0 ω optinen haara akustinen haara Optisessa haarassa erityyppiset atomit värähtelevät toisiaan vastaan, kun taas akustisessa haarassa värähtelyt ovat samansuuntaisia (ainakin pienillä k π/a). Optisen haaran taajuudet ν ovat luokkaa Hz. Tämä vastaa sähkömagneettisen säteilyn infrapuna-aluetta. rityisesti ionikiteissä optinen haara kytkeytyy voimakkaasti sähkömagneettisen säteilyn kanssa, koska säteilyn sähkökenttä ajaa vastakkaisvarauksisia ioneja vastakkaisiin suuntiin. Tästä seuraa säteilyn voimakas absorptio optisen haaran taajuuksilla. a π k Hilavärähtelyjen kvanttiteoria Tarkastellaan hilavärähtelyjen yhtä moodia: kiinnitetään jokin arvo aaltovektorille k ja valitaan jokin mahdollisista värähtelysuunnasta (jota kuvaa jokin indeksi s). Jokaisella moodilla (k, s) on jokin tietty kulmataajuus ω, millä se värähtelee. Värähtely on harmonista sillä ξ fysikaalinen n (29) = Re(Ae ikan ) cos(ωt) + Im(Ae ikan ) sin(ωt). Voidaan siis sanoa, että jokainen moodi muodostaa harmonisen värähtelijän. Kuhunkin värähtelymoodiin liittyy energia = kin + pot, joka muodostuu atomien yhteenlasketuista kineettisistä ja sidosten (=jousien) potentiaalienergioista. dellä tarkasteltiin hilavärähtelyjä klassisen mekaniikan mukaan [lähtien Newtonin liikeyhtälöstä (16)]. Siinä värähtelyjen amplitudi A voi olla mielivaltainen. Siten myös moodin energialla voi olla mielivaltainen einegatiivinen arvo. Kun siirrytään kvanttimekaniikkaan, edellinen lasku on muuten voimassa, mutta moodin energia voi saada vain tiettyjä diskreettejä arvoja. Atomifysiikan kurssissa johdettiin, että harmonisen värähtelijän mahdolliset energiaarvot ovat j = hω(j ), j = 0, 1, 2, 3,... (30) Tässä h = h/2π = Js. Alinta energiaa 0 = 1 2 hω kutsutaan nollapiste-energiaksi. 7 2 ħω Hilavärähtelyt kolmessa ulottuvuudessa Yllä on tarkasteltu yksiulotteista kidettä. Kolmessa ulottuvuudessa on otettava huomioon että värähtelyt voivat olla kolmeen eri suuntaan. Tästä aiheutuu, että edellä tarkastellut värähtelymoodit yleisessä tapauksessa jakautuvat kolmeksi. Lisäksi kaikki värähtelymoodit riippuvat aallon etenemissuunnasta kiteessä, mitä kuvastaa aaltovektori k = (2π/λ)ˆk. Tietyissä erityissuunnissa värähtelymoodit voidaan jakaa kahteen poikittaisen (transverse) värähtelyn ja yhteen pitkittäisen (longitudinal) värähtelyn moodiin. Oheinen kuva esittää kuviteltua tilannetta missä esim. T A 1 = transverse acoustic mode 1 jne ħω ħω ħω Kaava (30) pätee myös hilavärähtelymoodeihin. Tällä on olennainen vaikutus moniin kiteiden ominaisuuksiin. Tarkastellaan tässä lämpökapasiteettia. Tässä on olennaista että kiteen täsmällistä värähtelytilaa ei voida tietää. Sen asemesta lasketaan todennäköisyyksiä eri tiloille. Lyhyt johdanto todennäköisyyslaskuun on esitetty liitteessä A. 11
13 Harmonisen värähtelijän lämpökapasiteetti Otetaan lähtökohdaksi Gibbsin jakauma. Tämä johdetaan termofysiikan kurssissa, ja siitä on kerrottu myös liitteessä A. (Termofysiikan kurssissa samaa jakaumaa on kutsuttu Boltzmannin jakaumaksi.) Gibbsin jakauma sanoo, että jos meillä on joukko tiloja, joiden energiat ovat j, niin tasapainossa tilan j esiintymistodennäköisyys on p j = 1 Z e βj. (31) Tässä Z on normalisointitekijä, joka määräytyy ehdosta, että kaikkien tilojen yhteenlaskettu todennäköisyys on yksi: p j = 1 Z = e βj. (32) j j Vakio β taas β = 1 k B T, (33) missä T on absoluuttinen lämpötila ja k B = J/K Boltzmannin vakio. Sovelletaan jakaumaa (31) harmoniseen värähtelijään. Saadaan Z = j = e β hω/2 j=0 e βj = e β hω/2 j=0 e β hωj ( e β hω ) j = e β hω/2 1, (34) 1 e β hω missä viimeisessä vaiheessa on käytetty geometrisen sarjan lauseketta. nergian odotusarvon laskemiseksi johdetaan ensin kätevä kaava = j p j = 1 j e βj = 1 d e βj Z Z dβ j j j = 1 dz Z dβ. (35) Soveltamalla tätä harmoniseen värähtelijään (34) saadaan pienellä laskulla energiaksi = hω 2 + hω e β hω 1. (36) Tämä tulos on esitetty kuvassa jatkuvalla viivalla. 2 ħ Ω 3 ħ Ω 2 ħ Ω ħ Ω 2 0 ħ Ω k B 2 ħ Ω k B T Tulos voidaan ymmärtää seuraavasti. Matalassa lämpötilassa, T hω/k B, harmoninen värähtelijä on perustilassaan (alimmassa energiatilassa). Tällöin energian odotusarvo on sama kuin perustilan energia, = 1 2 hω. Korkeassa lämpötilassa, T hω/k B, useat värähtelijän tilat ovat mahdollisia, ja keskimääräinen energia lähestyy termistä energiaa, k B T, mikä on esitetty kuvassa katkoviivalla. Lämpökapasiteetti määritellään keskimääräisen energian derivaattana lämpötilan suhteen, C = d dt. (37) Lämpökapasiteetti kuvaa kuinka paljon lämpöenergiaa on järjestelmään tuotava, että sen lämpötila nousisi tietyllä määrällä. Kaavasta (36) saadaan laskemalla harmonisen värähtelijän lämpökapasiteetti C = d dt = h2 ω 2 e β hω k B T 2 (e β hω 1) 2 = h 2 ω 2 4k B T 2 sinh 2 hω. (38) 2k BT Tämä on esitetty seuraavassa kuvassa jatkuvalla viivalla. C k B k B 2 0 ħ Ω k B 2 ħ Ω k B Suurissa lämpötiloissa, joissa k B T > hω, on lämpökapasiteetti lähes vakio, C k B. Klassisen fysiikan mukaan C on vakio, C k B (katkoviiva), mikä saadaan rajalla h 0. Matalissa lämpötiloissa, joissa k B T hω, lähestyy lämpökapasiteetti voimakkaasti nollaa. Tämä voidaan ymmärtää siten, että kun terminen energia k B T on pieni verrattuna perustilan ja ensimmäisen viritetyn tilan energiaeroon hω, pysyy viritetyn tilan todennäköisyys vielä pienenä eikä värähtelijä siten ota vastaan energiaa lämpötilan nostosta huolimatta. Nostettaessa lämpötilaa korkeammaksi myös ylemmät energiatilat tulevat mahdollisiksi, kun terminen energia k B T alkaa olla samaa suuruusluokkaa kuin alin viritysenergia hω. Sovelletaan edellistä tulosta hilavärähtelyihin. Kaikkein yksinkertaisin malli kiinteän aineen värähtelyille olisi että kaikki atomit värähtelisivät samalla taajuudella ω. Tällaisia värähtelymoodeja on kaikkiaan 3N kappaletta, missä N on atomien lukumäärä hilassa. Tekijä 3 tulee siitä, että atomit voivat värähdellä kolmeen toisiaan vastaan kohtisuoraan suuntaan. Tällaista mallia kutsutaan insteinin malliksi. insteinin mallissa lämpökapasiteetti on sama kuin yhdellä harmonisella värähtelijällä paitsi että se pitää kertoa moodien lukumäärällä 3N. Siis korkeissa lämpötiloissa värähtelijät noudattavat klassista tulosta T 12
14 ja lämpökapasiteetti C 3Nk B. Matalissa lämpötiloissa (T < hω/k B ) taas lämpökapasiteetti on pienentynyt ja lähenee nollaa kun T 0. Kokeellisesti on havaittu, että monien kiteiden lämpökapasiteetti korkeissa lämpötiloissa lähestyy klassista arvoa C 3Nk B, mutta pienenee matalammissa lämpötiloissa. instein osoitti mallillaan, että tämä lämpötilariippuvuus voidaan selittää kvanttimekaniikasta lähtien. Kehittyneempi malli on ns. Debyen malli. Siinä otetaan huomioon, että kiteessä yhden värähtelytaajuuden sijasta esiintyy monia eri taajuuksia, kuten olemme jo edellä johtaneet [kaava (21)]. Kun lämpötila on niin korkea, että k B T > hω max noudattavat kaikki värähtelijät klassista tulosta ja lämpökapasiteetti C 3Nk B. Matalissa lämpötiloissa, joissa k B T hω max, on osa värähtelijöistä jäätynyt koska niiden energia on niin korkea, että ne eivät virity. Ne eivät siten vaikuta lämpökapasiteettiin. Vain niillä moodeilla, joiden värähtelytaajuus on pieni (k on pieni), on vaikutusta lämpökapasiteettiin matalissa lämpötiloissa. 3 N k B C hω. Koko hilan värähdysenergia kirjoitetaan = k s hω k,s (j k,s + 1 ), (39) 2 missä j k,s on moodissa (k, s) olevien fononien lukumäärä. nergian odotusarvo (36) tulkitaan että fononien lukumäärän odotusarvo on j = 1 e β hω 1, (40) mikä on erikoistapaus ns. Bose-instein-jakaumasta. Fononit ovat analogisia sähkömagneettisen kentän kvanteille, fotoneille (photon). (Nimi fononi on tarkoituksella väännetty fotonista.) Yhden fotonin energia on hν = hω. Fotoniin voidaan liittää myös liikemäärä p = hk. Jos uskotaan tätä analogiaa, voidaan myös fononiin liittää liikemäärä p = hk. Fononikäsite on kätevä tutkittaessa mm. lämmönjohtavuutta. Fononit kuljettavat energiaa korkeammasta lämpötilasta matalampaan päin. Kun fononit törmäävät esim. epäpuhtausatomeihin, ne siroavat eri suuntiin ja energiavirta heikkenee. 3 N k B 2 0 D 2 D T Kuvassa on Debyen mallin mukainen lämpökapasiteetti, joka varsin hyvin kuvaa monia kiinteitä aineita. Suuretta Θ D hω max /k B kutsutaan Debyen lämpötilaksi. Alkuaineilla se on tyypillisesti noin muutama sata kelviniä. aine Debyen lämpötila (K) C (timantti) 1860 Na 150 Al 394 Si 625 Fe 420 Cu 315 Hg 100 NaCl 321 Fononit Hilavärähtelyistä puhuttaessa käytetään usein käsitettä fononi (phonon). Puhutaan esim. tapauksesta, jossa moodi (k, s) on tilassa j, ts. moodin energia = hω(j ). Täsmälleen sama asia voidaan ilmaista sanomalla, että moodissa on j kappaletta fononeja. Fononeista voidaan puhua kuin ne olisivat hiukkasia, vaikka oikeasti tarkoitetaan vain eri värähtelytiloja. sim. yhden fononin energia on 13
15 4. lektronirakenne Lähdetään tutkimaan kiinteän aineen elektronirakennetta. Kerrataan aluksi yhden atomin elektronirakennetta. Atomiytimen positiivinen varaus muodostaa elektroneille Coulombin potentiaalin, joka on kuvattu oheisessa kuvassa. energia 2p 2s 1s energiatasot 6 tasoa 2 tasoa 2 tasoa lektronit ovat tietyillä energia-arvoilla, joista kuvassa on piirretty kolme alinta vastaten orbitaaleja 1s, 2s ja 2p. Paulin kieltosäännön mukaan kahdella elektronilla ei voi olla kaikkia samoja kvanttilukuja. Koska elektronilla on spin, joka saa kaksi arvoa (± 1 2 ), voi 1s-orbitaalille mennä kaksi elektronia. Samoin 2s orbitaalille. Koska 2p orbitaaleja on 3, voi niille mennä yhteensä 6 elektronia. Jatkossa käytetään seuraavaa energiatason määritelmää: Paulin kieltosäännön mukaan jokaiselle energiatasolle menee enintään yksi elektroni. Siis kuvan mukaisesti 1sorbitaalia vastaten on kaksi energiatasoa ja 2p-orbitaaleja vastaten on 6 energiatasoa. Usein kahdella tai useammalla energiatasolla on sama energia. Tällöin sanotaan että tasot ovat degeneroituneita. Atomin perustilassa elektronit täyttävät sen energiatasot järjestyksessä pienimmän energian tasosta lähtien. Tämän perusteella voidaan mm. selittää alkuaineiden jaksollinen järjestelmä. Tarkastellaan seuraavaksi mitä energiatasoille tapahtuu kun atomit muodostavat kiinteän aineen. Alla olevassa kuvassa on tarkasteltu kolmea eri energian energiatasoa, joita on merkitty a, b ja c:llä. c b a energia Kun kaksi atomia tuodaan lähekkäin, madaltuu niiden välissä oleva energiavalli. Vaikka elektronin tunneloituminen viereiselle atomille on mahdollista, ei sitä juuri tapahdu tasolla a, sillä siitä nähtynä energiavalli on vielä liian korkea. Tämä on tärkeä tulos: atomin alimmat energiatasot pysyvät muuttumattomina sidoksia muodostettaessa. Tasolla b elektronien tunneloituminen on merkittävää. lektronit näillä tasoilla osallistuvat sidoksen muodostamiseen. Tasolla c pääsevät elektronit täysin vapaasti liikkumaan molekyylissä. Atomien yhdistyessä elektronitasot järjestyvät uudelleen. Kahden atomin yhdisteessä jokaista yhden atomin energiatasoa vastaa kaksi eri energialla olevaa tasoa. Näiden tasojen energiaero on sitä suurempi mitä voimakkaampaa elektronien tunneloituminen atomien välillä on. Neljän atomin ketjussa jokainen atomin energiataso on jakautunut neljään. Kiinteässä aineessa on hyvin suuri joukko atomeja yhdessä, N Tällöin saadaan yksittäisten energiatasojen sijasta energiakaistoja eli energiavöitä. Siis sallitut energia-arvot muodostavat kaistoja. Niiden väleissä on kiellettyjä energia-arvoja, joita kutsutaan energiaraoiksi tai energia-aukoiksi. Joissain tapauksissa kaistat menevät päällekkäin, jolloin energiarakoja ei jää. Kiinteässä aineessa elektronit täyttävät energiakaistat pienimmästä energiasta lähtien. Sitä kaistaa, joka täyttyy vain osittain kutsutaan johtavuuskaistaksi. Metallien sähkönjohtokyky perustuu tällaisen kaistan olemassaoloon, sillä täydet kaistat eivät johda sähköä, kuten pian tullaan tutkimaan tarkemmin. Jos kaikki kaistat ovat joko täynnä tai tyhjiä, on kyseessä eriste. Metallien johtavuuskaistassa olevia elektroneja kutsutaan johtavuuselektroneiksi. Nämä elektronit pääsevät liikkumaan varsin vapaasti metallikappaleen läpi. Seuraavassa pyritään tarkastelemaan niiden ominaisuuksia tarkemmin. 4.1 Vapaaelektronimalli Kvanttimekaniikkaa Tarkastellaan aluksi elektronia yhdessä ulottuvuudessa. lektronin tilaa kuvaa aaltofunktio ψ(x). Tämä funktio määräytyy Schrödingerin yhtälöstä h2 d 2 ψ(x) 2m dx 2 + U(x)ψ(x) = ψ(x). (41) Tässä m on elektronin massa, U(x) elektronin potentiaalienergia ja elektronin kokonaisenergia. Tässä oletetaan, että yhtälö (41) on perusteltu aiemmissa kursseissa. Huomautetaan ainoastaan, että jos kirjoitetaan liikemäärälle p = i h d dx, (42) niin yhtälön (41) vasemman puolen ensimmäinen termi voidaan kirjoittaa p 2 ψ. (43) 2m Tässä ψ:n kerroin on hiukkasen kineettinen energia kin = p 2 /2m ja Schrödingerin yhtälö (41) voidaan siten tulkita lausumaksi = kin + U. 14
16 Muistutetaan vielä aaltofunktion fysikaalinen tulkinta: Ψ(x) 2 on todennäköisyystiheys. Se kuvaa todennäköisyyttä, että mittausta tehdessä hiukkanen löytyy paikasta x. Yleisemmin minkä tahansa suureen O odotusarvo O voidaan laskea kaavasta O = ψ (x)oψ(x)dx. (44) simerkiksi liikemäärä ( p = ψ (x) i h d ) ψ(x)dx (45) dx tai potentiaalienergia U = ψ (x)u(x)ψ(x)dx = ψ(x) 2 U(x)dx. (46) Näissä kaavoissa on oletettu, että ψ(x) on normalisoitu ψ(x) 2 dx = 1. (47) Jos aaltofunktio ψ ei alun perin ole normalisoitu, voidaan se normalisoida jakamalla normalisaatiointegraalin I = ψ(x) 2 dx neliöjuurella, Vapaat hiukkaset ψ(x) = 1 I ψ(x). (48) Seuraavassa tutkitaan vapaata elektronia, ts. tapausta jossa U(x) 0. (Voitaisiin myös valita jokin muu vakio kuin nolla, mutta tällä ei ole olennaista vaikutusta tuloksiin.) Tässä tapauksessa saa Schrödingerin yhtälö muodon Ratkaistaan tämä yritteellä h2 d 2 ψ(x) 2m dx 2 = ψ(x). (49) ψ(x) = Ae ikx. (50) [Huom. paikkariippuvuuden osalta on yrite samanlainen kuin hilavärähtelyillä (17). Aikariippuvuutta ei tässä tarvita.] Sijoittamalla yrite yhtälöön (49) saadaan se toteutumaan kun = h2 k 2 2m. (51) Tietäen = kin = p 2 /2m saadaan lisäksi liikemäärälle p = hk. (52) Muistaen kaavan k = 2π/λ (19) voidaan tämä kirjoittaa myös muotoon p = h/λ, minkä de Broglie ensimmäisenä esitti vuonna Oletetaan seuraavaksi, että hiukkanen onkin rajoitettu liikkumaan vain tietyllä välillä 0 < x < L. Luonnollinen reunaehto välin päissä olisi, että aaltofunktion täytyy hävitä, ψ(0) = ψ(l) = 0. (53) (Tämä vastaa tapausta jossa potentiaali U(x) sallitun alueen ulkopuolella on ääretön.) n=3 n=2 n=1 0 L x Yritteen (50) sijasta onkin nyt kätevämpi käyttää ψ(x) = A cos(kx) + B sin(kx). (54) Sijoittamalla todetaan, että myös tämä toteuttaa yhtälön (49). Reunaehdosta ψ(0) = 0 seuraa A = 0. Reunaehto ψ(l) = 0 vaatii, että B sin(kl) = 0. Jotta tämä saataisiin toteutettua siten että ψ(x) 0, täytyy kl = πn, missä n = 1, 2, 3,.... Siis k = nπ L. (55) Kolme alinta funktiota on piirretty edellä olevaan kuvaan. Todetaan ehdon (55) tarkoittavan, että väliin L mahtuu tasamäärä puolia aallonpituuksia. Kolmiulotteinen tapaus Yleistetään edellinen tulos kolmeen ulottuvuuteen. Kolmessa ulottuvuudessa Schrödingerin yhtälö (41) saa muodon h2 2m ( 2 ) ψ x ψ y ψ z 2 + U(x, y, z)ψ = ψ. (56) Sen ratkaisu on aaltofunktio ψ(x, y, z), joka siis riippuu kaikista kolmesta koordinaatista. Myöskään yhtälöä (56) ei perustella tässä mutta huomautetaan, että jos kirjoitetaan liikemäärän x-komponentille p x = i h x, (57) ja vastaavasti y ja z komponenteille, voidaan myöskin yhtälön (56) vasemman puolen ensimmäinen termi kirjoittaa muotoon (43). Tarkastellaan nyt elektronia, joka voi vapaasti liikkua kuution muotoisen laatikon sisäpuolella. x L L z L y Yleistämällä yksiulotteisesta tapauksesta voidaan nyt arvata, että ratkaisu olisi ψ(x, y, z) = A sin n 1πx L sin n 2πy L sin n 3πz L, (58) 15
17 missä n 1, n 2 ja n 3 ovat positiivisia kokonaislukuja. [Harjoitus: totea että ψ toteuttaa yhtälön (56) ja häviää kaikilla kuution seinillä.] Kaavasta (56) saadaan energiaksi = π2 h 2 2mL 2 (n2 1 + n n 2 3). (59) Tästä voidaan myös päätellä liikemäärän komponenteiksi p x = π hn 1 L, p y = π hn 2 L, p z = π hn 3 L. (60) nergiatasojen tiheys Pyritään seuraavaksi määräämään niiden tasojen määrä, joiden energia on pienempi kuin joku annettu energia. Tällaisten tasojen n 1, n 2 ja n 3 toteuttavat yhtälön n n n 2 3 < 2mL2 π 2 h 2 = κ 2. (61) Piirretään avaruus jonka akselit ovat n 1, n 2 ja n 3. Tässä avaruudessa ehto (61) tarkoittaa pisteitä, jotka ovat ensimmäisessä oktantissa κ-säteisen pallopinnan sisällä. n 1 n 3 (1,3,1) n 2 Tutkitaan rajaa jossa laatikon koko on suuri. Tällöin pisteet ovat hyvin tiheässä pallon säteeseen nähden (κ 1). Pisteiden määrä N p () voidaan tällöin arvioida suoraan kappaleen tilavuudesta N p () = 1 ( ) πκ3 2m3 V = 3π 2 h 3 3/2, (62) missä kuution tilavuus V = L 3. Halutaan seuraavaksi laskea energiatasojen määrä. Tällöin pitää ottaa huomioon, että elektronilla on spin 1 2. Se tarkoittaa, että kukin aaltofunktio (58) muodostaa kaksi tasoa, joille kummallekin mahtuu yksi elektroni. Määritellään energiatasojen määrä n() lisäksi tilavuutta V kohti. delliseen verrattuna n() = 2N p ()/V ja siis n() = 2 2m 3 3π 2 h 3 3/2. (63) Määritellään energiatasojen tiheys g() = dn 2m d = 3 π 2 h. (64) 3 Tässä siis tiheys tarkoittaa energiatasojen määrää energiaväliä kohti. (Lisäksi muistetaan että tasot lasketaan myös tilavuutta V kohti.) Niiden tasojen määrä, jotka ovat energiavälillä (, + d), saadaan laskemalla g()d. Tämä on verrannollinen energian neliöjuureen. dn d nergiaa alempien tasojen määrä (63) saadaan takaisin g:n integraalina n() = 0 g()d = 2 2m 3 3π 2 h 3 3/2. (65) Oletetaan, että elektronien tiheys on n e (lukumäärä/tilavuus). Nämä täyttävät energiatasot alhaalta lukien johonkin tiettyyn energiaan asti. Tätä energiaa kutsutaan Fermi-energiaksi ja merkitään ɛ F. dn d täydet tasot ε F tyhjät tasot hdosta n e = n(ɛ F ) saadaan kaavan (65) avulla määrättyä ɛ F : ɛ F = h2 ( 3π 2 ) 2/3 n e. (66) 2m dellinen on täsmällisesti totta vain absoluuttisessa nollalämpötilassa. Kun lämpötila on suurempi, on osa elektroneista virittynyt korkeamman energian tasoihin. lektronien jakauma voisi olla oheisen kuvan mukainen. täyttötodennäköisyys dn d täydet tasot k B T osittain täytetyt tasot µ tyhjät tasot Tässä tasot, joiden energia on lähellä Fermi-energiaa, ovat osittain täyttyneet. Jakauma poikkeaa olennaisesti nollalämpötilan jakaumasta energiavyöhykkeessä, joka on 16
18 termisen energian k B T suuruusluokkaa. Suurenergiset tasot, joilla ɛ F k B T, ovat edelleen tyhjiä ja matalaenergiset tasot, joilla ɛ F k B T, ovat täynnä. nergiaa, jolla täyttötodennäköisyys on tasan 1/2, kutsutaan Fermi-tasoksi ja merkitään µ. Nollalämpötilassa µ = ɛ F. (Tämän ns. Fermi-jakauman täsmälliseen muotoon palataan myöhemmin.) Sovellus johtavuuselektroneihin Sovelletaan vapaiden elektronien teoriaa metallien johtavuuskaistassa oleviin elektroneihin. nsiksi halutaan tietää Fermi-energian suuruusluokka. Oletetaan että kustakin atomista tulee johtavuuskaistaan Z elektronia, joka luku on arvioitu seuraavassa taulukossa muutamille alkuaineille. Kun tiedetään aineen tiheys, voidaan laskea johtavuuselektronitiheys n e, ja Fermi-energia saadaan kaavasta (66). Z ɛ F (ev) T F (10 4 K) Na Cu Fe Al Pb Fermi-lämpötila T F määritellään kaavalla T F = ɛ F k B. (67) Se on oleellisesti sama asia kuin Fermi-energia mutta lausuttuna lämpötilayksiköissä. Nähdään että Fermilämpötilat ovat suuruusluokka K. Siksi Fermijakauman pyöristyminen esim. huoneenlämpötilassa on varsin vähäistä. Fermi-pinta dellä johdettiin, että elektronitasot ovat täyttyneet Fermi-energiaan (66) asti. nergia riippuu aaltovektorista kaavan = h 2 k 2 /2m (51) mukaan. Vastaten Fermienergiaa, on myös k:lla arvo, johon asti tasot on täytetty: jota kutsutaan Fermi-aaltoluvuksi. ε F = ħ 2 k 2 2m k F k F = ( 3π 2 n e ) 1/3, (68) k Lisäksi määritellään Fermi-liikemäärä ja Fermi-nopeus kaavoilla p F = hk F, v F = p F m. (69) Laskemalla saadaan suuruusluokat k F /m ja v F 10 6 m/s. Kun ajatellaan kolmiulotteista avaruutta jonka akselit ovat k x, k y ja k z, ovat täynnä olevat tasot k F -säteisen pallon sisällä. Pallon pintaa sanotaan Fermi-pinnaksi. k x k z k y 4.2 lektroni jaksollisessa potentiaalissa dellä tutkittiin vapaita elektroneja, joita sitten käytettiin mallina metallin johtavuuselektroneille. Vapaaelektronimallissa oletettiin, että potentiaali häviää. Todellisuudessa ionit aiheuttavat aina paikasta riippuvan potentiaalin U(x), mitä tapausta nyt tutkitaan. Kiteisessä aineessa potentiaalin U(x) huomioon ottaminen on suhteellisen helppoa, koska sillä on erittäin merkittävä symmetria. Tutkitaan yksiulotteista tapausta jossa hilavakio on a. Tällöin U(x + a) U(x). (70) Toisin sanoen, U(x) on jaksollinen funktio, jonka jakso on a. Tämä tarkoittaa, että meidän tarvitsee tietää potentiaali vain yhdessä alkeiskopissa, niin sitten jaksollisuuden (70) perusteella tiedämme sen koko kiteessä. Tehtävänä on nyt ratkaista Schrödingerin yhtälö h2 d 2 ψ(x) 2m dx 2 + U(x)ψ(x) = ψ(x). (41) Tässä on merkittävänä apuna Blochin teoreema. Se sanoo että aaltofunktio ψ(x) voidaan kirjoittaa muotoon ψ(x) = e ikx u(x), u(x + a) = u(x). (71) Tämä on kahden tekijän tulo. Näistä u on jaksollinen funktion, jonka jakso on a. ksponenttiosa ei ole a-jaksollinen, sillä e ik(x+a) = e ika e ikx e ikx. (72) Nähdään siis että ψ(x) ei ole jaksollinen, mutta ψ(x) on. Blochin teoreemalle voidaan esittää erilaisia enemmän tai vähemmän uskottavia todistuksia. Yritetään tässä seuraavaa. Sijoitetaan muoto (71) Schrödingerin yhtälöön. Pienellä laskulla saadaan h2 d 2 u 2m dx 2 i h2 k du m dx + U(x)u = ( h2 k 2 2m ) u. (73) Tämä yhtälö on a-jaksollinen. Toisin sanoen, jos se ratkaistaan yhdessä alkeiskopissa, saadaan ratkaisu kaikkialla. Nähdään siis että Blochin muoto (71) on ainakin mahdollinen. Täydellisessä todistuksessa vaadittaisiin lisäksi, että näin saadaan todella kaikki ratkaisut. 17
PHYS-C0240 Materiaalifysiikka (5op), kevät 2016
 PHYS-C0240 Materiaalifysiikka (5op), kevät 2016 Prof. Martti Puska Emppu Salonen Tomi Ketolainen Ville Vierimaa Luento 7: Hilavärähtelyt tiistai 12.4.2016 Aiheet tänään Hilavärähtelyt: johdanto Harmoninen
PHYS-C0240 Materiaalifysiikka (5op), kevät 2016 Prof. Martti Puska Emppu Salonen Tomi Ketolainen Ville Vierimaa Luento 7: Hilavärähtelyt tiistai 12.4.2016 Aiheet tänään Hilavärähtelyt: johdanto Harmoninen
Braggin ehdon mukaan hilatasojen etäisyys (111)-tasoille on
 763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
763343A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 2 Kevät 2018 1. Tehtävä: Kuparin kiderakenne on pkk. Käyttäen säteilyä, jonka aallonpituus on 0.1537 nm, havaittiin kuparin (111-heijastus sirontakulman θ arvolla
ψ(x) = A cos(kx) + B sin(kx). (2) k = nπ a. (3) E = n 2 π2 2 2ma 2 n2 E 0. (4)
 76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
76A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 4 Kevät 214 1. Tehtävä: Yksinkertainen malli kovalenttiselle sidokselle: a) Äärimmäisen yksinkertaistettuna mallina elektronille atomissa voidaan pitää syvää potentiaalikuoppaa
E p1 = 1 e 2. e 2. E p2 = 1. Vuorovaikutusenergian kolme ensimmäistä termiä on siis
 763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
763343A IINTEÄN AINEEN FYSIIA Ratkaisut 3 evät 2017 1. Tehtävä: CsCl muodostuu Cs + - ja Cl -ioneista, jotka asettuvat tilakeskeisen rakenteen vuoropaikoille (kuva). Laske tämän rakenteen Madelungin vakion
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
Chem-C2400 Luento 2: Kiderakenteet Ville Jokinen
 Chem-C2400 Luento 2: Kiderakenteet 11.1.2019 Ville Jokinen Oppimistavoitteet Metalli-, ioni- ja kovalenttinen sidos ja niiden rooli metallien ja keraamien kiderakenteissa. Metallien ja keraamien kiderakenteen
Chem-C2400 Luento 2: Kiderakenteet 11.1.2019 Ville Jokinen Oppimistavoitteet Metalli-, ioni- ja kovalenttinen sidos ja niiden rooli metallien ja keraamien kiderakenteissa. Metallien ja keraamien kiderakenteen
Mustan kappaleen säteily
 Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Mustan kappaleen säteily Musta kappale on ideaalisen säteilijän malli, joka absorboi (imee itseensä) kaiken siihen osuvan säteilyn. Se ei lainkaan heijasta eikä sirota siihen osuvaa säteilyä, vaan emittoi
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen)
 Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
Vapaan hiukkasen Schrödingerin yhtälö (yksiulotteinen Vapaaseen hiukkaseen ei vaikuta voimia, joten U(x = 0. Vapaan hiukkasen energia on sen liike-energia eli E=p /m. Koska hiukkasella on määrätty energia,
1240eV nm. 410nm. Kun kappaleet saatetaan kontaktiin jännite-ero on yhtä suuri kuin työfunktioiden erotus ΔV =
 S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
S-47 ysiikka III (ST) Tentti 88 Maksimiaallonpituus joka irroittaa elektroneja metallista on 4 nm ja vastaava aallonpituus metallille on 8 nm Mikä on näiden metallien välinen jännite-ero? Metallin työfunktio
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Fononit. Värähtelyt lineaarisessa atomiketjussa Dispersiorelaatio Kaksi erilaista atomia ketjussa Fononit kolmessa dimensiossa
 Fononit Värähtelyt lineaarisessa atomiketjussa Dispersiorelaatio Kaksi erilaista atomia ketjussa Fononit kolmessa dimensiossa Atomien lämpövärähtely Mikä on atomien värähtelyn taajuus ja amplitudi? Tarkastellaan
Fononit Värähtelyt lineaarisessa atomiketjussa Dispersiorelaatio Kaksi erilaista atomia ketjussa Fononit kolmessa dimensiossa Atomien lämpövärähtely Mikä on atomien värähtelyn taajuus ja amplitudi? Tarkastellaan
Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa
 Potentiaalikuoppa Luento 9 Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa U( x ) = U U( x ) = 0 0 kun x < 0 tai x > L, kun 0 x L. Kuopan kohdalla hiukkanen on vapaa,
Potentiaalikuoppa Luento 9 Potentiaalikuopalla tarkoitetaan tilannetta, jossa potentiaalienergia U(x) on muotoa U( x ) = U U( x ) = 0 0 kun x < 0 tai x > L, kun 0 x L. Kuopan kohdalla hiukkanen on vapaa,
Luento 1: Sisältö. Vyörakenteen muodostuminen Molekyyliorbitaalien muodostuminen Atomiketju Energia-aukko
 Luento 1: Sisältö Kemialliset sidokset Ionisidos (suolat, NaCl) Kovalenttinen sidos (timantti, pii) Metallisidos (metallit) Van der Waals sidos (jalokaasukiteet) Vetysidos (orgaaniset aineet, jää) Vyörakenteen
Luento 1: Sisältö Kemialliset sidokset Ionisidos (suolat, NaCl) Kovalenttinen sidos (timantti, pii) Metallisidos (metallit) Van der Waals sidos (jalokaasukiteet) Vetysidos (orgaaniset aineet, jää) Vyörakenteen
Työn tavoitteita. 1 Teoriaa
 FYSP103 / K3 BRAGGIN DIFFRAKTIO Työn tavoitteita havainnollistaa röntgendiffraktion periaatetta konkreettisen laitteiston avulla ja kerrata luennoilla läpikäytyä teoriatietoa Röntgendiffraktio on tärkeä
FYSP103 / K3 BRAGGIN DIFFRAKTIO Työn tavoitteita havainnollistaa röntgendiffraktion periaatetta konkreettisen laitteiston avulla ja kerrata luennoilla läpikäytyä teoriatietoa Röntgendiffraktio on tärkeä
, m s ) täytetään alimmasta energiatilasta alkaen. Alkuaineet joiden uloimmalla elektronikuorella on samat kvanttiluvut n,
 S-114.6, Fysiikka IV (EST),. VK 4.5.005, Ratkaisut 1. Selitä lyhyesti mutta mahdollisimman täsmällisesti: a) Keskimääräisen kentän malli ja itsenäisten elektronien approksimaatio. b) Monen fermionin aaltofunktion
S-114.6, Fysiikka IV (EST),. VK 4.5.005, Ratkaisut 1. Selitä lyhyesti mutta mahdollisimman täsmällisesti: a) Keskimääräisen kentän malli ja itsenäisten elektronien approksimaatio. b) Monen fermionin aaltofunktion
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Aaltojen heijastuminen ja taittuminen
 Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
12. Eristeet Vapaa atomi. Muodostuva sähköinen dipolimomentti on p =! " 0 E loc (12.4)
 12. Eristeet Eristeiden tyypillisiä piirteitä ovat kovalenttiset sidokset (tai vahvat ionisidokset) ja siitä seuraavat mekaaniset ja sähköiset ominaisuudet. Makroskooppisen ulkoisen sähkökentän E läsnäollessa
12. Eristeet Eristeiden tyypillisiä piirteitä ovat kovalenttiset sidokset (tai vahvat ionisidokset) ja siitä seuraavat mekaaniset ja sähköiset ominaisuudet. Makroskooppisen ulkoisen sähkökentän E läsnäollessa
23 VALON POLARISAATIO 23.1 Johdanto. 23.2 Valon polarisointi ja polarisaation havaitseminen
 3 VALON POLARISAATIO 3.1 Johdanto Mawellin htälöiden avulla voidaan johtaa aaltohtälö sähkömagneettisen säteiln etenemiselle väliaineessa. Mawellin htälöiden ratkaisusta seuraa aina, että valo on poikittaista
3 VALON POLARISAATIO 3.1 Johdanto Mawellin htälöiden avulla voidaan johtaa aaltohtälö sähkömagneettisen säteiln etenemiselle väliaineessa. Mawellin htälöiden ratkaisusta seuraa aina, että valo on poikittaista
1 2 x2 + 1 dx. (2p) x + 2dx. Kummankin integraalin laskeminen oikein (vastaukset 12 ja 20 ) antaa erikseen (2p) (integraalifunktiot
 Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Helsingin yliopisto, Itä-Suomen yliopisto, Jyväskylän yliopisto, Oulun yliopisto, Tampereen yliopisto ja Turun yliopisto Matematiikan valintakoe (Ratkaisut ja pisteytys) 500 Kustakin tehtävästä saa maksimissaan
Kiinteän aineen ominaisuuksia I. Kiteisen aineen perusominaisuuksia
 Kiinteän aineen ominaisuuksia I Kiteiden perustyypit Kiderakenteiden peruskäsitteitä Kiteisen aineen perusominaisuuksia Kide on suuresta atomijoukosta muodostunut säännöllinen ja stabiili, atomiseen skaalaan
Kiinteän aineen ominaisuuksia I Kiteiden perustyypit Kiderakenteiden peruskäsitteitä Kiteisen aineen perusominaisuuksia Kide on suuresta atomijoukosta muodostunut säännöllinen ja stabiili, atomiseen skaalaan
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 7 Harmonisen värähdysliikkeen energia Jousen potentiaalienergia on U k( x ) missä k on jousivakio ja Dx on poikkeama tasapainosta. Valitaan
Materiaalifysiikan perusteet P Ratkaisut 1, Kevät 2017
 Materiaalifysiikan perusteet 51104P Ratkaisut 1, Kevät 017 1. Kiderakenteen alkeiskopin hahmottamiseksi pyritään löytämään kuvitteellisesta rakenteesta sen pienin toistuva yksikkö (=kanta). Kunkin toistuvan
Materiaalifysiikan perusteet 51104P Ratkaisut 1, Kevät 017 1. Kiderakenteen alkeiskopin hahmottamiseksi pyritään löytämään kuvitteellisesta rakenteesta sen pienin toistuva yksikkö (=kanta). Kunkin toistuvan
Kiteinen aine. Kide on suuresta atomijoukosta muodostunut säännöllinen ja stabiili, atomiseen skaalaan nähden erittäin suuri, rakenne.
 Kiteinen aine Kide on suuresta atomijoukosta muodostunut säännöllinen ja stabiili, atomiseen skaalaan nähden erittäin suuri, rakenne. Kiteinen aine on hyvä erottaa kiinteästä aineesta, johon kuuluu myös
Kiteinen aine Kide on suuresta atomijoukosta muodostunut säännöllinen ja stabiili, atomiseen skaalaan nähden erittäin suuri, rakenne. Kiteinen aine on hyvä erottaa kiinteästä aineesta, johon kuuluu myös
Aaltojen heijastuminen ja taittuminen
 Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
Luku 11 Aaltojen heijastuminen ja taittuminen Tässä luvussa käsitellään sähkömagneettisten aaltojen heijastumista ja taittumista väliaineiden rajapinnalla. Rajoitutaan monokromaattisiin aaltoihin ja oletetaan
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2012 Insinöörivalinnan fysiikan koe 30.5.2012, malliratkaisut
 A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
A1 Kappale, jonka massa m = 2,1 kg, lähtee liikkeelle levosta paikasta x = 0,0 m pitkin vaakasuoraa alustaa. Kappaleeseen vaikuttaa vaakasuora vetävä voima F, jonka suuruus riippuu paikasta oheisen kuvan
FYSA230/2 SPEKTROMETRI, HILA JA PRISMA
 FYSA230/2 SPEKTROMETRI, HILA JA PRISMA 1 JOHDANTO Työssä tutustutaan hila- ja prismaspektrometreihin, joiden avulla tutkitaan valon taipumista hilassa ja taittumista prismassa. Samalla tutustutaan eräiden
FYSA230/2 SPEKTROMETRI, HILA JA PRISMA 1 JOHDANTO Työssä tutustutaan hila- ja prismaspektrometreihin, joiden avulla tutkitaan valon taipumista hilassa ja taittumista prismassa. Samalla tutustutaan eräiden
Häiriöt kaukokentässä
 Häiriöt kaukokentässä eli kun ollaan kaukana antennista Tavoitteet Tuntee keskeiset periaatteet radioteitse tapahtuvan häiriön kytkeytymiseen ja suojaukseen Tunnistaa kauko- ja lähikentän sähkömagneettisessa
Häiriöt kaukokentässä eli kun ollaan kaukana antennista Tavoitteet Tuntee keskeiset periaatteet radioteitse tapahtuvan häiriön kytkeytymiseen ja suojaukseen Tunnistaa kauko- ja lähikentän sähkömagneettisessa
Havaitsevan tähtitieteen peruskurssi I
 Havaintokohteita 9. Polarimetria Lauri Jetsu Fysiikan laitos Helsingin yliopisto Havaintokohteita Polarimetria Havaintokohteita (kuvat: @phys.org/news, @annesastronomynews.com) Yleiskuvaus: Polarisaatio
Havaintokohteita 9. Polarimetria Lauri Jetsu Fysiikan laitos Helsingin yliopisto Havaintokohteita Polarimetria Havaintokohteita (kuvat: @phys.org/news, @annesastronomynews.com) Yleiskuvaus: Polarisaatio
S-108-2110 OPTIIKKA 1/10 Laboratoriotyö: Polarisaatio POLARISAATIO. Laboratoriotyö
 S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
Voima ja potentiaalienergia II Energian kvantittuminen
 Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Voima ja potentiaalienergia II Energian kvantittuminen Mene osoitteeseen presemo.helsinki.fi/kontro ja vastaa kysymyksiin Tavoitteena tällä luennolla Miten määritetään voima kun potentiaalienergia U(x,y,z)
Infrapunaspektroskopia
 ultravioletti näkyvä valo Infrapunaspektroskopia IHMISEN JA ELINYMPÄ- RISTÖN KEMIAA, KE2 Kertausta sähkömagneettisesta säteilystä Sekä IR-spektroskopia että NMR-spektroskopia käyttävät sähkömagneettista
ultravioletti näkyvä valo Infrapunaspektroskopia IHMISEN JA ELINYMPÄ- RISTÖN KEMIAA, KE2 Kertausta sähkömagneettisesta säteilystä Sekä IR-spektroskopia että NMR-spektroskopia käyttävät sähkömagneettista
Luento 8. Lämpökapasiteettimallit Dulong-Petit -laki Einsteinin hilalämpömalli Debyen ääniaaltomalli. Sähkönjohtavuus Druden malli
 Luento 8 Lämpökapasiteettimallit Dulong-Petit -laki Einsteinin hilalämpömalli Debyen ääniaaltomalli Sähkönjohtavuus Druden malli Klassiset C V -mallit Termodynamiikka kun Ei ennustetta arvosta! Klassinen
Luento 8 Lämpökapasiteettimallit Dulong-Petit -laki Einsteinin hilalämpömalli Debyen ääniaaltomalli Sähkönjohtavuus Druden malli Klassiset C V -mallit Termodynamiikka kun Ei ennustetta arvosta! Klassinen
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Vyöteoria. Orbitaalivyöt
 Vyöteoria Elektronirakenne ja sähkönjohtokyky: Metallit σ = 10 4-10 6 ohm -1 cm -1 (sähkönjohteet) Epämetallit σ < 10-15 ohm -1 cm -1 (eristeet) Puolimetallit σ = 10-5 -10 3 ohm -1 cm -1 σ = neµ elektronien
Vyöteoria Elektronirakenne ja sähkönjohtokyky: Metallit σ = 10 4-10 6 ohm -1 cm -1 (sähkönjohteet) Epämetallit σ < 10-15 ohm -1 cm -1 (eristeet) Puolimetallit σ = 10-5 -10 3 ohm -1 cm -1 σ = neµ elektronien
KIINTEÄN AINEEN FYSIIKKA A. Erkki Thuneberg
 KIINTÄN AINN FYSIIKKA 763333A rkki Thuneberg Fysiikan laitos Oulun yliopisto 2014 Järjestelyjä Kurssin verkkosivu on https://noppa.oulu.fi/noppa/kurssi/763333a Verkkosivulta tai löytyy luentomateriaali
KIINTÄN AINN FYSIIKKA 763333A rkki Thuneberg Fysiikan laitos Oulun yliopisto 2014 Järjestelyjä Kurssin verkkosivu on https://noppa.oulu.fi/noppa/kurssi/763333a Verkkosivulta tai löytyy luentomateriaali
KIINTEÄN AINEEN FYSIIKKA a a a. Erkki Thuneberg
 KIINTÄN AINN FYSIIKKA 763343a 766330a-01 763333a rkki Thuneberg Fysiikan laitos Oulun yliopisto 2018 Järjestelyjä Kurssin verkkosivu on https://www.oulu.fi/tf/kaf/index.html Verkkosivulta löytyy luentomateriaali
KIINTÄN AINN FYSIIKKA 763343a 766330a-01 763333a rkki Thuneberg Fysiikan laitos Oulun yliopisto 2018 Järjestelyjä Kurssin verkkosivu on https://www.oulu.fi/tf/kaf/index.html Verkkosivulta löytyy luentomateriaali
KIINTEÄN AINEEN FYSIIKKA a a a. Erkki Thuneberg
 KIINTÄN AINN FYSIIKKA 763343a 766330a-01 763333a rkki Thuneberg Fysiikan laitos Oulun yliopisto 2017 Järjestelyjä Kurssin verkkosivu on https://noppa.oulu.fi/noppa/kurssi/763343a Verkkosivulta löytyy luentomateriaali
KIINTÄN AINN FYSIIKKA 763343a 766330a-01 763333a rkki Thuneberg Fysiikan laitos Oulun yliopisto 2017 Järjestelyjä Kurssin verkkosivu on https://noppa.oulu.fi/noppa/kurssi/763343a Verkkosivulta löytyy luentomateriaali
1 WKB-approksimaatio. Yleisiä ohjeita. S Harjoitus
 S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
S-114.1427 Harjoitus 3 29 Yleisiä ohjeita Ratkaise tehtävät MATLABia käyttäen. Kirjoita ratkaisut.m-tiedostoihin. Tee tuloksistasi lyhyt seloste, jossa esität laskemasi arvot sekä piirtämäsi kuvat (sekä
Kvantittuminen. E = hf f on säteilyn taajuus h on Planckin vakio h = 6, Js = 4, evs. Planckin kvanttihypoteesi
 Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
Kvantittuminen Planckin kvanttihypoteesi Kappale vastaanottaa ja luovuttaa säteilyä vain tietyn suuruisina energia-annoksina eli kvantteina Kappaleen emittoima säteily ei ole jatkuvaa (kvantittuminen)
12. Eristeet Vapaa atomi
 12. Eristeet Eristeiden tyypillisiä piirteitä ovat kovalenttiset sidokset (tai vahvat ionisidokset) ja siitä seuraavat mekaaniset ja sähköiset ominaisuudet. Makroskooppisen ulkoisen sähkökentän E läsnäollessa
12. Eristeet Eristeiden tyypillisiä piirteitä ovat kovalenttiset sidokset (tai vahvat ionisidokset) ja siitä seuraavat mekaaniset ja sähköiset ominaisuudet. Makroskooppisen ulkoisen sähkökentän E läsnäollessa
LIITE 11A: VALOSÄHKÖINEN ILMIÖ
 LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
LIITE 11A: VALOSÄHKÖINEN ILMIÖ Valosähköisellä ilmiöllä ymmärretään tässä oppikirjamaisesti sitä, että kun virtapiirissä ja tyhjiölampussa olevan anodi-katodi yhdistelmän katodia säteilytetään fotoneilla,
Luku 9: Atomien rakenne ja spektrit. https://www.youtube.com/watch? v=bmivwz-7gmu https://www.youtube.com/watch? v=dvrzdcnsiyw
 Luku 9: Atomien rakenne ja spektrit Vedyn kaltaiset atomit Atomiorbitaalit Spektrisiirtymät Monielektroniset atomit https://www.youtube.com/watch? v=bmivwz-7gmu https://www.youtube.com/watch? v=dvrzdcnsiyw
Luku 9: Atomien rakenne ja spektrit Vedyn kaltaiset atomit Atomiorbitaalit Spektrisiirtymät Monielektroniset atomit https://www.youtube.com/watch? v=bmivwz-7gmu https://www.youtube.com/watch? v=dvrzdcnsiyw
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 206 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 2: BE- ja FD-jakaumat, kvanttikaasut Pe 5.4.206 AIHEET. Kvanttimekaanisesta vaihtosymmetriasta
Nyt n = 1. Tästä ratkaistaan kuopan leveys L ja saadaan sijoittamalla elektronin massa ja vakiot
 S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
S-1146 Fysiikka V (ES) Tentti 165005 1 välikokeen alue 1 a) Rubiinilaserin emittoiman valon aallonpituus on 694, nm Olettaen että fotonin emissioon tällä aallonpituudella liittyy äärettömän potentiaalikuopan
Luento 13: Periodinen liike. Johdanto Harmoninen värähtely Esimerkkejä F t F r
 Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
KRISTALLOGRAFIASSA TARVITTAVAA MATEMA- TIIKKAA
 KRISTALLOGRAFIASSA TARVITTAVAA MATEMA- TIIKKAA Aloita kertaamalla hilan indeksointi niin, että osaat kuutiollisen kiteen tasojen ja suuntien Miller-indeksit. Vektorit määritellään yleisessä muodossa r
KRISTALLOGRAFIASSA TARVITTAVAA MATEMA- TIIKKAA Aloita kertaamalla hilan indeksointi niin, että osaat kuutiollisen kiteen tasojen ja suuntien Miller-indeksit. Vektorit määritellään yleisessä muodossa r
Alikuoret eli orbitaalit
 Alkuaineiden jaksollinen järjestelmä Alkuaineen kemialliset ominaisuudet määräytyvät sen ulkokuoren elektronirakenteesta. Seuraus: Samanlaisen ulkokuorirakenteen omaavat alkuaineen ovat kemiallisesti sukulaisia
Alkuaineiden jaksollinen järjestelmä Alkuaineen kemialliset ominaisuudet määräytyvät sen ulkokuoren elektronirakenteesta. Seuraus: Samanlaisen ulkokuorirakenteen omaavat alkuaineen ovat kemiallisesti sukulaisia
Kuva 6.6 esittää moniliitosaurinkokennojen toimintaperiaatteen. Päällimmäisen
 6.2 MONILIITOSAURINKOKENNO Aurinkokennojen hyötysuhteen kasvattaminen on teknisesti haastava tehtävä. Oman lisähaasteensa tuovat taloudelliset reunaehdot, sillä tekninen kehitys ei saisi merkittävästi
6.2 MONILIITOSAURINKOKENNO Aurinkokennojen hyötysuhteen kasvattaminen on teknisesti haastava tehtävä. Oman lisähaasteensa tuovat taloudelliset reunaehdot, sillä tekninen kehitys ei saisi merkittävästi
TASASUUNTAUS JA PUOLIJOHTEET
 TASASUUNTAUS JA PUOLIJOHTEET (YO-K06+13, YO-K09+13, YO-K05-11,..) Tasasuuntaus Vaihtovirran suunta muuttuu jaksollisesti. Tasasuuntaus muuttaa sähkövirran kulkemaan yhteen suuntaan. Tasasuuntaus toteutetaan
TASASUUNTAUS JA PUOLIJOHTEET (YO-K06+13, YO-K09+13, YO-K05-11,..) Tasasuuntaus Vaihtovirran suunta muuttuu jaksollisesti. Tasasuuntaus muuttaa sähkövirran kulkemaan yhteen suuntaan. Tasasuuntaus toteutetaan
KIINTEÄN AINEEN FYSIIKKA
 KIINTEÄN AINEEN FYSIIKKA 766330a-01 Fysiikan laitos Oulun yliopisto 2016 Järjestelyjä Kurssin verkkosivu on https://noppa.oulu.fi/noppa/kurssi/766330a-01 Verkkosivulta löytyy luentomateriaali (tämä moniste),
KIINTEÄN AINEEN FYSIIKKA 766330a-01 Fysiikan laitos Oulun yliopisto 2016 Järjestelyjä Kurssin verkkosivu on https://noppa.oulu.fi/noppa/kurssi/766330a-01 Verkkosivulta löytyy luentomateriaali (tämä moniste),
SPEKTROMETRI, HILA JA PRISMA
 FYSA234/K2 SPEKTROMETRI, HILA JA PRISMA 1 Johdanto Kvanttimekaniikan mukaan atomi voi olla vain tietyissä, määrätyissä energiatiloissa. Perustilassa, jossa atomi normaalisti on, energia on pienimmillään.
FYSA234/K2 SPEKTROMETRI, HILA JA PRISMA 1 Johdanto Kvanttimekaniikan mukaan atomi voi olla vain tietyissä, määrätyissä energiatiloissa. Perustilassa, jossa atomi normaalisti on, energia on pienimmillään.
766334A Ydin- ja hiukkasfysiikka
 1 76633A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 3 5-3 Kuorimalli Juhani Lounila Oulun yliopisto, Fysiikan laitos, 011 Kuva 7-13 esittää, miten parillis-parillisten ydinten ensimmäisen
1 76633A Ydin- ja hiukkasfysiikka Luentomonistetta täydentävää materiaalia: 3 5-3 Kuorimalli Juhani Lounila Oulun yliopisto, Fysiikan laitos, 011 Kuva 7-13 esittää, miten parillis-parillisten ydinten ensimmäisen
763628S Kondensoidun materian fysiikka
 763628S Kondensoidun materian fysiikka Jani Tuorila Fysiikan laitos Oulun yliopisto 10. tammikuuta 2012 Yleistä Kurssin verkkosivu löytyy osoitteesta: https://wiki.oulu.fi/display/763628s/ Etusivu Se sisältää
763628S Kondensoidun materian fysiikka Jani Tuorila Fysiikan laitos Oulun yliopisto 10. tammikuuta 2012 Yleistä Kurssin verkkosivu löytyy osoitteesta: https://wiki.oulu.fi/display/763628s/ Etusivu Se sisältää
Ydin- ja hiukkasfysiikka: Harjoitus 1 Ratkaisut 1
 Ydin- ja hiukkasfysiikka: Harjoitus Ratkaisut Tehtävä i) Isotoopeilla on sama määrä protoneja, eli sama järjestysluku Z, mutta eri massaluku A. Tässä isotooppeja keskenään ovat 9 30 3 0 4Be ja 4 Be, 4Si,
Ydin- ja hiukkasfysiikka: Harjoitus Ratkaisut Tehtävä i) Isotoopeilla on sama määrä protoneja, eli sama järjestysluku Z, mutta eri massaluku A. Tässä isotooppeja keskenään ovat 9 30 3 0 4Be ja 4 Be, 4Si,
Molekyylit. Helsinki University of Technology, Laboratory of Computational Engineering, Micro- and Nanosciences Laboratory. Atomien väliset sidokset
 Molekyylit. Atomien väliset sidokset. Vetymolekyyli-ioni 3. Kaksiatomiset molekyylit ja niiden molekyyliorbitaalit 4. Muutamien kaksiatomisten molekyylien elektronikonfiguraatio 5. Moniatomiset molekyylit
Molekyylit. Atomien väliset sidokset. Vetymolekyyli-ioni 3. Kaksiatomiset molekyylit ja niiden molekyyliorbitaalit 4. Muutamien kaksiatomisten molekyylien elektronikonfiguraatio 5. Moniatomiset molekyylit
5.10. HIUKKANEN POTENTIAALIKUOPASSA
 5.10. HIUKKANEN POTENTIAALIKUOPASSA eli miten reunaehdot ja normitus vaikuttavat aaltofunktioihin Yleensä Schrödingerin yhtälön ratkaiseminen matemaattisesti on hyvin työlästä ja edellyttää vahvaa matemaattista
5.10. HIUKKANEN POTENTIAALIKUOPASSA eli miten reunaehdot ja normitus vaikuttavat aaltofunktioihin Yleensä Schrödingerin yhtälön ratkaiseminen matemaattisesti on hyvin työlästä ja edellyttää vahvaa matemaattista
PHYS-C0240 Materiaalifysiikka kevät 2017
 PHYS-C0240 Materiaalifysiikka kevät 2017 Prof. Martti Puska Emppu Salonen Ville Vierimaa Janika Tang Luennot 9 ja 10: Sironta kiteistä torstait 13.4. ja 20.4.2017 Aiheet Braggin sirontaehto Lauen sirontaehto
PHYS-C0240 Materiaalifysiikka kevät 2017 Prof. Martti Puska Emppu Salonen Ville Vierimaa Janika Tang Luennot 9 ja 10: Sironta kiteistä torstait 13.4. ja 20.4.2017 Aiheet Braggin sirontaehto Lauen sirontaehto
Miehitysluvuille voidaan kirjoittaa Maxwell Boltzmann jakauman mukaan. saamme miehityslukujen summan muodossa
 S-4.7 Fysiia III (EST) Tetti..6. Tarastellaa systeemiä, jossa ullai hiuasella o olme mahdollista eergiatasoa, ε ja ε, missä ε o eräs vaio. Oletetaa, että systeemi oudattaa Maxwell-Boltzma jaaumaa ja, että
S-4.7 Fysiia III (EST) Tetti..6. Tarastellaa systeemiä, jossa ullai hiuasella o olme mahdollista eergiatasoa, ε ja ε, missä ε o eräs vaio. Oletetaa, että systeemi oudattaa Maxwell-Boltzma jaaumaa ja, että
Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus
 Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus värähtelytiheyden. 1 Funktiot ja aallot Aiemmin käsiteltiin funktioita ja miten niiden avulla voidaan kuvata fysiikan
Kuva 1: Yksinkertainen siniaalto. Amplitudi kertoo heilahduksen laajuuden ja aallonpituus värähtelytiheyden. 1 Funktiot ja aallot Aiemmin käsiteltiin funktioita ja miten niiden avulla voidaan kuvata fysiikan
Muodonmuutostila hum 30.8.13
 Muodonmuutostila Tarkastellaan kuvan 1 kappaletta Ω, jonka pisteet siirtvät ulkoisen kuormituksen johdosta siten, että siirtmien tapahduttua ne muodostavat kappaleen Ω'. Esimerkiksi piste A siirt asemaan
Muodonmuutostila Tarkastellaan kuvan 1 kappaletta Ω, jonka pisteet siirtvät ulkoisen kuormituksen johdosta siten, että siirtmien tapahduttua ne muodostavat kappaleen Ω'. Esimerkiksi piste A siirt asemaan
MUUTOKSET ELEKTRONI- RAKENTEESSA
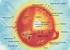 MUUTOKSET ELEKTRONI- RAKENTEESSA KEMIAA KAIK- KIALLA, KE1 Ulkoelektronit ja oktettisääntö Alkuaineen korkeimmalla energiatasolla olevia elektroneja sanotaan ulkoelektroneiksi eli valenssielektroneiksi.
MUUTOKSET ELEKTRONI- RAKENTEESSA KEMIAA KAIK- KIALLA, KE1 Ulkoelektronit ja oktettisääntö Alkuaineen korkeimmalla energiatasolla olevia elektroneja sanotaan ulkoelektroneiksi eli valenssielektroneiksi.
Hiukkasfysiikan luento 21.3.2012 Pentti Korpi. Lapuan matemaattisluonnontieteellinen seura
 Hiukkasfysiikan luento 21.3.2012 Pentti Korpi Lapuan matemaattisluonnontieteellinen seura Atomi Aine koostuu molekyyleistä Atomissa on ydin ja fotonien ytimeen liittämiä elektroneja Ytimet muodostuvat
Hiukkasfysiikan luento 21.3.2012 Pentti Korpi Lapuan matemaattisluonnontieteellinen seura Atomi Aine koostuu molekyyleistä Atomissa on ydin ja fotonien ytimeen liittämiä elektroneja Ytimet muodostuvat
3 Ääni ja kuulo. Ihmiskorva aistii paineen vaihteluita, joten yleensä äänestä puhuttaessa määritellään ääniaalto paineen vaihteluiden kautta.
 3 Ääni ja kuulo 1 Mekaanisista aalloista ääni on ihmisen kannalta tärkein. Ääni on pitkittäistä aaltoliikettä, eli ilman (tai muun väliaineen) hiukkaset värähtelevät suuntaan joka on sama kuin aallon etenemissuunta.
3 Ääni ja kuulo 1 Mekaanisista aalloista ääni on ihmisen kannalta tärkein. Ääni on pitkittäistä aaltoliikettä, eli ilman (tai muun väliaineen) hiukkaset värähtelevät suuntaan joka on sama kuin aallon etenemissuunta.
Yhtälöryhmä matriisimuodossa. MS-A0004/A0006 Matriisilaskenta. Tarkastellaan esimerkkinä lineaarista yhtälöparia. 2x1 x 2 = 1 x 1 + x 2 = 5.
 2. MS-A4/A6 Matriisilaskenta 2. Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.9.25 Tarkastellaan esimerkkinä lineaarista yhtälöparia { 2x x 2 = x + x 2
2. MS-A4/A6 Matriisilaskenta 2. Nuutti Hyvönen, c Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.9.25 Tarkastellaan esimerkkinä lineaarista yhtälöparia { 2x x 2 = x + x 2
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina
 Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Jakso 6: Värähdysliikkeet Tämän jakson tehtävät on näytettävä viimeistään torstaina 31.5.2012. T 6.1 (pakollinen): Massa on kiinnitetty pystysuoran jouseen. Massaa poikkeutetaan niin, että se alkaa värähdellä.
Preliminäärikoe Pitkä Matematiikka 3.2.2009
 Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, PITKÄ OPPIMÄÄRÄ 4.9.09 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio.
 MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
ja KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
ja KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka WYP2005 ja KVANTTITEORIA 24.1.2006 WYP 2005
Shrödingerin yhtälön johto
 Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Shrödingerin yhtälön johto Tomi Parviainen 4. maaliskuuta 2018 Sisältö 1 Schrödingerin yhtälön johto tasaisessa liikkeessä olevalle elektronille 1 2 Schrödingerin yhtälöstä aaltoyhtälöön kiihtyvässä liikkeessä
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
Mekaniikan jatkokurssi Fys102 Syksy 2009 Jukka Maalampi LUENTO 12 Aallot kahdessa ja kolmessa ulottuvuudessa Toistaiseksi on tarkasteltu aaltoja, jotka etenevät yhteen suuntaan. Yleisempiä tapauksia ovat
MIKKELIN LUKIO SPEKTROMETRIA. NOT-tiedekoulu La Palma
 MIKKELIN LUKIO SPEKTROMETRIA NOT-tiedekoulu La Palma Kasper Honkanen, Ilona Arola, Lotta Loponen, Helmi-Tuulia Korpijärvi ja Anastasia Koivikko 20.11.2011 Ryhmämme työ käsittelee spektrometriaa ja sen
MIKKELIN LUKIO SPEKTROMETRIA NOT-tiedekoulu La Palma Kasper Honkanen, Ilona Arola, Lotta Loponen, Helmi-Tuulia Korpijärvi ja Anastasia Koivikko 20.11.2011 Ryhmämme työ käsittelee spektrometriaa ja sen
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
 Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Jukka Tulkki 8. Laskuharjoitus (ratkaisut) Palautus torstaihin 3.4 klo 12:00 mennessä. x 2
 S 437 Fysiikka III Kevät 8 Jukka Tulkki 8 askuharjoitus (ratkaisut) Palautus torstaihin 34 klo : mennessä Assistentit: Jaakko Timonen Ville Pale Pyry Kivisaari auri Salmia (jaakkotimonen@tkkfi) (villepale@tkkfi)
S 437 Fysiikka III Kevät 8 Jukka Tulkki 8 askuharjoitus (ratkaisut) Palautus torstaihin 34 klo : mennessä Assistentit: Jaakko Timonen Ville Pale Pyry Kivisaari auri Salmia (jaakkotimonen@tkkfi) (villepale@tkkfi)
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Luku 3: Virheetön kide
 Luku 3: Virheetön kide Suurin osa teknisistä materiaaleista ovat kiteisiä. Materiaalit voidaan kiderakenteensa puolesta jakaa 7:ään kidesysteemiin ja 14:sta piste- eli Bravais-hilaan. Metallien kiderakenne
Luku 3: Virheetön kide Suurin osa teknisistä materiaaleista ovat kiteisiä. Materiaalit voidaan kiderakenteensa puolesta jakaa 7:ään kidesysteemiin ja 14:sta piste- eli Bravais-hilaan. Metallien kiderakenne
on radan suuntaiseen komponentti eli tangenttikomponentti ja on radan kaarevuuskeskipisteeseen osoittavaan komponentti. (ks. kuva 1).
 H E I L U R I T 1) Matemaattinen heiluri = painottoman langan päässä heilahteleva massapiste (ks. kuva1) kuva 1. - heilurin pituus l - tasapainoasema O - ääriasemat A ja B - heilahduskulma - heilahdusaika
H E I L U R I T 1) Matemaattinen heiluri = painottoman langan päässä heilahteleva massapiste (ks. kuva1) kuva 1. - heilurin pituus l - tasapainoasema O - ääriasemat A ja B - heilahduskulma - heilahdusaika
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 7: Ekvipartitioteoreema, partitiofunktio ja ideaalikaasu Ke 16.3.2016 1 KURSSIN
Luvun 10 laskuesimerkit
 Luvun 10 laskuesimerkit Esimerkki 10.1 Tee-se-itse putkimies ei saa vesiputken kiinnitystä auki putkipihdeillään, joten hän päättää lisätä vääntömomenttia jatkamalla pihtien vartta siihen tiukasti sopivalla
Luvun 10 laskuesimerkit Esimerkki 10.1 Tee-se-itse putkimies ei saa vesiputken kiinnitystä auki putkipihdeillään, joten hän päättää lisätä vääntömomenttia jatkamalla pihtien vartta siihen tiukasti sopivalla
KJR-C2002 Kontinuumimekaniikan perusteet
 KJR-C2002 Kontinuumimekaniikan perusteet Luento 23.11.2015 Susanna Hurme, Yliopistonlehtori, TkT Luennon sisältö Hooken laki lineaaris-elastiselle materiaalille (Reddy, kpl 6.2.3) Lujuusoppia: sauva (Reddy,
KJR-C2002 Kontinuumimekaniikan perusteet Luento 23.11.2015 Susanna Hurme, Yliopistonlehtori, TkT Luennon sisältö Hooken laki lineaaris-elastiselle materiaalille (Reddy, kpl 6.2.3) Lujuusoppia: sauva (Reddy,
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Suunnattu derivaatta Aluksi tarkastelemme vektoreita, koska ymmärrys vektoreista helpottaa alla olevien asioiden omaksumista. Kun liikutaan tasossa eli avaruudessa
Matematiikan tukikurssi Kurssikerta 8 1 Suunnattu derivaatta Aluksi tarkastelemme vektoreita, koska ymmärrys vektoreista helpottaa alla olevien asioiden omaksumista. Kun liikutaan tasossa eli avaruudessa
2 Yhtälöitä ja epäyhtälöitä
 2 Yhtälöitä ja epäyhtälöitä 2.1 Ensimmäisen asteen yhtälö ja epäyhtälö Muuttujan x ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan kirjoittaa muotoon ax + b = 0, missä vakiot a ja b ovat reaalilukuja
2 Yhtälöitä ja epäyhtälöitä 2.1 Ensimmäisen asteen yhtälö ja epäyhtälö Muuttujan x ensimmäisen asteen yhtälöksi sanotaan yhtälöä, joka voidaan kirjoittaa muotoon ax + b = 0, missä vakiot a ja b ovat reaalilukuja
a b c d + + + + + + + + +
 28. 10. 2010!"$#&%(')'+*(#-,.*/1032/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + + + 2. 3. 4. 5. 6. + + + + + + + + + + P1. Valitaan kannaksi sivu, jonka pituus on 4. Koska toinen jäljelle jäävistä sivuista
28. 10. 2010!"$#&%(')'+*(#-,.*/1032/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + + + 2. 3. 4. 5. 6. + + + + + + + + + + P1. Valitaan kannaksi sivu, jonka pituus on 4. Koska toinen jäljelle jäävistä sivuista
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys12 Kevät 21 Jukka Maalampi LUENTO 11 Mekaaninen aaltoliike alto = avaruudessa etenevä järjestäytynyt häiriö. alto altoja on kahdenlaisia: Poikittainen aalto - poikkeamat kohtisuorassa
Mekaniikan jatkokurssi Fys12 Kevät 21 Jukka Maalampi LUENTO 11 Mekaaninen aaltoliike alto = avaruudessa etenevä järjestäytynyt häiriö. alto altoja on kahdenlaisia: Poikittainen aalto - poikkeamat kohtisuorassa
Funktion määrittely (1/2)
 Funktion määrittely (1/2) Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon a täsmälleen yhden B:n alkion b. Merkitään b = f (a). Tässä A = M f on f :n määrittelyjoukko, B on f :n maalijoukko.
Funktion määrittely (1/2) Funktio f : A B on sääntö, joka liittää jokaiseen joukon A alkioon a täsmälleen yhden B:n alkion b. Merkitään b = f (a). Tässä A = M f on f :n määrittelyjoukko, B on f :n maalijoukko.
FYSIIKKA (FY91): 9. KURSSI: Kertauskurssi KOE 30.01.2014 VASTAA KUUTEEN (6) TEHTÄVÄÄN!!
 FYSIIKKA (FY91): 9. KURSSI: Kertauskurssi KOE 30.01.2014 VASTAA KUUTEEN (6) TEHTÄVÄÄN!! 1. Vastaa, ovatko seuraavat väittämät oikein vai väärin. Perustelua ei tarvitse kirjoittaa. a) Atomi ei voi lähettää
FYSIIKKA (FY91): 9. KURSSI: Kertauskurssi KOE 30.01.2014 VASTAA KUUTEEN (6) TEHTÄVÄÄN!! 1. Vastaa, ovatko seuraavat väittämät oikein vai väärin. Perustelua ei tarvitse kirjoittaa. a) Atomi ei voi lähettää
Sähköstaattinen energia
 Luku 4 Sähköstaattinen energia oiman, työn ja energian käsitteet ovat keskeisiä fysiikassa. Sähkö- ja magneettikenttiä mitataan voimavaikutuksen kautta. Kun voima vaikuttaa varaukselliseen hiukkaseen,
Luku 4 Sähköstaattinen energia oiman, työn ja energian käsitteet ovat keskeisiä fysiikassa. Sähkö- ja magneettikenttiä mitataan voimavaikutuksen kautta. Kun voima vaikuttaa varaukselliseen hiukkaseen,
KVANTTITEORIA MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA
 KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
KVANTTITEORIA 1 MODERNI FYSIIKKA KVANTTITEORIAN SYNTY AALTO HIUKKAS-DUALISMI EPÄTARKKUUSPERIAATE TUNNELOITUMINEN ELEKTRONIRAKENNE UUSI MAAILMANKUVA Fysiikka KVANTTITEORIA Metso Tampere 13.11.2005 MODERNI
4757 4h. MAGNEETTIKENTÄT
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
Atomien rakenteesta. Tapio Hansson
 Atomien rakenteesta Tapio Hansson Ykköskurssista jo muistamme... Atomin käsite on peräisin antiikin Kreikasta. Demokritos päätteli alunperin, että jatkuva aine ei voi koostua äärettömän pienistä alkeisosasista
Atomien rakenteesta Tapio Hansson Ykköskurssista jo muistamme... Atomin käsite on peräisin antiikin Kreikasta. Demokritos päätteli alunperin, että jatkuva aine ei voi koostua äärettömän pienistä alkeisosasista
Osallistumislomakkeen viimeinen palautuspäivä on maanantai
 Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
Jakso : Materiaalihiukkasten aaltoluonne. Teoriaa näihin tehtäviin löytyy Beiserin kirjasta kappaleesta 3 ja hyvin myös peruskurssitasoisista kirjoista. Seuraavat videot demonstroivat vaihe- ja ryhmänopeutta:
FYSA220/K2 (FYS222/K2) Vaimeneva värähtely
 FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
Erityinen suhteellisuusteoria (Harris luku 2)
 Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
Erityinen suhteellisuusteoria (Harris luku 2) Yliopistonlehtori, TkT Sami Kujala Mikro- ja nanotekniikan laitos Kevät 2016 Ajan ja pituuden suhteellisuus Relativistinen työ ja kokonaisenergia SMG-aaltojen
S Fysiikka III (EST) Tentti ja välikoeuusinta
 S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
S-437 Fysiikka III (EST) Tentti ja välikoeuusinta 65007 Välikoeuusinnassa vastataan vain kolmeen tehtävään Kokeesta saatu pistemäärä kerrotaan tekijällä 5/3 Merkitse paperiin uusitko jommankumman välikokeen,
Luku 2: Atomisidokset ja ominaisuudet
 Luku 2: Atomisidokset ja ominaisuudet Käsiteltävät aiheet: Mikä aikaansaa sidokset? Mitä eri sidostyyppejä on? Mitkä ominaisuudet määräytyvät sidosten kautta? Chapter 2-1 Atomirakenne Atomi elektroneja
Luku 2: Atomisidokset ja ominaisuudet Käsiteltävät aiheet: Mikä aikaansaa sidokset? Mitä eri sidostyyppejä on? Mitkä ominaisuudet määräytyvät sidosten kautta? Chapter 2-1 Atomirakenne Atomi elektroneja
B sivu 1(6) AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE
 B sivu 1(6) TEHTÄVÄOSA 7.6.2004 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän
B sivu 1(6) TEHTÄVÄOSA 7.6.2004 AMMATTIKORKEAKOULUJEN TEKNIIKAN JA LIIKENTEEN VALINTAKOE YLEISOHJEITA Tehtävien suoritusaika on 2 h 45 min. Osa 1 (Tekstin ymmärtäminen) Osassa on 12 valintatehtävää. Tämän
Kertausta 1.kurssista. KEMIAN MIKROMAAILMA, KE2 Atomin rakenne ja jaksollinen järjestelmä. Hiilen isotoopit
 KEMIAN MIKROMAAILMA, KE2 Atomin rakenne ja jaksollinen järjestelmä Kertausta 1.kurssista Hiilen isotoopit 1 Isotoopeilla oli ytimessä sama määrä protoneja, mutta eri määrä neutroneja. Ne käyttäytyvät kemiallisissa
KEMIAN MIKROMAAILMA, KE2 Atomin rakenne ja jaksollinen järjestelmä Kertausta 1.kurssista Hiilen isotoopit 1 Isotoopeilla oli ytimessä sama määrä protoneja, mutta eri määrä neutroneja. Ne käyttäytyvät kemiallisissa
