Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
|
|
|
- Kirsi Saarnio
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa 1. Satunnaismuuttujien X ja Y yhteistiheysfunktio on f X,Y (x, y) c (3 + x y) 1 < x < 1, < y < x } a) Laske vakion c arvo. (p) b) Laske ehdollinen odotusarvo E( Y X x ), kun < x < 1. (4p) Ratkaisuehdotus: Huomautus! Alla oleva ehdotus on hyvin seikkaperäinen kuvaus jokaisesta askeleesta. En luonnollisestikaan esitä, että tämä olisi mallivastaus vaan ainoastaan vastaus, jossa jokainen kohta on kirjoitettu näkyviin. Kohdassa a) vakion c arvo selviää yhtälöstä f X,Y (x, y)dxdy 1. Tämä yhtälö seuraa siis siitä, että funktio f X,Y on yhteistiheysfunktio. Fubinin lauseen avulla voimme laskea vasemman puolen tasointegraalin f X,Y (x, y)dxdy 1 dx dy c (3 + x y) missä käytimme apuna sitä, että indikaattorifunktiosta tiedämme suoraan, että < y < x, joten on helpompi integroida ensin muuttujan y suhteen ja sitten integroida x yli välin (, 1). Nyt sisempi integraali on c (3 + x y)dy c (3 + x y)dy c(f 1 (x ) F 1 ()) kun F 1 on funktion (3 + x y) (eräs) antiderivaatta muuttujan y suhteen, eli F 1 (y) (3 + x y)dy 3y + 1 x y (+vakio) Sijoittamalla tähän t, havaitsemme F 1 () ja sijoittamalla t x päädymme F 1 (x ) 3x + 1 x (x ) 3x + 1 x x 4 3x + 1 x6.
2 Siispä Olemme siten jo päätelleet, että f X,Y (x, y)dxdy c (3 + x y)dy c(f 1 (x ) F 1 ()) c (3x + 1 x6 ). 1 dx dy c (3 + x y) c 1 (3x + 1 x6 )dx c (F (1) F ()) Vastaavasti voimme laskea antiderivaatan F funktiolle 3x + 1 x6, mikä on F (x) x x7 ja siispä F () ja F (1) Kaiken kaikkiaan olemme päätelleet, että 1 f X,Y (x, y)dxdy c (F (1) F ()) c joten kysytty vakio c Kohdassa b) kysyttiin ehdollista odotusarvoa E( Y X x ) ehdolla satunnaismuuttujan arvo. Luentojen määritelmän mukaan tämä on E( Y X x ) y f Y X (y x)dy Edelleen ehdollinen tiheysfunktio on luentojen määritelmän mukaan silloin kun f X (x) > yhtä kuin f Y X (y x) f X,Y (x, y) 1 f X (x) > } f X (x) joten integraalin laskemiseksi tarvitsemme satunnaismuuttujan X reunajakauman f X. Tämä on luentojen määritelmän nojalla f X (x) f X,Y (x, y)dy c 1 < x < 1 } (3 + x y)dy. Olemme jo kohdassa a) laskeneet tämän määrätyn integraalin ( F 1 (x )), joten havaitsemme, että f X (x) f X,Y (x, y)dy c 1 < x < 1 }(3x + 1 x6 ) Voimme nyt laskea ehdollisen tiheysfunktion f Y X. Kun < x < 1, niin f X (x) >, joten f Y X (y x) c(3 + x y) c(3x + 1 x6 ) 1 < x < 1, < y < x } 3 + x y 3x < y < x } x6 Kun taas x tai x 1, niin f X (x), joten määrittelemme f Y X (y x) Toisaalta, tehtävänannossa pyydettiin käsittelemään vain tapaus < x < 1, joten tällä ei ole juurikaan merkitystä.
3 Kun < x < 1, niin tiedämme siis että ja siten E( Y X x ) f Y X (y x) y(3 + x y) 3x + 1 dy 1 x6 3x + 1 x6 3 + x y 3x + 1 x6 1 < y < x } kun F 3 on funktion (3y + x y ) antiderivaatta muuttujan y suhteen, eli F 3 (y) 3 y x y 3 Tästä näemme, että F 3 () ja F 3 (x ) 3 x x x 6 3 x x8. Siispä olemme laskeneet, että kun < x < 1, niin E( Y X x ) F 3(x ) F 3 () 3x + 1 x6 (3y + x y )dy F 3(x ) F 3 () 3x + 1 x6, 3 x x8 3 3x + 1 x x6 x x + x 6 x x 4. Olkoon X ja Y satunnaismuuttujia, joiden yhteistiheysfunktio on Määritellään satunnaismuuttujat f X,Y (x, y) x 8y 1 < x <, y > 1 4 x } U X, V 1 X 4Y Laske satunnaismuuttujien U ja V yhteistiheysfunktio (4p) ja vastaa lyhyesti perustellen seuraaviin kysymyksiin (vihje: ainakin toinen vastauksista on kyllä): a) Noudattaako (U, V ) tasajakaumaa jossakin tasoalueessa? b) Ovatko U ja V riippumattomia? Ratkaisuehdotus: Huomautus! Alla oleva ehdotus on hyvin seikkaperäinen kuvaus jokaisesta askeleesta. En luonnollisestikaan esitä, että tämä olisi mallivastaus vaan ainoastaan vastaus, jossa jokainen (tarvittava) kohta on kirjoitettu näkyviin. Koska on täysin vaihtoehtoisia tapoja lähestyä tehtävää, niin kaikkia mahdollisuuksia ei ehdotus myöskään kata. Edelleen, suosittelen katsomaan kertaustehtävissä ollutta tehtävää, jonka ratkaisussa käytin suoraviivaisempaa muistisääntöä. Tämä suoraviivaisempi tapa on aivan riittävä. Luentojen perusteella meillä on kaksi erityyppistä tapaa lähestyä muunnoksen yhteistiheysfunktiota: kertymäfunktiotekniikka ja diffeomorfismin käyttö. Sovellamme tässä jälkimmäistä. Diffeomorfismin käytön voi myös jakaa eksplisiittiseen ja implisiittiseen tapaan. Edellisessä kirjoitamme näkyviin muunnokset (U, V ) g(x, Y ) ja h(u, V ) (X, Y ) ja jälkimmäisessä ajattelemme, että (u, v) on tarvittaessa (x, y):n funktio ja (x, y) on tarvittaessa (u, v):n funktio. Käytämme seuraavassa eksplisiittistä tapaa, mutta implisiittinen tapa on suoraviivaisempi ja ehkä helpommin lähestyttävä. 3
4 Tehtävänannon mukaan (U, V ) g(x, Y ), kun g on kahden muuttujan vektoriarvoinen funktio ( ) ( ) ( ) x x g1 (x, y) g(x, y) g y g (x, y) 1 x 4y Näytämme aluksi, että g : A B on diffeomorfismi, kun A on tehtävänannon joukko A < x <, y > 1 4 x }. Voimme suoraan sanoa, että g 1 on jatkuvasti derivoituva koko tasossa R eli g 1 on jatkuvasti derivoituva määrittelyjoukossamme A. Vastaavasti voimme suoraan sanoa, että g on jatkuvasti derivoituva, kunhan y, joten g ja siten myös g (g 1, g ) on jatkuvasti derivoituva koko määrittelyjoukossamme A. Seuraavaksi tarkastamme että g : A B on bijektio. Tätä varten etsimme sen mahdollisen käänteisfunktion h: B A. Löydämme funktion h ratkaisemalla yhtälön ( ( ( ( x u u x g h y) v) v) y) Jos yhtälöllä on yksikäsitteinen ratkaisu, niin g on bijektio A g(a) h 1 (A). Nyt ( ) ( x u x g y v) u x u 1 x 4y v 1 4 x y 1 1 v x u x u 1 4 (u) y 1 1 v yu 1 1 v x u y u (1 v) 1 eli löysimme käänteisfunktion ehdokkaan ( ) ( ) u h1 (u, v) h v h (u, v) ( u u (1 v) 1 ja koska ratkaisu oli yksikäsitteinen on g bijektio A h 1 (A). Määräämme joukon B h 1 (A) selvittämällä, milloin h(u, v) A. Tämä on yhtäpitävää sen kanssa, että < u < < u < 1 < u < 1 u (1 v) 1 > 1 4 h 1(u, v) u (1 v) 1 > u (1 v) 1 > 1 Nyt ehdosta (1 v) 1 > 1 seuraa, että 1 v >, sillä muuten (1 v) 1 <. Siispä v < 1. Kun v < 1, niin ehdosta (1 v) 1 > 1 seuraa, että 1 v < 1 eli v >. Olemme siis päätelleet, että h(u, v) A on yhtäpitävää sen kanssa, että u, v (, 1). Siispä joukko B (, 1) (, 1) ja g : A B on siis bijektio. Koska suoraan havaitsemme, että kuvaus h 1 on jatkuvasti derivoituva koko tasossa ja h on jatkuvasti derivoituva, kunhan v 1, joten h on jatkuvasti derivoituva joukossa B. Siispä g : A B on myös diffeomorfismi. Luentojen (esimerkiksi muistisäännön) perusteella voimme nyt todeta, että f U,V (u, v) (u, v) f X,Y (x, y) (x, y) ) 4
5 eli toisin sanoen, f U,V (u, v) f X,Y (x, y) (x, y) (u, v) f X,Y (h 1 (u, v), h (u, v)) J h (u, v) missä J h on käänteisfunktion h jacobiaani, joka voidaan nyt laskea: ( ) ( ) u h det 1 (u, v) v h 1 (u, v) det u (u) v (u) u h (u, v) v h (u, v) u (u (1 v) 1 ) v (u (1 v) 1 ) ( ) det u (u (1 v) 1 ) u (1 v) Siispä olemme jo päätelleet, että u (1 v) u(u (1 v) 1 ) u (1 v) u f U,V (u, v) f X,Y (h 1 (u, v), h (u, v)) (1 v) Enää tarvitsee sijoittaa h 1 ja h satunnaismuuttujien X ja Y yhteistiheysfunktion: joten kaiken kaikkiaan, f X,Y (h 1 (u, v), h (u, v)) (h 1(u, v)) 1 h(u, v) A } 8(h (u, v)) (u) 8(u (1 v) 1 ) 1 (u, v) h 1 (A) } 4u 8(u 4 (1 v) 1 (u, v) B } ) (1 v) u 1 (u, v) B } (1 v) u f U,V (u, v) u 1 (u, v) B } 1 (u, v) B } (1 v) Nyt kysymyksiin a) ja b) voidaan vastata. Koska yhteistiheysfunktio f U,V on vakio 1 alueessa B, niin määritelmän mukaan (U, V ) on tasajakautuneita joukossa B (, 1) (, 1). Siispä vastaus kysymykseen a) on kyllä. Myös kysymyksen b) vastaus on kyllä. Tämän huomaa helpoiten siten, että f U,V (u, v) 1 < u, v < 1 } 1 < u < 1 }1 < v < 1 } eli f U,V (u, v) voidaan esittää tulona k 1 (u)k (v), joten luentojen nojalla tiedämme, että f U,V (u, v) f U (u)f V (v). Siispä U ja V ovat riippumattomia. Vaikka U ja V riippuvatkin satunnaismuuttujasta X, niin tämä ei vielä tee U:sta ja V :stä riippuvia toisistaan. 5
6 3. Olkoon X, Y ja W satunnaismuuttujia, joiden jakauman kuvaa hierarkinen malli X Y N(, Y ) Y W + 1, Z Bin(3, 1 ) a) Kerro mallin avulla, mikä on ehdollinen tiheysfunktio f X Y ja kerro mallin avulla, mikä on ehdollinen odotusarvo E(X Y ). (p) b) Laske EX. (p) c) Laske var X. (p) Ratkaisuehdotus: Huomautus! Alla oleva ehdotus on hyvin seikkaperäinen kuvaus jokaisesta askeleesta. En luonnollisestikaan esitä, että tämä olisi mallivastaus vaan ainoastaan vastaus, jossa jokainen kohta on kirjoitettu näkyviin. Esimerkiksi kohdassa a) tehtäväannossa sanottiin, että riittää kertoa, mikä on ehdollinen odotusarvo ja ehdollinen tiheysfunktio, kun ehdollinen jakauma on annettu suoraan. Kohdassa a) riittää lukea suoraan kysytyt tiedot. Tehtävänannon mukaan jokaisella y R on X (Y y) N(, y ), sillä tehtävänanto on sopimuksen mukaan lyhennys tästä. Jos kiinnitämme y:n ja merkitsemme Z N(, y ), niin satunnaismuuttujalla Z on siten sama jakauma kuin X:llä, ehdolla että Y y. Toisin sanoen, f X Y f Z sekä E(X Y y) EZ. Nyt luentojen nojalla tiedämme, että normaalijakautuneen satunnaismuuttujan Z odotusarvo on ja varianssi y sekä tiheysfunktio 1 f X Y (x y) f Z (x) 1 πy e x y kaikilla y, joilla f Y (y) >. Edelleen tiedämme, että E(X Y y) EZ m(y) Koska luentojen mukaan E(X Y ) m(y ), kun m(y) E(X Y y), niin olemme siis päätelleet että E(X Y ) m(y ) Kohdassa b) haluamme laskea satunnaismuuttujan X odotusarvon. Käytämme tässä apuna luentojen iteroidun odotusarvon kaavaa, jonka mukaan EX EE(X Y ) Koska a)-kohdassa luimme mallista, että E(X Y ), niin saamme sijoittamalla EX EE(X Y ) E. Kohdassa c) haluamme laskea satunnaismuuttujan X varianssin. Käytämme tässä apuna luentojen kaavaa varianssille, jonka mukaan se on ehdollisen varianssin odotusarvon ja ehdollisen odotusarvon varianssin summa eli var X E var(x Y ) + var E(X Y ) 6
7 Koska a)-kohdan mukaan E(X Y ), niin var E(X Y ) var. Toistamalla a)- kohdan päätelmät, voimme todeta, että var(x Y y) var Z, kun Z N(, y ). Siispä var(x Y y) y, joten luentojen määritelmän mukaan var(x Y ) Y. Olemme siten johtaneet, että var X E var(x Y ) + var E(X Y ) EY + EY Satunnaismuuttujan Y toisen momentin laskemiseen on monta tapaa. Voimme esimerkiksi käyttää identiteettiä EY var Y + (EY ) var(w + 1) + ( EW + 1 ) var W + (EW + 1) tai mallin antamaa identiteettiä joka johtaa samaan, sillä EY E(W + 1) EW + EW + 1 EW + EW + 1 var W + (EW ) + EW + 1 var W + (EW + 1) Koska W Bin(3, 1 ), niin tiedämme luentojen perusteella, että EW sekä var W 3 1 (1 1 ) 3 4. Siispä var X EY var W + (EW + 1) (1 + 3 ) ( 5 ) Olkoon X (X 1, X ) ja Y (Y 1, Y, Y 3 ) riippumattomia standardinormaalijakautuneita satunnaisvektoreita ja olkoon Z (X 1 Y + 3, 3Y 1 X, X 1 + Y 3 ) (Z 1, Z, Z 3 ). a) Määrää satunnaisvektorin Z jakauma. (4 p) b) Selitä miksi satunnaismuuttujat Z 1 ja exp(z 3) ovat riippumattomia. ( p) Ratkaisuehdotus: Huomautus! Alla oleva ehdotus on hyvin seikkaperäinen kuvaus jokaisesta askeleesta. En luonnollisestikaan esitä, että tämä olisi mallivastaus vaan ainoastaan vastaus, jossa jokainen kohta on kirjoitettu näkyviin. Kohdassa a) haluamme selvittää satunnaisvektorin Z jakauman. Huomaamme, että Z saadaan satunnaisvektoreista X ja Y affiinina muunnoksena, sillä Z 1 X 1 Y + 3 X 1 Y 3 Z 3Y 1 X X + 3Y 1 + Z 3 X 1 + Y 3 X 1 Y 3 1 ( ) 1 Y 1 1 X1 + 3 Y X + b AX + BY + b 1 Y 3 kun A 1 1, B 1 3 ja b 3 1 7
8 Koska X Y, niin satunnaisvektori (X, Y ) noudattaa luentojen mukaan myös multinormaalijakaumaa. Siispä Z AX + BY + b ( A B ) ( ) X + b, Y eli Z on affiini muunnos multinormaalista satunnaisvektorista (X, Y ) eli Z noudattaa multinormaalijakaumaa. Luentojen mukaan jakauman täydelliseksi kuvaamiseksi tämän jälkee riittää siis kertoa odotusarvovektori EZ sekä kovarianssimatriisi Cov Z. Koska EX (, ) ja EY (,, ), niin AEX + BEY (,, ) joten 3 EZ E(AX + BY + b) AEX + BEY + b b Kovarianssimatriisin Cov Z laskemiseen käytämme luentojen tietoa Cov(AZ) A Cov ZA sekä sitä, että riippumattomien satunnaisvektorien summan kovarianssimatriisi on niiden kovarianssimatriisien summa. Koska X Y, niin tiedämme, että AX BY. Edelleen vakiovektori b (AX + BY ), joten Cov Z Cov(AX + BY + b) Cov(AX) + Cov(BY ) + Cov(b) A Cov XA + B Cov Y B + (,, ) AI A + BI 3 Y B AA + BB Satunnaisvektorien X ja Y kovarianssimatriisit tiesimme tehtävänannon mukaan olevan yksikkömatriisi I ja yksikkömatriisi I 3 vastaavasti. Olemme siis määränneet kovarianssimatriisin Cov Z lähes täysin, sillä tiedämme matriisit A ja B sekä niiden transpoosit. Siispä Cov Z AA + BB 1 ( ) Olemme näin päätelleet, että Z on multinormaalijakautunut satunnaisvektori, jonka odotusarvovektori on b ja kovarianssimatriisi kuten yllä. Kohdassa b) voimme nyt suoraan lukea kovarianssimatriisista, että cov(z 1, Z ) eli satunnaismuuttujat Z 1 ja Z ovat korreloimattomia. Koska kohdan a) nojalla (Z 1, Z ) on multinormaalijakautunut, niin luentojen mukaan Z 1 Z. Siispä niiden muunnokset ovat myös riippumattomia, eli erityisesti Z1 ja exp(z 3) ovat riippumattomia. Toinen tapa päätellä tämä on suoraan huomaamalla, että Z 1 f 1 (X 1, Y ) ja Z f (Y 1, X ) ja päättelemällä tehtävänannon perusteella, että (X 1, Y ) (Y 1, X ), voidaan myös päätellä että kysytyt muunnokset Z 1 f 1 (X 1, Y ) ja exp(z 3) exp(f (Y 1, X ) 3) ovat riippumattomia. 8
Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe (kesto 2h 30 min)
 Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe 8..7 (kesto h 3 min) Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu. Ei
Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe 8..7 (kesto h 3 min) Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu. Ei
1. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden heittojen lukumäärä, joilla tuli 1, 2, 3 tai 4.
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu. f(x, y) = k x y, kun 0 < y < x < 1,
 Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X Y Bin(Y, θ) Y Poi(λ) λ y. f X (x) (λθ)x
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
0 3 y4 dy = 3 y. 15x 2 ydx = 15. f Y (y) = 5y 4 1{0 y 1}.
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 18 Harjoitus Ratkaisuehdotuksia Tehtäväsar I 1. Satunnaismuuttujilla X Y on tkuva yhteiskauma yhteistiheysfunktiolla f
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 18 Harjoitus Ratkaisuehdotuksia Tehtäväsar I 1. Satunnaismuuttujilla X Y on tkuva yhteiskauma yhteistiheysfunktiolla f
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
0 kun x < 0, 1/3 kun 0 x < 1/4, 7/11 kun 1/4 x < 6/7, 1 kun x 1, 1 kun x 6/7,
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
Yleistä tietoa kokeesta
 Yleistä tietoa kokeesta Kurssikoe on ma 18.12. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 10.1.2018 klo 10-14, johon ilmoittaudutaan Oodissa (ilmoittautumisaika
Yleistä tietoa kokeesta Kurssikoe on ma 18.12. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 10.1.2018 klo 10-14, johon ilmoittaudutaan Oodissa (ilmoittautumisaika
Harjoitus 4 Tehtävä 1
 Harjoitus 4 Tehtävä 1 19:39» Hei olen jumissa 1a) tehtävässä. Yritin näyttää että kovarianssi on nolla siten että E(Z m(x))(m(x) h(x)) E(Z m(x))(e(m(x) h(x)) = 0. Laskuista tuli aika raskaita enkä heti
Harjoitus 4 Tehtävä 1 19:39» Hei olen jumissa 1a) tehtävässä. Yritin näyttää että kovarianssi on nolla siten että E(Z m(x))(m(x) h(x)) E(Z m(x))(e(m(x) h(x)) = 0. Laskuista tuli aika raskaita enkä heti
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3
 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
7 Kaksiulotteinen jakauma
 7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
13. Ratkaisu. Kirjoitetaan tehtävän DY hieman eri muodossa: = 1 + y x + ( y ) 2 (y )
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Differentiaaliyhtälöt, kesä 00 Tehtävät 3-8 / Ratkaisuehdotuksia (RT).6.00 3. Ratkaisu. Kirjoitetaan tehtävän DY hieman eri muodossa: y = + y + y = + y + ( y ) (y
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Differentiaaliyhtälöt, kesä 00 Tehtävät 3-8 / Ratkaisuehdotuksia (RT).6.00 3. Ratkaisu. Kirjoitetaan tehtävän DY hieman eri muodossa: y = + y + y = + y + ( y ) (y
Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ
![1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ 1. Olkoon f :, Ratkaisu. Funktion f kuvaaja välillä [ 1, 3]. (b) Olkoonε>0. Valitaanδ=ε. Kun x 1 <δ, niin. = x+3 2 = x+1, 1< x<1+δ](/thumbs/67/57751673.jpg) Matematiikan tilastotieteen laitos Differentiaalilaskenta, syksy 2015 Lisätehtävät 1 Ratkaisut 1. Olkoon f :, x+1, x 1, f (x)= x+3, x>1 Piirrä funktion kuvaa välillä [ 1, 3]. (a) Tutki ra-arvon (ε, δ)-määritelmän
Matematiikan tilastotieteen laitos Differentiaalilaskenta, syksy 2015 Lisätehtävät 1 Ratkaisut 1. Olkoon f :, x+1, x 1, f (x)= x+3, x>1 Piirrä funktion kuvaa välillä [ 1, 3]. (a) Tutki ra-arvon (ε, δ)-määritelmän
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
Johdatus tn-laskentaan torstai 16.2.2012
 Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
10 Moniulotteinen normaalijakauma
 10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
k S P[ X µ kσ] 1 k 2.
![k S P[ X µ kσ] 1 k 2. k S P[ X µ kσ] 1 k 2.](/thumbs/92/110318530.jpg) HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia: Mitä opimme?
 TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
Odotusarvo. Odotusarvon ominaisuuksia Satunnaismuuttujien ominaisuuksia 61
 3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
TKK @ Ilkka Mellin (2008) 1/5
 Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät Ratkaisuehdotuksia
 HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 14..2017 Ratkaisuehdotuksia 1. Olkoon θ positiivinen parametri, ja asetetaan 2θ 1 y exp y 2 /θ), kun y > 0 fy; θ) = 0, muuten
HY / Matematiikan ja tilastotieteen laitos Tilastollinen päättely II, kevät 2017 14..2017 Ratkaisuehdotuksia 1. Olkoon θ positiivinen parametri, ja asetetaan 2θ 1 y exp y 2 /θ), kun y > 0 fy; θ) = 0, muuten
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset
 Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
Todennäköisyyslaskenta IIa, syys lokakuu 2019 / Hytönen 3. laskuharjoitus, ratkaisuehdotukset 1. Olkoon X satunnaismuuttuja, ja olkoot a R \ {0}, b R ja Y = ax + b. (a) Olkoon X diskreetti ja f sen pistetodennäköisyysfunktio.
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa
 MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat TKK (c) Ilkka Mellin (2006) 1 Moniulotteiset satunnaismuuttujat ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat TKK (c) Ilkka Mellin (2006) 1 Moniulotteiset satunnaismuuttujat ja
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Yleistä tietoa kokeesta
 Yleistä tietoa kokeesta Kurssikoe on pe 27.10. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 1.11 klo 16-20, johon ilmoittaudutaan Oodissa (ilmoittautumisaika erilliskokeeseen
Yleistä tietoa kokeesta Kurssikoe on pe 27.10. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 1.11 klo 16-20, johon ilmoittaudutaan Oodissa (ilmoittautumisaika erilliskokeeseen
Mat Sovellettu todennäköisyyslasku A. Moniulotteiset jakaumat. Avainsanat:
 Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
Satunnaismuuttujien muunnokset ja niiden jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
9 Moniulotteinen jakauma
 9 Moniulotteinen jakauma Moniulotteisella satunnaisvektorilla voi olla useampi kuin kaksi komponenttia. Sen jakaumaa kuvaillaan samaan tapaan kuin kaksiulotteisen satunnaisvektorin jakaumaa. Suurin osa
9 Moniulotteinen jakauma Moniulotteisella satunnaisvektorilla voi olla useampi kuin kaksi komponenttia. Sen jakaumaa kuvaillaan samaan tapaan kuin kaksiulotteisen satunnaisvektorin jakaumaa. Suurin osa
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Kertausluento. Tilastollinen päättely II - 2. kurssikoe
 Kertausluento Tilastollinen päättely II - 2. kurssikoe Yleistä tietoa TP II -2. kurssikokeesta 2. kurssikoe maanantaina 6.5.2019 klo 12.00-14.30 jossakin Exactumin auditoriossa Kurssikokeeseen ilmoittaudutaan
Kertausluento Tilastollinen päättely II - 2. kurssikoe Yleistä tietoa TP II -2. kurssikokeesta 2. kurssikoe maanantaina 6.5.2019 klo 12.00-14.30 jossakin Exactumin auditoriossa Kurssikokeeseen ilmoittaudutaan
7 Kaksiulotteinen jakauma
 7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
Matematiikan ja tilastotieteen laitos Stokastiset differentiaaliyhtälöt Ratkaisuehdotelma Harjoitukseen 5
 Matematiikan ja tilastotieteen laitos Stokastiset differentiaaliyhtälöt Ratkaisuehdotelma Harjoitukseen 5 1. Näytä, että X t := Bt 3 3tB t on martingaali Brownin liikkeen B historian suhteen. Ratkaisuehdotus:
Matematiikan ja tilastotieteen laitos Stokastiset differentiaaliyhtälöt Ratkaisuehdotelma Harjoitukseen 5 1. Näytä, että X t := Bt 3 3tB t on martingaali Brownin liikkeen B historian suhteen. Ratkaisuehdotus:
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat. TKK (c) Ilkka Mellin (2004) 1
 Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Moniulotteiset satunnaismuuttujat ja jakaumat
 Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
8.1 Ehdolliset jakaumat
 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
Kertausluento. Tilastollinen päättely II - 1. kurssikoe
 Kertausluento Tilastollinen päättely II - 1. kurssikoe Yleistä tietoa TP II -1. kurssikokeesta 1. Kurssikoe on to 7.3 klo 12.00-14.30 (jossakin Exactumin auditorioista, salijako selvinnee tuolloin torstiana).
Kertausluento Tilastollinen päättely II - 1. kurssikoe Yleistä tietoa TP II -1. kurssikokeesta 1. Kurssikoe on to 7.3 klo 12.00-14.30 (jossakin Exactumin auditorioista, salijako selvinnee tuolloin torstiana).
P (X B) = f X (x)dx. xf X (x)dx. g(x)f X (x)dx.
 Yhteenveto: Satunnaisvektorit ovat kuvauksia tn-avaruudelta seillaiselle avaruudelle, johon sisältyy satunnaisvektorin kaikki mahdolliset reaalisaatiot. Satunnaisvektorin realisaatio eli otos on jokin
Yhteenveto: Satunnaisvektorit ovat kuvauksia tn-avaruudelta seillaiselle avaruudelle, johon sisältyy satunnaisvektorin kaikki mahdolliset reaalisaatiot. Satunnaisvektorin realisaatio eli otos on jokin
2. Jatkoa HT 4.5:teen ja edelliseen tehtavään: Määrää X:n kertymäfunktio F (x) ja laske sen avulla todennäköisyydet
 Tilastotieteen jatkokurssi Sosiaalitieteiden laitos Harjoitus 5 (viikko 9) Ratkaisuehdotuksia (Laura Tuohilampi). Jatkoa HT 4.5:teen. Määrää E(X) ja D (X). E(X) = 5X p i x i =0.8 0+0.39 +0.4 +0.4 3+0.04
Tilastotieteen jatkokurssi Sosiaalitieteiden laitos Harjoitus 5 (viikko 9) Ratkaisuehdotuksia (Laura Tuohilampi). Jatkoa HT 4.5:teen. Määrää E(X) ja D (X). E(X) = 5X p i x i =0.8 0+0.39 +0.4 +0.4 3+0.04
Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi on lineaarinen projektio.
 Määritelmä 4.3. Estimaattoria X(Y ) nimitetään lineaariseksi projektioksi, jos X on lineaarinen kuvaus ja E[(X X(Y )) Y] 0 }{{} virhetermi Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi
Määritelmä 4.3. Estimaattoria X(Y ) nimitetään lineaariseksi projektioksi, jos X on lineaarinen kuvaus ja E[(X X(Y )) Y] 0 }{{} virhetermi Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi
Olkoon R S otosavaruuksien R ja S karteesinen tulo: Satunnaismuuttujien X ja Y järjestetty pari (X, Y) määrittelee kaksiulotteisen satunnaismuuttujan:
 Mat-.6 Sovellettu todennäköisslaskenta B Mat-.6 Sovellettu todennäköisslaskenta B / Ratkaisut Aiheet: Moniulotteiset satunnaismuuttujat ja todennäköissjakaumat Moniulotteisia jakaumia Avainsanat: Diskreetti
Mat-.6 Sovellettu todennäköisslaskenta B Mat-.6 Sovellettu todennäköisslaskenta B / Ratkaisut Aiheet: Moniulotteiset satunnaismuuttujat ja todennäköissjakaumat Moniulotteisia jakaumia Avainsanat: Diskreetti
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M)
 MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
MATEMATIIKAN JA TILASTOTIETEEN LAITOS Analyysi I Harjoitus 7. 2. 2009 alkavalle viikolle Ratkaisuehdotuksia (7 sivua) (S.M) Luennoilla on nyt menossa vaihe, missä Hurri-Syrjäsen monistetta käyttäen tutustutaan
Todennäköisyyslaskenta, syksy Petri Koistinen Matematiikan ja tilastotieteen laitos Helsingin yliopisto
 Todennäköisyyslaskenta, syksy 2013 Petri Koistinen Matematiikan ja tilastotieteen laitos Helsingin yliopisto 14. lokakuuta 2013 2 Sisältö 1 Tapahtumat ja niiden todennäköisyydet 1 1.1 Todennäköisyyden
Todennäköisyyslaskenta, syksy 2013 Petri Koistinen Matematiikan ja tilastotieteen laitos Helsingin yliopisto 14. lokakuuta 2013 2 Sisältö 1 Tapahtumat ja niiden todennäköisyydet 1 1.1 Todennäköisyyden
Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat. Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat
 TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat Johdatus todennäköisyyslaskentaan todennäköisyysjakaumat TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat: Mitä opimme? /5 hden satunnaismuuttujan todennäköisyysjakaumat
TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat Johdatus todennäköisyyslaskentaan todennäköisyysjakaumat TKK (c) Ilkka Mellin (4) todennäköisyysjakaumat: Mitä opimme? /5 hden satunnaismuuttujan todennäköisyysjakaumat
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
H5 Malliratkaisut - Tehtävä 1
 H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa
H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Demonstraatiot III, 4.5..06. Mikä on funktion f suurin mahdollinen määrittelyjoukko, kun f(x) x? Mikä on silloin f:n arvojoukko? Etsi f:n käänteisfunktio f ja tarkista, että löytämäsi
Matematiikan peruskurssi Demonstraatiot III, 4.5..06. Mikä on funktion f suurin mahdollinen määrittelyjoukko, kun f(x) x? Mikä on silloin f:n arvojoukko? Etsi f:n käänteisfunktio f ja tarkista, että löytämäsi
Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat TKK (c) Ilkka Mellin (2005) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat Kaksiulotteiset todennäköisyysjakaumat
Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat TKK (c) Ilkka Mellin (2005) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat Kaksiulotteiset todennäköisyysjakaumat
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Tentti ja välikokeiden uusinta 8..206 Gripenberg, Nieminen, Ojanen, Tiilikainen, Weckman Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi
Matematiikan perusteet taloustieteilij oille I
 Matematiikan perusteet taloustieteilijöille I Harjoitukset syksy 2006 1. Laskeskele ja sieventele a) 3 27 b) 27 2 3 c) 27 1 3 d) x 2 4 (x 8 3 ) 3 y 8 e) (x 3) 2 f) (x 3)(x +3) g) 3 3 (2x i + 1) kun, x
Matematiikan perusteet taloustieteilijöille I Harjoitukset syksy 2006 1. Laskeskele ja sieventele a) 3 27 b) 27 2 3 c) 27 1 3 d) x 2 4 (x 8 3 ) 3 y 8 e) (x 3) 2 f) (x 3)(x +3) g) 3 3 (2x i + 1) kun, x
Keskihajonta ja korrelaatio
 Luku 4 Keskihajonta ja korrelaatio Lasse Leskelä Aalto-yliopisto 19. syyskuuta 2017 4.1 Jakauman varianssi ja keskihajonta Edellisessä luvussa opittiin, että satunnaismuuttujan odotusarvo on X:n jakauman
Luku 4 Keskihajonta ja korrelaatio Lasse Leskelä Aalto-yliopisto 19. syyskuuta 2017 4.1 Jakauman varianssi ja keskihajonta Edellisessä luvussa opittiin, että satunnaismuuttujan odotusarvo on X:n jakauman
Satunnaisluvut, satunnaisvektorit ja niiden jakaumat
 1A Satunnaisluvut, satunnaisvektorit ja niiden jakaumat Ensimmäisen harjoituksen tavoitteena on kerrata todennäköisyyden peruskäsitteitä, jotka ovat välttämättömiä stokastisten prosessien käsittelyssä.
1A Satunnaisluvut, satunnaisvektorit ja niiden jakaumat Ensimmäisen harjoituksen tavoitteena on kerrata todennäköisyyden peruskäsitteitä, jotka ovat välttämättömiä stokastisten prosessien käsittelyssä.
Ratkaisuehdotus 2. kurssikoe
 Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
Ratkaisuehdotus 2. kurssikoe 4.2.202 Huomioitavaa: - Tässä ratkaisuehdotuksessa olen pyrkinyt mainitsemaan lauseen, johon kulloinenkin päätelmä vetoaa. Näin opiskelijan on helpompi jäljittää teoreettinen
M 2 M = sup E M 2 t. E X t = lim. niin martingaalikonvergenssilauseen oletukset ovat voimassa, eli löydämme satunnaismuuttujan M, joka toteuttaa ehdon
 Matematiian ja tilastotieteen laitos Stoastiset differentiaaliyhtälöt Rataisuehdotelma Harjoituseen 7 1. Näytä, että uvaus M M M 2, un M 2 M = sup E M 2 t 2 t 0 on normi jouossa M 2 = { M : M on martingaali
Matematiian ja tilastotieteen laitos Stoastiset differentiaaliyhtälöt Rataisuehdotelma Harjoituseen 7 1. Näytä, että uvaus M M M 2, un M 2 M = sup E M 2 t 2 t 0 on normi jouossa M 2 = { M : M on martingaali
4.1 Diskreetin satunnaismuuttujan odotusarvo
 4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
Analyysi I (sivuaineopiskelijoille)
 Analyysi I (sivuaineopiskelijoille) Mika Hirvensalo mikhirve@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2017 Mika Hirvensalo mikhirve@utu.fi Luentoruudut 19 1 of 18 Kahden muuttujan funktioista
Analyysi I (sivuaineopiskelijoille) Mika Hirvensalo mikhirve@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2017 Mika Hirvensalo mikhirve@utu.fi Luentoruudut 19 1 of 18 Kahden muuttujan funktioista
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
10 Moniulotteinen normaalijakauma
 10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
Johdatus tn-laskentaan perjantai 17.2.2012
 Johdatus tn-laskentaan perjantai 17.2.2012 Kahden diskreetin muuttujan yhteisjakauma On olemassa myös monen muuttujan yhteisjakauma, ja jatkuvien muuttujien yhteisjakauma (jota ei käsitellä tällä kurssilla;
Johdatus tn-laskentaan perjantai 17.2.2012 Kahden diskreetin muuttujan yhteisjakauma On olemassa myös monen muuttujan yhteisjakauma, ja jatkuvien muuttujien yhteisjakauma (jota ei käsitellä tällä kurssilla;
Matematiikan peruskurssi 2
 Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Matematiikan peruskurssi Tentti, 9..06 Tentin kesto: h. Sallitut apuvälineet: kaavakokoelma ja laskin, joka ei kykene graaseen/symboliseen laskentaan Vastaa seuraavista viidestä tehtävästä neljään. Saat
Poisson-prosessien ominaisuuksia ja esimerkkilaskuja
 4B Poisson-prosessien ominaisuuksia ja esimerkkilaskuja Tuntitehtävät 4B1 Eksponentiaalisten odotusaikojen toistuva odottaminen. Satunnaisluvun X sanotaan noudattavan Gamma-jakaumaa parametrein k ja λ,
4B Poisson-prosessien ominaisuuksia ja esimerkkilaskuja Tuntitehtävät 4B1 Eksponentiaalisten odotusaikojen toistuva odottaminen. Satunnaisluvun X sanotaan noudattavan Gamma-jakaumaa parametrein k ja λ,
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
Luento 9: Yhtälörajoitukset optimoinnissa
 Luento 9: Yhtälörajoitukset optimoinnissa Lagrangen kerroin Oletetaan aluksi, että f, g : R R. Merkitään (x 1, x ) := (x, y) ja johdetaan Lagrangen kerroin λ tehtävälle min f(x, y) s.t. g(x, y) = 0 Olkoon
Luento 9: Yhtälörajoitukset optimoinnissa Lagrangen kerroin Oletetaan aluksi, että f, g : R R. Merkitään (x 1, x ) := (x, y) ja johdetaan Lagrangen kerroin λ tehtävälle min f(x, y) s.t. g(x, y) = 0 Olkoon
3.6 Su-estimaattorien asymptotiikka
 3.6 Su-estimaattorien asymptotiikka su-estimaattorit ovat usein olleet puutteellisia : ne ovat usein harhaisia ja eikä ne välttämättä ole täystehokkaita asymptoottisilta ominaisuuksiltaan ne ovat yleensä
3.6 Su-estimaattorien asymptotiikka su-estimaattorit ovat usein olleet puutteellisia : ne ovat usein harhaisia ja eikä ne välttämättä ole täystehokkaita asymptoottisilta ominaisuuksiltaan ne ovat yleensä
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Ratkaisu: (i) Joukko A X on avoin jos kaikilla x A on olemassa r > 0 siten että B(x, r) A. Joukko B X on suljettu jos komplementti B c on avoin.
 Matematiikan ja tilastotieteen laitos Topologia I 1. kurssikoe 26.2.2013 Malliratkaisut ja tehtävien tarkastamiset Tehtävät 1 ja 2 Henrik Wirzenius Tehtävät 3 ja 4 Teemu Saksala Jos sinulla on kysyttävää
Matematiikan ja tilastotieteen laitos Topologia I 1. kurssikoe 26.2.2013 Malliratkaisut ja tehtävien tarkastamiset Tehtävät 1 ja 2 Henrik Wirzenius Tehtävät 3 ja 4 Teemu Saksala Jos sinulla on kysyttävää
TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä
 J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.2012 klo 10 13 Ratkaisut ja pisteytysohjeet
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.01 klo 10 13 t ja pisteytysohjeet 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 x 3 3 x 1 4, (b)
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.01 klo 10 13 t ja pisteytysohjeet 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 x 3 3 x 1 4, (b)
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
Matemaattinen tilastotiede. Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto
 Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
EX1 EX 2 EX =
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
V ar(m n ) = V ar(x i ).
 Mat-.3 Stokastiset prosessit Syksy 007 Laskuharjoitustehtävät 6 Poropudas/Kokkala. Olkoon M n = X +... + X n martingaali ja M 0 = 0. Osoita, että V ar(m n ) = n V ar(x i ). i= Huomattavaa on, että muuttujia
Mat-.3 Stokastiset prosessit Syksy 007 Laskuharjoitustehtävät 6 Poropudas/Kokkala. Olkoon M n = X +... + X n martingaali ja M 0 = 0. Osoita, että V ar(m n ) = n V ar(x i ). i= Huomattavaa on, että muuttujia
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
Tilastollinen päättömyys, kevät 2017 Harjoitus 6B
 Tilastollinen päättömyys, kevät 7 Harjoitus 6B Heikki Korpela 8. helmikuuta 7 Tehtävä. Monisteen teht. 6... Olkoot Y,..., Y 5 Nµ, σ, ja merkitään S 5 i Y i Y /4. Näytä, että S/σ on saranasuure eli sen
Tilastollinen päättömyys, kevät 7 Harjoitus 6B Heikki Korpela 8. helmikuuta 7 Tehtävä. Monisteen teht. 6... Olkoot Y,..., Y 5 Nµ, σ, ja merkitään S 5 i Y i Y /4. Näytä, että S/σ on saranasuure eli sen
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe klo 10 13
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.2012 klo 10 13 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 2 x 2 3 2 3 x 1 4, (b) (x + 1)(x 2)
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.2012 klo 10 13 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 2 x 2 3 2 3 x 1 4, (b) (x + 1)(x 2)
Tilavuus puolestaan voidaan esittää funktiona V : (0, ) (0, ) R,
 Vektorianalyysi Harjoitus 9, Ratkaisuehdotuksia Anssi Mirka Tehtävä 1. ([Martio, 3.4:1]) Millä suoralla sylinterillä, jonka tilavuus on V > on pienin vaipan ja pohjan yhteenlaskettu pinta-ala? Ratkaisu
Vektorianalyysi Harjoitus 9, Ratkaisuehdotuksia Anssi Mirka Tehtävä 1. ([Martio, 3.4:1]) Millä suoralla sylinterillä, jonka tilavuus on V > on pienin vaipan ja pohjan yhteenlaskettu pinta-ala? Ratkaisu
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit
 MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 8: Newtonin iteraatio. Taso- ja avaruusintegraalit Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
Gripenberg. MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Tentti ja välikoeuusinta
 MS-A00 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Tentti ja välikoeuusinta 7.. Gripenberg Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot ja minkä kokeen suoritat! Laskin,
MS-A00 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Tentti ja välikoeuusinta 7.. Gripenberg Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot ja minkä kokeen suoritat! Laskin,
Satunnaisluvut, satunnaisvektorit ja niiden jakaumat
 1A Satunnaisluvut, satunnaisvektorit ja niiden jakaumat Ensimmäisen harjoituksen tavoitteena on kerrata todennäköisyyden peruskäsitteitä, jotka ovat välttämättömiä stokastisten prosessien käsittelyssä.
1A Satunnaisluvut, satunnaisvektorit ja niiden jakaumat Ensimmäisen harjoituksen tavoitteena on kerrata todennäköisyyden peruskäsitteitä, jotka ovat välttämättömiä stokastisten prosessien käsittelyssä.
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
8.1 Ehdolliset jakaumat
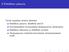 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
Epäyhtälöt ovat yksi matemaatikon voimakkaimmista
 6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
4.1. Olkoon X mielivaltainen positiivinen satunnaismuuttuja, jonka odotusarvo on
 Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
