9 Moniulotteinen jakauma
|
|
|
- Jussi Mäkinen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 9 Moniulotteinen jakauma Moniulotteisella satunnaisvektorilla voi olla useampi kuin kaksi komponenttia. Sen jakaumaa kuvaillaan samaan tapaan kuin kaksiulotteisen satunnaisvektorin jakaumaa. Suurin osa tämän luvun ideoista on ennestään tuttuja, eikä tuttuja tuloksia enää perustella uudestaan. Tilastotieteilijä tarvitsee moniulotteisia jakaumia sen takia, että hän voisi määritellä ja analysoida tilastollisia malleja.
2 Moniulotteisuudesta johtuvia uusia asioita Reunajakauma voidaan määritellä mille tahansa komponenttien osajoukolle. Ehdollisia jakaumia voidaan laskea ehdollistamalla millä tahansa komponenttien osajoukolla. Ehdollinen riippumattomuus on käsite, joka ei ole mielekäs kuin vasta dimensioissa kolmesta eteenpäin. Moniulotteisten jakaumien havainnollistaminen on hankalaa. Kuvien piirtäminen ei onnistu korkeissa dimensioissa, vaan niiden sijasta pitää luottaa kaavojen manipulointiin.
3 9.1 Satunnaisvektori Jos X 1,..., X n ovat samalla perusjoukolla Ω määriteltyjä satunnaismuuttujia, niin X = (X 1,..., X n ) on n-ulotteinen satunnaisvektori (lyh. sv). Ts. satunnaisvektori on kuvaus Ω R n siten, että X 1 (ω) X(ω) = X (ω) = (X 1 (ω),..., X n (ω)) =. X n (ω)
4 Diskreetisti jakautunut satunnaisvektori Jos kaikki satunnaisvektorin X komponentit X i ovat diskreettejä sm:ia, niin sen ptnf eli sm:ien X i yhteispistetodennäköisyysfunktio (yptnf) on f X (x) = P(X = x) = P(X 1 = x 1,..., X n = x n ). (9.1) Jos g(x ) on sv:n X reaaliarvoinen muunnos, niin sen odotusarvo saadaan kaavalla (tiedostamattoman tilastotieteilijän laki diskreetissä tapauksessa). Eg(X) = x g(x) f X (x), (9.2) mikäli kyseinen summa suppenee itseisesti
5 Jatkuvasti jakautunut satunnaisvektori Satunnaisvektorilla X on jatkuva jakauma, mikäli sillä on tiheysfunktio f X. Tämä tarkoittaa sitä, että P(X B) = f X = B B f X (x) dx, kaikilla B R n. Tällöin sen komponenteilla X 1,..., X n on jatkuva yhteisjakauma, ja tiheysfunktiota f X1,...,X n (x 1,..., x n ) = f X (x), x = (x 1,..., x n ) kutsutaan sm:ien X 1,..., X n yhteistiheysfunktioksi. (9.3)
6 Kuinka n-kertainen integraali lasketaan Edellä kyseessä on n-kertainen integraali, f X (x) dx = 1 B (x) f X (x) dx 1 dx n, B joka voidaan laskea iteroituna integraalina käyttämällä mielivaltaista integrointijärjestystä.
7 Tiedostamattoman tilastotieteilijän laki jatkuvassa tapauksessa Jos g(x) on sv:n X reaaliarvoinen muunnos, niin sen odotusarvo saadaan kaavalla Eg(X) = g(x) f X (x) dx (9.4) mikäli kyseinen integraali suppenee itseisesti. Tämä integraali voidaan laskea iteroituna integraalina käyttäen mielivaltaista integrointijärjestystä. Kun integrointijoukkoa ei merkitä näkyviin, tarkoitetaan koko avaruuden (tässä R n ) yli laskettua integraalia. Jos dimensio n 2, niin tämä merkintä ei sekaannu määrämättömän integraalin (engl. indefinite integral) merkinnän kanssa, sillä määräämättömän integraalin käsitettä käytetään vain dimensiossa yksi.
8 Ytf:n ja ykf:n välinen yhteys Jatkuvan (yhteis)jakauman tapauksessa ykf on F X (x) = x1 s 1 =... xn s n= f X (s 1,..., s n ) ds 1 ds n. Kun tätä funktiota derivoidaan osittain jokaisen argumenttinsa suhteen, nähdään että n F X (x 1,..., x n ) x 1 x n = f X (x 1,..., x n ), ainakin niissä pisteissä (x 1,..., x n ), joissa f X on jatkuva. Voidaan osoittaa, että tämä funktio kelpaa jatkuvasti jakautuneen sv:n tiheysfunktioksi (kun se jatketaan mielivaltaisesti niissä pisteissä, joissa ko. derivaatta ei ole olemassa).
9 Diskreetin ja jatkuvan sv:n yhteisjakauma Jos X on diskreetti sv, ja Y on jatkuvasti jakautunut sv, ja ne on määritelty samalla perusjoukolla Ω, niin silloin niiden yhteisjakauma voidaan esittää funktiolla f X,Y (x, y) = f X (x) f Y X (y x), jossa f X on sv:n X reunajakauman (yhteis-)ptnf, ja f Y X (y x) on sv:n Y ehdollinen (yhteis-)tf ehdolla X = x. Jos g(x, Y) on reaaliarvoinen sm, niin sen odotusarvo saadaan kaavalla Eg(X, Y) = g(x, y) f X,Y (x, y) dy, (9.5) x mikäli kyseinen odotusarvo on olemassa.
10 9.2 Odotusarvovektori ja kovarianssimatriisi Asetamme seuraavat määritelmät, mikäli kyseessä olevat odotusarvot ovat olemassa. Satunnaisvektorin X = (X 1,..., X n ) odotusarvo tai odotusarvovektori on n-komponenttinen vakiovektori EX 1 EX = E(X) = (EX 1,..., EX n ) =.. EX n
11 Satunnaismatriisin odotusarvo Dimensioltaan m n olevan satunnaismatriisin Z = Z = (Z ij ) odotusarvo tai odotusarvomatriisi on se m n-vakiomatriisi, jonka alkio (i, j) on alkion Z ij odotusarvo, ts. Z 11 Z Z 1n EZ 11 EZ EZ 1n Z 21 Z Z 2n EZ = E = EZ 21 EZ EZ 2n Z m1 Z m2... Z mn EZ m1 EZ m2... EZ mn
12 Kahden satunnaisvektorin kovarianssi Satunnaisvektorien X = (X 1,..., X n ) ja Y = (Y 1,..., Y k ) (välinen) kovarianssi on n k-matriisi cov(x, Y) = E ( (X EX)(Y EY) ) cov(x 1, Y 1 ) cov(x 1, Y 2 )... cov(x 1, Y k ) cov(x 2, Y 1 ) cov(x 2, Y 2 )... cov(x 2, Y k ) = cov(x n, Y 1 ) cov(x n, Y 2 )... cov(x n, Y k ) cov(x, Y) on matriisi, joka sisältää kaikkien parien (X i, Y j ) kovarianssit cov(x i, Y j ). Mikäli cov(x, Y) = 0, niin sanotaan, että satunnaisvektorit X ja Y eivät korreloi eli että ne ovat korreloimattomat (engl. uncorrelated).
13 Satunnaisvektorin kovarianssimatriisi Satunnaisvektorin X = (X 1,..., X n ) kovarianssimatriisi on n n-matriisi Cov(X) = cov(x, X) = E ( (X EX)(X EX) ) cov(x 1, X 1 ) cov(x 1, X 2 )... cov(x 1, X n ) cov(x 2, X 1 ) cov(x 2, X 2 )... cov(x 2, X n ) = cov(x n, X 1 ) cov(x n, X 2 )... cov(x n, X n ) Satunnaisvektorin kovarianssimatriisi on symmetrinen ja sen päälävistäjällä on komponenttisatunnaismuuttujien varianssit. Näissä merkinnöissä Cov() on yhden argumentin funktio, ja cov(, ) on kahden argumentin funktio.
14 Laskusääntöjä odotusarvolle Palautetaan mieleen, että määritelmästä odotusarvolle seuraa suoraan, että E(Z ) = (EZ). (9.6) Laskusääntö E ( AZB + C ) = A(EZ)B + C, (9.7) on voimassa kun Z on satunnaismatriisi ja A, B ja C ovat vakiomatriiseja, joiden dimensiot ovat sellaiset, että lauseke on määritelty. Ts. vakiomatriisit saadaan vetää ulos odotusarvosta, jos ne sijaitsevat matriisitulossa äärimmäisenä vasemmalla tai äärimmäisenä oikealla.
15 Riippumattomuus Mikäli Y ja Z ovat satunnaisvektoreita, ja G(Y) ja H(Z) ovat matriisiarvoisia lausekkeita, niin Y Z G(Y) H(Z). (9.8) Matriisilausekkeiden riippumattomuus tarkoittaa sitä, että kaikki matriisin G(Y) komponentit ovat riippumattomia kaikista matriisin H(Z) komponenteista. Riippumattomien satunnaisvektorien funktiot ovat keskenään riippumattomia. Koska tämä asia pätee matrisiarvoisille funktioille, se pätee tietenkin myös vektori- tai skalaariarvoisille funktioille.
16 Riippumattomien satunnaismatriisien tulon odotusarvo Riippumattomuudesta ja matriisikertolaskun määritelmästä seuraa, että Y Z E ( G(Y) H(Z) ) = E ( G(Y) ) E ( H(Z) ) (9.9) mikäli dimensiot ovat matriisitulossa G(Y) H(Z) yhteensopivat ja mikäli odotusarvot ovat olemassa.
17 Kahden satunnaisvektorin kovarianssin ominaisuuksia Jos X Y, ja X on m-komponenttinen ja Y on n-komponenttinen, niin cov(x, Y) = 0 m n. Sv:ien X ja Y kovarianssi voidaan laskea myös kaavalla cov(x, Y) = E ( XY ) (EX)(EY). Jos v R m on vakiovektori, ja X on n-komponenttinen sv, niin cov(v, X) = 0 m n, cov(x, v) = 0 n m.
18 Kahden satunnaisvektorin kovarianssin ominaisuuksia cov(x, Y) = cov(y, X). Jos X 1, X 2 ja Y ovat satunnaisvektoreita, niin cov(x 1 + X 2, Y) = cov(x 1, Y) + cov(x 2, Y), cov(y, X 1 + X 2 ) = cov(y, X 1 ) + cov(y, X 2 ). Jos A ja B ovat vakiomatriiseja ja v ja w ovat vakiovektoreja, niin cov(ax + v, BY + w) = A cov(x, Y) B. (9.10) Erityisesti Cov(AX + v) = A Cov(X)A. (9.11)
19 Esimerkki: summan kovarianssimatriisi Jos satunnaisvektorit X ja Y ovat samanpituisia, niin Cov(X + Y) = cov(x + Y, X + Y) = cov(x, X + Y) + cov(y, X + Y) = cov(x, X) + cov(x, Y) + cov(y, X) + cov(y, Y) = Cov(X) + Cov(Y) + cov(x, Y) + cov(y, X). Jos X ja Y eivät korreloi, niin cov(x, Y) = 0 ja cov(y, X) = 0. Korreloimattomille satunnaisvektoreille summan kovarianssimatriisi on summattavien satunnaisvektoreiden kovarianssimatriisien summa. Tämä pitää erityisesti paikkansa riippumattomille satunnaisvektoreille.
20 Neliömatriisin mahdollisia ominaisuuksia Neliömatriisi B on säännöllinen eli kääntyvä eli ei-singulaarinen, jos sillä on olemassa käänteismatriisi B 1 ; symmetrinen, jos B = B; positiivisesti semidefiniitti, jos v Bv 0 kaikilla v; positiivisesti definiitti, jos v Bv > 0 kaikilla v 0.
21 Definiittisyys ja ominaisarvot On olemassa matriiseja, joiden kaikki alkiot ovat positiivisia, mutta jotka eivät ole positiivisesti semidefiniittejä, kuten esim. ( ) 1 2 B =. 2 1 Valitsemalla v = ( 1, 1) saadaan v Bv = 2. Definittisyyden voi käsittää helposti ominaisarvojen etumerkkien avulla (mikäli ominaisarvot ovat tuttu käsite): Symmetrinen matriisi B on positiivisesti semidefiniitti jos ja vain jos kaikki sen ominaisarvot ovat suurempia tai yhtä kuin nolla. Symmetrinen matriisi B on positiivisesti definiitti jos ja vain jos kaikki sen ominaisarvot ovat aidosti suurempia kuin nolla. Myös Sylvesterin kriteeri (jos tuttu) on toimiva tapa selvittää definiittisyys
22 Satunnaisvektorin kovarianssimatriisin definiittisyys Lause 9.2 Sv:n X kovarianssimatriisi on symmetrinen ja positiivisesti semidefiniitti matriisi. Jos se ei ole positiivisesti definiitti, niin sv:n X komponenttien välillä on lineaarisia sidosehtoja, eli X saa todennäköisyydellä yksi arvoja vain tietyltä kiinteältä hypertasolta. Seuraus: Jos Cov X ei ole positiivisesti definiitti, niin X:llä ei voi olla jatkuva jakauma, sillä hypertaso on alempiulotteisena pintana nollamittainen. Huomaa analogia satunnaismuuttujan Z varianssin var(z) ominaisuuksien kanssa.
23 Todistus Kovarianssimatriisin symmetrisyys seuraa sen määritelmästä. Positiivinen semidefiniittisyys seuraa siitä, että v Cov(X)v = v E ( (X EX)(X EX) ) v = E ( v (X EX)(X EX) v ) ( ( ) ) 2 = E v (X EX) 0, sillä ei-negatiivisen sm:n odotusarvo on ei-negatiivinen. Jos kovarianssimatriisi ei ole positiivisesti definiitti, niin on olemassa v 0 siten, että ( ( ) ) 2 0 = v Cov(X) v = E v (X EX), joten todennäköisyydellä yksi on v (X EX) = 0.
24 9.3 Ehdolliset jakaumat, kertolaskusääntö ja ehdollinen odotusarvo Tarkastellaan sv:ia Z, jonka r ensimmäistä koordinaattia muodostavat sv:n X ja loput s koordinaattia sv:n Y, Z = (X, Y) = (X 1,..., X r, Y 1,..., Y s ). Ehdolliset jakaumat Y (X = x) ja X (Y = y) hallitaan tutuilla kaavoilla: f Y X (y x) = f X,Y(x, y) f X (x), f X Y (x y) = f X,Y(x, y). f Y (y) Miten reunajakaumien tiheydet lasketaan? Pitääkö kaikkien komponenttien olla joko disreettejä tai jatkuvia?
25 Diskreettejä vai jatkuvia komponentteja? Oletamme, että sv:n Z = (X, Y) yhteisjakauman esittää tiheys f Z (z) = f X,Y (x, y), z = (x, y). Sallimme sen tilanteen, että jotkut Z:n koordinaatit ovat diskreettejä sm:ia ja lopuilla on jatkuva yhteisjakauma.
26 Marginalisointi: yhteisjakaumasta reunajakaumaan Osavektorin X:n reunajakauman esittää tiheys f X, joka saadaan summaamalla pois tiheydestä f X,Y sv:n Y diskreetit komponentit ja integroimalla pois sen jatkuvat komponentit. Merkintöjä väärinkäyttämällä, f X (x) = f X,Y (x, y) dy, (9.12) missä integraalimerkki tarkoittaa summaamista diskreettien komponenttien kohdalla. X:n jakauma saadaan marginalisoimalla yhteisjakaumasta. Vastaavasti f Y saadaan kaavalla f Y (y) = f X,Y (x, y) dx.
27 Marginalisointi, kun komponentit ovat hujan hajan vektorissa Z Edellä marginalisoitiin satunnaisvektorin Z = (X, Y) yhteisjakaumasta joko ensimmäisten komponenttien X tai viimeisten komponenttien Y reunajakauma. Se tilanne, missä pitää reunajakauma pitää etsiä mielivaltaiselle osajoukolle Z:n komponentteja saadaan palautettua edelliseen tilanteeseen permutoimalla koordinaatteja. Menettely selviää esimerkistä.
28 Esimerkki kahden muuttujan reunajakauman laskemisesta nejän muuttujan yhteisjakaumasta Olkoot U ja V diskreettejä sm:ia ja (X, Y ) jatkuvasti jakautunut sv. Yhteisjakauman esittää tiheys f U,V,X,Y (u, v, x, y) Etsitään komponenttien V ja Y reunajakauma (ts. niiden yhteisjakauma). Jotta päästäisiin soveltamaan em. kaavoja, permutoidaan V ja Y ensimmäisiksi f V,Y,U,X (v, y, u, x) = f U,V,X,Y (u, v, x, y), (kaikilla kyseeseen tulevilla arvoilla u, v, x, y). Tämän jäkeen vektori (V, Y ) on ensimmäisenä, joten sm:ien V ja Y yhteisjakauman esittää tiheys f V,Y (v, y) = f V,Y,U,X (v, y, u, x) dx, u
29 Esimerkki jatkuu Nyt muistetaan, että f V,Y,U,X (v, y, u, x) on sama asia kuin f U,V,X,Y (u, v, x, y). Siispä sm:ien V ja Y yhteisjakauman esittää tiheys f V,Y (v, y) = f U,V,X,Y (u, v, x, y) dx. u Käytännön laskuissa siirryttäisiin suoraan viimeiseen vaiheeseen ilman välissä esitettyjä permutointivälivaiheita. Diskreetit komponentit yksinkertaisesti marginalisoidaan pois summaamalla ja jatkuvat komponentit integroimalla.
30 Kertolaskusääntö Kertolaskusääntö (eli ketjusääntö) on voimassa, eli f X,Y (x, y) = f X (x) f Y X (y x) = f Y (y) f X Y (x y). Kertolaskusääntöä voidaan iteroida. Oletetaan, että sv X = (U, V). Tällöin minkä takia f U,V (u, v) = f U (u) f V U (v u), f U,V,Y (u, v, y) = f U (u) f V U (v u) f Y U,V (y u, v).
31 Lisää kertolaskusäännöstä Kertolaskusäännön soveltamista voidaan jatkaa, kunnes ollaan päästy skalaarikomponentteihin asti. Esimerkiksi neljän sm:n U, V, X, Y tiheys voidaan esittää muodossa f U,V,X,Y (u, v, x, y) = f U (u) f V U (v u) f X U,V (x u, v) f Y X,U,V (y x, u, v). Kertolaskusääntöä voidaan soveltaa yhtä hyvin käyttämällä jotakin muuta sm:ien permutaatiota.
32 Kertolaskusääntö pätee myös ehdollisille jakaumille Esim. f U,V Y (u, v y) = f U,V,Y(u, v, y) f Y (y) = f U,Y(u, y) f Y (y) = f U Y (u y) f V U,Y (v u, y). f U,V,Y (u, v, y) f U,Y (u, y) Ensimmäinen tekijä on komponentin U reunajakauma ehdollisessa yhteisjakaumassa (ehtona Y = y) ja toisena tekijänä komponentin V ehdollinen jakauma ehdolla U = u (kun edelleen ehdollistetaan arvolla Y = y).
33 Marginalisointi ehdollisesta yhteisjakaumasta Ehdollisen jakauman reunajakauman voi laskea marginalisoimalla tuttuun tapaan ehdollista yhteisjakaumaa. Esim. f U Y (u y) = f U,Y(u, y) = 1 f U,V,Y (u, v, y) dv f Y (y) f Y (y) = f U,V Y (u, v y) dv.
34 Merkintöjä mielellään yksinkertaistetaan Kun jakaumien välisiä yhteyksiä johdetaan tähän tapaan kertolaskukaavan ja marginalisoinnin kautta, niin tiheysfunktioiden alaindeksit jätetään usein kirjoittamatta, koska ne selviävät tiheysfunktion argumenteista. Muussa tapauksessa kaikki argumentit joudutaan kirjoittamaan kahteen kertaan: alaindekseissä esiintyvät satunnaismuuttujat (tai -vektorit) ja funktion argumentteina niiden mahdolliset arvot. Tämä merkintöjen väärinkäyttö ei johda sekaannukseen, kunhan pidetään mielessä, että esim. f (x), f (y), f (x y) ja f (y x) ovat tyypillisesti kaikki eri funktioita.
35 Ehdollistaminen satunnaisvektorin kiinteällä arvolla Seuraavassa g = (g 1,..., g n ), kun n 1, on jokin (vektoriarvoinen) muunnos. Satunnaisvektorin g(x, Y) ehdollinen odotusarvo(vektori) ehdolla X = x määritellään siten, että se on satunnaisvektorin g(x, Y) odotusarvovektori, kun Y:n jakaumana käytetään ehdollista jakaumaa f Y X ( x). Merkintöjä väärinkäyttämällä E(g(X, Y) X = x) = g(x, y) f Y X (y x) dy. Tässä integraalimerkki voi tarkoittaa summausta joidenkin vektorin y komponenttien suhteen.
36 Ehdollistaminen satunnaisvektorilla Jos ehdollistetaan satunnaisvektorilla X, niin satunnaisvektori E(g(X, Y) X) määritellään niin, että se on m(x), kun m(x) = E(g(X, Y) X = x), Edellä funktion m määritelmä jatketaan tarvittaessa nollavektoriksi niillä argumentin arvoilla, jolla se ei luonnostaan ole määritelty.
37 Ehdollinen kovarianssimatriisi Satunnaisvektorin g(x, Y) ehdollinen kovarianssimatriisi ehdolla X = x määritellään satunnaisvektorin g(x, Y) kovarianssimatriisina, kun Y:n jakaumana käytetään ehdollista jakaumaa f Y X ( x). Voidaan käyttää merkintää Cov(g(X, Y) X = x). Jos ehdollistetaan satunnaisvektorilla X, niin ehdollinen kovarianssimatriisi on satunnaismatriisi, ja sitä merkitään Cov(g(X, Y) X).
38 9.4 Ehdollinen riippumattomuus Palautetaan mieleen, mitä (ei-ehdollinen) riippumattomuus tarkoittaa. Satunnaisvektorit X ja Y ovat riippumattomia, jos kaikilla argumenteilla x, y. f X,Y (x, y) = f X (x) f Y (y). Vastaavasti satunnaisvektorit X 1,..., X n ovat riippumattomia, jos kaikilla argumenteilla. f X1,...,X n (x 1,..., x n ) = f X1 (x 1 ) f Xn (x n )
39 Ehdollinen riippumattomuus Määritelmä 9.2 Satunnaisvektorit X ja Y ovat riippumattomia ehdolla Z, mikä voidaan merkitä (X Y) Z, jos ne ovat riippumattomia niiden ehdollisessa yhteisjakaumassa ehdolla Z = z kaikilla z, ts. mikäli f X,Y Z (x, y z) = f X Z (x z) f Y Z (y z), kaikilla x, y ja z (9.13) Vastaavasti, satunnaisvektorit X 1,..., X n ovat riippumattomia ehdolla Z, mikäli f X1,...,X n Z(x 1,..., x n z) = kaikilla x 1,..., x n ja kaikilla z. n f Xi Z(x i z) i=1
40 Riippumattomuus ja ehdollinen riippumattomuus ovat eri asioita Ehdollisesti riippumattomat satunnaisvektorit eivät tyypillisesti ole marginaalisesti riippumattomia, eli riippumattomia niiden (reuna-)yhteisreunajakaumassa. Esim. jos (X Y) Z, niin f X,Y (x, y) = f X,Y Z (x, y z) f Z (z) dz = f X Z (x z) f Y Z (y z) f Z (z) dz, eikä tämä tyypillisesti enää faktoroidu.
41 9.5 Tilastollisia malleja Tilastolliseen päättelyyn on kaksi pääasiallista lähestymistapaa: ns. frekventistinen päättely ja Bayes-päättely. Ne molemmat perustuvat uskottavuusfunktion käyttöön. Jotta uskottavuusfunktio saataisiin selville, pitää selvittää havaintosatunnaisvektorin tiheys (esim. ypntf tai ytf).
42 Tilastollisen päättelyn perusasetelma Meillä on numeerinen aineisto vektorin y = (y 1,..., y n ) muodossa. Ennen havaintojen tekoa aineiston arvot ovat epävarmoja (mittausvirheiden, populaation luonnollisen vaihtelun tms. syyn takia). Mallinnamme tilanteen niin, että y on jollakin perusjoukolla Ω määritellyn satunnaisvektorin Y havaittu arvo, ts. y = Y(ω act ), jossa ω act on todennäköisyysmallissa aktualisoitunut alkeistapaus.
43 Tilastollinen malli Tyypillisesti vektorin Y jakauma mallinnetaan parametrisella mallilla, jossa on yksi tai useampia parametreja θ 1,..., θ p, jotka kootaan parametrivektoriksi θ. Kun parametrivektorin arvo on kiinnitetty, niin tilastollisessa mallissa sv:n Y jakauman esittää tiheys y f (y θ). Kiinnostuksen kohteena on sv:n Y jakauma. Sitä voidaan arvoida, jos ensin arvioidaan eli estimoidaan tuntematonta parametrivektoria θ.
44 Uskottavuusfunktio Kun aineisto y on havaittu, ja havaittua arvoa käytetään funktion f (y θ) ensimmäisenä argumenttina, niin funktiota θ f (y θ) kutsutaan uskottavuusfunktioksi (engl. likelihood function). Tässä yhteydessä tiheysfunktiosta saatetaan jättää pois kertoimia, jotka eivät riipu parametrivektorista θ, ja silti kyseistä funktiota edelleen kutsutaan uskottavuusfunktioksi.
45 Frekventistinen päättely Ns. klassisessa eli frekventistisessä tilastotieteessä parametrivektoria θ pidetään tuntemattomana vakiona, josta tiedetään vain, missä joukossa (eli parametriavaruudessa) sen arvot voivat olla. Tällöin merkintään f (y θ) ei liitetä tulkintaa ehdollisena jakaumana, koska parametrivektorille ei ole olemassa mitään todennäköisyysjakaumaa. Tyypillisempi merkintä olisikin f (y; θ). Uskottavuusfunktiota esim. maksimoidaan, jolloin saadaan määriteltyä suurimman uskottavuuden estimaatti.
46 Bayes-päättely Bayes-päättelyssä parametrivektoria pidetään satunnaisvektorin Θ arvona. Funktio f (y θ) ja ehdollinen jakauma f Y Θ (y θ) samastetaan. Bayes-päättelyssä tilastollisessa mallissa tarvitaan uskottavuusfunktion lisäksi reunajakauma vektorille Θ. Tätä kutsutaan priorijakaumaksi. Sen on tarkoitus kuvata ennen havaintoja olevaa tietoa parmetrien järkevistä arvoista.
47 Bayes-päättely: uskottavuusfunktiosta ja priorista posterioriin Parametrivektorin ja havaintovektorin yhteisjakauman esittää tiheys (y, θ) f Θ,Y (θ, y) = f Θ (θ) f Y Θ (y θ). Kun on saatu havainto Y = y, niin tilastolliset päätelmät tehdään karakterisoimalla parametrivektorin posteriorijakaumaa, joka on ehdollinen jakauma f Θ Y (θ y) = f Θ,Y(θ, y) f Y (y) = f Θ(θ) f Y Θ (y θ) fθ (t) f Y Θ (y t) dt
48 Mihin tilastotieteessä tarvitaan moniulotteisia jakaumia? Kummassakin tilastollisen päättelyn lähestymistavassa tarvitaan konkreettinen kaava uskottavuusfunktiolle. Uskottavuusfunktio on havaintosatunnaisvektorin yhteisjakauman tiheys (esim. yptnf tai ytf) ajateltuna tuntemattoman parametrivektorin funktiona, kun havainnot on siihen sijoitettu. Tämän takia tilastotieteilijän pitää osata johtaa moniulotteisten satunnaisvektoreiden tiheyksiä. Monisteessa on tästä joitakin esimerkkejä.
49 9.6 Tiheysfunktion muuntokaava Tarkastelemme diffeomorfisimia g : A B, jossa A, B R n ovat avoimia joukkoja. Tällöin g:llä on käänteisfunktio h : B A, ja sekä g että h ovat jatkuvasti derivoituvia. Näiden kuvausten komponenttifunktiot ovat g = (g 1,..., g n ), h = (h 1,..., h n ). Nämä funktiot määrittelevät bijektiivisen vastaavuuden koordinaattien x ja y välillä kaavoilla y = g(x) x = h(y). Tätä ajatusta voidaan merkitä vaihtoehtoisesti kaavoilla y = y(x) x = x(y).
50 Merkintä osittaisderivaatoille Otamme käyttöön merkinnän D i h j (y) tarkoittamaan reaaliarvoisen funktion h j osittaisderivaattaa sen i:nnen argumentin suhteen pisteessä y, ts. D i h j (y) = y i h j (y).
51 Derivaattamatriisi ja jacobiaani Kuvauksen h = (h 1,..., h n ) derivaatta tai derivaattamatriisi (tai Jacobin matriisi) pisteessä y B on D 1 h 1 (y) D 2 h 1 (y)... D n h 1 (y) D 1 h 2 (y) D 2 h 2 (y)... D n h 2 (y) D 1 h n (y) D 2 h n (y)... D n h n (y) Kuvauksen h jacobiaani, eli Jacobin determinantti eli funktionaalideterminantti J h (y) = x y = (x 1,..., x n ) (y 1,..., y n ) on derivaattamatriisin determinantti.
52 Tiheysfunktion muuntokaava Lause 9.3 Jos g : A B on diffeomorfismi, h : B A on sen käänteiskuvaus, eli h = g 1, ja sv:lla X on jatkuva jakauma, ja P(X A) = 1, niin sv:lla Y = g(x) on jatkuva jakauma tf:lla ja nolla muualla. f Y (y) = f X (h(y)) J h (y), kun y B, Todistus on suora seuraus n-ulotteisten integraalien muuntokaavasta (jossa integraali pitää ymmärtää Lebesguen integraaliksi).
53 Muistisääntö Tiheysfunktion muuntokaava (diffeomorfismille) kannattaa pitää mielessään muodossa f X (x) x = f Y (y) y, kun (9.14) y = g(x) x = h(y), x A, y B (9.15)
54 Tiheysfunktion muuntuminen affiinissa muunnoksessa Jos A on vakiomatriisi ja b on vakiovektori siten, että seuraavassa kaavassa dimensiot ovat yhteensopivia, niin funktiota g(x) = Ax + b, x R n. kutsutaan affiiniksi muunnokseksi. Jos A on kääntyvä matriisi (jolloin se on neliömatriisi), niin tämän kuvauksen käänteiskuvaus on myös affiini, sillä y = g(x) = Ax + b x = A 1 (y b) = h(y)
55 Muuntokaava affiinille kuvaukselle jatkoa Kuvauksen h(y) = A 1 (y b) derivaattamatriisi on A 1, joten jacobiaaniksi saadaan J h (y) = x y = det(a 1 ) = 1 det(a). Jos X on n-ulotteinen sv, jolla on jatkuva jakauma, ja sv Y määritellään kaavalla Y = g(x), niin muistisäännöstä f X (x) x = f Y (y) y saadaan tulos f Y (y) = f X (x) x y = f X(A 1 (y b)) 1 det(a).
56 9.7 Satunnaisvektorin momenttiemäfunktio Määritelmä 9.3 Satunnaisvektorin X = (X 1,..., X n ) momenttiemäfunktio, eli satunnaismuuttujien X 1,..., X n yhteismomenttiemäfunktio on ( n M(t) = M X (t) = E exp(t X) = E exp t j X j ), niillä t = (t 1,..., t n ) R n, joilla odotusarvo on määritelty. Sv:n X kumulanttiemäfunktio (eli sm:ien X 1,... X n yhteiskumulanttiemäfunktio) on K(t) = K X (t) = ln M X (t), niillä t R n, joilla M(t) on määritelty. j=1
57 Momenttiemäfunktion ominaisuuksia Lause 9.4 Jos M X (t) on olemassa jossakin epätyhjässä origon ympäristössä, niin M X määrää sv:n X jakauman. Kertaluvun (k 1,..., k n ) momentti saadaan laskettuna tiettynä momenttiemäfunktion osittaisderivaattana (ks. moniste).
58 Osista kootun satunnaisvektorin momenttiemäfunktio Lause 9.6 Olkoon X = (Y, Z) sellainen sv, että sen momenttiemäfunktio M X (t) on olemassa jossakin origon ympäristössä. Olkoon t = (u, v) ositettu samandimensioisiin osiin kuin Y and Z. Tällöin (a) Sv:ien Y ja Z momenttiemäfunktiot ovat M Y (u) = M X (u, 0), M Z (v) = M X (0, v). (b) Y Z jos ja vain jos kaikilla riittävän pienillä u ja v. M X (u, v) = M Y (u) M Z (v). Todistus taululla. Hankalinta on todistaa, että riippumattomuus seuraa momenttiemäfunktion jakautumisesta tekijöihin.
1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X Y Bin(Y, θ) Y Poi(λ) λ y. f X (x) (λθ)x
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 017 Harjoitus 5 Ratkaisuehdotuksia Tehtäväsarja I 1. Jatketaan luentojen esimerkkiä 8.3. Oletetaan kuten esimerkissä X
Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe (kesto 2h 30 min)
 Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe 8..7 (kesto h 3 min) Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu. Ei
Matemaattisten tieteiden kandiohjelma / MTL Todennäköisyyslaskenta IIb Kurssikoe 8..7 (kesto h 3 min) Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu. Ei
0 3 y4 dy = 3 y. 15x 2 ydx = 15. f Y (y) = 5y 4 1{0 y 1}.
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 18 Harjoitus Ratkaisuehdotuksia Tehtäväsar I 1. Satunnaismuuttujilla X Y on tkuva yhteiskauma yhteistiheysfunktiolla f
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 18 Harjoitus Ratkaisuehdotuksia Tehtäväsar I 1. Satunnaismuuttujilla X Y on tkuva yhteiskauma yhteistiheysfunktiolla f
Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu. f(x, y) = k x y, kun 0 < y < x < 1,
 Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
Todennäköisyyslaskenta, 2. kurssikoe 7.2.22 Sallitut apuvälineet: MAOL-taulukot, kirjoitusvälineet, laskin sekä itse laadittu, A4-kokoinen lunttilappu.. Satunnaismuuttujien X ja Y yhteistiheysfunktio on
7 Kaksiulotteinen jakauma
 7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
8.1 Ehdolliset jakaumat
 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
10 Moniulotteinen normaalijakauma
 10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
 Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe 18.1.15 Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II. kurssikoe 18.1.15 Sallitut apuvälineet: kirjoitusvälineet, laskin sekä käsinkirjoitettu, A4-kokoinen lunttilappu ja MAOL taulukkokirjaa
1. Tilastollinen malli??
 1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
0 kun x < 0, 1/3 kun 0 x < 1/4, 7/11 kun 1/4 x < 6/7, 1 kun x 1, 1 kun x 6/7,
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä niistä
7 Kaksiulotteinen jakauma
 7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
7 Kaksiulotteinen jakauma Diskreetti kaksiulotteinen jakauma ks. luku 3. Uutta asiaa tässä kappaleessa: jatkuva kaksiulotteinen jakauma satunnaisvektorin muunnoksen odotusarvo odotusarvovektori ja kovarianssimatriisi
Todennäköisyyslaskenta, syksy Petri Koistinen Matematiikan ja tilastotieteen laitos Helsingin yliopisto
 Todennäköisyyslaskenta, syksy 2013 Petri Koistinen Matematiikan ja tilastotieteen laitos Helsingin yliopisto 14. lokakuuta 2013 2 Sisältö 1 Tapahtumat ja niiden todennäköisyydet 1 1.1 Todennäköisyyden
Todennäköisyyslaskenta, syksy 2013 Petri Koistinen Matematiikan ja tilastotieteen laitos Helsingin yliopisto 14. lokakuuta 2013 2 Sisältö 1 Tapahtumat ja niiden todennäköisyydet 1 1.1 Todennäköisyyden
1. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden heittojen lukumäärä, joilla tuli 1, 2, 3 tai 4.
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta II, syksy 206 Kurssikoe 28.0.206 Ratkaisuehdotuksia. Kuusisivuista noppaa heitetään, kunnes saadaan silmäluku 5 tai 6. Olkoon X niiden
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
8.1 Ehdolliset jakaumat
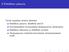 8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
8 Ehdollinen jakauma Tämän kappaleen tärkeitä käsitteitä: Ehdollinen jakauma; ehdollinen ptnf/tf. Kertolaskusääntö eli ketjusääntö yhteisjakauman esittämiseksi. Ehdollinen odotusarvo ja ehdollinen varianssi.
Odotusarvo. Odotusarvon ominaisuuksia Satunnaismuuttujien ominaisuuksia 61
 3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
3.3. Satunnaismuuttujien ominaisuuksia 61 Odotusarvo Määritelmä 3.5 (Odotusarvo) Olkoon X diskreetti satunnaismuuttuja, jonka arvojoukko on S ja todennäköisyysfunktio f X (x). Silloin X:n odotusarvo on
Yleistä tietoa kokeesta
 Yleistä tietoa kokeesta Kurssikoe on ma 18.12. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 10.1.2018 klo 10-14, johon ilmoittaudutaan Oodissa (ilmoittautumisaika
Yleistä tietoa kokeesta Kurssikoe on ma 18.12. klo 12.00-14.30 (jossakin auditorioista). Huomaa tasatunti! Seuraava erilliskoe on ke 10.1.2018 klo 10-14, johon ilmoittaudutaan Oodissa (ilmoittautumisaika
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3
 Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
Todennäköisyyslaskennan ja tilastotieteen peruskurssi Esimerkkikokoelma 3 Aiheet: Satunnaisvektorit ja moniulotteiset jakaumat Tilastollinen riippuvuus ja lineaarinen korrelaatio Satunnaisvektorit ja moniulotteiset
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Mitkä seuraavista funktioista F, F, F ja F 4 ovat kertymäfunktioita? Mitkä
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
10 Moniulotteinen normaalijakauma
 10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
10 Moniulotteinen normaalijakauma Tässä luvussa tarkastellaan normaalijakauman moniulotteista yleistystä eli moniulotteista (eli monimuuttujaista) normaalijakaumaa (engl. multivariate normal distribution).
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Inversio-ongelmien laskennallinen peruskurssi Luento 7
 Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
Inversio-ongelmien laskennallinen peruskurssi Luento 7 Kevät 2012 1 Tilastolliset inversio-ongelmat Tilastollinen ionversio perustuu seuraaviin periaatteisiin: 1. Kaikki mallissa olevat muuttujat mallinnetaan
4.1 Diskreetin satunnaismuuttujan odotusarvo
 4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
4 Odotusarvo Seuraavaksi kertaamme, miten satunnaismuuttujan odotusarvo (sv. väntevärde) määritellään diskreetissä ja jatkuvassa tapauksessa. Odotusarvolle käytetään englannikielisessä kirjallisuudessa
P (X B) = f X (x)dx. xf X (x)dx. g(x)f X (x)dx.
 Yhteenveto: Satunnaisvektorit ovat kuvauksia tn-avaruudelta seillaiselle avaruudelle, johon sisältyy satunnaisvektorin kaikki mahdolliset reaalisaatiot. Satunnaisvektorin realisaatio eli otos on jokin
Yhteenveto: Satunnaisvektorit ovat kuvauksia tn-avaruudelta seillaiselle avaruudelle, johon sisältyy satunnaisvektorin kaikki mahdolliset reaalisaatiot. Satunnaisvektorin realisaatio eli otos on jokin
Maximum likelihood-estimointi Alkeet
 Maximum likelihood-estimointi Alkeet Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Maximum likelihood-estimointi p.1/20 Maximum Likelihood-estimointi satunnaismuuttujan X
Maximum likelihood-estimointi Alkeet Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Maximum likelihood-estimointi p.1/20 Maximum Likelihood-estimointi satunnaismuuttujan X
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (006) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Epäyhtälöt ovat yksi matemaatikon voimakkaimmista
 6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
6 Epäyhtälöitä Epäyhtälöt ovat yksi matemaatikon voimakkaimmista työvälineistä. Yhtälö a = b kertoo sen, että kaksi ehkä näennäisesti erilaista asiaa ovat samoja. Epäyhtälö a b saattaa antaa keinon analysoida
Moniulotteisia todennäköisyysjakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (007) 1 Moniulotteisia todennäköisyysjakaumia >> Multinomijakauma Kaksiulotteinen
2. Uskottavuus ja informaatio
 2. Uskottavuus ja informaatio Aluksi käsittelemme uskottavuus- ja log-uskottavuusfunktioita Seuraavaksi esittelemme suurimman uskottavuuden estimointimenetelmän Ensi viikolla perehdymme aiheeseen lisääkö
2. Uskottavuus ja informaatio Aluksi käsittelemme uskottavuus- ja log-uskottavuusfunktioita Seuraavaksi esittelemme suurimman uskottavuuden estimointimenetelmän Ensi viikolla perehdymme aiheeseen lisääkö
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 9 1 Implisiittinen derivointi Tarkastellaan nyt yhtälöä F(x, y) = c, jossa x ja y ovat muuttujia ja c on vakio Esimerkki tällaisesta yhtälöstä on x 2 y 5 + 5xy = 14
Matematiikan tukikurssi Kurssikerta 9 1 Implisiittinen derivointi Tarkastellaan nyt yhtälöä F(x, y) = c, jossa x ja y ovat muuttujia ja c on vakio Esimerkki tällaisesta yhtälöstä on x 2 y 5 + 5xy = 14
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Sovellettu todennäköisyyslaskenta B Antti Rasila 21. syyskuuta 2007 Antti Rasila () TodB 21. syyskuuta 2007 1 / 19 1 Satunnaismuuttujien riippumattomuus 2 Jakauman tunnusluvut Odotusarvo Odotusarvon ominaisuuksia
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (005) 1 Moniulotteisia todennäköisyysjakaumia Multinomijakauma Kaksiulotteinen normaalijakauma TKK (c) Ilkka
Luento 9: Yhtälörajoitukset optimoinnissa
 Luento 9: Yhtälörajoitukset optimoinnissa Lagrangen kerroin Oletetaan aluksi, että f, g : R R. Merkitään (x 1, x ) := (x, y) ja johdetaan Lagrangen kerroin λ tehtävälle min f(x, y) s.t. g(x, y) = 0 Olkoon
Luento 9: Yhtälörajoitukset optimoinnissa Lagrangen kerroin Oletetaan aluksi, että f, g : R R. Merkitään (x 1, x ) := (x, y) ja johdetaan Lagrangen kerroin λ tehtävälle min f(x, y) s.t. g(x, y) = 0 Olkoon
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Mat Sovellettu todennäköisyyslasku A. Moniulotteiset jakaumat. Avainsanat:
 Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
Mat-.9 Sovellettu todennäköisyyslasku A Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Moniulotteiset jakaumat Diskreetti jakauma, Ehdollinen jakauma, Ehdollinen odotusarvo, Jatkuva
TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä
 J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
J. Virtamo 38.3143 Jonoteoria / Todennäköisyyslaskenta 1 TODENNÄKÖISYYSLASKUN KERTAUS Peruskäsitteitä Otosavaruus S S on satunnaiskokeen E kaikkien mahdollisten alkeistapahtumien e joukko. Esim. 1. Noppaa
4.2.2 Uskottavuusfunktio f Y (y 0 X = x)
 Kuva 4.6: Elektroniikassa esiintyvän lämpökohinan periaate. Lämpökohinaa ε mallinnetaan additiivisella häiriöllä y = Mx + ε. 4.2.2 Uskottavuusfunktio f Y (y 0 X = x) Tarkastellaan tilastollista inversio-ongelmaa,
Kuva 4.6: Elektroniikassa esiintyvän lämpökohinan periaate. Lämpökohinaa ε mallinnetaan additiivisella häiriöllä y = Mx + ε. 4.2.2 Uskottavuusfunktio f Y (y 0 X = x) Tarkastellaan tilastollista inversio-ongelmaa,
l (φ; y) = l(θ(φ); y) Toinen derivaatta saadaan tulon derivaatan laskusäännöllä Uudelleenparametroidun mallin Fisherin informaatio on
 HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 018 Harjoitus B Ratkaisuehdotuksia Tehtäväsarja I 1 (Monisteen tehtävä 14) Olkoon f Y (y; θ) tilastollinen malli, jonka
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Johdatus tn-laskentaan torstai 16.2.2012
 Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi on lineaarinen projektio.
 Määritelmä 4.3. Estimaattoria X(Y ) nimitetään lineaariseksi projektioksi, jos X on lineaarinen kuvaus ja E[(X X(Y )) Y] 0 }{{} virhetermi Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi
Määritelmä 4.3. Estimaattoria X(Y ) nimitetään lineaariseksi projektioksi, jos X on lineaarinen kuvaus ja E[(X X(Y )) Y] 0 }{{} virhetermi Lause 4.2. Lineearinen pienimmän keskineliövirheen estimaattoi
Satunnaismuuttujien muunnokset ja niiden jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2007) 1 Satunnaismuuttujien muunnokset ja
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat. TKK (c) Ilkka Mellin (2004) 1
 Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Johdatus todennäköisyyslaskentaan Satunnaismuuttujien muunnokset ja niiden jakaumat TKK (c) Ilkka Mellin (2004) 1 Satunnaismuuttujien muunnokset ja niiden jakaumat Satunnaismuuttujien muunnosten jakaumat
Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia. Moniulotteisia todennäköisyysjakaumia: Mitä opimme?
 TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia Johdatus todennäköisyyslaskentaan Moniulotteisia todennäköisyysjakaumia TKK (c) Ilkka Mellin (4) Moniulotteisia todennäköisyysjakaumia: Mitä
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
Sovellettu todennäköisyyslaskenta B Antti Rasila 4. lokakuuta 2007 Antti Rasila () TodB 4. lokakuuta 2007 1 / 17 1 Moniulotteiset todennäköisyysjakaumat Johdanto Kaksiulotteiset satunnaismuuttujat Kaksiulotteisen
3.1 Kaksiulotteinen satunnaisvektori ja sen jakauma
 3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
3 Yhteisjakauma Kappaleessa 2 tarkastelimme aina yhtä satunnaismuuttujaa kerrallaan. Tässä kappaleessa näemme, miten aikaisemmat käsitteet yleistyvät siihen tilanteeseen, jossa samalla perusjoukolla on
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2018 Harjoitus 3 Ratkaisuehdotuksia.
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy 08 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var
Mallipohjainen klusterointi
 Mallipohjainen klusterointi Marko Salmenkivi Johdatus koneoppimiseen, syksy 2008 Luentorunko perjantaille 5.12.2008 Johdattelua mallipohjaiseen klusterointiin, erityisesti gaussisiin sekoitemalleihin Uskottavuusfunktio
Mallipohjainen klusterointi Marko Salmenkivi Johdatus koneoppimiseen, syksy 2008 Luentorunko perjantaille 5.12.2008 Johdattelua mallipohjaiseen klusterointiin, erityisesti gaussisiin sekoitemalleihin Uskottavuusfunktio
k S P[ X µ kσ] 1 k 2.
![k S P[ X µ kσ] 1 k 2. k S P[ X µ kσ] 1 k 2.](/thumbs/92/110318530.jpg) HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 28 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Pelaisitko seuraavaa peliä?
 Lisätehtävä 1 seuraavassa on esitetty eräs peli, joka voidaan mallintaa paramterisena tilastollisena mallina tehtävänä on selvittää, kuinka peli toimii ja näyttää mallin takana oleva apulause (Tehtävä
Lisätehtävä 1 seuraavassa on esitetty eräs peli, joka voidaan mallintaa paramterisena tilastollisena mallina tehtävänä on selvittää, kuinka peli toimii ja näyttää mallin takana oleva apulause (Tehtävä
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat TKK (c) Ilkka Mellin (2006) 1 Moniulotteiset satunnaismuuttujat ja
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat TKK (c) Ilkka Mellin (2006) 1 Moniulotteiset satunnaismuuttujat ja
Satunnaismuuttujat Satunnaismuuttuja kuvaa kokeen tuloksen reaaliakselille Satunnaismuuttuja on siis funktio X(s) joka saa reaalisia arvoja Koe s
 Satunnaismuuttujat Satunnaismuuttuja kuvaa kokeen tuloksen reaaliakselille Satunnaismuuttuja on siis funktio X(s) joka saa reaalisia arvoja Koe s kuuluu todennäköisyysavaruuteen S (s S) Esimerkkejä Kolikonheitossatodennäköisyysavaruus
Satunnaismuuttujat Satunnaismuuttuja kuvaa kokeen tuloksen reaaliakselille Satunnaismuuttuja on siis funktio X(s) joka saa reaalisia arvoja Koe s kuuluu todennäköisyysavaruuteen S (s S) Esimerkkejä Kolikonheitossatodennäköisyysavaruus
Tässä luvussa mietimme, kuinka paljon aineistossa on tarpeellista tietoa Sivuamme kysymyksiä:
 4. Tyhjentyvyys Tässä luvussa mietimme, kuinka paljon aineistossa on tarpeellista tietoa Sivuamme kysymyksiä: Voidaanko päätelmät perustaa johonkin tunnuslukuun t = t(y) koko aineiston y sijasta? Mitä
4. Tyhjentyvyys Tässä luvussa mietimme, kuinka paljon aineistossa on tarpeellista tietoa Sivuamme kysymyksiä: Voidaanko päätelmät perustaa johonkin tunnuslukuun t = t(y) koko aineiston y sijasta? Mitä
P(X = x T (X ) = t, θ) = p(x = x T (X ) = t) ei riipu tuntemattomasta θ:sta. Silloin uskottavuusfunktio faktorisoituu
 1. Tyhjentävä tunnusluku (sucient statistics ) Olkoon (P(X = x θ) : θ Θ) todennäköisyysmalli havainnolle X. Datan funktio T (X ) on Tyhjentävä tunnusluku jos ehdollinen todennäköisyys (ehdollinen tiheysfunktio)
1. Tyhjentävä tunnusluku (sucient statistics ) Olkoon (P(X = x θ) : θ Θ) todennäköisyysmalli havainnolle X. Datan funktio T (X ) on Tyhjentävä tunnusluku jos ehdollinen todennäköisyys (ehdollinen tiheysfunktio)
Tilastomatematiikka Kevät 2008
 Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Tilastomatematiikka Kevät 2008 Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastomatematiikka p.1/19 4.3 Varianssi Satunnaismuuttuja on neliöintegroituva, jos odotusarvo
Johdatus tn-laskentaan perjantai 17.2.2012
 Johdatus tn-laskentaan perjantai 17.2.2012 Kahden diskreetin muuttujan yhteisjakauma On olemassa myös monen muuttujan yhteisjakauma, ja jatkuvien muuttujien yhteisjakauma (jota ei käsitellä tällä kurssilla;
Johdatus tn-laskentaan perjantai 17.2.2012 Kahden diskreetin muuttujan yhteisjakauma On olemassa myös monen muuttujan yhteisjakauma, ja jatkuvien muuttujien yhteisjakauma (jota ei käsitellä tällä kurssilla;
9. Tila-avaruusmallit
 9. Tila-avaruusmallit Aikasarjan stokastinen malli ja aikasarjasta tehdyt havainnot voidaan esittää joustavassa ja monipuolisessa muodossa ns. tila-avaruusmallina. Useat aikasarjat edustavat dynaamisia
9. Tila-avaruusmallit Aikasarjan stokastinen malli ja aikasarjasta tehdyt havainnot voidaan esittää joustavassa ja monipuolisessa muodossa ns. tila-avaruusmallina. Useat aikasarjat edustavat dynaamisia
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 2017 Harjoitus 1 Ratkaisuehdotuksia
 HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
HY, MTL / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIb, syksy 07 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Osa tämän viikon tehtävistä ovat varsin haastavia, joten ei todellakaan
Tilastollinen päättely II, kevät 2017 Harjoitus 1A
 Tilastollinen päättely II, kevät 207 Harjoitus A Heikki Korpela 23. tammikuuta 207 Tehtävä. Kertausta todennäköisyyslaskennasta. Ilmoita satunnaismuuttujan Y jakauman nimi ja pistetodennäköisyys- tai tiheysfunktio
Tilastollinen päättely II, kevät 207 Harjoitus A Heikki Korpela 23. tammikuuta 207 Tehtävä. Kertausta todennäköisyyslaskennasta. Ilmoita satunnaismuuttujan Y jakauman nimi ja pistetodennäköisyys- tai tiheysfunktio
031021P Tilastomatematiikka (5 op) viikko 7
 0302P Tilastomatematiikka (5 op) viikko 7 Jukka Kemppainen Mathematics Division Yhteisjakauma Edellä on tarkasteltu yksiulotteista satunnaismuuttujaa. Sovelluksissa joudutaan usein tarkastelemaan samanaikaisesti
0302P Tilastomatematiikka (5 op) viikko 7 Jukka Kemppainen Mathematics Division Yhteisjakauma Edellä on tarkasteltu yksiulotteista satunnaismuuttujaa. Sovelluksissa joudutaan usein tarkastelemaan samanaikaisesti
12. Hessen matriisi. Ääriarvoteoriaa
 179 12. Hessen matriisi. Ääriarvoteoriaa Tarkastelemme tässä luvussa useamman muuttujan (eli vektorimuuttujan) n reaaliarvoisia unktioita : R R. Edellisessä luvussa todettiin, että riittävän säännöllisellä
179 12. Hessen matriisi. Ääriarvoteoriaa Tarkastelemme tässä luvussa useamman muuttujan (eli vektorimuuttujan) n reaaliarvoisia unktioita : R R. Edellisessä luvussa todettiin, että riittävän säännöllisellä
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 2016 Antti Rasila
Matemaattinen tilastotiede. Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto
 Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
Matemaattinen tilastotiede Erkki Liski Matematiikan, Tilastotieteen ja Filosofian Laitos Tampereen Yliopisto Alkusanat Tämä moniste perustuu vuosina 2002-2004 pitämiini matemaattisen tilastotieteen luentoihin
Moniulotteiset satunnaismuuttujat ja jakaumat
 Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Moniulotteiset satunnaismuuttujat ja jakaumat KE (2014) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat >> Kaksiulotteiset
Tilastollinen päättömyys, kevät 2017 Harjoitus 6B
 Tilastollinen päättömyys, kevät 7 Harjoitus 6B Heikki Korpela 8. helmikuuta 7 Tehtävä. Monisteen teht. 6... Olkoot Y,..., Y 5 Nµ, σ, ja merkitään S 5 i Y i Y /4. Näytä, että S/σ on saranasuure eli sen
Tilastollinen päättömyys, kevät 7 Harjoitus 6B Heikki Korpela 8. helmikuuta 7 Tehtävä. Monisteen teht. 6... Olkoot Y,..., Y 5 Nµ, σ, ja merkitään S 5 i Y i Y /4. Näytä, että S/σ on saranasuure eli sen
EX1 EX 2 EX =
 HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
HY, MTL / Matemaattiste tieteide kadiohjelma Todeäköisyyslasketa IIb, syksy Harjoitus Ratkaisuehdotuksia Tehtäväsarja I. Olkoot X ja X riippumattomia satuaismuuttujia, joille ja olkoo X EX, EX, var X,
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat.
 MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 6: Ääriarvojen luokittelu. Lagrangen kertojat. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2016 1 Perustuu
Antti Rasila. Kevät Matematiikan ja systeemianalyysin laitos Aalto-yliopisto. Antti Rasila (Aalto-yliopisto) MS-A0204 Kevät / 16
 MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Antti Rasila Matematiikan ja systeemianalyysin laitos
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Antti Rasila Matematiikan ja systeemianalyysin laitos
Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat TKK (c) Ilkka Mellin (2005) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat Kaksiulotteiset todennäköisyysjakaumat
Johdatus todennäköisyyslaskentaan Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat TKK (c) Ilkka Mellin (2005) 1 Moniulotteiset satunnaismuuttujat ja todennäköisyysjakaumat Kaksiulotteiset todennäköisyysjakaumat
Tilastollinen päättely II, kevät 2017 Harjoitus 2A
 Tilastollinen päättely II, kevät 07 Harjoitus A Heikki Korpela 3. tammikuuta 07 Tehtävä. (Monisteen tehtävä.3 Olkoot Y,..., Y n Exp(λ. Kirjoita vastaava tilastollisen mallin lauseke (ytf. Muodosta sitten
Tilastollinen päättely II, kevät 07 Harjoitus A Heikki Korpela 3. tammikuuta 07 Tehtävä. (Monisteen tehtävä.3 Olkoot Y,..., Y n Exp(λ. Kirjoita vastaava tilastollisen mallin lauseke (ytf. Muodosta sitten
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä
 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a 21
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a 21
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
MS-A0207 Differentiaali- ja integraalilaskenta 2 (Chem) Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 21. tammikuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0207 Differentiaali- ja integraalilaskenta
r > y x z x = z y + y x z y + y x = r y x + y x = r
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Osoita, että avoin kuula on avoin joukko ja suljettu kuula on suljettu joukko. Ratkaisu.
Lineaarikuvauksen R n R m matriisi
 Lineaarikuvauksen R n R m matriisi Lauseessa 21 osoitettiin, että jokaista m n -matriisia A vastaa lineaarikuvaus L A : R n R m, jolla L A ( v) = A v kaikilla v R n. Osoitetaan seuraavaksi käänteinen tulos:
Lineaarikuvauksen R n R m matriisi Lauseessa 21 osoitettiin, että jokaista m n -matriisia A vastaa lineaarikuvaus L A : R n R m, jolla L A ( v) = A v kaikilla v R n. Osoitetaan seuraavaksi käänteinen tulos:
TKK @ Ilkka Mellin (2008) 1/5
 Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 3, 6, 7 Pistetehtävät: 2, 4, 5, 9 Ylimääräiset tehtävät: 8, 10, 11 Aiheet: Moniulotteiset jakaumat Avainsanat: Diskreetti jakauma,
Luento 8: Epälineaarinen optimointi
 Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
Luento 8: Epälineaarinen optimointi Vektoriavaruus R n R n on kaikkien n-jonojen x := (x,..., x n ) joukko. Siis R n := Määritellään nollavektori 0 = (0,..., 0). Reaalisten m n-matriisien joukkoa merkitään
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio.
 MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
MS-A0207 Differentiaali- ja integraalilaskenta 2 Luento 5: Gradientti ja suunnattu derivaatta. Vektoriarvoiset funktiot. Taylor-approksimaatio. Riikka Korte Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus
 Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Inversio-ongelmien laskennallinen peruskurssi Luento 2
 Inversio-ongelmien laskennallinen peruskurssi Luento 2 Kevät 2012 1 Lineaarinen inversio-ongelma Määritelmä 1.1. Yleinen (reaaliarvoinen) lineaarinen inversio-ongelma voidaan esittää muodossa m = Ax +
Inversio-ongelmien laskennallinen peruskurssi Luento 2 Kevät 2012 1 Lineaarinen inversio-ongelma Määritelmä 1.1. Yleinen (reaaliarvoinen) lineaarinen inversio-ongelma voidaan esittää muodossa m = Ax +
11 Raja-arvolauseita ja approksimaatioita
 11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
11 Raja-arvolauseita ja approksimaatioita Tässä luvussa esitellään sellaisia kuuluisia todennäköisyysteorian raja-arvolauseita, joita sovelletaan usein tilastollisessa päättelyssä. Näiden raja-arvolauseiden
802320A LINEAARIALGEBRA OSA II
 802320A LINEAARIALGEBRA OSA II Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 64 Sisätuloavaruus Määritelmä 1 Olkoon V reaalinen vektoriavaruus. Kuvaus on reaalinen
802320A LINEAARIALGEBRA OSA II Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 64 Sisätuloavaruus Määritelmä 1 Olkoon V reaalinen vektoriavaruus. Kuvaus on reaalinen
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi. Viikko 3. Kaksiulotteiset satunnaismuuttujat
 .9. Kaksiulotteiset satunnaismuuttujat MS-A Todennäköisslaskennan ja tilastotieteen peruskurssi Viikko Moniulotteiset satunnaismuuttujat sekä niiden jakaumat ja tunnusluvut; Moniulotteisia jakaumia Usein
.9. Kaksiulotteiset satunnaismuuttujat MS-A Todennäköisslaskennan ja tilastotieteen peruskurssi Viikko Moniulotteiset satunnaismuuttujat sekä niiden jakaumat ja tunnusluvut; Moniulotteisia jakaumia Usein
Ominaisarvo ja ominaisvektori
 Määritelmä Ominaisarvo ja ominaisvektori Oletetaan, että A on n n -neliömatriisi. Reaaliluku λ on matriisin ominaisarvo, jos on olemassa sellainen vektori v R n, että v 0 ja A v = λ v. Vektoria v, joka
Määritelmä Ominaisarvo ja ominaisvektori Oletetaan, että A on n n -neliömatriisi. Reaaliluku λ on matriisin ominaisarvo, jos on olemassa sellainen vektori v R n, että v 0 ja A v = λ v. Vektoria v, joka
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 4: Ketjusäännöt ja lineaarinen approksimointi
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 4: Ketjusäännöt ja lineaarinen approksimointi Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 4: Ketjusäännöt ja lineaarinen approksimointi Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1
Kuva 1: Funktion f tasa-arvokäyriä. Ratkaisu. Suurin kasvunopeus on gradientin suuntaan. 6x 0,2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä
 1 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a
1 3 Lineaariset yhtälöryhmät ja Gaussin eliminointimenetelmä Lineaarinen m:n yhtälön yhtälöryhmä, jossa on n tuntematonta x 1,, x n on joukko yhtälöitä, jotka ovat muotoa a 11 x 1 + + a 1n x n = b 1 a
Harjoitus 4 Tehtävä 1
 Harjoitus 4 Tehtävä 1 19:39» Hei olen jumissa 1a) tehtävässä. Yritin näyttää että kovarianssi on nolla siten että E(Z m(x))(m(x) h(x)) E(Z m(x))(e(m(x) h(x)) = 0. Laskuista tuli aika raskaita enkä heti
Harjoitus 4 Tehtävä 1 19:39» Hei olen jumissa 1a) tehtävässä. Yritin näyttää että kovarianssi on nolla siten että E(Z m(x))(m(x) h(x)) E(Z m(x))(e(m(x) h(x)) = 0. Laskuista tuli aika raskaita enkä heti
Johdatus tilastotieteeseen Estimointi. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia
 Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Estimointi. Estimointi. Estimointi: Mitä opimme? 2/4. Estimointi: Mitä opimme? 1/4. Estimointi: Mitä opimme? 3/4. Estimointi: Mitä opimme?
 TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
Liite. Matriisilaskentaa
 Liite A Matriisilaskentaa A. Matriisinormi Jos A = [a ij ] on dimensiota n m oleva reaalinen matriisi, niin sen (Euklidinen) normi on määritelmän mukaan v u nx kak = t a ij : i= On selvää, että määritelmä
Liite A Matriisilaskentaa A. Matriisinormi Jos A = [a ij ] on dimensiota n m oleva reaalinen matriisi, niin sen (Euklidinen) normi on määritelmän mukaan v u nx kak = t a ij : i= On selvää, että määritelmä
