REAALIOPTIOAJATTELU SUOMALAISTEN PÖRSSIYRITYSTEN INVESTOINTILASKENNASSA
|
|
|
- Hanna Rantanen
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 TAMPEREEN YLIOPISTO Taloustieteiden laitos REAALIOPTIOAJATTELU SUOMALAISTEN PÖRSSIYRITYSTEN INVESTOINTILASKENNASSA Yrityksen taloustiede, laskentatoimi Pro gradu -tutkielma Tammikuu 2006 Ohjaaja: Eeva-Mari Ihantola Antti Lyytikäinen
2 TIIVISTELMÄ Tampereen yliopisto Taloustieteiden laitos; yrityksen taloustiede, laskentatoimi Tekijä: Tutkielman nimi: LYYTIKÄINEN, ANTTI Reaalioptioajattelu suomalaisten pörssiyritysten investointilaskennassa 73 sivua, 3 liitesivua Pro gradu -tutkielma: Aika: Tammikuu 2006 Avainsanat: investoinnit, reaalioptiot, epävarmuus Perinteiset investointilaskentamenetelmät eivät huomioi investointeihin liittyvää joustavuutta. Reaalioptioajattelun avulla tämä voi olla mahdollista. Reaalioptioajattelussa investointeihin liittyvien joustokohtien eli reaalioptioiden arvoja määritetään finanssioptioiden arvonmääritysmalleilla. Reaalioptioiden arvonmäärityksessä voidaan käyttää finanssioptioiden arvonmääritysmalleja, sillä reaalioptioita voidaan finanssioptioiden tapaan käsitellä osto- ja myyntioptioina. Menetelmään liittyy myös investointien käsitteleminen käyttämällä arvioinnissa reaalioptioajatteluun liittyvää käsitteistöä. Reaalioptioajattelun avulla yritysjohto voi tunnistaa investointiin liittyvät lisäarvoa luovat tekijät ja ongelmakohdat sekä monipuolistaa arviointiin liittyvää kommunikointia. Optioperusteisen arvioinnin avulla yritys kykenee hallitsemaan investointiin liittyvää epävarmuutta, koska arvioinnissa säilytetään jousto ja mahdollisuus muutoksille. Tutkimuksen empiirinen osuus toteutettiin kyselytutkimuksena, jossa Helsingin Pörssin päälistalla noteeratuille yrityksille lähetettiin postitse kyselylomake. Tutkimuksen tavoitteena oli kartoittaa reaalioptioajattelun käyttöä suomalaisten pörssiyritysten investointilaskennassa. Menetelmän käyttöä pyrittiin analysoimaan sekä niiden yritysten näkökulmasta, jotka soveltavat optioperusteista investointien arviointia, että niiden, jotka eivät sovella. Lisäksi tutkimuksessa pyrittiin saamaan käsitys yritysten soveltamista muista investointilaskentamenetelmistä. Suomalaiset yritykset suosivat edelleen takaisinmaksuajan menetelmää. Investointiteorian suosittaman nettonykyarvon soveltaminen on vuosien mittaan kuitenkin yleistynyt. Investointipäätöksenteko näyttäisi perustuvan usean menetelmä käyttöön, sillä valtaosa yrityksistä soveltaa kahta tai useampaa menetelmää. Suomalaiset pörssiyritykset eivät sovella reaalioptioajattelua, joten menetelmän käyttöä ei voitu analysoida menetelmää soveltavien yritysten näkökulmasta. Noin viidesosa yrityksistä on kuitenkin joskus harkinnut optioperusteisen investointien arvioinnin käyttöönottoa. Kyseiset yritykset ovat pitäneet menetelmää kuitenkin liian vaikeana. Myös reaalioptioajattelun soveltaminen tulevaisuudessa näyttää epätodennäköiseltä. Valtaosa tutkimukseen vastanneista yrityksistä ei näe reaalioptioajattelussa merkittävää hyötyä.
3 SISÄLTÖ 1 JOHDANTO Tutkimuksen tausta Tutkimuksen tavoitteet Tutkimusmenetelmä ja -ote Tutkimuksen rajaukset Aikaisemmat tutkimukset Tutkimusraportin rakenne REAALIOPTIOIDEN ESITTELY Reaalioptioiden luokittelutapoja Reaalioptiotyypit Lykkäysoptio Vaiheistusoptio Skaalausoptio Hylkäysoptio Vaihto-optio Kasvuoptio Moniulotteiset vuorovaikutusoptiot Yhteenveto reaalioptiotyypeistä Esimerkki erilaisista reaalioptioista REAALIOPTIOIDEN ARVONMÄÄRITYS Arvonmääritysmallit Binomimalli Black & Scholes -malli Reaali- ja finanssioptioiden yhteys Reaali- ja finanssioptioiden yhtäläisyyksiä Reaali- ja finanssioptioiden eroja Reaalioption arvoon vaikuttavat tekijät Arvonmääritykseen liittyviä erityistekijöitä Volatiliteetin määrittäminen Reaalioptioiden arvojen yhteenlaskettavuus REAALIOPTIOAJATTELUN KÄYTTÖ Perinteisten investointilaskentamenetelmien kritiikki Reaalioptioajattelun peruslähtökohtia Laajennettu nettonykyarvo Reaalioptioajattelun vaiheet Reaalioptioajattelun sovelluskohteet Strategiset käyttöomaisuusinvestoinnit Tutkimus- ja tuotekehitysinvestoinnit Informaatioteknologiainvestoinnit Esimerkki reaalioptioajattelun soveltamisesta Soveltaminen binomimallilla Soveltaminen Black & Scholes -mallilla Reaalioptioajattelun käytön arviointi Reaalioptioajattelun hyötyjä...49
4 4.5.2 Reaalioptioajattelun ongelmia Yhteenveto käytön arvioinnista REAALIOPTIOAJATTELU JA MUUT INVESTOINTILASKENTAMENETELMÄT SUOMALAISISSA PÖRSSIYRITYKSISSÄ Tutkimusaineiston kuvaus ja käsittely Tutkimuksen rajoituksia Perinteisten investointilaskentamenetelmien soveltaminen Reaalioptioajattelun soveltaminen YHTEENVETO JA PÄÄTELMÄT...68 LÄHTEET...71 LIITE: Kyselylomake...74
5 5 1 JOHDANTO 1.1 Tutkimuksen tausta Yritysten toimintaan liittyy nykyisin yhä enemmän epävarmuus, joka asettaa haasteita koko yritystoiminnan lisäksi myös investointipäätöksentekoon. Yritysjohdon tulisi löytää investointikohteiden joukosta yrityksen kannalta parhaat vaihtoehdot myös epävarmoissa tilanteissa. Investointipäätökset ovat tärkeitä, sillä investoinnit luovat puitteet toiminnalle. Investoinneilla on huomattava merkitys yritysten taloudelliseen menestykseen ja toiminnan jatkuvuuteen. Perinteiset investointilaskentamenetelmät eivät aina kykene arvioimaan investoinnin todellista kannattavuutta luotettavalla tavalla. Investointeihin sisältyy joustokohtia, joita nämä menetelmät eivät huomioi. Menetelmät, kuten nettonykyarvo, sisäinen korkokanta ja takaisinmaksuaika, olettavat, että investointi toteutetaan ennalta tehdyn suunnitelman mukaan epävarmuudesta huolimatta. Ne eivät huomio yrityksen mahdollisuutta muuttaa investointipäätöstä ajan kuluessa, ja niitä kritisoidaankin liian yksinkertaisina. Investointeihin liittyviä joustokohtia kutsutaan reaalioptioiksi. Reaalioptiot tarjoavat oikeuden säilyttää tietty investointiin liittyvä vaihtoehto avoimena sitomatta siihen pääomia. Yrityksellä saattaa olla mahdollisuus esimerkiksi laajentaa hyväksi osoittautunutta hanketta tai luopua kannattamattomasta hankkeesta. Tämänkaltaisilla reaalioptioilla voi olla huomattavaa arvoa, joka olisi hyvä huomioida investointilaskelmissa. Koska investoinnit ovat merkittävä tekijä yrityksen taloudellisen menestymisen kannalta, on tärkeää, että niihin liittyvät laskelmat voidaan tehdä mahdollisimman todenmukaisesti. Perinteisiä investointilaskentamenetelmiä on mahdollista täydentää reaalioptioajattelulla, jolloin laskelmista voidaan saada todenmukaisempia. Reaalioptioajattelussa investointeihin liittyvien reaalioptioiden arvoja määritetään finanssioptioiden arvonmääritysmalleilla. Menetelmään liittyy myös investointien
6 6 käsitteleminen käyttämällä arvioinnissa reaalioptioajatteluun liittyvää käsitteistöä. Tämän avulla yritysjohto voi tunnistaa investointiin liittyvät lisäarvoa luovat tekijät ja ongelmakohdat sekä monipuolistaa arviointiin liittyvää kommunikointia. Reaalioptioajattelun avulla yritys kykenee hallitsemaan investointiin liittyvää epävarmuutta, koska arvioinnissa säilytetään jousto ja mahdollisuus muutoksille. (Ståhle, Kyläheiko, Sandström & Virkkunen 2002, 119) 1.2 Tutkimuksen tavoitteet Tutkimuksen ongelma-alueena on investointilaskenta ja erityisesti reaalioptioajattelu. Tutkimuksen tavoitteena on kartoittaa reaalioptioajattelun käyttöä suomalaisten pörssiyritysten investointilaskennassa. Menetelmän käyttöä pyritään analysoimaan sekä niiden yritysten näkökulmasta, jotka soveltavat optioperusteista investointien arviointia, että niiden, jotka eivät sovella. Lisäksi pyritään saamaan käsitys yritysten soveltamista muista investointilaskentamenetelmistä. Tässä tutkimuksessa investoinneilla tarkoitetaan reaali-investointeja eli yrityksen toiminnassa tarvittavia aineellisia ja aineettomia pitkävaikutteisia tuotannontekijöitä. 1.3 Tutkimusmenetelmä ja -ote Investointitutkimus voidaan jakaa normatiiviseen ja behavioristiseen lähestymistapaan (Kasanen, Virtanen, Laine & Matinpalo 1993, 15). Normatiivinen investointitutkimus keskittyy tarkastelemaan investoinnin valintapäätöstä ja investointivaihtoehtojen taloudellista arvottamista erilaisilla menetelmillä. Behavioristinen tutkimus puolestaan keskittyy yritysten tosiasiallisen investointikäyttäytymisen kuvaamiseen ja analysointiin empiirisen aineiston perusteella. Behavioristista tutkimusta tehdään kyselylomakkeiden ja haastattelujen avulla. Pääosin behavioristinen investointitutkimus on ollut kyselylomakkeilla tehtyä. Suomessa investointiprosessia ovat kyselylomakkeiden avulla tutkineet aiemmin esimerkiksi Keloharju ja Puttonen (1995) sekä Liljeblom ja Vaihekoski (2004).
7 7 Tutkimusmenetelmänä tässä tutkimuksessa on kysely, eli kyseessä on niin sanottu behavioristinen investointitutkimus. Kyselytutkimuksen otos muodostuu Helsingin Pörssin päälistalla noteeratuista yrityksistä. Varsinaista otantamenetelmää ei tällöin tarvita, koska kyseessä on perusjoukko. Tutkimuksen kohdejoukkoon kuuluu yhteensä 105 yritystä kymmeneltä eri toimialalta (Helsingin Pörssin www-sivu: < _paivitys.xls>). Kyselytutkimuksen tulokset analysoidaan tilastollisesti jakaumia tutkimalla. Tulosten analysoinnissa hyödynnetään taulukkolaskentaohjelmaa. Tutkimuksessa ei perusjoukon pienuuden vuoksi analysoida riippuvuuksia. Tutkimusotteena tässä tutkimuksessa on lähinnä nomoteettinen tutkimusote. Nomoteettisessa tutkimuksessa pyritään kuvaamaan, selittämään ja ennustamaan tutkittavaa asiaa. Tutkimusotteessa deduktiolla on yleensä keskeinen rooli. Teorioiden perusteella rakennetaan hypoteeseja tai malleja, joiden validiteettia testataan empiirisen havaintoaineiston avulla. Erityisen selkeästi tämä tulee esille, kun tutkimuksen aiheeseen liittyy selkeä teoriavaranto, jonka toimivuutta arvioidaan. (Salmi & Järvenpää 2000, ) Nomoteettisessa tutkimuksessa on kyse empiirisestä tutkimuksesta, joka on luonteeltaan deskriptiivinen eli kuvaileva. Tämän tutkimuksen empirian muodostaa Helsingin Pörssin päälistalla noteeratuille yrityksille suunnattu kyselytutkimus, jolla pyritään kuvailemaan investointilaskennan ja reaalioptioajattelun soveltamista kyseisissä yrityksissä. Yleensä nomoteettisessa tutkimuksessa teorialla on keskeinen merkitys. Tyypillisesti tutkimuksessa keskitytään yhteen teoriaan kerrallaan ja vähintään kohtuulliseen määrään tilastollisia havaintoja. (Salmi & Järvenpää 2000, 264) Tässä tutkimuksessa nojaudutaan erityisesti reaalioptioteoriaan, ja havaintoaineiston muodostavat kyselyn avulla saadut vastaukset.
8 8 1.4 Tutkimuksen rajaukset Tutkimuksen kohteena oleva yritysjoukko rajataan tarkoituksenmukaisesti pörssiyrityksiin. Ensinnäkin pörssiyrityksillä on resursseja palkata laskentahenkilöstöä, joka pystyy suorittamaan erityistä investointien arviointia kuten reaalioptioajattelu. Toiseksi näiden yritysten investoinnit ovat merkittävämpiä kuin pienempien ja einoteerattujen yritysten, joten myös arviointiprosessissa voisi olla tarvetta edistyneimmille menetelmille. Lisäksi pörssilistatut yritykset voivat käyttää hyväksi pörssistä saatavaa tietoa investointien arvioinnissa. Myös eri maissa tehdyt investointiprosessia koskevat tutkimukset ovat kohdistuneet ensisijaisesti suuryrityksiin, joissa investointisuunnittelun voidaan olettaa olevan pisimmälle formalisoitua (Kasanen ym. 1993, 19). Pörssiyrityksistä tarkastellaan päälistan yrityksiä, eli tutkimuksen ulkopuolelle rajataan I-, NM- ja PRE-listojen yritykset. Optioiden arvonmääritysmalleista tutkimuksessa esitellään binomimalli ja Black & Scholes -malli, joilla reaalioptioiden arvoja voidaan märittää. Arvonmääritysmallit esitellään riittävässä laajuudessa niiden perusperiaatteiden ymmärtämiseksi. Tutkimuksessa käsitellään myös muita investointilaskentamenetelmiä kuin reaalioptioajattelua. Näiden perinteisten menetelmien toimintaperiaatteiden esittely rajataan kuitenkin tutkimusraportinlaajuuden vuoksi tutkimuksen ulkopuolelle. 1 Investointilaskelmiin liittyy olennaisesti myös tuottovaatimuksen määrittäminen sekä verojen ja inflaation huomioiminen. Näiden tarkastelu rajataan tutkimuksen ulkopuolelle. Samoin investointihankkeiden rahoitukseen liittyviä ongelmia ei käsitellä tässä tutkimuksessa, vaikka rahoitusvaihtoehtojen arviointi onkin keskeinen asia investointiprosessissa. 1.5 Aikaisemmat tutkimukset Reaalioptio-termi esitettiin ensimmäisen kerran vuonna 1977 Stewart C. Myersin toimesta. Tällöin hän julkaisi artikkelin Determinants of corporate borrowing, jossa todettiin, että yrityksen arvo muodostuu sekä sen hetkisistä varoista että 1 Kyseisten menetelmien soveltamistavoista voi lukea tarkemmin esimerkiksi teoksesta Aho (1982).
9 9 mahdollisuuksista ostaa omaisuutta suotuisaan hintaan. Tästä mahdollisuudesta Myers käytti nimitystä reaalioptio ja rinnasti sen ominaisuudet finanssimarkkinoiden ostooptioon. (Myers 1977) Varsinaisesti reaalioptioajattelun alkujuuret ovat kuitenkin jo vuodessa 1973, jolloin Fischer Black ja Myron Scholes esittelivät arvonmääritysmallin osakkeen osto-optiolle (Black & Scholes 1973). Reaalioptioteoria pohjautuukin pitkälti finanssioptioiden teoriaan luoden samalla yhteyden rahoitus- ja investointiteorian välille. Myersin (1977) keksinnön jälkeen reaalioptioajattelu on ollut aktiivisen teoreettisen kehittelyn kohteena. Erityisen vilkasta keskustelu on ollut 1990-luvun loppupuolella ja 2000-luvulla. Pääosin reaalioptiotutkimus on ollut teoreettista, mutta myös menetelmän käytännön soveltamista on alettu tutkia viimeisen kymmenen vuoden aikana yhä enemmän. Busbyn ja Pittsin (1997) tutkimuksen kohteena olivat Lontoon pörssin markkinaarvoltaan sata suurinta yritystä. Kyselynä toteutetussa tutkimuksessa havaittiin, että yrityksillä ei ollut käytössä arvonmääritysmallia reaalioptioille. Busby ja Pitts (1997) keskittyivät tutkimuksessaan erityisesti investointeihin tyypillisesti liittyviin reaalioptioihin ja niiden hyötyarvoon investoinnin kannalta. Tyypillisimpiä optiotyyppejä olivat kasvu- ja lykkäysoptiot, ja hyödyllisimmiksi optioiksi arvioitiin skaalaus- ja kasvuoptiot. Busbyn ja Pittsin (1997) tutkimukseen vastanneista yrityksistä vain harvat olivat tietoisia optioperusteisesta investointien arvioinnista. Hieman alle puolet yrityksistä arvioi, että menetelmästä voisi tietyin varauksin kuitenkin olla hyötyä. Triantis ja Borison (2003) tutkivat reaalioptioajattelua soveltavia eri alojen kansainvälisiä suuryrityksiä. Tutkimuksen tavoitteena oli arvioida, miksi menetelmä oli otettu käyttöön ja kuinka sitä sovellettiin. Valtaosalle yrityksistä motivaatio menetelmän käyttöönottoon oli syntynyt sen mahdollisuudesta hallita investointiin liittyvää epävarmuutta ja mahdollisuudesta tunnistaa kasvua luovia tekijöitä. Osa yrityksistä käytti menetelmää vasta ajatuskehikkona ja osa arvonmääritystyökaluna, jossa koko organisaatio oli mukana. Suomessa reaalioptioajattelun tutkiminen on ollut melko vähäistä. Menetelmä oli kuitenkin mukana, kun Liljeblom ja Vaihekoski (2004) tutkivat vuonna 2002
10 10 suomalaisten pörssiyritysten investointilaskentamenetelmien soveltamista ja tuottovaatimuksen asettamista. 2 Kyseisen tutkimuksen mukaan 4 % yrityksistä sovelsi optioperusteista arviointia. Yhdysvalloissa menetelmän osuudet ovat olleet huomattavasti suurempia. Esimerkiksi Grahamin ja Harveyn (2001) tutkimuksessa reaalioptioajattelua soveltavia yrityksiä oli 27 %. 1.6 Tutkimusraportin rakenne Tutkimusraportin toisessa luvussa esitellään erilaisia reaalioptioita. Aluksi käydään läpi luokittelutapoja, joiden mukaan reaalioptioita voidaan jaotella. Tämän jälkeen esitellään yleisimmät reaalioptiotyypit ja niiden ominaisuudet. Lopuksi esimerkin avulla vielä havainnollistetaan eri luokittelutapojen mukaisia reaalioptioita. Kolmannessa luvussa käsitellään reaalioptioiden arvonmääritystä. Arvonmääritysmalleista esitellään binomimalli ja Black & Scholes -malli. Lisäksi tuodaan esille reaali- ja finanssioptioiden välistä yhteyttä. Kolmannen luvun lopussa käydään läpi reaalioption arvoon vaikuttavia tekijöitä ja arvonmääritykseen liittyviä erityistekijöitä. Tutkimusraportin neljännessä luvussa käsitellään reaalioptioajattelun käyttöä. Aluksi tuodaan esille perinteisten investointilaskentamenetelmien ongelmia, joita reaalioptioajattelulla voisi olla mahdollista ratkaista. Tämän jälkeen käydään läpi reaalioptioajattelun peruslähtökohtia ja sovelluskohteita. Neljännen luvun loppuosassa reaalioptioajattelun soveltamista havainnollistetaan kahden esimerkin avulla sekä arvioidaan menetelmän käyttöä. Viidennessä luvussa käsitellään kyselytutkimuksen tulokset. Luvun alussa kuvataan tutkimuksen kohdeyrityksiä ja tutkimusaineiston käsittelyä. Tämän jälkeen käydään läpi kohdeyrityksissä käytettäviä investointilaskentamenetelmiä ja reaalioptioajattelua. Kuudennessa ja viimeisessä luvussa esitetään tutkimuksen päätelmät. 2 Liljeblom ja Vaihekoski (2004) keskittyivät tutkimuksessaan suomalaisten pörssiyritysten tuottovaatimuksen asettamiseen, eikä investointilaskentamenetelmiä ja niiden käyttötilanteita tutkittu yksityiskohtaisemmin.
11 11 2 REAALIOPTIOIDEN ESITTELY 2.1 Reaalioptioiden luokittelutapoja Reaalioptioita voidaan luokitella niiden luomien mahdollisuuksien mukaan. Yrityksestä löytyviä optiota on mahdollista jakaa kasvua ja joustoa luoviin optioihin. Joustoa luoviin optioihin liittyy myös suojauselementti. Reaalioptiot jaetaan finanssioptioiden tapaan osto- ja myyntioptioihin. Kasvuoptiot ovat aina osto-optioita. Joustavuus- ja suojausoptioista löytyy osto- ja myyntioptioita. Osto-optio antaa oikeuden mutta ei velvollisuutta jonkin hyödykkeen tai kyvykkyyden hankkimiseen tulevaisuudessa. Myyntioptio puolestaan luo oikeuden mutta ei velvollisuutta myydä jokin hyödyke tai kyvykkyys. Kasvuoptioita ovat esimerkiksi: (Ståhle ym. 2002, 140) uuden tuotantolaitoksen rakentaminen uuden tuotteen kehittäminen yritysosto asiantuntijan rekrytoiminen patentin hankkiminen laaja koulutusohjelma henkilöstölle yhteisyrityksen perustaminen erityisosaamisen hankkiminen. Jousto- ja suojausoptioita puolestaan ovat esimerkiksi: tärkeän investoinnin viivyttäminen luopuminen yhteisyrityksestä ulkoistamispäätökset osa-aikaisen työvoiman käyttö liiketoiminnan osittainen myyminen yrityksen uudelleenorganisointi
12 12 kehityshankkeen porrastaminen ohjausjärjestelmän kehittäminen investointi monikäyttöiseen tuotantokalustoon. Reaalioptioita on mahdollista luokitella myös sen mukaan, onko yrityksellä yksinoikeus kyseiseen optioon, vai onko optio jaettu. Jaetuissa optioissa myös kilpailijoilla on mahdollisuus käyttää kyseinen optio. Patentit ja ainutlaatuinen teknologinen osaaminen ovat esimerkkejä yksinoikeusoptioista. Jaettu optio puolestaan on esimerkiksi uuden markkina-alueen valtaaminen, johon myös kilpailijoilla on mahdollisuus. Se kumpaan ryhmään optio kuuluu vaikuttaa luonnollisesti yrityksen toimiin. Yrityksen tulee päättää, mitä optioita se voi antaa kilpailijoiden hyödynnettäväksi, ja mitä sen tulee käyttää itse. Lisäksi tulee huomioida, että yksinoikeusoption toteuttamista voidaan tarvittaessa viivästyttää, mutta jaetuissa optioissa tämä mahdollisuus riippuu pitkälti kilpailijoiden toimista. Jako yksinoikeus ja jaettuihin optioihin ei kuitenkaan välttämättä ole aina selkeä. (Smit & Trigeorgis 2004, 23 24) Reaalioptioita voidaan jakaa myös sen mukaan, löytyvätkö ne yrityksestä luonnostaan, vai pitääkö niitä erikseen hankkia. Luonnostaan löytyvät optiot yritysjohdon tulisi aina tunnistaa. Luonnostaan löytyvät optiot kytkevät yrityksen eri osat, toiminnot ja hankkeet toisiinsa. Hankittavia optioita taas ovat esimerkiksi yritysostot, patentit ja panostukset yrityksen kyvykkyyksien lisäämiseen. (Ståhle ym. 2002, 131) Yrityksestä löytyviä optioita on mahdollista jaotella myös yksinkertaisiin optioihin (simple option) ja yhdistelmäoptioihin (compound option). Yksinkertaisella optiolla tarkoitetaan investointimahdollisuutta, johon liittyvä hyöty realisoituu ainoastaan hankkeen kassavirtoina. Niihin liittyvä analyysi onkin melko yksinkertaista. Huomattavasti monimutkaisempia ovat niin sanotut yhdistelmäoptiot, jotka luovat kassavirtojen lisäksi muita investointimahdollisuuksia. Yksinkertaisia optioita ovat esimerkiksi yrityksen organisatoriset järjestelyt ja tuotannonylläpitoon liittyvät investoinnit. Yhdistelmäoptioita ovat esimerkiksi yritysostot ja tuotekehityshankkeet. (Smit & Trigeorgis 2004, ) Lisäksi reaalioptioita voidaan finanssioptioiden tapaan jakaa amerikkalaisiin ja eurooppalaisiin optioihin. Eurooppalainen optio voidaan käyttää ainoastaan option
13 13 päättymispäivänä, kun taas amerikkalainen optio voidaan käyttää koska tahansa ennen option päättymispäivää. (Brealey & Myers 2000, ) 2.2 Reaalioptiotyypit Edellä käsiteltyjen tapojen lisäksi reaalioptioita voidaan luokitella erilaisiin tyyppeihin. Yritysjohdon tulee tuntea ja havaita nämä reaalioptiotyypit, jotta se voi hyödyntää niitä yrityksen investoinneissa. Trigeorgis (1996, 2 14) jakaa reaalioptiot seitsemään ryhmään: lykkäys-, vaiheistus-, skaalaus-, hylkäys-, vaihto-, kasvu- ja moniulotteisiin vuorovaikutusoptioihin. Tätä luokittelutapaa on pidetty onnistuneena, ja sitä sovelletaan yleisesti (ks. esim. Lander & Pinches 1998, 540; Perlitz, Peske & Schrank 1999, 256; Fichman, Keil & Tiwana 2005, 80). Seuraavaksi optiotyypit käydään läpi yksityiskohtaisesti Lykkäysoptio Yritysjohto voi viivästyttää investoinnin toteutusta lykkäysoption (option to defer; wait; learn) avulla. Johdolla voi olla mahdollisuus hankkia lisätietoa investoinnin kannattavuuteen vaikuttavista tekijöistä, tarkkailla markkinoiden muutoksia ja kilpailijoiden toimintaa. Investointipäätöstä voidaan lykätä option pitoajan puitteissa niin pitkälle tulevaisuuteen, kunnes investoinnin toteuttaminen on kannattavaa. Tämä on hyödyllistä etenkin silloin, kun markkinat ovat epävarmat ja uhkana ovat investoinnista aiheutuneet suuret uponneet kustannukset. (Smit & Trigeorgis 2004, ) Lykkäämisestä ei kuitenkaan ole hyötyä, mikäli yritys ei option pitoaikana hanki lisätietoa kannattavuuteen vaikuttavista tekijöistä, kuten markkinoista, teknologian kehittymisestä, kilpailijoiden toimista tai kustannuksista. Tämän optiotyypin avulla yritys kykenee siis oppimaan investointihankkeesta enemmän. Mikäli hanke ei ole lykättävissä, kyseessä on erääntyvä investointimahdollisuus. (Dixit & Pindyck 1994, 6 9) Lykkäysoption voi tulkita amerikkalaiseksi osto-optioksi. Tämä tarkoittaa sitä, että optio on mahdollista toteuttaa milloin vain sen voimassaoloaikana. Yrityksellä on siis
14 14 mahdollisuus siirtää investointia tulevaisuuteen, mutta ei velvollisuutta toteuttaa sitä. Mikäli hanke alkaa näyttää kannattamattomalta, se voidaan hylätä. Lykkäysoptio sisältääkin tyypillisesti monia optioita, kuten hylkäys-, vaihto- ja skaalausoptioita. Odottaminen ei kuitenkaan kannata, mikäli kilpailijoille on tarjolla kyseinen optio, vaan etua voidaan päinvastoin saavuttaa investoinnin nopealla toteutuksella. Muissa tilanteissa toteuttaminen kannattaa yleensä siirtää option voimassaoloajan loppuun, jotta tarpeellista tietoa kannattavuuteen vaikuttavista tekijöistä voidaan hankkia. Tällöin on kuitenkin tarpeen, että hankkeen tuottoja ja kustannuksia seurataan jatkuvasti. Lykkäyksen mahdollisesti tuomaa etua tulee verrata esimerkiksi menetettyihin tuloihin tai heikentyneeseen markkina-asemaan. (Trigeorgis 1996, 2 10; Ståhle ym. 2002, ) Investoinnin lykkääminen edellyttää, että kyseinen kohde on ainutlaatuinen, ja että kilpailijoilla ei ole mahdollisuutta toteuttaa kyseistä optiota ennen yritystä. Lykkääminen ei kuitenkaan ole tarpeen, mikäli investoinnin nykyarvo on selvästi positiivinen tai markkinaolosuhteet muuten edellyttävät hankkeen nopeaa toteuttamista. (Dixit & Pindyck 1994, 6 9) Lykkäysoptio on erityisen arvokas pääomavaltaisilla teollisuudenaloilla, kuten metalli- ja metsäteollisuudessa. Tämä johtuu muun muassa investointien suuresta koosta, epävarmuudesta ja hankkeiden pitkästä vaikutusajasta. (Trigeorgis 1996, 2 10) Vaiheistusoptio Vaiheistusoptio (time to built option) perustuu investoinnin pilkkomiseen osiksi. Useimmissa yrityksen hankkeista ei olekaan kysymys vain yhdestä suuresta investoinnista, vaan hanke on pienempien investointien sarja, jonka osat seuraavat toisiaan. Suurille investointihankkeille on tyypillistä, että investointiin liittyvä päätöksenteko sekä tuotot ja kustannukset jakautuvat pitkälle ajanjaksolle. Vaiheistusoption avulla yritys kykenee hallitsemaan investointiin liittyvää epävarmuutta ja kontrolloimaan uponneita kustannuksia. (Dixit & Pindyck 1994, ) Vaiheistusoptiotilanteessa investointihankkeen eri osat suoritetaan valitulla hetkellä, ja johdolla on mahdollisuus jatkaa tai keskeyttää hanke milloin tahansa. Mikäli hanke
15 15 keskeytetään, käytetään hylkäysoptiota, jonka voi tulkita myyntioptioksi. Investointihankkeen hylkääminen voi olla tarpeen, mikäli markkinaolosuhteissa tapahtuu odottamattomia muutoksia, kuten lopputuotteen voimakas hinnanalennus tai kustannusten äkillinen nousu. Mikäli markkinaolosuhteet osoittautuvat suotuisiksi, toteutetaan hankkeen seuraava vaihe suunnitelmien mukaan. Yksittäisen vaiheen voi siis nähdä optioksi seuraavan osan toteuttamiselle, silloin kun investointi jatkuu vaiheittain. (Trigeorgis 1996, 2 11; Ståhle ym. 2002, ) Vaiheistusoptio on arvokas kaikilla tutkimus- ja kehitysintensiivisillä teollisuuden aloilla, kuten lääketeollisuudessa ja informaatioteknologia-alan yrityksissä. Tutkimusja kehityshanke voidaan keskeyttää tai sitä voidaan jatkaa, mikäli markkinaolosuhteet niin osoittavat. Lisäksi vaiheistusoptio on arvokas pääomaintensiivisillä aloilla, joissa vaarana ovat suuret uponneet kustannukset. (Trigeorgis 1996, 2 11; Ståhle ym. 2002, ) Skaalausoptio Skaalausoptio (option to alter operating scale) sallii yrityksen muuttaa toiminta-astetta ja kapasiteettia markkinaolosuhteiden mukaan. Markkinoiden osoittautuessa suotuisiksi yritys voi laajentaa tuotantoa ja näin maksimoida tuottojaan. Laajennusmahdollisuuden voi tulkita osto-optioksi. Vastaavasti huonoina aikoina yritys voi pienentää tuotantoa, joka voidaan puolestaan tulkita myyntioptioksi. Tuotanto voidaan ääritapauksissa myös pysäyttää, mikäli olosuhteet ovat niin heikot. Tämän jälkeen toiminta voidaan aloittaa uudelleen, kun markkinaolosuhteet ovat taas suotuisat. (Smit & Trigeorgis 2004, ) Tuotannonsopeuttamismahdollisuus voi muodostua tärkeäksi tekijäksi, kun yritys tekee päätöstä käytettävästä tuotantoteknologiasta. Sopeuttamistoimien avulla voidaan saavuttaa suuria kustannussäästöjä tai kasvattaa tuottoja. Sopeuttamismahdollisuudet voivat muodostua yritykselle erittäin tärkeiksi, sillä niiden avulla voi olla mahdollista saavuttaa asetetut taloudelliset tavoitteet. Sopeuttamistoimia varten yrityksen tulee määrittää rajat, jolloin tuotantoa supistetaan tai laajennetaan. (Trigeorgis 1996, 2 12)
16 16 Skaalausoptiot ovat arvokkaita luonnonvaroja hyödyntävillä teollisuuden aloilla, kuten kaivos-, öljy-, metalli- ja metsäteollisuudessa. Näillä aloilla lopputuotteiden hinnat saattavat vaihdella voimakkaasti. Lisäksi skaalausoptiot ovat tärkeitä kausiluoteisilla aloilla, kuten muoti- ja kulutustavarateollisuudessa, jossa tuotteiden elinkaaret voivat olla huomattavan lyhyitä. (Trigeorgis 1996, 2 12; Ståhle ym. 2002, ) Hylkäysoptio Hylkäysoptio (option to abandon) mahdollistaa käynnissä olevan investointiprojektin hylkäämisen, mikäli markkinaolosuhteet heikkenevät ankarasti. Hylkäysmahdollisuuden voi tulkita amerikkalaiseksi myyntioptioksi. Hylkäysoption avulla pystytään välttämään projektista aiheutuvia tappioita. Optioon sisältyy myös mahdollisuus realisoida hankkeeseen liittyvät tuotannontekijät. Yleensä monikäyttöiseen omaisuuteen liittyy korkeampi realisointiarvo, ja sitä kautta korkeampi hylkäysoption arvo, kuin erityiskäyttöön tarkoitetulla omaisuuserällä. Tämä johtuu siitä, että monikäyttöiselle omaisuudelle on helppo löytää myöhempää käyttöä. (Trigeorgis 1996, 2 13) Hylkäysoption avulla yritys voi lähteä helpommin mukaan investointihankkeisiin, koska sillä on mahdollisuus luopua projektista, mikäli se osoittautuu kannattamattomaksi. Hylkäysoptio toimii siis eräänlaisena vakuutuksena hankkeeseen liittyen. (Brealey & Myers 2000, 623) Hylkäysoptiota ei kuitenkaan tule toteuttaa, ellei hylkäämisestä ole tehty tarkkoja laskelmia ja arvioita option toteuttamisen vaikutuksesta. Seurauksena saattaa olla tärkeän osaamisen menettäminen ja suuret tappiot, mikäli optio toteutetaan ilman tarkkaa harkintaa. Yrityksen tulisi myös huomioida investointiprojektiin liittyvät mahdolliset muut reaalioptiot ennen kuin se luopuu hankkeesta. (Trigeorgis 1996, 12 13) Hylkäysoptiot ovat arvokkaita pääomaintensiivisillä aloilla, kuten lento- ja rautatieliikenteessä. Mikäli yritys havaitsee, että pääomat eivät ole tuottavassa käytössä, se voi hylätä kyseisen hankkeen ja suunnata pääomat tuottavampiin kohteisiin. Optio voi olla tärkeä myös lanseerattaessa uutta tuotetta epävarmoille markkinoille. Hylkääminen voi muodostua arvokkaaksi vaihtoehdoksi, mikäli markkinat osoittautuvat
17 17 epäsuotuisiksi. Hylkäysoptio voi olla arvokas myös rahoituspalveluja tarjoaville yrityksille. (Trigeorgis 1996, 2 13; Smit & Trigeorgis 2004, ) Vaihto-optio Yritys voi muuttaa tuotevalikoimaansa vaihto-option (option to switch) avulla. Tästä mahdollisuudesta käytetään nimitystä tuotejoustavuus (product flexibility). Mahdollisuus muuttaa tuotevalikoimaa saattaa olla erityisen tärkeää, mikäli hinnat tai kysyntä vaihtelevat voimakkaasti. Vaihto-optio voi sallia myös tuotantomenetelmien tai raaka-aineiden muuttamisen, kuitenkin siten, että tuotetaan samoja tuotteita. Tätä mahdollisuutta kutsutaan prosessijoustavuudeksi (process flexibility). Tuote- ja prosessijoustavuus saattavat merkitä yritykselle erittäin tärkeää kilpailuetua. Yrityksen tulisikin olla valmis maksamaan enemmän tämänkaltaisesta joustavasta tuotantoteknologiasta. (Trigeorgis 1996, 2 13) Prosessijoustavuutta voidaan teknologisen joustavuuden lisäksi saavuttaa esimerkiksi ylläpitämällä suhteita useisiin tavarantoimittajiin. Tämänkaltaisessa tilanteessa yrityksen on mahdollista vaihtaa tavarantoimittajaa hintojen muutosten mukaan. Joustavuutta voidaan saavuttaa myös hajauttamalla toimintoja eri maihin. Tällöin yrityksen on mahdollista toimia siellä maassa, missä markkinaolosuhteet ovat kulloinkin suotuisimmat. Tämä on ollut yksi syy, miksi esimerkiksi autoteollisuuden yritykset ovat hajauttaneet toimintaansa useisiin maihin. (Brealey & Myers 2000, 629) Tuotevalikoiman muuttamisen mahdollistava vaihto-optio on arvokas muun muassa lääke-, auto- ja elektroniikkateollisuudessa. Näillä aloilla tuotteiden erilaistaminen on tärkeää, ja varsinkin autoteollisuudessa valmistetaan paljon tuotteita asiakkaiden toiveiden mukaan. Lisäksi näille aloille on ominaista kysynnän voimakas vaihtelu. Tuotantomenetelmien tai raaka-aineiden muuttamisen mahdollistava optio on puolestaan tärkeä esimerkiksi öljy- ja kemikaaliteollisuudessa. Nämä alat ovat yleensä voimakkaasti riippuvaisia raaka-aineesta. (Trigeorgis 1996, 2 13; Ståhle ym. 2002, )
18 Kasvuoptio Kasvuoptiot (growth options) luovat tulevaisuuden kasvu- ja investointimahdollisuuksia, ja ne voidaan tulkita osto-optioiksi. Kasvuoptiot ovat tyypillisimpiä ja käytetyimpiä optiotyyppejä kasvuhakuisten yritysten toiminnassa. Investointi esimerkiksi tuotekehitykseen voi olla edellytys tuleville projekteille. Investoinnin toteuttaminen ei välttämättä ole kannattavaa lyhyellä aikavälillä, mutta tulevaisuudessa saatavat hyödyt voivat olla erittäin merkittäviä. Projekti voi toimia ponnahduslautana esimerkiksi tuleville täysin uusille tuotteille tai kustannussäästöille. (Trigeorgis 1996, 2 14) Kasvumahdollisuuksia sisältävät investoinnit ovat tärkeitä myös siinä mielessä, että yrityksen markkina-arvosta huomattava osa voi perustua tuleville investointi- ja kasvumahdollisuuksille. Yrityksen ei tulisikaan arvioida sen investointiprojekteja liian lyhytnäköisesti, vaan sen olisi hyvä ottaa huomioon myös hankkeisiin liittyvät kasvumahdollisuudet. (Ståhle ym. 2002, 154) Kasvuoptioita hankitaan usein yritysostojen kautta. Yritysoston avulla on mahdollista saada kasvuoptioita, joiden hankkiminen olisi muuten vaikeaa tai niiden luominen aiheuttaisi liian suuria kustannuksia. Tyypillisesti kasvuoptioita hankitaan myös kansainvälistymishankkeiden avulla. (Damodaran 2003, ) Kasvuoptiot ovat arvokkaita toimialoilla, jotka perustuvat korkeaan teknologiaan ja ovat tuotekehitysintensiivisiä. Näille aloille on erityisen tärkeää, että hanketta voidaan laajentaa, mikäli se osoittautuu onnistuneeksi. Kasvumahdollisuuksia on tärkeää pitää avoimina myös aloilla, joilla on paljon eri sovelluksia yrityksen tarjoamasta tuotteesta. Kasvuoption avulla tämänkaltainen yritys voi erottautua kilpailijoista ja saavuttaa kilpailuetua. (Trigeorgis 1996, 2 14; Ståhle ym. 2002, ) Moniulotteiset vuorovaikutusoptiot Moniulotteiset vuorovaikutusoptiot (multiple integrating options) ovat lukuisten optioiden kokoelmia. Todellisuudessa investoinnit sisältävät usein monia erityyppisiä optioita yhtä aikaa. Reaalioptioiden arvoja on kuitenkin tapana määrittää yksi optio kerrallaan, koska arvonmääritys vuorovaikutteisille optioille on erittäin vaikeaa.
19 19 Arvonmääritys on vaikeaa juuri optioiden vuorovaikutuksen takia. Moniulotteisille vuorovaikutusoptioille on tyypillistä, että aiemmin toteutettu optio vaikuttaa useimmiten myöhemmin toteutettavaan optioon. Aiemmat reaalioptiot reagoivat uusien optioiden huomioimiseen laskelmissa, eikä reaalioptioiden joukon arvoa ole yleensä mahdollista laskea summaamalla optioiden arvoja yhteen. Option arvo saattaa olla yhdessä tarkasteltuna suurempi tai pienempi kuin itsenäisesti tarkasteltuna. Se, kuinka paljon optiot vaikuttavat toisiinsa, riippuu optioiden ominaisuuksista, kuten esimerkiksi siitä, onko kyseessä myynti- vai osto-optio. Moniulotteisia vuorovaikutusoptioita löytyy esimerkiksi edellä muiden optiotyyppien yhteydessä mainituilta toimialoilta. (Trigeorgis 1996, 227; Ståhle ym. 2002, )
20 Yhteenveto reaalioptiotyypeistä Kunkin reaalioptiotyypin ominaisuudet esitetään vielä tiivistetysti taulukossa 1. TAULUKKO 1 Yhteenveto reaalioptiotyypeistä Vaiheistusoptio Skaalausoptio Hylkäysoptio Vaihto-optio Kasvuoptio Moniulotteiset vuorovaikutusoptiot OMINAISUUDET Mahdollistaa investoinnin lykkäämisen. Johdolla voi olla mahdollisuus viivästyttää investoinnin toteutusta ja hankkia lisätietoa investoinnin kannattavuuteen vaikuttavista tekijöistä. Perustuu investoinnin pilkkomiseen osiksi. Investoinnin eri osat suoritetaan valitulla hetkellä. Yksittäisen vaiheen voi nähdä optioksi seuraavan vaiheen toteuttamiselle. Sallii yrityksen muuttaa tuotantoaan. Markkinoiden osoittautuessa suotuisiksi yritys voi laajentaa tuotantoa tai vastaavasti huonoina aikoina pienentää sitä. Tuotanto voidaan ääritapauksissa myös pysäyttää ja aloittaa uudelleen. Mahdollistaa käynnissä olevan investointiprojektin hylkäämisen, mikäli markkinaolosuhteet heikkenevät ankarasti. Hylkäysoptioon liittyy myös mahdollisuus realisoida hankkeeseen liittyvät tuotannontekijät. Sallii yrityksen muuttaa esimerkiksi tuotevalikoimaansa, mikäli hinnat tai kysyntä vaihtelevat voimakkaasti. Tämä optio voi sallia myös tuotantomenetelmien tai teknologian muuttamisen. Luo tulevaisuuden kasvu- ja investointimahdollisuuksia. Investointi esimerkiksi tuotekehitykseen voi olla edellytys tuleville projekteille. Moniulotteiset vuorovaikutusoptiot ovat lukuisten yksittäisten optiotyyppien kokoelmia. Todellisuudessa investoinnit sisältävät usein monia erityyppisiä optioita yhtä aikaa. REAALIOPTIO- TYYPPI Lykkäysoptio MYYTI/OS- TO-OPTIO Osto-optio Myyntija/tai ostooptio Myyntija/tai ostooptio Myyntioptio Myyntija/tai ostooptio Osto-optio Myyntija/tai ostooptio TOIMIALAT, JOILLA TÄRKEÄ Pääomavaltaiset teollisuudenalat, kuten metalli- ja metsäteollisuus T & k-intensiiviset alat, kuten lääketeollisuus ja informaatioteknologia sekä pääomaintensiiviset alat Luonnonvaroja hyödyntävät teollisuuden alat sekä kausiluoteiset alat Pääomaintensiiviset alat, lanseerattaessa uutta tuotetta epävarmoille markkinoille sekä rahoituspalvelualat Alat, joilla kysyntä vaihtelee voimakkaasti sekä raaka-aine riippuvaiset alat Korkeaan teknologiaan perustuvat alat sekä alat, joilla on paljon tarjontaa lopputuotteelle Investointiprojektit mm. yllä mainituilla aloilla
21 Esimerkki erilaisista reaalioptioista Tässä kuvitteellisessa esimerkissä (muunneltu Kester 2001, 43; ks. myös Ståhle ym. 2002, 137) käydään läpi eri luokittelutapojen mukaisia reaalioptioita, joita yrityksen investointihankkeeseen saattaa liittyä. Teollisuusyritys haluaa rakentaa tehtaan, jolla se pystyy laajentamaan tuotantoaan. Yrityksen asiakas sitoutuu ostamaan kiinteän osuuden tehtaan tuotannosta. Vaikka asiakas ei vastaanottaisikaan tuotetta, se maksaa sovitusta vuositoimituksesta. Mikäli yritys ei heti rakenna tehdasta, sopimus raukeaa ja asiakas rakentaa oman tehtaan. Yrityksellä on siis hallussa kasvuoptio, joka on yksinkertainen ja erääntyvä yksinoikeusoptio. Oletetaan, että edellä kuvattu mahdollisuus ei katoa vuodessa, ja että vuoden kuluttua tehtaan rakentamiskustannukset olisivat huomattavasti edullisemmat. Lisäksi asiakas on pyytänyt samanlaiset tarjoukset yrityksen kilpailijoilta. Nyt kyseessä on siis yksinkertainen, lykättävä ja jaettu kasvuoptio. Tilanteessa hankkeelle lasketaan nettonykyarvo sekä verrataan sitä reaalioption arvoon. Lopuksi tarkastellaan vielä tilannetta, jossa yrityksen lopputuote muodostuu innovaatioksi, ja se pystyy korvaamaan muita vastaavia tuotteita. Lopputuotteen kysynnän oletetaan kasvavan voimakkaasti, mikäli yritys pystyy tuottamaan tuotetta riittävästi ja tuotteen erityiset ominaisuudet havaitaan markkinoilla. Kysynnän kasvun myötä yrityksen on mahdollista rakentaa uusia tuotantolaitoksia. Uhkana hankkeessa on lopputuotteen vaikea valmistusprosessi sekä mahdollisesti kiristyvä lainsäädäntö, joka vaikeuttaisi tuotantoa. Lisäksi asiakas on pyytänyt tarjouksen myös nykyisen tuotteen muilta toimittajilta. Nyt kyseessä on kasvuoptio, joka on jaettu ja lykättävä yhdistelmäoptio. Vaikka kassavirran nykyarvon perusteella näyttäisi siltä, että yrityksen tulisi hylätä hanke, johto saattaa hyväksyä sen välittömästi. Näin tapahtuu, mikäli kilpailijoilla on mahdollisuus investoida samankaltaiseen tuotteeseen ja muuttaa yrityksen kasvuoptio arvottomaksi.
22 22 3 REAALIOPTIOIDEN ARVONMÄÄRITYS 3.1 Arvonmääritysmallit Reaalioptioiden arvonmääritys perustuu finanssioptioiden arvonmääritysmalleihin. Perinteisesti optioiden arvoja on määritetty binomimallilla tai Black & Scholes - mallilla. Binomimalli kuuluu niin sanottuihin numeerisiin menetelmiin, ja se juontaa juurensa William Sharpen ja Cox-Ingersoll-Rossin töistä vuosilta Black & Scholes -malli kuuluu analyyttisiin menetelmiin, ja sen juuret ovat Fischer Blackin ja Myron Scholesin tutkimuksessa vuodelta Myöhemmin näistä malleista on julkaistu erilaisia muunnelmia, joissa malleihin liittyviä rajoituksia on pyritty huomioimaan. (Puttonen & Valtonen 1996, 109) Seuraavaksi esitellään binomimallin toimintaperiaatteita, ja tämän jälkeen käsitellään Black & Scholes -mallia Binomimalli Binomimalli perustuu periaatteeseen, että osakkeen tämänhetkinen hinta S voi hetkeen t mennessä joko nousta arvoon Su tai laskea arvoon Sd. Tässä u ja d ovat nousun ja laskun suuruutta kuvaavia kertoimia. Periodin lopussa hinta voi olla tämänhetkistä arvoa korkeampi tai matalampi, eli hinnalla on kaksi vaihtoehtoista tulevaisuuden tulemaa. Hinnan nousun todennäköisyyttä kuvaa termi q. Tällöin laskun todennäköisyys on 1 q. Edellä kuvattu tieto voidaan tiivistää kuviossa 1, josta käytetään nimitystä yksiperiodinen binomipuu. Tämä kuvio kuvaa siis osakkeen hinnan kehitystä. (Puttonen & Valtonen 1996, 99)
23 23 q Su S 1 q Sd KUVIO 1 Yksiperiodinen binomipuu (Puttonen & Valtonen 1996, 99) Edellä mainittujen tekijöiden lisäksi option arvonmääritystä varten tarvitaan korkotekijä R. Oletetaan, että alkuhetkellä tehty riskitön sijoitus kasvaa R-kertaiseksi hetkeen t mennessä. Jotta niin sanottuja arbitraasimahdollisuuksia 3 ei olisi, pitää ehdon u > R > d olla voimassa. Jos korko olisi suurempi kuin arvonnousu (R > u), ei osake voisi parhaimmillaankaan tuottaa yli riskittömän koron. Jos taas korko olisi pienempi kuin arvonlasku (R < d), ei osake voisi huonoimmillaankaan tuottaa alle riskittömän koron. Oletetaan lisäksi, että option toteutushinta on X, jolloin option arvo päättymispäivänä on aina korkeintaan [0, S* X]. Merkitään option arvoa C:llä ja osakkeen hintaa päättymispäivänä S*:llä. Binomimallin mukaan osake voi saada tasan kaksi arvoa, joten option arvolle saadaan vastaavanlainen puu. Kuvio 2 kuvaa osto-option arvon kehitystä. q Cu = max (Su X, 0) C =? 1 q Cd = max (Sd X, 0) KUVIO 2 Osto-option arvon kehitys (Puttonen & Valtonen 1996, 99) Koska osake saavuttaa haaroissa olevat arvonsa Su ja Sd option päättymispäivänä, voidaan option hinnan odotusarvo päättymispäivään laskea painotettuna keskiarvona 3 Arbitraasi tarkoittaa mahdollisuutta riskittömiin voittoihin. Tehokkailla markkinoilla kenelläkään ei ole mahdollisuutta siihen.
24 24 seuraavasti q* Cu + (1 q)* Cd. Arvonmäärityksessä ollaan kuitenkin kiinnostuneita option arvosta tänään, minkä vuoksi oikean diskonttaustekijän valinta on ainoa jäljellä oleva ongelma. Option nykyarvon laskemiseksi käytetään niin sanottua riskineutraliteettiperiaatetta, jolla on kaksi tärkeää seurausta: kaikkien sijoituskohteiden odotettu tuotto on sama kuin riskitön korko kaikkien kassavirtojen nykyarvot voidaan laskea diskonttaamalla ne riskittömällä korolla. On huomattava, että tämä periaate ei pidä paikkaansa todellisessa maailmassa, mutta optioita hinnoiteltaessa oletus ei vaikuta hintaan, joten se kannatta tehdä. Option arvoksi saadaan näin ollen (kaava 1): (Puttonen & Valtonen 1996, 100) (1) C = qcu + ( 1 q) Cd R Soveltamalla riskineutraliteettiperiaatetta uudemman kerran saadaan kaavassa esiintyvä todennäköisyystermi sievennettyä pois. Voidaan nimittäin olettaa, että myös osakkeen odotettu tuotto on sama kuin riskitön korko. Näin ollen osakkeen hinnan odotusarvo E(S) hetkellä t on oltava sama kuin alkuhetkellä tehdyn S:n suuruisen talletuksen arvo hetkellä t (kaava 2). (2) E ( S) = qsu + (1 q) Sd = SR Tästä q saadaan ratkaistua eli q = (R d)/(u d). Sijoittamalla tämä kaavaan 1 saadaan yksiperiodinen binomimalli (kaava 3). Kaavassa ei ole enää lainkaan todennäköisyystermejä q ja 1 q, joten osakkeen tuotto-odotus ei vaikuta option arvoon. Edellä q:n arvo laskettiin olettaen, että maailma on riskineutraali. Tällöin q:n arvo pätee vain riskineutraalissa maailmassa. Optioteoriassa voidaan kuitenkin työskennellä riskineutraalissa maailmassa, sillä option hinta ei riipu sijoittajien riskipreferensseistä. Tällöin sijoittajat ovat riskineutraaleja, ja kaikkien sijoituskohteiden odotettu tuotto on sama kuin riskitön korko. (Puttonen & Valtonen 1996, 101)
25 25 (3) R d Cu C = u d u + Cd u R R d Kun option arvosta halutaan saada tarkempi kuva, voidaan option voimassaoloaika pilkkoa useampaan periodiin (Puttonen & Valtonen 1996, 104). Yksiperiodisen mallin jälkeen tarkastellaan kahta periodia, jolloin osakkeen hintapuu näyttää kuvion 3 mukaiselta. Kuten kuviosta voidaan havaita binomimalli käy läpi kaikki mahdolliset vaihtoehdot eri tulemille option voimassaoloaikana. Suu S q 1 q Su Sd Sud Sdd KUVIO 3 Kaksiperiodinen binomipuu (Puttonen & Valtonen 1996, 104) Kuviossa 3 Suu kuvaa tilannetta, jossa osakkeen hinta nousee molemmilla periodeilla. Vastaavasti Sud kuvaa tilannetta, jossa hinta ensin nousee ja sitten laskee tai päinvastoin, jolloin hinta ensin laskee ja sitten nousee. Tilanteeseen Sdd puolestaan päästään kahden laskun myötä. Suu kuvaa siis kannattavinta tulemaa ja sdd tappiollisinta. Kuvion 3 mukaiseen tilanteeseen on edelleen mahdollista lisätä kausia, jolloin on kyse moniperiodisesta binomimallista. Kausien lisäämisen myötä option arvosta saadaan entistä tarkempi kuva, sillä mitä pienempiin periodeihin voimassaoloaika jaetaan, sitä tarkemmin pystytään jäljittelemään todellista tilannetta. Moniperiodisessa mallissa option arvo voidaan laskea yksiperiodisen mallin avulla jakamalla binomipuu yhden haaraan osiin. Option arvon ratkaiseminen aloitetaan loppuhetkestä liikkuen takaisin nykyhetkeen.
26 Black & Scholes -malli Tunnetuin optioiden arvonmääritysmalleista on Black & Scholes -malli, jonka perusteella eurooppalaiselle osto-optiolle saadaan laskettua arvo (kaava 4). Option arvo riippuu Black & Scholes -mallin mukaan ainoastaan viidestä tekijästä, jotka ovat osakkeen hinta, option toteutushinta, voimassaoloaika, riskitön korkokanta ja osakkeen volatiliteetti. 4 (Black & Scholes 1973, ) Kaikki nämä tekijät olivat mukana myös binomimallissa, mutta volatiliteettiä käsiteltiin arvon nousun ja laskun muodossa. (4) C = [ N ( d1) * S] N( d 2) * Xe rt missä, 2 t ln( S / X ) + rt + σ d1 = 2 σ t d2 = d1 σ t C = osto-optio osakkeelle N(d) = standardisoidun kumulatiivisen normaalijakauman arvo d:lle e = Neperin luku, noin 2,71828 ln = luonnollinen logaritmi S X t r σ = osakkeen hinta = option toteutushinta = option voimassaoloaika = riskitön korko = osakkeen volatiliteetti Black & Scholes -mallissa käytetyt korot ovat jatkuva-aikaisia, jolloin rahamarkkinakorot täytyy ensin annualisoida ja sitten muuttaa jatkuva-aikaisiksi. 4 Volatiliteetillä tarkoitetaan kohde-etuuden arvon vaihtelua tarkasteluhetkestä option päättymispäivään.
27 27 Kaavassa esiintyvä funktio N(d) on niin sanottu kumulatiivinen normaalijakaumafunktio. Funktion arvo N(x) kertoo, mikä on pisteen x vasemmalle puolelle jäävän alueen pinta-ala normaalijakauman kellokäyrässä. Tämä ala on se todennäköisyys, jolla normaalisti jakautuneen muuttujan arvo on pienempi kuin x. (Puttonen & Valtonen 1996, ) Black & Scholes -mallin taustalla on muutamia tärkeitä oletuksia, jotka eivät rahoitusmarkkinoilla kuitenkaan aina toteudu. Malli olettaa, että: (Hull 1989, 92 93) osakkeen tuotot ovat normaalisti jakautuneita osakkeiden lyhyeksimyynti 5 on mahdollista markkinoilla ei ole transaktiokustannuksia tai veroja osakkeelle ei makseta osinkoja markkinoilla ei ole arbitraasimahdollisuuksia osakekaupankäynti on jatkuvaa riskitön korko on vakio. Kun osto-option arvo on saatu määritettyä, voidaan myyntioption (P) hinta laskea seuraavan kaavan mukaan (kaava 5) (Puttonen & Valtonen 1996, 120). (5) P = C S + Xe rt 3.2 Reaali- ja finanssioptioiden yhteys Tässä luvussa käsitellään reaali- ja finanssioptioiden välistä yhteyttä. Ensin esitellään reaali- ja finanssioptioiden yhtäläisyyksiä, joiden myötä reaalioptioiden arvonmäärityksessä voidaan käyttää finanssioptioiden arvonmääritysmalleja. Lopuksi esitellään reaali- ja finanssioptioiden välisiä eroja. 5 Lyhyeksimyynti tarkoittaa sitä, että myydään osakkeita, joita ei omisteta. Lyhyeksimyyjä lainaa osakkeet toiselta osapuolelta, myy ne ja ostaa myöhemmin takaisin.
28 Reaali- ja finanssioptioiden yhtäläisyyksiä Reaali- ja finanssioptioilla on yhtenäisiä piirteitä, joiden myötä finanssioptioteoriaa voidaan soveltaa myös reaalioptioihin. Finanssioptio antaa option haltijalle oikeuden ostaa tai myydä osake. Reaalioptio puolestaan antaa yritykselle oikeuden ostaa tai myydä jokin hyödyke tai kyvykkyys. Taulukko 2 havainnollistaa osakkeen osto-option ja investoinnin reaalioption välistä yhteyttä. TAULUKKO 2 Osakkeen osto-option ja investoinnin reaalioption yhteys (Luehrman 1998 a, 52) OSTO-OPTIO OSAKKEELLE INVESTOINNIN REAALIOPTIO Osakkeen hinta S Investoinnin tuottojen nykyarvo Option toteutushinta X Investoinnin hankintameno Option voimassaoloaika t Option voimassaoloaika Riskitön korko r Riskitön korko Osakkeen volatiliteetti σ Investointikohteen epävarmuus, volatiliteetti Osto-option kohteena olevan osakkeen hinta vastaa investoinnista saatavien tuottojen nykyarvoa (termi S). Option toteutushinta puolestaan vastaa investoinnin hankintamenoa eli hankkeeseen käytettyä rahamäärää (termi X). Option voimassaoloaika kuvastaa sitä mahdollisuutta, kuinka kauan päätöstä voi lykätä menettämättä optiota (termi t). Rahan aika-arvoa kuvataan sekä osakeoptiossa että reaalioptiossa riskittömällä korolla (termi r). Osakkeen volatiliteetti vastaa investoinnin tapauksessa hankkeeseen liittyvää epävarmuutta (termi σ). (Luehrman 1998 a, 52) Epävarmuutta on mahdollista kuvata esimerkiksi tuotannossa vaadittavan raaka-aineen tai lopputuotteen hinnan vaihtelulla. Finanssi- ja reaalioption välinen yhteys pätee sekä binomimalliin että Black & Scholes -malliin. Tekijöiden vaikutuksia reaalioption arvoon käsitellään luvussa 3.3.
29 Reaali- ja finanssioptioiden eroja Reaali- ja finanssioptioiden yhtenäisistä piirteistä huolimatta optioiden välillä löytyy myös lukuisia eroavaisuuksia, jotka omalta osaltaan vaikeuttavat finanssioptioteorian suoraa soveltamista reaalioptioihin. Seuraavaksi esitellään reaali- ja finanssioptioiden keskeisimpiä eroja. (Kautt 2003, 74) Reaalioptio ei ole johdannainen, vaikka sen arvo määräytyy samoin periaattein kuin optiojohdannaisen. Finanssioptiot ovat kaupattavissa likvideillä markkinoilla, mutta reaalioptioilla ei useimmiten käydä kauppaa. Finanssioption arvo riippuu kohde-etuuden arvosta. Reaalioptioissa arvoon vaikuttavat kassavirrat ja optioiden luomat mahdollisuudet. Finanssioptioissa option haltijalla on yksinoikeus kohteeseen, kun reaalioptioissa optio voi olla jaettu. Yksittäisen finanssioption arvo on yleensä melko pieni, kun taas reaalioption arvo voi olla huomattavan suuri. Option haltijan toimet eivät vaikuta finanssioptiossa option arvoon. Sen sijaan reaalioptioissa ne voivat vaikuttaa. Finanssioptioiden voimassaoloaika on yleensä lyhyempi verrattuna reaalioptioihin, joissa maturiteetti voi olla vuosia. 3.3 Reaalioption arvoon vaikuttavat tekijät Reaalioption arvo muodostuu kahdesta tekijästä eli option perusarvosta ja aika-arvosta. Option perusarvoon vaikuttavat reaalioptioiden tapauksessa investoinnin odotetut tuotot ja hankintameno. Osto-option perusarvo on tuottojen nykyarvon ja hankintamenon välinen erotus. Myyntioption perusarvon laskentatapa on käänteinen verrattuna ostooptioon. Myyntioption perusarvo saadaan, kun hankintamenosta vähennetään tuottojen nykyarvo. Option perusarvo on siis se rahamääräinen hyöty, joka saataisiin jos optio toteutettaisiin heti. Perusarvo voi olla haltijan kannalta vain positiivinen, koska optio on oikeus eikä velvollisuus. Tuottojen ja hankintamenon suhde, option voimassaoloaika,
Rahoitusriskit ja johdannaiset Matti Estola. luento 8 Optioiden hinnoittelusta
 Rahoitusriskit ja johdannaiset Matti Estola luento 8 Optioiden hinnoittelusta 1. Optioiden erilaiset kohde-etuudet 1.1. Osakeoptiot Yksi optio antaa yleensä oikeuden ostaa/myydä 1 kpl kohdeetuutena olevia
Rahoitusriskit ja johdannaiset Matti Estola luento 8 Optioiden hinnoittelusta 1. Optioiden erilaiset kohde-etuudet 1.1. Osakeoptiot Yksi optio antaa yleensä oikeuden ostaa/myydä 1 kpl kohdeetuutena olevia
Reaalioptioden käsitteen esittely yksinkertaisen esimerkin avulla
 Reaalioptioden käsitteen esittely yksinkertaisen esimerkin avulla Optimointiopin seminaari - Syksy 2000 / 1 Esitelmän sisältö Investointien peruuttamattomuuden vaikutus investointipäätökseen Investointimahdollisuuksien
Reaalioptioden käsitteen esittely yksinkertaisen esimerkin avulla Optimointiopin seminaari - Syksy 2000 / 1 Esitelmän sisältö Investointien peruuttamattomuuden vaikutus investointipäätökseen Investointimahdollisuuksien
Kuntasektorin toiminnanohjausjärjestelmäinvestointien arvonmääritys
 Tampereen yliopisto Taloustieteiden laitos TAMPEREEN Y L I O P I S T O Kuntasektorin toiminnanohjausjärjestelmäinvestointien arvonmääritys Kansantaloustiede Pro gradu -tutkielma Syyskuu 2006 Ohjaaja: Markus
Tampereen yliopisto Taloustieteiden laitos TAMPEREEN Y L I O P I S T O Kuntasektorin toiminnanohjausjärjestelmäinvestointien arvonmääritys Kansantaloustiede Pro gradu -tutkielma Syyskuu 2006 Ohjaaja: Markus
Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia
 Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia { z(t k+1 ) = z(t k ) + ɛ(t k ) t t k+1 = t k + t, k = 0,..., N, missä ɛ(t i ), ɛ(t j ), i j ovat toisistaan riippumattomia siten, että
Wiener-prosessi: Tarkastellaan seuraavanlaista stokastista prosessia { z(t k+1 ) = z(t k ) + ɛ(t k ) t t k+1 = t k + t, k = 0,..., N, missä ɛ(t i ), ɛ(t j ), i j ovat toisistaan riippumattomia siten, että
Rahoitusriskit ja johdannaiset Matti Estola. luento 2 Termiini- ja futuurihintojen määräytyminen
 Rahoitusriskit ja johdannaiset Matti Estola luento 2 ermiini- ja futuurihintojen määräytyminen 1. ermiinien hinnoittelusta Esimerkki 1 Olkoon kullan spot -hinta $ 300 unssilta, riskitön korko 5 % vuodessa
Rahoitusriskit ja johdannaiset Matti Estola luento 2 ermiini- ja futuurihintojen määräytyminen 1. ermiinien hinnoittelusta Esimerkki 1 Olkoon kullan spot -hinta $ 300 unssilta, riskitön korko 5 % vuodessa
OPTIOT Vipua ja suojausta - mutta mitä se maksaa? Remburssi Investment Group 23.5.2000
 OPTIOT Vipua ja suojausta - mutta mitä se maksaa? Remburssi Investment Group 23.5.2000 MARKKINAKATSAUS AGENDA Lyhyt johdanto optioihin Näkemysesimerkki 1: kuinka tehdä voittoa kurssien laskiessa Näkemysesimerkki
OPTIOT Vipua ja suojausta - mutta mitä se maksaa? Remburssi Investment Group 23.5.2000 MARKKINAKATSAUS AGENDA Lyhyt johdanto optioihin Näkemysesimerkki 1: kuinka tehdä voittoa kurssien laskiessa Näkemysesimerkki
10.8 Investoinnin sisäinen korkokanta
 154 108 Investoinnin sisäinen korkokanta Investoinnin sisäinen korkokanta on se laskentakorko, jolla investoinnin nettonykyarvo on nolla Investointi on tuottava (kannattava), jos sen sisäinen korkokanta
154 108 Investoinnin sisäinen korkokanta Investoinnin sisäinen korkokanta on se laskentakorko, jolla investoinnin nettonykyarvo on nolla Investointi on tuottava (kannattava), jos sen sisäinen korkokanta
Investointiajattelu ja päätöksenteko
 Investointiajattelu ja päätöksenteko Ismo Vuorinen yliopettaja (laskentatoimi ja rahoitus) Investointien suunnittelu / erikoistumisopinnot 2010 Hämeenlinna / syksy 2010 Investointi käsitteenä investointi
Investointiajattelu ja päätöksenteko Ismo Vuorinen yliopettaja (laskentatoimi ja rahoitus) Investointien suunnittelu / erikoistumisopinnot 2010 Hämeenlinna / syksy 2010 Investointi käsitteenä investointi
Rahoitusriskit ja johdannaiset Luentokurssi kevät 2011 Lehtori Matti Estola
 Rahoitusriskit ja johdannaiset Luentokurssi kevät 2011 Lehtori Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Oikeustieteiden laitos, kansantaloustiede Luennot 22 t, harjoitukset
Rahoitusriskit ja johdannaiset Luentokurssi kevät 2011 Lehtori Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Oikeustieteiden laitos, kansantaloustiede Luennot 22 t, harjoitukset
Tietoa hyödykeoptioista
 Tietoa hyödykeoptioista Tämä esite sisältää tietoa Danske Bankin kautta tehtävistä hyödykeoptiosopimuksista. Hyödykkeet ovat jalostamattomia tuotteita tai puolijalosteita, joita tarvitaan lopputuotteiden
Tietoa hyödykeoptioista Tämä esite sisältää tietoa Danske Bankin kautta tehtävistä hyödykeoptiosopimuksista. Hyödykkeet ovat jalostamattomia tuotteita tai puolijalosteita, joita tarvitaan lopputuotteiden
Optiot 1. Tervetuloa webinaariin!
 Optiot 1 Tervetuloa webinaariin! Optiot 1 on peruskurssi optioista kiinnostuneelle sijoittajalle. Webinaarissa käydään läpi mm. mikä optio on, miten sitä voi käyttää ja mistä kannattaa lähteä liikkeelle.
Optiot 1 Tervetuloa webinaariin! Optiot 1 on peruskurssi optioista kiinnostuneelle sijoittajalle. Webinaarissa käydään läpi mm. mikä optio on, miten sitä voi käyttää ja mistä kannattaa lähteä liikkeelle.
Mat-2.11 4 Investointiteoria. Tentti 6.9.2005. Mitd
 .* Mat-2.11 4 Investointiteoria Tentti 6.9.2005 Ki{oita jokaiseen koepapcriin selveisti: o Mat-2.114 Investointiteoria o opintoki{'an numero sekii sukunimi ja viralliset etunimet tekstaten o koulutusohjelma
.* Mat-2.11 4 Investointiteoria Tentti 6.9.2005 Ki{oita jokaiseen koepapcriin selveisti: o Mat-2.114 Investointiteoria o opintoki{'an numero sekii sukunimi ja viralliset etunimet tekstaten o koulutusohjelma
Investointilaskentamenetelmiä
 Investointilaskentamenetelmiä Laskentakorkokannan käyttöön perustuvat menetelmät (netto)nykyarvomenetelmä suhteellisen nykyarvon menetelmä eli nykyarvoindeksi annuiteettimenetelmä likimääräinen annuiteettimenetelmä
Investointilaskentamenetelmiä Laskentakorkokannan käyttöön perustuvat menetelmät (netto)nykyarvomenetelmä suhteellisen nykyarvon menetelmä eli nykyarvoindeksi annuiteettimenetelmä likimääräinen annuiteettimenetelmä
a) 3500000 (1, 0735) 8 6172831, 68. b) Korkojaksoa vastaava nettokorkokanta on
 Kotitehtävät 4 Ratkaisuehdotukset. 1. Kuinka suureksi 3500000 euroa kasvaa 8 vuodessa, kun lähdevero on 30% ja vuotuinen korkokanta on 10, 5%, kun korko lisätään a) kerran vuodessa b) kuukausittain c)
Kotitehtävät 4 Ratkaisuehdotukset. 1. Kuinka suureksi 3500000 euroa kasvaa 8 vuodessa, kun lähdevero on 30% ja vuotuinen korkokanta on 10, 5%, kun korko lisätään a) kerran vuodessa b) kuukausittain c)
Hyödykebarrieroptioiden hinnoittelu
 Hyödykebarrieroptioiden hinnoittelu Kandidaattiseminaari 2010 1.11.2010 Esityksen rakenne Yleistä barrieroptioista Taustaa barrieroptioiden hinnoittelusta Työn tavoitteet ja rajaukset Sovellettava aineisto
Hyödykebarrieroptioiden hinnoittelu Kandidaattiseminaari 2010 1.11.2010 Esityksen rakenne Yleistä barrieroptioista Taustaa barrieroptioiden hinnoittelusta Työn tavoitteet ja rajaukset Sovellettava aineisto
Nyt ensimmäisenä periodina (ei makseta kuponkia) odotettu arvo on: 1 (qv (1, 1) + (1 q)v (0, 1)) V (s, T ) = C + F
 Mat-2.34 Investointiteoria Laskuharjoitus 2/2008, Ratkaisut 29.04.2008 Binomihilan avulla voidaan laskea T vuoden ja tietyn kupongin sisältävän joukkovelkakirjan arvo eli hinta rekursiivisesti vaihtelevan
Mat-2.34 Investointiteoria Laskuharjoitus 2/2008, Ratkaisut 29.04.2008 Binomihilan avulla voidaan laskea T vuoden ja tietyn kupongin sisältävän joukkovelkakirjan arvo eli hinta rekursiivisesti vaihtelevan
Talousmatematiikan perusteet
 kevät 219 / orms.1 Talousmatematiikan perusteet 1. Laske integraalit a 6x 2 + 4x + dx, b 5. harjoitus, viikko 6 x + 1x 1dx, c xx 2 1 2 dx a termi kerrallaan kaavalla ax n dx a n+1 xn+1 +C. 6x 2 + 4x +
kevät 219 / orms.1 Talousmatematiikan perusteet 1. Laske integraalit a 6x 2 + 4x + dx, b 5. harjoitus, viikko 6 x + 1x 1dx, c xx 2 1 2 dx a termi kerrallaan kaavalla ax n dx a n+1 xn+1 +C. 6x 2 + 4x +
Tietoja osakeoptioista
 Tietoja osakeoptioista Tämä esite sisältää yleisiä tietoja osakeoptioista, joilla voidaan käydä kauppaa Danske Bankin välityksellä. AN OTC TRANSACTION WITH DANSKE BANK AS COUNTERPARTY. ESITTELY Osakeoptioilla
Tietoja osakeoptioista Tämä esite sisältää yleisiä tietoja osakeoptioista, joilla voidaan käydä kauppaa Danske Bankin välityksellä. AN OTC TRANSACTION WITH DANSKE BANK AS COUNTERPARTY. ESITTELY Osakeoptioilla
b) Arvonnan, jossa 50 % mahdollisuus saada 15 euroa ja 50 % mahdollisuus saada 5 euroa.
 2.9. Epävarmuus ja odotetun hyödyn teoria Testi. Kumman valitset a) 10 euroa varmasti. b) Arvonnan, jossa 50 % mahdollisuus saada 15 euroa ja 50 % mahdollisuus saada 5 euroa. Odotettu arvo 0,5* 15 + 0,5*5
2.9. Epävarmuus ja odotetun hyödyn teoria Testi. Kumman valitset a) 10 euroa varmasti. b) Arvonnan, jossa 50 % mahdollisuus saada 15 euroa ja 50 % mahdollisuus saada 5 euroa. Odotettu arvo 0,5* 15 + 0,5*5
Investoinnin takaisinmaksuaika
 Investoinnin takaisinmaksuaika Takaisinmaksuaika on aika, jona investointi maksaa hintansa takaisin eli nettotuottoja kertyy perushankintamenon verran Investointi voidaan tehdä, jos takaisinmaksuaika
Investoinnin takaisinmaksuaika Takaisinmaksuaika on aika, jona investointi maksaa hintansa takaisin eli nettotuottoja kertyy perushankintamenon verran Investointi voidaan tehdä, jos takaisinmaksuaika
KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN
 00 N:o 22 LIITE KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN. Positioriskin laskemisessa käytettävät määritelmät Tässä liitteessä tarkoitetaan: arvopaperin nettopositiolla samanlajisen arvopaperin pitkien
00 N:o 22 LIITE KAUPANKÄYNTIVARASTON POSITIORISKIN LASKEMINEN. Positioriskin laskemisessa käytettävät määritelmät Tässä liitteessä tarkoitetaan: arvopaperin nettopositiolla samanlajisen arvopaperin pitkien
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Hanken Svenska handelshögskolan / Hanken School of Economics www.hanken.fi
 Sijoittajan sanastoa Pörssisäätiön sijoituskoulu VERO 2014 Prof. Minna Martikainen Hanken School of Economics, Finland Sijoitusmaailman termistö ja logiikka, omat toimet ja näin luen. SIJOITUSMAAILMAN
Sijoittajan sanastoa Pörssisäätiön sijoituskoulu VERO 2014 Prof. Minna Martikainen Hanken School of Economics, Finland Sijoitusmaailman termistö ja logiikka, omat toimet ja näin luen. SIJOITUSMAAILMAN
Valuuttariskit ja johdannaiset
 Valuuttariskit ja johdannaiset Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Sosiaali- ja terveysjohtamisen laitos, kansantaloustiede Lähde: Hull, Options, Futures, & Other
Valuuttariskit ja johdannaiset Matti Estola Itä-Suomen yliopisto, Yhteiskunta- ja Kauppatieteiden tiedekunta, Sosiaali- ja terveysjohtamisen laitos, kansantaloustiede Lähde: Hull, Options, Futures, & Other
Kansainvälinen rahatalous Matti Estola. Termiinikurssit ja swapit valuuttariskien hallinnassa
 Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Investointimahdollisuudet ja niiden ajoitus
 Investointimahdollisuudet ja niiden ajoitus Ratkaisu optiohinnoitteluteorian avulla Esitelmä - Eeva Nyberg Optimointiopin seminaari - Syksy 000 / Tähän asti opittua NP:n rajoitteet vaikka NP negatiivinen
Investointimahdollisuudet ja niiden ajoitus Ratkaisu optiohinnoitteluteorian avulla Esitelmä - Eeva Nyberg Optimointiopin seminaari - Syksy 000 / Tähän asti opittua NP:n rajoitteet vaikka NP negatiivinen
Suojaa ja tuottoa laskevilla markkinoilla. Johannes Ankelo Arvopaperi Aamuseminaari
 Suojaa ja tuottoa laskevilla markkinoilla Commerzbank AG Saksan toiseksi suurin pankki Euroopan johtavia strukturoitujen tuotteiden liikkeellelaskijoita Yli 50 erilaista tuotetyyppiä listattuna Saksan
Suojaa ja tuottoa laskevilla markkinoilla Commerzbank AG Saksan toiseksi suurin pankki Euroopan johtavia strukturoitujen tuotteiden liikkeellelaskijoita Yli 50 erilaista tuotetyyppiä listattuna Saksan
Ratkaisu: a) Koroton takaisinmaksuaika on 9000 = 7,5 vuotta. 1200 b) Kun vuosituotot pysyvät vakiona, korollinen takaisinmaksuaika määräytyy
 Kotitehtävät 7. Aihepiirinä Investointi Ratkaisuehdotuksia 1. Investoinnin hankintameno on 9000 euroa ja siitä saadaan seuraavina vuosina vuosittain 1200 euron tulot. Määritä a) koroton takaisinmaksuaika
Kotitehtävät 7. Aihepiirinä Investointi Ratkaisuehdotuksia 1. Investoinnin hankintameno on 9000 euroa ja siitä saadaan seuraavina vuosina vuosittain 1200 euron tulot. Määritä a) koroton takaisinmaksuaika
10 Liiketaloudellisia algoritmeja
 218 Liiketaloudellisia algoritmeja 10 Liiketaloudellisia algoritmeja Tämä luku sisältää liiketaloudellisia laskelmia. Aiheita voi hyödyntää vaikkapa liiketalouden opetuksessa. 10.1 Investointien kannattavuuden
218 Liiketaloudellisia algoritmeja 10 Liiketaloudellisia algoritmeja Tämä luku sisältää liiketaloudellisia laskelmia. Aiheita voi hyödyntää vaikkapa liiketalouden opetuksessa. 10.1 Investointien kannattavuuden
r1 2 (1 0,02) 1 0,027556 (1 0, 0125) A250A0100 Finanssi-investoinnit 6. harjoitukset 21.4.2015 Futuuri, termiinit ja swapit
 A50A000 Finanssi-investoinnit 6. harjoitukset.4.05 Futuuri, termiinit ja swapit Tehtävä 6. Mikä on kahden vuoden bonditermiinin käypä markkinahinta, kun kohdeetuutena on viitelaina, jonka nimellisarvo
A50A000 Finanssi-investoinnit 6. harjoitukset.4.05 Futuuri, termiinit ja swapit Tehtävä 6. Mikä on kahden vuoden bonditermiinin käypä markkinahinta, kun kohdeetuutena on viitelaina, jonka nimellisarvo
Selvitetään korkokanta, jolla investoinnin nykyarvo on nolla eli tuottojen ja kustannusten nykyarvot ovat yhtä suuret (=investoinnin tuotto-%)
 Sisäisen korkokannan menetelmä Selvitetään korkokanta, jolla investoinnin nykyarvo on nolla eli tuottojen ja kustannusten nykyarvot ovat yhtä suuret (=investoinnin tuotto-%) Sisäinen korkokanta määritellään
Sisäisen korkokannan menetelmä Selvitetään korkokanta, jolla investoinnin nykyarvo on nolla eli tuottojen ja kustannusten nykyarvot ovat yhtä suuret (=investoinnin tuotto-%) Sisäinen korkokanta määritellään
Arvo (engl. value) = varmaan attribuutin tulemaan liittyvä arvo. Päätöksentekijä on riskipakoinen, jos hyötyfunktio on konkaavi. a(x) = U (x) U (x)
 Arvo (engl. value) = varmaan attribuutin tulemaan liittyvä arvo. Hyöty (engl. utility) = arvo, jonka koemme riskitilanteessa eli, kun teemme päätöksiä epävarmuuden (todennäköisyyksien) vallitessa. Vrt.
Arvo (engl. value) = varmaan attribuutin tulemaan liittyvä arvo. Hyöty (engl. utility) = arvo, jonka koemme riskitilanteessa eli, kun teemme päätöksiä epävarmuuden (todennäköisyyksien) vallitessa. Vrt.
Tietoja koron-ja valuutanvaihtosopimuksista
 Tietoja koron-ja valuutanvaihtosopimuksista Tämä esite sisältää tietoja Danske ankin kautta tehtävistä koron- ja valuutanvaihtosopimuksista. Koron- ja valuutanvaihtosopimuksilla voidaan käydä Danske ankin
Tietoja koron-ja valuutanvaihtosopimuksista Tämä esite sisältää tietoja Danske ankin kautta tehtävistä koron- ja valuutanvaihtosopimuksista. Koron- ja valuutanvaihtosopimuksilla voidaan käydä Danske ankin
RAHOITUS JA RISKINHALLINTA
 RAHOITUS JA RISKINHALLINTA Opintojaksosuunnitelma deadlines 2.9. 9.9. 30.9. 12.11. 2.12. Kohdeyritysvaraus Rahan sitoutuminen yritystoiminnassa käyttöomaisuuteen ja käyttöpääomaan pohdinta Case Rahoitustilanne
RAHOITUS JA RISKINHALLINTA Opintojaksosuunnitelma deadlines 2.9. 9.9. 30.9. 12.11. 2.12. Kohdeyritysvaraus Rahan sitoutuminen yritystoiminnassa käyttöomaisuuteen ja käyttöpääomaan pohdinta Case Rahoitustilanne
KANSANTALOUSTIETEEN PÄÄSYKOE : Mallivastaukset
 KANSANTALOUSTIETEEN PÄÄSYKOE.6.016: Mallivastaukset Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti Pohjola, Taloustieteen oppikirja, 014] sivuihin. (1) (a) Julkisten menojen kerroin (suljetun
KANSANTALOUSTIETEEN PÄÄSYKOE.6.016: Mallivastaukset Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti Pohjola, Taloustieteen oppikirja, 014] sivuihin. (1) (a) Julkisten menojen kerroin (suljetun
Talousmatematiikan perusteet
 kevät 2019 / orms.1030 Talousmatematiikan perusteet 5. harjoitus, viikko 7 11.02. 15.02.2019 R01 Ma 12 14 F453 R08 Ke 10 12 F453 R02 Ma 16 18 F453 L To 08 10 A202 R03 Ti 08 10 F425 R06 To 12 14 F140 R04
kevät 2019 / orms.1030 Talousmatematiikan perusteet 5. harjoitus, viikko 7 11.02. 15.02.2019 R01 Ma 12 14 F453 R08 Ke 10 12 F453 R02 Ma 16 18 F453 L To 08 10 A202 R03 Ti 08 10 F425 R06 To 12 14 F140 R04
Mat-2.3114 Investointiteoria Laskuharjoitus 3/2008, Ratkaisut 05.02.2008
 Korko riippuu usein laina-ajan pituudesta ja pitkille talletuksille maksetaan korkeampaa korkoa. Spot-korko s t on se korko, joka kertyy lainatulle pääomalle hetkeen t (=kokonaisluku) mennessä. Spot-korot
Korko riippuu usein laina-ajan pituudesta ja pitkille talletuksille maksetaan korkeampaa korkoa. Spot-korko s t on se korko, joka kertyy lainatulle pääomalle hetkeen t (=kokonaisluku) mennessä. Spot-korot
Mat Investointiteoria Laskuharjoitus 1/2008, Ratkaisu Yleistä: Laskarit tiistaisin klo luokassa U352.
 Yleistä: Laskarit tiistaisin klo 14-16 luokassa U352. Kysyttävää laskareista yms. jussi.kangaspunta@tkk. tai huone U230. Aluksi hieman teoriaa: Kassavirran x = (x 0, x 1,..., x n ) nykyarvo P x (r), kun
Yleistä: Laskarit tiistaisin klo 14-16 luokassa U352. Kysyttävää laskareista yms. jussi.kangaspunta@tkk. tai huone U230. Aluksi hieman teoriaa: Kassavirran x = (x 0, x 1,..., x n ) nykyarvo P x (r), kun
Nykyarvo ja investoinnit, L7
 Nykyarvo ja investoinnit, L7 netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k n k 1 k 2 k 3 k 4 k 5 k 6... 0 1 2 3 4 5 6... n j netto
Nykyarvo ja investoinnit, L7 netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k n k 1 k 2 k 3 k 4 k 5 k 6... 0 1 2 3 4 5 6... n j netto
Alustava liiketoimintasuunnitelma. Miksi alustava LTS? Ajattele vaikkapa näin. Hyvin suunniteltu on jo melkein puoleksi perustettu
 Alustava liiketoimintasuunnitelma Hyvin suunniteltu on jo melkein puoleksi perustettu 15.1.2013/LTPT1013 22.4.2013/EO1213 HM Miksi alustava LTS? Jäsennetään ja selvennetään aiotun yritystoiminnan kannattavuutta
Alustava liiketoimintasuunnitelma Hyvin suunniteltu on jo melkein puoleksi perustettu 15.1.2013/LTPT1013 22.4.2013/EO1213 HM Miksi alustava LTS? Jäsennetään ja selvennetään aiotun yritystoiminnan kannattavuutta
Rahoitusriskit ja johdannaiset Matti Estola Luento 5. Termiinihinnan määräytyminen
 Rahoitusriskit ja johdannaist Matti Estola Lunto 5 rmiinihinnan määräytyminn 1. rmiinin ylinn hinnoittlukaava Mrkitään trmiinisopimuksn kohd-tuudn spot hintaa sopimuksn tkopäivänä S :lla, kohd-tuudn trmiinihintaa
Rahoitusriskit ja johdannaist Matti Estola Lunto 5 rmiinihinnan määräytyminn 1. rmiinin ylinn hinnoittlukaava Mrkitään trmiinisopimuksn kohd-tuudn spot hintaa sopimuksn tkopäivänä S :lla, kohd-tuudn trmiinihintaa
Optiot 2. Tervetuloa webinaariin!
 Optiot 2 Tervetuloa webinaariin! Optiot 2 on jatkokurssi optioista kiinnostuneelle sijoittajalle. Webinaarissa jatketaan optioiden käsittelyä ja syvennymme johdannaisten maailmaan. Webinaarissa käydään
Optiot 2 Tervetuloa webinaariin! Optiot 2 on jatkokurssi optioista kiinnostuneelle sijoittajalle. Webinaarissa jatketaan optioiden käsittelyä ja syvennymme johdannaisten maailmaan. Webinaarissa käydään
Pääsykoe 2001/Ratkaisut Hallinto
 Pääsykoe 2001/Ratkaisut Hallinto 1. Osio 3/Tosi; Organisaatiokenttää ei mainita (s.35). 2. Osiot 1 ja 2/Epätosia; Puppua. Osio 3/Lähellä oikeata kuvion 2.1 mukaan (s.30). Osio 4/Tosi (sivun 30 tekstin
Pääsykoe 2001/Ratkaisut Hallinto 1. Osio 3/Tosi; Organisaatiokenttää ei mainita (s.35). 2. Osiot 1 ja 2/Epätosia; Puppua. Osio 3/Lähellä oikeata kuvion 2.1 mukaan (s.30). Osio 4/Tosi (sivun 30 tekstin
Käy kauppaa RBS minifutuureilla FIM Direct Pro -palvelulla
 Käy kauppaa RBS minifutuureilla FIM Direct Pro -palvelulla Kaupankäynti RBS minifutuureilla on kasvanut voimakkaasti viimeisen kahden vuoden aikana. Haluamme tällä lyhyellä oppaalla lisätä ymmärrystä näihin
Käy kauppaa RBS minifutuureilla FIM Direct Pro -palvelulla Kaupankäynti RBS minifutuureilla on kasvanut voimakkaasti viimeisen kahden vuoden aikana. Haluamme tällä lyhyellä oppaalla lisätä ymmärrystä näihin
Kirjanpito ja laskentatoimi A-osa
 1. Arvon määritys a) Mitkä tekijät vaikuttavat osto- ja myyntioptioiden arvoon ja miten? b) Yrityksen osingon oletetaan olevan ensi vuonna 3 euroa per osake ja osinkojen uskotaan kasvavan 6 % vuosivauhtia.
1. Arvon määritys a) Mitkä tekijät vaikuttavat osto- ja myyntioptioiden arvoon ja miten? b) Yrityksen osingon oletetaan olevan ensi vuonna 3 euroa per osake ja osinkojen uskotaan kasvavan 6 % vuosivauhtia.
KANSANTALOUSTIETEEN PÄÄSYKOE 4.6.2015 MALLIVASTAUKSET
 KANSANTALOUSTIETEEN ÄÄSYKOE 4.6.05 MALLIVASTAUKSET Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti ohjola, Taloustieteen oppikirja,. painos, 04] sivuihin. () (a) Bretton Woods -järjestelmä:
KANSANTALOUSTIETEEN ÄÄSYKOE 4.6.05 MALLIVASTAUKSET Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti ohjola, Taloustieteen oppikirja,. painos, 04] sivuihin. () (a) Bretton Woods -järjestelmä:
12. Korkojohdannaiset
 2. Korkojohdannaiset. Lähtökohtia Korkojohdannaiset ovat arvopapereita, joiden tuotto riippuu korkojen kehityksestä. korot liittyvät lähes kaikkiin liiketoimiin korkojohdannaiset ovat tärkeitä. korkojohdannaisilla
2. Korkojohdannaiset. Lähtökohtia Korkojohdannaiset ovat arvopapereita, joiden tuotto riippuu korkojen kehityksestä. korot liittyvät lähes kaikkiin liiketoimiin korkojohdannaiset ovat tärkeitä. korkojohdannaisilla
(1) Katetuottolaskelma
 (1) Katetuottolaskelma Katetuottolaskelmalla tarkastellaan yrityksen kannattavuutta myyntituotto - muuttuvat kustannukset (mukut) = katetuotto katetuotto - kiinteät kustannukset (kikut) = tulos (voitto
(1) Katetuottolaskelma Katetuottolaskelmalla tarkastellaan yrityksen kannattavuutta myyntituotto - muuttuvat kustannukset (mukut) = katetuotto katetuotto - kiinteät kustannukset (kikut) = tulos (voitto
www.tulosakatemia.fi Toivo Koski Liiketoiminnan käynnistäminen, liiketoiminnan suunnittelu ja taloudelliset laskelmat
 Liiketoiminnan käynnistäminen, liiketoiminnan suunnittelu ja taloudelliset laskelmat Jäljempänä esitetty vaiheistettu konsultoinnin sisältökuvaus sopii mm. uuden liiketoiminnan käynnistämiseen (kaupallistamiseen),
Liiketoiminnan käynnistäminen, liiketoiminnan suunnittelu ja taloudelliset laskelmat Jäljempänä esitetty vaiheistettu konsultoinnin sisältökuvaus sopii mm. uuden liiketoiminnan käynnistämiseen (kaupallistamiseen),
Mat-2.3114 Investointiteoria - Kotitehtävät
 Mat-2.3114 Investointiteoria - Kotitehtävät Kotitehtäviä on yhteensä kahdeksan ja ne ratkeavat tavallisilla taulukkolaskentaohjelmistoilla. Jokaisesta kotitehtävistä saa maksimissaan 5 pistettä: 4p/oikea
Mat-2.3114 Investointiteoria - Kotitehtävät Kotitehtäviä on yhteensä kahdeksan ja ne ratkeavat tavallisilla taulukkolaskentaohjelmistoilla. Jokaisesta kotitehtävistä saa maksimissaan 5 pistettä: 4p/oikea
Rahoitusriskit ja johdannaiset Matti Estola. luento 7 Swap sopimuksista lisää
 Rahoitusriskit ja johdannaiset Matti Estola luento 7 Swap sopimuksista lisää 1. Pankki swapin välittäjänä Yleensä 2 eri-rahoitusalan yritystä eivät tee swap sopimusta keskenään vaan pankin tai yleensäkin
Rahoitusriskit ja johdannaiset Matti Estola luento 7 Swap sopimuksista lisää 1. Pankki swapin välittäjänä Yleensä 2 eri-rahoitusalan yritystä eivät tee swap sopimusta keskenään vaan pankin tai yleensäkin
Kvalitatiivinen analyysi. Henri Huovinen, analyytikko Osakesäästäjien Keskusliitto ry
 Henri Huovinen, analyytikko Osakesäästäjien Keskusliitto ry Laadullinen eli kvalitatiiivinen analyysi Yrityksen tutkimista ei-numeerisin perustein, esim. yrityksen johdon osaamisen, toimialan kilpailutilanteen
Henri Huovinen, analyytikko Osakesäästäjien Keskusliitto ry Laadullinen eli kvalitatiiivinen analyysi Yrityksen tutkimista ei-numeerisin perustein, esim. yrityksen johdon osaamisen, toimialan kilpailutilanteen
Nollasummapelit ja bayesilaiset pelit
 Nollasummapelit ja bayesilaiset pelit Kristian Ovaska HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Seminaari: Peliteoria Helsinki 18. syyskuuta 2006 Sisältö 1 Johdanto 1 2 Nollasummapelit 1 2.1
Nollasummapelit ja bayesilaiset pelit Kristian Ovaska HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Seminaari: Peliteoria Helsinki 18. syyskuuta 2006 Sisältö 1 Johdanto 1 2 Nollasummapelit 1 2.1
Päiväkohtaista vipua Bull & Bear -sertifikaateilla
 Päiväkohtaista vipua Bull & Bear -sertifikaateilla Matias Juslin Equity Derivatives Public Distribution 21. marraskuuta 2013 Bull & Bear -sertifikaatit: Johdanto Pörssissä treidattu sertifikaatti, jolla
Päiväkohtaista vipua Bull & Bear -sertifikaateilla Matias Juslin Equity Derivatives Public Distribution 21. marraskuuta 2013 Bull & Bear -sertifikaatit: Johdanto Pörssissä treidattu sertifikaatti, jolla
Aloitamme yksinkertaisella leluesimerkillä. Tarkastelemme yhtä osaketta S. Oletamme että tänään, hetkellä t = 0, osakkeen hinta on S 0 = 100=C.
 Luku 1 Johdatteleva esimerkki Herra K. tarjoaa osto-option Aloitamme yksinkertaisella leluesimerkillä. Tarkastelemme yhtä osaketta S. Oletamme että tänään, hetkellä t = 0, osakkeen hinta on S 0 = 100=C.
Luku 1 Johdatteleva esimerkki Herra K. tarjoaa osto-option Aloitamme yksinkertaisella leluesimerkillä. Tarkastelemme yhtä osaketta S. Oletamme että tänään, hetkellä t = 0, osakkeen hinta on S 0 = 100=C.
Ajatuksia hinnoittelusta. Hinta on silloin oikea, kun asiakas itkee ja ostaa, mutta ostaa kuitenkin.
 Ajatuksia hinnoittelusta Hinta on silloin oikea, kun asiakas itkee ja ostaa, mutta ostaa kuitenkin. Hinnoittelu Yritystoiminnan tavoitteena on aina kannattava liiketoiminta ja asiakastyytyväisyys. Hinta
Ajatuksia hinnoittelusta Hinta on silloin oikea, kun asiakas itkee ja ostaa, mutta ostaa kuitenkin. Hinnoittelu Yritystoiminnan tavoitteena on aina kannattava liiketoiminta ja asiakastyytyväisyys. Hinta
Moduuli 7 Talouden hallinta
 2O16-1-DEO2-KA2O2-003277 Moduuli 7 Talouden hallinta Osa 3 Talouden suunnittelu ja ennusteet Hanke on rahoitettu Euroopan komission tuella. Tästä julkaisusta (tiedotteesta) vastaa ainoastaan sen laatija,
2O16-1-DEO2-KA2O2-003277 Moduuli 7 Talouden hallinta Osa 3 Talouden suunnittelu ja ennusteet Hanke on rahoitettu Euroopan komission tuella. Tästä julkaisusta (tiedotteesta) vastaa ainoastaan sen laatija,
KUVAT. Kansainvälisen toiminnan rahoitus
 Kansainvälisen toiminnan rahoitus KUVAT 1 Rahoitussuunnittelu REAALIPROSESSI Tuotannontekijämarkkinat Meno MOBILA OY Tulo Suoritemarkkinat Kassa RAHAPROSESSI Kassastamaksut Kassaanmaksut Korot Verot Osingot
Kansainvälisen toiminnan rahoitus KUVAT 1 Rahoitussuunnittelu REAALIPROSESSI Tuotannontekijämarkkinat Meno MOBILA OY Tulo Suoritemarkkinat Kassa RAHAPROSESSI Kassastamaksut Kassaanmaksut Korot Verot Osingot
Yrittäjän oppikoulu. Johdatusta yrityksen taloudellisen tilan ymmärtämiseen (osa 2) 23.10.2015. Niilo Rantala, Yläneen Tilikeskus Oy
 Yrittäjän oppikoulu Johdatusta yrityksen taloudellisen tilan ymmärtämiseen (osa 2) 23.10.2015 Niilo Rantala, Yläneen Tilikeskus Oy Sisältö Mitä on yrityksen taloudellinen tila? Tunnuslukujen perusteet
Yrittäjän oppikoulu Johdatusta yrityksen taloudellisen tilan ymmärtämiseen (osa 2) 23.10.2015 Niilo Rantala, Yläneen Tilikeskus Oy Sisältö Mitä on yrityksen taloudellinen tila? Tunnuslukujen perusteet
Nykyarvo ja investoinnit, L14
 Nykyarvo ja investoinnit, L14 netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n netto 0 1 2 3 4 5 6...
Nykyarvo ja investoinnit, L14 netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n netto 0 1 2 3 4 5 6...
BL20A1200 Tuuli- ja aurinkoenergiateknologia ja liiketoiminta
 BL20A1200 Tuuli- ja aurinkoenergiateknologia ja liiketoiminta Tuulipuiston investointi ja rahoitus Tuulipuistoinvestoinnin tavoitteet ja perusteet Pitoajalta lasketun kassavirran pitää antaa sijoittajalle
BL20A1200 Tuuli- ja aurinkoenergiateknologia ja liiketoiminta Tuulipuiston investointi ja rahoitus Tuulipuistoinvestoinnin tavoitteet ja perusteet Pitoajalta lasketun kassavirran pitää antaa sijoittajalle
Palvelusetelihanke Hinnoitteluprojekti / hinnoittelupolitiikan vaihtoehtoja ja malleja 16.4.2010
 Palvelusetelihanke Hinnoitteluprojekti / hinnoittelupolitiikan vaihtoehtoja ja malleja 16.4.2010 Sisältö Sivu Johdanto 3 Palvelusetelin hinnoittelun elementit 5 Palvelun hinta: hintakatto tai markkinahinta
Palvelusetelihanke Hinnoitteluprojekti / hinnoittelupolitiikan vaihtoehtoja ja malleja 16.4.2010 Sisältö Sivu Johdanto 3 Palvelusetelin hinnoittelun elementit 5 Palvelun hinta: hintakatto tai markkinahinta
Asiantuntija ostajan/jatkajan apuna yrityskaupan valmistelussa. Osmo Leppiniemi Visma Services Teemuaho Oy
 Asiantuntija ostajan/jatkajan apuna yrityskaupan valmistelussa Osmo Leppiniemi Visma Services Teemuaho Oy Asiantuntija ostajan/jatkajan apuna yrityskaupan valmistelussa Yrittäjät ovat parhaita asiantuntijoita
Asiantuntija ostajan/jatkajan apuna yrityskaupan valmistelussa Osmo Leppiniemi Visma Services Teemuaho Oy Asiantuntija ostajan/jatkajan apuna yrityskaupan valmistelussa Yrittäjät ovat parhaita asiantuntijoita
FiSERN 1. Tutkija Harri Kostilainen, Diak Vanhempi tutkija Jari Karjalainen, Aalto yliopiston kauppakorkeakoulu, PYK
 Näkökulmia sosiaalisten yritysten kilpailuedusta alustavia tuloksia FiSERN 1. Tutkija Harri Kostilainen, Diak Vanhempi tutkija Jari Karjalainen, Aalto yliopiston kauppakorkeakoulu, PYK Lähtökohdat Miten
Näkökulmia sosiaalisten yritysten kilpailuedusta alustavia tuloksia FiSERN 1. Tutkija Harri Kostilainen, Diak Vanhempi tutkija Jari Karjalainen, Aalto yliopiston kauppakorkeakoulu, PYK Lähtökohdat Miten
Rahoitusriskit ja johdannaiset Matti Estola Luento 6. Swap -sopimukset
 Rahoitusriskit ja johdannaiset Matti Estola Luento 6 Swap -sopimukset 1. Swapit eli vaihtosopimukset Swap -sopimus on kahden yrityksen välinen sopimus vaihtaa niiden saamat tai maksamat rahavirrat keskenään.
Rahoitusriskit ja johdannaiset Matti Estola Luento 6 Swap -sopimukset 1. Swapit eli vaihtosopimukset Swap -sopimus on kahden yrityksen välinen sopimus vaihtaa niiden saamat tai maksamat rahavirrat keskenään.
Investointipäätöksenteko
 Investointipäätöksenteko Ekstralaskuesimerkkejä Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Neppi Oy valmistaa neppejä ja nappeja. Käsityöpiireissä se on tunnettu laadukkaista
Investointipäätöksenteko Ekstralaskuesimerkkejä Laskentatoimen Perusteet, Syksy 2015 Katja Kolehmainen KTT, Apulaisprofessori Neppi Oy valmistaa neppejä ja nappeja. Käsityöpiireissä se on tunnettu laadukkaista
Korko ja inflaatio. Makrotaloustiede 31C00200 Kevät 2016
 Korko ja inflaatio Makrotaloustiede 31C00200 Kevät 2016 Sisältö Nimellis ja reaalikorot, Fisher yhtälö Lyhyt ja pitkä korko Rahapolitiikka ja korot Korko ja inflaatio Nimellinen korko i: 1 tänä vuonna
Korko ja inflaatio Makrotaloustiede 31C00200 Kevät 2016 Sisältö Nimellis ja reaalikorot, Fisher yhtälö Lyhyt ja pitkä korko Rahapolitiikka ja korot Korko ja inflaatio Nimellinen korko i: 1 tänä vuonna
Pyhäjärven kaupungin 100 % tytäryhtiö Rekisteröity 6/2013 Yhtiön toiminta-ajatuksena on omistaa, vuokrata ja rakentaa tietoliikenneverkkoja ja
 Pyhäjärven kaupungin 100 % tytäryhtiö Rekisteröity 6/2013 Yhtiön toiminta-ajatuksena on omistaa, vuokrata ja rakentaa tietoliikenneverkkoja ja tuottaa tietoliikennepalveluita Pyhäjärven ja Kärsämäen kuntien
Pyhäjärven kaupungin 100 % tytäryhtiö Rekisteröity 6/2013 Yhtiön toiminta-ajatuksena on omistaa, vuokrata ja rakentaa tietoliikenneverkkoja ja tuottaa tietoliikennepalveluita Pyhäjärven ja Kärsämäen kuntien
Todellinen vuosikorko. Efektiivinen/sisäinen korkokanta. Huomioitavaa
 Todellinen vuosikorko Huomioitavaa Edellinen keskimaksuhetkeen perustuva todellinen vuosikorko antaa vain arvion vuosikorosta. Tarkempi arvio todellisesta korosta saadaan ottamalla huomioon mm. koronkorko.
Todellinen vuosikorko Huomioitavaa Edellinen keskimaksuhetkeen perustuva todellinen vuosikorko antaa vain arvion vuosikorosta. Tarkempi arvio todellisesta korosta saadaan ottamalla huomioon mm. koronkorko.
ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2010 Harjoitus 3
 ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2010 Harjoitus 3 Ratkaisuehdotuksia 1. (a) Päätöspuu on matala, jos mitään sattumasolmua ei välittömästi seuraa sattumasolmu eikä mitään päätössolmua
ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2010 Harjoitus 3 Ratkaisuehdotuksia 1. (a) Päätöspuu on matala, jos mitään sattumasolmua ei välittömästi seuraa sattumasolmu eikä mitään päätössolmua
diskonttaus ja summamerkintä, L6
 diskonttaus ja summamerkintä, L6 1 Edellä aina laskettiin kasvanut pääoma alkupääoman ja koron perusteella. Seuraavaksi pohdimme käänteistä ongelmaa: Miten suuri tulee alkupääoman K 0 olla, jotta n jakson
diskonttaus ja summamerkintä, L6 1 Edellä aina laskettiin kasvanut pääoma alkupääoman ja koron perusteella. Seuraavaksi pohdimme käänteistä ongelmaa: Miten suuri tulee alkupääoman K 0 olla, jotta n jakson
Mitä tilinpäätös kertoo?
 Kati Leppälä 2018 Mitä tilinpäätös kertoo? Tilinpäätös on yrityksestäsi tilikaudelta eli vuosittain tehtävä laskelma, josta selviää yrityksesi tulos ja varallisuus. Tilinpäätös on osa yrityksen valvontajärjestelmää
Kati Leppälä 2018 Mitä tilinpäätös kertoo? Tilinpäätös on yrityksestäsi tilikaudelta eli vuosittain tehtävä laskelma, josta selviää yrityksesi tulos ja varallisuus. Tilinpäätös on osa yrityksen valvontajärjestelmää
ALUSTAVA LIIKETOIMINTASUUNNITELMA
 ALUSTAVA LIIKETOIMINTASUUNNITELMA 1 Alustavan liiketoimintasuunnitelman tarkoituksena on jäsentää ja selventää aiotun yritystoiminnan kannattavuutta ja menestymisen mahdollisuuksia. Liiketoimintasuunnitelma
ALUSTAVA LIIKETOIMINTASUUNNITELMA 1 Alustavan liiketoimintasuunnitelman tarkoituksena on jäsentää ja selventää aiotun yritystoiminnan kannattavuutta ja menestymisen mahdollisuuksia. Liiketoimintasuunnitelma
Tehtävä 1: Maakunta-arkisto
 Tehtävä 1: Maakunta-arkisto Maakunta-arkisto aikoo ostaa uuden laitteen avustamaan ja nopeuttamaan henkilöstönsä työskentelyä. Laitteen hinta on 36 000 ja sen arvioitu taloudellinen pitoaika on 5 vuotta.
Tehtävä 1: Maakunta-arkisto Maakunta-arkisto aikoo ostaa uuden laitteen avustamaan ja nopeuttamaan henkilöstönsä työskentelyä. Laitteen hinta on 36 000 ja sen arvioitu taloudellinen pitoaika on 5 vuotta.
Kokonaisvaltaista tilanpitoa - kannattavasti eteenpäin. Reijo Käki www.reijokaki.com
 Kokonaisvaltaista tilanpitoa - kannattavasti eteenpäin Reijo Käki www.reijokaki.com 1. PÄIVÄ I Voitto ja arvopohjainen päätöksenteko? II Kassavirta ja katetuotto III Heikot lenkit IV Marginaalituottavuus
Kokonaisvaltaista tilanpitoa - kannattavasti eteenpäin Reijo Käki www.reijokaki.com 1. PÄIVÄ I Voitto ja arvopohjainen päätöksenteko? II Kassavirta ja katetuotto III Heikot lenkit IV Marginaalituottavuus
Mat Investointiteoria Laskuharjoitus 4/2008, Ratkaisut
 Projektien valintapäätöksiä voidaan pyrkiä tekemään esimerkiksi hyöty-kustannus-suhteen (so. tuottojen nykyarvo per kustannusten nykyarvo) tai nettonykyarvon (so. tuottojen nykyarvo - kustannusten nykyarvo)
Projektien valintapäätöksiä voidaan pyrkiä tekemään esimerkiksi hyöty-kustannus-suhteen (so. tuottojen nykyarvo per kustannusten nykyarvo) tai nettonykyarvon (so. tuottojen nykyarvo - kustannusten nykyarvo)
INVESTOINTIEN EDULLISUUSVERTAILU. Tero Tyni Erityisasiantuntija (kuntatalous)
 INVESTOINTIEN EDULLISUUSVERTAILU Tero Tyni Erityisasiantuntija (kuntatalous) 25.5.2007 Mitä tietoja laskentaan tarvitaan Investoinnista aiheutuneet investointikustannukset Investoinnin pitoaika Investoinnin
INVESTOINTIEN EDULLISUUSVERTAILU Tero Tyni Erityisasiantuntija (kuntatalous) 25.5.2007 Mitä tietoja laskentaan tarvitaan Investoinnista aiheutuneet investointikustannukset Investoinnin pitoaika Investoinnin
Reaalioptiot investointipäätösten tukena
 Reaalioptiot investointipäätösten tukena Kandidaatintutkielma Artturi Hannula Aalto-yliopiston Kauppakorkeakoulu Laskentatoimi Kesä 2018 1 Tekijä Artturi Hannula Työn nimi Reaalioptiot investointipäätösten
Reaalioptiot investointipäätösten tukena Kandidaatintutkielma Artturi Hannula Aalto-yliopiston Kauppakorkeakoulu Laskentatoimi Kesä 2018 1 Tekijä Artturi Hannula Työn nimi Reaalioptiot investointipäätösten
Nykyarvo ja investoinnit, L9
 Nykyarvo ja investoinnit, L9 netto netto netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n 0 1 2 3 4 5
Nykyarvo ja investoinnit, L9 netto netto netto netto 1 Tarkastellaan tulovirtaa, joka kestää n jakson ajana, ja jossa jakson j lopussa kassaan tulee tulo k j. k 1 k 2 k 3 k 4 k 5 k 6... k n 0 1 2 3 4 5
Rahoitusinnovaatiot kuntien teknisellä sektorilla
 Rahoitusinnovaatiot kuntien teknisellä sektorilla Oma ja vieras pääoma infrastruktuuri-investoinneissa 12.5.2010 Tampereen yliopisto Jari Kankaanpää 6/4/2010 Jari Kankaanpää 1 Mitä tiedetään investoinnin
Rahoitusinnovaatiot kuntien teknisellä sektorilla Oma ja vieras pääoma infrastruktuuri-investoinneissa 12.5.2010 Tampereen yliopisto Jari Kankaanpää 6/4/2010 Jari Kankaanpää 1 Mitä tiedetään investoinnin
SOCIÉTÉ GÉNÉRALE LISTALLEOTTOESITTEEN PERUSOSAN TÄYDENNYSOSA TEKNISET EHDOT WARRANTEILLE, JOIDEN KOHDE-ETUUTENA ON VALUUTTAKURSSI
 SOCIÉTÉ GÉNÉRALE LISTALLEOTTOESITTEEN PERUSOSAN TÄYDENNYSOSA TEKNISET EHDOT WARRANTEILLE, JOIDEN KOHDE-ETUUTENA ON VALUUTTAKURSSI Tämä Listalleottoesitteen perusosan täydennysosa ( Täydennysosa ) täydentää
SOCIÉTÉ GÉNÉRALE LISTALLEOTTOESITTEEN PERUSOSAN TÄYDENNYSOSA TEKNISET EHDOT WARRANTEILLE, JOIDEN KOHDE-ETUUTENA ON VALUUTTAKURSSI Tämä Listalleottoesitteen perusosan täydennysosa ( Täydennysosa ) täydentää
Yrityksen taloudellisen tilan analysointi ja oma pääoman turvaaminen. Toivo Koski
 1 Yrityksen taloudellisen tilan analysointi ja oma pääoman turvaaminen SISÄLLYS Mitä tuloslaskelma, tase ja kassavirtalaskelma kertovat Menojen kirjaaminen tuloslaskelmaan kuluksi ja menojen kirjaaminen
1 Yrityksen taloudellisen tilan analysointi ja oma pääoman turvaaminen SISÄLLYS Mitä tuloslaskelma, tase ja kassavirtalaskelma kertovat Menojen kirjaaminen tuloslaskelmaan kuluksi ja menojen kirjaaminen
YRITYKSEN ARVONMÄÄRITYS
 YRITYKSEN ARVONMÄÄRITYS ARVONMÄÄRITYSTILANTEITA 1. Luovutushinnan määrittäminen kauppa ulkopuolisen kanssa kauppa läheisten kanssa lahjan luonteiset kaupan lahjoitukset omien osakkeiden lunastus avioero-ositukset
YRITYKSEN ARVONMÄÄRITYS ARVONMÄÄRITYSTILANTEITA 1. Luovutushinnan määrittäminen kauppa ulkopuolisen kanssa kauppa läheisten kanssa lahjan luonteiset kaupan lahjoitukset omien osakkeiden lunastus avioero-ositukset
Luento 9. June 2, Luento 9
 June 2, 2016 Otetaan lähtökohdaksi, että sopimuksilla ei voida kattaa kaikkia kontingensseja/maailmantiloja. Yksi kiinnostava tapaus on sellainen, että jotkut kontingenssit ovat havaittavissa sopimusosapuolille,
June 2, 2016 Otetaan lähtökohdaksi, että sopimuksilla ei voida kattaa kaikkia kontingensseja/maailmantiloja. Yksi kiinnostava tapaus on sellainen, että jotkut kontingenssit ovat havaittavissa sopimusosapuolille,
laskuperustekorkoisia ja ns. riskihenkivakuutuksia), yksilöllisiä eläkevakuutuksia, kapitalisaatiosopimuksia sekä sairauskuluvakuutuksia.
 SHV - TUTKINTO Vakavaraisuus 30.9.2010 klo 9-15 1(5) 1. Henkivakuutusosakeyhtiö Tuoni myöntää yksilöllisiä henkivakuutuksia (sijoitussidonnaisia, laskuperustekorkoisia ja ns. riskihenkivakuutuksia), yksilöllisiä
SHV - TUTKINTO Vakavaraisuus 30.9.2010 klo 9-15 1(5) 1. Henkivakuutusosakeyhtiö Tuoni myöntää yksilöllisiä henkivakuutuksia (sijoitussidonnaisia, laskuperustekorkoisia ja ns. riskihenkivakuutuksia), yksilöllisiä
Riski ja velkaantuminen
 Riski ja velkaantuminen TU-C1030 Laskelmat liiketoiminnan päätösten tukena Luento 28.1.2016 I vaiheen luentokokonaisuus INVESTOINNIN KANNATTAVUUS YRITYKSEN KANNATTAVUUS 1. Vapaa rahavirta (FCF) 2. Rahavirtojen
Riski ja velkaantuminen TU-C1030 Laskelmat liiketoiminnan päätösten tukena Luento 28.1.2016 I vaiheen luentokokonaisuus INVESTOINNIN KANNATTAVUUS YRITYKSEN KANNATTAVUUS 1. Vapaa rahavirta (FCF) 2. Rahavirtojen
Korkojen aikarakenne
 Korkojen aikarakenne opetusnäyte: osa kuvitteellista Raha- ja pankkiteorian aineopintojen kurssia Antti Ripatti Taloustiede 4.11.2011 Antti Ripatti (Taloustiede) Korkojen aikarakenne 4.11.2011 1 / 30 2003),
Korkojen aikarakenne opetusnäyte: osa kuvitteellista Raha- ja pankkiteorian aineopintojen kurssia Antti Ripatti Taloustiede 4.11.2011 Antti Ripatti (Taloustiede) Korkojen aikarakenne 4.11.2011 1 / 30 2003),
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
PK -yritykset rahoitusmarkkinoilla
 PK -yritykset rahoitusmarkkinoilla Mervi Niskanen Kuopion yliopisto Kauppatieteiden laitos Suomalaiset rahoitusmarkkinat Rahoitusmarkkinoilla tarkoitetaan kaikkien rahoitusvaateiden markkinoita Rahamarkkinat
PK -yritykset rahoitusmarkkinoilla Mervi Niskanen Kuopion yliopisto Kauppatieteiden laitos Suomalaiset rahoitusmarkkinat Rahoitusmarkkinoilla tarkoitetaan kaikkien rahoitusvaateiden markkinoita Rahamarkkinat
TUKIMATERIAALI: Arvosanan kahdeksan alle jäävä osaaminen
 KEMIA Kemian päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Merkitys, arvot ja asenteet T1 kannustaa ja innostaa oppilasta kemian opiskeluun T2 ohjata ja
KEMIA Kemian päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Merkitys, arvot ja asenteet T1 kannustaa ja innostaa oppilasta kemian opiskeluun T2 ohjata ja
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
Matematiikan tukikurssi Kurssikerta 6 1 Korkolaskentaa Oletetaan, että korkoaste on r Jos esimerkiksi r = 0, 02, niin korko on 2 prosenttia Tätä korkoastetta käytettään diskonttaamaan tulevia tuloja ja
Markkinariskipreemio Suomen osakemarkkinoilla
 Sisältö Yhteenveto s2 / Markkinariskipreemio Suomen osakemarkkinoilla s3 / Suomen osakemarkkinoiden kasvu ja uudet listautumiset s5 / Aikaisemmat tutkimustulokset s6 Markkinariskipreemio Suomen osakemarkkinoilla
Sisältö Yhteenveto s2 / Markkinariskipreemio Suomen osakemarkkinoilla s3 / Suomen osakemarkkinoiden kasvu ja uudet listautumiset s5 / Aikaisemmat tutkimustulokset s6 Markkinariskipreemio Suomen osakemarkkinoilla
Yrityskaupan toteuttaminen - ostajan ja myyjän ajatuksia
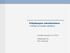 Yrityskaupan toteuttaminen - ostajan ja myyjän ajatuksia Nordea Tampere, 8.5.2014 Riku Salomaa Yrityskaupan kulku Strategian ja kohteen valinta Kaupan toteuttamisvaihtoehdot Arvonmääritys Esisopimus Kaupan
Yrityskaupan toteuttaminen - ostajan ja myyjän ajatuksia Nordea Tampere, 8.5.2014 Riku Salomaa Yrityskaupan kulku Strategian ja kohteen valinta Kaupan toteuttamisvaihtoehdot Arvonmääritys Esisopimus Kaupan
Optioiden hinnoittelu binomihilassa
 Mat-2.3114 Investointiteoria Optioien hinnoittel binomihilassa 26.3.2015 Yksiperioiset optiot 1/3 Olkoon S kohe-eten arvo perioin alssa siten, että perioin päättyessä sen arvo on S toennäköisyyellä p tai
Mat-2.3114 Investointiteoria Optioien hinnoittel binomihilassa 26.3.2015 Yksiperioiset optiot 1/3 Olkoon S kohe-eten arvo perioin alssa siten, että perioin päättyessä sen arvo on S toennäköisyyellä p tai
Referaatti Jaakko Ollila 46016V
 PÄÄTÖSPUUT PITKÄN AIKAVÄLIN INVESTOINTILASKELMISSA Referaatti Jaakko Ollila 46016V Syksy 1999 Päätöspuut pitkän aikavälin investointilaskelmissa, referaatti 2 Päätöspuiden ongelmakohtia pitkän aikavälin
PÄÄTÖSPUUT PITKÄN AIKAVÄLIN INVESTOINTILASKELMISSA Referaatti Jaakko Ollila 46016V Syksy 1999 Päätöspuut pitkän aikavälin investointilaskelmissa, referaatti 2 Päätöspuiden ongelmakohtia pitkän aikavälin
Talousmatematiikan perusteet: Luento 1. Prosenttilaskentaa Korkolaskentaa Lukujonot: aritmeettinen ja geometrinen
 Talousmatematiikan perusteet: Luento 1 Prosenttilaskentaa Korkolaskentaa Lukujonot: aritmeettinen ja geometrinen Luennon sisältö Prosenttilaskennan kertausta Korkolaskentaa Käsitteitä Koron lisäys kerran
Talousmatematiikan perusteet: Luento 1 Prosenttilaskentaa Korkolaskentaa Lukujonot: aritmeettinen ja geometrinen Luennon sisältö Prosenttilaskennan kertausta Korkolaskentaa Käsitteitä Koron lisäys kerran
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Laadullinen tutkimus. KTT Riku Oksman
 Laadullinen tutkimus KTT Riku Oksman Kurssin tavoitteet oppia ymmärtämään laadullisen tutkimuksen yleisluonnetta oppia soveltamaan keskeisimpiä laadullisia aineiston hankinnan ja analysoinnin menetelmiä
Laadullinen tutkimus KTT Riku Oksman Kurssin tavoitteet oppia ymmärtämään laadullisen tutkimuksen yleisluonnetta oppia soveltamaan keskeisimpiä laadullisia aineiston hankinnan ja analysoinnin menetelmiä
Samuli Knüpfer Vesa Puttonen MODERNI RAHOITUS. Talentum Media Oy Helsinki
 Samuli Knüpfer Vesa Puttonen MODERNI RAHOITUS Talentum Media Oy Helsinki 7., uudistettu painos Copyright 2014 Talentum Media Oy ja kirjoittajat Toimitus: Saara Palmberg Taitto: Marja-Leena Saari ISBN 978-952-14-2312-3
Samuli Knüpfer Vesa Puttonen MODERNI RAHOITUS Talentum Media Oy Helsinki 7., uudistettu painos Copyright 2014 Talentum Media Oy ja kirjoittajat Toimitus: Saara Palmberg Taitto: Marja-Leena Saari ISBN 978-952-14-2312-3
hyvä osaaminen
 MERKITYS, ARVOT JA ASENTEET FYSIIKKA T2 Oppilas tunnistaa omaa fysiikan osaamistaan, asettaa tavoitteita omalle työskentelylleen sekä työskentelee pitkäjänteisesti. T3 Oppilas ymmärtää fysiikkaan (sähköön
MERKITYS, ARVOT JA ASENTEET FYSIIKKA T2 Oppilas tunnistaa omaa fysiikan osaamistaan, asettaa tavoitteita omalle työskentelylleen sekä työskentelee pitkäjänteisesti. T3 Oppilas ymmärtää fysiikkaan (sähköön
