Telecommunication engineering I A Exercise 3
|
|
|
- Johanna Mattila
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Teleouao egeerg I 5359A xere 3 Proble elaodulaaor lohkokaavo o eey oppkrja kuvaa Pulodulaaor ääuloa o aoagaal ja reeregaal erou d. Tää gaal kerroaa pulgeeraaor gaallla rajouke, el erouke erk elväe, jälkee.
2 Teleouao egeerg I 5359A xere 3 δ T x Käyäöä delaodulaaor uloulo e uodou pulea, vaa hyv kapea pulea. Reeregaal uodoeaa egroalla x T δ T dα jollo aadaa porraapprokaao gaala. elaodulodu gaal deodulo vodaa uoraa egroalla x, el uodoeaa uudeaa porraapprokaao, ja e jälkee uoreaa alpääöuodau porae reuoje pyöräek. elaodulaaor vodaa oeuaa vahoehoe yö ao. kuva ukae koparaaor ja vvee avulla e, eä xk eduaa y äyeä k aoagaala. Kapea pul ε ± polaree rppuu ä, oko k k q x uurep ε k va peep ε k ku k q äyeä approkova gaal x q k edelle arvo k q ~ x q. x -
3 Teleouao egeerg I 5359A xere 3 elaodulaaor äyeeooopeu 44, khz ja porragaal akelee aplud o,v. Modulova aoagaal o uooa V. aoagaal uur uuoopeu o: ax d d ax o V V Modulaaor pyyy euraaaa korkeaa ouujyrkkyydellä kulakerro: δ T gaal lekkauue ja äröyye eäek o olava voaa eho: δ d ax T d δ V δ V 7Hz,V 44,kHz V 3
4 Teleouao egeerg I 5359A xere 3 Proble PCM gaal uodoaek aoagaal äyeeää aplg yqu äyeeooeoreea ukaella opeudella. äyeey arvo kvaodaa quazg, joka jälkee kvaodu arvo koodaaa bäärk PCM-koodauk aok. Käyäöä operaao oeueaa aple & hold prllä ja aaloga-dgaaluuella. Kvaoao o koodau bäärkood avulla, jollo arvave be lukuäärä, ku kvaoaoje kokoaäärä o q, aadaa kaavaa olava kokoaluku: q log q log l x x l Kvaoa yyvä vrhe kvaokoha rajouu vällle o kvaoväl uuruu. Ku kvaoja oa-alue o [ A, A] lukuääräk aadaa A q ±, joa vola, kvaoaoje 4
5 Teleouao egeerg I 5359A xere 3 uur kvaoa yyvä vrhejäe äyää epäyhälö:, A A, A A, A, A, A q 5 log 5 5,64 Valaa 6 Jo kaaaajue aoagaal kaalevey o W, o e yqv eoreea ukae äyeeävä vähää äyeeooopeudella W. Tällö PCM - gaal arveak kaaleveydek aadaa karkea arvoua B W 6 4kHz 48kHz Arvoa oleeu, eä bvrra kaalevey o aa ku bopeu. Käyäöä arvava kaalevey kaavaa rppuu yö perupul uodoa, el ä aalouodoa jolla olla ja ykköe eeää joko kaaaajue a kaoaalooduloua. odulaaoeeelä vala vakuaa. 5
6 Teleouao egeerg I 5359A xere 3 Proble 3 Läheeyy gaal vaaaoeu gaal o x uauuu kaavaa AWG-kohaa x o r, jollo joka kaapääöuodaeaa pre-deeo ler ee laua hyöygaal pääee läp ellaeaa ja koha uodauu W-kaalle y o Kapeakaae gaal karkea: BW < % BW Kohaproe o kapeakaaa, koka yyplle kaalevey ää B:lle W o pe verraua kaoaaloaajuuee. Tällö kohaproe joa vodaa laa kvadrauurkopoeea avulla: o voa eää vekoreykeä yö euraava: 6
7 Teleouao egeerg I 5359A xere 3 7 o R φ ω ku R verhokäyrä ara φ vahe { } o y gaal eho ee laua ollakekarvoe gaal oe oe: { } { } [ ] { } { } o4 o4 o o Koha eho ee laua { } W W B H joa
8 Teleouao egeerg I 5359A xere 3 B o kakpuole koha ehohey valkoelle AWG kohalle kaapääöuodae uloa kaapääöuodae kaalevey W H uodae rouko vahvu oleeaa Koherea laea y kerroaa kaoaallolla ja ulo alpääöuodaeaa po-deeo ler y y [ ] o [ ] o o o o 4 4 o [ o4 ] llä o α α α oα [ o α ] 8
9 Teleouao egeerg I 5359A xere 3 y gaal eho lau jälkee alpääöuoda pääää aoagaal ellaeaa läve: { } ja koha eho lau jälkee o { } W W { } y W 5kHz a R 4dB W / Hz Vaaaoea haluaa aavuaa 4dB gaalkohauhde, jollo R 4 db log 4 koka hyöygaal eho ee ja jälkee lau aa R W 5 5 W,5W 9
10 Teleouao egeerg I 5359A xere 3 b Vaaaoe lähdö kohaeho 4 8 W 5 W 5 W 5W
KOHINAN JA VAIHEVIRHEEN VAIKUTUS VAIHEKOHERENTEILLA JÄRJESTELMILLÄ
 KOHINAN JA VAIHVIRHN VAIKUTUS VAIHKOHRNTILLA JÄRJSTLMILLÄ Mie vaihee epävaruu vaikuaa kohereia ilaiua? Mikä o piloiigaali? 557A Tieoliikeeekiikka I Oa 6 Kari Kärkkäie Kevä 05 VAIHVIRHN YLINN ANALYYSI QSB
KOHINAN JA VAIHVIRHN VAIKUTUS VAIHKOHRNTILLA JÄRJSTLMILLÄ Mie vaihee epävaruu vaikuaa kohereia ilaiua? Mikä o piloiigaali? 557A Tieoliikeeekiikka I Oa 6 Kari Kärkkäie Kevä 05 VAIHVIRHN YLINN ANALYYSI QSB
KVANTISOINTIKOHINA JA KANAVAN AWGN- KOHINA PULSSIKOODIMODULAATIOSSA
 KVANTIOINTIKOHINA JA KANAVAN AWGN- KOHINA PULIKOODIMODULAATIOA Teolkenneeknkka I 5359A Kar Kärkkänen Osa 6 5 Kvansonkohna PCM-järjeselmässä PCM:ssa on kaks vrhelähdeä:. kvansonkohna,. kanavan kohnan aheuama
KVANTIOINTIKOHINA JA KANAVAN AWGN- KOHINA PULIKOODIMODULAATIOA Teolkenneeknkka I 5359A Kar Kärkkänen Osa 6 5 Kvansonkohna PCM-järjeselmässä PCM:ssa on kaks vrhelähdeä:. kvansonkohna,. kanavan kohnan aheuama
DIGITAALISET PULSSIMODULAATIOT M JA PCM
 DIGITAALISET PULSSIMODULAATIOT M JA PCM 1 (10) Deltamodulaatio ( M) M koodaa informaation ± polariteetin omaavaki binääriiki impuleiki. Menetelmä on ykinkertainen. Idea perutuu ignaalin m(t) muutoken binäärieen
DIGITAALISET PULSSIMODULAATIOT M JA PCM 1 (10) Deltamodulaatio ( M) M koodaa informaation ± polariteetin omaavaki binääriiki impuleiki. Menetelmä on ykinkertainen. Idea perutuu ignaalin m(t) muutoken binäärieen
DIGITAALISET PULSSIMODULAATIOT M JA PCM A Tietoliikennetekniikka I Osa 21 Kari Kärkkäinen Kevät 2015
 1 DIGITAALISET PULSSIMODULAATIOT M JA PCM 521357A Tietoliikennetekniikka I Oa 21 Kari Kärkkäinen DELTAMODULAATIO M 2 M koodaa näytteen ± polariteetin omaavaki binääripuliki. Idea perutuu ignaalin m(t muutoken
1 DIGITAALISET PULSSIMODULAATIOT M JA PCM 521357A Tietoliikennetekniikka I Oa 21 Kari Kärkkäinen DELTAMODULAATIO M 2 M koodaa näytteen ± polariteetin omaavaki binääripuliki. Idea perutuu ignaalin m(t muutoken
Rak-54.116 Rakenteiden mekaniikka C, RM C (4 ov) Tentti 30.8.2007
 Rak-54.116 Rakeneden mekankka, RM (4 ov) Ten.8.7 Krjoa jokaeen koepapern elvä - koko nme, puhuelunm allevvauna - oao, vuokur, enn pävämäärä ekä enävä opnojako koodeneen - opkeljanumero, mukaan luken arkukrjan
Rak-54.116 Rakeneden mekankka, RM (4 ov) Ten.8.7 Krjoa jokaeen koepapern elvä - koko nme, puhuelunm allevvauna - oao, vuokur, enn pävämäärä ekä enävä opnojako koodeneen - opkeljanumero, mukaan luken arkukrjan
RATKAISUT: 3. Voimakuvio ja liikeyhtälö
 Phyica 9. paino (8) 3. Voiakuvio ja liikeyhtälö : 3. Voiakuvio ja liikeyhtälö 3. a) Newtonin I laki on nieltään jatkavuuden laki. Kappale jatkaa liikettään uoraviivaieti uuttuattoalla nopeudella tai pyyy
Phyica 9. paino (8) 3. Voiakuvio ja liikeyhtälö : 3. Voiakuvio ja liikeyhtälö 3. a) Newtonin I laki on nieltään jatkavuuden laki. Kappale jatkaa liikettään uoraviivaieti uuttuattoalla nopeudella tai pyyy
12. ARKISIA SOVELLUKSIA
 MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
Eo C)sl. oarl. d to E= J. o-= o cy) =uo. f,e. ic v. .o6. .9o. äji. :ir. ijo 96. {c o o. ';i _o. :fe. C=?i. t-l +) (- c rt, u0 C.
 C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
Vallox TEKNINENOHJE. Vallox SILENT. Tyyppi 3510 Mallit: VALLOX 75 VALLOX 75 VKL VALLOX 95 VALLOX 95 VKL VALLOX 95 SILENT VALLOX 95 SILENT VKL
 75 95.9.59F 9.. yyppi 5 VAOX yyppi 5 Mallit: VAOX 75 VAOX 75 VK VAOX 95 VAOX 95 VK Huoneitokohtaieen ilanvaihtoon pien-, rivi- ja kerrotaloihin ulo-/poitoilanvaihto läöntalteenotolla Hyvä uodatu Siäänrakennettu
75 95.9.59F 9.. yyppi 5 VAOX yyppi 5 Mallit: VAOX 75 VAOX 75 VK VAOX 95 VAOX 95 VK Huoneitokohtaieen ilanvaihtoon pien-, rivi- ja kerrotaloihin ulo-/poitoilanvaihto läöntalteenotolla Hyvä uodatu Siäänrakennettu
BINÄÄRINEN SYNKRONINEN TIEDONSIIRTO KAISTARAJOITTAMATTOMILLA MIELIVALTAISILLA PULSSIMUODOILLA SOVITETTU SUODATIN JA SEN SUORITUSKYKY AWGN-KANAVASSA
 BINÄÄRINN SYNKRONINN IDONSIIRO KAISARAJOIAMAOMILLA MILIVALAISILLA PULSSIMUODOILLA SOVIU SUODAIN JA SN SUORIUSKYKY AWGN-KANAVASSA Millaiia aalomuooja perupuleja yypilliei käyeään? 536A ieoliikenneekniikka
BINÄÄRINN SYNKRONINN IDONSIIRO KAISARAJOIAMAOMILLA MILIVALAISILLA PULSSIMUODOILLA SOVIU SUODAIN JA SN SUORIUSKYKY AWGN-KANAVASSA Millaiia aalomuooja perupuleja yypilliei käyeään? 536A ieoliikenneekniikka
FCG Planeko Oy HELSINGIN KAUPUNKI MUNKKINIEMEN KÄYTTÄJÄKYSELY. Yhteenveto ja johtopäätökset 0100-D1194
 FCG P Oy HELSINGIN AUPUNI UNINIEEN ÄYÄJÄYSELY Yhv hääö -D9..9 FCG P Oy Yhv hääö () SISÄLLYSLUEELO YLEISÄ... YSELY.... V d.... Y d h....3 Ad v.... Ad äyö.... Lh.... Eöyy v... LIIEE (CD)...... yyyh v...
FCG P Oy HELSINGIN AUPUNI UNINIEEN ÄYÄJÄYSELY Yhv hääö -D9..9 FCG P Oy Yhv hääö () SISÄLLYSLUEELO YLEISÄ... YSELY.... V d.... Y d h....3 Ad v.... Ad äyö.... Lh.... Eöyy v... LIIEE (CD)...... yyyh v...
RATKAISUT: 8. Momentti ja tasapaino
 Phyica 9. paino (7) : 8. Voian vari r on voian vaikutuuoran etäiyy pyöriiakelita. Pyöriiakeli on todellinen tai kuviteltu akeli, jonka ypäri kappale pyörii. Voian oentti M kuvaa voian vääntövaikututa tietyn
Phyica 9. paino (7) : 8. Voian vari r on voian vaikutuuoran etäiyy pyöriiakelita. Pyöriiakeli on todellinen tai kuviteltu akeli, jonka ypäri kappale pyörii. Voian oentti M kuvaa voian vääntövaikututa tietyn
KULMAMODULOITUJEN SIGNAALIEN SPEKTRIN LASKEMINEN
 1 KULMMODULOITUEN SIGNLIEN SPEKTRIN LSKEMINEN Mie laskea eroaa lieaarise odulaaioide apauksesa? Milä spekri äyää epälieaarise prosessi jälkee? 51357 Tieoliikeeekiikka I Osa 15 Kari Kärkkäie Kevä 015 SPEKTRIN
1 KULMMODULOITUEN SIGNLIEN SPEKTRIN LSKEMINEN Mie laskea eroaa lieaarise odulaaioide apauksesa? Milä spekri äyää epälieaarise prosessi jälkee? 51357 Tieoliikeeekiikka I Osa 15 Kari Kärkkäie Kevä 015 SPEKTRIN
4.3 Liikemäärän säilyminen
 Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Tämän kappaleen aihe liikemäärän äilyminen törmäykiä. Törmäy on uora ja kekeinen, jo törmäävät kappaleet liikkuvat maakekipiteitten kautta kulkevaa uoraa pitkin ja jo törmäykohta on tällä amalla uoralla.
Derivoimalla ensimmäinen komponentti, sijoittamalla jälkimmäisen derivaatta siihen ja eliminoimalla x. saadaan
 87 5. Eliminoinimeneely Tarkaellaan -kokoia vakiokeroimia yeemiä + x a a x a x + a x b() x = = = +. a a x a x a x b () (3) b() x + Derivoimalla enimmäinen komponeni, ijoiamalla jälkimmäien derivaaa iihen
87 5. Eliminoinimeneely Tarkaellaan -kokoia vakiokeroimia yeemiä + x a a x a x + a x b() x = = = +. a a x a x a x b () (3) b() x + Derivoimalla enimmäinen komponeni, ijoiamalla jälkimmäien derivaaa iihen
Physica 9 1. painos 1(8) 20. Varattu hiukkanen sähkö- ja magneettikentässä
 Phyica 9 aino (8) 0 Varattu hiukkann ähkö- ja agnttikntää : 0 Varattu hiukkann ähkö- ja agnttikntää 0 a) Sähköknttä aikuttaa arattuun hiukkan oialla F = QE Poitiiiti aratull hiukkall oian uunta on ähkökntän
Phyica 9 aino (8) 0 Varattu hiukkann ähkö- ja agnttikntää : 0 Varattu hiukkann ähkö- ja agnttikntää 0 a) Sähköknttä aikuttaa arattuun hiukkan oialla F = QE Poitiiiti aratull hiukkall oian uunta on ähkökntän
b) Laskiessani suksilla mäkeä alas ja hypätessäni laiturilta järveen painovoima tekee työtä minulle.
 nergia. Työ ja teho OHDI JA TSI -. Opettaja ja opikelija tekevät hyvin paljon aanlaita ekaanita työtä, kuten liikkuinen, kirjojen ja eineiden notainen, liikkeellelähtö ja pyähtyinen. Uuien aioiden oppiinen
nergia. Työ ja teho OHDI JA TSI -. Opettaja ja opikelija tekevät hyvin paljon aanlaita ekaanita työtä, kuten liikkuinen, kirjojen ja eineiden notainen, liikkeellelähtö ja pyähtyinen. Uuien aioiden oppiinen
RATKAISUT: 14. Aaltoliike, heijastuminen ja taittuminen
 Phya 9 pao (7) 4 Aaltolke, hejatue ja tattue : 4 Aaltolke, hejatue ja tattue 4 a) Aalloptuu o kahde lähä aaa aheea olea ärähteljä älatka b) Aaltolkkee peruyhtälö o = λ f, joa λ o aalloptuu, f o taajuu
Phya 9 pao (7) 4 Aaltolke, hejatue ja tattue : 4 Aaltolke, hejatue ja tattue 4 a) Aalloptuu o kahde lähä aaa aheea olea ärähteljä älatka b) Aaltolkkee peruyhtälö o = λ f, joa λ o aalloptuu, f o taajuu
X 2 = k 21X 1 + U 2 s + k 02 + k 12. (s + k 02 + k 12 )U 1 + k 12 U 2. s 2 + (k 01 + k 21 + k 02 + k 12 ) s + k
 Aalto-yliopiton Perutieteiden korkeakoulu Matematiikan ja yteemianalyyin laito Mat-49 Syteemien Identifiointi 0 harjoituken ratkaiut äytetään enin iirtofunktiomalli Tehdään Laplace-muunno: ẋ k 0 k x +
Aalto-yliopiton Perutieteiden korkeakoulu Matematiikan ja yteemianalyyin laito Mat-49 Syteemien Identifiointi 0 harjoituken ratkaiut äytetään enin iirtofunktiomalli Tehdään Laplace-muunno: ẋ k 0 k x +
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKKA A KTONKKA. välkoe 9.3.2007. Saat vatata van neljään tehtävään!. ake pteden A ja B välnen potentaalero el jännte AB. =4Ω, 2 =2Ω, =0 V, 2 =4V, =2A, =3A A + 2 2 B + 2. Kytkn ljetaan hetkellä.
S-55.00 SÄHKÖTKNKKA A KTONKKA. välkoe 9.3.2007. Saat vatata van neljään tehtävään!. ake pteden A ja B välnen potentaalero el jännte AB. =4Ω, 2 =2Ω, =0 V, 2 =4V, =2A, =3A A + 2 2 B + 2. Kytkn ljetaan hetkellä.
HERNESAARI OSAYLEISKAAVAEHDOTUS VESIHUOLLON YLEISSUUNNITELMA
 HERNESAAR OSAYLESKAAAEHDOTUS ESHUOLLON YLESSUUNNTELMA KS/TEK SSÄLLYSLUETTELO Yä S- v p äöd d ävvä Hvvä K äää ää Nyy S Yä d ävvä Hvvä v v L: L y HELSNGN KAUUNK KAUUNKSUUNNTTELURASTO Y Td Yä y vää H yv-
HERNESAAR OSAYLESKAAAEHDOTUS ESHUOLLON YLESSUUNNTELMA KS/TEK SSÄLLYSLUETTELO Yä S- v p äöd d ävvä Hvvä K äää ää Nyy S Yä d ävvä Hvvä v v L: L y HELSNGN KAUUNK KAUUNKSUUNNTTELURASTO Y Td Yä y vää H yv-
Vallox TEKNINENOHJE. Vallox SILENT. Tyyppi 3510 Mallit: VALLOX 75 VALLOX 75 VKL VALLOX 95 VALLOX 95 VKL VALLOX 95 SILENT VALLOX 95 SILENT VKL
 Vallox 75 95.9.59F.5.9 yyppi 5 VAOX yyppi 5 Mallit: VAOX 75 VAOX 75 VK VAOX 95 VAOX 95 VK Huoneitokohtaieen ilanvaihtoon pien-, rivi- ja kerrotaloihin ulo-/poitoilanvaihto läöntalteenotolla Hyvä uodatu
Vallox 75 95.9.59F.5.9 yyppi 5 VAOX yyppi 5 Mallit: VAOX 75 VAOX 75 VK VAOX 95 VAOX 95 VK Huoneitokohtaieen ilanvaihtoon pien-, rivi- ja kerrotaloihin ulo-/poitoilanvaihto läöntalteenotolla Hyvä uodatu
OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA 2 OV. Isto Jokinen 2012. 1. Mekaniikka 2
 OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA OV Io Jokinen 01 SISÄLTÖ SIVU 1. Mekaniikka Nopeu Kekinopeu Kehänopeu 3 Kiihyvyy 3 Puoamikiihyvyy 4 Voima 5 Kika 6 Työ 7 Teho 8 Paine 9
OPINTOJAKSO FYSIIKKA 1 OV OPINTOKOKONAISUUTEEN FYSIIKKA JA KEMIA OV Io Jokinen 01 SISÄLTÖ SIVU 1. Mekaniikka Nopeu Kekinopeu Kehänopeu 3 Kiihyvyy 3 Puoamikiihyvyy 4 Voima 5 Kika 6 Työ 7 Teho 8 Paine 9
Johda jakauman momenttiemäfunktio ja sen avulla jakauman odotusarvo ja varianssi.
 / Raaisu Aihee: Avaisaa: Momeiemäfuio Sauaismuuujie muuose ja iide jaauma Kovergessiäsiee ja raja-arvolausee Biomijaauma, Espoeijaauma, Geomerie jaauma, Jaaumaovergessi, Jauva asaie jaauma, Kolmiojaauma,
/ Raaisu Aihee: Avaisaa: Momeiemäfuio Sauaismuuujie muuose ja iide jaauma Kovergessiäsiee ja raja-arvolausee Biomijaauma, Espoeijaauma, Geomerie jaauma, Jaaumaovergessi, Jauva asaie jaauma, Kolmiojaauma,
Luento 6 Luotettavuus ja vikaantumisprosessit
 Tkll korkakoulu ysmaalyys laboraoro Luo 6 Luoavuus a vkaaumsrosss Ah alo ysmaalyys laboraoro Tkll korkakoulu PL 00, 005 TKK Tkll korkakoulu ysmaalyys laboraoro Määrlmä Tarkaslava ykskö luoavuus o s odäkösyys,
Tkll korkakoulu ysmaalyys laboraoro Luo 6 Luoavuus a vkaaumsrosss Ah alo ysmaalyys laboraoro Tkll korkakoulu PL 00, 005 TKK Tkll korkakoulu ysmaalyys laboraoro Määrlmä Tarkaslava ykskö luoavuus o s odäkösyys,
KULMAMODULOITUJEN SIGNAALIEN SPEKTRIN LASKEMINEN
 KULMMODULOITUJEN SIGNLIEN SPEKTRIN LSKEMINEN 1 (3) (3) Spekri laskeie siisaoalle Kulaoduloidu sigaali spekri johaie o yöläsä epälieaarisuudesa johue (epälieaarise aalyysi ova yleesä hakalia). Se voidaa
KULMMODULOITUJEN SIGNLIEN SPEKTRIN LSKEMINEN 1 (3) (3) Spekri laskeie siisaoalle Kulaoduloidu sigaali spekri johaie o yöläsä epälieaarisuudesa johue (epälieaarise aalyysi ova yleesä hakalia). Se voidaa
8 USEAN VAPAUSASTEEN SYSTEEMIN VAIMENEMATON PAKKOVÄRÄHTELY
 Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
PD-säädin PID PID-säädin
 -äädin - äätö on ykinkertainen äätömuoto, jota voidaan kutua myö uhteuttavaki äädöki. Sinä lähtöignaali on uoraa uhteea tuloignaalin. -äätimen uhdealue kertoo kuinka paljon mittauuure aa muuttua ennen
-äädin - äätö on ykinkertainen äätömuoto, jota voidaan kutua myö uhteuttavaki äädöki. Sinä lähtöignaali on uoraa uhteea tuloignaalin. -äätimen uhdealue kertoo kuinka paljon mittauuure aa muuttua ennen
Mat Koesuunnittelu ja tilastolliset mallit
 Mat-.03 Koeuuttelu tlatollet mallt. harjotuket Mat-.03 Koeuuttelu tlatollet mallt. harjotuket / Ratkaut Aheet: Avaaat: Tlatollte aetoje kuvaame Oto otokaumat Etmot Etmotmeetelmät Väletmot Artmeette kekarvo,
Mat-.03 Koeuuttelu tlatollet mallt. harjotuket Mat-.03 Koeuuttelu tlatollet mallt. harjotuket / Ratkaut Aheet: Avaaat: Tlatollte aetoje kuvaame Oto otokaumat Etmot Etmotmeetelmät Väletmot Artmeette kekarvo,
Älä tee mitään merkintöjä kaavakokoelmaan!
 AS-74. Alogie ääö vkokoelm v. Plu ei jälkee! Trk kokoelm ivumäärä! Älä ee miää merkiöjä kvkokoelm! Dymie mllie perukompoei. Sähköie kompoei Vu (reii) u() Ri() el (iduki) u() L di() d odeori i() C du()
AS-74. Alogie ääö vkokoelm v. Plu ei jälkee! Trk kokoelm ivumäärä! Älä ee miää merkiöjä kvkokoelm! Dymie mllie perukompoei. Sähköie kompoei Vu (reii) u() Ri() el (iduki) u() L di() d odeori i() C du()
1. välikoe
 Jan Loto TA7 Ekonometan johdantok Nm: Opkeljanmeo: välkoe 77 Vataa alla olevn kyymykn ympäömällä okea vahtoehto Kakn tehtävää on neljä vahtoehtoa, jota yk on oken Okeata vataketa aa pteen ja vääätä vataketa
Jan Loto TA7 Ekonometan johdantok Nm: Opkeljanmeo: välkoe 77 Vataa alla olevn kyymykn ympäömällä okea vahtoehto Kakn tehtävää on neljä vahtoehtoa, jota yk on oken Okeata vataketa aa pteen ja vääätä vataketa
Mat-2.091 Sovellettu todennäköisyyslasku. Tilastolliset testit. Avainsanat:
 Mat-.090 Sovellettu todeäköiyylaku A 0. harjoituket Mat-.09 Sovellettu todeäköiyylaku 0. harjoituket / Ratkaiut Aiheet: Avaiaat: Tilatolliet tetit Aritmeettie kekiarvo, Beroulli-jakauma, F-jakauma, F-teti,
Mat-.090 Sovellettu todeäköiyylaku A 0. harjoituket Mat-.09 Sovellettu todeäköiyylaku 0. harjoituket / Ratkaiut Aiheet: Avaiaat: Tilatolliet tetit Aritmeettie kekiarvo, Beroulli-jakauma, F-jakauma, F-teti,
Esitä koherentin QAM-ilmaisimen lohkokaavio, ja osoita matemaattisesti, että ilmaisimen lähdöstä saadaan kantataajuiset I- ja Q-signaalit ulos.
 Sgnaalt ja järjestelmät Laskuharjotukset Svu /9. Ampltudmodulaato (AM) Spektranalysaattorlla mtattn 50 ohmn järjestelmässä ampltudmodulaattorn (AM) lähtöä, jollon havattn 3 mpulssa spektrssä taajuukslla
Sgnaalt ja järjestelmät Laskuharjotukset Svu /9. Ampltudmodulaato (AM) Spektranalysaattorlla mtattn 50 ohmn järjestelmässä ampltudmodulaattorn (AM) lähtöä, jollon havattn 3 mpulssa spektrssä taajuukslla
11. Takaisinkytketyt vahvistimet
 Kar berg Kar berg. akankykey vahvme. ahvn yyppejä Jännevahvn Ohjaun läheen pääyyppejä Jänne hjau jännelähde ra hjau jännelähde Jänne hjau vralähde ra hjau vralähde v kun >> v kun >> ja >> njänne n en uraan
Kar berg Kar berg. akankykey vahvme. ahvn yyppejä Jännevahvn Ohjaun läheen pääyyppejä Jänne hjau jännelähde ra hjau jännelähde Jänne hjau vralähde ra hjau vralähde v kun >> v kun >> ja >> njänne n en uraan
7.lk matematiikka. Geometria 1. Janne Koponen versio 2.0
 7.lk matematiikka 1 Janne Koponen verio 2.0 Tämä monite on tehty 7.lk. geometrian opetukeen ja olen käyttänyt itä ite Hatanpään koulua. Jo joku opettaja haluaa tätä kuitenkin käyttää omaa opetukeaan, on
7.lk matematiikka 1 Janne Koponen verio 2.0 Tämä monite on tehty 7.lk. geometrian opetukeen ja olen käyttänyt itä ite Hatanpään koulua. Jo joku opettaja haluaa tätä kuitenkin käyttää omaa opetukeaan, on
INTERFERENSSIN VAIKUTUS LINEAARISESSA MODULAATIOSSA
 INTERFERENSSIN VIUTUS LINERISESS MOULTIOSS Teolkenneeknkka I 521359 a äkkänen Osa 15 1 19 Inefeenssn vakuus lneaasessa odulaaossa Radoaausa nefeenssä RFI sn usa äeselsä, kun oa kanoaaloaauus on lähellä
INTERFERENSSIN VIUTUS LINERISESS MOULTIOSS Teolkenneeknkka I 521359 a äkkänen Osa 15 1 19 Inefeenssn vakuus lneaasessa odulaaossa Radoaausa nefeenssä RFI sn usa äeselsä, kun oa kanoaaloaauus on lähellä
YKSISIVUKAISTAMODULAATIO (SSB)
 YKSISIVUKISTODULTIO SSB Tieoliikenneekniikka I 5359 Kari Kärkkäinen Osa 6 0 Yksisivukaisamodulaaion idea DSB:ssa inormaaio on redundanisesi kaheen keraan, s. LSB & USB. Toisen kaisan läheys riiää, olloin
YKSISIVUKISTODULTIO SSB Tieoliikenneekniikka I 5359 Kari Kärkkäinen Osa 6 0 Yksisivukaisamodulaaion idea DSB:ssa inormaaio on redundanisesi kaheen keraan, s. LSB & USB. Toisen kaisan läheys riiää, olloin
1 Määrittele lyhyesti seuraavat käsitteet. a) Kvantisointivirhe. b) Näytetaajuuden interpolointi. c) Adaptiivinen suodatus.
 TL536DSK-algoritmit (J. Laitinen) 6.4.5 Määrittele lyyeti euraavat käitteet a) Kvantiointivire. b) äytetaajuuden interpolointi. ) Adaptiivinen uodatu. a) Kvantiointivire yntyy, kun ignaalin ykittäinen
TL536DSK-algoritmit (J. Laitinen) 6.4.5 Määrittele lyyeti euraavat käitteet a) Kvantiointivire. b) äytetaajuuden interpolointi. ) Adaptiivinen uodatu. a) Kvantiointivire yntyy, kun ignaalin ykittäinen
ää*r: rfrtlqäe'räs rr[; äsüä FäF r."f F'*üe ;=v* tr, $rr;gt :r1 älfese li ä; äepö* l4:e x1;'.äö l--g! li r: ; ;;*; ssü ntirs E,pä ;;qi?
 j X \: c : 1:8" : Z : : ) ) c 1 T [ b[ ]4 ) < c 1 ü ]T G \\ e p > : [ : e L [? p 2 9 Z S: c? [:? " : e :: [ : >9 Y :[ p e ß < 1 9 1 \ c 4 > ) 1 :91$ :e h b 1 6 " ö:p:?e S9e R ü e $ :1 ee \ eö 4:e 1ö X
j X \: c : 1:8" : Z : : ) ) c 1 T [ b[ ]4 ) < c 1 ü ]T G \\ e p > : [ : e L [? p 2 9 Z S: c? [:? " : e :: [ : >9 Y :[ p e ß < 1 9 1 \ c 4 > ) 1 :91$ :e h b 1 6 " ö:p:?e S9e R ü e $ :1 ee \ eö 4:e 1ö X
Luonnos 1 (13) 17.6.2011 Sosiaali- ja terveystoimialan palvelustrategia (linjaukset) Yleistä
 L 1 (13) - j rv pvrg (j) Yä Pvrg - j rv rg ä r pvrg. Pvrg j: 1. j v (= rppv pvj) 2. ä - j rvpv järjää 3. äärää pv p j j - j rvh v EU- ääöä j äääöä hj. Thj rää fr-hj p rhj. Nää vv r p h j r r. K -hää äääö
L 1 (13) - j rv pvrg (j) Yä Pvrg - j rv rg ä r pvrg. Pvrg j: 1. j v (= rppv pvj) 2. ä - j rvpv järjää 3. äärää pv p j j - j rvh v EU- ääöä j äääöä hj. Thj rää fr-hj p rhj. Nää vv r p h j r r. K -hää äääö
S Piirianalyysi 2 2. välikoe
 S-55.22 Piirianalyyi 2 2. välikoe 6.5.23 Lake tehtävät 2 eri paperille kuin tehtävät 3 5. Muita kirjoittaa jokaieen paperiin elväti nimi, opikelijanumero, kurin nimi ja koodi. Epäelvät vataupaperit voidaan
S-55.22 Piirianalyyi 2 2. välikoe 6.5.23 Lake tehtävät 2 eri paperille kuin tehtävät 3 5. Muita kirjoittaa jokaieen paperiin elväti nimi, opikelijanumero, kurin nimi ja koodi. Epäelvät vataupaperit voidaan
S Piirianalyysi 2 1. Välikoe
 S-55.0 Piirianalyyi. Välioe.3.0 ae ehävä eri paperille uin ehävä 3 5. Muia irjoiaa joaieen paperiin elväi nimi, opielijanumero, urin nimi ja oodi. Tehävä laeaan oreaoulun oepaperille. Muia papereia ei
S-55.0 Piirianalyyi. Välioe.3.0 ae ehävä eri paperille uin ehävä 3 5. Muia irjoiaa joaieen paperiin elväi nimi, opielijanumero, urin nimi ja oodi. Tehävä laeaan oreaoulun oepaperille. Muia papereia ei
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Yhden vapausasteen värähtely - harjoitustehtäviä
 Dynaiia 1 Liie luuun 8. g 8.1 Kuvan jousi-assa syseeissä on = 10 g ja = 2,5 N/. Siiryä iaaan saaisesa asapainoaseasa lähien. luheellä = 0 s assa on saaisessa asapainoaseassaan ja sillä on nopeus 0,5 /
Dynaiia 1 Liie luuun 8. g 8.1 Kuvan jousi-assa syseeissä on = 10 g ja = 2,5 N/. Siiryä iaaan saaisesa asapainoaseasa lähien. luheellä = 0 s assa on saaisessa asapainoaseassaan ja sillä on nopeus 0,5 /
MO-teoria ja symmetria
 MO-teora ja symmetra () Kaks atomorbtaaa vovat muodostaa kaks moekyyorbtaaa - Stova orbtaa - ajottava orbtaa () Atomorbtaaen energoden otava keskenään samansuurusa () Atomorbtaaen symmetravaatmukset LCAO
MO-teora ja symmetra () Kaks atomorbtaaa vovat muodostaa kaks moekyyorbtaaa - Stova orbtaa - ajottava orbtaa () Atomorbtaaen energoden otava keskenään samansuurusa () Atomorbtaaen symmetravaatmukset LCAO
RATKAISUT: Kertaustehtäviä
 Phyica 1 uuditettu paino OPETTAJAN OPAS 1(9) Kertautehtäiä RATKAISUT: Kertautehtäiä LUKU 3. Luua on a) 4 eriteää nueroa b) 3 eriteää nueroa c) 7 eriteää nueroa. 4. Selitetään erieen yhtälön olepien puolien
Phyica 1 uuditettu paino OPETTAJAN OPAS 1(9) Kertautehtäiä RATKAISUT: Kertautehtäiä LUKU 3. Luua on a) 4 eriteää nueroa b) 3 eriteää nueroa c) 7 eriteää nueroa. 4. Selitetään erieen yhtälön olepien puolien
Kirjainkiemurat - mallisivu (c)
 Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
Aa Ii Uu Ss Aa Ii Uu Ss SII-LIN VII-LI-KUP-PI I-sot, pie-net kir-jai-met, sii-li neu-voo aak-ko-set. Roh-ke-as-ti mu-kaan vaan, kaik-ki kyl-lä op-pi-vat! Ss Har-joit-te-le kir-jai-mi-a li-sää vih-koo-si.
Intensiteettitaso ja Doplerin ilmiö
 Inteniteettitao ja Doplerin ilmiö Tehtävä Erkki työkentelee airaalaa. Sairaalalta 6,0 km päää on tapahtunut tieliikenneonnettomuu ja onnettomuupaikalta lähteneen ambulanin ireenin ääni kuuluu Erkille 60,0
Inteniteettitao ja Doplerin ilmiö Tehtävä Erkki työkentelee airaalaa. Sairaalalta 6,0 km päää on tapahtunut tieliikenneonnettomuu ja onnettomuupaikalta lähteneen ambulanin ireenin ääni kuuluu Erkille 60,0
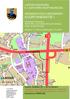
Ei asemakaavaa. E3 Söörmarkun eritasoliittymä
 X= Värn slyks Suunnllu : Y = Tään suunnlan ukaan Y = raknnaa a parannaa X= Mudn suunnln ukaan raknnaa E asakaaaa Tdn hallnnllsssa järjslyssä apahdu uusa Y E Söörarkun raslyä Y Y M a s a Va Y P r R R Va
X= Värn slyks Suunnllu : Y = Tään suunnlan ukaan Y = raknnaa a parannaa X= Mudn suunnln ukaan raknnaa E asakaaaa Tdn hallnnllsssa järjslyssä apahdu uusa Y E Söörarkun raslyä Y Y M a s a Va Y P r R R Va
Luento 6 Luotettavuus Koherentit järjestelmät
 Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Aalto-ylosto erustetede korkeakoulu Matematka a systeemaalyys latos Lueto 6 Luotettavuus Koherett ärestelmät Aht Salo Systeemaalyys laboratoro Matematka a systeemaalyys latos Aalto-ylosto erustetede korkeakoulu
Analyysi A. Harjoitustehtäviä lukuun 1 / kevät 2018
 Aalyysi A Harjoitustehtäviä lukuu / kevät 208 Ellei toisi maiita, tehtävissä esiityvät muuttujat ja vakiot ovat mielivaltaisia reaalilukuja.. Aa joki ylä- ja alaraja joukoille { x R x 2 + x 6 ja B = {
Aalyysi A Harjoitustehtäviä lukuu / kevät 208 Ellei toisi maiita, tehtävissä esiityvät muuttujat ja vakiot ovat mielivaltaisia reaalilukuja.. Aa joki ylä- ja alaraja joukoille { x R x 2 + x 6 ja B = {
Videokoulu PASSE LEI TA VI NKKE JÄ TA RIN A N K E RT OJ A L L E
 Vdeool PASSE LEI TA VI NKKE JÄ TA RIN A N K E RT OJ A L L E v 1.0 29.10.2015 Mely j ome m Te o e m m oll eem j m. M l ed j vdeo? Keelle vdeo oll eem? M vdeoll l d e? Mllo olemme vee pee, jollo vomme o
Vdeool PASSE LEI TA VI NKKE JÄ TA RIN A N K E RT OJ A L L E v 1.0 29.10.2015 Mely j ome m Te o e m m oll eem j m. M l ed j vdeo? Keelle vdeo oll eem? M vdeoll l d e? Mllo olemme vee pee, jollo vomme o
Mat-2.090 Sovellettu todennäköisyyslasku A
 Mat-.090 Sovellettu todeäköiyylaku A Mat-.090 Sovellettu todeäköiyylaku A / Ratkaiut Aiheet: Avaiaat: Tilatollite aieito keräämie ja mittaamie Tilatollite aieitoje kuvaamie Oto ja otojakaumat Aritmeettie
Mat-.090 Sovellettu todeäköiyylaku A Mat-.090 Sovellettu todeäköiyylaku A / Ratkaiut Aiheet: Avaiaat: Tilatollite aieito keräämie ja mittaamie Tilatollite aieitoje kuvaamie Oto ja otojakaumat Aritmeettie
Tekes: Korjausrakentamisen kehittäminen -teema TEEMAN TILANNEKUVA
 eke: Krurkee kehäe ee EEMN ILNNEKUV J Sre, kvr, V llce Prer Oy 20.11.2013 J Sre Älykä rkeeu elypärö: V Lkee Rkeuke Su edelläkävä älykkää re plvelu eklg, k udv u ue, yö vp kkuuk. eke edää käyäe, yrye ekä
eke: Krurkee kehäe ee EEMN ILNNEKUV J Sre, kvr, V llce Prer Oy 20.11.2013 J Sre Älykä rkeeu elypärö: V Lkee Rkeuke Su edelläkävä älykkää re plvelu eklg, k udv u ue, yö vp kkuuk. eke edää käyäe, yrye ekä
MONIKAPPALEMEKANIIKAN MALLINTAMINEN PARAMETRISOIMALLA SIDOSMONISTO
 IIVISELMÄ MONIKAPPALEMEKANIIKAN MALLINAMINEN PARAMERISOIMALLA SIDOSMONISO J. MÄKINEN & H. MARJAMÄKI eknllen ekankan a optonnn lato apereen teknllnen ylopto PL 589 33101 AMPERE ää etykeä kuvataan lyhyet
IIVISELMÄ MONIKAPPALEMEKANIIKAN MALLINAMINEN PARAMERISOIMALLA SIDOSMONISO J. MÄKINEN & H. MARJAMÄKI eknllen ekankan a optonnn lato apereen teknllnen ylopto PL 589 33101 AMPERE ää etykeä kuvataan lyhyet
Luento 9. Epälineaarisuus
 Lueno 9 Epälineaarisuus 9..7 Epälineaarisuus Tarkasellaan passiivisa epälineaarisa komponenia u() y() f( ) Taylor-sarjakehielmä 3 y f( x) + f '( x) ( x x) + f ''( x) ( x x) + f ''( x) ( x x) +...! 3! 4!
Lueno 9 Epälineaarisuus 9..7 Epälineaarisuus Tarkasellaan passiivisa epälineaarisa komponenia u() y() f( ) Taylor-sarjakehielmä 3 y f( x) + f '( x) ( x x) + f ''( x) ( x x) + f ''( x) ( x x) +...! 3! 4!
1. (Jatkoa Harjoitus 5A tehtävään 4). Monisteen esimerkin mukaan momenttimenetelmän. n ne(y i Y (n) ) = 2E(Y 1 Y (n) ).
 HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
S Signaalit ja järjestelmät Tentti
 S-7. Signaali ja järjeselmä eni..6 Vasaa ehävään, ehävisä 7 oeaan huomioon neljä parhaien suorieua ehävää.. Vasaa lyhyesi seuraaviin osaehäviin, käyä arviaessa kuvaa. a) Mikä kaksi ehoa kanaunkioiden φ
S-7. Signaali ja järjeselmä eni..6 Vasaa ehävään, ehävisä 7 oeaan huomioon neljä parhaien suorieua ehävää.. Vasaa lyhyesi seuraaviin osaehäviin, käyä arviaessa kuvaa. a) Mikä kaksi ehoa kanaunkioiden φ
MUODONMUUTOKSET. Lähtöotaksumat:
 MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
MUODONMUUTOKSET Lähöoaksuma:. Maeraal on sorooppsa ja homogeensa. Hooken lak on vomassa (fyskaalnen lneaarsuus) 3. Bernoulln hypoees on vomassa (eknnen avuuseora) 4. Muodonmuuokse ova nn penä rakeneen
Taustaa KOMPLEKSILUVUT, VÄRÄHTELIJÄT JA RADIOSIGNAALIT. Jukka Talvitie, Toni Levanen & Mikko Valkama TTY / Tietoliikennetekniikka
 IMA- Exurso: Kompleksluvu ja radosgnaal / KOMPLEKSILUVUT, VÄRÄHTELIJÄT JA RADIOSIGNAALIT Tausaa IMA- Exurso: Kompleksluvu ja radosgnaal / Kakk langaon vesnä ja radoeolkenne (makapuhelme, WLAN, ylesrado
IMA- Exurso: Kompleksluvu ja radosgnaal / KOMPLEKSILUVUT, VÄRÄHTELIJÄT JA RADIOSIGNAALIT Tausaa IMA- Exurso: Kompleksluvu ja radosgnaal / Kakk langaon vesnä ja radoeolkenne (makapuhelme, WLAN, ylesrado
12. laskuharjoituskierros, vko 16, ratkaisut
 1. lakuharjoitukierro, vko 16, ratkaiut D1. Muuttujien x ja Y havaitut arvot ovat: x 1 3 4 6 8 9 11 14 Y 1 4 4 5 7 8 9 a) Määrää regreiomallin Y i = α +βx i +ǫ i regreiokertoimien PNS-etimaatit ja piirrä
1. lakuharjoitukierro, vko 16, ratkaiut D1. Muuttujien x ja Y havaitut arvot ovat: x 1 3 4 6 8 9 11 14 Y 1 4 4 5 7 8 9 a) Määrää regreiomallin Y i = α +βx i +ǫ i regreiokertoimien PNS-etimaatit ja piirrä
DEE-53000 Sähkömagneettisten järjestelmien lämmönsiirto
 DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
DEE-53000 Sähkömageese järjeselme lämmösro Lueo 8 1 Sähkömageese järjeselme lämmösro Rso Mkkoe Dfferessmeeelmä Numeersa rakasua haeaa aluee dskreeesä psesä. Muodoseaa verkko ja eseää dervaaa erousosamäärä.
Kahdeksansolmuinen levyelementti
 Levy8 ja RS hm 7.. Kahdekanolminen levyelementti akatellaan kvan kahdekanolmita levyelementtiä. q 6 y (,y q 8 ( 8,y 8 8 q 7 q 6 (,y q 5 q q q 7 q q ( 7,y 7 v ( 6,y 6 P 5 ( 5,y 5 q 9 6 q 5 (,y q (,y q q
Levy8 ja RS hm 7.. Kahdekanolminen levyelementti akatellaan kvan kahdekanolmita levyelementtiä. q 6 y (,y q 8 ( 8,y 8 8 q 7 q 6 (,y q 5 q q q 7 q q ( 7,y 7 v ( 6,y 6 P 5 ( 5,y 5 q 9 6 q 5 (,y q (,y q q
Soorrea. OUTC'KUMPU Oy.' Malminetsintä. O. POhjamies/pAL ,4 1 (3) VLF -MI'ITAUS. Periaate. Lähetysase.mat
 - OUTCKUMPU Oy Malmnesnä O POhames/pAL 94 (3) VLF -MTAUS Peraae Läheysasema VU (= Very M Frequency) -ruauks$sa käyeään apuna 5-0 khz aauusaueea omva asea Näden asemen anenrrl ova pysyä a nssä kulkeva vra
- OUTCKUMPU Oy Malmnesnä O POhames/pAL 94 (3) VLF -MTAUS Peraae Läheysasema VU (= Very M Frequency) -ruauks$sa käyeään apuna 5-0 khz aauusaueea omva asea Näden asemen anenrrl ova pysyä a nssä kulkeva vra
VÄRÄHTELYMEKANIIKKA SESSIO 24: Usean vapausasteen vaimenematon ominaisvärähtely osa 2
 / ÄRÄHELYMEKANIIKKA SESSIO : Usea vapausastee vaeeato oasvärähtely osa MONINKERAISE OMINAISAAJUUDE Sesso MS oreeratu oasuodo { lasetaeetelässä oletett, että o ysertae oasulataauus. arastellaa velä tapausta,
/ ÄRÄHELYMEKANIIKKA SESSIO : Usea vapausastee vaeeato oasvärähtely osa MONINKERAISE OMINAISAAJUUDE Sesso MS oreeratu oasuodo { lasetaeetelässä oletett, että o ysertae oasulataauus. arastellaa velä tapausta,
Voiman momentti. Momentin yksikkö on [M] = [F] [r] = 1 Nm (newtonmetri) Voiman F vaikutussuora
![Voiman momentti. Momentin yksikkö on [M] = [F] [r] = 1 Nm (newtonmetri) Voiman F vaikutussuora Voiman momentti. Momentin yksikkö on [M] = [F] [r] = 1 Nm (newtonmetri) Voiman F vaikutussuora](/thumbs/62/47972980.jpg) Voa oett Moett o oa ja oa ae tulo Täsällse ääteltä oa F oett (aksel A suhtee) o M A = F, ssä o oa akutussuoa (kohtsuoa) etäss akselsta A Voa ae sjasta odaa kättää ös oa akutuspstee ja akselpstee lhtä etästtä,
Voa oett Moett o oa ja oa ae tulo Täsällse ääteltä oa F oett (aksel A suhtee) o M A = F, ssä o oa akutussuoa (kohtsuoa) etäss akselsta A Voa ae sjasta odaa kättää ös oa akutuspstee ja akselpstee lhtä etästtä,
VÄRÄHTELYMEKANIIKKA SESSIO 18: Yhden vapausasteen pakkovärähtely, transienttikuormituksia
 8/ VÄRÄHTELYMEKANIIKKA SESSIO 8: Yhen vapausaseen paovärähely, ransieniuormiusia JOHDANTO c m x () Kuva. Syseemi. Transieniuormiusella aroieaan uormiusheräeä, joa aiheuaa syseemiin lyhyaiaisen liieilan.
8/ VÄRÄHTELYMEKANIIKKA SESSIO 8: Yhen vapausaseen paovärähely, ransieniuormiusia JOHDANTO c m x () Kuva. Syseemi. Transieniuormiusella aroieaan uormiusheräeä, joa aiheuaa syseemiin lyhyaiaisen liieilan.
S Fysiikka III (Est) Tentti
 S-114137 Fyiikka III (Et) Tentti 9008 1 Vetyatomin elektronin kulmaliikemäärää kuvaa kvanttiluku l =3 Lake miä kaikia kulmia kulmaliikemäärävektori voi olla uhteea kulmaliikemäärän z-komponenttiin ( )
S-114137 Fyiikka III (Et) Tentti 9008 1 Vetyatomin elektronin kulmaliikemäärää kuvaa kvanttiluku l =3 Lake miä kaikia kulmia kulmaliikemäärävektori voi olla uhteea kulmaliikemäärän z-komponenttiin ( )
Kokonaistodennäköisyys ja Bayesin kaava. Kokonaistodennäköisyys ja Bayesin kaava. Kokonaistodennäköisyys ja Bayesin kaava: Esitiedot
 TKK (c) Ilkka Mell (2004) Kokoastodeäkösyys ja Kokoastodeäkösyys ja : Johdato Kokoastodeäkösyyde ja Bayes kaavoje systeemteoreette tulkta Johdatus todeäkösyyslasketaa Kokoastodeäkösyys ja TKK (c) Ilkka
TKK (c) Ilkka Mell (2004) Kokoastodeäkösyys ja Kokoastodeäkösyys ja : Johdato Kokoastodeäkösyyde ja Bayes kaavoje systeemteoreette tulkta Johdatus todeäkösyyslasketaa Kokoastodeäkösyys ja TKK (c) Ilkka
KANTATAAJUINEN BINÄÄRINEN SIIRTOJÄRJESTELMÄ AWGN-KANAVASSA
 KJUI BIÄÄRI SIIROJÄRJSLMÄ WG-KVSS Kaajaajui siiro iformaaio siiro johdossa sllaisaa ilma kaoaalo- ai pulssimodulaaioa 536 ioliikkiikka II Osa 3 Kari Kärkkäi Syksy 5 JÄRJSLMÄMLLI Bii kso. Symboli {} ja
KJUI BIÄÄRI SIIROJÄRJSLMÄ WG-KVSS Kaajaajui siiro iformaaio siiro johdossa sllaisaa ilma kaoaalo- ai pulssimodulaaioa 536 ioliikkiikka II Osa 3 Kari Kärkkäi Syksy 5 JÄRJSLMÄMLLI Bii kso. Symboli {} ja
F Y S I I K K A KERTAUSTEHTÄVIÄ 1-20
 F Y S I I K K A KERTAUSTEHTÄVIÄ - 0 Oalla eieyiä kyyykiä vaauke ova huoaavai pidepiä kuin iä eierkiki kokeea vaaukela vaadiaan. Kokeea on oaava vain olennainen aia per ehävä. . Muua SI järjeelän ykiköihin
F Y S I I K K A KERTAUSTEHTÄVIÄ - 0 Oalla eieyiä kyyykiä vaauke ova huoaavai pidepiä kuin iä eierkiki kokeea vaaukela vaadiaan. Kokeea on oaava vain olennainen aia per ehävä. . Muua SI järjeelän ykiköihin
LAPUAN KAUPUNKI 8. LIUHTARIN KAUPUNGINOSA ASEMAKAAVAN KUMOAMINEN KUORTANEENTIE I
 . G ä y, ä y-, y-.., äydy.... äyö- ö.. yäyy g xx.xx. xx yäyy g xx.xx. xx - . - D.. d.. ääyä. ä y-, - y., ö ---, ---, ---, --- (ä) - --... - g - -. y - y d ä. - -,. - .., Ä, yydä g d ää :., ä äy äää ä-.
. G ä y, ä y-, y-.., äydy.... äyö- ö.. yäyy g xx.xx. xx yäyy g xx.xx. xx - . - D.. d.. ääyä. ä y-, - y., ö ---, ---, ---, --- (ä) - --... - g - -. y - y d ä. - -,. - .., Ä, yydä g d ää :., ä äy äää ä-.
VÄRÄHTELYMEKANIIKKA SESSIO 06: Ekvivalentti systeemi
 6/ VÄRÄHTEYMEKANKKA SESS 6: Evvle sysee JHDANT Use äyä pplee uodos sysee vod orv yhde vpussee evvlell llll os se pplede se/ul-se vod lusu s oord vull. Tällö sysee geoers vod uodos yheyde se e pplede leloe
6/ VÄRÄHTEYMEKANKKA SESS 6: Evvle sysee JHDANT Use äyä pplee uodos sysee vod orv yhde vpussee evvlell llll os se pplede se/ul-se vod lusu s oord vull. Tällö sysee geoers vod uodos yheyde se e pplede leloe
RATKAISUT: 7. Gravitaatiovoima ja heittoliike
 Phyica 9. paino () 7. Gaitaatiooia ja heittoliike : 7. Gaitaatiooia ja heittoliike 7. a) Gaitaatiooia aikuttaa kaikkien kappaleiden älillä. Gaitaatiooian uuuu iippuu kappaleiden aoita ja niiden älietä
Phyica 9. paino () 7. Gaitaatiooia ja heittoliike : 7. Gaitaatiooia ja heittoliike 7. a) Gaitaatiooia aikuttaa kaikkien kappaleiden älillä. Gaitaatiooian uuuu iippuu kappaleiden aoita ja niiden älietä
Juuri 13 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. K1. A: III, B: I, C: II ja IV.
 Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 Keraus K. A: III, B: I, C: II ja IV Kuvaaja: I II III IV Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 K. a) lim ( ) Nimiäjä ( ) o aia
Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 Keraus K. A: III, B: I, C: II ja IV Kuvaaja: I II III IV Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 K. a) lim ( ) Nimiäjä ( ) o aia
LUKION FYSIIKKAKILPAILU 8.11.2005 avoimen sarjan vast AVOIN SARJA
 LKION FYSIIKKAKILPAIL 8..5 avoien arjan vat AVOIN SARJA Kirjoita tektaten koepaperiin oa niei, kotiooitteei, ähköpotiooitteei, opettajai nii ekä koului nii. Kilpailuaikaa on inuuttia. Sekä tehtävä- että
LKION FYSIIKKAKILPAIL 8..5 avoien arjan vat AVOIN SARJA Kirjoita tektaten koepaperiin oa niei, kotiooitteei, ähköpotiooitteei, opettajai nii ekä koului nii. Kilpailuaikaa on inuuttia. Sekä tehtävä- että
TL5362DSK-algoritmit (J. Laitinen) TTE2SN4X/4Z, TTE2SN5X/5Z Välikoe 1, ratkaisut
 TL536DSK-algoritmit (J. Laitie) 4. - 5..4 TTESN4X/4Z, TTESN5X/5Z Välikoe, ratkaiut a) Maiite väitää kaki digitaalite FIR-uotimie etua verrattua IIR-uotimii. b) Mite Reme-meetelmällä uuitellu FIR-uotime
TL536DSK-algoritmit (J. Laitie) 4. - 5..4 TTESN4X/4Z, TTESN5X/5Z Välikoe, ratkaiut a) Maiite väitää kaki digitaalite FIR-uotimie etua verrattua IIR-uotimii. b) Mite Reme-meetelmällä uuitellu FIR-uotime
KUINKA PALJON VAROISTA OSAKKEISIIN? Mika Vaihekoski, professori. Lappeenrannan teknillinen yliopisto
 KUINKA PALJON VAROISTA OSAKKEISIIN? Mika Vaihekoki, proeori Lappeenrannan teknillinen yliopito Näin uuden vuoden alkaea ueat meitä miettivät ijoitualkkuna kootumuta. Yki kekeiitä kyymykitä on päätö eri
KUINKA PALJON VAROISTA OSAKKEISIIN? Mika Vaihekoki, proeori Lappeenrannan teknillinen yliopito Näin uuden vuoden alkaea ueat meitä miettivät ijoitualkkuna kootumuta. Yki kekeiitä kyymykitä on päätö eri
2.4 Erikoistapaus kantalukuna 10 eli kymmenen potenssit
 2.4 Kyenen potenit 2.4 Erikoitapau kantaukuna ei kyenen potenit Potenin kantaukuna käytetään kyentä erityieti, kun uku on erittäin uuri tai erittäin pieni. Tää auttaa näitten ääritapauten hahottaiea. Tarkateaan
2.4 Kyenen potenit 2.4 Erikoitapau kantaukuna ei kyenen potenit Potenin kantaukuna käytetään kyentä erityieti, kun uku on erittäin uuri tai erittäin pieni. Tää auttaa näitten ääritapauten hahottaiea. Tarkateaan
HY, MTO / Matemaattisten tieteiden kandiohjelma Tilastollinen päättely II, kevät 2018 Harjoitus 6A Ratkaisuehdotuksia.
 HY, MTO / Matemaattiste tieteide adiohjelma Tilastollie päättely II, evät 2018 Harjoitus 6A Rataisuehdotusia Tehtäväsarja I 1. (Moistee tehtävä 5.4) Kauppias myy mäysiemeiä, joide itävyyde väitetää oleva
HY, MTO / Matemaattiste tieteide adiohjelma Tilastollie päättely II, evät 2018 Harjoitus 6A Rataisuehdotusia Tehtäväsarja I 1. (Moistee tehtävä 5.4) Kauppias myy mäysiemeiä, joide itävyyde väitetää oleva
MATA172 Sami Yrjänheikki Harjoitus Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki!
 MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
Flow shop, työnvaiheketju, joustava linja, läpivirtauspaja. Kahden koneen flow shop Johnsonin algoritmi
 Flow shop önvaheeju jousava lnja läpvrauspaja Flow shopssa önvaheden järjess on sama alla uoella Kosa vahea vo edelää jono vova ö olla vaheleva ja ö vova ohaa osensa äl ö evä oha osaan puhuaan permuaaoaaaulusa
Flow shop önvaheeju jousava lnja läpvrauspaja Flow shopssa önvaheden järjess on sama alla uoella Kosa vahea vo edelää jono vova ö olla vaheleva ja ö vova ohaa osensa äl ö evä oha osaan puhuaan permuaaoaaaulusa
Osakeoptioiden markkinahinnoittelu, volatiliteetti ja kohde-etuuden hintadynamiikka
 Oaeopode marahoelu volalee a ohde-euude hadyama Kaaalouede Pro-radu Kaaaloueee lao Tamperee ylopo 8 Teemu Krau TIIVISTELMÄ Tamperee ylopo Teä: Tuelma m: Taloueede lao; aaalouede KRAUS TEEMU Oaeopode marahoelu
Oaeopode marahoelu volalee a ohde-euude hadyama Kaaalouede Pro-radu Kaaaloueee lao Tamperee ylopo 8 Teemu Krau TIIVISTELMÄ Tamperee ylopo Teä: Tuelma m: Taloueede lao; aaalouede KRAUS TEEMU Oaeopode marahoelu

