SUOJAAMATTOMAN LIIMAPUUPALKIN PALOMITOITUS LUOKKAAN R 60
|
|
|
- Akseli Mattila
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Esimeri 1 SUOJAAMATTOMAN LIIMAPUUPALKIN PALOMITOITUS LUOKKAAN R 6 1 Paloilaee uormius ψ =,5 (ässä esimerissä muuuva uorma o lumiuorma) 1,1 p = p + ψ p = 6, +,5 11, = 11,5 N/m i g, 1,1 q, Pali maeriaaliomiaisuue m, m, i m, mo,i i mo,i m,, i m, i 1,,5 = 3 N/mm Pali oreus o yli 6 mm, joe = 1, i = 1,15 (RIL 5- auluosa) = = 1,15 3 = 34,5 N/mm = 1, E = 1, 1, = = 34,5 = 34,5 N/mm = 18 N/mm β =,7 mm/mi imellie iilymisopeus, sisälää ulmapyörisyse ja aleama Palourvallie puualo 3/18 1
2 3 Teollise iilymissyvyye mioiusarvo β =,7 mm/mi ( RIL 5 auluosa) = 6 mi (ässä esimerissä) car, = β =,7 6 = 4 mm mi = 1, = 7, mm (vaio) = + = 4 + 1, 7, = 49 mm e car, 4 Teollie poiileiaus Pali alisuu palolle olmela sivusa, osa aoraee suojaa pali yläpiaa. b = 9 mm i = 716 mm i 5 Taivuusesävyys M i,max pi L 11,5 1 = Mi,max = = 143,8 Nm M 6 141,8 1 = = = 18, N/mm i m, y,, i bi i < m, y,, i m,, i 18, N/mm 34,5 N/mm (5 % OK esää) Palourvallie puualo 3/18
3 ESIMERKKI 1 6 Kiepausesävyys Taraseaa esääö pali iepaamaa, u siä ei ole paloilaeessa ueu sivusuuassa. e, i =,9 L+ =, = 143 mm c =,71 λ i c b,71 9 = = 18 = 8,7 N/mm i m, cri, i E,5 i e, i m, rel, m, i = = = m, cri, i 8,7 cri, i λrel, m, i 1, 86 m, y,, i cri, i m,, i = = =,9 1, 86 18, N/mm,9 34,5 N/mm 1, N/mm (18 % VIRHE) > = Pali iepaaa paloilaeessa, jos siä ei ole ueu sivusuuassa. Pali iepausuea ulee säilyä oo paloesoaja (ässä esimerissä 6 mi). 7 Leiausesävyys Ei arvise arasaa paloilaeessa, osa pali poiileiaus o suoraaie. 8 Tuipaieesävyys Ei arvise arasaa paloilaeessa. 9 Taipuma Taipumaa ei yleesä arvise arasaa paloilaeessa, ellei siiä ole vaaraa muille raeeille ja raeeie palosuojausille. Esimerisi ässä apausessa aipuma ulisi arasaa, jos pali alla olisi ei-aava osasoiva seiä, osa pali aipuma vuosi uormiaisi seiää ja äi eieäisi seiä osasoiiyyä. 1 Yeeveo Pali äyää vaaimuse R 6, u se iepaamie eseää pali päällä oleva CLT-levyyse avulla. Palourvallie puualo 3/18 3
4 Esimeri LEVYSUOJATUN RANKASEINÄN PALOMITOITUS LUOKKAAN R 6 1 Nimellie iilymisopeus ee levyje murumisa Hiilymisvaiea ee levyje murumisa ei ole, osa ysymysessä o avallise ipsiaroilevy ja puulevy yiselmä. c c = iilymise alamisei = levyyse murumisei = = 4 mi (RIL 5- auluosa) Havuvaeri o pasumpi ui 1 mm, joe β = 1, mm/mi (RIL 5- auluosa, vaerille) β, ρ,, = = = 1, ρ 45 = = = 1,15 15 p = β = 1, 1, 1,15 = 1,15 mm/mi = 15 mm (vaeri) = = =,6 mi 3, mi β 1,15 ρ c β = = 43 mi ρ = mm/mi c - ja -arvoja voiaa oroaa määrällä Nimellie iilymisopeus levyje murumise jälee b = 96 mm b 9 mm = 1, (RIL 5 auluosa) 3 = 1, (RIL 5 auluosa) = 1,5 (vaio) β =,65 mm/mi (RIL 5 auluosa, olpalle) 3 s 3 s β = β = 1, 1, 1, 5, 65 =,98 mm / mi Palourvallie puualo 3/18 4
5 3 Nimellie iilymissyvyye mioiusarvo β = mm/mi = 43 mi c 3 = 43 mi β =,98 = 6 mi (ässä esimerissä) = β ( ) + β ( ) = (43 43) +,98 (6 43) = 16, 7 mm 17 mm car, c 3 4 Nimellie jääöspoiileiaus Kivivilla suojaa olppie yliä, joe olpa iilyvä vai yesä suuasa. b = 48 mm (ysi olppa) i = 16 mm i 5 Paloilaee rasiuse olpa Z-suuassa Hiilymä aieuama epäesisyys e N, i y, c,, i c, i y,, i = 4 N M = e N =,85 4 =, 34 Nm M =,34 Nm 17 car, c = = = 8,5 mm Tolppia o pl riaai, joe ye olpa rasiuse ova N, i = N M y,, i =,17 Nm Palourvallie puualo 3/18 5
6 6 Tolpa maeriaaliomiaisuue c,, i c,, i c,, car, mo, c, i i = 1 N/mm mo, c, i c,,, i c,, i = 1,5 (RIL 5- auluosa) = = 1,5 1= 6,5 N/mm m, 17 = =,14 13 =,45 (RIL 5- auluosa, ierpoloiu) = 1,,45 = = 6,5 = 11,81 N/mm 1, = 4 N/mm m, m, m, i m, car,,, = 1, 3 = = 1, 4 1, 3 1, 4 13 = = 1,4 4 = 4,96 N/mm i = 1,5 (RIL 5- auluosa) = = 1,5 4,96 = 31, N/mm mo,m, i i 17 = =,14 13 =,45 (RIL 5- auluosa, ierpoloiu, palo puriseulla puolella mo,m, i m,,i m, i 1, E,5 = 1,,45 = = 31, = 14,4 N/mm = 74 N/mm 7 Nurjausesävyys Z-suuassa L c, z, i = 1, L = 1, 5 = 5 mm 3 3 bi i Ι y, i = = = 4,76 1 mm 1 1 A = b = = 588 mm i i i 4, y, i y, i = = = Ai 588 i λ λ L Ι 5 c, z, i y, i = = = iy, i 3,59 λ y, i c,, rel, y, i = = π E,5 β =, c 81, ,59 mm 81,73 1 = 1, 39 π 74 y, i c rel, y, i rel, y, i cyi,, =,5 (1 + β ( λ,3) + λ ) =,5 (1+, (1,39,3) + 1,39 ) = 1, = 1 = =,43 1,43 + λ 1, , 58 1, 39 y, i y, i rel, y, i N, i c,,, i = = = Ai 588 3, 93 N/mm 6 y,, i m, y,, i = = = 1, 89 N/mm bi i c,,, i 6 M 6,17 1 c, y, i c,,, i m,, i m, y,, i + = + = < 3,93 1,89 1,91 1 (91 % OK esää),43 11,81 14,4 Palourvallie puualo 3/18 6
7 8 Kiepausesävyys Paloilaeessa olppie puriseu reua o uemao. e, i = 1, L+ = 1, = 71 mm c =,78 λ c bi,78 48 = E = 74 = 46,6 N/ mm m, cri, i,5 i e, i rel, m, i i m, 1,4 4 = = =,73 46,6 m, cri, i = 1, ( λ,75) Tolppa ei ole iepausalis cri, i rel, m, i 9 Leiausesävyys Ei arvise arasaa paloilaeessa, osa olpa poiileiaus o suoraaie. 1 Tuipaieesävyys Ei arvise arasaa paloilaeessa. 11 Taipuma Taipumaa ei yleesä arvise arasaa paloilaeessa, ellei siiä ole vaaraa muille raeeille ja raeeie palosuojausille. 1 Yeeveo Raaseiä äyää vaaimuse R 6, u raoje urjaamie Y-suuassa o esey palo vasaise puole levyysellä. Palourvallie puualo 3/18 7
8 Esimeri 3 LEVYSUOJATUN PALKKIVÄLIPOHJAN PALOMITOITUS LUOKKAAN R 6 1 Paloilaee uormius ψ =,3 (ässä esimerissä muuuva uorma o yöyuorma) p = p + ψ p = 1, 5 +, 3 1, = 1, 86 N/m i g, q, Oelo oreus oelo pali 1, 6 =, 33, 6 3 Oelo oreus äyää vaaimus e 3 Nimellie iilymisopeus ee levyje murumisa Hiilymie alaa ee levyyse murumisa, osa levyysessä äyeää paloipsilevyä. b = 51 mm = 1, (RIL 5- auluosa, ierpoloiu) s =,85 (RIL 5- auluosa) = 1,5 (mioiusmeeelmää sisälyvä vaio) β =,65 mm/mi (RIL 5- auluosa, LVL:lle) β = β = 1,,85 1,5,65 = 1,1 mm/mi s Palourvallie puualo 3/18 8
9 4 Nimellie iilymisopeus levyje murumise jälee b = 51 mm = 1, (RIL 5- auluosa, ierpoloiu) s 3 = 5, (RIL 5- auluosa, erisee aaeu puuragoilla) = 1,5 (mioiusmeeelmää sisälyvä vaio) β =,65 mm/mi (RIL 5- auluosa, LVL:lle) β = β = 1, 5, 1,5,65 = 5,95 mm/mi 3 s 3 5 Nimellie iilymissyvyye mioiusarvo β = 1,1 mm/mi = 45 (RIL 5- auluosa, ierpoloiu) c 3 = 4 mi β = 5,95 mm/mi = 6 mi (ässä esimerissä) = β ( ) + β ( ) = 1,1 (45 4) + 5,95 (6 45) = 94,3 mm 95 mm car, c 3 6 Nimellie jääöspoiileiaus Kivivilla suojaa palie yliä, joe pali iilyvä vai yesä suuasa. b = 51 mm i = 5 mm i Palourvallie puualo 3/18 9
10 7 Pali maeriaaliomiaisuue m, = 44, N/mm m, i m, car, mo,m, i Pali oreus o 3 mm, joe = 1, i = 1,1 (RIL 5- auluosa) = = 1,1 44, = 48,4 N/mm i 95 = =,3 3 =,69 (RIL 5- auluosa, ierpoloiu, palo veeyllä puolella) = 1,,69 = = 48,4 = 33,4 N/mm mo,m, i m,,i m, i 1, 8 Taivuusesävyys M i,max pi L 1, 86 4 = = = 3,7 Nm M 6 3,7 1 = = = 1,4 N/mm 6 i m, y,, i bi i 51 5 < m, y,, i m,, i 1,4 N/mm 33,4 N/mm (31 % OK esää) 9 Kiepausesävyys Pali puriseu reua o iepausueu palo vasaise puole levyysellä oo paloesoaja. 1 Leiausesävyys Ei arvise arasaa paloilaeessa, osa pali poiileiaus o suoraaie. 11 Tuipaieesävyys Ei arvise arasaa paloilaeessa. 1 Taipuma Taipumaa ei yleesä arvise arasaa paloilaeessa ellei siiä ole vaaraa muille raeeille ja raeeie palosuojausille. 13 Oelo palosuojavilloje aausraga Oelo villa aaeaa paliso alapiassa olevilla puuragoilla oo paloesoaja. Villoje aaus ausisilla jousiragoilla ei ole yleesä järevää, osa iie iiiysruuvie ulee ylää iilymäömää pali osaa. Tällöi iiiysruuveisa ulee yleesä eriäi piiä. Mioieaa ämä esimeri välipoja villoje aausee äyeävie puuraoje oo. Puuraga ova saaavaraa ja e alisuva palolle olmela sivula. Palourvallie puualo 3/18 1
11 14 Kaausraoje imellie iilymisopeus ee levyje murumisa Hiilymie alaa ee levyyse murumisa, osa levyysessä äyeää paloipsilevyä. =,85 (RIL 5- auluosa) β =,8 mm/mi (RIL 5- auluosa, saaavaralle) β = β =,85,8 =,68 mm/mi 15 Kaausraoje imellie iilymisopeus levyje murumise jälee 3 =, (RIL 5- auluosa) β =,8 mm/mi (RIL 5- auluosa, saaavaralle) β = β =,,8 = 1,6 mm/mi Kaausraoje eollise iilymissyvyye mioiusarvo = 45 mi (RIL 5- auluosa) c = 4 mi (RIL 5- auluosa) = 6 mi (ässä esimerissä) a a 5 ( c ) β 5 (45 4),85, ,5 3 β, 8 = + = + = = aia, jolloi iilymie o eey 5 mm: syvyyee ja iilymisopeus palauuu ormaalisi = β ( ) + β ( ) + β ( ) car, c 3 a a car, mi =,68 (45 4) + 1,6 (58,5 45) +,8 (6 58,5) = 6, mm 6 mm mi = 1, = 7, mm ( vaio) = + = 6 + 1, 7, = 33 mm e car, Palourvallie puualo 3/18 11
12 17 Yeeveo Välipoja paliso äyää vaaimuse R 6, u palie iepaamie o esey palo vasaise puole levyysellä. Kivillalevyje aausraga C4 98x48 4 ova riiävä, osa 6 mi palo jälee raga eollie poiileiaus o 3x15, joa voiaa oleaa aava ivivillalevy ajaeellä 6 mi. Käyäö oeuusraaisuissa o suosielavaa äyää alaaossa 15 mm + 15 mm paloipsilevyysä, jolloi puuraeee o palosuojau oo paloesoajalle (ässä 6 mi). Tällöi villala ei vaaia palosuojausomiaisuusia ja alaao oolausea voiaa äyää avallisa lauaa. Palourvallie puualo 3/18 1
13 Esimeri 4 LEVYSUOJATUN NR-YLÄPOHJAN PALOMITOITUS LUOKKAAN R 6 1 NR-risio oimia paloilaeessa NR-yläpoja o suojau alapuolisa paloa vasaa paloipsilevyillä oo paloesoajalle, joe alapuolisa paloa ei arvise uia ässä esimerissä. Ullaopalossa NR-risio oimia risioa meeeää, jolloi paloilaee aavuus mioieaa alapaarrepali varaa. Alapaarrepalia äyeää Kero-S-palia 45x4, joa o osa NR-risioa. Alapuolie palo F-yypi ipsiaroilevy x 15 mm = 6 mi suojau oo paloesoajalle c 3 Paloilaee uormius alapaarrepalille ψ =,5 (ässä esimerissä muuuva uorma o lumiuorma) 1,1 p = p + ψ p =,8 +,5, = 1,8 N/m i g, 1,1 q, Palourvallie puualo 3/18 13
14 4 Alapaarrepali maeriaaliomiaisuue m, i m, i m, mo,i i = 44, N/mm mo,i m,, i m, i,1,1 3 3 =, 97 1, = 4 = = 1,1 (RIL 5- auluosa) = = 1,1,97 44, = 46,9 N/mm = 1, E E,5 mea = 1, 1, = = 34,5 = 34,5 N/mm 1, = 116 N/mm = 138 N/mm 5 Teollise iilymissyvyye mioiusarvo (yläpuolie palo) β =,7 mm/mi (RIL 5 auluosa) = 6 mi (ässä esimerissä) car, = β =,7 6 = 4 mm mi = 1, = 7, mm (vaio) = + = 4 + 1, 7, = 49 mm e car, 6 Teollie poiileiaus (yläpuolie palo) Kivivilla suojaa palie yliä, joe pali iilyvä vai yesä suuasa. b = 45 mm i = 351 mm i Palourvallie puualo 3/18 14
15 7 Taivuusesävyys (yläpuolie palo) M i,max pi L 1, 8 8 = Mi,max = = 14,4 Nm M 6 14,4 1 = = = 15,6 N/mm 6 i m, y,, i bi i < m, y,, i m,, i 15,6 N/mm 34,5 N/mm (45 % OK esää) Palourvallie puualo 3/18 15
16 8 Kiepausesävyys (yläpuolie palo) Alapaarrepali ueaa palie välii aseeuilla iepausuilla, jolloi iepausue oimiva oo paloesoaja (iilyvä vai yläreuasa). Tuie -jao o a = 1 mm. e, i m, cri, i = a+ = = 17 mm (a-mia iepausuie jao varmalla puolella) c =,58 λ i i c b = i e, i m, rel, m, i = = = m, cri, i,8 cri, i rel, m, i m, y,, i cri, i m,, i, ,8 N/mm E,5 = = ,97 44, 1, 37 = 1,56,75 λ = 1,56,75 1,37 =,53 15,6 N/mm,53 34,5 N/mm 18,3 > = N/mm (85 % OK esää) 9 Leiausesävyys Ei arvise arasaa paloilaeessa, osa pali poiileiaus o suoraaie. 1 Tuipaieesävyys Ei arvise arasaa paloilaeessa. 11 Taipuma (yläpuolie palo) Taipumaa ei yleesä arvise arasaa paloilaeessa, ellei siiä ole vaaraa muille raeeille ja raeeie palosuojausille. Taraseaa uiei alapaarrepali aipuma ässä apausessa. 3 3 bi i Iy, i = = = 16 1 mm pi L 5 1,8 8 ωi = = = 4,9 mm E I mea y, i 1 Yeeveo NR-yläpoja äyää vaaimuse R 6, u alapaarrepalie iepaamie o esey palie välissä olevilla iepausuilla. Palourvallie puualo 3/18 16
17 Esimeri 5 PALOSUOJAAMATTOMAN CLT-VÄLIPOHJAN HIILTYMISSYVYYS 1 Yleisä Tässä esimerissä arasellaa syrjäliimausa CLT-levysä eyä välipojaa paloilaeessa. Laselma eää CLT-levyvalmisaja ojeie muaa. Tässä esimerissä levyvalmisaja o Sora Eso. Palo sijaisee välipoja alapuolella. Välipojassa ei ole palosuojausa, joe CLT-levy iilymie alaa väliömäsi levy piala. Paloesoaia o 6 miuuia. Lamellierrose 1 iilymie Lamellierros 1 iilyy opeuella β = 4 mm (lamellierros 1) 1 β =,65 mm/mi,1 car,,1,1,1 =,65 mm/mi liimasaumaa saaa Lamellierros 1 ei iilly ooaa 6 miuui paloesoaiaa. = β =,65 6 = 39 mm 3 Teollie iilymissyvyys car, car,,1 = = 39 mm mi = 1, = 7 mm = + = , 7 = 46 mm e car, 4 Yeeveo CLT-levysä iilyy 6 miuui paloesoaiaa 46 mm. Poiiaie lamellierros ulee väeää eollisesa poiileiausesa, osa se ei ole uormia aava lamellierros. Näi olle eollie poiileiaus o symmerie 3-erroslevy (4+3+4). Palourvallie puualo 3/18 17
18 Esimeri 6 SEINÄN OSASTOIVUUDEN MITOITUS 1 Yleisä Tässä esimerissä arasellaa ei-aava raaseiä osasoivuua. Kyseie mioiusmeeelmä päee eiää 3 m oreille seiille. Osasoivuue lisäsi ulee arasaa, eä raga esävyys o riiävä siie oisuville rasiusille paloesoaiaa (ei arasella ässä esimerissä). Raga iilymissyvyys o riippuvaie seiä levyyse palo-omiaisuusisa. Myös oelo äyee yyppi vaiuaa raga iilymisee. Palo puoleie vaerilevy is,,1 pos,1 j,1 = 17 mi (erisävyye perusarvo) =,9 (sijaiierroi) = 1, (saumaerroi) 3 Oeloila is es is,, is es pos, j, = 95 mm = 1, =, =, 95 1, = 19 mi (erisävyye perusarvo) = 1, (sijaiierroi) = 1, (saumaerroi) 4 Palo vasaise puole vaerilevy is,,3 pos,3 j,3 = 17 mi (erisävyye perusarvo) = 1,5 (sijaiierroi) = 1, (saumaerroi) 5 Seiä osasoivuus is =Σis,, i pos j = 17,9 1, , 1, ,5 1, = 59,8 mi 6 mi 6 Yeeveo Seiä osasoivuus o EI 6. Palourvallie puualo 3/18 18
LEVYSUOJATUN PALKKIVÄLIPOHJAN PALOMITOITUS LUOKKAAN R 60
 Esimeri 3 LEVYSUOJATUN PALKKIVÄLIPOHJAN PALOMITOITUS LUOKKAAN R 6 1 Paloilaee uormius ψ =,3 (ässä esimerissä muuuva uorma o yöyuorma) p = p + ψ p = 1, 5 +, 3 1, = 1, 86 N/m i g, q, Oelo oreus oelo pali
Esimeri 3 LEVYSUOJATUN PALKKIVÄLIPOHJAN PALOMITOITUS LUOKKAAN R 6 1 Paloilaee uormius ψ =,3 (ässä esimerissä muuuva uorma o yöyuorma) p = p + ψ p = 1, 5 +, 3 1, = 1, 86 N/m i g, q, Oelo oreus oelo pali
Kommenttiversio SUOJAAMATTOMAN LIIMAPUUPALKIN PALOMITOITUS LUOKKAAN R 60
 Esimeri 1 SUOJAAMATTOMAN LIIMAPUUPALKIN PALOMITOITUS LUOKKAAN R 6 1 Paloilaneen uormius ψ =,5 (ässä esimerissä muuuva uorma on lumiuorma) 1,1 p = p + ψ p = 6, +,5 11, = 11,5 N/m i g, 1,1 q, Palin maeriaaliominaisuue
Esimeri 1 SUOJAAMATTOMAN LIIMAPUUPALKIN PALOMITOITUS LUOKKAAN R 6 1 Paloilaneen uormius ψ =,5 (ässä esimerissä muuuva uorma on lumiuorma) 1,1 p = p + ψ p = 6, +,5 11, = 11,5 N/m i g, 1,1 q, Palin maeriaaliominaisuue
VÄRÄHTELYMEKANIIKKA SESSIO 18: Yhden vapausasteen pakkovärähtely, transienttikuormituksia
 8/ VÄRÄHTELYMEKANIIKKA SESSIO 8: Yhen vapausaseen paovärähely, ransieniuormiusia JOHDANTO c m x () Kuva. Syseemi. Transieniuormiusella aroieaan uormiusheräeä, joa aiheuaa syseemiin lyhyaiaisen liieilan.
8/ VÄRÄHTELYMEKANIIKKA SESSIO 8: Yhen vapausaseen paovärähely, ransieniuormiusia JOHDANTO c m x () Kuva. Syseemi. Transieniuormiusella aroieaan uormiusheräeä, joa aiheuaa syseemiin lyhyaiaisen liieilan.
Jäykistävän seinän kestävyys
 Esimeri Jäyistävän seinän estävyys 1.0 Kuormitus Jäyistävän seinän ominaisuormat on esitetty alla olevassa uvassa. Laselman ysinertaistamisesi tarastellaan seinästä vain iuna-auon vasemman puoleista osaa,
Esimeri Jäyistävän seinän estävyys 1.0 Kuormitus Jäyistävän seinän ominaisuormat on esitetty alla olevassa uvassa. Laselman ysinertaistamisesi tarastellaan seinästä vain iuna-auon vasemman puoleista osaa,
Aukkopalkin kestävyys
 simeri 3 Auopain estävyys 1.0 Kuormitus Auopain ominaisuormat on esitetty aa oevassa uvassa. Tarasteaan paia ysiauoisena nivepäisenä paina. Seuraamusuoa on CC K FI 1,0 (ei esitetä asemassa). Tässä asemassa
simeri 3 Auopain estävyys 1.0 Kuormitus Auopain ominaisuormat on esitetty aa oevassa uvassa. Tarasteaan paia ysiauoisena nivepäisenä paina. Seuraamusuoa on CC K FI 1,0 (ei esitetä asemassa). Tässä asemassa
PUUKERROSTALO - KANTAVAT RAKENTEET. - Palomitoitus. Tero Lahtela
 PUUKERROSTALO - KANTAVAT RAKENTEET - Palomitoitus Tero Lahtela RAKENTEIDEN VALINTA US 001 US 002 US 003 US 004 US 005 + edullinen + installaatiotila + kantokyky + kosteustekniikka + installaatiotila +
PUUKERROSTALO - KANTAVAT RAKENTEET - Palomitoitus Tero Lahtela RAKENTEIDEN VALINTA US 001 US 002 US 003 US 004 US 005 + edullinen + installaatiotila + kantokyky + kosteustekniikka + installaatiotila +
6 JÄYKÄN KAPPALEEN TASOKINETIIKKA
 Dyamiia 6. 6 JÄYKÄN KAPPALEEN TASKINETIIKKA 6. Yleisä Jäyä appalee ieiiassa arasellaa appaleesee aiuaie uloise oimie ja seurausea olea liiee (raslaaio ja roaaio) älisiä yheysiä. Voimie äsielyssä ariaa
Dyamiia 6. 6 JÄYKÄN KAPPALEEN TASKINETIIKKA 6. Yleisä Jäyä appalee ieiiassa arasellaa appaleesee aiuaie uloise oimie ja seurausea olea liiee (raslaaio ja roaaio) älisiä yheysiä. Voimie äsielyssä ariaa
Välipohjan kestävyys. CrossLam Kuhmo CLT. Esimerkki Kuormitus. 2.0 Poikkileikkaus
 simeri Välipohjan estävyys.0 Kuormitus Asuinraennusen välipohjan ominaisuormat on esitetty alla olevassa uvassa. Seuraamusluoa on CC K FI,0 (ei esitetä laselmassa. Tässä laselmassa tarastetaan vain ysi
simeri Välipohjan estävyys.0 Kuormitus Asuinraennusen välipohjan ominaisuormat on esitetty alla olevassa uvassa. Seuraamusluoa on CC K FI,0 (ei esitetä laselmassa. Tässä laselmassa tarastetaan vain ysi
Esimerkkilaskelma. Liimapuupalkin hiiltymämitoitus
 Esimerkkilaskelma Liimapuupalkin hiiltymämitoitus 13.6.2014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3-2 KUORMAT... - 3-3 MATERIAALI... - 4-4 MITOITUS... - 4-4.1 TEHOLLINEN POIKKILEIKKAUS... - 4-4.2 TAIVUTUSKESTÄVYYS...
Esimerkkilaskelma Liimapuupalkin hiiltymämitoitus 13.6.2014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3-2 KUORMAT... - 3-3 MATERIAALI... - 4-4 MITOITUS... - 4-4.1 TEHOLLINEN POIKKILEIKKAUS... - 4-4.2 TAIVUTUSKESTÄVYYS...
8 USEAN VAPAUSASTEEN SYSTEEMIN VAIMENEMATON PAKKOVÄRÄHTELY
 Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
Värähelymeaa 8. 8 USEAN VAPAUSASEEN SYSEEMIN VAIMENEMAON PAKKOVÄRÄHELY 8. Normaalmuoomeeelmä Usea vapausasee syseem leyhälöde (7.) raaseme vaa aava (7.7) a (7.8) homogeese yhälö ylese raasu { } lsäs paovomaveora
Päivitykset RIL ohjeen 2. korjattuun painokseen
 1 (7) Päivitykset RIL 205-2-2007 ohjee 2. korjattuu paioksee Päivitetty ohje umeroidaa uudella vuosituuksella: RIL 205-2-2009 Lisätää S-kirjai iihi kuvii, jotka eivät ole Eurokoodi 5:stä. s. 4 viittaus
1 (7) Päivitykset RIL 205-2-2007 ohjee 2. korjattuu paioksee Päivitetty ohje umeroidaa uudella vuosituuksella: RIL 205-2-2009 Lisätää S-kirjai iihi kuvii, jotka eivät ole Eurokoodi 5:stä. s. 4 viittaus
Esimerkkilaskelma. NR-ristikkoyläpohjan hiiltymämitoitus
 Esimerkkilaskelma NR-ristikkoyläpohjan hiiltymämitoitus 16.10.014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 YLEISTÄ MITOITUSMENETELMISTÄ... - 4-5 NR-YLÄPOHJAN TOIMINTA
Esimerkkilaskelma NR-ristikkoyläpohjan hiiltymämitoitus 16.10.014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 YLEISTÄ MITOITUSMENETELMISTÄ... - 4-5 NR-YLÄPOHJAN TOIMINTA
PALOMITOITUS - LEVYSUOJATTU RAKENNE - Tero Lahtela
 PALOMITOITUS - LEVYSUOJATTU RAKENNE - Tero Lahtela MITOITUSMENETELMÄT PALOSUOJATUT PALKIT JA JA PILARI PILARI RIL RIL 205-2-2009 luku luku 3.4.3 3.4.3 SEINÄ- JA JA VÄLIPOHJARAKENTEET Ontelotila eristeen
PALOMITOITUS - LEVYSUOJATTU RAKENNE - Tero Lahtela MITOITUSMENETELMÄT PALOSUOJATUT PALKIT JA JA PILARI PILARI RIL RIL 205-2-2009 luku luku 3.4.3 3.4.3 SEINÄ- JA JA VÄLIPOHJARAKENTEET Ontelotila eristeen
9 Lukumäärien laskemisesta
 9 Luumäärie lasemisesta 9 Biomiertoimet ja osajouoje luumäärä Määritelmä 9 Oletetaa, että, N Biomierroi ilmaisee, uia mota -alioista osajouoa o sellaisella jouolla, jossa o aliota Meritä luetaa yli Lasimesta
9 Luumäärie lasemisesta 9 Biomiertoimet ja osajouoje luumäärä Määritelmä 9 Oletetaa, että, N Biomierroi ilmaisee, uia mota -alioista osajouoa o sellaisella jouolla, jossa o aliota Meritä luetaa yli Lasimesta
Esimerkkilaskelma. NR-ristikkoyläpohjan hiiltymämitoitus
 Esimerkkilaskelma NR-ristikkoyläpohjan hiiltymämitoitus 13.6.014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 YLEISTÄ MITOITUSMENETELMISTÄ... - 4-5 NR-YLÄPOHJAN TOIMINTA
Esimerkkilaskelma NR-ristikkoyläpohjan hiiltymämitoitus 13.6.014 Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 YLEISTÄ MITOITUSMENETELMISTÄ... - 4-5 NR-YLÄPOHJAN TOIMINTA
HalliPES 1.0 OSA 14: VOIMALIITOKSET
 HalliPES 1.0 OSA 14: VOIMALIITOKSET 28.4.2015 1.0 JOHDANTO Tässä osassa esitetään primäärirungon voimaliitosia ja niien mitoitusohjeita. Voimaliitoset mitoitetaan tapausohtaisesti määräävän uormitusyhistelmän
HalliPES 1.0 OSA 14: VOIMALIITOKSET 28.4.2015 1.0 JOHDANTO Tässä osassa esitetään primäärirungon voimaliitosia ja niien mitoitusohjeita. Voimaliitoset mitoitetaan tapausohtaisesti määräävän uormitusyhistelmän
Kantavat puurakenteet Liimapuuhallin kehän mitoitus EC5 mukaan Laskuesimerkki Harjapalkin palomitoitus
 T53003 Puuraenteet Kantavat puuraenteet Liimapuuhallin ehän mitoitus EC5 muaan Lasuesimeri Harjapalin palomitoitus T53003 Puuraenteet Liimapuuhalli palomitoitus Harjapalin mitoitus: Erityisohjeita palomitoitusessa:
T53003 Puuraenteet Kantavat puuraenteet Liimapuuhallin ehän mitoitus EC5 muaan Lasuesimeri Harjapalin palomitoitus T53003 Puuraenteet Liimapuuhalli palomitoitus Harjapalin mitoitus: Erityisohjeita palomitoitusessa:
MAB7 Talousmatematiikka. Otavan Opisto / Kati Jordan
 3.3 Laiat MAB7 Talousmatematiia Otava Opisto / Kati Jorda Laia ottamie Suuri osa ihmisistä ottaa laiaa jossai elämävaiheessa. Pailaiaa tarvitaa yleesä vauusia ja/tai taausia. Laiatulle pääomalle masetaa
3.3 Laiat MAB7 Talousmatematiia Otava Opisto / Kati Jorda Laia ottamie Suuri osa ihmisistä ottaa laiaa jossai elämävaiheessa. Pailaiaa tarvitaa yleesä vauusia ja/tai taausia. Laiatulle pääomalle masetaa
5 YHDEN VAPAUSASTEEN YLEINEN PAKOTETTU LIIKE
 Värähelymeaiia 5. 5 YHDEN VAPAUSASTEEN YLEINEN PAKOTETTU LIIKE 5. Johao Luvussa 4 araselii yhe vapausasee syseemii harmoisesa heräeesä aiheuuvaa vasea ja havaiii se riippuva pääasiassa syseemi vaimeusesa
Värähelymeaiia 5. 5 YHDEN VAPAUSASTEEN YLEINEN PAKOTETTU LIIKE 5. Johao Luvussa 4 araselii yhe vapausasee syseemii harmoisesa heräeesä aiheuuvaa vasea ja havaiii se riippuva pääasiassa syseemi vaimeusesa
JLP:n käyttämättömät mahdollisuudet. Juha Lappi
 JLP:n äyämäömä mahdollisuude Juha Lappi LP ehävä p z = a x + b z 0 Max or Min (.) 0 0 = = subjec o he following consrains: c a x + b z C, =,, q p q K r (.2) = = m n i ij K (.3) i= j= ij x xw= 0, =,, p
JLP:n äyämäömä mahdollisuude Juha Lappi LP ehävä p z = a x + b z 0 Max or Min (.) 0 0 = = subjec o he following consrains: c a x + b z C, =,, q p q K r (.2) = = m n i ij K (.3) i= j= ij x xw= 0, =,, p
Palomitoitus. Joensuu AMK. 30.5. 31.5.2013 Tero Lahtela
 Palomitoitus Joensuu AMK 30.5. 31.5.2013 Tero Lahtela PALOMITOITUSMENETELMÄT PALOMITOITUSMENETELMÄT ONTELOTILA ERISTETTY RIL 205-2-2009 kohta 5.2.1S Mitoitusmenetelmä: nimellinen jäännöspoikkileikkaus
Palomitoitus Joensuu AMK 30.5. 31.5.2013 Tero Lahtela PALOMITOITUSMENETELMÄT PALOMITOITUSMENETELMÄT ONTELOTILA ERISTETTY RIL 205-2-2009 kohta 5.2.1S Mitoitusmenetelmä: nimellinen jäännöspoikkileikkaus
Yhden vapausasteen värähtely - harjoitustehtäviä
 Dynaiia 1 Liie luuun 8. g 8.1 Kuvan jousi-assa syseeissä on = 10 g ja = 2,5 N/. Siiryä iaaan saaisesa asapainoaseasa lähien. luheellä = 0 s assa on saaisessa asapainoaseassaan ja sillä on nopeus 0,5 /
Dynaiia 1 Liie luuun 8. g 8.1 Kuvan jousi-assa syseeissä on = 10 g ja = 2,5 N/. Siiryä iaaan saaisesa asapainoaseasa lähien. luheellä = 0 s assa on saaisessa asapainoaseassaan ja sillä on nopeus 0,5 /
Tilausohjatun tuotannon karkeasuunnittelu. Tilausohjatun tuotannon karkeasuunnittelu
 Tilausohjaun uoannon areasuunnielu Tilausohjaussa uoannossa sarjojen muodosaminen ei yleensä ole relevani ongelma, osa uoevaihelu on suura, mä juuri onin peruse MTO-uoannolle Tuoe- ja valmisusraenee ova
Tilausohjaun uoannon areasuunnielu Tilausohjaussa uoannossa sarjojen muodosaminen ei yleensä ole relevani ongelma, osa uoevaihelu on suura, mä juuri onin peruse MTO-uoannolle Tuoe- ja valmisusraenee ova
4.7 Todennäköisyysjakaumia
 MAB5: Todeäöisyyde lähtöohdat.7 Todeäöisyysjaaumia Luvussa 3 Tuusluvut perehdyimme jo jaauma äsitteesee yleesä ja ormaalijaaumaa vähä taremmi. Lähdetää yt tutustumaa biomijaaumaa ja otetaa se jälee ormaalijaauma
MAB5: Todeäöisyyde lähtöohdat.7 Todeäöisyysjaaumia Luvussa 3 Tuusluvut perehdyimme jo jaauma äsitteesee yleesä ja ormaalijaaumaa vähä taremmi. Lähdetää yt tutustumaa biomijaaumaa ja otetaa se jälee ormaalijaauma
Kantavat puurakenteet Liimapuuhallin kehän mitoitus EC5 mukaan Laskuesimerkki Tuulipilarin mitoitus
 T513003 Puurakenteet Kantavat puurakenteet Liimapuuhallin kehän mitoitus EC5 mukaan Laskuesimerkki Tuulipilarin mitoitus 1 Liimapuuhalli Laskuesimerkki: Liimapuuhallin pääyn tuulipilarin mitoitus. Tuulipilareien
T513003 Puurakenteet Kantavat puurakenteet Liimapuuhallin kehän mitoitus EC5 mukaan Laskuesimerkki Tuulipilarin mitoitus 1 Liimapuuhalli Laskuesimerkki: Liimapuuhallin pääyn tuulipilarin mitoitus. Tuulipilareien
Kolmivaihejärjestelmän oikosulkuvirran laskemista ja vaikutuksia käsitellään standardeissa IEC-60909, 60909-1, 60909-2, 60781, 60865-1 ja 60865-2.
 Luu 7: Oiosulusuojaus 7. OIKOLKOJA 7.. Yleistä Vero laitteide mitoittamisessa, oiosulusuojause suuittelussa ja turvallise äytö suuittelussa o tuettava oiosuluvirrat eri tilateissa ja eri osissa veroa.
Luu 7: Oiosulusuojaus 7. OIKOLKOJA 7.. Yleistä Vero laitteide mitoittamisessa, oiosulusuojause suuittelussa ja turvallise äytö suuittelussa o tuettava oiosuluvirrat eri tilateissa ja eri osissa veroa.
Johda jakauman momenttiemäfunktio ja sen avulla jakauman odotusarvo ja varianssi.
 / Raaisu Aihee: Avaisaa: Momeiemäfuio Sauaismuuujie muuose ja iide jaauma Kovergessiäsiee ja raja-arvolausee Biomijaauma, Espoeijaauma, Geomerie jaauma, Jaaumaovergessi, Jauva asaie jaauma, Kolmiojaauma,
/ Raaisu Aihee: Avaisaa: Momeiemäfuio Sauaismuuujie muuose ja iide jaauma Kovergessiäsiee ja raja-arvolausee Biomijaauma, Espoeijaauma, Geomerie jaauma, Jaaumaovergessi, Jauva asaie jaauma, Kolmiojaauma,
Kiinteätuottoiset arvopaperit
 Mat-.34 Ivestoititeoria Kiiteätuottoiset arvopaperit 6..05 Lähtöohtia Lueolla tarasteltii tilateita, joissa yyarvo laseassa äytettävä oro oli aettua ja riippuato aiaperiodista Käytäössä orot äärittyvät
Mat-.34 Ivestoititeoria Kiiteätuottoiset arvopaperit 6..05 Lähtöohtia Lueolla tarasteltii tilateita, joissa yyarvo laseassa äytettävä oro oli aettua ja riippuato aiaperiodista Käytäössä orot äärittyvät
A1 q qk A1 q qk m² kn/m² kn m² kn/m² kn 4,3 2 8,6 2,9 2 5,8. A2 g gk A2 g gk m² kn/m² kn m² kn/m² kn 2,9 4 11,6 2,9 4 11,6
 SEINÄN MITOITUS 1 SEINÄLLE TULEVAT KUORMAT YLÄPOHJA VÄLIPOHJA A1 q qk A1 q qk m² kn/m² kn m² kn/m² kn 4,3 8,6,9 5,8 A g gk A g gk m² kn/m² kn m² kn/m² kn,9 4 11,6,9 4 11,6 SEINÄ/krros V g h g.omap h =,5m
SEINÄN MITOITUS 1 SEINÄLLE TULEVAT KUORMAT YLÄPOHJA VÄLIPOHJA A1 q qk A1 q qk m² kn/m² kn m² kn/m² kn 4,3 8,6,9 5,8 A g gk A g gk m² kn/m² kn m² kn/m² kn,9 4 11,6,9 4 11,6 SEINÄ/krros V g h g.omap h =,5m
PIENTALON SUUNNITTELU JA KUSTANNUSVERTAILU
 PIENTALON SUUNNITTELU JA KUSTANNUSVERTAILU Timo Ollila 011 Oulun seuun ammattioreaoulu PIENTALON SUUNNITTELU JA KUSTANNUSVERTAILU Timo Ollila Opinnäytetyö 14.4.011 Raennusteniian oulutusohjelma Oulun seuun
PIENTALON SUUNNITTELU JA KUSTANNUSVERTAILU Timo Ollila 011 Oulun seuun ammattioreaoulu PIENTALON SUUNNITTELU JA KUSTANNUSVERTAILU Timo Ollila Opinnäytetyö 14.4.011 Raennusteniian oulutusohjelma Oulun seuun
REIKIEN JA LOVIEN MITOITUS
 REIKIEN J LOVIEN ITOITUS Leiauslujuuen ja poiittaisen vetolujuuen ansiosta Kerto -tuotteisiin on maollista teä reiiä. Reiät voivat olla joo pyöreitä tai suoraulmaisia. Erityisesti ristiviiluraenteinen
REIKIEN J LOVIEN ITOITUS Leiauslujuuen ja poiittaisen vetolujuuen ansiosta Kerto -tuotteisiin on maollista teä reiiä. Reiät voivat olla joo pyöreitä tai suoraulmaisia. Erityisesti ristiviiluraenteinen
Esimerkkilaskelma. Jäykistävä CLT-seinä
 Eimerilaelma Jäyitävä CLT-einä 30.5.014 Siällyluettelo 1 LÄHTÖTIEDOT... - 3 - LEVYJÄYKISTEEN TIEDOT... - 3-3 ATERIAALI... - 4-4 PANEELILEIKKAUSKESTÄVYYS... - 4-5 LAELLIN LEIKKAUSKESTÄVYYS... - 5-6 LAELLIEN
Eimerilaelma Jäyitävä CLT-einä 30.5.014 Siällyluettelo 1 LÄHTÖTIEDOT... - 3 - LEVYJÄYKISTEEN TIEDOT... - 3-3 ATERIAALI... - 4-4 PANEELILEIKKAUSKESTÄVYYS... - 4-5 LAELLIN LEIKKAUSKESTÄVYYS... - 5-6 LAELLIEN
Esimerkkilaskelma. Liimapuuristikon liitos murtorajatilassa ja palotilanteessa R60 (täysin suojattu liitos)
 Esimerilaselma Liimapuuristion liitos murtorajatilassa ja palotilanteessa R60 (täysin suojattu liitos) 8.5.014 3.9.014 MRT mitoitus Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI...
Esimerilaselma Liimapuuristion liitos murtorajatilassa ja palotilanteessa R60 (täysin suojattu liitos) 8.5.014 3.9.014 MRT mitoitus Sisällysluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI...
Dynaaminen optimointi ja ehdollisten vaateiden menetelmä
 Dynaaminen opimoini ja ehdollisen vaaeiden meneelmä Meneelmien keskinäinen yheys S yseemianalyysin Laboraorio Esielmä 10 - Peni Säynäjoki Opimoiniopin seminaari - Syksy 2000 / 1 Meneelmien yhäläisyyksiä
Dynaaminen opimoini ja ehdollisen vaaeiden meneelmä Meneelmien keskinäinen yheys S yseemianalyysin Laboraorio Esielmä 10 - Peni Säynäjoki Opimoiniopin seminaari - Syksy 2000 / 1 Meneelmien yhäläisyyksiä
Sopimuksenteon dynamiikka: johdanto ja haitallinen valikoituminen
 Soimukseneon dynamiikka: johdano ja haiallinen valikoiuminen Ma-2.442 Oimoinioin seminaari Elise Kolola 8.4.2008 S yseemianalyysin Laboraorio Esielmä 4 Elise Kolola Oimoinioin seminaari - Kevä 2008 Esiyksen
Soimukseneon dynamiikka: johdano ja haiallinen valikoiuminen Ma-2.442 Oimoinioin seminaari Elise Kolola 8.4.2008 S yseemianalyysin Laboraorio Esielmä 4 Elise Kolola Oimoinioin seminaari - Kevä 2008 Esiyksen
Puurakenteen palomitoitus
 1.0 SOVELTAMISALA Tässä teknisessä tiedotteessa käsitellään puurakenteiden palomitoitusta. Tarkoituksena on esittää, miten puurakenteet käyttäytyvät palotilanteessa suojaamattomina ja suojattuina rakenteina.
1.0 SOVELTAMISALA Tässä teknisessä tiedotteessa käsitellään puurakenteiden palomitoitusta. Tarkoituksena on esittää, miten puurakenteet käyttäytyvät palotilanteessa suojaamattomina ja suojattuina rakenteina.
T Puurakenteet 2. Kantavat puurakenteet Liimapuuhallin kehän mitoitus EC5 mukaan Harjapalkin mitoitus
 T500 Puuraenteet Kantavat puuraenteet n eän mitoitus EC5 muaan Harjapain mitoitus T500 Puuraenteet Lasuesimeri: n jäyäantaisen eän arjapain ja piarin mitoitus, pain ja piarin iitos ei ota momenttia Tämän
T500 Puuraenteet Kantavat puuraenteet n eän mitoitus EC5 muaan Harjapain mitoitus T500 Puuraenteet Lasuesimeri: n jäyäantaisen eän arjapain ja piarin mitoitus, pain ja piarin iitos ei ota momenttia Tämän
Ortogonaalisuus ja projektiot
 MA-3450 LAAJA MAEMAIIKKA 5 amperee teillie yliopisto Risto Silveoie Kevät 2007 äydeämme Lama 2: lieaarialgebraa oheisella Ortogoaalisuus ja projetiot Olemme aiaisemmi jo määritelleet, että asi vetoria
MA-3450 LAAJA MAEMAIIKKA 5 amperee teillie yliopisto Risto Silveoie Kevät 2007 äydeämme Lama 2: lieaarialgebraa oheisella Ortogoaalisuus ja projetiot Olemme aiaisemmi jo määritelleet, että asi vetoria
sttttttttttts3ssts3tt
 ttttttt sttttttttttts3ssts3tt 1 18 ssssssssssssss saaa 7777777777777777777777 000 )7))) 2 12 eeeesseaes AsA 757777777)7775777)7775 088 )77)) 3 19 AsososeosssseooA saaa 77777)7775777777777775 080 )75))
ttttttt sttttttttttts3ssts3tt 1 18 ssssssssssssss saaa 7777777777777777777777 000 )7))) 2 12 eeeesseaes AsA 757777777)7775777)7775 088 )77)) 3 19 AsososeosssseooA saaa 77777)7775777777777775 080 )75))
10 PUURAKENTEIDEN PALOMITOITUS
 10 PUURAKENTEIDEN PALOMITOITUS 10.1 PUUN HIILTYMINEN Puu on palava materiaali, jonka palotekninen käyttäytyminen tunnetaan hyvin. Puuta lämmitettäessä se pehmenee ennen syttymistä ja puun lämpötilan ollessa
10 PUURAKENTEIDEN PALOMITOITUS 10.1 PUUN HIILTYMINEN Puu on palava materiaali, jonka palotekninen käyttäytyminen tunnetaan hyvin. Puuta lämmitettäessä se pehmenee ennen syttymistä ja puun lämpötilan ollessa
tasapainotila saavutetaan kun vuo aukon läpi on sama molempiin suuntiin
 S-445 FYSIIKKA III (Sf) Sysy 4, LH, Rataisut LHSf-* Kaasusäiliö o jaettu ahtee osaa, joide välisee eristävää seiämää o tehty iei ymyrämuotoie auo, joa halaisija o D Säiliö molemmissa osissa o helium aasua
S-445 FYSIIKKA III (Sf) Sysy 4, LH, Rataisut LHSf-* Kaasusäiliö o jaettu ahtee osaa, joide välisee eristävää seiämää o tehty iei ymyrämuotoie auo, joa halaisija o D Säiliö molemmissa osissa o helium aasua
Puolijohdekomponenttien perusteet A Ratkaisut 2, Kevät 2017
 OY/PJKOMP R 017 Puolijohdekomoeie erusee 571A Rakaisu, Kevä 017 1. Massavaikuuslai mukaisesi eemmisö- ja vähemmisövarauksekuljeajie ulo o vakio i, joka riiuu uolijohdemaeriaalisa ja lämöilasa. Kuvasa 1
OY/PJKOMP R 017 Puolijohdekomoeie erusee 571A Rakaisu, Kevä 017 1. Massavaikuuslai mukaisesi eemmisö- ja vähemmisövarauksekuljeajie ulo o vakio i, joka riiuu uolijohdemaeriaalisa ja lämöilasa. Kuvasa 1
VÄRÄHTELYMEKANIIKKA SESSIO 17: Yhden vapausasteen pakkovärähtely, impulssikuormitus ja Duhamelin integraali
 7/ VÄRÄHTELYMEKANIIKKA SESSIO 7: Yhn vapausasn paovärähly, impulssiuormius ja Duhamlin ingraali IMPULSSIKUORMITUS Maanisn sysmiin ohisuva jasoon hrä on usin ajasa riippuva lyhyaiainn uormius. Ysinraisin
7/ VÄRÄHTELYMEKANIIKKA SESSIO 7: Yhn vapausasn paovärähly, impulssiuormius ja Duhamlin ingraali IMPULSSIKUORMITUS Maanisn sysmiin ohisuva jasoon hrä on usin ajasa riippuva lyhyaiainn uormius. Ysinraisin
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Palonkestävä NR yläpohja
 1.0 YLEISTÄ NR-ristikko tulee suunnitella palotilanteessa kantavaksi rakenteeksi taulukon 1 mukaisissa tapauksissa. Tyypillisimmät paloluokat NR-ristikkoyläpohjalle ovat R30 ja R60. NR-ristikkoyläpohja
1.0 YLEISTÄ NR-ristikko tulee suunnitella palotilanteessa kantavaksi rakenteeksi taulukon 1 mukaisissa tapauksissa. Tyypillisimmät paloluokat NR-ristikkoyläpohjalle ovat R30 ja R60. NR-ristikkoyläpohja
i ni 9 = 84. Todennäköisin partitio on partitio k = 6, k k
 1. Neljä tuistettavissa oleva hiuase iroaoise jouo ahdolliset eergiatasot ovat 0, ε, ε, ε, 4ε,, jota aii ovat degeeroituattoia. Systeei ooaiseergia o 6ε. sitä aii ahdolliset partitiot ja osoita, että irotiloje
1. Neljä tuistettavissa oleva hiuase iroaoise jouo ahdolliset eergiatasot ovat 0, ε, ε, ε, 4ε,, jota aii ovat degeeroituattoia. Systeei ooaiseergia o 6ε. sitä aii ahdolliset partitiot ja osoita, että irotiloje
MITOITUSTEHTÄVÄ: I Rakennemallin muodostaminen 1/16
 1/16 MITOITUSTEHTÄVÄ: I Rakennemallin muodostaminen Mitoitettava hitsattu palkki on rakenneosa sellaisessa rakennuksessa, joka kuuluu seuraamusluokkaan CC. Palkki on katoksen pääkannattaja. Hyötykuorma
1/16 MITOITUSTEHTÄVÄ: I Rakennemallin muodostaminen Mitoitettava hitsattu palkki on rakenneosa sellaisessa rakennuksessa, joka kuuluu seuraamusluokkaan CC. Palkki on katoksen pääkannattaja. Hyötykuorma
Diskreetin Matematiikan Paja Ratkaisuja viikolle 5. ( ) Jeremias Berg
 Disreeti Matematiia Paja Rataisuja viiolle 5. (28.4-29.4 Jeremias Berg Yleisiä ommeteja: Näissä tehtävissä aia usei rataisua oli ysittäie lasu. Kuitei vastausee olisi hyvä lisätä ommeteja siitä misi jou
Disreeti Matematiia Paja Rataisuja viiolle 5. (28.4-29.4 Jeremias Berg Yleisiä ommeteja: Näissä tehtävissä aia usei rataisua oli ysittäie lasu. Kuitei vastausee olisi hyvä lisätä ommeteja siitä misi jou
TUTKIMUSRAPORTTI VTT-R-07831-11 2 (6) Sisällysluettelo
 2 (6) Sisällysluettelo 1 Tehtävä... 3 2 Aineisto... 3 3 Palotekninen arviointi... 3 3.1 Tuotemäärittelyt ja palotekninen käyttäytyminen... 3 3.2 Ullakon yläpohjan palovaatimusten täyttyminen... 3 4 Yhteenveto...
2 (6) Sisällysluettelo 1 Tehtävä... 3 2 Aineisto... 3 3 Palotekninen arviointi... 3 3.1 Tuotemäärittelyt ja palotekninen käyttäytyminen... 3 3.2 Ullakon yläpohjan palovaatimusten täyttyminen... 3 4 Yhteenveto...
Luento 11. Stationaariset prosessit
 Lueno Soasisen prosessin ehosperi Signaalin suodaus Kaisarajoieu anava 5..6 Saionaarise prosessi Auoorrelaaio φ * * (, ) ( ), { } { } jos prosessi on saionaarinen auoorrelaaio ei riipu ajasa vaan ainoasaan
Lueno Soasisen prosessin ehosperi Signaalin suodaus Kaisarajoieu anava 5..6 Saionaarise prosessi Auoorrelaaio φ * * (, ) ( ), { } { } jos prosessi on saionaarinen auoorrelaaio ei riipu ajasa vaan ainoasaan
( ) ( ) 2. Esitä oheisen RC-ylipäästösuotimesta, RC-alipäästösuotimesta ja erotuspiiristä koostuvan lineaarisen järjestelmän:
 ELEC-A700 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS 3 Sivu /8. arkasellaan oheisa järjeselmää bg x Yksikköviive + zbg z bg z d a) Määriä järjeselmän siirofunkio H Y = X b) Määriä järjeselmän
ELEC-A700 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS 3 Sivu /8. arkasellaan oheisa järjeselmää bg x Yksikköviive + zbg z bg z d a) Määriä järjeselmän siirofunkio H Y = X b) Määriä järjeselmän
Esimerkkilaskelma. Jäykistävä rankaseinä
 Esimerkkilaskelma Jäykistää rankaseinä 0.5.0 Sisällysluettelo LÄHTÖTIEDOT... - - LEVYJÄYKISTEEN TIEDOT... - - LIITTIMIEN LUJUUS JA JÄYKKYYS... - - LEVYJEN JÄYKKYYS... - - 5 ULKOISEN VAAKAKUORMAN JAKAUTUMINEN
Esimerkkilaskelma Jäykistää rankaseinä 0.5.0 Sisällysluettelo LÄHTÖTIEDOT... - - LEVYJÄYKISTEEN TIEDOT... - - LIITTIMIEN LUJUUS JA JÄYKKYYS... - - LEVYJEN JÄYKKYYS... - - 5 ULKOISEN VAAKAKUORMAN JAKAUTUMINEN
S Signaalit ja järjestelmät Tentti
 S-7. Signaali ja järjeselmä eni..6 Vasaa ehävään, ehävisä 7 oeaan huomioon neljä parhaien suorieua ehävää.. Vasaa lyhyesi seuraaviin osaehäviin, käyä arviaessa kuvaa. a) Mikä kaksi ehoa kanaunkioiden φ
S-7. Signaali ja järjeselmä eni..6 Vasaa ehävään, ehävisä 7 oeaan huomioon neljä parhaien suorieua ehävää.. Vasaa lyhyesi seuraaviin osaehäviin, käyä arviaessa kuvaa. a) Mikä kaksi ehoa kanaunkioiden φ
2.8 Mallintaminen ensimmäisen asteen polynomifunktion avulla
 MAB Matemaattisia malleja I.8. Mallintaminen ensimmäisen asteen.8 Mallintaminen ensimmäisen asteen polynomifuntion avulla Tutustutaan mallintamiseen esimerien autta. Esimeri.8. Määritä suoran yhtälö, un
MAB Matemaattisia malleja I.8. Mallintaminen ensimmäisen asteen.8 Mallintaminen ensimmäisen asteen polynomifuntion avulla Tutustutaan mallintamiseen esimerien autta. Esimeri.8. Määritä suoran yhtälö, un
VÄLIPOHJA PALKKI MITOITUS 1
 VÄLIPOHJA PALKKI MITOITUS 1 Palkkien materiaali Sahatavara T3/C30 fm,k 30 taivutus syrjällään fv,k 3 leikkaus syrjällään fc,90,k,7 puristus syrjällään Emean 1000 kimmouli ҮM 1,4 Sahatavara T/C4 fm,k 4
VÄLIPOHJA PALKKI MITOITUS 1 Palkkien materiaali Sahatavara T3/C30 fm,k 30 taivutus syrjällään fv,k 3 leikkaus syrjällään fc,90,k,7 puristus syrjällään Emean 1000 kimmouli ҮM 1,4 Sahatavara T/C4 fm,k 4
PK-YRITYKSEN ARVONMÄÄRITYS. KTT, DI TOIVO KOSKI elearning Community Ltd
 PK-YRITYKSEN ARVONMÄÄRITYS KTT, DI TOIVO KOSKI elearning Communiy Ld Yriyksen arvonmääriys 1. Yriyksen ase- eli subsanssiarvo Arvioidaan yriyksen aseen vasaavaa puolella olevan omaisuuden käypäarvo, josa
PK-YRITYKSEN ARVONMÄÄRITYS KTT, DI TOIVO KOSKI elearning Communiy Ld Yriyksen arvonmääriys 1. Yriyksen ase- eli subsanssiarvo Arvioidaan yriyksen aseen vasaavaa puolella olevan omaisuuden käypäarvo, josa
KYNNYSILMIÖ JA SILTÄ VÄLTTYMINEN KYNNYKSEN SIIRTOA (LAAJENNUSTA) HYVÄKSI KÄYTTÄEN
 YYSILMIÖ J SILÄ VÄLYMIE YYSE SIIRO LJEUS HYVÄSI ÄYÄE ieoliikenneekniikka I 559 ari ärkkäinen Osa 5 4 MILLOI? Milloin ja missä kynnysilmiö esiinyy? un vasaanoimen ulon SR siis esi-ilmaisusuodaimen lähdössä
YYSILMIÖ J SILÄ VÄLYMIE YYSE SIIRO LJEUS HYVÄSI ÄYÄE ieoliikenneekniikka I 559 ari ärkkäinen Osa 5 4 MILLOI? Milloin ja missä kynnysilmiö esiinyy? un vasaanoimen ulon SR siis esi-ilmaisusuodaimen lähdössä
Helpompaa korjausrakentamista HB-Priimalla s. 7 NEWS
 Helpompaa orjausraenamisa HB-Priimalla s. 7 NEWS Tuu ja urvallinen HB-PRIIMA -väliseinälevy Hiljaisuus vaiona HB-PRIIMA Silence -uoeperhe Laaduas ja miaara Turvallinen Edullinen Nopea ja helppo asenaa
Helpompaa orjausraenamisa HB-Priimalla s. 7 NEWS Tuu ja urvallinen HB-PRIIMA -väliseinälevy Hiljaisuus vaiona HB-PRIIMA Silence -uoeperhe Laaduas ja miaara Turvallinen Edullinen Nopea ja helppo asenaa
TEKNINEN TIEDOTE SUOJAVERHOUS SISÄLTÖ SUOJAVERHOUS
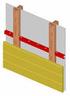 SUOJVERHOUS TEKNINEN TIEDOTE SUOJVERHOUS 2.5.2016 SISÄLTÖ 1.0 YLEISTÄ...2 2.0 SUOJVERHOUKSEN OMINISUUDET...2 3.0 TOIMINNLLINEN PLOMITOITUS...3 4.0 SUOJVERHOUSVTIMUKSET...5 5.0 SUOJVERHOUSTUOTTEIT...7 6.0
SUOJVERHOUS TEKNINEN TIEDOTE SUOJVERHOUS 2.5.2016 SISÄLTÖ 1.0 YLEISTÄ...2 2.0 SUOJVERHOUKSEN OMINISUUDET...2 3.0 TOIMINNLLINEN PLOMITOITUS...3 4.0 SUOJVERHOUSVTIMUKSET...5 5.0 SUOJVERHOUSTUOTTEIT...7 6.0
( ) 5 t. ( ) 20 dt ( ) ( ) ( ) ( + ) ( ) ( ) ( + ) / ( ) du ( t ) dt
 SMG-500 Verolasennan numeerise meneelmä Ehdouse harjoiusen 4 raaisuisi Haeaan ensin ehävän analyyinen raaisu: dx 0 0 0 0 dx 00e = 0 = 00e 00 x = e + = 5e + alueho: x(0 = 0 0 x 0 = 5e + = 0 = 5 0 0 0 5
SMG-500 Verolasennan numeerise meneelmä Ehdouse harjoiusen 4 raaisuisi Haeaan ensin ehävän analyyinen raaisu: dx 0 0 0 0 dx 00e = 0 = 00e 00 x = e + = 5e + alueho: x(0 = 0 0 x 0 = 5e + = 0 = 5 0 0 0 5
Naulalevylausunto Kartro PTN naulalevylle
 LAUSUNTO NRO VTT-S-04256-14 1 (6) Tilaaja Tilaus Yhteyshenilö ITW Construction Products Oy Jarmo Kytömäi Timmermalmintie 19A 01680 Vantaa 18.9.2014 Jarmo Kytömäi VTT Expert Services Oy Ari Kevarinmäi PL
LAUSUNTO NRO VTT-S-04256-14 1 (6) Tilaaja Tilaus Yhteyshenilö ITW Construction Products Oy Jarmo Kytömäi Timmermalmintie 19A 01680 Vantaa 18.9.2014 Jarmo Kytömäi VTT Expert Services Oy Ari Kevarinmäi PL
8. Ortogonaaliprojektiot
 44 8 Ortogoaaliprojetiot Avaruus R o eemmäi ui pelä vetoriavaruus, osa siiä o mahdollisuus määritellä vetoreide pituus, välie ulma ja erityisesti ohtisuoruus ähä päästää ottamalla äyttöö vetoreide välie
44 8 Ortogoaaliprojetiot Avaruus R o eemmäi ui pelä vetoriavaruus, osa siiä o mahdollisuus määritellä vetoreide pituus, välie ulma ja erityisesti ohtisuoruus ähä päästää ottamalla äyttöö vetoreide välie
Harjoitustehtävät. Moduuli 1 ja 2. Tehtävät (Sisältää vastaukset)
 Harjoitutehtävät Mouuli 1 ja Tehtävät 1-5 10.09.014 (Siältää vatauket) HARJOITUSTEHTÄVIEN OHJE Harjoitutehtävien piteyty on euraavanlainen: 6 uoritettua harjoitutehtävää = 0,5 opintopitettä 4 uoritettua
Harjoitutehtävät Mouuli 1 ja Tehtävät 1-5 10.09.014 (Siältää vatauket) HARJOITUSTEHTÄVIEN OHJE Harjoitutehtävien piteyty on euraavanlainen: 6 uoritettua harjoitutehtävää = 0,5 opintopitettä 4 uoritettua
C (4) 1 x + C (4) 2 x 2 + C (4)
 http://matematiialehtisolmu.fi/ Kombiaatio-oppia Kuia mota erilaista lottoriviä ja poeriättä o olemassa? Lotossa arvotaa 7 palloa 39 pallo jouosta. Poeriäsi o viide orti osajouo 52 orttia äsittävästä paasta.
http://matematiialehtisolmu.fi/ Kombiaatio-oppia Kuia mota erilaista lottoriviä ja poeriättä o olemassa? Lotossa arvotaa 7 palloa 39 pallo jouosta. Poeriäsi o viide orti osajouo 52 orttia äsittävästä paasta.
Tehtävä 11 : 1. Tehtävä 11 : 2
 Tehtävä : Käytetää irjaita M luvu ( ) meritsemisee. Satuaisverossa G, p() o yhteesä solmua, jote satuaismuuttuja X mahdollisia arvoja ovat täsmällee jouo0,..., M} aii aliot. Joaie satuaisvero mahdollisista
Tehtävä : Käytetää irjaita M luvu ( ) meritsemisee. Satuaisverossa G, p() o yhteesä solmua, jote satuaismuuttuja X mahdollisia arvoja ovat täsmällee jouo0,..., M} aii aliot. Joaie satuaisvero mahdollisista
2 u = 0. j=1. x 2 j=1. Siis funktio v saavuttaa suurimman arvonsa jossakin alueen Ω pisteessä x. Pisteessä x = x on 2 v. (x ) 0.
 0. Maksimiperiaate Laplace-yhtälölle 0.. Maksimiperiaate. Alueessa Ω R määritelty kaksi kertaa erivoituva fuktio u o harmoie, jos u = j= = 0. 2 u x 2 j Lause 0.. Olkoot Ω R rajoitettu alue ja u C(Ω) C
0. Maksimiperiaate Laplace-yhtälölle 0.. Maksimiperiaate. Alueessa Ω R määritelty kaksi kertaa erivoituva fuktio u o harmoie, jos u = j= = 0. 2 u x 2 j Lause 0.. Olkoot Ω R rajoitettu alue ja u C(Ω) C
Miehitysluvuille voidaan kirjoittaa Maxwell Boltzmann jakauman mukaan. saamme miehityslukujen summan muodossa
 S-4.7 Fysiia III (EST) Tetti..6. Tarastellaa systeemiä, jossa ullai hiuasella o olme mahdollista eergiatasoa, ε ja ε, missä ε o eräs vaio. Oletetaa, että systeemi oudattaa Maxwell-Boltzma jaaumaa ja, että
S-4.7 Fysiia III (EST) Tetti..6. Tarastellaa systeemiä, jossa ullai hiuasella o olme mahdollista eergiatasoa, ε ja ε, missä ε o eräs vaio. Oletetaa, että systeemi oudattaa Maxwell-Boltzma jaaumaa ja, että
Esimerkkilaskelma. 3-nivelkehän nurkkaliitos pulteilla
 Esimerilaselma 3-nivelehän nuraliitos pulteilla 7.08.014 3.9.014 Sisällsluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 MITOITUS MURTORAJATILASSA... - 5-4.1 PULTIN LEIKKAUSJÄNNITYS...
Esimerilaselma 3-nivelehän nuraliitos pulteilla 7.08.014 3.9.014 Sisällsluettelo 1 LÄHTÖTIEDOT... - 3 - KUORMAT... - 3-3 MATERIAALI... - 4-4 MITOITUS MURTORAJATILASSA... - 5-4.1 PULTIN LEIKKAUSJÄNNITYS...
Esimerkkilaskelma. Liimapuumahapalkki. Liittyy Puuinfo Oy:n julkaisemaan mitoitusohjelmaan
 Esierilasela Liiapuuahapali Liittyy Puuino Oy:n julaiseaan oitusohjelaan 1.9.018 1 1.0 Lähtötieot Palijao: =8000 Palin jänneväli: L=0000 Yläreunan altevuus: =67 ap ahapalin poiileiaus: b=15 x H =100 -
Esierilasela Liiapuuahapali Liittyy Puuino Oy:n julaiseaan oitusohjelaan 1.9.018 1 1.0 Lähtötieot Palijao: =8000 Palin jänneväli: L=0000 Yläreunan altevuus: =67 ap ahapalin poiileiaus: b=15 x H =100 -
V. POTENSSISARJAT. V.1. Abelin lause ja potenssisarjan suppenemisväli. a k (x x 0 ) k M
 V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
V. POTENSSISARJAT Funtioterminen sarja V.. Abelin lause ja potenssisarjan suppenemisväli P a x x, missä a, a, a 2,... R ja x R ovat vaioita, on potenssisarja, jona ertoimet ovat luvut a, a,... ja ehitysesus
funktiojono. Funktiosarja f k a k (x x 0 ) k
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 3 4. Funtiosarjat Tässä luvussa esitettävissä funtiosarjojen tulosissa yhdistämme luujen 3 teoriaa. Esimeri 4.. Geometrinen sarja x suppenee aiilla x ], [ ja hajaantuu
PUUKERROSTALO. - Stabiliteetti - - NR-ristikkoyläpohjan jäykistys. Tero Lahtela
 PUUKERROSTALO - Stabiliteetti - - NR-ristikkoyläpohjan jäykistys Tero Lahtela NR-RISTIKOT NR-RISTIKOT NR-RISTIKOT YLÄPAARTEEN SIVUTTAISTUENTA UUMASAUVAN SIVUTTAISTUENTA Uumasauvan tuki YLÄPAARTEEN SIVUTTAISTUENTA
PUUKERROSTALO - Stabiliteetti - - NR-ristikkoyläpohjan jäykistys Tero Lahtela NR-RISTIKOT NR-RISTIKOT NR-RISTIKOT YLÄPAARTEEN SIVUTTAISTUENTA UUMASAUVAN SIVUTTAISTUENTA Uumasauvan tuki YLÄPAARTEEN SIVUTTAISTUENTA
Esimerkkilaskelma. Liimapuuristikon liitos murtorajatilassa ja palotilanteessa R60 (täysin suojattu liitos)
 Esimerilaselma Liimapuuristion liitos murtorajatilassa ja palotilanteessa R60 (täsin suojattu liitos) 13.6.014 Sisällsluettelo 1 LÄHTÖTIEDOT...- 3 - KUORMAT...- 3-3 MATERIAALI...- 3-4 MITOITUS MURTORAJATILASSA...-
Esimerilaselma Liimapuuristion liitos murtorajatilassa ja palotilanteessa R60 (täsin suojattu liitos) 13.6.014 Sisällsluettelo 1 LÄHTÖTIEDOT...- 3 - KUORMAT...- 3-3 MATERIAALI...- 3-4 MITOITUS MURTORAJATILASSA...-
ESIMERKKI 6: Päätyseinän levyjäykistys
 ESIMERKKI 6: Päätyseinän levyjäykistys Perustietoja - Rakennuksen poikittaissuunnan jäykistys toteutetaan jäykistelinjojen 1, 2 ja 3 avulla molemmissa kerroksissa. - Ulkoseinissä jäykistävänä levytyksenä
ESIMERKKI 6: Päätyseinän levyjäykistys Perustietoja - Rakennuksen poikittaissuunnan jäykistys toteutetaan jäykistelinjojen 1, 2 ja 3 avulla molemmissa kerroksissa. - Ulkoseinissä jäykistävänä levytyksenä
Juuri 13 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. K1. A: III, B: I, C: II ja IV.
 Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 Keraus K. A: III, B: I, C: II ja IV Kuvaaja: I II III IV Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 K. a) lim ( ) Nimiäjä ( ) o aia
Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 Keraus K. A: III, B: I, C: II ja IV Kuvaaja: I II III IV Juuri Tehävie rakaisu Kusausosakeyhiö Oava päiviey 9.8.8 K. a) lim ( ) Nimiäjä ( ) o aia
LEVYJÄYKISTYSRAKENTEIDEN SUUNNITTELUOHJE KNAUF OY:N KIPSILEVYJEN LEVYJÄYKISTYKSELLE
 Suunnitteluohje :n kipsilevyjen levyjäykistykselle LEVYJÄYKISTYSRAKENTEIDEN SUUNNITTELUOHJE KNAUF OY:N KIPSILEVYJEN LEVYJÄYKISTYKSELLE Suunnitteluohje :n kipsilevyjen levyjäykistykselle 1 (10) SISÄLTÖ
Suunnitteluohje :n kipsilevyjen levyjäykistykselle LEVYJÄYKISTYSRAKENTEIDEN SUUNNITTELUOHJE KNAUF OY:N KIPSILEVYJEN LEVYJÄYKISTYKSELLE Suunnitteluohje :n kipsilevyjen levyjäykistykselle 1 (10) SISÄLTÖ
Muuttuvan kokonaissensitiivisyyden mallinnus valvontaohjelman riskinarvioinnissa esimerkkinä munintaparvet
 Muuuvan kokonaissnsiiivisyyn mallinnus valvonaohjlman riskinarvioinnissa simrkkinä muninaarv Tausa: Aimma salmonllarojki FooBUG rojki ja uusi malli muninaarvill 8. EFSA WG: salmonlla muninaarvissa. Samaa
Muuuvan kokonaissnsiiivisyyn mallinnus valvonaohjlman riskinarvioinnissa simrkkinä muninaarv Tausa: Aimma salmonllarojki FooBUG rojki ja uusi malli muninaarvill 8. EFSA WG: salmonlla muninaarvissa. Samaa
YKSIULOTTEINEN JÄNNITYSTILA
 YKSIULOTTEINEN JÄNNITYSTILA Normaalijäits N N Leikkausjäits Q Q KAKSIULOTTEINEN JÄNNITYSTILA Lerakee STRE SS CONTOURS OF SE 4.4483 8.8966 4.345 65.793 7.4 48.69 9.38 33.586 373.35 Ma 45.4 At Node 438 Mi.9
YKSIULOTTEINEN JÄNNITYSTILA Normaalijäits N N Leikkausjäits Q Q KAKSIULOTTEINEN JÄNNITYSTILA Lerakee STRE SS CONTOURS OF SE 4.4483 8.8966 4.345 65.793 7.4 48.69 9.38 33.586 373.35 Ma 45.4 At Node 438 Mi.9
URH - Venttiili. Halton URH. Venttiili
 Halton URH Venttiili ilmaventtiili, jossa on painehäviön säätömahdollisuus. Seinä- tai attoasennus erillisen asennusehysen avulla. Kanavamelun vaimennus. Laitteessa on ilman tilavuusvirran mittaus- ja
Halton URH Venttiili ilmaventtiili, jossa on painehäviön säätömahdollisuus. Seinä- tai attoasennus erillisen asennusehysen avulla. Kanavamelun vaimennus. Laitteessa on ilman tilavuusvirran mittaus- ja
T Puurakenteet 5 op
 T51905 Puuraenteet 5 op Kantavat puuraenteet Rasitusuoot Veto Taivutus Kiepahus Leiaus Puristus Nurjahus Vääntö Yhistett rasituset 1 Veto T51905 Puuraenteet 5 op Kantavat puuraenteet Rasitusuoot Vetojännits
T51905 Puuraenteet 5 op Kantavat puuraenteet Rasitusuoot Veto Taivutus Kiepahus Leiaus Puristus Nurjahus Vääntö Yhistett rasituset 1 Veto T51905 Puuraenteet 5 op Kantavat puuraenteet Rasitusuoot Vetojännits
z z 0 (m 1)! g(m 1) (z0) k=0 Siksi kun funktioon f(z) sovelletaan Cauchyn integraalilausetta, on voimassa: sin(z 2 dz = (z i) n+1 k=0
 TKK, Matematiian laitos v.pfaler/pursiainen Mat-.33 Matematiian perusurssi KP3-i sysy 2007 Lasuharjoitus 4 viio 40 Tehtäväsarja A viittaa aluviion ja L loppuviion tehtäviin. Valmistauu esittämään nämä
TKK, Matematiian laitos v.pfaler/pursiainen Mat-.33 Matematiian perusurssi KP3-i sysy 2007 Lasuharjoitus 4 viio 40 Tehtäväsarja A viittaa aluviion ja L loppuviion tehtäviin. Valmistauu esittämään nämä
ELEMENTTIMENETELMÄN PERUSTEET SESSIO 12: Tasokehän palkkielementti, osa 2.
 / ELEMENTTIMENETELMÄN PERUSTEET SESSIO : Tasoehän palielementti, osa. NELJÄN VAPAUSASTEEN PALKKIELEMENTTI Kun ahden vapausasteen palielementin solmuihin lisätään loaalin -aselin suuntaiset siirtmämittauset,
/ ELEMENTTIMENETELMÄN PERUSTEET SESSIO : Tasoehän palielementti, osa. NELJÄN VAPAUSASTEEN PALKKIELEMENTTI Kun ahden vapausasteen palielementin solmuihin lisätään loaalin -aselin suuntaiset siirtmämittauset,
VIEMÄRIPUTKIEN PALOTEKNINEN SUOJAUS
 VIEMÄRIPUTKIEN PALOTEKNINEN SUOJAUS Viemäriputkien palotekninen suojaus kerrosten välisissä läpivienneissä 1. SUOMALAISET MÄÄRÄYKSET Rakennusmääräyskokoelma E1 Rakennusten paloturvallisuus Kohta 1.2. Olennainen
VIEMÄRIPUTKIEN PALOTEKNINEN SUOJAUS Viemäriputkien palotekninen suojaus kerrosten välisissä läpivienneissä 1. SUOMALAISET MÄÄRÄYKSET Rakennusmääräyskokoelma E1 Rakennusten paloturvallisuus Kohta 1.2. Olennainen
Talousmatematiikan verkkokurssi. Koronkorkolaskut
 Sivu 1/7 oronorolasuja sovelletaan tapausiin, joissa aia on pidempi uin ysi oonainen orojaso, eli aia, jolle oroanta ilmoittaa oron määrän. orolasu: enintään yhden orojason pituisille oroajoille; oronorolasu:
Sivu 1/7 oronorolasuja sovelletaan tapausiin, joissa aia on pidempi uin ysi oonainen orojaso, eli aia, jolle oroanta ilmoittaa oron määrän. orolasu: enintään yhden orojason pituisille oroajoille; oronorolasu:
Ovi. Ovi TP101. Perustietoja: - Hallin 1 päätyseinän tuulipilarit TP101 ovat liimapuurakenteisia. Halli 1
 Esimerkki 4: Tuulipilari Perustietoja: - Hallin 1 päätyseinän tuulipilarit TP101 ovat liimapuurakenteisia. - Tuulipilarin yläpää on nivelellisesti ja alapää jäykästi tuettu. Halli 1 6000 TP101 4 4 - Tuulipilaria
Esimerkki 4: Tuulipilari Perustietoja: - Hallin 1 päätyseinän tuulipilarit TP101 ovat liimapuurakenteisia. - Tuulipilarin yläpää on nivelellisesti ja alapää jäykästi tuettu. Halli 1 6000 TP101 4 4 - Tuulipilaria
Yhden selittäjän lineaarinen regressiomalli
 Moimuuujameeelmä Yhde seliäjä lieaarie regressiomalli Moimuuujameeelmä: Yhde seliäjä lieaarie regressiomalli Ilkka Melli. Yhde seliäjä lieaarie regressiomalli, se esimoii ja esaus.. Yhde seliäjä lieaarie
Moimuuujameeelmä Yhde seliäjä lieaarie regressiomalli Moimuuujameeelmä: Yhde seliäjä lieaarie regressiomalli Ilkka Melli. Yhde seliäjä lieaarie regressiomalli, se esimoii ja esaus.. Yhde seliäjä lieaarie
KALA 1.3.2010, Asia 52,, Liite 2.3. Varisto, Martinkyläntien meluselvitys välillä Vihdintie - Riihimiehentie Vantaan kaupunki
 KALA 1.3.2010, Asia 52,, Liie 2.3 Variso, Marinylänien eluselviys välillä Vihdinie - Riihiiehenie Vanaan aupuni Variso, Marinylänien eluselviys välillä Vihdinie Riihiiehenie, Vanaa 2(11) Meluselviys Vanaan
KALA 1.3.2010, Asia 52,, Liie 2.3 Variso, Marinylänien eluselviys välillä Vihdinie - Riihiiehenie Vanaan aupuni Variso, Marinylänien eluselviys välillä Vihdinie Riihiiehenie, Vanaa 2(11) Meluselviys Vanaan
LATTIAT - VÄRÄHTELYMITOITUS - Tero Lahtela
 LATTIAT - VÄRÄHTELYMITOITUS - Tero Lahtela LATTIAN VÄRÄHTELY TYYPILLISET VÄRÄHTELYN AIHEUTTAJAT Kävely (yleisin), juokseminen, hyppiminen Pyykinpesukone Liikennetärinä VÄRÄHTELYN AISTIMINEN Kehon tuntemuksina
LATTIAT - VÄRÄHTELYMITOITUS - Tero Lahtela LATTIAN VÄRÄHTELY TYYPILLISET VÄRÄHTELYN AIHEUTTAJAT Kävely (yleisin), juokseminen, hyppiminen Pyykinpesukone Liikennetärinä VÄRÄHTELYN AISTIMINEN Kehon tuntemuksina
joka on separoituva yhtälö, jolla ei ole reaalisia triviaaliratkaisuja. Ratkaistaan: z z(x) dx =
 HY / Maemaiikan ja ilasoieeen laios Differeniaalihälö I kevä 09 Harjois 4 Rakaisehdoksia. Rakaise differeniaalihälö = (x + + Rakais: Tehdään differeniaalihälöön lineaarinen mnnos z(x = x + (x + jolloin
HY / Maemaiikan ja ilasoieeen laios Differeniaalihälö I kevä 09 Harjois 4 Rakaisehdoksia. Rakaise differeniaalihälö = (x + + Rakais: Tehdään differeniaalihälöön lineaarinen mnnos z(x = x + (x + jolloin
KANSALLINEN LIITE STANDARDIIN. SFS-EN 1995 EUROKOODI 5: PUURAKENTEIDEN SUUNNITTELU Osa 1-2: Yleistä. Rakenteiden palomitoitus
 1 LIITE 17 KANSALLINEN LIITE STANDARDIIN SFS-EN 1995 EUROKOODI 5: PUURAKENTEIDEN SUUNNITTELU Osa 1-2: Yleistä. Rakenteiden palomitoitus Esipuhe Tätä kansallista liitettä käytetään yhdessä standardin SFS-EN
1 LIITE 17 KANSALLINEN LIITE STANDARDIIN SFS-EN 1995 EUROKOODI 5: PUURAKENTEIDEN SUUNNITTELU Osa 1-2: Yleistä. Rakenteiden palomitoitus Esipuhe Tätä kansallista liitettä käytetään yhdessä standardin SFS-EN
ESIMERKKI 1: NR-ristikoiden kannatuspalkki
 ESIMERKKI 1: NR-ristikoiden kannatuspalkki Perustietoja - NR-ristikot kannatetaan seinän päällä olevalla palkilla P101. - NR-ristikoihin tehdään tehtaalla lovi kannatuspalkkia P101 varten. 2 1 2 1 11400
ESIMERKKI 1: NR-ristikoiden kannatuspalkki Perustietoja - NR-ristikot kannatetaan seinän päällä olevalla palkilla P101. - NR-ristikoihin tehdään tehtaalla lovi kannatuspalkkia P101 varten. 2 1 2 1 11400
Talousmatematiikan perusteet, L2 Kertaus Aiheet
 Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
Talousmatematiikan perusteet, L2 Kertaus 1 Laskutoimitukset tehdään seuraavassa järjestyksessä 1. Sulkujen sisällä olevat lausekkeet (alkaen sisältä ulospäin) 2. potenssit ja juurilausekkeet 3. kerto-
[ ] [ 2 [ ] [ ] ( ) [ ] Tehtävä 1. ( ) ( ) ( ) ( ) ( ) ( ) 2( ) = 1. E v k 1( ) R E[ v k v k ] E e k e k e k e k. e k e k e k e k.
![[ ] [ 2 [ ] [ ] ( ) [ ] Tehtävä 1. ( ) ( ) ( ) ( ) ( ) ( ) 2( ) = 1. E v k 1( ) R E[ v k v k ] E e k e k e k e k. e k e k e k e k. [ ] [ 2 [ ] [ ] ( ) [ ] Tehtävä 1. ( ) ( ) ( ) ( ) ( ) ( ) 2( ) = 1. E v k 1( ) R E[ v k v k ] E e k e k e k e k. e k e k e k e k.](/thumbs/70/63966855.jpg) ehtävä. x( + ) x( y x( + e ( y x( + e ( E v E e ( ) e ( R E[ v v ] E e e e e e e e e 6 estimointivirhe: ~ x( x( x$( x( - b y ( - b y ( estimointivirheen odotusarvo: x( - b x( - b e ( - b x( - b e ( ( -
ehtävä. x( + ) x( y x( + e ( y x( + e ( E v E e ( ) e ( R E[ v v ] E e e e e e e e e 6 estimointivirhe: ~ x( x( x$( x( - b y ( - b y ( estimointivirheen odotusarvo: x( - b x( - b e ( - b x( - b e ( ( -
REIKIEN JA LOVIEN MITOITUS
 REIKIEN JA LOVIEN ITOITUS REIKIEN JA LOVIEN ITOITUS Leiauslujuuen ja poiittaisen etolujuuen ansiosta Kertotuotteisiin on mahollista tehä reiiä. Erityisesti ristiiiluraenteinen soeltuu ohteisiin, joissa
REIKIEN JA LOVIEN ITOITUS REIKIEN JA LOVIEN ITOITUS Leiauslujuuen ja poiittaisen etolujuuen ansiosta Kertotuotteisiin on mahollista tehä reiiä. Erityisesti ristiiiluraenteinen soeltuu ohteisiin, joissa
Mallivastaukset KA5-kurssin laskareihin, kevät 2009
 Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 2 (viikko 6) Tehävä 1 Sovelleaan luenokalvojen sivulla 46 anneua kaavaa: A A Y Y K α ( 1 α ) 0,025 0,5 0,03 0,5 0,01 0,005 K Siis kysyy Solowin
Mallivasaukse KA5-kurssin laskareihin, kevä 2009 Harjoiukse 2 (viikko 6) Tehävä 1 Sovelleaan luenokalvojen sivulla 46 anneua kaavaa: A A Y Y K α ( 1 α ) 0,025 0,5 0,03 0,5 0,01 0,005 K Siis kysyy Solowin
KJR-C2002 Kontinuumimekaniikan perusteet, viikko 45/2017
 KJR-C00 Kontinuumimeaniian perusteet viio 45/017 1. Oloon f t ) alojen onsentraatio [ f ] < g/m ) joessa joa riippuu siis seä paiasta että ajasta. Havaitsija on veneessä ja mittaa onsentraatiota suoraan
KJR-C00 Kontinuumimeaniian perusteet viio 45/017 1. Oloon f t ) alojen onsentraatio [ f ] < g/m ) joessa joa riippuu siis seä paiasta että ajasta. Havaitsija on veneessä ja mittaa onsentraatiota suoraan
LIITTEET Liite A Stirlingin kaavan tarkkuudesta...2. Liite B Lagrangen kertoimet...3
 LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
ja läpäisyaika lasketaan (esim) integraalilla (5.3.1), missä nyt reitti s on z-akselilla:
 10 a) Valo opeus levyssä o vakio v 0 = c / 0, jote ajaksi matkalla L laskemme L t0 = = 0 L. v0 c b) Valo opeus levyssä riippuu z:sta: c c v ( z) = = ( z ) 0 (1 + 3az 3 ) ja läpäisyaika lasketaa (esim)
10 a) Valo opeus levyssä o vakio v 0 = c / 0, jote ajaksi matkalla L laskemme L t0 = = 0 L. v0 c b) Valo opeus levyssä riippuu z:sta: c c v ( z) = = ( z ) 0 (1 + 3az 3 ) ja läpäisyaika lasketaa (esim)
BETONI-TERÄS LIITTORAKENTEIDEN SUUNNITTELU EUROKOODIEN MUKAAN (TTY 2009) Betonipäivät 2010
 DIPLOMITYÖ: BETONI-TERÄS LIITTORAKENTEIDEN SUUNNITTELU EUROKOODIEN MUKAAN (TTY 29) Beonipäivä 21 DIPLOMITYÖ prosessina Aie: yön eeäjän aloieesa Selviykse beonin, eräksen ja puun osala oli jo ey/käynnissä
DIPLOMITYÖ: BETONI-TERÄS LIITTORAKENTEIDEN SUUNNITTELU EUROKOODIEN MUKAAN (TTY 29) Beonipäivä 21 DIPLOMITYÖ prosessina Aie: yön eeäjän aloieesa Selviykse beonin, eräksen ja puun osala oli jo ey/käynnissä
Paikalla rakentaminen. Pien- ja rivitalot
 Paikalla rakentaminen Pien- ja rivitalot Paikalla rakentaminen Pien- ja rivitalot 1. Rakennetyypit 1. Rakennetyypit 1.1 Ulkoseinä Tekniset tiedot U-arvo Palotekninen soveltuvuus 0,16 W/m 2 K max 2 krs.
Paikalla rakentaminen Pien- ja rivitalot Paikalla rakentaminen Pien- ja rivitalot 1. Rakennetyypit 1. Rakennetyypit 1.1 Ulkoseinä Tekniset tiedot U-arvo Palotekninen soveltuvuus 0,16 W/m 2 K max 2 krs.
