Matematyka 1. Šukasz Dawidowski. Instytut Matematyki, Uniwersytet l ski
|
|
|
- Olavi Honkanen
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski
2 Elementy logiki i teorii mnogo±ci Zdanie (w sensie logicznym) takie zdanie w sensie gramatycznym, które jest prawdziwe lub faªszywe. je»eli zdanie jest prawdziwe, to przypisujemy mu warto± logiczn 1, je»eli jest faªszywe, to przypisujemy warto± logiczn 0. Oznaczenia zda«: p, q, r,....
3 Elementy logiki i teorii mnogo±ci Spójniki logiczne: negacja zdania p: p, p koniunkcja zda«p i q: p q p p p q p q
4 Elementy logiki i teorii mnogo±ci alternatywa zda«p i q: p q p q p q implikacja zda«p i q: p q, p q p q p q
5 Elementy logiki i teorii mnogo±ci równowa»no± zda«p i q: p q, p q p q p q
6 Elementy logiki i teorii mnogo±ci Przykªad: Drzewo ma li±cie. (nie jest to zdanie w sensie logicznym) Funkcja zdaniowa wypowied¹ jest funkcj zdaniow o dziedzinie X, je±lipo podstawieniu dowolnego elementu zbioru X za zmienn otrzymamy zdanie. Niech α(x) b dzie funkcj zdaniow. Wtedy zbiór wszystkich (i tylko tych) elementów x 0 X takich,»e α(x 0 ) jest zdaniem prawdziwym oznacza b dziemy symbolem {x X : α(x)}
7 Elementy logiki i teorii mnogo±ci Prawa rachunku zda«(zdania zawsze prawdziwe, tautologie): prawa de Morgana (p q) p q (p q) p q ª czno± alternatywy i koniunkcji p (q r) (p q) r p (q r) (p q) r rozdielno±ci: p (q r) (p q) (p r) p (q r) (p q) (p r)
8 Elementy logiki i teorii mnogo±ci prawo kontrapozycji (p q) ( q p) negacja implikacji (p q) (p q) prawo wyª czonego ±rodka p ( p)
9 Elementy logiki i teorii mnogo±ci Elementy rachunku kwantykatorów Niech p(x) b dzie funkcj zdaniow zmiennej x o dziedzinie X. Zdanie: Istnieje x w zbiorze X taki,»e p(x) zapisujemy w postaci x X p(x) p(x) x X Zdanie: Dla ka»dego x ze zbioru X takiego,»e p(x) zapisujemy w postaci x X p(x) p(x) x X
10 Elementy logiki i teorii mnogo±ci Zwroty istnieje i dla ka»dego oraz odpowiadaj ce im symbole, nazywamy kwantykatorami: egzystencjalnym (maªym), ogólnym (du»ym).
11 Elementy logiki i teorii mnogo±ci Prawa logiczne dla kwantykatorów: x X p(x) q(x) (p(x) q(x)) x X x X (p(x) q(x)) p(x) q(x) x X x X x X prawa de Morgana: p(x) p(x) x X x X p(x) p(x) x X x X
12 Rachunek zbiorów = teoria mnogo±ci Zbiór i element zbioru longrightarrow poj cia pierwotne x X x jest elementem zbioru X x / X x nie jest elementem zbioru X A B x A x B zbiór A zawiera si w zbiorze B
13 Rachunek zbiorów = teoria mnogo±ci X przestrze«, A, B X. dopeªnienie zbioru A ró»nica zbiorów A i B suma zbiorów A i B A = {x X : x / A} A \ B = {x A: x / B} A B = {x X : x A x B} iloczyn (przekrój) zbiorów A i B A B = {x X : x A x B}
14 Rachunek zbiorów = teoria mnogo±ci Mówimy,»e zbiory A i B s rozª czna, je»eli A B = Mówimy,»e A = B, je»eli x A x B A B B A Zbiór maj cy skpo«czon ilo± elementów nazywamy zbiorem sko«czonym; zbiór maj cy niesko«czon ilo± elementów nazywamy zbiorem niesko«czonym.
15 Rachunek zbiorów = teoria mnogo±ci Niektóre wªasno±ci dziaªa«na zbiorach: (A B) C = A (B C) (A B) C = A (B C) A B = B A A B = B A A (B C) = (A B) (A C) A (B C) = (A B) (A C) (A B) = A B (A B) = A B
16 Rachunek zbiorów = teoria mnogo±ci Zbiór, którego elementy s zbiorami nazywamy rodzin zbiorów. Niech T b dzie dowolnym zbiorem wska¹ników oraz niech {A t : t T } b dzie rodzin zbiorów. Wtedy: x t T x t T A t t T x A t A t x A t t T
17 Funkcje Niech X oraz Y b d niepustymi zbiorami (X, Y ). f : X Y funkcja, je»eli ka»demu elementowi x zbioru X przyporz dkowany jest dokªadnie jeden element y zbioru Y. X dziedzina funkcji f Y przeciwdziedzina funkcji f je±li x X, to piszemy: y = f (x) warto± funkcji f dla argumentu x
18 Funkcje Niech f : X 1 Y 1 i g : X 2 Y 2 b d funkcjami. Wtedy f = g je»eli X 1 = X 2, f (x) = g(x) x X 1
19 Funkcje Niech f : X Y, A X, B Y. Zbiór f (A) = {y Y : y = f (x)} x A nazywamy obrazem zbioru A poprzez funkcj f. Zbiór f 1 (B) = {x X : f (x) B} nazywamy przeciwobrazem zbioru B poprzez funkcj f.
20 Funkcje Niech f : X Y. Wtedy: f nazywamy surjekcj (odwzorowaniem na), je±li f (X ) = Y, f nazywamy funkcj ró»nowarto±ciow, je»eli x 1,x 2 X (x 1 x 2 f (x 1 ) f (x 2 )) albo x 1,x 2 X (f (x 1 ) = f (x 2 ) x 1 = x 2 ), f jest odwracalna, je»eli jest surjekcj i jest ró»nowarto±ciowa.
21 Funkcje Zªo»enie funkcji Niech f : X Y, g : Y Z. Wtedy odwzorowanie g f : X Z dane wzorem (g f )(x) = g(f (x)), x X nazywamy zªo»eniem (superpozycj ) funkcji f i g. Uwaga: Skªadanie funkcji nie jest przemienne, tzn. f g g f!
22 Funkcje Równoliczno± zbiorów (kilka uwag) Zbiory A i B nazywamy równolicznymi, je»eli istnieje odwracalna funkcja f (tzn. jest surjekcj i jest ró»nowarto±ciowa) taka,»e f : A B Uwagi: zbiory sko«czone s równoliczne, kiedy maj tak sam liczb elementów, zbiór N jest równoliczny ze zbiorami Z i Q, ka»dy niezdegenerowany przedziaª liczb rzeczywistych jest równoliczny ze zbiorem R, zbiory N i R nie s równoliczne.
23 Funkcje Zbiór nazywamy przeliczalnym, je»eli jest równoliczny z pewnym podzbiorem zbioru liczb naturalnych, tzn.: albo jest sko«czony albo jest równoliczny ze zbiorem N. Zbiory, które nie s przeliczalne, nazywamy zbiorami nieprzeliczalnymi. Przykªady: R, (a, b), [a, b] dla a < b.
24 Funkcje Iloczyn kartezja«ski X, Y X Y = {(x, y): x X y Y } Je±li X = Y, to b dziemy pisali X 2 = X X. Niech X 1, X 2,..., X n, to X 1 X 2... X n = {(x 1, x 2,..., x n ): i {1,...,n} x i X i } Je±li X = X 1 =... = X n, to piszemy: X n = X 1... X n. Je±li X = R, to R n = R... R. }{{} n razy
25 Funkcje Wykres odwzorowania f : X Y gr(f ) = {(x, y) X Y : y = f (x)} Twierdzenie: Je±li f : X Y jest odwzorowaniem odwracalnym, to odwzorowanie g : Y na X jest odwzorowaniem odwrotnym do f wtedy i tylko wtedy, gdy: (g f )(x) = x (f g)(y) = y x X y Y
Matematyka 1. Šukasz Dawidowski. Instytut Matematyki, Uniwersytet l ski
 Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Granica ci gu Niech Y, A N. Dowoln funkcj f : A Y nazywamy ci giem elementów zbioru Y. Najcz ±ciej mamy: A = N, tzn. f : N Y. Je»eli
Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Granica ci gu Niech Y, A N. Dowoln funkcj f : A Y nazywamy ci giem elementów zbioru Y. Najcz ±ciej mamy: A = N, tzn. f : N Y. Je»eli
Matematyka 1. Šukasz Dawidowski. Instytut Matematyki, Uniwersytet l ski
 Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Macierze Niech dane b d liczby n, m N Ka»d funkcj okre±lon na iloczynie kartezja«skim {1,, m} {1,, n} o warto±ciach w zbiorze liczb
Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Macierze Niech dane b d liczby n, m N Ka»d funkcj okre±lon na iloczynie kartezja«skim {1,, m} {1,, n} o warto±ciach w zbiorze liczb
Zamykanie otworów w trójwymiarowych obiektach wolumetrycznych
 AUTOMATYKA 2009 Tom 13 Zeszyt 3 Marcin Janaszewski*, **, Laurent Babout*, Micha³ Postolski*, **, ukasz Jopek*, ** Zamykanie otworów w trójwymiarowych obiektach wolumetrycznych 1. Wprowadzenie W niniejszym
AUTOMATYKA 2009 Tom 13 Zeszyt 3 Marcin Janaszewski*, **, Laurent Babout*, Micha³ Postolski*, **, ukasz Jopek*, ** Zamykanie otworów w trójwymiarowych obiektach wolumetrycznych 1. Wprowadzenie W niniejszym
Zastosowanie zbiorów rozmytych do ewaluacji ró nych aspektów systemów kszta³cenia
 AUTOMATYKA 2008 Tom 12 Zeszyt 3 Kzysztof Pzybyszewski* Zastosowanie zbioów ozmytych do ewaluacji ó nych aspektów systemów kszta³cenia 1. Wpowadzenie Ka dy system nauczania mo na ozpatywaæ jako system infomacyjny.
AUTOMATYKA 2008 Tom 12 Zeszyt 3 Kzysztof Pzybyszewski* Zastosowanie zbioów ozmytych do ewaluacji ó nych aspektów systemów kszta³cenia 1. Wpowadzenie Ka dy system nauczania mo na ozpatywaæ jako system infomacyjny.
bab.la Zwroty: Korespondencja osobista Życzenia fiński-fiński
 Życzenia : Ślub Onnittelut! Toivomme teille molemmille kaikkea onnea maailmassa. Onnittelut! Toivomme teille molemmille kaikkea onnea maailmassa. młodej parze Lämpimät onnentoivotukset teille molemmille
Życzenia : Ślub Onnittelut! Toivomme teille molemmille kaikkea onnea maailmassa. Onnittelut! Toivomme teille molemmille kaikkea onnea maailmassa. młodej parze Lämpimät onnentoivotukset teille molemmille
Seurauksia. Seuraus. Seuraus. Jos asteen n polynomilla P on n erisuurta nollakohtaa x 1, x 2,..., x n, niin P on muotoa
 Seurauksia Seuraus Jos asteen n polynomilla P on n erisuurta nollakohtaa x 1, x 2,..., x n, niin P on muotoa P(x) = a n (x x 1 )(x x 2 )... (x x n ). Seuraus Astetta n olevalla polynomilla voi olla enintään
Seurauksia Seuraus Jos asteen n polynomilla P on n erisuurta nollakohtaa x 1, x 2,..., x n, niin P on muotoa P(x) = a n (x x 1 )(x x 2 )... (x x n ). Seuraus Astetta n olevalla polynomilla voi olla enintään
Matkustaminen Liikkuminen
 - Sijainti Zgubiłem/Zgubiłam się. Et tiedä missä olet. Czy mógłby Pan/mogłaby Pani pokazać mi gdzie to jest na mapie? Tietyn sijainnin kysymistä kartalta Gdzie jest? Tietyn rakennuksen / n sijainnin tiedustelu...
- Sijainti Zgubiłem/Zgubiłam się. Et tiedä missä olet. Czy mógłby Pan/mogłaby Pani pokazać mi gdzie to jest na mapie? Tietyn sijainnin kysymistä kartalta Gdzie jest? Tietyn rakennuksen / n sijainnin tiedustelu...
Karta Praw dla Dzieci z Trudnościami
 Karta Praw dla Dzieci z Trudnościami Jeśli nie zaczniemy dobrze traktować dzieci ze społecznymi, emocjonalnymi i behawioralnymi wyzwaniami, utracimy ich ze zdumiewającą szybkością. Właściwe postępowanie
Karta Praw dla Dzieci z Trudnościami Jeśli nie zaczniemy dobrze traktować dzieci ze społecznymi, emocjonalnymi i behawioralnymi wyzwaniami, utracimy ich ze zdumiewającą szybkością. Właściwe postępowanie
a 1 y 1 (x) + a 2 y 2 (x) = 0 vain jos a 1 = a 2 = 0
 6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
Rekrutacja Referencje
 - Wstęp Hyvä Herra, Hyvä Herra, Formalny, odbiorcą jest mężczyzna, którego nazwiska nie znamy Hyvä Rouva Hyvä Rouva Formalny, odbiorcą jest kobieta, której nazwiska nie znamy Hyvä Herra / Rouva Formalny,
- Wstęp Hyvä Herra, Hyvä Herra, Formalny, odbiorcą jest mężczyzna, którego nazwiska nie znamy Hyvä Rouva Hyvä Rouva Formalny, odbiorcą jest kobieta, której nazwiska nie znamy Hyvä Herra / Rouva Formalny,
Johdatus reaalifunktioihin P, 5op
 Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Johdatus reaalifunktioihin 802161P, 5op Osa 2 Pekka Salmi 1. lokakuuta 2015 Pekka Salmi FUNK 1. lokakuuta 2015 1 / 55 Jatkuvuus ja raja-arvo Tavoitteet: ymmärtää raja-arvon ja jatkuvuuden määritelmät intuitiivisesti
Adaptacyjny uk³ad regulacji z predyktorem Smitha z mo liwoœci¹ zastosowania w systemach rozproszonych
 AUTOMATYKA 2008 Tom 12 Zeszyt 2 Andrzej Tutaj* Adaptacyjny uk³ad regulacji z predyktorem Smitha z mo liwoœci¹ zastosowania w systemach rozproszonych 1. Wstêp Sterowanie w uk³adach z opóÿnieniem przedstawia
AUTOMATYKA 2008 Tom 12 Zeszyt 2 Andrzej Tutaj* Adaptacyjny uk³ad regulacji z predyktorem Smitha z mo liwoœci¹ zastosowania w systemach rozproszonych 1. Wstêp Sterowanie w uk³adach z opóÿnieniem przedstawia
Matkustaminen Yleistä
 - Olennaiset Voisitko auttaa minua? Avun pyytäminen Puhutko englantia? Tiedustelu henkilöltä puhuuko hän englantia Możesz mi pomóc? [form.:] Może Pan(i) mi pomóc? Czy mówisz po angielsku? [form.:] Czy
- Olennaiset Voisitko auttaa minua? Avun pyytäminen Puhutko englantia? Tiedustelu henkilöltä puhuuko hän englantia Możesz mi pomóc? [form.:] Może Pan(i) mi pomóc? Czy mówisz po angielsku? [form.:] Czy
CERTYFIKAT JĘZYKOWY UNIWERSYTETU WARSZAWSKIEGO EGZAMIN Z JĘZYKA OBCEGO NA POZIOMIE B1 TEST PRZYKŁADOWY
 CERTYFIKAT JĘZYKOWY UNIWERSYTETU WARSZAWSKIEGO EGZAMIN Z JĘZYKA OBCEGO NA POZIOMIE B1 TEST PRZYKŁADOWY odpowiedzi na pytania do testów 1.1, 2.1, 2.2, 2.3, 3.1 wpisuj na kartę odpowiedzi numer 1 odpowiedzi
CERTYFIKAT JĘZYKOWY UNIWERSYTETU WARSZAWSKIEGO EGZAMIN Z JĘZYKA OBCEGO NA POZIOMIE B1 TEST PRZYKŁADOWY odpowiedzi na pytania do testów 1.1, 2.1, 2.2, 2.3, 3.1 wpisuj na kartę odpowiedzi numer 1 odpowiedzi
Analiza sceny przy u yciu deskryptorów punktów charakterystycznych**
 AUTOMATYKA 2011 Tom 15 Zeszyt 3 Piotr Szymczyk*, Magdalena Szymczyk* Analiza sceny przy u yciu deskryptorów punktów charakterystycznych** 1. Wprowadzenie Analiza sceny polega na wyodrêbnieniu z obrazu
AUTOMATYKA 2011 Tom 15 Zeszyt 3 Piotr Szymczyk*, Magdalena Szymczyk* Analiza sceny przy u yciu deskryptorów punktów charakterystycznych** 1. Wprowadzenie Analiza sceny polega na wyodrêbnieniu z obrazu
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 4.7 Syklisen koodin jälkiesitys Olkoon F = F q ja K = F q m kunnan F laajennuskunta. Määritelmä 4.7.1. Kuntalaajennuksen K/F jälkifunktioksi
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 4.7 Syklisen koodin jälkiesitys Olkoon F = F q ja K = F q m kunnan F laajennuskunta. Määritelmä 4.7.1. Kuntalaajennuksen K/F jälkifunktioksi
Reaalilukuvälit, leikkaus ja unioni (1/2)
 Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Luvut Luonnolliset luvut N = {0, 1, 2, 3,... } Kokonaisluvut Z = {..., 2, 1, 0, 1, 2,... } Rationaaliluvut (jaksolliset desimaaliluvut) Q = {m/n m, n Z, n 0} Irrationaaliluvut eli jaksottomat desimaaliluvut
Toispuoleiset raja-arvot
 Toispuoleiset raja-arvot Määritelmä Funktiolla f on oikeanpuoleinen raja-arvo a R pisteessä x 0 mikäli kaikilla ɛ > 0 löytyy sellainen δ > 0 että f (x) a < ɛ aina kun x 0 < x < x 0 + δ; ja vasemmanpuoleinen
Toispuoleiset raja-arvot Määritelmä Funktiolla f on oikeanpuoleinen raja-arvo a R pisteessä x 0 mikäli kaikilla ɛ > 0 löytyy sellainen δ > 0 että f (x) a < ɛ aina kun x 0 < x < x 0 + δ; ja vasemmanpuoleinen
Säilytetään paikallisesti
 OUTCOME + määrä: Sairaalan koodi määrä 3.. esimerkki Max Muster Ma Mu 5 1 1 17.0.08 B x 1 1 1 1 3 Hiesmayr/Schindler (ESPEN/AKE Austria)_v/010 OUTCOME + määrä: Sairaalan koodi määrä 3.. 1 4 1 5 1 6 1 7
OUTCOME + määrä: Sairaalan koodi määrä 3.. esimerkki Max Muster Ma Mu 5 1 1 17.0.08 B x 1 1 1 1 3 Hiesmayr/Schindler (ESPEN/AKE Austria)_v/010 OUTCOME + määrä: Sairaalan koodi määrä 3.. 1 4 1 5 1 6 1 7
Kunnossapitoyksikön päällikkö
 RATAHALLINTO KESKUS BANFÖRVALTNINGS CENTRALEN 8.11.2004 1277/731/2004 STANDARDIN SFSEN 13450 RAIDESEPELIKIVIAINEKSET KANSALLINEN SOVELTAMISOHJE Ratahallintokeskus on hyväksynyt standardin SFSEN 13450 Raidesepelikiviainekset
RATAHALLINTO KESKUS BANFÖRVALTNINGS CENTRALEN 8.11.2004 1277/731/2004 STANDARDIN SFSEN 13450 RAIDESEPELIKIVIAINEKSET KANSALLINEN SOVELTAMISOHJE Ratahallintokeskus on hyväksynyt standardin SFSEN 13450 Raidesepelikiviainekset
KÄYTTÖOHJE BRUKSANVISNING OPERATING INSTRUCTION INSTRUKCJA MONTAŻU
 SYSTEM CERTIFICATION 14001 9001 KÄYTTÖOHJE BRUKSANVISNING ORATING INSTRUCTION INSTRUKCJA MONTAŻU RAK 17 22.01.2008 ESSI I ( INDUSTRY ) ESSI I 12-18 - 24-30 - 36 IP X4 SYSTEM CERTIFICATION ISO ISO ME04
SYSTEM CERTIFICATION 14001 9001 KÄYTTÖOHJE BRUKSANVISNING ORATING INSTRUCTION INSTRUKCJA MONTAŻU RAK 17 22.01.2008 ESSI I ( INDUSTRY ) ESSI I 12-18 - 24-30 - 36 IP X4 SYSTEM CERTIFICATION ISO ISO ME04
Yksityinen kirjeenvaihto Yksityiskirje
 - Osoite Matti Meikäläinen Puistokatu 17 A 01234 Helsinki Finland Osoitteen ulkomuoto Suomessa: kadun nimi + katunumero postiosoite + kaupungin nimi maa. Sz.P. Michał Kopiejka ul. B. Prusa 32/29 91-075
- Osoite Matti Meikäläinen Puistokatu 17 A 01234 Helsinki Finland Osoitteen ulkomuoto Suomessa: kadun nimi + katunumero postiosoite + kaupungin nimi maa. Sz.P. Michał Kopiejka ul. B. Prusa 32/29 91-075
Luoki?elua: tavallinen vs osi?ais. Osa 11. Differen0aaliyhtälöt. Luoki?elua: kertaluku. Luoki?elua: lineaarisuus 4/13/13
 4/3/3 Osa. Differen0aaliyhtälöt Differen0aaliyhtälö = yhtälö jossa esiintyy jonkin funk0on derivaa?a. Esim: dx = x2 f x + f xy 2 2m d 2 ψ = Eψ dx 2 Luoki?elua: tavallinen vs osi?ais Differen0aaliyhtälöt
4/3/3 Osa. Differen0aaliyhtälöt Differen0aaliyhtälö = yhtälö jossa esiintyy jonkin funk0on derivaa?a. Esim: dx = x2 f x + f xy 2 2m d 2 ψ = Eψ dx 2 Luoki?elua: tavallinen vs osi?ais Differen0aaliyhtälöt
(2006/C 274/02) (Tekst mający znaczenie dla EOG)
 C 274/2 POMOC PAŃSTWA FINLANDIA Pomoc państwa C 7/06 (ex NN83/05) Finnish Road Enterprise (Fińskie Przedsiębiorstwo Drogowe) Zaproszenie do przedkładania uwag zgodnie z art. 88 ust. 2 traktatu WE (2006/C
C 274/2 POMOC PAŃSTWA FINLANDIA Pomoc państwa C 7/06 (ex NN83/05) Finnish Road Enterprise (Fińskie Przedsiębiorstwo Drogowe) Zaproszenie do przedkładania uwag zgodnie z art. 88 ust. 2 traktatu WE (2006/C
w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1.
 Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
Kotitehtävät, tammikuu 2011 Vaikeampi sarja 1. Ratkaise yhtälöryhmä w + x + y + z =4, wx + wy + wz + xy + xz + yz =2, wxy + wxz + wyz + xyz = 4, wxyz = 1. Ratkaisu. Yhtälöryhmän ratkaisut (w, x, y, z)
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Sprzêtowa implementacja czêœci wielomianowej funkcji orbitalnej na potrzeby obliczeñ kwantowo-chemicznych
 AUTOMATYKA 2010 Tom 14 Zeszyt 3/2 Maciej Wielgosz*, Ernest Jamro*, Pawe³ Russek*, Kazimierz Wiatr* Sprzêtowa implementacja czêœci wielomianowej funkcji orbitalnej na potrzeby obliczeñ kwantowo-chemicznych
AUTOMATYKA 2010 Tom 14 Zeszyt 3/2 Maciej Wielgosz*, Ernest Jamro*, Pawe³ Russek*, Kazimierz Wiatr* Sprzêtowa implementacja czêœci wielomianowej funkcji orbitalnej na potrzeby obliczeñ kwantowo-chemicznych
Travel Getting Around
 - Location Zgubiłem/Zgubiłam się. Not knowing where you are Czy mógłby Pan/mogłaby Pani pokazać mi gdzie to jest na mapie? Asking for a specific location on a map Gdzie jest? Asking for a specific Olen
- Location Zgubiłem/Zgubiłam się. Not knowing where you are Czy mógłby Pan/mogłaby Pani pokazać mi gdzie to jest na mapie? Asking for a specific location on a map Gdzie jest? Asking for a specific Olen
saadaan kvanttorien järjestystä vaihtamalla ehto Tarkoittaako tämä ehto mitään järkevää ja jos, niin mitä?
 ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
ANALYYSI A, HARJOITUSTEHTÄVIÄ, KEVÄT 208 4 Funktion raja-arvo 4 Määritelmä Funktion raja-arvon määritelmän ehdosta ε > 0: δ > 0: fx) A < ε aina, kun 0 < x a < δ, saadaan kvanttorien järjestystä vaihtamalla
Podróże Poruszanie się
 - Lokalizacja Jag har gått vilse. Nie wiemy, gdzie się znajdujemy Kan du visa mig var det är på kartan? Pytanie o na mapie Var kan jag hitta? Pytanie o konkretny Olen eksyksissä. Voisitko näyttää kartalta
- Lokalizacja Jag har gått vilse. Nie wiemy, gdzie się znajdujemy Kan du visa mig var det är på kartan? Pytanie o na mapie Var kan jag hitta? Pytanie o konkretny Olen eksyksissä. Voisitko näyttää kartalta
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
Generowanie danych z obrazów bronchoskopowych w celu póÿniejszej klasyfikacji***
 AUTOMATYKA 2009 Tom 13 Zeszyt 3 Zbigniew Mikrut*, Mariusz Duplaga** Generowanie danych z obrazów bronchoskopowych w celu póÿniejszej klasyfikacji*** 1. Wprowadzenie Koncepcje i eksperymenty opisywane w
AUTOMATYKA 2009 Tom 13 Zeszyt 3 Zbigniew Mikrut*, Mariusz Duplaga** Generowanie danych z obrazów bronchoskopowych w celu póÿniejszej klasyfikacji*** 1. Wprowadzenie Koncepcje i eksperymenty opisywane w
Funktioista. Esimerkki 1
 Funktio eli kuvaus on matematiikan keskeisimpiä käsitteitä. Seuraavaksi tarkastellaan funktioita ja todistetaan niiden ominaisuuksia. Määritelmä 1 Olkoot A ja B. Kuvaus eli funktio f : A B on sääntö, joka
Funktio eli kuvaus on matematiikan keskeisimpiä käsitteitä. Seuraavaksi tarkastellaan funktioita ja todistetaan niiden ominaisuuksia. Määritelmä 1 Olkoot A ja B. Kuvaus eli funktio f : A B on sääntö, joka
Suomi Svenska Polski Lietuvių Deutsch... 55
 Suomi... 2 Svenska... 15 Polski... 28 Lietuvių... 42 Deutsch... 55 V 1.8 Sisällysluettelo 1. Määräystenmukainen käyttö... 3 2. Toimituksen sisältö... 3 3. Yhteenveto... 3 3.1 Nestekidenäyttö... 4 4. Tekniset
Suomi... 2 Svenska... 15 Polski... 28 Lietuvių... 42 Deutsch... 55 V 1.8 Sisällysluettelo 1. Määräystenmukainen käyttö... 3 2. Toimituksen sisältö... 3 3. Yhteenveto... 3 3.1 Nestekidenäyttö... 4 4. Tekniset
Marû ja modaalit. Aleksi Sahala
 Marû ja modaalit Aleksi Sahala 27.09.2015 Marû Intransitiivitaivutus Marûn intransitiivinen persoonataivutus muodostetaan ensimmäisellä suffiksisarjalla, sekä preesens-futurin tunnuksella {ed} Yksikkö
Marû ja modaalit Aleksi Sahala 27.09.2015 Marû Intransitiivitaivutus Marûn intransitiivinen persoonataivutus muodostetaan ensimmäisellä suffiksisarjalla, sekä preesens-futurin tunnuksella {ed} Yksikkö
Valtuuskunnille toimitetaan oheisena asiakirja COM(2017) 112 final LIITTEET 1 9.
 Euroopan unionin neuvosto Bryssel, 7. maaliskuuta 2017 (OR. en) 7057/17 ADD 1 TRANS 97 SAATE Lähettäjä: Saapunut: 6. maaliskuuta 2017 Vastaanottaja: Euroopan komission pääsihteerin puolesta Jordi AYET
Euroopan unionin neuvosto Bryssel, 7. maaliskuuta 2017 (OR. en) 7057/17 ADD 1 TRANS 97 SAATE Lähettäjä: Saapunut: 6. maaliskuuta 2017 Vastaanottaja: Euroopan komission pääsihteerin puolesta Jordi AYET
Korespondencja osobista Życzenia
 - Ślub Congratulations. Wishing the both of you all the happiness in the world. Używane, gdy gratulujemy młodej parze Congratulations and warm wishes to both of you on your wedding day. Używane, gdy gratulujemy
- Ślub Congratulations. Wishing the both of you all the happiness in the world. Używane, gdy gratulujemy młodej parze Congratulations and warm wishes to both of you on your wedding day. Używane, gdy gratulujemy
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 17. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 17. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
BRUKSANVISNING KÄYTTÖOHJE MÙKÖDÉSI ÉS HASZNÁLATI UTASÍTÁS INSTRUKCJA OBS UGI NÁVOD NA INSTALACI A POUÎITÍ
 Kyl-och frysskåp / Jääkaappipakastin / HıtŒ-Fagyasztó szekrény / Ch odziarko - zamra arka / Chladniãka s mrazákem BRUKSANVISNING KÄYTTÖOHJE MÙKÖDÉSI ÉS HASZNÁLATI UTASÍTÁS INSTRUKCJA OBS UGI NÁVOD NA INSTALACI
Kyl-och frysskåp / Jääkaappipakastin / HıtŒ-Fagyasztó szekrény / Ch odziarko - zamra arka / Chladniãka s mrazákem BRUKSANVISNING KÄYTTÖOHJE MÙKÖDÉSI ÉS HASZNÁLATI UTASÍTÁS INSTRUKCJA OBS UGI NÁVOD NA INSTALACI
Virtapainike. Virran merkkivalo. Bluetooth-merkkivalo. Bluetooth-painike. Päälle tai pois kytkeminen
 Pakkauksen sisältö Painikkeet ja portit Bluetooth-kuulokkeet USB - 3,5 mm -latauskaapeli 3,5 mm:n audiokaapeli Pikaopas Kantokotelo Äänenvoimakkuus ylös -painike Äänenvoimakkuus alas -painike Virtapainike
Pakkauksen sisältö Painikkeet ja portit Bluetooth-kuulokkeet USB - 3,5 mm -latauskaapeli 3,5 mm:n audiokaapeli Pikaopas Kantokotelo Äänenvoimakkuus ylös -painike Äänenvoimakkuus alas -painike Virtapainike
Konfiguracja sceny w systemie wizyjnym z nieruchom¹ kamer¹**
 AUTOMATYKA 2011 Tom 15 Zeszyt 3 Miros³aw Jab³oñski* Konfiguracja sceny w systemie wizyjnym z nieruchom¹ kamer¹** 1. Wprowadzenie Jednym z celów stosowania systemów wizyjnych jest pozyskiwanie informacji
AUTOMATYKA 2011 Tom 15 Zeszyt 3 Miros³aw Jab³oñski* Konfiguracja sceny w systemie wizyjnym z nieruchom¹ kamer¹** 1. Wprowadzenie Jednym z celów stosowania systemów wizyjnych jest pozyskiwanie informacji
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + 2 ( 1) ( 1) 3 = = 4
 KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
( )
 ( www.padasalai.net ) TET TET TET ReExam Paper I Paper II. 8015118094 sivatvmalai@yahoo.co.in Questions TRB - Page 1 II ( 7, 21 ) ( 3, 15 ) ( 3, 5) ( 6,2) (3,5) 1 ( 3, 5 ) (2 + ) ( - 2 ) (2 + ) ( - 2 )
( www.padasalai.net ) TET TET TET ReExam Paper I Paper II. 8015118094 sivatvmalai@yahoo.co.in Questions TRB - Page 1 II ( 7, 21 ) ( 3, 15 ) ( 3, 5) ( 6,2) (3,5) 1 ( 3, 5 ) (2 + ) ( - 2 ) (2 + ) ( - 2 )
(0 desimaalia, 2 merkitsevää numeroa).
 NUMEERISET MENETELMÄT DEMOVASTAUKSET SYKSY 20.. (a) Absoluuttinen virhe: ε x x ˆx /7 0.4 /7 4/00 /700 0.004286. Suhteellinen virhe: ρ x x ˆx x /700 /7 /00 0.00 0.%. (b) Kahden desimaalin tarkkuus x ˆx
NUMEERISET MENETELMÄT DEMOVASTAUKSET SYKSY 20.. (a) Absoluuttinen virhe: ε x x ˆx /7 0.4 /7 4/00 /700 0.004286. Suhteellinen virhe: ρ x x ˆx x /700 /7 /00 0.00 0.%. (b) Kahden desimaalin tarkkuus x ˆx
2 Keminmaa 3 4 5 6. Haaparanta TORNIO. > 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db. Vt 4 Kemi
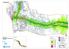 LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
LIITE.. Pek ka ti injun Heik rä npe ä nper kkaa u u L joki Kylä L LIITE.. i aar Na u ska ang as ik ju Koi vuh ar Ru u tti Mä nt Väi nöl ä y lä Ma rtta Vai n io n ine Tor v o Paa tti Las si ik ko Kem inm
Badania nad automatyzacj¹ procesu tworzenia serwisów internetowych
 AUTOMATYKA 2010 Tom 14 Zeszyt 3/2 Lidia Dutkiewicz*, Katarzyna Grobler*, Patryk Orzechowski*, Dariusz Pa³ka**, Cezary Piskor-Ignatowicz*, Marek Zachara* Badania nad automatyzacj¹ procesu tworzenia serwisów
AUTOMATYKA 2010 Tom 14 Zeszyt 3/2 Lidia Dutkiewicz*, Katarzyna Grobler*, Patryk Orzechowski*, Dariusz Pa³ka**, Cezary Piskor-Ignatowicz*, Marek Zachara* Badania nad automatyzacj¹ procesu tworzenia serwisów
Monika Kociuba 500 najbardziej przydatnych fińskich słówek
 1 ISBN 978-83-947303-4-5 Wersja 1.0 (16.12.2017) Gdynia 2017 Wszelkie prawa zastrzeżone. Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci jest zabronione.
1 ISBN 978-83-947303-4-5 Wersja 1.0 (16.12.2017) Gdynia 2017 Wszelkie prawa zastrzeżone. Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci jest zabronione.
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
LUKUJÄRJESTYS (SHH11) kevät 2014 kevät lukukausi 2.1.2014-30.5.2014
 Sosiaali- terveys- ja liikunta-ala LUKUJÄRJESTYS () kevät 2014 kevät lukukausi 2.1.2014-30.5.2014 Ryhmä: 1 2 kello 30.12 31.12 ke.1.1 to 2.1 pe 3.1 ma 6.1 ti 7.1 ke.8.1 to 9.1 pe 10.1 8.00-8.45 sis.kir
Sosiaali- terveys- ja liikunta-ala LUKUJÄRJESTYS () kevät 2014 kevät lukukausi 2.1.2014-30.5.2014 Ryhmä: 1 2 kello 30.12 31.12 ke.1.1 to 2.1 pe 3.1 ma 6.1 ti 7.1 ke.8.1 to 9.1 pe 10.1 8.00-8.45 sis.kir
KUNTOUTUS- PROTOKOLLA
 KUNTOUTUS- PROTOKOLLA IMPLANTIN ASETTAMISEN JÄLKEEN Jotta leikatun polven kuntoutus sujuu oikein, on tärkeää noudattaa tätä kuntoutusohjelmaa ammattimaisen fysioterapeutin ohjauksessa. Ohjelmassa kiinnitetään
KUNTOUTUS- PROTOKOLLA IMPLANTIN ASETTAMISEN JÄLKEEN Jotta leikatun polven kuntoutus sujuu oikein, on tärkeää noudattaa tätä kuntoutusohjelmaa ammattimaisen fysioterapeutin ohjauksessa. Ohjelmassa kiinnitetään
2. Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä. y = 2xy, Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä käyristä on kyse?
 2. Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä 2.1. Ensimmäisen kertaluvun yhtälöt 30. Ratkaise alkuarvotehtävä y = 2xy, y(0)=1. Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä
2. Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä 2.1. Ensimmäisen kertaluvun yhtälöt 30. Ratkaise alkuarvotehtävä y = 2xy, y(0)=1. Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä
Suosituimmat kohdemaat
 Suosituimmat kohdemaat Maakuntanro Maakunta Kohdemaa Maakoodi sum_lah_opisk 21 Ahvenanmaa - Kreikka GR 3 Åland Italia IT 3 Turkki TR 2 Saksa DE 1 09 Etelä-Karjala Venäjä RU 328 Britannia GB 65 Ranska FR
Suosituimmat kohdemaat Maakuntanro Maakunta Kohdemaa Maakoodi sum_lah_opisk 21 Ahvenanmaa - Kreikka GR 3 Åland Italia IT 3 Turkki TR 2 Saksa DE 1 09 Etelä-Karjala Venäjä RU 328 Britannia GB 65 Ranska FR
Koncepcja i realizacja molekularnego modelu obliczeñ w analizie paradygmatu niewidzialnej rêki rynku Adama Smitha
 AUTOMATYKA 2009 Tom 13 Zeszyt 3 Pawe³ Skrzyñski*, Tadeusz Szuba* Koncepcja i realizacja molekularnego modelu obliczeñ w analizie paradygmatu niewidzialnej rêki rynku Adama Smitha 1. Wprowadzenie Pomimo
AUTOMATYKA 2009 Tom 13 Zeszyt 3 Pawe³ Skrzyñski*, Tadeusz Szuba* Koncepcja i realizacja molekularnego modelu obliczeñ w analizie paradygmatu niewidzialnej rêki rynku Adama Smitha 1. Wprowadzenie Pomimo
Metody kalibracji urz¹dzeñ do akwizycji sygna³ów okoruchowych***
 AUTOMATYKA 2010 Tom 14 Zeszyt 3/1 Jacek Chodak*, Tomasz Kryjak* Metody kalibracji urz¹dzeñ do akwizycji sygna³ów okoruchowych*** 1. Wprowadzenie Urz¹dzenie do akwizycji sygna³u okoruchowego (eye-traker)
AUTOMATYKA 2010 Tom 14 Zeszyt 3/1 Jacek Chodak*, Tomasz Kryjak* Metody kalibracji urz¹dzeñ do akwizycji sygna³ów okoruchowych*** 1. Wprowadzenie Urz¹dzenie do akwizycji sygna³u okoruchowego (eye-traker)
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
MATA172 Sami Yrjänheikki Harjoitus Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki!
 MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
Satunnaislukujen generointi
 Satunnaislukujen generointi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo Tutkimustiedonhallinnan peruskurssi Satunnaislukujen generointi 1/27 Kevät 2003 Lähteet Knuth, D., The Art of Computer Programming,
Satunnaislukujen generointi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo Tutkimustiedonhallinnan peruskurssi Satunnaislukujen generointi 1/27 Kevät 2003 Lähteet Knuth, D., The Art of Computer Programming,
Matkustaminen Yleistä
 - Olennaiset Możesz mi pomóc? [form.:] Może Pan(i) mi pomóc? Avun pyytäminen Czy mówisz po angielsku? [form.:] Czy mówi Pan(i) po angielsku? Tiedustelu henkilöltä puhuuko hän englantia Can you help me,
- Olennaiset Możesz mi pomóc? [form.:] Może Pan(i) mi pomóc? Avun pyytäminen Czy mówisz po angielsku? [form.:] Czy mówi Pan(i) po angielsku? Tiedustelu henkilöltä puhuuko hän englantia Can you help me,
Psalmin kertosäkeitä
 Psalmin kertosäkeitä Kaste Tämän päivän on Herra tehnyt Ps. 118:24. Virsikirjan jumalanpalvelusliitteessä nro 852. Tuomo Nikkola 2001 Tä - män päi - vän on Her - ra teh - nyt, i - loit - kaa ja rie - muit
Psalmin kertosäkeitä Kaste Tämän päivän on Herra tehnyt Ps. 118:24. Virsikirjan jumalanpalvelusliitteessä nro 852. Tuomo Nikkola 2001 Tä - män päi - vän on Her - ra teh - nyt, i - loit - kaa ja rie - muit
BI.21 Biurko Game Box BI.21 Desk Game Box BI.21 Письменный стол Game Box BI.21 Birou Game Box BI.21 Schreibtisch Game Box BI.
 BI.21 Biurko Game Box BI.21 Desk Game Box BI.21 Письменный стол Game Box BI.21 Birou Game Box BI.21 Schreibtisch Game Box BI.21 Pöytä Game Box 1m 1 9 18 8 15 7 6 10 17 14 5 16 3 13 2 11 12 11 1 2 12 12
BI.21 Biurko Game Box BI.21 Desk Game Box BI.21 Письменный стол Game Box BI.21 Birou Game Box BI.21 Schreibtisch Game Box BI.21 Pöytä Game Box 1m 1 9 18 8 15 7 6 10 17 14 5 16 3 13 2 11 12 11 1 2 12 12
BI.22 Biurko Game Print BI.22 Desk Game Print BI.22 Письменный стол Game Print BI.22 Birou Game Print BI.22 Schreibtisch Game Print BI.
 BI. Biurko Game Print BI. Desk Game Print BI. Письменный стол Game Print BI. Birou Game Print BI. Schreibtisch Game Print BI. Pöytä Game Print m 9 8 8 9 7 6 0 7 5 5 6 3 0 0 3 4 4 d a e c b W78 W W4 W5
BI. Biurko Game Print BI. Desk Game Print BI. Письменный стол Game Print BI. Birou Game Print BI. Schreibtisch Game Print BI. Pöytä Game Print m 9 8 8 9 7 6 0 7 5 5 6 3 0 0 3 4 4 d a e c b W78 W W4 W5
Nuorisotyöttömyys Euroopassa. Eurooppafoorumi: Työläisten Eurooppa, Tampere, 6.9.2013 Liisa Larja (liisa.larja@stat.fi)
 Nuorisotyöttömyys Euroopassa Eurooppafoorumi: Työläisten Eurooppa, Tampere, 6.9.2013 Liisa Larja (liisa.larja@stat.fi) 2 Talouskriisin vaikutus nuorisotyöttömyyteen (15-24 v.) 25,0 20,0 15,0 23,3 20,1
Nuorisotyöttömyys Euroopassa Eurooppafoorumi: Työläisten Eurooppa, Tampere, 6.9.2013 Liisa Larja (liisa.larja@stat.fi) 2 Talouskriisin vaikutus nuorisotyöttömyyteen (15-24 v.) 25,0 20,0 15,0 23,3 20,1
BH.22 Biurko Biurko Snap Print BH.22 Desk Snap Print BH.22 Письменный стол Snap Print BH.22 Birou Snap Print BH.22 Schreibtisch Snap Print BH.
 BH. Biurko Biurko Snap Print BH. Desk Snap Print BH. Письменный стол Snap Print BH. Birou Snap Print BH. Schreibtisch Snap Print BH. Pöytä Snap Print m 9 8 6 7 5 3 0 0 3 d a e c b OKUCIA / FITTINGS / ФУРНИТУРА
BH. Biurko Biurko Snap Print BH. Desk Snap Print BH. Письменный стол Snap Print BH. Birou Snap Print BH. Schreibtisch Snap Print BH. Pöytä Snap Print m 9 8 6 7 5 3 0 0 3 d a e c b OKUCIA / FITTINGS / ФУРНИТУРА
Osa 11. Differen-aaliyhtälöt
 Osa 11. Differen-aaliyhtälöt Differen-aaliyhtälö = yhtälö jossa esiintyy jonkin funk-on derivaa
Osa 11. Differen-aaliyhtälöt Differen-aaliyhtälö = yhtälö jossa esiintyy jonkin funk-on derivaa
Biurko 160 Desk 160 Письменный стол 160 Birou 160 Schreibtisch 160 Pöytä 160
 Biurko 60 Desk 60 Письменный стол 60 Birou 60 Schreibtisch 60 Pöytä 60 m 0 5 8 7 6 9 a e c d b OKUCIA / FITTINGS / ФУРНИТУРА / FERONERIE / BESCHLÄGE / KIINNITTIMET ELEMENTS / CZĘŚĆI / ДЕТАЛИ / COMPONENTE
Biurko 60 Desk 60 Письменный стол 60 Birou 60 Schreibtisch 60 Pöytä 60 m 0 5 8 7 6 9 a e c d b OKUCIA / FITTINGS / ФУРНИТУРА / FERONERIE / BESCHLÄGE / KIINNITTIMET ELEMENTS / CZĘŚĆI / ДЕТАЛИ / COMPONENTE
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio
 MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
MAT-13510 Laaja Matematiikka 1U. Hyviä tenttikysymyksiä T3 Matemaattinen induktio Olkoon a 1 = a 2 = 5 ja a n+1 = a n + 6a n 1 kun n 2. Todista induktiolla, että a n = 3 n ( 2) n, kun n on positiivinen
Kuvaus. Määritelmä. LM2, Kesä /160
 Kuvaus Määritelmä Oletetaan, että X ja Y ovat joukkoja. Kuvaus eli funktio joukosta X joukkoon Y on sääntö, joka liittää jokaiseen joukon X alkioon täsmälleen yhden alkion, joka kuuluu joukkoon Y. Merkintä
Kuvaus Määritelmä Oletetaan, että X ja Y ovat joukkoja. Kuvaus eli funktio joukosta X joukkoon Y on sääntö, joka liittää jokaiseen joukon X alkioon täsmälleen yhden alkion, joka kuuluu joukkoon Y. Merkintä
TARKISTUKSET FI Moninaisuudessaan yhtenäinen FI 2012/0266(COD) Mietintöluonnos Dagmar Roth-Behrendt (PE507.
 EUROOPAN PARLAMENTTI 2009-2014 Ympäristön, kansanterveyden ja elintarvikkeiden turvallisuuden valiokunta 14.5.2013 2012/0266(COD) TARKISTUKSET 297-449 Mietintöluonnos Dagmar Roth-Behrendt (PE507.972v02-00)
EUROOPAN PARLAMENTTI 2009-2014 Ympäristön, kansanterveyden ja elintarvikkeiden turvallisuuden valiokunta 14.5.2013 2012/0266(COD) TARKISTUKSET 297-449 Mietintöluonnos Dagmar Roth-Behrendt (PE507.972v02-00)
IAN HAND-HELD VACUUM CLEANER SAS 7.4 LI B3 HANDDAMMSUGARE RIKKAIMURI ODKURZACZ SAMOCHODOWY RANKINIS DULKIŲ SIURBLYS HANDSTAUBSAUGER
 HAND-HELD VACUUM CLEANER RIKKAIMURI Käyttöohje HANDDAMMSUGARE Bruksanvisning ODKURZACZ SAMOCHODOWY Instrukcja obsługi RANKINIS DULKIŲ SIURBLYS Naudojimo instrukcija HANDSTAUBSAUGER Bedienungsanleitung
HAND-HELD VACUUM CLEANER RIKKAIMURI Käyttöohje HANDDAMMSUGARE Bruksanvisning ODKURZACZ SAMOCHODOWY Instrukcja obsługi RANKINIS DULKIŲ SIURBLYS Naudojimo instrukcija HANDSTAUBSAUGER Bedienungsanleitung
POSTĘPOWANIA ZWIĄZANE Z REALIZACJĄ POLITYKI KONKURENCJI KOMISJA EUROPEJSKA
 C 249/12 Dziennik Urzędowy Unii Europejskiej 16.9.2010 POSTĘPOWANIA ZWIĄZANE Z REALIZACJĄ POLITYKI KONKURENCJI KOMISJA EUROPEJSKA POMOC PAŃSTWA FINLANDIA Pomoc państwa C 9/10 (ex N 417/09) Tymczasowa ulga
C 249/12 Dziennik Urzędowy Unii Europejskiej 16.9.2010 POSTĘPOWANIA ZWIĄZANE Z REALIZACJĄ POLITYKI KONKURENCJI KOMISJA EUROPEJSKA POMOC PAŃSTWA FINLANDIA Pomoc państwa C 9/10 (ex N 417/09) Tymczasowa ulga
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 14. helmikuuta 2011 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun olemassaolosta ja yksikäsitteisyydestä...........
Dierentiaaliyhtälöistä Markus Kettunen 14. helmikuuta 2011 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun olemassaolosta ja yksikäsitteisyydestä...........
Sivu 1 / 8. A31C00100 Mikrotaloustieteen perusteet: matematiikan tukimoniste. Olli Kauppi
 Sivu 1 / 8 A31C00100 Mikrotaloustieteen perusteet: matematiikan tukimoniste Olli Kauppi Monisteen ensimmäinen luku käsittelee derivointia hieman yleisemmästä näkökulmasta. Monisteen lopussa on kurssilla
Sivu 1 / 8 A31C00100 Mikrotaloustieteen perusteet: matematiikan tukimoniste Olli Kauppi Monisteen ensimmäinen luku käsittelee derivointia hieman yleisemmästä näkökulmasta. Monisteen lopussa on kurssilla
Lapsiperheiden kotipalveluiden myöntämisperusteet ja asiakasmaksut 1.1.2016 alkaen
 Hallitus 267 16.12.2015 Lapsiperheiden kotipalveluiden myöntämisperusteet ja asiakasmaksut 1.1.2016 alkaen H 267 (Valmistelija: perhepalvelujohtaja Matti Heikkinen ja vastuualuepäällikkö Tarja Rossinen)
Hallitus 267 16.12.2015 Lapsiperheiden kotipalveluiden myöntämisperusteet ja asiakasmaksut 1.1.2016 alkaen H 267 (Valmistelija: perhepalvelujohtaja Matti Heikkinen ja vastuualuepäällikkö Tarja Rossinen)
Matematiikka B3 - Avoin yliopisto
 2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
Differentiaaliyhtälöt I Ratkaisuehdotuksia, 2. harjoitus, kevät Etsi seuraavien yhtälöiden yleiset ratkaisut (Tässä = d
 Differentiaaliyhtälöt I Ratkaisuehdotuksia,. harjoitus, kevät 016 1. Etsi seuraavien yhtälöiden yleiset ratkaisut (Tässä = d dx ): (a) y + xy = xe x, (b) (1 + x ) y xy = (1 + x ), (c) y sin x y = 1 cos
Differentiaaliyhtälöt I Ratkaisuehdotuksia,. harjoitus, kevät 016 1. Etsi seuraavien yhtälöiden yleiset ratkaisut (Tässä = d dx ): (a) y + xy = xe x, (b) (1 + x ) y xy = (1 + x ), (c) y sin x y = 1 cos
Bedienungs- und Sicherheitshinweise. Käyttöja turvaohjeet. Användaroch Säkerhetsanvisning. Wskazówki dotyczàce obs ugi i bezpieczeƒstwa
 D Bedienungs- und Sicherheitshinweise Wskazówki dotyczàce obs ugi i bezpieczeƒstwa Käyttöja turvaohjeet S Användaroch Säkerhetsanvisning D S Bedienungsanleitung Seite 4-6 Instrukcja obs ugi Strona 7-10
D Bedienungs- und Sicherheitshinweise Wskazówki dotyczàce obs ugi i bezpieczeƒstwa Käyttöja turvaohjeet S Användaroch Säkerhetsanvisning D S Bedienungsanleitung Seite 4-6 Instrukcja obs ugi Strona 7-10
Fysiikan laboratoriotyöt 1, työ nro: 3, Vastuksen ja diodin virta-jänniteominaiskäyrät
 Fysiikan laboratoriotyöt 1, työ nro: 3, Vastuksen ja diodin virta-jänniteominaiskäyrät Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä:
Fysiikan laboratoriotyöt 1, työ nro: 3, Vastuksen ja diodin virta-jänniteominaiskäyrät Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä:
Asemakaavan muutos hyvinvointikeskuksen alueella korttelissa 46
 Kunnanhallitus 81 15.04.2019 Kunnanhallitus 95 13.05.2019 Kaava- ja maapoliittinen 6 22.05.2019 työryhmä Kunnanhallitus 123 03.06.2019 Asemakaavan muutos hyvinvointikeskuksen alueella korttelissa 46 2004/55.551/2019
Kunnanhallitus 81 15.04.2019 Kunnanhallitus 95 13.05.2019 Kaava- ja maapoliittinen 6 22.05.2019 työryhmä Kunnanhallitus 123 03.06.2019 Asemakaavan muutos hyvinvointikeskuksen alueella korttelissa 46 2004/55.551/2019
Johdatus matemaattiseen päättelyyn (5 op)
 Johdatus matemaattiseen päättelyyn (5 op) Tero Vedenjuoksu Oulun yliopisto Matemaattisten tieteiden laitos 2014 Johdatus matemaattiseen päättelyyn 2014 Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi
Johdatus matemaattiseen päättelyyn (5 op) Tero Vedenjuoksu Oulun yliopisto Matemaattisten tieteiden laitos 2014 Johdatus matemaattiseen päättelyyn 2014 Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi
* Hyödyn maksimointi on ihmisten toimintaa ja valintoja ohjaava periaate.
 KANSANTALOUSTIETEEN PERUSTEET Yrityksen teoria (Economics luvut 13-14) 14) KTT Petri Kuosmanen Optimointiperiaate a) Yksilöt pyrkivät maksimoimaan hyötynsä. * Hyödyn maksimointi on ihmisten toimintaa ja
KANSANTALOUSTIETEEN PERUSTEET Yrityksen teoria (Economics luvut 13-14) 14) KTT Petri Kuosmanen Optimointiperiaate a) Yksilöt pyrkivät maksimoimaan hyötynsä. * Hyödyn maksimointi on ihmisten toimintaa ja
renkaissa. 0 R x + x =(0 R +1 R )x =1 R x = x
 8. Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme näiltä kahdella laskutoimituksella varustetuilta
8. Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme näiltä kahdella laskutoimituksella varustetuilta
T Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut
 T-79.146 Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun
T-79.146 Kevät 2005 Logiikka tietotekniikassa: erityiskysymyksiä I Kertausta Ratkaisut 1. Jokaiselle toteutuvalle lauselogiikan lauseelle voidaan etsiä malli taulumenetelmällä merkitsemällä lause taulun
Nakkilan kunta ja Lions Club Nakkila ry sopivat keskenään seuraavaa:
 HOHTARINPUISTON KÄYTTÖO IKEUDEN LUOVUTUSSOPIMUS Nakkilan kunta ja Lions Club Nakkila ry sopivat keskenään seuraavaa: 1. Luavut uksen kohde Nakkilan kunnan Arantilan kylässä Alaviinikka -nimisellä tilalla
HOHTARINPUISTON KÄYTTÖO IKEUDEN LUOVUTUSSOPIMUS Nakkilan kunta ja Lions Club Nakkila ry sopivat keskenään seuraavaa: 1. Luavut uksen kohde Nakkilan kunnan Arantilan kylässä Alaviinikka -nimisellä tilalla
Juuri 2 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Kertaus K. a) E Nouseva suora. b) A 5. asteen polynomifunktio, pariton funktio Laskettu piste f() = 5 =, joten piste (, ) on kuvaajalla. c) D Paraabelin mallinen, alaspäin aukeava. Laskettu piste f() =
Kertaus K. a) E Nouseva suora. b) A 5. asteen polynomifunktio, pariton funktio Laskettu piste f() = 5 =, joten piste (, ) on kuvaajalla. c) D Paraabelin mallinen, alaspäin aukeava. Laskettu piste f() =
5 Differentiaalilaskentaa
 5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
5 Differentiaalilaskentaa 5.1 Raja-arvo Esimerkki 5.1. Rationaalifunktiota g(x) = x2 + x 2 x 1 ei ole määritelty nimittäjän nollakohdassa eli, kun x = 1. Funktio on kuitenkin määritelty kohdan x = 1 läheisyydessä.
DRUKUJ, WYMAZUJ, POPRAWIAJ I DRUKUJ PONOWNIE
 Broszura produktowa Pierwszy na świecie system wielofunkcyjny z funkcją wymazywania. Dzięki unikalnej technologii druku hybrydowego jedno urządzenie potrafi drukować standardowe dokumenty jak i takie,
Broszura produktowa Pierwszy na świecie system wielofunkcyjny z funkcją wymazywania. Dzięki unikalnej technologii druku hybrydowego jedno urządzenie potrafi drukować standardowe dokumenty jak i takie,
Tutkimustiedonhallinnan peruskurssi
 Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
IAN TOASTER STC 920 A1. LEIVÄNPAAHDIN Käyttöohje. BRÖDROST Bruksanvisning. SKRUDINTUVAS Naudojimo instrukcija. TOSTER Instrukcja obsługi
 TOASTER LEIVÄNPAAHDIN Käyttöohje BRÖDROST Bruksanvisning TOSTER Instrukcja obsługi SKRUDINTUVAS Naudojimo instrukcija TOASTER Bedienungsanleitung IAN 315615 Käännä ennen lukemista kuvallinen sivu esiin
TOASTER LEIVÄNPAAHDIN Käyttöohje BRÖDROST Bruksanvisning TOSTER Instrukcja obsługi SKRUDINTUVAS Naudojimo instrukcija TOASTER Bedienungsanleitung IAN 315615 Käännä ennen lukemista kuvallinen sivu esiin
Todistus. Eliminoidaan Euleideen algoritmissa jakojäännökset alhaaltaylöspäin.
 18 ALGEBRA II missä r n (x) =syt(f(x),g(x)). Lause 2.7. Olkoot f(x),g(x) K[x]. Silloin syt(f(x),g(x)) = a(x)f(x)+b(x)g(x), joillakin a(x),b(x) K[x]. Todistus. Eliminoidaan Euleideen algoritmissa jakojäännökset
18 ALGEBRA II missä r n (x) =syt(f(x),g(x)). Lause 2.7. Olkoot f(x),g(x) K[x]. Silloin syt(f(x),g(x)) = a(x)f(x)+b(x)g(x), joillakin a(x),b(x) K[x]. Todistus. Eliminoidaan Euleideen algoritmissa jakojäännökset
Lähentyminen Yhteisestä käytännöstä usein kysytyt kysymykset Lähentymisohjelma 3. Erottamiskyky:
 FI FI Lähentyminen Yhteisestä käytännöstä usein kysytyt kysymykset Lähentymisohjelma 3. Erottamiskyky: kuvailevia/erottamiskyvyttömiä sanoja sisältävät kuviomerkit A. YHTEINEN KÄYTÄNTÖ 1. Mitkä virastot
FI FI Lähentyminen Yhteisestä käytännöstä usein kysytyt kysymykset Lähentymisohjelma 3. Erottamiskyky: kuvailevia/erottamiskyvyttömiä sanoja sisältävät kuviomerkit A. YHTEINEN KÄYTÄNTÖ 1. Mitkä virastot
BM20A0900, Matematiikka KoTiB3
 BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
BM20A0900, Matematiikka KoTiB3 Luennot: Matti Alatalo Oppikirja: Kreyszig, E.: Advanced Engineering Mathematics, 8th Edition, John Wiley & Sons, 1999, luvut 1 4. 1 Sisältö Ensimmäisen kertaluvun differentiaaliyhtälöt
MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen
 MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen Tehtävä 1. Onko joukon X potenssijoukon P(X) laskutoimitus distributiivinen laskutoimituksen suhteen? Onko laskutoimitus distributiivinen laskutoimituksen
MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen Tehtävä 1. Onko joukon X potenssijoukon P(X) laskutoimitus distributiivinen laskutoimituksen suhteen? Onko laskutoimitus distributiivinen laskutoimituksen
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos Koodausteoria 10 op Kontaktiopetusta 50 h, 26.5. - 26.6. ma 10-14, ti 10-13, to 10-13 Aloitusviikolla poikkeuksellisesti ke 10-13 torstain
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos Koodausteoria 10 op Kontaktiopetusta 50 h, 26.5. - 26.6. ma 10-14, ti 10-13, to 10-13 Aloitusviikolla poikkeuksellisesti ke 10-13 torstain
12 Jatkuva-aikaisten tehtävien numeerinen ratkaiseminen
 12 Jatkuva-aikaisten tehtävien numeerinen ratkaiseminen Ratkaisumenetelmät jaetaan epäsuoriin ja suoriin menetelmiin Epäsuora menetelmä yrittää ratkaista Pontryaginin minimiperiaatteen mukaiset vättlämättömät
12 Jatkuva-aikaisten tehtävien numeerinen ratkaiseminen Ratkaisumenetelmät jaetaan epäsuoriin ja suoriin menetelmiin Epäsuora menetelmä yrittää ratkaista Pontryaginin minimiperiaatteen mukaiset vättlämättömät
Todista suoraan integraalin määritelmään perustuen tasointegraalin ominaisuus. λ f = λ f,
 7. Taso- ja avaruusintegraali 7.1. Tasointegraalin määrittely 205. Tarkastellaan funktiota f (x,y) = x+y neliössä {(x,y) 0 x 1, 0 y 1}. Neliö jaetaan suorilla x = a ja y = b neljään osasuorakulmioon; 0
7. Taso- ja avaruusintegraali 7.1. Tasointegraalin määrittely 205. Tarkastellaan funktiota f (x,y) = x+y neliössä {(x,y) 0 x 1, 0 y 1}. Neliö jaetaan suorilla x = a ja y = b neljään osasuorakulmioon; 0
Osoita, että eksponenttifunktio ja logaritmifunktio ovat differentiaaliyhtälön
 3. Lineaariset differentiaaliyhtälöt 3.1. Lineaariyhtälöiden teoriaa 99. Onko differentiaaliyhtälö y + x(y y )=y + 1 a) lineaarinen, b) homogeeninen? 100. Olkoot funktiot f (x) ja g(x) jatkuvasti derivoituvia
3. Lineaariset differentiaaliyhtälöt 3.1. Lineaariyhtälöiden teoriaa 99. Onko differentiaaliyhtälö y + x(y y )=y + 1 a) lineaarinen, b) homogeeninen? 100. Olkoot funktiot f (x) ja g(x) jatkuvasti derivoituvia
Johdatus matemaattiseen päättelyyn
 Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä 2 Todistamisesta 3 Joukko-oppia 4 Funktioista Funktio eli kuvaus on matematiikan
Johdatus matemaattiseen päättelyyn Maarit Järvenpää Oulun yliopisto Matemaattisten tieteiden laitos Syyslukukausi 2015 1 Merkintöjä 2 Todistamisesta 3 Joukko-oppia 4 Funktioista Funktio eli kuvaus on matematiikan
OUTOKUMPU OY KAIRAUSNAYTTEISTA - 1. Kalibrointi Kanavarajojen asetuksen jälkeen mitattiin 40 kpl ns.
 Q * Q>~/X - 4514 02 0 K MALMNETSNTA X-MET -ANALYSAATSORN TESTAUS NOLYBDEENN ANALYSOMSESSSA ATTOJARVEN KARAUSNAYTTESTA - Työn tarkoituksena on ollut tutkia X-Metin soveltuvuutta geologisten näytteiden analysointiin
Q * Q>~/X - 4514 02 0 K MALMNETSNTA X-MET -ANALYSAATSORN TESTAUS NOLYBDEENN ANALYSOMSESSSA ATTOJARVEN KARAUSNAYTTESTA - Työn tarkoituksena on ollut tutkia X-Metin soveltuvuutta geologisten näytteiden analysointiin
TILAX - UUDEN SUKUPOLVEN TERÄSRAKENNEJÄRJESTELMÄ
 1 2 3 4 5 4255 2980 4080 2980 4255 MMA-9 MMA-8 IPE240 403 402 403 IPE240 106 108 106 107 Pxx3.0 Pxx3.0 Pxx3.0 1014 1011 1012 1013 1015 1016 Pxx3.0 IPE240 402 406 IPE240 101 Pxx3.0 IPE240 402 406 IPE240
1 2 3 4 5 4255 2980 4080 2980 4255 MMA-9 MMA-8 IPE240 403 402 403 IPE240 106 108 106 107 Pxx3.0 Pxx3.0 Pxx3.0 1014 1011 1012 1013 1015 1016 Pxx3.0 IPE240 402 406 IPE240 101 Pxx3.0 IPE240 402 406 IPE240
